作业解答

合集下载

四年级下册语文作业本参考解答(部编版)

四年级下册语文作业本参考解答（部编版）第一单元作业1：生字词书写参考答案：- 定价：dìng jià- 购买：gòu mǎi- 拆穿：chāi chuān- 姓：xìng- 机会：jī huì- 课堂：kè táng- 准备：zhǔn bèi- 葡萄：pú táo- 发生：fā shēng- 尤其：yóu qí作业2：古诗背诵参考答案：- 《静夜思》- 床前明月光，- 疑是地上霜。

- 举头望明月，- 低头思故乡。

第二单元作业1：词语接龙参考答案：- 蓝天 - 天高 - 高楼 - 楼宇 - 体重作业2：课后习题参考答案：1. 因为“我”看到草地变色，很奇怪，所以“我”询问爸爸。

2. 爸爸告诉“我”草地变色是因为夜晚气温低，草叶里的水分凝结成露珠，露珠的颜色把草叶染变了。

第三单元作业1：语法填空参考答案：- 我____（1）书桌上____（2）一本有趣的书。

- 今天____（3）晴天，我们____（4）去公园玩。

填空：1. 在 2. 有一本 3. 因为 4. 决定作业2：作文练习参考答案：- 我的家人- 我有一个幸福的家人。

爸爸是一位工程师，他很勤奋。

妈妈是一位教师，她很温柔。

我有一个弟弟，他叫小明。

我们一家人常常一起去公园玩。

第四单元作业1：阅读理解参考答案：1. 文章讲述了作者童年时和伙伴们一起捉迷藏、放风筝、游泳等快乐的事情。

2. 文章表达了作者对童年时光的怀念和对家乡的热爱。

作业2：课后习题参考答案：1. 因为“我”小时候常常和伙伴们一起玩耍，所以“我”怀念童年。

2. “我”喜欢家乡，因为家乡有很多美好的回忆。

第五单元作业1：生字词书写参考答案：- 暖和：nuǎn huo- 凉爽：liáng shuǎng- 温暖：wēn nuǎn- 融化：róng huà- 春天：chūn tiān- 冰雪：bīng xuě- 融化：róng huà- 太阳：tài yáng作业2：古诗背诵参考答案：- 《春晓》- 春眠不觉晓，- 处处闻啼鸟。

作业解答第二版

2 F1<0
3 F2<0
4 F3<0
坐标进给
-x +y +y +y
偏差计算`
F0=0
F1=F0–2X0+1 =–11 F2=F1+2Y1+1 =–10 F3=F2+2Y2+1 =-7
F4=F3+ Y3+1 =–2
坐标计算
X0=6 Y0=0 X1=X0–1=5 Y1=0
X2=5 Y2=Y1+1=1
X3=5 Y3=Y2+1=2
答：(1) 第一象限直线插补程序设内存中三个单元XE、YE、FM分别存放直线终点横坐标、终点纵坐标、加工点偏差。
data segment XE DB xe YE DB yz FM DB 0 ZF DB 0
data ends
MOV ADD MOV LAB1：MOV CMP
AL，XE AL，YE CL，AL ；CL存NXY AL，FM AL，00H
1)
(1
z 1)Z
10
s
2
(0.1s
1)
10(1
z
1
)Z
1 s2
0.1 s
0.1 s 10
10(1
z
1
)
(1
z 1 z 1
)
2
0.1
1
1 z
1
0.1 1
1 z 1e101
(1
9z1(1 0.1z1) z1)(1 4.5105
z
1 )
阶跃输入对应 q 1 由被控对象传递函数，得 d 0 由广义对象传递函数，得 v 1, j 1,u 0
修改通道号和计数器修改采样值缓冲区指针

经济学基础作业及参考解答

作业一选择题1．经济学可定义为（）。

A．政府对市场制度的干预 B.企业赚取利润的活动 C.研究稀缺资源如何有效配置的问题 D.个人的生财之道2．“资源是稀缺的”是指（）A．资源是不可再生的 B.资源必须留给下一代 C.资源终将被耗费殆尽 D.相对于需求而言,资源总是不足的.3．失业问题如果反映在生产可能性曲线图上，可记为（）A．生产可能性曲线内的一点 B.生产可能性曲线上的一点 C.生产可能性曲线以外的一点 D.不在该平面直角坐标系上.4．下列哪一项会导致一国生产可能性曲线的外移？（）A．股市持续走强 B.通货膨胀 C.有用资源被发掘或技术进步 D.消费品生产增加,资本品生产下降.5．一个经济体系必须作出的基本选择是（）。

A．生产什么，生产多少 B.如何生产 C.为谁生产 D.以上都包括6．计划经济体制解决资源配置问题的方式有（）。

A．分散决策 B.竞争生产 C.纵向传递信息 D.要素市场定价7．在市场经济体制中，价格不发挥哪个功能（）？A．激励功能 B.集中资源办大事 C.收入再分配功能 D.信息传递功能8.下列哪个陈述不属于实证主义陈述( )?A.1990年的海湾危机引起石油价格上升，并导致了汽油消费的下降。

B.穷人应该不纳税。

C.美国经济比俄罗斯经济增长的更快。

D.“让一部分人先富起来”政策，拉开了中国居民收入的贫富差距。

9．政府税收政策和转移支付政策直接关系到（）。

A．生产什么 B.如何生产 C.为谁生产 D.生产多少10.经济均衡是指( ).A．在其他条件不变时，经济行为或经济状态不再改变；B．无论发生什么情况，这种状态都将处于稳定状况；C．一种理想状况，现实中并不会发生；D.规范分析中才使用的范畴。

问答题1．微观经济学研究什么？2．每个经济体系都面临的基本选择有哪些？3．资源配置的有效性有哪几个方面的含义？它们分别如何表示？4．实证经济学与规范经济学各自的特点是什么？相互关系如何？5．微观经济学为什么又叫价格理论？6．什么是经济理性主义假定？为何要作出该假定？7．市场机制的特点是什么？包含哪些要素？作业一参考解答：选择题1．C．A、B、D都是经济学所考察的某一个方面，不能作为经济学的定义。

第3章--作业解答

（2）C1C2=01时， F AB
（3）C1C2=10时， F A B
（4）C1C2=11时， F AB
试设计符合上述要求旳逻辑电路（器件不限）。
解：题目中要求控制信号对不同功能进行选择，故选用数据选择器实现，分析设计要求，得到逻辑体现式：
F C1C 2( A B ) C C1 2( AB ) C1C 2( A B ) C1C2( AB )
1
0
1
1
0
1
0
0
0
1
1
1
1
0
0
0
0
0
1
1
1
10
0
1
1
习题3.19 用8选1数据选择器设计一种组合逻
辑电路。该电路有3个输入逻辑变量A、B、C 和1个工作状态控制变量M。当M=0时电路实现“意见一致”功能（A、B、C状态一致时输出为1，不然输出为0），而M=1时电路实现“多数表决”功能，即输出与A、B、C中多数旳状
B1B0 A1A0
00
01
11
10
00 1 0 0
0
B1 B0
01 1
10
0
A B0 1 11 1
1
11
10 1 1 0 1
A1 B1
A1 A0
A1 B0
F1 A1 B1 B1 B0 A1 A0 A1B0 A0 B1
（3）卡诺图化简函数，得到最简与或式
F1 A1 B1 B1 B0 A1 A0 A1B0 A0 B1
outp(0)<='1' WHEN inp="000" ELSE '0'; outp(1)<='1' WHEN inp="001" ELSE '0'; outp(2)<='1' WHEN inp="010" ELSE '0'; outp(3)<='1' WHEN inp="011" ELSE '0'; outp(4)<='1' WHEN inp="100" ELSE '0'; outp(5)<='1' WHEN inp="101" ELSE '0'; outp(6)<='1' WHEN inp="110" ELSE '0'; outp(7)<='1' WHEN inp="111" ELSE '0'; END behave;

C语言基础知识作业(含解答)

基础知识作业解答（1）一、选择题：1.下面叙述错误的是：a)C程序中，各种括号应成对出现。

b)C程序中，赋值号的左边不可以是表达式。

c)C程序中，变量名的大小是有区别的。

d)C程序中，若未给变量赋初值，则变量的初值自动为0。

答案：d）解答：C程序中，若未给变量赋初值，则变量的初值不一定为0。

按变量被定义的位置来区分，变量可分为局部变量和全局变量；在{ … } 之间定义的变量称为局部变量，编译系统对局部变量是不进行初始化的，即，不赋初值。

未赋初值的局部变量的值为机内随机值。

在{ … } 之外定义的变量称为全局变量，编译系统自动对全局变量进行初始化。

未赋初值的全局部变量的值为0。

2.下面叙述正确的是：a)C程序中的变量定义语句可以写在函数体中任何位置。

b)C程序中不能有空语句。

c)C程序中的变量必须先定义后使用。

d)C程序中所有简单数据类型都可以准确无误的表示。

答案：c）解答：C程序中，变量定义语句的作用是通知编译系统为变量分配存储空间，所以必须先定义后使用。

3.以下合法的用户标识符的是：a)long b）\t c）5a d）user答案：d）解答：C程序中，合法的用户标识符的定义是：以字母或下划线开头的由字母、数字和下划线组成的字符串，不可以使用系统的关键字作为用户的标识符。

常见的关键字有：int, float ,char ,double ,long, short,unsigned,if,switch,case,break, continue ,do ,for ,while ,struct ,union, auto, static, extern, register;标准函数名可以用作用户标识符，但不提倡。

4.C程序中，合法的关键字的是：a)Float b）while c）Int d）Integer答案：b）5.下面选项中，优先级最高的运算符是：a)&& b）/= c) ! d)<=答案：c）6.下面选项中，优先级最低的运算符是：a)！= b) || c)++ d)，答案：d）7.C程序中，运算对象必须为整型数据的运算符是a)++ b) % c) / d) *答案：b）8.假设x，y，z为整型变量，且x=2，y=3，z=10，则下列表达式中值为1的是：a)x && y||z b)x>z c) (!x && y)||(y>z) d)x && !z ||!(y && z)答案：a）解答：C程序中，进行逻辑运算时，所有的非0数都处理成逻辑真；0处理成逻辑假。

作业解答-1-new高等教育出版社

新1-23.
解：如图
v船对地 = v船对水 + v水对地
正北偏东36.9º。
v船对地
v船对地 5m/s,
100 t 25s, l 3 25 75m 4
正对岸下游75米处。
v船对地 = v船对水 + v水对地
Y 北
t
新1-20
假设一电子在电场中运动，其运动方程为
x 3t
，
y 12 3t 2
（SI)。（1）计算电子的运动轨迹；（2）计算
t 1s 时电子的切向加速度、法向加速度及轨道上该点处
的曲率半径； *（3）在什么时刻电子的位矢与其速度矢量恰好垂直。
x 3t , y 12 3t ,
1-13.飞机以100m/s的速度沿水平直线飞行，在距离地面100m高处驾驶员要将救灾物资投放到前方预定地点。求：（1）此时目标应在飞机下前方多远？（2）物品投出2.0s后的切向加速度和法向加速度各为多少？
解：向下为y轴正方向，取g=9.8m/s
(1)v0 v0 x 100m/s, h 100m, v y gt 1 2 200 200 x v0t , y gt h 100, t , x 100 452m 2 9.8 9.8
v船对地
西
O 南
东X
v 船对地 = (3 i + 4 j )( m / s )
r = (7 5 i + 1 0 0 j )( m )
2 新1-7 ． v 0 . 1 0 . 02 t 一物体沿直线运动，其速度和时间的关系为
，当
t
t 0 时，物体在坐标原点右方0.2m处。求：（1） t 2.0s t 0 末时物体的加速度；（2）和 t 2 . 0 s 和 0

概率论与数理统计作业及解答

概率论与数理统计作业及解答第一次作业★1. 甲乙丙三门炮各向同一目标发射一枚炮弹设事件A B C 分别表示甲乙丙击中目标则三门炮最多有一门炮击中目标如何表示. 事件E {事件,,A B C 最多有一个发生},则E 的表示为;E ABC ABC ABC ABC =+++或;AB AC BC =U U 或;AB AC BC =U U或;AB ACBC =或().ABC ABC ABC ABC =-++(和A B +即并A B U ,当,A B 互斥即AB φ=时A B U 常记为A B +) 2. 设M 件产品中含m 件次品计算从中任取两件至少有一件次品的概率.221M mM C C --或1122(21)(1)m M m m MC C C m M m M M C -+--=- ★3. 从8双不同尺码鞋子中随机取6只计算以下事件的概率.A {8只鞋子均不成双},B {恰有2只鞋子成双},C {恰有4只鞋子成双}. ★4. 设某批产品共50件其中有5件次品现从中任取3件求 (1)其中无次品的概率 (2)其中恰有一件次品的概率(1)34535014190.724.1960C C == (2)21455350990.2526.392C C C ==5. 从1～9九个数字中任取3个排成一个三位数求(1)所得三位数为偶数的概率 (2)所得三位数为奇数的概率(1){P 三位数为偶数}{P =尾数为偶数4},9=(2){P 三位数为奇数}{P =尾数为奇数5},9=或{P 三位数为奇数}1{P =-三位数为偶数45}1.99=-=6. 某办公室10名员工编号从1到10任选3人记录其号码求(1)最小号码为5的概率(2)最大号码为5的概率记事件A {最小号码为5}, B {最大号码为5}.(1) 253101();12C P A C ==(2) 243101().20C P B C ==7. 袋中有红、黄、白色球各一个每次从袋中任取一球记下颜色后放回共取球三次求下列事件的概率:A ={全红}B ={颜色全同}C ={颜色全不同}D ={颜色不全同}E ={无黄色球}F ={无红色且无黄色球}G ={全红或全黄}.☆.某班n 个男生m 个女生(mn 1)随机排成一列计算任意两女生均不相邻的概率.☆.在[0 1]线段上任取两点将线段截成三段计算三段可组成三角形的概率. 第二次作业1. 设A B 为随机事件 P (A ) P (B ) (|)0.85P B A = 求(1)(|)P A B (2)()P A B ∪(1) ()()0.85(|),()0.850.080.068,()10.92P AB P AB P B A P AB P A ====⨯=- (2)()()()()P A B P A P B P AB =+-U 0.920.930.8620.988.=+-= 2. 投两颗骰子已知两颗骰子点数之和为7求其中有一颗为1点的概率. 记事件A {(1,6),(2,5),(3,4),(4,3),(5,2),(6,1)}, B {(1,6),(6,1)}.★.在1—2000中任取一整数求取到的整数既不能被5除尽又不能被7除尽的概率记事件A {能被5除尽}, B {能被7除尽}.4001(),20005P A ==取整2000285,7⎡⎤=⎢⎥⎣⎦28557(),2000400P B ==200057,57⎡⎤=⎢⎥⨯⎣⎦57(),2000P AB = 3. 由长期统计资料得知某一地区在4月份下雨(记作事件A )的概率为4/15刮风(用B 表示)的概率为7/15 既刮风又下雨的概率为1/10 求P (A |B )、P (B |A )、P (AB )4 设某光学仪器厂制造的透镜第一次落下时摔破的概率是1/2若第一次落下未摔破第二次落下时摔破的概率是7/10若前二次落下未摔破第三次落下时摔破的概率是9/10试求落下三次而未摔破的概率．记事件i A ={第i 次落下时摔破}1,2,3.i =5 设在n 张彩票中有一张奖券有3个人参加抽奖分别求出第一、二、三个人摸到奖券概率．记事件i A ={第i 个人摸到奖券}1,2,3.i =由古典概率直接得1231()()().P A P A P A n ===或212121111()()()(|),1n P A P A A P A P A A n n n -====-或第一个人中奖概率为11(),P A n=前两人中奖概率为12122()()(),P A A P A P A n +=+=解得21(),P A n=前三人中奖概率为1231233()()()(),P A A A P A P A P A n ++=++=解得31().P A n=6 甲、乙两人射击甲击中的概率为08 乙击中的概率为07 两人同时射击假定中靶与否是独立的求(1)两人都中靶的概率 (2)甲中乙不中的概率 (3)甲不中乙中的概率记事件A ={甲中靶}B ={乙中靶}.(1) ()()()0.70.70.56,P AB P A P B ==⨯= (2) ()()()0.80.560.24,P AB P A P AB =-=-= (3) ()()()0.70.560.14.P AB P B P AB =-=-=★7 袋中有a 个红球 b 个黑球有放回从袋中摸球计算以下事件的概率 (1)A {在n 次摸球中有k 次摸到红球}(2)B {第k 次首次摸到红球}(3)C {第r 次摸到红球时恰好摸了k 次球}(1) ();()k n kk n kk k nnna b a b P A C C a b a b a b --⎛⎫⎛⎫== ⎪ ⎪+++⎝⎭⎝⎭(2) 11();()k k kb a ab P B a b a b a b --⎛⎫== ⎪+++⎝⎭ (3) 1111().()rk rr k rr r k k ka b a b P C CCa b a b a b ------⎛⎫⎛⎫== ⎪ ⎪+++⎝⎭⎝⎭8一射手对一目标独立地射击4次已知他至少命中一次的概率为80.81求该射手射击一次命中目标的概率设射击一次命中目标的概率为,1.p q p =-4801121,,1.818133q q p q =-===-=9 设某种高射炮命中目标的概率为问至少需要多少门此种高射炮进行射击才能以的概率命中目标(10.6)10.99,n -<-0.40.01,n <由50.40.01024,=60.40.01,<得 6.n ≥ ☆.证明一般加法(容斥)公式证明只需证分块111,,k k n k i i i i i i A A A A A A +⊂L L L 只计算1次概率．(1,,n i i L 是1,,n L 的一个排列1,2,,.k n =L )分块概率重数为1,,k i i A A L 中任取1个-任取2个1(1)k -++-L 任取k 个即将,U I 互换可得对偶加法(容斥)公式☆.证明若A B 独立 A C 独立则A B ∪C 独立的充要条件是A BC 独立. 证明充分性:⇐(())()()()()(),P A B C P A P B P A P C P ABC =+-U 代入()()()P ABC P A P BC = ()(()()())P A P B P C P BC =+-()(),P A P B C =U 即,A B C U 独立. 必要性:⇒()()(),P ABC P A P BC =即,A BC 独立.☆.证明：若三个事件A 、B 、C 独立，则A ∪B 、AB 及A －B 都与C 独立．证明因为所以A ∪B 、AB 及A －B 都与C 独立. 第三次作业1 在做一道有4个答案的选择题时如果学生不知道问题的正确答案时就作随机猜测设他知道问题的正确答案的概率为p 分别就p 和p 两种情形求下列事件概率(1)学生答对该选择题 (2)已知学生答对了选择题求学生确实知道正确答案的概率记事件A ={知道问题正确答案}B ={答对选择题}.(1) 由全概率公式得()()(|)()(|)P B P A P B A P A P B A =+113,444p pp -=+=+当0.6p =时13130.67()0.7,444410p P B ⨯=+=+== 当0.3p =时13130.319()0.475.444440p P B ⨯=+=+==(2) 由贝叶斯公式得()4(|),13()1344P AB p pP A B p P B p ===++当0.6p =时440.66(|),13130.67p P A B p ⨯===++⨯ 当0.3p =时440.312(|).13130.319p P A B p ⨯===++⨯ 2 某单位同时装有两种报警系统A 与B 当报警系统A 单独使用时其有效的概率为当报警系统B 单独使用时其有效的概率为.在报警系统A 有效的条件下报警系统B 有效的概率为.计算以下概率 (1)两种报警系统都有效的概率 (2)在报警系统B 有效的条件下报警系统A 有效的概率 (3)两种报警系统都失灵的概率.(1) ()()(|)0.70.840.588,P AB P A P B A ==⨯=(2) ()0.588(|)0.735,()0.8P AB P A B P B === (3) ()()1()1()()()P AB P A B P A B P A P B P AB ==-=--+U U☆.为防止意外在矿内同时设有两种报警系统A 与B 每种系统单独使用时其有效的概率系统A 为0 92 系统B 为在A 失灵的条件下 B 有效的概率为求: (1)发生意外时两个报警系统至少有一个有效的概率 (2) B 失灵的条件下 A 有效的概率3 设有甲、乙两袋甲袋中有n 只白球 m 只红球乙袋中有N 只白球 M 只红球从甲袋中任取一球放入乙袋在从乙袋中任取一球问取到白球的概率是多少记事件A ={从甲袋中取到白球}B ={从乙袋中取到白球}. 由全概率公式得☆.设有五个袋子其中两个袋子每袋有2个白球 3个黑球另外两个袋子每袋有1个白球 4个黑球还有一个袋子有4个白球 1个黑球 (1)从五个袋子中任挑一袋并从这袋中任取一球求此球为白球的概率 (2)从不同的三个袋中任挑一袋并由其中任取一球结果是白球问这球分别由三个不同的袋子中取出的概率各是多少★4 发报台分别以概率06和04发出信号 “·” 及 “” 由于通信系统受到于扰当发出信号 “·” 时收报台分别以概率08及02收到信息 “·” 及 “” 又当发出信号 “” 时收报台分别以概率09及0?l 收到信号 “” 及 “·” 求: (1)收报台收到 “·”的概率(2)收报台收到“”的概率(3)当收报台收到 “·” 时发报台确系发出信号 “·” 的概率(4)收到 “” 时确系发出 “” 的概率记事件B ={收到信号 “·”}1A ={发出信号 “·”}2A ={发出信号“”}. (1) )|()()|()()(2211A B P A P A B P A P B P +=;52.01.04.0)2.01(6.0=⨯+-⨯= (2) ()1()10.520.48;P B P B =-=-=(3) 1111()()(|)(|)()()P A B P A P B A P A B P B P B ==0.60.8120.923;0.5213⨯=== (4)2222()()(|)(|)()()P A B P A P B A P A B P B P B ==0.40.930.75.0.484⨯=== 5 对以往数据分析结果表明当机器调整良好时产品合格率为90% 而机器发生某一故障时产品合格率为30% 每天早上机器开动时机器调整良好的概率为75%(1)求机器产品合格率(2)已知某日早上第一件产品是合格品求机器调整良好的概率记事件B ={产品合格}A ={机器调整良好}. (1) 由全概率公式得(2) 由贝叶斯公式得()()(|)(|)()()P AB P A P B A P A B P B P B ==0.750.90.9.0.75⨯== ☆.系统(A) (B) (C)图如下系统(A) (B)由4个元件组成系统(C)由5个元件组成每个元件的可靠性为p 即元件正常工作的概率为p 试求整个系统的可靠性.(A) (B) (C) 记事件A ={元件5正常}B ={系统正常}.(A) 222(|)(1(1)(1))(44),P B A p p p p p =---=-+(B) 2222(|)1(1)(1)(2),P B A p p p p =---=- (C) 由全概率公式得第四次作业1 在15个同型零件中有2个次品从中任取3个以X 表示取出的次品的个数求X 的分布律.☆.经销一批水果第一天售出的概率是每公斤获利8元第二天售出的概率是每公斤获利5元第三天售出的概率是每公斤亏损3元求经销这批水果每公斤赢利X2 抛掷一枚不均匀的硬币每次出现正面的概率为2/3 连续抛掷8次以X 表示出现正面的次数求X 的分布律.3 一射击运动员的击中靶心的命中率为以X 表示他首次击中靶心时累计已射击的次数写出X 的分布律并计算X 取偶数的概率解得0.6513()=0.394.110.6533q P X q ==++B 偶 4 一商业大厅里装有4个同类型的银行刷卡机调查表明在任一时刻每个刷卡机使用的概率为求在同一时刻(1)恰有2个刷卡机被使用的概率(2)至少有3个刷卡机被使用的概率 (3)至多有3个刷卡机被使用的概率(4)至少有一个刷卡机被使用的概率在同一时刻刷卡机被使用的个数(4,0.1).X B n p ==:(1) 2224(2)0.10.90.00486,P X C ==⨯⨯= (2) 3344(3)(3)(4)0.10.90.10.0037,P X P X P X C ≥==+==⨯⨯+= (3) 4(3)1(4)10.10.9999,P X P X ≤=-==-=(4)4(1)1(0)10.910.65610.3439.P X P X ≥=-==-=-=5 某汽车从起点驶出时有40名乘客设沿途共有4个停靠站且该车只下不上每个乘客在每个站下车的概率相等并且相互独立试求 (1)全在终点站下车的概率 (2)至少有2个乘客在终点站下车的概率 (3)该车驶过2个停靠站后乘客人数降为20的概率记事件A ={任一乘客在终点站下车}乘客在终点站下车人数(40,1/4).X B n p ==:(1) 40231(40)8.271810,4P X -⎛⎫===⨯ ⎪⎝⎭(2) 403940140313433(2)1(0)(1)1144434P X P X P X C ⎛⎫⎛⎫⎛⎫≥=-=-==--⨯=-⨯ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭(3) 记事件B ={任一乘客在后两站下车}乘客在后两站下车人数(40,1/2).Y B n p ==:2020202040404011(20)0.1268.222C P Y C ⎛⎫⎛⎫==== ⎪ ⎪⎝⎭⎝⎭(精确值)应用斯特林公式!,nn n e ⎫⎪⎭其中 1.7724538509.π==参贝努利分布的正态近似6 已知瓷器在运输过程中受损的概率是有2000件瓷器运到求 (1)恰有2个受损的概率 (2)小于2个受损的概率 (3)多于2个受损的概率 (4)至少有1个受损的概率受损瓷器件数(2000,0.002),X B n p ==:近似为泊松分布(4).P n p λ=⨯=(1) 2441480.146525,2!P e e --=== (2) 4424150.0915782,1!P e e --⎛⎫=+== ⎪⎝⎭(3) 431211130.761897,P P P e-=--=-= (4) 4410.981684.P e -=-=7 某产品表面上疵点的个数X 服从参数为的泊松分布规定表面上疵点的个数不超过2个为合格品求产品的合格品率产品合格品率2 1.2 1.21.2 1.212.920.879487.1!2!P e e --⎛⎫=+=== ⎪⎝⎭★8 设随机变量X求X 的分布函数 5),(||5).P X ≤ 随机变量X 的分布函数为第五次作业1 学生完成一道作业的时间X 是一个随机变量(单位小时) 其密度函数是试求 (1)系数k (2)X 的分布函数 (3)在15分钟内完成一道作业的概率 (4)在10到20分钟之间完成一道作业的概率 (1) 0.50.52320111(0.5),21,32248kk F kx xdx x x k ⎛⎫==+=+=+= ⎪⎝⎭⎰(2) 23200,01()()217,00.5,2(0.5)1,0.5.x x F x P X x x xdx x x x F x <⎧⎪⎪=≤=+=+≤<⎨⎪=≥⎪⎩⎰(3) 322011119()2170.140625,442464x F P X x x xdx ⎛⎫⎛⎫⎛⎫=≤=+=+== ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎰(4) 3212316111111129217.6336424108P X F F x xdx ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫≤≤=-=+=+= ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎰2 设连续型随机变量X 服从区间[a a ](a 0)上的均匀分布且已知概率1(1)3P X >= 求 (1)常数a (2)概率1()3P X <(1) 1111(1),3,223aa P X dx a a a ->====⎰(2) 13311115()3.36639P X dx -⎛⎫<==+= ⎪⎝⎭⎰3 设某元件的寿命X 服从参数为的指数分布且已知概率P (X 50)e4 试求(1)参数的值 (2)概率P (25X 100)补分布()()|,0.x x xx x S x P X x e dx e ex θθθθ+∞--+∞->==-=>⎰@ (1) 504502(50)(50),0.08,25x S P X e dx e e θθθθ+∞---=>=====⎰(2) 由()(),,0,rx r S rx e S x r x θ-==>取50,x =依次令1,2,2r =得其中 2.7182818284.e B4 某种型号灯泡的使用寿命X (小时)服从参数为1800的指数分布求 (1)任取1只灯泡使用时间超过1200小时的概率 (2)任取3只灯泡各使用时间都超过1200小时的概率 (1) 1312008002(1200)0.2231301602,P X ee-⨯->===1.6487212707001.= (2) 932(1200)0.0111089965.P X e->==5 设X ~N (0 1) 求 P (X 061) P (262X 125) P (X 134) P (|X |213) (1) (0.61)(0.61)0.72907,P X <=Φ=(2) ( 2.62 1.25)(1.25)( 2.62)(1.25)(2.62)1P X -<<=Φ-Φ-=Φ+Φ- (3) ( 1.34)1(1.34)10.909880.09012,P X >=-Φ=-= (4)(|| 2.13)22(2.13)220.983410.03318.P X >=-Φ=-⨯=6 飞机从甲地飞到乙地的飞行时间X ~N (4 19) 设飞机上午10 10从甲地起飞求 (1)飞机下午2 30以后到达乙地的概率 (2)飞机下午2 10以前到达乙地的概率 (3)飞机在下午1 40至2 20之间到达乙地的概率 (1)131331/34111(1)10.841340.15866,331/3P X P X -⎛⎫⎛⎫⎛⎫>=-≤=-Φ=-Φ=-= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭(2) (4)(0)0.5,P X <=Φ=(3) 72525/647/24261/31/3P X --⎛⎫⎛⎫⎛⎫<<=Φ-Φ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭★7 设某校高三女学生的身高X ~N (162 25) 求 (1)从中任取1个女学生求其身高超过165的概率 (2)从中任取1个女学生求其身高与162的差的绝对值小于5的概率 (3)从中任取6个女学生求其中至少有2个身高超过165的概率 (1)162165162(165)0.61(0.6)10.72580.2742,55X P X P --⎛⎫>=>==-Φ=-= ⎪⎝⎭(2) 162(|162|5)12(1)120.8413410.6827,5X P X P ⎛-⎫-<=<=Φ-=⨯-= ⎪⎝⎭(3) 记事件A ={任一女生身高超过165} ()(165)0.2742,p P A P X ==>= 随机变量Y :贝努利分布(6,0.2742),B n p == 第六次作业★1.设随机变量X 的分布律为 (1)求Y |X |的分(2)求YX 2X 的分布律(1)(2)★.定理设连续型变量X 密度为()X f x ,()y g x =严格单调,反函数()x x y =导数连续,则()Y g X =是连续型变量,密度为证明 1)若()0,x x y ''=>{}{()()}{},Y y g X g x X x ≤=≤=≤ 两边对y 求导,2)若()0,x x y ''=<{}{()()}{},Y y g X g x X x ≤=≤=≥ 两边对y 求导,因此总有()(())|()|,.Y X f y f x y x y y αβ'=<< 或证明两边对y 求导,或两边微分2 设随机变量X 的密度函数是f X (x ) 求下列随机变量函数的密度函数 (1)Y tan X (2)1Y X=(3)Y |X | (1) 反函数()arctan ,x y y ='21(),1x y y =+由连续型随机变量函数的密度公式得或反函数支()arctan ,i x y i y i π=+为整数，'21(),1i x y y=+(2) 1,X Y =反函数1,y x y ='211()()().Y X y y X f y f x x f y y==(3) ()()(||)()()()Y X X F y P Y y P X y P y X y F y F y =≤=≤=-≤≤=-- 两边对y 求导得Y 的密度函数为()()(),0.Y X X f y f y f y y =+-> ★3 设随机变量X ~U [2 2] 求Y 4X 21的密度函数两边对y 求导得随机变量Y 的密度为或解反函数支12()()x y x y ==★4 设随机变量X 服从参数为1的指数分布求YX 2的密度函数(Weibull 分布) 当0y ≤时, 2Y X =的分布()0Y F y =,当0y >时, 两边对y 求导得或反函数y x ='()()0.Y X y y f y f x x y ==>★5 设随机变量X~N (0 1) 求(1)Ye X 的密度函数 (2)YX 2的密度函数(Gamma 分布)(1) 当0y ≤时, e X Y =的分布()0Y F y =,当0y >时, 因而Y 的密度为或反函数ln ,X Y =ln ,y x y ='1()()(ln )Y y y f y x x y y ϕϕ=={}2(ln ),0.2y y =->(2) 当0y ≤时,()0Y F y =;当0Y >时,2()()()((Y X X F y P Y y P X y P X F F =≤=≤=≤=-两边对y 求导得Y的密度函数为2,0,()0.yY y f y ->=⎩或反函数支12()()x y x y ==6 设随机变量X 的密度函数是21,1()0,1X x f x x x ⎧>⎪=⎨⎪≤⎩ 求Y ln X 的概率密度反函数,y y x e ='()()(),0.y y y Y X y y X f y f x x f e e e y -===>第七次作业☆.将8个球随机地丢入编号为1 2 3 4 5的五个盒子中去设X 为落入1号盒的球的个数 Y 为落入2号盒的球的个数试求X 和Y 的联合分布律 1 袋中装有标上号码1 2 2的3个球从中任取一个并且不再放回然后再从袋中任取一球以X Y 分别记第一、二次取到球上的号码数求 (1)(X Y )的联合分布律(设袋中各球被取机会相等) (2)X Y 的边缘分布律 (3)X 与Y 是否独立 (1)(X Y )的联合分布律为(2) X Y 的分布律相同12(1),(2).33P X P X ==== (3) X 与Y 不独立2 设二维连续型变量(,)X Y 的联合分布函数35(1)(1),,0,(,)0,.x y e e x y F x y --⎧-->=⎨⎩其它求(,)X Y 联合密度★3 设二维随机变量(X Y )服从D 上的均匀分布其中D 是抛物线yx 2和xy 2所围成的区域试求它的联合密度函数和边缘分布密度函数并判断Y X ,是否独立分布区域面积213123200211,333x S x dx x x ⎛⎫===-= ⎪⎝⎭⎰⎰联合密度213,1,(,)0,.x y f x y S ⎧=<<<⎪=⎨⎪⎩其它边缘X的密度为22()),01,X x f x dy x x ==<<边缘Y的密度为22()),0 1.Y yf y dy y y ==<<(,)()(),X Y f x y f x f y ≠⋅因此X 与Y 不独立.或(,)f x y 非零密度分布范围不是定义在矩形区域上,因此X 与Y 不独立.4. 设二维离散型变量),(Y X 联合分布列是问,p q 取何值时X 与Y 两行成比例1/151/52,1/53/103q p ===解得12,.1015p q == ★5.设(,)X Y 的联合密度为2,11,0,(,)0,.y Ax e x y f x y -⎧-<<>=⎨⎩其它求(1)常数A (2)概率1(0,1);2P X Y <<>(3)边缘概率密度f X (x ) f Y (y ) (4)X 与Y 是否相互独立(1) 2220()(,),11,y y X f x f x y dy Ax e dy Axe dy Ax x +∞+∞+∞--====-<<⎰⎰⎰(2) 112201113(0,1)(0)(1).22216y e P X Y P X P Y x dx e dy -+∞-<<>=<<>==⎰⎰ (3) 23(),11,2X f x x x =-<<(4)由23,11,0()()(,),20,yX Yx e x y f x f y f x y -⎧-<<>⎪⋅==⎨⎪⎩其它得X 与Y 独立. 或因为2(,),11,0,y f x y Ax e x y -=-<<>可表示为x 的函数与y 的函数的积且分布在矩形区域上,所以X 与Y 相互独立.由此得(),0;y Y f y e y -=>2(),11,X f x Ax x =-<<6. 设X 服从均匀分布(0,0.2),U Y 的密度为55,0,()0,y Y e y f y -⎧>=⎨⎩其它.且,X Y 独立.求(1)X 的密度(2) (,)X Y 的联合密度 (1)X 的密度为()5,00.2,X f x x =≤≤(2)(,)X Y 的联合密度为525,00.2,0,(,)0,y e x y f xy -⎧≤≤>=⎨⎩其它.第八次作业★1 求函数(1)Z 1XY (2) Z 2min{X Y } (3) Z 3max{X Y }的分布律 (1)11(0)(0),6P Z P X Y =====1111(1)(0,1)(1,0),362P Z P X Y P X Y ====+===+=(2)2111(1)(1,1)(1,2),1264P Z P X Y P X Y ====+===+=223(0)1(1).4P Z P Z ==-==(3) 31(0)(0),6P Z P X Y =====2 设随机变量求函数Z X /Y 的分布律3 设X 与Y 相互独立概率密度分别为220()00,xX e x f x x -⎧>=⎨≤⎩0()00,y Y e y f y x -⎧>=⎨≤⎩试求ZXY 的概率密度★4 设X ~U (0 1) Y ~E (1) 且X 与Y 独立求函数ZXY 的密度函数当01z <≤时当1z >时因此★5 设随机变量(X Y )的概率密度为()101,0(,)10x y e x y f x y e -+-⎧⎪<<<<+∞=⎨-⎪⎩其它(1)求边缘概率密度f X (x ) f Y (y ) (2)求函数U max (X , Y )的分布函数 (3)求函数V min (X , Y )的分布函数(1) 1,01,()10,x X e x f x e --⎧<<⎪=-⎨⎪⎩其它.,0,()0,yY e y f y -⎧>=⎨⎩其它. (2) 11000,0,1()(),01,111,1x xx x X X x e e F x f x dx dx x e e x ----≤⎧⎪-⎪===<<⎨--⎪≥⎪⎩⎰⎰.min{,1}10,0,1,01x x e x e --≤⎧⎪=⎨->⎪-⎩. (3) 111,0,()1(),01,10,1x X X x e eS x F x x e x ---≤⎧⎪-⎪-=<<⎨-⎪≥⎪⎩@.6 设某种型号的电子管的寿命(以小时计)近似地服从N (160 202)分布随机地选取4只求其中没有一只寿命小于180小时的概率随机变量2(160,20),X N :180160(180)(1)0.84134,20P X -⎛⎫≤=Φ=Φ= ⎪⎝⎭没有一只寿命小于180小时的概率为第九次作业★1.试求 E (X ) E (X 25) E (|X |)2. 设随机变量X 的概率密度为0 0,() 01, 1.x x f x x x Ae x -⎧≤⎪=<≤⎨⎪>⎩求 (1)常数A (2)X 的数学期望(1) 1100111(),2x f x dx xdx Ae dx Ae +∞+∞--==+=+⎰⎰⎰,2e A =(2) 12100114()2.2323x e e EX xf x dx x dx xe dx e +∞+∞--==+=+⨯=⎰⎰⎰★3. 设球的直径D 在[a b ]上均匀分布试求 (1)球的表面积的数学期望(表面积2D π)(2)球的体积的数学期望(体积316D π)(1) 22222()();3ba x E D ED dx a ab b b a ππππ===++-⎰ (2) 33322()().6624b a x E D ED dx a b a b b a ππππ⎛⎫===++ ⎪-⎝⎭⎰ ★4.求E (X ) E (Y ) E (XY ) ★ 5. 设随机变量X 和Y 独立且具有概率密度为2,01,()0,X x x f x <<⎧=⎨⎩其它,3(1)3,1,()0, 1.y Y e y f y y --⎧>=⎨≤⎩(1)求(25)E X Y + (2)求2()E X Y(1) 112002()2,3X EX xf x dx x dx ===⎰⎰或随机变量1Z Y =-:指数分布(3),E 141,,33EZ EY EY =-==(2) 11223001()2,2X EX x f x dx x dx ===⎰⎰由X 和Y 独立得22142().233E X Y EX EY ==⨯=第十次作业1.试求 (1) D (X ) (2) D (3X 2)(1) 20.110.210.320.130.10.4,i i iEX x p ==-⨯-⨯+⨯+⨯+⨯=∑(2) 2(32)(3)9 2.0418.36.D X DX -+=-=⨯=★2. 设随机变量X 具有概率密度为22,02,()0,Ax x x f x ⎧+<<=⎨⎩其他，试求 (1)常数A (2)E (X ) (3) D (X ) (4) D (2X 3)(1) 22081()(2)4,3f x dx Ax x dx A +∞-∞==+=+⎰⎰解得9.8A =-(2) 22095()(2).86EX xf x dx x x x dx +∞-∞==-+=⎰⎰(3)22222094()(2),85EX x f x dx x x x dx +∞-∞==-+=⎰⎰2224519.56180DX EX E X ⎛⎫=-=-= ⎪⎝⎭(4) 21919(23)24.18045D X DX -==⨯=★ 3. 设二维随机变量(,)X Y 联合概率密度为2,01,01,(,)0,x y x y f x y --<<<<⎧=⎨⎩其他，试求 (1),X Y 的协方差和相关系数A (2)(21).D X Y -+(1) 103()(,)(2),01,2X f x f x y dy x y dy x x +∞-∞==--=-<<⎰⎰由,x y 的对称性3(),0 1.2Y f y y y =-<<因此(2) 由随机变量和的方差公式()2(,)D X Y DX DX Cov X Y +=++得 ★4. 设二维随机变量(,)X Y 具有联合分布律试求,,,EX DX EY DY 以及X 和Y 的相关系数 (1) X 的分布列为由变量X 分布对称得0,EX =或10.4500.4510.450,i i iEX x p ==-⨯+⨯+⨯=g(2) Y(,)X Y 取值关于原点中心对称由变量Y分布对称得0,EY =或20.20.250.2520.20,j j iEY y p ==-⨯-++⨯=∑g(3) 由二维变量(,)X Y 的联合分布列关于两坐标轴对称得,()0,i j i j ijE XY x y p ==∑∑(,)()0,Cov X Y E XY EXEY =-=因此,0.X Y ρ==5. 设随机变量X 服从参数为2的泊松分布(2)P 随机变量Y 服从区间(0,6)上的均匀分布(0,6),U 且,X Y 的相关系数,X Y ρ=记2,Z X Y =-求,.EZ DZ (1) 2,EX =063,2EY +==(2)2223 4.EZ E X Y EX EY =-=-=-⨯=-(2) 2(60)2, 3.12DX DY -===由,X Y ρ==得(,)1,Cov X Y = 由随机变量和的方差公式()2(,)D X Y DX DY Cov X Y +=++得第十一次作业★1. 试用切比雪夫不等式估计下一事件概率至少有多大掷1000次均匀硬币出现正面的次数在400到600次之间出现正面的次数~(1000,0.5),X B n p == 应用切比雪夫不等式有2. 若每次射击目标命中的概率为不断地对靶进行射击求在500次射击中击中目标的次数在区间(49 55)内的概率击中目标的次数~(500,0.1),X B n p ==根据中心极限定理,X 近似服从正态分布(50,45).N EX DX ==★3. 计算器在进行加法时将每个加数舍入最靠近它的整数.设所有舍入误差是独立的且在( 上服从均匀分布 (1)若将1500个数相加问误差总和的绝对值超过15的概率是多少(2)最多可有几个数相加使得误差总和的绝对值小于10的概率不小于(1) 误差变量,1,2,.i X i =⋅⋅⋅独立同均匀分布(0.5,0.5),X U -:10,.12EX DX ==由独立变量方差的可加性150011500125,12i i D X =⎛⎫== ⎪⎝⎭∑15001i i X =∑近似(0,125).N :(2) 1||10n i i P X =⎧⎫<⎨⎬⎩⎭∑1|n i P X =⎧⎪=<=⎨⎪⎩210.90,⎛≈Φ-≥ ⎝ 因此最多可有4个数相加误差总和的绝对值小于10的概率不小于★4. 一个系统由n 个相互独立的部件所组成每个部件的可靠性(即部件正常工作的概率)为至少有80%的部件正常工作才能使整个系统正常运行问n 至少为多大才能使系统正常运行的可靠性不低于正常工作的部件数~(,),X B n p 其中0.9.p =0.9,EX np n ==0.09.DX npq n ==1.645,24.354.n ≥≥因此n 至少取25. ★5. 有一大批电子元件装箱运往外地正品率为为保证以的概率使箱内正品数多于1000只问箱内至少要装多少只元件正品数~(,),X B n p 其中0.8.p =0.8,EX np n ==0.16.DX npq n == 解得1637.65,n ≥因此n 至少取1638.★.贝努利分布的正态近似.投掷一枚均匀硬币40次出现正面次数20X =的概率.正面次数(40,1/2),X B n p ==:400.520,400.50.510.EX np DX npq ==⨯===⨯⨯=离散值20X =近似为连续分组区间19.520.5,X << 第十二次作业★1. 设X 1 X 2 X 10为来自N (0 032)的一个样本求概率1021{ 1.44}i i P X =>∑标准化变量(0,1),1,2,...,10.0.3iX N i =:由卡方分布的定义10222211~(10).0.3i i X χχ==∑略大卡方分布上侧分位数20.1(10)15.9872.χ= ★2. 设X 1 X 2 X 3 X 4 X 5是来自正态总体X ~(0 1)容量为5的样本试求常数c 使得统计量服从t 分布并求其自由度由独立正态分布的可加性12(0,2),X X N +:标准化变量(0,1),U N =:由卡方分布的定义22222345~(3),X X X χχ=++U 与2χ独立由t 分布的定义(3),T t ===:因此c =自由度为3. ★3 设112,,,n X X X L 为来自N (1 2)的样本 212,,,nY Y Y L为来自N (2 2)的样本且两样本相互独立 2212,S S 分别为两个样本方差 222112212(1)(1)2pn S n S S n n -+-=+- 试证明22().p E S σ=证由221112(1)~(1),n S n χσ--及()211(1)1E n n χ-=-得类似地222.ES σ=★4 设1,...,n X X 为总体2(,)N μσ的简单样本样本均值和样本方差依次为2,.X S 求满足下式的k 值()0.95.P X kS μ>+=统计量(1),X T t n =-:因此k = ☆.设正态总体2(,)N μσ的容量为12n =的简单样本为112,...,X X 样本均值和样本方差依次为2,.X S 求满足下式的k 值()0.95.P X kS μ>+=正态总体样本方差未知统计量(1),12.X T t n n =-=:★5 设N ( 2)的样本记11nii X X n ==∑ 2211()1ni i S X X n ==--∑ 证明 T (1)t n - 证由独立正态分布的可加性21(,),ni i XN n n μσ=∑:211,,ni i X X N n n σμ=⎛⎫= ⎪⎝⎭∑:1n X +及2S 相互独立()2110,n n X X N nσ++-:和2S 独立标准化变量(0,1),U N =:2222(1)~(1),n S n χχσ-=-/,S σ=由t 分布的定义第十三次作业★1 设总体的密度函数为22(),0,(;)0,x x f x αααα-⎧<<⎪=⎨⎪⎩其他，求参数α的矩估计总体期望23220002()2(;),33x x x EX xf x dx x dx ααααααααα⎛⎫-==⋅=-= ⎪⎝⎭⎰⎰3,EX α= 用样本均值X 估计（或替换）总体期望EX 即ˆ,EXX =得α矩估计为ˆ3.X α= ★2 设总体的密度函数为1(1)(1),01(;)0,x x x f x θθθθ-⎧+-<<=⎨⎩其他求参数的矩估计总体期望解得2,1EX EX θ=-用样本均值X 估计（或替换）总体期望EX 即ˆ,EX X =得矩估计为2ˆ.1X Xθ=- 3 设总体的密度函数为||1(;),2x f x e x σσσ-=-∞<<+∞ 求参数的最大似然估计似然函数1111()(;)exp ||,2nn i i n n i i L f x x σσσσ==⎧⎫==-⎨⎬⎩⎭∑∏取对数得对数似然函数11ln ()ln 2ln ||,ni i L n n x σσσ==---∑令21ln ()1||0,ni i L n x σσσσ=∂=-+=∂∑ 解得σ的最大似然估计为11ˆ||.nL i i x n σ==∑ 4 设总体的密度函数为222,0(;)0,0x x e x f x x θθθ-⎧⎪>=⎨⎪<⎩求参数的最大似然估计似然函数2122111()(;)exp ,ninn i i i ni i xL f x x θθθθ===⎧⎫==-⎨⎬⎩⎭∏∑∏取对数得对数似然函数22111ln ()ln 2ln ,nn i i i i L x n x θθθ===--∑∑令231ln ()220,n i i L n x θθθθ=∂=-+=∂∑ 解得θ的最大似然估计为ˆLθ= ★5 设总体X 的均值和方差分别为与 2 X 1 X 2 X 3是总体的一个样本, 试验证统计量(1)112311ˆ4412X X X μ=++; (2)2123111ˆ333X X X μ=++; (3)3123311ˆ882X X X μ=++均为的无偏估计量, 并比较其有效性(1)1123123111111ˆ.442442E E X X X EX EX EX μμ⎛⎫=++=++= ⎪⎝⎭ (2)1123123111111ˆ.333333E E X X X EX EX EX μμ⎛⎫=++=++= ⎪⎝⎭ (3)1123123311311ˆ.882882E E X X X EX EX EX μμ⎛⎫=++=++= ⎪⎝⎭ 因此123ˆˆˆ,,μμμ均为μ的无偏估计量由独立变量方差的可加性因此无偏估计量123ˆˆˆ,,μμμ中2ˆμ最有效,1ˆμ比3ˆμ有效 ★7. 设2ˆθ为 2的无偏估计, 且ˆ()0D θ>, 试证ˆθ不是的无偏估计反之, 若ˆθ为的无偏估计, ˆ()0D θ>, 则2ˆθ也不是 2的无偏估计证(1) 22ˆ,E θθ=2222ˆˆˆˆ0,D E E E θθθθθ=-=->22ˆˆ,,E E θθθθ<≠得ˆθ不是的无偏估计(2) ˆ,E θθ=222222ˆˆˆˆˆ0,,D E E E E θθθθθθθ=-=->>得2ˆθ不是2θ的无偏估计 8设$$12,θθ是参数θ的两个相互独立的无偏估计量,且$$124D D θθ=,找出常数12,k k ,使$$1212k k θθ+也是θ的无偏估计量,并使它在所有这种形状的估计量中方差最小.$$$$1212121212()()E k k k E k E k k θθθθθθ+=+=+=,121k k +=,$$$$$222212122121212()(4)D k k k D k D k k D θθθθθ+=+=+,121222121,0,1,min{4}.k k k k s k k +=≤≤⎧⎨=+⎩ 求最小值得1214,55k k ==,4min 5s =,$$$121124min ().5D k k D θθθ+=第十四次作业★1. 某车间生产滚珠, 从长期实践中知道, 滚珠直径X 可以认为服从正态分布.从某天的产品里随机抽取6个, 测得直径(单位:mm)为, , , , ,若已知总体方差为, 试求平均直径的置信区间.(置信度为若总体方差未知, 试求平均直径的置信区间.(置信度为 (1)μ的置信区间中心当20.06σ=时,μ的95.01=-α置信区间半长为因此μ的0.95置信区间为(2) 样本方差2211()0.051,1ni S X X n =-=-∑ μ的95.01=-α置信区间半长为因此μ的0.95置信区间为★2. 为了解某型号灯泡使用寿命X (单位:小时)的均值μ和标准差今测量10只灯泡测得1500x = S20 若已知X 服从正态分布N ( 2), 求 (1)置信度为的总体均值的置信区间 (2)置信度为的总体方差2的置信区间(1) 置信区间半长/20.025( 2.262 6.32214.3,t n t α-==⨯= 当2σ未知时,μ的95.01=-α置信区间为(2) 已知参数2210,20,0.10,n S α===上侧分位数为置信区间两端(下限,上限)为因此灯泡使用寿命方差2σ置信度为10.90α-=的置信区间为★3. 对方差220σσ=为已知的正态总体问须抽取容量n 为多大的样本, 方能使总体均值的置信度为1的置信区间的长度不大于L总体均值μ的置信区间长度为/22,u L α≤取220/224n u L ασ≥的整数 ★4 已知某种元件的寿命X ~N ( 2) 现随机地抽取10个试件进行试验, 测得数据如下82, 93, 57, 71, 10, 46, 35, 18, 94, 69. (1)若已知 3, 求平均抗压强度的95%的置信区间(2)求平均抗压强度的95%的置信区间 (3)求的95%的置信区间 (1)μ的置信区间中心当223σ=时,μ的95.01=-α置信区间半长/2 1.96 1.861,u α==因此μ的0.95置信区间为(2) 上侧分位数220.02510.025(9)19.023,(9) 2.700,χχ-== 样本方差σ的10.95α-=的置信区间两端(下限,上限)为因此元件寿命标准差σ的0.95置信区间为★.两正态总体均值差21μμ-的1α-置信区间．当22212σσσ==未知时由于22,,,x y X Y S S 相互独立构造服从分布(2)t m n +-的统计量(枢轴量) 记222(1)(1)2x ywm S n S S m n -+-=+-，则21μμ-的二样本t 置信区间为★5 随机地抽取A 批导线4根 B 批导线5根测得起电阻为(单位欧姆)A B设测得数据分别服从正态分布N (1 2) N (2 2) 且它们相互独立 1 2 均未知求12的95%的置信区间上侧分位数20.025(2)(7) 2.3646,t m n t α+-==当22212σσσ==未知时,21μμ-的1α-置信区间半长为 21μμ-的95.01=-α置信区间为★6 假设人体身高服从正态分布, 今抽测甲、乙两地区18岁~ 25岁女青年身高得数据如下: 甲地区抽取10名, 样本均值米, 样本标准差0.2米; 乙地区抽取10名, 样本均值米, 样本标准差0.4米. 求 (1)两正态总体均值差的95%的置信区间 (2)两正态总体方差比的95%的置信区间 (1) 分位数20.025(2)(18) 2.1009,t m n t α+-==当22212σσσ==未知时,21μμ-的1α-置信区间半长为 21μμ-的95.01=-α置信区间为★(2)两正态总体(期望未知)的方差比2212/σσ的1α-置信区间．由于22111(1)/n S σ-~21(1),n χ-22222(1)/n S σ-~22(1),n χ-且2212,S S 独立,构造统计量(枢轴量) 2211122222~(1,1),S F F n n S σσ=-- 对给定的置信度α-1,由其中/2211/2121(1,1),(1,1)F n n F n n αα-=---- 因此2212/σσ的α-1置信区间为第十五次作业★1 某工厂生产的固体燃料推进器的燃烧率服从正态分布N ( 2) 40cm/s, 2cm/s 现在用新方法生产了一批推进器从中随机抽取25只测得燃烧率的样本均值为X s 设在新方法下总体均方差仍为2cm/s 问这批推进器的燃烧率是否较以往生产的推进器的燃烧率有显着的改变取显着性水平 1).提出原假设及备择假设.0010:40;:.H H μμμμ==≠ 2).选取统计量并确定其分布.~(0,1).X U N =3).确定分位数及拒绝域.上侧分位数0.025 1.96,u =拒绝域{|| 1.96}.W U =≥4).计算统计量的观测值并作出统计推断.因此拒绝原假设,认为在显着性水平0.05α=下,推进器的燃烧率显着改变.★2 某苗圃规定平均苗高60(cm)以上方能出圃今从某苗床中随机抽取9株测得高度分别为 62 61 59 60 62 58 63 62 63 已知苗高服从正态分布试问在显着性水平下这些苗是否可以出圃 1).原假设及备择假设0010:60;:.H H μμμμ≥=< 2).取统计量(8).X T t =: 3).上侧分位数0.05(8) 1.8595,t =得拒绝域(, 1.8595).W =-∞-4).由样本计算得61.11,X=0,.T T W S ==>∉因此接受原假设0,H 即认为在显着性水平0.05α=下,这些苗可以出圃.★3 5名测量人员彼此独立地测量同一块土地分别测得这块土地面积(单位 km 2)为, , , ,算得平均面积为设测量值总体服从正态分布由这批样本值能否说明这块土地面积不到(1).原假设及备择假设0010: 1.25;:.H H μμμμ≥=< 2).取统计量(4).X T t =:3).上侧分位数0.05(4) 2.1318,t =得拒绝域(, 2.1318).W =-∞-4).样本方差为2211()0.00123,1ni S X X n =-=-∑0.035,S = 统计量的实现值为因此接受原假设0,H 认为在显着性水平0.05下,这块土地面积达到. ★4 设某电缆线的抗拉强度X 服从正态分布N (10600 822) 现从改进工艺后生产的一批电缆线中随机抽取10根测量其抗拉强度计算得样本均值x 10653 方差S 26962 当显着水平时能否据此样本认为(1)新工艺下生产的电缆线抗拉强度比过去生产的电缆线抗拉强度有显着提高 (2)新工艺下生产的电缆线抗拉强度的方差有显着变化 (1)提出原假设及备择假设.0010:10600;:.H H μμμμ≥=< 选取统计量并确定其分布.(9).X T t =: 确定分位数及拒绝域.0.05(9) 1.8331,t =得拒绝域(, 1.8331).W =-∞- 计算统计量的观测值并作出统计推断.因此接受原假设,认为在显着性水平0.05α=下,新工艺电缆抗拉强度比过去工艺有显着提高.(2)提出原假设及备择假设222220010:82;:.H H σσσσ==≠ 在原假设成立的前提下,构造统计量2222(1)~(9).n S χχσ-=确定上侧分位数2210.0250.025(9) 2.700,(9)19.023,χχ-==得拒绝域计算2χ统计量的观测值并作出统计推断因而接受原假设0,H 即认为新工艺下的电缆抗拉强度的方差无显着变化.★5 设某涤纶强度X ~N ( 2) 用老方法制造的涤纶强度均值是标准差现改进工艺后从新生产的产品中随机抽取9个样品测得起强度如下在显着性水平0.05α=下,涤纶强度的均值和标准差是否发生了改变 (1)提出原假设及备择假设.0010:0.528;:.H H μμμμ==≠ 选取统计量并确定其分布.~(0,1).X U N =确定分位数及拒绝域.上侧分位数0.025 1.96,u =拒绝域{|| 1.96}.W U =≥ 计算统计量的实现值并作出统计推断.样本均值为统计量的实现值为因此接受原假设0,H 即认为在显着性水平0.05α=下,涤纶强度均值未改变.(2)提出原假设及备择假设222220010:0.016;:,H H σσσσ==≠ 在原假设成立的前提下,构造统计量2222(1)~(8).n S χχσ-=确定上侧分位数2210.0250.025(8) 2.180,(8)17.535,χχ-==得拒绝域计算2χ统计量的观测值并作出统计推断样本平方和样本偏差平方和统计量的观测值因而接受原假设0,H 即认为涤纶强度的标准差未改变.★6 测定某饮料中糖份的含量测得10个观察值的均值X %标准差S % 设饮料中糖份的含量服从正态分布N ( 2) 试在显着性水平下分别检验(1) 0010:0.05%;:.H H μμμμ==≠ (2) 0010:0.04%;:.H H σσσσ==≠ (1)提出原假设及备择假设.0010:0.05%;:.H H μμμμ==≠ 选取统计量并确定其分布.~(1).X T t n =-。

作业(2)解答

Fe Fe 同素异构转变点（1394℃，0%C ） • N：
• G： Fe Fe 同素异构转变点（912℃，0%C）
三、绘出Fe-Fe3C相图（2），标明各区域的组织成分，并说明各特性点S 、E 、 P、N 、G （2.5）和各特性线GS源自、SE 、PQ 、PSK（2）的含义。
• 0.60% C：充分奥氏体化后，冷到1点时奥氏体开始析出铁素体F，12点之间奥氏体A成分沿GS线变化，铁素体F成分沿GP线变化，当温度到2点时，奥氏体的成分达到S点成分（含碳0.77%），便发生共析转变，形成珠光体，此时，原先析出的铁素体保持不变，称为先析铁素体，其成分为0.02%C，所以共析转变结束后，合金的组织为先析铁素体和珠光体，当温度继续下降时，铁素体的溶碳量沿PQ线变化，析出三次渗碳体Fe3CIII ，同样量很少，可忽略。所以室温平衡组织为：铁素体F+珠光体P 或者：充分奥氏体化 1 奥氏体开始析出铁素体， 1-2 奥氏体析出铁素体，奥氏体A成分沿GS线变化，铁素体 F成分沿GP线变化 2 发生共析转变 Fe3C ，形成珠光体组织温度继续下降铁素体的溶碳量沿PQ线变化，析出三次渗碳体 Fe3CIII ，同样量很少，可忽略。室温平衡组织为：铁素体F+珠光体P
• S：共析点（727℃，0.77%C）在这一点上发生共析转变， Fe 反应式：，当冷却到 727℃时从具有S点成 3C 分的奥氏体中同时析出具有P点成分的铁素体和渗碳体的两相混合物——珠光体P • E：碳在γ -Fe中的最大溶解度点（1148℃，2.11%C）
• P：碳α-Fe在中的最大溶解度点（0.0218%C，727℃ ）
四、根据Fe-Fe3C相图，分析含碳量分别为 0.60% 、 0.77% 、 1.0% 的铁碳合金在充分奥氏体化以后缓慢冷却至室温时的相转变过程和室温平衡组织（3）。

规范作业12解答

= k 2 λ2 ,
3 即： k1
= 5k 2 ,
3 k 2 = k1 5
（K1、K2必须为整数）
∴ k 2 = 3,6,9,12,L
2.一束光是自然光和线偏振光的混合光, 2.一束光是自然光和线偏振光的混合光,让它垂直穿过一束光是自然光和线偏振光的混合光一偏振片,若以此入射光束为轴旋转偏振片,测得透射光一偏振片,若以此入射光束为轴旋转偏振片, 强最大值是最小值的5 强最大值是最小值的5倍,那么入射光束中自然光和线偏振光的光强比值为：振光的光强比值为：（A））（A） 1/2; （B） 1/5; （C） 1/3; （D） 2/3 ））））分析：设自然光光强为I0，线偏振光光强为I1。根据马吕斯定律，有：I max
大学物理规范作业
12
一、选择题 1.某元素的特征光谱中含有波长分别为λ =450nm和 1.某元素的特征光谱中含有波长分别为λ1=450nm和某元素的特征光谱中含有波长分别为 =750nm的光谱线在光栅光谱中, 的光谱线。 λ2=750nm的光谱线。在光栅光谱中,这两种波长原谱线有重叠现象,重叠处λ 的谱线的级数将是: 线有重叠现象,重叠处λ2的谱线的级数将是:
I max
I0 = 4
3.在双折射晶体内部, 3.在双折射晶体内部,频率相同而电振动方向不同的线在双折射晶体内部偏振光,沿光轴传播时, 偏振光,沿光轴传播时,它们的传播速度是相同的(填相同” 不同” “相同”或“不同”)。
三、计算题波长为λ=500nm单色光, 30° 入射角照射在光栅上, λ=500nm单色光 1. 波长为 λ=500nm 单色光 , 以 30° 入射角照射在光栅上 , 发现原在垂直入射时的中央明纹的位置现在改变为第2 发现原在垂直入射时的中央明纹的位置现在改变为第2级光谱线的位置, 此光栅每厘米上共有多少条缝?( ?(2 光谱线的位置,求:(1)此光栅每厘米上共有多少条缝?(2) 最多能看到几级光谱线?共可看到几条谱线? 最多能看到几级光谱线?共可看到几条谱线? 解：（1） ′ (a 垂直入射时光栅干涉的主极大条件为： + b) sin ϕ k = k ′λ 中央明纹处，对应的级数为K/=0，

第一章作业参考解答

∞
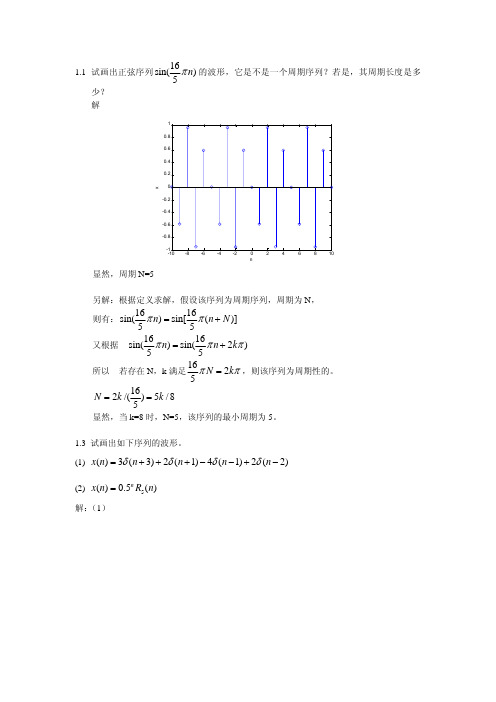
注：该题反映了对原序列 2 倍内插后的频谱变化。 1.7 求以下序列的 z 变换、收敛域及零极点分布图（1） δ ( n − n0 ) 解： Ζ[δ ( n − n0 )] =
n=-∞
∑ δ (n − n ) z
0
∞
−n
= z − n0
ROC：若 n0 ≠ 0 ,则 0 <| z |≤ ∞ ，在 z=0 处存在极点；若 n0 = 0 ，则 0 ≤| z |≤ ∞ ，无零极点（2） 0.5 u ( n) 解： Ζ[0.5 u (n)] =
1 xa2 0 -1 -4 -3 0 1 2 3 n xa3(t)=cos(10*pi*t)以角频率 8pi rad/s 采样后的序列 -2 -1 4
1 xa3 0 -1 -4 -3 -2 -1 0 n 1 2 3 4
图 3 采样后得到的序列
xa1(t)=cos(2*pi*t)的幅频响应 60 Xa1(omega)
xa 3 (t ) 的波形及采样点位置并解释频谱混叠现象。
解：
xa1(t)=cos(2*pi*t) 1 xa1 0 -1 -1 -0.8 -0.6 -0.4 -0.2 0 0.2 t xa2(t)=-cos(6*pi*t) 0.4 0.6 0.8 1
1 xa2 0 -1 -1 -0.8 -0.6 -0.4 -0.2 0 0.2 t xa3(t)=cos(10*pi*t) 0.4 0.6 0.8 1
mΩ sτ τ sin( 2 ) − jmΩ τ / 2 jmΩ t − jΩt = ∫ xa (t ) ∑ ( e e dt )e −∞ mΩ sτ m =−∞ T
∞ ∞
s s
mΩ sτ τ sin( 2 ) − jmΩ τ / 2 ∞ = ∑( e ) ∫ xa (t )e − j ( Ω− mΩ )t dt −∞ Ω τ m T s m =−∞

大物静电场作业解答

[A ]
高斯定理推导过程中考虑了各种
+q
静电场和任意曲面。
物理系：史彭
静电场作业解
4．边长为 L 的正方形，在其四个顶点上各放有等量的点电
荷，若正方形中心O处的场强不为零，则
[B]
(A) 顶点a、b、c、d处都是正电荷;
(B) 顶点a、b处是正电荷，c、d处是负电荷;
(C) 顶点a、c处是正电荷，b、d处是负电荷;
(D) 0
物理系：史彭
静电场作业解
4. 在静电场中，下列说法中哪一个是正确的？ [ D ] （A）带正电荷的导体，其电势一定是正值。（B）等势面上各点的场强一定相等。（C）场强为零处，电势也一定为零。（D）场强相等处，电势梯度矢量一定相等。（A）带正电荷的导体，其电势不一定是正值。电势的正负与零点选取有关。（B）等势面上各点的场强不一定相等。场强与电势梯度有关。（C）场强为零处，电势不变但不一定为零。（D）场强相等处，电势梯度矢量一定相等。
静电场作业解
( C ) E O 0U O 0
+q
+q
-q
O -q
( D ) E O 0U O 0
-q
+q
+q
O -q
物理系：史彭
静电场作业解
二.填空题:
2q
1.如图所示，一等边三角形边
长为a，三个顶点上分别放置着电量为q,2q,3q的三个正点电荷。
a
设无穷远处为电势零点，则三角形中心处O的电势
侧上S总S下总总 S总
侧4r24(rh22R2)q0
物理系：史彭
静电场作业解
侧4r24(rh22R2)q0
由几何关系 r 2R

流体力学课后作业答案

49
2.37 圆柱体直径d=2m，长l=5m，放置于60°的斜
面上，求水作用于圆柱体上的静水总压力大小及其
流
作用方向。
体
力
解： Px ghxC Ax
学
9800 d cos 60 d cos 60 5
2
60°
24.5kN
V

1 2
V圆

V三角
[1 (d )2
22
1 d sin 60 2
0

R3 H3
h3dh
=39.6N m
33
1-13 水暖系统为防止水温升高时体积膨胀将水管胀裂，在系统顶部设膨胀水箱，若系统内水的总体积V=8m3，
流体力
加温前后温差为50ºC，水的体膨胀系数为0.0005 1/ºC，学
求膨胀水箱的最小容积。
dV
解：由
V

V dt
dV V dt V 0.0005508 0.2m3
若反向流动，Q不变，Re不变，λ不变，hf不变，
所以h不变，只是反向高差为9cm。
26
4-20 环形断面管道中水温10℃，流量Q=400L/min，
当量粗糙高度K=0.15mm，d=75mm，D=100mm。求流
在管长l=300m管段上的沿程水头损失。
体
解： v Q 4Q 1.94m/s
34
第二章习题解答
2-29 有一容器上部盛油h1=1m，ρ1=800kg/m3，下部盛水 h2=2m，侧壁倾角θ=60º。求容器壁上单宽静水压力及作用位置。
解：F1 1gh1C A1
油 h1
8009.8 0.5 (1/ sin 60) 1 4.52kN

物理班静电部分作业参考解答

练习一1、三个电量为q -的点电荷各放在边长为r 的等边三角形的三个顶点上，电荷)(0>Q Q 放在三角形的重心上。

为使每个负电荷受力为零，Q 之值应为多大？解：如图， 0321=++F F F030cos 2301=-F F 04234220202=-⨯⨯l qQrq πεπε 3r l =3/3q Q =2、一均匀带电直线长为L ，线电荷密度为λ。

求直线的延长线上距L 中点为)(2L r r >处的场强。

解：如图，电荷元dx dq λ=在P 点的场强为 20)(4x r dxdE -=πελ，水平向右整个带电直线在P 点的场强为)4/(4)(42202/2/20L r Lx r dxdE E L L -=-==⎰⎰-πελπελ方向沿x e λ方向。

3、一根不导电的细塑料杆，被弯成近乎完整的圆，圆的半径为0.5m ，杆的两端有2cm 的缝隙，910123-⨯.C 的正电荷均匀地分布在杆上，求圆心处电场的大小和方向。

解：圆心处的电场应等于完整的均匀圆周电荷和相同线电荷密度填满缝隙的负电荷的电场的叠加，由于前者在圆心处的电场为零，所以圆心处的电场为)2(420d r r d E -=ππελm V /72.0)02.05.02(5.002.01012.3109299=-⨯⨯⨯⨯⨯⨯=-π 方向指向负电荷，即指向缝隙。

4、一个电偶极子的电矩为l q p=，证明此电偶极子轴线上距其中心为)(l r r >>处的一点的场强为3042r p E πε=。

证：2211[]4()()22P E E E q l l r r πε+-=+=--+q-F2xdx2-q-Oq+PE -E +2322002244()4r lqrl qll rr πεπε>>=−−−→- 方向与E +同即： 3024pE rπε=轴，证毕。

5、电偶极子电场的一般表示式。

将电矩为p的电偶极子所在位置取作原点，电矩方向取作x 轴正向。

第3章作业解答

(2)
Pi

Po

Po
vm
1800 2105W 0.9 0.95
台州学院机械工程学院
3-2 设液压泵转速为950r/min，排量V=168mL/r，在额定压力
29.5MPa和同样转速下，测得的实际流量为150L/min，额定工况
下的总效率为0.87，试求：1）泵的理论流量。2）泵的容积效率。
解:
1）活塞运动时，液压缸的负载压力为：p负

F A

1200 15 104
8105 Pa
0.8MPa
p负<pj1,pj2, 两个减压阀都不起作用, 阀口全开，即：
pA pB pC 0.8MPa
2）当达到终点时，相当于负载无穷大，两个减压阀均起作用； PJ2< PJ1,减压阀2出口先关闭，减压阀1出口后关闭，出口压力均等于各自的减压阀调定压力，即三点压力如下：
压力为 1MPa, 容积效率ηv=0.96，机械效率ηm= 0.86，若输入流量为q=40L/min，试求：
（1）液压马达的输出转速；
（2）液压马达的输出转矩。
解：
(1) n qv 40 L / min 0.96 384 r / min
V 100 mL / r
(2) T

pV 2π
2)
Ppi

Ppo
p
Ppo
pm pv

2175 0.9 0.9
2685W
3)
nm

qmv
Vm
=
217.5106 60 0.9 10 106
1175
r
/
min
TmBiblioteka pVm2mm =

作业参考解答（精）

3.1证明对六边形系统，同频复用因子为N Q 3=，其中ij j i N ++=22。

证明：同频复用因子（co-channel reuse ratio ，同信道复用比？） Q=D/R对于六边形系统，D 与R 有下图的关系由余弦定理22222222(2)(2)23cos120(333)3D R ij R i j ij R NR =+-=++=D Q R ⇒===3.3证明蜂窝系统的频率复用因子为k/S ，其中k 为每个小区的平均信道数，S 为蜂窝系统的可用信道总数。

证明：频率复用因子(frequency reuse factor)是簇中小区数目N 的倒数， S/k=N ，因此频率复用因子=1/N=k/S3.5有一个蜂窝电话运营商约定使用TDMA 方案，该方案可以容忍的最低信噪比为15dB ，求最理想的N 值：（a ）全向天线；（b ）120º裂向；（c ）60º裂向。

并回答应该使用裂向吗？如果应该，那么应该使用哪种裂向方式(60º还是120º)？(假设路径损耗指数n=4，并考虑中继效率)解：由题意可得01.5001(/)151031.62()nn i nii SR D R dB Ii D --====≥==∑由于ij j i N ++=22，其中i 、j 为整数，所以簇大小N=3,4,7…… 不同簇大小和裂向情况下，仅考虑最近的干扰小区数量i 0，如下表：N=7（i=2，j=1）：N=4（i=2，j=0）：N=3（i=1，j=1）：取路径损耗指数4n = (a) 使用全向天线06,7,4,3i for N ==于是59.4)106(31215.1=⨯≥N故N=7(b) 使用120º裂向027,433N i N =⎧=⎨=⎩于是11.5211.521(210)2.657,431(310) 3.2533N N N ⎧⨯==⎪⎪≥⎨⎪⨯==⎪⎩故N=4(c) 使用60º裂向，017,423N i N =⎧=⎨=⎩于是11.5211.521(110) 1.877,431(210) 2.6533N N N ⎧⨯==⎪⎪≥⎨⎪⨯==⎪⎩故N=3使用裂向技术，减小了蜂窝小区簇的大小，增大了频率复用因子，提高了蜂窝系统的容量，所以应该使用裂向技术。

环境化学作业题解答

5
2、逆温现象对大气中污染物的迁移有什么影响?
一般情况下，大气温度随着高度增加而下降，每上升100 米，温度降低0.6℃左右。即是说在数千米以下，总是低层大气温度高、密度小，高层大气温度低、密度大，显得 “头重脚轻”。这种大气层结容易发生上下翻滚即“对流” 运动，可将近地面层的污染物向高空乃至远方输散，从而使城市上空污染程度减轻。因而在通常情况下，城市上空为轻度污染，对人体健康影响不大。可是在某些天气条件下，一地上空的大气结构会出现气温随高度增加而升高的反常现象，从而导致大气层结“脚重头轻”，气家学家称之为“逆温”，发生逆温现象的大气层称为“逆温层”。它像一层厚厚的被子罩在我们城乡上空，上下层空气减少了流动，近地面层大气污染物“无路可走”，只好原地不动，越积越多，空气污染势必加重。
（2）含氮化合物
氧化亚氮(N2O)、一氧化氮(NO)和二氧化氮(NO2)。N2O是低层大气含量最高的含氮化合物，由于其非常稳定，一般认为其没有明显的污染效应。 NOX来源与消除：NO和N02是大气中主要含氮污染物。其人为来源是燃料燃烧。燃烧源分为流动和固定燃烧源。城市大气中NOX 2/3来自汽车排放，1/3来自固定源排放。燃烧产生的NOX主要是NO，占90％以上；NO2 约占O.5％～10％。大气中NOX最终将转化为硝酸和硝酸盐微粒经湿沉降和干沉降从大气中去除，其中湿沉降是最主要的消除方式。
③中间层： 50～80km；空气较稀薄；臭氧层消失；温度随海拔高度的增加而迅速降低；大气的垂直对流强烈。 ④热层：80～500km；在太阳紫外线照射下空气处于高度电离状态（电离层），能反射无线电波，人类可利用它进行远距离无线电通讯；大气温度随高度增加而升高；空气更加稀薄，大气质量仅占大气总质量的 0．5％。热层以上的大气层称为逃逸层。这层空气在太阳紫外线和宇宙射线的作用与大气温度不同，大气的压力总是随着海拔高度的增加而减小。

下册作业参考答案

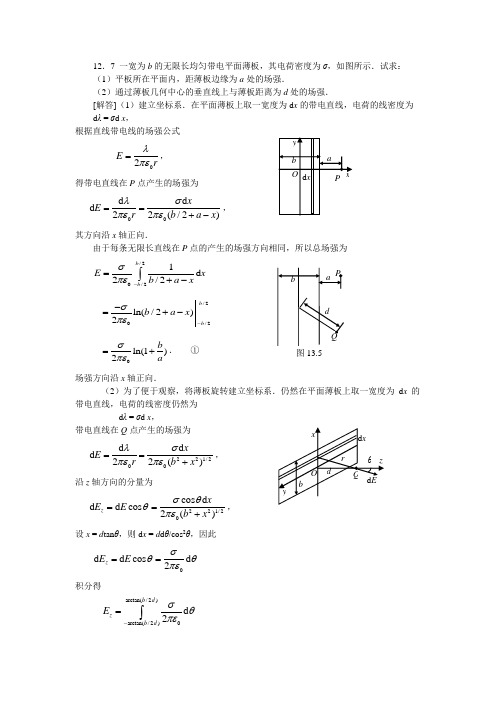
12．7 一宽为b 的无限长均匀带电平面薄板，其电荷密度为ζ，如图所示．试求：（1）平板所在平面内，距薄板边缘为a 处的场强．（2）通过薄板几何中心的垂直线上与薄板距离为d 处的场强．[解答]（1）建立坐标系．在平面薄板上取一宽度为d x 的带电直线，电荷的线密度为 d λ = ζd x ，根据直线带电线的场强公式02E rλπε=，得带电直线在P 点产生的场强为00d d d 22(/2)xE rb a x λσπεπε==+-，其方向沿x 轴正向．由于每条无限长直线在P 点的产生的场强方向相同，所以总场强为/20/21d 2/2b b E x b a x σπε-=+-⎰ /2/2ln(/2)2b b b a x σπε--=+-0ln(1)2baσπε=+． ① 场强方向沿x 轴正向．（2）为了便于观察，将薄板旋转建立坐标系．仍然在平面薄板上取一宽度为d x 的带电直线，电荷的线密度仍然为d λ = ζd x ，带电直线在Q 点产生的场强为 221/200d d d 22()xE rb x λσπεπε==+，沿z 轴方向的分量为221/20cos d d d cos 2()z xE E b x σθθπε==+，设x = d tan θ，则d x = d d θ/cos 2θ，因此d d cos d 2z E E σθθπε==积分得arctan(/2)0arctan(/2)d 2b d z b d E σθπε-=⎰图13.50arctan()2bdσπε=． ② 场强方向沿z 轴正向．[讨论]（1）薄板单位长度上电荷为λ = ζb ，①式的场强可化为0ln(1/)2/b a E a b aλπε+=，当b →0时，薄板就变成一根直线，应用罗必塔法则或泰勒展开式，场强公式变为02E aλπε→， ③这正是带电直线的场强公式．（2）②也可以化为0arctan(/2)2/2z b d E d b dλπε=，当b →0时，薄板就变成一根直线，应用罗必塔法则或泰勒展开式，场强公式变为02z E dλπε→，这也是带电直线的场强公式．当b →∞时，可得2z E σε→， ④ 这是无限大带电平面所产生的场强公式．12．9 面电荷密度为ζ的均匀无限大带电平板，以平板上的一点O 为中心，R 为半径作一半球面，如图所示．求通过此半球面的电通量．[解答]设想在平板下面补一个半球面，与上面的半球面合成一个球面．球面内包含的电荷为q = πR 2ζ，通过球面的电通量为Φe = q /ε0，通过半球面的电通量为Φ`e = Φe /2 = πR 2ζ/2ε0．图12.912．10 两无限长同轴圆柱面，半径分别为R 1和R 2(R 1 > R 2)，带有等量异号电荷，单位长度的电量为λ和-λ，求（1）r < R 1；（2） R 1 < r < R 2；（3）r > R 2处各点的场强．[解答]由于电荷分布具有轴对称性，所以电场分布也具有轴对称性．（1）在内圆柱面内做一同轴圆柱形高斯面，由于高斯内没有电荷，所以E = 0，（r < R 1）．（2）在两个圆柱之间做一长度为l ，半径为r 的同轴圆柱形高斯面，高斯面内包含的电荷为 q = λl ，穿过高斯面的电通量为d d 2e SSE S E rl Φπ=⋅==⎰⎰E S Ñ，根据高斯定理Φe = q /ε0，所以02E rλπε=， (R 1 < r < R 2)．（3）在外圆柱面之外做一同轴圆柱形高斯面，由于高斯内电荷的代数和为零，所以E = 0，（r > R 2）．12．16 一半径为R 的均匀带电球面，带电量为Q ．若规定该球面上电势值为零，则无限远处的电势为多少？[解答]带电球面在外部产生的场强为204Q E r πε=，由于 d d R RRU U E r ∞∞∞-=⋅=⎰⎰E l200d 44RR QQr r r πεπε∞∞-==⎰04Q Rπε=，当U R = 0时，04Q U Rπε∞=-．12．17 电荷Q 均匀地分布在半径为R 的球体内，试证明离球心r （r <R ）处的电势为2230(3)8Q R r U Rπε-=． [证明]球的体积为343V R π=，电荷的体密度为 334Q QV R ρπ==．利用13．10题的方法可求球内外的电场强度大小为30034QE r r Rρεπε==，（r ≦R ）； 204Q E rπε=，（r ≧R ）．取无穷远处的电势为零，则r 处的电势为d d d RrrRU E r E r ∞∞=⋅=+⎰⎰⎰E l3200d d 44RrRQ Qr r r R r πεπε∞=+⎰⎰230084R rRQQ r R rπεπε∞-=+22300()84Q Q R r RRπεπε=-+2230(3)8Q R r Rπε-=．14．3 如图所示的正方形线圈ABCD ，每边长为a ，通有电流I ．求正方形中心O 处的磁感应强度B = ？[解答]正方形每一边到O 点的距离都是a /2，在O 点产生的磁场大小相等、方向相同．以AD 边为例，利用直线电流的磁场公式：012(cos cos )4IB Rμθθπ=-，令θ1 = π/4、θ2 = 3π/4、R = a /2，AD 在O 产生的场强为02AD IB aπ=， O 点的磁感应强度为04ADIB B aπ==，方向垂直纸面向里．14．6 在半径为R = 1.0cm 的无限长半圆柱形导体面中均匀地通有电流I =5.0A ，如图所示．求圆柱轴线上任一点的磁感应强度B = ？[解答]取导体面的横截面，电流方向垂直纸面向外．半圆的周长为 C = πR ，电流线密度为 i = I/C = IπR ．在半圆上取一线元d l = R d φ代表无限长直导线的截面，电流元为 d I = i d l = I d φ/π，在轴线上产生的磁感应强度为 002d d d 22I I B R Rμμϕππ==，方向与径向垂直．d B 的两个分量为 d B x = d B cos φ，d B y = d B sin φ．积分得002200cos d sin 022x I IB R R ππμμϕϕϕππ===⎰，02sin d 2y IB R πμϕϕπ=⎰00220(cos )2II RRπμμϕππ=-=．由对称性也可知B x = 0，所以磁感应强度B = B y = 6.4×10-5(T)，方向沿着y 正向．14．10 半径为R 的无限长直圆柱导体，通以电流I ，电流在截面上分布不均匀，电流密度δ = kr ，求：导体内磁感应强度？[解答]在圆柱体内取一半径为r 、宽度为d r 的薄圆环，其面积为 d S = 2πr d r ，电流元为 d I = δd S = 2πk r 2d r ，从0到r 积分得薄环包围的电流强度为I r = 2πkr 3/3；从0到R 积分得全部电流强度I = 2πkR 3/3，因此I r /I = r 3/R 3．根据安培环路定理可得导体内的磁感应强度200322r I IB r r Rμμππ==．14．12 二条长直载流导线与一长方形线圈共面，如图所示．已知a = b = c = 10cm ，l = 10m ，I 1 = I 2 = 100A ，求通过线圈的磁通量．[解答]电流I 1和I 2在线圈中产生的磁场方向都是垂直纸面向里的，在坐标系中的x 点，它们共同产生的磁感应强度大小为01022(/2)2(/2)I I B a b x c b x μμππ=++++-．在矩形中取一面积元d S = l d x ，通过面积元的磁通量为d Φ = B d S = Bl d x ，图15.13通过线圈的磁通量为/2012/2()d 2/2/2b b l I I x a b x c b xμΦπ-=++++-⎰ 011(ln ln )2l a b cI I a c bμπ+=-+ =2×10-7×10×100×2ln2=2.77×10-4(Wb)．。

材料力学作业参考解答

2-2（b）答：
2-3答：以B点为研究对象，由平面汇交力系的平衡条件
2-2求下列结构中指定杆内的应力。已知(a)图中杆的横截面面积A1=A2=1150mm2；
解：（1）分析整体，作示力图
：
（2）取部分分析，示力图见（b）
：
（3）分析铰E，示力图见（c）
：
2-3求下列各杆内的最大正应力。
（3）图(c)为变截面拉杆，上段AB的横截面积为40mm2，下段BC的横截面积为30mm2，杆材料的ρg=78kN/m3。
解：（1）求①、②杆轴力
由平衡方程可以求出:
（2）求杆的变形
（压缩）
（拉伸）
（压缩）
（3）由几何关系：（下降）
2-9答：任一截面上轴力为F，由
得面积为
伸长量为
2-11图示一挡水墙示意图，其中AB杆支承着挡水墙，各部分尺寸均已示于图中。若AB杆为圆截面，材料为松木，其容许应力［σ］=11MPa，试求AB杆所需的直径。
：
（2）由强度条件求
2-14图示AB为刚性杆，长为3a。A端铰接于墙壁上，在C、B两处分别用同材料、同面积的①、②两杆拉住，使AB杆保持水平。在D点作用荷载F后，求两杆内产生的应力。设弹性模量为E，横截面面积为A。
解：
1．本题为超静定问题，
见图(a),设AB杆产生角位移，则
，
2．由Hooke定律：
由平衡条件可知：
所以B,C截面相对位移为
3-1试作下列各杆的扭矩图。
3-2一直径d=60mm的圆杆，其两端受外力偶矩T=2kN·m的作用而发生扭转。试求横截面上1，2，3点处的切应力和最大切应变，并在此三点处画出切应力的方向。(G=80GPa)。
解：横截面上切应力大小沿半径线性分布，方向垂直半径

淘师湾作业内容及答案

淘师湾作业内容及答案淘师湾作业内容及答案。

一、数学作业。

1. 计算下列各题。

（1）30 ÷ 5 × 3 = （）。

（2）（3 + 4）× 5 2 = （）。

（3）（8 3）× 2 ÷ 5 = （）。

2. 解方程。

（1）3x 5 = 7。

（2）2y + 4 = 10。

3. 计算三角形的面积。

（1）底边长为6cm，高为4cm。

（2）底边长为8cm，高为5cm。

4. 用比例尺表示下列各长度。

（1）实际长度为12m，比例尺为1:50。

（2）实际长度为30cm，比例尺为1:100。

5. 简答题。

（1）什么是最大公约数和最小公倍数？（2）如何判断一个数是不是另一个数的因数？二、语文作业。

1. 阅读理解。

（1）阅读课文《荷塘月色》，回答问题，作者在课文中通过怎样的描写表现了荷塘的美丽？（2）阅读课文《岳阳楼记》，回答问题，作者写《岳阳楼记》的目的是什么？2. 写作。

请根据所学课文或自己的生活经历，写一篇不少于800字的作文，题目自拟。

三、英语作业。

1. 单词拼写。

（1）He is very (h o n e s t) and always tells the truth.（2）The (c o m p e t i t i o n) will be held next week.2. 选择填空。

（1）—Would you like (some/any) tea?—Yes, please.（2）—What does your brother do?—He is (a/an) engineer.3. 完形填空。

Long long ago, there was a poor family in a small village. The 1 didn’t have much food to eat. They were often 2 . One day, the father 3 to his children, "I have no money to buy food. What can we do?" The children thoughtfor a while and said, "We can 4 the cow. We can get some money from it." The father thought it was a good 5 . So he went to the market and sold the cow. He got 6 money and bought some food. The family had a good meal that day. And the father 7 to his children, "It's really a good idea. We can 8 the cow again next time."4. 翻译。

大学物理作业解答

解：m在下滑过程中，机械能守恒；且系统在水平方向上不受外力，系统动量也守恒:
m gR1m2v1MV 2 22
mv M V 0
AR
O
Vm 2M gR; M mM
V
N
G
v
v 2M gR
M
B
m M 大家好
7
物体m 下滑至B处时，M所受合外力为零，没有加速度，所以M是惯性系，则相对此惯性系可写出对m的牛二定律方程∶
MVx m(u cos Vx ) 0 Vx mu cos /(M m)
即炮车向后退．
(2) 以 u 表示发炮过程中任一时刻炮弹相对于炮身的速度，则该瞬时炮车的速度应为
Vx mu cos / (M m)
积分求炮车后退距离
t
t
x Vx d t m cos / (M m) u d t
的匀速圆周运动,现在向下拉绳，当小球半径减少到 r0/2时，向下拉的速度为v，求这一过程中拉力的功。
大家好
0
m r0 o
v
14
解小球所受的力中,重力和桌面的支持力抵消,只有绳的拉力影响小球的运动。
拉力的作用线通过o点,对o点
的力矩为零,故小球在运动中
对o点的角动量守恒,于是有
m0r20
m(r0)2
0
0
x ml cos /(M m)
即向后退了 ml cos /(M m) 的距大离家好．
m
3
练习4-2（1）
假设子弹离开枪口时合力刚好为零
大家好
4
练习 4-2(2)：质量为 m 的小球自高为 y0 处沿水平方向以速率 v0 抛出,与
地面碰撞后跳起的最大高度为
1 2