轴对称图形(章复习)

合集下载

第一章轴对称图形复习课

第一章轴对称图形复习课学习目标：1、回顾和整理本章所学知识，用自己喜欢的方式进行总结的归纳，构建本章知识结构框架，使所学知识系统化；2、进一步巩固轴对称性质和简单的轴对称图形——线段、角、等腰三角形、等边三角形、等腰梯形的性质，并能运用这些性质解决问题；学习重点:轴对称图形的性质，以及运用于解题学习难点:有条理地表达，熟练地运用已知结论解决问题学习过程:一、【知识梳理】1. ，那么称这个图形是轴对称图形.2．线段的对称轴是，线段的垂直平分线有什么性质？3．角的对称轴是，角平分线有什么性质？4.等腰三角形的判定：有相等的三角形是等腰三角形；有相等的三角形是等腰三角形5.等边三角形的判定：都相等的三角形是等边三角形；都相等的三角形是等边三角形；有一个角是的等腰三角形是等边三角形.6.等腰三角形的性质：等腰三角形的相等；等腰三角形的、、互相重合.7．直角三角形斜边上的中线 .8.等腰梯形的性质：（1）边：；（2）角：；（3）对角线：.9.等腰梯形的判定： .二、【热身练习】1．下列图形中，轴对称图形有（）．（A ）1个（B ）2个（C ）3个（D ）4个2. 右图是从镜中看到的一串数字，这串数字应为 .3.如右图，在△ABC 中，∠B ＝90°，∠A ＝36°，AC 的垂直平分线MN 与AB 交于点D ，则∠BCD 的度数是____________. 4．已知AB 垂直平分CD ，AC=6cm,BD=4cm ，则四边形ADBC 的周长是 .5．如图，以正方形ABCD 的一边CD 为边向形外作等边三角形CDE ，则∠AEB= .6. 等腰三角形ABC 中，（1）若∠A=80°，则∠B= °；（2）若周长为8cm ，AB=3cm ，则BC= cm7.等腰梯形的腰长为2，上、下底之和为10且有一底角为60°，则它的两底长分别为____________．三、【典型例题】例1、已知∆ABC 中，AB=AC=10，DE 垂直平分AB ，交AC 于E ，已知∆BEC 的周长是16.求∆ABC 的周长.例2、如图，已知D 、E 两点在线段BC 上，AB ＝AC ，AD ＝AE ，试说明BD=CE 的理由?B C D N M AA B CED例3、如图，等腰梯形ABCD 中，AD ∥BC ，对角线AC 、BD 相交于点O ．试说明：AO ＝DO ．测试题1.下列图形不是轴对称图形的是（）A 、有两个外角相等的三角形.B 、有一个内角为45°的直角三角形.C 、有一个内角为60°的等腰三角形.D 、有一个内角为40°的直角三角形.2．下列命题中，正确的是 ( )A ．等腰三角形底边上的中线就是底边的垂直平分线B ．等腰三角形的对称轴是底边上的高C ．一条线段可看作是以它的垂直平分线为轴的轴对称图形D ．等腰三角形的对称轴就是顶角平分线3．下列说法正确的是 ( )A ．等腰梯形的对角线互相平分B ．有两个角相等的梯形是等腰梯形C ．对角线相等的四边形是等腰梯形D ．等腰梯形的对角线相等4.如果等腰三角形两边长是6㎝和3㎝，那么它的周长是（） A 、9㎝ B 、12㎝ C 、12㎝或15㎝ D 、15㎝5.等腰三角形是对称图形，它至少有条对称轴.6.若等腰三角形的一个角为50°，则其他两个角的度数为________________．7.等腰梯形的腰长为12cm ，上底长为15cm ，上底与腰的夹角为120°，则下底长为 cm ．8.如图，在梯形ABCD 中，AD ∥BC ，AB ＝CD ，∠A ＝120°，对角线BD 平分∠ABC ，则∠BDC 的度数是；又若AD ＝5，则BC ＝．OCDA B D E A9.如图，△ABC 中，AB =AC ，∠A =36°，AB 的中垂线DE 交AC 于D ，交AB 于E ，下述结论：（1）BD 平分∠ABC ；（2）AD =BD =BC ；（3）△BDC 的周长等于AB +BC ；（4）D 是AC 中点.其中正确的命题序号是 .10.在△ABC 中，∠C =90°，DE 垂直平分斜边AB ，分别交AB ，BC 于D ，E .若∠CAE = ∠B +30°，求∠AEB .11如图，已知：△ABC 中，BD 、CE 分别是AC 、AB 边上的高，G 、F 分别是BC 、DE 的中点.试探索FG 与DE 的关系.12.如图，AD 平分∠BAC ，EF 垂直平分AD 交BC 的延长线于F ，连结AF.求证：∠B=∠CAF.F E D C BA EB DC A G F ED C BA · ·。

人教版初二数学13章轴对称图形复习知识点

线段垂直平分线上的点到线段两个端点的距离相等；（3）线段垂直平分线的判定：到一条线段两个端点距离相等的点，在这条线段的垂直平分线上。
如图，AD与BC相交于点O，OA=OC，∠A=∠C，BE=DE．求证：OE垂直平分BD．
５．如图，AC＝AD，BC＝BD，则有（）
A
A．AB垂直平分CD
B．CD垂直平分AB
底边上的高互相重合。
(3)判别方法：①有两条边相等（概念）
②等角对等边
2.等边三角形 (1)三边都相等的三角形叫做等边三角形，它是轴对称图形，有三条对称轴。
(2)性质：等边三角形的三个角都是60° (3)判定： ①三个角都相等的三角形是等边三角形 ②有一个角是60°的等腰三角形是等边三角形 ③有三个边都相等的三角形是等边三角形
∴ AE+EF+AF =BE+EF+CF=10cm
C∠EAF= ∠BAC-∠BAE-∠CAF =120°- ∠B- ∠C=60°
例6 如图，△ABC中，AB=AC，∠A=50°，AB的垂直平分线交AC于D，求∠ FBC的度数。
A
解：∵ AB=AC， ∠A=50°
∴ ∠ABC= ∠C=65°
又∵ AC是线段AB的垂直平分线
；
（x，－y）
（－x，y）
1．已知点P1（a，3）和点P2（4，b）关于y轴对称，则（a+b）2007= -1
2．点A（2，5）与点B（2，-3）关于直线 y=1
对称．
知识点6
•等腰三角形的性质：等边对等角三线合一
• 等腰三角形的判定： ①有两条边相等（概念） ②等角对等边
知识点7
初中阶段五种基本的尺规作图 (1)作一条线段等于已知线段； (2)作一个角等于已知角； (3)作已知角的平分线； (4)作线段的垂直平分线； (5)过直线外一点作已知直线的垂线。

第一章轴对称图形-复习课课件1

(2)图②由5张全等的正方形组成，只移动其中一张纸片，你能使它变成轴对称图形吗？
辨析与思考：
(1)如果一个图形沿着某条直线对折，两侧的图形能够完
全重合，这个图形就是轴对称图形
（）
(2)全等图形不一定是轴对称图形。（）
(3)线段的对称轴是它的垂直平分线
Байду номын сангаас
（）
(4)等边三角形有３条对称轴。
（）
(5)一个角的角平分线就是这个角的对称轴（）
(2)小丽用如图①的直角三角形铁皮，烙一块与铁皮形状、大小相同的饼。如果烙好一面后就把饼翻身，那么这块并不能正好落在“锅”中。如图②，小丽将饼切了一刀，然后将两小块都翻身，结果饼就能正好落在“锅”中了，这是为什么？
(3)如果用来烙饼的既不是等腰三角形也不是直角三角形 (如图③)，那么烙好一面后，怎样将烙饼翻身，才能使烙饼仍能正好落在锅中？
20世纪著名数学家赫尔曼·外尔所说的，“对称是一种思想，人们毕生追求，并创造次序、美丽和完善……”
知识点复习：
轴对称一个图形沿着某一条直线折叠,
如果它能够与另一个图形______,那么就
说这两个图形成轴对称.这条直线就是
______.两个图形中的对应点叫做
.
轴对称图形一个图形沿着某条直线对折,
CF⊥BD于F，交DE于G，DF= 1 BC，试
说明∠FCB= 1∠B
2
2
D
F
A
G
B
E
C
本节课小结：
本节课我们复习了哪些知识点？你对本节课所复习的知识又有了哪些新的
认识？
设计轴对称图案
图案的对称不但要求图形对称外，有时颜色也“对称”。

章复习第12章轴对称

章复习第12章轴对称一、轴对称图形和轴对称1、轴对称图形如果一个图形沿一条直线折叠，直线两旁的部分能够____________，这个图形就叫做轴对称图形，这条直线就是它的__________．这时，我们也说这个图形关于这条直线____或____________．2、线段的垂直平分线⑴垂直平分线的定义．经过____________并且____________这条线段的直线，叫做这条线段的垂直平分线，垂直平分线也称__________．⑵垂直平分线的性质．①线段垂直平分线上的点②与一条线段两个端点距离相等的点，注：三角形三边的垂直平分线交于一点，并且交点____________3、轴对称⑴定义：把一个图形沿着某一条直线折叠，如果能够________________，那么就说这两个图形关于这条直线对称，也叫做这两个图形____________，这条直线叫做________，折叠后重合的对应点，叫做________．⑵轴对称的性质：①如果两个图形关于某条直线对称，那么对称轴是____________②轴对称图形的对称轴是____________成轴对称的两个图形是____形；成轴对称的两个图形，它们的对应线段或延长线如果相交，则交点在______上．注：轴对称与轴对称固形的区别与联系：区别：轴对称是指____个图形的位置关系；轴对称图形是指____个具有特殊形状的图形．联系：①它们的定义中都是沿某直线____，图形____．②如果把两个成轴对称的图形看成一个整体，那么它就是一个____________；反过来，把轴对称图形的对称的两部分当作两个图形，那么这两个图形____________．4、轴对称变换⑴定义：由一个平面图形得到它的____________的图形变换叫做轴对称变换．⑵利用坐标表示轴对称．利用平面直角坐标系中与已知点关于x轴或y，轴对称点的坐标的规律，可以在平面直角坐标系中作出与一个图形关于x轴或y轴对称的图形．点（x，y）关于x轴对称的点的坐标为________ ；关于y轴对称的点的坐标为________．二、等腰三角形1、等腰三角形⑴定义：____________的三角形，叫做等腰三角形．相等的两条边叫做____，另一条边叫做____，两腰所夹的角叫做____，底边和腰的夹角叫做____．⑵性质：①等腰三角形的两腰____；②等腰三角形的两个底角____（即____________）；③等腰三角形的顶角平分线、底边上的中线、高相互重合，简称为____________．⑶等腰三角形的判定（等角对等边）：如果一个三角形____________，那么____________________，（简称为____________）即____________2、等边三角形⑴定义：注：等边三角形是一种特殊的等腰三角形。

八年级数学上第13章《轴对称》期末复习课件

用
折叠（对折）
这条直线就是
对称轴
1.轴对称图形的定义：如果一个图形沿着一条直线对折，两侧的
图形能够完全重合，这个图形就是轴对称图形。折痕所在的这条直线叫做__对__称__轴。
图(1)能与图(2)重合吗？
这条直线也是
___对_称__轴___
2.两个图形关于某直线对称：
把一个图形沿着某一条直线折叠，如果它能与另一个图形重合，那么我们就说这两个图_____关__于__这__条__直__线__对_。称
A
图中有哪些等腰三角形？
解：∠1=720 ∠2=360
2
等腰三角形有：
B
⊿ABC 、⊿ABD 和 ⊿BCD
D 1
C
等边三角形的定义：三条边都相等的三角形叫做等边三角形。
A
B
C
11.等边三角形的性质：
等边三角形的三个内角都相等，并且每一个内角都等于60 °
12.等边三角形的判定：
判定1：
三个角都相等的三角形是等边三角形。
判定2：
有一个角是 60°的等腰三角形是等边三角形。
13.用法归纳
1、等腰三角形的判定方法有下列几种：1定义 2判定定理。
2、等边三角形的判定方法有以下几
种：1定义 2判定1 3判定2
。
3、等腰三角形的判定定理与性质定理的区别是条件和结论刚好相反。
4、运用等腰三角形的判定定理时，应注意在同一个三角形中。
(D)
特殊的轴对称图形:
正方形、长方形、等腰三角形、等腰梯形和圆都是轴对称图形。有的轴对称图形有不止一条
1.找到一组对应点， 2.画出以这两点为顶点的线段的垂直平分线。
练习４：如图，已知△ABC和直线，作出与△ABC 关于直线对称的图形。

苏科版数学九上第二章轴对称图形--圆复习

A．150°
B．130°
C．120°
D．60°
2.5.直线与圆的位置关系
一、直线与圆的位置关系
r
O
┐d
●
相交
r
O
┐d
●
相切
1、直线和圆相交
d < r.
2、直线和圆相切
d = r.
3、直线和圆相离
d > r.
r
O
d
●
┐
相离
2.5 直线与圆的位置关系
二、切线的判定定理
经过半径的外端,并且垂直于这条半径的直线是圆的切线
线平分两条切线的夹角.
A
∵PA,PB切⊙O于A,B
∴PA=PB ∠1=∠2
P
1
2
O
●
B
练习
1、已知：如图1，△ABC中，AC＝BC，以BC为直径的⊙O交
AB于点D，过点D作DE⊥AC于点E，交 BC的延长线于点F．
求证：（1）AD＝BD；（2）DF是⊙O的切线．
A
A
D
E
B
O
C
P
F
C
图1
B
图2
2、如图2，PA、PA是圆的切线，A、B为切点，AC为
．
练习
三、选择题：
下列命题正确的是（ C ）
A、三角形外心到三边距离相等
B、三角形的内心不一定在三角形的内部
C、等边三角形的内心、外心重合
D、三角形一定有一个外切圆
四、一个三角形,它的周长为30cm,它的内切圆半径为2cm,则这个三
30
角形的面积为______．
2.5直线与圆的位置关系
七、圆线与圆的位置关系
⌒ ⌒

(完整)初二数学八上第十三章轴对称知识点总结复习和常考题型练习,推荐文档

第十三章轴对称、知识框架:二、知识概念：1.基本概念：⑴轴对称图形：如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形就叫做轴对称图形•⑵两个图形成轴对称：把一个图形沿某一条直线折叠，如果它能够与另一个图形重合，那么就说这两个图形关于这条直线对称 •铀对称图形AA\L区別只对f —冲-)ft-fKmr150对裤轴CF 一佥只冇一舉>(“轴对称旳睛(WK 予秤瓚的俭M 工菲.矗麹»JSt :t 鹽个、曲擢：心)只有1一頭〉对務柄联系却晁把射对材囲宼泊对禅轴曲卿撷甘"么卿牛曲癣轶夭于迭条 W 鑽處抽对耕-如杲把.阿十庇抽对秤的国招拼& — 妊呑虑一* 益林.外也亡赣足一亍轴对STSJ 搭-(4) 线段的垂直平分线：经过线段中点并且垂直于这条线段的直线，叫做这条线段的垂直平分线• (5) 等腰三角形：有两条边相等的三角形叫做等腰三角形 •相等的两条边叫做腰，另一条边叫做底边，两腰所夹的角叫做顶角，底边与腰的夹角叫做底角(6) 等边三角形：三条边都相等的三角形叫做等边三角形 2.基本性质：⑴对称的性质：① 不管是轴对称图形还是两个图形关于某条直线对称，对称轴都是任何一对对应点所连线段的垂直平分线.② 对称的图形都全等•③ 如果两个图形的对应点连线被同条直线垂直平分，那么这两个图形关于这条直线对称。

④ 两个图形关于某条直线成轴对称，如果它们的对应线段或延长线相交，那么交点在对称轴上。

⑵线段垂直平分线的性质：① 线段垂直平分线上的点与这条线段两个端点的距离相等 ② 与一条线段两个端点距离相等的点在这条线段的垂直平分线上 ⑶关于坐标轴对称的点的坐标性质①点(x, y )关于x 轴对称的点的坐标为(x, -y ).②点（x, y ）关于y轴对称的点的坐标为（-x, y ）.③点（x, y ）关于原点对称的点的坐标为（-x,- y ）⑷等腰三角形的性质：①等腰三角形两腰相等•②等腰三角形两底角相等（等边对等角）③等腰三角形的顶角角平分线、底边上的中线，底边上的高相互重合•④等腰三角形是轴对称图形，对称轴是三线合一（1条）.⑸等边三角形的性质：①等边三角形三边都相等•②等边三角形三个内角都相等，都等于60 °③等边三角形每条边上都存在三线合一④等边三角形是轴对称图形，对称轴是三线合一（3条）.（6）三角形三条边的垂直平分线相交于一点，这个点到三角形三个顶点的距离相等3.基本判定：⑴等腰三角形的判定：①有两条边相等的三角形是等腰三角形•②如果一个三角形有两个角相等，那么这两个角所对的边也相等（等角对等边）•⑵等边三角形的判定：①三条边都相等的三角形是等边三角形•②三个角都相等的三角形是等边三角形•③有一个角是60°的等腰三角形是等边三角形.4.基本方法：⑴做已知直线的垂线：⑵做已知线段的垂直平分线：⑶作对称轴：连接两个对应点，作所连线段的垂直平分线⑷作已知图形关于某直线的对称图形：⑸在直线上做一点，使它到该直线同侧的两个已知点的距离之和最短•常考例题精选1. （2015 •三明中考）下列图形中，不是轴对称图形的是（）2. （2015 •日照中考）下面所给的交通标志图中是轴对称图形的是（）ABC3. （2015 •杭州中考）下列“表情图”中，属于轴对称图形的是（）4. （2015 •凉山州中考）如图，/ 3=30°,为了使白球反弹后能将黑球直接撞入袋中，那么击打白球时，必须保证/ 1的度数为（）A.30 °B.45 °C.60 °D.755. （2015 •德州中考）如图，动点P从（0，3）出发，沿所示的方向运动，每当碰到矩形的边时反弹，反弹时反射角等于入射角，当点P第2013次碰到矩形的边时，点P的坐标为（）771 ~1 ~2 ~~ ~~6 ~7 d F A.（1，4） B.（5，0） C.（6，4）D.（8，3）6. （2015 •南充中考）如图，△ ABC中, AB=AC Z B=70，则/A的度数是（）A.70 ° B.55C.50 °D.407. （2015 •玉溪中考）若等腰三角形的两边长分别为4和8,贝尼的周长为（）A.12B.16C.20D.16 或208. （2014 •海门模拟）如图，在边长为1的正方形网格中，将△ ABC向右平移两个单位长度得到△ A B' C',则与点B'关于x轴对称的点的坐标是（）A.（0，-1） B.（1，1） C.（2，-1）D.（1，-1）9. （2015 •绵阳中考）如图，AC BD相交于O, AB// DC AB=BC / D=40，/ ACB= 35°，则/ AOD= ______ .10. （2015 •丽水中考）如图，在等腰厶ABC中，AB=AC Z BAC=50，/ BAC的平分线与AB的中垂线交于点O,点C沿EF折叠后与点O重合，则/ CEF的度数1. （2015遵义）观察下列图形，是轴对称图形的是（）2. 点P（5，—4）关于y轴的对称点是（）A. （5，4）B. （5，—4）C. （4，—5）D. （—5，—4）3. 如图，△ ABC与厶ADC关于AC所在的直线对称，/ BCD= 70° ，/ BA B C D=80°，则/ DAC的度数为（）D. 854. 如图，在Rt A ABC 中，/ C= 90° ，/ B = 15° ，DE 垂直平分AB 交BC于点E，BE = 4，则AC长为（），第4题图）A. 2B. 3C. 4 D .以上都不对6. 如图是一台球桌面示意图，图中小正方形的边长均相等，黑球放在如图所示的位置，经白球撞击后沿箭头方向运动，经桌边反弹最后进入球洞的序号是8. 如图，D ABC 内一点，CD 平分Z ACB ，BE 丄CD ，垂足为D ，交AC 于点 E ，Z A ABE ，AC = 5，BC = 3，贝U BD 的长为（）9.如图，已知S A ABC = 12, AD 平分Z BAC ，且AD 丄BD 于点D ，则S ^ADC的值是（）5. 如图，AB = AC = AD ,若/ BAD = 80则/ BCD =(C. 140 D . 1607. （2015玉林）如图，在厶ABC正确的是（）EC C . 中，AB = AC ，DE // BC ，则下列结论中不 Z ADE = Z C D . DE = *BC，第5题图）(A . 10 B. 8 C . 610. 如图，C为线段AE上一动点（不与点A , E重合）,在AE同侧分别作正三角形ABC和正三角形CDE, AD 与BE交于点O, AD与BC交于点P，BE 与CD交于点Q,连接PQ.以下五个结论：①AD = BE;②PQ// AE ;③AP= BQ; ④DE= DP;⑤/ AOB = 60° .其中正确的结论的个数是（）A. 2个B. 3个C. 4个D. 5个12. 如图，D, E ABC两边AB , AC的中点,将厶ABC沿线段DE折叠，使点A落在点F处，若/ B = 55° ,则/BDF等于____________ .A「，第12题图）13. ____________________________________________________________ 如图，在3X 3的正方形网格中，已有两个小正方形被涂黑，再将图中其余小正方形任意涂黑一个,使整个图案构成一个轴对称图形的方法有________________________ 种.14. 如图，在厶ABC中，AB = AC , AB的垂直平分线交BC于点D ,垂足15. _______ 在厶ABC中，AC = BC,过点A作厶ABC的高AD ,若/ ACD = 30 贝B = __________ .16. ____ 如图，△ ABC中，D, E分别是AC , AB上的点，BD与CE交于点O. 给出下列三个条件：①/ EBO = /DCO;②/ BEO = /CDO:③BE = CD.上述三个条件中，哪两个条件可判定△ ABC是等腰三角形（用序号写出一种情形）：.，第16题图）17. _________________________ 如图是由9个等边三角形拼成的六边形，若已知中间的小等边三角形的边长是2,则六边形的周长是 .' ，第17题图）18. __ 如图，已知/AOB = 30° ，OC平分/ AOB，在OA上有一点M，OM =10 cm,现要在OC, OA上分别找点Q，N，使QM + QN最小，则其最小值为.，第18题图）19. 如图，某校准备在校内一块四边形草坪内栽上一棵银杏树，要求银杏树的位置点P到边AB，BC的距离相等，并且点P到点A，D的距离也相等.请用尺规作图作出银杏树的位置点P.不写作法，保留作图痕迹）23.如图，△ ABC，△ ADE是等边三角形，B，求证：(1)CE=AC + DC; (2)Z ECD = 60° . C，D在同一直线上.20. 如图，在平面直角坐标系中，A( —2, 2), B( —3, —2).(1) 若点D与点A关于y轴对称，则点D的坐标为__________ ;(2) 将点B先向右平移5个单位再向上平移1个单位得到点C，则点C的坐标为________ ;(3) 求A，B，C，D组成的四边形ABCD的面积.■I r厂m ! I I_ ■i == = Ji1 l:-一十一4二* t： 1 ER I r21. 如图，在厶ABC 中，AB = AC, D 为BC 为上一点，/ B = 30° ，/ DAB45(1) 求/ DAC的度数；(2)求证：DC = AB.22. (2015潜江)我们把两组邻边分别相等的四边形叫做“筝形”，如图，四边形ABCD是一个筝形，其中AB = CB，AD = CD，角或者对角线有关的一个结论，并证明你的结论.请你写出与筝形ABCD的24. 如图,在等腰Rt A ABC中,/ ACB = 90° , D为BC的中点,DE丄AB , 垂足为E,过点B作BF // AC交DE的延长线于点F,连接CF.(1) 求证：AD丄CF;(2) 连接AF ,试判断△ ACF的形状，并说明理由.25. 如图，已知AE丄FE,垂足为E,且E是DC的中点.(1) 如图①，如果FC丄DC, AD丄DC,垂足分别为C, D,且AD = DC,判断AE是/ FAD的角平分线吗？(不必说明理由)(2) 如图②，如果(1)中的条件“ AD = DC”去掉，其余条件不变，⑴中的结论仍成立吗？请说明理由；(3) 如图③，如果⑴的条件改为“ AD // FC” , (1)中的结论仍成立吗？请说明理由.。

轴对称及轴对称图形(复习课)

A 10 D 8 -x 10 6 F 8 -x 4 E x C
8 B
⒊如图,在梯形ABCD中，AD∥BC，如图,在梯形ABCD中 AD∥BC， ABCD DC的中点 EF⊥AB于点的中点，于点F E是DC的中点，EF⊥AB于点F．求证：S梯形ABCD=AB×EF．求证： =AB×EF．
A F E D
B
C
G
平移底,梯形转化成:三角形. 平移底,梯形转化成:三角形.
5．在梯形ABCD中，AB∥DC，AD＝在梯形ABCD中 AB∥DC，AD＝ ABCD BC，AB=1，DC=5，AC⊥BD，BE⊥CD， BC，AB=1，DC=5，AC⊥BD，BE⊥CD，则梯形的面积= 则梯形的面积= ．
A B
D
E
C
F
6．如图,梯形ABCD中，AD∥BC，E、F 如图,梯形ABCD中 AD∥BC， ABCD 分别是AD BC的中点,∠B+∠C=90° AD、的中点,∠B+∠C=90 分别是AD、BC的中点,∠B+∠C=90°，请说明EF= （BC-AD）．请说明EF= 1 BC-AD）．
D C B
E
5、如图，△ABC中，AB的垂直平分线如图， ABC中分别交AB BC于点 AB、于点D AC的垂直分别交AB、BC于点D、E，AC的垂直平分线分别交AC BC于点 AC、于点F 平分线分别交AC、BC于点F、G，若 BC=20， AEG的周长为多少的周长为多少？ BC=20，则△AEG的周长为多少？
A
F
N E
B M
C
10、已知△ABC是等腰三角形，过 10、已知 ABC是等腰三角形，过
△ABC的一个顶点的一条直线，把 ABC的一个顶点的一条直线，把 △ABC分成两个小三角形，如果这 ABC分成两个小三角形，如果这两个小三角形也是等腰三角形，问 △ABC顶角的度数是多少？ ABC顶角的度数是多少？

章节复习(三)轴对称

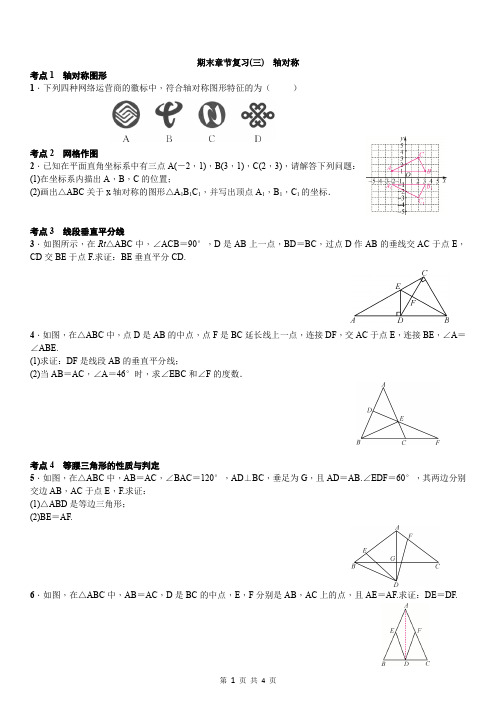
期末章节复习(三)轴对称考点1轴对称图形1．下列四种网络运营商的徽标中，符合轴对称图形特征的为（）考点2网格作图2．已知在平面直角坐标系中有三点A(－2，1)，B(3，1)，C(2，3)，请解答下列问题：(1)在坐标系内描出A，B，C的位置；(2)画出△ABC关于x轴对称的图形△A1B1C1，并写出顶点A1，B1，C1的坐标．考点3线段垂直平分线3．如图所示，在Rt△ABC中，∠ACB＝90°，D是AB上一点，BD＝BC，过点D作AB的垂线交AC于点E，CD交BE于点F.求证：BE垂直平分CD.4．如图，在△ABC中，点D是AB的中点，点F是BC延长线上一点，连接DF，交AC于点E，连接BE，∠A＝∠ABE.(1)求证：DF是线段AB的垂直平分线；(2)当AB＝AC，∠A＝46°时，求∠EBC和∠F的度数．考点4等腰三角形的性质与判定5．如图，在△ABC中，AB＝AC，∠BAC＝120°，AD⊥BC，垂足为G，且AD＝AB.∠EDF＝60°，其两边分别交边AB，AC于点E，F.求证：(1)△ABD是等边三角形；(2)BE＝AF.6．如图，在△ABC中，AB＝AC，D是BC的中点，E，F分别是AB，AC上的点，且AE＝AF.求证：DE＝DF.7．如图，在△ABC中，AB＝AC，∠BAC＝120°，AD⊥BC，垂足为G，且AD＝AB.∠EDF＝60°，其两边分别交边AB，AC于点E，F.求证：(1)△ABD是等边三角形；(2)BE＝AF.考点5等边三角形的性质与判定8．如图，已知△ABC是等边三角形，E，D，G分别在AB，BC，AC边上，且AE＝BD＝CG.连接AD，BG，CE，相交于点F，M，N.(1)求证：AD＝CE；(2)求∠DFC的度数；(3)试判断△FMN的形状，并说明理由．考点630°角的直角三角形的性质9．如图，如图，一艘轮船以每小时20海里的速度沿正北方航行，在A处测得灯塔C在北偏西30°方向上，轮船航行2小时后到达B处，在B处测得灯塔C在北偏西60°方向上，当轮船到达灯塔C的正东方向D处时，则轮船航程AD的距离是（）A．20海里B．40海里C．60海里D．80海里第9题图第10题图第1题图第3题图考点7最短路径问题10．如图，在等边△ABC中，BD平分∠ABC交AC于点D，点E，F分别是线段BD，BC上的动点，则CE＋EF 的最小值等于（）A．BD B．CD C．CE D．AC一、选择题(每小题3分，共30分)1．誉为全国第三大露天碑林的“浯溪碑林”，摩崖上铭刻着500多方古今名家碑文，其中悬针篆文具有较高的历史意义和研究价值，下面四个悬针篆文明显不是轴对称图形的是（）2．点(3，－2)关于x轴对称的点的坐标是（）A．(3，2) B．(－3，－2) C．(－3，2) D．(3，－2)3．如图，△ABC与△A′B′C′关于直线MN对称，P为MN上任一点，下列结论中错误的是（）A．△AA′P是等腰三角形B．MN垂直平分AA′，CC′C．△ABC与△A′B′C′面积相等D．直线AB，A′B′的交点不一定在MN上4．等腰三角形的一边长为6，另一边长为13，则它的周长为（）A．25 B．25或32 C．32 D．195．如图，将△ABC沿直线DE折叠后，使得点B与点A重合，已知AC＝5 cm，△ADC的周长为17 cm，则BC的长为（）A．7 cm B．10 cm C．12 cm D．22 cm第5题图第6题图第7题图第8题图第9题图第10题图6．如图，AD，CE分别是△ABC的中线和角平分线．若AB＝AC，∠CAD＝20°，则∠ACE的度数是（）A．20°B．35°C．40°D．70°7．如图，在等边△ABC中，D是AC边上的中点，延长BC到点E，使CE＝CD，则∠E的度数为（）A．15°B．20°C．30°D．40°8．如图，点P是∠AOB外的一点，点M，N是∠AOB两边上的点，点P关于OA的对称点Q恰好落在MN上，点P关于OB的对称点R落在MN的延长线上．若PM＝2.5 cm，PN＝3 cm，MN＝4 cm，则线段QR的长为（）A．4.5 cm B．5.5 cm C．6.5 cm D．7 cm9．如图，A，B两点在正方形网格的格点上，每个方格都是边长为1的正方形，点C也在格点上，且△ABC为等腰三角形，满足条件的点C有（）A．6个B．7个C．8个D．9个10．如图，在△ABC中，AB＝20 cm，AC＝12 cm，点P从点B出发以3 cm/s的速度向点A运动，点Q从点A同时出发以2 cm/s的速度向点C运动，其中一个动点到达端点时，另一个动点也随之停止运动，当△APQ是以∠A为顶角的等腰三角形时，运动的时间是（）A．2.5 s B．3 s C．3.5 s D．4 s二、填空题(每小题4分，共20分)11．如图，△ABC与△A1B1C1关于某条直线成轴对称，则∠A1＝_______．第11题图第12题图第13题图第14题图第15题图12．如图，AB＝AC，BD＝BC，若∠A＝40°，则∠ABD的度数是______．13．如图，在等边△ABC中，AC＝9，点O在AC上，且AO＝3，点P是AB上一动点，连接OP，以O为圆心，OP长为半径画弧交BC于点D，连接PD.如果PO＝PD，那么AP的长是______．14．如图，在△ABC中，AB＝4，BC＝6，∠B＝60°，将△ABC沿着射线BC的方向平移2个单位长度后，得到△A′B′C′，连接A′C，则△A′B′C的周长为_______．15．如图，点P是∠AOB内部的一点，∠AOB＝30°，OP＝8 cm，M，N是OA，OB上的两个动点，则△MPN周长的最小值为______cm.三、解答题(共50分)16．(7分)某科技公司研制开发了一种监控违章车辆的电子仪器．如图，有三条两两相交的公路，你认为这个监控仪器安装在什么位置可离三个路口的交叉点的距离相等，以便及时进行监控？17．(8分)如图，在△ABC中，AD平分∠BAC，BD⊥AD，垂足为D，过点D作DE∥AC，交AB于点E.求证：△BDE是等腰三角形．18．(10分)如图，△ABC为等边三角形，∠1＝∠2＝∠3.(1)求∠BEC的度数；(2)△DEF是等边三角形吗？为什么？19．(12分)如图，已知在等腰Rt△OAB中，∠AOB＝90°，在等腰Rt△EOF中，∠EOF＝90°，连接AE，BF.求证：(1)AE＝BF；(2)AE⊥BF.20．(13分)如图，已知等腰△ABC中，AB＝AC，点D，E分别在边AB，AC上，且AD＝AE，连接BE，CD交于点F.(1)判断∠ABE与∠ACD的数量关系，并说明理由；(2)求证：过点A，F的直线垂直平分线段BC.。

第二章轴对称图形总复习

1 l AB 第二章轴对称图形总复习一、必备知识点1.轴对称定义：如果把一个图形沿着后，能够重合，那么这两个图形关于这条直线成轴对称，这条直线叫做，两个图形中的对应点叫做。

2.轴对称图形定义：如果把一个图形沿着，直线两旁的部分能够，那么这个图形叫做轴对称图形，这条直线叫做。

3.轴对称的性质： ⑴成轴对称的两个图形。

⑵如果两个图形成轴对称，那么对称轴是。

4．线段的垂直平分线定义：垂直并且平分一条线段的直线，叫做这条线段的垂直平分线。

（也称线段的中垂线）5．线段的轴对称性：①线段是轴对称图形，对称轴有两条，一条是，另一条是。

②性质：线段的垂直平分线上的点到相等。

③判定：到的点，在这条线段的上。

结论：线段的垂直平分线是到线段两端距离相等的点的集合6．角的轴对称性：①角是图形，对称轴是。

②性质：角平分线上的点到相等。

③判定：在角的内部，到的点，在上。

7．等腰三角形定义：有的三角形叫等腰三角形，其中相等的边叫做腰，另一条边叫做底。

等腰三角形是，对称轴是。

性质：等腰三角形相等，相等（简称）；等腰三角形的互相重合。

（三线合一）8．判定：如果一个三角形，那么（简称）；9．等边三角形是特殊的，具备的一切性质。

除此之外，等边三角形有，，。

10．等边三角形的判定：是等边三角形；的三角形是等边三角形；是等边三角形。

11.直角三角形的性质：① 直角三角形两锐角② 直角三角形斜边上的中线是斜边的。

B AC E DO P l A B M2 二、学力检测一、选择题1．下列命题中：①两个全等三角形合在一起是一个轴对称图形；②等腰三角形的对称轴是底边上的中线；③等边三角形一边上的高就是这边的垂直平分线；④一条线段可以看着是以它的垂直平分线为对称轴的轴对称图形. 正确的说法有（）个 A ．1个 B ．2个 C ．3个 D ．4个2．下列图形中：①平行四边形；②有一个角是30°的直角三角形；③长方形；④等腰三角形. 其中是轴对称图形有（）个A ．1个B ．2个C ．3个D ．4个3．已知∠AOB ＝30°，点P 在∠AOB 的内部，P 1与P 关于OA 对称，P 2与P 关于OB 对称，则△P 1OP 2是（） A ．含30°角的直角三角形； B ．顶角是30的等腰三角形；C ．等边三角形D ．等腰直角三角形. 4．如图：等边三角形ABC 中，BD ＝CE ，AD 与BE 相交于点P ，则 ∠APE 的度数是（） A ．45° B ．55°C ．60°D ．75°5. 下列关于等腰三角形的性质叙述错误的是（） A ．等腰三角形两底角相等B ．等腰三角形底边上的高、底边上的中线、顶角的平分线互相重合C ．等腰三角形是中心对称图形D ．等腰三角形是轴对称图形6．已知点P 在线段AB 的垂直平分线上，点Q 在线段AB 的中垂线外，则（） A ．PA+PB ＞QA+QB B ．PA+PB ＜QA+QB D ．PA+PB ＝QA+QB D ．不能确定7．已知△ABC 与△A 1B 1C 1关于直线MN 对称，且BC 与B 1C 1交与直线MN 上一点O ，则（） A ．点O 是BC 的中点 B ．点O 是B 1C 1的中点 C ．线段OA 与OA 1关于直线MN 对称 D ．以上都不对8．如图：已知∠AOP=∠BOP=15°，PC ∥OA ，PD ⊥OA ，若PC=4，则PD= （） A ．4 B ．3C ．2D ．1 9．∠AOB 的平分线上一点P 到OA 的距离为5，Q 是OB 上任一点，则（） A ．PQ ＞5 B ．PQ≥5C ．PQ ＜5D ．PQ≤510．等腰三角形的周长为15cm ，其中一边长为3cm ．则该等腰三角形的底长为（） A ．3cm 或5cm B ．3cm 或7cm C ．3cm D ．5cmB AD PO C P AEC B D3 二．填空题11．线段轴是对称图形，它有_______条对称轴． 12．等腰△ABC 中，若∠A=30°，则∠B=________．13．在Rt △ABC 中，∠C=90°，AD 平分∠BAC 交BC 于D ，若CD=4，则点D 到AB 的距离是__________． 14．等腰△ABC 中，AB=AC=10，∠A=30°，则腰AB 上的高等于___________． 15．如图，在△ABC 中，∠ABC=∠ACB=72°，BD 、CE 分别是∠ABC 和∠A CB 的平分线，它们的交点为F ，则图中等腰三角形有___________个．16．（2012•梧州）如图，在△ABC 中，AB=AD=DC ，∠BAD=32°，则∠BAC= °___________．17．若D 为△ABC 的边BC 上一点，且AD=BD ，AB=AC=CD ，则∠BAC=____________．18．△ABC 中，AB 、AC 的垂直平分线分别交BC 于点E 、F ，若∠BAC=115°，则∠EAF=___________．三．解答题19．如图：已知∠AOB 和C 、D 两点，求作一点P ，使PC=PD ，且P 到∠AOB 两边的距离相等．A C··DOB4 20．如图：AD 为△ABC 的高，∠B=2∠C ，用轴对称图形说明：CD=AB+BD ．21．有一本书折了其中一页的一角，如图：测得AD=30cm,BE=20cm ，∠BEG=60°，求折痕EF的长．22．如图：△ABC 中，AB=AC=5，AB 的垂直平分线DE 交AB 、AC 于E 、D ，① 若△BCD 的周长为8，求BC 的长；② 若BC=4，求△BCD 的周长．ACDBBCDEA5 23．等边△ABC 中，点P 在△ABC 内，点Q 在△ABC 外，且∠ABP=∠ACQ ，BP=CQ ，问 △APQ是什么形状的三角形？试说明你的结论．24. 如图1，已知矩形ABED ，点C 是边DE 的中点，且AB=2AD ．（1）判断△ABC 的形状，并说明理由；（2）保持图1中△ABC 固定不变，绕点C 旋转DE 所在的直线MN 到图2中（当垂线段AD 、BE 在直线MN 的同侧），试探究线段AD 、BE 、DE 长度之间有什么关系？并给予证明；（3）保持图2中△ABC 固定不变，继续绕点C 旋转DE 所在的直线MN 到图3中的位置（当垂线段AD 、BE 在直线MN 的异侧）．试探究线段AD 、BE 、DE 长度之间有什么关系？并给予证明．A CBPQ。

第一章轴对称图形(复习课)079PPT课件

①在BC上取一点D,使BD<CD,连结AD; ②作线段AF,使AF与AB关于AD所在的直线对称; ③作线段AE,使E在BC上,且AF与AC关于AE所在的
直线对称; ④连结DF,EF. (2)通过观察和测量,猜想△DEF是什么三角形.
等腰三角形、梯形的轴对称性
回顾与复习
等腰三角形的性质： A
= （
P
且PC＝PD
O
∴点P在∠AOB的平分线上．
DB
简单应用
1. 指出下列图案是否是轴对称图形，如果是请指出有几条对称轴
（5）
（6）
简单应用
2. 下列说法正确的是( B )
⑴ 全等的两个图形一定对称.
⑵ 成轴对称的两个图形一定全等. √
⑶ 若两个图形关于某直线对称,则它们的对应点一定位于对称轴的两侧.
线段的垂直平分线上的点到线段两端的距离相等．
A
·P
a
B
练：《补充》/17（1）
动脑筋
12 如图,要在河边
修建一个水泵站, 向张庄、李庄送水. 修
在河边什么地方,可使使用的水管B最短？
A
∟
· ·P
a
把问题转化成第10题的形式画图。
练：《补充》/17（2）课本38页/9
练一练
《课本》37-38页复习巩固/1.2.3.4.5，9
4
形，首先应确定对称轴，然后找
·D2
C·
出对称点。且点D 必须在格点上
·A ·B
综上所述：
·D 3
·D1
方格纸中符合要求的点D有4个。
8.分别画出（1）（2）（3）中,已知△ABC 关于直线l 的对称△A′B′C′
l
A
∟

第2章轴对称图形复习苏科版八年级数学上册课件

轴对称图形、成轴对称定义
轴对称图形的应用—镜面与反射
轴对称图形性质
P42
轴对称图形、成轴对称定义
轴对称图形的应用—镜面与反射
轴对称图形性质
P42
轴对称图形、成轴对称定义
轴对称图形的应用—镜面与反射
轴对称图形性质
角度相等：入射角=反射角对称轴垂直反射面
轴对称图形、成轴对称定义
轴对称图形的应用—镜面与反射
P44
轴对称图形、成轴对称定义
轴对称图形的应用—翻折与抠图
轴对称图形性质
P44
轴对称图形、成轴对称定义
轴对称图形的应用—镜面与反射
轴对称图形性质民间良方对称轴方向
镜面与实物平行前后、左右颠倒
镜面与实物垂直
前后、上下颠倒
轴对称图形、成轴对称定义
轴对称图形的应用—镜面与反射
轴对称图形性质
P42
轴对称图形性质
补充
轴对称图形、成轴对称定义
轴对称图形的应用—翻折与抠图
轴对称图形性质
关键翻折前后对应边角相等，折痕所在直线是对称轴
考点一：利用全等性质求边、角（周长）解题要点：对应边相等，对应角相等
考点二：翻折抠图解题方法：还原→折痕所在直线为对称轴
轴对称图形、成轴对称定义
轴对称图形的应用—翻折与抠图
轴对称图形性质
补充
下课啦
轴对称图形性质
P42
轴对称图形、成轴对称定义
轴对称图形的应用—翻折与抠图
轴对称图形性质
P43
轴对称图形、成轴对称定义
轴对称图形的应用—翻折与抠图
轴对称图形性质
P43
轴对称图形、成轴对称定义
轴对称图形的应用—翻折与抠图

第二章+轴对称图形(小结与思考)(单元复习)2023-2024学年八年级数学上册同步精品课堂

∴AD是BC的垂直平分线，
A
∴AB＝AC.∵AB＋BD＝DE，
B
D
C
E
∴AB＋BD＝DC＋CE，∴AC＝
CE，
巩固练习
3.如图，已知直线a和直线a同侧的两点A、B，
(1)在直线a上求作一点，使得PA=PB;
Ｂ
Ａ
a
●
P
巩固练习
(2)在直线a上求作一点，使得PA+PB最小．
Ｂ
Ａ
●
a
●
A'
P
考点分析
巩固练习
3. 如图，在△ABC中，D点在BC边上，将D点分别以AB，AC边所在直
线为对称轴，画出对称点E，F，并连接AE，AF.根据图中标示的角度，
则∠EAF的度数为___________.
140°
A
E
●
●
60°
B
●
D
F
50°
C
当堂检测
4. 如图，已知O是∠APB内的一点，M，N分别是点O关于PA，PB的对
PN⊥CD，垂足分别是M、N.
证明：∵BD是∠ABC的平分线,
求证：PM=PN.
∴∠ABD=∠CBD.
A M
D
P
B
N
C
在△ABD和△CBD中,
= ，
∠ = ∠，
= ，
∴△ABD≌△CBD,
∴∠ADB=∠CDB.
∵点P在BD上，PM⊥AD，PN⊥CD，
∴PM=PN.
考点分析
巩固练习
1.如图，在△ABC中，∠ACB＝90°，AD平分∠BAC交BC于点D，CD
＝3，DB＝5，点E在边AB上运动，连接DE，则线段DE长度的最小值