2020年四年级奥数春季班-第5讲等积变形(下)
等积变形问题归纳总结

等积变形问题归纳总结等积变形是数学中一个经典而重要的问题,涉及到几何和代数两个方面。
这类问题一般给定一个几何形状,然后要求找到一个变形的方法,使得该形状在变形后保持等面积不变。
在这篇文章中,我将对等积变形问题进行归纳和总结,介绍常见的等积变形方法及其应用。
一、等积变形的概念和意义等积变形是指通过某种方式改变一个几何形状,使得变形后的形状与原来的形状面积相等。
这个问题在工程、建筑、地理测量等领域有着广泛的应用。
等积变形的主要目的是在不改变面积的情况下,改变某个几何形状的外观或者其他性质。
在实际应用中,等积变形可以用于设计优化、曲面造型、地图绘制等方面。
二、等积变形的常见方法1. 平移变形:平移是最简单的等积变形方法之一。
平移变形是通过将几何形状整体平行地移动,使得形状的外观发生变化,但面积保持不变。
平移变形的关键是保持对称性,即移动后的形状与原来的形状在空间中仍具有相同的位置关系。
2. 旋转变形:旋转变形是通过将几何形状绕一个确定的旋转点旋转一定角度,使得形状的外观发生变化,但面积保持不变。
旋转变形的关键是确定旋转中心和旋转角度,以及保持旋转后的形状与原来的形状在空间中具有相同的位置关系。
3. 缩放变形:缩放变形是通过改变几何形状的尺寸,使得形状的外观发生变化,但面积保持不变。
缩放变形可以分为等比例缩放和非等比例缩放两种方式。
等比例缩放是将形状的所有尺寸同时按照相同的比例进行缩放;非等比例缩放是将形状的各个尺寸分别按照不同的比例进行缩放。
4. 拉伸变形:拉伸变形是通过改变几何形状的某个方向的尺寸,使得形状的外观发生变化,但面积保持不变。
拉伸变形可以在一维、二维和三维空间中进行。
在一维空间中,拉伸变形是指改变线段的长度;在二维空间中,拉伸变形是指改变面的某个方向的尺寸;在三维空间中,拉伸变形是指改变体的某个方向的尺寸。
5. 弯曲变形:弯曲变形是通过施加外力将几何形状弯曲,使得形状的外观发生变化,但面积保持不变。
四年级下册数学奥数试题-培优拓展训练--第4讲:等积变形(学生版)

第4讲 等积变形(不用添加内容,任课老师根据学生情况自行添加)(不用添加内容,也不做修改)1、三角形的面积=21底边长 高;所以,两个面积相等的三角形,当底边相等时,高也相等;反之亦然。
2、当两个三角形高相等时,面积之比等于底边长之比。
3、当两个三角形的底边长相等时,面积之比等于高之比。
4、在等底等高的情况下,三角形面积是平行四边形面积的一半;5、底边之和等于平行四边形的一边,且高相等的所有三角形,面积之和是平行四边形面积的一半;6、高之和等于平行四边形的高,且分别以这条高的两边为底的所有三角形,面积之和是平行四边形面积的一半。
1、灵活运用三角形和四边形的面积公式2、掌握三角形的等积变形技巧(不用添加内容,任课老师根据学生情况自行添加)例1:如图,三角形ABC的面积为1,其中AE=3AB,BD=2BC,三角形BDE的面积是多少?A B EC例2:正方形ABCD和正方形CEFG,且正方形ABCD边长为10厘米,则图中三角形BDF面积为多少平方厘米?GFHEC例3:图中三角形AOB的面积为15平方厘米,线段OB的长度为OD的3倍,求梯形ABCD的面积。
A DO例4:如下图,在平行四边形ABCD中,直线CF交AB于E,交DA延长线于F,若三角形ADE 的面积为1,求三角形BEF的面积。
例5:如图,三角形ABC中,AB是AD的5倍,AC是AE的3倍,如果三角形ADE的面积等于1,那么三角形ABC的面积是多少?ADEB C例6:B C如图所示,长方形ABCD的长是12厘米,宽是8厘米,三角形CEF的面积是32平方厘米,则OG是多少厘米?1、如图,在梯形ABCD中,AC与BD是对角线,其交点O,求证:△AOB与△COD 面积相等.2、如图,已知在△ABC中,BE=3AE,CD=2AD.若△ADE的面积为1平方厘米.求三角形ABC的面积.3、如下图,在△ABC中,BD=2AD,AG=2CG,BE=EF=FC=4、如右图,ABCD为平行四边形,EF平行AC,如果△ADE的面积为4平方厘米.求三角形CDF的面积.5、如右图,四边形ABCD 面积为1,且AB=AE ,BC=BF ,DC=CG ,AD=DH .求四边形EFGH 的面积.6、如右图,在平行四边形ABCD 中,直线CF 交AB 于E ,交DA 延长线于F ,若S △ADE=1,求△BEF 的面积.1、如右图,AD DB =,AE EF FC ==,已知阴影部分面积为5平方厘米,ABC ∆的面积是 平方厘米.DA2、图中三角形ABC 的面积是180平方厘米,D 是BC 的中点,AD 的长是AE 长的3倍,EF 的长是BF 长的3倍.那么三角形AEF 的面积是多少平方厘米?CB3、如图,在长方形ABCD 中,Y 是BD 的中点,Z 是DY 的中点,如果24AB =厘米,8BC =厘米,求三角形ZCY 的面积.ABC DZ Y4、如图,三角形ABC 的面积是24,D 、E 和F 分别是BC 、AC 和AD 的中点.求三角形DEF 的面积.FE DCBA5、图中两个正方形的边长分别是6厘米和4厘米,则图中阴影部分三角形的面积是多少平方厘米.6、右图是由大、小两个正方形组成的,小正方形的边长是4厘米,求三角形ABC 的面积.G4ABCDEF(不用添加内容,也不做修改)1、如图所示,平行四边形的面积是50平方厘米,则阴影部分的面积是 平方厘米.2、如下图,长方形AFEB 和长方形FDCE 拼成了长方形ABCD ,长方形ABCD 的长是20,宽是12,则它内部阴影部分的面积是 .F E DCBA3、图中的E 、F 、G 分别是正方形ABCD 三条边的三等分点,如果正方形的边长是12,那么阴影部分的面积是 .E D GCBA4、在边长为6厘米的正方形ABCD 内任取一点P ,将正方形的一组对边二等分,另一组对边三等分,分别与P 点连接,求阴影部分面积.5、如图,BD 长12厘米,DC 长4厘米,B 、C 和D 在同一条直线上。
小学四年级奥数下册三角形的等积变形教案

三一文库()/小学四年级〔小学四年级奥数下册三角形的等积变形教案〕小学四年级小学四年级奥数下册三角形的等积变形教案,供大家学习参考。
我们已经掌握了三角形面积的计算公式:# 三角形面积=底×高÷2# 这个公式告诉我们:三角形面积的大小,取决于三角形底和高的乘积.如果三角形的底不变,高越大(小),三角形面积也就越大(小).同样若三角形的高不变,底越大(小),三角形面积也就越大(小).这说明;当三角形的面积变化时,它的底和高之中至少有一个要发生变化.但是,当三角形的底和高同时发生变化时,三角形的面积不一定变化.比如当高变为原来#角形的面积变化与否取决于它的高和底的乘积,而不仅仅取决于高或底的变化.同时也告诉我们:一个三角形在面积不改变的情况下,可以有无数多个不同的形状.本讲即研究面积相同的三角形的各种形状以及它们之间的关系.# 为便于实际问题的研究,我们还会常常用到以下结论:# ①等底等高的两个三角形面积相等.# ②底在同一条直线上并且相等,该底所对的角的顶点是同一个点或在与底平行的直线上,这两个三角形面积相等.# ③若两个三角形的高(或底)相等,其中一个三角形的底(或高)是另一个三角形的几倍,那么这个三角形的面积也是另一个三角形面积的几倍.# #,它们所对的顶点同为A点,(也就是它们的高相等)那么这两个三角形的面积相等.#同时也可以知道△ABC的面积是△ABD或△AEC面积的3倍.#例如在右图中,△ABC与△DBC的底相同(它们的底都是BC),它所对的两个顶点A、D在与底BC平行的直线上,(也就是它们的高相等),那么这两个三角形的面积相等.#例如右图中,△ABC与△DBC的底相同(它们的底都是BC),△ABC的高是△DBC高的2倍(D是AB中点,AB=2BD,有AH=2DE),则△ABC的面积是△DBC面积的2倍.###。
五年级奥数第5讲等积变形

学生课程讲义
两个平面图形面积相等,称为这两个图形等积.解决平面图形面积问题的主要渠道是将欲求的图形的面积转化为已经学过的基本图形的面积问题.其中三角形的等积变形的技巧是各种
等积变形的核心,都要运用到“等(同)底、等(同)高的两个三角形面积相等”这个基本规则,并由此衍生出因题而宜的种种精巧的等积变形的技巧。
【例1】计算:
如图,5-1,ABCD 是直角梯形,两条对角线把梯形分为4个三角形,已知其中两个三角形的面积为3平方厘米和6平方厘米,求直角梯形ABCD 的面积。
【例2】
其中A、B、C都是大于0且互不相同的自然数,则(A+B)÷C=。
四年级奥数之等积变形(上)
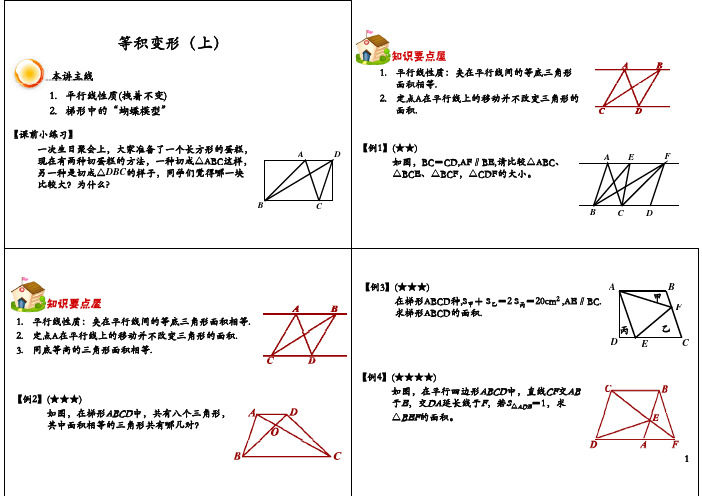
本讲主线
1.平行线性质:夹在平行线间的等底三角形
面积相等
面积相等.2.定点A在平行线上的移动并不改变三角形的
面积
面积.【例1】(★★)
如图,BC=CD,AF∥BE,请比较△ABC、F
E A 如图,BC CD,AF∥BE,请比较△ABC、△BCE、△BCF,△CDF的大小。
1.平行线性质:夹在平行线间的等底三角形面积相等.
2.定点A在平行线上的移动并不改变三角形的面积.
3.同底等高的三角形面积相等.
【例2】(★★★)
如图在梯形如图,在梯形其中面积相等的三角形共有哪几对?
D F
G H
B
C
A C
B
E
1.平行线性质:夹在平行线间的等底三角形面积相等.
2梯形蝴蝶模型:任意等积变形(上)
2.梯形蝴蝶模型:任意一个梯形中,都可以找到三对面积相等的三角形.
A
D
B
C
___________________________________________。
________________________________________________________________________________________。
奥数几何专题:等积变形(基础篇)

等积变形(上)
例1
(★★)
⑴图中每个小正方形面积都是1平方厘米,那么下面的三角形面积各是多少?
⑵图中每个小正方形面积都是1平方厘米,那么下面的三角形面积各是多少?
⑶图中每个小正方形面积都是1平方厘米,那么下面的三角形面积各是多少?
例2
(★★★)
如图,在梯形ABCD中,共有八个三角形,其中面积相等的三角形共有哪几对?
例3
(★★★)
正方形ABCD和正方形CEFG,且正方形ABCD边长为10厘米,则图中阴影面积为多少平方厘米?
例4
(★★★)
下图是由大、小两个正方形组成的,小正方形的边长是4厘米,求三角形ABC的面积。
例5
(★★★★)
如图,有三个正方形的顶点D、G、K恰好在同一条直线上,其中正方形GFEB的边长为10厘米,求阴影部分的面积。
例6
(★★★)
在平行四边形ABCD中,直线CF交AB于E,交DA延长线于F,若S△ADE=1,求△BEF的面积。
例7
(★★★★)
如图,ABCD为平行四边形,EF平行AC,如果△ADE的面积为4平方厘米。
求三角形CDF的面积。
⑴夹在一组平行线之间的等积变形,如下图,△ACD和△BCD夹在一组平行线之间,且有公共底边CD,反之,如果S△ACD=S△BCD,且A、B在CD同侧,则可知直线AB平行于CD。
⑵平行线藏在哪里?
——并列正方形的同方向对角线
【先睹为快】
(★★★★)
如图,已知三角形ABC面积为1,延长AB至D,使BD=AB;延长BC至E,使CE=BC;延长CA至F,使AF=2AC,求三角形DEF的面积。
四年级奥数之等积变形(下)
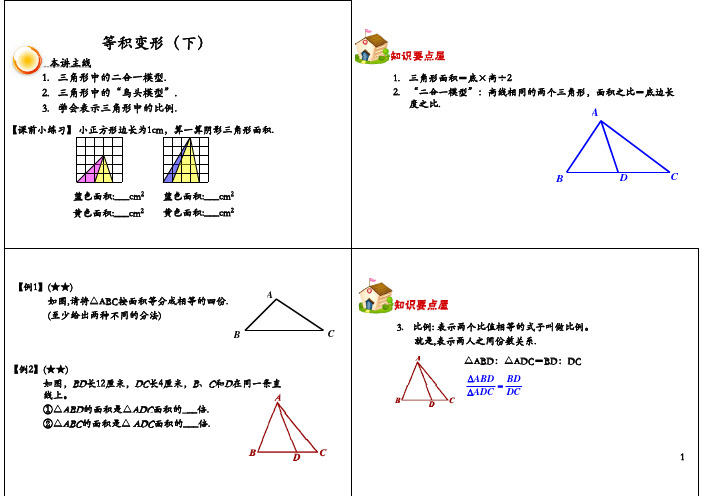
ABD BD ADC DC
1
【例3】(★★★) 如图,△ABC中,DC=2BD,CE=3AE,△ADE的面积是20cm2, △ABC的面积是多少?
【例4】(★★★) 如图,△ABC的面积是40,D、E和F分别是BC、 AC和AD的中点。求: △DEF的面积。
4. “鸟头”模型:有角共线的两个三角形,它们的面积之比等于相 应边长乘积之比。
A D
E
E C
D
D
A
B
C
B
A
E
B
C
ห้องสมุดไป่ตู้
ABC AB AC ADE AD AE
2
【今日讲题】 例3,例5,超常大挑战
【讲题心得】 ___________________________________________ __________________________________________。
A
C
E
D E
D
D
A
B
CB
ABC AB AC ADE AD AE
A
E
B
C
【例5】(★★★★) 如图,△ABC中,AB是AD的5倍,AC是AE的3倍,如果△ADE的面 积等于1,那么△ABC的面积是多少?
等积变形(下)
1. 三角形中的“二合一”模型。 2. 三角形中的“鸟头”模型。
【超常大挑战】(★★★★) 如图,△ABC的面积为2,其中AE=3AB,BD= 2BC,△BDE的面积是多少?
【家长评价】
____________________________________________ ____________________________________________ ________________________________________。
2020年四年级奥数春季班-第4讲等积变形(上)
2020年四年级奥数春季班
【动手试一试】
你有多少种方法可以将任意一个三角形分成4个面积相等的三角形?
你有什么方法将任意一个三角形分成6个面积相等的三角形?
如图,在梯形ABCD中,共有八个三角形,其中面积相等的三角形共有哪几对?
如图,在平行四边形ABCD中,EF平行AC,连结BE、AE、CF、BF那么与△BEC等积的三角形一共有哪几个三角形?
如图,ABCD为平行四边形,EF平行AC,如果△ADE的面积为4平方厘米。
求三角形CDF 的面积。
等积变形(上)
(★★)
(★★★)
(★★★★)
(★★★★)
在梯形ABCD中,OE平行于AD。
如果三角形AOB的面积是7平方厘米,则三角形DEC 的面积是______平方厘米。
正方形ABCD和正方形CEFG,且正方形ABCD边长为20厘米,则图中阴影面积为多少平方厘米?
如图,有三个正方形的顶点D、G、K恰好在同一条直线上,其中正方形GFEB的边长为16厘米,求阴影部分的面积。
(★★★★) (★★★)。
最新小学奥数 三角形的等积变形教师版

A
乙 E
甲
B
D
C
连接 AD.因为 BE=3,AE=6,所以 BE:AE=3:6=1:2,设甲部分的面积为 1 个单位,那么三角形
AED 的面积为 2 个单位,这样 ABD 的面积为 3 个单位,因为 BD:CD=1:1,所以三角形 ADC
的面积也为 3 个单位,这样乙部分的面积为 3+3-1=5 个单位,所以乙部分是甲部分面积的 5
,它们 所对的顶点同为 A 点,(也就是它们的高相等)那么这两个三角形的面积相
等. 同时也可以知道△ABC 的面积是△ABD 或△AEC 面积的 3 倍.
例如在右图中,△ABC 与△DBC 的底相同(它们的底都是 BC),它所对的两个顶 点 A、D 在与底 BC 平行的直线上,(也就是它们的高相等),那么这两个三角形 的面积相等.
-1-
例如右图中,△ABC 与△DBC 的底相同(它们的底都是 BC),△ABC 的高是△DBC 高的 2 倍(D 是 AB 中点,AB=2BD,有 AH=2DE),则△ABC 的面积是△DBC 面积的 2 倍.
上述结论,是我们研究三角形等积变形的重要依据. 例 1 用三种不同的方法,把任意一个三角形分成四个面积相等的三角形.
方法 2:如右图,先将 BC 二等分,分点 D、连结 AD,得到两个等积 三角形,即△ABD 与△ADC 等积.然后取 AC、AB 中点 E、F,并连结 DE、 DF.以而得到四个等积三角形,即△ADF、△BDF、△DCE、△ADE 等积.
-2-
例 2 用三种不同的方法将任意一个三角形分成三个小三角形,使它们的面积比 为及 1∶3∶4.
A
B
E
C
D
如图,连接 AD,因为 BC:CE=1:1,所以三角形 ACD 的面积:三角形 ABC 的面积=1:1, 所以三角形 ACD 的面积=1,三角形 ABD 的面积=2,因为 AB:BE=1:2,所以三角形 ADE 的 面积为 4. 5、三角形 ABC 被分成了甲、乙两部分,BD=DC=4,BE=3,AE=6,乙部分面积是甲部分面积的 几倍?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2020年四年级奥数春季班
【动手算一算】
⑴
⑵
⑴如图,BD长12厘米,DC长4厘米,B、C和D在同一条直线上。
①求三角形ABC的面积是三角形ADC面积的多少倍?
②求三角形ABD的面积是三角形ADC面积的多少倍?
⑵如图,E在AD上,AD垂直BC,AD=12厘米,DE=3厘米。
求三角形ABC的面积是三角形EBC面积的几倍?
如图,三角形ABC的面积是40,D、E和F分别是BC、AC和AD的中点。
求:三角形DEF 的面积。
等积变形(下)
(★★)
(★★★)
如图,在三角形ABC中,BC=8厘米,高是6厘米,E、F分别为AB和AC的中点,那么三角形EBF的面积是多少平方厘米?
如图所示,在平行四边形ABCD中,E为AB的中点,AF=2CF,三角形AFE(图中阴影部分)的面积为10平方厘米。
平行四边形ABCD的面积是多少平方厘米?
如图,三角形ABC被分成了甲、乙两部分,BD=DC=4,BE=3,AE=6,乙部分面积是甲部分面积的几倍?
如图,三角形ABC的面积为1,其中AE=3AB,BD=2BC,三角形BDE的面积是多少?
(★★★)
(★★★★) (★★★) (★★★★) (★★★)
如图,已知三角形ABC面积为1,延长AB至D,使BD=AB;延长BC至E,使CE=BC;延长CA至F,使AF=2AC,求三角形DEF的面积。
(★★★★★)
如图,D是三角形ABC一边上的中点,两个长方形分别以B、D为顶点,并且有一个公共顶点E,已知两块阴影部分的面积分别是100和120,则三角形BDE的面积是多少?
【大海点睛】
一、重要结论
1.结论㈠:等底等高的两个三角形面积相等
结论㈠拓展:夹在平行线间的一组同底三角形面积相等
如下图,△ACD和△BCD夹在一组平行线之间,且有公共底边CD,那么S△ACD=S △BCD
2.结论㈡
⑴若两个三角形的高相等,其中一个三角形的底是另一个三角形的几倍,那么这个
三角形的面积也是另一个三角形面积的几倍。
⑵若两个三角形的底相等,其中一个三角形的高是另一个三角形的几倍,那么这个
三角形的面积也是另一个三角形面积的几倍。
二、技巧方法
1.平行线的来源
⑴平行四边形(包括长方形和正方形)和梯形
⑵已知平行
⑶并排摆放的正方形的同方向对角线
2.已知做底边,等高优先找
三、经典例题
等积变形(上):例3,例5,例6,例7
等积变形(下):例2,例4,例5,例7。
