高二数学理科期末试卷
高二数学(理科)期末试卷

高二数学(理科)期末试卷
本文档为高二数学(理科)期末试卷的题目和答案。
试卷题目包
括选择题、填空题、计算题和证明题。
试卷内容涵盖了高二数学课
程的各个知识点。
选择题部分包括了多项选择题和单项选择题,考察了学生对数
学概念和定理的理解和应用能力。
填空题部分要求学生填写正确的数值或表达式,考察了学生对
问题的分析和解决能力。
计算题部分要求学生进行具体的计算操作,涉及到数值运算、
代数运算、几何运算等,考察了学生对运算方法和计算规则的掌握。
证明题部分要求学生运用已学的数学理论和方法进行推导和证明,考察了学生的逻辑思维能力和数学推理能力。
试卷内容难度适中,旨在检测学生对高二数学知识的掌握程度
和应用能力。
根据试卷得分,可以评估学生的数学水平,并作出针
对性的教学调整。
希望本次期末试卷能够促进学生对数学学科的兴趣和研究动力,帮助他们提升数学能力和解决问题的能力。
对于学生来说,认真复课堂内容和做好试卷的备考是取得好成
绩的关键。
希望学生们抓住这次机会,全力以赴,取得优秀的成绩。
祝愿每位学生都能在高二数学(理科)期末试卷中取得好成绩!。
人教版高二数学下册期末考试理科数学试卷(附答案)
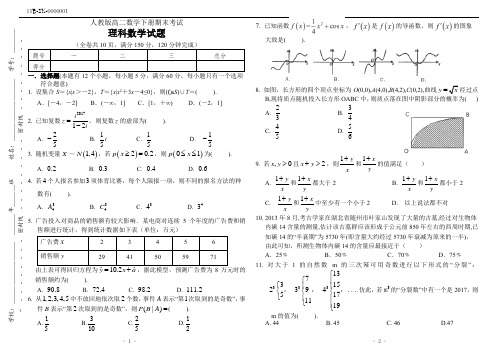
( ) 即 a 2x −1 = 2x −1对一切实数 x 都成立.
∴ a = 1,∴ a = b = 1 .……5 分
f ( x) 是 R 上的减函数。……6 分
⑵ 不等式 f (t2 − 2t) + f (2t2 − k ) 0等价于 f (t2 − 2t) f (k − 2t2 ) .
又 f ( x) 是 R 上的减函数,∴ t2 − 2t k − 2t2 . ……8 分
内碳 14 含量的测量,估计该古墓群应该形成于公元前 850 年左右的西周时期,已
知碳 14 的“半衰期”为 5730 年(即含量大约经过 5730 年衰减为原来的一半),
由此可知,所测生物体内碳 14 的含量应最接近于( )
A.25﹪
B.50﹪
C.70﹪
D.75﹪
11. 对 大 于 1 的 自 然 数 m 的 三 次 幂 可 用 奇 数 进 行 以 下 形 式 的 “ 分 裂 ” :
地运往 C 地, 现在 AB 上的距点 B 为 x 的点 M 处修一公路至点 C.已知铁路运 费为每公里 2 元,公路运费为每公里 4 元. (1)将总运费 y 表示为 x 的函数. (2)如何选点 M 才使总运费最小?
-5-
-6-
11B-SX-0000001 20. (本小题满分 12 分)
已知数列an 的前 n 项和为 Sn ,且 a1 = 1, Sn = n2an (n N+ )
( ) ( ) ⑵ 若对任意的 t R ,不等式 f t2 − 2t + f 2t2 − k 0恒成立,求实数 k 的取
值范围.
18. (本小题满分 12 分)
为了增强环保意识,某社团从男生中随机抽取了 60 人,从女生中随机抽取了
高二数学期末试卷

高二年级数学(理科)试题一、选择题(本卷共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知集合N M x x N x x M 则},1log |{},3|{2<=<== ( )A .φB .}32|{<<x xC .}20|{<<x xD .}2|{<x x2.在ABC ∆中,“ 60>A ”是“23sin >A ”的 ( )A .充分而不必要条件B .必要而不充分条件C .充要条件D .既不充分也不必要条件 3.有关命题的说法错误的是 ( )A .若p q ∧为假命题,则p 、q 均为假命题B .“x=1”是“x 2-3x+2=0”的充分不必要条件C .命题“若x 2-3x+2=0,则x=1”的逆否命题为:“若x≠1,则x 2-3x+2≠0”D .对于命题p: x R ∃∈,使得x 2+x+1<0,则2:,10p x R x x ⌝∀∈++≥均有 4.在ABC ∆中, 120,3,33===A b a ,则B的值为( ) A、 30 B、 45 C、 60 D、 905.若直线mx + 2ny -4 = 0(m ,n ∈R )始终平分圆042422=---+y x y x 的周长,则mn 的取值范围是( ) A 、(0,1) B 、(0,1] C 、(-∞,1] D 、(-∞,1)6.已知函数xxx f -+=11ln )(,若b a f -=-)(,则=)(a f ( ) A .b1B .b1- C .b D .b -7.如图,ABCD —A 1B 1C 1D 1是正方体,B 1E 1=D 1F 1=411B A ,则BE 1与DF 1所成角的余弦值是( )A .1715 B .21 C .178D .238.已知向量)0,1,1(=,)2,0,1(-=,且k +与-2互相垂直,k 等于( )A.1B.51C.57D. 539.若a 、b 、c ∈R ,则下列命题正确的是( )A 、a >b , c >d >⇒a c >b dB 、c a >cb⇒a >bC 、a 3>b 3且a b >0⇒a 1<b 1D 、a 2>b 2且a b >0⇒a 1<b 110.设函数f (x )满足f (n +1)=2)(2nn f +(n ∈N *)且f (1)=2,则f (20)为( ) A .95 B .97 C .105 D .192 二、填空题:(本大题共5小题,每小题5分,共25分。
高二数学期末考试试题高二数学(理科)

秋季期末考试试题高二数学(理科)说明:本试题分选择题和非选择题两部分. 满分150分. 考试时间120分钟 .一、选择题:(本大题共10小题;每小题5分;共50分;在每小题所给的四个选项中;只有一个是正确的。
请把答案写在答题卡上。
) 1.命题2222:0(,),:0(,)p a b a b R q a b a b R +<∈+≥∈.下列结论正确的是( ) A. ""q p ∨为真 B. ""q p ∧为真 C. ""p ⌝为假 D. ""q ⌝为真 2.设原命题:若a+b ≥2;则a ;b 中至少有一个不小于1.则原命题与其逆命题的真假情况是( ) A .原命题真;逆命题假B .原命题假;逆命题真C .原命题与逆命题均为真命题D .原命题与逆命题均为假命题3.抛物线22y x =- 的焦点坐标是 ( )A .1(0,)8B .1(,0)4-C .1(0,)8- D . 1(0,)4-4.若f (x )=sin α-cos x ;则f ′(α)等于( )A 、sin αB 、cos αC 、sin α+cos αD 、2sin α5、方程my x ++16m -2522=-1表示焦点在y 轴上的双曲线;则m 的取值范围是 ( )A. -16<m<25B.m<-16C.m<-16或m>25D. m>256. 过椭圆2222x y +=的左焦点F 引一条倾斜角为45︒的直线;则以此直线与椭圆的两个交点及椭圆中心为顶点的三角形面积为 ( )A.21B.23C.32D.27.下列求导运算正确的是( ) A 、3211)1(xx x -='+B 、2222(log )ln 2x x x '= C 、2(cos )2sin x x x x '=- D 、 3(3)3log x x e '=8.函数323922yx x x x 有( )A 、极大值5;极小值-27B 、极大值5;极小值-11C 、极大值5;无极小值D 、极小值-27;无极大值9. 1F 是22195x y +=的左焦点;P 为随圆上的动点A (1;1)为定点;则1PA PF +的最小值为 ( )A 、9B 、6C 、3D 、6+10(3,)3与抛物线22y x =上的点P 之间距离为1d ;P 到抛物线准线l 的距离为2d ;则当12d d +取最小值时;P 点坐标为 ( )A. (1;.(0;0) C. (2 ;2 ) D. 11(,)82-二、填空题(每小题5分;共20分;请把答案写在答题卡上。
高二数学(理科)下学期期末考试试题(带参考答案)

高二数学(理科)下学期期末考试试题第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.用反证法证明命题“设a ,b 为实数,则方程31x ax be ++=至少有一个实根”时,要做的假设是( )A .方程31x ax be ++=没有实根 B .方程31x ax b e ++=至多有一个实根 C .方程31x ax be++=至多有两个实根 D .方程31x ax b e ++=恰好有两个实根2.设i 是虚数单位,若2i 1iz=+-,则复数z 的共轭复数是( ) A .1i + B .2i + C .3i - D .3i + 3.13aedx x=⎰,则a =( ) A .212e B .4e C .3e D .2e 4.已知随机变量ξ服从正态分布(),16N μ,且()()261P P <-+≤=ξξ,则=μ( ) A .4- B .4 C .2- D .25.已知直线l 过点()1,1P ,且与曲线3y x =在点P 处的切线互相垂直,则直线l 的方程为( ) A .340x y ++= B .340x y +-= C .320x y -+= D .320x y --= 6.用数学归纳法证明“11112321n n ++++<-L (2n ≥)”时,由n k =的假设证明1n k =+时,不等式左边需增加的项数为( ) A .12k - B .21k - C .2k D .21k+7.一批产品的合格率为90%,检验员抽检时出错率为10%,则检验员抽取一件产品,检验为合格品的概率是( )A .0.81B .0.82C .0.90D .0.918.为大力提倡“厉行节约,反对浪费”,某市通过随机询问100名性别不同的居民是否能做到“光盘”行动,得到如下的22⨯列联表:附:()()()()()22n ad bc K a b c d a c b d -=++++参照附表,得到的正确结论是( )A .在犯错误的概率不超过5%的前提下,认为“该市居民能否做到‘光盘’与性别有关”B .在犯错误的概率不超过2.5%的前提下,认为“该市居民能否做到‘光盘’与性别有关”C .有90%以上的把握认为“该市居民能否做到‘光盘’与性别无关”D .有90%以上的把握认为“该市居民能否做到‘光盘’与性别有关”9.如果42a x x x x ⎛⎫⎛⎫+- ⎪⎪⎝⎭⎝⎭的展开式中各项系数之和为2,则展开式中x 的系数是( )A .8B .8-C .16D .16-10.已知()2cos 4f x x x =+,()f x '为()f x 的导函数,则()f x '的图象大致是( )A .B .C .D .11.已知6件不同产品中有2件是次品,现对它们依次进行测试,直至找出所有次品为止.若恰在第4次测试后,就找出了所有次品,则这样的不同测试方法数是( ) A .24 B .72 C .96 D .36012.已知()y f x =为定义在R 上的单调递增函数,()y f x '=是其导函数,若对任意x ∈R 总有()()12017f x f x <',则下列大小关系一定正确的是( )A .()102017f e f ⎛⎫>⋅⎪⎝⎭ B .()102017f e f ⎛⎫<⋅ ⎪⎝⎭C .()2102017f e f ⎛⎫>⋅⎪⎝⎭D .()2102017f e f ⎛⎫<⋅ ⎪⎝⎭第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13.曲线2y x =与y =所围成的封闭图形的面积为 .14.设某种机械设备能够连续正常工作10000小时的概率为0.85,能够连续正常工作15000小时的概率为0.75,现有一台连续工作了10000小时的这种机械,它能够连续正常工作到15000小时的概率是 . 15.若()2017201212x a a x a x -=++20172017a x ++L (x ∈R ),则12323111222a a a ++2017201712a ++L 的值为 .16.如果对定义在区间D 上的函数()f x ,对区间D 内任意两个不相等的实数1x ,2x ,都有()()1122x f x x f x +()()1221x f x x f x >+,则称函数()f x 为区间D 上的“H 函数”.给出下列函数及函数对应的区间 ①()32111322f x x x x =-+,(x ∈R );②()3cos sin f x x x x =+-,0,2x ⎛⎫∈ ⎪⎝⎭π; ③()()1xf x x e -=+,(),1x ∈-∞;④()ln f x x x =,10,x e ⎛⎫∈ ⎪⎝⎭.以上函数为区间D 上的“H 函数”的序号是 .(写出所有正确的序号)三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.已知复数()22431233a a z a a i a --=++-+(a ∈R ). (Ⅰ)若z z =,求a ;(Ⅱ)a 取什么值时,z 是纯虚数. 18.已知函数()321233f x x x x b =-++(b ∈R ). (Ⅰ)当0b =时,求()f x 在[]1,4上的值域;(Ⅱ)若函数()f x 有三个不同的零点,求b 的取值范围.19.在一次抽样调查中测得样本的6组数据,得到一个变量y 关于x 的回归方程模型,其对应的数值如下表:(Ⅰ)请用相关系数r 加以说明y 与x 之间存在线性相关关系(当0.81r >时,说明y 与x 之间具有线性相关关系);(Ⅱ)根据(Ⅰ)的判断结果,建立y 关于x的回归方程并预测当9x =时,对应的y 值为多少(ˆb精确到0.01).附参考公式:回归方程ˆˆa =+中斜率和截距的最小二乘法估计公式分别为: 1221ˆni ii nii x y nx ybxnx==-=-∑∑,ˆˆ=-ay bx ,相关系数r公式为:ni ix y nx yr -=∑参考数据:6147.64i ii x y==∑,621139i i x ==∑ 4.18= 1.53=.20.近几年来,我国许多地区经常出现干旱现象,为抗旱经常要进行人工降雨.现由天气预报得知,某地在未来5天的指定时间的降雨概率是:前3天均为12,后2天均为45,5天内任何一天的该指定时间没有降雨,则在当天实行人工降雨,否则,当天不实施人工降雨. (Ⅰ)求至少有一天需要人工降雨的概率; (Ⅱ)求不需要人工降雨的天数X 的分布列和期望. 21.已知函数()21ln 2f x x ax =-,a ∈R . (Ⅰ)求函数()f x 的单调区间;(Ⅱ)若关于x 的不等式()()11f x a x ≤--恒成立,求整数a 的最小值.请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分.22.选修4-4:坐标系与参数方程在直角坐标系xOy 中,曲线1C 的参数方程为cos x y =⎧⎪⎨=⎪⎩αα(α为参数),以原点O 为极点,x 轴正半轴为极轴,建立极坐标系,曲线2C 的极坐标方程为sin 4⎛⎫+= ⎪⎝⎭πρθ(Ⅰ)求直角坐标系下曲线1C 与曲线2C 的方程;(Ⅱ)设P 为曲线1C 上的动点,求点P 到2C 上点的距离的最大值,并求此时点P 的坐标. 23.选修4-5:不等式选讲 已知函数()1f x x x a =++-. (Ⅰ)当3a =时,解不等式()5f x >;(Ⅱ)若关于x 的不等式()21f x a ≥-恒成立,求实数a 的取值范围.高二数学(理科)试题参考答案一、选择题1-5:ADBDB 6-10:CBDCA 11、12:CA二、填空题13.13 14.151715.1- 16.①② 三、解答题17.解:(Ⅰ)230230a a a +≠⎧⎨+-=⎩解得331a a a ≠-⎧⎨=-=⎩或所以1a =(Ⅱ)22304310230a a a a a +≠⎧⎪--=⎨⎪+-≠⎩解得311413a a a a a ≠-⎧⎪⎪==-⎨⎪≠≠-⎪⎩或且所以14a =-18.解:(Ⅰ)当0b =时,()321233f x x x x =-+,()243f x x x '=-+=()()13x x --, 当()1,3x ∈时,()0f x '<,故函数()f x 在()1,3上单调递减, 当()3,4x ∈时,()0f x '>,故函数()f x 在()3,4上单调递增. 由()30f =,()()4143f f ==. ∴()f x 在[]1,4上的值域为40,3⎡⎤⎢⎥⎣⎦;(Ⅱ)由(Ⅰ)可知,()243f x x x '=-+()()13x x =--,由()0f x '<得13x <<,由()0f x '>得1x <或3x >所以()f x 在()1,3上单调递减,在(),1-∞,()3,+∞上单调递增;所以()()413f x f b ==+极大值,()()3f x f b ==极小值 所以当403b +>且0b <,即403b -<<时,()10,1x ∃∈,()21,3x ∈,()33,4x ∈.使得()()()1230f x f x f x ===. 由()f x 的单调性知,当且仅当4,03b ⎛⎫∈- ⎪⎝⎭时,()f x 有三个不同零点. 19.解:(Ⅰ)由题意,计算()1234567 4.56x =⨯+++++=, ()13 2.48 2.08 1.86 1.48+1.10=26y =⨯++++,且6147.64i ii x y==∑4.18=1.53=ni ix y nx yr -=∑47.646 4.52 6.36=4.18 1.53 6.3954-⨯⨯=-⨯0.99≈-;∵0.81r >,说明y 与x 之间存在线性相关关系;(Ⅱ)1221ˆni ii ni i x y nx ybx nx==-=-∑∑247.646 4.52 6.360.361396 4.517.5-⨯⨯==-≈--⨯, ∴ˆˆ2ay bx =-=+0.36 4.5 3.62⨯= ∴y 与x 的线性回归方程是ˆ0.369 3.62y=-⨯+, 将9x =代入回归方程得ˆ0.369 3.620.38y=-⨯+=. 20.解:(Ⅰ)5天全不需要人工降雨的概率是3211422525P ⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭ 故至少有1天需要人工降雨的概率是123125P -=.(Ⅱ)X 的取值是0,1,2,3,4,5()32111025200P X ⎛⎫⎛⎫==⨯=⎪ ⎪⎝⎭⎝⎭()321311125P X C ⎛⎫⎛⎫==⨯⨯+ ⎪ ⎪⎝⎭⎝⎭31211411255200C ⎛⎫⨯⨯⨯=⎪⎝⎭()32321331112252P X C C ⎛⎫⎛⎫⎛⎫==⨯⨯+⨯ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭121455C ⨯⨯⨯+32144325200⎛⎫⎛⎫⨯= ⎪ ⎪⎝⎭⎝⎭ ()321314325P X C ⎛⎫⎛⎫==⨯⨯+ ⎪ ⎪⎝⎭⎝⎭32132114255C C ⎛⎫⨯⨯⨯⨯+⎪⎝⎭32117325200⎛⎫⎛⎫⨯= ⎪ ⎪⎝⎭⎝⎭ ()3121414255P X C ⎛⎫==⨯⨯⨯ ⎪⎝⎭3223145672520025C ⎛⎫⎛⎫+⨯⨯==⎪ ⎪⎝⎭⎝⎭ ()3214252525P X ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭∴不需要人工降雨的天数X 分布列是不需要人工降雨的天数X 的期望是()11143012200200200E X =⨯+⨯+⨯7372345 3.12002525+⨯+⨯+⨯= 21.解:(Ⅰ)()211ax f x ax x x-'=-=,函数()f x 的定义域为()0,+∞当0a ≤时,()0f x '>,则()f x 在()0,+∞上单调递增 当0a >时,令()0f x '=,则x =当0x <<()0f x '>,()f x 为增函数;当x >()0f x '<,()f x 为减函数.∴当0a ≤时,()f x 的单调递增区间为()0,+∞,无减区间. 当0a >时,()f x的单调递增区间为⎛ ⎝,单调递减区间为⎫+∞⎪⎪⎭(Ⅱ)由()21ln 112x ax a x -≤--得()()22ln 12x x a x x ++≤+ ∵0x >∴原命题等价于()22ln 12x x a x x++≥+在()0,+∞上恒成立.令()()22ln 12x x g x x x++=+, 则()()()()22212ln 2x x x g x xx -++'=+令()2ln h x x x =+,则()h x 在()0,+∞上单调递增 由()110h =>,112ln 2022h ⎛⎫=-+<⎪⎝⎭∴存在唯一01,12x ⎛⎫∈⎪⎝⎭,使()00h x =,002ln 0x x += ∴当00x x <<时,()0g x '>,()g x 为增函数 当0x x >时,()0g x '<,()g x 为减函数 ∴0x x =时()()002max 002ln 12x x g x x x ++==+()0000112x x x x +=+ ∴01a x ≥又01,12x ⎛⎫∈⎪⎝⎭,则()011,2x ∈由a ∈Z ,所以2a ≥ 故整数a 的最小值为2.22.解:(Ⅰ)由曲线1C:cos x y =⎧⎪⎨=⎪⎩αα,可得cos sin x =⎧⎪=αα,两式两边平方相加得:2213y x +=, 即曲线1C 在直角坐标系下的方程为:2213y x +=. 由曲线2C:()sin sin cos 4⎛⎫+=+= ⎪⎝⎭πρθθθ,即s i n c o s 80+-=ρθρθ,所以80x y +-=,即曲线2C 在直角坐标系下的方程为:80x y +-=.(Ⅱ)由(Ⅰ)知椭圆1C 与直线2C无公共点,椭圆上的点()cos P αα到直线80x y +-=的距离为d ==46⎛⎫=+- ⎪⎝⎭πα,∴当sin 16⎛⎫+=- ⎪⎝⎭πα即43=πα时,d的最大值为 此时点P 的坐标为13,22⎛⎫-- ⎪⎝⎭. 23.解:(Ⅰ)当3a =时,()135f x x x =++->,等价于:①1135x x x ≤-⎧⎨---+>⎩,得32x <-;②13135x x x -<<⎧⎨+-+>⎩,无解;③3135x x x ≥⎧⎨++->⎩,得72x >;综上,解集为32x x ⎧<-⎨⎩或72x ⎫>⎬⎭. (Ⅱ)()1f x x x a =++-=1x a x ++-≥1x a x ++-121a a =+≥-,则121a a +≥-或()121a a +≤--,11 得2a ≤,所以a 的取值范围为(],2-∞.。
学高二第二学期期末考试理科数学试题及答案

试卷类型:A高二数学(理科)试题注意事项:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共5页。
2.答题前,考生务必在答题卡上用直径毫米的黑色字迹签字笔将自己的姓名、准考证号填写清楚,并粘好条形码。
请认真核准条形码上的准考证号、姓名和科目。
3.答第Ⅰ卷时,选出每题答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
答在本试卷上无效。
4.答第Ⅱ卷时,请用直径毫米的黑色字迹签字笔在答题卡上各题的答题区域内作答。
答在本试卷上无效。
5.第(22)、(23)小题为选考题,请按题目要求从中任选一题作答,并用2B 铅笔在答题卡上把所选题目题号后的方框涂黑。
6.考试结束后,将本试卷和答题卡一并收回。
附:回归方程ˆˆˆybx a =+中斜率与截距的最小二乘估计公式分别为: ∑∑∑∑====--=---=ni ini ii ni ini iixn xy x n yx x x y yx x b1221121)())((ˆ,x b y aˆˆ-= 第Ⅰ卷一、选择题:本题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
(1)已知复数iiz +-=122,其中i 是虚数单位,则z 的模等于 (A )2- (B) 3 (C) 4 (D) 2(2)用反证法证明某命题时,对结论:“自然数c b a ,,中恰有一个偶数”正确的反设为(A) c b a ,,中至少有两个偶数 (B)c b a ,,中至少有两个偶数或都是奇数 (C) c b a ,,都是奇数 (D) c b a ,,都是偶数(3)用数学归纳法证明:对任意正偶数n ,均有41212111 (41)31211+++=--++-+-n n n n ( )21...n++,在验证2=n 正确后,归纳假设应写成 (A )假设)(*N k k n ∈=时命题成立 (B )假设)(*N k k n ∈≥时命题成立(C )假设)(2*N k k n ∈=时命题成立 (D )假设))(1(2*N k k n ∈+=时命题成立(4)从3男4女共7人中选出3人,且所选3人有男有女,则不同的选法种数有(A )30种 (B) 32 种 (C) 34种 (D) 35种(5)曲线xey =在点()22e ,处的切线与坐标轴所围三角形的面积为(A)22e (B)2e (C) 22e (D) 492e(6)已知随机变量X服从正态分布()2,3σN ,且)3(41)1(>=<X P X P ,则)5(<X P 等于(A)81 (B) 85 (C) 43 (D) 87 (7)已知⎰≥3sin 2πxdx a ,曲线)1ln(1)(++=ax aax x f 在点())1(,1f 处的切线的斜率为k ,则k 的最小值为(A)1 (B)23(C)2 (D) 3 (8)甲、乙、丙三人独立参加体育达标测试,已知甲、乙、丙各自通过测试的概率分别为p ,4332,,且他们是否通过测试互不影响.若三人中只有甲通过的概率为161,则甲、丙二人中至少有一人通过测试的概率为(A)87 (B) 43 (C) 85 (D) 76 (9)函数)1(2)(3-'+=f x x x f ,则函数)(x f 在区间[]3,2-上的值域是 (A) ]9,24[- (B) ]24,24[- (C) ]24,4[ (D)[]9,4 (10)设()()5522105)1(...1)1(1x a x a x a a x +++++++=-,则420a a a ++等于 (A) 242 (B) 121 (C) 244 (D)122(11)已知函数)()()(2R b x bx x e x f x ∈-=.若存在⎥⎦⎤⎢⎣⎡∈2,21x ,使得0)()(>'+x f x x f ,则实数b 的取值范围是(A) ⎪⎭⎫ ⎝⎛∞-65, (B) ⎪⎭⎫ ⎝⎛∞-38, (C) ⎪⎭⎫ ⎝⎛-65,23 (D) ⎪⎭⎫⎝⎛∞+,38(12)中国南北朝时期的着作《孙子算经》中,对同余除法有较深的研究.设)0(,,>m m b a 为整数,若a 和b 被m 除得的余数相同,则称a 和b 对模m 同余,记为)(mod m b a =.如9和21被6除得的余数都是3,则记)6(mod 219=.若20202022201200202...22⋅++⋅+⋅+=C C C C a ,)10(mod b a =,则b 的值可以是(A) 2011 (B) 2012 (C) 2013 (D) 2014第II 卷本卷包括必考题和选考题两部分。
(完整版)高二数学理科期末试卷

高二数学(上)期末考一、选择题:本小题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1. 不等式0322<--x x 的解集是( )A .()1,3-B .()3,1-C .()3,-∞-Y ()+∞,1D .()1,-∞-Y ()+∞,32. 已知平面α的法向量是()2,3,1-,平面β的法向量是()4,,2λ-,若//αβ,则λ的值是( ) A .103-B .6-C .6D .1033.已知, , a b c 满足c b a <<,且0ac <,那么下列选项中一定成立的是( ) A. ab ac > B. ()0c b a -< C. 22cb ab < D. ()0ac a c ->4. 已知{}n a 是由正数组成的等比数列,n S 表示{}n a 的前n 项的和.若13a =,24144a a =,则10S 的值是( ) A .511 B .1023 C .1533 D .30695. 下列有关命题的说法正确的是( ) A .命题“若21x =,则1=x ”的否命题为:“若21x =,则1x ≠”. B .“1x =-”是“2560x x --=”的必要不充分条件.C .命题“x R ∃∈,使得210x x ++<”的否定是:“x R ∀∈, 均有210x x ++<”. D .命题“若x y =,则sin sin x y =”的逆否命题为真命题6. 设21,F F 为双曲线1422=-y x 的两个焦点,点P 在双曲线上且02190=∠PF F ,则21PF F ∆的面积是( ) A.1 B.25C.2D.57. 已知向量)0,1,1(=→a ,)2,0,1(-=→b ,且→→+b a k 与→→-b a 2互相垂直,则k 的值是( ) A. 1 B.51 C. 53 D. 57 8. 若ABC ∆的内角,,A B C 所对的边,,a b c 满足22()4a b c +-=,且060C =,则a b +的最小值为( )A .3 B . 3C .43D .8-9.若双曲线22221(0,0)x y a b a b-=>>的右焦点为F ,若过F 且倾斜角为︒60的直线与双曲线的右支有且只有一个交点,则此双曲线离心率e 的取值范围是( ) A .[]2,1B .()2,1C .()+∞,2D . [)+∞,210.若抛物线24y x =的焦点是F ,准线是l ,则经过点F 、M (4,4)且与l 相切的圆共有( ). A.4个 B.2个 C.1个 D.0个二、填空题:本大题共5小题,每小题4分,满分20分.请把答案填在答题纸的相应位置.11.等差数列{}n a 中,若34512,a a a ++=则71a a += .12. 已知1,10,220x x y x y ≥⎧⎪-+≤⎨⎪--≤⎩则z x y =+的最小值是 .13. 已知正方体1111D C B A ABCD -中,E 为11D C 的中点,则异面直线AE 与BC 所成角的余弦值为 . 14. 点P 是抛物线x y 42=上一动点,则点P 到点)1,0(-A 的距离与P 到直线1-=x 的距离和的最小值是 . 15.设{}n a 是公比为q 的等比数列,其前n 项积为n T ,并满足条件011,01,110099100991<-->->a a a a a ,给出下列结论:(1)10<<q ; (2)1198<T ;(3)110199<a a ;(4)使1<n T 成立的最小自然数n 等于199,其中正确的编号为 (写出所有正确的编号) 三、解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤. 16. (本小题满分13分)已知数列}{n a 的前n 项和为n S ,且n a 是n S 与2的等差中项,⑴求12,a a 的值;⑵求数列{}n a 的通项公式。
高二数学下学期期末考试理科试题含答案

第二学期高二年级期末考试数学试卷(理科)一、选择题:本大题共12小题,每小题5分,共60分.每小题给出的四个选项中只有一项是符合题目要求的.1.复数z 满足()134i z i -=+,则z =( )A.52B.2C. D.52.设集合{}419A x x =-≥,03x B xx ⎧⎫=≤⎨⎬+⎩⎭,则A B ⋂等于( )A.(3,2]--B.5(3,2]0,2⎡⎤--⋃⎢⎥⎣⎦C.5(,2],2⎛⎫-∞-⋃+∞ ⎪⎝⎭ D.5(,3),2⎡⎫-∞-⋃+∞⎪⎢⎣⎭3.二项式(52x +的展开式中,3x 的系数为( )A.80B.40C.20D.104.由直线2y x =及曲线24y x x =-围成的封闭图形的面积为( ) A.1B.43C.83D.45.已知命题:p 若0x >,则sin x x <,命题 :q 函数2()2xf x x =-有两个零点,则下列说法正确的是( )①p q ∧为真命题;②p q ⌝∨⌝为真命题;③p q ∨为真命题;④p q ⌝∨为真命题 A.①②B.①④C.②③D.①③④6.函数3()1f x ax x =++有极值的一个充分不必要条件是( ) A.1a <- B.1a <C.0a <D.0a >7.为了解某社区居民的家庭年收入年支出的关系,随机调查了该社区5户家庭,得到如下统计数据表:但是统计员不小心丢失了一个数据(用m 代替),在数据丢失之前得到回归直线方程为0.760.4y x =+,则m 的值等于( )A.8.60B.8.80C.9.25D.9.528.2020年全国高中生健美操大赛,某市高中生代表队运动员由2名男生和3名女生共5名同学组成,这5名同学站成一排合影留念,则3名女生中有且只有两位女生相邻的排列种数共有( ) A.36B.54种C.72种D.144种9.《易经》是中国传统文化中的精髓.下图是易经先天八卦图(记忆口诀:乾三连、坤六断、巽下断、震仰盂、坎中满、离中虚、艮覆碗、兑上缺),每一卦由三根线组成(“”表示一根阳线,“”表示一根阴线),现从八卦中任取两卦,已知每卦都含有阳线和阴线,则这两卦的六根线中恰有四根阳线和两根阴线的概率为( )A.13B.514C.314D.1510.观察下列算式:311=3235=+ 337911=++ 3413151719=+++若某数3n 按上述规律展开后,发现等式右边含有“2021”这个数,则n =( ) A.42B.43C.44D.4511.如图是一个质地均匀的转盘,一向上的指针固定在圆盘中心,盘面分为A ,B ,C 三个区域,每次转动转盘时,指针最终都会随机停留在A ,B ,C 中的某一个区域,且指针停留在区域A ,B 的概率分别是p 和1206p p ⎛⎫<<⎪⎝⎭.每次转动转盘时,指针停留在区域A ,B ,C 分别获得积分10,5,0.设某人转动转盘3次获得总积分为5的概率为()f p ,则()f p 的最大值点0p 的值为( )A.17B.18C.19D.11012.定义在(2,2)-上的函数()f x 的导函数为()f x ',已知2(1)f e =,且()2()f x f x '>,则不等式24(2)xe f x e -<的解集为( )A.(1,4)B.(2,1)-C.(1,)+∞D.(0,1)二、填空题:本大题共4小题,每小题5分,共20分. 13.命题“0x ∃<,220x x -->”的否定是“______”. 14.曲线1ln y x x=-在1x =处的切线在y 轴上的截距为______. 15.我国在2020年11月1日零时开始展开第七次全国人口普查,甲、乙等5名志愿者参加4个不同社区的人口普查工作,要求每个社区至少安排1名志愿者,每名志愿者只去一个社区,则不同的安排方法共有______种.16.甲乙两人进行乒乓球比赛,约定每局胜者得1分,负者得0分,比赛进行到有一人比对方多2分或打满6局时停止.设甲、乙在每局中获胜的概率均为12,且各局胜负相互独立,比赛停止时一共打了ξ局,则ξ的方差()D ξ=______.三、解答题:本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤. 17.(本小题满分10分)已知函数()|3|f x x =-,()|4|g x x m =-++. (1)当9m =时,解关于x 的不等式()()f x g x >;(2)若()()f x g x >对任意x R ∈恒成立,求实数m 的取值范围. 18.(本小题满分12分)盲盒里面通常装的是动漫、影视作品的周边,或者设计师单独设计出来的玩偶.由于盒子上没有标注,购买者只有打开才会知道自己买到了什么,因此这种惊喜吸引了众多年轻人,形成了“盲盒经济”.某款盲盒内可能装有某一套玩偶的A ,B ,C 三种样式,且每个盲盒只装一个.(1)某销售网点为调查该款盲盒的受欢迎程度,随机发放了200份问卷,并全部收回.经统计,有30%的人购买了该款盲盒,在这些购买者当中,女生占23;而在未购买者当中,男生女生各占50%.请根据以上信息填写下表,并判断是否有95%的把握认为购买该款盲盒与性别有关?附:)22()()()()()n ad bc K a b c d a c b d -=++++,其中n a b c d =+++.参考数据:(2)该销售网点已经售卖该款盲盒6周,并记录了销售情况,如下表:由于电脑故障,第二周数据现已丢失,该销售网点负责人决定用第4、5、6周的数据求线性回归方程,再用第1,3周数据进行检验.①请用4,5,6周的数据求出)关于x 的线性回归方程y bx a =+;(注:()()()1122211n niii ii i nniii i x x y y x y nx yb x x xnx====---==--∑∑∑∑,a y bx =-)②若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2盒,则认为得到的线性回归方程是可靠的,试问①中所得的线性回归方程是否可靠? 19.(本小题满分12分)在某学校某次射箭比赛中,随机抽取了100名学员的成绩(单位:环),并把所得数据制成了如下所示的频数分布表; (1)求抽取的样本平均数x (同一组中的数据用该组区间的中点值作代表);(2)已知这次比赛共有2000名学员参加,如果近似地认为这次成绩Z 服从正态分布()2,N μσ(其中μ近似为样本平均数x ,2σ近似为样本方差2 1.61s =),且规定8.27环是合格线,那么在这2000名学员中,合格的有多少人?(3)已知样本中成绩在[9,10]的6名学员中,有4名男生和2名女生,现从中任选3人代表学校参加全国比赛,记选出的男生人数为ξ,求ξ的分布列与期望E ξ. [附:若()2~,Z N μσ,则()0.6827P Z μσμσ-<<+=,(22)0.9545P Z μσμσ-<<+=, 1.27≈,结果取整数部分]20.(本小题满分12分) 已知()23x x f e x e =--. (1)求函数()f x 的解析式; (2)求函数()f x 的值域;(3)若函数1()g x f kx x ⎛⎫=-⎪⎝⎭在定义域上是增函数,求实数k 的取值范围. 21.(本小题满分12分)随着5G 通讯技术的发展成熟,移动互联网短视频变得越来越普及,人们也越来越热衷于通过短视频获取资讯和学习成长.某短视频创作平台,为了鼓励短视频创作者生产出更多高质量的短视频,会对创作者上传的短视频进行审核,通过审核后的短视频,会对用户进行重点的分发推荐.短视频创作者上传一条短视频后,先由短视频创作平台的智能机器人进行第一阶段审核,短视频审核通过的概率为35,通过智能机器人审核后,进入第二阶段的人工审核,人工审核部门会随机分配3名员工对该条短视频进行审核,同一条短视频每名员工审核通过的概率均为12,若该视频获得2名或者2名以上员工审核通过,则该短视频获得重点分发推荐.(1)某创作者上传一条短视频,求该短视频获得重点分发推荐的概率;(2)若某创作者一次性上传3条短视频作品,求其获得重点分发推荐的短视频个数的分布列与数学期望.22.(本小题满分12分)已知2()sin sin xxf x x e xe x ax a x =--+. (1)当()f x 有两个零点时,求a 的取值范围; (2)当1a =,0x >时,设()()sin f x g x x x=-,求证:()ln g x x x ≥+.六安一中2020~2021学年第二学期高二年级期末考试数学试卷(理科)参考答案一、选择题:二、填空题:13.0x ∀<,220x x --≤ 14.-315.240 16.114三、解答题:17.解:(1)当9m =时,由()()f x g x >,得341x x -++>,4349x x x <-⎧⎨--->⎩或43349x x x -≤≤⎧⎨-++>⎩或3349x x x >⎧⎨-++>⎩ 解得,5x <-或x 无解或4x >, 故不等式的解集为(,5)(4,)x ∈-∞-⋃+∞.(2)因为()()f x g x >恒成立,即|3||4|x x m ->-++恒成立, 所以|3||4|m x x <-++恒成立,所以min (|3||4|)m x x <-++, 因为|3||4||(3)(4)|7x x x x -++≥--+=(当43x -≤≤时取等号)所以min (|3||4|)7x x -++=,所以实数m 的取值范围是(,7)-∞. 18.解:(1)则2 4.714 3.8411109060140K =≈>⨯⨯⨯,故有95%的把握认为“购买该款盲盒与性别有关”. (2)①由数据,求得5x =,27y =,由公式求得222(45)(2527)(55)(2627)(65)(3027)5ˆ(45)(55)(65)2b--+--+--==-+-+-, 5ˆˆ27514.52ay bx =-=-⨯=, 所以y 关于x 的线性回归方程为ˆ 2.514.5yx =+. ②当1x =时,ˆ 2.5114.517y=⨯+=,|1716|2-<; 同样,当3x =时,ˆ 2.5314.522y=⨯+=,|2223|2-<. 所以,所得到的线性回归方程是可靠的.19.解:(1)由所得数据列成的频数分布表,得样本平均数4.50.055.50.186.50.287.50.268.50.179.50.067x =⨯+⨯+⨯+⨯+⨯+⨯=(2)由(1)知~(7,1.61)Z N ,10.6827(8.27)0.158652P Z -∴≥==∴在这2000名学员中,合格的有:20000.15865317⨯≈人(3)由已知得ξ的可能取值为1,2,31242361(1)5C C P C ξ===,2142363(2)5C C P C ξ===,3042361(3)5C C P C ξ===, ξ∴的分布列为:1232555E ξ=⨯+⨯+⨯=(人)20.解:(1)令x e t =,(0)t >,则ln x t =,由()23x x f e x e =--,得()ln 23f t t t =--, 所以函数()f x 的解析式为()ln 23f x x x =--.(2)依题意知函数的定义域是(0,)+∞,且1()2f x x'=-, 令()0f x '>,得102x <<,令()0f x '<,得12x >,故()f x 在10,2⎛⎫ ⎪⎝⎭上单调递增,在1,2⎛⎫+∞⎪⎝⎭上单调递减, 所以max 1()ln 242f x f ⎛⎫==--⎪⎝⎭;又因为0x →,()f x →-∞, 所以函数()f x 的值域为(,ln 24]-∞--.(3)因为12()ln 3g x f kx x kx x x ⎛⎫=-=---- ⎪⎝⎭在(0,)+∞上是增函数, 所以212()0g x k x x '=-+-≥在(0,)+∞上恒成立, 则只需2min 12k x x ⎛⎫≤-+ ⎪⎝⎭,而221211112488x x x ⎛⎫-+=--≥- ⎪⎝⎭(当4x =时取等号),所以实数k 的取值范围为1,8⎛⎤-∞- ⎥⎝⎦.21.解:(1)设“该短视频获得重点分发推荐”为事件A ,则21302333311113()C 115222210P A C ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=⨯⨯-+⨯-=⎢⎥ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎢⎥⎣⎦ (2)设其获得重点分发推荐的短视频个数为随机变量X ,X 可取0,1,2,3.则3~3,10X B ⎛⎫⎪⎝⎭, 030333343(0)110101000P X C ⎛⎫⎛⎫==⨯-= ⎪ ⎪⎝⎭⎝⎭;121333441(1)110101000P X C ⎛⎫⎛⎫==⨯-= ⎪ ⎪⎝⎭⎝⎭; 212333189(2)110101000P X C ⎛⎫⎛⎫==⨯-= ⎪ ⎪⎝⎭⎝⎭;30333327(3)110101000P X C ⎛⎫⎛⎫==⨯-= ⎪ ⎪⎝⎭⎝⎭, 所以随机变量X 的分布列如下:343441189279()0123100010001000100010E X =⨯+⨯+⨯+⨯=(或39()31010E X =⨯=) 22.解:(1)由题知,()()(sin )x f x xe a x x =--有两个零点,sin 0x x -=时,0x =故当0x xe a -=有一个非零实根设()x h x xe =,得()(1)xh x x e '=+,()h x ∴在(,1)-∞-上单调递减,在(1,)-+∞上单调递增.又1(1)h e-=-,(0)0h =,0x >时,(0)0h >;0x <时,(0)0h <. 所以,a 的取值范围是1a e=-或0a >. (2)由题,()()1sin x f x g x xe x x==--法一:()1ln ln x x xe x x xe -≥+=,令0x t xe =>,令()ln 1(0)H t t t t =-->11()1t H t t t -'=-=()H x ∴在(0,1)上单调递减,在(1,)+∞上单调递增. ()(1)0H x H ∴≥=.1ln x xe x x ∴-≥+法二:要证1ln x xe x x -≥+成立故设()ln 1xM x xe x x =---,1()(1)xM x x e x ⎛⎫'=+-⎪⎝⎭,(0)x >, 令1()x N x e x =-,则21()0x N x e x'=+>,()N x ∴在(0,)+∞上单调递增又1202N ⎛⎫=<⎪⎝⎭,(1)10N e =->, 01,12x ⎛⎫∴∃∈ ⎪⎝⎭使()00N x =.001x e x ∴=,00ln x x =-,()M x ∴在()00,x 上单调递减,在()0,x +∞上单调递增.()0min 0000[()]ln 10x M x M x x e x x ∴==---=.1ln x xe x x ∴-≥+。
完整版高二数学期末试卷理科及含

高二数学期末考试卷〔理科〕一、选择题〔本大题共 11 小题,每题 3 分,共 33 分〕r 1、与向量 a (1, 3, 2)平行的一个向量的坐标是〔 〕A .〔 1 3,1,1〕 B .〔-1,-3,2〕C .〔- 1 2 , 3 2,-1〕 D .〔 2 ,- 3,-2 2 〕2、设命题 p :方程 2 3 1 0x x 的两根符号不一样;命题 q :方程2 3 1 0x x 的两根之和为 3,判断命题“ p 〞、“ q 〞、“ p q 〞、“ p q 〞为假命题的个数为 ( ) A .0 B .1 C .2 D .3 3、“a >b >0〞是“ ab <a 2b 22〞的 〔 〕A .充足而不用要条件B .必需而不充足条件C .充要条件D .既不充足也不用要条件2y 2 x的焦距为 2,那么 m 的值等于 〔 〕. 4、椭圆 1m 4A .5B .8C .5 或 3D .5 或 85、空间四边形 OABC 中, OA a ,OB b ,OC c ,点 M 在 OA 上,且 OM=2MA ,N 为 BC 中点,那么 MN =〔 〕1 2 1A . a b c2 3 22 1 1 B . a b c3 2 21 1 1 C . a b c2 2 22 2 1 D . a b c3 3 26、抛物线 2y 4x 上的一点 M 到焦点的距离为 1,那么点 M 的纵坐标为〔 〕A .17 16B .1516C .78D .07、对称轴为坐标轴的双曲线有一条渐近线平行于直线 x +2y -3=0,那么该双曲线的离心率为〔 〕或5 4B. 5 或52C. 3 或3 2或5 38、假定不等式 |x -1| <a 成立的充足条件是 0<x<4,那么实数 a 的取值范围是 ( )A .a 1B .a 3C .a 1D .a 39、a (1 t,1 t,t),b (2,t,t) ,那么| a b |的最小值为〔〕A .55 B.555C.3 55 D.11510、动点 P(x、y)知足 10 2 ( 2)2(x 1 y =|3x+4y+2|,那么动点 P 的轨迹是〔〕)A .椭圆 B.双曲线 C.抛物线 D.没法确立2 y2x11、 P 是椭圆125 9上的一点, O 是坐标原点, F 是椭圆的左焦点且1OQ (OP OF ), | OQ | 4,那么点 P 到该椭圆左准线的距离为〔〕25D.2高二数学期末考试卷〔理科〕答题卷一、选择题〔本大题共 11 小题,每题 3 分,共 33 分〕题号 1 2 3 4 5 6 7 8 9 10 11答案二、填空题〔本大题共 4 小题,每题 3 分,共 12 分〕2 x12、命题:x R, x 1 0的否定是2 y213、假定双曲线x 4 4 的左、右焦点是F1、F2 ,过F1 的直线交左支于 A、B 两点,假定|AB|=5 ,那么△ AF2B 的周长是 .14、假定a ( 2,3, 1),b ( 2 ,1,3) ,那么a,b为邻边的平行四边形的面积为.15、以下四个对于圆锥曲线的命题中:u uur uuur ①设A、B 为两个定点, k 为正常数,| PA| | PB | k ,那么动点P 的轨迹为椭圆;②双曲线2 2x y25 91 与椭圆2x352 1y 有同样的焦点;2 x③方程2x 5 2 0 的两根可分别作为椭圆和双曲线的离心率;25④和定点A( 5, 0) 及定直线l : x 的距离之比为4此中真命题的序号为 _________.54的点的轨迹方程为2 2x y16 91.三、解答题〔本大题共 6 小题,共 55 分〕2 2x y16、〔本题总分值 8 分〕命题 p:方程1表示焦点在 y 轴上的椭圆,命题 q:2m m 12 2y x 双曲线15 m 的离心率e (1, 2) ,假定p,q只有一个为真,务实数m 的取值范围.17、〔本题总分值 8 分〕棱长为 1 的正方体 AB CD-A1B1C1D1,试用向量法求平面 A1BC1与平面 AB CD 所成的锐二面角的余弦值。
高二理科数学下学期期末考试

1 1
(k 1) 0 成立
k1
由①②可知,对 n 3, f (n) (1 1 ) n n 0 成立 n
……………… 10 分
x 19.解:( 1) l 的参数方程 y
高二数学理期末测试(二)
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分共 钟.
150 分,考试时间 120 分
第Ⅰ 卷 (选择题 共 60 分)
一. 选择题(本大题共 12 个小题,每小题 5 分,共 60 分 .在每个小题的四个选项中,只有 一项是符合题目要求的 .)
(1 3i )2
1.复数
( 4)当 变化时,求弦 BC 的中点的轨迹方程.
20.(本小题满分 9 分)设在一个盒子中,放有标号分别为 1, 2,3 的三张卡片,现从这个
盒 子 中 , 有 放 回 地 先 后 抽 得 两 张 卡 片 , 标 号 分 别 记 为 x, y , 设 随 机 变 量 x 2 y x.
( 1)写出 x, y 的可能取值,并求随机变量
∵ lg(| x 3| | x 7 |) a 解集为 R .∴ a 1………………………… 8 分
1
17
18.解:( 1) f (1) 1, f (2) , f (3)
2
27
( 2)猜想: n 3, f ( n) (1 1 ) n n 0 n
证明:①当 n 3 时, f (3)
17 0 成立 27
②假设当 n k (n 3, n N * ) 时猜想正确,即 f k
装箱分配给这 3 台卡车运送,则不同的分配方案的种数为
()
A . 168
B .84
C. 56
D. 42
第Ⅱ 卷(非选择题满分 90)
高二数学下学期期末考试理科试题(解析版)

由于直线 过原点,且倾斜角为 ,故其极坐标方程为 .
(2)由 得 ,
设 , 对应的极径分别为 ,则 , ,
三、解答题:(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)
17.已知集合 , .
(1)若 , ,求实数 的取值范围;
(2)若 ,且 ,求实数 取值范围.
【答案】(1) ;(2) .
【解析】
【分析】
(1)先求出 ,再根据包含关系可得关于 的不等式组,从而求实数 的取值范围,注意对 是否为空集分类讨论;
所以p∧q为假命题,p∨q为真命题,p∧( q)为假命题, q为假命题.
故选B.
【点睛】(1)本题主要考查命题的真假和复合命题的真假的判断,意在考查学生对这些知识的掌握水平和分析推理能力.(2)复合命题真假判定的口诀:真“非”假,假“非”真,一真“或”为真,两真“且”才真.
8.甲、乙两位射击运动员的5次比赛成绩(单位:环)如茎叶图所示,若两位运动员平均成绩相同,则成绩较稳定(方差较小)的那位运动员成绩的方差为
【详解】依题意,产品的质量X(单位:千克)服从正态分布N(90,64),得 ,
,
质量在区间 内的产品估计有 件.
故选A.
【点睛】本题考查正态分布曲线的特点及曲线所表示的意义,考查曲线的对称性,属于基础题.
11.2021年广东新高考将实行 模式,即语文数学英语必选,物理历史二选一,政治地理化学生物四选二,共有12种选课模式.今年高一的小明与小芳都准备选历史,假若他们都对后面四科没有偏好,则他们选课相同的概率( )
公园
甲
乙
丙
丁
获得签名人数
45
60
30
15
高二下期末统一考试数学试题(理)含答案

高二数学试卷(理科)本试卷共4页,22小题,满分150分.考试用时120分钟.注意事项:1、答卷前,考生务必用2B铅笔在答题卡“考生号”处填涂考生号,用黑色字迹钢笔或签字笔将自己姓名、考生号、试室号、座位号填写在答题卡上.2、选择题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案,答案不能答在试卷上.3、非选择题必须用黑色字迹钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上.如需改动,先划掉原来的答案,然后再写上新的答案.不准使用铅笔和涂改液.不按以上要求作答的答案无效.4、考生必须保持答题卡的整洁.考试结束,将答题卡交回,试卷不用上交.一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个备选项中,只有一项是符合题目要求的.)1. 若复数满足,则A. B. C. D.【答案】C【解析】,故选C.2. 设随机变量X~B(8,p),且D(X)=1.28,则概率p的值是A. 0.2B. 0.8C. 0.2或0.8D. 0.16【答案】C【解析】∵随机变量X~B(8,p),且D(X)=1.28,∴8P(1-p)=1.28,∴p=0.2或0.8故选:C3. 某研究型学习小组调查研究学生使用智能手机对学习的影响.部分统计数据如下表:附表:经计算的观测值为10,,则下列选项正确的是( )A. 有99.5%的把握认为使用智能手机对学习有影响B. 有99.5%的把握认为使用智能手机对学习无影响C. 在犯错误的概率不超过0.001的前提下认为使用智能手机对学习有影响D. 在犯错误的概率不超过0.001的前提下认为使用智能手机对学习无影响 【答案】A【解析】因为7.879<K 2=10<10.828,对照数表知,有99.5%的把握认为使用智能手机对学习有影响. 故选:A .4. 用反证法证明:若整系数一元二次方程有有理数根,那么中至少有一个是偶数.下列假设正确的是 A. 假设都是偶数; B. 假设都不是偶数C. 假设至多有一个偶数D. 假设至多有两个偶数【答案】B【解析】试题分析:“中至少有一个是偶数”包括一个、两个或三个偶数三种情况,其否定应为不存在偶数,即“假设都不是偶数”,故选B...............................考点:命题的否定.5. 函数的单调递减区间是A. B.C. ,D.【答案】A【解析】函数y=x2﹣lnx的定义域为(0,+∞).令y′=2x﹣= ,解得,∴函数y=x2﹣lnx的单调递减区间是.故选:A .点睛:求函数的单调区间的“两个”方法方法一(1)确定函数y=f(x)的定义域;(2)求导数y′=f′(x);(3)解不等式f′(x)>0,解集在定义域内的部分为单调递增区间;(4)解不等式f′(x)<0,解集在定义域内的部分为单调递减区间.方法二(1)确定函数y=f(x)的定义域;(2)求导数y′=f′(x),令f′(x)=0,解此方程,求出在定义区间内的一切实根;(3)把函数f(x)的间断点(即f(x)的无定义点)的横坐标和上面的各实数根按由小到大的顺序排列起来,然后用这些点把函数f(x)的定义区间分成若干个小区间;(4)确定f′(x)在各个区间内的符号,根据符号判定函数在每个相应区间内的单调性6. 已知X的分布列为设Y=2X+3,则E(Y)的值为A. B. 4 C. -1 D. 1 【答案】A【解析】由条件中所给的随机变量的分布列可知 EX=﹣1×+0×+1×=﹣, ∵E (2X+3)=2E (X )+3,∴E (2X+3)=2×(﹣)+3= .故答案为:A .7. 从1,2,3,4,5中任取2个不同的数,事件A 为“取到的2个数之和为偶数”,事件B 为“取到的2个数均为偶数”,则P (B |A )等于( )A. B. C. D. 【答案】B【解析】事件A=“取到的2个数之和为偶数”所包含的基本事件有:(1,3)、(1,5)、(3,5)、(2,4),∴p(A)= ,事件B=“取到的2个数均为偶数”所包含的基本事件有(2,4),∴P(AB)= ∴.本题选择B 选项.8. 在如图所示的正方形中随机投掷10 000个点,则落入阴影部分(曲线C 为正态分布 N(-1,1)的部分密度曲线)的点的个数的估计值为附:若X ~N(μ,σ2),则P(μ-σ<X<μ+σ)=0.682 6,P(μ-2σ<X<μ+2σ)=0.954 4.A. 1 193B. 1 359C. 2 718D. 3 413【答案】B【解析】正态分布的图象如下图:正态分布N(﹣1,1)则在(0,1)的概率如上图阴影部分,其概率为×[P(μ﹣2σ<X≤μ+2σ)﹣P(μ﹣σ<X≤μ+σ)]= ×(0.9544﹣0.6826)=0.1359;即阴影部分的面积为0.1359;所以点落入图中阴影部分的概率为p==0.1359;投入10000个点,落入阴影部分的个数期望为10000×0.1359=1359.故选B.点睛:正态曲线的性质:(1)曲线在轴的上方,与轴不相交 .(2)曲线是单峰的,它关于直线=μ对称(由得)(3)曲线在=μ处达到峰值(4)曲线与轴之间的面积为19. 下表提供了某厂节能降耗技术改造后在生产A产品过程中记录的产量x(吨)与相应的生产能耗y(吨)的几组对应数据,根据表中提供的数据,求出y关于x的线性回归方程为=0.7x+0.35,则下列结论错误的是( )A. 产品的生产能耗与产量呈正相关B. t的值是3.15C. 回归直线一定过(4.5,3.5)D. A产品每多生产1吨,则相应的生产能耗约增加0.7吨【答案】B【解析】由题意,故选:B.10. 将5件不同的奖品全部奖给3个学生,每人至少一件奖品,则不同的获奖情况种数是A. 150B. 210C. 240D. 300【答案】A【解析】将5本不同的书分成满足题意的3组有1,1,3与2,2,1两种,分成1、1、3时,有C53•A33=60种分法,分成2、2、1时,根据分组公式90种分法,所以共有60+90=150种分法,故选A.点睛:一般地,如果把不同的元素分配给几个不同对象,并且每个不同对象可接受的元素个数没有限制,那么实际上是先分组后排列的问题,即分组方案数乘以不同对象数的全排列数。
高二理科数学及答案

高二数学(理科)期末考试卷 (选修2-1)第一卷 选择题 一、 选择题(每题5分,共60分) 1.下列命题中的假命题是( )A .∃x ∈R ,lg x =0B .∃x ∈R ,tan 1x =C .∀x ∈R ,3x >0 D .∀x ∈R, 2x>02.设A 、B 、C 、D 是空间不共面的四点,且满足0,0,0=⋅=⋅=⋅AD AC AD AB AC AB 则△BCD 是( ) A .钝角三角形 B .直角三角形 C .锐角三角形D .不确定3.设向量},,{c b a 是空间一个基底,则一定可以与向量b a q b a p -=+=,成空间的另一个基底的向量是( )A .cB . a C. b D .b a 或4.已知条件p :1-x <2,条件q :2x -5x -6<0,则p 是q 的 ( )A 充要条件B 充分不必要条件C 必要不充分条件D 既不充分也不必要条件5. 在集合{x | m x }0122=++x 的元素中,有且仅有一个元素是负数的充要条件( )A. m 1≤ B .m<0或m=1 C .m<1 D. m 0≤或m=1 6.椭圆14222=+ay x与双曲线1222=-yax有相同的焦点,则a 的值是 ( )A 12B 1或–2C 1或12D 17.已知椭圆192522=+yx上的一点M 到焦点F 1的距离为2,N 是MF 1的中点,O 为原点,则|ON|等于 ( ) A 2B 4C 8D238.若椭圆的两个焦点与它的短轴的两个端点是一个正方形的四个顶点,则椭圆的离心率为( )A.32 B. 53 C. 22 D. 639.若向量)2,1,2(),2,,1(-==b aλ,且a 与b 的夹角余弦为31,则λ等于( )A .2B .2-C .1231 D . 1231-10. 抛物线y 2= 4x 上一点P 到焦点F 的距离是10, 则P 点的坐标是 ( )A (9,±6)B (6, 9)C (±6, 9)D (9, 6)11.若A )12,5,(--x x x ,B )2,2,1(x x -+,当B A取最小值时,x 的值等于( )A . 19B .78 C . 78-D .141912.空间四边形O A B C 中,O B O C =,3A OB A OC π∠=∠=,则cos <,O A BC>的值是 ( ) A .21 B .22 C .-21 D .0第二卷 非选择题 二、填空题(每题5分,共20分)13.抛物线2(0)x ay a =>的焦点坐标是 ;14.若双曲线1922=-myx的渐近线l 方程为x y 35±=,则双曲线焦点F 到渐近线l 的距离为 ; 15.在棱长为1的正方体ABCD —A 1B 1C 1D 1中,M 和N 分别为A 1B 1和BB 1的中点,那么直线AM 与CN 所成角的余弦值是 ;16.下列命题①“A ∩B =A ”成立的必要条件是“A B ”; ②“若x 2+y 2=0,则x ,y 全为0”的否命题; ③“全等三角形是相似三角形”的逆命题;④“圆内接四边形对角互补”的逆否命题.中的真命题是高二数学第一学期期末试题答案卷(理科)一、选择题(每小题5分,共60分)二、填空题(每小题5分,共20分)13. _____________________. 14. _____________________.15. _____________________. 16. _____________________.三、解答题(10分)斜率为1的直线l经过抛物线2417.的焦点,且与抛物线相交于,A By x两点,求线段A B的长。
高二下学期期末考试数学理科Word版含答案

遂宁市高中级第四学期期末教学水平监测数学(理科)试题本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分。
总分150分。
考试时间120分钟。
第Ⅰ卷(选择题,满分60分)注意事项:1.答题前,考生务必将自己的姓名、班级、考号用0.5毫米的黑色墨水签字笔填写在答题卡上。
并检查条形码粘贴是否正确。
2.选择题使用2B 铅笔填涂在答题卡对应题目标号的位置上,非选择题用0.5毫米黑色墨水签字笔书写在答题卡对应框内,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。
3.考试结束后,将答题卡收回。
一、选择题(本大题共12小题,每小题5分,共计60分。
在每小题给出的四个选项中,只有一项是符合题目要求。
) 1.已知是虚数单位,则11z i=-在复平面内对应的点位于 A .第一象限 B .第二象限 C .第三象限 D .第四象限 2.已知命题52,:>∈∀xR x P ,则P ⌝为A .52,>∉∀xR x B .52,≤∈∀xR xC .52,00≤∈∃x R x D .52,00>∈∃x R x3.设抛物线22y px =的焦点与椭圆221204x y +=的右焦点重合,则该抛物线的准线方程为 A .1x =- B .2x =- C .3x =- D .4x =-4.某家具厂的原材料费支出x 与销售量y (单位:万元)之间有如下数据,根据表中提供的ˆˆA .5B .10C .12D .205.“m ≥”是“函数221y x mx =-+在(),-∞+∞内存在零点”的A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件6.观察下面“品”字形中各数之间的规律,根据观察到的规律得出a 的值为A .23B .75C .77D .139 7.运行下列程序,若输入的,p q 的值分 别为65,36,则输出的p q -的值为 A .47 B .57 C .61 D .678.根据党中央关于“精准”脱贫的要求,我市 某农业经济部门决定派出五位相关专家对三 个贫困地区进行调研,每个地区至少派遣一 位专家,其中甲、乙两位专家需要派遣至同 一地区,则不同的派遣方案种数为A .18B .24C .28D .369.已知函数()f x 在0x >上可导且满足()()0xf x f x '->,则下列一定成立的为 A .()()f f e eππ>B .()()f f e π<C .()()f f e eππ<D .()()f f e π> 10.若函数32()21f x ax x x =+++在()1,2上有最大值无最小值,则实数a 的取值范围为A .34a >-B .53a <-C .5334a -<<-D .5334a -≤≤-11.已知抛物线22(0)y px p =>上一动点到其准线与到点M (0,4)的距离之和的最小值为32,F 是抛物线的焦点,O 是坐标原点,则MOF ∆的内切圆半径为 A .2 B .3 C .21+ D .22-12.已知函数32()312()f x x mx nx m N *=-++∈在1x =-处取得极值,对任意,()270x R f x '∈+>恒成立,则1240344035()()...()()2018201820182018f f f f ++++= A .4032 B .4034 C .4035 D .4036第Ⅰ卷(非选择题,满分90分)注意事项:1.请用蓝黑钢笔或圆珠笔在第Ⅱ卷答题卡上作答,不能答在此试卷上。
高二理科数学下学期期末试卷

高二理科数学下学期期末试卷(理科)班级 学号 姓名 分数第I 卷(选择题共60分)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.复数(2)12i i i+-等于( D ) A .i B .i - C .1 D .1-2.函数1()f x x x =-的图像关于( C )A .y 轴对称B . 直线x y -=对称C . 坐标原点对称D . 直线x y =对称3.记等差数列{}n a 的前n 项和为n S ,若112a =,420S =,则6S =( D ) A .16B .24C .36D .484.已知a ,b 都是实数,那么“22b a >”是“a >b ”的D(A )充分而不必要条件 (B )必要而不充分条件 (C )充分必要条件 (D )既不充分也不必要条件5.在△ABC 中,角ABC 的对边分别为a 、b 、c ,若(a 2+c 2-b 2)tan B ,则角B 的值为DA. 6π B.3π C.6π或56πD.3π或23π6.设,M N 是球心O 的半径OP 上的两点,且NP MN OM ==,分别过,,N M O 作垂直于OP 的面截球得三个圆,则这三个圆的面积之比为:( D ) (A)3,5,6 (B)3,6,8 (C)5,7,9 (D)5,8,97.在ABC △中,AB =c ,AC =b .若点D 满足2BD DC =,则AD =( A )A .2133+b cB .5233-c bC .2133-b cD .1233+b c 若函数9.若双曲线12222=-by a x 的两个焦点到一条准线的距离之比为3:2,则双曲线的离心率是D(A )3 (B )5 (C )3 (D )58.()y f x =的值域是1[,3]2,则函数1()()()F x f x f x =+的值域是BA .1[,3]2B .10[2,]3C .510[,]23D .10[3,]310.已知函数3()2x f x +=,1()f x -是()f x 的反函数,若16mn =(m n ∈+R ,),则11()()f m f n --+的值为( A ) A .2-B .1C .4D .1011.设曲线11x y x +=-在点(32),处的切线与直线10ax y ++=垂直,则a =( D )A .2B .12C .12- D .2-12.函数y =lncos x (-2π<x <)2π的图象是A第Ⅱ卷(非选择题 共90分)考生注意事项:请用0.5毫米黑色墨水签字笔在答题卡上书写作答,在试题卷上书写作答无效....................... 二、填空题:本大题共4小题,每小题5分,共20分.把答案填在答题卡的相应位置.13.在)5)(4)(3)(2)(1(-----x x x x x 的展开式中,含4x 的项的系数是 。
高二数学(理科)下学期期末试卷
高二数学(理科)下学期期末试卷本试卷共4页,21小题,满分150分.考试用时120分钟.一、选择题(本大题共8小题,每小题5分,满分40分,在每小题给出的四个选项中,只有一项是符合题目要求的)1. 若集合M 是函数x y lg =的定义域,N 是函数x y -=1的定义域,则N M ⋂等于( )(]()[)+∞+∞,1..,0.1,0.D C B A φ2. 在复平面内,复数311i i+-对应的点位于( ) 第四象限第三象限第二象限第一象限....D C B A3. 一简单组合体的三视图及尺寸如图所示(单位:cm )则该组合体的体积为( )333344000.56000.64000.72000.cm D cm C cm B cm A4. 已知等比数列{}n a 中,各项都是正数,且2312,21,a a a 成等差数列, 则7698a a a a ++等于( )223.223.21.21.-+-+D C B A5. 某程序框图如图1所示,则输出的结果S= ( )247.120.57.26.D C B A6. 平面向量060b 的夹角为与 a ,=+==b a b a ,1),0,2(( )7.3.7.3.D C B A50 1040 20 20 20主视图侧视图俯视图开始 S=1,k=1k=k+1S=2S+k K>4输出S 结束 是 否图17. 已知{}{},02,0,4|),(,0,0,6|),(≥-≥≤=≥≥≤+=Ωy x y x y x A y x y x y x 若向区域Ω内随机投一点P,则点P 落在区域A 内的概率为 ( )92.91.32.31.D C B A 8. 方程1916-=+y y x x 的曲线即为函数)(x f y =,有如下结论:①)(x f 在R 上单调递减;②函数x x f x F 3)(4)(+=不存在零点;③函数)(x f y =的值域是R;④)(x f 的图像不经过第一象限,其中正确的个数是( )个个个个4.3.2.1.D C B A二、填空题(本大题共7小题,考生作答6小题,每小题5分,满分30分) 9. ()82x -展开式中含4x 项的系数为 .10. 2个好朋友一起去一家公司应聘,公司人事主管通知他们面试时间时说:“我们公司要从面试的人中招3个人,你们都被招进来的概率是701”,若每个人都被招进来的概率是均等的,根据他的话可推断去面试的人有 个(用数字作答). 11. 若圆04122=-++mx y x 与直线1-=y 相切,其圆心在y 的左侧,则m= . 12. 在ABC ∆中,060,2,7=∠==B BC AC ,则ABC ∆的面积等于 .13. 函数)(x f 的定义域为D,若对任意的D x ∈21x 、,当21x <x 时,都有),()(21x f x f ≤则称函数)(x f 在D 上为“非减函数”.设函数)(x g 在[]1,0上为“非减函数”,且满足以下三个条件:(1)=-=-==)1(),(1)1()3();(21)3()2(;0)0(g x g x g x g x g g 则 ,=)125(g .(二)选做题(14、15题,考生只能从中选做一题) 14. (坐标系与参数方程选做题)已知直线⎩⎨⎧-=+=ty tx l 4231:1(t 为参数)与直线542:2=-y x l 相交于点B,又点A(1,2),则=AB .15. (几何证明选讲选做题)如图,PA 切ΘO 于点A ,割线PBC 经过圆心O,OB=PB=1,OA 绕点O 逆时针旋转060到OD,则PD 的长为 .D CABO P三、解答题(本大题共6小题,满分80分,解答应写出文字说明、证明过程或演算步骤) 16. (本小题满分12分)已知函数.cos sin 2)(sin 3)(22x x x con x x f --= (1)求)(x f 的最小正周期;(2)设⎥⎦⎤⎢⎣⎡-∈3,3ππx ,求)(x f 的值域和单调递增区间.17. (本小题满分12分)近年空气质量逐步恶化,雾霾天气现象出现增多,大气污染危害加重,大气污染可引起心悸、呼吸困难等心肺疾病,为了解某市心肺疾病是否与性别有关,在某医院随机地对入院50人进行了问卷调查,得到如下的列联表:患心肺疾病 不患心肺疾病 合计 男 5 女 10 合计50已知在全部50人中随机抽取1人,抽到患心肺疾病的人的概率为53, (1)请将上面的列联表补充完整;(2)是否有99.5%的把握认为患心肺疾病与性别有关?说明你的理由;(3)已知在患心肺疾病的10女性中,有3位又患有胃病,现在从患心肺疾病的10位女性中,选出3名进行其它方面的排查,记选出患胃病的女性人数为ξ,求ξ的分布、数学期望以及方差。
高二下学期期末考试理科数学试题 (含答案)

高二下学期期末考试理科数学试题(含答案)一、选择题(本题共12道小题,每小题5分,共60分)1.已知集合A=﹛-2,0,2﹜,B=﹛x |x 2-x -2=0﹜,则A∩B= ( )(A) ∅ (B ){2} (C ){0} (D) {-2}2.复数的共轭复数是( )A .2+iB .2-iC .-1+iD .-1-i3.已知命题p :∃x 0∈R ,lg x 0<0,那么命题 ⌝p 为A. ∀x ∈R ,lg x >0B. ∃x 0∈R ,lg x 0>0C. ∀x ∈R ,lg x ≥0D. ∃x 0∈R ,lg x 0≥04.已知向量(2,1)a =,(3,)b m =,若(2)//a b b +,则m 的值是( )A .32B .32-C .12D .12- 5.已知实数,x y 满足3141y x x y y ≤-⎧⎪+≤⎨⎪≥⎩,则目标函数z x y =-的最大值为( )A .-3B .3C .2D .-26.钝角三角形ABC 的面积是12,AB=1,,则AC=( ) (A ) 5 (B(C ) 2 (D ) 17.如图,网格纸上正方形小格的边长为1(表示1cm ),图中粗线画出的是某零件的三视图,该零件由一个底面半径为3cm ,高为6c m 的圆柱体毛坯切削得到,则切削掉部分的体积与原来毛坯体积的比值为( )(A )1727 (B ) 59 (C )1027 (D) 13 8.若21()nx x -展开式中的所有二项式系数之和为512,则该开式中常数项为( ) A. 84- B. 84 C. 36- D. 369.已知三棱锥P ABC -的三条棱PA ,PB ,PC 长分别是3、4、5,三条棱PA ,PB ,PC 两两垂直,且该棱锥4个顶点都在同一球面上,则这个球的表面积是 ( )A .25π B.50π C. 125π D.都不对10.已知ω>0,函数f(x)=sin(ωx +4π)在(2π,π)上单调递减,则ω的取值范围是( ) (A )[21,45] (B )[21,43] (C )(0,21] (D )(0,2] 11.已知双曲线2222:1x y C a b-=(0a >,0b >)的左顶点为M ,右焦点为F ,过左顶点且斜率为l 的直线l 与双曲线C 的右支交于点N ,若MNF ∆的面积为232b ,双曲线C 的离心率为( ) A . 3 B .2 C. 53 D .4312.若存在实数[ln3,)x ∈+∞,使得(3)21x a e a -<+,则实数a 的取值范围是( )A .(10,+∞)B .(-∞,10) C. (-∞,3) D .(3,+∞)二、填空题(本题共4道小题,每小题5分,共20分)13.已知向量()1,3a =-,()3,b t =,若a b ⊥,则2a b += .14.已知3()5sin 8f x x a x =+-,且(2)4f -=-,则(2)f = .15.函数)sin()(ϕ+=x x f —2ϕsin x cos 的最大值为_________.16.定义: 区间[](),c d c d <的长度为d c -. 已知函数3log y x =的定义域为[],a b , 值域为[]0,2,则区间[],a b 长度的最大值与最小值的差等于________.三、解答题(本题共6道小题,第1题0分,第2题0分,第3题0分,第4题0分,第5题0分,第6题0分,共0分)17.在ABC ∆中,角,,A B C 所对应的边分别为,,a b c ,且()2cos cos a b C c B -⋅=⋅.(1)求角C 的大小;(2)若2c =,ABC ∆.18.设数列{}n a 的前n 项和为n S ,满足112n n a S -=,又数列{}n b 为等差数列,且109b =,2346b b b ++=. (1)求数列{}n a 的通项公式;(2)记112n n n a c b b ++=,求数列{}n c 的前n 项和n T .19.某基地蔬菜大棚采用水培、无土栽培方式种植各类蔬菜.过去50周的资料显示,该地周光照量X (小时)都在30小时以上,其中不足50小时的周数有5周,不低于50小时且不超过70小时的周数有35周,超过70小时的周数有10周.根据统计,该基地的西红柿增加量y (百斤)与使用某种液体肥料x (千克)之间对应数据为如图所示的折线图.(1)依据数据的折线图,是否可用线性回归模型拟合y 与x 的关系?请计算相关系数r 并加以说明(精确到0.01).(若75.0||>r ,则线性相关程度很高,可用线性回归模型拟合)(2)蔬菜大棚对光照要求较大,某光照控制仪商家为该基地提供了部分光照控制仪,但每周光照控制仪最多可运行台数受周光照量X 限制,并有如下关系:制仪周亏损1000元.若商家安装了3台光照控制仪,求商家在过去50周周总利润的平均值. 附:相关系数公式∑∑∑===----=n i i n i in i ii y y x x y y x x r 12121)()())((,参考数据55.03.0≈,95.09.0≈.20.如图,正方形ADEF 与梯形ABCD 所在的平面互相垂直,,//AD CD AB CD ⊥,122AB AD CD ===,点M 是线段EC 的中点.(1)求证://BM 面ADEF ;(2)求平面BDM 与平面ABF 所成锐二面角的余弦值.21.已知椭圆C :12222=+by a x (a >b >0)的焦点在圆x 2+y 2=3上,且离心率为23. (Ⅰ)求椭圆C 的方程;(Ⅱ)过原点O 的直线l 与椭圆C 交于A ,B 两点,F 为右焦点,若△F AB 为直角三角形,求直线l 的方程.22.已知函数()ln a f x x x=+. (1)求函数()f x 的单调区间;(2)证明:当2a e≥时, ()x f x e ->.试卷答案1.BB=﹛-1,2﹜,故A B=﹛2﹜.2.D略3.C4.A5.C6.BAC=1,但ABC ∆为直角三角形不是钝角三7.C该零件是一个由两个圆柱组成的组合体,其体积为π×32×2+π×22×4=34π(cm 3),原毛坯的体积为π×32×6=54π(cm 3),切削掉部分的体积为54π-34π=20π(cm 3),故所求的比值为ππ5420=2710. 8.B略9.B10.A 592()[,]444x πππωω=⇒+∈ 不合题意 排除()D 351()[,]444x πππωω=⇒+∈ 合题意 排除()()B C 另:()22πωππω-≤⇔≤,3()[,][,]424422x ππππππωωπω+∈++⊂得:315,2424224πππππωπωω+≥+≤⇔≤≤11.B12.B13.14.-1215.1(x )=sin(x +φ)-2sin φcos x =sin x cos φ-sin φcos x =sin(x -φ),故其最大值为1.16.817.(1)由()2cos cos a b C c B -⋅=⋅得2sin sin cos AcosC BcosC BsinC =+∴2sin cos sin A C A = ∴1cos 2C =∵0C π<< ∴3C π=(2)∵1sin 2ABC S ab C ∆=∴4ab = 又2222()23c a b abcosC a b ab =+-=+-∴2()16a b += ∴4a b += ∴周长为6.18.(1)设{}n b 的公差为d ,则1199366b d b d +=⎧⎨+=⎩ ∴101b d =⎧⎨=⎩∴1n b n =-当1n =时,11112a S -=,∴12a =当2n ≥时,()111222222n n n n n n n a S S a a a a ---=-=---=-∴12n n a a -= ∴2n n a =(2)由(1)知 11,2n b n a =-=,()211211n c n n n n ⎛⎫==- ⎪++⎝⎭ ∴1211111212231n n T c c c n n ⎛⎫=+++=-+-++- ⎪+⎝⎭122111n n n ⎛⎫=-= ⎪++⎝⎭ 19.(1)由已知数据可得2456855x ++++==,3444545y ++++==.………1分 因为51()()(3)(1)000316i i i x x y y =--=-⨯-++++⨯=∑, …………………2分 ,52310)1()3()(22222512=+++-+-=-∑=i ix x …………………………3分==…………………………4分所以相关系数()()0.95n i i x x y y r --===≈∑.………5分 因为0.75r >,所以可用线性回归模型拟合y 与x 的关系.……………6分(2)记商家周总利润为Y 元,由条件可得在过去50周里:当70X >时,共有10周,此时只有1台光照控制仪运行,周总利润Y =1×3000-2×1000=1000元.…………8分当5070X ≤≤时,共有35周,此时有2台光照控制仪运行,周总利润Y =2×3000-1×1000=5000元. ……………………………9分当50X <时,共有5周,此时3台光照控制仪都运行,周总利润Y =3×3000=9000元.…………………10分所以过去50周周总利润的平均值10001050003590005460050Y ⨯+⨯+⨯==元, 所以商家在过去50周周总利润的平均值为4600元. ………………………12分20.(1)证明:取DE 中点N ,连,MN AN 则//MN AB ,且MN AB =∴ABMN 是平行四边形,∴//BM AN∵BM ⊄平面ADEF ,AN ⊂平面ADEF ,∴//BM 平面ADEF(2)如图,建立空间直角坐标系,则()()()()()2,0,0,2,2,0,0,4,0,0,0,0,0,0,2A B C D E因为点M 是线段EC 的中点,则()0,2,1M ,()0,2,1DM =,又()2,2,0DB =.设()111,,n x y z =是平面BDM 的法向量,则1111220,20DB n x y DM n y z ⋅=+=⋅=+=.取11x =,得111,2y z =-=,即得平面BDM 的一个法向量为()1,1,2n =-.由题可知,()2,0,0DA =是平面ABF 的一个法向量.设平面BDM 与平面ABF 所成锐二面角为θ,因此,cos 2DA n DA n θ⋅===⨯⋅. 21.解:(Ⅰ)因为椭圆的焦点在x 轴上,所以焦点为圆x 2+y 2=3与xa=2.分 (Ⅱ)当△FAB 为直角三角形时,显然直线l 斜率存在,可设直线l 方程为y=kx ,设A(x 1,y 1),B(x 2,y 2).(ⅰ)当FA ⊥FB消y 得(4k 2+1)x 2-4=0.则x 1+x 2=0此时直线l 分 (ⅱ)当FA 与FB此时直线l综上,直线l 分 22.(1)函数()ln a f x x x =+的定义域为()0,+∞. 由()ln a f x x x =+,得()221a x a f x x x x ='-=-.………1分 ①当0a ≤时, ()0f x '>恒成立, ()f x 递增,∴函数()f x 的单调递增区间是()0,+∞ ………2分②当0a >时,则()0,x a ∈时,()0,f x '<()f x 递减,(),x a ∈+∞时, ()0f x '>,()f x 递增.∴函数()f x 的单调递减区间是(0,)a ,单调递增区间是(),a +∞.………4分(2)要证明当2a e ≥时, ()x f x e ->,即证明当20,x a e >≥时, ln x a x e x-+>,………5分 即ln x x x a xe -+>,令()ln h x x x a =+,则()ln 1h x x ='+, 当10x e <<时, ()0h x '<;当1x e>时, ()0h x '>. 所以函数()h x 在10,e ⎛⎫ ⎪⎝⎭上单调递减,在1,e ⎛⎫+∞ ⎪⎝⎭上单调递增. 当1x e =时, ()min 1h x a e ⎡⎤=-+⎣⎦.于是,当2a e ≥时, ()11h x a e e≥-+≥.①………8分 令()x x xe φ-=,则()()1x x x x e xe e x φ---'=-=-.当01x <<时, ()0x ϕ'>;当1x >时, ()0x φ'<.所以函数()x φ在()0,1上单调递增,在()1,+∞上单调递减.当1x =时, ()max 1x e φ⎡⎤=⎣⎦.于是,当0x >时, ()1x eφ≤.②………11分 显然,不等式①、②中的等号不能同时成立.故当2a e ≥时, (f x )x e ->.………12分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高二数学(上)期末考一、选择题:本小题共 小题,每小题 分,共 分 在每小题给出的四个选项中,只有一项是符合题目要求的 不等式0322<--x x 的解集是( )✌.()1,3- .()3,1- .()3,-∞- ()+∞,1.()1,-∞- ()+∞,3 已知平面α的法向量是()2,3,1-,平面β的法向量是()4,,2λ-,若//αβ,则λ的值是( ) ✌.103-.6- . .103.已知, , a b c 满足c b a <<,且0ac <,那么下列选项中一定成立的是☎ ✆✌ ab ac > ()0c b a -< 22cb ab < ()0ac a c -> 已知{}n a 是由正数组成的等比数列,n S 表示{}n a 的前n 项的和.若13a =,24144a a =,则10S 的值是☎ ✆✌. . . . 下列有关命题的说法正确的是☎ ✆ ✌.命题“若21x =,则1=x ”的否命题为:“若21x =,则1x ≠”. .“1x =-”是“2560x x --=”的必要不充分条件..命题“x R ∃∈,使得210x x ++<”的否定是:“x R ∀∈, 均有210x x ++<”. .命题“若x y =,则sin sin x y =”的逆否命题为真命题 设21,F F 为双曲线1422=-y x 的两个焦点,点P 在双曲线上且02190=∠PF F ,则21PF F ∆的面积是( )✌ 25 5 已知向量)0,1,1(=→a ,)2,0,1(-=→b ,且→→+b a k 与→→-b a 2互相垂直,则k 的值是( ) ✌ 51 53 57 若ABC ∆的内角,,A B C 所对的边,,a b c 满足22()4a b c +-=,且060C =,则a b +的最小值为☎ ✆ ✌..43.8- .若双曲线22221(0,0)x y a b a b-=>>的右焦点为☞,若过☞且倾斜角为︒60的直线与双曲线的右支有且只有一个交点,则此双曲线离心率e 的取值范围是( ) ✌.[]2,1.()2,1 .()+∞,2 . [)+∞,2若抛物线24y x =的焦点是F 准线是l 则经过点F 、M ( , )且与l 相切的圆共有( ). ✌个 个 个 个二、填空题 本大题共 小题,每小题 分,满分 分 请把答案填在答题纸的相应位置.等差数列{}n a 中,若34512,a a a ++=则71a a + 已知1,10,220x x y x y ≥⎧⎪-+≤⎨⎪--≤⎩则z x y =+的最小值是 已知正方体1111D C B A ABCD -中,E 为11D C 的中点,则异面直线AE 与BC 所成角的余弦值为 点P 是抛物线x y 42=上一动点,则点P 到点)1,0(-A 的距离与P 到直线1-=x 的距离和的最小值是 .设{}n a 是公比为q 的等比数列,其前n 项积为n T ,并满足条件011,01,110099100991<-->->a a a a a ,给出下列结论:( )10<<q ; ( )1198<T ;( )110199<a a ;( )使1<n T 成立的最小自然数n 等于199,其中正确的编号为 (写出所有正确的编号)三、解答题 本大题共 小题,共 分 解答应写出文字说明 证明过程或演算步骤 (本小题满分 分)已知数列}{n a 的前n 项和为n S ,且n a 是n S 与 的等差中项, ⑴求12,a a 的值;⑵求数列{}n a 的通项公式。
.(本小题满分 分)已知0,1a a >≠,命题:p ❽函数xa x f =)(在(0,)+∞上单调递减❾,命题:q ❽关于x 的不等式21204x ax -+≥对一切的x R ∈恒成立❾,若p q ∧为假命题,p q ∨为真命题,求实数a 的取值范围.(本小题满分 分)在 ✌中,♋、♌、♍分别是角✌、 、 的对边,且cab b ac a -=++, ( )求角 的大小;( )若ABC △最大边的边长为7,且A C sin 2sin =,求最小边长..(本小题满分 分)运货卡车以每小时⌧千米的速度匀速行驶 千米☎♎⌧♎✆☎单位:千米 小时✆.假设汽油的价格是每升 元,而汽车每小时耗油☎+⌧✆升,司机的工资是每小时 元.☎✆求这次行车总费用⍓关于⌧的表达式;☎✆当⌧为何值时,这次行车的总费用最低,并求出最低费用的值. .(本小题满分 分)如图,在四棱锥 —✌中, ⊥ 底面✌, 底面✌是正方形, ,☜、☞分别为✌、 的中点。
( )求证:☜☞⊥ ;( )求 与平面 ☜☞所成角的正弦值; ( )在平面 ✌内求一点☝,使☝☞⊥ 平面 ,并证明你的结论。
.(本小题满分 分)已知椭圆)0(12222>>=+b a by a x 的左、右焦点分别是☞ (-♍, )、☞ (♍, ),✈是椭圆外的动点,满足.2||1a Q F =点 是线段☞ ✈与该椭圆的交点,点❆在线段☞ ✈上,并且满足.0||,022≠=⋅TF TF PT ( )设x 为点 的横坐标,证明x aca F +=||1;( )求点❆的轨迹 的方程;( )试问:在点❆的轨迹上,是否存在点 , 使△☞ ☞ 的面积 .2b 若存在,求∠☞ ☞ 的正切值;若不存在,请说明理由高二(上)期末联考数学试卷参考答案(理科)一、选择题 — 、 ✌ — 、✌二、填空题 、 、 、32、2 、( )( )( ) 三、解答题 、2n S =+n 解:由已知得2a ① 分☞由①得:122S =+⇒=112a a 分2224S =+=++⇒=21222a a a a 分☎✆解:12n S +=+n+12a ②② ①得12n n S S +-=-=∴=n+1n n+1n+1n2a 2a a a a 分∴数列}{n a 以 为首项,以 为公比的等比数列分即1222n n-=⋅=n a 分、解:p 为真:01a <<;⑤⑤分;q 为真:0142≤-=∆a ,得2121≤≤-a ,又0,1a a >≠,210≤<∴a ⑤⑤⑤分因为p q ∧为假命题,p q ∨为真命题,所以,p q 命题一真一假⑤⑤分 ( )当p 真q 假1212110<<⇒⎪⎩⎪⎨⎧><<a a a ⑤⑤⑤⑤⑤分( )当p 假q 真⎪⎩⎪⎨⎧≤<>2101a a 无解 ⑤⑤⑤⑤分综上,a 的取值范围是1(,1)2⑤⑤⑤⑤⑤⑤⑤分、解:(♊)由ca b b a c a -=++整理得))(()(b a a b c c a +-=+,即222a b c ac -=+, 分 ∴2122cos 222-=-=-+=ac ac ac b c a B , ∵π<<B 0,∴32π=B 。
(♋)∵32π=B ∴最长边为b ,∵A C sin 2sin =,∴a c 2=, ∴a 为最小边,由余弦定理得)21(2247222-⋅⋅-+=a a a a ,解得12=a , ∴1=a ,即最小边长为、解:☎✆行车所用时间为♦= ⌧☎♒✆,⍓= ⌧ ☎+⌧ ✆+ ⌧,⌧∈☯. 所以,这次行车总费用⍓关于⌧的表达式是⍓= ⌧+ ⌧,⌧∈☯.☎✆⍓= ⌧+ ⌧♏ ,当且仅当 ⌧= ⌧,即⌧= 时,上述不等式中等号成立. 当⌧= 时,这次行车的总费用最低,最低费用为 元. 、PD ⊥面ABCD ∴,PD DA PD DC ⊥⊥,又底面✌是正方形,∴DA DC ⊥(0,0,0)000000022200.222DA DC DP x y z AD a a a aD A a B a a C aE aF a a a F P a =以、、所在直线为轴、轴、轴建立空间直角坐标系,设,则、(,,)、(,,)、(,,)、(,,)、(,,)(,,)、(,,)10000.22a aEF DC a EF DC ⋅=-⋅=∴⊥()(,,)(,,),(,,).(,,)(,,)0,()0.02222(,,)(,,0)0,0.221,2,1,(1,2,1).cos ,62DEF n x y z a a a ax y z x y z n DF a a n DE x y z a ax y BD n x y z n BD n a BD nDB DEF =⎧⎧⋅=++=⎪⎪⎧⋅=⎪⎪⎪⇒⎨⎨⎨⋅=⎪⎪⎪⎩⋅=+=⎪⎪⎩⎩⋅==-=∴=-<>===∴(2)设平面的法向量为由,得取则与平面所成角的正弦20.,,,222,,(,0,0)()0,;22222,,(0,,)()0,0.2222200.2a a aG x z G PAD FG x z a a a a aFG CB x z a a x x a a a a aFG CP x z a a a z z aG G AD ∈=---⋅=---⋅=-==⋅=---⋅-=+-==∴(3)设(,,),则平面。
()()()点坐标为(,,),即点为的中点 解法二、☎✆证明:PD ⊥面ABCD ∴PD CD ⊥,又ABCD 是正方形∴AD CD ⊥PDAD D =∴CD ⊥面PAD ∴CD PA ⊥☜、☞分别为✌、 的中点∴EFPA ,故CD EF ⊥AD OE EB AE OE FO O BD //.∴=,、,连结的中点(证法二)取.//.PD FO FB FP CD OE CD AD ∴=⊥∴⊥,,又PD ABCD FO ABCD ⊥∴⊥∴底面,底面,FO CD ⊥OE OF O = ∴CD ⊥面OEF EF ⊂面OEF ∴CD EF ⊥☞22211..33111224221153.224B DEF F DEB DEF DEBDEBB DEF d d FO aa FO a a EF AP a DF PB a DE a V V S S S --∆∆∆=∴⋅=⋅=======+=(2)设到平面的距离为,设底面边长为,则,,,, .6363sin .6121418686.90454342222222222所成角的正弦值为与平面,,则所成角与平面设,,DEF DB DB d DEF DB a d a a d a a DEF DE a a a DF EF S DEF o ∴===⇒⋅=⋅∴=∴=∠∴==+=+∆θθ .G AD (3)答:是的中点.PC H DH PD DC DH PC =∴⊥(方法一)取的中点,连结,.BC PDC BC DH DH PCB ⊥∴⊥∴⊥又平面,,平面1.////2DA G GF FH HF BC DG DGFH ∴取中点,连结、,四边形为平行四边形 //.DH GF GF PCB ∴∴⊥,平面.....AD G PG GB GF PGD BGA PG GB F PB GF PB GO FO ABCD OG AD FG AD FG BCFG PBC ∆≅∆∴=∴⊥⊥⊥∴⊥∴⊥∴⊥(方法二)取中点,连结、、,又为中点,连结底面,,,平面、解:( )证法一:设点 的坐标为).,(y x 由 ),(y x 在椭圆上,得.)()()(||222222221x aca xa b b c x y c x P F +=-++=++=由0,>+-≥+≥a c x a c a a x 知,所以 .||1x aca F +=……………………… 分 证法二:设点 的坐标为).,(y x 记,||,||2211r F r F ==则.)(,)(222221y c x r y c x r ++=++=由.||,4,211222121x aca r F cx r r a r r +===-=+得 ( )解法一:设点❆的坐标为).,(y x 当0||=时,点(a , )和点(-a , )在轨迹上当 0||0|2≠≠TF PT 且时,由0||||2=⋅TF PT ,得2TF PT ⊥ 又||||2PF PQ =,所以❆为线段☞ ✈的中点在△✈☞ ☞ 中,a F ==||21||1,所以有.222a y x =+综上所述,点❆的轨迹 的方程是.222a y x =+ 解法二:设点❆的坐标为).,(y x 当0||=时,点(a , )和点(-a , )在轨迹上 当 0||0|2≠≠TF 且时,由02=⋅TF ,得2TF ⊥ 又||||2PF =,所以❆为线段☞ ✈的中点设点✈的坐标为(y x '',),则⎪⎪⎩⎪⎪⎨⎧'=+'=.2,2y y c x x 因此⎩⎨⎧='-='.2,2y y c x x ①由a Q F 2||1=得.4)(222a y c x ='++' ② 将①代入②,可得.222a y x =+综上所述,点❆的轨迹 的方程是.222a y x =+…………………… 分( )解法一: 上存在点 (00,y x )使 2b 的充要条件是⎪⎩⎪⎨⎧=⋅=+.||221,2022020b y c a y x 由③得a y ≤||0,由④得.||20c b y ≤ 所以,当cb a 2≥时,存在点 ,使 2b ; 当cb a 2<时,不存在满足条件的点 ……………………… 分当cb a 2≥时,),(),,(002001y x c MF y x c MF --=---=, 由2222022021b c a y c x MF MF =-=+-=⋅, 212121cos ||||MF F MF MF MF ∠⋅=⋅,22121sin ||||21b MF F MF MF S =∠⋅=,得.2tan 21=∠MF F 解法二: 上存在点 (00,y x )使 2b 的充要条件是③ ④⎪⎩⎪⎨⎧=⋅=+.||221,2022020b y c a y x由④得.||20c b y ≤ 上式代入③得.0))((2224220≥+-=-=c b a c b a cb a x于是,当cb a 2≥时,存在点 ,使 2b ; 当cb a 2<时,不存在满足条件的点 ……………………… 分当cb a 2≥时,记c x y k k c x y k k M F M F -==+==00200121,, 由,2||21a F F <知︒<∠9021MF F ,所以.2|1|tan 212121=+-=∠k k k k MF F ………… 分③ ④。
