六年级数学找规律练习
(完整版)六年级数学经典找规律专题

找规律专题一.解答题(共30小题)1.(2015•深圳)在生活中,经常把一些同样大小的圆柱管如图捆扎起来,下面我们来探索捆扎时绳子的长度,图中,每个圆的直径都是8厘米,当圆柱管放置放式是“单层平放”时,捆扎后的横截面积如图所示:那么,当圆柱管有100个时需要绳子厘米(π取3)2.(2015•龙泉驿区校级三模)摆一个六边形需要六根小棒,摆2个六边形需要11根小棒,3个需要16根小棒…问:摆10个六边形需要根小棒,摆100个六边形需要根小棒,摆n个六边形需要根小棒.3.(2015春•淮安校级期中)用计算器计算,再根据规律编写一道算式并直接写出得数.(24+25)×5=;(872+873)×5=;(2830+2831)×5=;(+)×=.4.(2015春•射阳县校级期中)根据规律填数.9×9+9=90 9876×9+6=8889098×9+8=890 98765×9+5=987×9+7=8890 987654×9+4=.5.(2015春•成都校级期中)如图表示“宝塔”,它们的层数不同,但都是由一样大的小三角形摆成的.仔细观察后,请回答:(1)五层的“宝塔”最下层包含多少个小三角形?六层呢?七层呢?n层呢?(2)整个五层“宝塔”一共包含多少个小三角形?六层呢?七层呢?n层呢?6.(2015春•西安校级期中)仔细观察,根据发现的规律把表格填完整.第几幅图 1 2 3 5 …n共几个面在外面…7.(2015春•盐城校级期中)用小棒如图的方式搭正方形.搭1个正方形要4根小棒,搭2个正方形要7根小棒.(1)搭3个正方形要根小棒;(2)搭8个正方形要根小棒;8.(2015春•团风县期中)一串珠子按照3颗黑珠,2颗白珠,3颗红珠,2颗蓝珠的顺序排列.(1)第14颗珠子是珠子.(2)第998颗珠子是颜色珠子.9.(2015春•射阳县校级期中)想一想,填一填.用上面的图形在左边表里框出5个数,先算出这5个数的和,再想想算出的和与中间一个数有什么关系?如果5个数的和为795,请在上面图形里写出这5个数.10.(2015春•威宁县校级期中)表中一共有50个奇数,黑线框出的5个数之和是115;仔细观察后回答问题.(1)你能发现每次框出的5个数的和与中间数有什么关系吗?(2)如果框出5个数的和要是375,应该怎么框?(先在图中框一框,并在下面用文字说明)(3)能框出和是295的5个数吗?为什么?(4)一共可以框出多少个大小不同的和?11.(2015春•株洲校级月考)不计算,运用规律在横线上填上合适的数.7×9=6377×9=693777×9=69937777×9=69993…777777777×9=1÷7=0.142857142857…2÷7=0.285714285714…3÷7=0.428571428571…4÷7=0.575÷7=0.76÷7=7÷7=12.(2014•涟水县模拟)观察与计算.计算:1+2+3+…+99+100+99+98+…+3+2+1=13.(2014•金寨县校级模拟)找规律,填表.序号①②③④⑤…⑩数列A 1 3 5 7 9 …数列B 0 1 4 9 (81)14.(2014•宝安区校级模拟)观察下面3题的规律,然后算出(1)(2)两小题的结果.1+2+1=2×2=41+2+3+2+1=3×3=91+2+3+4+3+2+1=16(1)1+2+3+…+99+100+99+…+3+2+1=(2)+++…+++1+++…+++=15.(2014•绍兴)有些题目可以通过观察找出规律,知道答案.按照下图算式的规律不变,如果商是123456,括号中的“减数”应该是.(3﹣3)÷27=0(33﹣6)÷27=1(333﹣9)÷27=12(3333﹣12)÷27÷=123.16.(2014•武平县)观察图形找规律:(1)按照图形变化规律填表:1 2 3 4 5 …正方形个数直角三角0 4 8 …形个数(2)如果画8个正方形能得到个直角三角形,画n个正方形能得到个直角三角形.17.(2014•东莞)探寻规律.如图 是一块瓷砖的图案,用这种瓷砖来铺设地面.如果铺成一个2×2的正方形图案(如图‚),其中完整的圆共有5个,如果铺成一个3×3的正方形图案(如图ƒ),其中完整的圆共有13个,如果铺成一个4×4的正方形图案(如图④),其中完整的圆共有25个.若这样铺成一个10×10的正方形图案,则其中完整的圆共有个.18.(2014•东台市)准备(1)每个都是棱长为1厘米的正方体.(2)一个挨着一个排成一排你要研究的问题是:正方体个数与拼成的长方体表面积之间的关系.探索过程:根据你的发现填空.当正方体个数为10时,所拼成的长方体表面积是平方厘米.当正方体个数为a时,所拼成的长方体表面积是平方厘米.当拼成的长方体表面积是202平方厘米时,正方体个数是.19.(2014•长沙)在如图所示的数表中,第100行左边的第一个数是.20.(2014•成都)有甲、乙两个同样的杯子,甲杯装满水,乙杯是空的.第一次将甲杯里的倒入乙杯,第二次将乙杯中水的倒回甲杯,第三次将甲杯中的倒回乙杯,第四次将乙杯中的倒回甲杯,…,这样反复倒2015 次后,甲杯中的水是原来的几分之几?21.(2014•陕西校级模拟)有一列数2,9,8,2,6,…从第3个数起,每个数都是前面两个数乘积的个位数字.例如第四个数就是第二、第三两数乘积9×8=72的个位数字2.问这一列数第1997个数是几?22.(2014•江油市校级模拟)有一串数,,,,,,,,,,…则是第个分数.23.(2014•临夏县模拟)找规律填数.1,4,9,16,,,49,,81.24.(2014•湖南模拟)分析推理找规律①1+2+1=4②1+2+3+2+1=9③1+2+3+4+3+2+1=16④1+2+…+49+50+49+…+2+1=⑤1+2+…+(n﹣1)+n+(n﹣1)+…+2+1=(n为自然数)25.(2014•江油市校级模拟)1+3=4=22,1+3+5=9=32,1+3+5+7=16=42,…1+3+5+…+(2n ﹣1)=20132,则n=.26.(2014•宁远县校级模拟)如图,第6个图形一共由个小三角形组成,第n 个图形,一共由个小角形组成.27.(2014•广州模拟)为了美化城市,某商场在门前的空地上用花盆按如图所示的方式搭正方形.(1)填写下表正方形的层数 1 2 3 4 5该层所需花盆的个数 4 12(2)按这种规律搭下去,搭第n(n为正整数)层正方形,需要盆花.28.(2014•台湾模拟)如图所示,按一定规律用棉花棒摆放图案:第一组的图案用棉花棒2枝,第二组用棉花棒7枝,第三组用棉花棒15枝,如此类推,问第二十组的图案用棉花棒多少枝﹖29.(2014•成都校级模拟)下面的小点按如图所示的规律摆放:第1个图形有6个小点,第2个图形有10个小点,第3个图形有16个小点,第4个图形有24个点…,依次规律,第10个图形中点的个数是30.(2014•海安县模拟)用小棒按照如下的方式摆图形.摆1个八边形需要8根小棒,摆2个八边形需要15根小棒,…摆50个八边形需要根小棒;如果摆这样的八边形用了771根小棒,你知道摆了个八边形.。
小学六年级百以内数的找规律练习题

小学六年级百以内数的找规律练习题题目一:填空题1. 填写下列数列的规律:a) 2, 4, 6, 8, __, __, __, __b) 10, 20, 30, 40, __, __, __, __2. 填写下列数列中的数字:a) 1, 3, 5, 7, __, 11, __, 15b) 6, 12, 18, __, __, __, 36, 423. 请找出下面数列的规律并填写空缺的数字:a) 2, 4, 8, 16, __, __, __, __b) 5, 10, 15, __, __, __, 35, 40题目二:选择题1. 以下哪一个数字不符合规律?a) 12b) 15c) 18d) 202. 填写下列数列的规律,并选择正确的选项:4, 9, 14, 19, __, __, __, __a) 22, 27, 32, 37b) 23, 29, 35, 41c) 24, 30, 36, 42d) 25, 31, 37, 433. 填写下列数列的规律,并选择正确的选项:3, 6, 12, 24, __, __, __, __a) 36, 48, 60, 72b) 48, 60, 70, 84c) 36, 48, 60, 84d) 24, 36, 48, 60题目三:应用题1. 请通过找规律的方法填写下列表格中的空白部分: | 数字 | 数字的倍数 ||--------|-----------|| 2 | __ || 5 | __ || 7 | __ || 10 | __ || 15 | __ || 20 | __ || 25 | __ || 30 | __ |2. 根据规律,完成下列加法填空:a) 48 + 12 + __ + 12 = 96b) 72 + __ + 8 + 8 = 1203. 将下列数按照某种规律进行分类:12, 15, 18, 20, 23, 25, 28, 30, 33, 35题目四:解答题1. 找出下列数列的规律:a) 3, 6, 9, 12, 15b) 10, 14, 18, 22, 262. 填写下列数列中的数字,并说明规律:a) 2, 5, 9, 14, __, __, __, __b) 11, 22, 33, __, __, __, 66, 773. 某规律数列的前几项如下:1, 4, 9, 16, 25, 36a) 该数列的规律是什么?b) 写出该数列的通项公式。
六年级数学找规律试卷答案

一、选择题(每题2分,共20分)1. 下面哪个数列是等差数列?A. 1, 4, 7, 10, 13, ...B. 1, 3, 6, 10, 15, ...C. 1, 2, 4, 8, 16, ...D. 2, 4, 8, 16, 32, ...答案:B2. 下面哪个数列是等比数列?A. 1, 3, 9, 27, 81, ...B. 1, 2, 3, 4, 5, ...C. 1, 3, 6, 10, 15, ...D. 2, 4, 8, 16, 32, ...答案:A3. 下面哪个数列是斐波那契数列?A. 1, 2, 3, 5, 8, 13, ...B. 1, 3, 6, 10, 15, ...C. 2, 4, 8, 16, 32, ...D. 1, 2, 4, 8, 16, ...答案:A4. 下面哪个数列是平方数列?A. 1, 4, 9, 16, 25, ...B. 1, 3, 6, 10, 15, ...C. 1, 2, 4, 8, 16, ...答案:A5. 下面哪个数列是立方数列?A. 1, 8, 27, 64, 125, ...B. 1, 2, 3, 4, 5, ...C. 1, 3, 6, 10, 15, ...D. 2, 4, 8, 16, 32, ...答案:A二、填空题(每题3分,共15分)6. 下列数列中,缺失的数是:2, 4, 8, __, 32, ...答案:167. 下列数列中,缺失的数是:1, 4, 9, 16, __, ...答案:258. 下列数列中,缺失的数是:1, 2, 4, 8, __, ...答案:169. 下列数列中,缺失的数是:2, 4, 8, 16, __, ...答案:3210. 下列数列中,缺失的数是:1, 3, 6, 10, __, ...答案:15三、解答题(每题10分,共30分)11. 写出一个公差为3的等差数列,并写出前5项。
答案:2, 5, 8, 11, 1412. 写出一个公比为2的等比数列,并写出前5项。
六年级数学总复习--找规律练习题
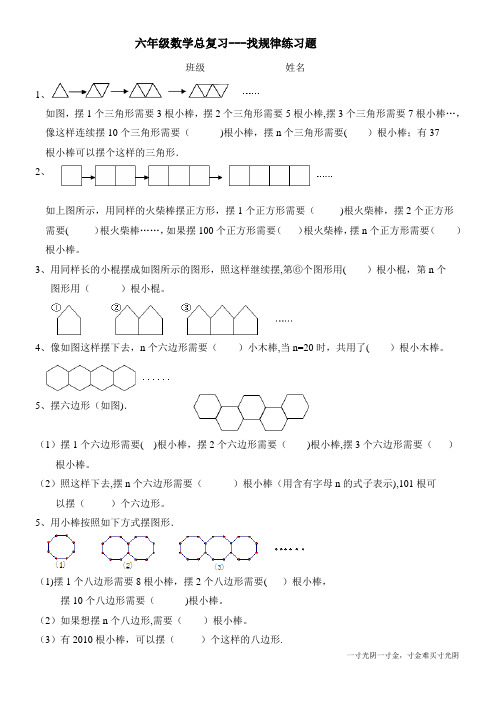
班级姓名1、如图,摆1个三角形需要3根小棒,摆2个三角形需要5根小棒,摆3个三角形需要7根小棒…,像这样连续摆10个三角形需要()根小棒,摆n个三角形需要( )根小棒;有37根小棒可以摆个这样的三角形.2、如上图所示,用同样的火柴棒摆正方形,摆1个正方形需要()根火柴棒,摆2个正方形需要( )根火柴棒……,如果摆100个正方形需要()根火柴棒,摆n个正方形需要()根小棒。
3、用同样长的小棍摆成如图所示的图形,照这样继续摆,第⑥个图形用()根小棍,第n个图形用()根小棍。
4、像如图这样摆下去,n个六边形需要()小木棒,当n=20时,共用了( )根小木棒。
5、摆六边形(如图).(1)摆1个六边形需要( )根小棒,摆2个六边形需要()根小棒,摆3个六边形需要()根小棒。
(2)照这样下去,摆n个六边形需要()根小棒(用含有字母n的式子表示),101根可以摆()个六边形。
5、用小棒按照如下方式摆图形.(1)摆1个八边形需要8根小棒,摆2个八边形需要( )根小棒,摆10个八边形需要()根小棒。
(2)如果想摆n个八边形,需要()根小棒。
(3)有2010根小棒,可以摆()个这样的八边形.6、用小棒可摆成小鱼,摆要8根,摆要14根,摆要20根…像这样,当摆成10条小鱼连在一起的时,需要()根小棒。
7、如下图,用同样大小的黑色棋子按图所示的方式摆图案,按照这样的规律摆下去,第10个图案需棋子()枚,第n个图案需棋子()枚。
8、用长度相等的小木棒按照下图的方式搭塔式三角形,按照这样的规律搭下去,搭第5个图形需要( )根小木棒,搭第m个图形需要( )根小木棒.9、猜猜用火柴棒摆出大小不同的长方形(如下图).第1个长方形需要()根火柴棒,第2个长方形需要()根小棒,如果按这样的规律摆下去,第10个长方形共需要( )根火柴棒。
8、如图所示:用黑白两种颜色的正五边形地砖按下图所示的规律,拼成若干个蝴蝶图案,则第7幅蝴蝶图案中白色地砖有()块.9、用黑白两种颜色的正六边形地面砖按如图所示的规律,拼成若干个图案,则第2012个图案中有白色地面砖()块.10、用同样规格的黑白两种颜色的正方形,按如图方式拼图,如果继续铺下去,那么第n个图形要用()块黑色正方形。
六年级的数学找规律练习题.doc

六年级数学找规律练习题班级 姓名等级例 1 假设 a#b=( a+b ) +(a —b );求 13#5 和 13#(5#4) 练习一1、将新运算定义为 a *b=(a+b )×(a —b );求 27*92、设 a *b=a 2 +2b ;求 10* 6 和 5*( 2*8)3、设 a *b=3a —b ×1;求 (15* 24)*( 10 *12)2例 2 设 p 、q 是两个数;规定: p # q=4×q —( p +q )÷2;求 3 #( 4# 6) 练习二1、设 p 、q 是两个数;规定: p # q=4×q —( p +q )÷2;求 5#( 6# 4)2、设 p 、q 是两个数;规定: p # q=p 2 +(p —q ) ×2;求 30#(5# 3)、设 M 、 N 是两个数;规定:MN ;求 10#20—13M # N=+4N M例 3 如果 1&5=1+11+111+1111+11111;2&4=2+22+222+2222;3&3=3+33+333 ;4&2=4+44 ; 那么 7&4= ;210&2= 。
练习三1、如果 1&5=1+11+111+1111+11111; 2&2=2+22 ;3&3=3+33+333 ⋯⋯ 那么 4&4= 。
2、规定 a&b=a+aa+aaa+aaaa+a ⋯⋯ a ( b 个 a );那么 8&5= 。
、如果1 ;3&2= 1 ; 4&3=1;那么( 6&3 )÷(2&6 )= 。
33 4442例 4 设 a@b=4a —2b+ 1ab ;求 x@(4@1) =34 中的未知数 x2练习四1、设 a@b=3a —2b ;已知 x@(4@1)=7;求 x、对两个整数 a 和 b 定义新运算“ & ”;a&b= 2a b ;求 6&4+9&82ba ba4xyx 和 y 定义新运算“ #”: x#y= (其中 m 是一个确定的整数) 。
六年级数学找规律练习题

六年级数学找规律练习题班级 姓名 等级例1 假设a#b=(a+b )+(a —b );求13#5和13#(5#4)练习一1、将新运算定义为a *b=(a+b )×(a —b );求27*92、设a *b=a 2+2b ;求10*6和5*(2*8)3、设a *b=3a —b ×21;求(15*24)*(10*12)例2 设p 、q 是两个数;规定:p # q=4×q —(p +q )÷2;求3 #(4# 6)练习二1、设p 、q 是两个数;规定:p # q=4×q —(p +q )÷2;求5#(6# 4)2、设p 、q 是两个数;规定:p # q=p 2+(p —q )×2;求30#(5# 3)3、设M 、N 是两个数;规定:M # N=N M +MN ;求10#20—41例3如果1&5=1+11+111+1111+11111;2&4=2+22+222+2222;3&3=3+33+333;4&2=4+44;那么7&4= ;210&2= 。
练习三1、如果1&5=1+11+111+1111+11111;2&2=2+22;3&3=3+33+333……那么4&4= 。
2、规定a&b=a+aa+aaa+aaaa+a ……a (b 个a );那么8&5= 。
3、如果2&1=21;3&2=331;4&3=4441;那么(6&3)÷(2&6)= 。
例4 设a@b=4a —2b+21ab ;求x@(4@1)=34中的未知数x练习四1、设a@b=3a —2b ;已知x@(4@1)=7;求x2、对两个整数a 和b 定义新运算“&”;a&b=()()b a b a ba -⨯+-2;求6&4+9&83、对任意两个整数x 和y 定义新运算“#”:x#y=ymx xy34+(其中m 是一个确定的整数)。
六年级数学探索规律题练习卷(含解析)

小学生规律探索题(二)1.如图,摆一个△用3根小棒,摆2个△用5根小棒,摆3个△用7根小棒.照这样,摆5个△用多少根小棒?用21根小棒可以摆多少△?2.现有若干圆环,它的外直径5厘米,环宽0.5厘米,将它们(如图)扣在一起,拉紧后测其长度.(1)根据规律,则2个圆环拉紧后的长度是多少厘米?10个圆环拉紧后的长度是多少厘米?(2)若拉紧后的长度是77厘米,它由多少个环扣成的?(3)设环的个数为a,拉紧后总长为S,请你用一个关系式表示你发现的规律。
3.甲种茶叶每千克40元,乙种茶叶每千克24元,按3:2的比例混合后共80千克,求混合后的茶叶每千克至少要卖多少元?4.某省原来用电收费标准统一为每度电0.65元.但由于当前物价上涨,省物价局决定,从2012年6月1日起,全省5.“学雷锋见行动”活动中,六年级部分学生为社区服务,其中男生人数和女生人数比是2:3.后来又有3名男生参加,有3名女生有事离开,这时男生人数是女生的75%.原来参加社区服务的男、女生各有多少人?6.(2014•荔波县模拟)有A、B两个容器,如图先把A装满水,然后倒入B中,B中水的深度是多少厘米?7.一件商品打九折后,现在的价格是990元,仍可获利10%.这件商品的成本价是多少元?这件商品的原来的价格是多少元?8.一个边长为8厘米的正方体,从如图示挖掉一侧面为正方形(边长为2厘米)的长方体,求剩余部分的表面积.元?(2)小文乘出租车从家到外婆家,共付费22.6元,小文家到外婆家相距多少千米?10.张华中心小学为了增强学生体质打算买60个足球,现有三个超市可以选择,三个超市足球的价格都是25元,但各规律探索题参考答案与试题解析一.填空题(共2小题)1.如图,摆一个△用3根小棒,摆2个△用5根小棒,摆3个△用7根小棒.照这样,摆5个△用11根小棒,用21根小棒可以摆10△.2.现有若干圆环,它的外直径5厘米,环宽0.5厘米,将它们(如图)扣在一起,拉紧后测其长度.(1)根据规律,则2个圆环拉紧后的长度是9厘米,10个圆环拉紧后的长度是41厘米.(2)若拉紧后的长度是77厘米,它由19个环扣成的.(3)设环的个数为a,拉紧后总长为S,请你用一个关系式表示你发现的规律.S=4a+1.二.解答题(共7小题)3.甲种茶叶每千克40元,乙种茶叶每千克24元,按3:2的比例混合后共80千克,求混合后的茶叶每千克至少要卖由题意可知:混合后甲种茶叶的重量占总重的,乙种茶叶的重量占总重量的,把茶叶总重(×=48×=324.某省原来用电收费标准统一为每度电0.65元.但由于当前物价上涨,省物价局决定,从2012年6月1日起,全省李华家6月用电量为500度,则李华家6月份的电费一共是多少元?5.“学雷锋见行动”活动中,六年级部分学生为社区服务,其中男生人数和女生人数比是2:3.后来又有3名男生参加,V=sh解:×=此题是考查圆柱、圆锥的体积计算,可利用它们的体积公式解答,同时不要漏了多少元?8.一个边长为8厘米的正方体,从如图示挖掉一侧面为正方形(边长为2厘米)的长方体,求剩余部分的表面积.(1)、张老师从学校到相距5千米的教育局取文件并立即回到学校,他应该怎样坐车比较合算?需付出租车车费多少元?(2)小文乘出租车从家到外婆家,共付费22.6元,小文家到外婆家相距多少千米?10、张华中心小学为了增强学生体质打算买60个足球,现有三个超市可以选择,三个超市足球的价格都是25元,但。
六年级毕业找规律练习题

六年级毕业找规律练习题在六年级毕业之际,当我们回顾所学的数学知识时,发现找规律是我们数学学习中最重要且有趣的一部分。
通过找规律,我们不仅能更好地理解数学概念,还能提高问题解决能力。
为了帮助大家巩固与提升这一技能,下面将提供一系列六年级毕业找规律练习题。
希望大家通过解答这些题目,能够更好地应用和运用找规律方法。
1. 找规律:下图为一个数字组成的三角形。
12 34 5 67 8 9 1011 12 13 14 15请写出这个三角形的第n行的数字。
2. 找规律:观察下图数列。
1, 4, 9, 16, 25, ...根据观察,写出这个数列的第n项。
3. 找规律:在下面的数表中,填上相应的数字。
12 63 5 84 9 12 145 7 10 13 154. 找规律:观察下列数表,写出每行中的 "?" 所代表的数字。
1, 4, 9, 16, 252, 6, 12, 20, ?3, 8, 15, ?, ?5, 14, ?, ?, ?5. 找规律:观察下列图案,写出每个图案中 "?" 所代表的数字。
□ □ □ □ □□ □ □ □□ □ □□ □□♦♦♦♦♦♦♦♦♦♦★★★★★★★★★★以上是一些六年级毕业找规律练习题,希望大家通过这些题目的练习,能够熟练应用找规律方法来解决问题。
找规律是数学学习中非常重要的一种技能,它不仅有助于提高数学成绩,也培养了我们的观察能力和逻辑思维能力。
祝愿同学们在六年级毕业后的学习中能够继续保持对数学的兴趣和热爱,不断挑战自己,取得更好的成绩!。
小学六年级数学找规律练习题

小学六年级数学找规律练习题六年级学生每天坚持做找规律的数学题目可以锻炼思维,在期末考试中取得优异的成绩。
为六年级师生整理了六年级数学找规律练习题,希望大家有所收获!小学六年级数学找规律练习题11、一座拱形桥的两根望柱间隔1米,每侧各有15根望柱,这座拱形桥长几米?2、四年级一班有60人,排成两队,每两个同学相隔1米,队伍前后长几米?3、公园圆形草坪四周有10个小喷水池,每两个喷水池中间有2把休息椅。
你知道一共有几把休息椅吗?4、张强家住在6楼,从1楼到3楼需要走34级台阶。
如果各层楼台阶数相同,张强到家需要走多少级台阶?5、在一条路的两边装路灯,每隔15米装一盏。
如果路的两端都要装,一共需要装162盏。
这条路全长多少米?6、在一条公路的两侧栽树,每隔5米栽一棵,公路的两端都有树,公路长400米,公路每侧要植几棵树?两侧一共要植几棵树?7、张老师要沿200米圆形跑道每隔5米插一面彩旗,一共需要几面彩旗?8、在一张边长为3米的方桌周围摆水果,每个角上都要摆一盘。
如果每隔1米摆一盘,这张方桌上能摆几盘水果?每条边上有几盘?9、学校林荫路长54米,路的一边从一端到另一端一共栽了19棵树,每两棵树之间相距几米?10、为美化环境,园林公司在草坪的一侧每隔2米摆了一盆花,两端都摆共摆了56盆花,现在全部换成木桩做成护拦,这一侧共用了111根木桩,相邻两根木桩间相距几米?11、某人到高层建筑的10层去,他从1层到5层用了100秒,如果用同样的速度走到10层,还需要多少秒?12、科学家进行一项实验,每隔5小时做一次记录。
做第12次记录时,挂钟的时针正好指向9,问做第一次记录时,时针指向几?13、两棵树相隔115米,中间以相等距离增加22棵后,第16棵与第1棵之间相隔几米?14、有一条植着等距离树的路,哥哥和弟弟同时出发,从第一棵数到最后一棵树方向走去,哥哥每分钟走84米,弟弟每分钟走36米。
哥哥走到第22棵树时,弟弟走到第几棵树?15、一列火车共20节,每节长5米,每两节之间相距1米,这列火车以每分钟20米的速度通过81米长的隧道,需要几分钟?16、请你把9棵树平均栽成8行,每行栽3棵,你能否做到?如果能请画出栽树的示意图。
小学六年级数学找规律专项练习题,孩子提高必备!

小学六年级数学找规律专项练习题,孩子提高必备!经典例题例1:找规律填数。
(1)1,3,5,7,(),()。
(2)65,60,55,50,(),()。
(3)1,10,100,1000,(),()。
(4)1,2,4,7,11,(),()。
(5)1,2,4,8,(),()。
(6)1,3,4,7,11,(),(),()。
思路点拨第(1)题,从左往右依次增加;第(2)题从左往右依次减少;第(3)题,从左往右依次在末尾添加一个,或者说依次乘;第(4)题从左往右,相邻两个数相差1,2,3,4……第(5)题中,1×2=2,2×2=4,4×2=8,所以,8×2=……第(6)题中,从第三个数开始,每个数都等于前面两个数的和。
模仿练习找规律填数。
(1)2,4,6,8,(),()。
(2)1,5,9,13,(),()。
(3)2,20,200,2000,(),()。
(4)1,2,2,4,3,6,4,8,(),()。
(5)49,42,35,(),(),()。
(6)4,6,9,13,(),24,()。
(7)100,81,64,(),36,25,(),9,4,1例2:仔细观察下列组图,在每一组的“?”处填上合适的数。
(1)(2)(3)(4)(5)思路点拨第(1)题中,3+4+8=15;第(2)题中,2×3+1=7;第(3)题中,3×4+5=17;第(4)题中4×5-5=20;第(5)题中,5+3+7=15,15+15=30。
模仿练习仔细观察每组图的规律,在空白处填合适的数。
(1)(2)例3:根据下表中的排列规律,在空格里填上适当的数。
思路点拨分析表格中的数可以发现,按行看,12+6=18,8+7=15,也就是说每一行中间的数等于两边的两个数的和。
依此规律可以填出空格中的数。
找规律练习题1.按照下面所绘图形的排列规律,第25个图形是________.(画出草图)□△○△□△○△□△○△……2.仔细观察下面的图,想一想,第3幅图问号处应填什么图形?3.仔细观察下面的图形,想一想,第4幅图应画怎样的图形?4.根据下面前三幅图的变化规律,在第4幅图中画出阴影部分.5.想一想,方框内应有多少个小圆点?6.按照图形的变化规律,在“?”处画出相符的图形.7.观察图的排列规律,在“?”处填上恰当的图形.8.下面哪个图形和其他几个图形不一样,找出来,并打上“√”.9.观察下列黑白小球的排列规律,然后回答方框内有几个白球,几个黑球?10.四个小动物排座位,如下图:一开始,小老鼠坐在第1号,小猴子坐第2号,小兔坐第3号,小猫坐第4号.以后它们多次地交换位子:第一次上下两排交换,第二次(在第一次交换之后)左右两列交换,第三次上下两排交换,第四次左右两列交换,……这样换下去,问:第十次交换后,小兔子坐在第几号位子上?答案解析1.□提示:在这列图形中出现的图形有:正方形、三角形、圆,且三种图形出现的规律是:按照正方形→三角形→圆→三角形的顺序4个一组循环出现.因25÷4=6……1,所以横线上应填第一个图形,即正方形.2.☆△提示:观察前两组图形可知,第一、二组都是由□○☆△组成,但顺序不同.第一组中的左边两个,在第二组中变为右边两个,而另外三个按原来的顺序移到了最左边.按此规律,“?”处应分别填上“☆”“△”.3.提示:观察前三幅图,大圆内都是■○△◇组成的,第一幅图中的图形按逆时针方向旋转可得到第二幅图形,第二幅图形按逆时针方向旋转可得到第三幅图形,同理可推得第四幅图形.4.提示:第一幅图的阴影部分均按顺时针方向旋转一格便可得到第二幅图,第二幅图中的阴影部分均按顺时针方向旋转一格便可得到第三幅图,由此,第三幅图中的阴影部分均按顺时针方向旋转一格便可得到第四幅图.5.方框内应填25个圆点.6.提示:观察前三幅图可知,前一幅图按逆时针方向旋转一格便可得到下一幅图.7.△提示:通过观察可知,从上到下每一横行圆的个数逐次减少1,三角的个数逐次增加1,由此推得“?”处的图形.8.(1)提示:图中的几何图形的共同特点是在图形内部都有一个同一类型的图形.但1、3、4、5内部的图形都较小,只有2内部图形较大,且位置和其它几个图形不同.(2)提示:这五幅图形都是由相同的两个图形重叠而成的,但不同的是前四个图形都是下面的图形盖住了上面的图形,只有5不同,是上面的图形盖住了下面的图形.9.9个白球,3个黑球.提示:观察图形可知,黑、白小球按照2个黑球,1个白球,2个黑球,3个白球,2个黑球,5个白球……的规律排列,即每组都是先有2个黑球,白球的个数每次增加2.10.小兔坐在第2号位置上.提示:小兔子开始在第3号位置上,第四次交换后,小兔子又回到原位,因10÷4=2……2,所以小兔第十次交换后应与第二次交换后的位置相同.。
六年级数学找规律练习题

六年级数学找规律练习题【六年级数学找规律练习题】(注意:以下习题适用于六年级学生,题目形式和结构遵循试卷格式,请根据实际情况自行适当调整)第一部分:选择题(每小题2分,共20分)请在括号内选择正确的答案填入。
1. 下列数列中,找不到规律的是()A. 2,4,8,16,32,64B. 1,3,6,10,15,21C. 4,7,11,16,22,29D. 1,2,4,7,11,162. 以下数列中,规律是每一项比前一项少1的是()A. 3,5,8,12,17B. 10,7,4,1,-2C. 6,10,15,21,-8D. 2,6,11,17,243. 当n=2时,数列2n-1的值为()A. 0B. 1C. 2D. 34. 数列1,4,9,16,25,...,是由什么公式得到的?()A. n²B. 2nC. n+1D. n(n+1)5. 某个数列的前4项是9,14,19,24,那么这个数列的第6项是多少?()A. 28B. 29C. 30D. 316. 以下数列的规律是:每一项都是前一项的两倍,那么它的第7项是多少?()A. 32B. 48C. 64D. 967. 小明在一个数列中发现了如下规律:每一项都是前一项的负数,那么第5项是多少?()A. -8B. -16C. -32D. -648. 小明根据某个规律列出了数列0,3,8,15,...,则它的第10项是多少?()A. 42B. 45C. 48D. 519. 某个数列的规律为:第1项是4,第2项是8,第3项是12,以此类推。
那么它的第6项是多少?()A. 22B. 24C. 26D. 2810. 数列1,3,6,10,...,的规律是:每一项都比前一项多1,那么它的第8项是多少?()A. 27B. 28C. 29D. 30第二部分:填空题(每小题3分,共30分)请根据数列的规律,填写相应的数值。
11. 数列2,4,6,8,...,的第10项是______。
小学六年级数学找规律练习题-

小学六年级数学找规律练习题|相关热词搜索:六年级学生每天坚持做找规律的数学题目可以锻炼思维,在期末考试中取得优异的成绩。
WTT为六年级师生整理了六年级数学找规律练习题,希望大家有所收获!小学六年级数学找规律练习题11、一座拱形桥的两根望柱间隔1米,每侧各有15根望柱,这座拱形桥长几米?2、四年级一班有60人,排成两队,每两个同学相隔1米,队伍前后长几米?3、公园圆形草坪四周有10个小喷水池,每两个喷水池中间有2把休息椅。
你知道一共有几把休息椅吗?4、张强家住在6楼,从1楼到3楼需要走34级台阶。
如果各层楼台阶数相同,张强到家需要走多少级台阶?5、在一条路的两边装路灯,每隔15米装一盏。
如果路的两端都要装,一共需要装162盏。
这条路全长多少米?6、在一条公路的两侧栽树,每隔 5米栽一棵,公路的两端都有树,公路长400米,公路每侧要植几棵树?两侧一共要植几棵树?7、张老师要沿200米圆形跑道每隔5米插一面彩旗,一共需要几面彩旗?8、在一张边长为3米的方桌周围摆水果,每个角上都要摆一盘。
如果每隔1米摆一盘,这张方桌上能摆几盘水果?每条边上有几盘?9、学校林荫路长 54米,路的一边从一端到另一端一共栽了19棵树,每两棵树之间相距几米?10、为美化环境,园林公司在草坪的一侧每隔2米摆了一盆花,两端都摆共摆了56盆花,现在全部换成木桩做成护拦,这一侧共用了111根木桩,相邻两根木桩间相距几米?11、某人到高层建筑的10层去,他从1层到5层用了100秒,如果用同样的速度走到10层,还需要多少秒?12、科学家进行一项实验,每隔5小时做一次记录。
做第12次记录时,挂钟的时针正好指向9,问做第一次记录时,时针指向几?13、两棵树相隔115米,中间以相等距离增加22棵后,第16棵与第1棵之间相隔几米?14、有一条植着等距离树的路,哥哥和弟弟同时出发,从第一棵数到最后一棵树方向走去,哥哥每分钟走 84米,弟弟每分钟走 36米。
六年级数学总复习--找规律练习题

六年级数学总复习--找规律练习题1.如图.摆1个三角形需要3根小棒.摆2个三角形需要5根小棒.摆3个三角形需要7根小棒….像这样连续摆10个三角形需要()根小棒.摆n个三角形需要()根小棒;有37根小棒可以摆个这样的三角形.2.如上图所示.用同样的火柴棒摆正方形.摆1个正方形需要()根火柴棒.摆2个正方形需要()根火柴棒…….如果摆100个正方形需要()根火柴棒.摆n个正方形需要()根小棒·3.用同样长的小棍摆成如图所示的图形.照这样继续摆.第⑥个图形用()根小棍.第n个图形用()根小棍·4.像如图这样摆下去.n个六边形需要()小木棒.当n=20时.共用了()根小木棒·5、摆六边形(如图).(1)摆1个六边形需要()根小棒.摆2个六边形需要()根小棒.摆3个六边形需要()根小棒·(2)照这样下去.摆n个六边形需要()根小棒(用含有字母n的式子表示).101根可以摆()个六边形·5.用小棒按照如下方式摆图形.(1)摆1个八边形需要8根小棒.摆2个八边形需要()根小棒.摆10个八边形需要()根小棒·(2)如果想摆n个八边形.需要()根小棒·(3)有2010根小棒.可以摆()个这样的八边形·6.用小棒可摆成小鱼.摆要8根.摆要14根.摆要20根…像这样.当摆成10条小鱼连在一起的时.需要()根小棒·7.如下图.用同样大小的黑色棋子按图所示的方式摆图案.按照这样的规律摆下去.第10个图案需棋子()枚.第n个图案需棋子()枚·8.用长度相等的小木棒按照下图的方式搭塔式三角形.按照这样的规律搭下去.搭第5个图形需要()根小木棒.搭第m个图形需要()根小木棒·9.猜猜用火柴棒摆出大小不同的长方形(如下图).第1个长方形需要()根火柴棒.第 2个长方形需要()根小棒.如果按这样的规律摆下去.第10个长方形共需要()根火柴棒·8、如图所示:用黑白两种颜色的正五边形地砖按下图所示的规律.拼成若干个蝴蝶图案.则第7幅蝴蝶图案中白色地砖有()块.9、用黑白两种颜色的正六边形地面砖按如图所示的规律.拼成若干个图案.则第2012个图案中有白色地面砖()块·10、用同样规格的黑白两种颜色的正方形.按如图方式拼图.如果继续铺下去.那么第n个图形要用()块黑色正方形·。
六年级数学找规律练习题

六年级数学找规律练习题第一节:数列找规律一、让我们来找找这些数列的规律吧!写出下一个数和数列的规律。
1. 2, 4, 6, 8, 10, ___, 规律:每次加22. 1, 4, 9, 16, 25, ___, 规律:每次加上前一个数字的连续奇数3. 3, 6, 12, 24, 48, ___, 规律:每次乘以24. 1, 3, 6, 10, 15, ___, 规律:每次加上连续的自然数二、数列中,有些数字被隐藏了,你能找到它们的规律吗?1. 2, 4, __, 8, __, 16, __, __, __, 32, 规律:每次乘以22. 1, __, 9, __, 25, __, __, __, 81, 规律:每次平方3. __, 6, __, __, 24, __, __, __, 48, 规律:每次乘以24. __, __, 6, __, __, __, 14, __, __, __, 规律:每次加上连续的自然数第二节:解决问题一、小明共有64个乒乓球,每天都比前一天多2个,经过几天后他会有100个乒乓球?二、班级一共有30个学生,每天都会有3个学生请假,经过几天后班级中只剩下10个学生?三、有一列数:7, 10, 13, 16, 19, ___. 请你写出下一个数,并简单解释规律。
四、小红练习算术题,她发现两个偶数相加得到的结果总是偶数,两个奇数相加得到的结果总是奇数。
这是不是一个规律?为什么?第三节:数列运算一、写出满足下列要求的数列,并计算数列的和。
1. 2 + 5 + 8 + 11 + 14 + ___ + 23, 共有9个数,数列的和是多少?2. 10 + 9 + 8 + 7 + 6 + ___ + 2, 共有12个数,数列的和是多少?3. 3 + 7 + 11 + 15 + ___ + 27, 共有7个数,数列的和是多少?4. 1 + 4 + 7 + 10 + 13 + ___ + 31, 共有9个数,数列的和是多少?二、小明想知道前100个奇数的和是多少,请用数列的运算法则计算一下。
数学六年级找规律练习题

数学六年级找规律练习题在数学学习的过程中,找规律是一个重要的能力培养方面。
让学生通过观察数列中的数字,找到其中的规律,进而预测未来的数字,不仅能锻炼学生的逻辑思维能力,也有助于提高他们解决问题的能力。
下面就让我们来一起解答一些六年级的数学找规律练习题。
1. 找规律填空(1)2,5,8,11,__,__,__,__,__,__(2)1,10,19,__,__,__,__,__,__,__(3)0,-1,-2,__,__,__,__,__,__,__(4)11,8,__,__,__,__,__,__,__,__(5)10,9,__,__,__,__,__,__,__,__这些题目中,我们需要找到数列中每个数字之间的规律,然后根据这个规律填写空缺的数字。
(1)这个数列中,每一项都比前一项大3,因此可以填写为14,17,20,23,26。
(2)这个数列中,每一项都比前一项大9,因此可以填写为28,37,46,55,64。
(3)这个数列中,每一项都比前一项减1,因此可以填写为-3,-4,-5,-6,-7。
(4)这个数列中,每一项都比前一项减3,因此可以填写为5,2,-1,-4,-7。
(5)这个数列中,每一项都比前一项减1,因此可以填写为8,7,6,5,4。
这些题目可以让学生分析数字之间的关系,通过观察找出规律,进而预测未来的数字。
这种能力对于日常生活中的问题解决也是很有帮助的。
2. 找规律继续下一项(1)2,4,6,8,__(2)3,6,9,12,__(3)1,4,7,10,__(4)100,90,80,70,__(5)8,6,4,2,__这些题目中,我们需要找到数列中每个数字之间的规律,并推测下一个数字是多少。
(1)这个数列中,每一项都比前一项大2,因此下一个数字是10。
(2)这个数列中,每一项都比前一项大3,因此下一个数字是15。
(3)这个数列中,每一项都比前一项大3,因此下一个数字是13。
(4)这个数列中,每一项都比前一项减10,因此下一个数字是60。
最新小学六年级数学找规律练习题

最新小学六年级数学找规律练习题小学六年级数学找规律练习题11、一座拱形桥的两根望柱间隔1米,每侧各有15根望柱,这座拱形桥长几米?2、四年级一班有60人,排成两队,每两个同学相隔1米,队伍前后长几米?3、公园圆形草坪四周有10个小喷水池,每两个喷水池中间有2把休息椅。
你知道一共有几把休息椅吗?4、张强家住在6楼,从1楼到3楼需要走34级台阶。
如果各层楼台阶数相同,张强到家需要走多少级台阶?5、在一条路的两边装路灯,每隔15米装一盏。
如果路的两端都要装,一共需要装162盏。
这条路全长多少米?6、在一条公路的两侧栽树,每隔5米栽一棵,公路的两端都有树,公路长400米,公路每侧要植几棵树?两侧一共要植几棵树?7、张老师要沿200米圆形跑道每隔5米插一面彩旗,一共需要几面彩旗?8、在一张边长为3米的方桌周围摆水果,每个角上都要摆一盘。
如果每隔1米摆一盘,这张方桌上能摆几盘水果?每条边上有几盘?9、学校林荫路长54米,路的一边从一端到另一端一共栽了19棵树,每两棵树之间相距几米?10、为美化环境,园林公司在草坪的一侧每隔2米摆了一盆花,两端都摆共摆了56盆花,现在全部换成木桩做成护拦,这一侧共用了111根木桩,相邻两根木桩间相距几米?11、某人到高层建筑的10层去,他从1层到5层用了100秒,如果用同样的速度走到10层,还需要多少秒?12、科学家进行一项实验,每隔5小时做一次记录。
做第12次记录时,挂钟的时针正好指向9,问做第一次记录时,时针指向几?13、两棵树相隔115米,中间以相等距离增加22棵后,第16棵与第1棵之间相隔几米?14、有一条植着等距离树的路,哥哥和弟弟同时出发,从第一棵数到最后一棵树方向走去,哥哥每分钟走84米,弟弟每分钟走36米。
哥哥走到第22棵树时,弟弟走到第几棵树?15、一列火车共20节,每节长5米,每两节之间相距1米,这列火车以每分钟20米的速度通过81米长的隧道,需要几分钟?16、请你把9棵树平均栽成8行,每行栽3棵,你能否做到?如果能请画出栽树的示意图。
找规律练习题六年级下册

找规律练习题六年级下册找规律练习题是数学课堂上常见的一种题型,通过观察数字序列中的规律,找出下一个数或者填写缺失的数字。
这种练习可以锻炼学生的观察能力、逻辑思维和数学思维。
下面将介绍一些六年级下册的找规律练习题,帮助学生更好地掌握这个问题类型。
练习题1:2,4,6,8,10,__,__,__观察数字序列,我们可以发现每个数都是前一个数加2。
所以,下一个数字是前一个数字12,再加2得到14;再加2得到16。
因此,答案是12,14,16。
练习题2:5,10,15,20,25,__,__,__观察数字序列,我们可以发现每个数都是前一个数加5。
所以,下一个数字是前一个数字30,再加5得到35;再加5得到40。
因此,答案是30,35,40。
练习题3:3,6,12,24,48,__,__,__观察数字序列,我们可以发现每个数都是前一个数乘以2。
所以,下一个数字是前一个数字96,再乘以2得到192;再乘以2得到384。
因此,答案是96,192,384。
练习题4:1,4,9,16,25,__,__,__观察数字序列,我们可以发现每个数都是前一个数的平方。
所以,下一个数字是前一个数字36,再平方得到1296;再平方得到46656。
因此,答案是36,1296,46656。
练习题5:2,5,10,17,26,__,__,__观察数字序列,我们可以发现第一个数加1,第二个数加3,第三个数加5,第四个数加7,以此类推。
所以,下一个数字是前一个数字37,再加9得到46;再加11得到57。
因此,答案是37,46,57。
通过这些练习题,我们可以看到找规律练习题的解题思路。
首先,我们要观察数字序列中的数字,寻找数字之间的关系和规律。
根据规律,我们可以找出下一个数字或填写缺失的数字。
这种练习可以培养学生的观察能力和逻辑思维,对于正确解题有很大的帮助。
总结:找规律练习题是六年级下册数学中的重要题型。
通过观察数字序列中的关系和规律,学生可以找出下一个数或填写缺失的数字。
六年级找规律数学题

六年级找规律数学题一、数字规律1. 按规律填数:1,3,6,10,15,(),28。
- 解析:观察这组数字,1到3增加了2,3到6增加了3,6到10增加了4,10到15增加了5。
可以发现相邻两个数的差值在依次递增1。
那么15后面的数应该比15大6,即15 + 6 = 21。
验证一下,21到28增加了7,符合规律。
所以括号里应填21。
2. 数列:2,4,8,16,32,()。
- 解析:这组数列中,2×2 = 4,4×2 = 8,8×2 = 16,16×2 = 32。
可以得出规律是后一个数是前一个数的2倍。
所以括号里的数应该是32×2 = 64。
二、图形规律1. 用小棒按照如下方式摆三角形:摆1个三角形需要3根小棒;摆2个三角形需要5根小棒;摆3个三角形需要7根小棒……(1)摆10个三角形需要多少根小棒?- 解析:观察可得,摆1个三角形用3根小棒(3 = 2×1+1);摆2个三角形用5根小棒(5 = 2×2 + 1);摆3个三角形用7根小棒(7 = 2×3+1)。
可以总结出规律,摆n个三角形需要2n + 1根小棒。
当n = 10时,2×10+1 = 21根小棒。
(2)有21根小棒,可以摆多少个三角形?- 解析:根据前面总结的规律2n+1。
设可以摆n个三角形,则2n + 1 = 21,2n = 20,解得n = 10。
所以21根小棒可以摆10个三角形。
2. 下列图形是由同样大小的小圆圈按照一定规律所组成的,其中第1个图形中一共有6个小圆圈,第2个图形中一共有9个小圆圈,第3个图形中一共有12个小圆圈……(1)第5个图形中有多少个小圆圈?- 解析:观察图形,第1个图形有6 = 3×1+3个小圆圈;第2个图形有9 = 3×2 + 3个小圆圈;第3个图形有12 = 3×3+3个小圆圈。
可以得出规律,第n个图形有3n+3个小圆圈。
六年级下册找规律练习题

六年级下册找规律练习题找规律是数学中一项重要的能力训练内容,对于六年级学生来说,掌握找规律的方法和技巧有助于提高解题能力和数学思维能力。
下面我将给出一些六年级下册的找规律练习题,帮助学生们加深对这一概念的理解和应用。
1. 数列规律练习题(1) 请找出下列数列的规律,并继续下一个数:a) 2, 4, 6, 8, 10, ...b) 3, 6, 9, 12, 15, ...c) 1, 4, 9, 16, 25, ...d) 5, 10, 20, 40, 80, ...(2) 根据下列数列的规律,填写空缺处的数字:a) 3, 5, 8, 12, _, _, _, ...b) 2, 4, 8, 16, _, _, _, ...c) 1, 1, 2, 3, 5, _, _, ...d) 10, 7, 4, 1, _, _, _, ...2. 图形规律练习题(1) 找出下列图形的规律,并画出下一个图形:a)◻︎◻︎◻︎◻︎◻︎◻︎◻︎◻︎b)☰☰☰☰☰☰☰☰c)△△△△△△△△△△d)□□ □□ □ □□ □ □ □□ □ □(2) 根据下列图形的规律,填写空缺处的图形:a)☰☰☰☰☰☰☰☰☰☰☰☰☰☰b)〇〇〇〇〇〇〇〇〇〇c)■■■■ ■■■■ ■■ ■■3. 算式规律练习题(1) 找出下列算式的规律,并继续下一个算式:a) 2 + 4 = 6, 3 + 6 = 9, 4 + 8 = 12, ...b) 5 - 2 = 3, 8 - 3 = 5, 11 - 4 = 7, ...c) 3 × 2 = 6, 5 × 3 = 15, 7 × 4 = 28, ...d) 12 ÷ 4 = 3, 20 ÷ 5 = 4, 30 ÷ 6 = 5, ...(2) 根据下列算式的规律,填写空缺处的算式:a) 6 + 10 = 16, 9 + 15 = 24, 12 + 20 = _, ...b) 8 - 4 = 4, 11 - 5 = 6, 14 - 6 = _, ...c) 3 × 4 = 12, 6 × 5 = 30, 9 × 6 = _, ...d) 16 ÷ 2 = 8, 25 ÷ 5 = 5, 36 ÷ 6 = _, ...通过以上的六年级下册找规律练习题,学生们可以锻炼他们发现规律、分析规律以及推广规律的能力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
六年级找规律练习题班级姓名等级
1、观察下面的几个算式:
1+2+1=4,
1+2+3+2+1=9,
1+2+3+4+3+2+1=16,
1+2+3+4+5+4+3+2+1=25,…
根据你所发现的规律,请你直接写出下面式子的结果:
1+2+3+…+99+100+99+…+3+2+1=_ ___。
2、已知下列等式:
① 13=12;
② 13+23=32;
③ 13+23+33=62;
④ 13+23+33+43=102;
…… ……
由此规律知,第⑤个等式是。
3、如图是用火柴棍摆成边长分别是1、2、3根火柴棍时的正方形,当边长为n根火柴棍时,若摆出的正方形所用的火柴棍的根数为S,则S=(用含n的
三层二杈树二层二杈树一层二杈树代数式表示,n 为正整数).
4、如图是五角星灯连续旋转闪烁所成的三个图形。
照此规律闪烁,下一个呈现出来的图形是
5、如下图是小明用火柴搭的1条、2条、3条“金鱼”……,则搭n 条“金鱼”需要火柴 根。
……
6、如图,在图1中,互不重叠的三角形共有4个,在图2中,互不重叠的三角形
共有7个,在图3中,互不重叠的三角形共有10个,……,则在第n 个图形中,互不重叠的三角形共有 个(用含n 的代数式表示)。
7、小的黑、白两种颜色的棋子摆设如下图所示的正方形图案,则第n 个图案需要
用白色棋子 ( )枚(用含有n 的代数式表示)
8、在计算机程序中,二杈树是一种表示数据结构的方法。
如图,一层二杈树的结点总数是1,二层二杈树的结点总数是3,三层二杈树的结点总数是7,四层二杈树的结点总数是15……照此规律七层二杈树的结点总数是 。
9、瑞士中学教师巴尔末成功地从光谱数据
、591216⋯⋯32
36
2125、、中得到巴尔末公式,从而打开了光谱奥妙的大门。
请你按这种规律写出第七个数据是_________。
10、观察右面的图形(每个正方形的边长均为1)和相应等式,控究其中的规律;
①2
11211-=⨯
A B C D
1条
2条
3条
……
图③
图②
图①
(3)
(2)
(1)1B 2
C 2
A B
C 1B 1
C
1A 2
C
1B 11C B
A …
第5题 ②322322-=⨯
③433433-=⨯
④5
44544
-=⨯
⑴写出第五个等式,并在右边给出的五个正方形上画出与之对应的图示: ⑵猜想并写出与第n 个图形相对应的等式。
11、填在下面各正方形中的四个数之间都有相同的规律,根据此规律,
m 的值是
A .38
B .52 C
.66 12、如图,将第一个图(图①)所示的正三角形连结各边中点进行分割,得到第二
个图(图②);再将第二个图中最中间的小正三角形按同样的方式进行分割,得到第三个图(图③);再将第三个图中最中间的小正三角形按同样的方式进行分割,……,则得到的第五个图中,共有________个正三角形。
13、如图4,在图(1)中,A 1、B 1、C 1分别是△ABC 的边BC 、CA 、AB 的中点,在图
(2)中,A 2、B 2、C 2分别是△A 1B 1C 1的边B 1C 律,则第n 个图形中平行四边形的个数共有14、2个图案由7个基础图形组成,……,第n (n 是正整数)个图案中由 个基础图形组成。
-
15、
它们是按一定规律排列的,依照此规律,第9个图形中共有 个★。
16、如图3,有一个形如六边形的点阵,它的中心是一个点,作为第一层,第
0 2 8 4
2 4 6
24 6 8
4(1
(2(3……
二层每边有两个点,第三层每边有三个点,依次类推,如果n 层六边形点阵的总点数为331, 则n 等于 。
17、下图表示“宝塔”,它们的层数不同,但都是由一样大的小三角形摆成的.仔细观察后,请回答:
(1)五层的“宝塔”最下层包含多少个小三角形六层呢七层呢n 层呢 (2)整个五层“宝塔”一共包含多少个小三角形六层呢七层呢n 层呢 18、观察下列图形,则第n 个图形中三角形的个数是( )
A .22n +
B .44n +
C .44n -
D .4n
19、将一些半径相同的小圆按如图所示的规律摆放:第1个图形有6个小圆,第2个图形有10个小圆,第3个图形有16个小圆,第4个图形有24个小圆,……,依次规律,第6个图形有 个小圆.
20、观察下列等式:
221.4135-=⨯; 22
2.5237-=⨯; 22
3.6339-=⨯; 22
4.74311-=⨯
…………
则第n (n 是正整数)个等式为 .
21、王婧同学用火柴棒摆成如下的三个“中”字形图案,依此规律,
第1个图形
第2个图形
第3个图形
第4个图形
…
……
第1个 第2个
第3个
第n 个“中”字形图案需 根火柴棒.
22、如图7-①,图7-②,图7-③,图7-④,…,是用围棋棋子按照某种规律摆成的一行“广”字,按照这种规律,第5个“广”字中的棋子个数是________,第n 个“广”字中的棋子个数是____________
23、下图是一组有规律的图案,第1个图案由4个基础图形组成,第2个 图案由7个基础图形组成……第n (n 是正整数)个图案中由 个基础图形组成.
24、观察图中每一个大三角形中白色三角形的排列规律,则第5个大三角形中白色
三角形有 个 .
25、下图是用火柴棍摆成的边长分别是1,2,3 根火柴棍时的正方形.当边长为n 根火柴棍时,设摆出的正方形所用的火柴棍的根数为s ,则s = . (用
n 的代数式表示s )
26、下列图案是晋商大院窗格的一部分,其中“○”代表窗纸上所贴的剪纸,则第n 个图中所贴剪纸“○”的个数为 .
27、用同样规格的黑白两种颜色的正方形瓷砖,按下图的方式铺地板,则第(3)
个图形中有黑色瓷砖________块,第n 个图形中需要黑色瓷砖__________块(用含n 的代数式表示).
(1(2(3……
……
……
n =1 n =2 n =3
(1
(2(3……
123。
