初高中数学衔接内容调测卷含答案
初高中衔接型数学试题(1)及参考答案

初高中衔接型数学试题(1)及参考答案一、选择题1.点P (-1,2)关于y 轴对称的点的坐标是( ).A .(1,2)B .(-1,2)C .(1,-2)D .(-1,-2) 2.在△ABC 中,∠C =90°,53sin =A ,则cosA 的值是( ).A .54B .53 C .43 D .34 3.方程2650x x +-=的左边配成完全平方后所得方程为( )A . 2(3)14x +=B . 2(3)14x -=C . 21(6)2x +=D . 以上答案都不对 4.如图3—1,在正方形铁皮上剪下一个圆形和扇形,使之恰好围成图3—2所示的一个圆锥模型.设圆的半径为r ,扇形半径为 R ,则圆的半径与扇形半径之间的关系为( ) A .R =2r B .R =94r C .R =3r D .R =4r二、填空题5.已知A 是锐角,且31sin =A ,则cos (90°-A )=___________.6.如图,为了求出湖两岸A 、B 两点之间的距离,观测者从测点A 、B 分别测得∠BAC =90°,∠ABC =30°,又量得BC =160 m ,则A 、B 两点之间的距离为 m (结果保留根号)三、解答题7.如图,在△ABC 中,AB =AC =5,BC =6,F 为BC 的中点.P 是BF 上的一点,过点P作BC 的垂线交AB 于D ,交CA 的延长线于E .若设 BP =x ,那么,图中有些量(线段、面积等)可以看作x 的函数,如,PC =6-x ,PF =3-x 等.除以上两例外,请你再写出一个关于x 的函数解析式,并加以证明.(不要添加辅助线和其它字母)图3—1图3—2第6题图8.如图14—1是某段河床横断面的示意图.查阅该 河段的水文资料,得到下表中的数据:x /m510 20 30 4050y /m 0.125 0.5 2 4.5 8 12.5(1)请你以上表中的各对数据(x ,y )作为点的坐标, 尝试在图14—2所示的坐标系中画出y 关于x 的 函数图象;(2)①填写下表: x5 10 20 30 40 50 2x y②根据所填表中数据呈现的规律,猜想出用x 表示y的二次函数的表达式: .(3)当水面宽度为36米时,一艘吃水深度(船底部到水面的距离)为1.8米的货船能 否在这个河段安全通过?为什么?9.如图15—1和15—2,在20×20的等距网格(每格的宽和高均是1个单位长)中, Rt △ABC 从点A 与点M 重合的位置开始,以每秒1个单位长的速 QM CAB O 10 20 30 40 50 60x /m214 12 10 86 4 y /m 图14—2你能行,加 油呀!xxy图14—1度先向下平移,当BC 边与网的底部重合时,继续同样的速度向右 平移,当点C 与点P 重合时,Rt △ABC 停止移动.设运动时间 为x 秒,△QAC 的面积为y .(1)如图15—1,当Rt △ABC 向下平移到Rt △A 1B 1C 1的位置时,请你在网格中画出Rt △A 1B 1C 1关于直线QN 成轴对称的图形; (2)如图15—2,在Rt △ABC 向下平移的过程中,请你求出y 与x 的函数关系式,并说明当x 分别取何值时,y 取得最大值和最小值?最大值和最小值分别是多少?(3)在Rt △ABC 向右平移的过程中,请你说明当x 取何值时,y 取得最大值和最小值?最大值和最值分别是多少?为什么?(说明:在(3)中,将视你解答方法的创新程度,给予1~4分的加分)ONPQM CAB图15—2参考答案一、1、答:A2、答:A 分析:可用两种方法解。
初高中衔接型中考数学试题(11)及参考答案

初高中衔接型中考数学试题(11)及参考答案一、选择题1.(浙江富阳)数轴上有两点A 、B 分别表示实数a 、b ,则线段AB 的长度是( )A 、b a -B 、b a +C 、b a -D 、b a + 2.(浙江富阳)二次函数2332+-=x x y 的图象与x 轴交点的个数是( ) A 、0个 B 、1个 C 、2个 D 、不能确定3.某种细菌在营养过程中,细菌每半小时分裂一次(由一个分裂为两个),经过两小时,这种细菌由1个可分裂繁殖成( ).(A )8个 (B )16个 (C )4个 (D )32个二、填空题 4.(浙江宁波)等腰三角形ABC 中,8=BC ,AB 、AC 的长是关于x 的方程0102=+-m x x 的两根,则m 的值是___________.5.(浙江富阳)方程0)2)(1(=--x x x 的解是 ;三、解答题6.(资阳市)已知等式 (2A -7B ) x +(3A -8B )=8x +10对一切实数x 都成立,求A 、B 的值.7.(浙江富阳)已知一个长方体的木箱高为80cm ,底面的长比宽多10cm ,(1)求这个长方体的体积y (3cm )与长方体的宽x (cm )之间的函数关系式;(2)问当该木箱的体积为0.723m 时,木箱底面的长与宽各为多少cm ?8. (河北省)某化工材料经销公司购进了一种化工原料共7000知克,购进价格为每千克30.物价部门规定其销售单价不得高于每千克70元,也不得低于30元.市场调查发现:单价定为70元时,日均销售60千克;单价每降低1元,日均多售出2千克.在销售过程中,每天还要支出其他费用500元(天数不足一天时,按整天计算).设销售单价为x 元,日均获利为y 元.第8题图(1)求y 关于x 的二次函数关系式,并注明x 的取值范围;(2)将(1)中所求出的二次函数配方成y =a (x +a b 2)2 +ab ac 442的形式,写出顶点坐标;在图9所示的坐标系中画出草图;观察图像,指出单价定为多少元时日均获利最多,是多少?(3)若将这种化工原料全部售出,比较日均获利最多和销售单价最高这两种销售方式,哪一种获总利较多,多多少?9.(北京西城)已知:Rt △ABC 中,∠C =90°. (1)若AB =c ,∠A =θ,用c 和θ表示BC 、AC ; (2)若AB =5,sin A =54,P 是AB 边上一动点(不与点A 、B 重合),过点P A 分别作PM ⊥AC 于点M ,PN ⊥BC 于点N .设△AMP 的面积为S 1、△PNB 的面积为S 2、四边形CMPN 的面积为S 3、AP =x .分别求出S 1、S 2、S 3关于x 的函数解析式;(3)试比较S 1+S 2与S 3的大小,并说明理由.初高中衔接型中考数学试题(11)参考答案一、 1、 答:C 2、 答:C 3、 答:B 二、4、 答:25或165、 答:2,1,0321===x x x三、6、解:由题意有⎩⎨⎧=-=-.1083,872B A B A(正确建立关于A 、B 的一个方程,给1分.)解得:⎪⎪⎩⎪⎪⎨⎧-==.54,56B A即A 、B 的值分别为65、45- .7、解:(1)因为木箱的长、宽、高分别为:10+x cm 、x cm 、80cm ……2分 所以 x x x x y 80080)10(802+=+= …………………………………………4分(2)因为 0.723m =703cm所以 720000800802=+x x 即 09000102=-+x x ……6分 解得:1001-=x (舍去)902=x …………………………………7分10010=+x所以当木箱体积为0.723m 时,底面的长和宽分别为100cm 和90cm 。
2024年新高一数学初升高衔接《函数的概念与性质》综合检测卷含答案解析

第三章:函数的概念与性质综合检测卷(试卷满分150分,考试用时120分钟)一、选择题:本题共8小题,每小题5分,共40分。
在每小题给出的四个选项中,只有一项是符合题目要求的.1.(23-24高一上·山东济宁·期中)下列函数是幂函数且在(),0∞-是增函数的是( )A .1y x=B .31y x =+C .2y x -=D.y =2.(23-24高一下·河北石家庄·开学考试)已知函数1()2f x x =+,其定义域为( )A .RB .{3}xx >-∣C .{}32xx x ≥-≠-∣且D .{3}x x ≤-∣3.(23-24高一上·安徽阜阳·月考)设偶函数()f x 的定义域为R ,当[0,)x ∈+∞时,()f x 是增函数,则((π),(3)f f f -的大小关系是( )A.(π)(3)(f f f >->B.(π)((3)f f f >>-C.(π)(3)(f f f <-<D.(π)((3)f f f <<-4.(23-24高一下·云南昆明·期中)已知函数()()22,023,0f x x f x x x x ⎧-≥=⎨-<⎩,则(1)f =( )A .14B .5C .1D .-15.(23-24高一上·广东深圳·期末)已知()533f x x ax bx =+++且()25f -=,则()2f 的值是( )A .3-B .1-C .1D .36.(23-24高一上·吉林延边·月考)已知定义在()0,∞+上的函数()f x 满足()1154f x f x x ⎛⎫-=- ⎪⎝⎭,则()2f 的值为( )A .152B .154C .174D .1727.(23-24高一上·江苏无锡·月考)已知函数29,1(),1x ax x f x a x x⎧---≤⎪=⎨>⎪⎩在R 上满足不等式2121()()0f x f x x x ->-,则实数a 的取值范围为( )A .[5,0)-B .(,2]-∞-C .[5,2]--D .(,0)-∞8.(23-24高一上·山东烟台·月考)已知()f x 是定义在R 上的偶函数,且在()0,∞+上是增函数,若()30f -=,则()0xf x >的解集是( )A .(3,0)(3,)-⋃+∞B .(,3)(3,)-∞-⋃+∞C .(,3)(0,3)-∞-⋃D .(3,0)(0,3)-⋃二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.9.(23-24高一上·福建龙岩·月考)下列各组函数是同一个函数的是( )A .()f x =与()g x =B .()221f x x x =--与()221g s s s =--C .()x f x x=与()01g x x =D .()f x x =与()g x =10.(23-24高一上·河南新乡·月考)关于幂函数()()1mf x m x -=-,下列结论正确的是( )A .()f x 的图象经过原点B .()f x 为偶函数C .()f x 的值域为()0,∞+D .()f x 在区间()0,∞+上单调递增11.(23-24高一上·河北邢台·月考)已知定义在R 上的函数()f x ,对任意实数,x y ,都有()()()f xy yf x xf y =+,则( )A .()00f =B .()10f =C .()()16162f f =D .()f x 为奇函数三、填空题:本题共3小题,每小题5分,共15分.12.(23-24高一上·重庆·月考)已知幂函数()y f x =的图象经过1(2,8,则(3)f =.13.(23-24高一下·广东广州·月考)函数()425x f x x -=+在[2,1]--上的值域是 .14.(23-24高一上·云南昆明·月考)已知函数2()26f x x kx =-+在[1,3]上的最大值为10-,则实数k 的值为.四、解答题:本题共5小题,共77分。
初升高数学衔接带答案

初升高数学衔接带答案一、选择题1. 已知函数\( f(x) = 2x^2 - 3x + 5 \),求\( f(2) \)的值。
A. 7B. 9C. 11D. 13答案:B2. 一个直角三角形的两条直角边分别为3和4,求斜边的长度。
A. 5B. 6C. 7D. 8答案:A3. 一个数列的前三项为1, 2, 3,且每一项都是前一项的两倍加一,求第4项的值。
A. 7B. 8C. 9D. 10答案:A二、填空题1. 计算\( \sqrt{64} \)的值是______。
答案:82. 一个圆的半径为7,求该圆的面积。
面积公式为\( A = \pi r^2 \),所以面积是______。
答案:\( 49\pi \)三、简答题1. 解释什么是二项式定理,并给出一个例子。
答案:二项式定理是代数学中的一个重要定理,它描述了(a+b)^n展开成多项式的形式。
例如,\( (x+y)^2 = x^2 + 2xy + y^2 \)。
2. 给定一个函数\( g(x) = 3x - 4 \),求\( g^{-1}(x) \)。
答案:为了求\( g^{-1}(x) \),我们首先设\( y = g(x) \),即\( y = 3x - 4 \)。
解出x,得到\( x = \frac{y+4}{3} \),所以\( g^{-1}(x) = \frac{x+4}{3} \)。
四、计算题1. 解不等式\( |x - 5| < 2 \)。
答案:解这个绝对值不等式,我们得到两个不等式:\( -2 < x - 5 < 2 \)。
解这两个不等式,我们得到\( 3 < x < 7 \)。
2. 计算\( \int_{0}^{1} (3x^2 + 2x) \, dx \)。
答案:首先找到被积函数的原函数,即\( F(x) = x^3 + x^2 \)。
然后计算定积分:\[ \int_{0}^{1} (3x^2 + 2x) \, dx = F(1) - F(0) = (1^3 + 1^2) - (0^3 + 0^2) = 1 + 1 = 2 \]。
初高中衔接型数学试题(8)及参考答案
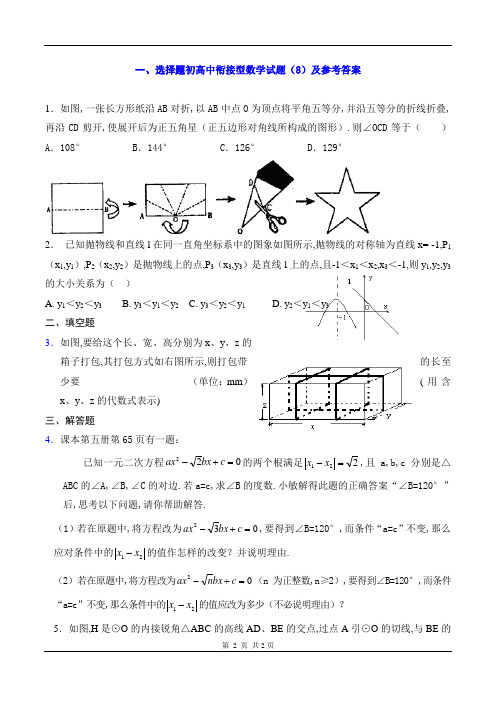
一、选择题初高中衔接型数学试题(8)及参考答案1.如图,一张长方形纸沿AB 对折,以AB 中点O 为顶点将平角五等分,并沿五等分的折线折叠,再沿CD 剪开,使展开后为正五角星(正五边形对角线所构成的图形).则∠OCD 等于( )A .108°B .144°C .126°D .129°2. 已知抛物线和直线l 在同一直角坐标系中的图象如图所示,抛物线的对称轴为直线x= -1,P 1(x 1,y 1),P 2(x 2,y 2)是抛物线上的点,P 3(x 3,y 3)是直线l 上的点,且-1<x 1<x 2,x 3<-1,则y 1,y 2,y 3的大小关系为( )A. y 1<y 2<y 3B. y 3<y 1<y 2C. y 3<y 2<y 1D. y 2<y 1<y 3二、填空题3.如图,要给这个长、宽、高分别为x 、y 、z 的箱子打包,其打包方式如右图所示,则打包带的长至少要____________________ (单位:mm )(用含x 、y 、z 的代数式表示)三、解答题4.课本第五册第65页有一题:已知一元二次方程022=+-c bx ax 的两个根满足221=-x x ,且a,b,c 分别是△ABC 的∠A,∠B,∠C 的对边.若a=c,求∠B 的度数.小敏解得此题的正确答案“∠B=120°”后,思考以下问题,请你帮助解答.(1)若在原题中,将方程改为032=+-c bx ax ,要得到∠B=120°,而条件“a=c ”不变,那么应对条件中的21x x -的值作怎样的改变?并说明理由.(2)若在原题中,将方程改为02=+-c bx n ax (n 为正整数,n ≥2),要得到∠B=120°,而条件“a=c ”不变,那么条件中的21x x -的值应改为多少(不必说明理由)?5.如图,H 是⊙O 的内接锐角△ABC 的高线AD 、BE 的交点,过点A 引⊙O 的切线,与BE 的延长线相交于点P,若AB 的长是关于x 的方程0)1cos (cos 363622=+-+-C C x x 的实数根。
初升高数学衔接试卷及答案

初升高数学衔接试卷及答案一、选择题(每题3分,共30分)1. 下列哪个数是无理数?A. 0.33333...(无限循环)B. πC. √2D. 1/32. 一个圆的半径为5,那么它的直径是多少?A. 10B. 15C. 20D. 253. 如果一个二次方程 \( ax^2 + bx + c = 0 \) 有两个相等的实根,那么 \( b^2 - 4ac \) 等于多少?A. 0B. 1C. -1D. 44. 函数 \( y = 3x + 2 \) 的斜率是多少?A. 2B. 3C. 5D. 45. 以下哪个表达式是正确的因式分解?A. \( x^2 - 1 = x + 1 \)B. \( x^2 - 1 = x - 1 \)C. \( x^2 - 1 = (x + 1)(x - 1) \)D. \( x^2 - 1 = (x - 1)^2 \)6. 一个三角形的三边长分别是3,4,5,那么这个三角形是:A. 锐角三角形B. 直角三角形C. 钝角三角形D. 不能构成三角形7. 一个数的平方根是2,那么这个数是:A. 4B. -4C. 2D. -28. 如果一个函数 \( f(x) \) 是奇函数,那么 \( f(-x) \) 等于:A. \( f(x) \)B. \( -f(x) \)C. \( x \cdot f(x) \)D. \( x^2 \cdot f(x) \)9. 以下哪个选项是不等式 \( x^2 - 4x + 3 < 0 \) 的解集?A. \( x < 1 \) 或 \( x > 3 \)B. \( x < 3 \) 或 \( x > 1 \)C. \( 1 < x < 3 \)D. \( x < -3 \) 或 \( x > 1 \)10. 一个数列的前5项为1,3,5,7,9,这个数列是:A. 等差数列B. 等比数列C. 既不是等差数列也不是等比数列D. 几何数列二、填空题(每题2分,共20分)11. 一个直角三角形的两条直角边长分别是6和8,那么斜边长是________。
【初升高衔接】初升高开学考数学模拟卷01-2024年数学无忧衔接(通用版)含解析

【分析】利用韦恩图法即可快速求解.【详解】设同时学习必修二和选修一的有x人,则28=15+8+14-3-3-x,解得x=3,即同时学习必修二和选修一的有3人,则只学习必修一的有15-3-3=9(人),故选:D..6.手卷是国画装裱中横幅的一种体式,以能握在手中顺序展开阅览得名,它主要由“引首”、“画心”、“拖尾”三部分组成(这三部分都是矩形形状),分隔这三部分的其余部分统称为“隔水”.如图,墨涵同学装裱了一幅《雀华秋色图》的手卷,手卷长1000厘米,宽40厘米.引首和拖尾完全相同,其宽度都为100厘米,若隔水的宽度为x厘米,画心的面积为15200厘米2,根据题意,可列方程是()A.(1000-4x)(40-2x)=15200B.(1000-2⨯100-2x)(40-4x)=15200C.(1000-2⨯100-2x)(40-2x)=15200D.(1000-2⨯100-4x)(40-2x)=15200【答案】D【分析】此题主要考查一元二次方程的应用,设隔水的宽度为x cm,分别表示出画心的长和宽,根据面积列出方程.【详解】解:根据题意,得(1000-2⨯100-4x)(40-2x)=15200.故选:D.7.一家金店使用一架两臂不等长的天平称黄金.一位顾客到店内购买20g黄金,店员先将10g的砝码放在天平左盘中,取出一些黄金放在天平右盘中,使天平平衡;再将10g的砝码放在天平右盘中,再取出一些黄金放在天平左盘中,使得天平平衡;最后将两次称得的黄金交给顾客.记顾客实际购得的黄金为xg,则x与20的大小关系为()【点睛】易错点睛:利用基本不等式求最值时,要注意其必须满足的三个条件:(1)“一正二定三相等”“一正”就是各项必须为正数;(2)“二定”就是要求和的最小值,必须把构成和的二项之积转化成定值;要求积的最大值,则必须把构成积的因式的和转化成定值;(3)“三相等”是利用基本不等式求最值时,必须验证等号成立的条件,若不能取等号则这个定值就不是所求的最值,这也是最容易发生错误的地方.10.对于一元二次方程ax 2+bx +c =0(a ≠0),下列说法正确的是()A .若a -b +c =0,则b 2-4ac ≥0B .若方程ax 2+c =0有两个不相等的实根,则方程ax 2+bx +c =0必有两个不相等的实根C .若c 是方程ax 2+bx +c =0的一个根,则一定有ac +b +1=0成立D .若am 2+bm +c =an 2+bn +c ,则m =n【答案】AB 【分析】本题考查了一元二次方程的解、根的判别式,以及因式分解等知识点,熟记相关结论是解题关键.本题考查根据判别式判断一元二次方程根的情况.对于一元二次方程ax 2+bx +c =0(a ≠0),若∆=b 2-4ac >0,则方程有两个不相等的实数根;若∆=b 2-4ac =0,则方程有两个相等的实数根;若∆=b 2-4ac <0,则方程没有实数根.据此即可判断①②;将x =c 代入方程ax 2+bx +c =0,进行因式分解即可判断③;根据⎣am 2+bm +c -(an 2+bn +c )=(m -n )⎡a (m +n )+b ⎤即可判断④⎦.【详解】解:∵a -b +c =0,∴一元二次方程ax 2+bx +c =0(a ≠0)有一个根是x =-1,∴b 2-4ac ≥0,故A 正确;∵方程ax 2+c =0有两个不相等的实根,∴∆=-4ac >0,∴b 2-4ac >0,∴则方程ax 2+bx +c =0必有两个不相等的实根,故B 正确;∵c 是方程ax 2+bx +c =0的一个根,∴ac 2+bc +c =0,∴c (ac +b +1)=0,∴ac +b +1=0或c =0,故C 错误;∵am 2+bm +c =an 2+bn +c ,∴am 2+bm +c -(an 2+bn +c )=0,∴am 2+bm +c -(an 2+bn +c )=a (m 2-n 2⎣)+b (m -n )=(m -n )⎡a (m +n )+b ⎤=0⎦,∴(m -n )=0或a (m +n )+b =0,。
初升高衔接数学测试(附解答)

初升高衔接数学测试(附解答)初升高衔接数学测试(附解答)一.填空题。
(每题3分,共30分)1. 已知函数f(x) = x^2 - 4x + 3,则f(1) = ______。
解答:f(1) = 1^2 - 4 × 1 + 3 = 1 - 4 + 3 = 0。
2. 设x = 2,则函数f(x) =x^3 - 3|x|的值为______。
解答:f(2) = 2^3 - 3 × 2 = 8 - 6 = 2。
3. 设一次函数y = kx + 3的图象过点(2, 7),则k的值为______。
解答:代入已知点得7 = k × 2 + 3,整理得k = (7 - 3)/2 = 4/2 = 2。
4. 已知x^2 + k = (x - 2)(x + 3),则k的值为______。
解答:展开右侧得x^2 + k = x^2 + x - 6,比较系数得k = -6。
5. 一个三位数的1/10是5,将这个三位数加上55后得到一个四位数,这个四位数是________。
解答:设三位数为xyz,其中x、y、z表示个位、十位和百位数字。
根据题意得到两个方程:(1)1/10 * 100 * x + 1/10 *10 * y + 1/10 * z = 5;(2)100 * x + 10 * y + z + 55 = 1000 * x+ 100 * y + 10 * z。
计算得x = 4,y = 4,z = 5,所以四位数为4445。
6. 一根绳子长45米,把它剪成3段,第一段比第二段短3米,第二段比第三段短2米,则第一段的长度是________。
解答:设第一段的长度为x,根据题意得到两个方程:(1)x + (x + 3) + (x + 3 + 2) = 45;(2)x + 5 = x + 3。
解得x = 13,所以第一段的长度是13米。
7. 甲、乙两人连续投掷硬币,甲方先开始,投得正面得1分,反面得0分;乙方投得正面得2分,反面得0分。
历年初高中数学衔接型中考试题四及答案

初高中衔接型中考数学试题1. 把抛物线c bx x y ++=2的图象向右平移3个单位,再向下平移2个单位,所得图象的解析式是2(1)2y x =++,则有b = ,c = 。
2. 已知:如图,梯形ABCD 中,AD ∥BC ,∠B =45°,∠C =120°,AB =8,则CD 的长为( ) A 、638 B 、64 C 、238 D 、243. 如图,在△ABC 中,已知∠ACB=90°,CD⊥AB 于D ,AC =36,BD =3。
(1)请根据下面求cosA 的解答过程,在横线上填上适当的结论,使解答正确完整: ∵CD⊥AB ,∠ACB=90°,∴AC = cosA , =AC·cosA,由已知AC =36,BD =3 ∴36=AB cosA =(AD +BD )cosA =(36cosA +3)cosA设=cosA ,则t >0,且上式可化为322t + =0,则此解得cosA =t =23 (2)求BC 的长及△ABC 的面积。
4. (本题满分8分)(1)如图1,在△ABC 中,∠B 、∠C 均为锐角,其对边分别为b 、c,求证:B b sin =Cc sin ; (2)在△ABC 中,AB=3,AC=2,∠B =450,问满足这样的△ABC 有几个?在图2中作出来(不写作法,不述理由)并利用(1)的结论求出∠ACB 的大小。
450 1200 第8题图D C B A D C BAA B C A B C(图1) (图2) 19题图参考答案1、答:b =8,c =20。
分析:抛物线2(1)2y x =++的顶点是(-1,2),向左平移3个单位,横坐标-1变-4,再向上平移2个单位,纵坐标2变4,顶点变为(-4,4),而抛物线的大小形状开口方向都不改变,故解析式为2(4)4y x =++,即2820y x x =++,与c bx x y ++=2比较得b =8,c =20。
初高中衔接_数学试题_含答案

保密★启用前高中第二次阶段性考试初高中衔接考试题数学(含答案)数学本试卷分为试题卷和答题两部分,其中试题卷由第I卷(选择题)和第II卷(非选择题)组成,共4页;答题卡共2页。
满分100分,考试时间120分钟。
注意事项:1.答题前,考生务必将自己的学校、班级,姓名用0.5毫米黑色签字笔填写清楚,同时用2B铅笔将考号准确填涂在“准考证号”栏目内。
2.选择题使用2B铅笔填涂在答题卡对应题目标号的位置上,如需改动,用橡皮擦擦干净后再选涂其它答案;非选择题用0.5毫米黑色签字笔书写在答题卡的对应框内,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。
3.考试结束后将答题卡收回。
第I卷一、本大题10小题,每小题4分,共40分。
在每小题给出的四个选项中有一个选项正确,1.设集合U={1,2,3,4,5,6},M={1,2,4},则∁U M等于A.U B.{1,3,5} C.{3,5,6} D.{2,4,6}2.已知集合M={0,1,2,3,4},N={1,3,5},P=M∩N,则P的子集共有A.2个B.4个C.6个D.8个3.若函数y=f(x)的定义域为M={x|-2≤x≤2},值域为N={y|0≤y≤2},则函数y=f(x)的图象可能是中学第二次阶段性考试数学第1页共4页4.下列函数中,在(-∞,0)上为增函数的是A.y=1-x2B.y=x2+2xC.y =11+xD.y=xx-15. 已知函数f(x)=x2-2x+2的定义域和值域均为[1,b],则b等于A.3 B.2或3 C.2 D.1或2 6.函数y=1-1x-1的图象是7.设函数f(x)=⎩⎪⎨⎪⎧x2+1,x≤1,2x,x>1,则f(f(3))等于A.15B.3 C.23 D.1398.设abc>0,二次函数f(x)=ax2+bx+c的图象可能是中学第二次阶段性考试数学第2页共4页9.若函数f (x )=x(2x +1)(x -a )为奇函数,则a 等于( )A.12B.23C.34 D .110.函数f (x )的定义域为R ,若f (x +1)与f (x -1)都是奇函数,则 ( )A .f (x )是偶函数B .f (x )是奇函数C .f (x )=f (x +2)D .f (x +3)是奇函数第Ⅱ卷二、填空题,本大题5小题,每小题4分,共20分。
初高中数学衔接内容调测卷含答案编辑版

初高中数学衔接内容调测卷注意事项:1、本试卷分为3大题,其中选择题8题,填空题4题,解答题3题;满分100分,考试时间60分钟.2、请按照题号顺序在各题目的答题区域内作答;在草稿纸上答题无效.3、答题必须使用黑色签字笔或钢笔书写,字体工整,笔迹清楚;严禁使用计算器......... 一、选择题:本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.073|2|=-++-y x y x 已知, 则xy y x --2)(的值为( ) 1.-A 21.B 0.C 1.D2.化简: ( ) ABC.D.3.若02522<+-x x ,则221442-++-x x x 等于( ).A 54-x .B 3- .C 3 .D x 45-4.已知一个直角三角形的两条直角边长恰好是方程2x 2-8x +7=0的两根,则这个直角三角形的斜边长等于 ( ).A .B 3 .C 6 .D 95.已知关于x 不等式2x 2+bx -c >0的解集为{}31|>-<x x x 或,则关于x 的不等式042≥++cx bx 的解集为 ( ).A }212|⎩⎨⎧≥-≤x x x 或 .B }221|⎩⎨⎧≥-≤x x x 或 .C }221|{≤≤-x x .D }212|⎩⎨⎧≤≤-x x 6.关于x 的一元二次方程mx 2+(m -1)x+m=0有实根,则实数m 的取值范围是( ).A }311|{<<-m m .B }311|{≤≤-m m.C }0311|{≠≤≤-m m m 且 .D }311|⎩⎨⎧≥-≤m m m 或密封线内不要答题学校 姓名准考证号7.当11≤≤-x 时,函数a ax x y 21222-+-=有最小值是23-,则a 的值为( ) .A 1 .B 3 .C 1或3 .D 878.设βα、是方程)( 02442R x m mx x ∈=++-的两实根,则22βα+的最小值为( ).A 1617 .B 21 .C 2 .D 1615二、填空题:本大题共4小题,每小题5分,共20分.9.二次函数c bx ax y ++=2的图象如图,则a ______0;b _____0; c ______0;ac b 42-_______0.(填“>”或“<”、“=”) 10.已知4a b c ++=,4ab bc ac ++=,则222a b c ++_____________. 11.计算:1111132435911++++⨯⨯⨯⨯=____________. 12.若二次函数c bx ax y ++=2的顶点为)25,21(,与x 轴交于两点,且这两点的横坐标的立方和为19,则这个二次函数的表达式为 .三、解答题:本大题共3小题, 共40分,解答应写出文字说明、证明过程或演算步骤. 13.(本题满分12分)已知21=x ,31=y ,求yx yy x x +--的值.14.(本题满分14分)分解因式:(1)3722+-x x ;(2)8)2(7)2(222-+-+x x x x ; (3)a ax x x 51522---+ .15.(本题满分14分)设函数R x x x y ∈+-+=,1222. (1)作出函数的图象;(2)求函数y 的最小值及y 取最小值时的x 值.初高中数学衔接内容测试参考答案一.选择题DCCBC CAB 二.填空题9.a ___>___0;b ___>__0;c ___>__0;ac b 42-___>__0. 10. 8 11.553612. 24442++-=x x y 三:解答题 13.解:yx yxy xy x yx y x y yx y x x yx y yx x -+-+=----+=+--)()(531213121=-+=-+y x y x . 14.解:(1))3)(12(3722--=+-x x x x ;(2))12)(82(8)2(7)2(22222++-+=-+-+x x x x x x x x =2)1)(2)(4(+-+x x x ;(3))3)(5()5()3)(5(51522a x x x a x x a ax x x --+=+--+=---+. 15.(1)图略;(2)当x =1时,y 最小值4.。
初高中衔接数学试题(含答案)

.初高中衔接数学试题第Ⅰ卷(共42 分)一、选择题:本大题共14 个小题 ,每小题 3 分 ,共 42 分 .在每小题给出的四个选项中,只有一项是符合题目要求的.1. 观察下列四个图形,中心对称图形是()A .B .C. D .2.斑叶兰被列为二级保护植物,它的一粒种子重约0.0000005克 .将 0.0000005用科学记数法表示为()77C. 0.566A.5 10B.5 1010D.5 10 3.如图,点 A 所表示的数的绝对值是()A . 3B .3C.1D .1 334.某校排球队 10 名队员的身高(厘米)如下:195,,182, 188,182,,188 , ,188.这组数据的众数和中位数分别是()A . ,188B . 188,187C. 187,188 D .188,5. 计算 a 2 35a 3 a3的结果是()A . a55a 6B. a65a9C. 4a 6 D . 4a66.不等式组A.C.2x13x213 23 x 2的解集在数轴上表示正确的是()B.D.7 .二次方程ax2+bx+c=0的两根为-2,3,a<0,那么ax2+bx+c>0的解集为()A .{x| x >3 或 x <- 2}B.{x| x >2 或 x <- 3}.C.{x | -2 <x <3} D . {x| - 3< x <2}8. 如图,三角形纸片ABC ,AB AC , BAC 90 ,点E为AB中点 . 沿过点E的直线折叠,使点 B 与点 A 重合,折痕现交于点 F .已知EF3 ,则BC的长是()2A.3 2B.3 2C. 3D.3 3 29. 如图,将线段AB 绕点 P 按顺时针方向旋转90 ,得到线段 A B ,其中点 A、 B 的对应点分别是点 A 、B ,,则点A 的坐标是()A.1,3B.4,0C. 3, 3D. 5, 110. 已知二次函数y ax 2bx c(a 0) 的图象如图所示,则正比例函y (b c) x 与反比例函数y a b c在x同一坐标系中的大致图象是().A B C D.11. 甲、乙两人用如图所示的两个转盘(每个转盘被分成面积相等的 3 个扇形)做游戏 . 游戏规则:转动两个转盘各一次,当转盘停止后,指针所在概率是()1 4 52 A .B .C.D .399312 .若关于 x 的一元二次方程x 2- 2 x + k =0 有两个不相等的实数根,则 k 的取值围是()A . k < 1B . k ≤1C . k >- 1D . k > 113 .大明湖畔的“超然楼”被称作“江北第一楼” .某校数学社团的同学对超然楼的高度进行了测量.如图,他们在 A 处仰望塔顶,测得仰角为 30 °,再往楼的方向前进 60m 至 B 处,D测得仰 角为 60 °,若学生的身高忽略不计, 3 ≈1.7 ,结果精确到 1m ,则该楼的高度 CD 为()BCA第 12 题图A . 47mB . 51mC . 53mD . 54m14. 甲、乙两组各有12 名学生,组长绘制了本组 5 月份家庭用水量的统计图表,如图,比较5 月份两组家庭用水量的中位数,下列说确的是()A .甲组比乙组大B .甲、乙两组相同C .乙组比甲组大D .无法判断第Ⅱ卷(共 96 分)二、填空题(每题 3 分,满分 18 分,将答案填在答题纸上)15. 已知甲、乙两组数据的折线图如图,设甲、乙两组数据的方差分别为S 甲2、S 乙2,16. 5 月份,甲、乙两个工厂用水量共为200 吨 .进入夏季用水高峰期后,两工厂积极响应号召,采取节水措施.6月份,甲工厂用水量比 5 月份减少了15%,乙工厂用水量比 5 月份减少了10%,两个工厂 6 月份用水量共为174吨,求两个工厂 5 月份的用水量各是多少. 设甲工厂 5 月份用水量为x 吨,乙工厂 5 月份用水量为y 吨,根据题意列关于 x, y 的方程组为.17. 如图,Rt ABC, B 90 , C 30 ,O为AC上一点,OA 2 ,以 O 为圆心,以 OA 为半径的圆与CB 相切于点 E ,与 AB 相交于点 F ,连接 OE、OF ,则图中阴影部分的面积是.318.已知一个圆锥体的三视图如图所示,则这个圆锥体的侧面积为.819. 对于实数p , q ,我们用符号min p, q 表示 p , q 两数中较小的数,如min 1,2 1 ,因此min2,3;若min ( x1)2 , x21,则x.20.阅读理解:如图 1 ,⊙O与直线a, b都相切 . 不论⊙O如何转动,直线a,b之间的距离始终保持不变(等于⊙O 的半径).我们把具有这一特性的图形称为“等宽曲线”.图 2 是利用圆的这一特性的例子.将等直径的圆棍放在物体下面,通过圆棍滚动,用较小的力就可以推动物体前进.据说,古埃及就是利用只有的方法将巨石推到金字塔顶的.拓展应用:如图 3 所示的弧三角形(也称为莱洛三角形)也是“等宽曲线”.如图 4 ,夹在平行线c,d 之间的莱洛三角形无论怎么滚动,平行线间的距离始终不变.若直线c, d之间的距离等于2cm ,则莱洛三角形的周长为cm .三、解答题(本大题共 5 小题,共60 分 .解答应写出文字说明、证明过程或演算步骤.)21.求下列关于 x 的不等式的解:(1)x 2-(2 m +1) x+ m 2+m < 0.(2) .求不等式 ax +1 <a2+ x 的解.22. 八年级( 1 ) 班研究性学习小组为研究全校同学课外阅读情况,在全校随机邀请了部分同学参与问卷调查,统计请根据图息解决下列问题:( 1 )共有名同学参与问卷调查;( 2 )补全条形统计图和扇形统计图;( 3 )全校共有学生1500人,请估计该校学生一个月阅读 2 本课外书的人数约为多少.23. 某区域平面示意图如图,点O 在河的一侧,AC 和 BC 表示两条互相垂直的公路.甲勘测员在 A 处测得点 O 位于北偏东 45 ,乙勘测员在 B 处测得点 O 位于南偏西 73.7 ,测得AC840m, BC 500m .请求出点O到BC的距离 .24 ,cos73.77 ,tan 73.724参考数据:sin 73.72525724. 已知反比例函数的图象经过三个点 A 4, 3 , B 2m, y1 , C 6m, y2,其中m0 .( 1)当 y1 y2 4 时,求 m 的值;( 2)如图,过点 B、 C 分别作x轴、 y 轴的垂线,两垂线相交于点D,点P在 x 轴上,若三角形PBD的面积是8 ,请写出点 P 坐标(不需要写解答过程).25. 某公司投入研发费用80 万元( 80 万元只计入第一年成本),成功研发出一种产品.公司按订单生产(产量销售量),第一年该产品正式投产后,生产成本为 6 元/件. 此产品年销售量y (万件)与售价x ( 元/件)之间满足函数关系式 y x26 ..(2 )该产品第一年的利润为 20 万元,那么该产品第一年的售价是多少?(3 )第二年,该公司将第一年的利润 20 万元( 20 万元只计入第二年成本)再次投入研发,使产品的生产成本降为 5元/件 .为保持市场占有率,公司规定第二年产品售价不超过第一年的售价,另外受产能限制,销售量无法超过12 万件 .请计算该公司第二年的利润W2至少为多少万元.新预科部数学试题答案1-5 CBABC6-10BCBDC11-14CABBx y2007416.17.3(1 15%) x(110%)y 1742015.___>___2 3 18.19.3; 2 或-1..20. 2 π21(1) 解 x 2- (2 m + 1) x +m 2+m < 0 ,因式分解得 (x -m )[ x - (m + 1)] < 0.∵m < m +1 ,∴m < x <m +1.即不等式的解为m <x <m + 1(2)解:将原不等式化为 (a-1) x < a2-1.①当 a-1 >0 ,即 a >1 时, x <a+1.②当 a-1 <0 ,即 a <1 时, x >a+1.③当 a-1 =0 ,即 a =1 时,不等式无解.综上所述,当 a> 1 时,不等式的解集为 x <a +1 ;当 a< 1 时,不等式的解集为 x >a +1 ;当 a= 1 时,不等式无解22 232425。
初高中数学衔接测试卷(含答案)

初高中数学衔接测试卷1 不等式053<--xx 的解集是_________。
2. 方程04)1(222=-+--m x m x 的两根异号,则m 的取值范围是_________。
3. 若方程01222=-+-m mx x 有两根,且方程的两根介于-2与4之间,则实数m 的取值范围是 。
4. 若不等式02<--b ax x 的解是2<x <3,则不等式012>--ax bx 的解集为 。
5.若一个正方形面积是一个正三角形面积的倍,则其边长的比为________________6.已知关于x 不等式2x 2+bx -c >0的解集为{}31|>-<x x x 或,则关于x 的不等式042≥++cx bx 的解集为_________7、已知⊙O 1的半径为1,⊙O 2的半径为2,两圆的圆心距O 1O 2为3,则两圆的位置关系是______________________8、函数xy 1=与x y =的图象在同一平面直角坐标系内的交点的个数是_________________9、2009年7月22日发生了百年不遇的天文现象——日全食,现代快报记者在安徽某地目睹了整个日全食奇观,上午9时34分看到了生光现象,此时钟面上时针与分针的夹角是________________________________________10. 某公司销售A 、B 、C 三种产品,在去年的销售中,高新产品C 的销售金额占总销售金额的40%.由于受国际金融危机的影响,今年A 、B 两种产品的销售金额都将比去年减少20%,因而高新产品C 是今年销售的重点.若要使今年的总销售金额与去年持平,那么今年高新产品C 的销售金额应比去年增加 %.11、 a 、b 为实数,且ab =1,设P =11a b a b +++,Q =1111a b +++,则P Q (填“>”、“<”或“=”). 12、. 观察下列各式:11111323⎛⎫=- ⎪⨯⎝⎭,111135235⎛⎫=- ⎪⨯⎝⎭,111157257⎛⎫=- ⎪⨯⎝⎭,…,根据观察计算:1111133557(21)(21)n n ++++⨯⨯⨯-+= (n 为正整数).13. 化简381--=____________ ,324- =___________; 14. 如果2a b c x y z ===,则456456a b cx y z+++-= ; 15. 如图,梯形ABCD 中,DC ∥AB ,DC =3cm ,AB =6cm ,且MN ∥PQ ∥AB ,DM =MP =PA , 则MN = ,PQ = 。
2024年新高一数学初升高衔接《一元二次函数、方程和不等式》含答案解析

第二章:一元二次函数、方程和不等式综合检测卷(试卷满分150分,考试用时120分钟)一、选择题:本题共8小题,每小题5分,共40分。
在每小题给出的四个选项中,只有一项是符合题目要求的.1.(23-24高一下·河南开封·期中)不等式220x x +-<的解集为( )A .{21}x x -<<∣B .{12}x x -<<∣C .{2xx <-∣或1}x >D .{1x x <-∣或2}x >2.(23-24高一上·湖南衡阳·月考)若2x >-,则12y x x =++的最小值为( )A .-2B .0C .1D .123.(23-24高一上·广东珠海·期中)已知25P a =+,41Q a =+,则P ,Q 的大小关系是( )A .P Q<B .P Q>C .P Q≤D .P Q≥4.(23-24高一上·江苏盐城·月考)已知实数x ,y 满足41x y -≤-≤-,145x y -≤-≤,则9x y -的取值范围是( )A .[7,26]-B .[1,20]-C .[]4,15D .[]1,155.(23-24高一上·湖南衡阳·月考)已知不等式230ax x b +->的解集为{}12x x -<<,则a 、b 的值等于( )A .3a =,6b =-B .3a =,6b =C .3a =-,6b =-D .3a =-,6b =6.(23-24高一上·贵州黔南·月考)已知,0x y >且41x y +=,则11x y +的最小值为( )A .B .8C .9D .107.(23-24高一下·河南·月考)若命题“x ∃∈R ,20x ax a --≤”为假命题,则实数a 的取值范围是( )A .(,4][0,)-∞-+∞B .(,4)(0,)∞∞--⋃+C .[]4,0-D .()4,0-8.(23-24高一上·广东广州·月考)一家金店使用一架两臂不等长的天平称黄金.一位顾客到店内购买20g 黄金,店员先将10g 的砝码放在天平左盘中,取出一些黄金放在天平右盘中,使天平平衡;再将10g 的砝码放在天平右盘中,再取出一些黄金放在天平左盘中,使得天平平衡;最后将两次称得的黄金交给顾客.记顾客实际购得的黄金为xg ,则x 与20的大小关系为( )A .20x <B .20x >C .20x =D .无法确定二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.9.(23-24高一上·江苏苏州·月考)若0a b <<,则下列结论正确的是( )A .11a b>B .01a b<<C .2ab b >D .b a a b>10.(22-23高一上·山西大同·月考)下列结论正确的是( )A .当0x >时,2≥B .当2x >时,1x x+的最小值是2C .当0,0x y >>时,2x y y x+≥D .当2x <时,112y x x =-+-的最小值为311.(23-24高一上·湖北武汉·月考)已知01b a <<+,若关于x 的不等式22()()x b ax ->的解集中的整数恰有3个,则a 的值可以为( )A .12-B .12C .32D .52三、填空题:本题共3小题,每小题5分,共15分.12.(23-24高一上·河北沧州·期末)不等式302x x+≥-的解集为 .13.(23-24高一上·江苏连云港·月考)已知方程22240x ax a -+-=的一个实根小于2,另一个实根大于2,求实数a 的取值范围.14.(23-24高一上·山东菏泽·月考)若两个正实数x y ,满足3x y +=,且不等式4161m x y+>+恒成立,则实数m 的取值范围为.四、解答题:本题共5小题,共77分。
初高中衔接数学试题及答案

初高中衔接数学试题及答案一、选择题(每题3分,共30分)1. 下列哪个数是无理数?A. 0.33333(无限循环)B. πC. √2D. 1/32. 函数y = 2x^2 + 3x + 1的顶点坐标是:A. (-3/4, -1)B. (-1/2, -1)C. (-1, 0)D. (0, 1)3. 已知a + b = 5,a - b = 3,求a^2 + b^2的值。
A. 13B. 14C. 15D. 164. 一个圆的半径为5,求圆的面积。
A. 25πB. 50πC. 75πD. 100π5. 一个直角三角形的两直角边长分别为3和4,求斜边长。
A. 5B. 6C. 7D. 86. 以下哪个是二次方程的解?A. x = 1B. x = -1C. x = 2D. x = 37. 一个数列的前三项为2, 4, 6,这是一个:A. 等差数列B. 等比数列C. 几何数列D. 既不是等差也不是等比数列8. 已知x + y = 7,2x - y = 1,求x和y的值。
A. x = 2, y = 5B. x = 3, y = 4C. x = 4, y = 3D. x = 5, y = 29. 一个长方体的长、宽、高分别为2, 3, 4,求其体积。
A. 24B. 26C. 28D. 3010. 下列哪个是正弦函数的图像?A. 直线B. 抛物线C. 正弦曲线D. 余弦曲线二、填空题(每题2分,共20分)11. 一个数的平方根是4,这个数是________。
12. 圆的周长公式是________。
13. 一个数的绝对值是其本身,这个数是________。
14. 一个二次方程的一般形式是________。
15. 等差数列的通项公式是________。
16. 函数y = 3x + 2的斜率是________。
17. 一个直角三角形的斜边长是13,一个直角边长是5,另一个直角边长是________。
18. 一个数的立方根是2,这个数是________。
初高中衔接型中考数学试题及参考答案

一、选择题
.(浙江富阳2004)数轴上有两点A、B分别表示实数 、 ,则线段AB的长度是( )
A、 B、 C、 D、
.(浙江富阳2004)二次函数 的图象与 轴交点的个数是( )
A、0个B、1个C、2个D、不能确定
.某种细菌在营养过程中,细菌每半小时分裂一次(由一个分裂为两个),通过两小时,这种细菌由1个可分裂繁育成().
单价为65元日均销售602706570千克那么获总利为1950707000当销售单价最高时单价为70元日均销售60千克将这种化工原料全部售完需607000117天那么获总利为70307000117500221500因为22150019500且2215001950026500元所以销售单价最高时获总利较多且多获利26500在rtabc中c90abca如图第9sinaabbcbcabsinacsin
∵∠ACB=90°,∴AP=CP=BP.(这种方法“巧”在何处?)
不难推出:
△APM≌△CPM,△BPN≌△CPN.
∴
当P在AB中点左侧时,如图[第9题(4)],作∠EPM=∠APM,分别交MC于点F,交BC延长线于点E.
不难推出:
[第七题(3)] [第七题(4)]
△FPM≌△APM,△EPN≌△BPN.
(3)试比较S +S 与S 的大小,并说明理由.
初高中衔接型中考数学试题(11)参考答案
一、
1、答:C
2、答:C
3、答:B
二、
4、答:25或16
5、答:
三、
6、解:由题意有
(正确建立关于A、B的一个方程,给1分.)
解得:
即A、B的值分别为 、 .
7、解:(1)因为木箱的长、宽、高分别为:t△ABC中,∠C=90°.
初高中衔接型中考数学

初高中衔接型中考数学试题(5)及参考答案1、(河北03/20)如图:是用火柴棍摆出的一系列三角形图案,按这种方式摆下去,当每边上摆20(即n =20)根时,需要的火柴棍总数为 根。
••••••••••••••••••••••••••••••1=n 2=n 3=n 2、观察下列图形,并阅读图形下面的相关文字:两条直线相交, 三条直线相交, 四条直线相交,……最多有1个交点; 最多有3个交点; 最多有6个交点;……像这样,十条直线相交,最多交点的个数是 ( )A.40个B.45个C.50个D.55个3.一种浓度是15%的溶液30千克,现要用浓度更高的同种溶液50千克和它混合,使混合后的浓度大于20%,而小于35%,则所用溶液浓度x 的取值范围是( )(A )15%<x<23% (B )15%<x<35% (C )23%<x<47% (D )23%<x<50%4、(贵阳03/25)如图,圆柱的轴截面ABCD 是边长为4的正方形,动点P 从A 点出发,沿着圆柱的侧面移动到BC 的中点S 的最短距离是( )(A )212π+ (B )2412π+ (C )214π+ (D )242π+ 5、(黄冈市2003年)同学们都做过《代数》课本第三册87页第4题:某礼堂共有25排座位,第一排有20个座位,后面每一排都比前一排多1个座位,写出每排的座位数m 与这排的排数n 的函数关系式并写出自变量n 的取值范围.答案是:每排的座位数m 与这排的排数n 的函数关系式是m=n+19;自变量n 的取值范围是1≤n ≤25,且n 是整数.上题中,在其它条件不变的情况下,请探究下列问题:(1)当后面每一排都比前一排多2个座位,则每排的座位数m 与这排的排数n 的函数关系式是 m=2n+18 (1≤n ≤25, 且n 是整数).(2)当后面每一排都比前一排多3个座位、4个座位时,则每排的座位数m 与这排的排数n 的函数关系式分别是 m=3n+17, m=4n+16, , (1≤n ≤25, 且n 是整数).(3)某礼堂共有p排座位,第一排有a 个座位,后面每一排都比前一排多b 个座位,试写出每排的座位数m 与这排的排数n 的函数关系式,并指出自变量n 的取值范围.75S PD C BA初高中衔接型中考数学试题(5)及参考答案1、答:630根。
2024年新高一数学初升高衔接《指数函数与对数函数》综合检测卷含答案解析

第四章:指数函数与对数函数综合检测卷(试卷满分150分,考试用时120分钟)一、选择题:本题共8小题,每小题5分,共40分。
在每小题给出的四个选项中,只有一项是符合题目要求的.1.(23-24高一上·宁夏吴忠·月考)若12a <)A .12a+B .12a-C .12a--D .21a -2.(23-24高一上·湖南郴州·期末)函数()42xf x x =-+的零点所在的区间为( )A .()1,2B .()2,3C .()3,4D .()4,53.(23-24高二下·山东济宁·月考)函数()()log 21a f x x =+(0a >,且1a ≠)的图象一定过点( )A .1,02⎛⎫- ⎪⎝⎭B .()1,0C .()0,0D .()0,14.(23-24高一上·河南信阳·期末)我国某科技公司为突破“芯片卡脖子问题”实现芯片国产化,加大了对相关产业的研发投入.若该公司计划2020年全年投入芯片制造研发资金120亿元,在此基础上,每年投入的研发资金比上一年增长9%,则该公司全年投入的研发资金开始超过200亿元的年份是( )参考数据:lg1.090.037,lg20.3010,lg30.4771≈≈≈A .2024年B .2023年C .2026年D .2025年5.(23-24高三上·陕西西安·月考)已知函数()f x 为R 上的奇函数,当0x <时,()128x f x =-,则()0f x ≤的解集为( )A .][(),30,3∞--⋃B .[]3,3-C .][(,30,3∞⎤--⋃⎦D .[)(]3,00,3- 6.(23-24高一下·辽宁辽阳·月考)若9log 6a =,3log b =0.32c =,则( )A .c b a<<B .c<a<bC .a b c<<D .b a c<<7.(23-24高一下·河南信阳·月考)已知()()5121(0,1)log 1a a x a x f x a a x x ⎧-+≤=>≠⎨>⎩,,是减函数,则a 的取值范围是( )A .10,7⎛⎤⎥⎝⎦B .10,5⎛⎫ ⎪⎝⎭C .1,17⎛⎫ ⎪⎝⎭D .11,75⎡⎫⎪⎢⎣⎭8.(23-24高一下·安徽·月考)已知函数()442x x f x --=的反函数为()1y f x -=,那么()()122g x f x -=-+在[]2,6-上的最大值与最小值之和为( )A .4B .2C .1D .0二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.9.(23-24高一上·河北石家庄·月考)下列各式中一定成立的有( )A .7177n n m m ⎛⎫= ⎪⎝⎭B.=C34()x y =+D=10.(23-24高一上·山东青岛·期末)已知函数||1()3x f x a b ⎛⎫=+ ⎪⎝⎭的图象过原点,且无限接近直线1y =但又不与该直线相交,则( )A .0a b +=B .||1()13x f x ⎛⎫=- ⎪⎝⎭C .()f x 是偶函数D .()f x 在(,0]-∞上单调递增11.(23-24高一上·广东韶关·期中)给出下列命题,其中正确的是()A .幂函数()R ay x a =∈图象一定不过第四象限B .函数()12(0,1)x f x a a a +=->≠的图象过定点()1,2--C .1lg1xy x+=-是奇函数D .248log 3log 5log 9>>三、填空题:本题共3小题,每小题5分,共15分.12.(23-24高一下·云南昆明·期中)函数()()215log 232f x x x =-++的单调递减区间为 .13.(23-24高一上·江苏无锡·月考)用二分法求方程22x =的正实数根的近似解(精确度0.0001)时,如果我们选取初始区间是[]1.4,1.5,则要达到精确度至少需要计算的次数是 .14.(23-24高一上·浙江杭州·月考)若关于x 的不等式()21212180x x m +-+⋅+≤在[]0,1上有解,则实数m的最小值为.四、解答题:本题共5小题,共77分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.已知 | 2x - y | + x + 3 y - 7 = 0 , 则 ( x - y ) 的值为(
)
........
5.已知关于 x 不等式 2x 2+bx -c >0 的解集为 x | x < -1或x > 3} ,则关于 x 的不等式 A . ⎨ x | x ≤ -2或x ≥ }
B . ⎨x | x ≤ - 或x ≥ 2} ≤ x ≤ 2}
D . ⎨x | -2 ≤ x ≤ } C . {m | -1 ≤ m ≤ 且m ≠ 0}
D . ⎨m | m ≤ -1或m ≥ }
号 证 考 准
题
答
要
不
初高中数学衔接内容调测卷
注意事项:
1、本试卷分为 3 大题,其中选择题 8 题,填空题 4 题,解答题 3 题;满分 100 分,考
试时间 60 分钟.
2、请按照题号顺序在各题目的答题区域内作答;在草稿纸上答题无效.
3、答题必须使用黑色签字笔或钢笔书写,字体工整,笔迹清楚;严禁使用计算器.
一、选择题:本大题共 8 小题,每小题 5 分,共 40 分,在每小题给出的四个选项中,
只有一项是符合题目要求的.
2
y - x
1
A . - 1
B .
C .0
D .1
2
2.化简: a - 1
等于 ( )
a
A . -a
B . a
C . - -a D. - a
3.若 2 x 2 - 5 x + 2 < 0 ,则 4x 2 - 4x + 1 + 2 x - 2 等于( )
名
姓
A . 4 x - 5
B . - 3
C . 3
D . 5 - 4 x
4.已知一个直角三角形的两条直角边长恰好是方程 2x 2-8x +7=0 的两根,则这个直角
内 三角形的斜边长等于 ( )
A . 3
B . 3
C . 6
D . 9
{
线
封
bx 2 + cx + 4 ≥ 0 的解集为 ( )
⎧ 1 ⎧ 1
⎩ 2 ⎩ 2
C . {x | - 1 2
⎧ 1 ⎩ 2
校 学
密 6.关于 x 的一元二次方程 mx 2+(m -1)x+m=0 有实根,则实数 m 的取值范围是( )
1 1
A . {m | -1 < m < }
B . {m | -1 ≤ m ≤ }
3 3
1 ⎧ 1
3 ⎩ 3
衔接内容调测卷第 1 页共 4 页
.
12.若二次函数 y = ax 2 + bx + c 的顶点为 ( ,25) ,与 x 轴交于两点,且这两点的横坐标
1
1 y x
2
3
7.当 - 1 ≤ x ≤ 1时,函数 y = 2 x 2
- 2ax + 1 - 2a 有最小值是 - 3
,则 a 的值为(
2
)
A . 1
B . 3
C . 1 或 3
D .
7 8
8.设 α、β 是方程 4 x 2 - 4mx + m + 2 = 0 ( x ∈ R ) 的两实根,则 α 2 + β 2 的最小值为
( )
A . 17
16
1 15 B . C .
2 D .
2 16
二、填空题:本大题共 4 小题,每小题 5 分,共 20 分.
9.二次函数 y = ax 2 + bx + c 的图象如图,则 a ______0;b _____0;
c ______0; b 2 - 4ac _______0 (填“>”或“<”、“=”)
10.已知 a + b + c = 4 , ab + bc + ac = 4 ,则 a 2 + b 2 + c 2 _____________.
11.计算:
1 1 1 1
+ + + + =____________. 1⨯ 3 2 ⨯ 4 3 ⨯ 5 9 ⨯11
1
2
的立方和为 19,则这个二次函数的表达式为
.
三、解答题:本大题共 3 小题, 共 40 分,解答应写出文字说明、证明过程或演算步骤.
13.(本题满分 12 分)已知 x =
, y = ,求 -
x - y x + y
的值.
衔接内容调测卷第 2 页共 4 页
14.(本题满分14分)分解因式:(1)2x2-7x+3;
(2)(x2+2x)2-7(x2+2x)-8;(3)x2+2x-15-ax-5a.
15.(本题满分14分)设函数y=x2+2x-2+1,x∈R.
(1)作出函数的图象;
(2)求函数y的最小值及y取最小值时的x值.
衔接内容调测卷第3页共4页
x+y
x-y11初高中数学衔接内容测试参考答案
一.选择题
DCCBC CAB
二.填空题
9.a___>___0;b___>__0;c___>__0;b2-4ac___>__0.
10.811.三:解答题36
5512.y=-4x2+4x+24
13.解:
x
x-y
-
y
x+y
=
x(x+
x-y
y)
-
y(x-
x-y
y)
=
x+xy-xy+y
x-y
11
+
=
23=5.
-
23
14.解:
(1)2x2-7x+3=(2x-1)(x-3);
(2)(x2+2x)2-7(x2+2x)-8=(x2+2x-8)(x2+2x+1)
=(x+4)(x-2)(x+1)2;
(3)x2+2x-15-ax-5a=(x+5)(x-3)-a(x+5)=(x+5)(x-3-a). 15.(1)图略;
(2)当x=1时,y最小值4.
衔接内容调测卷第4页共4页。
