运筹学 邮递员问题
运筹学最短路邮递员问题

算法是1959年首次被提出来的。该算法适用于每条弧的权数ωij ≥0 情形。算法的基本思路:从发点vs 出发,有一个假想的流沿网络一 切可能的方向等速前进,遇到新节点后,再继续沿一切可能的方向 继续前进,则最先到达终点vt 的流所走过的路径一定是最短的。为 了实现这一想法,对假想流依次到达的点,依次给予p标号,表示vs 到这些点的最短距离。对于假想流尚未到达的点给予T标号,表示vs 到这些点的最短距离的估计值。具体作法如下:
或v1 →v4。
v1 →vv31→5v36 或
v1 →v4→v6
22
30
41
59
23
16
v2v24→1 v61262
v3v33→1 v6 17 30
v4v42→3 v167 23
v5v51→8 v618 v6
41
31
21
2
6
5
08
7
1
17
2
1
9
32
5
9 3
79
66
11 2 13
431 4
9
1
10
21
p(v2)=3 3
v2
p(v1)=0 v1
p(v3)=4
6
51 1
v4
7 4
v5
v3 2 3
5
v7
26 v6 9
15
v8
T(v4)=min{6,4+1}=5, k(v4 )=v3
T(v6)=min{7,4+2}=6, k(v6 )=v3
目前,点v4 具有最小T标号,将其标号改为p标号: p(v4)=5;
数学与应用数学论文-中国邮递员问题的数学模型名师教案与资料

目录前言 (1)第一章中国邮递员问题的整数规划模型 (2)1.1 图论中模型 (2)1.2 中国邮递员问题的整数规划模型[5] (6)1.2.1 传统中国邮递员问题的建模 (6)1.2.2 广义中国邮递员问题及其建模 (7)1.2.3随机中国邮递员问题及其建模[7] (11)第二章中国邮递员问题的DNA计算 (14)2.1 DNA计算模型 (14)2.2 中国邮递员问题的图论模型变换 (15)2.3中国邮递员问题的DNA算法[11] (16)2.4 总结 (19)第三章中国邮路问题的数学模型 (20)3.1 问题的重述 (20)3.2 需解决的问题 (21)3.3 问题假设 (21)3.4 符号说明 (22)3.5 问题一的建模与求解 (23)(一)模型的分析与建立 (24)3.6 模型的求解 (27)结语 (30)致谢 (31)参考文献 (32)前言图论是一个新的数学分支,也是一门很有实用价值的学科,它在自然科学,社会科学等各领域均有很多应用。
近年来,计算机技术在图论中的应用使得图论得到飞速的发展,应用范围也不断拓广,已渗透到诸如语言学,逻辑学,物理学,化学,电讯工程,计算机科学以及数学的其它分支中。
特别在计算机科学中,如形式语言,数据结构,分布式系统,操作系统等方面均扮演着重要的角色。
最早的图论问题要追溯到1736年的哥尼斯堡七桥问题,而且在19世纪关于图论的许多重要结论都已相继提出。
但是直到20世纪20年代图论才引起广大学者的注意并得以广泛接受和传播。
其实现实生活中的许多问题都是可以通过图论中的相关知识得以解决的,这些例子俯拾即是。
例如,住在城市里的人出行的街道, 抽象出来就是由顶点(结点)和边(线) 构成的图, 在这个图上, 清洁工人必须把这个城市的所有街道清扫一遍,也就是走完所有的边,于是, 清洁工人马上遇到一个十分重要的图论问题: 怎样扫才能一条不落地把所有街道扫上一遍,而且使得所走的总路程最短,这就是典型的欧拉回路问题。
运筹学课件4.8 中国邮递员问题

哥尼斯堡七桥问题与欧拉图 中国邮递员问题 求解中国邮递员问题的奇偶点图作业法 奇偶点图作业法的改进方法
一、哥尼斯堡七桥问题与欧拉图
哥尼斯堡七桥问题 欧拉图与一笔画问题
A
A C B 哥尼斯堡七桥问题 C D
D
B
二、中国邮递员问题
1962年,管梅谷先生提出 中国邮递员问题 若图中无奇点,欧拉圈即为所求 若图中有奇点,则奇点必为偶数,在奇点间加边 (重复走),使其变为偶数而成欧拉图。 中国邮递员问题是要求所加边的权之和最小。
三、求解中国邮递员问题的奇偶点图作业法
在奇点间加边,构造初始可行方案。 寻找改进可行方案:在两奇点间检查所有链,若 某链的长度小于已加重复边的长度,则在该链的 每边加上重复边,去掉原重复边。 重复以上步骤,直到任意两奇点间加重复边的链 是最短的为止。
求解中国邮递员问题:例子
v2
1 2 3 6
v3
4 2
5 1 2 2
v1
v6
v4
3
v5
例子的初始可行解
v2
1 2 3 6
v3
v4
4 2 3
5 1 2 2
5
v1
v6
2
v5
例子的修正解
v2
1 1 2 3 6
v3
v4
4 2 3
5 1 2 2 2
v1
v6
v5Leabharlann 四、奇偶点作业法的改进方法
奇偶点作业法的瓶颈是需检查太多的链 可以首先求出任意一对奇点之间的最短路, 从中选出总路长最小的组合方案。 也可以由奇点构成偶图,求最小匹配得到 最优解。
运筹学 中国邮递员问题

§4.中国邮递员问题(Chinese Postman Problem)1.问题的提出例5. 一个邮递员从邮局出发投递信件, 然后再返回邮局, 如果他必须至少一次地走过他负责投递范围内的每条街道, 街道路线如下图所示, 问选择怎样的路线才能使所走的路为最短?5 6 78问题的图论表述:在赋权G=[V, E]上找一条经每条边至少一次的权最小的圈。
1960年山东师范学院管梅谷教授首先提出此问题,并设计了一个“奇偶点表上作业法”,后来发现此法不是多项式算法,1973年,Edmonds和Johnson给出一个多项式算法。
2.哥尼斯堡七桥问题18世纪在哥尼斯堡城(今俄罗斯加里宁格勒)的普莱格尔河上有7座桥,将河中的两个岛和河岸连结,如下图所示。
城中的居民经常沿河过桥散步,于是提出了一个问题:能否一次走遍7座桥,而每座桥只许通过一次,最后仍回到起始地点。
3.Euler圈Euler圈:经图G的每条边的简单圈Euler图:具有Euler圈的图Euler图非Euler图下面讨论的图G允许有重边,且重边被认为是有区别的边。
伪Euler 圈:经图G 的每条边至少一次的圈点v 的次:与点V 关联的边的数目奇(偶)点:该点的次为奇(偶)数命题1:G 的奇点个数为偶数命题2:G 中有伪Euler 圈 ⇔ G 无奇点中国邮递员问题可表述为:在图G 中找一条权最小的伪Euler 圈。
对于邮递员来说,有些街道可能会重复走,原问题便转化为尽可能少走重复的 街道。
我们将这些重复的边组成的集合称可行集,即找最小的可行集。
命题3:E *是最小可行集 ⇔ωωμμμ()()()()*()*()e e e E E E e E E ≤∑∑∀μ∈∩∈∩\初等圈重复的边 非重复的边4.算法思路由命题1,简单图G 的奇点个数为偶数,可设为v 1 , v 2 , …, v 2k , 对每个1≤ i ≤k, 找v 2i − 1 至v 2i 的链p i ,将p i 的边重复一次。
中国邮递员问题 ppt课件

中国邮递员问题
管梅谷教授首先提出的方法是奇偶点图上作业 法(1962年)
Edmonds,Johnson(1973年)给出有效算法。
复杂度为 O(|V(G)|2|E(G)|)
中国邮递员问题
中国邮递员问题
解决这样的问题,可以采用奇偶 点图上作业法:如果在配送范围 内,街道中没有奇点,那么他就 可以从配送中心出发,走过每条 街道一次,且仅一次,最后回到 配送中心,这样他所走的路程也 就是最短的路程。
原来的问题可以叙述为在一个有奇点的图中, 要求增加一些重复边,使新图不含奇点,并且 重复边的总权为最小。
我们把使新图不含奇点而增加的重复边简称为 可行(重复边)方案,使总权最小的可行方案 为最优方案。
现在的问题是第一个可行方案如何确定? 在确定一个可行方案后,怎么判断这个方案是
否为最优方案? 若不是最优方案,如何调整这个方案?
Fleury算法的复杂度是 O(| E(G)|2)
中国邮递员问题
求欧拉回路的算法(回路算法)
算法思想: 首先得到一个回路C1, 再在剩
下的图G- C1中求一条与C1有公共顶点的
回路C2, 则C1与 C2构成一个更长的回路,
继续下去可得到含所有边恰好一次的回
路. 回路算法的复杂度是
O(|
E(G) |)
这个问题就是一笔画问题。
中国邮递员问题
管梅谷教授。
上海市人。1957年毕业于华 东师范大学数学系。历任 山东师范大学讲师、副教 授、教授、校长,中国运 筹学会第一、二届常务理 事,山东省数学学会第四 届副理事长,山东省运筹 学会第一届副理事长,山 东省世界语协会理事长。 是第六届全国政协委员。 从事运筹学及其应用的研 究,对最短投递路线问题 的研究取得成果。所提模 型在国外称为中国投递问 题。
中国邮递员问题

中国邮递员问题第一篇:中国邮递员问题运筹学第六组运筹学个人心得之中国邮递员问题我们第六组做的第二次案例就是中国邮递员问题,这个问题是运筹学中的经典命题。
这个案例讲的是:在中国的六个县城,每个县城都有一个县局,县局下面设立若干个邮政所,每天邮递员的任务就是从县局出发,依次到每一个邮政所送邮件,要求每个邮政所都必须去,而且只能去一次。
这就涉及到一个路线的规划问题,怎么走才能使得邮递员走的路最少,而且能够完成任务。
在做题之前考虑了很久,真不知道从何着手,国为以前确实没有接触过这个类型的题,没有一个能够行得通的办法。
后来,我们选定了一个代表性的区域,来尝试求解,国为第六个区域的变量最多,所以就选择这个区域作为突破口。
只要第六个区域求解成功,其它五个区域便迎刃而解了。
首先,我们画了一个由第六区域的十七个点所组成的17*17矩阵,一一对应设定变量,在去除对角线的17个变量之后,我们得到272个变量。
这是一个非常庞大的变量群体,若按传统的线性规划方法求解,求解过程将会变得异常艰辛,而且以前的模板,求解工具都不能求解这么多变量。
所以我们一度陷入混乱,求解工作停滞不前。
后来老师在对这价目案例作初步的讲解的时候,提出了用运输模型来对这个问题进行求解,此话一出,真是如醍醐灌顶,酣畅极了,眼前简直豁然一亮,真想“拍案而起”。
若用运输模型求解,这个问题将会变得非常简单。
一方面由于每行的出发点只能有一个,而每列的终点也只能有一个,这样看来,邮运筹学第六组递员总是变成了一个产销平衡的运输问题,产量和销量都有是1。
这样我们就完成了求解工作,在第一次求解得出结论后,我们画了一个路线图,发现有几个两点循环,没有形成一条大通路,于是我们重新加入了两点循环约束,进行二次求解;在第二次求解完成后,我们又重新画了路线图,结果发现有四点循环于是我们又加入四点循环约束,进行第三次求解,在得到第三次求解的结果后,我们又画出了路线图,这次刚好形成了一个完整的通路,保证了邮递员每点都走到且行走的路线最合理。
中国邮递员问题

管梅谷
管梅谷教授。 上海市人。1957年毕业于华 东师范大学数学系。历任 山东师范大学讲师、副教 授、教授、校长,中国运 筹学会第一、二届常务理 事,山东省数学学会第四 届副理事长,山东省运筹 学会第一届副理事长,山 东省世界语协会理事长。 是第六届全国政协委员。 从事运筹学及其应用的研 究,对最短投递路线问题 的研究取得成果。所提模 型在国外称为中国投递问 题。
求解。
推广的中国邮递员问题: 混合图的中国邮递员问题,有各种限制 的中国邮递员问题,动态网络的中国邮 递员问题。 其他相关问题-旅行售货员(TSP)问题, 灾清巡视路线。
谢谢!
v1 2 5 v2 5 9 v3 v4 图2 3 v8
4
3
v7
6
v9 4 4 4
v6
4
v5
这样就得到初始方案.在这个图中,没有奇点, 故称它为欧拉图。对应于这个可行方案,重复 边总权为51。
思考
这样的可行方案是不是只有一种呢? 在确定一个可行方案后,怎么判断这个方案是 否为最优方案? 若不是最优方案,如何调整这个方案?
欧拉图及求欧拉回路的算法
欧拉行迹—含所有边恰好一次的行迹 欧拉回路—含所有边恰好一次的回路 欧拉图—存在欧拉回路的图
设G是连通图, 下列命题等价: (1) G是欧拉图. (2) 每个顶点的度数都是偶数. (3) G是两两无公共边的圈的并.
欧拉图及求欧拉回路的算法
求欧拉回路的算法(Fleury算法,1921年) 算法思想: “过河拆桥,尽量不走独木桥”. 即若已选定迹 Wi v0e1v1e2 eivi , 从 G Wi 中选 取下一条边 ei 1 使得ei 1 与 vi 相关联, 且ei 1 不是 G Wi 的桥, 除非无边可选.
中国邮递员问题

h
5
v1 a
b
c
v2
v3
v4
图1
图2
图1和图2当中哪一个图满足:从图中任何一点出 发,途径每条边,最终还能回到出发点?
试想:一个图应该满足什么条件才能达到上面要
求呢?
h
6
一笔画问题
凡是能一笔画出的图,奇点的个数最多 有两个。始点与终点重合的一笔画问题, 奇点的个数必是0。
求解。
推广的中国邮递员问题: 混合图的中国邮递员问题,有各种限制
的中国邮递员问题,动态网络的中国邮 递员问题。 其他相关问题-旅行售货员(TSP)问题, 灾清巡视路线。
谢谢!
上述两算法都是在连通欧拉图中求欧拉 回路的算法.
h
11
中国邮递员问题
一个邮递员送信,要走完他负责投递的 全部街道,投完后回到邮局,应该怎样 走,使所走的路程最短?
这个问题是我国管梅谷同志1960年首先 求出来的,因此在国际上通称为中国邮 递员问题。在物流活动中,经常会遇到 这样的问题,如:每天在大街小巷行驶 的垃圾车、洒水车、各售货点的送货车 等都需要解决一个行走的最短路程问题。
h
15
求解中国邮递员问题的算法
管梅谷教授首先提出的方法是奇偶点图上作业 法(1962年)
Edmonds,Johnson(1973年)给出有效算法。
复杂度为 O(|V(G)|2|E(G)|)
h
16
求解中国邮递员问题的算法(例)
h
17
求解中国邮递员问题的算法(例)
h
18
解决这样的问题,可以采用奇偶 点图上作业法:如果在配送范围 内,街道中没有奇点,那么他就 可以从配送中心出发,走过每条 街道一次,且仅一次,最后回到 配送中心,这样他所走的路程也
中国邮递员问题

(割边)
FE算法复习:
(1)任取 v0属于V(G),令W0=v0. (2)设行迹Wi=v0v1v2…vi已选定,则从E(G)-E(W)中 选一条边ei+1,使得ei+1与vi相关联,且非必要时, ei+1 不要选G-E(W)的桥(所谓桥是一条删除后使连通图 不再连通的边)。 (3)反复执行(2), 直至每边e属于E(G)皆入选为止。
情况2:加权图G中有奇次顶时中国邮路问 题的解法(某些边要通过两次)
解法步骤:设G是连通加权图 1)求G中奇次顶集合V0; 2)对V0中的每个顶对u,v,用Dijkstra算法求距离d(u,v); 3)构造加权完全图K|V0|,完全图中顶点即为V0中顶点,边uv 之权为d(u,v); 4)求加权图K|V0|的总权最小的完备匹配M。 5)在G中求M中同一边之端点间的最短轨。 6)把G中在(5)求得的每条最短轨之边变成同权倍边,得 Euler图G’. 7)用FE算法求G’的一条Euler回路W’,W’即为中国邮路。 实例探讨
中国邮递员问题--邮递员从选好邮件去投递,然后返回邮 局,必须经过由他负责的每条街道至少 一次,怎么走耗时最少?
情况 1:邮路可抽象为 Euler图,则所有路经过恰好一次。 情况 2:邮路抽象成的图 G中包含奇次顶。(有的路径需要 重复走)
情况1:仍要遵循一定规则走
定理6.3
若G是Euler图,FE算法终止时得 到的W是Euler回路。
本质:此算法能实现无重复边的一笔画,且
回到出发点。
证明思路 (1)证明是闭行迹。 (2)证明能够经过一切边。(反证不能经过一切边)
基本概念复习
行迹:各边相异的道路。 Euler行迹:在图G中含一切边的行迹。 Euler回路:含一切边的闭行迹。 Euler图:若G中存在Euler回路。
中国邮递员问题算法

G-E(C)仍然无奇数度结点。
?
由于G是连通的,C中应至少存在一点v,使G-
E(C)中有一条包含v的回路C′。(见示意图)
2019/7/8
计算机学院
7
C
v
C'
这样,就可以构造出一条由C和C′组成的 G的回路,其包含的边数比C多,与假设矛盾。 因此,C必是Euler回路,结论成立。
2019/7/8
计算机学院
类似于无向图的讨论,对有向图我们有以下 结论: 定理13-1.2 ⅰ)有向连通图G含有有向欧拉道路,当且仅当
除了两个结点以外,其余结点的入度等于出度, 而这两个例外的结点中,一个结点的入度比出 度大1,另一个结点的出度比入度大1。 ⅱ)有向连通图G含有有向欧拉回路,当且仅当G 中的所有结点的入度等于出度。
计算机学院
16
显然,当这个图是欧拉图时,任何一条欧拉回路都 符合要求;当这个图不是欧拉图时,所求回路必然要重复 通过某些边。
对此,管梅谷曾证明,若图的边数为m,则所求回 路的长度最小是m,最多不超过2m,并且每条边在其中 最多出现两次。中国邮递员问题,一般为在带权连通图 中找一条包括全部边的且权最小的关回键路是。:复制哪些边?
V6
d(V2,V5)=3, d(V3,V5)=4
G
各路径:V1V2(3),V3V5(4)—7
V1V3(5),V2V5(3)—8
V1
V1V5(4),V2V3(2)—6
∴两条长度最短P1=V1V7V5,P2=V2V3
3.构造G’的任一E图就是中国邮递员 V6
问题的解。
G′
V2
3
2
1 3
3 6
V3
3
V7
7
中国邮递员问题(第五版)
中国邮递员问题引言H T T P ://W W W .588K U .C O M /P P Tu 中国邮递员问题是由山东师范大学管梅谷同志1960年首先提出的。
u 该问题涉及著名的的哥尼斯堡(Königsberg)七桥问题。
u 这是数学中为数不多的几个以“中国”命名的问题或定理之一。
u 七桥问题是图论和拓扑学的起源。
引言1哥尼斯堡七桥问题2欧拉图及判定定理3Fleury算法4中国邮递员问题5奇偶点图上作业法6理论根据(选讲)哥尼斯堡(Königsberg)今称加里宁格勒,建城于1255年,是位于波罗的海海岸的俄罗斯海港城市与加里宁格勒州的首府。
加里宁格勒州位于波兰北方、立陶宛西南,原为德国东普鲁士一部分,现为俄罗斯的外飞地。
图1 加里宁格勒图2 哥尼斯堡七桥示意图有一条普雷格尔(Pregel)河流经哥尼斯堡,河上有七个桥。
一个散步者能否从某处出发走遍七个桥且每个桥只走一次,最后回到出发点?哥尼斯堡七桥问题大数学家欧拉在1736年解决了这个问题。
欧拉Euler(1707-1783)莱昂哈德·欧拉(Leonhard Euler,1707年4月15日-1783年9月18日)u瑞士数学家和物理学家,近代数学先驱之一。
u欧拉是18世纪数学界最杰出的人物之一。
u欧拉是科学史上最多产的一位杰出的数学家,据统计他那不倦的一生,共写下了886本书籍和论文。
u30岁左右右眼几乎完全失明,60岁左右左眼又几乎完全失明。
u在1775年,他平均每周就完成一篇数学论文。
u1783年9月18日于俄国彼得堡去逝。
n 将上图中A,B,C和D这四个区域各看成一个顶点,两区域之间有一个桥相连,就将相应的两个顶点连一条边,得到一个图。
AB CD图3 七桥问题对应图欧拉Euler(1707-1783)的走法为一个欧拉通路。
n如果进一步该走法还回到出发点,则称之为欧拉环游(回路)。
n具有欧拉环游的图称之为欧拉图。
中国邮递员问题的求解实例

中国邮递员问题的求解实例前面已经讲过,对于欧拉图,可以直接用Fleury算法找出一条欧拉巡回路线;对于半欧拉图,可以先求出奇点u和v之间的最短路径P,令G =G P,贝U G *为欧拉图,然后用Fleury算法来确定一个G *的欧拉巡回,它就是G的最优巡回。
当G有2n个奇点(n>1),可以用Edmonds算法解决,步骤如下:(1) 用Floyd算法求出所有奇点之间的最短路径和距离矩阵。
(2) 用匈牙利法或0-1规划法求出所有奇点之间的最佳配对。
(3) 在原图上添加最佳配对所包含的两两顶点之间的最短路得到欧拉图G *。
⑷用Fleury算法确定一个G *的欧拉巡回,这就是G的最优巡回。
以上步骤的关键是找出2n个奇点的最佳配对,举例如下。
例图3是某区街道示意图,各边的长度数据如下表所示。
现在需要对每条街道找最优巡回,需要先求26个奇点的最佳配对。
先用Floyd算法求出所有42个顶点之间的最短路距离和路径。
程序如下:E=[1 2 10261 4 402........ 注:每一行代表一条边(两个顶点和边长),此处省略59行40 39 198];for i=1:42for j=1:42if j==ia(i,j)=0; elsea(i,j)=inf; end end endfor k=1:62 i=E(k,1);j=E(k,2);a(i,j)=E(k,3);a(j,i)=E(k,3); end[D,R]=floyd(a);图3某区街道示意图然后求26个奇点的最优配对,这可以用Lin go 求解,编写程序如下:MODEL: SETS:4U12°26"30 O3539 40413*27 21 4128* 3338仆2934O114251015• 1724,25201922 23 32313637dot/2,4,5,6,8,9,10,11,12,13,14,15,17,18,19,20,22,24,25,26,28,29,30,36,40,41/;LINKS(dot,dot)| &2 # GT # & 1:C,X;ENDSETSDATA:C=1319 1065 651 650 939 1228 1463 1500 1213 617 895 1590 1709 1377 1033 1112 1652 1761 1853 1418 1832 2124 2151 2479 1687254 668 1173 1462 1751 198 181 402 1140 1418 2113 453 601 945 1635 2175 2284 597 1941 2355 868 1463 1498 2104414 919 1208 1497 1732 435 148 886 1164 1859 679 347 691 1381 1921 2030 823 1687 2101 1094 1689 1724 1850505 794 1083 1318 849 562 472 750 1445 1058 726 382 967 1507 1616 1202 1273 1687 1473 2005 2103 1541289 578 813 1354 1067 471 245 940 1563 1231 887 462 1002 1111 1707 768 1182 1978 2005 2333 1541 289 524 1643 1356 760 534 651 1852 1520 1176 504 828 886 1996 594 1008 2267 2197 2525 1733235 1932 1645 1049 823 362 2141 1809 1465 793 706 597 2285 883 890 2556 2486 2814 20222167 1880 1284 1058 163 2376 2044 1700 1028 507 398 2520 1105 691 2766 2658 2986 2194306 1321 1599 2294 272 505 849 1571 2111 2220 416 1877 2291 687 1282 1317 20081034 1312 2007 531 199 543 1265 1805 1914 675 1571 1985 946 1541 1576 1702360 1411 1203 871 527 577 1117 1226 1347 883 1297 1618 1534 1862 10701101 1563 1231 887 217 757 866 1707 523 937 1978 1894 2222 14302282 1950 1606 884 344 235 2426 942 528 2603 2495 2823 2031332 676 1398 1938 2047 144 1704 2118 415 1010 1045 1824344 1066 1606 1715 476 1372 1786 747 1342 1377 1503722 1262 1371 820 1028 1442 1091 1623 1721 1159540 649 1542 306 720 1813 1729 2057 1265109 2082 598 184 **** **** 2479 16872191 707 293 2368 2260 2588 17961848 2262 271 866 901 1680414 1711 1603 1931 11392075 1967 2295 1503595 630 1409360 832792;ENDDATA图4 26个奇点的最优配对MIN=@SUM(LINKS:C *X);@FOR(LINKS:@BIN(X));@FOR(dot(l):@SUM(LINKS(J,K)| J #EQ# I #OR# K #EQ# I:X(J,K))=1);END运行以上程序,得到最优配对结果为:2与6、4与12、5与13、8与9、10与11、14 与15、17 与25、18 与26、19 与20、22 与28、24 与29、30 与36、40 与41。
运筹学-邮递员问题

值得注意的是,这个方法主要困难在于检查判定标准2。它要求对于图中的每一个圈都检查一遍。当一个连通图所包含的圈数比较多时,将会大大提高运算的工作量,比如“田”字型的图就有13个圈。
到目前为止,关于中国邮递员问题,已经找到了更好的算法,由于篇幅所限,我们就不去介绍它了。
当q=3时,显然G是欧拉图。假设q=n时成立,看q=m+1的情形:由于G是无奇点的连通图,并且G的点数p>=3,因此存在三个点μ,v,w,使得[μ,v],[w,v]∈E。从G中去掉边[μ,v],[w,v],增加新的边[μ,w],得到一个新的多重图G1,G1有q-1条边,且仍不含奇点,G1至多有两个分图。
推论 一个多重连通图G有欧拉链的充分必要条件是G有且仅有两个奇点。
这个推论的证明留给读者作为习题。
从这个定理的证明可以看出,识别一个连通图能否一笔画出的条件是它是否有奇点。若有奇点,就不能一笔画出。若没有奇点,就能够一笔画出,并回到原出发地。
比如前面提到的哥尼斯堡七桥问题,欧拉把它抽象成具有四个项点,并且都是奇点的图8.26的形状。很明显,一个漫步者无论如何也不可能重复的走完七座桥,并最终回到原出发地。图8.27。仅有两个奇点,可以一笔画出。
v1-v2-v4-v3-v2-v4-v6-v5-v4-v6-v5-v3-v1, 总长是12。 也可以按照另一条路线走: v1-v2-v3-v2-v4-v5-v6-v4-v3-v5-v3-v1, 总长是11。 按照第1条路线走,在边[v2,v4],[v4,v6],[v6,v5]上各走3两次,按照第2条路线走,在边[v3,v2],[v3,v5]上各走了两次。
图8.26
B
A
D
C
图8.27
v5
v6
v4
运筹学最短路邮递员问题PPT课件

•
新的T(vj)=min{老的T(vj),p(vi)+ ωij }
• 若T(vj)= p(vi)+ ωij ,则记k(vj )=vi(前点标记);
• 3°找出具有最小T标号的点,将其标号改为p标号。若vt 已获得p
标号,则已找到最短路,由k(vt)反向追踪,就可找出vs 到vt 的最
短路径,p(vt)就是vs 到vt 的最短距离。否则,转2°。
p(v2)
=3 3
p(v1) v1
p(v=30)
=4
6
v2
51 1
v4
7 4
v5
v3 3 2
5
v7
26 v6 9 15
v8
T(v4)=min{6,4+1}=5, k(v4 )=v3
T(v6)=min{7,4+2}=6, k(v6 )=v3
目前,点v4 具有最小T标号,将其标号改为p标号: p(v4)=5;
向继续前进,则最先到达终点vt 的流所走过的路径一定是最短的。
为了实现这一想法,对假想流依次到达的点,依次给予p标号,表
示vs到这些点的最短距离。对于假想流尚未到达的点给予T标号,
表示vs到这些点的最短距离的估计值。具体作法如下:
• 1°标p(vs)=0,其余点标T(vi)=+∞;
• 2°由刚刚获得p标号的vi 点出发,改善它的相邻点vj 的T标号,即
对于点v2 :d(v2)=min{16+31,22+23,30+18,41}=41, v对2→于v点6 v;1 :d(v1)=min{16+41,22+31,30+23,41+18,59}
试确定一个五年内的设备更新计划,使五年内总支出最小。
邮递员问题

运输优化的基本问题
V7
图 3-22ຫໍສະໝຸດ (二)奇偶点图上作业法(P92-96)
V2 5 9
V9 6 4
V6 5
V1 2 V8 4
V7 3
V3
V4
图 3-21
V5 V2
6
V9
4
V6
V3
第三章 运输合理化
V4
V5
Transportation
第二节
V1 V8
运输优化的基本问题
V7
图 3-22
(二)奇偶点图上作业法(P92-96)
Transportation
第二节
运输优化的基本问题
二.最小费用最大流问题 (P87) 三.(中国)邮递员问题 (P90)
连通图:图G中,若任何两个点之间,至少有一条链, 则称G是连通图,否则称为不连通图。
给图G,对G中的每一条边[ Vi, Vj ],相应地有 一个数Wij ,则称这样的图G为赋权图,Wij 称为边 [ Vi, Vj ]上的权。 这里所说的“权”,是指与边有关的数量指标。 根据实际问题的需要,可以赋予它不同的含义,例 如表示距离、时间、费用等。
V2
V9 4
V6 5
V1 2 V8 4
V7 3
V3
V4
图 3-23
V5 V2
6
V9
4
V6
V3
第三章 运输合理化
V4
V5
V3
V5
V1
V3
V5
V2
V4
(a)
V6
V2
V4
(b)
V6
图 3-18
第三章 运输合理化
Transportation
1478.安排邮筒邮递员问题(dp绝对值不等式)
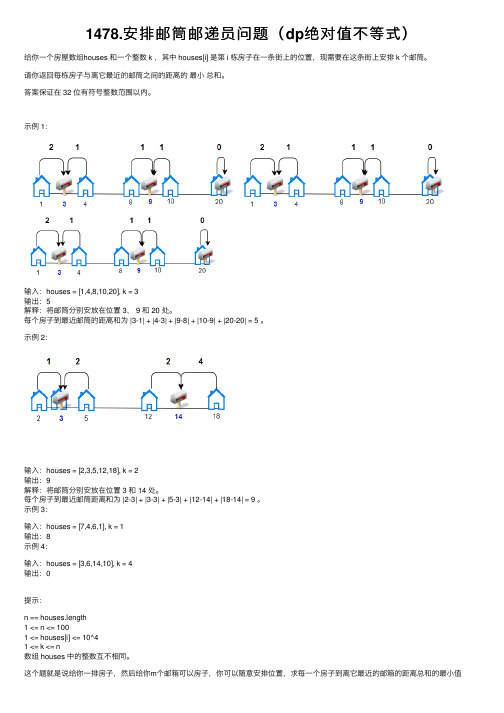
1478.安排邮筒邮递员问题(dp绝对值不等式)给你⼀个房屋数组houses 和⼀个整数 k ,其中 houses[i] 是第 i 栋房⼦在⼀条街上的位置,现需要在这条街上安排 k 个邮筒。
请你返回每栋房⼦与离它最近的邮筒之间的距离的最⼩总和。
答案保证在 32 位有符号整数范围以内。
⽰例 1:输⼊:houses = [1,4,8,10,20], k = 3输出:5解释:将邮筒分别安放在位置 3, 9 和 20 处。
每个房⼦到最近邮筒的距离和为 |3-1| + |4-3| + |9-8| + |10-9| + |20-20| = 5 。
⽰例 2:输⼊:houses = [2,3,5,12,18], k = 2输出:9解释:将邮筒分别安放在位置 3 和 14 处。
每个房⼦到最近邮筒距离和为 |2-3| + |3-3| + |5-3| + |12-14| + |18-14| = 9 。
⽰例 3:输⼊:houses = [7,4,6,1], k = 1输出:8⽰例 4:输⼊:houses = [3,6,14,10], k = 4输出:0提⽰:n == houses.length1 <= n <= 1001 <= houses[i] <= 10^41 <= k <= n数组 houses 中的整数互不相同。
这个题就是说给你⼀排房⼦,然后给你m个邮箱可以房⼦,你可以随意安排位置,求每⼀个房⼦到离它最近的邮箱的距离总和的最⼩值⾸先我们先考虑⼀个问题就是假如给你n个房⼦的坐标,然后你只能有⼀个邮箱怎么求这个最⼩的距离总和呢?这个问题涉及到绝对值不等式,就是先拍个序,然后求这个中位数(a[(1+n)/2)然后每⼀个数,跟他做差求和就是答案然后这个题是⼀个dp,f[i][j]数组代表的是前i个数组,分到j个邮箱的最⼩值然后我们⼀层枚举i,⼀层枚举j,然后⼀层枚举枚举这⼀段的起点然后转移⽅程就是转移时,对于 i 和 j,枚举当前段的起点 l,令闭区间 [l, i] 使⽤同⼀个邮筒,则转移 f(i,j)=min(f(l−1,j−1)+cost(l,i))。
