§2.4 粘弹性流体
粘弹性流体的特性及其在药物输送和生物流体力学中的应用

粘弹性流体的特性及其在药物输送和生物流体力学中的应用粘弹性流体是一种特殊的流体,具有粘性和弹性的双重特性。
在物理学、化学和工程学等领域中,粘弹性流体的研究与应用日益受到关注。
本文将介绍粘弹性流体的特性,并探讨其在药物输送和生物流体力学中的应用。
一、粘弹性流体的特性粘弹性流体的特性可以归结为两个方面:粘性和弹性。
1. 粘性:粘弹性流体表现出与黏度相关的特性。
黏度是流体内部分子间相互作用引起的阻力大小。
粘性使得粘弹性流体具有黏滞的特性,即流动缓慢且阻力较大。
2. 弹性:粘弹性流体在受力后能够产生应力,当施加的力消失后,流体能够恢复原貌。
这种特性使得粘弹性流体具有一定的形变能力。
二、粘弹性流体在药物输送中的应用1. 控释药物输送系统:粘弹性流体可用于制备控释药物输送系统。
通过调节粘弹性流体的黏度和弹性,可以使药物以缓慢且持续的方式释放,从而提高药物治疗效果并减少药物的频繁使用。
2. 口腔和皮肤黏附剂:粘弹性流体作为黏附剂可以在口腔和皮肤表面保持一定时间。
在药物输送中,它可以增加药物在局部的停留时间,从而提高药效。
三、粘弹性流体在生物流体力学中的应用1. 血液模拟体:粘弹性流体可以用于生物流体力学的研究中,模拟血液的流动行为。
通过调节粘弹性流体的黏度和弹性,可以模拟不同状态下的血流情况,研究血流动力学特性,从而为心血管疾病的诊断和治疗提供依据。
2. 细胞培养基:粘弹性流体还可以作为细胞培养基的替代品,提供更接近细胞体内环境的生物力学条件。
这可以帮助研究者更好地理解细胞生长、分化和迁移等过程,为组织工程和再生医学提供指导。
四、结语粘弹性流体作为一种特殊的流体,具有粘性和弹性的特性,广泛应用于药物输送和生物流体力学领域。
在药物输送中,粘弹性流体可以用于制备控释药物输送系统,以及口腔和皮肤黏附剂的制备。
在生物流体力学中,粘弹性流体可以模拟血液流动行为,用作血液模拟体,同时也可以作为细胞培养基,提供更接近细胞体内环境的生物力学条件。
黏弹性流体力学研究中的弹性效应分析

黏弹性流体力学研究中的弹性效应分析引言黏弹性流体是一种特殊的流体,其流动特性既受到黏性的影响,也受到弹性的影响。
在研究黏弹性流体力学时,必须考虑到弹性效应对流体流动行为的影响。
本文将详细分析黏弹性流体力学研究中的弹性效应,以期深入理解这一领域。
黏弹性流体的特性黏弹性流体具有独特的流动特性,其特点如下: 1. 延展性: 黏弹性流体能够以较小的应力下发生很大的变形。
2. 回弹性: 黏弹性流体在停止外力作用后能够恢复原状或接近原状。
3. 补偿时间: 黏弹性流体具有补偿能力,可以在流动中适应外界环境变化。
4. 结构耗散: 黏弹性流体的流动过程中存在结构的重组和破坏。
弹性效应对黏弹性流体力学研究的影响黏弹性流体力学研究在很大程度上依赖于弹性效应的考虑,弹性效应对流体流动的影响主要体现在以下几个方面:弹性模量的测定弹性模量是衡量黏弹性流体中弹性效应的重要参数,它可以通过实验方法测定得到。
常用的测定方法包括剪切杆测试、剪切振动测试和动态拉伸测试等。
这些方法通过施加外力并测量流体的应变来计算弹性模量,从而揭示流体中弹性效应的特征。
力学行为的描述黏弹性流体力学中,弹性效应对力学行为的描述起着重要的作用。
流体的粘滞效应和弹性效应共同决定了流体的力学行为。
根据流变学理论,可以通过引入弹性效应的流体模型来描述流体的力学行为,例如,Maxwell模型、Kelvin模型和Oldroyd模型等。
这些模型可用于模拟黏弹性流体的应力-应变关系。
流动行为的预测弹性效应在预测黏弹性流体流动行为中发挥着重要作用。
在模拟黏弹性流体的流动过程时,必须考虑到弹性效应对流体动力学行为的影响。
通过引入弹性效应的流体模型,可以预测黏弹性流体在不同流动条件下的行为,如层流和湍流过渡、流动的稳定性和剪切层的形成等。
弹性效应的尺度依赖性弹性效应在黏弹性流体力学中的研究中还表现出尺度依赖性。
尺度效应是指由于尺度效应引起的材料力学性质随尺度的改变而发生变化,在弹性效应的研究中,尺度效应尤为重要。
粘弹性流体力学的理论与实验研究

粘弹性流体力学的理论与实验研究引言粘弹性流体力学是研究流体在同时具有粘性和弹性特性时的行为的学科。
这一领域的研究在多个领域具有重要的应用,包括材料科学、生物医学以及地球科学等领域。
本文将深入探讨粘弹性流体力学的理论基础,并介绍一些经典的实验研究。
理论基础粘弹性流体的概念粘弹性流体是指既具有粘性又具有弹性的液体或软固体。
粘性是指流体内部分子之间相互摩擦的现象,而弹性是指流体内部分子在外力作用下出现回弹的现象。
粘弹性流体的宏观性质在很大程度上取决于物质的微观结构与分子间力的相互作用。
粘弹性流体的模型粘弹性流体的模型通常基于两种基本模型:弹性体模型和粘性流体模型。
弹性体模型可以用弹簧和阻尼器串联的方式来描述,而粘性流体模型则可以用牛顿黏滞定律来表示。
实际的粘弹性流体通常需要综合考虑这两种模型。
粘弹性流体的本构方程粘弹性流体的本构方程用于描述物质的应力-应变关系。
最常用的本构方程是Maxwell模型和Kelvin模型。
Maxwell模型将弹性元素和粘性元素串联起来,可以较好地描述物质的粘弹性行为。
而Kelvin模型通过并联弹性元素和粘性元素来描述物质的行为。
粘弹性流体的流变特性粘弹性流体的流变特性包括黏度、屈服应力、流变曲线等。
黏度是指流体流动时所表现出的阻力大小,是刻画流体流动难易程度的物理量。
屈服应力是指流体在外力作用下开始产生可观测的流动行为所需要的最小应力。
流变曲线则是描述流体在剪切应力施加下产生的剪切应变与时间的关系。
实验研究粘弹性流体的流变性能测试粘弹性流体的流变性能可以通过实验测试来获得。
常见的实验方法有旋转粘度计法、振荡剪切法、迎风试验法等。
旋转粘度计法是通过测量粘弹性流体在旋转圆盘上产生的剪切应力与剪切速率的关系来确定其黏度。
振荡剪切法则是通过频率和振幅的变化来研究粘弹性流体的流变特性。
迎风试验法则是在流体流动中施加外界气流压力来研究粘弹性流体的变形和流动行为。
粘弹性流体的微观结构表征粘弹性流体的微观结构对其宏观行为具有重要影响。
§2.4 粘弹性流体
τ13= τ31 , τ23= τ32 。对简单的剪切流动, τ13= τ31=0, τ23= τ32 =0, 故只有剪切应力τ12起作用。
τ 11-τ 22=N1 为 第 一 法 向 应 力 差 , 产 生 轴 向 压 力 , 引 起
Weissenberg效应和挤出物胀大现象。
τ 22-τ 33=N 2为第二法向应力差,产生径向压力,通常很小,
3.同心套管轴向流动现象
4.回弹现象
5.无管虹吸现象
6.次级流现象
7.紊流减阻现象
二、粘弹性流体的流变特征 1.法向应力与法向应力差 当力F作用于物体时,物体内部体积元所受的总应力(或物体内
τ 部某一点所受到的总应力) 可用九个应力分量τ
τ
可分解为九个应力分量 τ
ij
ij
表示,或者说
,其中i代表应力分量作用的平面
法向方向,j代表应力分量的方向,如下图所示,可用张量表示如 下。
τ 11 τ 12 τ 13 τ τ ij = 21 τ 22 τ 23 τ 31 τ 32 τ 33
其中,应力分量的下标1、2、3分别对应于x、y、z方向。τ11 、 τ
22、
τ33为法向应力,其它6个为剪切应力,并且, τ12= τ21 ,
并为负值。 为描述剪切流场中流体流变性随剪切速率的变化性质,需要 下面3个物料函数: (1)剪切粘度
µ (γɺ )=τ 12 γɺ
ψ 1 (γɺ )= N 1 2 (2)第一法向应力系数 γɺ
(3)第二法向应力系数
ψ 2 (γɺ )= N 2
γɺ 2
ψ µ对于牛顿流体, 1 (γɺ )和 ψ 2 (γɺ ) 均为0, (γɺ ) 为常数。
应力松弛曲线示意图
粘弹性流体物理特性的研究及其在工业化加工中的应用研究

粘弹性流体物理特性的研究及其在工业化加工中的应用研究第一章粘弹性流体的概念与分类粘弹性流体是指在应力下表现出固体特性和流体特性的一类复杂非牛顿流体,广泛应用于化工、生物医学、食品加工等领域。
粘弹性流体常见的物质有聚合物、胶体、水泥、淀粉等。
根据流变学的分类,粘弹性流体可以分为黏弹性体、黏塑性体、粘弹性液体三类。
第二章粘弹性流体的物理特性2.1 流动行为粘弹性流体与牛顿流体不同,其流动规律不同,随着剪切速率的增加,黏度呈现不同程度的变化,即存在剪切率的效应。
为了描述流体的这种特性,研究者提出了流变学的概念,即研究流体随剪切力的变化而产生的结构演变和性质变化。
2.2 破坏形变当粘弹性流体在剪切场中进行变形时,其分子链会因为外力而断裂,形成流化结构,导致物理性质的改变。
这种流化结构可以随着外力的停止而缓慢恢复,称为“记忆效应”。
2.3 外场响应在外力场的作用下,粘弹性流体内部会产生很大的内应变和相应的能量损失,具有优异的阻尼特性。
因此,在工程实践中可以利用这种特性来制作减震、隔音等工业产品。
第三章粘弹性流体在工业化加工中的应用研究3.1 液压系统液压系统在航空、机械、汽车等领域非常常见,而粘弹性流体的阻尼特性很适合用来制作减震器,提升车辆乘坐的舒适度和行驶的平稳性。
3.2 食品加工粘弹性流体在食品加工中的应用非常广泛,如在果酱、果泥等加工过程中,加入一定量的黏性增稠剂使其提高流动性。
3.3 生物医学在生物医学领域中,粘弹性流体的应用也得到了广泛的关注。
例如,利用粘弹性流体可以制作出仿生材料,来模拟肌肉组织及生物材料的特性。
第四章粘弹性流体应用的优点与不足4.1 优点①显著的阻尼特性:液压减震器、阻尼材料等领域中广泛使用这种特性。
②柔顺的流动性:在食品、化妆品、纺织品等领域中广泛应用于改善质地和流动性。
③增强的粘附性:在油墨、染料等工业中广泛应用,可以有效地提高粘附性。
4.2 不足由于粘弹性流体本身结构复杂,且理论研究尚未完备,因此在实际应用中容易出现应变失稳、流动不稳定等问题。
流体动力学中的黏弹性流体研究

流体动力学中的黏弹性流体研究引言流体动力学是研究流体运动规律的物理学科,黏弹性流体是其中的一个重要分支。
黏弹性流体具有介于液体和固体之间的特性,既具有流体的流动性,又具有固体的弹性。
在工程领域中,黏弹性流体的研究在物料加工、油田开发、生物医学等多个方面具有重要应用价值。
本文将探讨黏弹性流体的定义、性质、流动行为以及相关研究方法与应用领域。
一、黏弹性流体的定义与分类1.1 定义黏弹性流体是指在外力作用下具有应力和应变关系不仅取决于变形速度和应变量,而且还取决于变形历史的流体。
与牛顿流体和非牛顿流体相比,黏弹性流体展现出了更为复杂的性质。
1.2 分类黏弹性流体按照性质可分为两类:线性黏弹性流体和非线性黏弹性流体。
线性黏弹性流体的应力与应变呈线性关系,而非线性黏弹性流体的应力与应变则不是线性关系。
二、黏弹性流体的性质与特点黏弹性流体具有以下几个基本性质与特点:2.1 弹性本质黏弹性流体具有固体的形变回复能力,即具有弹性本质。
当外力停止作用时,黏弹性流体会恢复到初始状态,这与牛顿流体和非牛顿流体在停止外力作用后无法恢复的特性有所区别。
2.2 流变性黏弹性流体的应力-应变关系与变形速率密切相关,即流体的黏度会随着变形速度的变化而发生变化。
这种特性使得黏弹性流体具有复杂的流变性质。
2.3 液体性质与固体相比,黏弹性流体更接近液体,具有流动性。
黏弹性流体的流动性使得其在流体力学中具有重要地位,并广泛应用于工程领域。
黏弹性流体的流动行为比较复杂,受多个因素的影响。
主要包括应变速率、外力作用、温度等因素。
3.1 应变速率的影响黏弹性流体的黏度随应变速率的变化而变化。
当应变速率较低时,黏弹性流体呈现出较低的黏度值;当应变速率增加时,黏度也会随之增加。
这种应变速率对黏度的敏感性使得黏弹性流体在实际应用中需要进行合适的设定与控制,以满足不同流动条件的要求。
3.2 外力作用的影响外力的作用对黏弹性流体的流动行为具有重要影响。
流体动力学中的粘弹性流体研究

流体动力学中的粘弹性流体研究引言流体力学是研究流体运动规律的科学领域,其中粘弹性流体是一种特殊的流体,具有既有液体的流动性,又具有可变形的固体的特性。
粘弹性流体在工程和科学研究中具有重要应用价值,对其进行深入研究有助于我们更好地理解和掌握流体动力学的基本原理。
本文将介绍粘弹性流体的基本概念和特性,并介绍流体动力学中的粘弹性流体研究的主要内容和方法。
粘弹性流体的定义和特性粘弹性流体是介于固体和液体之间的一类流体。
与牛顿流体(如水和空气)不同,粘弹性流体在外力作用下不仅会流动,还会发生变形。
粘弹性流体的主要特性包括粘度、弹性、流变性和记忆效应。
粘度粘度是粘弹性流体的一种基本特性,它描述了流体内部的黏性阻力。
粘度可以分为静态粘度和动态粘度两种。
静态粘度指的是流体在不应变条件下的黏性阻力,动态粘度则指的是流体在受到应变时的黏性阻力。
粘度可用来描述流体的流动阻力大小,常用单位是帕斯卡·秒(Pa·s)。
弹性粘弹性流体的弹性是指其在受力作用下会发生恢复变形的特性。
与刚体不同,粘弹性流体在受到外力后会发生弹性变形,当外力去除时会恢复到原始状态。
粘弹性流体的弹性可用弹性模量来描述,常用单位是帕斯卡(Pa)。
流变性粘弹性流体的流变性是指其在外力作用下会发生非线性变形的特性。
由于流体具有粘度和弹性,其应力-应变关系不遵循线性规律,而呈现出非线性的行为。
流变性可用流变学来研究和描述。
记忆效应粘弹性流体的记忆效应是指其在经历过一定变形后,会在一定的时间范围内保持相同的应力-应变关系。
这使得粘弹性流体具有一定的时间依赖性。
记忆效应是粘弹性流体独特的特性之一。
粘弹性流体的研究内容和方法在流体动力学中,粘弹性流体的研究主要集中在以下几个方面:流变学、模型和仿真、实验测量和应用。
流变学研究流变学是研究粘弹性流体变形和流动规律的学科。
通过建立流变学模型来描述粘弹性流体的应力-应变关系,从而深入了解粘弹性流体的流变性质。
粘弹性流体的本构模型及其应用

粘弹性流体的本构模型及其应用随着人们对物质性质的深入研究,越来越多的特殊性质的物质被人们所发现,粘弹性流体就是其中之一。
粘弹性流体既具有粘性又具有弹性,被广泛运用于化学、医学、生物学和工程等领域中。
而对于粘弹性流体的本构模型的研究,则是这些应用的基础。
本篇文章将对粘弹性流体的本构模型及其应用进行详细的论述。
一、粘弹性流体的性质粘弹性流体是介于粘性流体和弹性体之间的物质,它既具有流变性质,也具有力学弹性。
它的流变特性表现为,当它受到作用力时会出现变形,而当这种作用力减小或消失时,它的变形又会逐渐恢复。
这种特殊的性质使得它在许多领域具有广泛的应用。
二、粘弹性流体的本构模型粘弹性流体的本构模型是用数学方式来描述流体变形特性的模型。
它是通过实验数据和理论推导确定的粘弹性流体性质的一种数学表示,用于预测和计算其在不同外力下的流变特性。
在粘弹性流体的本构模型中,最常见的是Maxwell模型、Kelvin模型以及Jeffreys模型。
1、Maxwell模型Maxwell模型是由Maxwell在1867年提出的一种模型,是最早被使用的粘弹性流体本构模型之一。
它被广泛应用于石油工程、高分子材料工程、生物领域等领域中。
Maxwell模型的基本原理是将粘性流体和弹性体的模型结合而成。
在Maxwell模型中,流体被视为一个简单的线性弹性体,它由一个弹簧和一个阻尼器组成。
当给该模型施加一个外力时,其中的弹簧会产生弹性变形,而其中的阻尼器会产生粘性变形,使模型发生流变。
而在外力消失后,这两种变形也会随之减小或消失。
2、Kelvin模型Kelvin模型是由Lord Kelvin在1855年提出的一种模型,它将Maxwell模型中的一个弹簧换成为一个螺旋状的弹性体。
和Maxwell模型一样,Kelvin模型也是一种线性的本构模型,它可以更好地描述时间依赖性粘弹性流体的行为。
3、Jeffreys模型Jeffreys模型是由Jeffreys在1927年提出的一种模型,它是Maxwell模型的一种变体。
黏弹性流体运动规律

黏弹性流体运动规律引言黏弹性流体是一类具有黏弹性特性的流体,其运动行为受到黏性和弹性的共同影响。
在工程和科研领域中,对于黏弹性流体的运动规律的研究具有重要的意义。
本文将从宏观和微观两个层面介绍黏弹性流体的运动规律,并对其应用进行探讨。
黏弹性流体的基本特性黏弹性流体是介于弹性体和牛顿流体之间的一种特殊流体。
其既具有牛顿流体的流变性质,又具有弹性体的回弹特性。
黏弹性流体的基本特性主要包括流变特性和弹性特性。
流变特性黏弹性流体的流变特性主要表现为剪切应力与切变速率之间的关系,并可以通过应力-应变关系描述。
不同于牛顿流体,黏弹性流体的应力-应变曲线呈现出非线性的特点,包括屈服应力、流动应力和稳态应力。
•屈服应力:当黏弹性流体受到较大的外力作用时,其初始阻力较大,需要超过一定的应力阈值才能开始流动。
这一阈值即为屈服应力。
•流动应力:在黏弹性流体开始流动之后,剪切应力与切变速率呈现非线性关系。
即切变速率越大,剪切应力越大。
•稳态应力:当黏弹性流体达到稳定流动状态时,其剪切应力保持稳定。
稳态应力与切变速率之间的关系呈线性关系。
弹性特性黏弹性流体的弹性特性主要表现为形变恢复能力和应力-应变之间的关系。
黏弹性流体在受力后,具有一定的形变恢复能力。
其应力-应变关系可以通过应力松驰曲线来描述。
•弹性模量:表示黏弹性流体在受力后发生变形的能力。
弹性模量越大,黏弹性流体的回弹性越强。
•应力松驰曲线:用于描述黏弹性流体在受力后弹性恢复的过程。
应力松驰曲线呈指数衰减趋势。
黏弹性流体的运动规律黏弹性流体的运动规律可以通过牛顿运动定律和黏弹性流体的流变特性来描述。
法则一:牛顿粘度法则牛顿粘度法则是描述黏弹性流体剪切应力与切变速率之间关系的基本法则。
根据牛顿粘度法则,剪切应力与切变速率成正比,比例系数即为黏度。
牛顿粘度法则的数学表达式为:$$\\tau = \\eta \\frac{du}{dy}$$其中,$\\tau$为剪切应力,$\\eta$为黏度,$\\frac{du}{dy}$为切变速率。
黏弹性流体运动特性数值模拟

黏弹性流体运动特性数值模拟黏弹性流体是指既有粘性又有弹性的流体。
它们的运动特性是非常复杂的,因为它们同时受到粘性和弹性的影响。
黏弹性流体的研究在各个领域都非常重要,比如食品加工、药物制备、航空航天等。
为了研究这种复杂的流体运动特性,数值模拟是一种非常有效的方法。
数值模拟的基本原理是根据偏微分方程和边界条件,将流体的运动过程分段离散化,最后得到整个系统的稳定解。
对于黏弹性流体的数值模拟,需要采用比传统的流体表征方法复杂得多的数学模型,同时需要考虑精度、运算速度和计算量的平衡问题。
黏性流体的数值模拟对于纯粘性流体,其运动特性可以通过纳维-斯托克斯方程组来描述。
对于黏性流体,我们需要对其进行粘弹性的扩展,来加入弹性特性。
比如在食品行业,豆浆和酸奶等材料具有黏弹性特性,它们的流动行为无法完全通过纯粘性模型来描述。
在数值模拟中,黏弹性流体的模型可以通过广义麦克斯韦模型(Generalized Maxwell Model)来表示。
这种模型通过线性组合多个弹性体系的弹簧和粘滞元素,来对复杂的流体动力学进行描述。
模型的参数可以通过实验得到,然后通过数值方法进行计算。
弹性体系的弹簧和粘滞元素分别表示流体的弹性和黏性特性。
模型中的常数称为弹簧常数和粘滞系数,用来描述流体沿着时间方向的历史依赖性。
可以使用有限元方法等数值算法来求解黏弹性流体的模型。
黏弹性流体的计算流体动力学模拟计算流体动力学(CFD)是数值模拟中的一种方法,用来模拟流体流动和热传输等物理过程,它可以非常准确地模拟黏弹性流体。
在CFD模拟中,可以采用有限体积法、有限元法、谱方法等数值算法来求解宏观流体的物理量,比如速度、压力、密度等。
在黏弹性流体的CFD模拟中,需要建立黏弹性模型,来描述复杂的流动特性。
目前常用的黏弹性模型有Maxwell模型、Kelvin模型等,其中Maxwell模型被广泛应用于食品和医药制品的研究中。
模型中的参数可以通过实验得到,然后通过数值方法进行计算,这样可以更加准确地预测流体的运动特性。
粘弹性流体

粘弹性流体引言粘弹性流体是指同时具有流体和固体特性的一类物质,具有流体的流动性和固体的弹性变形。
它在工程和科学领域中有着广泛的应用,例如聚合物溶液、涂料、凝胶等都属于粘弹性流体。
本文将介绍粘弹性流体的基本概念、特性及其在不同领域的应用。
粘弹性流体的定义粘弹性流体是一类在应力作用下既可以像固体一样变形,又可以像流体一样流动的物质。
粘弹性流体的特点是当受到应力时,既存在瞬时变形(弹性变形),也存在持续的变形(粘性变形)。
其粘性部分是由分子间的摩擦力所引起的,而弹性部分则是由分子间的弹力所引起的。
粘弹性流体的特性非线性流变性粘弹性流体的流变行为不符合线性黏度模型,其应力与应变之间的关系是非线性的。
在应力作用下,粘弹性流体会产生非常规的时间和频率相关的变形。
记忆效应粘弹性流体具有记忆效应,即它们可以保存之前的形状和结构,在受力解除后仍能保持原来的形态。
这种记忆效应使粘弹性流体具有较好的回弹性,能够在压力释放后迅速恢复到初始形状。
时间相关性粘弹性流体的性能与时间有关。
在应力施加之后,粘弹性流体会随时间的推移而发生变形,这种变形与历史应力有关。
因此,粘弹性流体的性质在单位时间内会随外界作用而发生变化。
剪切稀化和剪切增稠在剪切流动中,粘弹性流体可以表现出剪切稀化或剪切增稠的行为。
剪切稀化指的是粘弹性流体在受到高切变速率作用时,黏度逐渐减小的现象;而剪切增稠则是指在低切变速率下,黏度逐渐增大的现象。
粘弹性流体的应用污泥处理粘弹性流体在污泥处理中有着重要的应用。
通过添加粘弹性流体,可以使污泥更易于流动和处理,从而提高污泥的处理效率和降低处理成本。
聚合物溶液聚合物溶液是一种常见的粘弹性流体,广泛应用于工业生产和科研领域。
聚合物溶液的粘弹性特性使其能够在加工和使用过程中适应各种流动状态,从而满足不同需求。
塑性体粘弹性流体在塑性体的制备中起着重要作用。
通过调整粘弹性流体的组成和浓度,可以获得不同稠度和粘度的塑性体,用于各种应用,如模具制备、减震材料等。
粘弹性流体的流动特性研究

粘弹性流体的流动特性研究随着现代科技和工业发展的进步,粘弹性流体的流动特性研究日益成为热门话题。
粘弹性流体不同于牛顿流体,其流变学性质具有时间依赖性、剪切历史效应和非线性行为等特点。
这些特性为研究者深入探究这类流体的流动提出了巨大的挑战。
一、粘弹性流体的分类粘弹性流体是指当应力作用下会发生弹性变形和粘性变形的流体。
通常可以分为两类:常规非牛顿流体和非常规非牛顿流体。
常规非牛顿流体是指粘性变化与应变速率有关,例如聚合物溶液;而非常规非牛顿流体是指粘性变化与时间和历史应变有关,例如凝胶和生物流体。
二、粘弹性流体的流动特性粘弹性流体的流动特性与其类型有着密切的联系。
在聚合物溶液中,流动行为主要由凝聚、流化和沿流方向拉伸等操作所形成的不规则性状况所主导。
较之于常温下牛顿流体的流动情况,其瞬时流动性能非常差。
而凝胶和半凝胶由于固体和液体的混合,对于应力的反应不仅与剪切率有关,还与应变速率的改变有关,因此在应用上显得更为困难。
三、粘弹性流体的流动模型研究粘弹性流体流动的难点在于其不能通过牛顿流体的流动模型进行描述。
近年来,一些新的流动模型正在逐渐被采用,例如Maxwell-Wiechert模型和Jeffreys模型等。
这些模型充分考虑了流体历史变形带给其粘性和弹性的变化,具备了描述粘弹性流体的非线性动力学特性的能力。
四、粘弹性流体的应用粘弹性流体的应用范围非常广泛,例如在建筑行业、化妆品生产、冶金加工以及食品工业等方面都有着重要的应用价值。
在构建桥梁、隧道等大型基础设施的过程中,聚合物溶液和泥浆都在加强和保护结构,提高生产效率的同时能够减少能耗和成本。
此外,在化妆品、护肤品的生产过程中,各种黏稠度一定的乳液是非常重要的。
总之,粘弹性流体的研究和应用已经成为了科技界的热门话题。
未来需要进一步深入挖掘其流动特性和行为规律,以期更加高效、可靠地利用这类流体,为各领域的发展带来更多的创新和发展机遇。
黏弹性体流体

黏弹性体流体概述黏弹性体流体是一种特殊的流体,具有黏弹性质的流动行为。
在物理学中,黏弹性体流体是指其具有液体流动和固体变形的特征,具有比普通流体更复杂的运动和性质。
黏弹性体流体的研究对于理解流体力学和材料科学具有重要意义,广泛应用于工程、医学、化学等领域。
黏弹性体流体的特性黏性黏弹性体流体的黏性指的是其内部分子间的摩擦力。
黏性的不同使得黏弹性体流体在外力作用下表现出不同的流动行为。
黏性较大的黏弹性体流体流动缓慢,呈现粘稠的特点;而黏性较小的黏弹性体流体流动迅速,呈现流动性。
弹性黏弹性体流体的弹性特性表现为它具有一定范围内的形变后能自行恢复原状的能力。
当外力作用结束时,黏弹性体流体能够通过其分子间的力重新排列,使得形变消失。
流变学性质流变学性质是黏弹性体流体研究的重点内容之一。
流变学描述了黏弹性体流体在外力作用下的变形和流动行为。
黏弹性体流体的流变学性质包括剪切应力、流变应力、应变速率等。
通过研究这些性质,可以获取黏弹性体流体的流变学信息。
黏弹性体流体的应用工程领域在工程中,黏弹性体流体的应用十分广泛。
例如,在润滑油、涂料、胶粘剂和液压系统中,黏弹性体流体被用作传递动力、减小摩擦或固定组件的材料。
黏弹性体流体的流变学性质使得它们能够适应不同的工作环境和应用需求。
医学领域在医学领域,黏弹性体流体的应用主要集中在生物材料和医疗器械中。
例如,黏弹性体流体被制成人工关节润滑液,以减少关节疼痛和损伤。
此外,黏弹性体流体的流变学性质也被用于研究和治疗疾病,如心血管疾病和癌症。
化学领域在化学领域,黏弹性体流体的应用主要包括聚合物凝胶和液晶材料。
黏弹性体流体的流动性和变形性使得它们在聚合物合成和纳米材料制备中发挥重要作用。
此外,黏弹性体流体还可以用于药物传递系统、涂料和颜料的制备等。
黏弹性体流体的研究方法流变学实验流变学实验是研究黏弹性体流体的一种常用方法。
通过测量流体在不同应变速率下的剪切应力和应变,可以得到流体的流变学性质。
粘弹性流体的特性韦森堡数和约束松弛时间的定义和计算

粘弹性流体的特性韦森堡数和约束松弛时间的定义和计算粘弹性流体的特性:韦森堡数和约束松弛时间的定义和计算粘弹性流体是一种介于固体和液体之间的物质,它具有同时表现出粘性和弹性特性的特殊流体。
在许多工程和科学领域中,了解和掌握粘弹性流体的特性对于设计和分析具有重要意义。
本文将重点介绍粘弹性流体的两个关键特性:韦森堡数和约束松弛时间的定义和计算方法。
一、韦森堡数的定义和计算韦森堡数(Wi)是用来描述粘弹性流体中粘性和弹性之间相互作用程度的无量纲指标。
它定义为粘性应力和弹性应力比值的乘积。
Wi = (η ×γ̇) / G其中,η是粘性系数,γ̇是剪切速率,G是弹性模量。
韦森堡数的数值越大,表示粘性作用在流体运动中的影响越突出,反之则表示弹性作用占主导地位。
韦森堡数的计算可以通过实验方法得到,也可以通过粘弹性流体的流动模型来进行理论计算。
二、约束松弛时间的定义和计算约束松弛时间是用来描述粘弹性流体在受到外部扰动后,恢复到稳定状态所需的时间。
它是一个衡量粘弹性流体粘弹性特性的重要参数。
约束松弛时间(λ)的定义可以通过粘弹性流体的弛豫模型来理解。
在弛豫模型中,粘弹性流体的应力或应变在受到外部扰动后,会经历一个渐进逐渐减小的过程,最终趋于稳定。
约束松弛时间定义为应力或应变衰减到初始值的1/e(约等于0.368)所需的时间。
λ = η / G其中,η是粘性系数,G是弹性模量。
约束松弛时间越短,表示粘弹性流体能够更快地恢复到稳定状态,具有更强的弹性特性;相反,约束松弛时间越长,则表示流体粘性效应更为显著。
三、计算示例假设我们具有一个粘弹性流体样品,并进行了剪切实验以获得相关的物理参数。
已知该样品的粘性系数η为10 Pa·s,弹性模量G为5e3 Pa,剪切速率γ̇为1/s。
我们可以根据上述定义和计算公式来求解韦森堡数和约束松弛时间。
首先,计算韦森堡数:Wi = (10 Pa·s × 1/s) / 5e3 Pa = 2e-3接下来,计算约束松弛时间:λ = 10 Pa·s / 5e3 Pa = 2e-3 s通过以上计算,我们得到了该粘弹性流体样品的韦森堡数和约束松弛时间的数值。
力学中的流体力学及粘弹性流体的性质研究

力学中的流体力学及粘弹性流体的性质研究流体力学是力学的一个分支,主要研究流体的运动规律和性质,包括流体内部的流动状态、压力分布、阻力、混合等。
流体力学是许多领域的基础,比如工程、物理、化学、生物等。
本文将着重介绍流体力学中的粘弹性流体及其特性。
1. 粘弹性流体的性质粘弹性流体一般指那些既具有液体的流动性质,又具有固体的弹性性质,即既能够流动,又能够回复原来的状态。
这些物质的特性通常表现为粘性和弹性的耦合,即应力和应变的关系不再是线性的,而是非线性的。
因此,粘弹性流体是一类比较复杂的流体,具有复杂的流动特性。
粘弹性流体的流动特性可以用许多不同的方法来描述,其中最常用的方法是使用粘度和弹性来描述流体的流动行为。
粘度通常是指流体内部的阻力,而弹性通常是指流体内部的应变能。
这两个特性可以同时影响粘弹性流体的流动规律。
2. 粘弹性流体的流变学流变学是研究物质流动过程的科学,它涉及到物质的变形和变形速率。
在流变学中,粘弹性流体是一个十分重要的研究对象,因为它是一类具有复杂性的非牛顿流体。
不同于牛顿流体,粘弹性流体在受到剪切应力时,它的应变率不再是线性的。
为了描述这种非线性,人们提出了许多不同的流变模型,例如齐奇模型、Maxwell模型、Oldroyd模型等等。
这些模型在模拟不同类型的流体流动行为上具有广泛的应用。
3. 粘弹性流体的应用由于其独特的物理特性,粘弹性流体在许多实际应用中发挥了重要作用。
以下是一些具体的应用:3.1 生物医学粘弹性流体在医疗应用中具有广泛的应用,例如用来测试肌肉收缩情况、诊断和治疗疾病、设计人工关节等等。
3.2 工业应用许多工业应用需要使用粘弹性流体,例如制造环氧树脂、设计高分子半导体材料、生产润滑剂以及打印油墨等等。
3.3 土木工程在土木工程中,粘弹性流体的研究主要集中在软基土壤的力学性质方面。
这类土壤通常是由于各种原因引起的松软或压缩,以至于难以承受重压。
研究粘弹性流体在软基土壤中的特性和行为对于改善工程质量具有重要意义。
2.4 粘滞流体的运动规律

1 1 2 2 1 gh1 P 2 gh2 P2 E 1 2 2
2
如果流体在均匀水平管中稳
定流动,则:
P P E 1 2
可见:P1>P2,因此,水平 均匀细管中,必须保持一定 的压强差,才能使粘性流体
做稳定流动。
若是均匀的开放的管中维 持稳定流动,由 1
3
P=R f Q 5.97 104 1.0 104 5.97Pa
可见:在主动脉中,血压的下降是微不足道的。
10
第四节 粘滞流体的运动规律
一、粘滞性流体的伯努利方程 二、泊肃叶定律 三、斯托克斯定律
11
三、斯托克斯定律
物体在流体中作匀速运动时,表面附着一层流体,
是流体在半径r处的速度梯度。 由于流体做稳定流动,流体受力平衡,即:
d (P1-P2)r 2rL dr
2
6
P1 P2 所以:d rdr 2L
P P2 2 积分得: 1 r C 4 L
P1 P2 2 R 因为r =R时,v=0的条件,求得: C 4L P P2 2 2 所以: 1 (R r ) 4 L
与物体一起运动,因此受到粘性力的作用。若物体时
球形的,球体所受阻力大小为(R为球的半径,v为
球体相对于流体的速度 ) :
f 6R
此式即为斯托克斯定律
4 G R 3 g 3
球在流体中受到的重力为: 球受到的浮力为(流 体的密度为σ):
4 3 F浮 R g 3
球受到的流体的阻力:
2.4 粘滞流体的运动规律
14
4
R为管子半径,ŋ为流体粘度系数, L为管子的长度。此式即为泊肃叶定律。
粘弹性流体的微观结构特性与流动行为研究

粘弹性流体的微观结构特性与流动行为研究第一章:引言粘弹性流体是指具有粘性和弹性特性的流体。
这种流体在现实世界中处处可见,涉及到许多领域如化学工业、生物医学、环境科学等。
研究粘弹性流体的微观结构特性和流动行为,对于开发新的材料,研究生物体液的行为以及改进工业生产过程等具有重要意义。
本文将介绍粘弹性流体的微观结构特性、流动行为以及目前研究中的问题和挑战。
第二章:粘弹性流体的微观结构粘弹性流体的微观结构是决定其物理性质和流动行为的关键。
在微观尺度下,粘弹性流体是由高分子链所组成的,这些链之间会通过物理化学作用结合起来形成网络结构。
这种网络结构会决定粘弹性流体的高度可塑性和弹性行为。
其中,高分子的分子量、分子结构以及网络结构的均匀性和相互作用都会影响流体的物理性质。
粘弹性流体的物理性质与其的微观结构也有密切的关系。
当高分子链之间的相互作用力较小时,粘弹性流体表现出低弹性的特点,容易流动。
而当高分子链相互作用力较强时,会形成三维的网络结构,此时粘弹性流体表现出较强的弹性行为。
第三章:粘弹性流体的流动行为粘弹性流体的流动行为是研究粘弹性流体的一个关键问题。
粘弹性流体的流动行为不同于牛顿流体的行为,其流动性质与外部应力场的时间依赖特性紧密相关。
其缘由在于粘弹性流体的微观结构会对它的流动行为产生影响。
粘弹性流体在低剪切速率下呈现出黏弹性特性,而在高剪切速率下呈现出牛顿流体的行为。
当外部应力越来越大时,高分子链网络会断裂,从而使得粘弹性流体表现出牛顿液体的行为。
此时粘弹性流体的黏度与应力成正比。
粘弹性流体的流体行为具有时间依赖特性。
当外部应力作用于粘弹性流体上时,粘弹性流体会表现出瞬时反应,其粘性行为主要由高分子链所组成的网络结构控制。
当外部应力撤离时,粘弹性流体会慢慢恢复到原来的状态,此时高分子链的弹性特性会成为主要控制因素。
此种时间依赖的行为会影响粘弹性流体的流动稳定性,并增加其处理和控制的难度。
第四章:研究中的问题和挑战目前,研究人员仍然面临着粘弹性流体的许多难题和挑战。
黏弹性流体

黏弹性流体引言黏弹性流体是一种特殊的流体,具有介于固体和液体之间的性质。
其黏性使其能够流动,而其弹性使其能够恢复形状。
本文将介绍黏弹性流体的基本概念、性质以及在工程和科学领域中的应用。
基本概念黏性和弹性黏弹性流体的特性主要由黏性和弹性两个方面决定。
黏性是指流体抵抗形变和流动的能力,它使得流体能够流动并保持流动状态。
而弹性是指流体在受到应力后能够恢复原来的形状。
黏弹性流体的特殊之处在于其黏性和弹性之间的协调和平衡。
黏弹性流体的分类黏弹性流体可以分为线性黏弹性流体和非线性黏弹性流体两类。
线性黏弹性流体的应力和应变之间的关系具有线性性质,如胶水和某些塑料。
非线性黏弹性流体的应力和应变之间的关系则不是线性的,常见的例子有血液和胶体溶液。
黏弹性流体的性质流变学流变学是研究物质流动和变形行为的学科。
在黏弹性流体中,流变学描述了应力与变形速率之间的关系。
黏弹性流体的应力可以通过应力应变关系来描述,其中应力与应变率呈指数关系。
这种非线性关系表明黏弹性流体在流动过程中不同位置的变形速率不同。
粘度粘度是衡量黏弹性流体黏性的物理量。
它是指流体内部分子间作用力的大小和分子运动的速度之间的关系。
粘度越大,流体越黏稠;粘度越小,流体越稀薄。
黏弹性流体的粘度通常是变化的,随着应变率的增加而减小,这种现象称为剪切变稀。
刚性模量和阻尼比刚性模量是指黏弹性流体承受外力时的刚性程度。
它是流体中分子与分子之间相互作用力的大小。
阻尼比则衡量了流体内部能量耗散的大小。
阻尼比越大,流体的能量耗散越大,其刚性也相对较高。
黏弹性流体的应用工程领域在工程领域,黏弹性流体的应用非常广泛。
比如,黏弹性流体在润滑剂中的应用可以减少机械设备的摩擦和磨损,提高工作效率和寿命。
此外,黏弹性流体在混凝土工程中被用作掺和剂,以改善混凝土的流动性和抗压强度。
医学领域黏弹性流体在医学领域也有重要的应用。
例如,黏弹性流体被用来制造假肢和矫形器,以帮助残疾人恢复运动功能。
粘弹性流体力学模型与应用研究

粘弹性流体力学模型与应用研究粘弹性流体力学是研究粘弹性流体的运动行为和力学性质的学科领域。
粘弹性流体是指具有同时表现出粘性和弹性特性的流体,其运动行为不仅受到流体的黏度和密度等因素的影响,还受到流体的弹性特性的影响。
在实际应用中,粘弹性流体力学模型可以用于解释和预测各种流体的行为,包括聚合物溶液、胶体悬浮液、生物体液等。
粘弹性流体力学的研究对象通常是非牛顿流体,即流体的黏度随着应力的变化而变化。
与牛顿流体不同,非牛顿流体的流动行为无法用简单的线性关系来描述,而是需要引入更复杂的模型来描述其流动行为。
其中,最常用的模型包括Maxwell模型、Kelvin模型和Oldroyd模型等。
Maxwell模型是最简单的粘弹性流体模型之一,它将粘弹性流体的应力应变关系分为两个部分:弹性部分和粘性部分。
弹性部分描述了流体在受到应力时的弹性回复,而粘性部分则描述了流体在受到应力时的黏滞阻力。
Kelvin模型在Maxwell模型的基础上增加了一个弹性元件,用于描述流体的弹性特性。
而Oldroyd模型则是将Maxwell模型和Kelvin模型相结合,用于描述更复杂的粘弹性流体。
粘弹性流体力学模型的应用非常广泛。
在化工工艺中,粘弹性流体力学模型可以用于设计和优化各种流体的混合、输送和分离等过程。
在生物医学领域,粘弹性流体力学模型可以用于研究血液的流动行为、细胞的变形特性等。
在地质学和地球物理学领域,粘弹性流体力学模型可以用于模拟地下岩石和土壤的变形和流动行为。
此外,粘弹性流体力学模型还可以应用于材料科学、食品工程、环境工程等领域。
例如,在材料科学中,粘弹性流体力学模型可以用于研究聚合物材料的加工和成型过程,以及纳米颗粒的悬浮和固液分离等。
在食品工程中,粘弹性流体力学模型可以用于研究食品的流变性质和质感特性等。
在环境工程中,粘弹性流体力学模型可以用于研究水体和土壤的流动行为,以及废水处理和土壤污染修复等。
总之,粘弹性流体力学模型在科学研究和工程应用中具有重要的意义。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
并为负值。 为描述剪切流场中流体流变性随剪切速率的变化性质,需要 下面3个物料函数: (1)剪切粘度
µ (γɺ )=τ 12 γɺ
ψ 1 (γɺ )= N 1 2 (2)第一法向应力系数 γɺ
(3)第二法向应力系数
ψ 2 (γɺ )= N 2
γɺ 2
ψ µ 对于牛顿流体, 1 (γɺ )和 ψ 2 (γɺ ) 均为0, (γɺ ) 为常数。
蠕变与回复曲线
5.线性粘弹性与非线性粘弹性 流体的粘弹性可分为线性粘弹性和非线性粘弹性。线性粘弹 性即应力、应变和应变速率之间成线性关系。粘弹性流体往往 只能在较小的形变或形变速率下才出现线性特性。在较大的应 变或剪切速率下,应力、应变和应变速率之间一般不成线性关 系,即流体呈现非线性粘弹性。对非线性粘弹性状态下的流体, 所测的流变性数据受实验参数和测量系统几何尺寸的影响非常 大,不是绝对值,只能用作比较。目前人们对粘弹性流体流变 性的认识、描述在很大程度上仍停留在线性粘弹性范围。
2.应力松弛 对粘弹性流体施加一恒定的应变,即保持应变随时间不变 见 图中的曲线a,那么流体内所受到的应力随时间而逐渐减小,这 种特性称应力松弛。
τ → ∞ 时, > 0 当 t → ∞ 时, = 0 τ
当t
,称部分应力松弛,如图中的曲线b所示; ,称完全应力松弛,如图中的曲线c所示。
τ ϒ
a
b
c t
τ
a
b
ϒ
弹性滞后曲线示意图
4.蠕变与回复 对理想固体施加一恒定的应力时,固体中瞬间产生对应的 应变;当应力消除时,产生的应变也瞬间完全回复。对理想流 体施加恒定的应力时,流体内产生的应变会随应力作用时间的 增加而逐渐增大;当应力消除后,流体内产生的应变不会回复。 对粘弹性流体,对于应力的突然施加与突然消除,得到的应变 -时间曲线是介于理想固体与理想流体之间的独特的特性曲线。 在应力施加阶段的应变-时间曲线为蠕变曲线,在应力消除后 对应的应变-时间曲线为回复曲线变曲线为通过原点的直线,而且应力上 升与下降对应的应力-应变曲线完全重合,如图中的曲线a。 而粘弹性流体的应力-应变曲线不是直线,而且其应力上升与 下降对应的应力-应变曲线不重合,如图中的曲线b,这种特 性称弹性滞后。滞后环的面积与应变随时间的变化速率有关, 即应力是应变与时间的函数。
法向方向,j代表应力分量的方向,如下图所示,可用张量表示如 下。
τ 11 τ 12 τ 13 τ τ ij = 21 τ 22 τ 23 τ 31 τ 32 τ 33
其中,应力分量的下标1、2、3分别对应于x、y、z方向。τ11 、 τ
22、
τ33为法向应力,其它6个为剪切应力,并且, τ12= τ21 ,
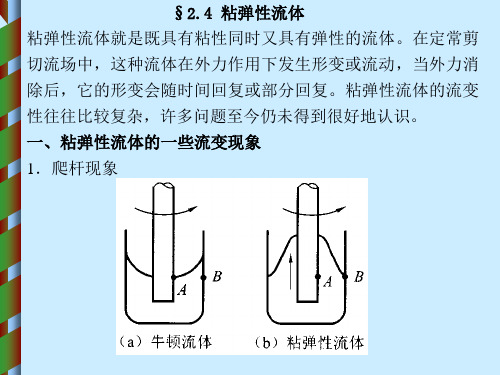
§2.4 粘弹性流体 粘弹性流体就是既具有粘性同时又具有弹性的流体。在定常剪 切流场中,这种流体在外力作用下发生形变或流动,当外力消 除后,它的形变会随时间回复或部分回复。粘弹性流体的流变 性往往比较复杂,许多问题至今仍未得到很好地认识。 一、粘弹性流体的一些流变现象 1.爬杆现象
2.挤出胀大现象
3.同心套管轴向流动现象
4.回弹现象
5.无管虹吸现象
6.次级流现象
7.紊流减阻现象
二、粘弹性流体的流变特征 1.法向应力与法向应力差 当力F作用于物体时,物体内部体积元所受的总应力(或物体内
τ 部某一点所受到的总应力) 可用九个应力分量τ
τ
可分解为九个应力分量 τ
ij
ij
表示,或者说
,其中i代表应力分量作用的平面
τ13= τ31 , τ23= τ32 。对简单的剪切流动, τ13= τ31=0, τ23= τ32 =0, 故只有剪切应力τ12起作用。
τ 11-τ 22=N1 为 第 一 法 向 应 力 差 , 产 生 轴 向 压 力 , 引 起
Weissenberg效应和挤出物胀大现象。
τ 22-τ 33=N 2为第二法向应力差,产生径向压力,通常很小,
