高等代数第九章 4第四节 正交变换
高等代数课件(北大版)第九章-欧式空间§9

中向量 Y 使 B 到它的距离 ( Y B ) 比到
L (1 ,2 , ,s)中其它向量的距离都短.
§9.7 向量到子空间的距离 数学与计算科学学院
设 C B Y B A X ,
为此必 C L (1 ,2 , ,s )
这等价于 ( C , 1 ) ( C , 2 ) ( C , s ) 0 , (4)
第九章 欧氏空间
§1 定义与基本性质 §2 标准正交基 §3 同构 §4 正交变换 §5 子空间
§6 对称矩阵的标准形 §7 向量到子空间的
距离─最小二乘法 §8酉空间介绍 小结与习题
2024/10/23
数学与计算科学学院
§9.7 向量到子空间的距离
一、向量到子空间的距离 二、最小二乘法
§9.7 向量到子空间的距离 数学与计算科学学院
§9.7 向量到子空间的距离 数学与计算科学学院
即为
1 0 6 . 7 5 a 2 7 . 3 b 1 9 . 6 7 5 0 2 7 . 3 a 7 b 5 . 1 2 0 解得 a 1 .0 5 , b 4 .8 1(取三位有效数字).
§9.7 向量到子空间的距离 数学与计算科学学院
可能无解, 即任意 x1,x2, ,xn都可能使
n
ai1x1ai2x2 ainxnbi 2
i 1
不等于零.
(2)
§9.7 向量到子空间的距离 数学与计算科学学院
设法找实数组 x10,x02,
,x0 使(2)最小, n
这样的 x10,x02,
,x0 为方程组(1)的最小二乘解, n
此问题叫最小二乘法问题.
最小二乘法的表示:
设
n
n
实数域上的正交变换

实数域上的正交变换学院:数学与计算机科学学院班级:2011级数学与应用数学姓名:***学号:指导教师:***日期:2012.06.01实数域上的正交变换的分类***(西北民族大学数学与应用数学专业,兰州730124)指导教师***摘要:在这里主要研究的是正交变换的分类,首先是从欧式空间到正交变换,然后从有限维数欧式空间研究正交变换,通过从简单的二维,三维到有限维向n维推广,最终掌握欧氏空间、性质、判别及其初步分类。
关键字:欧氏空间正交变换分类一.正交变换的定义欧氏空间V 的一个线性变换叫δ作一个正交变换,如果对于任意V∈ξ都有:|)(ξδ|=|ξ|注意:欧式空间中的正交变换是几何空间中保持长度不变的正交变换的推广。
二.欧氏空间的概念设V 是实数域R 上一个向量空间。
如果对于V 中任意一对向量ηξ,有一个确定的记作<ηξ,>的实数与他们对应,叫作向量ξ与η的内积(或标量积),并且下列条件被满足:(i)<ηξ,>=<ξη,> (ii)<ζηξ,+>=<ζξ,>+<ζη,>(iii)<a ηξ,>=a<ηξ,> (iv)当0≠ξ时,<ξξ,>>0这里ζηξ,,是V 中任意向量,a 是任意实数,那么V 叫作这个内积来说的一个欧氏空间。
三.正交变换的性质:定理1 欧氏空间V 的一个线性变换σ是正交变换的充分且必要条件是:对于V 中任意向量ξ,η,(1)<σ(ξ),σ(η)>=<ξ,η>.证明: 条件的充分性是明显的。
因为在(1)中取ξ=η,就得到⎥σ(ξ)⎥⎥2=⎥ξ⎥⎥2,从而⎥σ(ξ)⎥=⎥ξ⎥。
反过来,设σ是一个正交变换。
那么对于ξ,η∈V ,我们有⎥σ(ξ+η)|⎥2=⎥ξ+η⎥|2然而⎥σ(ξ+η)⎥=<σ(ξ+η),σ(ξ+η)>=<σ(ξ)+σ(η),σ(ξ)+σ(η)>=<σ(ξ)σ(ξ)+<σ(η),σ(η)>+2<σ(ξ),σ(η)>;⎥ξ+η⎥⎥2=<ξ+η,ξ+η>=<ξ,ξ>+<η,η>+2<ξ,η>.由于<σ(ξ),σ(ξ)>=<ξ,ξ>,<σ(η),σ(η)>=<η,η>,比较上面两面个等式就得到()(),,ηξησξσ=定理2 设V 是一个n 维欧氏向量空间,σ是V 的一个线性变换。
正交变换的应用及数学方法论意义

指导教师:赵峰2012年4 月25 日原创性声明本人郑重声明: 所提交的学位论文是本人在导师指导下, 独立进行研究取得的成果. 除文中已经注明引用的内容外, 论文中不含其他人已经发表或撰写过的研究成果, 也不包含为获得聊城大学或其他教育机构的学位证明书而使用过的材料. 对本文的研究做出重要贡献的个人和集体, 均已在文中以明确方式标明. 本人承担本声明的相应责任.学位论文作者签名: 日期指导教师签名: 日期目录引言 (1)1 正交变换的定义 (1)2 正交变换的性质 (2)3正交变换法化二次标准型 (2)3.1正交变换化二次标准型的步骤 (3)3.2正交变换在二次标准型中的应用 (3)4 正交变换在积分中的应用 (7)4.1在多元积分学中的应用 (7)4.2重积分在正交变换下形式不变性 (9)4.3 正交变换在区面积分中的应用 (10)5 正交变换的数学方法论的意义 (12)5.1一般化 (12)5.2代数化 (12)5.3 模型化 (12)结语 (13)参考文献 (14)致谢 (15)摘要正交变换是欧氏空间中一类重要的变换,是保持度量不变的变换,正因为它有这一特征,使正交变换在高等代数中起着重要的作用.不仅如此,它在其它领域也有着广泛的应用,如在积分应用中,在多重积分及其曲面积分等方面.本文简单的介绍了正交变换的定义及其性质,讨论了正交变换化二次标准型的步骤及其广泛应用,运用正交变换进行变量替换是将数学分析与代数方法结合的例证,证明了第一类曲面积分和重积分在正交变换下的不变性。
因而可将其应用于简化多元函数积分计算.正交变换的此类应用充分体现了一般化、代数化、模型化的数学方法论。
关键词:正交变换;二次型;变量替换;重积分;曲面积分;数学方法论AbstractThe orthogonal transformation, a transformation that maintains the measure invariable, is one of the most important transformations in the field of euclidean space.Benifiting from this feature, it plays an important role in the advanced algebra. Furthermore,it applies widely in many other fields,such as the applications of integration, like the multiple integrations , the surface integrations and so on.This paper introduces the definition and properties of the orthogonal transformation briefly,it also discusses the procedures and wide applications of the secondary standard of the orthogonal transformation,using the orthogonal transformation to make a variable substitution is a good instance to prove the perfect combination of the mathematical analysis and algebraic approach,it demonstrates the invariance of the the first class of the surface integrations and double integrations under the orthogonal transformation. Thus,the orthogonal transformation can be applied in( the numerical integration of simplifying the function of many cariables.This kind of application of the orthogonal transformation fully embodies such mathematical methodologies as the generalization,the algebraization, and the modeling.Keyword:Orthogonal transformation; Quadratic ;Variable Substitution;Multiple integral;Surface integrals;Mathematical methodology引 言随着近代数学的发展,数学的各学科间的相互渗透显得越来越重要,特别是代数的方法运用更为突出,在现行的数学分析教材中,某些内容也注意到代数的方法的运用,但还需进一步加强, 将数学分析与代数方法结合, 是解决问题的途径之一, 更是培养学生数学能力的重要内容,有利于培养学生综合运用基础知识的能力。
高等代数【北大版】9

| 1 | 2,
|
3
|
3
4 10
,
| 2 |
2, 6
|
4
|
5
4 14
.
§9.2 标准正交基
于是得 R[ x]4的标准正交基
1
|
1
1
| 1
2 ,
2
2
|
1
2
|
2
6 x
2
3
|
1
3
| 3
10 4
14 (5x3 3x) 4
§9.2 标准正交基
4.标准正交基间的基变换
设 1, 2 , , n与 1,2 , ,n 是 n 维欧氏空间V中的
1. 定义
设 A (aij ) Rnn , 若A满足 则称A为正交矩阵.
AA E
2. 简单性质
1)A为正交矩阵 A 1. 2)由标准正交基到标准正交基的过渡矩阵是正交
矩阵.
§9.2 标准正交基
3)设 1, 2 , , n 是标准正交基,A为正交矩阵,若 (1,2 , ,n ) (1, 2 , , n ) A
(6)
§9.2 标准正交基
由公式(3), 有
(i , j ) a1i1 j a2i 2 j
aninj
1 0
i i
j j
, (7)
把A按列分块为 A A1, A2, , An
由(7)有
A1
AA
A2
A1
,
A2
,
An
, An En
(8)
§9.2 标准正交基
三、正交矩阵
注:
① 由正交基的每个向量单位化, 可得到一组标准 正交基.
9.4 正交变换

A 是正交矩阵 → (A 1, A 2 , , A n ) (1, 2 , , n )A ,A 可逆
→ A 1, A 2 , , A n 是 V 的基,且
a1i
A i (1,2 ,
,
n
)
a
2i
n
一 正交变换的概念及性质 定义9 V是欧氏空间,A (∈L(V))称为正交变换,如 果对任意的α,β∈V, (Aα,Aβ) = (α,β).
性质1 (定理1) V是欧氏空间,A ∈L(V),则以下条 件等价:
1) A 是正交变换; 2) 对任意的α∈V,│Aα│=│α│(即保持向量的长
度不变);
3) ε1,ε2, ···,εn 是V的标准正交基,则Aε1,Aε2, ···,Aεn 是V的标准正交基;
σ(α)
准正
义,σ(ε1) =ε1, σ(ε2) =ε2, σ(ε3) = -ε3 . 对任意的α∈V3 ,设 α= x1ε1 + x2ε2 + x3ε3 , 则
σ(α) = x1σ(ε1) + x2σ(ε2) + x3σ(ε3) = x1ε1 + x2ε2 -x3ε3 ,
故 |σ(α)|2 = x12 + x22 + x32 = |α|, 即推出 |σ(α)|= |α|,所以σ是正交变换. 由如上过程可知
以下等式成立,即σ的行列式|B|= -1,即σ是第
二类正交变换.
1
(1,2 ,3 ) (1,2 ,3)B,
B
1
1
作业: P394 习题11,12,13,14,15.
9.4正交变换

正交变换
§9.4
正交变换
一、正交变换的定义及性质 二、正交变换的类型
第九章 欧几里得空间
线性空间的线性变换,实际上是保持向量线性运算的变换。 在欧氏空间中,除了向量的线性运算外,还有向量的度量性质, 因此有必要讨论保持度量关系不变的线性变换。其中保持长度 不变的线性变换无疑是重要的。 例9.4.1 在欧氏空间 R 2 中有一个坐标旋转变换,在把平面 围绕原点逆时针旋转 θ 角之后,平面上向量之间什么关系保持 不变? 向量的长度、向量的夹角、向量的距离等保持不变。 能否在一般欧氏空间也找到具有这种性质的线性变换? 这种线性变换就是本节要研究的正交变换。
充分性。 若 σ 保持向量的内积不变, 于是对 ∀α ∈ V , σα = (σα , σα ) = (α , α ) = α 故 σ 是正交变换。
第九章 欧几里得空间
定理9.4.2 设 σ 是n维欧氏空间V的一个线性变换。 σ 是 正交变换的充要条件是:σ 把V的标准正交基变为标准正交基。 证明:必要性。若 σ 是正交变换,由定理9.4.1知 σ 保持向量的内积不变。 ∀α , β ∈ V , (σα , σβ ) = (α , β ) ⎧1, i = j α1 , α 2 , , α n 是V的一个标准正交基,则有 (α i , α j ) = ⎨ 设 ⎩ 0, i ≠ j ⎧1, i = j (σα i , σα j ) = (α i , α j ) = ⎨ ⎩ 0, i ≠ j 因此 σα1 , σα 2 , , σα n 也是V的一个标准正交基。 充分性。若 σ 把V的标准正交基变为标准正交基。 设 α1 , α 2 , , α n 是V的一个标准正交基,则 σα1 , σα 2 , , σα n 也是V的一个标准正交基。 ∀α ∈ V , 设 α = k1α 1 + k2α 2 + + knα n , σα = k1σα1 + k2σα 2 + + knσα n , 则 于是 σα = ki2 = α , ∑ 故 σ 是正交变换。
关于正交变换的分类

实数域上正交变换的分类一、正交变换定义1.1 设A是欧氏空间V的一个线性变换,若A保持向量的内积不变,即对于任意的α,βεV都有(Aɑ,Aβ) = (ɑv,β),则称A为V的正交变换.二、等价条件定理2.1 设A是n维欧氏空间V的一个线性变换,则下列命题等价:1)A是正交变换;2)A保持向量的长度不变,即对于V,|Aα|=|ɑ|;3)A把V的规范正交基变为V的规范正交基;4)A在规范正交基下的矩阵是正交矩阵.⇒2)对于αεV, 由证:1)(Aɑ,Aɑ)=(ɑ,ɑ),即得:|Aɑ|=|ɑ|2)⇒3)设ε1,ε2,…,εn是V的任一规范正交基,记εi+εj=ɑεV.由|Aɑ|=|ɑ|或(Aɑ,Aɑ)=(ɑ,ɑ)得(A(εi+εj),A(εi+εj))=(εi+εj,εi+εj)而(A(εi+εj),A(εi+εj))=(Aεi,Aεi)+2(Aεi,Aεj)+(Aεj,Aεj)=(εi ,εi)+2(εi ,εj)+(εj ,εj)(εi+εj,εi+εj )=(εi ,εi)+2(εi ,εj)+(εj ,εj)故 A ε1,A ε2,…,A εn 是V 的一组规范正交基. 3)⇒4)设ε1,ε2,…,εn 是V的规范正交基,A(ε1,ε2,…,εn)=(A ε1, A ε2,…,A εn)= (ε1,ε2,…,εn)A由3), A ε1,A ε2,…,A εn 是0,(,)(,)1,i j i j i j A A i j εεεε≠⎧∴==⎨=⎩V的规范正交基,故A可看作是由规范正交基ε1,ε2,…,εn到规范正交基Aε1,Aε2,…,Aεn的过渡矩阵,A是正交矩阵.4) 1)设ε1,ε2,…,εn是V 的规范正交基,且A在此基下的矩阵A为正交矩阵.由(Aε1,Aε2,…,Aεn)= (ε1,ε2,…,εn)A,知Aε1,Aε2,…,Aεn也是V的规范正交基,设α=x1ε1+x2ε2+……x nεn,Β=y1ε1+y2ε2+……y nεn,Aɑ=x1Aε1+x2Aε2+…+xnAεnAβ=y1Aε1+y2Aε2+…+ynAεn (Aα,Aβ)= x1y1+x2y2+…+xnyn(α,β)= x1y1+x2y2+…+xnyn 所以 (A α,A β)=(α,β),故A 为正交变换.三、规范正交基到规范正交基的过渡矩阵。
高等代数-欧几里得空间

2) (, ) (, ) (, )
s
s
推广: ( , i ) ( , i )
i 1
i 1
3) (0, ) 0
§9.1 定义与基本性质
二、欧氏空间中向量的长度
1. 引入长度概念的可能性
1)在 R3向量 的长度(模) . 2) 欧氏空间V中, ,V , (, ) 0
使得 有意义.
③ ( , ) R.
§9.1 定义与基本性质
例1.在 Rn 中,对于向量
a1,a2, ,an , b1,b2, ,bn
1)定义 ( , ) a1b1 a2b2 anbn
(1)
易证 ( , ) 满足定义中的性质 1 ~ 4 .
所以, ( , ) 为内积. 这样Rn 对于内积 ( , ) 就成为一个欧氏空间.
2. 向量长度的定义
,V , ( , ) 称为向量 的长度. 特别地,当 1时,称 为单位向量.
§9.1 定义与基本性质
3. 向量长度的简单性质
1) 0; 0 0
2) k k
3)非零向量 的单位化:
1.
(3)
§9.1 定义与基本性质
三、欧氏空间中向量的夹角
1. 引入夹角概念的可能性与困难
注:
① 零向量与任意向量正交.
②
, ,
2
即 cos, 0
.
§9.1 定义与基本性质
5. 勾股定理
设V为欧氏空间, , V
2 2 2
证: 2 , , 2, ,
2 2 2
( , ) 0
.
§9.1 定义与基本性质
推广:若欧氏空间V中向量1,2 , ,m 两两正交,
当 n 3 时,1)即为几何空间 R3中内积在直角 坐标系下的表达式 . ( , )即 .
正交变换数学三

正交变换数学三正交变换是数学中的一个重要概念,广泛应用于线性代数、几何学和物理学等领域。
本文将从不同角度介绍正交变换的定义、性质及应用。
一、正交变换的定义正交变换是指保持向量长度和夹角不变的线性变换。
具体而言,对于任意两个向量u和v,如果它们的内积在正交变换后仍然保持不变,即有(u, v) = (T(u), T(v)),其中T表示正交变换,则称T为正交变换。
二、正交变换的性质1. 正交变换的矩阵表示是正交矩阵,即满足A^T * A = I,其中A^T表示A的转置矩阵,I表示单位矩阵。
2. 正交变换的逆变换也是正交变换,即正交变换的逆矩阵也是正交矩阵。
3. 正交变换保持向量长度不变,即对于向量v,有||v|| = ||T(v)||,其中||v||表示向量v的长度。
4. 正交变换保持向量夹角不变,即对于向量u和v,有(u, v) = (T(u), T(v))。
5. 任意两个不平行的向量在正交变换后仍然保持不平行。
三、正交变换的应用1. 几何变换:正交变换在几何学中有着广泛的应用,如旋转、镜像、平移等。
正交变换可以保持几何图形的形状和大小不变,常用于计算机图形学、计算机视觉等领域。
2. 物理学中的坐标变换:正交变换可以将一个坐标系转换为另一个坐标系,常用于解决物理学中的坐标变换问题,如刚体运动的描述、电磁场的变换等。
3. 数据压缩与降维:正交变换在数据处理中有着重要的应用,如主成分分析(PCA)就是一种基于正交变换的数据降维方法。
通过正交变换,可以将高维数据映射到低维空间,保留数据的主要信息。
4. 信号处理:正交变换在信号处理中也有广泛应用,如傅里叶变换、小波变换等。
正交变换可以将信号在不同域之间进行转换,常用于信号压缩、滤波、频谱分析等。
正交变换是一种保持向量长度和夹角不变的线性变换。
它具有许多重要的性质,如矩阵表示是正交矩阵、保持向量长度和夹角不变等。
正交变换在几何学、物理学、数据处理和信号处理等领域都有着广泛的应用。
M正交变换和仿射变换
如果保持所有的点不动,即是一个恒等变换
那 么 就 有 = , 这 和 不 是 刚 体 运 动 矛 盾 .所 以
所以不能保持所有的点不动.
设 P 是 的 动 点 , 记 P ' = ( P ).
由 于 是 正 交 变 换 , 所 以 的 不 动 点 都 会 位 于 PP ' 的 垂 直 平 分 面 P上 .
设 P1 , P2 , P3 是 直 线 l 上 的 三 点 , 经 过 仿 射 变 换 变 成 直 线 l ' 上 ' ' ' ' ' ' ' ' 的 三 点 P1 , P2 , P3 .如 果 P1 P 2 P2 P3 , P1 P2 P2 P3 , 要 证 明 = '
,
那 么 是 一 个 保 持 A ' B ' C ' 不 变 的 正 交 变 换
A ' B ' C ' A ' B ' C '.
同 时 , ( P ) ( ( P ))
-1
正交变换
( ( P )) ( P ),
这 表 明 = .
例 题 2: 分 别 对 于 两 个 相 交 平 面பைடு நூலகம்的 两 个 反 射 的 乘 积 是一个旋转.
作业
7,10,11
复习:坐标变换
旧 坐 标 系 [ O , e1 , e 2 , e 3 ]
O ( a1 , a 2 , a 3 )
'
新 坐 标 系 [ O , e1 , e 2 , e 3 ] ' O O a 1 e1 a 2 e 2 a 3 e 3 .
正交变换在积分中的应用

目录1.正交变换 (1)1.1正交变换的定义 (1)1.2正交变换的性质 (1)2.正交变换在重积分中的应用 (1)2.1正交变换在二重积分中的应用 (2)2.2正交变换在三重积分中的应用 (3)3.正交变换在曲面积分中的应用 (6)3.1正交变换在第一型曲面积分中的应用 (6)3.2正交变换在第二型曲面积分中的应用 (13)4.正交变换在曲线积分中的应用 (15)4.1正交变换在第一型曲线积分中的应用 (15)4.2正交变换在第二型曲线积分中的应用 (16)5. 结束语 (18)参考文献 (19)1.正交变换1.1正交变换的定义在解析几何里,允许使用的变换都是保持向量的长度不变的.在欧式空间里,保持长度不变的线性变换——正交变换无疑是重要的.高等代数中给出了一般欧式空间中关于正交变换的定义.欧氏空间V 的一个线性变换σ叫作一个正交变换,如果对于任意的V ∈ξ,都有()ξξσ=.正交变换的另一种定义:欧氏空间V 的一个线性变换σ叫作一个正交变换,如果对于任意的V ∈ηξ,,都有()()〉〈=〉〈ηξησξσ,,.1.2正交变换的性质实际上正交变换是欧氏空间V 到自身的一个同构映射,因而正交变换的乘积与正交变换的逆变换还是正交变换,在标准正交基下,正交变换与正交矩阵对应,因此正交矩阵的乘积与正交矩阵的逆矩阵也是正交矩阵.如果A 是正交矩阵,则由I AA T =可知12=A 即1±=A ,因此正交变换的行列式等于1或1-.行列式等于1的正交变换称为旋转或称为第一类的;行列式等于1-的正交变换称为第二类的.如果A 是正交矩阵,伴随矩阵*A 也是正交矩阵.若A 是()2>n n 阶正交矩阵时,当1=A 时,*A A T =,即ij ij A a =;当1-=A 时,*A A T -=,即ij ij A a -=.2.正交变换在重积分中的应用在多元函数积分中,变量替换法的选用与否,不只关系着积分计算的快与慢,有时甚至影响着积分的算得出与算不出.如计算⎰⎰≤++-22222)(R y x y xdxdy e .若要在直角坐标系下化为累次积分计算,则会遇到计算⎰⎰---2222x R dy e dx ey Rx 的问题,但我们无法将⎰-dy e y 2表示成初等函数,计算便无法进行下去.此题若用极坐标变换计算,则易于得出结果.由此可见,变量替换在多元函数积分中的重要作用.多元函数积分中的变量替换法是计算积分的重要方法,变量替换的目的使得被积函数简单或者是积分区域简化,但是实际应用时选择要用的替换有很大的随意性,并且存在一定的难度.因此引入新的积分变量的同时必须要考虑被积函数的性质和积分区域的形状,而对于某些多元函数积分问题应用“正交变换”的有关理论解决是一种较为简便且颇有成效的方法.2.1正交变换在二重积分中的应用引理2.1[1] 设变换T :()v u x x ,=,()v u y y ,=将uv 平面上由按段光滑封闭曲线所围的闭区域∆,一对一地映成xy 平面上的闭区域D ,函数()v u x ,,()v u y ,在∆内分别具有一阶连续偏导数且它们的函数行列式()()()∆∈≠∂∂=v u v u y x v u J ,,0),(,,, 则区域D 的面积())(⎰⎰∆=dudv v u J D ,μ.定理2.1[1] 设()y x f ,在有界闭区域D 上可积,变换T :()v u x x ,=,()v u y y ,=将uv 平面由按段光滑封闭曲线所围成的闭区域∆一对一地映成xy 平面上的闭区域D ,函数()v u x ,,()v u y ,在∆内分别具有一阶连续偏导数且它们的函数行列式()()()∆∈≠∂∂=v u v u y x v u J ,,0),(,,, 则 ()()()()()⎰⎰⎰⎰∆=dudv v u J v u y v u x f dxdy y x f D,,,,,.例1 进行适当的变量替换,化二重积分()⎰⎰≤+++122y x dxdy c by ax f ,()022≠+b a为一重的.解 设()b a ,为二维空间的一个向量,它的单位向量为⎪⎭⎫⎝⎛k b k a ,(其中22b a k +=),再将其扩充为二维空间的一个标准正交基,设为⎪⎭⎫⎝⎛k b k a ,,()11,b a 作正交变换⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛y x A v u ,这里⎪⎪⎭⎫ ⎝⎛=11b a k b k a A (1) 为正交矩阵,则 ⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛-v u A v u A y x T 1 两边转置得 ()()A v u y x ,,=∴()()1,,2222≤+=⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛=+v u v u AA v u y x y x y x T又因为1-=A A T 仍是正交矩阵且1±=T A ,于是变换的雅可比行列式为()()()1,,,±==∂∂=T A v u y x v u J 由(1)知ku by ax =+,于是由二重积分的变量替换公式得:()⎰⎰≤+++122y x dxdy c by ax f ()()⎰⎰≤++=122,v u dudv v u J c ku f()⎰⎰----+=221111u u dv du c ku f()⎰-+-=11212du c ku f u 即()=++⎰⎰≤+122y x dxdy c by ax f ()⎰-++-1122212du c u b afu此题选用正交变换兼顾了被积函数、积分区域的特点,较用其它的变换来解要简便.2.2正交变换在三重积分中的应用定理2.2[1] 设变换T :()w v u x x ,,=,()w v u y y ,,=,()w v u z z ,,=,将uvw 空间中的区域'V 一对一地映成xyz 空间中的区域V ,并设函数()w v u x ,,,()w v u y ,,,()w v u z ,,及它们的一阶偏导数在'V 内连续且函数行列式()0,,≠∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂=wz v z uz w yv y u yw x v x u x w v u J ,()',,V w v u ∈. 则 ()()()()()()⎰⎰⎰⎰⎰⎰=VV dudvdw w v u J w v u z w v u y w v u x f dxdydz z y x f ',,,,,,,,,,,,, 其中()z y x f ,,为V 上可积.例2 对于连续函数()z y x f ,,证明:()()()⎰⎰⎰⎰-≤++-=++11211222du ku f u dxdydz cz by ax f z y x π其中222c b a k ++=.证明 设()c b a ,,为三维空间的一个向量,它的单位向量为⎪⎭⎫⎝⎛k c k b k a ,,(其中222c b a k ++=),再将其扩充为三维空间的一个标准正交基,设为⎪⎭⎫⎝⎛k c k b k a ,,,()111,,c b a ,()222,,c b a 作正交变换⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛z y x A w v u ,这里⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=222111c b a c b a k c k b k a A (2) 为正交矩阵,则⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛-w v u A w v u A z y x T1 两边转置得 ()()A w v u z y x ,,,,=∴()()1,,,,222222≤++=⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛=++w v u w v u AA w v u z y x z y x z y x T又因为1-=A A T 仍是正交矩阵且1±=T A ,于是变换的雅可比行列式为()()()1,,,,,,±==∂∂=T A w v u z y x w v u J 由(2)知ku cz by ax =++,于是由三重积分的变量替换公式得:()()()()⎰⎰⎰⎰⎰⎰⎰⎰⎰≤++≤++≤++==++111222222222,,w v u w v u z y x dudvdw ku f dudvdw w v u J ku f dxdydz cz by ax f()()()⎰⎰⎰⎰--≤+--==1121111222du ku f u dvdw duku f u w v π其中222c b a k ++=证毕.化重积分为累次积分的变量替换,是计算重积分最常用的方法.但是,我们遇到的积分不一定能用它们算出来,所以有时不得不使用其它数学工具和方法.例3 设()33⨯=ija A 是正定矩阵,证明由椭球V :1a 31,ij ≤∑=j i j i x x 所围成的体积等于()21-detA 34π.证明 (即证()21321det 34-=⎰⎰⎰A dx dx dx Vπ)由于A 是对称正定矩阵,故∑=31,ij a j i j i x x 是正定二次型.由高等代数知,存在一个正交矩阵T ,使 ()321321',,diag 000000λλλλλλ=⎪⎪⎪⎭⎫ ⎝⎛=AT T 这里1λ,2λ,3λ是矩阵A 的三个正特征根.作正交变换⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛321321y y y T x x x ,及变换⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛3213213213211010001u u u U u u u y y y λλλ 则'U U =且I ATU T U =''是三阶单位矩阵,⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛321321u u u TU x x x 则变换的雅可比行列式为()()()=∂∂=321321321,,,,,,u u u x x x u u u J ()()⋅∂∂321321,,,,y y y x x x ()()321321,,,,u u u y y y ∂∂ ()()()2121321det det det det --==⋅==A U T TU λλλ,又()()()⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛=∑=321321321''32132132131,ij ,,,,,,a u u u I u u u u u u ATU T U u u u x x x A x x x x x j i j i 232221u u u ++=于是由三重积分的变量替换公式得:()()⎰⎰⎰⎰⎰⎰⎰⎰⎰≤++-≤++==1321211321321321232221232221det ,,u u u u u u Vdu du du A du du du u uu J dxdx dx ()21det 34-=A π 3.正交变换在曲面积分中的应用3.1正交变换在第一型曲面积分中的应用定理3.1[1] 设有光滑曲面S :()y x z z ,=,()D y x ∈,,()z y x f ,,为S 上的连续函数,则()()()⎰⎰⎰⎰++=SDy x dxdy z z y x z y x f dS z y x f 221,,,,,.定理3.2[1] 设有光滑曲面S :()()()⎪⎩⎪⎨⎧===,,,,,,v u z z v u y y v u x x ()D v u ∈,,则在S 上的第一型曲面积分的计算公式为()()()()()⎰⎰⎰⎰-=SDdudv F EG v u z v u y v u x f dS z y x f 2,,,,,,,,其中 222u u u z y x E ++=,v u v u v u z z y y x x F ++=,222v v v z y x G ++=. 这里还要求雅可比行列式()()v u y x ,,∂∂,()()v u z y ,,∂∂,()()v u x z ,,∂∂中至少有一个不等于零. 定理3.3[3] 设有光滑曲面S :()()()⎪⎩⎪⎨⎧===,,,,,,v u z z v u y y v u x x ()D v u ∈,,在正交变换⎪⎪⎪⎭⎫⎝⎛⎪⎪⎪⎭⎫ ⎝⎛==⎪⎪⎪⎭⎫ ⎝⎛=z y x a a a a a a a a a AX z y x X 3332312322211312111111之下变成曲面'S :()()()⎪⎩⎪⎨⎧===,,,,,,111111v u z z v u y y v u x x则对于S 上的连续函数()z y x f ,,有()()⎰⎰⎰⎰=SSdSX A f dS X f ''1'(3)证明 因为A 是正交矩阵,所以'212121222E z y x z y x E u u u u u u =++=++=, '111111F z z y y x x z z y y x x F v u v u v u v u v u v u =++=++=,'212121222G z y x z y x G v v v v v v =++=++=,因此()⎰⎰SdS X f ()()()()()⎰⎰⎰⎰-==SDdudv F EG v u z v u y v u x f dS z y x f 2,,,,,,,=()()()()⎰⎰-D dudv F G E v u z v u y v u x f 2'''111,,,,,()⎰⎰=''111,,S dS z y x f ()⎰⎰=''1'S dS X A f例1 证明普阿松公式()()⎰⎰⎰-++=++Sdu c b a u f dS cz by ax f 112222π,其中S 为单位球面1222=++z y x .证明 设()c b a ,,为三维空间的一个向量,它的单位向量为⎪⎭⎫⎝⎛k c k b k a ,,(其中222c b a k ++=),再将其扩充为三维空间的一个标准正交基,设为⎪⎭⎫⎝⎛k c k b k a ,,,()111,,c b a ,()222,,c b a 作正交变换⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛z y x A w v u ,这里⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=222111c b a c b a k c k b k a A 为正交矩阵,则⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛-w v u A w v u A z y x T1 两边转置得 ()()A w v u z y x ,,,,=∴()()1,,,,222222=++=⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛=++w v u w v u AA w v u z y x z y x z y x T由公式(3)得()()⎰⎰⎰⎰=++=++=++11222222z y x w v u dS ku f dS cz by ax f于是 ()D v u v u w ∈--=,,1222;w u u w -=∂∂,wvv w -=∂∂ 2222221111vu w v w u v w u w --=⎪⎭⎫⎝⎛-+⎪⎭⎫ ⎝⎛-+=⎪⎭⎫ ⎝⎛∂∂+⎪⎭⎫ ⎝⎛∂∂+()()()⎰⎰⎰⎰⎰⎰--==++=++=++Dz y x w v u dudv vu ku f dS ku f dS cz by ax f 221111222222令u u =,θsin 12u v -=,其中11≤≤-u ,πθ20≤≤. 于是 ()()()⎰⎰⎰⎰⎰--=--=--ππθθθ20112211222cos 1cos 111du ku f d u u du ku f dudv vu ku f D即 ()()⎰⎰⎰-++=++Sdu c b a u f dS cz by ax f 112222π.得证.例2 设()ds x m x m x m f n n n +++-⎰⎰⎰22111是展布在n 维空间中单位球面上的一曲面积分,则()()()()⎰∑⎰⎰⎰---=-=-⎪⎭⎫ ⎝⎛-Γ=⎪⎭⎫ ⎝⎛∑==113221111121212du uku f n ds x m f I n n n i i i n x n i i π(当3≥n 时)此处,令∑==ni imk 12,设函数()u f 当k u ≤时连续,其中()x Γ为Gamma 函数.证明 这里只要证: ()()()()⎰∑∑⎰⎰⎰----=-=-≤-⎪⎭⎫ ⎝⎛-Γ=-⋅⋅⋅⎪⎭⎫ ⎝⎛∑-=1123221112121111121212112du uku f n x dx dx dx x m f n n n i i n n i i i n x n i i π即可.设正交变换:⎪⎪⎪⎪⎪⎭⎫⎝⎛⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛n nn n n n n n u u u a a a a a a a a a x x x 2121222121211121 其中2n 个系数受制于()2121+=+n n C C n n 个条件:⎩⎨⎧=∑=,0,11nji a a τττ nj n i j i j i ,2,1,,2,1,==≠= 于是 11212==∑∑==n i i n i i x u ,∑-=-±=1121n i i n u u今取121,,,-n u u u 作为新的变量,系数选择的任意性很大,因此我们令()n i km a ii ,2,11==,同时我们可进一步要求由变换系数组成的行列式的值等于1,在这种假设下,对应于行列式任一元素的代数余子式等于元素的本身.所以雅可比行列式:()()121121,,,,,,--∂∂n n u u u x x xn n nn n n n nn n nnn n n n n n nn nn n n n n n n n n u ua a u ua a u ua a u ua a u ua a u ua a u u a a u u a a u u a a 111121121111121222221212111121211111---------------------=nn nn n n n n n n n nu x a u u a u ua u u a =++++=--112211 ()()()()nn n n n n x du du du u u u x x x ku f x dx dx dx ku f 12112112111211,,,,,,----∂∂=⋅⋅⋅∴ ()()∑-=---=⋅=1121211121111n i in n n n n u du du du ku f du du du x u x ku f , 从而()()∑⎰⎰⎰⎰∑⎰⎰⎰-=---≤--=--≤--∑=-∑=-=-=12221132211111112121111121212212112n i in n u u n i in n u u u du du du du ku f u du du du ku f I n i in i i对里面2-n 重积分实行变量替换:设⎪⎪⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎪⎭⎫ ⎝⎛---=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--22121212113210010001n n tt t u u u u u u, 则()()()()2212211321,,,,,,----=∂∂n n n u t t t u u u⇒ ()()∑⎰⎰⎰∑⎰⎰⎰-=---≤-=---≤--∑=--∑-=-=212221232121122211212111121212212n i in n n t n i in n u u t dt dt dt u u u du du du n i i n i i,再设⎪⎪⎪⎩⎪⎪⎪⎨⎧=====------3421234213321321211sin sin sin sin cos sin sin sin cos sin sin cos sin cos n n n n n n r t r t r t r t r t ϕϕϕϕϕϕϕϕϕϕϕϕϕϕ其中10≤≤r ,πϕϕϕ≤≤-421,,0n ,πϕ203≤≤-n .()()42514331221sin sin sin ,,,,,,------=∂∂n n n n n n r r t t t ϕϕϕϕϕ∑⎰⎰⎰-=--≤-∑-=212221211212n i in n t t dt dt dt n i i⎰⎰⎰⎰⎰-=------12320304402251141sin sinsindr rr d d d d n n n n n n ππππϕϕϕϕϕϕϕ⎰⎰⎰⎰-⋅=------12320442225211441sin sinsin22dr rr d d d n n n n n n πππϕϕϕϕϕϕπ⎰-⎪⎭⎫ ⎝⎛B ⎪⎭⎫ ⎝⎛-B ⎪⎭⎫ ⎝⎛-B ⋅⋅=---102344121,2221,2421,232122dr rrn n n n n π()⎰-⎪⎭⎫ ⎝⎛Γ⎪⎭⎫⎝⎛ΓΓ⎪⎭⎫ ⎝⎛-Γ⎪⎭⎫ ⎝⎛Γ⎪⎭⎫ ⎝⎛-Γ⎪⎭⎫ ⎝⎛-Γ⎪⎭⎫ ⎝⎛Γ⎪⎭⎫ ⎝⎛-Γ⎪⎭⎫ ⎝⎛-Γ⎪⎭⎫ ⎝⎛Γ⎪⎭⎫ ⎝⎛-Γ=-10231232112421252321242221232dr r r n n n n n n n π ⎰-⎪⎭⎫ ⎝⎛-Γ⎪⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛Γ=--1234122212dr r r n n n π(设v r =2)()()⎪⎭⎫ ⎝⎛-B ⎪⎭⎫ ⎝⎛-Γ⎪⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛Γ=-⎪⎭⎫ ⎝⎛-Γ⎪⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛Γ=----⎰22,2122211222141024214n n dv v v n n n n ππ()()⎪⎭⎫ ⎝⎛-Γ=⎪⎭⎫⎝⎛-Γ=⎪⎭⎫ ⎝⎛-Γ⎪⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛Γ=⎪⎭⎫ ⎝⎛-Γ⎪⎭⎫ ⎝⎛-Γ⎪⎭⎫ ⎝⎛Γ⎪⎭⎫ ⎝⎛-Γ⎪⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛Γ=----21212121212221222112334n n n n n n n n n n πππππ()()()()⎰----⎪⎭⎫ ⎝⎛-Γ=∴11232211212du uku f n I n n π若令λcos =u ()πλ≤≤0,则有()()()⎰--⎪⎭⎫⎝⎛-Γ=πλλλπ0221sin cos 212d k f n I n n 当3=n 时,且令c m b m a m ===321,,,z x y x x x ===321,,,得到著名的普阿松公式:()()⎰⎰⎰-++=++Sdu c b a u f dS cz by ax f 112222π,其中S 为单位球面1222=++z y x .运用正交变换仿上述命题推理过程可简快明了地处理以下n 重积分()2≥n 问题: 一、对连续函数()n x x x f ,,,21 ,证明:()()()()⎰∑⎰⎰⎰---=≤-⎪⎭⎫ ⎝⎛+Γ=⎪⎭⎫⎝⎛∑=1121221211112112du u ku f n dx dx dx x m f n n n n i i i n x n i i π,其中012≥=∑=ni i m k ,()u f 在k u ≤上连续,1≥n . 特别当3=n 时,设c m b m a m ===321,,,z x y x x x ===321,,有()()()⎰⎰⎰⎰-≤++-=++11211222du ku f u dxdydz cz by ax f z y x π其中222c b a k ++=.二、对连续函数()n x x x f ,,,21 ,证明:()()()()⎰∑⎰⎰⎰---=≤-+⎪⎭⎫ ⎝⎛+Γ=⎪⎭⎫ ⎝⎛+∑=111221211112112du u ku f n dx dx dx x m f n n n n i i i n x n i i ωπω其中012≥=∑=ni i m k ,()u f 在k ku ≤+ω上连续.当2=n 时,设,,,21c b m a m ===ωy x x x ==21,,有()=++⎰⎰≤+122y x dxdy c by ax f ()⎰-++-1122212du c u b afu3.2正交变换在第二型曲面积分中的应用定理3.4[4] 设S 为三维欧式空间内的光滑曲面,()z y x P ,,,()z y x Q ,,,()z y x R ,,均为S 上的连续函数,而⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛w v u a a a a a a a a a z y x 333231232221131211 ()A为欧式空间中的正交变换;'S 为S 在上述变换()A 下的象,()w v u P ,,,()w v u Q ,,,()w v u R ,,分别为P ,Q ,R 与变换()A 的复合函数,则()()⎰⎰⎰⎰⎪⎪⎪⎭⎫⎝⎛⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛'''''333231232221131211cos cos cos cos cos cos S S dS a a a a a a a a a R Q P A dS R Q P γβαγβα (4)其中1±=A 是正交变换()A 的行列式,()γβαcos ,cos ,cos 和()'''cos ,cos ,cos γβα分别为S 和'S 的单位法向量.证明 设S 的参数方程为()()()⎪⎩⎪⎨⎧===,,,,,,θθθr z z r y y r x x ()D r ∈θ,, 则'S 的参数方程为()()()⎪⎩⎪⎨⎧===,,,,,,θθθr w w r v v r u u 记()3,2,1321=++=i R a Q a P a F i i i i ,则θθθθθθθθθw v u w v u F F F A a a a a a a a a a w v u w v u F F F z y x z y x R Q P r r rr r r r r r 321332313322212312111321⋅=⋅= 于是()⎰⎰⎰⎰⎰⎰±=±=⎪⎪⎪⎭⎫⎝⎛Dr r rD r r rSdrd w v u w v u F F F A drd z y x z y x R Q P dS R QPθθγβαθθθθθθ321cos cos cos()⎰⎰⎪⎪⎪⎭⎫ ⎝⎛='''''321cos cos cos S dS F F F A γβα ()⎰⎰⎪⎪⎪⎭⎫⎝⎛⎪⎪⎪⎭⎫⎝⎛='''''333231232221131211cos cos cos S dS a a a a a a a a a R Q P A γβα例3 计算第二型曲面积分()⎰⎰++SdS z y x γβαcos cos cos其中S 为球面4222=++z y x 介于1≥++cz by ax 的外表面.解 设()c b a ,,为三维空间的一个向量,它的单位向量为⎪⎭⎫⎝⎛k c k b k a ,,(其中222c b a k ++=),再将其扩充为三维空间的一个标准正交基,设为⎪⎭⎫⎝⎛k c k b k a ,,,()111,,c b a ,()222,,c b a 作正交变换⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛z y x A w v u ,这里⎪⎪⎪⎪⎪⎭⎫⎝⎛=k c kb ka cb ac b a A 222111(5), 为正交矩阵,则由(5)知()cz by ax c b a w ++++=2221.变换将S 变为'S ,它为球面4222=++w v u 介于2221cb a w ++≥的外表面.由于正交变换保持向量的内积不变,故'''cos cos cos cos cos cos γβαγβαw v u z y x ++=++记222214cb a R ++-=,由(4)式得 ()()⎰⎰⎰⎰++=++'''''cos cos cos cos cos cos S SdS w v u dS z y x γβαγβα ⎰⎰≤+⎪⎭⎫ ⎝⎛--+∂∂-∂∂-=222224R v u dudv v u v w v u w u ⎰⎰≤+⎪⎪⎭⎫⎝⎛--+--+=22222222244R v u dudv v u v u v u ⎪⎪⎭⎫⎝⎛++-=--=⎰⎰≤+2222212844222c b a v u dudvR v u π 4.正交变换在曲线积分中的应用4.1正交变换在第一型曲线积分中的应用定理4.1[1] 设有光滑曲线()()()⎪⎩⎪⎨⎧===,,,:t z t y t x L χψϕ []βα,∈t , 函数()z y x f ,,为定义在L 上的连续函数,则()()()()()()()()⎰⎰++=βαχψϕχψϕdt t t t t t t f ds z y x f L2'2'2',,,,.定理4.2[4] 设L 为三维欧式空间内的光滑曲线,()z y x P ,,为L 上的连续函数,而⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛w v u a a a a a a a a a z y x 333231232221131211 ()A为欧式空间中的正交变换;'L 为L 在上述变换()A 下的象,()w v u P ,,为P 与变换()A 的复合函数,则()()⎰⎰='',,,,LLds w v u P ds z y x P (6).例1 计算第一型曲线积分()⎰-Lds y x ,其中L 为曲线()()3222223y x zx yz xy z y x -=+++++,02=++z y x ,上从点()0,0,0到点⎪⎪⎭⎫⎝⎛-+-+32,3221,3221的一段弧.解 L 是一条平面曲线,但是不易写出其参数方程.为此,作正交变换⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛--=⎪⎪⎪⎭⎫ ⎝⎛z y x w v u 62616131313102121, 此变换将平面02=++z y x 变成坐标面0=w .由于()zx yz xy z y x +++++23222()()()()222222222242323144243222231w v z y x z y x zx yz xy z y x zx yz xy z y x +=+++-+=++++++--+++=()3342u y x =-,且当()()0,0,0,,=z y x 时,()()0,0,0,,=w v u ;当()⎪⎪⎭⎫ ⎝⎛-+-+=32,3221,3221,,z y x 时,()()0,2,1,,=w v u ,故变换将曲线L 变为'L :324u v =,0=w 从()0,0,0到()0,2,1的弧.于是由(6)式得()⎪⎪⎭⎫ ⎝⎛+=+=⎪⎭⎫ ⎝⎛+==-⎰⎰⎰⎰15131025812491212210102''du u u du du dv u uds ds y x L L4.2正交变换在第二型曲线积分中的应用定理4.3[4] 设L 为三维欧式空间内的光滑曲线,()z y x P ,,,()z y x Q ,,,()z y x R ,,均为L 上的连续函数,而⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛w v u a a a a a a a a a z y x 333231232221131211()A为欧式空间中的正交变换;'L 为L 在上述变换()A 下的象,()w v u P ,,,()w v u Q ,,,()w v u R ,,分别为P ,Q ,R 与变换()A 的复合函数,则()()⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛⎰⎰dw dv du a a a a a a a a a R QP dz dy dx R QPLL333231232221131211' (7).例2 计算第二型曲线积分⎰Lxdy ,其中L 为圆周()34222=-++++zx yz xy z y x ,3=+-z y x ,从x 轴正向看去,圆周是沿逆时针方向进行的.解 作正交变换⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛--=⎪⎪⎪⎭⎫ ⎝⎛z y x w v u 31313161626121021 则w v u x 316121++=,w v y 3162-=且()()()zxyz xy z y x z y x zx yz xy z y x 222234222222222+--++-++=-++++()()()()2222222222236323wv u ww vuz y x z y x -+=-++=+--++=这样,由(7)式得⎰⎰⎪⎪⎭⎫⎝⎛-⎪⎪⎭⎫⎝⎛++='3162316121L L w v d w v u xdy 其中'L 为圆周3422==+w v u ,,从w 轴正向看去,圆周是沿逆时针方向进行的.因此⎰⎰⎪⎪⎭⎫⎝⎛++='6216121L L dv v u xdy πθθθθθθππ34cos 34cos 2621sin 261cos 22120220==⋅⎪⎪⎭⎫ ⎝⎛+⋅+⋅=⎰⎰d d5. 结束语上述诸例足以说明利用正交变换的方法去处理重积分和曲面积分的某些问题是卓有成效的(对于曲线积分亦是如此),并且不受空间维数的限制.而正交变换在物理学上、几何上、概率论上等学科有着广泛的应用前景,同时数学问题的代数化的方法是值得重视的.参考文献[1]华东师范大学数学系编.《数学分析》[M],高等教育出版社,2001[2]张禾瑞,郝鈵新编.《高等代数》[M],高等教育出版社,2007.6[3]邹晓范. 正交变换在多元函数积分中的应用[J],佳木斯大学学报(自然科学版), 2003,21(4):494-496[4]林元重. 正交变换在曲线、曲面积分计算中的应用[J],数学通报, 1996,(12):27-29。
高等代数9.4 正交变换

事实上由正交变换的定义及标准正交基的性质
即有,
( i ), ( j )
( i , j )
1 0
i j i j
2).若线性变换 使V的标准正交基 1, 2 ,, n 变成
标准正交基 (1), ( 2 ),, ( n ) ,则 为V的正交
在任一组标准正交基下的矩阵是正交矩阵. 证明:" " 设 1, 2 ,, n 为V的标准正交基,且
1,2,,n 1,2,,n 1,2,,n A
当 是正交变换时,由1知,1, 2 ,, n 也是V
的标准正交基, 而由标准正交基 1, 2 ,, n 到标准 正交基1, 2 ,, n的过渡矩阵是正交矩阵.
d ( ), ( ) ( ) ( )
( ) 根据2)
故 3)成立.
d( , )
3) 2) : 若 d ( ), ( ) d , , , V
则有, d ( ), (0) d ,0, V
作业
• P396 15
§1 定义与基本性质 §2 标准正交基
§3 同构
§4 正交变换
§5 子空间
§6 对称矩阵的标准形
§7 向量到子空间的 §8 酉空间介绍
距离─最小二乘法 小结与习题
一、一般欧氏空间中的正交变换 二、n 维欧氏空间中的正交变换
一、一般欧氏空间中的正交变换
1.定义
欧氏空间V的线性变换 如果保持向量的内积不变,
即,
( ), ( ) ( , ), , V
则称 为正交变换.
注:欧氏空间中的正交变换是几何空间中保持长度
不变的正交变换的推广.
正交变换与正交矩阵

(
A
i
,
A
j
)
(
i
,
j
)
0, i 1, i
j j
故 A1,A2,…,An是V的一组标准正交基.
3)4)设1,2,…,n是V的标准正交基, A(1,2,…,n)=(A1,A2,…,An) = (1,2,…,n)A 由3), A1,A2,…,An是V的标准正交基,
故A可看作是由标准正交基1,2,…,n到标 准正交基A1,A2,…,An的过渡矩阵,A是正 交矩阵.
AB-1,A-1BA等都是正交矩阵;
A
2)
0
0 B
,12
A A
A A
是正交矩阵.
证:1)由AT=A-1,BT=B-1可知
(AB)T=BTAT=B-1A-1=(AB)-1,
所以AB为正交矩阵,从而再由性质1可推知:
Am(m为自然数),ATB,ABT,A-1B,AB-1,A-1BA
等均为正交矩阵.
(A-1)T=(AT)T=A=(A-1)-1=E. 故A-1是正交矩阵.
3)由2)知AT=A-1,AT是正交矩阵.
而A*=|A|A-1= A-1,有 (A*)T=(A-1)T=A=(A*)-1,
故A*是正交矩阵.
性质3.2 设A,B都是正交矩阵,则:
1)AB , Am(m 为 自 然数 ),ATB , ABT ,A-1B ,
2)设为A,B奇数阶正交矩阵,且|A|=|B|,则必 A-B不可逆.
证:1)由|A+B|=|BBTA+BATA|=|B||BT+AT||A| =-|B|2|BT+AT|=-|(A+B)T|=-|A+B|
得|A+B|=0,即A+B不可逆. 2)由|A-B|=|BBTA-BATA|=|B||BT-AT||A| =|B|2|BT-AT|=|-(A-B)T|=(-1)n|A-B|
高等代数(第9章)

第9章 欧几里得空间
定义与简单性质 标准正交基
* 同构
正交变换 子空间 对称矩阵的标准形 * 向量到子空间的距离最小二乘法
§9.1 定义与基本性质
几何空间R3中向量与的内积是指实数 (, )=||| |cos= a1b1+ a2b2+a3b3 ||,| |分别为向量与的模(长度),为与的夹角. 利用内积概念也可以表示向量的长度及两个非 零向量的夹角: ( , ) | | (, )=0, 且具有以下 性质: (, )= (, ) (k , )=k (, ) (+ ,)= (, )+ (, ) (, )0,当且仅当=0时,(, )=0.
3.度量矩阵 定义 设V是n维欧氏空间, 1, 2,…,n为V的一组基.称 ( 1 , 1 ) ( 1 , 2 ) ( 1 , n ) ( , ) ( , ) ( , ) 2 1 2 2 2 n A ( n , 1 ) ( n , 2 ) ( n , n ) 为基1, 2,…,n的度量矩阵.
性质 (i) AT=A (ii) 对V中任意向量
基的度量矩阵完 全确定了内积!
x1 y1 = x11+x22+…+xnn , x 2 , Y y 2 . = y11+y22+…+ynn , 其中X x y 有 ( ,) =XTAY. n n
知 [2( , )]2 4( , )( , ) 0 即( , ) 2 ( , )( , ) 0
|( , ) |<|| | |.
(ii)若 , 线性相关,则当 , 至少有一为零向量时, 等号显然成立,否则可设 =k.由 |( ,)|=|(k ,)|= |k( , )| = |k|| |2 = |k|| || |= ||| | 即等号成立; 反之若等号成立,则为零向量时,,线性相关,
北京大学数学系《高等代数》(第3版)【教材精讲+考研真题解析】第9章 欧式空间 【圣才出品】

第9章欧式空间[视频讲解]9.1本章要点详解本章要点■欧式空间的定义■标准正交基■同构■正交变换■子空间■对称矩阵的标准型重难点导学一、定义与基本性质1.欧式空间的定义设V 是实数域R 上一线性空间,在V 上定义了一个二元实函数,记作(α,β),若(α,β)满足(1)(α,β)=(β,α);(2)(k α,β)=k (α,β);(3)(α+β,γ)=(α,γ)+(β,γ);(4)(α,α)≥0,当且仅当α=0时(α,α)=0.这里α,β,r 是V 中任意的向量,k 是任意实数,则称(α,β)为α和β的内积,并称线性空间V 为欧几里得空间.2.内积的简单性质V 为欧氏空间,∀α,β,γ,∀k ∈R ,则(1)(,)(,)k k =αβαβ;(2)(,)(,)(,)+=+αβγαβαγ;(3)(0,)=0β.2.欧氏空间中向量的长度(1)向量长度的定义非负实数称为向量α的长度,记为|α|.(2)关于长度的性质①零向量的长度是零;②|kα|=|k||α|;③长度为1的向量称为单位向量.如果α≠0,向量1αα就是一个单位向量,称此过程为把α单位化.3.欧氏空间中向量的夹角(1)柯西-布涅柯夫斯基不等式,即对于任意的向量α,β有|(α,β)|≤|α||β|当且仅当α,β线性相关时,等号才成立.(2)非零向量α,β的夹角<α,β>定义为(3)如果向量α,β的内积为零,即(α,β)=0,则称α,β为正交或互相垂直,记为α⊥β.注:零向量才与自己正交.(4)勾股定理:当α,β正交时,|α+β|2=|α|2+|β|2.4.有限维空间的讨论(1)度量矩阵设V是一个n维欧几里得空间,在V中取一组基ε1,ε2,…,εn,对V中任意两个向量α=x1ε1+x2ε2+…+x nεn,β=y1ε1+y2ε2+…+y nεn,由内积的性质得a ij=(εi,εj)(i,j=1,2,…,n)有a ij=a ji,则(α,β)还可写成(α,β)=X'AY,其中分别是α,β的坐标,而矩阵A=(a ij)nn称为基ε1,ε2,…,εn的度量矩阵.(2)性质①设η1,η2,…,ηn是空间V的另外一组基,而由ε1,ε2,…,εn到η1,η2,…,ηn的过渡矩阵为C,即(η1,η2,…,ηn)=(ε1,ε2,…,εn)C,于是基η1,η2,…,ηn的度量矩阵B=(b ij)=(ηi,ηj)=C'AC,则不同基的度量矩阵是合同的.②对于非零向量α,即有(α,α)=X'AX>0.因此,度量矩阵是正定的.二、标准正交基1.正交向量组欧式空间V中一组非零的向量,如果它们两两正交,称为正交向量组.按定义,由单个非零向量所成的向量组也是正交向量组.2.标准正交基(1)定义在n维欧氏空间中,由n个向量组成的正交向量组称为正交基;由单位向量组成的正交基称为标准正交基.注:①对一组正交基进行单位化就得到一组标准正交基.②一组基为标准正交基的充分必要条件是:它的度量矩阵为单位矩阵.(2)标准正交基的求法①n维欧氏空间中任一个正交向量组都能扩充成一组正交基.②对于n维欧氏空间中任意一组基ε1,ε2,…,εn,存在一组标准正交基η1,η2,…,η,使L(ε1,ε2,…,εi)=L(η1,η2,…,ηi),i=1,2,…,n.n把一组线性无关的向量变成一单位正交向量组的方法称为施密特正交化过程.3.标准正交基间的基变换设ε1,ε2,…,εn与η1,η2,…,ηn是欧氏空间V中的两组标准正交基,它们之间的过渡矩阵是A=(a ij),即因为η1,η2,…,ηn是标准正交基,所以矩阵A的各列就是η1,η2,…,ηn在标准正交基ε1,ε2,…,εn下的坐标.4.正交矩阵n级实数矩阵A称为正交矩阵,如果A'A=E.由标准正交基到标准正交基的过渡矩阵是正交矩阵;反过来,如果第一组基是标准正交基,同时过渡矩阵是正交矩阵,则第二组基一定也是标准正交基.三、同构。
正交变换的等价条件及其应用

正交变换的等价条件及其应⽤⽬录1引⾔ ................................................................................................................... 12正交变换的定义及其等价条件........................................................................ 12.1定义..................................................................................................................................12.2等价条件..........................................................................................................................23正交变换的应⽤................................................................................................ 43.1化⼆次型为标准形..........................................................................................................43.2解不变⼦空间相关问题..................................................................................................83.3求解矩阵问题..................................................................................................................83.4求解欧⽒空间中其它相关问题......................................................................................83.5在积分中的应⽤.......................................................................................................... 114结束语............................................................................................................ 12参考⽂献........................................................................................................... 13致谢语............................................................................................................... 14正交变换的等价条件及其应⽤数学系2013级1班许鹏指导教师:陈⾦梅摘要:正交变换在⼤学学习中是⼀个重要的概念,例如在代数中,它涉及到了线性代数中⼀⼤部分的基本概念,如矩阵、向量、线性变换、标准正交基等,深⼊探讨研究这个课题对学好⾼等代数和线性代数⼗分有帮助.不仅如此,它在其他的领域也有着⼤范围的普及,如在积分的应⽤中,在多重积分的⽅⾯。
正交变换

正交变换设M是对称矩阵, P是正交矩阵, N=P^tMP 称为 M的正交变换。
(正交矩阵的定义为:P.P^t = I)正交变换既是相似变换,也是相合变换。
正交变换不改变M的特征值。
正交变换最初来自于维基百科,这种矩阵元被称为简正坐标.用质量加权坐标表示的分子内部运动的动能,用质量加权坐标表示的分子内部势能,用质量加权坐标表示的分子内部势能,由力常数的数学表达式可以知道fij = fji因而矩阵为一个正交变换通过酉变换可以把矩阵变形成为对角矩阵的形式:。
则有:它的每一个矩阵元都是分子所有质量加权坐标的线性组合,总的矩阵元的数量恰巧等于质量加权坐标的个数,这些矩阵元就被称作简正坐标,而这些变换中分子的势能不变,所以正交变换又称为酉变换.采用OpenCV进行人脸识别一、实现原理本程序的实现方法请参看《face recognition using an embedded HMM》。
二、开发工具1、OpenCV视觉开发库2、MFC三、程序运行1、主界面主界面包括识别区域和结果区域。
如下:2、参数设置(Set Params)u状态数的设置,默认为5个超态,从上到下分别代表前额(3),眼睛(6),鼻子(6),嘴巴(6),下巴(3)u观察向量2D-DCT:包括观察向量大小(OBS),DCT大小和Delta大小u最大迭代次数,默认为80u混合高斯次数,默认为33、人员管理(Per Manage)人员管理界面如下:u添加人员信息:输入人员信息具有Name与NO属性,NO不可重复。
u删除人员信息:在人员列表中选择要删除的人员,然后进行删除,人员信息删除后,包括人员的图片也进行删除,该人员也不在识别范围内。
u添加人员图片:一个人可以多张图片,点击要添加的人员,可以通过此按钮添加图片。
添加前最好在.. \HMM\××文件夹里(××表示该人员名称)。
u删除人员图片:点击要删除的图片,按“Del Image”按钮进行删除,图片删除后只是该图片不在训练的区域。
正交变换原理讲解PPT

高了通信干线的传输效率,同时也可使计算机实时处理音频、视频信息,以保证播放出高
质量的视频、音频节目成为可能。用于声音图象数据压缩的编码方法甚多。
13
第一组
感谢观看
用这些少量的数据同样表述原有的信息。对这些系数进行量化、编码,就
可以达到压缩编码的目的。
正交变换应是可逆的,但是由于利用系数分布集中的特点,当舍去集
中区域外的那些系数后的逆变换就会产生一定的误差。一个好的正交变换 ,
舍去集中区域外的系数值后,进行的逆变换得到的图象和声音与原先图象
和声音质量相差不大。这就达到了在基本保质的前提下较大的提高数据压
那么称为正交矩阵,简称正交阵。
4. 若为正交矩阵,则线性变换 = 称为正交变换。设
= 为正交变换,则
有
y =
= = = .
由于 表示向量的长度,相当于线段的长度,
因此 y = 说明经正交变换线段长度不变。
4
Part 01
1.2 数字信号处理中的正交变换:
低次分量之中(M<N)。
(3)最佳特性
K-L变换是在均方误差测度下,失真最小的一种变换,其失真为被略去的各分量之和。
由于这一特性,K-L变换被称为最佳变换。许多其他变换都将K-L变换作为性能上比较的
参考标准。
(4)无快速算法,且变换矩阵随不同的信号样值集合而不同。
这是K-L变换的一个缺点,是K-L变换实际应用中的一个很大障碍。
正
交
变
换
的
性
质
1. 正交变换的基向量即是其对偶基向量。
2. 展开系数是信号在基向量上的准确投影。
正交变换论文

则有
关于该基的矩阵是U
那么
是正交变换
设 ,
于是
根据定理3有
σ是次正交变换
命题②得证。
结论
本文通过对正交变换相关概念的介绍,逐步总结出正交变换的几个等价条件。并对这些等价条件进行了理论推导证明。文末还对正交变换进行了理论推广证明。这就是本文创新之处。
参考文献:
[1]邱乾恒关于正交变换的几个问题庆阳师专学报1994年第2期
证明:充分性:
因 是确定的实数, 是正交变换
则 ,有
故σ是次正交变换。
必要性:
因σ是次正交变换,则 有 ,a是一确定的正实数,不难看出 满足
所以 是正交变换
设 ,可以得出
其中a是正实数, 是正交变换。
得证。
定理4设 ,则有
①如果σ是次正交变换,则σ关于任意标准正交基的矩阵是 ,这里b≠0是实数,U
是正交矩阵。
故由(1)←→(2)的证明,σ是V的一个正交变换。
得证。
注记:欧式空间的保长度变换不一定是正交变换。例如,在欧式空间R2中,定义
则σ是R2的一个保长度变换。但因
之故, ,从而σ不是R2的正交变换。
V的保夹角变换也不一定是正交变换,例如
是V的一个保夹角变换。但σ是不保长度变换,所以不是正交变换。
(1)←→(4)的证明
所以
故σ不是线性变换,因而不是正交变换。
(2)欧式空间V上的一个变换σ满足什么条件才能是正交变换?
对于这个问题已经有若干结论,列举如下:
定理1:欧式空间V上一个变换σ是正交变换的充分必要条件是对任意 ,都有 成立。
定理2:欧式空间V上一个变换σ是正交变换的充分必要条件是对任意 成立。
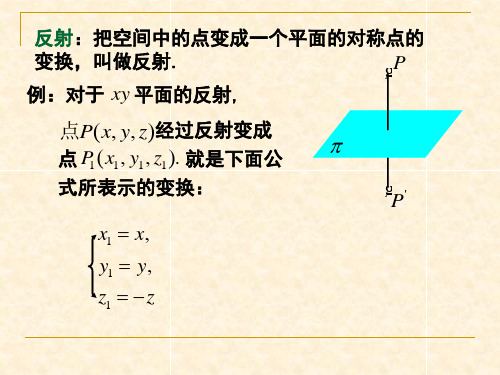
高等代数第九章 4第四节 正交变换

正交变换
在解析几何中,我们有正交变换的概念. 正交 变换就是保持点之间的距离不变的变换. 在一般的 欧氏空间中,我们有
定义9 欧氏空间V的线性变换A称为一个正交变换, 如果它保持向量的内积不变,即对任意的α, β∈V, 都有 (Aα, Aβ)=(α, β). 正交变换可以从几个不同方面公平加以刻划.
1)=>3)因为A是正交变换,所以有 1 ,当 i j ; (Aεi, Aεj)= ( i , j ) (i , j 1,2,, n) . 0 , 当i j . 这就是说,Aε1,Aε2,…,Aεn 是标准正交基. 1)<=3)因为Aε1,Aε2,…,Aεn 是标准正交基,则由 α=x1ε1+x2ε2+…+xnεn. β=y1ε1+y2ε2+…+ynεn. 与 Aα=x1Aε1+x2Aε2+…+xnAεn. Aβ=y1Aε1+y2Aε2+…+ynAεn. 即得 (α, β)=x1y1+x2y2+…+xnyn=(Aα, Aβ). 因而A是正交变换.
阵的乘积与正交矩阵的逆矩阵也是正交矩阵.
返回
上页
下页
如果A是正交矩阵,那么由 AAT=E 可知 |A|2=1或者|A|=±1. 因此,正交变换的行列式等于+1或-1. 行列式等于
+1的正交变换通常称为旋转,或者称为第一类的; 行列式等于-1的正交变换称为第二类的. 例如,在欧氏空间中任意取一组标准正交基 ε1,ε2,…,εn ,定义线性变换A为: Aε1=-ε1 , Aεi=εi , i=2,3, …,n. 那么,A就是一个第二类的正交变换. 从几何上看, 这是一个镜面反射 (参看本章习题15) .
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1)<=2)因为A保持向量的长度不变,即有 (Aα, Aα)=(α, α), (Aβ, Aβ)=(β, β), 及 (A(α+β), A(α+β))=(α+β, α+β) .
把最后的等式展开得 (Aα, Aα)+2(Aα, Aβ)+(Aβ, Aβ)=(α, α)+2(α, β)+(β, β).
0 0 1 0 0 1
以上两个矩阵都是正交矩阵.
返回 上页 下页
1)=>3)因为A是正交变换,所以有 1 ,当 i j ; (Aεi, Aεj)= ( i , j ) (i , j 1,2,, n) . 0 , 当i j . 这就是说,Aε1,Aε2,…,Aεn 是标准正交基. 1)<=3)因为Aε1,Aε2,…,Aεn 是标准正交基,则由 α=x1ε1+x2ε2+…+xnεn. β=y1ε1+y2ε2+…+ynεn. 与 Aα=x1Aε1+x2Aε2+…+xnAεn. Aβ=y1Aε1+y2Aε2+…+ynAεn. 即得 (α, β)=x1y1+x2y2+…+xnyn=(Aα, Aβ). 因而A是正交变换.
3)<=4) 因为A是正交矩阵,而ε1,ε2,…,εn是标准正 交基,则Aε1,Aε2,…,Aεn就是标准正交基. 这样,我们就证明了1),2),3),4)的等价性. 证毕.
返回 上页 下页
因为正交矩阵是可逆的,所以正交变换是可逆
的. 由定义不难看出,正交变换实际上就是一个欧 氏空间到自身的同构映射(§3),因而正交变换的 乘积与正交变换的逆变换还是正交变换. 在标准正 交基,正交变换与正交矩阵对应,因此,正交矩
第四节
正交变换
在解析几何中,我们有正交变换的概念. 正交 变换就是保持点之间的距离不变的变换. 在一般的 欧氏空间中,我们有
定义9 欧氏空间V的线性变换A称为一个正交变换, 如果它保持向量的内积不变,即对任意的α, β∈V, 都有 (Aα, Aβ)=(α, β). 正交变换可以从几个不同方面公平加以刻划.
阵的乘积与正交矩阵的逆矩阵也是正交矩阵.
返回
上页
下页
如果A是正交矩阵,那么由 AAT=E 可知 |A|2=1或者|A|=±1. 因此,正交变换的行列式等于+1或-1. 行列式等于
+1的正交变换通常称为旋转,或者称为第一类的; 行列式等于-1的正交变换称为第二类的. 例如,在欧氏空间中任意取一组标准正交基 ε1,ε2,…,εn ,定义线性变换A为: Aε1=-ε1 , Aεi=εi , i=2,3, …,n. 那么,A就是一个第二类的正交变换. 从几何上看, 这是一个镜面反射 (参看本章习题15) .
返回 上页 下页
③ (3)<=>4))
设A在标准正交基ε1,ε2,…,εn下的矩阵为A,即 (Aε1,Aε2,…,Aεn)=(ε1,ε2,…,εn)A.
3)=>4)由上因为Aε1,Aε2,…,Aεn也是标准正交基,
那么A就是由标准正交基ε1,ε2,…,εn到Aε1,Aε2,…,Aεn
的过渡矩阵,因而A是正交矩阵.
返回 上页 下页
定理4 设A是n维欧氏空间V的一个线性变换,于
是下面四个命题是相互等价的: 1)A是正交变换; 2)A保持向量的长度不变,即对于α∈V,|Aα|=|α|; 3)如果ε1,ε2,…,εn是标准正交基, 那么Aε1,Aε2,…,Aεn
也是标准正交基;
4)A在任一组标准正交基下的矩阵是正交矩阵. 证明 ① (1)<=>2)) 1)=>2)因为A是正交变换,即有(Aα, Aα) =(α, α), 两边开方即得 |Aα|=|α| .
返回 上页 下页
例3 将R2的每一向量旋转一个角φ的正交变换关于 R2的任意标准正交基的矩阵是
cos sin
sin cos
又令σ是例1中的正交变换. 在平面H内取两个 正交的单位向量γ1, γ2,再取一个垂直于H的单位向 量γ3,那么 {γ1,γ2,γ3}是R3的一个规范正交基,σ关于 这个基的矩阵是 1 0 0
返回 上页 下页
例1 令H是空间R3里过原点的一个平面,对任意
ξ∈R3 ,记ξ对于H的镜面反射的像是ξ. 则映射
σ :ξ|→ξ是R3的一个正交变换. 因为σ对应的矩阵是A=E-2ββT为一个正交矩
阵,其中β是平面H的单位法向量. 例2 设σ∈L(R3),对任意向量ξ=(x1,x2,x3)∈R3 ,令 σ(ξ)=(x2,x3,x1). 则σ是R3的一个正交变换. 0 1 0 因为σ对应的矩阵是 A 0 0 1 为一个正交矩阵. 1 0 0
再利用前两个等式,就有 (Aα, Aβ)=(α, β). 此即为,A是正交变换. ② (1)<=>3)) 设ε1,ε2,…,εn是一组标准正交基,即有 1 ,当 i j ; ( i , j ) (i , j 1,2,, n) . 0 , 当i j .
返回 上页 下页
