纯-弯曲梁的正应力实验
梁的纯弯曲正应力实验报告

梁的纯弯曲正应力实验报告梁的纯弯曲正应力实验报告一、实验目的本实验旨在通过对实验材料进行纯弯曲加载,测量其正应力和弯曲角度,从而掌握材料在纯弯曲状态下的应力特性,并探究材料性能的影响因素。
二、实验原理当梁在纯弯曲时,受到的载荷可以分解为一个弯矩和一个剪力。
由于实验中去除了外部作用力,剪力为零,因此我们只需要考虑弯矩作用下的应力情况。
在梁的截面上,由于受到弯曲,不同位置的应变不同,因此会形成不同大小的应力。
在正常情况下,当梁未发生破坏时,梁的内部应力呈线性分布,即受到的弯矩越大,所受到的应力也会相应增大。
三、实验设备本实验所使用的设备包括:1.纯弯曲实验台2.测力仪3.梁材料(一定长度的圆形钢管或方管)四、实验步骤1. 选择一段合适材质的梁进行实验。
2. 将梁固定在纯弯曲实验台上。
3. 在梁的一端加上一定荷载。
4. 通过测力仪测量在梁部位不同位置受到的正应力。
5. 在梁的另一端加上一定数量的荷载,并重复步骤4,记录正应力。
6. 重复以上操作,直到梁发生破坏。
五、实验结果在实验过程中,我们记录了梁不同位置受到的正应力,并根据实验数据分析了不同弯矩下的应力分布曲线。
实验结果表明,在纯弯曲状态下,梁的内部应力呈线性分布,随着弯矩的增大,所受应力也会逐渐增大,直到梁发生破坏。
六、实验分析根据实验结果,我们可以发现梁的性能会受到材料的影响。
不同的材料具有不同的弯曲特性,不同的性能和抗断性能。
而在实验中,我们也可以通过调整材料的材质和长度来控制弯曲的程度,从而控制梁的应力分布和破坏点位置。
七、实验结论本实验通过纯弯曲实验台对梁进行弯曲测试,得到了不同弯矩下的应力分布曲线。
实验结论表明,梁在纯弯曲状态下,其内部应力呈线性分布,随着弯矩的增大,所受应力也会逐渐增大,直到梁发生破坏。
同时,不同材质和长度的材料在弯曲状态下具有不同的弯曲特性和抗断性能。
梁的纯弯曲正应力实验报告

梁的纯弯曲正应力实验报告一、实验目的。
本实验旨在通过对梁的纯弯曲正应力实验,了解梁在纯弯曲状态下的受力情况,掌握梁的弯曲应力分布规律,加深对梁的力学性能的理解。
二、实验原理。
梁是一种常见的结构构件,在工程中应用广泛。
梁在受外力作用下会发生弯曲变形,产生弯曲应力。
在纯弯曲状态下,梁上任意截面的应力都是正应力,弯矩对梁上任意一点的作用会引起该点产生正应力。
梁的弯曲应力分布规律受到梁的截面形状、材料性质以及外力大小和作用形式的影响。
三、实验装置与仪器。
本次实验所使用的实验装置包括,梁的支撑装置、加载装置、测力传感器、位移传感器、数据采集系统等。
测力传感器用于测量梁上各点的受力情况,位移传感器用于测量梁上各点的位移情况,数据采集系统用于采集并记录实验数据。
四、实验步骤。
1. 将梁放置在支撑装置上,并调整支撑装置,使梁处于自由悬臂梁状态。
2. 将加载装置作用在梁的中央位置,施加均匀分布的外力。
3. 通过测力传感器和位移传感器采集梁上各点的受力和位移数据。
4. 记录实验数据,并进行数据处理和分析。
五、实验数据处理与分析。
通过对实验数据的处理和分析,得到了梁在纯弯曲状态下的应力分布规律。
实验结果表明,在梁的中央位置受力最大,呈现出最大的正应力;而在梁的两端位置受力较小,呈现出较小的正应力。
梁的弯曲应力分布呈现出一定的规律性,符合理论预期。
六、实验结论。
通过本次实验,我们深入了解了梁在纯弯曲状态下的受力情况,掌握了梁的弯曲应力分布规律。
实验结果表明,在纯弯曲状态下,梁上任意截面的应力都是正应力,呈现出一定的规律性。
这对于工程结构设计和实际应用具有一定的指导意义。
七、实验心得。
通过本次实验,我们对梁的纯弯曲正应力有了更深入的了解,也增强了对力学知识的理解和应用能力。
在今后的学习和工作中,我们将继续努力,不断提高自己的实验技能和科研能力,为工程实践和科学研究做出更大的贡献。
八、参考文献。
1. 钱七虎. 结构力学实验教程[M]. 北京,中国建筑工业出版社,2008.2. 吴光辉. 结构力学[M]. 北京,高等教育出版社,2011.以上为本次梁的纯弯曲正应力实验报告的全部内容。
梁的纯弯曲正应力实验

梁的纯弯曲正应力实验
梁的纯弯曲正应力实验是为了确定梁在弯曲的情况下的受力机制以及测定梁的弯曲刚
度和受力性能的试验。
在这项实验中,主要是测试梁的弯曲刚度性能,这样可以更清楚地
了解梁的特性,并且可以判断梁受到外力时应如何反应。
这项实验是建筑结构设计中的重
要内容,当结构受外力时,梁的刚度将决定结构的中止和模态。
梁的纯弯曲正应力实验,通常需要两个或三个支撑点。
它们可以是球形、凸形或圆形
的轴承。
其中,球形轴承最常用,其支撑的特性是最佳的,最不容易产生不必要的侧向力,影响试验的准确性。
在一个纯弯曲正应力实验中,支撑一端的梁头会受到一个外载荷,即弯矩,使其变形。
强度和刚度试验系统通常由模拟电源、试验控制台、力传感器等设备组成,力导致模拟器
输出同时加载在梁上,并通过力数据计算出受力的曲率系数和强度系数。
该实验的基本步骤是:(1)在梁上安装支持设备,并将梁放在试验台上;(2)给各
支撑点安装传感器,并通过模拟器输出同时加载在梁上;(3)测量梁承受的外载荷以及
梁的变形量;(4)分析测量结果,并计算出梁在弯曲时的曲率系数和受力
总之,梁的纯弯曲正应力实验是非常重要的,它可以查明梁的强度系数,曲率和强度
系数,以及梁受外力时的变形性能和应力变化规律。
实验结果对于确定结构抗震性能等具
有重大意义,在建筑结构分析和设计中扮演着巨大的作用。
纯弯曲梁的正应力实验

纯弯 曲梁 的正 应力 实验
(1)梁的基本参数。 (2)实验记录表格。 (3)将各点的σ实和σ理描绘在同一个σOy 坐标系中,分别作出σ实-y和σ理-y分布曲线, 以便进行比较,从而检验梁的弯曲正应力理论公 式的正确性。
15.4 材料 剪切 弹性 模量G 的测
定
实验用到的仪器包括WSG-80型纯弯曲正应力试 验台、静
实验梁为低碳钢制成的矩形截面梁,根据实验装置 图、实验受力图可知,施加的砝码重量通过杠杆以一定 的比例作用于副梁的中央并通过两个挂杆作用于实验梁 C,D处,其荷载各为F/2。CD段处于纯弯曲状态。
(1)测定矩形截面梁的宽度b和高度h,荷载作用点 至梁支座距离a,并测量各应变片距中性层的距离y。
(2)正确地将各测点应变片和温度补偿片分别接到 电阻应变仪的相应接线柱上。
(3)接通应变仪的电源,完成预热工作后,设置应 变仪的灵敏系数,并将各窗口读数清零。
(4)加载。首先挂上砝码托作为初荷载,记录各测 点的应变值εi。采用增量法逐级加载,分四次加载,每加 载一次记录一次应变值,直至加载完毕。
在梁中CD段任选一截面,距中性层不同高度处,等 距离地粘贴五片电阻应变片,每片相距h/4,此外还布 设一个温度补偿片。试验中,采用半桥接线法将各测点 的工作应变片和温度补偿片连接在应变电桥的相邻桥臂 上,按照电阻应变仪的操作规程将电桥预调平衡,加载 后即可从应变仪上读出各测点的应变值ε实。
纯弯 曲梁 的正 应力 实验
1.1实验目的及仪器设备
纯弯曲梁的正 应力实验
1.2实验原理 1.3实验步骤
1.4实验数据处理
理论分析可知,梁发生纯弯曲变形时,横截面 上只有正应力,以中性轴为界,一侧为拉应力,一 侧为压应力,且正应力的大小与点到中性轴的距离 成正比。本节用实验测定矩形截面简支梁承受纯弯 曲时横截面上正应力的大小及其分布规律,并与理 论值进行比较,以验证弯曲正应力公式,并初步掌 握电测法原理和静态电阻应变仪的使用方法。
梁的纯弯曲正应力实验

梁的纯弯曲正应力实验
工作片
R1
B
A
R2 温度补偿片 C 固定电阻
相同应变片R1.R2,R1贴 在构件受力处,R2贴在附 近不受力处,环境温度对 R1.R2引起的阻值变化相 同,为DRT,则
R4
R3
D
梁的纯弯曲正应力实验
五、实验数据的记录与计算
梁的纯弯曲正应力实验
六、注意事项
1.加载时要缓慢, 防止冲击。 2.读取应变值时, 应保持载荷稳定。 3.各引线的接线柱必须拧紧, 测量过程中不要触动引线, 以 免引起测量误差。
梁的纯弯曲正应力实验
一、实验目的
1.测定纯弯曲下矩形截面梁横截面上正应力的 分布规律,并与理论值比较;
2.熟悉电测法基本原理和电阻应变仪的使用。 二、实验仪器 1.纯弯曲试验装置;
2.YD-15型静态数字电阻应变仪。
梁的纯弯曲正应力实验
三、试验原理
1. 结构示意图及理论值计算
b hz
y
F/2 a
F/2
DR1 R1
-
DR2 R2
DR3 R3
-
DR4 R4
)
E 4
K
(
1
-
2
3
-
4
)
梁的纯弯曲正应力实验
4.电桥接法及温度补偿 1.电桥接法: 全桥接法(四个电阻均为应变片);
半桥接法(R1、R2为应变片, R3.R4为固定电阻)
两种接法中的应变片型号、阻值尽可能相同 或接近, 固定电阻与应变片阻值也应接近。
F F/2
ma m
FQ +
纯弯曲梁的正应力测定的实验报告
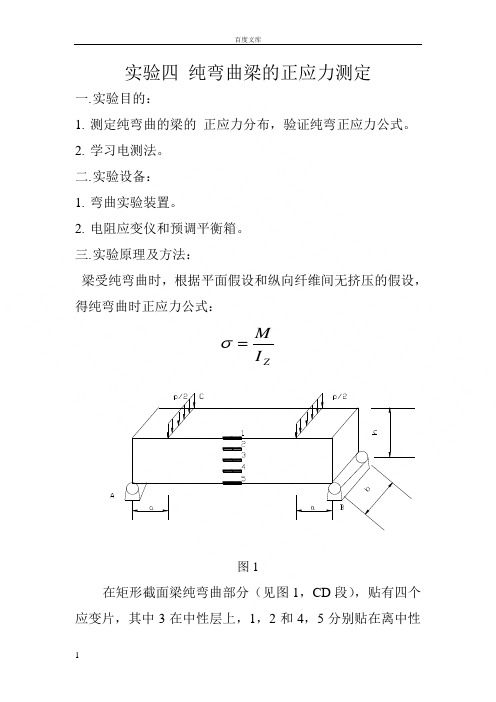
贴片位置
b
8
y3
0
h
16
y2(y4)
a
200
y1(y5)
3应变读数记录
读数A
应变片号
载荷
1
2
3
4
A
0
120
567
168
637
92
4500
0
7449
91
4
522
606
4500
7481
8
120
461
184
576
92
4500
0
7510
89
12
399
545
4500
7540
16
120
338
185
514
92
4500
0
7570
91
20
276
484
4500
7601
平均
179
92
0
0
4计算结果及误差
应变片号
1
2
3
4
0
18MPa
0
误差(%)
%
%
0
%
计算过程:
1计算梁的弯矩:
2计算不同应变片的应力
应变片1
应变片2
应变片4
2:学习电测法。
主要实验仪器:1:弯曲试验装置。
2:电阻应变仪和预调平衡箱。
主要实验步骤:
一:取一矩形截面的等截面剪支梁AB,其上作用两个对称的集中力P/2,未加载前,在中间CD段表面画些平行于梁轴线的纵向线和垂直于梁轴线的横向线。加载后在梁的AC和DB两段内,各横截面上有不同的剪力和弯矩M。
梁纯弯曲正应力测定实验(最全)word资料
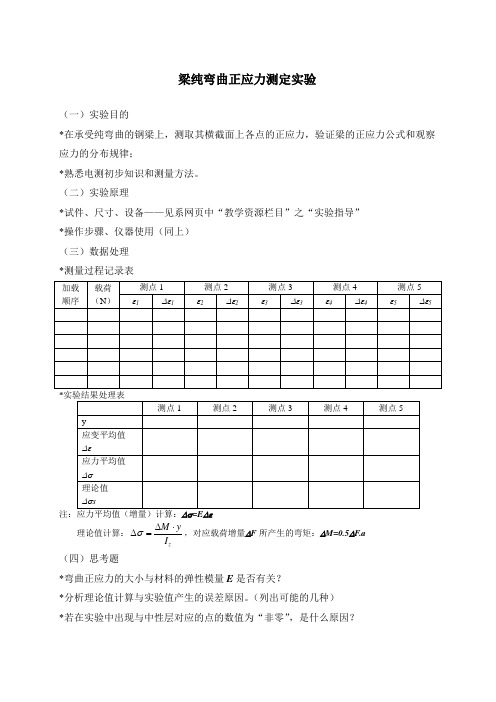
梁纯弯曲正应力测定实验(一)实验目的*在承受纯弯曲的钢梁上,测取其横截面上各点的正应力,验证梁的正应力公式和观察应力的分布规律;*熟悉电测初步知识和测量方法。
(二)实验原理*试件、尺寸、设备——见系网页中“教学资源栏目”之“实验指导” *操作步骤、仪器使用(同上) (三)数据处理 *测量过程记录表*注:应力平均值(增量)计算:=E 理论值计算:zM yI σ∆⋅∆=,对应载荷增量∆F 所产生的弯矩:∆M=0.5∆F .a (四)思考题*弯曲正应力的大小与材料的弹性模量E 是否有关?*分析理论值计算与实验值产生的误差原因。
(列出可能的几种) *若在实验中出现与中性层对应的点的数值为“非零”,是什么原因?临床实验室定量测定室内质量控制一术语和定义1偏倚 bias试验结果偏离可接受参考值的系统偏离(带有正负号)。
2不精密度 imprecision一组重复测定结果的随机离散,其值由统计量定量表示为标准差或变异系数。
3质量控制quality control质量管理的一部分,致力于满足质量要求。
[GB/T 19000-2000,]4 质量控制策略 quality control strategy质控品种类、每种检测频次、放置的位置,以及用于质控数据解释和确定分析批是在控还是失控的规则。
5 随机误差 random error测量结果与在重复性条件下对同一被测量进行无限多次测量所得结果的平均值之差。
6 系统误差 systematic error在重复性条件下,对同一被测量进行无限多次测量所得结果的平均值与被测量的真值之差。
7 可报告范围 reportable range在仪器、试剂盒或系统的测定响应之间的关系,显示是有效的期间内试验值范围。
8 标准差 standard deviation观察值或测定结果中不精密度的统计度量。
变异性/离散的度量是总体方差的正平方根。
二质量控制的目的质量控制方法是用来监测检验方法的分析性能,警告检验人员存在的问题。
纯弯曲梁正应力实验报告数据

纯弯曲梁正应力实验报告数据纯弯曲梁正应力实验报告数据引言:纯弯曲梁正应力实验是结构力学实验中的一项重要内容,通过对材料的弯曲变形进行测试,可以得到材料在不同载荷下的正应力分布情况。
本文将介绍一项纯弯曲梁正应力实验的数据结果,并对实验结果进行分析和讨论。
实验装置与方法:本次实验使用了一台万能材料试验机,悬臂梁的试件采用了标准的矩形截面,材料为钢。
实验过程中,通过加载试件的两端,使其产生弯曲变形,并通过应变计和测力计等传感器测量试件在不同载荷下的应变和力的变化。
实验结果:在不同的载荷下,测得悬臂梁试件的应变和力的变化数据如下:载荷(N)应变(με)力(N)100 500 10200 1000 20300 1500 30400 2000 40500 2500 50数据分析与讨论:通过对实验结果的分析,可以得到以下几个方面的结论:1. 应变与载荷的关系:从实验数据可以看出,应变随着载荷的增加而线性增加。
这是由于在纯弯曲梁实验中,试件的上表面受到拉应力,下表面受到压应力,而应变计测量的是试件的表面应变,因此随着载荷的增加,试件的弯曲变形增大,表面应变也相应增加。
2. 力与载荷的关系:实验数据表明,力与载荷之间呈线性关系,即力随着载荷的增加而增加。
这是因为在纯弯曲梁实验中,试件受到的弯曲力矩与载荷成正比,而力是力矩除以试件的截面积,因此力与载荷之间呈线性关系。
3. 正应力分布:根据弯曲梁的受力分析理论,试件上表面受到拉应力,下表面受到压应力。
通过实验数据可以得到,试件上表面的正应力随着载荷的增加而增大,而下表面的正应力随着载荷的增加而减小。
这与弯曲梁的受力分布规律一致。
结论:通过纯弯曲梁正应力实验的数据分析与讨论,可以得出以下结论:1. 在纯弯曲梁实验中,应变与载荷呈线性关系,力与载荷呈线性关系;2. 试件上表面的正应力随着载荷的增加而增大,下表面的正应力随着载荷的增加而减小。
这些结论对于理解材料在弯曲变形下的应力分布规律具有重要意义,对于结构设计和工程实践具有指导作用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
纯-弯曲梁的正应力实验
本实验旨在研究弯曲梁在受力时的正应力分布情况,通过实验数据的测量及分析,探
讨影响梁正应力分布的因素,并对梁的强度进行评估。
1. 实验原理
1.1 弯曲梁正应力分析
弯曲梁是一种常用的结构元件,例如桥梁、楼层结构等,她受到外力的作用会发生弯
曲形变,产生正应力和剪应力。
弯曲梁的正应力是沿着截面法向的应力,在梁的顶部为拉
应力,底部为压应力。
正应力的计算公式如下:
$$\sigma = \frac{My}{I}$$
其中,$\sigma$为正应力,$M$为弯矩,$y$为受力点到截面重心的距离,$I$为截面
惯性矩。
弯曲梁正应力的分布情况受到多种因素的影响,主要包括:
① 梁材料的弹性模量:弹性模量越大,弯曲梁的刚度越大,相同外力作用下,梁的
形变和正应力都会相应减小。
② 梁截面形状和尺寸:梁截面的惯性矩影响正应力的大小和分布情况。
截面抗弯性
能越强,正应力越小。
③ 受力位置和方向:受力位置和作用方向是影响正应力大小和分布情况的重要因素。
不同位置和方向的外力作用会导致不同的正应力分布规律。
2. 实验设备和方法
本实验采用的主要设备有:弯曲梁试验机、电子天平、千分尺等。
2.2 实验步骤
1. 准备弯曲梁样品,将其加工成常用的矩形截面和半圆形截面,分别测量其截面形
状和尺寸。
2. 调整弯曲梁试验机,设置好取样位置和取样方式。
3. 将弯曲梁放入试验机,设置试验参数,包括荷重大小、位移速率等。
4. 开始试验,记录每个荷载下的跨中挠度和荷载大小,并计算出弯矩大小。
5. 在试验过程中,用电子天平测量梁的重量,并用千分尺对梁的跨中直径和截面高度进行测量,计算出截面惯性矩。
6. 根据测量数据,计算出每个荷载下的正应力,并绘制出正应力分布图。
3. 结果分析
3.1 实验数据记录
本实验用常见的矩形和半圆形弯曲梁进行了试验,记录了不同工况下的荷载和跨中挠度等数据。
根据数据计算得出弯矩以及正应力等数据,具体数据结果如下表:
1. 矩形截面弯曲梁
(1)弯曲梁在起始荷载下出现了微小的振动,但并未发生失稳。
(2)随着荷载增加,弯曲梁出现了弯曲形变,且挠度增加越来越快。
(3)正应力分布在梁的顶部为拉应力,在底部为压应力,弯矩$\ M$与正应力$\
\sigma$成正比。
对比三种不同荷载下的正应力分布情况发现,正应力大小随荷载的增加而增加,应力分布最大值位置始终在距离梁两端等距离的中心位置,符合理论分析结果。
(3)大荷载下的半圆形截面弯曲梁出现了扭曲形变,导致正应力分布与矩形截面弯曲梁略有不同。
在跨中位置,弯曲梁的顶部和底部正应力分别接近于0,而在轴心位置,正应力最大,且呈压应力。
综合分析变形和正应力分布情况发现,矩形截面弯曲梁的负载能力较强,能够承受较大的荷载。
半圆形截面弯曲梁相比之下,不仅负载能力较小,而且变形形态也较大,不适合用于负载较大的情况。
4. 实验结论
通过本次实验,我们研究了弯曲梁受荷载下的变形和正应力分布规律,得出以下结论:
1. 弯曲梁的正应力分布情况受多种因素的影响,包括梁材料的弹性模量、梁截面形状和尺寸以及受力位置和方向等。
3. 对于弯曲梁的设计和使用,应该根据实际需求选择合适的截面形状和尺寸,以保证梁的安全稳定运行。
