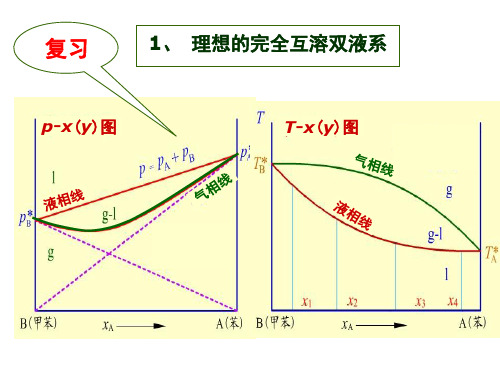
理想的完全互溶双液系
物理化学中国药科大学相平衡第三章2-4节

三相点与冰点的区别
三相点是物质自身的特性,不能加以改变, 如H2O的三相点 T 273.16 K , p 610.62 Pa . 冰点是在大气压力下,水、冰、气三相共存。当大 气压力为105 Pa时,冰点温度为273.15 K ,改变外压, 冰点也随之改变。
E B 冰 水 p 610.16Pa
• 解: T/T较小,
6 333 . 5 10 0 . 5 p2 p1 1 Pa 1 .2 0.9998 0.9165 273
6.74106 P a T2 6.8410 P a
6
• 欲使-5oC的冰熔化所需施加的最小压力 6.84106Pa.
第三节 完全互溶双液系统
fusVm T
• T1~T2 将fusHm Vm看成常数,作定积分
fus H m T2 p2 p1 ln fusVm T1 lnT2 /T1 (T2 T1 )/T1 fus H m T2 T1 p2 p1 fusVm T1
例题: 试计算-5oC,欲使冰熔化所需施加的 最小压力?已知:ice=0.9168gcm-3, water=0.9998gcm-3, SubHm=333.5Jg-1.
水
临界点 374oC, 2.23107Pa
气
lnp~1/T
B
T1273.16
T2 T
硫的相图
p
正交
液
p
X
Y
气
T
CO2的相图
一些有机化合物在熔点时的蒸气压
化合物
顺丁烯二酸酐 萘 苯甲酸 -萘酚
熔点/°C 熔点时的蒸气压/kPa
60 79 120 122 0.44 0.9 0.8 0.33
苯酐
物理化学第五章2

2、 等压T-x-y图( 沸点组成图 )
T x y
( yA )
p
等温p x
p
T4 T3 T2
T : 纯B物质的沸点 T : 纯A物质的沸点
A
B A
T1
B
x1
x2 xA
x3
x4
p xA yA p
T x y
气相线
A
T
TB
液相线
p
B
TA
xA
A
( yA )
T
B
T
A
T
B
T
A
l
完全互溶双液系
两个纯液体组分可以按任意比例相互混合 成均一液相的体系,称为完全互溶双液系(或 液体混合物)。
理想的完全互溶双液系
若混合溶液中任一组分在全部浓度范围内, 其蒸气压与液相组成的关系都符合Raoult定律, 则这样的双液系称为理想的完全互溶双液系(或 理想的液体混合物)。
B A
A A A B
说明1 液相线是直线,
p pA pB p ( p p ) xA
B B A
B
A
B
p p 气相线不是直线, p pA ( p pA ) yA
p
气相线
液相线
?
说明2
p p
A
B
yB pB p xB yA pA p xA
答案:A
三、杠杆规则
1、物系点与相点? 2、杠杆规则的内容? 3、杠杆规则推导的依据? 4、杠杆规则在相图中的应用?
三、杠杆规则 1、物系点与相点
物系点: 相图中表示体系总状态(总组 成、温度和压力)的点称为物系点。
4.3完全互溶双液系统讲解

T x1
x2
x3 x4
A
xB
B
一、理想的完全互溶的双液系统
T-p-x图
T
液 pA*
TA*
液
A
xB
pB* 气
气 气
TB* B
一、理想的完全互溶的双液系统
T-p-x图
二、杠杆规则
T g
TB*
DC E
l TA*
B
x1
xA x2
A
xA
物系点:系统物质的总组成点(不管相的存在状态)
二、杠杆规则
假设某压力下液态混合物沸腾时气液平衡的物系点为C点,那 么有: n总 nA nB nl ng
三、非理想的完全互溶双液系统
1. 正负偏差不大的体系
气液相图与理想液态混合物气液相图基本类似
p
p
T
A
xB
(a) p-x图
BA
xB
BA
xB
B
(b) p-x-y图
(c) T-x-y图
三、非理想的完全互溶双液系统
2. 正偏差很大的体系 有最高点
p-液相组成线
p
p
p-气相组成线
A
xB
B
(a) p-x图
A
xB
B
(b) p-x-y图
pA、pB偏离拉乌尔定律都很大,p-x图上形成最高点。
三、非理想的完全互溶双液系统
2. 正偏差很大的体系
g
T lg lg
(c) T-x-y图
l
l
A
x1
B
xB
在p-x图上有最高点,在T-x图上就有最低点,称最低恒沸点。 最低恒沸点对应的组成称最低恒沸组成。在此组成下蒸馏双 液系:yA = xA , yB= xB,A与B达不到分离目的,类似蒸馏 具有恒定沸点的纯物质,所以此点上混合物称恒沸混合物。
互溶双液系的相图及应用

精馏的原理:经过多次蒸馏达到提纯的目的。
定压
馏出液 Tb
馏出液 组成
二次蒸
g 馏馏出
液组成
l
A
xB
B
Tb - xB图
二、精馏的原理
馏出液
实验室的蒸馏装置
化工厂的精馏塔
二、精馏的原理
气相从塔顶蒸出
沸点高的物质留在塔底
液相留在 塔底
沸点低的 物质蒸出
塔顶
二、精馏的原理
1 精馏是经过多次蒸馏,达到提纯的目的。
A
Tb - xB图 B
自学 其他非理想完全互溶双液系相图及应用
预习 相图的绘制
谢谢大家!
定压
g
馏出液 组成
l
如果是理想完全互溶双液系,通过精馏 可以纯A和纯B。
Tb
沸点低的纯B被蒸馏出来 3 沸点高的纯A留在塔底被分离出来。
A
xB
B
Tb - xB图
三、 非理想互溶双液系的相图(具有最低恒沸点)
最低恒沸点:M点
xB=yB
恒沸物:混合物
组成随压强改变
注意:不能同时得到两种纯组分,
一定能得到恒沸物。
思考
思考
100 ℃ 78.13 ℃
pθ
g 78.3 ℃ l
95.57%
H2O 15%
C2H5OH
Tb - xB图
思考
酒厂的酒度计坏了,你 如何利用所学知识帮助酒 厂确定酒精度数?
预习相图的准确绘制 写出具体方案 抽签讲解
小结
小结 精馏的原理及应用
定压
g
Tb l
定压
g
Tb
l
A
B
Tb - xB图
理想完全互溶双液系相图的数学解析

理想完全互溶双液系相图的数学解析刘兴;屈景年;周立君;赖华;曾荣英;李俊华【摘要】理想完全互溶双液系是两个组分都严格遵守Raoult定律的体系,从数学角度看,其平面相图有着确定的函数关系。
本文以Clausius-Clapeyron方程为基础,推导了该类理想体系的p-x、T-x及p-T相图的函数解析式。
%In an ideal completely miscible two components liquid system, the two components strictly abide by the Raoult′s law, and their plane phase diagrams have a definite function relationship. Based on the Clausius-Clapeyron equation, the functional analytic formula of p-x、T-x and p-T phase diagrams in this ideal system were derived in the present paper.【期刊名称】《大学化学》【年(卷),期】2016(031)007【总页数】5页(P96-100)【关键词】理想完全互溶双液系;相图;函数解析式;Clausius-Clapeyron方程【作者】刘兴;屈景年;周立君;赖华;曾荣英;李俊华【作者单位】衡阳师范学院化学与材料科学学院,湖南衡阳421008;衡阳师范学院化学与材料科学学院,湖南衡阳421008;衡阳师范学院数学与统计学院,湖南衡阳421001;衡阳师范学院化学与材料科学学院,湖南衡阳421008;衡阳师范学院化学与材料科学学院,湖南衡阳421008;衡阳师范学院化学与材料科学学院,湖南衡阳421008【正文语种】中文【中图分类】G64;O6理想完全互溶双液系(双组分理想液态混合物)相图是双液系相图的基础。
二组分凝聚系统相图.

T
' c
等压
c'
两相
T/K
453
413
373
Tc
c
0.2 0.4 0.6
单相
0.8 1.0
0
水
质量分数 水-烟碱的溶解度图
烟碱
6.4 二组分凝聚系统相图 一、二组分固态完全不互溶系统液固平衡相图
1. 热分析法
基本原理:二组分系统 C=2,指定压力不变,
f * = C +1 -F =3 -F
F = 1
f f 1 ** f f 2
*
相点 表示某个相状态(如相态、组成、温度等)的 点称为相点。 物系点 相图中表示系统总状态的点称为物系点。在T-x 图上,物系点可以沿着与温度坐标平行的垂线上、 下移动;在水盐相图上,随着含水量的变化,物系 点可沿着与组成坐标平行的直线左右移动。
单相区,物系点与相点重合;两相区中,只有 物系点,它对应的两个相的组成由对应的相点表示
B
3. 全部变为固体Bi后
f * C 1 Φ 1
t /s
温度又可以下降 纯Cd步冷曲线与之相同
Cd-Bi二元相图的绘制
w(Cd) 0.2
的步冷曲线
b
T /K
f* 2
C
D
f * 1
1. 加热到b点,Bi-Cd全部熔化 Φ 1 f * 2 1 Φ 2 温度可以下降,组成也可变 2. 冷至C点,固体Bi开始析出 Φ 2 f * 2 1 Φ 1 温度可以下降 3.D点固体Bi、Cd同时析出
Φ 3
f* 0 温度不能改变 f * 1 4.熔液消失,Bi和Cd共存
f 2 1 Φ 0
*
5.3完全互溶双液系统

四、蒸馏、分馏与精馏
从图可看出:
Tn+1
Tn
y0 > y1 > y2 > y3 > y4 > y5 > y 6 > y7 > y8 反复将气相部分冷凝, 气相组成沿气相线下降,最 后得到的蒸气组成可接近纯B。
x8 < x7 < x6 < x5 < x4 < x3 < x2 < x1< x0 液相组成沿液相线 上升,xB下降,xA上升,最 后可得纯A。
三、非理想的完全互溶双液系统
2. 正偏差很大的体系
三、非理想的完全互溶双液系统
2. 正偏差很大的体系 具有最低恒沸点的相图可以看作 由两个简单的T-x(y)图的组合。 在组成处于恒沸点之左,精馏结果 只能得到纯B和恒沸混合物。组成 处于恒沸点之右,精馏结果只能得 到恒沸混合物和纯A 。
对于 H2 O - C2 H5OH 体系,若乙醇的含量小于95.57,无 论如何精馏,都得不到无水乙醇。只有加入 CaCl 2 ,分子筛 等吸水剂,使乙醇含量超过95.57,再精馏可得无水乙醇。
气相部分沿分馏柱上升,在刺形 物上实现多次蒸馏。气相部分在上升 过程中组成不断变化,沸点亦逐渐降 低。柱身在无外界热源情况下温度会 降低,若降的太多,起完全回流作用, 所以应注意柱身保温,控制回流比。
四、蒸馏、分馏与精馏
精馏塔
四、蒸馏、分馏与精馏
精馏塔
四、蒸馏、分馏与精馏
四、蒸馏、分馏与精馏
三、非理想的完全互溶双液系统
3. 负偏差很大的体系
三、非理想的完全互溶双液系统
3. 负偏差很大的体系 例:1atm下,H2O-HCl体系 Tb最高=108.5C 恒沸物组成 HCl% =20.24%
相平衡6-3
含B的量增多.
组成为y3的气体在塔中继续上升, 温度降为T2, 如此继续到塔顶, 温度为纯B的沸点, 蒸气冷凝物 几乎是纯B.
组成为x4的液相在塔板冷凝后滴下, 温度上升为 T5;又有部分液体气化, 气相组成为y5, 剩余的组成
为 x5的液体再流到下一层塔板, 温度继续升高; 如此
继续, 在塔底几乎得到的是纯A, 这时温度为A的沸点. 精馏塔中必需的塔板数可以从理论计算得到. 每一 个塔板上都经历了一个热交换过程: 蒸气中的高沸点 物在塔板上冷凝, 放出冷凝热后流到下一层塔板, 液
液相区 xA xA,0 xA yA L O 气相区
气相
G
气相
nl OG = ng LO
气相区 L O G
yA xA,0 nl = ng xA,0 xA
液相区 xA xA,0 xA yA
非理想的完全互溶双液系
(即§6.4)
构成理想液态混合物的系统极少, 绝大多数二 组分完全互溶系统是非理想的, 称为真实液态混 合物. 一定温度下, 真实液态混合物除了在xB=1 附近极小的浓度范围内, 组分B的蒸汽压近似遵 循Raoult定律外, 其它组成下均对Raoult定律 发生偏差: 蒸汽总压与组成不再呈线性关系.
剩余液组成为x2, A含量增加. 这样, 将A和B进行
了粗略分离.
精馏原理
精馏——精馏是多次简单蒸馏的组合。 精馏塔底部是加热区, 塔釜温度最高; 塔顶温度最低. 精馏结果,塔顶冷凝收集的是纯低沸点组分,纯高
沸点组分则留在塔底。
精馏塔有多种类型,泡罩塔、浮阀塔、筛板塔等. 如下图所示是泡罩式塔板状精馏塔的示意图。
334K)以下和在最高会
溶温度(约481K)以上,
两液体可完全互溶, 而在
物理化学第5章相平衡

(2) 保持压力不变,得 T-x 图 常用
这三个变量通常是T,p 和组成 x。所以要表示二组分系统状态图,需用三个坐标的立体图表示。
一. 合金体系 1、相图绘制—— 热分析法 §5.7 具有简单低共熔混合物的固液二组分系统 Cd-Bi二元相图
①对拉乌尔定律有较大正偏差:
在T-x图上就有最低点,这最低点称为最低恒沸点
最低恒沸混合物是混合物而不是化合物,它的组成在定压下有定值。
在标准压力下, 的最低恒沸点温度为351.28 K,含乙醇 95.57 。
改变压力,最低恒沸点的温度也改变,它的组成也随之改变。
属于此类的系统有:
5.8 有化合物生成的固液二组分系统
5.4 完全互溶的双液系统
5.2 单组分系统的克-克方程
5.9 三组分系统
5.7 具有简单低共熔混合物的固液二组分系统
5.1 相律
5.3 水的相图
第五章 相平衡
相平衡是热力学在化学领域中的重要应用之一 研究多相系统的平衡在化学、化工的科研和生产中有重要的意义,例如:溶解、蒸馏、重结晶、萃取、提纯及金相分析等方面都要用到相平衡的知识 相律(phase rule);相图(phase diagram)
2、分析相图
区:图上有4个相区 ( 1) AEH线之上, 熔液(l)单相区 (2) ABE之内, Bi(s)+ l 两相区 (3) HEM之内, Cd(s)+ l 两相区 (4)BEM线以下, Bi(s)+Cd(s)两相区
线:有三条多相平衡曲线
(1)ACE线,Bi(s)+熔液 共存时的熔液组成线。
组成为F的气体冷到E
有组成为x1的液体出现
物理化学Ⅱ6.4 相平衡体系热力学(四)-二组分气液及液液体系(曹勇) 2

p / Pa
pB*
p pA pB
液相线 l
g-l
g
气相线
pA
p* A
xA
pA*
yA
p A
xA
yB
p B
xB
B(甲苯)
pB
p* B
xB
xA
A(苯)
2019/10/15
物理化学II
7
相平衡体系热力学
二组分气液及液液体系
理想的完全互溶双液系
如果
p* A
p* B
,则
yA xA ,即易挥发的组分在气相
2
相平衡体系热力学
二组分气液及液液体系
p-x图 和 T-x图
对于二组分体系,K = 2, f =4 -, 至少为 1,
则 f 最多为 3。
这三个变量通常是T,p 和组成 x。故要表示二组分
体系状态图,需用三坐标的立体图表示。
保持一个变量为常量,从立体图上得到平面截面图。
(1) 保持温度不变,得 p-x 图 (2) 保持压力不变,得 T-x 图 (3) 保持组成不变,得 T-p 图
设 pA*和 pB*分别为液体A和B在指定温度时的饱和蒸气压,p 为体系的总蒸气压
pA
p* A
xA
pB
p* B
xB
p pA pB
2019/10/15
物理化学II
4
相平衡体系热力学
二组分气液及液液体系
理想的完全互溶双液系
p / Pa
p pA pB
pA*
pB*
pA
p* A
xA
2019/10/15
完全互溶双液系相图

4.3 完全互溶的双夜系相图4.3.1 二组分系统的相律的应用最多可有四相平衡共存,是无变量系统。
最多可有三个自由度-T ,p ,x 均可变,属三变量系统。
因此,要完整的描述二组分系统相平衡状态,需要三维坐标的立体图。
但为了方便,往往指定一个变量固定不变,观察另外两个变量之间的关系,这样就得到一个平面图。
如: 保持温度不变,得 p-x 图 较常用 保持压力不变,得 T-x 图 常用 保持组成不变,得 T-p 图 不常用。
若保持一个变量为常量,从立体图上得到平面图。
相律 单相,两个自由度。
最多三相共存。
二组分系统相图种类很多,以物态来区分,大致分为: 完全互溶双液系 气-液平衡相图 部分互溶双液系 完全不互溶双液系具有简单低共熔混合物 稳定化合物有化合物生成 不稳定化合物 固-液平衡相图 固相完全互溶 固相部分互溶固相部分互溶 等C 2C 24= f Φ+=Φ=--min max 1 3Φf ==min max 0 4f Φ==213f ΦΦ*=-+=-*min max1 2Φf ==*max min 3 0Φf ==4.3.2 理想的完全互溶双液系相图若A 、B 两种液体均能以任意比例相互混容形成均匀单一的液相,则该系统称为完全互溶双液系。
根据相似相容原理,它可以分为:理想的完全互溶双液系 和非理想的完全互溶双液系。
首先学习理想液态混合物的相图。
4.3.2.1. 理想溶液p-x 图设A 、B 形成理想溶液,其饱和蒸气压分别为P A * 和P B *,P 为体系的总蒸气压。
以x A 为横坐标,以P 蒸气压为纵坐标,在p-x 图上分别表示出P A 、P B 、P 与x A l 的关系。
p-x-y 图 同压下 , 之间的关系若知道一定温度下的P A *、P B *,就可据液相组成(x A /x B )求其气相组成(y A /y B )px p p p y A A A A *==BAB A B A x x p p y y **=若 则 此时 即蒸气压大的组分在气相中浓度更大。
物理化学之相平衡
通过升华从冻结的样品中除去水份的方法。
E
f=2
B
冰
水
f=2 A
C
气
D
f=2
s+g, f=1,冷冻干燥
T
一、单组分系统的相图
f f=K- +2 水的相图
E
B
冰
水
p
610.6Pa
A:三相点
C
A
气
f=0
D
T
0.0098℃
一、单组分系统的相图
f=K-f+2 水的三相点:水的气、液、固三相平衡点。 f=0,T=273.16K ( 0.01℃),p=610.6Pa 水的凝固点(冰点):水的液、固二相平衡点。
↑
l+g, f=1
l+g, f=1 TB
l, f=2
T
A
xB →
B
T
二、杠杆规则
TA
↑
f f=K- +2 g, f=2
l+g, f=1 TB
l, f=2
A
xB →
B
T
二、杠杆规则
TA
↑
f f=K- +2 g, f=2
l+g, f=1 TB
l, f=2
A
xB →
B
T
二、杠杆规则
TA
↑
f=K-f+2 g, f=2
单位与相图一致
A
x1 x0
y1
B
二、杠杆规则
f=K-f+2 系统温度变化时,相如何变化?
n1L1= n2L2
TA
L1
L2
气
T0时,L1=0,得 n2=0
实验5 完全互溶双液系的平衡相图

实验5 完全互溶双液系定压气液液相平衡图【实验目的】1.掌握阿贝折光仪的使用方法并通过测定混和物折光率确定其组成。
2.学习常压下完全互溶双液系定压气液液相平衡图的测绘方法,加深对相律、恒沸点的理解。
3.绘制常压下环己烷-乙醇双液系的T—X图,并找出恒沸点混合物的组成和最低恒沸点。
【实验原理】相图:描述相平衡系统温度、压力、组成之间关系的图形,通过实验测定相平衡系统的组成来绘制。
由液态物质混合而成的二组分系统称为双液系统。
若两液体能以任意比例互溶,称其为完全互溶双液系;若两液体只能部分互溶,称其为部分互溶双液系。
纯液体或液态混合物的蒸气压与外压相等时就会沸腾,此时气液两相呈平衡,所对应的温度为沸点。
双液系的沸点不仅取决于压力,还与液体的组成有关。
表示定压下双液系气液两相平衡时温度与组成关系的图称为Tx图或沸点组成图。
定压下完全互溶双液系的沸点组成图可分为三类:(1)各组分对拉乌尔定律的偏差不大,溶液的沸点介于两纯液体的沸点之间。
如苯与甲苯系统,其T-x图如图5.1 (a)所示;(2)各组分对拉乌尔定律有较大负偏差,其溶液有最高沸点。
如丙酮与氯仿系统,其T-X图如图5.1 (b)所示;(3)各组分对拉乌尔定律有较大正偏差,其溶液有最低沸点。
如乙醇与环己烷等系统,其T-X图如图5.1 (c)所示。
图5.1 完全互溶双液系的相图恒沸点与恒沸组:在最高沸点和最低沸点处,气相线与液相线相交,对应于此点组成的溶液,达到气液两相平衡时,气相与液相组成相同,沸腾的结果只使气相量增加,液相量减少,沸腾过程中温度保持不变,这时的温度叫恒沸点,相应的组成叫恒沸组成。
压力不同,同一双液系的相图不同,恒沸点及恒沸组成也不同。
平衡数据测定:配制不同组成的溶液,大气压下加热至沸腾,测定不同组分的体系在沸点温度时气相、液相的折射率,再从折射率—组成工作曲线上查得相应的组成,然后绘制T—x图。
图5.2 沸点测定装置1进样口 2气相冷凝液取样口 3气相冷凝液 4数字温度计5电加热套实验装置如图。
完全互溶双液系气液平衡相图相关知识

实验一 完全互溶双液系气液平衡相图的绘制一.实验目的1.测定常压下环己烷-乙醇二元系统的气液平衡数据,绘制沸点-组成相图。
2.掌握双组分沸点的测定方法,通过实验进一步理解分馏原理。
3.掌握阿贝折射仪的使用方法。
二.实验原理两种液体物质混合而成的两组分体系称为双液系。
根据两组分间溶解度的不同,可分为完全互溶、部分互溶和完全不互溶三种情况。
两种挥发性液体混合形成完全互溶体系时,如果该两组分的蒸气压不同,则混合物的组成与平衡时气相的组成不同。
当压力保持一定,混合物沸点与两组分的相对含量有关。
恒定压力下,真实的完全互溶双液系的气-液平衡相图(T -x ),根据体系对拉乌尔定律的偏差情况,可分为三类:(1)一般偏差:混合物的沸点介于两种纯组分之间,如甲苯-苯体系,如图1(a)所示。
(2)最大负偏差:混合物存在着最高沸点,如盐酸-水体系,如图1 (b)所示。
(3)最大正偏差:混合物存在着最低沸点,如正丙醇—水体系,如图1(c))所示。
t AtAt At Bt B t Bt / o Ct / o t / o x Bx Bx BABAABB(a)(b)(c)x 'x '图1 完全互溶双液系的相图 对于后两种情况,为具有恒沸点的双液系相图。
它们在最低或最高恒沸点时的气相和液相组成相同,因而不能象第一类那样通过反复蒸馏的方法而使双液系的两个组分相互分离,而只能采取精馏等方法分离出一种纯物质和另一种恒沸混合物。
为了测定双液系的T -x 相图,需在气-液平衡后,同时测定双液系的沸点和液相、气相的平衡组成。
本实验以环己烷-乙醇为体系,该体系属于上述第三种类型,在沸点仪(如图2)中蒸馏不同组成的混合物,测定其沸点及相应的气、液二相的组成,即可作出T -x 相图。
本实验中两相的成分分析均采用折光率法。
图2折光率是物质的一个特征数值,它与物质的浓度及温度有关,因此在测量物质的折光率时要求温度恒定。
溶液的浓度不同、组成不同,折光率也不同。
物理化学简明教程第四版第五章-1

f = K–F +2
式中2通常指T,p两个变量。相律最早由
Gibbs提出,所以又称为Gibbs相律。
f = K–F +1 指定温度或压力
f = K–F
指定温度和压力
上一内容 下一内容 回主目录
返回
2020/10/17
(4)相律
例题1.碳酸钠和水可以形成下列几种化合物: Na2CO3·H2O; Na2CO3·7H2O; Na2CO3·10H2O
时 f = 0。
f = 3的三个变量通常是T,p 和组成 x。所
以要表示二组分体系状态图,需用三个坐标的立 体图表示。
上一内容 下一内容 回主目录
返回
2020/10/17
5.4 完全互溶的双液系
通常保持一个变量为常量,从立体图上得到 平面截面图。
(1) 保持温度不变,得 p-x 图 (2) 保持压力不变,得 T-x 图 (3) 保持组成不变,得 T-p 图
5.2 克劳修斯-克拉贝龙方程
-S () dT + V () dp =-S () dT + V () dp [V ()-V ()] dp = [S ()-S ()] dT
即 : d dT pV S(( )) V S(( )) V Sm m
对 于 可 逆 相 变 : S m H T m H m 为 相 变 热 。
B
273.16
T /K
OA 不能任意延长,终止于临界 点A (T = 647 K, p = 2.2×107 Pa), 这时气-液界面消失。高于临界 温度,不能加压使气体液化。
OB 理论上可延长至0 K附近。
OC 当C点延长至压力等于 2×108 Pa 时,相图变得复 杂,有不同结构的冰生成。
物理化学课件二组分体系相图

假定 H vap m的值与温度无关,积分得:
lnp2 vapHm(11)
p1
R T1 T2
这公式可用来计算不同温度下的蒸气压或摩尔蒸发热。
6.2.2 Clapeyron方程
三条两相平衡线的斜率均可由Clausius-Clapeyron 方程或Clapeyron方程求得。
f * * = ( 3 - 1 ) - 1 + 0 = 1 ( X B )
d ) T = 4 5 0 ℃ , P = 1 5 0 P θ , 有 催 化 剂 , 发 生 反 应
投 料 比 : N 2 ∶ H 2 = 1 ∶ 3 R ’ = 1 f * * = ( 3 - 1 - 1 ) - 1 + 0 = 0
注意:
a ) 独 立 的 浓 度 限 制 条 件 ( 初 始 条 件 或 分 解 )
说明:不同物质在同一相中的浓度限制条件 R’=0 C a C O 3 ( s ) → C a O ( s ) + C O 2 ( g )
b ) 独 立 的 化 学 反 应 数 “ R ” 表 示
化 学 平 衡 时 , 平 衡 常 数 限 制 浓 度
d dT PV Sii,,m m
Si,m Vi ,m
Si,m Vi,m
相变摩尔熵 相变摩尔体积
Si,m
Hi,m T
得:
dP H i,m
Clapeyron equation 适用于纯物质两相
dT
TVi , m
平衡
6.2.2 Clapeyron方程
在一定温度和压力下,任何纯物质达到两相平 衡时,蒸气压随温度的变化率可用下式表示:
§ 6.1.1 基本概念
相(phase) 体系内部物理和化学性质完全均
物理化学 第四章 第三节 完全互溶双液体系

(2)若组分A原为缔合分子,在形成溶液 过程中A的缔合体发生解离,使A分子个数 增多,从而蒸气压增加,产生正偏差。
(3)如果二组分混合后A-B分子间能形成结合 较弱的化合物或者氢键,这就会A分子个数减 少,从而蒸气压减小,产生负偏差。 一般说来,凡是组分A发生正或负偏差,则 组分B亦发生相同类型的偏差。 当正负偏差较小时,溶液的总蒸气 压还介于两个纯组分蒸气压之间(见下图)。
在T-X图上P恒定,
f
ƒ* = K-Φ+1=1-2+1=0
即P恒定时,恒沸点的温度和组成都固定不变.
2 .恒沸物的沸点和组成随外压改变--恒沸物 不是化合物,而是混合物 同上, K=2-0-1=1 当外压P不恒定,则 f = K-Φ+2=1-2+2=1 f 不为零,则恒沸点可随外压改变而移动,这表 明恒沸物的沸点和组成可随外压改变而改变, 所以恒沸物不是化合物而是混合物.
pB p xB yB p p
若纯液体B比纯液体A易挥发,亦即pB*> pA*,则
y y
因为: 所以: 则
A B
XA XB
xA + xB=1
yA + yB=1 <
1 xB xB
1 yB yB
xB < yB
结论说明,在相同温度下有较高蒸气压的易挥发 组分B,在气相中的浓度要大于在液相中的浓度, 对于有较低蒸气压的难挥发组分A则相反,这个规 律称为柯诺瓦洛夫(konowalov)第一定律
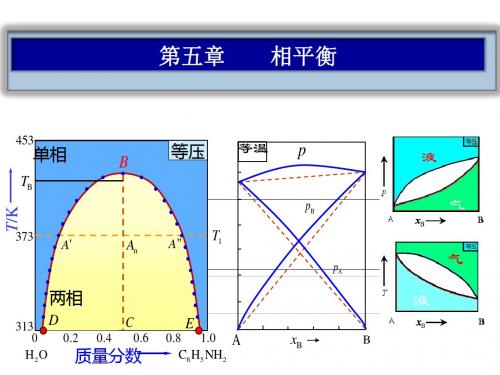
物系点--表示体系的温度、压力及 总组成在相图中的状态点称为物系 点。 相点--表示某个相状态(如相态,组 成,T,P等)的点称为相点。
当体系处于单相区 时,体系的总组成与 该相的组成是相同的 (即物系点与相点重合 为一点D);当物系点出 现在两相区时,体系 呈两相平衡形成两个 相点,它们的组成可 由通过物系点O的水 平连结线在气、液二 线上的交点决定(如上 图M、N点所示)。
第五章____相平衡5.2
§5.5
二组分系统的相图及应用
T,p , x1, y1。
两组分系统的特征
C=2, f =4 -, ≥ 1,R = 0, R’ = 0 则 f ≤ 3。
(1) T不变,得 p-x 图 (2) P不变,得 T-x 图 (3) x不变,得 T-p 图
一、理想的二组分液态混合物 ——完全互溶的双液系 1. 理想混合物的恒温相图p-x图
相点
系统点
液相线
• 点, 线, 区的含义 及各状态下自由 度数; T一定 • 会读系统总组成 g p 与相组成 ; yA yB pA pB 气相线 xA xB 相点 l 结线 •理想液态混合 物的气 - 液平衡
蒸气压组成相图
A和B均满足 pB = p*B xB
液相线 p-xB 线,直线 成对出现 气相线 p-yB 线(在液相线之下) p 两线交点 A pB 液相面 L 液相线以上 气相面 V 气相线以下 气液共存面 L + V 气相线和液相线之间
p
pB ( pB pA ) yB pA pB
以 p 对 yB 作图, 可得一曲线, 即压力-组成图上的气相线.
1. 理想混合物的恒温相图p-x 图
p / Pa
气相线: p ~ y, 恒温下蒸 气压随气 相组成的 变化。
pA pB p pB ( pB pA ) yB
p
* A
* pB
气相线
B
xA
A
1. 理想混合物的恒温相图p-x 图
p / Pa
p pA pB
液相线
p
p / Pa
* A
* pA
* pB
pA p xA
物理化学-第六章,相平衡-164

pC
A
临界点
647.30K
水
22.09MPa
ed c b a 冰
D O三相点 气
273.16K
B
610.62Pa
水的相图 T
OA、OB、OC三条线即两相平 衡线,可用克拉佩龙方程描述。
O:三相点 triple point(水在它 自身蒸气压力下的凝固点)。 通常所说的水的凝固点或冰点 (273.15 K)则是在101.325 kPa 下被空气所饱和的水的凝固点。
2020/9/7
相平衡
15
例4:某一纯理想气体的自由度为零,它必处于( )。 (A) 气液平衡共存; (B) 临界点; (C) 三相点; (D) 气相区
相律只能对系统作定性的描述,它只讨论“数目”而不 讨论“数值”:
根据相律可以确定有几个因素能对相平衡发生影响;在 一定条件下系统有几个相;等等。
但相律不能告诉我们这些数目具体代表哪些变量或哪些 相,也不知道各相的量之间的关系
2020/9/7
相平衡
29
第四节 理想的完全互溶双液系的相图
二组分系统: F = C – P + 2 = 4 – P
F最少为0,P最多为4; P最少为1,F最多为3——其相 图要用 p-T-x 三维立体图表示。
二组分系统相图的类型很多。
2020/9/7
相平衡
5
物种数 S:系统中所含化学物质的种数。 独立组分数 C:确定相平衡系统中所有各相组成所需的 最少物种数。
如:由 HI、H2、I2 三种气体组成的单相系统,S = 3。
① 如果各物质间没有任何化学反应,则组分数也是 3,即需要三 种物质才能确定气相的组成;
② 如果存在反应 2HI == H2 + I2,则组分数为 2,只需两种即可; ③ 如果还存在浓度限制如[H2]:[I2]=1:1,则组分数为1,只需一种
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
5.2几个基本概念
(2)组分数,独立组分数
在平衡体系所处的条件下,能够确保各相组成 所需的最少独立物种数称为独立组分数。 用符号C表示。
相对独立化学平衡数
浓度关系数
定义: 板书细讲
C S R R'
2019/5/13
5.2几个基本概念
3. 自由度 f
确定平衡体系的状态所必须的独立强度变量的 数目称为自由度,用符号f 表示。
OB 是气-固两相平衡线,即 冰的升华曲线,理论上可延长 至0 K附近。
OC 是液-固两相平衡线,当C点延长至压力大于 2108 Pa 时,相图变得复杂,有不同结构的冰生成。
2019/5/13
水的相图
OD 是AO的延长线,是过冷水和水蒸气的介稳平衡 线。因为在相同温度下,过冷水的蒸气压大于冰的蒸 气压,所以OD线在OB线之上。过冷水处于不稳定状 态,一旦有凝聚中心出现,就立即全部变成冰。
第五章概念 5.3 相律 5.4 单组分体系的相图 5.5 二组分体系的相图及其应用 5.6 三组分体系的相图及其应用
2019/5/13
5.1 引言
1.内容
(1)相律:讨论平衡体系中相数、独立组分数与描述 该平衡体系的变数之间的关系。 (2)相图:表达多相体系的状态随温度、压力、组成 等强度性质变化而变化的图形,称为相图。
相律(phase rule)
f F C 2
相律是相平衡体系中揭示相数 ,独立组分数C和
自由度 f 之间关系的规律,可用上式表示。式中2
通常指T,p两个变量。相律最早由Gibbs提出,所以 又称为Gibbs相律。如果除T,p外,还受其它力场影
响,则2改用n表示,即:
f F C n
2019/5/13
(1)处于f点的纯水,保持 温度不变,逐步减小压力, 在无限接近于P点之前,气 相尚未形成,体系自由度为2。 用升压或降温的办法保持液相 不变。
2019/5/13
水的相图
(2)到达P点时,气相出现, 在气-液两相平衡时,f 1 。 压力与温度只有一个可变。
(3)继续降压,离开P点时, 最后液滴消失,成单一气相,
(2)压力平衡条件:达到平衡时各相的压力相等
p p pF
2019/5/13
5.2几个基本概念
(3) 相平衡条件: 任一物质B在各相中的化学 势相等,相变达到平衡
B B FB
(4) 化学平衡条件:化学变化达到平衡
BB 0
B
2019/5/13
5.3 相律
O点 是三相点(triple point),气-液-固三相
共存,F 3, f 0 。三
相点的温度和压力皆由 体系自定。
H2O的三相点温度为273.16 K,压力为610.62 Pa。
2019/5/13
水的相图
两相平衡线上的相变过程 在两相平衡线上的任何
一点都可能有三种情况。如 OA线上的P点:
水的相图
水的相图是根据实验绘制的。图上有:
三个单相区 在气、液、固三个 单相区内, 1,f 2 ,温度和 压力独立地有限度地变化不会引 起相的改变。
三条两相平衡线 2,f 1 ,压力与温度只能改变 一个,指定了压力,则温度由体系自定。
2019/5/13
水的相图
OA 是气-液两相平衡线,即水的蒸气压曲线。它 不能任意延长,终止于临界点。临界点T 647 K , p 2.2107 Pa ,这时气-液界面消失。高于临界温 度,不能用加压的方法使气体液化。
5.4 单组分体系的相图
单组分体系 C 1
f 1 2 3
3,三相共存,f 0,无变量体系 max
2,两相共存,f 1,单变量体系
min
1,单相,f max
2,双变量体系
单组分体系的自由度最多为2,双变量体系的相 图可用平面图表示。
2019/5/13
2019/5/13
5.1 引言
2.特点
(1) 抽象 (2) 直观 (3)计算少,定性理解多
3.应用
(1)冶金 (2)化工分离,提纯 (3)寻找新材料、新化合物
2019/5/13
5.2几个基本概念
1.相 (1)定义:体系内部物理和化学性质完全均匀的部分 称为相。 相与相之间在指定条件下有明显的界面,在界面上 宏观性质的改变是飞跃式的。
体系中相的总数称为相数,用 表示
2019/5/13
5.2几个基本概念
(2)规律 ① 气相:一相 ② 液相:一相,两相或三相共存 ③ 固相:几种固体有几相;固溶体为一相
2. 物种数和组分数 (1)物种数: 体系中所含有的化学物质数称为体系的 物种数,用符号S表示。 物种数与状态无关,与化学式有关。
f 2 。 通常只考虑(2)的情况。
2019/5/13
两相平衡线的斜率
三条两相平衡线的斜率均可由Clausius-Clapeyron 方程或Clapeyron方程求得。
OA线 H vap m 0
d ln p H vap m 斜率为正。
dT
RT 2
OB线
H sub m 0
d ln p H sub m 斜率为正。
dT
RT 2
OC线 fus H 0, fusV 0 dp H fus m 0 斜率为负。 dT T V fus
2019/5/13
三相点与冰点的区别
三相点是物质自身的特性,不能加以改变, 如H2O的三相点 T 273.16 K , p 610.62 Pa . 冰点是在大气压力下,水、冰、气三相共存。当大 气压力为105 Pa时,冰点温度为273.15 K,改变外压, 冰点也随之改变。
2019/5/13
三相点与冰点的区别
冰点温度比三相点温度低 0.01 K 是由两种因素造成的:
(1)因外压增加,使凝固点下降 0.00748 K ;
如T,P,浓度(x,c,m…)
液态水f 2T,p
气 - 液平衡水f 1T或p
气 液 固平衡f 0三相点,固定
2019/5/13
5.2几个基本概念
4. 多相平衡条件
(1)热平衡条件:设体系有, , 时,各相具有相同温度
T T TF
,F 个相,达到平衡
