VLSI课内实验——RTL级并行前缀加法器设计

合集下载

VLSI电路系统与设计_32bit移位相加乘法器

《VLSI电路系统与设计》课程设计报告——32bit_32bit移位相加乘法器A 移位相加乘法器原理无符号二进制移位相加乘法器的基本原理是通过逐项移位相加来实现相乘的，从被乘数的最低为开始，若为1，则乘法左移后与上一次的和相加；若为0，左移后以全零相加，直至被乘数的最高位。

以下以4位二进制数为例进行说明：图1 移位相加乘法器原理图如图所示，就可以实现4位二进制数的相乘。

B 电路结构方案根据移位相加乘法器的基本原理，可以将整个电路划分为四个部分：32右移寄存器，32位加法器，乘1模块，64位锁存器。

原理框图如下所示：图2 移位相加乘法器原理框图在上图中，START信号的上跳沿及其高电平有两个功能，即32位寄存器清零和被乘数A[32:0]向移位寄存器SREG32B加载；它的低电平则作为乘法使能信号。

CLK为乘法时钟信号。

当被乘数被加载于32位右移寄存器SREG32B后，随着每一时钟节拍，最低位在前，由低位至高位逐位移出。

当为1时，与门ANDARITH打开，32位乘数B[32:0]在同一节拍进入32位加法器，与上一次锁存在64位锁存器REG16B中的高32位进行相加，其和在下一时钟节拍的上升沿被锁进此锁存器。

而当被乘数的移出位为0时，与门全零输出。

如此往复，直至32个时钟脉冲后，乘法运算过程中止。

此时REG64B的输出值即为最后的乘积。

此乘法器的优点是节省芯片资源，它的核心元件只是一个32位加法器，其运算速度取决于输入的时钟频率。

一、32位加法器模块的设计加法器模块是由8个四位全加器构成的，4位全加器是采用1位全加器构成的。

对于1位全加器，采用门级描述语言，使用了3个异或门和2个与门来实现的。

(1)1位加法器是采用门级描述语言，生成的库文件如图：仿真结果：图1 功能仿真图2 时序仿真(2)32位全加器32位全加器是采用8个4位全加器构成的，其电路原理图如下：图3-32位全加器原理图仿真结果：图4 功能仿真图5 时序仿真由以上的仿真结果可以看出，所设计电路在在功能上能满足要求，在时序上存在一定的时间延迟。

《FPGA入门教程》看书随笔——RTL设计

《FPGA入门教程》看书随笔——RTL设计1、使用verilog进行RTL设计一般可归纳为3种基本的描述方式：（1）数据流描述：采用assign连续赋值语句（2）行为描述：使用always语句或initial语句块的过程赋值语句（3）结构化描述：实例化已有的功能模块或原语，即平常所说的元件例化和IP core.过程赋值语句包括非阻塞过程赋值、阻塞过程赋值和连续过程赋值。

2、RTL级设计时需注意的问题（1）凡是在always或initial语句中赋值的变量，一定是reg类型变量；凡是在assign语句中赋值的变量，一定是wire类型变量、（2）定义存储器：reg[3:0] MEMAORY[0:7];地址为0~7，每个存储单元都是4bit；（3）由于硬件是并行工作的，在Verilog语言的module中，所有描述语句（包括连续辅助语句assign、行为语句块always和initial 语句块以及模块实例化）都是并发执行的。

（4）使用完备的if...else语句，使用个条件完备的case语句并设置default操作。

以防止产生锁存器latch，因为锁存器对毛刺敏感（5）严禁设计组合逻辑反馈环路，它最容易引起振荡、毛刺、时序违规等问题。

（6）不要在两个或两个以上的语句块（always或initial）中对同一个信号赋值3、阻塞赋值与非阻塞赋值（1）阻塞赋值的操作符号为“=”。

它的含义是在计算等式右侧表达式值及完成其赋值时不会被其他的verilog 语句打断，就是说，在当前赋值没有完成之前，它阻塞了其他 verilog 语句的执行。

（2）非阻塞赋值的操作符为“<>在实际使用中，应该遵循的原则是：（1）在时序逻辑中，使用非阻塞赋值（2）在组合逻辑中，使用阻塞赋值（3）在同一个always块中，不要混合使用阻塞赋值和非阻塞赋值（4）在同一个always块中，如果既有组合逻辑又有时序逻辑，使用非阻塞赋值（5）always模块的敏感表为电平敏感信号时，使用阻塞赋值（6）不要使用#0时延进行赋值（7）不要在阻塞赋值中使用时延语句（8）在行为级描述中，如语句间是顺序执行的关系，使用阻塞赋值4、哪些是不可综合的代码（1）对于一些抽象的行为描述代码是不可综合的。

高性能64位并行前缀加法器全定制设计_王仁平

第39卷第6期2011年12月福州大学学报（自然科学版）Journal of Fuzhou University（Natural Science Edition）Vol．39No．6Dec．2011DOI：CNKI：35－1117/N．20111220．1002．027文章编号：1000－2243（2011）06－0862－06高性能64位并行前缀加法器全定制设计王仁平，何明华，魏榕山，陈传东，戴惠明（福州大学物理与信息工程学院，福建福州350108）摘要：基于64位基4的Kogge－Stone树算法原理，采用多米诺动态逻辑、时钟延迟多米诺和传输管逻辑等技术来设计和优化并行前缀加法器的结构，达到减少了加法器各级门的延迟时间目的．为实现版图面积小、性能好，采用启发式欧拉路径算法来确定块进位产生信号电路结构，采用多输出多米诺逻辑来优化块进位传播信号，采用6管传输管逻辑的半加器．该加法器全定制设计采用SMIC0．18μm1P4M CMOS工艺，版图面积为0．1379mm2，在最坏情况下完成一次64位加法运算的时间为532．26ps．关键词：并行前缀加法器；基4点操作；多米诺逻辑；欧拉路径算法中图分类号：TN402文献标识码：AFull－custom design of high－performance64－bit Parall－Prefix adderWANG Ren－ping，HE Ming－hua，WEI Rong－shan，CHEN Chuan－dong，DAI Hui－ming （College of Physics and Information Engineering，Fuzhou University，Fuzhou，Fujian350108，China）Abstract：A parall－prefix adder based on64－bit radix－4Kogge－Stone tree algorithm principle isproposed in this paper．The architecture is optimized using domino dynamic logic，clock delayed domi-no and transmission pipes logic，which reduces the gate delay of each stage in the adder dramatically．In order to achieve small layout area and good performance，heuristic Euler algorithm is adopted to de-termine the block carry generation signals circuit structure，multi－output domino logic is adopted tooptimize the block carry propagate signals，and six transmission pipes logic is used to build a half－ad-der．Using SMIC0．18μm1P4M CMOS process for layout design，the adder’s area is0．1379mm2．In the worst case，the computation time is532．26ps．Keywords：parall－prefix adder；radix－4dot operation；dynamic logic；Euler algorithm；stick figure并行前缀加法器（PPA）是超前进位加法器的变种，由于具有速度和面积两方面的优势，被广泛应用于高性能微处理器设计中．在64位并行前缀加法器算法中，为进一步减少加法器的运算时间，人们提出多种变体算法［1－3］，其中基4的Kogge－Stone树算法因其卓越的性能而成为目前64位及以上快速运算加法器最常用的实现结构之一．如今，运算速度超过GHz的64位微处理器已成为主流产品，对加法器的运算速度要求也越来越高，因此，采用动态逻辑门设计高性能的并行前缀加法器变得更加广泛［4－6］．本研究设计的高性能64位并行前缀加法器应用于64位微处理器，在基4的Kogge－Stone树算法基础上，采用多米诺动态逻辑、时钟延迟多米诺和传输管逻辑等技术来优化加法器结构，采用启发式欧拉路径算法、逻辑图、棍棒图、多输出多米诺逻辑、6管传输管XOR逻辑等方法来减少版图面积，提高性能．采用SMIC0．18μm1P4M CMOS工艺进行设计，整个加法器的版图面积为0．1379mm2，仿真时在最坏情况下完成一次64位加法运算时间为532．26ps．1加法器算法分析和电路结构1．164位基4的Kogge－Stone树算法并行前缀运算基本思想：先计算每位的进位产生信号G i和进位传播信号P i，再通过前缀运算单元计收稿日期：2011－04－01通讯作者：王仁平（1972－），高级讲师，E－mail：rpwang@fzu．edu．cn基金项目：福建省科技重大专项基金资助项目（2009HZ010002）；福建省教育厅科研资助项目（JA09001）；福建省自然科学基金资助项目（2009J05143）第6期王仁平，等：高性能64位并行前缀加法器全定制设计算块进位产生信号G i ：j 和块进位传播信号P i ：j ，并将所有的前缀运算单元按照一定规律组织成递归的进位树，这样每一位的进位信号就可通过进位树的传递作用在运算结点中一步一步地计算出来．64位并行前缀加法器基于基4的Kogge －Stone 树算法如图1所示［7］，图中用“□”表示用两个加数A i 、B i 来建立相应进位产生信号G i 和进位传播信号P i ，“○”表示基4的Kogge －Stone 树算法中的点操作来计算块进位产生信号G i ：j 和块进位传播信号P i ：j ，“◇”表示用两个加数A i 、B i 和前一位进位C o ，i －1来计算该位的和S i ．这种算法计算块进位函数的最长时间是O （log N 4）级门延迟，其中N 是加法器位数，如计算其最高位的块进位函数G 63：0和P 63：0时间为3级门的延迟．图164位基4的Kogge －Stone 树算法Fig．1Arithmetic of 64－bit radix －4Kogge －Stone tree计算最高位的块进位产生函数G 63：0和块进位传播函数P 63：0，具体过程如下：第一级点操作输入在每相邻4位进行，如计算G 3：0和P 3：0的点操作如式（1）所示：（G 3：0，P 3：0）=（G 3，P 3）·（G 2，P 2）·（G 1，P 1）·（G 0，P 0）（1）第二级点操作输入在第一级输出基础上每隔4位进行，如计算G 15：0和P 15：0的点操作如式（2）所示：（G 15：0，P 15：0）=（G 15：12，P 15：12）·（G 11：8，P 11：8）·（G 7：4，P 7：4）·（G 3：0，P 3：0）（2）图2改进的64位基4的Kogge －Stone 树加法器结构Fig．2Modified adder structure of 64－bit radix －4Kogge －Stone tree第三级点操作输入在第二级输出基础上每隔16位进行，如计算G 63：0和P 63：0的点操作如式（3）所示：（G 63：0，P 63：0）=（G 63：48，P 63：48）·（G 47：32，P 47：32）·（G 31：16，P 31：16）（G 15：0，P 15：0）（3）当算出相应位的块进位产生函数G i ：0和块进位传播函数P i ：0，计算该位的进位输出如式（4）所示．若最低位进位C i ，0为0，则该位的进位输出C o ，i =G i ：0，（C o ，i ，0）=（G i ：0，P i ：0）·（C i ，0，0）=（G i ：0+P i ：0C i ，0，0）（4）1．264位基4的Kogge －Stone 树加法器结构为缩短加法器运算时间和减少版图面积，设计了改进的64位基4的Kogge －Stone 树加法器结构如图2所示，进位产生信号G i 、进位传播信号P i 和进位输出信号C o ，i 采用动态逻辑实现、块进位产生信号G i ：j 和块进位传播信号P i ：j采用多米诺动态逻辑实现；为减少多米诺动态逻辑的时钟负载并提高下拉驱动能力，取消了下拉网络预充电，但由于预充电是“行波”推进，为避免存在短路电流，采用时钟延迟多米诺技术为各级多米诺动态逻辑提供时钟信号；半·368·福州大学学报（自然科学版）第39卷加器采用面积小且运算速度快的6管传输管逻辑实现．2主要模块设计和优化基4的Kogge －Stone 树算法64位并行前缀加法器模块包括：进位产生信号和进位传播信号电路、块进位产生信号和块进位传播信号电路、时钟延时多米诺、计算进位电路和求和电路．进位产生信号、进位传播信号和计算进位的动态逻辑电路设计相对简单，因此，重点对块进位产生信号电路设计、块进位传播信号电路设计、求和电路设计和时钟延时多米诺技术等进行研究．2．1块进位产生信号和块进位传播信号电路设计用基4点操作计算块进位产生函数G i ：0和块进位传播函数P i ：0，由于各基4点操作的电路结构一致，以实现块进位产生信号G 3：0和块进位传播信号P 3：0来进行研究．2．1．1块进位产生信号电路设计复合逻辑门版图要实现面积小且性能好的条件是物理连接的晶体管能通过扩散区进行重叠，使复合逻辑门可用连续的扩散区来实现（即一个器件的漏区也是下一个器件的源区），这样即可以减少版图面积，又无需导线和过孔进行连接，减少寄生参数．为达到复合逻辑门的版图能用连续扩散区实现，采用逻辑图基于欧拉路径算法得到复合逻辑门输入端的排列顺序，然后用棍棒图［8］（不标尺寸器件、只注重器件相对位置和连接关系的象征性符号）研究版图绘制策略，得到版图的拓扑结构．根据点操作算法，G 3：0输出表达式可写成式（5）所示：G 3：0=G 3+P 3G 2+P 3P 2G 1+P 3P 2P 1G 0=P 3（P 2（P 1G 0+G 1）+G 2）+G 3（5）图3块进位产生信号G 3：0逻辑电路Fig．3Logic circuit of block carry generation signal G 3：0G 3：0对应组合逻辑电路如图3所示的实线部分，为6级两输入与或结构．对这种结构电路，可用基于启发式的欧拉路径算法来进行版图设计．启发式欧拉路径算法的理论基础是：对于多级与或结构的组合逻辑，如果每一个与/或门的输入端数目为奇数，则在相应的逻辑图中，下拉网络PDN 和上拉网络PUN 存在一致的欧拉路径．为满足启发式欧拉路径算法输入端数目为奇数要求，在每个与/或门加入一个用虚线表示的“假想”输入，这些“假想”输入统一放在图的上方．运用欧拉路径算法设计块进位产生信号G 3：0复合门版图步骤是先绘制逻辑图，逻辑图是用圆点代表电路节点，边是用控制晶体管的栅信号命名，再根据启发式欧拉路径算法的理论基础，研究得到下拉网络PDN 的逻辑图如图4所示．图4块进位产生信号G 3：0逻辑图Fig．4Logic diagram of block carry generation signal G 3：0图5块进位产生信号G 3：0电路原理图Fig．5Circuit schematic of block carry generation signal G 3：0·468·第6期王仁平，等：高性能64位并行前缀加法器全定制设计欧拉路径是通过逻辑图中所有节点并且只经过每条边一次的一条路径，在欧拉路径中边的顺序等于在复合门版图中输入端的顺序．本设计选择欧拉路径为G 3P 3G 2P 2G 1P 1G 0X 0X 1X 2X 3X 4X 5，X 0X 1X 2X 3X 4X 5是假想输入，在版图设计中不存在．根据所选择的欧拉路径，对应多米诺动态逻辑电路图如图5所示．图6块进位产生信号G 3：0棍棒图Fig．6Stick figure of block carry generationsignal G 3：0在设计块进位产生信号G 3：0复合门版图时，先用棍棒图来研究版图绘制策略，得到电路版图的拓扑结构．选择欧拉路径为G 3P 3G 2P 2G 1P 1G 0，在欧拉路径中边的顺序等于在复合门版图中输入端的顺序，得到的棍棒图如图6所示，物理连接的晶体管能通过扩散区进行重叠连接，这样即减少版图面积，又无需导线和过孔进行连接，减少寄生参数．2．1．2块进位传播信号电路设计为减少版图面积和提高性能，对块传播信号P 3：0=P 3P 2P 1P 0电路，利用多输出多米诺逻辑（动态逻辑门在一个门中可产生不同逻辑功能）特点，在图5基础上共享P 3P 1．这图7基4点操作的动态实现Fig．7Dynamic implementation of radix －4dotoperation种方法对预充电器件数目没有减少，但P 3P 1为两个输出所共享，减少求值晶体管数目，也减少前一级的扇出数，最终基4点操作的动态逻辑电路实现如图7所示．2．1．3基4点操作动态电路的优化基4点操作动态电路有多个输入端，为降低大扇入电路的延时，提高性能，根据Elmore 延时模型可知，最靠近输出的P 3管电阻在延时公式中出现的次数最多，应当使P 3管的电阻最小（即宽长比最大）．依次类推．因此，对下拉网络PDN ，从输出往下采用逐级加大晶体管尺寸，即P 2＜P 1=G 0＜P 3，能达到降低起主要作用的电阻，同时使器件电容的增加保持在一定的范围内．通过仿真分析可知，逐级加大晶体管尺寸与各个管子相同尺寸相比传播延时减少约10%．由64位基4的Kogge －Stone 树算法可知，输出的G 3：0和P 3：0要去驱动较大负载，如果由大扇入再直接去驱动大负载，则该电路的延时很长，性能差．可采用下面方法进行优化：引入静态反相器，在预充电期间n 型动态门输出充电至VDD ，通过反相器输出为0，而反相器输出又是下一级动态多米诺门输入，因此可取消下拉网络预充电管，减少时钟负载并提高下拉的驱动能力；同时引入的静态反相器隔离了由大扇入直接驱动大负载，提高了速度；另外该反相器还可用来驱动一个漏泄器件以抵抗漏电和电荷分享，解决了动态电路中信号完整性问题［9］．由于第一级与第二级的块信号输出要驱动较大负载，在估算出负载电容基础上，采用3个具有相同门努力的反相器组成反相器链来实现传播延时最小．图8基4点操作的版图Fig．8Layout of radix －4dot operation 对一个较大尺寸的晶体管意味着有较长栅线，较长栅线有较高电阻，从而降低器件的性能．本设计对一个较大尺寸的晶体管采用许多小的晶体管并联来构成，采用低电阻的金属线旁路连接较短的栅线可降低电阻，提高器件性能，同时各个模块的版图做到相同高度，便于集成和连接，最后得到基4点操作的版图如图8所示．2．2求和电路设计异或门XOR 是加法运算的基本单元，基于如图9（a ）所示CMOS 互补逻辑的10管XOR 在面积和功耗上都不经济，而基于如图9（b ）所示10管传输门XOR 逻辑，节省了面积和功耗，但是互补控制信号增加了电路的复杂度．由WangJyh －Ming 提出了6管传输管XOR 逻辑如图9（c ）所示［10］，结构简单，面积小，性能好，运算速度比10管CMOS 互补逻辑快27．9%，比10管传输门逻辑快20%，且无需互补信号．由于使用传输管逻辑，高电平输出时可能存在阀值压降导致反相器输出存在静态功耗．通过综合考虑面·568·福州大学学报（自然科学版）第39卷积和性能，半加器选择基于6管传输管XOR 逻辑．（a ）10管CMOS XOR （b ）10管传输门XOR （c ）6管传输管XOR图9异或门实现比较Fig．9Implementation Comparison of XOR gate2．3时钟延时多米诺和H树分布图10时钟延时多米诺逻辑和H 树分布Fig．10Clock －delay domino logic and H －tree distribution时钟延时匹配是采用时钟延时多米诺技术，它的每一级时钟由前一级时钟和后一级时钟推导来进行确定，具体的时钟延时要求如下：只有在当前这一级预充电稳定输出为0后才能对下一级开始进行预充电；在当前这一级求值边沿时，下一级必须充电结束，这样才能取消下拉网络预充电管和避免存在短路电流．由于每一级时钟信号都有较大的驱动负载，如计算第一级块进位产生信号和块进位传播信号的时钟信号CLK1就连接有126个PMOS 管，因此采用反相器延时加上时钟路径上的传输门以及H 树结构时钟分布技术来设计时钟延时驱动，具体电路如图10所示，形成16个子叶节点，每个子叶节点再去驱动8个PMOS 管，传输门总是导通，而时钟路径的延时则可能通过这些器件的尺寸来进行调整．3仿真结果分析和比较加法器版图设计完成后，用Assura 工具先对它进行物理验证，包括设计规则检查（DRC ）、电气规则检查（ERC ）和版图与原理图一致性检查（LVS ），物理验证通过后，再用Assura 工具提取版图的寄生参数并采用ss 的Spectre 模型基于最长进位传播路径条件下进行后仿真．根据块进位函数动态实现电路特点，可知当输入A 为全“0”，B 为全“1”，最低位进位C i ，0为“1”时，将使进位传播路径最长，即在该条件下可以得出整个加法器关键路径的延时，后仿真得CLK0、P 0、P 3：0、P 15：0、P 63：0、C o ，63和S 63波形如图11所示．在最坏条件下测得关键路径（从CLK0到第63位和输出S 63）的延时为532．26ps ，从中可知本文设计的64位整数加法器部件可运行在1．8GHz 的工作频率．在设计基4的Kogge －Stone 树算法64位并行前缀加法器同时，也用相同工艺的静态CMOS 技术来设计相同结构的加法器，对每个阶段的关键路径延时比较结果如表1所示，从中可知采用多米诺动态逻辑、时钟延迟多米诺和传输管逻辑等技术实现的电路性能有非常大改善．表1多米诺动态逻辑和静态CMOS 关键路径延时比较Tab．1Comparison domino dynamic logic with static CMOS on the critical path delay时钟延迟多米诺加法器逻辑t 延时/ps 静态CMOS 加法器逻辑t 延时/ps P i /G i 53P i /G i112P 4/G 4117P 4/G 4283P 16/G 16144P 16/G 16354P 64/G 64135P 64/G 64378进位（C o ，i ）52进位（C o ，i ）135求和（S i ）31求和（S i ）180·668·第6期王仁平，等：高性能64位并行前缀加法器全定制设计图11最坏情况下关键路径波形仿真结果Fig．11Wave simulation results on critical path in worst －case4结论设计高性能加法器部件需要在实现算法、电路结构、采用技术、器件参数、版图设计等各个方面进行优化和改进．本文实现算法和电路结构采用改进的64位基4的Kogge －Stone 树加法器结构，采用技术有多米诺动态逻辑、多输出多米诺逻辑、6管传输管实现XOR 逻辑、时钟延迟多米诺逻辑和H 树分布等，器件参数优化主要对基4点操作动态电路进行，版图设计采用启发式殴拉路径算法、逻辑图、棍棒图对基4点操作动态电路进行．最终设计的64位加法器面积为0．1379mm 2，在最坏情况下完成一次加法运算时间为532．26ps．本设计广泛采用动态电路实现，在速度和面积方面有很大的优势，但功耗相对较大以及动态结点易受到来自各方面噪声影响，因此还需要进一步研究动态电路工作在相对较低功耗且可靠性相对较高的设计技术．参考文献：［1］Dozza D ，Gaddoni M ，Baccarani G．A 3．5ns ，64bit carry －lookahead adder ［C ］//Proceedings of IEEE International Symposi-um on Circuit and Systems．1996：297－300．［2］Matthew S ，Krishnamurthy R ，Anders M ，et al ．Sub －500ps 64－b ALUs in 0．18mm SOI /Bulk CMOS ：design and scalingtrends ［J ］．IEEE Journal of Solid －State Circuits ，2001，36（11）：1636－1646．［3］孙旭光，毛志刚，来逢昌．改进结构的64位CMOS 并行加法器设计与实现［J ］．半导体学报，2003，24（3）：203－208．［4］Mathew S ，Anders M ，Krishnamurthy R ，et al ．A 4GHz 130nm address generation unit with 32b sparse －tree adder core ［J ］．IEEE Journal of Solid －State Circuits ，2003，38（5）：689－695．［5］Mathew S K ，Anders M A ，Bloechel B ，et al ．A 4GHz 300mW 64b integer execution ALU with dual supply voltages in 90nmCMOS ［J ］．IEEE Journal of Solid －State Circuits ，2005，40（1）：162－163．［6］Jin Zhan －peng ，Shen Xu －bang ，Bai Yong －qiang．A 64－bit fast adder with 0．18μm CMOS technology ［C ］//Proceedingsof IEEE International Symposium on Communications and Information Technologies．Beijing ：［s．n．］，2005：1167－1171．［7］王仁平，何明华，陈传东，等．64位超前进位对数加法器的设计与优化［J ］．半导体技术，2010，35（11）：1116－1121．［8］Rabeay J M．数字集成电路－电路、系统与设计［M ］．周润德，译．北京：清华大学出版社，2008：171－431．［9］David A Hodges．数字集成电路分析与设计－深亚微米工艺［M ］．将安平，译．北京：清华大学出版社，2005：235－266．［10］吴金，应征．高速浮点乘法器设计［J ］．电路与系统学报，2005，10（6）：6－10．（责任编辑：林晓）·768·。

RTL设计与仿真实验报告

综合课程设计8 路彩灯控制器RTL设计与仿真实验报告专业：集成电路设计与集成系统班级：2班指导老师：王忆文/杜涛学生：一、多路彩灯控制器设计原理（功能说明）：设计的是一个彩灯控制程序器。

可以实现四种花型循环变化，有复位开关。

整个系统共有三个输入信号CLK，RST，SelMode，八个输出信号控制八个彩灯。

时钟信号CLK脉冲由系统的晶振产生，各种不同花样彩灯的变换由SelMode控制。

设计方框图如下图1所示：图1：系统方框图硬件电路的设计要求在彩灯的前端加74373锁存器，用来对彩灯进行锁存控制。

此彩灯控制系统设定有四种花样变化，这四种花样可以进行切换，四种花样分别为：(1)彩灯从左到右逐次闪亮。

然后从右到左逐次熄灭。

(2)彩灯两边同时亮两个，然后逐次向中间点亮。

(3)彩灯从左到右两个两个点亮，然后从右到左两个两个逐次点亮。

(4)彩灯中间两个点亮。

然后同时向两边散开。

二、设计方案说明本控制电路采用VHDL语言设计，运用top-down自顶而下的设计思想，按功能逐层分割实现层次化设计。

根据多路彩灯控制器的设计原理，将整个控制器分为四个部分，分别对应彩灯的四种变化模式。

另外，由于灯的控制时钟的时钟频率要满足人眼识别的要求，而总时钟信号CLK由外部晶振产生，时钟频率一般在1MHz—数百MHz，很大，所以要有分频进程。

本设计主要由两个进程组成：时序控制进程和分频进程。

时序控制进程在分频后的时钟信号clk1ms的作用下，利用case语句实现不同selmode模式下的花型变化。

分频进程是在外部晶振产生的时钟CLK 信号的作用下，将CLK信号分频产生clk1ms这一时钟信号。

输出端口将信号输出给前端加有74373锁存器的彩灯（如8个LED数码管）来实现硬件电路。

具体模块设计:时序控制模块：CLK为输入时钟信号，电路在时钟上升沿变化；RST为复位清零信号，低电平有效，一旦有效时，电路无条件地回到初始状态；selmode 为变化模式选择信号，从00到11四种模式；Light[7:0]为输出信号，RST 有效时输出为零；RST无效时随selmode信号的变化而变化。

RTL基本知识：全加器设计（VHDL）

RTL基本知识：全加器设计（VHDL）
【设计要求】
使⽤层次化设计⽅法，⽤VHDL语⾔设计四位⼆进制全加器，并进⾏仿真。

【设计⽬的】
考查对于VHDL元件例化语法的熟悉程度；
考查对于数字电路中全加器⼯作原理的理解；
【设计思路】
⽤门实现两个⼆进制数相加并求出和的组合线路，称为⼀位全加器。

⼀位全加器可以处理低位进位，并输出本位加法进位。

多个⼀位全加器进⾏级联可以得到多位全加器。

第⼀步：⼀位全加器；
第⼆步：多位全加器，在其中例化⼀位全加器实现；
1 ⼀位全加器
a和b为两位⼆进制数据，cin为前级进位位，cout为当前计算后的进位位，sum为加法结果，电路结构和真值表如下：
2 四位全加器
四位全加器是在⼀位全加器的基础上利⽤进位进⾏串⾏级联实现，实现后的电路结构⽰意图如下：
【源代码】
1 ⼀位全加器源代码
2 四位全加器源代码
【实验结果】
【思考】
在仿真时，输⼊可能会存在⽑刺，采⽤什么⽅法可以消除⽑刺？
在设计多位全加器时，如果位数很多，⽤元件例化的⽅式程序会很长，可以采⽤什么⽅法可以改进实现？。

并行前缀加法器优化并行阵列乘法器的设计(IJEM-V3-N2-3)

I.J. Engineering and Manufacturing, 2013, 2, 40-50Published Online September 2013 in MECS ()DOI: 10.5815/ijem.2013.02.03Available online at /ijemDesign Of A Optimized Parallel Array MultiplierUsing Parallel Prefix AdderK.KalaiKaviya a, D.P.Balasubramanian b, S.Tamilselvan ca,b PG Student,S.M.K Fomra Institute of technology, Chennaic Asst Professor,S.M.K Fomra Institute of technology, ChennaiAbstractMultiplication is the basic building block for several DSP processors, Image processing and many other. Over the years the computational complexities of algorithms used in Digital Signal Processors (DSPs) have gradually increased. This requires a parallel array multiplier to achieve high execution speed or to meet the performance demands. A typical implementation of such an array multiplier is Braun design. Braun multiplier is a type of parallel array multiplier. The architecture of Braun multiplier mainly consists of some Carry Save Adders, array of AND gates and one Ripple Carry Adder. In this research work, a new design of Braun Multiplier is proposed and this proposed design of multiplier uses a very fast parallel prefix adder (Brent kung Adder) in place of Ripple Carry Adder. The architecture of standard Braun Multiplier is modified in this work for reducing the area and delay due to Ripple Carry Adder and performing faster multiplication of two binary numbers. The design is implemented using Microwind1, digital schematics (DSCH)Index Terms: Array multiplier, carry save adder (CSA), Kogge stone Adder, parallel prefix adder ripple carry adder, Microwind, DSCH.© 2013 Published by MECS Publisher. Selection and/or peer review under responsibility of the Research Association of Modern Education and Computer Science.1.IntroductionFor scientific computations, Multiplication is an important and predominance in all digital signal processing (DSP) applications and its subfields. Application Specific Integrated Circuits (ASICs) utilizes as special purpose processor for DSP algorithms [1]. Multiplication is a Repeated addition of n bits will give the solution for the multiplication. i.e.Multioperand addition process. The multioperand addition process needs two n – bit operands. It can be realized in n- cycles of shifting and adding. If the multiplicand is given be.* Corresponding author. Tel.: 00966; 533273146E-mail address: salem_farh@A= a n-1…a1a0 ---- (1) Multiplier is given byB=b n-1…b1b0, --- (2) Then product will beP=P2n P2n-1..p1p0 (3) Over the years the computational complexities of algorithms used in Digital Signal Processors (DSPs) have gradually increased. This requires a parallel multiplier to meet the performance demands.1.1.Parallel MultipliersThree important criteria to be considered in the design of multipliers are the chip area, speed of computation and power dissipation. Most advanced digital systems incorporate a parallel multiplication unit to carry out high speed mathematical operations. a microprocessor requires multipliers in its arithmetic logic unit and a digital signal processing system requires multipliers to implement algorithms such as convolution and filtering. Today, high speed parallel multipliers with much larger areas and higher complexity are used extensively in reduced Instruction set computers, digital signal processing and graphics accelerator. There are many different design methods of multipliers such as the serial-parallel multiplier,the baugh-wooley multiplier and wallace tree multiplier.to implement a multiplier a relatively simpler form of adders is the braun array.1.2 Parallel Prefix addersParallel prefix adder is the most flexible and widely used for binary addition. Parallel Prefix adders are best suited for VLSI implementation. Number of parallel prefix adder structures have been proposed over the past years intended to optimize area, fan out, logic depth and inter connect count.Binary addition is the most fundamental and frequently used arithmetic operation. A lot of work on adder design has been done so far and much architecture have been proposed. When high operation speed is required, tree structures like parallel prefix adders are used [2] [6] In [2], Sklansky proposed one of the earliest tree prefix is used to compute intermediate signals. In the Brent Kung approach [4], designed the computation graph for area optimization. The KS architecture [3] is optimized for timing. The LF architecture [11], is proposed, where the fan out of gates increased with the depth of the prefix computation tree.2.Research MethodologyThe architecture of Braun Multiplier is modified by replacing the Ripple Carry Adder with a Brent Kung Adder. The reason for selecting Brent Kung Adder is that it is the Fastest adder and low area consumption adder.2.1Braun MultiplierIt is a simple parallel multiplier generally called as carry save array multiplier. It has been restricted to perform signed bits. The structure consists of array of AND gates and adders arranged in the iterative manner and no need of logic registers. This can be called as non – addictive multipliers.Braun Multiplier in standard form has (n-1) Carry Save Adder stages for generating partial products and one Ripple Carry Adder [6] stagewhich give final 4 MSB.2.1.1Carry Save AdderCarry save adder is a digital adder which is used to compute sum of three or more n-bit binary numbers. Carry save adder is same as a full adder. It generates two outputs of equal dimensions as the inputs.This unique dual output consists of:One sequence of partial sum bitsOne sequence of carry bitsOne of the major speed enhancement techniques used in modern digital circuits is the ability to add numbers with minimal carry propagation. The basic idea is that three numbers can be reduced to 2, in a 3:2 compressor, by doing the addition while keeping the carries and the sum separate. This means that all of the columns can be added in parallel without relying on the result of the previous column, creating a two output "adder" with a time delay that is independent of the size of its inputs. The sum and carry can then be recombined in a normal addition to form the correct result. It is only the final recombination of the final carry and sum that requires a carry propagating addition.2.1.2. Ripple Carry AdderA simple ripple carry adder is a digital circuit that produces the arithmetic sum of two binary numbers. It can be constructed with full adders connected in cascade, with the carry output from each full adder connected to the carry input of the next full adder in the chain. Figure.1 shows the interconnection of four full adder (FA) circuits to provide a 4-bit ripple carry adder.The main drawback of this adder is that the total propagation delay, T is directly proportional to the total number of stages of Ripple Carry Adder. If the total no. of stages are N and propagation delay of each stage is D, then total propagation delay of ripple carry adder will be T. 2.2. Architecture:An n*n bit Braun multiplier [5],[6] is constructed with n (n-1) adders, n2 AND gates and (n-1) rows of Carry Save Adder as shown in the fig.1, whereX: 4 bit MultiplicandY: 4 bit MultiplierP: 8 bit Product of X & YPn: Xi Yi is a Product bitFig 1: 4x4 Braun Multiplier ArchitectureEach products can be generated in parallel with the AND gates. Each partial product can be added with the sum of partial product which has previously produced by using the row of adders. The carry out will be shifted one bit to the left or right and then it will be added to the sum which is generated by the first adder and the newly generated partial product. The shifting would carry out with the help of Carry Save Adder (CSA) [6] and the Ripple carry adder should be used for the final stage of the output. Braun multiplier [5] performs well for the unsigned operands that are less than 16 bits in terms of speed, power and area. But it is simplestructure when compared to the other multipliers.Fig 2 : Layout of Braun Multiplier using Ripple carry adder using Micro windFig 3:Transistor count using Tanner EDAThe main drawback of this multiplier is that the potential susceptibility of glitching problem due to the Ripple Carry Adder in the last stage. The delay depends on the delay of the Full Adder and also a final adder in the last stage. The delay depends on the delay of the Full Adder and also a final adder in the last stage. Delay due to the final ripple adder can be minimized by using very fast one of a Parallel Prefix Adder [2] “Brent kung adder” which is a type of carry look Head Adder.3.Proposed Work - Design Of Braun Multiplier With Brent Kung AdderThe objective of this research is to design a new architecture of Braun Multiplier with Brent kung Adder which gives fast multiplication and less area.3.1 ArchitectureThe proposed multiplier‟s block diagram is shown in fig.4 .The architecture of Braun multiplier with brent kung adder is shown in fig 5. where we have used a 3 bit Brent kung Adder in 4th stage of Braun multiplier[8].Fig 4: Block diagram of Braun multiplier with Brent Kung adder3.2Brent Kung AdderIn the following section, a structure known as the Brent Kung Structure which was first proposed by Brent and Kung in 1982 and which uses the logarithmic concept is discussed. This structure used an operator known as the dot (.) operator, which is explained in the architecture, for its basic blocks3.2.1. Brent Kung ArchitectureThe Brent Kung architecture is divided into three separate stages1. Generate/Propagate Generation2. The Dot (.) Operation3. Sum generationFig 5: Architecture of Braun Multiplier with Brent kung adder3.2.1.1 Generate/Propagate GenerationIf the inputs to the adder are given by the signals A and B, then the generate and propagate signals are obtained according to the following equations.G=A and B (4)P = A xor B (5)3.2.1.2 The Dot ( • ) OperationThe most important building block in the Brent Kung Structure is the dot (.) operator. The basic inputs to this structure are the generate and propagate signals obtained in the previous stage. The. operator is a function that takes in two sets of inputs-- (g, p) and (g', p')-and generates a set of outputs-- (g + pg', pp'). These building blocks are used for the generation of the carry signals in the structure. For the generation of the carry signals, the carry for the kth bit from the carry look-ahead concept is given by.Fig 6: Design of the dot ( • ) operationCo,k=Gk+Pk(Gk-1 +Pk-1 +P k-l (...+Pl(GO+Po Ci,o))) (6) Using the dot operator explained above the Equation 3.3 can be written for the different carry signals as Co,o = Go+P Ci,o = a ( Go,Po) (7) Co,l = G1 + GoPI = a ((G l , PI )e(Go, Po)) (8) where a is a function defined in order to access all the tuples. The 8-bit Brent Kung Structure is shown in Figure 7.This figure shows all the carry signals generated at different where a is a function defined in order to access all the tuples. The 8-bit Brent Kung Structure is shown in Figure7.this figure shows all the carry signals generated at different stages in the structure. In the structure, two binary tree organizations are represented –the forward and the reverse trees.The forward binary tree alone is not sufficient for generation of all the carry signals. It can only generate the signals shown as Co,o, Co,l, Co,3 and Co,7. The remaining carry signals.Fig 7:8-bit Brent Kung StructureFig 8:.Layout of proposed adder using MicrowindFig 9:Transistor Count of proposed adder using TanneTable 1. Result analysis4.ConclusionThe results shown in Table 1 are for the new Braun Multiplier which is designed for two inputs …A‟ and …B‟ each of width 4 bits. Hence, we can say that for the multiplier applications the proposed new design of Braun Multiplier using Brent Kung adder would provide the result in effectively lesser area than compared with Ripple Carry Adder we have a reduction in area of 194µm2.Reference[1]Muhammad H. Rais, “Hardware Implementation of Truncated Multipliers Using Sp artan-3AN, Virtex-4 and Virtex-5 FPGA Devices”, Am. J. Engg. & Applied Sci., 3 (1): 201-206, 2010.[2]Skalansky “conditional sum additions logic” IRE Transactions, Electronic Computers, vol, EC – 9, pp,226 - 231, June 1960.[3]Kogge P, Stone H, “A parallel algo rithm for the efficient solution of a general class Recurrencerelations”, IEEE Trans. Computers, vol.C-22, No.8, pp 786-793, Aug.1973.[4]Brent R, Kung H, “A regular layout for parallel adders”. IEEE Trans, computers, Vol.C-31, no.3, pp260-264, March1982 Academy of Science, Engineering and Technology.[5]R ,Anitha, and V, Bagyaveereswaran (September 2011). “Braun‟s Multiplier Implementation usingFPGA with Bypassing Techniques”, International Journal of VLSI design & Communicatio n Systems (VLSICS), Vol.2, No.3.[6]Seng, Yeo Kiat and Roy, Kaushik (2009). “Low Voltage, Low Power VLSI Subsystems”, TMC.[7]Wanhannar, Lars (May 2008). “DSP Integrated Circuits”, Academic Press.[8]Weste, Neil, Harris, David and Banerjee, Ayan (2009). “CMOS VLSI Design: A circuits and sys temperspective”, Pearson education.[9]Wen, M.-C., Wang, S.-J. and Lin Y.-N.(12th May 2005). “Low-power parallel multiplier with columnbypassing” ELECTRONICS LETTERS, Vol. 41 No. 10.[10]P.Ramanathan and.P.T.Vanathi, “Hybrid Prefix Adder Architecture for Minimi zing the Power DelayProduct”, 2009, World Academy of Science, Engineering and Technology.[11]Ladner R, Fischer M,” Parallel prefix computation “, J.ACM, vol.27, no. 4, pp 831-838, Oct.1980.50 Design Of A Optimized Parallel Array Multiplier Using Parallel Prefix Adder Authors Biography:Er. S.Tamil Selvan received the M. Tech degree in VLSI Design from SathyabamaUniversity in 2011. He is currently working as Assistant Professor in Department ofElectronics and Communication Engineering at SMK Fomra College of Engineering andtechnology in Chennai. Previously working at lecture in KCG College of technology inChennai. His main research interests are in High speed digital VLSI circuits, Low power,Area reduction, synthesis and Simulation of digital circuits and FPGA Implementation.D.P.Balasubramanian received his B.E. degree in Electronics and communicationengineering at k.v.c.e.t under Anna university, Chennai. Currently pursuing his M.TechDegree in S.M.K Fomra institute of technology.Area of interest is reversible logic,quantumelectronics and RFID has presented papers in various national and international conferences.K.Kalaikaviya received her B.E. degree in Electronics and communication engineering atPeriyar Maniammai college of technology for women under Anna university, Tiruchirapalli.Currently pursuing her M.Tech Degree in S.M.K Fomra institute of technology.Area ofinterest is digital electronics, vlsi design,Testing of vlsi.How tocitethis paper: K.KalaiKaviya,D.P.Balasubramanian,S.Tamilselvan,"Design Of A Optimized Parallel Array Multiplier Using Parallel Prefix Adder", IJEM, vol.3, no.2, pp.40-50, 2013.DOI: 10.5815/ijem.2013.02.03。

Verilog HDL《数字加法器》报告

实验三数字加法器的设计一、实验目的1. 掌握数字加法器的工作原理和逻辑功能。

2. 熟悉ISE集成开发环境。

3. 熟悉ISE中进行开发设计的流程。

二、实验环境1. 装有ModelSim和ISE的计算机。

2. Sword实验系统。

三、实验任务1. 用VerilogHDL语言设计实现4位串行数字加法器和4位并行加法器，在ModelSim上仿真实现。

2. 生成FPGA设计文件，下载到Sword实验系统上验证电路功能。

四、实验原理与实验步骤1. 实验原理数字加法器是一种较为常用的逻辑运算器件，被广泛用于计算机、通信和多媒体数字集成电路中。

广义的加法器包括加法器和减法器，在实际系统中加法器输入通常采用补码形式。

此次实验仅考虑加法运算，分别完成4位的串行进位加法器设计和4位的并行进位加法器设计。

(1) 1 bit全加器最简单的一位全加器的结构，设定两个二进制数字Ai ，Bi和一个进位输入C i 相加，产生一个和输出Si，以及一个进位输出Ci＋1。

Si＝ Ai⊕Bi⊕CiCi＋1＝ AiBi＋BiCi＋CiAi＝ AiBi＋﹙Ai⊕Bi﹚Ci(2) 4位串行进位加法器n位串行进位全加器原理示意图(3) 4位并行进位加法器超前进位加法器是一种高速加法器，每级进位由附加的组合电路产生，高位的运算不需等待低位运算完成，因此可以提高运算速度。

各级进位信号表达式的推导过程Ci＋1 ＝ AiBi＋(Ai⊕Bi)Ci设： Gi = AiBiPi= Ai⊕Bi则有： Si ＝ Pi⊕CiCi＋1＝ Gi＋PiCi4位并行进位的逻辑表达式为: CC 1＝ G＋PCC 2＝ G1＋P1C1= G1+ P1(G+PC)＝ G1+ GP1+PP1CC 3＝ G2＋P2C2= G2+ P2(G1+GP1+PP1C)＝ G2+ G1P2+GP1P2+PP1P2CC 4＝ G3＋P3C3=G3+ P3(G2+…+PP1P2C)＝ G3+G2P3+G1P2P3+GP1P2P3+PP1P2P3C2. 实验步骤（1）用连续赋值语句实现4位串行进位的全加器，并完成modelsim下的功能仿真。

并行前缀加法器的研究与实现

并行前缀加法器的研究与实现微电子学与计算机2005年第22卷第12期并行前缀加法器的研究与实现靳战鹏沈绪榜罗曼(西北工业大学计算机学院.陕西西安710072)摘要:随着微处理器运算速度的大幅度提高,对快速加法器的需求也越来越高.当VLSI工艺进入深亚微米阶段的时候,很多情况下,无论是在面积还是在时序上连线都起着决定性的作用.文章基于不同的CMOS工艺.针对三种不同结构的并行前缀加法器,在不同数据宽度的情况下进行性能比较.根据深亚微米下金属互连线对加法器性能的影响,挑选出适合深亚微米工艺的加法器结构.关键词:并行前缀加法器,KS结构,LF结构,BK结构中图法分类号:TF39文献标识码:A文章编号:1000—7180(2005)12—092—04 ResearchandImplementationofParallelPrefixAdderJINZhan—peng,SHENXu—bang,LUOMin(SchoolofComputerScience,NorthwesternPolytechnicalUniversity,Xi'an710072China) Abstract:Witlltllegreatincreaseofthespeedofmodernmicroprocessors.theneedoffastadde rsbecomesmoreexi.gent.Whenthetechnologyhasgotthestageofdeepsubmicron.theconnectivewirewillplaya nimportantroleeitherintheareaorinthetiming.BasedonvariousCMOStechnologies:O.181~m,O.151~m,O.131~ mand90nm,thisthesismakes aperformancecomparisonwithdifferentbitwidths,andthenselectstheadderarchitecturefitf ordeepsubmicrontech. nologyaccordingtotheimpactofconnectivewiresonadderperformanceindeepsubmicront echnology.Keywords:Parallelprefixadder,KSadder,LFadder,BKadder 1引言众所周知.在高性能微处理器和DSP处理器中.二进制加法器的运算时间至关重要,加法运算常常处于高性能处理器运算部件的关键路径中随着微处理器运算速度的大幅度提高.对快速加法器的需求也越来越高.因此,为了减少进位传输所耗的时间.提高计算速度,多年以来,人们提出了许多快速加法器结构.并且以不同的电路设计类型加以实现i1一.为了进一步提高加法器的运算速度.提出了并行前缀加法器(ParallelPrefixAdder)结构[3-5]由于采用了简单的标准单元以及规则的内部连接.并行前缀加法器非常适合于VLsI实现对于目前的并行前缀加法器而言.在逻辑层次已经最小的情况下.如何进一步提高加法器的性能是一个关键的问题.在影响性能的几个因素中.扇出(Fanout)和连线长度在其中起了关键作用当VLSI工艺进入深亚微米工艺阶段的时候.在很多情况下.连线的作用无论是在面积还是在时序上都起收稿日期:20o5—04—14基金项目:国防"十五"预研课题(41308010108)西北工业大学研究生创业种子基金(Z20040o5O)着决定性的作用[6一.因此,研究加法器中互连线的作用是非常有必要的本文基于不同的CMOS工艺:0.18m,0.15m,0.13m,以及90nm,针对三种不同结构的并行前缀加法器:LF结构[41,BK结构网,以及KS结构[3J.在不同数据宽度的情况下进行性能比较.根据深亚微米下金属互连线对加法器结构的影响.挑选出适合深亚微米工艺的加法器结构2并行前缀加法器对于并行前缀加法器,有如下定义:两个操作数A=aoa1..…a1.an_l'B=bob1...6.b.其中0<i<0—1,O<j<n一1.同时有操作:+6,.j}F+6l,pi=aiblO<i<n一1(1)定义前缀操作"?":()?()=()<(2)因此,加法进位可以表示为:(—Cnkn-lkk)=(卫k)(卫k)(卫k)卫kh\,….j}1o厂,?,,?,…()().(,nm(3)2005年第22卷第l2期微电子学与计算机93从式(1)～式(3)廿J以看出,日lJ缴加法器廿J以是一个级联进位加法器(ripplecalTyadder).但是由于前缀操作具有结合律(Associativity):(()¨?()?()J,=()¨?(()J?()『,h<i<j<k(4)其中,()=()?()?()?…?()J一让明如卜:(()¨?()?(,=(学).(铷=(舒)(6)()?(()?(=()?()一,岛.±墨!(臣止盘iJ:&l盘2,一,g±墨:臣.f±(盘!墨:臣&2, 一.j}^,磅,～kl,,.j}磅,:(啦)(7)一磅,前缀操作同时还具有冥等律(Idempotency),()¨=()¨?()h<k<i<j(8)证明如下:()?()=()蛐?(,.?()"?()=().(=(?()()=()蛐?()=()(9)但是前缀操作不支持交换率.证明如下:()?()『=()()『?()F()(10)以上两个鲁式不相等.根据结合律以及冥等律这两种重要的特性.可以将以上串行加法操作转化成为并行的加法操作.其中.结合律允许前缀等式中的每一个子项进行预计算.这也就意味着上面提到的串行计算可以被分解为多个并行计算的过程.同时,冥等律允许这些并行计算的子项相互之间可以重叠.这样就使并行计算具有很大的灵活性.目前.通常使用的并行前缀加法器有KS加法器[31,LF加法器网以及BK加法器【5】,这三种并行前缀加法器的结构分别如图l～图3所示.图1KS/JI]法器结构图2LFJJII法器结构图3BK~II法器结构在以上三种结构中.LF结构充分利用了前缀计算所具有的结合律特性.但是没有使用冥等律.图2 中显示了l6位加法器的每一级节点之间的互联关系输入在最顶层.输出在最低层,最高位在最左边图中仅仅显示了横向之间的联系,而没有显示纵向之间的联系在第一行中.每一个节点用来计算,p,k.在后面每行中,拥有横向连线的节点都是一个前缀计算节点最后一行用来计算加法的和.LF加法器结构具有最小的逻辑深度,但是同时也具有最大的扇出.在最后一级.最大扇出可以达到n,2.因此,对于LF加法器而言,连线长度与扇出成为影响延迟的主要因素.如图1所示.KS加法器在一定程度上缓解了微电子学与计算机2005年第22卷第12期LF加法器大扇出的问题KS加法器充分利用了冥等律的特点.通过限制每一个节点的输出来减小扇出.但是付出的代价就是每一级中使用了更多的横向连线.在KS加法器中.最长连线的长度与LF加法器中的一样如图3所示.为了改进LF加法器的扇出,BK加法器增加了逻辑层次深度3并行前缀加法器电路特性分析为了简化三种加法器结构的比较.假设加法器的输入是同时达到在没有考虑连线延迟和扇出影响的情况下.KS加法器和LF加法器拥有最小的加法器延迟.而BK加法器由于其逻辑层次深度多了一级.因此比起KS加法器和LF加法器而言,延迟较大.但是随着CMOS工艺的不断发展.扇出和连线对电路延迟的影响已经起着重要的作用.因此. 评判加法器延迟的大小.已经不能够仅仅只关注逻辑电路层次的多少.同时也更要考虑扇出和连线的影响.在电路中.一段连线的模型分割成为多个短线.其中每一短线可以抽象成为分布式的连线模型.如图4所示其中.逻辑输入电容C;输出电阻.;门延迟;(C和为每一个线段的电容,电阻;(CL)为连线每一个负载节点i的负载电容图4分布式连线模型因此.总延迟就是每一级逻辑的延迟与每一级线段延迟的总和,即=+.当不考虑连线延迟的时候,根据文献[8],可以将逻辑延迟模型简化为lumpedRC模型.Ⅳ=+o.7Ro(CL)(11)/=1然而.随着工艺特征尺寸的不断下降.连线所引起的延迟越来越占据总延迟中的较大比重.文献提出了一种连线延迟的估计模型.如式(12)所示: NNNN=∑∑=∑(∑(12)/=1j=l/=1j=l根据文献[8],整个连线延迟公式可以简化为:NNo.7.∑(c+∑(0.4(Cw)+o.7(CL)Ⅳ+o.7∑((+(c))(13)j=/+l其中,第一项是连线电容效应,也就是连线的lumpedRC模型.第二项是连线的电阻效应.也就是分布式RC模型.4实验结果在TSMC0.181~m1P6M工艺,0.151zm1P6M工艺,0.131zm1P7M工艺,以及90nm1P8M工艺下.针对16位宽加法器,32位宽加法器,64位宽加法器, 以及128位宽加法器的LF结构,KS结构,BK结构进行比较.如图5所示16bit32bit64bit128bitDelay(0.18n1)16bit32bit64bit128bitDelay(0.15m)16bit32bit64biL128biLDelay(0.15m)圜囵圈囵16bit32bit64bit128bitDelay(90nm1图5四种工艺和位宽下三种加法器结构性能对比从图5中可以看出.BK加法器虽然在O.181zm工艺下的延迟不是最小.但是随着工艺尺寸的不断缩小,其相对于其他结构的加法器而言,具有一定2005年第22卷第12期微电子学与计算机的优势.即使在O.181xm工艺下,64位加法器的BK结构加法器的延迟也能够满足时序要求.因此,为了满足今后设计对工艺要求不断提高.便于工艺上的转换,在实现上,宜选取BK结构作为加法器结构.5结束语随着微处理器运算速度的大幅度提高.对快速加法器的需求也越来越高.因此.人们提出了许多快速加法器结构.包括并行前缀加法器(Parallel PrefixAdder)结构由于采用了简单的标准单元以及规则的内部连接.并行前缀加法器非常适合于VLSI实现本文基于不同的CMOS工艺.针对三种不同结构的并行前缀加法器.在不同数据宽度的情况下进行性能比较.根据深亚微米下金属互连线对加法器结构的影响.挑选出了适合深亚微米工艺的加法器结构参考文献[1】KUdea,NSasaki,HSato,eta1.A64-BitCarryLookA—headUsingPassTransistorBiCMOSGate[J].IEEEJ.Sol—id—StateCircuits,1996,31:810-819.[2】KSuzuki,eta1.A500MHz32bit0.4txmCMOSRISCPro—cessor[J].IEEE,Solid-StateCircuits,1994,29(12):1464- 1476.f3】PMKogge,HSStone.AParallelAlgorithmfortheEttl—cientSolutionofaGeneralClassofRecurrenceEquationsputers,1973,22(8):786-793.f4】RELadner,MJFischer.ParallelPrefixCompu~fion[J]. JACM,1980,27(4):831-838.f5】RPBrent,HTKung.ARegularLayoutforParallel Adders[J]puters,1982,31(3):260-264.f6】JCong.ChallengesandOpportunitiesforDesignInnova—tionsinNanometerTechnologies.SRCWorkingPaper,/prg_mgmt/frontier.dgw,1997.f7】JCong,DZPan.InterconnectDelayEstimationModels forSynthesisandDesignPlanning[J]andSouth PacificDesignAutomationConf.,1999,97-100.[8】HBBakoglu.Circuit,InterconnectionsandPackagingfor VLSI[M].Addison-WesleyPublishingCompany,1990.f9】EElmore.TheTransientResponseofDampedLinearNet—workswithParticularRegardtoWidebandAmplifiers[J1. JournalofAppliedPhysics,1948,55-63.靳战鹏男,(1981~),硕士研究生.研究方向为计算机系统结构,专用微处理器设计.沈绪榜男.(1933一),博士生导师,中国科学院院士.研究方向为计算机体系结构,专用微处理器设计,超大规模集成电路设计罗晏男,(1975一),博士,讲师.研究方向为计算机系统结构,专用微处理器设计,ASIC设计.(上接第91页)型的自身结构,对其作进一步的优化,是提高FIRE—Agent求解效率的根本途径.本文进一步的工作将从上述2个方面展开.参考文献[1】eBaySite.http://www.eBay.eom.WorldWideWeb.[2】AmazonSite.http://www.amazon.eom.WorldWideWeb. [3】ZaehariaG,MacsP.TrustManagementThroughReputa—tionMechanisms.AppliedArtificialIntelligence,2000,14 (9):881-908.f4】HuynhTD,JenningsNR,ShadbohNR.FIRE:Aninte—gratedTrustandRepumtionModelforOpenMullti-agent Systems.Proc.16thEuropeanConferenceonArtificialIn—telligence,V alencia,Spain,2004:18-22.f5】ShehoryO,KrausS.CoalitionFormationAmongAu—tonomousAgents:Strategiesandcomplexity.Reactionto Cognition,LectureNotesinArtificialIntelligence,Berlin: Springer,1993,957:57-72.[6】KetchpelS.CoalitionFormationAmongAutonomousA—gents.ReactiontoCognition,LectureNotesinArtificial Intelligence,Berlin:Springer,1993,957:73～88.f7】SandholmTW,LesserVR.CoalitionAmongComputa—tionallyBoundedAgents.ArtificialIntelligence,1997,94 (1):99-137.[8】罗翊,石纯一.Agent协作求解中形成联盟的行为策略. 计算机学报,1997.20(11):961～965.『91徐晋晖,石纯一.一种基于等价的联盟演化机制.计算机研究与发展,1999,36(5):513～517.李凯男,(1977一),博士研究生,助教.研究方向为人工智能,企业建模与优化.杨善林男.(1948一),教授,博士生导师.研究方向为人工智能,信息管理与决策支持系统.刘桂庆女,(1978一),博士研究生,讲师.研究方向为供应链管理,人工智能.。

模2^n-2^k-1加法器高效VLSI设计与实现

模2^n-2^k-1加法器高效VLSI设计与实现
马上;叶燕龙;胡剑浩
【期刊名称】《微电子学与计算机》
【年(卷),期】2010(0)10
【摘要】模加法器是余数系统(Residue Number System,RNS)的基本运算单元,2n-2k-1形式的余数基易于构建大动态范围和具有优良复杂度平衡性的多通道余数基.基于前缀运算和进位修正算法提出了一类新的模2n-2k-1加法通用算法及其VLSI实现结构.该算法消除了重复的进位信息计算,且可采用任意已有的前缀运算结构.与同类型模加法器的分析对比结果表明,提出的模2n-2k-1加法器具有优良的"面积×时延"特性.
【总页数】7页(P1-7)
【关键词】余数系统;模加法器;并行前缀;进位修正;超大规模集成电路
【作者】马上;叶燕龙;胡剑浩
【作者单位】电子科技大学通信抗干扰技术国家级重点实验室
【正文语种】中文
【中图分类】TP338.6
【相关文献】
1.一种高效去块滤波结构设计与VLSI实现 [J], 胡红旗;许家栋;段哲民;孙景楠
2.高效缩1码模2n+1加法器设计与优化 [J], 吕晓兰
3.VLSI中加法器的一种高效自测试设计 [J], 肖继学;陈光(礻禹);谢永乐
4.一种规整高效的缩1码模2n+1乘法器的VLSI设计 [J], 王文瑞
5.有限域上模逆电路的VLSI设计与实现 [J], 韩永相;白国强;陈弘毅
因版权原因，仅展示原文概要，查看原文内容请购买。

VLSI课内实验——RTL级并行前缀加法器设计

VLSI课内实验RTL级并行前缀加法器设计班级：学号：姓名：RTL 级并行前缀加法器设计一、加法器简介算术逻辑部件主要处理算术运算指令和逻辑运算指令，它的核心单元是加法器。

这个加法器是影响算术逻辑部件整体性能的关键部分，因为几乎所有的算术运算和逻辑运算，都要通过它来完成。

加法器结构包括串行进位加法器(Carry Ripple Adder ，CRA)、进位跳跃加法器(Cany Skip Adder ，CKA)，以及较高速度的进位选择加法器(carry select Adder ，CSA)、超前进位加法器(Carry Look ahead Adder ，CLA)和并行前缀加法器(Parallel Prefix Adder)等。

除上述五种加法器结构外，还有采取多加法器并联的流水线加法器和专用的加法器，如支持向量的快速加法器等等，本设计主要是用VHDL 描述一个RTL 级并行前缀加法器。

二、原理及设计思路并行前缀加法器是超前进位的一种改进结构，它将n 位加法器的进位传播信号层次化地分解为m 位子组合，并将进位产生和进位传播组织成递归的树型结构。

并行前缀加法器使用一种特殊的方式产生各位的进位输出，这种方式称为“前缀运算(Prefix Compution)”。

所有进位产生和传播信号并行地通过前缀运算单元进行运算，同时输出进位信号。

各个前缀运算单元通过递归的方式连接起来，即可形成整个加法器。

对于并行前缀加法器，有以下定义：两个操作数：110......A -=n i a a a a ，110......B -=n j b b b b 。

其中1,0-<<n j i 。

同时有操作：i i i b a =g ，i i i b a p ⊕=，称g i 为进位产生位，p i 为进位传输位。

这两个操作很好理解：不计进位输入，当a i ，b i 同时为1时，g i 为1，此时会产生进位；如果有进位输入，则a i ，b i 有一个为1的时候就会产生进位。

基于并行前缀结构的十进制加法器设计

基于并行前缀结构的十进制加法器设计
王书敏;崔晓平
【期刊名称】《电子科技》
【年(卷),期】2016(029)006
【摘要】针对硬件实现BCD码十进制加法需要处理无效码的问题,设计了一种基于并行前缀结构的十进制加法器.该十进制加法器依据预先加6,配合二进制加法求中间和,然后再减6修正的算法,并将减6修正步骤整合到重新设计的减6修正进位选择加法器中,充分利用并行前缀结构大幅提高了电路运算的并行度.采用Verilog HDL对加法器进行实现并利用Design Compiler进行综合,得到设计的32位,64位,128位的十进制加法器的延时分别为0.56 ns,0.61 ns,0.71 ns,面积分别为1 310μm2,2 681 μm2,5 485 μm2.
【总页数】4页(P19-21,25)
【作者】王书敏;崔晓平
【作者单位】南京航空航天大学电子信息工程学院,江苏南京211100;南京航空航天大学电子信息工程学院,江苏南京211100
【正文语种】中文
【中图分类】TP332.2+1
【相关文献】
1.基于Sklansky结构的24位并行前缀加法器的设计与实现 [J], 姚若河;马廷俊;苏少妍
2.基于Verilog的并行前缀Ling型加法器的验证 [J], 肖九思;张磊
3.Sklansky并行前缀加法器的优化设计 [J], 王晓泾;崔晓平;王大宇
4.一种改进的基于Kogge-Stone结构的并行前缀加法器 [J], 赵翠华;娄冕;张洵颖;沈绪榜
5.并行前缀加法器的研究与实现 [J], 靳战鹏;沈绪榜;罗旻
因版权原因，仅展示原文概要，查看原文内容请购买。

数字逻辑实验报告。利用逻辑门构成半加器和全加器,设计一个2位并行加法器

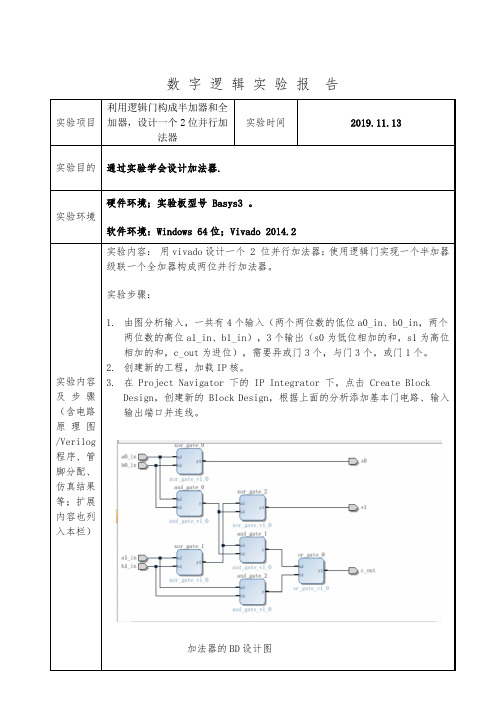
数字逻辑实验报告实验项目利用逻辑门构成半加器和全加器，设计一个2位并行加法器实验时间2019.11.13实验目的通过实验学会设计加法器.实验环境硬件环境；实验板型号 Basys3 。

软件环境：Windows 64位；Vivado 2014.2实验内容及步骤（含电路原理图/Verilog 程序、管脚分配、仿真结果等；扩展内容也列入本栏）实验内容：用vivado设计一个 2 位并行加法器：使用逻辑门实现一个半加器级联一个全加器构成两位并行加法器。

实验步骤：1.由图分析输入，一共有4个输入（两个两位数的低位a0_in、b0_in，两个两位数的高位a1_in、b1_in），3个输出（s0为低位相加的和，s1为高位相加的和，c_out为进位），需要异或门3个，与门3个，或门1个。

2.创建新的工程，加载IP核。

3.在 Project Navigator 下的 IP Integrator 下，点击 Create BlockDesign，创建新的 Block Design，根据上面的分析添加基本门电路、输入输出端口并连线。

加法器的BD设计图4.完成原理图设计后，生成顶层文件和HDL代码文件。

5.到 I/O PLANNING界面下方的I/O ports 窗口中将设计端口与 FPGA 引脚进行关联，在site栏将a0_in、a1_in、b0_in、b1_in、c_out、s0、s1分别设置为V16、V17、W16、W17、U16、E19、U19；I/O std 栏均设为 LVCMOS33。

实验3.2.2管脚约束图6.综合、实现、生成bitstream。

7.连接实验版进行板级验证。

实验结果分析实验4.2.1结果（部分）（a_in对应V16、b_in对应V17、c_in对应W16、c_out对应U16、s对应E19） A1 B1 Cin1→S1 Cout1A0 B1 Cin0→S1 Cout0A0 B1 Cin1→S0 Cout1实验4.2.2结果（部分）a0_in1 a1_in0 b0_in0 b1_in1→c_out0 s01 s11a0_in0 a1_in1 b0_in1 b1_in0→c_out0 s01 s11a0_in1 a1_in0 b0_in0 b1_in1→c_out1 s00 s10A1 A0 B1 B0 LED灯显示0 1 1 0 亮亮暗1 0 0 1 亮亮暗0 1 1 1 暗暗亮实验报告说明数字逻辑课程组实验名称列入实验指导书相应的实验题目。

并行加法器实验报告

《计算机组成原理》课程设计实验报告1 任务描述掌握运算器的原理及其设计方法的基础上，利用TD-CMA 计算机组成原理教学实验系统的CPLD单元或FPGA单元，使用Quartus II 软件,使用Verilog或VHDL语言设计方式实现一8位并行进位并行加法器,并进行验证。

2 实验设备该实验所使用的是TD-CMA实验箱及PC机一台。

3 设计原理和方法3.1 工作原理加法器是执行二进制加法运算的逻辑部件，也是CPU 运算器的基本逻辑部件（减法可以通过补码相加来实现）。

加法器又分为半加器和全加器（FA），不考虑低位的进位，只考虑两个二进制数相加，得到和以及向高位进位的加法器为半加器，而全加器是在半加器的基础上又考虑了低位过来的进位信号。

3.2 设计方法对加法器进位的逻辑表达式做推导：C0 = 0Ci+1 = AiBi + AiCi + BiCi设gi = AiBi；pi = Ai + Bi，则有Ci+1 = gi + piCi由于gi、pi 只和Ai、Bi 有关，这样Ci+1 就只和Ai、Ai-1、…、A0，Bi、Bi-1、…B0 及C0有关。

所以各位的进位Ci、Ci-1、…、C1 就可以并行地产生。

转化为VHDL语言即为：sum(n)<=ain(n) xor bin(n) xor h(n);h(n+1):=(ain(n) and bin(n)) or (h(n) and ain(n)) or (h(n) and bin(n));3.3设计思想本算法的核心思想是把8 位加法器分成两个4 位加法器，先求出低4 位加法器的各个进位，特别是向高4 位加法器的进位C4。

然后，高4 位加法器把C4 作为初始进位，使用低4 位加法器相同的方法来完成计算。

每一个4 位加法器在计算时，又分成了两个2 位的加法器。

4 设计过程（1）根据上述加法器的逻辑原理使用 Quartus II 软件编辑相应的电路原理图并进行编译，其在EPM1270 芯片中对应的引脚如图，框外文字表示I/O 号，框内文字表示该引脚的含义。

数电实验丨多路复用器-进位加法器-先行进位加法器

数字电路与逻辑设计实验二一、实验目的1．熟悉多路复用器、加法器的工作原理。

2．学会使用VHDL语言设计多路复用器、加法器。

3．掌握generic的使用，设计n-1多路复用器。

4．兼顾速度与成本，设计行波加法器和先行进位加法器。

二、实验内容1．用VHDL语言设计8重3-1多路复用器；2．用VHDL语言设计n-1多路复用器，调用该n-1多路复用器定制为8-1多路复用器。

53．用VHDL语言设计4位行波进位加法器。

4．用VHDL语言设计4位先行进位加法器。

第一部分：8重3-1多路复用器①实验方法1、实验方法采用基于FPGA进行数字逻辑电路设计的方法。

采用的软件工具是Quartus II。

2、实验步骤1、新建，编写源代码。

(1).选择保存项和芯片类型：【File】-【new project wizard】-【next】（设置文件路径+设置project name为multiplexer_3_to_1_st）-【next】（设置文件名multiplexer_3_to_1_st.vhd—在【add】）-【properties】（type=AHDL）-【next】（family=FLEX10K；name=EPF10K10TI144-4）-【next】-【finish】(2).新建：【file】-【new】（第二个AHDL File）-【OK】2、根据题意，写好源代码并保存文件。

3、编译与调试。

确定源代码文件为当前工程文件，点击【processing】-【start compilation】进行文件编译，编译成功。

4、波形仿真及验证。

新建一个vector waveform file。

按照程序所述插入S、I0-I2、Y五个八维向量节点（S、I0-I2为输入节点，Y为输出节点）。

(操作为：右击-【insert】-【insert node or bus】-【node finder】（pins=all；【list】）-【>>】-【ok】-【ok】)。

VLSI课内实验——RTL级并行前缀加法器设计

这个加法器是影响算术逻辑部件整体性能的关键部分，因为几乎所有的算术运算和逻辑运算，都要通过它来完成。

并行前缀加法器使用一种特殊的方式产生各位的进位输出，这种方式称为“前缀运算(Prefix Compution)”。

所有进位产生和传播信号并行地通过前缀运算单元进行运算，同时输出进位信号。

各个前缀运算单元通过递归的方式连接起来，即可形成整个加法器。

对于并行前缀加法器，有以下定义：两个操作数：110......A -=n i a a a a ，110......B -=n j b b b b 。

其中1,0-<<n j i 。

同时有操作：i i i b a =g ，i i i b a p ⊕=，称g i 为进位产生位，p i 为进位传输位。

这两个操作很好理解：不计进位输入，当a i ，b i 同时为1时，g i 为1，此时会产生进位；如果有进位输入，则a i ，b i 有一个为1的时候就会产生进位。

上海大学---Verilog-设计-32位浮点加法器设计

32位浮点加法器设计摘要：浮点数具有数值范围大，表示格式不受限制的特点，因此浮点数的应用是非常广泛的。

浮点数加法运算比较复杂，算法很多，但是为了提高运算速度，大部分均是基于流水线的设计结构。

本文介绍了基于IEE754标准的用Verilog语言设计的32位浮点加法器，能够实现32位浮点数的加法运算。

虽然未采用流水线的设计结构但是仍然对流水线结构做了比较详细的介绍。

关键字：浮点数，流水线，32位浮点数加法运算，Verilog语言设计32-bit floating point adder designCao Chi,Shen Jia- qi,Zheng Yun-jia[(School of Mechatronic Engineering and Automation, Shanghai University, Shanghai ,China)words：float; Assembly line; 32-bit floating-point adder浮点数的应用非常广泛，无论是在计算机还是微处理器中都离不开浮点数。

但是浮点数的加法运算规则比较复杂不易理解掌握，而且按照传统的运算方法，运算速度较慢。

因此，浮点加法器的设计采用了流水线的设计方法。

32位浮点数运算的摄入处理采用了IEE754标准的“0舍1入”法。

1.浮点数的介绍在处理器中，数据不仅有符号，而且经常含有小数，即既有整数部分又有小数部分。

根据小数点位置是否固定，数的表示方法分为定点表示和浮点表示。

浮点数就是用浮点表示法表示的实数。

浮点数扩大了数的表示范围和精度。

浮点数由阶符、阶码E、数符、尾数N构成。

任意一个二进制数N总可以表示成如下形式：N=±M×2±E。

通常规定：二进制浮点数，其尾数数字部分原码的最高位为1，叫作规格化表示法。

因此，扩大数的表示范围，就增加阶码的位数，要提高精度，就增加尾数的位数。

浮点数表示二进制数的优势显而易见。

加减法运算器的设计

中央民族大学数字电路实验报告加减法运算器的设计姓名：王瑞琦学号: ******** 班级：13级计算机一班所在院系：信息工程学院指导老师：***完成日期：2015/03/28-2015/03/29目录一、实验目的 (3)二、实验设备 (3)三、实验内容 (3)四、实验功能概要 (3)五、设计详细描述 (4)5.1四位行波进位加减法运算器 (4)5.1.1功能描述 (4)5.1.2封装模块图 (4)5.1.3总电路图 (4)5.1.4组成模块 (5)5.1.5程序设计 (6)5.1.6功能仿真波形图 (8)5.2四位超前进位加法运算器 (9)5.2.1功能概述 (9)5.2.2封装模块图 (9)5.2.3程序设计 (9)5.2.4功能仿真波形图 (11)六、实验注意事项 (11)七、实验问题及解决方法 (12)一、实验目的1、掌握加减法运算器的Verilog HDL语言描述方法2、理解超前进位算法的基本原理3、掌握基于模块的多位加减运算器的层次化设计方法4、掌握溢出检测方法和标志线的生成技术5、熟悉QuartusⅡ 10.0和DE2-115使用方法二、实验设备PC机+ QuartusⅡ10.0 + DE2-115三、实验内容1、在PC机上安装QuartusⅡ10.0或更高版本并破解。

（注意：QuartusⅡ10.0版本以上软件不再包含仿真组件，因此需要在安装QuartusⅡ10.0同时选择安装第三方仿真工具，我们可以选择安装免费的Modelsim-Altera，学习如何编写Verilog HDL格式的仿真测试文件Testbench。

）2、在PC机上安装DE2-115的驱动程序。

3、使用Verilog HDL语言实现一个4位行波（串行）进位的加减法运算器，要求有溢出和进位标志，仿真正确后封装成模块。

4、使用Verilog HDL语言实现一个4位超前（并行）进位加减运算器，要求有溢出和进位标志，仿真正确后封装成模块。

计算机组成原理实验_加减法运算器设计

计算机组成原理与汇编语言实验报告实验二: 加减法运算器的设计与实现专业班级：xxxxxxxxxx学号：xxxxxxx 姓名：xxx学号：xxxxxxx 姓名：xxx实验地点：实验时间：实验二加减法运算器的设计一、实验目的1、理解加减法运算器的原理图设计方法2、掌握加减法运算器的VERILOG语言描述方法3、理解超前进位算法的基本原理4、掌握基于模块的多位加减运算器的层次化设计方法5、掌握溢出检测方法和标志线的生成技术6、掌握加减运算器的宏模块设计方法二、实验任务1、用VERILOG设计完成一个4位行波进位的加减法运算器，要求有溢出和进位标志，并封装成模块。

模块的端口描述如下：module lab2_RippleCarry 宽度可定制（默认为4位）的行波进位有符号数的加减法器。

#(parameter WIDTH=4)( input signed [WIDTH-1:0] dataa,input signed [WIDTH-1:0] datab,input add_sub, // if this is 1, add; else subtractinput clk,input cclr,input carry_in, //1 表示有进位或借位output overflow,output carry_out,output reg [WIDTH-1:0] result)2、修改上述运算器的进位算法，设计超前进位无符号加法算法器并封装成模块。

模块的端口描述如下：module lab2_LookaheadCarry // 4位超前进位无符号加法器(input [3:0] a,input [3:0] b,input c0, //carry_ininput clk,input cclr,output reg carry_out,output reg [3:0]sum);3、在上述超前进位加法运算器的基础上，用基于模块的层次化设计方法，完成一个32位的加法运算器，组内超前进位，组间行波进位。

VLSI设计课件六设计实例

这个乘法器的VHDL源代码可如下所示：
8位移位相加乘法器 LIBRARY ieee; USE ieee.std_logic_1164.all; USE ieee.std_logic_unsigned.all;
ENTITY mult_8 IS PORT(product: a: b: rst: clk: END mult_8;
第6章设计实例
6.1 6.2
乘法器的设计 FIR滤波器的设计与实现
6.1 乘法器的FPGA设计与实现
• 6.1.1 乘法的基本原理在二进制乘法中，乘法的基本算法常可用所谓的一位乘法和两位乘法进行。进行这种乘法运算时，通常分别用乘数的一位或二位与被乘数相乘，再把部分积加起来。例分别用一位乘法和两位乘法求下式的积:
SIGNAL b_tmp: STD_LOGIC_VECTOR(7 DOWNTO 0);-------用于记录乘数 SIGNAL a_tmp: STD_LOGIC_VECTOR(15 DOWNTO 0);------用于记录被乘数 SIGNAL prod_tmp: STD_LOGIC_VECTOR(15 DOWNTO 0);---用于记录乘积 BEGIN PROCESS(a，b，clk，rst) BEGIN IF rst = ′1′ then ---------------------异步复位 product <= (others =>′0′);-----------输出清零 a_tmp <= ′′00000000′′ & a;-------寄存a b_tmp <= b; -------寄存b prod_tmp <= ′′0000000000000000′′;---寄存器清零 ELSIF (clk′EVENT AND clk = ′1′) THEN IF b_tmp(0) = ′1′ THEN prod_tmp <= prod_tmp + a_tmp;-------逐位累加