Java中AVL平衡二叉树实现Map (仿照TreeMap和TreeSet)
java treemap实现原理

java treemap实现原理Java TreeMap是Java中非常常用的一种数据结构,使用红黑树作为其底层实现。
它提供了一种将键映射到值的方式,键是唯一的,并且按照升序进行排序。
Java TreeMap的实现原理是非常有趣的,它主要涉及到红黑树、迭代器、比较器等知识点。
在本文中,我们将深入了解Java TreeMap的实现原理,并理解如何在代码中使用它。
1. 红黑树红黑树是一种自平衡的二叉搜索树。
它通过保持一些简单规则来保证树的平衡,以确保左右子树的高度之差不超过1,并且保证每个节点的颜色都为红色或黑色。
这些规则允许红黑树保持在O(log n)的时间复杂度下进行插入、搜索和删除操作。
在Java TreeMap中,红黑树被用作底层存储结构。
当添加一个新的键值对时,它会首先检查根节点是否为空。
如果是,则创建一个新的节点并将其设置为根节点。
否则,它会沿着树的路径查找适当的叶子节点,并将其插入为其左侧或右侧的子节点。
为了保持树的平衡,通过旋转和重新着色来调整节点的颜色和位置。
每个节点都有一个颜色标记,标记为红色或黑色,红色表示该节点是一个违反规则的节点,黑色表示该节点是一个符合规则的节点。
2. TreeMap的比较器Java TreeMap还有另一个重要的组件,即比较器。
所有元素的排序都是通过比较器来定义的。
比较器定义了如何将元素按照升序排列,应该提供一个实现了 Comparator 接口的类。
在Java TreeMap的实现中,比较器用来将元素按照顺序排列。
它允许 TreeMap 将元素按照自定义顺序排序而不是按照它们的自然顺序排序。
也就是说,比较器的作用是自定义元素排序的规则并将其存储在TreeMap中。
3. TreeMap的迭代器Java TreeMap还提供了迭代器,用于遍历TreeMap中的元素。
什么是迭代器?迭代器是用于遍历集合或列表中元素的指针。
在Java中,每个集合或列表都可以通过iterator() 方法返回它的迭代器。
TreeMap集合特点、排序原理

TreeMap集合特点、排序原理TreeMap特点(类似于TreeSet):1.⽆序,不允许重复(⽆序指元素顺序与添加顺序不⼀致)2.TreeMap集合默认会对键进⾏排序,所以键必须实现⾃然排序和定制排序中的⼀种3..底层使⽤的数据结构是⼆叉树两种排序的⽤法(参照TreeSet集合):练习:1,创建公司Company类,拥有属性:no(公司编号)、name(公司名称)、num(公司⼈数)、founder(创始⼈)、info(公司简介),要求属性进⾏封装即:属性私有并提供公有⽅法。
(a)请根据下列信息创建5个公司对象,各属性值来⾃下⾯的信息”1001,百度,2000,李彦宏,全球最⼤的中⽂搜索引擎、致⼒于让⽹民更便捷地获取信息,找到所求。
”“1010,腾讯,10000,马化腾,深圳市腾讯计算机系统有限公司成⽴于1998年11⽉,由马化腾、张志东、许晨晔、陈⼀丹、曾李青五位创始⼈共同创⽴。
”“1020,阿⾥巴巴,20000,马云,阿⾥巴巴⽹络技术有限公司(简称:阿⾥巴巴集团)”“1050,京东,8000,刘强东,京东()是中国最⼤的⾃营式电商企业,2015年第⼀季度在中国⾃营式B2C电商市场的占有率为56.3%。
”“1030,⼩⽶,5000,雷军,⼩⽶公司成⽴于2010年4⽉,是⼀家专注于智能产品⾃主研发的移动互联⽹公司。
”(b)请将上述的5个对象添加到TreeMappackage TreeMap;import java.text.CollationKey;import java.text.Collator;/*** 创建公司Company类,拥有属性:no(公司编号)、* name(公司名称)、num(公司⼈数)、founder(创始⼈)、* info(公司简介),要求属性进⾏封装即:属性私有并提供公有⽅法。
* @author Administrator**/public class Company implements Comparable<Company>{private int no;private String name;private int num;private String founder;private String info;public int getNo() {return no;}public void setNo(int no) {this.no = no;}public String getName() {return name;}public void setName(String name) { = name;}public int getNum() {return num;}public void setNum(int num) {this.num = num;}public String getFounder() {return founder;}public void setFounder(String founder) {this.founder = founder;}public String getInfo() {return info;}public void setInfo(String info) { = info;}@Overridepublic String toString() {return "Company [no=" + no + ", name=" + name + ", num=" + num + ", founder=" + founder + ", info=" + info+ "]";}public Company(int no, String name, int num, String founder, String info) {super();this.no = no; = name;this.num = num;this.founder = founder; = info;}public Company() {super();}//要求按照以下规则依次排序:公司编号、公司名称、创始⼈、公司⼈数,按升序排列@Overridepublic int compareTo(Company o) {//公司编号int a=this.no-o.no;if(a!=0){return a;}else{//公司名称CollationKey key=Collator.getInstance().getCollationKey();CollationKey key2=Collator.getInstance().getCollationKey();int b=pareTo(key2);if(b!=0){return b;}else{//创始⼈CollationKey key3=Collator.getInstance().getCollationKey(this.founder);CollationKey key4=Collator.getInstance().getCollationKey(o.founder);int c=pareTo(key4);if(c!=0){return c;}else {//公司⼈数return this.num-o.num;}}}}}测试代码:package TreeMap;import java.util.Set;import java.util.TreeMap;public class Test {public static void main(String[] args) {TreeMap<Company, String> map=new TreeMap<>();map.put(new Company(1001, "百度", 2000, "李彦宏", "全球最⼤的中⽂搜索引擎、致⼒于让⽹民更便捷地获取信息,找到所求"),"有钱的公司,任性!!");map.put(new Company(1010, "腾讯", 10000, "马化腾", "深圳市腾讯计算机系统有限公司成⽴于1998年11⽉,由马化腾、张志东、许晨晔、陈⼀丹、曾李青五位创始⼈共同创⽴"), "有钱的公司,任性!!");map.put(new Company(1020, "阿⾥巴巴", 20000, "马云", "阿⾥巴巴⽹络技术有限公司(简称:阿⾥巴巴集团)"),"有钱的公司,任性!!");map.put(new Company(1050, "京东", 8000, "刘强东", "京东()是中国最⼤的⾃营式电商企业,2015年第⼀季度在中国⾃营式B2C电商市场的占有率为56.3%"),"有钱的公司,任性!!");map.put(new Company(1030, "⼩⽶", 5000, "雷军", "⼩⽶公司成⽴于2010年4⽉,是⼀家专注于智能产品⾃主研发的移动互联⽹公司"),"有钱的公司,任性!!");Set<Company> set=map.keySet();for (Company company : set) {System.out.println(company+","+map.get(company));}}}。
平衡二叉树10.3.2

11
28
96 98
25
(1) LL型调整 型调整 p A 1 2
调整方法: 调整方法: 单向右旋平衡,即将 的左孩子 单向右旋平衡,即将A的左孩子 B 向右上旋转代替 成为根结点, 向右上旋转代替A成为根结点 成为根结点, 结点向右下旋转成为B的右 将A结点向右下旋转成为 的右 结点向右下旋转成为 子树的根结点, 子树的根结点,而B的原右子树 的原右子树 则作为A结点的左子树 结点的左子树. 则作为 结点的左子树. h d e B
1 38 -1 24 88
0 -1 -2
0
11
28 1
96
0
-1 0
25
0
98
1,平衡二叉树插入结点的调整方法
若向平衡二叉树中插入一个新结点后破坏了平衡二叉树的平衡性, 若向平衡二叉树中插入一个新结点后破坏了平衡二叉树的平衡性, 首先从根结点到该新插入结点的路径之逆向根结点方向找第一个失去平 衡的结点, 衡的结点,然后以该失衡结点和它相邻的刚查找过的两个结点构成调整 子树(最小不平衡子树 即调整子树是指以离插入结点最近,且平衡因子 最小不平衡子树), 子树 最小不平衡子树 ,即调整子树是指以离插入结点最近 且平衡因子 绝对值大于1的结点为根结点的子树 使之成为新的平衡子树. 的结点为根结点的子树,使之成为新的平衡子树 绝对值大于 的结点为根结点的子树 使之成为新的平衡子树. 38 24 88 -2
(2)RR型调整 型调整 p A -1 -2
调整方法: 调整方法: 单向左旋平衡:即将 的右孩子 的右孩子B向 单向左旋平衡:即将A的右孩子 向 左上旋转代替A成为根结点 成为根结点, 左上旋转代替 成为根结点,将A结 结 点向左下旋转成为B的左子树的根 点向左下旋转成为 的左子树的根 结点, 的原左子树则作为A结点 结点,而B的原左子树则作为 结点 的原左子树则作为 的右子树. 的右子树. B
数据结构与算法系列研究五——树、二叉树、三叉树、平衡排序二叉树AVL

数据结构与算法系列研究五——树、⼆叉树、三叉树、平衡排序⼆叉树AVL树、⼆叉树、三叉树、平衡排序⼆叉树AVL⼀、树的定义树是计算机算法最重要的⾮线性结构。
树中每个数据元素⾄多有⼀个直接前驱,但可以有多个直接后继。
树是⼀种以分⽀关系定义的层次结构。
a.树是n(≥0)结点组成的有限集合。
{N.沃恩}(树是n(n≥1)个结点组成的有限集合。
{D.E.Knuth})在任意⼀棵⾮空树中:⑴有且仅有⼀个没有前驱的结点----根(root)。
⑵当n>1时,其余结点有且仅有⼀个直接前驱。
⑶所有结点都可以有0个或多个后继。
b. 树是n(n≥0)个结点组成的有限集合。
在任意⼀棵⾮空树中:⑴有⼀个特定的称为根(root)的结点。
⑵当n>1时,其余结点分为m(m≥0)个互不相交的⼦集T1,T2,…,Tm。
每个集合本⾝⼜是⼀棵树,并且称为根的⼦树(subtree)树的固有特性---递归性。
即⾮空树是由若⼲棵⼦树组成,⽽⼦树⼜可以由若⼲棵更⼩的⼦树组成。
树的基本操作1、InitTree(&T) 初始化2、DestroyTree(&T) 撤消树3、CreatTree(&T,F) 按F的定义⽣成树4、ClearTree(&T) 清除5、TreeEmpty(T) 判树空6、TreeDepth(T) 求树的深度7、Root(T) 返回根结点8、Parent(T,x) 返回结点 x 的双亲9、Child(T,x,i) 返回结点 x 的第i 个孩⼦10、InsertChild(&T,&p,i,x) 把 x 插⼊到 P的第i棵⼦树处11、DeleteChild(&T,&p,i) 删除结点P的第i棵⼦树12、traverse(T) 遍历树的结点:包含⼀个数据元素及若⼲指向⼦树的分⽀。
●结点的度: 结点拥有⼦树的数⽬●叶结点: 度为零的结点●分枝结点: 度⾮零的结点●树的度: 树中各结点度的最⼤值●孩⼦: 树中某个结点的⼦树的根●双亲: 结点的直接前驱●兄弟: 同⼀双亲的孩⼦互称兄弟●祖先: 从根结点到某结点j 路径上的所有结点(不包括指定结点)。
java tree用法

java tree用法
Java中的Tree是一种数据结构,它可以用来表示层次关系的数据,比如文件系统、组织结构等。
在Java中,Tree的常见实现包括Binary Tree、Binary Search Tree、AVL Tree、Red-Black Tree等。
这些Tree结构在Java中都有对应的类库实现,可以直接使用。
在Java中,可以使用TreeMap和TreeSet来实现Tree结构。
TreeMap是基于红黑树实现的,它可以用来存储键值对,并且能够根据键进行排序。
TreeSet是基于TreeMap实现的,它是一个有序的集合,能够自动对元素进行排序。
在使用TreeMap和TreeSet时,需要注意以下几点:
1. 添加的元素必须实现Comparable接口或者在构造TreeMap 和TreeSet时传入Comparator对象,以便进行元素的比较和排序。
2. TreeMap和TreeSet是基于红黑树实现的,因此插入、删除和查找操作的时间复杂度都是O(logN),其中N为元素个数。
3. TreeMap和TreeSet是有序的,它们会根据元素的大小进行排序,因此在遍历时可以得到有序的结果。
除了TreeMap和TreeSet,Java中还有一些第三方库实现了更复杂的Tree结构,比如Apache Commons Collections中的TreeBag、TreeList等。
总之,Java中的Tree结构可以通过TreeMap和TreeSet来实现,它们能够提供高效的插入、删除和查找操作,并且能够自动对元素进行排序。
在实际开发中,可以根据具体的需求选择合适的Tree实现来处理层次关系的数据。
平衡二叉树

编辑
红黑树
红黑树是一种自平衡二叉查找树,是在计算机科学中用到的一种数据结构,典型的用途是实现关联数组。它是在1972年由Rudolf Bayer发明的,他称之为"对称二叉B树",它现代的名字是在 Leo J. Guibas 和 Robert Sedgewick 于1978年写的一篇论文中获得的。它是复杂的,但它的操作有着良好的最坏情况运行时间,并且在实践中是高效的: 它可以在O(log n)时间内做查找,插入和删除,这里的n是树中元素的数目。
伸展树
伸展树(Splay Tree)是一种二叉排序树,它能在O(log n)内完成插入、查找和删除操作。它由Daniel Sleator和Robert Tarjan创造。它的优势在于不需要记录用于平衡树的冗余信息。在伸展树上的一般操作都基于伸展操作。
SBT
Size Balanced Tree(简称SBT)是一自平衡二叉查找树,是在计算机科学中用到的一种数据结构。它是由中国广东中山纪念中学的陈启峰发明的。陈启峰于2006年底完成论文《Size Balanced Tree》,并在2007年的全国青少年信息学奥林匹克竞赛冬令营中发表。由于SBT的拼写很容易找到中文谐音,它常被中国的信息学竞赛选手和ACM/ICPC选手们戏称为“傻B树”、“Super BT”等。相比红黑树、AVL树等自平衡二叉查找树,SBT更易于实现。据陈启峰在论文中称,SBT是“目前为止速度最快的高级二叉搜索树”。SBT能在O(log n)的时间内完成所有二叉搜索树(BST)的相关操作,而与普通二叉搜索树相比,SBT仅仅加入了简洁的核心操作Maintain。由于SBT赖以保持平衡的是size域而不是其他“无用”的域,它可以很方便地实现动态顺序统计中的select和rank操作。
map的存储方式以及用法

map的存储方式以及用法Map是一种常用的数据结构,用于存储键值对(key-value)的映射关系。
Map有多种实现方式,包括哈希表、平衡二叉树等。
在Java中,常用的Map实现是HashMap和TreeMap。
本文将介绍Map的存储方式以及常见的用法。
一、Map的存储方式:1. 哈希表(HashMap):哈希表是一种通过计算哈希值并将键值对存储在数组中的数据结构。
在HashMap中,通过键的哈希值找到对应的数组索引位置,然后将键值对存储在该位置。
当存在哈希冲突时,使用链表或红黑树来解决冲突。
2. 平衡二叉树(TreeMap):平衡二叉树是一种树形结构,其中每个节点的键值都大于其左子树中的任意键值,小于其右子树中的任意键值。
在TreeMap中,键值对按照键的顺序进行存储,因此可以实现按照键的大小进行排序。
二、Map的用法:1. 添加键值对:通过put(key, value)方法添加键值对到Map中。
如果Map中已存在相同的键,则新值会替换旧值,并返回旧值;如果Map 中不存在相同的键,则返回null。
2. 获取值:通过get(key)方法获取指定键对应的值。
3. 删除键值对:通过remove(key)方法删除指定键对应的值,并返回被删除的值。
4. 判断键是否存在:通过containsKey(key)方法判断Map中是否存在指定的键。
5. 判断值是否存在:通过containsValue(value)方法判断Map中是否存在指定的值。
6. 获取所有键的集合:通过keySet(方法获取Map中所有键的集合。
7. 获取所有值的集合:通过values(方法获取Map中所有值的集合。
8. 获取所有键值对的集合:通过entrySet(方法获取Map中所有键值对的集合。
9. 遍历Map:可以使用for-each循环遍历Map中的键值对,也可以使用迭代器进行遍历。
下面是一个使用HashMap的例子:```import java.util.HashMap;import java.util.Map;public class MapExamplepublic static void main(String[] args)// 创建一个HashMapMap<String, Integer> map = new HashMap<>(;//添加键值对map.put("apple", 10);map.put("banana", 5);map.put("orange", 8);//获取值int appleCount = map.get("apple");System.out.println("apple count: " + appleCount);//判断键是否存在boolean hasKey = map.containsKey("banana");System.out.println("has banana: " + hasKey);//删除键值对int removedCount = map.remove("orange");System.out.println("removed orange count: " + removedCount); // 遍历Mapfor (Map.Entry<String, Integer> entry : map.entrySet() String key = entry.getKey(;int value = entry.getValue(;System.out.println(key + ": " + value);}}```输出结果为:```apple count: 10has banana: trueremoved orange count: 8apple: 10banana: 5```以上便是Map的存储方式以及常见用法的介绍。
Java篇:树和Map

Java篇:树和MapJava篇:树和Map每次涉及到集合就想将Map拎出来单独看看,每次开始了解⼜似乎觉得没必要,⽽每次想到相关问题⼜只有隐隐约约的印象。
⽽提到Map就会想到TreeMap,就会想到红⿊树。
有关于树的概念我也总是这个状态,所以⼀起拎出来看看总结下加深印象。
概念部分皆参考⾃列在参考链接中的博⽂。
1、数据结构:树树的部分主要参考:1.1 树作为计算机中常⽤的数据机构--树(Tree),随着在计算机中应⽤越发⼴泛,衍⽣出了许多结构:树、⼆叉树、⼆叉查找树、平衡⼆叉树(AVL 树)、红⿊树、哈夫曼树(Huffman Tree)、多路查找树、B树、B+树、B*树、R树。
在计算机科学中,树(英语:tree)是⼀种抽象数据类型或是实现这种抽象数据类型的数据结构,⽤来模拟具有树状结构性质的数据集合。
它是由n(n>0)个有限节点组成⼀个具有层次关系的集合。
把它叫做“树”是因为它看起来像⼀棵倒挂的树,也就是说它是根朝上,⽽叶朝下的。
它具有以下的特点:①每个节点有零个或多个⼦节点;②没有⽗节点的节点称为根节点;③每⼀个⾮根节点有且只有⼀个⽗节点;④除了根节点外,每个⼦节点可以分为多个不相交的⼦树;然后你要知道⼀⼤堆关于树的术语:度,叶⼦节点,根节点,⽗节点,⼦节点,深度,⾼度。
1.2 ⼆叉树1.2.1 ⼆叉树⼆叉树:每个节点最多含有两个⼦树的树称为⼆叉树。
(我们⼀般在书中试题中见到的树是⼆叉树,但并不意味着所有的树都是⼆叉树。
)在⼆叉树的概念下⼜衍⽣出满⼆叉树和完全⼆叉树的概念满⼆叉树:除最后⼀层⽆任何⼦节点外,每⼀层上的所有结点都有两个⼦结点。
也可以这样理解,除叶⼦结点外的所有结点均有两个⼦结点。
节点数达到最⼤值,所有叶⼦结点必须在同⼀层上完全⼆叉树:若设⼆叉树的深度为h,除第 h 层外,其它各层 (1~(h-1)层) 的结点数都达到最⼤个数,第h层所有的结点都连续集中在最左边,这就是完全⼆叉树。
java treemap用法

java treemap用法Java TreeMap是一个有序的键值对集合,它基于红黑树实现。
以下是Java TreeMap的详细用法:1. 导入TreeMap类:import java.util.TreeMap;2. 创建TreeMap对象:TreeMap<KeyType, ValueType> treeMap = new TreeMap<>();其中,`KeyType`为键的类型,`ValueType`为值的类型。
3. 添加键值对:treeMap.put(key, value);使用`put()`方法向TreeMap中添加键值对。
如果键已存在,则会更新对应的值。
4. 获取值:ValueType value = treeMap.get(key);使用`get()`方法根据键获取对应的值。
5. 删除键值对:treeMap.remove(key);使用`remove()`方法根据键删除对应的键值对。
6. 判断键是否存在:boolean containsKey = treeMap.containsKey(key);使用`containsKey()`方法判断TreeMap中是否存在指定的键。
7. 获取键的集合:Set<KeyType> keySet = treeMap.keySet();使用`keySet()`方法获取TreeMap中所有键的集合。
8. 获取值的集合:Collection<ValueType> values = treeMap.values();使用`values()`方法获取TreeMap中所有值的集合。
9. 遍历键值对:for (Map.Entry<KeyType, ValueType> entry :treeMap.entrySet()) {KeyType key = entry.getKey();ValueType value = entry.getValue();// 处理键值对}使用`entrySet()`方法获取TreeMap中所有键值对的集合,然后使用增强for循环遍历集合,通过`getKey()`和`getValue()`方法获取键和值。
平衡二叉树详解

平衡⼆叉树详解平衡⼆叉树详解简介平衡⼆叉树(Balanced Binary Tree)具有以下性质:它是⼀棵空树或它的左右两个⼦树的⾼度差的绝对值不超过1,并且左右两个⼦树都是⼀棵平衡⼆叉树。
平衡⼆叉树的常⽤实现⽅法有红⿊树、AVL、替罪⽺树、Treap、伸展树等。
其中最为经典当属AVL树,我们总计⽽⾔就是:平衡⼆叉树是⼀种⼆叉排序树,其中每⼀个结点的左⼦树和右⼦树的⾼度差⾄多等于1。
性值AVL树具有下列性质的⼆叉树(注意,空树也属于⼀种平衡⼆叉树):l 它必须是⼀颗⼆叉查找树l 它的左⼦树和右⼦树都是平衡⼆叉树,且左⼦树和右⼦树的深度之差的绝对值不超过1。
l 若将⼆叉树节点的平衡因⼦BF定义为该节点的左⼦树的深度减去它的右⼦树的深度,则平衡⼆叉树上所有节点的平衡因⼦只可能为-1,0,1.l 只要⼆叉树上有⼀个节点的平衡因⼦的绝对值⼤于1,那么这颗平衡⼆叉树就失去了平衡。
实现平衡⼆叉树不平衡的情形:把需要重新平衡的结点叫做α,由于任意两个结点最多只有两个⼉⼦,因此⾼度不平衡时,α结点的两颗⼦树的⾼度相差2.容易看出,这种不平衡可能出现在下⾯4中情况中:1.对α的左⼉⼦的左⼦树进⾏⼀次插⼊2.对α的左⼉⼦的右⼦树进⾏⼀次插⼊3.对α的右⼉⼦的左⼦树进⾏⼀次插⼊4.对α的右⼉⼦的右⼦树进⾏⼀次插⼊(1)LR型(2)LL型(3)RR型(4)RL型完整代码#include<stdio.h>#include<stdlib.h>//结点设计typedef struct Node {int key;struct Node *left;struct Node *right;int height;} BTNode;int height(struct Node *N) {if (N == NULL)return0;return N->height;}int max(int a, int b) {return (a > b) ? a : b;}BTNode* newNode(int key) {struct Node* node = (BTNode*)malloc(sizeof(struct Node));node->key = key;node->left = NULL;node->right = NULL;node->height = 1;return(node);}//ll型调整BTNode* ll_rotate(BTNode* y) {BTNode *x = y->left;y->left = x->right;x->right = y;y->height = max(height(y->left), height(y->right)) + 1;x->height = max(height(x->left), height(x->right)) + 1;return x;}//rr型调整BTNode* rr_rotate(BTNode* y) {BTNode *x = y->right;y->right = x->left;x->left = y;y->height = max(height(y->left), height(y->right)) + 1;x->height = max(height(x->left), height(x->right)) + 1;return x;}//判断平衡int getBalance(BTNode* N) {if (N == NULL)return0;return height(N->left) - height(N->right);}//插⼊结点&数据BTNode* insert(BTNode* node, int key) {if (node == NULL)return newNode(key);if (key < node->key)node->left = insert(node->left, key);else if (key > node->key)node->right = insert(node->right, key);elsereturn node;node->height = 1 + max(height(node->left), height(node->right)); int balance = getBalance(node);if (balance > 1 && key < node->left->key) //LL型return ll_rotate(node);if (balance < -1 && key > node->right->key) //RR型return rr_rotate(node);if (balance > 1 && key > node->left->key) { //LR型node->left = rr_rotate(node->left);return ll_rotate(node);}if (balance < -1 && key < node->right->key) { //RL型node->right = ll_rotate(node->right);return rr_rotate(node);return node;}//遍历void preOrder(struct Node *root) { if (root != NULL) {printf("%d ", root->key);preOrder(root->left);preOrder(root->right);}}int main() {BTNode *root = NULL;root = insert(root, 2);root = insert(root, 1);root = insert(root, 0);root = insert(root, 3);root = insert(root, 4);root = insert(root, 4);root = insert(root, 5);root = insert(root, 6);root = insert(root, 9);root = insert(root, 8);root = insert(root, 7);printf("前序遍历:");preOrder(root);return0;}。
AVL树与红黑树平衡树的应用与区别

AVL树与红黑树平衡树的应用与区别AVL树和红黑树都是常见的自平衡二叉查找树,它们在计算机科学领域中被广泛应用。
本文将探讨AVL树和红黑树的应用及它们之间的区别。
一、AVL树的应用与特点AVL树是一种高度平衡的二叉查找树,它的特点是任意节点的左右子树高度差不超过1。
AVL树通过旋转操作来保持树的平衡,以确保在最坏情况下的查找、插入和删除操作的时间复杂度为O(log n)。
AVL树的应用广泛,特别适用于对插入和删除操作较为频繁的场景,比如数据库索引、编译器中的符号表等。
由于AVL树的严格平衡性,它在某些场景下可能会比红黑树更快,尤其是对于查找操作。
二、红黑树的应用与特点红黑树是一种近似平衡的二叉查找树,它通过引入颜色标记和一些约束条件来保持树的平衡。
红黑树的特点是具有较好的平衡性能,插入和删除操作相对AVL树更为高效,适用于需要频繁插入和删除操作的场景。
红黑树广泛应用于各种编程语言的标准库中,比如C++的STL中的map和set,Java中的TreeMap和TreeSet等。
红黑树的平衡性能虽然不如AVL树那么严格,但在实际应用中往往能够提供更好的性能。
三、AVL树与红黑树的区别1. 平衡性要求不同:AVL树要求任意节点的左右子树高度差不超过1,而红黑树则通过引入颜色标记和约束条件来保持树的近似平衡。
2. 插入和删除操作的效率不同:红黑树在插入和删除操作上比AVL树更高效,因为红黑树的平衡性要求相对宽松,旋转操作相对较少。
3. 查询操作的效率可能有差异:由于AVL树的严格平衡性,它在某些情况下可能比红黑树更快,尤其是对于查找操作。
但在实际应用中,红黑树的性能往往更优秀。
4. 存储空间的利用率不同:由于红黑树的平衡性要求相对宽松,它在存储空间利用率上可能比AVL树更好,因为红黑树的高度不会像AVL树那样严格受限。
综上所述,AVL树和红黑树都是重要的平衡树结构,在不同的应用场景下有着各自的优势和特点。
java treeset 方法

java treeset 方法Java中的TreeSet是一种有序集合,它使用红黑树实现。
TreeSet继承自AbstractSet并实现了NavigableSet接口。
TreeSet通过Comparator或元素的自然排序来维护元素的有序性。
在本文中,我们将探讨TreeSet的各种方法,并深入了解其内部实现。
一、TreeSet的创建与基本操作方法:1. 创建一个空的TreeSet对象:可以使用无参构造函数创建一个空的TreeSet,例如:TreeSet<String> set = new TreeSet<>();2. 创建一个包含元素的TreeSet对象:可以使用带有Collection参数的构造函数创建一个包含指定元素的TreeSet,例如:Set<String> set = new TreeSet<>(Arrays.asList("apple", "banana", "cherry"));3. 添加元素:可以使用add()方法向TreeSet中添加元素,例如:set.add("orange");4. 删除元素:可以使用remove()方法从TreeSet中删除指定元素,例如:set.remove("banana");5. 判断元素是否存在:可以使用contains()方法判断指定元素是否存在于TreeSet中,例如:boolean contains = set.contains("apple");二、TreeSet的遍历方法:1. 使用增强for循环遍历:可以使用增强for循环遍历TreeSet中的所有元素,例如:for (String element : set) {System.out.println(element);2. 使用迭代器遍历:可以使用迭代器遍历TreeSet中的所有元素,例如:Iterator<String> iterator = set.iterator();while (iterator.hasNext()) {System.out.println(iterator.next());}三、TreeSet的元素访问方法:1. 获取第一个元素:可以使用first()方法获取TreeSet中的第一个(最小的)元素,例如:String firstElement = set.first();2. 获取最后一个元素:可以使用last()方法获取TreeSet中的最后一个(最大的)元素,例如:String lastElement = st();3. 获取小于等于给定元素的最大元素:可以使用floor()方法获取TreeSet中小于等于给定元素的最大元素,例如:String floorElement = set.floor("banana");4. 获取大于等于给定元素的最小元素:可以使用ceiling()方法获取TreeSet中大于等于给定元素的最小元素,例如:String ceilingElement = set.ceiling("banana");四、TreeSet的排序方法:1. 使用自然排序:如果元素实现了Comparable接口,TreeSet将使用元素自身的自然排序对元素进行排序,例如:TreeSet<Integer> set = new TreeSet<>();set.add(3);set.add(1);set.add(2);输出:1 2 3System.out.println(set);2. 使用Comparator排序:如果元素没有实现Comparable接口,可以通过传递一个Comparator对象给TreeSet的构造函数,来指定元素的排序方式,例如:Comparator<String> comparator = new Comparator<>() { public int compare(String str1, String str2) {return str1.length() - str2.length();}};TreeSet<String> set = new TreeSet<>(comparator);set.add("apple");set.add("banana");set.add("cherry");输出:apple cherry bananaSystem.out.println(set);五、TreeSet的性能分析:1. 添加元素的性能:TreeSet的添加元素的平均时间复杂度为O(log n),最坏情况下的时间复杂度为O(n)。
平衡二叉树-构造方法(绝妙)
平衡二叉树构造方法平衡二叉树对于二叉查找树,尽管查找、插入及删除操作的平均运行时间为O(logn),但是它们的最差运行时间都是O(n),原因在于对树的形状没有限制。
平衡二叉树又称为AVL树,它或者是一棵空树,或者是有下列性质的二叉树:它的左子树和右子树都是平衡二叉树,且左右子树的深度之差的绝对值不超过1。
二叉树的的平衡因子BF为:该结点的左子树的深度减去它的右子树的深度,则平衡二叉树的所有结点的平衡因子为只可能是:-1、0和1一棵好的平衡二叉树的特征:(1)保证有n个结点的树的高度为O(logn)(2)容易维护,也就是说,在做数据项的插入或删除操作时,为平衡树所做的一些辅助操作时间开销为O(1)一、平衡二叉树的构造在一棵二叉查找树中插入结点后,调整其为平衡二叉树。
若向平衡二叉树中插入一个新结点后破坏了平衡二叉树的平衡性。
首先要找出插入新结点后失去平衡的最小子树根结点的指针。
然后再调整这个子树中有关结点之间的链接关系,使之成为新的平衡子树。
当失去平衡的最小子树被调整为平衡子树后,原有其他所有不平衡子树无需调整,整个二叉排序树就又成为一棵平衡二叉树(1)插入点位置必须满足二叉查找树的性质,即任意一棵子树的左结点都小于根结点,右结点大于根结点(2)找出插入结点后不平衡的最小二叉树进行调整,如果是整个树不平衡,才进行整个树的调整。
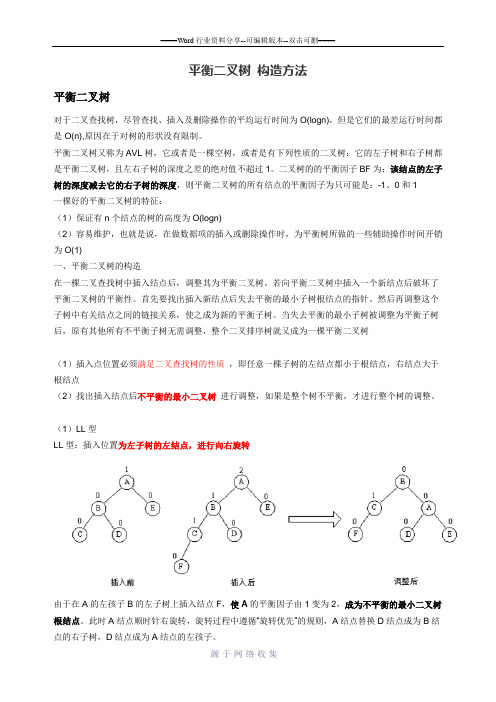
(1)LL型LL型:插入位置为左子树的左结点,进行向右旋转由于在A的左孩子B的左子树上插入结点F,使A的平衡因子由1变为2,成为不平衡的最小二叉树根结点。
此时A结点顺时针右旋转,旋转过程中遵循“旋转优先”的规则,A结点替换D结点成为B结点的右子树,D结点成为A结点的左孩子。
(2)RR型RR型:插入位置为右子树的右孩子,进行向左旋转由于在A的右子树C的右子树插入了结点F,A的平衡因子由-1变为-2,成为不平衡的最小二叉树根结点。
此时,A结点逆时针左旋转,遵循“旋转优先”的规则,A结点替换D结点成为C的左子树,D结点成为A的右子树。
java实现二叉树的基本操作

java实现二叉树的基本操作一、二叉树的定义树是计算机科学中的一种基本数据结构,表示以分层方式存储的数据集合。
树是由节点和边组成的,每个节点都有一个父节点和零个或多个子节点。
每个节点可以对应于一定数据,因此树也可以被视作提供快速查找的一种方式。
若树中每个节点最多只能有两个子节点,则被称为二叉树(Binary Tree)。
二叉树是一种递归定义的数据结构,它或者为空集,或者由一个根节点以及左右子树组成。
如果左子树非空,则左子树上所有节点的数值均小于或等于根节点的数值;如果右子树非空,则右子树上所有节点的数值均大于或等于根节点的数值;左右子树本身也分别是二叉树。
在计算机中实现二叉树,通常使用指针来表示节点之间的关系。
在Java中,定义一个二叉树节点类的代码如下:```public class BinaryTree {int key;BinaryTree left;BinaryTree right;public BinaryTree(int key) {this.key = key;}}```在这个类中,key字段表示该节点的数值;left和right字段分别表示这个节点的左右子节点。
1. 插入节点若要在二叉树中插入一个节点,首先需要遍历二叉树,找到一个位置使得插入新节点后,依然满足二叉树的定义。
插入节点的代码可以写成下面这个形式:```public void insert(int key) {BinaryTree node = new BinaryTree(key); if (root == null) {root = node;return;}BinaryTree temp = root;while (true) {if (key < temp.key) {if (temp.left == null) {temp.left = node;break;}temp = temp.left;} else {if (temp.right == null) {temp.right = node;break;}temp = temp.right;}}}```上面的代码首先创建了一个新的二叉树节点,然后判断二叉树根是否为空,若为空,则将这个节点作为根节点。
java treeset原理

java treeset原理Java中的TreeSet是一个基于红黑树实现的有序集合,具有自动排序和去重功能。
它是Set接口的实现类之一,继承自AbstractSet 类,实现了NavigableSet接口。
本文将深入介绍Java TreeSet的原理,包括红黑树、TreeSet的实现、遍历方式和常用操作等内容。
1. 红黑树红黑树是一种自平衡二叉查找树,它的每个节点都有一个颜色属性,可以是红色或黑色。
这种树具有以下特性:1. 每个节点要么是黑色,要么是红色。
2. 根节点是黑色。
3. 每个叶子节点(NIL节点,空节点)是黑色。
4. 如果一个节点是红色,那么它的子节点必须是黑色。
5. 从任意一个节点到其每个叶子节点的所有路径都包含相同数目的黑色节点。
这些特性确保了红黑树的平衡性和搜索效率。
插入、删除节点时,需要对树进行旋转和改变颜色等操作,以维持平衡。
2. TreeSet的实现Java TreeSet是基于红黑树实现的有序集合,它的元素按照自然顺序或者指定的比较器顺序进行排序。
TreeSet中的元素必须是可比较的,即实现了Comparable接口或者传入了Comparator比较器。
TreeSet的底层数据结构是红黑树,它的节点类是TreeMap中的Entry类,包含三个属性:key、value和color。
TreeSet的实现主要涉及以下几个方法:1. add(E e):向TreeSet中添加元素e。
首先通过比较器或者自然顺序找到要插入的位置,然后将元素包装成Entry对象,插入红黑树中,最后进行平衡操作。
2. remove(Object o):从TreeSet中删除元素o。
首先通过比较器或者自然顺序找到要删除的节点,然后进行删除操作,最后进行平衡操作。
3. clear():清空TreeSet中的所有元素。
4. iterator():返回一个迭代器,按照自然顺序或者指定的比较器顺序遍历元素。
5. size():返回TreeSet中元素的个数。
avl方案介绍

avl方案1. 引言AVL树是一种自平衡二叉查找树,它在操作过程中保持树的高度平衡,从而保证了各种基本操作的时间复杂度为O(log n)。
本文将介绍AVL树的原理、实现方法以及应用场景。
2. AVL树的原理AVL树是由G.M. Adelson-Velsky和E.M. Landis在1962年提出的,它的名称取自于他们的名字的首字母。
AVL树的特点是每个节点的左子树和右子树的高度差不超过1,即保证了树的高度平衡。
AVL树的插入和删除操作会导致树的失衡,为了维持树的平衡,AVL树使用了旋转操作。
旋转操作主要包括左旋和右旋,通过重新调整子树的结构来使得树重新达到平衡。
3. 实现AVL树实现AVL树可以采用递归或迭代的方式,这里以递归方式为例进行说明。
3.1 AVL树节点定义首先需要定义AVL树的节点结构,一个简单的AVL树节点可以包括以下几个字段:class AVLNode:def__init__(self, key):self.key = keyself.left =Noneself.right =Noneself.height =1其中,key字段用于存储节点的键值,left和right字段分别指向节点的左子树和右子树,height字段表示节点的高度。
3.2 AVL树的插入操作AVL树的插入操作分为以下几个步骤:1.找到插入位置,若树为空,则直接插入新节点。
2.根据插入节点的键值与当前节点的键值进行比较,决定向左子树或右子树递归插入。
行旋转操作。
4.若当前节点失衡,根据失衡情况选择合适的旋转操作进行平衡调整。
下面是插入操作的递归实现代码:def insert(root, key):if not root:return AVLNode(key)elif key < root.key:root.left = insert(root.left, key)else:root.right = insert(root.right, key)root.height =1+ max(get_height(root.left), get_height(root.right)) balance = get_balance(root)# 左旋if balance >1and key < root.left.key:return rotate_right(root)# 右旋if balance <-1and key > root.right.key:return rotate_left(root)# 左右旋if balance >1and key > root.left.key:root.left = rotate_left(root.left)return rotate_right(root)# 右左旋if balance <-1and key < root.right.key:root.right = rotate_right(root.right)return rotate_left(root)return root3.3 AVL树的删除操作AVL树的删除操作也需要进行树的平衡调整,它分为以下几个步骤:1.找到待删除的节点。
Java实现二叉树,Java实现队列

Java实现二叉树,Java实现队列实验 Java 实现二叉树一、实验目的利用JAVA的代码实现二叉树的结构二、实验代码定义一个结点类:package com.xiao.tree; /** ** @author WJQ 树结点类 */public class TreeNode { /*存数据的*/private Object value; /*左孩子结点*/private TreeNode leftChild; /*右孩子结点*/private TreeNode rightChild; /*以下是setter和getter方法*/ public Object getValue() { return value; }public void setValue(Object value) { this.value = value; }public TreeNode getLeftChild() {return leftChild;}public void setLeftChild(TreeNode leftChild) { this.leftChild = leftChild; }public TreeNode getRightChild() { return rightChild; }public void setRightChild(TreeNode rightChild) { this.rightChild = rightChild; } }定义一个树类:package com.xiao.tree; /** ** @author WJQ* 树的结构,树中只有结点 */public class Tree { /*结点属性*/private TreeNode node;public TreeNode getNode() { return node; }public void setNode(TreeNode node) { this.node = node; } }//定义一个队列类:package com.xiao.tree; /*** @author WJQ* 该类是在向树中加入结点时需要使用的*/import java.util.LinkedList;public class Queue {private LinkedList list; }/*一初始化就new一个list*/public Queue(){list = new LinkedList(); }/*结点入队列*/public void enQueue(TreeNode node){ this.list.add(node); } /*队首元素出队列*/public TreeNode outQueue(){return this.list.removeFirst(); }/*队列是否为空*/public boolean isEmpty(){return this.list.isEmpty(); }public LinkedList getList() { return list; }public void setList(LinkedList list) { this.list = list; }//定义一个二叉树类: package com.xiao.tree; /*** @author WJQ 二叉树,增加结点,前序遍历,中序遍历,后序遍历 */public class BinaryTree {private Tree tree; private Queue queue;/* 构造函数,初始化的时候就生成一棵树 */ public BinaryTree() { tree = new Tree(); }/* 向树中插入结点 */public void insertNode(TreeNode node) {/* 如果树是空树,则生成一颗树,之后把当前结点插入到树中,作为根节点 ,根节点处于第0层 */if (tree.getNode() == null) { tree.setNode(node); return; } else {/* 根节点入队列 */queue = new Queue();queue.enQueue(tree.getNode()); /** 队列不空,取出队首结点,如果队首结点的左右孩子有一个为空的或者都为空,则将新结点插入到相应的左右位置,跳出循环,如果左右孩子都不为空* ,则左右孩子入队列,继续while循环*/while (!queue.isEmpty()) {TreeNode temp = queue.outQueue(); if (temp.getLeftChild() == null){ temp.setLeftChild(node); return;} else if (temp.getRightChild() == null) { temp.setRightChild(node); return; } else {/* 左右孩子不空,左右孩子入队列 */}}}queue.enQueue(temp.getLeftChild());queue.enQueue(temp.getRightChild()); } }/* 中序遍历 */public void midOrder(TreeNode node) { if (node != null) {this.midOrder(node.getLeftChild()); System.out.println(node.getValue()); this.midOrder(node.getRightChild()); } }/* 先序遍历 */public void frontOrder(TreeNode node) { if (node != null) {System.out.println(node.getValue());this.frontOrder(node.getLeftChild());this.frontOrder(node.getRightChild()); } }/* 后序遍历 */public void lastOrder(TreeNode node) { if (node != null) {stOrder(node.getLeftChild());stOrder(node.getRightChild());System.out.println(node.getValue()); } }public Tree getTree() { return tree; }最好来一个客户端测试一下:package com.xiao.tree;感谢您的阅读,祝您生活愉快。
TreeSet和TreeMap排序

TreeSet和TreeMap排序TreeSet 有两种排序⽅式1. parble+compareTonew TreeSet()⽤这种⽅法必须要求实体类实现Comparable接⼝,也就是说要求添加到TreeSet中的元素是可排序的2. parator +compare举个TreeSet栗⼦:package com.etc.test;import parator;import java.util.TreeSet;import com.etc.entity.Person;public class TreeSetDemo {public static void main(String[] args) {Person p1=new Person("depp",100);Person p2=new Person("tom",90);Person p3=new Person("jack",50);TreeSet<Person> ts=new TreeSet<Person>(new Comparator<Person>() {public int compare(Person o1,Person o2){return o1.getHandsome()-o2.getHandsome();//升序}});ts.add(p1);ts.add(p2);ts.add(p3);System.out.println(ts);/** 排序结果没有改变,是因为TreeSet在添加元素的时候进⾏排序,需要注意,数据更改不会影响原来的顺序还有⼀点需要注意的是,TreeSet中不可以数据重复,所以⼀般不修改数据,为了确保这⼀点,我们可以在Person类为属性加上final关键字,删除setter⽅法 */p3.setHandsome(200);//改变数据,排序不会改变System.out.println(ts);}}举个TreeMap栗⼦:package com.etc.test;import parator;import java.util.Set;import java.util.TreeMap;import java.util.TreeSet;import com.etc.entity.Person;public class TreeMapDemo {public static void main(String[] args) {Person p1=new Person("depp",100);Person p2=new Person("tom",90);Person p3=new Person("jack",50);TreeMap<Person, String> tm=new TreeMap<Person, String>(new Comparator<Person>() {public int compare(Person o1,Person o2){return o1.getHandsome()-o2.getHandsome();//升序}});tm.put(p1, "ttt");tm.put(p2, "ttt");tm.put(p3, "ttt");System.out.println(tm);//也可以⽤set进⾏输出 TreeMap也是在添加元素时进⾏排序Set<Person> set=tm.keySet();System.out.println(set);}}。
平衡二叉树构造方法

平衡二叉树构造方法构造平衡二叉树的方法有很多,其中一种绝妙的方法是通过AVL树进行构造。
AVL树是一种平衡二叉树,它的左子树和右子树的高度差不超过1、利用这种特性,我们可以通过以下步骤构造平衡二叉树:1.将需要构造平衡二叉树的数据按照升序或者降序排列。
2.选择数据的中间元素作为根节点。
3.将数据分成左右两个部分,分别作为根节点的左子树和右子树的数据。
4.递归地对左子树和右子树进行构造。
下面我们通过一个例子来具体说明这个方法:假设我们需要构造一个平衡二叉树,并且数据为1,2,3,4,5,6,7,8,9首先,我们将数据按照升序排列得到1,2,3,4,5,6,7,8,9、选择中间的元素5作为根节点。
然后,我们将数据分成两部分:1,2,3,4和6,7,8,9、递归地对这两个部分进行构造。
对于左子树,我们选择中间元素2作为根节点,将数据分成两部分:1和3,4、递归地构造这两个部分。
对于右子树,我们选择中间元素8作为根节点,将数据分成两部分:6,7和9、递归地构造这两个部分。
重复这个过程,直到所有的数据都被构造为节点。
最后得到的树就是一个平衡二叉树。
这个构造方法的时间复杂度是O(nlogn),其中n是数据的数量。
虽然它的时间复杂度比较高,但是它保证了构造的树是一个平衡二叉树,从而提高了数据的查找、插入和删除等操作的效率。
总结起来,通过AVL树进行构造是一种有效的方法来构造平衡二叉树。
它将数据按照升序或者降序排列,选择中间元素作为根节点,然后递归地对左子树和右子树进行构造。
这种方法保证了构造的树是一个平衡二叉树,从而提高了数据的查找、插入和删除等操作的效率。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Java中A VL平衡二叉树实现Map (仿照TreeMap和TreeSet)1、下面是AVLTreeMap的实现package com;import java.io.IOException;import java.util.*;public class AVLTreeMap<K, V> extends AbstractMap<K, V> implements NavigableMap<K, V>, java.io.Serializable {private static final long serialVersionUID = 1731396135957583906L;private final Comparator<? super K> comparator;private transient Entry<K, V> root = null;private transient int size = 0;private transient int modCount = 0;public AVLTreeMap() {comparator = null;}public AVLTreeMap(Comparator<? super K> comparator) {parator = comparator;}public AVLTreeMap(Map<? extends K, ? extends V> m) {comparator = null;putAll(m);}public AVLTreeMap(SortedMap<K, ? extends V> m) {comparator = parator();try {buildFromSorted(m.size(), m.entrySet().iterator(), null, null);} catch (IOException e) {} catch (ClassNotFoundException e) {}}public int size() {return size;}public boolean containsKey(Object key) {return getEntry(key) != null;}public boolean containsValue(Object value) {for (Entry<K, V> e = getFirstEntry(); e != null; e = successor(e)) {if (valEquals(value, e.value))return true;}return false;}public V get(Object key) {Entry<K, V> p = getEntry(key);return p == null ? null : p.value;}public Comparator<? super K> comparator() {return comparator;}public K firstKey() {return key(getFirstEntry());}public K lastKey() {return key(getLastEntry());}@SuppressWarnings({ "rawtypes", "unchecked" })public void putAll(Map<? extends K, ? extends V> map) {int mapSize = map.size();if (size == 0 && mapSize != 0 && map instanceof SortedMap) {Comparable<? super K> cmp = (Comparable<? super K>) ((SortedMap) map).comparator();if (cmp == comparator || (cmp != null && cmp.equals(comparator))) {++modCount;try {buildFromSorted(mapSize, map.entrySet().iterator(), null, null);} catch (IOException e) {} catch (ClassNotFoundException e) {}return;}}super.putAll(map);}@SuppressWarnings("unchecked")final Entry<K, V> getEntry(Object key) {if (comparator != null) {return getEntryUsingComparator(key);}if (key == null)throw new NullPointerException();Comparable<? super K> k = (Comparable<? super K>) key;Entry<K, V> p = root;while (p != null) {int cmp = pareTo(p.key);if (cmp < 0) {p = p.left;} else if (cmp > 0) {p = p.right;} else {return p;}}return null;}@SuppressWarnings("unchecked")final Entry<K, V> getEntryUsingComparator(Object key) { K k = (K) key;Comparator<? super K> cpr = comparator;if (cpr != null) {Entry<K, V> p = root;while (p != null) {int cmp = pare(k, p.key);if (cmp < 0)p = p.left;else if (cmp > 0)p = p.right;elsereturn p;}}return null;}final Entry<K, V> getCeilingEntry(Object key) {Entry<K, V> p = root;while (p != null) {int cmp = compare(key, p.key);if (cmp < 0) {if (p.left != null)p = p.left;elsereturn p;} else if (cmp < 0) {if (p.right != null)p = p.right;else {Entry<K, V> parent = p.parent;Entry<K, V> ch = p;while (parent != null && ch == parent.right) {ch = parent;parent = parent.parent;}return parent;}} else {return p;}}return null;}final Entry<K, V> getFloorEntry(Object key) {Entry<K, V> p = root;while (p != null) {int cmp = compare(key, p.key);if (cmp > 0) {if (p.right != null)p = p.right;elsereturn p;} else if (cmp < 0) {if (p.left != null)p = p.left;else {Entry<K, V> parent = p.parent;Entry<K, V> ch = p;while (parent != null && ch == parent.left) {ch = parent;parent = parent.parent;}return parent;}} else {return p;}}return null;}final Entry<K, V> getHigherEntry(Object key) {Entry<K, V> p = root;while (p != null) {int cmp = compare(key, p.key);if (cmp < 0) {if (p.left != null)p = p.left;elsereturn p;} else {if (p.right != null)p = p.right;else {Entry<K, V> parent = p.parent;Entry<K, V> ch = p;while (parent != null && ch == parent.right) {ch = parent;parent = parent.parent;}return parent;}}}return null;}final Entry<K, V> getLowerEntry(Object key) {Entry<K, V> p = root;while (p != null) {int cmp = compare(key, p.key);if (cmp > 0) {if (p.right != null)p = p.right;elsereturn p;} else {if (p.left != null)p = p.left;else {Entry<K, V> parent = p.parent;Entry<K, V> ch = p;while (parent != null && ch == parent.left) {ch = parent;parent = parent.parent;}return parent;}}}return null;}@SuppressWarnings("unchecked")public V put(K key, V value) {Entry<K, V> t = root;if (t == null) {root = new Entry<K, V>(key, value, null);root.height = 1;size++;modCount++;return null;}int cmp;Entry<K, V> parent;Comparator<? super K> cpr = comparator;if (cpr != null) {do {parent = t;cmp = pare(key, t.key);if (cmp < 0)t = t.left;else if (cmp > 0)t = t.right;elsereturn t.setValue(value);} while (t != null);} else {do {parent = t;cmp = ((Comparable<? super K>) key).compareTo(t.key);if (cmp < 0)t = t.left;else if (cmp > 0)t = t.right;elsereturn t.setValue(value);} while (t != null);}Entry<K, V> e = new Entry<K, V>(key, value, parent);if (cmp < 0)parent.left = e;elseparent.right = e;fixAfterInsertion(e);size++;modCount++;return null;}public V remove(Object key) {Entry<K, V> p = getEntry(key);if (p == null) {return null;}V oldVal = p.value;deleteEntry(p);return oldVal;}public void clear() {size = 0;modCount++;root = null;}@SuppressWarnings("unchecked")public Object clone() {AVLTreeMap<K, V> clone = null;try {clone = (AVLTreeMap<K, V>) super.clone();} catch (CloneNotSupportedException e) {throw new InternalError();}clone.root = null;clone.size = 0;clone.modCount = 0;clone.entrySet = null;clone.keySet = null;clone.descendingMap = null;try {clone.buildFromSorted(size, entrySet().iterator(), null, null);} catch (IOException e) {} catch (ClassNotFoundException e) {}return clone;}public Map.Entry<K, V> firstEntry() {return exportEntry(getFirstEntry());}public Map.Entry<K, V> lastEntry() {return exportEntry(getLastEntry());}public Map.Entry<K, V> pollFirstEntry() {AVLTreeMap.Entry<K, V> p = getFirstEntry();Map.Entry<K, V> result = exportEntry(p);if (p != null)deleteEntry(p);return result;}public Map.Entry<K, V> pollLastEntry() {AVLTreeMap.Entry<K, V> e = getLastEntry();Map.Entry<K, V> result = exportEntry(e);if (e != null)deleteEntry(e);return result;}public Map.Entry<K, V> lowerEntry(K key) {return exportEntry(getLowerEntry(key));}public K lowerKey(K key) {return keyOrNull(getLowerEntry(key));}public Map.Entry<K, V> floorEntry(K key) {return exportEntry(getFloorEntry(key));}public K floorKey(K key) {return keyOrNull(getFloorEntry(key));}public Map.Entry<K, V> ceilingEntry(K key) {return exportEntry(getCeilingEntry(key));}public K ceilingKey(K key) {return keyOrNull(getCeilingEntry(key));}public Map.Entry<K, V> higherEntry(K key) {return exportEntry(getHigherEntry(key));}public K higherKey(K key) {return keyOrNull(getHigherEntry(key));}private transient EntrySet entrySet = null;private transient KeySet<K> navigableKeySet = null;private transient NavigableMap<K, V> descendingMap = null; @SuppressWarnings("unused")private transient Set<K> keySet = null;private transient Collection<V> values = null;public Set<K> keySet() {return navigableKeySet();}@SuppressWarnings({ "unchecked", "rawtypes" })public NavigableSet<K> navigableKeySet() {KeySet<K> ks = navigableKeySet;return (ks != null) ? ks : (navigableKeySet = new KeySet(this));}public NavigableSet<K> descendingKeySet() {return descendingMap().navigableKeySet();}public Set<Map.Entry<K, V>> entrySet() {EntrySet es = entrySet;return (es != null) ? es : (entrySet = new EntrySet());}public Collection<V> values() {Collection<V> vs = values;return (vs != null) ? vs : (values = new Values());}@SuppressWarnings({ "unchecked", "rawtypes" })public NavigableMap<K, V> descendingMap() {NavigableMap<K, V> km = descendingMap;return (km != null) ? km : (descendingMap = new DescendingSubMap(this, true, null, true, true, null, true));}@SuppressWarnings({ "unchecked", "rawtypes" })public NavigableMap<K, V> subMap(K fromKey, boolean fromInclusive, K toKey, boolean toInclusive) {return new AscendingSubMap(this, false, fromKey, fromInclusive, false, toKey, toInclusive);}@SuppressWarnings({ "unchecked", "rawtypes" })public NavigableMap<K, V> headMap(K toKey, boolean inclusive) {return new AscendingSubMap(this, true, null, true, false, toKey, inclusive);}@SuppressWarnings({ "unchecked", "rawtypes" })public NavigableMap<K, V> tailMap(K fromKey, boolean inclusive) {return new AscendingSubMap(this, false, fromKey, inclusive, true, null, true);}public SortedMap<K, V> subMap(K fromKey, K toKey) {return subMap(fromKey, true, toKey, false);}public SortedMap<K, V> headMap(K toKey) {return headMap(toKey, false);}public SortedMap<K, V> tailMap(K fromKey) {return tailMap(fromKey, true);}class Values extends AbstractCollection<V> {public Iterator<V> iterator() {return new ValueIterator(getFirstEntry());}public int size() {return AVLTreeMap.this.size();}public boolean contains(Object o) {return AVLTreeMap.this.containsValue(o);}public boolean remove(Object o) {for (Entry<K, V> e = getFirstEntry(); e != null; e = successor(e)) { if (valEquals(o, e.value)) {deleteEntry(e);return true;}}return false;}public void clear() {AVLTreeMap.this.clear();}}class EntrySet extends AbstractSet<Map.Entry<K, V>> {public Iterator<Map.Entry<K, V>> iterator() {return new EntryIterator(getFirstEntry());}public int size() {return AVLTreeMap.this.size();}@SuppressWarnings("unchecked")public boolean contains(Object o) {if (!(o instanceof Map.Entry)) {return false;}Map.Entry<K, V> entry = (Map.Entry<K, V>) o;V value = entry.getValue();Entry<K, V> p = getEntry(entry.getKey());return p != null && valEquals(p.getValue(), value);}@SuppressWarnings("unchecked")public boolean remove(Object o) {if (!(o instanceof Map.Entry)) {return false;}Map.Entry<K, V> entry = (Map.Entry<K, V>) o;V value = entry.getValue();Entry<K, V> p = getEntry(entry.getKey());if (p != null && valEquals(p.getValue(), value)) {deleteEntry(p);return true;}return false;}public void clear() {AVLTreeMap.this.clear();}}Iterator<K> keyIterator() {return new KeyIterator(getFirstEntry());}Iterator<K> descendingKeyIterator() {return new DescendingKeyIterator(getLastEntry());}static final class KeySet<E> extends AbstractSet<E> implements NavigableSet<E> { private final NavigableMap<E, Object> m;KeySet(NavigableMap<E, Object> m) {this.m = m;}@SuppressWarnings({ "unchecked", "rawtypes" })public Iterator<E> iterator() {if (m instanceof AVLTreeMap)return ((AVLTreeMap) m).keyIterator();elsereturn (Iterator<E>) (((AVLTreeMap.NavigableSubMap) m).keyIterator());}@SuppressWarnings({ "unchecked", "rawtypes" })public Iterator<E> descendingIterator() {if (m instanceof AVLTreeMap)return ((AVLTreeMap) m).descendingKeyIterator();elsereturn (Iterator<E>) (((AVLTreeMap.NavigableSubMap)m).descendingKeyIterator());}public int size() {return m.size();}public boolean isEmpty() {return m.isEmpty();}public boolean contains(Object o) {return m.containsKey(o);}public void clear() {m.clear();}public E lower(E e) {return m.lowerKey(e);}public E floor(E e) {return m.floorKey(e);}public E ceiling(E e) {return m.ceilingKey(e);}public E higher(E e) {return m.higherKey(e);}public E first() {return m.firstKey();}public E last() {return stKey();}public Comparator<? super E> comparator() {return parator();}public E pollFirst() {Map.Entry<E, Object> e = m.pollFirstEntry();return e == null ? null : e.getKey();}public E pollLast() {Map.Entry<E, Object> e = m.pollLastEntry();return e == null ? null : e.getKey();}public boolean remove(Object o) {int oldSize = m.size();m.remove(o);return oldSize != m.size();}public NavigableSet<E> descendingSet() {return new AVLTreeSet<E>(m.descendingMap());}public NavigableSet<E> subSet(E fromElement, boolean fromInclusive, E toElement, boolean toInclusive) {return new AVLTreeSet<E>(m.subMap(fromElement, fromInclusive, toElement, toInclusive));}public NavigableSet<E> headSet(E toElement, boolean inclusive) {return new AVLTreeSet<E>(m.headMap(toElement, inclusive));}public NavigableSet<E> tailSet(E fromElement, boolean inclusive) {return new AVLTreeSet<E>(m.tailMap(fromElement, inclusive));}public SortedSet<E> subSet(E fromElement, E toElement) {return subSet(fromElement, true, toElement, false);}public SortedSet<E> headSet(E toElement) {return headSet(toElement, false);}public SortedSet<E> tailSet(E fromElement) {return tailSet(fromElement, true);}}abstract class PrivateEntryIterator<T> implements Iterator<T> {Entry<K, V> next;Entry<K, V> lastReturned;int expectedModCount;PrivateEntryIterator(Entry<K, V> first) {expectedModCount = modCount;lastReturned = null;next = first;}public final boolean hasNext() {return next != null;}final Entry<K, V> nextEntry() {Entry<K, V> e = next;if (next == null)throw new NoSuchElementException();if (modCount != expectedModCount)throw new ConcurrentModificationException();next = successor(e);lastReturned = e;return e;}final Entry<K, V> prevEntry() {Entry<K, V> e = next;if (next == null)throw new NoSuchElementException();if (modCount != expectedModCount)throw new ConcurrentModificationException();next = predecessor(e);lastReturned = e;return e;}public void remove() {if (lastReturned == null)throw new IllegalStateException();if (modCount != expectedModCount)throw new ConcurrentModificationException();if (leftOf(lastReturned) != null && rightOf(lastReturned) != null) next = lastReturned;deleteEntry(lastReturned);expectedModCount = modCount;lastReturned = null;}}final class EntryIterator extends PrivateEntryIterator<Map.Entry<K, V>> { EntryIterator(Entry<K, V> first) {super(first);}public Map.Entry<K, V> next() {return nextEntry();}}final class ValueIterator extends PrivateEntryIterator<V> {ValueIterator(Entry<K, V> first) {super(first);}public V next() {return nextEntry().value;}}final class KeyIterator extends PrivateEntryIterator<K> {KeyIterator(Entry<K, V> first) {super(first);}public K next() {return nextEntry().key;}}final class DescendingKeyIterator extends PrivateEntryIterator<K> {DescendingKeyIterator(Entry<K, V> first) {super(first);}public K next() {return prevEntry().key;}}@SuppressWarnings("unchecked")final int compare(Object k1, Object k2) {return comparator == null ? ((Comparable<? super K>) k1).compareTo((K) k2) : pare((K) k1, (K) k2);}final static boolean valEquals(Object o1, Object o2) {return o1 == null ? o2 == null : o1.equals(o2);}@SuppressWarnings({ "unchecked", "rawtypes" })static <K, V> Map.Entry<K, V> exportEntry(Entry<K, V> e) {return e == null ? null : new AbstractMap.SimpleImmutableEntry(e);}static <K, V> K keyOrNull(Entry<K, V> e) {return e == null ? null : e.key;}static <K, V> K key(Entry<K, V> e) {if (e == null)throw new NoSuchElementException();return e.key;}final int max(int height1, int height2) {return (height1 > height2) ? height1 : height2;}static abstract class NavigableSubMap<K, V> extends AbstractMap<K, V> implements NavigableMap<K, V>, java.io.Serializable {private static final long serialVersionUID = 3330238317193227055L;final AVLTreeMap<K, V> m;final K lo, hi;final boolean fromStart, toEnd;final boolean loInclusive, hiInclusive;NavigableSubMap(AVLTreeMap<K, V> m, boolean fromStart, K lo, boolean loInclusive, boolean toEnd, K hi, boolean hiInclusive) {if (!fromStart && !toEnd) {if (pare(lo, hi) > 0)throw new IllegalArgumentException("fromKey > toKey");} else {if (!fromStart)pare(lo, lo);elsepare(hi, hi);}this.m = m;this.lo = lo;this.hi = hi;this.fromStart = fromStart;this.toEnd = toEnd;this.loInclusive = loInclusive;this.hiInclusive = hiInclusive;}final boolean tooLow(Object key) {if (!fromStart) {int c = pare(key, lo);if (c < 0 || (c == 0 && !loInclusive))return true;}return false;}final boolean tooHigh(Object key) {if (!toEnd) {int c = pare(key, hi);if (c > 0 || (c == 0 && !hiInclusive))return true;}return false;}final boolean inRange(Object key) {return !tooLow(key) && !tooHigh(key);}final boolean inClosedRange(Object key) {return (fromStart || pare(key, lo) >= 0) && (toEnd || pare(key, hi) <= 0);}final boolean inRange(Object key, boolean inclusive) {return inclusive ? inRange(key) : inClosedRange(key);}final AVLTreeMap.Entry<K, V> absLowest() {AVLTreeMap.Entry<K, V> e = fromStart ? m.getFirstEntry() : (loInclusive ?m.getCeilingEntry(lo) : m.getHigherEntry(lo));return (e == null || tooHigh(e.key)) ? null : e;}final AVLTreeMap.Entry<K, V> absHighest() {AVLTreeMap.Entry<K, V> e = toEnd ? m.getLastEntry() : (hiInclusive ?m.getFloorEntry(hi) : m.getLowerEntry(hi));return (e == null || tooLow(e.key) ? null : e);}final AVLTreeMap.Entry<K, V> absCeiling(K key) {if (tooLow(key))return absLowest();AVLTreeMap.Entry<K, V> e = m.getCeilingEntry(key);return (e == null || tooHigh(e.key)) ? null : e;}final AVLTreeMap.Entry<K, V> absHigher(K key) {if (tooLow(key))return absLowest();AVLTreeMap.Entry<K, V> e = m.getHigherEntry(key);return (e == null || tooHigh(e.key)) ? null : e;}final AVLTreeMap.Entry<K, V> absFloor(K key) {if (tooHigh(key))return absHighest();AVLTreeMap.Entry<K, V> e = m.getFloorEntry(key);return (e == null || tooLow(e.key)) ? null : e;}final AVLTreeMap.Entry<K, V> absLower(K key) {if (tooHigh(key))return absHighest();AVLTreeMap.Entry<K, V> e = m.getLowerEntry(key);return (e == null || tooLow(e.key)) ? null : e;}final AVLTreeMap.Entry<K, V> absHighFence() {return toEnd ? null : (hiInclusive ? m.getHigherEntry(hi) : m.getCeilingEntry(hi));}final AVLTreeMap.Entry<K, V> absLowFence() {return fromStart ? null : (loInclusive ? m.getLowerEntry(lo) :m.getCeilingEntry(lo));}abstract AVLTreeMap.Entry<K, V> subLowest();abstract AVLTreeMap.Entry<K, V> subHighest();abstract AVLTreeMap.Entry<K, V> subCeiling(K key);abstract AVLTreeMap.Entry<K, V> subHigher(K key);abstract AVLTreeMap.Entry<K, V> subFloor(K key);abstract AVLTreeMap.Entry<K, V> subLower(K key);abstract Iterator<K> keyIterator();abstract Iterator<K> descendingKeyIterator();public boolean isEmpty() {return (fromStart && toEnd) ? m.isEmpty() : entrySet().isEmpty(); }public int size() {return (fromStart && toEnd) ? m.size() : entrySet().size();}public final boolean containsKey(Object key) {return inRange(key) && m.containsKey(key);}public final V put(K key, V value) {if (!inRange(key))throw new IllegalArgumentException("key out of range");return m.put(key, value);}public final V get(Object key) {return !inRange(key) ? null : m.get(key);}public final V remove(Object key) {return !inRange(key) ? null : m.remove(key);}public Map.Entry<K, V> ceilingEntry(K key) {return exportEntry(subCeiling(key));}public K ceilingKey(K key) {return keyOrNull(subCeiling(key));}public Map.Entry<K, V> higherEntry(K key) {return exportEntry(subHigher(key));}public K higherKey(K key) {return keyOrNull(subHigher(key));}public Map.Entry<K, V> floorEntry(K key) { return exportEntry(subFloor(key));}public K floorKey(K key) {return keyOrNull(subFloor(key));}public Map.Entry<K, V> lowerEntry(K key) { return exportEntry(subLower(key));}public K lowerKey(K key) {return keyOrNull(subLower(key));}public K firstKey() {return key(subLowest());}public K lastKey() {return key(subHighest());}public Map.Entry<K, V> firstEntry() {return exportEntry(subLowest());}public Map.Entry<K, V> lastEntry() {return exportEntry(subHighest());}public Map.Entry<K, V> pollFirstEntry() { AVLTreeMap.Entry<K, V> e = subLowest();Map.Entry<K, V> result = exportEntry(e);if (e != null)m.deleteEntry(e);return result;}public Map.Entry<K, V> pollLastEntry() { AVLTreeMap.Entry<K, V> e = subHighest();Map.Entry<K, V> result = exportEntry(e);if (e != null)m.deleteEntry(e);return result;}transient NavigableMap<K, V> descendingMapView = null;transient EntrySetView entrySetView = null;transient KeySet<K> navigableKeySetView = null;@SuppressWarnings({ "unchecked", "rawtypes" })public final NavigableSet<K> navigableKeySet() {KeySet<K> nksv = navigableKeySetView;return nksv != null ? nksv : (navigableKeySetView = new AVLTreeMap.KeySet(this));}public final Set<K> keySet() {return navigableKeySet();}public NavigableSet<K> descendingKeySet() {return descendingMap().navigableKeySet();}public SortedMap<K, V> subMap(K fromKey, K toKey) {return subMap(fromKey, true, toKey, false);}public SortedMap<K, V> headMap(K toKey) {return headMap(toKey, false);}public SortedMap<K, V> tailMap(K fromKey) {return tailMap(fromKey, true);}abstract class EntrySetView extends AbstractSet<Map.Entry<K, V>> { private transient int size = -1, sizeModCount;public int size() {if (fromStart && toEnd)return m.size();if (size == -1 || sizeModCount != m.modCount) {size = 0;Iterator<Map.Entry<K, V>> i = iterator();while (i.hasNext()) {size++;i.next();}}return size;}public boolean isEmpty() {AVLTreeMap.Entry<K, V> e = absLowest();return (e == null || tooHigh(e));}@SuppressWarnings("unchecked")public boolean contains(Object o) {if (!(o instanceof Map.Entry))return false;Map.Entry<K, V> entry = (Map.Entry<K, V>) o;K key = entry.getKey();if (!inRange(key))return false;AVLTreeMap.Entry<K, V> node = m.getEntry(key);return node != null && valEquals(node.getValue(), entry.getValue());}@SuppressWarnings("unchecked")public boolean remove(Object o) {if (!(o instanceof Map.Entry))return false;Map.Entry<K, V> entry = (Map.Entry<K, V>) o;K key = entry.getKey();if (!inRange(key))return false;AVLTreeMap.Entry<K, V> node = m.getEntry(key);if (node != null && valEquals(node.getValue(), entry.getValue())) { m.deleteEntry(node);return true;}return false;}}abstract class SubMapIterator<T> implements Iterator<T> {AVLTreeMap.Entry<K, V> lastReturned;AVLTreeMap.Entry<K, V> next;final K fenceKey;int expectedModCount;SubMapIterator(AVLTreeMap.Entry<K, V> first, AVLTreeMap.Entry<K, V> fence) {expectedModCount = m.modCount;lastReturned = null;next = first;fenceKey = (fence == null ? null : fence.key);}public boolean hasNext() {return (next != null) && (next.key != fenceKey);}final AVLTreeMap.Entry<K, V> nextEntry() {AVLTreeMap.Entry<K, V> e = next;if (next == null)throw new NoSuchElementException();if (expectedModCount != m.modCount)throw new ConcurrentModificationException();next = successor(e);lastReturned = e;return e;}final AVLTreeMap.Entry<K, V> prevEntry() {AVLTreeMap.Entry<K, V> e = next;if (next == null)throw new NoSuchElementException();if (expectedModCount != m.modCount)throw new ConcurrentModificationException();next = predecessor(e);lastReturned = e;return e;}final void removeAscending() {if (lastReturned == null)throw new IllegalStateException();if (expectedModCount != m.modCount)throw new ConcurrentModificationException();if (lastReturned.left != null && lastReturned.right != null)next = lastReturned;m.deleteEntry(lastReturned);lastReturned = null;expectedModCount = m.modCount;}final void removeDescending() {if (lastReturned == null)throw new IllegalStateException();if (expectedModCount != m.modCount)throw new ConcurrentModificationException();m.deleteEntry(lastReturned);lastReturned = null;expectedModCount = m.modCount;}}final class SubMapEntryIterator extends SubMapIterator<Map.Entry<K, V>> { SubMapEntryIterator(AVLTreeMap.Entry<K, V> first, AVLTreeMap.Entry<K, V> fence) {super(first, fence);}public Map.Entry<K, V> next() {return nextEntry();}public void remove() {removeAscending();}}final class SubMapKeyIterator extends SubMapIterator<K> {SubMapKeyIterator(AVLTreeMap.Entry<K, V> first, AVLTreeMap.Entry<K, V> fence) {super(first, fence);}public K next() {return nextEntry().key;}。
