中考数学压轴题二.doc

合集下载

第十八章全国通用版中考数学：《平行四边形》与坐标系结合压轴题(二)—解析版

第十八章专题：《平行四边形》与坐标系结合压轴题(二)1.如图，在平面直角坐标系中，AB //OC, A (0, 12), B (a, c) , C (b, 0),并且a, b满足b= 府市 /口' + 16. 一动点P从点A出发，在线段AB上以每秒2个单位长度的速度向点 B 运动；动点Q 从点。

出发在线段OC上以每秒1个单位长度的速度向点C运动，点P、Q分别从点A、O同时出发，当点P 运动到点B时，点Q随之停止运动.设运动时间为t (秒)(1)求B、C两点的坐标；(2)当t为何值时，四边形PQCB是平行四边形？并求出此时P、Q两点的坐标；(3)当t为何值时，APQC是以PQ为腰的等腰三角形？并求出P、Q两点的坐标.(1) •, b= ^a-21 J^T^+16,••.a=21, b=16,故B (21, 12) C (16, 0)； (2)由题意得：AP=2t, QO=t,贝U： PB=21-2t , QC=16-t,•••当PB=QC时，四边形PQCB是平行四边形,.•.21-2t=16-t,解得：t=5,,P (10, 12) Q (5, 0);(3)当PQ=CQ 时，过Q 作QN^AB,由题意得：122+t2=(16-t) 2, 解得：t=3.5,故P (7, 12), Q (3.5, 0),当PQ=PC时，过P作PM ±x轴,由题意得：QM=t , CM=16-2t ,则t=16-2t,解得：t=16, 2t=32, 3 3故P( 32,12), Q(16,3 30).2.如图1,在平面直角坐标系中， AB ，y 轴于点A, BC ，x 轴于点B,点D 为线段BC 的中点，若AB=a , CD=b ,且J 2 a 8 v 5 +/4我 a +2屈=b .连接AD ,在线段OC 上取一点E,使/ EAD= / DAB .(1)贝U a=, b=(2)求证：AE=OE+CD ;【解答】(1) a =4 v15 , b =2 后,(2)由(1)可知 AB=4 75, CD=BD=2 V 5 , • . AB=CB ,,.AB ±y 轴于点 A, BC±x 轴于点 B,，乙 BAO= / B= / AOC=90° ,••・四边形ABCO 是矩形，••・AB=CB , ••・四边形ABCO 是正方形，延长 CO 至u M ,使得 OM=BD ,贝u ^ABD AOM , ，/4=/M, Z1 = Z2=Z3,. OA//BC, . ・/4=/2+/5=/5+/3=/EAM , . . / M= / EAM , • . AE=EM=OE+OM=OE+BD ••• BD=CD , .1. AE=OE+CD .(3)如图 2 中，设 AE=EM=x .在 RtAAOE 中，AO 2+OE 2=AE 2, - x 2= (4<5 ) 2+ (x-2 J 5 ) 2, . . x=5石, OE=3 而,•.D (4V 5, 2 45), E (3V5 , 0), •. F (0, -6V5 )风0)3.如图，在平面直角坐标系中，有一矩形ABCD，其中A(0, 0), B (m, 0) , D (0, n), m是最接近质的整数，n是16的算术平方根，若将4ABC沿矩形又•角线AC所在直线翻折，点B落在点E处，AE与边CD相交于点M .(1)求AC的长；(2)求4AMC的面积；(3)求点E的坐标.【解答】(1)•' m是最接近#5的整数,• ' m=8,.「n 是16 的算术平方根，，n=4,，B (8, 0), D (0, 4),.••点C 矩形ABCD 的一个顶点，..C (8, 4),，AB=8, BC=4 ,AC=4 J5 ,(2)由折叠有，CE=AD=BC=4 , AE=AB=8 ,设DM=x 则CM=8-x ,・. /ADM= / CEM , /AMD=/CME, /.A ADM ^ACEM , • .AM=CM=8-x , ME=MD , 在RtAADM 中，AD=4 , DM=x , AM=8-x ,根据勾股定理有：AD2+DM 2=AM 2,即：16+x2= (8-x) 2, •1- x=3 , DM=3 , CM=5 , S AAMC = —Ch/|X AD=)>^M=10,2 2(3)过点E作EFXCD,如图，由(2)有，CM=5 , CE=4, ME=DM=3在Rt^CEM 中，由射影定理得，CE2=CFXCM , 16=CFX5,，CF=3.2,••・Ma CE=CMK EF (直角三角形的面积的两种计算) ，，EF=2.4,• . DF=CD -CF=4.8 , BC+EF=6.4 , . . E (4.8, 6.4)4 .已知正方形OABC 在平面直角坐标系中，点 A, C 分别在x 轴，y 轴的正半轴上，等腰直角三角形OEF 的直角顶点O 在原点，E, F 分别在OA, OC 上，且OA=4 , OE=2 .将AOEF 绕点O 逆时针旋转，得△OE I F I ,点E, F 旋转后的对应点为Ei, Fi.(I )①如图①，求EiFi 的长；②如图②，连接CFi, AEi,求证△OAEi^^OCFi；「(II)将AOEF 绕点O 逆时针旋转一周，当 OEi//CFi 时，求点Ei 的坐标(直接写出结果即可)姝姝CB C 石【解答】(I )①解：二.等腰直角三角形 OEF 的直角顶点O 在原点，OE=2, / EOF=90 , OF=OE=2 ,「. EF=2 血，・ ••将AOEF 绕点 O 逆时针旋转，得△OE i F i, ••.E i F i =EF=2 J 2 ； ②证明：四边形OABC 为正方形，OC=OA .・ •・将AOEF 绕点 O 逆时针旋转，得 △OE i F i,AOE i =/COF i, • △OEF 是等腰直角三角形，・•.△OEiFi 是等腰直角三角形， ••OE i =OF i.在 AOAE i 和 ^OCF i 中，OA=OC, /AOEi=/COF i, OEi=OFi% E・•.△OAE 卢^OCF i (SAS)；(n)解：••• OEXOF,卜过点F与OE平行的直线有且只有一条，并与OF垂直，当三角板OEF绕。

2021年中考数学真题分类汇编--函数：函数与几何(压轴题2)(学生版)

中考真题分类汇编（函数）----函数与几何（2）1.（2021•四川省眉山市）如图，直线y＝x+6与x轴交于点A，与y轴交于点B．直线MN∥AB，且与△AOB的外接圆⊙P相切，与双曲线y＝﹣在第二象限内的图象交于C、D两点．（1）求点A，B的坐标和⊙P的半径；（2）求直线MN所对应的函数表达式；（3）求△BCN的面积．2.（2021•四川省南充市）如图，已知抛物线y＝ax2+bx+4（a≠0）与x轴交于点A（1，0）和B，与y轴交于点C，对称轴为直线x＝．（1）求抛物线的解析式；（2）如图1，若点P是线段BC上的一个动点（不与点B，C重合），过点P作y轴的平行线交抛物线于点Q，连接OQ，当线段PQ长度最大时，判断四边形OCPQ的形状并说明理由；（3）如图2，在（2）的条件下，D是OC的中点，过点Q的直线与抛物线交于点E，且∠DQE＝2∠ODQ．在y轴上是否存在点F，得△BEF为等腰三角形？若存在，求点F的坐标；若不存在，请说明理由．3.（2021•遂宁市）如图，已知二次函数的图象与x轴交于A和B（－3，0）两点，与y轴x=-，直线y＝－2x＋m经过点A，且与y轴交于点D，交于C（0，－3），对称轴为直线1与抛物线交于点E，与对称轴交于点F．（1）求抛物线的解析式和m的值；（2）在y轴上是否存在点P，使得以D、E、P为顶点的三角形与△AOD相似，若存在，求出点P的坐标；若不存在，试说明理由；（3）直线y＝1上有M、N两点（M在N的左侧），且MN＝2，若将线段MN在直线y＝1上平移，当它移动到某一位置时，四边形MEFN的周长会达到最小，请求出周长的最小值（结果保留根号）．4. (2021•四川省自贡市) 如图，抛物线(1)()y x x a =+-（其中1a >）与x 轴交于A 、B 两点，交y 轴于点C ．（1）直接写出OCA ∠的度数和线段AB 的长（用a 表示）；（2）若点D 为ABC 的外心，且BCD △与ACO △104，求此抛物线的解析式；（3）在（2）的前提下，试探究抛物线(1)()y x x a =+-上是否存在一点P ，使得CAP DBA ∠=∠？若存在，求出点P 的坐标；若不存在，请说明理由．5. （2021•天津市）已知抛物线22y ax ax c =-+（a ，c 为常数，0a ≠）经过点()0,1C -，顶点为D ．（Ⅰ）当1a =时，求该抛物线的顶点坐标；（Ⅱ）当0a >时，点()0,1E a +，若22DE DC =，求该抛物线的解析式；（Ⅲ）当1a <-时，点()0,1F a -，过点C 作直线l 平行于x 轴，(),0M m 是x 轴上的动点，()3,1N m +-是直线l 上的动点．当a 为何值时，FM DN +的最小值为10，并求此时点M ，N 的坐标．6. 2021•湖北省恩施州）如图，在平面直角坐标系中，四边形ABCD 为正方形，点A ，B 在x 轴上，抛物线y ＝x 2+bx +c 经过点B ，D （﹣4，5）两点，且与直线DC 交于另一点E ．（1）求抛物线的解析式；（2）F 为抛物线对称轴上一点，Q 为平面直角坐标系中的一点，是否存在以点Q ，F ，E ，B为顶点的四边形是以BE为边的菱形．若存在，请求出点F的坐标；若不存在，请说明理由；（3）P为y轴上一点，过点P作抛物线对称轴的垂线，垂足为M，连接ME，BP，探究EM+MP+PB是否存在最小值．若存在，请求出这个最小值及点M的坐标；若不存在，请说明理由．7.（2021•浙江省金华市）在平面直角坐标系中，点A的坐标为（﹣，0），点B在直线l：y＝x上，过点B作AB的垂线，过原点O作直线l的垂线，两垂线相交于点C．（1）如图，点B，C分别在第三、二象限内，BC与AO相交于点D．①若BA＝BO，求证：CD＝CO．②若∠CBO＝45°，求四边形ABOC的面积．（2）是否存在点B，使得以A，B，C为顶点的三角形与△BCO相似？若存在，求OB 的长；若不存在，请说明理由．8.（2021•湖北省荆门市）如图，抛物线y＝ax2+bx+c交x轴于A（﹣1，0），B（3，0）两点，交y轴于点C（0，﹣3），点Q为线段BC上的动点．（1）求抛物线的解析式；（2）求|QO|+|QA|的最小值；（3）过点Q作PQ∥AC交抛物线的第四象限部分于点P，连接P A，PB，记△P AQ与△PBQ面积分别为S1，S2，设S＝S1+S2，求点P坐标，使得S最大，并求此最大值．9.（2021•江苏省盐城市）学习了图形的旋转之后，小明知道，将点P绕着某定点A顺时针旋转一定的角度α，能得到一个新的点P′，经过进一步探究，小明发现，当上述点P在某函数图象上运动时，点P ′也随之运动，并且点P ′的运动轨迹能形成一个新的图形．试根据下列各题中所给的定点A 的坐标、角度α的大小来解决相关问题．【初步感知】如图1，设A （1，1），α＝90°，点P 是一次函数y ＝kx +b 图象上的动点，已知该一次函数的图象经过点P 1（﹣1，1）．（1）点P 1旋转后，得到的点P 1′的坐标为（1，3）；（2）若点P ′的运动轨迹经过点P 2′（2，1），求原一次函数的表达式．【深入感悟】如图2，设A （0，0），α＝45°，点P 是反比例函数y ＝﹣（x ＜0）的图象上的动点，过点P ′作二、四象限角平分线的垂线，垂足为M ，求△OMP ′的面积．【灵活运用】如图3，设A （1，﹣），α＝60°，点P 是二次函数y ＝x 2+2x +7图象上的动点，已知点B （2，0）、C （3，0），试探究△BCP ′的面积是否有最小值？若有，求出该最小值；若没有，请说明理由．10. （2021•重庆市A ）如图，在平面直角坐标系中，抛物线2y x bx c =++经过A （0，﹣1），B （4，1）．直线AB 交x 轴于点C ，P 是直线AB 下方抛物线上的一个动点．过点P 作PD ⊥AB ，垂足为D ，PE ∥x 轴，交AB 于点E ．（1）求抛物线的函数表达式；（2）当△PDE 的周长取得最大值时，求点P 的坐标和△PDE 周长的最大值；（3）把抛物线2y x bx c =++平移，使得新抛物线的顶点为（2）中求得的点P ．M 是新抛物线上一点，N 是新抛物线对称轴上一点，直接写出所有使得以点A ，B ，M ，N 为顶点的四边形是平行四边形的点M 的坐标，并把求其中一个点M 的坐标的过程写出来．11.（2021•重庆市B ）如图，在平面直角坐标系中，抛物线y ＝ax 2+bx ﹣4（a ≠0）与x 轴交于点A （﹣1，0），B （4，0），与y 轴交于点C ．（1）求该抛物线的解析式；（2）直线l 为该抛物线的对称轴，点D 与点C 关于直线l 对称，点P 为直线AD 下方抛物线上一动点，连接P A ，PD ，求△P AD 面积的最大值．（3）在（2）的条件下，将抛物线y ＝ax 2+bx ﹣4（a ≠0）沿射线AD 平移4个单位，得到新的抛物线y 1，点E 为点P 的对应点，点F 为y 1的对称轴上任意一点，在y 1上确定一点G ，使得以点D ，E ，F ，G 为顶点的四边形是平行四边形，写出所有符合条件的点G 的坐标，并任选其中一个点的坐标，写出求解过程．12. （2021•湖北省十堰市）已知抛物线25y ax bx =+-与x 轴交于点()1,0A -和()5,0B -，与y 轴交于点C ，顶点为P ，点N 在抛物线对称轴上且位于x 轴下方，连AN 交抛物线于M ，连AC 、CM ．（1）求抛物线的解析式；（2）如图1，当tan 2ACM ∠=时，求M 点的横坐标；（3）如图2，过点P 作x 轴的平行线l ，过M 作MD l ⊥于D ，若3MD MN =，求N 点的坐标．13. （2021•湖南省张家界市）如图，已知二次函数c bx ax y ++=2的图象经过点)3,2(-C ，且与x 轴交于原点及点)0,8(B .(1)求二次函数的表达式；(2)求顶点A 的坐标及直线AB 的表达式；（3）判断ABO 的形状，试说明理由；（4）若点P 为⊙O 上的动点，且⊙O 的半径为 22，一动点E 从点A 出发，以每秒2个单位长度的速度沿线段AP 匀速运动到点P ，再以每秒1个单位长度的速度沿线段PB 匀速运动到点B 后停止运动，求点E 的运动时间t 的最小值.14. （2021•海南省）已知抛物线y ＝ax 2+x +c 与x 轴交于A 、B 两点，与y 轴交于C 点，且点A 的坐标为（﹣1，0）、点C 的坐标为（0，3）．（1）求该抛物线的函数表达式；（2）如图1，若该抛物线的顶点为P ，求△PBC 的面积；（3）如图2，有两动点D 、E 在△COB 的边上运动，速度均为每秒1个单位长度，它们分别从点C 和点B 同时出发，点D 沿折线COB 按C →O →B 方向向终点B 运动，点E 沿线段BC 按B →C 方向向终点C 运动，当其中一个点到达终点时，另一个点也随之停止运动．设运动时间为t 秒，请解答下列问题： ①当t 为何值时，△BDE 的面积等于；②在点D 、E 运动过程中，该抛物线上存在点F ，使得依次连接AD 、DF 、FE 、EA 得到的四边形ADFE 是平行四边形，请直接写出所有符合条件的点F 的坐标．_y _x _ A_ B _ O _ C _ P15. （2021•广西玉林市）已知抛物线：234y ax ax a =--（0a >）与x 轴交点为A ，B（A 在B 的左侧），顶点为D ．（1）求点A ，B 的坐标及抛物线的对称轴；（2）若直线32y x =-与抛物线交于点M ，N ，且M ，N 关于原点对称，求抛物线的解析式；（3）如图，将（2）中抛物线向上平移，使得新的抛物线的顶点D 在直线7:8l y =上，设直线l 与y 轴的交点为O '，原抛物线上的点P 平移后的对应点为点Q ，若O P O Q ''=，求点P ，Q 的坐标．16. （2021•广西贺州市）如图，抛物线2y x bx c =++与x 轴交于A 、B 两点，且()1,0A -，对称轴为直线2x =．（1）求该抛物线的函数达式；（2）直线l 过点A 且在第一象限与抛物线交于点C ．当45CAB ∠=︒时，求点C 的坐标；（3）点D 在抛物线上与点C 关于对称轴对称，点P 是抛物线上一动点，令(,)P P P x y ，当1P x a ≤≤，15a ≤≤时，求PCD 面积的最大值（可含a 表示）．17. 2021•山东省济宁市）如图，直线y ＝﹣x +分别交x 轴、y 轴于点A ，B ，过点A 的抛物线y ＝﹣x 2+bx +c 与x 轴的另一交点为C ，与y 轴交于点D （0，3），抛物线的对称轴l 交AD 于点E ，连接OE 交AB 于点F ．（1）求抛物线的解析式；（2）求证：OE ⊥AB ；（3）P 为抛物线上的一动点，直线PO 交AD 于点M ，是否存在这样的点P ，使以A ，O ，M 为顶点的三角形与△ACD 相似？若存在，求点P 的横坐标；若不存在，请说明理由．18 . (2021•内蒙古包头市) 如图，在平面直角坐标系中，抛物线24y x x =-+经过坐标原点，与x 轴正半轴交于点A ，点(,)M m n 是抛物线上一动点．（1）如图1，当0m >，0n >，且3n m =时，①求点M 的坐标： ②若点15,4B y ⎛⎫ ⎪⎝⎭在该抛物线上，连接OM ，BM ，C 是线段BM 上一动点（点C 与点M ，B 不重合），过点C 作//CD MO ，交x 轴于点D ，线段OD 与MC 是否相等？请说明理由；（2）如图2，该抛物线的对称轴交x 轴于点K ，点7,3E x ⎛⎫ ⎪⎝⎭在对称轴上，当2m >，0n >，且直线EM 交x 轴的负半轴于点F 时，过点A 作x 轴的垂线，交直线EM 于点N ，G 为y 轴上一点，点G 的坐标为180,5⎛⎫ ⎪⎝⎭，连接GF ．若2EF NF MF +=，求证：射线FE 平分AFG ∠．19. （2021•齐齐哈尔市）综合与探究如图，在平面直角坐标系中，抛物线2()20y ax x c a =++≠与x 轴交于点A 、B ，与y 轴交于点C ，连接BC ，1OA =，对称轴为2x =，点D 为此抛物线的顶点．（1）求抛物线的解析式；（2）抛物线上C，D两点之间的距离是__________；（3）点E是第一象限内抛物线上的动点，连接BE和CE．求BCE面积的最大值；（4）点P在抛物线对称轴上，平面内存在点Q，使以点B、C、P、Q为顶点的四边形为矩形，请直接写出点Q的坐标．20.（2021•内蒙古通辽市）如图，抛物线y＝ax2+bx+3交x轴于A（3，0），B（﹣1，0）两点，交y轴于点C，动点P在抛物线的对称轴上．（1）求抛物线的解析式；（2）当以P，B，C为顶点的三角形周长最小时，求点P的坐标及△PBC的周长；（3）若点Q是平面直角坐标系内的任意一点，是否存在点Q，使得以A，C，P，Q为顶点的四边形是菱形？若存在，请直接写出所有符合条件的点Q的坐标；若不存在，请说明理由．。

2022年深圳中考数学各区压轴题2

2022年深圳中考数学各区压轴题2一．选择题（共15小题）1．（2019•鞍山）如图，正方形ABCD和正方形CGFE的顶点C，D，E在同一条直线上，顶点B，C，G在同一条直线上．O是EG的中点，∠EGC的平分线GH过点D，交BE 于点H，连接FH交EG于点M，连接OH．以下四个结论：①GH⊥BE；②△EHM∽△FHG；③＝﹣1；④＝2﹣，其中正确的结论是（）A．①②③B．①②④C．①③④D．②③④2．（2020秋•化州市期末）如图，已知E，F分别为正方形ABCD的边AB，BC的中点，AF 与DE交于点M，O为BD的中点，则下列结论：①∠AME＝90°，②∠BAF＝∠EDB，③AM＝MF，④ME+MF＝MB．其中正确结论的有（）A．4个B．3个C．2个D．1个3．（2021秋•宝安区校级期中）如图，在Rt△ABC中，∠ACB＝90°，AC＝3，∠BAC＝30°，把Rt△ABC沿AB翻折得到Rt△ABD，过点B作BE⊥BC，交AD于点E，点F是线段BE上一点，且∠ADF＝45°．则下列结论：①AE＝BE；②△BED∽△ABC；③BD2＝AD •DE；④AF＝，其中正确的有（）A．①④B．②③④C．①②③D．①②③④4．（2021秋•宝安区校级期中）如图，在▱ABCD中，点E在线段AB上，点F、G分别为对角线AC与DE、DB的交点．若AB：AE＝3：2，则四边形BGFE与▱ABCD的面积之比为（）A．7：60B．8：70C．5：43D．3：26 5．（2021秋•深圳期中）如图，在正方形ABCD中，F为CD上一点，AF交对角线BD于点E，过点E作EG⊥AF，交BC于点G，连结AG，交BD于点H．现给出下列结论：①AE＝EG；②BG+DF＝FG；③AH2＝HE•HD；④若F为CD中点，则CG＝2BG．其中正确的有（）个．A．1B．2C．3D．46．（2021秋•深圳期中）如图，▱ABCD中，点F为AD上一点，AF＝2DF，连结BF，交AC于点E，延长线交CD的延长线于点G，则的值为（）A．B．C．3D．2 7．（2020•遂宁）如图，在正方形ABCD中，点E是边BC的中点，连接AE、DE，分别交BD、AC于点P、Q，过点P作PF⊥AE交CB的延长线于F，下列结论：①∠AED+∠EAC+∠EDB＝90°，②AP＝FP，③AE＝AO，④若四边形OPEQ的面积为4，则该正方形ABCD的面积为36，⑤CE•EF＝EQ•DE．其中正确的结论有（）A．5个B．4个C．3个D．2个8．（2021•锡山区模拟）如图，正方形ABCD的边长为4，点E在边AB上，BE＝1，∠DAM ＝45°，点F在射线AM上，且AF＝，过点F作AD的平行线交BA的延长线于点H，CF与AD相交于点G，连接EC、EG、EF．下列结论：①CG＝；②△AEG的周长为8；③△EGF的面积为．其中正确的是（）A．①②③B．①③C．①②D．②③9．（2020秋•宝安区期末）如图，边长为4的正方形ABCD中，对角线AC，BD交于点O，E在BD上，连接CE，作EF⊥CE交AB于点F，连接CF交BD于点H，则下列结论：①EF＝EC；②CF2＝CG•CA；③BE•DH＝16；④若BF＝1，则DE＝，正确的是（）A．①②④B．②③④C．①②③D．①②③④10．（2021•龙岗区校级一模）如图，抛物线y＝x2﹣2x+m交x轴于点A（a，0），B（b，0），交y轴于点C，抛物线的顶点为D，下列四个结论：①无论m取何值，CD＝恒成立；②当m＝0时，△ABD是等腰直角三角形；③若a＝﹣2，则b＝6；④P（x1，y1），Q（x2，y2）是抛物线上的两点，若x1＜1＜x2，且x1+x2＞2，则y1＜y2．其中正确的有（）A．①②③④B．①②④C．①②D．②③④11．（2021•龙岗区校级一模）如图，正方形ABCD中，点E为对角线AC上一点，EF⊥DE 交边AB于F，连接DF交线段AC于点H，延长DE交边BC于点Q，连接QF．下列结论：①DE＝EF；②若AB＝6，CQ＝3，则AF＝2；③∠AFD＝∠DFQ；④若AH＝2，CE＝4，则AB＝3+；其中正确的有（）个．A．1个B．2个C．3个D．4个12．（2021秋•福田区校级月考）如图所示的是抛物线y＝ax2+bx+c（a≠0）的一部分，已知抛物线的对称轴为直线x＝2，与x轴的一个交点是（﹣1，0），有以下结论：①b2＞4ac；②4a﹣2b+c＜0；③c＝﹣6a；④若顶点的纵坐标为﹣1，则关于x的方程ax2+bx+c+1＝0有两个相等的实数根．其中正确的有（）A．1个B．2个C．3个D．4个13．（2021秋•仓山区校级期末）如图，正方形ABCD中，AB＝6，点E在边CD上，且CE ＝2DE．将△ADE沿AE对折至△AFE，延长EF交BC于点G，连结AG、BF、CF．下列结论：①△ABG≌△AFG；②FG＝CG；③AG∥CF；④S△BFC＝．其中正确结论的个数是（）A．1个B．2个C．3个D．4个14．（2021秋•罗湖区校级月考）如图，正方形ABCD中，AB＝1，连接AC，∠ACD的平分线交AD于点E，在AB上截取AF＝DE，连接DF，分别交CE，AC于点G，H，点P是线段GC上的动点，PQ⊥AC于点Q，连接PH，以下结论：①CE⊥DF；②DE+DC＝AC；③EA＝AH；④PH+PQ的最小值是，其中正确的结论有（）个．A．1B．2C．3D．415．（2021秋•罗湖区校级月考）如图，正方形ABCD中，AB＝6，点E在边CD上，且CE：ED＝2：1，将△ADE沿AE对折至△AFE，延长EF交边BC于点G，连接AG、CF，下列结论：①∠GAE＝45°；②GB＝GC＝GF；③S△GCF＝3.2；④AG∥CF；⑤图中与∠AGB 相等的角有5个，其中正确的结论的个数为（）A．2个B．3个C．4个D．5个二．填空题（共20小题）16．（2018春•江北区期末）如图，四边形ABCD是矩形，边AB长为6，∠ABD＝60°，点E在边AB上，BE＝4，过点E作EF∥BC，分别交BD，CD于G，F两点，若M，N分别是DG，CE的中点，则MN的长为．17．（2021秋•深圳期中）如图所示，已知AB∥EF∥CD，AC，BD相交于点E，AB＝3cm，CD＝6cm，则EF＝．18．（2021秋•罗湖区期中）如图，在正方形ABCD中，以AB为腰向正方形内部作等腰△ABE（AB＝AE），点G在CD上，且CG＝3DG，连接BG并延长，与AE交于点F，与AD延长线交于点H，连接DE交BH于点K，连接CK．若AE2＝BF•BH，FG＝，则S△BCK＝．19．（2021秋•罗湖区期中）如图，矩形ABCD的顶点D在反比例函数y＝的图象上，且点D在第一象限，顶点B，C在x轴上，对角线AC的延长线交y轴于点E，若△BCE的面积是12，则k＝．20．（2020秋•覃塘区期末）如图，在等腰△ABC中，AB＝AC，点P在BA的延长线上，P A ＝AB，点D在BC边上，PD＝PC，则的值是．21．（2021秋•宝安区校级期中）如图，在△ABC中，AC＞AB，AD是角平分线，AE是中线，BF⊥AD于点G，交AE于点F，交AC于点M，EG的延长线交AB于点H，若∠BAC＝60°，则＝．22．（2021秋•宝安区校级期中）如图，矩形OABC的两边OA、OC分别在x轴和y轴上，以AC为边作平行四边形ACDE，E点在CB的延长线上，反比例函数y＝（x＞0）过B 点且与CD交于F点，CF＝3DF，S△ABF＝6，则k的值为．23．（2021秋•深圳期中）如图，已知AB∥CD，AB＝CD，∠A＝∠D，E是AB边的中点，F为AD边上一点，∠DFC＝2∠BCE．若CE＝4，CF＝5，则AF的值为．24．（2021秋•罗湖区校级期中）如图，矩形ABCD中，AB＝8，点E是AD上的一点，若AE＝4，BE的垂直平分线交BC的延长线于点F，连结EF交CD于点G，若G是CD的中点，则CM的长是．25．（2021秋•龙岗区校级期中）如图，点A（0，4），点B（3，0），点P为线段AB上一个动点，作PM⊥y轴于点M，作PN⊥x轴于点N，连接MN，当MN取最小值时，则PN 为．26．（2021秋•龙岗区校级期中）如图，在四边形ABCD中，AE⊥BC，垂足为E，∠BAE＝∠ADC，BE＝CE＝2，CD＝5，AD＝kAB（k为常数），则BD的长为．（用含k 的式子表示）27．（2021•鹿城区校级三模）如图，点A在反比例函数y＝的图象上，点B在反比例函数y＝的图象上，且AB⊥x轴于点C，点D在y轴上，则△ABD的面积为．28．（2020•饶平县校级模拟）如图，四边形OABC是平行四边形，其面积为8，点A在反比例函数y＝的图象上，过点A作AD∥x轴交BC于点D，过点D的反比例函数图象关系式为y＝，则k的值是．29．（2020•饶平县校级模拟）如图，在矩形ABCD中，AC＝5，AE平分∠DAC交CD于E，CF平分∠ACD交AE于点F，且EF：AF＝1：2，则CF＝．30．（2020•成都）如图，六边形ABCDEF是正六边形，曲线F A1B1C1D1E1F1…叫做“正六边形的渐开线”，，，，，，，…的圆心依次按A，B，C，D，E，F循环，且每段弧所对的圆心角均为正六边形的一个外角．当AB＝1时，曲线F A1B1C1D1E1F1的长度是．31．（2021春•福田区校级月考）平面直角坐标系中，点A（0，5），点B（﹣5，3），点C 为x轴负半轴上一点，且∠BAC＝45°，则点C的横坐标为．32．（2021秋•福田区校级月考）如图，在平面直角坐标系中，A是反比例函数y＝（k＞0，x＞0）图象上一点，B是y轴正半轴上一点，以OA、AB为邻边作▱ABCO．若点C及BC 中点D都在反比例函数y＝﹣（x＜0）图象上，则k的值为．33．（2019秋•长兴县期末）如图，在平面直角坐标系中抛物线y＝x2﹣3x+2与x轴交于A、B两点，与y轴交于点C，点D是对称轴右侧抛物线上一点，且tan∠DCB＝3，则点D 的坐标为．34．（2021秋•罗湖区校级月考）在正方形ABCD中，AD＝4，点E是对角线AC上一点，连接DE，过点E作EF⊥ED，交AB于点F，连接DF，交AC于点G，将△EFG沿EF 所在直线翻折，得到△EFM，连接DM，若点F是线段AB的中点，则△DEM的周长是．35．（2021•江州区模拟）如图，在Rt△ABC中，∠ACB＝90°，AC＝6，BC＝8，AD平分∠CAB交BC于D点，E，F分别是AD，AC上的动点，则CE+EF的最小值为三．解答题（共25小题）36．（2021秋•深圳期中）如图1，矩形OABC在平面直角坐标系中的位置如图所示，点A，C分别在x轴，y轴上，点B的坐标为（8，4），点P，Q同时以相同的速度分别从点O，B出发，在边OA，BC上运动，连接OQ，BP，当点P到达A点时，运动停止．（1）求证：在运动过程中，四边形OPBQ是平行四边形；（2）如图2，在运动过程中，是否存在四边形OPBQ是菱形的情况？若存在，求出此时直线PQ的解析式；若不存在，请说明理由；（3）如图3，在（2）的情况下，直线PQ上是否存在一点D，使得△PBD是直角三角形？如果存在，请直接写出点D的坐标；如果不存在，请说明理由．37．（2008•新华区校级一模）把两块全等的直角三角形ABC和DEF叠放在一起，使三角板DEF的锐角顶点D与三角板ABC的斜边中点O重合，其中∠ABC＝∠DEF＝90°，∠C ＝∠F＝45°，AB＝DE＝4，把三角板ABC固定不动，让三角板DEF绕点O旋转，设射线DE与射线AB相交于点P，射线DF与线段BC相交于点Q．（1）如图，当射线DF经过点B，即点Q与点B重合时，易证△APD∽△CDQ．此时，AP•CQ＝．（2）将三角板DEF由图所示的位置绕点O沿逆时针方向旋转，设旋转角为α．其中0°＜α＜90°，问AP•CQ的值是否改变？说明你的理由．（3）在（2）的条件下，设2＜x＜4，两块三角板重叠面积为y，求y与x的函数关系式．（图2，图3供解题用）38．（2021秋•罗湖区期中）（问题发现）数学小组成员小明做作业时遇到以下问题：（1）若四边形ABCD是菱形，∠ABC＝60°，点P是射线BD上一动点，以AP为边向右侧作等边△APE，如图1，当点E在菱形ABCD内部或边上时，连接CE、CA，则BP 与CE有怎样的数量关系？请直接写出你的猜想．（类比探究）数学小组对该问题进行进一步探究：（2）若四边形ABCD是正方形，点P是射线BD上一动点，以AP为直角边在AP边的右侧作等腰Rt△APE，其中∠APE＝90°，AP＝PE．①如图2，当点P在对角线BD上时，小组发现点E恰好在射线CD上，求BP与CE之间的数量关系（过程只用说明点E在线段CD上的情况即可）；②如图3，当P是对角线BD的延长线上一动点时，小组发现点E恰好在射线CD上，连接BE，若BE＝6，AB＝2，求△BPE的面积．39．（2021秋•南山区校级期中）（1）如图1，Rt△ABC与与Rt△ADE，∠ADE＝∠ABC＝90°，，连接BD，CE．求证：．（2）如图2，四边形ABCD，∠BAD＝∠BCD＝90°，且，连接BD，AC，请问BC，AC，CD之间有何数量关系？小明在完成本题中，如图3，使用了“旋转放缩”的技巧，即将△ABC与绕点A逆时针旋转90°，并放大2倍，点B对应点为点D，点C 对应点为点E，连接DE，请你根据以上思路求出BC，AC，CD之间的关系．（3）拓展：如图4，矩形ABCD，E为线段AD上一点，以CE为边，在其右侧作矩形CEFG，且，AB＝5，连接BE，BF．直接写出BE+BF的最小值．40．（2021•宁波）【证明体验】（1）如图1，AD为△ABC的角平分线，∠ADC＝60°，点E在AB上，AE＝AC．求证：DE平分∠ADB．【思考探究】（2）如图2，在（1）的条件下，F为AB上一点，连结FC交AD于点G．若FB＝FC，DG＝2，CD＝3，求BD的长．【拓展延伸】（3）如图3，在四边形ABCD中，对角线AC平分∠BAD，∠BCA＝2∠DCA，点E在AC上，∠EDC＝∠ABC．若BC＝5，CD＝2，AD＝2AE，求AC的长．41．（2021秋•宝安区校级期中）如图1，在平面直角坐标系xOy中，直线l2：y＝﹣与x轴交于点B，与直线l1交于点C，C点到x轴的距离CD为2，直线l1交x轴于点A，且∠BAC＝60°．（1）求直线l1的函数表达式；（2）如图2，y轴上的两个动点E、F（E点在F点上方）满足线段EF的长为，连接CE、AF，当线段CE+EF+AF有最小值时，求出此时点F的坐标，以及CE+EF+AF的最小值；（3）如图3，将△ACB绕点B逆时针方向旋转60°，得到△BGH，使点A与点H重合，点C与点G重合，将△BGH沿直线BC平移，记平移中的△BGH为△B'G'H'，在平移过程中，设直线B'H'与x轴交于点M，是否存在这样的点M，使得△B'MG'为等腰三角形？若存在，请直接写出此时点M的坐标；若不存在，说明理由．42．（2021秋•深圳期中）在矩形ABCD中，OA＝3，AB＝6．分别以OA，OC边所在的直线为x轴，y轴建立如图所示的平面直角坐标系．（1）如图1，将△OAC沿对角线AC翻折，交AB于点P，求点P的坐标；（2）如图2，已知H是AB上一点，且S△HBC＝，OG⊥CH于点P，求四边形OAHP 的面积；（3）如图3，点D（0，5），点E是OB上一点，且OE＝2BE，M是直线DE上的一个动点，在x轴上方的平面内是否存在另一个点N，使以O、D、M、N为顶点的四边形是菱形？若存在，直接写出点N的坐标；若不存在，请说明理由．43．（2021秋•福田区校级期中）如图，在平面直角坐标系中，矩形ABCD的对角线AC的中点与坐标原点重合，点E是x轴上一点，连接AE、BE，若AD平分∠OAE，反比例函数y＝（k＜0，x＜0）的图象经过AE上的点A、F，且AF＝EF，△ABE的面积为18．（1）连接BD，证明AF∥BD．（2）连接OF，求△AOF的面积．（3）求k的值．44．（2021秋•福田区校级期中）在平面直角坐标系中，已知点A（0，3），点B在线段AO 上，且AB＝2BO，若点P在x轴的正半轴上，连接BP，过点P作PQ⊥PB．（1）如图1，点E是射线PQ上一点，过点E作EC⊥x轴，垂足为点C，求证：△BOP ∽△PCE；（2）在（1）的条件下，如图2，若点C坐标为（4，0）．过点A作DA⊥y轴，且和CE 的延长线交于点D，若点C关于直线PQ的对称点C′正好落在线段AD上．连接PC′，求点P的坐标．（3）如图3，若∠BPO＝60°，点E在直线PQ上，EC⊥x轴，垂足为点C，若以点E，P，C为顶点的三角形和△BPE相似，请直接写出点E的坐标．45．（2021秋•罗湖区校级期中）如图，点P是菱形ABCD的对角线BD上一点，连结CP 并延长，交AD于E，交BA的延长线于点F．问：如图1：（1）图中△APD≌；△APE∽；（2）猜想：线段PC、PE、PF之间存在什么数量关系（用等式表示）？说明理由；（3）如图2，连接AC交BD于O，连接OE，若CE⊥BC，且PE＝，OE＝，求菱形的边长．46．（2020•新都区模拟）如图，正方形ABCD的边长为4．点E，F分别在边AB，AD上，且∠ECF＝45°，CF的延长线交BA的延长线于点G，CE的延长线交DA的延长线于点H，连接AC，EF，GH．（1）填空：∠AHC∠ACG；（填“＞”或“＜”或“＝”）（2）设AE＝m，①△AGH的面积S有变化吗？如果变化，请求出S与m的函数关系式；如果不变化，请求出定值；②请直接写出使△CGH是等腰三角形的m值．47．（2018秋•福鼎市期中）如图，在矩形ABCD中，AB＝1，BC＝k，E是边BC上一个动点（不与B，C重合），连接AE，作EF⊥AE，EF交边CD于点F．（1）求证：△ABE∽△ECF；（2）若在动点E的运动过程中，一定存在点F，使得EF＝EA，求k的取值范围；（3）若点G是边AB上一点且∠GEB＝∠FEC，求EG，EF，EA的数量关系．48．（2020秋•太和县期末）某班“手拉手”数学学习互助小组对矩形内两条互相垂直的线段与矩形两邻边的数量关系进行探究时，遇到以下问题，请你逐一加以解答：（1）如图1，正方形ABCD中，EF⊥GH，EF分别交AB，CD于点E，F，GH分别交AD，BC于点G，H，则EF GH；（填“＞”“＝”或“＜”）（2）如图2，矩形ABCD中，EF⊥GH，EF分别交AB，CD于点E，F，GH分别交AD，BC于点G，H，求证：＝；（3）如图3，四边形ABCD中，∠ABC＝∠ADC＝90°，BC＝3，CD＝5，AD＝7.5，AM ⊥DN，点M，N分别在边BC，AB上，求的值．49．（2017•齐齐哈尔）如图，在平面直角坐标系中，把矩形OABC沿对角线AC所在直线折叠，点B落在点D处，DC与y轴相交于点E，矩形OABC的边OC，OA的长是关于x 的一元二次方程x2﹣12x+32＝0的两个根，且OA＞OC．（1）求线段OA，OC的长；（2）求证：△ADE≌△COE，并求出线段OE的长；（3）直接写出点D的坐标；（4）若F是直线AC上一个动点，在坐标平面内是否存在点P，使以点E，C，P，F为顶点的四边形是菱形？若存在，请直接写出P点的坐标；若不存在，请说明理由．50．（2020秋•宝安区期末）（1）阅读下列材料，填空：如图1，已知点C为线段AB的中点，AD＝BE．求证：∠D＝∠BEC．证明：作BF∥AD交DC延长线于点F，则＝∠F，∠A＝∠CBF．∵C为AB中点，∴AC＝BC．∴△ADC≌△BFC（AAS）．∴AD＝BF．∵AD＝BE，∴BE＝．∴∠BEC＝∠F＝∠D．（2）如图2，AD为△ABC的中线，E为线段AD上一点，∠BED＝∠BAC，F为线段AD 上一点，且CF＝BE．①求证：△AEB∽△CF A．②若AD＝4，CD＝2，当△ABC是以AB为腰的等腰三角形时，求线段AF的长．51．（2021•博山区一模）如图，抛物线y＝ax2+bx+c交轴于点A（﹣1，0），B（3，0），交y 轴于点C，∠CAB＝60°，点E是线段AB上一动点，作EF∥AC交线段BC于点F．（1）求抛物线的解析式；（2）如图1，延长线段EF交抛物线第一象限的部分于点G，点D是AC边中点，当四边形ADGF为平行四边形时，求出G点坐标；（3）如图2，M为射线EF上一点，且EM＝EB，将射线EF绕点E逆时针旋转60°，交直线AC于点N，连接MN，P为MN的中点，连接AP、BP，问：AP+BP是否存在最小值，若存在，请求出这个最小值，若不存在，请说明理由．52．（2021•罗湖区校级模拟）如图①，在平面直角坐标系中，已知抛物线y＝ax2+bx+3（a ≠0）与x轴交于A（﹣1，0），B（3，0）两点，与y轴交于点C．（1）求该抛物线的解析式；（2）如图②，若点D是抛物线上一动点，设点D的横坐标为m（0＜m＜3），连接CD，BD，当△BCD的面积等于△AOC面积的2倍时，求m的值；（3）抛物线上是否存在点P，使∠CBP+∠ACO＝∠ABC？若存在，请求出点P的坐标；若不存在，请说明理由．53．（2021•罗湖区校级模拟）如图1，在Rt△ABC中，∠C＝90°，∠A＝30°，BC＝1，点D，E分别为AC，BC的中点．△CDE绕点C顺时针旋转，设旋转角为α（0°≤α≤360°），记直线AD与直线BE的交点为点P．（1）如图1，当α＝0°时，AD与BE的数量关系为，AD与BE的位置关系为；（2）当0°＜α≤360°时，上述结论是否成立？若成立，请仅就图2的情形进行证明；若不成立，请说明理由；（3）△CDE绕点C顺时针旋转一周，请直接写出运动过程中P点运动轨迹的长度和P点到直线BC距离的最大值．54．（2021春•福田区校级月考）如图，AD∥BC，∠ABC＝90°，AD＝3，AB＝4，点P为射线BC上一动点以P为圆心，BP长为半径作⊙P，交射线BC于点Q，连接BD、AQ 相交于点G，⊙P与线段BD、AQ分别相交于点E、F．（1）如果⊙P过点G，求BP的长；（2）设BP＝x，FQ＝y，求y关于x的函数关系式；（3）如果△ADG是等腰三角形，求BP的长．55．（2021•商河县校级模拟）如图，在平面直角坐标系中，二次函数y＝﹣x2+bx+c的图象与坐标轴交于A、B、C三点，其中点A的坐标为（0，8），点B的坐标为（﹣4，0）．（1）求该二次函数的表达式及点C的坐标；（2）点D为该二次函数在第一象限内图象上的动点，连接AC、CD，以AC、CD为邻边作平行四边形ACDE，设平行四边形ACDE的面积为S．①求S的最大值；②当S取最大值时，P为该二次函数图象对称轴上一点，当点D关于直线CP的对称点E落在y轴上时，求点P的坐标．56．（2021秋•江夏区期中）如图，抛物线y＝ax2﹣2ax+c与x轴交于点A（﹣2，0）和B两点，点C（6，4）在抛物线上．（1）求抛物线解析式；（2）如图1，D为y轴左侧抛物线上一点，且∠DCA＝2∠CAB，求点D的坐标；（3）如图2，直线y＝mx+n与抛物线交于点E、F，连接CE、CF分别交y轴于点M、N，若OM•ON＝3．求证：直线EF经过定点，并求出这个定点的坐标．57．（2021秋•西湖区期中）如图，在矩形ABCD中，AB＝3，BC＝4，动点P从点A出发沿AC向终点C运动，同时动点Q从点B出发沿BA向终点A运动，P，Q运动速度均为每秒1个单位长度，当一个点到达终点时，另一个点也停止运动，连接PQ，设运动时间为t（t＞0）秒．（1）t为何值时，△AQP与△ABC相似？（2）t为何值时，△AQP的面积为0.8？58．（2021秋•罗湖区校级月考）如图，直线y＝﹣2x+12与x轴交于点A，与y轴交于点B，点C是线段AB的中点，点D在线段OC上，OD＝2CD，直线AD交y轴于点E．（1）点C的坐标为；（2）①求直线AD的解析式；②P是直线AD上的点，在平面内是否存在点Q，使以点O、A、P、Q为顶点的四边形是菱形？若存在，请直接写出点Q的坐标；若不存在，请说明理由；（3）F是线段AB上一动点，连接EF，将△EFB翻折得△EFB′，B′在直线AE的上方，若△EFB′与△AEF的重叠部分为直角三角形，请直接写出线段BF的长．59．（2018•乌鲁木齐）如图，在四边形ABCD中，∠BAC＝90°，E是BC的中点，AD∥BC，AE∥DC，EF⊥CD于点F．（1）求证：四边形AECD是菱形；（2）若AB＝6，BC＝10，求EF的长．60．（2021•永嘉县校级模拟）如图，在平面直角坐标系中，直线l1：y＝﹣x+4分别交x、y轴于B、A两点，将△AOB沿直线l2：y＝2x折叠，点B落在y轴的点C处．（1）点C的坐标为；（2）若点D沿射线BA运动，连接OD，当△CDB与△CDO面积相等时，求直线OD的解析式；（3）在（2）的条件下，当点D在第一象限时，沿x轴平移直线OD，分别交x，y轴于点E，F，在平面直角坐标系中，是否存在点M（m，3）和点P，使四边形EFMP为正方形？若存在，求出点P的坐标；若不存在，说明理由．2022年深圳中考各区压轴题2参考答案与试题解析一．选择题（共15小题）1．（2019•鞍山）如图，正方形ABCD和正方形CGFE的顶点C，D，E在同一条直线上，顶点B，C，G在同一条直线上．O是EG的中点，∠EGC的平分线GH过点D，交BE 于点H，连接FH交EG于点M，连接OH．以下四个结论：①GH⊥BE；②△EHM∽△FHG；③＝﹣1；④＝2﹣，其中正确的结论是（）A．①②③B．①②④C．①③④D．②③④【分析】由四边形ABCD和四边形CGFE是正方形，得出△BCE≌△DCG，推出∠BEC+∠HDE＝90°，从而得GH⊥BE；由GH是∠EGC的平分线，得出△BGH≌△EGH，再由O是EG的中点，利用中位线定理，得HO∥BG且HO＝BG；由△EHG是直角三角形，因为O为EG的中点，所以OH＝OG＝OE，得出点H在正方形CGFE的外接圆上，根据圆周角定理得出∠FHG＝∠EHF＝∠EGF＝45°，∠HEG＝∠HFG，从而证得△EHM ∽△FHG；设CG＝a，则BG＝GE＝a，BC＝a﹣a，即可得出＝＝﹣1，设正方形ECGF的边长是2b，则EG＝2b，得到HO＝b，通过证得△MHO∽△MFE，得到＝＝＝，进而得到＝＝＝﹣1，进一步得到＝＝﹣1．【解答】解：如图，∵四边形ABCD和四边形CGFE是正方形，∴BC＝CD，CE＝CG，∠BCE＝∠DCG，在△BCE和△DCG中，∴△BCE≌△DCG（SAS），∴∠BEC＝∠BGH，∵∠BGH+∠CDG＝90°，∠CDG＝∠HDE，∴∠BEC+∠HDE＝90°，∴GH⊥BE．故①正确；∵△EHG是直角三角形，O为EG的中点，∴OH＝OG＝OE，∴点H在正方形CGFE的外接圆上，∵EF＝FG，∴∠FHG＝∠EHF＝∠EGF＝45°，∠HEG＝∠HFG，∴△EHM∽△FHG，故②正确；∵△BGH≌△EGH，∴BG＝EG，设CG＝a，则BG＝GE＝a，∴BC＝a﹣a，∴＝＝﹣1；故③正确；∵△BGH≌△EGH，∴EG＝BG，∵HO是△EBG的中位线，∴HO＝BG，∴HO＝EG，设正方形ECGF的边长是2b，∴EG＝2b，∴HO＝b，∵OH∥BG，CG∥EF，∴OH∥EF，∴△MHO∽△MFE，∴＝＝＝，∴EM＝OM，∴＝＝＝﹣1，∴＝﹣1，∵EO＝GO，∴S△HOE＝S△HOG，∴＝﹣1，故④错误，故选：A．【点评】本题考查了正方形的性质，以及全等三角形的判定与性质，相似三角形的判定与性质，正确求得两个三角形的边长的比是解决本题的关键．2．（2020秋•化州市期末）如图，已知E，F分别为正方形ABCD的边AB，BC的中点，AF 与DE交于点M，O为BD的中点，则下列结论：①∠AME＝90°，②∠BAF＝∠EDB，③AM＝MF，④ME+MF＝MB．其中正确结论的有（）A．4个B．3个C．2个D．1个【分析】根据正方形的性质可得AB＝BC＝AD，∠ABC＝∠BAD＝90°，再根据中点定义求出AE＝BF，然后利用“边角边”证明△ABF和△DAE全等，根据全等三角形对应角相等可得∠BAF＝∠ADE，然后求出∠ADE+∠DAF＝∠BAD＝90°，从而求出∠AMD ＝90°，再根据邻补角的定义可得∠AME＝90°，得出①正确；根据中线的定义判断出∠ADE≠∠EDB，然后求出∠BAF≠∠EDB，判断出②错误；设正方形ABCD的边长为2a，利用勾股定理列式求出AF，再根据似三角形对应边成比例求出AM，然后求出MF，消掉a即可得到AM＝MF，判断出③正确；如图，过点M作MN⊥AB于N，于是得到＝＝，得到NB＝AB﹣AN＝2a﹣a＝a，根据勾股定理得到BM＝＝a，于是得到结论．【解答】解：在正方形ABCD中，AB＝BC＝AD，∠ABC＝∠BAD＝90°，∵E、F分别为边AB，BC的中点，∴AE＝BF＝BC，在△ABF和△DAE中，，∴△ABF≌△DAE（SAS），∴∠BAF＝∠ADE，∵∠BAF+∠DAF＝∠BAD＝90°，∴∠AME＝180°﹣∠AMD＝180°﹣90°＝90°，故①正确；∵DE是△ABD的中线，∴∠ADE≠∠EDB，∴∠BAF≠∠EDB，故②错误；设正方形ABCD的边长为2a，则BF＝a，在Rt△ABF中，AF＝＝a，∵∠BAF＝∠MAE，∠ABC＝∠AME＝90°，∴△AME∽△ABF，∴＝，即＝，解得：AM＝a，∴MF＝AF﹣AM＝a﹣a＝a，∴AM＝MF，故③正确；如图，过点M作MN⊥AB于N，则＝＝，即＝＝，解得MN＝a，AN＝a，∴NB＝AB﹣AN＝2a﹣a＝a，根据勾股定理，BM＝＝a，∵ME+MF＝a+a＝a，MB＝a＝a，∴ME+MF＝MB．综上所述，正确的结论有①③④共3个．故选：B．【点评】本题考查了正方形的性质，全等三角形的判定与性质，相似三角形的判定与性质，勾股定理的应用，勾股定理逆定理的应用，综合性较强，难度较大，仔细分析图形并作出辅助线构造出直角三角形与相似三角形是解题的关键．3．（2021秋•宝安区校级期中）如图，在Rt△ABC中，∠ACB＝90°，AC＝3，∠BAC＝30°，把Rt△ABC沿AB翻折得到Rt△ABD，过点B作BE⊥BC，交AD于点E，点F是线段BE上一点，且∠ADF＝45°．则下列结论：①AE＝BE；②△BED∽△ABC；③BD2＝AD •DE；④AF＝，其中正确的有（）A．①④B．②③④C．①②③D．①②③④【分析】由折叠的性质可求∠BAD＝∠BAC＝30°，AD＝AC＝3，BD＝BC＝，∠C ＝∠ADB＝90°，可得∠BAE＝∠EBA＝30°，可证BE＝AE，故①正确，由外角的性质可得∠BED＝∠ABC，可证△BED∽△ABC，故②正确；由相似三角形的性质可得，可得BD2＝AD•DE，故③正确；过点F作FH⊥AD于H，FG⊥BD于G，由面积法求出FH，DH的长，由勾股定理可求AF＝，故④正确，即可求解．【解答】解：∵∠ACB＝90°，AC＝3，∠BAC＝30°，∴∠ABC＝60°，BC＝，AB＝2BC＝2，∵BE⊥BC，∴∠EBA＝30°，∵把Rt△ABC沿AB翻折得到Rt△ABD，∴∠BAD＝∠BAC＝30°，AD＝AC＝3，BD＝BC＝，∠C＝∠ADB＝90°，∴∠BAE＝∠EBA＝30°，∴BE＝AE，故①正确，∵∠BED＝∠ABE+∠BAE＝60°，∴∠BED＝∠ABC，又∵∠C＝∠ADB，∴△BED∽△ABC，故②正确；∴，∴BD2＝AD•DE，故③正确；如图，过点F作FH⊥AD于H，FG⊥BD于G，∵∠DBE＝90°﹣∠BED＝30°，∠BDE＝90°，∴BD＝DE＝，BE＝2DE，∴DE＝1，BE＝2，∵∠ADF＝45°＝∠BDF，FH⊥AD，FG⊥BD，∴FH＝FG，∵S△BDE＝BD×DE＝×DE×HF+×BD×GF，∴HF＝，∵∠ADF＝45°，∠DHF＝90°，∴DH＝HF＝，∴AH＝AD﹣DH＝，∴AF＝＝，故④正确，故选：D．【点评】本题是三角形综合题，考查了直角三角形的性质，折叠的性质，相似三角形的判定和性质，三角形的面积公式，勾股定理等知识，求出AH的长是解题的关键．4．（2021秋•宝安区校级期中）如图，在▱ABCD中，点E在线段AB上，点F、G分别为对角线AC与DE、DB的交点．若AB：AE＝3：2，则四边形BGFE与▱ABCD的面积之比为（）A．7：60B．8：70C．5：43D．3：26【分析】根据平行四边形的性质得S△ABD＝S▱ABCD，S△AGB＝S▱ABCD，再根据AB：AE＝3：2得S△ADE＝S△ABD＝S▱ABCD，根据AB∥CD，推△AEF∽△CDF，得＝，从而得S△AEF＝S△AED＝S▱ABCD，再通过面积之差进而求出四边形BGFE与▱ABCD 的面积之比．【解答】解：∵四边形ABCD为平行四边形，∴S△ABD＝S▱ABCD，S△AGB＝S▱ABCD，∵AB：AE＝3：2，∴S△ADE＝S△ABD＝S▱ABCD，∵AB∥CD，∴△AEF∽△CDF，∴＝＝＝，∴＝，∴S△AEF＝S△AED＝S▱ABCD，∵S四BGFE＝S△AGB﹣S△AEF＝S▱ABCD﹣S▱ABCD＝S▱ABCD，∴S四BGFE：S▱ABCD＝7：60，故选：A．【点评】本题主要考查了相似三角形的判定与性质、平行四边形的性质，熟练应用平行四边形的性质和相似三角形的判断，根据线段之比求面积之比是解题关键．5．（2021秋•深圳期中）如图，在正方形ABCD中，F为CD上一点，AF交对角线BD于点E，过点E作EG⊥AF，交BC于点G，连结AG，交BD于点H．现给出下列结论：①AE＝EG；②BG+DF＝FG；③AH2＝HE•HD；④若F为CD中点，则CG＝2BG．其中正确的有（）个．A．1B．2C．3D．4【分析】连接CE，由“SAS”可证△ABE≌△CBE，可得AE＝CE，∠BAE＝∠BCE，根据四边形的内角和得∠BAE+∠BGE＝180°，可得∠EGC＝∠BCE，CE＝EG，即可得AE ＝EG；把△ADF顺时针旋转90°得到△ABM，由“SAS”可证△AGM≌△AGF，可得MG＝FG，即可得BG+DF＝FG；由AE＝EG，EG⊥AF，可得∠EAG＝∠EGA＝45°，由正方形的性质可得∠ADH＝∠EAG＝45°，可证得△AHE∽△DHA，根据相似三角形的性质可得AH2＝HE•HD；设正方形ABCD的边长为2a，BG＝m，表示出CG、CF、FG，利用勾股定理即可得出结论．【解答】解：如图①，连接CE，在正方形ABCD中，AB＝BC，∠ABE＝∠CBE＝45°，在△ABE和△CBE中，，∴△ABE≌△CBE（SAS），∴AE＝CE，∠BAE＝∠BCE，∵FG⊥AE，在四边形ABGE中，∠BAE+∠BGE＝360°﹣90°﹣90°＝180°，又∵∠BGE+∠CGE＝180°，∴∠BAE＝∠CGE，∴∠CGE＝∠BCE，∴CE＝EG，∴AE＝EG，故①正确；如图，把△ADF顺时针旋转90°得到△ABM，则AM＝AF，BM＝DF，∠BAM＝∠DAE，∵AE＝EG，EG⊥AE，∴△AEG是等腰直角三角形，∴∠EAG＝45°，∴∠MAG＝∠BAG+∠DAF＝90°﹣45°＝45°，∴∠F AG＝∠MAG，在△AMG和△AFG中，，∴△AMG≌△AFG（SAS），∴MG＝FG，∵FG＝BM+BG＝DF+BG，∴FG＝DF+BG，故②正确；∵AE＝EG，EG⊥AF，∴∠EAG＝∠EGA＝45°，∵四边形ABCD是正方形，∴∠ADH＝∠EAG＝45°，∵∠AHE＝∠DHA，∴△AHE∽△DHA，∴，∴AH2＝HE•HD；∴③正确，设正方形ABCD的边长为2a，BG＝m，∵F为CD中点，∴CF＝DF＝a，∴CG＝2a﹣m，CF＝DF＝a，FG＝DF+BG＝a+m，在Rt△FCG中，GC2+FC2＝GF2，即（2a﹣m）2+a2＝（a+m）2，∴m＝a，∴BG＝a，∴CG＝2a﹣a＝a，∴CG＝2BG．故④正确．故选：D．【点评】本题考查了正方形的性质，全等三角形的判定与性质，相似三角形的判定与性质，作辅助线构造出等腰三角形和全等三角形是解题的关键．6．（2021秋•深圳期中）如图，▱ABCD中，点F为AD上一点，AF＝2DF，连结BF，交AC于点E，延长线交CD的延长线于点G，则的值为（）A．B．C．3D．2【分析】由AF＝2DF，可以假设DF＝k，则AF＝2k，AD＝3k，证明AB＝AF＝2k，DF ＝DG＝k，再利用相似三角形的判定与性质即可解决问题．【解答】解：由AF＝2DF，可以假设DF＝k，则AF＝2k，AD＝3k，∵四边形ABCD是平行四边形，∴AD∥BC，AB∥CD，AD＝BC＝3k，∵AD∥BC，∴△AEF∽△CEB，∴，∴，∵AB∥CD，∴△AEB∽△CEG，∴＝，故选：B．【点评】本题考查平行四边形的性质，相似三角形的判定与性质，解题的关键是学会利用参数解决问题，属于中考常考题型．7．（2020•遂宁）如图，在正方形ABCD中，点E是边BC的中点，连接AE、DE，分别交BD、AC于点P、Q，过点P作PF⊥AE交CB的延长线于F，下列结论：①∠AED+∠EAC+∠EDB＝90°，②AP＝FP，③AE＝AO，④若四边形OPEQ的面积为4，则该正方形ABCD的面积为36，⑤CE•EF＝EQ•DE．其中正确的结论有（）A．5个B．4个C．3个D．2个【分析】①正确．证明∠EOB＝∠EOC＝45°，再利用三角形的外角的性质即可解决问题．②正确．利用四点共圆证明∠AFP＝∠ABP＝45°即可．③正确．设BE＝EC＝a，求出AE，OA即可解决问题．④错误，通过计算正方形ABCD的面积为48．。

2019中考数学压轴题专项训练题二(附答案)

2019中考数学压轴题专项训练题二1.如图1，OABC是一张放在平面直角坐标系中的矩形纸片，O为原点，点A在x轴的正半轴上，点C在y轴的正半轴上，OA=5，OC=4．（1）在OC边上取一点D，将纸片沿AD翻折，使点O落在BC边上的点E处，求D，E两点的坐标；（2）如图2，若AE上有一动点P（不与A，E重合）自A点沿AE方向E点匀速运动，运动的速度为每秒1个单位长度，设运动的时间为t秒（0＜t＜5），过P 点作ED的平行线交AD于点M，过点M作AE平行线交DE于点N．求四边形PMNE 的面积S与时间t之间的函数关系式；当t取何值时，s有最大值，最大值是多少？（3）在（2）的条件下，当t为何值时，以A，M，E为顶点的三角形为等腰三角形，并求出相应的时刻点M的坐标？2.（1）问题：如图1，在四边形ABCD中，点P为AB上一点，∠DPC=∠A=∠B=90°.求证：AD•BC=AP•BP．（2）探究：如图2，在四边形ABCD中，点P为AB上一点，当∠DPC=∠A=∠B=θ时，上述结论是否依然成立？说明理由．（3）应用：请利用（1）（2）获得的经验解决问题：如图3，在△ABD中，AB=12，AD=BD=10．点P以每秒1个单位长度的速度，由点A 出发，沿边AB向点B运动，且满足∠DPC=∠A．设点P的运动时间为t（秒），当以D为圆心，以DC为半径的圆与AB相切，求t的值．3.如图，在平面直角坐标系中，矩形OABC的边OA在x轴的负半轴上，边OC在y轴的正半轴上，且OA=1，tan∠ACB=2，将矩形OABC绕点O按顺时针方向旋转90°后得到矩形ODEF．点A的对应点为点D，点B的对应点为点E，点C的对应点为点F，抛物线y=ax2+bx+2的图象过点A，C，F．（1）求抛物线所对应函数的表达式；（2）在边DE上是否存在一点M，使得以O，D，M为顶点的三角形与△ODE相似，若存在，求出经过M点的反比例函数的表达式，若不存在，请说明理由；（3）在x轴的上方是否存在点P，Q，使以O，F，P，Q为顶点的平行四边形的面积是矩形OABC面积的2倍，且点P在抛物线上，若存在，请求出P，Q两点的坐标；若不能存在，请说明理由；（4）在抛物线的对称轴上是否存在一点H，使得HA﹣HC的值最大，若存在，直接写出点H的坐标；若不存在，请说明理由．4.如图,在直角坐标系中,Rt△OAB的直角顶点A在x轴上,OA=4,AB=3.动点M从点A出发，以每秒1个单位长度的速度,沿AO向终点O移动；同时点N从点O出发,以每秒1.25个单位长度的速度,沿OB向终点B移动.当两个动点运动了x秒（0＜x＜4）时,解答下列问题：（1）求点N的坐标（用含x的代数式表示）；（2）设△OMN的面积是S,求S与x之间的函数表达式；当x为何值时,S有最大值？最大值是多少？（3）在两个动点运动过程中,是否存在某一时刻,使△OMN是直角三角形？若存在,求出x的值；若不存在,请说明理由．5.如图所示，已知抛物线y=x2﹣1与x轴交于A、B两点，与y轴交于点C．（1）求A、B、C三点的坐标；（2）过点A作AP∥CB交抛物线于点P，求四边形ACBP的面积；（3）在x轴上方的抛物线上是否存在一点M，过M作MG⊥x轴于点G，使以A、M、G 三点为顶点的三角形与△PCA相似？若存在，请求出M点的坐标；否则，请说明理由．答案：1.解：（1）依题意可知，折痕AD是四边形OAED的对称轴，∴在Rt△ABE中，AE=AO=5，AB=4．BE==3．∴CE=2．∴E点坐标为（2，4）．在Rt△DCE中，DC2+CE2=DE2，又∵DE=OD．∴（4﹣OD）2+22=OD2．解得：OD=2.5．∴D点坐标为（0，2.5）．（2）如图②∵PM∥ED，∴△APM∽△AED．∴，又知AP=t，ED=2.5，AE=5，PM=0.5t×2.5=0.5t，又∵PE=5﹣t．而显然四边形PMNE为矩形．S矩形PMNE =PM•PE=0.5t×（5﹣t）=﹣0.5t2+2.5t；∴S四边形PMNE=﹣0.5（t﹣2.5）2+，又∵0＜2.5＜5．∴当t=2.5时，S矩形PMNE有最大值．（3）（i）若以AE为等腰三角形的底，则ME=MA（如图①）在Rt△AED中，ME=MA，∵PM⊥AE，∴P为AE的中点，∴t=AP=0.5AE=2.5．又∵PM∥ED，∴M为AD的中点．过点M作MF⊥OA，垂足为F，则MF是△OAD的中位线，∴MF=0.5OD=1.25，OF=0.5OA=2.5，∴当t=2.5时，（0＜2.5＜5），△AME为等腰三角形．此时M点坐标为（2.5，1.25）．（ii）若以AE为等腰三角形的腰，则AM=AE=5（如图②）在Rt△AOD中，AD===．过点M作MF⊥OA，垂足为F．∵PM∥ED，∴△APM∽△AED．∴．∴t=AP===2，∴PM=t=．∴MF=MP=，OF=OA﹣AF=OA﹣AP=5﹣2，∴当t=2时，（0＜2＜5），此时M点坐标为（5﹣2，）．综合（i）（ii）可知，t=2.5或t=2时，以A，M，E为顶点的三角形为等腰三角形，相应M点的坐标为（2.5，1.25）或（5﹣2，）．2.（1）证明：如图1，∵∠DPC=∠A=∠B=90°，∴∠ADP+∠APD=90°，∠BPC+∠APD=90°，∴∠APD=∠BPC，∴△ADP∽△BPC，∴，∴AD•BC=AP•BP；（2）结论AD•BC=AP•BP仍成立；理由：证明：如图2，∵∠BPD=∠DPC+∠BPC，又∵∠BPD=∠A+∠APD，∴∠DPC+∠BPC=∠A+∠APD，∵∠DPC=∠A=θ，∴∠BPC=∠APD，又∵∠A=∠B=θ，∴△ADP∽△BPC，∴，∴AD•BC=AP•BP；（3）解：如下图，过点D作DE⊥AB于点E，∵AD=BD=10，AB=12，∴AE=BE=6∴DE==8，∵以D为圆心，以DC为半径的圆与AB相切，∴DC=DE=8，∴BC=10﹣8=2，∵AD=BD，∴∠A=∠B，又∵∠DPC=∠A，∴∠DPC=∠A=∠B，由（1）（2）的经验得AD•BC=AP•BP，又∵AP=t，BP=12﹣t，∴t（12﹣t）=10×2，∴t=2或t=10，∴t的值为2秒或10秒．3.解：（1）∵矩形OABC，∴BC=OA=1，OC=AB，∠B=90°，∵tan∠ACB=2，∴AB:BC=2∴OC:OA=2，则OC=2，∵将矩形OABC绕点O按顺时针方向旋转90°后得到矩形ODEF，∴OF=2，则有A（﹣1，0）C（0，2）F（2，0）∵抛物线y=ax2+bx+2的图象过点A，C，F，把点A、C、F坐标代入得a-b+c=0,4a+2b+c=0,c=2∴解得a=-1,b=1,c=2∴函数表达式为y=﹣x2+x+2，（2）存在，当∠DOM=∠DEO时，△DOM∽△DEO∴此时有DM:DO=DO:DE.∴DM2=0.5,∴点M坐标为（0.5，1），设经过点M的反比例函数表达式为y=kx-1，把点M代入解得k=0.5∴经过M点的反比例函数的表达式为y=0.5x-1，（3）存在符合条件的点P，Q．∵S矩形ABCD=2×1=2，∴以O，F，P，Q为顶点平行四边形的面积为4，∵OF=2，∴以O，F，P，Q为顶点平行四边形的高为2，∵点P在抛物线上，设点P坐标为（m，2），∴﹣m2+m+2=2，解得m1=0，m2=1，∴点P坐标为P1（0，2），P2（1，2）∵以O，F，P，Q为顶点的四边形为平行四边形，∴PQ∥OF，PQ=OF=2．∴当点P坐标为P1（0，1）时，点Q的坐标分别为Q1（2，2），Q2（﹣2，2）；当点P坐标为P2（1，2）时，点Q的坐标分别为Q3（3，2），Q4（﹣1，2）；（4）若使得HA﹣HC的值最大，则此时点A、C、H应在同一直线上，设直线AC的函数解析式为y=kx+b，把点A（﹣1，0），点C（0，2）代入得-k+b=0,b=2解得k=2,b=2∴直线AC的函数解析式为y=2x+2，∵抛物线函数表达式为y=﹣x2+x+2，∴对称轴为x=0.5∴把x=0.5代入y=2x+2 解得y=3∴点H的坐标为（0.5，3）4.解：（1）根据题意得：MA=x，ON=1.25x，在Rt△OAB中，由勾股定理得：OB===5，作NP⊥OA于P，如图1所示：则NP∥AB，∴△OPN∽△OAB，∴，即，解得：OP=x，PN=，∴点N的坐标是（x，）；（2）在△OMN中，OM=4﹣x，OM边上的高PN=，∴S=0.5OM•PN=0.5（4﹣x）•=﹣x2+1.x，∴S与x之间的函数表达式为S=﹣x2+1.x（0＜x＜4），配方得：S=﹣（x﹣2）2+1.5，∵﹣＜0，∴S有最大值，当x=2时，S有最大值，最大值是1.5；（3）存在某一时刻，使△OMN是直角三角形，理由如下：分两种情况：①若∠OMN=90°，如图2所示：则MN∥AB，此时OM=4﹣x，ON=1.25x，∵MN∥AB，∴△OMN∽△OAB，∴，即，解得：x=2；②若∠ONM=90°，如图3所示：则∠ONM=∠OAB，此时OM=4﹣x，ON=1.25x，∵∠ONM=∠OAB，∠MON=∠BOA，∴△OMN∽△OBA，∴，即，解得：x=；综上所述：x的值是2秒或秒．5.。

《2020年中考数学保A必刷压轴题(湖南长沙专版)》(二)：最值问题专题(解析版)

《2020年中考数学保A必刷压轴题(湖南长沙专版)》（二）最值问题专题1.（2019•十堰）如图，正方形ABCD和Rt△AEF，AB＝5，AE＝AF＝4，连接BF，DE．若△AEF绕点A旋转，当∠ABF最大时，S△ADE＝6．解：作DH⊥AE于H，如图，∵AF＝4，当△AEF绕点A旋转时，点F在以A为圆心，4为半径的圆上，∴当BF为此圆的切线时，∠ABF最大，即BF⊥AF，在Rt△ABF中，BF＝＝3，∵∠EAF＝90°，∴∠BAF+∠BAH＝90°，∵∠DAH+∠BAH＝90°，∴∠DAH＝∠BAF，在△ADH和△ABF中，∴△ADH≌△ABF（AAS），∴DH＝BF＝3，∴S△ADE＝AE•DH＝×3×4＝6．故答案为6．2.（2019•黄冈）如图，AC，BD在AB的同侧，AC＝2，BD＝8，AB＝8，点M为AB的中点，若∠CMD＝120°，则CD的最大值是．解：如图，作点A关于CM的对称点A′，点B关于DM的对称点B′．∵∠CMD＝120°，∴∠AMC+∠DMB＝60°，∴∠CMA′+∠DMB′＝60°，∴∠A′MB′＝60°，∵MA′＝MB′，∴△A′MB′为等边三角形∵CD≤CA′+A′B′+B′D＝CA+AM+BD＝2+4+8＝14，∴CD的最大值为14，故答案为14．3.（2019•南京）在△ABC中，AB＝4，∠C＝60°，∠A＞∠B，则BC的长的取值范围是4＜BC≤．解：作△ABC的外接圆，如图所示：∵∠BAC＞∠ABC，AB＝4，当∠BAC＝90°时，BC是直径最长，∵∠C＝60°，∴∠ABC＝30°，∴BC＝2AC，AB＝AC＝4，∴AC＝，∴BC＝；当∠BAC＝∠ABC时，△ABC是等边三角形，BC＝AC＝AB＝4，∵∠BAC＞∠ABC，∴BC长的取值范围是4＜BC≤；故答案为：4＜BC≤．4.（2019•连云港）如图，在矩形ABCD 中，AB ＝4，AD ＝3，以点C 为圆心作⊙C 与直线BD 相切，点P 是⊙C 上一个动点，连接AP 交BD 于点T ，则的最大值是 3 ．方法1、解：设C 的半径为R ，如图，作BD 的平行线P E '，使P E '切C 于P '，则PE 与BD 的最大距离为2R ，BD 与C 相切，∴点C 到BD 的距离为R ，∴四边形ABCD 是矩形，∴点A 到BD 的距离为R ，∴点A 到PE 的最大距离为3R ，∴AP AT 的最大值为33R R=；方法2、解：如图，过点A 作AG BD ⊥于G ，BD 是矩形的对角线，90BAD ∴∠=︒，5BD ∴==，1122AB AD BD AG =， 125AG ∴=，BD 是C 的切线，C ∴的半径为125过点P 作PE BD ⊥于E ，AGT PET ∴∠=∠，ATG PTE ∠=∠，AGT PET ∴∆∆∽， ∴AG AT PE PT=， ∴512PT PE AT =⨯ 1AP AT PT PTAT AT AT+==+，要AP AT最大，则PE 最大，点P 是C 上的动点，BD 是C 的切线，PE ∴最大为C 的直径，即：245PE =最大， ∴AP AT 最大值为8134+=，故答案为3．方法3、解：如图，过点P 作//PE BD 交AB 的延长线于E ，AEP ABD ∴∠=∠，APE ATB ∆∆∽， ∴AP AE AT AB=， 4AB =，4AE AB BE BE ∴=+=+， ∴14AP BE AT =+， BE ∴最大时，AP AT最大，四边形ABCD 是矩形，3BC AD ∴==，4CD AB ==，过点C 作CH BD ⊥于H ，交PE 于M ，并延长交AB 于G ， BD 是C 的切线，90GME ∴∠=︒，在Rt BCD ∆中，5BD ，90BHC BCD ∠=∠=︒，CBH DBC ∠=∠，BHC BCD ∴∆∆∽， ∴BH CH BC BC DC BD==， ∴3345BH CH ==， 95BH ∴=，125CH =， 90BHG BAD ∠=∠=︒，GBH DBA ∠=∠，BHG BAD ∴∆∆∽， ∴HG BG BH AD BD AB==， ∴95354HG BG ==，2720HG ∴=，94BG =，在Rt GME ∆中，33sin 55GM EG AEP EG EG =∠=⨯=，而94BE GE BG GE =-=-， GE ∴最大时，BE 最大，GM ∴最大时，BE 最大，2720GM HG HM HM =+=+，即：HM 最大时，BE 最大，延长MC 交C 于P '，此时，HM 最大2425HP CH '===， 1234GP HP HG ''∴=+=，过点P '作//P F BD '交AB 的延长线于F ，BE ∴最大时，点E 落在点F 处，即：BE 最大BF =，在Rt △GP F '中，1234143sin sin 45GP GP FG F ABD ''====∠∠， 8BF FG BG ∴=-=， ∴AP AT 最大值为8134+=，故答案为：3．5.（2019•镇江）已知抛物线y＝ax2+4ax+4a+1（a≠0）过点A（m，3），B（n，3）两点，若线段AB的长不大于4，则代数式a2+a+1的最小值是．解：∵抛物线y＝ax2+4ax+4a+1（a≠0）过点A（m，3），B（n，3）两点，∴＝﹣＝﹣2∵线段AB的长不大于4，∴4a+1≥3∴a≥∴a2+a+1的最小值为：（）2++1＝；故答案为．6.（2019•潍坊）如图，直线y＝x+1与抛物线y＝x2﹣4x+5交于A，B两点，点P是y轴上的一个动点，当△P AB的周长最小时，S△P AB＝．解：，解得，或，∴点A的坐标为（1，2），点B的坐标为（4，5），∴AB＝＝3，作点A关于y轴的对称点A′，连接A′B与y轴的交于P，则此时△P AB的周长最小，点A′的坐标为（﹣1，2），点B的坐标为（4，5），设直线A′B的函数解析式为y＝kx+b，，得，∴直线A′B的函数解析式为y＝x+，当x＝0时，y＝，即点P的坐标为（0，），将x＝0代入直线y＝x+1中，得y＝1，∵直线y＝x+1与y轴的夹角是45°，∴点P到直线AB的距离是：（﹣1）×sin45°＝＝，∴△P AB的面积是：＝，故答案为：．7.（2019•泰安）如图，矩形ABCD中，AB＝4，AD＝2，E为AB的中点，F为EC上一动点，P为DF中点，连接PB，则PB的最小值是（）A．2B．4C．D．解：如图：当点F与点C重合时，点P在P1处，CP1＝DP1，当点F与点E重合时，点P在P2处，EP2＝DP2，∴P1P2∥CE且P1P2＝CE当点F在EC上除点C、E的位置处时，有DP＝FP由中位线定理可知：P1P∥CE且P1P＝CF∴点P的运动轨迹是线段P1P2，∴当BP⊥P1P2时，PB取得最小值∵矩形ABCD中，AB＝4，AD＝2，E为AB的中点，∴△CBE、△ADE、△BCP1为等腰直角三角形，CP1＝2∴∠ADE＝∠CDE＝∠CP1B＝45°，∠DEC＝90°∴∠DP2P1＝90°∴∠DP1P2＝45°∴∠P2P1B＝90°，即BP1⊥P1P2，∴BP的最小值为BP1的长在等腰直角BCP1中，CP1＝BC＝2∴BP1＝2∴PB的最小值是2故选：D．8.（2019•东营）如图所示是一个几何体的三视图，如果一只蚂蚁从这个几何体的点B出发，沿表面爬到AC的中点D处，则最短路线长为（）A．3B．C．3D．3解：如图将圆锥侧面展开，得到扇形ABB′，则线段BF为所求的最短路程．设∠BAB′＝n°．∵＝4π，∴n＝120即∠BAB′＝120°．∵E为弧BB′中点，∴∠AFB＝90°，∠BAF＝60°，∴BF＝AB•sin∠BAF＝6×＝3，∴最短路线长为3．故选：D．9.（2019•自贡）如图，已知A、B两点的坐标分别为（8，0）、（0，8），点C、F分别是直线x＝﹣5和x轴上的动点，CF＝10，点D是线段CF的中点，连接AD交y轴于点E，当△ABE面积取得最小值时，tan∠BAD的值是（）A．B．C．D．解：如图，设直线x＝﹣5交x轴于K．由题意KD＝CF＝5，∴点D的运动轨迹是以K为圆心，5为半径的圆，∴当直线AD与⊙K相切时，△ABE的面积最小，∵AD是切线，点D是切点，∴AD⊥KD，∵AK＝13，DK＝5，∴AD＝12，∵tan∠EAO＝＝，∴＝，∴OE＝，∴AE＝＝，作EH ⊥AB 于H ．∵S △ABE ＝•AB •EH ＝S △AOB ﹣S △AOE ，∴EH ＝，∴AH ＝＝，∴tan ∠BAD ＝＝＝，故选：B ．10.（2019•台州）如图，直线l 1∥l 2∥l 3，A ，B ，C 分别为直线l 1，l 2，l 3上的动点，连接AB ，BC ，AC ，线段AC 交直线l 2于点D ．设直线l 1，l 2之间的距离为m ，直线l 2，l 3之间的距离为n ，若∠ABC ＝90°，BD ＝4，且＝，则m +n 的最大值为．解：过B 作1BE l ⊥于E ，延长EB 交3l 于F ，过A 作2AN l ⊥于N ，过C 作2CM l ⊥于M ，设AE x =，CF y =，BN x =，BM y =，4BD =，4DM y ∴=-，4DN x =-，90ABC AEB BFC CMD AND ∠=∠=∠=∠=∠=︒，90EAB ABE ABE CBF ∴∠+∠=∠+∠=︒，EAB CBF ∴∠=∠，ABE BFC∴∆∆∽，∴AE BEBF CF=，即x mn y=，xy mn∴=，ADN CDM∠=∠，CMD AND∴∆∆∽，∴AN DNCM DM=，即4243m xn y-==-，3102y x∴=-+，23mn=，32n m∴=，5()2m n m∴+=最大，∴当m最大时，5()2m n m+=最大，22333(10)10222mn xy x x x x m ==-+=-+=，∴当1010332()2x=-=⨯-时，250332mn m==最大，103m∴=最大，m n∴+的最大值为51025233⨯=．故答案为：253．。

2020年中考数学压轴题(含答案) (2)

2020年中考数学压轴题一、选择题1．如图，在△ABC中，点D、E、F分别在AB、AC、BC边上，DE∥BC，EF∥AB，则下列比例式中错误的是（）A．B．C．D．第1题第2题2．如图，在平面直角坐标系xOy中，A（﹣3，0），B（3，0），若在直线y＝﹣x+m上存在点P满足∠APB＝60°，则m的取值范围是（）A．≤m≤B．﹣﹣5≤m≤+5C．﹣2≤m≤+2D．﹣﹣2≤m≤+2二、填空题18．如图，点G是矩形ABCD的对角线BD上一点，过点G作EF∥AB交AD于E，交BC 于F，若EG＝5，BF＝2，则图中阴影部分的面积为．第3题第4题24．如图为二次函数y＝ax2+bx+c图象，直线y＝t（t＞0）与抛物线交于A，B两点，A，B 两点横坐标分别为m，n．根据函数图象信息有下列结论：①abc＞0；②若对于t＞0的任意值都有m＜﹣1，则a≥1；③m+n＝1；④m＜﹣1；⑤当t为定值时，若a变大，则线段AB变长．其中，正确的结论有（写出所有正确结论的序号）三、解答题5．如图，已知点A（1，0），B（0，3），将△AOB绕点O逆时针旋转90°，得到△COD，设E为AD的中点．（1）若F为CD上一动点，求出当△DEF与△COD相似时点F的坐标；（2）过E作x轴的垂线l，在直线l上是否存在一点Q，使∠CQO＝∠CDO？若存在，求出Q点的坐标；若不存在，请说明理由．6．如图1，在平面直角坐标系中，直线y＝x+4与抛物线y＝﹣x2+bx+c（b，c是常数）交于A、B两点，点A在x轴上，点B在y轴上．设抛物线与x轴的另一个交点为点C．（1）求该抛物线的解析式；（2）P是抛物线上一动点（不与点A、B重合），①如图2，若点P在直线AB上方，连接OP交AB于点D，求的最大值；②如图3，若点P在x轴的上方，连接PC，以PC为边作正方形CPEF，随着点P的运动，正方形的大小、位置也随之改变．当顶点E或F恰好落在y轴上，直接写出对应的点P的坐标．【答案与解析】一、选择题1．【分析】根据平行线分线段成比例定理列出比例式，再分别对每一项进行判断即可．【解答】A．∵EF∥AB，∴＝，故本选项正确，B．∵DE∥BC，∴＝，∵EF∥AB，∴DE＝BF，∴＝，∴＝，故本选项正确，C．∵EF∥AB，∴＝，∵CF≠DE，∴≠，故本选项错误，D．∵EF∥AB，∴＝，∴＝，故本选项正确，故选：C．2．【分析】作等边三角形ABE，然后作外接圆，求得直线y＝﹣x+m与外接圆相切时的m的值，即可求得m的取值范围．【解答】解：如图，作等边三角形ABE，∵A（﹣3，0），B（3，0），∴OA＝OB＝3，∴E在y轴上，当E在AB上方时，作等边三角形ABE的外接圆⊙Q，设直线y＝﹣x+m与⊙Q相切，切点为P，当P与P1重合时m的值最大，当P与P1重合时，连接QP1，则QP1⊥直线y＝﹣x+m，∵OA＝3，∴OE＝3，设⊙Q的半径为x，则x2＝32+（3﹣x）2，解得x＝2，∴EQ＝AQ＝PQ＝2，∴OQ＝，由直线y＝﹣x+m可知OD＝OC＝m，∴DQ＝m﹣，CD＝m，∵∠ODC＝∠P1DQ，∠COD＝∠QP1D，∴△QP1D∽△COD，∴＝，即＝，解得m＝+2，当E在AB下方时，作等边三角形ABE的外接圆⊙Q，设直线y＝﹣x+m与⊙Q相切，切点为P，当P与P2重合时m的值最小，当P与P2重合时，同理证得m＝﹣﹣2，∴m的取值范围是﹣﹣2≤m≤+2，故选：D．二、填空题3．【分析】由矩形的性质可证明S矩形AEGM＝S矩形CFGN＝2×5＝10，即可求解．【解答】解：作GM⊥AB于M，延长MG交CD于N．则有四边形AEGM，四边形DEGN，四边形CFGN，四边形BMGF都是矩形，∴AE＝BF＝2，S△ADB＝S△DBC，S△BGM＝S△BGF，S△DEG＝S△DNG，∴S矩形AEGM＝S矩形CFGN＝2×5＝10，∴S阴＝S矩形CFGN＝5，故答案为：5．4．【分析】由图象分别求出a＞0，c＝﹣2，b＝﹣a＜0，则函数解析式为y＝ax2﹣ax﹣2，则对称轴x＝，由开口向上的函数的图象开口与a的关系可得：当a变大，函数y＝ax2﹣ax﹣2的开口变小，依据这个性质判断m的取值情况．【解答】解：由图象可知，a＞0，c＝﹣2，∵对称轴x＝﹣＝，∴b＝﹣a＜0，∴abc＞0；∴①正确；A、B两点关于x＝对称，∴m+n＝1，∴③正确；a＞0时，当a变大，函数y＝ax2﹣ax﹣2的开口变小，则AB的距离变小，∴⑤不正确；若m＜﹣1，n＞2，由图象可知n＞1，∴④不正确；当a＝1时，对于t＞0的任意值都有m＜﹣1，当a＞1时，函数开口变小，则有m＞﹣1的时候，∴②不正确；故答案①③．三、解答题5．【分析】（1）当△DEF∽△COD时，＝，DF＝DE cos∠CDO＝，据此求出EF的长度和点F的坐标即可；（2）首先以CD为直径作圆，设其圆心为P，交直线a于点Q、Q′，连接PQ，P Q′，由圆周角定理，可得∠CQO＝∠CQ′O＝∠CDO，在Rt△CDO中，由勾股定理可得CD＝，则PQ＝CD＝；然后求出点P的坐标是多少；设Q（﹣1，a），则（）2+（a﹣）2＝，据此求出a的值是多少，进而求出Q点坐标是多少即可．【解答】解：（1）∵A（1，0），B（0，3），∴OA＝1，OB＝3，∵将△AOB绕点O逆时针旋转90°，得到△COD，∴OC＝1，OD＝3，∴C（0，1），D（﹣3，0），如图1，当△DEF∽△COD时，＝∴EF＝，∴F（﹣1，）；当△DEF∽△COD时，DF＝DE cos∠CDO＝，作FK⊥OD于K，则FK＝DF sin∠CDO＝，DK＝DF cos∠CDO＝，∴F（﹣，）；（2）如图2，以CD为直径作圆，设其圆心为P，交直线a于点Q、Q′，连接PQ，P Q′，由圆周角定理，可得∠CQO＝∠CQ′O＝∠CDO，在Rt△CDO中，由勾股定理可得CD＝，则PQ＝CD＝，又∵P为CD中点，P（﹣，），设Q（﹣1，a），则（）2+（a﹣）2＝，解得a＝2或﹣1，∴Q（﹣1，2）或（﹣1，﹣1）．6．【分析】（1）利用直线解析式求出点A、B的坐标，再利用待定系数法求二次函数解析式解答；（2）作PF∥BO交AB于点F，证△PFD∽△OBD，得比例线段，则PF取最大值时，求得的最大值；（3）（i）点F在y轴上时，P在第一象限或第二象限，如图2，3，过点P作PH⊥x轴于H，根据正方形的性质可证明△CPH≌△FCO，根据全等三角形对应边相等可得PH＝CO＝2，然后利用二次函数解析式求解即可；（ii）点E在y轴上时，过点PK⊥x轴于K，作PS⊥y轴于S，同理可证得△EPS≌△CPK，可得PS＝PK，则P点的横纵坐标互为相反数，可求出P点坐标；点E在y轴上时，过点PM⊥x轴于M，作PN⊥y轴于N，同理可证得△PEN≌△PCM，可得PN＝PM，则P点的横纵坐标相等，可求出P点坐标．由此即可解决问题．【解答】解：（1）直线y＝x+4与坐标轴交于A、B两点，当x＝0时，y＝4，x＝﹣4时，y＝0，∴A（﹣4，0），B（0，4），把A，B两点的坐标代入解析式得，，解得，，∴抛物线的解析式为；（2）如图1，作PF∥BO交AB于点F，∴△PFD∽△OBD，∴，∵OB为定值，∴当PF取最大值时，有最大值，设P（x，），其中﹣4＜x＜0，则F（x，x+4），∴PF＝＝，∵且对称轴是直线x＝﹣2，∴当x＝﹣2时，PF有最大值，此时PF＝2，；（3）∵点C（2，0），∴CO＝2，（i）如图2，点F在y轴上时，若P在第二象限，过点P作PH⊥x轴于H，在正方形CPEF中，CP＝CF，∠PCF＝90°，∵∠PCH+∠OCF＝90°，∠PCH+∠HPC＝90°，∴∠HPC＝∠OCF，在△CPH和△FCO中，，∴△CPH≌△FCO（AAS），∴PH＝CO＝2，∴点P的纵坐标为2，∴，解得，，x＝﹣1+（舍去）．∴，如图3，点F在y轴上时，若P在第一象限，同理可得点P的纵坐标为2，此时P2点坐标为（﹣1+，2）（ii）如图4，点E在y轴上时，过点PK⊥x轴于K，作PS⊥y轴于S，同理可证得△EPS≌△CPK，∴PS＝PK，∴P点的横纵坐标互为相反数，∴，解得x＝2（舍去），x＝﹣2，∴，如图5，点E在y轴上时，过点PM⊥x轴于M，作PN⊥y轴于N，同理可证得△PEN≌△PCM，∴PN＝PM，∴P点的横纵坐标相等，∴，解得，（舍去），∴，综合以上可得P点坐标为，，．。

2021年九级中考数学压轴题满分训练 –几何综合问题(圆的专题)(二)

2021年中考数学压轴题满分训练–几何综合问题（圆的专题）（二）1．如图，以△ABC的边AC为直径的⊙O恰好经过顶点B，∠ABC的平分线交⊙O于点D，过点D作⊙O的切线交BC的延长线于点E．（1）求证：DE∥AC；（2）若AB＝8，BC＝4，求DE的长．2．如图，⊙O经过Rt△ABC的顶点A，与BC相切于点D，交AC于E，交AB于F，连接AD，DE，DF，EF，∠C＝90°．（1）求证：DE＝DF．（2）若AE＝3，CD＝2，求BD的长．3．如图，在△ABC中，AB＝AC，以AB为直径作⊙O，交BC于点D，连接AD，过点D 作⊙O的切线交AC于点E，交AB的延长线于点F．（1）求证：DE⊥AC．（2）如果⊙O的半径为5，cos∠DAB＝，求BF的长．4．如图，在Rt△OAB中，∠AOB＝90°，OA＝OB＝4，以点O为圆心、2为半径画圆，过点A作⊙O的切线，切点为P，连接OP．将OP绕点O按逆时针方向旋转到OH时，连接AH，BH．设旋转角为α（0°＜α＜360°）．（1）当α＝90°时，求证：BH是⊙O的切线；（2）当BH与⊙O相切时，求旋转角α和点H运动路径的长；（3）当△AHB面积最大时，请直接写出此时点H到AB的距离．5．如图，在⊙O中，AB是直径，AC是弦，AC＝AD，连接CD交⊙O于点E，∠ACD ＝∠DAE．（1）求证：AD是⊙O的切线；（2）过点E作EF⊥AB于F，交AC于G，已知，EG＝3．求AG的长；（3）在（2）的条件下，求△ACE的面积．6．如图，在▱ABCD中，AD＝8，▱ABCD的面积是72，⊙O与▱ABCD的三条边分别相切于点D、E、F，交AD于点G，DG＝3AG．（1）求⊙O的半径的长；（2）求阴影部分的面积（保留π）．7．[提出问题]如图1，△ABC是圆O的内接三角形，且AB＝AC，D是圆上一点，作AE⊥BD于E．要研究BE，DE，CD之间的关系．[特例分析]（1）如图2，当△ABC是等边三角形时，且当D在∠ABC的平分线上时，假设DE＝a，则DC＝，BE＝，BE，DE，CD之间的关系为．[猜想探究]（2）在图1中，上述结论是否依然成立，请证明你的猜想．[结论应用]（3）如图3，△ABC是等边三角形，∠CBD＝15°，AC＝，则△BCD的周长为．8．问题发现：（1）如图1，P是半径为2的⊙O上一点，直线m是⊙O外一直线，圆心O到直线m的距离为3，PQ⊥m于点Q，则PQ的最大值为；问题探究：（2）如图2，将两个含有30°角的直角三角板的60°角的顶点重合（其中∠A＝∠A'＝30°，∠C＝∠C'＝90°），绕点B旋转△C'A'B，当旋转至CC′＝4时，求AA'的长；问题解决：（3）如图3，点O为等腰Rt△ABC的斜边AB的中点，AC＝BC＝5，OE＝2，连接BE，作Rt△BEF，其中∠BEF＝90°，tan∠EBF＝，连接AF，求四边形ACBF的面积的最大值．9．如图，在△ABC中，AB＝AC＝2，∠BAC＝120°，点D在AB上，AD＝2，以点A为圆心，AD长为半径的弧交AC于点E，与BC交于点F，G，P是上一点．将AP绕点A逆时针旋转120°，得到AQ，连接CQ，AF．（1）若BP与所在圆相切，判断CQ与所在圆的位置关系．并加以证明；（2）求BF的长及扇形EAF的面积；（3）若∠PAB＝m°，当∠ACQ＝30°，直接写出m的值．10．如图，⊙O是△ABC的外接圆，AB＝AC，BO的延长线交AC于点D．（1）求证：∠BAC＝2∠ABD；（2）若＝，求tan∠ABD．11．已知：如图，在△ABC中，点I是△ABC的内心（三角形三条角平分线的交点），延长AI与△ABC的外接圆交于点D，连接BD，DC．求证：（1）DI＝DB；（2）若∠BAC＝60°，BC＝2，求DI的长．12．有一些代数问题，我们也可以通过几何方法进行求解，例如下面的问题：已知：a＞b＞0，求证：＞．经过思考，小明给出了几何方法的证明，如图：①在直线l上依次取AB＝a，BC＝b；②以AC为直径作半圆，圆心为O；③过B点作直线l的垂线，与半圆交于点D，连接OD．请回答：（1）连接AD，CD，由作图的过程判断，∠ADC＝90°，其依据是；（2）根据作图过程，试求线段BD、OD（用a，b的代数式表示），请写出过程；（3）由BD⊥AC，可知BD＜OD，其依据是，由此即证明了这个不等式．13．如图，⊙O是△ABC的外接圆，∠ACB＝90°．D是⊙O上一点，连接CD，与AB 交于点F，过点A作⊙O的切线交DC延长线于点E，已知AC＝EC．（1）求证：AD＝AE；（2）若AE＝2，EF＝2，求⊙O的直径．14．如图，已知扇形AOB的半径OA＝4，∠AOB＝90°，点C、D分别在半径OA、OB 上（点C不与点A重合），联结CD．点P是弧AB上一点，PC＝PD．（1）当cot∠ODC＝，以CD为半径的圆D与圆O相切时，求CD的长；（2）当点D与点B重合，点P为弧AB的中点时，求∠OCD的度数；（3）如果OC＝2，且四边形ODPC是梯形，求的值．15．如图，已知半圆O的直径AB＝4，点P在线段OA上，半圆P与半圆O相切于点A，点C在半圆P上，CO⊥AB，AC的延长线与半圆O相交于点D，OD与BC相交于点E．（1）求证：AD•AP＝OD•AC；（2）设半圆P的半径为x，线段CD的长为y，求y与x之间的函数解析式，并写出定义域；（3）当点E在半圆P上时，求半圆P的半径．参考答案1．（1）证明：连接CD，∵AC是⊙O的直径，∴∠ABC＝90°，∵BD是∠ABC的平分线，∴∠ABD＝∠CBD＝∠ABC＝45°，又∵DE是⊙O的切线，∴∠CDE＝∠CBD＝45°，∵∠ABD＝∠ACD＝45°，∴∠ACD＝∠CDE，∴AC∥DE；（2）解：连接OD，过点C作CF⊥DE，垂足为F，则四边形ODFC是正方形，在Rt△ABC中，AC＝＝＝4，∴DF＝FC＝OC＝OD＝2，∵∠E＝∠ACB，∠CFE＝∠ABC＝90°，∴△ABC∽△CFE，∴＝＝＝，∴EF＝CF＝，∴DE＝DF+EF＝2+＝3．2．（1）证明：如图，连接OD交EF于G，∵BC是⊙O的切线，∴∠ODB＝90°，∵∠C＝90°，∴OD∥AC，∴∠ODA＝∠EAD，∵OA＝OD，∴∠ODA＝∠OAD，∴∠OAD＝∠EAD，∴＝，∴DE＝DF；（2）解：∵＝，∴OD垂直平分EF，∵∠C＝∠CDG＝∠DGE＝90°，∴四边形CDGE为矩形，∴EG＝CD＝2，∠AEF＝90°，∴EF＝2EG＝4，在R△AEF中，AF＝＝5，∵O是AF的中点，G是EF的中点，∴OG＝AE＝，∴CE＝DG＝OD﹣OG＝＝1，∴AC＝AE+CE＝4，∵OD∥AC，∴△BOD∽△ABC，∴，∴，∴BD＝．3．（1）证明：连接OD，如图，∵AB为⊙O的直径，∴AD⊥BC，∵AB＝AC，∴AD平分BC，∴∠CAD＝∠BAD，∵OA＝OD，∴∠DAO＝∠ADO，∴∠EAD＝∠ADO，∴AE∥OD，∵EF是⊙O的切线，∴OD⊥EF，∴DE⊥AC；（2）解：∵cos∠DAB＝，而AB＝10，∴AD＝8，在Rt△ADE中，cos∠DAE＝＝，∴AE＝，∵OD∥AE，∴△FDO∽△FEA，∴，即＝，∴BF＝．4．解：（1）证明：∵α＝90°，∠AOB＝90°，∴∠AOP＝∠BOH，又OA＝OB＝4，OP＝OH，在△AOP和△BOH中，，∴△AOP≌△BOH（SAS），∴∠OPA＝∠OHB，∵AP是⊙O的切线，∴∠OPA＝90°，∠OHB＝90°，即OH⊥BH于点H，∴BH是⊙O的切线；（2）如图，过点B作⊙O的切线BC，BD，切点分别为C，D，连接OC，OD，则有OC⊥BC，OD⊥BD，∵OC＝2，OB＝4，∴，∴∠BOC＝60°，同理∠BOD＝60°，当点H与点C重合时，由（1）知：α＝90°，∴∠OHB＝90°．∵圆弧PH的长为；当点H与点D重合时，α＝∠POC+∠BOC+∠BOD＝90°+2×60°＝210°，∴圆弧PH的长为，∴当BH与⊙O相切时，旋转角α＝90°或210°，点H运动路径的长为π或；（3）S△AHB＝AB•h，h表示点H到直线AB的距离，作ON⊥AB于点N，H在圆O上，在Rt△ONB中，∠OBN＝45°，OB＝4，∴ON＝4cos45°＝2，∴h min＝ON﹣r＝2，h max＝2+2，∴当△AHB面积最大时，点H到AB的距离为2．5．（1）证明：如图1，连接BE，则∠B＝∠C，∵AB是⊙O的直径，∴∠ACB＝90°，∵∠BCE+∠BAE＝180°，∴∠ACD+∠DAE＝90°，∵∠ACD＝∠DAE，∴∠DAE+∠BAE＝90°，∴∠BAD＝90°，∴BD是⊙O的切线；（2）如图2，延长EF，交⊙O于H，∵EF⊥AB，AB是⊙O的直径，∴＝，∴∠ECA＝∠AEH，∵∠EAC＝∠GAE，∴△EAC∽△GAE，∴＝，∵AC＝AD，∴∠C＝∠D，∵∠C＝∠DAE，∴∠D＝∠DAE，∴AE＝DE＝2，∵∠BFE＝∠BAD＝90°，∴AD∥EF，∴∠D＝∠CEF，∴∠C＝∠CEF，∴CG＝GE＝3，∴AC＝AG+CG＝AG+3，∴＝，∴AG＝5（负值舍去）；（3）如图3，由（2）知，AG＝5，CG＝3，∵EG∥DA，∴△CEG∽△CDA，∴，∴＝，∴CE＝，过点E作EM⊥AC于M，设CM＝x，在Rt△CME中，根据勾股定理得，EM2＝CE2﹣CM2＝（）2﹣x2，在Rt△AME中，根据勾股定理得，EM2＝AE2﹣AM2＝（2）2﹣（8﹣x）2，∴（）2﹣x2＝（2）2﹣（8﹣x）2，∴x＝，∴EM2＝（）2﹣x2，∴EM＝（舍去负值），∴S△ACE＝AC•EM＝×8×＝．6．解：（1）连接FO并延长交AD于点H，∵BC与⊙O相切于点F，∴HF⊥BC，∴HF＝÷＝9，又∵平行四边形ABCD中，AD∥BC，∠HFC＝90°，∴∠FHD＝90°，∴HF⊥AD，∴DH＝DG＝3，设⊙O的半径为r，在Rt△DOH中，（3）2+（9﹣r）2＝r2，∴r＝3；（2）连接OD，OG，在Rt△DOH中，sin∠ODG＝，∴∠ODG＝30°，又∵OD＝OG，∴∠OGD＝∠ODG，∴∠GOD＝120°，∴阴影部分的面积等于＝．7．解：（1）如下图：∵△ABC是等边三角形，∴∠ABC＝60°．∵BD是∠ABC的平分线，∵∠DCA＝∠ABD，∴∠DCE＝30°．∵AE⊥BD，∴CD＝2DE＝2a．∵BD是圆的直径，∴∠BCD＝90°．∵∠DBC＝30°∴AB＝2CD＝4a．∴BE＝BD﹣DE＝3a．∵DE+CD＝3a，∴BE＝DE+CD．故答案为：2a；3a；BE＝DE+CD．（2）成立．理由：如图，过A作AF⊥CD，交DC延长线于F，连接AD，∵AF⊥CD，AE⊥BD，∴∠AEB＝∠AFC＝90°．∵同弧所对的圆周角相等，∠ABE＝∠ACD．在△ABE和△ACD中，．∴△ABE≌△ACD（AAS）．∴AE＝AF，BE＝CF．在Rt△ADE和Rt△ADF中，．∴Rt△ADE≌Rt△ADF（HL）．∴DE＝DF．∵CF＝CD+DF＝CD+DE，∴BE＝DE+CD．故结论成立．（3）∵AB＝AC，D是圆上一点，AE⊥BD于E，由（2）的结论可得：BE＝DE+CD．∵△ABC是等边三角形，∴AB＝BC＝AC＝，∠ABC＝60°．∵∠CBD＝15°，∴∠ABE＝∠ABC﹣∠CBD＝45°．∵AE⊥BD，∴AE＝BE＝AB＝×＝．∴BE＝DE+CD＝．∴△BCD的周长为：BC+CD+BD＝BC+CD+DE+BE＝BC+2BE＝+2．故答案为：+2．8．解：（1）如图1，当点P距离直线m最远时，即过点P且垂直于m的直线经过圆心O时，PQ最大，最大值为2+3＝5．故答案为：5．（2）如图2，由已知可得：BC＝BC′，BA＝BA′，∠CBA＝∠C′BA′＝60°．∴．∵∠CBA＝∠C′BA′＝60°，∴∠CBA+∠ABC′＝∠C′BA′+∠ABC′．即∠CBC′＝∠ABA′．∴△CBC′～△ABA′．∴．∵，∴．∴AA′＝2CC′＝2×4＝8．（3）∵四边形ACBF的面积＝S△ABC+S△FAB，△ABC的面积为定值，∴△ABF面积最大时，四边形ACBF的面积最大．∵AB＝5且位置不变，∴点F距离AB最大时，△ABF面积最大．∵OE＝2，∴点E在以O为圆心，半径为2的圆上，如下图所示：∵∠BEF＝90°，∴当O，E，F三点在一条直线上，即BE与该圆相切时，△ABF面积最大．过F作FD⊥OB于D，∵AC＝BC＝5，∴AB＝AC＝10．∵O为AB的中点，∴BO＝5．∵BE⊥OF，∴BE＝．∵tan∠EBF＝，∴．∴EF＝．∴OF＝OE+EF＝2+．在Rt△BEO中，sin∠EOB＝．在Rt△ODF中，sin∠EOB＝＝．∴DF＝OF••（2+）＝+．∴△ABF面积最大值为×AB×DF＝2+．∴四边形ACBF的面积的最大值＝S△ABC+S△FAB＝×AC×BC+2+＝2+．9．解：（1）CQ与所在圆相切；证明：由旋转知，AP＝AQ，∠PAQ＝120°，∵∠BAC＝120°，∴∠PAQ＝∠BAC，∴∠PAQ﹣∠PAC＝∠BAC﹣∠PAC，∴∠ACQ＝∠ABP，∵AC＝AB，∴△ACQ≌△ABP（SAS），∴∠AQC＝∠APB，∵BP与所在圆相切，∴∠APB＝90°，∴∠AQC＝90°，∵AQ＝AP，∴CQ与所在圆相切；（2）如图，过点A作AN⊥BC于N，∵AB＝AC＝2，∠BAC＝120°，∴∠ABC＝30°，∴AN＝AB＝，∴BN＝AN＝3，①当点F在点G的左边时，过点F作FM⊥AB于M，设FM＝m，在Rt△BMF中，BF＝2m，BM＝m，∴AM＝AB﹣BM＝（2﹣m），在Rt△AMF中，根据勾股定理得，FM2+AM2＝AF2，∴m2+[（2﹣m）]2＝22，∴m＝1或m＝2，∴BF＝2m＝2或4（舍），∴BF＝AF，∴∠BAF＝∠ABC＝30°，∴∠EAF＝90°，∴S扇形EAF＝＝π；②当点F在点G的右边时，同①的方法得，BF＝4，S扇形EAF＝﹣＝；即当BF＝2时，扇形EAF的面积为π，当BF＝4时，扇形EAF的面积为；（3）由（1）知，△ACQ≌△ABP，∴∠ABP＝∠ACQ＝30°，∵∠ABP＝30°，∴点P在BC上，即点P与点F或G重合，当点P与点F重合时，∠PAB＝∠BAF，由（2）知，∠BAF＝30°，∴m＝30，当点P与点G重合时，∠PAB＝∠BAG＝90°，∴m＝90，即m的值为30或90．10．解：（1）连接AO，并延长交BC于点H，∵AB＝AC，∴．∴AH⊥BC．∴AH平分∠BAC．∴∠BAC＝2∠BAH．∵OA＝OB，∴∠ABD＝∠BAH．∴∠BAC＝2∠ABD．（2）过A作AE∥BC，交BD延长线于点E，∴．∵AB＝AC，AH⊥BC，∴BH＝BC．∴．∵AE∥BC，∴．设OB＝OA＝4a，则OH＝3a．∴BH＝．AH＝OA+OH＝7a．∵∠ABD＝∠BAH，∴tan∠ABD＝tan∠BAH＝．11．（1）证明：连接BI，如图1所示：∵点I是△ABC的内心，∴AD平分∠BAC，∴∠BAD＝∠CAD，∠ABI＝∠CBI，∵∠BID＝∠BAI+∠IBA，∠IBD＝∠CBI+∠CBD，∠CBD＝∠CAD，∴∠BID＝∠IBD，∴DI＝DB；（2）解：过点D作DE⊥BC于E，如图2所示：由（1）得：∠BAD＝∠CAD，∴，∵DE⊥BC，∴BE＝CE＝BC＝，∵∠BAC＝60°，∴∠BAD＝∠CAD＝30°，∴∠DBC＝∠BCD＝30°，∴DE＝BE＝1，BD＝2DE＝2，∴DI＝BD＝2．12．解：（1）∵AC为直径，∴∠ADC＝90°（直径所对的圆周角是直角）．故答案为：直径所对的圆周角是直角；（2）∵BD⊥AC，∴∠ABD＝∠CBD＝90°．∴∠BAD+∠ADB＝90°．∵∠ADC＝90°，∴∠CDB+∠ADB＝90°．∴∠BAD＝∠CDB．∴．∴BD2＝AB•BC＝ab．∴BD＝．∵AB＝a，BC＝b，∴AC＝a+b．∴OD＝．（3）∵BD⊥AC，∴BD＜OD（直线外一点到直线上各点的所有连线中，垂线段最短）．∴＞．故答案为：垂线段最短．13．（1）证明：∵∠ACB＝90°．∴AB是⊙O的直径，∵EA是⊙O的切线，∴BA⊥EA，∴∠EAC+∠CAB＝90°，∵∠B+∠CAB＝90°，∴∠EAC＝∠B，∵AC＝EC，∴∠EAC＝∠E，∴∠E＝∠B，∵∠B＝∠D，∴∠E＝∠D，∴AD＝AE；（2）解：∵∠EAF＝90°，AE＝2，EF＝2，∴AF＝＝2，由（1）知：AD＝AE＝2，∵∠B＝∠E，∠ACB＝∠EAF＝90°，∴＝，∴AB＝AC，如图，过点A作AG⊥CD于点G，设AC＝EC＝t，则CF＝2﹣t，∵tan∠E＝＝，sin∠E＝＝＝，∴AG＝，∴FG＝＝，∴EG＝EC+CG，∴CG＝CF﹣FG＝2﹣t﹣＝﹣t，∵AC2＝AG2+CG2，∴t2＝（）2+（﹣t）2，解得t＝，∴AB＝AC＝t＝3．∴⊙O的直径是3．14．解：（1）如图1中，∵∠COD＝90°，cot∠ODC＝＝，∴可以假设OD＝3k，OC＝4k，则CD＝5k，∵以CD为半径的圆D与圆O相切，∴CD＝DB＝5k，∴OB＝OC＝8k，∴AC＝OC＝4k＝2，∴k＝，∴CD＝．（2）如图2中，连接OP，过点P作PE⊥OA于E，PF⊥OB于F．∵＝，∴∠AOP＝∠POB，∵PE⊥OA，PF⊥OB，∴PE＝PF，∵∠PEC＝∠PFB＝90°，PD＝PC，∴Rt△PEC≌Rt△PFB（HL），∴∠EPC＝∠FPB，∵∠PEO＝∠EOF＝∠OFP＝90°，∴∠EPF＝90°，∴∠EPF＝∠CPB＝90°，∴∠PCB＝∠PBC＝45°，∵OP＝OB，∠POB＝45°，∴∠OBP＝∠OPB＝67.5°，∴∠CBO＝67.5°﹣45°＝22.5°，∴∠OCD＝90°﹣22.5°＝67.5°．（3）如图3﹣1中，当OC∥PD时，∵OC∥PD，∴∠PDO＝∠AOD＝90°，∵CE⊥PD，∴∠CED＝90°，∴四边形OCED是矩形，∴OC＝DE＝2，CE＝OD，设PC＝PD＝x，EC＝OD＝y，则有，可得x＝2﹣2（不合题意的已经舍弃），∴PD＝2﹣2，∴＝＝﹣1．如图3﹣2中，当PC∥OD时，∴∠COD＝∠OCE＝∠CED＝90°，∴四边形OCED是矩形，∴OC＝DE＝2，CE＝OD，∵OP＝4，OC＝2，∴PC＝＝＝2，∴PD＝PC＝2，∴PE＝＝＝2，∴EC＝OD＝2﹣2，∴＝＝＝3+，综上所述，的值为﹣1或3+．15．解：（1）连接CP，如图：∵AP＝CP，AO＝DO，∴∠A＝∠ACP＝∠ADO，∴△ACP∽△ADO，∴，∴AD•CP＝OD•AC，∴AD•AP＝OD•AC；（2）∵半圆O的直径AB＝4，∴AO＝2，∵半圆P的半径为x，∴OP＝2﹣x，∴∠COP＝90°，∴CO2＝CP2﹣OP2＝x2﹣（2﹣x）2＝4x﹣4，Rt△AOC中，AC＝＝2，∵∠A＝∠ACP＝∠ADO，∴CP∥DO，∴，又线段CD的长为y，∴，变形得：y＝，x范围是0＜x≤2；（3）设半圆P与AB交于G，连接EG，过E作EH⊥AB于H，如图：设半圆P的半径为x，由（2）知AC＝2，∵CO⊥AB，∴BC＝AC＝2，∵CP∥DO，∴，而OB＝2，PB＝4﹣x，∴，∴BE＝，∵点E在半圆P上，∴∠EGB＝∠ACB，且∠B＝∠B，∴△CAB∽△GEB，∴＝，∴，∴EG＝，∵AC＝BC，∴EG＝BG，而BG＝AB﹣AG＝4﹣2x，∴＝4﹣2x，解得x＝或（大于2，舍去），∴半圆P的半径为x＝．。

全国中考数学压轴题精选(2)(含答案)

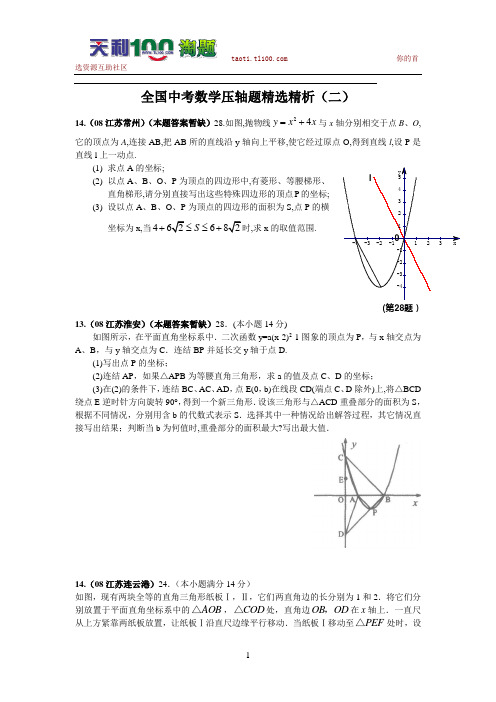
全国中考数学压轴题精选精析（二）14.（08江苏常州）（本题答案暂缺）28.如图,抛物线24y x x =+与x 轴分别相交于点B 、O ,它的顶点为A ,连接AB,把AB 所的直线沿y 轴向上平移,使它经过原点O,得到直线l ,设P 是直线l 上一动点.(1) 求点A 的坐标;(2) 以点A 、B 、O 、P 为顶点的四边形中,有菱形、等腰梯形、直角梯形,请分别直接写出这些特殊四边形的顶点P 的坐标;(3) 设以点A 、B 、O 、P 为顶点的四边形的面积为S,点P 的横坐标为x,当46S +≤≤+,求x 的取值范围.13.（08江苏淮安）（本题答案暂缺）28．(本小题14分)如图所示，在平面直角坐标系中．二次函数y=a(x-2)2-1图象的顶点为P ，与x 轴交点为 A 、B ，与y 轴交点为C ．连结BP 并延长交y 轴于点D.(1)写出点P 的坐标；(2)连结AP ，如果△APB 为等腰直角三角形，求a 的值及点C 、D 的坐标；(3)在(2)的条件下，连结BC 、AC 、AD ，点E(0，b)在线段CD(端点C 、D 除外)上,将△BCD 绕点E 逆时针方向旋转90°，得到一个新三角形．设该三角形与△ACD 重叠部分的面积为S ，根据不同情况，分别用含b 的代数式表示S ．选择其中一种情况给出解答过程，其它情况直接写出结果；判断当b 为何值时,重叠部分的面积最大?写出最大值．14.（08江苏连云港）24．（本小题满分14分）如图，现有两块全等的直角三角形纸板Ⅰ，Ⅱ，它们两直角边的长分别为1和2．将它们分别放置于平面直角坐标系中的AO B △，C O D △处，直角边O B O D ，在x 轴上．一直尺从上方紧靠两纸板放置，让纸板Ⅰ沿直尺边缘平行移动．当纸板Ⅰ移动至P E F △处时，设(第28题）（第24题图）P E P F ，与O C 分别交于点M N ，，与x 轴分别交于点G H ，．（1）求直线A C 所对应的函数关系式；（2）当点P 是线段A C （端点除外）上的动点时，试探究： ①点M 到x 轴的距离h 与线段B H 的长是否总相等？请说明理由；②两块纸板重叠部分（图中的阴影部分）的面积S 是否存在最大值？若存在，求出这个最大值及S 取最大值时点P 的坐标；若不存在，请说明理由．（08江苏连云港24题解析）24．解：（1）由直角三角形纸板的两直角边的长为1和2，知A C ，两点的坐标分别为(12)(21)，，，．设直线A C 所对应的函数关系式为y kx b =+． ······················································ 2分有221k b k b +=⎧⎨+=⎩，．解得13k b =-⎧⎨=⎩，．所以，直线A C 所对应的函数关系式为3y x =-+． ·············································· 4分（2）①点M 到x 轴距离h 与线段B H 的长总相等．因为点C 的坐标为(21)，，所以，直线O C 所对应的函数关系式为12y x =．又因为点P 在直线A C 上，所以可设点P 的坐标为(3)a a -，．过点M 作x 轴的垂线，设垂足为点K ，则有M K h =．因为点M 在直线O C 上，所以有(2)M h h ，．················· 6分因为纸板为平行移动，故有EF O B ∥，即E F G H ∥．又EF PF ⊥，所以P H G H ⊥．法一：故R t R t R t M K G P H G P F E △∽△∽△，（第24题答图）从而有12G KG HE FM K P H P F ===．得1122G K M K h ==，11(3)22G H PH a ==-．所以13222O G O K G K h h h =-=-=．又有13(3)(1)22O G O H G H a a a =-=--=-． ················································· 8分所以33(1)22h a =-，得1h a =-，而1B H O H O B a =-=-，从而总有h B H =． ·······························································································10分法二：故R t R t P H G P F E △∽△，可得12G H E F P HP F=-．故11(3)22G H PH a ==-．所以13(3)(1)22O G O H G H a a a =-=--=-．故G 点坐标为3(1)02a ⎛⎫-⎪⎝⎭，．设直线P G 所对应的函数关系式为y cx d =+，则有330(1)2a ca d c a d -=+⎧⎪⎨=-+⎪⎩，．解得233c d a =⎧⎨=-⎩ 所以，直线P G 所对的函数关系式为2(33)y x a =+-． ········································ 8分将点M 的坐标代入，可得4(33)h h a =+-．解得1h a =-．而1B H O H O B a --=-，从而总有h B H =． ···················································10分 ②由①知，点M 的坐标为(221)a a --，，点N 的坐标为12a a ⎛⎫⎪⎝⎭，．O N H O N G S S S =-△△1111133(1)222222a N H O H O G h a a a -=⨯-⨯=⨯⨯-⨯⨯-22133133224228a a a ⎛⎫=-+-=--+ ⎪⎝⎭． ·······························································12分当32a =时，S 有最大值，最大值为38．S 取最大值时点P 的坐标为3322⎛⎫⎪⎝⎭，． ···································································14分15.（08江苏连云港）25．（本小题满分12分）我们将能完全覆盖某平面图形的最小圆称为该平面图形的最小覆盖圆．例如线段A B 的最小覆盖圆就是以线段A B 为直径的圆．（1）请分别作出图1中两个三角形的最小覆盖圆（要求用尺规作图，保留作图痕迹，不写作法）；（2）探究三角形的最小覆盖圆有何规律？请写出你所得到的结论（不要求证明）；（3）某地有四个村庄E F G H ，，，（其位置如图2所示），现拟建一个电视信号中转站，为了使这四个村庄的居民都能接收到电视信号，且使中转站所需发射功率最小（距离越小，所需功率越小），此中转站应建在何处？请说明理由．（08江苏连云港25题解析）25．解：（1）如图所示： ················································· 4分A AB BCC 80100（第25题图1）E F（第25题图2）C（第25题答图1）（注：正确画出1个图得2分，无作图痕迹或痕迹不正确不得分）（2）若三角形为锐角三角形，则其最小覆盖圆为其外接圆； ·································· 6分若三角形为直角或钝角三角形，则其最小覆盖圆是以三角形最长边（直角或钝角所对的边）为直径的圆．········································································································· 8分（3）此中转站应建在EFH △的外接圆圆心处（线段E F 的垂直平分线与线段E H 的垂直平分线的交点处）． ···················································· 10分理由如下：由47.835.182.9HEF HEG GEF ∠=∠+∠=+=50.0EHF ∠=，47.1EFH ∠=，故EFH △是锐角三角形，所以其最小覆盖圆为EFH △的外接圆，设此外接圆为O ，直线E G 与O 交于点E M ，，则50.053.8EMF EHF EGF ∠=∠=<=∠ ．故点G 在O 内，从而O 也是四边形E F G H 的最小覆盖圆．所以中转站建在EFH △的外接圆圆心处，能够符合题中要求． ·················································································· 12分16（08江苏南京）28．（10分）一列快车从甲地驶往乙地，一列慢车从乙地驶往甲地，两车同时出发，设慢车行驶的时间为(h )x ，两车之间的距离．．．．．．．为(km )y ，图中的折线表示y 与x 之间的函数关系．根据图象进行以下探究：信息读取（1）甲、乙两地之间的距离为 km ；（2）请解释图中点B 的实际意义；图象理解（3）求慢车和快车的速度；（4）求线段B C 所表示的y 与x 之间的函数关系式，并写出自变量x 的取值范围；问题解决（5）若第二列快车也从甲地出发驶往乙地，速度与第一列快车相同．在第一列快车与慢车相遇30分钟后，第二列快车与慢车相遇．求第二列快车比第一列快车晚出发多少小时？（08江苏南京28题解析）28．（本题10分）解：（1）900； ········································································································ 1分（2）图中点B 的实际意义是：当慢车行驶4h 时，慢车和快车相遇． ····················· 2分（3）由图象可知，慢车12h 行驶的路程为900km ，F（第25题答图2）（第28题）y所以慢车的速度为90075(km /h )12=； ··································································· 3分当慢车行驶4h 时，慢车和快车相遇，两车行驶的路程之和为900km ，所以慢车和快车行驶的速度之和为900225(km /h )4=，所以快车的速度为150km/h ． ·························· 4分（4）根据题意，快车行驶900km 到达乙地，所以快车行驶9006(h )150=到达乙地，此时两车之间的距离为675450(km )⨯=，所以点C 的坐标为(6450)，．设线段B C 所表示的y 与x 之间的函数关系式为y kx b =+，把(40)，，(6450)，代入得044506.k b k b =+⎧⎨=+⎩，解得225900.k b =⎧⎨=-⎩，所以，线段B C 所表示的y 与x 之间的函数关系式为225900y x =-． ·················· 6分自变量x 的取值范围是46x ≤≤． ······································································· 7分（5）慢车与第一列快车相遇30分钟后与第二列快车相遇，此时，慢车的行驶时间是4.5h ．把 4.5x =代入225900y x =-，得112.5y =．此时，慢车与第一列快车之间的距离等于两列快车之间的距离是112.5km ，所以两列快车出发的间隔时间是112.51500.75(h )÷=，即第二列快车比第一列快车晚出发0.75h ．10分 17.（08江苏南通）（第28题14分）28．已知双曲线k y x=与直线14y x=相交于A 、B 两点．第一象限上的点M （m ，n ）（在A 点左侧）是双曲线k y x=上的动点．过点B 作BD ∥y轴交x 轴于点D ．过N （0，－n ）作NC ∥x 轴交双曲线k y x=于点E ，交BD 于点C ．（1）若点D 坐标是（－8，0），求A 、B 两点坐标及k 的值．（2）若B 是CD 的中点，四边形OBCE 的面积为4，求直线CM 的解析式．（3）设直线AM 、BM 分别与y 轴相交于P 、Q 两点，且MA =pMP ，MB =qMQ ，求p －q 的值．（08江苏南通28题解析）28．解：（1）∵D （－8，0），∴B 点的横坐标为－8，代入14y x=中，得y =－2．∴B 点坐标为（－8，－2）．而A 、B 两点关于原点对称，∴A （8，2）．从而8216k =⨯=．……………………3分（2）∵N （0，－n ），B 是CD 的中点，A 、B 、M 、E 四点均在双曲线上，∴m n k =，B （－2m ，－2n ），C （－2m ，－n ），E （－m ，－n ）． ……4分S 矩形DCNO 22m n k ==，S △DBO =1122m n k=，S △OEN =1122m n k=， …………7分∴S 四边形OBCE = S 矩形DCNO －S △DBO － S △OEN =k ．∴4k =． ……………………8分由直线14y x=及双曲线4y x=，得A （4，1），B （－4，－1），∴C （－4，－2），M （2，2）．………………………………………………9分设直线CM 的解析式是y ax b =+，由C 、M 两点在这条直线上，得42,2 2.a b a b -+=-⎧⎨+=⎩ 解得23a b ==． ∴直线CM 的解析式是2233y x =+．………………………………………11分（3）如图，分别作AA 1⊥x 轴，MM 1⊥x 轴，垂足分别为A 1、M 1．设A 点的横坐标为a ，则B 点的横坐标为－a111A M M A a m p M PM Om-===．同理M B m a q M Qm+==，…………13分∴2a m m a p q mm-+-=-=-．……………14分18.（08江苏宿迁）27．（本题满分12分）（第28题）如图，⊙O 的半径为1，正方形ABCD 顶点B 坐标为)0,5(，顶点D 在⊙O 上运动．(1)当点D 运动到与点A 、O 在同一条直线上时,试证明直线CD 与⊙O 相切；(2)当直线CD 与⊙O 相切时，求CD 所在直线对应的函数关系式；(3)设点D 的横坐标为x ，正方形ABCD 的面积为S ，求S 与x 之间的函数关系式，并求出S 的最大值与最小值．（08江苏宿迁27题解析）27．解：(1) ∵四边形ABCD 为正方形 ∴CD AD ⊥ ∵A 、O 、D 在同一条直线上 ∴︒=∠90ODC ∴直线CD 与⊙O 相切； (2)直线CD 与⊙O 相切分两种情况: ①如图1, 设1D 点在第二象限时,过1D 作x E D ⊥11轴于点1E ,设此时的正方形的边长为a ,则2225)1(=+-a a ,解得4=a 或3-=a (舍去)．由BOA Rt ∆∽11OE D Rt ∆ 得OBOD BAE D OAOE 1111==∴54,53111==E D OE ∴)54,53(1-D ，故直线OD 的函数关系式为x y 34-=；②如图2, 设2D 点在第四象限时,过2D 作x E D ⊥22轴于点2E ,设此时的正方第27题第27题图1形的边长为b ,则2225)1(=++b b ,解得3=b 或4-=b (舍去)．由BOA Rt ∆∽22OE D Rt ∆ 得OBOD BAE D OAOE 2222==∴53,54222==E D OE∴)53,54(2-D ，故直线OD 的函数关系式为x y 43-=.(3)设),(0y x D ,则201x y -±=,由)0,5(B 得x x x DB 1026)1()5(22-=-+-=∴x x BDS 513)1026(21212-=-==∵11≤≤-x∴851318513=-==+=最小值最大值，S S .（08江苏泰州29题解析）九、（本题满分14分）20.（08江苏无锡）27．（本小题满分10分）如图，已知点A 从(10)，出发，以1个单位长度/秒的速度沿x 轴向正方向运动，以O A ，为顶点作菱形O A B C ，使点B C ，在第一象限内，且60AOC ∠=；以(03)P ，为圆心，P C 为半径作圆．设点A 运动了t 秒，求：（1）点C 的坐标（用含t 的代数式表示）；（2）当点A 在运动过程中，所有使P 与菱形O A B C 的边所在直线相切的t 的值．（08江苏无锡27题解析）27．解：（1）过C 作C D x ⊥轴于D ，1O A t =+ ，1O C t ∴=+，1cos 602t O D O C +∴==，sin 602D C O C ==，∴点C 的坐标为1)22t t ⎛⎫++ ⎪ ⎪⎝⎭，． ········ （2分）（2）①当P 与O C 相切时（如图1），切点为C ，此时P C O C ⊥，cos 30OC OP ∴=，132t ∴+=，12t ∴=． ············· （4分） ②当P 与O A ，即与x 轴相切时（如图2），则切点为O ，P C O P =，过P 作PE O C ⊥于E ，则12O E O C =，······················································· （5分）1cos 3022t O P +∴==，1t ∴=-． ················································ （7分）③当P 与A B 所在直线相切时（如图3），设切点为F ，P F 交O C 于G ，则PF O C ⊥，2FG C D ∴==，sin 302PC PF O P ∴==+． ·························································· （8分）过C 作CH y ⊥轴于H ，则222PH CH PC +=，2221)3)32222t t t ⎛⎫⎛⎫+++⎛⎫∴+-=+⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，化简，得2(1)1)270t t +-++=，解得1t +=±，10t =-< ，xx1t ∴=．∴所求t12，1和1． ···································（10分）21.（08江苏无锡）28．（本小题满分8分）一种电讯信号转发装置的发射直径为31km ．现要求：在一边长为30km 的正方形城区选择若干个安装点，每个点安装一个这种转发装置，使这些装置转发的信号能完全覆盖这个城市．问：（1）能否找到这样的4个安装点，使得这些点安装了这种转发装置后能达到预设的要求？（2）至少需要选择多少个安装点，才能使这些点安装了这种转发装置后达到预设的要求？答题要求：请你在解答时，画出必要的示意图，并用必要的计算、推理和文字来说明你的理由．（下面给出了几个边长为30km 的正方形城区示意图，供解题时选用）（08江苏无锡28题解析）28．解：（1）将图1中的正方形等分成如图的四个小正方形，将这4个转发装置安装在这4个小正方形对角线的交点处，此时，每个小正方形的对角线长为1312=< ，每个转发装置都能完全覆盖一个小正方形区域，故安装4个这种装置可以达到预设的要求．···························································································（3分）（图案设计不唯一）（2）将原正方形分割成如图2中的3个矩形，使得BE D G C G ==．将每个装置安装在这些矩形的对角线交点处，设A E x =，则30E D x =-，15D H =．由BE D G =，得22223015(30)x x +=+-，22515604x ∴==，30.231BE ∴=≈<，即如此安装3个这种转发装置，也能达到预设要求． ······································· （6分）或：将原正方形分割成如图2中的3个矩形，使得31B E =，H 是C D 的中点，将每个图1 图2 图3 图4装置安装在这些矩形的对角线交点处，则AE ==，30D E =-，26.831DE ∴=<，即如此安装三个这个转发装置，能达到预设要求．······················································································································· （6分）要用两个圆覆盖一个正方形，则一个圆至少要经过正方形相邻两个顶点．如图3，用一个直径为31的O 去覆盖边长为30的正方形A B C D ，设O 经过A B ，，O 与A D 交于E ，连B E ，则1152A E A D ==<=，这说明用两个直径都为31的圆不能完全覆盖正方形A B C D ．所以，至少要安装3个这种转发装置，才能达到预设要求．····························· （8分）评分说明：示意图（图1、图2、图3）每个图1分．22.（08江苏徐州）（本题答案暂缺）28.如图1，一副直角三角板满足AB ＝BC ，AC ＝DE ，∠ABC ＝∠DEF ＝90°，∠EDF ＝30°【操作】将三角板DEF 的直角顶点E 放置于三角板ABC 的斜边AC 上，再将三角板．．．．DEF ．．．绕点．．E ．旋转．．，并使边DE 与边AB 交于点P ，边EF 与边BC 于点Q 【探究一】在旋转过程中，（1）如图2，当C E 1E A ＝时，EP 与EQ 满足怎样的数量关系？并给出证明.（2）如图3，当C E 2E A＝时EP 与EQ 满足怎样的数量关系？，并说明理由.（3）根据你对（1）、（2）的探究结果，试写出当C E E A＝m 时，EP 与EQ 满足的数量关系式为_________,其中m 的取值范围是_______(直接写出结论，不必证明)【探究二】若，AC ＝30cm ，连续PQ ，设△EPQ 的面积为S(cm 2)，在旋转过程中：（1） S 是否存在最大值或最小值？若存在，求出最大值或最小值，若不存在，说明理由. （2）随着S 取不同的值，对应△EPQ 的个数有哪些变化？不出相应S 值的取值范围.AD CB图1BF D A E H O 图2图3FA(D)EAPEA23.（08江苏盐城）（本题答案暂缺）28．（本题满分12分）如图甲，在△ABC 中，∠ACB 为锐角．点D 为射线BC 上一动点，连接AD ，以AD 为一边且在AD 的右侧作正方形ADEF ．解答下列问题：（1）如果AB=AC ，∠BAC=90º．①当点D 在线段BC 上时（与点B 不重合），如图乙，线段CF 、BD 之间的位置关系为 ▲ ，数量关系为 ▲ ． ②当点D 在线段BC 的延长线上时，如图丙，①中的结论是否仍然成立，为什么？（2）如果AB≠AC ，∠BAC≠90º，点D 在线段BC 上运动．试探究：当△ABC 满足一个什么条件时，CF ⊥BC （点C 、F 重合除外）？画出相应图形，并说明理由．（画图不写作法）（3）若AC＝BC=3，在（2）的条件下，设正方形ADEF 的边DE 与线段CF相交于点P ，求线段CP 长的最大值．24.（08江苏扬州）（本题答案暂缺）26．（本题满分14分）已知：矩形ABCD 中，AB=1，点M 在对角线AC 上，直线l 过点M 且与AC 垂直，与AD 相交于点E 。

挑战中考数学压轴题1-2

因动点产生的相似三角形问题1、直线113y x =-+分别交x 轴、y 轴于A 、B 两点，△AOB 绕点O 按逆时针方向旋转90°后得到△COD ，抛物线y ＝ax 2＋bx ＋c 经过A 、C 、D 三点． (1) 写出点A 、B 、C 、D 的坐标；(2) 求经过A 、C 、D 三点的抛物线表达式，并求抛物线顶点G 的坐标；(3) 在直线BG 上是否存在点Q ，使得以点A 、B 、Q 为顶点的三角形与△COD 相似？若存在，请求出点Q 的坐标；若不存在，请说明理由．2、Rt △ABC 在直角坐标系内的位置如图1所示，反比例函数(0)ky k x=≠在第一象限内的图像与BC 边交于点D （4，m ），与AB 边交于点E （2，n ），△BDE 的面积为2．（1）求m 与n 的数量关系；（2）当tan ∠A ＝12时，求反比例函数的解析式和直线AB 的表达式；（3）设直线AB 与y 轴交于点F ，点P 在射线FD 上，在（2）的条件下，如果△AEO 与△EFP 相似，求点P 的坐标．图1图13、如图，已知点A (-2，4) 和点B (1，0)都在抛物线22=++上．y mx mx n（1）求m、n；（2）向右平移上述抛物线，记平移后点A的对应点为A′，点B的对应点为B′，若四边形A A′B′B为菱形，求平移后抛物线的表达式；（3）记平移后抛物线的对称轴与直线AB′的交点为C，试在x轴上找一个点D，使得以点B′、C、D为顶点的三角形与△ABC相似．4、如图1，抛物线经过点A(4，0)、B（1，0)、C（0，－2）三点．（1）求此抛物线的解析式；（2）P是抛物线上的一个动点，过P作PM⊥x轴，垂足为M，是否存在点P，使得以A、P、M为顶点的三角形与△OAC相似？若存在，请求出符合条件的点P的坐标；若不存在，请说明理由；（3）在直线AC上方的抛物线是有一点D，使得△DCA的面积最大，求出点D 的坐标．,5、如图1，在直角坐标系xOy 中，设点A （0，t ），点Q （t ，b ）．平移二次函数2tx y -=的图象，得到的抛物线F 满足两个条件：①顶点为Q ；②与x 轴相交于B 、C 两点（∣OB ∣<∣OC ∣），连结A ，B ．（1）是否存在这样的抛物线F ，使得OC OB OA ⋅=2？请你作出判断，并说明理由；（2）如果AQ ∥BC ，且tan ∠ABO ＝23，求抛物线F 对应的二次函数的解析式．因动点产生的等腰三角形问题1、如图1，已知正方形OABC 的边长为2，顶点A 、C 分别在x 、y 轴的正半轴上，M 是BC 的中点．P (0,m )是线段OC 上一动点（C 点除外），直线PM 交AB 的延长线于点D ．（1）求点D 的坐标（用含m 的代数式表示）；（2）当△APD 是等腰三角形时，求m 的值；（3）设过P 、M 、B 三点的抛物线与x 轴正半轴交于点E ，过点O 作直线ME 的垂线，垂足为H （如图2）．当点P 从O 向C 运动时，点H 也随之运动．请直接写出点H 所经过的路长（不必写解答过程）．图1 图22、如图1，已知一次函数y ＝－x ＋7与正比例函数43y x 的图象交于点A ，且与x 轴交于点B ．（1）求点A 和点B 的坐标；（2）过点A 作AC ⊥y 轴于点C ，过点B 作直线l //y 轴．动点P 从点O 出发，以每秒1个单位长的速度，沿O —C —A 的路线向点A 运动；同时直线l 从点B 出发，以相同速度向左平移，在平移过程中，直线l 交x 轴于点R ，交线段BA 或线段AO 于点Q ．当点P 到达点A 时，点P 和直线l 都停止运动．在运动过程中，设动点P 运动的时间为t 秒．①当t 为何值时，以A 、P 、R 为顶点的三角形的面积为8？②是否存在以A 、P 、Q 为顶点的三角形是等腰三角形？若存在，求t 的值；若不存在，请说明理由．3、如图1，在直角坐标平面内有点A (6, 0)，B (0, 8)，C (－4, 0)，点M 、N 分别为线段AC 和射线AB 上的动点，点M 以2个单位长度/秒的速度自C 向A 方向作匀速运动，点N 以5个单位长度/秒的速度自A 向B 方向作匀速运动，MN 交OB 于点P ．(1)求证：MN ∶NP 为定值；(2)若△BNP 与△MNA 相似，求CM 的长； (3)若△BNP 是等腰三角形，求CM 的长．图14、如图1，在矩形ABCD 中，AB ＝m （m 是大于0的常数），BC ＝8，E 为线段BC 上的动点（不与B 、C 重合）．连结DE ，作EF ⊥DE ，EF 与射线BA 交于点F ，设CE ＝x ，BF ＝y ．（1）求y 关于x 的函数关系式；（2）若m ＝8，求x 为何值时，y 的值最大，最大值是多少？（3）若12y m，要使△DEF 为等腰三角形，m 的值应为多少？5、已知：如图1，在平面直角坐标系xOy 中，矩形OABC 的边OA 在y 轴的正半轴上，OC 在x 轴的正半轴上，OA ＝2，OC ＝3，过原点O 作∠AOC 的平分线交AB 于点D ，连接DC ，过点D 作DE ⊥DC ，交OA 于点E ．（1）求过点E 、D 、C 的抛物线的解析式；（2）将∠EDC 绕点D 按顺时针方向旋转后，角的一边与y 轴的正半轴交于点F ，另一边与线段OC 交于点G ．如果DF 与（1）中的抛物线交于另一点M ，点M 的横坐标为56，那么EF ＝2GO 是否成立？若成立，请给予证明；若不成立，请说明理由；（3）对于（2）中的点G ，在位于第一象限内的该抛物线上是否存在点Q ，使得直线GQ 与AB 的交点P 与点C 、G 构成的△PCG 是等腰三角形？若存在，请求出点Q 的坐标；若不存在成立，请说明理由．。

2023年中考数学第二轮高频压轴题：二元一次方程组-试卷

2023年人教版中考数学第二轮高频压轴题：二元一次方程组一、选择题（本大题共10道小题）1. (2022春•博白县期末)下列方程中是二元一次方程的是( )A.x ﹣5＝3B.x 3C.x+y ＝1D.xy ＝3 2. (2022·无锡)方程组⎩⎪⎨⎪⎧x ＋y ＝5，x －y ＝3的解是( ) A.⎩⎪⎨⎪⎧x ＝2，y ＝3 B.⎩⎪⎨⎪⎧x ＝3，y ＝2 C.⎩⎪⎨⎪⎧x ＝4，y ＝1D.⎩⎪⎨⎪⎧x ＝1，y ＝4 3. (2022北京石景山)方程组326x y x y -=⎧⎨+=⎩的解为( ) A.30x y =⎧⎨=⎩ B.03x y =⎧⎨=⎩ C.14x y =⎧⎨=⎩ D.41x y =⎧⎨=⎩4. (2022•嘉兴)用加减消元法解二元一次方程组时,下列方法中无法消元的是( )A.①×2-②B.②×(-3)-①C.①×(-2)+②D.①-②×35. (2022·定海)已知t=x 2-2x+4,x,y 满足⎩⎨⎧+=++=33m y x 1m y -x ,且-1≤y ≤1,则t 的取值范围是( )A.4≤t ≤12B.3≤t ≤12C.3≤t ≤4D.4≤t ≤76. (2022·攀枝花模拟)若方程组⎩⎪⎨⎪⎧3x －y ＝4k －5①2x ＋6y ＝k ② 的解中x ＋y ＝16,则k 等于( ) A.15 B.18 C.16 D.177. (2022•齐齐哈尔)母亲节来临,小明去花店为妈妈准备节日礼物.已知康乃馨每支2元,百合每支3元.小明将30元钱全部用于购买这两种花(两种花都买),小明的购买方案共有( )A.3种B.4种C.5种D.6种8. (2022·新疆生产建设兵团中考)某校举行篮球赛,每场比赛都要分出胜负,每队胜一场得2分,负一场得1分.八年级一班在16场比赛中得26分.设该班胜x 场,负y 场,则根据题意,下列方程组中正确的是( )A.⎩⎪⎨⎪⎧x ＋y ＝26x ＋2y ＝16B.⎩⎪⎨⎪⎧x ＋y ＝262x ＋y ＝16C.⎩⎪⎨⎪⎧x ＋y ＝16x ＋2y ＝26D.⎩⎪⎨⎪⎧x ＋y ＝162x ＋y ＝26 9. (2022•黑龙江)在抗击疫情网络知识竞赛中,为奖励成绩突出的学生,学校计划用200元钱购买A 、B 、C 三种奖品,A 种每个10元,B 种每个20元,C 种每个30元,在C 种奖品不超过两个且钱全部用完的情况下,有多少种购买方案( )A.12种B.15种C.16种D.14种10. (2022·湖北武汉)在平面直角坐标系中,我们把横纵坐标均为整数的点称为格点,若一个多边形的顶点全是格点,则称该多边形为格点多边形.例如:图中△ABC 的与四边形DEFG 均为格点多边形.格点多边形的面积记为S,其内部的格点数记为N,边界上的格点记为L,已知格点多边形的面积可表示为S=N+aL+B(a,b 为常数),若某格点多边形对应的N=14,L=7,则S=( )A.16.5B.17C.17.5D.18二、填空题（本大题共8道小题）11. (2022•南京)已知x 、y 满足方程组,则x+y 的值为______.12. (2022·贵州·仁怀市教育研究室二模)若x,y 满足二元一次方程组521122x y x y +=⎧⎨-=⎩,则x+y 的值为______.13. (2022·绍兴中考)我国明代数学读本《算法统宗》有一道题,其题意为:客人一起分银子,若每人7两,还剩4两；若每人9两,则差8两.银子共有____两.14. (2022•北京模拟)我国古代数学名著《孙子算经》中记载了一道题,大意是:100匹马恰好拉了100片瓦,已知3匹小马能拉1片瓦,1匹大马能拉3片瓦,求小马、大马各有多少匹.若设小马有x 匹,大马有y 匹,依题意,可列方程组为__________.15. (2022•无锡)我国古代问题:以绳测井,若将绳三折测之,绳多四尺,若将绳四折测之,绳多一尺,井深几何？这段话的意思是:用绳子量井深,把绳三折来量,井外余绳四尺,把绳四折来量,井外余绳一尺,井深几尺？则该问题的井深是尺.16. (2022·大庆)某酒店客房都有三人间普通客房,双人间普通客房,收费标准为:三人间150元/间,双人间140元/间.为吸引游客,酒店实行团体入住五折优惠措施,一个46人的旅游团,优惠期间到该酒店入住,住了一些三人间普通客房和双人间普通客房,若每间客房正好住满,且一天共花去住宿费1310元,则该旅游团住了三人间普通客房和双人间普通客房共____间.17. (2022•岳阳)我国古代数学名著《九章算术》上有这样一个问题:“今有醇酒一斗,直钱五十;行酒一斗,直钱一十.今将钱三十,得酒二斗.问醇、行酒各得几何？”其大意是:今有醇酒(优质酒)1斗,价值50钱;行酒(劣质酒)1斗,价值10钱.现用30钱,买得2斗酒.问醇酒、行酒各能买得多少？设醇酒为x 斗,行酒为y 斗,根据题意,可列方程组为 .18. (2022•重庆)火锅是重庆的一张名片,深受广大市民的喜爱.重庆某火锅店采取堂食、外卖、店外摆摊(简称摆摊)三种方式经营,6月份该火锅店堂食、外卖、摆摊三种方式的营业额之比为3:5:2.随着促进消费政策的出台,该火锅店老板预计7月份总营业额会增加,其中摆摊增加的营业额占总增加的营业额的则摆摊的营业额将达到7月份总营业额的为使堂食、外卖7月份的营业额之比为8:5,则7月份外卖还需增加的营业额与7月份总营业额之比是 .三、解答题（本大题共6道小题）19. (2022·扬州)已知方程组⎩⎪⎨⎪⎧2x ＋y ＝7，x ＝y －1的解也是关于x,y 的方程ax ＋y ＝4的一个解,求a 的值.20. (2022秋•建平县期末)列二元一次方程组解应用题:某大型超市投入15000元资金购进A 、B 两种品牌的矿泉水共600箱,矿泉水的成本价和销售价如下表所示:(1)该大型超市购进A 、B 品牌矿泉水各多少箱?(2)全部销售完600箱矿泉水,该超市共获得多少利润?21. (2022秋•铁西区期末)列二元一次方程组解应用题:小颖家离学校1880米,其中有一段为上坡路,另一段为下坡路.她跑步去学校共用了16分钟,已知小颖在上坡路上的平均速度是80米/分钟,在下坡路上的平均速度是200米/分钟.求小颖上坡、下坡各用了多长时间？22. (2022秋•普宁市期末)某超市对甲、乙两种商品进行打折销售,其中甲种商品打八折,乙种商品打七五折,已知打折前,买6件甲种商品和3件乙种商品需600元;打折后,买50件甲种商品和40件乙种商品需5200元.(1)打折前甲、乙两种商品每件分别为多少元?(2)某人购买甲种商品80件,乙种商品100件,问打折后购买这些商品比不打折可节省多少元?23. (2022•江西)放学后,小贤和小艺来到学校附近的地摊上购买一种特殊型号的笔芯和卡通笔记本,这种笔芯每盒10支,如果整盒买比单支买每支可优惠0.5元.小贤要买3支笔芯,2本笔记本需花费19元;小艺要买7支笔芯,1本笔记本需花费26元.(1)求笔记本的单价和单独购买一支笔芯的价格;(2)小贤和小艺都还想再买一件单价为3元的小工艺品,但如果他们各自为要买的文具付款后,只有小贤还剩2元钱.他们要怎样做才能既买到各自的文具,又都买到小工艺品,请通过运算说明.24. (2022•扬州)阅读感悟:有些关于方程组的问题,欲求的结果不是每一个未知数的值,而是关于未知数的代数式的值,如以下问题:已知实数x、y满足3x﹣y＝5①,2x+3y＝7②,求x﹣4y和7x+5y的值.本题常规思路是将①②两式联立组成方程组,解得x、y的值再代入欲求值的代数式得到答案,常规思路运算量比较大.其实,仔细观察两个方程未知数的系数之间的关系,本题还可以通过适当变形整体求得代数式的值,如由①﹣②可得x﹣4y＝﹣2,由①+②×2可得7x+5y＝19.这样的解题思想就是通常所说的“整体思想”.解决问题:(1)已知二元一次方程组则x﹣y＝,x+y＝;(2)某班级组织活动购买小奖品,买20支铅笔、3块橡皮、2本日记本共需32元,买39支铅笔、5块橡皮、3本日记本共需58元,则购买5支铅笔、5块橡皮、5本日记本共需多少元？(3)对于实数x、y,定义新运算:x*y＝ax+by+c,其中a、b、c是常数,等式右边是通常的加法和乘法运算.已知3*5＝15,4*7＝28,那么1*1＝.。

2020年九年级中考数学压轴题专题训练二次函数含答案.docx

2020年九年级中考数学压轴题专题训练二次函数一、选择题（本大题共7道小题）1.己知二次函数y=x2+bx+c与x轴只有一个交点，且图象过，加）、B（Xi+n，m）两点，则加、"的关系为（）1 1 1 , 1 ,A.加=B.加=才〃C.加=D.加=玄〃2.下列函数中，满足y的值随x的值增大而增大的是（）1 °A. y= ~2xB. y=3x~ 1C. y=~D. y=x'3.下列说法正确的是（）A.抛物线的开口向下B.当x> —3时，y随x的增大而增大C.二次函数的最小值是一2D.抛物线的对称轴是x=~l4.已知二次函数y=a.x5 6+bx+c的图象如图所示，则下列结论正确的个数为（）A-2 / -1 Ho 1\①c>0；②a<b<0；③2b+c>0；④当x>—时，y随x的增大而减小.A. 1个B.2个C. 3个D.4个5 点Pi（-1，力），P2（3，y2） ' P3（5，旳）均在二次函数-x2+2x+c的图象上，则”，y2 9旳的大小关系是（）A.旳〉y2>y\B.旳> 旳=旳C.刃>力>旳D.刃=力>旳6 二次函数y=ax1+bx+c（a，b，c为常数且°主0）的图象如图所示，则一次函数y=ax7.若二次函数y=x2+nu的对称轴是x=3 >则关于x的方程?+/^=7的解为()A.兀1=0、兀2=6B.兀1 = 1、兀2=7C.兀i =］，兀2=_7D.兀i = —1，兀2=7二' 填空题(本大题共6道小题)&己知A(0 ‘ 3)，B(2 ‘ 3)是抛物线y=—F+加+c上两点‘该抛物线的顶点坐标是9. _____________________________________________ 如图，抛物线y=c/ + i>x+c与x 轴相交于点A > B(m+2 > 0) 1与y轴相交于点C > 点D在该抛物线上'坐标为(m > c)'则点A的坐标是_____________________________________________________ .10.某农场拟建三间长方形种牛饲养室，饲养室的一面靠墙(墙长50 m)，中间用两道墙隔开(如图).己知计划中的建筑材料可建墙的总长度为48 m，则这三间长方形种牛饲养室的总占地面积的最大值为.11.已知二次函数y=3.r+c 与正比例函数y=4x的图象只有一个交点‘则c的值为X-2 — 1.5 -1 —0.5 0 0.5 1 1.5 2 ・・•y 2 0.75 0 -0.25 0 -0.25 0 m 213.如图，抛物线H+2X+3与y轴交于点C，点D(0，1)，点P在抛物线上，且△ PCD是以CD为底的等腰三角形，则点P的坐标为___________ .三' 解答题(本大题共4道小题)14.凯里市某文具店某种型号的计算器每只进价12元，售价20元，多买优惠，优惠方法是：凡是一次买10只以上的，每多买一只，所买的全部计算器每只就降价0.1元，例如：某人买18只计算器，于是每只降价0.1X(18 —10)=0.8(元)，因此所买的18只计算器都按每只19.2元的价格购买，但是每只计算器的最低售价为16元.(1)求一次至少购买多少只计算器，才能以最低售价买？(2)写岀该文具店一次销售x(x>10)只时，所获利润y(元)与x(只)之间的函数关系式，并写出自变量尢的取值范围；(3)—天，甲顾客购买了46只，乙顾客购买了50只，店主发现卖46只赚的钱反而比卖50只赚的钱多，请你说明发生这一现象的原因；当10V150时，为了获得最大利润，店家一次应卖多少只？这时的售价是多少？15.如图，抛物线cix2+2ax+1与x轴仅有一个公共点A >经过点A的直线交该抛物线于点交y轴于点C，且点C是线段AB的中点.(1)求这条抛物线对应的函数解析式；(2)求直线AB对应的函数解析式.16.如图，抛物线y=$ + bx+c与x轴交于A(-l，0) ' B(3，0)两点，顶点M关于x轴的对称点是M'.(1)求抛物线的解析式；(2)若直线AM，与此抛物线的另一个交点为C ‘求4 CAB的面积；(3) 是否存在过A 、B 两点的抛物线，其顶点P 关于x 轴的对称点为Q ，使得四边形APBQ 为正方形？若存在，求出此抛物线的解析式；若不存在，请说明理由.17.如图 > 已知抛物线y=x 1— (m+3')x+9的顶点C 在x 轴正半轴上，一次函数y=x+3 与抛物线交于A 、B 两点，与x 、y 轴分别交于D 、E 两点.⑴求"2的值；(2) 求A 、B 两点的坐标；(3) 点P(a /)( —3<a<l)是抛物线上一点，当△ PAB 的面积是△ ABC 面积的2倍时，求“、b 的值.答案b=-|n|-2xi, .*.c=— ~ =1»1 +4|n|xi+4xi ,.，人匕］,m)在 y=x?+bx+c 上，.I m=x?+bxi+c > m=x?+(—|n|—2xi)- xi +回 + 網xi+例,化简整理得 m =i n2 ,故选D.2. 【答案】B 【解析】一次函数y =—2x 中，y 随x 增大而减小；一次函数y=3x —1 中，y 随一、选择题(本大题共7道小题)1.【答案】D 【解析】因为二次函数y=x 2+bx+c 的图象与x —4c=0 '即C =Y ，由题意知，点A ，B 关于抛物线的对称轴对称，轴只有一个交点， •■•|AB=2 =b-2:.b- ■xi 'x的增大而增大；反比例函数y=|•中，在每一个分支上，y随x的增大而减小；二次函数y=x?中，当x>0时，y随x增大而增大，当x<0时，y随x的增大而减小，故答案为B.3.【答案】D【解析】从表中选取三组值（一4，0），（― 1，0），（0，4），由此设抛物线的解析式为y=G U+4）（A-+1）.将（0，4）代入y=a（x+4）（x+l），求得a=l.：.抛物线的解析式为y=x+5x+4 '即j=（x+|）2—由此可见 ' 只有选项D中的说法是正确的.4.【答案】C【解析】•••抛物线与y轴交点在正半轴，••,>（），故①正确；抛物线开口向下，.•.“<（），对称轴在y轴左侧，，血同号，.•』<0.由图象知，二次函数图象经过点（1，0），.•.d+b+c=0 ? c= —a—b，又4a—2b+cV0 j»\4a—2b—a—b<0 f .*.3a—3b VO 5 .*.«—b<0，故②正确；V^+/?+c=O，•: a= —c—b 5 4a—2b+cV0，・；一. A4c—4/?—2b+cV0，・；一6Z?—3cV0 5 /.2/?+c>0，故③正确；丁― IV—不VO，若对称轴兀h 1=—石〉一㊁时5y随兀增大不一定减小，故④不正确.5.【答案】D【解析】此类题利用图象法比较大小更直观简单.容易求出二次函数y = -x+2x+c 图象的对称轴为直线x=l ‘可画草图如解图：由解图知，Pi（-1，刃），P2（3，力）关于直线x=l对称，P3（5，旳）在图象的右下方部分上，因此，刃=力>旳・6.【答案】C【解析】抛物线开口向上，所以a>0，对称轴在y轴右侧，所以a、b 异号，所以b<0，抛物线与y轴交于负半轴5所以c<0，所以直线y=ax+b过第一、三、四象限，反比例函数立于第二、四象限，故答案为C.7.【答案】D【解析】•.•二次函数y=x2+mx的对称轴为,r=-y=3 >解得心一6，则关于X的方程为.r —6.¥=7 >解得> .¥1 = — 1 ' .¥2 = 7.二、填空题（本大题共6道小题）8.【答案】（1，4）【解析］VA（O，3）、B（2，3），两点纵坐标相同，.・.A、B两点关于直线x=l对称，.•.抛物线的对称轴是直线x=l >即—2x （^1） =1 '解得b = 2，［当x =0 时，y=3 > /.c = 3，抛物线的解析式为y= —x?+2x+3，当x = l 时，y = —x?+2x+ 3 = -l2+2xl + 3=4，.I 抛物线的顶点坐标是（1 ‘ 4）.9.【答案】（-2，0）【解析】如解图，过D作DM±x轴于点M - :.M（m，0），又B（m+2，0） - .-.MB = 2，由C（0，c），D（m，c）知：OC=DM，即点C、D 关于对称轴对称，故点O、M也关于对称轴对称，.・.OA=MB=2，...AC —2，0）.10.【答案】144【解析】T围墙的总长为50 m?设3间饲养室合计长x m»则饲养室48——x48——x 1 1的宽=——m，・••总占地面积为y=x・一—=—/?+12x（0VxV48），由y=—Q'+IQX =-|（X-24）2+144 ' Vx=24 在0 Vx<48 范围内，a=-|<0，.•.在0 Vx《24 范围内，丫随x的增大而增大-.'.x=24时，y取得最大值，y **=144 m.411.【答案】扌【解析】本题考查了己知二次函数的图象与一次函数的图象的交点个数，求字母未知数的值.把y=3x2+c与y=4x联立方程组并消去y得3x2+c=4x，化简得3x2 -4x+c=0，由于它们的图象只有一个交点，故此方程有两个相等的实数根，所以b2-4ac =（—4）2—4x3c=0，解得c=|.12.【答案】0.75【解析】根据表格可得该图象关于y轴对称，故当x=1.5和x=-1.5 时1 y 的值相等..".m=0.75.13.【答案】（1+迈，2）或（1—迈，2）【解析】抛物线y =-X2+2X+3与y轴交于点C，则点C坐标是（0，3），［点D（0，1），点P在抛物线上，且4 PCD是以CD 为底的等腰三角形，・••易得点P的纵坐标是2 5当y=2时，二一x?+2x+3=2，则x2—2x— 1 =0，解得方程的两根是x=2，・••点P的坐标是（1+迈，2）或（1 一迈，2）.三、解答题（本大题共4道小题）14.【答案】解：⑴设一次至少买X只计算器，才能以最低售价购买，则每只降价为：O.I(X-IO)元，由题意得，20-0.1(x-10)=16，解得x=50.答：一次至少购买50只计算器，才能以最低售价购买.(2分)【一题多解】设一次购买x只计算器1才能以最低售价购买 ' 则每只降低为：0.1(x —10)元，由题意得，20-0.1(x-10)<16 > 解得xV50，.•.最大整数x=50.答：一次至少购买50只计算器，才能以最低售价购买.(2)由题意得 > 当10<x<50 时'y=[20—12—0.1(x—10)]x >即y=—0.1X2+9X(3分)当x>50时，则每只计算器都按16元销售..".y= 16x— 12x=4x ‘—0.1x+x (10<x<50)综上可得y=•(5 分)4x (x>50)h Q(3)由y =-0.1X2+9X得，其图象的对称轴为x=—石=—2x(_。

2024年中考数学高频压轴题训练——二次函数压轴题(角度问题)(含答案)

2024年中考数学高频压轴题训练——二次函数压轴题（角度问题）（1）求抛物线的解析式；（2）抛物线上是否存在点，使P存在，请说明理由．(1)求该抛物线的函数表达式；(2)在直线上是否存在点，使说明理由．(3)为第一象限内抛物线上的一个动点，且在直线，垂足为，以点为圆心，，且不经过点l C P PM l ⊥M M 2PAB PT S =V M e (4．如图，已知顶点为的抛物线与x 轴交于A ，B 两点，且．(1)求点B 的坐标；(2)求二次函数的解析式；(3)作直线，问抛物线上是否存在点M ，使得，若存在，求出点M 的坐标；若不存在，请说明理由．5．如图，抛物线与x 轴交于A 、B 两点，，，与y 轴交于点C ，连接．()0,6C -()20y ax b a =+≠OC OB =()20y ax b a =+≠CB ()20y ax b a =+≠15MCB ∠=︒24y ax bx =+-()2,0A -()8,0B AC BC 、(1)求抛物线的解析式；(2)求证：；(3)点P 在抛物线上，且，求点P的坐标．6．如图，在平面直角坐标系中，已知抛物线与x 轴交于、两点，与y 轴交于点C ，连接．(1)求抛物线的解析式；(2)在对称轴上是否存在一点M ，使，若存在，请求出点M 的坐标；若不存在，请说明理由；(3)若点P 是直线下方的抛物线上的一个动点，作于点D ，当的值最大时，求此时点P 的坐标及的最大值．∠=∠ACO ABC PCB ACO ∠=∠()230y ax bx a =+-≠()3,0A ()1,0B -AC MCA MAC ∠=∠AC PD AC ⊥PD PD(1)试求抛物线的解析式；(2)点P 是直线下方抛物线上一动点，当的面积最大时，求点P 的坐标；(3)若M 是抛物线上一点，且，请直接写出点M 的坐标．BC BCP V MCB ABC ∠=∠(1)求此抛物线的解析式；(2)点E 是AC 延长线上一点，的平分线CD 交⊙于点D ，连接BD ，求点D 的坐标；(3)在（2）的条件下，抛物线上是否存在点P ，使得？如果存在，请求出点P 的坐标；如果不存在，请说明理由．9．综合与实践：如图，抛物线与x 轴交于点和点，与y 轴交于点C ，连接，点D 在抛物线上．(1)求抛物线的解析式；(2)小明探究点D 位置时发现：如图1，点D 在第一象限内的抛物线上，连接，，面积存在最大值，请帮助小明求出面积的最大值；(3)小明进一步探究点D 位置时发现：点D 在抛物线上移动，连接，存在BCE ∠O 'PDB CBD ∠=∠22y ax bx =++()1,0A -()4,0B BC BD CD BCD △BCD △CD(1)求抛物线的解析式．(2)如图1，过点D 作轴，垂足为M ，点P 在直线P 作，，求的最大值，以及此时点(3)将原抛物线沿射线方向平移个单位长度，在平移后的抛物线上存在点得，请写出所有符合条件的点G 的横坐标，并写出其中一个的求解过DM x ⊥PE AD ⊥PF DM ⊥2PE PF +CA 5245CAG ∠=︒(1)填空：___________，___________；(2)点为直线上方抛物线上一动点．①连接、，设直线交线段于点，求的最大值；②过点作于点，连接，是否存在点，使得中的，若存在，求出点的坐标；若不存在，请说明理由．(1)求抛物线的解析式；b =c =D AC BC CD BD AC E DE EBD DF AC ⊥F CD D CDF V 2DCF BAC ∠=∠D(1)求抛物线的解析式；(2)抛物线上是否存在点D ，使得？若存在，求出所有点不存在，请说明理由；(3)如图2，点E 是点B 关于抛物线对称轴的对称点，点F 是直线OB 动点，EF 与直线OB 交于点G ．设和的面积分别为值．DOB OBC ∠=∠BFG V BEG V S14．如图，在平面直角坐标系中，点为坐标原点，抛物线与轴交于、两点且点，，与轴的负半轴交于点，．(1)求此抛物线的解析式；(2)在(1)的条件下，连接，点为直线下方的抛物线上的一点，过点作交于点，交直线于点，若，求点的坐标．(3)在(1)的条件下，点为该抛物线的顶点，过点作轴的平行线交抛物线于另一点，过点作于点，该抛物线对称轴右侧的抛物线上有一点，连接交于点，当时，求的度数．15．已知抛物线与轴相交于点，，与轴相交于点．O 2y x bx c =++x A B (3B 0)y C OB OC =AC P BC P PQ AC ∥AB Q BC D PD DQ =P D C x R R RH AB ⊥H M DM RH Q 2MQ RQ =MQH ∠24y ax bx =++x ()1,0A ()4,0B y C参考答案：的值最大时，此时，。

中考数学压轴题含答案

中考数学压轴题含答案一、选择题1、下列图形中，既是轴对称图形，又是中心对称图形的是（）A.菱形B.平行四边形C.矩形（答案：C）2、如果一个三角形的三条边的平方相等，那么这个三角形一定是（）A.等边三角形B.直角三角形C.等腰三角形D.等腰直角三角形（答案：A）3、下列说法正确的是（）A.所有的质数都是奇数B.所有的偶数都是合数C.一个数的因数一定比它的倍数小D.自然数一定是正数（答案：A）二、填空题1、若a-b=2，a+b=7，则a²-b²=（答案：14）2、我们学过的数有整数和分数，整数的运算律在分数运算中（答案：同样适用）。

3、一个长方形的周长是20cm，长和宽的比是3:2，则长方形的面积是（答案：60平方厘米）。

三、解答题1、一个圆柱体底面半径为r，高为h，它的体积是多少？（答案：πr²h）2、有一块三角形的土地，底边长为120米，高为90米，这块土地的面积是多少？（答案：5400平方米）3、对于一个给定的整数n，如果它是3的倍数，那么我们就称它为“三的倍数”，否则我们就称它为“非三的倍数”。

现在有一个整数n，它是“三的倍数”，我们可以得出哪些结论？（答案：n+1、n+2、n+3、...、2n都是“三的倍数”，因为它们都可以被3整除。

）中考数学压轴题100题及答案在中考数学考试中，压轴题往往是最具挑战性和最能检验考生数学能力的题目。

为了帮助同学们更好地理解和掌握中考数学的压轴题，本文将分享100道经典的中考数学压轴题及其答案。

一、选择题1、在一个等边三角形中，边长为6，下列哪个选项的面积最接近这个等边三角形的面积？A. 20B. 25C. 30D. 35答案：B解析：等边三角形的面积可以通过计算得出，边长为6的等边三角形的面积为：436293约为28.2，因此选项B最接近。

2、如果一个多边形的内角和是外角和的2倍，那么这个多边形的边数是多少？A. 4B. 6C. 8D. 10答案：C解析：根据多边形的内角和公式和外角和为360度，可列出方程求解。

中考数学压轴题及答案(共20题) 2百度文库

一、中考数学压轴题1．在平面直角坐标系中，直线4(0)3y x b b =-+>交x 轴于点A ，交y 轴于点B ，10AB =．（1）如图1，求b 的值；（2）如图2，经过点B 的直线(4)(40)y n x b n =++-<<与直线y nx =交于点C ，与x 轴交于点R ，//CD OA ，交AB 于点D ，设线段CD 长为d ，求d 与n 的函数关系式；（3）如图3，在（2）的条件下，点F 在第四象限，CF 交OA 于点E ，45AEF ∠=︒,点P 在第一象限，PH OA ⊥，点N 在x 轴上，点M 在PH 上，MN 交PE 于点G ，PH EN =，过点E 作EQ CF ⊥，交PH 于点Q ， 32==EQ EF PM ，∠=∠OBR HNM ，BC CR =，点G 的坐标为1927,55⎛⎫ ⎪⎝⎭，连接FN ，求EFN 的面积．2．已知：如图，在平面直角坐标系中，点O 为坐标原点，()2,0C ．直线26y x =+与x 轴交于点A ，交y 轴于点B ．过C 点作直线AB 的垂线，垂足为E ，交y 轴于点D ．（1）求直线CD 的解析式；（2）点G 为y 轴负半轴上一点，连接EG ，过点E 作EH EG ⊥交x 轴于点H ．设点G 的坐标为()0,t ，线段AH 的长为d ．求d 与t 之间的函数关系式（不要求写出自变量的取值范围）（3）过点C 作x 轴的垂线，过点G 作y 轴的垂线，两线交于点M ，过点H 作HN GM ⊥于点N ，交直线CD 于点K ，连接MK ，若MK 平分NMB ∠，求t 的值．3．如图1，抛物线2(0)y ax bx c a =++≠的顶点为C （1，4），交x 轴于A 、B 两点，交y 轴于点D ，其中点B 的坐标为（3，0）．（1）求抛物线的解析式；（2）如图2，点E 是BD 上方抛物线上的一点，连接AE 交DB 于点F ，若AF=2EF ，求出点E 的坐标．（3）如图3，点M 的坐标为（32，0），点P 是对称轴左侧抛物线上的一点，连接MP ，将MP 沿MD 折叠，若点P 恰好落在抛物线的对称轴CE 上，请求出点P 的横坐标．4．如图，在四边形ABCD中，∠B=90°，AD//BC，AD=16，BC=21，CD=13．（1）求直线AD和BC之间的距离；（2）动点P从点B出发，沿射线BC以每秒2个单位长度的速度运动，动点Q从点A出发，在线段AD上以每秒1个单位长度的速度运动，点P、Q同时出发，当点Q运动到点D 时，两点同时停止运动，设运动时间为t秒．试求当t为何值时，以P、Q、D、C为顶点的四边形为平行四边形？（3）在（2）的条件下，是否存在点P，使△PQD为等腰三角形？若存在，请直接写出相应的t值，若不存在，请说明理由．5．如图，AB∥CD，定点E，F分别在直线AB，CD上，平行线AB，CD之间有一动点P．（1）如图1，当P点在EF的左侧时，∠AEP，∠EPF，∠PFC满足数量关系为，如图2，当P点在EF的右侧时，∠AEP，∠EPF，∠PFC满足数量关系为．（2）如图3，当∠EPF＝90°，F P平分∠EFC时，求证：EP平分∠AEF；（3）如图4，QE，QF分别平分∠PEB和∠PFD，且点P在EF左侧．①若∠EPF＝60°，则∠EQF＝．②猜想∠EPF与∠EQF的数量关系，并说明理由；6．定义：如果一个三角形一条边上的高与这条边的比值是3：5，那么称这个三角形为“准黄金”三角形，这条边就叫做这个三角形的“金底”．（概念感知）（1）如图1，在ABC 中，12AC =，10BC =，30ACB ∠=︒，试判断ABC 是否是“准黄金”三角形，请说明理由．（问题探究）（2）如图2，ABC 是“准黄金”三角形，BC 是“金底”，把ABC 沿BC 翻折得到DBC △，连AB 接AD 交BC 的延长线于点E ，若点C 恰好是ABD △的重心，求AB BC的值．（拓展提升）（3）如图3，12l l //，且直线1l 与2l 之间的距离为3，“准黄金”ABC 的“金底”BC 在直线2l 上，点A 在直线1l 上．10AB BC =，若ABC ∠是钝角，将ABC ∠绕点C 按顺时针方向旋转()090αα︒<<︒得到A B C ''，线段A C '交1l 于点D ．①当30α=︒时，则CD =_________；②如图4，当点B 落在直线1l 上时，求AD CD 的值．7．如图①，四边形ABCD 中，//,90AB CD ADC ∠=︒．（1）动点M 从A 出发，以每秒1个单位的速度沿路线A B C D →→→运动到点D 停止，设运动时间为a ，AMD ∆的面积为,S S 关于a 的函数图象如图②所示，求AD CD 、的长．（2）如图③动点P 从点A 出发，以每秒2个单位的速度沿路线A D C →→运动到点C 停止，同时，动点Q 从点C 出发，以每秒5个单位的速度沿路线C D A →→运动到点A 停止，设运动时间为t ，当Q 点运动到AD 边上时，连接CP CQ PQ 、、，当CPQ ∆的面积为8时，求t 的值．8．如图，在菱形ABCD 中，AB a ，60ABC ∠=︒，过点A 作AE BC ⊥，垂足为E ，AF CD ⊥，垂足为F ．（1）连接EF ，用等式表示线段EF 与EC 的数量关系，并说明理由；（2）连接BF ，过点A 作AK BF ⊥，垂足为K ，求BK 的长(用含a 的代数式表示)；（3）延长线段CB 到G ，延长线段DC 到H ，且BG CH =，连接AG ，GH ，AH ． ①判断AGH 的形状，并说明理由； ②若12,(33)2ADH a S ==+，求sin GAB ∠的值．9．∠MON=90°，点A ，B 分别在OM 、ON 上运动（不与点O 重合）．（1）如图①，AE 、BE 分别是∠BAO 和∠ABO 的平分线，随着点A 、点B 的运动，∠AEB= °（2）如图②，若BC 是∠ABN 的平分线，BC 的反向延长线与∠OAB 的平分线交于点D ①若∠BAO=60°，则∠D= °．②随着点A ，B 的运动，∠D 的大小会变吗？如果不会，求∠D 的度数；如果会，请说明理由．（3）如图③，延长MO 至Q ，延长BA 至G ，已知∠BAO ，∠OAG 的平分线与∠BOQ 的平分线及其延长线相交于点E 、F ，在△AEF 中，如果有一个角是另一个角的3倍，求∠ABO 的度数．10．对于平面直角坐标系xOy 中的任意点()P x y ，，如果满足x y a += (x ≥0，a 为常数)，那么我们称这样的点叫做“特征点”．（1）当2≤a ≤3时，①在点(1,2),(1,3),(2.5,0)A B C 中，满足此条件的特征点为__________________；②⊙W 的圆心为(,0)W m ，半径为1，如果⊙W 上始终存在满足条件的特征点，请画出示意图，并直接写出m 的取值范围；（2）已知函数()10Z x x x=+>，请利用特征点求出该函数的最小值．11．问题背景：如图（1），ABC 内接于O ，过点A 作O 的切线l ，在l 上任取一个不同于点A 的点P ，连接PB PC 、，比较BPC ∠与BAC ∠的大小，并说明理由．问题解决：如图（2），A （0，2）、B （0，4），在x 轴正半轴上是否存在一点P ，使得cos APB ∠最小？若存在，求出点P 的坐标；若不存在，请说明理由．拓展应用：如图（3），四边形ABCD 中，//AB CD ，AD CD ⊥于D ，E 是AB 上一点，AE AD =，P 是DE 右侧四边形ABCD 内一点，若8AB =，11CD =，tan 2C =，9DEP S =，求sin APB ∠的最大值．12．注意：为了使同学们更好地解答本题的第（Ⅱ）问，我们提供了一种分析问题的方法，你可以依照这个方法按要求完成本题的解答，也可以选用其他方法，按照解答题的一般要求进行解答即可．如图，将一个矩形纸片ABCD ，放置在平面直角坐标系中，()0,0A ，()4,0B ，()0,3D ，M 是边CD 上一点，将ADM 沿直线AM 折叠，得到ANM ．（Ⅰ）当AN 平分MAB ∠时，求DAM ∠的度数和点M 的坐标；（Ⅱ）连接BN ，当1DM =时，求ABN 的面积；（Ⅲ）当射线BN 交线段CD 于点F 时，求DF 的最大值．（直接写出答案）在研究第（Ⅱ）问时，师生有如下对话：师：我们可以尝试通过加辅助线，构造出直角三角形，寻找方程的思路来解决问题．小明：我是这样想的，延长MN 与x 轴交于P 点，于是出现了Rt NAP △．小雨：我和你想的不一样，我过点N 作y 轴的平行线，出现了两个Rt NAP △．13．如图，在等边△ABC 中，AB =BC =AC =6cm ，点P 从点B 出发，沿B →C 方向以1．5cm/s 的速度运动到点C 停止，同时点Q 从点A 出发，沿A →B 方向以1cm/s 的速度运动，当点P 停止运动时，点Q 也随之停止运动，连接PQ ，过点P 作BC 的垂线，过点Q 作BC 的平行线，两直线相交于点M ．设点P 的运动时间为x （s ），△MPQ 与△ABC 重叠部分的面积为y （cm 2）（规定：线段是面积为0的图形）．（1）当x =（s ）时，PQ ⊥BC ；（2）当点M 落在AC 边上时，x = （s ）；（3）求y 关于x 的函数解析式，并写出自变量x 的取值范围．14．新定义，若关于x ，y 的二元一次方程组①111222a x b y c a x b y c +=⎧⎨+=⎩的解是00x x y y =⎧⎨=⎩，关于x ，y 的二元一次方程组②111222e x f y d e x f y d +=⎧⎨+=⎩的解是11x x y y =⎧⎨=⎩，且满足1000.1x x x -≤，1000.1y y y -≤，则称方程组②的解是方程组①的模糊解．关于x ，y 的二元一次方程组222104x y m x y m +=+⎧⎨-=+⎩的解是方程组10310x y x y +=⎧⎨+=-⎩的模糊解，则m 的取值范围是________． 15．AB 是O 直径，,C D 分别是上下半圆上一点，且弧BC =弧BD ，连接,AC BC ，连接CD 交AB 于E ，（1）如图(1)求证：90AEC ∠=︒；（2）如图(2)F 是弧AD 一点，点,M N 分别是弧AC 和弧FD 的中点，连接FD ，连接MN 分别交AC ，FD 于,P Q 两点，求证：MPC NQD ∠=∠（3）如图(3)在(2)问条件下，MN 交AB 于G ，交BF 于L ，过点G 作GH MN ⊥交AF 于H ，连接BH ，若,6,BG HF AG ABH ==∆的面积等于8，求线段MN 的长度16．如图，在平面直角坐标系中，矩形ABCD 的顶点,A D 在坐标轴上，两点的坐标分别是点()0,,A m 点(),0,D m 且m 满足：322m m -+62=边AB 与x 轴交于点,E 点F 是边AD 上一动点，连接FB ，分别与x 轴，y 轴交于点,P 点,H 且FD BE =．（1）求m 的值；（2）若45,APF ∠=︒求证：AHF HFA ∠=∠；（3）若点F 的纵坐标为,n 则线段HF 的长为．(用含n 的代数式表示)17．已知抛物线2y ax bx c =++过点(6,0)A -，(2,0)B ，(0,3)C -．（1）求此抛物线的解析式；（2）若点H 是该抛物线第三象限的任意一点，求四边形OCHA 的最大面积；（3）若点Q 在y 轴上，点G 为该抛物线的顶点，且45GQA ∠=︒，求点Q 的坐标．18．如图，在⊙O 中，直径AB ＝10，tanA 3 （1）求弦AC 的长；（2）D 是AB 延长线上一点，且AB ＝kBD ，连接CD ，若CD 与⊙O 相切，求k 的值；（3）若动点P 以3cm/s 的速度从A 点出发，沿AB 方向运动，同时动点Q 以32cm/s 的速度从B 点出发沿BC 方向运动，设运动时间为t （0＜t ＜103），连结PQ ．当t 为何值时，△BPQ为Rt△？19．如图1，以AB为直径作⊙O，点C是直径AB上方半圆上的一点，连结AC，BC，过点C作∠ACB的平分线交⊙O于点D，过点D作AB的平行线交CB的延长线于点E．（1）如图1，连结AD，求证：∠ADC＝∠DEC．（2）若⊙O的半径为5，求CA•CE的最大值．（3）如图2，连结AE，设tan∠ABC＝x，tan∠AEC＝y，①求y关于x的函数解析式；②若CBBE＝45，求y的值．20．如图1，在平面直角坐标系中，O是坐标原点，矩形OACB的顶点A、B分别在x轴和y轴上，已知OA=5，OB=3，点D的坐标是（0，1），点P从点B出发以每秒1个单位的速度沿折线BCA的方向运动，当点P与点A重合时，运动停止，设运动的时间为t秒．（1）点P运动到与点C重合时，求直线DP的函数解析式；（2）求△OPD的面积S关于t的函数解析式，并写出对应t的取值范围；（3）点P在运动过程中，是否存在某些位置使△ADP是不以DP为底边的等腰三角形，若存在，请求出点P 的坐标；若不存在，请说明理由．21．（操作发现）如图1，ABC ∆为等腰直角三角形，90ACB ∠=︒，先将三角板的90︒角与ACB ∠重合，再将三角板绕点C 按顺时针方向旋转（旋转角大于0︒且小于45︒），旋转后三角板的一直角边与AB 交于点D ．在三角板另一直角边上取一点F ，使CF CD =，线段AB 上取点E ，使45DCE ∠=︒，连接AF ，EF ．（1）请求出EAF ∠的度数？（2）DE 与EF 相等吗？请说明理由；（类比探究）如图2，ABC ∆为等边三角形，先将三角板中的60︒角与ACB ∠重合，再将三角板绕点C 按顺时针方向旋转（旋转角大于0︒且小于30）.旋转后三角板的一直角边与AB 交于点D .在三角板斜边上取一点F ，使CF CD =，线段AB 上取点E ，使30DCE ∠=︒，连接AF ，EF .（3）直接写出EAF ∠=_________度；（4）若1AE =，2BD =，求线段DE 的长度.22．如图，二次函数23y x x m =-++的图象与x 轴的一个交点为(4,0)B ，另一个交点为A ，且与y 轴相交于C 点（1）则m =_________；C 点坐标为___________；（2）在直线BC 上方的抛物线上是否存在一点M ，使得它与B ，C 两点构成的三角形面积最大，若存在，求出此时M 点坐标；若不存在，请简要说明理由．（3）P 为抛物线上一点，它关于直线BC 的对称点为Q①当四边形PBQC 为菱形时，求点P 的坐标；②点P 的横坐标为(04)t t <<，当t =________时，四边形PBQC 的面积最大．23．综合与探究：如图1，抛物线24832999y x x =-++与x 轴交于,A B 两点（点A 在点B 的左侧），顶点为D ，P 为对称轴右侧抛物线的一个动点，直线AD 与y 轴于点C ，过点P 作//PF AD ，交x 轴于点F ．（1）求直线AD 的函数表达式及点C 的坐标；（2）如图2，当//PC x 轴时，将AOC ∆以每秒1个单位长度的速度沿x 轴的正方向平移，当点C 与点P 重合时停止平移．设平移t 秒时，在平移过程中AOC ∆与四边形AFPC 重叠部分的面积为S ，求S 关于t 的函数关系式，并写出自变量t 的取值范围；（3）如图3，过点P 作x 轴的平行线，交直线AD 于点E ，直线DF 与PE 交于点M ，设点P 的横坐标为m ．①当3DM MF =时，求m 的值；②试探究点P 在运动过程中，是否存在值m ，使四边形AFPE 是菱形？若存在，请直接写出点P 的坐标；若不存在，请说明理由．24．（1）探究发现数学活动课上，小明说“若直线21y x =-向左平移3个单位，你能求平移后所得直线所对应函数表达式吗？”经过一番讨论，小组成员展示了他们的解答过程：在直线21y x =-上任取点()01A -，，向左平移3个单位得到点()31，'--A 设向左平移3个单位后所得直线所对应的函数表达式为2y x n =+．因为2y x n =+过点()31，'--A ，所以61n -+=-，所以5n =，填空：所以平移后所得直线所对应函数表达式为（2）类比运用已知直线21y x =-，求它关于x 轴对称的直线所对应的函数表达式；（3）拓展运用将直线21y x =-绕原点顺时针旋转90°，请直接写出：旋转后所得直线所对应的函数表达式．25．小明研究了这样一道几何题：如图1，在ABC 中，把AB 绕点A 顺时针旋转()0180a a ︒<<︒得到AB '，把AC 绕点A 逆时针旋转β得到AC '，连接B C ''．当180a β+=︒时，请问AB C ''△边B C ''上的中线AD 与BC 的数量关系是什么？以下是他的研究过程：特例验证：（1）①如图2，当ABC 为等边三角形时，猜想AD 与BC 的数量关系为AD =_______BC ；②如图3，当90BAC ∠=︒，8BC =时，则AD 长为________．猜想论证：（2）在图1中，当ABC 为任意三角形时，猜想AD 与BC 的数量关系，并给予证明．拓展应用：（3）如图4，在四边形ABCD ，90C ∠=︒，120A B ∠+∠=︒，3BC =6CD =，3DA =P ，使PDC △与PAB △之间满足小明探究的问题中的边角关系？若存在，请画出点P 的位置（保留作图痕迹，不需要说明）并直接写出PDC △的边DC 上的中线PQ 的长度；若不存在，说明理由．【参考答案】***试卷处理标记，请不要删除一、中考数学压轴题1．B解析：（1）8b =；（2）382d n =+；（3）92EFN S =△ 【解析】【分析】（1）先用b 表示出点B 和点A 的坐标，然后利用勾股定理列出方程即可求出b 的值；（2）联立直线BC 的解析式和直线AB 的解析式即可用n 表示出点C 的坐标，从而求出点D 的坐标，从而求出d 与n 的函数关系式；（3）过点C 作CS ⊥x 轴于S ，过点F 作FT ⊥x 轴于T ，过点G 作GD ⊥y 轴于D ，MN 与y 轴交于点I ，根据相似三角形判定可得△RSC ∽△ROB ，列出比例式即可求出OR 和CS ，然后根据等角的锐角三角函数相等求出ON ，再根据等腰直角三角形的性质求出NE ，然后结合已知条件和等角的锐角三角函数相等求出TF ，即可求出结论．【详解】解：（1）当x=0时，y=b ；当y=0时，x=34b∴点B 的坐标为（0，b ），点A 的坐标为（34b ，0） ∴OB=b ，OA=34b 根据勾股定理OB 2＋OA 2=AB 2b 2＋（34b ）2=102 解得：b=8或-8（不符合已知条件，舍去）∴b=8（2）直线BC 的解析式为(4)8=++y n x ，直线AB 的解析式为483y x =-+ 联立(4)8y n x y nx =++⎧⎨=⎩解得：22x y n =-⎧⎨=-⎩∴点C 的坐标为（-2，-2n ）∵//CD OA∴点D 的纵坐标为-2n将y=-2n 代入483y x =-+中，解得：x=362+n ∴点D 的坐标为36,22⎛⎫+- ⎪⎝⎭n n ∴线段CD 长d =362+n －（-2）=382+n （3）过点C 作CS ⊥x 轴于S ，过点F 作FT ⊥x 轴于T ，过点G 作GD ⊥y 轴于D ，MN 与y 轴交于点I∴OD=275，GD=195由（2）知点C 坐标为（-2，-2n ）∴CS=-2n ，OS=2∵BC CR =，CS ∥y 轴∴RB=2RC ，△RSC ∽△ROB ∴12===CS RS RC OB OR RB 即22182--==n OR OR 解得：n=-2，OR=4∴CS=4∵∠=∠OBR HNM ，GD ∥x 轴∴∠=∠OBR HNM =∠DGI∴tan tan ∠=∠OBR HNM =tan ∠DGI ∴==OR OI ID OB ON GD即48927515-==ID ID ON解得：1910,7==ID ON ∵45AEF ∠=︒∴∠CES=∠AEF=45°，∠QEH=∠QEF －∠AEF=45°∴△CES 、△EFT 和△EHQ 都是等腰直角三角形∴CS=SE=4，ET=TF=2EF ， EH=HQ ，设EH=HQ=a ，则∴EN=ON ＋OE=ON ＋SE －OS=9∵3==EQ EF ，PH EN = ∴，PM=a ，PH=9， ∴NH=EN ＋EH=9＋a ，MH=PH －PM=9－a ∴tan ∠HNM =12==MH OI NH ON ∴9192-=+a a 解得：a=3∴EF=33⨯=∴TF=12=∴S△EFN =12EN·TF=12×9×1=92【点睛】此题考查的是一次函数与几何图形的综合题型，此题难度较大，掌握勾股定理、联立方程求交点坐标、锐角三角函数的性质、勾股定理、等腰直角三角形的性质和相似三角形的判定及性质是解决此题的关键．2．C解析：（1）112y x=-+；（2）1d t=-+；（3）64215t-=【解析】【分析】（1）根据互相垂直两直线斜率积为-1，设出直线CE的解析式，再将点C坐标代入即可求解；（2）过点E作EM⊥y轴于点M，过点E作EN x⊥轴于点N，通过解直角三角形可证EDM≌EAN，ENH≌EMG，得到AN=DM，HN=GM，进而得到AH DG=，再根据CE解析式求出D点坐标，即可找出d与t之间的函数关系式；（3）过点B作BT CM⊥于点T，在直线BT上截取TL NK=，证四边形BGMT与四边形HNMC均为矩形，得MN MT=，再进一步证明ENH≌EMG，利用全等三角形的性质通过角度计算，得出△BML为等腰三角形且BM BL=，再用含有t的代数式表示BM，最后在Rt△BMG中利用勾股定理建立等式，求出t的值．【详解】解：（1）∵CE⊥AB，∴设直线CE的解析式为：12y x c=-+，把点C（2，0）代入上述解析式，得1c=，∴直线CD的解析式为：112y x=-+；（2）过点E作EM⊥y轴于点M，过点E作EN x⊥轴于点N，令26112y xy x=+⎧⎪⎨=-+⎪⎩，解得22x y =-⎧⎨=⎩， ∴()2,2E -，易证EDM ≌EAN ，ENH ≌EMG ，∴AN =DM ，HN =GM ，∴AH DG =，由直线CE 的解析式112y x =-+，可求点D （0，1） ∴DG =1—t ，∴1d t =-+；（3）过点B 作BT CM ⊥于点T ，在直线BT 上截取TL NK =，易证四边形BGMT 与四边形HNMC 均为矩形，由（2）问可知1t AH GD ==-，则6t HC =-∴6t BG MT ==-，∴MN MT =，∵90KNM LTM ∠=∠=︒，∴ENH ≌EMG ，∴L NKM ∠=∠，设KMN α∠=，则KMB KMN α∠=∠=，∴90NKM α∠=︒-，∴90NKM L α∠=∠=︒-， ∵//BL MN ，∴2MBL BMN α∠=∠=，∴18090BML MBL L α∠=︒-∠-∠=︒-，∴BM BL =，∵1tan 2KCH ∠=， ∴11322KH CH t ==-，∴133322KN KH HN t t t TL =+=--=-=， ∴352BL BT TL t BM =+=-=，在Rt BMG △中， 222BM BG GM =+，解得65t +=（不合题意舍去）或65t -=故，65t -=．【点睛】本题一次函数综合题，考查了待定系数法求解析式，一次函数的性质，全等三角形的判定与性质，角平分线的性质，勾股定理等，利用已知条件求相等交，相等线段是解决本题的关键．3．E解析：（1）2y x 2x 3=-++；（2）E （2，3）或（1，4）；（3）P 点横坐标为【解析】【分析】(1) 抛物线2(0)y ax bx c a =++≠的顶点为C （1，4），设抛物线的解析式为2(1)4y a x =-+，由抛物线过点B,（3，0），即可求出a 的值，即可求得解析式；（2）过点E 、F 分别作x 轴的垂线，交x 轴于点M 、N ，设点E 的坐标为()2,23x xx -++，求出A 、D 点的坐标，得到OM=x ，则AM=x+1，由AF=2EF 得到22(1)33x AN AM +==，从而推出点F 的坐标21210(,)3333x x --+，由23FN EM =，列出关于x 的方程求解即可；（3）先根据待定系数法求出直线DM 的解析式为y=-2x+3，过点P 作PT ∥y 轴交直线DM 于点T ，过点F 作直线GH ⊥y 轴交PT 于点G ，交直线CE 于点H.证明△FGP ≌△FHQ ，得到FG=FH ，PT=45GH.设点P （m ，-m²+2m+3），则T （m ，-2m+3），则PT=m²-4m ，GH=1-m ，可得m²-4m=45（1-m ），解方程即可. 【详解】（1）∵抛物线的顶点为C （1，4），∴设抛物线的解析式为2(1)4y a x =-+，∵抛物线过点B,（3，0），∴20(31)4a =-+，解得a=-1，∴设抛物线的解析式为2(1)4y x =--+，即2y x 2x 3=-++；（2）如图，过点E 、F 分别作x 轴的垂线，交x 轴于点M 、N ，设点E 的坐标为()2,23x x x -++，∵抛物线的解析式为2y x 2x 3=-++，当y=0时，2023x x =-++，解得x=-1或x=3，∴A （-1.0），∴点D （0,3），∴过点BD 的直线解析式为3y x =-+，点F 在直线BD 上，则OM=x ，AM=x+1， ∴22(1)33x AN AM +==， ∴2(1)2111333x x ON AN +=-=-=-， ∴21210(,)3333x x F --+， ∴2210332233FN EM x x x +--++==，解得x=1或x=2， ∴点E 的坐标为（2，3）或（1，4）；（3）设直线DM 的解析式为y=kx+b ，过点D （0,3），M （32，0），可得，3023k b b ⎧+=⎪⎨⎪=⎩，解得k=-2，b=3，∴直线DM的解析式为y=-2x+3，∴32OM=，3OD=，∴tan∠DMO=2，如图，过点P作PT∥y轴交直线DM于点T，过点F作直线GH⊥y轴交PT于点G，交直线CE于点H.∵PQ⊥MT，∴∠TFG=∠TPF，∴TG=2GF，GF=2PG，∴PT=25 GF，∵PF=QF，∴△FGP≌△FHQ，∴FG=FH，∴PT=45 GH.设点P（m，-m²+2m+3），则T（m，-2m+3），∴PT=m²-4m，GH=1-m，∴m²-4m=45（1-m），解得：111201m-=211201m+=（不合题意，舍去），∴点P的横坐标为112018-.【点睛】本题考查二次函数综合题、平行线分线段成比例定理、轴对称性质等知识，解题的关键是学会用转化的思想思考问题，学会用数形结合的思想解决问题，有一定难度.4．A解析：（1）12；（2）5s或373s；（3）163s或685s或72s【解析】【分析】（1）AD与BC之间的距离即AB的长，如下图，过点D作BC的垂线，交BC于点E，在RtDEC中可求得DE的长，即AB的长，即AD与BC间的距离；（2）四边形QDCP为平行四边形，只需QD=CP即可；（3）存在3大类情况，情况一：QP=PD，情况二：PD=QD，情况三：QP=QD，而每大类中，点P存在2种情况，一种为点P还未到达点C，另一种为点P从点C处返回．【详解】（1）如下图，过点D作BC的垂线，交BC于点E∵∠B=90°，AD∥BC∴AB⊥BC，AB⊥AD∴AB的长即为AD与BC之间的距离∵AD=16，BC=21，∴EC=5∵DC=13∴在Rt DEC中，DE=12同理，DE的长也是AD与BC之间的距离∴AD与BC之间的距离为12（2）∵AD∥BC∴只需QD=PC，则四边形QDCP是平行四边形QD=16－t，PC=21－2t或PC=2t－21∴16－t=21－2t或16－t=2t－21解得：t=5s或t=37 3s（3）情况一：QP=PD图形如下，过点P作AD的垂线，交AD于点F∵PQ=PD，PF⊥QD，∴QF=FD∵AF ∥BP ，AB ∥FP ，∠B=90°∴四边形ABPF 是矩形，∴AF=BP由题意得：AQ=t ，则QD=16－t ，QF=8－2t ，AF=8+2t BP=2t 或BP=21－(2t －21)=42－2t∵AF=BP∴8+2t =2t 或8+2t =42－2t 解得：t=163或t=685情况二：PD=QD ，图形如下，过点P 作AD 的垂线，交AD 于点F同理QD=16－t ，PF=AB=12BP=2t 或21－(2t －21)=42－2t则FD=AD －AF=AD －BP=16－2t 或FD=16－(42－2t)=2t －26∴在Rt PFD 中，()22212162PD t =+-或()22212226PD t =+-∵PD=QD ，∴22PD QD =∴()()22216t 12162t =+-－或()()22216t 12226t =+-－解得：2个方程都无解情况三：QP=QD ，图形如下，过点P 作AD 的垂线，交AD 于点F同理：QD=16－t ，FP=12BP=2t 或BP=42－2tQF=AF －AQ=BP －AQ=2t －t=t 或QF=42－2t －t=42－3t在Rt QFP 中，22212PQ t =+或()22212423PQ t =+- ∵PQ=QD ，∴22PQ QD =∴()22216t 12t =+－或()()22216t 12423t =+-－第一个方程解得：t=72，第二个方程解得：无解综上得：t=163或685或72 【点睛】本题考查四边形中的动点问题，用到了勾股定理、平行四边形的性质、矩形的性质，解题关键是根据点Q 运动的轨迹，得出BP 的长度． 5．E解析：（1）∠EPF=∠AEP+∠PFC，∠AEP+∠EPF+∠PFC=360°；（2）见解析；（3）①150°，∠EQF=180°－12∠EPF 【解析】【分析】（1）如下图，过点P 作AB 的平行线，根据平行线的性质可推导出角度关系；（2）如下图，根据（1）的结论，可得∠AEP+∠PFC=∠EPF=90°，利用△EPF 内角和为180°可推导得出∠PEF+∠PFE=90°，从而得出∠PEF=∠AEP ；（3）①根据（1）的结论知：∠AEP+∠PFC=∠EPF=60°，再利用角平分线的性质得出∠PEQ+∠PFQ=150°，最后在四边形EPFQ 中得出结论；②根据（1）的结论知：∠AEP+∠PFC=∠EPF°，再利用角平分线的性质得出∠PEQ+∠PFQ=180°－1EPF 2∠，最后在四边形EPFQ 中得出结论．【详解】（1）如下图，过点P 作PQ ∥AB∵PQ ∥AB ，AB ∥CD ，∴PQ ∥CD∴∠AEP=∠EPQ ，∠QPF=∠PFC又∵∠EPF=∠EPQ+∠QPF∴∠EPF=∠AEP+∠PFC如下图，过点P 作PQ ∥AB同理，AB ∥QP ∥CD∴∠AEP+∠QPE=180°，∠QPF+∠PFC=180°∴∠AEP+∠EPF+∠PFC=∠AEP+∠EPQ+∠QPF+∠PFC=360°（2）根据（1）的结论知：∠AEP+∠PFC=∠EPF=90°∵PF 是∠CFE 的角平分线，∴∠PFC=∠PFE在△PEF 中，∵∠EPF=90°，∴∠PEF+∠PFE=90°∴∠PEF+∠PFE=∠AEP+∠PFC∴∠PEF=∠AEP ，∴PE 是∠AEF 的角平分线（3）①根据（1）的结论知：∠AEP+∠PFC=∠EPF=60°∴∠BEP+∠PFD=180°－∠AEP+180°－∠PFC=300°∵EQ 、QF 分别是∠PEB 和∠PFD 的角平分线∴∠PEQ=QEB ，∠PFQ=∠QFD∴∠PEQ+∠PFQ=150°在四边形PEQF 中，∠EQF=360°－∠EPF －(∠PEQ+∠PFQ)=360°－60°－150°=150° ②根据（1）的结论知：∠AEP+∠PFC=∠EPF∴∠BEP+∠PFD=180°－∠AEP+180°－∠PFC=360°－∠EPF∵EQ 、QF 分别是∠PEB 和∠PFD 的角平分线∴∠PEQ=∠QEB ，∠PFQ=∠QFD∴∠PEQ+∠PFQ=()1360EPF 2∠︒－=180°－1EPF 2∠ ∴在四边形PEQF 中： ∠EQF=360°－∠EPF －(∠PEQ+∠PFQ)=360°－EPF ∠－(180°－1EPF 2∠)=180°－1EPF 2∠ 【点睛】本题考查“M ”型模型，解题关键在过两条平行线中间的点作已知平行线的平行线，然后利用平行线的性质进行角度转化可推导结论．6．A解析：（1）ABC 是“准黄金”三角形，理由见解析；（2）329AB BC =3）①12561535AD CD =．【解析】【分析】（1）过点A 作AD BC ⊥于点D ，先求出AD 的长度，然后得到61035AD BC ==，即可得到结论；（2）根据题意，由“金底”的定义得:3:5AE BC =，设3AE k =，5BC k =，由勾股定理求出AB 的长度，根据比值即可求出AB BC的值；（3）①作AE ⊥BC 于E ，DF ⊥AC 于F ，先求出AC 的长度，由相似三角形的性质，得到AF=2DF ，由解直角三角形，得到3CF DF =，则(23)35AC x =+=，即可求出DF 的长度，然后得到CD 的长度；②由①可知，得到CE 和AC 的长度，分别过点B '，D 作B G BC '⊥，DF AC ⊥，垂足分别为点G ，F ，然后根据相似三角形的判定和性质，得到DF AF AE EC=，然后求出CD 和AD 的长度，即可得到答案．【详解】解：（1）ABC 是“准黄金”三角形．理由：如图，过点A 作AD BC ⊥于点D ，∵12AC =，30ACB ∠=︒， ∴162AD AC ==． ∴:6:103:5AD BC ==． ∴ABC 是“准黄金”三角形．（2）∵点A ，D 关于BC 对称，∴BE AD ⊥，AE ED =．∵ABC 是“准黄金”三角形，BC 是“金底”，∴:3:5AE BC =．不防设3AE k =，5BC k =，∵点C 为ABD △的重心，∴:2:1BC CE =．∴52k CE =，152k BE =． ∴2215329(3)22k AB k k ⎛⎫=+= ⎪⎝⎭．∴329329:5210AB k k BC ==．（3）①作AE ⊥BC 于E ，DF ⊥AC 于F ，如图：由题意得AE=3， ∵35AE BC =， ∴BC=5， ∵10AB BC =， ∴10AB ，在Rt △ABE 中，由勾股定理得：22(10)31BE =-=，∴156EC =+=， ∴223635AC =+=∵∠AEC=∠DFA=90°，∠ACE=∠DAF ，∴△ACE ∽△DAF ， ∴3126AE E D C F AF ===，设DF x =，则2AF x =，∵∠ACD=30°， ∴3CF x =， ∴(23)35AC x ==解得：65315DF x == ∴2125615CD DF == ②如图，过点A 作AE BC ⊥于点E ，则3AE =．∵ABC 是“准黄金”三角形，BC 是“金底”，∴:3:5AE BC =．∴5BC =．∵10AB BC =，∴10AB． ∴221BE AB AE =-=．∴6CE BE BC =+=，2236935AC CE AE =+=+=．分别过点B '，D 作B G BC '⊥，DF AC ⊥，垂足分别为点G ，F ，∴90B GC DFC '∠=∠=︒，3B G '=，5C B B C '==，则CG 4=．∵GCB FCD α'∠=∠=，∴AEC DFA ∽△△．∴::::3:4:5DF FC CD B G GC CB ''==． ∴设3DF k =，4FC k =，5CD k =．∵12l l //，∴ACE CAD ∠=∠，且90AEC AFD ∠=∠=︒．∴AEC DFA ∽△△．∴DF AF AE EC =． ∴335436k k =，解得3510k =． ∴3552CD k ==，2222959595102AF DF AD ⎛⎫⎛⎫+=+= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭=． ∴93525355AD CD ===．【点睛】本题属于相似形综合题，主要考查了重心的性质，等腰直角三角形的性质，勾股定理，解直角三角形，旋转的性质以及勾股定理的综合运用，解决问题的关键是依据题意画出图形，根据数形结合的思想进行解答．7．C解析：（1）12,16AD CD ==；（2）277和297. 【解析】【分析】（1）根据题意由函数图象可知动点M 从A 出发，以每秒1个单位的速度从C 到D 耗时16秒求出CD ，再利用三角形面积公式求得AD 即可；（2）由题意可知只能有P 和Q 点都在AD 边上，此时分当P 在Q 上方时以及当P 在Q 下方时两种情况运用数形结合思维进行分析得出答案.【详解】解：（1）由函数图象可知动点M 从A 出发，以每秒1个单位的速度从C 到D 耗时36-20=16秒，即CD=16，而此时AMD ∆的面积为96，又因为90ADC ∠=︒，即有11169622CD AD AD =⨯=,解得12AD =. 所以12,16AD CD ==. （2）由题意可知Q 运动到点A 停止的时间为285，而P 运动到点D 停止的时间为6，所以只能有P 和Q 点都在AD 边上，此时以PQ 为底边，CD 为高，设运动时间为t ，则AP=2t ，QD=5t-16，（162855t ≤<）， ①当P 在Q 上方时，则有PQ=AD-AP-QD= 122516287t t t --+=-，可知CPQ ∆的面积为8时即11(287)16822PQ CD t =⨯-⨯=，解得277t =（满足条件）；②当P 在Q 下方时，则有PQ=QD-（AD-AP ）= 516(122)728t t t ---=-，可知CPQ ∆的面积为8时即11(728)16822PQ CD t =⨯-⨯=，解得297t =（满足条件）. 所以当CPQ ∆的面积为8时，t 的值为277和297. 【点睛】本题考查四边形动点问题和一次函数结合，熟练掌握四边形动点问题的解决办法和一次函数图象的相关性质，运用数形结合思维分析是解题的关键.8．E解析：（1）EF =，见解析；（2）BK =；（3）①AGH 是等边三角形，见解析；②14【解析】【分析】（1）连接EF ，AC ，由菱形的性质，可证Rt AEB Rt AFD ∆≅∆，然后得到AEF ∆为等边三角形，由解直角三角形得到3AE EC =，即可得到答案；（2）由菱形的性质和等边三角形的性质，求出AF 的长度，然后得到BF 的长度，然后由相似三角形的性质，得到AB BK FB BA=，即可求出答案；（3）①由等边三角形的性质，先证明ABG ACH ≅，然后得到AG AH =，然后得到60BAH GAB GAH ︒∠+∠=∠=，即可得到答案；②由三角形的面积公式得到31DH =+，然后得到AHF △为等腰直角三角形，再由解直角三角形的性质，即可求出答案．【详解】解：（1）3EF EC =；理由：∵四边形ABCD 是菱形，60ABC ∠=︒，,60,//AB AD BC ABC ADC AD BC ︒∴==∠=∠=，120BAD ︒∴∠=，∵AE BC ⊥，垂足为E ，AF CD ⊥，垂足为F ，90AEB AFD ︒∴∠=∠=Rt AEB Rt AFD ∴∆≅∆，,30AE AF BAE DAF ∴=∠=∠=︒，60EAF ∴∠=︒，AEF ∴∆为等边三角形，EF AE ∴=.连接AC ，1602BAC BAD ︒∴∠=∠= 30EAC ︒∴∠= 在Rt AEC ∆中，tan EC EAC AE ∠=3AE EC ∴=，3EF EC ∴=（2）如图：∵四边形ABCD 是菱形，60,ABC AB a ︒∠==， ACD ∴是等边三角形，//,,60AB CD AD CD a ADC ︒==∠=. AF CD ⊥，垂足为F ， 1,902CF DF a BAF AFD ︒∴==∠=∠= 在Rt ADF 中，sin AF ADF AD ∠=， 23AF a ∴=在Rt ABF 中，22BF AB AF =+， 7BF a ∴= AK BF ⊥，垂足为K ，90AKB FAB ︒∴∠=∠=ABK FBA ∠=∠~Rt AKB Rt FAB ∴∆∆，AB BK FB BA∴=， 27BK a ∴=，（3）如图：①AGH 是等边三角形.理由：连接AC .,60AB BC ABC ︒=∠=，ABC ∴为等边三角形，,60AB AC ABC ACB ︒∴=∠=∠=，120ABG ︒∴∠=.//AB CD ，60BCH ABC ︒∴∠=∠=，120ACH ︒∴∠=ABG ACH ∴∠=∠，又BG CH =，ABG ACH ∴≅，,AG AH GAB HAC ∴=∠=∠.60BAH HAC BAC ︒∠+∠=∠=，60BAH GAB GAH ︒∴∠+∠=∠=，AGH ∴为等边三角形；②ADC 为等边三角形，2,1AD DC AC CF DF ∴=====，AF ∴=.1(32ADH S =， 11(322DH ∴⨯=，1DH ∴=1CH DH CD ∴=-=，HF DH DF =-=AF HF ∴=，AHF ∴为等腰直角三角形，45AHF ︒∴∠=.过点C 作CM AH ⊥，垂足为M .在Rt CMH 中，sin CM CHM CH∠=， 12CM ∴=，在Rt AMC 中，sin CM MAC AC ∠=， 1sin 4MAC ∴∠=. 又GAB HAC ∠=∠， 1sin sin 4GAB HAC ∴∠=∠=；【点睛】本题考查了解直角三角形，相似三角形的判定和性质，等边三角形的判定和性质，菱形的性质，等腰三角形的判定和性质，全等三角形的判定和性质，解题的关键是熟练掌握所学的定理和性质，正确作出辅助线进行解题．9．A解析：（1）135°；（2）①45°，②不发生变化，45°；（3）60°或45°【解析】【分析】（1）利用三角形内角和定理、两角互余、角平分线性质即可求解；（2）①利用对顶角相等、两角互余、两角互补、角平分线性质即可求解；②证明和推理过程同①的求解过程；（3）由（2）的证明求解思路，不难得出EAF ∠=90°，如果有一个角是另一个角的3倍，所以不确定是哪个角是哪个角的三倍，所以需要分情况讨论；值得注意的是，∠MON=90°，所以求解出的∠ABO 一定要小于90°，注意解得取舍.【详解】（1）()11801802118090180451352AEB EBA BAE OBA BAO ∠=︒-∠-∠=︒-∠+∠=︒-⨯︒=︒-︒=︒（2）①如图所示AD 与BO 交于点E ，()9060301180307521909030602180180756045OBA DBO NBC DEB OEA OAB D DBE DEB ∠=︒-︒=︒∠=∠=︒-︒=︒∠=∠=︒-∠=︒-︒=︒∠=︒-∠-∠=︒-︒-︒=︒②∠D 的度数不随A 、B 的移动而发生变化设BAD α∠=，因为AD 平分∠BAO ，所以2BAO α∠=，因为∠AOB=90°，所以180902ABN ABO AOB BAO α∠=︒-∠=∠+∠=+。

2023年九年级数学中考复习：旋转(面积问题)综合压轴题(Word版,含答案)

2023年九年级数学中考复习：旋转（面积问题）综合压轴题1．一节数学课上，老师提出一个这样的问题：如图，点P是正方形ABCD内一点，P A=1，PB=2，PC=3，你能求出∠APB的度数吗？小明通过观察、分析、思考，形成了如下思路：思路一：将∠PBC绕点B逆时针旋转90°，得到∠P'BA，连接P P'，求出∠APB的度数．思路二：将∠APB绕点B顺时针旋转90°，得到∠C P'B，连接P P'，求出∠APB的度数．请参考小明的思路，任选一种写出完整的解答过程．2．如图，已知在∠ABC中，AB＝AC，D、E是BC边上的点，将∠ABD绕点A旋转，得到∠AC D，连接D E．(1)当∠BAC＝120°，∠DAE＝60°时，求证：DE＝D E；(2)当DE＝D E时，∠DAE与∠BAC有怎样的数量关系？请写出，并说明理由．(3)在（2）的结论下，当∠BAC＝90°，BD与DE满足怎样的数量关系时，∠D EC是等腰直角三角形？（直接写出结论，不必证明）AC BD相交于点O，3．如图，平行四边形ABCD中，,1,5AB AC AB BC⊥==,BC AD于点E，F．将直线AC绕点O顺时针旋转，分别交,(1)证明：当旋转角为90°时，四边形ABEF 是平行四边形；(2)证明：在旋转过程中，线段AF 与EC 总保持相等；(3)在旋转过程中，当AC 绕点O 顺时针旋转多少度时，四边形BEDF 是菱形，请给出证明．4．如图1所示，将一个边长为2的正方形ABCD 和一个长为2、宽为1的长方形CEFD 拼在一起，构成一个大的长方形ABEF ．现将小长方形CEFD 绕点C 顺时针旋转至''CE FD ，旋转角为α．(1)当点D 恰好落在边EF 上时，点D 到边DC 的距离为____________，旋转角α=____________︒；(2)如图2，G 为BC 的中点，且090α︒<<︒，求证：GD E D ''=；(3)小长方形CEFD 绕点C 顺时针旋转一周的过程中，DCD '与CBD '△能否全等？若能，直接写出旋转角α的值；若不能，说明理由．5．将两块完全相同的且含60°角的直角三角板ABC 和AFE 按如图1所示位置放置，现将Rt AEF 绕A 点按逆时针方向旋转()090αα︒<<︒．如图2，AE 与BC 交于点M ，AC 与EF 交于点N ，BC 与EF 交于点P ．(1)若AMC 是等腰三角形，则旋转角α的度数为______．(2)在旋转过程中，连接AP ，CE ，求证：AP 所在的直线是线段CE 的垂直平分线．(3)在旋转过程中，CPN是否能成为直角三角形？若能，直接写出旋转角α的度数；若不能，说明理由．6．旋转是一种重要的图形变换，当图形中有一组邻边相等时，往往可以通过旋转解决问题．如图∠，在四边形ABCD中，AD CDADC∠=︒，2∠=︒，60=，120ABCAB=，1BC=．【问题提出】(1)如图∠，在图∠的基础上连接BD，由于AD CD=，所以可将DCB绕点D顺时针方向旋转60°，得到DAB'，则BDB'的形状是_______；【尝试解决】(2)在（1）的条件下，求四边形ABCD的面积；【类比应用】(3)如图∠，等边ABC的边长为2，BDC是顶角120∠=︒的等腰三角形，以D为顶BDC点作一个60°的角，角的两边分别交AB于点M，交AC于点N，连接MN，求AMN的周长．7．如图1，在等腰三角形ABC中，∠A＝120°，AB＝AC，点D、E分别在边AB、AC上，AD＝AE，连接BE，点M、N、P分别为DE、BE、BC的中点．。

中考数学压轴题专集 2一元二次方程试题

2021年全国各地中考数学压轴题专集：2一元二次方程1．△ABC的两边AB、AC的长是关于x的一元二次方程x2－(2k＋3)x＋k2＋3k＋2＝0的两个实数根，第三边长为5．〔1〕当k为何值时，△ABC是以BC为斜边的直角三角形；〔2〕当k为何值时，△ABC是等腰三角形，并求△ABC的周长．2．△ABC的三边长为a、b、c，关于x的方程x2－2(a＋b)x＋c2＋2ab＝0有两个相等的实数根，又sin A、sin B是关于x的方程(m＋5)x2－(2m－5)x＋m－8＝0的两个实数根．〔1〕求m的值；〔2〕假设△ABC的外接圆面积为25π，求△ABC的内接正方形的边长．3．关于x的方程x2－(m＋n＋1)x＋m＝0〔n≥0〕的两个实数根为α、β，且α≤β．〔1〕试用含有α、β的代数式表示m和n；〔2〕求证：α≤1≤β；〔3〕假设点P〔α，β〕在△ABC的三条边上运动，且△ABC顶点的坐标分别为A〔1，2〕，B〔12，1〕，C〔1，1〕，问是否存在点P，使m＋n＝54？假设存在，求出点P的坐标；假设不存在，请说明理由．4．请阅读以下材料：问题：方程x2＋x－1＝0，求一个一元二次方程，使它的根分别是方程根的2倍．解：设所求方程的根为y，那么y＝2x，所以x＝y2．把x＝y2代入方程，得(y2)2＋y2－1＝0．化简，得y2＋2y－4＝0．故所求方程为y2＋2y－4＝0．这种利用方程根的代换求新方程的方法，我们称为“换根法〞．请用阅读材料提供的“换根法〞求新方程〔要求：把所求方程化为一般形式〕；〔1〕方程x2＋x－2＝0，求一个一元二次方程，使它的根分别是方程根的相反数，那么所求方程为：___________________；〔2〕关于x的一元二次方程ax2＋bx＋c＝0〔a≠0〕有两个不等于零的实数根，求一个一元二次方程，使它的根分别是方程根的倒数．5．关于x的一元二次方程x2－2x－a2－a＝0〔a＞0〕．〔1〕证明这个方程的一个根比2大，另一个根比2小；〔2〕假如当a＝1，2，3，…，2021时，对应的一元二次方程的两个根分别为α1、β1，α2、β2，α3、β3，…，α2021、β2021，求1α1＋1β1＋1α2＋1β2＋1α3＋1β3＋…＋1α2021＋1β2021的值．6．关于x的一元二次方程x2－(a＋b＋c)x＋ab＋bc＋ca＝0，且a＞b＞c＞0．〔1〕假设方程有实数根，求证：a，b，c不能构成一个三角形的三边长；〔2〕假设方程有实数根x0，求证：b＋c＜x0＜a；〔3〕假设方程的实数根为6和9，求正整数a，b，c的值．7．方程x2＋2ax＋a－4＝0有两个不同的实数根，方程x2＋2ax＋k＝0也有两个不同的实数根，且其两根介于方程x2＋2ax＋a－4＝0的两根之间，求k的取值范围．8．关于x的方程x2－4|x|＋3＝k．〔1〕当k为何值时，方程有4个互不相等的实数根？〔2〕当k为何值时，方程有3个互不相等的实数根？〔3〕当k为何值时，方程有2个互不相等的实数根？〔4〕是否存在实数k，使得方程只有1个实数根？假设存在，求k的值和方程的根；假设不存在，请说明理由．9．x1，x2是关于x的一元二次方程4x2＋4(m－1)x＋m2＝0的两个非零实数根，那么x1与x2能否同号？假设能同号，恳求出相应的m的取值范围；假设不能同号，请说明理由．10．α、β为关于x的方程x2－2mx＋3m＝0的两个实数根，且(α－β)2＝16，假如关于x 的另一个方程x2－2mx＋6m－9＝0的两个实数根都在α和β之间，求m的值．11．a为实数，且关于x的二次方程ax2＋(a2＋1)x－a＝0的两个实数根都小于1，求这两个实数根的最大值．12．务实数a的取值范围，使关于x的方程x2＋2(a－1)x＋2a＋6＝0〔1〕有两个实根x1、x2，且满足0＜x1＜1＜x2＜4；〔2〕至少有一个正根．13．x1、x2是方程x2－mx－1＝0的两个实数根，满足x1＜x2，且x2≥2．〔1〕求m的取值范围；〔2〕假设x2＋mx1－m＋x1＋mx2－m＝2，求m的值．14．关于x的方程x2－(m－2)x－m24＝0〔m≠0〕〔1〕求证：这个方程总有两个异号实根；〔2〕假设这个方程的两个实根x1、x2满足|x2|＝|x1|＋2，求m的值及相应的x1、x2．15．△ABC的一边长为5，另两边长恰是方程2x2－12x＋m＝0的两个根，求m的取值范围．16．：α，β〔α＞β〕是一元二次方程x2－x－1＝0的两个实数根，设s1＝α＋β，s2＝α2＋β2，…，s n＝αn＋βn．根据根的定义，有α2－α－1＝0，β2－β－1＝0，将两式相加，得(α2＋β2)－(α＋β)－2＝0，于是，得s2－s1－2＝0．根据以上信息，解答以下问题：〔1〕利用配方法求α，β的值，并直接写出s1，s2的值；〔2〕猜测：当n≥3时，s n，s n-1，s n-2之间满足的数量关系，并证明你的猜测的正确性；〔3〕根据〔2〕中的猜测，求(1＋52)8＋(1－52)8的值．17．方程(x－1)(x2－2x＋m)＝0的三个实数根恰好构成△ABC的三条边长．〔1〕务实数m的取值范围；〔2〕当△ABC为直角三角形时，求m的值和△ABC的面积．励志赠言经典语录精选句；挥动**，放飞梦想。

2021年九级中考数学压轴题满分训练 –几何综合问题(圆的专题)(二)

2021年九级中考数学压轴题满分训练–几何综合问题（圆的专题）（二）1．如图，AB为⊙O直径，C为⊙O上的一点，过点C的切线与AB的延长线相交于点D，CA＝CD．（1）连接BC，求证：BC＝OB；（2）E是中点，连接CE，BE，若BE＝4，求CE的长．2．如图，AB为⊙O的直径，点C在⊙O上，AD与过点C的切线互相垂直，垂足为D．连接BC并延长，交AD的延长线于点E．（1）求证：AE＝AB；（2）若AB＝20，BC＝16，求CD的长．3．如图，在△ABC中，AB＝AC，以AC为直径的⊙O交BC于点D，过点D作⊙O的切线DE交AB于E．（1）求证：DE⊥AB；（2）如果tan B＝，⊙O的直径是5，求AE的长．4．阅读以下材料，并按要求完成相应的任务：莱昂哈德•欧拉（LeonhardEuler）是瑞士数学家，在数学上经常见到以他的名字命名的重要常数，公式和定理，下面就是欧拉发现的一个定理：在△ABC中，R和r分别为外接圆和内切圆的半径，O和I分别为其中外心和内心，则OI2＝R2﹣2Rr．如图1，⊙O和⊙I分别是△ABC的外接圆和内切圆，⊙I与AB相切于点F，设⊙O的半径为E，⊙I的半径为r，外心O（三角形三边垂直平分线的交点）与内心I（三角形三条角平分线的交点）之间的距离OI＝d，则有d2＝R2﹣2Rr．下面是该定理的证明过程（部分）：延长AI交⊙O于点D，过点I作⊙O的直径MN，连接DM，AN．∵∠D＝∠N，∴∠DMI＝∠NAI（同弧所对的圆周角相等）．∴△MDI∽△ANI．∴＝，∴IA•ID＝IM•IN，①如图2，在图1（隐去MD，AN）的基础上作⊙O的直径DE，连接BE，BD，BI，IF．∵DE是⊙O的直径，∴∠DBE＝90°．∵⊙I与AB相切于点F，∴∠AFI＝90°，∴∠DBE＝∠IFA．∵∠BAD＝∠E（同弧所对的圆周角相等），∴△AIF∽△EDB，∴＝．∴IA•BD＝DE•IF②任务：（1）观察发现：IM＝R+d，IN＝（用含R，d的代数式表示）；（2）请判断BD和ID的数量关系，并说明理由．（3）请观察式子①和式子②，并利用任务（1），（2）的结论，按照上面的证明思路，完成该定理证明的剩余部分；（4）应用：若△ABC的外接圆的半径为6cm，内切圆的半径为2cm，则△ABC的外心与内心之间的距离为cm．5．【发现】如图（1），AB为⊙O的一条弦，点C在弦AB所对的优弧上，根据圆周角性质，我们知道∠ACB的度数（填“变”或“不变”）；若∠AOB＝150°，则∠ACB ＝°．爱动脑筋的小明猜想，如果平面内线段AB的长度已知，∠ACB的大小确定，那么点C是不是在某一个确定的圆上运动呢？【研究】为了解决这个问题，小明先从一个特殊的例子开始研究．如图（2），若AB＝2，直线AB上方一点C满足∠ACB＝45°，为了画出点C所在的圆，小明以AB为底边构造了一个等腰Rt△AOB，再以O为圆心，OA为半径画圆，则点C在⊙O上．请根据小明的思路在图（2）中完成作图（要求尺规作图，不写作法，保留作图痕迹，并用2B 铅笔或黑色水笔加黑加粗）．后来，小明通过逆向思维及合情推理，得出一个一般性的结论，即：若线段AB的长度已知，∠ACB的大小确定，则点C一定在某一个确定的圆上，即定弦定角必定圆，我们把这样的几何模型称之为“定弦定角”模型．【应用】（1）如图（3），AB＝2，平面内一点C满足∠ACB＝60°，则△ABC面积的最大值为．（2）如图（4），已知正方形ABCD，以AB为腰向正方形内部作等腰△BAE，其中BE ＝BA，过点E作EF⊥AB于点F，点P是△BEF的内心．①∠BPE＝°，∠BPA＝°；②连接CP，若正方形ABCD的边长为2，则CP的最小值为．6．如图，BE为⊙O的直径，C为线段BE延长线上一点，CA为⊙O的切线，A为切点，连接AB，AE，AO．∠C＝30°．（1）求∠ABC的度数；（2）求证：BO＝CE；（3）已知⊙O的半径为6，求图中阴影部分的面积．（结果保留π）7．如图，在△ABC中，点D是AC边上一点，以AD为直径的⊙O与边BC切于点E，且AB＝BE．（1）求证：AB是⊙O的切线；（2）若BE＝3，BC＝7，求⊙O的半径长；（3）求证：CE2＝CD•CA．8．如图，AB是⊙O的直径，AC⊥AB，BC交⊙O于点D，点E在劣弧BD上，DE的延长线交AB的延长线于点F，连接AE交BD于点G．（1）求证：∠AED＝∠CAD；（2）若点E是劣弧BD的中点，求证：ED2＝EG•EA；（3）在（2）的条件下，若BO＝BF，DE＝1.5，求EF的长．9．定义：三角形一边上的点将该边分为两条线段，且这两条线段的积等于这个点到这边所对顶点连线的平方，则称这个点为三角形该边的“好点”．如图1，△ABC中，点D是BC边上一点，连接AD，若AD2＝BD•CD，则称点D是△ABC中BC边上的“好点”．（1）如图2，△ABC的顶点是4×4网格图的格点，请仅用直尺画出（或在图中直接描出）AB边上的“好点”；（2）△ABC中，BC＝14，tan B＝，tan C＝1，点D是BC边上的“好点”，求线段BD的长；（3）如图3，△ABC是⊙O的内接三角形，点H在AB上，连接CH并延长交⊙O于点D．若点H是△BCD中CD边上的“好点”．①求证：OH⊥AB；②若OH∥BD，⊙O的半径为r，且r＝3OH，求的值．10．如图，DE是△DBC的外角∠FDC的平分线，交BC的延长线于点E，DE的延长线与△DBC的外接圆交于点A．（1）求证：AB＝AC；（2）若∠DCB＝90°，sin E＝，AD＝4，求BD的长．11．已知⊙O为△ABC的外接圆，点E是△ABC的内心，AE的延长线交BC于点F，交⊙O于点D．（1）如图1，求证：BD＝ED．（2）如图2，AD为⊙O的直径．若BC＝12，sin∠BAC＝，求OE的长．12．如图，AB是大半圆O的直径．OA是小半圆O1的直径，点C是大半圆O上的一个动点（不与点A、B重合），AC交小半圆O1于点D，DE⊥OC，垂足为E．（1）求证：AD＝DC；（2）求证：DE是半圆O1的切线；（3）如果OE＝EC，请判断四边形O1OED是什么四边形，并证明你的结论．13．已知△ABC是⊙O的内接三角形，AB为⊙O的直径．点D是⊙O外一点，连接AD 和OD，OD与AC相交于点E，且OD⊥AC．（1）如图1，若AD是⊙O的切线，tan∠BAC＝，证明：AD＝AB；（2）如图2，延长DO交⊙O于点F，连接CD，CF，AF．当四边形ADCF为菱形，且∠BAC＝30°，BC＝1时，求DF的长．14．如图1，在△ABC中，AB＝AC，⊙O是△ABC的外接圆，过C作CD∥AB，CD交⊙O于D，连接AD交BC于点E，延长DC至点F，使CF＝AC，连接AF．（1）求证：AF是⊙O的切线；（2）求证：AB2﹣BE2＝BE•EC；（3）如图2，若点G是△ACD的内心，BC•BE＝64，求BG的长．15．已知：△ABC内接于⊙O，连接CO并延长交AB于点E，交⊙O于点D，满足∠BEC ＝3∠ACD．（1）如图1，求证：AB＝AC；（2）如图2，连接BD，点F为弧BD上一点，连接CF，弧CF＝弧BD，过点A作AG⊥CD，垂足为点G，求证：CF+DG＝CG；（3）如图3，在（2）的条件下，点H为AC上一点，分别连接DH，OH，OH⊥DH，过点C作CP⊥AC，交⊙O于点P，OH：CP＝1：，CF＝12，连接PF，求PF的长．参考答案1．解：（1）如图，连接OC，AE，过点A作AM⊥CE，垂足为M，∵PC是⊙O的切线，∴∠CAB＝∠DCB，又∵CA＝CD，∴∠CAB＝∠CDB，∴∠DCB＝∠CDB，∴BC＝BD，又∵AB是⊙O的直径，∴∠ACB＝90°，∴∠CAB+∠CBA＝90°，∵∠CBA＝2∠CDB＝2∠CAB，∴∠CBA＝90°×＝60°，∵OC＝OB，∴△OBC是正三角形，∴BC＝OB；（2）连接AE，过点A作AM⊥CE，垂足为M，∵E是中点，∴AE＝BE＝4，∠ACE＝∠BCE＝∠ACB＝×90°＝45°，在Rt△AEM中，AE＝4，∠AEM＝∠CBA＝60°，∴EM＝AE＝2，AM＝AE＝2，在Rt△ACM中，AM＝2，∠ACM＝45°，∴CM＝AM＝2，∴CE＝EM+CM＝2+2，答：CE的长为2+2．2．（1）证明：连接OC，∵DC切⊙O于C，∴OC⊥CD，∵AE⊥CD，∴AE∥OC，∵AO＝BO，∴EC＝BC，∴OC＝AE，∵OC＝OA＝OB＝AB，∴AE＝AB；（2）解：连接AC，∵AB是⊙O的直径，∴∠ACB＝90°，∴∠ACE＝90°，AC⊥BE，∵由（1）知：AB＝AE，∴EC＝BC，∵BC＝16，∴EC＝16，在RtACB中，由勾股定理得：AC＝＝＝12，在Rt△ACE中，S△ACE＝＝，∵AE＝AB＝20，∴＝CD，解得：CD＝9.6．3．（1）证明：连接AD，OD，∵AC为⊙O的直径，∴AD⊥BC，∵AB＝AC，∴∠BAD＝∠CAD，∵OA＝OD，∴∠OAD＝∠ODA，∴∠BAD＝∠ODA，∴AB∥OD，∵DE是⊙O的切线，∴OD⊥DE，∴DE⊥AB；（2）解：∵tan B＝＝，∴设AD＝k，BD＝2k，∴AB＝＝k，∵AB＝AC＝5，∴k＝，∴AD＝，BD＝2，∵S△ABD＝AB•DE＝AD•BD，∴DE＝＝2，∴AE＝＝＝1．4．解：（1）∵O、I、N三点共线∴OI+IN＝ON∴IN＝ON﹣OI＝R﹣d故答案为：R﹣d．（2）BD＝ID．理由如下：∵点I是△ABC的内心∴∠BAD＝∠CAD，∠CBI＝∠ABI∵∠DBC＝∠CAD，∠BID＝∠BAD+∠ABI ∠DBI＝∠DBC+∠CBI∴∠BID＝∠DBI∴BD＝ID．（3）由（2）知BD＝ID∴式子②可改写为IA•ID＝DE•IF又∵IA•ID＝IM•IN∴DE•IF＝IM•IN∴2R•r＝（R+d）（R﹣d）∴R2﹣d2＝2Rr∴d2＝R2﹣2Rr．（4）∵d2＝R2﹣2Rr＝62﹣2×6×2＝12∴d＝2．故答案为：2．5．解：【发现】根据圆周角性质，∠ACB的度数不变，∵∠AOB＝150°，∴∠ACB＝∠AOB＝75°，故答案为：不变，75°；【研究】补全图形如图1所示，【应用】（1）如图2，记△ABC的外接圆的圆心为O，连接OA，OB，∵∠ACB＝60°，∴∠AOB＝2∠ACB＝120°，∵OA＝OB，∴∠OAB＝30°，过点O作OH⊥AB于H，∴AH＝AB＝，在Rt△AHO中，设⊙O的半径为2r，则OH＝r，根据勾股定理得，（2r）2﹣r2＝3，∴r＝1（舍去负数），∴OA＝2，OH＝1，∵点C到AB的最大距离h为r+OH＝2+1＝3，∴S△ABC最大＝AB•h＝×2×3＝3，故答案为：3；（2）①∵EF⊥AB，∴∠EFB＝90°，∴∠BEF+∠EBF＝90°，∵点P是△BEF的内心，∴PE，PB分别是∠BEF和∠EBF的角平分线，∴∠BEP＝∠BEF，∠EBP＝∠ABP＝∠ABE，∴∠BPE＝180°﹣（∠BEP+∠EBP）＝180°﹣（∠BEF+∠EBF）＝180°﹣×90°＝135°；在△BPE和△BPA中，，∴△BPE≌△BPA（SAS）．∴∠BPA＝∠BPE＝135°，故答案为：135°，135°；②如图3，作△ABP的外接圆，圆心记作点O，连接OA，OB，在优弧AB上取一点Q，连接AQ，BQ，则四边形APBQ是⊙O的圆内接四边形，∴∠AQB＝180°∠BPA＝45°，∴∠AOB＝2∠AQB＝90°，∴OA＝OB＝AB＝，连接OC，与⊙O相交于点P'此时，CP'是CP的最小值，过点O作OM⊥AB于M，ON⊥CB，交CB的延长线于N，则四边形OMBN是正方形，∴ON＝BN＝BM＝AB＝1，∴CN＝BC+BN＝3，在Rt△ONC中，OC＝＝，∴CP的最小值＝CP'＝OC﹣OP'＝﹣，故答案为：﹣．6．（1）解：∵CA为⊙O的切线，∴∠OAC＝90°，∴∠AOC＝90°﹣∠C＝60°，由圆周角定理得，∠ABC＝∠AOC＝30°；（2）证明：在Rt△AOC中，∠C＝30°，∴OA＝OC，∵OA＝OB＝OE，∴OB＝CE；（3）解：在Rt△AOC中，AC＝＝6，∴图中阴影部分的面积＝×6×6﹣＝18﹣6π．7．（1）证明：连接OB、OE，如图所示：在△ABO和△EBO中，，∴△ABO≌△EBO（SSS），∴∠BAO＝∠BEO，∵⊙O与边BC切于点E，∴OE⊥BC，∴∠BEO＝∠BAO＝90°，即AB⊥AD，∴AB是⊙O的切线；（2）解：∵BE＝3，BC＝7，∴AB＝BE＝3，CE＝4，∵AB⊥AD，∴AC＝＝＝2，∵OE⊥BC，∴∠OEC＝∠BAC＝90°，∠ECO＝∠ACB，∴△CEO∽△CAB，∴，即，解得：OE＝，∴⊙O的半径长为．（3）证明：连接AE，DE，∵AD是⊙O的直径，∴∠AED＝90°，∴∠AEB+∠DEC＝90°，∵BA是⊙O的切线，∴∠BAC＝90°，∴∠BAE+∠EAD＝90°，∵AB＝BE，∴∠BAE＝∠BEA，∴∠DEC＝∠EAD，∴△EDC∽△AEC，∴，∴CE2＝CD•CA．8．（1）证明：∵AB是⊙O的直径，∴∠ADB＝90°，∵AC⊥AB，∴∠CAB＝90°，∴∠ABD＝∠CAD，∵＝，∴∠AED＝∠ABD，∴∠AED＝∠CAD；（2）证明：∵点E是劣弧BD的中点，∴＝，∴∠EDB＝∠DAE，∵∠DEG＝∠AED，∴△EDG∽△EAD，∴，∴ED2＝EG•EA；（3）解：连接OE，∵点E是劣弧BD的中点，∴∠DAE＝∠EAB，∵OA＝OE，∴∠OAE＝∠AEO，∴∠AEO＝∠DAE，∴OE∥AD，∴，∵BO＝BF＝OA，DE＝，∴，∴EF＝3．9．解：（1）如图：D即为△ABC边AB上的“好点”；（2）如答图1：过A作AH⊥BC于H，∵tan B＝，tan C＝1，∴，＝1，设AH＝3k，则BH＝4k，CH＝3k，∵BC＝14，∴3k+4k＝14，解得k＝2，∴BH＝8，AH＝CH＝6，设BD＝x，则CD＝14﹣x，DH＝8﹣x，Rt△ADH中，AD2＝AH2+DH2＝62+（8﹣x）2，而点D是BC边上的“好点”，有AD2＝BD•CD＝x•（14﹣x），∴62+（8﹣x）2＝x•（14﹣x），解得x＝5或x＝10，∴BD＝5或BD＝10；（3）①∵∠CAH＝∠HDB，∠AHC＝∠BHD，∴△ACH∽△DBH，∴，∴AH•BH＝CH•DH，∵点H是△BCD中CD边上的“好点”，∴BH2＝CH•DH，∴AH＝BH，∴OH⊥AB；②如答图2：连接AD，∵OH⊥AB，OH∥BD，∴AB⊥BD，∴AD是直径，∵r＝3OH，设OH＝m，则OA＝3m，BD＝2m，Rt△AOH中，AH＝＝2m，∴BH＝2m，Rt△BHD中，HD＝＝2m，∵点H是△BCD中CD边上的“好点”，∴BH2＝CH•DH，∴CH＝＝m，∴＝＝．10．（1）证明：∵DE是△DBC的外角∠FDC的平分线，∴∠FDE＝∠CDE，∵∠ADB＝∠ACB＝∠FDE，∠ABC＝∠CDE，∴∠ABC＝∠ACB，∴AB＝AC；（2）解：∵∠DCB＝90°，∴∠DCE＝∠BAD＝90°，∴∠E+∠CDE＝∠ABD+∠ADB＝90°，∵∠ADB＝∠FDE＝∠CDE，∴∠ABD＝∠E，∵sin E＝，∴sin∠ABD＝＝，∵AD＝4，∴BD＝4．11．（1）证明：如图1，连接BE．∵E是△ABC的内心，∴∠ABE＝∠CBE，∠BAD＝∠CAD，∵∠DBC＝∠CAD．∴∠DBC＝∠BAD，∵∠BED＝∠BAD+∠ABE，∴∠DBE＝∠DEB，∴BD＝ED；（2）如图2 所示；连接OB．∵AD是直径，AD平分∠BAC，∴AD⊥BC，且BF＝FC＝6，∵，∴OB＝10．在Rt△BOF中，BF＝6，OB＝10，∴，∴DF＝2，在Rt△BDF中，BF2+DF2＝BD2，∴，∴，∴．12．证明：（1）连接OD，∵AO为圆O1的直径，则∠ADO＝90°．∵AC为⊙O的弦，OD为弦心距，∴AD＝DC．（2）证明：∵D为AC的中点，O1为AO的中点，∴O1D∥OC．又DE⊥OC，∴DE⊥O1D∴DE与⊙O1相切．（3）如果OE＝EC，又D为AC的中点，∴DE∥O1O，又O1D∥OE，∴四边形O1OED为平行四边形．又∠DEO＝90°，O1O＝O1D，∴四边形O1OED为正方形．13．解：（1）证明：∵OD⊥AC，∴AE＝EC＝AC，∠DEA＝90°，∵AB为⊙O的直径，∴∠ACB＝90°，∵tan∠BAC＝＝，∴BC＝AC，∴AE＝BC，∵AD是⊙O的切线，∴DA⊥AB，∴∠DAO＝∠ACB＝90°，∴∠DAE+∠CAB＝∠ABC+∠CAB＝90°，∴∠DAE＝∠ABC，在△DAE和△ABC中，，∴△DAE≌△ABC（ASA），∴AD＝AB；（2）在Rt△ABC中，∠BAC＝30°，BC＝1，∵∠ABC＝∠AFC＝60°，∵四边形ADCF为菱形，∴AC＝FC＝，∴△AFC是等边三角形，∴∠DFC＝AFC＝30°，∴CE＝FC＝，∴EF＝CE＝，∴DF＝2EF＝3．14．解：（1）如图1，连接OA，∵AB＝AC，∴＝，∠ACB＝∠B，∴OA⊥BC，∵CA＝CF，∴∠CAF＝∠CFA，∵CD∥AB，∴∠BCD＝∠B，∴∠ACB＝∠BCD，∴∠ACD＝∠CAF+∠CFA＝2∠CAF，∵∠ACB＝∠BCD，∴∠CAF＝∠ACB，∴AF∥BC，∴OA⊥AF，∴AF为⊙O的切线；（2）∵∠BAD＝∠BCD＝∠ACB，∠B＝∠B，∴△ABE∽△CBA，∴，∴AB2＝BC•BE＝BE（BE+CE）＝BE2+BE•CE，∴AB2﹣BE2＝BE•EC；（3）由（2）知：AB2＝BC•BE，∵BC•BE＝64，∴AB＝8，如图2，连接AG，∴∠BAG＝∠BAD+∠DAG，∠BGA＝∠GAC+∠ACB，∵点G为内心，∴∠DAG＝∠GAC，又∵∠BAD+∠DAG＝∠GAC+∠ACB，∠BAD＝∠ACB，∴∠BAG＝∠BGA，∴BG＝AB＝8．15．（1）证明：如图1中，连接AD．设∠BEC＝3α，∠ACD＝α．∵∠BEC＝∠BAC+∠ACD，∴∠BAC＝2α，∵CD是直径，∴∠DAC＝90°，∴∠D＝90°﹣α，∴∠B＝∠D＝90°﹣α，∵∠ACB＝180°﹣∠BAC﹣∠ABC＝180°﹣2α﹣（90°﹣α）＝90°﹣α．∴∠ABC＝∠ACB，∴AB＝AC．（2）证明：如图2中，连接AD，在CD上取一点Z，使得CZ＝BD．∵＝，∴DB＝CF，∵∠DBA＝∠DCA，CZ＝BD，AB＝AC，∴△ADB≌△AZC（SAS），∴AD＝AZ，∵AG⊥DZ，∴DG＝GZ，∴CG＝CZ+GZ＝BD+DG＝CF+DG．（3）解：连接AD，PA，作OK⊥AC于K，OR⊥PC于R，CT⊥FP交FP的延长线于T．∵CP⊥AC，∴∠ACP＝90°，∴PA是直径，∵OR⊥PC，OK⊥AC，∴PR＝RC，∠ORC＝∠OKC＝∠ACP＝90°，∴四边形OKCR是矩形，∴RC＝OK，∵OH：PC＝1：，∴可以假设OH＝a，PC＝2a，∴PR＝RC＝a，∴RC＝OK＝a，sin∠OHK＝＝，∴∠OHK＝45°，∵OH⊥DH，∴∠DHO＝90°，∴∠DHA＝180°﹣90°﹣45°＝45°，∵CD是直径，∴∠DAC＝90°，∴∠ADH＝90°﹣45°＝45°，∴∠DHA＝∠ADH，∴AD＝AH，∵∠COP＝∠AOD，∴AD＝PC，∴AH＝AD＝PC＝2a，∴AK＝AH+HK＝2a+a＝3a，在Rt△AOK中，tan∠OAK＝＝，OA＝＝＝a，∴sin∠OAK＝＝，∵∠ADG+∠DAG＝90°，∠ACD+∠ADG＝90°，∴∠DAG＝∠ACD，∵AO＝CO，∴∠OAK＝∠ACO，∴∠DAG＝∠ACO＝∠OAK，∴tan∠ACD＝tan∠DAG＝tan∠OAK＝，∴AG＝3DG，CG＝3AG，∴CG＝9DG，由（2）可知，CG＝DG+CF，∴DG+12＝9DG，∴DG＝，AG＝3DG＝3×＝，∴AD＝＝＝，∴PC＝AD＝，∵sin∠F＝sin∠OAK，∴sin∠F＝＝，∴CT＝×FC＝×12＝，FT＝＝＝，PT＝＝＝，∴PF＝FT﹣PT＝﹣＝．。

中考数学压轴题二

1．如图，点P是反比例函数y＝－2x（x＜0）图象上一动点，点A、B分别在x轴，y轴上，且OA＝OB＝2，PM⊥x轴于M，交AB于E，PN⊥y轴于N，交AB于F．（1）当动点P的纵坐标为53时，连接OE（2）设动点P的坐标为P（a，b）（－2＜探索：以AE、EF、BF2、如图，在△OAB中，OA＝OB，点A坐标为（－33，3），点B在x轴负半轴上．（1）将△OAB沿x轴向右平移a个单位后，点A恰好落在反比例函数y＝63x的图象上，求a的值；（2）将△OAB绕点O按逆时针方向旋转α角（0°＜α＜90°）．①当α＝30°时，点B恰好落在反比例函数y＝k的图象上，求k的值；②点A、B请说明理由．3．如图1，在Rt△ABC中，∠C＝90°，AC＝BC，D是AB边上一点，E是AC边上的一个动点（与点A、C不重合），DF⊥DE，DF与射线BC相交于点F．（1）如图2，若点D是边AB的中点，求证：DE＝DF；（2）若AD:DB＝m，求DE:DF的值；（3）若AC＝BC＝6，AD:DB＝1:2，设AE＝x，BF＝y．①求y关于x的函数关系式，并写出自变量x的取值范围；②以CE为直径的圆与直线AB是否可相切，若可能，求出此时x的值，若不可能，请说明理由．B图1B图2B 备用图B 备用图4．Rt △ABC 的直角顶点B 在Rt △DEF 的斜边DF 上，已知AB ＝DF ，DE ＝EF ，∠A ＝30°．固定△DEF 不动，将△ABC 绕点B 旋转，并使边AB 与边DE 交于点P ，边BC 与边EF 于点Q ．（1）如图1，若FBBD ＝m ，求BPBQ的值，并确定m 的取值范围；（2）若DF ＝30， FBBD＝2，连接PQ ，设△BPQ 的面积为S ，在旋转过程中：①如图2，当点E 恰好落在边AC 上时，求AE 的长；②S 是否存在最大值或最小值？若存在，求出最大值或最小值，若不存在，请说明理由； ③随着S 取不同的值，对应△BPQ 的个数有哪些变化？求相应S 值的取值范围．Q E D F B A PC 图1 Q ED FBA PC图2 H5．如图，已知抛物线y＝(3－m)x2＋2(m－3)x＋4m－m2的顶点A在双曲线y＝3x上，直线y＝mx＋b经过点A，与y轴交于点B，与x轴交于点C．（1）求直线AB的解析式；（2）将直线AB绕点O顺时针旋转90°，与x轴交于点D，与y轴交与点E，求sin∠BDE 的值；（3）过点B作x轴的平行线与双曲线交于点F，点M在直线BF上，且到抛物线的对称轴的距离为6．若点N在直线BF上，直接写出使得∠AMB＋∠ANB＝45°的点N的坐标．6．如图，在平面直角坐标系中，直线y＝mx（m＞0）与双曲线y＝kx交于A、B两点，过点A作AC∥x轴，过点B作BC∥y轴，AC与BC交于点C，AC与y轴交于点M，BC与x 轴交于点N，若∠BAC＝60°，AB＝4．（1）求m、k的值；（2）将一把三角尺的直角顶点放在原点O处，绕着点O旋转三角尺，三角尺的两直角边分别交射线CA、射线BC于点P、Q，设点P的横坐标为x，PQ的长为L，当点P在边AC上运动时，求L与x的函数关系式；（3）当△PQC的面积为32时，求点P的坐标．7．如图，矩形ABCD的顶点A在坐标原点，顶点B坐标为（－2，1），顶点C在y轴上．（1）求顶点D的坐标；（2）将矩形ABCD绕点O顺时针旋转，使点D落在x轴的点G处，得到矩形AEFG，EF 与AD交于点M，过点M的反比例函数图象交FG于点N（3）求证：△AMN是直角三角形．8．在平面直角坐标系中，点A （3，0），B （0，4）．以点A 为旋转中心，把△ABO 顺时针旋转，得△ACD ．记旋转转角为α，∠ABO 为β．（1）如图①，当旋转后点D 恰好落在AB 边上时，求点D 的坐标；（2）如图②，当旋转后满足BC ∥x 轴时，求α与β之间的数量关系；（3）当旋转后满足∠AOD ＝β时，求直线CD 的解析式．图①图②9．已知∠MON ＝60°，射线OT 是∠MON 的平分线，点P 是射线OT 上的一个动点，射线PB 交射线ON 于点B ．（1）如图，若射线PB 绕点P 顺时针旋转120°后与射线OM 交于点A ，求证：P A ＝PB ；（2）在（1）的条件下，若点C 是AB 与OP 的交点，且满足PC ＝32PB ，求△POB 与△PBC 的面积之比；（3）当OB ＝2时，射线PB 绕点P 顺时针旋转120°后与直线OM 交于点A （点A 不与点O 重合），直线P A 交射线ON 于点D ，且满足∠PBD ＝∠ABO ，求OP 的长．B C M A N PT M N T 备用图MNT 备用图10．已知一次函数y＝－12x＋b的图象与反比例函数y＝6x（x＞0）的图象交于A、B两点，与x轴、y轴分别交于C、D两点．（1）如图1，若AB＝2AC，求b的值；（2）在（1）的条件下，将一块直角三角板的直角顶点P放在反比例函数y＝6x（x＞0）图象的AB段上滑动，两直角边始终与坐标轴平行，且与线段AB分别交于Q、R两点．设点P 的横坐标为x，QR的长为L，求L关于x的函数关系式，并求L的最大值；（3）如图2，过点A作直线AE∥x轴，交轴于点E；过点B作直线BF∥轴交x轴于点F，交直线AE于点并说明理由．11．如图，在直角梯形ABCD 中，AD ∥BC ，AB ⊥BC ，AD ＝AB ＝1，BC ＝2．将点A 折叠到CD 边上，记折叠后A 点对应的点为P （P 与D 点不重合），折痕EF 只与边AD 、BC 相交，交点分别为E 、F ．过点P 作PN ∥BC 交AB 于N ，交EF 于M ，连结P A 、PE 、AM ，EF 与P A 相交于O ．（1）指出四边形PEAM 的形状（不需证明）；（2）记∠EPM ＝α，△AOM 、△AMN 的面积分别为S 1、S 2．①求证：S 1tanα2＝18P A 2；②设AN ＝x ，y ＝S 1－S 2tanα2，试求出以x 为自变量的函数y 的解析式，并确定y 的取值范围．OABCDPE FMN12．已知：在△ABC 中，BC ＝2AC ，∠DBC ＝∠ACB ，BD ＝BC ，CD 交线段AB 于点E ．（1）如图l ，当∠ACB ＝90°时，则线段DE 、CE 之间的数量关系为____________________；（2）如图2，当∠ACB ＝120°时，求证：DE ＝3CE ；（3）如图3，在（2）的条件下，点F 是BC 边的中点，连接DF ，DF 与AB 交于点G ，△DKG 和△DBG 关于直线DG 对称（点B 的对称点是点K ），延长DK 交AB 于点H ．若BH ＝10，求CE 的长．C A B DE 图1C A BDE 图2C AB D E 图3K HG F13．如图，在平面直角坐标系中，已知点A（－1，0），点B（9，0），以AB为直径作⊙M，交y轴的负半轴于点C，连接AC、BC，抛物线经过A、B、C三点．（2）点E是AC延长线上一点，∠BCE的平分线CD交⊙M于点D，连接BD，求直线BD的解析式；（3）在（2）的条件下，抛物线上是否存在点P，使得∠PDB＝∠CBD？若存在，求出P点坐标；若不存在，请说明理由．14．如图，二次函数y＝ax2＋bx（a＞0）的图象与反比例函数y＝kx的图象相交于A，B两点，且点A的坐标为（1，4），点B在第三象限．（1）求该二次函数的表达式；（2）设二次函数图象与x轴的另一个交点为D，E点为线段OD上的动点（与O，D不重合），过E点作EF∥OB，交BD于F，连接BE①设OE的长为m，△BEF的面积为S，求S②当△BEF为等腰三角形时，求点E15．如图，在Rt△ABC中，∠C＝90°，AC＝BC＝6，点D为AC中点，点E为边AB上一动点，点F为射线BC上一动点，且∠FDE＝90°．（1）当DF∥AB时，连接EF，求cos∠DEF的值；（2）当点F在线段BC上时，设AE＝x，BF＝y，求y关于x的函数关系式，并写出自变量x的取值范围；（3）连接CE，若△CDE为等腰三角形，求BF的长．ACB DEF16．如图，Rt△ABC中，∠ACB＝90°，AC＝3cm，CB＝4cm．点P、Q分别是AB、CB上动点，它们分别从A、C同时出发向B点匀速移动，移动速度为1cm/秒，设P、Q移动时间为t秒（0≤t≤4）．（1）当∠CPQ＝90°时，求t的值；（2）是否存在t，使△CPQ成为等边三角形？若存在，求出t的值；若不存在，能否改变Q 的运动速度（P的速度不变），使△CPQ成为等边三角形？如何改变？并求出相应的t值．17．如图，抛物线y＝－14x2＋4交x轴于A、B两点（A在B的左侧），交y轴于点C，连接AC、BC，D是线段OB上一动点，以CD为一边向右侧作正方形CDEF，连接BF，交DE于点P．（1）试判断△ABC的形状，并说明理由；（2）求证：BF⊥AB；（3）连接CP，记△CPF的面积为S1，△CPB的面积为S2，若S＝S1－S2，试探究S的最小值．18．如图，Rt△ABC中，∠A＝30°，BC＝10cm，点Q在线段BC上从B向C运动，点P在线段BA上从B向A运动．Q、P两点同时出发，运动的速度相同，当点Q到达点C时，两点都停止运动．作PM⊥PQ交CA于点M，过点P分别作BC、CA的垂线，垂足分别为E、F．（1）求证：△PQE∽△PMF；（2）当点P、Q运动时，请猜想线段PM与MA的大小有怎样的关系？并证明你的猜想；（3）设BP＝x，△PEM的面积为y，求y关于x的函数关系式，当x为何值时，y有最大值，并将这个值求出来．EQAC19．在△ABC中，AB＝AC，∠BAC＝α，点D是BC上一动点（不与B、C重合），将线段AD绕点A逆时针旋转α后到达AE位置，连接DE、CE，设∠BCE＝β．（1）如图1，若α＝90°，求β的大小；（2）如图2，当点D在线段BC上运动时，试探究α与β之间的数量关系，并证明你的结论；（3）当点D在线段BC的反向延长线上运动时，（2）中的结论是否仍然成立？若成立，请证明，若不成立，请写出α与β之间的数量关系，并说明理由．EA图1E A图220．如图1，已知正方形OABC的边长为2，顶点A、C分别在x、y轴的正半轴上，M是BC的中点，P（0，m）是线段OC上一动点（C点除外），直线PM交AB的延长线于点D．（1）求点D的坐标（用含m的代数式表示）；（2）当△APD是等腰三角形时，求m的值；（3）设过P、M、B三点的抛物线与x轴正半轴交于点E，过点O作直线ME的垂线，垂足为H（如图2）．当点P从点O向点C运动时，点H也随之运动，请直接写出点H所经过的路径长．（不必写解答过程）图121．在四边形ABCD 中，对角线AC 、BD 相交于点O ，设锐角∠DOC ＝α，将△DOC 绕点O 按逆时针方向旋转得到△D ′OC ′（0°＜旋转角＜90°），连接AC ′、BD ′，AC ′ 与BD ′ 相交于点M ．（1）当四边形ABCD 是矩形时，如图1，请猜想AC ′ 与BD ′ 的数量关系以及∠AMB 与α的大小关系，并证明你的猜想；（2）当四边形ABCD 是平行四边形时，如图2，已知AC ＝kBD ，请猜想此时AC ′ 与BD ′ 的数量关系以及∠AMB 与α的大小关系，并证明你的猜想；（3）当四边形ABCD 是等腰梯形时，如图3，AD ∥BC ，此时（1）AC ′ 与BD ′ 的数量关系是否成立？∠AMB 与α的大小关系是否成立？不必证明，直接写出结论．M B C A O D C ′ D ′ 图1MB C A O D C ′D ′ 图2MB C A O D C ′ D ′图322．在矩形ABCD中，点E是AD边上一点，∠ABE＝30°，BE＝DE，连接BD．动点M从点E出发沿射线ED运动，过点M作MN∥BD交直线BE于点N．（1）如图1，当点M在线段ED上时，求证：BE＝PD＋33MN；（2）若BC＝6，设MN长为x，以M、N、D为顶点的三角形面积为y，求y关于x的函数关系式；（3）在（2）的条件下，当点M运动到线段ED的中点时，连接NC，过点M作MF⊥NC 于F，MF交对角线BD于点G（如图2），求线段MG的长．A E M DNC图1 A E DC备用图A E M DN图2GF23．如图1，边长为2的正方形ABCD 中，E 是BA 延长线上一点，且AE ＝AB ，点P 从点D 出发，以每秒1个单位长度的速度沿D →C →B 向终点B 运动，直线EP 交AD 于F ，过点F 作直线FG ⊥DE 于G ，交AB 于Q ．设点P 运动时间为t （秒）．（1）求证：AF ＝AQ ；（2）当t 为何值时，四边形PQBC 是矩形？（3）如图2，连接PB ，当t 为何值时，△PQB 是等腰三角形？A B C E D F G Q P 图1 A B C E D FG Q P 图224．如图，已知抛物线y＝ax2＋bx＋8（a≠0）与x轴交于点A（－2，0）、B，与y轴交于点C，tan∠ABC＝2．（1）求抛物线的解析式及其顶点D的坐标；（2）设直线CD交x轴于点E．在线段OB的垂直平分线上是否存在点P，使得经过点P 的直线PM垂直于直线CD，且与直线OP的夹角为75°？若存在，求出点P的坐标；若不存在，请说明理由；（3）过点B作x轴的垂线，交直线CD于点F，将抛物线沿其对称轴向上平移，使抛物线与线段EF25．已知正方形ABCD，点P是对角线AC所在直线上的动点，点E在DC边所在直线上，且始终保持PE＝PD．（1）如图1，当点P在对角线AC上时，请你通过测量、观察，猜想PE与PB有怎样的关系？（直接写出结论不必证明）；（2）如图2，当点P运动到CA的延长线上时，（1）中猜想的结论是否成立？如果成立，请给出证明；如果不成立，请说明理由；（3）如图3，当点P运动到CA的反向延长线上时，请你利用图3画出满足条件的图形，并判断此时PE与PB有怎样的关系？（直接写出结论不必证明）B 图1B 图226．如图，在直角梯形ABCD 中，AD ∥BC ，∠A ＝90°，AB ＝6，BC ＝8，AD ＝14，点E 、F 、G 分别在BC 、AB 、AD 上，且BE ＝3，BF ＝2，以EF 、FG 为邻边作□EFGH ，连接CH 、DH ．（1）直接写出点H 到AD 的距离；（2）若点H 落在梯形ABCD 内或其边上，求△HGD 面积的最大值与最小值；（3）当△EHC 为等腰三角形时，求AG 的长．A D C GB F E H27．如图，四边形OABC的四个顶点坐标分别为O（0，0），A（8，0），B（4，4），C（0，4），直线l：y＝kx＋b保持与四边形OABC的边交于点M、N（M在折线AOC上，N在折线ABC上）设四边形OABC在l右下方部分的面积为S1，在l左上方部分的面积为S2，记S＝|S1－S2|．（1）求∠OAB的大小；（2）当M、N重合时，求l的解析式；（3）当b≤0时，问线段AB上是否存在点N使得S＝0？若存在，求b的值；若不存在，请说明理由；（4）求S与b的函数关系式。

2024年长沙中考数学压轴题

2024年长沙中考数学压轴题一、在直角坐标系中，点A的坐标为(1,0)，点B的坐标为(0,2)，以原点O为圆心，半径为r的圆与线段AB有且仅有一个公共点，则r的值不可能是？A. 1B. 根号2C. 根号5D. 3（答案）D。

解析：线段AB的长度为根号下(12+22)=根号5，当r=1时，圆与线段AB的端点A相切；当r=根号2时，圆过线段AB的中点；当r=根号5时，圆与线段AB的端点B相切；而当r=3时，圆会同时与线段AB的两个端点都相交，或与线段AB无交点，故r不可能为3。

二、已知二次函数y=ax2+bx+c的图像经过点(1,0)，(2,0)，(3,4)，则a的值为？A. 1B. 2C. 3D. 4（答案）B。

解析：由题意知，二次函数的图像经过点(1,0)，(2,0)，所以其对称轴为x=1.5，且可设二次函数为y=a(x-1)(x-2)，将点(3,4)代入得4=a(3-1)(3-2)，解得a=2。

三、在三角形ABC中，AB=AC，D为BC的中点，E为AB上的一点，且AE=1:2，AD与CE相交于点F，则S三角形ADF三角形ABC等于？A. 1:6B. 1:8C. 1:9D. 1:12（答案）A。

解析：过点D作AB的平行线交CE于点G，由于D是BC的中点，所以DG是三角形CBE的中位线，有DG=0.5BE，且DG平行于BE，所以三角形ADG与三角形ABE相似，且相似比为1:2，又因为AE=1:2，所以AE=DG，所以三角形ADG与三角形AEF全等，所以S三角形ADF=S三角形AGD=0.5S三角形ADG，而S三角形ADG=0.25S三角形ABC，所以S三角形ADF三角形ABC=1:6。

四、若关于x的一元二次方程x2-2x+m=0有两个不相等的实数根，则m的取值范围是？A. m<1B. m>1C. m<0D. m>0（答案）A。

解析：一元二次方程有两个不相等的实数根，需要满足判别式Δ=b2-4ac>0，将方程的系数代入得Δ=(-2)2-41m=4-4m>0，解得m<1。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2019-2020 年中考数学压轴题精选二1、如图，在菱形ABCD中， AB=2，∠ A=60°，以点D为圆心的⊙D 与边 AB 相切于点E．（1）求证：⊙D 与边 BC也相切；（2）设⊙D与 BD相交于点 H，与边 CD相交于点 F，连接 HF，求图中阴影部分的面积（结果保留π）；（3）⊙D上一动点 M从点 F 出发，按逆时针方向运动半周，当S△HDF=S△MDF时，求动点M经过的弧长（结果保留π ）．思路点拨：（ 1）过 D 作 DQ⊥BC 于 Q，连接 DE，根据切线性质得出⊥ AB，根据菱形性质求出BD平分∠ ABC，根据角平分线性质得出DE=DQ，根据切线判定推出即可；（ 2）根据菱形性质和等边三角形判定得出等边三角形ADB，求出 DE值，即可得出圆的半径长，得出等边三角形DCB和等边三角形DHF，求出△ DFH 的高 FN，求出△ DFH的面积和扇形FDH的面积，相减即可得出答案；（3）根据△ FDH 的面积和已知求出△ MDF 边 DF 上的高 MZ，求出∠ MDF，同理得出另一点 M′也符合，且圆心角是 150°，根据弧长公式求出即可．（1）证明：满分解答：过 D 作 DQ⊥BC 于 Q，连接 DE，∵⊙D切 AB 于 E，∴DE⊥AB，∵四边形ABCD是菱形，∴BD 平分∠ ABC，∴DE=DQ（角平分线性质），∵DQ⊥BC，∴⊙D与边 BC也相切；（2）解：过 F 作 FN⊥DH于 N，∵四边形 ABCD是菱形，∴AD=AB=2 ，∵∠ A=60°，∴△ ABD是等边三角形，∴∠ DBA=60°， DC∥AB， AD=BD=AB=2∵DE⊥AB，∴A E=BE= ，由勾股定理得： DE=3=DH=DF，∵四边形 ABCD是菱形，∴∠ C=∠A=60°，DC=BC，∴△ DCB是等边三角形，∴∠ CDB=60°，∵DF=DH，∴△ DFH是等边三角形，∵FN⊥DH，∴DN=NH=，由勾股定理得：FN=，∴S阴影 =S扇形FDH﹣ S△FDH=﹣× 3×=π﹣；（ 3）解：过M作 MZ⊥DF 于 Z，∵由（ 2）知： S△HDF=×3×=，DF=3，又∵S△HDF=S△DFM，∴= ×× 3×MZ，∴MZ=，在Rt△DMZ中， sin ∠MDZ= =，∴∠ MDZ=30°，同理还有另一点M′也符合，此时MM′∥ CD，∠ M′DC=180°﹣ 30°=150°，∴弧MC的长是=π；弧 CM′的长是=π；π 或π ．答：动点M经过的弧长是本题考查的知识点是三角形的面积，等边三角形的性质和判定，勾股定理，菱形的性点评：质，扇形的面积，锐角三角函数的定义，弧长公式等，主要考查学生综合运用性质进行推理和计算的能力，题目综合性比较强，难度偏大．2、如图 1，抛物线 y ＝ ax 2＋ bx ＋ c 经过 A ( － 1,0) 、B (3, 0) 、C (0 ,3) 三点，直线 l 是抛物线的对称轴．（ 1）求抛物线的函数关系式；（ 2）设点 P 是直线 l 上的一个动点，当△ PAC 的周长最小时，求点 P 的坐标；（ 3）在直线 l 上是否存在点 M ，使△ MAC 为等腰三角形，若存在，直接写出所有符合条件的点 M 的坐标；若不存在，请说明理由．图 1思路点拨1．第（ 2）题是典型的“牛喝水”问题，点 P 在线段 BC 上时△ PAC 的周长最小．2．第（ 3）题分三种情况列方程讨论等腰三角形的存在性．满分解答（ 1）因为抛物线与 x 轴交于 A ( －1,0) 、 B (3, 0) 两点，设 y ＝ a ( x ＋ 1)( x － 3) ，代入点 C (0 ,3) ，得－ 3a ＝ 3．解得 a ＝－ 1．所以抛物线的函数关系式是 y ＝－ ( x ＋ 1)( x － 3) ＝－ x 2＋ 2x ＋3．（ 2）如图 2，抛物线的对称轴是直线 x ＝ 1．当点 P 落在线段 BC 上时， PA ＋ PC 最小，△ PAC 的周长最小．设抛物线的对称轴与 x 轴的交点为 H ．由 BHPH， BO ＝ CO ，得 PH ＝ BH ＝2．BOCO所以点 P 的坐标为 (1, 2)．图 2（ 3）点的坐标为 (1, 1) 、 (1,6 ) 、 (1,6 ) 或(1,0) ．M考点伸展第（ 3）题的解题过程是这样的：设点 M 的坐标为 (1, m ) ．22222在△ MAC 中， AC ＝10， MC ＝ 1＋ ( m － 3) ，MA ＝ 4＋ m ．①如图 2222，得 m ＝ 1．3，当 MA ＝ MC 时， MA ＝ MC ．解方程 4＋m ＝ 1＋ ( m －3)此时点的坐标为 (1, 1) ．M②如图 2226 ．4，当 AM ＝ AC 时， AM ＝ AC ．解方程 4＋m ＝ 10，得 m此时点 M 的坐标为 (1, 6 ) 或 (1,6 ) ．③如图 2225，当 CM ＝ CA 时， CM ＝ CA ．解方程 1＋( m － 3) ＝ 10，得 m ＝0 或 6．当 M (1, 6) 时， M 、 A 、 C 三点共线，所以此时符合条件的点 M 的坐标为 (1,0) ．图 3图 4 图 53、如图 1，已知一次函数 y ＝－ x ＋ 7 与正比例函数y4x 的图象交于点 A ，且与 x 轴交于3点 B ．（ 1）求点 A 和点 B 的坐标；（ 2）过点 A 作 AC ⊥ y 轴于点 C ，过点 B 作直线 l // y 轴．动点 P 从点 O 出发，以每秒 1 个单位长的速度，沿 O — C — A 的路线向点 A 运动；同时直线l 从点 B 出发，以相同速度向左平移，在平移过程中，直线l 交 x 轴于点 R ，交线段 BA 或线段于点．当点 P 到达点 A 时，点 P 和直线 l 都停止运AOQ动．在运动过程中，设动点P 运动的时间为 t 秒．①当 t 为何值时，以、、为顶点的三角形的面积为 8？A P R②是否存在以 A 、 P 、 Q 为顶点的三角形是等腰三角形？图 1若存在，求 t 的值；若不存在，请说明理由．思路点拨1．把图 1 复制若干个，在每一个图形中解决一个问题．2．求△ APR 的面积等于 8，按照点 P 的位置分两种情况讨论．事实上， P 在 CA 上运动时，高是定值 4，最大面积为 6，因此不存在面积为 8 的可能．3．讨论等腰三角形，按照点 P 的位置分两种情况讨论，点P 的每一种位置又要讨APQ论三种情况．满分解答（ 1）解方程组 yx 7,x 3, 所以点 A 的坐标是 (3 ， 4) ．4 得y y 4. x,3令 yx 7 0 ，得 x 7 ．所以点 B 的坐标是 (7 ， 0) ．（ 2）①如图 2，当 P 在 OC 上运动时， 0≤ t ＜ 4．由 S △ APRS 梯形 CORA S △ACP S △POR8 ，1 1 1 8 ．整理，得 t 28t 12 0．解得 t ＝ 2 或 t ＝ 6得（3+7 t) 44 (4 t)t(7 t)222（舍去）．如图 3，当 P 在 CA 上运动时，△ APR 的最大面积为 6．因此，当 t ＝ 2 时，以 A 、P 、R 为顶点的三角形的面积为 8．图 2图 3图 4②我们先讨论 P 在 OC 上运动时的情形， 0≤t ＜ 4．如图 1，在△ 中，∠ ＝45°，∠ ＞45°，＝ 7，AB 4 2 ，所以＞．因 AOB B AOB OBOB AB 此∠ OAB ＞∠ AOB ＞∠ B ．如图 4，点 P 由 O 向 C 运动的过程中， OP ＝ BR ＝ RQ ，所以 PQ // x 轴．此时点 A 在 PQ 的垂直平分线上， OR ＝ 2CA ＝ 6．所以 BR ＝ 1，t ＝ 1．我们再来讨论 P 在 CA 上运动时的情形， 4≤t ＜ 7．在△ APQ 中， cosA3为定值， AP 7 t ， AQ OA OQ OA 5OR5t 20 ．53 33如图 5，当 AP ＝AQ 时，解方程 7 t5 t 20，得t 41．3 3 8如图 6，当 QP ＝ QA 时，点 Q 在 PA 的垂直平分线上， AP ＝ 2( OR － OP ) ．解方程7 t 2[(7 t )(t 4)，得] t 5 ．1AQ如 7 ，当 PA ＝ PQ 时，那么cos A2．因此A Q 2 A P c o s ．解方程APA5t 20 2(7 t)3，得t 226．3 3543综上所述， t＝1 或41或 5 或226时，△是等腰三角形．843APQ图 5 图 6 图 7考点伸展当 P 在 CA 上， QP ＝ QA 时，也可以用 AP 2AQ cos A 来求解．3、如图 1，抛物线 y 1 x 2 3x 4 与 x 轴交于 A 、B 两点（点 B 在点 A 的右侧），与42y 轴交于点，连结，以为一边，点为对称中心作菱形，点 P 是 x 轴上的一个CBCBCOBDEC动点，设点 P 的坐标为 ( m , 0) ，过点 P 作 x 轴的垂线 l 交抛物线于点 Q ．（ 1）求点 A 、 B 、 C 的坐标；（ 2）当点 P 在线段 OB 上运动时，直线 l 分别交 BD 、BC 于点 M 、N ．试探究 m 为何值时，四边形 CQMD 是平行四边形，此时，请判断四边形CQBM 的形状，并说明理由；（ 3）当点 P 在线段上运动时，是否存在点，使△ 为直角三角形，若存在，请EB Q BDQ直接写出点 Q 的坐标；若不存在，请说明理由．图 1思路点拨1．第（ 2）题先用含 m 的式子表示线段 MQ 的长，再根据 MQ ＝ DC 列方程． 2．第（ 2）题要判断四边形CQBM 的形状，最直接的方法就是根据求得的 m 的值画一个准确的示意图，先得到结论．3．第（ 3）题△ BDQ 为直角三角形要分两种情况求解，一般过直角顶点作坐标轴的垂线可以构造相似三角形．满分解答（ 1）由 y 1 x 23 x4 1(x 2)(x 8) ，得 A ( －2,0) ， B (8,0) ， C (0, － 4) ．42 4（ 2）直线 DB 的解析式为 y1．x 42由点 P 的坐标为 ( m , 0)，可得M (m,1 m 4) ， Q( m, 1m 23 m4) ．24 2所以 MQ ＝ (1m 4) ( 1m 23m 4) 1 m 2 m 8 ． 2 4 2 4当 MQ ＝ DC ＝ 8 时，四边形 CQMD 是平行四边形．解方程1 m2 m 8 8 ，得 m ＝4，或 m ＝0（舍去）． 4此时点 P 是 OB 的中点， N 是 BC 的中点， N (4, － 2) ，Q (4, － 6) ．所以＝＝ 4．所以与互相平分．MN NQBC MQ所以四边形 CQBM 是平行四边形．图 2 图 3 （ 3）存在两个符合题意的点Q，分别是(－2,0) ， (6, － 4) ．考点伸展第（ 3）题可以这样解：设点Q的坐标为( x,18)) ．( x 2)( x4QG BH1．所以1(x 2)(x 8)1 ．①如图 3，当∠DBQ＝ 90°时， 4GB HD 2 8 x 2 解得 x＝6．此时 Q(6,－4)．QG DH 41( x 2)(x 8)②如图 4，当∠＝ 90°时，2 ．所以42．BDQ GD HB x解得 x＝－2．此时 Q(－2,0)．图 3图 44、为表彰在“缔造完美教室”活动中表现积极的同学，老师决定购买文具盒与钢笔作为奖品．已知 5 个文具盒、 2 支钢笔共需100 元； 4 个文具盒、7 支钢笔共需161 元．（1）每个文具盒、每支钢笔各多少元？（2）时逢“五一”，商店举行优惠促销活动，具体办法如下：文具盒九折，钢笔10 支以上超出部分八折．设买x 个文具盒需要y1元，买 x 支钢笔需要y2元，求 y1、y2关于关系式；（3）若购买同一种奖品，并且该奖品的数量超过10 件，请分析买哪种奖品省钱．x 的函数考点：一次函数的应用；二元一次方程组的应用。

中考数学压轴题二.doc

第十八章全国通用版中考数学：《平行四边形》与坐标系结合压轴题(二)—解析版

2021年中考数学真题分类汇编--函数：函数与几何(压轴题2)(学生版)

2022年深圳中考数学各区压轴题2

2019中考数学压轴题专项训练题二(附答案)

《2020年中考数学保A必刷压轴题(湖南长沙专版)》(二)：最值问题专题(解析版)

2020年中考数学压轴题(含答案) (2)

2021年九级中考数学压轴题满分训练 –几何综合问题(圆的专题)(二)

全国中考数学压轴题精选(2)(含答案)

挑战中考数学压轴题1-2

2023年中考数学第二轮高频压轴题：二元一次方程组-试卷

2020年九年级中考数学压轴题专题训练 二次函数含答案.docx

2024年中考数学高频压轴题训练——二次函数压轴题(角度问题)(含答案)

中考数学压轴题含答案

中考数学压轴题及答案(共20题) 2百度文库

2023年九年级数学中考复习：旋转(面积问题)综合压轴题(Word版,含答案)

中考数学压轴题专集 2一元二次方程 试题

2021年九级中考数学压轴题满分训练 –几何综合问题(圆的专题)(二)

中考数学压轴题二

2024年长沙中考数学压轴题

2020年九年级中考数学压轴题专题训练二次函数含答案.docx

中考数学压轴题专集 2一元二次方程试题