第7章(热力学与统计物理) 玻耳兹曼统计
合集下载
热力学统计 第七章玻尔兹曼统计
al !
al lal ln ln N ! N ln N al ln al ! l l l x 1 ln x ! x ln x x S k ln S
0
设＝1时，S＝0 S0＝0
ln Z S Nk (ln Z )
2.内能U与广义力Y的统计表达式
2.1 内能U的统计表达式
N N l U al l ll e Z Z l l N Z ln Z N Z
e l l
N al l e l Z Z l e l
配分函数Z ：
l
Z l e l
l
分布在能级l 的粒子数：
N al l e l Z
已知（l, l），可求Z——并不容易！
经典粒子： 配分函数Z ：
Z l e l
l
Z e
( q . p )
dqdp e D( )d r h
积分因子：
如果 X ( x, y )dx Y ( x, y )dy 不是全微分，但存在函数 ( x, y ) ，使得
( x, y ) X ( x, y )dx ( x, y )Y ( x, y )dy 为全微分， 即
( x, y ) X ( x, y )dx ( x, y )Y ( x, y )dy ds ( x, y )
S k ln
满足经典极限的非定域系统：
ln
l
la
l
al !
al S k N ln N al ln l l
S0
lal al ln ln N ln N al ln ln N ! l l al ! l
第7章(热力学与统计物理) 玻耳兹曼统计解析
(V )1 3 h( 1 )1 2
N
2mkT
用分子的德布罗义波长
h p h 2m h 2mkT 分子数密度
N e Z1
U N ln Z1
Y
N
y
ln
Z1
S
Nk (ln
Z1
ln
Z1 )
k
ln
N!
S k ln M .B. N!
F NkT ln z1 kT ln N!
经典系统
Z1
l
el
l
h0r
el
d
h0r
e( p,q)
dq1dq2
dqrdp1dp2 h0r
dpr
N e Z1
U
N
ln
dW Ydy dy
l
l
y
al
l
al d l
考虑内能 U l al 的全微分 l
dU l dal al dl
l
。
ቤተ መጻሕፍቲ ባይዱ
与热力学第一定律
dU dQ dW dQ aldl
l
比较，有
dQ ldal
以上两式说明，在准静态过程中系统从外界吸收的热 量等于粒子在各能级重新分布所增加的内能：外界对系统 所作的功等于粒子分布不变时由于能级改变所引起的内能 变。 化。
l
与（6.6.4） ln N ln N al ln al al ln l
l
l
比较，有玻耳兹曼关系
S k ln
该关系反映了熵的统计意义。
自由能
由自由能的定义，
F U TS
N
ln
Z1
TNk (ln
Z1
ln
Z1 )
TNk ln Z1
热力学与统计物理：第七章 玻耳兹曼统计
双原子能量：
1 2m
(
px2
p
2 y
pz2 )
1 2I
( p2
p2
sin2
)
1
2
pr2
1 2
k
(r
r0
)2
上式中： m
m1
m2 ,
m1m2 m1 m2
,I
r2
r02
其中： t
1 2m
( px2
p
2 y
pz2 )
v
1 2I
( p2
p2
sin2
)
1
2
pr2
1 2
k(r
r0 )2
配分函数的计算
00
ex2 dx
1
ex2 dx
0
2
2
由此求
e x2
xdx
1
0
2
I n ex2 xndx
0
I 0 e x2 dx
0
2 1/2
I 1 ex2 xdx
1
0
2
I n I n 2
§7.3 麦克斯韦速度分布率
系统：V，N
al
e l l
as e s
体积V内，在dpxdpydpz的动量范围内，分子质心 平动的状态数为：
CVt
U t (
T
)V
3 Nk 2
平动配分函数的量子计算与经典计算的不同点 只在于用h取代h0，因此对热容的贡献与经典 计算结果相同。
振动配分函数的经典计算：
zv 1
h
e dp pr2 / 2
v
e d (r k (rr0 )2 / 2
r0 )
2 h
第七章 玻尔兹曼统计
1 宏观热力学量的统计表达式
1.1 单粒子配分函数 Z1 及其与参数 α 的关系
粒子数约束
N
al
w e l l
e
wl el
l
l
l
定义单粒子配分函数 Z1 为 Z1 wlel l
N e Z1 或
e N Z1
• 配分函数是统计物理的重要概念，甚至可以说是统计物理 的核心概念。如果知道某个系统的配分函数随热力学参量 （如温度 T ，压强 p 或体积 V ）的函数，系统的物理量 都可以表达成为配分函数对某个参量的一次或高阶次偏微 分。
N
d
(
f1
)
(df1
f1d
)
Nd
f1
f1
(N const.)
即 也是 Q 的积分因子
概据微分方程关于积分因子的理论（参阅汪志诚书附录）：
当微分方程有一个积分因子时，它就有无穷多个积分因 子，任意两个积分因子之比是 S 的函数（dS 是用积分因
子乘以变分 Q 后所得的完整微分）。
即有 1 k(S) 1
2.1 单粒子平均量与系统的宏观平均量的关系 由于整个系统是近独立系统
系统内能：U N : 一个粒子的平均能量
系统压强：p N p p : 一个粒子对器壁的压强贡献
2.2 近独立粒子玻尔兹曼系统的单粒子统计行为
微观状态由 μ 空间 (x, y, z, px , py , pz )的相格描述。
1
若将
V 3 N
理解为气体中分子的平均距离：d ave
，
则经典极限条件可以表述为：
d thermal _ ave
ave
若令 n N V
，则经典极限条件可以表述为：
第七章节-玻尔兹曼统计
在准静态过程中,系统从外界所吸收的热量等于 粒子在各能级重新分布所增加的内能. 根据热力学第二定律
dQ不是全微分，与过程有关，有一积分因子， 除以T后得全微分dS,dS是全微分
BEIJING NORMAL UNIVERSITY
BEIJING NORMAL UNIVERSITY
积分因子
熵的统计表达式
3 U = NkT 2
BEIJING NORMAL UNIVERSITY
麦克斯韦速度分布律
讨论气体分子作无规热运动时，气体分子质心的平移 运动速度所表现出来的统计分布规律。 一、麦克斯韦速度分布律 1859年，麦克斯韦在研究分子相互碰撞作无规则运 动时，得到了气体分子按其质心速度分布的统计规律 麦克斯韦速度分布律
物态方程
∂ ln Z 注：也可直接利用公式 p = NkT 计算 ∂V
⎛ ∂F ⎞ S = −⎜ ⎟ ⎝ ∂T ⎠V
2πmk 3 3 3 = Nk ln V + Nk ln 2 + Nk ln T + Nk 2 h 2 2
3 = Nk ln V + Nk ln T + S 0 2
BEIJING NORMAL UNIVERSITY
熵的统计表达式，Boltzmann 关系
BEIJING NORMAL UNIVERSITY
由于
特性函数，自由能
量子情况下，粒子不可分辨性带来的差别
BEIJING NORMAL UNIVERSITY
计算单原子分子理想气体的熵：
3 3 2πmkT S = Nk + Nk ln V + Nk ln( ) 2 2 2 h
(ⅰ)系统在热力学过程中的规律 (ⅱ)系统的基本热力学函数
第七章 玻耳兹曼统计教案..
热力学与统计物理课程教案第七章 玻耳兹曼统计 7.1 热力学量的统计表达式一、 定域系统的内能、广义力和熵统计表达式在§6.8说过,定域系统和满足经典极限条件的玻色系统都遵从玻耳兹曼分布。
本章根据玻耳兹曼分布讨论这两类系统的热力学性质。
本节首先推导热力学量的统计表达式。
内能是系统中粒子无规则运动总能量的统计平均值.所以 ∑∑--==lβεαl l ll l l e ωεεa U ①引入函数1Z :∑-=lβεl l e εZ 1 ②名为粒子配分函数。
由式∑--=lβεαl l e ωN ②，得：1Z e e ωe N αlβεl αl ---==∑ ③上式给出参量α与N 和1Z 的关系,可以利用它消去式①中的α。
经过简单的运算,可得：11ln Z βZ N e ωβe e ωεe U l βεl αl βεl l αll ⎪⎪⎭⎫ ⎝⎛∂∂-=⎪⎪⎭⎫ ⎝⎛∂∂-==∑∑---- ④ 式④是内能的统计表达式。
在热力学中讲过,系统在程中可以通过功和热量两种方法与外界交换能量。
在无穷小过程中，系统在过程前后内能的变化dU 等于在过程中外界对系统所作的功W d 及系统从外界吸收的热量Q d 之和：Q d W d dU +=。
如果过程是准静态的, W d 可以表达为Ydy 的形式,其中dy 是外参量的改变量,Y 是外参量y 相应的外界对系统的广义作用力。
粒子的能量是外参量的函数。
由于外参量的改变,外界施于处于能级l ε的一个粒子的力为yεl∂∂。
因此，外界对系统的广义作用力Y 为： 11ln 11Z y βN Z y βe e ωy βe e ωyεa y εY αl βεl αβεαl l l l ll l l ∂∂-=⎪⎪⎭⎫ ⎝⎛∂∂-=⎪⎪⎭⎫ ⎝⎛∂∂-=∂∂=∂∂=-----∑∑∑⑤式⑤是广义作用力的统计表达式。
它的一个重要例子是：1ln Z VβN P ∂∂=在无穷小的准静态过程中,当外参量有dy 的改变时,外界对系统所作的功是：l ll l llεd a a y εdy Ydy ∑∑=∂∂= 将内能∑=ll l εa U 求全微分,有：l ll ll l da εεd a dU ∑∑+=上式指出,内能的改变可以分成两项，第一项是粒子分布不变时由于能级改变而引起的内能变化，第二项是粒子能级不变时由于粒子分布改变所引起的内能变化。
7玻耳兹曼统计
3
因此,所有经典粒子体系都是定域粒子体系.由于 量子统计在数学处理上的困难,在处理实际问题时, 引入一些近似条件,使费米-狄拉克统计,玻色-爱因 斯坦统计退化成为经典的麦克斯韦-玻尔兹曼统计.
在第六章中,得到近独立粒子最概然分布:
麦克斯韦 — 玻耳兹曼分布:
al
l exp(
l )
玻
色 — 爱因斯坦分布:
N
(ln Z y
)
y V
N
(ln Z ) V
青海民族大学电信系 李林
第七章 玻尔兹曼统计
9
在无穷小准静态过程中,当外参量改变dy时,外界 对系统所作功,
dW Ydy dy
l
l
y
al
l
al d l
对内能U求全微分,得
dU d l all l aldl l ldal
内能改变 : dU l aldl l ldal
y
青海民族大学电信系 李林
第七章 玻尔兹曼统计
8
Y
l
l
y
al
l
l
y
l exp(
l
)
1
exp
1
y
l
l exp( l )
N Z
1
y
Z
N
(ln Z ) y
al
l exp(
l )
例: 当系统在准静态过程中,体积变化为dV,外界 对系统所作的功为dW=-pdV=Ydy时,
p
Y
y V
粒子分布确定,由能级 粒子能级确定,由分布 改变引起的内能变化. 改变引起的内能变化.
青海民族大学电信系 李林
第七章 玻尔兹曼统计
10
第七章玻耳兹曼统计教学内容1、玻尔兹曼统计中粒子配分
第七章 玻耳兹曼统计教学内容：1、玻尔兹曼统计中粒子配分函数的量子和经典表达式、热力学量的统计表达式；2、由玻尔兹曼统计求理想气体的物态方程；3、由玻尔兹曼分布推求麦克斯韦速度、速率分布律，碰壁数；4、爱因斯坦固体热容量理论的假设和结论。
教学目的：1、理解玻耳兹曼分布是近独立粒子孤立系统在统计平衡态下处于热力学几率最大的宏观分布时粒子数按能量分布的规律。
粒子的配分函数是由和外参量等决定的状态函数。
理解玻耳兹曼关系式。
理解经典的能量均分定理应用于固体和双原子分子理想气体系统求热容量严重偏离实验结果的原因，并由能量的量子化定性解释实验结果。
2、简单应用：由玻耳兹曼分布律求其它分布律，由配分函数求理想气体（单原子分子）系统的热力学函数。
3、综合运用：应用压强的微观实质思想计算分子的碰壁数，用量子玻耳兹曼分布律求理想固体（爱因斯坦模型）的热容量。
玻耳兹曼统计：假设系统由大量定域的全同近独立粒子组成，具有确定的粒子数N ，能量E ，体积V 。
N 个粒子的在各能级的分布可以描述如下： 能 级 12,,,,l εεε … 简 并 度 12,,,,l ωωω … 粒 子 数 12,,,,l a a a … 约束条件：l la N =∑，l l la E ε=∑定域系统和满足经典极限条件的玻色和费米系统都遵从玻耳兹曼分布：l l l a e αβεω--=。
其中系数α与β由l la N =∑与l l la E ε=∑确定。
总能量是系统在某平衡态下的全部能量，包括系统作整体运动时的宏观动 能，在重力场中的势能，以及与系统整体运动和重力场存在无关的内能，是系统内部分子无规则热运动的全部能量。
因此在这里我们所说的总能量E 即总的内能U 。
§7.1 热力学量的统计表达式在§6.8说过，定域系统以及满足经典极限条件的玻色系统和费米系统都遵从玻耳兹曼分布。
本章根据玻耳兹曼分布讨论这两类系统的热力学性质。
本节首先推导热力学量的统计表达式。
热力学_统计物理学答案第七章
− β (ε x + ε y ) − ( pz + ) 1 2m β N( )2∫e dp x dp y dpz = ∫ f ( px , p y , p z )dp x dp y dp z 2πmkT 3
mγ
2
由条件（3）知 计算得
∫p
z
f ( p x , p y , p z ) dp x dp y dp z = Np0
co m
∑
⎞ ⎟ ⎟ ⎠
⎛ Sk ⎞ ⎜ e −α − βε s′′ ⎟ ⎜ ⎟ S ′′ ⎝ S = S1 ⎠
∑
⎤ ……⎥ ⎥ ⎦
)
离开正 常位置而占据图中×位置时，晶体中就出现缺位和填隙原子，晶体这种缺陷 叫做弗伦克缺陷。 (1)假设正常位置和填隙位置数都是 N，试证明由于在晶体中形成 n 个缺位和 填隙原子而具有的熵等于 S = 2k ln
S
习题 7.5 固体含有 A、B 两种原子。试证明由于原子在晶体格点的随机分布引起 的混 合熵为 S = k ㏑
ww
是A 原子的百分比， （1-x ）是 B 原子的百分比。注意 x<1，上式给出的熵为正值。 证： 显然 Ω=
习题 7.6 晶体含有 N 个原子。原子在晶体中的正常位置如图中 O 所示。当原子
P = −∑ a l
∂ε l ； ∂V
co m
5
2U ,上述结论对玻耳兹曼分布、玻色分布和费米分布都成立。 3V
对极端相对论粒子 类似得
ε = cp = c P = −∑ al
l
1 2πℏ 2 ( nx + n y 2 + n z 2 ) 2 L 1 1 − ∂ 2 ( 2πℏ )( ∑ ni ) 2 V 3 ∂V 1 4 3
mγ
2
由条件（3）知 计算得
∫p
z
f ( p x , p y , p z ) dp x dp y dp z = Np0
co m
∑
⎞ ⎟ ⎟ ⎠
⎛ Sk ⎞ ⎜ e −α − βε s′′ ⎟ ⎜ ⎟ S ′′ ⎝ S = S1 ⎠
∑
⎤ ……⎥ ⎥ ⎦
)
离开正 常位置而占据图中×位置时，晶体中就出现缺位和填隙原子，晶体这种缺陷 叫做弗伦克缺陷。 (1)假设正常位置和填隙位置数都是 N，试证明由于在晶体中形成 n 个缺位和 填隙原子而具有的熵等于 S = 2k ln
S
习题 7.5 固体含有 A、B 两种原子。试证明由于原子在晶体格点的随机分布引起 的混 合熵为 S = k ㏑
ww
是A 原子的百分比， （1-x ）是 B 原子的百分比。注意 x<1，上式给出的熵为正值。 证： 显然 Ω=
习题 7.6 晶体含有 N 个原子。原子在晶体中的正常位置如图中 O 所示。当原子
P = −∑ a l
∂ε l ； ∂V
co m
5
2U ,上述结论对玻耳兹曼分布、玻色分布和费米分布都成立。 3V
对极端相对论粒子 类似得
ε = cp = c P = −∑ al
l
1 2πℏ 2 ( nx + n y 2 + n z 2 ) 2 L 1 1 − ∂ 2 ( 2πℏ )( ∑ ni ) 2 V 3 ∂V 1 4 3
玻尔兹曼统计
al
e l l
ln l
al
l
ln M .B. N ln N al ( l )
l
N (ln N ) all l
又
e
N Z1
f1
ln Z1
ln N
l
al l
U
N
f1
ln
M .B.
Nf1
N
f1
N (
f1
f1 )
所以 S k ln M .B.
S k ln M .B.
率（未归一化）
Z1 wlel ：未归一化的概率之和，或者说归一化常数
l
pl
el Z1
：粒子处于能级 l 的一个量子态的概率
粒子的平均能量为
1
l
l wl pl
1 Z1
l
l wlel
1.2.2 U 与配分函数 Z1 的关系
N
U Z1
l
l wl el
N Z1
l
wl el
N Z1
Z1
N ln Z1
第七章 玻尔兹曼统计
对于可分辨的近独立系统，我们推导了：
一个粒子数分布 {al } 对应的微观状态数为
M .B.
N! al !l来自 al ll最可几分布 {al }m. p.
al
e l l
式中 , 为待定参数，其值由孤立系统粒子数及能量
约束 N al
l
E= lal 求解得到。
l
本章将从玻尔兹曼统计的这几个方程出发，求解宏观热力 学量的统计表达式，讲参数 α 及 β 的物理意义，以及玻 尔兹曼统计的几个重要应用。
U
N
f1
1.3 广义力的统计表达
粒子的能量是外参量的函数。外参量的改变导致能级 的改变：
热力学统计物理玻耳兹曼统计
义
粒子处在该
能级的几率
有效状 态数
al
N Z1
l
e
l
al
el l
N
Z1
el l el l
玻耳兹
曼因子 粒子总是优先占据较低能级；温度升高，占 据该能级的几率增大。
Z1——有效状态和 一个粒子所有可能达到的有效状态的总和。
热统 西华大学 理化学院
6
f e s
l 能量为εl的一个量子态s上的平均粒子数
p
3.粒子配分函数的经典表达式
处元于内能层的l 粒l内子，数运为动：状态处于相体积
al
l
h0r
fs
l h0r
e l
N Z1
l
h0r
el
l x
Z1
l
el l
h0r
al
N Z1
l
h0r
el
取 l 足够小，求和可化为积分：
Z1
el d
h0r
e ( p,q) dq1dq2 dqr dp1dp2 dpr h0r
l l
FD l l! BE
l
l
l
e l
ln
l l
l
对于满足非兼并条件的处
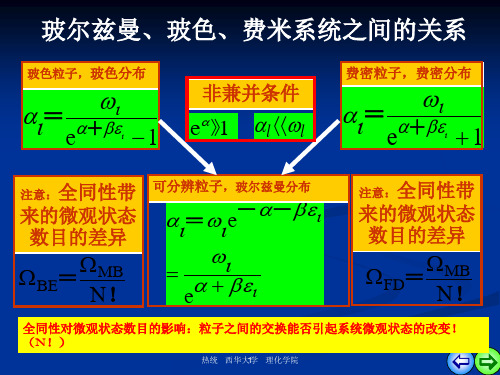
于平衡态（最可几分布） lnFD lnBE l ln l lnl !
的非定域（玻色、费米） 系统，通过对所对应的系 统微观状态数目取对数， 得到了微观状态数目的对 数ln与系统包含的粒子数
l
l
l ln l l ln l 1
玻尔兹曼、玻色、费米系统之间的关系
玻色粒子，玻色分布
＝
e＋
1
非兼并条件
e》1 l l
费密粒子，费密分布
统计物理学第7章
ln Z1 ln Z1 ln Z1 d ( N ) N d ( )N d
(dU Ydy )
ln Z1 ln Z1 ln Z1 N d d (N ) N dy y
17
ln Z1 ln Z1 ln Z1 (dU Ydy) N d d (N ) N dy y
dQ 1 (dU Ydy ) dS T T
热力学基本方程
说明1/T是积分因子，根据积分因子的理论，1/T
与β应同为积分因子，两者相差一个常数 k，称为玻耳
兹曼常数：
1 kT ,
k R N0
16
dQ (dU Ydy )
ln Z1 N d ( ln Z1 ) N dy y
V 3 e h
2m
2 2 ( px p2 p y z)
dpx dp y dpz
2m
2 px
dpx e
2 px
2m
p2 y
dp y e
0
2m
2 pz
dpz
V 3 ( e h
2m
dpx )
3
I (0)
e
x 2
l
l
受到外界 的作用力
N 1 ( ) Z1 N e Z1 Z1 y
N ln Z 1 y
8
N Y ln Z1 y
当
Y p y V ，
时，
这时广义力的统计表达式简化为：
N p ln Z 1 V
(dU Ydy )
ln Z1 ln Z1 ln Z1 N d d (N ) N dy y
17
ln Z1 ln Z1 ln Z1 (dU Ydy) N d d (N ) N dy y
dQ 1 (dU Ydy ) dS T T
热力学基本方程
说明1/T是积分因子，根据积分因子的理论，1/T
与β应同为积分因子，两者相差一个常数 k，称为玻耳
兹曼常数：
1 kT ,
k R N0
16
dQ (dU Ydy )
ln Z1 N d ( ln Z1 ) N dy y
V 3 e h
2m
2 2 ( px p2 p y z)
dpx dp y dpz
2m
2 px
dpx e
2 px
2m
p2 y
dp y e
0
2m
2 pz
dpz
V 3 ( e h
2m
dpx )
3
I (0)
e
x 2
l
l
受到外界 的作用力
N 1 ( ) Z1 N e Z1 Z1 y
N ln Z 1 y
8
N Y ln Z1 y
当
Y p y V ，
时，
这时广义力的统计表达式简化为：
N p ln Z 1 V
07 玻耳兹曼统计
例:1)当平动时,
(即定义广义力延广义位移方向)
ε l=
v v 1 mv 2 , δ w = F d x 2
(取广义位移为沿x轴平动)
∴
dε l = dx
d(
1 mv 2 ) 2 dx
= m
dv v dx
2)当转动时,
在系统的无穷小准静态过程中,系统的广义力为
ε l=
dv dt dt dx dv = m dt = ma = mv
ln z1 ) + Nd ln z1 β ln z1 = Nd (ln z1 β ) β Q dN = 0 ln z1 ∴ βδ Q = d [ N (ln z1 β )] β ∴ βδ Q = Nd ( β
∴β 和
由积分因子的理论,微分方程有一个积分因子 时,它就有无穷多个积分因子,且任意两个因子之比 是全微分函数的函数,即:
= V h3
β
dω h3
(
V 2πm 3 / 2 ( ) h3 β
(h:本质还是玻尔兹曼理论)
p2 + y
2 pz )
---即得到单原子分子理想气体的的配分函数
2m
p2 + x
dxdydzdp x dp y dpz h3
β
2
∴ 根据压强的统计表达,得
p=
+ ∞ 2 m pz ∞
+∞ 2m px ∞
1),若将分子热运动的平均能量理解为 ---- ε 热平均 = π kT 则: 2πmkT = 2m ε 热平均 = p 2
d 分子平均 >> λ热平均
或
1 1 ∴h( )2 = h = λ热平均 2πmkT p热平均
1
nλ3热平均 << 1
(即定义广义力延广义位移方向)
ε l=
v v 1 mv 2 , δ w = F d x 2
(取广义位移为沿x轴平动)
∴
dε l = dx
d(
1 mv 2 ) 2 dx
= m
dv v dx
2)当转动时,
在系统的无穷小准静态过程中,系统的广义力为
ε l=
dv dt dt dx dv = m dt = ma = mv
ln z1 ) + Nd ln z1 β ln z1 = Nd (ln z1 β ) β Q dN = 0 ln z1 ∴ βδ Q = d [ N (ln z1 β )] β ∴ βδ Q = Nd ( β
∴β 和
由积分因子的理论,微分方程有一个积分因子 时,它就有无穷多个积分因子,且任意两个因子之比 是全微分函数的函数,即:
= V h3
β
dω h3
(
V 2πm 3 / 2 ( ) h3 β
(h:本质还是玻尔兹曼理论)
p2 + y
2 pz )
---即得到单原子分子理想气体的的配分函数
2m
p2 + x
dxdydzdp x dp y dpz h3
β
2
∴ 根据压强的统计表达,得
p=
+ ∞ 2 m pz ∞
+∞ 2m px ∞
1),若将分子热运动的平均能量理解为 ---- ε 热平均 = π kT 则: 2πmkT = 2m ε 热平均 = p 2
d 分子平均 >> λ热平均
或
1 1 ∴h( )2 = h = λ热平均 2πmkT p热平均
1
nλ3热平均 << 1
第七章_玻尔兹曼统计
曼分布一样，但系统的微观状态数为 ΩB(F )
=
ΩM ⋅B N!
，所以直接由分布函数导出的内能和广义
力的表达式与玻尔兹曼系统一样。（∵ 它由分布函数直接导出）
而由系统的微观状态数决定的熵
SB( F )
=
k
ln
ΩB(F )
=
k
ln
⎛ ⎜⎝
ΩM ⋅B N!
⎞ ⎟⎠
=
k
ln
ΩM ⋅B
−k
ln
N!=
SM ⋅B
玻尔兹曼系统的一样。
不同的 h0 的值对经典统计结果的影响。
经典玻尔兹曼分布
al
= e−α −βεl
Δωl h0r
由 e−α = N 得： Z1
al
=
N e−βεl Z1
Δωl h0r
式中的 h0r 与配分函数 Z1 所含的 h0r 相互抵消，与 h0 无关。
一个粒子的运动状态处于 Δωl 的概率：
n
n
n
∴ S = k ln Ω = k ln ∏ Ωi = ∑ k ln Ωi = ∑ Si 。
i =1
i =1
i =1
（2）非平衡态的熵： S = k ln Ω 可推广到非平衡态只不过在平衡态时， Ω 是系统最多的微观 状态数，而在非平衡态时， Ω 也是系统的微观状态数，但不是最多的，所以系统在由非平衡
k = 1.381×10−23 J ⋅ K −1 玻尔兹曼常数
玻尔兹曼常数 k 在统计物理学中所起的作用相当于普朗克常数 在量子力学中所起的作用。
dS
=
dQ T
= kβ dQ
=
Nkd
⎛ ⎜ ⎝
ln
Z1
热力学与统计物理 第七章 玻尔兹曼统计
e Z1 r dq1 dqr dp1 dpr h0
粒子自由度为3
e Z1 3 dxdydzdpx dp y dpz h0
15
Z1
V Z1 3 h0
方法一：
e
2 2 px p2 y pz
2m
h
3 0
dxdydzdp x dp y dp z
ln Z1 S Nk ln Z1
7
ln Z1 S Nk ln Z1 ln Z1 Nk ln Z1 T Nk ln Z1 自由能 F U TS N kT F NkT ln Z1
l l Z1 r e h0
体积元 l 取得足够小时，
l d dq1 dqr dp1 dpr
l l Z1 r e h0
Z1
e
h
r 0
dq1 dqr dp1 dpr
14
§7.2
理想气体的物态方程
N ln Z1 p V
Z1 l e l
Z1 l ln Z1 U N
l e l
l l e l l
2
三、广义力
Y 广义力
dW pdV
y
外参量
dW Ydy
Y l作用在该粒子上 当某个粒子处在 l 能级上，若有一“外力”
e
2 2 px p2 y pz
2m
dp x dp y dp z
V Z1 3 h0
4V Z1 3 h0
则
1 e t t 2 dt
第七章玻尔兹曼统计
分子光谱学：通过玻尔兹曼分布解释光谱线强度和偏振现象
化学反应动力学：通过玻尔兹曼分布描述反应速率常数和活化能
在生物学中的应用
分子动力学模拟
蛋白质折叠研究
生物膜与跨膜运输
基因表达调控
在其他领域的应用
物理学：描述气体分子在平衡态时的分布情况
化学：研究反应速率和化学平衡
工程学：热传导、热力学等领域
信息科学：数据压缩、信息编码等方面
1896年：玻尔兹曼提出了熵的概念，为热力学第二定律提供了微观解释
1900年：玻尔兹曼提出了玻尔兹曼统计，用于描述气体分子的分布状态
重要人物和事件
背景：对气体分子运动的研究
影响：奠定了统计力学的理论基础
人物：路德维希·玻尔兹曼
事件：1877年提出玻尔兹曼统计
理论的意义和影响
玻尔兹曼统计的方法和思想对其他学科领域的发展也产生了积极的影响，如化学反应动力学、材料科学等。
玻尔兹曼统计在复杂系统中的应用
玻尔兹曼统计与机器学习算法的结合
对未来发展的展望和预测
新的理论框架的建立
跨学科研究的融合
人工智能和大数据的应用
实验验证和观测技术的发展
汇报人：XX
感谢观看
05
玻尔兹曼统计的局限性和发展
理论局限性和不足之处
玻尔兹曼统计不适用于描述具有高度非线性的复杂系统
玻尔兹曼统计无法准确描述微观粒子的量子行为
玻尔兹曼统计无法解释某些特殊系统的相变现象
玻尔兹曼统计在处理多体问题时存在困难
理论的发展和改进方向
统计力学的其他理论：如微正则分布、巨正则分布等，可作为玻尔兹曼统计的补充或替代。
玻尔兹曼统计的提出为现代科学和技术的发展奠定了重要的基础。
热力学统计物理_第七章_玻耳兹曼统计
ln Z ' S S Nk ln Z
ln Z S' S Nk ln Z U Nk ln N S ' N k N ln N N U S '
Z1 l e l
l
粒子 配分 函数
1 kT
热统 西华大学 理化学院
e
N Z1
6
2、粒子配分函数的物理意义
粒子处在该 能级的几率
有效状 态数
N l al l e Z1
玻耳兹 曼因子
al l e N Z1
l
l e l e
S k N ln N N U S '
lnMB N ln N N U
lnFD lnBE N U N
S MB k ln MB
e ' S k ( N ln N N ) Nk ln N
14 热统 西华大学 理化学院
我们已经学习了什么？
1、粒子运动状态的描述
经典粒子：－空间、相轨道的概念、 量子粒子：量子数、可能量子状态数目的计算
2、系统微观状态的经典和量子描述
经典系统：－空间中的N个点 量子系统：定域和非定域、全同性、统计特性
3、等几率原理
平衡状态下系统的任何微观状态出现的几率都相等
4、系统的微观状态数 目的计算及其关系
对于遵从玻尔兹曼分 U＝－N lnZ 布的定域系统、满足 经典极限条件的玻色、 费米系统，从玻尔兹 N Y － lnZ 曼分布得到系统的内 y 能和广义力的统计表 达式： 可分辨粒子系统：
相关主题
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2m
在体积 V 内，在 dpx dpy dpz 的动量范围内，分子质心平动的状态数为
V 3 dpx dpy dpz 3 h0 h0
分子数为
l l al 3 e h0
对经典粒子，物理量是连续的，可以去掉下标，于是
V a 3 e 3e dpx dpy dpz h0 h0
f (v, , )v 2 sin dv dd
m 2
m 3 2 2 kT v 2 2 n( ) e v dv 2kT 0
0
sin dd
则在单位体积内，速率在 dv 范围内的分子数，称为麦氏速率分布律
m 32 f (v)dv 4n( ) e 2kT
m 2 v 2 kT
V 13 1 ( ) h( )1 2 N 2mkT
用分子的德布罗义波长 分子数密度 代入上式
h ph
2m h
2mkT
nN V
1 13 ( ) n
满足经典极限条件可等价表示为
n 1
3
7.3麦克斯韦速度分布律 一、 根据玻耳兹曼分布研究气体分子质心的平动，导出气体 分子的速度分布律。在这问题上，由量子统计理论和由经典统计 理论得到的结果相同。以下采用经典统计理论讨论。 设气体含有N个分子，体积为V, 分子质心平动动能 1 2 2 2 ( px py pz )
2m
2 px
dpx ) (
3
2m
)3 2
得
e
h N 32 ( ) V 2m kT
2 0
得质心动量在 dpx dpy dpz 范围内的分子数为
1 32 a N( ) e 2m kT
1 2 2 ( px p2 y pz ) 2 kmT
dpx dpy dpz
如果用速度作变量，作代换 px mvx
ln N ln Z1
有
S Nk (ln Z1 ln Z1 ) k ( N ln N N U ) k[ N ln N ( l )al ]
l
又由玻耳兹曼分布
al l e
l ln al l
参数由总分子数决定，
V 3 h0
e
2m
2 2 ( px p2 y pz )
dpx dpy dpz N
V 2m px2 3 e ( e dp ) N x 3 h0
利用
I (0)
0
e
x
2
1 dx 2
( e
l l l
e (
e
l l
l
Z N Z ) e ( ) ( ) N ln Z Z
三.广义力的统计表达式
1 l l l l e ( ) e Y al l e l y l y y l l
0 0
7.2理想气体的物态方程
一般气体满足经典极限条件，遵从玻耳兹曼分布。 以下将理想气体看作满足经典极限条件的粒子，用玻 耳兹曼分布导出单原子分子理想气体的物态方程。组 成理想气体的单个粒子的能量，
配分函数
Z1 l e l
l
1
l
1 2 2 2 ( px py pz ) 2m
ln Z1 ln Z1 ln Z1 ln Z1 Nd ( )N d Nd ( ) d ( N )
移项得
ln Z1 ln Z1 ln Z1 Nd ( )N d d ( N )
所以
ln Z1 ln Z1 ln Z1 (dU Ydy) N d d ( N ) N dy ln Z1 d ( N ln Z1 ) d ( N )
v 2 dv
f (v) 称为速率分布函数，满足条件
f (v)dv n
0
麦氏速度概率分布 w(v x, v y , v z )dvx dvy dvz f (vx , v y , vz )dvx dvy dvz / n
麦氏速度概率密度分布
w(vx, v y , vz ) f (vx , v y , vz ) / n
2 px
V 2m 3 2 2m 3 2 dpx ) 3 ( ) V( 2 ) h h
3
根据广义力的统计表达式，求出理想气体的物态方程
N N 3 2m p ln Z1 [lnV ln( 2 )] V V 2 h
N ln V N V V
1
经典极限条件对气体性质的要求 将单原子分子组成的理想气体的配分函数 极限条件
Z1
代入经典
V 2mkT 3 2 e Z1 N ( ) 1 2 N h
满足经典极限条件
e 1 ，意味着要求理想气体
（1）气体很稀薄； （2）温度很高； （3）分子质量大。
另外，满足经典极限条件 e 1 还可等价地表述为
称为麦氏速度分布律
2 y vz ) m 3 2 2 kT ( vx2 v 2 f (v x , v y , v z )dvx dvy dvz n( ) e dvx dvy dvz 2kT
m
函数
f (vx , v y , vz )
称为麦氏速度分布函数，满足条件
f (v , v
x
p y mvy
p z mvz
m 32 a N( ) e 2kT
m 2 2 ( vx v 2 y vz ) 2 kT
dvx dvy dvz
或
a N m 32 ( ) e V V 2kT
m 2 2 2 ( vx v y vz ) 2 kT
dvx dvy dvz
则在单位体积内，速度在 dvx dvy dvz 范围内的分子数，
S Nk (ln Z1
S k ln
M . B. N!
F NkT ln z1 kT ln N!
经典系统
Z1 e
l l
l l d ( p , q ) dq 1dq2 dqr dp 1dp2 dpr e e r r r h0 h0 h0
。
四.
与熵的统计表达式
N ln Z1 dQ dU Ydy Nd ( ln Z1 ) dy y
由内能、广义力的统计表达式和热力学第一定律，有
两边同乘以
dQ (dU Ydy)
ln Z1 Nd ( ln Z1 ) N dy y
N 1 N ( ) Z1 ln Z 1 Z1 y y
当
y V
Y p
时，对应的广义力为压强，
这时广义力的统计表达式简化为
N p ln Z 1 V
广义功和热量的微观含义 在准静态过程中，外参量发生 统所作的功是
dy
改变时，外界对系
l dW Ydy dy al y l
ln Z1 d ( N ln Z1 N )
与热力学基本方程 (dU Ydy) T dS
比较，得熵的统计表达式
S Nk (ln Z1 ln Z1 )
玻耳兹曼关系 利用
N al
l
U l ln Z1
F U TS
N ln Z1 TNk (ln Z1 ln Z1 )
TNk ln Z1
满足经典极限条件的玻色(费米)系统
Z1 l e l
N e Z1
U N ln Z1
Y
N ln Z1 y
ln Z1 ) k ln N!
V 3 h
e
2m
2 px
dpx
e
2m
p2 y
dp y
e
2m
2 pz
dp z
V 2 m px2 3 ( e dpx ) 3 h
由积分公式
I (0)
2m
0
e
x 2
1 dx 2
V Z1 3 ( e h
即
pV kTN
pV nkTN0
与热力学中根据实验定理推出的理想气体物态方程
pV nRT
比较，可得普适气体常数、阿伏加德罗常数和玻耳兹曼 常数之间的关系，
R kN0
对双原子分子组成的理想气体，单个粒子 的能量表达式中增加了转动能量和振动能量， 由于计及转动能量和振动能量后不改变配分 V 函数 对Z 的依赖关系，所以求得的物态 方程与单原子分子组成的理想气体具有相同 的形式。
麦氏速率概率分布
w(v)dv f (v)dv / n
麦氏速率概率密度分布
w(v) f (v) / n
最可几速率 最可几速率：使速率分布函数 关于 v 求导，令
f (v )
取极大值的速率。对 f (v)
考虑内能
U l al
l
a d
l l
l
的全微分
dU l dal al d l
l
。
与热力学第一定律
dU dQ dW dQ al d l
l
比较，有
dQ l dal
以上两式说明，在准静态过程中系统从外界吸收的热 量等于粒子在各能级重新分布所增加的内能：外界对系统 所作的功等于粒子分布不变时由于能级改变所引起的内能 变化。
在体积 V 内，在 dpx dpy dpz 的动量范围内，分子质心平动的状态数为
V 3 dpx dpy dpz 3 h0 h0
分子数为
l l al 3 e h0
对经典粒子，物理量是连续的，可以去掉下标，于是
V a 3 e 3e dpx dpy dpz h0 h0
f (v, , )v 2 sin dv dd
m 2
m 3 2 2 kT v 2 2 n( ) e v dv 2kT 0
0
sin dd
则在单位体积内，速率在 dv 范围内的分子数，称为麦氏速率分布律
m 32 f (v)dv 4n( ) e 2kT
m 2 v 2 kT
V 13 1 ( ) h( )1 2 N 2mkT
用分子的德布罗义波长 分子数密度 代入上式
h ph
2m h
2mkT
nN V
1 13 ( ) n
满足经典极限条件可等价表示为
n 1
3
7.3麦克斯韦速度分布律 一、 根据玻耳兹曼分布研究气体分子质心的平动，导出气体 分子的速度分布律。在这问题上，由量子统计理论和由经典统计 理论得到的结果相同。以下采用经典统计理论讨论。 设气体含有N个分子，体积为V, 分子质心平动动能 1 2 2 2 ( px py pz )
2m
2 px
dpx ) (
3
2m
)3 2
得
e
h N 32 ( ) V 2m kT
2 0
得质心动量在 dpx dpy dpz 范围内的分子数为
1 32 a N( ) e 2m kT
1 2 2 ( px p2 y pz ) 2 kmT
dpx dpy dpz
如果用速度作变量，作代换 px mvx
ln N ln Z1
有
S Nk (ln Z1 ln Z1 ) k ( N ln N N U ) k[ N ln N ( l )al ]
l
又由玻耳兹曼分布
al l e
l ln al l
参数由总分子数决定，
V 3 h0
e
2m
2 2 ( px p2 y pz )
dpx dpy dpz N
V 2m px2 3 e ( e dp ) N x 3 h0
利用
I (0)
0
e
x
2
1 dx 2
( e
l l l
e (
e
l l
l
Z N Z ) e ( ) ( ) N ln Z Z
三.广义力的统计表达式
1 l l l l e ( ) e Y al l e l y l y y l l
0 0
7.2理想气体的物态方程
一般气体满足经典极限条件，遵从玻耳兹曼分布。 以下将理想气体看作满足经典极限条件的粒子，用玻 耳兹曼分布导出单原子分子理想气体的物态方程。组 成理想气体的单个粒子的能量，
配分函数
Z1 l e l
l
1
l
1 2 2 2 ( px py pz ) 2m
ln Z1 ln Z1 ln Z1 ln Z1 Nd ( )N d Nd ( ) d ( N )
移项得
ln Z1 ln Z1 ln Z1 Nd ( )N d d ( N )
所以
ln Z1 ln Z1 ln Z1 (dU Ydy) N d d ( N ) N dy ln Z1 d ( N ln Z1 ) d ( N )
v 2 dv
f (v) 称为速率分布函数，满足条件
f (v)dv n
0
麦氏速度概率分布 w(v x, v y , v z )dvx dvy dvz f (vx , v y , vz )dvx dvy dvz / n
麦氏速度概率密度分布
w(vx, v y , vz ) f (vx , v y , vz ) / n
2 px
V 2m 3 2 2m 3 2 dpx ) 3 ( ) V( 2 ) h h
3
根据广义力的统计表达式，求出理想气体的物态方程
N N 3 2m p ln Z1 [lnV ln( 2 )] V V 2 h
N ln V N V V
1
经典极限条件对气体性质的要求 将单原子分子组成的理想气体的配分函数 极限条件
Z1
代入经典
V 2mkT 3 2 e Z1 N ( ) 1 2 N h
满足经典极限条件
e 1 ，意味着要求理想气体
（1）气体很稀薄； （2）温度很高； （3）分子质量大。
另外，满足经典极限条件 e 1 还可等价地表述为
称为麦氏速度分布律
2 y vz ) m 3 2 2 kT ( vx2 v 2 f (v x , v y , v z )dvx dvy dvz n( ) e dvx dvy dvz 2kT
m
函数
f (vx , v y , vz )
称为麦氏速度分布函数，满足条件
f (v , v
x
p y mvy
p z mvz
m 32 a N( ) e 2kT
m 2 2 ( vx v 2 y vz ) 2 kT
dvx dvy dvz
或
a N m 32 ( ) e V V 2kT
m 2 2 2 ( vx v y vz ) 2 kT
dvx dvy dvz
则在单位体积内，速度在 dvx dvy dvz 范围内的分子数，
S Nk (ln Z1
S k ln
M . B. N!
F NkT ln z1 kT ln N!
经典系统
Z1 e
l l
l l d ( p , q ) dq 1dq2 dqr dp 1dp2 dpr e e r r r h0 h0 h0
。
四.
与熵的统计表达式
N ln Z1 dQ dU Ydy Nd ( ln Z1 ) dy y
由内能、广义力的统计表达式和热力学第一定律，有
两边同乘以
dQ (dU Ydy)
ln Z1 Nd ( ln Z1 ) N dy y
N 1 N ( ) Z1 ln Z 1 Z1 y y
当
y V
Y p
时，对应的广义力为压强，
这时广义力的统计表达式简化为
N p ln Z 1 V
广义功和热量的微观含义 在准静态过程中，外参量发生 统所作的功是
dy
改变时，外界对系
l dW Ydy dy al y l
ln Z1 d ( N ln Z1 N )
与热力学基本方程 (dU Ydy) T dS
比较，得熵的统计表达式
S Nk (ln Z1 ln Z1 )
玻耳兹曼关系 利用
N al
l
U l ln Z1
F U TS
N ln Z1 TNk (ln Z1 ln Z1 )
TNk ln Z1
满足经典极限条件的玻色(费米)系统
Z1 l e l
N e Z1
U N ln Z1
Y
N ln Z1 y
ln Z1 ) k ln N!
V 3 h
e
2m
2 px
dpx
e
2m
p2 y
dp y
e
2m
2 pz
dp z
V 2 m px2 3 ( e dpx ) 3 h
由积分公式
I (0)
2m
0
e
x 2
1 dx 2
V Z1 3 ( e h
即
pV kTN
pV nkTN0
与热力学中根据实验定理推出的理想气体物态方程
pV nRT
比较，可得普适气体常数、阿伏加德罗常数和玻耳兹曼 常数之间的关系，
R kN0
对双原子分子组成的理想气体，单个粒子 的能量表达式中增加了转动能量和振动能量， 由于计及转动能量和振动能量后不改变配分 V 函数 对Z 的依赖关系，所以求得的物态 方程与单原子分子组成的理想气体具有相同 的形式。
麦氏速率概率分布
w(v)dv f (v)dv / n
麦氏速率概率密度分布
w(v) f (v) / n
最可几速率 最可几速率：使速率分布函数 关于 v 求导，令
f (v )
取极大值的速率。对 f (v)
考虑内能
U l al
l
a d
l l
l
的全微分
dU l dal al d l
l
。
与热力学第一定律
dU dQ dW dQ al d l
l
比较，有
dQ l dal
以上两式说明，在准静态过程中系统从外界吸收的热 量等于粒子在各能级重新分布所增加的内能：外界对系统 所作的功等于粒子分布不变时由于能级改变所引起的内能 变化。