奥数第12讲.竞赛123班.教师版
小学数学奥数基础教程12讲.docx

小学奥数基础教程第1讲速算与巧算第2讲高斯求和第3讲找规律第4讲最不利原则第5讲归一问题与归总问题第6讲年龄问题第7讲鸡兔同笼问题与假设法第8将乘法原理第9讲加法原理第10讲还原问题第11讲逻辑问题第12讲抽屉原理第1讲速算与巧算计算是数学的基础,小学生要学好数学,必须具有过硬的计算本领。
准确、快速的计算能力既是一种技巧, 也是一种思维训练,既能提高讣算效率、节省计算时间,更可以锻炼记忆力,提髙分析、判断能力,促进思维和智力的发展。
我们在三年级已经讲过一些四则运算的速算与巧算的方法,本讲和下一讲主要介绍加法的基准数法和乘法的补同与同补速算法。
例1四年级一班第一小组有10名同学,某次数学测验的成绩(分数)如下:86, 78, 77, 83, 91, 74, 92,69, 84, 750求这10名同学的总分。
分析与解:通常的做法是将这10个数直接相加,但这些数杂乱无章,直接相加既繁且易错。
观察这些数不难发现,这些数虽然大小不等,但相差不大。
我们可以选择一个适当的数作“基准”,比如以“80”作基准,这10个数与80的差如下:6, —2, -3, 3, 11, 一6, 12, -11, 1, -5,其中“-”号表示这个数比80 小。
于是得到总和=80X10+ (6-2-3+3 + 11-= 800 + 9=809。
实际计算时只需口算,将这些数与80的差逐一累加。
为了清楚起见,将这一过程表示如下:通过口算,得到差数累加为9,再加上80X10,就可口算出结果为809。
例1所用的方法叫做加法的基准数法。
这种方法适用于加数较多,而冃所有的加数相差不大的情况。
作为“基准”的数(如例1的80)叫做基准数,各数与基准数的差的和叫做累计差。
由例1得到:总和数二基准数X加数的个数+累计差.平均数二基准数+累计差三加数的个数。
在使用基准数法时,应选取与各数的差较小的数作为基准数,这样才容易讣算累计差。
同时考虑到垒准数与加数个数的乘法能够方便地计算出來,所以基准数应尽最选取整十、整百的数。
最新北师大版小学四年级数学下册奥数知识讲解第十二课(数字综合题选讲)

四年级下册数学奥数知识讲解第十二课《数字综合题选讲》奥数练习题和答案四年级奥数下册:第十二讲数字综合题选讲
四年级奥数下册:第十二讲数字综合题选讲习题
四年级奥数下册:第十二讲数字综合题选讲习题解答
给读者的一封信
你好!读者朋友。
本文档是本人精心为您准备的,用于我们彼此交流、探讨,希望你有用的到的地方。
在使用过程中如有不妥或许改进之处,请您在下方留言栏告诉我。
我收到你的信息之后,我会尽快进行更新优化。
希望通过你我的共同交流、共同探讨,以促进我们共同提高的目的。
俗话说:一个人的能力是有限的,但众人拾柴火焰高,相信有您的帮助,我会进步更大,提升更快。
在此非常感谢您提出的宝贵意见。
祝:生活安康、学习进步、工作顺利。
奥数精品讲义第12讲.竞赛1班.教师版--深圳清华实验学校佘珊珊

第十二讲期末考试一、 填空题(每题6分,共60分。
如有两个空,只对一个给3分)1.有17个队参加篮球比赛,比赛分两个组,第一组七个队,第二组八个队,各组先进行单循环赛(即每队都要与其它各队比赛一场),然后由各组的前三名共六个队再进行单循环赛决定冠亚军。
问:共需比赛__________场。
【分析】 分三部分考虑,第一组预赛、第二组预赛和最后的决赛。
第一组要赛2721C =(场),第二组要赛2828C =(场),决赛阶段要赛2615C =(场),所以总场数为: 21281564++=(场)。
2. 将前100个自然数依次无间隔地写成一个192位数:1234567891011129899100L ,从中划去170个数字,那么剩下的22位数最大是__________,最小是__________。
【分析】 在前100个自然数中,共有20个9,再保留后面的“10”,即得到最大数:209999910L 1442443个;最小数的第一位是“1”,再保留1090:中的9个“0”,再在91100:中留下12个尽量小的数,即得最小数:1000000000123456789100。
3.有一个展览会场如右图所示,共有16个展室,每两个相邻的展室之间都有门相通,问__________(填能或不能)从入口进去,不重复地参观完所有的展室后从出口出来。
【分析】 黑白相间染色后发现,入口和出口都是黑色,但每次都是从黑格到白格或从白格到黑格,这样应是从黑格进去,白格出来,但出口也是白格,所以不可能。
4. 设自然数n 有下列性质:从1、2、…、n 中任取65个不同的数,其中必有两数之差等于8,这样的n 最大不能超过__________。
【分析】 当128n =时,将1、2、…、128按每组中两数的差为8的规则分成64组,所以当任取65个数时,必有两个数在同一组,它们的差等于8。
当129n =时,取上面每组中的前一个数,和129,一共65个数,而它们中任两个数的差不为8。
奥数 六年级竞赛 数论(二).教师版word

小学奥数数论内容中,余数相关问题是最成体系的,也是各类竞赛考试中的重点.⑴同余性质是解决同余问题的重要依据,复习简单同余问题,学会灵活运用同余性质解决同余问题. ⑵熟练掌握余数定理在多位数除法以及高次冥末尾数字求解中的基本运用.⑶能用凑同余的办法解决一个数除以多个数,得不同余数的问题,学会使用中国剩余定理.带余除法:一般地,如果a 是整数,b 是整数()0b ≠,那么一定有另外两个整数q 和r ,0r b ≤<,使得a b q r =⨯+.当0r =时,我们称a 能被b 整除.当0r ≠时,我们称a 不能被b 整除,r 为a 除以b 的余数,q 为a 除以b 的不完全商(亦简称为商).用带余数除式又可以表示为a b q r ÷= ,0r b ≤<.同余式:若两个整数a ,b 被自然数m 除有相同的余数,那么称a ,b 对于模m 同余,用“同余式”表示为()mod a b m ≡意味着(我们假设a b ≥)a b mk -=,k 是整数,即()|m a b -.若两个数a ,b 除以同一个数c 得到的余数相同,则a ,b 的差一定能被c 整除.余数定理:①两数的和除以m 的余数等于这两个数分别除以m 的余数和.实例:7321÷= ,5312÷= ,这样()753+÷的余数就等于()123+÷的余数.②两数的差除以m 的余数等于这两个数分别除以m 的余数差.实例:8322÷= ,4311÷= ,这样()843-÷的余数就等于()213-÷的余数.③两数的积除以m 的余数等于这两个数分别除以m 的余数积.实例:7321÷= ,5312÷= ,这样()753⨯÷的余数就等于()123⨯÷的余数. 第 6讲数论(二)【例 1】 有一个整数,用它去除70,110,160所得到的3个余数之和是50,那么这个整数是______.【分析】 (70110160)50290++-=,503162÷= ,除数应当是290的大于17小于70的约数,只可能是29和58,11058152÷= ,5250>,所以除数不是58.7029212÷= ,11029323÷= ,16029515÷= ,12231550++=,所以除数是29.【例 2】 一个两位数被它的各位数字之和去除,问余数最大是多少?【分析】 设两位数ab (a 表示十位数字,b 表示个位数字)1091ab a b a a b a b a b+==++++ 由于余数不会超过除数a b +的值,所以我们对a b +的值从最大值18开始往小进行尝试搜索:当18a b +=,此时余数为9. 当17a b +=,则两位数为89、98,余数为4、13.当16a b +=,则两位数为97、88、79,余数为1、8、15.则余数最大的为15,因为接下来,除数最大为15,这样余数中最大的也只可能为14,所以余数最大的是15.【例 1】 一个自然数除429、791、500所得的余数分别是5a +、2a 、a ,求这个自然数和a 的值. [分析] 将这些数转化被该自然数除后余数为2a 的数:()42952848-⨯=,791、50021000⨯=,这些数被这个自然数除所得的余数都是2a ,同余. 将这三个数相减,得到84879157-=、1000848152-=,所求的自然数一定是57和152的公约数,而()57,15219=,所以这个自然数是19的约数,显然1是不符合条件的,经过验证,当这个自然数是19时,除429、791、500所得的余数分别为11、12、6,6a =时成立,所以这个自然数是19,6a =.[拓展]已知60,154,200被某自然数除所得余数分别是1a -,2a ,31a -,求该自然数的值. [分析] 自然数61,154,201被该数除所得余数分别是a ,2a ,3a .自然数2613721=与154同余,611549394⨯=与201同余,所以除数是3567和9193的公约数,运用辗转相除法可得到该除数为29.经过检验成立.[拓展]甲、乙、丙三数分别为603,939,393.某数A 除甲数所得余数是A 除乙数所得余数的2倍,A 除乙数所得余数是A 除丙数所得余数的2倍.求A 等于多少?[分析] 设这个数为M ,则11603M A r ÷=22939M A r ÷=33393M A r ÷=122r r =,232r r =,要消去余数1r ,2r ,3r ,我们只能先把余数处理成相同的,再两数相减.这样我们先把第二个式子乘以2,这样被除数和余数都扩大2倍,同理,第三个式子乘以4. 这样我们可以得到下面的式子:11603M A r ÷=()22939222M A r ⨯÷=()33393424M A r ⨯÷=这样余数就处理成相同的.最后两两相减消去余数,意味着能被M 整除.93926031275⨯-=,3934603969⨯-=,()1275,30651317==⨯.603,939,393这三个数有公约数3.51317÷=.则A 等于17.【例 2】 一个自然数减去它的各位数字之和得到的差值,称为“好数”.例如,根据()757757738-++=是“好数”.在四位数20□○的方框中填入某个恰当的数字后,可以使得无论圆圈内填入09 中的哪个数字,该四位数都不是“好数”,那么在方框中应填写数字__________.【分析】 注意到所有“好数”都是9的倍数,但9的倍数不一定都是好数.200x 对应的“好数”是20021998x x --=;201x 对应的“好数”是201212007x x ---=;202x 对应的“好数”是202222016x x ---=;…… …… ……209x 对应的“好数”是209292079x x ---=;210x 对应的“好数”是210212097x x ---=;即在20□○中“好数”只能是2007、2016、2025、2034、2043、2052、2061、2070、2079、2097. 所以,如果在20□○的“□”内填入8,则不管“○”填入什么数都不能是“好数”.【例 3】 (南京市“兴趣杯”少年数学邀请赛决赛)现有糖果254粒,饼干210块和桔子186个.某幼儿园大班人数超过40.每人分得一样多的糖果,一样多的饼干,也分得一样多的桔子.余下的糖果、饼干和桔子的数量的比是:1:3:2,这个大班有_____名小朋友,每人分得糖果_____粒,饼干_____块,桔子_____个.【分析】 法一:设大班共有a 名小朋友.由于余下的糖果、饼干和桔子的数量之比是1:3:2,所以余下的糖果、桔子数目的和正好等于余下的饼干数,从而254186210+-一定是a 的倍数,即2541862102301230102325+-==⨯=⨯=⨯⨯是a 的倍数.同样,225418632223142327⨯-==⨯=⨯⨯也一定是a 的倍数.所以,a 只能是232⨯的因数.但40a >,所以46a =.此时25446524=⨯+,21046372=⨯+,18646348=⨯+.故大班有小朋友46名,每人分得糖果5粒,饼干3块,桔子3个.法二:如果糖果有25461524⨯=粒,饼干有2102420⨯=块,橘子有1863558⨯=个,那么余下的糖果、饼干、橘子的个数相等,所以1524、420、558这三个数的相互之差是大班人数的倍数,152********-=,558420138-=,()1104,138138=,所以幼儿园大班人数是138的大于40的约数,即138、69、46,经过检验,其中只有46满足条件.每人分得糖果5粒、饼干3块、橘子3块.【例 4】 试求105253168⨯的末两位数.【分析】 分别考虑这两个幂除以4和25所得的余数.首先考虑4,253除以4余数是1,所以25310除以4的余数仍是1;168是4的倍数,它的5次方仍是4的倍数,即除以4的余数为0,则原数除以4的余数也是0.再考虑25,253除以25余3,则只需看310除以25的余数,又310=27×27×27×3,则310除以25的余数为2×2×2×3=24;168除以25余18,则只需看51832432418=⨯⨯除以25的余数,可知余数为18;又2418432⨯=除以25的余数为7,所以原式除以25的余数即为7.两位数中,能被4整除,除以25余7的数只有32,则原式的末两位即为32.[拓展]试求20082007的末两位数.[分析]200720007=+,所以20082007的末两位数与20087的末两位数相同. ()()100450220082100425027749492401====,2401被100除余1所以5022401被100除得的余数等于5021,所以20082007的末两位数是01.[拓展]求89143除以7的余数.[分析] 法一:∵()1433mod7≡(143被7除余3)∴()89891433mod7≡(89143被7除所得余数与893被7除所得余数相等)而63729=,()7291mod7≡∴()8966655143333335mod7≡⨯⨯⨯⨯≡≡个. 89于是余数以6为周期变化.所以335mod7≡≡.【例 5】1234200512342005+++++ 除以10所得的余数为多少? 【分析】 求结果除以10的余数即求其个位数.从1到2005这2005个数的个位数字是10个一循环的,而对一个数的幂方的个位数,我们知道它总是4个一循环的,因此把每个加数的个位数按20个(20是4和10的最小公倍数)一组,则不同组中对应的数字应该是一样的.首先计算123420123420+++++ 的个位数字,为4.2005个加数中有100组另5个数,100组的个位数是4100400⨯=的个位数即0,另外5个数为20012001、20022002、20032003、20042004、20052005,它们和的个位数字是1476523++++=的个位数 3,所以原式的个位数字是3,即除以10的余数是3.【例 6】 求{10031203308L 个除以19的余数. 【分析】 法一:{{{10161003101312033081266406332=-L L L 个个个 {{101310132063326332=⨯-L L 个个 {1013196332=⨯L 个 所以{10031203308L 个除以19的余数为0. 法二:首先计算120308被19除所得余数为0,120330812030810228=⨯+,228也是19的倍数,所以1203308也是19的倍数.12033308120330810228=⨯+,所以1203308也是19的倍数.以此递推可得到{10031203308L 个也是19的倍数.[拓展](2008年奥数网杯)已知20082008200820082008a = 个,问:a 除以13所得余数是______.[分析]2008除以13余6,10000除以13余3, 注意到200820082008100002008=⨯+;20082008200820082008100002008=⨯+;2008200820082008200820082008100002008=⨯+;根据这样的递推规律求出余数的变化规律:20082008除以13余6361311⨯+-=,200820082008除以13余1136390⨯+-=,即200820082008是13的倍数,而2008除以3余1,所以20082008200820082008a = 个除以13的余数与2008除以13的余数相同,为6.【例 7】 对任意的自然数n ,证明2903803464261n n n n A =--+能被1897整除.【分析】18977271=⨯,7与271互质,因为29035(mod 7)≡,8035(mod7)≡,4642(mod 7)≡,2612(mod7)≡,所以,290380346426155220(mod7)n n n n n n n n A =--+≡--+≡,故A 能被7整除.又因为2903193(mod 271)≡,803261(mod 271)≡,464193(mod 271)≡,所以29038034642611932611932610(mod271)n n n n n n n n A =--+≡--+≡,故A 能被271整除. 因为7与271互质,所以A 能被1897整除.【例 8】 在下表中填入自然数,要求第一行中所填入的自然数从左到右依次是31,32,33, ,第中填入的自然数从左到右依次是13,23,33, ,第三行中填入的自然数是同一列当中第一行、7【分析】 第一行的数被7除所得余数依次是1,1,6,1,6,6,0,……,以7为周期.第二行的数被7除所得的余数依次是3,2,6,4,5,1……,以6为周期.第三行的自然数如果除以7余1,那么对应第一行、第二行的自然数被7除,只有0+1和6+2两种情况,其中第一种情况下,对应的列数能被7和6整除,所以在第42列才能出现该情况,第二种情况下,对应的列数被7除余3,5,6,被6除余2,符合条件的最小列数是20.“物不知数问题”一般解题步骤:①凑“多”相同,即把余数处理成相同 条件:余数与除数的和相同②凑“缺”相同,即把余数处理成缺的数字相同 条件:除数与余数的差相同③先考虑上面两种,如果都不行,可使用逐步满足法或使用“中国剩余定理” .④逐步满足法:先满足条件一,得N ,再用“M N =+已满足除数公倍数”来满足下一个条件.《孙子算经》中有记载:“今有物不知其数:三三数之余二,五五数之余三,七七数之余二,问物几何?”它的意思就是,有一些物品,如果3个3个的数,最后剩2个;如果5个5个的数,最后剩3个;如果7个7个的数,最后剩2个;求这些物品一共有多少?这个问题人们通常把它叫作“孙子问题”, 西方数学家把它称为“中国剩余定理”.到现在,这个问题已成为世界数学史上闻名的问题.到了明代,数学家程大位把这个问题的算法编成了四句歌诀:三人同行七十稀,五树梅花廿一枝;七子团圆正半月,除百零五便得知.用现在的话来说就是:一个数用3除,除得的余数乘70;用5除,除得的余数乘21;用7除,除得的余数乘15.最后把这些乘积加起来再减去105的倍数,就知道这个数是多少.《孙子算经》中这个问题的算法是:702213152233⨯+⨯+⨯=;23310510523--=;所以这些物品最少有23个.得出问题中的系数70、21、15,实际上是非常巧妙的构造过程,这三个数满足以下条件70是5和7的公倍数,且被3除余1;21是3和7的公倍数,且被5除余1;15是3和5的公倍数,且被7除余1.在这样的条件下,任意一个系数乘以对应余数所得的积,被对应除数除后所得的余数恰好等于对应余 数,且该积仍然能被其他两个除数整除,因此三个积相加并不相互影响各自被对应除数除后所得的余数. 即702115a b c ++是被3除余a ,被5除余b ,被7除余c 的数.【例 9】 一个大于10的数,除以3余1,除以5余2,除以11余7,问满足条件的最小自然数是多少?【分析】 法一:仔细分析可以发现321527⨯+=+=,所以这个数可以看成被3、5、11除余7,[]3,5,11165=,所以这个数最小是1657172+=.法二:事实上,如果没有“大于10”这个条件,7即可符合条件,在7的基础上加上3,5,11的最小公倍数,得到172即为所求的数.[铺垫]一个大于10的数,除以5余3,除以7余1,除以9余8,问满足条件的最小自然数为____. [分析] 根据总结,我们发现三个数中两个数的除数与余数的和都是53718+=+=,这样我们可以把余数都处理成8,所以[]5,7,9315=,所以这个数最小为3158323+=.[铺垫]一个小于200的数,它除以11余8,除以13余10,这个数是多少?[分析] 根据总结,我们发现这两个除数与余数的差都等于11813103-=-=,观察发现这个数加上3后就能同时被11和13整除,所以[]11,13143=,所以这个数是1433140-=.【例10】 一个数除以3余2,除以5余3,除以7余4,问满足条件的最小自然数为____.【分析】 法一:根据总结,我们发现前面两种都不符合,所以可以使用普遍适用的“中国剩余定理”,步骤如下:分别找出除以7余7的公倍数,除以3余2的5、7的公倍数,分别是:60、63、35可见60+63+35=158满足我们的条件,但不是最小的自然数,处理方法就是减去最小公倍数的若干倍,使结果小于最小公倍数.所以答案为:158-105=53.法二:逐步构造符合条件的最小自然数,首先求符合前两个条件的最小自然数,用3不断加2,当2被加上两个3时得到8,检验符合前两个条件,再用3和5的最小公倍数不断加8,当8被加上3个15,得到53,检验符合三个条件.法三:逐步构造符合条件的最小自然数,首先求符合后面两个条件的最小自然数,用7不断加4,当4被加上两个7时得到18,检验符合后两个条件,再用7和5的最小公倍数不断加18,当18被加上1个35,得到53,检验符合三个条件.【例11】有连续的三个自然数a、1a+,它们恰好分别是9、8、7的倍数,求这三个自然数中最a+、2小的数至少是多少?【分析】法一:由1a+是7的倍数,得到a被7除余5,运用中国a+是8的倍数,得到a被8除余7,由2剩余定理求a:(⨯+⨯=495是满足各个余数条件的最小441728854527值,所以a至少是495.法二:a、1a++也分别是9、a++、27a+、18a+、2a+恰好分别是9、8、7的倍数,那么9a+的最小值是987504⨯⨯=,即a至少是495.8、7的倍数,即9a+是9、8、7的倍数,9【例12】一个数除以3、5、7、11的余数分别是2、3、4、5,求符合条件的最小的数:【分析】将33210×5=1050被11除余5,由此可知770+693+165+1050=2678是符合条件的一个值,又3、5、7、11的最小公倍数是1155,所以2678-1155×2=368是符合条件的最小值.[拓展]一个数除以2、3、5、7、11的余数分别是1、2、3、4、5,求符合条件的最小数.[分析]本题实际上就是求被3、5、7、11除的余数分别是2、3、4、5的最小奇数,符合条件的最小偶数是368,只要将368加上3×5×7×11就能求得符合条件的最小奇数,这个数是368+3×5×7×11=1523.1. 有一个自然数,用它分别去除63,90,130都有余数,3个余数的和是25.这3个余数中最大的一个是多少?【分析】 由于这三个数除以这个自然数后所得的余数和为25,所以63、90、130的和除以这个自然数后所得的余数为25,所以63+90+130-25=258能被这个自然数整除.258=2×3×43,显然当除数为2、3、6时,3个余数的和最大为3×(2-1)=3,3×(3-1)=6,3×(6-1)=15,所以均不能满足条件.当除数为43×2、43×3、43×6时,它除63的余数均是63,所以也不满足.那么除数只能是43,它除63,90,130的余数依次为20,4,1,余数的和为25,满足. 显然这3个余数中最大的为20.2. ()200831312008+被13除所得的余数是多少?【分析】31被13除所得的余数为5,31n 当n 取1,2,3, 时31n 被13除所得余数分别是5,12,8,1,5,12, 所以200831被13除余1.2008被13除所得的余数是6,6n 当n 取1,2,3, 时,6n 被13除所得的余数分别是6,10,8,9,2,12,7,3,5,4,11,1,6, 所以316被13除所得的余数等于76被13除所得的余数,即7,所以()200831312008+被13除所得的余数是178+=.3. 一个自然数除以7、8、9后分别余3、5、7,而所得的三个商的和是758,这个数是___________.【分析】 这个数加上11后能被7、8、9整除.7、8、9的最小公倍数是789504⨯⨯=,所以除以7,8,9后分别余3、5、7的数最小为50411-.504分别除以7、8、9所得的商之和是897879191⨯+⨯+⨯=,则50411-分别除以7、8、9所得的商之和是19123185-⨯=.7581851913=+⨯,所以这个数为5041150432005-+⨯=.4. 一个数除以5余3,除以6余4,除以7余1,求适合条件的最小的自然数.【分析】 “除以5余3”即“加2后被5整除”,同样“除以6余4”即“加2后被6整除”.[]5,6228-=,即28适合前两个条件.分析[]285,6x +⨯中能满足“除以7余1”的x 的值.可得到4x =是满足条件的最小值,所以,适合条件的最小的自然数是28304148+⨯=.5. 将一些水果装盘(少于100)个,如果7个7个装盘则剩下2个不能装,如果11个11个装盘则剩下6个不能装盘,如果13个13个装盘,那么还剩下7个不能装盘,那么这些水果有多少个?【分析】 11×13的倍数:143、286、429,……其中被7除余2的有429;7×13的倍数:91,182,……除以11余6的有182;7×11的倍数:77,154,……除以13余7的有462.1824624291073++=,由于水果数少于100,所以水果数有1073100172-=个.选绿色包装——减少垃圾灾难每人每年丢掉的垃圾重量超过人体平均重量的五六倍.北京年产垃圾430万吨,日产垃圾1.2万吨,人均每天扔出垃圾约1千克,相当于每年堆起两座景山.我国目前垃圾的产生量是1989年的4倍,其中很大一部分是过度包装造成的.不少商品特别是化妆品、保健品的包装费用已占到成本的30%—50%.过度包装不仅造成了巨大的浪费,也加重了消费者的经济负担,同时还增加了垃圾量,污染了环境.我们选购产品的时候还是以使用价值为主,尽量避免选购过度包装的产品,减少垃圾的制造量.拒子入门子发是战国时期楚国的一位将军.一次,他带兵与秦国作战,前线断了粮草,他派人向楚王告急.使者顺便去看望子发的老母.老人问使者:“兵士都好吗?”使者回答:“还有点儿豆子,只能一粒一粒分着吃.”“你们将军呢?”母亲问.使者回答道:“将军每餐都能吃到肉和米饭,身体很好.”子发得胜归来,母亲紧闭大门不让他进家门,并派人去告诉子发:“你让士兵饿着肚子打仗,自己却有吃有喝,这样做将军,打了胜仗也不是你的功劳.”母亲又说:“越王勾践伐吴的时候,有人献给他一罐酒,越王让人把酒倒在江的上游,叫士兵们一起饮下游的水.虽然大家没尝到酒味,却鼓舞了全军的士气,提高了战斗力.现在你却只顾自己不顾士兵,你不是我的儿子,你不要进我的门.”子发听了母亲的批评,向母亲认了错,决心改正,才得以进家门.俗话说:“子不教,父之过.”子女成长的好坏,长辈有着极大的责任.父母为了使孩子成长成参天大树,就必须在我们心中植下博爱之心,有了博爱之心,才有施爱于他人的可能.多以有时候,责备也蕴涵着父母对子女深沉的爱.。
三年级奥数第12讲乘法速算(教师版)

三年级奥数第12讲乘法(chéngfǎ)速算(教师版)教学目标多位数与一些特殊(tèshū)的数相乘,也可以(kěyǐ)用简便的方法来计算。
知识梳理我们(wǒ men)已经学会了整数乘法的计算方法,但计算(jì suàn)多位数乘法要一位一位地乘,运算起来比较麻烦。
其实,多位数与一些特殊的数相乘,也可以用简便的方法来计算。
计算乘法时,如果一个因数是25,另一个因数考虑可拆成4×几,这样可“先拆数再扩整”。
两位数、三位数及更高位数乘以11,可采用“两头一拉,中间相加”的办法,但要注意相邻两位相加作积的中间数时,哪一位上满十要向前一位进一。
比如两位数乘以11,我们有“两位数与11相乘,首尾不变中间变,左右相加放中间,满十进一头就变。
”典例分析例1、试着计算下列各题,你发现了什么规律?(1)26×11 (2)57×11 (3)253×11 (4)467×11【解析】通过计算、观察可以发现,一个数与11相乘,所得的结果就是将这个数的首位和末位拉开分别作为积的最高位和最低位,再依次将这个数相邻两位由个位加起,和写在十位、百位……,哪一位上满十就向前一位进一。
(1)26×11=286 (2)57×11=627 (3)253×11=2783 (4)247×11=2717例2、很快算出下面各题的结果。
(1)12×11 (2)11×75 (3)87×11 (4)124×11【解析】(1)132;(2)825;(3)957;(4)1364例3、下面的乘法(chéngfǎ)计算有规律吗?(1)25×24 (2)21×25 (3)25×427 (4)1998×25【解析(jiě xī)】因为(yīn wèi)25×4=100,因此(yīncǐ),一个(yī ɡè)数与25相乘,我们就看这个数里有几个4,有几个4就有几个100,余1就加25,余2就加50,余3就加75。
小学数学奥数基础教程(三年级)目30讲全

小学奥数基础教程(三年级)- 1 -小学奥数基础教程(三年级)第1讲加减法的巧算第2讲横式数字谜(一)第3讲竖式数字谜(一)第4讲竖式数字谜(二)第5讲找规律(一)第6讲找规律(二)第7讲加减法应用题第8讲乘除法应用题第9讲平均数第10讲植树问题第11讲巧数图形第12讲巧求周长第13讲火柴棍游戏(一)第14讲火柴棍游戏(二)第15讲趣题巧解第16讲数阵图(一)第17讲数阵图(二)第18讲能被2,5整除的数的特征第19讲能被3整除的数的特征第20讲乘、除法的运算律和性质第21讲乘法中的巧算第22讲横式数字谜(二)第23讲竖式数字谜(三)第24讲和倍应用题第25讲差倍应用题第26讲和差应用题第27讲巧用矩形面积公式第28讲一笔画(一)第29讲一笔画(二)第30讲包含与排除一、两、三位数乘一位数(一)二、两、三位数乘一位数(二)三、乘法分配律数学智慧园(一)四、等量替换五、两、三位数除以一位数(一)六、两、三位数除以一位数(二)七、和差问题数学智慧园(二)八、图形空格填数九、归一问题十、和倍问题十一、差倍问题数学智慧园(三)十二、两积之和第2讲横式数字谜(一)在一个数学式子(横式或竖式)中擦去部分数字,或用字母、文字来代替部分数字的不完整的算式或竖式,叫做数字谜题目.解数字谜题就是求出这些被擦去的数或用字母、文字代替的数的数值。
例如,求算式324+□=528中□所代表的数。
根据“加数=和—另一个加数”知,□=582-324=258。
又如,求右竖式中字母A,B所代表的数字。
显然个位数相减时必须借位,所以,由12—B=5知,B=12—5=7;由A—1=3知,A=3+1=4。
解数字谜问题既能增强数字运用能力,又能加深对运算的理解,还是培养和提高分析问题能力的有效方法。
这一讲介绍简单的算式(横式)数字谜的解法.解横式数字谜,首先要熟知下面的运算规则:(1)一个加数+另一个加数=和;(2)被减数-减数=差;(3)被乘数×乘数=积;(4)被除数÷除数=商。
小学数学奥数基础教程(三年级)目30讲全

小学奥数基础教程(三年级)- 1 -小学奥数基础教程(三年级)第1讲加减法的巧算第2讲横式数字谜(一)第3讲竖式数字谜(一)第4讲竖式数字谜(二)第5讲找规律(一)第6讲找规律(二)第7讲加减法应用题第8讲乘除法应用题第9讲平均数第10讲植树问题第11讲巧数图形第12讲巧求周长第13讲火柴棍游戏(一)第14讲火柴棍游戏(二)第15讲趣题巧解第16讲数阵图(一)第17讲数阵图(二)第18讲能被2,5整除的数的特征第19讲能被3整除的数的特征第20讲乘、除法的运算律和性质第21讲乘法中的巧算第22讲横式数字谜(二)第23讲竖式数字谜(三)第24讲和倍应用题第25讲差倍应用题第26讲和差应用题第27讲巧用矩形面积公式第28讲一笔画(一)第29讲一笔画(二)第30讲包含与排除一、两、三位数乘一位数(一)二、两、三位数乘一位数(二)三、乘法分配律数学智慧园(一)四、等量替换五、两、三位数除以一位数(一)六、两、三位数除以一位数(二)七、和差问题数学智慧园(二)八、图形空格填数九、归一问题十、和倍问题十一、差倍问题数学智慧园(三)十二、两积之和第2讲横式数字谜(一)在一个数学式子(横式或竖式)中擦去部分数字,或用字母、文字来代替部分数字的不完整的算式或竖式,叫做数字谜题目。
解数字谜题就是求出这些被擦去的数或用字母、文字代替的数的数值。
例如,求算式324+□=528中□所代表的数.根据“加数=和-另一个加数”知,□=582-324=258.又如,求右竖式中字母A,B所代表的数字。
显然个位数相减时必须借位,所以,由12—B=5知,B=12-5=7;由A—1=3知,A=3+1=4.解数字谜问题既能增强数字运用能力,又能加深对运算的理解,还是培养和提高分析问题能力的有效方法.这一讲介绍简单的算式(横式)数字谜的解法.解横式数字谜,首先要熟知下面的运算规则:(1)一个加数+另一个加数=和;(2)被减数-减数=差;(3)被乘数×乘数=积;(4)被除数÷除数=商.由它们推演还可以得到以下运算规则:由(1),得和-一个加数=另一个加数;其次,要熟悉数字运算和拆分.例如,8可用加法拆分为8=0+8=1+7=2+6=3+5=4+4;24可用乘法拆分为24=1×24=2×12=3×8=4×6(两个数之积)=1×2×12=2×2×6=…(三个数之积)=1×2×2×6=2×2×2×3=…(四个数之积)例1下列算式中,□,○,△,☆,*各代表什么数?(1)□+5=13-6;(2)28-○=15+7;(3)3×△=54;(4)☆÷3=87;(5)56÷*=7。
第5讲.竞赛123班.教师版

第五讲应用问题综合强化1. 掌握和差倍分、年龄、盈亏问题的解题方法;2. 利用基本方法解答复杂应用题。
应用题的种类有许多,一般可以按照如下三类来划分、归类:第一类:按照题目内容划分,如行程问题、年龄问题、时钟问题等;第二类:按照题目本质划分,如和差倍分问题、盈亏问题、鸡兔同笼问题等,这一类题涉及的是思想方法,可以变成第一类中的任何一种问题;第三类:按照解题方法划分,如从反面考虑问题、还原问题等。
本讲是对原来学过的和差倍分问题、年龄问题、盈亏问题进行总结强化,同时帮助同学们不断回顾已有知识,更加深刻掌握解题的思路和方法!【例1】 某项竞赛分一等奖、二等奖和三等奖,每个一等奖的奖金是每个二等奖奖金的2倍,每个二等奖的奖金是每个三等奖奖金的2倍。
如果评出一、二、三等奖各2人,那么每个一等奖的奖金是308元。
如果评出1个一等奖,2个二等奖,3个三等奖,那么一等奖的奖金是多少元?【分析】 我们把每个三等奖奖金看作1份,那么每个二等奖奖金是2份,每个一等奖奖金则是4份。
当一、二、三等奖各评2人时,2个一等奖的奖金之和是(3082)⨯元,2个二等奖的奖金之和等于1个一等奖的奖金308元,2个三等奖的奖金等于1个二等奖奖金(3082)÷元。
所以奖金总额是:308230830821078⨯++÷=元。
当评1个一等奖,2个二等奖,3个三等奖时,1个一等奖奖金看做4份,2个二等奖奖金224⨯=(份),3个三等奖奖金的份数是133⨯=(份),总份数就是:44311++=(份)。
这样,可以求出1份数为10781198÷=元,一等奖奖金为:984392⨯=(元)。
[前铺] 甲、乙、丙三所小学学生人数的总和为1999,已知甲校学生人数的2倍,乙校学生人数减3,丙校学生人数加4都是相等的,问:甲、乙、丙各校的人数是多少?[分析] 甲校学生人数为:(199934)(122)400⨯+=,-+÷++=,乙校学生人数为:40023803丙校学生人数为:40024796⨯-=。
奥数第11讲竞赛123班.教师版
第十一讲逻辑推理1.掌握逻辑推理的解题思路与基本方法;2.能够解决较复杂的逻辑推理问题。
逻辑推理问题是一类很少进行计算的数学问题,它主要运用严密的逻辑推理来解决问题。
所谓逻辑推理,就是依据逻辑规律,从已知的结论为出发点,推出新的结论的过程。
在解决这类问题时,必须依据事情的逻辑关系进行合情的推理,最后作出正确的判断。
逻辑推理题的特点是条件繁杂交错,必须仔细分析,选择突破口,并且借助于图表,步步深入,这样才能使问题得到较快的解决。
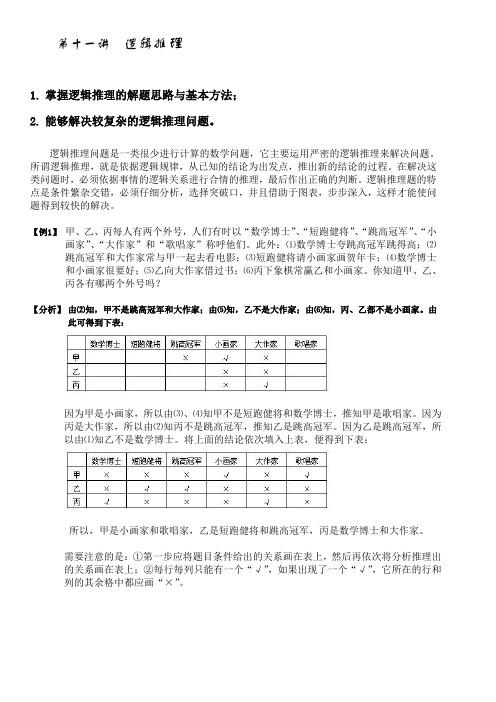
【例1】甲、乙、丙每人有两个外号,人们有时以“数学博士”、“短跑健将”、“跳高冠军”、“小画家”、“大作家”和“歌唱家”称呼他们。
此外:⑴数学博士夸跳高冠军跳得高;⑵跳高冠军和大作家常与甲一起去看电影;⑶短跑健将请小画家画贺年卡;⑷数学博士和小画家很要好;⑸乙向大作家借过书;⑹丙下象棋常赢乙和小画家。
你知道甲、乙、丙各有哪两个外号吗?【分析】由⑵知,甲不是跳高冠军和大作家;由⑸知,乙不是大作家;由⑹知,丙、乙都不是小画家。
由此可得到下表:因为甲是小画家,所以由⑶、⑷知甲不是短跑健将和数学博士,推知甲是歌唱家。
因为丙是大作家,所以由⑵知丙不是跳高冠军,推知乙是跳高冠军。
因为乙是跳高冠军,所以由⑴知乙不是数学博士。
将上面的结论依次填入上表,便得到下表:所以,甲是小画家和歌唱家,乙是短跑健将和跳高冠军,丙是数学博士和大作家。
需要注意的是:①第一步应将题目条件给出的关系画在表上,然后再依次将分析推理出的关系画在表上;②每行每列只能有一个“√”,如果出现了一个“√”,它所在的行和列的其余格中都应画“×”。
[前铺] 小王、小张和小李一位是工人,一位是农民,一位是教师,现在只知道:小李比教师年龄大;小王与农民不同岁;农民比小张年龄小。
问:谁是工人?谁是农民?谁是教师?[分析] 由题目条件可以知道:小李不是教师,小王不是农民,小张不是农民。
由此得到左下表。
表格中打“√”表示肯定,打“×”表示否定。
奥数讲座4年级综合练习12讲

四年级奥数讲座综合练习目录第一讲:乘法原理第二讲:加法原理第三讲:排列第四讲:组合第五讲:排列、组合第六讲:排列组合的综合应用第七讲:有趣的数阵第八讲:数学游戏第九讲:简单的幻方及其他数阵图第十讲:数字综合题选讲第十一讲:数字谜第十二讲:数学竞赛试题选讲第一讲:乘法原理基础班1、有五顶不同的帽子,两件不同的上衣,三条不同的裤子。
从中取出一顶帽子、一件上衣、一条裤子配成一套装束。
问:有多少种不同的装束?2、四角号码字典,用4个数码表示一个汉字。
小王自编一个"密码本",用3个数码(可取重复数字)表示一个汉字,例如,用"011"代表汉字"车"。
问:小王的"密码本"上最多能表示多少个不同的汉字?3、"IMO"是国际数学奥林匹克的缩写,把这3个字母写成三种不同颜色。
现在有五种不同颜色的笔,按上述要求能写出多少种不同颜色搭配的"IMO"?4、在右图的方格纸中放两枚棋子,要求两枚棋子不在同一行也不在同一列。
问:共有多少种不同的放法?5、要从四年级六个班中评选出学习和体育先进集体各一个(不能同时评一个班),共有多少种不同的评选结果?6、甲组有6人,乙组有8人,丙组有9人。
从三个组中各选一人参加会议,共有多少种不同选法?7、如下图,在三条平行线上分别有一个点,四个点,三个点(且不在同一条直线上的三个点不共线).在每条直线上各取一个点,可以画出一个三角形.问:一共可以画出多少个这样的三角形?8、在自然数中,用两位数做被减数,用一位数做减数.共可以组成多少个不同的减法算式?9、一个篮球队,五名队员A、B、C、D、E,由于某种原因,C不能做中锋,而其余四人可以分配到五个位置的任何一个上.问:共有多少种不同的站位方法?10、由数字1、2、3、4、5、6、7、8可组成多少个①三位数?②三位偶数?③没有重复数字的三位偶数?④百位为8的没有重复数字的三位数?⑤百位为8的没有重复数字的三位偶数?11、某市的电话号码是六位数的,首位不能是0,其余各位数上可以是0~9中的任何一个,并且不同位上的数字可以重复.那么,这个城市最多可容纳多少部电话机?解答1.30种。
奥数第9讲[1].竞赛123班.教师版
![奥数第9讲[1].竞赛123班.教师版](https://img.taocdn.com/s3/m/3d29d14df7ec4afe04a1dfea.png)
操作类问题与计数类问题由于其灵活性和本身的趣味性,非常受出题和供题者青睐,如今各类数学竞赛的出题越来越趋向于新奇和趣味化,因此操作类问题和计数问题在竞赛中的比重将会加大。
鉴于操作类问题和计数问题没有一般性的算法或解题通式,本讲将以近年来各类竞赛以及小升初考试中的出现过的真题为例,引导学生发现关键并解决问题。
1. 常见操作类问题2. 计数技巧与操作【例1】 (2006年《小学生数学报》读报竞赛)把一张正方形的餐巾纸先上下对折,再左右对折(如右图),然后用剪刀将所得的小正方形沿直线剪一刀。
问能把餐巾纸: ⑴剪成2块吗? ⑵剪成3块吗? ⑶剪成4块吗? ⑷剪成5块吗?如果你认为能剪成,请在下面图中各画出一种你的剪法;如果你认为不能,那么只需回答“不行”即可。
【分析】⑴剪开成两块,如下图:⑵剪开成3块,如下图:操作与计数技巧第九讲⑶剪开成4块,如下图:⑷剪开成5块,如下图:【巩固】(2008年华杯赛)将等边三角形纸片按图所示的步骤折迭3次(图中的虚线是三边中点的连线),然后沿两边中点的连线剪去一角。
将剩下的纸片展开、铺平,得到的图形是( ).【分析】折迭3次,纸片的厚度为4,所以剪去的面积即应等于4倍小三角形的面积,所以答案是A。
【例2】A、B、C、D四个盒子中依次放有6,4,5,3个球。
第1个小朋友找到放球最少的盒子,从其他盒子中各取一个球放入这个盒子;然后第2个小朋友找到放球最少的盒子,从其他盒子中合取一个球放入这个盒子;如此进行下去,……。
求当34位小朋友放完后,B盒子中放有球多少个?【分析】盒子A B C D初始状态 6 4 5 3第1人放过后 5 3 4 6第2人放过后 4 6 3 5第3人放过后 3 5 6 4第4人放过后 6 4 5 3第5人放过后 5 3 4 6由此可知:每经过4人,四个盒子中球的情况重复出现一次,因为34482÷= ,所以第34次后的情况与第2次后的情况相同,即B盒子中有球6个。
小学一年级奥数:第12讲 猫捉老鼠 - 教师版(含答案)

第12讲猫捉老鼠【专题导引】在我们的日常生活中,经常会遇到一些十分有趣的数学问题。
思考这类问题时,要联系我们的生活实际来思考,如不小心,你就可能落入“圈套”。
解答这些题目,不仅能激发我们的思维,使我们的头脑越来越灵活。
小朋友,“智力趣事”中所讲的这些题,非常有趣,兴趣是最好的老师,一旦你对数学产生了兴趣,有了学好数学的信心,你就有了克服困难的勇气和毅力。
相信:你会越来越喜欢数学的。
【典型例题】【B1】有10个小朋友在玩“猫捉老鼠”的游戏,现在已经捉到了5人。
还有几个人没有被捉到?解答:10-1-5=4(人)【试一试】有12个小朋友在一起玩捉迷藏的游戏,现在已经捉到了7人。
还有几个人没有被捉到?解答:12-1-7=4(人)【B2】一只船上坐着一家人。
数一数,有两个爸爸,两个儿子。
船上一共有几个人?解答:3个人。
【试一试】一只船上坐着一家人。
数一数,有两个妈妈,两个女儿。
船上一共有几个人?解答:3个人。
【B3】房间的桌子上有10支刚刚点燃的蜡烛,风从窗户吹进来,吹灭了2支蜡烛。
过了一会儿,又有1支蜡烛被风吹灭。
把窗户关起来以后,再没有蜡烛被吹灭。
最后还剩几支蜡烛?解答:2+1=3(支)【试一试】妈妈在房间里点燃了8支蜡烛,风从窗户吹来,吹灭了1支,后来又吹灭了1支。
妈妈关好了窗户,再没有蜡烛被吹灭。
房间里最后还剩下几支蜡烛?解答:1+1=2(支)【A1】小明和小亮同买一本书,小明缺1元5角,小亮缺1元3角。
如果用他们俩的钱合买这本书,钱正好。
这本书的价钱是多少?他们各带了多少钱?解答:1元5角+1元3角=2元8角,小明带了1元3角,小亮带了1元5角。
【试一试】东东和华华买同一本《科学画报》,东东缺1元2角,华华缺1元4角。
把他俩的钱合起来,正好是一本书的价钱,这本《科学画报》的价钱是多少?他们各带了多少钱?解答:1元2角+1元4角=2元6角,东东带了1元4角,华华带了1元2角。
【A2】一个正方形有4个角,直直的剪去1个角,还剩几个角?解答:4+1=5(个)【试一试5】一块正方形木板,直直的锯下一个角,还剩几个角?解答:4+1=5(个)课外作业家长签名:1、连长带着10名战士过河,已经有6名战士过了河,没过河的还有几人?解答:10-6+1=5(人)2、一天,一家人中3个爸爸、3个儿子一同去公园玩,他们至少有多少个人?解答:4个。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.如果()3a b +是7的倍数,那么下面算式中______一定也是7的倍数。
(a 、b 都是自然数)⑴a b -⑵2a b -⑶4a b -⑷23a b +⑸3a b-【分析】()3a b +是7的倍数,()62a b +也是7的倍数,所以()2762a b a a b -=-+也是7的倍数。
()473a b a a b -=-+也是7的倍数,()2373223a b a a b a b +=-+÷=+⎡⎤⎣⎦也是7的倍数。
所以只有⑵⑶⑷一定是7的倍数。
2.在一次考试中,甲乙两人考试结果如下:甲答错了全部试题的13,乙答错了7道题,甲乙都答错的题目占全部试题的15,则甲、乙两人都答对的题目最少有______道。
【分析】容斥原理。
甲答错,乙答对的题占全部试题的13-15=215。
那么甲乙都答对的题目有1315的全部试题减去7道乙答错的题目。
可见全部试题越少,甲、乙都答对的题目就越少。
则至少有15道全部试题,则15×1315-7=6道。
3.在1到100中,恰好有6个约数的数有______个。
【分析】6只能表示为()51+或()()1121++,所以恰好有6个约数的数要么能表示成某个质数的5次方,要么表示为某个质数的平方再乘以另一个质数,100以内符合前者的只有32,符合后者的数枚举如下:2222222222222222325272112132172192238323537311452532721⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯ 种种种种所以符合条件的自然数一共有1842116++++=种。
4.某地收费的标准是:若每月用电不超过50度,则每度收5角;若超过50度,则超出部分按每度8角收费。
某月甲用户比乙用户多交3元3角电费,这个月乙用了______度电。
【分析】因为33既不是5的倍数又不是8的倍数,所以甲用电超过50度,乙用电不足50度。
设甲用电()50x +度时,乙用电()50y -度时。
因为甲比乙多交33角电费,所以有8533x y +=。
容易看出1x =,5y =,推知甲用电51度,乙用电45度。
期末考试第十二讲5.如果一个质数加上2,8,14,26以后,得到的和都是质数,那么,原来的质数是______。
【分析】因为2,8,24,26除以5,余数依次为2,3,4,1,所以这四个数加上一个比5大的质数,得到的和必有一个能被5整除,不是质数,所以原来的质数不大于5,通过尝试可得到这个质数是5。
6.四组平行线(每组两条,共八条直线)最多能将平面划分成______个部分。
【分析】两组平行线能将平面分割成9个部分,再加一组平行线,每条直线最多能和原来的直线有4个交点,被分割成5段,所以一组平行线一共是10段,所以平面上的分区增加10快,即分成19块。
增加到四组平行线,新增加()26114⨯+=段线段,所以最多能将平面分成191433+=个部分。
7.将3,5,7,11,13,17,19,23,29这9个数分别填人右图的9个○中,使3条直线上的○中的数之和都相等。
请分别求出满足上述条件的最大的和与最小的和的差:______。
【分析】设三个交点○内所填的数为a ,b ,c ,每条边上的和为K ,三个顶点上的数在求和时各用了2次,所以条边上的三数之和相加得()()3571113171923291273a b c a b c K +++++++++++=+++=;由于所得的和必须能被3整除,而1273421÷= ,所以()a b c ++的和应被3除余2,a b c++的最小值是571123++=,最大值是29231971++=,所以K 的最小值是()12723350+÷=,最大值是()12771366+÷=。
差为16。
8.甲、乙、丙三队要完成A ,B 两项工程,B 工程的工作量是A 工程工作量再增加14,如果让甲、乙、丙三队单独做,完成A 工程所需时间分别是20天,24天,30天.现在让甲队做A 工程,乙队做B 工程,为了同时完成这两项工程,丙队先与乙队合做B 工程若干天,然后再与甲队合做A 工程若干天.问丙队与乙队合做了______天。
【分析】三队合做完成二项工程所用的天数111111184202430⎛⎫⎛⎫++÷++= ⎪ ⎪⎝⎭⎝⎭天,丙帮乙队做的天数:1111181542430⎛⎫+-⨯÷= ⎪⎝⎭天。
9.小李小张和小朱三人参加灯谜会,他们分别猜对了一条二条三条灯谜。
小赵问他们各猜对了几条。
小李说:“我猜对了两条”。
小朱说:“我猜对的灯谜最多”。
小张说:“我猜对的不是偶数条。
”他三人只有一人说的不对。
请问,小朱猜对了______条灯谜。
【分析】分别假设没有猜对的人是小李、小张、小朱,可以发现只有小朱没有猜对时,不会有矛盾,所以,此时小李猜对两条,小朱猜对的不是最多,所以1条。
10.在一次象棋比赛中,每两人之间都要比赛两盘,每盘比赛胜者得2分,负者得0分,平局两人各得1分。
现有6名同学统计全部选手的总分,分别是920,921,922,923,924,925分。
但只有一个数据是正确的,共有_______名选手参加了这次比赛。
【分析】n 个人之间比赛场数为()1n n -,每一场产生2分,所以比赛的分数一定能写成()21n n -,在920,921,922,923,924,925这几个分数当中,只有92422221=⨯⨯,所以其中正确的分数是924,共有22名选手参加了这次比赛。
1.如图相邻两个格点间的距离是1,则图中阴影三角形的面积为多少?【分析】三角形ABD 的面积为162347---=,四边形ABCD 的面积为162329---=,三角形ACD的面积等于122325---=,所以:5:9OD BD =,阴影部分的面积等于535799⨯=。
2.一次足球比赛,有A ,B ,C ,D 四队参加,每两队都比赛一场,按规定胜一场得2分,平一场各得1分,负一场得0分。
比赛结果,B 队得了5分,C 队得3分,A 队得1分,所有场次共进9个球,B 队进球最多,共进4个球,C 队共失3个球,D 队一个球未进,A 队与C 队的比分为2:3,则A 队与B 队的比分是多少?【分析】3:0,首先由D 队一个球未进,可得到D 从来没有赢过,A 队得1分,所以A 队也没有赢过,所以A 和D 之间是平局,并且A 负于B 和C ,而C 队得3分,所以C 对B 和D 的两场比赛一平一负,而D 从来没有赢过,所以C 对D 是平局,由此可得到对阵图:D CA D 的三场比赛都是平局,根据D 队一个球未进,可得出,这三场比赛的比分为0:0,C 队在与A 的比赛当中失球2个,所以在与B 的比赛当中失球1个,所以B 与C 的比赛只能是1:0,B 与A 的比赛当中进球413-=个,这时除了A 与B 的比赛中的进球外,其它的进球已经达到31329+++=,所以A 队与B 队的比分是3:0。
3.甲、乙合作一件工程:由于配合得好,甲的工作效率比单独做时提高110,乙的工作效率比单独做时提高15.甲、乙两人合作6小时,完成全部工作的25,第二天乙又单独做了6小时,还留下这件工作的1330尚未完成,如果这件工作始终由甲一人单独来做,需要多少小时?【分析】第二天乙单独做了6小时完成了213115306--=,所以第一天乙工作6小时完成了1111655⎛⎫⨯+= ⎪⎝⎭,所以第一天甲完成了211555-=,这样甲和乙合作时甲每小时完成116530÷=,所以甲单独做的时候每小时完成1101301133⨯=,所以甲单独做需要33小时。
4.一些学生在老师的带领下去郊区游玩,男生小刚发现,学生的人数(当然包括了他自己)不到老师人数的3倍,而女生人数比女老师人数的3倍还多,已知学生和老师一共有20人,并且女老师比男老师人数多,求女生人数。
【分析】由学生的人数不到老师人数的3倍可以得到学生的人数不到15人,否则学生人数达到老师人数的3倍,所以学生人数最多有14人,老师人数至少有6,再由“女老师比男老师人数多”可得到女老师人数至少有4人,再根据女生人数比女老师人数的3倍还多,可以得到女生人数至少有43113⨯+=人,而之前我们得到学生人数最多有14人,并且包括男生小刚,所以学生人数只能是14人,女生人数只能是13人。
1.小明的妈妈买了葡萄、苹果、雪梨和芒果的果脯各若干袋(每种至少一袋),用了340元.葡萄、苹果、雪梨和芒果果脯每袋售价分别为14元、22元、28元、42元.小明的妈妈至少买了多少袋果脯?其中苹果果脯是多少袋?【分析】因为葡萄、雪梨和芒果果脯的价格都是7的倍数,苹果的价格除以7余1,妈妈花的钱数除以7余4,所以苹果果脯买了4袋或11袋.当买11袋苹果果脯时,剩余的钱必然是买2袋葡萄,1袋雪梨,1袋芒果,共15袋果脯.当买4袋苹果果脯时,还剩下252元,为了使买的果脯的袋数尽量少,应该尽量多买最贵的芒果果脯,所以应该买1袋葡萄,1袋雪梨,5袋芒果,共11袋果脯.所以小明的妈妈至少买了11袋果脯,其中苹果果脯是4袋。
2.在下图的乘法算式中,每个□表示一个数字,那么计算所得的乘积应该是多少?51105⨯【分析】被乘数和乘数的百位都是1,乘数的十位是0,个位是奇数,由被乘数与乘数的个位数字相乘,即15105⨯=。
可知乘数的个位数字只能是7或9。
经检验,只能是9,而且14591305⨯=。
所以原式的乘积为14510915805⨯=。
1.一个回文数是指从首位数读到末尾数,与末尾数读到首位数都相同的数(如11511、14041)。
请问,可被11整除的五位数的回文数个数与全部五位数的回文数的个数之比是什么?答案用分数表示:【分析】显然五位回文数为abcba 的形式,其中a 为1~9有9种取法,b 和c 可为0~9有10种取法。
故5位回文数有91010900⨯⨯=个。
若11abcba ,则有()11|2,a b c -+又由C 可为0~9中的任意数知当()2a b -除以11的余数不为1时,C 有且只有一种取法使()11|2a b c -+。
而a 与b 的取法共有91090⨯=种,其中()2a b -除以11余1时,只有()212a b -=,故能被11整除的五位回文数有90783=个。
所以可被11整除的五位数的回文数个数与全部五位数的回文数的个数之比是83900。
2.有一个面积为34562cm的矩形,它的四个边都在如图所示的网格线上,图中每个小正方形的边长为1cm。
格点我们称图中每个小正方形的顶点为“格点”,例如:24⨯的矩形的一条对角线正好通过3cm cm个格点。
请问:上述面积为34562cm的矩形的对角线最多可能通过多少个格点。
【分析】因为73=⨯,当矩形的的长和宽的最大公约数越大时,对角线所经过的格点也越多,345623将3456分解成两个数相乘,这两个数的公约数的标准分解式中2的次数不会超过7的一半,3的次数不会超过3的一半,所以这个最大公约数最大是31⨯=,此时长和宽的取值可以是232472和48。
