2010.8溷凝土随机损伤力学(教育部暑期学校讲座,长沙)
冲击荷载作用下岩石压动态和拉动态损伤模型

第50卷第2期中南大学学报(自然科学版) V ol.50No.2 2019年2月Journal of Central South University (Science and Technology)Feb. 2019 DOI: 10.11817/j.issn.1672−7207.2019.02.022冲击荷载作用下岩石压动态和拉动态损伤模型谢福君,张家生,陈俊桦(中南大学土木工程学院,湖南长沙,410075)摘要:根据经典岩石冲击动态损伤模型和统计损伤力学理论,提出冲击荷载加载条件下的岩石压、拉统计损伤本构模型和冲击损伤判据模型。
在该损伤模型中,将损伤演化关系分为体积压缩损伤和体积拉伸损伤2种。
应用提出的损伤模型和经典动态拉伸损伤模型分别进行爆破损伤数值模拟,并将数值计算结果和现场实测结果进行对比。
研究结果表明:与炮孔轴向相比,炮孔径向是爆破破裂延伸的主方向;沿炮孔径向主要发生拉伸破裂,孔底下方主要发生压缩破裂;与基于经典冲击动态拉伸损伤模型的数值计算结果相比,根据损伤模型得到的爆破破裂范围特别是孔底正下方破裂深度与实测值相差不大且最接近实测值,表明所提出的损伤模型是合理的,具有实用性。
关键词:岩石;动力损伤作用;压缩; 拉伸;爆破数值模拟中图分类号:TU45;TD235 文献标志码:A 文章编号:1672−7207(2019)02−0420−08 Dynamic damage model of rock under impact loads ofcompression and tensionXIE Fujun, ZHANG Jiasheng, CHEN Junhua(School of Civil Engineering, Central South University, Changsha 410075, China)Abstract: An impact-induced damage constitutive model based on classical impact-induced constitutive models and statistic damage mechanics was presented. In the model, damage evolutions were considered to be caused by volume compression and volume tension, respectively, and the presented model considered that compression strength of rock was much bigger than its tension strength. Numerical simulation of blasting was conducted according to the presented model.Results of blasting-induced fracture zone among the numerical simulation based on presented model and those of the blasting numerical simulation based on current tension damage model and actual measurement in field were comparied.The results show that the cardinal extension direction of fracture zone is the radial direction of blast hole rather than the axial direction of blast hole. The tension-induced fracture mainly appears along the radial direction while the compression-induced fracture mainly appears along the axial direction. The blasting-induced fracture zone obtained from the numerical simulation based on the presented model, especially the fracture depth under blast hole, is much closer to the actual measurement result than that obtained from the numerical simulation based on the current dynamic tension damage models. There is little difference between the numerical simulation results based on the presented model and actual measurement, indicating that the presented model is reasonable and useful.Key words: rock; dynamic damage; compression; tension; numerical simulation of blasting在冲击荷载作用下,岩石动态本构关系是爆破工程、地下防护工程等领域的研究热点。
岩土塑性力学原理—广义塑性力学(郑颖人)

2 zx
I
3
x
y
z
2
xy
yz zx
x
2 yz
2
y zx
2
z xy
II121(12
3 2
2
3
3
1
)
I31 2 3
应力张量第一 不变量 I1 ,是平均应力p的三倍。
26
应力张量分解及其不变量
应力张量
岩土材料的稳定性、应变软化、损伤、应变局部化
(应力集中)与剪切带等问题
11
岩土材料的试验结果
土的单向或三向固结压缩试验:土有塑性体变
初始加载:
卸载与再加载:
e e0 ln p
e ek k ln p
12
岩土材料的试验结果
土的三轴剪切试验结果:
(1)常规三轴
土有剪胀(缩)性; 土有应变软化现象;
3
第1章 概 论
岩土塑性力学的提出 岩土塑性力学及其本构模型发展方向 岩土材料的试验结果 岩土材料的基本力学特点 岩土塑性力学与传统塑性力学不同点 岩土本构模型的建立
4
岩土塑性力学的提出
材料受力三个阶段: 弹性 → 塑性 → 破坏
弹性力学 塑性力学 破坏力学 断裂力学等
19世纪40年代末,提出Drucker塑性公论,经典塑性 力学完善;
1773年Coulomb提出的土质破坏条件,其后推广为 莫尔—库仑准则;
1957年Drucker提出考虑岩土体积屈服的帽子屈服面;
1958年Roscoe等人提出临界状态土力学,1963年提出 剑桥模型。岩土塑性力学建立。
土_结构动力相互作用体系阻尼及地震反应分析_夏栋舟

2924
岩
土
力
学
2009 年
2
土 - 结构动力相互作用体系阻尼的 简化分析方法
文献 [8] 根据直接分析法提出不考虑基础质量
构与基础、基础与地基土之间,因而忽略基础质量 是不妥的。笔者提出一个改进的简化分析方法,能 考虑基础质量 m0 、基础的等效半径 a ,同时也考虑 了柔性地基土本身的黏滞材料阻尼 ξs 。其简化模型 如图 2 所示,根据简化模型建立体系的整体运动方 程:
m
Kθ cθ
图 2 土-结构动力相互作用体系简化模型 2 Fig.2 The simplified model 2 for soil-structureinteraction system
ξ=
xg m
xu
hθ m
x m
c k ; ω2 = m 2mω 2 K u = mωu {1 + 2i[ξs + (ω / ωu ) ξ u ]} K θ = mh 2ωθ2 {1 + 2i[ξs + (ω / ωθ ) ξθ ]}
⎡⎛ ImK θ ⎢⎜ ⎢⎝ ReK θ ⎣
⎤ ⎞ ⎟ − 2ξs ⎥ ⎥ ⎠ ⎦
(7)
但是,在土-结构动力相互作用时,其非线性接 触及动力相互作用往往导致的能量损耗就发生在结
式中:Re 为复数函数的实部;Im 为复数函数的虚 部;ω 、ξ 为刚性地基上结构的自振频率与阻尼比;
第 10 期
夏栋舟等:土-结构动力相互作用体系阻尼及地震反应分析
[1-4]
能的研究国内外还为之甚少,因此,笔者提出了一 种新的考虑土 -结构动力相互作用体系阻尼的简化 分析方法,得到了耦合阻尼比公式,并结合大西洋 地震工程研究中心 102 个强震中的 1 037 条实际地 震时程记录中的地震加速度反应谱数据和《建筑抗 震设计规范》[7] 的规定,提出基于加速度反应谱的 阻尼影响因子 η ,并将其用于抗震设计,建立阻尼 影响因子 η 与地震影响系数 α 间的关系式,从而根 据现有的抗震规范求得上部结构的地震作用。通过 算例分析可知,考虑土与上部结构的相互作用后能 够增加体系的阻尼,并大大降低上部结构的地震作 用,为未来抗震研究与工程的抗震设计提供了理论 依据。
会议时间2012年11月8日830–1730会议地点西安交通

DAAD von Alumni fü r Alumni BMP课题组照片
DAAD von Alumni fü r Alumni
DAAD “校友为校友”项目
DAAD北京办事处在2010与2011年通过“校友 为校友”(von Alumni für Alumni)项目协助多位校友 成功举办了自己的专题活动并收获到了很好的效果。 这些活动促进了同行业和同领域的留德校友之间的 交流,DAAD留德校友专业网络得以进一步的扩大。
Birgit Stender (Institute for Robotics and Gognitive Systems, University of Luebeck, Luebeck, Germany)
堡大学医学院肿瘤医院、威廉港应用大学和吕贝克应用
大学从事科学研究。目前发表论文百余篇。获部 级科技
进步三等奖二项、2006年度陕西省科学技术奖二等奖一 项、2006年享受政府特殊津贴。2012获陕西省师德教育模范个人奖。 教育部高等学校生物医学工程专业教学指导委员会委员(2006-2010年)。 《激光生物学报》副主任编委、《中国激光》、《光电子·激光》、 Optoelectronics Letters、《国际生物医学工程杂志》、《世界医疗器械》 编委。
张镇西 (西安交通大学生命科学与技术学院生物医学分析技术与仪器研究所,710049, 西安)
摘 要: 现代生命科学的发展在很大程度上依赖于对活细胞的加工 和操纵, 比如切除细胞内的某些特定蛋白或细胞器等。激光细胞微手术 是一个强有力的工具, 近年来在细胞微手术精度控制方面取得很大的进 展。综述了激光细胞微手术的最新发展及其在生物学和生物医学工程 中的应用, 对目前激光细胞微手术中存在的主要问题进行了讨论, 对比 了普通激光聚焦法、飞秒激光聚焦法以及纳米金辅助的激光照射法的 优点和不足。
混凝土随机损伤力学

3.5
3.5
30
Karsan and Jirsa (1969)
Model result
25
Stress(MPa)
Stress(MPa) Stress(MPa)
3.0
3.0
20
2.5
2.5
2.0
2.0
1.5
1.5
1.0
1.0
0.5
0.5
0.0
0.0
-1.4
0.0 0.5 1.0 1.5 2.0 2.5 3.0 3.5 4.0 0.0 0.5 1.0 1.5 2.0 2.5 3.0 3.5 4.0
ID:C0 :(εp)
建模基本过程(4)
由材料的弹塑性Helmholtz自由能势得到损伤能释放率表 达式,基于损伤能释放率,建立材料的损伤准则和损伤变量的 演化法则.
损伤能 释放率
Yt
t dt
te0(εe)
Y s d s ss0(εe,q )s e 0(εe)s p 0(q )
损伤准则 与演化法则
5
x 10 5
4
3
2
1
0
-1
-2
-3
-4
-5
-0.04 -0.03 -0.02 -0.01
0
0.01 0.02 0.03 0.04
Inter-floor Displacement (m)
损伤机制、受力形式与结构滞回耗能机制的关系?
3)损伤扩散与多尺度随机涨落
静力作用下的损伤
动力作用下的损伤
研究在不同尺度上的损伤扩散、转移、随机涨落及其跨尺度影
-1.2 -1.0 -0.8 -0.6 -0.4
强度 准则
2
精品课程《损伤力学》ppt课件全共236页文档

传统材料力学的强度问题
两大假设:均匀、连续
σC
评选寿
定材命
s
b 强度指标
1
应用
材料力学
SU
强度分析
强度理论
f , k , NC f C
断裂力学的韧度问题
均匀性假设仍成立,但且仅在缺陷处不连续
σC
K IC i,C Ji, JC JR TR
阻力C
选 工 维 缺陷 材 艺 修 评定
应用
断裂力学
裂纹扩展准则 f i C T TC N f f i , a,...
a
SU
K
响应 i
C
奇异场
控制参量 T
损伤力学的评定方法
均匀性和连续性假设均不成立
设选寿 计材命
应用
损伤临界 ~ C 参量
损伤力学
Damage Mechanics
• 过程:
– 选取物体内某点的代表性体积单元,需满足尺度的双重性 – 连续介质力学及热力学分析膝关节够的损伤演化、变形 – 通过细观尺度上的平均化方法将细观结果反映到宏观本构、损
伤演化、断裂等行为上
• 能量损伤理论:
– 以连续介质力学和热力学为基础 – 损伤过程视为不可逆能量转换过程 – 由体系的自由能和耗散势导出损伤演化方程和本构关
损伤的宏观测量
损伤变量和结构寿命预报
损伤演变依赖于: • 延性失效或疲劳失效中的应力 • 蠕变、腐蚀或辐照过程中的应力 • 疲劳损伤时载荷循环周数
三、损伤力学的发展历程
• Kachanov,1958,连续性因子和有效应力的概念 • Rabotnov,1963,损伤因子的概念 • Lemaitre,1971,损伤的概念重新提出 • Leckie & Hult,1974,蠕变损伤研究的推进 • 70年代中末期,CDM的框架逐步形成 • Murakami,1980s’,几何损伤理论 • 80年代中Bui、Dyson、Krajcinovic、Sidoroff等人的工
中国矿业大学大学生课外科技竞赛项目分类分级汇总表
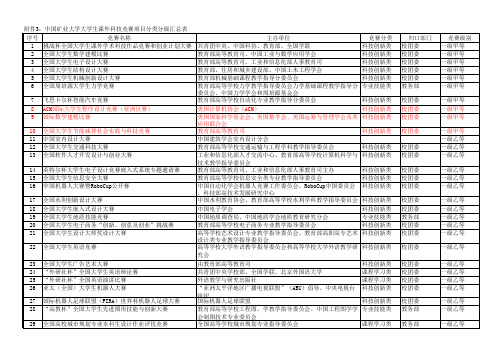
归口部门 研究生院 研究生院 研究生院 研究生院 教务部 校团委 校团委 教务部 学工处 教务部 校团委 校团委 校团委 校团委 校团委 校团委 校团委 校团委 教务部 教务部 校团委 校团委 校团委 校团委 校团委 教务部 教务部 教务部 校团委 教务部
竞赛级别 一级乙等 一级乙等 一级乙等 一级乙等 二级 二级 二级 二级 二级 二级 二级 二级 二级 二级 二级 二级 二级 二级 二级 二级 二级 二级 二级 二级 二级 二级 二级 二级 二级 二级
序号 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84
竞赛名称 中国研究生电子设计竞赛 全国研究生智慧城市技术与创意设计大赛 全国研究生数学建模竞赛 全国石油工程设计大赛 江苏省高等数学竞赛 “挑战杯”大学生课外学术科技作品竞赛和创业计划大赛 江苏省选拔赛 全国数学建模比赛江苏赛区选拔赛 江苏省大学生工程训练综合能力竞赛暨全国选拔赛 江苏省大学生职业生涯规划大赛 江苏省高校测绘技能大赛 五一数学建模联赛 全国信息技术应用水平大赛 全国普通高校信息技术创新与实践活动(含竞赛) “艾默生创新杯”全国大学生金相大赛 全国大学生UML建模创造力大赛
序号竞赛名称主办单位竞赛分类归口部门竞赛级别挑战杯全国大学生课外学术科技作品竞赛和创业计划大赛共青团中央中国科协教育部全国学联科技创新类校团委一级甲等全国大学生数学建模比赛教育部高等教育司中国工业与数学应用学会科技创新类校团委一级甲等全国大学生电子设计大赛教育部高等教育司工业和信息化部人事教育司科技创新类校团委一级甲等全国大学生结构设计大赛教育部住房和城乡建设部中国土木工程学会科技创新类校团委一级甲等全国大学生机械创新设计大赛教育部机械基础课程教学指导分委员会科技创新类校团委一级甲等全国周培源大学生力学竞赛专业技能类教务部一级甲等飞思卡尔杯智能汽车竞赛教育部高等学校自动化专业教学指导分委员会科技创新类校团委一级甲等科技创新类校团委一级甲等国际数学建模比赛美国国家科学基金会美国数学会美国运筹与管理学会及其应用联合会科技创新类教务部一级甲等10全国大学生节能减排社会实践与科技竞赛教育部高等教育司科技创新类校团委一级甲等11中国室内设计大赛中国建筑学会室内设计分会一级乙等12全国大学生交通科技大赛教育部高等学校交通运输与工程学科教学指导委员会科技创新类校团委一级乙等13全国软件人才开发设计与创业大赛科技创新类校团委一级乙等14英特尔杯大学生电子设计竞赛嵌入式系统专题邀请赛教育部高等教育司工业和信息化部人事教育司主办科技创新类校团委一级乙等15全国大学生信息安全大赛教育部高等学校信息安全类专业教学指导委员会科技创新类校团委一级乙等16科技创新类校团委一级乙等17全国水利创新设计大赛中国水利教育协会教育部高等学校水利学科教学指导委员会科技创新类校团委一级乙等18全国大学生嵌入式设计大赛中国电子学会科技创新类校团委一级乙等19全国大学生地质技能竞赛中国地质调查局中国地质学会地质教育研究分会专业技能类教务部一级乙等20全国大学生电子商务创新创意及创业挑战赛教育部高等学校电子商务专业教学指导委员会科技创新类校团委一级乙等21全国大学生设计大师奖设计大赛科技创新类校团委一级乙等22全国大学生英语竞赛高等学校大学外语教学指导委员会和高等学校大学外语教学研究会科技创新类教务部一级乙等23全国大学生广告艺术大赛由教育部高等教育司科技创新类校团委一级乙等24外研社杯全国大学生英语辩论赛共青团中央学校部全国学联北京外国语大学课程学习类教务部一级乙等25外研社杯全国英语演讲比赛外语教学与研究出版社课程学习类教务部一级乙等26亚太全国大学生机器
损伤力学课件第二章

B2 , C2 为曲线参数
力学与建筑工程学院力学系弹性力学电子教案
CHINA UNIVERSITY OF MINING AND TECHNOLOGY
四、分段曲线模型( 分段曲线模型(钱济成, 钱济成,1989) 1989)
σ
σ
f
D
D =1
εf
ε ≤ 0.4 时,无损伤 εf
ε
εf
ε
以
ε ε ≤ 0.8 时,损伤较小,裂纹扩展 作为对象变量: 0.4 < εf εf
上节内容回顾
一是定义损伤变量并将其视为内变量引入到材料的本构 方程中, 方程中,发展含损伤内变量的本构理论 二是寻找基于试验结果之上的损伤演化方程 归结为求塑性势函数和自由能函数 建立损伤力学的全部方程--建立损伤力学的全部方程---及其初边值问题与变分问 ---及其初边值问题与变分问 题的提法--题的提法---求解 ---求解
ɶ A ϕ= A
A
无承载能力、破坏
~ A
0 取值范围: ϕ = 1
无损伤
力学与建筑工程学院力学系弹性力学电子教案
CHINA UNIVERSITY OF MINING AND TECHNOLOGY
第一节 损伤变量及有效应力
有效应力:
~= = σ ~
Cauchy 应力:
F A
σ ϕ
σ=
F A
~ A σ = ~ σ A
0≤ε ≤εf
~
~ =σ ~ = Eε σ y f
ε f ≤ ε ≤ εu
εf
ε uε
力学与建筑工程学院力学系弹性力学电子教案
5
CHINA UNIVERSITY OF MINING AND TECHNOLOGY
韶关学院2010-2011第1学期评教结果

必修课 53.69 选修课 54.03 必修课 52.01 必修课 53.47 必修课 52.98 选修课 53.55 选修课 53.31 必修课 53.59 必修课 53.88 全校性选修课 53.99 必修课 53.83 选修课 53.93 选修课 53.78 必修课 51.78 选修课 52.93 选修课 52.88 必修课 53.56 必修课 54.05 必修课 53.67 选修课 53.71 选修课 54.19 选修课 54.03 必修课 53.45 选修课 54.39 必修课 53.88 必修课 53.79 必修课 53.9 选修课 54.35 必修课 53.98 选修课 53.02 必修课 53.56 选修课 52.31 选修课 54.03 必修课 53.91 必修课 53.6 选修课 54.14 选修课 53.18 选修课 53.16 必修课 53.24 必修课 53.67 必修课 53.57 选修课 53.79 必修课 53.08 选修课 54.26 必修课 53.15 必修课 54.04 选修课 54.18 选修课 53.2 选修课 53.98 选修课 54.33 必修课 53.24 选修课 53.41 必修课 53.23 必修课 53.17 必修课 54.38 选修课 54.24
55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110
干湿循环作用下基于Laplace分布的裂土应变硬化损伤模型

第51卷第12期2020年12月中南大学学报(自然科学版)Journal of Central South University (Science and Technology)V ol.51No.12Dec.2020干湿循环作用下基于Laplace 分布的裂土应变硬化损伤模型周峙1,2,张家铭1,2,宁伏龙1,2,罗易1,2(1.中国地质大学(武汉)工程学院,湖北武汉,430074;2.地质探测与评估教育部重点实验室,湖北武汉,430074)摘要:为了建立干湿循环作用下裂土应变硬化损伤模型,提出裂土微元强度服从Laplace 分布的假定,同时考虑初始损伤门槛影响,引入干湿循环损伤变量和荷载作用损伤变量,分别描述裂土干湿循环开裂和应力水平作用下损伤演化规律。
基于不同干湿循环阶段裂土的固结不排水三轴剪切试验,探究围压对不同干湿循环开裂损伤的影响;利用线性拟合确定应变硬化损伤模型参数,探讨围压和干湿循环次数对初始损伤应力门槛值的影响,并对比验证不同干湿循环次数与应力水平作用下的试验结果。
研究结果表明:干湿循环对裂土平均微元强度影响显著,5次循环后,微元平均强度降幅显著,相比初始状态降低39.7%~78.5%;反映平均微元强度与弹性模量的Laplace 分布参数m 0和T 0均与围压呈正相关;围压提高了初始应力损伤门槛值,降低了干湿循环作用造成的损伤,相比初始状态试样,5,8和12次干湿循环后试样的初始损伤应力门槛值分别降低37.77%,45.67%和57.43%。
建立的基于Laplace 分布的损伤本构模型能充分反映干湿循环作用后裂土受荷时的应变硬化特征,并可模拟裂土在干湿循环和围压共同作用下的全应力−应变曲线,其模型参数易获取,且具有明确的物理意义;干湿循环次数愈多,围压愈高,模型与土体应力−应变试验曲线吻合程度越高。
关键词:裂土;干湿循环;Laplace 分布;应变硬化;统计损伤模型中图分类号:TU45文献标志码:A开放科学(资源服务)标识码(OSID)文章编号:1672-7207(2020)12-3484-09Strain hardening damage model of cracked soil during dry-wetcirculation based on Laplace distributionZHOU Zhi 1,2,ZHANG Jiaming 1,2,NING Fulong 1,2,LUO Yi 1,2(1.School of Engineering,China University of Geosciences,Wuhan 430074,China;2.Key Laboratory of Geological Survey and Evaluation of Ministry of Education,Wuhan 430074,China)Abstract:In order to establish the strain hardening damage model of cracked soil during the drying-wetting cycles,the hypothesis that the strength of cracked soil obeys Laplace distribution was proposed.Considering the influence of initial damage threshold,the damage evolution law of cracked soil during drying-wetting cycles andDOI:10.11817/j.issn.1672-7207.2020.12.022收稿日期:2020−02−21;修回日期:2020−05−12基金项目(Foundation item):地质探测与评估教育部重点实验室主任基金和中央高校基本科研业务费(GLAB2019ZR05);国家自然科学基金资助项目(41372311);安徽省交通运输厅科技进步计划项目(2018030)(Project(GLAB2019ZR05)supported by the Opening Fund of Key Laboratory of Geological Survey and Evaluation of Ministry of Education and the Fundamental Research Funds for the Central Universities;Project(41372311)supported by the National Science Foundation of China;Project(2018030)supported by the Science and Technology Plan of Anhui Provincial Department of Transport)通信作者:张家铭,博士,副教授,从事特殊性岩土工程防治研究;E-mail :*************第12期周峙,等:干湿循环作用下基于Laplace分布的裂土应变硬化损伤模型at different stress levels was described by introducing the damage variable of drying-wetting cycles and load.Based on the triaxial consolidation undrained shear test(CU)of cracked soil during different drying-wetting cycles, the influence of confining pressure on cracking damage during drying-wetting cycles was investigated.The parameters of damage model were determined by linear fitting,the effects of confining pressure and drying-wetting cycles on the threshold value of initial damage stress were discussed,and the results were compared with those during different dry wet cycles and at different stress levels.The results show that the drying-wetting cycle has a significant effect on the average micro element strength.After five cycles,the average micro element strength decreases significantly,which is39.7%−78.5%lower than that of the initial state.The parameters of theLaplace distribution,m0and T,which reflect the mean strength and elastic modulus of the microelements,arelinearly and positively correlated with confining pressure.Confining pressure can improve the initial damage threshold and reduce the damage caused by the drying-wetting pared with the initial state of samples, the initial damage stress threshold of samples after5,8and12cycles reduces by37.77%,45.67%,and57.43%, respectively.The damage constitutive model based on Laplace distribution can fully reflect the strain hardening characteristics of cracked soil under load after dry and wet cycles,and can simulate the stress−strain curve of cracked soil under the combined action of dry and wet cycles and confining pressures.The model parameters are easy to obtain and have clear physical significance.The more the number of drying-wetting cycles,the higher the confining pressure,the more the model is consistent with the stress-strain test curve of soil.Key words:cracked soil;wet-dry circulation;Laplace distribution;strain hardening;statistical damage model裂土是一种弱膨胀和强收缩的黏性土,在安徽沿江垄岗地区广泛发育。
混凝土随机损伤力学 读书报告

混凝土随机损伤力学的研究思想(混凝土随机损伤力学读书报告)2010年12月目录0 前言 (1)1 为什么要进行随机结构非线性分析? (2)2 损伤力学的基本原理是什么? (3)3 什么是经典混凝土本构? (5)3.1 经典弹性本构 (5)3.2 经典塑性本构 (6)4 什么是弹塑性损伤本构? (6)5 什么是随机损伤本构? (9)6 怎么进行混凝土随机损伤非线性反应分析? (10)7 小结 (10)附录作业 (12)参考文献 (13)0 前言由于混凝土材料抗压强度高,钢筋抗拉强度高,两者结合后协同工作,利用混凝土抗压和钢筋抗拉,能使得两者材料各尽其能,组成性能良好的结构构件。
同时,由于混凝土的包裹,钢筋不容易被腐蚀,使得钢筋混凝土结构耐久性较好。
正是钢筋混凝土结构的这些优点,从其出现于中国至今,已在建筑、隧道、桥梁、高速公路、地铁、大坝、港口等各个领域都得到了广泛的应用。
混凝土是以水泥为胶结材料,以天然砂石为骨料加水拌合,经过浇筑成型、凝结硬化形成的固体材料[1]。
它是一种多相颗粒复合材料,从宏观结构来看,它是骨料分散在水泥浆基体中的二相材料;从微观来看,它是由水泥凝胶、氢氧化钙结晶、未水化的水泥颗粒、毛细管及孔隙水、空气泡等组成。
对于混凝土力学性能的研究,固体力学假设其为处处连续,毫无初始缺陷的均匀各向同性材料,这与混凝土材料的实际情况不一致。
经典材料强度理论假设材料为均匀连续,分析结构的应力状态,根据材料的屈服或者极限应力判断结构是否达到屈服或者破坏,即在此理论下,混凝土只有两个状态:正常服役状态(无损伤)和破坏状态。
然而,结构的破坏一般不会突然发生,它是由于结构在建造过程中产生的微裂纹在外界荷载的作用下长大、汇合成宏观裂纹,并继续扩展,导致结构强度、刚度持续下降,最终失去承载能力,也就是说,混凝土的全寿命分析与微裂纹的产生、扩展密不可分。
为了确定微裂纹的演化,必须对裂纹的产生、扩展的规律有所研究,才能深入分析裂纹的扩展规律及其对结构的影响。
基于受压裂隙开裂准则的损伤模型

第50卷第3期中南大学学报(自然科学版) V ol.50No.3 2019年3月Journal of Central South University (Science and Technology)Mar. 2019 DOI: 10.11817/j.issn.1672-7207.2019.03.023基于受压裂隙开裂准则的损伤模型马秋峰,田静,周天白(中国矿业大学(北京) 资源与安全学院,北京,100083)摘要:为了反映岩石内部裂隙对岩石本构关系的影响,建立受裂隙分布及裂隙面摩擦因数共同影响的损伤模型。
类比弹簧束模型,定义与开裂裂隙长度有关的损伤模型。
基于受压裂隙的开裂准则,对不同应力状态下的开裂裂隙长度范围进行求解,通过概率统计的方法计算开裂裂隙长度的数学期望,将其代入建立的损伤模型中得到损伤变量。
利用模型对岩石应力−应变曲线进行计算。
研究结果表明:建立的损伤模型能够反映裂隙面摩擦因数与裂隙角度对岩石强度的影响。
当摩擦因数为0时,裂隙角度45º对应的岩石强度最小,随着裂隙摩擦因数增大,最小峰值强度对应的裂隙倾角逐渐减小;当裂隙角度一定时,摩擦因数越大,峰值强度越大;数值计算结果与实验结果一致。
该模型还能够反映裂隙长度分布对岩石强度的影响。
当长裂隙数占比较大时,岩石强度较小;反之,岩石强度较大。
计算结果能够反映岩石在塑性阶段的变形特征,该损伤模型具有合理性。
关键词:开裂准则;裂隙长度;裂隙角度;概率统计;损伤模型中图分类号:TU452 文献标志码:A 文章编号:1672−7207(2019)03−0687−07Damage model based on fracture cracking criteriaMA Qiufeng, TIAN Jing, ZHOU Tianbai(College of Resources and Safety Engineer, China University of Mining and Technology, Beijing 100083, China)Abstract: In order to reflect the influence of rock internal fracture on rock constitutive relation, a damage model affected by fracture distribution and friction coefficient of fracture surface was established. Analogous to the spring beam model, a damage model related to the length of cracked fissure was defined. Based on the cracking criterion of the compression fracture, the length range of crack fracture in different stress states was solved, the mathematical expectation of crack length was calculated by probability statistics, and the damage variable was obtained in the damage model. The stress−strain curve of rock was calculated by this model. The results show that the model can reflect the influence of fracture surface friction coefficient and angle on rock strength. When the friction coefficient is 0, the corresponding angle of minimum strength of rock is 45º. With the increase of the friction coefficient, the crack angle corresponding to the minimum peak strength decreases gradually. When the angle is constant, the greater the friction coefficient is, the larger the peak strength is. The calculated results are in agreement with the experimental results. The model can also reflect the effect of crack length distribution on rock strength. When the long crack occupies a larger proportion of the crack, the strength of rock is smaller. When the long crack occupies a smaller proportion, the strength of rock is larger. The calculated results reflect he deformation characteristics of rock at plastic stage, which shows the reliability of the model.Key words: crack criterion; crack length; crack angle; probability statistics; damage model收稿日期:2018−04−23;修回日期:2018−06−04基金项目(Foundation item):国家自然科学基金资助项目(50904071,51274207) (Projects(50904071, 51274207) supported by the National Natural Science Foundation of China)通信作者:马秋峰,博士研究生,从事煤岩动力研究;E-mail:*********************中南大学学报(自然科学版) 第50卷688岩石内部存在大量的微裂隙,在加载过程中,微裂隙开裂扩展导致应力−应变曲线呈现出非线性特征。
课程教学大纲

课程教学大纲土木建筑工程学院2009年9月目录课程目录 (1)研究生课程汇总表 (1)课程大纲 (11)土木工程专题讲座 (11)现代混凝土结构设计理论及其应用 (12)结构可靠度理论 (13)建设项目管理理论与方法 (14)高等地震工程 (15)钢筋混凝土非线性有限元分析 (16)钢筋混凝土力学 (17)建设工程招标投标理论与方法 (18)现代钢结构理论与应用 (19)钢结构疲劳与断裂理论 (20)灾害学 (21)决策理论与风险分析 (22)细观力学 (23)计算结构动力学 (24)岩土工程中的数值方法 (26)人工神经网络方法在土木工程中的应用 (28)非连续介质的数值方法 (30)结构随机振动 (31)高等结构风工程 (32)非饱和土力学 (33)高等岩石力学 (34)土动力学 (35)岩土工程中的可靠度理论及应用 (36)桥梁结构空间计算理论 (37)桥梁结构非线性计算理论与仿真分析 (38)隧道结构可靠度 (39)钢桥 (40)隧道力学 (41)围岩稳定性分析及支护技术 (42)水处理高级教程 (43)建筑性能化防火设计理论 (44)活性污泥生物反应动力学 (45)连续介质力学 (46)有限单元法 (47)弹塑性力学 (48)专业外语(英语) (50)结构动力学 (51)断裂与损伤力学 (52)结构分析程序设计 (53)大型有限元软件及应用 (54)复合材料力学 (55)板壳理论 (56)结构优化设计 (57)结构动力试验与检测 (58)非线性有限元法 (59)摩擦磨损原理 (60)结构抗风理论与实验 (61)材料强度特性参数的现代试验方法 (62)路基路面设计理论 (63)公路边坡稳定性分析原理及数值方法 (64)沥青路面抗裂设计理论与方法 (65)高等桥梁结构理论 (66)现代预应力混凝土结构 (67)隧道结构计算与分析 (68)岩土塑性力学 (70)复合式路面设计原理与施工技术 (71)公路与桥梁结构检测 (72)桥梁结构抗震设计 (73)GIS基本原理及其在道桥工程中的应用 (74)工程经济学 (75)土工试验 (76)结构稳定理论 (77)高等钢结构学 (78)高等钢筋混凝土结构学 (79)现代施工技术 (80)现代企业管理 (81)水质控制原理 (82)给水排水工程专题讲座 (83)工程结构抗震 (84)工程结构可靠性理论与应用 (85)工程结构加固理论和应用 (86)混凝土结构的耐久性与损伤防治 (87)工程结构试验与测试 (88)高层建筑结构设计 (89)现代钢筋混凝土结构新理论与新技术 (90)钢筋混凝土结构分析程序设计 (91)工程结构安全监测 (92)结构控制理论与应用 (93)板壳稳定理论 (94)大跨度钢结构 (95)钢与混凝土组合结构设计原理 (96)钢结构事故分析与处理 (97)投资管理学 (98)项目风险分析 (100)城市土地经济与管理 (101)国际工程项目管理 (102)房地产投资分析与决策 (103)管网非稳定流分析与控制 (104)建筑消防理论及应用 (105)水质分析方法及仪器 (106)岩土流变学原理和应用 (107)智能岩石力学 (108)土的本构关系 (109)滑坡学 (110)土工合成材料 (111)环境岩土工程 (112)土坡渗流和稳定 (113)桩基理论 (114)岩质边坡稳定分析的原理、方法和程序设计 (115)道路与铁道工程试验检测技术 (116)桥梁结构抗震分析 (117)信号处理 (118)模态识别理论 (119)课程目录研究生课程汇总表课程大纲.。
考虑地震动力响应的复杂地基碾压混凝土重力坝分缝优化研究

http://www.renminzhujiang.cnDOI:10 3969/j issn 1001 9235 2023 06 008第44卷第6期人民珠江 2023年6月 PEARLRIVER基金项目:湖南省自然科学基金资助项目(2020JJ5317);湖南省教育厅优秀青年项目(22B1005);湖南省水利科技项目(XSKJ2019081-20)收稿日期:2022-12-10作者简介:李金友(1984—),男,博士,高级工程师,研究方向为水工结构工程抗震评价。
E-mail:lijinyou2003@163.com李金友,胡江,顾振华.考虑地震动力响应的复杂地基碾压混凝土重力坝分缝优化研究[J].人民珠江,2023,44(6):63-69.考虑地震动力响应的复杂地基碾压混凝土重力坝分缝优化研究李金友1,胡 江2,顾振华3(1.湖南水利水电职业技术学院,湖南 长沙 410131;2.南京水利科学研究院大坝安全与管理研究所,江苏 南京 210029;3.上海勘测设计研究院有限公司,上海 200434)摘要:为了探究高碾压混凝土重力坝横缝切割对坝体抗震性能的影响,以高地震烈度、砂泥岩互层地基的巴基斯坦玛尔水电站碾压混凝土重力坝工程为研究对象,通过建立三维整体有限元模型,并引入自编黏弹性动力边界程序,分别计算了设计地震、最大可信地震(MaximumCredibleEarthquake,MCE)作用下,输入规范波、场地波、Koyna波时坝体的动力响应及差异;通过模拟横缝切割1/3高度、2/3高度和全分缝3个对比方案,并以承载能力极限状态设计式定义的比值为依据,综合评价了碾压混凝土重力坝抗震安全状态。
结果表明:当输入波为规范波时,在MCE作用下,横缝切割1/3高度和2/3高度方案坝基面的抗力效应比系数(η)均大于1,全分缝方案下ηmin=0.91,且总计6次在0.6s时长内η值均小于1,经综合考虑,横缝切割2/3高度可作为施工推荐方案。
非均质地基中V·T联合受荷桩承载力分析

第49卷第10期中南大学学报(自然科学版) V ol.49No.10 2018年10月Journal of Central South University (Science and Technology)Oct. 2018 DOI: 10.11817/j.issn.1672−7207.2018.10.023非均质地基中V−T联合受荷桩承载力分析邹新军,夏尉桓,王亚雄(湖南大学土木工程学院,湖南长沙,410082)摘要:为研究非均质地基中单桩基础在桩顶竖向力(V)和扭矩(T)联合作用下的承载特性,假定桩侧地基土剪切模量和极限侧摩阻力沿深度呈指数函数非线性增加,并考虑桩−土接触面上位移的非协调性,根据剪切位移法和桩身荷载传递函数建立桩身位移控制方程,引入相应的力和位移边界条件,导出桩周土体处于理想弹性和塑性受力状态时的桩身内力位移解答,由此求得不同桩顶载荷工况(不同V−T组合与加载顺序)下的桩身承载力及其包络线。
在此基础上,进一步采用ABAQUS对V−T联合受荷桩进行数值模拟对比分析,获得不同工况下的桩身破坏机理、影响桩身承载力的关键因素及其规律。
研究结果表明:桩身承载力随桩身长径比L/D的增大而增大,但随桩土刚度比λ的增大而逐渐减小;桩顶可承受的竖向力V(扭矩T)随扭矩T(竖向力V)增加不断减小而趋于零。
关键词:桩基础;V−T联合荷载;非均质地基;荷载传递函数;数值分析中图分类号:TU473.1 文献标志码:A 文章编号:1672−7207(2018)10−2553−08Bearing capacity analysis of a single pile undercombined V−T Loads in non-homogeneous subsoilZOU Xinjun, XIA Weihuan, WANG Yaxiong(College of Civil Engineering, Hunan University, Changsha 410082, China)Abstract: To discuss the bearing behavior of a single pile under combined loading of vertical force V and torsion T in non-homogeneous subsoil, the control equation of the pile shaft was set up by using the pile shaft load transferring function and shear displacement method, in which the exponential function model was adopted to simulate the increasing change of subsoil shear modulus and ultimate side resistance with depth, and the non-coordination deformation along the pile-soil interface was considered as well. Then, force and displacement boundary conditions were introduced to deduce the analytical solutions for the inner forces and deformation of the pile shaft under ideal elastic-plastic bearing stages of subsoil. Based on the obtained solutions, various combined values and loading sequences of V and T at the pile top were adopted to determine the bearing capacity of the pile shaft, from which failure envelops were plotted correspondingly.Further numerical analyses were carried out by ABAQUS to find out the failure mechanism and the key factors that affect the bearing capacity of V−T combined loaded piles. The results show that the bearing capacity of pile shaft increases with the increase of aspect ratio L/D, while decreases with the increase of the ratio of the constant coefficient of the subsoil shear modulus distribution function to that in the stiffness ratio (λ) of pile shaft to subsoil. Increasing the torsion (or the vertical force) at the pile top will decrease the vertical (or torsional) bearing capacity of a final zero value.Key words: pile foundations; V−T combined loads; non-homogeneous subsoil; load transfer functions; numerical analysis收稿日期:2017−10−12;修回日期:2017−12−21基金项目(Foundation item):国家自然科学基金资助项目(51578231,51378197)(Projects(51578231, 51378197) supported by the National Natural Science Foundation of China)通信作者:邹新军,博士,副教授,从事地基基础与支挡结构研究;E-mail:***************.cn中南大学学报(自然科学版) 第49卷2554随着我国基础设施建设的不断推进特别是近海资源的持续性开发,城市立体交通的弯梁桥、跨海大桥、海上风力发电塔等结构物不断兴建。
冰雹作用下土质边坡模型试验方法

第50 卷第 3 期2023年3 月Vol.50,No.3Mar. 2023湖南大学学报(自然科学版)Journal of Hunan University(Natural Sciences)冰雹作用下土质边坡模型试验方法赵明华,刘洲,赵衡†,徐泽宇,彭文哲,杨凯旋(湖南大学岩土工程研究所,湖南长沙 410082)摘要:为研究冰雹灾害对土质边坡稳定性的影响,自主设计了一套冰雹降落装置,采用自制冰球对模型边坡进行加载. 共进行了3组试验,通过高灵敏度动土压力监测系统获得土压力,拟合冲击力;通过摄影测量技术(PIV)监测冰球冲击坡面时的速度向量,计算法向和切向恢复系数,同时监测加载过程中位移变化规律;通过含水率监测系统监测坡体含水率,分析试验前后的水分迁移规律. 试验结果表明:在加载密度和加载次数较大时,冲击会使边坡产生浅层滑动,落于坡顶面的冰球重新分布形成堆积,逐渐融化,向下形成渗流;加载瞬时形成冲击荷载,可将其拟合为衰减的半正弦波形;法向恢复系数较小,切向恢复系数较大,冰球在冲击过程中倾向于沿坡面运动;含水率传感器从上到下依次响应,边坡后端融水渗流速度比前端更快,融水主要影响坡顶平台,坡顶平台中层水分迁移速度最快;静土压力与坡顶堆载和冰球融化渗流有直接联系;坡体整体变形较小,最大变形位于坡顶转角处;试验结果反映了冰雹降落对边坡稳定性影响的3个方面:冲击作用、堆载作用、渗透作用,可为冰雪极端灾害条件下的边坡安全预警提供参考和依据.关键词:土质边坡;冰雹作用;模型试验;冲击响应;水分迁移中图分类号:P642.22 文献标志码:AModel Test Method of Soil Slope under Hail ActionZHAO Minghua,LIU Zhou,ZHAO Heng†,XU Zeyu,PENG Wenzhe,YANG Kaixuan(Geotechnical Institute, Hunan University, Changsha 410082, China)Abstract:In order to study the influence of hail disaster on the stability of soil slope, a set of hail falling device was designed independently and the model slope was loaded with self-made ice balls. Three groups of tests were car‐ried out in this paper. The earth pressure was obtained through a high-sensitivity dynamic earth pressure monitoring system, and the impact force was fitted. Particle Image Velocimetry (PIV) was used to monitor the velocity vector change when the puck impinged on the slope, and the normal and tangential restitution coefficients were calculated. At the same time, the displacement change law during the loading process was monitored. The moisture content of slope was monitored by a moisture content monitoring system, and the rule of the water migrating before and after the test was analyzed. The experimental results show that when the loading density and loading times are large, the im‐pact causes shallow sliding of the slope, and the ice puck on the top surface of the slope can redistribute and form ac‐∗收稿日期:2022-01-09基金项目:国家自然科学基金资助项目(51978255),National Natural Science Foundation of China(51978255);湖南省交通科技项目(201808), Hunan Transportation Technology Project(201808)作者简介:赵明华(1956—),男,湖南邵阳人,湖南大学教授,博士生导师† 通信联系人,E-mail:*****************.cn文章编号:1674-2974(2023)03-0217-10DOI:10.16339/ki.hdxbzkb.2023046湖南大学学报(自然科学版)2023 年cumulation, gradually melt, and form seepage downward. The impact load is formed instantaneously after loading,and it can be fitted as a decaying half-sine waveform. The normal recovery coefficient is small, and the tangential re‐covery coefficient is large. The puck tends to move along the slope during impact. The water content sensor responds sequentially from top to bottom, the melt water seepage velocity at the rear end of the slope is faster than that at the front end, and water mainly affects the slope top platform. The middle layer of the slope top platform has the fastest water migration speed. The static earth pressure is directly related to the load on the slope top and the seepage of the ice ball melting. The overall deformation of the slope is small, and the maximum deformation is located at the corner of the top of the slope. The experimental results reflect three aspects of the influence of hail falling on slope stability:impact, stacking and infiltration, which can provide a reference and basis for slope safety warning under the condi‐tion of extreme snow and ice disasterKey words:soil slopes;hail role;model test;impact response;water migration边坡稳定性一直是工程界的重点研究领域,其中,极端降雨、降雪、冰雹等灾害天气下高速公路沿线边坡的稳定性研究尤为重要. 冰雹作用对边坡的稳定性影响较为复杂. 冰雹降落会对边坡产生较大的冲击荷载;冰雪的堆积会产生堆积荷载;冰雪的融化渗流会增加土体重度,减小土体强度. 综合上述各类作用,边坡可能出现失稳状态.目前,冰雹降落条件下的边坡稳定性研究似未见报道,现有相关研究重点集中在雪荷载、落石冲击荷载、降雨入渗对边坡的稳定性影响等方面. 在雪荷载对边坡的稳定性影响方面,钱晓慧等[1]利用饱和非饱和渗流有限元方法,对积雪深度、气温变化以及坡度等不同条件进行了边坡融雪入渗渗流计算及稳定性分析;缪海波等[2]探讨了极端冰雪灾害条件下均质松散堆积体边坡的演化特征,比较了融雪与降雨触发滑坡的异同点. 在落石冲击对边坡的稳定性影响方面,张东亮等[3]采用显式动力学程序LSDYNA,研究了不同下落高度及入射角度的落石冲击作用下路基边坡的力学响应,揭示了落石冲击力和路基边坡的变形、能量转化与落石高度和入射角度正相关;胡杰等[4]研发了大型落石冲击边坡模型试验系统,通过开展物理模型试验研究了近长方体落石初始滑移角度、形状、质量等3种因素对碰撞恢复系数这一落石运动轨迹模拟中关键参数的影响. 降雨入渗被认为是使边坡破坏的首要因素,国内外学者进行了大量的研究. 赵明华等[5]通过室内抗冲刷试验得到了不同草种与固土结构在不同降雨强度及不同坡度条件下与边坡冲刷的关系. Lourenço 等[6]通过试验研究渗透系数变化对边坡特性的影响,认为边坡破坏模式主要取决于渗透层及孔隙水压力对其所施加的渗透方向. Tohari等[7]研究了粉粒含量、密实度、水位等因素对滑坡启动和发展及破坏模式的影响. 李焕强等[8-9]对不同坡角边坡物理模型进行人工模拟降雨试验,揭示了降雨诱发的均质土坡破坏容易出现在浅层的原因,并考虑隔水层的影响,认为隔水层的存在会使其上部土体重度大幅提升. 左自波等[10]研究了降雨条件下颗粒级配对边坡破坏模式的影响,结果表明级配对边坡破坏模式和细颗粒流失影响显著. 姬猛等[11]研究了滑坡安全系数与降雨强度和降雨历时的关系,拟合出相关公式. 朱元甲等[12]研究了间歇型降雨作用下缓倾堆积层斜坡的变形破坏特征. 苏永华等[13]改进了传统GA模型,并将其运用到间歇型降雨条件下的边坡稳定性分析.综上可知,现有研究大多探讨在雨雪条件下边坡的应力与变形规律、失稳破坏模式,似未涉及冰雹降落条件下的边坡稳定性研究. 鉴于此,本文设计了冰雹降落条件下的模型试验. 自制冰球,设计了一套冰雹加载系统和模型箱,采用粉质砂土进行试验. 揭示了在不同加载密度和降落时长下冰雹冲击力、恢复系数、基质吸力、含水率、变形变化规律. 这些参数反映边坡稳定性变化,可为冰雪极端灾害条件下的边坡安全预警提供参考和依据.1 冰雹的作用特性空气中的水蒸气遇冷后温度急剧下降,会结成较大的冰团,即形成了冰雹. 王晓明等[14]统计了吉林省1960—1999年的冰雹资料,对冰雹天气发生的规律进行了详尽的分析,结果表明:冰雹灾害天气多发生于5月—6月,持续时间几分钟至数小时,冰雹直218第 3 期赵明华等:冰雹作用下土质边坡模型试验方法径由1 mm到几十毫米不等. 上述文献说明冰雹降落时长不一,大小差异很大,难以进行量化统计. 冰雹作用兼有落石冲击和积雪的作用特征,研究较多的落石冲击和雪荷载对边坡稳定性的影响,对本研究具有借鉴作用. 研究落石冲击的主要手段有数值模拟和模型试验,主要研究最大冲击力和恢复系数两个参数. 研究雪荷载一般将其等效为雪雨当量,以理论、数值等手段从孔隙水压力、基质吸力、变形、稳定性系数等方面展开研究. 值得注意的是,冰雹作用并不是落石冲击和积雪作用的简单叠加. 冰雹通常呈圆形,不考虑风速的情况下一般考虑为垂直降落,而落石可以呈现不同的形态,对坡面的冲击入射角度也不是固定的;对于有限长边坡,积雪按全长覆盖,而圆形冰雹会沿坡面滚落,仅在坡顶面形成堆积. 冰雹作用下边坡的物理力学响应更为复杂,形成冲击—堆积—融化—渗流全过程,是落石冲击与融雪的有机结合.2 模型试验设计2.1 模型设计边坡原型取自湖南省内衡枣高速路堤边坡,坡面平整,坡顶平台长3.3 m,坡长4.5 m,坡高4.5 m,坡角为45°,填土为粉质黏土. 边坡的物理力学特性以及边坡坡度与其受载荷作用下的稳定性密切相关. 边坡土体的物理力学特性影响冲击作用效果,对于土质边坡,冲击会使土体产生振荡,并使土体表面形成裂隙,成为融水快速下渗的通道. 坡度则直接影响边坡的稳定状态,坡角较大时较小的荷载作用也可能使边坡破坏.张果军等[15]统计了湖南省冰雹的降落规律,冰雹一般从3~5 km高空降落,平均直径2 cm,最大直径4 cm,持续时间5~50 min. 以文献[15]为依据,考虑最不利因素,取冰雹降落高度为5 km,冰雹直径为4 cm. 忽略风速等次要因素的影响,仅考虑重力和空气阻力,计算收尾速度.空气阻力与速度的平方成反比,则有:m d2x d t2=mg-k(d x d t)2.(1)式中:m为冰雹质量;g为重力加速度;x为降落距离;t为降落时间;k为风阻系数,k=0.5cps,c为空气阻力系数,对于球体,c=0.5;p为空气密度,取p=1.29 kg/m3;s为球体投影面积.冰球达最大速度v max时,加速度为0,则有:mg-kv2max=0.(2)解得v max=27 m/s,即收尾速度为27.0 m/s.采用无量纲分析法,只考虑边坡高度h、边坡长度l、冰雹质量m、冰雹收尾速度v、土体重度γ、应力σ、变形量s,这7个与试验结果密切相关的参数,列方程得:φ(σ,s,m,v,γ,h,l)=0.(3)根据量纲和谐得不变量为π1=mv2/σs3,π2=γs/σ,π3=h/s. 为方便试验进行,取试验坡高为0.7 m,自制等直径冰球,将模拟加载装置设为2 m高,采用粉质砂土进行试验. 则试验中冰球的收尾速度为:v=2gh.(4)解得v=4.85 m/s.相似比定义为现场物理量与试验物理量的比值,试验中所测得的某物理量的数值乘以相似比即为实际值. 通过上述条件可得边坡高度、冰雹质量、冰雹收尾速度、土体密度的相似比,进而求得其他3个物理量的相似比. 各物理量相似比见表1.加载中测量冰雹冲击力和恢复系数,坡顶堆积冰球融化过程测量土压力、含水率、变形. 冲击力测试采用由孔压计改装的高精度DMTY应变式土压力盒,量程0~10 kPa,分辨率0.005 kPa,准确度误差≤0.3%FS. 含水率测试选用美国Decagon生产的ECH2O-5 体积含水率传感器,测试范围0~100%,精度±2%. 落球轨迹捕捉和变形测试采用英国艾美创非接触式视频测量系统,如图1所示.系统采用亚像素技术,可动态实时精确测量摄表1 相似比Tab.1 Simila scale物理量原状试验相似比h/m4.500.706.43m/g59591v/(m•s-1)27.004.855.57γ/(N•cm-3)19.317.81.1l/m4.500.706.43σ/Pa——2.53s/m——2.30注:σ和s为待测量.(a)摄影镜头(b)控制器图1 变形测量系统Fig.1 Deformation measurement system219湖南大学学报(自然科学版)2023 年像机图像上目标点的位置. 本试验选用单镜头2D 测量,测量误差±0.001 mm.数据采集系统方面,冲击力和静土压力采集选用武汉优泰电子技术有限公司生产的动态应变采集仪,冲击力采集时选用10 kHz 高频,静土压力采集时则选用1 Hz 低频. 含水率采集采用美国Campbell 生产的CR1000数据采集仪.测点物理量变化应反映试验规律,本文测点布置如图2所示.2.2 试验材料原状土为粉质黏土,为方便试验进行且符合工程实际,选用砂土与重塑黏土按9∶1的质量比均匀拌合. 土工试验测得最大干密度为1.85 g/cm 3,最小干密度为1.39 g/cm 3,泊松比为0.3,黏聚力为9.6 kPa ,内摩擦角为30°,土分类为粉质砂土. 试验中设置初始含水率为5%,填筑密度为1.78 g/cm 3.选用直径4 cm 圆形制冰模具,盛满水后放入冰箱进行冷冻制作冰球,成型冰球如图3所示.2.3 装置设计试验装置分为模型箱和加载系统,二者通过四根角钢连接,如图4所示. 模型箱尺寸为1.5 m× 0.8 m×0.8 m ,底座和四周的骨架均采用型钢和钢板,模型箱前侧、后侧、底板由3 mm 厚钢板整体弯折而成,左右两侧为12 mm 厚透明的钢化玻璃,以便于观察坡体变形情况. 在模型箱前侧,等距钻设排水孔,为防止颗粒流失,在排水孔内侧设置一层滤布. 组成冰雹模拟系统的构件有支承角钢、加载板、滑板、连接槽钢,各构件的连接皆选择栓接. 该试验装置已授权国家发明专利(一种模拟冰雹降落的试验方法).在考虑地震作用的模型试验中一般需考虑边界效应,本试验重点研究的是冰雹冲击力的作用形式与大小、冰雹融化渗流作用,可以忽略边界效应,不对边界进行柔性处理.2.4 试验过程组装模型箱和加载系统,配置试验用土,制作冰球,取土样进行土工试验. 分四层进行阶梯形填坡,对接触面进行粗糙处理,每层按设计密度1.78 g/cm 3击实至指定高度,全部填筑完成后,切削至指定坡角. 安装相机,进行标定,对各测量仪器进行测试. 提前准备好冰球,将冰球迅速放入加载板的孔中,抽动拉板,冰球落下,控制加载速率为3 min/板. 清理坡脚冰球,持续观测各测量值的变化,直到数值稳定为止. 冰雹降落的数量和密度对边坡稳定性可能有较大影响,故以表2所示作参数分析,以S1组和S2组对比来分析冰雹降落密度的影响,S2组和S3组对比来分析降落数量的影响.3 模型试验结果与分析3.1 试验现象加载瞬时产生冲击波,模型箱轻微震动. 冲击使边坡表面开裂,坡面处冰球迅速滚落,坡肩处冰球少图2 测量位置布置Fig.2 Measurement location layout(a )试验装置效果图 (b )实际效果图4 模拟冰雹降落试验装置Fig.4 Test device for simulating hail fall图3 成型冰球Fig.3 Forming ice hockey表2 试验分组Tab.2 Test grouping试验编号S1S2S3加载密度/(个•板-1)3×67×127×12加载板数101020加载间隔/min 333降落冰球总数/个1808401 680220第 3 期赵明华等:冰雹作用下土质边坡模型试验方法部分滚落,坡顶处冰球重新分布,形成堆积. S1、S2组未观察到明显的破坏现象. S3组在第14次加载时坡肩处观察到浅层滑动现象,如图5所示,破坏土体堆积于坡底. 考虑极端情况,S3组共加载20次,故堆积的冰球会较厚. 继续加载,边坡未产生进一步破坏,加载完成后无明显破坏现象.3.2 碰撞恢复系数与冲击力落石与边坡接触碰撞后的法向恢复系数和切向恢复系数是两个重要的参数,这两个参数的大小直接说明了碰撞的能量变化情况. 恢复系数定义为:R n =v r n v i n ,R t =v r tv i t .(5)式中:R n 和R t 分别为碰撞速度法向恢复系数和切向恢复系数;v i n 和v i t 分别为入射前落石的法向和切向速度;v r n 和v r t 分别为落石撞击坡面反弹后的法向与切向速度.本试验采用的高速摄影系统,可以将落石轨迹拍摄成180帧/s 的超慢视频. 后期采用视频处理软件分析落石碰撞前后的速度,并根据公式求得恢复系数.影响恢复系数的因素有边坡材质、密实度、坡角以及冲击物的材料、形状、质量、入射速度、入射角度等,3组试验中上述参数相同. 理论上3组试验的恢复系数应趋于一致,故仅对加载系数的分布特征进行研究. 碰撞监测点X1处的R n 和R t 都趋向于0,这是由于3组试验中,第一次加载时冰球均陷入土体中,未产生回弹,土体缓冲了所有的冲击能量;另外,冰雹堆积后,随后的冰雹冲击被原有堆积冰雹阻挡,无法作用至坡面. 综上,可忽略冰雹对坡顶平台的冲击破坏作用. 坡面(即监测点X2)处的恢复系数分布情况,如图6所示,法向恢复系数介于0.1~0.2,切向恢复系数介于0.6~0.8. 这表明冰球与坡面碰撞后在法向损失了较多的能量,倾向于沿坡面弹跳,这可能会剪切土体造成破坏.在冲击瞬时,3组试验中T1、T2、T3、T5、T7、T9土压力盒均监测到了动土压力变化,其他土压力盒无反应. 因3组试验所采用的冰球大小及自由落体的高度相同,故所测瞬时冲击反应基本一致. 位于坡顶平台的T1、T2、T3土压力盒监测到最大冲击力分别为2 634 Pa 、1 984 Pa 、150 Pa ,T2、T3能量骤减. 沿深度方向损失能量,T1至T2层为3.61 Pa/mm ,T2至T3层为7.34 Pa/mm ,这说明土层越深,单位深度能量损耗越大. 位于边坡表层的T1、T5、T7、T9土压力响应特征是类似的,以位于坡顶平台的T1进行说明. S2组T1土压力盒的第一次加载瞬态土压力反应如图7所示.整个动态反应持续约10 ms ,第一个波峰值为2 634 Pa ,在6 ms 左右恢复到50 Pa ,然后出现第二个波,第二个波峰较小,为200 Pa. 最终土压力稳定在50 Pa ,这是由冰球堆积引起的恒载. 整个图形呈现为一个衰减的半正弦波,将其拟合为:F (t )=A +B |sin ωt |e -ωt .(6)式中:ω为频率;A 、B 为待定常数.图7 动土压力瞬时反应及其拟合曲线Fig.7 Instantaneous response of earth-moving pressureand its fitting curve图5 S3组破坏现象Fig.5 Destruction phenomenon of S3 group图6 法向、切向恢复系数分布Fig.6 Distribution of normal and tangential recovery coefficients221湖南大学学报(自然科学版)2023 年拟合得ω=490 Hz ,A =52,B =8 290.3.3 含水率变化规律图8反映了S3试验组的冰雹融水下渗情况. 湿润线近似后端深前端浅的斜直线,这说明坡顶平台竖向水分迁移速度比坡面更快.图9~图11反映了各试验组不同位置质量含水率的变化情况. S1组坡顶平台的H1、H2及坡肩的H5发生了变化. H1迅速增长至饱和含水率20%左右维持6 h ,再减速回落至10%左右,H2从5 h 开始减速增长至9%后保持稳定. H1、H5位于坡体表层,受融水影响最快,土层迅速达到饱和,而后含水率下降则可能是因为表面的蒸发作用. 最终坡体表面含水率维持在10%左右,这是由于试验在室内进行,空气湿度相对稳定,表面土体与空气的水汽交换达到了动态平衡.S2组坡顶平台的H1、H2、H3和坡肩的H5、H6及坡中的H7含水率发生了变化. H1迅速增长至饱和含水率20%左右维持15 h 再减速至12%后保持稳定,H2和H3分别于5 h 和10 h 减速增长至19%和9%左右,H5迅速增长至饱和含水率18%左右维持5 h 再减速下降至8%,H6和H7于7 h 和10 h 分别减速增长至18%和8%左右. 相比于S1组,S2组堆积冰球更多,下渗的水量更大,表层的含水率维持饱和的时间更长,H2处维持了饱和,H3、H6、H7位置处含水率也发生了变化.S3组仅位于坡角下层的H10未发生响应,变化规律与S2组类似,不再赘述. 坡顶平台底层H4缓速增长至8%,而坡角处的H10未发生变化,这说明在竖向水分的迁移并不均匀.3组试验表层的含水率都是呈现迅速增长至峰值—维持峰值一段时间—减速衰减—稳定于某一数值的规律,而内部变化的含水率呈现减速增长至某一数值的规律. 由于冰球融化需要数小时甚至十数小时,融水持续不断地往下渗,故表面土体的含水率会维持一段峰值,后面逐渐减小则是由于冰雹完全融化后的风干作用.土体内部含水率的增长是因为(a )加载结束时 (b )加载结束后12 h图8 S3组湿润锋变化Fig.8 Wetting front change of S3 group(a )坡顶平台 (b )坡肩(c )坡中 (d )坡脚图9 S1组含水率变化趋势Fig.9 Water-cut trend of S1 group222第 3 期赵明华等:冰雹作用下土质边坡模型试验方法融水的渗透作用. 从竖向来看,坡顶范围内土层越深,开始增长得越慢,除浅层外稳定的数值也越小;从纵向来看,坡顶平台同一深度处后端总比前端含水率开始响应要快,这也与宏观上观察到的湿润锋(a )坡顶平台 (b )坡肩(c )坡中 (d )坡脚图10 S2组含水率变化趋势Fig.10 Water-cut trend of S2 group(a )坡顶平台 (b )坡肩(c )坡中 (d )坡脚图11 S3组含水率变化趋势Fig.11 Water-cut trend of S3 group223湖南大学学报(自然科学版)2023 年变化规律相互印证.为分析竖向水分迁移规律,引入竖向平均迁移速率的概念:v ver=h a-h bt a-t b.(7)式中:v ver为水分在a点和b点的竖向平均迁移速率;h a、h b为a、b两点距地表的深度;t a、t b为a、b两点含水率响应时刻.试验中坡面并无直接的冰球堆积,故仅计算坡顶平台的水分迁移速率,如表3所示.可以看出,坡顶平台H2-H3层有着最大的水分迁移速率,其次为H3-H4层,最小的为H1-H2层. 表层的水分迁移较慢,是因为冰球冲击产生了压密作用,使土体孔隙率变小,以至渗透系数变小.3.4 土压力变化规律S1组仅T1、T2位置处土压力产生变化;S2组T1、T2、T3、T5、T6、T8处土压力产生变化;S3组土压力除上述S2组位置处产生变化外,在T4位置处土压力亦产生变化. 各组相同位置处变化规律相同,故以S3组说明土压力的变化规律.图12呈现了S3组在整个试验过程中的静土压力增量变化规律. 在加载过程中,坡顶平台的T1、T2和坡肩的T5、T6呈线性增长,峰值分别为1 000 Pa、400 Pa、600 Pa、200 Pa,这是坡顶平台冰球产生的堆载作用,加载是均匀的,故呈线性增长. 加载结束后,冰球融化,荷载逐渐减小,位于坡体表面的T1、T5减速下降至0. 位于T1下方的T2土压力维持400 Pa约400 min后减速下降至200 Pa,这可能是由于其上层的水部分渗透到下层,荷载减小. T6变化规律同T2. T3、T4、T7依次响应,减速增长至固定值,这是因为融水逐渐渗透到了这些位置.静土压力的变化与冰球的堆积、冰球融化、融水渗流密切相关. 冰球堆积产生了堆载,坡顶平台浅层土压力产生响应. 冰球融化,融水向下渗流的过程,一方面是卸载作用,同时改变了土体的含水率、重度、黏聚力等物理性质,使土压力产生变化.3.5 位移变化规律图13显示了PIV监测范围在加载完成时的变形情况. S1组仅在坡肩处出现较大位移,其他位置基表3 坡顶平台水分迁移速率Tab.3 Law of water migration in sloping platform mm/h 试验组S1S2S3位置H1-H2303036H2-H3—50125H3-H4——83.33(a)坡顶平台(b)坡肩(c)坡中(d)坡脚图12 S3组静土压力增量Fig.12 Static earth pressure increment of S3 group224第 3 期赵明华等:冰雹作用下土质边坡模型试验方法本不变. S2、S3组变形情况与S1组类似,不再列出.T1最大值为0.4 mm ,T2为1.4 mm ,T3为2.4 mm. 边坡模型按1.78 g/cm 3的密度填筑,土体较为紧密,故在加载过程中,土体内部的变形较小. 而坡面受到冰雹的直接冲击,且坡顶面接近坡顶转角处的冰球沿着坡面滚落,沿着坡面形成了滚落通道,坡顶转角处受到的约束亦较小,故位移最大.图14、图15反映了加载过程中监测点位移变化规律. X 轴向和Y 轴向的位移都呈阶梯形上升,每次加载会产生一个瞬时位移增量,随着加载的进行,土体逐渐紧密,每次加载产生的位移增量越来越小,加载完成时位移为X 向0.42 mm 、1.4 mm 、2.0 mm ,Y 向0.14 mm 、0.42 mm 、0.56 mm.3.6 冰雹降落条件下边坡稳定性探讨冰雹降落对边坡稳定性的影响,主要体现在3个方面:冰雹的瞬时冲击、坡顶平台内冰球的堆积、冰球融化对边坡土体物理性质的影响.冲击主要引起坡体变形、土体滑塌等灾害,需要重点关注冲击力和恢复系数两个指标,这二者分别代表了冲击能量的大小及其耗散程度. 试验中测得冰雹的冲击力可拟合为衰减的半正弦波,最大值约为2.6 kPa. 测得法向恢复系数介于0.1~0.2,切向恢复系数介于0.6~0.8,冰球回弹后倾向于沿坡面运动.总体来看,冰雹冲击很难使边坡产生直接破坏,仅在加载密度较大且加载次数较多时在坡顶产生了浅层滑动现象. 从整个试验过程来看,冰雹冲击使边坡土体产生的变形是微小的,仅在坡顶转角处产生了较大位移. 加载完成后边坡未进一步产生破坏,加载瞬时为边坡最不稳定时刻.堆载作用会使坡体的应力重分布,引起坡体局部破坏,甚至导致边坡失稳. 本试验中坡顶平台堆积冰球数量较少,仅在边坡上层观测到了土压力改变. 同时,堆载冰球是渗流的水源,冰球的融化,在卸载的同时对坡体产生了湿化作用. 冰球融化所产生的湿化作用与降雨的入渗作用是类似的,会使坡体含水率增加,影响土体的黏聚力和内摩擦角,在坡体中形成渗流作用,从而影响边坡的稳定性. 但二者又有所差异,降雨作用于整个边坡,可能对坡体表面产生冲刷和形成坡面径流,而冰球的融化仅作用于坡顶平台. 冰球的融化持续数小时甚至十数小时,融化速率也不均匀. 试验中,坡顶平台后端比前端入渗快,同一深度处坡顶平台的含水率比坡体大,说明冰球融水主要对坡顶平台产生影响.总之,冰雹对边坡稳定性的影响,首先体现在碰撞瞬间的冲击作用,其次体现在落球在坡顶面的堆载,最后体现在冰球融化后使土体重度增大,力学参数减弱. 冰雹作用主要影响坡顶平台和坡顶范围内的较浅层土体. 鉴于此,为防范边坡冰雹灾害,可在浅层设置伸入坡顶平台的排水管,在坡肩采取加固措施.4 结论本文分析了冰雹的作用特性,设计了一套冰雹模拟降落装置,自制冰球对边坡进行试验. 测量了各阶段含水率、土压力、位移变化,分析了其变化规律. 最后,讨论了冰雹对土质边坡稳定性的影响,得出结论如下:(a )变形 (b ) 比色卡图13 S1组测量区域变形分布Fig.13 S1 deformation of the measurement area图15 监测点Y 轴向位移Fig.15 Yaxis displacement of monitoring point图14 监测点X 轴向位移Fig.14 X axis displacement of monitoring point225。
土力学教学中学生科研能力训练探索_以讲授土层应力历史为例_卢萌盟

. 高等建筑教育, 2017 , 26 — —以讲授土层应力历史为例[J] 刘志强, 王博. 土力学教学中学生科研能力训练探索— 欢迎按以下格式引用 : 卢萌盟, ( 1 ) : 89 - 92.
目前, 各高校在本科教育阶段都非常注重对创新人才的培养, 而科研训练 是推动创新人才成长的驱动力, 因此, 通过选择合适的课程对学生进行一定的 科研训练无疑对人才培养的质量起着重要的促进作用 。 土力学是研究土体的应力、 变形、 强度、 渗流及长期稳定性的一门学科。 其 很多课程内容和研究方法均借鉴于其他的力学学科 。 例如, 土中应力计算来源 于弹性力学中的布辛奈斯克( Boussinesq ) 解, 土中的渗流计算源于流体力学, 土 中的应力状态和挡土墙土压力计算来自于材料力学中的强度理论 , 地基的极限 承载力计算源于塑性力学中的滑移线理论。 因此, 通过对土力学的学习, 学生 除了可以更加深入地理解相关力学知识外 , 还可以学会如何用一般的力学原理 来解决实际工程问题。 另外, 除了具有深厚的理论背景外, 土力学还是一门实践性较强的课程 。 事实上, 作为土力学的研究对象, 土是一种非均质、 非弹性、 多孔的三相介质, 与以往的各种力学学科所研究的对象有着本质的区别 。 因此, 在沿用以往力学知
( 中国矿业大学 力学与土木工程学院, 江苏 徐州 221116 )
其教学内容无论从深度还是广度来讲都非常适合用来训练学生的 摘要: 土力学是一门理论性较强的课程 , 探索性思维能力。文章以讲授土层的应力历史为例, 对土力学面向研究的教学方法进行探索。 教师在授课 时可围绕知识点设置一系列的问题来引导学生主动思考 , 通过解决问题的方式来理解知识点。 在理解知识 点的前提下, 教师进一步就该问题进行拓展, 引导学生进入更广阔的层面深入思考 , 使学生了解目前的研究 概况, 以及与知识点相关的科学研究前沿问题 。 通过教师引导、 学生主动思考的教学方式既使学生更加深 刻理解知识点, 又能使学生的科研创新能力得以启蒙 , 从而达到良好的教学效果。 关键词: 土力学; 教学改革; 科研训练; 应力历史 中图分类号: G642 ; TU43 文献标志码: A 2909 ( 2017 ) 01008904 文章编号: 1005-
地震波斜入射下混凝土重力坝的塑性损伤响应分析

地震波斜入射下混凝土重力坝的塑性损伤响应分析李明超; 张佳文; 张梦溪; 闵巧玲; 史博文【期刊名称】《《水利学报》》【年(卷),期】2019(050)011【总页数】14页(P1326-1338,1349)【关键词】混凝土重力坝; 地震波斜入射; 塑性损伤模型; 地震破坏评价模型; 黏弹性人工边界【作者】李明超; 张佳文; 张梦溪; 闵巧玲; 史博文【作者单位】水利工程仿真与安全国家重点实验室天津大学天津300350; 华电重工股份有限公司北京 100070【正文语种】中文【中图分类】TV642.31 研究背景我国西南部强震区拥有全国约80%的水能资源,随着近年来西南地区不断修建200米级、300米级的高坝,对高坝大库的抗震安全评价提出了严峻的挑战[1-2]。
以往大坝安全性评价在地震输入机制方面考虑略有不足[3],高坝坝趾地震动参数确定方法复杂[4]。
用有限元法模拟结构地震响应时,多将坝体-地基体系作为封闭系统,并采用一致性激励方法输入地震,未考虑到行波效应和地基能量辐射。
为此,Deeks等[5]推导了二维时域人工边界来模拟无限地基辐射阻尼;王进廷等[6]验证了考虑地基辐射阻尼对坝体非线性地震反应的必要性;刘晶波等[7-8]结合球面波动理论推导了三维黏弹性人工边界,并将波动问题转换为等效荷载的输入。
波动输入方法较封闭系统改进较大,但由于地震波经过地壳中复杂介质时要进行多次折射、反射,很难确定入射方向,目前多假定为垂直向上的平面体波进行输入,这对于远场波动是合理的,但震源距场地较近时地震波通常是倾斜入射的[9],地震动呈现出更为复杂的空间变化特性。
随着大型结构和建坝地区地形的复杂性,单一方向的垂直入射无法真实反映地震输入状态,且地面运动的非一致变化对大型结构的影响难以预测。
廖河山等[10]利用特征线法分析了地震SH波斜入射时层状半空间的动力响应,结果表明入射角度对地表加速度放大倍数有显著影响。
Heymsfield等[11]利用边界积分方程法求解,指出倾斜基岩在SH波斜入射角度为60°时位移幅值最大。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Model Results Kupfer et al. (1969)
-1.2
0.5
2
0.2 0.0 -0.2 0.0 -0.2 3.0 -0.4 -0.6 -0.8
Stress(MPa)
Stress(MPa)
3.0
3.0
20 15 10
fc
1
fc
4.0 0
1 2 3
-1.0
1.0
-0.8
1.5
-0.6
-0.4 -0.6 -0.8 -1.0
强度提高
-1.2 -1.4
经典力学对混凝土本构行为的反映方式
1、弹性力学模型
能量耗散
强度退化
线弹性模型
刚度退化
非线性线弹性模型
经典力学对混凝土本构行为的反映方式
2、弹塑性力学模型
强度退化
能量耗散
刚度退化
强化法则
等向强化
随动强化
混合强化
经典力学对混凝土本构行为的反映方式
E0 ( p )
一些国际知名的混凝土损伤力学模型
Mazars模型(1984, 1986):弹性损伤模型,未反映塑性变形的影响; Resende模型(1987) :弹塑性损伤模型,损伤演化法则完全依赖于试 验; Ju模型(1989):各向同性弹塑性损伤模型,不能反映混凝土材料的单 边效应; Lubliner模型(1989):各向异性塑性-损伤模型,纯经验的损伤演化 法则,在Cauchy应力空间考虑塑性应变的演化; Faria 模型(1998):双标量弹塑性损伤模型,纯经验的损伤演化法则, 经验的塑性应变演化法则,未考虑塑性变形对损伤能的影响;
1997至2007年,我国在土木工程领域发表刊物研究
论文约66100篇,其中,涉及混凝土材料、混凝土结
构和混凝土力学的研究达29600篇,占上述研究论文 总数的45%。 如何正确地反映混凝土结构的受力力学行为、 尤其是动力荷载作用下的力学行为,仍然是呈现
在研究工作者面前的巨大挑战。
1. 混凝土结构分析中的关键科学问题
σ (1 dt )σ (1 d s )σ I D : C0 : (ε p )
建模基本过程(4)
由材料的弹塑性Helmholtz自由能势得到损伤能释放率表 达式,基于损伤能释放率,建立材料的损伤准则和损伤变量的 演化法则. 损伤能 释放率
t e Yt te ( ε ) 0 dt s Ys s 0 (εe , q) se0 (εe ) sp0 (q) d s
4.0 3.5
Test Result(Gopalarantam and Shah, 1985) Model Result 25
Karsan and Jirsa (1969) Model result
Stress(MPa)
Stress(MPa)
2.5 2.0 1.5 1.0 0.5
2.5 2.0 1.5 1.0 0.5 -1.4
对于带有根本性的损伤演化法则,经典质损伤力学理论
在逻辑上只能采用经验归纳或理论假设的方式给出,而难以
说明损伤演化的内在物理机制。
研究切入点
混凝土材料在其形成之初,内部即已存在着随机分布的
初始缺陷(如初始裂纹、空隙和微缺陷),从而形成初始随
机损伤场。在荷载等外界作用下,结构损伤的演化与初始的 损伤状态密切相关,在物理本质上是一个随机的损伤演化过 程,具有很强的离散性和不确定性。 概率观点的引入即随机损伤本构关系的研究将有助于更合 理地反映混凝土破坏的本质特征。也有助于说明损伤演化的 内在物理机制。
化 、单边效应 、拉压软化效应…)。
20世纪80年代中期以来,混凝土损伤力学的研究为混凝 土本构关系的研究开辟了新的道路。
损伤力学模型的基本原理
A d A0
1 d
在未受损伤部分,虎克定律依然成立
E0 e
当考虑塑性变形时
(1 d ) E0 e
(1 d ) E0 ( p )
退化:单轴受拉和单轴受压应力应变关系
t (1 dt )E0te
c (1 ds )E0 ce
建模基本过程(2)
在有效应力空间的塑性力学理论基础上,定义塑性 Helmholtz自由能势的显式表达式,得到混凝土材料的弹塑性 Helmholtz自由能势。 塑性自由能
p (q, dt , ds ) 1 ds sp0 (q)
1 d s se0 (ε e ) sp0 (q)
建模基本过程(3)
根据弹塑性Helmholtz自由能,根据热力学基本原理给出 本构关系。在等温绝热条件下, Clausius-Duheim不等式为
σ : ε 0
t (ε e ) s (ε e ) σ 1 dt 1 d s e ε ε e
3、断裂力学模型
从单个微裂缝及其扩展机制入手研究混凝土的非线性,建立了 一套描述混凝土中单个微裂缝及其稳定性的方法; 将裂缝扩展所需能量在给定体积上积分,可以得到本构关系。
?
断裂力学基本模型 混凝土中的缺陷
研究背景
经典力学(弹性力学、塑性力学、断裂力学等)很难
全面反映混凝土的复杂力学性质(例如:刚度退化和强度软
基于能量建模的基本原理
1 2 ( ) E 2
( ) E
( ) d
ij
( ij ) ij
建模基本过程(1)
根据材料损伤的物理机制,选取受拉损伤变量和受剪损伤变量 描述基本的损伤机制。与之相应,引入有效应力张量的正、负分解
和科学反映这些特征?
混凝土损伤过程中 典型的非线性表现 混凝土损伤过程中 典型的随机性表现
刚度退化
2)动力加载条件下混凝土损伤的率敏感性
细观物理与科学反映方式?
蠕变
静态 10 地震
8
碰撞 爆炸
101 10 2 103
107 106 105 104 103 102 101 1
应变率 (S-1)
科学问题聚焦 混凝土的本构关系
结构非线性的正确反映
随机性的传播规律
2、混凝土随机损伤本构关系研究
混凝土材料受力非线性特征
能量耗散
强度退化
拉压软化
0.2
2
fc
0.0 -1.4 -1.2 -1.0 -0.8 -0.6 -0.4 -0.2 0.0 -0.2
1
0.2 f c
拉压软化
刚度退化
1 ) 确定性弹塑性损伤本构关系
从基本的材料损伤物理机制出发选取损伤变量; 同时反映弹性损伤与塑性变形两种机制;
利用连续介质力学和热力学基本原理建模;
全面反映混凝土材料的非线性特性:刚度退化和强度软
化 、单边效应 、拉压软化效应、有侧限时材料强度和 延性提高等。
李杰,吴建营,2005,“混凝土弹塑性损伤本构模型研究Ⅰ:基本公式”,土木 工程学报,38(9):14-20 Wu Jianying, Li Jie * & Faria R., 2006, “An energy release rate-based plastic-damage model for concrete”, International Journal of Solids and Structures, 43(3), 583-612.
0.04
损伤机制、受力形式与结构滞回耗能机制的关系?
3)损伤扩散与多尺度随机涨落
静力作用下的损伤度上的损伤扩散、转移、随机涨落及其跨尺度影 响规律,是理解结构破坏规律、发现复杂结构整体可靠性形成机 动力作用下损伤出现弥散! 制,实现重大工程结构灾变过程控制的重要基础。
4)结构非线性反应的随机演化规律
3)结构滞回耗能的物理机制
4 3 2
Restoring force (N)
x 10
5
Fz Fx
1 0 -1 -2 5 -3 4 -4 -0.05 -0.04 -0.03 -0.02 -0.01 0 0.01 Inter-floor Displacement (m) 0.02 0.03 0.04 3 2
弹塑性自由能
(εe , q, dt , ds ) t (εe , q, dt ) s (εe , q, ds )
t (εe , q, dt ) te (εe , q, dt ) (1 dt ) te0 (εe )
s (εe , q, d s ) se (εe , d s ) sp (q, d s ) 1 d s s 0 (εe , q)
混凝土随机损伤力学 研究进展
李 杰
同济大学 2010年8月2日
混凝土材料与混凝土结构
至2009年,我国混凝土用量已达 每人每年5.5吨的水平。
作为一种主导性建筑材料,混凝土在我国重大工程建设中发挥着重要 支撑作用。20世纪90年代以来,我国混凝土工程一直保持持续增长势头。
混凝土材料与混凝土结构研究
与混凝土结构分析相关的关键科学问题
混凝土损伤过程中非线性与随机性及其耦合效应 动力加载条件下混凝土损伤的率敏感性 结构滞回耗能的物理机制 损伤扩散与多尺度随机涨落 结构非线性反应的随机演化规律
1)混凝土损伤过程中的非线性与随机性
能量耗散
在损伤及其演化进程中,非线性
材料软化
与随机性互相耦合! 如何正确认识
e e (εe , dt , ds ) te (εe , dt ) s (εe , ds )
