M序列自相关辨识与机理分析结合法
通信原理精品课-第七章m序列(伪随机序列)

04
m序列在扩频通信中的应用
扩频通信的基本原理和特点
扩频通信的基本原理
扩频通信是一种利用信息信号对一个很宽频带的载波进行调制,以扩展信号频谱 的技术。通过扩频,信号的频谱被扩展,从而提高了信号的抗干扰能力和隐蔽性 。
扩频通信的特点
扩频通信具有抗干扰能力强、抗多径干扰能力强、抗截获能力强、可实现码分多 址等优点。同时,扩频通信也存在一些缺点,如信号的隐蔽性和保密性可能受到 影响,信号的带宽较宽,对信道的要求较高。
在无线通信中,由于信号传播路径的不同,接收端可能接收到多个不同路径的信号,形成多径干 扰。
抗多径干扰
m序列具有良好的自相关和互相关特性,可以用于抗多径干扰。通过在发射端加入m序列,可以 在接收端利用相关器检测出原始信号,抑制多径干扰的影响。
扩频通信
m序列可以用于扩频通信中,将信息信号扩展到更宽的频带中,提高信号的抗干扰能力和隐蔽性 。
离散性
m序列是一种周期性信号,其 功率谱具有离散性,即只在某 些特定的频率分量上有能量分 布。
带宽有限
m序列的功率谱具有有限的带 宽,其带宽与序列的长度和多 项式的系数有关。
旁瓣抑制
m序列的功率谱具有较好的旁 瓣抑制特性,即除了主瓣外的 其他频率分量的能量较小。
m序列在多径干扰抑制中的应用
多径干扰
抗截获能力
m序列扩频通信系统具有较强 的抗截获能力。由于信号的频 谱被扩展,敌方难以检测和识 别信号,从而提高了通信的保 密性。
码分多址能力
m序列扩频通信系统具有较强 的码分多址能力。不同的用户 可以使用不同的扩频码进行通 信,从而实现多用户共享同一 通信信道。
05
m序列的未来发展与研究方向
m序列与其他通信技术的融合应用
m序列的特点与应用 ppt课件

m序列的产生 m序列的性质 m序列的应用
11
测量房间脉冲效应 测距回答概率控制中的应用
系统辨识中的应用
12
m序列是一种伪随机序列,在通信、雷达、密码学等领域都有应 用。近几十年来,运用m序列测量房间声学系统脉冲响应的技术研究也 受到了人们的关注。m序列法测量技术有两大优点,其一是较强的抗噪 声性能,其二是运算速度快、效率高。
系统辨识的方法主要分为非参数模型辨识和参数模型辨识,在假定系 统是线性的前提下,通过对系统施加特定的信号,测定输出,即可求得系 统的非参数模型,进而转换为参数模型。因而这类方法可适用于任何复 杂系统。用于非参数模型辨识的信号一般有正弦信号;阶跃信号;脉冲信 号。
19
20
一. 实验目的:利用matlab验证m序列的产生方法及其自相关特性 二. 实验要求:设m序列的生成多项式为g(x)=1+x3+ x4,求 (1)m序列的输出及其自相关序列; (2)设脉冲成形为p(t)= 1 0<t<Ts 0 其他 画出其m序列信号的自相关函数; (3)设脉冲波形为升余弦成形(α=0),画出其m序列信号的自相关 函数。 实验源码 clear all; close all; g=19;%G=10011; state=8;%state=1000 L=1000; %m序列产生 N=15; mq=mgen(g,state,L); %m序列自相关
22
st=s(1:length(st)); rt1=conv(mt,st(end:-1:1))/(N*N_sample); subplot(223) plot(t,rt1(length(st):length(st)+length(t)-1)); axis([0 63 -0.3 1.2]);title('m序列矩形成型信号的自相关');xlabel('t'); Tc=1; dt=Tc/N_sample; t=-20:dt:20; gt=sinc(t/Tc); mt=sigexpand(1-2*mq,N_sample); mt=conv(mt,gt); st2=sigexpand(1-2*mq(1:15),N_sample); s2=conv(st2,gt); st2=s2; rt2=conv(mt,st2(end:-1:1))/(N*N_sample); subplot(224); t1=-55+dt:dt:Tc*L-dt; %plot(t,mt(1:length(t)));
m序列辨识原理__解释说明以及概述

m序列辨识原理解释说明以及概述1. 引言1.1 概述m序列是一种具有良好性质的伪随机序列,广泛应用于通信、密码学和编码等领域。
m序列辨识原理是指通过对已知的m序列进行分析和处理,从中提取特征并判断其生成方式的过程。
准确地辨识出m序列的生成方法能够帮助我们更好地理解和应用这一伪随机序列。
1.2 文章结构本文将围绕m序列辨识原理展开详细说明,并介绍相关的定义、特点、辨识过程以及算法和技术。
文章将分为五个部分组成:引言、m序列的定义和特点、m序列辨识原理与过程、m序列辨识算法与技术以及结论。
1.3 目的本文旨在通过对m序列辨识原理的深入研究和分析,进一步探索该领域内的关键概念、方法和工具,并提供给读者一个清晰全面的认识。
通过阅读本文,读者将能够了解什么是m序列以及其在实际应用中所起到的重要作用。
另外,通过对不同辨识算法和技术的比较与选择指南,本文还可为读者提供一些实用性的建议和参考。
最后,本文也将以对未来m序列研究方向的建议,为该领域内进一步研究工作提供一定的借鉴和指导。
这样设计文章结构,能够使读者逐步深入了解m序列辨识原理,并全面回顾相关概念、方法和技术,并为进一步探索和应用m序列提供指导。
2. m序列的定义和特点:2.1 m序列的概念和起源:m序列是一种特殊的二进制序列,也被称为最长线性反馈移位寄存器(LFSR)序列。
它是由一个长度为m的线性反馈移位寄存器生成的序列,在信息科学和通信领域有广泛应用。
m序列最早由亚当斯(J. W. Adams)于1965年引入。
2.2 m序列的生成方法:m序列可通过使用线性反馈移位寄存器(LFSR)来生成。
LFSR是一种采用线性组合和位移操作产生下一个状态的寄存器。
它由一系列触发器组成,每个触发器都保存一个二进制值,并且输出总是满足某个线性方程式。
在生成m序列时,通常会选择长度为m-1或m的LFSR作为产生器。
这样可以保证生成的序列具有周期性,且周期长度为(2^m) - 1。
基于matlab的m序列的产生和特性分析

基于matlab的m序列的产生和特性分析作者:耿亚南来源:《中国新通信》 2017年第15期【摘要】 m 序列是一种重要的伪随机序列。
本文借助MATLAB 平台,详细介绍了m 序列的产生原理,并仿真了由移位寄存器产生的m 序列,同时研究了m 序列的自相关函数并得到了m 序列自相关函数的图像。
仿真结果验证了该方法的正确性和可行性。
【关键字】 m 序列自相关函数 MATLAB一、引言m 序列是最长线性移位寄存器序列的简称,有着良好的自相关性,易于产生和复制,是目前广泛应用的一种伪随机序列。
其在通信领域有着广泛的应用,如扩频通信,卫星通信的码分多址,数字数据中的加密、加扰、同步、误码率测量等领域。
近几十年来,运用m 序列测量房间声学系统脉冲响应的技术研究也受到了人们的关注。
m 序列法测量技术有两大优点其一是较强的抗噪声性能,其二是运算速度快、效率高。
二、m 序列的产生2.1 m 序列的产生原理m 序列是由带线性反馈的移位寄存器产生的。
由n 级串联的移位寄存器和反馈逻辑线路可组成动态移位寄存器,如果反馈逻辑线路只由模2 和构成,则称为线性反馈移位寄存器。
m 序列的产生框图如图1 所示。
图中C0、C1…Cn 均为反馈线,其中C0= Cn=1,表示反馈连结。
因为m 序列是由循环序列发生器产生的,因此C0和Cn 肯定为1,即参与反馈。
而反馈系数C1、C2…Cn - 1若为1,参与反馈,若为0,则表示断开反馈线,即开路、无反馈连线。
2.2 MATLAB 仿真MATLAB 产生m 序列的部分程序:function[mseq]=m_sequence(fbconnection)n=length(fbconnection);N=2^n-1;register=[zeros(1,n-1) 1];mseq(1)=register(n);for i=2:Nnewregister(1)=mod(sum(fbconnection.*register),2);for j=2:nnewregister(j)=register(j-1);end;三、m 序列的自相关函数3.1 自相关函数自相关是指m 序列与逐位移位后的序列相关性的一种度量。
Matlab实现M序列的产生和自相关序列
电子信息工程专业课程设计任务书1 需求分析伪随机信号既有随机信号所具有的优良的相关性,又有随机信号所不具备的规律性. 因此,伪随机信号既易于从干扰信号中被识别和分离出来,又可以方便地产生和重复,其相关函数接近白噪声的相关函数, 有随机噪声的优点,又避免了随机噪声的缺点. 伪随机序列具有可确定性、可重复性,易于实现相关接受或匹配接受,故有很好的抗干扰性能. 因此伪随机序列在相关辩识、伪码测距、导航、遥控遥测、扩频通信、多址通信、分离多径、误码测试、线形系统测量、数据加扰、信号同步等方面均有广泛的应用. m 序列是伪随机序列中最重要的一种,是最长线性移位寄存器序列,m 序列易于实现,具有优良的自相关特性,在直扩通信系统中用于扩展要传递的信号。
可以通过移位寄存器,利用MATLAB 编程产生m 序列。
2 概要设计m 序列是最长线性反馈移位寄存器序列的简称,m 序列是由带线性反馈的移位寄存器产生的.由n 级串联的移位寄存器和和反馈逻辑线路可组成动态移位寄存器,如果反馈逻辑线路只由模2和构成,则称为线性反馈移位寄存器。
带线性反馈逻辑的移位寄存器设定初始状态后,在时钟触发下,每次移位后各级寄存器会发生变化。
其中任何一级寄存器的输出,随着时钟节拍的推移都会产生一个序列,该序列称为移位寄存器序列。
n 级线性移位寄存器的如图1所示:图1 n 级线性移位寄存器图中i C 表示反馈线的两种可能连接方式,i C =1表示连线接通,第n-i 级输出加入反馈中;i C =0表示连接线断开,第n-i 级输出未参加反馈。
因此,一般形式的线性反馈逻辑表达式为112201(mod 2)n n n n n i n i i a C a C a C a C a ---==⊕⊕⊕=∑L将等式左面的n a 移至右面,并将00(1)n n a C a C ==代入上式,则上式可改写为100n i n i C a -==∑定义一个与上式相对应的多项式()ni i i F x C x ==∑其中x 的幂次表示元素的相应位置。
试验八:M序列产生及特性分析实验

试验八:m序列产生及特性分析实验一实验目的1.了解m序列的性质和特点;2.熟悉m序列的产生方法;3.了解m序列的DSP或CPLD实现方法。
二实验内容1.熟悉m序列的产生方法;2.测试m序列的波形;3*.用DSP或CPLD编程产生m序列。
三实验原理m序列是最长线性反馈移存器序列的简称,是伪随机序列的一种。
它是由带线性反馈的移存器产生的周期最长的一种序列。
m序列在一定的周期内具有自相关特性。
它的自相关特性和白噪声的自相关特性相似。
虽然它是预先可知的,但性质上和随机序列具有相同的性质。
比如:序列中“0”码与“1”码等抵及具有单峰自相关函数特性等。
1.m序列的产生m序列是由带线性反馈的移存器产生的。
结构如图:图1-1-1 反馈移位寄存器的结构其中an-i为移位寄存器中每位寄存器的状态,C i为第i位寄存器的反馈系数。
C i=1表示有反馈,C i=0表示无反馈。
我们先给出一个m序列的例子。
在图1-1-1中示出一个4级反馈移存器。
若其初始状态为(a3, a2, a1, a)=(1,0,0,0),则在移位一次时,由a3和a模2相加产生新的输入a4=1⊕0=1新的状态变为(a4, a3, a2, a1)=( 1, 1, 0, 0)这样移位15次后又回到初始状态(1,0,0,0),不难看出,若初始状态为全“0”,即“0,0,0,0”,则移位后得到的仍为全“0”状态。
这就意味着在这种反馈移存器中应避免出现全“0”状态。
不然移存器的状态将不会改变。
因为4级移存器共有24=16种可能的不同状态。
除全“0”状态外,只剩15种状态可用。
即由任何4级反馈移存器产生的序列的周期最长为15。
我们常常希望用尽可能小的级数产生尽可能长的序列。
由上例可见,一般说来,一个n 级反馈移存器可能产生的最长周期等于(2n –1)。
我们将这种最长的序列称为最长线性反馈1 1 1 1 0 1 0 1 1 0 0 1 0 0 00 1 1 1 1 0 1 0 1 1 0 0 1 0 00 0 1 1 1 1 0 1 0 1 1 0 0 1 00 0 0 1 1 1 1 0 1 0 1 1 0 0 1移存器序列,简称m 序列。
M序列的产生及特性分析实验

M 序列的产生及特性分析实验一:实验目的1、了解m 序列的特性及产生。
二:实验模块1、 主控单元模块2、 14号 CDMA 扩频模块3、示波器三:实验原理1、14号模块的框图14号模块框图2、14号模块框图说明(m 序列)127位128位该模块提供了四路速率为512K 的m 序列,测试点分别为PN1、PN2、PN3、PN4。
其中,PN2和PN4分别由PN 序列选择开关S2、S3控制;不同的开关码值,可以设置m 序列码元的不同偏移量。
开关S6是PN 序列长度设置开关,可选127位或128位,其中127位是PN 序列原始码长,128位是在原始码元的连6个0之后增加一个0得到。
Gold 序列测试点为G1和G2,其中G1由PN1和PN2合成,G2由PN3和PN4合成。
拨码开关S1和S4是分别设置W1和W2产生不同的Walsh 序列。
实验中还可以观察不同m 序列(或Gold 序列)和Walsh 序列的合成波形。
注意,每次设置拨码开关后,必须按复位键S7。
3、实验原理框图m 序列相关性实验框图为方便序列特性观察,本实验中将Walsh 序列码型设置开关S1和S4固定设置为某一种。
4、实验框图说明 m 序列的自相关函数为()R A D τ=-式中,A 为对应位码元相同的数目;D 为对应位码元不同的数目。
自相关系数为()A D A DP A Dρτ--==+ 对于m 序列,其码长为P=2n -1, 在这里P 也等于码序列中的码元数,即“0”和“1”个数的总和。
其中“0”的个数因为去掉移位寄存器的全“0”状态,所以A 值为121n A -=-“1”的个数(即不同位)D 为12n D -=m 序列的自相关系数为1 0()1 0,1,2,p τρτττ=⎧⎪=⎨-≠=⎪⎩…,p-1cT τm 序列的自相关函数四:实验步骤(注:实验过程中,凡是涉及到测试连线改变或者模块及仪器仪表的更换时,都需先停止运行仿真,待连线调整完后,再开启仿真进行后续调节测试。
m序列产生及自相关和互相关函数曲线

1、m序列产生及自相关和互相关函数曲线function PN=makem(x) %m序列产生函数ss1=num2str(x);ss2=dec2bin(base2dec(ss1,8)); %先把八进制转换为十进制,再把十进制转换为二进制G=2^(length(ss2)-1)-1; %最大周期sd=[];for j=1:(length(ss2)-2)sd=[sd 0];endsd=[sd 1]; %寄存器初始状态0 0 0...0 1PN=[];for j=1:GPN=[PN sd(length(sd))]; %m序列输出的第一位onenum=[];for jj=1:length(ss2)if str2num(ss2(jj))==1onenum=[onenum jj-1]; %存储二进制反馈系数里面“1”的位置-1,即进行异或的位置endendtemp=sd(onenum(2));for jj=3:length(onenum) %根据“1”的位置进行异或运算temp=xor(temp,sd(onenum(jj)));endfor jj=length(ss2)-1:-1:2 %移位(序列后一位值等于前一位值)sd(jj)=sd(jj-1);endsd(1)=temp; %序列第一位等于反馈出来的值endfunction mandzi(ss) %m序列曲线及自相关函数曲线绘图函数ss1=num2str(ss);ss2=dec2bin(base2dec(ss1,8)); %转换为二进制G=2^(length(ss2)-1)-1; %最大周期PN=makem(ss); %调用函数计算m序列pp=(-2).*PN+1; %0→1 1→-1pp2=[];for tao=-(G-1):G-1pp1=circshift(pp,[0,tao]);pp2=[pp2 sum(pp.*pp1)/G]; %计算自相关函数endsubplot(2,1,1)stem(PN)grid on;title(['使用生成多项式(',num2str(ss),')8=(',ss2,')2产生的m序列']) subplot(2,1,2)tao=-(G-1):G-1;plot(tao,pp2)grid on;title('自相关函数曲线')function huxg(x,y) %m序列互相关绘图函数x1=num2str(x);x2=dec2bin(base2dec(x1,8)); %转换为二进制G1=2^(length(x2)-1)-1; %最大周期y1=num2str(y);y2=dec2bin(base2dec(y1,8)); %转换为二进制G2=2^(length(y2)-1)-1; %最大周期if G1~=G2error('周期不同,无法计算')returnendpn1=makem(x); %分别调用函数计算出m序列pn2=makem(y);pp=[];for tao=-(G1-1):G1-1pn1tao=circshift(pn1,[0,tao]); %计算互相关函数%pp=[pp sum(pn2.*pn1tao)/G1];pp=[pp sum(pn2.*pn1tao)];endtao=-(G1-1):G1-1;plot(tao,pp)grid on;title(['反馈系数(',num2str(x),')8和(',num2str(y),')8的互相关函数曲线'])2、Rake接收机仿真clear all;clcNumusers=1;Nc=16; %扩频因子ISI_Length=1; %每径延时为ISI_Lengh/2 EbN0db=[0:1:30]; %信噪比,单位dBTlen=8000; %数据长度Bit_Error_Number1=0; %误比特率初始值Bit_Error_Number2=0;Bit_Error_Number3=0;power_unitary_factor1=sqrt(6/9); %每径功率因子power_unitary_factor2=sqrt(2/9);power_unitary_factor3=sqrt(1/9);s_initial=randsrc(1,Tlen); %数据源wal2=[1 1;1 -1]; %产生walsh矩阵wal4=[wal2 wal2;wal2 wal2*(-1)];wal8=[wal4 wal4;wal4 wal4*(-1)];wal16=[wal8 wal8;wal8 wal8*(-1)];s_spread=zeros(Numusers,Tlen*Nc); %扩频ray1=zeros(Numusers,2*Tlen*Nc);ray2=zeros(Numusers,2*Tlen*Nc);ray3=zeros(Numusers,2*Tlen*Nc);for i=1:Numusersx0=s_initial(i,:).'*wal16(8,:);x1=x0.';s_spread(i,:)=(x1(:)).';end%将每个扩频后的输出重复为两次,有利于下面的延迟(延迟半个码元)ray1(1:2:2*Tlen*Nc-1)=s_spread(1:Tlen*Nc);ray1(2:2:2*Tlen*Nc)=ray1(1:2:2*Tlen*Nc-1);%产生第二径和第三径信号ray2(ISI_Length+1:2*Tlen*Nc)=ray1(1:2*Tlen*Nc-ISI_Length);ray2(2*ISI_Length+1:2*Tlen*Nc)=ray1(1:2*Tlen*Nc-2*ISI_Length);for nEN=1:length(EbN0db)en=10^(EbN0db(nEN)/10); %将Eb/N0的dB值转化为十进制数值sigma=sqrt(32/(2*en)); %将收到的信号dempdemp=power_unitary_factor1*ray1+...power_unitary_factor2*ray2+...power_unitary_factor3*ray3+...(randn(1,2*Tlen*Nc)+randn(1,2*Tlen*Nc)*i)*sigma;dt=reshape(demp,32,Tlen)';wal16_d(1:2:31)=wal16(8,1:16); %将walsh码重复为两次wal16_d(2:2:32)=wal16(8,1:16);rdata1=dt*wal16_d(1,:).'; %解扩后rdata1为第一径输出wal16_delay1(1,2:32)=wal16_d(1,1:31); %将walsh码延迟半个码元rdata2=dt*wal16_delay1(1,:).'; %解扩后rdata2为第二径输出wal16_delay2(1,3:32)=wal16_d(1,1:30); %将walsh码延迟一个码元wal16_delay2(1,1:2)=wal16_d(1,31:32);rdata3=dt*wal16_delay2(1,:).'; %解扩后rdata3为第三径输出p1=rdata1'*rdata1;p2=rdata2'*rdata2;p3=rdata3'*rdata3;p=p1+p2+p3;u1=p1/p;u2=p2/p;u3=p3/p;rd_m1=real(rdata1*u1+rdata2*u2+rdata3*u3); %最大比合并rd_m2=(real(rdata1+rdata2+rdata3))/3; %等增益合并u=[u1,u2,u3]; %选择式合并maxu=max(u);if(maxu==u1)rd_m3=real(rdata1);elseif(maxu==u2)rd_m3=real(rdata2);else rd_m3=real(rdata3);endendr_Data1=sign(rd_m1)'; %三种方法判决输出r_Data2=sign(rd_m2)';r_Data3=sign(rd_m3)';%计算误比特率Bit_Error_Number1=length(find(r_Data1(1:Tlen)~=s_initial(1:Tlen)));Bit_Error_Rata1(nEN)=Bit_Error_Number1/Tlen;Bit_Error_Number2=length(find(r_Data2(1:Tlen)~=s_initial(1:Tlen)));Bit_Error_Rata2(nEN)=Bit_Error_Number2/Tlen;Bit_Error_Number3=length(find(r_Data3(1:Tlen)~=s_initial(1:Tlen)));Bit_Error_Rata3(nEN)=Bit_Error_Number3/Tlen;endsemilogy(EbN0db,Bit_Error_Rata1,'r*-');hold on;semilogy(EbN0db,Bit_Error_Rata2,'bo-');hold on;semilogy(EbN0db,Bit_Error_Rata3,'g.-');legend('最大比合并','等增益合并','选择式合并');xlabel('信噪比');ylabel('误比特率');title('三种主要分集合并方式性能比较');。
M序列自相关辨识与机理分析结合法

M序列自相关辨识与机理分析结合法M序列自相关辨识与机理分析结合法是一种用于分析和探索M序列机理的方法。
M序列是一种伪随机序列,具有良好的自相关性质和伪随机性质,因此被广泛应用于通信、密码学和系统辨识等领域。
M序列自相关辨识与机理分析结合法通过对M序列的自相关函数进行分析,推导出M序列产生的机理,并进一步探索其应用潜力。
M序列是由一个初值和一组特定的生成矩阵确定的。
生成矩阵的选取是关键,不同的生成矩阵会导致不同类型的M序列。
M序列的自相关函数可以用来表示序列中元素之间的相关性。
M序列的自相关函数具有周期性,通过对自相关函数的周期性分析,可以推导出M序列的生成机理。
对于给定的M序列,首先需要计算其自相关函数。
自相关函数的定义是序列与其延迟序列的内积。
通过计算不同延迟下的自相关函数,可以观察到自相关函数的周期性特征。
根据周期性特征,可以推断M序列的位移寄存器长度和生成矩阵的特征。
在推导了M序列的位移寄存器长度和生成矩阵的特征之后,可以进一步分析M序列的机理。
M序列的机理涉及到位移寄存器之间的互屏蔽和非线性函数的作用。
通过对位移寄存器和非线性函数的动态分析,可以了解M序列的产生过程和特性。
M序列自相关辨识与机理分析结合法在通信、密码学和系统辨识等领域具有广泛的应用。
在通信领域,M序列的自相关辨识可以用于信号调制和信道估计;在密码学领域,M序列的自相关辨识可以用于密码分析和密钥生成;在系统辨识领域,M序列的自相关辨识可以用于系统模型辨识和参数估计。
总之,M序列自相关辨识与机理分析结合法是一种用于分析和探索M 序列机理的方法。
通过对M序列的自相关函数进行分析,可以推导出M序列的生成机理,并进一步探索其应用潜力。
该方法在通信、密码学和系统辨识等领域具有广泛的应用前景。
自相关(序列相关)

常用的方法有: (1)科克伦-奥科特(Cochrane-Orcutt)迭代法。 (2)杜宾(durbin)两步法
附:杜宾(durbin)两步法
该方法仍是先估计1,2,,L,再对差分 模型进行估计。
第一步,变换差分模型为下列形式:
Yi 1Yi 1 l Yi l 0 (1 1 l ) 1 ( X i 1 X i 1 l X i l ) i
利用
ut ut 1 vt
有
ut 1 ut 2 vt 1,, ut m1 ut m vt m1
ut mut m m1vt ( m1) m2vt ( m2) vt 1 vt
1 2 Cov N , N u n 1
i 1 l ,2 l , , n
(2.5.13)
采用 OLS 法估计该方程,得各Y j ( j i 1, i 2, i l ) 前的
ˆ1 , ˆ 2 , , ˆl 。 系数 1 , 2 , , l 的估计值
ˆ1 , ˆ 2 ,, ˆ l 代入差分模型 第二步,将估计的
i
对各方程估计并进行显著性检验,如果存在某 一种函数形式,使得方程显著成立,则说明原模 型存在序列相关性。
具体应用时需要反复试算。 回归检验法的优点是:
一旦确定了模型存在序列相关性,也就同时知 道了相关的形式;
它适用于任何类型的序列相关性问题的检验。
(2)杜宾-瓦森(Durbin-Watson)检验法
三、序列相关性的后果
1、参数估计量无偏但非有效 ; 2、变量的显著性检验失去意义 ; 3、模型的预测失效 ;
多次采样m序列法辨识LTI脉冲响应计算方法

多次采样m序列法辨识LTI脉冲响应计算方法
方俊初;聂启燕
【期刊名称】《河北工程大学学报(自然科学版)》
【年(卷),期】2016(033)003
【摘要】研究一个时钟周期内多次采样条件下m序列法辨识线性时不变系统脉冲响应的计算方法,推导出脉冲响应序列与m序列周期、幅度及采样率之间的关系表达式.将双极性m序列信号的自相关特性进行均匀抽样,写成全周期内的统一表达式,代入维纳-何甫方程,再利用循环右移矩阵将脉冲响应用输入、输出采样序列表达出来.在matlab平台上对算法进行仿真实验,结果证明这种算法是正确的.
【总页数】4页(P109-112)
【作者】方俊初;聂启燕
【作者单位】安徽工程大学电气工程学院,安徽芜湖241000;安徽工程大学电气工程学院,安徽芜湖241000
【正文语种】中文
【中图分类】TN91;TP202
【相关文献】
1.m序列的完备递归采样法 [J], 唐朝京;肖戎
2.m序列法测量房间脉冲响应中截断点的选择 [J], 杨春花;黄翔东;李文元;王兆华
3.m序列法测量室内脉冲响应的非线性失真分析 [J], 杨春花;黄翔东;李文元;王兆华
4.离散LTI系统单位脉冲响应求解方法研究 [J], 钱琳琳;牛瑞燕;李秀丽
5.运用gold伪随机序列测量LTI系统的脉冲响应 [J], 杨春花;李文元;王兆华因版权原因,仅展示原文概要,查看原文内容请购买。
(完整word版)m序列产生及其特性实验.doc
实验九m 序列产生及其特性实验一、实验目的和要求通过本实验掌握m 序列的特性、产生方法及应用。
二、实验内容和原理1)、实验内容1、观察 m 序列,识别其特征。
2、观察 m 序列的自相关特性。
2)、基本原理m序列是有 n级线性移位寄存器产生的周期为 2 n 1 的码序列,是最长线性移位寄存器序列的简称。
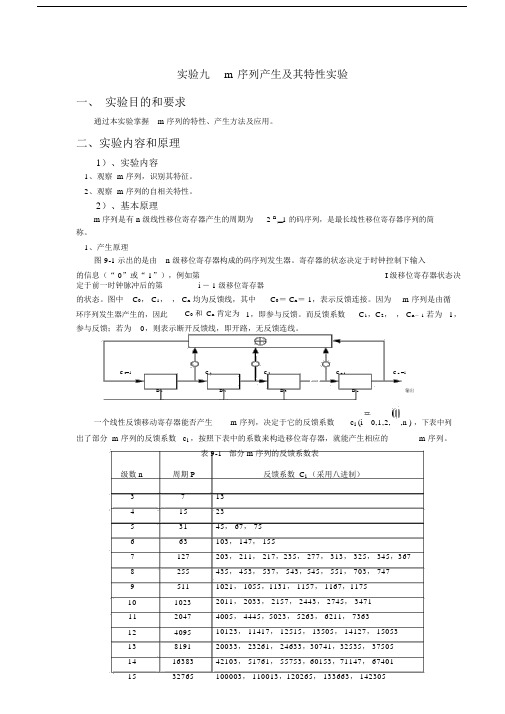
1、产生原理图 9-1 示出的是由n 级移位寄存器构成的码序列发生器。
寄存器的状态决定于时钟控制下输入的信息(“ 0”或“ 1”),例如第I 级移位寄存器状态决定于前一时钟脉冲后的第i - 1 级移位寄存器的状态。
图中C0, C1,, C n均为反馈线,其中C0= C n= 1,表示反馈连接。
因为m 序列是由循环序列发生器产生的,因此C0和C n肯定为1,即参与反馈。
而反馈系数C1,C2,, C n-1若为1,参与反馈;若为0,则表示断开反馈线,即开路,无反馈连线。
C 0=1 C 1 C 2 C n-1 C n =1D 1 D 2 D 3 D n 输出一个线性反馈移动寄存器能否产生m 序列,决定于它的反馈系数c i (i 0,1,2,,n ) ,下表中列出了部分 m 序列的反馈系数 c i,按照下表中的系数来构造移位寄存器,就能产生相应的m 序列。
表 9-1 部分 m 序列的反馈系数表级数 n 周期 P 反馈系数 C i(采用八进制)3 7 134 15 235 31 45, 67, 756 63 103, 147, 1557 127 203, 211, 217,235, 277, 313, 325, 345,3678 255 435, 453, 537, 543,545, 551, 703, 7479 511 1021, 1055,1131, 1157, 1167,117510 1023 2011, 2033, 2157, 2443, 2745, 347111 2047 4005, 4445,5023, 5263, 6211, 736312 4095 10123, 11417, 12515, 13505, 14127, 1505313 8191 20033, 23261, 24633,30741,32535, 3750514 16383 42103, 51761, 55753,60153,71147, 6740115 32765 100003, 110013,120265, 133663, 142305根据表 9-1 中的八进制的反馈系数,可以确定 m 序列发生器的结构。
m序列自相关

m序列自相关
M序列是一种在电信和通信系统中广泛应用的伪随机数序列,其自相关性质是M序列的重要特征之一。
M序列具有很长的长度和非常好的自相关特性,其自相关函数(ACF)形状类似于矩形脉冲,并在正常化的自相关函数中具有明显的
峰值。
这种自相关性质使得M序列在通信系统中的应用非常广泛,因
为其可以用于同步信号的产生和检测,以及在CDMA系统中作为扩频码。
然而,M序列也存在一些自相关性弱点,例如其自相关峰值幅度不尽相同,而且其峰值之间存在周期性交替。
这些限制使得M序列不适
用于某些应用,例如在特定应用中需要高度精确定时的高速数据传输
系统。
总之,M序列自相关性是其重要的特性之一,也是其在通信和电信系统中广泛应用的关键特性之一。
实验一 m序列相关特性

其正/负峰波形及峰值电压,而波形中的小毛刺、小起伏不要理睬,这是步进延时跳变瞬间 PNi 及 PNj 码型的短暂混乱所造成。 说明:在“自动延时”方式下,因 Ri,j(τ)是 PNi(t)×PNj(t-τ)经窄带低通滤波形成的,故 Ri,j(τ)的时序比SYR(τ)的稍有延时。 5. 按 K3 键使 K3 键 LED 灯亮,选择“互相关” 。选择了“5 阶 m 序列-互相关特性测 量”方式。重复步骤 4。 6. 按 K2 键使 K2 键 LED 灯亮,选择“m7” ;按 K3 键使 K3 键 LED 灯灭,选择“自相 关” 。选择了“7 阶 m 序列-自相关特性测量”方式。重复步骤 4。 7. 按 K3 键使 K3 键 LED 灯亮,选择“互相关” 。选择了“7 阶 m 序列-互相关特性测 量”方式。重复步骤 4。
Ri ( )
T
0
p , 0 ci (t ) ci (t )dt p , Tp | | T Tp
(3-1-3)
具有这种与白噪声相似的自相关特性的序列称为 PN 序列(PseudoNoise sequence 伪噪声序 列) ,例如 m 序列及其派生出来的 M 序列及 Gold 序列;而不具有这种自相关特性的序列, 就不能称为 PN 序列,例如 Walsh 序列。 实验一~实验四观测 m 序列、M 序列、Gold 序列、截短的 Gold 序列及 Walsh 序的自 关特性及互相关特性。由“监控及 Pe/Rij 测量”模块中的单片机 CPU1 产生各种正交序列, 再与其外围电路一起按式(3-1-1)及式(3-1-2)实行相关运算,如图 3-1-1 所示。图中用 到第 1 章所述模二加与乘法器等效的关系。用示波器观测各点波形即可了解它们的相关特 性。
传递函数频域辨识及M序列生成指南甄选范文

传递函数频域辨识及M序列生成指南12自动化摘要:系统辨识、状态估计和控制理论是现代控制论中相互渗透的三个领域。
控制理论的应用离不开系统辨识技术,实际中,许多控制系统的模型在工作中是变化的,为了实现自适应控制,需要系统辨识技术不断更新模型参数。
通过学习使用MATLAB软件,初步体验系统辨识方法。
关键字:系统辨识,控制理论,MATLAB。
Abstract: System identification, State estimation and The Principle of Automatic Control are three different disciplines of the modern control theory, which are interpenetrated with one another. In practice, the model of system is changing all the time. To control adaptively, the system model should be update its parameters, by the method of System identification. By learning the using of MATLAB, we are supposed to practice the method of system identification.Key Words: System identification, System identification, MATLAB目录一、引言 (2)1.1介绍 (2)1.2实验目的 (2)二、实验内容和方法 (2)2.1实验内容 (2)2.1.1实验一: (2)2.1.2实验二: (3)2.2实验步骤 (3)2.2.1实验一: (3)非周期激励信号 (4)2.2.2实验二:M序列 (6) (9)三、实验分析分析 (9)一、引言1.1介绍在自然科学和社会科学的许多领域中,人们越来越重视对系统进行定量的系统分析、系统综合、仿真、控制和预测。
m序列及相关理论分析

m 序列及相关理论分析摘要:本文阐述了常用伪随机序列m 序列的产生方法,对其自相关性和互相关性等主要性质进行简要分析。
关键字:m 序列;伪随机序列;相关性;m code sequence and relevant theory analysesAbstict : This paper expounds the generation method of commonly used pseudo-random sequence: m sequence and carries the brief analys on auto correlation mutual correlation.Keywords :m sequence; pseudo-random sequence; correlation1 引言在通信系统中,随机噪声会使数字信号出现误码和使模拟信号产生失真和,而且随机噪声也是限制信道容量的一个重要因素。
因此人们经常希望消除或减少通信系统中的随机噪声。
另一方面,在实际需要时人们产生随机噪声并利用随机噪声。
例如,在实验室中可能要故意加入一定的随机噪声对通信设备或系统的各个性能指标进行测试。
又如通过利用掺入随机噪声来提高通信的可靠性。
为了满足上述实际应用要求,则需要产生满足对应要求的随机噪声信号。
实际中,难以重复产生和处理随机噪声是利用随机噪声的最大困难。
2 m 序列的产生m 序列又称伪随机序列、伪噪声码(PN)或伪随机码。
其中:确定序列是可以预先确定并且可以重复实现的序列;随机序列是既不能预先确定又不能重复实现的序列;伪随机序列是不能预先确定但可以重复产生的序列。
m 序列(全称:最长线性反馈移位寄存器序列)是最为常用的一种伪随机序列。
m 序列是由带线性反馈的移位寄存器产生的序列,并且具有最长的周期。
由n 级串接的移位寄存器和对应级别的反馈逻辑电路可组成动态移位寄存器,如果反馈逻辑线路只用线性模2和构成,那么就称此寄存器为线性反馈移位寄存器;但是反馈逻辑线路中出现如“与”、“或”等运算,那么称此寄存器为非线性反馈移位寄存器。
m序列的原理

m序列的原理
M序列(Maximum Length Sequence)是一种伪随机序列生成
方法,也称为伪随机二进制序列。
它具有自相关性和互相关性很小的特点,并且具有最长周期。
M序列的生成原理基于反馈移位寄存器(Feedback Shift Register,FSR)。
FSR是由多个D触发器(D Flip-Flop)组
成的,每个D触发器的输出作为下一个D触发器的输入,并
形成移位链。
M序列的开始状态可以是任意的,并通过逻辑运算(如异或
运算)将连续的寄存器输出进行组合,生成伪随机序列。
M
序列的周期取决于FSR的长度,理论上可以达到2的n次方-1,其中n为FSR的长度。
生成M序列的特点如下:
1. 周期最长:当FSR的长度为n时,M序列的周期为2的n
次方-1。
2. 互相关性和自相关性较小:M序列具有较小的相互相关性
和自相关性,适合用于通信系统中的扩频技术。
3. 均匀性:M序列的值为+1或-1,每个值出现的概率相等,
具有较好的均匀性。
4. 硬件实现简单:使用FSR和逻辑运算可以很容易地生成M
序列,不需要复杂的计算。
M序列在通信系统中的应用广泛,主要用于扩频通信中的伪
随机序列生成、同步检测以及信号捕获等方面。
m序列的仿真验证

m序列的仿真验证一:实验目的:利用matlab验证m序列的产生方法及其自相关特性二:实验要求:设m序列的生成多项式为g(x)=1+x3+ x4,求(1)m序列的输出及其自相关序列;(2)设脉冲成形为p(t)= 1 0<t<T s0 其他画出其m序列信号的自相关函数;(3)设脉冲波形为升余弦成形(α=0),画出其m序列信号的自相关函数。
三:实验原理:m序列即为maximal length linear feedback shift register sequence 它具有类似与随机噪声的某些统计特性,有是可以重复产生的。
四:实验源码:clear all;close all;g=19;state=8;L=1000;%m序列产生N=15;mq=mgen(g,state,L);%求序列自相关ms=conv(1-2*mq,1-2*mq(15:-1:1))/N;figure(1)subplot(222)stem(ms(15:end));axis([0 63 -0.3 1.2]);title('m序列自相关')%m序列构成的信号(矩形脉冲)N_sample=8;Tc=1;dt=Tc/N_sample;t=0:dt:Tc*L-dt;gt=ones(1,N_sample);mt=sigexpand(1-2*mq,N_sample);mt=conv(mt,gt);figure(1)subplot(221);plot(t,mt(1:length(t)));axis([0 63 -1.2 1.2]);title('m序列矩形形成信号')st=sigexpand(1-2*mq(1:15),N_sample);s=conv(st,gt);st=s(1:length(st));rt1=conv(mt,st(end:-1:1))/(N*N_sample);subplot(223);plot(t,rt1(length(st):length(st)+length(t)-1));axis([0 63 -1.2 1.2]);title('m序列矩形形成信号的自相关');xlabel('t');%sinc脉冲Tc=1;dt=Tc/N_sample;t=-20:dt:20;gt=sinc(t/Tc);mt=sigexpand(1-2*mq,N_sample);mt=conv(mt,gt);st2=sigexpand(1-2*mq(1:15),N_sample);s2=conv(st2,gt);st2=s2;rt2=conv(mt,st2(end:-1:1))/(N*N_sample);subplot(224);t1=-55+dt:dt:Tc*L-dt;%plot(t,mt(1:length(t)));plot(t1,rt2(1:length(t1)));axis([0 63 -0.5 1.2]);title('m序列sinc形成信号的自相关');xlabel('t');调用函数:sigexpand(d,M)function[out]=sigexpand(d,M)N=length(d);out=zeros(M,N);out(1,:)=d;out=reshape(out,1,M*N);五:实验结果及分析:m序列的输出波形在每次运行程序后不尽相同,这是由m序列特性决定的,它是一种伪随机序列。
系统辨识M序列

1.M序列的产生因为Np=15,所以应该用4个移位寄存器。
连接图如下:仿真图如下:表如下:用程序实现如下:X1=0;X2=0;X3=0;X4=0; %定义移位寄存器Xi初态(1000),Yi为移位寄存器各级输出m=32; %置M序列总长度for i=1:m %1#Y4=X4; Y3=X3; Y2=X2; Y1=X1;X4=Y3; X3=Y2; X2=Y1;X1=xor(Y3,Y4); %异或运算if Y4==0U(i)=0.03;elseU(i)=Y4*(-0.03);endendM=U;figure(1) %绘M序列图i1=ik=1:1:i1;stairs(M,'g-')xlabel('k')ylabel('M序列')title('移位寄存器产生的M序列')2.从图形得到数据Y=[2.05 1.80 1.84 1.79 1.08 0.68 0.44 0.80 1.91 2.38 2.47 2.51 3.05 2.69 1.94 1.82 1.82 2.03 2.03 1.03 0.68 0.52 0.86 1.78 2.50 2.50 2.32 3.28 2.82 2.04 2.01 1.67 1.70 1.82 1.04 0.59 0.38 0.81 1.91 2.55 2.28 2.56 3.13 2.70 2.01];3.相关函数s=0;c=0; %设置中间变量,初始化R=zeros(1,15);r=zeros(1,32);%初始化相关数组for i=1:15 %计算相关函数for j=16:32r(j)=U(j-i+1)*Y(j)/30;s=s+r(j)endR(i)=s;s=0;endc=(-1)*R(15); %求补偿量cfor i=1:15 %求脉冲响应g(k)g(i)=15*(R(i)+c)/(4*0.03^2*16)endfigure(3)plot(R)xlim([1,15])ylabel('Rym')title('互相关函数');4.脉冲响应曲线hold onfigure(4)plot(g)xlim([1,15])ylabel('g')title('脉冲响应');5.阶跃响应曲线hold onp=0;for k=1:15 %用积分法求阶跃响应for l=1:kp=g(l)+pendv(k)=p;p=0;endfigure(5)plot(v)title('阶跃响应')xlim([1,15]);hold on6.得出加热炉的数学模型选择采样间隔T=1,于是得g(t)在t=[1:1:15]这15个时刻对应的值为:0.2813, 0.3177, 0.6094, 3.896,9.021, 12.76,15.97,18.14,19.82, 21.21,21.79, 21.74 21.86, 22.1, 22.1用Z 变换的方法来求解系统的传递函数,设2121)(a z a z z b z G ++= (1) 由实验曲线阶跃响应曲线可得其Z 变换G (z )(采样间隔为T=1)为0.2813/z +0.3177 /z^2+0.6094/z^3 (2)要使(1)式与(2)式相等,则应取 b 1=0.3201 a 1= -1.2158 a 2= -1.2369 则可以得到:()20.32011.2158 1.2369s G s s s =--。
M序列自相关辨识与机理分析结合法

PLC
电压u与高度 H之间的非线
性关系
电压u
1
Ts +1
设定高度h
图 2-9 整体模型方框图
第三章 总结
本文 Airball Demo 建模涉及机理建模与使用自相关辨识的暗箱建模。M 序 列自相关辨识法使用简单,实践也证明其有很好的复现性,仿真的结果接近实际 模型。但是,选择合适的 M 序列又因实际模型不同而相差交大,有时甚至需要 多次测量系统的固有特性参数。机理建模理论上能跟实际系统模型完全吻合,但 由于存在随机的,不确定的因素,往往有一定的偏差。无论如何,系统模型辨识 永远无法反映真实的系统,所以单单依据辨识得到的模型进行控制仿真得到的控 制方法需要再实际系统中运行、多次改进之后才有实用性。现在出现了很多更为 先进的控制方法,例如把系统辨识融合到控制算法中,不断改变控制参数以适应 系统模型的改变,对与模型的准确性要求不高。
(2.4)所示。
F
−
mg
=
m
d 2v dt 2
(2.3)
v
=
1 m
∫∫
(F
−
mg
)dt
(2.4)
乒乓球子系统方框图如图 2-3 所示。
风扇作用力F+ -
1
1
1 乒乓球高度H
m
s
s
mg
乒乓球自身重力G
图 2-3 乒乓球子系统方框图
2.2 M 序列自相关法辨识
2.2.1M 序列产生 M 序列属于伪随即信号,其自相关函数和功率谱在一定条件下接近于白噪声
f
=
−
1 2
ρv 2 ACd
(2.1)
其中 v 为乒乓球运动速度空气密度 ρ =1.19kg/m3,乒乓球截面积 A = 0.001256m2 ,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
f
=
−
1 2
ρv 2 ACd
(2.1)
其中 v 为乒乓球运动速度空气密度 ρ =1.19kg/m3,乒乓球截面积 A = 0.001256m2 ,
空气阻力系数 Cd = 0.1。
2
(1) 乒乓球向上运动时, ma = F − mg − f 。
(2) 乒乓球向下运动时, ma = F − mg + f 。
PLC
电压u与高度 H之间的非线
性关系
电压u
1
Ts +1
设定高度h
图 2-9 整体模型方框图
第三章 总结
本文 Airball Demo 建模涉及机理建模与使用自相关辨识的暗箱建模。M 序 列自相关辨识法使用简单,实践也证明其有很好的复现性,仿真的结果接近实际 模型。但是,选择合适的 M 序列又因实际模型不同而相差交大,有时甚至需要 多次测量系统的固有特性参数。机理建模理论上能跟实际系统模型完全吻合,但 由于存在随机的,不确定的因素,往往有一定的偏差。无论如何,系统模型辨识 永远无法反映真实的系统,所以单单依据辨识得到的模型进行控制仿真得到的控 制方法需要再实际系统中运行、多次改进之后才有实用性。现在出现了很多更为 先进的控制方法,例如把系统辨识融合到控制算法中,不断改变控制参数以适应 系统模型的改变,对与模型的准确性要求不高。
因为乒乓球运动的速度 v 较小,最高不会超过 0.1m/s。则空气阻力
f max
=
1 2
× 0.12
× 0.001256× 0.1 =
7.4 ×10−7
N
(2.2)
由式(2.2)看出,空气阻力与 F 或者 G 相比相差太大,可以忽略。则乒乓球向
上和向下运动的过程可以统一为 ma = F − mg ,微分与积分方程分别如式(2.3)与
N −1
∑ RMz (k) ≈ g( j)RMM (k − j)Δt j=0
M 序列的响应函数可写成
⎧
∑ ⎪
⎪
RMz (k )
⎨
∑ ⎪⎪⎩RMM (k)
= =
1 Np 1 Np
N p −1
M (i
i=0 N p −1
M (i
i=0
− k)z(i) − k)M (i)
从式(2.11)和(2.12),可推导出 M 序列的自相关函数为
1
电压u
Ts +1
电压u与高度H 之间的非线性
对应
运算处理
图 2-8 红外高度传感器子系统方框图
2.4 系统整体模型
到目前为止,三个子系统的模型都已建立。系统的整体模型如图 2-9 所示。
7
电机输入电压U U与F的响应函数 风扇作用力F+
1
g(k)
-
m
mg
乒乓球自身重力G
1
1 乒乓球高度H
s
s
运算处理
2.1 乒乓球子系统机理建模
在整个模型中,机理最为明确的的是乒乓球的受力过程。乒乓球受到三个力 作用分别是自身重力 G,风力 F 和空气阻力 f。乒乓球上升和下降过程受力分别 如图 2-1、2-2 所示。
F
Ff
v
v
Gf 图2-1 乒乓球上升过程受力图
G 图2-2 乒乓球下降过程受力图
根据牛顿第二定理, F合 = ma 。空气阻力计算公式[1],
RMM
⎧ (k )⎪⎩⎪⎨−
a2 , a2 , Np
k = 0, N p ,2N p,L , k ≠ 0, N p ,2N p,L
系统输入输出的互相关函数为
RMz
(k)
=
(N
p
+ 1)a 2Δt Np
g(k)
−
c
∑ 式中
c
=
a 2 Δt
N p −1
g (i)
。对于稳定的系统,
c
是有界常数,而且很小。
(2.4)所示。
F
−
mg
=
m
d 2v dt 2
(2.3)
v
=
1 m
∫∫
(F
−
mg
)dt
(2.4)
乒乓球子系统方框图如图 2-3 所示。
风扇作用力F+ -
1
1
1 乒乓球高度H
m
s
s
mg
乒乓球自身重力G
图 2-3 乒乓球子系统方框图
2.2 M 序列自相关法辨识
2.2.1M 序列产生 M 序列属于伪随即信号,其自相关函数和功率谱在一定条件下接近于白噪声
第一章 模型简介
Airball Demo 实验装置由贝加莱公司提供,该系统由控制器、风扇、玻璃管、 乒乓球组成,如图 1-1 所示。各部件描述如下。 1. 底座:系统的支撑部分,主要是固定管道部分和乒乓球。此外,
还在底部安装了吹动乒乓球的直流风扇,与检测乒乓球 高度的红外传感器。 2. 管道:与底座相连,是乒乓球竖直运行的通道。管道外直径为 50mm,壁厚为 4mm, 可保证乒乓球在管道内自由(无 摩擦)运行。管道有效长度:400mm。 3. 乒乓球:标准乒乓球,直径 40mm,重量 2.7g。 接通风扇电源,风扇转动形成的气流将对乒乓球作用一个向 上的力,通过控制风扇的转速,可以调节对乒乓球的作用力,使 之在管道内上下运行并稳定在某一设定高度。 总的来说,整个系统的输入为电机的电压 U,输出为乒乓球 的高度 H。其控制方框图如图 1-2 所示。
的确定性、周期性的信号。M 序列是由 N 级串联的移位寄存器,按照一定的反 馈联结而产生的周期性方波。四级移位寄存器产生 M 序列结构图如图 2-4[2]所示。
图 2-4 四级移位寄存器产生 M 序列结构图
3
图中,⊕ 表示异或运算,C1 、C2 、C3 、C4 表示四个移位寄存器,x1 、x2 、 x3 、 x4 分别表示各移位寄存器的输出, x4 输出为 M 序列。四级移位寄
H
0
2 34 5
图 2-7 传感器阶跃响应曲线
可以使用一阶惯性环节近似,如下
C(s) = 1 Ts + 1
(2.16)
其中,T 为传感器的时间常数,T 越小,传感器器响应越快。可以通过测得
传感器阶跃响应曲线,类似图 2-7,得到时间常数T 。红外高度传感器子系统方
框图如图 2-8 所示。
PLC
高度H
图 2-6 高度与输出电压曲线 传感器存在惯性,它的输出不能立即复现输入信号,而是从零开始,按指数 规律上升,最终达到稳态值。使用阶跃相应法测传感器惯性的传递函数。使 t0 时
6
刻传感器输出 0 高度(经过非线性转换), t1 时刻传感器输入 h 的高度并同时记 录传感器的经过转换的输出高度 H 的时间响应曲线,其一般形式如图 2-7 所示。
存器的连接方式可用式(2.5)表示。
⎧ x2 (k +1) = x1(k)
⎪⎪ ⎨ ⎪
x3 (k +1) = x2 (k) x3(k +1) = x3(k)
⎪⎩x1(k +1) = x3 (k) ⊕ x4 (k)
(2.5)
设初始状态为 1010,在移位脉冲 CP 作用下,寄存器各级状态的变化如表 2.1[2]
2.2.2 相关辨识原理
相关辨识的理论较为复杂,涉及使用变分法求泛函最小值函数问题,此处作 简要说明。相关辨识的基础是 Wiener – Hopf 方程,如式(2.6)所示。
∫ Rxy (τ ) =
∞ 0
g (t ) R xx
(t
−
τ
)dt
ቤተ መጻሕፍቲ ባይዱ
(2.6)
使用 M 序列相关辨识过程中,式(2.6)中的 g(t) 为系统输出 y(t) 与输入 x(t) 的比
可很大程度上简化计算过程,此时 Wiener – Hopf 变换为
∫ RMz (τ ) ≈
N 0
p Δt
g
(t
)RMM
(t
−
τ
)dt
(2.9)
式中,N p 是 M 序列的循环长度;Δt 是 M 序列移位脉冲的周期。当 N p 充分大时,
RMz (τ ) ≈ a2 g(τ )
当数据采集时间和 Δt 相等时,式(2.9)的离散形式为
N p i=0
到目前为止,可以得到 M 序列自相关辨识法求响应函数为
(2.10) (2.11) (2.12) (2.13) (2.14)
5
g(k)
=
(Np
Np + 1)a 2 Δt
[RMz
(k)
+
c]
(2.15)
2.2.3 电机输入电压 U 与风扇输出作用力 F 关系辨识
由于不能输出负电压给电机,M 序列输出的两极电压可取 0 与 24V。使用 PLC 编程实现 M 序列输出,通过 PWM 模块向电机供电。由于风扇对乒乓球的 作用力 F 无法直接测得,可以通过测乒乓球的高度 H,通过式(2.3)转换为 F。此 时得到 M 序列与 F 的离散值(注意数据采集时间和 Δt 相等才能使得两个数组同 维),根据式(2.15)可以推导出 U 与 F 之间的关系,其方框图如图 2-5 所示。
当前值的依赖关系的统计测度。对于离散系统,
Rxx
(τ
)
=
Lim
N →∞
1 N
[x(k)x(k
−τ
)]
(2.8)
由式(2.6)可知,如果知道输入的自相关函数 Rxx 和输入与输出的自相关函数 Rxy ,可以求得输入与输出之间的函数关系 g(t) 。但存在的问题是,由于存在积 分关系, g(t) 的求解过程并不简单。使用 M 序列伪随机信号作为激励输入,则
电机输入电压U U与F的响应函数 风扇对乒乓球作用力F g(k)
