和、差、积、商变化规律
运算定律 和差积商的变化 规律

名称定义字母表示加法交换律几个数相加,任意交换加数的位置,它们的和不变。
a+b=b+a加法结合律三个数相加,先把前两个数相加,再同第三个数相加;或者先把后两个数相加,再同第一个数相加,它们的和不变。
(a+b)+c=a+(b+c)乘法交换律几个数相乘,任意交换因数的位置,它们的积不变。
ab=ba乘法结合律三个数相乘,先把前两个数相乘,再同第三个数相乘;或者先把后两个数相乘,再同第一个数相乘,它们的积不变。
(ab)c=a(bc)乘法分配律☆两个数的和同第三个数相乘,可以把和里的每个加数分别同第三个数相乘,再把两个积相加,结果不变。
☆两个数的差同第三个数相乘,可以把被减数和减数分别同第三个数相乘,再把两个积相减,结果不变。
(a+b)c=ac+bc(a-b)c=ac-bc乘法分配律逆运算☆一个数分别乘以两个数,然后把所得的积相加,等于这个数乘以这两个数的和,结果不变。
☆一个数分别乘以两个数,然后把所得的积相减,等于这个数乘以这两个数的差,结果不变。
ac+bc=(a+b)cac-bc=(a-b)cac+c=(a+1)cac-c=(a-1)c减法运算的性质☆一个数连续减去两个数,等于这个数减去这两个数的和,结果不变。
☆一个数减去两个数的和,等于这个数连续减去这两个数,结果不变。
a-b-c=a-(b+c)a-(b+c)=a-b-c除法运算的性质☆一个数连续除以两个数,等于这个数除以这两个数的积,结果不变。
☆一个数除以两个数的积,等于这个数连续除以这两个数,结果不变。
a÷b÷c=a÷(bc)a÷(bc)=a÷b÷c运算定律和差积商的变换规律名称文字叙述字母表示和的变化规律☆若一个加数增加(或减少)一个数,另一个加数不变,则它们的和也增加(或减少)同一个数。
☆若一个加数增加一个数,另一个加数减少同一个数,则它们的和不变若a+b=c则(a+d)+b=c+d(a-d)+b=c-d,(a+d)+(b-d)=c☆当减数不变,被减数增加(或减少),差也若a-b=c则(a+d)-b=c+d差的变化规律增加(或减少)相同的数☆当被减数不变,减数增加(或减少),差反而减少(或增加)相同的数☆若被减数和减数同时增加(或都减少)相同的数,差不变(a-d)-b=c-d a-(b+d)=c-da-(b-d)=c+d (a+d)-(b+d)=c (a-d)-(b-d)=c (a>b+d)积的变化规律☆当一个因数不变,另一个因数扩大(或缩小)若干倍,它们的积也扩大(或缩小)同样的倍数☆若一个因数扩大若干倍,另一个因数缩小同样的倍数,它们的积不变若ab=c则(an)b=cn (a÷n)b=c÷n,(an)(b÷n)=c(a÷n)(bn)=c商的变化规律(整除时)☆当除数不变,被除数扩大(或缩小),商也随着扩大(或缩小)同样的倍数☆当被除数不变,除数扩大(或缩小),商反而缩小(或扩大)同样的倍数。
(完整版)和差积商的变化规律
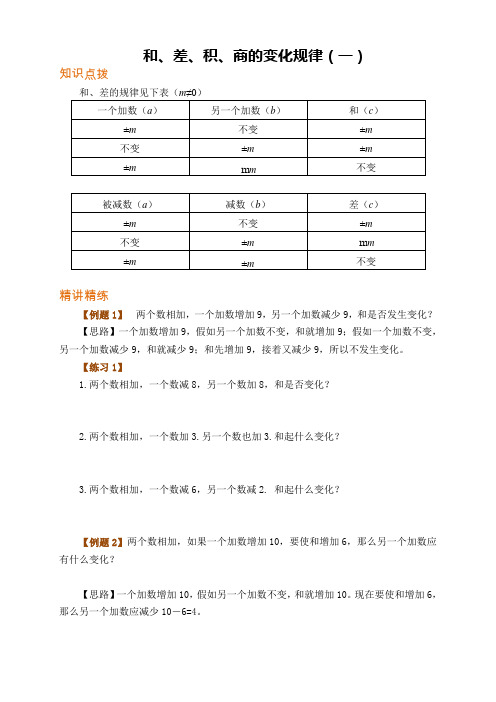
和、差、积、商的变化规律(一)知识点拨和、差的规律见下表(m≠0)精讲精练【例题1】两个数相加,一个加数增加9,另一个加数减少9,和是否发生变化?【思路】一个加数增加9,假如另一个加数不变,和就增加9;假如一个加数不变,另一个加数减少9,和就减少9;和先增加9,接着又减少9,所以不发生变化。
【练习1】1.两个数相加,一个数减8,另一个数加8,和是否变化?2.两个数相加,一个数加3.另一个数也加3.和起什么变化?3.两个数相加,一个数减6,另一个数减2. 和起什么变化?【例题2】两个数相加,如果一个加数增加10,要使和增加6,那么另一个加数应有什么变化?【思路】一个加数增加10,假如另一个加数不变,和就增加10。
现在要使和增加6,那么另一个加数应减少10-6=4。
【练习2】1.两个数相加,如果一个加数增加8,要使和增加15,另一个加数应有什么变化?2.两个数相加,如果一个加数增加8,要使和减少15,另一个加数应有什么变化?3.两个数相加,如果一个加数减少8,要使和减少8,另一个加数应有什么变化?【例题3】两数相减,如果被减数增加8,减数也增加8,差是否起变化?【思路】被减数增加8,假如减数不变,差就增加8;假如被减数不变,减数增加8,差就减少8。
两个数的差先增加8,接着又减少8,所以不起什么变化。
【练习3】1.两数相减,被减数减少6,减数也减少6,差是否起变化?2.两数相减,被减数增加12.减数减少12.差起什么变化?3.两数相减,被减数减少10,减数增加10,差起什么变化?【例题4】两数相乘,如果一个因数扩大8倍,另一个因数缩小2倍,积将有什么变化?【思路】如果一个因数扩大8倍,另一个因数不变,积将扩大8倍;如果一个因数不变,另一个因数缩小2倍,积将缩小2倍。
积先扩大8倍又缩小2倍,因此,积扩大了8÷2=4倍。
【练习4】1.两数相乘,如果一个因数缩小4倍,另一个因数扩大4倍,和是否起变化?2.两数相乘,如果一个因数扩大3倍,另一个因数缩小12倍,积将有什么变化?3.两数相乘,如果一个因数扩大3倍,另一个因数扩大6倍,积将有什么变化?【例题5】两数相除,如果被除数扩大4倍,除数缩小2倍,商将怎样变化?【思路】如果被除数扩大4倍,除数不变,商就扩大4倍;如果被除数不变,除数缩小2倍,商就扩大2倍。
商和积的变化规律

1、商不变的性质:
被除数和除数同时扩大或缩小(乘以或除以)相同的数 (0除外),商不变。
2、商的变化规律: 被除数÷除数=商
a、除数(老二)不变,被除数(老大)扩大或缩小几倍, 商也跟着扩大或者缩小几倍。
b、被除数(老大)不变,除数(老二)扩大或缩小几倍, 商反而缩小或扩大几倍。
C、如果被除数和除数都变化,则根据具体情况判断商的 变化情况。
5.22÷1.8=
52.2÷0.18=
52.2÷18=
522÷0.18=
0.522÷0.18=
大家好
5
大家好
6
大家好
7
大家好
8
结束
大家好
9
大家好
1
二、积的规律
1、积不变的规律:
一个因数扩大或缩小几倍,另一个因数缩小或者 扩大相同的倍数,积不变。
2、积的变化规律:(因数×因数=积)
a、一个因数不变,另一个因数扩大或者缩小几倍, 积也跟着扩大或者缩小相同的倍数。
b、一个因数扩大m倍,另一个因数扩大n倍,则 积扩大m×n倍。
大家好
2
大家好
3
根据125×48=6000,直接写出下面各式的积。
1、1.25×4.8=
2、1.25×0.048=
3、0.125×4.8=
4、0.125×0.48=
大家好
4
根据47×14=658,直接写出下面各式的积。
0.47×14=
4.7×14=
47×0.14=
பைடு நூலகம்
0.47×0.14=
根据522÷18=29
52.2÷1.8=
小学数学四则运算的变化规则(和差积商变化规律)

四则运算的变化规则一、加法的变化规则(1)加法公式:加数+ 加数= 和加数= 和—另一个加数(2)加法的变化规则有:(一)如果一个加数增加几,另一个加数不变,那么和也增加几。
例如:13+5=18(13+2)+5=18+2题型1小丽在做一道加法题,一个加数十位上的4看作了7,个位上的5看作了2,算得的和是87。
正确的和是多少?一个加数十位4——7,个位5——2 增加 72-45=27另一个加数不变正确的和增加27即正确的和+27=87 => 正确的和=87-27=60(二)如果一个加数减少几,另一个加数不变,那么和也减少几。
例如:28+16=44(28-12)+16=44-12题型1小强在计算加法时,把一个加数十位上的7错写成1,把个位上的8错写成0,所得的和是285。
正确的和是多少?一个加数十位7——1,个位8——0 减少 78-10=68另一个加数不变正确的和减少68即正确的和-68=285 => 正确的和=285+68=353题型2两个数相加,一个加数减少29,另一个加数不变,和将有什么变化?一个加数减少29另一个加数不变和减少29题型3两个数相加,和是100,一个加数减少48,另一个加数不变,现在和是多少?一个加数减少48另一个加数不变和减少48即现在的和=100-48=52(三)如果一个加数增加几,另一个加数减少同样的几,那么和不变。
例如:112+23=135(112+3)+(23-3)=135题型1:两个加数的和是378,其中一个加数增加245,另一个加数减少245,现在这两个加数的和是(378 )。
题型2:一个加数增加6,要使和保持不变,另一个加数应(减少6 )。
(四)如果一个加数增加几,另一个加数增加另一个几,那么和增加了(几+另一个几)。
例如:35+48=83(35+12)+(48+5)=83+(12+5)题型1:小明在计算加法时,把一个加数十位上的0错写成8,把另一个加数个位上的6错写成9,所得的和是532。
四年级奥数和差积商的变化规律
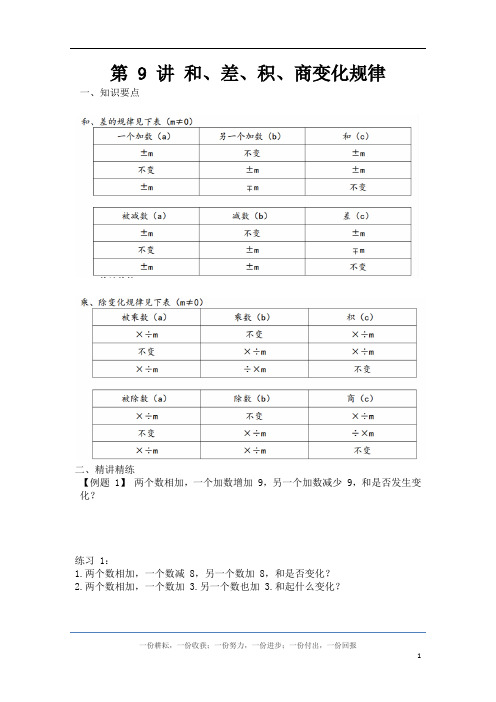
第 9 讲和、差、积、商变化规律一、知识要点二、精讲精练【例题 1】两个数相加,一个加数增加 9,另一个加数减少 9,和是否发生变化?练习 1:1.两个数相加,一个数减 8,另一个数加 8,和是否变化?2.两个数相加,一个数加3.另一个数也加 3.和起什么变化?【例题 2】两个数相加,如果一个加数增加 10,要使和增加 6,那么另一个加数应有什么变化?练习 2:1.两个数相加,如果一个加数增加 8,要使和增加 15,另一个加数应有什么变化?2.两个数相加,如果一个加数增加 8,要使和减少 15,另一个加数应有什么变化?【例题 3】两数相减,如果被减数增加 8,减数也增加 8,差是否起变化?练习 3:1.两数相减,被减数减少 6,减数也减少 6,差是否起变化?2.两数相减,被减数增加 12.减数减少 12.差起什么变化?【例题 4】两数相乘,如果一个因数扩大 8 倍,另一个因数缩小 2 倍,积将有什么变化?练习 4:1.两数相乘,如果一个因数缩小 4 倍,另一个因数扩大 4 倍,和是否起变化?2.两数相乘,如果一个因数扩大 3 倍,另一个因数缩小 12 倍,积将有什么变化?【例题 5】两数相除,如果被除数扩大 4 倍,除数缩小 2 倍,商将怎样变化?练习 5:1.两数相除,被除数扩大 30 倍,除数缩小 5 倍,商将怎样变化?2.两数相除,被除数缩小 12 倍,除数缩小 2 倍,商将怎样变化?【例题 6】两数相减,被减数减少 8,要使差减少 12.减数应有什么变化?练习6:1.两数相减,如果被减数增加 6,要使差增加 15,减数应有什么变化?2.两数相减,如果被减数增加 20,要使差减少 12.减数应有什么变化?【例题7】两个数相除,商是 8,余数是 20,如果被除数和除数同时扩大 10 倍,商是多少?余数是多少?练习7:1.两数相除,商是 6,余数是 30,如果被除数和除数同时扩大 10 倍,商是多少?余数是多少?2.两个数相除,商是 9,余数是 3。
四年级上册数学思维拓展题:和差积商变化规律

四年级上册数学思维拓展题:和差积商变化规律和的变化规律:如果一个加数增加(或减少)一个数(不为0),另一个加数不变,则它们的和也增加(或减少)同一个数。
如果一个加数增加一个数(不为0),另一个加数减少同一个数,和不变。
差的变化规律:如果一个被减数增加(或减少)一个数(不为0),减数不变,则差增加(或减少)同一个数。
如果一个被减数和减数同时增加(或减少)一个数(不为0),差不变。
如果被减数不变,一个减数增加(或减少)一个数(不为0),差也减少(或增加)同一个数。
积的变化规律:1.一个因数扩大(或缩小)若干倍,另一个因数不变,积也扩大(或缩小)相同的倍数。
2.一个因数扩大(或缩小)若干倍,而另一个因数缩小(或扩大)相同的倍数,它们的积不变。
3.一个因数乘以(或除以)a,另一个因数乘以(或除以)b,积就乘以(或除以)ab的积。
商的变化规律:1.被除数扩大(或缩小)若干倍,除数不变,商也扩大(或缩小)同样的倍数。
2.被除数不变,除数扩大(或缩小)若干倍,商反而缩小(或扩大)相同的倍数。
3.被除数乘以a,除数除以b,商就乘以ab的积。
4.被除数除以a,除数乘以b,商就除以ab的积。
参考答案:1、两个数相加,如果一个加数减少9,要使和增加9,另一个加数应该有什么变化?解题思路:一个加数减少9,假设另一个加数不变,和就减少了9;题目要求和增加9,所以另一个加数应该增加9+9=18。
2、两个数相减,如果被减数减少10,减数也减少10,差是否有变化?解题思路:被减数减少10,假设减数不变,差就减少10;假设被减数不变,减数减少10,和就增加10;差先减少10,再增加10,所以无变化。
3、被减数、减数、差相加得2076,差是减数的一半。
如果被减数不变,差增加42,减数应该变成多少?解题思路:减数与差的和即是被减数,2076里有2个被减数,被减数等于2076÷2=1038。
差是减数的一半,也就是说减数是差的2倍,差应该为1038÷(2+1)=346,减数为346×2=692。
六年级上册数学讲义-和、差、积、商的变化规律-人教版(含答案)

和、差、积、商的变化规律学生姓名年级学科授课教师日期时段核心内容和、差、积、商的变化规律课型一对一/一对N教学目标1.掌握和、差、积、商的变化规律2.学会根据规律进行速算重、难点根据积、商的变化规律速算课首沟通1、上讲回顾(错题管理);检查作业;2、询问学生加减乘除的运算公式知识导图课首小测1.两个数相加,一个加数增加25,另一个加数也增加15,和()。
2.两数相减,如果被减数减少18,减数减少8,差()。
3.两个因数相乘,如果一个因数缩小5倍,另一个因数扩大5倍,积()。
4.根据每组第一个算式的结果,直接写出第二、第三个算式的得数。
(1)18÷6=3(18×2)÷(6×2)= (18×3)÷(6×3)= (2)480÷10=48(480÷2)÷(10÷2)= (480÷5)÷(10÷5)= (3)420÷6=70(420×2)÷(6÷2)= (420÷5)÷(6×2)=知识梳理导学一:和的变化规律例 1. 按题目要求解答下列各题。
(1)两个数相加,一个数减8,另一个数加8,和是否变化?(2)两个数相加,一个数加3,另一个数也加3,和有什么变化?(3)两个数相加,一个数减6,另一个数减2,和有什么变化?例 2. 按要求解答下列各题。
(1)两个数相加,如果一个加数增加8,要使和增加15,另一个加数应有什么变化?(2)两个数相加,如果一个加数增加8,要使和减少15,另一个加数应有什么变化?例 3. 小华在计算两个数相加时,把一个加数个位上的1错误地写成7,把另一个加数十位上的3错误地写成8,所得的和是1996。
原来两个数相加的正确答案是多少?例 4. 两个加数都扩大了8倍,则和扩大()倍。
【学有所获】两个加数都乘以(或除以)同一个数(零除外),和也乘以(或除以)同一个数。
《和、差、积、商》的变化规律例题与练习

《和、差、积、商》的变化规律例题与练习
例题1、两个数相加,一个加数增加8,另一个加数较少8,和有什么变化?
练习:两个数相加,一个加数增加26,另一个加数较少26,和有什么变化?
例题2、两个数相加,如果一个加数增加18,要使和增加6,那么另一个加数应有什么变化?
练习:两个数相加,如果一个加数减少16,要使和减少9,那么另一个加数怎样变化?
例题3、两数相减,被减数减少15,如果要使差减少20,减数应怎样变化?
练习:.两数相减,被减数增加12,如果要使差增加5,减数应怎样变化?
例题4、两数相乘,如果一个因数扩大6倍,另一个因数缩小2倍,积怎样变化?
练习:两数相乘,如果一个因数扩大12倍,另一个因数缩小4倍,积怎样变化?
例题5、两数相除,如果被除数扩大6倍,除数缩小3倍,商怎样变化?
练习:两数相除,如果被除数扩大5倍,除数缩小5倍,商怎样变化?
例题6、两个因数的积是72,如果一个因数扩大2倍,另一个因数缩小 3倍,这时两数的积是多少?
练习:两个数的积是42,其中一个因数扩大2倍,另一个因数缩小6倍,这时积应是多少?。
著名机构五升六数学讲义和、差、积、商的变化规律

和、差、积、商的变化规律学生姓名年级学科授课教师日期时段核心内容和、差、积、商的变化规律课型一对一/一对N教学目标1.掌握和、差、积、商的变化规律2.学会根据规律进行速算重、难点根据积、商的变化规律速算课首沟通1、上讲回顾(错题管理);检查作业;2、询问学生加减乘除的运算公式知识导图课首小测1.两个数相加,一个加数增加25,另一个加数也增加15,和()。
2.两数相减,如果被减数减少18,减数减少8,差()。
3.两个因数相乘,如果一个因数缩小5倍,另一个因数扩大5倍,积()。
4.根据每组第一个算式的结果,直接写出第二、第三个算式的得数。
(1)18÷6=3(18×2)÷(6×2)= (18×3)÷(6×3)= (2)480÷10=48(480÷2)÷(10÷2)= (480÷5)÷(10÷5)= (3)420÷6=70(420×2)÷(6÷2)= (420÷5)÷(6×2)=知识梳理例 1. 按题目要求解答下列各题。
(1)两个数相加,一个数减8,另一个数加8,和是否变化?(2)两个数相加,一个数加3,另一个数也加3,和有什么变化?(3)两个数相加,一个数减6,另一个数减2,和有什么变化?例 2. 按要求解答下列各题。
(1)两个数相加,如果一个加数增加8,要使和增加15,另一个加数应有什么变化?(2)两个数相加,如果一个加数增加8,要使和减少15,另一个加数应有什么变化?例 3. 小华在计算两个数相加时,把一个加数个位上的1错误地写成7,把另一个加数十位上的3错误地写成8,所得的和是1996。
原来两个数相加的正确答案是多少?例 4. 两个加数都扩大了8倍,则和扩大()倍。
【学有所获】两个加数都乘以(或除以)同一个数(零除外),和也乘以(或除以)同一个数。
四上《和、差、积、商》的变化规律例题与练习

四上《和、差、积、商》的变化规律例题与练习姓名:________ 家长签字:_________ 例题1、两个数相加,一个加数增加8,另一个加数较少8,和有什么变化?练习:两个数相加,一个加数增加26,另一个加数较少26,和有什么变化?例题2、两个数相加,如果一个加数增加18,要使和增加6,那么另一个加数应有什么变化?练习:两个数相加,如果一个加数减少16,要使和减少9,那么另一个加数怎样变化?例题3、两数相减,被减数减少15,如果要使差减少20,减数应怎样变化?练习:.两数相减,被减数增加12,如果要使差增加5,减数应怎样变化?例题4、两数相乘,如果一个因数扩大6倍,另一个因数缩小2倍,积怎样变化?练习:两数相乘,如果一个因数扩大12倍,另一个因数缩小4倍,积怎样变化?例题5、两数相除,如果被除数扩大6倍,除数缩小3倍,商怎样变化?练习:两数相除,如果被除数扩大5倍,除数缩小5倍,商怎样变化?例题6、两个因数的积是72,如果一个因数扩大2倍,另一个因数缩小 3倍,这时两数的积是多少?练习:两个数的积是42,其中一个因数扩大2倍,另一个因数缩小6倍,这时积应是多少?课内练习1、两个数相加,一个加数增加a,另一个加数减少a,和有什么变化?2、两个数相加,一个加数减少20,要使和减少16,另一个加数应怎样变化?3、两个数相减,被减数增加20,要使差增加26,减数应怎样变化?4、两数相乘,一个因数扩大5倍,另一个因数也扩大5倍,积怎样变化?5、两数相除,如果除数扩大2倍,要使商扩大4倍,被除数应怎样变化?6、两个数的积是126,如果一个因数缩小7倍,另一个因数扩大5倍,积是多少?7、两个数相除商16,余数是25,如果把被除数和除数同时缩小5倍,那么商和余数各是多少?课外练习1、两个数相加,一个加数增加12,另一个加数也增加12,和有什么变化?2、两个数相加,一个加数增加12,要使和减少12,另一个加数应怎样变化?3、两个数相减,减数减少8,要使差减少8,被减数应怎样变化?4、a乘b ,如果a缩小4倍,要使积扩大4倍,b应怎样变化?5、两数相除,如果被除数扩大6倍后又缩小2倍,要使商扩大12倍,除数应怎样变化?6、两数相除,商是18,如果被除数扩大20倍,除数缩小5倍,那么商是多少?7、一个三位数,个位是0,百位数字比十位数字少6,如果把这个数拨在算盘上,一共要用8个算珠,这个三位数是多少?。
积商变化规律

和、差、积、商的变化规律1、和的变化规律(1)如果一个加数增加(或减少)一个数,另一加数不变,那么它们的和也增加(或减少)同一个数。
用字母表示:a+b= c→(a+m)+b=c+m或(a-m)+b=c-m(2)如果一个加数增加一个数,另一个加数减少同一个数,那么它们的和不变。
用字母表示:a+b=c→(a+m)+(b-m)=c2、差的变化规律(1)如果被减数增加(或减少)一个数,减数不变,那么它们的差也增加(或减少)一个数。
用字母表示:a-b= c→(a+ m)- b= c+ m或a- b= c→(a- m)- b = c- m(2)如果被减数不变,减数增加(或减少)一个数,那么它们差反而减少(或增加)同一个数。
用字母表示:a- b= c→a-(b+ m)= c- m或a-(b- m)= c+ m(3)如果被减数和减数都增加(或减少)同一个数,那么它们的差不变。
用字母表示:a- b= c→(a+ m)-(b+ m)= c或(a- m)-(b- m)= c3、积的变化规律(1)一个因数扩大(或缩小)若干倍,另一个因数缩小(或扩大)相同的倍数,积不变。
用字母表示:a×b=c→(a×m)×(b÷m)=c或(a÷m)×(b×m)=c(2)一个因数扩大(或缩小)若干倍,另一个因数不变,积也扩大(或缩小)相同的倍数。
用字母表示:a×b=c→(a×m)×b=c×m或(a÷m)×b=c÷m4、商的变化规律(1)商不变的性质:在除法里,被除数和除数同时乘或除以相同的数(0除外),商不变。
用字母表示:a÷b=c→(a×m)÷(b×m)=c或(a÷m)÷(b÷m)=c(2)除数不变,被除数扩大(或缩小)若干倍,商也扩大(或缩小)相同的倍数。
小学数学奥数解题技巧 第90讲根据和、差、积、商变化规律速算

利用这一规律,可以使计算简便、快速。
例如:645+203=645+200+3 =845+3 =848 397+468=400+468-3 =868-3
同步教材视频
11
小升初数学解题技巧 第90讲 根据和、差、积、商变化规律速算
【根据商的变化规律速算】商的变化规律,有如下三条: (3)被除数和除数都扩大(或者都缩小)同样的倍数,它们的商不变。 运用这一规律速算
例如:690000÷23000=(690000÷1000)÷(23000÷1000) =690÷23 =30 12000÷25=(12000×4)÷(25×4) =48000÷100 =480
小升初数学 总复习
小学数学奥数解题技巧
第九十讲 根据和、差、积、商变化规 律速算
1
小升初数学解题技巧 第90讲 根据和、差、积、商变化规律速算
【根据和的变化规律速算】和的变化规律有以下两条。 (1)如果一个加数增加(或减少)一个数,另一个加数不变,那么它们的 和也增加(或减少)同一个数。
利用这一规律,可以使计算简便、快速。
8
小升初数学解题技巧 第90讲 根据和、差、积、商变化规律速算
【根据积的变化规律速算】积的变化规律有如下两条。 (2)如果一个因数扩大若干倍,另一个因数缩小同样的倍数,那么它
们的积不变。 运用这一规律速算,
例如:240×25=(240÷4)×(250×4) =60×1000 =60000 45×14=(45×2)×(14÷2) =90×2 =180
注意:在有余数的除法里,如果被除数和除数都扩大(或者都缩小)同样的倍数,不 完全商虽然不会变化,但余数会跟着扩大(或者缩小)同样的倍数。要使余数不变, 所得的余数必须缩小(或者扩大)同样的倍数。
积和商“变与不变”规律及练习

积和商“变与不变”规律及练习积和商的“变与不变”规律积的变化规律:1.一个因数不变,另一个因数乘(或除以)几,积就相应的乘(或除以)几。
例如:如果a×b=c,则(a×3)×b=c×3,举例:a×b=12,如果(a×3),则积就是12×3=36.2.一个数乘一个比1大的数,积比原数大;一个数乘一个比1小的数,积比原数小。
积不变规律:1.一个因数乘(或除以)几,另一个因数相应的除以(或乘)几,积不变。
例如:如果a×b=c,则(a×5)×(b÷5)=c。
商的变化规律:1.被除数不变,除数乘或除以几,商就相应的除以或乘几。
例如:如果a÷b=c,则a÷(b×3)=c÷3,举例:a÷b=12,如果(b×3),则商就是12÷3=4.2.除数不变,被除数乘或除以几,商就相应的乘或除以几。
例如:如果a÷b=c,则(a×3)÷b=c×3,举例:a÷b=12,如果(a×3),则商就是12×3=36.被除数大于除数,商就大于1;被除数小于除数,商就小于1.一个数除以一个比1大的数,商比被除数要小;一个数除以一个比1小的数,商比被除数要大。
商不变规律:被除数和除数同时乘或除以几,商不变。
练题:1.根据78×12=936,填写下面各题的结果。
7.8×12=(93.6),0.78×12=(9.36),7.8×(93.6)=(734.88)2.根据414÷18=23,填写下面各题的结果。
4.14÷1.8=(2.3),4140÷1.8=(2300),0.414÷0.18=(2.3),41.4÷18=(2.3)3.根据45×63=2835,填写下面各题的结果。
六年级下册奥数专题练习-根据和、差、积、商变化规律速算-全国通用

根据和、差、积、商变化规律速算【根据和的变化规律速算】和的变化规律有以下两条。
(1)如果一个加数增加(或减少)一个数,另一个加数不变,那么它们的和也增加(或减少)同一个数。
利用这一规律,可以使计算简便、快速。
例如645+203=645+200+3=845+3=848397+468=400+468-3=868-3(2)如果一个加数增加一个数,另一个加数减少同一个数,那么它们的和不变。
利用这一规律,也可以使计算简便、快速。
例如657+309=(657+9)+(309-9)=666+300=966154+286=(154—4)+(286+4)=150+290=(150-10)+(290+10)=140+300=440【根据差的变化规律速算】差的变化规律有如下三条。
(1)如果被减数增加(或减少)一个数,那么它们的差也增加(或减少)同一个数。
运用这一规律的速算,如804—355=800—355+4=445+4=449593—264=600—264—7=336—7=329(2)如果减数增加(或减少)一个数,被减数不变,那么它们的差反而减少(或增加)同一个数。
运用这一规律的速算,如675—298=675—300+2=375+2=377458—209=458—200—9=258—9=249(3)如果被减数和减数都增加(或都减少)同一个数,那么它们的差不变。
运用这一规律的速算,如3520—984=(3520+16)-(984+16)=3536—1000=2526803—345=(803—3)-(345—3)=800—342=458【根据积的变化规律速算】积的变化规律有如下两条。
(1)如果一个因数扩大(或者缩小)若干倍,另一个因数不变,那么它们的积也扩大(或者缩小)同样的倍数。
运用这一规律的速算,如175×4=(25×7)×4=[(25×7)÷25]×4×25=7×4×25=7×(4×25)=70068×25=68×100÷4=6800÷4=1700(2)如果一个因数扩大若干倍,另一个因数缩小同样的倍数,那么它们的积不变。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(a≥b且a≥m,b>m)。
例如:
500-200=300→(500+100)-(200+100)=300,
500-200=300→(500-100)-(200-100)=300
积的变化规律:
积的变化规律
字母表示及举例
如果一个因数扩大到原来的几倍或缩小到原来的几分之一,另一个因数不变,那么它们的积也相应地扩大到
或(a÷n)÷b=c÷n
(a、c都是n的倍数)。
例如:
40÷5=8→ (40×5)÷5=8×5
或(40÷4)÷5=8÷4
如果被除数不变,除数扩大到原来的几倍或缩小到原来的几分之一,那么它们的商反而缩小到原来的几分之一或扩大到原来的几倍
用字母表示:
a÷b=c→ a÷(b×n)=c÷n
(a是b×n的倍数)
或a÷(b÷n)=c×n
(b是n的倍数)
例如:
120÷20=6→120÷(20×3)=6÷3
或120÷(20÷2)=6×2
商不变的性质:
在除法里,被除数和除数同时乘或除以相同的数(0除外),商不变。这个性质
通常被称为“商不变的性质”。
用字母表示:如果a÷b=c→ (a×n)÷(b×n)=c(n≠0),
减少)同一个数
字母表示:
a-b=c →(a+m)-b=c+m,
(a-m)-b=c-m(a≥m)。
例如:
100-60=40→(100+50) -60=40+50,
100-60=40→(100-10)-60=40-10
如果被减数不变,减数增加(或减
少)一个数,那么它们的差反而减
少(或增加)同一个数
字母表示:
和的变化规律:
和的变化规律
字母表示及举例
如果一个加数增加一个数,另一个加数不变,那么它们的和也增加同一个数
字母表示:a+b=c→(a+m)+b=c+m.
例如:10+5=15→(10&#个加数不变,那么它们的和也减少同一个数
字母表示:a+b=c→(a-m)+b=c-m(a≥m)。
例如:10+5=15→(10-5)+5=15-5
如果一个加数增加一个数,另一个加数同时减少同一个数,那么它们的和不变
字母表示:a+b=(a+m)+(b-m)(b≥m)。
例如:598+327=(598+2)+(327-2)
差的变化规律:
差的变化规律
字母表示及举例
如果被减数增加(或减少)一个数,减数不变,那么它们的差也增加(或
用字母表示:
a×b=c →(a×n)×(b÷n)=c
(n≠0,b能被n整除)。
例如:
5×6=30→ (5×2)×(6÷2)=30
商的变化规律:
商的变化规律
字母表示及举例
如果被除数扩大到原来的几倍或缩小到原来的几分之一,除数不变,那么它们的商也随着扩大到原来的几倍或缩小到原来的几分之一
用字母表示:
a÷b=c→ (a×n)÷b=c×n
原来的几倍或缩小到原来的几分之一
用字母表示:
a×b=c→(a×n)×b=c×n
或(a÷n)×b=c÷n
(n≠0,a能被n整除)。
例如:
8×4=32→(8×2)×4=32×2,
25×4=100→(25÷5)×4=100÷5
如果一个因数扩大到原来的几倍,另一个因数缩小到原来的几(与前面的“几”相等)分之一,则它们的积不变
或(a÷n)÷(b÷n)=c(n≠0,a、b是n的倍数)。
例如:1200÷25
=(1200×4)÷(25×4)
=4800÷100
=48
a-b=c →a-(b+m)=c-m(c≥m),
a-(b-m)=c+m(b≥m)。
例如:
180-60=120→ 180-(60+20)=120-20,
180-60=120→ 180-(60-20) =120+20
如果被减数和减数都增加(或减少)同一个数,那么它们的差不变
字母表示:
a-b=c→(a+m)-(b+m)=c,
