格林公式例题与习题
格林公式与曲线积分路径无关

4 2 2 6 4 2 2 8
-1
重要意义:
1.它建立了二重积分与曲线积分的一种等式关系
2.它揭示了函数在区域内部与边界之间的内在联系 3.从它出发,可以导出数学物理中的许多重要公式
四、曲线积分与路径无关的定义
如果对于区域 G 内任意指定的两点 A、B 以及 G 内
从点 A 到点 B 的任意两条曲线 L1,yL2 有
L
练习1 计算积分 (ex sin y y)dx (ex cos y 1)dy
L
y
其中L是曲线|x|+|y|=1围成的区域D的正向边界。
1
解 (ex sin y y)dx (ex cos y 1)dy
L
②
L①
D
(ex cos y ex cos y 1) dxdy
D
-1
O
③
1x ④
x0
=
Px, y
同理可证 u Q x, y.因此
y du Pdx Qdy.
(ⅲ) (ⅳ)设存在u x , y ,使得 du Pdx Qdy
所以P x, y u x, y,Q x, y u x, y.因此
x
y
P 2u , Q 2u . y xy x yx
因 Px, y,Qx, y在区域 D 内有连续的偏导数,所以
o
x
x1
x0
P(
x,
y0
)dx
y1Q( y0
x1 ,
y)dy
或
y1Q( y0
x0
,
y)dy
x1
x0
P(
x,
y1
)dx
AC CB
AD DB
例 5 验证 (e y x)dx ( xe y 2 y)dy.与路径无关,
第四节格林公式

EAC c
⌒
证明(2) 若区域D由按段光滑的 闭曲线围成.如图, 将D分成三个既是 x 型又是 y 型的 区域D1, D2, D3.
L3 D3
D2
L2
L1
D1
D
L
Q P Q P ( x y )dxdy ( x y )dxdy D D1 D2 D3
(
D1 D2 D3
Q P )( )dxdy x y
(
D1
D2
D3
) Pdx Qdy
D
Pdx Qdy.
证明(3) 若D是复连通区域 ,添加直线段
AB,CE. 则D由AB, BA,AFC,CE, EC 及CGA构成. 由(2)知 ( Q P )dxdy D y D x
y2
1
x
e
D
y2
dxdy
x2
OA AB BO
xe
dy
OA
xe
y2
dy
0 xe
1
1 1 x2 1 dx [ e ] 0 (1 e 1 ). 2 2
3) 利用第二类曲线积分可求闭曲线所围区域的面积.
Q P )dxdy Pdx Qdy 格林公式: ( y D x D
y
解 记 L 所围闭区域为 D ,
则原积分
( y
D
2
x )dxdy
2
O
2 x
d 0
2 2
2 cos
d 8
3
2 0
3 cos d . 2
格林公式例题与习题

y dy 0 x2 y2
目录 上页 下页 返回 结束
或
y dy 0 1 y2
π arctan x
2
y
y (1, y) (x, y) O (1,0) ( x,0) x
目录 上页 下页 返回 结束
例7. 设质点在力场
作用下沿曲线 L :
由 A( 0, π ) 移动到 2
求力场所作的功W
y
A
解:
W
Fds
L
L
k r2
( ydx
x d y)
L
令
则有
O Bx
P y
k(x2 y2) r4
Q x
( x2 y2 0)
可见, 在不含原点的单连通区域内积分与路径无关.
目录 上页 下页 返回 结束
取圆弧 AB : x π cos , y π sin ( : π 0)
2
2
2
W
AB
k r2
(y
一、 格林公式
区域 D 分类
单连通区域 ( 无“洞”区 域 多连) 通区域 ( 有“洞”区
L D
规定:域 D 边域界L) 的正向: 域的内部靠左
定理1. 设区域 D 是由分段光滑正向曲线 L 围成, 函数 在 D 上具有连续一阶偏导数, 则有
Q P dxdy Pdx Qdy
D x y
0
1 (1 e1) 2
目录 上页 下页 返回 结束
二、平面上曲线积分与路径无关的等价条件
定理2. 设D 是单连通域 , 函数
在D 内
具有一阶连续偏导数, 则以下四个条件等价:
(1) 沿D 中任意光滑闭曲线 L , 有 L Pdx Qdy 0.
格林公式习题解析

“ u(x, y) (x,y) 2x ydx x2 d y ”. ( x0 , y0 )
图1
又由于积分 u(x, y) (x,y) 2X Y d X X 2 dY 与路径无关, ( x0 , y0 )
也就意味着,我们可以选取使计算简便的路径,通常我们选择 折线路径,如图 1 和图 2 所示.
y
x
y x
符合定理 9.3.2 中的充要条件,因此,积分与路径无关.
再来计算积分值——
本题中并没有指定积分弧段,只取定了起点 (1,1) 和终点 (2,3) . 由于积分与路径无关,
因此,无论沿哪条积分弧段计算曲线积分,积分值都是相同的, 我们可以选择较简便的折线路径(如图 3 所示)进行计算,记
因此,无论沿哪条积分弧段计算曲线积分,积分值都是相同的, 我们可以选择较简便的折线路径(如图 4 所示)进行计算,记
x x
LAB
:
y
2
(x
:1
3)
,
LBC
:
x y
3 y
( y : 2 4) ,则有
图4
(3,4) (6 x y2 y3)dx (6 x2 y 3 x y2 )d y (1,2)
的正向边界;
答案: 1 (e 1) 5
解析: 本题考查课本第 137~138 页知识点——
可简单地理解为曲线上无“尖点”(导数或偏导数不存在的点), 即曲线上处处有切线,且切线随切点的移动而连续转动.
简单地讲,格林公式就是把闭区域内的二重积分和该闭区域边界上的曲线积分联系了起 来,这两种积分可以根据我们的需要相互转化,从而简化计算.
u(x, y) y0 (x2 x02 ) x2 ( y y0) 的全微分,随着 (x0, y0 ) 的不同, u(x, y) 也不同.
数学分析21.3格林公式、曲线积分与路线的无关性(含习题及参考答案)

第二十一章 重积分3格林公式、曲线积分与路线的无关性一、格林公式概念:当区域D 的边界L 由一条或几条光滑曲线所组成时,规定边界曲线的正方向为:当人沿边界行走时,区域D 总在他的左边. 与正方向相反的方向称为负方向,记为-L.定理21.11:若函数P(x,y), Q(x,y)在闭区域D 上连续,且有连续的一阶偏导数,则有格林公式:⎰⎰⎪⎪⎭⎫ ⎝⎛∂∂-∂∂D d y P x Q σ=⎰+L Qdy Pdx . L 为区域D 的边界曲线,并取正方向.证:根据区域D 的不同形状,可分三种情形来证明: (1)若区域D 既是x 型区域,又是y 型区域(如图1),即 平行于坐标轴的直线和L 至多交于两点,该区域D 可表示为: φ1(x)≤y ≤φ2(x), a ≤x ≤b 或ψ1(x)≤x ≤ψ2(x), c ≤y ≤d.这里y=φ1(x)和y=φ2(x)分别为曲线⌒ACB 和⌒AEB 的方程, x=ψ1(x)和x=ψ2(x) 分别为曲线⌒CAE 和⌒CBE的方程, ∴⎰⎰∂∂Dd x Qσ=⎰⎰∂∂)()(21y y d c dx x Q dy ψψ=⎰d c dy y y Q )),((2ψ-⎰d c dyy y Q )),((1ψ=⎰⋂CBE dy y x Q ),(-⎰⋂CAE dy y x Q ),(=⎰⋂CBE dy y x Q ),(+⎰⋂EAC dy y x Q ),(=⎰L dy y x Q ),(.同理可证:-⎰⎰∂∂Dd y Pσ=⎰L dx y x P ),(. 即有⎰⎰⎪⎪⎭⎫ ⎝⎛∂∂-∂∂D d y P x Q σ=⎰+L Qdy Pdx . (2)若区域D 是一条按段光滑的闭曲线围成(如图2),则先用几段光滑曲线将D 分成有限个既是x 型又是y 型的子区域,然后逐块按(1)得到它们的格林公式,相加即可.图2中区域D 可分成三个既是x 型又是y 型的区域D 1,D 2,D 3,则有⎰⎰⎪⎪⎭⎫⎝⎛∂∂-∂∂D d y P x Q σ=⎰⎰⎪⎪⎭⎫ ⎝⎛∂∂-∂∂1D d y P x Q σ+⎰⎰⎪⎪⎭⎫ ⎝⎛∂∂-∂∂2D d y P x Q σ+⎰⎰⎪⎪⎭⎫ ⎝⎛∂∂-∂∂3D d y P x Q σ =⎰+1L Qdy Pdx +⎰+2L Qdy Pdx +⎰+3L Qdy Pdx =⎰+L Qdy Pdx.(3)若区域D 由几条闭曲线所围成(如图3), 可适当添加直线AB, CE,把区域转化为(2)的情况处理.图D 的边界线由AB,L 2,BA,⌒AFC ,CE,L 3,EC 及⌒CGA构成. 由(2)知 ⎰⎰⎪⎪⎭⎫ ⎝⎛∂∂-∂∂D d y P x Q σ=⎪⎭⎫ ⎝⎛+++++++⎰⎰⎰⎰⎰⎰⎰⎰⋂⋂CGA EC l CE AFCBA l AB32(Pdx+Qdy)=()⎰⎰⎰++132L L L (Pdx+Qdy)=⎰+L Qdy Pdx .注:格林公式可写为:⎰⎰∂∂∂∂Dd QP y x σ=⎰+L Qdy Pdx .例1:计算⎰AB xdy ,其中曲线AB 为半径为r 的圆在第一象限部分. 解:如图,对半径为r 的四分之一圆域D 应用格林公式有⎰⎰-D d σ=⎰-L xdy =⎰OA xdy +⎰AB xdy +⎰BO xdy =⎰AB xdy . ∴⎰AB xdy =⎰⎰-Dd σ=-41πr 2.例2:计算I=⎰+-Ly x ydxxdy 22, 其中L 为任一不包含原点的闭区域的边界线.解:⎪⎪⎭⎫ ⎝⎛+∂∂22y x x x =22222)(y x x y +-, ⎪⎪⎭⎫ ⎝⎛+-∂∂22y x y y =22222)(y x x y +- 在上述区域D 上连续且有界,∴⎰⎰⎥⎦⎤⎢⎣⎡⎪⎪⎭⎫ ⎝⎛+-∂∂-⎪⎪⎭⎫ ⎝⎛+∂∂Dd yx yx y x x x σ2222=0. 由格林公式可得I=0.注:在格林公式中,令P=-y, Q=x ,则得到一个计算平面区域D 的面积S D 的公式:S D =⎰⎰Dd σ=⎰-L ydx xdy 21.例3:如图,计算抛物线(x+y)2=ax (a>0)与x 轴所围的面积.解:曲线⌒AMO由函数y=x ax -, x ∈[0,a], 直线OA 为直线y=0, ∴S D =⎰-ydx xdy 21=⎰-OA ydx xdy 21+⎰⋂-AMO ydx xdy 21=⎰⋂-AMO ydx xdy 21=dx x ax ax ax a ⎰⎥⎦⎤⎢⎣⎡--⎪⎪⎭⎫ ⎝⎛-0)(1221=dx ax a ⎰-02121=dx x a a⎰4=62a .二、曲线积分与路线的无关性概念:若对于平面区域D 上任一封闭曲线,皆可不经过D 以外的点而连续收缩于属于D 的某一点,则称此平面区域为单连通区域,否则称为复连通区域。
第三节 格林公式及其应用

第三节 格林公式及其应用一、选择题 1. 设L 为椭圆12222=+by ax 的顺时针路径,则⎰=--+Ldy y x dx y x )()(( )A . ab π4-;B . ab π2-;C . 0 ;D . ab π2. 2. 设区域B : x 2 + y 2 ≤ a 2, 积分路线L 是B 的负向边界, 则=-⎰Lxdy ydx( )A . 22a π;B . 22a π-;C . 2a π- ;D . 2a π.3. 设L 是正向椭圆周: x = a cos t , y = b sin t (0 ≤ t ≤ 2π), 则线积分⎰+Lxdy ydx =( )A . 0 ;B . 2π ;C . π ab ;D . 2π ab . 4.⎰+++)2,1()0,0()()(dy y x f dx y x f =( )A .⎰30)(dx x f ; B .⎰10)(dx x f ;C . f (3) - f (0);D . 0.二、填空题1. 设L 为任意正向简单闭曲线, a 、b 为常数, 则曲线积分=+⎰Lbdy adx .2. 设L 是由曲线y = x 2及y = 1所围成的区域D 的正向边界, 则=+++⎰Ldy y x x dx y x xy )()(24233_____.3. 设L 是正向圆周922=+y x , 则=-+-⎰Ldy x x dx y xy )4()22(2 .三、解答题 1. 计算曲线积分⎰-+-Ldy xy y dx xy x )2()(232, 其中L 是四个顶点分别为(0, 0)、(2, 0)、(2, 2)和(0, 2)的正方形区域的正向边界. 2. 计算曲线积分⎰-+-Lx x dy m y e dx my y e )cos ()sin (, 其中L 为从点O (0, 0)到点A (a , 0)的上半圆周:)0(22>=+a ax y x .3. 验证曲线积分⎰-+-)4,3()2,1(2232)36()6(dy xy y x dx y xy 在xOy 面内与路径无关, 并求其值.4. 验证dy x y x dx x y y )cos cos ()sin (sin ++-为某二元函数F (x , y )的全微分, 并求F (x , y )及积分:⎰++-)0,1()1,0()cos cos ()sin (sin dy x y x dx x y y .。
格林定理练习题

格林定理练习题格林定理是数学中的一个重要定理,它与曲线积分和曲面积分之间的关系密切相关。
为了帮助读者更好地理解和运用格林定理,本文将介绍一些格林定理的练习题,以便读者加深对于该定理的理解和应用能力。
练习题一:计算曲线积分考虑曲线C:y = x^2,从点A(0, 0)到点B(2, 4)。
我们要计算函数P(x, y) = x^2 + y^2在曲线C上的曲线积分。
首先,我们需要计算曲线的参数方程。
由于曲线是由y = x^2给出的,我们可以将x作为参数,然后得到参数方程为:(x, y) = (t, t^2),其中0 <= t <= 2。
然后,我们需要计算函数P(x, y)在曲线参数方程上的切向量。
切向量的计算公式为:P(x, y) = (P/∂x)(dx/dt) + (P/∂y)(dy/dt)。
其中(∂x/∂t,∂y/∂t)为曲线参数方程的导数,(dx/dt, dy/dt)为曲线上任意一点的切向量。
对于本题中的函数P(x, y) = x^2 + y^2,可以求得∂P/∂x = 2x和∂P/∂y = 2y。
曲线参数方程的导数为(dx/dt, dy/dt) = (1, 2t)。
将以上结果带入切向量的计算公式,我们可以得到切向量为:(2x)(1) + (2y)(2t) = 2x + 4yt。
由此,我们可以得到函数P(x, y)在曲线C上的曲线积分表达式为∫(2x + 4yt)dt。
继续计算曲线积分,我们得到∫(2x + 4yt)dt = 2∫xdt + 4y∫tdt = 2x^2 +2yt^2 + C,其中C为常数。
最后,我们将曲线积分的结果代入曲线C的参数方程,即可得到函数P(x, y)在曲线C上的曲线积分为:2(2)^2 + 2(4)(2)^2 + C = 32 + C。
练习题二:计算曲面积分考虑曲面S:z = x^2 + y^2,其中S是单位半球体的上表面。
我们要计算函数Q(x, y, z) = z在曲面S上的曲面积分。
格林公式及其应用

易于计算时,可应用格林公式计算
O
L2 L L1 L3
x
(2)L不封闭时,采取“补线”的方法:
L L l lD ( Q x P y)dx d l y
要求右端的二重积分及曲线l积分易于计算。l 选用直线段、折线、圆、半圆、椭圆、抛物线等。
(3)如在D上P、Q一阶偏导连续,且处处有
(1) 沿D中任意光滑闭曲线 L,有 LPdxQdy0。
(2) 对 D中任一分段光滑曲线 L, 曲线积分
PdxQdy与路径无关, 只与起止点有关.
L
(3)PdxQdy在 D内是某一函数 u(x, y)的全微分, 即 d u ( x ,y ) P d x Q d y
(4) 在 D内每一点都有 P Q 。 y x
注意本题只在不含原点的单连通区域内积分与路径无关内有设pq在单连通域d内具有一阶连续偏导数则有思考与练习且都取正向问下列计算是否正确的半圆计算质点m沿着以ab为直径的半圆从a12运动到故所求功为ab锐角其方向垂直于om且与y轴正向夹角为对质点m所作的功
8.2 格林公式及其应用
8.2.1 格林公式 8.2.2 平面上曲线积分与路径无关的条件
a a xdx1a2
40
6
8.2.2 平面上曲线积分与路径无关的条件
如果在区域G内有
y
PdxQdy L1
PdxQdy L2
B G
L1
A
L2
o
x
则称曲线积分L Pdx Qdy在G 内与路径无关,
否则与路径有关。
平面上曲线积分与路径无关的等价条件 定理8.2.2 设 D是单连通域,函数P (x ,y)Q ,(x ,y)在D内 具有一阶连续偏导数, 则以下四个条件等价:
典型习题:(120212)用格林公式计算曲线积分

典型习题:(120212)用格林公式计算曲线积分解析视频习题解答相关小结“用格林公式计算曲线积分”题型的求解思路以及相关的知识点:1.格林公式当(1)积分曲线为闭曲线L;(2)积分曲线L的方向相对于其围成的封闭区域D以左手法则判定为正方向;(3)在闭区域上,两个二元函数P(x,y)和Q(x,y)存在有一阶连续偏导数,则有【注1】正确使用以上标准格林公式,三个条件:闭曲线、正方向、闭区域上的偏导连续性,一个都不能少。
【注2】格林公式中闭区域的边界曲线不取由左手法则确定的正向,而是取相反的方向时,则借助于对坐标的曲线积分的方向性计算性质,有即不管边界曲线取什么方向,有利用“左手法则”判断为正方向,则取正;否则取负。
【注3】判断平面区域的边界曲线正向的“左手法则”:当沿着边界曲线的正方向行走时,平面区域应该位于我们左手一侧,所以对于单连通区域,即只有外边界曲线的实心区域来说,曲线的正方向为逆时钟方向;对于多连通区域,则边界曲线由内外边界曲线构成,外边界曲线的正方向为逆时钟方向,内边界的边界曲线为顺时钟方向。
【注4】注意封闭曲线切向量方向与外法线方向的关系。
如果切向量方向为T0=(cosα,cosβ)(T=(x’(t),y’(t))),则当曲线的切向量指向为逆时钟方向时,则外法线方向的方向向量为n0=(cosβ,-cosα)(n=(y’(t),-x’(t)));当曲线的切向量指向为顺时钟方向时,则外法线方向的方向向量为n0=(-cosβ,cosα)(n=-(y’(t),-x’(t)))。
即曲线的法向量与切向量的关系为:n=±(y’(t),-x’(t))。
取正号时,法向量为切向量顺时钟旋转90度得到;取负号时,法向量为切向量逆时钟旋转90度得到。
2.利用格林公式计算对坐标的曲线积分的基本思路与步骤依据以上定理,有如下使用格林公式计算关于平面上的积分曲线对坐标的曲线积分计算步骤:第一步:明确被积表达式中的P(x,y)和Q(x,y)函数(dx前面的函数为P(x,y),dy前面的函数为Q(x,y),如果有负号,记得带上负号)。
格林公式练习题

格林公式练习题为了更好地理解和应用格林公式,我们可以通过一些练习题来加深对该公式的理解和掌握。
下面将给出一些关于格林公式的练习题,希望能够帮助大家更好地应用这个定理。
1. 练习题一:计算曲线C围成的面积设曲线C为:x^2 + y^2 = 1,从点(1,0)到点(0,1)。
现在需要计算曲线C围成的面积S。
解析:首先,我们需要确定边界曲线C是一个圆。
根据格林公式,计算曲线C围成的面积可以转化为计算曲线C的线积分。
设曲线C的参数方程为x(t)和y(t),其中t∈[a,b]。
由于边界曲线C 为一个圆,我们可以使用参数方程表示,令x(t) = cos(t),y(t) = sin(t),其中t∈[0,π/2]。
然后,我们需要计算曲线C的线积分∮C P dx + Q dy。
根据题目中的曲线C和格林公式,我们可以得到:∮C P dx + Q dy = ∫[a,b] (P(x(t), y(t)) * x'(t) + Q(x(t), y(t)) * y'(t)) dt代入曲线C的参数方程,可以得到:∮C P dx + Q dy = ∫[0,π/2] (P(cos(t), sin(t)) * (-sin(t)) + Q(cos(t), sin(t)) * cos(t)) dt接下来,我们需要确定P(x,y)和Q(x,y)的具体值。
根据题目中要计算曲线C围成的面积S,我们可以令P(x,y) = 0 和 Q(x,y) = x。
因此,我们有:∮C P dx + Q dy = ∫[0,π/2] (0 * (-sin(t)) + cos(t) * cos(t)) dt对上述积分进行计算,可以得到:∮C P dx + Q dy = ∫[0,π/2] (cos^2(t)) dt = π/4因此,曲线C围成的面积S = π/4。
2. 练习题二:计算二维区域D的边界曲线C上某个函数f(x,y)的线积分设二维区域D为:0 ≤ x ≤ 1,0 ≤ y ≤ x,并且边界曲线C为D的周长曲线。
格林公式挖洞法例题

格林公式挖洞法例题
格林公式挖洞法例题是指使用格林公式解决一些具体的例题,这些例题通常涉及到在某个区域上对一个向量场进行积分,通过引入一个“洞”来简化或解决这个问题。
以下是一些示例:
1.计算曲线积分:
题目:计算曲线积分∫(x^2 + y^2)dx + (x - y)dy,其中L是从点(0,0)到点(1,1)的上半圆周 x^2 + y^2 = 1,且方向为逆时针。
解答:首先,我们引入一个“洞”D,使得上半圆周L是D的边界。
然后,我们使用格林公式计算出向量场在区域D上的散度为0,从而简化了曲线积分的计算。
2.计算面积:
题目:计算曲线围成的区域的面积。
解答:我们可以使用格林公式计算出围成的区域的边界上的曲线积分,由于围成的区域内的向量场满足格林公式的条件,我们可以通过求解相应的偏微分方程来计算出区域的面积。
总结:格林公式挖洞法是一种通过引入一个“洞”来简化或解决一些积分问题的方法。
这种方法在计算曲线积分、面积等方面有着广泛的应用。
在解题过程中,需要注意格林公式的条件和适用的范围,同时要注意对区域内的向量场进行准确的计算和分析。
高等数学 曲线积分和曲面积分 (10.3.2)--格林公式及其应用

0,
其中 C
为平面区域
x
内的
任一封闭曲线.
6. 设函数 Q(x, y) 在 xOy 平面上具有一阶连续偏导数,曲线积分 2xydx Q(x, y)dy 与 C 路径无关,并且对任意 t 恒有
(2xydx Q(x, y)dy 2xydx Q(x, y)dy ,
(0, 0)
(0, 0)
求 Q(x, y) .
7. 确定常数 p , 使得在任何不含 y 的点的区域上, 曲线积分
C
x y2
(x2
y2)p
ydx
xdy
与路径无关,并求当 C 从点 (1, 1) 到点 (0, 2) 时的积分值.
8. 求下列微分方程的通解:
(1) [ y ln(1 x)]dx (x 1 ey )dy 0 ;
C
a b
(3)
C
(x2
y
2 y)dx
x3 3
x
dy
,其中 C
是直线
x
1,
y
x,
y
2x
所围三角形区
域的正向边界.
(4) (ex sin y my)dx (ex cos y m)dy ,其中 C 为由点 A(a,) 到点 O(,) 的上 C 半圆周 x y ax ;
t
2π
)与
x
轴.
2. 利用 Green 公式, 计算下列第二类曲线积分:
(1) (2x sin y 4y)dx (x2 cos y x)dy ,其中 C 为圆周 x2 y2 3 , 并取逆时针 C 方向;
习题二十一格林公式及其应用(续)
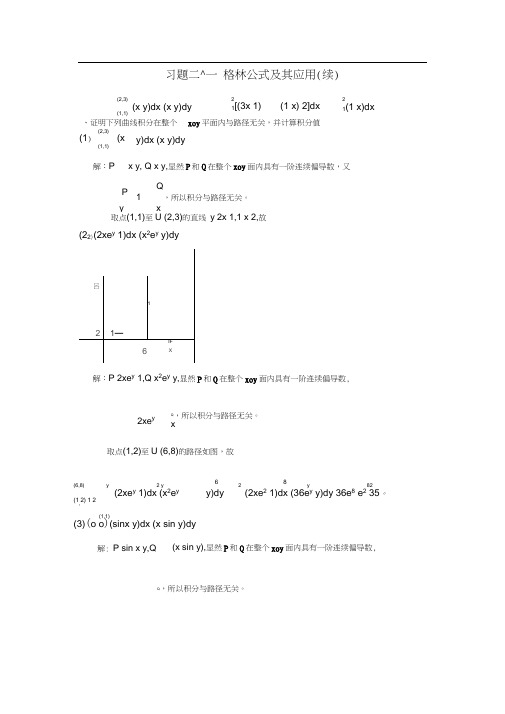
习题二^一 格林公式及其应用(续)、证明下列曲线积分在整个 xoy 平面内与路径无关,并计算积分值 (2,3)(1) (x (1,1) y)dx (x y)dy解:P x y, Q x y,显然P 和Q 在整个xoy 面内具有一阶连续偏导数,又PQ 1 ,所以积分与路径无关。
y x取点(1,1)至U (2,3)的直线 y 2x 1,1 x 2,故(22)(2xe y 1)dx (x 2e y y)dy解:P 2xe y 1,Q x 2e y y,显然P 和Q 在整个xoy 面内具有一阶连续偏导数,取点(1,2)至U (6,8)的路径如图,故(6,8) y2 y 6 2 8y 82 (2xe y 1)dx (x 2e y y)dy (2xe 2 1)dx (36e y y)dy 36e 8 e 2 35。
(1,2) 1 2(1,1) (3)(o o )(sinx y)dx (x sin y)dy(x sin y),显然P 和Q 在整个xoy 面内具有一阶连续偏导数,Q ,所以积分与路径无关。
(2,3) (1,1)(x y)dx (x y)dy 21[(3x 1) (1 x) 2]dx 2 1(1 x)dx 2xe yQ ,所以积分与路径无关。
x 解: P sin x y,Q取点(0,0)至U (1,1)的直线 y x,0 x 1,故(1,1) i(0,0)(sinx y)dx (x siny)dy °[(sinx 2x 上从点(0,0)到点(4,8)。
( )e sin ydx e cos ydy L 1 L 248 4 0 dx e cos ydy 0 04 e sin 8三、设IJe x 2f (x)] ydx f (x)dy 与积分路径L 无关,且f(1) 1 ,求(1,1) I (0,0)[e 2f(x)]ydx f (x)dy 之值。
1x) (x sin x)]dx o 2xdx 1。
高数-格林公式

2(
y),
y]d
y
d c
{Q[
2
(
y),
y]
Q[ 1
(
y),
y]}d
y
D
Q x
dxdy
则有
Q P
(
D
x
y
)dxdy
L
Pdx
Qdy
(1)
证明:(1)设 D 既是 X 型,又是 Y 型区域。
X 型: a x b, 1( x) y 2( x),
L Pdx
D
P y
dxdy
y d
L2 : x 2( y)
D L2
L3
L1
(2)格林公式建立了平面上的曲线积分与二重积分 的关系,它是牛顿莱布尼茨公式在平面上的推广。
主要用途:实现曲线积分与二重积分之间的转换,而 经常用来将复杂的曲线积分转化为二重积分。
D
(
Q x
P y
)dxdy
L
Pdx
Qdy
(1)
(3)便于记忆的形式
若记
Q P x y
x P
y Q
则格林公式可表示为
(
D
x
y
)dxdy
L
Pdx
Qdy
(1)
证明:(1)设 D 既是 X 型,又是 Y 型区域。
X 型: a x b, 1( x) y 2( x),
y L2 : y 2( x)
P
D
y
dxdy
b
a
dx
2 (x) 1 ( x)
P y
dy
ab{
P[
ab
x,2(
2 (x)
P(x, y) | 1 (x)
应用格林公式计算下列曲线积分;

1. 应用格林公式计算下列曲线积分; (1)dy y x dx y x L)()(222+-+⎰,其中L 是以)5,2(),2,3(),1,1(C B A 为顶点的三角形,方向取正向; (2)⎰-+-ABx x dy m y e dx my y e )cos ()sin (,其中m 为常数,AB 为由)0,(a 到)0,0(经过圆ax y x =+22上半部的路线.分析:(1)首先应画出曲线L 的图形,并求出AB ,BC ,CA 的方程;(2)应用格林公式时,首先应是封闭曲线,因此(2)题应补上直线段OA 解:(1) AB 的方程为:)31)(1(21≤≤+=x x y , BC 的方程为: )32(113≤≤+-=x x y CA 的方程为: )21(34≤≤-=x x y , 设)(,)(222y x Q y x P +-=+=,则.24)(22y x y x x yPx Q --=+--=∂∂-∂∂ 把三角形域分成两部分1S 和2S ,于是 原式=⎰⎰⎰⎰⎰⎰--+=--SS S d y x d y x 12)24)(()24(σσ=⎰⎰⎰⎰+-+-+--+--32113)1(212134)1(21)24()24(x x x x dy y x dx dy y x dx=.3246)4483249421()2352774119(232221-=-++-+-⎰⎰dx x x dx x x (2)在Ox 轴上连接点)0,0(O 与点)0,(a A 这样就构成封闭的半圆形A AO,且在线段OA上,0,0==dy y 于是.0)cos ()sin (=-+-⎰dy m y e dx my y e OAx x而⎰⎰⎰⎰=+=OA AAO OA AO .由格林公式得:8)2(21)cos ()sin (22:22a m a m mdxdy dy m y e dx my y e axy x D xA AO xππ=⋅==-+-⎰⎰⎰≤+因此,原式=28a m π. 2. 应用格林公式计算下列曲线所围的平面面积:(1) 星形线:;sin ,cos 33t a y t a x == (2) 双纽线:).()(222222y x a y x -=+分析:封闭曲线L : (),()x x t y y t ==所围的面积公式是:⎰⎰⎰-==LS D ydx xdy d S D21σ 解: (1)⎰⎰⎰-==L S D ydx xdy d S D21σ =dt t t a t a t t a t a )sin cos 3sin cos sin 3cos (21220323⋅+⋅⎰π=dt t t t t a )cos sin sin (cos 232204242⎰+π=tdt t a 22022cos sin 23⎰π=tdt a ⎰π20222sin 83 =dt ta ⎰-π20224cos 183 =ππ83|)4sin 8121(832202a t t a =-. (2) 化双纽线的极坐标方程为参数方程,2cos cos cos )(θθθθa r x == ,2cos sin θθa y =应用面积公式并利用图形的对称性可得.2cos 2142402a d a ydx xdy S L==-⋅=⎰⎰θθπ3. 证明:若L 为平面上封闭曲线,l 为任意方向向量,则⎰=Lds n l ,0),cos(其中n 为曲线L 的外法线方向.分析:设l 与n 的方向余弦分别为βαcos ,cos 与),,cos(),,cos(y n x n 则cos(,)cos cos(,)cos cos(,)l n n x n y αβ=+,又cos(,),cos(,)n y ds dx n x ds dy =-=证: 设l 与n 的方向余弦分别为βαcos ,cos 与),,cos(),,cos(y n x n 则⎰⎰+=ds y n x n ds n l L L)],cos(cos ),cos([cos ),cos(βα由第一、二型曲线积分的关系,有上式=cos cos Ldx dy βα-+⎰由βαcos ,cos 均为常数,故0cos cos =∂∂=∂∂xy αβ 从而由格林公式知⎰=.0),cos(ds n l L4. 求积分值⎰+=,)],cos(),cos([ds y n y x n x I 其中L 为包围有界区域的封闭曲线,n 为L的外法线方向。
格林公式题目

格林公式题目好嘞,以下是为您生成的关于“格林公式题目”的文章:在数学的奇妙世界里,格林公式就像是一把神奇的钥匙,能为我们打开许多复杂问题的大门。
记得我当初刚开始接触格林公式的时候,那可真是一头雾水。
就像在黑暗中摸索,找不到方向。
有一次,在课堂上,老师在黑板上写下了一道格林公式的题目,那密密麻麻的符号和线条,看得我眼花缭乱。
题目是这样的:计算曲线积分∮(x² - y²)dx + 2xydy,其中曲线 C 是由抛物线 y = x²和直线 y = 1 所围成的闭区域的正向边界。
我当时看着这道题,心里直发怵。
心想:“这可咋办呀?” 但我还是硬着头皮开始尝试。
首先,我们需要判断是否满足格林公式的条件。
这里,被积函数 P= x² - y²,Q = 2xy,它们在整个闭区域上都具有连续的一阶偏导数。
接下来,使用格林公式,将曲线积分转化为二重积分。
根据公式,原积分等于∬(Q'x - P'y)dxdy,其中 Q'x 表示 Q 对 x 的偏导数,P'y 表示P 对 y 的偏导数。
经过一番计算,Q'x = 2y,P'y = -2y,所以 Q'x - P'y = 4y。
然后,我们要确定积分区域。
由抛物线 y = x²和直线 y = 1 所围成的闭区域,横坐标的范围是 -1 到 1。
于是,原积分就变成了:∫∫ 4ydxdy,积分区域为 -1 到 1 以及 x²到1 。
这时候,我们先对 y 积分,得到:∫[-1, 1] 2(1 - x⁴)dx再计算这个定积分,最终得出答案。
在这个过程中,每一步都需要小心翼翼,一个小错误就可能导致满盘皆输。
就像走在钢丝上,稍有不慎就会掉下去。
经过那次的磨练,我对格林公式的理解更加深刻了。
往后再遇到类似的题目,心里也有了底。
其实啊,学习格林公式就像是一场冒险,每一道题目都是一个关卡,需要我们运用智慧和勇气去突破。
积分与路径无关后的计算例题

积分与路径无关后的计算例题积分是数学中的一种重要概念,它的出现可以帮助我们解决一些与路径相关的问题。
但是在某些情况下,这些积分与路径无关,也就是说无论我们选择怎样的路径,最终得到的积分结果都是相同的。
在这篇文章中,我们将通过一个具体的计算例题来介绍积分与路径无关的情况以及相关的参考内容。
首先,让我们来考虑一个简单的例题:计算积分 $\int_C ydx + xdy$ ,其中 $C$ 是以原点为起点,半径 $r$ 的圆周路径。
要计算这个积分,我们可以使用格林公式,即 $\int_C Pdx + Qdy = \iint_D \left(\frac{\partial Q}{\partial x} - \frac{\partialP}{\partial y}\right)dxdy$ ,其中 $D$ 是 $C$ 所围成的区域,$P$ 和 $Q$ 是函数 $F(x,y) = (P(x,y),Q(x,y))$ 的分量函数。
在这个例题中,$P = y$ , $Q = x$ ,所以我们需要计算$\frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y}$ 。
对于该函数$F(x,y)=(y,x)$,有 $\frac{\partial Q}{\partial x} =1$ , $\frac{\partial P}{\partial y} = 1$ ,因此 $\frac{\partialQ}{\partial x} - \frac{\partial P}{\partial y} = 0$ 。
根据格林公式,我们可以将要求的积分转换为对区域 $D$ 的二重积分,即$\iint_D 0dxdy$ 。
接下来,我们需要确定区域 $D$ 。
根据问题描述, $C$ 是以原点为起点,半径 $r$ 的圆周路径,因此区域 $D$ 就是圆$x^2 + y^2 = r^2$ 所围成的区域。
格林公式-习题共36页

8、法律就是秩序,有好的法律才有好的秩序。——亚里士多德 9、上帝把法律和公平凑合在一起,可是人类却把它拆开。——查·科尔顿 10、一切法律都是无用的,因为好人用不着它们,而坏人又不会因为它们而变得规矩起来。——德谟耶克斯
格林公式-习题
16、业余生活要有意义,不要越轨。——华盛顿 17、一个人即使已登上顶峰,也仍要自强不息。——罗素·贝克 18、最大的9、自己活着,就是为了使别人过得更美好。——雷锋 20、要掌握书,莫被书掌握;要为生而读,莫为读而生。——布尔沃
END
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
D
利用格林公式 , 有
yx
O
D
x
xe xe
y2
dy dy 0 ye
1 y2
y2
OA
dy
1 (1 e 1 ) 2
目录 上页 下页 返回 结束
二、平面上曲线积分与路径无关的等价条件
定理2. 设D 是单连通域 , 函数 具有一阶连续偏导数, 则以下四个条件等价: (1) 沿D 中任意光滑闭曲线 L , 有 在D 内
L Pd x Qd y 0 .
L
(2) 对D 中任一分段光滑曲线 L, 曲线积分 Pd x Qd y
与路径无关, 只与起止点有关.
(3) 在 D 内是某一函数 的全微分,
d u( x, y) P d x Q d y P Q . (4) 在 D 内每一点都有 y x
Q( x, y )d y
或 u ( x, y )
பைடு நூலகம்
Q( x0 , y )d y P( x, y)d x
定理2
y0 O x0
x x
目录 上页 下页 返回 结束
3) 若已知 d u = P dx + Q dy , 则对D内任一分段光滑曲 线 AB ,有
AB
B A
B
P ( x , y )d x Q ( x , y )d y
0 x
y
0
dy x2 y 2
目录 上页 下页 返回 结束
或
y (1, y) ( x, y)
dy 0 1 y2
y
O (1,0)
( x,0 )
x
π x arctan 2 y
目录 上页 下页 返回 结束
例7. 设质点在力场
作用下沿曲线 L : 求力场所作的功W
π 移动到 由 A( 0, ) 2
D
A
B
P( x, y ) d x Q( x, y )d y d u u
A
B A
u ( B) u ( A)
注: 此式称为曲线积分的基本公式(P213定理4). 它类似于微积分基本公式:
定理2
目录 上页 下页 返回 结束
例4. 计算 圆周
其中L 为上半
从 O (0, 0) 到 A (4, 0).
解: 为了使用格林公式, 添加辅助线段 AO , 它与L 所围 区域为D , 则
原式
L AO
( x 3 y ) d x ( y x) d y
2
2
( 4)d xd y ( x 2 3 y )d x D OA y 4 2 4 d xd y x d x
D
0
AO
( x 3 y )d x ( y x ) d y
2 2
L D Ax
64 8π 3
O
目录 上页 下页 返回 结束
例5. 验证 出这个函数及
2 2
是某个函数的全微分, 并求
P Q 证: 设 P x y , Q x y, 则 2x y y x ( x, y ) 由定理2 可知, 存在函数 u (x , y) 使
即
目录 上页 下页 返回 结束
P Q 说明: 根据定理2 , 若在某区域D内 , 则 y x 1) 计算曲线积分时, 可选择方便的积分路径; 注: 求曲线积分时,若积分路径不是闭曲线,且难计 算,则可添加辅助线后,利用格林公式简化计算。
2) 可用积分法求d u = P dx + Q dy在域 D 内的原函数:
利用格林公式 , 得
L
2x y d x x 2 d y 0 d x d y 0
D
目录 上页 下页 返回 结束
例2. 计算
y2
其中D 是以 O(0,0) , A(1,1) ,
B(0,1) 为顶点的三角形闭域 . 解: 令P 0, Q x e ,则
y
B(0,1) A(1,1)
du x y 2 d x x 2 yd y
(0,0) ( x,0)
0 0 x y d y
2
y
y 2 x y 0
dy
目录 上页 下页 返回 结束
xd y yd x 在右半平面 ( x > 0 ) 内存在原函 例6. 验证 2 2 x y y 数 , 并求出它. ( x, y ) y x , Q 2 证: 令 P 2 2 x y x y2 2 2 O (1,0) ( x,0 ) x P y x Q 则 2 ( x 0) 2 2 x ( x y ) y 由定理 2 可知存在原函数
解: W F ds
L
y
L
k ( y dx x d y) 2 r
A L
O
令
2
则有
B x
P k ( x y ) Q 4 x y r
2
( x2 y2 0 )
可见, 在不含原点的单连通区域内积分与路径无关.
目录 上页 下页 返回 结束
π π π 取圆弧 AB : x cos , y sin ( : 0 ) 2 2 2 k W ( y dx x d y) 2 y AB r A L π O B x k 2 思考: 积分路径是否可以取 AO OB ? 为什么?
L
xd y y d x
L
1 2π (ab cos 2 ab sin 2 ) d π ab 2 0
定理1 目录 上页 下页 返回 结束
例1. 设 L 是一条分段光滑的闭曲线, 证明
L
2x y d x x 2 d y 0
证: 令 P 2 x y , Q x 2 , 则
取定点 ( x0 , y0 ) D 及动点 ( x , y ) D , 则原函数为 ( x, y ) y u ( x, y ) P( x, y )d x Q( x, y )d y y
P( x, y0 )d x
x0 y y0
( x0 , y0 ) x
y y0 x x0
Q P d xd y P d x Q d y 格林公式 x y D L
推论: 正向闭曲线 L 所围区域 D 的面积
x a cos (0 2π) 所围面积 例如, 椭圆 L : y b sin
1 A xd y y d x 2 L
