空间直角坐标系、大地坐标系、平面坐标系、高斯平面直角坐标系
空间直角坐标系、大地坐标系、平面坐标系、高斯平面直角坐标系

空间直角坐标系、大地坐标系、平面坐标系、高斯平面直角坐标系本篇学习了空间直角坐标系、大地坐标系、平面坐标系、高斯平面直角坐标系。
这个个坐标系有时很容易弄混淆!(一)空间直角坐标系空间直角坐标系的坐标原点位于参考椭球的中心,Z轴指向参考椭球的北极,X轴指向起始子午面与赤道的交点,Y轴位于赤道面上切按右手系于X轴呈90度夹角,某点中的坐标可用该点在此坐标系的各个坐标轴上的投影来表示。
空间直角坐标系可用如下图所示:(二)大地坐标系大地坐标系是采用大地纬度、经度和大地高程来描述空间位置的。
纬度是空间的点与参考椭球面的法线与赤道面的夹角;经度是空间的点与参考椭球的自转轴所在的面与参考椭球的起始子午面的夹角;大地高程是空间的点沿着参考椭球的法线方向到参考椭球面的距离。
地面点的高程和国家高程基准(1)绝对高程。
地面点沿垂线方向至大地水准面的距离称为绝对高程或称海拔。
过去我国采用青岛验潮站(tide gauge station)1950~1956年观测成果求得的黄海平均海水面作为高程的零点,称为“1956年黄海高程系”(Huanghai height system 1956水准原点高程为72.289m)。
后经复查,发现该高程系的验潮资料时间过短,准确性较差,改用青岛验潮站1950~1979年的观测资料重新推算,并命名为“1985年国家高程基准”(Chinese height datum 1985)。
国家水准原点(leveling origin高程为72.260m)设于青岛市观象山附近,作为我国高程测量的依据。
它的高程值是以“1985年国家高程基准”所确定的平均海水面为零点测算而得。
在使用原“1956年黄海高程系”的高程成果时,应注意将其换算为新的高程基准系统。
(2)相对高程。
地面点沿铅垂线方向至任意假定的水准面的距离称为该点的相对高程,亦称假定高程。
在图l—5中,地面点A和B的相对高程分别为H'A 和H'B 。
空间大地坐标系与平面直角坐标系转换公式

空间大地坐标系与平面直角坐标系转换公式空间大地坐标系和平面直角坐标系是两种不同的坐标系统,用于描述地球上的点的位置。
在进行空间大地坐标系与平面直角坐标系之间的转换时,需要考虑到地球的椭球体形状和投影方式。
下面将详细介绍空间大地坐标系与平面直角坐标系的转换方法。
1.空间大地坐标系经度:经度是指地球上特定点与本初子午线之间的角度差,用度、分、秒的形式表示。
纬度:纬度是指地球上特定点距离赤道的角度,用度、分、秒的形式表示。
大地高:大地高是指地球表面特定点到参考椭球体上其中一参考面的高度差,可分为正高和负高。
2.平面直角坐标系平面直角坐标系是以地球上一些基准点为原点建立的二维坐标系。
在平面直角坐标系下,点的位置通常用东方向坐标值X和北方向坐标值Y来表示。
3.空间大地坐标系到平面直角坐标系的转换公式3.1平面直角投影平面直角投影是将地球表面上的点投影到一个水平的平面上。
其转换公式为:X = k₀ + R * cosL * sin(λ - λ₀)Y = k₀ + R * (cosφ₀ * sinL - sinφ₀ * cosL * cos(λ - λ₀))其中,X和Y为平面直角坐标系下的坐标值,L为参考点与待转换点的经度差,λ为待转换点的经度,φ₀为参考点的纬度,λ₀为参考点的经度,k₀为常数,R为参考点到地心的距离。
3.2高斯投影高斯投影是将地球上的点投影到一个平面上,使得该平面上的距离尽可能与大地距离一致。
其转换公式为:X = X₀ + N * cosB * (λ - L₀)Y = Y₀ + N * (tanB * cos(λ - L₀) - sinB * (B - B₀))其中,X和Y为平面直角坐标系下的坐标值,X₀和Y₀为参考点的平面坐标,N为法向子午线长度,B为待转换点的纬度,λ为待转换点的经度,L₀为参考点的经度,B₀为参考点的纬度。
4.平面直角坐标系到空间大地坐标系的转换公式平面直角坐标系到空间大地坐标系的转换公式为空间大地坐标系到平面直角坐标系的逆运算,可以通过解方程组或迭代法来进行计算。
GPS定位的坐标系统类型

CPS定位的坐标系统类型
GPS 定位是以 GPS 卫星为动态已知点,根据 GPS 接收机观测的星站距离来确定接收机或测站的位置的。
可将 GPS 定位中所采用的坐标系进行如下分类:
1.空固坐标系与地固坐标系
空固坐标系与天球固连,与地球自转无关,用来确定天体位置较方便。
地固坐标系与地球固连,随地球一起转动,用来确定地面点位置较方便。
2.地心坐标系与参心坐标系
地心坐标系以地球的质量中心为原点,如 WGS -84坐标系和ITRF 参考框架均为地心坐标系。
而参心坐标系以参考椭球体的几何中心为原点,如北京54坐标系和80国家大地坐标系。
3.空间直角坐标系、球面坐标系、大地坐标系及平面直角坐标系经典大地测量采用的坐标系通常有两种:一是以大地经纬度表示点位的大地坐标系,二是将大地经纬度进行高斯投影或横轴墨卡托投影后的平面直角坐标系。
在 GPS 测量中,为进行不同大地坐标系之间的坐标转换,还会用到空间直角坐标系和球面坐标系。
4.国家统一坐标系与地方独立坐标系
我国国家统一坐标系常用的是80国家大地坐标系和北京54坐标系,采用高斯投影,分6°带和3°带,而对于诸多城市和工程建设来说,因高斯投影变形以及高程归化变形而引起实地上两点间的距离与高斯平面距离有较大差异,为便于城市建设和工程的设计、施工,
常采用地方独立坐标系,即以通过测区中央的子午线为中央子午线,以测区平均高程面代替参考椭球体面进行高斯投影而建立的坐标系。
空间直角坐标系、大地坐标系、平面坐标系、高斯平面直角坐标系

本篇学习了空间直角坐标系、大地坐标系、平面坐标系、高斯平面直角坐标系。
这个个坐标系有时很容易弄混淆!(一)空间直角坐标系空间直角坐标系的坐标原点位于参考椭球的中心,Z轴指向参考椭球的北极,X轴指向起始子午面与赤道的交点,Y轴位于赤道面上切按右手系于X轴呈90度夹角,某点中的坐标可用该点在此坐标系的各个坐标轴上的投影来表示。
空间直角坐标系可用如下图所示:(二)大地坐标系大地坐标系是采用大地纬度、经度和大地高程来描述空间位置的。
纬度是空间的点与参考椭球面的法线与赤道面的夹角;经度是空间的点与参考椭球的自转轴所在的面与参考椭球的起始子午面的夹角;大地高程是空间的点沿着参考椭球的法线方向到参考椭球面的距离。
地面点的高程和国家高程基准(1)绝对高程。
地面点沿垂线方向至大地水准面的距离称为绝对高程或称海拔。
过去我国采用青岛验潮站(tide gauge station)1950~1956年观测成果求得的黄海平均海水面作为高程的零点,称为“1956年黄海高程系”(Huanghai height system 1956水准原点高程为72.289m)。
后经复查,发现该高程系的验潮资料时间过短,准确性较差,改用青岛验潮站1950~1979年的观测资料重新推算,并命名为“1985年国家高程基准”(Chinese height datum 1985)。
国家水准原点(leveling origin高程为72.260m)设于青岛市观象山附近,作为我国高程测量的依据。
它的高程值是以“1985年国家高程基准”所确定的平均海水面为零点测算而得。
在使用原“1956年黄海高程系”的高程成果时,应注意将其换算为新的高程基准系统。
(2)相对高程。
地面点沿铅垂线方向至任意假定的水准面的距离称为该点的相对高程,亦称假定高程。
在图l—5中,地面点A和B的相对高程分别为H'A 和H'B。
(3)高差。
地面上任意两点的高程(绝对高程或相对高程)之差称为高差。
测量中的常用坐标系及坐标转换概述

三、坐标转换
5、高斯投影的邻带换算
应用高斯投影正反算公式间接进行换带计算:实质是把椭球 面上的大地坐标作为过渡坐标,首先把某投影带(比如I带)内 有关点的平面坐标(x,y) I ,利用高斯投影反算公式换算成椭球 面上的大地坐标(B ,ι),进而得到L=L10+ ι,然后再由大地坐 标(B ,ι),利用投影正算公式换算成相邻带第Ⅱ带的平面坐标 (x,y) Ⅱ,在这一步计算中,要根据第Ⅱ带的中央子午线L20来 计算经差ι,此时ι=L- L20
大地高H:某点沿投影方向到基准面(参考椭球面)的距离。
在大地坐标系中,某点的位置用(B , L,H)来表示。
二、测量中的各种坐标系
2、空间直角坐标系
定义:以椭球体中心为原点,起始子午面与赤道面交线为X轴,在赤 道面上与X轴正交的方向为Y轴,椭球体的旋转轴为Z轴。
在空间直角坐标系中,某点的位置用(X,Y,Z)来表示。
二、测量中的各种坐标系
3、平面直角坐标系
在小区域进行测量工作若采用大地坐标来表示地面点位置是不方便的, 通常采用平面直角坐标系。 测量工作以x轴为纵轴,以y轴为横轴 投影坐标:为了建立各种比例尺地形图的控制及工程测量控制,一般应 将椭球面上各点的大地坐标按照一定的规律投影到平面上,并以相应的 平面直角坐标表示。
三、坐标转换
3、大地坐标同空间直角坐标的变换
X N cos B cos L Y N cos B sin L Z N (1 e 2 ) sin B
三、坐标转换
4、大地坐标与高斯平面坐标的变换
将大地坐标转换为高斯平面坐标,按照高斯投影正算公式 进行。
高斯投影正算公式:
x X 0 0.5 N sin B cos B l 2 y N cos B l 1 / 6 N cos3 B l 3 (1 t 2 2 )
空间大地坐标系与平面直角坐标系转换公式

§坐标系的分类正如前方所说起的 ,所谓坐标系指的是描绘空间地点的表达形式 ,即采纳什么方法来表示空间地点。
人们为了描绘空间地点,采纳了多种方法,进而也产生了不一样的坐标系,如直角坐标系、极坐标系等。
在丈量中常用的坐标系有以下几种:一、空间直角坐标系空间直角坐标系的坐标系原点位于参照椭球的中心,Z 轴指向参照椭球的北极,X 轴指向开端子午面与赤道的交点,Y 轴位于赤道面上且按右手系与X 轴呈 90°夹角。
某点在空间中的坐标可用该点在此坐标系的各个坐标轴上的投影来表示。
空间直角坐标系可用图2-3来表示:图 2-3 空间直角坐标系二、空间大地坐标系空间大地坐标系是采纳大地经、纬度和大地高来描绘空间地点的。
纬度是空间的点与参考椭球面的法线与赤道面的夹角;经度是空间中的点与参照椭球的自转轴所在的面与参照椭球的开端子午面的夹角;大地高是空间点沿参照椭球的法线方向到参照椭球面的距离。
空间大地坐标系可用图2-4 来表示:图 2-4 空间大地坐标系三、平面直角坐标系平面直角坐标系是利用投影变换,将空间坐标空间直角坐标或空间大地坐标经过某种数学变换映照到平面上,这类变换又称为投影变换。
投影变换的方法有好多,如横轴墨卡托投影、 UTM 投影、兰勃特投影等。
在我国采纳的是高斯-克吕格投影也称为高斯投影。
UTM 投影和高斯投影都是横轴墨卡托投影的特例,不过投影的个别参数不一样而已。
高斯投影是一种横轴、椭圆柱面、等角投影。
从几何意义上讲,是一种横轴椭圆柱正切投影。
如图左边所示,假想有一个椭圆柱面横套在椭球外面,并与某一子午线相切(此子午线称为中央子午线或轴子午线),椭球轴的中心轴CC’经过椭球中心而与地轴垂直。
高斯投影知足以下两个条件:1、它是正形投影;2、中央子午线投影后应为x 轴,且长度保持不变。
将中央子午线东西各必定经差(一般为 6 度或 3 度)范围内的地域投影到椭圆柱面上,再将此柱面沿某一棱线睁开,便组成了高斯平面直角坐标系,以以下图2-5右边所示。
坐 标 系 讲 义

坐标转换软件GEOTRANS
主要功能
在相同的参心或地心系统下进行大 地坐标, 空间直角坐标和高斯平面坐 标相互间的转换。 高斯平面坐标的换带、换投影计算。 通用墨卡托投影(UTM投影)。
上 表 中 一 区 取 y0=542800 , H0=1250 ; 二 区 y0=621641,H0=850,计算结果均满足要求。 根据测区平均纬度及y0值,利用近似公式 或利用坐标转换软件计算两区中央子午线经 度:一区为117º 31′36″, 二区为118º 29′49″。
工程坐标系
ቤተ መጻሕፍቲ ባይዱ
坐标转换软件GEOTRANS
地方坐标系建立需给定的元素
起算点坐标 起算方位 选定中央子午线 投影面高程
隐含参考椭球参数
地方独立坐标系也隐含一个参考椭球体, 即该椭球体的中心、轴向、扁率与国家 坐标系的参考椭球相同,但其长半径则 有一定改进量da。设某地方独立坐标系 的投影面高程取为H0,该地区平均高 程异常为ζ0,则长半径改正量da= H0+ζ0, 长半径a1=a+da。
投影长度变形
高斯投影的长度比是纬度和离开中央子 午线距离的函数,计算公式如下:
表一
表二
我国国家坐标系
1954北京坐标系 1980年西安大地坐标系
1954北京坐标系
1954北京坐标系采用克拉索夫斯基 椭球体 椭球参数为:长半径a=6378245m, 扁率α=1/298. 3
1954北京坐标系存在明显缺点
用人为地改变归化高程来使与高斯投 影的长度改化相抵偿,但并不改变统一 3°带的投影改化方法,称为抵偿高程 面的高斯正形投影统一3°带平面直角 坐标系,简称抵偿坐标系 经过抵偿修正后的归化高程值计算:
测量坐标系

方位角的互算
A A m
A A
m
真 北
Am A α
O
P
三种方位角的关系
正、反方位角
✓ 正、反坐标方位角:
✓ 正、反真方位角: ✓ 正、反磁方位角:
180
12
21
A A ( ) 180
12
21
2
1
A A ( ) 180
磁12
磁 21
m1
m2
真 北
γ1
α12
A12
➢ 方位角及其互换
由直线一端的标准方向线北端起,顺时针量至该直线的 水平角。其取值范围:0°~360°。
方位角的种类 ✓真方位角
由子午线北端起算的方位角 ,用A表示。
✓磁方位角
由磁北方向起算的方位角 ,用A磁 表示。
✓坐标方位角
由X坐标轴北端起算的方位角 ,用α表示 。
真 北
Aα
Am
O
P
三种方位角的关系
(3)P点距离中央子午线和赤道的投影距离各为多少米? 10. 什么叫绝对高程?什么叫相对高程? 11. 用水平面代替水准面,地球曲率对水平距离、水平角和高
程有何影响?
12.根据“1956年黄海高程系”算得地面上A点高程为 63.464m,B点高程为44.529m。若改用“1985国家 高程基准”,则A、B两点的高程各应为多少?
1
3
γ2
A21
2
α21
Quadrantal Angle(象限角)
✓ 象限角
从标准方向线的北端或南端,顺时针或逆时针量至某直线的
水平锐角,以R表示,取值范围为0°~90°。
✓ 象限角与坐标方位角的换算
N
第一象限
我国三大坐标系

我国三大常用坐标系区别(北京54、西安80和WGS-84)我国三大常用坐标系区别(北京54、西安80和WGS-84)1、北京54坐标系(BJZ54)北京54坐标系为参心大地坐标系,大地上的一点可用经度L54、纬度M54和大地高H54定位,它是以克拉索夫斯基椭球为基础,经局部平差后产生的坐标系。
1954年北京坐标系的历史:新中国成立以后,我国大地测量进入了全面发展时期,再全国范围内开展了正规的,全面的大地测量和测图工作,迫切需要建立一个参心大地坐标系。
由于当时的“一边倒”政治趋向,故我国采用了前苏联的克拉索夫斯基椭球参数,并与前苏联1942年坐标系进行联测,通过计算建立了我国大地坐标系,定名为1954年北京坐标系。
因此,1954年北京坐标系可以认为是前苏联1942年坐标系的延伸。
它的原点不在北京而是在前苏联的普尔科沃。
北京54坐标系,属三心坐标系,长轴6378245m,短轴6356863,扁率1/298.3;2、西安80坐标系1978年4月在西安召开全国天文大地网平差会议,确定重新定位,建立我国新的坐标系。
为此有了1980年国家大地坐标系。
1980年国家大地坐标系采用地球椭球基本参数为1975年国际大地测量与地球物理联合会第十六届大会推荐的数据,即IAG 75地球椭球体。
该坐标系的大地原点设在我国中部的陕西省泾阳县永乐镇,位于西安市西北方向约60公里,故称1980年西安坐标系,又简称西安大地原点。
基准面采用青岛大港验潮站1952-1979年确定的黄海平均海水面(即1985国家高程基准)。
西安80坐标系,属三心坐标系,长轴6378140m,短轴6356755,扁率1/298.257221013、WGS-84坐标系WGS-84坐标系(World Geodetic System)是一种国际上采用的地心坐标系。
坐标原点为地球质心,其地心空间直角坐标系的Z轴指向国际时间局(BIH)1984.0定义的协议地极(CTP)方向,X轴指向BIH1984.0的协议子午面和CTP赤道的交点,Y轴与Z轴、X轴垂直构成右手坐标系,称为1984年世界大地坐标系。
测绘各种坐标系

测绘各种坐标系1 大地坐标系:设P点的子午面NPS与起始子午面NGS所构成的二面角L,即P点的大地经度;P点的法线Pn与赤道的夹角B,即P点的大地纬度;从观测点沿椭球的法线方向大到椭球面的距离,即大地高H。
注意:内业的基准线是法线,基准面是参考椭球面;外业的基准线是铅垂线,基准面是大地水准面,此时高程为正高。
以似大地水准面为参照面的高程系统为正常高。
2 空间直角坐标系:空间任意点的坐标用(X,Y,Z)表示,坐标原点位于总地球质心或参考椭球中心,Z轴与地球平均自转轴相重合,即指向某一时刻的平均北极点,X轴指向平均自转轴与平均格林尼治天文台所决定的子午面与赤道面的交点Ge而Y轴与XOZ平面垂直,且指向东为正。
坐标参考系统:分为天球坐标系和地球坐标系。
天球坐标系用于研究天体和人造卫星的定位与运动。
地球坐标系用于研究地球上物体的定位与运动,是以旋转椭球为参照体建立的坐标系统,分为大地坐标系和空间直角坐标系。
即地固坐标系3 天球直角坐标系:原点位于地球质心O,z轴指向天球北极Pn,x轴指向春分点r,y轴垂直于xOz平面,从而建立起来的坐标系即为天球直角坐标系;天球直角坐标也可转化为赤经(a)、赤纬()、向径(d)构成的球面坐标。
春分点和天球赤道面,是建立天球坐标系的重要基准点和基准面。
4 惯性坐标系:是指在空间固定不动或做匀速直线运动的坐标系。
一般很难建立,通常约定建立近似的惯性坐标系,即协议惯性坐标系。
5 协议天球坐标系:由于地球的旋转轴是不断变化的,通常约定某一时刻t作为参考历元,把该时刻对应的瞬时自转轴经岁差和章动改正后的指向作为z轴,以对应的春分点为x 轴的指向点,以xoz的垂直方向为y轴建立的球坐标系协议天球坐标系与瞬时真天球坐标系的差异是由地球旋转轴的岁差和章动引起的,两者之间有其转换关系。
6 瞬时真天球坐标系:是一时刻t的瞬时北天极和真春分点为参考建立的天球坐标系。
它与瞬时平天球坐标系的差异主要是地球自转轴的章动造成的。
坐标转换

《坐标转换的基础知识》一、坐标体系(大类)坐标用来表示地球表面各点的空间位置。
坐标体系通常分为空间直角坐标系、大地坐标系(俗称经纬度坐标)、平面直角坐标系(俗称公里网坐标)三大类。
① 空间直角坐标系常用于宇宙空间科研或参数中间转换,日常生活中使用较少,在此不多做介绍;常规测量一般使用大地坐标系及平面直角坐标系坐标。
② 大地坐标系俗称经纬度坐标,是球面坐标体系,经纬度---竖向记作纬度X(B)、横向记作经度Y(L)。
纬度采用赤道为起始0度、北极为90度、南极为-90度,向北增大、向南减小,北半球记作北纬XX度,南半球记作南纬XX度。
经度采用英国伦敦的格林威治天文台作为起始0度,向东为正记作东经XX度,向西为负记作西经XX 度。
经度按每15度划分时区,共24个时区,对应24小时,我国首都处于东经117度、北纬40度附近,属于东8时区(105-120度),时区与坐标分带无关。
③ 通常我们使用的都是平面地图,能表示地物点的方位、距离及高程等信息。
使用大地坐标系的球面坐标研究整个地球是合适的,显然采用度分秒格式无法表示地物点间的距离,不利于日常使用。
当针对某个地区绘制平面地图时,需要采用地球中心作为参考中心进行平面投影,这就形成了平面直角坐标体系(俗称公里网坐标),一般以米作为计量单位。
公里网坐标都采用北方为上-X-正,东方为右-Y-正,上北下南左西右东的绘图方式,这与平时的数学坐标系统右为X 正、上为Y正不同,需要特别注意。
二、平面坐标投影方式将球面坐标投影为平面坐标,常用墨卡托投影、等角圆锥投影、高斯克吕格投影、UTM投影等。
① 正轴墨卡托投影(简称墨卡托投影,是正轴等角圆柱投影,适合编制航海图,经纬线都是直角正交的),于1569年创立。
假想一个与地轴方向一致的圆柱切或割于地球,按等角条件,将经纬网投影到圆柱面上,将圆柱面展为平面后,即得本投影。
墨卡托投影有切圆柱投影与割圆柱投影之分。
② 等角圆锥投影(适合编制区域性专题地图),是用圆锥切割地球的两条标准纬线,又称双标准纬线等角圆锥投影(适合编制全国地图),其变种为单标准纬线等角圆锥投影(适合编制省级地图)。
测量学课件——1 测绘基础知识

➢1954年北京坐标系存在着很多缺点,主要表现在以 下几个方面:
•1.克拉索夫斯基椭球参数同现代精确的椭球参数的差异较大,并且不包含 表示地球物理特性的参数,因而给理论和实际工作带来了许多不便。
•2.椭球定向不十分明确,椭球的短半轴既不指向国际通用的CIO极,也不 指向目前我国使用的JYD极。参考椭球面与我国大地水准面呈西高东低的 系统性倾斜,东部高程异常达60余米,最大达67米。
克拉索夫斯基椭球
1954年坐标系
IAG-75椭球 WGS84椭球
1980年坐标系 GPS坐标系
地球自然表面
水准面
大地水准面
地球的形状和大小
参考椭球面
地球的形状是一个南北极稍扁的,类似于一个 椭圆绕其短轴旋转的椭球体。 测量工作的基准面是大地水准面,基准线是铅垂线
测量计算的基准面是参考椭球面,基准线是法线
为: L0 6N 3
高斯投影 3° 带: 3°带的分带是在 6°带的基础上进行分带。自东经 1° 30' 开始,每隔 3°由西向东按 1,2, 3 …120顺序编号。
如果知道某点的经度,就可以求出该点 所在3°带的带号n ,该3°带的中央子 午线的经度L为: L=3n。
大比例尺测图和工程测量常采用 3°带、 1.5°带投影或者以任意经度的子午线作为
数学中的笛卡儿 平面直角坐标系
投影变换
正规的平面直角坐标系是利用投影变换,将 空间坐标(空间直角坐标或大地坐标)通过某 种数学变换投影到平面上。这种变换又称为投 影变换。
常见的投影变换 高斯-克吕格投影(也称高斯投影) UTM投影 Lambuda投影
3.1.4 高斯投影
高斯—克吕格投影
将一个椭圆柱面横向 切于一条子午线(称 中央子午线)上,椭 球赤道与柱面相交成 直线。
土地信息系统的几种坐标系
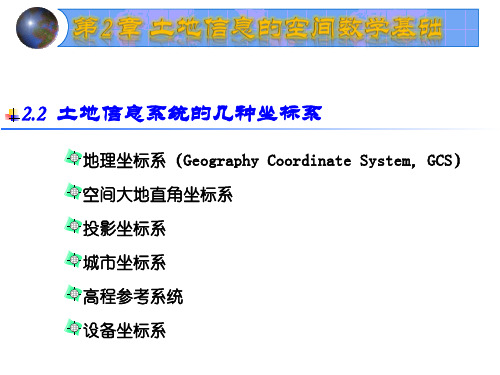
正交成90°夹角 ▪ 空间直角坐标系可用如图所示,某点的坐标
可用该点在此坐标系的各个坐标轴上的投影 (X、Y、Z)来表示。
坐标系应用
▪ 在卫星大地测量中,常采用空间大地直角坐 标系来确定地面点的三维坐标。
▪ 目前,空间大地直角坐标已为很多部门采用 ,但仍有很多部门,由于传统习惯等原因, 通过地面联测,将空间大地直角坐标换算为 全国统一坐标系和高程系的坐标和高程。
▪ 我国高程参考系统
新中国成立后我国大地水准面取青岛验潮站1950年至1956年验潮结果推算的黄海平 均海水面,原点高程值为72.289米,并以此作为全国的高程起算面,亦称1956年黄 海高程系。
1988年1月1日起,我国又启用了1985年国家高程基准,原点高程为72.260米。 1985年与1956年国家高程基准之水准原点间的转换关系为:H85=H56–0.029 。
• 对于绝大多数地理坐标系,本初子午线是指通过英国格林尼治的经线。 • 其他国家/地区使用通过伯尔尼、波哥达和巴黎的经线作为本初子午线。
• 原点——经纬网的原点(0,0) 定义在赤道和本初子午线的交点处。 经度和纬度——经度和纬度是从地心到地球表面上某点的测量角,通常十进制度为单
位或以度、分和秒 (DMS) 为单位进行测量该角度。
三、投影坐标系
坐标系定义
▪ 由地理坐标系经过地图投影变换在二维平面中进行建 立的坐标系即投影坐标系。如图所示:
南北方向为坐标纵轴X′ oX,东西方向为坐标横轴Y′ oY ,交点为坐标原点o;
原点上方的水平线oX、原点右侧的垂直线oY具有正值 ,原点下方的水平线oX′、原点左侧的垂直线oY′具有负 值,在 x 和 y 值域范围内,单位保持不变且间隔相等。
从东北象限开始顺时针记为Ⅰ、Ⅱ、Ⅲ、Ⅳ象限。4个 象限分别表示正负 X 坐标和 Y 坐标的四种可能组合。
坐标系之间的换算

sin X sin Z cos X sinY cos Z
sin X cos Z cos X sinY sin Z
cos X cosY
当已知转换参数⊿X0、dK、R( )时,可按上式将Pi点的X坐标系坐标换算为XT坐 标系的坐标。
A1
X Y Z
A1
X Y Z
A1C
da d
A1
X 0 Y0 Z0
A1dKB
A1QB
A1C
da d
上式中
X ( N H )cos B cos L B Y ( N H )cos B sin L
Z B Y L Z H
0
(M H )cos B
sin B
sin B cos L (M H ) A1 secB sin L (N H )
cos B cos L
sinB sin L (M H ) secB cos L (N H )
X,Y,Z是B,L,H,a, 的函数,全微分有
顾及到
dX dY dZ
A
dB dL dH
C
da
d
0 Z Y X i 0 Zi Yi X
QXi Z 0 X Yi Zi 0 X i Y
X 0 Y0 Z0
sin L
大地测量中常用的坐标系

B) 椭球大地测量学:研究坐标系建立及地球椭球性 质以及投影数学变换为主要内容。
C) 大地天文测量学:以研究测量天文经度、纬度及 天文方位角为中心内容。 D) 大地重力测量学:以研究重力场及重力测量方法 为中心内容。
E) 测量平差:以研究大地测量控制网平差计算为主 要内容。
高斯平面直角坐标系
高斯投影平面特点 1,中央子午线是直线,其长度 不变,离开中央子午线的其它 子午线是弧形,凹向中央子午 线。离开中央子午线越远,变 形越大; 2,投影后赤道是一条直线,赤 道与中央子午线保持正交; 3 离开赤道的纬线是弧线,凸 向赤道。
高斯平面直角坐标系
高斯投影可以将椭球面变成平 面,但是离开中央子午线越远 变形越大。实际中采用分带投 影的方法。投影带宽度是以两 相邻子午线的径差l来划分。有 6°带和3 °带等不同投影方法。
a) 几何大地测量学:基本任务是确定地球的形状和 大小及确定地面点的几何位置。 B) 物理大地测量学:基本任务是用物理方法(重力 测量)确定地球形状及其外部重力场。 C) 空间大地测量学:以人造地球卫星及格其他空间 探测器为代表的空间大地测量的理论、技术与方法。
二 大地测量的基本概念
2.3 大地测量学的基本体系
a=6378137米, α =1:298.257223563
新华网北京2001年2月23日电(记者张继民)覆盖我国全部国土,其分 辨率东部为30公里见方格网、西部为60公里见方格网,精度为30厘 米至60厘米的2000中国似大地水准面,近日通过国家验收。这表明, 新一代分米级精度大地水准面已在我国建立。 曾确定了被称为1980中国大地水准面。这一水准面的精度为±3 米至±5米,分辨率为220公里见方网格。随着科学技术特别是卫星空 间技术的飞速发展,测绘生产技术发生了重大变革,1980中国大地水 准面已远远不能满足现代大地测量发展以及地学研究、国民经济建设的需 要。为此,国家测绘局在“九五”期间设立了重点科技攻关项目——建立 我国分米级精度大地水准面研究。 使用大量我国大陆及其周边海洋地区的重力、高精度GPS水准、 多代卫星测高数据和数字高程模型及海深模型等国内外资料,并结合国情, 最终建立了我国新一代分米级精度大地水准面。通过用中国地壳运动观测 网络的73个GPS水准点进行独立检核,表明其精度在我国东部即东经 102度以东地区,优于0.3米。西部即东经102度以西、北纬36 度以北优于0.4米,东经102度以西、北纬36度以南优于0.6米。 首次以整体分米级精度覆盖了我国全部国土。
各种坐标系的定义

各种坐标系的定义一:空间直角坐标系空间直角坐标系的坐标原点位于参考椭球的中心,Z轴指向参考椭球的北极,X轴指向起始子午面与赤道的交点,Y轴位于赤道面上切按右手系于X轴呈90度夹角,某点中的坐标可用该点在此坐标系的各个坐标轴上的投影来表示。
空间直角坐标系可用如下图所示:二:大地坐标系:大地坐标系是采用大地纬度、经度和大地高程来描述空间位置的。
纬度是空间的点与参考椭球面的法线与赤道面的夹角;经度是空间的点与参考椭球的自转轴所在的面与参考椭球的起始子午面的夹角;大地高师空间的点沿着参考椭球的法线方向到参考椭球面的距离。
附:经度和纬度的详细概念,呵呵。
经度和纬度都是一种角度。
经度是个面面角,是两个经线平面的夹角。
因所有经线都是一样长,为了度量经度选取一个起点面,经1884年国际会议协商,决定以通过英国伦敦近郊、泰晤士河南岸的格林尼治皇家天文台(旧址)的一台主要子午仪十字丝的那条经线为起始经线,称为本初子午线。
本初子午线平面是起点面,终点面是本地经线平面。
某一点的经度,就是该点所在的经线平面与本初子午线平面间的夹角。
在赤道上度量,自本初子午线平面作为起点面,分别往东往西度量,往东量值称为东经度,往西量值称为西经度。
由此可见,一地的经度是该地对于本初子午线的方向和角距离。
本初子午线是0°经度,东经度的最大值为180°,西经度的最大值为180°,东、西经180°经线是同一根经线,因此不分东经或西经,而统称180°经线。
纬度是个线面角。
起点面是赤道平面,线是本地的地面法线。
所谓法线,即垂直于参考扁球体表面的线。
某地的纬度就是该地的法线与赤道平面之间的夹角。
纬度在本地经线上三:平面坐标系(这里主要将gis中高斯-克吕格尔平面直角坐标系,不是数学里面的平面坐标系)高斯-克吕格尔平面直角坐标系Gauss-Krüger plane rectangular coordinates system 根据高斯-克吕格尔投影所建立的平面坐标系,或简称高斯平面坐标系。
坐标系简介

p 11
大地坐标系和高程
大地坐标系(Geodetic
Coordinate System)
大地坐标系是大地测量中以参考椭球面为基准 面建立起来的坐标系。地面点的位臵用大地经度(L)、 大地纬度(B)和大地高度(H)表示。 过地面点P的子午面与起始子午面间的夹角叫P 点的大地经度L。由起始子午面起算,向东为正,叫 东经(0°-180°),向西为负,叫西经(0°-180°)。 过P点的椭球法线与赤道面的夹角叫P点的大地纬度B。 由赤道面起算,向北为正,叫北纬(0°-90°),向 南为负,叫南纬(0°-90°)。从地面点P沿椭球法线 到参考椭球面的距离叫大地高度H。如图4:
坐 标 系 简 介
邹 晶 2011年2月
1
坐标系
坐标系(Coordinate System)
定义:在一个国家或一个地区范围内统一规定 地图投影的经纬线作为坐标轴,以确定国家或某一 地区所有测量成果在平面或空间上的位臵的坐标系 统 。
坐标系种类
坐标系的种类很多,常用的坐标系有:笛卡尔 直角坐标系、平面极坐标系、柱面坐标系(或称柱坐 标系)、独立坐标系和球面坐标系(或称球坐标系)等。
p 12
高程
一般测量中以大地水 准面作为基准面。某点到 基准面的高度是指某点沿 铅垂线方向到大地水准面 的距离,通常称为绝对高 程或海拔,简称高程。 我国的绝对高程是以 青岛港验潮站历年纪录的 黄海平均海水面高为准, 并在青岛建立水准原点, 高程为72.260m。(1985国 家高程基准;原1956年黄 海高程系为72.289m。)
数学上的平面直角坐标系
概念:在平面“二维”内画两条互相垂直,并 且有公共原点的数轴。简称直角坐标系。平面直角 坐标系有两个坐标轴,其中横轴为x轴(x-axis),取 向右方向为正方向;纵轴为y轴(y-axis) ,取向上 为正方向。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
空间直角坐标系、大地坐标系、平面坐标系、
高斯平面直角坐标系
本篇学习了空间直角坐标系、大地坐标系、平面坐标系、高斯平面直角坐标系。
这个个坐标系有时很容易弄混淆!
(一)空间直角坐标系
空间直角坐标系的坐标原点位于参考椭球的中心,Z轴指向参考椭球的北极,X轴指向起始子午面与赤道的交点,Y轴位于赤道面上切按右手系于X轴呈90度夹角,某点中的坐标可用该点在此坐标系的各个坐标轴上的投影来表示。
空间直角坐标系可用如下图所示:
(二)大地坐标系
大地坐标系是采用大地纬度、经度和大地高程来描述空间位置的。
纬度是空间的点与参考椭球面的法线与赤道面的夹角;经度是空间的点与参考椭球的自转轴所在的面与参考椭球的起始子午面的夹角;大地高程是空间的点沿着参考椭球的法线方向到参考椭球面的距离。
地面点的高程和国家高程基准
(1)绝对高程。
地面点沿垂线方向至大地水准面的距离称为绝对高程或称海拔。
过去我国采用青岛验潮站(tide gauge station)1950~1956年观测成果求得的黄海平均海水面作为高程的零点,称为“1956年黄海高程系”(Huanghai height system 1956水准原点高程为72.289m)。
后经复查,发现该高程系的验潮资料时间过短,准确性较差,改用青岛验潮站1950~1979年的观测资料重新推算,并命名为“1985年国家高程基准”(Chinese height datum 1985)。
国家水准原点(leveling origin高程为72.260m)设于青岛市观象山附近,作为我国高程测量的依据。
它的高程值是以“1985年国家高程基准”所确定的平均海水面为零点测算而得。
在使用原“1956年黄海高程系”的高程成果时,应注意将其换算为新的高程基准系统。
(2)相对高程。
地面点沿铅垂线方向至任意假定的水准面的距离称为该点的相对高程,亦称假定高程。
在图l—5中,地面点A和B的相对高程分别为H'A 和H'B 。
(3)高差。
地面上任意两点的高程(绝对高程或相对高程)之差称为高差。
如图l—5中,A、B 两点的高差:
hAB=HB—HA =H'B—H'A
(1-1)
上式中,当 HB (H'B)>HA (H'A) 时,hAB为正;当HB (H'B)<HA (H'A) 时,hAB为‘负’。
确定地面点相互位置的几何要素与测量的基本工作
水平距离、水平角及高程是确定地面点相对位置的三个基本几何要素(图 1-6)距离测量
测量的三项基本工作:水平角(方向)测量
高程测量。
(三)平面直角坐标
瓶面直角坐标:如坐标原点o是任意假定的,则为独立的平面直角坐标系。
由于测量上所用的方向是从北方向(纵轴方向)起按顺时针方向以角度计值(象限也按顺时针编号)。
因此,将数学上平面直角坐标系(角值从横轴正方向起按逆时针方向计值)的 x 和 y轴互换后,数学上的三角函数计算公式可不加改变直接用于测量数据的计算。
(四)高斯-克吕格尔平面直角坐标系(这里主要将gis中高斯-克吕格尔平面直角坐标系,不是数学里面的平面坐标系)
根据高斯-克吕格尔投影所建立的平面坐标系,或简称高斯平面坐标系。
它是大地测量、城市测量、普通测量、各种工程测量和地图制图中广泛采用的一种平面坐标系。
高斯-克吕格尔投影是德国的 C.F.高斯于1822年提出的,后经德国的克吕格尔(J.H.L.Krüger)于1912年加以扩充而完善。
用大地经度和纬度表示的大地坐标是一种椭球面上的坐标,不能直接应用于测图。
因此,需要将它们按一定的数学规律转换为平面直角坐标。
大地坐标(B,L)转换为平面直角坐标(X,Y)的一般数学表示法为:X=F1(B,L), Y=F2(B,L), 式中F1、F2为投影函数。
高斯-克吕格尔投影的投影函数是根据以下两个条件确定的:第一,投影是正形的,即椭球面上无穷小的图形和它在平面上的表象相似,故又称保角投影或保形投影;投影面上任一点的长度比(该点在椭球面上的微分距离与其在平面上相应的微分距离之比)同方位无关。
第二,椭球面上某一子午线在投影平面上的表象是一直线,而且长度保持不变,即长度比等于1。
该子午线称为中央子午线,或称轴子午线。
这两个条件体现了高斯-克吕格尔投影的特性。
大地坐标系是大地测量的基本坐标系。
常用于大地问题的细算,研究地球形状和大小,编制地图,火箭和卫星发射及军事方面的定位及运算,若将其直接用于工程建设规划、设计、施工等很不方便。
所以要将球面上的大地坐标按一定数学法则归算到平面上,即采用地图投影的理论绘制地形图,才能用于规划建设。
椭球体面是一个不可直接展开的曲面,故将椭球体面上的元素按一定条件投影到平面上,总会产生变形。
测量上常以投影变形不影响工程要求为条件选择投影方法。
地图投影有等
角投影、等面积投影和任意投影三种。
其中等角投影又称为正形投影,它保证在椭球体面上的微分图形投影到平面后将保持相似。
这是地形图的基本要求。
正形投影有两个基本条件:①保角条件,即投影后角度大小不变。
②长度变形固定性,即长度投影后会变形,但是在一点上各个方向的微分线段变形比m是个常数k。
