应用光学课件--APP_OPT2
合集下载
应用光学课件-PPT

4)若视阑为长方形或正方形,其线视场按对角线计算。
5)入射窗、出射窗、视阑之间得相互共轭关系。
大家应该也有点累了,稍作休息
大家有疑问得,可以询问与交流
10
例:有一光学系统,透镜O1、O2得口径D1=D2=50mm,焦距 f1′= f2′=150mm,两透镜间隔为300mm,并在中间置一光 孔O3,口径D3=20mm,透镜O2右侧150mm处再置一光孔O4,口 径D4=40mm,平面物体处于透镜O1左侧150mm处。求该系统 得孔径光阑、入瞳、出瞳、视场光阑、入窗、出窗得位 置与大小。
两正薄透镜组L1与L2得焦距分别为100mm与50mm,通光口径 分别为60mm与30mm,两透镜之间得间隔为50mm,在透镜L2之 前30mm处放置直径为40mm得光阑,问 1)当物体在无穷远处时,孔径光阑为哪个? 2)当物体在L1前方300mm处时,孔径光阑为哪个?
4、说明: 1)物体位置改变,原孔阑可能失去控制轴上点孔径角得作用,要重复上述 三个步骤确定孔阑。
工具显微镜中(β 准确)被测物得像与刻度尺相比较,可测物之长度。
物体不论处于何位 置,发出得主光线 都不随物体位置得 移动而变化;读出 刻尺面上光斑得中 心示值,即可求出 准确得象高。
三、 象方远心光路
1、 概念: 某些大地测量仪器或投影仪器中,为了消除像平面与标尺分划刻
线面不重合而引起得测量误差,在物镜得物方焦平面上加入一个光 阑作为孔径光阑,出瞳则位于像方无穷远,称为“像方远心光路”。 2、 应用:
3)物点在无限远时,各光孔像中,直径最小者即为入瞳。入瞳对应得实际 光孔即为孔径光阑。
例:有两个薄透镜L1与L2 ,焦距分别为90mm与30mm,孔径分 别为60mm与40mm,相隔50mm,在两透镜之间,离L2为 20mm处放置一直径为10mm得圆光阑,试对L1前120mm处 得轴上物点求孔阑、入瞳、出瞳得位置与大小。
5)入射窗、出射窗、视阑之间得相互共轭关系。
大家应该也有点累了,稍作休息
大家有疑问得,可以询问与交流
10
例:有一光学系统,透镜O1、O2得口径D1=D2=50mm,焦距 f1′= f2′=150mm,两透镜间隔为300mm,并在中间置一光 孔O3,口径D3=20mm,透镜O2右侧150mm处再置一光孔O4,口 径D4=40mm,平面物体处于透镜O1左侧150mm处。求该系统 得孔径光阑、入瞳、出瞳、视场光阑、入窗、出窗得位 置与大小。
两正薄透镜组L1与L2得焦距分别为100mm与50mm,通光口径 分别为60mm与30mm,两透镜之间得间隔为50mm,在透镜L2之 前30mm处放置直径为40mm得光阑,问 1)当物体在无穷远处时,孔径光阑为哪个? 2)当物体在L1前方300mm处时,孔径光阑为哪个?
4、说明: 1)物体位置改变,原孔阑可能失去控制轴上点孔径角得作用,要重复上述 三个步骤确定孔阑。
工具显微镜中(β 准确)被测物得像与刻度尺相比较,可测物之长度。
物体不论处于何位 置,发出得主光线 都不随物体位置得 移动而变化;读出 刻尺面上光斑得中 心示值,即可求出 准确得象高。
三、 象方远心光路
1、 概念: 某些大地测量仪器或投影仪器中,为了消除像平面与标尺分划刻
线面不重合而引起得测量误差,在物镜得物方焦平面上加入一个光 阑作为孔径光阑,出瞳则位于像方无穷远,称为“像方远心光路”。 2、 应用:
3)物点在无限远时,各光孔像中,直径最小者即为入瞳。入瞳对应得实际 光孔即为孔径光阑。
例:有两个薄透镜L1与L2 ,焦距分别为90mm与30mm,孔径分 别为60mm与40mm,相隔50mm,在两透镜之间,离L2为 20mm处放置一直径为10mm得圆光阑,试对L1前120mm处 得轴上物点求孔阑、入瞳、出瞳得位置与大小。
最新应用光学课件第二章幻灯片课件

靠近光轴的区域叫近轴区,近轴区域内的光 线叫近轴光线
• 近轴光路计算公式有误差 • 相对误差范围
s
in sin
0.100
5
应用光学§讲2稿-3 球面近轴范围内成像性质和近轴光路计算公式
1. 轴上点
近轴光线的成像性质
ilru kilrku
r
r
i'ni n'
k'inki n'
u ' u i i ' k ' u k u k k i' i
应用光学课件第二章
应用光学讲稿
§ 2-1 共轴球面系统中的光路计算公式
求一物点的像,即求所有出射光线位置,交点就是 该物点的像点。
因为所有出射光线位置的求法是相同的,只须找出 求一条出射光线的方法即可。
因为所有的球面的特性是一样的,只须导出光线经 过一个球面折射时由入射光线位置计算出射光线位置 的公式, 即球面折射的光路计算公式。
sinU=u sinU'=u' sinI=i sinI'=i’
得到新的公式组
应用光学§讲2稿-3 球面近轴范围内成像性质和近轴光路计算公式
sin I L r sin U r
sin I ' n sin I n'
i lru r
i' n i n'
U'U I I'
u' u i i'
L' r sin I ' r sin U '
-1°
- 100 10
0.1920 0.1932弧度
0.1266 0.1269弧度 0.0488弧度
u1 l1 r1 i1=(l1-r1)÷ r1×u1
应用光学第二版胡玉禧课件第二章

−l
β =
y' y
y' nl ' = β = y n ' l (2.15) -------垂轴放大率仅取决于共轭面的位置。
l'
第二章
高斯光学
四、近轴光学公式的实际意义 1、作为衡量光学系统成像质量的标准; 2、近似确定光学系统的成像尺寸。 例1.(习题1)一根长500mm, n =1.5的玻璃棒,两端面为凸 球面,半径分别为50mm和100mm,高1mm的物体位于左端 球面顶点之前200mm处,
图2.11 过节点的光线
第二章
高斯光学
B A′ A F H H′ F′ B′
§2-5 由基面、基点求理想像
一、作图法求像 1、典型光线及性质 2、用作图法求光学系统的理想像 1) 轴外 点B或 一垂 轴线 段AB 的像 (图2.14-5)
B′ B A′ F A N H M M ′ N′ H′ F′
M 2 ' A2 ' // N 2 ' F2 '
图(d):为(a)、(b)、(c)的总结果图。
B′ A2 F2 H2 H F1′ 2′ A2′ F2′ A1′ A1 F1 M1′
M1 H1 F2
M2
M2′ A2′ F ′ 2
H1′ H2 F1′ 2′ H
图 (c)
图 (d )
第二章
二、解析法求像
高斯光学
3、作图注意几点(P.37)
图2. 16
作图法求轴上点的像
第二章
高斯光学
图(b):同2)中法一;
轴上点经两个光组的像 图(a):作A1M1 ;
M1
A F1 F2 H1 H1′H2 F ′H2′ 1 F2′ A1
应用光学第二,三章ppt课件

r d 2 2
r d 1 3
14. 假定显微镜物镜由相隔20mm的两个薄透镜组 构成,物平面和像平面之间的距离为180mm, 放大率β=-10×,要求近轴光线通过二透镜组时 的偏角Δu1和Δu2相等,求二透镜 组的焦距。 解:
' u u u 1 1 1
' u u u 2 2 2
应用视度公式就可以了
1 1 SD 1 l 1
注意符号,这里是-1
3、假定用眼睛直接观察敌人的坦克时,可以在400m的距离上看清
坦克上的编号,如果要求距离2km也能看清,问应使用几倍的望远镜 ?
l ' 36 . 12 m
若 l'50 m
l ' 1 1 1 300 l l ' l f '
3 50 10 f' 166 . 11 mm 301
16. 一个投影仪用5×的投影物镜,当像平面与投影屏不重合而
外伸10mm时,则须移动物镜使其重合,试问物镜此时应向 物平面移动还是向像平面移动?移动距离多少?
x 8 m x ' 0 . 703 mm
x 6 m x ' 0 . 9375 mm
x 4 m x ' 1 . 406 mm
x 2 m x ' 2 . 813 mm
7. 设一物体对正透镜成像,其垂轴放大率等于-1,
试求物平面与像平面的位置,并用作图法验证。
ห้องสมุดไป่ตู้
解:
2 2 dx 5 25
dx ' 25 dx
dx ' 10 dx ' 10
应用光学教学课件第二章1

sin sin
的大小来确定。
例: sin sin 0.001 θ<5o
2024/2/18
39
The final image formed by a lens of a small planar object normal to the optical axis will itself be a small plane normal to that axis.
A’
O
r
-L
L’
第四步:在△EA’C中,CA’ = L’-r, 由正弦定理,可得
L' r r sin I ' sinU '
L' r(1 sin I ' ) sinU '
2024/2/18
21
sin I L r sinU r
sin I ' n sin I n'
U' U I I'
子午面内光路计 算大L计算公式
2024/2/18
从左向右为正向光路,反之为反向光路。
正向光路
反向光路
2024/2/18
7
(二)线段
1. 沿轴线段:从起点(原点)到终点的方向与光 线传播方向相同,为正;反之为负。
即线段的原点为起点,向右为正,向左为负。
原点
+
-
原点
2024/2/18
8
※ 原点规定:
(1)曲率半径 r ,以球面顶点O为原点,球心
C在右为正,在左为负。
光轴 为起始边。
B
y -U
A
-L
E I
h
I’
φ
C
U’
A’
O
r
的大小来确定。
例: sin sin 0.001 θ<5o
2024/2/18
39
The final image formed by a lens of a small planar object normal to the optical axis will itself be a small plane normal to that axis.
A’
O
r
-L
L’
第四步:在△EA’C中,CA’ = L’-r, 由正弦定理,可得
L' r r sin I ' sinU '
L' r(1 sin I ' ) sinU '
2024/2/18
21
sin I L r sinU r
sin I ' n sin I n'
U' U I I'
子午面内光路计 算大L计算公式
2024/2/18
从左向右为正向光路,反之为反向光路。
正向光路
反向光路
2024/2/18
7
(二)线段
1. 沿轴线段:从起点(原点)到终点的方向与光 线传播方向相同,为正;反之为负。
即线段的原点为起点,向右为正,向左为负。
原点
+
-
原点
2024/2/18
8
※ 原点规定:
(1)曲率半径 r ,以球面顶点O为原点,球心
C在右为正,在左为负。
光轴 为起始边。
B
y -U
A
-L
E I
h
I’
φ
C
U’
A’
O
r
应用光学 ppt课件

当光线遇到障碍物时会发生光的衍射现象,从而偏离光线的直线 传播。
衍射
双折射
梯度折射率
2.2 光的独立传播定律
在光相交的区域可能发生叠加,甚至发生干涉。不管是哪一种情 况,在光离开相交区域后,光波继续沿着既定的方向向前传播,该 光波身上找不到其他光波对其产生的任何影响,此现象称为光的独 立传播定律。
1.1.2 电磁波谱
400~760nm
380~760nm 390~780nm
1nm 103 μm 106 mm 109 m
1.1.2 电磁波谱
在电磁波谱里,可见光大约在380~760nm之间,按波长从长到 短依次分别呈现红、橙、黄、绿、蓝、靛、紫等七种颜色。这七种 色光其实分界并不完全准确,因为两种色光之间的界限本身就不明 显,过渡是一种渐进的过程。
色光 红 橙 黄 绿
范围/nm 640-760 600-640 550-600 480-550
色光 蓝 靛 紫
范围/nm 450-480 430-450 380-430
1.1.3 可见光
可见光(Visible light)是波 长大约在380~760nm之间的波 段范围,由于人眼对此波段的 光线敏感,可以引起视网膜的 感光,传递到大脑后,经过大 脑处理后可以分辨出光线的颜 色及与光线相关的物体。
则光的折射定律(Snell law, refraction law of light)可以表示为
1.折射光线也在入射面内; 2.入射角和折射角正弦之比为一个常数,与入射角大小无关。
sin I sin I ' n12
其中为 n12 比例常数
2.4 光的折射定律
海市蜃楼的形成
2.5 光路可逆
光的反射定律和折射定律一个直接的应用就是光路可逆。光在空 间传播时,在光学系统中行进,无外乎有三种情况:
衍射
双折射
梯度折射率
2.2 光的独立传播定律
在光相交的区域可能发生叠加,甚至发生干涉。不管是哪一种情 况,在光离开相交区域后,光波继续沿着既定的方向向前传播,该 光波身上找不到其他光波对其产生的任何影响,此现象称为光的独 立传播定律。
1.1.2 电磁波谱
400~760nm
380~760nm 390~780nm
1nm 103 μm 106 mm 109 m
1.1.2 电磁波谱
在电磁波谱里,可见光大约在380~760nm之间,按波长从长到 短依次分别呈现红、橙、黄、绿、蓝、靛、紫等七种颜色。这七种 色光其实分界并不完全准确,因为两种色光之间的界限本身就不明 显,过渡是一种渐进的过程。
色光 红 橙 黄 绿
范围/nm 640-760 600-640 550-600 480-550
色光 蓝 靛 紫
范围/nm 450-480 430-450 380-430
1.1.3 可见光
可见光(Visible light)是波 长大约在380~760nm之间的波 段范围,由于人眼对此波段的 光线敏感,可以引起视网膜的 感光,传递到大脑后,经过大 脑处理后可以分辨出光线的颜 色及与光线相关的物体。
则光的折射定律(Snell law, refraction law of light)可以表示为
1.折射光线也在入射面内; 2.入射角和折射角正弦之比为一个常数,与入射角大小无关。
sin I sin I ' n12
其中为 n12 比例常数
2.4 光的折射定律
海市蜃楼的形成
2.5 光路可逆
光的反射定律和折射定律一个直接的应用就是光路可逆。光在空 间传播时,在光学系统中行进,无外乎有三种情况:
应用光学第七章2-课件

• 物体被物镜成的像A’ B’ 位于目镜的物方焦点上或附近,此像相 对于物镜像方焦点的距离为Δ(物镜和目镜的光学间隔),在显 微镜系统中称为光学筒长
• 设物镜的焦距为f1′, 则物镜的放大率为
x'
f1' f1'
• 物镜的像被目镜放大,其放大率为
e
250 f2'
• 式中: f2' 为目镜的焦距。由此,显微镜系统的总放大率为
• 利用体视仪器可以提高人眼的体视能 力
• 双眼仪器的体视放大率
仪
•
人眼直接观察时的视角差α眼为
眼
B
αB
A
αA
眼
b l
αA-αB
• 假设双眼望远镜的二个入射光轴之间为距离B,称为该仪器的基 线长,则同一物体对仪器的二入射瞳孔所构成的视角差α为
B l
• 若系统的视放大率Г为,则物方视角差α和像方视角 差α’在不大条件下存在以下关系
• 人眼瞳孔之间的平均距离为b=62mm,min10"
lmi n bmin 01 .0"062 20"61 02 0m 00
• Lmax称为立体视觉半径
b l
lb 2 l
或 l l2
b
双眼观察仪器
• 利用仪器观察物体时,必须采用双眼
仪器来保持人眼的体视能力,这种仪 器称为“双眼望远镜”和“双眼显微镜”
应用光学第七章2
精品
• 双眼观察的深度感觉除上述因素外:
• 5)物体的距离越近,视轴之间的夹角越大,这种感 觉使眼球发生转动的肌肉紧张程度就不同,据此就 能判断物体的远近;
• 6)双眼立体视觉(简称体视)
• α称为“视差角” B
• 设物镜的焦距为f1′, 则物镜的放大率为
x'
f1' f1'
• 物镜的像被目镜放大,其放大率为
e
250 f2'
• 式中: f2' 为目镜的焦距。由此,显微镜系统的总放大率为
• 利用体视仪器可以提高人眼的体视能 力
• 双眼仪器的体视放大率
仪
•
人眼直接观察时的视角差α眼为
眼
B
αB
A
αA
眼
b l
αA-αB
• 假设双眼望远镜的二个入射光轴之间为距离B,称为该仪器的基 线长,则同一物体对仪器的二入射瞳孔所构成的视角差α为
B l
• 若系统的视放大率Г为,则物方视角差α和像方视角 差α’在不大条件下存在以下关系
• 人眼瞳孔之间的平均距离为b=62mm,min10"
lmi n bmin 01 .0"062 20"61 02 0m 00
• Lmax称为立体视觉半径
b l
lb 2 l
或 l l2
b
双眼观察仪器
• 利用仪器观察物体时,必须采用双眼
仪器来保持人眼的体视能力,这种仪 器称为“双眼望远镜”和“双眼显微镜”
应用光学第七章2
精品
• 双眼观察的深度感觉除上述因素外:
• 5)物体的距离越近,视轴之间的夹角越大,这种感 觉使眼球发生转动的肌肉紧张程度就不同,据此就 能判断物体的远近;
• 6)双眼立体视觉(简称体视)
• α称为“视差角” B
应用光学课件新

第一章
几何光学基本定律
本章要解决的问题:
光是什么?--光的本性问题 光是怎么走的?--光的传播规律
像与成像的概念
对成像的要求
第一节 念
几何光学的基本概
研究光的意义: 90%信息由视觉获得,光波是视觉的 载体 光是什么?弹性粒子-弹性波-电磁波-波粒二象 性 1666年:牛顿提出微粒说,弹性粒子
1678年:惠更斯提出波动说,以太中传播的弹性波 1873年:麦克斯韦提出电磁波解释,电磁波 1905年:爱因斯坦提出光子假设 20世纪:人们认为光具有波粒二象性
B
反射:I1=R1
R1=I1 A I1 R1 C
折射:
n1
O I2 B n2
n1 Sin I1 = n2 Sin I2 n2 Sin I2 = n1 Sin I1
3、应用 光路可逆:
求焦点 光学设计中,逆向计算:目镜,显微 物镜等
• 全反射
1、定义:当光从光密介质射入到光疏介质,并且当入 射角大于某值时,在二种介质的分界面上光全部返回 到原介质中的现象。 空气
所以称之为几何光学 当几何光学不能解释某些光学现象,例如干涉、衍射 时,再采用物理光学的原理
波面:在某一时刻,同一光源辐射场的位相相 同的点构成的曲面。
t + Δt 时刻 t 时刻 A
光线是波面的法线 波面是所有光线的垂直曲
面
光线与波面之间的关系:波面的法线即为几何
光学中所指的光线。
1.1 光源、波面、光线和光束(续)
υ1 υ2
C
第一种介质的绝对折射率 : 第二种介质的绝对折射率 : n2
n1 =
n2 =
υ1
C
υ2
所以
n 1, 2 =
几何光学基本定律
本章要解决的问题:
光是什么?--光的本性问题 光是怎么走的?--光的传播规律
像与成像的概念
对成像的要求
第一节 念
几何光学的基本概
研究光的意义: 90%信息由视觉获得,光波是视觉的 载体 光是什么?弹性粒子-弹性波-电磁波-波粒二象 性 1666年:牛顿提出微粒说,弹性粒子
1678年:惠更斯提出波动说,以太中传播的弹性波 1873年:麦克斯韦提出电磁波解释,电磁波 1905年:爱因斯坦提出光子假设 20世纪:人们认为光具有波粒二象性
B
反射:I1=R1
R1=I1 A I1 R1 C
折射:
n1
O I2 B n2
n1 Sin I1 = n2 Sin I2 n2 Sin I2 = n1 Sin I1
3、应用 光路可逆:
求焦点 光学设计中,逆向计算:目镜,显微 物镜等
• 全反射
1、定义:当光从光密介质射入到光疏介质,并且当入 射角大于某值时,在二种介质的分界面上光全部返回 到原介质中的现象。 空气
所以称之为几何光学 当几何光学不能解释某些光学现象,例如干涉、衍射 时,再采用物理光学的原理
波面:在某一时刻,同一光源辐射场的位相相 同的点构成的曲面。
t + Δt 时刻 t 时刻 A
光线是波面的法线 波面是所有光线的垂直曲
面
光线与波面之间的关系:波面的法线即为几何
光学中所指的光线。
1.1 光源、波面、光线和光束(续)
υ1 υ2
C
第一种介质的绝对折射率 : 第二种介质的绝对折射率 : n2
n1 =
n2 =
υ1
C
υ2
所以
n 1, 2 =
应用光学课件

有渐晕时,斜光束的宽度不单由孔径光阑的口径确定, 有渐晕时,斜光束的宽度不单由孔径光阑的口径确定,而且还 与其余光学零件或光阑的口径有关
应用光学讲稿
§5-2 望远系统中成像光束的选择 一、双目望远镜
1、光学系统图 、 视放大率: 视放大率: Г=6 成像范围(视场角):2ω=8°30’ 成像范围(视场角):2 =8° ): 出瞳直径: 出瞳直径: 出瞳距离: 出瞳距离: 物镜焦距: 物镜焦距: 目镜焦距: 目镜焦距: D´=5mm l´z≥11mm f´物=108mm f´目=18mm
10 (1) tg ω = ,所以 240
(2)
1 ω = arctg 即为物方视角。 24
1 ω ′ = arctg 即为像方视角。 3
10 tg ω ′ = ,所以 30
(3)出瞳是孔径光阑在系统像空间所成的像,对目镜来说:
l = −240 mm − 30 mm = − 270 mm
应用光学讲稿
出瞳:是光能最集中的地方, 出瞳:是光能最集中的地方,为了看清整个视场 眼睛的瞳孔应该和出瞳重合。 ,眼睛的瞳孔应该和出瞳重合。 对出瞳距离必须有一定的要求,一般仪器大于6毫米, 对出瞳距离必须有一定的要求,一般仪器大于 毫米, 毫米 对于军用仪器,要大一些,可能大于20毫米 毫米。 对于军用仪器,要大一些,可能大于 毫米。 出瞳直径的大小,直接与像的亮暗有关 出瞳直径的大小, 问题:是否出瞳直径越大越好,出瞳距离越长越好? 问题:是否出瞳直径越大越好,出瞳距离越长越好?
应用光学讲稿
二 光阑概念 1、孔径光阑(Aperture Stop) 、孔径光阑( ) 光束口径的光阑 2、视场光阑(Field Stop) 、视场光阑( ) 限制成像范围的光阑 底片框 3、消杂光光阑(False 、消杂光光阑( Light Stop) )
应用光学讲稿
§5-2 望远系统中成像光束的选择 一、双目望远镜
1、光学系统图 、 视放大率: 视放大率: Г=6 成像范围(视场角):2ω=8°30’ 成像范围(视场角):2 =8° ): 出瞳直径: 出瞳直径: 出瞳距离: 出瞳距离: 物镜焦距: 物镜焦距: 目镜焦距: 目镜焦距: D´=5mm l´z≥11mm f´物=108mm f´目=18mm
10 (1) tg ω = ,所以 240
(2)
1 ω = arctg 即为物方视角。 24
1 ω ′ = arctg 即为像方视角。 3
10 tg ω ′ = ,所以 30
(3)出瞳是孔径光阑在系统像空间所成的像,对目镜来说:
l = −240 mm − 30 mm = − 270 mm
应用光学讲稿
出瞳:是光能最集中的地方, 出瞳:是光能最集中的地方,为了看清整个视场 眼睛的瞳孔应该和出瞳重合。 ,眼睛的瞳孔应该和出瞳重合。 对出瞳距离必须有一定的要求,一般仪器大于6毫米, 对出瞳距离必须有一定的要求,一般仪器大于 毫米, 毫米 对于军用仪器,要大一些,可能大于20毫米 毫米。 对于军用仪器,要大一些,可能大于 毫米。 出瞳直径的大小,直接与像的亮暗有关 出瞳直径的大小, 问题:是否出瞳直径越大越好,出瞳距离越长越好? 问题:是否出瞳直径越大越好,出瞳距离越长越好?
应用光学讲稿
二 光阑概念 1、孔径光阑(Aperture Stop) 、孔径光阑( ) 光束口径的光阑 2、视场光阑(Field Stop) 、视场光阑( ) 限制成像范围的光阑 底片框 3、消杂光光阑(False 、消杂光光阑( Light Stop) )
应用光学教学课件完整

※从上述定律可以得到光线传播的一 个重要原理—光路的可逆性原理。利 用这一原理,可以由物求像,也可以 由像求物。
• 图1-9
※光学系统 的作用之一是对物体成像,因此必须搞 清物像的基本概念和它们的关系。
※物体通过光学系统(光组)成像,光学系统(各 种光学仪器)由一系列光学零件 组成。。
※光学系统一般是轴对称的,有一条公共轴线,
全反射现象
当
一般情况下,光线射至透明介质的分界面时将发 生反射和折射现象。
光 由
由公式 n sin I n' sin I ' 可知
光
密
sin I sin I '
介 质
射
即折射光线较入射光线偏离法线
向
光
疏
sin I ' 不可能大于1,此时入射光线将不能射入
另一介质。
按照反射定律在介面上全部被反射回原介质
原点
+
-
原点
※ 原点规定:
(1)曲率半径 r ,以球面顶点O为原点,球
心C在右为正,在左为负。
E
A
C
O +r
E
A
C
-r O
(2)物方截距L 和像方截距L’ 也以顶点O为原点,到光线
与光轴交点,向右为正,向左为负。
E
A
A’
O
C
-L
+L’
E
A
A’
O
C
-L’
-L
(3)球面间隔 d 以前一个球面的顶点为原点, 向右为正,向左为负。
(在折射系统中总为正,在反射和折反系统中才有为负的情况)
O1
O2
+d
O1
O2
• 图1-9
※光学系统 的作用之一是对物体成像,因此必须搞 清物像的基本概念和它们的关系。
※物体通过光学系统(光组)成像,光学系统(各 种光学仪器)由一系列光学零件 组成。。
※光学系统一般是轴对称的,有一条公共轴线,
全反射现象
当
一般情况下,光线射至透明介质的分界面时将发 生反射和折射现象。
光 由
由公式 n sin I n' sin I ' 可知
光
密
sin I sin I '
介 质
射
即折射光线较入射光线偏离法线
向
光
疏
sin I ' 不可能大于1,此时入射光线将不能射入
另一介质。
按照反射定律在介面上全部被反射回原介质
原点
+
-
原点
※ 原点规定:
(1)曲率半径 r ,以球面顶点O为原点,球
心C在右为正,在左为负。
E
A
C
O +r
E
A
C
-r O
(2)物方截距L 和像方截距L’ 也以顶点O为原点,到光线
与光轴交点,向右为正,向左为负。
E
A
A’
O
C
-L
+L’
E
A
A’
O
C
-L’
-L
(3)球面间隔 d 以前一个球面的顶点为原点, 向右为正,向左为负。
(在折射系统中总为正,在反射和折反系统中才有为负的情况)
O1
O2
+d
O1
O2
应用光学课件完整版

球面波,会聚为物体的完善象。
物象都有虚实之分: 实物— 物方实际光线直接相交而成的点。 虚物— 物方实际光线不能相交,延长线相交而成的点。 实象— 象方实际光线直接相交的点。 虚象— 象方实际光线不能直接相交,反向延长相交。 物空间— 构成物的光线所处的空间。(实物、虚物) 象空间— 构成象的光线所处的空间。(实象、虚象)
由一点A发出的光线经过光学系统后聚交或近似的聚 交在一点A′,则A为物点, A′为物点A通过光学系统 所成的像点。物与象之间的对应关系称为“共轭”。
一个物点,总是发出同心光束,与球面波相对应; 一个像点,理想情况应该由球面波对应的同心光束汇交 而成,称这种像点为完善像点。
3. 成完善象的条件 发光体每一物点发出球面波,通过光学系统后仍为
1. 共轴球面系统的结构参量: 各球面半径:r1 、 r2 …… rk-1 、 rk 相邻球面顶点间隔:d1 、 d2 …… dk-1 各球面间介质折射率:n1 、 n2 …… nk-1 、 nk n 、 k+1
2. 转面公式
原则:前一折射面的象为后一面的物 ,前一面的象空间为后一面的物空间
n2 = n1′, n3 = n2′ …… nk = nk-1′
3)在光学设计中有重要作用。为了设计出一定垂 轴倍率的光学系统,在物方参数nuy固定的条件下,常通 过改变像方孔径角u′的大小来改变y′的数值,使得y′与y 的比值满足系统设计的要求。
§ 2-3 共轴球面系统
探讨方法— 将光线的光路计算公式及放大率公式反复应 用于各个折射面,分别求出各面的u、 u′、l 、 l′、 β、α、γ、y、y′J、J′、Q、 Q′。 转面公式— 前后相邻面之间的基本量的转化关系。
反射定律可表示为 I I ''
物象都有虚实之分: 实物— 物方实际光线直接相交而成的点。 虚物— 物方实际光线不能相交,延长线相交而成的点。 实象— 象方实际光线直接相交的点。 虚象— 象方实际光线不能直接相交,反向延长相交。 物空间— 构成物的光线所处的空间。(实物、虚物) 象空间— 构成象的光线所处的空间。(实象、虚象)
由一点A发出的光线经过光学系统后聚交或近似的聚 交在一点A′,则A为物点, A′为物点A通过光学系统 所成的像点。物与象之间的对应关系称为“共轭”。
一个物点,总是发出同心光束,与球面波相对应; 一个像点,理想情况应该由球面波对应的同心光束汇交 而成,称这种像点为完善像点。
3. 成完善象的条件 发光体每一物点发出球面波,通过光学系统后仍为
1. 共轴球面系统的结构参量: 各球面半径:r1 、 r2 …… rk-1 、 rk 相邻球面顶点间隔:d1 、 d2 …… dk-1 各球面间介质折射率:n1 、 n2 …… nk-1 、 nk n 、 k+1
2. 转面公式
原则:前一折射面的象为后一面的物 ,前一面的象空间为后一面的物空间
n2 = n1′, n3 = n2′ …… nk = nk-1′
3)在光学设计中有重要作用。为了设计出一定垂 轴倍率的光学系统,在物方参数nuy固定的条件下,常通 过改变像方孔径角u′的大小来改变y′的数值,使得y′与y 的比值满足系统设计的要求。
§ 2-3 共轴球面系统
探讨方法— 将光线的光路计算公式及放大率公式反复应 用于各个折射面,分别求出各面的u、 u′、l 、 l′、 β、α、γ、y、y′J、J′、Q、 Q′。 转面公式— 前后相邻面之间的基本量的转化关系。
反射定律可表示为 I I ''
应用光学第二章2.ppt
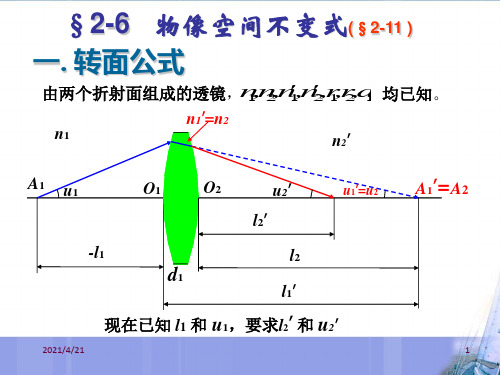
§2-6 物像空间不变式(§2-11 )
一. 转面公式
由两个折射面组成的透镜,n1,n2,n'1,n'2,r1,r2,d1 均已知。
n1’=n2
n1
n2’
A1 u1
O1
O2
u2’
l2’
u1’=u2
-l1
l2
d1
l1’
现在已知 l1 和 u1,要求l2’ 和 u2’
2021/4/21
A1’=A2
1
问题分两步解决:
12
方法2: 对每一面应用物像位置公式
n' n n' n
l' l
r
及转面公式
l 2 l ' 1 d 1 , l 3 l '2 d 2 . . . . . . l k l 'k 1 d k 1
当只关心物像位置且折射面很少时,用方法2较为 方便。如需知道一些中间量且折射面较多时,多 采用方法1。
2021/4/21
4
反复应用小 l 公式进行计算,此时,前一 个面的像空间就是后一个面的物空间。
参数关系:
n2 n'1,n3 n'2......nk n'k1 ul22lu'1'1,ud13,l3u'2l,'2.....d.u2k.....u.lk'k1l'k1dk1 y2 y'1,y3 y'2......yk y'k1
只能对细光束成完善像的光学系统是无实用价值的!
寻找一个能对较大范围、较粗光束及较宽波段 范围都能成满意像的光学系统,就是应用光学所需 要解决的中心问题。
到哪里找这样 的系统呢?
2021/4/21
一. 转面公式
由两个折射面组成的透镜,n1,n2,n'1,n'2,r1,r2,d1 均已知。
n1’=n2
n1
n2’
A1 u1
O1
O2
u2’
l2’
u1’=u2
-l1
l2
d1
l1’
现在已知 l1 和 u1,要求l2’ 和 u2’
2021/4/21
A1’=A2
1
问题分两步解决:
12
方法2: 对每一面应用物像位置公式
n' n n' n
l' l
r
及转面公式
l 2 l ' 1 d 1 , l 3 l '2 d 2 . . . . . . l k l 'k 1 d k 1
当只关心物像位置且折射面很少时,用方法2较为 方便。如需知道一些中间量且折射面较多时,多 采用方法1。
2021/4/21
4
反复应用小 l 公式进行计算,此时,前一 个面的像空间就是后一个面的物空间。
参数关系:
n2 n'1,n3 n'2......nk n'k1 ul22lu'1'1,ud13,l3u'2l,'2.....d.u2k.....u.lk'k1l'k1dk1 y2 y'1,y3 y'2......yk y'k1
只能对细光束成完善像的光学系统是无实用价值的!
寻找一个能对较大范围、较粗光束及较宽波段 范围都能成满意像的光学系统,就是应用光学所需 要解决的中心问题。
到哪里找这样 的系统呢?
2021/4/21
光学的应用PPT课件

第5页/共14页
光的反射与折射
• 海市蜃楼 海市蜃楼是非常神奇又难得一见的自然景观之一,在我国沿海省份的夏季经常可以看到此奇景,在我国
古代经常被神化,其实它的的形成主要是由于光的折射和全反射造成的。
第6页/共14页
生活中光的反射应用
• 镜面的反射
•
根据镜面反射、漫反射特点,反射在我们的日常生活中有着极其广泛的应用。我们每天都接触镜子,
第8页/共14页
干涉、衍射在生活中的应用
电子显微镜
光谱仪
第9页/共14页
光学在高新技术中的应用
• X光线在医学中的应用
从1895年德国物理学家伦琴发现X线至今已有100多年的历史,X线透
视和摄片为人类的健康做出了巨大的贡献,而。今影像医学作为一门崭新
的学科。
X线穿透密度不同的组织时,密度高的组织被吸收
第1页/共14页
光源
•
顾名思义,也就是任何能够发出可见光的物体,太阳、萤火虫等发出的光(自然光源),蜡烛、火焰、
各种各样的灯(人造光源)等所发出的光,都是我们日常生活中所熟悉的光源。光源不仅用来照明,在科
学实验中为了各种科学研究课题的需要,人们常使用形式多样的特殊光源,尤其是在上世纪六十年代美国
红宝石激光器的成功发射,更是人们在探索光的路途中的一项重大里程碑。
正是有了光的反射,镜子才可以把接收到的光反射过来。例如:汽车后视镜,公路上的标志牌,潜望镜。
第7页/共14页
光的干涉与衍射
• 两列或几列光波在空间相遇时相互叠加,在某些区域始终加强,在另一些区域则始终削弱,形成稳定的强 弱分布的现象。这种现象叫作光的干涉。
光在传播过程中,遇到障碍物或小孔时,光将偏离直线传播的途径 而绕到障碍物后面传播的现象,叫光的衍射。 光的衍射和光的干 涉一样证明了光具有波动性。
光的反射与折射
• 海市蜃楼 海市蜃楼是非常神奇又难得一见的自然景观之一,在我国沿海省份的夏季经常可以看到此奇景,在我国
古代经常被神化,其实它的的形成主要是由于光的折射和全反射造成的。
第6页/共14页
生活中光的反射应用
• 镜面的反射
•
根据镜面反射、漫反射特点,反射在我们的日常生活中有着极其广泛的应用。我们每天都接触镜子,
第8页/共14页
干涉、衍射在生活中的应用
电子显微镜
光谱仪
第9页/共14页
光学在高新技术中的应用
• X光线在医学中的应用
从1895年德国物理学家伦琴发现X线至今已有100多年的历史,X线透
视和摄片为人类的健康做出了巨大的贡献,而。今影像医学作为一门崭新
的学科。
X线穿透密度不同的组织时,密度高的组织被吸收
第1页/共14页
光源
•
顾名思义,也就是任何能够发出可见光的物体,太阳、萤火虫等发出的光(自然光源),蜡烛、火焰、
各种各样的灯(人造光源)等所发出的光,都是我们日常生活中所熟悉的光源。光源不仅用来照明,在科
学实验中为了各种科学研究课题的需要,人们常使用形式多样的特殊光源,尤其是在上世纪六十年代美国
红宝石激光器的成功发射,更是人们在探索光的路途中的一项重大里程碑。
正是有了光的反射,镜子才可以把接收到的光反射过来。例如:汽车后视镜,公路上的标志牌,潜望镜。
第7页/共14页
光的干涉与衍射
• 两列或几列光波在空间相遇时相互叠加,在某些区域始终加强,在另一些区域则始终削弱,形成稳定的强 弱分布的现象。这种现象叫作光的干涉。
光在传播过程中,遇到障碍物或小孔时,光将偏离直线传播的途径 而绕到障碍物后面传播的现象,叫光的衍射。 光的衍射和光的干 涉一样证明了光具有波动性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
正负含义? φ = n'−n r
f
'=
l'l
→
−∞
=
n' n '− n
r
f
=
ll
'
→
∞
=
−
n n '− n
r
光焦度 (折射面偏折光线的能力)
ቤተ መጻሕፍቲ ባይዱ
f’像方焦距(点),后焦距(点)
l→-∞
l’→∞
F -f O
f’
F’
由上三式得
φ = n' = − n
f'
f
f ' = − n'
f
n
f 物方焦距(点),前焦距(点)
二、近轴光线经折射球面折射并成像 1.近轴光线:与光轴很靠近的光线,即-U很小, sin(-U)≈-U,此时用小写: sin(-U)= - u sinI=i L=l
近轴光线所在的区域叫近轴区
对近轴光,已知入射光线求折射球面的出射光线:即由 l, u — >l’,u’ ,以上公式组变为:
i= l− r u r
光轴以锐角方向转到光线,顺时针正逆时针负 光线与法线组成角度(I,I’)
光线以锐角方向转到法线,顺正逆负 光轴与法线组成角度(φ)
光轴以锐角方向转到法线,顺正逆负
§2-2 折射球面
A -U
E I
I’ h
φ
r -L
n’>n
U’
A’
L’
一、由折射球面的入射光线求出射光线 即已知:r, n, n’,L, U 求 : L’, U’
i'= n i n'
u '= u + i − i'
当u改变时,l’不变! 点——》点,完善成像
此时A,A’互为物像,称共轭点
l'= r + r i' u'
近轴光所成像称为高斯像 仅考虑近轴光的光学叫高斯光学
1
2.近轴光线经折射球面计算的其他形式
(为计算方便,根据不同情况可使用不同公式)
利用 lu = h = l'u'
利用三角形相似、折射定律及U+I=U’+I’=φ 得
sin I = L − r sin U r
sin I ' = n sin I n'
U '= U + I − I'
L ' = r + r sin I ' sin U '
可见,L’=f(U) 不同U的光线经折射 后不能相交于一点 点-》斑,不完善成像
A Aa’ Ab’ Ac’
不再是平面:像面弯曲
2. 细小平面以细光束经折射球面成像: 平面物——》平面像,完善成像
3. 细小平面以细光束成像的三种放大率与拉氏不变量
B
n
n’
y
A’
A
r
-y’ B’
-l
l’
①横向放大率(垂轴放大率)β
β = y' = nl' = nu (利用三角形相似和阿贝不变量) y n'l n'u'
②轴向(沿轴)放大率α α = dl ' = nl '2 = n' β 2 dl n' l 2 n
描述光轴上一对共轭点沿轴 移动量之间的关系
③角度放大率
γ = u' = l = n 1 u l' n' β
描述折射前后一对光线与光轴夹 角之间的关系
讨论:
β = nl' n'l
β = y' y
当n,n’一定, l不同,则β不同 垂轴物像
当l一定(l’一定)时,β为常量。 相似 β>0时,y,y’同号,成正像,否则成倒像 |β|>1时,|y’|>|y|, 成放大像,否则成缩小像
φ = h / r = u + i = u'+i'
ni = n'i'
可导出
n(1 − 1) = n'(1 − 1) = Q
rl
r l'
n' − n = n'−n l' l r
n'u'−nu = n'−n h r
阿贝不变量
折射球面的物像位置关系
光线经折射球面时 的u,u’关系
3.(近轴区)折射球面的光焦度,焦点和焦距 可见,当(n’-n)/r一定时,l’仅与l有关。
1+1= 2 l' l r
φ = − 2n r
r<0, φ>0会聚 r>0, φ<0发散
二、焦距 f ' = f = r
2
f ’,f 与 r 同号
C
F F’
FF’ C
f’<0为实焦点
f’>0为虚焦点
β = − l'
三、放大率与拉氏不变量
α
l = −β 2
(物像反向移动)
γ =− 1 β
j = nyu = n ' y ' u ' ∴ yu = − y ' u '
讨论经共轴球面系统成像的几个光路计算问题。
一、由入射光线求出射光线 对一个面的操作 + 过渡 过渡公式:
ni' = ni + 1, (i = 1,2,..., k ) yi' = yi + 1, (i = 1,2,..., k − 1) ui' = ui + 1, (i = 1,2,..., k − 1) li + 1 = li'− di, (i = 1,2,..., k − 1) hi + 1 = hi − diui' , (i = 1,2,..., k − 1)
第二章 球面和球面系统
§2-1 概念与符号规则 §2-3 反射球面
§2-2 折射球面 §2-4 共轴球面系统
§2-1 概念与符号规则
一、概念
①子午平面——包含光轴的平面
②截距:物方截距——物方光线与光轴的交点到顶点的距离 像方截距——像方光线与光轴的交点到顶点的距离
③倾斜角:物方倾斜角——物方光线与光轴的夹角
2
B1
y1
A1
-u1
-l1
§2-4 共轴球面系统
n1
n1’=n2
u1’ A1’(A2) O2
O1
C1
-y1’ -y2 u2
B1’(B2) r1
l1’
-l2
d1
n2’=n3 C2
r2 l2’
B2’
y2’ -u2’ A2’
已知:1、各球面曲率半径 r1,r2,……rk 2、各表面顶点的间隔 d1, d2, ….. ,dk-1 3、折射率 n1, n2, ……, nk+1
α = n' β 2 n
α>0, 像移动方向与物移动方向相同 一般α≠β,立体物与像不再相似
αγ = β β、α、γ之间的关系
由
y' = β = nu
y
n'u'
得 nyu = n' y'u' =
j
j为拉氏不变量, 它是表征光学系统
性能的重要参数
§2-3 反射球面——球面镜
一、物像公式 n' − n = n'−n n’=-n l' l r
普适于任何 光学系统 及
f'+ f =1 l' l f '+ f = r
三、物平面以细光束经折射球面成像
1.物平面以细小光束成像 B1 A1
B2’ A2’
A
C
A’
B2 A2
细光束,A——》A’ 完善成像
B1’ A1’
同心球面A1AA2——》曲面A1’A’A2’ 完善成像 由公式,l变小,l’也变小,平面B1AB2——》曲面B1’A’B2’
像方倾斜角——像方光线与光轴的夹角
E
I
n’>n
A -U
I’ h
φ
U’
A’
O
C
r
-L
L’
分界面有左右,球面有凹凸,光轴有上方下方,区别?
二、符号规则:规定 a. 光线传播方向:从左向右 b. 线段:沿轴线段(L,L’,r)以顶点O为基准,左负右正
垂轴线段(h)以光轴为准,上正下负 间隔d (O1O2=d)以前一个面为基准,左负右正 c. 角度:光轴与光线组成角度(U,U’)
