二十三章反比例函数单元测试卷.doc
第一章《反比例函数》(基础卷)(原卷版)

2022-2023学年湘教版九年级上册期末真题单元冲关测卷(基础卷)第一章反比例函数一、选择题(每小题4分,共40分)1.(2021-2022·湖南·期末试卷)下列函数中,是反比例函数的是()A.y=5xB.y=x2C.y=2x+1D.2y=x2.(2021-2022·广东·单元测试)若函数y=(m2−1)x m2−m−3是反比例函数,则m的值是()A.±1B.2C.−1或2D.−13.(2021-2022·河南·月考试卷)下列关于反比例函数y=−3x的结论中正确的是()A.图象过点(1,3)B.图象在一、三象限内C.当x<0时,y随x的增大而增大D.当x>−1时,y>34.(2021-2022·河南·月考试卷)已知电流I(安培)、电压U(伏特)、电阻R(欧姆)之间的关系为I=UR,当电压为定值时,关于R的函数图象是()A. B. C. D.5.(2021-2022·广东·单元测试)已知反比例函数y=kx的图象经过点P(3,−4),则这个反比例函数的解析式为()A.y=12x B.y=−12xC.y=3xD.y=4x6.(2021-2022·安徽·期末试卷)若点A(−3,2)关于x轴的对称点A′恰好在反比例函数y=kx(k≠0)的图象上,则k的值为()A.−5B.−1C.6D.−67.(2021-2022·广东·同步练习)如图,点P在反比例函数y=k(k≠0)的图象上,PA⊥x轴于点A,x△PAO的面积为2,则k的值为()A.1B.2C.4D.68.(2021-2022·广东·月考试卷)若点A(−3,y1),B(−1,y2),C(3,y3)都在反比例函数y=k(k>0)的x图象上,则y1,y2,y3的大小关系是()A.y1>y2>y3B.y3>y1>y2C.y2>y1>y3D.y1>y3>y29.(2021-2022·安徽·月考试卷)已知正比例函数y=k1x和反比例函数y=k2,在同一直角坐标x系下的图象如图所示,其中符合k1⋅k2>0的是()A.①②B.①④C.②③D.③④10.(2021-2022·广东·单元测试)如图,在直角坐标系中,正方形的中心在原点O,且正方形的一组对边与x轴平行,点P(4a,a)是反比例函数y=k(k>0)的图象上与正方形的一个交点,若x图中阴影部分的面积等于16,则k的值为( )A.16B.1C.4D.−16二、填空题(本题共计6小题,每题4分,共计24分)11.(2021-2022·广东·期末试卷)若函数y=mx m2+3m−1是反比例函数,则m=________.12.(2020-2021·湖南·期中试卷)已知反比例函数y=(m−2)x m2−10的图象,在每一象限内y随x 的增大而减小,则反比例函数的解析式为________.13.(2021-2022·全国·中考复习)计划修建铁路1200km,那么铺轨天数y(d)是每日铺轨量x的________比例函数解,其表达式为________.14.(2021-2022·河南·中考复习)已知函数y=−1,当自变量的取值为−1<x<0或x≥2时,x函数值y的取值为________.15.(2021-2022·河南·月考试卷)已知(−3, y1),(−2, y2),(1, y3)是抛物线y=3x2+12x+m上的点,则y1,y2,y3的大小关系为________.A.y2<y3<y1B.y1<y2=y3C.y2<y1<y3D.y3<y2<y116.(2021-2022·河南·中考复习)如图,在平面直角坐标系中,菱形OBCD的边OB在x轴正半的图象经过菱形OB-CD对角线的交点A,若点D的坐标为(6,8),则k 轴上,反比例函数y=kx的值为________.三、解答题(本题共计8小题,每题10分,共计86分)17.(2021-2022·广东·单元测试)已知函数y=(m2+2m)x m2−m−1.(1)如果y是x的正比例函数,求m的值;(2)如果y是x的反比例函数,求出m的值,并写出此时y与x的函数关系式.18.(2020·广东·单元测试)已知函数y=(k−2)x k2−5为反比例函数.(1)求k的值;(2)它的图象在第________象限内,在各象限内,y随x增大而________;(填变化情况)时,y的取值范围.(3)求出−2≤x≤−1219.(2021-2022·吉林·月考试卷)如图,在平面直角坐标系xOy中,一次函数y=x+b的图象与在第一象限内的图象交于点C,连接CO x轴交于点A(−4,0),与y轴交于点B,与反比例函数y=kx.(1)求b的值;(2)若S△OBC=2,则k的值是________.20.(2021-2022·甘肃·月考试卷)如图,一次函数y=kx+b与反比例函数y=m的图象相交于xA(−1, 4),B(2, n)两点,直线AB交x轴于点D.(1)求一次函数与反比例函数的表达式;(2)过点B作BC⊥y轴,垂足为C,连接AC交x轴于点E,求△AED的面积S· .21.(2021-2022·山东·月考试卷)Rt△OAB在直角坐标系内的位置如图所示,BA⊥OA,反比例函数y=k(k≠0)在第一象限内的图像与AB交于点C(8,1)与OB交于点D(4,m).x(1)求该反比例函数的解析式及图像为直线OB的正比例函数解析式;(2)求BC的长.22.(2021-2022·河南·月考试卷)如图,平行四边形OABC的边OA在x轴上,点D是对角线OB 的中点,反比例函数y=k(x>0)的图象经过点D.点B的坐标为(10,4),点C的坐标为(3,4)x(1)求反比例函数的解析式;(2)求平行四边形OABC的周长.23.(2021-2022·山东·月考试卷)如图,在平面直角坐标系中,直线y=x+2与双曲线y=k交x 于A,B两点,已知点A的横坐标为1.(1)求k的值;(2)求△OAB的面积;的解集.(3)直接写出关于x的不等式x+2>kx24.(2021-2022·安徽·月考试卷)校园里的饮水机接通电源就进入自动程序,开机加热时每分钟上升10∘C,加热到100∘C停止加热,水温开始下降,此时水温y(∘C)与开机后用时x(min)成反比例关系,直至水温降至40∘C,饮水机关机,饮水机关机后即刻自动开机,重复上述自动程序.若在水温为40∘C时接通电源,水温y(∘C)与时间x(min)的关系如图所示:(1)分别写出图中水温上升和下降阶段y与x之间的函数关系式;(2)小明同学想喝高于50∘C的水,请问他最多需要等待多长时间?。
反比例函数单元测试卷

.已知反比例函数y =xk的图象经过点(m ,3m ),则此反比例函数的图象(.第一、二象限 B .第一、三象限 .C .第二、四象限 D .第三、四象限P (kPa)例函数,其图象如图所示.当气球内的气压大于120 kPa 时,气球发将爆炸.为了安全起见,气球的体积应 ( )A .不小于54m 3 B .小于54m 3 C .不小于45m 3 D .小于45m 37.如果点P 为反比例函数xy 4=的图象上一点,PQ ⊥x 轴,垂足为Q ,那么△POQ 的面积为( )A .2B . 4C .6D . 8 8.已知:反比例函数xmy 21-=的图象上两点A (x 1,y 1),B (x 2, y 2)当x 1<0<x 2时,y 1<y 2,则m 的取值范围 ( ) A .m <0 B .m >0 C .m <21 D .m >21二、填空题.(共10小题,每小题3分,共30分)9.有m 台完全相同的机器一起工作,需m 小时完成一项工作,当由x 台机器(x 为不大于m 的正整数)完成同一项工作时,所需的时间y 与机器台数x 的函数关系式是___ _.10.已知y 与x 成反比例,且当x 32=-时,y =5,则y 与x 的函数关系式为__________.11.反比例函数xy 3=的图象在第一象限与第 象限.12.某食堂现有煤炭500吨,这些煤炭能烧的天数y 与平均每天烧煤的吨数x 之间的函数关系式是 .13.若n x m y ++=2)5(是反比例函数,则m 、n 的取值是 .14.两位同学在描述同一反比例函数的图象时,甲同学说:这个反比例函数图象上任意一点到两坐标轴的距离的积都是3;乙同学说:这个反比例函数的图象与直线y =x 有两个交点,你认为这两位同学所描述的反比例函数的解析式是 . 15.在ABC △的三个顶点A (2,-3)、B (-4,-5)、C (-3,2)中,可能在反比例函数(0)ky k x=>的图象上的点是 . 16.如果反比例函数4ny x-=的图象位于第二、四象限,则n 的取值范围是_______;如果图象在每个象限内,y 随x 的增大而减小,则n 的取值范围是 .17.如图,△P 1OA 1、△P 2A 1 A 2是等腰直角三角形,点P 1、P 2在函数4(0)y x x=>的图象上,斜边OA 1、A 1 A 2都在x 轴上,则点A 2的坐标是 . 18.两个反比例函数k y x =和1y x=在第一象限内的图象如图所示,点P 在k y x=的图象上,PC ⊥x 轴于点C ,交1y x=的图象于点A ,PD ⊥y 轴于点D ,交1y x=的图象于点B ,当点P 在ky x=的图象上运动时,以下结论:①△ODB 与△OCA 的面积相等;②四边形PAOB 的面积不会发生变化;③PA 与PB 始终相等;④当点A 是PC 的中点时,点B 一定是PD 的中点. 其中一定正确的是 (把你认为正确结论的序号都填上,少填或错填不给分).三、解答题(7小题,共46分)19.(6分)反比例函数xky =的图象经过点A (2 ,3).(1)求这个函数的解析式;(2)请判断点B (1 ,6)是否在这个反比例函数的图象上,并说明理由.20.(6分)已知三角形的一边为x ,这条边上的高为y ,三角形的面积为3,写出y 与x 的函数表达式,并画出函数的图象.21.(10分)某蓄水池的排水管每时排水8 m 3,6h 可将满池水全部排空. (1)蓄水池的容积是多少?(2)如果增加排水管,使每时排水量达到Q (m 3),那么将满池水排空所需的时间t (h )将如何变化?(3)写出t 与Q 之间的函数关系式.12第17题(4)如果准备在5小时之内将满水池排空,那么每时的排水量至少为多少? (5)已知排水管的最大排水量为每时12m 3,那么最少多长时间可将满池水全部排空?22.(8分)近视眼镜的度数y (度)与镜片焦距x (米)成反比例,已知800度近视眼镜镜片的焦距为0.125米, (1)求y 与x 的函数关系;(2)若张华同学近视眼镜镜片的焦距为0.25米,你知道他的眼睛近视多少度吗?23.(9分)对于取消市场上使用的杆秤的呼声越来越高,原因在于一些不法商贩在卖货时将秤砣挖空,或更换较小称砣,使砣较轻,从而欺骗顾客.(1)如图,对于同一物体,哪个图用的是标准秤砣,哪个用的是较轻的秤砣?(2)在称同一物体时,所称得的物体质量y (千克)与所用秤砣质量x (千克)之间满足 关系.(3)当砣较轻时,称得的物体变重,这正好符合哪个函数的哪些性质?24.6分)联想电脑公司新春期间搞活动,规定每台电脑0.7万元,交首付后剩余的钱数y 与时间t 的关系如图所示:(1)根据图象写出y 与t 的函数关系式. (2)求出首付的钱数.(3)如果要求每月支付的钱数不少于400元,那么还至少几个才能将所有的钱全部还清? (4)图1图2月)y ()新人教八年级(下)第17章《反比例函数》答案一、选择题1.B ;2. A ;3. B ;4. A ;5. B ;6. C ;7.A ;8. C . 二、填空题9.y =x m 2 10.152y x=- 11.三 12.y =x 50013.m ≠-5 n =-3 14.y =x 3 15.B16.n >4,n <4 17.(0) 18.①②④ 三、解答题 19.(1)y =x 6;(2)在 20. y =6x ,图像略 21.(1)348m ;(2)t 将减小;(3)48t Q=;(4)4859.6Q Q ==,;(5)48412t ==22. 23. 24.(1)12--=x y ;(2)略 25.(1)100y x =,(2)400度 26.(1)图②是用与秤配套的秤砣,图①则使用较轻的秤砣.(2)反比例. (3)函数y =x k(k >0),当x 变小时,y 增大 27.(1)y =t 6000 ;(2)7000-6000=1000(元);(3)400=t6000,t =15。
反比例函数全章测试卷

《反比例函数》单元测试题班级_____________姓名____________得分______________一、选择题(30分)1、若反比例函数22)12(--=mx m y 的图像在第二、四象限,则m 的值是( ) (A )-1或1 (B )小于21 的任意实数 (C ) -1 (D) 不能确定 2、在反比例函数1k y x-=的图象的每一条曲线上,y x 都随的增大而增大,则k 的值可以是( ) A .1- B .0 C .1 D .23、已知点(-1,y 1)、(2,y 2)、(π,y 3)在双曲线xk y 12+-=上,则下列关系式正确的是( )(A )y 1>y 2>y 3 (B )y 1>y 3>y 2 (C )y 2>y 1>y 3 (D )y 3>y 1>y 24、已知反比例函数y=2x,下列结论中,不正确...的是( )A .图象必经过点(1,2)B .y 随x 的增大而减少C .图象在第一、三象限内D .若x >1,则0<y <25、如图是三个反比例函数312,,k k k y y y x x x===,在x 轴 上方的图像,由此观察得到k l 、k 2、k 3的大小关系为( )(A ) k 1>k 2>k 3 (B ) k 3>k 1>k 2 (C ) k 2>k 3>k 1 (D ) k 3>k 2>k 16、反比例函数k y x=在第一象限的图象如图所示,则k 的值可能是( ) A .1 B .2 C .3 D .47、如图,直线l 和双曲线k y x=(0k >)交于A 、B 两点,P 是线段 AB 上的点(不与A 、B 重合),过点A 、B 、P 分别向x 轴作垂线,垂足分别为C 、D 、E ,连接OA 、OB 、OP ,设△AOC 的面积为1S 、△BOD的面积为2S 、△POE 的面积为3S ,则有( ) A .123S S S << B .123S S S >> C . 123S S S =< D .123S S S =>8、如图,直线y=mx 与双曲线y=xk 交于A 、B 两点,过点A 作AM ⊥x 轴, 垂足为M ,连结BM,若ABM S ∆=2,则k 的值是( )A .2B 、m-2C 、mD 、49、已知甲、乙两地相s (千米),汽车从甲地匀速行驶到达乙地,如果汽车每小时耗油量为a(升),那么从甲地到乙地汽车的总耗油量y(升)与汽车的行驶速度v(千米/时)的函数图象大致是()10.如图,已知关于x的函数y=k(x-1)和y=-kx(k≠0), 它们在同一坐标系内的图象大致是( )11、两位同学在描述同一反比例函数的图象时,甲同学说:“从这个反比例函数图象上任意一点向x轴、y轴作垂线,与两坐标轴所围成的矩形的面积为6.”乙同学说:“这个反比例函数图象与直线y=-x有两个交点.”你认为这两位同学所描述的反比例函数的表达式为.12、已知:点A(m,m)在反比例函数1yx=的图象上,点B与点A关于坐标轴对称,以AB为边作等边△ABC,则满足条件的点C有个.13、若反比例函数的表达式为3yx=,则当1x<-时,y的取值范围是14、反比例函数1kyx=与一次函数2y x b=-+的图象交于点(23)A,和点(2)B m,.若12y y>,则x的取值范围是______ ________.15、如图,正方形OABC的面积是4,点B在反比例函数(00)ky k xx=><,的图象上.若点R是该反比例函数图象上异于点B的任意一点,过点R分别作x轴、y轴的垂线,垂足为M、N,从矩形OMRN的面积中减去其与正方形OABC重合部分的面积,记剩余部分的面积为S.则当S=m(m为常数,且0<m<4)时,点R的坐标是_______________ (用含m的代数式表示)16、两个反比例函数k y x =和1y x=在第一象限内的图象如图所示,点P 在k y x =的图象上,PC ⊥x 轴于点C ,交1y x =的图象于点A ,PD ⊥y 轴于点D ,交1y x=的图象于点B ,当点P 在k y x=的图象上运动时,以下结论:①△ODB 与△OCA 的面积相等;②四边形PAOB 的面积不会发生变化;③PA 与PB 始终相等;④当点A 是PC 的中点时,点B 一定是PD 的中点. 其中一定正确的是 (把你认为正确结论的序号都填上,少填或错填不给分).三、解答题17(10分)、已知y=y 1+y 2 ,y 1与x+1成正比例,y2与x+1成反比例,当x=0时,y=-5;当x=2时,y=-7. (1)求y与x的函数关系式; (2)当2y x =-时,求x的值。
(名师整理)数学九年级下册《第26章 反比例函数》单元检测试题(含答案解析)

第26章《反比例函数》单元测试卷一.选择题1.下列函数中,y是x的反比例函数的是()A.=﹣1 B.xy=﹣C.y=x﹣p D.y=﹣52.若y=(m﹣1)x|m|﹣2是反比例函数,则m的值为()A.m=2 B.m=﹣1 C.m=1 D.m=03.在同一坐标系中(水平方向是x轴),函数y=和y=kx+3的图象大致是()A.B.C.D.4.一次函数y=kx+2k与反比例函数y=(k≠0)在同一直角坐标系内的图象可能是()A.B.C.D.5.若一个正比例函数的图象与一个反比例函数图象的一个交点坐标是(2,3),则另一个交点的坐标是()A.(2,3)B.(3,2)C.(﹣2,3)D.(﹣2,﹣3)6.关于双曲线的对称性叙述错误的是()A.关于原点对称B.关于直线y=x对称C.关于x轴对称D.关于直线y=﹣x对称7.若一元二次方程x2﹣2x﹣m=0无实数根,则反比例函数y=的图象所在的象限是()A.第一、二象限B.第一、三象限C.第二、四象限D.第三、四象限8.反比例函数y=的图象位于()A.第一、二象限B.第一、三象限C.第二、三象限D.第二、四象限9.在反比例函数y=的图象的每一个象限内,y都随x的增大而减小,则k的取值范围是()A.k>3 B.k>0 C.k≥3 D.k<310.对于反比例函数y=,下列说法正确的是()A.图象经过点(2,﹣1)B.图象位于第二、四象限C.图象是中心对称图形D.当x<0时,y随x的增大而增大11.如图,在平面直角坐标系中,△OAB的顶点A在x轴正半轴上,OC是△OAB 的中线,点B、C在反比例函数y=(x>0)的图象上,则△OAB的面积等于()A.2 B.3 C.4 D.612.如图,在平面直角坐标系中,双曲线y=,y=﹣与⊙O相交,以交点为顶点的八边形ABCDEFGH是正八边形,则此正八边形的面积为()A.32 B.64 C.16D.16+1613.已知点A(2,3)在双曲线y=上,则下列哪个点也在该双曲线上()A.(﹣1,6)B.(6,﹣1)C.(﹣2,﹣3)D.(﹣2,3)14.若反比例函数y=(k≠0)的图象经过点P(2,﹣3),则该函数的图象不经过的点是()A.(3,﹣2)B.(1,﹣6)C.(﹣1,6)D.(﹣1,﹣6)15.如图,点P(3a,a)是反比例函数y=(k>0)与⊙O的一个交点,图中阴影部分的面积为10π,则反比例函数的解析式为()A.y=B.y=C.y=D.y=16.如图,过点A(4,5)分别作x轴、y轴的平行线,交直线y=﹣x+6于B、C两点,若函数y=(x>0)的图象△ABC的边有公共点,则k的取值范围是()A.5≤k≤20 B.8≤k≤20 C.5≤k≤8 D.9≤k≤20二.填空题17.下列函数中,哪些是y关于x的反比例函数?A.y=B.y=﹣C.y=D.y=(a为常数)E.y=+1018.函数y=(m+1)x是y关于x的反比例函数,则m=.19.如果直线y=mx与双曲线y=的一个交点A的坐标为(3,2),则它们的另一个交点B的坐标为.20.如图,已知双曲线y=(k<0)经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C.若点A的坐标为(﹣8,6),则△AOC的面积为.21.已知反比例函数y=在第二象限内的图象如图,经过图象上两点A、E 分别引y轴与x轴的垂线,交于点C,且与y轴与x轴分别交于点M、B.连接OC交反比例函数图象于点D,且=,连接OA,OE,如果△AOC的面积是15,则△ADC与△BOE的面积和为.22.如图,在平面直角坐标系xOy中,点A,B在双曲线y=(k是常数,且k≠0)上,过点A作AD⊥x轴于点D,过点B作BC⊥y轴于点C,已知点A的坐标为(4,),四边形ABCD的面积为4,则点B的坐标为.23.已知一菱形的面积为12cm2,对角线长分别为xcm和ycm,则y与x的函数关系式为三.解答题(共1小题)24.已知反比例函数y=(k≠0)的图象经过点A(﹣3,﹣6).(1)求这个函数的表达式;(2)点B(4,),C(2,﹣5)是否在这个函数的图象上?(3)这个函数的图象位于哪些象限?函数值y随自变量x的增大如何变化?参考答案一.选择题1.解:A、该函数是一次函数,故本选项错误;B、该函数符合反比例函数的定义,故本选项正确;C、该函数不符合反比例函数的定义,故本选项错误;D、该函数不符合反比例函数的定义,故本选项错误.故选:B.2.解:依题意得:|m|﹣2=﹣1且m﹣1≠0,解得m=﹣1.故选:B.3.解:A、由函数y=的图象可知k>0与y=kx+3的图象k>0一致,故A 选项正确;B、因为y=kx+3的图象交y轴于正半轴,故B选项错误;C、因为y=kx+3的图象交y轴于正半轴,故C选项错误;D、由函数y=的图象可知k>0与y=kx+3的图象k<0矛盾,故D选项错误.故选:A.4.解:①当k>0时,y=kx+2k过一、二、三象限;y=过一、三象限;②当k<0时,y=kx+2k二、三、四象象限;y=过二、四象限.观察图形可知只有D符合②.故选:D.5.解:∵反比例函数的图象与经过原点的直线的两个交点一定关于原点对称,∴另一个交点的坐标与点(2,3)关于原点对称,∴该点的坐标为(﹣2,﹣3).故选:D.6.解:∵双曲线的两个分支分别在二、四象限,∴两个分支关于原点对称,关于直线y=x对称,故A、B选项正确;此双曲线的每一个分支关于直线y=﹣x对称,故D选项正确;故选:C.7.解:∵一元二次方程x2﹣2x﹣m=0无实数根,∴△=4+4m<0,解得m<﹣1,∴m+1<0,∴反比例函数y=的图象所在的象限是第二、四象限.故选:C.8.解:∵反比例函数y=中,k=3>0,∴反比例函数y=的图象在一、三象限.故选:B.9.解:∵在反比例函数y=的图象的每一个象限内,y都随x的增大而减小,∴3﹣k>0,即k<3,故选:D.10.解:∵当x=2时,可得y=1≠﹣1,∴图象不经过点(2,﹣1),故A不正确;∵在y=中,k=2>0,∴图象位于第一、三象限,且在每个象限内y随x的增大而减小,故B、D不正确;又双曲线为中心对称图形,故C正确,故选:C.11.解:如图,过点B、点C作x轴的垂线,垂足为D,E,则BD∥CE,∴==,∵OC是△OAB的中线,∴===,设CE=x,则BD=2x,∴C的横坐标为,B的横坐标为,∴OD=,OE=,∴DE=OE﹣OD=,∴AE=DE=,∴OA=OE+AE=,∴S△OAB=OA•BD=××2x=3.故选:B.12.解:连接AO,HO,∵点A在双曲线y=﹣上,∴S△AOM=×|﹣4|=2,∵点H在双曲线y=上,∴S△HOM=×4=2,∴S△AOH=4,∴此正八边形的面积=8×4=32,故选:A.13.解:∵点A(2,3)在双曲线y=上,∴k=xy=2×3=6,∴只需把各点横纵坐标相乘,结果为6的点在函数图象上.A、因为﹣1×6=﹣6≠6,所以该点不在双曲线y=上.故A选项错误;B、因为6×(﹣1)=﹣6≠6,所以该点不在双曲线y=上.故B选项错误;C、因为﹣2×(﹣3)=6,所以该点在双曲线y=上.故C选项正确;D、因为﹣2×3=﹣6≠6,所以该点不在双曲线y=上.故D选项错误.故选:C.14.解:∵反比例函数y=(k≠0)的图象经过点P(2,﹣3),∴k=2×(﹣3)=﹣6∴解析式y=当x=3时,y=﹣2当x=1时,y=﹣6当x=﹣1时,y=6∴图象不经过点(﹣1,﹣6)故选:D.15.【解答】解:设圆的半径是r,根据圆的对称性以及反比例函数的对称性可得:πr2=10π解得:r=2.∵点P(a,b)是反比例函y=(k>0)与⊙O的一个交点.∴ab=k且=r∴a2=×(2)2=4.∴k=3×4=12,则反比例函数的解析式是:y=.故选:C.16.解:∵过点A(4,5)分别作x轴、y轴的平行线,交直线y=﹣x+6于B、C两点,∴点B的纵坐标为5,点C的横坐标为4,将y=5代入y=﹣x+6,得x=1;将x=4代入y=﹣x+6得,y=2,∴点B的坐标为(1,5),点C的坐标为(4,2),∵函数y=(x>0)的图象与△ABC的边有公共点,点A(4,5),点B(1,5),∴1×5≤k≤4×5即5≤k≤20,故选:A.二.填空题(共7小题)17.解:A、该函数是关于(x+1)的反函数,故本选项错误;B、该函数是y关于x的反函数,故本选项正确;C、y=不是反比例函数,故本选项错误;D、符合反比例函数的定义,故本选项正确;E、该函数是y﹣10关于x的反函数,故本选项错误;故答案为:B、E18.解:∵函数y=(m+1)x是y关于x的反比例函数,∴m2﹣2m﹣4=﹣1且m+1≠0,解得m=3.故答案是:3.19.解:因为直线y=mx与双曲线y=的交点均关于原点对称,所以另一个交点坐标为(﹣3,﹣2).20.解:∵点D为线段OA的中点,且点A的坐标为(﹣8,6),∴点D的坐标为(﹣4,3).将点D(﹣4,3)代入到y=中得:3=,解得:k=﹣12.∴双曲线的解析式为y=﹣.令x=﹣8,则有y=﹣=,即点C的坐标为(﹣8,).∵AB⊥BO,∴点B(﹣8,0),AC=6﹣=,OB=0﹣(﹣8)=8,∴△AOC的面积S=AC•OB=××8=18.故答案为:18.21.解:连结AD,过D点作DG∥CM.∵=,△AOC的面积是15,∴CD: CO=1:3,OG:OM=2:3,∴△ACD的面积是5,△ODF的面积是15×=,∴四边形AMGF的面积=,∴△BOE的面积=△AOM的面积=×=12,∴△ADC与△BOE的面积和为5+12=17.故答案为:17.22.解:连接BO、BD,∵点A在双曲线y=(k是常数,且k≠0)上,点A的坐标为(4,),∴k=4×=6,又∵BC⊥y轴于点C,∴BC∥OD,∴△BOC的面积=△BCD的面积=3,又∵四边形ABCD的面积为4,∴△ABD的面积=4﹣3=1,设B(a,),∵AD⊥x轴于点D,A的坐标为(4,),∴AD=,∵××(4﹣a)=1,解得a=,∴=,∴点B的坐标为(,).故答案为:(,).23.解:由题意得:y与x的函数关系式为y==.故本题答案为:y=.三.解答题(共1小题)24.解:(1)∵反比例函数y=(k≠0)的图象经过点A(﹣3,﹣6).∴﹣6=,解得,k=18则反比例函数解析式为y=;(2)点B(4,),C(2,﹣5),∴4×=18,2×(﹣5)=10,∴点B(4,)在这个函数的图象上,点C(2,﹣5)不在这个函数的图象上;(3)∵k=18>0,∴这个函数的图象位于一、三象限,在每一个象限内,函数值y随自变量x的增大而减小.。
反比例函数单元测试题(含答案)

反比例函数练习题一. 选择题1. 函数y m x m m =+--()2229是反比例函数,则m 的值是( )A. m =4或m =-2B. m =4C. m =-2D. m =-1 2. 下列函数中,是反比例函数的是( ) A. y x =-2 B. y x =-12 C. y x =-11 D. y x =123. 函数y kx =-与y k x=(k ≠0)的图象的交点个数是( ) A. 0 B. 1 C. 2 D. 不确定 4. 函数y kx b =+与y k x kb =≠()0的图象可能是( )A B C D5. 若y 与x 成正比,y 与z 的倒数成反比,则z 是x 的( )A. 正比例函数B. 反比例函数C. 二次函数D. z 随x 增大而增大6. 下列函数中y 既不是x 的正比例函数,也不是反比例函数的是( )A. y x =-19B. 105=-x y :C. y x =412 D.152xy =- 二. 填空题7. 一般地,函数__________是反比例函数,其图象是__________,当k <0时,图象两支在__________象限内。
8. 已知反比例函数y x=2,当y =6时,x =_________。
9. 反比例函数y a x a a =---()3224的函数值为4时,自变量x 的值是_________。
10. 反比例函数的图象过点(-3,5),则它的解析式为_________11. 若函数y x =4与y x =1的图象有一个交点是(12,2),则另一个交点坐标是_________。
三. 解答题12. 直线y kx b =+过x 轴上的点A (32,0),且与双曲线y k x =相交于B 、C 两点,已知B 点坐标为(-12,4),求直线和双曲线的解析式。
13. 已知一次函数y x =+2与反比例函数y k x =的图象的一个交点为P (a ,b ),且P 到原点的距离是10,求a 、b 的值及反比例函数的解析式。
反比例函数》单元测试题(含答案)-

反比例函数》单元测试题(含答案)-1.给定双曲线经过点(-2,3),求解析式。
解析:双曲线的一般式为y=k/x,代入点(-2,3)可得3=k/(-2),解得k=-6,所以双曲线的解析式为y=-6/x。
2.已知y与x成反比例,且y=1时,x=4,求x=2时的y 值。
解析:由反比例函数的定义可知,y1*x1=y2*x2,代入y=1,x=4可得1*4=y2*2,解得y2=2,所以当x=2时,y=2.3.已知反比例函数和正比例函数的图象都经过点A(-1,-2),求它们的解析式。
解析:正比例函数的图象为直线y=kx,代入点A可得-2=k*(-1),解得k=2,所以正比例函数的解析式为y=2x。
反比例函数的图象为双曲线y=k/x,代入点A可得-2=k/(-1),解得k=2,所以反比例函数的解析式为y=2/x。
4.某厂有1500吨煤,求这些煤能用的天数y与每天用煤的吨数x之间的函数关系式。
解析:假设每天用煤的吨数为x,那么1500吨煤能用的天数为y=1500/x,所以函数关系式为y=1500/x。
5.若点(3,6)在反比例函数y=k/x(k≠0)的图象上,那么下列各点在此图象上的是()解析:由反比例函数的图象可知,其图象为双曲线,因此点(3,6)在图象上,而点(-3,-6)、(2.-9)、(2.9)、(3.-6)不在图象上。
6.已知反比例函数的图象过(2,-2)和(-1,n),求n的值。
解析:反比例函数的图象为双曲线,过点(2,-2)和(-1,n)的双曲线有两个分支,分别为y=k/x和y=-k/x,因此可列出方程组-2=k/2和n=-k/-1,解得k=4,n=4,所以n的值为4.7.反比例函数y=k^3/x的图像经过(-,5)点、(a,-3)及(10,b)点,求k、a、b的值。
解析:代入三个点可得5=k^3/-,-3=k^3/a^3,b=k^3/10,解得k=∛(-50),a=∛(k^3/-3),b=10∛(-50)。
第26章反比例函数单元测试(含答案)2024-2025学年数学人教版九年级下册

第26章反比例函数一、选择题:本题共10小题,每小题3分,共30分。
在每小题给出的选项中,只有一项是符合题目要求的。
1.如图是反比例函数的图象,它的函数表达式是( ).A. y=5xB. y=2x C. y=−1xD. y=−2x2.对于反比例函数y=−5x,下列说法错误的是( )A. 图象经过点(1,−5)B. 图象位于第二、四象限C. 当x<0时,y随x的增大而减小D. 当x>0时,y随x的增大而增大3.如图,点A在双曲线y=kx上,B在y轴上,且AO=AB.若△ABO的面积为6,则k的值为 ( )A. 6B. −6C. 12D. −124.如图,直线y1=kx+1与反比例函数y2=2x的图象在第一象限交于点P(1,t),与x轴、y轴分别交于A,B 两点,则下列结论错误的是 ( )A. t=2B. △AOB是等腰直角三角形C. k=1D. 当x>1时,y2>y15.当x<0时,函数y=(k−1)x与y=2−k的y值都随x的增大而增大,则k的取值范围是( ).3xA. k>1B. 1<k<2C. k>2D. k<16.函数y=k和y=−kx+2(k≠0)在同一平面直角坐标系中的大致图象可能是( )xA. B.C. D.7.若点A(−3,y1),B(−1,y2),C(2,y3)都在反比例函数y=k(k<0)的图象上,则y1,y2,y3的大小关系是( )xA. y3<y1<y2B. y2<y1<y3C. y1<y2<y3D. y3<y2<y18.在大棚中栽培新品种的蘑菇,在18℃的条件下生长最快,因此用装有恒温系统的大棚栽培,如图是某天恒温系统从开启升温到保持恒温及关闭,大棚内温度y(℃)随时间x(时)变化的函数图象,其中BC段是函数(k>0)图象的一部分.若该蘑菇适宜生长的温度不低于12℃,则这y=kx天该品种蘑菇适宜生长的时间为( )A. 18小时B. 17.5小时C. 12小时D. 10小时9.设A,B,C,D是反比例函数y=k图象上的任意四点,现有以下结论:x①四边形ABCD可以是平行四边形;②四边形ABCD可以是菱形;③四边形ABCD不可能是矩形;④四边形ABCD不可能是正方形.其中正确的是( ).A. ①②B. ①④C. ②③D. ③④10.如图,点P、Q是反比例函数y=k(k≠0)图象上的两点,PA⊥y轴于点A,QN⊥x轴于点N,作PM⊥xx轴于点M,QB⊥y轴于点B,连接PB、QM.记SΔABP=S1,SΔQMN=S2,则S1与S2的大小关系为 ( )A. S1>S2B. S1<S2C. S1=S2D. 无法判断二、填空题:本题共6小题,每小题3分,共18分。
反比例函数单元测试题及答案(供参考)

第17章反比例函数综合检测题一、选择题(每小题3分,共30分)1、反比例函数y =x n 5+图象经过点(2,3),则n 的值是( ). A 、-2 B 、-1 C 、0 D 、12、若反比例函数y =xk(k ≠0)的图象经过点(-1,2),则这个函数的图象一定经过点( ). A 、(2,-1) B 、(-21,2) C 、(-2,-1) D 、(21,2) 3、(08双柏县)已知甲、乙两地相距s (km ),汽车从甲地匀速行驶到乙地,则汽车行驶的时间t (h )与行驶速度v (km/h )的函数关系图象大致是( )、若y 与x 成正比例,x 与z 成反比例,则y 与z 之间的关系是( ). A 、成正比例 B 、成反比例 C 、不成正比例也不成反比例 D 、无法确定、一次函数y =kx -k ,y 随x 的增大而减小,那么反比例函数y =x k 满足( ). A 、当x >0时,y >0 B 、在每个象限内,y 随x 的增大而减小 C 、图象分布在第一、三象限 D 、图象分布在第二、四象限6、如图,点P 是x 轴正半轴上一个动点,过点P 作x 轴的垂 线PQ 交双曲线y =x1于点Q ,连结OQ ,点P 沿x 轴正方向运动时,Rt △QOP 的面积( ).A 、逐渐增大B 、逐渐减小C 、保持不变D 、无法确定7、在一个可以改变容积的密闭容器内,装有一定质量m 的某种气体,当改变容积V 时,气体的密度ρ也随之改变. ρ与V 在一定范围内满足ρ=Vm ,它的图象如图所示,则该 气体的质量m 为( ).A 、1.4kgB 、5kgC 、6.4kgD 、7kg8、若A (-3,y 1),B (-2,y 2),C (-1,y 3)三点都在函数y =-x1的图象上,则y 1,y 2,y 3的大小关系是( ).A 、y 1>y 2>y 3B 、y 1<y 2<y 3C 、y 1=y 2=y 3D 、y 1<y 3<y 29、已知反比例函数y =xm 21-的图象上有A (x 1,y 1)、B (x 2,y 2)两点,当x 1<x 2<0时,y 1<y 2,则m 的取值范围是( ). A 、m <0 B 、m >0 C 、m <21 D 、m >21 10、如图,一次函数与反比例函数的图象相交于A 、B 两点,则图中使反比例函数的值小于一次函数的值的x 的取值范围是( ).A 、x <-1B 、x >2C 、-1<x <0或x >2D 、x <-1或0<x <2Q p xy o t /h O t /h O t /hO t /h v /(km/h) OA .B .C .D .二、填空题(每小题3分,共30分)11.某种灯的使用寿命为1000小时,它的可使用天数y 与平均每天使用的小时数x 之间的函数关系式为 . 12、已知反比例函数x k y =的图象分布在第二、四象限,则在一次函数b kx y +=中,y 随x 的增大而 (填“增大”或“减小”或“不变”).13、若反比例函数y =xb 3-和一次函数y =3x +b 的图象有两个交点,且有一个交点的纵坐标为6,则b = .14、反比例函数y =(m +2)x m 2-10的图象分布在第二、四象限内,则m 的值为 .15、有一面积为S 的梯形,其上底是下底长的31,若下底长为x ,高为y ,则y 与x 的函数关系是 .16、如图,点M 是反比例函数y =xa (a ≠0)的图象上一点, 过M 点作x 轴、y 轴的平行线,若S 阴影=5,则此反比例函数解析式为 .17、使函数y =(2m 2-7m -9)x m 2-9m +19是反比例函数,且图象在每个象限内y 随x 的增大而减小,则可列方程(不等式组)为 .18、过双曲线y =x k (k ≠0)上任意一点引x 轴和y 轴的垂线,所得长方形的面积为______.19. 如图,直线y =kx(k >0)与双曲线xy 4=交于A (x 1,y 1), B (x 2,y 2)两点,则2x 1y 2-7x 2y 1=___________.20、如图,长方形AOCB 的两边OC 、OA 分别位于x 轴、y 轴上,点B 的坐标为B (-320,5),D 是AB 边上的一点, 将△ADO 沿直线OD 翻折,使A 点恰好落在对角线OB 上的点E 处,若点E 在一反比例函数的图象上,那么该函数的解析式是 .三、解答题(共60分)21、(8分)如图,P 是反比例函数图象上的一点,且点P 到x轴的距离为3,到y 轴的距离为2,求这个反比例函数的解析式.22、(9分)请你举出一个生活中能用反比例函数关系描述的实例,写出其函数表达式,并画出函数图象.举例:函数表达式:23、(10分)如图,已知A (x 1,y 1),B (x 2,y 2)是双曲线y =xk 在第一象限内的分支上的两点,连结OA 、OB .(1)试说明y 1<OA <y 1+1y k ; (2)过B 作BC ⊥x 轴于C ,当m =4时,求△BOC 的面积.24、(10分)如图,已知反比例函数y =-x8与一次函数 y =kx +b 的图象交于A 、B 两点,且点A 的横坐标和点B 的纵坐标都是-2.求:(1)一次函数的解析式;(2)△AOB 的面积.25、(11分)如图,一次函数y =ax +b 的图象与反比例函数y =xk的图象交于M 、N 两点.(1)求反比例函数与一次函数的解析式;(2)根据图象写出使反比例函数的值大于一次函数的值的x 的取值范围.26、(12分)如图, 已知反比例函数y =xk 的图象与一次函 数y =a x +b 的图象交于M (2,m )和N (-1,-4)两点.(1)求这两个函数的解析式;(2)求△MON 的面积;(3)请判断点P (4,1)是否在这个反比例函数的图象上,并说明理由.参考答案:一、选择题1、D ;2、A ;3、C ;4、B ;5、D ;6、C7、D ;8、B ;9、D ; 10、D .二、填空题11、y =x 1000; 12、减小; 13、5 ; 14、-3 ;15、y =xs 23 ; 16、y =-x 5; 17、⎩⎨⎧---=+-0972119922>m m m m ; 18、|k|; 19、 20; 20、y =-x 12. 三、解答题21、y =-x6. 22、举例:要编织一块面积为2米2的矩形地毯,地毯的长x (米)与宽y (米)之间的函数关系式为y =x2(x >0). x… 1 2 …y … 4 2 1 …(只要是生活中符合反比例函数关系的实例均可)画函数图象如右图所示.23、(1)过点A 作AD ⊥x 轴于D ,则OD =x 1,AD =y 1,因为点A (x 1,y 1)在双曲线y =xk 上,故x 1=1y k ,又在Rt △OAD 中,AD <OA <AD +OD ,所以y 1<OA <y 1+1y k ; (2)△BOC 的面积为2.24、(1)由已知易得A (-2,4),B (4,-2),代入y =kx +b 中,求得y =-x +2;(2)当y =0时,x =2,则y =-x +2与x 轴的交点M (2,0),即|OM|=2,于是S △AOB=S △AOM +S △BOM =21|OM|·|y A |+21|OM|·|y B |=21×2×4+21×2×2=6. 25、(1)将N (-1,-4)代入y =x k ,得k =4.∴反比例函数的解析式为y =x 4.将M (2,m )代入y =x 4,得m =2.将M (2,2),N (-1,-4)代入y =ax +b ,得⎩⎨⎧-=+-=+.b a ,b a 422解得⎩⎨⎧-==.b ,a 22∴一次函数的解析式为y =2x -2. (2)由图象可知,当x <-1或0<x <2时,反比例函数的值大于一次函数的值. 26、解(1)由已知,得-4=1-k ,k =4,∴y =x 4.又∵图象过M (2,m )点,∴m =24=2,∵y =a x +b 图象经过M 、N 两点,∴,422⎩⎨⎧-=+-=+b a b a 解之得,22⎩⎨⎧-==b a ∴y =2x -2. (2)如图,对于y =2x -2,y =0时,x =1,∴A (1,0),OA =1,∴S △MON =S △MOA +S △NOA =21OA ·MC +21OA ·ND =21×1×2+21×1×4=3. (3)将点P (4,1)的坐标代入y =x 4,知两边相等,∴P 点在反比例函数图象上.。
人教版九年级数学26章反比例函数单元测试卷(含答案)(K12教育文档)

人教版九年级数学26章反比例函数单元测试卷(含答案)(word版可编辑修改) 编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(人教版九年级数学26章反比例函数单元测试卷(含答案)(word版可编辑修改))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为人教版九年级数学26章反比例函数单元测试卷(含答案)(word版可编辑修改)的全部内容。
第二十六章反比例函数一、填空题(本大题共6小题,每小题3分,共18分)1、若反比例函数y=kx经过点(-1,2),则一次函数y=-kx+2的图象一定不经过第__________象限。
2、函数 y=2x,当 x<0 时,y 随 x 的增大而。
3、如图,点P是反比例函数2yx=-上的一点,PD⊥x轴于点D,则△POD的面积为。
4、已知反比例函数kyx=与一次函数2y x k=+的图象一个交点的纵坐标是4-,则k的值为_________。
5、如果一次函数mxy=与反比例函数xmny-=3的图象交于点)2,21(,那么这条直线与双曲线的另一个交点是。
6、如图,一次函数与反比例函数的图像相交于A、B两点,则图中使反比例函数的值小于一次函数的值的x的取值范围是。
二、选择题(本大题共8小题,每小题4分,共32分)7、已知y与x—1成反比例)0k(≠,那么它的解析式是()A。
1xky-= B。
)1x(ky-= C.1xky-= D。
k1xy-=8、在函数 y=kx(k<0)的图象上有A(1,y1)、B(-1,y)、C(-2,y)三个点,则下列各式中正确()A、y1<y2<y3B、y1<y3<y2C、y3<y2<y1D、y2<y3<y13题图6题图9、 函数xky =的图象在第二、四限象,则函数1+=kx y 的图象所在限象是( ) A .一、二、三 B .二、三、四 C .一、三、四 D .一、二、四10、已知反比例函数xmy 21-=的图象上两点),(),,(2211y x B y x A ,当21x O x <<时,有21y y <,则m 的取值范围是( )A.0<mB.0>m C 。
反比例函数单元测试卷含答案

反比例函数单元测试卷含答案一、选择题1. 反比例函数的一般形式是:A. y = kxB. y = ax + bC. y = k/xD. y = mx + c答案: C2. 当x为0时,反比例函数的值为:A. 0B. 1C. 无定义D. 任意值答案: C3. 若反比例函数的k值为正数,x趋近于无穷大,y会趋近于:A. 正无穷大B. 负无穷大C. 0D. 不存在极限答案: B4. 反比例函数的图像是一条:A. 直线B. 抛物线C. 余弦曲线D. 双曲线答案: D5. 若反比例函数的x值为正数,y值为负数,那么k值是:A. 正数B. 负数C. 零D. 无法确定答案: B二、计算题1. 已知反比例函数y = 5/x,当x = 2时,求y的值。
答案: 2.52. 已知反比例函数y = 3/x,当y = 6时,求x的值。
答案: 0.5三、简答题1. 什么是反比例函数?答案: 反比例函数是一种函数关系,当自变量x的值增大时,因变量y的值会减小,并且二者之间呈现出一种倒数关系。
它的一般形式为y = k/x,其中k为常数。
2. 反比例函数的图像有什么特点?答案: 反比例函数的图像是一条双曲线。
当x趋近于无穷大或无穷小时,函数的值趋近于零。
两支曲线的对称轴为y轴,并在y 轴上有一个渐近线。
3. 如何确定反比例函数的常数k的值?答案: 可以通过已知点的坐标进行求解。
将已知的x和y的值代入反比例函数的一般形式中,解方程得到k的值。
以上就是反比例函数单元测试卷的答案。
希望能对你的学习有所帮助!。
反比例函数单元测试题二及答案

第17章反比例函数综合检测题一、选择题(每小题3分,共30分) 1、反比例函数y =xn 5+图象经过点(2,3),则n 的值是( ). A 、-2 B 、-1 C 、0 D 、12、若反比例函数y =xk(k ≠0)的图象经过点(-1,2),则这个函数的图象一定经过点( ).A 、(2,-1)B 、(-21,2) C 、(-2,-1) D 、(21,2) 3、(08双柏县)已知甲、乙两地相距s (km ),汽车从甲地匀速行驶到乙地,则汽车行驶的时间t (h )与行驶速度v (km/h )的函数关系图象大致是( )4、若y 与x 成正比例,x 与z成反比例,则y 与z 之间的关系是().A 、成正比例B 、成反比例C 、不成正比例也不成反比例D 、无法确定 5、一次函数y =kx -k ,y 随x 的增大而减小,那么反比例函数y =xk 满足( ).A 、当x >0时,y >0B 、在每个象限内,y 随x 的增大而减小C 、图象分布在第一、三象限D 、图象分布在第二、四象限6、如图,点P 是x 轴正半轴上一个动点,过点P 作x 轴的垂 线PQ 交双曲线y =x1于点Q ,连结OQ ,点P 沿x 轴正方向运动时, Rt △QOP 的面积( ).A 、逐渐增大B 、逐渐减小C 、保持不变D 、无法确定 7、在一个可以改变容积的密闭容器内,装有一定质量m 的某种气体,当改变容积V 时,气体的密度ρ也随之改变. ρ与V 在一定范围内满足ρ=Vm,它的图象如图所示,则该 气体的质量m 为( ).A 、1.4kgB 、5kgC 、6.4kgD 、7kg 3,y 1),B (-2,y 2),C (-1,y 3)三点都在函数y =-x 1的y 1,y 2,y 3的大小关系是( ). y 3 B 、y 1<y 2<y 3 C 、y 1=y 2=y 3 D 、y 1<y 3<y 2 y =xm 21-的图象上有A (x 1,y 1)、B (x 2,y 2)两点,12时,y 1<y 2,则m 的取值范围是( ). A 、m <0 B 、m >0 C 、m <21 D 、m >2110、如图,一次函数与反比例函数的图象相交于A 、B 两点,则图中使反比例函数的值小于一次函数的值的x 的取值范围是( ). A . B . C . .A 、x <-1B 、x >2C 、-1<x <0或x >2D 、x <-1或0<x <2 二、填空题(每小题3分,共30分)11.某种灯的使用寿命为1000小时,它的可使用天数y 与平均每天使用的小时数x 之间的函数关系式为 .12、已知反比例函数xky =的图象分布在第二、四象限,则在一次函数b kx y +=中,y 随x 的增大而 (填“增大”或“减小”或“不变”).13、若反比例函数y =xb 3-和一次函数y =3x +b 的图象有两个交点,且有一个交点的纵坐标为6,则b = . 14、反比例函数y =(m +2)x m 2-10的图象分布在第二、四象限内,则m的值为 .15、有一面积为S 的梯形,其上底是下底长的31,若下底长为x ,高为y ,则y 与x 的函数关系是 . 16、如图,点M 是反比例函数y =xa(a ≠0)的图象上一点, 过M 点作x 轴、y 轴的平行线,若S 阴影=5,则此反比例函数解析 式为 .17、使函数y =(2m 2-7m -9)x m2-9m +19是反比例函数,且图象在每个象限内y 随x 的增大而减小,则可列方程(不等式组)为 .18、过双曲线y =xk(k ≠0)上任意一点引x 轴和y 轴的垂线,所得长方形的面积为______.19. 如图,直线y =kx(k >0)与双曲线xy 4=交于A (x 1,y 1), B (x 2,y 2)两点,则2x 1y 2-7x 2y 1=___________.20、如图,长方形AOCB 的两边OC 、OA 分别位于x 轴、 y 轴上,点B 的坐标为B (-320,5),D 是AB 边上的一点, 将△ADO 沿直线OD 翻折,使A 点恰好落在对角线OB 上的 点E 处,若点E 在一反比例函数的图象上,那么该函数的解析 式是 .三、解答题(共60分) 21、(8分)如图,P 是反比例函数图象上的一点,且点P 到x 轴的距离为3,到y 轴的距离为2,求这个反比例函数的解析式. 22、(9分)请你举出一个生活中能用反比例函数关系描 述的实例,写出其函数表达式,并画出函数图象. 举例:函数表达式:23、(10分)如图,已知A (x 1,y 1),B (x 2,y 2)是双曲线y =xk在第一象限内的分支上的两点,连结OA 、OB .(1)试说明y 1<OA <y 1+1y k;(2)过B 作BC ⊥x 轴于C ,当m =4时, 求△BOC 的面积.24、(10分)如图,已知反比例函数y =-x8与一次函数 y =kx +b 的图象交于A 、B 两点,且点A 的横坐标和点B 的 纵坐标都是-2. 求:(1)一次函数的解析式; (2)△AOB 的面积.25、(11分)如图,一次函数y =ax +b 的图象与反比例函数y =xk的图象交于M 、N 两点.(1)求反比例函数与一次函数的解析式; (2)根据图象写出使反比例函数的值大于一次函数的值的x 的取值范围.26、(12分)如图, 已知反比例函数y =xk的图象与一次函 数y =a x +b 的图象交于M (2,m )和N (-1,-4)两点. (1)求这两个函数的解析式; (2)求△MON 的面积;(3)请判断点P (4,1)是否在这个反比例函数的图象上, 并说明理由.参考答案:一、选择题 1、D ; 2、A ; 3、C ; 4、B ; 5、D ; 6、C 7、D ; 8、B ; 9、D ; 10、D .二、填空题 11、y =x 1000; 12、减小; 13、5 ; 14、-3 ;15、y =xs23 ; 16、y =-x 5; 17、⎩⎨⎧---=+-0972119922>m m m m ; 18、|k|; 19、 20; 20、y =-x12.三、解答题21、y =-x6. 22、举例:要编织一块面积为2米2的矩形地毯,地毯的长x (米)与宽y (米)之间的函数关系式为y =2(x >0). (只要是生活中符合反比例函数关系的实例均可)画函数图象如右图所示. 23、(1)过点A 作AD ⊥x 轴于D ,则OD =x 1,AD =y 1,因为点A (x 1,y 1)在双曲线y =x k 上,故x 1=1y k,又在Rt △OAD 中,AD <OA <AD +OD ,所以y 1<OA <y 1+1y k; (2)△BOC 的面积为2. 24、(1)由已知易得A (-2,4),B (4,-2),代入y =kx +b 中,求得y =-x +2;(2)当y =0时,x =2,则y =-x +2与x 轴的交点M (2,0),即|OM|=2,于是S △AOB =S △AOM +S △BOM =21|OM|·|y A |+21|OM|·|y B |=21×2×4+21×2×2=6. 25、(1)将N (-1,-4)代入y =xk,得k =4.∴反比例函数的解析式为y =x 4.将M (2,m )代入y =x4,得m =2.将M (2,2),N (-1,-4)代入y =ax +b ,得⎩⎨⎧-=+-=+.b a ,b a 422解得⎩⎨⎧-==.b ,a 22∴一次函数的解析式为y =2x -2.(2)由图象可知,当x <-1或0<x <2时,反比例函数的值大于一次函数的值.26、解(1)由已知,得-4=1-k ,k =4,∴y =x4.又∵图象过M (2,m )点,∴m =24=2,∵y =a x +b 图象经过M 、N 两点,∴,422⎩⎨⎧-=+-=+b a b a 解之得,22⎩⎨⎧-==b a ∴y =2x -2. (2)如图,对于y =2x -2,y =0时,x =1,∴A (1,0),OA =1,∴S △MON =S △MOA +S △NOA =21OA ·MC +21OA ·ND =21×1×2+21×1×4=3. (3)将点P (4,1)的坐标代入y =x4,知两边相等,∴P 点在反比例函数图象上.。
反比例函数全章测试题

反比例函数单元测试题班级 姓名一、精心选一选(每小题5分,共25分) 1.下列函数中,反比例函数是( )A 、()11x y -=B 、11y x =+ C 、21y x = D 、 13y x = 2.若y 与x 成反比例,x 与z 成反比例,则y 是z 的( ) A 、正比例函数 B 、反比例函数 C 、一次函数 D 、不能确定3. 在同一直角坐标系中,函数y=kx-k 与(0)ky k x=≠的图像大致是( )4. 面积为2的△ABC,一边长为x ,这边上的高为y ,则y 与x 的变化规律用图象表示大致是( )5.已知112233(,),(,),(,)x y x y x y 是反比例函数xy 4-=的图象上三点,且1230x x x <<<,则123,,y y y 的大小关系是( )A 、1230y y y <<<B 、1230y y y >>>C 、1320y y y <<<D 、1320y y y >>> 二、耐心填一填(每空5分,共40分)1. 一批零件300个,一个工人每小时做15个,用关系式表示人数x•与完成任务所需的时间y 之间的函数关系式为________.2. 已知y -2与x 成反比例,当x =3时,y =1,则y 与x 间的函数关系式为 ;(1,4)y xAO 32y x BO (1,4)y xCO 44y xO3. 已知A (-3,3m -)和B (m+3,2)都是反比例函数xky =的图像上的两点,则m=______. 4. 对于函数xy 2=,当2x >时,y 的取值范围是______y <<______;当2x ≤时且0x ≠时,y 的取值范围是y ______1或y ______。
(提示:利用图像解答) 5. 反比例函数)0(>=k xky 在第一象限内的图象如图,点M 是图像上一点,MP 垂直x 轴于点P ,如果△MOP 的面积为1,那么k 的值是 ;三、用心想一想(共55分)1.已知正比例函数x y 31=与反比例函数xky =的图象都过A (m,1)点。
九下《第26章 反比例函数》2021年单元测试卷(广东省潮州市饶平县英才实验中学)(1)

人教新版九年级下册《第26章反比例函数》2021年单元测试卷(广东省潮州市饶平县英才实验中学)(1)试题数:30,总分:01.(单选题,0分)下列函数是y关于x的反比例函数的是()A.y= 1x+1B.y= 1x2C.y=- 12xD.y=- x22.(填空题,0分)若函数y=(m-2)x m2−5是反比例函数,则m=___ .在同一平面直角坐标系3.(单选题,0分)已知ab<0,一次函数y=ax-b与反比例函数y= ax中的图象可能()A.B.C.D.4.(单选题,0分)正比例函数y=2x和反比例函数y=2x的一个交点为(1,2),则另一个交点为()A.(-1,-2)B.(-2,-1)C.(1,2)D.(2,1)5.(填空题,0分)如图,反比例函数y= kx(k<0)的图象与经过原点的直线相交于A、B两点,已知A点坐标为(-2,1),那么B点的坐标为___ .6.(单选题,0分)反比例函数y= m−2x(m为常数),在每个象限内,y随x的增大而减小,则m取值范围是()A.m>0B.m>2C.m<0D.m<27.(填空题,0分)若反比例函数y=1−3kx的图象经过第一、三象限,则k的取值范围是___ .8.(单选题,0分)给出函数:① y=3x;② y=-3x+1;③ y= 3x (x<0);④ y=- 3x,其中y随x的增大而减小的函数的个数为()A.1个B.2个C.3个D.4个9.(填空题,0分)若双曲线y= mx|m|−2的图象在第一、三象限,那么m的值为___ .10.(单选题,0分)反比例函数y= k的图象经过点A(-2,3),则此图象一定经过下列哪个x点()A.(3,2)B.(-3,-2)C.(-3,2)D.(-2,-3)的11.(单选题,0分)若点A(x1,1),B(x2,-2),C(x3,-3)在反比例函数y=- k2+1x图象上,则x1、x2、x3的大小关系是()A.x1<x2<x3B.x1<x3<x2C.x3<x1<x2D.x2<x1<x3(m为常12.(单选题,0分)如图,一次函数y1=kx+b(k≠0)的图象与反比例函数y2= mx的解集数且m≠0)的图象都经过A(-1,2),B(2,-1),结合图象,则不等式kx+b>mx是()A.x<-1B.-1<x<0C.x<-1或0<x<2D.-1<x<0或x>213.(问答题,0分)如图,在平面直角坐标系xOy中,直线y=kx+3(k≠0)与x轴交于点A,(m≠0)的一个交点为B(-1,4).与双曲线y= mx(1)求直线与双曲线的表达式;上,且△PAC的面积为4,求点P的坐(2)过点B作BC⊥x轴于点C,若点P在双曲线y= mx标.14.(单选题,0分)如果等腰三角形的面积为10,底边长为x,底边上的高为y,则y与x 的函数关系式为()A.y= 10xB.y= 5xC.y= 20xD.y= x20图象上一点,MA⊥y轴于A,S△MAO=4时,15.(填空题,0分)如图:M为反比例函数y= kxk=___ .16.(填空题,0分)如图,P是反比例函数y=k图象上一点,点P与坐标轴围成的矩形面积x为3,则解析式为___ .17.(填空题,0分)如图,在平面直角坐标系xOy中,已知函数y1= 3x (x>0)和y2=- 1x(x<0),点M为y轴正半轴上一点,N为x轴上一点,过M作y轴的垂线分别交y1,y2的图象于A,B两点,连接AN,BN,则△ABN的面积为___ .18.(填空题,0分)如图,四边形OABC是矩形,四边形ADEF是正方形,点A、D在x轴的负半轴上,点C在y轴的正半轴上,点F在AB上,点B、E在反比例函数y= kx(k为常数,k≠0)的图象上,正方形ADEF的面积为4,且BF=2AF,则k值为___ .19.(单选题,0分)如图,A、B是曲线y= 5x上的点,经过A、B两点向x轴、y轴作垂线段,若S阴影=1,则S1+S2=()A.4B.5C.6D.820.(单选题,0分)如图,在平面直角坐标系中,△OAB的顶点A在x轴正半轴上,OC是△OAB的中线,点B、C在反比例函数y= 2x(x>0)的图象上,则△OAB的面积等于()A.2B.3C.4D.621.(问答题,0分)如图,一次函数y=kx+b的图象与反比例函数y= mx的图象相交于A(1,2),B(-2,n)两点.(1)求一次函数和反比例函数的表达式.(2)直线AB交x轴于点C,点P是x轴上的点,若△ACP的面积是4,求点P的坐标.22.(问答题,0分)如图,已知一次函数y= 12 x+b的图象与反比例函数y= kx(x<0)的图象交于点A(-1,2)和点B.(1)求b和k的值;(2)请求出点B的坐标,并观察图象,直接写出关于x的不等式12 x+b>kx的解集;(3)若点P在y轴上一点,当PA+PB最小时,求点P的坐标.23.(问答题,0分)如图,直线y=- 1x+m与x轴,y轴分别交于点B、A两点,与双曲线相3交于C、D两点,过C作CE⊥x轴于点E,已知OB=3,OE=1.(1)求直线AB和双曲线的表达式;(2)设点F是x轴上一点,使得S△CEF=2S△COB,求点F的坐标.24.(问答题,0分)为了做好校园疫情防控工作,校医每天早上对全校办公室和教室进行药物喷洒消毒,她完成3间办公室和2间教室的药物喷洒要19min;完成2间办公室和1间教室的药物喷洒要11min.(1)校医完成一间办公室和一间教室的药物喷洒各要多少时间?(2)消毒药物在一间教室内空气中的浓度y(单位:mg/m3)与时间x(单位:min)的函数关系如图所示:校医进行药物喷洒时y与x的函数关系式为y=2x,药物喷洒完成后y与x成反比例函数关系,两个函数图象的交点为A(m,n).当教室空气中的药物浓度不高于1mg/m3时,对人体健康无危害,校医依次对一班至十一班教室(共11间)进行药物喷洒消毒,当她把最后一间教室药物喷洒完成后,一班学生能否进入教室?请通过计算说明.25.(问答题,0分)已知:一次函数y=-2x+10的图象与反比例函数y= k(k>0)的图象相x交于A,B两点(A在B的右侧).(1)当A(4,2)时,求反比例函数的解析式及B点的坐标;(2)在(1)的条件下,反比例函数图象的另一支上是否存在一点P,使△PAB是以AB为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,请说明理由.在第一象限内的图象上的一个26.(填空题,0分)如图,点P(a,a)是反比例函数y=16x点,以点P为顶点作等边△PAB,使A、B落在x轴上(点A在点B左侧),则△POA的面积是___ .,将▱ABCD放置在平面直角坐标27.(填空题,0分)如图,在▱ABCD中,AB⊥BD,sinA= 45(k>0)系中,且AD⊥x轴,点D的横坐标为1,点C的纵坐标为3,恰有一条双曲线y= kx同时经过B、D两点,则点B的坐标是___ .28.(问答题,0分)如图,点A(5,2),B(m,n)(m<5)在反比例函数y= k的图象上,x作AC⊥y轴于点C.(1)求反比例函数的表达式;(2)若△ABC的面积为10,求点B的坐标.29.(问答题,0分)我市某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18℃的条件下生长最快的新品种.图是某天恒温系统从开启到关闭及关闭的一部后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线y= kx分.请根据图中信息解答下列问题:(1)恒温系统在这天保持大棚内温度18℃的时间有多少小时?(2)求k的值;(3)当棚内温度不低于16℃时,该蔬菜能够快速生长,请问这天该蔬菜能够快速生长多长时间?30.(问答题,0分)教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升10℃,加热到100℃停止加热,水温开始下降,此时水温y(℃)与开机后用时x(min)成反比例关系,直至水温降至30℃,饮水机关机,饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时接通电源,水温y(℃)与时间x(min)的关系如图所示:(1)分别写出水温上升和下降阶段y与x之间的函数关系式;(2)怡萱同学想喝高于50℃的水,请问她最多需要等待多长时间?人教新版九年级下册《第26章反比例函数》2021年单元测试卷(广东省潮州市饶平县英才实验中学)(1)参考答案与试题解析试题数:30,总分:01.(单选题,0分)下列函数是y关于x的反比例函数的是()A.y= 1x+1B.y= 1x2C.y=- 12xD.y=- x2【正确答案】:C【解析】:直接利用反比例函数的定义分别判断得出答案.是y与x+1成反比例,故此选项不合题意;【解答】:解:A、y= 1x+1B、y= 1,是y与x2成反比例,不符合反比例函数的定义,故此选项不合题意;x2C、y=- 1,符合反比例函数的定义,故此选项符合题意;2x是正比例函数,故此选项不合题意.D、y=- x2故选:C.【点评】:此题主要考查了反比例函数的定义,正确把握定义是解题关键.2.(填空题,0分)若函数y=(m-2)x m2−5是反比例函数,则m=___ .【正确答案】:[1]-2【解析】:根据反比例函数的定义可得出关于m的一元一次不等式以及一元二次方程,解之即可得出m的值,此题得解.【解答】:解:∵解:∵函数y=(m-2)x m2−5是反比例函数,∴ {m−2≠0,m2−5=−1解得:m=-2.故答案为:-2.【点评】:本题考查了反比例函数的定义,熟练掌握反比例函数的定义是解题的关键.在同一平面直角坐标系3.(单选题,0分)已知ab<0,一次函数y=ax-b与反比例函数y= ax中的图象可能()A.B.C.D.【正确答案】:A【解析】:根据反比例函数图象确定b的符号,结合已知条件求得a的符号,由a、b的符号确定一次函数图象所经过的象限.经过第一、三象限,则a>0.所以b<0.则一次函数【解答】:解:若反比例函数y= axy=ax-b的图象应该经过第一、二、三象限;经过第二、四象限,则a<0.所以b>0.则一次函数y=ax-b的图象应该若反比例函数y= ax经过第二、三、四象限.故选项A正确;故选:A.【点评】:本题考查了反比例函数的图象性质和一次函数函数的图象性质,要掌握它们的性质才能灵活解题.的一个交点为(1,2),则另一个4.(单选题,0分)正比例函数y=2x和反比例函数y=2x交点为()A.(-1,-2)B.(-2,-1)C.(1,2)D.(2,1)【正确答案】:A【解析】:根据反比例函数的关于原点对称的性质知,正比例函数y=2x和反比例函数y=2x的另一个交点与点(1,2)关于原点对称.的一个交点为(1,2),【解答】:解:∵正比例函数y=2x和反比例函数y=2x∴另一个交点与点(1,2)关于原点对称,∴另一个交点是(-1,-2).故选:A.【点评】:本题考查了反比例函数图象的对称性.关于原点对称的两点的横纵坐标互为相反数.5.(填空题,0分)如图,反比例函数y= k(k<0)的图象与经过原点的直线相交于A、B两x点,已知A点坐标为(-2,1),那么B点的坐标为___ .【正确答案】:[1](2,-1)【解析】:反比例函数的图象是中心对称图形,则经过原点的直线的两个交点一定关于原点对称.【解答】:解:∵点A与B关于原点对称,点A的坐标为(-2,1),∴B点的坐标为(2,-1).故答案是:(2,-1).【点评】:本题主要考查了反比例函数图象的中心对称性,要求同学们要熟练掌握.6.(单选题,0分)反比例函数y= m−2(m为常数),在每个象限内,y随x的增大而减小,x则m取值范围是()A.m>0B.m>2C.m<0D.m<2【正确答案】:B(m为常数),在每个象限内,y随x的增大而减小,可【解析】:根据反比例函数y= m−2x知m-2>0,从而可以取得m的取值范围,本题得以解决.(m为常数),在每个象限内,y随x的增大而减小,【解答】:解:∵反比例函数y= m−2x∴m-2>0,解得,m>2,故选:B.【点评】:本题考查反比例函数的性质,解答本题的关键是明确题意,利用反比例函数的性质解答.的图象经过第一、三象限,则k的取值范围是___ .7.(填空题,0分)若反比例函数y=1−3kx【正确答案】:[1]k<13【解析】:先根据反比例函数的性质列出关于k的不等式,求出k的取值范围即可.的图象经过第一、三象限,【解答】:解:∵反比例函数y=1−3kx.∴1-3k>0,解得k<13.故答案为:k<13【点评】:本题考查的是反比例函数的性质,熟知反比例函数y= kx(k≠0)的图象是双曲线;当k>0,双曲线的两支分别位于第一、第三象限是解答此题的关键.8.(单选题,0分)给出函数:① y=3x;② y=-3x+1;③ y= 3x (x<0);④ y=- 3x,其中y随x的增大而减小的函数的个数为()A.1个B.2个C.3个D.4个【正确答案】:B【解析】:分别根据正比例函数、一次函数及反比例函数的性质进行解答即可.【解答】:解:① y=3x中的k=3>0,y随x的增大而增大;② y=-3x+1中的k=-3<0,y随x的增大而减小;③ y= 3x(x<0)中k=3>0,y随x的增大而减小;④ y=- 3x中的k=-3<0,在每一象限内,y随x的增大而增大.综上所述,符合题意的结论有2个.故选:B.【点评】:本题考查的是正比例函数、一次函数及反比例函数的性质,熟知反比例函数的增减性是解答此题的关键.9.(填空题,0分)若双曲线y= mx|m|−2的图象在第一、三象限,那么m的值为___ .【正确答案】:[1]3【解析】:根据反比例函数的定义及性质列出关于m的不等式组,求出m的值即可.【解答】:解:∵双曲线y= mx|m|−2的图象在第一、三象限,∴ {m>0|m|−2=1,解得m=3.故答案为:3.【点评】:本题考查的是反比例函数的性质,在解答此类题目时要注意反比例函数的定义等知识.10.(单选题,0分)反比例函数y= k的图象经过点A(-2,3),则此图象一定经过下列哪个x点()A.(3,2)B.(-3,-2)C.(-3,2)D.(-2,-3)【正确答案】:C【解析】:根据反比例函数图象上点的坐标特征即可求解.的图象经过点A(-2,3),【解答】:解:∵反比例函数y= kx∴k=-2×3=-6,的解析式,只有C选项符合题意,将四个选项代入反比例函数y= kx故选:C.【点评】:本题考查了反比例函数图象上点的坐标特征,解题的关键是根据A点的坐标求出k 值.的11.(单选题,0分)若点A(x1,1),B(x2,-2),C(x3,-3)在反比例函数y=- k2+1x图象上,则x1、x2、x3的大小关系是()A.x1<x2<x3B.x1<x3<x2C.x3<x1<x2D.x2<x1<x3【正确答案】:B【解析】:利用反比例函数的性质得到反比例函数图象分布在第,二、四象限,在每一象限内,y随x的增大而增大,所以x1<0,x2>x3>0,从而可对各选项进行判断.【解答】:解:∵-(k2+1)<0,∴反比例函数图象分布在第,二、四象限,在每一象限内,y随x的增大而增大,∴x1<0,x2>x3>0,∴x1<x3<x2.故选:B.【点评】:本题考查了反比例函数图象上点的坐标特征:反比例函数图象上点的坐标满足其解析式.也考查了反比例函数的性质.(m为常12.(单选题,0分)如图,一次函数y1=kx+b(k≠0)的图象与反比例函数y2= mx的解集数且m≠0)的图象都经过A(-1,2),B(2,-1),结合图象,则不等式kx+b>mx是()A.x<-1B.-1<x<0C.x<-1或0<x<2D.-1<x<0或x>2【正确答案】:C的【解析】:根据一次函数图象在反比例函数图象上方的x的取值范围便是不等式kx+b>mx解集.【解答】:解:由函数图象可知,当一次函数y1=kx+b(k≠0)的图象在反比例函数y2= mx(m为常数且m≠0)的图象上方时,x的取值范围是:x<-1或0<x<2,的解集是x<-1或0<x<2∴不等式kx+b>mx故选:C.【点评】:本题是一次函数图象与反比例函数图象的交点问题:主要考查了由函数图象求不等式的解集.利用数形结合是解题的关键.13.(问答题,0分)如图,在平面直角坐标系xOy中,直线y=kx+3(k≠0)与x轴交于点A,(m≠0)的一个交点为B(-1,4).与双曲线y= mx(1)求直线与双曲线的表达式;上,且△PAC的面积为4,求点P的坐(2)过点B作BC⊥x轴于点C,若点P在双曲线y= mx标.【正确答案】:【解析】:(1)将点B(-1,4)代入直线和双曲线解析式求出k和m的值即可;AC•|y P|=4求得点P的纵坐标,继而可(2)根据直线解析式求得点A坐标,由S△ACP=12得答案.(m≠0)都经过点B(-1,4),【解答】:解:(1)∵直线y=kx+3(k≠0)与双曲线y= mx∴-k+3=4,m=-1×4.∴k=-1,m=-4..∴直线的表达式为y=-x+3,双曲线的表达式为y=−4x(2)由题意,得点C的坐标为C(-1,0),直线y=-x+3与x轴交于点A(3,0).∴AC=4.AC•|y P|=4,∵ S△ACP=12∴y P=±2.上,∵点P在双曲线y=−4x∴点P的坐标为P1(-2,2)或P2(2,-2).【点评】:本题主要考查反比例函数和一次函数的交点问题,熟练掌握待定系数法求函数解析式及三角形的面积是解题的关键.14.(单选题,0分)如果等腰三角形的面积为10,底边长为x,底边上的高为y,则y与x的函数关系式为()A.y= 10xB.y= 5xC.y= 20xD.y= x20【正确答案】:C【解析】:利用三角形面积公式得出12xy=10,进而得出答案.【解答】:解:∵等腰三角形的面积为10,底边长为x,底边上的高为y,∴ 12xy=10,∴y与x的函数关系式为:y= 20x.故选:C.【点评】:此题主要考查了根据实际问题抽象出反比例函数解析式,根据已知得出12xy=10是解题关键.15.(填空题,0分)如图:M为反比例函数y= kx图象上一点,MA⊥y轴于A,S△MAO=4时,k=___ .【正确答案】:[1]-8【解析】:根据反比例函数y= kx (k≠0)系数k的几何意义得到S△AOM= 12|k|=4,然后根据k<0去绝对值得到k的值.【解答】:解:∵MA⊥y轴,∴S△AOM= 12|k|=4,∵k<0,∴k=-8.故答案为-8.【点评】:本题考查了反比例函数y= kx (k≠0)系数k的几何意义:从反比例函数y= kx(k≠0)图象上任意一点向x轴和y轴作垂线,垂线与坐标轴所围成的矩形面积为|k|.16.(填空题,0分)如图,P是反比例函数y=kx图象上一点,点P与坐标轴围成的矩形面积为3,则解析式为___ .【正确答案】:[1]y=- 3x【解析】:因为过双曲线上任意一点引x轴、y轴垂线,所得矩形面积S是个定值,即S=|k|,再由函数图象所在的象限确定k的值,则该解析式即可求出.【解答】:解:∵P是反比例函数y=kx图象上一点,∴S=|k|=3,又函数图象位于第二象限,k<0,则k=-3.故反比例函数的解析式为y=- 3x.故答案为:y=- 3x.【点评】:主要考查了反比例函数y=kx中k的几何意义,即过双曲线上任意一点引x轴、y轴垂线,所得矩形面积为|k|,是经常考查的一个知识点;这里体现了数形结合的思想,做此类题一定要正确理解k的几何意义.17.(填空题,0分)如图,在平面直角坐标系xOy中,已知函数y1= 3x (x>0)和y2=- 1x(x<0),点M为y轴正半轴上一点,N为x轴上一点,过M作y轴的垂线分别交y1,y2的图象于A,B两点,连接AN,BN,则△ABN的面积为___ .【正确答案】:[1]2【解析】:直接利用反比例函数的性质结合矩形的性质得出矩形BEOM面积为:1,矩形MOFA面积为:3,则矩形BEFA的面积为4,进而得出答案.【解答】:解:过点B作BE⊥x轴于点E,过点A作AF⊥x轴于点F,由题意可得,四边形BEFA是矩形,∵函数y1= 3x (x>0)和y2=- 1x(x<0),∴矩形BEOM面积为:1,矩形MOFA面积为:3,则矩形BEFA的面积为4,则△ABN的面积为:12S矩形BEFA=2.故答案为:2.【点评】:此题主要考查了反比例函数系数k的几何意义,正确得出各矩形面积是解题关键.18.(填空题,0分)如图,四边形OABC是矩形,四边形ADEF是正方形,点A、D在x轴的负半轴上,点C在y轴的正半轴上,点F在AB上,点B、E在反比例函数y= kx(k为常数,k≠0)的图象上,正方形ADEF的面积为4,且BF=2AF,则k值为___ .【正确答案】:[1]-6【解析】:先由正方形ADEF的面积为4,得出边长为2,BF=2AF=4,AB=AF+BF=2+4=6.再设B点坐标为(t,6),则E点坐标(t-2,2),根据点B、E在反的图象上,利用根据反比例函数图象上点的坐标特征得k=6t=2(t-2),即可比例函数y= kx求出k=-6.【解答】:解:∵正方形ADEF的面积为4,∴正方形ADEF的边长为2,∴BF=2AF=4,AB=AF+BF=2+4=6.设B点坐标为(t,6),则E点坐标(t-2,2),的图象上,∵点B、E在反比例函数y= kx∴k=6t=2(t-2),解得t=-1,k=-6.故答案为-6.(k为常数,k≠0)【点评】:本题考查了反比例函数图象上点的坐标特征:反比例函数y= kx的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.上的点,经过A、B两点向x轴、y轴作垂线段,19.(单选题,0分)如图,A、B是曲线y= 5x若S阴影=1,则S1+S2=()A.4B.5C.6D.8【正确答案】:D【解析】:首先根据反比例函数y= kx中k的几何意义,可知S1+S阴影=S2+S阴影=5,又S阴影=1,则S1=S2=5-1=4,从而求出S1+S2的值.【解答】:解:∵A、B是曲线y= 5x上的点,经过A、B两点向x轴、y轴作垂线段,∴S1+S阴影=S2+S阴影=5,又∵S阴影=1,∴S1=S2=5-1=4,∴S1+S2=8.故选:D.【点评】:主要考查了反比例函数y= kx中k的几何意义,即过双曲线上任意一点引x轴、y轴垂线,所得矩形面积为|k|,是经常考查的一个知识点;这里体现了数形结合的思想,做此类题一定要正确理解k的几何意义.20.(单选题,0分)如图,在平面直角坐标系中,△OAB的顶点A在x轴正半轴上,OC是△OAB的中线,点B、C在反比例函数y= 2x(x>0)的图象上,则△OAB的面积等于()A.2B.3C.4D.6【正确答案】:B【解析】:过点B、点C作x轴的垂线,垂足为D,E,则BD || CE,得出∴ CEBD = AEAD= ACAB,设CE=x,则BD=2x,根据反比例函数的解析式表示出OD= 1x ,OE= 2x,OA= 3x,然后根据三角形面积公式求解即可.【解答】:解:如图,过点B、点C作x轴的垂线,垂足为D,E,则BD || CE,∴ CE BD = AEAD= ACAB,∵OC是△OAB的中线,∴ CE BD = AEAD= ACAB= 12,设CE=x,则BD=2x,∴C的横坐标为2x ,B的横坐标为1x,∴OD= 1x ,OE= 2x,∴DE=OE-OD= 1x,∴AE=DE= 1x,∴OA=OE+AE= 3x,∴S△OAB= 12OA•BD= 12× 3x×2x=3.故选:B.【点评】:本题考查了反比例函数图象上点的坐标特征,反比例函数系数k的几何意义,平行线分线段成比例定理,求得BD,OA的长是解题关键.21.(问答题,0分)如图,一次函数y=kx+b的图象与反比例函数y= mx的图象相交于A(1,2),B(-2,n)两点.(1)求一次函数和反比例函数的表达式.(2)直线AB交x轴于点C,点P是x轴上的点,若△ACP的面积是4,求点P的坐标.【正确答案】:【解析】:(1)先根据点A 坐标求出反比例函数解析式,再求出点B 的坐标,继而根据点A 、B 坐标可得直线解析式;(2)先根据直线解析式求出点C 的坐标,根据S △ACP = 12 •PC•y A =4求出PC 的长,即可得出答案.【解答】:解:(1)∵反比例函数y= mx 经过点A (1,2), ∴2= m 1, ∴m=2,∴反比例函数的表达式为y= 2x,把点B 的坐标 (-2,n )代入y= 2x 得,n= 2−2 ,解得n=-1, ∴点B 的坐标为(-2,-1),分别把点A ,点B 的坐标代入y=kx+b 得 {k +b =2−2k +b =−1 ,解得 {k =1b =1,∴一次函数的表达式为y=x+1; (2)把y=0代入y=x+1,解得x=-1, ∴点C 的坐标为(-1,0),∵△ACP 的面积是4,点A 的纵坐标等于2, ∴ 12 •PC×2=4, 解得CP=4,∴点P 的坐标为(-5,0)或(3,0).【点评】:本题主要考查反比例函数与一次函数的交点问题,解题的关键是掌握待定系数法求函数解析式、三角形的面积问题.22.(问答题,0分)如图,已知一次函数y= 12 x+b 的图象与反比例函数y= kx (x <0)的图象交于点A (-1,2)和点B . (1)求b 和k 的值;(2)请求出点B 的坐标,并观察图象,直接写出关于x 的不等式 12 x+b > kx 的解集; (3)若点P 在y 轴上一点,当PA+PB 最小时,求点P 的坐标.【正确答案】:【解析】:(1)根据待定系数法即可求得;(2)联立两函数解析式成方程组,解方程组即可求出点A 、B 的坐标,根据两函数图象的上下关系结合点A 、B 的坐标,即可得出不等式的解集.(3)作点A 关于y 轴对称点A′,设出直线A′B 的解析式为y=mx+n ,结合点的坐标利用待定系数法即可求出直线A′B 的解析式,令直线A′B 解析式中x 为0,求出y 的值,即可得出结论.【解答】:解:(1)∵一次函数y= 12x+b 的图象与反比例函数y= k x(x <0)的图象交于点A (-1,2),把A (-1,2)代入两个解析式得:2= 12 ×(-1)+b ,2=-k , 解得:b= 52,k=-2;(2)联立一次函数解析式与反比例函数解析式成方程组: {y =12x +52y =−2x , 解得: {x =−4y =12或 {x =−1y =−2 ,∴点A 的坐标为(-1,2)、点B 的坐标为(-4, 12 ).观察函数图象可知:关于x 的不等式 12 x+b > kx 的解集x 为-4<x <-1或x >0.(3)作点A 关于y 轴的对称点A′,连接A′B 交y 轴于点P ,此时点P 即是所求,如图所示.∵点A′与点A 关于y 轴对称, ∴点A′的坐标为(1,2), 设直线A′B 的解析式为y=mx+n , ∴ {m +n =2−4m +n =12,解得: {m =310y =1710 ,∴直线A′B 的解析式为y= 310 x+ 1710 . 令x=0,则y= 1710 , ∴点P 的坐标为(0, 1710 ).【点评】:本题考查了反比例函数与一次函数的交点问题、轴对称中的最短线路问题、利用待定系数法求函数解析式以及反比例函数图象上点的坐标特征,解题的关键是:(2)找出交点坐标;(3)求出直线A′B 的解析式;本题属于中档题,难度不大,但解题过程稍显繁琐,解决该题型题目时,找出点的坐标,利用待定系数法求出函数解析式是关键.23.(问答题,0分)如图,直线y=- 13 x+m 与x 轴,y 轴分别交于点B 、A 两点,与双曲线相交于C 、D 两点,过C 作CE⊥x 轴于点E ,已知OB=3,OE=1. (1)求直线AB 和双曲线的表达式;(2)设点F 是x 轴上一点,使得S △CEF =2S △COB ,求点F 的坐标.【正确答案】:【解析】:(1)根据已知条件求出A、B、C点坐标,用待定系数法求出直线AB和反比例函数的解析式;(2)根据三角形面积公式求得EF的长,即可求得点F的坐标;【解答】:解:(1)∵OB=3,OE=1,∴B(3,0),C点的横坐标为-1,∵直线y=- 13x+m经过点B,∴0=- 13×3+m,解得m=1,∴直线为:y=- 13x+1,把x=-1代入y=- 13 x+1得,y=- 13×(-1)+1= 43,∴C(-1,43),∵点C在双曲线y= kx(k≠0)上,∴k=-1× 43 =- 43,∴双曲线的表达式为:y=- 43x;(2)∵OB=3,CE= 43,∴S△COB= 12 ×3× 43=2,∵S△CEF=2S△COB,∴S△CEF= 12 ×EF× 43=4,∴EF=6,∵E(-1,0),∴F(-7,0)或(5,0);【点评】:本题考查了反比例函数与一次函数的交点问题:求反比例函数与一次函数的交点坐标,把两个函数关系式联立成方程组求解,若方程组有解则两者有交点,方程组无解,则两者无交点.24.(问答题,0分)为了做好校园疫情防控工作,校医每天早上对全校办公室和教室进行药物喷洒消毒,她完成3间办公室和2间教室的药物喷洒要19min ;完成2间办公室和1间教室的药物喷洒要11min .(1)校医完成一间办公室和一间教室的药物喷洒各要多少时间?(2)消毒药物在一间教室内空气中的浓度y (单位:mg/m 3)与时间x (单位:min )的函数关系如图所示:校医进行药物喷洒时y 与x 的函数关系式为y=2x ,药物喷洒完成后y 与x 成反比例函数关系,两个函数图象的交点为A (m ,n ).当教室空气中的药物浓度不高于1mg/m 3时,对人体健康无危害,校医依次对一班至十一班教室(共11间)进行药物喷洒消毒,当她把最后一间教室药物喷洒完成后,一班学生能否进入教室?请通过计算说明.【正确答案】:【解析】:(1)设完成一间办公室和一间教室的药物喷洒各要xmin 和ymin ,则 {3x +2y =192x +y =11,即可求解; (2)点A (5,10),则反比例函数表达式为y= 50x ,当x=55时,y= 5055 <1,即可求解.【解答】:解:(1)设完成一间办公室和一间教室的药物喷洒各要xmin 和ymin , 则 {3x +2y =192x +y =11,解得 {x =3y =5 ,故校医完成一间办公室和一间教室的药物喷洒各要3min 和5min ;(2)一间教室的药物喷洒时间为5min ,则11个房间需要55min , 当x=5时,y=2x=10,故点A (5,10),设反比例函数表达式为:y= kx ,将点A 的坐标代入上式并解得:k=50, 故反比例函数表达式为y= 50x ,当x=55时,y= 5055<1,故一班学生能安全进入教室.【点评】:本题主要考查反比例函数的应用,现实生活中存在大量成反比例函数的两个变量,解答该类问题的关键是确定两个变量之间的函数关系,然后利用待定系数法求出它们的关系式.25.(问答题,0分)已知:一次函数y=-2x+10的图象与反比例函数y= kx(k>0)的图象相交于A,B两点(A在B的右侧).(1)当A(4,2)时,求反比例函数的解析式及B点的坐标;(2)在(1)的条件下,反比例函数图象的另一支上是否存在一点P,使△PAB是以AB为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,请说明理由.【正确答案】:【解析】:(1)只需把点A的坐标代入反比例函数的解析式,就可求出反比例函数的解析式;解一次函数与反比例函数的解析式组成的方程组,就可得到点B的坐标;(2)△PAB是以AB为直角边的直角三角形,可分两种情况讨论:① 若∠BAP=90°,过点A作AH⊥OE于H,设AP与x轴的交点为M,如图1,易得OE=5,OH=4,AH=2,HE=1.易证△AHM∽△EHA,根据相似三角形的性质可求出MH,从而得到点M的坐标,然后用待定系数法求出直线AP的解析式,再解直线AP与反比例函数的解析式组成的方程组,就可得到点P的坐标;② 若∠ABP=90°,同理即可得到点P的坐标.【解答】:解:(1)把A(4,2)代入y= kx,得k=4×2=8.∴反比例函数的解析式为y= 8x.解方程组{y=−2x+10y=8x,得{x=1y=8或{x=4y=2,∴点B的坐标为(1,8);(2)存在,理由:① 若∠BAP=90°,过点A作AH⊥OE于H,设AP与x轴的交点为M,如图1,对于y=-2x+10,当y=0时,-2x+10=0,解得x=5,∴点E(5,0),OE=5.∵A(4,2),∴OH=4,AH=2,∴HE=5-4=1.∵AH⊥OE,∴∠AHM=∠AHE=90°.又∵∠BAP=90°,∴∠AME+∠AEM=90°,∠AME+∠MAH=90°,∴∠MAH=∠AEM,∴△AHM∽△EHA,∴ AH EH =MHAH,即21=MH2,∴MH=4,∴M(0,0),可设直线AP的解析式为y=mx,则有4m=2,解得m= 12,∴直线AP的解析式为y= 12x,。
人教版九年级数学下册《第26章 反比例函数》单元测试卷-带参考答案

人教版九年级数学下册《第26章 反比例函数》单元测试卷-带参考答案(考试时间:90分钟 试卷满分:100分)一、选择题:(本大题共10小题,每小题3分,满分30分) 1.在下列函数中,y 是x 的反比例函数的是( ) A .2y x = B .2x y =C .2y x=D .21yx【答案】C【详解】A .该函数是正比例函数,故本选项错误; B .该函数是正比例函数,故本选项错误; C .该函数符合反比例函数的定义,故本选项正确; D .y 是()1x -的反比例函数,故本选项错误; 故选:C . 2.若双曲线(0)ky k x=<,经过点()12,A y -,()25,B y -则1y 与2y 的大小关系为( ) A .12y y < B .12y y > C .12y y = D .无法比䢂1y 与2y 的大小 【答案】B【详解】解: (0)ky k x=< ∴ 在同一象限内,y 随着x 的增大而增大即可求解()12,A y -,()25,B y -都在第二象限,且25->-∴12y y >.故选:B .3.已知反比例函数4y x=,则它的图象经过点( ) A .(2,8) B .(1,4)- C .(4,1) D .(2,2)-【答案】C【详解】解:由反比例函数4y x=可得:4xy = 2816⨯=,故A 选项不符合题意; 144-⨯=-,故B 选项不符合题意; 414⨯=,故C 选项符合题意;()224⨯-=-,故D 选项不符合题意.故选:C4.反比例函数5m y x-=的图象在第一、三象限,则m 的取值范围是( ) A .5m ≥ B .5m > C .5m ≤ D .5m <【答案】B【详解】解:∵反比例函数5m y x-=图象在第一、三象限 50m ∴->解得5m >. 故选:B5.如图,一次函数1y ax b 的图象与反比例函数2ky x=图象交于()2,A m 、()1,B n -两点,则当12y y >时,x 的取值范围是( )A .1x <-或2x >B .10x -<<或2x >C .12x -<<D .1x <-或02x <<【答案】B【详解】解:∵图象交于()2,A m 、()1,B n -两点 ∵当12y y >时,10x -<<或2x >. 故选B .6.若0ab >,则反比例函数aby x=与一次函数y ax b =+在同一坐标系中的大致图象可能是( )A .B .C .D .【答案】A【详解】解:0ab > ∴aby x=的图象在第一、三象限,排除B ,D ; 0ab >∴a ,b 同号当0a >,0b >时,y ax b =+的图象经过第一、二、三象限 当a<0,0b <时,y ax b =+的图象经过第二、三、四象限 综上可知,只有A 选项符合条件 故选A .7.在平面直角坐标系中,若反比例函数()0ky k x=≠的图像经过点()1,2A 和点()2,B m -,则m 的值为( ) A .1 B .1- C .2 D .2-【答案】B【详解】解:根据题意,将点()1,2A 代入()0ky k x =≠中得:21k =解得:2k =∵反比例函数解析式为2y x =将()2,B m -代入2y x =中得212m ==--故选:B .8.如图1是一个亮度可调节的台灯,其灯光亮度的改变,可以通过调节总电阻控制电流的变化来实现.如图2是该台灯的电流(A)I 与电阻()R Ω成反比例函数的图像,该图像经过点()880,0.25P .根据图像可知,下列说法正确的是( )A .当0.25I <时,880R <B .I 与R 的函数关系式是()2000I R R=> C .当1000R >时,0.22I >D .当8801000R <<时,I 的取值范围是0.220.25I <<【答案】D【详解】解:设I 与R 的函数关系式是(0)UI R R=>∵该图像经过点()880,0.25P ∵0.25880U= ∵220U =∵I 与R 的函数关系式是220(0)I R R=>,故选项B 不符合题意; 当0.25I =时,880R =,当1000R =时0.22I = ∵反比例函数(0)UI R R=>I 随R 的增大而减小 当0.25R <时880I >,当1000R >时0.22I <,故选项A ,C 不符合题意; ∵0.25R =时880I =,当1000R =时0.22I =∵当8801000R <<时,I 的取值范围是0.220.25I <<,故D 符合题意; 故选:D .9.正比例函数y x =与反比例函数1y x=的图象相交于A 、C 两点,AB x ⊥轴于点B ,CD x ⊥轴于点D (如图),则四边形ABCD 的面积为( )A .1B .32C .2D .52【答案】C【详解】解:解方程组1y xy x =⎧⎪⎨=⎪⎩,得:11x y =⎧⎨=⎩或11x y =-⎧⎨=-⎩ 即:正比例函数y x =与反比例函数1y x=的图象相交于两点的坐标分别为(1,1)A (1,1)C -- ∵AB x ⊥ CD x ⊥ ∵(1,0)D - (1,0)B ∵1111212122222四边形=⋅+⋅=⨯⨯+⨯⨯=ABCD S BD AB BD CD 即:四边形ABCD 的面积是2. 故选:C10.如图,正方形ABCD 的顶点分别在反比例函数11(0)k y k x=>和22(0)ky k x =>的图象上.若BD y ∥轴,点C 的纵坐标为4,则12k k +=( )A .32B .30C .28D .26【答案】A【详解】解:连接AC 交BD 于E ,延长BD 交x 轴于F ,连接OD 、OB 如图:四边形ABCD 是正方形AE BE CE DE ∴===设AE BE CE DE m ==== (,4)C aBD y ∥轴(,4)B a m m ∴++ (2,4)A a m + (,4)D a m m +-A ,B 都在反比例函数11(0)k y k x=>的图象上 14(2)(4)()k a m m a m ∴=+=++0m ≠4m a ∴=- (4,8)B a ∴-()4,D a(4,8)B a -在反比例函数11(0)k y k x=>的图象上,(4,)D a 在22(0)ky k x =>的图象上14(8)324k a a ∴=-=- 24k a =12324432k k a a ∴+=-+=;故选:A .二、填空题:(本大题共6小题,每小题3分,满分18分)11.已知反比例函数(0)ky kx=≠ 当x = y =- 则比例系数k 的值是______.【答案】4-【详解】解:把x = y =-4k =-=-;故答案为4-.12.如图 若反比例函数(0)ky x x=<的图像经过点A AB x ⊥轴于B 且AOB 的面积为5 则k =______.【答案】10-【详解】解:∵反比例函数(0)ky x x=<的图像经过点A AB OB ⊥ ∵设,k A a a ⎛⎫ ⎪⎝⎭∵12AOB k S a a=△ ∵反比例函数的图像在第二象限 ∵0k < a<0 则0ka> ∵11522AOB k S a k a ===△ ∵10k =- 故答案为:10-. 13.已知反比例函数3ky x-=的图像在每一个象限内 y 随x 的增大而增大 则k 的取值范围是_____.【答案】3k >##3k < 【详解】解:∵反比例函数3ky x-=的图像在每一个象限内 y 随x 的增大而增大 ∵30k -< ∵3k >.故答案为:3k >.14.如图 点M 和点N 分别是反比例函数a y x =(0x <)和by x=(0x >)的图象上的点MN x ∥轴 点P 为x 轴上一点 若4b a -= 则MNP S △的值为_______.【答案】2【详解】解:如图 连接,OM ON∵MN x ∥轴 ∵ ||||22MNP MNO a b S S ∆∆==+ ∵点M 和点N 分别是反比例的数(0)ay x x =<和(0)b y x x=> 的图象上的点 ∵0,0a b <> ∵||||4222222a b a b b a -+=-+== ∵2MNP S =△; 故答案为:2.15.已知点(3,)C n 在函数ky x=(k 是常数 0k ≠)的图象上 若将点C 先向下平移2个单位 再向左平移4个单位 得点D 点D 恰好落在此函数的图象上 n 的值是______. 【答案】12##0.5【详解】解:点(3,)C n 向下平移2个单位 再向左平移4个单位得(,)n --12; ∵(,)D n --12 ∵点C 、点D 均在函数k y x=上 ∵3k n = ()k n =--2 ∵()n n =--32 解得:12n =故答案为:1216.如图 正方形ABCD 的边长为5 点A 的坐标为(4,0) 点B 在y 轴上 若反比例函数(0)ky k x=≠的图象过点C 则k 的值为_______.【答案】3-【详解】解:如图 过点C 作CE y ⊥轴于E 在正方形ABCD 中 AB BC = 90ABC ∠=︒90ABO CBE ∴∠+∠=︒ 90OAB ABO ∠+∠=︒ OAB CBE ∴∠=∠点A 的坐标为(4,0)4∴=OA 5AB =3OB ∴= 在ABO 和BCE 中OAB CBE AOB BEC AB BC ∠=∠⎧⎪∠=∠⎨⎪=⎩()AAS ABO BCE ∴≌4OA BE ∴== 3CE OB ==431OE BE OB ∴=-=-= ∴点C 的坐标为(3,1)-反比例函数(0)ky k x=≠的图象过点C 313k xy ∴==-⨯=-故答案为:3-.三、解答题(本大题共6题 满分52分) 17.(8分)已知反比例函数12y x=-. (1)说出这个函数的比例系数和自变量的取值范围. (2)求当3x =-时函数的值.(3)求当y =x 的值. 【答案】(1)12,0k x =-≠ (2)4(3)【详解】(1)解:∵12y x=- ∵12,0k x =-≠;(2)解:把3x =- 代入12y x =-得:1243y =-=-; ∵当3x =-时函数的值为:4;(3)解:把y = 代入12y x =-得:12x - 解得:43x ;∵当y =x 的值为:18.(9分)已知一次函数y =kx +b 与反比例函数y mx=的图像交于A (﹣3 2)、B (1 n )两点.(1)求一次函数和反比例函数的表达式; (2)求∵AOB 的面积;(3)结合图像直接写出不等式kx +b mx>的解集. 【答案】(1)一次函数的解析式为y =﹣2x ﹣4 反比例函数的解析式为y 6x=- (2)8(3)x <﹣3或0<x <1【详解】(1)解:∵反比例函数y mx =的图象经过点A (﹣3 2)∵m =﹣3×2=﹣6∵点B (1 n )在反比例函数图象上 ∵n =﹣6. ∵B (1 ﹣6)把A B 的坐标代入y =kx +b 则326k b k b -+=⎧⎨+=-⎩ 解得k =﹣2 b =﹣4∵一次函数的解析式为y =﹣2x ﹣4 反比例函数的解析式为y 6x=-; (2)解:如图 设直线AB 交y 轴于C则C (0 ﹣4)∵S △AOB =S △OCA +S △OCB 12=⨯4×312+⨯4×1=8; (3)解:观察函数图象知 不等式kx +b mx>的解集为x <﹣3或0<x <1. 19.(6分)某气球内充满一定质量的气体 当温度不变时 气球内气体的压强(kPa)p 与气体的体积()3m V 成反比例.当气体的体积30.8m V =时 气球内气体的压强112.5kPa p =.(1)当气体的体积为31m 时 它的压强是多少?(2)当气球内气体的压强大于150kPa 时 气球就会爆炸.问:气球内气体的体积应不小于多少气球才不会爆炸?【答案】(1)当气体的体积为31m 时 它的压强是90kPa (2)当气球内气体的体积应不小于30.6m 时 气球才不会爆炸 【详解】(1)解:设k V p=由题意得:0.8112.5k= ∵90k = ∵90V p=∵当1V =时 90p =∵当气体的体积为31m 时 它的压强是90kPa ; (2)解:当150p =时 900.6150V == ∵900k =>∵V 随p 的增大而增大∵要使气球不会爆炸 则0.6V ≥∵当气球内气体的体积应不小于30.6m 时 气球才不会爆炸.20.(9分)如图 一次函数28y x =-+与函数(0)ky x x=>的图像交于(,6)A m (,2)B n 两点 AC y ⊥轴于C BD x ⊥轴于D .(1)求k 的值;(2)连接OA OB 求AOB 的面积;(3)在x 轴上找一点P 连接AP BP 使ABP 周长最小 求点P 坐标. 【答案】(1)6 (2)8 (3)5,02⎛⎫ ⎪⎝⎭【详解】(1)解:∵一次函数28y x =-+与函数(0)k y x x=>的图像交于(,6)A m (,2)B n 两点 ∵628m =-+ 228n =-+ 解得1m = 3n = ∵点(1,6)A (3,2)B 代入反比例函数得 61k= ∵616k =⨯=.(2)解:如图所示设一次函数图像与x 轴的交点为M 在一次函数28y x =-+中 令0y = 则4x = ∵(4,0)M 且(1,6)A (3,2)B∵114642822AOB AOM BOM S S S =-=⨯⨯-⨯⨯=△△△.(3)解:已知(1,6)A (3,2)B 则点A 关于x 轴的对称点A '的坐标(1,6)- 如图所示 A P AP '= 则ABP 的周长为AP BP AB A P BP AB '++=++设直线BA '的解析式为y kx b =+将点(3,2)B 、(1,6)A '-代入 得326k b k b +=⎧⎨+=-⎩解得410k b =⎧⎨=-⎩ ∵直线BA '的解析式为410=-y x 当0y =时 则4100x -= 解方程得 52x = ∵点P P 的坐标为5,02⎛⎫⎪⎝⎭.21.(10分)已知一次12y x a =-+的图象与反比例函数()20ky k x=≠的图象相交. (1)判断2y 是否经过点(),1k .(2)若1y 的图象过点(),1k 且25a k +=. ∵求2y 的函数表达式.∵当0x >时 比较1y 2y 的大小. 【答案】(1)过 (2)∵21=y x;∵当01x <<时 12y y < 当1x >时 12y y > 当1x =时 12y y = 【详解】(1)∵()20ky k x =≠∵把点(),1k 代入反比例函数 得1kk= ∵2y 经过点(),1k . (2)①∵1y 的图象过点(),1k∵把点(),1k 代入12y x a =-+ 得12k a =-+ 又∵25a k += ∵解得2a = 1k = ∵21=y x∵2y 的函数表达式为:21=y x②如图所示:由函数图象得 当01x <<时 12y y <;当1x >时 12y y >;当1x =时 12y y =.22.(10分)图1 已知双曲线(0)ky k x=>与直线y k x '=交于A 、B 两点 点A 在第一象限 试回答下列问题:(1)若点A 的坐标为(3,1) 则点B 的坐标为 ;(2)如图2 过原点O 作另一条直线l 交双曲线(0)ky k x=>于P Q 两点 点P 在第一象限.∵四边形ABPQ 一定是 ;∵若点A 的坐标为(3,1) 点P 的横坐标为1 求四边形ABPQ 的面积.(3)设点A 、P 的横坐标分别为m 、n 四边形ABPQ 可能是矩形吗?可能是正方形吗?若可能 直接写出m 、n 应满足的条件;若不可能 请说明理由. 【答案】(1)(3,1)-- (2)∵平行四边形;∵16(3)mn k =时 四边形ABPQ 是矩形 不可能是正方形 理由见解析 【详解】(1)A 、B 关于原点对称 (3,1)A ∴点B 的坐标为(3,1)--故答案为:(3,1)--(2)∵A 、B 关于原点对称 P 、Q 关于原点对称 ∴OA OB = OP OQ = ∴四边形ABPQ 是平行四边形故答案为:平行四边形 ∵点A 的坐标为(3,1) ∴313k =⨯=∴反比例函数的解析式为3y x=点P 的横坐标为1 ∴点P 的纵坐标为3∴点P 的坐标为(1,3)由双曲线关于原点对称可知 点Q 的坐标为(1,3)-- 点B 的坐标为(3,1)--如图 过点A 、B 分别作y 轴的平行线 过点P 、Q 分别作x 轴的平行线 分别交于C 、D 、E 、F则四边形CDEF 是矩形 6CD = 6DE = 4DB DP == 2CP CA ==则四边形ABPQ 的面积=矩形CDEF 的面积-ACP △的面积-PDB △的面积-BEQ 的面积-AFQ △的面积36282816=----=(3)当AB PQ ⊥时四边形ABPQ 是正方形 此时点A 、P 在坐标轴上 由于点A P 不可能在坐标轴上且都在第一象限故不可能是正方形 即90POA ∠≠︒ PO AO BO QO ===时 四边形ABPQ 是矩形此时P 、A 关于直线y x =对称 即22k k m n m n ++=化简得mn k =∴mn k =时 四边形ABPQ 是矩形 不可能是正方形。
人教版初中数学九年级数学下册第一单元《反比例函数》测试题(包含答案解析)

一、选择题1.正比例函数1y 的图像与反比例函数2y 的图像相交于点(2,4)A ,下列说法正确的是( )A .反比例函数2y 的解析式是28y x=-B .两个函数图像的另一个交点坐标为(2,4)C .当2x <-或02x <<时,12y y <D .正比例函数1y 与反比例函数2y 都随x 的增大而增大2.在同一平面直角坐标系中,函数y =kx +1(k ≠0)和ky x=(k ≠0)的图象大致是( )A .B .C .D .3.如图,正比例函数y = ax 的图象与反比例函数ky x=的图象相交于A ,B 两点,其中点A 的横坐标为2,则不等式ax<kx的解集为( )A .x < - 2或x > 2B .x < - 2或0 < x < 2C .-2 < x < 0或0 < x < 2D .-2 < x < 0或 x > -24.已知()()()112233,,,,,A x y B x y C x y 是反比例函数2y x=上的三点,若123x x x <<,213y y y <<,则下列关系式不正确的是 ( )A .120x x <B .130x x <C .230x x <D .120x x +<5.对于反比例函数21k y x+=,下列说法错误的是( )A .函数图象位于第一、三象限B .函数值y 随x 的增大而减小C .若A (-1,y 1)、B (1,y 2)、C (2,y 3)是图象上三个点,则y 1<y 3<y 2D .P 为图象上任意一点,过P 作PQ ⊥y 轴于Q ,则△OPQ 的面积是定值6.如图,过y 轴上一个动点M 作x 轴的平行线,交双曲线y=4x-于点A ,交双曲线10y x=于点B ,点C 、点D 在x 轴上运动,且始终保持DC =AB ,则平行四边形ABCD 的面积是( )A .7B .10C .14D .287.在平面直角坐标系xOy 中,对于横、纵坐标相等的点称为“好点”.下列函数的图象中不存在...“好点”的是( ) A .y x =- B .2y x =+C .2y x=D .22y x x =-8.若函数5y x=与1y x =+的图像交于点(),A a b ,则11a b -的值为 ( )A .15-B .15C .5-D .59.同一坐标系中,函数()1y k x +=与ky x=的图象正确的是( ) A . B .C .D .10.已知点()1,3M -在双曲线ky x=上,则下列各点一定在该双曲线上的是( ) A .()3,1-B .()1,3--C .()1,3D .()3,111.给出下列函数:①y =﹣3x +2:②y =3x ;③y =﹣5x:④y =3x ,上述函数中符合条件“当x >1时,函数值y 随自变量x 增大而增大”的是( ) A .①③ B .③④ C .②④ D .②③12.已知点A (x 1,y 1),B (x 2,y 2)是反比例函数ky x=(k <0)的图象上的两点,若x 1<0<x 2,则下列结论正确的是( )A .y 1<0<y 2B .y 2<0<y 1C .y 1<y 2<0D .y 2<y 1<0二、填空题13.双曲线y =kx经过点A (a ,﹣2a ),B (﹣2,m ),C (﹣3,n ),则m _____n (>,=,<).14.若点()()125,,3,A y B y --在反比例函数3y x=的图象上,则12,y y ,的大小关系是_________.15.如图,平面直角坐标系中,矩形ABCD 的顶点B 在x 轴负半轴上,边CD 与x 轴交于点E ,连接AE ,//AE y 轴,反比例函数()0ky x x=>的图象经过点A ,及AD 边上一点F ,4AF FD =,若,2DA DE OB ==,则k 的值为________.16.有5张正面分别有数字-1,14-,0,1,3的卡片,它们除数字不同外全部相同,将它们背面朝上,洗匀后从中随机的抽取一张.记卡片上的数字为a ,则使以x 为自变量的反比例函数37a y x-=经过二、四象限,且关于x 的一元二次方程2230ax x -+=有实数解的概率是__________.17.如图,B(2,﹣2),C(3,0),以OC ,CB 为边作平行四边形OABC ,则经过点A 的反比例函数的解析式为_____.18.反比例函数16y x =与2ky x=()0k <的图像如图所示,点P 是x 正半轴上一点,过点P 作x 轴的垂线,分别交反比例函数16y x =与2ky x=()0k <的图像于点A ,B ,若4AB PB =,则k 的值为_______.19.如图,在平面直角坐标系中,菱形ABCD 的顶点A 、B 在反比例函数y kx=(k >0,x >0)的图象上,横坐标分别为1,4,对角线BD ∥x 轴,若菱形ABCD 的面积为9.则k 的值为____.20.如图,点()11,P x y ,点()22,P x y ,…点(),n n P x y 在函数()90y x x=>的图象上, 112123231,,n n n POA P A A P A A P A A -⋅⋅⋅都是等腰直角三角形,斜边112231,,,n n OA A A A A A A -⋅⋅⋅都在x 轴上(n 是大于或等于2的正数数),则12n y y y ++⋅⋅⋅+=__________.(用含n 的式子表示)三、解答题21.如图,一次函数y kx b =+的图象交反比例函数()0ay x x=>的图象于()()2,4,,1A B m --两点,交x 轴于点C .(1)求反比例函数与一次函数的关系式. (2)求ABO ∆的面积.(3)根据图象回答:当x 为何值时,一次函数的值大于反比例函数的值? 22.如图,Rt △ABO 的顶点A 是双曲线y =kx与直线y =﹣x +(k +1)在第四象限的交点,AB ⊥x 轴于点B ,且S △ABO =32.(1)求这两个函数的表达式;(2)求直线与双曲线的交点A 和C 的坐标及△AOC 的面积. (3)写出反比例函数y =kx的值大于一次函数y =﹣x +(k +1)时的x 的取值范围. 23.已知A (-2n ,n )、B (n ,-4)两点是一次函数y kx b =+和反比例函数my x=图像的两个交点.(1)求一次函数与反比例函数的解析式; (2)求△AOB 的面积;(3)观察图像,写出不等式0mkx b x+->的解集.24.已知:如图,一次函数的图象与反比例函数ky x=的图象交于A 、B 两点,且点B 的坐标为.(1)求反比例函数ky x=的表达式; (2)点在反比例函数ky x=的图象上,求△AOC 的面积;(3)在(2)的条件下,在坐标轴上找出一点P ,使△APC 为等腰三角形,请直接写出所有符合条件的点P 的坐标.25.某校园艺社计划利用已有的一堵长为10m 的墙,用篱笆围一个面积为212m 的矩形园子.(1)如图,设矩形园子的相邻两边长分别为()x m 、()y m . ①求y 关于x 的函数表达式; ②当4y 时,求x 的取值范围;(2)小凯说篱笆的长可以为9.5m ,洋洋说篱笆的长可以为10.5m.你认为他们俩的说法对吗?为什么?26.已知反比例函数y =12mx-(m 为常数)的图象在第一、三象限.(1)求m的取值范围;(2)如图,若该反比例函数的图象经过▱ABOD的顶点D,点A,B的坐标分别为(0,3),(﹣2,0),求出该反比例函数的解析式;(3)若E(x1,y1),F(x2,y2)都在该反比例函数的图象上,且x1>x2>0,则y1和y2有怎样的大小关系?【参考答案】***试卷处理标记,请不要删除一、选择题1.C解析:C【分析】由题意可求正比例函数解析式和反比例函数解析式,由正比例函数和反比例函数的性质可分别进行判断求解,即可得出结论.【详解】解:∵正比例函数y1的图象与反比例函数y2的图象相交于点A(2,4),∴正比例函数12y x=,反比例函数28yx=,∴两个函数图象的另一个交点为(−2,−4),∴A,B选项错误;∵正比例函数12y x=中,y随x的增大而增大,反比例函数28yx=中,在每个象限内y随x的增大而减小,∴D选项错误;∵当x<−2或0<x<2时,y1<y2,∴选项C正确;故选:C.【点睛】本题考查了反比例函数与一次函数的交点问题,熟练运用反比例函数与一次函数的性质解决问题是本题的关键.2.C解析:C 【分析】分两种情况讨论,当k>0时,分析出一次函数和反比例函数所过象限;再分析出k<0时,一次函数和反比例函数所过象限,符合题意者即为正确答案. 【详解】①当k> 0时,y=kx+1过第一、二、三象限,ky x =过第一、三象限; ②当k<0时,y= kx+1过第一、二、四象限,ky x=过第二、四象限,观察图形可知,只有C 选项符合题意, 故选:C . 【点睛】此题考查了依据一次函数与反比例函数的图象,正确掌握各函数的图象与字母系数的关系是解题的关键.3.B解析:B 【分析】先根据反比例函数与正比例函数的性质求出B 点横坐标,再由函数图象即可得出结论. 【详解】∵正比例函数y ax =的图象与反比例函数ky x=的图象相交于A ,B 两点, ∴A ,B 两点坐标关于原点对称, ∵点A 的横坐标为2, ∴B 点的横坐标为-2, ∵k ax x<, ∴在第一和第三象限,正比例函数y ax =的图象在反比例函数ky x=的图象的下方, ∴2x <-或02x <<, 故选:B . 【点睛】本题考查了反比例函数与一次函数的交点问题,关键是掌握正比例函数与反比例函数图象交点关于原点对称.4.A解析:A 【分析】 根据反比例函数2y x=和x 1<x 2<x 3,y 2<y 1<y 3,可得点A ,B 在第三象限,点C 在第一象限,得出x1<x2<0<x3,再选择即可.【详解】解:∵反比例函数2yx=中,2>0,∴在每一象限内,y随x的增大而减小,∵x1<x2<x3,y2<y1<y3,∴点A,B在第三象限,点C在第一象限,∴x1<x2<0<x3,∴x1•x2>0,x1•x3<0,x2•x3<0,x1+x2<0,故选:A.【点睛】本题考查了反比例函数图象上点的坐标特征,解答此题的关键是熟知反比例函数的增减性,本题是逆用,难度有点大.5.B解析:B【分析】先判断出k2 +1的符号,再根据反比例函数的性质即可得出结论.【详解】A、∵k2+1>0,∴它的图象分布在第一、三象限,故本选项正确;B、∵它的图象分布在第一、三象限,∴在每一象限内y随x的增大而减小,故本选项错误;C、∵它的图象分布在第一、三象限,在每一象限内y随x的增大而减小,∵x1=-1<0,∴y1<0,∵x2=1>0,x3=2>0,∴y2>y3,∴y1<y3<y2故本选项正确;D、∵P为图象上任意一点,过P作PQ⊥y轴于Q,∴△OPQ的面积=12(k2+1)是定值,故本选项正确.故选B.【点睛】本题考查的是反比例函数的性质,熟知反比例函数y=kx(k≠0)中,当k>0时函数图象的两个分支分别位于一三象限是解答此题的关键.6.C解析:C【分析】设出M点的坐标,可得出过M与x轴平行的直线方程为y=m,将y=m代入反比例函数y=4x-中,求出对应的x的值,即为A的横坐标,将y=m代入反比例函数10yx=中,求出对应的x 的值,即为B 的横坐标,用B 的横坐标减去A 的横坐标求出AB 的长,根据DC=AB ,且DC 与AB 平行,得到四边形ABCD 是平行四边形,过B 作BN 垂直于x 轴,平行四边形底边为DC ,DC 边上的高为BN ,由B 的纵坐标为m得到BN=m ,再由求出的AB 的长,得到DC 的长,利用平行四边形的面积等于底乘以高可得出平行四边形ABCD 的面积. 【详解】解:设M 的坐标为(0,m )(m >0)则直线AB 的方程为:y=m , 将y=m 代入y=4x-中得:4x m =-,∴A (4m -,m )将y=m 代入10y x=中得:10x m =,∴B (10m ,m )∴DC=AB=10m -(4m -)=14m过B 作BN ⊥x 轴,则有BN=m ,则平行四边形ABCD 的面积S=DC·BN=14m×m=14. 故选C . 【点睛】本题考查反比例函数综合题.7.B解析:B 【分析】根据“好点”的定义判断出“好点”即是直线y=x 上的点,再各函数中令y=x ,对应方程无解即不存在“好点”. 【详解】解:根据“好点”的定义,好点即为直线y=x 上的点,令各函数中y=x , A 、x=-x ,解得:x=0,即“好点”为(0,0),故选项不符合; B 、2x x =+,无解,即该函数图像中不存在“好点”,故选项符合; C 、2x x=,解得:2x =2x =“好点”22)和(2,2),故选项不符合;D 、22x x x =-,解得:x=0或3,即“好点”为(0,0)和(3,3),故选项不符合; 故选B. 【点睛】本题考查了函数图像上的点的坐标,涉及到解分式方程,一元二次方程,以及一元一次方程,解题的关键是理解“好点”的定义.8.B解析:B【分析】先把A (a ,b )分别代入两个解析式得到5b a =,b =a +1,则ab =5,b -a =1,再变形11a b -得到b a ab-,然后利用整体思想进行计算即可. 【详解】解:把A (a ,b )代入5y x=与y =x +1, 得5b a=,b =a +1, 即ab =5,b -a =1, 所以11a b -=b a ab -=15. 故选:B.【点睛】 本题考查了反比例函数与一次函数的交点问题:反比例函数图象与一次函数图象的交点坐标满足两函数的解析式.9.D解析:D【分析】先根据四个选项的共同点确定k 的符号,再根据各函数图象的性质确定图象所在的象限即可.【详解】解:A 、反比例函数图象位于一、三象限,0k >,则一次函数图象应该交y 轴于正半轴,故本选项错误;B 、反比例函数图象位于二、四象限,k 0<,则一次函数图象应该交y 轴于负半轴,故本选项错误;C 、反比例函数图象位于二、四象限,k 0<,则一次函数应该是个减函数,故本选项错误;D 、反比例函数图象位于一、三象限,0k >,则一次函数图象应该交y 轴于正半轴,故本选项正确;故选:D .【点睛】此题考查反比例函数的图象性质和一次函数的图象性质,解题关键是由k 的取值确定函数所在的象限.10.A解析:A【分析】先求出k=-3,再依次判断各点的横纵坐标乘积,等于-3即是在该双曲线上,否则不在.【详解】∵点()1,3M -在双曲线k y x=上, ∴133k =-⨯=-,∵3(1)3⨯-=-,∴点(3,-1)在该双曲线上,∵(1)(3)13313-⨯-=⨯=⨯=,∴点()1,3--、()1,3、()3,1均不在该双曲线上,故选:A.【点睛】此题考查反比例函数解析式,正确计算k 值是解题的关键. 11.B解析:B【分析】分别利用一次函数、正比例函数、反比例函数的增减性分析得出答案.【详解】解:①y =﹣3x +2,当x >1时,函数值y 随自变量x 增大而减小,故此选项不符合题意; ②y =3x,当x >1时,函数值y 随自变量x 增大而减小,故此选项不符合题意; ③y =﹣5x,当x >1时,函数值y 随自变量x 增大而增大,故此选项符合题意; ④y =3x ,当x >1时,函数值y 随自变量x 增大而增大,故此选项符合题意; 故选:B .【点睛】此题考查一次函数、正比例函数、反比例函数,正确把握相关性质是解题关键. 12.B解析:B【分析】首先根据系数判定函数的图象在二、四象限,再根据x 1<0<x 2,可比较出y 1、y 2的大小,进而得到答案.【详解】 解:由反比例函数k y x=(k <0),可知函数的图象在二、四象限, ∵x 1<0<x 2,∴A (x 1,y 1)在第二象限,y 1>0,B (x 2,y 2)在第四象限,y 2<0,∴y 2<0<y 1,故选:B .【点睛】此题主要考查了反比例函数图象上的点的坐标特征,熟练掌握是解题的关键.二、填空题13.>【分析】先求出反比例函数解析式判断函数的增减性﹣2>﹣3即可判断mn 的大小【详解】∵双曲线y =经过点A (a ﹣2a )∴k =﹣2a2<0∴双曲线在二四象限在每个象限内y 随x 的增大而增大∵B (﹣2m )C解析:>.【分析】先求出反比例函数解析式,判断函数的增减性﹣2>﹣3,即可判断m ,n 的大小..【详解】∵双曲线y =k x经过点A (a ,﹣2a ), ∴k =﹣2a 2<0, ∴双曲线在二、四象限,在每个象限内,y 随x 的增大而增大,∵B (﹣2,m ),C (﹣3,n ),﹣2>﹣3,∴m >n ,故答案为:>.【点睛】本题利用函数的性质比较大小,关键是求出函数解析式,掌握反比例函数的性质. 14.【分析】根据反比例函数的性质解答【详解】∵反比例函数中∴此函数图象的两个分支分别位于一三象限并且在每一象限内随的增大而减小这两点都在反比例函数的图象上在第三象限故答案为:【点睛】此题考查反比例函数的 解析:21y y <【分析】根据反比例函数的性质解答.【详解】∵反比例函数3y x=中30k =>, ∴此函数图象的两个分支分别位于一三象限,并且在每一象限内,y 随x 的增大而减小. ()()125,,3,A y B y --这两点都在反比例函数3y x =的图象上,A B ∴、在第三象限,21y y ∴<,故答案为:21y y <.【点睛】此题考查反比例函数的性质:当k>0时,函数图象的两个分支分别位于一三象限,并且在每一象限内,y 随x 的增大而减小;当k<0时,函数图象的两个分支分别位于二四象限,并且在每一象限内,y 随x 的增大而增大.15.【分析】根据矩形的性质已知条件可得均为等腰直角三角形进而根据点在坐标系中的位置设并过点作于再根据点与点之间的相对位置反比例函数的解析式用含表示出然后利用反比例函数的解析式得到关于的方程解方程即可得解 解析:15【分析】根据矩形的性质、已知条件可得ADE 、ABE △、BCE 均为等腰直角三角形,进而根据点在坐标系中的位置设(),0E x ,并过D 点作DHAE ⊥于H ,再根据点与点之间的相对位置、反比例函数的解析式用含x 、k 表示出,k A x x ⎛⎫ ⎪⎝⎭、7436,55x x F ++⎛⎫ ⎪⎝⎭,然后利用反比例函数的解析式得到关于k 的方程,解方程即可得解.【详解】∵AD AE =,90ADE ∠=︒∴ADE 为等腰直角三角形∴45DAE ∠=︒ ∴9045BAE DAE ∠=︒-∠=︒∴ABE △为等腰直角三角形∴45ABE ∠=︒∴45CBE ∠=︒∴BCE 为等腰直角三角形设(),0E x ,则,k A x x ⎛⎫ ⎪⎝⎭,过D 点作DH AE ⊥于H ,如图:∴()1112222DH AE BE x ===+ ∴()132222x DH OE x x ++=++=∴322,22x x D ++⎛⎫ ⎪⎝⎭ ∵4AF FD =∴点F 的横坐标为32217422415x x x +++-⋅=+、纵坐标为2213622145x x x ++++⋅=+ ∴7436,55x x F ++⎛⎫ ⎪⎝⎭∵,k A x x⎛⎫ ⎪⎝⎭ ∴2k AE x x ==+ ∴()2k x x =+ ∴()7436255x x k x x ++=⋅=⋅+ ∴()()()7436252x x x x ++=+∴3x =或2x =-(不合题意舍去)∴()()233215k x x =+=⨯+=.【点睛】本题考查了反比例函数、矩形的性质、等腰直角三角形的判定和性质等,能够表示出点F 坐标是解题的关键.16.【分析】根据反比例函数图象经过第二四象限关于x 的一元二次方程ax2-2x+3=0有实数解列出不等式求出a 的取值范围从而确定出a 的值再根据概率公式计算即可【详解】解:∵反比例函数图象经过第二四象限∴3 解析:25【分析】根据反比例函数图象经过第二、四象限,关于x 的一元二次方程ax 2-2x+3=0有实数解,列出不等式求出a 的取值范围,从而确定出a 的值,再根据概率公式计算即可.【详解】解:∵反比例函数图象经过第二、四象限,∴3a-7<0,解得73a < 关于x 的一元二次方程ax 2-2x+3=0有实数解,则△=4-12a≥0,且a≠0,解得:,a≤13,且(a≠0), 综上,a≤13,且(a≠0), ∴ a 可取-1,-14,∴使以x 为自变量的反比例函数37a y x -=经过二、四象限,且关于x 的一元二次方程ax 2-2x+3=0有实数解的概率是25. 故答案为:25. 【点睛】 本题考查了概率公式,用到的知识点是反比例函数图象的性质、根的判别式、概率公式,熟记性质以及判别式求出a 的值是解题的关键.17.y =【分析】设A 坐标为(xy )根据四边形OABC 为平行四边形利用平移性质确定出A 的坐标利用待定系数法确定出解析式即可【详解】解:设A 坐标为(xy )∵B (2﹣2)C (30)以OCCB 为边作平行四边形O解析:y =2x【分析】设A 坐标为(x ,y ),根据四边形OABC 为平行四边形,利用平移性质确定出A 的坐标,利用待定系数法确定出解析式即可.【详解】解:设A 坐标为(x ,y ),∵B (2,﹣2),C (3,0),以OC ,CB 为边作平行四边形OABC ,∴x+3=0+2,y+0=0﹣2,解得:x =﹣1,y =﹣2,即A (﹣1,﹣2), 设过点A 的反比例解析式为y =k x, 把A (﹣1,﹣2)代入得:k =2, 则过点A 的反比例函数解析式为y =2x , 故答案为:y =2x. 【点睛】此题考查了待定系数法求反比例函数解析式,以及平行四边形的性质,熟练掌握待定系数法是解本题的关键. 18.-2【分析】设点A 横坐标为m 分别表示出ABPB 根据得到关于k 的方程解方程即可【详解】解:设点A 横坐标为m 则点A 纵坐标为∵AB ⊥x 轴∴点B 纵坐标为∴AB=PB=∵∴∴∴故答案为:-2【点睛】本题考查了解析:-2【分析】设点A 横坐标为m ,分别表示出AB 、PB ,根据4AB PB =,得到关于k 的方程,解方程即可.【详解】解:设点A 横坐标为m ,则点A 纵坐标为6m , ∵ AB ⊥x 轴,∴点B 纵坐标为k m , ∴AB =66k k m m m--= ,PB =k k m m =-, ∵4AB PB =,∴64k k m m-=- , ∴64k k -=- ,∴2k =-.故答案为:-2【点睛】本题考查了反比例函数图象上点的表示,解题的关键是根据4AB PB =列出方程,注意表示PB 时,注意式子符号问题.19.2【分析】根据题意利用面积法求出AE 设出点B 坐标表示点A 的坐标应用反比例函数上点的横纵坐标乘积为k 构造方程求k 【详解】连接AC 分别交BDx 轴于点EF 由已知AB 横坐标分别为14∴BE=3∵四边形ABC解析:2.【分析】根据题意,利用面积法求出AE ,设出点B 坐标,表示点A 的坐标.应用反比例函数上点的横纵坐标乘积为k 构造方程求k .【详解】连接AC 分别交BD 、x 轴于点E 、F .由已知,A 、B 横坐标分别为1,4,∴BE =3.∵四边形ABCD 为菱形,AC 、BD 为对角线,∴S 菱形ABCD =412⨯AE •BE =9,∴AE 32=,设点B 的坐标为(4,y ),则A 点坐标为(1,y 32+) ∵点A 、B 同在y k x =图象上, ∴4y =1•(y 32+), ∴y 12=, ∴B 点坐标为(4,12), ∴k =2故答案为:2.【点睛】 此题考查菱形的性质,反比例函数图象上点的坐标与k 之间的关系,解题关键在于掌握其性质定义.20.【分析】过过点P1作P1E ⊥x 轴于点E 过点P2作P2F ⊥x 轴于点F 过点P3作P3G ⊥x 轴于点G 根据△P1OA1△P2A1A2△P3A2A3都是等腰直角三角形可求出A1A2A3的横坐标从而总结出一般规解析:3n【分析】过过点P 1作P 1E ⊥x 轴于点E ,过点P 2作P 2F ⊥x 轴于点F ,过点P 3作P 3G ⊥x 轴于点G ,,根据△P 1OA 1,△P 2A 1A 2,△P 3A 2A 3都是等腰直角三角形,可求出A 1,A 2,A 3的横坐标,从而总结出一般规律得出点A n 的坐标,再求12n y y y ++⋅⋅⋅+的值即可.【详解】解:过点P 1作P 1E ⊥x 轴于点E ,过点P 2作P 2F ⊥x 轴于点F ,过点P 3作P 3G ⊥x 轴于点G ,∵△P 1OA 1是等腰直角三角形,∴P 1E=OE=A 1E ,设点P 1的坐标为(a,a),(a>0),将点P 1(a,a)代入()90y x x=>,可得a=3, 故点A 1的坐标为(6,0), 设点P 2的纵坐标为b ,则P 2的横坐标为6+b ,将点(b+6,b)代入()90y x x=>,可得b=3,故点A 2的横坐标为同理可以得到A 3的横坐标是A n 的横坐标是,根据等腰三角形的性质得到12n y y y ++⋅⋅⋅+=A n 的横坐标的一半,∴12n y y y ++⋅⋅⋅+=故答案为:【点睛】本题考查了反比例函数的综合应用,涉及了点的坐标的规律变化,解答本题的关键是根据等腰三角形的性质结合反比例函数解析式求出A 1,A 2,A 3的横坐标,从而总结出一般规律,难度较大.三、解答题21.(1)81;52y y x x =-=-;(2)15;(3)02x <<或8x > 【分析】(1)根据点A 坐标求出反比例函数的系数,再利用反比例函数解析式求出点B 坐标,再用待定系数法求出一次函数解析式;(2)分别过A 点,B 点作x 轴的垂线,垂足为,E F ,可知三角形ABO 的面积等于梯形ABFE 的面积,就可以算出结果;(3)根据图象找出一次函数在反比例函数上面时x 的取值范围,就可以得到结果.【详解】(1)∵()2,4A -在反比例函数()0a y x x =>上, ∴代入得24k -=, ∴8k =-,∴反比例函数的关系数8y x =-, ∵(),1B m 在8y m =-上, ∴代入得81m -=-, ∴8m =,∴()8,1B -,又∵()()2,4,8,1A B --在一次函数y kx b =+上,∴代入得4218k bk b-=+⎧⎨-=+⎩,解得125kb⎧=⎪⎨⎪=-⎩,∴一次函数的解析式为152y x=-;(2)如图,分别过A点,B点作x轴的垂线,垂足为,E F,∵()()2,4,8,1A B--,∴ABO EABFS S∆=梯()()141822=⨯+⨯-1562=⨯⨯15=,∴ABOS∆的面积是15;(3)一次函数的值大于反比例函数的值,即一次函数的图象在上方,∴由图知02x<<或8x>.【点睛】本题考查反比例函数和一次函数综合,解题的关键是掌握反比例函数的图象和性质,特殊三角形的面积求法,利用函数图象解不等式的方法.22.(1)y=3x-和y=-x-2;(2)交点A为(1,-3),C为(-3,1);4;(3)-3<x<0或x>1.【分析】(1)设出A坐标(x,y),表示出OB与AB,进而表示出三角形ABO面积,由已知面积确定出反比例函数k的值,进而确定出一次函数;(2)联立反比例函数与一次函数解析式,求出A与C坐标即可;由一次函数解析式求出交点的坐标,然后三角形AOC面积=两个三角形面积的和,求出即可;(3)根据图象即可求得.【详解】解:(1)设A 点坐标为(x ,y ),且x >0,y <0, 则113||||(),222ABO S OB AB x y ∆=⋅⋅=⋅⋅-= ∴xy=-3,∴k=xy=-3,代入y =﹣x +(k +1),得y=-x-2;∴所求的两个函数的解析式分别为y=3x-和y=-x-2; (2)解:求两个函数图象交点,得 32y x y x ⎧=-⎪⎨⎪=--⎩ 13,?31x x y y ==-⎧⎧⎨⎨=-=⎩⎩∴交点A 为(1,-3),C 为(-3,1);由y=-x-2,令x=0,得y=-2.∴直线y=-x+2与y 轴的交点的坐标为(0,-2), 则112123422AOC S ∆=⨯⨯+⨯⨯= (3)∵交点A 为(1,-3),C 为(-3,1),∴由图象可知:反比例函数y=k x的值大于一次函数y=-x+(k+1)时, x 的取值范围为-3<x <0或x >1.【点睛】 此题考查了一次函数与反比例函数的交点问题,以及三角形面积,解题关键是熟练掌握待定系数法.23.(1)8y x=-,2y x =--;(2)6AOB S ∆=;(3)4x <-或02x << 【分析】(1)根据反比例函数图像上任意一点的横坐标与纵坐标的乘积相等可得到-2n²=-4n 求出n 的值,进而确定A 、B 两点坐标,求出反比例函数的解析式,然后利用待定系数法确定一次函数的解析式;(2)先求出直线y=-x-2与x 轴交点C 的坐标,然后利用S △AOB =S △AOC +S △BOC 进行计算;(3)观察函数图象得到当x <-4或0<x <2时,一次函数的图象在反比例函数图象上方,据此可得不等式的解集.【详解】解:(1)由“反比例函数上任意一点的横坐标与纵坐标的乘积相等”可知:-2n²=-4n ,求得n=0(舍去)或n=2,∴A(-4,2),B(2,-4),∴m=-4×2=-8,故反比例函数的解析式为:8y x =-, 将A 、B 两点代入一次函数y kx b =+中: ∴2442k b k b =-+⎧⎨-=+⎩,解得12k b =-⎧⎨=-⎩, ∴一次函数的解析式为:2y x =--,故答案为:8y x=-,2y x =--; (2) y=-x-2中,令y=0,则x=-2, 即直线y=-x-2与x 轴交于点C (-2,0),∴S △AOB =S △AOC +S △BOC =112224622⨯⨯+⨯⨯=, 故答案为:6;(3)0m kx b x+->,变形为:m kx b x +>, 观察图形,即要求一次函数的图像在反比例函数图像的上方,∴解集为:x <-4或0<x <2,故答案为:x <-4或0<x <2.【点睛】本题考查了反比例函数与一次函数的交点问题:反比例函数与一次函数的交点坐标满足两函数的解析式.解决问题的关键是掌握用待定系数法确定一次函数的解析式.24.(1);(2)32;(3)(-1,0)、(0,0)、(0,1). 【详解】(1)一次函数的图象过点B , ∴∴点B 坐标为∵反比例函数k y x=的图象经过点B反比例函数表达式为(2)设过点A 、C 的直线表达式为,且其图象与轴交于点D ∵点在反比例函数的图象上 ∴∴点C 坐标为∵点B 坐标为∴点A 坐标为解得:过点A 、C 的直线表达式为∴点D 坐标为∴(3)①当点P 在x 轴上时,设P(m ,0)∵AC=2,AP=22(1)2m ++,CP=22(2)1m ++,∴22(1)2m ++=22(2)1m ++或22(2)1m ++=2,解得:m=0或-1 ②当点P 在y 轴上时,设P(0,n),∵AC=2,AP=221(2)n +-,CP=222(1)n +-,∴221(2)n +-=222(1)n +-或221(2)n +-=2解得:n=0或1 综上所述:点P 的坐标可能为、、 25.(1)①1265y x x ⎛⎫=⎪⎝⎭,②635x ;(2)小凯的说法错误,洋洋的说法正确. 【分析】(1)①根据矩形的面积公式计算即可,注意自变量的取值范围;②构建不等式即可解决问题;(2)构建方程求解即可解决问题;【详解】(1)①由题意xy =12, 1265y x x ⎛⎫∴= ⎪⎝⎭②y ⩾4时,124x ≥,解得3x ≤ 所以635x . (2)当1229.5x x +=时,整理得:2419240,0x x -+=∆<,方程无解.当12210.5xx+=时,整理得2421240,570x x-+=∆=>,符合题意;∴小凯的说法错误,洋洋的说法正确.【点睛】本题考查反比例函数的应用.(1)①中需注意,因为墙的宽度为10m,所以y≤10,据此可求得自变量x的取值范围;②中求得x的取值要与①中取公共解集;(2)能根据根的判别式判断一元二次方程解的情况是解决此问的关键.26.(1)m<12;(2)该反比例函数的解析式为y=6x;(3)y1<y2.【分析】(1)由图象在第一、三象限可得关于m的不等式,然后解不等式即可;(2)先根据平行四边形的性质求出D点的坐标,然后将D点的坐标代入y=12mx-可求得1-2m的值即可;(3)利用反比例函数的增减性解答即可.【详解】解:(1)∵y=12mx-的图象在第一、三象限,∴1﹣2m>0,∴m<12;(2)∵四边形ABOD为平行四边形,∴AD∥OB,AD=OB=2,∴D点坐标为(2,3),∴1﹣2m=2×3=6,∴该反比例函数的解析式为y=6x;(3)∵x1>x2>0,∴E,F两点都在第一象限,又∵该反比例函数在每一个象限内,函数值y都随x的增大而减小,∴y1<y2.【点睛】本题考查了反比例函数的解析式、反比例函数的性质以及反比例函数与几何的综合,掌握反比例函数的定义及性质是解答本题的关键.。
人教版九年级下册第二十六章《反比例函数》单元测试及答案【2】
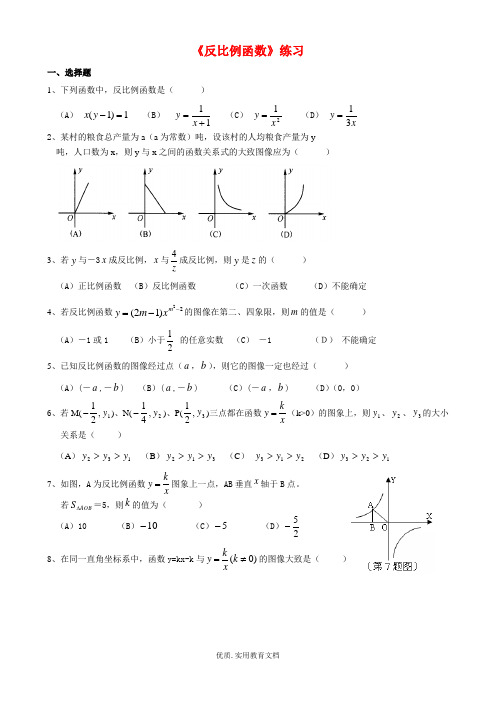
《反比例函数》练习一、选择题1、下列函数中,反比例函数是( ) (A ) 1)1(=-y x (B ) 11+=x y (C ) 21xy = (D ) x y 31= 2、某村的粮食总产量为a (a 为常数)吨,设该村的人均粮食产量为y 吨,人口数为x ,则y 与x 之间的函数关系式的大致图像应为( )3、若y 与-3x 成反比例,x 与z4成反比例,则y 是z 的( ) (A )正比例函数 (B )反比例函数 (C )一次函数 (D )不能确定 4、若反比例函数22)12(--=m x m y 的图像在第二、四象限,则m 的值是( )(A )-1或1 (B )小于21的任意实数 (C ) -1 (D) 不能确定 5、已知反比例函数的图像经过点(a ,b ),则它的图像一定也经过( ) (A )(-a ,-b ) (B )(a ,-b ) (C )(-a ,b ) (D )(0,0) 6、若M(12-,1y )、N(14-,2y )、P(12,3y )三点都在函数ky x=(k>0)的图象上,则1y 、2y 、3y 的大小关系是( )(A )132y y y >> (B )312y y y >> (C ) 213y y y >> (D )123y y y >> 7、如图,A 为反比例函数ky x=图象上一点,AB 垂直x 轴于B 点。
若AOB S ∆=5,则k 的值为( ) (A )10 (B )10-(C )5- (D )25-8、在同一直角坐标系中,函数y=kx-k 与(0)ky k x=≠的图像大致是( )9、如图是三个反比例函数312,,k k ky y y x x x===,在x 轴上方的图像,由此观察得到k l 、k 2、k 3的大小关系为( ) (A )k 1>k 2>k 3 (B )k 3>k 1>k 2 (C )k 2>k 3>k 1 (D )k 3>k 2>k 110、在同一直角坐标平面内,如果直线1y x k =与双曲线2k y x=没有交点,那么1k 和2k 的关系一定是( )(A) 1k 、2k 异号 (B) 1k 、2k 同号 (C) 1k >0, 2k <0 (D) 1k <0, 2k >0二、填空题 11、已知22)1(--=a xa y 是反比例函数,则a=____ .12、在函数13x -中自变量x 的取值范围是_________. 13、在反比例函数xk y 1+=的图象上有两点11()x y ,和22()x y ,,若120x x <<时,210y y >>,则k 的取值范围是 .14、已知圆柱的侧面积是π102cm ,若圆柱底面半径为r cm ,高为h cm ,则h 与r 的函数关系式是 。
18人教版九年级下《第26章反比例函数》单元测试卷94

人教版九年级下《第26章反比例函数》单元测试卷一、选择题1. 对于反比例函数y=2x,下列说法正确的是( )A.点(-2,1)在它的图象上 B.它的图象经过原点C.它的图象在第一、三象限 D.当x>0时,y随x的增大而增大2. 如图,正比例函数y=k1x与反比例函数y=的图象相交于A、B两点,若点A的坐标为(2,1),则点B的坐标是( )A.(1,2) B.(-2,1) C.(-1,-2) D.(-2,-1)3. 反比例函数y=ax(a>0,a为常数)和y=2x在第一象限内的图象如图所示,点M在y=ax的图象上,MC⊥x轴于点C,交y=2x的图象于点A;MD⊥y轴于点D,交y=2x的图象于点B,连接OA,OB.当点M在y=ax的图象上运动时,以下结论:①S△ODB=S△OCA;②四边形OAMB的面积不变;③当点A是MC的中点时,则点B是MD 的中点.其中正确的个数是( )A.0个 B.1个 C.2个 D.3个4. 如图,若点M是x轴正半轴上任意一点,过点M作PQ∥y轴,分别交函数y=k1x (x>0)和y=k2x(x>0)的图象于点P和Q,连接OP和OQ.则下列结论正确的是( )A.∠POQ不可能等于90° B.PM QM=k1k2C.这两个函数的图象一定关于x轴对称D.△POQ的面积是12(|k1|+|k2|)5. 若一次函数y=mx+6的图象与反比例函数y=nx在第一象限的图象有公共点,则有()A.mn≥﹣9 B.﹣9≤mn≤0 C.mn≥﹣4 D.﹣4≤mn≤06. 若点(x1,y1),(x2,y2)都是反比例函数y=-1x图象上的点,并且y1<0<y2,则下列结论中正确的是( )A.x1<x2 B.x2<x1C.y随x的增大而增大 D.两点有可能在同一象限7. 若是反比例函数,则m的取值为( )A.1 B.-1 C.±1 D.任意实数8. 如图,已知A,B是反比例函数y=(k>0,x>0)图象上的两点,BC∥x轴,交y轴于点C,动点P从坐标原点O出发,沿O→A→B→C(图中“→”所示路线)匀速运动,终点为C,过P作PM⊥x轴,垂足为M.设三角形OMP的面积为S,P点运动时间为t,则S关于x的函数图象大致为()A. B. C.D.9. 在平面直角坐标系中,直线y=-x+2与反比例函数y=1x的图象有唯一公共点,若直线y=-x+b与反比例函数y=1x的图象有2个公共点,则b的取值范围是( )A.b>2 B.-2<b<2 C.b>2或b<-2 D.b<-210. 已知点A(2,y1)、B(4,y2)都在反比例函数y=kx(k<0)的图象上,则y1、y2的大小关系为( )A.y1>y2 B.y1<y2C.y1=y2 D.无法确定二、填空题1. 如果点A(﹣2,y1),B(﹣1,y2),C(2,y3)都在反比例函数y=(k>0)的图象上,那么y1,y2,y3的大小关系是________(请用“<”表示出来)2. 如图,在平面直角坐标系xOy中,函数y=(x>0)的图象经过Rt△OAB的斜边OA的中点D,交AB于点C.若点B在x轴上,点A的坐标为(6,4),则△BOC的面积为__________.3. 若梯形的下底长为x,上底长为下底长的13,高为y,面积为60,则y与x的函数关系为___________.(不考虑x的取值范围)4. 如图,已知一次函数y=ax+b和反比例函数y=的图象相交于A(﹣2,y1)、B(1,y2)两点,则不等式ax+b<的解集为__________.5. 请写出一个图象在第二、四象限的反比例函数的解析式:________.6. 在第一象限内,点P(2,3),M(a,2)是双曲线kyx=(0k≠)上的两点,PA⊥x轴于点A,MB⊥x轴于点B,PA与OM交于点C,则△OAC的面积为___ _______.7. 如图,在反比例函数y=2x(x>0)的图象上,有点P1,P2,P3,P4,它们的横坐标依次为1,2,3,4.分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次为S1,S2,S3,则S1+S2+S3=___________.8. 如图,反比例函数y=的图象经过点(﹣1,-2),点A是该图象第一象限分支上的动点,连结AO并延长交另一分支于点B,以AB为斜边作等腰直角三角形ABC,顶点C在第四象限,AC与x轴交于点D,当=时,则点C的坐标为________.三、解答题1. 已知双曲线y=如图所示,点A(﹣1,m),B(n,2).求S△AOB.2. 已知反比例函数y1=的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,﹣2),(1)求这两个函数的关系式;(2)观察图象,写出使得y1>y2成立的自变量x的取值范围;(3)如果点C与点A关于x轴对称,求△ABC的面积.3. 如图,科技小组准备用材料围建一个面积为60m²的矩形科技园ABCD,其中一边AB靠墙,墙长为12m,设AD的长为xm,DC的长为ym.(1)求y与x之间的函数关系式;(2)若围成矩形科技园ABCD的三边材料总长不超过26m,材料AD和DC的长都是整米数,求出满足条件的所有围建方案.4. 如图,在正方形中,点在轴正半轴上,点的坐标为,反比例函数的图象经过点.求点的坐标;若点是反比例函数图象上的一点且;求点的坐标.5. 画出反比例函数y=6x的图象,并根据图象回答问题:(1)根据图象指出当y=-2时x的值;(2)根据图象指出当-2<x<1且x≠0时y的取值范围;(3)根据图象指出当-3<y<2且y≠0时x的取值范围.6. 如图,过点C(1,2)分别作x轴,y轴的平行线,交直线y=-x+6于点A,B,若反比例函数y=kx(x>0)的图象与△ABC有公共点,求k的取值范围.7. 阅读下列材料:实验数据显示,一般成人喝250毫升低度白酒后,其血液中酒精含量(毫克/百毫升)随时间的增加逐步增高达到峰值,之后血液中酒精含量随时间的增加逐渐降低.小明根据相关数据和学习函数的经验,对血液中酒精含量随时间变化的规律进行了探究,发现血液中酒精含量y是时间x的函数,其中y表示血液中酒精含量(毫克/百毫升),x表示饮酒后的时间(小时).下表记录了6小时内11个时间点血液中酒精含量y(毫克/百毫升)随饮酒后的时间x(小时)(x>0)的变化情况.下面是小明的探究过程,请补充完整:(1)如图,在平面直角坐标系xOy中,以上表中各对数值为坐标描点,图中已给出部分点,请你描出剩余的点,画出血液中酒精含量y随时间x变化的函数图象;(2)观察表中数据及图象可发现此函数图象在直线x=32两侧可以用不同的函数表达式表示,请你任选其中一部分写出表达式;(3)按国家规定,车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升时属于“酒后驾驶”,不能驾车上路.参照上述数学模型,假设某驾驶员晚上20:00在家喝完250毫升低度白酒,第二天早上6:30能否驾车去上班?请说明理由.8. 求反比例函数y=kx(k≠0)关于x轴对称的函数的解析式.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二十三章反比例函数单元测试卷
一、填空题:
2
1.反比例函数y =--的图像的两个分支在象
限,y随x的增大而o
2.已知反比例函数y=-(x> 0)的图像如图所示,则k=
k一I
3.已知反比例函数),=J 的图像的每一分支上,y都随x的
增大而减小,则k的取值范围是。
4.三角形的面积是12,它的底边a (单位:cm)与这个底边上的高h(单位:cm)的函
数关系是o
5.在同一坐标系中,反比例函数),= &与正比例函数y = k2x没有交点,则两个常数
象限,并且的乘积kik2的取伯.范围是。
6.宜线y=kx+b过第一、三、四象限,则函数y =—的图象在___
kx
在每个象限内y随x的增大而。
k
7.已知反比例函数y=-的图像上两点A (xi,yD、B (x2, y2),
x
若xi<0<x2, yi>y2,则k的取值范围是。
k
8.直线 > =心与双曲线y =-交于A、B两点。
过点A作AM±x轴
x
垂足为点M,连接BMo若S MBM=1,则k的值是。
9.如图所示是三个反比例函数y = n =的图象,V
XXX
由此观察k” k2, k3的大小关系是(用“V”连接)
二、选择题:
1.下列函数中,y是x的反比例函数的是()
D y = l-~
X
2. 如果反比例函数y=-的图像经过点(-3, -4),那么函数的图像应在( )
A 第一、三象限
B 第一、二象限
C 第二、四象限
D 第三、四象限 2 函数y = --的图象与x 轴的交点个数是( )
Ay = —
B )‘ = v
C y =—-—
2x
JC
X + 1
k
A 1个
B 2个
C
没有交点
D 不能确定
4. 当乂〈0时,,y =-的图像在(
)
A 第一象限
B 第二象限
C 第三象限
D 第四象限
5. 双曲线y =—与直线y = mx 相交于两点,其中一个交点坐
x
标为(・2, -1),则它的另一个交点坐标是( ) A (2, 1) B (-2, 1) C (・2,-l ) D (2,-l )
如图所示,P 是反比例函数的图像上一点,过点P 分别向x 轴、y 轴作垂线,所得
到的图形的阴影面积为6,则这个反比例函数的解析式为(
)
3
3
C y = —
D y =— x x
之间的函数关系的图象大致应为(
如图,在同一坐标系中,函数),=灯"1)与),,=4的图象只能是图中的( )
A”/ B
),M
)
9.已知反比例函数y = —(SO)的图像上有两点A (工],力),8(工2,力)其工^工2,则yi-y2
的值是()
A正数B负数C非正数D不能确定
三、解答题:
1.已知变量y与(x+1)成反比例,且当x=2时,y=—1,求y与x之间的函数关系。
2.某空调厂的装配车间计划组装9000台空调:
(1)从组装空调开始,每天组装的台数m (单位:台/天)与生产的时间t (单位:天)
之间有怎样的函数关系?
⑵原计划用2个月时间(每月以30天计算)完成,由于气温升高,厂家决定这批空
调提前十天上市,那么装配车间每天至少要比原来多组装多少台空调?
3.市政府计划建设一项水利工程,工程需要运送土石方总量为1.5X1()6立方米,某运
输公司承办了该项工程运送土石方的任务。
(1)匀速公司平均每天的工作量u (单位:立方米/)与完成运输任务所需时间t (单位:
天)之间具有怎样德函数关系?
(2)这个运输公司共有100辆卡车,每天一共可运送土石方IO"立方米,则公司运完
全部运输任务需要多长时间?
(3)当公司以问题⑵中的速度工作了80天后,由丁•工程进度的需要,剩下的所有
运输任务必须在50天内完成,公司至少需要再增加多少量卡车才能按时完成任务?
4.一次函数y=kx+b的图象与反比例函数y =竺的图像交于A、B两点,且已知点A
X
的横坐标与点B的纵坐标都是2,点C ( — 1,8)在反比例函数,y=-的图象上。
⑴求一次函数和反比例函数的解析式。
(2)求左AOB的面积。
5.如图所示,正方形OABC的面积为9,点0为坐标原点,点B在函数y=- (k>0,
X x>0)的图象上。
点P (m,n)是函数图象上任意一点,过点P分别作x轴、y轴的垂线,垂足分别为E、F,并设矩形OEPF和正方形OABC不重合部分的面积为S。
(提示考虑点P在点B的左侧或右侧两种情况)
(1)求点B的坐标和k值。
Q
(2)当S=—时,求点P的坐标。
(3)写出S关于m的函数关系式。
