薄膜渗透率的测定
细胞膜渗透率的测定

三、材料与仪器设备 1.材料 低温处理过的黄瓜、番茄。 去离子水。 2.仪器设备 DDS——11A型电导仪;751——型紫外分光 光度计;真空泵;真空干燥器;三用水浴; 打孔器;剪刀;洗瓶;试管;移液管;玻 棒;滤纸。
四、方法与步骤 1.清洗器具:由于电导仪变化非常灵敏,稍有杂质即产生很大误差。因 此所用玻璃器具均需先用热肥皂水洗,再用洗液洗涤,然后用自来水、 无离子水各冲四到五遍(最好是容器口朝下用水冲)。向洗净的试管 中加入去离子水,用电导仪测定电导值,检查试管是否确实冼净。 2.取样及处理:自购样品,设计不同贮藏条件,作为处理。用打孔器及 切片器将样品制成厚薄均匀,大小一致的组织圆片,精确称取2g(或 10个圆片),放入试管内,用去离子水冲洗三次,然后加入20mL去离 子水。对照和处理均设3~4个重复。 将试管放入真空干燥器内,开动真空泵抽气10min,压力控制在 0.04-0.06MPa,以抽出细胞间隙空气。缓慢放入空气,水即渗入细胞 间隙,组织圆片变成透明状,细胞内溶质易于渗出,取出试管,间隔 几分钟振荡一次,在室温下保持30min。 3.测定:将DDS——11A型电导仪电极插入试管,测定外渗液的电导值。 测定之后,将试管放入水浴锅沸水中5min 以杀死组织。待冷至室温后, 再次测定外渗液的电导值。
在电解质外渗透的同时细胞内可溶性有机物也随之渗出引起外渗液在电解质外渗透的同时细胞内可溶性有机物也随之渗出引起外渗液可溶性糖氨基酸核苷酸等含量增加氨基酸和核苷酸对紫外光有吸收可溶性糖氨基酸核苷酸等含量增加氨基酸和核苷酸对紫外光有吸收用紫外分光光度计测定受伤害组织外渗液消光值同样可反映出质膜受伤害用紫外分光光度计测定受伤害组织外渗液消光值同样可反映出质膜受伤害的程度
实验 细胞膜渗透率的测定 一.目的: 了解测定果蔬细胞膜渗透率的意义,果蔬 成熟衰老或受到外界环境影响是细胞膜渗透 率变化规律,掌握果蔬组织细胞膜渗透率的 测定原理和方法。
薄膜渗透率的测定
薄膜渗透率的测定摘要根据问题的要求,我们对题目进行恰当的分析,通过合理的假设,们建立微积分数学模型和数据拟合数学模型,求出不同关系量之间的关系。
对于问题,我们运用高等数学和高中物理和生物学的相关知识,同时也用MATLAB进行求解,得出A=0.00006985525148 B=-0.00002994067803 K=0.10117070586401 关键词:数据拟合,渗透率,质量守恒一、问题的重述某种医用薄膜有允许一种物质的分子穿透它,从高浓度的溶液向低浓度的溶液扩散的功能,在试制时,需要测定薄膜被这种分子穿透的能力。
测定方法如下:用面积S的薄膜将容器分成体积分别为V A,V B的两部分,在两部分中分别注满该物质的两种不同浓度的溶液。
此时该物质分子就会从高浓度溶液穿过薄膜向低浓度溶液中扩散。
通过单位面积膜分子扩散的速度与膜两侧溶液的浓度差成正比,比例系数K表示薄膜被该物质分子穿透的能力,称为渗透率。
的值。
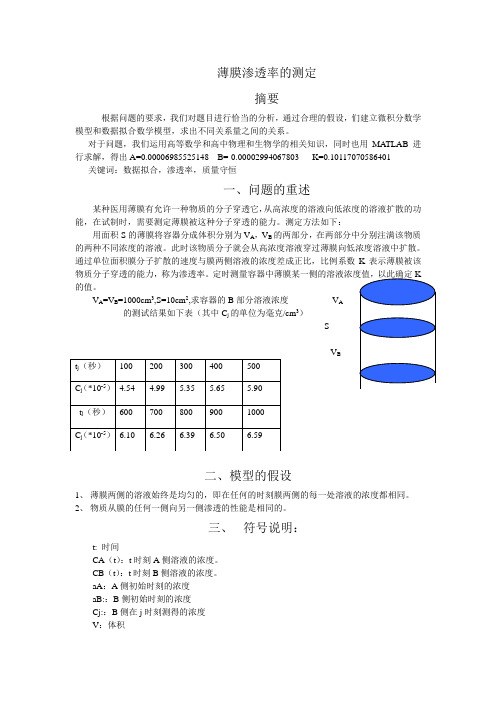
V A=V B=1000cm3,S=10cm2,求容器的B部分溶液浓度V A的测试结果如下表(其中C j的单位为毫克/cm3)SV B二、模型的假设1、薄膜两侧的溶液始终是均匀的,即在任何的时刻膜两侧的每一处溶液的浓度都相同。
2、物质从膜的任何一侧向另一侧渗透的性能是相同的。
三、符号说明:t: 时间CA(t):t时刻A侧溶液的浓度。
CB(t):t时刻B侧溶液的浓度。
aA:A侧初始时刻的浓度aB::B侧初始时刻的浓度Cj::B侧在j时刻测得的浓度V:体积SK:物质质量的增加四、问题的分析渗透率和浓度差是本文所要求的关系量,我们先用质量守恒建立溶质间的渗透关系,用微分方程,建立微分数学模型来求t时刻薄膜两侧的浓度,体积差。
最后通过数据拟合,得出K的值。
四、模型的建立与求解令时刻t,膜两侧溶液的浓度分别为CA(t)和CB(t), 初始时刻两侧的浓度分别为aA和aB,单位为mg/cm3. 又设B侧在tj时刻测得的浓度为cj(j=1,2,3……n).在A侧经△t 物质质量增加为:V ACA(t+△t)-V ACA(t)从B侧渗透到A侧的物质质量为:SK(CB-CA)△t.由质量守恒:V(CA(t+△t)-CA(t))=SK(CB-CA)△t两边同除V A△t得:dCA/dt=SK(CB-CA)/V A (1)在B侧,经△t 物质增加为:VBCB(t+△t)-VBCB(t)从A侧渗透到B侧的物质质量为:SK(CA-CB)△t由质量守恒定律得:VB(CB(t+△t)-CB(t))=SK(CA-CB)△tdCB/dt=SK(CA-CB)/VB (2)得到薄膜两侧溶液满足微分方程组的初值问题:dCA/dt=SK(CB-CA)/V A (1)dCB/dt=SK(CA-CB)/VB (2)CA(0)=Aa,CB(0)=aB又能有整个容器的溶液中含有该物质的质量不变,即成立V ACA(t)+VBCB(t)=常数=V AaA+VbaB (3)即:CA(t)=Aa+VB*Ab/V A-VB*CB(t)/V A (4)将(4)式代入(2 )式;根据积分中值定理:dCB/dt=SK(Aa+VB*Ab/V A-VB*CB(t)/VA -CB)/VB (5)dCB/dt=a-bCBCB(0)=aB其中a= SK(Aa/VB+Ab/V A)b=SK(1/V A+1/VB);解得:CB(t)=(aA V A+aBVB)/(V A+VB)+(V A(aB-aA)/(VA+VB))*e.^(-sk(1/VA+1/VB)*t 令A=(aA V A+aBVB)/(V A+VB)=0.2B=V A(aB-aA)/(V A+VB)=0.05CB(t)=A+B*E.^(-SK(1/V A+1/VB)*t将已知数据代入,通过数据拟合求参数k :s=10,V A==VB=1000A=0.00006985525148 B=-0.00002994067803 K=0.10117070586401附录:运用MATLAB:函数一:function f=curvefun1(x,tdata)f=x(1)+x(2)*exp(-0.02*x(3)*tdata) %其中x(1)=a;x(2)=b;x(3)=k;调用函数一:tdata=100:100:1000;cdata=1e-05*[4.54,4.99,5.35,5.65,5.90,6.10,6.26,6.39,6.50,6.59];x0=[0.2,0.05,0.05];x=curvefit('curvefun1',x0,tdata,cdata);f=curvefun1(x,tdata);x,fx =0.00006985525148 -0.00002994067803 0.10117070586401f =1.0e-004 *0.45399226319512 0.49879178593386 0.53538475333677 0.565274474956340.58968887810267 0.60963095346149 0.62591995988254 0.639225081110450.65009291714129 0.65896993960280。
膜渗透系数测定

膜渗透系数测定
膜渗透系数是指单位时间内经过单位面积膜的物质流量与膜上浓度差的比值,是评价
膜分离效果的重要参数之一,也是影响膜分离过程的关键性因素之一。
因此,测定膜的渗
透系数具有重要的意义。
测定膜渗透系数常常采用实验室装置进行,实验装置的结构一般由供液泵、膜组件和
回流管三部分组成。
实验过程中首先将待测液体通过膜组件,使其在膜的两侧形成不同的
浓度差;接着,泵送一定量的超纯水使回流管中形成压力差,促进液体的通过。
最后,测
量流量,并据此计算膜渗透系数。
不同的膜材质和膜结构间,膜渗透系数的值会有所不同。
在膜分离应用中,通常会选
择与分离物分子大小相仿的膜材质和膜结构,以达到最佳的分离效果。
同时,温度、pH值等外在因素也会影响膜的渗透性能。
常用的膜渗透系数测定方法包括两种:一种为浓度极限模型法,另一种为剖面模型法。
浓度极限模型法是采用初始浓度较高的液体,在连续流过膜的过程中,膜上浓度变化很小,而膜的另一侧的浓度极度降低。
根据初始浓度和时间与膜上浓度与时间之间的规律,确定
膜的渗透系数。
而剖面模型法则是在连续流过膜的过程中采用两个浓度较小的液体,通过
在时间和浓度的变化范围内进行采样分析,计算出膜的渗透系数。
总之,膜渗透系数是膜分离工艺中必不可少的指标之一,对其进行准确测定有助于了
解膜的性能、优化分离工艺、提高膜分离效率。
三种聚合物薄膜氦渗透率的测试

书山有路勤为径,学海无涯苦作舟
三种聚合物薄膜氦渗透率的测试
本文提出利用氦质谱检漏仪测量聚合物薄膜渗透性能的方法,即通过
聚对苯二甲酸乙二醇酯(PET)、聚二甲基硅氧烷(PDMS)、聚酰亚胺(P 由于气体分子的扩散性和材料的缺陷,气体渗透在聚合物薄膜中是一种
常见的现象。
近年来,聚合物薄膜广泛应用于食品包装、军事、发光显示等领域,因此对薄膜渗透率的测量越显重要。
在食物包装工业方面,包装新鲜食物
的塑料薄膜应具有高的渗透率;为保存油腻类食物,要求包装膜对氧气的渗透
率极小而对充氮包装用膜,则要求其它气体几乎不渗透;在发光显示方面,聚合物薄膜广泛应用于有机发光二极管(OLED);军事方面所用到的平流层飞艇,组成飞艇的聚合物材料对氦的渗透率必须达到一定的要求以保证飞艇良好的整
体漏率,从而确保飞艇良好的工作性能,因此本文进行薄膜对氦渗透率的研究
具有实践意义。
目前,气体累积法是国内外测试薄膜对气体渗透率的主要方法。
气体累
积法:测试初始阶段,薄膜两侧需要保持一定的真空度;测试时,测试气体充
满与薄膜一侧相连的腔体(高压室)并保持压强为1atm;测试气体通过薄膜渗透到另一侧,并利用真空计记录与薄膜另一侧相连腔体(被检室) 的压强随时间变化的规律。
Xue FengYao 等人便是利用此方法研究计算薄膜对气体渗透率的理论方法,
由于气体累积法测量时间较长,被检室内的本底漏率是影响结果的一个
重要因素,同时环境温度的波动也影响着结果的准确度。
因此真空技术网(chvacuum/)认为该测试方法要求实验在恒温室内进行,且需要单独测量被检室内的本底漏率,测量过程较复杂,测量时间长。
15光学薄膜透、反射率的常用测量方法

I Ix I y
偏振棱镜的测试方法
图〔a放置:
IIT
x s IyT
p
/I
T
I
(
I
TI
T
)
/I
xs
yp
图〔b放置:
T
(IT
IT
x P
y s)/I
Iy
Ix
T
T
T
T
T
(T
P
s)
P
s
I
对自然光透射率
1
1
T (T
T
TT)
P
s) (
按测试原理不同划分为:单色仪分光光度计和干涉型光谱测试系统;
➢单色仪型分光光度计原理
光源
照明光
学系统
单
单
色
仪
样品池
色
仪
传感器
处理
系统
• 光源:稳压电源、可见<钨丝灯或卤钨灯>、紫外<氙灯>、红外<卤钨
灯>;
• 照明系统:光束整形与会聚;
• 单色仪:由色散原件、狭缝机构以及色散原件的扫描驱动;光栅和棱镜
样品形状和尺寸的影响,一部分测量光没有
经过样品,需要选择合适的小孔光阑.
• 大气吸收对测量结果的影响,二氧化碳吸收
带水蒸气的吸收带回对测量结果带来较大
影响.
• 样品楔角对测量结果的影响,锲形的测试样
品会影响测量精度.
• 测试样品厚度对测试结果的影响,较厚的高
折射率基片会使光束在接受器光敏面的汇
分光光度计中影响测量的因素:
➢ 特点
需要2次测量,测量速度慢;
聚乙烯薄膜试验方法:熔融指数、摩擦系数、光泽度、光雾度、渗透性

聚乙烯薄膜试验方法:熔融指数、摩擦系数、光泽度、光雾度、渗透性PE(聚乙烯)膜具有防潮性,透湿性小。
聚乙烯薄膜(PE)根据制造方法与控制手段的不同,可制造出低密度、中密度、高密度的聚乙烯与交联聚乙烯等不同性能的产品。
检测橡塑材料检测实验室可聚乙烯薄膜试验服务。
作为第三方检测中心,机构拥有CMA、CNAS检测资质,检测设备齐全、数据科学可靠。
聚乙烯薄膜的五种试验方法(01)熔融指数熔融指数表明在十分钟内,在190°C的温度下和在0.3MPa(3公斤力/厘米2)的压力下有多少克的聚乙烯可从2.08毫米的模头里挤出。
此方法已被国际标准化组织ISO(R292一1963方法a)批准,并用它表示聚合物材料的熔体粘度。
此方法需要价格较高的设备,并且一般不由薄膜供应商测量熔融指数。
然而,有关各种聚乙烯材料的熔融指数,密度,摩擦力,强度性能和光学性能等完整资料,可从原料供应商那里得到。
(02)摩擦系数测量同一薄膜的两个表面之间的摩擦阻力所获得的数量就是摩擦系数。
做法是:使用一个可调整自身重量以适应滑动表面面积的滑动体,将其在薄膜的表面上拉过,并且用应变计测定滑动摩擦力。
把仪器调至零位,滑动体和薄膜要自由悬垂着,滑动摩擦力的zui大值就是一。
(03)光泽度光泽度是薄膜表面平滑度的一个量度。
把一片薄膜试样用胶条贴在标准测试装置的黑玻璃片上面,用同平面成45或60度角的光线照射薄膜。
然后测量出反射光线的强度,并以此强度和由未贴薄膜的玻璃片反射的光线强度相比较,求得光泽度值。
(04)光雾度薄膜光雾度一般用薄膜的光线散射能力来表示。
试验方法规定,试样厚度为0.038毫米,将试样固定好,以便使光线通过薄膜。
光雾度是与入射光束方向的偏差大于2.5度的透射光的强度和总的透射光强度的比率来测定的。
光雾度是薄膜混浊外观的一种量度。
(05)渗透性渗透性是气体在一定的气候条件下,能透过薄膜的一种量度。
试验方法的zui简单说明就是将气体或蒸气溶解于薄膜的一面,在浓度梯度的作用下透过薄膜在相反的一面上蒸发。
数学建模-薄膜分子穿透力

分子穿透能力的测定摘要通过对问题的分析,根据质量守恒,利用微分方程模型,得到了关于浓度低一侧浓度对时间的微分方程模型,通过求解参数和简化以后确定了浓度与时间的指数关系。
运用MATLAB编程进行拟合,求得参数,从而得到渗透率K。
最后,对拟合结果进行检验,检验结果见图5.2.1和图5.3.1。
关键字:渗透率MATLAB软件参数估计微分方程模型一、问题重述某种医用薄膜有允许一种物质的分子穿透它从高浓度的溶液向低浓度的溶液扩散的功能,在测试时需测定薄膜被这种分子穿透的能力。
测定方法如下:用面积10cm2的薄膜将分成体积分别为100cm3和100cm3的两部分,在两部分中分别注满该物质的两种不同浓度的溶液。
此时该物质分子就会从高浓度溶液穿过薄膜向低浓度溶液中扩散。
通过单位面积膜分子扩散的速度与膜两侧溶液的浓度差成正比,比例系数K表征了薄膜被该物质分子穿透的能力,称为渗透率。
定时测量容器中薄膜某一侧的溶液浓度值,以此确定K的数值。
对容器一侧溶液浓度的测试结果如下:试建立一个较好的数学模型并给出相应的算法和程序。
二、问题分析用单位体积溶液中所含的溶质质量数来表示的浓度叫质量-体积浓度,题中给出的浓度为质量-体积浓度。
通过薄膜单位面积分子扩散速度与膜两侧溶液浓度差成正比例,比例系数K被称为渗透率,它表征了薄膜被分子穿透的能力。
要确定渗透率,需要建立通过薄膜单位面积分子扩散速与薄膜两侧浓度差的关系模型。
在本题中我们可以根据质量守恒来进行求解,考察时段[]t,薄膜两侧容+t t∆器中该物质质量的变化,可以用两种形式表示出来,薄膜的一侧在时段[]t+,内t t∆物质质量的增加,以及根据渗透率K表示的一侧渗透至另一侧的物质的质量,两者相等可得到等式(1)。
其次,整个容器的溶液中含有该物质的质量不变,与初始时刻该物质的含量相同,也是质量守恒,可得到等式(2),即联立两个等式,可以得到浓度与时间的表达式,代入数据,对等式的系数进行求解。
凝胶类薄膜气体渗透性能的测试方法介绍

摘要:气体渗透性能是影响凝胶类薄膜使用性能的重要指标参数。
本文通过对凝胶膜氧气透过量的测试及对试验过程、试验原理、设备参数及适用范围等内容的描述,介绍了如何利用压差法测试凝胶类薄膜的气体渗透性能,为凝胶膜使用性能的监控提供参考。
关键词:气体渗透性能、氧气透过量、气体渗透仪、压差法、凝胶膜1、意义凝胶膜是一种具有广泛应用的高分子材料,在气体分离、生物科技、医疗、电子、汽车等行业均有应用,适宜的透气性及选择渗透性能是凝胶膜得到如此广泛应用的重要条件之一。
如用于气体分离的凝胶膜应具有高选择性与高渗透性;用于微生物载体的凝胶膜应在保证不泄漏微生物的基础上,能够提供保持微生物正常活性所需的氧气;在疤痕治疗应用中,通过凝胶膜降低微血管及胶原纤维水蒸气的蒸发及氧气供应,减少疤痕的再生。
因此,通过对凝胶膜相应气体透过量的检测,及时了解凝胶膜的气体渗透性能,可为凝胶膜使用性能的控制与改善提供有效的数据依据。
本文以凝胶膜氧气透过量的测试过程为例,介绍该类材料气体渗透性能的检测方法。
2、试验样品本次试验测试了某种凝胶膜材料的氧气渗透性能。
3、试验依据材料氧气透过量的测试方法主要分为压差法与等压法两种原理,鉴于压差法可测试气体种类较多,如氧气、氮气、二氧化碳、空气等,本次试验采用压差法原理测试凝胶膜样品的氧气透过量,依据的标准为GB/T 1038-2000 《塑料薄膜和薄片气体透过性试验方法压差法》。
4、试验设备本次试验利用VAC-V2压差法气体渗透仪对样品进行测试,该设备由济南兰光机电技术有限公司自主研发生产。
图1 VAC-V2压差法气体渗透仪4.1 试验原理压差法是根据渗透气体压力随渗透时间的变化情况得到试样的气体透过量。
装夹的试样将设备的测试腔分为高压腔与低压腔,高压腔内充填的是一定压力的待测试气体,低压腔内通过抽真空形成低压环境。
试验时,气体在压力差的作用下由高压腔通过试样渗透到低压腔,低压腔内压力逐渐增加,当气体在试样两侧的渗透达到稳定状态时,低压腔内压力的增加量与渗透时间呈线性关系,通过测量此时单位时间内低压腔内压力的变化值计算试样的气体透过量。
光学薄膜透反射率的常用测量方法

光学薄膜透反射率的常用测量方法
1.透射法
透射法是一种常见的测量光学薄膜透反射率的方法。
它利用透射光的强度对薄膜进行测量。
首先,将薄膜样品放置于光源前方,透过光源照射到样品上,然后测量透射光的强度。
通过与样品前后的基板透射光强度进行比较,就可以得到薄膜透射率的信息。
2.反射法
反射法是另一种常用的测量光学薄膜透反射率的方法。
它利用薄膜反射光的强度进行测量。
首先,将薄膜样品放置在光源前方,让光照射到样品上,然后测量反射光的强度。
通过与空气或基板的反射光进行比较,就可以得到薄膜透射率的信息。
3.光谱透射法
光谱透射法是测量光学薄膜透反射率的一种精确方法。
它利用的是薄膜样品的透射光谱特征。
首先,将薄膜样品置于光源前方,然后使用光谱仪测量透射光的光谱特征。
通过分析透射光的波长和强度信息,就可以得到薄膜的透反射特性。
4.激光参比法
激光参比法是测量光学薄膜透反射率的一种高精度测量方法。
它利用激光器作为参比光源。
首先,将激光光束通过参比光路照射到参比探测器上,同时将激光光束通过薄膜样品照射到样品探测器上。
通过比较参比探测器和样品探测器接收到的光信号,就可以得到薄膜的透反射率。
除了以上四种常用的测量方法外,还存在其他一些用于测量光学薄膜透反射率的方法,例如自脉冲法、透微量测量法等。
每种方法都有其适用的场合和特点,根据具体的需求选择合适的测量方法是至关重要的。
总的来说,测量光学薄膜透反射率的常用方法有透射法、反射法、光谱透射法、激光参比法等。
第6章_医用薄膜渗透率的

f=x(1)+x(2)*exp(-0.02*x(3)*tdata);
其中x(1)=a x(2)=b x(3)=K
15
6.4 用曲线拟合方法确定医用薄膜渗透率
2)编写程序(nihe2.m)
tdata=linspace(100,1000,10); cdata=[4.54,4.99,5.35,5.65,5.9,6.1,6.26,6.39,6.5,6.59]*10^ (-3); x0=[0.2,0.05,0.05]; [x,resnorm,residual]=lsqcurvefit('nongdu',x0,tdata,cdata) t=linspace(100,1000,100); c=nongdu(x,t); plot(tdata,cdata,'o',t,c) c1=nongdu(x,tdata); e=c1-cdata; e1=sum(e.*e) 输出结果: x =0.0063 -0.0034 0.2542 e1=3.5604e-007 16
输出结果: a=0.0886 -1.9701 50.0594 拟合的多项式为 d=0.0886v2-1.9701v+50.0594
21
6.4 用曲线拟合方法确定医用薄膜渗透率
拟合数据与实测数据比较
22
6.4 用曲线拟合方法确定医用薄膜渗透率
模型二 通过观测散点图,还可以假设刹车距离d与v刹车速度之 间的函数关系为 d a1 v a0 ,下面为编写求未知参数 的a1、a0的matlab程序 v=[20 25 30 35 40 45 50 55 60 65 70 75 80]; d=[42 56 73.5 91.5 116 142.5 173 209.5 248 292.5 343 401 464]; v=sqrt(v); a=polyfit(v,d,1) dl=polyval(a,v); plot(v,d,'ro',v,dl,'b.'); box off 输出结果:a=91.4428 -430.1865
《医用薄膜渗透率的》课件

通过优化生产工艺,降低生产过程中可能引入的不稳定因素,提 高医用薄膜渗透率的重复性和可靠性。
质量控制
建立严格的质量控制体系,对医用薄膜进行全面的性能检测和质量 控制,确保产品质量的稳定可靠。
长期性能监测
对医用薄膜进行长期性能监测和研究,了解其在不同条件下的性能 变化,为临床应用提供可靠依据。
2023
REPORTING
《医用薄膜渗透率的 》ppt课件
2023
目录
• 医用薄膜渗透率的概述 • 医用薄膜渗透率的测试方法 • 医用薄膜渗透率的性能影响因素 • 医用薄膜渗透率的实际应用案例 • 医用薄膜渗透率的未来发展趋势与挑战
2023
PART 01
医用薄膜渗透率的概述
REPORTING
医用薄膜的定义与特性
感谢观看
医用薄膜渗透率的法规与标准制定
国际标准
积极参与国际标准的制定和修订,推动医用薄膜 渗透率的标准化和规范化。
国内标准
根据国内市场需求和技术发展状况,制定符合国 情的医用薄膜渗透率相关标准。
法规监管
加强医用薄膜渗透率的法规监管,规范市场秩序 ,保障产品质量和安全。
2023
REPORTING
THANKS
环境因素对医用薄膜渗透率的影响
温度
光照
温度会影响材料的热膨胀和分子运动 ,进而影响其渗透率。
紫外线照射会使一些材料发生光氧化 ,导致性能下降。
湿度
湿度会影响材料的吸湿性能,从而影 响其阻水性和透气性。
2023
PART 04
医用薄膜渗透率的实际应 用案例
REPORTING
医用薄膜在医疗器械中的应用
医用薄膜在生物医学工程中也有广泛的应用,如组织工程、再生医学和细胞培养 等。这些应用需要使用医用薄膜作为细胞培养基质、组织工程支架或再生医学材 料等。
薄膜渗透率

tdata = linspace(100,1000,10); cdata = 1e-05.*[454 499 535 565 590... 610 626 639 650 659]; [d,ifail]=e01bef(tdata,cdata); [cj,dcj]=e01bgf(tdata,cdata,d,tdata);
SK (
1 1 )t VA VB
将 VA VB 1000cm 3 , S 10cm 2 代入上式有:
CB( t ) a be 0.02Kt
用函数CB(t)来拟合所给的实验数据, 从而估计出其中的参数a,b,K。
用MATLAB软件进行计算. 1)编写函数M-文件 nongdu.m function f = nongdu(x,tdata) f = x(1)+x(2)*exp(-0.02*x(3)*tdata); 其中 x(1) = a;x(2) = b;x(3) = k; 2) 在工作空间中执行以下命令(test1.m) tdata = linspace(100,1000,10); cdata =[4.54 4.99 5.35 5.65 5.90 6.10 ... 6.26 6.39 6.50 6.59]; x0 = [0.2,0.05,0.05]; x = curvefit(‘nongdu’,x0,tdata,cdata) 3) 输出结果: x = 0.007 -0.003 0.1012 即 k = 0.1012, a = 0.007, b = -0.003,
dt
%作函数拟合
x0=[0.2,0.1]; x=curvefit('baomof',x0,cdata,dcj') 3) 输出结果: x = 0.1009 0.014 即 k = 0.1009, h = 0.014 五、结果及误差分析 几种方法得出的结果及相应的误差总结于 下表,误差为计算数据与实验数据之差的平方 和。
利用调幅红外传感器对水蒸气透过塑料薄膜和薄板渗透率的标准测试方法

利⽤调幅红外传感器对⽔蒸⽓透过塑料薄膜和薄板渗透率的标准测试⽅法利⽤调幅红外传感器对⽔蒸⽓透过塑料薄膜和薄板渗透率的标准测试⽅法1. 范围该测试⽅法涵盖了⽔蒸⽓通过柔韧的屏障性材料的透过率测定步骤。
该⽅法适⽤于3毫⽶(0.1英⼨)以下的⽚材和薄膜,包含单层或多层合成的天然聚合物或⾦属箔,涂层材料。
它提供了(1)⽔蒸⽓透过速率(WVTR )的决定因素,(2)薄膜的⽔蒸⽓透过速率,(3)均质材料中,⽔蒸⽓的透过系数。
2. 试验⽅法综述⼀个⽤阻隔材料与已知温度和湿度的湿室分开的⼲燥室将被⽤来测试。
待测试薄膜被密封在⼲燥室和湿室构成的扩散单元⾥。
⽔蒸⽓在⼲燥室内扩散混合着⽓体通过薄膜,并被传输到压⼒调制红外传感器。
这种传感器测量被⽔蒸⽓吸收的⼀⼩部分红外能量,并产⽣⼀个电⼦信号,信号强度跟⽔蒸⽓浓度成正⽐。
将测试薄膜与⼀个已知⽔蒸⽓渗透速率的校准薄膜所产⽣的电⼦信号强度相⽐,然后使⽤这些信息来计算⽔蒸⽓透过被测材料的速率。
3. 仪器本⽅法采⽤⽔蒸⽓传输设备(图1)包括以下内容:图1 测量系统流量计测量空⽓流量调节阀清除红外探测放⼤器红外光源⾦属波纹管泵四通空⽓流量电磁阀⼲燥剂旁通长图记录仪试验箱测试单元阀插⼊3.1 扩散单元——由两种⾦属组成的装置,放⼊试样关闭后,将准确地定义⼀个圆形区域。
⼀般可接受的扩散单元⾯积为50 cm2。
由每个半单元封闭的体积,当夹紧时,不是很关键;它应该⾜够⼩允许进⾏快速的⽓体交换,但不能太⼩,否则⼀个不受⽀持的薄膜发⽣凹陷或弯曲将接触单元的顶部或底部。
已发现约6毫⽶(0.250英⼨)的深度适合50平⽅厘⽶的单元。
3.1.1 O形圈扩散单元——⼀个适当⼤⼩的槽被加⼯成扩散单元潮湿室⼀侧保留了氯丁橡胶的O形圈。
测试区被认为是当扩散单元被夹紧关闭时试样与压缩O形圈内径接触形成的区域。
3.1.2 扩散单元表⾯密封——平坦的边缘围绕着扩散单元⼲燥侧。
这是⼀个关键的表⾯密封,当试样被按下时,它应是光滑,⽆径向划痕的。
《医用薄膜渗透率的》课件

薄膜材料的可持续性
研发环保、可回收的薄膜材料,减少对环境的负面影响,是医用薄膜产业未来的一个重要发展方向。
医用薄膜的市场需求
随着医疗技术的进步和人们对保健意识的提高,医用薄膜的市场需求将会持续增长。
《医用薄膜渗透率的》 PPT课件
了解医用薄膜的渗透率是非常重要的。本课件将介绍医用薄膜的定义、分类、 应用领域以及渗透率的测定方法和影响因素等内容。让我们一起来探索医用 薄膜的奥秘吧!
什么是医用薄膜?
医用薄膜是一种被广泛应用于医学领域的薄膜材料,具有特殊的渗透性能和 生物相容性。
医用薄膜的分类
可吸收薄膜
渗透率的测定方法
蒸发法测定
通过测量物质在薄膜上的蒸发速率来间接推断 渗透率。
液体扩散法测定
将待测物质溶解在液体中,通过测量溶液在薄 膜上的扩散速率来直接测定渗透率。
渗透率的影响因素
1 薄膜厚度
厚度越小,渗透率越大。
3 温度和湿度
温度和湿度对渗透率有显著影响。
2 材料性质
不同材料的渗透率差异很大。
医用薄膜的商业前景
医用薄膜作为一个高附加值的产品,将有着广阔的商业前景和经济效益。
医用薄膜的更广泛应用
除了现有的医疗领域,医用薄膜还有着许多可以开拓的更广泛的应用领域, 如食品包装、能源等。
渗透率的了解和测定在医学、药学、材料科学等领域具有广泛的实际应用价值。
医用薄膜的生产过程
医用薄膜的生产过程包括颗粒制备、薄膜成型、后处理等多个环节,确保薄膜的质量和性能。
薄膜渗透率的质量控制
通过严格的质量控制流程,确保每批医用薄膜的渗透率符合要求,并保证产 品的一致性和可靠性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
薄膜渗透率的测定
摘要
根据问题的要求,我们对题目进行恰当的分析,通过合理的假设,们建立微积分数学模型和数据拟合数学模型,求出不同关系量之间的关系。
对于问题,我们运用高等数学和高中物理和生物学的相关知识,同时也用MATLAB进行求解,得出A=0.00006985525148 B=-0.00002994067803 K=0.10117070586401 关键词:数据拟合,渗透率,质量守恒
一、问题的重述
某种医用薄膜有允许一种物质的分子穿透它,从高浓度的溶液向低浓度的溶液扩散的功能,在试制时,需要测定薄膜被这种分子穿透的能力。
测定方法如下:
用面积S的薄膜将容器分成体积分别为V A,V B的两部分,在两部分中分别注满该物质的两种不同浓度的溶液。
此时该物质分子就会从高浓度溶液穿过薄膜向低浓度溶液中扩散。
通过单位面积膜分子扩散的速度与膜两侧溶液的浓度差成正比,比例系数K表示薄膜被该
物质分子穿透的能力,称为渗透率。
的值。
V A=V B=1000cm3,S=10cm2,求容器的B部分溶液浓度V A
的测试结果如下表(其中C j的单位为毫克/cm3)
S
V B
二、模型的假设
1、薄膜两侧的溶液始终是均匀的,即在任何的时刻膜两侧的每一处溶液的浓度都相同。
2、物质从膜的任何一侧向另一侧渗透的性能是相同的。
三、符号说明:
t: 时间
CA(t):t时刻A侧溶液的浓度。
CB(t):t时刻B侧溶液的浓度。
aA:A侧初始时刻的浓度
aB::B侧初始时刻的浓度
Cj::B侧在j时刻测得的浓度
V:体积
SK:物质质量的增加
四、问题的分析
渗透率和浓度差是本文所要求的关系量,我们先用质量守恒建立溶质间的渗透关系,用微分方程,建立微分数学模型来求t时刻薄膜两侧的浓度,体积差。
最后通过数据拟合,得出K的值。
四、模型的建立与求解
令时刻t,膜两侧溶液的浓度分别为CA(t)和CB(t), 初始时刻两侧的浓度分别为aA和aB,单位为mg/cm3. 又设B侧在tj时刻测得的浓度为cj(j=1,2,3……n).
在A侧经△t 物质质量增加为:V ACA(t+△t)-V ACA(t)
从B侧渗透到A侧的物质质量为:SK(CB-CA)△t.
由质量守恒:
V(CA(t+△t)-CA(t))=SK(CB-CA)△t
两边同除V A△t得:
dCA/dt=SK(CB-CA)/V A (1)
在B侧,经△t 物质增加为:
VBCB(t+△t)-VBCB(t)
从A侧渗透到B侧的物质质量为:
SK(CA-CB)△t
由质量守恒定律得:
VB(CB(t+△t)-CB(t))=SK(CA-CB)△t
dCB/dt=SK(CA-CB)/VB (2)
得到薄膜两侧溶液满足微分方程组的初值问题:
dCA/dt=SK(CB-CA)/V A (1)
dCB/dt=SK(CA-CB)/VB (2)
CA(0)=Aa,CB(0)=aB
又能有整个容器的溶液中含有该物质的质量不变,即成立
V ACA(t)+VBCB(t)=常数=V AaA+VbaB (3)
即:CA(t)=Aa+VB*Ab/V A-VB*CB(t)/V A (4)
将(4)式代入(2 )式;根据积分中值定理:
dCB/dt=SK(Aa+VB*Ab/V A-VB*CB(t)/VA -CB)/VB (5)
dCB/dt=a-bCB
CB(0)=aB
其中a= SK(Aa/VB+Ab/V A)
b=SK(1/V A+1/VB);
解得:
CB(t)=(aA V A+aBVB)/(V A+VB)+(V A(aB-aA)/(VA+VB))*e.^(-sk(1/VA+1/VB)*t 令
A=(aA V A+aBVB)/(V A+VB)=0.2
B=V A(aB-aA)/(V A+VB)=0.05
CB(t)=A+B*E.^(-SK(1/V A+1/VB)*t
将已知数据代入,通过数据拟合求参数k :
s=10,V A==VB=1000
A=0.00006985525148 B=-0.00002994067803 K=0.10117070586401
附录:
运用MATLAB:
函数一:function f=curvefun1(x,tdata)
f=x(1)+x(2)*exp(-0.02*x(3)*tdata) %其中x(1)=a;x(2)=b;x(3)=k;
调用函数一:
tdata=100:100:1000;
cdata=1e-05*[4.54,4.99,5.35,5.65,5.90,6.10,6.26,6.39,6.50,6.59];
x0=[0.2,0.05,0.05];
x=curvefit('curvefun1',x0,tdata,cdata);
f=curvefun1(x,tdata);
x,f
x =
0.00006985525148 -0.00002994067803 0.10117070586401
f =1.0e-004 *
0.45399226319512 0.49879178593386 0.53538475333677 0.56527447495634
0.58968887810267 0.60963095346149 0.62591995988254 0.63922508111045
0.65009291714129 0.65896993960280。
