八年级数学平行四边形、矩形、菱形、正方形知识点总结
1.3平行四边形,矩形,菱形,正方形的性质和判定
第三节 平行四边形,矩形,菱形,正方形的性质和判定(一)平行四边形的性质和判定 一.教学重难点:重点：平行四边形的性质证明． 难点：分析、综合思考的方法．二.知识点和考点:1.平行四边形的定义2.平行四边形的性质,面积3.平行四边形的判定4.三角形的中位线及其性质三.知识点讲解考点一: 平行四边形的定义考点二:平行四边形的性质(1)平行四边形的对边相等注：在证明题时使用格式是：∵四边形ABCD 是平行四边形，定义:有两组对边分别平行的四边形叫做平行四边形。
记做例1：如图：在中，如果E F ∥AD ，GH ∥CD ，EF 与GH 相交于点O ，那么图中的平行四边形一共有 （ ） A ．4个 B 、5个 C 、8个 D 、9个例2:如图，E 、F 分别是边AD 、BC 上的点，并且AF ∥CE ，求证：∠AFB=∠DEC 。
∴AB=DC，AD=BC例1、如图，在平行四边形ABCD中，AE=CF，求证：AF=CE。
例2.平行四边形的周长等于56cm，两邻边长的比为3：1，那么这个平行四边形较长的边长为(2).平行四边形的对角相等注：在证明题时使用格式是：∵四边形ABCD是平行四边形∴∠A=∠C，∠B=∠D例1.已知中，E、F是对角线AC上的两点，且AE=CF。
求证：∠ADF=∠CBE。
例2、在中，∠A、∠B的度数之比为5：4，则∠C等于（）A、 B、 C、 D、(3)、平行四边形的对角线互相平分注：在证明题时使用格式是：∵四边形ABCD是平行四边形∴OA=OC，OB=OD例3.如图，，过其对角线交点O，引一直线交BC于E，交AD于F，若AB=2.4cm，BC=4cm，OE=1.1cm，求四边形ABEF的周长。
例4.如图，已知：中，AC、BD相交于O点，OE⊥AD于E，OF⊥BC于F，求证：OE=OF。
例5.如图，如果的周长之差为8，而AB:AD=3:2，那么的周长为多少？例6.如图，已知的周长为60cm，对角线AC、BD相交于点O，的周长长8cm，求这个四边形各边长.(4)平行四边形的面积如图（1），，也就是边长×高=ah(2）、同底（等底）同高（等高）的平行四边形面积相等。
初中数学知识点归纳总结(全)
初中数学知识点1、一元一次方程根的情况△=b2-4ac当△〉0时，一元二次方程有2个不相等的实数根；当△=0时,一元二次方程有2个相同的实数根；当△〈0时，一元二次方程没有实数根2、平行四边形的性质:①两组对边分别平行的四边形叫做平行四边形。
②平行四边形不相邻的两个顶点连成的线段叫他的对角线.③平行四边形的对边/对角相等。
④平行四边形的对角线互相平分。
菱形：①一组邻边相等的平行四边形是菱形②领心的四条边相等，两条对角线互相垂直平分，每一组对角线平分一组对角。
③判定条件:定义/对角线互相垂直的平行四边形/四条边都相等的四边形.矩形与正方形：①有一个内角是直角的平行四边形叫做矩形.②矩形的对角线相等,四个角都是直角。
③对角线相等的平行四边形是矩形.④正方形具有平行四边形，矩形，菱形的一切性质.⑤一组邻边相等的矩形是正方形。
多边形：①N边形的内角和等于(N—2）180度②多边心内角的一边与另一边的反向延长线所组成的角叫做这个多边形的外角，在每个顶点处取这个多边形的一个外角,他们的和叫做这个多边形的内角和(都等于360度）平均数：对于N个数X1,X2…X N，我们把（X1+X2+…+X N）/N叫做这个N个数的算术平均数，记为X加权平均数:一组数据里各个数据的重要程度未必相同，因而，在计算这组数据的平均数时往往给每个数据加一个权,这就是加权平均数。
二、基本定理1、过两点有且只有一条直线2、两点之间线段最短3、同角或等角的补角相等4、同角或等角的余角相等5、过一点有且只有一条直线和已知直线垂直6、直线外一点与直线上各点连接的所有线段中，垂线段最短7、平行公理经过直线外一点，有且只有一条直线与这条直线平行8、如果两条直线都和第三条直线平行,这两条直线也互相平行9、同位角相等，两直线平行10、内错角相等，两直线平行11、同旁内角互补，两直线平行12、两直线平行，同位角相等13、两直线平行,内错角相等14、两直线平行,同旁内角互补15、定理三角形两边的和大于第三边16、推论三角形两边的差小于第三边17、三角形内角和定理三角形三个内角的和等于180°18、推论1 直角三角形的两个锐角互余19、推论2 三角形的一个外角等于和它不相邻的两个内角的和20、推论3 三角形的一个外角大于任何一个和它不相邻的内角21、全等三角形的对应边、对应角相等22、边角边公理(SAS）有两边和它们的夹角对应相等的两个三角形全等23、角边角公理（ASA）有两角和它们的夹边对应相等的两个三角形全等24、推论(AAS）有两角和其中一角的对边对应相等的两个三角形全等25、边边边公理(SSS）有三边对应相等的两个三角形全等26、斜边、直角边公理（HL）有斜边和一条直角边对应相等的两个直角三角形全等27、定理1 在角的平分线上的点到这个角的两边的距离相等28、定理2 到一个角的两边的距离相同的点,在这个角的平分线上29、角的平分线是到角的两边距离相等的所有点的集合30、等腰三角形的性质定理等腰三角形的两个底角相等（即等边对等角）31、推论1 等腰三角形顶角的平分线平分底边并且垂直于底边32、等腰三角形的顶角平分线、底边上的中线和底边上的高互相重合33、推论3 等边三角形的各角都相等，并且每一个角都等于60°34、等腰三角形的判定定理如果一个三角形有两个角相等，那么这两个角所对的边也相等（等角对等边）35、推论1 三个角都相等的三角形是等边三角形36、推论2 有一个角等于60°的等腰三角形是等边三角形37、在直角三角形中，如果一个锐角等于30°那么它所对的直角边等于斜边的一半38、直角三角形斜边上的中线等于斜边上的一半39、定理线段垂直平分线上的点和这条线段两个端点的距离相等40、逆定理和一条线段两个端点距离相等的点,在这条线段的垂直平分线上41、线段的垂直平分线可看作和线段两端点距离相等的所有点的集合42、定理1 关于某条直线对称的两个图形是全等形43、定理2 如果两个图形关于某直线对称，那么对称轴是对应点连线的垂直平分线44、定理3 两个图形关于某直线对称,如果它们的对应线段或延长线相交,那么交点在对称轴上45、逆定理如果两个图形的对应点连线被同一条直线垂直平分，那么这两个图形关于这条直线对称46、勾股定理直角三角形两直角边a、b的平方和、等于斜边c的平方，即a2+b2=c247、勾股定理的逆定理如果三角形的三边长a、b、c有关系a2+b2=c2,那么这个三角形是直角三角形48、定理四边形的内角和等于360°49、四边形的外角和等于360°50、多边形内角和定理n边形的内角的和等于(n-2）×180°51、推论任意多边的外角和等于360°52、平行四边形性质定理1 平行四边形的对角相等53、平行四边形性质定理2 平行四边形的对边相等54、推论夹在两条平行线间的平行线段相等55、平行四边形性质定理3 平行四边形的对角线互相平分56、平行四边形判定定理1 两组对角分别相等的四边形是平行四边形57、平行四边形判定定理2 两组对边分别相等的四边形是平行四边形58、平行四边形判定定理3 对角线互相平分的四边形是平行四边形59、平行四边形判定定理4 一组对边平行相等的四边形是平行四边形60、矩形性质定理1 矩形的四个角都是直角61、矩形性质定理2 矩形的对角线相等62、矩形判定定理1 有三个角是直角的四边形是矩形63、矩形判定定理2 对角线相等的平行四边形是矩形64、菱形性质定理1 菱形的四条边都相等65、菱形性质定理2 菱形的对角线互相垂直，并且每一条对角线平分一组对角66、菱形面积=对角线乘积的一半,即S=（a×b）÷267、菱形判定定理1 四边都相等的四边形是菱形68、菱形判定定理2 对角线互相垂直的平行四边形是菱形69、正方形性质定理1 正方形的四个角都是直角，四条边都相等70、正方形性质定理2正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角71、定理1 关于中心对称的两个图形是全等的72、定理2 关于中心对称的两个图形,对称点连线都经过对称中心,并且被对称中心平分73、逆定理如果两个图形的对应点连线都经过某一点，并且被这一点平分，那么这两个图形关于这一点对称74、等腰梯形性质定理等腰梯形在同一底上的两个角相等75、等腰梯形的两条对角线相等76、等腰梯形判定定理在同一底上的两个角相等的梯形是等腰梯形77、对角线相等的梯形是等腰梯形78、平行线等分线段定理如果一组平行线在一条直线上截得的线段相等，那么在其他直线上截得的线段也相等79、推论1 经过梯形一腰的中点与底平行的直线，必平分另一腰80、推论2 经过三角形一边的中点与另一边平行的直线，必平分第三边81、三角形中位线定理三角形的中位线平行于第三边，并且等于它的一半82、梯形中位线定理梯形的中位线平行于两底,并且等于两底和的一半L=（a+b）÷2 S=L×h83、(1)比例的基本性质：如果a：b=c：d，那么ad=bc如果ad=bc ,那么a:b=c：d84、（2)合比性质:如果a／b=c／d,那么（a±b）／b=(c±d）／d85、（3)等比性质:如果a／b=c／d=…=m／n(b+d+…+n≠0)，那么（a+c+…+m）／(b+d+…+n）=a／b86、平行线分线段成比例定理三条平行线截两条直线,所得的对应线段成比例87、推论平行于三角形一边的直线截其他两边(或两边的延长线)，所得的对应线段成比例88、定理如果一条直线截三角形的两边(或两边的延长线）所得的对应线段成比例，那么这条直线平行于三角形的第三边89、平行于三角形的一边,并且和其他两边相交的直线，所截得的三角形的三边与原三角形三边对应成比例90、定理平行于三角形一边的直线和其他两边（或两边的延长线）相交，所构成的三角形与原三角形相似91、相似三角形判定定理1 两角对应相等，两三角形相似(ASA)92、直角三角形被斜边上的高分成的两个直角三角形和原三角形相似93、判定定理2 两边对应成比例且夹角相等，两三角形相似（SAS)94、判定定理3 三边对应成比例，两三角形相似（SSS)95、定理如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例，那么这两个直角三角形相似96、性质定理1 相似三角形对应高的比，对应中线的比与对应角平分线的比都等于相似比97、性质定理2 相似三角形周长的比等于相似比98、性质定理3 相似三角形面积的比等于相似比的平方99、任意锐角的正弦值等于它的余角的余弦值，任意锐角的余弦值等于它的余角的正弦值100、任意锐角的正切值等于它的余角的余切值，任意锐角的余切值等于它的余角的正切值101、圆是定点的距离等于定长的点的集合102、圆的内部可以看作是圆心的距离小于半径的点的集合103、圆的外部可以看作是圆心的距离大于半径的点的集合104、同圆或等圆的半径相等105、到定点的距离等于定长的点的轨迹，是以定点为圆心,定长为半径的圆106、和已知线段两个端点的距离相等的点的轨迹，是着条线段的垂直平分线107、到已知角的两边距离相等的点的轨迹，是这个角的平分线108、到两条平行线距离相等的点的轨迹,是和这两条平行线平行且距离相等的一条直线109、定理不在同一直线上的三点确定一个圆.110、垂径定理垂直于弦的直径平分这条弦并且平分弦所对的两条弧111、推论1①平分弦（不是直径)的直径垂直于弦，并且平分弦所对的两条弧②弦的垂直平分线经过圆心,并且平分弦所对的两条弧③平分弦所对的一条弧的直径,垂直平分弦，并且平分弦所对的另一条弧112、推论2 圆的两条平行弦所夹的弧相等113、圆是以圆心为对称中心的中心对称图形114、定理在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦相等，所对的弦的弦心距相等115、推论在同圆或等圆中,如果两个圆心角、两条弧、两条弦或两弦的弦心距中有一组量相等那么它们所对应的其余各组量都相等116、定理一条弧所对的圆周角等于它所对的圆心角的一半117、推论1 同弧或等弧所对的圆周角相等；同圆或等圆中,相等的圆周角所对的弧也相等118、推论2 半圆(或直径）所对的圆周角是直角；90°的圆周角所对的弦是直径119、推论3 如果三角形一边上的中线等于这边的一半，那么这个三角形是直角三角形120、定理圆的内接四边形的对角互补，并且任何一个外角都等于它的内对角121、①直线L和⊙O相交d﹤r②直线L和⊙O相切d=r③直线L和⊙O相离d﹥r122、切线的判定定理经过半径的外端并且垂直于这条半径的直线是圆的切线123、切线的性质定理圆的切线垂直于经过切点的半径124、推论1 经过圆心且垂直于切线的直线必经过切点125、推论2 经过切点且垂直于切线的直线必经过圆心126、切线长定理从圆外一点引圆的两条切线,它们的切线长相等圆心和这一点的连线平分两条切线的夹角127、圆的外切四边形的两组对边的和相等128、弦切角定理弦切角等于它所夹的弧对的圆周角129、推论如果两个弦切角所夹的弧相等,那么这两个弦切角也相等130、相交弦定理圆内的两条相交弦，被交点分成的两条线段长的积相等131、推论如果弦与直径垂直相交，那么弦的一半是它分直径所成的两条线段的比例中项132、切割线定理从圆外一点引圆的切线和割线，切线长是这点到割线与圆交点的两条线段长的比例中项133、推论从圆外一点引圆的两条割线,这一点到每条割线与圆的交点的两条线段长的积相等134、如果两个圆相切,那么切点一定在连心线上135、①两圆外离d﹥R+r ②两圆外切d=R+r ③两圆相交R-r﹤d﹤R+r(R﹥r) ④两圆内切d=R—r(R﹥r)⑤两圆内含d﹤R—r（R﹥r)136、定理相交两圆的连心线垂直平分两圆的公共弦137、定理把圆分成n(n≥3):⑴依次连结各分点所得的多边形是这个圆的内接正n边形⑵经过各分点作圆的切线,以相邻切线的交点为顶点的多边形是这个圆的外切正n边形138、定理任何正多边形都有一个外接圆和一个内切圆，这两个圆是同心圆139、正n边形的每个内角都等于（n-2）×180°／n140、定理正n边形的半径和边心距把正n边形分成2n个全等的直角三角形141、正n边形的面积Sn=pnrn／2 p表示正n边形的周长142、正三角形面积√3a／4 a表示边长143、如果在一个顶点周围有k个正n边形的角,由于这些角的和应为360°，因此k×(n—2）180°／n=360°化为(n—2)(k—2)=4144、弧长计算公式：L=n兀R／180145、扇形面积公式：S扇形=n兀R^2／360=LR／2 146、内公切线长= d—(R—r) 外公切线长= d-（R+r）三、常用数学公式公式分类公式表达式乘法与因式分解a2-b2=(a+b)(a-b）a3+b3=(a+b)(a2-ab+b2) a3-b3=（a—b(a2+ab+b2)一元二次方程的解-b+√(b2—4ac）/2a -b-√(b2—4ac）/2a根与系数的关系X1+X2=-b/aX1*X2=c/a 注：韦达定理某些数列前n项和1+2+3+4+5+6+7+8+9+…+n=n(n+1)/2 1+3+5+7+9+11+13+15+…+（2n-1）=n22+4+6+8+10+12+14+…+（2n)=n(n+1) 12+22+32+42+52+62+72+82+…+n2=n(n+1)(2n+1)/613+23+33+43+53+63+…n3=n2(n+1)2/4 1*2+2*3+3＊4+4*5+5＊6+6*7+…+n（n+1）=n(n+1)（n+2）/3正弦定理a/sinA=b/sinB=c/sinC=2R注：其中R 表示三角形的外接圆半径余弦定理b2=a2+c2—2accosB注：角B是边a和边c的夹角。
特殊平行四边形知识点总结
特殊平行四边形知识点总结
平行四边形、矩形、菱形、正方形的性质：
所有这些图形都有对边相等且平行的性质，四条边都相等的图形是正方形，对角线互相平分的图形是平行四边形，对角线相等的图形是矩形，有一组邻边相等的图形是菱形。
判定方法小结：
判定平行四边形的方法有五种：①两组对边分别平行；②两组对边分别相等；③两组对角分别相等；④对角线互相平分；
⑤一组对边平行且相等。
判定矩形的方法有四种：①有一个角是直角的平行四边形；
②对角线相等的平行四边形；③有三个角是直角的四边形；④对角线相等且互相平分的四边形。
判定菱形的方法有四种：①有一组邻边相等的平行四边形；
②对角线互相垂直的平行四边形；③四边都相等的四边形；④对角线互相垂直平分的四边形。
判定正方形的方法有七种：①有一组邻边相等且有一个角是直角的平行四边形；②对角线互相垂直且相等的平行四边形；
③有一组邻边相等的矩形；④对角线互相垂直的矩形；⑤有一
个角是直角的菱形；⑥对角线相等的菱形；⑦对角线互相垂直平分且相等的四边形。
基础达标训练：
1.两条对角线的四边形是平行四边形；
2.两条对角线的四边形是矩形；
3.两条对角线的四边形是菱形；
4.两条对角线的四边形是正方形；
5.两条对角线的平行四边形是矩形；
6.两条对角线的平行四边形是菱形；
7.两条对角线的平行四边形是正方形；
8.两条对角线的矩形是正方形；
9.两条对角线的菱形是正方形。
新人教版八年级数学全册知识点总结
新人教版八年级数学上册知识点总结第十一章 三角形1.三角形：由不在同一直线上的三条线段首尾顺次相接所组成的图形叫做三角形.2.三边关系：三角形任意两边的和大于第三边，任意两边的差小于第三边.3.高：从三角形的一个顶点向它的对边所在直线作垂线，顶点和垂足间的线段叫做三角形的高.4.中线：在三角形中，连接一个顶点和它对边中点的线段叫做三角形的中线.5.角平分线：三角形的一个内角的平分线与这个角的对边相交，这个角的顶点和交点之间的线段叫做三角形的角平分线.6.三角形的稳定性：三角形的形状是固定的，三角形的这个性质叫三角形的稳定性.7.多边形：在平面内，由一些线段首尾顺次相接组成的图形叫做多边形.8.多边形的内角：多边形相邻两边组成的角叫做它的内角.9.多边形的外角：多边形的一边与它的邻边的延长线组成的角叫做多边形的外角. 10.多边形的对角线：连接多边形不相邻的两个顶点的线段，叫做多边形的对 角线.11.正多边形：在平面内，各个角都相等，各条边都相等的多边形叫正多边形. 12.平面镶嵌：用一些不重叠摆放的多边形把平面的一部分完全覆盖，叫做用 多边形覆盖平面， 13.公式与性质：⑴三角形的内角和：三角形的内角和为180° ⑵三角形外角的性质：性质1：三角形的一个外角等于和它不相邻的两个内角的和. 性质2：三角形的一个外角大于任何一个和它不相邻的内角. ⑶多边形内角和公式：n 边形的内角和等于(2)n -·180° ⑷多边形的外角和：多边形的外角和为360°.⑸多边形对角线的条数：①从n 边形的一个顶点出发可以引(3)n -条对角线，把多边形分成(2)n -个三角形.②n 边形共有(3)2n n -条对角线. 第十二章 全等三角形1.基本定义：⑴全等形：能够完全重合的两个图形叫做全等形.⑵全等三角形：能够完全重合的两个三角形叫做全等三角形. ⑶对应顶点：全等三角形中互相重合的顶点叫做对应顶点. ⑷对应边：全等三角形中互相重合的边叫做对应边. ⑸对应角：全等三角形中互相重合的角叫做对应角. 2.基本性质：⑴三角形的稳定性：三角形三边的长度确定了，这个三角形的形状、大小就全确定，这个性质叫做三角形的稳定性.⑵全等三角形的性质：全等三角形的对应边相等，对应角相等. 3.全等三角形的判定定理：⑴边边边（SSS ）：三边对应相等的两个三角形全等.⑵边角边（SAS ）：两边和它们的夹角对应相等的两个三角形全等. ⑶角边角（ASA ）：两角和它们的夹边对应相等的两个三角形全等. ⑷角角边（AAS ）：两角和其中一个角的对边对应相等的两个三角形全等. ⑸斜边、直角边（HL ）：斜边和一条直角边对应相等的两个直角三角形 全等. 4.角平分线： ⑴画法：⑵性质定理：角平分线上的点到角的两边的距离相等.⑶性质定理的逆定理：角的内部到角的两边距离相等的点在角的平分线上. 5.证明的基本方法：⑴明确命题中的已知和求证.（包括隐含条件，如公共边、公共角、对顶 角、角平分线、中线、高、等腰三角形等所隐含的边角关系） ⑵根据题意，画出图形，并用数字符号表示已知和求证.⑶经过分析，找出由已知推出求证的途径，写出证明过程.第十三章 轴对称1.基本概念：⑴轴对称图形：如果一个图形沿一条直线折叠，直线两旁的部分能够互相 重合，这个图形就叫做轴对称图形.⑵两个图形成轴对称：把一个图形沿某一条直线折叠，如果它能够与另一 个图形重合，那么就说这两个图形关于这条直线对称.⑶线段的垂直平分线：经过线段中点并且垂直于这条线段的直线，叫做这 条线段的垂直平分线.⑷等腰三角形：有两条边相等的三角形叫做等腰三角形.相等的两条边叫 做腰，另一条边叫做底边，两腰所夹的角叫做顶角，底边与腰的夹角叫做 底角.⑸等边三角形：三条边都相等的三角形叫做等边三角形. 2.基本性质： ⑴对称的性质：①不管是轴对称图形还是两个图形关于某条直线对称，对称轴都是任何一 对对应点所连线段的垂直平分线. ②对称的图形都全等. ⑵线段垂直平分线的性质：①线段垂直平分线上的点与这条线段两个端点的距离相等. ②与一条线段两个端点距离相等的点在这条线段的垂直平分线上. ⑶关于坐标轴对称的点的坐标性质①点P (,)x y 关于x 轴对称的点的坐标为'P (,)x y -. ②点P (,)x y 关于y 轴对称的点的坐标为"P (,)x y -.⑷等腰三角形的性质： ①等腰三角形两腰相等.②等腰三角形两底角相等（等边对等角）.③等腰三角形的顶角角平分线、底边上的中线，底边上的高相互重合. ④等腰三角形是轴对称图形，对称轴是三线合一（1条）. ⑸等边三角形的性质： ①等边三角形三边都相等.②等边三角形三个内角都相等，都等于60° ③等边三角形每条边上都存在三线合一.④等边三角形是轴对称图形，对称轴是三线合一（3条）. 3.基本判定：⑴等腰三角形的判定：①有两条边相等的三角形是等腰三角形.②如果一个三角形有两个角相等，那么这两个角所对的边也相等（等角对 等边）.⑵等边三角形的判定：①三条边都相等的三角形是等边三角形. ②三个角都相等的三角形是等边三角形. ③有一个角是60°的等腰三角形是等边三角形. 4.基本方法：⑴做已知直线的垂线： ⑵做已知线段的垂直平分线：⑶作对称轴：连接两个对应点，作所连线段的垂直平分线. ⑷作已知图形关于某直线的对称图形：⑸在直线上做一点，使它到该直线同侧的两个已知点的距离之和最短.第十四章 整式的乘除与分解因式1.基本运算：⑴同底数幂的乘法：mnm na a a+⨯=⑵幂的乘方：()nm mn aa =⑶积的乘方：()nn nab a b = 2.整式的乘法：⑴单项式⨯单项式：系数⨯系数，同字母⨯同字母，不同字母为积的因式. ⑵单项式⨯多项式：用单项式乘以多项式的每个项后相加.⑶多项式⨯多项式：用一个多项式每个项乘以另一个多项式每个项后相加. 3.计算公式：⑴平方差公式：()()22a b a b a b -⨯+=-⑵完全平方公式：()2222a b a ab b +=++；()2222a b a ab b -=-+4.整式的除法：⑴同底数幂的除法：mnm na a a-÷=⑵单项式÷单项式：系数÷系数，同字母÷同字母，不同字母作为商的因式. ⑶多项式÷单项式：用多项式每个项除以单项式后相加. ⑷多项式÷多项式：用竖式.5.因式分解：把一个多项式化成几个整式的积的形式,这种变形叫做把这个式 子因式分解.6.因式分解方法：⑴提公因式法：找出最大公因式. ⑵公式法：①平方差公式：()()22a b a b a b -=+-②完全平方公式：()2222a ab b a b ±+=±③立方和：3322()()a b a b a ab b +=+-+ ④立方差：3322()()a b a b a ab b -=-++⑶十字相乘法：()()()2x p q x pq x p x q +++=++⑷拆项法 ⑸添项法第十五章 分式1.分式：形如AB，A B 、是整式，B 中含有字母且B 不等于0的整式叫做分式.其中A 叫做分式的分子，B 叫做分式的分母.2.分式有意义的条件：分母不等于0.3.分式的基本性质：分式的分子和分母同时乘以（或除以）同一个不为0的整式，分式的值不变.4.约分：把一个分式的分子和分母的公因式(不为1的数）约去，这种变形称为约分.5.通分：异分母的分式可以化成同分母的分式，这一过程叫做通分.6.最简分式:一个分式的分子和分母没有公因式时，这个分式称为最简分式，约分时，一般将一个分式化为最简分式. 7.分式的四则运算：⑴同分母分式加减法则：同分母的分式相加减，分母不变，把分子相加减.用字母表示为：a b a bc c c±±=⑵异分母分式加减法则：异分母的分式相加减，先通分，化为同分母的分 式，然后再按同分母分式的加减法法则进行计算.用字母表示为：a c ad cbb d bd±±=⑶分式的乘法法则：两个分式相乘，把分子相乘的积作为积的分子，把分 母相乘的积作为积的分母.用字母表示为：a c acb d bd⨯=⑷分式的除法法则：两个分式相除,把除式的分子和分母颠倒位置后再与 被除式相乘.用字母表示为：a c a d adb d bc bc÷=⨯= ⑸分式的乘方法则：分子、分母分别乘方.用字母表示为：nn n a a b b⎛⎫= ⎪⎝⎭8.整数指数幂： ⑴mnm na a a +⨯=（m n 、是正整数）⑵()nm mn aa =（m n 、是正整数）⑶()nn n ab a b =（n 是正整数） ⑷mnm na a a-÷=（0a ≠，m n 、是正整数，m n >）⑸n n n a a b b⎛⎫= ⎪⎝⎭（n 是正整数） ⑹1nn aa-=（0a ≠，n 是正整数） 9.分式方程的意义:分母中含有未知数的方程叫做分式方程.10.分式方程的解法:①去分母(方程两边同时乘以最简公分母,将分式方程化为整式方程);②按解整式方程的步骤求出未知数的值;③验根(求出未知数的值后必须验根,因为在把分式方程化为整式方程的过程中,扩大了未知数的取值范围,可能产生增根).新人教版八年级数学下册知识点总结第16章 二次根式1.二次根式：式子a （a ≥0）叫做二次根式。
初二数学平行四边形知识点归纳
初二数学平行四边形知识点归纳一、平行四边形的定义与性质。
1. 定义。
- 两组对边分别平行的四边形叫做平行四边形。
平行四边形用符号“▱”表示，例如平行四边形ABCD记作“▱ABCD”。
2. 性质。
- 边的性质。
- 平行四边形的两组对边分别平行且相等。
即AB∥CD，AD∥BC，AB = CD，AD = BC。
- 角的性质。
- 平行四边形的两组对角分别相等，邻角互补。
即∠A = ∠C，∠B = ∠D，∠A+∠B = 180°，∠B + ∠C=180°等。
- 对角线的性质。
- 平行四边形的对角线互相平分。
即若AC、BD是▱ABCD的对角线，则AO = CO，BO = DO（O为AC、BD交点）。
二、平行四边形的判定。
1. 边的判定。
- 两组对边分别平行的四边形是平行四边形（定义判定）。
- 两组对边分别相等的四边形是平行四边形。
即若AB = CD，AD = BC，则四边形ABCD是平行四边形。
- 一组对边平行且相等的四边形是平行四边形。
例如AB∥CD且AB = CD，则四边形ABCD是平行四边形。
2. 角的判定。
- 两组对角分别相等的四边形是平行四边形。
即若∠A = ∠C，∠B = ∠D，则四边形ABCD是平行四边形。
3. 对角线的判定。
- 对角线互相平分的四边形是平行四边形。
若AO = CO，BO = DO，则四边形ABCD 是平行四边形。
三、平行四边形的面积。
1. 面积公式。
- 平行四边形的面积 = 底×高，即S = ah（a为底边长，h为这条底边对应的高）。
例如在▱ABCD中，若以AB为底，AB边上的高为h，则S▱ABCD=AB×h。
2. 等底等高的平行四边形面积关系。
- 等底等高的平行四边形面积相等。
如果有▱ABCD和▱EFGH，AB = EF，且它们对应的高相等，那么S▱ABCD = S▱EFGH。
四、特殊的平行四边形（矩形、菱形、正方形）与平行四边形的关系。
四边形知识点总结大全
四边形知识点总结大全1.四边形的内角和与外角和定理：四边形的内角和等于360度；四边形的外角和等于360度。
2.多边形的内角和与外角和定理：n边形的内角和等于(n-2)180度；任意多边形的外角和等于360度。
3.平行四边形的性质：两组对边分别平行；两组对边分别相等；两组对角分别相等；对角线互相平分；邻角互补。
4.平行四边形的判定：若两组对边分别平行、相等、对角分别相等或一组对边平行且相等，则四边形为平行四边形。
5.矩形的性质：具有平行四边形的所有通性；四个角都是直角；对角线相等。
6.矩形的判定：若四边形为平行四边形且至少有一个直角，则为矩形；若对角线相等且为平行四边形，则为矩形。
7.菱形的性质：具有平行四边形的所有通性；四个边都相等；对角线垂直且平分对角。
8.菱形的判定：若四边形为平行四边形且一组邻边相等，则为菱形；若四边形四边相等且对角线垂直，则为菱形。
9.正方形的性质：具有平行四边形的所有通性；四个边都相等，四个角都是直角；对角线相等垂直且平分对角。
10.正方形的判定：若四边形为平行四边形且至少有一组邻边相等且有一个直角，则为正方形；若为菱形且有一个直角，则为正方形；若为矩形且一组邻边相等，则为正方形。
11.等腰梯形的性质：两底平行，两腰相等；同一底上的底角相等；对角线相等。
12.等腰梯形的判定：若四边形两底平行且两腰相等，则为等腰梯形；若同一底上的底角相等且对角线相等，则为等腰梯形。
1.等腰梯形的定义：一个四边形，其中两边是平行的且相等，另外两边也相等，但不平行。
根据这个定义，可以得出等腰梯形的性质：底角相等，对角线相等。
2.三角形中位线定理：三角形的中位线是连接一个角的顶点和对边中点的线段。
根据中位线定理，三角形的中位线平行于第三边，并且等于它的一半。
3.梯形中位线定理：梯形的中位线是连接两个非平行边中点的线段。
根据梯形中位线定理，梯形的中位线平行于两底，并且等于两底和的一半。
公式部分：1.菱形的面积公式：S=ab=ch，其中a、b为菱形的对角线，c为菱形的边长，h为c边上的高。
人教版初二数学下册第18章《平行四边形》讲义第11讲菱形及正方形
人教版初二数学下册第18章《平行四边形》讲义第11讲菱形及正方形1、定义：有一组邻边相等的平行四边形叫做菱形。
2、基本性质：〔1〕边：菱形的四条边都相等；〔2〕角：菱形的对角相等，邻角互补；〔3〕对角线：菱形的对角线相互垂直平分，且每一条对角线平分一组对角： 〔4〕对称性：菱形是轴对称图形，中心对称图形，对称轴有两条；〔5〕面积：S=21ab(其中a 、b 区分是菱形的两条对角线的长). 或 S=底×高。
〔1〕有一组邻边相等的平行四边形是菱形;〔2〕四边都相等的四边形是菱形;〔3〕对角线相互垂直平分的四边形是菱形;〔4〕对角线相互垂直的平行四边形是菱形.1、正方形的定义：有一组邻边相等并且有一个角是直角的平行四边形叫做正方形。
2、基本性质：〔1〕边：正方形四条边都相等；〔2〕角：正方形的四个角都相等；〔3〕对角线：对角线相等且相互垂直平分，并且每条对角线平分一组对角； 〔4〕对称性：是中心对称图形，又是轴对称图形，对称轴有四条；〔1〕有一组邻边相等的矩形是正方形；〔2〕对角线相互垂直的矩形是正方形；〔3〕有一个角是直角的菱形是正方形；〔4〕对角线相等的菱形是正方形。
考点1、菱形的性质例1、菱形的一个内角是120°，一条较短的对角线的长为10，那么菱形的周长是________ 例2、如图，菱形ABCD 的两条对角线区分长6和8，点P 是对角线AC 上的一个动点，点M 、N 区分是边AB 、BC 的中点，那么PM +PN 的最小值是________．例3、菱形的一条对角线长为12cm ，面积为30cm 2，那么这个菱形的另一条对角线长为_______cm 。
例4、如图，菱形ABCD ，E ，F 区分是BC ，CD 上的点，∠B ＝∠EAF ＝60°，∠BAE ＝18°，求∠CEF 的度数。
例5、如图，在菱形ABCD 中，对角线AC 、BD 相交于点O ，过点D 作对角线BD 的垂线交BA 的延伸线于点E ．〔1〕证明：四边形ACDE 是平行四边形；〔2〕假定AC=8，BD=6，求△ADE 的周长．例6、如图，在菱形ABCD 中，F 为对角线BD 上一点，点E 为AB 延伸线上一点，DF=BE ，CE=CF.求证：〔1〕△CFD ≌△CEB ；〔2〕∠CFE=60°.例7、：如图，在菱形ABCD 中，F 为边BC 的中点，DF 与对角线AC 交于点M ，过M 作ME ⊥CD 于点E ，∠1=∠2．〔1〕、假定CE=1，求BC 的长；〔2〕、求证：AM=DF+ME ．1、菱形ABCD 中，∠A ＝60o ，对角线BD 长为7cm ，那么此菱形周长 cm 。
正方形、矩形、菱形和平行四边形四者知识点详细总结汇总
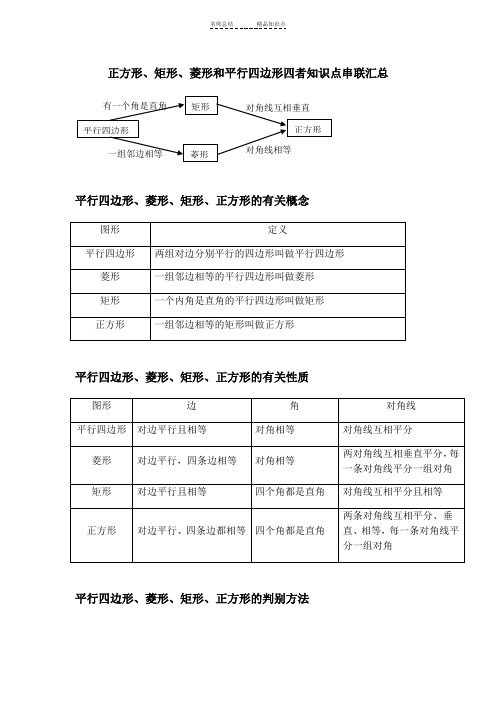
正方形、矩形、菱形和平行四边形四者知识点串联汇总平行四边形、菱形、矩形、正方形的有关概念图形 定义平行四边形 两组对边分别平行的四边形叫做平行四边形 菱形 一组邻边相等的平行四边形叫做菱形 矩形 一个内角是直角的平行四边形叫做矩形 正方形 一组邻边相等的矩形叫做正方形平行四边形、菱形、矩形、正方形的有关性质图形边角对角线平行四边形 对边平行且相等 对角相等 对角线互相平分菱形 对边平行，四条边相等 对角相等 两对角线互相垂直平分，每一条对角线平分一组对角 矩形对边平行且相等四个角都是直角对角线互相平分且相等 正方形 对边平行、四条边都相等 四个角都是直角两条对角线互相平分、垂直、相等，每一条对角线平分一组对角平行四边形、菱形、矩形、正方形的判别方法对角线相等对角线互相垂直有一个角是直角 一组邻边相等平行四边形矩形菱形正方形图形 判别方法平行四边形 两组对边分别平行的四边形是平行四边形 一组对边平行且相等的四边形是平行四边形两组对边分别相等的四边形是平行四边形 两组对角分别相等的四边形是平行四边形 对角线互相平分的四边形是平行四边形菱形 一组邻边相等的平行四边形是菱形四条边都相等的四边形是菱形 对角线互相垂直的平行四边形是菱形 矩形一个内角是直角的平行四边形是矩形对角线相等的平行四边形是矩形 正方形一组邻边相等的矩形是正方形 对角线互相垂直的矩形是正方形有一个角是直角的菱形是正方形 对角线相等的菱形是正方形二、梯形常见的辅助线 1.延长两腰交于一点作用：使梯形问题转化为三角形问题。
若是等腰梯形则得到等腰三角形。
2.平移一腰作用：使梯形问题转化为平行四边形及三角形问题。
3.作高作用：使梯形问题转化为直角三角形及矩形问题。
4.平移一条对角线作用：（1）得到平行四边形ACED，使CE=AD，BE等于上、下底的和=S△DBE（2）S梯形ABCD5.当有一腰中点时，连结一个顶点与一腰中点并延长交一个底的延长线。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
说明四边形ABCD的四条相等．
（3）识别正方形的常用方法
先说明四边形ABCD为平行四边形，再说明平行四边形ABCD的一个角为直角且有一组邻边相等．
先说明四边形ABCD为平行四边形，再说明对角线互相垂直且相等．
先说明四边形ABCD为矩形，再说明矩形的一组邻边相等．
平行四边形、矩形、菱形、正方形知识点总结
平行四边形：
性质：
边：对边平行且相等；
角：对角相等、邻角互补；
对角线：对角线互相平分；
判定：
①定义：两组对边分别平行的四边形
②方法1：两组对角分别相等的四边形
③方法2：两组对边分别相等的四边形
④方法3：对角线互相平分的四边形
⑤方法4：一组平行且相等的四边形
矩形：
性质：
边：对边平行且相等；
角：对角相等、邻角互补；
对角线：对角线互相平分且相等；
判定：
有一个角是直角的平行四边形；
对角线相等的平行四边形；
四个角都相等
菱形：
性质：
边：四条边都相等；
角：对角相等、邻角互补；
对角线：对角线互相垂直平分且每条对角线平分每组对角；
面积：则S菱形=底×高=ah；或者S菱形= （对角线乘积的一半）．
几种特殊四边形的常用说理方法与解题思路分析
（1）识别矩形的常用方法
先说明四边形ABCD为平行四边形，再说明平行四边形ABCD的任意一个角为直角．
先说明四边形ABCD为平行四边形，再说明平行四边形ABCD的对角线相等．
说明四边形ABCD的三个角是直角．
（2）识别菱形的常用方法
先说明四边形ABCD为平行四边形，再说明平行四边形ABCD的任一组邻边相等．
先说明四边形ABCD为菱形，再说明菱形ABCD的一个角为直角．
判定：
有一组邻边相等的平பைடு நூலகம்四边形；
对角线互相垂直的平行四边形；
四条边都相等．
正方形：
性质：
边：四条边都相等；
角：四角相等；
对角线：对角线互相垂直平分且相等，对角线与边的夹角为450；
判定：
有一组邻边相等且有一个直角的平行四边形
有一组邻边相等的矩形；
对角线互相垂直的矩形．
有一个角是直角的菱形
对角线相等的菱形；