离散系统的时域分析共67页
合集下载
第3章离散系统的时域分析ppt课件
3.1.1离散时间信号 连续系统的激励和响应都是连续时间信号,它们是
连续变量t的函数,离散系统的激励与响应都是离散时间 信号,表示这种信号的函数,只在一系列互相分离的时间 点上才有定义,而在其它点上则未定义,所以它们是离散 变量tk的函数〔或称序列〕.
《 信号与线性系统》
第3章 离散系统的时域分析
行取样.进行取样的取样器一般由电子开关组成.其工作 原理如图3.2所示.
x(t)
y(t)
T
x(t) 脉冲 y(t) 调制
p(t)
《 信号与线性系统》
图3.2 取样原理图
第3章 离散系统的时域分析
x (t)
p (t)
T
y (t)
(a ) t
(b ) t
(c ) t
图 3.3 信号的取样 <a>连续信号x<t>波形；<b>取样脉冲p<t>波形；<c>取样信号y<t> 波形
=sin<n ω0 ＋2kπ>
=sin<n ω0 >=x<n>
所以,x<n>=sin<n ω0 >是一个周期序列.
《 信号与线性系统》
第3章 离散系统的时域分析
3.3 离散时间系统的描述和响应
3.3.1 离散时间系统的描述 离散时间系统的输入和输出信号都是离散时间函
数〔序列〕.这种系统的工作情况,不能用连续时间系统 的微分方程来描述,而必须采用差分方程来描述.
y<2>=1,y<3>=2,y<4>=3,y<5>=5,…
《 信号与线性系统》
第3章 离散系统的时域分析
连续变量t的函数,离散系统的激励与响应都是离散时间 信号,表示这种信号的函数,只在一系列互相分离的时间 点上才有定义,而在其它点上则未定义,所以它们是离散 变量tk的函数〔或称序列〕.
《 信号与线性系统》
第3章 离散系统的时域分析
行取样.进行取样的取样器一般由电子开关组成.其工作 原理如图3.2所示.
x(t)
y(t)
T
x(t) 脉冲 y(t) 调制
p(t)
《 信号与线性系统》
图3.2 取样原理图
第3章 离散系统的时域分析
x (t)
p (t)
T
y (t)
(a ) t
(b ) t
(c ) t
图 3.3 信号的取样 <a>连续信号x<t>波形；<b>取样脉冲p<t>波形；<c>取样信号y<t> 波形
=sin<n ω0 ＋2kπ>
=sin<n ω0 >=x<n>
所以,x<n>=sin<n ω0 >是一个周期序列.
《 信号与线性系统》
第3章 离散系统的时域分析
3.3 离散时间系统的描述和响应
3.3.1 离散时间系统的描述 离散时间系统的输入和输出信号都是离散时间函
数〔序列〕.这种系统的工作情况,不能用连续时间系统 的微分方程来描述,而必须采用差分方程来描述.
y<2>=1,y<3>=2,y<4>=3,y<5>=5,…
《 信号与线性系统》
第3章 离散系统的时域分析
第3章离散系统的时域分析精品精品文档
《 信号与线性系统》
第3章 离散系统的时域分析
(4)序列的标乘：A·x=Ax(n)=y(n)表示序列x的每个取 样值同乘以常数A所形成的新序列，其运算符号如图3.8(c) 所示。
(5)序列的延时：若序列y(n)满足取值y(n)=x(n-n0)，则 称序列y(n)是序列x(n)延时n0个取样间隔的复现，式中n0 为整数。当n0=1时，称为单位延时 ，其运算符号如图 3.8(d)所示。
《 信号与线性系统》
第3章 离散系统的时域分析
例3―1 试用单位跃迁序列表示单位序列。
解由
u(n)
0 1
n0 n0
可知
即
u (n
1)
0
1
n1 0 n1 0
而
u (n
1)
0
1
n0 n0
(n )
0
n0
1 n 0
输 入 转 换 器 处 理 器 转 换 器输 出
图3.6 模拟信号转换成数字信号进行处理 《 信号与线性系统》
第3章 离散系统的时域分析
3.2 离散时间信号的表示
3.2.1 序列的表示方法
序列本来就是离散时间信号或是从数字处理过程
中得到的，所以序列不必以kT作为变量，而直接以x(k) 表示一数字序列x的第k个数字，k表示x［k］在数字序 列x前后变量的序号，则x可以用公式表示为
第3章 离散系统的时域分析
第3章 离散系统的时域分析
3.1 连续时间信号的取样 3.2 离散时间信号的表示 3.3 离散时间系统的描述和响应 3.4 卷积和 3.5 卷积和的计算机模拟 3.6 离散时间系统与连续时间系统时域分析法的比较
第3章 离散系统的时域分析
(4)序列的标乘：A·x=Ax(n)=y(n)表示序列x的每个取 样值同乘以常数A所形成的新序列，其运算符号如图3.8(c) 所示。
(5)序列的延时：若序列y(n)满足取值y(n)=x(n-n0)，则 称序列y(n)是序列x(n)延时n0个取样间隔的复现，式中n0 为整数。当n0=1时，称为单位延时 ，其运算符号如图 3.8(d)所示。
《 信号与线性系统》
第3章 离散系统的时域分析
例3―1 试用单位跃迁序列表示单位序列。
解由
u(n)
0 1
n0 n0
可知
即
u (n
1)
0
1
n1 0 n1 0
而
u (n
1)
0
1
n0 n0
(n )
0
n0
1 n 0
输 入 转 换 器 处 理 器 转 换 器输 出
图3.6 模拟信号转换成数字信号进行处理 《 信号与线性系统》
第3章 离散系统的时域分析
3.2 离散时间信号的表示
3.2.1 序列的表示方法
序列本来就是离散时间信号或是从数字处理过程
中得到的，所以序列不必以kT作为变量，而直接以x(k) 表示一数字序列x的第k个数字，k表示x［k］在数字序 列x前后变量的序号，则x可以用公式表示为
第3章 离散系统的时域分析
第3章 离散系统的时域分析
3.1 连续时间信号的取样 3.2 离散时间信号的表示 3.3 离散时间系统的描述和响应 3.4 卷积和 3.5 卷积和的计算机模拟 3.6 离散时间系统与连续时间系统时域分析法的比较
第7章 离散时间系统的时域分析1PPT课件
1 o 1 2 3
N 1 n
与 u n 的R N 关 ( n ) u ( n ) 系 u ( n N )：
18
4．斜变序列
x(n)nu (n)
x(n)
1 1 O 1 2 3 4 n
19
5．单边指数序列 x n an u n
anun
a 1
1 1 O 1 2 3 4 n
a nun
a 1
1 1 O
x(n) x(n)
xn
x n
x 1
x0 x1
x3
x0 x1 x 1 x3
2
1 o 1 3 n
1 o 1 n
x2
x2
x(n) x(n1)
xn 1 x0
x 1 x1 x3
3 1 o 1 2 4 n
x2
10
例：已知序列
f (k) 6
f(n) n(n1)
则
2
3
…1
…
3 1 1 3 k
f (n) n(n1) 2
两个序列同序号的数值逐项对应相乘。
例：已知序列
0 n1 f1(n)2n5 n1
2n n0 f2(n)n2 n0
求 f 1 ( n ) f 2 ( n ) 和 f 1 ( n )f 2 ( n )
8
0 n1 f1(n)2n5 n1
2n n0 f2(n)n2 n0
0 n1 解 ： f1(n) 7 n1
f(n1)(n1)n 2
f(k2)(k2)k (3) 2
f ቤተ መጻሕፍቲ ባይዱk) 6
f (k1) 6
f (k 2) 6
3 …1
3 ……
1
……
3 …
1
3 1 1 3 k 3 1 1 3 k
N 1 n
与 u n 的R N 关 ( n ) u ( n ) 系 u ( n N )：
18
4．斜变序列
x(n)nu (n)
x(n)
1 1 O 1 2 3 4 n
19
5．单边指数序列 x n an u n
anun
a 1
1 1 O 1 2 3 4 n
a nun
a 1
1 1 O
x(n) x(n)
xn
x n
x 1
x0 x1
x3
x0 x1 x 1 x3
2
1 o 1 3 n
1 o 1 n
x2
x2
x(n) x(n1)
xn 1 x0
x 1 x1 x3
3 1 o 1 2 4 n
x2
10
例：已知序列
f (k) 6
f(n) n(n1)
则
2
3
…1
…
3 1 1 3 k
f (n) n(n1) 2
两个序列同序号的数值逐项对应相乘。
例：已知序列
0 n1 f1(n)2n5 n1
2n n0 f2(n)n2 n0
求 f 1 ( n ) f 2 ( n ) 和 f 1 ( n )f 2 ( n )
8
0 n1 f1(n)2n5 n1
2n n0 f2(n)n2 n0
0 n1 解 ： f1(n) 7 n1
f(n1)(n1)n 2
f(k2)(k2)k (3) 2
f ቤተ መጻሕፍቲ ባይዱk) 6
f (k1) 6
f (k 2) 6
3 …1
3 ……
1
……
3 …
1
3 1 1 3 k 3 1 1 3 k
离散时间系统的时域分析-PPT精品
解：
x(n)
y(n)
y ( n ) a y ( n 1 ) x ( n )
y ( n ) a y ( n 1 ) x ( n ) a
1
常系数线性差分方程
E
*差分方程的阶:差分方程的阶数等于未知序列变量 序号最高与最低值之差.
未知序列的序号自n以递减的方式给出，称为后向 形式的(或向右移序)差分方程。
完全响应
y(n)01.5440.4254(40.93)n 01.942(04.93)n
R
R
R
E
R
R
R
R
R
解： v ( n 1 ) v ( n ) v ( n 1 ) v ( n 2 ) v ( n 1 )
RR
R
v ( n ) 3 v ( n 1 ) v ( n 2 ) 0
此例中的差分方程v(n)的自变量n不表示时 间，而是代表电路图中结点序号。
例4 假定每对兔子每月可以生育一对小兔，新生的
i0
若 Tx(n)y(n) 则 Tax1(n)ay1(n);Tbx2(n)by2(n)
T a x 1 ( n ) b x 2 ( n ) a T x 1 ( n ) b T x 2 ( n ) a y 1 ( n ) b y 2 ( n )
3.时不变系统：系统的运算关系T[ ]在整个运 算过程中不随时间(不随序列的先后)而变化。
(1)2(21)0
特征根为
1 2 1 ,3 j ,4 j
奇次解：y h (n ) (C 0 C 1 n ) P c o s n 2 Q s in n 2
y (1) C 0 C1 Q 1
y(2)
C0
2C1
P
0
信号与系统第6章离散信号与系统的时域分析PPT
x(n)
y(n)
n
0
N
x(n m)
n
0
m m N
h(n)
(b) 非时变特性 图 6.1-2 线性非时变系统
n
0
N
y(n m)
n
0
m m N
第 6 章 离散信号与系统的时域分析
离散时间信号与系统的分析，归根到底也是求解建立的常系数线性差分方程的过程，概括起来其方法包 括以下几种：
1．递归迭代法 递归迭代法包括手算逐次代入求解或利用计算机求解。这种方法简单、概念清楚，但是不易得到系统响 应的数值解，一般很难给出一个完整的解析表达式。 2．时域经典法 与连续时间系统微分方程的时域经典解法相类似。离散系统的经典解法也是先分别求齐次解和特解，然 后代入边界条件求待定系数，这种方法便于从物理概念上说明各响应分量之间的关系，但求解过程相对比较 麻烦。 3．时域近代解法 该方法主要是分别求零输入响应和零状态响应，具体来说就是，利用类似经典法中求齐次解的方法求零 输入响应，利用卷积(和)的方法求零状态响应。与连续时间系统的情况类似，卷积法在离散时间系统分析中占 有十分重要的地位。 4．变换域求解法 类似于连续时间信号与系统的傅立叶变换和拉普拉斯变换法，利用 z 变换法求解差分方程是实用中简便 而有效的方法。 在以上方法中，迭代法、经典时域法和时域近代解法都是时域分析方法，将在本章介绍，变换域法将在 第 7 章中讨论，而零输入响应与零状态响应可以在时域求解，也可以在变换域求解。
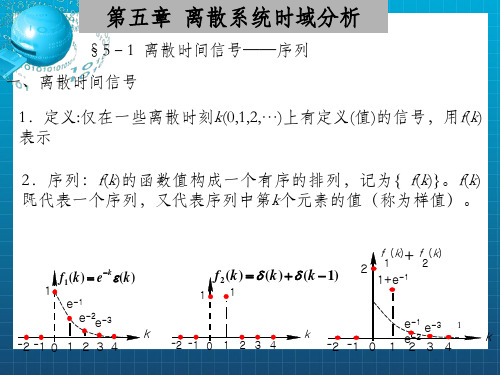
fk={f(tk)} k=0, ±1, ±2, … 式中，k为整数，表示信号值在序列中出现的序号。
第 6 章 离散信号与系统的时域分析
其中tk和tk-1之间的间隔(tk-tk-1)可以是常数，也可以随k变化。在实际应用 中，一般取为常数。例如，对连续时间信号均匀取样后得到的离散时间 信号便是如此。对于这类离散时间信号，若令tk-tk-1=T，则信号仅在均 匀时刻t=kT(k=0,±1,±2,…)上取值。此时， {f(tk)}可以改写为{f(kT)}， 为了简便，我们用序列值的通项f(kT)表示集合{f(kT)}，并将常数T省略， 则简写为
第六章——离散时间系统的时域分析
第六章 离散时间系统的时域分析6.1离散时间信号—序列（一）序列运算[1] 相加()()()z n x n y n =+[2] 相乘()()()z n x n y n =[3] 延时()()z n x n m =-[4] 反褶()()z n x n =-[5] 前向差分()()()1x n x n x n ∆=+-[6] 后向差分()()()1x n x n x n ∇=--[7] 累加()()NK z n x K =-∞=∑[8] 倍乘序列的尺度倍乘将波形压缩或拓展，若将自变量n 乘以正整数a ，构成()x an 为压缩，而n x a ⎛⎫⎪⎝⎭则为波形扩展。
必须注意，这时要按规律去除某些点或者补足相应的零值。
因此，也称这种运算为序列的“重排”。
(二)常见序列1. 单位样值信号()()()1000n n n δ=⎧⎪=⎨≠⎪⎩2. 单位阶跃序列()()()1000n u n n ≥⎧⎪=⎨<⎪⎩ 3. 矩形序列()()()10100,N n N R n n n N ≤≤-⎧⎪=⎨<≥⎪⎩4. 斜变序列()()x n nu n =5. 指数序列()()n x n a u n =6. 正余弦序列()()0sin x n n ω= ()()0cos x n n ω=7. 复指数序列()()()0j 00cos jsin nx n e n n ωωω==+6.2离散时间系统的数学模型（一）三种方框图在时间域描述中，以符号1E表示单位延时（也可用符号“T ”或者符号“D ”表示单位延时）；以符号∑表示两个序列相加；以符号⊗表示序列与系数相乘。
三种运算的方框图如下：单位延时相加乘系数例 一个离散时间系统如下图所示，写出描述系统工作的差分方程。
解 延时器的输入端应为序列()1y n +。
于是，围绕相加器可以写出()()()1y n ay n x n +=+或者()()()11y n y n x n a=+-⎡⎤⎣⎦a()y n ()ay n6.3常系数线性差分方程的求解(一)求解常系数线性差分方程的方法[1]时域经典法与微分方程的时域经典法类似，先分别求齐次解与特解，然后代入边界条件求待定系数。
《离散系统时域分析》课件
总结和结论
《离散系统时域分析》是一门重要的课程，通过学习时域分析的基本概念和 方法，我们能够更好地理解和分析离散系统的时域行为和特性。
实例分析：时域分析在离散系统中的应 用
数字信号处理
时域分析在数字信号处理中广 泛应用，可用于滤波器设计、 音频处理和图像处理等领域。
控制系统分析
时域分析可用于控制系统的动 态响应分析和控制器的设计， 以实现系统的稳定性和性能要 求。
通信系统分析
时域分析在通信系统中起着重 要的作用，可用于信号传输和 信道估计等方面的分析和优化。
《离散系统时域分析》 PPT课件
本课程将介绍《离散系统时域分析》的重要概念和方法，帮助学生深入理解 离散系统在时域中的行为和特性。
课程概述
《离散系统时域分析》PPT课件将探讨离散系统在时域中的分析方法和应用。 通过本课程，学生将学习如何分析离散系统的时域响应和特性。
时域分析的定义
时域分析是研究系统在时间上的行为和特性的一种方法。通过对信号的时域分析，我们可以了解系统的 时域响应和时域特性。
时域分析的目的
时域分析的目的是通过观察系统在时间上的行为，了解系统的动态行为和特性。通过时域分析，我们可 以提取系统的时域响应和时域特性，进而优化系统设计和调整系统参数。
时域分析的基本概念
时域分析涉及到信号的时域表示、时域响应和时域特性。常用的时域分析方法包括时域卷积、时域离散 傅里叶变换和时域差分方程等。
常见的时域分析方法
时域卷积
时域卷积是一种用于分析两个信号之间的线性叠加关系的方法，常用于系统的时域分析和滤 波器的设计。
时域离散傅里叶变换
时域离散傅里叶变换是一种将时域信号变换到频域的方法，可时域差分方程是一种描述离散系统行为的数学模型，常用于分析系统的时域响应和特性。
离散时间系统的时域分析
T 是抽样间隔 ，n= 0,1,2…。 5
§3.2差分方程法
dy(t) ay(t) x(t), a 0
●一阶导数与一阶dt差分：
dy(t) lim y(t) y(t t)
dt t0
t
y(nT ) y(nT T ) T
y(nT-T)
y（nT) y (t ) y[n]
T
y[n] y[n 1] T
x[n]
dy(t) y[n] dt T dy(t) ay(t)
dt
y[n] y[n 1] T
x(t) , a 0
●二阶导数与二阶差分：
d 2 y(t) dt 2
d dy(t) ()
dt dt tnT
y[n] T T
T
y[n]
y[n T
1]
y[n]
y[n T2
1]
( y[n] y[n 1]) ( y[n 1] y[n 2]) T2
后代入边界条件求出待定系数。 该法求解过程繁琐，现已很少采用。（略）
C.零输入、零状态响应法 y[n]=y0[n]+ yx[n]
y0[n]——零输入响应 yx[n]——零状态响应
17
§3.2差分方程法
● 用奇次解的方法求零输入响应y0[n]。
N
方程： ak y[n k] 0 k 0
● 用卷积和的方法求零状态响应yx[n] ： yx[n]= x[n]* h[n]
§3.1 引言1．离散源自间系统x[n]系统 h[n]
y[n] x(t)
系统
y(t)
h(t)
已知
差分方程 求解
离散系统
已知——>微分方程——>求解
连续时间系统
离散系统：
§3.2差分方程法
dy(t) ay(t) x(t), a 0
●一阶导数与一阶dt差分：
dy(t) lim y(t) y(t t)
dt t0
t
y(nT ) y(nT T ) T
y(nT-T)
y（nT) y (t ) y[n]
T
y[n] y[n 1] T
x[n]
dy(t) y[n] dt T dy(t) ay(t)
dt
y[n] y[n 1] T
x(t) , a 0
●二阶导数与二阶差分：
d 2 y(t) dt 2
d dy(t) ()
dt dt tnT
y[n] T T
T
y[n]
y[n T
1]
y[n]
y[n T2
1]
( y[n] y[n 1]) ( y[n 1] y[n 2]) T2
后代入边界条件求出待定系数。 该法求解过程繁琐，现已很少采用。（略）
C.零输入、零状态响应法 y[n]=y0[n]+ yx[n]
y0[n]——零输入响应 yx[n]——零状态响应
17
§3.2差分方程法
● 用奇次解的方法求零输入响应y0[n]。
N
方程： ak y[n k] 0 k 0
● 用卷积和的方法求零状态响应yx[n] ： yx[n]= x[n]* h[n]
§3.1 引言1．离散源自间系统x[n]系统 h[n]
y[n] x(t)
系统
y(t)
h(t)
已知
差分方程 求解
离散系统
已知——>微分方程——>求解
连续时间系统
离散系统：
离散系统时域分析_OK
例：设 y(k)+3y(k-1)+2y(k-2)=2k (k)，y(0)=0， y(1)=2，求y(k)。
f(k)=ak(k)
|a| >
1
f(k)=ak(k)
|a| <
11
1
-2 -1 0 1 2 3
k
-2 -1 0 1 2 3
k
3
发散
收敛
5．正弦序列
f (k) Acos(kω0 )
0序列依次重复出现的频率。
2
ω 0
为有理数，正弦序列为周期序列。
f (k N ) A cosω[ 0(k N ) ] A cosω[ 0k ω0 N ]
any(k)+an-1y(k-1)+…+a1y(k-n+1)+a0y(k-n)=0(后向)
any(k+n)+an-1y(k+n-1)+…+a1y(k+1)+a0y(k)=0(前向)
对应的特征方程为：ann+an-1n-1+ + …+a1 + a0=0
1．特征根均为单根： 则齐次通解为：
1≠2≠…≠n
10
§5–2 离散时间系统的数学模型
一、线性时不变离散时间系统
1．离散系统：激励和响应都是离散信号的系统
f(k)
y(k)
离散时间系统
2．分类：亦可分为线性与非线性；时不变与时变；因果与非 因果等。
时不变： f(k) → y(k) f(k-m) → y(k-m)
因果系统：响应总是出现在激励之后。即： 当k < k0 ，f(k)
(2) 初始条件y(0), y(1),…, y(n-1)(与外施激励有关)代入完全解，可确 定待定常数Ci 。
离散系统时域分析
n n 1
基本运算：各阶导数，系数乘，相加
20
二、离散系统的数学模型
• 输入是离散序列及其时移函数
• 输出是离散序列及其时移函数
x(n), x(n 1), x(n 2),....
y(n), y(n 1), y(n 2),....
• 系统模型是输入输出的线性组合 系数乘，相加，延时单元
b2
a2
y(n 2)
29
§7.4常系数差分方程的求解
• 迭代法 • 时域经典法 • 离散卷积法：利用齐次解得零输入 解，再利用卷积和求零状态解。 • 变换域法（Z变换法） • 状态变量分析法
30
一、迭代法
• 当差分方程阶次较低时常用此法
y (n) ay(n 1) x(n) n0 n2 nn y (n) ay(n 1) x(n) a
x(n)
y(n)
1 a
1 E
1 y(n) y(n 1) x(n) a
26
1
x(n 1)
E
b1
y(n)
1
x(n)
b0
E
a1
y(n 1)
y ( n) a1 y ( n 1) b0 x(n) b1 x(n 1)
27
y(n)
x(n)
1 E
y (n) a1 y (n 1) a2 y (n 2) x(n)
n
例7-3
已知描述某系统的差分方程为
yn 3 yn 1 2 yn 2 xn 1 且 y 1 0, y 2 ; 2 设激励 xn 2n , n 0; 求响应序列 yn。
12
基本运算：各阶导数，系数乘，相加
20
二、离散系统的数学模型
• 输入是离散序列及其时移函数
• 输出是离散序列及其时移函数
x(n), x(n 1), x(n 2),....
y(n), y(n 1), y(n 2),....
• 系统模型是输入输出的线性组合 系数乘，相加，延时单元
b2
a2
y(n 2)
29
§7.4常系数差分方程的求解
• 迭代法 • 时域经典法 • 离散卷积法：利用齐次解得零输入 解，再利用卷积和求零状态解。 • 变换域法（Z变换法） • 状态变量分析法
30
一、迭代法
• 当差分方程阶次较低时常用此法
y (n) ay(n 1) x(n) n0 n2 nn y (n) ay(n 1) x(n) a
x(n)
y(n)
1 a
1 E
1 y(n) y(n 1) x(n) a
26
1
x(n 1)
E
b1
y(n)
1
x(n)
b0
E
a1
y(n 1)
y ( n) a1 y ( n 1) b0 x(n) b1 x(n 1)
27
y(n)
x(n)
1 E
y (n) a1 y (n 1) a2 y (n 2) x(n)
n
例7-3
已知描述某系统的差分方程为
yn 3 yn 1 2 yn 2 xn 1 且 y 1 0, y 2 ; 2 设激励 xn 2n , n 0; 求响应序列 yn。
12