化工热力学相平衡
化工热力学第五章

比较泡点计算、露点计算和闪蒸计算可 知,在泡点时,液相组成等于总组成,汽 相分率等于0;在露点时,汽相组成等于总 组成,汽相分率等于1;闪蒸时,汽、液相 组与总组成均不相等,汽相分率在0和1之 间。
4 状态方程法(EOS法) 计算混合物的汽液平衡 状态方程法计算混合物汽液平衡的主要 步骤如下: (1) 选定的一个能适用于汽、液两相的状 态方程,并结合混合法则推导出组分逸 度系数 i 的表达式(能用于汽、液两相的 组分逸度的计算);
l s Vi ( p pi ) l s s f i pi exp pi i RT
平衡关系是一个固定的三相点。
图5-4 二元部分互溶系统的等压相图
2 汽液平衡的准则和计算方法
1) 汽液平衡的准则
N元系统的汽液平衡准则可以表示如下:
fi fi
v
l
( i 1, 2, , N )
2)汽液平衡的计算方法 2.1) EOS法:
若汽、液相的组分逸度系数可以用一个 同时适合于汽、液两相的状态方程及其 混合法则来计算,这种方法称为状态方 程法,或简称EOS法。
j
组合:OB4 OB2 OB3 (是加权因子)
6 状态方程+活度系数法(EOS+法)
计算混合物的汽液平衡
EOS+法分别采用两个模型来分别计
算汽相和液相的组分逸度。若采用对称归
一化定义的活度系数,则平衡准则可以转
化为
yi i p f i x i i
l
v
(i 1, 2, , N )
l l
数),则汽液平衡准则为
fi fi
pห้องสมุดไป่ตู้i yi f i xi i
化工热力学 第五章 相平衡

A)汽相为理想气体混合物,液相为理想溶液。 B)汽相和液相都是理想溶液。 C)汽相是理想气体混合物,而液相是非理想溶液。 D)两相都是非理想溶液。 5.2.1、相平衡的处理方法 状态方程法:用状态方程来解决相平衡中的逸度系数
ˆ iv yi P li xi P ˆ
活度系数法:液相的逸度用活度系数来计算
s s i i
5.3.2.2) 泡点温度和组成的计算(BUBLT)
已知:平衡压力P,液相组成xi,求 平衡温度T,汽相组成 yi 假设T,确定Pis 计算yi 否
y
i
1
是
园整
5.3.2.3 露点压力和组成计算(DEWP)
已知 平衡温度T,汽相组成yi , 求平衡压力 P,液相组成xi 假设 P 计算Pis及xi
第5章
相 平 衡
在化工生产中,原料由于含有各种杂质,需要提纯进入反 应器;反应又常常是不完全的并伴有副产物,因而产物也是不 纯的,也需要进一步处理,才能得到产品。所有这些都离不开 分离操作,典型的分离操作有精馏(VLE)、吸收(GLE)、 萃取(LLE)、结晶(SLE)等,他们的投资常达整个工厂投 资的一半以上,对有些行业如石油和煤焦油加工等,甚至达到 80%--90%,这些分离都需要相平衡数据。 5.1 相平衡基础 5.1.1、相平衡的判据 何谓相平衡:
例:乙醇(1)----苯(2)溶液,含乙醇80%(mol%),求该溶液在 750mmHg时,的沸点及饱和蒸汽组成。已知乙醇---苯系统有一恒沸 混合物,此混合物含44.8%乙醇,在760mmHg时的沸点为68.24oC (忽略温度对活度系数的影响。 乙醇
苯
lg P1S 8.04494
1554 .3 222 .65 t
化工热力学 第五章

露点:当第一个液滴在一定压力下出现时的温度。
恒沸点: 达到平衡时汽液两相组成相等,即xi=yi。
沸程:
南阳理工学院
生化学院
化工热力学
第五章
相平衡热力学
二元组分汽液平衡关系,不是一条
线来描述的,而是用一个区域来描
述的,图中实线为泡点线MCm,虚线 为露点线NCm,不同的溶液组成,就 对应不同的汽液平衡关系,在整个 溶液范围内组成了一个上拱形的泡 K P
p2
液
C1 T C1
p
等压面
p1
等温面
K
0 汽
x1 , y1
TB1
1
T
U
图5-2二元汽-液平衡图
南阳理工学院
生化学院
化工热力学
第五章
相平衡热力学
T y1露点线
p=常数 A B C D E C” D” V
等x,y面线
T2
T
V/L B’ T’ C’ D’
等压面
T1
T x1泡点线 x1 y1 x1 , y1 0 1 图5-3(a) 二元气液平衡T-x-y图
化工热力学
第五章
相平衡热力学
第五章
第七章
相平衡
南阳理工学院
相 平 衡 热 力 学
生化学院
化工热力学
第五章
相平衡热力学
目的和要求:
混合物相平衡理论是论述相平衡时系统T、p 和各 相组成以及其它热力学函数之间的关系与相互间的 推算。 相平衡是分离技术及分离设备开发、设计的理论 基础。
即在一定温度T,压力p下处于平衡状态的多相多组分 系统中,任一组分 i 在各相中的组分逸度必定相等。
南阳理工学院
高等化工热力学PPT.

由于实验条件的限制,大部分气体溶解度数据或Henry常数 是在298.15K下测定的,需要建立气体溶解度与温度的关系。
Hildebrand法 ln x2 ΔS2
ln T p R
ln
x2 T T2
ln
x2 T T1
ΔS2 R
ln
T2 T1
S2 为气体溶质的微分溶解熵。
7相平衡计算—有模型法
7相平衡计算—有模型法
泡点温度计算
已知x和p计算y和T,根据相平衡方程及平衡常数的定义,有:
yi Ki xi
计算所得的气相组成必须满足归一化条件,即
iK1 yi iK1Ki xi 1
上式即为泡点方程。若汽液相用统一的状态方程,则:
f (T ) iK1i(L)xi /i(V) 1 0
若汽液用状态方程,液相用活度系数模型,则:
K
*( ) Hi ( m )
(mi(
)
/
mo )
( ) i,III
K
*( ) Hi ( c )
(ci(
)
/
co )
( ) i,IV
K ( ) i
f *( ) i
( ) i,I
/
p
( ) i
K *( ) Hi
( ) i,II
/
p
( ) i
f *( ) i
pi*i*
exp[Vm*,(iL) ( p
p1* p2*
1
7相平衡计算—有模型法
已知各组分的无限稀释活度系数,则
12 (x1
0)
1,I
p1*
/
p2*
12 (x1
1)
p1*
/
2,I
p2*
化工热力学第6章 相平衡

^
由前知,逸度系数的定义为:
^
i
fi xiP
^^
fi i xiP
^^
写成通式: fi i ZiP
^V ^V
对 V 相 iyiZfi i yiP
^L ^L
对 L 相 ixiZfi i xiP
汽液平衡的准则和计算方法
(2)由活度定义式计算
^
^
ai
fi fi0
^
(3)EOS+γi法 对汽相逸度用逸度系数来表示
对液相逸度用活度系数来表示
VLE时
^V ^L
fi fi
^V ^ V
fi i yiP
^L
fi ixifi0L
相平衡的判据与相律
⒊ 由逸度的定义 dG idRT ln ˆfd i等温 和积分上式可得
fˆi fˆi .. .fˆi...i 1 ,2 ,.N .( ..T ,P ) 恒 ,
各相在同样的温度、压力下达到平衡 时,每一个组分在各相中的逸度相等。实 际当中,这个式子最具有实用价值。
自由度为1,平衡时 ,只要P 一定,对应 的T 也一定,也就是 说对于纯物质具有固 定的沸点。
汽气液平衡的相图
二元体系的P-T 图 对于二元组分,它没有固定的沸点,沸点
是对纯物质来说的,混合物只有泡点。
所谓泡点就是当第一个气泡在一定压力下 出现时的温度。与泡点相对应的还有露点,所 谓露点就是当最后一滴液体在一定压力下全部 汽化时的温度。
当恒温时的P-x 曲线低于拉乌尔定律P-x 直线 ,叫做负偏差,
3.最高正偏差体系(乙醇-苯体系)
低压下互溶体系的汽液平衡相图
在恒温时,当正偏差较小时,在整个温度 范围内不会出现总压高于轻组分处于同温下 纯态时的蒸汽压,但是当正偏差较大时,在
化工热力学--相平衡与化学反应平衡PPT(38张)

ni0
i
0 id
ni nio i
n n i( n i0 i) n 0
n n i n 0 n i0 i
yi
ni n
ni0 n0
i
如果系统中有N个组分,同时有r个独立反应发生
r
dni d i,j j
——微分检验法或点检验法
x11 x10
ln
1 2
d
x1
0——积分检验法或总体检验法
SA SB SA SB
0.02——符合热力学一致性校验
SA
A
SB
B
ln 1 2
0
x0
x1
1
汽液平衡数据的面积校验法
恒压数据检验 d p 0
x11ln
x10
12dx1xx1101
1)
,上式变为:
lnH 1lnH 1 (S )V 1 (R p T p 2 S)R A T(x2 2 1 )
该式称为Kritchevsky-Kasarnovsky方程。
溶解度与温度的关系 考虑纯溶质气体与溶液呈平衡:G1G G1
G 1G 1Gf(T,p,x1)
在等压的条件下,微分上式:
重要内容
相平衡的判据与相律
相平衡的判据
含有个相和N个组分的系统达到相平衡时
ii ....i ( i 1 ,2 ,....,N )
由逸度的定义dGi di RTdlnfˆi(等T )和上式可得
f ˆ i f ˆ i ...... f ˆ i ( i 1 ,2 ,....,N )
?相平衡的判据与相律?单元系统的汽液相平衡及其计算?液液平衡固液平衡和含超临界组分的相平衡?二元系统的汽液相平衡及其计算?第5章相平衡热力学?汽液相平衡实验数据的热力学一致性检验?重要内容??书山有路勤为径学海无涯苦作舟书到用时方恨少事非经过不知难?相平衡的判据与相律?相平衡的判据含有??个相和n个组分的系统达到相平衡时由逸度的定义等t和上式可得因此系统达到相平衡时除了各相的温度t压力p相同外组分i在各相中的逸度应相等??书山有路勤为径学海无涯苦作舟书到用时方恨少事非经过不知难?相律?表征相平衡系统强度状态的变量称作相律变量
化工热力学 第七章 相平衡

, y1
x1 p1S p
py2 x2 p2S
x2
p p1S p2S p1S
, y2
x2 p2S p
例题
7
上一内容气液平衡问题:
(1)已知:体系的压力与液相组成xi; 求:泡点温度T与气相组成yi。
(2)已知:体系的压力与气相组成yi; 求:露点温度T与液相组成xi 。
上一内容
下一内容
回主目录
例题
7
9
7.3.2 状态方程法
汽相: 液相: 平衡时
fˆiV pyiˆiV fˆi L pxiˆiL
yiˆiV xiˆiL
计算时选择一个既适合汽相又适合液
相的状态方程求 ˆiV 和ˆiL
上一内容
下一内容
回主目录
例题
7
10
补充:低压汽液平衡计算
对非极性或弱极性溶液,在温度接近或高
ˆi T , p, yi
i T , p, xi
fi0 f T , p 以Lewis-Randall定则为基准的标准态
上一内容
下一内容
回主目录
例题
7
8
dGi ViLdp RTd ln fiL 恒T
d
ln
fiL
Vi L RT
dp恒T
T , piS , fiS T , p, fi0 :
上一内容
下一内容
回主目录
7
7.3 汽液平衡的计算 根据以逸度表示的相平衡判据
fˆiV fˆiL
i 1,2,, N
7.3 .1 活度系数法
汽相: 液相: 平衡时
fˆiV pyiˆi
fˆi L fi0ˆi fi0 i xi
pyiˆi fi0 i xi
化工热力学第四章

St ,Vt ,ni
dni
0
H t ni
St , p,ni
U t ni
St ,Vt ,ni
❖ 2)意义: ❖ 化学势体现了不同条件下热力学性
质随构成旳变化,可用以描述相平衡。
❖ §4-3 相平衡准则及相律
❖ 1 相平衡准则 相平衡准则能够由均相敞开系统旳 热力学关系来推导。
V RT p
ay12 by22 2cy1 y2
dV dy1 2ay1 2by2 2cy1 2cy2
dV V 1 V (1 y1 ) dy1
RT p
ay12 by22 2cy1 y2
(1 y1 )(2ay1 2by2 2cy1 2cy2 )
RT p
a( y12
dni dni( ) dni( ) 0 dni( ) dni( ) (i 1, 2, , N )
dUt T ( )dSt( ) T ( )dSt( )
p( )dVt( ) p( )dVt( )
N
i( )dni( ) i( )dni( ) i
T ( ) T ( ) dSt( ) p( ) p( ) dVt( )
M1
M
(1
x1 )
dM dx1
dM M 2 M x1 dx1
二元混合物旳偏摩尔性质和摩尔性质图示
T,p一定
dM x1 d x1 M
M1
1
x1
d d
M x1
M1
M
M2
M M ( x1 )
M2
0
x1
1
❖ 对于N元系统,各组分旳偏摩尔性质与 摩尔性质之间旳关系是:
N M
Mi
M
j1
xj
化工热力学第七章相平衡

采用状态方程法的重点在于 ˆiV
ˆ L
,, i
的求取:
lnˆiV
ln
fˆiV pyi
1 RT
VmV
0
[
RT VmV
(
p ni
)T
,V
,nj
[ i ] ]dVmV
ln ZV
lnˆil
ln
fˆil pxi
1 RT
Vml
0
[
RT Vml
(
p ni
)T
,V
,nj
[ i ] ]dVml
ln Z l
2
ln 1
A12
A21 x2 A12 x1 A21 x2
2
ln 2
A21
A12 x1 A12 x1 A21 x2
x1 0; ln 1 A 12
x2 0; ln 2 A 21
3.如何得到模型参数A12和A21?
1) 利 1, 用 2
无论是Margules方程还是van Laar 方程均有:
有的人领带被肉汁弄脏,他会用清洁剂溶解并除 去油渍。
在这些普通的日常经历以及生理学、家庭生活、 工业等方面的许多例子中,都有一种物质从一相 到另一相的转化,这是因为当两相相互接触时, 它们倾向于交换其中的成分直至各相组成恒定。 这时,我们就说这些相处于平衡状态。
两个相的平衡组成通常有很大的不同,正是这种 差别使我们可以利用蒸馏、萃取和其它的相接触 操作来分离混合物。
§7.1 相平衡判据与相律 §7.2 汽液平衡的相图 §7.3 活度系数与组成关系式 §7.4 汽液平衡计算
§7.1 相平衡判据与相律
§7.1.1 相平衡( Phase Equilibrium) – 相平衡讲的就是物系组成(x,y)与T、
化工热力学-相平衡例题
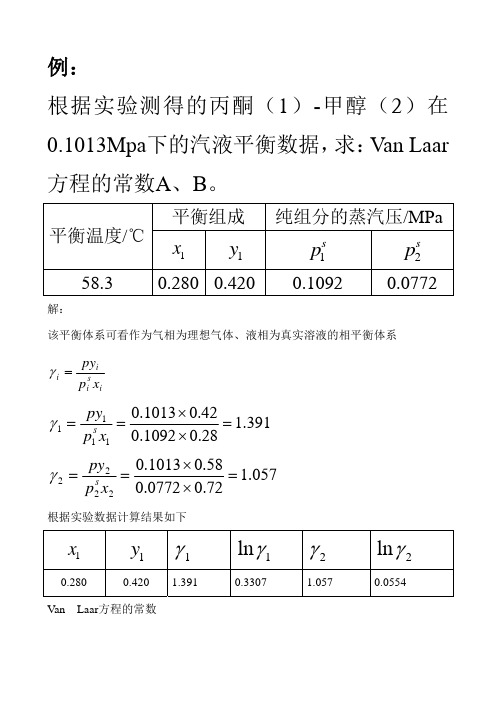
平衡组成 平衡温度/℃ 58.3
解: 该平衡体系可看作为气相为理想气体、液相为真实溶液的相平衡体系
纯组分的蒸汽压/MPa
x1
y1
ห้องสมุดไป่ตู้
p1s
0.1092
s p2
0.280 0.420
ln 1
1.652 1.082 0.693 0.432 0.372 0.202 0.148 0.0677 0.0296 0.00995
1
5.22 2.95 2.00 1.54 1.45 1.30 1.16 1.07 1.03 1.01
ln 2
0.0392 0.140 0.270 0.412 0.457 0.554 0.693 0.829 0.959 1.078
p1s x1 1 y1 p
本体系看作相对挥发度为常数,则
y1
1 s p2 x 1 s 2 2 p1 x1 1
s s p2 p2 483 0.923 上式中 s 可看作为常数,并等于恒沸点时的值, s p1 p1 524
把计算结果列成表格
x1
0.1 0.2 0.3 0.4 0.432 0.5 0.6 0.7 0.8 0.9
例: 正丙醇(1)-水(2)在 101.3kPa 下形成均 相恒沸物,恒沸温度 87.8℃,恒沸组成
x1 y1 0.432 ,此时 p1s 524mmHg ,
s p2 483mmHg , 试用 Van Laar 方程求 101.3kPa
下的 VLE 关系。
解: 该平衡体系可看作为气相为理想气体、液相为真实溶液的相平衡体系
化工热力学第4章

G
( 2) i
G
(M ) i
( I 1,2, N )
二、摩尔性质与偏摩尔性质间的关系 溶液性质M:如H,S,A,U,G,V等
纯组分性质Mi: 如 Hi,Si,Ai,Ui,Gi,Vi 等
偏摩尔性质 M :如
i
Hi ,..Si ,..Ai ,..Ui ,..Gi ,..Vi 等
偏摩尔性质与摩尔性质在热力学关系式形式上相似:
( nM ) ( n1 n2 ) M M2 n n 2 2 T , P ,n1 T , P ,n1
M M n1 n2 n2 T , P , n1 n1 因为: x1 n1 n2
(A)
H K A
F 0
B
α
J
C x2'
G
如果能证得: M dM M 2 M x1 x M x1 dx 1 1 T , P 比较式(A)和式(B),即得
(B)
x2
1
M2 GE
M为溶液的摩尔性质,则有: nM=(n1+n2)M
将nM在T,P,n1不变的条件下对n2求导,则有:
i [ ]T , P ,n ji ni
2、物理意义:
在保持T,P,{n}≠i不变的条件下,在系统中加入极少 量的i组分dni,引起系统的某一容量性质的变化。
体积增加 1.78cm3
0.1mol水 1.81cm3
甲醇(1)-水(2) X1=0.3 X2=0.7
3
加0.1mol水后的甲醇(1)-水 (2)X1=0.3 X2=0.7
U t 则: S t
对于含N个组分的敞开系统:
化工热力学_Chapter5-01_201505

i 1
高温低压下,构成物系的组份,其分子结构差异较大。低 压下的非轻烃类,如水与醇、醛、酮…… 所组成的物系。
27
(3)理想体系 ——V、L两相都符合L-R定则 石油化工过程中,中压(1.5~3.5 MPa)下轻烃物系或 裂解气均可视为理想体系。 (4)非理想体系 V相是非理想溶液 L相符合L-R定则
i i i i
fi 为标准态的逸度。
取以Lewis-Randall定则为基准的标准态:
L V fi fi L is pis exp s i dp pi RT p
Poynting 因 子,对压力 影响的校正
20
完全理想系的p-x-y相图 服从Raoult定律
s pA xA pA s p B xB p B
p p A pB
s s xA pA 1 x A pB s s s pB xA pA pB
21
1)一般正偏差体系 当 恒 温 时 的 px 曲 线 高 于 Raoult 定 律 的 px 直 线 , 此 体 系 为 正偏差体系,γi>1
22
2)一般负偏差体系 当 恒 温 时 的 p-x 曲 线低于Raoult定律 的 p-x 直 线 , 此 体 系为负偏差体系。 γi<1
23
3)最大正偏差体系
当正偏差较大时,在p-x曲线上 就可以出现极大值,γi>1; 该点x=y, 称为共沸点; 由 于 该 点 压 力 最 大 , 温 度 最 低,所以称为最大压力(或最低 温度)共沸点; 对于这类体系,采用一般的精 馏方法难以实现分离,必须采用 特殊分离法。
ˆV f ˆL f i i
i 1, 2,, N
(5-7)
化工热力学

(nU ) [ ] nS ,n P (nV )
6/129
化工热力学
Chemical Engineering Thermodynamics
( nU ) d ( nU ) d ( nS ) ( nS ) nV ,n
T
( nU ) d ( nV ) ( nV ) nS ,n
中组分i 在各相中的化学势相等,即:
i i
混合物中组分i 在各相中的逸度相等,即:
ˆ ˆ fi fi
在模型导出及计算中具有非常重要的应用价值。
14/129
化工热力学
Chemical Engineering Thermodynamics
4. 相平衡的应用
相平衡是一切分离 技术及分离设备开 发、设计的理论基 础和关键。 分离技术:精馏、 吸收、吸附、萃取、 结晶。
10/129
化工热力学
Chemical Engineering Thermodynamics
对于上面推导出的热力学关系式,使用时要
注意以下几点:
⑴适用于敞开体系、封闭体系;
⑶当dni=0时,简化成适用于定组成、定质量体系; ⑷Maxwell关系式用于可变组成体系时,要考虑组成 不变的因素,如:
(
(
第四章 均相敞开系统热力学及相平衡准 第四章 均相敞开系统热力学及相平衡准
dU TdS PdV
dH TdS VdP dA SdT PdV
dG SdT VdP
U f S、V H f S、P
A f T、V G f衡准 第四章 均相敞开系统热力学及相平衡准 可通过H=U+PV;A=U-TS;G=H-TS来证明。
化工热力学习题七(附参考答案)

4.
汽液平衡关系
ϕˆ
v i
yi
=
ϕˆ
l i
xi
的适用的条件
(A)
A 无限制条件 B 低压条件下的非理想液相 C 理想气体和理想溶液 D 理想溶液和 非理想气体
5. 汽液平衡关系 Pyi = Pisγ i xi 的适用的条件 (B)
A 无限制条件 B 低压条件下的非理想液相 C 理想气体和理想溶液 和非理想气体
(错) 3. 在一定压力下,组成相同的混合物的露点温度和泡点温度不可能相同。
(错,在共沸点时相同) 4. 一定压力下,纯物质的泡点温度和露点温度是相同的,且等于沸点。
(对) 5. 纯物质的汽液平衡常数K等于1。
(对,因为 x1 = y1 = 1)
6. 理想系统的汽液平衡Ki等于1。 (错,理想系统即汽相为理想气体,液相为理想溶液,)
D 理想溶液
6. 汽液平衡关系 Pyi = Pis xi 的适用的条件 (C)
A 无限制条件 B 低压条件下的非理想液相 C 理想气体和理想溶液 和非理想气体
D 理想溶液
二、选择题
1. 欲找到活度系数与组成的关系,已有下列二元体系的活度系数表达式,α, β 为常数,
请决定每一组的可接受性 。 (D)
A γ 1 = αx1;γ 2 = βx2
B γ 1 = 1 + αx2 ;γ 2 = 1 + βx1
C ln γ 1 = αx2 ;ln γ 2 = βx1
D ln γ 1 = αx22 ; ln γ 2 = βx12
2. 二元气体混合物的摩尔分数y1=0.3,在一定的T,P下,ϕˆ1 = 0.9381,ϕˆ 2 = 0.8812 ,则此
时混合物的逸度系数为 。 (C)
化工热力学第6章 相平衡

3.闪蒸计算。
泡点计算:即确定某一组成的液体混合物在一定压力 的沸点(泡点)或一定温度下的蒸汽压,以及平衡汽相 组成。
露点计算,即确定某一组成的汽体混合物在一温度 下的露点压力或一定压力下的露点温度,以及平衡液 相组成。。
闪蒸计算:液体流过阀门等装置.由于压力突然降 低而引起急骤蒸发,产生部分汽化,形成互成平衡的 汽、液两相(也可以是汽相产生部分冷凝)。在T、p条 件下,对于总组成为zi的混合物分为相互成平衡的汽、 液两相,闪蒸计算的目的是确定汽化(或冷凝)分率 和平衡时气、液相的组成。
汽液平衡的准则和计算方法
点Mp是这种组成体系中 两相共存的最高压力,通称” 临界冷凝压力”。
饱 和
Mp
液
体
Cm
MT
0. 9
饱和蒸 汽
T
临界区域相特征部分的P-T 图
K——L逆向冷凝 M——J逆向蒸发
等压过程
J——M逆向蒸发 M——J逆向冷凝
等温过程
气液平衡的相图
3.逆向凝聚现象的意义
逆向现象在天然气深井的开采过程中很重要,油 品自地底层向地面举升的过程,可以近似看作是 等温减压的过程。由于出油管的体积是一定的, 为了单位时间油品的产量最大,油品以液相采出 最为经济。根据相图,在1-2线上,J点的液相量 最大。于是,控制出口压力为J点的压力,可以保 证油品的举升产量最大。
汽液平衡的准则(计算理论基础式)
ˆ fivˆ fil i 1 ,2 , ,N
各相在同样的温度、压力下达到平衡 时,每一个组分在各相中的逸度相等。
化工热力学

气液两相平衡相是指系统的某一部分具有相的物理和化学性质,具有相同的组成,并且与另外的相以一定的边界隔开。
出现在世有产品里的大多数的相相是液态烃和气相。
水也是普遍存在的另一个液态相。
在给定的系统里,当描述变化的变量随着时间和位置的改变而保持恒定时,液态烃、气相和水这些相将会平衡共存。
而决定平衡状态的主要变量是系统的温度,压力和组分。
对于设计表面分离装置和改进组分模型,不同相能够共存的条件是非常值得考虑并且具有实践价值的重要问题。
这些计算的类型是以平衡常数的原理为基础的。
一、 平衡常数一给定组分的平衡常数i K 是指组分的气相的摩尔分数yi与液相摩尔分数xi 之比。
在数学上,它们的关系是i i i x y K /= (5----1)在41003.7⨯2/m kg (100磅/2英寸)的压力下,Raoult 和Dalton 的定律为对于理想溶液方法提供了一个预测平衡常数的简化的方法。
Raoult 定律是指多组分系统中单一组分所产生的局部压力i P 等于它的液相摩尔分数i x 与该祖父的气相压力Pvi 的乘积即i P =i x Pvi (5----2) i P ------组分i 的局部压力,磅/2英寸)Pvi ------组分i 的气相压力,磅/2英寸)i x ------组分i 的液相摩尔分数Dalton 定律是指某一组分的局部压力等于它的气相摩尔分数与系统的总压力的乘积,即iP =iy P(5----3)P------系统总压力,磅/2英寸在平衡状态下,根据上面的定律可知,被某一组分气相作用产生的局部压力必须与该液相作用产生的局部压力平衡。
因此,将描述两大定律的方程结合得i x Pvi =i y P ,整理以上关系式并代入平衡常数定义式得iy /ix =Pvi/P=i K(5----4)这个方程表明对理想溶液,不管烃类混合物的组分如何,平衡常数仅仅有体现系统压力和温度的作用。
(第一章表明,组分的气相压力有体现温度的作用。
化工热力学 第六章 相平衡.

5
2019/9/8
2 相律
F N 2
相律是各种平衡系统都必须遵守的规律。
相数π讨论:
(1)甲醇-水二元汽液平衡 甲醇-水全浓度下互溶, 仅存在一个液相, 和一个与
之平衡的汽相. π = 2
(2)戊醇-水二元汽液平衡 戊醇-水不能在全浓度下互溶, 存在两个液相, 和一
个汽相. π = 3 在有限浓度范围内, 戊醇-水能够互溶, 仅存在一个
fˆil
fi
l i
xi
(i
1,2,, N )
分析:
v难于
i
计算,
l i
重点计算
2019/9/8
8
1 状态方程法 (Equitions of States)
汽、液相逸度均用逸度系数表示
pyi iv pxi il yi iv xi il
ln i
fi是i组元标准态下的逸度(L R) fi fil (i 1,2,, N )
2019/9/8
10
fi fil (i 1,2,, N )
fi1
fis
exp[ Vil ( p RT
pis )]
Pi sis
exp[ Vil ( p RT
pis )]
pyiˆiv
pyi pis i xi (i 1,2,, N )
对于低压的二元汽液平衡:
p1 py1 p1s1x1
p2 py2 p2s 2 x2
p p1 p2 p1s1x1 p2s 2 x2
2019/9/8
y1
p1s 1x1 p1s 1x1 p2s 2 x2
相平衡名词解释

相平衡名词解释
相平衡(phase equilibrium)是指多相系统中各相变化达到的极限状态。
此时在宏观上已经没有任何物质在相际传递,但在微观上仍有方向相反的物质在相际传递,且速度相等,故传递的净速度为零.化工热力学研究的两相系统的平衡,有气液平衡、气固平衡、汽液平衡、汽固平衡、液液平衡、液固平衡和固固平衡;相数多于2的系统,有气液固平衡、汽液液平衡等。
相平衡是热力学在化学领域中的重要应用之一。
研究多相体系的平衡在化学、化工的科研和生产中有重要的意义,例如:溶解、蒸馏、重结晶、萃取、提纯及金相分析等方面都要用到相平衡的知识。
一个系统可以是多组分的并含有许多相。
当相与相间达到物理的和化学的平衡时,则称系统达到了相平衡。
相平衡的热力学条件是各相的温度和压力相等,任一组分在各相的化学势相等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(4) 非理想体系
V相是非理想溶液 L相符合L-R定则
如压力较高的烃类物系。
第三类和第四类都是碳氢化合物的混合物所组成的物系, 所不同的是第四类的压力比第三类的高。
(5) 完全非理想体系 V、L两相都是非理想溶液。
高压下,构成物系的组份,其分子结构差异较 大,皆属于这类体系。
18
2.VLE计算的基本问题:
dGT,P 0
对于封闭体系,满足其中一个条件即为平衡态。
2
二. 相平衡的判据
相平衡的判据,较常用的有三个
1. dGT,P 0
2.
i
i
i
i
^ ^ ^
^
3. f i f i f i f i
三. 相律
由物化知:相律
F=N –π+2
(7-4) (7-5)
(7-6)
3
5.2 互溶体系VLE相图
0 i
—液态标准态的逸度
fi0 f T , P
基于L-R定则
f
0 i
fiL T , P
23
由P56 式(3-90)
f
L i
s i
Pis
exp
1 RT
P psi
ViL dP
^
i
yiP
ixiiSPiSexp
1 RT
P
ViLdP (5-8)
PiS
该式是用于汽液平衡计算的通式。
24
(2)EOS法
(三)热力学计算
若体系为化学体系
yi P i x i PiS
12
1P1S 2 P2S
P=P1+P2= 1x1P1S + 2 x 2 P2S
对多元体系
P yiP i xiPiS
28
(2)汽液平衡比Ki和相对挥发度 ij
汽液平衡比:在汽液平衡时,组分i
在汽相中的摩尔分数与液相中的摩尔 即 分数的比值.
相对挥发度:两组份汽液平衡比的比值。
对于化学体系,由上边知:
汽液平衡比 相对挥发度 对二元体系
fi fi
两种基础式
一种是基于逸度定义的基础式; 另一种是基于活度定义的基础式.
(1)由逸度系数的定义式计算
^
由前知,逸度系数的定义为:
^
i
fi xiP
^^
f i i xiP
^^
写成通式: f i i ZiP
^V ^ V
对V相 Z i yi f i i yiP
^L ^ L
对L相 Z i xi f i i xiP
已知数据:60℃时,两组分的饱和蒸气压
P1S 52.39kPa
P2S 52.26kPa
该温度下体系的无限稀释活度系数为
二元体系1-2,
1
1.96,
2
1.48
二元体系1-3,
1
3.55,
3
15.1
二元体系2-3,
1
2.04,
3
3 .89
31
分析:已知 2,4-二甲基戊烷(1)+苯(2) 2-甲基戊醇-2,4(3)
60℃时, P1S 52.39kPa
P2S 52.26kPa
二元体系:
i
物系
i
1-2 1.96 1.48
1-3 3.55 15.1
2-3 2.04 3.89
恒沸点时 xi=yi 求:x3=?
12 =1
要解决这一问题,必须具备萃取精馏的热力学基础。
32
(一)为何加入第三组分
当体系偏离理想溶液的程度很大时,就会出现恒沸点, 在这一点,用简单的精馏法是无法将其混合物分开的, 必须采用特殊的分离方法。萃取精馏就是通过加入第 三组分,改变了原溶液组分的相对挥发度,使在全浓 度范围内不出现相对挥发度等于1的现象。并不是随 便加入任何物质就能使其分开的,第三组份必须满足 一定条件才能够起到萃取剂的作用。
二. 低压下互溶体系的汽液平衡相图
对理想溶液(或拉乌尔定律)产生偏差的情况有四种。 1.一般正偏差体系(甲醇-水体系) 2.一般负偏差体系(氯仿-苯体系) 3.最大正偏差体系(乙醇-苯体系) 4.最小负偏差体系(氯仿-丙酮体系)
12
1.一般正偏差体系
当恒温时的P~x曲线 高于拉乌尔定律的 P~x直线,此体系为 正偏差体系。γi>1
P 在正常情况下,当在恒温下,
压力升高 气相 (V)
液相(L)
在 CmMT区域内,恒温下,随压力升高,
出现液相(L)
气相 (V)
这个区域就成为等温逆向凝聚区。
Cm MT
T
9
(2)等压逆向凝聚现象
在正常情况下,当在恒压下,
P
温度升高
液相(L)
气相 (V)
在 MpCm区域内,恒压下, 温度升高
气相(V)
P
等温
共沸点
➢当正偏差较大时,在P~x曲线上
就可以出现极大值,γi> 1 ;
➢在这一点上,x=y, 此点称为
共沸点;
0
➢由于这一点压力最大,温度最
T
低,所以称为最大压力(或最
低温度)共沸点;
➢对于这种体系,用一般精馏法
是不能将此分离开的,必须要
采用特殊分离法。
0
x1,y1
1
等压
1
x1,y1
15
4.最小负偏差体系
33
(二)第三组分(萃取剂)应具备的特点
1. 第三组份与原体系组分能互溶 2. 对体系中某组分有选择性作用
3. 在体系温度下, P3S 较小,使其能很容易地从原组分中分离。
当第三组份满足以上条件,就可以作为萃取剂加入体系。但加入第 三组分的量多少为宜?加入量多了,造成了浪费,加入量少了又不 能把原体系组分分开,到底加多少为合适?
1 RT
P psi
ViL dP
26
二.低压下VLE的计算
1.完全理想体系(物理化学讲过) 2.化学体系 对于低压高温的体系,当其组成体系的各组分的
分子结构差异较大时,汽相可以看作是理想气体, 但其液相由于分子间作用力差异较大,因而不能 看作是理想溶液。对于这类体系,称为化学体系.
27
(1) 计算式:
➢泡点:当第一个气泡在一定压力下出现时的温度。 ➢露点:当最后一滴液体在一定压力下全部汽化时的 温度。
5
➢二元组分汽液平衡关系,不是 一条线来描述的,而是用一个区 域来描述的,图中实线为泡点线 MCm,虚线为露点线NCm,不 同的溶液组成,就对应不同的汽 液平衡关系,在整个溶液范围内 组成了一个上拱形的泡点面和下 拱形的露点面。 ➢混合物的临界点Cm ➢泡点面的上方为过冷液体,露 点面的下方为过热蒸汽。
^V ^ V
f i i yiP
^L ^ L
f i i xiP
^V ^L
fi fi
^V
^L
i yiP i xiP
式中:
^V ^L
i , i
由EOS计算
^V
^L
i yi i xi
(5-9)
这种方法是今后发展的方向,难度还是比较大的。
25
(3)γi法
活度系数法是将汽液两相都用活度系数来表示
L 相: V 相:
yi
i x i PiS
P
i x i PiS i x i PiS
y1
1x1P1S
P
1x1P1S
1x1P1S 2 x 2P2S
对二元体系
y2
2x2P2S
P
2x2P2S 1x1P1S 2x2P2S
P 1x1P1S 2 x2 P2S
30
(4)应用举例[P166-172 例7-1~7-5]
(2) 化学体系
V相是理想气体 L相是非理想溶液
^
i 1
i 1
高温低压下,构成物系的组份,其分子结构差异较大。
低压下的非轻烃类,如水与醇、醛、酮……….所组成的
物系就属于这一类。
17
(3) 理想体系 V、L两相都符合L-R定则。
石油化工,中压(1.5~3.5MPa)下轻烃物 系或裂解气都视为理想体系
一. 二元体系的P-T图
纯组分的PT图可用两维坐 标表示出来。
L 3相
c 临界点
溶化线 P
汽化线
S相 2 三相点 V相
1 升华线
T
4
➢纯组分的汽液平衡表现为自由度为1; ➢汽液平衡时,当P一定,对应的T也一定,也就是说对 于纯物质具有固定的沸点。 ➢对于二元组分,它没有固定的沸点,沸点是对于纯物 质而言的; ➢对于混合物,只有泡点。
P
等温
最小压力(最高温度)
共沸点
共沸点x=y, γi<1
0
x1,y1
1
T 等压
0
1
x1,y1
16
5.3 VLE的计算
一.概述
1.VLE的分类
五种类型:
(1) 完全理想体系
V相是理想气体 L相是理想溶液
Pi=yiP
Pi=xiPis
高温低压下,构成物系的组份,其分子结构相似,如
0.2MPa下的轻烃混合物系。
前面我们已经推出VLE的基本计算式为
^
i
yiP
i
x
i
S i
PiS
exp
1 RT
P
ViL dP
PiS
(5-8)
^
∵低压高温 i 1
∴式(5-8)可写为
S i
1
VLi<<RT
yi P i x i PiS
exp
1 RT
P PiS
ViL dP
1
对于二元溶液
P1 y1P 1x1P1S P2 y2P 2 x 2P2S 2 (1 - x1 )P2S
