非参数统计十道题
非参数统计答案范文

非参数统计答案范文1. 考察Mann-Whitney U检验:问题:对两组数据进行比较,数据不符合正态分布,要判断两组数据是否有显著差异。
如何选择合适的非参数检验方法?答案:Mann-Whitney U检验是一种适用于比较两组独立样本的非参数检验方法,适用于数据不符合正态分布的情况。
2. 考察Wilcoxon符号秩和检验:问题:对同一组数据进行配对比较,数据不符合正态分布,如何选择合适的非参数检验方法?答案:Wilcoxon符号秩和检验是一种适用于配对样本的非参数检验方法,适用于数据不符合正态分布的情况。
3. 考察Kruskal-Wallis检验:问题:有三组数据需要比较,但数据不符合正态分布,如何选择合适的非参数检验方法?答案:Kruskal-Wallis检验是一种适用于比较多组独立样本的非参数检验方法,适用于数据不符合正态分布的情况。
4. 考察Friedman检验:问题:有三组配对数据需要比较,但数据不符合正态分布,如何选择合适的非参数检验方法?答案:Friedman检验是一种适用于比较多组配对样本的非参数检验方法,适用于数据不符合正态分布的情况。
5. 考察Mood's中位数差异检验:问题:有两组独立样本数据需要比较,数据不符合正态分布,如何选择合适的非参数检验方法?答案:Mood's中位数差异检验是一种适用于比较两组独立样本的非参数检验方法,适用于数据不符合正态分布的情况。
6.考察符号检验:问题:对一组配对数据进行比较,但数据不符合正态分布,如何选择合适的非参数检验方法?答案:符号检验是一种适用于配对样本的非参数检验方法,适用于数据不符合正态分布的情况。
7.考察秩和检验:问题:有两组独立样本数据需要比较,如何选择合适的非参数检验方法?答案:秩和检验是一种适用于比较两组独立样本的非参数检验方法。
8. 考察Kolmogorov-Smirnov检验:问题:有一组数据需要验证其服从一些特定分布,如何进行检验?答案:Kolmogorov-Smirnov检验是一种非参数检验方法,可以用于验证数据是否符合一些特定分布。
非参数统计作业

非参数统计2010-11-14一、思考题1.当一组配对计量资料既可作参数又可作非参数检验,应首选何种检验方法,为什么?2.两小样本比较的假设检验首先应如何考虑?3.当总体分布类型不清楚时最好采用何种检验方法?4.参数检验和非参数检验的区别何在,各有何优缺点?5.非参数检验是针对总体分布之间的比较吗?6.简要回答进行非参数统计检验的适用条件。
7.你学过哪些设计的秩和检验,各有什么用途?8.试写出非参数统计方法的主要有缺点。
二、选择题1.配对比较秩和检验的基本思想是:若检验假设成立,则对样本来说( )。
A .正秩和与负秩和的绝对值不会相差很大 B .正秩和与负秩和的绝对值相等 C .正秩和与负秩和的绝对值相差很大 D .不能得出结论 E .以上都不对2.设配对资料的变量值为1X 和2X ,则配对资料的秩和检验是( )。
A .把1X 和2X 的差数从小到大排序 B .分别按1X 和2X 从小到大排序 C .把1X 和2X 综合从小到大排序 D .把1X 和2X 的和数从小到大排序 E .把1X 和2X 的差数的绝对值从小到大排序 3.下列哪项不是非参数统计的优点( )。
A .不受总体分布的限制 B .适用于等级资料 C .适用于未知分布型资料 D .适用于正态分布资料 E .适用于分布呈明显偏态的资料 4.等级资料的比较宜采用( )。
A .秩和检验B .F 检验C .t 检验D .2检验 E .u 检验 5.在进行成组设计两样本秩和检验时,以下检验假设哪种是正确的( )。
A .两样本均数相同B .两样本的中位数相同C .两样本对应的总体均数相同D .两样本对应的总体分布相同E .两样本对应的总体均数不同6.以下检验方法中,不属于非参数检验方法的是( )。
A .Friedman 检验 B .符号检验 C .Kruskal-Wallis 检验 D .Wilcoxon 检验 E .t 检验7.成组设计两样本比较的秩和检验中,描述不正确的是( )。
非参数统计

1.某航空公司为了了解旅客对公司的服务态度的满意程度,对50名旅客作调查.要求他们写出对乘机服务,机上服务和到到达机场服务的满意程度.满意程度的评分从0到100.分数越大,满意程度越高.下表是收集到的数据.乘机服务机上服务到达机场服务71 49 5884 53 6384 74 3787 66 4972 59 7972 37 8672 57 4063 48 7884 60 2990 62 6672 56 5594 60 5284 42 6685 56 6488 55 5274 70 5171 45 6888 49 4290 27 6785 89 4679 59 4172 60 4588 36 4777 60 7564 43 6172 76 3771 25 7469 47 1690 56 2384 28 6286 37 5970 38 5486 72 7287 51 5777 90 5171 36 5575 53 9274 59 8276 51 5495 66 5289 66 62 85 57 67 65 42 68 82 37 54 82605689 80 64 74 47 63 82 49 92 90 76 7078 52 72由Minitab 得乘机服务,机上服务和到达机场服务直方图为:F r e q u e n c y968880726412108642His togr am ofF r e q u e n c y908070605040309876543210His togr am ofF r e q u e n c y908070605040302014121086420His togr am of箱线图:Boxplot of 9590858075706560Boxplot of 9080706050403020Boxplot of1009080706050403020102.为检验两种燃料添加剂对客车每加仑汽油行使里程数的影响是否不同,随即挑选12辆,让每一辆车都能先后使用这两种添加剂,12辆汽车使用这两种添加剂每加仑汽油行使里程数的检测结果如下:添加剂1 添加剂222.32 21.2525.76 23.9724.23 24.7721.35 19.2623.43 23.1226.97 26.0018.36 19.4020.75 17.1824.07 22.2326.43 23.3525.41 24.9827.22 25.90分别用符号秩和检验法和符号检验法检验两种添加剂有没有差异,试比较两种方法哪一比较可信?解:一.符号秩和检验法:(1).用minitab计算出差值得表:添加剂1 添加剂2 差值22.32 21.25 1.0725.76 23.97 1.7924.23 24.77 -0.5421.35 19.26 2.0923.43 23.12 0.3126.97 26.00 0.9718.36 19.40 -1.0420.75 17.18 3.5724.07 22.23 1.8426.43 23.35 3.0825.41 24.98 0.4327.22 25.90 1.32(2).minitab进行检验得:Wilcoxon Signed Rank Test: C3Test of median = 0.000000 versus median not = 0.000000Nfor Wilcoxon EstimatedN Test Statistic P MedianC3 12 12 70.0 0.017 1.230二:符号检验法:Sign Test for Median: C3Sign test of median = 0.00000 versus > 0.00000N Below Equal Above P MedianC3 12 2 0 10 0.0193 1.195One-Sample T: C3Variable N Mean StDev SE Mean 95% CIC3 12 1.24083 1.35497 0.39115 (0.37992, 2.10174)1某部门有26位女职工和24位男职工.他们的年收入如下:女职工男职工28500 30650 39700 3370031000 35050 33250 3630022800 35600 31800 3725032350 26900 38200 3395030450 31350 30800 3775038200 28950 32250 3670034100 32900 380503610030150 31300 34800 2655033550 31350 32750 3920027350 35700 38800 4100025200 35900 29900 4040032050 35200 37400 3550026550 30450(1)使用Mood中位数检验法回答问题:收入和性别有没有关系?女职工的收入是否比男职工的收入低?(2)使用Wilcoxon秩和检验法回答上述问题。
非参数统计题

一、填空题(每空2分,共计30分)1、性别属于_______ 尺度的测量层次,文化程度属于___________ 尺度的测量层次,温度属于__________ 尺度的测量层次,年龄属于__________ 尺度的测量层次。
2、某一序列的观察值为2,5,3,乙8,9,6,4,16,10,则上游程数为 ___________ ,下游程为_______ ,第一个下游程的长度是__________ 。
3、两组独立的随机样本的观察值分别为:第一组(XX): 9,12,3,7 第二组(Y): 5,8,6,14,16则第一组X的等级和T x= _________ ,第二组Y的等级和T y= _________ ,Y的评分值先于X的总次数U= ______ ,游程的总数目V= _________ 。
4、妇女的教育水平对志愿的影响,交叉列联表如下:则列边缘次数为 ___________ ,不考虑X,直接预测Y时产生的误差巳= _____________ ,用X预测Y时产生的误差E2 = ______ ,非对称形式的A系数hyx = ____________。
(10分)某地一周内个日患忧郁症的人数分布如表所示,请用2检验法检验一周内个日人们忧郁数是否满足1:1:2: 2: 1:1: 1?(显著性水平〉=0.05)三、(20分)试根据下表的数据分别用符号检验和Wilcox on符号秩检验法检验学生接受某种方法训练前后成绩是否存在显著差异,训练能否提高学生的成绩?(显著性水平二=0.05)四、(10分)随机抽取3个班级的学生,得到21个成绩样本,如表所示,试用Kruskal-Wallis检验法检验3五、(10三个月后的体重,试用Friedman检验法检验在这4个时期,10个人的体重有无发生显著的变化?(显著性水平:.=0.05)X 的秩:1,2,5,6,4,3Y 的秩:5,3,6,4,2,1分别用S p e a r m a n等级相关系数及K e n d a l l秩相关系数分析两位裁判员评分的相关程度。
非参数统计题目及答案

1.人们在研究肺病患者的生理性质时发现,患者的肺活量与他早在儿童时期是否接受过某种治疗有关,观察3组病人,第一组早在儿童时期接受过肺部辐射,第二组接受过胸外科手术,第三组没有治疗过,现观察到其肺活量占其正常值的百分比如下:这一经验是否可靠。
解:H 0:θ2≤θ1≤θ3 H 1:至少有一个不等式成立可得到 N=15由统计量H=)112+N N (∑=Ki i N R 1i 2-3(N+1)=)(1151512+(32×6.4+29×5.8+59×11.8)-3×(15+1)=5.46查表(5,5,5)在P(H ≥4.56)=0.100 P(H ≥5.66)=0.0509 即P (H ≥5.46)﹥0.05 故取α=0.05, P ﹥α ,故接受零假设即这一检验可靠。
2.关于生产计算机公司在一年中的生产力的改进(度量为从0到100)与它们在过去三年中在智力投资(度量为:低,中等,高)之间的关系的研究结果列在下表中:值等等及你的结果。
(利用Jonkheere-Terpstra 检验) 解:H 0:M 低=M 中=M 高 H 1:M 低﹤M 中﹤M 高U 12=0+9+2+8+10+9+10+2+10+10+8+0.5+3=82.5 U 13=10×8=80U 23=12+9+12+12+12+11+12+11=89 J=∑≤jijUi =82.5+80+89=251.5大样本近似 Z=[]72)32()324121i 222∑∑==+-+--ki i i ki n n N N n N J ()(~N (0,1)求得 Z=3.956 Ф(3.956)=0.9451取α=0.05 , P >α,故接受原假设,认为智力投资对改进生产力有帮助。
非参数统计题目及答案

1.人们在研究肺病患者的生理性质时发现,患者的肺活量与他早在儿童时期是否接受过某种治疗有关,观察3组病人,第一组早在儿童时期接受过肺部辐射,第二组接受过胸外科手术,第三组没有治疗过,现观察到其肺活量占其正常值的百分比如下:这一经验是否可靠。
解:H 0:θ2≤θ1≤θ3 H 1:至少有一个不等式成立可得到 N=15由统计量H=)112+N N (∑=Ki i N R 1i 2-3(N+1)=)(1151512+(32×6.4+29×5.8+59×11.8)-3×(15+1)=5.46查表(5,5,5)在P(H ≥4.56)=0.100 P(H ≥5.66)=0.0509 即P (H ≥5.46)﹥0.05 故取α=0.05, P ﹥α ,故接受零假设即这一检验可靠。
2.关于生产计算机公司在一年中的生产力的改进(度量为从0到100)与它们在过去三年中在智力投资(度量为:低,中等,高)之间的关系的研究结果列在下表中:值等等及你的结果。
(利用Jonkheere-Terpstra 检验) 解:H 0:M 低=M 中=M 高 H 1:M 低﹤M 中﹤M 高U 12=0+9+2+8+10+9+10+2+10+10+8+0.5+3=82.5 U 13=10×8=80U 23=12+9+12+12+12+11+12+11=89 J=∑≤jijUi =82.5+80+89=251.5大样本近似 Z=[]72)32()324121i 222∑∑==+-+--ki i i ki n n N N n N J ()(~N (0,1)求得 Z=3.956 Ф(3.956)=0.9451取α=0.05 , P >α,故接受原假设,认为智力投资对改进生产力有帮助。
(完整版)非参数统计试题

非参数统计试题
一、试比较参数统计与非参数统计的区别和联系。
(15)
二、请你结合实际谈谈非参数统计的应用。
(15)
三、试验者把一只老鼠放入一个有两扇门的笼子里,并且把门都关上,一扇涂红色一扇涂
蓝
色,然后给老鼠播放一段音乐,再同时打开两扇门,记录老鼠逃出选择的门的颜色,重复了10次,发现有7次从红色门中出来,他的结论是:此时老鼠更喜欢红色。
他同时做另一个试验向10只老鼠注射某种药物,5分钟后有7只死亡,他断定这个结果具有偶然性,即药物不具有危险性。
试分析他的结论的合理性,如果是你,你怎样分析这一问题?可以通过适当计算来说明你的结论。
(20)
四、下列数据是从某个总体中,随机抽取的,数据如下:
34 38 56 23 41 52 37 53 46 37 29 48 35 43试问利用这一组数据我们能分析什么?(不需要计算,只说明怎样分析);若还有一组数据,如:38 45 27 34 46 63 34 48 30 43,我们又如何分析他们?写出你的分析思路。
(20)
五、下面是关于非参数统计的一段文献,试叙述其主要意思(30)。
非参数统计十道题
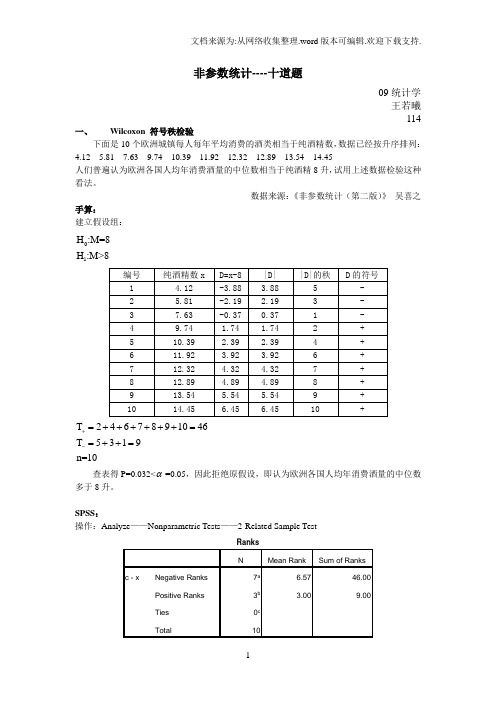
非参数统计----十道题09统计学 王若曦114一、 Wilcoxon 符号秩检验下面是10个欧洲城镇每人每年平均消费的酒类相当于纯酒精数,数据已经按升序排列: 4.12 5.81 7.63 9.74 10.39 11.92 12.32 12.89 13.54 14.45 人们普遍认为欧洲各国人均年消费酒量的中位数相当于纯酒精8升,试用上述数据检验这种看法。
数据来源:《非参数统计(第二版)》 吴喜之手算:建立假设组:01H :M=8H :M>8T 2467891046T 5319n=10+-=++++++==++=查表得P=0.032<α=0.05,因此拒绝原假设,即认为欧洲各国人均年消费酒量的中位数多于8升。
SPSS :操作:Analyze ——Nonparametric Tests ——2-Related Sample TestRanksNMean RankSum of Ranksc - xNegative Ranks 7a 6.57 46.00 Positive Ranks 3b 3.009.00Ties 0c Total10由输出结果可知,单侧精确显著性概率P=0.032<=0.05,因此拒绝原假设,即认为欧洲各国人均年消费酒量的中位数多于8升。
与手算结果相同。
R语言:> x=c(4.12,5.81,7.63,9.74,10.39,11.92,12.32,12.89,13.54,14.45)> wilcox.test(x-8,alt="greater")Wilcoxon signed rank testdata: x - 8V = 46, p-value = 0.03223alternative hypothesis: true location is greater than 0由输出结果可知,P=0.03223<α=0.05,因此拒绝原假设,即认为欧洲各国人均年消费酒量的中位数多于8升。
非参数统计题目及答案

非参数统计题目及答案标准化管理处编码[BBX968T-XBB8968-NNJ668-MM9N]1.人们在研究肺病患者的生理性质时发现,患者的肺活量与他早在儿童时期是否接受过某种治疗有关,观察3组病人,第一组早在儿童时期接受过肺部辐射,第二组接受过胸外科手术,第三组没有治疗过,现观察到其肺活量占其正常值的百分比如下:以往的经验告诉我们,这三组病人的肺活量有如下关系:第二组≤第一组≤第三组,试判断这一经验是否可靠。
解:H 0:θ2≤θ1≤θ3 H 1:至少有一个不等式成立可得到 N=15由统计量H=)112+N N (∑=Ki i N R 1i 2-3(N+1)=)(1151512+(32×+29×+59×-3×(15+1)= 查表(5,5,5)在P(H ≥= P(H ≥= 即P (H ≥)﹥故取α=, P ﹥α ,故接受零假设即这一检验可靠。
2.关于生产计算机公司在一年中的生产力的改进(度量为从0到100)与它们在过去三年中在智力投资(度量为:低,中等,高)之间的关系的研究结果列在下表中:是否智力投资对改进生产力有帮助说明检验的步骤,包括零假设,备选假设,统计量,P值等等及你的结果。
(利用Jonkheere-Terpstra检验)解:H0:M低=M中=M高H1:M低﹤M中﹤M高U 12=0+9+2+8+10+9+10+2+10+10+8++3=U 13=10×8=80U 23=12+9+12+12+12+11+12+11=89J=∑≤jij U i =+80+89=大样本近似 Z=[]72)32()324121i 222∑∑==+-+--k i i i k i n n N N n N J ()(~N (0,1)求得 Z= Ф=取α= , P >α, 故接受原假设,认为智力投资对改进生产力有帮助。
非参数统计和回归分析习题参考答案

非参数统计和回归分析习题参考答案班级: 姓名: 学号: 得分一、单项选择题:1、相关关系是指变量间的 ( D )A 、严格的函数关系B 、简单关系和复杂关系C 、严格的依存关系D 、不严格的依存关系 2、进行简单直线回归分析时,总是假定 ( A )。
A 自变量是非随机变量、因变量是随机变量 B 两变量都是随机变量 C 自变量是随机变量、因变量是确定性变量 D 两变量都不是随机变量 3、回归方程i i x y5.1123ˆ+=中的回归系数数值表明:当自变量每增加一个单位时,因变量 ( B )。
A 增加1.5个单位 B 平均增加1.5个单位 C 增加123个单位 D 平均增加123个单位4、设某种产品产量为 1000 件时,其生产成本为 30000 元,其中固定成本 6000 元,则总生产成本对产量的一元线性回归方程为: ( B ) A 、y=6+0.24x B 、y=6000+24x C 、y=24000+6x D 、y=24+6000x5、在回归分析中,要求对应的两个变量 ( B ) A.都是随机变量 B.不是对等关系 C.是对等关系 D.都不是随机变量6、下列现象的相关密切程度高的是 ( B )。
A 某商店的职工人数与商品销售额之间的相关系数为0.87B 流通费用率与商业利润率之间的相关系数为-0.94C 商品销售额与商业利润率之间的相关系数为0.51D 商品销售额与流通费用率之间的相关系数为-0.817.相关系数r =0表示 ( D ) (A )不存在相关关系 (B )存在平衡关系(C )两变量独立 (D )不存在线性相关关系8.若物价上涨,商品的需求量相应减少,那么物价与商品需求量之间的关系为 ( B )A 、不相关B 、负相关C 、正相关D 、复相关9、回归估计标准误差的剂量单位与 ( B )A 、自变量单位相同B 、因变量单位相同C 、相关系数单位相同D 、自变量、因变量的单位都不同10、在回归分析中,F 检验主要是用来检验 ( C )A 、相关系数的显著性B 、回归系数的显著性C 、线性关系的显著性D 、估计标准误差的显著性11、下列检验中不属于非参数统计方法的是 ( B )A 、总体是否服从正态分布B 、总体的方差值是否为某一个值C 、两组随机变量之间是否独立D 、样本的取得是否具有独立性12、下列情况中,最适合非参数统计方法的是 ( C ) A 、反映两个大学新生成绩的差别B 、反映两个法学毕业英语六级的及格率的差别C 、反映两个大学四年级同学对于就业前景看法的差别D 、反映两个大学在校生平均月支出的差别二、计算题1、一农场10年前在一鱼塘中按比例20:15:40:25投放了四种鱼,鲑鱼、鲈鱼、2、在对某城市家庭社会经济特性的调查中,一个市场研究公司想确定电话拥有数与汽车拥有数是否独立。
非参数统计题目及答案
种治疗有关,观察3组病人,第一组早在儿童时期接受过肺部辐射,第二组接受过胸外科 手术,第三组没有治疗过,现观察到其肺活量占其正常值的百分比如下:
第一组
71
57
85
67
66
第二组
76
94
61
36
42
第三组
80
104
81
90
故取a=0.05,P>a,故接受零假设即这一检验可靠
2.关于生产计算机公司在一年中的生产力的改进(度量为从0到100)与它们在过去三年中
在智力投资(度量为:低,中等,高)之间的关系的研究结果列在下表中:
智
力 投 资
生产力改进
低
9.1
7.0
6.4
8.0
7.3
6.1
7.5
7.3
6.8
7.8
中
5.1
8.7
6.6
7.9
10.1
8.5
9.8
6.6
9.5
9.9
8.1
7.0
高
10.4
9.2
10.6
10.9
10.7
10.0
10.1
10.0
力
资
改
生
力
帮
?
明
验
步
骤, 括零假设,备选假设,统计量,P值等等及你的结果。(利用Jonkheere-Terpstra佥验)
解:
H0:M低=M中=M高Hi:M低vM中<M高
智力投资
36(1)
67(6)
90(12)
42(2)
66(5)
非参数统计期末九道题(手算+机算)

非参数统计—期末九题汇总目录1.单样本Wilcoxon符号秩检验〔SAS〕 (2)2.Wald-Wolfowitz游程检验法 (4)3.两样本的Kolmogorov-Smirnov检验 (5)4.两个独立样本的M-W-W检验〔SAS〕 (6)5.k个样本的2 检验 (9)6.k个独立样本的Kruskal-Wallis检验(R) (10)7.k个相关样本的Friedman检验〔R〕 (11)8.k个相关样本的Cochran Q检验 (12)9.完全秩评定的Kendall协和系数〔R〕 (14)1.单样本Wilcoxon 符号秩检验〔SAS 〕设5.0ε是对称的连续型分布的中位数,现随机抽查了10名普通男子的血压如下: 98 160 136 128 130 114 123 134 129 107试用Wilcoxon 符号检验法检验假设0H :5.0ε=130,1H :5.0ε≠130,显著性水平为α=0.05。
解 手算:i)秩次和计算表ii)根据表中D 的符号和D 的秩,可以计算得到-T =9+2+6+5+1+7=30 +T =8+4+3=15根据n=9,+T =15,-T =30,查表得-T 的右尾概率为0.213,P=0.213⨯2=0.426,P 值相对于显著性水平α=0.05已足够大,因此抽查数据不拒绝0H ,即认为5.0ε=130。
机算:SPSS 输出结果表2Test Statistics by – xZ -.889aAsymp. Sig. (2-tailed) .374Exact Sig. (2-tailed) .426Exact Sig. (1-tailed) .213Point Probability .033a. Based on positive ranks.b. Wilcoxon Signed Ranks Test表1显示:y-x的负秩即满足y<x的为6,而y-x的正秩即满足y-x>3的为3,同分的既满足x=y的为1,总共10。
非参数统计试题及答案

非参数统计试题及答案一、选择题1. 非参数统计方法是指在统计分析中不依赖于数据的分布形态的统计方法。
以下哪项不是非参数统计方法的特点?A. 不需要预先假定总体分布B. 对数据的分布形态要求严格C. 适用于小样本数据D. 可用于顺序变量和计数数据答案:B2. 以下哪个统计量是用来检验两个独立样本的中位数是否有显著差异的?A. t检验B. 方差分析C. Wilcoxon秩和检验D. 卡方检验答案:C3. 在非参数统计中,如果样本量很小,以下哪个方法可以用来估计总体分布?A. 直方图B. 箱线图C. 核密度估计D. 以上都是答案:D二、简答题1. 请简述非参数统计方法相对于参数统计方法的优势。
答案:非参数统计方法的优势在于它们不依赖于数据的分布形态,因此对于不符合正态分布的数据集也能适用。
此外,非参数方法通常对异常值不敏感,适用于小样本数据,并且可以处理顺序变量和计数数据。
2. 描述一下Kruskal-Wallis H检验的基本原理及其适用场景。
答案:Kruskal-Wallis H检验是一种非参数方法,用于比较三个或更多个独立样本的中位数是否存在显著差异。
其基本原理是将所有数据合并并进行秩次排序,然后比较各组的秩和。
如果所有组的中位数相同,则各组的秩和应该大致相等。
如果发现某个组的秩和显著高于或低于其他组,则该组的中位数可能与其他组存在显著差异。
该检验适用于样本量不均等、数据不满足正态分布或未知分布的情况。
三、计算题1. 假设有四个独立样本的数据如下,使用Kruskal-Wallis H检验来检验这四个样本的中位数是否有显著差异。
样本1: 10, 12, 8样本2: 15, 18, 20, 17样本3: 22, 25, 23, 24, 21样本4: 30, 28, 29, 27, 26答案:首先,将所有数据合并并进行秩次排序。
然后计算每个样本的秩和,接着使用Kruskal-Wallis H检验的公式计算H值。
非参数统计(附答案).wps

《非参数统计》试卷注意事项:1.本试卷适用于经济统计专业学生使用。
2.本试卷共6 页,满分100分,答题时间120分钟。
题号一二三四总分得分一、选择题(本大题共10小题,每小题1分,共10分)评卷人1、以下对非参数检验的描述,哪一项是错误的()。
A.非参数检验方法不依赖于总体的分布类型B.应用非参数检验时不考虑被研究对象的分布类型C.非参数检验的假定条件比较宽松D.非参数检验比较简便2、秩和检验又叫做()A、参数检验B、Wilcoxon检验C、非参数检验D、近似正态检验3、()同分校正后,统计量会变小。
A. Kruskal-Wallis检验B.弗里德曼(Friedman)检验C. Mann-Whitney检验D. Spearman等级相关检验4、配对比较的秩和检验的基本意思是:如果检验假设成立,则对样本来说()。
A.正秩和的绝对值小于负秩和的绝对值B.正秩和的绝对值大于负秩和的绝对值C.正秩和的绝对值与负秩和的绝对值不会相差很大D.正秩和的绝对值与负秩和的绝对值相等5、成组设计多个样本比较的秩和检验,当组数大于3时,统计量H近似()分布A、正态B、2C、FD、二项6、Wilcoxon符号秩检验不适用于()。
A 位置的检验B 连续总体C 随机性的检验D 配对样本的检验7、成组设计两样本比较的秩和检验中,描述不正确的是()。
A.遇有相同数据,若在同一组,取平均秩次B.遇有相同数据,若在同一组,按顺序编秩C.遇有相同数据,若不在同一组,按顺序编秩D.遇有相同数据,若不在同一组,取其秩次平均值8、m=4,n=7,Tx=14的双侧检验,则()A. Ty=41,在显著性水平0.05时接受原假设B. Ty=41,在显著性水平0.05时拒绝原假设C. Ty=42,在显著性水平0.05时拒绝原假设D. Ty=42,在显著性水平0.05时接受原假设9、序列3 5 2 7 9 8 6的一致对数目为()。
A.14B.15C.16D.1310、X的秩为1 2 3.5 3.5 5 Y相应的秩为2.5 1 2.5 5 4,则V、U分别为()。
非参数统计题目及答案

非参数统计题目及答案 Document number:WTWYT-WYWY-BTGTT-YTTYU-2018GT1.人们在研究肺病患者的生理性质时发现,患者的肺活量与他早在儿童时期是否接受过某种治疗有关,观察3组病人,第一组早在儿童时期接受过肺部辐射,第二组接受过胸外科手术,第三组没有治疗过,现观察到其肺活量占其正常值的百分比如下:以往的经验告诉我们,这三组病人的肺活量有如下关系:第二组≤第一组≤第三组,试判断这一经验是否可靠。
解:H 0:θ2≤θ1≤θ3 H 1:至少有一个不等式成立可得到 N=15由统计量H=)112+N N (∑=Ki i N R 1i 2-3(N+1)=)(1151512+(32×+29×+59×-3×(15+1)= 查表(5,5,5)在P(H ≥= P(H ≥= 即P (H ≥)﹥ 故取α=, P ﹥α ,故接受零假设即这一检验可靠。
2.关于生产计算机公司在一年中的生产力的改进(度量为从0到100)与它们在过去三年中在智力投资(度量为:低,中等,高)之间的关系的研究结果列在下表中:是否智力投资对改进生产力有帮助说明检验的步骤,包括零假设,备选假设,统计量,P 值等等及你的结果。
(利用Jonkheere-Terpstra 检验) 解:H 0:M 低=M 中=M 高 H 1:M 低﹤M 中﹤M 高U 12U 13=10×8=80U 23=12+9+12+12+12+11+12+11=89 J=∑≤jij U i =+80+89=大样本近似 Z=[]72)32()324121i 222∑∑==+-+--ki i i ki n n N N n N J ()(~N (0,1)求得 Z= Ф=取α= , P >α, 故接受原假设,认为智力投资对改进生产力有帮助。
非参数统计题目及答案

1.人们在研究肺病患者的生理性质时发现,患者的肺活量与他早在儿童时期是否接受过某种治疗有关,观察3组病人,第一组早在儿童时期接受过肺部辐射,第二组接受过胸外科手术,第三组没有治疗过,现观察到其肺活量占其正常值的百分比如下:这一经验是否可靠。
解:H 0:θ2≤θ1≤θ3 H 1:至少有一个不等式成立可得到 N=15由统计量H=)112+N N (∑=Ki i N R 1i 2-3(N+1)=)(1151512+(32×6.4+29×5.8+59×11.8)-3×(15+1)=5.46查表(5,5,5)在P(H ≥4.56)=0.100 P(H ≥5.66)=0.0509 即P (H ≥5.46)﹥0.05 故取α=0.05, P ﹥α ,故接受零假设即这一检验可靠。
2.关于生产计算机公司在一年中的生产力的改进(度量为从0到100)与它们在过去三年中在智力投资(度量为:低,中等,高)之间的关系的研究结果列在下表中:值等等及你的结果。
(利用Jonkheere-Terpstra 检验) 解:H 0:M 低=M 中=M 高 H 1:M 低﹤M 中﹤M 高U 12=0+9+2+8+10+9+10+2+10+10+8+0.5+3=82.5 U 13=10×8=80U 23=12+9+12+12+12+11+12+11=89 J=∑≤jijUi =82.5+80+89=251.5大样本近似 Z=[]72)32()324121i 222∑∑==+-+--ki i i ki n n N N n N J ()(~N (0,1)求得 Z=3.956 Ф(3.956)=0.9451取α=0.05 , P >α,故接受原假设,认为智力投资对改进生产力有帮助。
非参数试题A

广东财经大学13级非参数统计方法试题A(上机开卷考试)1.(10分) Rotherford观察了每分钟内一放射性物质放射粒子数,他观察了2612次,结果如下:α05=.02.(10分)某药厂的质检科,希望知道两种不同的生产法生产出来的药片厚度是否有区。
现从这两种方法生产出来的药片中随机地抽取一部分,测其厚度如下:α=.0053. (10分)一个监听装置收到如下的信号0 1 0 1 1 1 0 0 1 1 0 0 0 0 1 1 1 1 1 1 1 1 1 0 1 0 0 1 1 1 0 1 0 1 01 0 0 0 0 0 0 0 0 1 0 1 1 0 0 1 1 1 0 1 0 1 0 0 0 1 0 0 1 0 1 0 1 0 0 0 0 0 0 0 0这些信号是不是纯粹随机干扰?(05α).0=4. (10分)一个大工厂的管理人员在随机抽样中发现20个雇员的年平均请假天数为:1915 18 16 12 13 17 12 18 141614 14 17 13 16 12 13 12 14请问雇员们的请假天数是否大于13天?(用Wilcoxon符号秩检验)(05α).0=5. (10分)以A、B两种饲料喂猪,喂A饲料的16只猪月增重(斤)为:34.2 28.4 36.6 39.2 25.8 39.5 37.1 34.2 33.4 36.6 42.7 31.3 32.1 34.7 29.5 26.8;喂B饲料的14只猪月增重(斤)为:31.5 25.6 24.4 22.8 19.7 26.3 29.7 29.5 34.2 27.5 36.1 29.5 28.2 30.0 。
问两种饲料对猪的月增重是否有不同效果(用wlicoxon秩和检验)(05α)?.0=6.(10分)开摩托车的用户对油的粘性都很感兴趣。
假设现有两种型号的油在不同的条件下,从中随机地抽取部分,测其粘性如下:α=05.07. (10分)在500人身上实验某种血清预防感冒的作用,把他们一年中的记录与另外500名未用血清处理的人做比较,结果如下:是否与在未用血清处理的人中,这些情况的人所占的比例一致?(05α)=.08. (10分)人们在研究肺病患者的生理性质时发现患者的肺活量与他早在儿童时期是否接受某种治疗有关,现观察3组病人,第一组6个人,早在儿童时期接受过肺部辐射;第二组6个人,接受过胸外科手术;第三组8个人,没有治疗过。
非参数统计——期末试卷

每小题20分1. 下面是DMBA 公司为了研究某一种癌症所做的试验。
Group 1和2分别代表试验的控制组和对照组。
下面是所得的试验老鼠的生存数据,*代表数据被右删失。
请回答下面问题:Group 1: 164 188 190 192 206 209 213 216 220 230 234 246265 304 216* 244*Group 2: 156 163 198 205 232 233 239 240 261 280 296 323204* 344*1)请给出非参数的Kaplan-Meier 估计的公式,并计算在时间点t=156,164这两点的具体估计值,若假设在t=164处被删失,计算此处的估计值。
2)如果协变量分别取为1和0,请用Cox 模型模拟上述数据,给出计算协变量的系数的相关公式;3)给出Kaplan-Meier 估计的Matlab 程序。
2. 下面是16个学生的体能测试数据: P81例3.1482 53 70 73 103 71 69 80 54 38 87 91 62 75 65 77。
1) 请用顺序统计量方法构造置信度为95%的中位数的置信区间;2) 编写上述计算的Matlab 程序3. 下面是申请进入法学院学习的学生的LSAT 测试成绩和GPA 成绩。
LSAT: 576 635 558 578 666 580 555 661 651 605 653 575 545 572 594GPA: 3.39 3.30 2.81 3.03 3.44 3.07 3.00 3.43 3.36 3.13 3.12 2.742.76 2.883.96每个数据点用(,),i i i X Y Z 其中i Y 表示LSAT 成绩,i Z 表示GPA 成绩1) 计算i Y 和i Z 的Pearson 相关系数 (只写出公式); (5分)2) 使用Boostrap 方法估计相关系数的标准误差(只写出算法步骤);(5分)3) 编写相应的Matlab 程序。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
非参数统计----十道题09统计学 王若曦 32009121114一、 Wilcoxon 符号秩检验下面是10个欧洲城镇每人每年平均消费的酒类相当于纯酒精数,数据已经按升序排列: 4.12 5.81 7.63 9.74 10.39 11.92 12.32 12.89 13.54 14.45 人们普遍认为欧洲各国人均年消费酒量的中位数相当于纯酒精8升,试用上述数据检验这种看法。
数据来源:《非参数统计(第二版)》 吴喜之手算:建立假设组:01H :M=8H :M>8T 2467891046T 5319n=10+-=++++++==++=查表得P=0.032<α=0.05,因此拒绝原假设,即认为欧洲各国人均年消费酒量的中位数多于8升。
SPSS :操作:Analyze ——Nonparametric Tests ——2-Related Sample TestRanksNMean RankSum of Ranksc - xNegative Ranks 7a 6.57 46.00 Positive Ranks 3b 3.009.00Ties 0c Total10由输出结果可知,单侧精确显著性概率P=0.032<=0.05,因此拒绝原假设,即认为欧洲各国人均年消费酒量的中位数多于8升。
与手算结果相同。
R语言:> x=c(4.12,5.81,7.63,9.74,10.39,11.92,12.32,12.89,13.54,14.45)> wilcox.test(x-8,alt="greater")Wilcoxon signed rank testdata: x - 8V = 46, p-value = 0.03223alternative hypothesis: true location is greater than 0由输出结果可知,P=0.03223<α=0.05,因此拒绝原假设,即认为欧洲各国人均年消费酒量的中位数多于8升。
与以上结果一致。
二、Mann-Whitney-Wilcoxon检验下表为8个亚洲国家和8个欧美国家2005年的人均国民收入数据。
检验亚洲国家和欧美国家的人均国民收入是否有显著差异(α=0.05)。
数据来源:《统计学(第三版)》 贾俊平手算:设亚洲国家为X ,欧美国家为Y 建立假设组:0x y 1x yH :M =M H :M M ≠x y x T 12346891548T 5710111213141688N m n 16m n 8U T m(m 1)/212=+++++++==+++++++==+====-+=,,查表得,T x =48的右尾概率的2倍为0.019*2=0.038< α=0.05,因此拒绝原假设,即认为亚洲国家和欧美国家的人均国民收入有显著差异。
SPSS :操作:Data ——Sort CasesAnalyze ——Nonparametric Tests ——2-Independent SamplesRanks分组 NMean RankSum of Ranks收入亚洲国家 8 6.00 48.00 欧美国家 8 11.0088.00Total16Test Statistics b收入 Mann-Whitney U 12.000 Wilcoxon W 48.000 Z-2.100 Asymp. Sig. (2-tailed) .036 Exact Sig. [2*(1-tailed Sig.)] .038a Exact Sig. (2-tailed).038由输出结果可知,精确双尾概率P=0.038<=0.05,因此拒绝原假设,即认为亚洲国家和欧美国家的人均国民收入有显著差异。
与手算结果一致。
R语言:> x<-c(1740,38980,1280,4960,2750,27490,15830,720)> y<-c(43740,32600,34580,37600,34810,30010,7310,3460)> wilcox.test(x,y,exact=F,cor=F)Wilcoxon rank sum testdata: x and yW = 12, p-value = 0.03569alternative hypothesis: true location shift is not equal to 0由输出结果可知,P=0.03569< α=0.05,因此拒绝原假设,即认为亚洲国家和欧美国家的人均国民收入有显著差异。
与以上结果一致。
三、两样本的Kolmogorov-Smirnov检验下面是13个非洲地区和13个欧洲地区的人均酒精年消费量,试分析这两个地区的酒精人均年消费量是否分布相同。
》吴喜之手算:建立假设组:012112H :F (x)=F (x)H :F (x)F (x)≠D=max D =0769231mnD=130().,查表得,当mnD=130时,双侧检验的概率P<0.01,所以P<α=0.05,因此拒绝原假设,即认为这两个地区的酒精人均年消费量分布有显著差异。
SPSS :操作:Analyze ——由输出结果可知,双侧精确显著性概率P =0.05,因此拒绝原假设,即认为这两个地区的酒精人均年消费量分布有显著差异。
与手算结果一致。
四、 Cochran Q 检验下面是某村村民对四个候选人(A ,B ,C ,D )的赞同与否的调查(“1”代表同意,“0”代表不同意);最后一列为行总和,最后一行为列总和,全部“1”的总和为42。
试分析4手算:建立假设组:01H 4H 4:位候选人在村民眼中没有差异:位候选人在村民眼中有差异k k 22j j 22222j=1j=1n n 2222i i i=1i=1k-1k x -x (41)[4(161196)42]Q =9.35294(42)(518273)k y -y df 413⎡⎤⎢⎥-+++-⎣⎦==-⨯+⨯+⨯=-=∑∑∑∑()() 查表得20.057.82Q 9.3529χ=<=,因此在5%的显著性水平上拒绝原假设,即认为4位候选人在村民眼中有显著差异。
SPSS :操作:Analyze ——Test StatisticsN20 Cochran's Q 9.353adf3 Asymp. Sig. .025 Exact Sig. .025 Point Probability.006a. 0 is treated as a success.由输出结果可知,Q=9.353,精确的显著性概率P=0.025< α=0.05,因此拒绝原假设,即认为4位候选人在村民眼中有显著差异。
与手算结果一致。
R 语言:> x=read.table("f:/CochranQ.txt") > n=apply(x,2,sum) > N=sum(n)> L=apply(x,1,sum) > k=dim(x)[2]> Q=(k*(k-1)*sum((n-mean(n))^2))/(k*N-sum(L^2)) > Q[1] 9.352941> pvalue=pchisq(Q,k-1,low=F) > pvalue[1] 0.02494840由输出结果可知,Q=9.352941, P=0.02494840< α=0.05,因此拒绝原假设,即认为4位候选人在村民眼中有显著差异。
与以上结果一致。
五、 Friedman 检验一项关于销售茶叶的研究报告说明销售方式可能和售出率有关。
三种方式为:在商店内等待,在门口销售和当面表演炒制茶叶。
对一组商店在一段时间的调查结果列再下表中(单位为购买者人数)。
试问三种不同的销售方式是否有显著差异(α=0.05)。
手算:建立假设组:01H H :三种销售方式无差异:三种销售方式有差异k22222rjj=11212R 3n(k 1)(101424)38(31)13nk(k 1)83(31)df 312χ=-+=++-⨯+=+⨯+=-=∑ 查表得220.05r 5.9913χχ=<=,因此在5%的显著性水平上拒绝原假设,即认为三种销售方式有显著差异。
SPSS :操作:Analyze ——Nonparametric Tests ——K Related SamplesTest Statistics aN8 Chi-Square 13.000df2 Asymp. Sig. .002 Exact Sig. .000 Point Probability .000a. Friedman Test由输出结果可知,22r 0.0513 5.99χχ=>=,精确的显著性概率P<0.001,因此在5%的显著性水平上拒绝原假设,即认为三种销售方式有显著差异。
与手算结果一致。
R 语言:> d=read.table("f:/Friedman.txt") > friedman.test(as.matrix(d))Friedman rank sum testdata: as.matrix(d)Friedman chi-squared = 13, df = 2, p-value = 0.001503由输出结果可知,213χ=, P=0.001503<α=0.05,因此拒绝原假设,即认为三种销售方式有显著差异。
与以上结果一致。
六、 K 个样本的卡方检验在一个有三个主要百货商场的商贸中心,调查者问479个不同年龄段的人首先去三个商王星手算:建立假设组:01H H :人们去三个商场的概率相同:人们去三个商场的概率不同()2rkij ij i=1j=1ijf -e Q==0.685+2.274+15.691=18.651e df=(k-1)(r-1)=4∑∑查表得20.05=9.49χ,因为Q=18.651>20.05=9.49χ,因此拒绝原假设,即认为人们去三个商场的概率不同。
SPSS :操作:Data ——Weight Cases由输出结果可知,卡方统计量为18.651,精确双尾检验概率P=0.01<=0.05,因此拒绝原假设,即认为人们去三个商场的概率不同。
与手算结果一致。
七、 Kruskal-Wallis 检验某制造商雇用了来自三个本地大学的雇员作为管理人员。
最近,公司的人事部门已经收集信息并考核了年度工作成绩。
从三个大学来的雇员中随机地抽取了三个独立样本。
制造商想知道是否来自这三个不同的大学的雇员在管理岗位上的表现有所不同。
数据来源:百度文库 SAS 讲义手算:建立假设组:01H H :三个总体的考核成绩分布相同:三个总体的考核成绩分布不同各雇员的成绩等级2222k jj=1j R 1212(95)(27)(88)KW H 3(N+1)=3(201)8.9163N(N+1)n 20(21)767⎡⎤=-++-+=⎢⎥⎣⎦∑统计量因为出现同分的情况,应对H 进行校正,校正系数3333322u u (33332222)C 1=10.9925N(N +1)20(20+1)H 8.9163/0.99258.9839df=k 12--+-+-+-=--===-=∑∑校正后的统计量查表得,在05.0=α的显著性水平上,20.05χ=5.99,由于H=8.9839>20.05χ=5.99,因此拒绝原假设,即三个总体的考核成绩分布不同。
