信号检测与估计仿真作业
信号检测与估计试题——答案(不完整版)

一、概念:1. 匹配滤波器。
概念:所谓匹配滤波器是指输出判决时刻信噪比最大的最佳线性滤波器。
应用:在数字信号检测和雷达信号的检测中具有特别重要的意义。
在输出信噪比最大准则下设计一个线性滤波器是具有实际意义的。
2. 卡尔曼滤波工作原理及其基本公式(百度百科)首先,我们先要引入一个离散控制过程的系统。
该系统可用一个线性随机微分方程(Linear Stochastic Difference equation)来描述:X(k)=A X(k-1)+B U(k)+W(k)再加上系统的测量值:Z(k)=H X(k)+V(k)上两式子中,X(k)是k时刻的系统状态,U(k)是k时刻对系统的控制量。
A和B是系统参数,对于多模型系统,他们为矩阵。
Z(k)是k时刻的测量值,H是测量系统的参数,对于多测量系统,H为矩阵。
W(k)和V(k)分别表示过程和测量的噪声。
他们被假设成高斯白噪声(White Gaussian Noise),他们的covariance 分别是Q,R(这里我们假设他们不随系统状态变化而变化)。
对于满足上面的条件(线性随机微分系统,过程和测量都是高斯白噪声),卡尔曼滤波器是最优的信息处理器。
下面我们来用他们结合他们的covariances 来估算系统的最优化输出(类似上一节那个温度的例子)。
首先我们要利用系统的过程模型,来预测下一状态的系统。
假设现在的系统状态是k,根据系统的模型,可以基于系统的上一状态而预测出现在状态:X(k|k-1)=A X(k-1|k-1)+B U(k) (1)式(1)中,X(k|k-1)是利用上一状态预测的结果,X(k-1|k-1)是上一状态最优的结果,U(k)为现在状态的控制量,如果没有控制量,它可以为0。
到现在为止,我们的系统结果已经更新了,可是,对应于X(k|k-1)的covariance还没更新。
我们用P表示covariance:P(k|k-1)=A P(k-1|k-1) A’+Q (2)式(2)中,P(k|k-1)是X(k|k-1)对应的covariance,P(k-1|k-1)是X(k-1|k-1)对应的covariance,A’表示A的转置矩阵,Q是系统过程的covariance。
信号处理仿真题作业

信号处理基础仿真作业学号:S1201010573.17在计算机上用如下方法产生随机信号()u n的观测样本:首先产生一段零均值、方差为2σ的复高斯白噪声序列()v n;然后在()v n上叠加三个复正弦信号,它们的归一化频率分别是f1=0.15,f2=0.17和f3=0.26。
调整2σ和正弦信号的幅度,使在f1、f2和f3处得信噪比分别为30dB、30dB和27dB。
(1)令信号观测样本长度N=32,试用3.1.1节讨论的基于FFT的自相关函数快速计算方法估计出自相关函数^()mr,并与教材式(3.1.2)估计出的自相关函数^()mr做比较。
产生零均值、方差为1的复高斯白噪声序列y >> y=randn(1,32);>> y=y-mean(y);>> y=y/std(y);>> a=0;>> b=sqrt(2);>> y=a+b*y产生三个复正弦信号并产生观察样本:>> N=32;>> f1=0.15;>> f2=0.17;>> f3=0.26;>> SNR1=30;>> SNR2=30;>> SNR3=27;>> A1=10^(SNR1/20);>> A2=10^(SNR2/20);>> A3=10^(SNR3/20);>> signal1=A1*exp(j*2*pi*f1*(0:N-1));>> signal2=A2*exp(j*2*pi*f2*(0:N-1));>> signal3=A3*exp(j*2*pi*f3*(0:N-1));>> un=signal1+signal2+signal3+y基于FFT的自相关函数快速计算方法:N=32;>> Uk=fft(un, 2*N);Sk=(1/N)* abs(Uk).^2;r0=ifft(Sk);r1=[r0(N+2:2*N),r0(1:N)];>> figure(1);>> stem(real(r1));>> figure(2);>> stem(imag(r1))输出结果为:图 1 基于FFT的自相关函数快速计算实部:虚部:教材中式(3.1.2)估计自相关函数>> r=xcorr(un, N-1,'biased');>> figure(1);>> stem(real(r))>> figure(2);>> stem(imag(r))输出结果为:图 2 教材式(3.1.2)估计的自相关函数实部:虚部:(2)令信号观测样本长度N=256,试用BT法和周期图法估计()u n的功率谱,这里设BT法中所用自相关函数的单边长度M=64。
现代数字信号处理仿真作业
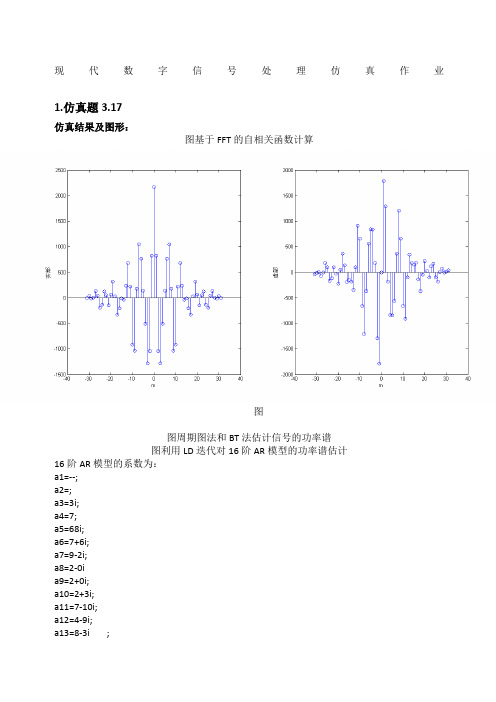
现代数字信号处理仿真作业1.仿真题3.17仿真结果及图形:图基于FFT的自相关函数计算图图周期图法和BT法估计信号的功率谱图利用LD迭代对16阶AR模型的功率谱估计16阶AR模型的系数为:a1=--;a2=;a3=3i;a4=7;a5=68i;a6=7+6i;a7=9-2i;a8=2-0ia9=2+0i;a10=2+3i;a11=7-10i;a12=4-9i;a13=8-3i ;a14=2+4i;a15=2+1i;a16=3i.仿真程序(3_17):clear allclc%%产生噪声序列N=32;%基于FFT的样本长度%N=256;%周期图法,BT法,AR模型功率谱估计的长度vn=(randn(1,N)+1i*randn(1,N))/sqrt(2);%%产生复正弦信号f=[0.150.170.26];%归一化频率SNR=[303027];%信噪比A=10.^(SNR./20);%幅度signal=[A(1)*exp(1i*2*pi*f(1)*(0:N-1));%复正弦信号A(2)*exp(1i*2*pi*f(2)*(0:N-1));A(3)*exp(1i*2*pi*f(3)*(0:N-1))];%%产生观察样本un=sum(signal)+vn;%%利用3.1.1的FFT估计Uk=fft(un,2*N);Sk=(1/N)*abs(Uk).^2;r0=ifft(Sk);r1=[r0(N+2:2*N),r0(1:N)];%%r2=xcorr(un,N-1,'biased');%画图k=-N+1:N-1;figure(1)subplot(1,2,1)stem(k,real(r1))xlabel('m');ylabel('实部');subplot(1,2,2)stem(k,imag(r1))xlabel('m');ylabel('虚部');figure(2)subplot(1,2,1)stem(k,real(r2))xlabel('m');ylabel('实部');subplot(1,2,2)stem(k,imag(r2))xlabel('m');ylabel('虚部');%%周期图法NF=1024;Spr=fftshift((1/NF)*abs(fft(un,NF)).^2);kk=-0.5+(0:NF-1)*(1/(NF-1));Spr_norm=10*log10(abs(Spr)/max(abs(Spr)));%%BT法M=64;r3=xcorr(un,M,'biased');BT=fftshift(fft(r3,NF));BT_norm=10*log10(abs(BT)/max(abs(BT)));figure(3)subplot(1,2,1)plot(kk,Spr_norm)xlabel('w/2pi');ylabel('归一化功率谱/DB');title('周期图法')subplot(1,2,2)plot(kk,BT_norm)xlabel('w/2pi');ylabel('归一化功率谱/DB');title('BT法')%%LD迭代算法p=16;r0=xcorr(un,p,'biased');r4=r0(p+1:2*p+1);%计算自相关函数a(1,1)=-r4(2)/r4(1);sigma(1)=r4(1)-(abs(r4(2))^2)/r4(1);for m=2:p%LD迭代算法k(m)=-(r4(m+1)+sum(a(m-1,1:m-1).*r4(m:-1:2)))/sigma(m-1);a(m,m)=k(m);for i=1:m-1a(m,i)=a(m-1,i)+k(m)*conj(a(m-1,m-i));endsigma(m)=sigma(m-1)*(1-abs(k(m))^2);endPar=sigma(p)./fftshift(abs(fft([1,a(p,:)],NF)).^2);%p阶AR模型的功率谱Par_norm=10*log10(abs(Par)/max(abs(Par)));figure(4)plot(kk,Par_norm)xlabel('w/2pi');ylabel('归一化功率谱/DB');title('16阶AR模型')2.仿真题3.20仿真结果及图形:单次Root-MUSIC算法中最接近单位圆的两个根为:+-对应的归一化频率为:相同信号的MUSIC谱估计结果如下图对3.20信号进行MUSIC谱估计的结果仿真程序(3_20):clear allclc%%信号样本和高斯白噪声的产生N=1000;vn=(randn(1,N)+1i*randn(1,N))/sqrt(2);signal=[exp(1i*0.5*pi*(0:N-1)+1i*2*pi*rand);%复正弦信号exp(-1i*0.3*pi*(0:N-1)+1i*2*pi*rand)];un=sum(signal)+vn;%%计算自相关矩阵M=8;for k=1:N-Mxs(:,k)=un(k+M-1:-1:k).';endR=xs*xs'/(N-M);%%自相关矩阵的特征值分解[U,E]=svd(R);%%Root-MUSIC算法的实现G=U(:,3:M);Gr=G*G';co=zeros(2*M-1,1);for m=1:Mco(m:m+M-1)=co(m:m+M-1)+Gr(M:-1:1,m);endz=roots(co);ph=angle(z)/(2*pi);err=abs(abs(z)-1);%%计算MUSIC谱En=U(:,2+1:M);NF=2048;for n=1:NFAq=exp(-1i*2*pi*(-0.5+(n-1)/(NF-1))*(0:M-1)');Pmusic(n)=1/(Aq'*En*En'*Aq);endkk=-0.5+(0:NF-1)*(1/(NF-1));Pmusic_norm=10*log10(abs(Pmusic)/max(abs(Pmusic))); plot(kk,Pmusic_norm)xlabel('w/2*pi');ylabel('归一化功率谱/dB')3.仿真题3.21仿真结果及图形:单次ESPRIT算法中最接近单位元的两个特征值为:+-对应的归一化频率为:仿真程序(3_21):clear allclc%%信号样本和高斯白噪声的产生N=1000;vn=(randn(1,N)+1i*randn(1,N))/sqrt(2);signal=[exp(1i*0.5*pi*(0:N-1)+1i*2*pi*rand);%复正弦信号exp(-1i*0.3*pi*(0:N-1)+1i*2*pi*rand)];un=sum(signal)+vn;%%自相关矩阵的计算M=8;for k=1:N-Mxs(:,k)=un(k+M-1:-1:k).';endRxx=xs(:,1:end-1)*xs(:,1:end-1)'/(N-M-1);Rxy=xs(:,1:end-1)*xs(:,2:end)'/(N-M-1);%%特征值分解[U,E]=svd(Rxx);ev=diag(E);emin=ev(end);Z=[zeros(M-1,1),eye(M-1);0,zeros(1,M-1)];Cxx=Rxx-emin*eye(M);Cxy=Rxy-emin*Z;%%广义特征值分解[U,E]=eig(Cxx,Cxy);z=diag(E);ph=angle(z)/(2*pi);err=abs(abs(z)-1);4.仿真题4.18仿真结果及图形:步长为0.05时失调参数为m1=0.0493;步长为0.005时失调参数为m2=0.0047。
信号检测与估计作业第一二三八章答案

时间:6月16日(星期一)晚上6:30-8:30 地点:六教104室(上课教室)试卷共8题,其中4题属于教材第一章内容,其余4题分别的其他章节。
请同学们对匹配滤波器,离散卡尔曼滤波,离散维纳滤波,高斯白噪声下确知信号的检测,K -L 展开,高斯白噪声信道中的单参量信号估计等内容重点关注。
1.1 (付柏成 20060150)在例1.2中,设噪声均方差电压值为σ=2v ,代价为f c =2,m c =1。
信号存在的先验概率P =0.2。
试确定贝叶斯意义下最佳门限β,并计算出相应的平均风险。
解:根据式(1-15),可以算出00.8280.21f mQc Pc ⨯Λ===⨯ 而判决门限2201ln 0.52ln 88.822βσ=+Λ=+= 根据式(1-21)可知平均风险1010Pr 0.2r 0.8R Qr r =+=+01100.2(|)0.8(|)m f c P D H c P D H =+ 而011(|)(|)D P D H p x H dx =⎰1100(|)(|)D P D H p x Hdx =⎰而2121(1)(|)exp[]22x p x H σπσ-=- 2021(|)exp[]22x p x H σπσ=-所以201121(1)(|)(|)exp[]22D D x P D H p x H dx dx σπσ-==-⎰⎰221(1)e x p []22x dx βσπσ-∞-=-⎰=17.82()()(3.91)22β-Φ=Φ=Φ 同理11210021(|)(|)exp[]22D D x P D H p x Hdx dx σπσ==-⎰⎰221e x p ()22x dx βσπσ∞=-⎰8.821()1()1(4.41)22β=-Φ=-Φ=-Φ 所以0.21(3.91)0.82[1(4.41)]R =⨯⨯Φ+⨯⨯-Φ 1.2 (关瑞东 20060155)假定加性噪声()n t 服从均值为零,方差为的正态分布。
信号检测与估值matlab仿真报告

信号检测与估值仿真报告题目信号检测与估值的MATLAB仿真学院通信工程学院专业通信与信息系统学生姓名学号导师姓名作业1试编写程序,画出相干移频键控、非相干移频键控(无衰落)和瑞利衰落信道下非相干移频键控的性能曲线。
(1)根据理论分析公式画性能曲线;(2)信噪比范围(0dB-10dB),间隔是1dB;(3)信噪比计算SNR=10lg(Es/N0)一、脚本文件1、主程序%********************************************************%二元移频信号检测性能曲线(理论分析)%FSK_theo.m%********************************************************clear all;clc;SNRindB=0:1:20;Pe_CFSK=zeros(1,length(SNRindB));Pe_NCFSK=zeros(1,length(SNRindB));Pe_NCFSK_Rayleigh=zeros(1,length(SNRindB));for i=1:length(SNRindB)EsN0=exp(SNRindB(i)*log(10)/10);Es_aveN0=exp(SNRindB(i)*log(10)/10);Pe_CFSK(i)=Qfunct(sqrt(EsN0));%相干移频键控系统Pe_NCFSK(i)=0.5*exp(-EsN0/2);%非相干移频键控系统(无衰落)Pe_NCFSK_Rayleigh(i)=1/(2+Es_aveN0);%非相干移频键控系统(瑞利衰落)endsemilogy(SNRindB,Pe_CFSK,'-o',SNRindB,Pe_NCFSK,'-*',SNRindB,Pe_NC FSK_Rayleigh,'-');xlabel('Es/No或平均Es/No(dB)');ylabel('最小平均错误概率Pe');legend('相干移频','非相干移频(无衰落)','非相干移频(瑞利衰落)');title('二元移频信号检测性能曲线');axis([02010^-71]);grid on;2、调用子函数%********************************************************%Q函数%Qfunct.m%********************************************************function[y]=Qfunct(x)%[y]=Qfunct(x)%QFUNCT evaluates the Q-function.%y=1/sqrt(2*pi)*integral from x to inf of exp(-t^2/2)dt.%y=(1/2)*erfc(x/sqrt(2)).y=(1/2)*erfc(x/sqrt(2));二、仿真结果作业2试编写程序,仿真BPSK,4PSK调制信号在高斯信道下的性能,画出误码率(误比特和误符号)的性能曲线,并与理论分析结果相比。
信号检测与估计第四章计算机仿真作业

信号检测与估计第四章计算机仿真作业题目1:试编写程序,仿真4PSK 调制信号在高斯信道下的性能,并与理论分析结果相比。
(1). 解题思路:图1-1 QPSK 的调制原理框图如图1-1所示,QPSK 实质上是一种正交调制,它等于两路(I 路与Q 路)正交的BPSK 的叠加。
图中串/并变换器将输入的二进制序列分为速度减半的两个并行双极性序列a 和b (a,b 码元在事件上是对齐的),再分别进行极性变换,把极性码变为双极性码(0→-1,1→+1)然后分别调制到cosωc t 和sinωc t 两个载波上,两路相乘器输出的信号是相互正交的抑制载波的双边带调制(DSB )信号,其相位与各路码元的极性有关,分别由a 和b 码元决定。
经相加电路后输出两路的合成波形,即是4PSK 信号。
图中两个乘法器,其中一个用于产生0o 与180o 两种相位状态,另一个用于产生90o 与270o 两种相位状态,相加后就可以得到45o ,135o ,225o ,和315o 四种相位在时隙(1)s s n T t nT -≤≤上_Q_cos 2cos 2()()]QPSK In c Qn c I PSK PSK s f t f t s t s t ππ==-(1.1)那么,它的解调可以采用与2PSK 信号类似的解调方法进行解调,同相支路和正交支路分别采用相干解调方式解调,之后可以得到二者的和,经过抽样判决和串、并变换器,将上图1-2 QPSK 解调原理框图下之路得到的并行数据恢复为串行数据。
那么此时就得到我们最初的原始信号,它的解调原理图如图1-2所示。
再来分析QPSK 的误比特性能,因为QPSK 的每个四元符号所包含的两个比特都独立,并行地按照BPSK 传输,各比特的传输误比特率均为_2s psk P (相当于2PSK 的无比特率),显然QPSK 系统与2PSK 系统具有完全相同的误比特性能,即_412e PSK P erfc =(1.2)(2). 仿真结果仿真性能曲线如图1-3所示:图1-3 QPSK 高斯信道下的性能仿真曲线101010101010101010SNRQPSK,高斯信道下的性能曲线误比特率题目2:试编写程序,画出相干移频键控、非相干移频键控(无衰落)和瑞利衰落信道下非相干移频键控的性能曲线。
信号检测与估计试卷

XXX 大学(学院)试卷《信号检测与估计》试卷 第 1 页 共 2 页 《信号检测与估计》模拟试卷一、填空题(每空1分,共10分)1.广义匹配滤波器可通过 和 级联而构成。
2.卡亨南-洛维展开是把平稳随机信号表示成 的形式,并使 。
3.修正的奈曼-皮尔逊准则是在给定 和 的条件下,从第一个观测数据开始就进行似然比检测,直至能做出判决为止。
4.秩检测是一种利用观测样本的 和 的一种非参量检测方法。
5.最小二乘估计的使用条件:含有被估计参量的信号模型已知, 和 的任何统计知识均未知。
二、简答题(每题4分,共20分)1.概述高斯白噪声情况下和高斯色噪声情况下信号检测所采用方法的特点。
2.简述序列检测的概念与特点。
3.简述非参量检测的概念、特点及基本原理。
4.简要说明在似然函数对的频率偏导数难以求解情况下,信号频率估计的方法。
5.说明参量的最小二乘估计方法的基本思路。
三、(10分)设线性滤波器的输入为)()()(t n t s t x +=,其中)(t n 是功率谱密度为2/0N 的白噪声,信号为⎩⎨⎧><≤<-=T t t T t t T A t s ,000)()( 式中,0>A ,且为常数。
(1)试求匹配滤波器的冲激响应及对应于)(t s 的输出信号。
(2)求匹配滤波器输出的信噪比。
四、(10分)对于二元随机参量信号的检测问题,若两个假设下观测信号分别为:n x H =:0,n s x H +=:1,其中,信号s 和噪声n 是相互统计独立的随机变量,其概率密度函数分别为⎩⎨⎧<>≥-=0,00,0,)exp()(s a s s a a s p ⎩⎨⎧<>>≥-=0,00,0,)exp()(n a b b n n b b n p 且 设似然比检验门限为0Λ,试证明信号的似然比检测判决式可化简为γ10H H x<>。
五、(15分)在T t ≤≤0时间范围内,二元通信系统发送的二元信号为t A t s 00sin )(ω=,。
信号检测与估计课后习题

三、(15分)在二元信号的检测中,若两个假设下的观测信号分别为:0122112::H x r H x r r ==+其中,和是独立同分布的高斯随机变量,均值为零,方差为1。
若似然比检测门限为1r 2r ,求贝叶斯判决表示式。
η解 假设下,观测信号的概率密度函数为0H x 1/2201(|)exp 22x p x H π⎛⎫⎛⎫=- ⎪⎪⎝⎭⎝⎭假设下,,而,且相互统计独立。
大家知1H 2212x r r =+12(0,1),(0,1)r N r N ::道,若,且之间相互统计独立,则(0,1)k r N :(1,2,,)k r k N =L 21Nk k x x ==∑是具有个自由度的分布。
现在,所以假设下,观测信号的概率密度函数N 2χ2N =1H x 为22/2112/221(|)exp()2(2/2)21exp(),022x p x H x x x -=-Γ=-≥当时,。
0x <1(|)0p x H =于是,似然比函数为1/2210exp ,0(|)()222(|)0,0x x x p x H x p x H x πλ⎧⎛⎫⎛⎫-≥⎪ ⎪ ⎪==⎨⎝⎭⎝⎭⎪<⎩当似然比检测门限为时,判决表达式为η11/220exp ,0222,0H H x x x H x πη⎧⎛⎫>⎛⎫⎪-≥⎪ ⎪ ⎪<⎝⎭⎨⎝⎭⎪⎪<⎩成立对的情况,化简整理得判决表达式为0x ≥11/2222ln H H x x ηπ⎡⎤>⎛⎫-⎢⎥⎪<⎝⎭⎢⎥⎣⎦四、(15分)已知被估计参量的后验概率密度函数为θ2(|)()exp[()],0p x x x θλθλθθ=+-+≥(1)求的最小均方误差估计量 。
θ^mse θ(2)求 的最大后验估计量 。
θ^map θ 解 (1)参量的最小均方误差估计量是的条件均值,即θ^mse θθ^0220221(|)()[()]1()()2,mse p x d x exp x d x x x x θθθθλθλθθλλλλ∞∞+==+-+=++=≥-+⎰⎰^0,mse x θλ=<-(2)由最大后验方程^ln (|)|0map p x θθθθ=∂=∂得^2[ln()ln ()]1()|0mapx x x θθλθλθθλθ=∂++-+∂=-+=解得^^1,0,map map x x x θλλθλ=≥-+=<-七、(15分)若对未知参量进行了六次测量,测量方程和结果如下:θ182222202384404384n θ⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦设初始估计值和估计量的均方误差分别为:^2000,θε==∞试用递推估计求的线性最小二乘估计量和估计量的均方误差θ^^1def s k θθ=;并将最终结果与非递推估计的结果进行比较。
信号检测与估计理论计算机仿真题 (1)

信号检测与估计理论计算机仿真题
1 由M个接收机接收同一入射电磁波,每个接收机接收信号为:
2 通过计算机运用MUSIC、ESPRIT、GEESE等方法进行非相关源的模拟测向并比较各种算法的性能。
3 通过计算机仿真非平稳噪声(噪声协方差矩阵为对角阵,但对角元素值不一样)以及色噪声(噪声协方差矩阵不为对角阵)对MUSIC、ESPRIT、GEESE等方法性能的影响。
注:1 原则上要求独立设计,联合设计最多不超过两人;
2 提交仿真报告(论述清楚主要设计步骤),报告保存为Office word 2003版本;
3 用文件夹打包提交所有仿真程序和仿真报告;
4 文件夹和文件名命名为:学号+姓名.doc(如果两人联合,文件加及文件命名如上,但是文件中必须有合作者学号和姓名);
5 资料提交到ligun@(邮件主题写XXX同学信号检测估计计算机仿真报告,以免被邮件系统过滤为垃圾邮件);
6 报告提交截止日期:2013年11月30日12:00,过期不候;
7 雷同资料一律视为无效。
信号检测与估计(1)

1
xx
(
s)
[
S xs ( S xx
s)e s (s)
]
22
g(t) 1
2
1 Sxx (s)
[
S xs (s)et S xx (s)
] ds
g(t) 0 (t 0)
(t 0)
I E[e2 ]min
{Sss (s)
Sxx (s) S xx (s)
[
S xs ( S xx
s)et (s)
x(t) s(t) n(t) (0 t T )
1) =0,则为滤波。 2) >0,则为预测(外推)。 3) <0,则为平滑(内插)。
2
例1: 设信号为S(t)为均值为零的平稳随机过程。
求 S(t ), 0的估计
S(t ), 0
解: 采用线性最小均方误差估计
Sˆ(t ) aS(t)
Rs (0)
E{[S (t
)
Rs ( ) ]S (t
Rs (0)
)}
Rs
(0)
Rs 2 ( )
Rs (0)
4
例2: 设信号为S(t)为均值为零的平稳随机过程。
用 S(t) 及其导数 S / (t) 对 S(t ), 进0 行预测。
解:
Sˆ(t ) aS(t) bS / (t)
由线性最小均方误差估计和正交原理
S y ( j)
R
y
()e
j
d
1
S y () 2
S
y
(
j)e
j
d
21
如
S
y
(s)
Sy
(s)S
y
(s)
则 G(s)Sxx (s)Sxx (s) Sxs (s)es A(s)
信号检测与估计作业参考(电子科大)

对于两种假设下的条件概率密度函数为
则似然比
p(x | H0) =
1 2π σ
e−
x2 2σ 2
;
p(x
|
H1)
=
1
e−
(
x −1)2 2σ 2
2π σ
有贝叶斯准则得
Λ(x) =
p(x | H1)
2 x−1
= e 2σ 2
p(x | H0)
Λ0 =
p(H0 ) ⋅ c10 − c00 p(H1) c01 − c11
4
(2)与 β 相应的各假设先验概率。
解:
(1)求判决门限 β :
由题设可得相应假设的似然函数 p(x | H1) 和 p(x | H0 )
⎧
⎪ ⎪
p(
x
|
H1
)
=
⎨
⎪ ⎪⎩
p(
x
|
H
0
)
=
1
− ( x−1)2
e 2σ 2
2π σ
1
− x2
e 2σ 2
2π σ
则相应的似然比为
Λ(x) =
p(x | H1)
(2)相应的检测概率 P(D1|H1) .
解:
(1)求最佳判决门限 β
单个样本所对应的似然函数为:
p(xi | H0 ) =
1 2π σ
− xi2
e 2σ 2
;
p( xi
|
H1)
=
1
− ( xi −2)2
e 2σ 2
2π σ
由于样本相互独立且服从正态分布,则可得此时依据 M 个独立样本所得似然函数为:
>
1 2
信号检测与估计实验指导书

1实验1 匹配滤波器的仿真验证............................................................................ 1 实验2 信号检测的仿真验证 ............................................................................... 3 第验3 信号参量估计的仿真验证........................................................................ 6 实验4 卡尔曼滤波的仿真验证. (8)实验1 匹配滤波器的仿真验证一、实验目的通过利用Matlab 编程,验证匹配滤波器的基本原理和特性,进一步掌握匹配滤波器的基本概念和基本原理,加深对匹配滤波器性质的理解,掌握匹配滤波器的一般设计方法,深刻认识匹配滤波器的一些实际应用,熟悉用计算机进行数据分析的方法。
二、实验仪器1.硬件实验平台:通用个人计算机;2.软件实验平台:32位或64位Windows 操作系统,Matlab 软件。
三、实验原理在输入为确定信号加平稳噪声的情况下,使输出信噪比达到最大的线性系统称为匹配滤波器。
假设确定信号加平稳噪声的输入信号模型为)()()(t n t s t x += (3.1)式中:)(t s 为确定信号,并存在于时间间隔],0[T 内;)(t n 为平稳噪声,其均值为0,自相关函数为)(τn R 。
设)(0t h 是匹配滤波器的冲激响应,则匹配滤波器方程为2 T t t T s t R h Tn ≤≤-=-⎰0)(d )()(00τττ (3.2)匹配滤波器的最大输出信噪比为⎰-=TT s h 00max d )()(SNR τττ (3.3)设白噪声的自相关函数为)()2/()(0τδτN R n =,功率谱密度为2/)(0N S n =ω。
信号检测与估计仿真作业

信号检测与估计计算机仿真作业一.实验目的1.学习Matlab软件在信号检测与估计中的应用2.学习MUSIC、ESPRIT、GEESE等的空间谱估计算法的原理,并通过仿真分析比较这三种算法的不同及性能特点3.通过仿真分析了解非平稳噪声和色噪声对MUSIC、ESPRIT、GEESE方法性能的影响二.实验原理2.1最小错误概率准则出发点是如何使译码后的错误概率PE为最小。
其基本思路为:收到yj后,对于所有的后验概率P(x1|yj),P(x2|yj), …,P(xi|yj),…,若其中P(x*|yj)具有最大值,则将x*判决为yj的估值。
由于这种方法是通过寻找最大后验概率来进行译码的,故又常称之为最大后验概率准则。
最大后验概率译码方法是理论上最优的译码方法,但在实际译码时,既要知道先验概率又要知道后验概率,而后验概率的定量计算有时比较困难,需要寻找更为实际可行的译码准则。
2.2 MUSIC原理MUSIC算法是一种基于矩阵特征空间分解的方法。
从几何角度讲,信号处理的观测空间可以分解为信号子空间和噪声子空间,显然这两个空间是正交的。
信号子空间由阵列接收到的数据协方差矩阵中与信号对应的特征向量组成,噪声子空间则由协方差矩阵中所有最小特征值(噪声方差)对应的特征向量组成。
MUSIC算法就是利用这两个互补空间之间的正交特性来估计空间信号的方位。
噪声子空间的所有向量被用来构造谱,所有空间方位谱中的峰值位置对应信号的来波方位。
MUSIC算法大大提高了测向分辨率,同时适应于任意形状的天线阵列,但是原型MUSIC算法要求来波信号是不相干的。
2.3 ESPRIT算法原理ESPRIT算法估计信号参数时要求阵列的几何结构存在所谓的不变性,这个不变性可以通过两种手段得到:一是阵通过某些变换获得两个或两个以上的相同子阵。
由于这种算法在有效性和方面都有非常突出的表现,已经被公认为空间谱估计的一种经典算法,随着ESPRIT 算法的深入研究,ESPRIT算法进一步被广大学者接受并推广。
信号处理仿真题作业

信号处理基础仿真作业学号:S*********姓名:***3.17在计算机上用如下方法产生随机信号()u n的观测样本:首先产生一段零均值、方差为2σ的复高斯白噪声序列()v n;然后在()v n上叠加三个复正弦信号,它们的归一化频率分别是f1=0.15,f2=0.17和f3=0.26。
调整2σ和正弦信号的幅度,使在f1、f2和f3处得信噪比分别为30dB、30dB和27dB。
(1)令信号观测样本长度N=32,试用3.1.1节讨论的基于FFT的自相关函数快速计算方法估计出自相关函数^()0mr,并与教材式(3.1.2)估计出的自相关函数^()mr做比较。
产生零均值、方差为1的复高斯白噪声序列y >> y=randn(1,32);>> y=y-mean(y);>> y=y/std(y);>> a=0;>> b=sqrt(2);>> y=a+b*y产生三个复正弦信号并产生观察样本:>> N=32;>> f1=0.15;>> f2=0.17;>> f3=0.26;>> SNR1=30;>> SNR2=30;>> SNR3=27;>> A1=10^(SNR1/20);>> A2=10^(SNR2/20);>> A3=10^(SNR3/20);>> signal1=A1*exp(j*2*pi*f1*(0:N-1));>> signal2=A2*exp(j*2*pi*f2*(0:N-1));>> signal3=A3*exp(j*2*pi*f3*(0:N-1));>> un=signal1+signal2+signal3+y基于FFT的自相关函数快速计算方法:N=32;>> Uk=fft(un, 2*N);Sk=(1/N)* abs(Uk).^2;r0=ifft(Sk);r1=[r0(N+2:2*N),r0(1:N)];>> figure(1);>> stem(real(r1));>> figure(2);>> stem(imag(r1))输出结果为:图 1 基于FFT的自相关函数快速计算实部:虚部:教材中式(3.1.2)估计自相关函数>> r=xcorr(un, N-1,'biased');>> figure(1);>> stem(real(r))>> figure(2);>> stem(imag(r))输出结果为:图 2 教材式(3.1.2)估计的自相关函数实部:虚部:(2)令信号观测样本长度N=256,试用BT法和周期图法估计()u n的功率谱,这里设BT法中所用自相关函数的单边长度M=64。
通信信号处理仿真大作业
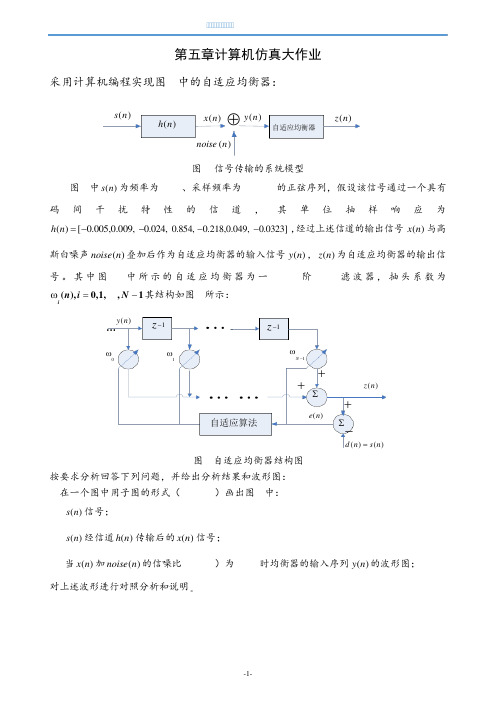
第五章计算机仿真大作业采用计算机编程实现图1中的自适应均衡器:()h n ()s n ()x n ⊕()noise n ()y n 自适应均衡器()z n图1 信号传输的系统模型图1中()s n 为频率为10Hz 、采样频率为1000Hz 的正弦序列,假设该信号通过一个具有码间干扰特性的信道,其单位抽样响应为()[0.005,0.009,0.024,h n =--0.854,0.218,0.049,0.0323]--,经过上述信道的输出信号()x n 与高斯白噪声()noise n 叠加后作为自适应均衡器的输入信号()y n ,()z n 为自适应均衡器的输出信号。
其中图1中所示的自适应均衡器为一N=31阶FIR 滤波器,抽头系数为(),0,1,,1in i N ω=-其结构如图2所示: 1z -()y n 0ω1ω∑∑++()()d n s n =+-()z n ()e n 1z -1N ω-自适应算法图2自适应均衡器结构图按要求分析回答下列问题,并给出分析结果和波形图: 1.在一个图中用子图的形式(subplot )画出图1中: (1)()s n 信号;(2)()s n 经信道()h n 传输后的()x n 信号;(3)当()x n 加()noise n 的信噪比SNR(dB )为20dB 时均衡器的输入序列()y n 的波形图; 对上述波形进行对照分析和说明。
01002003004005006007008009001000-101正弦信号s(n)01002003004005006007008009001000-101x(n)序列1002003004005006007008009001000-101y(n)序列分析说明:s(n)通过具有码间干扰特性的信道h(n),由于信道存在一定的误差和码间干扰使系统的性能下降,x(n)的波形密度减小了,但整体波形没有发生变化。
加入噪声后,y (n )的幅值没有变化,但整个波形由于受到噪声干扰浮现“毛刺”现象,波形不在平滑。
2021年信号检测与估计各章作业参考答案(1~9章)

其中 是常数, 是 上均匀分布的随机参量; 是高斯白噪声。
(a)求判决公式及最正确接收机结构形式。
(b)如果 ,证明最正确接收机可用 作为检验统计量,并对此加以讨论。
解:〔a〕设 是均值为0、功率谱密度为 的正态白噪声,那么有
由于
所以
按照贝叶斯准那么
或者
两边取对数得到
最正确接
因此 的均值、二阶原点矩和方差分别为
9.假设随机过程 的自相关函数为 ,求 的功率谱密度。
解:自相关函数与功率谱密度函数是一对傅立叶变换对,所以有
利用欧拉公式,可得
11.平稳随机过程 具有如下功率谱密度
求 的相关函数 及平均功率 。
解:
而自相关函数 与功率谱密度 是一对傅立叶变换,
〔b〕不管是否有条件 ,
都可选 作为检验统计量。
当 时,由于
所以判决规那么为
第六章多重信号检测
思考题1:为何要进行多重信号的检测?
答:利用多重信号检测的优势是可以增加检测系统的信噪比,从而增强系统的检测性能。
思考题3:何谓随机相位相干脉冲串信号和随机相位非相干脉冲串信号?
答:通常把多个脉冲信号组成的一串信号称为脉冲串信号,各个脉冲叫做子脉冲,整个信号叫做脉冲串信号。如果脉冲串信号的初相随机,但各个子脉冲信号的相位一致,那么称之为随机相位相干脉冲串信号。如果各子脉冲信号的相位都是随机变化的,且彼此独立变化,那么称之为随机相位非相干脉冲串信号。
〔1〕求 的最大似然估计。
〔2〕假设 的概率密度
求 的最大后验概率估计。
解:〔1〕由题意可写出似然函数
按最大似然估计方程 ,由此解得
〔2〕当 时,可按最大后验概率方程 求解,得到
信号检测与估计仿真实验

MATLAB仿真实验(1)单频信号,f=100KHz,T=1ms,采样率fs=500KHz,输入SNR=6dB,脉冲压缩后脉宽,信噪比等参数的变化?(2)线性调频信号,f=90—100KHz,T=20ms,采样率fs=500KHz,输入SNR=6dB,脉冲压缩后脉宽,信噪比等参数的变化?要求:仿真作业需提交MATLAB程序(m文件)和仿真结果分析报告电子版仿真实验(1)1.单频信号脉冲压缩程序clc;clear;close all;f=100e3;%信号频率T=1e-3;%脉宽1msfl=90e3;f2=110e3;B=20e3;%系统带宽fs=500e3;%采样频率m=T*fs;%采样点个数t1=1/fs:1/fs:T;SNR_1=6; %输入信噪比S=sin(2*pi*f*t1);S_max=max(S);%单频信号最大值figure(1); %画出单频信号波形图plot(t1,S);xlabel('t/s');ylabel('单频信号幅度');title('单频信号时域波形图');Noise=randn(1,3*length(S)); %高斯白噪声序列[b,a]=butter(8,[fl,f2]/(fs/2),'bandpass');Noise_filter=filter(b,a,Noise); %白噪声通过滤波器std_Noise=(S_max/sqrt(2))/(10^(SNR_1/20)); %高斯白噪声的标准偏差std_Noise_1=Noise_filter/std(Noise_filter);%通过滤波器后噪声的标准偏差Noise_f_s=std_Noise_1*std_Noise; %满足输入信噪比下的带限白噪声std_Noise_filter_s=std(Noise_f_s);%带限白噪声的标准偏差figure(2);%画出带通滤波后噪声时域图像t2=linspace(0,3*T,1500);%产生时间数组plot(t2,Noise_f_s);xlabel('t/s');ylabel('噪声幅度');title('带通滤波后噪声时域图像');P_Noise=fft(Noise_f_s);%对带限白噪声作快速傅里叶变换figure(3) %画出带通滤波后噪声频域图像t3=linspace(1,500000,1500);plot(t3,abs(P_Noise));xlim([0 200000]);xlabel('f/Hz');ylabel('噪声频谱');title('带通滤波后噪声频域图像');S_send=[zeros(1,500),S,zeros(1,500)];%信号补零,使之处于噪声之中Rec=S_send+Noise_f_s;%接受混有噪声的信号figure(4);%接收信号时域波形t4=linspace(0,3*T,1500);plot(t4,Rec);xlabel('t/s');ylabel('接受信号幅度');title('接受信号');figure(7)P_Rec=fft(Rec);t7=linspace(0,fs,length(P_Rec));plot(t7,abs(P_Rec));xlim([50000 150000]);xlabel('f/Hz');ylabel('接收信号频谱');title('接收信号频谱图像');Rec_x=xcorr(Rec,S_send);figure(5);t5=linspace(0,6*T,length(Rec_x));plot(t5,Rec_x);xlabel('t/s');ylabel('信号幅度');title('脉冲压缩后图像');R_dB=20*log10(abs(hilbert(Rec_x))/max(Rec_x));%归一化并取分贝值figure(6)plot(t5,R_dB);xlabel('t/s');ylabel('信号幅度/dB');title('脉冲压缩后图像');Rec_S=xcorr(S,S);max_Rec_S=max(Rec_S);Rec_max=max(Rec_x);%接收信号最大值Rec_std=std(Rec_x);%接受信号标准值SNR_2=20*log10(Rec_max/Rec_std); %输出信噪比2.仿真结果仿真实验(2)1.线性调频信号脉冲压缩程序clc;clear;close all;T=0.02;%脉宽20msfl=90e3;f2=110e3;B=20e3;%系统带宽f0=100e3;SNR=6;%信噪比6dBfs=500e3;%采样频率m=T*fs;k=B/T;%调频斜率t1=1/fs:1/fs:T;LFM=sin(2*pi*fl*t1+pi*k*t1.^2);%LFM信号figure(1); %画出线性调频信号幅度图像plot(t1,LFM);title('LFM信号时域图像');xlabel('t/s');ylabel('幅度');P_LFM=fft(LFM);%对LFM信号做快速傅里叶变换figure(2);%画出线性调频信号频谱图像t2=linspace(0,fs,length(P_LFM));plot(t2,abs(P_LFM));xlim([50000 150000]);xlabel('f/Hz');ylabel('线性调频信号频谱');title('调频信号频谱图像');Noise=randn(1,3*length(LFM)); %高斯白噪声序列[b,a]=butter(10,[fl,f2]/(fs/2),'bandpass');Noise_f=filter(b,a,Noise); %白噪声通过滤波器std_Noise=(max(LFM)/sqrt(2))/(10^(SNR/20)); %噪声的标准偏差std_Noise_f=Noise_f/std(Noise_f);%通过滤波器后噪声标准偏差Noise_f_s=std_Noise_f*std_Noise; %满足条件的带限白噪声std_Noise_f_s=std(Noise_f_s);%带限白噪声的标准偏差figure(3);%画出瞒住条件的带限噪声信号幅度谱图像t3=linspace(0,3*T,length(Noise_f_s));%产生时间数组plot(t3,Noise_f_s);xlabel('t/s');ylabel('噪声幅度');title('带限噪声信号幅度谱');P_N=fft(Noise_f_s);%对带限噪声做快速傅里叶变换figure(4);%画出带限噪声频谱图像t4=linspace(0,fs,length(P_N));%产生时间数组plot(t4,abs(P_N));xlim([0 200000]);xlabel('f/Hz');ylabel('噪声频谱');title('带限噪声频谱图像');LFM_send=[zeros(1,10000),LFM,zeros(1,10000)];%信号补零,使信号处于噪声中Rec=LFM_send+Noise_f_s;%接收混有噪声的线性调频信号figure(5);%画出接收信号幅度谱图像t5=linspace(0,3*T,length(Rec));%产生时间数组plot(t5,Rec);xlabel('t/s');ylabel('接收信号幅度');title('接受信号幅度谱');Rec_x=xcorr(Rec,LFM_send);%计算自相关函数figure(6); %画出脉冲压缩后幅度谱t6=linspace(0,6*T,length(Rec_x));plot(t6,Rec_x);xlabel('t/s');ylabel('信号幅度');title('脉冲压缩后幅度谱');Max_x_H=max(Rec_x);Rec_x_H=20*log10(abs(hilbert(Rec_x))/max(Rec_x));%取分贝并且归一化figure(7);%画出脉冲压缩后信号级图像t7=linspace(0,6*T,length(Rec_x));%产生时间数组plot(t7,Rec_x_H);xlabel('时间');ylabel('分贝');title('脉冲压缩后信号级图像');Rec_max=max(Rec_x);Rec_std=std(Rec_x);SNR_out=20*log10(Rec_max/Rec_std); %输出信噪比2.仿真结果仿真结果分析:单频信号与线性调频信号脉冲压缩后输出的信噪比都比输入的信噪比高,但对比两种信号的信噪比变大倍数,显然线性调频信号的信噪比变化更大。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
信号检测与估计计算机仿真作业一.实验目的1.学习Matlab软件在信号检测与估计中的应用2.学习MUSIC、ESPRIT、GEESE等的空间谱估计算法的原理,并通过仿真分析比较这三种算法的不同及性能特点3.通过仿真分析了解非平稳噪声和色噪声对MUSIC、ESPRIT、GEESE方法性能的影响二.实验原理2.1最小错误概率准则出发点是如何使译码后的错误概率PE为最小。
其基本思路为:收到yj后,对于所有的后验概率P(x1|yj),P(x2|yj), …,P(xi|yj),…,若其中P(x*|yj)具有最大值,则将x*判决为yj的估值。
由于这种方法是通过寻找最大后验概率来进行译码的,故又常称之为最大后验概率准则。
最大后验概率译码方法是理论上最优的译码方法,但在实际译码时,既要知道先验概率又要知道后验概率,而后验概率的定量计算有时比较困难,需要寻找更为实际可行的译码准则。
2.2 MUSIC原理MUSIC算法是一种基于矩阵特征空间分解的方法。
从几何角度讲,信号处理的观测空间可以分解为信号子空间和噪声子空间,显然这两个空间是正交的。
信号子空间由阵列接收到的数据协方差矩阵中与信号对应的特征向量组成,噪声子空间则由协方差矩阵中所有最小特征值(噪声方差)对应的特征向量组成。
MUSIC算法就是利用这两个互补空间之间的正交特性来估计空间信号的方位。
噪声子空间的所有向量被用来构造谱,所有空间方位谱中的峰值位置对应信号的来波方位。
MUSIC算法大大提高了测向分辨率,同时适应于任意形状的天线阵列,但是原型MUSIC算法要求来波信号是不相干的。
2.3 ESPRIT算法原理ESPRIT算法估计信号参数时要求阵列的几何结构存在所谓的不变性,这个不变性可以通过两种手段得到:一是阵通过某些变换获得两个或两个以上的相同子阵。
由于这种算法在有效性和方面都有非常突出的表现,已经被公认为空间谱估计的一种经典算法,随着ESPRIT 算法的深入研究,ESPRIT算法进一步被广大学者接受并推广。
2.4 GEESE算法基本原理信号子空间特征向量的广义特征值法(GEESE),可以在简化计算的情况下解决ESPRIT算法中实际噪声测量有误差的问题。
它利用信号子空间的一个显著特征,那就是真实方向向量所张成的子空间与除了阵列输出互相关矩阵的最小多重特征值之外的所有相应特征向量所张成的子空间是一样的。
2.5非相关源的数学模型图2.1 .阵元接收信号与位置的关系阵元接收信号与位置的关系如图 2-1 所示。
假设空间有M 个阵元组成阵列,将阵元从1到M 编号,并以阵元 1 作为参考点。
由于各阵元无方向性,相对于基准点的位置向量分别为1(1,2,...,,0)i i N r r ==令信源信号为 s(t),信号的载波为iwt e,则基准点处的接收信号为()jwt s t e ,各阵元上的接收信号的表达式为1()()exp[()]T i i i c s t s t r j wt rk α=--式中k 为波数向量,α为入射信号传播的传播方向,单位向量,1T i c r α为信号相对于基准点的延迟时间,i r k 为信号传播到基准点r 处的阵元相对于信号传播到基准点的滞后相位(弧度)。
图中θ为入射信号传播方向角,k = k[cos θ,sin θ]。
天线阵列中,信号的带宽B 一般比载波频率ω小得多,所以就有1()()T i c s t r s t -≈,即信号在各阵元上的差异可以忽略不计,称为窄带信号。
因此,阵列信号用向量形式可以表示为: 1212()[(),(),...,()]()[,,...,]TT T N TN jr k jr k jr k T s t s t s t s t s t e e e ---==选定第一个阵元为基准点,则方向向量为 2()[1,,...,]TT N jr k jr k T e e αθ--= 式中,1i i r r r =-当有P 个信源时,波束的方向向量可分别表达为1()αθ,2()αθ,…,()p αθ。
这P 个方向向量组成的矩阵 12[(),(),...,()]p A αθαθαθ=称为阵列的方向矩阵或响应矩阵,它表示所有信源的方向信息。
当有N个窄带信号入射到空间M 个阵元上时候,接收的信号可以写成如下的矢量形式:()()()X t AS t N t=+式中,X(t)为阵列的M×1维快拍数据矢量,N(t)为阵列的M ×1维噪声数据矢量,S(t)为空间信号的N×1维矢,A空间阵列的M×N维响应矩阵(导向矢量阵)。
三.实验过程3.1 实验1首先,当M=1,实验1就变成了一般二元随机振幅与随机相位信号的波形检测问题。
这样,就有如下模型:H0: x(t)=B1cos(ω0t+θ0)+n(t), 0≤t≤TH1: x(t)=A1cos(ω1t+θ0)+n(t), 0≤t≤T其中,噪声n(t)是均值为零,功率谱密度为P n(ω)=N02⁄的高斯白噪声;信号的振幅服从瑞丽分布,随机相位服从均匀分布。
由于功率信噪比早0~60dB范围内,取A0=100,N0=2,T=1us。
根据教材的推导,得到错误判决概率的表达式如下:P(H0|H1)=N02N0+σa2TP(H1|H0)=N02N0+σa2T从上面可以看到,当M=1时,模型很简单。
当M>1时,我们选取一个M值,用MA TLAB 软件进行仿真,得到仿真结果如下图所示(MATLAB仿真程序见附录1):3.2 实验23.2.1. MUSIC 算法过程及仿真1).收集阵列接收的数据样本,0,1,,1i x i p =-得到数据协方差矩阵xx R1,,01p H xx i i i R x x P -==∑ 2).对协方差矩阵xx R 进行特征分解,分解为特征值和特征向量的形式xx R V V =Λ式中,0,1,1,[]N V q q q -=是xx R 对应的特征向量所组成的矩阵,011011{,},N N V diag λλλλλλ--=≥≥为xx R 的特征值。
3).利用最小特征值min λ的重数M 来估计信号源数KK N M =-4).计算MUSIC 算法的功率谱()()()()H MUSIC H H N N a a P a V V a θθθθ= 5).MUSIC P 中极大值对应的角度就是信号入射方向。
在Matlab 的命令窗口输入仿真程序,见附录2,得到如下结果:A =-10 23 45DOA =44.9986 23.0019 -10.0519图3.1 MUSIC 算法非相关源的模拟测向仿真3.2.2 ESPRIT 算法过程及仿真1).由快拍数据X 可以得到数据相关矩阵R 的估计R2).对相关矩阵的估计R 做特征分解H R U U =∑(33) 特征值矩阵011{,}N diag λλλ-=∑,0,1,1,[]N U q q q -=。
3).利用小特征值的重数估计M 得到信号源的估计数K N M =-。
4).将特征向量矩阵分解为子阵列矩阵得到:12s s U U U ⎡⎤=⎢⎥⎢⎥⎣⎦5). 得到ψ112()s s U U -ψ=6). 对Ψ进行特征分解,得到K 个特征值,就可以得到对应K 个信号的到达角。
在Matlab 的命令窗口输入仿真程序,见附录3,得到如下结果:A =-10 23 45DOA =44.9986 23.0019 -10.0519图3.2 ESPRIT 算法非相关源的模拟测向仿真3.2.3 GEESE 算法:1).收集阵列接收的数据样本,0,1,...,1i x i P =-得到数据协方差矩阵xx R11P H xx i i i R x x P -==∑ 2). 对xx R 进行特征分解,得到s V '和s '∑:xx s s s R V V '''=∑3). 选定J 的值,将s V '代入式中得到1E ',2E ':1,[]JJ N J s E I O V -''= 2,1,1[]J J J N J s E O I O V --''=4). 将1S V ,2S V 代入式得到k η';5). 将k η'代入式中即得到信号源的波达方向:arg()k k θη''= 1,2,...,k K =在Matlab 的命令窗口输入仿真程序,见附录4,得到如下结果:DOA =-30.02440.000030.0244图3.3 GEESE算法非相关源的模拟测向仿真3.2.4 三种算法性能比较MUSIC算法就是多重信号分类算法,它是一种信号参数估计算法,利用输入信号协方差矩阵的特征结构,给出的信息包括入射信号的数目、各个信号的波达方向、强度以及入射信号和噪声间的互相关。
ESPRIT算法就是旋转不变子空间算法,也是一种基于子空间的波达方向估计技术,与MUSIC算法不同的是,ESPRIT 算法不需要精确知道阵列的方向向量,仅需各子需各子阵列之间保持一致,因此降低了对阵列校准的严格性。
GEESE算法是指信号子空间特征向量的广义特征值法,可以在简化计算的情况下解决ESPRIT算法中实际噪声测量有误差的问题。
它利用信号子空间的一个显著特征,那就是真实方向向量所张成的子空间与除了阵列输出互相关矩阵的最小多重特征值之外的所有相应特征向量所张成的子空间是一样的。
这三种算法是空间谱估计中最经典的算法。
MUSIC算法估计值接近克拉美—罗界算法(CRB),对参数的少量偏差不敏感,更接近实际应用,具有较好的应用前景,但需要对参数空间进行搜索,计算量大。
随着信噪比的增加,MUSIC功率谱的峰值越高,估计精度越精确。
在阵元数目不同,其他条件相同的情况下,阵元数目越大,旁瓣干扰越小,DOA估计越精确。
在条件相同的情况下,相邻信号(以50为例)的MUSIC功率谱随着角度的增加而降低,信号源相关,MUSIC算法失效。
色噪声下,MUSIC算法方位估计不准确。
与MUSIC算法相比,ESPRIT算法还降低了计算量和存储量,且避免了参数空间的搜索,计算量小于MUSIC算法,但是算法数据协方差矩阵中提取噪声方差的估计,有时会使估计结果变坏,当信号高度相关时估计性能同样会变坏,且对所设的参数有较高的要求,少量的误差也会导致算法的失败。
在ESPRIT算法中随着信噪比的增加,均方误差越小,DOA估计效果越好。
在阵元数目不同,其他条件相同的情况下,阵元数目越大,均方误差越小,ESPRIT算法的估计精度越高。
在条件相同的情况下,相邻信号(以100为例)的均方差与信噪比关系随着角度的增加而性能降低。
ESPRIT 算法对相干信号的 DOA 估计失效。
