nurbs曲线和贝塞尔曲线
贝塞尔曲线B样条NURBS样条学习总结

Bezier曲线、B样条曲线和NURBS曲线0.概述1. 贝塞尔曲线(Bezier Curve):贝塞尔曲线由一组控制点和控制点上的权重组成。
贝塞尔曲线的阶数由控制点的数量决定,阶数为n的贝塞尔曲线需要n+1个控制点。
贝塞尔曲线具有局部控制的特性,即曲线上的一段由相邻的几个控制点决定,不受其他控制点的影响。
贝塞尔曲线的计算相对简单,但在变形过程中可能会出现形状扭曲的问题。
2. B样条(B-Spline): B样条曲线是一种基于分段多项式的曲线表示方法。
与贝塞尔曲线不同,B样条曲线的每个控制点都有一个关联的基函数。
这些基函数决定了曲线上每一点的形状。
B样条曲线的阶数可以是任意的,较高阶的B样条曲线能够更灵活地描述复杂的曲线形状。
B样条曲线具有良好的局部控制性和平滑性,可以很好地避免贝塞尔曲线的形状扭曲问题。
3. NURBS曲线(Non-Uniform Rational B-Spline Curve):NURBS曲线是对B样条曲线的扩展,它引入了有理权重的概念。
NURBS曲线的每个控制点都有一个关联的权重,这些权重可以调节曲线上各个点的影响程度。
NURBS曲线能够表示更复杂的曲线形状,如圆弧和椭圆等。
总的来说Bezier曲线中的每个控制点都会影响整个曲线的形状,而B样条中的控制点只会影响整个曲线的一部分,显然B样条提供了更多的灵活性;Bezier和B样条都是多项式参数曲线,不能表示一些基本的曲线,比如圆,所以引入了NURBS,即非均匀有理B样条来解决这个问题;贝塞尔曲线适用于简单的曲线形状设计,B样条曲线具有更好的局部控制和平滑性,适用于复杂曲线的建模而NURBS曲线在B样条的基础上引入了有理权重,可以更准确地描述各种曲线形状Bezier曲线是B样条的一个特例,而B样条又是NURBS的一个特例1.Bezier曲线1.1 贝塞尔曲线的历史:贝塞尔曲线于 1962 年,由法国工程师皮埃尔·贝济埃(PierreBézier)所广泛发表,他运用贝塞尔曲线来为汽车的主体进行设计,贝塞尔曲线最初由保尔·德·卡斯特里奥于1959年运用德卡斯特里奥算法开发,以稳定数值的方法求出贝塞尔曲线。
Nurbs曲线详解

Nurbs曲线详解NURBS(Non Uniform Rational B-spline)曲线通常称为非均匀有理B样条曲线,其数学定义如下:基函数由递推公式定义:非均匀:指节点向量的值与间距可以为任意值。
这样我们可以在不同区间上得到不同的混合函数形状,为自由控制曲线形状提供了更大自由。
均匀与非均匀的主要区别在于节点向量的值。
如果适当设定节点向量,可以生成一种开放均匀样条,它是均匀与非均匀的交叉部分。
开放样条在两端的节点值会重复d次,其节点间距是均匀的。
例如:{0,0,1,2,3,3},(d=2,n=3){0,0,0,1,2,2,2},(d=4,n=4)开放均匀B样条与贝泽尔样条性质非常类似,如果d=n+1(即多项式次数为n),那么开放B样条就变成了贝泽尔样条,所有节点值为0或1。
如四个控制点的三次开放B样条,节点向量为:{0,0,0,0,1,1,1}。
有理B样条:有理函数是两个多项式之比,有理样条(rationalspline)是两个样条函数之比,有理B样条用向量描述。
URBS曲线由以下三个参数定义:(1)控制点:确定曲线的位置,通常不在曲线上,形成控制多边形。
(见图1,图中)图1 控制点移动对曲线的影响(2)权因子:确定控制点的权值,它相当于控制点的“引力”,其值越大曲线就越接近控制点(见图2,Bi为控制点)。
图2 曲线随权因子变化(3)节点矢量K:NURBS曲线随着参数K的变化而变化,与控制顶点相对应的参数化点K称为节点,节点的集合Ki:[K0,K1…,Kn…,Kn+m+1]称为节点矢量。
节点:在曲线上任意一点有多于一个控制点产生影响(除了bezier的端点),节点就象一种边界,在这个边界上一个控制点失去影响作用,另一个控制点取得影响。
2、NURBS曲线怎样通过首末节点多重节点序列使得样条曲线更靠近于重复节点位置。
如果末端节点重复d+1次,则d 阶B-样条必须插值最后一个控制点。
因此,解决样条曲线不能横跨整个控制顶点序列的一个方法是,重复首尾两个节点,这样得到的样条曲线将插值首尾两个控制点。
nurbs曲线和贝塞尔曲线

Nurbs曲线和贝塞尔曲线1. 引言曲线在计算机图形学中扮演着重要的角色,用于绘制平滑的形状和路径。
Nurbs曲线(Non-Uniform Rational B-Spline)和贝塞尔曲线是两种常用的数学表示方法,被广泛应用于计算机图形学、CAD设计、动画制作等领域。
本文将介绍Nurbs曲线和贝塞尔曲线的基本概念、数学表示方法以及应用场景。
2. Nurbs曲线2.1 基本概念Nurbs曲线是一种由多个控制点和权重组成的数学曲线。
它通过插值或逼近这些控制点来定义一个平滑的曲线。
Nurbs曲线具有以下特点:•非均匀性(Non-Uniformity):相邻控制点之间可以有不同的距离,从而使得曲线更加灵活。
•有理性(Rationality):每个控制点都有一个权重值,可以调整该点对整体形状的影响程度。
•B样条插值(B-Spline Interpolation):通过插值控制点来得到平滑的曲线。
2.2 数学表示方法Nurbs曲线可以通过以下数学公式表示:其中,u为参数,P为控制点,N为基函数,w为权重。
基函数N是由B样条插值算法计算得到的。
2.3 应用场景Nurbs曲线广泛应用于计算机图形学和CAD设计领域。
它们可以用于绘制平滑的曲线、曲面和体积模型。
例如,在三维建模软件中,设计师可以使用Nurbs曲线来创建汽车的车身曲线、船体曲线等复杂形状。
3. 贝塞尔曲线3.1 基本概念贝塞尔曲线是一种由多个控制点组成的数学曲线。
它通过控制点之间的插值来定义一个平滑的路径或形状。
贝塞尔曲线具有以下特点:•控制点决定形状:贝塞尔曲线的形状由控制点的位置决定。
•插值特性:贝塞尔曲线经过起始和结束控制点,并且在两个端点处切线方向与控制点的切线方向一致。
3.2 数学表示方法贝塞尔曲线可以通过以下数学公式表示:其中,t为参数,P为控制点,B为贝塞尔基函数。
贝塞尔基函数由二项式系数和控制点的位置决定。
3.3 应用场景贝塞尔曲线广泛应用于计算机图形学和动画制作领域。
NURBS曲线理论

第三章 NURBS 曲线理论基础NURBS 方法的提出是基于描述自由曲面曲线的B 样条方法。
B 样条基函数和B 样条曲线是UURBS 曲线的基础,UURBS 是非均匀有理B 样条的英文缩写。
因此在给出UURBS 曲线定义之前,先介绍一下B 样条基函数和B 样条曲线的相关知识。
3.1 B 样条基函数定义和性质B-Spline Function (简称B 样条)就是B 样条基函数,是样条函数的一种。
B 样条不但具有一般样条函数所具有的分段光滑又在各段交接处具有一定光滑性等特点,而且具有许多其他优良性质,如连续阶数可调、局部支撑性、递推性等。
有很多种方法可以用来定义B 样条基函数,我们这里采用de Boor-Cox 递推定义方法,是由这种递推法很容易和有效地在计算机上实现。
而且de Boor-Cox 递推定义很好地揭示了B 样条基函数的性质。
B 样条基函数的de Boor-Cox 递推定义如下:1,01,,11,1i 111[,N 0()()000i i i i i k i k i k i k i k i k i u u u u u u u N N u N u u u u u +++-+-++++⎧∈⎧=⎨⎪⎩⎪⎪--⎪=+⎨--⎪⎪=⎪⎪⎩)其他规定: (3. 1) 上式(3.1)中k 为B 样条的次数(k+1阶);令U={u 0,u 1,…,u m }是一个单调不减的实数序列,u i 称为节点序列,U 称为节点矢量,若存在ui-1,<u i =u i+1=…=u i+r-1<u i+r 则称节点u i 的重复度为r ,其中,r 、n 均为整数;N i,k (u )表示参数为u 时,k 次B 样条序号为i 的基函数值。
B 样条具有良好的性质,简单概括主要有【18,20】: ● 递推性:定义式(3.1)很好的说明了这个性质。
● 规范性:对于定义域内任意参数u ,所有的k 次B 样条基函数之和恒为1,即1)(0,=∑=u N mi k i 。
grasshopper运算器名称总结
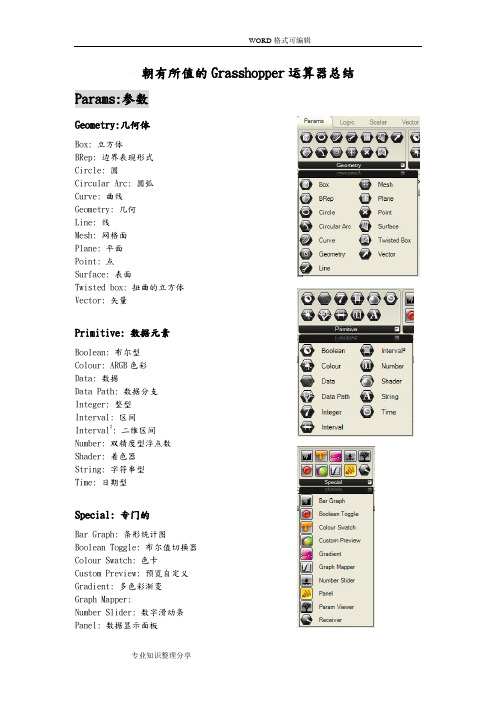
朝有所值的Grasshopper运算器总结Params:参数Geometry:几何体Box: 立方体BRep: 边界表现形式Circle: 圆Circular Arc: 圆弧Curve: 曲线Geometry: 几何Line: 线Mesh: 网格面Plane: 平面Point: 点Surface: 表面Twisted box: 扭曲的立方体Vector: 矢量Primitive: 数据元素Boolean: 布尔型Colour: ARGB色彩Data: 数据Data Path: 数据分支Integer: 整型Interval: 区间Interval2: 二维区间Number: 双精度型浮点数Shader: 着色器String: 字符串型Time: 日期型Special: 专门的Bar Graph: 条形统计图Boolean Toggle: 布尔值切换器Colour Swatch: 色卡Custom Preview: 预览自定义Gradient: 多色彩渐变Graph Mapper:Number Slider: 数字滑动条Panel: 数据显示面板Param Viewer: 参数结构查看器Receiver: 数据接收器Logic 逻辑Boolean: 布尔运算Gate And: 并集Gate And Ternary: 三元并集Gate Majority:Gate Nand:Gate Nor:Gate Not:Gate Or:Gate Or Ternary:Gate Xnor:Gate Xor:List: 列表Dispatch: 分配(把一个列表中的项目分派到两个目标列表中)List Item: 清单项List Length: 列表长度(计算列表的长度)Null Item:空值(测试一个数据项是否无效)Reverse List: 反转列表Shift List: 移动列表Sort List: 分类列表Split List: 分拆列表Sub List: 次级列表(从一个列表中提取子集)Weave: 编排(使用自定义的式样编排输入流的设置)Script: 脚本DotNET C# Script: C#脚本DotNET VB Script: VB脚本F1 : 一元函数F2 : 二元函数F3 : 三元函数Variable Expression : 多元函数Sets: 集合Cull Nth : 选取元素(在列表中每n个选取元素)Cull Pattern : 选取图案(使用反复的掩码在列表中选取元素)Duplicate Date : 复制数据Fibonacci: 费班纳赛(创建一个费班纳赛序列)Jitter: 振动Random:Range: 范围Series: 数列Trees: 设计树Clean Tree: 清理设计树(把数据树中所有空项和无效数据清除掉)Create Branch: 创建分支(创建一个分支访问路径)Decompose Branch: 分解分支(分解分支访问路径)Flatten Tree: “夷平”设计树(把设计树中所有分支路径去除)Graft tree: 续接设计树Merge: 合并(把两个数据流合二为一)Merge Multiple: 合并多项(合并多个输入数据流为一个)Simplify Tree : 简化设计树(通过清除重复的可共享的分支简化设计树)Prune Tree: 修剪设计树(从设计树中去掉小的分支路径)Stream Filter: 数据流过滤器(过滤输入的数据流)Stream Gate: 数据流闸口(向一个指定的输出项重新传入数据流)Tree Branch: 设计树分支(从数据树中取回一个指定的分支)Tree Item: 设计树项目(从数据树中取回一个指定的项目)Scalar:标量Constants:常数:Epsilon: 艾普西龙(四舍五入双精度浮点数)Golden Ratio: 黄金分割比(1.618)Natural logarithm: 自然对数(2.718)Pi: 圆周率(3.14)Interval:区间:Bounds: 界限(围绕数字列表创建一个区间)Bounds 2D: 二维界限(围绕坐标列表创建一个二维的区间)Divide Interval: 均分区间Divide Interval2: 均分二维区间Interval: 区间Interval Components: 分解一维区间Interval2: 通过两个一维区间创建二维区间Interval2: 通过四个数字创建二维区间Interval2 Components: 分解一个二维区间到四个数字Interval2 Components: 分解一个二维区间到独立的一维区间Operators:运算符:Addition: 加法运算Division: 除法运算Equality: 等量代换Larger Than: 比较运算(大于)Modulus: 取模运算Multiplication: 乘法运算Power: 乘方运算Similarity: 近似运算Smaller Than: 比较运算(小于)Subtraction: 减法运算Polynomials:多项式:Factorial: 阶乘Log N: 求底数为N的对数Logarithm: 求10为底的对数Natural logarithm: 求以e为底的对数Power of 10: 10的乘方Power of 2: 2的乘方Power of E: E的乘方Trig:三角函数:ArcCosine: 反余弦函数ArcSine: 反正弦函数ArcTangent: 反正切函数Cosine: 余弦函数Sine: 正弦函数Tangent: 正切函数Util:公用:Mass Addition: 并集运算Maximum: 取最大值Mean: 取平均值Minimum: 取最小值Truncate:Vector:矢量:Colour: 色彩Add Colours : 颜色相加AHSV : 创建一个HSV色彩通道(浮点色彩)ARGB : 创建一个RGB色彩通道ARGB Fractional : 创建一个浮点RGB色彩通道Blend Colours : 混合色彩(在两个颜色中取插值)Create Shader : 创建OpenGL着色器Multiply Colours: 色彩倍增Split AHSV: 将颜色分解为HSV通道Split ARGB: 将颜色分解为RGB通道Subtract Colours: 减去颜色通道Constants: 常数:Unit X : 与X轴平行的矢量Unit Y : 与Y轴平行的矢量Unit Z : 与Z轴平行的矢量XY Plane : XY平面XZ Plane : XZ平面YZ Plane : YZ平面Plane:平面:Align Plane : 调整平面(执行最小的旋转调整平面到矢量指向)Align Planes :Plane : 在XY平面上创建一个平面Plane 3Pt : 过三点创建一个平面Plane Components: 把平面分解到其组成元素Plane Normal: 创建平面法线Rotate Plane : 绕Z轴旋转平面Point:点:Closest Point: 查找最近点Decompose : 把点分解到其组成元素Distance : 计算连个点坐标间的欧几里得距离Grid Hexagonal : 在每六个点之间生成六边形网格Grid Rectangular : 在点之间生成矩形网格Plane CP: 查找离平面最近的点Point Cylindrical: 在柱面坐标上创建点(角度,半径,标高)Point List: 点列表(显示坐标点的顺序列表)Point Oriented: 通过UVW坐标创建点Point Polar: 在球面坐标上创建点Point XYZ: 通过XYZ坐标创建点Pull Point: 把点拉至几何体Text Tag: 在Rhino视图中创建文字标签Text Tag 3D: 在Rhino视图中创建三维文字标签Vector:矢量:Amplitude : 振幅(设置矢量的振幅)Angle : 角度(计算两个矢量间的夹角)Cross Product : 矢量叉积Decompose: 把矢量分解到其组成元素Dot Product: 矢量点积(计算连个矢量的数量积)Multiply: 执行矢量和标量的乘法运算Reverse: 矢量反向Summation: 求矢量的和Unit Vector:Vector 2Pt: 在两点间创建矢量Vector Length: 计算矢量的振幅Vector XYZ: 通过XYZ创建矢量Curve:曲线:Analysis:分析:Center: 查找圆或圆弧的圆点和半径Closed: 测试一条曲线是闭合的还是周期性的Curvature: 曲率(在指定的部位上评估一条曲线的曲率)Curvature Graph: 曲率图表(绘制Rhino的曲率图表)Curve CP: 在曲线上查找离指定点最近的点Curve Frame: 曲线骨架(在指定的部位上得到曲率骨架)Discontinuity: 不连续(沿曲线找出所有不连续点)End Points: 提取曲线端点Evaluate Curve: 评估曲线(在指定的部位上评估曲线)Evaluate Length: 评估长度(根据长度上一个特定的因子评估曲线,长度因子可以由曲线单元和法线单元提供,可以通过改变N参数来切换这两种模式)Explode: 炸开(把曲线分解到其组成元素)Horizontal Frame: 水平框架(在曲线上一个特定部位获取一个水平基准的框架)Length: 计算曲线长度Perp Frame: 垂直框架(在曲线上一个特定部位获取一个垂直基准的框架)Planer: 测试曲线平面性Division:分割:Curve Frames: 生成一系列等距曲线骨架Divide Curve: 等长度分割曲线Divide Distance: 用预设距离的点分割曲线Divide Length: 用预设长度分割曲线Hortzontal Frames: 产生一系列等位等高的曲线骨架Perp Frames: 用一系列垂直方向的等位骨架分割曲线Shatter: 按分段数打碎曲线Primitive:基本曲线:Arc: 圆弧(由基准面、半径、角度区间决定)Arc 3Pt: 过指定三点的圆弧Arc SED: SED圆弧(由起点、终点、切线矢量决定)BiArc: Bi曲线(由端点和切线决定)Circle : 圆(由指定平面和半径决定)Circle 3Pt: 过三个定点的圆Circle CNR: CNR圆(由圆心、旋转轴、半径决定)Ellipse : 椭圆(由指定平面和两个焦点决定)Line : 两点确定的线段Line SDL : SDL线段(由起点、正切方向、长度决定)Polygon : 多边形Rectangle: 矩形Spline:样条曲线:Bezier Span: 贝塞尔曲线Curve: 控制点曲线Curve On Surface: 创建一个在指定曲面上的内插点曲线Interpolate: 内插点曲线Iso Curve: ISO曲线(从曲线上提取的uv曲线)Kinky Curve: 混合式曲线(贝赛尔角点控制曲线)Poly Arc: 复合弧线(由圆弧和线段拼接而成)Poly Line: 复合线(连接各点组成的折线段)Sub Curve: 子曲线(从一条基本曲线上获得)Util:公用:Fillet: 接触点圆角Fillet Distance: 断点圆角Flip: 翻转曲线Join Curves: 结合曲线Offset: 偏移曲线Project: 投射曲线到复合曲面上(BRep曲面集合,即Rhino中的多重曲面)Surface:曲面:Analysis:分析:Box Components: 立方体元素(把立方体分解到其组成元素)Box Corners: 提取立方体角点BRep Area: 计算BRep(边界表示)的面积BRep Components: 把BRep(边界表示)分解到其组成元素BRep CP: 在BRep(边界表示)上查找离指定点最近的点BRep Volune: 计算BRep(边界表示)的体积BRep Wireframe: 提取BRep(边界表示)物体的线框Dimensions : 尺寸Evaluate Box: 在UVW空间评估一个立方体Evaluate Surface: 在UV坐标系上评估局部曲面特性Osc Circles: 圆上接触点(在指定的UV坐标系上计算出圆周上和曲面的交点)Principal Curvature: 助率(在指定的UV坐标系上计算出曲面的主曲率)Surface CP : 在曲面上查找离指定点最近的点Surface Curvature: 表面曲率在(指定的UV坐标系上计算出曲面的曲率)Trim Inclusion : 测试被修剪部分以内的UV点Freeform:自由曲面:4Point Surface: 由四点创建曲面Extrude: 沿矢量方向拉伸曲线或曲面Extrude Linear: 沿笔直路径拉伸曲线或曲面Extrude Point: 把曲面或曲线拉伸到指定点Loft: 沿界面曲线方向Offset: 定量偏移曲面Pipe: 沿轨道产生管状曲面Planar Srf: 从一系列边界曲线生成平坦面Rail Revolution: 通过绕轨道旋转生成曲面Revolution: 通过旋转生成曲面Sum Surface: 通过两条边界线生成曲面Surface From Point: 通过网格点生成nurbs曲面Sweep1 : 单轨扫描曲面Sweep2 : 双轨扫描曲面Primitive:基本曲面:Bounding Box: 边界立方体(边界范围由需要被包含的集合体决定)Box 2Pt: 空间上两点决定的立方体Box Plane: 创建与一个矩形所在平面相匹配的立方体Center Box: 在平面的中心点创建立方体Cone: 圆锥体Cylinder: 圆柱体Interval Box: 由基准面和边长创建一个立方体Plane Srf: 平面Sphere: 球体Util:公用:Brep Join: 结合Brep(复合曲面)Cap Holes: 封闭所有Brep形(复合曲面)的平面开口Copy Trim: 复制修剪数据(将UV修剪数据从一个曲面复制到另一个)Divide Surface: 产生UV网格点分割曲面Flip: 翻转曲面法线Isotrim: 等参修剪(在曲面上提取由等参线分割的子集)Retrim: 再修剪(基于其它曲面的三维修剪数据)Surface Frames: 曲面框架(在曲面表面生成UV框架网格)Untrim: 撤销修剪(移除曲面上的所有切割线)Mesh:网格面:Primitive:基本网格面:Mesh: 网格面Mesh Box: 网格面立方体Mesh Plane: 网格平面Mesh Quad: 四边形网格Mesh Sphere: 网格球体Mesh Triangle: 三角面网格Triangulation:三角细分关系:Mesh BRep: 创建一个与现有BRep几何体相似的网格面Mesh Surface: 网格表面Settings (Custom): 描绘自定义网格设置Settings (Quality): 描绘高质量光滑曲面设置Settings (Speed): 快速描绘不带抗锯齿的曲面设置Util:公用:Face Components: 分解一个单元网格面到其组成元素Mesh Components: 分解一个网格面到其组成元素Mesh Paint: 指派一个反复的色彩图案到网格面物体Intersect:交集:Boolean:布尔:Region Difference: 差集(适用于平面闭合曲线)Region Intersection: 交集(适用于平面闭合曲线)Region Union: 并集(适用于平面闭合曲线)Solid Difference: 实体差集(适用于BRep形)Solid Intersection: 实体交集(适用于BRep形)Solid Union: 实体并集(适用于BRep形)Mathematical:数学:BRep | Line: 处理复合曲面和线段的交集问题BRep | Plane: 处理复合曲面和平面的交集问题(计算剖面)Curve | Line: 处理曲线和线段的交集问题Curve | Plane: 处理曲线和平面的交集问题Line | Plane: 处理平面和线段的交集问题Plane | Plane: 处理平面和平面的交集问题(计算面面交线)Plane | Plane | Plane: 处理三个平面的交集问题Surface | Line: 处理曲面和线段的交集问题Physical:物理:BRep | BRep: 处理两个复合曲面的交集问题BRep | Curve: 处理复合曲面和曲线的交集问题Curve | Curve: 处理曲线和曲线的交集问题Surface | Curve: 处理曲面和曲线的交集问题Region:区域:Split with BRep: 用复合曲面分割曲线Split with BReps: 用多个符合曲面分割曲线Trim with BRep: 用复合曲面修剪曲线Trim with BReps: 用多个符合曲面修剪曲线Trim with Region: 用一个范围修剪曲线Trim with Regions: 用多个范围修剪曲线XForm:变换:Affine:仿射:Orient Direction: 指定方向Project: 将物体映射到平面Scale: 缩放物体(所有方向均匀缩放)Scale NU: 非均匀缩放物体Shear : 扭曲(按矢量扭曲方向扭曲变换物体)Shear Angle: 角度扭曲(按倾斜角度扭曲物体)Euclidian:欧几里得:Mirror: 镜像Move: 移动Orient: 转向(将几何体从一个坐标系重映射到另一个坐标系)Rotate: 旋转(在平面内旋转物体)Rotate Axis: 绕轴旋转物体Morph:变形:Blend Box: 在两个平面间建立立方体Box Morph: 扭曲立方体Camera Obscura: 针孔照相机Mirror Curve: 以自由曲线为基准镜像Mirror Surface: 以自由曲面为基准镜像Surface Box: 在曲面块上创建扭曲立方体Surface Morph: 将几何体变形到曲面UVW坐标系Twisted Box: 利用角点创建扭曲立方体。
课件 计算机图形学 贝塞尔曲线及B样条

n
p(t) pi Bi,n (t)
(0 t 1)
i0
p(t) (1 t)3 p0 3t(1 t)2 p1 3t 2 (1 t) p2 t3 p3
其中混合函数分别为:
B0,3 = 1- 3t + 3t2 - t3 =
B1,3 = 3t - 6t2 + 3t3 =
B2,3 = 3t2 - 3t3 =
(2)通过控制点即顶点直观而方便地调整曲线的形状, (3)仅通过起始点和终止点,而不通过其它的型值点。
三 贝塞尔曲线举例 曲线仅通过起始点和终止点,而不通过其它的型值点。
四 贝塞尔曲线的性质:
1 该曲线由一组多边形折线的多个顶点唯一地定义出来。
多边形折线又称特征多边形,顶点又称为控制点。
2 在多边折线的各个顶点中,只有第1点和最后1点在曲线上。
1 n!
nk j0
(1)
j
j (t n k j)n (0 t 1, k 0,1, n)
n1
P’(0) B2
2 例:n=3,m=1,
B1
P’(1)
表示有5个顶点, 能画出两段3次曲线
B02
B3
B0
P’’(0) P’’(1)
B4
3 n次B样条曲线
连接全部曲线段所组成的整条曲线称为n次B样条曲线。
j 0
j (t 2 j)2 1 (t 1)2
3
2
F1,2 (t)
1 2
(2t
2
2t
1)
t F2,2 (t)
1 2
2
因此,二次 B 样条曲线的分段表达式可以写成如下的形式:
Pi (t) F0,2 (t)Pi F1,2 (t)Pi1 F2,2 (t)Pi2
maya建模教程NURBS曲线

Maya 主要是制作复杂的数学模型和动画,而这些都是以曲线为基础创建的。
下面介绍NURBS 曲线的基本概念。
NURBS 曲线的特点直线没有任何的弯曲,仅由两个端点定义,可以有一个斜率但角度不变。
曲线的曲率是变化的,而直线的斜率是不变的。
曲线通常是由几个点定义的,而且从一条没有任何在角度上突变的直线路径推导而来。
曲线有时候也成为曲线段,而且能够用于定义曲面或曲面网。
曲线也常被称为样条,因为它们看起来就像物理样条,即一个长长的木头或者金属条。
所有的样条都有一个共同的特征,即它们都是从定义一个多边形产生的。
由于这个共同的特征,所以将样条称为受控曲线。
包含在不同类型样条中的控制包括:控制线、控制多边形或者外壳、控制点或者控制定点、控制切线和节点或者权重。
NURBS 通过权重或者结点提供高级的局部曲线控制。
这些控制允许样条的一部分被修改时不会影响到另外一部分。
权重与每一个控制点相结合,它们指定控制点与曲线的定点之间的距离。
默认设置下,样条上所有控制点具有相同的权重因子,称为非实数曲线。
当修改曲线的权重时,曲线称为实数曲线。
处理 NURBS 曲线的权重可能改善一条曲线的细微形状,但通常也减慢了最后模型的渲染速度。
使用不同权重的另一个坏处是,当交换模型文件时,许多系统会忽略该数据。
NURBS 上的结点决定一条曲线上点的分布的局部密度。
形成一个曲线段的最小结点数等于一条曲线的阶加 1 ,再加控制点的数目,曲线的阶涉及产生曲线的数学公式中高次幂指数。
曲线的阶越高,则产生该曲线所需要的计算越多。
一阶曲线相应于直线段;二阶曲线相应于二次曲线;三阶曲线相应于三次曲线。
曲线的阶越多,曲线段所需要的控制点或者结点就越多。
一般而言创建曲线的方法各式各样,但在创建之前,一定要把曲线的度数和跨度等要素掌握清楚,它们是产生一条“完美”曲线的决定性因素。
在计算机中画的曲线实际上是一个曲线段或是一个连续的线段,一个线段被称为一个Span 。
一种简化计算的s型加减速nurbs插补算法

一种简化计算的s型加减速nurbs插补算法一种简化计算的S型加减速NURBS插补算法NURBS曲线插补算法是现代数控系统中的重要算法之一,用于控制加工设备完成高精度的加工任务。
其中,S型加减速是常用的运动控制方式之一,能够保证机床在开始加工、过程中和结束加工时都具有很好的平稳性。
本文将介绍一种简化计算的S型加减速NURBS插补算法,以提高机床的控制精度和加工效率。
一、S型加减速运动控制原理S型加减速是一种基于速度的控制方法,其核心原理是根据速度变化规律来控制机床的运动。
具体来说,S型加减速运动分为加速段、匀速段和减速段三个阶段。
在加速阶段,机床匀加速运动,使速度随时间线性增加,到达一定速度后,进入匀速阶段,使速度恒定不变。
在减速阶段,速度随时间线性减小,直到机床停止。
该方法可以避免机床突然加速或停止时产生的惯性冲击,从而保证了机床的运动平稳。
二、NURBS插补算法NURBS插补算法是一种基于贝塞尔曲线的算法,通过多个曲线段的拼接来实现曲线的绘制。
其优点是可以绘制复杂的曲线形状,并且对于曲线的控制点位置和权重系数都具有很好的控制性。
三、S型加减速NURBS插补算法该算法核心思想是在NURBS曲线上进行S型加减速运动控制,以实现更加平稳的加工运动。
具体来说,该算法的步骤如下:1. 将NURBS曲线按照一定间隔进行采样,得到离散点序列。
2. 对离散点序列进行处理,获取三个阶段的状态点:起始点、加速段末点、减速段起点、最终点。
3. 对加速段末点和减速段起点进行插值,获取中间匀速段起点和末点。
4. 根据三个状态点之间的距离和时间进行速度和加速度控制计算。
5. 根据速度和加速度计算出每个采样点的位置坐标,使用NURBS 插值得到平滑的曲线。
6. 基于机床的动力学模型,通过PID算法进行控制,实现机床的运动。
该算法的优点在于简化了S型加减速的计算过程,同时保持了曲线的平滑性,提高了机床的运动精度。
blender曲线类型

Blender曲线类型
Blender中的曲线类型主要有以下几种:
1. 曲线(Curve):表示一系列点的集合,可以通过调整点的位置和控制点来创建曲线。
2. 贝塞尔曲线(Bezier Curve):一种由控制点和中间点组成的曲线类型,可用于创建平滑的曲线形状。
3. NURBS曲线(Non-Uniform Rational B-Splines):一种基于贝塞尔曲线的高级曲线类型,可以通过调整控制点和权重来创建更复杂的曲线形状。
4. 样条曲线(Spline Curve):一种由一系列曲线段组成的曲线类型,可用于创建平滑的曲线形状,并且可以在曲线段之间创建光滑的过渡。
5. 圆弧(Arc):表示一个圆形路径,可以通过调整弧度和半径来创建不同形状的圆弧。
6. 椭圆(Ellipse):表示一个椭圆形路径,可以通过调整长轴和短轴的长度来创建不同形状的椭圆。
7. 多边形(Polygon):由多个线段组成的路径,可以用于创建复杂的多边形形状。
以上是Blender中常见的曲线类型,每种曲线类型都有其独特的特点和用途,可以根据需要选择不同的曲线类型来创建所需的形状。
nurbs曲线和贝塞尔曲线

nurbs曲线和贝塞尔曲线一、简介在计算机图形学和三维建模领域,NURBS曲线和贝塞尔曲线是两种常用的曲线表示方法。
它们在实际应用中具有一定的联系,但也存在明显的区别。
本文将对这两种曲线进行简要介绍,并分析它们之间的联系与区别。
二、NURBS曲线1.定义与特点URBS(Non-Uniform Rational B-Spline)曲线是一种非均匀有理贝塞尔曲线。
它通过基函数和控制点加权求和来表示一条曲线。
NURBS曲线具有以下特点:- 参数化表示,易于调整曲线形状- 具有良好的连续性,可以轻松实现平滑过渡- 具有较高的计算效率,适用于实时渲染和交互式设计- 局限性:处理复杂曲线时,计算量较大,容易出现过拟合现象2.在三维建模中的应用URBS曲线在三维建模中的应用广泛,如汽车、飞机等复杂几何体的建模。
通过调整基函数和控制点,可以轻松地实现曲面的生成和调整。
3.NURBS曲线的优势与局限性优势:- 参数化表示,易于调整曲线形状- 具有良好的连续性,可以轻松实现平滑过渡- 适用于复杂曲面的建模局限性:- 处理复杂曲线时,计算量较大- 容易出现过拟合现象三、贝塞尔曲线1.定义与特点贝塞尔曲线(Bézier curve)是一种通过基函数和控制点加权求和的曲线表示方法。
它具有以下特点:- 非参数化表示,直接控制曲线形状- 具有良好的连续性,可以实现平滑过渡- 计算效率较高,适用于实时渲染和交互式设计- 局限性:在处理复杂曲线时,控制点数量较多,计算量较大2.在三维建模中的应用贝塞尔曲线在三维建模中也具有广泛的应用,如角色建模、场景搭建等。
通过调整控制点,可以实现曲线的平滑过渡和复杂形状的生成。
3.贝塞尔曲线的优势与局限性优势:- 非参数化表示,直接控制曲线形状- 具有良好的连续性,可以实现平滑过渡- 适用于简单和复杂曲线的建模局限性:- 在处理复杂曲线时,控制点数量较多,计算量较大四、比较与总结1.NURBS曲线与贝塞尔曲线的异同- 相同点:两者都具有良好的连续性和较高的计算效率,适用于三维建模中的应用- 不同点:NURBS曲线是参数化表示,易于调整曲线形状,但处理复杂曲线时计算量较大;贝塞尔曲线是非参数化表示,直接控制曲线形状,但在处理复杂曲线时计算量较大。
nurbs曲线和贝塞尔曲线

nurbs曲线和贝塞尔曲线
NURBS(Non-Uniform Rational B-Spline,非均匀有理B样条曲线)是一种用于描述曲线和曲面的数学模型,在计算机图形学领域得到了广泛应用。
NURBS曲线由一系列控制点、权重和节点向量组成。
NURBS曲线相比于其他曲线模型具有以下特点:
1. 非均匀性:NURBS曲线的节点向量可以非均匀地分布,使得曲线在不同区域有不同的曲率和细节。
2. 有理性:NURBS曲线的控制点可以有不同的权重值,这使得曲线可以具有更多的灵活性和控制性。
3. 兼容性:NURBS曲线可以与其他几何对象(如直线、圆、曲面等)进行无缝连接和平滑过渡。
贝塞尔曲线(Bézier curve)是另一种常用的曲线模型,最早由法国工程师Pierre Bézier在20世纪50年代提出。
贝塞尔曲线也由一系列控制点来定义,通过调整这些控制点的位置和权重,可以实现曲线的形状和曲率变化。
贝塞尔曲线相比于NURBS曲线具有以下特点:
1. 受限性:贝塞尔曲线的形状受控制点的位置限制,难以实现复杂曲线的定义。
2. 难以编辑:贝塞尔曲线的形状调整需要重新调整控制点的位置,较为繁琐。
3. 简单性:贝塞尔曲线的数学计算较为简单,适用于一些简单的曲线绘制任务。
总结来说,NURBS曲线相对于贝塞尔曲线拥有更大的灵活性和控制性,适用于绘制复杂曲线和曲面;而贝塞尔曲线相对简单,适用于一些简单曲线绘制任务。
贝塞尔曲线介绍

贝塞尔曲线
贝塞尔曲线跟PS里的钢笔的意思大概差不多,不过贝塞尔曲线没有选取的功能。
在这里,要切记,不要和轮廓工具弄混,前者是通过调节点调节形状,后者是调节形状轮廓的粗细以及样式。
补充几点:
1、在任意工具情况下,在曲线上双击都可以换为形状工具对曲线进行编辑;
2、在曲线上用形状工具双击可以增加一个节点;
3、在曲线的节点上双击形状工具可以删除一个节点;
4、位图可以用形状工具点击再拖动某一点可以进行任意形状的编辑;
5、用形状工具同时选中几个节点可以进行移动;
6、在微调距离中设定一个数值再用形状工具选中曲线的某一节点敲方向箭头可以进行精确位移;
7、将某一个汉字或字母转换为曲线就可以用形状工具进行修理如将“下”的右边的点拿掉等。
贝塞尔曲线的介绍

贝塞尔曲线的介绍
贝塞尔曲线是一种基于贝塞尔曲线插值的曲线,通常用于建立光滑的曲线轨迹,例如在计算机图形学、工业设计和动画制作中。
贝塞尔曲线的主要特点是它可以通过相互连接的锚点来定义曲线,而锚点之间的曲线可以被平滑地调整。
贝塞尔曲线有两种类型:贝塞尔曲线和贝塞尔曲面。
贝塞尔曲线是二维的,而贝塞尔曲面可以具有三维形状。
在贝塞尔曲线中,每一个控制点都表示曲线的一部分,通过调节控制点的位置,可以改变曲线的形状。
贝塞尔曲线有许多应用,例如在图形软件中进行编辑曲线、建模和动画、绘制自然风景和地形等。
NURBS曲线

• 齐次坐标表示形式说明:NURBS曲线是它的控制顶 点的齐次坐标或带权控制点在高一维空间里所定义 的非有理B样条曲线在ω=1超平面上的投影。 • 不仅包含了明确的几何意义,而且也说明:非 有理B样条曲线的大多数算法都可以推广应用于 NURBS曲线。
NURBS曲线有理分式表示
• 一条k次NURBS曲线可表示为一分段有理多项式矢函数:
n
i Pi Bi,k u
P u
i0 n
i Bi,k u
i0
• 这给出了NURBS的数学定义,也是有理的由来。
• 参数ωi是控制顶点权因子,分别与n+1个控制顶点 Pi(i=0,1,2,…,n)相联系。 • 首末权因子ω0,ωn>0,其余ωi≥0,以防止分母为 零、保留凸包性质及曲线不致于权因子而退化为
• 若移动k次NURBS曲线的一个控制顶点Pi或改变所 联系的权因子将仅仅影响定义在区间[ui,ui+k+1]上那 部分曲线的形状,对NURBS曲线的其它部分不发 生影响。
• 变差减少性质:
• 平面内任一直线与B样条曲线的交点各数不多于该 直线与曲线控制多边形的交点数目。
☆NURBS曲线 ● 有理样条曲线 ● NURBS 曲 线 表
质
● NURBS 形 状 因
子 ☆ 三次曲线比较
有理/非有理样条比较
• 有理样条与非有理样条相比有两个重要的优点: – 有理样条提供了二次曲线的精确表达式; – 非有理样条表达式为多项式,仅能逼近二次曲线。 • 这使图形包能用一个表达式(有理样条)来模拟所 有曲线形状,无需用一个曲线函数库去处理不 同的形状。 – 有理样条对于透视观察变换是不变的。 – 非有理样条关于透视观察变换是可变的。 • 这意味着可对有理曲线上的控制点应用一个透 视观察变换,来得到曲线的正确视图,
曲线数学NURBS之B样条曲线

曲线数学NURBS之B样条曲线上一篇博客已经讲到了bezier曲线,本篇接着讲解B样条曲线。
B样条曲线是bezier曲线的更一般化,bezier曲线是B样条曲线的特列。
相比于Bezier曲线,B样条曲线是分段组成的,每一段参数的区间都是[0,1],这就克服了Bezier曲线改变任意一个控制点,曲线上所有的点都要改变的缺点。
B样条曲线的数学公式如下:其中di(i=0,1…n)为控制点,K为规定的基函数的次数,Ni,k(i=0,1…n)即为k次B样条基函数,最高次数为k。
u表示参数序列,即B样条分段函数中的参数。
B样条基函数的公式如下:其中i为节点序号,k是基函数的次数,规定:0/0等于0。
这就是Cox-deBoor算法公式。
节点和控制点是不一样的,满足控制关系m+1=n+k+2.即假如有3个控制点控制的2次B样条曲线,其节点的数量为3+2+2=7.Boehm 给出了节点的插入公式:其中r是新插入的节点t在节点序列中的重复度。
如上图,控制点Pj生成新的控制点Pj’。
B样条曲线总的分为均匀和非均匀的。
根据如上的讲解为了设计一个B-样条曲线,我们需要一系列的控制点,一系列的节点和一系列的系数,每个系数对应一个控制点,所有曲线段连接在一起满足某个连续条件,即为B样条曲线。
有了上边整体的了解,接着从B样条基函数开始讲起,如何根据几个控制点,以及给定的B样条基函数次数k画出B样条曲线。
如上图,基函数的系数定义如图中所述,可以看出,每一个系数范围都为(0,1)区间。
而基函数中的Ni,k(u) 可以表示为如下的杨辉三角形状,比如求第1段区间1次基函数N1,1 就要求出N1,0 和N2,0,其他依次类推。
如下三图为本人从基函数推导出来的B样条曲线。
其中控制点个数为3(n=2),基函数最高次数为2(k=2),则节点总数为m+1=n+k+2=6.推导中,为了便于计算,各个节点赋值分别为0,1,2,3,4,5。
最后得出B样条曲线的每一段的函数表示。
maya约束路径

maya约束路径Maya约束路径Maya是一款广泛应用于电影、动画、游戏等行业的三维计算机图形软件,它提供了丰富的工具和功能,使得用户可以创建和编辑复杂的三维场景。
在Maya中,约束路径是一种常用的技术,可以用来控制物体在三维空间中的运动轨迹,本文将介绍Maya约束路径的基本原理和使用方法。
一、约束路径的原理约束路径是一种基于曲线的约束技术,它可以将一个物体沿着一个或多个曲线进行运动。
在Maya中,可以使用NURBS曲线、贝塞尔曲线或者自定义曲线作为约束路径。
当物体被约束到路径上时,它的运动将会受到路径的控制,可以沿着路径进行平移、旋转或缩放。
二、创建约束路径在Maya中,创建约束路径非常简单。
首先,选择一个曲线作为路径,然后选择需要被约束的物体,使用"Constrain"菜单中的"Motion Path"命令进行约束。
在约束路径的属性面板中,可以设置路径的参数,如路径长度、速度、是否循环等。
此外,还可以调整物体在路径上的初始位置和朝向,以及物体在路径上的运动方式。
三、约束路径的控制一旦物体被约束到路径上,它的运动将会受到路径的控制。
在Maya中,可以通过调整路径的形状、曲率、控制点等属性来改变物体的运动轨迹。
此外,还可以通过添加控制器、调整控制器的位置和旋转角度等方式来进一步控制物体的运动。
通过灵活运用这些控制手段,可以实现各种复杂的动画效果。
四、约束路径的应用约束路径在动画制作中有广泛的应用。
例如,可以使用约束路径来模拟飞行器在空中的飞行轨迹,或者模拟汽车在道路上的行驶轨迹。
此外,还可以使用约束路径来控制角色的动作,使其沿着特定的路径进行行走、奔跑或攀爬。
约束路径还可以用于模拟物体的自然运动,如河流的流动、海浪的翻滚等。
五、约束路径的进阶技巧除了基本的约束路径技术外,Maya还提供了一些高级的约束路径技巧,用于实现更加复杂的动画效果。
例如,可以使用多个路径约束物体,使其在不同的路径上同时运动。
第3章 NURBS基本概念

3.3.2 连续性的检测
Rhino提供多种工具链检测物件的连续性,包括:曲率图形、两条 曲线的几何连续性、斑马纹分析(曲面连续性检测工具)。
3.3.3 曲率图形
Rhino提供的【开启曲率图形】工具以曲率梳的形式显示曲线内部 或曲线间的连续性。用户可以通过观察曲率图形在曲线端点处的方向和 高度来判断曲线之间的连续性。 由于直线曲率为0 ,所以看不到曲率图形。
一、Non-Uniform:非均匀分布(包含均匀分布)
Uniform(均匀)与Non-Uniform(非均匀)是NURBS曲线节点赋值的方式,图 3-1所示,以两条相同的曲线为例,第一条曲线是Uniform(均匀)曲线,它是以每 一个节点(Knot)或每一跨距(span)为曲线的参数铺设的依据,故第一条曲线每 一节点的参数刚好是1,2,3…的整数,而不论其节点之间距离的长短。第二条曲线 则是Non-Uniform(非均匀)曲线,它是以节点与节点之间的弦长(Chord length) 为曲线的参数铺设的依据,故其曲线上每一节点的参数值是随距离而改变。
3.2 NURBS的属性
伴随着数字技术手段的成熟,能够应用于工业设计的相关软件也越来越 多,按其在设计环节中的应用可以划分为数字草绘软件、二维图形图像软 件、三维造型、渲染和动画软件、CAD/CAM软件和设计评估演示软件5大 类。下面就常用的相关软件做简要介绍。
1.3.1 数字草绘软件
此类软件的最大特点是完全以数字模拟的手段将纸上作业的传统过程转 移到电脑屏幕上来,通过模拟各种传统绘画工具的特性和图层的叠加来达 到表现目的,在过程和效果上更加自由、出色,但前提是必须配备专门的 数字输入设备,如数位手绘板(屏)等。
(2)相切连续(G1)。 G1连续在满足G0连续的基础上,还满足两条曲线在相接端点的切线方
Bezier和NURBS曲线、曲面

void glMapGrid2{fd}(GLint nu, TYPE u1, TYPE u2, GLint nv, TYPE v1, TYPE v2) void glEvalMesh2(GLenum mode, GLint i1, GLint i2, GLint j1, GLint j2)
定义二维图形网格,从u1到u2经历nu个均匀 分布的阶段,从v1和v2经历nv个均匀分布的 阶段,并把这个网格应用于所有被启用的求 值器。 mode参数在GL_POINT和GL_LINE的基础 上增加了GL_FILL。它使用四边形网格图元 生成填充多边形。
void gluNurbsProperty(GLUnurbsObj *nobj, GLenum property, GLfloat value) 控制NURBS对象nobj的属性。property参数指定了 属性。 当property是GLU_DISPLAY_MODE,value是 GLU_FILL表示将表面渲染成多边形。 当property是GLU_SAMPLING_TOLERANCE, value(使用像素为单位或者物体空间的单位)用于控 制分格化多边形的最大长度。
Bezier和NURBS曲 线、曲面
void glMap2{fd}(GLenum target, TYPE u1, TYPE u2, GLint ustride, GLint uorder, TYPE v1, TYPE v2, GLint vstride, GLint vorder, TYPE points) target: GL_MAP_VERTEX_3 为x,y,z顶点坐标 u1,u2:变量u的变化范围 v1,v2:变量v的变化范围 ustride:u方向一个控制点的起始位置和下一个控 制点的起始位置之间的偏移量。 vstride:v方向一个控制点的起始位置和下一个控 制点的起始位置之间的偏移量。 uorder:u方向控制点数量 vorder:v方向控制点数量 points:存放控制点数组的起始地址
快速学习Blender中的模型曲线建模技巧

快速学习Blender中的模型曲线建模技巧Blender是一款功能强大的三维建模软件,拥有丰富的工具和功能,可以用于创建各种各样的模型。
本教程将介绍Blender中的模型曲线建模技巧,帮助您更快速地学习和掌握这一方面的技术。
1. 创建曲线在Blender中,可以通过多种方式创建曲线。
最简单的方式是按下Shift +A选择"曲线",然后选择想要创建的曲线类型,如贝塞尔曲线或NURBS曲线。
您也可以使用其他工具,如"画笔"或"边"来创建曲线。
2. 修改曲线一旦创建了曲线,您可以使用各种编辑工具来修改它的形状。
例如,您可以使用"选择"工具选择曲线上的点,并通过移动它们来改变曲线的形状。
您还可以使用"旋转"和"缩放"工具对曲线进行进一步的调整。
3. 添加混合曲线在Blender中,您可以将多个曲线合并成一个混合曲线。
要做到这一点,选择两个或多个曲线,然后按下Ctrl + J将它们合并为一个曲线对象。
您可以使用混合曲线的各种工具和功能来进一步编辑它的形状。
4. 添加材质和纹理在Blender中,您可以为曲线添加材质和纹理,使其更加逼真。
通过选择曲线并在"材质"选项卡中进行设置,您可以调整曲线的颜色、反射和折射等属性。
您还可以为曲线添加纹理,如木纹或纹理贴图,以增加细节和真实感。
5. 渲染和导出最后,当您完成了曲线建模,并对其进行了调整和编辑后,您可以使用Blender的渲染功能将曲线渲染成图像或动画。
通过选择渲染设置和设置所需的输出格式,您可以将曲线渲染为高质量的图像,并保存到您的计算机上。
总结:Blender中的模型曲线建模技巧非常广泛和多样化。
本教程提供了一些基本的技巧和步骤,帮助您快速学习和掌握这一方面的技术。
通过不断练习和尝试,您可以进一步提高和发展您的技能,创造出更加出色和逼真的模型。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
NURBS曲线和贝塞尔曲线
1. 引言
在计算机图形学中,曲线是一种重要的数学工具,用于描述平面或空间中的形状。
NURBS(Non-Uniform Rational B-Spline)曲线和贝塞尔(Bezier)曲线是两种常见的曲线表示方法。
它们在计算机图形学、计算机辅助设计(CAD)、动画和游戏
开发等领域中被广泛应用。
本文将介绍NURBS曲线和贝塞尔曲线的原理、特点以及应用。
2. NURBS曲线
2.1 原理
NURBS曲线是一种基于B样条(B-spline)的数学表示方法,它通过控制点和权重
来描述一条平滑的曲线。
与贝塞尔曲线不同,NURBS曲线可以具有非均匀节点向量,这使得它更加灵活。
2.2 特点
•控制点与权重: NURBS曲线由一系列控制点和对应的权重组成。
每个控制点都有一个权重值,用于调整其对整个曲线的影响程度。
•非均匀节点向量: 节点向量决定了参数空间中的曲线形状。
NURBS曲线允许节点向量非均匀,从而可以创建更加复杂的曲线形状。
•局部控制: 修改一个控制点只会影响其附近的局部区域,不会对整个曲线产生影响。
这使得NURBS曲线具有较好的局部编辑性。
•数学精度: NURBS曲线可以通过增加控制点数量来提高其数学精度,从而更好地逼近所需的形状。
2.3 应用
NURBS曲线在计算机图形学和CAD领域中得到广泛应用。
它们常用于描述和绘制复
杂的二维和三维形状,如汽车外壳、船体、人体模型等。
此外,NURBS曲线还被用
于动画和游戏开发中的角色建模、场景设计等方面。
3. 贝塞尔曲线
3.1 原理
贝塞尔曲线是一种基于贝塞尔多项式的数学表示方法。
它通过控制点来定义一条平滑的曲线。
贝塞尔曲线具有递归性质,即高阶贝塞尔曲线可以由低阶贝塞尔曲线递归计算得到。
3.2 特点
•控制点: 贝塞尔曲线由一系列控制点组成,这些控制点决定了曲线的形状。
•局部控制: 修改一个控制点只会影响其附近的局部区域,不会对整个曲线产生影响。
这使得贝塞尔曲线具有较好的局部编辑性。
•平滑性: 贝塞尔曲线在控制点上保持C0连续,即曲线在连接处没有明显的拐角。
通过增加控制点数量,可以增加曲线的平滑程度。
3.3 应用
贝塞尔曲线在计算机图形学和CAD领域中也得到广泛应用。
它们常用于绘制二维图形、字体设计、动画和游戏开发中的路径运动等方面。
贝塞尔曲线还被用于图像处理中的插值和边缘检测等算法。
4. NURBS曲线与贝塞尔曲线的比较
4.1 控制灵活性
NURBS曲线相比贝塞尔曲线具有更高的灵活性。
非均匀节点向量和权重调节使得NURBS曲线能够描述更加复杂的形状。
贝塞尔曲线的控制点数量和位置对曲线形状
的影响较大。
4.2 局部编辑性
NURBS曲线和贝塞尔曲线都具有良好的局部编辑性,但NURBS曲线在修改一个控制
点时只影响附近区域,而贝塞尔曲线会影响整个曲线。
这使得NURBS曲线更适用于需要局部调整的场景。
4.3 数学精度
由于可以通过增加控制点数量来提高数学精度,NURBS曲线在逼近所需形状时具有
更高的灵活性和准确性。
贝塞尔曲线的数学精度取决于控制点数量。
5. 结论
NURBS曲线和贝塞尔曲线作为常见的数学表示方法,在计算机图形学、CAD、动画
和游戏开发等领域中发挥着重要作用。
它们各自具有特点,适用于不同的场景。
NURBS曲线通过非均匀节点向量和权重调节实现了更高的灵活性和数学精度,而贝
塞尔曲线则以其简单直观的控制方式和局部编辑性受到广泛应用。
在实际应用中,开发者可以根据具体需求选择适合的曲线表示方法,以达到最佳效果。
