2019北京市各区初三一模数学分类汇编——几何综合题1

合集下载

2019年北京市初三一模数学-几何综合专题(教师版)

2019年北京市初三一模数学-(学生版)

2019一模几何综合专题一、旋转变换1.(2019通州一模27)如图，在等边ABC △中，点D 是线段BC 上一点.作射线AD ，点B 关于射线AD 的对称点为E .连接CE 并延长，交射线AD 于点F . （1）设BAF α∠=，用α表示BCF ∠的度数；（2）用等式表示线段AF 、CF 、EF 之间的数量关系，并证明.2.(2019平谷一模27)在△ABC中，∠ABC=120°，线段AC绕点A逆时针旋转60°得到线段AD，连接CD，BD交AC于P．（1）若∠BAC=α，直接写出∠BCD的度数（用含α的代数式表示）；（2）求AB，BC，BD之间的数量关系；（3）当α=30°时，直接写出AC，BD的关系．H O DBA3.(2019延庆一模27)已知：四边形ABCD 中，120ABC ∠=︒，60ADC ∠=︒，AD =CD ，对角线AC ，BD相交于点O ，且BD 平分∠ABC ，过点A 作AH BD ⊥，垂足为H ．（1）求证：ADB ACB ∠=∠；（2）判断线段BH ，DH ，BC 之间的数量关系；并证明．4.(2019密云一模27)已知ABC ∆为等边三角形，点D 是线段AB 上一点（不与A 、B 重合）.将线段CD 绕点C 逆时针旋转60︒得到线段CE.连结DE 、BE. （1）依题意补全图1并判断AD 与BE 的数量关系.（2）过点A 作AF EB ⊥交EB 延长线于点F.用等式表示线段EB 、DB 与AF 之间的数量关系并证明.图2D CBA图1A B CD5.(2019东城一模27)如图，在正方形ABCD中，E是边BC上一动点（不与点B，C重合），连接DE，点C 关于直线DE的对称点为Cʹ，连接ACʹ并延长交直线DE于点P，F是AC′中点，连接DF．（1）求∠FDP的度数；（2）连接BP，请用等式表示AP，BP，DP三条线段之间的数量关系，并证明．（3）连接ACACC′的面积最大值．PBA6.(2019房山一模27)已知：Rt △ABC 中，∠ACB =90°，AC =BC .(1) 如图1，点D 是BC 边上一点(不与点B ，C 重合)，连接AD ，过点B 作BE ⊥AD ，交AD 的延长线于点E ，连接CE . 若∠BAD =α，求∠DBE 的大小 (用含α的式子表示) ；(2) 如图2，点D 在线段BC 的延长线上时，连接AD ，过点B 作BE ⊥AD ，垂足E 在线段AD 上，连接CE .①依题意补全图2；②用等式表示线段EA ，EB 和EC 之间的数量关系，并证明.图1 图2ABA7.(2019门头沟一模27)如图，∠AOB = 90°，OC 为∠AOB 的平分线，点P 为OC 上一个动点，过点P 作射线PE 交OA 于点E ．以点P 为旋转中心，将射线PE 沿逆时针方向旋转90°，交OB 于点F ．（1）根据题意补全图1，并证明PE = PF ；（2）如图1，如果点E 在OA 边上，用等式表示线段OE ，OP 和OF 之间的数量关系，并证明；（3）如图2，如果点E 在OA 边的反向延长线上，直接写出线段OE ，OP 和OF 之间的数量关系．图1 图2PPEECCBBOOAA8.(2019燕山一模27)如图，在△ABC 中，AB ＝BC ，∠B ＝90°，点D 为线段BC 上一个动点(不与点B ，C 重合)，连接AD ，将线段AD 绕点D 顺时针旋转90°得到线段DE ，连接EC ．(1) ① 依题意补全图1；② 求证：∠EDC ＝∠BAD ； (2) ① 小方通过观察、实验，提出猜想：在点D 运动的过程中，线段CE 与BD 的数量关系始终不变，用等式表示为：； ② 小方把这个猜想与同学们进行交流，通过讨论，形成了证明该猜想的几种想法：想法1：过点E 作EF ⊥BC ，交BC 延长线于点F ，只需证△ADB ≌△DEF ．想法2：在线段AB 上取一点F ，使得BF ＝BD ，连接DF ，只需证△ADF ≌△DEC ．想法3：延长AB 到F ，使得BF ＝BD ，连接DF ，CF ，只需证四边形DFCE 为平行四边形． ……请你参考上面的想法，帮助小方证明①中的猜想．(一种方法即可)图1 D C B A 备用图 AB C D9.(2019丰台一模27)在△ABC中，∠ACB=90°，AC=BC，D为AB的中点，点E为AC延长线上一点，连接DE，过点D作DF⊥DE交CB的延长线于点F．（1）求证：BF= CE；（2）若CE=AC，用等式表示线段DF与AB的数量关系，并证明．10.(2019朝阳一模27)如图，在Rt△ABC中，∠A=90°，AB=AC，将线段BC绕点B逆时针旋转α°（0<α<180），得到线段BD，且AD∥BC．（1）依题意补全图形；（2）求满足条件的α的值；（3）若AB=2，求AD的长．11.(2019怀柔一模27)如图，等边△ABC中，P是AB上一点，过点P作PD⊥AC于点D，作PE⊥BC于点E，M是AB的中点，连接ME，MD．（1）依题意补全图形；（2）用等式表示线段BE ，AD 与AB的数量关系，并加以证明；（3）求证：MD=ME．C二、轴对称变换12.(2019西城一模27)如图，在△ABC中，∠ABC=90°，BA=BC．将线段AB绕点A逆时针旋转90°得到线段AD，E是边BC上的一动点，连接DE交AC于点F，连接BF．（1）求证：FB=FD；（2）点H在边BC上，且BH=CE，连接AH交BF于点N．①判断AH与BF的位置关系，并证明你的结论；②连接CN．若AB=2，请直接写出线段CN长度的最小值．13．(2019顺义一模27)已知：如图，在△ABC 中，AB >AC ，∠B =45°，点D 是BC 边上一点，且AD=AC ，过点C 作CF ⊥AD 于点E ，与AB 交于点F ．（1）若∠CAD =α，求∠BCF 的大小（用含α的式子表示）；（2）求证：AC =FC ；（3）用等式直接表示线段BF 与DC 的数量关系．ABCDFE三、平移变换14.(2019石景山一模27)如图，在等边△ABC 中，D 为边AC 的延长线上一点()CD AC ，平移线段BC ，使点C 移动到点D ，得到线段ED ，M 为ED 的中点，过点M 作ED 的垂线，交BC 于点F ，交AC 于点G ．（1）依题意补全图形；（2）求证：AG = CD ；（3）连接DF 并延长交AB 于点H ，用等式表示线段AH 与CG 的数量关系，并证明．B四、其它15.(2019海淀一模27)如图，在等腰直角△ABC中，90CA CD>），?°，D是线段AC上一点（2ABC连接BD，过点C作BD的垂线，交BD的延长线于点E，交BA的延长线于点F．（1）依题意补全图形；?，求ABDÐ的大小（用含α的式子表示）；（3）若点G在线段CF上，CG BD=，连接DG．①判断DG与BC的位置关系并证明；②用等式表示DG，CG，AB之间的数量关系为．。

2019年北京市各区县初三一模数学试卷-共10套2019.1

图1
图2
下列说法中错误的是
A．勒洛三角形是轴对称图形 B．图 1 中，点 A 到 BC 上任意一点的距离都相等
C．图 2 中，勒洛三角形上任意一点到等边三角形 DEF 中心 O1 的距离都相等 D．图 2 中，勒洛三角形的周长与圆的周长相等
二、填空题（本题共 16 分，每小题 2 分）
09. 如图，在线段 AD、AE、AF 中，△ABC 的高是线段
B．4×1012 千米 D．9.5×1012 千米
06．如果
a2+3a+1=0，那么代数式
a2 (
+9
+ 6)?
2a2
的值为
a
a +3
【】
A．1
B．-1
C．2
D．-2
07．三名快递员某天的工作情况如图所示，其中点 A1，A2，A3 的横、纵左边分别表示甲、乙、丙三名快递
员上午派送快递所用的时间和件数；点 B1，B2，B3 的横、纵左边分别表示甲、乙、丙三名快递员下午
一模试题
（2019 届北京中考数学）
2019 初三一模·数学试题
02.北京市西城区 2019 年初三一模数学试卷...........................................01/答案 112 05.北京市丰台区 2019 年初三一模数学试卷...........................................12/答案 114 07.北京市通州区 2018 年初三一模数学试卷...........................................22/答案 118 09.北京市石景山 2018 年初三一模数学试卷.......................................... 33/答案 123 11.北京市平谷区 2018 年初三一模数学试卷.......................................... 43/答案 128 12.北京市房山区 2019 年初三一模数学试卷.......................................... 55/答案 132 13.北京市门头沟 2019 年初三一模数学试卷.......................................... 66/答案 137 14.北京市延庆区 2018 年初三一模数学试卷.......................................... 78/答案 141 15.北京市燕山区 2018 年初三一模数学试卷.......................................... 80/答案 141 16.北京市密云区 2019 年初三一模数学试卷........................................ 101/答案 150

2019北京中考数学一模16区-分类汇编-07 几何综合(学生版)

第 15 页共 17 页
燕山一模 27．如图，在△ABC 中，AB＝BC，∠B＝90°，点 D 为线段 BC 上一个动点(不与点 B，C 重合)，连接 AD，
将线段 AD 绕点 D 顺时针旋转 90°得到线段 DE，连接 EC．
图1
备用图
(1) ① 依题意补全图 1；
② 求证：∠EDC＝∠BAD；
丰台一模 27．在△ABC 中，∠ACB=90°，AC=BC， D 为 AB 的中点，点 E 为 AC 延长线上一点，连接 DE，过点 D 作 DF⊥DE 交 CB 的延长线于点 F．
（1）求证：BF= CE；（2）若 CE=AC，用等式表示线段 DF 与 AB 的数量关系，并证明．
第 6 页共 17 页
第 12 页共 17 页
平谷一模
27．在△ABC 中，∠ABC=120°，线段 AC 绕点 A 逆时针旋转 60°得到线段 AD，连接 CD，BD 交 AC 于 P．
（1）若∠BAC=α，直接写出∠BCD 的度数
（用含α的代数式表示）；
（2）求 AB，BC，BD 之间的数量关系；
（3）当α=30°时，直接写出 AC，BD 的关系．
(2) 如图 2，点 D 在线段 BC 的延长线上时，连接 AD，过点 B 作 BE⊥AD，垂足 E 在线段 AD 上，连接 CE. ①依题意补全图 2； ②用等式表示线段 EA，EB 和 EC 之间的数量关系，并证明.
图1
图2
第 9 页共 17 页
大兴一模 27．在 Rt△ABC 中，∠ACB=90°，CA =CB．点 D 为线段 BC 上一个动点（点 D 不与点 B，C 重合），连接
AD，点 E 在射线 AB 上，连接 DE，使得 DE=DA．作点 E 关于直线 BC 的对称点 F，连接 BF， DF. （1）依题意补全图形；（2）求证：∠CAD=∠BDF；（3）用等式表示线段 AB，BD，BF 之间的数量关系，并证明．

(完整)2019年北京市初三一模数学-几何综合专题(教师版)

2019一模几何综合专题一、旋转变换1.（等边三角形+对称＋旋转）(2019通州一模27)如图，在等边ABC △中，点D 是线段BC 上一点.作射线AD ，点B 关于射线AD 的对称点为E .连接CE 并延长，交射线AD（1）设BAF α∠=，用α表示BCF ∠的度数；（2）用等式表示线段AF 、CF、EF 之间的数量关系，并证明. 解：（1）连接AE . ∵点B 关于射线AD 的对称点为E ，∴AE =AB ，BAF EAF α∠=∠=∵ABC △是等边三角形， ∴AB AC =，60BAC ACB ∠=∠=︒. ∴602EAC α∠=︒-，AE AC =. 1分∴()1180602602ACE αα∠=︒-︒-=︒+⎡⎤⎣⎦. ∴6060BCF ACE ACB αα∠=∠-∠=︒+-︒=. ……………… 2分另解：借助圆. （2）AF EF CF -=证明：如图，作60FCG ∠=︒交AD 于点G ，连接BF . ……………… 3分 ∵BAF BCF α∠=∠=，ADB CDF ∠=∠， ∴60ABC AFC ∠=∠=︒. ∴△FCG 是等边三角形.∴GF = FC . ……………… 4分 ∵ABC △是等边三角形，∴BC AC =，60ACB ∠=︒. ∴ACG BCF α∠=∠=.在△ACG 和△BCF 中，CA CB ACG BCF CG CF =⎧⎪∠=∠⎨⎪=⎩，，， ∴△ACG ≌△BCF .∴AG BF =. ……………… 5分 ∵点B 关于射线AD 的对称点为E ， ∴BF EF =. ……………… 6分 ∴AF AG GF -=.∴AF EF CF -=. ……………… 7分另一种证法：作60FAH ∠=︒交FC 的延长线于点H ，连接BF .2.（等边三角形＋旋转）(2019平谷一模27)在△ABC中，∠ABC=120°，线段AC绕点A逆时针旋转60°得到线段AD，连接CD，BD交AC于P．（1）若∠BAC=α，直接写出∠BCD的度数（用含α的代数式表示）；（2）求AB，BC，BD之间的数量关系；（3）当α=30°时，直接写出AC，BD的关系．解：（1）∠BCD=120°－α． ······························································（2）解：方法一：延长BA使AE=BC，连接DE． (2)由（1）知△ADC是等边三角形，∴AD=CD．∵∠DAB+∠DCB=∠DAB+∠DAE=180°，∴∠DAB=∠DAE．∴△ADE≌△CDB． (3)∴BD=BE．∴BD=AB+BC． (4)方法二：延长AB使AF=BC，连接CF． (2)∠BDC=∠ADE．∵∠ABC=120°，∴∠CBF=60°．∴△BCF是等边三角形．∴BC=CF．∵∠DCA=∠BCF=60°，∴∠DCA+∠ACB=∠BCF+∠ACB．即∠DCB=∠ACF．∵CA=CD，∴△ACF≌△DCB． (3)∴BD=AF．∴BD=AB+BC． (4)（3）AC，BD的数量关系是：AC ； (5)位置关系是：AC⊥BD于点P． (6)H O DBA3.（等边三角形＋旋转）(2019延庆一模27).已知：四边形ABCD 中，120ABC ∠=︒，60ADC ∠=︒，AD =CD ，对角线AC ，BD相交于点O ，且BD 平分∠ABC ，过点A 作AH BD ⊥，垂足为H ．（1）求证：ADB ACB ∠=∠；（2）判断线段BH ，DH ，BC 之间的数量关系；并证明．解：（1）证明：∵∠ADC =60°，DA=DC∴△ADC 是等边三角形． ……1分 ∴∠DAC =60°,AD=AC ． ∵∠ABC=120°,BD 平分∠ABC ∴∠ABD=∠DBC =60°．∴∠DAC =∠DBC =60° ∵∠AOD =∠BOC∠ADB=180°- ∠DAC -∠AOD∠ACB=180°- ∠DBC -∠BOC∴∠ADB=∠ACB ……3分（2）结论：DH=BH+BC ……4分证明：在HD 上截取HE=HB ……5分∵AH ⊥BD∴∠AHB=∠AHE =90° ∵AH =AH∴△ABH ≌△AEH ∴AB=AE, ∠AEH=∠ABH =60° ……6分 ∴∠AED=180°-∠AEH=120° ∴∠ABC=∠AED=120° ∵AD=AC, ∠ADB=∠ACB ∴△ABC ≌△AED∴DE=BC ……7分 ∵DH=HE+ED∴DH=BH+BC ……8分4.（等边三角形+旋转）(2019密云一模27)已知ABC ∆为等边三角形，点D 是线段AB 上一点（不与A 、B 重合）.将线段CD 绕点C 逆时针旋转60︒得到线段CE.连结DE 、BE. （1）依题意补全图1并判断AD 与BE 的数量关系.（2）过点A 作AF EB ⊥交EB 延长线于点F.用等式表示线段EB 、DB 与AF 之间的数量关系并证明.27.（1）补全图形AD 与BE 的数量关系为AD=BE .................................2分（2）∵∠ACB=∠DCE= 60°, ∴∠ACD=∠BCE 又∵AC=BC,CD=CE ∴△ACD ≌△BCE∴AD=BE, ∠CBE=∠CAD=60°∴∠ABF=180°-∠ABC-∠CBE=60° 在Rt AFB ∆中，3AF AB = ∴BE+BD=3AB.................................7分图2D CBA图1A B CD DEBA5.（正方形+旋转+最值）(2019东城一模27)如图，在正方形ABCD 中，E 是边BC 上一动点（不与点B ，C 重合），连接DE ，点C 关于直线DE 的对称点为C ʹ，连接ACʹ并延长交直线DE 于点P ，F 是AC ′中点，连接DF ．（1）求∠FDP 的度数；（2）连接BP ，请用等式表示AP ，BP ，DP 三条线段之间的数量关系，并证明．（3）连接ACACC ′的面积最大值．解：（1）由对称可知 CD ＝C ′D ，∠CDE ＝∠C ′DE ．在正方形ABCD 中，AD ＝CD ，∠ADC ＝90°， ∴AD ＝C ′D ．又∵F 为AC ′中点，∴DF ⊥AC ′，∠ADF ＝∠C ′DF ．……………………………………………………1分∴∠FDP ＝∠FDC ′＋∠EDC ′=12∠ADC ＝45°．…………………2分（2）结论：BP ＋DPAP ．……………………………………………………3分如图，作AP ′⊥AP 交PD 延长线于P ′， ∴∠P AP ′＝90°．在正方形ABCD 中，DA ＝BA ，∠BAD ＝90°， ∴∠DAP ′＝∠BAP ．由（1）可知∠APD ＝45°， ∴∠P ′＝45°．∴AP ＝AP ′……………………………………………………4分在△BAP 和△DAP ′中，BA DA BAP DAP AP AP =⎧⎪'∠=∠⎨⎪'=⎩，∴△BAP ≌△DAP ′（SAS ）……………………………………………………5分 ∴BP ＝DP ′．P BAP BA∴DP＋BP＝PP′＝．（3－1……………………………………………………7分P'B A6.（等腰直角三角形+旋转）(2019房山一模27).已知：Rt△ABC中，∠ACB=90°，AC=BC.(1) 如图1，点D是BC边上一点(不与点B，C重合)，连接AD，过点B作BE⊥AD，交AD的延长线于点E，连接CE.若∠BAD=α，求∠DBE的大小(用含α的式子表示) ；(2) 如图2，点D在线段BC的延长线上时，连接AD，过点B作BE⊥AD，垂足E在线段AD上，连接CE.①依题意补全图2；②用等式表示线段EA，EB和EC之间的数量关系，并证明.图1 图2解：（1）解: 依题意，∠CAB=45°，∵∠BAD=α，∴∠CAD=45α︒-.∵∠ACB=90°，BE⊥AD，∠ADC=∠BDE，∴∠DBE=∠CAD=45α︒-. …………………………………2分（2）解：①补全图形如图…………………………………4分②猜想：当D在BC边的延长线上时，EB - EAEC.…………………………………5分证明：过点C作CF⊥CE，交AD的延长线于点F.∵∠ACB=90°，∴∠ACF=∠BCE.∵CA=CB，∠CAF =∠CBE，∴△ACF≌△BCE.…………………………………6分∴AF=BE，CF=CE.∵∠ECF=90°，∴EFEC.即AF-EAEC.AB A∴7分7.（等腰直角三角形+旋转）(2019门头沟一模27). 如图，∠AOB = 90°，OC 为∠AOB 的平分线，点P 为OC 上一个动点，过点P 作射线PE 交OA 于点E ．以点P 为旋转中心，将射线PE 沿逆时针方向旋转90°，交OB 于点F ．（1）根据题意补全图1，并证明PE = PF ；（2）如图1，如果点E 在OA 边上，用等式表示线段OE ，OP 和OF 之间的数量关系，并证明；（3）如图2，如果点E 在OA 边的反向延长线上，直接写出线段OE ，OP 和OF 之间的数量关系．图1 图227．（本小题满分7分）解：（1）补全图形（如图1）； ……………………………… 1分证明：略. ……………………………………… 3分（2）线段OE ，OP 和OF 之间的数量关系是OF +OE =2OP . ……………………………… 4分证明：如图2，作PQ ⊥PO 交OB 于Q .∴ ∠2+∠3 = 90°，∠1+∠2 = 90°. ∴ ∠1=∠3.又∵ OC 平分∠AOB ，∠AOB =90°， ∴∠4 =∠5 = 45°. 又∵ ∠5 +∠6 = 90°， ∴∠6 = 45°，∴∠4 = ∠6 . ∴ PO = PQ .∴ △EPO ≌ △FPQ . ……………………… 5分 ∴ PE =PF ，OE = FQ .又∵OQ = OF +FQ = OF + OE .又∵ OQ =2OP ，∴OF + OE =2OP . ……………………… 6分（3）线段OE ，OP 和OF 之间的数量关系是OF - OE =2OP . ………………………… 7分PPEECCBBOOAA图2图18.（等腰直角三角形+旋转）(2019燕山一模27)如图，在△ABC 中，AB ＝BC ，∠B ＝90°，点D 为线段BC 上一个动点(不与点B ，C 重合)，连接AD ，将线段AD 绕点D 顺时针旋转90°得到线段DE ，连接EC ．(1) ① 依题意补全图1；② 求证：∠EDC ＝∠BAD ； (2) ① 小方通过观察、实验，提出猜想：在点D 运动的过程中，线段CE 与BD 的数量关系始终不变，用等式表示为：； ② 小方把这个猜想与同学们进行交流，通过讨论，形成了证明该猜想的几种想法：想法1：过点E 作EF ⊥BC ，交BC 延长线于点F ，只需证△ADB ≌△DEF ．想法2：在线段AB 上取一点F ，使得BF ＝BD ，连接DF ，只需证△ADF ≌△DEC ．想法3：延长AB 到F ，使得BF ＝BD ，连接DF ，CF ，只需证四边形DFCE 为平行四边形． ……请你参考上面的想法，帮助小方证明①中的猜想．(一种方法即可)27．(1)①补全的图形如图的所示；………………………………1分②证明：∵∠ADE ＝∠B ＝90°，∴∠EDC ＋∠ADB ＝∠BAD ＋∠ADB ＝90°，∴∠EDC ＝∠BAD ． ………………………………3分(2) ①CE ＝2BD ． ………………………………4分②想法1：证明：如图，过点E 作EF ⊥BC ，交BC 延长线于点F ，∴∠F ＝90°．在△ADB 和△DEF 中，∠B ＝∠F ＝90°，∠EDC ＝∠BAD ，AD ＝DE ， ∴△ADB ≌△DEF ， ∴AB ＝DF ，BD ＝EF ．图1 D C B A 备用图 A B CD AB ECD EA∵AB＝BC，∴DF＝BC，即DC＋CF＝BD＋DC，∴CF＝BD＝EF，∴△CEF是等腰直角三角形，∴CECFBD．………………………………7分想法2：证明：在线段AB上取一点F，使得BF＝BD，连接DF，∵∠B＝90°，AB＝BC，∴DFBD，∵AB＝BC，BF＝BD，∴AB－BF＝BC－BD，即AF＝DC．在△ADF和△DEC中，AF＝DC，∠BAD＝∠EDC，AD＝DE，∴△ADF≌△DEC，∴CE＝DFBD．………………………………7分∴AD＝CF，∠BAD＝∠BCF．∵AD＝DE，∴DE＝CF．∵∠EDC＝∠BAD，∴∠EDC＝∠BCF，∴DE∥CF，∴四边形DFCE为平行四边形，9.（等腰直角三角形+旋转）(2019丰台一模27)在△ABC 中，∠ACB =90°，AC =BC ， D 为AB 的中点，点E 为AC 延长线上一点，连接DE ，过点D 作DF ⊥DE 交CB 的延长线于点F ．（1）求证：BF= CE ；（2）若CE =AC ，用等式表示线段DF 与AB 的数量关系，并证明．解：（1）连接CD.在△ABC 中，∠ACB=90°，AC=BC ，D 为AB 中点，∴CD ⊥BD , CD=BD=DA. ...............1分∵DF ⊥DE ， ∴∠BDF =∠CDE . ∵∠F =∠E ，∴△DBF ≌△DCE .∴BF=CE. ..................3分（2）52DF AB =. ..................4分理由如下：由（1）知△DBF ≌△DCE ，∴DF=DE. ..................5分连接BE.∵CE=CA ， ∴BA=BE.∴∠A=∠BEA=45°. ∴∠ABE=90°. 设AD=BD=a ， ∴AB=BE=2a. ∴5DF DE a ==.∴52DF AB =. .........................7分FA EC DB10.（等腰直角三角形+旋转＋解直角三角形）(2019朝阳一模27)如图，在Rt △ABC 中，∠A =90°，AB =AC ，将线段BC 绕点B 逆时针旋转α°（0<α<180），得到线段BD ，且AD ∥BC ．（1）依题意补全图形；（2）求满足条件的α的值；（3）若AB =2，求AD 的长．解：（1）满足条件的点D 有两个，补全图形如图1所示．………………………………………2分（2）如图2，过点B 作BE ⊥D 1D 2于点E ．由题意可知，BD 1=BD 2 =BC ，AE ∥BC ． ∴∠AEB =90°．∵在Rt △ABC 中，∠BAC =90°，AB =AC ， ∴∠EAB =∠ABC =45°．∴在Rt △ABE 中，22BE AB =，在Rt △ABC 中，22AB BC =． ∴11122BE BC BD ==．……………………………………………………………………4分∴∠D 1=∠D 2=30°． ∵D 1D 2∥BC ，∴30α=或150．……………………………………………………………………………5分（3）∵AB =2，∴2BE AE ==．∴D 1E = D 2E =6．∴AD 的长为62-或62+．………………………………………………………7分图1图2CFE CAB11.（等边三角形+旋转）(2019怀柔一模27)如图，等边△ABC 中，P 是AB 上一点，过点P 作PD ⊥AC 于点D ，作PE ⊥BC 于点E ，M 是AB 的中点，连接ME ，MD ．（1）依题意补全图形；（2）用等式表示线段BE ，AD 与AB 的数量关系，并加以证明；（3）求证：MD=ME ．（1）补全图形如图：（2）线段BE ，AD 与AB 的数量关系是：AD+ BE=12AB ． ∵△ABC 是等边三角形，∴∠A=∠B=60°． ∵PD ⊥AC ，PE ⊥BC ，∴∠APD=∠BPE=30°， ∴AD=AP ，AD=AP ． ∴AD+ BE=（AP+ BP ）=AB ．………………………………3分（3）取BC 中点F ，连接MF ．∴MF=AC ．MF ∥AC ． ∴∠MFB=∠ACB=60°．∴∠A=∠MFE=60°． ∵AM=AB ，AB=AC ，∴MF=MA ． ∵EF+ BE=BC ， ∴AD + BE=AB ．∴EF=AD. ∴△MAD ≌△MFE （SAS ）．∴MD=ME ．…………………………………7分212121212121212121二、轴对称变换12.（正方形+对称）(2019西城一模27)如图，在△ABC中，∠ABC=90°，BA=BC．将线段AB绕点A逆时针旋转90°得到线段AD，E是边BC上的一动点，连接DE交AC于点F，连接BF．（1）求证：FB=FD；（2）点H在边BC上，且BH=CE，连接AH交BF于点N．①判断AH与BF的位置关系，并证明你的结论；②连接CN．若AB=2，请直接写出线段CN长度的最小值．解：（1）证明：∵∠ABC=90°，BA=BC，∴∠BAC=∠ACB=45°．∵AB绕点A逆时针旋转90°得到AD，∴∠BAD=90°，AB=AD．∴∠DAF=∠BAD－∠BAC=45°．∴∠BAF=∠DAF．…………………………………………………………1分∵AF=AF，∴△BAF≌△DAF．∴FB=FD．…………………………………………………………………2分（2）①AH与BF的位置关系：AH⊥BF．……………………………………………3分证明：连接DC，如图．∵∠ABC+∠BAD=180°，∴AD∥BC．∵AB=BC=AD，∴四边形ABCD是平行四边形．∵∠ABC=90°，∴四边形ABCD是矩形．∴AB=DC，∠ADC=∠DCB=90°．∴∠ABH=∠DCE．∵BH=CE，∴△ABH≌△DCE．∴∠BAH=∠CDE．∵△BAF≌△DAF，∴∠ABF=∠ADF．∴∠BAH＋∠ABF=∠CDE＋∠ADF=∠ADC=90°．∴∠ANB=180°－(∠BAH＋∠ABF)=90°．∴AH⊥BF．……………………………………………………………5分1．…………………………………………………………………………7分13．（等腰三角形+对称）(2019顺义一模27)已知：如图，在△ABC中，AB>AC，∠B=45°，点D是BC边上一点，且AD=AC，过点C作CF⊥AD于点E，与AB交于点F．（1）若∠CAD=α，求∠BCF的大小（用含α的式子表示）；（2）求证：AC=FC；（3）用等式直接表示线段BF与DC的数量关系．解：（1）过点A作AG⊥BC于点G，…………………1分∴∠2+∠4=90°，∵AD=AC，∴∠1=∠2=12∠CAD=12α，…………………………2分∵CF⊥AD于点E，∴∠3+∠4=90°，∴∠3=∠2=12∠CAD=12α，…………………………3分即∠BCF=12α．（2）证明：∵∠B=45°，∴∠BAG=45°，………………………………………4分∵∠BAC=45°+∠1，∠AFC=45°+∠3，∴∠BAC=∠AFC，∴AC=FC．………………………………………………5分（3）DC．…………………………………7分AB CDFE4231GEFD CBA三、平移变换14.（等边三角形+平移）(2019石景山一模27). 如图，在等边△ABC 中，D 为边AC 的延长线上一点()CD AC <，平移线段BC ，使点C 移动到点D ，得到线段ED ，M 为ED 的中点，过点M 作ED 的垂线，交BC 于点F ，交AC 于点G ．（1）依题意补全图形；（2）求证：AG = CD ；（3）连接DF 并延长交AB 于点H ，用等式表示线段AH 与CG 的数量关系，并证明．27．（1）补全的图形如图1所示． …………… 1分（2）证明：Q △ABC 是等边三角形， ∴AB BC CA ==．60ABC BCA CAB ∠=∠=∠=︒．由平移可知ED ∥BC ，ED =BC ．………… 2分 60ADE ACB ∴∠=∠=︒． 90GMD ∠=︒Q ，2DG DM DE ∴==． …………… 3分 DE BC AC ==Q ， DG AC ∴=．AG CD ∴=． …………… 4分（3）线段AH 与CG 的数量关系：AH = CG ．…………… 5分证明：如图2，连接BE ，EF ．,ED BC =Q ED ∥BC ，BEDC ∴四边形是平行四边形．BE CD CBE ADE ABC ∴=∠=∠=∠，． GM ED Q 垂直平分，EF DF ∴=．DEF EDF ∴∠=∠．Q ED ∥BC ，BFE DEF BFH EDF ∴∠=∠∠=∠，． BFE BFH ∴∠=∠． BF BF =Q ，BEF BHF ∴△≌△． …………… 6分 BE BH CD AG ∴===． AB AC =Q ，AH CG ∴=．…………… 7分B图1图2四、其它15.（等腰直角三角形+全等）(2019海淀一模27)如图，在等腰直角△ABC 中，90ABC ?°，D 是线段AC 上一点（2CA CD > ），连接BD ，过点C 作BD 的垂线，交BD 的延长线于点E ，交BA 的延长线于点F ．（1）依题意补全图形；（2）若ACE α?，求ABD Ð的大小（用含α的式子表示）；（3）若点G 在线段CF 上，CG BD =，连接DG ．①判断DG 与BC 的位置关系并证明；②用等式表示DG ，CG ，AB 之间的数量关系为．（1）补全图形，如图．（2）解：∵ AB =BC ，∠ABC =90°，∴ ∠BAC =∠BCA =45°．∵ ∠ACE =α， ∴ 45ECB α??．∵ CF ⊥BD 交BD 的延长线于点E ， ∴ ∠BEF =90°． ∴ ∠F +∠ABD =90°． ∵ ∠F +∠ECB =90°， ∴45ABD ECB α???．（3）① DG 与BC 的位置关系：DG ⊥BC ．证明：连接BG 交AC 于点M ，延长GD 交BC 于点H ，如图．∵ AB =BC ，∠ABD =∠ECB ，BD =CG ， ∴ △ABD ≌△BCG ． ∴ ∠CBG =∠BAD =45°． ∴ ∠ABG =∠CBG =∠BAC =45°． ∴ AM =BM ，∠AMB =90°． ∵ AD =BG ， ∴ DM =GM ．∴ ∠MGD =∠GDM =45°． ∴ ∠BHG =90° ∴ DG ⊥BC ．H。

2019年5月北京市初三数学一模全市各区全部试卷的分类整理——直线与双曲线的小综合(含参考答案)

201905初三数学一模试题整理：直线与双曲线的小综合（教师版）本题主要考察根据已知条件，分析、确定一次函数图象的变化情况，从运动与变化的角度，结合函数图象，观察、分析、发现与变量对应的数量关系的规律，考察函数思想、数形结合、分类与整合的数学思想.解决方法主要是要正确并准确的画图，借助图象（图形）的直观性，找出临界位置的点，将其坐标带入相应函数的表达式计算参数的值，进而得出参数的取值范围. 注意在写取值范围时，别将参数取值范围的大小写反.一、直线与双曲线综合----与面积有关的问题1.（2019西城一模第22题）在平面直角坐标系xOy 中，直线l ：y x b =+与x 轴交于点A （2-，0），与y 轴交于点B ．双曲线ky x=与直线l 交于P ，Q 两点，其中点P 的纵坐标大于点Q 的纵坐标．（1）求点B 的坐标；（2）当点P 的横坐标为2时，求k 的值；（3）连接PO ，记△POB 的面积为S ，若112S <<，直接写出k 的取值范围．答案：22．解：（1）∵直线l ：y x b =+与x 轴交于点A （2-，0），∴02b =-+，解得2b =． …………………………………………………1分 ∵直线l ：2y x =+与y 轴交于点B ，令0x =，则2y =，∴点B 的坐标为（0，2）． …………………………………………………2分（2）∵点P 在直线l ：2y x =+上，且点P 的横坐标为2，∴点P 的纵坐标为4． ∵点P 在双曲线ky x=上， ∴8k =． ………………………………………………………………………3分（3）314k -<<-或534k <<． …………………………………………………5分2.（2019密云一模第23题）. 已知直线3y kx k =+ 与函数(0)my x x=> 交于A （3，2）. （1）求k ，m 值.（2）若直线3y kx k =+与x 轴交于点P ，与y 轴交于点Q.点B 是y 轴上一点，且ABQ S ∆=2POQ S ∆.求点B 的纵坐标.答案：（1）由已知，直线3y kx k =+ 与函数(0)my x x=> 交于A （3，2）. ∴ 3k+3k=2,23m = 解得13k =,m=6 .................................2分(2)由（1），13k =，故此直线表达式为113y x =+令x=0,则y=1；令y=0,则3x =-. ∴P(-3，0)，Q(0,1).过点A 作AD ⊥y 轴，垂足为D. ∵ABQ S ∆=2POQ S ∆∴122BQ AD OP OQ ⨯⨯=⨯⨯ 即11323222BQ ⨯⨯=⨯⨯⨯ ∴BQ=2，∴B 点纵坐标为3或-1. .................................6分答案：（1）由题意可求：m = 2，n = -1．………………………………………………………………… 2分将（2，3），B （-6，-1）带入y kx b =+，得 32,16.k b k b =+⎧⎨-=-+⎩ 解得 1,22.k b ⎧=⎪⎨⎪=⎩ ∴ 直线的解析式为122y x =+. …………… 3分（2）（-2，0）或（-6，0）. …………………………………………………………………… 5分4.（2019顺义一模第23题）在平面直角坐标系xOy 中，直线26y x =-与双曲线ky x=(0≠k )的一个交点为A (m ，2)，与x 轴交于点B ，与y 轴交于点C .（1）求点B 的坐标及k 的值；（2）若点P 在x 轴上，且∆APC 的面积为16，求点P 的坐标.答案：23．解：（1）令0y =，则260x -=，可得3x =，∴直线26y x =-与x 轴交点B 的坐标为（3，0），……………1分将A (m ，2)，代入26y x =-，得4m =，将A (4，2)，代入ky x=，得8k =，………………3分（2）过点A 作AM ⊥x 轴于点M ，∵A (4，2)，C (0，-6)，…………………………4分 ∴OC =6，AM =2， ∵1126422APC APB CPB S S S PB PB PB ∆∆∆=+==⨯⨯+⨯⨯=， ∵16APC S ∆=， ∴PB =4，∴1P (-1，0)，2P (7，0) ……………………………………6分二、直线与双曲线综合----图象的上下左右位置关系问题1.（2019海淀一模第23题）在平面直角坐标系xOy 中，直线2y x=（1）求b 和m 的值；（2）将点B 向右平移到y 轴上，得到点C ，设点B 关于原点的对称点为D ，记线段BC 与AD 组成的图形为G ．① 直接写出点C ，D 的坐标； ② 若双曲线ky x=与图形G 恰有一个公共点，结合函数图象，求k 的取值范围．答案：（1）∵直线2y x b =+经过点A （1，m ），B （1-，1-），∴1b =．又∵直线2y x b =+经过点A （1，m ）， ∴3m =．（2）①C （0，1-），D （1，1）．②函数ky x=的图象经过点A 时，3k =．函数ky x=的图象经过点D 时，1k =，此时双曲线也经过点B ，结合图象可得k 值得范围是0113k k <<<≤或．2.（2019燕山一模第24题）如图，在平面直角坐标系xOy 中，直线l ：1(0)y kx k =-≠与函数(0)my x x=>的图象交于点B (3，2)． (1) 求k ，m 的值；(2) 将直线l 沿y 轴向上平移t 个单位后，与y 轴交于点C ，与函数(0)my x x=>的图象交于点D ． ① 当t ＝2时，求线段CD 的长；②≤CD≤，结合函数图象，直接写出t 的取值范围．答案：(1) 将点A (3，2)的坐标分别代入1y kx =-和my x=中，得 0＝k ×1－1， 23m =， ∴k ＝1，m ＝3×2＝6． ………………………………2分(2) ① ∵直线1y x =-与y 轴交于点B (0，－1)，∴当t ＝2时，C (0，1)． ………………………………3分此时直线解析式为1y x =+，代入函数6y x=中整理得， (1)6x x +=，解得13x =-(舍去)，22x =， ∴D (2，3)，∴CD＝． ………………………………4分② 2≤ t ≤6． ………………………………6分在第一象限内，∠OAB =90°，（1）求k 的值；（2）已知点P 坐标为（a ，0），过点P 作直线OB 的垂线l ，点O ，A 关于直线l 的对称点分别为O ’，A ’，若线段O ’A’与反比例函数ky x=的图象有公共点，直接写出a 的取值范围． 23．（1）解：∵△OAB 的面积为2， ∴22k=．∴4k =．………………………………………………………………………2分（2）21a -≤≤-21a ≤≤ ………………………………………………………6分三、直线与双曲线综合----线段倍数关系问题1.（2019石景山一模第23题）如图，在平面直角坐标系xOy 中，函数()0ky x x=<的图象经过点()16A -，，直线2y mx =-与x 轴交于点()10B -，．（1）求k ，m 的值；（2）过第二象限的点P ()2n n -，作平行于x 轴的直线，交直线y =函数()0ky x x=<的图象于点D .①当1=-n 时，判断线段PD 与PC ②若2PD PC ≥，结合函数的图象，直接写出n 的取值范围．答案：（1）∵函数()0ky x x=<的图象G 经过点A （-1，6）， ∴6k =-． …………… 1分∵直线2y mx =-与x 轴交于点B （-1，0）， ∴2m =-． ……………………… 2分（2）①判断：PD =2PC ．理由如下： ……… 3分当1n =-时，点P 的坐标为(-1,2)，∴点C 的坐标为(-2,2)，点D 的坐标为(-3,2)．∴PC =1，PD =2．∴PD =2PC ． …………… 4分②10n -<≤或3n -≤． …………… 6分2.（2019通州一模第22题）如图，在平面直角坐标系xOy 中，直线2y x =与函数()0my x x=>的图象交于点A （1，2）. （1）求m 的值；（2）过点A 作x 轴的平行线l ，直线2y x b =+与直线l 交于点B ，与函数()0my x x=>的图象交于点C ，与x 轴交于点D .①当点C 是线段BD 的中点时，求b 的值； ②当BC BD >时，直接写出b 的取值范围.答案：（1）把A （1，2）代入函数(0)my x x=>中， ∴21m =. ∴2m =. ……………… 1分（2）①过点C 作x 轴的垂线，交直线l 于点E ，交x 轴于点F .当点C 是线段BD 的中点时，1CE CF ==.∴点C 的纵坐标为1.……………… 2分把1y =代入函数2y x=中，得2x =.∴点C 的坐标为（2，1）. ……………… 3分把C （2，1）代入函数2y x b =+中，得3b =-. ……………… 4分 ②3b >. ……………… 5分3.（2019丰台一模第23题）如图，在平面直角坐标系xOy 中，直线l ：y =x +1与y 轴交于点A ，与函数xky =（x ＞0）的图象交于点B （2，a ）. （1）求a 、k 的值；（2）点M 是函数xky =（x ＞0）图象上的一点，过点M 作平行于y 轴的直线，交直线l 于点P ，过点A 作平行于x 轴的直线交直线MP 于点N ，已知点M 的横坐标为m .①当23=m 时，求MP 的长； ②若MP ≥PN ，结合函数的图象，直接写出m 的取值范围.答案：23.解：（1）由题意，得A (0,1) .∵直线l 过点B (2,a ),∴3a =. .................…..........1分∵反比例函数(0)k y x x=>的图象经过点B (2,3)，∴6k =. .................…..........2分（2）①由题意，得335(,4),(,)222M P .∴32MP =； .................…..........4分 ②3062m m <≤≥或. .................…..........6分4.（2019大兴一模第23题）如图，在平面直角坐标系xOy 中，直线y=x 与函数y =kx(x <0)的图象交于点A（m ）. （1）求m ，k 的值；（2）点P （x P ，y P ）为直线y=x 上任意一点，将直线y=x 沿y 轴向上平移两个单位得到直线l ，过点P 作x 轴的垂线交直线l 于点C ，交函数y =kx(x < 0)的图象于点D . ①当x P = -1时，判断PC 与PD 的数量关系，并说明理由； ②若PC+PD ≤4时，结合函数图象，直接写出x P 的取值范围. 23.解：（1）∵直线y=x 经过点A （m ）∴m =1分又∵函数y =kx(x <0)的图象经过点A （ ∴k =3 …………………………………………………………………2分（2）①PC=PD ……………………………………………………………3分∵点P 为直线y =x 上一点，x p =－1， ∴y P =－1， ∴P （－1，－1）∵y =x 向上平移两个单位， ∴l ：y =x +2∴C （－1，1） ……………………………………………………… 4分把x =－1代入3y x=∴y =－3∴点D 的坐标为（－1，－3）∴PC=PD =2 ………………………………………………………… 5分 ②－3≤x P ≤－1 ……………………………………………………6分四、直线与双曲线综合----特殊三角线问题1.（2019东城一模第22题）在平面直角坐标系xOy 中，直线(0)y kx k =≠与双曲线y ＝8(0)x x> 交于点A（2，n ）（1）求n 及k 的值；（2）点B 是y 轴正半轴上一点，且△OAB 是等腰三角形，请直接写出所有．．符合条件的点B 坐标．答案：22.解：（1）点A （2，n ）在双曲线8y x=上， ∴n ＝842= ………………………………………………………………1分 ∵点A （2，4）在直线y kx =上，∴k＝2……………………………………………………………………2分（2）（0,8）（0，0，52）…………………………………5分五、直线与双曲线综合----整数点问题1.（2019延庆一模第22题）在平面直角坐标系xOy 中，函数ky x=（0x >）的图象经过边长为2的正方形OABC 的顶点B ，如图，直线1y mx m =++与k y x=（0x >）的图象交于点D （点D 在直线BC 的上方），与x轴交于点E ．（1）求k 的值；（2）横、纵坐标都是整数的点叫做整点．记ky x=（0x >）的图象在点B ，D 之间的部分与线段AB ，AE ，DE 围成的区域（不含边界）为W ． ①当12m =时，直接写出区域W 内的整点个数； ②若区域W 内恰有3个整点，结合函数图象，求m 的取值范围．答案：（1）由题意可知：边长为2的正方形OABC 的顶点B 的坐标为（2，2）∵函数ky x=（0x >）的图象经过B （2，2） ∴ 4k =． ……2分（2）①2个． ……3分 ②112m <≤． ……5分 2（2019平谷一模第21题）如图，在平面直角坐标系xOy 中，函数()0ky x x=>的图象经过点A ，作AC ⊥x 轴于点C ．（1）求k 的值；（2）直线AB ：()0y ax b a =+>图象经过点A 交x 轴于点B ．横、纵坐标都是整数的点叫做整点．线段AB ，AC ，BC 围成的区域（不含边界）为W ．①直线AB 经过()0,1时，直接写出区域W 内的整点个数； ②若区域W 内恰有1个整点，结合函数图象，求a 的取值范围．答案：（1）k =4； (1)（2）①1个； (2)②当直线AB 经过点A （2，﹣2），（0,1）时区域W 内恰有1个整点， ∴12a =．当直线AB 经过点A （2，﹣2），（1,1）时区域W 内没有整点，∴a =1． (3)∴当112a ≤<时区域W 内恰有1个整点． · (5)3.（2019怀柔一模第23题）在平面直角坐标系xoy 中，直线y=kx+b (k<0),经过点（6，0），且与坐标轴围成的三角形的面积是9，与函数xm=y （0x >）的图象G 交于A ，B 两点. （1）求直线的表达式；（2）横、纵坐标都是整数的点叫作整点.记图像G 在点A 、B 之间的部分与线段AB 围成的区域（不含边界）为W.①当m=2时，直接写出区域W 内的整点的坐标；②若区域W 内恰有3个整数点，结合函数图象，求m 的取值范围.答案：：如图，（1）设直线与y 轴的交点为C （0，b ），∵直线与两坐标轴围成的三角形的面积是9， ∴9621=⋅⨯b .3±=b . ∵k<0，∴3=b .∴直线y=kx+b 经过点（6，0）和（0，3）∴表达式为321-+=x y ………………………2分（2）①（3，1）…………………………………4分②当x m=y 图象经过点（1,1）时,则m=1. 当xm=y 图象经过点（2,1）时,则m=2.所以，21<≤m ………………6分六、直线与双曲线综合----线段最小值问题1.（2019房山一模第23题）已知一次函数2y x =的图象与反比例函数x ky =(k ≠ 0) 在第一象限内的图象交于点A （1，m ）. (1) 求反比例函数的表达式；(2) 点B 在反比例函数的图象上，且点B 的横坐标为2.若在x 轴上存在一点M ，使MA +MB 的值最小，求点M 的坐标.答案：（1）∵A （1，m ）在一次函数y =2x 的图象上∴m =2， ………………………………… 1分将A （1,2）代入反比例函数xky =得k =2 ∴反比例函数的表达式为x y 2=………………………………… 3分（2）作点A 关于x 轴的对称点A '，连接B A '交x 轴于点M ，此时MA +MB 最小 ………………………………… 4分 A 关于x 轴的对称点A '（1，-2）， ∵B （2,1）………………………………… 5分………………………………… 6分。

2018-2019北京四中初三数学一模几何综合汇编

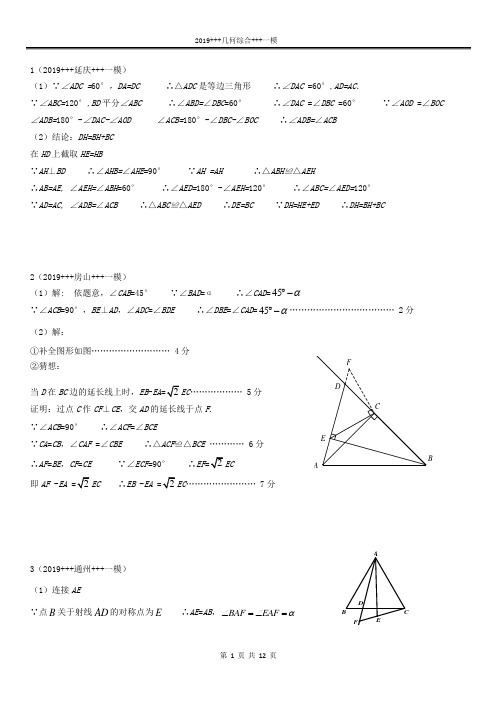
1（2019+++延庆+++一模）（1）∵∠ADC =60°，DA=DC ∴△ADC是等边三角形∴∠DAC =60°,AD=AC．∵∠ABC=120°,BD平分∠ABC ∴∠ABD=∠DBC=60°∴∠DAC =∠DBC =60°∵∠AOD =∠BOC ∠ADB=180°-∠DAC-∠AOD∠ACB=180°-∠DBC-∠BOC ∴∠ADB=∠ACB（2）结论：DH=BH+BC在HD上截取HE=HB∵AH⊥BD ∴∠AHB=∠AHE=90°∵AH =AH ∴△ABH≌△AEH ∴AB=AE,∠AEH=∠ABH=60°∴∠AED=180°-∠AEH=120°∴∠ABC=∠AED=120°∵AD=AC, ∠ADB=∠ACB ∴△ABC≌△AED ∴DE=BC ∵DH=HE+ED ∴DH=BH+BC2（2019+++房山+++一模）（1）解: 依题意，∠CAB=45°∵∠BAD=α∴∠CAD=45α︒-∵∠ACB=90°，BE⊥AD，∠ADC=∠BDE ∴∠DBE=∠CAD=45α︒-……………………………… 2分（2）解：①补全图形如图……………………… 4分②猜想：当D在BC边的延长线上时，EB-EA EC……………… 5分证明：过点C作CF⊥CE，交AD的延长线于点F.∵∠ACB=90°∴∠ACF=∠BCE∵CA=CB，∠CAF =∠CBE ∴△ACF≌△BCE………… 6分∴AF=BE，CF=CE ∵∠ECF=90°∴EF EC即AF -EA EC ∴EB -EA…………………… 7分3（2019+++通州+++一模）（1）连接AE∵点B关于射线AD的对称点为E∴AE=AB，BAF EAFα∠=∠=∵ABC △是等边三角形 ∴AB AC =，60BAC ACB ∠=∠=︒ ∴602EAC α∠=︒-，AE AC =………1分∴()1180602602ACE αα∠=︒-︒-=︒+⎡⎤⎣⎦ ∴6060BCF ACE ACB αα∠=∠-∠=︒+-︒=……………2分另解：借助圆（2）AF EF CF -=证明：如图，作60FCG ∠=︒交AD 于点G ，连接BF ……………3分 ∵BAF BCF α∠=∠=，ADB CDF ∠=∠ ∴60ABC AFC ∠=∠=︒ ∴△FCG 是等边三角形 ∴GF =FC ……………… 4分 ∵ABC △是等边三角形 ∴BC AC =，60ACB ∠=︒∴ACG BCF α∠=∠= 在△ACG 和△BCF 中CA CB ACG BCF CG CF =⎧⎪∠=∠⎨⎪=⎩，，， ∴△ACG ≌△BCF∴AG BF =……………5分 ∵点B 关于射线AD 的对称点为E ∴BF EF =……………6分 ∴AF AG GF -= ∴AF EF CF -=………………7分另一种证法：作60FAH ∠=︒交FC 的延长线于点H ，连接BF4（2019+++平谷+++一模）（1）∠BCD =120°－α （2）解：方法一：延长BA 使AE=BC ，连接DE 由（1）知△ADC 是等边三角形 ∴AD=CD ∵∠DAB +∠DCB =∠DAB +∠DAE =180°∴∠DAB =∠DAE ∴△ADE ≌△CDB ∴BD=BE ∴BD=AB+BC 方法二：延长AB 使AF=BC ，连接CF∠BDC =∠ADE ∵∠ABC =120° ∴∠CBF =60°∴△BCF 是等边三角形 ∴BC=CF ∵∠DCA =∠BCF =60°∴∠DCA +∠ACB =∠BCF +∠ACB 即∠DCB =∠ACF ∵CA=CD ∴△ACF ≌△DCB ∴BD=AF ∴BD=AB+BC （3）AC ，BD 的数量关系是：2AC BD 位置关系是：AC ⊥BD 于点P5（2019+++门头沟+++一模）（1）补全图形（如图1）…………… 1分证明：略………… 3分（2）线段OE ，OP 和OF 之间的数量关系是OF +OE OP …… 4分证明：如图2，作PQ ⊥PO 交OB 于Q∴∠2+∠3=90°，∠1+∠2=90° ∴∠1=∠3 又∵OC 平分∠AOB ，∠AOB =90° ∴∠4=∠5=45°又∵∠5+∠6=90° ∴∠6=45° ∴∠4=∠6 ∴PO =PQ ∴△EPO ≌ △FPQ …………… 5分 ∴PE =PF ，OE =FQ 又∵OQ =OF +FQ =OF +OE又∵OQ ∴OF+OE …………… 6分（3）线段OE ，OP 和OF 之间的数量关系是OF- OE …………… 7分6（2019++石景山+++一模）（1）补全的图形如图1所示（2）△ABC 是等边三角形∴AB BC CA ==，60ABC BCA CAB ∠=∠=∠=︒由平移可知ED ∥BC ，ED =BC ……… 2分60ADE ACB ∴∠=∠=︒ 90GMD ∠=︒ 2DG DM DE ∴==…… 3分DE BC AC == DG AC ∴= AG CD ∴=……… 4分（3）线段AH 与CG 的数量关系：AH = CG ……… 5分如图2，连接BE ，EF,ED BC =ED ∥BC BEDC ∴四边形是平行四边形 BE CD CBE ADE ABC ∴=∠=∠=∠， GM ED 垂直平分EF DF ∴= DEF EDF ∴∠=∠ ED ∥BCBFE DEF BFH EDF ∴∠=∠∠=∠， BFE BFH ∴∠=∠BF BF = BEF BHF ∴△≌△………… 6分BE BH CD AG ∴===AB AC = AH CG ∴=……… 7分7（2019+++西城+++一模）D8（2019+++燕山+++一模）(1)①补全的图形如图的所示………1分 ②证明：∵∠ADE ＝∠B ＝90°∴∠EDC ＋∠ADB ＝∠BAD ＋∠ADB ＝90° ∴∠EDC ＝∠BAD ……………3分 (2)①CE BD ……………4分 ②想法1：如图，过点E 作EF ⊥BC ，交BC 延长线于点F ∴∠F ＝90° 在△ADB 和△DEF 中，∠B ＝∠F ＝90°，∠EDC ＝∠BAD ，AD ＝DE ∴△ADB ≌△DEF ∴AB ＝DF ，BD ＝EF ∵AB ＝BC ∴DF ＝BC 即DC ＋CF ＝BD ＋DC ∴CF ＝BD ＝EF ∴△CEF 是等腰直角三角形∴CECF BD ……………7分想法2：证明：在线段AB 上取一点F ，使得BF ＝BD ，连接DF∵∠B ＝90°，AB ＝BC ∴DF BD ∵AB ＝BC ，BF ＝BD ∴AB －BF ＝BC －BD 即AF ＝DC 在△ADF 和△DEC 中AF ＝DC ，∠BAD ＝∠EDC ，AD ＝DE ∴△ADF ≌△DEC∴CE＝DF BD ……………7分想法3：证明：延长AB 到F ，使得BF ＝BD ，连接DF ，CF∵∠B ＝90°∴DF 在Rt △ABD 和Rt △CBF 中 ∠ABD ＝∠CBF ＝90°，AB ＝BC ，BD ＝BF ∴△ABD ≌△CBFFABECD∴AD＝CF，∠BAD＝∠BCF ∵AD＝DE ∴DE＝CF∵∠EDC＝∠BAD ∴∠EDC＝∠BCF ∴DE∥CF∴四边形DFCE为平行四边形∴CE＝DF BD……………7分9（2019+++丰台+++一模）10（2019+++密云+++零模）（1）补全图形AD与BE的数量关系为AD=BE（2）∵∠ACB=∠DCE= 60°∴∠ACD=∠BCE 又∵AC=BC,CD=CE ∴△ACD≌△BCE ∴AD=BE, ∠CBE=∠CAD=60°∴∠ABF=180°-∠ABC-∠CBE=60°在Rt AFB∆中，AFAB=∴ABDB AH O DBA1已知：四边形ABCD 中，120ABC ∠=︒，60ADC ∠=︒，AD =CD ，对角线AC ，BD 相交于点O ，且BD 平分∠ABC ，过点A 作AH BD ⊥，垂足为H （1）求证：ADB ACB ∠=∠（2）判断线段BH ，DH ，BC 之间的数量关系；并证明 2已知：Rt △ABC 中，∠ACB =90°，AC =BC(1) 如图1，点D 是BC 边上一点(不与点B ，C 重合)，连接AD ，过点B 作BE ⊥AD ，交AD 的延长线于点E ，连接CE . 若∠BAD =α，求∠DBE 的大小 (用含α的式子表示)(2) 如图2，点D 在线段BC 的延长线上时，连接AD ，过点B 作BE ⊥AD ，垂足E 在线段AD 上，连接CE . ①依题意补全图2 ②用等式表示线段EA ，EB 和EC 之间的数量关系，并证明AA3如图，在等边ABC △中，点D 是线段BC 上一点.作射线AD ，点B 关于射线AD 的对称点为E .连接CE 并延长，交射线AD 于点F（1）设BAF α∠=，用α表示BCF ∠的度数（2）用等式表示线段AF 、CF 、EF 之间的数量关系，并证明 4在△ABC 中，∠ABC =120°，线段AC 绕点A 逆时针旋转60°得到线段AD ，连接CD ，BD 交AC 于P （1）若∠BAC =α，直接写出∠BCD 的度数（用含α的代数式表示）（2）求AB ，BC ，BD 之间的数量关系（3）当α=30°时，直接写出AC ，BD 的关系5如图，∠AOB = 90°，OC 为∠AOB 的平分线，点P 为OC 上一个动点，过点P 作射线PE 交OA 于点E ．以点P 为旋转中心，将射线PE 沿逆时针方向旋转90°，交OB 于点F （1）根据题意补全图1，并证明PE = PF（2）如图1，如果点E 在OA 边上，用等式表示线段OE ，OP 和OF 之间的数量关系，并证明（3）如图2，如果点E 在OA 边的反向延长线上，直接写出线段OE ，OP 和OF 之间的数量关系6如图，在等边△ABC 中，D 为边AC 的延长线上一点()CD AC ，平移线段BC ，使点C 移动到点D ，得到线段ED ，M 为ED 的中点，过点M 作ED 的垂线，交BC 于点F ，交AC 于点G （1）依题意补全图形（2）求证：AG = CD（3）连接DF 并延长交AB 于点H ，用等式表示线段AH 与CG 的数量关系，并证明PPEECCBBOOAADB A7如图，在△ABC 中，∠ABC =90°，BA=BC .将线段AB 绕点A 逆时针旋转90°得到线段AD ，E 是边BC 上的一动点，连接DE 交AC 于点F ，连接BF(1) 求证：FB=FD(2) 点H 在边BC 上，且BH=CE ，连接AH 交BF 于点N①判断AH 与BF 的位置关系，并证明你的结论②连接CN .若AB =2，请直接写出线段CN 长度的最小值8如图，在△ABC 中，AB ＝BC ，∠B ＝90°，点D 为线段BC上一个动点(不与点B ，C 重合)，连接AD ，将线段AD 绕点 D 顺时针旋转90°得到线段DE ，连接EC(1) ① 依题意补全图1② 求证：∠EDC ＝∠BAD (2) ① 小方通过观察、实验，提出猜想：在点D 运动的过程中，线段CE 与BD 的数量关系始终不变，用等式表示为 ② 小方把这个猜想与同学们进行交流，通过讨论，形成了证明该猜想的几种想法想法1：过点E 作EF ⊥BC ，交BC 延长线于点F ，只需证△ADB ≌△DEF ．想法2：在线段AB 上取一点F ，使得BF ＝BD ，连接DF ，只需证△ADF ≌△DEC ．想法3：延长AB 到F ，使得BF ＝BD ，连接DF ，CF ，只需证四边形DFCE 为平行四边形．……请你参考上面的想法，帮助小方证明①中的猜想(一种方法即可)备用图AB C D 图1 D C B A9在ABC ∆中，090=∠ACB ，AC=BC ，D 为AB 的中点，点E 为AC 延长线上一点，连接DE ，过点D 作DF ⊥DE交CB 的延长线于点F（1）求证:BF=CE（2）若CE=AC ，用等式表示线段DF 与AB 的数量关系，并证明10已知ABC ∆为等边三角形，点D 是线段AB 上一点（不与A 、B 重合）.将线段CD 绕点C 逆时针旋转60︒得到线段CE.连结DE 、BE（1）依题意补全图1并判断AD 与BE 的数量关系（2）过点A 作AF EB ⊥交EB 延长线于点F ，用等式表示线段EB 、DB 与AF 之间的数量关系并证明图2D C BA 图1ABC D。

2019年北京市各区九年级上册期末数学试卷分类汇编：几何综合【标准版】

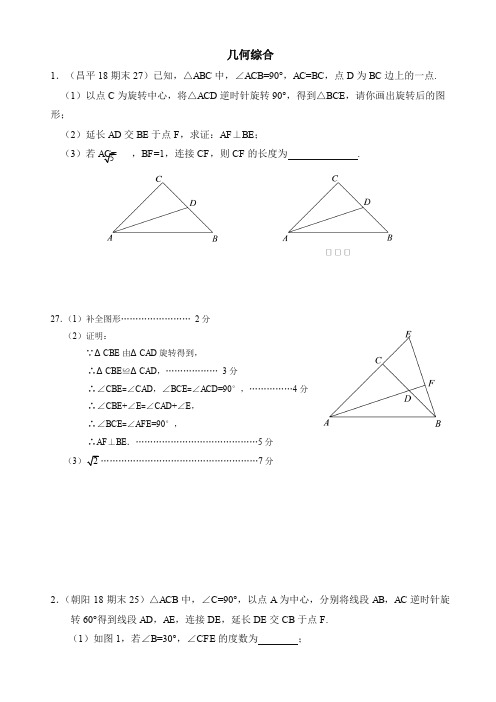
几何综合1．（昌平18期末27）已知，△ABC 中，∠ACB =90°，AC =BC ，点D 为BC 边上的一点. （1）以点C 为旋转中心，将△ACD 逆时针旋转90°，得到△BCE ，请你画出旋转后的图形；（2）延长AD 交BE 于点F ，求证：AF ⊥BE ；（3）若，BF =1，连接CF ，则CF 的长度为 .27．（1）补全图形…………………… 2分（2）证明：∵ΔCBE 由ΔCAD 旋转得到，∴ΔCBE ≌ΔCAD ，……………… 3分∴∠CBE =∠CAD ，∠BCE =∠ACD =90°，……………4分 ∴∠CBE +∠E =∠CAD +∠E ， ∴∠BCE =∠AFE =90°，∴AF ⊥BE ．……………………………………5分（3………………………………………………7分2．（朝阳18期末25）△ACB 中，∠C =90°，以点A 为中心，分别将线段AB ，AC 逆时针旋转60°得到线段AD ，AE ，连接DE ，延长DE 交CB 于点F . （1）如图1，若∠B =30°，∠CFE 的度数为；（2）如图2，当30°<∠B <60°时，①依题意补全图2；②猜想CF 与AC 的数量关系，并加以证明.图1 图23．（西城18期末27）如图1，在Rt △AOB 中，∠AOB =90°，∠OAB =30°，点C 在线段OB上，OC =2BC ，AO 边上的一点D 满足∠OCD =30°．将△OCD 绕点O 逆时针旋转α度（90°<α<180°）得到△OC D ''，C ，D 两点的对应点分别为点C '，D '，连接AC '，BD '，取AC'的中点M，连接OM．（1）如图2，当C D''∥AB时，α=°，此时OM 和BD'之间的位置关系为；（2）画图探究线段OM和BD'之间的位置关系和数量关系，并加以证明．4．（丰台18期末27）如图，∠BAD=90°，AB=AD ，CB=CD ，一个以点C 为顶点的45°角绕点C 旋转，角两边与BA ，DA 交于点M ，N ，与BA ，DA 延长线交于点E ，F ，连接AC . （1）在∠FCE 旋转的过程中，当∠FCA =∠ECA 时，如图1，求证：AE =AF ；（2）在∠FCE 旋转的过程中，当∠FCA ≠∠ECA 时，如图2，如果∠B=30°，CB=2，用等式表示线段AE ，AF 之间的数量关系，并证明.27.解：（1）证明：∵AB=AD ，BC=CD ，AC=AC ，∴△ABC ≌△ADC . …1分∴∠BAC =∠DAC =45°，可证∠FAC =∠EAC =135°. ……2分又∵∠FCA =∠ECA ，∴△ACF ≌△ACE . ∴AE =AF . ……3分其他方法相应给分.（2）过点C 作CG ⊥AB 于点G ，求得AC =2.……4分∵∠FAC =∠EAC =135°，∴∠ACF +∠F =45°. 又∵∠ACF +∠ACE =45°，∴∠F =∠ACE . ∴△ACF ∽△AEC. ……5分 ∴ACAF AE AC =，即AF AE AC ⋅=2. ……6分 ∴2=⋅AF AE . ……7分5．（怀柔18期末27）在等腰△ABC 中，AB =AC ，将线段BA 绕点B 顺时针旋转到BD，使图1图2BD⊥AC于H，连结AD并延长交BC的延长线于点P.（1）依题意补全图形；（2）若∠BAC=2α，求∠BDA的大小（用含α的式子表示）；（3）小明作了点D关于直线BC的对称点点E，从而用等式表示线段DP与BC之间的数量关系.请你用小明的思路补全图形并证明线段DP与BC之间的数量关系.27.解：(1)如图……………………………………………1分(2) ∵∠BAC=2α，∠AHB=90°∴∠ABH=90°-2α…………………………………………………………………………… 2分∵BA=BD∴∠BDA=45°+α………………………………………………………………………………3分(3)补全图形，如图………………4分证明过程如下：∵D关于BC的对称点为E，且DE交BP于G∴DE⊥BP，DG=GE，∠DBP=∠EBP，BD=BE；…………………………………………5分∵AB=AC，∠BAC=2α∴∠ABC=90°-α由(2)知∠ABH=90°-2α∠DBP=90°-α-（90°-2α）=α∴∠DBP=∠EBP=α∴∠BDE=2α∵AB=BD∴△ABC ≌△BDE ………………………………………………………………………………6分 ∴BC =DE∴∠DPB =∠ADB -∠DBP =45°+α-α=45° ∴DP DG =21, ∴DP DE=2, ∴DPBC=2, ∴BC =2DP .………………………………………………………………………………7分6．（平谷18期末27）如图，在Rt △ABC 中，∠BAC =90°，AB=AC ．在平面内任取一点D ，连结AD （AD ＜AB ），将线段AD 绕点A 逆时针旋转90°得到线段AE ，连结DE ，CE ，BD ．（1）请根据题意补全图1；（2）猜测BD 和CE 的数量关系并证明；（3）作射线BD ，CE 交于点P ，把△ADE 绕点A 旋转，当∠EAC =90°，AB =2，AD =1时，补全图形，直接写出PB 的长．27．解：（1）如图 (1)（2）BD 和CE 的数量是：BD =CE ；·················································································2B图1B备用图∵∠DAB +∠BAE =∠CAE +∠BAE =90°，∴∠DAB=∠CAE ． ················································································································· 3 ∵AD=AE ，AB=AC ， ∴△ABD ≌△ACE ．∴BD =CE ． (4)（3）PB ． (7)7．（密云18期末27）如图，已知Rt ABC ∆中，90ACB ∠=︒，AC=BC ，D 是线段AB 上的一点（不与A 、B 重合）. 过点B 作BE ⊥CD ，垂足为E.将线段CE 绕点C 顺时针旋转90︒，得到线段CF ，连结EF.设BCE ∠度数为α.（1）①补全图形； ②试用含α的代数式表示CDA ∠.（2）若EF AB = ，求α的大小. （3）直接写出线段AB 、BE 、CF 之间的数量关系.27.（1）①补全图形.……………………………..1分②45α︒+ ……………………………..3分（2）在FCE ∆和ACB ∆中，45CFE CAB ∠=∠=︒ ，90FCE ACB ∠=∠=︒ F C E ∆∽ ACB ∆CF EFAC AB =EF AB =2CF AC = ………………………………..5分连结FA.90,ECB 90FCA ACE ACE ∠=︒-∠∠=︒-∠ECB FCA ∠=∠=α在Rt CFA ∆中，90CFA ∠=︒，cos FCA ∠=30FCA ∠=︒即30α=︒. ………………………………6分（3）22222AB CF BE =+ …………………………………………8分8．（石景山18期末27）在正方形ABCD中，点P在射线AC上，作点P关于直线CD的对称点Q，作射线BQ交射线DC于点E，连接BP．（1）当点P在线段AC上时，如图1．①依题意补全图1；②若EQ=BP，则∠PBE的度数为，并证明；（2）当点P在线段AC的延长线上时，如图2．若EQ=BP，正方形ABCD的边长为1，请写出求BE长的思路．（可以不写出计算结果）27．（本小题满分7分）（1）解：①正确作图………………………1分②45°………………………2分连接PD，PE易证△CPD≌△CPB∴DP=BP，∠CDP=∠CBP∵P、Q关于直线CD对称∴EQ=EP∵EQ=BP∴DP=EP∴∠C D P=∠D E P………………………………………………3分∵∠CEP+∠DEP=180°∴∠CEP+∠CBP=180°∵∠BCD=90°∴∠BPE=90°∵BP=EP∴∠PBE =45°． …………………………………………………………4分（2）解：连接PD ，PE易证△CPD ≌△CPB ∴DP =BP ，∠1=∠2 ∵P 、Q 关于直线CD 对称， ∴EQ =EP ，∠3=∠4 ∵EQ =BP ， ∴DP =EP ∴∠3=∠1， ∴∠3=∠2 ∴∠5=∠BCE =90° ∵BP =EP ， ∴∠PEB =45° ∴∠3=∠4=22.5°，在△BCE 中，已知∠4=22.5°，BC =1，可求BE 长． ……………7分9．（东城18期末27）如图1，在△ABC 中，∠ACB =90°，AC =2，BC =B 为圆心，为半径作圆．点P 为B 上的动点，连接PC ，作PCPC '⊥，使点P '落在直线BC 的上方，且满足:P C PC '=BP ，AP '．（1）求∠BAC 的度数，并证明△AP C '∽△BPC ；（2）若点P 在AB 上时，①在图2中画出△AP’C ； ②连接BP '，求BP '的长；图1图2（3）点P 在运动过程中，BP '是否有最大值或最小值？若有，请直接写出BP '取得最大值或最小值时∠PBC 的度数；若没有，请说明理由．备用图10．（顺义18期末27）综合实践课上，某小组同学将直角三角形纸片放到横线纸上（所有横线都平行，且相邻两条平行线的距离为1），使直角三角形纸片的顶点恰巧在横线上，发现这样能求出三角形的边长．（1）如图1，已知等腰直角三角形纸片△ABC，∠ACB=90°，AC=BC，同学们通过构造直角三角形的办法求出三角形三边的长，则AB= ；（2）如图2，已知直角三角形纸片△DEF，∠DEF=90°，EF=2DE，求出DF的长；（3）在（2）的条件下，若橫格纸上过点E的横线与DF相交于点G，直接写出EG的长．27．（1）AB ；……………………….2分（2）解：过点E 作横线的垂线，交l 1，l 2于点M ，N ，……………………………..….3分∴∠DME =∠EDF = 90°，∵∠DEF =90°，∴∠2+∠3=90°，∵∠1+∠3=90°，∴∠1=∠2，∴△DME ∽△ENF ，………….…….4分 ∴DM ME DE EN NF EF==， ∵EF =2DE ， ∴12DM ME DE EN NF EF ===， ∵ME =2，EN =3，∴NF =4，DM =1.5，根据勾股定理得DE =2.5，EF =5，DF =……………………….5分（3）EG=2.5．…………………………………………………………..…….7分11．（门头沟18期末27）如图1有两条长度相等的相交线段AB 、CD ，它们相交的锐角中有一个角为60°，为了探究AD 、CB 与CD (或AB )之间的关系，小亮进行了如下尝试：（1）在其他条件不变的情况下使得AD BC ∥，如图2，将线段AB 沿AD 方向平移AD 的长度，得到线段DE ,然后联结BE ,进而利用所学知识得到AD 、CB 与CD (或AB )之间的关系：____________________；(直接写出结果)（2）根据小亮的经验，请对图27-1的情况（AD 与CB 不平行）进行尝试，写出AD 、CB 与CD (或AB )之间的关系，并进行证明；（3）综合（1）、（2）的证明结果，请写出完整的结论 __________________________.27．（本小题满分7分）（1） AD CB AB += ……………………………………………1分（2）补全图形正确 ………………………………………2分结论：AD CB AB +＞………………………………………3分理由：如图：将线段AB 沿AD 方向平移AD 的长度，得到线段DE ,联结BE 、CE ，且可得AB DE ∥且AB DE =∴四边形A 、B 、E 、D 是平行四边形………………………4分∴AD BE =∵AB CD =∴DE CD =∵AB DE ∥,60AOD ∠=︒∴DCE △是等边三角形……………………………………5分∴CE AB =由于AD 与CB 不平行，所以C 、B 、E 构成三角形∴BE CB CE +＞……………………………………………6分∴AD CB AB +＞（3）AD CB AB +≥ …………………………………………7分12．（通州18期末24）如图1，在矩形ABCD 中，点E 为AD 边中点，点F 为BC边中点；图1 图2点G ，H 为AB 边三等分点，I ，J 为CD 边三等分点.小瑞分别用不同的方式连接矩形对边上的点，如图2，图3所示.那么，图2中四边形GKLH 的面积与图3中四边形KPOL 的面积相等吗？（1）小瑞的探究过程如下在图2中，小瑞发现， ABCD GKLH S S _______=；在图3中，小瑞对四边形KPOL 面积的探究如下. 请你将小瑞的思路填写完整：设a S DEP =△，b S AKG =△∵AF EC ∥∴DAK DEP ∽△△，且相似比为2:1，得到a S DAK 4=△∵BI GD ∥∴ABM AGK ∽△△，且相似比为3:1，得到b S ABM 9=△ 又∵ABCD DAG S b a S 614=+=△，ABCD ABF S a b S 419=+=△ ∴a b b a S ABCD 436624+=+=∴b a ____=，b S ABCD _____=，b S KPOL _____=∴ABCD KPOL S S _____=，则GKLH KPOL S S ____（填写“”，“”或“”）（2）小瑞又按照图4的方式连接矩形ABCD 对边上的点.则ABCD ANML S S _____=.13．（海淀18期末28）在△ABC 中，∠A 90°，ABAC ．（1）如图1，△ABC 的角平分线BD ，CE 交于点Q ，请判断“QB =”是否正确：_______（填“是”或“否”）；（2）点P 是△ABC 所在平面内的一点，连接P A ，PB ，且P A ．①如图2，点P 在△ABC 内，∠ABP 30°，求∠P AB 的大小；②如图3，点P 在△ABC 外，连接PC ，设∠APCα，∠BPCβ，用等式表示α，β之间的数量关系，并证明你的结论．图1 图2图3 28．解：（1）否. ………………1分（2）① 作PD ⊥AB 于D ，则∠PDB =∠PDA =90°，∵ ∠ABP =30°，∴ 12PD BP =. ………………2分∵ PB =，∴ 2PD PA =.∴ sin PD PAB PA ∠== 由∠P AB 是锐角，得∠P AB =45°. ………………3分另证：作点P 关于直线AB 的对称点'P ，连接',',B P P A P P ，则',',','P B A P B A P A B P A B B P B P A P A P∠=∠∠=∠==.∵∠ABP =30°，∴'60P BP ∠=︒.∴△'P BP 是等边三角形.∴'P P BP =.∵PB =，∴'P P =. ………………2分 ∴222''P P PA P A =+.∴'90PAP ∠=︒.∴45PAB ∠=︒. ………………3分② 45αβ+=︒，证明如下： ………………4分作AD ⊥AP ，并取AD =AP ，连接DC ，DP .∴ ∠DAP =90°.∵ ∠BAC =90°，∴ ∠BAC +∠CAP =∠DAP +∠CAP ,即 ∠BAP =∠CAD .∵ AB =AC ，AD =AP ，∴ △BAP ≌△CAD .∴ ∠1=∠2，PB =CD . ………………5分 ∵ ∠DAP =90°，AD =AP ，∴ PD =，∠ADP =∠APD =45°.∵ PB =，∴ PD =PB =CD .∴ ∠DCP =∠DPC .∵ ∠APCα，∠BPCβ，∴ 45DPC α∠=+︒，12αβ∠=∠=-.∴ 31802902DPC α∠=︒-∠=︒-.∴ 139045ADP αβ∠=∠+∠=︒--=︒.∴45αβ+=︒. ………………7分。

2019年北京市各区中考数学一模试题卷分类汇编：几何压轴题(无答案)

2019年北京市各区一模数学试题分类汇编——几何综合题（房山）27．已知：Rt △ABC 中，∠ACB =90°，AC =BC ．（1）如图1，点D 是BC 边上一点(不与点B ，C 重合)，连接AD ，过点B 作BE ⊥AD ，交AD 的延长线于点E ，连接CE ．若∠BAD =α，求∠DBE 的大小 (用含α的式子表示) ；（2）如图2，点D 在线段BC 的延长线上时，连接AD ，过点B 作BE ⊥AD ，垂足E 在线段AD 上，连接CE ． ①依题意补全图2；②用等式表示线段EA ，EB 和EC 之间的数量关系，并证明．图1 图2B AA（门头沟）27．如图，∠AOB = 90°，OC 为∠AOB 的平分线，点P 为OC 上一个动点，过点P 作射线PE 交OA 于点E ．以点P 为旋转中心，将射线PE 沿逆时针方向旋转90°，交OB 于点F ．（1）根据题意补全图1，并证明PE = PF ；（2）如图1，如果点E 在OA 边上，用等式表示线段OE ，OP 和OF 之间的数量关系，并证明；（3）如图2，如果点E 在OA 边的反向延长线上，直接写出线段OE ，OP 和OF 之间的数量关系．图1 图2（密云）27．已知△ABC 为等边三角形，点D 是线段AB 上一点（不与A 、B 重合）．将线段CD 绕点C 逆时针旋转60°得到线段CE ．连结DE 、BE ．（1）依题意补全图1并判断AD 与BE 的数量关系．（2）过点A 作AF EB 交EB 延长线于点F ．用等式表示线段EB 、DB 与AF 之间的数量关系并证明．PPEECCBBOOAA图2D CBA图1A B CD（平谷）27．在△ABC 中，∠ABC =120°，线段AC 绕点A 逆时针旋转60°得到线段AD ，连接CD ，BD 交AC 于P ．（1）若∠BAC =α，直接写出∠BCD 的度数（用含α的代数式表示）；（2）求AB ，BC ，BD 之间的数量关系；（3）当α=30°时，直接写出AC ，BD 的关系．（石景山）27．如图，在等边△ABC 中，D 为边AC 的延长线上一点()CD AC ，平移线段BC ，使点C 移动到点D ，得到线段ED ，M 为ED 的中点，过点M 作ED 的垂线，交BC 于点F ，交AC 于点G ．（1）依题意补全图形；（2）求证：AG = CD ；（3）连接DF 并延长交AB 于点H ，用等式表示线段AH 与CG 的数量关系，并证明．DB A。

2019年北京市各区一模数学试题分类汇编——几何压轴题;

2019年北京市各区一模数学试题分类汇编——几何综合题（海淀）27．如图，在等腰直角△ABC 中，90ABC ?°，D 是线段AC 上一点（2CA CD > ），连接BD ，过点C 作BD 的垂线，交BD 的延长线于点E ，交BA 的延长线于点F ．（1）依题意补全图形；（2）若ACE α?，求ABD Ð的大小（用含α的式子表示）；（3）若点G 在线段CF 上，CG BD =，连接DG ．①判断DG 与BC 的位置关系并证明；②用等式表示DG ，CG ，AB 之间的数量关系为．（西城）27．如图，在△ABC中，∠ABC=90°，BA=BC．将线段AB绕点A逆时针旋转90°得到线段AD，E是边BC上的一动点，连接DE交AC于点F，连接BF.（1）求证：FB=FD；（2）点H在边BC上，且BH=CE，连接AH交BF于点N．①判断AH与BF的位置关系，并证明你的结论；②连接CN．若AB=2，请直接写出线段CN长度的最小值.（东城）27．如图，在正方形ABCD 中，E 是边BC 上一动点（不与点B ，C 重合），连接DE ，点C 关于直线DE 的对称点为C ʹ，连接ACʹ并延长交直线DE 于点P ，F 是AC ′中点，连接DF ．（1）求∠FDP 的度数；（2）连接BP ，请用等式表示AP ，BP ，DP 三条线段之间的数量关系，并证明．（3）连接AC△ACC ′的面积最大值．PBA(朝阳）27.如图,在Rt△ABC中,∠A=90°,AB=AC,将线段BC绕点B逆时针旋转a°(0<a<180)，得到线段BD,且AD∥BC.(1)依题意补全图形;(2)求满足条件的a的值;(3)若AB=2,求AD的长.（石景山）27．如图，在等边△ABC中，D为边AC的延长线上一点()，平移线段BC，CD AC使点C移动到点D，得到线段ED，M为ED的中点，过点M作ED的垂线，交BC于点F，交AC于点G．（1）依题意补全图形；（2）求证：AG = CD；（3）连接DF并延长交AB于点H，用等式表示线段AH与CG的数量关系，并证明．BD（丰台）27．在△ABC中，∠ACB=90°，AC=BC， D为AB的中点，点E为AC延长线上一点，连接DE，过点D作DF⊥DE交CB的延长线于点F．（1）求证：BF= CE；（2）若CE=AC，用等式表示线段DF与AB的数量关系，并证明．（房山）27．已知：Rt △ABC 中，∠ACB =90°，AC =BC ．（1）如图1，点D 是BC 边上一点(不与点B ，C 重合)，连接AD ，过点B 作BE ⊥AD ，交AD 的延长线于点E ，连接CE ．若∠BAD =α，求∠DBE 的大小 (用含α的式子表示) ；（2）如图2，点D 在线段BC 的延长线上时，连接AD ，过点B 作BE ⊥AD ，垂足E 在线段AD 上，连接CE ． ①依题意补全图2；②用等式表示线段EA ，EB 和EC 之间的数量关系，并证明．图1 图2B AA（门头沟）27．如图，∠AOB = 90°，OC 为∠AOB 的平分线，点P 为OC 上一个动点，过点P 作射线PE 交OA 于点E ．以点P 为旋转中心，将射线PE 沿逆时针方向旋转90°，交OB 于点F ．（1）根据题意补全图1，并证明PE = PF ；（2）如图1，如果点E 在OA 边上，用等式表示线段OE ，OP 和OF 之间的数量关系，并证明；（3）如图2，如果点E 在OA 边的反向延长线上，直接写出线段OE ，OP 和OF 之间的数量关系．图1 图2PPEECCBBOOAA（密云）27．已知△ABC 为等边三角形，点D 是线段AB 上一点（不与A 、B 重合）．将线段CD 绕点C 逆时针旋转60°得到线段CE ．连结DE 、BE ．（1）依题意补全图1并判断AD 与BE 的数量关系．（2）过点A 作AF EB 交EB 延长线于点F ．用等式表示线段EB 、DB 与AF 之间的数量关系并证明．图2DCBA图1ABCD（平谷）27．在△ABC中，∠ABC=120°，线段AC绕点A逆时针旋转60°得到线段AD，连接CD，BD交AC于P．（1）若∠BAC=α，直接写出∠BCD的度数（用含α的代数式表示）；（2）求AB，BC，BD之间的数量关系；（3）当α=30°时，直接写出AC，BD的关系．（通州）27．如图，在等边△ABC中，点D是线段BC上一点．作射线AD，点B关于射线AD 的对称点为E．连接CE并延长，交射线AD于点F．（1）设∠BAF＝α，用α表示∠BCF的度数；（2）用等式表示线段AF、CF、EF之间的数量关系，并证明．（延庆）27．已知：四边形ABCD 中，120ABC ∠=︒，60ADC ∠=︒，AD =CD ，对角线AC ，BD 相交于点O ，且BD 平分∠ABC ，过点A 作AH BD ⊥，垂足为H ．（1）求证：ADB ACB ∠=∠；（2）判断线段BH ，DH ，BC 之间的数量关系；并证明．H O DBA（燕山）27．如图，在△ABC 中，AB ＝BC ，∠B ＝90°，点D 为线段BC 上一个动点(不与点B ，C 重合)，连接AD ，将线段AD 绕点D 顺时针旋转90°得到线段DE ，连接EC ．(1) ① 依题意补全图1；② 求证：∠EDC ＝∠BAD ；(2) ① 小方通过观察、实验，提出猜想：在点D 运动的过程中，线段CE 与BD 的数量关系始终不变，用等式表示为：；② 小方把这个猜想与同学们进行交流，通过讨论，形成了证明该猜想的几种想法：想法1：过点E 作EF ⊥BC ，交BC 延长线于点F ，只需证△ADB ≌△DEF ．想法2：在线段AB 上取一点F ，使得BF ＝BD ，连接DF ，只需证△ADF ≌△DEC ．想法3：延长AB 到F ，使得BF ＝BD ，连接DF ，CF ，只需证四边形DFCE 为平行四边形． ……请你参考上面的想法，帮助小方证明①中的猜想．(一种方法即可)备用图AB CD 图1D C B A（顺义）27．已知：如图，在△ABC 中，AB >AC ，∠B =45°，点D 是BC 边上一点，且AD=AC ，过点C 作CF ⊥AD 于点E ，与AB 交于点F ．（1）若∠CAD =α，求∠BCF 的大小（用含α的式子表示）；（2）求证：AC =FC ；（3）用等式直接表示线段BF 与DC 的数量关系．ABCDFE（怀柔）27.如图，等边△ABC中，P是AB上一点，过点P作PD⊥AC于点D，作PE⊥BC于点E，M是AB的中点，连接ME，MD．（1）依题意补全图形；（2）用等式表示线段BE，AD与AB的数量关系，并加以证明；（3）求证：MD=ME．C。

2019年北京初三数学汇编几何综合答案

1（2019.1+++昌平+++初三上+++期末）（1）①圆心O 的位置在线段AB 的中点,正确画出图②∵AE ⊥BD ∴△AEB 为直角三角形 ∵点O 为线段AB 的中点 ∴OE =OA =OB =r ∴点E 在⊙O 上（2）①补全图形=AB证明如下： ∵AC =BC ，∠ACB =90° ∴∠BAC =∠CBA = 45° ∵BC BC =∴∠BEC =∠BAC = 45° ∵AE ⊥BD ∴∠BEA =90° ∴∠CEA =90°+ 45°= 135° ∵∠CEF =180°－∠CEB =135° ∴∠CEA =∠CEF ∵AE =EF ,∠CEA =∠CEF ,CE =C E ∴△CEA ≌△CEF ∴CF =CA ∵在等腰t ∆R ACB中，=AB∴=AB2（2019.1+++丰台+++初三上+++期末）（1）60° （2）1 （3）11AF BF n =- 证明：延长FE 至G ，使FG =FB 连接GB ，GC由（1）知，∠BFG=60° ∴△BFG 为等边三角形 ∴BF =BG ，∠FBG=∠FGB=60° ∵△ABC 是等边三角形 ∴AB=BC ，∠ABC=60° ∴∠ABF=∠CBG ∴△ABF ≌△CBG ∴∠BFA=∠BGC=120° ∴∠FGC=60° ∴∠FGC=∠BFG ∴FB ∥CG ∴AF AD FG DC = ∵1AD AC n = ∴11AF FG n =- ∴11AF BF n =-CAE BD F3（2019.1+++海淀+++初三上+++期末）（1）①证明：连接AD ，如图1∵点C 与点D 关于直线l 对称 ∴AC AD = ∵AB AC = ∴AB AC AD ==∴点B C D ，，在以A 为圆心，AB 为半径的圆上 ②12α（2）证法一：证明：连接CE ，如图2 ∵=60α°∴1302BDC α∠==° ∵DE BD ⊥ ∴90CDE ∠=°60BDC -∠=° ∵点C 与点D 关于直线l 对称 ∴EC ED = ∴CDE △是等边三角形∴CD CE =，60DCE ∠=° ∵AB AC =，60BAC ∠=° ∴ABC △是等边三角形 ∴CA CB =，60ACB ∠=° ∵ACE DCE ACD ∠=∠+∠，BCD ACB ACD ∠=∠+∠ ∴ACE BCD ∠=∠ ∴ACE BCD △≌△ ∴AE BD = 证法二：证明：连接AD ，如图2 ∵点C 与点D 关于直线l 对称∴AD AC AE CD =，⊥ ∴12DAE DAC ∠=∠∵12DBC DAC ∠=∠∴DBC DAE ∠=∠∵AE CD ⊥，BD DE ⊥∴90BDC CDE DEA CDE ∠+∠=∠+∠=°∴BDC DEA ∠=∠ ∵60AB AC BAC =∠=，° ∴ABC △是等边三角形 ∴CA CB AD == ∴BCD △≌ADE △ ∴AE BD = （3）134（2019.1+++怀柔+++初三上+++期末）（1）补全图形，如图所示（2）AH 与PH 的数量关系：AH =PH ，∠AHP =120°图2lD A 图1lE DA图2证明：如图，由平移可知，PQ=DC ∵四边形ABCD 是菱形，∠ADC=60° ∴AD=DC ，∠ADB =∠BDQ =30° ∴AD=PQ∵HQ=HD ∴∠HQD =∠HDQ =30° ∴∠ADB =∠DQH ，∠D HQ=120°∴△ADH ≌△PQH ∴AH =PH ，∠A HD =∠P HQ ∴∠A HD+∠DHP =∠P HQ+∠DHP ∴∠A HP=∠D HQ ∵∠D HQ=120° ∴∠A HP=120° （3）求解思路如下：由∠A HQ=141°，∠B HQ=60°解得∠A HB=81°a.在△ABH 中，由∠A HB=81°，∠A BD=30°，解得∠BA H=69°b.在△AHP 中，由∠A HP=120°，AH=PH ，解得∠PA H=30°c.在△ADB 中，由∠A DB=∠A BD= 30°，解得∠BAD =120° 由a 、b 、c 可得∠DAP =21°在△DAP 中，由∠A DP= 60°，∠DAP =21°，AD=1，可解△DAP ，从而求得DP 长5（2019.1+++通州+++初三上+++期末）（1）BF =（2）①依据题意补全图形 ②证明：如图，连接BF 、GB ∵四边形ABCD 是正方形∴AD =AB ，90ABC BAD ∠=∠=︒，AC 平分BAD ∠ ∴45BAC DAC ∠=∠=︒.在△ADF 和△ABF 中 AD AB DAC BAC AF AF =⎧⎪∠=∠⎨⎪=⎩，，，∴△ADF ≌△ABF ∴DF BF = ∵EF ⊥AC ，90ABC ∠=︒，点G 是AE 的中点 ∴AG EG BG FG === ∴点A 、F 、E 、B 在以点G 为圆心，AG 长为半径的圆上 ∵BF BF =，45BAC ∠=︒ ∴290BGF BAC ∠=∠=︒∴△BGF 是等腰直角三角形∴BF =∴DF =A BCDP HQ6（2019.1+++燕山+++初三上+++期末）(1) ① ∠BCE ＝35° ② AE ＝CE证明：过点B 作BG ⊥BE ，交AM 于点G∴∠GBE ＝∠GBC ＋∠2＝90° ∵正方形ABCD ∴AB ＝BC ，∠ABC ＝∠1＋∠GBC ＝90° ∴∠1＝∠2 ∵∠ABC ＝∠CEA ＝90°，∠4＝∠5 ∴△ABF ∽△CEF∴∠α＝∠3 ∴在△ABG 和△CBE 中 ∠1＝∠2，AB ＝BC ，∠α＝∠3∴△ABG ≌△CBE ∴AG ＝CE ，BG ＝BE ∵在△BEG 中，∠GBE ＝90°，BG ＝BE ∴GE∴AE ＝AG ＋GE ＝CE(2) AE ＋CE7（2019.1+++房山+++初三上+++期末）（1）补全图形如图分（2）证明:∵AD 平分∠BAC∴∠BAD =∠CAD ∵FE ⊥AD , ∠ACF =90°∴∠CFH =∠CAD ∴∠BAD =∠CFH , 即∠（3）猜想: 222AB FD FB += 证明：连接AF∵EF 为AD 的垂直平分线 ∴AF=FD ，∠ ∴∠DAC +∠CAF =∠B +∠BAD ∵AD 是角平分线 ∴∠BAD =∠CAD ∴∠CAF =∠B ∴∠BAF =∠BAC +∠CAF =∠BAC +∠B =90° ∴222AB AF FB += ∴222+=AB FD FB8（2019.1+++门头沟+++初三上+++期末）（1）证明：如图1，∵∠ACB = 90°，AE⊥BD ∴∠ACB =∠AEB = 90°又∵∠1=∠2 ∴∠CAE =∠CBD（2）①补全图形如图2②EF BE =+证明：在AE上截取AM，使AM=BE又∵AC=CB，∠CAE =∠CBD ∴△ACM≌△BCE∴CM=CE，∠ACM=∠BCE 又∵∠ACB =∠ACM+∠MCB=90°∴∠MCE=∠BCE+∠MCB=90°∴.ME=又∵射线AE绕点A顺时针旋转45°，后得到AF，且∠AEF=90°∴EF=AE=AM+ME=BE9（2019.1+++朝阳+++初三上+++期末）图2 图110（2019.1+++西城+++初三上+++期末）11（2019.1+++大兴+++初三上+++期末）（1）补全的图形如图所示 (2)解:由题意可知，∠ECF=∠ACG=90° ∴∠FCG=∠ACE=α∵过点A 作AB 的垂线AD ∴∠BAD=90° ∵AB=BC,∠ABC =90° ∴∠ACB=∠CAD= 45° ∵∠ACG=90° ∴∠AGC=45° ∴∠AFC =α+45°（3）AE ,AF 与BC 之间的数量关系为2AE AF BC += 由（2）可知∠DAC=∠AGC=45° ∴CA=CG ∵∠ACE =∠GCF ，∠CAE =∠CGF ∴△ACE ≌△GCF ∴AE =FG 在Rt △ACG 中∴AG =∴AE AF +=∵AC = ∴2AE AF BC +=12（2019.1+++东城+++初三上+++期末）无答案27.解：（1）…………………………………………………………1分（2）∵点P 为线段DE 的中点 ∴DP ＝EP在△MPE 和△FPD 中 MP FP MPEFPD EP DP =⎧⎪∠=∠⎨⎪=⎩∴△MPE≌△FPD（SAS）…………………………………………………………2分∴DF＝ME∵E为MN的中点∴MN＝2ME∵MN＝2MB∴MB＝ME＝D F．…………………………………………………………3分（3）结论：AM …………………………………………………………4分连接AF由（2）可知：△MPE≌△FPD∴∠DFP＝∠EMP.∴DF∥ME.∴∠FDN＝∠MND.在正方形ABCD中，AD＝AB，∠BAD＝90°又∵∠BMN＝90°∴∠MBA＋∠MNA＝180°又∵∠MNA＋∠MND＝180°∴∠MBA＝∠MND∴∠FDN ＝∠MBA …………………………………………………………5分在△FAD 和△MAB 中 FD MB FDA MBA DA BA =⎧⎪∠=∠⎨⎪=⎩∴△F AD ≌△MAB （SAS ） ∴∠FAD ＝∠MAB FA ＝MA∴∠FAM ＝∠DAB ＝90°∴△FAM 为等腰直角三角形…………………………………………………………6分∴FM 又∵FM ＝2PM∴AM = …………………………………………………………7分13（2019.1+++平谷+++初三上+++期末）。

北京市2019年5月初三数学一模全市十六区全部试卷的分类整理——圆(含答案)

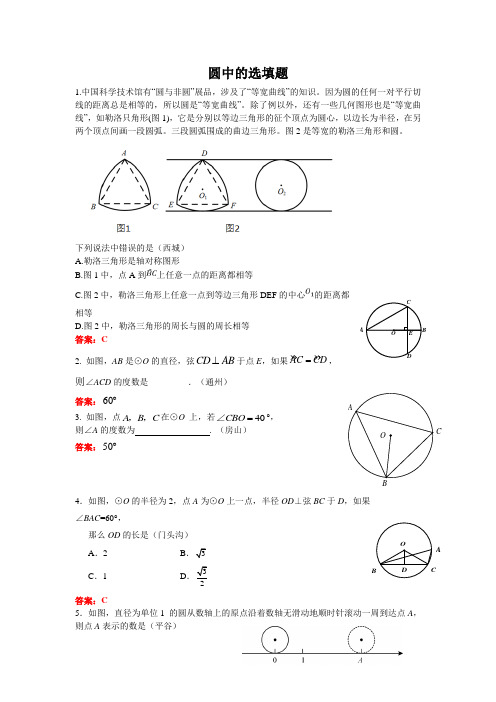
A 圆中的选填题1.中国科学技术馆有“圆与非圆”展品，涉及了“等宽曲线”的知识。

因为圆的任何一对平行切线的距离总是相等的，所以圆是“等宽曲线”。

除了例以外，还有一些几何图形也是“等宽曲线”，如勒洛只角形(图1)，它是分别以等边三角形的征个顶点为圆心，以边长为半径，在另两个顶点间画一段圆弧。

三段圆弧围成的曲边三角形。

图2是等宽的勒洛三角形和圆。

下列说法中错误的是（西城） A.勒洛三角形是轴对称图形 B.图1中，点A 到上任意一点的距离都相等C.图2中，勒洛三角形上任意一点到等边三角形DEF 的中心的距离都相等D.图2中，勒洛三角形的周长与圆的周长相等答案：C2. 如图，AB 是⊙O 的直径，弦CD AB ⊥于点E ，如果AC CD =，则∠ACD 的度数是_________．（通州）答案：60︒3. 如图，点A B C ，，在⊙O 上，若40CBO =∠°，则∠A 的度数为 . （房山）答案：50︒4．如图，⊙O 的半径为2，点A 为⊙O 上一点，半径OD ⊥弦BC 于D ，如果 ∠BAC =60°，那么OD 的长是（门头沟）A ．2 BC ．1D答案：C5．如图，直径为单位1 的圆从数轴上的原点沿着数轴无滑动地顺时针滚动一周到达点A ，则点A 表示的数是（平谷）ACBA(A)2(C) π (D)4答案：C6．如图，点A ，B ，C ，D 在⊙O 上，AC 是⊙O 的直径，∠BAC =40°，则∠D 的度数是（平谷）(A) 40° (B)50° (C)60° (D)90° 答案：B7.如图，AB 为⊙O 的直径，C 、D 是⊙O 上两点，AC=BC ，AD 与CB 交于点 E.25DAB ∠=︒，则E ∠=_______.（密云）答案：20︒8．下列图形中，21∠>∠的是（延庆）答案：C9．如图，⊙O 的直径AB 垂直于弦CD ，垂足是E ，已知22.5A ∠=︒，2OC =，则CD 的长为．（延庆）答案：10. 如图，点 A ，B ，C ，D 在⊙O 上，且AD 为直径，如果∠BAD =70°，∠CDA=50°，BC =，那么AD =．（丰台）答案：11．如图，AB 为⊙O 的直径，C ，D ，E 为⊙O 上的点，CD ︵＝DB ︵， ∠ABD ＝60°，则∠CEB ＝ °．（燕山）答案：6012．如图，AB 是⊙O 的一条弦，P 是⊙O 上一动点（不与点A ，B 重合），C ，D 分别是AB ，BP 的中点．若AB = 4，∠APB = 45°，则CD 长的最大值为．答案：13．如图，等边三角形ABC 内接于⊙O ，点D 在⊙O 上，25∠=︒ABD ,则AA ．B ．C ．D ．121212D∠=BAD ︒.（顺义）答案：9514．如图，AD 为△ABC 的外接圆⊙O 的直径，若∠BAD ＝50°，则∠ACB ＝________°．（东城）答案：4015．如图，AB 是⊙O 的直径，C ，D 为⊙O 上的点．若=20CAB Ð°，则D Ð= °．（海淀）答案：11016．如图，过⊙O 外一点P 作⊙O 的两条切线P A ，PB ，切点分别为A ， B ，作直径BC ，连接AB ，AC ，若∠P =80°，则∠C =_____°．（朝阳）答案：5017. 如图，△ABC 的内切圆⊙O 与AB ，BC ，CA 分别相切于点D ，E ，F ，且AD=2，△ABC 的周长为14，则BC 的长为（怀柔） A ．3 B ．4 C ．5 D ．6 答案：C18 将一块含30°角的三角板如图放置，三角板的一个顶点C 落在以AB 为直径的半圆上，斜边恰好经过点B ，一条直角边与半圆交于点D ，若AB = 2，则BD 的长为__________（结果保留π）. （大兴）答案：3π圆综——教师版1、（东城）如图，AB与⊙O相切于点A，P为OB上一点，且BP＝BA，连接AP并延长交⊙O于点C，连接OC．（1）求证：OC⊥OB；（2）若⊙O的半径为4，AB＝3，求AP的长．解：（1）证明:∵AB＝BP，∴∠BAP＝∠BP A．…………………………………………………………………1分∵AB与⊙O相切于点A，∴OA⊥BA．∴∠BAO＝90°，即∠BAP＋∠P AO＝90°．…………………………………………………………2分又∵OA＝OC，∴∠P AO＝∠C．∵∠BP A＝∠CPO，∴∠C＋∠CPO＝90°．∴∠COP＝90°，即CO⊥OB．………………………………………………………………………3分（2）解：如图，作BD⊥AP于点DA在Rt△ABO中，AB＝3，OA＝4，则BO＝5，OP＝2．在Rt △CPO 中，PO ＝2，CO ＝4，则CP ＝………………………………………………………………………4分 ∵BA ＝BP ， ∴AD ＝PD ．由（1）知∠COP ＝90°．∵∠BDP ＝90°，∠BPD ＝∠CPO ，∴△BPD ∽△CPO ．………………………………………………………………5分 ∴=2PD．∴PD ＝5．∴AP ＝2PD ＝5．………………………………………………………………6分2、（西城）如图，AB是⊙O的直径，CB与⊙O相切于点B．点D在⊙O上，且BC=BD，连接CD交⊙O于点E．过点E作EF⊥AB于点H，交BD于点M，交⊙O于点F．（1）求证：∠MED=∠MDE；（2）连接BE，若ME=3，MB=2，求BE的长．（1）证明：∵AB是⊙O的直径，CB与⊙O相切于点B，∴CB⊥AB．………………………………………………………………1分∴∠ABC=90°．∵EF⊥AB于点H，∴∠AHE=90°．∴∠ABC=∠AHE．∴CB∥EF．∴∠C=∠MED．……………………………………………………………2分∵BC=BD，∴∠C=∠MDE．∴∠MED=∠MDE．………………………………………………………3分（2）解：如图．∵AB是⊙O的直径，AB⊥EF，∴BE=BF．……………………………………………………………………4分∴∠BDE=∠BEF．∵∠DBE=∠EBM，∴△DBE ∽△EBM ． …………………………………………………………5分 ∴BD BEBE BM=． ∴2BE BD BM =⋅． ∵∠MED =∠MDE ， ∴ME =MD =3． ∵MB =2，∴BD = MB +MD =5． ∴210BE =．∴BE = ………………………………………………………………6分3、（海淀）如图，AB 是⊙O 的直径，弦CD ⊥AB 于点E ，在⊙O 的切线CM 上取一点P ，使得∠CPB =∠COA ．（1）求证：PB 是⊙O 的切线；（2）若AB =CD =6，求PB 的长．（1）证明：∵ PC 与⊙O 相切于点C ， ∴ OC ⊥PC ． ∴ ∠OCP =90°．∵ ∠AOC =∠CPB ，∠AOC +∠BOC =180°， ∴ ∠BOC +∠CPB =180°．在四边形PBOC 中，∠PBO =360°-∠CPB -∠BOC -∠PCO =90°． ∴ 半径OB ⊥PB ． ∴ PB 是⊙O 的切线．（2）解法1：连接OP ，如图．∵ AB 是⊙O的直径，AB = ∴12OC OB AB === ∵弦CD ⊥AB 于点E ，CD =6，∴132CE CD ==．在Rt △CEO 中，sin CE COE CO ∠==． ∴∠COE =60°．∵ PB ，PC 都是⊙O 的切线， ∴∠CPO =∠BPO ，∠OCP =∠OBP ． ∴ ∠COP=∠BOP =60°． ∴PB = OB · tan60°= 6．解法2：连接BC ，如图．∵ AB 是⊙O的直径，AB =∴12OC AB ==． ∵弦CD ⊥AB 于点E ，CD =6， ∴132CE CD ==．在Rt △CEO 中，sin CE COE CO ∠==． ∴∠COE =60°．∴∠CPB =∠COE =60°，1302ABC COE ∠=∠=︒．∴ BC =2CE = 6．∵ PB ，PC 都是⊙O 的切线， ∴ PB =PC ．∴△PBC 为等边三角形． ∴PB =BC = 6．4、（朝阳）如图，四边形ABCD 内接于⊙O ，点O 在AB 上，BC =CD ，过点C 作⊙O 的切线，分别交AB ，AD 的延长线于点E ，F ．（1）求证：AF ⊥EF ；（2）若cos A =45，BE =1，求AD 的长．解：（1）证明：如图1，连接OC ．图1∵EF 是⊙O 的切线， ∴∠OCE =90°． ……………………1分 ∵BC =CD ， ∴BC CD =．∴∠COB =∠DAB ．……………………2分 ∴AF ∥CO ．∴∠AFE =∠OCE =90°．即AF ⊥EF ． ……………………3分（2）解：如图2，连接BD ，∴∠ADB =90°．由（1）可知cos ∠COE =cos A =45．设⊙O 的半径为r ， ∵BE =1，∴415r r =+．解得4r =．……………………4分∴AB =8．5、（丰台）如图，AB 是⊙O 的直径，AE 是弦，C 是AE 的中点，过点C 作⊙O 的切线交BA 的延长线于点G ，过点C 作CD ⊥AB 于点D ，交AE 于点F ．（1）求证：GC ∥AE ；（2）若sin ∠EAB =53，ODAE 的长．图2（1）证明：连接OC ，交AE 于H.∵C 是弧AE 的中点，∴OC ⊥AE . ............ ......1分 ∵GC 是⊙O 的切线， ∴OC ⊥GC .∴∠OHA=∠OCG =90°.∴GC ∥AE . .............. .....2分（2）解： ∵OC ⊥AE ,CD ⊥AB , ∴∠OCD =∠EAB . ∴3sin sin 5OCD EAB ∠=∠=.在Rt △CDO 中，OD∴OC =.∴AB 连接BE.∵AB 是⊙O 的直径， ∴∠AEB =90°. 在Rt △A EB 中， ∵3sin 5BE EAB AB ∠==,∴BE =∴AE = ...................….........5分6、（石景山）如图，AB 是⊙O 的直径，过⊙O 上一点C 作⊙O 的切线CD ，过点B 作BE ⊥CD 于点E ，延长EB 交⊙O 于点F ，连接AC ，AF ．（1）求证：12CE AF =；（2）连接BC ，若⊙O 的半径为5，tan 2CAF ∠=，求BC 的长．（1）证明：连接CO 并延长交AF 于点G ．∵CD 是⊙O 的切线， ∴90ECO ∠=︒． ∵AB 是⊙O 的直径， ∴90AFB ∠=︒． ∵BE CD ⊥， ∴90CEF ∠=︒． ∴四边形CEFG 是矩形．∴GF CE =，90CGF ∠=︒． ∴CG AF ⊥． ∴12GF AF =． ………1分………………………………2分∴12CE AF =．（2）解：∵CG AF ⊥， ∴CF CA =．∴CBA CAF ∠=∠．∴tan tan 2CBA CAF ∠=∠=．∵AB 是⊙O 的直径，∴90ACB ∠=︒．在Rt △CBA 中，设BC x =，2AC x =，则=52AB =⨯．∴BC x ==7、（房山）如图，在△ABC 中，AB = AC ，以AB 为直径的⊙O 分别交AC ，BC 于点 D ，E ，过点B 作⊙O 的切线，交AC 的延长线于点F ．(1) 求证：∠CBF =12∠CAB ； (2) 若CD = 2，1tan 2CBF ∠=，求FC 的长．（1）证明：∵AB 为⊙O 的直径， ∴∠AEB =90°. ∴∠BAE +∠ABC =90°， ∵AB = AC ，………………………………3分………………………………4分………………………………5分∴∠BAE =∠EAC =12∠CAB . ∵BF 为⊙O 的切线， ∴∠ABC +∠CBF =90°. ∴∠BAE =∠CBF . ∴∠CBF =12∠CAB . ………………………………… 2分（2）解：连接BD ，F∵AB 为⊙O 的直径，∴∠ADB =90°.∵∠DBC =∠DAE ， ∴∠DBC =∠CBF .∵tan ∠CBF =12. ∴tan ∠DBC =12.∵CD =2，∴BD =4. ………………………………… 3分设AB =x ，则AD =2x - ，在RtΔABD 中，∠ADB =90°，由勾股定理得x=5.∴AB =5，AD =3. ……………………………… 4分 ∵∠ABF =∠ADB =90°，∠BAF =∠BAF . ∴ΔABD ∽ΔAFB . ∴2AB AD AF =⋅. ∴AF =253.∴FC=AF-AC=103. ……………………………… 5分8、（门头沟）如图，点D在⊙O上，过点D的切线交直径AB的延长线于点P，DC⊥AB于点C．（1）求证：DB平分∠PDC；（2）如果DC = 6，3tan4P∠=，求BC的长．P A（1）证明：如图1，连接OD．A图1∵DP是⊙O的切线，∴OD⊥DP．∴90ODP∠=︒．……………………………………………………………………… 1分∴90.ODB BDP∠+∠=︒又∵DC⊥OB，∴90DCB∠=︒．……………………………………………………………………… 2分∴90BDC OBD∠+∠=︒．∵OD=OB，∴.ODB OBD∠=∠∴BDP BDC∠=∠．∴DB平分∠PDC ．……………………………………………………………………… 3分（2）解：如图2，过点B 作BE ⊥DP 于点E ．A图2∵,BDP BDC ∠=∠ BC ⊥DC ，∴BC =BE . ………………………………………………………………………………… 4分 ∵DC =6，3tan 4P ∠=， ∴DP =10，PC =8．………………………………… 5分设CB = x , 则BE = x ，BP = 8 - x ． ∵ △PEB ∽△PCD ， ∴8610x x-=． ∴ 3=x ．∴ 3BC = …………………………………………………………………………… 6分9、（通州）如图，△ABC 内接于⊙O ，AB 为⊙O 的直径，过点A 作⊙O 的切线交BC 的延长线于点E ，在弦BC 上取一点F ，使AF =AE ，连接AF 并延长交⊙O 于点D ．（1）求证：B CAD ∠=∠；（2）若CE ＝2，30B ∠=︒，求AD 的长．（1）证明：∵AE 是⊙O 的切线，AB 为⊙O 的直径，∴90BAE ∠=︒， 90ACB ∠=︒. ……………… 1分 ∴90BAC CAE ∠+∠=︒ . ∴90BAC B ∠+∠=︒.∴B CAE ∠=∠. ……………… 2分 ∵AF =AE ，90ACB ∠=︒，∴CAD CAE ∠=∠.∴B CAD ∠=∠. ……………… 3分（2）解：连接CD .∵B CAD ∠=∠，∴AC CD =. ……………… 4分 ∴AC CD =.∵90ACE ∠=︒，CE ＝2，30CAE CAF B ∠=∠=∠=︒， ∴tan CECAE AC∠=. ∴tan 30︒=2AC. ∴AC = ……………… 5分过点C 作CG ⊥AD 于点G . ∴cos AGCAFAC∠=. ∴cos 30︒. ∴3AG =. ∵AC ＝CD ，90ACB ∠=︒，∴ 26AD AG ==. ……………… 6分另解一：连接BD . 先求AB 的长，再求AD . 另解二：连接CD . 先求AE 的长，再证FC =FD .10、（平谷）如图，AB是⊙O的直径，AC切⊙O于点A，连接BC交⊙O于点D，点E是BD 的中点，连接AE交BC于点F．（1）求证：AC=CF；（2）若AB=4，AC=3，求∠BAE的正切值．C（1）证明：∵AC切⊙O于点A，∴∠BAC=90°． (1)连接AD．∵点E是BD的中点，∴∠BAE=∠DAE．∵AB是⊙O的直径，∴∠ADB=90°．∵∠CAD+∠DAB=∠DAB+∠B=90°，∴∠CAD=∠B．∵∠CAD+∠DAE =∠B+∠BAE，∴∠CAF=∠CFA． (2)∴AC=CF． (3)（2）解：∵AB=4，AC=3，∴BC=5． (4)CQ CP ⊥43tan CPB ∠=∵AC=CF =3， ∴BF =2． ∵4cos 5BD AB B AB BC ===， ∴BD =165． ············································································· 5 ∴AD=125，DF =65．∴tan ∠BAE = tan ∠DAE =12 (6)11、（延庆）如图，AB 是⊙O 的直径，点C 在⊙O 上，点P 是AB 上一动点，且与点C 分别位于直径AB 的两侧，，过点C 作交PB 的延长线于点Q ；（1）当点P 运动到什么位置时，CQ 恰好是⊙O 的切线？（2）若点P 与点C 关于直径AB 对称，且AB =5，求此时CQ 的长．备用图解：（1）当点P 运动到直线OC 与的交点处． ……2分（说明：用语言描述或是画出图形说明均可）（2）连接CB ，∵AB 是直径， ∴∠ACB=90°．∵∠P=∠A ， 43tan CPB tan A ∴∠== ∵AB=5，∴AC=3，BC=4．∵点P 与点C 关于直径AB 对称 ∴CP ⊥AB ．在Rt △ABC 中，∴CP=4.8，在Rt△PCQ中，43CQ tan CPB tan ACP ∠===∴CQ=6.4．……6分12、（密云）如图，AB为⊙O的直径，E为OB中点，过E作AB垂线与⊙O 交于C、D两点.过点C作⊙O的切线CF与DB延长线交于点F.（1）求证：CF⊥DF；（2）若，求OF长.F证明：连结OC.∵AB为⊙O直径,CD为弦，AB⊥CD于E ∴CE=ED又∵OE=EB，∠CEO=∠BED∴△OCE≌△BDE∴∠OCE=∠CDB∵CF切⊙O于点C∴∠OCF=90°∴∠ODB+∠OCF =90°∴∠CFD=90°即CF⊥FD.................................3分(2) ∵1,2OE OB OB OC ==∴12 OE OC=∵在Rt△OEC中，1 sin2OCE∠=∴∠OCE=30°∴∠CDF=30°∴12 FC CD=即在Rt△OEC中，2cosCEOCOCE===∠在Rt△OCF中，OF=.................................6分13、（燕山）如图，Rt△ABC中，∠ACB＝90°，点D在AC边上，以AD为直径作⊙O交BD 的延长线于点E，CE＝BC．(1) 求证：CE是⊙O的切线；(2) 若CD＝2，BD＝O的半径．(1)证明：如图，连接OE，A∵∠ACB＝90°，∴∠1＋∠5＝90°．………………………………1分∵CE＝BC，∴∠1＝∠2．∵OE＝OD，∴∠3＝∠4．又∵∠4＝∠5，∴∠3＝∠5，∴∠2＋∠3＝90°，即∠OEC＝90°，∴OE⊥CE．∵OE是⊙O的半径，∴CE是⊙O的切线．………………………………2分(2) 解法一：在Rt△BCD中，∠DCB＝90°，CD＝2，BD＝∴BC＝CE＝4．………………………………3分设⊙O的半径为r，则OD＝OE＝r，OC＝r＋2，在Rt△OEC中，∠OEC＝90°，∴OE2＋CE2＝OC2，∴r2＋42＝(r＋2)2，………………………………4分解得r＝3，∴⊙O的半径为3．………………………………5分解法二：如图，连接AE，A∵AD为⊙O直径，∴∠AED＝90°．………………………………3分∵∠AED＝∠ACB＝90°，∠4＝∠5，∴∠6＝∠1．∵∠1＝∠2，∴∠6＝∠2．又∵∠ACE＝∠ECD，∴△ACE∽△ECD，∴CD CECE AC=．………………………………4分在Rt△BCD中，∠DCB＝90°，CD＝2，BD＝∴BC＝CE＝4．∴2CEACCD=＝8，∴AD＝AC－CD＝6，∴⊙O的半径为3．………………………………5分14、（怀柔）如图，AB为⊙O的直径，点C，D在⊙O上，且点C是BD的中点. 连接AC，过点C作⊙O的切线EF交射线AD于点E.（1）求证：AE⊥EF；（2）连接BC. 若165AE=，AB=5，求BC的长.F解：（1）证明：连接OC.F ∵OA OC=，∴∠1=∠2.∵点C是BD的中点.∴∠1=∠3.∴∠3=∠2.∴AE OC∥.∵EF是⊙O的切线，∴OC⊥EF.∴AE⊥EF. ………………………………… 2分（2）∵AB为O的直径，∴∠ACB=90°.∵AE EF⊥，∴∠AEC=90°.∴△AEC∽△ACB.又∵∠1=∠3，∴AE ACAC AB=,AC2=AE.AB=165165⨯=.∴AC=4.根据勾股定理，由AB=5, AC=4,求得BC=3. ………………………………… 5分15、（顺义）已知：如图，AB是⊙O的直径，点C是⊙O上一点，点P在AB的延长线上，且∠A=∠P=30O。

北京市各区2019届中考数学一模试卷精选汇编几何综合

几何综合东城区27. 已知△ABC 中，AD 是BAC ∠的平分线，且AD =AB ，过点C 作AD 的垂线，交 AD的延长线于点H ．（1）如图1，若60BAC ∠=︒①直接写出B ∠和ACB ∠的度数； ②若AB =2，求AC 和AH 的长；（2）如图2，用等式表示线段AH 与AB +AC 之间的数量关系，并证明．27. （1）①75B ∠=︒，45ACB ∠=︒；--------------------2分②作DE ⊥AC 交AC 于点E .Rt △ADE 中，由30DAC ∠=︒，AD=2可得DE =1，AE = Rt △CDE 中，由45ACD ∠=︒，DE=1，可得EC =1.∴AC 1=.Rt △ACH 中，由30DAC ∠=︒，可得AH =； --------------4分（2）线段AH 与AB +AC 之间的数量关系：2AH =AB +AC证明：延长AB 和CH 交于点F ，取BF 中点G ，连接GH . 易证△ACH ≌△AFH . ∴AC AF =,HC HF =. ∴GH BC ∥. ∵AB AD =， ∴ ABD ADB ∠=∠. ∴ AGH AHG ∠=∠ . ∴ AG AH =.∴()2222AB AC AB AF AB BF AB BG AG AH +=+=+=+==. --------------7分西城区27．正方形ABCD 的边长为2，将射线AB 绕点A 顺时针旋转α，所得射线与线段BD 交于点M ，作CE AM ⊥于点E ，点N 与点M 关于直线CE 对称，连接CN ．（1）如图，当045α︒<<︒时， ①依题意补全图．②用等式表示NCE ∠与BAM ∠之间的数量关系：__________．（2）当4590α︒<<︒时，探究NCE ∠与BAM ∠之间的数量关系并加以证明．（3）当090α︒<<︒时，若边AD 的中点为F ，直接写出线段EF 长的最大值．CDBA图1备用图C DBAM【解析】（1）①补全的图形如图所示：NEMABD C②2NCE BAM ∠=∠．（2）1902MCE BAM ∠+∠=︒，连接CM ，NQMABDC EDAM DCM ∠=∠，DAQ ECQ ∠=∠，∴2NCE MCE DAQ ∠=∠=∠，∴12DCM NCE ∠=∠，∵BAM BCM ∠=∠，90BCM DCM ∠+∠=︒，∴1902NCE BAM ∠+∠=︒．（3）∵90CEA ∠=︒， ∴点E 在以AC 为直径的圆上，E∴max 1EF FO r =+= 海淀区27（（27．.解：（1）作PF ⊥DE 交DE 于F . ∵PE ⊥BO ，60AOB ∠=，∴30OPE ∠=.∴30DPA OPE ∠=∠=.∴120EPD ∠=. ……………1分 ∵DP PE =,6DP PE +=, ∴30PDE∠=,3PD PE ==.∴cos30DF PD =⋅︒=∴2DE DF ==………………3分（2）当M 点在射线OA上且满足OM =DMME的值不变，始终为1.理由如下： ………………4分当点P 与点M 不重合时，延长EP 到K 使得PK PD =. ∵,DPA OPE OPE KPA ∠=∠∠=∠, ∴KPA DPA ∠=∠. ∴KPM DPM ∠=∠. ∵PK PD =,PM 是公共边, ∴KPM △≌DPM △.∴MK MD =. ………………5分作ML ⊥OE 于L ,MN ⊥EK 于N .∵60MO MOL =∠=， ∴sin 603ML MO =⋅=. ………………6分∵PE ⊥BO ,ML ⊥OE ,MN ⊥EK ， ∴四边形MNEL 为矩形. ∴3EN ML ==.∵6EK PE PK PE PD =+=+=, ∴EN NK =. ∵MN ⊥EK , ∴MK ME =. ∴ME MK MD ==,即1DMME=. 当点P 与点M 重合时，由上过程可知结论成立. ……………7分丰台区27．如图，Rt△ABC中，∠ACB = 90°，CA = CB，过点C在△ABC外作射线CE，且∠BCE = α，点B关于CE的对称点为点D，连接AD，BD，CD，其中AD，BD分别交射线CE于点M，N.（1）依题意补全图形；（2）当α= 30°时，直接写出∠CMA的度数；（3）当0°<α< 45°时，用等式表示线段AM，CN之间的数量关系，并证明．A BCE27．解：（1）如图；…………………1分（2）45°；…………………2分（3）结论：AM．…………………3分证明：作AG⊥EC的延长线于点G．∵点B与点D关于CE对称，∴CE是BD的垂直平分线．∴CB=CD．∴∠1=∠2=α．∵CA=CB，∴CA=CD．∴∠3=∠CAD．∵∠4=90°，∴∠3=12（180°-∠ACD）=12（180°-90°-α-α）=45°-α．∴∠5=∠2+∠3=α+45°-α=45°．…………………5分∵∠4=90°，CE是BD的垂直平分线，∴∠1+∠7=90°，∠1+∠6=90°．∴∠6=∠7．∵AG⊥EC，∴∠G =90°=∠8． ∴在△BCN 和△CAG 中， ∠8=∠G ， ∠7=∠6，BC =CA ，∴△BCN ≌△CAG ．∴CN =AG ． ∵Rt △AMG 中，∠G =90°，∠5=45°，∴AM ．∴AM ． …………………7分（其他证法相应给分.）石景山区27．在正方形ABCD 中，M 是BC 边上一点，点P 在射线AM 上，将线段AP 绕点A 顺时针旋转90°得到线段AQ ，连接BP ，DQ ．（1）依题意补全图1；（2）①连接DP ，若点P ，Q ，D 恰好在同一条直线上，求证：2222DP DQ AB +=； ②若点P ，Q ，C 恰好在同一条直线上，则BP 与AB 的数量关系为：．27．（1）补全图形如图1. ………………… 1分（2）①证明：连接BD ，如图2，∵线段AP 绕点A 顺时针旋转90°得到线段AQ ， ∴AQ AP =，90QAP ∠=°． ∵四边形ABCD 是正方形， ∴AD AB =，90DAB ∠=°． ∴12∠=∠．∴△ADQ ≌△ABP ． ………………… 3分 ∴DQ BP =，3Q ∠=∠．∵在Rt QAP ∆中，90Q QPA ∠+∠=°， ∴390BPD QPA ∠=∠+∠=°． ∵在Rt BPD ∆中，222DP BP BD +=，又∵DQ BP =，222BD AB =，∴2222DP DQ AB +=． ………………… 5分 ②BP AB =． ………………… 7分证明：过点A 作AE ⊥PQ 于E ，连接BE AC ∴AE 是△PAQ 的垂线∵三△PAQ 是等腰直角三角形（已证） ∴AE 是等腰直角三角形PAQ 的垂线，角平分线 ∴∠AEP=90°，AE=PEC图1∵正方形ABCD∴∠ABC=90°∠ACB=∠BAC=45°∠AEP+∠ABC=180°∴A ，B，C，E四点共圆∴∠AEB=∠ACB=45°，∠CEB=∠BAC=45°∴∠AEB=∠CEB=45°∵BE=BE∴△ABE≌△PBE (SAS)∴BP=AB朝阳区27. 如图，在菱形ABCD中，∠DAB=60°，点E为AB边上一动点（与点A，B不重合），连接CE，将∠ACE的两边所在射线CE，CA以点C为中心，顺时针旋转120°，分别交射线AD于点F，G.（1）依题意补全图形；（2）若∠ACE=α，求∠AFC的大小（用含α的式子表示）；（3）用等式表示线段AE、AF与CG之间的数量关系，并证明．27.（1）补全的图形如图所示.……………………………………1分（2）解：由题意可知，∠ECF=∠ACG=120°.∴∠FCG=∠ACE=α.∵四边形ABCD 是菱形，∠DAB=60°，∴∠DAC=∠BAC= 30°. ……………………………………………2分 ∴∠AGC=30°.∴∠AFC =α+30°. …………………………3分（3）用等式表示线段AE 、AF 与CG 之间的数量关系为CG AF AE 3=+.证明：作CH ⊥AG 于点H.由（2）可知∠BAC=∠DAC=∠AGC=30°.∴CA=CG. …………………………………………………5分∴HG =21AG. ∵∠ACE =∠GCF ，∠CAE =∠CGF ，∴△ACE ≌△GCF. ……………………………6分 ∴AE =FG .在Rt △HCG 中， .23cos CG CGH CG HG =∠⋅= ∴AG =3CG . …………………………………………7分即AF+AE =3CG .燕山区27．如图，抛物线)0(2>++=a c bx ax y 的顶点为M ，直线y=m 与抛物线交于点A ，B ，若△AMB 为等腰直角三角形，我们把抛物线上A ，B 两点之间的部分与线段AB 围成的图形称为该抛物线对应的准蝶形，线段AB 称为碟宽，顶点M 称为碟顶．(1)由定义知，取AB 中点N ，连结MN ，MN 与AB 的关系是 (2)抛物线221x y =对应的准蝶形必经过B (m ，m ),则m = ，对应的碟宽AB 是 (3)抛物线)0(3542>--=a a ax y 对应的碟宽在x 轴上，且AB =6. ①求抛物线的解析式；②在此抛物线的对称轴上是否有这样的点P （p x ，p y ），使得∠APB 为锐角，若有，请求出p y 的取值范围.若没有，请说明理由. ,备用图27.解：(1)MN 与AB 的关系是 MN ⊥AB ，MN=21AB…………………………………2′（2） m= 2 对应的碟宽是4…………………………………4′(3) ①由已知，抛物线必过（3，0），代入)0(3542>--=a a ax y准蝶形AMBABM得，03549=--a a31=a ∴抛物线的解析式是3312-=x y …………………………………5′ ② 由①知，3312-=x y 的对称轴上P （0，3），P （0，-3）时，∠APB 为直角， ∴在此抛物线的对称轴上有这样的点P ，使得∠APB 为锐角，p y 的取值范围是33〉〈-p p y y 或…………………………………7′门头沟区27. 如图，在△ABC 中，AB =AC ，2A α∠=，点D 是BC 的中点，DE AB E ⊥于点，DF AC F ⊥于点.（1）EDB ∠=_________°；（用含α的式子表示）（2）作射线DM 与边AB 交于点M ，射线DM 绕点D 顺时针旋转1802α︒-，与AC 边交于点N ．①根据条件补全图形；②写出DM 与DN 的数量关系并证明；③用等式表示线段BM CN 、与BC 之间的数量关系，（用含α的锐角三角函数表示）并写出解题思路.27．（本小题满分7分）（1） EDB α∠= ……………………………………………1分（2）①补全图形正确 ……………………………………2分 ②数量关系：DM DN =…………………………………3分 ∵,AB AC BD DC == ∴DA 平分BAC ∠∵DE AB E ⊥于点，DF AC F ⊥于点∴DE DF = ， MED NFD ∠=∠ ……………………4分BB∵2Aα∠=∴1802EDFα∠=︒-∵1802MDNα∠=︒-∴MDE NDF∠=∠∴MDE NDF△≌△……………………5分∴DM DN=③数量关系：sinBM CN BCα+=⋅……………………6分证明思路：a.由MDE NDF△≌△可得EM FN=b. 由AB AC=可得B C∠=∠,进而通过BDE CDF△≌△,可得BE CF=进而得到2BE BM CN=+c.过BDERt△可得sinBEBDα=,最终得到sinBM CN BCα+=⋅……………7分大兴区27．如图，在等腰直角△ABC中，∠CAB=90°，F是AB边上一点，作射线CF，过点B作BG⊥C F于点G，连接AG．（1）求证：∠ABG=∠ACF；（2）用等式表示线段C G，AG，BG之间的等量关系，并证明．27.（1）证明:∵∠CAB=90°.∵BG⊥CF于点G，∴∠BGF=∠CAB=90°.∵∠GFB=∠CFA. ………………………………………………1分∴∠ABG=∠ACF. ………………………………………………2分（2）CG+BG. …………………………………………………3分证明：在CG上截取CH=BG，连接AH，…………………………4分∵△ABC是等腰直角三角形，∴ ∠CAB =90°，AB =AC . ∵ ∠ABG =∠ACH .∴ △ABG ≌△ACH . …………………………………………………… 5分 ∴ AG =AH ,∠GAB =∠HAC . ∴ ∠GAH =90°.∴ 222AG AH GH +=.∴ GH. ………………………………………………………6分 ∴ CG =CH +GH+BG . ………………………………………7分平谷区27．在△ABC 中，AB=AC ，CD ⊥BC 于点C ，交∠ABC 的平分线于点D ，AE 平分∠BAC 交BD 于点E ，过点E 作EF ∥BC 交AC 于点F ，连接DF ．（1）补全图1；（2）如图1，当∠BAC =90°时，①求证：BE=DE ；②写出判断DF 与AB 的位置关系的思路（不用写出证明过程）；（3）如图2，当∠BAC=α时，直接写出α，DF ，AE 的关系．27．解：（1）补全图1； (1)图1BB图2B（2）①延长AE ，交BC 于点H ． ····· 2 ∵AB=AC ， AE 平分∠BAC ，∴AH ⊥BC 于H ，BH=HC ．∵CD ⊥BC 于点C ， ∴EH ∥CD ．∴BE=DE ． (3)②延长FE ，交AB 于点G ．由AB=AC ，得∠ABC =∠ACB ．由EF ∥BC ，得∠AGF =∠AFG ．得AG=AF ．由等腰三角形三线合一得GE=E F ． ·· 4 由∠GEB =∠FED ，可证△BEG ≌△DEF ．可得∠ABE =∠FDE ． (5)从而可证得DF ∥AB ． ······· 6 （3）tan 2DF αAE ． (7)怀柔区27.如图，在△ABC 中，∠A=90°，AB=AC ，点D 是BC 上任意一点，将线段AD 绕点A 逆时针方向旋转90°，得到线段AE ，连结EC. (1)依题意补全图形； (2)求∠ECD 的度数；(3)若∠CAE=7.5°，AD=1，将射线DA 绕点D 顺时针旋转60°交EC 的延长线于点F ，请写出求AF 长的思路．BBB27.(1)如图………………………………………………1分(2) ∵线段AD 绕点A 逆时针方向旋转90°，得到线段AE. ∴∠DAE=90°，AD=AE. ∴∠DAC+∠CAE =90°. ∵∠BAC=90°, ∴∠BAD+∠DAC =90°.∴∠BAD=∠CAE . …………………………………………………………………………2分又∵AB=AC, ∴△ABD ≌△ACE. ∴∠B=∠ACE.∵△ABC 中，∠A=90°，AB=AC,∴∠B=∠ACB=∠ACE=45°. ∴∠ECD=∠ACB+∠ACE=90°. ……………………………………………………………4分(3)Ⅰ.连接DE,由于△ADE 为等腰直角三角形，所以可求DE=2；……………………5分 Ⅱ.由∠ADF=60°,∠CAE=7.5°，可求∠EDC 的度数和∠CDF 的度数，从而可知DF 的长； …………………………………………………………………………………………………6分Ⅲ.过点A 作AH ⊥DF 于点H ，在Rt △ADH 中, 由∠ADF=60°，AD=1可求AH 、DH 的长； Ⅳ. 由DF 、DH 的长可求HF 的长；Ⅴ. 在Rt △AHF 中, 由AH 和HF,利用勾股定理可求AF 的长．…………………………7分延庆区27．如图1，正方形ABCD 中，点E 是BC 延长线上一点，连接DE ，过点B 作BF ⊥DE 于点F ，连接FC ．（1）求证：∠FBC =∠CDF ．（2）作点C 关于直线DE 的对称点G ，连接CG ，FG ．①依据题意补全图形；②用等式表示线段DF ，BF ，CG 之间的数量关系并加以证明．27.（1）证明：∵四边形ABCD 是正方形，∴∠DCB =90°． ∴∠CDF +∠E =90°． ∵BF ⊥DE ，∴∠FBC +∠E =90°． ∴∠FBC =∠CDF ．……2分（2）①图1FDEC BA GFDECBA……3分②猜想：数量关系为：BF=DF+CG．证明：在BF上取点M使得BM=DF连接CM．∵四边形ABCD是正方形，∴BC=DC．∵∠FBC =∠CDF，BM=DF，∴△BMC≌△DFC．∴CM=CF，∠1=∠2．∴△MCF是等腰直角三角形．∴∠MCF =90°，∠4=45°．……5分∵点C与点G关于直线DE对称，∴CF=GF，∠5=∠6．∵BF⊥DE，∠4=45°，∴∠5=45°，∴∠CFG =90°，∴∠CFG=∠MCF，∴CM∥GF．∵CM=CF，CF=GF，∴CM=GF，∴四边形CGFM是平行四边形，∴CG=MF．∴BF=DF+CG．……7分顺义区27. 如图，在正方形ABCD中，E是BC边上一点，连接AE，延长CB至点F，使BF=BE，过点F作FH⊥AE于点H，射线FH分别交AB、CD于点M、N，交对角线AC于点P，连接AF．（1）依题意补全图形；（2）求证：∠FAC=∠APF；（3）判断线段FM与PN的数量关系，并加以证明．27．（1）补全图如图所示． ………………………………………………………… 1分（2）证明∵正方形ABCD ，∴∠BAC =∠BCA =45°，∠ABC =90°， ∴∠PAH =45°-∠BAE ． ∵FH ⊥AE ．∴∠APF =45°+∠BAE ． ∵BF=BE ，∴AF=AE ，∠BAF =∠BAE ． ∴∠FAC =45°+∠BAF ．∴∠FAC =∠APF ．…………………………… 4分（3）判断：FM =PN ． …………………………………… 5分证明：过B 作BQ ∥MN 交CD 于点Q ，∴MN =BQ ，BQ ⊥AE ． ∵正方形ABCD ，∴AB =BC ，∠ABC =∠BCD=90°． ∴∠BAE =∠CBQ ． ∴△ABE ≌△BCQ ． ∴AE =BQ ． ∴AE =MN ． ∵∠FAC =∠APF ， ∴AF =FP ． ∵AF=AE ， ∴AE =FP ． ∴FP =MN ．∴FM =PN ．…………………………………………………………… 8分。

2019北京各区初三一模数学分类汇编——几何综合题

2019北京各区初三一模数学分类汇编——几何综合题（房山）26．在平面直角坐标系xOy 中，二次函数2y x mx n =++的图象经过点 A (−1，a )，B (3，a )，且顶点的纵坐标为 -4．（1）求 m ，n 和 a 的值；（2）记二次函数图象在点 A ，B 间的部分为 G (含点A 和点B )，若直线 2y kx =+与图象G 有公共点，结合函数图象，求 k 的取值范围．（门头沟）26．在平面直角坐标系xOy 中，一次函数4y x =+的图象与x 轴交于点A ，与过点（0，5）平行于x 轴的直线l 交于点B ，点A 关于直线l 的对称点为点C ．（1）求点B 和点C 坐标；（2）已知某抛物线的表达式为222y x mx m m =-+-．① 如果该抛物线顶点在直线4y x =+上，求m 的值；② 如果该抛物线与线段BC 有公共点，结合函数图象，直接写出m 的取值范围．（密云）26.已知抛物线，抛物线的顶点为P.（1）求点P 的纵坐标.（2）设抛物线x 轴交于A 、B 两点，1122(,),(,)A x y B x y ，21x x >. ①判断AB 长是否为定值，并证明.②已知点M （0，-4），且MA≥5，求21-x x m +的取值范围.（平谷）26．平面直角坐标系xOy 中，抛物线3222-+-=m mx x y 与y 轴交于点A ，过A 作AB ∥x 轴与直线x =4交于B 点．（1）抛物线的对称轴为x = （用含m 的代数式表示）；（2）当抛物线经过点A ，B 时，求此时抛物线的表达式；（3）记抛物线在线段AB 下方的部分图象为G （包含A ，B 两点），点P （m ,0）是x 轴上一动点，过P 作PD ⊥x 轴于P ，交图象G 于点D ，交AB 于点C ，若CD ≤1，求m 的取值范围．（石景山）26．在平面直角坐标系xOy 中，直线1y kx =+(0)k ≠经过点(2,3)A ，与y 轴交于点B ，与抛物线2y ax bx a =++的对称轴交于点(,2)C m .（1）求m 的值；（2）求抛物线的顶点坐标；（3）11(,)N x y 是线段AB 上一动点，过点N 作垂直于y 轴的直线与抛物线交于点22(,)P x y ,33(,)Q x y （点P 在点Q 的左侧）．若213x x x <<恒成立，结合函数的图象，求a 的取值范围．（通州）26. 已知二次函数2y x ax b =-+在0x =和4x =时的函数值相等．（1）求二次函数2y x ax b =-+的对称轴；（2）过P （0，1）作x 轴的平行线与二次函数2y x ax b =-+的图象交于不同的两点M 、N .①当2MN =时，求b 的值；②当=4PM PN +时，请结合函数图象，直接写出b 的取值范围．（延庆）26．在平面直角坐标系xOy 中，抛物线2432y ax ax a =-+-（0a ≠）的对称轴与x轴交于点A ，将点A 向右平移3个单位长度，向上平移2个单位长度，得到点B ．（1）求抛物线的对称轴及点B 的坐标；（2）若抛物线与线段AB 有公共点，结合函数图象，求a 的取值范围．（燕山）26．在平面直角坐标系xOy 中，抛物线223(0)y ax ax a a =--≠的顶点为D ，与x 轴交于A ，B 两点(A 在B 的左侧)．(1) 当1a =时，求点A ，B ，D 的坐标；(2) 横，纵坐标都是整数的点叫做整点．若抛物线在点A ，B 之间的部分与线段AB 所围成的区域内(不含边界)恰有7个整点，结合函数图象，求a 的取值范围．（西城）26．在平面直角坐标系xOy 中，已知抛物线2y x mx n =-+．（1）当2m =时，①求抛物线的对称轴，并用含n 的式子表示顶点的纵坐标；②若点1(2,)A y -，22(,)B x y 都在抛物线上，且21y y >，则2x 的取值范围是_______；（2）已知点P (－1,2)，将点P 向右平移4个单位长度，得到点Q ．当n ＝3时，若抛物线与线段PQ 恰有一个公共点，结合函数图像，求m 的取值范围．（顺义）26.在平面直角坐标系xOy 中，抛物线 2(3)3y mx m x =+--（0m >）与x 轴交于A 、B 两点（点A 在点B 左侧），与y 轴交于点C , 4=AB ，点D 为抛物线的顶点.（1）求点A 和顶点D 的坐标；（2）将点D 向左平移4个单位长度，得到点E ,求直线BE 的表达式；（3）若抛物线26=-y ax 与线段DE 恰有一个公共点，结合函数图象，求a 的取值范围.（丰台）26．在平面直角坐标系xOy 中，抛物线c bx ax y ++=2过原点和点A （-2，0）.（1）求抛物线的对称轴；（2）横、纵坐标都是整数的点叫做整点．已知点B （0AB 围成的封闭区域（不含边界）为W ．①当=1a 时，求出区域W 内的整点个数；②若区域W 内恰有3个整点，结合函数图象，直接写出a 的取值范围．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2019北京市各区初三一模数学分类汇编——几何综合题（房山）27．已知：Rt △ABC 中，∠ACB =90°，AC =BC ．
（1）如图1，点D 是BC 边上一点(不与点B ，C 重合)，连接AD ，过点B 作BE ⊥AD ，交AD 的延长线于点E ，连接CE ．若∠BAD =α，求∠DBE 的大小 (用含α的式子表示) ；
（2）如图2，点D 在线段BC 的延长线上时，连接AD ，过点B 作BE ⊥AD ，垂足E 在线段AD 上，连接CE ． ①依题意补全图2；
②用等式表示线段EA ，EB 和EC 之间的数量关系，并证明．
图1 图2
（门头沟）27．如图，∠AOB = 90°，OC 为∠AOB 的平分线，点P 为OC 上一个动点，过点P 作射线PE 交OA 于点E ．以点P 为旋转中心，将射线PE 沿逆时针方向旋转90°，交OB 于点F ．
（1）根据题意补全图1，并证明PE = PF ；
（2）如图1，如果点E 在OA 边上，用等式表示线段OE ，OP 和OF 之间的数量关系，并证明；
（3）如图2，如果点E 在OA 边的反向延长线上，直接写出线段OE ，OP 和OF 之间的数量关系．
图
1 图2
（密云）27．已知△ABC 为等边三角形，点D 是线段AB 上一点（不与A 、B 重合）．将线段CD 绕点C 逆时针旋转60°得到线段CE ．连结DE 、BE ．
（1）依题意补全图1并判断AD 与BE 的数量关系．
（2）过点A 作AF EB 交EB 延长线于点F ．用等式表示线段EB 、DB 与AF 之间的数量关系并证明．
（平谷）27．在△ABC 中，∠ABC =120°，线段AC 绕点A 逆时针旋转60°得到线段AD ，连接CD ，BD 交AC 于P ．
（1）若∠BAC =α，直接写出∠BCD 的度数（用含α的代数式表示）；
（2）求AB ，BC ，BD 之间的数量关系；
（3）当α=30°时，直接写出AC ，BD 的关系． B A A P
P E E
C
C B
B O
O
A A
图2D C
B
A 图1A
B
C D
（石景山）27．如图，在等边△ABC 中，D 为边AC 的延长线上一点()CD AC <，平移线段BC ，
使点C 移动到点D ，得到线段ED ，M 为ED 的中点，过点M 作ED 的垂线，交BC
于点F ，交AC 于点G ．
（1）依题意补全图形；
（2）求证：AG = CD ；
（3）连接DF 并延长交AB 于点H ，用等式表示线段AH 与CG 的数量关系，并证明．
（通州）27．如图，在等边△ABC 中，点D 是线段BC 上一点．作射线AD ，点B 关于射线AD 的对称点为E ．连接CE 并延长，交射线AD 于点F ．
（1）设∠BAF ＝α，用α表示∠BCF 的度数；
（2）用等式表示线段AF 、CF 、EF 之间的数量关系，并证明．
（延庆）27．已知：四边形ABCD 中，120ABC ∠=︒，60ADC ∠=︒，AD =CD ，对角线AC ，BD 相交于点O ，且BD 平分∠ABC ，过点A 作AH BD ⊥，垂足为H ．
（1）求证：ADB ACB ∠=∠；
（2）判断线段BH ，DH ，BC 之间的数量关系；并证明．
B
H
O
D
C B A
（燕山）27．如图，在△ABC 中，AB ＝BC ，∠B ＝90°，点D 为线段BC 上一个动点(不与点B ，C 重合)，连接AD ，将线段AD 绕点D 顺时针旋转90°得到线段DE ，连接EC ．
(1) ① 依题意补全图1；
② 求证：∠EDC ＝∠BAD ；
(2) ① 小方通过观察、实验，提出猜想：在点D 运动的过程中，线段CE 与BD 的数量关系始终不变，用等式表示为：；
② 小方把这个猜想与同学们进行交流，通过讨论，形成了证明该猜想的几种想法：
想法1：过点E 作EF ⊥BC ，交BC 延长线于点F ，只需证△ADB ≌△DEF ．
想法2：在线段AB 上取一点F ，使得BF ＝BD ，连接DF ，只需证△ADF ≌△DEC ．
想法3：延长AB 到F ，使得BF ＝BD ，连接DF ，CF ，只需证四边形DFCE 为平行四边形．
……
请你参考上面的想法，帮助小方证明①中的猜想．(一种方法即可)
（西城）27．如图，在△ABC 中，∠ABC =90°，BA=BC ．将线段AB 绕点A 逆时针旋转90°得到线段AD ，E 是边BC 上的一动点，连接DE 交AC 于点F ，连接BF .
（1）求证：FB=FD ；
（2）点H 在边BC 上，且BH=CE ，连接AH 交BF 于点N ．
①判断AH 与BF 的位置关系，并证明你的结论；
②连接CN ．若AB =2，请直接写出线段CN 长度的最小值.
（顺义）27．已知：如图，在△ABC 中，AB >AC ，∠B =45°，点D 是BC 边上一点，且AD=AC ，过点C 作CF ⊥AD 于点E ，与AB 交于点F ．
（1）若∠CAD =α，求∠BCF 的大小（用含α
的式子表示）；
（2）求证：AC =FC ；
（3）用等式直接表示线段BF 与DC 的数量关系．
（丰台）27．在△ABC 中，∠ACB =90°，AC =BC ， D 为AB 的中点，点E 为AC 延长线上一点，连接DE ，过点D 作DF ⊥DE 交CB 的延长线于点F ．
（1）求证：BF= CE ；
（2）若CE =AC ，用等式表示线段DF 与AB 的数量关系，并证明．
A B C
D F
E
备用图 A
B C
D 图1 D C B A。