2021年上海市金山区初三数学一模试卷
2021年上海市16区中考数学一模考点分类汇编专题05圆(学生版)

5. (2021・上海金山区•九年级一模)正十边形的中心角等于 度.2021年上海市16区中考数学一模汇编一、单选题L (2021・上海金山区•九年级一模)如图,己知必AA3C 中,ZC = 90 , AC = 3, 8c = 4,如果以点C 为圆心的圆与斜边43有公共点,那么回C 的半径,,的取值范围是( )12 B. —<r<3 5 2 . (2021 ・上海闵行区,九年级一模)己知。
A 与。
8的半径分别是6和8,圆心距A3 = 2,那么。
A 与 的位置关系是() A.相交 B.内切 C.外切 D.内含3 .(2021 ・上海崇明区•九年级一模)如果某正多边形的外接圆半径是其内切圆半径的四倍,那么这个正多 边形的边数是() A. 3 B. 4 C. 5 D.无法确定 4.(2021 ・上海奉贤区•九年级一模)如果和内含,圆心距。
2 = 4,的半径长是6,那么。
? 的半径,•的取值范围是().A. 0<r<2B. 2<r<4C. r>10D. 0<r<2或厂>10二、填空题专题05圆12 C. — < r < 45 D. 3<r<412 A. 0<r< — 56.(2021・上海崇明区,九年级一模)如果大小不同的两个圆外切时的圆心距为5厘米,并且它们内切时的圆心距为1厘米,那么其中较大圆的半径为厘米.7.(2021・上海金山区•九年级一模)已知日和同。
2的半径长分别为3和4,若回01和回。
2内切,那么圆心距Op.的长等于.8.(2021・上海崇明区•九年级一模)如图,在直角坐标系中,以点尸为圆心的弧与X轴交于A、3两点,已知点。
的坐标为(l,y),点A的坐标为(-L0),那么点8的坐标为.9.(2021 •上海闵行区•九年级一模)正六边形的边心距与半径的比值为(结果保留根号).10.(2021•上海金山区•九年级一模)如图,已知目。
2021年上海市16区中考数学一模考点分类汇编专题10锐角三角函数(解析版)

2021年上海市16区中考数学一模汇编专题10锐角三角函数一、单选题1.(2021·上海金山区·九年级一模)在Rt ABC ∆中,90C ∠=,那么锐角A 的正弦等于( )A .A A 锐角的对边锐角的邻边B .A 锐角的对边斜边C .A 锐角的邻边斜边D .A A 锐角的邻边锐角的对边.【答案】B【分析】根据锐角三角函数的定义可直接得出结果.【详解】在Rt ABC ∆中,90C ∠=,那么锐角A 的正弦=A 锐角的对边斜边,故选:B .【点睛】本题考查锐角三角函数的定义,属于基础题,需要熟练掌握锐角三角函数的定义.2.(2021·上海杨浦区·九年级一模)在ABC 中,如果1sin 2A =,cot 3=B ,那么这个三角形一定是( ) A .等腰三角形 B .锐角三角形C .钝角三角形D .直角三角形【答案】D【分析】根据特殊的三角函数值可知,∠A =30°,∠B =60°,即可判断三角形的形状.【详解】∠ 1sin 2A =,cot 3=B ,∠∠A =30°,∠B =60°,∠ ∠A +∠B =90°, ∠ 这个三角形一定是直角三角形,故选:D .【点睛】本题考查特殊角的三角函数值,三角形内角和定理,属于基础题型.3.(2021·上海宝山区·九年级一模)在Rt ABC △中,90C ∠=︒,5AB =,3BC =,那么sin A 的值为( ).A .35B .34C .45D .43【答案】A【分析】根据正弦的定义解答即可.【详解】解:在Rt∠ABC 中,∠C=90°,AB=5,BC=3,则sinA=35BC AB =,故选:A . 【点睛】本题考查了锐角三角函数的定义,掌握锐角A 的对边a 与斜边c 的比叫做∠A 的正弦是解题的关键.4.(2021·上海奉贤区·九年级一模)在 Rt ABC ∆中,90C =∠,如果33,4AC cosA == ,那么 AB 的长为( )A .94B .4C .5D .254【答案】B【分析】根据cosA 34==AC AB ,即可得出AB 的值 【详解】解:在Rt∠ABC 中,∠C=90°,AC=3,又∠,osA 34c ==AC AB ∠AB=4故选:B . 【点睛】本题考查锐角三角函数的定义,解题的关键是熟练掌握基本知识,属于中考常考题型. 5.(2021·上海虹口区·九年级一模)在Rt ABC ∆中,90C ∠=︒,3BC =,4AC =,那么tan A 的值等于( )A .34B .43C .35D .45【答案】A【分析】在直角三角形中,锐角的正切等于对边比邻边,由此可得tan A . 【详解】解:如图90C ∠=︒,3tan 4BC A AC ∴==.故选:A. 【点睛】本题主要考查了锐角三角函数中的正切,熟练掌握正切的表示是解题的关键.6.(2021·上海徐汇区·九年级一模)已知海面上一艘货轮A 在灯塔B 的北偏东30方向,海监船C 在灯塔B 的正东方向5海里处,此时海监船C 发现货轮A 在它的正北方向,那么海监船C 与货轮A 的距离是( )A .10海里B .C .5海里D 【答案】B【分析】根据题意先建立直角三角形,然后结合三角函数中正切的定义求解即可. 【详解】根据题意建立如图所示Rt∠ABC ,其中∠C=90°,∠B=60°,BC=5,∠560AC BC tan B tan ==⨯︒=B .【点睛】本题考查解直角三角形的实际应用,准确根据题意构建直角三角形并灵活运用三角函数求解是解题关键.7.(2021·上海徐汇区·九年级一模)在Rt ABC 中,90A ∠=︒,6AB =,10BC =,那么下列结论正确的是( )A.4tan3C=B.4cot5C=C.3sin4C=D.4cos5C=【答案】D【分析】先根据勾股定理解出AB,再逐项根据三角函数的定义判断即可.【详解】根据勾股定理可得:8AC==,则3tan4ABCAC==;4cot3ACCAB==;3sin5ABCBC==;4cos5ACCBC==;故选:D.【点睛】本题考查锐角三角函数的定义,熟悉基本定义是解题关键.8.(2021·上海长宁区·九年级一模)已知在∠ABC中,∠C=90°,∠B=50°,AB=10,那么BC的长为()A.10cos50°B.10sin50°C.10tan50°D.10cot50°【答案】A【分析】根据三角函数的定义即可求解.【详解】解:∠cosB=BCAB,∠BC=ABcosB=10cos50°.故选:A.【点睛】此题主要考查三角函数的定义.余弦:锐角A的邻边b与斜边c的比叫做∠A的余弦,记作cosA.即cosA=bc.9.(2021·上海杨浦区·九年级一模)如果小丽在楼上点A处看到楼下点B处小明的俯角是35°,那么点B处小明看点A处小丽的仰角是()A.35°B.45°C.55°D.65°【答案】A【分析】根据两点之间的仰角与俯角构成的两条水平线夹角的内错角相等,即可得出答案.【详解】解:根据两点之间的仰角与俯角构成的两条水平线夹角的内错角相等,可知,点B 处小明看点A 处小丽的仰角是35°,故选:A .【点睛】本题考查解直角三角形的应用-仰角俯角问题,正确理解是解题的关键. 10.(2021·上海黄浦区·九年级一模)对于锐角α,下列等式中成立的是( ) A .sin cos tan ααα=⋅ B .cos tan cot ααα=⋅ C .tan cot sin ααα=⋅ D .cot sin cos ααα=⋅【答案】A【分析】根据同角的三角函数关系逐一判断即可. 【详解】解:A .sin cos tan ααα=⋅,故本选项正确; B .tan cot 1cos ααα⋅=≠,故本选项错误; C .cot sin cos tan αααα⋅=≠ ,故本选项错误; D .cos cot sin cos sin ααααα=≠⋅ ,故本选项错误.故选A . 【点睛】此题考查的是同角的三角函数关系,掌握同角的三角函数关系是解题关键.11.(2021·上海松江区·九年级一模)如图,一艘船从A 处向北偏东30°的方向行驶10千米到B 处,再从B 处向正西方向行驶20千米到C 处,这时这艘船与A 的距离( )A .15千米B .10千米C .D .千米【答案】C【分析】根据题意,利用30BAD ∠=︒,根据锐角三角函数求出AD 和BD 的长,从而得到CD 的长,再用勾股定理求出AC 的长. 【详解】解:如图,根据题意,10AB km =,30BAD ∠=︒,∠1sin 301052BD AB km =⋅︒=⨯=,cos30102AD AB =⋅︒=⨯=,∠20BC km =,∠15CD km =,∠AC ==.故选:C .【点睛】本题考查解直角三角形,解题的关键是掌握利用锐角三角函数解直角三角形的方法.12.(2021·上海浦东新区·九年级一模)已知在Rt ABC ∆中,90C ∠=︒,,2A BC α∠==,那么AB 的长等于( )A .2sin αB .2sin αC .2cos αD .2cos α【答案】A【分析】根据锐角三角函数的定义得出sinA =BCAB,代入求出即可. 【详解】解:∠在Rt∠ABC 中,∠C =90°,∠A =α,BC =2,∠sinA =BCAB, ∠AB =sin BC A =2sin α,故选:A .【点睛】本题考查了锐角三角函数的定义,能熟记锐角三角函数的定义是解此题的关键.13.(2021·上海金山区·九年级一模)若α是锐角,()2sin 152α+=,那么锐角α等于( ) A .15 B .30 C .45D .60【答案】B【分析】由sin45°=2可得()15α+=45°即可确定α.【详解】解:∠sin45°=2,()2sin 152α+=,α是锐角∠()15α+=45°,即α=30°.故选:B .【点睛】本题主要考查特殊角的三角函数值,根据特殊角的三角函数值确定()15α+=45°成为解答本题的关键.14.(2021·上海九年级一模)在Rt ABC 中,90C ∠=︒,那么cosA 等于( ) A .BCABB .ACABC .BCACD .ACBC【答案】B【分析】作出草图,根据锐角的正弦=邻边斜边列式即可. 【详解】解:如图,∠∠C=90°,∠cosA=ACAB.故选:B . .【点睛】本题考查了锐角三角函数的定义,能熟记锐角三角函数的定义是解题的关键.15.(2021·上海静安区·九年级一模)在Rt∠ABC 中,∠C =90°,CD 是高,如果AB =m ,∠A =α,那么CD 的长为( )A .sin tan m αα⋅⋅B .sin cos m αα⋅⋅C .cos tan m αα⋅⋅D .cos cot m αα⋅⋅【答案】B【分析】此题根据题意作图根据锐角三角函数表示出AC ,再表示出CD 即可求出结果. 【详解】解:根据题意作图如下:由题意知:AB =m ,∠A =α,∠cos AC AB α=⋅,∠sin cos sin CD AC AB ααα=⋅=⋅⋅, 即cos sin CD m αα=⋅⋅,故选:B .【点睛】此题考查锐角三角函数的应用,主要涉及到正弦和余弦,找准对应边是解题关键.16.(2021·上海静安区·九年级一模)如果锐角α ) A .30α=︒ B .60α=︒ C .3045α︒<<︒D .4560α︒<<︒【答案】C【分析】利用30度角和45度角的正切值与角α的正切值比较,即可得到答案.【详解】∠tan 30tan tan 451α︒==︒=,22213,1134===, 而13134<<,∠3045α︒<<︒,故选:C . 【点睛】此题考查各角的正切值,实数的平方运算,实数的大小比较,熟记各角度的三角函数值是解题的关键.17.(2021·上海崇明区·九年级一模)倍,那么这个正多边形的边数是( ) A .3 B .4C .5D .无法确定【答案】B【分析】如图,画出简图,根据切线的性质可得∠OCA=90°,根据∠AOC 的余弦可得∠AOC=45°,即可得出此多边形的中心角为90°,即可求出多边形的边数.【详解】如图,OA 、OC 分别为此多边形的外接圆和内切圆的半径,AB 为边长,∠OC∠AB ,∠∠OCA=90°,∠倍,∠cos∠AOC=OC OA =2, ∠∠AOC=45°,∠∠AOB=90°,即此多边形的中心角为90°,∠此多边形的边数=360°÷90°=4,故选:B .【点睛】本题考查正多边形和圆及三角函数的定义,熟练掌握余弦的定义并熟记特殊角的三角函数值是解题关键.18.(2021·上海崇明区·九年级一模)在ABC 中,90C ∠=︒,如果8AC =,6BC =,那么A ∠的正弦值为( )A .35B .45C .34D .43【答案】A【分析】利用勾股定理可求出AB 的长,根据正弦函数的定义即可得答案.【详解】∠90C ∠=︒,8AC =,6BC =,,∠sinA=BC AB =35,故选:A . 【点睛】本题考查解直角三角形,解题的关键是熟练掌握各三角函数的定义,属于中考常考题型. 19.(2021·上海虹口区·九年级一模)如图,在Rt ABC 中,90ACB ∠=︒,D 是边AB 上一点,过D 作DF AB ⊥交边BC 于点E ,交AC 的延长线于点F ,联结AE ,如果1tan 3EAC ∠=,1CEFS=,那么ABCS的值是( )A .3B .6C .9D .12【答案】C【分析】证明∠BAC∠∠FEC ,得219EFC BAC S EC S AC ∆∆⎛⎫== ⎪⎝⎭,进一步得出结论.【详解】解:∠90ACB ∠=︒,DF∠AB ,∠∠ACB=∠FCE=∠BDE=90° 又∠FEC=∠BED∠∠F=∠B∠∠ABC∠∠EFC∠()22211tan 39EFC BAC S EC EAC S AC ∆∆⎛⎫⎛⎫==∠== ⎪ ⎪⎝⎭⎝⎭∠1CEFS =∠99BAC FEC S S ∆∆== 故选:C【点睛】此题主要考查了相似三角形的判定与性质以及三角函数的应用,熟练掌握相似三角形的判定与性质是解本题的关键.20.(2021·上海普陀区·九年级一模)如图,在∠ABC 中,∠C =90°.若AB =3,BC =2,则sin A 的值为( )A .23BCD 【答案】A【分析】根据在直角三角形中,正弦为对边比斜边,可得答案.【详解】解:∠ABC 中,∠C =90°,AB =3,BC =2,得sin A =2 3BC AB =,故选A . 【点睛】本题考查三角函数,熟记公式是解题关键.21.(2021·上海松江区·九年级一模)已知在Rt∠ABC 中,∠C=90°,如果BC=2,∠A=α,则AC 的长为( ) A .2sinαB .2cosαC .2tanαD .2cotα【答案】D 试题分析:根据锐角三角函数的定义得出cotA=,代入求出即可.∠在Rt∠ABC 中,∠C=90°, ∠cotA=,∠BC=2,∠A=α,∠AC=2cotα,故选D .考点:锐角三角函数的定义.二、填空题22.(2021·上海九年级一模)在ABC 中,90C ∠=︒,如果cot 2A ∠=,3BC =,那么AC =________________.【答案】6 【分析】直接根据cot AC A BC∠=,将已知条件代入,便可求出AC.【详解】∠cot AC A BC∠==2,3BC =,∠cot 326AC BC A =⋅∠=⨯=,故答案为:6. 【点睛】本题考查余切的定义,正确掌握余切的公式是解题的关键.23.(2021·上海九年级专题练习)已知某斜坡的坡度1:3,当铅垂高度为3米时,水平宽度为_________________米【答案】9【分析】根据斜坡是铅垂高度与水平距离的比值,而这个斜坡的坡度为1:3,铅垂高度为3米,从而求出斜坡的水平宽度.【详解】解:∠斜坡的坡度为1:3,其铅垂高度为3米,∠这个斜坡的水平宽度为:3×3=9米,故答案为:9.【点睛】本题考查解直角三角形的应用中的坡度坡角问题,解题的关键是明确坡度是指斜坡的铅直高度与水平距离的比值.24.(2021·上海松江区·九年级一模)在Rt ABC 中,90C ∠=︒,6AC =,3cos 4A =,那么AB 的长为__.【答案】8【分析】根据余弦函数的定义即可直接求解. 【详解】解:∠3cos 4AC A AB ==,∠AB=34AC =634=8,故答案为:8. 【点睛】本题考查了余弦函数的定义,是所邻的直角边与斜边的比,理解定义是关键.25.(2021·上海徐汇区·九年级一模)如图,点P 在线段BC 上,AB BC ⊥,DP AP ⊥, CD DP ⊥,如果10BC =,2AB =, 1tan 2C =,那么 DP 的长是 _____ .【答案】5【分析】由已知条件,根据同角的余角相等得APB C ∠=∠,根据1tan 2C =得1tan 2AB APB BP ==∠,求出4BP =,得出6PC =,利用1tan 2C =和勾股定理即可得DP 的长. 【详解】解:∠AB BC ⊥,DP AP ⊥,CD DP ⊥,∠90B APD PDC ∠=∠=∠=︒,90C DPC ∠+∠=︒,90APB DPC ∠+∠︒=,∠APB C ∠=∠, ∠1tan 2C =,∠1tan tan 2AB APB C BP ===∠,∠2AB =,10BC =,∠4BP =,6PC =, 设DP 的长是x ,∠1tan 2DP C CD ==,∠22CD DP x ==,∠222PC DP CD =+,即()22262x x =+,解得x =(舍去负值). 【点睛】本题考查三角函数-正切,勾股定理等知识,解题的关键是学会利用数形结合的思想解决问题. 26.(2021·上海杨浦区·九年级一模)如果小明沿着坡度为1:2.4的山坡向上走了130米,那么他的高度上升了______米.【答案】3256【分析】设高度上升了h ,则水平前进了2.4h ,然后根据勾股定理解答即可.【详解】解:设高度上升了h ,则水平前进了2.4h ,130= ,解得h=50.故答案为50.【点睛】本题主要考查了坡度比与勾股定理得应用,根据坡度比和勾股定理列出关于h 的方程成为解答本题的关键.27.(2021·上海黄浦区·九年级一模)如果视线与水平线之间的夹角为36°,那么该视线与铅垂线之间的夹角为________度.【答案】126°或54°【分析】根据仰角或俯角是36°分类讨论,画出图形即可分别求出结论.【详解】解:当仰角是36°时,如下图所示由图可知:该视线与铅垂线之间的夹角为36°+90°=126°;当俯角是36°时,如下图所示由图可知:该视线与铅垂线之间的夹角为90°-36°=54°;综上:该视线与铅垂线之间的夹角为126°或54°.故答案为:126°或54°.【点睛】此题考查的是仰角和俯角的定义,根据仰角或俯角是36°分类讨论是解题关键.OP ,且OP与x轴负半轴夹角的正切28.(2021·上海黄浦区·九年级一模)已知点P位于第二象限内,5值为2,则点P的坐标是________.【答案】(【分析】根据题意,画出图形,过点P 作PA∠x 轴于A ,根据正切值可知2PA OA=,设OA=x ,则PA=2x ,利用勾股定理列出方程即可求出x ,从而求出OA 和PA ,即可求出结论.【详解】解:如下图所示,过点P 作PA∠x 轴于A由题意可知:tan∠POA=2∠2PA OA=设OA=x ,则PA=2x∠OA 2+PA 2=OP 2∠x 2+(2x )2=52 解得:x=PA=∠点P 在第二象限∠点P的坐标为((.【点睛】此题考查的是解直角三角形和求点的坐标,掌握利用锐角三角函数和勾股定理解直角三角形是解题关键.29.(2021·上海黄浦区·九年级一模)已知一个锐角的正切值比余切值大,且两者之和是133,则这个锐角的正切值为________.【答案】3【分析】设这个锐角为α,根据题意和三角函数的性质可知:1tan cot 33tan cot 1αααα⎧+=⎪⎨⎪⋅=⎩,解方程即可. 【详解】解:设这个锐角为α,∠1tan cot 33tan cot 1αααα⎧+=⎪⎨⎪⋅=⎩①②由①,得10cot tan 3αα=-③将③代入②,得tan tan 0131αα⎛⎫⋅-= ⎪⎝⎭解得:1tan 3α=或tan 3α= 当1tan 3α=时,∠cot α=3>tan α∠α的正切值比余切值大∠此时不符合题意,舍去; 当tan 3α=时,cot α=13<tan α∠此时符合题意.故答案为:3. 【点睛】此题考查的是锐角三角函数值的运算,掌握三角函数的性质是解题关键.30.(2021·上海浦东新区·九年级一模)如果从某一高处甲看低处乙的俯角为36度,那么从低处乙看高处甲的仰角是______度.【答案】36【分析】根据仰角以及俯角的定义,画出图形进而求出即可.【详解】解:如图所示:∠甲处看乙处为俯角∠DBA=36°,//AC BD ,∠乙处看甲处为:仰角∠CAB=∠DBA=36°.故答案为:36.【点睛】此题主要考查了仰角、俯角的定义以及平行线的性质,仰角是向上看的视线与水平线的夹角;俯角是向下看的视线与水平线的夹角.31.(2021·上海嘉定区·九年级一模)已知一个斜坡的坡度i =______.【答案】30【分析】坡度=坡角的正切值,据此直接解答.【详解】解:∠3tan α==,∠坡角=30°.【点睛】此题主要考查学生对坡度及坡角的理解及掌握.32.(2021·上海长宁区·九年级一模)如图,一辆汽车沿着坡度为1:i =50米,则它距离地面的垂直高度下降了 米.【答案】25【分析】设出垂直高度,表示出水平距离,利用勾股定理求解即可.【详解】解:设垂直高度下降了x 米.根据勾股定理可得:x 2+)2=502.解得x=25,即它距离地面的垂直高度下降了25米.【点睛】此题考查三角函数的应用.关键是熟悉且会灵活应用公式:tanα(坡度)=垂直高度÷水平宽度,综合利用了勾股定理.33.(2021·上海金山区·九年级一模)在Rt ABC ∆中,90C ∠=,15AB =,4sin 5A =,那么BC =______. 【答案】12【分析】直接利用正弦的定义列式求解即可.【详解】解:∠90C ∠=︒,4sin 5A =,∠4sin 5CB A AB == ∠15AB =∠4155CB =,解得:BC=12.故填:12. 【点睛】本题主要考查了正弦的定义,正确理解正弦的定义是解答本题的关键.34.(2021·上海金山区·九年级一模)在ABC ∆中,::1:2AB AC BC =tan B =______.【答案】2【分析】先由勾股定理逆定理判断出ABC ∆是直角三角形,再根据正切的定义求解即可.【详解】设2AB x AC x BC ===,,,则()22222225AB AC x x x BC +=+==, ABC ∆∴是直角三角形,且90A ∠=︒,2tan 2AC x B AB x∴===,故答案为:2 【点睛】此题考查了正切的定义.再直角三角形中锐角的正切值等于对边和邻边的比是解答此题的关键. 35.(2021·上海徐汇区·九年级一模)如图,在ABC 中,120ABC ∠=︒,12AB =,点D 在边AC 上,点E 在边BC 上,4sin 5ADE ∠=,5ED =,如果ECD 的面积是6,那么BC 的长是_____.【答案】6【分析】过点F 作EF AC ⊥交AC 于F ,过点A 作BC 的垂线交CB 的延长线于点H ,通过解直角三角形、勾股定理及三角形面积公式求出CF ,再通过解直角三角形求出CH ,即可解得答案.【详解】解;过点F 作EF AC ⊥交AC 于F ,∠4sin =5EF ADE ED∠=,又∠5ED =,∠4EF =,∠3DF ==,又∠114622ECD S CD EF CD =⋅=⋅=,∠3CD =,6CF =, 过点A 作BC 的垂线交CB 的延长线于点H ,∠90AHB ∠=︒,又∠120ABC ∠=︒,∠60ABH ∠=︒,∠12AB =,∠1cos602BH AB ︒==,∠6BH =,sin 602AH AB ︒==AH =在CEF △和ACH 中,tan EF AH ACH CF CH ∠== 即46=CH =6BC CH BH =-=【点睛】本题考查了解直角三角形及勾股定理,解题的关键是根据题意做出辅助线.36.(2021·上海徐汇区·九年级一模)如图,已知ABC 是边长为2的等边三角形,正方形DEFG 的顶点,D E 分别在边,AC AB 上,点,F G 在边BC 上,那么AD 的长是_____.【答案】6【分析】根据等边三角形以及正方形的性质,在Rt∠CDG 中运用正弦的定义建立方程求解即可.【详解】根据题可知,∠ADE 为等边三角形,即:AD=DE ,根据正方形的性质可知DE=DG ,DG∠BC ,∠C=60°,设AD=x ,则DG=x ,DC=AC -AD=2-x ,∠在Rt∠CDG 中,DG sinC CD =,即:602DG x sinC sin CD x =︒===-解得:6=x ,经检验6=x 是上述分式方程的解,故答案为:6.【点睛】本题考查正方形和等边三角形的性质,以及利用锐角三角函数解直角三角形,灵活根据题意找准合适的直角三角形是解题关键.37.(2021·上海徐汇区·九年级一模)已知甲、乙两楼相距30米,如果从甲楼底看乙楼顶,测得仰角为45︒,从乙楼顶看甲楼顶,测得俯角为30,那么甲楼高是_____米.【答案】(30-【分析】先依据题意画出图形,再根据等腰直角三角形的判定与性质可得30AB BC ==米,再根据解直角三角形可得CF 的长,然后根据线段的和差即可得.【详解】由题意,画出图形如下,其中AD 长表示甲楼的高度,BC 长表示乙楼的高度,AB 表示地面,且,,AD AB BC AB EC BC ⊥⊥⊥,45,30BAC ECD ∠=︒∠=︒,30AB =米,过点D 作DF BC ⊥于点F ,则四边形ABFD 是矩形,AD BF ∴=,30DF AB ==米,,45BC AB BAC ⊥∠=︒,Rt ABC ∴是等腰三角形,30AB BC ∴==米,30,ECD EC BC ∠=︒⊥,60DCF ∴∠=︒,在Rt CDF 中,30tan tan 60DF CF DCF ===∠︒(米),30BF BC CF ∴=-=-,则甲楼高30AD =-,故答案为:(30-. 【点睛】本题考查了等腰直角三角形的判定与性质、解直角三角形等知识点,依据题意,正确画出图形,并通过作辅助线,构造直角三角形是解题关键.38.(2021·上海九年级一模)如图,A 、B 、C 是小正方形的顶点,且每个小正方形的边长相同,那么BAC ∠的正弦值为_________________.【答案】2【分析】连接BC ,根据网格求出AB,BC,AC ,得到∠ABC 是直角三角形,再进行求解.【详解】∠每个小正方形的边长均为1,∠AB =BC =AC =∠AB 2=BC 2+AC 2,∠∠ABC 是直角三角形,∠sin∠BAC =2BC AB ==,故答案为2. 【点睛】此题主要考查正弦的求解,解题的关键熟知勾股定理的运用.39.(2021·上海杨浦区·九年级一模)如图,已知在ABC 中,90ACB ∠=︒,点G 是ABC 的重心,2CG =,4BC =,那么cos GCB ∠=______.【答案】23【分析】根据重心的性质和余弦函数的定义可以得到解答.【详解】解:如图,延长CG 与AB 交于点D ,过D 作DE∠CB 于点E ,∠G是∠ABC 的重心,∠CG=2GD,∠CG=2,∠GD=1,∠CD=2+1=3,∠∠ACB=90°,∠AC∠CB,∠AC∠DE,∠D是AB中点,∠E是CB中点,∠CE=122CB=,∠cos∠GCB=23CECD=,故答案为23.【点睛】本题考查三角形的综合运用,熟练掌握重心的性质和余弦函数的定义是解题关键.40.(2021·上海宝山区·九年级一模)如图,某堤坝的坝高为12米,如果迎水坡的坡度为1:0.75,那么该大坝迎水坡AB的长度为______米.【答案】15【分析】过点B作BC∠AC于C,由迎水坡的坡度为1:0.75,得到tan∠BAC=43=BCAC,求出AC=9米,再利用勾股定理求出答案.【详解】过点B作BC∠AC于C,∠迎水坡的坡度为1:0.75,∠tan∠BAC=43=BCAC,∠BC=12米,∠AC=9米,=15(米),故答案为:15..【点睛】此题考查坡度的定义,解直角三角形的实际应用,勾股定理,正确理解迎水坡的坡度为1:0.75得到tan∠BAC=43=BC AC 是解题的关键. 41.(2021·上海宝山区·九年级一模)已知等腰梯形上底为5,高为4,底角的余弦值为35,那么其周长为______. 【答案】26 【分析】作DF∠BC 于F ,AE∠BC 于E ,根据等腰梯形的性质就可以得出∠AEB∠∠DFC 就可以求出FC=BE ,然后根据底角的余弦值为35,求得BE ,AB ,从而求出周长. 【详解】解:如图示,作DF∠BC 于F ,AE∠BC 于E ,∠四边形ABCD 是等腰梯形,∠∠B=∠C ,AB=CD ,AD∠BC ,∠∠ADF=∠DFC=90°,∠∠AEF=∠DFE=∠ADF=90°,∠四边形AEFD 是矩形,5EF AD ,在∠AEB 和∠DFC 中 ∠∠AEB∠∠DFC (AAS ),∠BE=CF ;∠35cos E AB B B ,设3BE x =,则5AB x =, 根据勾股定理,有:2222534AEAB BE x x ,解之得:1x =(取正值), ∠3BE =,5AB =,∠3FCBE ,5DC AB ==, ∠周长AB BE EF FC CDAD 53535526, 故答案是:26.【点睛】本题考查了等腰梯形的性质的运用,三角函数,矩形的判定及性质的运用,等腰三角形的性质的运用,全等三角形的判定及性质的运用,能熟练应用相关性质是解题的关键.42.(2021·上海闵行区·九年级一模)在直角坐标平面内有一点(12,5)A ,点A 与原点O 的连线与x 轴的正半轴的夹角为θ,那么cos θ=_________.【答案】1213【分析】根据锐角三角函数的定义、坐标与图形性质以及勾股定理的知识求解即可.【详解】解:∠在直角坐标平面内有一点A (12,5)=13∠cos θ=1213.故答案为:1213. 【点睛】本题主要考査了解直角三角形、锐角三角函数的定义、坐标与图形性质以及勾股定理等知识点,掌握锐角三角函数的定义成为解答本题的关键.43.(2021·上海松江区·九年级一模)如图,ABC 在边长为1个单位的方格纸中,ABC 的顶点在小正方形顶点位置,那么ABC ∠的正弦值为_____.【分析】利用勾股定理可求出AC 、BC 、AB 的值,利用勾股定理逆定理可得∠ACB=90°,根据正弦的等于即可得答案.【详解】∠ABC 在边长为1个单位的方格纸中,ABC 的顶点在小正方形顶点位置,,BC=,∠(2+)2=2,∠∠ACB=90°,∠sin∠ABC=ACAB 【点睛】本题考查网格的特征、勾股定理及正弦的定义,在直角三角形中,锐角的正弦是角的对边与斜边的比;熟练掌握三角函数的定义是解题关键.44.(2021·上海嘉定区·九年级一模)如图,正方形ABEF 和正方形BCDE 的边长相等,点A 、B 、C 在同一条直线上.连接AD 、BD ,那么cot ADB ∠的值为______.【答案】3【分析】先构造以∠ADB 为内角的直角三角形,根据余切的定义求解即可.【详解】解:如图,作正方形ABEF 关于直线AB 对称的正方形ABGH ,连接AG ,BH ,相交于点O ;∠正方形ABGH ,∠∠AOD=90°,OA=OB=12AG , ∠正方形ABEF 和正方形BCDE 的边长相等,∠正方形ABGH 和正方形BCDE 的边长相等,∠AG=BD=2OA ,∠OD=OB+BD=3OA ,∠在Rt∠AOD 中,cot ADB ∠=3OD OA OA OA==3. 故答案为3.【点睛】本题考查了求角的余切值,掌握相关知识是解题的关键.45.(2021·上海金山区·九年级一模)已知在Rt ABC ∆中,90C ∠=,1BC =,2AC =,以点C 为直角顶点的Rt DCE ∆的顶点D 在BA 的延长线上,DE 交CA 的延长线于点G ,若1tan 2CED ∠=,CE GE =,那么BD 的长等于______.【答案】2【分析】根据题意画图,作AH∠CE 于H ,根据1tan tan 2CED BAC ∠==∠得出E BAC ∠=∠,由等边对等角得CGE ECG ∠=∠,根据三角形的内角和可得出AKC ECG ∠=∠,得出AK=AC ,利用等腰三角形三线合一得KH=CH ,再证出AH 为KCD △的中位线,可得出AK ,AD 的长,利用勾股定理求出AB ,AB+AD 即可得BD 的长.【详解】解:如图,作AH∠CE 于H ,∠1tan tan 2CED BAC ∠==∠,∠E BAC ∠=∠,∠CE GE =,∠CGE ECG ∠=∠, ∠AKC ECG ∠=∠,∠AK=AC=2,∠AH∠CE ,90ECD ∠=,∠KH=CH ,//AH CD ,∠AH 为KCD △的中位线,∠A 为DK 的中点,DK=2AK=4,AD=AK=2,∠90ACB ∠=,1BC =,2AC =,=∠BD=AD+AB=2+.故答案为:2.【点睛】本题考查三角函数-正切,等腰三角形的判定和性质,三角形的中位线,勾股定理等知识,作垂线构造三角形的中位线是解题的关键.。
2020-2021学年上海市金山区九年级(上)期末数学试卷(一模)

2020-2021学年上海市金山区九年级(上)期末数学试卷(一模)题号一二三总分得分第I卷(选择题)一、选择题(本大题共6小题,共24.0分)1.下列二次函数的图象中,其对称轴是x=1的为()A. y=x2+2xB. y=x2−2xC. y=x2−2D. y=x2−4x2.下列各点中,在二次函数y=−x2的图象上的是()A. (1,−1)B. (2,−2)C. (−2,4)D. (2,4)3.已知Rt△ABC中,∠A=90°,则bc是∠B的()A. 正切B. 余切C. 正弦D. 余弦4.已知α是锐角,且满足2sin(α+20°)=√3,则α的度数为()A. 80°B. 60°C. 40°D. 10°5.如果a⃗=2b⃗ (a⃗,b⃗ 均为非零向量),那么下列结论错误的是()A. a⃗//b⃗B. a⃗−2b⃗ =0C. b⃗ =12a⃗ D. |a⃗|=2|b⃗ |6.如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,以点A为圆心作圆,如果圆A与线段BC没有公共点,那么圆A的半径r的取值范围是()A. 5≥r≥3B. 3<r<5C. r=3或r=5D. 0<r<3或r>5第II卷(非选择题)二、填空题(本大题共12小题,共48.0分)7.化简:32a⃗−(a⃗−32b⃗ )=______.8.已知函数f(x)=x−22x,那么f(3)=______.9. 如图,二次函数y =ax 2+bx +c 的图象与x 轴交于(3,0),对称轴是直线x =1,当函数值y >0时,自变量x 的取值范围是____.10. 正五边形的中心角的度数是______ .11. 已知⊙O 1的半径长为4,⊙O 2的半径长为r ,圆心距O 1O 2=6,当⊙O 1与⊙O 2外切时,r 的长为______.12. 在Rt △ABC 中,∠ACB =90°,BC =6,sinA =35,则AB =______. 13. 如图,在△ABC 中,∠B =45°,tanC =12,AB =√2,则AC =______.14. 如图.△ABC 的中线AD 、BE 相交于点G ,过点G 作GH//AC 交BC 于点H ,如果GH =2,那么AC =______.15. 如图,在△ABC 中,点D 在边AC 上,且CD =2AD.设AB ⃗⃗⃗⃗⃗ =a ⃗ ,AC ⃗⃗⃗⃗⃗ =b ⃗ ,那么BD ⃗⃗⃗⃗⃗⃗ =______.(结果用向量a ⃗ 、b ⃗ 的式子表示)16.如图,B,C,D,E为⊙A上的点,DE=5,∠BAC+∠DAE=180°,则圆心A到弦BC的距离为______.17.如图所示,在▱ABCD中,点E在边DC上,DE:EC=3:1,连接AE交BD于点F,则△DEF的面积与△BAF的面积之比为______.18.如图,点D在△ABC的边BC上,∠C+∠BAD=∠DAC,tan∠BAD=4,AD=√65,CD=13,则7线段AC的长为______.三、解答题(本大题共7小题,共78.0分)19.如图,在Rt△ABC中,∠C=90°,点D是AC边上一点,tan∠DBC=4,且BC=6,3 AD=4.求cos A的值.20.如图,已知AC和BD相交于点O,且AB//DC,OA=OB.求证:OC=OD.21.如图,已知二次函数y=ax2−4x+c的图象经过点A和点B.(1)求该二次函数的表达式;(2)写出该抛物线的对称轴及顶点坐标;(3)若点P(m,m)在该函数图象上,求m的值.22.如图,小山的一个横断面是梯形BCDE,EB//DC,其中斜坡DE的坡长为13米,坡度i=1:2.4,小山上有一座铁塔AB,在山坡的坡顶E处测得铁塔顶端A的仰角为45°,在与山坡的坡底D相距5米的F处测得铁塔顶端A的仰角为31°(点F、D、C在一直线上),求铁塔AB的高度.(参考数值:sin31°≈0.52,cos31°≈0.86,tan31°≈0.6)23.如图,四边形ABCD是菱形,点E在AB延长线上,连接AC,DE.DE分别交BC,AC于点F,G,且CD·AE=AC·AG.求证:(1)△ABC∽△AGE;(2)AB2=DE·DG.<a<0) 24.如图,点A,B,C都在抛物线y=ax2−2amx+am2+2m−5(其中−14上,AB//x轴,∠ABC=135°,且AB=4.(1)填空:抛物线的顶点坐标为_____(用含m 的代数式表示); (2)求△ABC 的面积(用含a 的代数式表示);(3)若△ABC 的面积为2,当2m −5≤x ≤2m −2时,y 的最大值为2,求m 的值.25. 如图①,在Rt △ABC 中,∠ABC =90°,AB 是⊙O 的直径,⊙O 交AC 于点D ,过点D 的直线交BC 于点E ,交AB 的延长线于点P ,∠A =∠PDB . (1)求证:PD 是⊙O 的切线;(2)若AB =4,DA =DP ,试求弧BD 的长;(3)如图②,点M 是AB ⏜的中点,连结DM ,交AB 于点N.若tanA =12,求DNMN的值.答案和解析1.【答案】B【解析】解:∵y=x2+2x=(x+1)2−1,∴y=x2+2x的对称轴是直线x=−1,故选项A不符合题意;∵y=x2−2x=(x−1)2−1,∴y=x2−2x的对称轴是直线x=1,故选项B符合题意;y=x2−2的对称轴是直线x=0,故选项C不符合题意,∵y=x2−4x=(x−2)2−4,∴y=x2−4x的对称轴是直线x=2,故选项D不符合题意;故选:B.根据各个选项中的函数解析式可以得到相应的对称轴,从而可以解答本题.本题考查二次函数的图象、二次函数的性质,解答本题的关键是明确题意,利用二次函数的性质解答.2.【答案】A【解析】解:当x=1时,y=−x2=−1,当x=−2时,y=−x2=−4,当x=2时,y=−x2=−4,所以点(1,−1)在二次函数y=−x2的图象上.故选:A.分别计算自变量为1和−2、2所对应的函数值,然后根据二次函数图象上点的坐标特征进行判断.本题考查了二次函数图象上点的坐标特征:二次函数图象上点的坐标满足其解析式.3.【答案】A【解析】解:如图,tanB=b.c故选A.根据题意画出直角三角形,根据锐角三角函数的定义便可直接解答.本题考查锐角三角函数的定义及运用:在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边.4.【答案】C【解析】解:∵2sin(α+20°)=√3,∴sin(α+20°)=√3,2∴α+20°=60°,∴α=40°.故选C.首先利用特殊角的三角函数值求出α+20°的值,进而求出α即可.此题主要考查了特殊角的三角函数值,得出α+20°的值是解题关键.5.【答案】B【解析】解:A、正确.因为a⃗=2b⃗ (a⃗,b⃗ 均为非零向量),所以a⃗与b⃗ 是方向相同的向量,即a⃗//b⃗ ;B、错误.应该是a⃗−2b⃗ =0⃗;a⃗;C、正确.由a⃗=2b⃗ 可得b⃗ =12D、正确.因为a⃗=2b⃗ 所以|a⃗|=2|b⃗ |;故选B.根据平行向量以及模的定义的知识求解即可求得答案,注意掌握排除法在选择题中的应用.本题考查了平面向量,注意,平面向量既有大小,又由方向,平行向量,也叫共线向量,是指方向相同或相反的非零向量.零向量和任何向量平行.6.【答案】D【解析】解:∵在Rt△ABC中,∠C=90°,AC=3,BC=4,以点A为圆心作圆,当圆A的半径0<r<3或r>5时,圆A与线段BC没有公共点;故选:D.根据直线与圆的位置关系得出相切时有一交点,再结合图形即可得出答案.此题主要考查了直线与圆的位置关系,结合题意画出符合题意的图形,从而得出答案.7.【答案】12a⃗+32b⃗【解析】解:原式=32a⃗−a⃗+32b⃗ =12a⃗+32b⃗ .故答案是:12a⃗+32b⃗ .平面向量的加减计算法则与实数的加减计算法则相同.考查了平面向量,解答此类题目时,直接去括号,然后计算加减法即可.8.【答案】16【解析】解:当x=3时,f(3)=3−22×3=16.故答案为:16.【分析】把x=3代入函数关系式,计算求值即可.本题考查求函数值.题目比较简单,已知函数解析式时,求函数值就是求代数式的值.9.【答案】−1<x<3【解析】解:∵二次函数y=ax2+bx+c的图象与x轴交于(3,0),对称轴是直线x=1,∴图象与x轴的另一个交点为:(−1,0),故当函数值y>0时,自变量x的取值范围是:−1<x<3.故答案为:−1<x<3.直接利用二次函数的对称性得出图象与x轴的另一个交点,进而得出答案.此题主要考查了抛物线与x轴的交点以及二次函数的性质,正确利用数形结合分析是解题关键.10.【答案】72°【解析】解:正五边形的中心角为:360°5=72°.故答案为:72°.根据正多边形的圆心角定义可知:正n边形的圆中心角为360°n,则代入求解即可.此题考查了正多边形的中心角的知识.题目比较简单,注意熟记定义.11.【答案】2【解析】解:∵⊙O1的半径长为4,⊙O2的半径长为r,圆心距O1O2=6,当⊙O1与⊙O2外切时,∴r+4=6,解得:r=2,故答案为:2;根据两圆的位置关系和数量之间的联系解答即可.本题考查的是圆与圆的位置关系与数量之间的联系,关键是根据两圆外切⇔d=R+r 解答.12.【答案】10【解析】【分析】本题主要考查锐角三角函数的定义,解题的关键是熟练掌握正弦函数的定义.由sinA=BCAB 知AB=BCsinA,代入计算可得.【解答】解:在Rt△ABC中,∵sinA=BCAB,BC=6,∴AB=BCsinA =635=10,故答案为10.13.【答案】√5【解析】解:过点A作AD⊥BC,垂足是点D,∵AB=√2,∴AD2+BD2=AB2=2,∵∠B=45°,∴∠BAD=∠B=45°,∴AD=BD,∴AD2=BD2=1,∴AD=BD=1,∵tanC=12,∴ADCD =12,∴CD=2,∴AC=√AD2+CD2=√12+22=√5.故答案为:√5.先过点A作AD⊥BC,垂足是点D,得出AD2+BD2=AB2=2,再根据∠B=45°,得出AD=BD=1,然后根据tanC=12,得出ADCD=12,CD=2,最后根据勾股定理即可求出AC.此题考查了解直角三角形,用到的知识点是勾股定理、解直角三角形等,关键是作出辅助线,构造直角三角形.14.【答案】6【解析】解:∵△ABC的中线AD、BE相交于点G,∴AGGD=2,∵GH//AC,∴GHAC =GDAD=13,∵GH=2∴AC=6,故答案为:6根据三角形重心的性质和平行线分线段成比例解答即可.本题考查的是平行线分线段成比例和三角形的重心的概念和性质,掌握三角形的重心是三角形三条中线的交点,且重心到顶点的距离是它到对边中点的距离的2倍是解题的关键.15.【答案】13b⃗ −a⃗【解析】解:∵CD =2AD ,AC ⃗⃗⃗⃗⃗ =b ⃗ , ∴AD ⃗⃗⃗⃗⃗⃗ =13AC ⃗⃗⃗⃗⃗ =13b ⃗ ,∵BD ⃗⃗⃗⃗⃗⃗ =BA ⃗⃗⃗⃗⃗ +AD⃗⃗⃗⃗⃗⃗ , ∴BD ⃗⃗⃗⃗⃗⃗ =−a ⃗ +13b ⃗ ,故答案为:13b⃗ −a ⃗ . 求出AD ⃗⃗⃗⃗⃗⃗ ,根据BD ⃗⃗⃗⃗⃗⃗ =BA ⃗⃗⃗⃗⃗ +AD⃗⃗⃗⃗⃗⃗ 求解即可. 本题考查平面向量,三角形法则等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.16.【答案】52【解析】 【分析】本题考查的是垂径定理、三角形中位线定理、圆心角、弧、弦之间的关系,掌握垂径定理、三角形中位线定理是解题的关键.延长CA 交⊙A 于F ,连接BF ,作AH ⊥BC 于H ,根据圆心角、弧、弦之间的关系定理求出BF ,根据垂径定理得到CH =HB ,根据三角形中位线定理计算即可. 【解答】解:延长CA 交⊙A 于F ,连接BF ,作AH ⊥BC 于H ,∵∠BAC +∠DAE =180°,∠BAC +∠BAF =180°, ∴∠BAF =∠DAE , ∴BF⏜=DE ⏜, ∴BF =DE =5, ∵AH ⊥BC ,∴CH =HB ,又CA =AF , ∴AH =12BF =52, 故答案为:52.17.【答案】9:16【解析】【分析】可证明△DFE∽△BFA,根据相似三角形的面积之比等于相似比的平方即可得出答案.本题考查了平行四边形的性质以及相似三角形的判定和性质,注:相似三角形的面积之比等于相似比的平方.【解答】解:∵四边形ABCD为平行四边形,∴DC//AB,∴△DFE∽△BFA,∵DE:EC=3:1,∴DE:DC=3:4,∴DE:AB=3:4,∴S△DFE:S△BFA=9:16.故答案为:9:16.18.【答案】4√13【解析】解:作∠DAE=∠BAD交BC于E,作DF⊥AE交AE于F,作AG⊥BC交BC于G.∵∠C+∠BAD=∠DAC,∴∠CAE=∠ACB,∴AE=EC,∵tan∠BAD=4,7∴设DF=4x,则AF=7x,在Rt△ADF中,AD2=DF2+AF2,即(√65)2=(4x)2+(7x)2,解得x1=−1(不合题意舍去),x2=1,∴DF=4,AF=7,设EF=y,则CE=7+y,则DE=6−y,在Rt△DEF中,DE2=DF2+EF2,即(6−y)2=42+y2,,解得y=53∴DE =6−y =133,AE =263,∴设DG =z ,则EG =133−z ,则(√65)2−z 2=(263)2−(133−z)2, 解得z =1, ∴CG =12,在Rt △ADG 中,AG =√AD 2−DG 2=8, 在Rt △ACG 中,AC =2+CG 2=4√13. 故答案为:4√13.作∠DAE =∠BAD 交BC 于E ,作AF ⊥BC 交BC 于F ,作AG ⊥BC 交BC 于G.根据三角函数设DF =4x ,则AF =7x ,在Rt △ADF 中,根据勾股定理得到DF =4,AF =7,设EF =y ,则CE =7+y ,则DE =6−y ,在Rt △DEF 中,根据勾股定理得到DE =133,AE =263,设DG =z ,则EG =133−z ,则(√65)2−z 2=(263)2−(133−z)2,依此可得CG =12,在Rt △ADG 中,据勾股定理得到AG =8,在Rt △ACG 中,据勾股定理得到AC =4√13. 考查了勾股定理,等腰三角形的判定与性质,解直角三角形,解题的关键是根据勾股定理得到AG 和CG 的长.19.【答案】解:在Rt △DBC 中,∵∠C =90°,BC =6,∴tan∠DBC =CD BC=43. ∴CD =8.∴AC =AD +CD =12. 在Rt △ABC 中,由勾股定理得, AB =√AC 2+BC 2=√122+62=6√5, ∴cosA =ACAB =65=25√5.【解析】先解Rt △DBC ,求出DC 的长,然后根据AC =AD +DC 即可求得AC ,再由勾股定理得到AB ,最后再求cos A 的值即可.本题主要考查了解直角三角形.熟练掌握三角函数的定义是解题的关键.20.【答案】证明:∵AB//DC ,∴∠A =∠C ,∠B =∠D , ∵OA =OB , ∴∠A =∠B ,∴∠C =∠D , ∴OC =OD .【解析】利用平行线的性质可求得∠A =∠C ,∠B =∠D ,利用OA =OB ,可求得∠A =∠B ,则可求得∠C =∠D ,则可证得OC =OD .本题主要考查等腰三角形的判定和性质及平行线的性质,利用平行线的性质及等腰三角形的性质证得∠C =∠D 是解题的关键.21.【答案】解:(1)将A(−1,−1),B(3,−9)代入,得{a +4+c =−19a −12+c =−9, ∴a =1,c =−6, ∴y =x 2−4x −6;(2)由y =x 2−4x −6=(x −2)2−10, 对称轴:直线x =2, 顶点坐标:(2,−10);(3)∵点P(m,m)在函数图象上, ∴m 2−4m −6=m , ∴m =6或−1.【解析】本题主要考查待定系数法求二次函数解析式及二次函数的对称轴、顶点坐标,掌握二次函数的性质及待定系数法是解题的关键.(1)由条件可知点A 和点B 的坐标,代入解析式可得到关于a 和c 的二元一次方程组,解得a 和c ,可写出二次函数的解析式;(2)利用配方法写出把二次函数写成顶点式,即可得其对称轴与顶点坐标; (3)把点的坐标代入可求得m 的值.22.【答案】解:延长AB 交DC 于G ,过E 作EH ⊥CD 于H ,则四边形EHGB 是矩形,∵斜坡DE 的坡长为13米,坡度i =1:2.4, ∴设EH =5x ,则DH =12x ,∵EH2+DH2=DE2,∴(5x)2+(12x)2=132,∴x=1(负值舍去),∴EH=5,DH=12,∵EB//DC,∴∠ABE=∠AGH=90°,∵∠AEB=45°,∴AB=BE,∴HG=AB,∴FG=5+12+AB,AG=AB+5,∵∠F=31°,∴tanF=tan31°=AGFG =AB+517+AB=0.6,∴AB=13米,答:铁塔AB的高度是13米.【解析】延长AB交DC于G,过E作EH⊥CD于H,则四边形EHGB是矩形,根据勾股定理得到EH=5,DH=12,根据三角函数的定义解直角三角形,然后列方程可得到结论.本题考查了解直角三角形的应用−仰角俯角问题,解直角三角形的应用−坡度坡角问题,矩形的性质,掌握的作出辅助线是解题的关键.23.【答案】证明:(1)∵CD⋅AE=AC⋅AG.∴CDAG =ACAE,∵四边形ABCD是菱形,∴AB=CD,∴ABAG =ACAE,∵∠BAC=∠GAE,∴△ABC∽△AGE;(2)∵△ABC∽△AGE,∴∠ACB=∠E,∵四边形ABCD是菱形,∴AB=AD,BC//AD,∴∠ACB =∠CAD =∠E , ∵∠ADG =∠ADE , ∴△ADG∽△EDA , ∴AD DE=DG AD,∴AD 2=DE ⋅DG , ∴AB 2=DE ⋅DG .【解析】本题考查相似三角形的判定与性质、菱形的性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.(1)只要证明ABAG =ACAE ,又∠BAC =∠GAE ,即可证明△ABC∽△AGE ; (2)只要证明△ADG∽△EDA ,可得ADDE =DGAD ,推出AD 2=DE ⋅DG 即可证明.24.【答案】(1)(m,2m −5);(2)S △ABC =−8a+2a;(3)72或10+2√10.【解析】[分析](1)利用配方法将二次函数解析式由一般式变形为顶点式,此题得解;(2)过点C 作直线AB 的垂线,交线段AB 的延长线于点D ,由AB//x 轴且AB =4,可得出点B 的坐标为(m +2,4a +2m −5),设BD =t ,则点C 的坐标为(m +2+t,4a +2m −5−t),利用二次函数图象上点的坐标特征可得出关于t 的一元二次方程,解之取其正值即可得出t 值,再利用三角形的面积公式即可得出S △ABC 的值;(3)由(2)的结论结合S △ABC =2可求出a 值,分三种情况考虑:①当m >2m −2,即m <2时,x =2m −2时y 取最大值,利用二次函数图象上点的坐标特征可得出关于m 的一元二次方程,解之可求出m 的值;②当2m −5≤m ≤2m −2,即2≤m ≤5时,x =m 时y 取最大值,利用二次函数图象上点的坐标特征可得出关于m 的一元一次方程,解之可求出m 的值;③当m <2m −5,即m >5时,x =2m −5时y 取最大值,利用二次函数图象上点的坐标特征可得出关于m 的一元一次方程,解之可求出m 的值.综上即可得出结论. [详解]解:(1)∵y =ax 2−2amx +am 2+2m −5=a(x −m)2+2m −5, ∴抛物线的顶点坐标为(m,2m −5), 故答案为:(m,2m −5);(2)过点C 作直线AB 的垂线,交线段AB 的延长线于点D ,如图所示,∵AB//x轴,且AB=4,∴点B的坐标为(m+2,4a+2m−5),∵∠ABC=135°,∴设BD=t,则CD=t,∴点C的坐标为(m+2+t,4a+2m−5−t),∵点C在抛物线y=a(x−m)2+2m−5上,∴4a+2m−5−t=a(2+t)2+2m−5,整理,得:at2+(4a+1)t=0,解得:t1=0(舍去),t2=−4a+1a,∴S△ABC=12AB⋅CD=−8a+2a;(3)∵△ABC的面积为2,∴−8a+2a=2,解得:a=−15,∴抛物线的解析式为y=−15(x−m)2+2m−5.分三种情况考虑:①当m>2m−2,即m<2时,则当x=2m−2时,y取最大值,有−15(2m−2−m)2+2m−5=2,整理,得:m2−14m+39=0,解得:m1=7−√10(舍去),m2=7+√10(舍去);②当2m−5≤m≤2m−2,即2≤m≤5时,则当x=m时,y取最大值,有2m−5=2,解得:m=72;③当m<2m−5,即m>5时,则当x=2m−5时,y取最大值,(2m−5−m)2+2m−5=2,有−15整理,得:m2−20m+60=0,解得:m3=10−2√10(舍去),m4=10+2√10.或10+2√10.综上所述:m的值为72[点睛]本题考查了二次函数解析式的三种形式、二次函数图象上点的坐标特征、等腰直角三角形、解一元二次方程以及二次函数的最值,解题的关键是:(1)利用配方法将二次函数解析式变形为顶点式;(2)利用等腰直角三角形的性质找出点C的坐标;(3)分m<2、2≤m≤5及m>5三种情况考虑.25.【答案】证明:(1)连结OD,∵AB是⊙O的直径,∴∠ADB=90°,∴∠A+∠ABD=90°,又∵OA=OB=OD,∴∠BDO=∠ABD,又∵∠A=∠PDB,∴∠PDB+∠BDO=90°,即∠PDO=90°,且D在圆上,∴PD是⊙O的切线(2)设∠A=x°,∵DA=DP,∴∠A=∠P=x°,∴∠DBA=∠P+∠BDP=x°+x°=2x°,在△ABD中,∠A+∠ABD=90°,∴x°+2x°=90o,即x=30,∴∠DOB=60°,∴弧BD长=60°×π×2180∘=23π(3)连结OM,过D作DF⊥AB于点F,∴点M是的AB⏜的中点,∴OM⊥AB,∵tanA=12=BDAD,∴设BD=x,则AD=2x,AB=√5x=2OM,∴OM=√5x2,在Rt△BDF中,S△ADB=12×AB×DF=12×AD×DB∴DF=2√55x,∵∠MON=∠DFN=90°,∠DNF=∠MNO ∴△OMN∽△FDN∴DNMN =DFOM=2√55x√52x=45.【解析】(1)由圆周角的定理可得∠ADB=90°,可得∠A+∠ABD=90°,可求∠PDB+∠BDO=90°,可得结论;(2)设∠A=x,由等腰三角形的性质和三角形外角的性质可得∠DBA=∠P+∠BDP= x+x=2x,由三角形内角和可求x的值,由弧长公式可求弧BD的长;(3)连结OM,过D作DF⊥AB于点F,设BD=x,则AD=2x,AB=√5x=2OM,可求OM,DF的长,通过证明△OMN∽△FDN,可求DNMN的值.本题是圆的综合题,考查了圆的知识,弧长公式,相似三角形的判定和性质,勾股定理等知识,添加恰当辅助线构造相似三角形是本题的关键.。
上海市金山区2021届九年级第一学期期末质量检测数学试题(一模)

上海市金山区2019届九年级第一学期期末质量检测数学试题(一模)学校:___________姓名:___________班级:___________考号:___________一、单选题1.下列函数是二次函数的是( )A .y x =B .1y x =C .22y x x =-+D .21y x = 2.在Rt △ABC 中,∠C =90°,那么sin ∠B 等于( )A .AC AB B .BC AB C .AC BCD .BC AC 3.如图,已知BD 与CE 相交于点A ,ED∥BC,AB=8,AC=12,AD=6,那么AE 的长等于( )A .4B .9C .12D .164.已知e 是一个单位向量,a 、b 是非零向量,那么下列等式正确的是( ) A .a e a = B .e b b = C .1a e a = D .11a b a b = 5.二次函数y=ax 2+bx+c(a≠0)的图象如图,a ,b ,c 的取值范围( )A .a<0,b<0,c<0B .a<0,b>0,c<0C .a>0,b>0,c<0D .a>0,b<0,c<06.如图,在Rt△ABC 中,∠C=90°,BC=2,∠B=60°,⊙A 的半径为3,那么下列说法正确的是( )A .点B 、点C 都在⊙A 内B .点C 在⊙A 内,点B 在⊙A 外 C .点B 在⊙A 内,点C 在⊙A 外D .点B 、点C 都在⊙A 外二、填空题 7.已知二次函数f(x)=x 2-3x+1,那么f(2)=_________.8.已知抛物线y=2112x -,那么抛物线在y 轴右侧部分是_________(填“上升的”或“下降的”).9.已知52x y =,那么x y y+=__. 10.已知α是锐角1sin 2α=,那么cos α=_________. 11.一个正n 边形的中心角等于18°,那么n =_____.12.已知点P 是线段AB 的黄金分割点,P A >PB ,AB =4 cm ,则P A =____cm . 13.如图,为了测量铁塔AB 高度,在离铁塔底部(点B )60米的C 处,测得塔顶A 的仰角为30°,那么铁塔的高度AB=________米.14.已知⊙O 1、⊙O 2的半径分别为2和5,圆心距为d,若⊙O 1与⊙O 2相交,那么d 的取值范围是_________.15.如图,已知O 为△ABC 内一点,点D 、E 分别在边AB 和AC 上,且25AD AB =,DE∥BC,设OB b =、OC C =,那么DE ______(用b 、c 表示).16.如图,已知⊙O 1与⊙O 2相交于A 、B 两点,延长连心线O 1O 2交⊙O 2于点P ,联结PA 、PB ,若∠APB=60°,AP=6,那么⊙O 2的半径等于________.17.如图,在△ABC 中,AD 、BE 分别是边BC 、AC 上的中线,AB=AC=5,cos∠C=45,那么GE=_______.18.如图,在Rt△ABC 中,∠C=90°,AC=8,BC=6.在边AB 上取一点O ,使BO=BC ,以点O 为旋转中心,把△ABC 逆时针旋转90°,得到△A′B′C′(点A 、B 、C 的对应点分别是点A′、B′、C′、),那么△ABC 与△A′B′C′的重叠部分的面积是_________.三、解答题19.计算:2cot 30cos 45tan 60cos 45sin 302sin 60︒︒-+︒-︒⋅︒︒. 20.已知二次函数y=x 2-4x-5,与y 轴的交点为P ,与x 轴交于A 、B 两点.(点B 在点A 的右侧)(1)当y=0时,求x 的值.(2)点M (6,m )在二次函数y=x 2-4x-5的图像上,设直线MP 与x 轴交于点C ,求cot∠MCB 的值.21.如图,已知某水库大坝的横断面是梯形ABCD,坝顶宽AD是6米,坝高24米,背水坡AB的坡度为1:3,迎水坡CD的坡度为1:2.求:(1)背水坡AB的长度.(2)坝底BC的长度.⌢的中点,CH⊥AB于H,垂22.如图,己知AB是⊙C的直径,C为圆上一点,D是BC足为H,连OD交弦BC于E,交CH于F,联结EH.(1)求证:△BHE∽△BCO.(2)若OC=4,BH=1,求EH的长.23.如图,M是平行四边形ABCD的对角线上的一点,射线AM与BC交于点F,与DC的延长线交于点H.(1)求证:AM2=MF.MH(2)若BC2=B D.DM,求证:∠AMB=∠AD C.24.已知抛物线y=x2+bx+c经过点A(0,6),点B(1,3),直线l1:y=kx(k≠0),直线l2:y=-x-2,直线l1经过抛物线y=x2+bx+c的顶点P,且l1与l2相交于点C,直线l2与x轴、y轴分别交于点D、E.若把抛物线上下平移,使抛物线的顶点在直线l2上(此时抛物线的顶点记为M),再把抛物线左右平移,使抛物线的顶点在直线l1上(此时抛物线的顶点记为N).(1)求抛物y=x2+bx+c线的解析式.(2)判断以点N为圆心,半径长为4的圆与直线l2的位置关系,并说明理由.(3)设点F、H在直线l1上(点H在点F的下方),当△MHF与△OAB相似时,求点F、H的坐标(直接写出结果).参考答案1.C【解析】【分析】根据一次函数的定义,二次函数的定义对各选项分析判断利用排除法求解.【详解】A. y=x 是一次函数,故本选项错误;B. y=1x是反比例函数,故本选项错误; C.y=x-2+x 2是二次函数,故本选项正确; D.y=21x 右边不是整式,不是二次函数,故本选项错误. 故答案选C.【点睛】本题考查的知识点是二次函数的定义,解题的关键是熟练的掌握二次函数的定义. 2.A【分析】根据锐角三角函数的定义得出sinB 等于∠B 的对边除以斜边,即可得出答案.【详解】根据在△ABC 中,∠C=90°,那么sinB=B 的对边斜边 =AC AB, 故答案选A.【点睛】本题考查的知识点是锐角三角函数的定义,解题的关键是熟练的掌握锐角三角函数的定义. 3.B【解析】【分析】由于ED∥BC,可证得△AB C ∽△ADE ,根据相似三角形所得比例线段,即可求得AE 的长.【详解】∵ED∥BC,∴△AB C∽△ADE,∴BADA=ACAE,∴BADA=ACAE=86,即AE=9;∴AE=9.故答案选B.【点睛】本题考查的知识点是相似三角形的判定与性质,解题的关键是熟练的掌握相似三角形的判定与性质.4.B【解析】【分析】长度不为0的向量叫做非零向量,向量包括长度及方向,而长度等于1个单位长度的向量叫做单位向量,注意单位向量只规定大小没规定方向,则可分析求解.【详解】A. 由于单位向量只限制长度,不确定方向,故错误;B. 符合向量的长度及方向,正确;C. 得出的是a的方向不是单位向量,故错误;D. 左边得出的是a的方向,右边得出的是b的方向,两者方向不一定相同,故错误.故答案选B.【点睛】本题考查的知识点是平面向量,解题的关键是熟练的掌握平面向量.5.D【解析】试题分析:根据二次函数的图象依次分析各项即可。
2021上海初三数学一模试题分类整理(几何综合题)
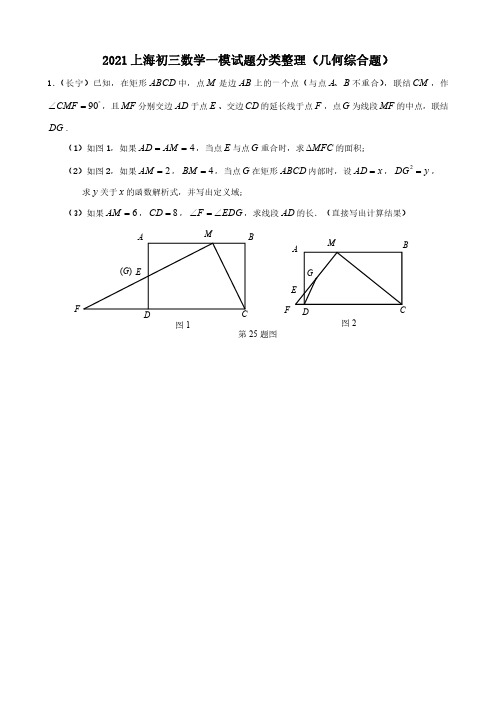
2021上海初三数学一模试题分类整理(几何综合题)1.(长宁)已知,在矩形ABCD 中,点M 是边AB 上的一个点(与点A B 、不重合),联结CM ,作90CMF ︒∠=,且MF 分别交边AD 于点E 、交边CD 的延长线于点F ,点G 为线段MF 的中点,联结DG .(1)如图1,如果4AD AM ==,当点E 与点G 重合时,求MFC ∆的面积;(2)如图2,如果2AM =,4BM =,当点G 在矩形ABCD 内部时,设AD x =,2DG y =,求y 关于x 的函数解析式,并写出定义域;(3)如果6AM =,8CD =,F EDG ∠=∠,求线段AD 的长.(直接写出计算结果)ABCDEF(G )M图1ABCDEFGM图2第25题图2.(杨浦)如图,已知在Rt△ABC 中,∠ACB =90°,AC =BC =4,点D 为边BC 上一动点(与点B 、C 不重合),点E 为边AB 上一点,∠EDB =∠ADC ,过点E 作EF ⊥AD ,垂足为点G ,交射线AC 于点F .(1)如果点D 为边BC 的中点,求∠DAB 的正切值;(2)当点F 在边AC 上时,设CD =x ,CF =y ,求y 关于x 的函数解析式及定义域;(3)联结DF ,如果△CDF 与△AGE 相似,求线段CD 的长.备用图ABC第25题图ABCEDG F3.(徐汇)如图,在ABC Rt ∆中,︒=∠90ACB ,12=AC ,5=BC ,点D 是边AC 上的动点,以CD 为边在ABC ∆外作正方形CDEF ,分别联结AE 、BE ,BE 与AC 交于点G .(1)当BE AE ⊥时,求正方形CDEF 的面积;(2)延长ED 交AB 于点H ,如果BEH ∆和ABG ∆相似,求ABE ∠sin 的值;(3)当AE AG =时,求CD 的长.(备用图)BAC(第25题图)GFED BAC4.(松江)如图,已知在等腰△ABC中,AB=AC=,tan∠ABC=2,BF⊥AC,垂足为F,点D是边AB上一点(不与A,B重合).(1)求边BC的长;(2)如图2,延长DF交BC的延长线于点G,如果CG=4,求线段AD的长;(3)过点D作DE⊥BC,垂足为E,DE交BF于点Q,联结DF,如果△DQF和△ABC相似,求线段BD的长.D·B AFC(图1)DBAFC(图2)G BAFC(备用图)5.(普陀)如图,矩形ABCD 中,1AB =,3BC =,点E 是边BC 上一个动点(不与点B 、C 重合),AE 的垂线AF 交CD 的延长线于点F .点G 在线段EF 上,满足:1:2FG GE =.设BE x =.(1)求证:AD DFAB BE=;(2)当点G 在△ADF 的内部时,用x 的代数式表示ADG ∠的余切;(3)当∠FGD =∠AFE 时,求线段BE 的长.F图14CB A DE G备用图CBAD6.(浦东)四边形ABCD 是菱形,∠B ≤90°,点E 为边BC 上一点,联结AE ,过点E 作EF ⊥AE ,EF 与边CD 交于点F ,且EC =3CF .(1)如图1,当∠B =90°时,求ABE S △与ECF S △的比值;(2)如图2,当点E 是边BC 的中点时,求cos B 的值;(3)如图3,联结AF ,当∠AFE =∠B 且CF =2时,求菱形的边长.(第25题图3)(第25题图2)(第25题图1)7.(闵行)如图,在矩形ABCD 中,2AB =,1AD =,点E 在边AB 上(点E 与端点A 、B 不重合),联结DE ,过点D 作DF ⊥DE ,交BC 的延长线于点F ,联结EF ,与对角线AC 、边CD 分别交于点G 、H .设AE x =,DH y =.(1)求证:△ADE ∽△CDF ,并求EFD ∠的正切值;(2)求y 关于x 的函数解析式,并写出该函数的定义域;(3)联结BG .当△BGE 与△DEH 相似时,求x 的值.(第25题图)B A CF ED GH(备用图)B A CFEDGH8.(静安)已知∠MAN 是锐角,点B 、C 在边AM 上,点D 在边AN 上,∠EBD =∠MAN ,且CE //BD ,sin∠MAN=35,AB =5,AC =9.(1)如图1,当CE 与边AN 相交于点F 时,求证:DF ·CE=BC ·BE ;(2)当点E 在边AN 上时,求AD 的长;(3)当点E 在∠MAN 外部时,设AD =x ,△BCE 的面积为y ,求y 与x 之间的函数解析式,写出定义域.(第25题图)(备用图)(图1)FAB DCE NM9.(嘉定)在矩形ABCD 中,6AB =,8AD =,点E 在CD 边上,1tan 2DAE ∠=.点F 是线段AE 上一点,联结BF ,CF.(1)如图11,如果3tan 4CBF ∠=,求线段AF 的长;(2)如图12,如果12CF BC =,①求证:∠CFE =∠DAE ;②求线段EF 的长.图11图12备用图10.(黄浦)如图10,四边形ABCD 中,AB =AD =4,CB =CD =3,∠ABC =∠ADC =90°,点M 、N 是边AB 、AD 上的动点,且∠MCN =12∠BCD ,CM 、CN 与对角线BD 分别交于点P 、Q .(1)求sin∠MCN 的值;(2)当DN =DC 时,求∠CNM 的度数;(3)试问:在点M 、N 的运动过程中,线段比PQMN的值是否发生变化?如不变,请求出这个值;如变化,请至少给出两个可能的值,并说明点N 相应的位置.P NM DC BAQ(图10)11.(虹口)如图12,在△ABC 中,∠ABC =90°,AB =3,BC =4,过点A 作射线AM //BC ,点D、E 是射线AM 上的两点(点D 不与点A 重合,点E 在点D 右侧),联结BD 、BE 分别交边AC 于点F 、G ,∠DBE =∠C .(1)当AD =1时,求FB 的长;(2)设AD =x ,FG =y ,求y 关于x 的函数关系式,并写出x 的取值范围;(3)联结DG 并延长交边BC 于点H ,如果△DBH 是等腰三角形,请直接写出AD 的长.C FGE D A B 图12C A B 备用图MM12.(奉贤)已知⊙O 的直径AB =4,点P 为弧AB 上一点,联结PA 、PO ,点C 为劣弧AP 上一点(点C 不与点A 、P 重合),联结BC 交PA 、PO 于点D 、E .(1)如图10,当cos∠CBO =87时,求BC 的长;(2)当点C 为劣弧AP 的中点,且△EDP 与△AOP 相似时,求∠ABC 的度数;(3)当AD =2DP ,且△BEO 为直角三角形时,求四边形AOED 的面积.备用图备用图A B图10PA BC D EO A B13.(崇明)如图,Rt△ABC 中,90ACB ∠=︒,6AC =,8BC =.点D 为斜边AB 的中点,ED ⊥AB ,交边BC 于点E .点P 为射线AC 上的动点,点Q 为边BC 上的动点,且运动过程中始终保持PD QD ⊥.(1)求证:△ADP ∽△EDQ ;(2)设AP x =,BQ y =.求y 关于x 的函数解析式,并写出该函数的定义域;(3)联结PQ ,交线段ED 于点F .当△PDF 为等腰三角形时,求线段AP 的长.A D BCPEQ 第25题图A D B C P E Q 第25题备用图F14.(宝山)如图3,已知Rt△ABC 中,∠ACB =90°,AC =BC ,点D、E 在边AB 上,∠DCE =45°,过点A 作AB 的垂线交CE 的延长线于点M ,联结MD.(1)求证:DE BE CE ⋅=2;(2)当AC =3,AD =2BD 时,求DE 的长;(3)过点M 作射线CD 的垂线,垂足为点F .设x BCBD =,y FMD =∠tan ,求y 关于x 的函数关系式,并写出定义域.EM DCAB (图3)15.(青浦)在△ABC 中,∠C=90°,AC =2,BC =23,点D 为边AC 的中点(如图),点P 、Q 分别是射线BC 、BA 上的动点,且BQ =32BP ,联结PQ 、QD 、DP .(1)求证:PQ ⊥AB ;(2)如果点P 在线段BC 上,当△PQD 是直角三角形时,求BP 的长;(3)将△PQD 沿直线QP 翻折,点D 的对应点为点'D ,如果点'D 位于△ABC 内,请直接写出BP 的取值范围.(第25题图)(备用图)A C O 第25题备用图16.(金山)定理:一条弧所对的圆周角等于这条弧所对的圆心角的一半.如图1中,O A ∠=∠21.已知:如图2,AC 是⊙O 的一条弦,点D 在⊙O 上(与A 、C 不重合),联结DC 交射线AO 于点E ,联结OD ,⊙O 的半径为5,43tan =∠OAC .(1)求弦AC 的长.(2)当点E 在线段OA 上时,若DOE ∆与AEC ∆相似,求DCA ∠的正切值.(3)当1=OE 时,求点A 与点D 之间的距离(直接写出答案).AB CO第25题图1第25题图2E D C A O。
2021年上海市16区中考数学一模考点分类汇编专题03三角形(逐题详解版)

2021年上海市16区中考数学一模汇编专题03三角形一、单选题1.(2021・上海崇明区•九年级一模)已知点G是△ A3C的重心,如果连接AG,并延长AG交边BC于点D, 那么下列说法中错误的是()A. BD = CDB. AG = GDC. AG = 2GDD. BC = 2BD2.( 2021•上海松江区•九年级一模)如图,已知在Rs ABC中,NC = 90。
,点G是△ ABC的重心,GE1AC, 垂足为如果C8 = 8,则线段GE的长为()二、填空题3.(2021・上海长宁区•九年级一模)如果一条对角线把凸四边形分成两个相似的三角形,那么我们把这条对角线叫做这个凸四边形的相似对角线,在凸四边形A8CD中,AB = AC = ^3, AD = CD = j,点E、点 F分别是边4D,边8c上的中点.如果4c是凸四边形A8C。
的相似对角线,那么EF的长等于.4.(2021•上海黄浦区•九年级一模)己知一个直角三角形的两条直角边长分别为3和6.则该三角形的重心到其直角顶点的距离是.5.(2021•上海浦东新区•九年级一模)已知AD、BE是△ ABC的中线,AD、BE相交于点F,如果AD=3,那么 AF=.6.(2021・上海长宁区•九年级一模)如图,一辆汽车沿着坡度为i = l:/的斜坡向下行股50米,则它距离地而的垂直高度下降了米.7.(2021・上海金山区•九年级一模)己知:如图,AABC的中线4E与3。
交于点G, DF//AE交BC于DF8.(2021 •上海徐汇区•九年级一模)如图,在A ABC中,ZABC = 120% AB = n.点。
在边AC上,4点、E在边BC上,sin ZADE = - , ED = 5,如果△&?£>的面积是6,那么8C的长是59.(2021 ・上海徐汇区•九年级一模)如图,己知443c是边长为2的等边三角形,正方形OEFG的顶点DE 分别在边AC,A8上,点£G在边3c上,那么A0的长是10. (2021,上海长宁区•九年级一模)如图,点G为酎8c的重心.如果AG=CG, 8G=2, 4c=4,那么48的长等于_________11.(2021•上海九年级一模)如图,A、3、。
2021届金山区中考数学一模(含答案)

上海市金山区2021届初三一模数学试卷2021.01一. 选择题(本大题共6题,每题4分,共24分)1. 已知二次函数2(2)1y x ,那么该二次函数图像的对称轴是( )A. 直线2xB. 直线2xC. 直线1xD. 直线1x 2. 下列各点在抛物线22y x 上的是( )A. (2,2)B. (2,4)C. (2,8)D. (2,16) 3. 在Rt △ABC 中,90C ,那么锐角A 的正弦等于( ) A.A A 锐角的对边锐角的斜边 B. A 锐角的对边斜边 C. A 锐角的邻边斜边D.A A 锐角的邻边锐角的对边4. 若 是锐角,sin(15)2,那么锐角 等于( ) A. 15° B. 30° C. 45°°5. 如图,已知点D 、E 分别在△ABC 的边AB 、AC 上,DE ∥BC ,2AD ,3BD ,BC a ,那么ED等于( )A. 23aB. 23aC. 25aD. 25a6. 如图,已知Rt △ABC 中,90C ,3AC ,4BC ,如果以点C 为圆心的圆与斜边AB 有公共点,那么C 的半径r 的取值范围是( ) A. 1205r B. 1235r C. 1245r D. 34r二. 填空题(本大题共12题,每题4分,共48分)7. 计算:32()2a a b8. 已知2()3f x x x ,那么(2)f9. 抛物线22y x 沿着x 轴正方向看,在y 轴左侧部分的是 (填“上升”或“下降”)10. 正十边形的中心角等于 度11. 已知1O 和2O 的半径长分别为3和4,若1O 和2O 内切,那么圆心距12O O 的长 等于12. 在Rt △ABC 中,90C ,15AB ,4sin 5A,那么BC13. 在Rt △ABC 中,::1:2AB AC BC tan B14. 已知:如图,△ABC 的中线AE 与BD 交于点G ,DF ∥AE 交BC 于F ,那么DFAG15. 如图,在梯形ABCD 中,AD ∥BC ,2BC AD ,设AB a ,AD b ,那么向量CD 用向量a 、b表示为16. 如图,已知O 中,120AOB ,弦18AB ,那么O 的半径长等于 17. 如图,在ABCD 中,点E 在边BC 上,DE 交对角线AC 于F ,若2CE BE , △ABC 的面积等于15,那么△FEC 的面积等于18. 已知在Rt △ABC 中,90C ,1BC ,2AC ,以点C 为直角顶点的 Rt △DCE 的顶点D 在BA 的延长线上,DE 交CA 的延长线于点G ,若1tan 2CED, CE GE ,那么BD 的长等于三. 解答题(本大题共7题,共10+10+10+10+12+12+14=78分) 19. 如图,已知在Rt △ABC 中,90C ,3AC ,4BC ,求2tan tan sin |1cos |4tan 30AB A B的值.20. 已知:如图,1O 与2O 外切于点T ,经过点T 的直线与1O 、2O 分别相交于点A 和点B .(1)求证:1O A ∥2O B ;(2)若12O A ,23O B ,7AB ,求AT 的长.21. 已知抛物线22y x bx c 经过点(0,1)A 、(1,5)B . (1)求抛物线的表达式;(2)把表达式化成22()y x m k 的形式,并写出顶点坐标与对称轴.22. 如图,在距某输电铁塔GH (GH 垂直地面)的底部点H 左侧水平距离60米的点B 处有一个山坡,山坡AB 的坡度1:i ,山坡坡底点B 到坡顶A 的距离AB 等于40米,在坡顶A 处测得铁塔顶点G 的仰角30°(铁塔GH 与山坡AB 在同一平行面内). (1)求山坡的高度;(2)求铁塔的高度GH .(结果保留根号)23. 已知:如图,四边形ABCD 是菱形,点M 、N 分别在边BC 、CD 上,联结AM 、AN 交对角线BD 于E 、F 两点,且MAN ABD . (1)求证:2AB BF DE ;(2)若BE DNDE DC,求证:EF ∥MN .24. 在平面直角坐标系xOy 中,直线324y x 与直线132y x相交于点A ,抛物线 21y ax bx (0a )经过点A .(1)求点A 的坐标;(2)若抛物线21y ax bx 向上平移两个单位后,经过点(1,2) ,求抛物线21y ax bx 的表达式;(3)若抛物线2y a x b x c (0a )与21y ax bx 关于x 轴对称,且这两条抛 物线的顶点分别是点P 与点P ,当3OPP S 时,求抛物线21y ax bx 的表达式.25. 定理:一条弧所对的圆周角等于这条弧所对的圆心角的一半,如图1中,12A O. 已知:如图2,AC 是O 的一条弦,点D 在O 上(与A 、C 不重合),联结DC 交射线AO 于点E ,联结OD ,O 的半径为5,3tan 4OAC . (1)求弦AC 的长;(2)当点E 在线段OA 上时,若△DOE 与△AEC 相似,求DCA 的正切值; (3)当1OE 时,求点A 与点D 之间的距离.(直接写出答案)参考答案一. 选择题1. A2. C3. B4. B5. D6. C二. 填空题7. 42a b8. 2 9. 上升 10. 3611. 1 12. 12 13. 2 14.3415. a b16. 17. 4 18. 2三. 解答题 19.95. 20.(1)证明略;(2)145AT. 21.(1)2241y x x ;(2)22(1)3y x ,顶点坐标为:(1,3) ,对称轴为:直线1x .22.(1)山坡的高度为20米;(2)铁塔的高度GH 为(40 米. 23.(1)证明略;(2)证明略.24.(1)(4,1) ;(2)241y x x ;(3)211182y x x .25.(1)8AC ;(2)1tan 3DCA ;(3)AD 的长是.。
2021年上海市16区中考数学一模考点分类汇编专题05 圆(解析版)

2021年上海市16区中考数学一模汇编专题05 圆一、单选题1.(2021·上海金山区·九年级一模)如图,已知Rt ABC ∆中,90C ∠=,3AC =,4BC =,如果以点C 为圆心的圆与斜边AB 有公共点,那么⊙C 的半径r 的取值范围是( )A .1205r ≤≤B .1235r ≤≤C .1245r ≤≤D .34r ≤≤【答案】C 【分析】作CD⊙AB 于D ,根据勾股定理计算出AB=13,再利用面积法计算出125CD =然后根据直线与圆的位置关系得到当1254≤≤r 时,以C 为圆心、r 为半径作的圆与斜边AB 有公共点. 【详解】解:作CD⊙AB 于D ,如图,⊙⊙C=90°,AC=3,BC=4,⊙22AB 5AC BC =+=1122⋅=⋅CD AB BC AC ⊙CD 125= ⊙以C 为圆心、r 为半径作的圆与斜边AB 有公共点时,r 的取值范围为1254≤≤r故选:C【点睛】本题考查了直线与圆的位置关系:设⊙O 的半径为r ,圆心O 到直线l 的距离为d :直线l 和⊙O 相交⊙d <r ;直线l 和⊙O 相切⊙d=r ;直线l 和⊙O 相离⊙d >r .2.(2021·上海闵行区·九年级一模)已知A 与B 的半径分别是6和8,圆心距2AB =,那么A 与B 的位置关系是( )A .相交B .内切C .外切D .内含 【答案】B【分析】根据圆心距等于两圆半径的差,判断两圆的位置关系即可解题.【详解】A 与B 的半径分别是6和8,圆心距2AB =,又8-6=2AB =∴A 与B 的位置关系是内切,故选:B .【点睛】本题考查两圆的位置关系,涉及圆心距,是重要考点,难度较易,掌握相关知识是解题关键.3.(2021·上海崇明区·边形的边数是( )A .3B .4C .5D .无法确定【答案】B【分析】如图,画出简图,根据切线的性质可得⊙OCA=90°,根据⊙AOC 的余弦可得⊙AOC=45°,即可得出此多边形的中心角为90°,即可求出多边形的边数.【详解】如图,OA 、OC 分别为此多边形的外接圆和内切圆的半径,AB 为边长,⊙OC⊙AB ,⊙⊙OCA=90°,⊙倍,⊙cos⊙AOC=OC OA =2, ⊙⊙AOC=45°,⊙⊙AOB=90°,即此多边形的中心角为90°,⊙此多边形的边数=360°÷90°=4,故选:B .【点睛】本题考查正多边形和圆及三角函数的定义,熟练掌握余弦的定义并熟记特殊角的三角函数值是解题关键.4.(2021·上海奉贤区·九年级一模)如果1O 和2 O 内含,圆心距12 4O O =,1O 的半径长是6,那么2 O 的半径r 的取值范围是( ).A .02r <<B .24r <<C .10r >D .02r <<或10r >【答案】D 【分析】根据题意得1206OO r ≤<-,结合124O O =,通过求解不等式,即可得到答案. 【详解】根据题意得:1206OO r ≤<-,0r >⊙124O O =⊙46r <-⊙64r ->或64r -<-⊙02r <<或10r >⊙2O 的半径r 的取值范围是:02r <<或10r > 故选:D .【点睛】本题考查圆与圆内含、绝对值、一元一次不等式的知识;解题的关键是熟练掌握圆与圆内含、绝对值、一元一次不等式的性质,从而完成求解.二、填空题5.(2021·上海金山区·九年级一模)正十边形的中心角等于______度.【答案】36【分析】根据正多边形的中心角的定义即可求解.【详解】正十边形的中心角等于360°÷10=36°。
初中数学上海市金山区中考模拟数学一模(即期末)考试题考试卷及答案.docx

xx学校xx学年xx学期xx试卷姓名:_____________ 年级:____________ 学号:______________题型选择题填空题简答题xx题xx 题xx题总分得分一、xx题评卷人得分(每空xx 分,共xx分)试题1:抛物线的顶点坐标是()(A);(B);(C );(D ).试题2:在中, ,,那么的值等于()(A);(B);(C);(D).试题3:已知∽,点、、对应点分别是、、,,那么等于()(A):;(B):;(C):;(D):.试题4:正多边形的中心角是º,那么这个正多边形的边数是()(A);(B);(C);(D).试题5:已知⊙与⊙的半径分别为和,若两圆相切,那么这两圆的圆心距的长等于()(A);(B);(C)或;(D)或试题6:已知反比例函数,当时,它的图像随的增大而减小,那么二次函数的图像只可能是()(A) (B) (C)(D)试题7:已知,那么试题8:计算:试题9:将抛物线向上平移3个单位,那么平移后得到的抛物线的解析式是试题10:如图,已知中,点、分别在边、上,∥,若,,,那么试题11:在中,,如果,那么的值为试题12:已知⊙的半径为,点在⊙外,那么线段的的取值范围是试题13:如图,斜坡的坡度,该斜坡的水平距离米,那么斜坡的长等于米试题14:如图,已知直线与⊙O相交于、两点,,半径,那么弦=_________试题15:已知⊙与⊙的半径分别为和,若两圆相交,那么这两圆的圆心距的取值范围是试题16:如图,在中,,⊥,=,=,那么=试题17:如图, 在中,分别是边上的中线,相交于点.设, ,那么(用、的式子表示)试题18:如图,在中,,,.将绕着点旋转,点、的对应点分别是、,那么的值为试题19:计算:试题20:如图,中,平分, (1)求证:∽;(2)若,,求的长.试题21:如图,小明在广场上的处用测角仪正面测量一座楼房墙上的广告屏幕的长度,测得屏幕下端处的仰角为,然后他正对大楼方向前进米到达处,又测得该屏幕上端处的仰角为,已知该楼高米,测角仪、的高度为1.7米.求广告屏幕的长.试题22:抛物线向右平移个单位得到抛物线,且平移后的抛物线经过点.(1)求平移后抛物线的解析式;(2)设原抛物线与轴的交点为,顶点为,平移后抛物,求的面积.线的对称轴与轴交于点如图,已知⊙与⊙外离,与分别是⊙与⊙的半径,∥.直线交于点,交⊙于点,交⊙于点.求证:(1)∥;(2)试题24:如图,已知直线与轴、轴分别交于、两点,抛物线经过点和点.(1)求抛物线的解析式;(2)在线段上取一点(点不与点重合),过点作轴的垂线交抛物线于点、交轴于点.当时,求点的坐标;(3)设抛物线的对称轴与直线交于点,抛物线与轴的交点为,点在线段上,当与相似时,求点的坐标.试题25:如图,在中,,,点、分别在边、上(点不与点、重合)∥.把沿直线翻折,点与点重合,设.(1)求的余切值;(2)当点在的外部时,、分别交于、,若,求关于的函数关系式并写出定义域;(3)(下列所有问题只要直接写出结果即可)以为圆心、长为半径的⊙与边①没有公共点时,求的取值范围.②一个公共点时,求的取值范围.③两个公共点时,求的取值范围.试题1答案:B试题2答案:C试题3答案:D试题4答案:A试题5答案:D试题6答案:B试题7答案:试题8答案:试题9答案:试题10答案:试题11答案:试题12答案:试题13答案:试题14答案:试题15答案:试题16答案:试题17答案:试题18答案:试题19答案:试题20答案:试题21答案:试题22答案:试题23答案:试题24答案:试题25答案:。
2021年上海市长宁区、金山区中考数学一模试题

3.将抛物线y=(x+1)2﹣3向右平移2个单位后得到的新抛物线的表达式为( )
A.y=(x﹣1)2﹣3B.y=(x+3)2﹣3C.y=(x+1)2﹣1D.y=(x+1)2﹣5
4.下列命题正确的是( )
A.如果| |=| |,那么 =
B.如果 、 都是单位向量,那么 =
C.如果 =k (k≠0),那么 ∥
D.如果m=0或 = ,那么m =0
5.已知在矩形ABCD中,AB=5,对角线AC=13.⊙C的半径长为12,下列说法正确的是( )
A.⊙C与直线AB相交B.⊙C与直线AD相切
C.点A在⊙C上D.点D在⊙C内
6.如果点D、E,F分别在△ABC的边AB、BC,AC上,联结DE、EF,且DE∥AC,那么下列说法错误的是( )
将图2中的BC绕点B向下旋转45°,使得BCD落在BC′D′的位置(如图3所示),此时C′D′⊥OM,AD′∥OM,AD′=16cm,求点B到水平桌面OM的距离,(参考数据:sin70°≈0.94,cos70°≈0.34,cot70°≈0.36,结果精确到1cm)
23.如图,在△ABC中,点D、E分别在边AB、BC上,AE与CD交于点F,若AE平分∠BAC,AB•AF=AC•AE.
解:过点A作AB⊥x轴,垂足为B,则OB=2,AB=3,
B.y=(x+3)2﹣x2Biblioteka 6x+9,化简后为一次函数;
D.y=x(x﹣1)=x2﹣x,为二次函数;
故选:D.
【点睛】
本题考查二次函数的概念和解析式的形式,知识点简单,比较容易掌握.
2.B
【分析】
过点A作AB⊥x轴,构造直角三角形,由坐标得出OB=2,AB=3,再根据余切的意义求出结果即可.
2021年上海市金山区初三数学一模试卷

2021年上海市金山区初三数学一模试卷金山区2020学年第一学期期末质量检测初三数学试卷一、选择题:(本大题共6题,每题4分,满分24分)1.已知二次函数$y=(x-2)^2-1$,那么该二次函数图像的对称轴是()。
A)直线$x=2$;(B)直线$x=-2$;(C)直线$x=1$;(D)直线$x=-1$.2.下列各点在抛物线$y=2x^2$上的是()。
A)$(2,2)$;(B)$(4,16)$;(C)$(2,8)$;(D)$(2,16)$.3.在Rt$\triangle ABC$中,$\angle C=90^{\circ}$,那么锐角A的正弦等于()。
A)$\frac{\text{锐角A的对边}}{\text{斜边}}$;(B)$\frac{\text{锐角A的邻边}}{\text{斜边}}$;(C)$\frac{\text{锐角A的对边}}{\text{锐角A的邻边}}$;(D)$\frac{\text{锐角A的邻边}}{\text{锐角A的对边}}$.4.若$\alpha$是锐角,$\sin(\alpha+15^{\circ})=\frac{\sqrt{2}}{2}$,那么锐角$\alpha$等于()。
A)$15^{\circ}$;(B)$30^{\circ}$;(C)$45^{\circ}$;(D)$60^{\circ}$.5.如图,已知点D、E分别在$\triangle ABC$的边AB、AC上,DE//BC,AD=2,BD=3,BC=a,那么ED等于()。
A)$\frac{2}{5}a$;(B)$-\frac{3}{5}a$;(C)$\frac{3}{5}a$;(D)$-\frac{2}{5}a$.6.如图,已知Rt$\triangle ABC$中,$\angle C=90^{\circ}$,AC=3,BC=4,如果以点C为圆心的圆与斜边AB有公共点,那么⊙C的半径r的取值范围是()。
上海市2022-2021年中考数学一模试卷含答案解析

中考数学一模试卷一、选择题(本大题共8小题,每小题4分,满分32分)1.若(x+2)(x﹣1)=x2+mx+n,则m+n=()A.1 B.﹣2 C.﹣1 D.22.我国计划在2022年左右发射火星探测卫星,据科学研究,火星距离地球的最近距离约为5500万千米,这个数据用科学记数法可表示为()A.5.5×106千米B.5.5×107千米C.55×106千米D.0.55×108千米3.如图是一个由4个相同的正方体组成的立体图形,它的主视图是()A. B.C. D.4.如图,在Rt△ABC中,∠BAC=90°,将Rt△ABC绕点C按逆时针方向旋转48°得到Rt△A′B′C′,点A在边B′C上,则∠B′的大小为()A.42° B.48° C.52° D.58°5.若关于x的一元二次方程方程(k﹣1)x2+4x+1=0有实数根,则k的取值范围是()A.k<5 B.k≥5,且k≠1 C.k≤5,且k≠1 D.k>56.如图,AB∥CD,直线EF分别交AB、CD于E、F两点,∠BEF的平分线交CD于点G,若∠EFG=52°,则∠EGF等于()A.26° B.64° C.52° D.128°7.如图,平面直角坐标系中,△ABC的顶点坐标分别是A(1,1),B(3,1),C(2,2),当直线与△ABC有交点时,b的取值范围是()A.﹣1≤b≤1 B.﹣≤b≤1 C.﹣≤b≤D.﹣1≤b≤8.如图,已知点A(﹣8,0),B(2,0),点C在直线y=﹣上,则使△ABC 是直角三角形的点C的个数为()A.1 B.2 C.3 D.4二、填空题(本大题共7小题,每小题4分,共20分)9.不等式组的解集是.10.分解因式:x3﹣2x2+x=.11.妈妈给小明买笔记本和圆珠笔.已知每本笔记本4元,每支圆珠笔3元,妈妈买了m本笔记本,n支圆珠笔.妈妈共花费元.12.如图,⊙O的内接四边形ABCD中,∠A=115°,则∠BOD等于.13.如图,在平行四边形ABCD中,点E是边AD的中点,EC交对角线BD于点F,若S△DEC=3,则S△BCF=.14.如图所示,反比例函数y=(k≠0,x>0)的图象经过矩形OABC的对角线AC 的中点D.若矩形OABC的面积为8,则k的值为.15.如图,正方形ABCD的边长为1,AC,BD是对角线.将△DCB绕着点D顺时针旋转45°得到△DGH,HG交AB于点E,连接DE交AC于点F,连接FG.则下列结论:①四边形AEGF是菱形②△AED≌△GED③∠DFG=112.5°④BC+FG=1.5其中正确的结论是.三、解答题(本大题共7小题,每小题5分,满分60分)16.计算:|﹣3|+tan30°﹣﹣10.17.先化简,再求值:(﹣x﹣1)÷,选一个你喜欢的数代入求值.18.已知:如图,在△ABC中,∠BAC=90°,DE、DF是△ABC的中位线,连接EF、AD.求证:EF=AD.19.某高校学生会在食堂发现同学们就餐时剩余饭菜较多,浪费严重,为了让同学们珍惜粮食,养成节约的好习惯,校学生会随机抽查了午餐后部分同学饭菜的剩余情况,并将结果统计后绘制成了如图所示的不完整的统计图.(1)这次被调查的同学共有名.(2)把条形统计图补充完整.(3)校学生会通过数据分析,估计这次被调查的所有学生一餐浪费的食物可以供200人用一餐.据此估算,该校18000名学生一餐浪费的食物可供多少人食用一餐?20.已知,如图,一次函数y=kx+b(k、b为常数,k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y=(n为常数且n≠0)的图象在第二象限交于点C.CD ⊥x轴,垂足为D,若OB=2OA=3OD=6.(1)求一次函数与反比例函数的解析式;(2)求两函数图象的另一个交点坐标;(3)直接写出不等式;kx+b≤的解集.21.如图,以△ABC的BC边上一点O为圆心,经过A,C两点且与BC边交于点E,点D为CE的下半圆弧的中点,连接AD交线段EO于点F,若AB=BF.(1)求证:AB是⊙O的切线;(2)若CF=4,DF=,求⊙O的半径r及sinB.22.如图,△ABC是等边三角形,AB=4cm,CD⊥AB于点D,动点P从点A出发,沿AC以1cm/s的速度向终点C运动,当点P出发后,过点P作PQ∥BC交折线AD ﹣DC于点Q,以PQ为边作等边三角形PQR,设四边形APRQ与△ACD重叠部分图形的面积为S(cm2),点P运动的时间为t(s).(1)当点Q在线段AD上时,用含t的代数式表示QR的长;(2)求点R运动的路程长;(3)当点Q在线段AD上时,求S与t之间的函数关系式;(4)直接写出以点B、Q、R为顶点的三角形是直角三角形时t的值.参考答案与试题解析一、选择题(本大题共8小题,每小题4分,满分32分)1.若(x+2)(x﹣1)=x2+mx+n,则m+n=()A.1 B.﹣2 C.﹣1 D.2【考点】多项式乘多项式.【分析】依据多项式乘以多项式的法则,进行计算,然后对照各项的系数即可求出m,n的值.【解答】解:∵原式=x2+x﹣2=x2+mx+n,∴m=1,n=﹣2.∴m+n=1﹣2=﹣1.故选:C.【点评】本题考查了多项式的乘法,熟练掌握多项式乘以多项式的法则是解题的关键.2.我国计划在2022年左右发射火星探测卫星,据科学研究,火星距离地球的最近距离约为5500万千米,这个数据用科学记数法可表示为()A.5.5×106千米B.5.5×107千米C.55×106千米D.0.55×108千米【考点】科学记数法—表示较大的数.【分析】科学记数法的表示形式为a×10n的形式.其中1≤|a|<10,n为整数,确定n 的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>10时,n是正数;当原数的绝对值<1时,n是负数.【解答】解:5500万=5.5×107.故选:B.【点评】此题考查科学记数法的表示方法,表示时关键要正确确定a的值以及n的值.3.如图是一个由4个相同的正方体组成的立体图形,它的主视图是()A. B.C. D.【考点】简单组合体的三视图.【分析】找到从正面看所得到的图形即可,注意所有的看到的棱都应表现在主视图中.【解答】解:从正面看易得第一层有2个正方形,第二层左边有一个正方形,第三层左边有一个正方形.故选A.【点评】本题考查了简单组合体的三视图的知识,主视图是从物体的正面看得到的视图.4.如图,在Rt△ABC中,∠BAC=90°,将Rt△ABC绕点C按逆时针方向旋转48°得到Rt△A′B′C′,点A在边B′C上,则∠B′的大小为()A.42° B.48° C.52° D.58°【考点】旋转的性质.【分析】先根据旋转的性质得出∠A′=∠BAC=90°,∠ACA′=48°,然后在直角△A′CB′中利用直角三角形两锐角互余求出∠B′=90°﹣∠ACA′=42°.【解答】解:∵在Rt△ABC中,∠BAC=90°,将Rt△ABC绕点C按逆时针方向旋转48°得到Rt△A′B′C′,∴∠A′=∠BAC=90°,∠ACA′=48°,∴∠B′=90°﹣∠ACA′=42°.故选A.【点评】本题考查了转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了直角三角形两锐角互余的性质.5.若关于x的一元二次方程方程(k﹣1)x2+4x+1=0有实数根,则k的取值范围是()A.k<5 B.k≥5,且k≠1 C.k≤5,且k≠1 D.k>5【考点】根的判别式.【分析】根据一元二次方程的定义以及根的判别式即可得出关于k的一元一次不等式组,解之即可得出结论.【解答】解:∵关于x的一元二次方程方程(k﹣1)x2+4x+1=0有实数根,∴,解得:k≤5且k≠1.故选C.【点评】本题考查了根的判别式以及一元二次方程的定义,根据根的判别式以及二次项系数非零找出关于k的一元一次不等式组是解题的关键.6.如图,AB∥CD,直线EF分别交AB、CD于E、F两点,∠BEF的平分线交CD于点G,若∠EFG=52°,则∠EGF等于()A.26° B.64° C.52° D.128°【考点】平行线的性质.【分析】根据平行线及角平分线的性质解答.【解答】解:∵AB∥CD,∴∠BEF+∠EFG=180°,∴∠BEF=180°﹣52°=128°;∵EG平分∠BEF,∴∠BEG=64°;∴∠EGF=∠BEG=64°(内错角相等).故选:B.【点评】本题考查了平行线的性质,解答本题用到的知识点为:两直线平行,内错角相等;角平分线分得相等的两角.7.如图,平面直角坐标系中,△ABC的顶点坐标分别是A(1,1),B(3,1),C(2,2),当直线与△ABC有交点时,b的取值范围是()A.﹣1≤b≤1 B.﹣≤b≤1 C.﹣≤b≤D.﹣1≤b≤【考点】一次函数的性质.【分析】将A(1,1),B(3,1),C(2,2)的坐标分别代入直线中求得b 的值,再根据一次函数的增减性即可得到b的取值范围.【解答】解:将A(1,1)代入直线中,可得+b=1,解得b=;将B(3,1)代入直线中,可得+b=1,解得b=﹣;将C(2,2)代入直线中,可得1+b=2,解得b=1.故b的取值范围是﹣≤b≤1.故选B.【点评】考查了一次函数的性质:k>0,y随x的增大而增大,函数从左到右上升;k <0,y随x的增大而减小,函数从左到右下降.8.如图,已知点A(﹣8,0),B(2,0),点C在直线y=﹣上,则使△ABC 是直角三角形的点C的个数为()A.1 B.2 C.3 D.4【考点】一次函数图象上点的坐标特征;勾股定理的逆定理.【分析】根据∠A为直角,∠B为直角与∠C为直角三种情况进行分析.【解答】解:如图,①当∠A为直角时,过点A作垂线与直线的交点W(﹣8,10),②当∠B为直角时,过点B作垂线与直线的交点S(2,2.5),③若∠C为直角则点C在以线段AB为直径、AB中点E(﹣3,0)为圆心的圆与直线y=﹣的交点上.过点E作x轴的垂线与直线的交点为F(﹣3,),则EF=∵直线y=﹣与x轴的交点M为(,0),∴EM=,FM==∵E到直线y=﹣的距离d==5∴以线段AB为直径、E(﹣3,0)为圆心的圆与直线y=﹣恰好有一个交点.所以直线y=﹣上有一点C满足∠C=90°.综上所述,使△ABC是直角三角形的点C的个数为3,故选:C.【点评】本题考查的是一次函数综合题,在解答此题时要分三种情况进行讨论,关键是根据圆周角定理判断∠C为直角的情况是否存在.二、填空题(本大题共7小题,每小题4分,共20分)9.不等式组的解集是x<1 .【考点】解一元一次不等式组.【分析】首先解每个不等式,两个不等式的解集的公共部分就是不等式组的解集.【解答】解:,解①得x<,解②得x<1,则不等式组的解集是x<1.故答案是:x<1.【点评】本题考查了一元一次不等式组的解法:解一元一次不等式组时,一般先求出其中各不等式的解集,再求出这些解集的公共部分,解集的规律:同大取大;同小取小;大小小大中间找;大大小小找不到.10.分解因式:x3﹣2x2+x= x(x﹣1)2.【考点】提公因式法与公式法的综合运用.【分析】首先提取公因式x,进而利用完全平方公式分解因式即可.【解答】解:x3﹣2x2+x=x(x2﹣2x+1)=x(x﹣1)2.故答案为:x(x﹣1)2.【点评】此题主要考查了提取公因式法以及公式法分解因式,熟练应用完全平方公式是解题关键.11.妈妈给小明买笔记本和圆珠笔.已知每本笔记本4元,每支圆珠笔3元,妈妈买了m本笔记本,n支圆珠笔.妈妈共花费4m+3n 元.【考点】列代数式.【分析】先求出买m本笔记本的钱数和买n支圆珠笔的钱数,再把两者相加即可.【解答】解:每本笔记本4元,妈妈买了m本笔记本花费4m元,每支圆珠笔3元,n 支圆珠笔花费3n,共花费(4m+3n)元.故答案为:4m+3n.【点评】此题考查了列代数式,关键是读懂题意,找出题目中的数量关系,列出代数式.12.如图,⊙O的内接四边形ABCD中,∠A=115°,则∠BOD等于130°.【考点】圆内接四边形的性质;圆周角定理.【分析】根据圆内接四边形的对角互补求得∠C的度数,再根据圆周角定理求解即可.【解答】解:∵∠A=115°∴∠C=180°﹣∠A=65°∴∠BOD=2∠C=130°.故答案为:130°.【点评】本题考查的是圆内接四边形的性质,熟知圆内接四边形的对角互补是解答此题的关键.13.如图,在平行四边形ABCD中,点E是边AD的中点,EC交对角线BD于点F,若S△DEC=3,则S△BCF= 4 .【考点】相似三角形的判定与性质;平行四边形的性质.【分析】根据平行四边形的性质得到AD∥BC和△DEF∽△BCF,由已知条件求出△DEF的面积,根据相似三角形的面积比是相似比的平方得到答案.【解答】解:∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC,∴△DEF∽△BCF,∴,=()2,∵E是边AD的中点,∴DE=AD=BC,∴=,∴△DEF的面积=S△DEC=1,∴=,∴S△BCF=4;故答案为:4.【点评】本题考查的是平行四边形的性质、相似三角形的判定和性质;掌握三角形相似的判定定理和性质定理是解题的关键,注意:相似三角形的面积比是相似比的平方.14.如图所示,反比例函数y=(k≠0,x>0)的图象经过矩形OABC的对角线AC 的中点D.若矩形OABC的面积为8,则k的值为 2 .【考点】反比例函数系数k的几何意义.【分析】过D作DE⊥OA于E,设D(m,),于是得到OA=2m,OC=,根据矩形的面积列方程即可得到结论.【解答】解:过D作DE⊥OA于E,设D(m,),∴OE=m.DE=,∵点D是矩形OABC的对角线AC的中点,∴OA=2m,OC=,∵矩形OABC的面积为8,∴OA•OC=2m•=8,∴k=2,故答案为:2.【点评】本题考查了反比例函数系数k的几何意义,矩形的性质,根据矩形的面积列出方程是解题的关键.15.如图,正方形ABCD的边长为1,AC,BD是对角线.将△DCB绕着点D顺时针旋转45°得到△DGH,HG交AB于点E,连接DE交AC于点F,连接FG.则下列结论:①四边形AEGF是菱形②△AED≌△GED③∠DFG=112.5°④BC+FG=1.5其中正确的结论是①②③.【考点】旋转的性质;全等三角形的判定;菱形的判定;正方形的性质.【分析】首先证明△ADE≌△GDE,再求出∠AEF、∠AFE、∠GEF、∠GFE的度数,推出AE=EG=FG=AF,由此可以一一判断.【解答】证明:∵四边形ABCD是正方形,∴AD=DC=BC=AB,∠DAB=∠ADC=∠DCB=∠ABC=90°,∠ADB=∠BDC=∠CAD=∠CAB=45°,∵△DHG是由△DBC旋转得到,∴DG=DC=AD,∠DGE=∠DCB=∠DAE=90°,在RT△ADE和RT△GDE中,,∴AED≌△GED,故②正确,∴∠ADE=∠EDG=22.5°,AE=EG,∴∠AED=∠AFE=67.5°,∴AE=AF,同理△AEF≌△GEF,可得EG=GF,∴AE=EG=GF=FA,∴四边形AEGF是菱形,故①正确,∵∠DFG=∠GFC+∠DFC=∠BAC+∠DAC+∠ADF=112.5°,故③正确.∵AE=FG=EG=BG,BE=AE,∴BE>AE,∴AE<,∴CB+FG<1.5,故④错误.故答案为①②③.【点评】本题考查正方形的性质、全等三角形的判定和性质、菱形的判定和性质、等腰直角三角形的性质等知识,解题的关键是通过计算发现角相等,学会这种证明角相等的方法,属于中考常考题型.三、解答题(本大题共7小题,每小题5分,满分60分)16.计算:|﹣3|+tan30°﹣﹣10.【考点】实数的运算;零指数幂;特殊角的三角函数值.【分析】将tan30°=、10=1代入原式,再根据实数的运算即可求出结论.【解答】解:|﹣3|+tan30°﹣﹣10,=3+×﹣2﹣1,=3+1﹣2﹣1,=3﹣2.【点评】本题考查了实数的运算、绝对值、零指数幂以及特殊角的三角函数值,熟练掌握实数混合运算的运算顺序是解题的关键.17.先化简,再求值:(﹣x﹣1)÷,选一个你喜欢的数代入求值.【考点】分式的化简求值.【分析】首先把括号内的分式约分,然后通分相加,把除法转化为乘法,计算乘法即可化简,然后化简x的值,代入求解即可.【解答】解:原式=[﹣(x+1)]•=[﹣(x+1)]•=•=1﹣(x﹣1)=2﹣x.当x=0时,原式=2.【点评】本题考查了分式的化简求值,正确对所求的分式进行通分、约分是关键.18.已知:如图,在△ABC中,∠BAC=90°,DE、DF是△ABC的中位线,连接EF、AD.求证:EF=AD.【考点】平行四边形的判定与性质;三角形中位线定理.【专题】证明题.【分析】由DE、DF是△ABC的中位线,根据三角形中位线的性质,即可求得四边形AEDF是平行四边形,又∠BAC=90°,则可证得平行四边形AEDF是矩形,根据矩形的对角线相等即可得EF=AD.【解答】证明:∵DE,DF是△ABC的中位线,∴DE∥AB,DF∥AC,∴四边形AEDF是平行四边形,又∵∠BAC=90°,∴平行四边形AEDF是矩形,∴EF=AD.【点评】此题考查了三角形中位线的性质,平行四边形的判定与矩形的判定与性质.此题综合性较强,但难度不大,解题的关键是注意数形结合思想的应用.19.某高校学生会在食堂发现同学们就餐时剩余饭菜较多,浪费严重,为了让同学们珍惜粮食,养成节约的好习惯,校学生会随机抽查了午餐后部分同学饭菜的剩余情况,并将结果统计后绘制成了如图所示的不完整的统计图.(1)这次被调查的同学共有1000 名.(2)把条形统计图补充完整.(3)校学生会通过数据分析,估计这次被调查的所有学生一餐浪费的食物可以供200人用一餐.据此估算,该校18000名学生一餐浪费的食物可供多少人食用一餐?【考点】条形统计图;用样本估计总体;扇形统计图.【分析】(1)用没有剩的人数除以其所占的百分比即可;(2)用抽查的总人数减去其他三类的人数,再画出图形即可;(3)根据这次被调查的所有学生一餐浪费的食物可以供200人用一餐,再根据全校的总人数是18000人,列式计算即可.【解答】解:(1)这次被调查的同学共有400÷40%=1000(名);故答案为:1000;(2)剩少量的人数是;1000﹣400﹣250﹣150=200,补图如下;(3)18000×=3600(人).答:该校18000名学生一餐浪费的食物可供3600人食用一餐.【点评】本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.20.已知,如图,一次函数y=kx+b(k、b为常数,k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y=(n为常数且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂足为D,若OB=2OA=3OD=6.(1)求一次函数与反比例函数的解析式;(2)求两函数图象的另一个交点坐标;(3)直接写出不等式;kx+b≤的解集.【考点】反比例函数与一次函数的交点问题.【分析】(1)先求出A、B、C坐标,再利用待定系数法确定函数解析式.(2)两个函数的解析式作为方程组,解方程组即可解决问题.(3)根据图象一次函数的图象在反比例函数图象的下方,即可解决问题,注意等号.【解答】解:(1)∵OB=2OA=3OD=6,∴OB=6,OA=3,OD=2,∵CD⊥OA,∴DC∥OB,∴=,∴=,∴CD=10,∴点C坐标(﹣2,10),B(0,6),A(3,0),∴解得,∴一次函数为y=﹣2x+6.∵反比例函数y=经过点C(﹣2,10),∴n=﹣20,∴反比例函数解析式为y=﹣.(2)由解得或,故另一个交点坐标为(5,﹣4).(3)由图象可知kx+b≤的解集:﹣2≤x<0或x≥5.【点评】本题考查一次函数与反比例函数的交点问题,解题的关键是学会利用待定系数法确定函数解析式,知道两个函数图象的交点坐标可以利用解方程组解决,学会利用图象确定自变量取值范围,属于中考常考题型.21.如图,以△ABC的BC边上一点O为圆心,经过A,C两点且与BC边交于点E,点D为CE的下半圆弧的中点,连接AD交线段EO于点F,若AB=BF.(1)求证:AB是⊙O的切线;(2)若CF=4,DF=,求⊙O的半径r及sinB.【考点】切线的判定.【分析】(1)连接OA、OD,如图,根据垂径定理得OD⊥BC,则∠D+∠OFD=90°,再由AB=BF,OA=OD得到∠BAF=∠BFA,∠OAD=∠D,加上∠BFA=∠OFD,所以∠OAD+∠BAF=90°,则OA⊥AB,然后根据切线的判定定理即可得到AB是⊙O切线;(2)先表示出OF=4﹣r,OD=r,在Rt△DOF中利用勾股定理得r2+(4﹣r)2=()2,解方程得到r的值,那么OA=3,OF=CF﹣OC=4﹣3=1,BO=BF+FO=AB+1.然后在Rt△AOB中利用勾股定理得AB2+OA2=OB2,即AB2+32=(AB+1)2,解方程得到AB=4的值,再根据三角函数定义求出sinB.【解答】(1)证明:连接OA、OD,如图,∵点D为CE的下半圆弧的中点,∴OD⊥BC,∴∠EOD=90°,∵AB=BF,OA=OD,∴∠BAF=∠BFA,∠OAD=∠D,而∠BFA=∠OFD,∴∠OAD+∠BAF=∠D+∠BFA=90°,即∠OAB=90°,∴OA⊥AB,∴AB是⊙O切线;(2)解:OF=CF﹣OC=4﹣r,OD=r,DF=,在Rt△DOF中,OD2+OF2=DF2,即r2+(4﹣r)2=()2,解得r1=3,r2=1(舍去);∴半径r=3,∴OA=3,OF=CF﹣OC=4﹣3=1,BO=BF+FO=AB+1.在Rt△AOB中,AB2+OA2=OB2,∴AB2+32=(AB+1)2,∴AB=4,OB=5,∴sinB==.【点评】本题考查了切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.也考查了勾股定理以及锐角三角函数的定义.22.如图,△ABC是等边三角形,AB=4cm,CD⊥AB于点D,动点P从点A出发,沿AC以1cm/s的速度向终点C运动,当点P出发后,过点P作PQ∥BC交折线AD ﹣DC于点Q,以PQ为边作等边三角形PQR,设四边形APRQ与△ACD重叠部分图形的面积为S(cm2),点P运动的时间为t(s).(1)当点Q在线段AD上时,用含t的代数式表示QR的长;(2)求点R运动的路程长;(3)当点Q在线段AD上时,求S与t之间的函数关系式;(4)直接写出以点B、Q、R为顶点的三角形是直角三角形时t的值.【考点】四边形综合题.【分析】(1)当点Q在线段AD上时,如图1,根据四边相等的四边形是菱形证明四边形APRQ是菱形,则QR=AP=t;(2)如图2,当点Q在线段AD上运动时,点R的运动的路程长为AR,当点Q在线段CD上运动时,点R的运动的路程长为CR,分别求长并相加即可;(3)分两种情况:①当0<t≤时,四边形APRQ与△ACD重叠部分图形的面积是菱形APRQ的面积,②当<t≤2时,四边形APRQ与△ACD重叠部分图形的面积是五边形APFMQ的面积,分别计算即可;(4)分两种情况:①当∠BRQ=90°时,如图6,根据BQ=2RQ列式可得:t=;②当∠BQR=90°时,如图7,根据BR=2RQ列式可得:t=.【解答】解:(1)由题意得:AP=t,当点Q在线段AD上时,如图1,∵△ABC是等边三角形,∴∠A=∠B=60°,∵PQ∥BC,∴∠PQA=∠B=60°,∴△PAQ是等边三角形,∴PA=AQ=PQ,∵△PQR是等边三角形,∴PQ=PR=RQ,∴AP=PR=RQ=AQ,∴四边形APRQ是菱形,∴QR=AP=t;(2)当点Q在线段AD上运动时,如图2,点R的运动的路程长为AR,由(1)得:四边形APRQ是菱形,∴AR⊥PQ,∵PQ∥BC,∴AR⊥BC,∴RC=BC=×4=2,由勾股定理得:AR===2;当点Q在线段CD上运动时,如图2,点R的运动的路程长为CR,∴AR+CR=2+2,答:点R运动的路程长为(2+2)cm;(3)当R在CD上时,如图3,∵PR∥AD,∴△CPR∽△CAD,∴,∴,4t=8﹣2t,t=,①当0<t≤时,四边形APRQ与△ACD重叠部分图形的面积是菱形APRQ的面积,如图4,过P作PE⊥AB于E,∴PE=AP•sin60°=t,∴S=AQ•PE=t2,②当<t≤2时,四边形APRQ与△ACD重叠部分图形的面积是五边形APFMQ的面积,如图5,在Rt△PCF中,sin∠PCF=,∴PF=PC•sin30°=(4﹣t)=2﹣t,∴FR=t﹣(2﹣t)=t﹣2,∴tan60°=,∴FM=×(t﹣2),∴S=S菱形APRQ﹣S△FMR=t2﹣FR•FM=﹣(t﹣2)××(t﹣2),∴S=﹣+3﹣2;综上所述,当点Q在线段AD上时,S与t之间的函数关系式为:S=;(4)①当∠BRQ=90°时,如图6,∵四边形APRQ是菱形,∴AP=AQ=RQ=t,∴BQ=4﹣t,∵∠AQP=∠PQR=60°,∴∠RQB=180°﹣60°60°=60°,∴∠RBQ=30°,∴BQ=2RQ,4﹣t=2t,3t=4,t=;②当∠BQR=90°时,如图7,同理得四边形CPQR是菱形,∴PC=RQ=RC=4﹣t,∴BR=t,∵∠CRP=∠PRQ=60°,∴∠QRB=60°,∴∠QBR=30°,∴BR=2RQ,∴t=2(4﹣t),t=,综上所述,以点B、Q、R为顶点的三角形是直角三角形时t的值是或.【点评】本题是四边形和三角形的综合题,考查了等边三角形的性质和判定、菱形的性质和判定、动点运动问题、二次函数等知识,熟练掌握菱形和等边三角形的性质与判定是关键,利用数形结合的思想解决重叠部分图形的面积问题.精品Word 可修改欢迎下载。
(数学3份试卷)2021年上海市金山区中考一模化学试题

中考数学模拟试卷一、选择题(本题包括10个小题,每小题只有一个选项符合题意)1.如图,等边△ABC的边长为1cm,D、E分别AB、AC是上的点,将△ADE沿直线DE折叠,点A落在点A′处,且点A′在△ABC外部,则阴影部分的周长为()cmA.1 B.2 C.3 D.4【答案】C【解析】由题意得到DA′=DA,EA′=EA,经分析判断得到阴影部分的周长等于△ABC的周长即可解决问题.【详解】如图,由题意得:DA′=DA,EA′=EA,∴阴影部分的周长=DA′+EA′+DB+CE+BG+GF+CF=(DA+BD)+(BG+GF+CF)+(AE+CE)=AB+BC+AC=1+1+1=3(cm)故选C.【点睛】本题考查了等边三角形的性质以及折叠的问题,折叠问题的实质是“轴对称”,解题关键是找出经轴对称变换所得的等量关系.2.在一个不透明的袋中装有10个只有颜色不同的球,其中5个红球、3个黄球和2个白球.从袋中任意摸出一个球,是白球的概率为()A.12B.13C.310D.15【答案】D【解析】一个不透明的袋中装有10个只有颜色不同的球,其中5个红球、3个黄球和2个白球.从袋中任意摸出一个球,共有10种等可能的结果,其中摸出白球的所有等可能结果共有2种,根据概率公式即可得出答案.【详解】根据题意:从袋中任意摸出一个球,是白球的概率为=210=15.故答案为D【点睛】此题主要考查了概率的求法,如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=m n.3.如图所示的几何体的俯视图是()A.B.C.D.【答案】D【解析】找到从上面看所得到的图形即可,注意所有看到的棱都应表现在俯视图中.【详解】从上往下看,该几何体的俯视图与选项D所示视图一致.故选D.【点睛】本题考查了简单组合体三视图的知识,俯视图是从物体的上面看得到的视图.4.一、单选题在反比例函数4yx=的图象中,阴影部分的面积不等于4的是()A.B.C.D.【答案】B【解析】根据反比例函数kyx=中k的几何意义,过双曲线上任意一点引x轴、y轴垂线,所得矩形面积为|k|解答即可.【详解】解:A、图形面积为|k|=1;B、阴影是梯形,面积为6;C、D面积均为两个三角形面积之和,为2×(12|k|)=1.故选B.【点睛】主要考查了反比例函数kyx中k的几何意义,即过双曲线上任意一点引x轴、y轴垂线,所得矩形面积为|k|,是经常考查的一个知识点;这里体现了数形结合的思想,做此类题一定要正确理解k的几何意义.图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S的关系即S=12|k|.5.某商品价格为a元,降价10%后,又降价10%,因销售量猛增,商店决定再提价20%,提价后这种商品的价格为()A.0.96a元B.0.972a元C.1.08a元D.a元【答案】B【解析】提价后这种商品的价格=原价×(1-降低的百分比)(1-百分比)×(1+增长的百分比),把相关数值代入求值即可.【详解】第一次降价后的价格为a×(1-10%)=0.9a元,第二次降价后的价格为0.9a×(1-10%)=0.81a元,∴提价20%的价格为0.81a×(1+20%)=0.972a元,故选B.【点睛】本题考查函数模型的选择与应用,考查列代数式,得到第二次降价后的价格是解决本题的突破点;得到提价后这种商品的价格的等量关系是解决本题的关键.6.下列图形中,周长不是32 m的图形是( )A.B.C.D.【答案】B【解析】根据所给图形,分别计算出它们的周长,然后判断各选项即可.【详解】A. L=(6+10)×2=32,其周长为32.B. 该平行四边形的一边长为10,另一边长大于6,故其周长大于32.C. L=(6+10)×2=32,其周长为32.D. L=(6+10)×2=32,其周长为32.采用排除法即可选出B故选B.【点睛】此题考查多边形的周长,解题在于掌握计算公式.7.甲、乙两人加工一批零件,甲完成240个零件与乙完成200个零件所用的时间相同,已知甲比乙每天多完成8个零件.设乙每天完成x 个零件,依题意下面所列方程正确的是( )A .2402008x x =- B .2402008x x =+ C .2402008x x =+ D .2402008x x =- 【答案】B 【解析】根据题意设出未知数,根据甲所用的时间=乙所用的时间,用时间列出分式方程即可.【详解】设乙每天完成x 个零件,则甲每天完成(x+8)个.即得,2402008x x+= ,故选B. 【点睛】找出甲所用的时间=乙所用的时间这个关系式是本题解题的关键.8.已知关于x 的一元二次方程2230x kx -+=有两个相等的实根,则k 的值为( )A .±B .C .2或3D 【答案】A【解析】根据方程有两个相等的实数根结合根的判别式即可得出关于k 的方程,解之即可得出结论.【详解】∵方程2230x kx -+=有两个相等的实根,∴△=k 2-4×2×3=k 2-24=0,解得:k=±故选A .【点睛】本题考查了根的判别式,熟练掌握“当△=0时,方程有两个相等的两个实数根”是解题的关键. 9.二次函数2(0)y ax bx c a =++≠的图像如图所示,下列结论正确是( )A .0abc >B .20a b +<C .30a c +<D .230ax bx c ++-=有两个不相等的实数根【答案】C 【解析】观察图象:开口向下得到a <0;对称轴在y 轴的右侧得到a 、b 异号,则b >0;抛物线与y 轴的交点在x 轴的上方得到c >0,所以abc <0;由对称轴为x=2b a -=1,可得2a+b=0;当x=-1时图象在x 轴下方得到y=a-b+c <0,结合b=-2a 可得 3a+c <0;观察图象可知抛物线的顶点为(1,3),可得方程230ax bx c ++-=有两个相等的实数根,据此对各选项进行判断即可.【详解】观察图象:开口向下得到a <0;对称轴在y 轴的右侧得到a 、b 异号,则b >0;抛物线与y 轴的交点在x 轴的上方得到c >0,所以abc <0,故A 选项错误;∵对称轴x=2b a-=1,∴b=-2a ,即2a+b=0,故B 选项错误; 当x=-1时, y=a-b+c <0,又∵b=-2a ,∴ 3a+c <0,故C 选项正确;∵抛物线的顶点为(1,3),∴230ax bx c ++-=的解为x 1=x 2=1,即方程有两个相等的实数根,故D 选项错误,故选C.【点睛】本题考查了二次函数图象与系数的关系:对于二次函数y=ax 2+bx+c (a≠0)的图象,当a >0,开口向上,函数有最小值,a <0,开口向下,函数有最大值;对称轴为直线x=2b a-,a 与b 同号,对称轴在y 轴的左侧,a 与b 异号,对称轴在y 轴的右侧;当c >0,抛物线与y 轴的交点在x 轴的上方;当△=b 2-4ac >0,抛物线与x 轴有两个交点.10.若ab <0,则正比例函数y=ax 与反比例函数y=b x在同一坐标系中的大致图象可能是( ) A . B . C . D .【答案】D【解析】根据ab <0及正比例函数与反比例函数图象的特点,可以从a >0,b <0和a <0,b >0两方面分类讨论得出答案.【详解】解:∵ab<0,∴分两种情况:(1)当a>0,b<0时,正比例函数y=ax数的图象过原点、第一、三象限,反比例函数图象在第二、四象限,无此选项;(2)当a<0,b>0时,正比例函数的图象过原点、第二、四象限,反比例函数图象在第一、三象限,选项D符合.故选D【点睛】本题主要考查了反比例函数的图象性质和正比例函数的图象性质,要掌握它们的性质才能灵活解题.二、填空题(本题包括8个小题)11.袋中装有一个红球和二个黄球,它们除了颜色外都相同,随机从中摸出一球,记录下颜色后放回袋中,充分摇匀后,再随机摸出一球,两次都摸到红球的概率是_____.【答案】1 9【解析】首先根据题意画出树状图,由树状图求得所有等可能的结果与两次都摸到红球的情况,然后利用概率公式求解即可求得答案.注意此题属于放回实验.【详解】画树状图如下:由树状图可知,共有9种等可能结果,其中两次都摸到红球的有1种结果,所以两次都摸到红球的概率是19,故答案为19.【点睛】此题考查的是用列表法或树状图法求概率的知识.注意画树状图与列表法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;解题时要注意此题是放回实验还是不放回实验.12.一个两位数,个位数字比十位数字大4,且个位数字与十位数字的和为10,则这个两位数为_______.【答案】37【解析】根据题意列出一元一次方程即可求解.【详解】解:设十位上的数字为a,则个位上的数为(a+4),依题意得:a+a+4=10,解得:a=3,∴这个两位数为:37【点睛】本题考查了一元一次方程的实际应用,属于简单题,找到等量关系是解题关键.13.如图,CE 是▱ABCD 的边AB 的垂直平分线,垂足为点O ,CE 与DA 的延长线交于点E .连接AC ,BE ,DO ,DO 与AC 交于点F ,则下列结论:①四边形ACBE 是菱形;②∠ACD =∠BAE ;③AF :BE =2:1;④S 四边形AFOE :S △COD =2:1.其中正确的结论有_____.(填写所有正确结论的序号)【答案】①②④.【解析】根据菱形的判定方法、平行线分线段成比例定理、直角三角形斜边中线的性质一一判断即可.【详解】∵四边形ABCD 是平行四边形,∴AB ∥CD ,AB=CD ,∵EC 垂直平分AB ,∴OA=OB=12AB=12DC ,CD ⊥CE , ∵OA ∥DC , ∴EA EO OA ED EC CD ===12, ∴AE=AD ,OE=OC ,∵OA=OB ,OE=OC ,∴四边形ACBE 是平行四边形,∵AB ⊥EC ,∴四边形ACBE 是菱形,故①正确,∵∠DCE=90°,DA=AE ,∴AC=AD=AE ,∴∠ACD=∠ADC=∠BAE ,故②正确,∵OA ∥CD ,∴AF OA 1CF CD 2==, ∴AF AF 1AC BE 3==,故③错误, 设△AOF 的面积为a ,则△OFC 的面积为2a ,△CDF 的面积为4a ,△AOC 的面积=△AOE 的面积=1a , ∴四边形AFOE 的面积为4a ,△ODC 的面积为6a∴S 四边形AFOE :S △COD =2:1.故④正确.故答案是:①②④.【点睛】此题考查平行四边形的性质、菱形的判定和性质、平行线分线段成比例定理、等高模型等知识,解题的关键是灵活运用所学知识解决问题,学会利用参数解决问题.14.如图所示,在四边形ABCD 中,AD ⊥AB ,∠C=110°,它的一个外角∠ADE=60°,则∠B 的大小是_____.【答案】40°【解析】根据外角的概念求出∠ADC 的度数,再根据垂直的定义、四边形的内角和等于360°进行求解即可得.【详解】∵∠ADE=60°,∴∠ADC=120°,∵AD ⊥AB ,∴∠DAB=90°,∴∠B=360°﹣∠C ﹣∠ADC ﹣∠A=40°,故答案为40°.【点睛】本题考查了多边形的内角和外角,掌握四边形的内角和等于360°、外角的概念是解题的关键.15.将23x =代入函数1y x =-中,所得函数值记为1y ,又将11x y =+代入函数1y x=-中,所得的函数值记为2y ,再将21x y =+代入函数中,所得函数值记为3y …,继续下去.1y =________;2y =________;3y =________;2006y =________.【答案】32- 213- 2【解析】根据数量关系分别求出y1,y2,y3,y4,…,不难发现,每3次计算为一个循环组依次循环,用2006除以3,根据商和余数的情况确定y2006的值即可.【详解】y1=32 -,y2=−1312-+=2,y3=−112+=13-,y4=−1113-+=32-,…,∴每3次计算为一个循环组依次循环,∵2006÷3=668余2,∴y2006为第669循环组的第2次计算,与y2的值相同,∴y2006=2,故答案为32-;2;13-;2.【点睛】本题考查反比例函数的定义,解题的关键是多运算找规律.16.如图,矩形ABCD中,AB=3,BC=5,点P是BC边上的一个动点(点P与点B,C都不重合),现将△PCD 沿直线PD折叠,使点C落到点F处;过点P作∠BPF的角平分线交AB于点E.设BP=x,BE=y,则下列图象中,能表示y与x的函数关系的图象大致是()【答案】C【解析】先证明△BPE∽△CDP,再根据相似三角形对应边成比例列出式子变形可得.【详解】由已知可知∠EPD=90°,∴∠BPE+∠DPC=90°,∵∠DPC+∠PDC=90°,∴∠CDP=∠BPE ,∵∠B=∠C=90°,∴△BPE ∽△CDP ,∴BP :CD =BE :CP ,即x:3=y:(5-x),∴y=253x x -+(0<x<5); 故选C .考点:1.折叠问题;2.相似三角形的判定和性质;3.二次函数的图象.17.对于实数a ,b ,定义运算“※”如下:a ※b=a 2﹣ab ,例如,5※3=52﹣5×3=1.若(x+1)※(x ﹣2)=6,则x 的值为_____.【答案】2【解析】根据新定义运算对式子进行变形得到关于x 的方程,解方程即可得解.【详解】由题意得,(x+2)2﹣(x+2)(x ﹣2)=6,整理得,3x+3=6,解得,x=2,故答案为2.【点睛】本题考查了解方程,涉及到完全平方公式、多项式乘法的运算等,根据题意正确得到方程是解题的关键.18.16的算术平方根是 .【答案】4【解析】正数的正的平方根叫算术平方根,0的算术平方根还是0;负数没有平方根也没有算术平方根 ∵2(4)16±=∴16的平方根为4和-4∴16的算术平方根为4三、解答题(本题包括8个小题)19.如图,已知抛物线的顶点为A (1,4),抛物线与y 轴交于点B (0,3),与x 轴交于C 、D 两点.点P 是x 轴上的一个动点.求此抛物线的解析式;求C、D两点坐标及△BCD的面积;若点P在x轴上方的抛物线上,满足S△PCD=12S△BCD,求点P的坐标.【答案】(1)y=﹣(x﹣1)2+4;(2)C(﹣1,0),D(3,0);6;(3)P(10,32),或P(110,32)【解析】(1)设抛物线顶点式解析式y=a(x-1)2+4,然后把点B的坐标代入求出a的值,即可得解;(2)令y=0,解方程得出点C,D坐标,再用三角形面积公式即可得出结论;(3)先根据面积关系求出点P的坐标,求出点P的纵坐标,代入抛物线解析式即可求出点P的坐标.【详解】解:(1)、∵抛物线的顶点为A(1,4),∴设抛物线的解析式y=a(x﹣1)2+4,把点B(0,3)代入得,a+4=3,解得a=﹣1,∴抛物线的解析式为y=﹣(x﹣1)2+4;(2)由(1)知,抛物线的解析式为y=﹣(x﹣1)2+4;令y=0,则0=﹣(x﹣1)2+4,∴x=﹣1或x=3,∴C(﹣1,0),D(3,0);∴CD=4,∴S△BCD=12CD×|y B|=12×4×3=6;(3)由(2)知,S△BCD=12CD×|y B|=12×4×3=6;CD=4,∵S△PCD=12S△BCD,∴S△PCD=12CD×|y P|=12×4×|y P|=3,∴|y P|= 32,∵点P在x轴上方的抛物线上,∴y P>0,∴y P= 32,∵抛物线的解析式为y=﹣(x﹣1)2+4;∴32=﹣(x﹣1)2+4,∴x=1±102,∴P(1+ 102,32),或P(1﹣102,32).【点睛】本题考查的是二次函数的综合应用,熟练掌握二次函数的性质是解题的关键.20.如图,△ABC中,CD是边AB上的高,且AD CD CD BD=.求证:△ACD∽△CBD;求∠ACB的大小.【答案】(1)证明见试题解析;(2)90°.【解析】试题分析:(1)由两边对应成比例且夹角相等的两个三角形相似,即可证明△ACD∽△CBD;(2)由(1)知△ACD∽△CBD,然后根据相似三角形的对应角相等可得:∠A=∠BCD,然后由∠A+∠ACD=90°,可得:∠BCD+∠ACD=90°,即∠ACB=90°.试题解析:(1)∵CD是边AB上的高,∴∠ADC=∠CDB=90°,∵AD CDCD BD=.∴△ACD∽△CBD;(2)∵△ACD∽△CBD,∴∠A=∠BCD,在△ACD中,∠ADC=90°,∴∠A+∠ACD=90°,∴∠BCD+∠ACD=90°,即∠ACB=90°.考点:相似三角形的判定与性质.21.我们已经知道一些特殊的勾股数,如三连续正整数中的勾股数:3、4、5;三个连续的偶数中的勾股数6、8、10;事实上,勾股数的正整数倍仍然是勾股数.另外利用一些构成勾股数的公式也可以写出许多勾股数,毕达哥拉斯学派提出的公式:a=2n+1,b=2n2+2n,c=2n2+2n+1(n为正整数)是一组勾股数,请证明满足以上公式的a、b、c的数是一组勾股数.然而,世界上第一次给出的勾股数公式,收集在我国古代的着名数学着作《九章算术》中,书中提到:当a=12(m2﹣n2),b=mn,c=12(m2+n2)(m、n为正整数,m>n时,a、b、c构成一组勾股数;利用上述结论,解决如下问题:已知某直角三角形的边长满足上述勾股数,其中一边长为37,且n=5,求该直角三角形另两边的长.【答案】(1)证明见解析;(2)当n=5时,一边长为37的直角三角形另两边的长分别为12,1.【解析】(1)根据题意只需要证明a2+b2=c2,即可解答(2)根据题意将n=5代入得到a=12(m2﹣52),b=5m,c=12(m2+25),再将直角三角形的一边长为37,分别分三种情况代入a=12(m2﹣52),b=5m,c=12(m2+25),即可解答【详解】(1)∵a2+b2=(2n+1)2+(2n2+2n)2=4n2+4n+1+4n4+8n3+4n2=4n4+8n3+8n2+4n+1,c2=(2n2+2n+1)2=4n4+8n3+8n2+4n+1,∴a2+b2=c2,∵n为正整数,∴a、b、c是一组勾股数;(2)解:∵n=5∴a=12(m2﹣52),b=5m,c=12(m2+25),∵直角三角形的一边长为37,∴分三种情况讨论,①当a=37时,12(m2﹣52)=37,解得m=(不合题意,舍去) ②当y=37时,5m=37,解得m=375(不合题意舍去);③当z=37时,37=12(m2+n2),解得m=±7,∵m>n>0,m、n是互质的奇数,∴m=7,把m=7代入①②得,x=12,y=1.综上所述:当n=5时,一边长为37的直角三角形另两边的长分别为12,1.【点睛】此题考查了勾股数和勾股定理,熟练掌握勾股定理是解题关键22.关于x的一元二次方程20x m +=有两个实数根,则m 的取值范围是( )A .m≤1B .m <1C .﹣3≤m≤1D .﹣3<m <1【答案】C 【解析】利用二次根式有意义的条件和判别式的意义得到230(3)40m m m +≥⎧⎪⎨+-≥⎪⎩=,然后解不等式组即可. 【详解】根据题意得230(3)40m m m +≥⎧⎪⎨+-≥⎪⎩=, 解得-3≤m≤1.故选C .【点睛】本题考查了根的判别式:一元二次方程ax 2+bx+c=0(a≠0)的根与△=b 2-4ac 有如下关系:当△>0时,方程有两个不相等的两个实数根;当△=0时,方程有两个相等的两个实数根;当△<0时,方程无实数根.23.计算:11|12sin 60(2016)3π-︒︒⎛⎫+-+-- ⎪⎝⎭先化简,再求值:2344111x x x x x ++⎛⎫-+÷ ⎪++⎝⎭,其中2x =.【答案】 (1)1;(2)【解析】(1)分别计算负指数幂、绝对值、零指数幂、特殊角的三角函数值、立方根;(2)先把括号内通分相减,再计算分式的除法,除以一个分式,等于乘它的分子、分母交换位置.【详解】(1)原式1﹣﹣﹣1﹣2=1. (2)原式=[31x +﹣(1)(1)1x x x +-+]•21(2)x x ++ =(2)(2)1x x x -+-+•21(2)x x ++=22x x -+, 当2时,原式-1. 【点睛】 本题考查负指数幂、绝对值、零指数幂、特殊角的三角函数值、立方根以及分式的化简求值,解题关键是熟练掌握以上性质和分式的混合运算.24.计算532224m m m m -⎛⎫+-÷ ⎪--⎝⎭. 【答案】26m + 【解析】分析:先计算522m m +--,再做除法,结果化为整式或最简分式. 详解: 532224m m m m -⎛⎫+-÷ ⎪--⎝⎭()()()2252423m m m m m +---=⋅-- ()222923m m m m --=⋅-- ()()()332223m m m m m -+-=⋅-- 26m =+.点睛:本题考查了分式的混合运算.解题过程中注意运算顺序.解决本题亦可先把除法转化成乘法,利用乘法对加法的分配律后再求和.25.在平面直角坐标系中,一次函数34y x b =-+的图象与反比例函数k y x=(k≠0)图象交于A 、B 两点,与y 轴交于点C ,与x 轴交于点D ,其中A 点坐标为(﹣2,3).求一次函数和反比例函数解析式.若将点C 沿y 轴向下平移4个单位长度至点F ,连接AF 、BF ,求△ABF 的面积.根据图象,直接写出不等式34k x b x-+>的解集. 【答案】(1)y =﹣34x+32,y =-6x ;(2)12;(3) x <﹣2或0<x <4. 【解析】(1)将点A 坐标代入解析式,可求解析式;(2)一次函数和反比例函数解析式组成方程组,求出点B 坐标,即可求△ABF 的面积;(3)直接根据图象可得.【详解】(1)∵一次函数y =﹣34x+b 的图象与反比例函数y = k x (k≠0)图象交于A (﹣3,2)、B 两点, ∴3=﹣34×(﹣2)+b ,k =﹣2×3=﹣6∴b =32,k =﹣6 ∴一次函数解析式y =﹣3342x +,反比例函数解析式y =6x -. (2)根据题意得:33426y x y x ⎧+⎪⎪⎨-⎪⎪⎩=﹣= , 解得:211242,332x x y y ⎧=⎧=-⎪⎪⎨⎨==-⎪⎪⎩⎩, ∴S △ABF =12×4×(4+2)=12 (3)由图象可得:x <﹣2或0<x <4【点睛】本题考查了反比例函数图象与一次函数图象的交点问题,待定系数法求解析式,熟练运用函数图象解决问题是本题的关键.26.在□ABCD ,过点D 作DE ⊥AB 于点E ,点F 在边CD 上,DF =BE ,连接AF ,BF.求证:四边形BFDE 是矩形;若CF =3,BF =4,DF =5,求证:AF 平分∠DAB .【答案】(1)见解析(2)见解析【解析】试题分析:(1)根据平行四边形的性质,可得AB 与CD 的关系,根据平行四边形的判定,可得BFDE 是平行四边形,再根据矩形的判定,可得答案;(2)根据平行线的性质,可得∠DFA=∠FAB ,根据等腰三角形的判定与性质,可得∠DAF=∠DFA ,根据角平分线的判定,可得答案.试题分析:(1)证明:∵四边形ABCD 是平行四边形,∴AB ∥CD .∵BE ∥DF ,BE=DF ,∴四边形BFDE 是平行四边形.∵DE ⊥AB ,∴∠DEB=90°,∴四边形BFDE 是矩形;(2)∵四边形ABCD 是平行四边形,∴AB ∥DC ,∴∠DFA=∠FAB .在Rt△BCF中,由勾股定理,得=,∴AD=BC=DF=5,∴∠DAF=∠DFA,∴∠DAF=∠FAB,即AF平分∠DAB.【点睛】本题考查了平行四边形的性质,利用了平行四边形的性质,矩形的判定,等腰三角形的判定与性质,利用等腰三角形的判定与性质得出∠DAF=∠DFA是解题关键.中考数学模拟试卷一、选择题(本题包括10个小题,每小题只有一个选项符合题意)1.不等式组12342x x +>⎧⎨-≤⎩的解集表示在数轴上正确的是( ) A .B .C .D .【答案】C 【解析】根据题意先解出12342x x +>⎧⎨-≤⎩的解集是, 把此解集表示在数轴上要注意表示时要注意起始标记为空心圆圈,方向向右; 表示时要注意方向向左,起始的标记为实心圆点,综上所述C 的表示符合这些条件.故应选C.2.如图所示是小孔成像原理的示意图,根据图中所标注的尺寸,求出这支蜡烛在暗盒中所成像CD 的长( )A .16cmB .13cm C .12cm D .1cm【答案】D【解析】过O 作直线OE ⊥AB ,交CD 于F ,由CD//AB 可得△OAB ∽△OCD ,根据相似三角形对应边的比等于对应高的比列方程求出CD 的值即可.【详解】过O 作直线OE ⊥AB ,交CD 于F ,∵AB//CD ,∴OF ⊥CD ,OE=12,OF=2,∴△OAB ∽△OCD ,∵OE 、OF 分别是△OAB 和△OCD 的高, ∴OF CD OE AB =,即2126CD =, 解得:CD=1.故选D.【点睛】本题考查相似三角形的应用,解题的关键在于理解小孔成像原理给我们带来的已知条件,熟记相似三角形对应边的比等于对应高的比是解题关键.3.在△ABC中,∠C=90°,sinA=45,则tanB等于()A.43B.34C.35D.45【答案】B【解析】法一,依题意△ABC为直角三角形,∴∠A+∠B=90°,∴cosB=45,∵22cos sin1B B+=,∴sinB=35,∵tanB=sincosBB=34故选B法2,依题意可设a=4,b=3,则c=5,∵tanb=34ba故选B4.如图,一圆弧过方格的格点A、B、C,在方格中建立平面直角坐标系,使点A的坐标为(﹣3,2),则该圆弧所在圆心坐标是()A.(0,0)B.(﹣2,1)C.(﹣2,﹣1)D.(0,﹣1)【答案】C【解析】如图:分别作AC与AB的垂直平分线,相交于点O,则点O即是该圆弧所在圆的圆心.∵点A的坐标为(﹣3,2),∴点O 的坐标为(﹣2,﹣1). 故选C .5.如图,已知11(,)3A y ,2(3,)B y为反比例函数1y x=图象上的两点,动点(,0)P x 在x 轴正半轴上运动,当线段AP 与线段BP 之差达到最大时,点P 的坐标是( )A .1(,0)3B .4(,0)3C .8(,0)3D .10(,0)3【答案】D【解析】求出AB 的坐标,设直线AB 的解析式是y=kx+b ,把A 、B 的坐标代入求出直线AB 的解析式,根据三角形的三边关系定理得出在△ABP 中,|AP-BP|<AB ,延长AB 交x 轴于P′,当P 在P′点时,PA-PB=AB ,此时线段AP 与线段BP 之差达到最大,求出直线AB 于x 轴的交点坐标即可. 【详解】把11(,)3A y ,2(3,)B y 代入反比例函数1y x =,得:13y =,213y =, 11(,3),(3,)33A B ∴,在ABP ∆中,由三角形的三边关系定理得:AP BP AB -<,∴延长AB 交x 轴于P',当P 在P'点时,PA PB AB -=,即此时线段AP 与线段BP 之差达到最大, 设直线AB 的解析式是y kx b =+,把A ,B 的坐标代入得:133133k b k b ⎧=+⎪⎪⎨⎪=+⎪⎩,解得:101,3k b =-=, 1215x ->∴直线AB 的解析式是103y x =-+, 当0y =时,103x =,即10(,0)3P ,故选D. 【点睛】本题考查了三角形的三边关系定理和用待定系数法求一次函数的解析式的应用,解此题的关键是确定P 点的位置,题目比较好,但有一定的难度.6.如图,在矩形ABCD 中,AB=2,AD=3,点E 是BC 边上靠近点B 的三等分点,动点P 从点A 出发,沿路径A→D→C→E 运动,则△APE 的面积y 与点P 经过的路径长x 之间的函数关系用图象表示大致是( )A .B .C .D .【答案】B【解析】由题意可知, 当03x ≤≤时,11222y AP AB x x =⋅=⨯=; 当35x <≤时,ABE ADP EPC ABCD y S S S S ∆∆∆=---矩形()()11123123325222x x =⨯-⨯⨯-⨯--⨯-1922x =-+; 当57x <≤时,()1127722y AB EP x x =⋅=⨯⨯-=-.∵3x =时,3y =;5x =时,2y =.∴结合函数解析式, 可知选项B 正确. 【点睛】考点:1.动点问题的函数图象;2.三角形的面积.7.在如图所示的数轴上,点B 与点C 关于点A 对称,A 、B 两点对应的实数分别是3和﹣1,则点C 所对应的实数是( )A .3B .3C .3 1D .3【答案】D【解析】设点C 所对应的实数是x .根据中心对称的性质,对称点到对称中心的距离相等,则有()x 3=31-,解得x=23+1.故选D.8.如图是某公园的一角,∠AOB=90°,弧AB 的半径OA 长是6米,C 是OA 的中点,点D 在弧AB 上,CD ∥OB ,则图中休闲区(阴影部分)的面积是()A.91032π⎛⎫-⎪⎝⎭米2B.932π⎛⎫-⎪⎝⎭米2C.9632π⎛⎫-⎪⎝⎭米2D.()693π-米2【答案】C【解析】连接OD,∵弧AB的半径OA长是6米,C是OA的中点,∴OC=12OA=12×6=1.∵∠AOB=90°,CD∥OB,∴CD⊥OA.在Rt△OCD中,∵OD=6,OC=1,∴2222CD OD OC6333=-=-=.又∵CD333sin DOCOD62∠===,∴∠DOC=60°.∴2606193336336022DOCAODS S Sππ∆⋅⋅=-=-⨯⨯=-阴影扇形(米2).故选C.9.对于一组统计数据1,1,6,5,1.下列说法错误的是()A.众数是1 B.平均数是4 C.方差是1.6 D.中位数是6【答案】D【解析】根据中位数、众数、方差等的概念计算即可得解.【详解】A、这组数据中1都出现了1次,出现的次数最多,所以这组数据的众数为1,此选项正确;B、由平均数公式求得这组数据的平均数为4,故此选项正确;C、S2=15[(1﹣4)2+(1﹣4)2+(6﹣4)2+(5﹣4)2+(1﹣4)2]=1.6,故此选项正确;D、将这组数据按从大到校的顺序排列,第1个数是1,故中位数为1,故此选项错误;故选D.考点:1.众数;2.平均数;1.方差;4.中位数.10.如图,△ABC的面积为8cm2,AP垂直∠B的平分线BP于P,则△PBC的面积为()A.2cm2B.3cm2C.4cm2D.5cm2【答案】C【解析】延长AP交BC于E,根据AP垂直∠B的平分线BP于P,即可求出△ABP≌△BEP,又知△APC和△CPE等底同高,可以证明两三角形面积相等,即可求得△PBC的面积.【详解】延长AP交BC于E.∵AP垂直∠B的平分线BP于P,∴∠ABP=∠EBP,∠APB=∠BPE=90°.在△APB和△EPB中,∵,∴△APB≌△EPB(ASA),∴S△APB=S△EPB,AP=PE,∴△APC 和△CPE等底同高,∴S△APC=S△PCE,∴S△PBC=S△PBE+S△PCE S△ABC=4cm1.故选C.【点睛】本题考查了三角形面积和全等三角形的性质和判定的应用,关键是求出S△PBC=S△PBE+S△PCE S△ABC.二、填空题(本题包括8个小题)11.亚洲陆地面积约为4400万平方千米,将44000000用科学记数法表示为_____.【答案】4.4×1【解析】分析:科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n 是正数;当原数的绝对值<1时,n是负数.详解:44000000=4.4×1,故答案为4.4×1.点睛:此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.12.如图,是用火柴棒拼成的图形,则第n 个图形需_____根火柴棒.【答案】2n+1.【解析】解:根据图形可得出:当三角形的个数为1时,火柴棒的根数为3; 当三角形的个数为2时,火柴棒的根数为5; 当三角形的个数为3时,火柴棒的根数为7; 当三角形的个数为4时,火柴棒的根数为9; ……由此可以看出:当三角形的个数为n 时,火柴棒的根数为3+2(n ﹣1)=2n+1. 故答案为:2n+1.13.如图所示,点C 在反比例函数ky (x 0)x=>的图象上,过点C 的直线与x 轴、y 轴分别交于点A 、B ,且AB BC =,已知AOB 的面积为1,则k 的值为______.【答案】1【解析】根据题意可以设出点A 的坐标,从而以得到点C 和点B 的坐标,再根据AOB 的面积为1,即可求得k 的值.【详解】解:设点A 的坐标为()a,0-,过点C 的直线与x 轴,y 轴分别交于点A ,B ,且AB BC =,AOB 的面积为1,∴点k C a,a ⎛⎫ ⎪⎝⎭,∴点B 的坐标为k 0,2a ⎛⎫⎪⎝⎭,1k a 122a∴⋅⋅=, 解得,k 4=, 故答案为:1. 【点睛】本题考查了反比例函数系数k 的几何意义、一次函数图象上点的坐标特征、反比例函数图象上点的坐标特征,解题关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答. 14.下表记录了甲、乙、丙、丁四名跳远运动员选拔赛成绩的平均数与方差s 2:甲 乙 丙 丁 平均数(cm ) 561 560 561 560 方差s 2(cm 2)3.53.515.516.5根据表中数据,要从中选择一名成绩好又发挥稳定的运动员参加比赛,应该选择_____. 【答案】甲【解析】首先比较平均数,平均数相同时选择方差较小的运动员参加. 【详解】∵==x x x x 甲乙丁丙> , ∴从甲和丙中选择一人参加比赛, ∵22S S 甲丙< , ∴选择甲参赛, 故答案为甲. 【点睛】此题考查了平均数和方差,关键是根据方差反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.15.如图,以扇形OAB 的顶点O 为原点,半径OB 所在的直线为x 轴,建立平面直角坐标系,点B 的坐标为(2,0),若抛物线21y x k 2=+与扇形OAB 的边界总有两个公共点,则实数k 的取值范围是 .【答案】-2<k <12。
学长宁、金山区初三数学一模试卷

2021 学年长宁、金山区调研测试九年级数学〔总分值 150 分,考试时间100 分钟〕考生注意:1. 本试卷含三个大题,共 25 题,答题时,考生务必按答题要求在答题纸规定位置上作答,在草稿纸、本试卷上大题一律无效。
2. 除第一、二大题外,其余各题如无特别说明,都必须在答题纸的相应位置上写出证明或计算的主要步骤。
一、选择题〔本大题共6 题,每题 4 分,总分值24 分〕1.在平面直角坐标系中,抛物线y x 122 的顶点坐标是〔〕A. 〔 -1, 2〕B. 〔 1, 2〕C. 〔 2, -1〕D. 〔 2, 1〕E D2.在 ABC 中,C 90 , AB5 , BC 4 ,那么A 的正弦值是〔 〕343D.4A.B.C.A43 553.如图,以下能判断 BC ∥ ED 的条件是〔〕ED ADED AEA. ABB. AC BCBC BCAD AEAD AC第3题图C.ACD.AEABAB4.O 1 与 O 2 的半径分别是 2 和 6,假设O 1 与 O 2 相交,那么圆心距 O 1O 2 的取值范围是〔〕A. 2< O 1O 2 <4B.2< O 1O 2 <6C. 4< O 1O 2 <8D. 4< O 1O 2 <105.非零向量 a 与 b ,那么以下说法正确的选项是〔 〕A. 如果 ab ,那么 a b ;B. 如果C. 如果 a ∥b ,那么 ab ;D. 如果ab ,那么 a ∥ba b ,那么 ab6.等腰三角形的腰长为6 cm ,底边长为 4 cm ,以等腰三角形的顶角的顶点为圆心 5 cm 为半径画圆,那么该圆与底边的位置关系是〔 〕A. 相离B. 相切C. 相交D. 不能确定二、填空题〔本大题共 12 题,每题 4 分,总分值 48 分〕7. 如果 3x4y x 0 ,那么x=__________.y8.二次函数 yx 2 2x 1,那么该二次函数的图像的对称轴是__________.9. 抛物线y 3x 2 x c 与 y 轴的交点坐标是〔, -3 〕,那么c =__________.10. 抛物线 y1 x2 3x 经过点〔 -2, m 〕,那么 m =___________.211. 设是锐角,如果 tan 2 ,那么 cot =___________.12. 在直角坐标平面中,将抛物线 y 2x 2 先向上平移 1 个单位,再向右平移1 个单位,那么平移后的抛物线解析式是 __________.13.A 的半径是 2,如果B 是 A 外一点,那么线段 AB 长度的取值范围是 __________.14. 如图,点 G 是 ABC 的重心,联结 AG 并延长交 BC 于点 D , GE ∥ AB 交 BC 与 E ,假设AB 6,那么 GE =___________.15. 如图,在地面上离旗杆BC 底部 18 米的 A 处,用测角仪测得旗杆顶端C 的仰角为 30°,测角仪AD 的高度为 1.5 米,那么旗杆BC 的高度为 _________米 .ACAA DGDO 1O 2OBEDCABBEBC第14题图第 15题图第 16题图第17题图16. 如图, O 1 与O 2 相交于 A 、B 两点, O 1 与O 2 的半径分别是1 和 3 , O 1O2 =2 ,那么两圆公共弦 AB 的长为 ___________.17. 如图,在梯形ABCD中,AD ∥ BC,AC与 BD交于O点,DO : BO1: 2 ,点 E 在 CB 的延长线上,如果S AOD: SABE =1:3 ,那么BC : BE =_________.18.沿如图,在ABC 中, C DE 翻折,使得点 A 落在点90 A ' , AC 处,当8 , BC A ' E AC6 , D 是 AB 的中点, 点时, A ' B =___________.E 在边AC上,将ADEBAC第18题图三、解答题〔本大题共 7 题,总分值 78 分〕19 . 〔此题总分值 10 分〕计算: sin 30 tan 301cos60 cot 30tan 453sin 2 4520.〔此题总分值10 分,第〔1〕小题总分值4 分,第〔2〕小题总分值6 分〕如图,在ABC 中,D 是AB中点,联结CD.〔 1〕假设AB10 且ACD B ,求AC的长 .〔 2〕过D点作BC 的平行线交AC于点E ,设DE a , DC b ,请用向量 a 、 b 表示AC 和AB 〔直接写出结果〕ADB C第20题图21.〔此题总分值10 分,第〔 1〕小题总分值5 分,第〔 2〕小题总分值 5 分〕如图, ABC中,CD AB 于点D, D 经过点 B ,与 BC 交于点 E ,与 AB 交与点 F . tan A 1,2cot ABC 38., AD4求〔 1〕 D 的半径;CE 〔 2〕CE的长 .A F D B第21 题图22.〔此题总分值10 分,第〔 1〕小题总分值 5 分,第〔 2〕小题总分值如图,拦水坝的横断面为梯形ABCD , AB∥ CD ,坝顶宽 DC5 分〕为 6 米,坝高DG为 2 米,迎水坡BC的坡角为30°,坝底宽AB为〔 8+2 3 〕米.(1〕求背水坡AD的坡度;(2〕为了加固拦水坝,需将水坝加高 2 米,并保持坝顶宽度不变,迎水坡和背水坡的坡度也不变,求加高后坝底 HB 的宽度.MED CHN A GFB第 22题图23.〔此题总分值 12 分,第〔 1〕小题总分值 6 分,第〔 2〕小题总分值 6 分〕如图,正方形 ABCD ,点 E 在 CB 的延长线上, 联结 AE 、 DE ,DE 与边 AB 交于点 F ,FG ∥ BE 且与AE 交于点 G.( 1〕求证: GF =BF .〔 2〕在 BC 边上取点 M ,使得 BMBE ,联结 AM 交 DE 于点 O .求证: FO ED OD EFADGFE BC第 23题图24.〔此题总分值 12 分,第〔 1〕小题总分值4 分,第〔 2〕小题总分值 4 分,第〔 3〕小题总分值 4 分〕在平面直角坐标系中,抛物线y x 2 2bx c 与 x 轴交于点 A 、 B 〔点 A 在点 B 的右侧〕,且与 y 轴正半轴交于点 C , A 〔 2, 0〕〔 1〕当 B 〔 -4, 0〕时,求抛物线的解析式;〔 2〕 O 为坐标原点,抛物线的顶点为P ,当 tan OAP 3时,求此抛物线的解析式;〔 3〕 O 为坐标原点,以 A 为圆心 OA 长为半径画A ,以 C 为圆心, 1OC 长为半径画圆C ,当 A2与C 外切时,求此抛物线的解析式.y10987654321A-5-4-3-2-1O123456x-1-2-3第24题图25.〔此题总分值14 分,第〔 1〕小题总分值4 分,第〔 2〕小题总分值 4 分,第〔 3〕小题总分值6 分〕ABC , AB AC 5, BC 8,PDQ 的顶点D在BC边上, DP 交 AB 边于点 E ,DQ 交 AB 边于点 O 且交 CA 的延长线于点 F 〔点 F 与点 A 不重合〕,设PDQB , BD 3 .〔 1〕求证:BDE∽ CFD ;〔 2〕设BE x , OA y ,求 y 关于x的函数关系式,并写出定义域;〔 3〕当AOF 是等腰三角形时,求BE 的长.QFA APOEB DC BD C第 25题图第 25题备用图参考答案:1-6: BDCCDA417、38、直线x19、 -310、411、2、 y 2 x 2121113、AB 214、 215、16、317、 2: 118、7 2或219、220〔1〕5 2〔 2〕AC2a2b, AB4a 2b7 21〔 1〕 3〔 2〕522〔 1〕i1:1 〔2〕104 3 米23、略2 x 8 〔3〕y x22824〔 1〕yx22x 8 〔2〕 y x2 3x3 y7525 x 0 x31211225〔 1〕略〔 2〕245x〔 3〕5或 65。
上海2020-2021学年初三数学一模考1-17题(锐角三角比+解直角三角形汇编)教师版

锐角三角比一、锐角三角比的定义如图,在Rt ABC∆中,90C∠=︒,A B C∠∠∠、、所对的边分别记为a b c、、(1)把锐角A的对边与邻边的比叫做A∠的正切,记作:tan AtanA a AA b∠==∠的对边的邻边(2)把锐角A的邻边与对边的比叫做A∠的余切,记作:cot AcotA b AA a∠==∠的邻边的对边(3)把锐角A的对边与邻边的比叫做A∠的正弦,记作:sin AsinA a Ac ∠==的对边斜边(4)把锐角A的邻边与对边的比叫做A∠的余弦,记作:cos AcosA b Ac ∠==的邻边斜边二、特殊角的锐角三角比值(2021金山一模3)在ABC Rt ∆中, 90=∠C ,那么锐角A 的正弦等于( ) (A )的邻边锐角的对边锐角A A ;(B )斜边的对边锐角A ;(C )斜边的邻边锐角A ;(D )的对边锐角的邻边锐角A A .【参考答案】B(2021虹口一模1)在△ABC 中,∠C =90°,如果BC =3,AC =4,那么tan A 的值是( )A .34; B .43; C .35; D .45. 【参考答案】A(2021宝山一模2) 在ABC △Rt 中,∠C =90°,AB =5,BC =3,那么A sin 的值为( )(A )53;(B )43; (C )54; (D )34. 【参考答案】A(2021崇明一模4)在△ABC 中,90C =︒∠,如果8AC =,6BC =,那么A ∠的正弦值为( ) (A)35; (B)45;(C)34;(D)43.【参考答案】A(2021奉贤一模4)在Rt △ABC 中,∠C =90°,如果AC =3,43=cos A ,那么AB 的长为( ) (A )49; (B )4; (C )5; (D )425. 【参考答案】B(2021闵行一模2)已知在Rt △ABC 中,90C ∠=︒,B β∠=,AB = 5,那么AC 的长为( ) (A )5cos β; (B )5sin β; (C )5cos β; (D )5sin β. 【参考答案】B(2021崇明一模12)已知锐角△ABC 中,5AB =,7BC =,4sin 5B =,那么C =∠ 度. 【参考答案】45(2021金山一模4)若α是锐角,()2215sin =+α,那么锐角α等于( ) (A ) 15; (B ) 30; (C ) 45; (D ) 60. 【参考答案】B(2021金山一模12)在ABC Rt ∆中, 90=∠C ,15=AB ,54in =A s ,那么=BC . 【参考答案】12(2021普陀一模3)已知在Rt △ABC 中,90C ∠=︒,3AB =,2BC =,那么tan B 的值等于( )(A )23; (B ); (C ; (D . 【参考答案】C(2021浦东新区一模2)已知在Rt △ABC 中,∠C =90°,∠B=α,AC =2,那么AB 的长等于( ) (A )2sin α; (B )2sin α; (C )2cos α; (D )2cos α.【参考答案】A(2021青浦一模3)在Rt △ABC 中,∠C =90º,那么cos A 等于( ) (A )BC AB; (B )AC AB; (C )BCAC; (D )AC BC.【参考答案】B(2021青浦一模13)在△ABC 中,∠C =90º,如果cot ∠A=2,BC =3,那么AC = . 【参考答案】6(2021松江一模10)在Rt △ABC 中,∠C =90°,AC=6,cos A =34,那么AB 的长为________.【参考答案】8(2021长宁一模1)已知在ABC ∆中,90C ∠=,50B ∠=,10AB =,那么BC 的长为( ) (A )10cos50; (B )10sin 50; (C )10tan50; (D )10cot 50︒.【参考答案】A(2021闵行一模13)在直角坐标平面内有一点A (12,5),点A 与原点O 的连线与x 轴的正半轴的夹角为θ,那么cos θ= .【参考答案】1312 (2021嘉定一模2)在平面直角坐标系xOy 中,已知点,3P (1),点P 与原点O 的连线与x 轴的正半轴的夹角为(090)αα︒<<︒,那么tan α的值是( )(A )10; (B )13; (C 10; (D )3.【参考答案】D(2021静安一模5)如果锐角α,那么下列结论中正确的是( ) (A )︒=30α; (B )︒=60α; (C )︒<<︒4530α; (D )︒<<︒6045α. 【参考答案】C(2021杨浦一模2)在△ABC 中,如果sin A =12,cot B ,那么这个三角形一定是( )(A )等腰三角形; (B )锐角三角形; (C )钝角三角形;(D )直角三角形. 【参考答案】D(2021松江一模2)在Rt △ABC 中,∠C =90°,∠A=α,BC =2,那么AC 的长为( )(A )2sin α;(B )2cos α;(C )2tan α;(D )2cot α.【参考答案】D(2021徐汇一模2)在ABC Rt ∆中,︒=∠90A ,6=AB ,10=BC ,那么下列结论正确的是( ) (A )34tan =C ; (B )54cot =C ;(C )43sin =C ; (D )54cos =C . 【参考答案】D(2021浦东新区一模9)计算:2sin30tan 45-= . 【参考答案】0(2021松江一模9)计算:sin30cot 60︒⋅︒=___________. 【参考答案】63(2021长宁一模9245sin 60︒︒+= .【参考答案】47解直角三角形的类型与解法:知二求三,至少一边类型一︰已知一边一角(角为两锐角之一)=sinA ctanB=tanA=tanAcotB 类型二︰已知两边(两直角边或一条直角边与斜边)2b+a(2021黄浦一模12)已知点P 位于第二象限内,OP =5,且OP 与x 轴负半轴夹角的正切值为 2,则点P 的坐标是 . 【参考答案】()52,5-(2021嘉定一模5)在Rt △ABC 中,90ACB ∠=︒,30A ∠=︒,CD AB ⊥,垂足为D .下列四个选项中,不正确的是( )(A )2AC AB=; (B )2BC CD=(C )3BD CD=(D )3BC AC=.【参考答案】B(2021黄浦一模11)在△ABC 中,AB =5,BC =8,∠B =60°,则△ABC 的面积是 . 【参考答案】310(2021黄浦一模3)对于锐角α,下列等式中成立的是( ) (A )sin cos tan ααα=⋅; (B )cos tan cot ααα=⋅;(C )tan cot sin ααα=⋅;(D )cot sin cos ααα=⋅.【参考答案】A(2021金山一模13)在ABC ∆中,5:2:1::=BC AC AB ,那么=B tan . 【参考答案】2(2021宝山一模11)已知等腰梯形上底为5,高为4,底角的余弦值为53,那么其周长为______【参考答案】26(2021黄浦一模10)已知一个锐角的正切值比余切值大,且两者之和是133,则这个锐角的正切值为 . 【参考答案】3(2021静安一模6)在Rt △ABC 中,∠C =90°,CD 是高,如果AB =m ,∠A =α, 那么CD 的长为_______(A )sin tan m αα⋅⋅; (B )sin cos m αα⋅⋅; (C )cos tan m αα⋅⋅; (D )cos cot m αα⋅⋅.【参考答案】B(2021徐汇一模14)如图,点P 在线段BC 上,BC AB ⊥,AP DP ⊥,DP CD ⊥,如果10=BC ,2=AB ,21tan =C ,那么DP 的长是_____.【参考答案】556(2021嘉定一模17)如图4,正方形ABEF和正方形BCDE的边长相等,点A、B、C 三个点在同一条直线上.联结AD BD、,那么cot ADB的值为.【参考答案】3(2021青浦一模16)如图,A、B、C是小正方形的顶点,且每个小正方形的边长相同,那么∠BAC的正弦值为.CBA【参考答案】22(2021松江一模14)如图,△ABC在边长为1个单位的方格纸中,△ABC的顶点在小正方形顶点位置,那么∠ABC的正弦值为___ _____.【参考答案】55图4BA(2021虹口一模6)如图2,在Rt △ABC 中,∠ACB =90°,D 是边AB 上一点,过D 作DF ⊥AB交边BC 于点E ,交AC 的延长线于点F ,联结AE .如果1tan 3EAC ∠=,1CEF S =△,那么ABC S △的值是( )A .3;B .6;C .9;D .12.【参考答案】C(2021虹口一模17)如图5,图中提供了一种求cot15°的方法.作Rt △ABC ,使∠C=90°,∠ABC =30°,再延长CB 到点D ,使BD =BA ,联结AD ,即可得∠D =15°.如果设AC =t ,则可得(23)CD t =+,那么cot15°= cot D ==2+3CDAC.运用以上方法,可求得cot22.5°的值是 .【参考答案】12+(2021普陀一模17)勾股定理是世界文明宝库中的一颗璀璨明珠,我国汉代数学家赵爽将四个全等的直角三角形拼成了一个大正方形ABCD ,同时留下一个小正方形EFGH 的空隙(如图7),利用面积证明了勾股定理.如果小正方形EFGH 的面积是4,10sin GBC ∠,那么大正方形ABCD 的面积等于 .【参考答案】10(2021徐汇一模16)《周髀算经》中的“赵爽弦图”(如图),图中的四个直角三角形都全等,如果正方形ABCD的面积是正方形EFGH面积的13倍,那么ABE∠的余切值是_____.【参考答案】23(2021杨浦一模16)如图,已知在△ABC中,∠C=90°,AB=10,cot12B=,正方形DEFG的顶点G、F分别在边AC、BC上,点D、E在斜边AB上,那么正方形DEFG的边长为 .【参考答案】720。
┃精选3套试卷┃2021年上海市金山区中考数学1月质量监测试题

中考数学模拟试卷一、选择题(本题包括10个小题,每小题只有一个选项符合题意)1.若关于x 的一元二次方程(k ﹣1)x 2+2x ﹣2=0有两个不相等的实数根,则k 的取值范围是( ) A .k >12B .k≥12C .k >12且k≠1 D .k≥12且k≠1 【答案】C【解析】根据题意得k-1≠0且△=2²-4(k-1)×(-2)>0,解得:k >12且k≠1. 故选C 【点睛】本题考查了一元二次方程ax²+bx+c=0(a≠0)的根的判别式△=b²-4ac ,关键是熟练掌握:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根. 2.一次函数y=ax+b 与反比例函数y=cx在同一平面直角坐标系中的图象如左图所示,则二次函数y=ax 2+bx+c 的图象可能是()A .B .C .D .【答案】B【解析】根据题中给出的函数图像结合一次函数性质得出a <0,b >0,再由反比例函数图像性质得出c <0,从而可判断二次函数图像开口向下,对称轴:2bx a=->0,即在y 轴的右边,与y 轴负半轴相交,从而可得答案.【详解】解:∵一次函数y=ax+b 图像过一、二、四, ∴a <0,b >0, 又∵反比例 函数y=cx图像经过二、四象限, ∴c <0,∴二次函数对称轴:2bx a=->0, ∴二次函数y=ax 2+bx+c 图像开口向下,对称轴在y 轴的右边,与y 轴负半轴相交, 故答案为B. 【点睛】本题考查了二次函数的图形,一次函数的图象,反比例函数的图象,熟练掌握二次函数的有关性质:开口方向、对称轴、与y 轴的交点坐标等确定出a 、b 、c 的情况是解题的关键.3.如图:A 、B 、C 、D 四点在一条直线上,若AB =CD ,下列各式表示线段AC 错误的是( )A .AC =AD ﹣CDB .AC =AB+BC C .AC =BD ﹣AB D .AC =AD ﹣AB【答案】C【解析】根据线段上的等量关系逐一判断即可. 【详解】A 、∵AD-CD=AC , ∴此选项表示正确; B 、∵AB+BC=AC , ∴此选项表示正确; C 、∵AB=CD , ∴BD-AB=BD-CD , ∴此选项表示不正确; D 、∵AB=CD , ∴AD-AB=AD-CD=AC , ∴此选项表示正确. 故答案选:C. 【点睛】本题考查了线段上两点间的距离及线段的和、差的知识,解题的关键是找出各线段间的关系. 4.二次函数2y ax bx c =++的图象如图所示,则一次函数24y bx b ac =+-与反比例函数a b c y x++=在同一坐标系内的图象大致为( )A .B .C .D .【答案】D【解析】根据二次函数图象开口向上得到a>0,再根据对称轴确定出b ,根据二次函数图形与x 轴的交点个数,判断24b ac -的符号,根据图象发现当x=1时y=a+b+c<0,然后确定出一次函数图象与反比例函数图象的情况,即可得解.【详解】∵二次函数图象开口方向向上, ∴a>0,∵对称轴为直线02bx a=->, ∴b<0,二次函数图形与x 轴有两个交点,则24b ac ->0, ∵当x=1时y=a+b+c<0,∴24y bx b ac =+-的图象经过第二四象限,且与y 轴的正半轴相交, 反比例函数a b cy x++=图象在第二、四象限, 只有D 选项图象符合. 故选:D. 【点睛】考查反比例函数的图象,一次函数的图象,二次函数的图象,掌握函数图象与系数的关系是解题的关键. 5.已知不透明的袋中只装有黑、白两种球,这些球除颜色外都相同,其中白球有30个,黑球有n 个.随机地从袋中摸出一个球,记录下颜色后,放回袋子中并摇匀,再从中摸出一个球,经过如此大量重复试验,发现摸出的黑球的频率稳定在0.4附近,则n 的值约为( ) A .20 B .30C .40D .50【答案】A【解析】分析:根据白球的频率稳定在0.4附近得到白球的概率约为0.4,根据白球个数确定出总个数,进而确定出黑球个数n. 详解:根据题意得:.n0430n=+ ,计算得出:n=20, 故选A.点睛:根据概率的求法,找准两点:①全部情况的总数;②符合条件的情况数目;二者的比值就是其发生的概率.6.若关于x 的一元二次方程2210x x kb -++=有两个不相等的实数根,则一次函数y kx b =+的图象可能是:A .B .C .D .【答案】B【解析】由方程2210x x kb ++=-有两个不相等的实数根, 可得()4410kb =-+>, 解得0kb <,即k b 、异号,当00k b >,<时,一次函数y kx b =+的图象过一三四象限,当00k b <,>时,一次函数y kx b =+的图象过一二四象限,故答案选B.7.如图,A 、B 、C 是小正方形的顶点,且每个小正方形的边长为1,则tan ∠BAC 的值为( )A .12B .1C .33D 3【答案】B【解析】连接BC ,由网格求出AB ,BC ,AC 的长,利用勾股定理的逆定理得到△ABC 为等腰直角三角形,即可求出所求.【详解】如图,连接BC ,由网格可得510AB 2+BC 2=AC 2, ∴△ABC 为等腰直角三角形, ∴∠BAC=45°, 则tan ∠BAC=1, 故选B .【点睛】本题考查了锐角三角函数的定义,解直角三角形,以及勾股定理,熟练掌握勾股定理是解本题的关键. 8.如果数据x 1,x 2,…,x n 的方差是3,则另一组数据2x 1,2x 2,…,2x n 的方差是( ) A .3 B .6 C .12 D .5【答案】C【解析】根据题意,数据x 1,x 2,…,x n 的平均数设为a ,则数据2x 1,2x 2,…,2x n 的平均数为2a ,再根据方差公式进行计算:()()()()222221231n S x x x x x x x x n⎡⎤=-+-+-++-⎣⎦即可得到答案.【详解】根据题意,数据x 1,x 2,…,x n 的平均数设为a , 则数据2x 1,2x 2,…,2x n 的平均数为2a , 根据方差公式:()()()()222221231n S x a x a x a x a n ⎡⎤=-+-+-++-⎣⎦=3,则()()()()22222123122222222n S x a x a x a x a n ⎡⎤=-+-+-++-⎣⎦=()()()()222212314444n x a x a x a x a n ⎡⎤-+-+-++-⎣⎦=4×()()()()22221231n x a x a x a x a n ⎡⎤-+-+-++-⎣⎦=4×3 =12, 故选C .【点睛】本题主要考查了方差公式的运用,关键是根据题意得到平均数的变化,再正确运用方差公式进行计算即可.9.为考察两名实习工人的工作情况,质检部将他们工作第一周每天生产合格产品的个数整理成甲,乙两组数据,如下表: 甲 2 6 7 7 8 乙23488关于以上数据,说法正确的是( ) A .甲、乙的众数相同 B .甲、乙的中位数相同 C .甲的平均数小于乙的平均数 D .甲的方差小于乙的方差【答案】D【解析】分别根据众数、中位数、平均数、方差的定义进行求解后进行判断即可得. 【详解】甲:数据7出现了2次,次数最多,所以众数为7,排序后最中间的数是7,所以中位数是7,26778==65x ++++甲,()()()()()2222221S =26666767865⎡⎤⨯-+-+-+-+-⎣⎦甲=4.4,乙:数据8出现了2次,次数最多,所以众数为8, 排序后最中间的数是4,所以中位数是4,23488==55x 乙++++,()()()()()2222221S =25354585855乙⎡⎤⨯-+-+-+-+-⎣⎦=6.4,所以只有D 选项正确, 故选D. 【点睛】本题考查了众数、中位数、平均数、方差,熟练掌握相关定义及求解方法是解题的关键.10.若二次函数22y ax ax c =-+的图象经过点(﹣1,0),则方程220ax ax c -+=的解为( ) A .13x =-,21x =- B .11x =,23x = C .11x =-,23x = D .13x =-,21x =【答案】C【解析】∵二次函数22y ax ax c =-+的图象经过点(﹣1,0),∴方程220ax ax c -+=一定有一个解为:x=﹣1,∵抛物线的对称轴为:直线x=1,∴二次函数22y ax ax c =-+的图象与x 轴的另一个交点为:(3,0),∴方程220ax ax c -+=的解为:11x =-,23x =. 故选C .考点:抛物线与x 轴的交点. 二、填空题(本题包括8个小题) 11.若反比例函数y =﹣6x的图象经过点A(m ,3),则m 的值是_____. 【答案】﹣2【解析】∵反比例函数6y x=-的图象过点A (m ,3), ∴63m=-,解得=2-. 12.将一些形状相同的小五角星如图所示的规律摆放,据此规律,第10个图形有_______个五角星.【答案】1.【解析】寻找规律:不难发现,第1个图形有3=22-1个小五角星;第2个图形有8=32-1个小五角星;第3个图形有15=42-1个小五角星;…第n个图形有(n+1)2-1个小五角星.∴第10个图形有112-1=1个小五角星.13.如图,已知点A(a,b),0是原点,OA=OA1,OA⊥OA1,则点A1的坐标是.【答案】(﹣b,a)【解析】解:如图,从A、A1向x轴作垂线,设A1的坐标为(x,y),设∠AOX=α,∠A1OD=β,A1坐标(x,y)则α+β="90°sinα=cosβ" cosα="sinβ" sinα==cosβ=同理cos α==sinβ=所以x=﹣b,y=a,故A1坐标为(﹣b,a).【点评】重点理解三角函数的定义和求解方法,主要应用公式sinα=cosβ,cosα=sinβ.14.圆锥的底面半径为3,母线长为5,该圆锥的侧面积为_______.【答案】15π【解析】试题分析:利用圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和扇形的面积公式求解.圆锥的侧面积=12•2π•3•5=15π.故答案为15π.考点:圆锥的计算.15.甲乙两人进行飞镖比赛,每人各投5次,所得平均环数相等,其中甲所得环数的方差为15,乙所得环数如下:0,1,5,9,10,那么成绩较稳定的是_____(填“甲”或“乙”).【答案】甲.【解析】乙所得环数的平均数为:0159105++++=5,S2=1n[21x x(-)+22x x(-)+23x x(-)+…+2nx x(-)]=15[205(-)+215(-)+255(-)+295(-)+2105(-)]=16.4,甲的方差<乙的方差,所以甲较稳定.故答案为甲.点睛:要比较成绩稳定即比方差大小,方差越大,越不稳定;方差越小,越稳定.16.如图,是由形状相同的正六边形和正三角形镶嵌而成的一组有规律的图案,则第n个图案中阴影小三角形的个数是.【答案】4n﹣1.【解析】由图可知:第一个图案有阴影小三角形1个,第二图案有阴影小三角形1+4=6个,第三个图案有阴影小三角形1+8=11个,···那么第n个就有阴影小三角形1+4(n﹣1)=4n﹣1个.17.A、B两地相距20km,甲乙两人沿同一条路线从A地到B地.甲先出发,匀速行驶,甲出发1小时后乙再出发,乙以2km/h的速度度匀速行驶1小时后提高速度并继续匀速行驶,结果比甲提前到达.甲、乙两人离开A地的距离y(km)与时间t(h)的关系如图所示,则甲出发_____小时后和乙相遇.【答案】16 5【解析】由图象得出解析式后联立方程组解答即可.【详解】由图象可得:y甲=4t(0≤t≤5);y乙=()() 2112 916(24)t tt t<⎧-≤≤⎨-≤⎩;由方程组4916y ty t⎧⎨-⎩==,解得t=165.故答案为165.【点睛】此题考查一次函数的应用,关键是由图象得出解析式解答.18.如图,矩形ABCD中,AB=3,对角线AC,BD相交于点O,AE垂直平分OB于点E,则AD的长为____________.【答案】33【解析】试题解析:∵四边形ABCD 是矩形, ∴OB=OD ,OA=OC ,AC=BD , ∴OA=OB , ∵AE 垂直平分OB , ∴AB=AO , ∴OA=AB=OB=3, ∴BD=2OB=6,∴AD=22226333BD AB -=-=.【点睛】此题考查了矩形的性质、等边三角形的判定与性质、线段垂直平分线的性质、勾股定理;熟练掌握矩形的性质,证明三角形是等边三角形是解决问题的关键. 三、解答题(本题包括8个小题)19.如图,抛物线y =ax 2+bx+c (a >0)的顶点为M ,直线y =m 与抛物线交于点A ,B ,若△AMB 为等腰直角三角形,我们把抛物线上A ,B 两点之间的部分与线段AB 围成的图形称为该抛物线对应的准蝶形,线段AB 称为碟宽,顶点M 称为碟顶.由定义知,取AB 中点N ,连结MN ,MN 与AB 的关系是_____.抛物线y =212x 对应的准蝶形必经过B (m ,m ),则m =_____,对应的碟宽AB 是_____.抛物线y =ax 2﹣4a ﹣53(a >0)对应的碟宽在x 轴上,且AB =1. ①求抛物线的解析式;②在此抛物线的对称轴上是否有这样的点P (x p ,y p ),使得∠APB 为锐角,若有,请求出y p 的取值范围.若没有,请说明理由.【答案】(1)MN 与AB 的关系是:MN ⊥AB ,MN =12AB ,(2)2,4;(2)①y =13x 2﹣2;②在此抛物线的对称轴上有这样的点P ,使得∠APB 为锐角,y p 的取值范围是y p <﹣2或y p >2. 【解析】(1)直接利用等腰直角三角形的性质分析得出答案;(2)利用已知点为B (m ,m ),代入抛物线解析式进而得出m 的值,即可得出AB 的值; (2)①根据题意得出抛物线必过(2,0),进而代入求出答案;②根据y =13x 2﹣2的对称轴上P (0,2),P (0,﹣2)时,∠APB 为直角,进而得出答案. 【详解】(1)MN 与AB 的关系是:MN ⊥AB ,MN =12AB ,如图1,∵△AMB 是等腰直角三角形,且N 为AB 的中点,∴MN ⊥AB ,MN =12AB , 故答案为MN ⊥AB ,MN =12AB ;(2)∵抛物线y =212x 对应的准蝶形必经过B (m ,m ), ∴m =12m 2, 解得:m =2或m =0(不合题意舍去), 当m =2则,2=12x 2, 解得:x =±2, 则AB =2+2=4; 故答案为2,4;(2)①由已知,抛物线对称轴为:y 轴,∵抛物线y =ax 2﹣4a ﹣53(a >0)对应的碟宽在x 轴上,且AB =1. ∴抛物线必过(2,0),代入y =ax 2﹣4a ﹣53(a >0),得,9a ﹣4a ﹣53=0,解得:a =13,∴抛物线的解析式是:y =13x 2﹣2;②由①知,如图2,y =13x2﹣2的对称轴上P (0,2),P (0,﹣2)时,∠APB 为直角,∴在此抛物线的对称轴上有这样的点P ,使得∠APB 为锐角,y p 的取值范围是y p <﹣2或y p >2.【点睛】此题主要考查了二次函数综合以及等腰直角三角形的性质,正确应用等腰直角三角形的性质是解题关键.20.某中学课外活动小组准备围建一个矩形生物苗圃园,其中一边靠墙,另外三边用长为30米的篱笆围成.已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边的长为x米.若平行于墙的一边长为y米,直接写出y与x的函数关系式及其自变量x的取值范围.垂直于墙的一边的长为多少米时,这个苗圃园的面积最大,并求出这个最大值.【答案】112.1【解析】试题分析:(1)根据题意即可求得y与x的函数关系式为y=30﹣2x与自变量x的取值范围为6≤x <11;(2)设矩形苗圃园的面积为S,由S=xy,即可求得S与x的函数关系式,根据二次函数的最值问题,即可求得这个苗圃园的面积最大值.试题解析:解:(1)y=30﹣2x(6≤x<11).(2)设矩形苗圃园的面积为S,则S=xy=x(30﹣2x)=﹣2x2+30x,∴S=﹣2(x﹣7.1)2+112.1,由(1)知,6≤x<11,∴当x=7.1时,S最大值=112.1,即当矩形苗圃园垂直于墙的一边的长为7.1米时,这个苗圃园的面积最大,这个最大值为112.1.点睛:此题考查了二次函数的实际应用问题.解题的关键是根据题意构建二次函数模型,然后根据二次函数的性质求解即可.21.为了了解某校学生对以下四个电视节目:A《最强大脑》,B《中国诗词大会》,C《朗读者》,D《出彩中国人》的喜爱情况,随机抽取了部分学生进行调查,要求每名学生选出并且只能选出一个自己最喜爱的节目,根据调查结果,绘制了如下两幅不完整的统计图.请你根据图中所提供的信息,完成下列问题:本次调查的学生人数为________;在扇形统计图中,A部分所占圆心角的度数为________;请将条形统计图补充完整:若该校共有3000名学生,估计该校最喜爱《中国诗词大会》的学生有多少名?【答案】(1)120;(2)54;(3)答案见解析;(4)1650.【解析】(1)依据节目B的数据,即可得到调查的学生人数;(2)依据A部分的百分比,即可得到A部分所占圆心角的度数;(3)求得C部分的人数,即可将条形统计图补充完整;(4)依据喜爱《中国诗词大会》的学生所占的百分比,即可得到该校最喜爱《中国诗词大会》的学生数量.【详解】()16655%120÷=,故答案为120;()18236054120⨯=,故答案为54;()3C:12025%30⨯=,如图所示:()4300055%1650⨯=,答:该校最喜爱《中国诗词大会》的学生有1650名.【点睛】本题考查了条形统计图、扇形统计图、用样本估计总体,解答本题的关键是明确题意,找出所求问题需要的条件,利用数形结合思想解答.22.解方程311(1)(2)xx x x-=--+.【答案】原分式方程无解.【解析】根据解分式方程的方法可以解答本方程,去分母将分式方程化为整式方程,解整式方程,验证. 【详解】方程两边乘(x﹣1)(x+2),得x(x+2)﹣(x﹣1)(x+2)=3即:x2+2x﹣x2﹣x+2=3整理,得x=1检验:当x=1时,(x﹣1)(x+2)=0,∴原方程无解.【点睛】本题考查解分式方程,解题的关键是明确解放式方程的计算方法.23.先化简,再求值:22144(1)1a a a a a-+-÷--,其中a 是方程a (a+1)=0的解. 【答案】13【解析】根据分式运算性质,先化简,再求出方程的根a=0或-1,分式有意义分母不等于0,所以将a=-1代入即可求解.【详解】解:原式=()()2a a 1a 11a 1a 2---⨯-- =a a 2- ∵a(a+1)=0,解得:a=0或-1,由题可知分式有意义,分母不等于0,∴a=-1,将a=-1代入a a 2-得, 原式=13【点睛】本题考查了分式的化简求值,中等难度,根据分式有意义的条件代值计算是解题关键.24.如图:求作一点P ,使PM PN =,并且使点P 到AOB ∠的两边的距离相等.【答案】见解析【解析】利用角平分线的作法以及线段垂直平分线的作法分别得出进而求出其交点即可.【详解】如图所示:P 点即为所求.【点睛】本题主要考查了复杂作图,熟练掌握角平分线以及线段垂直平分线的作法是解题的关键.25.为有效治理污染,改善生态环境,山西太原成为国内首个实现纯电动出租车的城市,绿色环保的电动出租车受到市民的广泛欢迎,给市民的生活带来了很大的方便,下表是行驶路程在15公里以内时普通燃油出租车和纯电动出租车的运营价格: 车型 起步公里数 起步价格 超出起步公里数后的单价 普通燃油型 3 13元 2.3元/公里纯电动型 3 8元 2元/公里张先生每天从家打出租车去单位上班(路程在15公里以内),结果发现,正常情况下乘坐纯电动出租车比乘坐燃油出租车平均每公里节省0.8元,求张先生家到单位的路程.【答案】8.2 km【解析】首先设小明家到单位的路程是x 千米,根据题意列出方程进行求解.【详解】解:设小明家到单位的路程是x 千米.依题意,得13+2.3(x -3)=8+2(x -3)+0.8x .解得:x=8.2答:小明家到单位的路程是8.2千米.【点睛】本题考查一元一次方程的应用,找准等量关系是解题关键.26.在平面直角坐标系中,一次函数y ax b =+(a≠0)的图象与反比例函数(0)k y k x=≠的图象交于第二、第四象限内的A 、B 两点,与y 轴交于点C ,过点A 作AH ⊥y 轴,垂足为点H ,OH=3,tan ∠AOH=43,点B 的坐标为(m ,-2).求该反比例函数和一次函数的解析式;求△AHO 的周长.【答案】(1)一次函数为112y x =-+,反比例函数为12y x=-;(2)△AHO 的周长为12 【解析】分析:(1)根据正切函数可得AH=4,根据反比例函数的特点k=xy 为定值,列出方程,求出k 的值,便可求出反比例函数的解析式;根据k 的值求出B 两点的坐标,用待定系数法便可求出一次函数的解析式.(2)由(1)知AH 的长,根据勾股定理,可得AO 的长,根据三角形的周长,可得答案.详解:(1)∵tan ∠AOH=AH OH =43 ∴AH=43OH=4 ∴A (-4,3),代入k y x =,得 k=-4×3=-12∴反比例函数为12y x =-∴122m-=-∴m=6∴B (6,-2) ∴4362a b a b -+=⎧⎨+=-⎩∴a =12-,b=1 ∴一次函数为112y x =-+ (2)2222345OA AH OH +=+=△AHO 的周长为:3+4+5=12点睛:此题考查的是反比例函数图象上点的坐标特点及用待定系数法求一次函数及反比例函数的解析式.中考数学模拟试卷一、选择题(本题包括10个小题,每小题只有一个选项符合题意)1.下列分式是最简分式的是( )A .223a a bB .23a a a -C .22a b a b ++D .222a ab a b -- 【答案】C【解析】解:A .22233a a b ab =,故本选项错误; B .2133a a a a =--,故本选项错误; C .22a b a b++,不能约分,故本选项正确; D .222()()()a ab a a b a a b a b a b a b--==-+-+,故本选项错误. 故选C .点睛:本题主要考查对分式的基本性质,约分,最简分式等知识点的理解和掌握,能根据分式的基本性质正确进行约分是解答此题的关键.2.下列每组数分别是三根小木棒的长度,用它们能摆成三角形的是( )A .3cm ,4cm ,8cmB .8cm ,7cm ,15cmC .13cm ,12cm ,20cmD .5cm ,5cm ,11cm【答案】C【解析】根据三角形的三边关系“任意两边之和大于第三边,任意两边之差小于第三边”,进行分析.【详解】A 、3+4<8,不能组成三角形;B 、8+7=15,不能组成三角形;C 、13+12>20,能够组成三角形;D 、5+5<11,不能组成三角形.故选:C .【点睛】本题考查了三角形的三边关系,关键是灵活运用三角形三边关系.3.一条数学信息在一周内被转发了2180000次,将数据2180000用科学记数法表示为( ) A .2.18×106 B .2.18×105 C .21.8×106 D .21.8×105【答案】A【解析】科学记数法的表示形式为a×10n 的形式,其中1≤|a|<10,n 为整数.确定n 的值时,要看把原数变成a 时,小数点移动了多少位,n 的绝对值与小数点移动的位数相同.当原数绝对值>1时,n 是正数;当原数的绝对值<1时,n 是负数.【详解】2180000的小数点向左移动6位得到2.18,所以2180000用科学记数法表示为2.18×106,故选A.【点睛】本题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.4.如图,比例规是一种画图工具,它由长度相等的两脚AC和BD交叉构成,利用它可以把线段按一定的比例伸长或缩短.如果把比例规的两脚合上,使螺丝钉固定在刻度3的地方(即同时使OA=3OC,OB=3OD),然后张开两脚,使A,B两个尖端分别在线段a的两个端点上,当CD=1.8cm时,则AB的长为()A.7.2 cm B.5.4 cm C.3.6 cm D.0.6 cm【答案】B【解析】由已知可证△ABO∽CDO,故CD OCAB OA=,即1.813AB=.【详解】由已知可得,△ABO∽CDO,所以,CD OC AB OA=,所以,1.813 AB=,所以,AB=5.4故选B【点睛】本题考核知识点:相似三角形. 解题关键点:熟记相似三角形的判定和性质.5.我国古代数学名著《孙子算经》中记载了一道题,大意是:100匹马恰好拉了100片瓦,已知1匹大马能拉3片瓦,3匹小马能拉1片瓦,问有多少匹大马、多少匹小马?若设大马有x匹,小马有y匹,那么可列方程组为()A.10033100x yx y+=⎧⎨+=⎩B.1003100x yx y+=⎧⎨+=⎩C.100131003x yx y+=⎧⎪⎨+=⎪⎩D.1003100x yx y+=⎧⎨+=⎩【答案】C【解析】设大马有x匹,小马有y匹,根据题意可得等量关系:①大马数+小马数=100;②大马拉瓦数+小马拉瓦数=100,根据等量关系列出方程组即可.【详解】解:设大马有x匹,小马有y匹,由题意得:100131003x yx y+=⎧⎪⎨+=⎪⎩,故选C.【点睛】此题主要考查了由实际问题抽象出二元一次方程组,关键是正确理解题意,找出题目中的等量关系,列出方程组.6.如图,在⊙O中,直径CD⊥弦AB,则下列结论中正确的是()A.AC=AB B.∠C=12∠BOD C.∠C=∠B D.∠A=∠B0D【答案】B【解析】先利用垂径定理得到弧AD=弧BD,然后根据圆周角定理得到∠C=12∠BOD,从而可对各选项进行判断.【详解】解:∵直径CD⊥弦AB,∴弧AD =弧BD,∴∠C=12∠BOD.故选B.【点睛】本题考查了垂径定理和圆周角定理,垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.7.如图所示的几何体的俯视图是()A.B.C.D.【答案】D【解析】找到从上面看所得到的图形即可,注意所有看到的棱都应表现在俯视图中.【详解】从上往下看,该几何体的俯视图与选项D所示视图一致.故选D.【点睛】本题考查了简单组合体三视图的知识,俯视图是从物体的上面看得到的视图.8.二次函数y=ax2+bx+c(a≠0)的部分图象如图,图象过点(-1,0),对称轴为直线x=2,下列结论:①4a+b=0;②9a+c>3b;③8a+7b+2c>0;④当x>-1时,y的值随x值的增大而增大.其中正确的结论有()A.1个B.2个C.3个D.4个【答案】B【解析】根据抛物线的对称轴即可判定①;观察图象可得,当x=-3时,y<0,由此即可判定②;观察图象可得,当x=1时,y>0,由此即可判定③;观察图象可得,当x>2时,的值随值的增大而增大,即可判定④.【详解】由抛物线的对称轴为x=2可得=2,即4a+b=0,①正确;观察图象可得,当x=-3时,y<0,即9a-3b+c<0,所以,②错误;观察图象可得,当x=1时,y>0,即a+b+c>0,③正确;观察图象可得,当x>2时,的值随值的增大而增大,④错误.综上,正确的结论有2个.故选B.【点睛】本题考查了二次函数图象与系数的关系:二次函数y=ax2+bx+c(a≠0),二次项系数a决定抛物线的开口方向和大小,当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;一次项系数b和二次项系数a共同决定对称轴的位置,当a与b同号时(即ab>0),对称轴在y轴左;当a与b异号时(即ab<0),对称轴在y轴右;常数项c决定抛物线与y轴交点.抛物线与y轴交于(0,c);抛物线与x轴交点个数由△决定,△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac <0时,抛物线与x轴没有交点.9.如图,桌面上放着1个长方体和1个圆柱体,按如图所示的方式摆放在一起,其左视图是()A.B.C.D.【答案】C【解析】根据左视图是从左面看所得到的图形进行解答即可.【详解】从左边看时,圆柱和长方体都是一个矩形,圆柱的矩形竖放在长方体矩形的中间.故选:C.【点睛】本题考查了三视图的知识,左视图是从物体的左面看得到的视图.10.如图,直线m∥n,直角三角板ABC的顶点A在直线m上,则∠α的余角等于()A.19°B.38°C.42°D.52°【答案】D【解析】试题分析:过C作CD∥直线m,∵m∥n,∴CD∥m∥n,∴∠DCA=∠FAC=52°,∠α=∠DCB,∵∠ACB=90°,∴∠α=90°﹣52°=38°,则∠a的余角是52°.故选D.考点:平行线的性质;余角和补角.二、填空题(本题包括8个小题)11.图1是我国古代建筑中的一种窗格,其中冰裂纹图案象征着坚冰出现裂纹并开始消溶,形状无一定规则,代表一种自然和谐美.图2是从图1冰裂纹窗格图案中提取的由五条线段组成的图形,则∠1+∠2+∠3+∠4+∠5=度.【答案】360°.【解析】根据多边形的外角和等于360°解答即可.【详解】由多边形的外角和等于360°可知,∠1+∠2+∠3+∠4+∠5=360°,故答案为360°.【点睛】本题考查的是多边形的内角和外角,掌握多边形的外角和等于360°是解题的关键.12.如图,若正五边形和正六边形有一边重合,则∠BAC =_____.【答案】132°【解析】解:∵正五边形的内角=180°-360°÷5=108°,正六边形的内角=180°-360°÷6=120°,∴∠BAC=360°-108°-120°=132°.故答案为132°.13.让我们轻松一下,做一个数字游戏:第一步:取一个自然数15n =,计算211n +得1a ;第二步:算出1a 的各位数字之和得2n ,计算221n +得2a ;第三步:算出2a 的各位数字之和得3n ,再计算231n +得3a ;依此类推,则2019a =____________【答案】1 【解析】根据题意可以分别求得a 1,a 2,a 3,a 4,从而可以发现这组数据的特点,三个一循环,从而可以求得a 2019的值.【详解】解:由题意可得,a 1=52+1=26,a 2=(2+6)2+1=65,a 3=(6+5)2+1=1,a 4=(1+2+2)2+1=26,…∴2019÷3=673,∴a 2019= a 3=1,故答案为:1.【点睛】本题考查数字变化类规律探索,解题的关键是明确题意,求出前几个数,观察数的变化特点,求出a 2019的值.14.把球放在长方体纸盒内,球的一部分露出盒外,其截面如图,已知EF=CD=80cm,则截面圆的半径为cm.【答案】1【解析】过点O作OM⊥EF于点M,反向延长OM交BC于点N,连接OF,设OF=r,则OM=80-r,MF=40,然后在Rt△MOF中利用勾股定理求得OF的长即可.【详解】过点O作OM⊥EF于点M,反向延长OM交BC于点N,连接OF,设OF=x,则OM=80﹣r,MF=40,在Rt△OMF中,∵OM2+MF2=OF2,即(80﹣r)2+402=r2,解得:r=1cm.故答案为1.15.如图,在平面直角坐标系中,已知点A(﹣4,0)、B(0,3),对△AOB连续作旋转变换依次得到三角形(1)、(2)、(3)、(4)、…,则第(5)个三角形的直角顶点的坐标是_____,第(2018)个三角形的直角顶点的坐标是______.【答案】(1645,125)(806845,125)【解析】利用勾股定理列式求出AB的长,再根据图形写出第(5)个三角形的直角顶点的坐标即可;观察图形不难发现,每3个三角形为一个循环组依次循环,用2018除以3,根据商和余数的情况确定出第(2018)个三角形的直角顶点到原点O的距离,然后写出坐标即可.【详解】∵点A(﹣4,0),B(0,3),∴OA=4,OB=3,∴2243,∴第(2)个三角形的直角顶点的坐标是(445,125);∵5÷3=1余2,∴第(5)个三角形的直角顶点的坐标是(1645,125),∵2018÷3=672余2,∴第(2018)个三角形是第672组的第二个直角三角形,其直角顶点与第672组的第二个直角三角形顶点重合,∴第(2018)个三角形的直角顶点的坐标是(806845,125).故答案为:(1645,125);(806845,125)【点睛】本题考查了坐标与图形变化-旋转,解题的关键是根据题意找出每3个三角形为一个循环组依次循环. 16.某物流仓储公司用如图A,B两种型号的机器人搬运物品,已知A型机器人比B型机器人每小时多搬运20kg,A型机器人搬运1000kg所用时间与B型机器人搬运800kg所用时间相等,设B型机器人每小时搬运x kg物品,列出关于x的方程为_____.【答案】100080020x x=+【解析】设B型机器人每小时搬运x kg物品,则A型机器人每小时搬运(x+20)kg物品,根据“A型机器人搬运1000kg所用时间与B型机器人搬运800kg所用时间相等”可列方程.【详解】设B型机器人每小时搬运x kg物品,则A型机器人每小时搬运(x+20)kg物品,根据题意可得100080020x x=+,故答案为100080020x x=+.【点睛】本题考查了由实际问题抽象出分式方程,解题的关键是根据数量关系列出关于x的分式方程.本题属于基础题,难度不大,解决该题型题目时,根据数量关系列出方程是关键.17.下列图形是用火柴棒摆成的“金鱼”,如果第1个图形需要8根火柴,则第2个图形需要14根火柴,第n根图形需要____________根火柴.【答案】62n+【解析】根据图形可得每增加一个金鱼就增加6根火柴棒即可解答.【详解】第一个图中有8根火柴棒组成,。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
金山区2020学年第一学期期末质量检测初三数学试卷(满分150分,考试时间100分钟)(2021.1)一、选择题:(本大题共6题,每题4分,满分24分)【下列各题的四个选项中,有且只有一个选项是正确的,选择正确项的代号并填涂在答题纸的相应位置上.】 1.已知二次函数()122--=x y ,那么该二次函数图像的对称轴是( )(A )直线2=x ; (B )直线2-=x ; (C )直线1=x ; (D )直线1-=x . 2.下列各点在抛物线22x y =上的是( )(A )()2,2; (B )()42,; (C ))(8,2; (D )()16,2. 3.在ABC Rt ∆中,90=∠C ,那么锐角A 的正弦等于( ) (A )的邻边锐角的对边锐角A A ;(B )斜边的对边锐角A ;(C )斜边的邻边锐角A ;(D )的对边锐角的邻边锐角A A .4.若α是锐角,()2215sin =+α,那么锐角α等于( ) (A )15; (B )30; (C )45; (D )60.5.如图,已知点D 、E 分别在ABC ∆的边AB 、AC 上,BC DE //,2=AD ,3=BD ,a BC =,那么ED 等于( )(A )a 32; (B )a 32-; (C )a 52; (D )a 52-. 6.如图,已知ABC Rt ∆中,90=∠C ,3=AC ,4=BC ,如果以点C 为圆心的圆与斜边AB 有公共点,那么⊙C 的半径r 的取值范围是( ) (A )5120≤≤r ; (B )3512≤≤r ; (C )4512≤≤r ; (D )43≤≤r .二、填空题:(本大题共12题,每题4分,满分48分) 【请直接将结果填入答题纸的相应位置】第6题图BCAA第5题图7.计算:=⎪⎭⎫⎝⎛-+b a a 232 . 8.已知()x x x f 32+=,那么()=-2f .9.抛物线22x y -=沿着x 轴正方向看,在y 轴的左侧部分是 .(填“上升”或“下降”) 10.正十边形的中心角等于 度.11.已知⊙1O 和⊙2O 的半径长分别为3和4,若⊙1O 和⊙2O 内切,那么圆心距21O O 的长等于 .12.在ABC Rt ∆中,90=∠C ,15=AB ,54in =A s ,那么=BC . 13.在ABC ∆中,5:2:1::=BC AC AB ,那么=B tan .14.已知:如图,ABC ∆的中线AE 与BD 交于点G ,AE DF //交BC 于F ,那么=AGDF. 15.如图,在梯形ABCD 中,BC AD //,AD BC 2=,设a AB =,b AD =,那么向量CD 用向量a 、b 表示为 .16.如图,已知⊙O 中,120=∠AOB ,弦18=AB ,那么⊙O 的半径长等于 .17.如图,在□ABCD 中,点E 在边BC 上,DE 交对角线AC 于F ,若BE CE 2=,ABC ∆的面积等于15,那么FEC ∆的面积等于 .18.已知在ABC Rt ∆中,90=∠C ,1=BC ,2=AC ,以点C 为直角顶点的DCE Rt ∆的顶点D 在BA 的延长线上,DE 交CA 的延长线于点G ,若21tan =∠CED ,GE CE =,那么BD 的长等于 .第17题图BACDEF第16题图A B O AGDC B E F 第14题图 第15题图ACB第18题图三、解答题(本大题共7题,满分78分) 19.(本题满分10分)如图,已知在ABC Rt ∆中,90=∠C ,3=AC ,4=BC .求:30tan 4tan cos 1sin tan 2AB A B +-+⋅的值.20. (本题满分10分,每小题满分5分)已知:如图,⊙1O 与⊙2O 外切于点T ,经过点T 的直线与⊙1O 、⊙2O 分别相交于点A 和点B .(1)求证:B O A O 21//;(2)若21=A O ,32=B O ,7=AB ,求AT 的长.21. (本题满分10分,每小题满分5分)已知抛物线c bx x y ++-=22经过点()1,0A 、()5,1-B .(1)求抛物线的表达式;(2)把表达式化成()k m x y ++-=22的形式,并写出顶点坐标与对称轴.22. (本题满分10分,每小题满分5分)如图,在距某输电铁塔GH (GH 垂直地面)的底部点H 左侧水平距离60米的点B 处有一个山坡,山坡AB 的坡度3:1=i ,山坡坡底点B 到坡顶A 的距离AB 等于40米,在坡顶A 处测得铁塔顶点G 的仰角为30(铁塔GH 与山坡AB 在同一平面内).(1)求山坡的高度;(2)求铁塔的高度GH .(结果保留根号)23. (本题满分12分,每小题满分6分)已知:如图,四边形ABCD 是菱形,点M 、N 分别在边BC 、CD 上,联结AM 、AN 交对角线BD 于E 、F 两点,且ABD MAN ∠=∠. (1)求证:DE BF AB ⋅=2;(2)若DCDNDE BE =,求证:MN EF //.C第19题图BAT 第20题图BAO 1 O 2G第22题图 AB HA BF E C第23题图DMN第24题图第25题备用图24. (本题满分12分,每小题满分4分) 在平面直角坐标系xoy 中,直线243+-=x y 与直线321-=x y 相交于点A ,抛物线)0(12≠-+=a bx ax y 经过点A .(1)求点A 的坐标;(2)若抛物线12-+=bx ax y 向上平移两个单位后,经过点()2,1-,求抛物线12-+=bx ax y 的表达式;(3)若抛物线c x b x a y +'+'=2()0<'a 与2+=ax y 对称,且这两条抛物线的顶点分别是点P '与点P ,当S 求抛物线12-+=bx ax y 的表达式.25. (本题满分14分,第(1)分4分,第(2)分6分,第(3)分4分)定理:一条弧所对的圆周角等于这条弧所对的圆心角的一半.如图1中,O A ∠=∠21. 已知:如图2,AC 是⊙O 的一条弦,点D 在⊙O 上(与A 、C 不重合),联结DC 交射线AO 于点E ,联结OD ,⊙O 的半径为5,43tan =∠OAC .(1)求弦AC 的长.(2)当点E 在线段OA 上时,若DOE ∆与AEC ∆相似,求DCA ∠的正切值. (3)当1=OE 时,求点A 与点D 之间的距离(直接写出答案).ABCO第25题图1第25题图2参考答案和评分标准一.选择题: 1.A ; 2.C ; 3.B ; 4.B ; 5.D ; 6.C .二.填空题: 7.b a 24-; 8.2-; 9.上升;10.36;11.1;12.12;13.2; 14.43;15.b a --;16.36;17.4;18.52+. 19.解:在ABC Rt ∆中, 90=∠C ,3=AC ,4=BC ,由勾股定理得,222BC AC AB +=, ∴5432222=+=+=BC AC AB ;……………………………………(2分)∴43tan ==BC AC B ;54sin ==AB BC A ;54cos ==AB BC B ;34tan ==AC BC A ……(4分)∴原式2334345415443⎪⎪⎭⎫⎝⎛⨯+-+⨯=;……………………(2分)59154=+=.………………(2分) 20.(1)证明:联结21O O ,即21O O 为连心线,又∵⊙1O 与⊙2O 外切于点T ,……(1分) ∴21O O 经过点T ;………………………………………(1分)∵T O B O T O A O 2211,==;∴TB O B TA O A 21,∠=∠∠=∠;……………………(1分) ∵TB O TA O 21∠=∠; ∴B A ∠=∠;……………(1分) ∴B O A O 21//.……………………(1分) (2)∵B O A O 21// ∴BTATBO AO =21;……………………………(2分) ∵21=A O ,32=B O ,7=AB ; ∴AT AT -=732,解得:514=AT .……………(3分) 21.解:(1)由抛物线c bx x y ++-=22经过点()1,0A 、()5,1-B 两点可得:⎩⎨⎧-=++-=521c b c ………………(2分)解得:⎩⎨⎧=-=14c b ;…………………(2分) ∴抛物线的解析式为:1422+--=x x y .……………………(1分) (2)1422+--=x x y ()3122++-=x ;……………(3分)∴()3122++-=x y ,顶点坐标为:()3,1-,对称轴为:直线1-=x .……………(1+1分)22.解:(1)过点A 作AD 垂直HB ,交HB 的延长线于点D .……………(1分) 即 90=∠ADB ;由题意得:3:1=i ,60=AB (米); ∴31=BD AD ,即AD BD 3=;………(1分) 又∵222BD AD AB +=,即()222340AD AD +=……………(1分)∴20=AD (米).……………(1分)答:山坡的高度为20米.…………………(1分) (2)作BH AE //交GH 于点E .………………(1分) ∵BH AD ⊥,BH GH ⊥;∴GH AD //; 即:四边形ADHE 是平行四边形;由题意可知: 30=∠GAE ,60=BH (米);∵3203==AD BD (米); ∴30260+==DH AE (米);……………(1分) 在AGE R ∆t 中,AEGEGAE =∠tan ; ∴32020+=GE (米).……………(1分) 又∵20==AD EH (米);∴32040+=+=EH GE GH (米);……………(1分)答:铁塔的高度GH 为)(32040+米.……………(1分)23.证明:(1)∵四边形ABCD 是菱形; ∴AD AB =;……………(1分) ∴ADB ABD ∠=∠;……………(1分)∵BAE ABD AED ∠+∠=∠,BAE MAN BAF ∠+∠=∠; 又∵ABD MAN ∠=∠;∴BAF AED ∠=∠;……………(1分) ∴AED ∆∽FAB ∆;……………(1分) ∴ABDEBF AD =,即DE BF AB AD ⋅=⋅;……………(1分) ∴DE BF AB ⋅=2.……………(1分) (2)∵四边形ABCD 是菱形;∴BC AD =,BC AD //;……………(1分)∴AD BM DE BE =;……………(2分) ∵DC DNDE BE =; ∴DC DN AD BM =,……………(1分)∴DCDN BC BM =;……………(1分) ∴BD MN //,即MN EF //.……………(1分) 24.解:(1)∵直线243+-=x y 与直线321-=x y 相交于点A , ∴⎪⎪⎩⎪⎪⎨⎧-=+-=321243x y x y ,解得:⎩⎨⎧-==14y x ;……………(3分)∴点A 的坐标为()14-,.……………(1分) (2)∵抛物线)0(12≠-+=a bx ax y 经过点A ()14-,, ∴11416-=-+b a 即a b 4-=……………(1分) ∴142--=ax ax y∴平移后的抛物线的表达式是142+-=ax ax y ;……………(1分) ∴142+-=-a a ,解得:1=a ………………(1分)∴抛物线12-+=bx ax y 的表达式是:142--=x x y .……………(1分) (3)∵142--=ax ax y()1422---=a x a∴()142--a P ,……………(1分) ∵抛物线()02<'+'+'=a c x b x a y 与142--=ax ax y关于x 轴对称,∴()142+'a P ,……………(1分) ∵0<'a ,∴0>a ; ∴28+='a P P ;又∵2=OD ,P P OD S P OP '⋅⋅='∆21; ∴()328221=+⨯⨯a ,解得:81=a .………(1分) ∴抛物线12-+=bx ax y 的表达式是121812--=x x y .………………(1分)25.(1)解:作AC OH ⊥垂足为点H ,OH 过圆心,由垂径定理得:AC CH AH 21==;……………………………(1分) ∵在OAH R ∆t 中43tan ==∠AH OH OAC ,设x AH x OH 4,3==,……………(1分)∴在OAH R ∆t 中,可得:222OA AH OH =+,由⊙O 的半径为5可得:()()222543=+x x , 解得:1±=x ,(1-=x 舍去)∴4,3==AH OH ,………………………(1分) ∴82==AH AC .………………………(1分) (2)∵AEC DEO ∠=∠,∴当DOE ∆与AEC ∆相似时可得:A DOE ∠=∠或者ACD DOE ∠=∠; 由定理:一条弧所对的圆周角等于这条弧所对的圆心角的一半.可知:DOE ACD ∠=∠21,∴DOE ACD ∠≠∠∴当DOE ∆与AEC ∆相似时不存在ACD DOE ∠=∠情况.………………………(1分) ∴当DOE ∆与AEC ∆相似时,A DOE ∠=∠,∴AC OD //,∴AEOEAC OD =;……………(1分) ∵8,5===AC OA OD ,得AE AE -=585,∴1340=AE ;…………………(1分)作AC EG ⊥垂足为G ,可得:90=∠=∠AHO AGE ,∴OH GE //,∴AH AG OH EG AO AE ==即4351340AG EG ==, ∴1324=EG ,……………(1分)1332=AG ,137213328=-=CG ,…………(1分)∴在CEG R ∆t 中,3113721324tan ===∠CG EG DCA .…………………………(1分)(3)当1=OE 时,AD 的长是52或1452918.……………………………(2+2分)。
