六方晶格第一布里渊区
布里渊区图示
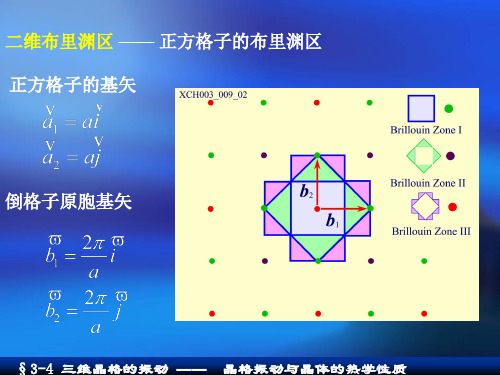
a 3 正格子原胞基矢 a1 ai, a2 i aj 2 2 取单位矢量k垂直于i, j 则,a1,a2和k构成的体积 3 2 a 2
§3-4 三维晶格的振动 ——
晶格振动与晶体的热学性质
倒格子原胞的基矢为 2 (a2 k ) 2 2 b1 i j a 3a 2 (k a1 ) 4 b2 j 3a
的垂直平分线和第一 布里渊区边界所围成 —— 第二布里渊区大小
§3-4 三维晶格的振动 ——
晶格振动与晶体的热学性质
第三布里渊区
由4个倒格点
的垂直平分线和第二布 里渊区边界边界所围成 第三布里渊区大小
§3-4 三维晶格的振动 ——
晶格振动与晶体的热学性质
第一、第二和第三布里渊区
§3-4 三维晶格的振动 ——
§3-4 三维晶格的振动 ——
晶格振动与晶体的热学性质
选一个倒格点为原点,原点的最近邻倒格矢有6个,分别是
b1 , b2 , (b1 b2 )
§3-4 三维晶格的振动 —— 晶格振动与晶体的热学性质
§3-4 三维晶格的振动 ——
晶格振动与晶体的热学性质
晶格振动与晶体的热学性质
正方格子其它布里渊区的形成
§3-4 三维晶格的振动 ——
晶格振动与晶体的热学性质
正方格子其它布里渊 和第一布里渊 区重合
§3-4 三维晶格的振动 ——
晶格振动与晶体的热学性质
二维斜格子的第一布里渊区
§3-4 三维晶格的振动 ——
晶格振动与晶体的热学性质
二维斜格子其它布里渊区的形成
§3-4 三维晶格的振动 ——
晶格振动与晶体的热学性质
二维斜格子其它布里渊区的形状
固体物理基础课后1到10题答案

一.本章习题P272习题1.试证理想六方密堆结构中c/a=.一. 说明:C 是上下底面距离,a 是六边形边长。
二. 分析:首先看是怎样密堆的。
如图(书图(a),P8),六方密堆结构每个格点有12个近邻。
(同一面上有6个,上下各有3个)上下底面中间各有一个球,共有六个球与之相切,每个球直径为a 。
中间层的三个球相切,又分别与上下底面的各七个球相切。
球心之间距离为a 。
所以球心之间即格点之间距离均为a (不管是同层还是上下层之间)。
三. 证明:如图OA=a ,OO ’=C/2(中间层是上下面层的一半),AB=a O ’是ΔABC 的三垂线交点33'a AB AO ==∴(由余弦定理)330cos 2,30cos 230cos 2222a a x x a ax x a x ===-+=οοο633.1322384132)2()2()3()2(2222222222''≈===∴+=+=+=a c c a ac a ac OA AO OO2.若晶胞基矢c b a ρρρ,,互相垂直,试求晶面族(hkl )的面间距。
一、分析:我们想到倒格矢与面间距的关系G d ρπ2=。
倒格矢与晶面族 (hkl )的关系321b l b k b h G ρρρρ++=写出)(321b b b ρρρ与正格子基矢 )(c b a ρρρ的关系。
即可得与晶面族(hkl ) 垂直的倒格矢G ρ。
进而求得此面间距d 。
二、解:c b a ρρρΘ,,互相垂直,可令k c c j b b i a a ρρρρρρ===,,晶胞体积abc c b a v =⨯⋅=)(ρρρ倒格子基矢:kcj b i a abc b a v b j b i a k c abc a c v b ia k c jb abc c b v b ρρρρρρρρρρρρρρρρρρπππππππππ2)(2)(22)(2)(22)(2)(2321=⨯=⨯==⨯=⨯==⨯=⨯=而与 (hkl )晶面族垂直的倒格矢 222321)()()(2)(2cl b k a h G k cl j b k i a h b l b k b h G ++=∴++=++=ππρρρρρρρρ故(hkl ) 晶面族的面间距222222)()()(1)()()(222cl b k a h cl b k a h G d ++=++==πππρ3.若在体心立方晶胞的每个面中心处加一个同类原子,试说明这种晶体的原胞应如何选择?每个原胞含有几个原子?1.分析:考虑选取原胞的条件:(即布拉菲晶格的最小单元)(1)体积最小的重复结构单元(2)只包含一个格点(3)能反映晶格的周期性应将几个原子组合成一个格点,然后构成原胞。
晶体的倒格子和布里渊区

倒易点阵仍是简立方点阵:
2 2 2 b1 i, b2 j , b3 k, a a a
所以倒格子也是布拉菲格子。 六角点阵: 六角点阵的倒易点阵: 见Ashcroft p88 c 轴方向不变,a 轴在垂直于c 轴的 平面上旋转30度。
正格子空间六方结构,在倒格子空间亦为六方结 构。不过其基矢尺寸关系发生变化,基矢方向也转了 一个角度。
五. 布里渊区: 第一布里渊区的确定:取法和正点阵中Wigner-Seitz 原胞取法相同。它是倒易点阵的原胞。
Léon Brilliouin
(1889-1969)
布里渊区定义:在倒易点阵中,以某一格点为坐标原点,做所有 倒格矢的垂直平分面,倒易空间被这些平面分成许多包围原 点的多面体区域,这些区域称作布里渊区,其中最靠近原点 的平面所围成的区域称作第一布里渊区,第一布里渊区界面
Face-centered cubic
K L
Middle of an edge joining two hexagonal faces Center of a hexagonal face
U
W X
Middle of an edge joining a hexagonal and a square face
与正格子的晶面系 (h1h2h3 ) 正交。 如图所示,晶面系 (h1h2h3 ) 中最靠近原点的晶面(ABC) 在正格子基矢 a1 , a 2 , a 3 的截距分别为: a1 , a 2 , a 3 h1 h2 h3
a1 a 3 CA OA OC h1 h3 a 2 a 3 CB OB OC h2 h3
二. 倒易点阵和晶体点阵之间的关系:
布里渊区

2
a
i
b2
2
a
j
2
b3 a k
所以,倒格子也是简立方结构,其第一布里渊区仍然是一个简立方。
(4)体心立方结构晶体点阵的布里渊区 对于体心立方结构晶体点阵,如果正格子基矢取为:
a1
a 2
(i
j
k)
a2
a 2
(i
j
k)
a a3 2 (i j k )
原胞体积为 a1 (a2 a3 ) a3 / 2
b1(h1 1, h2 1), b2(h1 1, h2 1)
通过这四个倒个是的中点,即
1 2
b1
1 2
b2
a
i
a
j
分别作四个垂直平分面,即可得到第二布里渊区的边界。
照此可以画出第二布区、第三布区等。如右图所示。 可以看出,布区的序号越大,分离的区域越多;但不论分离的区域数
目是多少,各布区的面积是相等的。
The first Brillouin zone is the Wigner-Seitz primitive cell in the reciprocal lattice.
§2.4 原子的形状因子和结构因子 (atomic form factor and structure factor )
一、散射波振幅(Diffraction amplitude)
可以展开为傅立叶级数
2
2
f (x) f0 p1 Cp cos( a
px)
p 1
S p sin( a
px)
(2.4.6)
其中 p 是整数, f0 ,Cp , S p 是傅立叶系数。
这个展开式可以写成更简洁的形式
2
1-6 倒格子与布里渊区

(3)正格子元胞与倒格子元胞 倒格子元胞体积:
b1 (b2 b3 ) (2 )3 (a2 a3 ) [(a3 a1 ) (a1 a2 )] 3 A ( B C ) ( A C ) B ( A B) C
(a3 a1 ) (a1 a2 ) {(a3 a1 ) a2 } a1 {(a3 a1 ) a1} a2 a1 0 a1 (2 ) (a2 a3 ) a1 3 (2 )3
三、典型晶格的倒格子与布里渊区
1、一维格子的布里渊区
a ai
2 b i a
2、二维正方格子的布里渊区 二维正方格子的原胞基矢为:
a1 ai , a2 aj
则其相应的倒格子原胞基矢为:
2 2 b1 i , b2 j a a
在倒格子空间中,距离原点最近的倒格点 有四个,其相应的倒格矢为:b , b , b
1 1 2
, b2
这四个倒格矢的垂直平分线的方程为:
kx
a
, ky
a
由这四个垂直平分线所围成的区域就是第一布 里渊区。
第一布里渊区
原点的次近邻四个到格点相应的倒格矢为:
b1 b2 , (b1 b2 ), b1 b2 , (b1 b2 )
它们的垂直平分线以及第一布里渊区边界 所共同围成的区域称为第二布里渊区。
二、特性:
1、第一布里渊区: 在倒格子点阵中,做某一倒格点到其最近邻 倒格点连线的垂直平分面,由这些垂直平分面所 围成的多面体就是第一布里渊区。 除第一布里渊区之外,还有第二布里渊区、第 三布里渊区以及更高阶的布里渊区。
2、第二、第三布里渊区可以由平移倒格矢的 整数倍至第一布里渊区。 3、每个布里渊区的体积都等于倒格子原胞的 体积。 4、布里渊区应选尽可能高的对称性。
布里渊区图示

a 3 正格子原胞基矢 a1 = ai, a2 = i + aj 2 2 取单位矢量k垂直于i, j 则,a1,a2和k构成的体积 3 2 Ω= a 2
§3-4 三维晶格的振动 ——
晶格振动与晶体的热学性质
倒格子原胞的基矢为 2π (a2 × k ) 2π 2π b1 = i− j = Ω a 3a 2π (k × a1 ) 4π b2 = = j Ω 3a
§3-4 三维晶格的振动 ——
晶格振动与晶体的热学性质
正方格子其它布里渊区的形成
§3-4 三维晶格的振动 ——
晶格振动与晶体的热学性质
正方格子其它布里渊区的形状
—— 每个布 里渊区经过适 当的平移之后 和第一布里渊 区重合
§3-4 三维晶格的振动 ——
晶格振动与晶体的热学性质
二维斜格子的第一布里渊区
§3-4 三维晶格的振动 ——
晶格振动与晶体的热学性质
二维斜格子其它布里渊区的形成
§3-4 三维晶格的振动 ——
晶格振动与晶体的热学性质
二维斜格子其它布里渊区的形状
—— 每个布里 渊区经过适当 的平移之后和 第一布里渊区 重合
§3-4 三维晶格的振动 ——
晶格振动与晶体的热学性质
平面正三角形,相邻原子间距为 求正格矢和倒格矢 求正格矢和倒格矢, 平面正三角形,相邻原子间距为a,求正格矢和倒格矢,画 出第一和第二布里渊区
的垂直平分线和第一 布里渊区边界所围成 —— 第二布里渊区大小
§3-4 三维晶格的振动 ——
晶格振动与晶体的热学性质
第三布里渊区 由4个倒格点 个倒格点
的垂直平分线和第二布 里渊区边界边界所围成 第三布里渊区大小
§3-4 三维晶格的振动 ——
23布里渊区
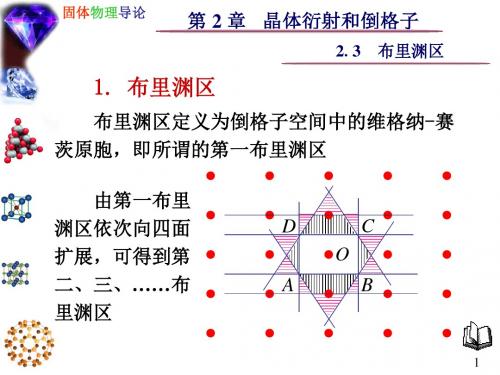
将任一布里渊 区的各部分平移适 当的位矢就可合并 成第一布里渊区
D
O A
C
B
由于倒格子的周期性,很多时候我们 只需关心第一布里渊区
2
固体物理导论
第 2 章 晶体衍射和倒格子
2.3 布里渊区
2. 衍射条件的布里渊区诠释
2k G G 2
D
GD
k1
1 1 2 k G G 2 2
体心立方
x
a3
Ω a1 (a2 a3 ) 1 3 a 2
Ω b1 (b2 b3 )
*
4π a
2( 2 π ) 3 / a 3
5
固体物理导论
第 2 章 晶体衍射和倒格子
2.3 布里渊区
倒格矢可以表示为
G v1b1 v2b2 v3b3 4π 2π [(v2 v3 )i (v3 v1 ) j (v1 v2 )k ] a a
最短的倒格矢是以下12个矢量
2π 2π 2π ( j k ); ( k i ); (i j ) a a a
第一布里渊区由上述12个矢量的 垂直平分面围成,是一个正十二面体
6
固体物理导论
第 2 章 晶体衍射和倒格子
2.3 布里渊区
体心立方晶格的布里渊区中一些 具有较高对称性的点或轴的坐标
其中
2π X: (1,0,0) a 2π 1 1 1 L: ( , , ) a 2 2 2 2π 3 3 K: ( , ,0 ) a 4 4 1 3 0 1, 0 , 0 2 4
10
k2
O
GC
C
任何从原点到 G 的垂直平分面的矢量都满足衍射 条件,这些平面正是布里渊区的边界。布里渊区包含 了所有能在晶体上发生布拉格反射的波的波矢 k
布里渊区

布里渊区
主讲人: 主讲人:许本超 答疑人: 答疑人:李海龙 封福明
固体物理 固体物理
内容
• • • • • • • • • 1.倒易空间 2. 布里渊区基本概念 3. 典型格子的第一布里渊区 4.布里渊区的几何性质 5. 衍射条件在布里渊区诠释 6.布里渊区中的K点 7.布里渊区和能带的关系 8.布里渊区和费米面 9.MS计算能带实例图
14
固体物理 固体物理
7.2布里渊区和能带的关系
能带论的基本出发点: 能带论的基本出发点 固体中的电子可以在整个固体中运动 电子在运动过程中要受晶格原子势场的作用 由于周期场的微扰, 由于周期场的微扰,
E
E6
E(k)函数在布里渊区 函数在布里渊区
允许带
E5
边界k=± 边界 ±nπ/a处出现 处出现
3.2体心立方晶格的F.B.Z 体心立方晶格的F.B.Z 体心立方晶格的 体心立方晶格的倒格子为面心立方晶格
可以看出, 可以看出,面心立方倒 格子(即体心立方晶格) 格子(即体心立方晶格) 的F.B.Z为正菱形十二 为正菱形十二 面体(非正十二面体) 面体(非正十二面体)
8
固体物理 固体物理
3.3面心立方晶格的F.B.Z 面心立方晶格的 面心立方晶格的F.B.Z 面心立方晶格的倒格子为体心立方晶格
如右图所示, 如右图所示,黑框为体心立方 倒格子,取其体心(黄点) 倒格子,取其体心(黄点)作 为原点,红点(8个 为原点,红点(8个)为此原 点最相邻的倒格点,蓝点(6 点最相邻的倒格点,蓝点( 个)为此原点次相邻倒格点 可以看出, 可以看出,体心立方倒 格子(即面心立方晶格) 格子(即面心立方晶格) 的F.B.Z为截角的八面体 为截角的八面体 十四面体) (十四面体)
固体电子物理5

固
体
电
子
理
论
—— 第一布里渊区
固
② 体心立方格子 正格子基矢 倒格子基矢 倒格矢
体
电
子
理
论
2π kn = n1b1 +n2b2 +n3b3 = [(n2 +n3)i +(n1 +n3) j +(n1 +n2)k] a
2π ( n 2 + n 3 , n1 + n 3 , n1 + n 2 ) a
固
体
电
子
理
论
—— 第一布里渊区在 方向上能量最高点 , 方向上能量最高点 方向上能量最高点A, 方向上能量最高点C —— C点的能量比第二布里渊区 点高 点的能量比第二布里渊区B点高 点的能量比第二布里渊区
k
k'
固
体
电
子
理
论
—— 第一布里渊区和第二布里渊区 能带的重叠
固
体
电
子
理
论
其它二维晶格的布里渊区
a
固
2π j a
体
b1 + b2
电
子
理
论
ky
M Σ
2π i a
kx
Г
∆
X
Γ
离中心点次近的四个倒格点相应的倒格矢是: 离中心点次近的四个倒格点相应的倒格矢是: b1 + b 2 , −(b1 + b2 ) , b1 − b2, −(b1 − b2 ) 其垂直平分线同第一布里渊区边界线围成的区域合起来为第二布里渊 这个区的各部分分别平移一个倒格矢,可以同第一个区重合。 区。这个区的各部分分别平移一个倒格矢,可以同第一个区重合。第 三布里渊区是2 四个倒格矢的垂直平分线同第一、 三布里渊区是2b1,2b2,-2b1,-2b2 四个倒格矢的垂直平分线同第一、 二布里渊区的边界线围成的。 二布里渊区的边界线围成的。
30 布里渊区的知识

*简谐近似是晶格动力学处理许多物理问题的出发点!
* 对热膨胀和热传导等问题必须考虑高阶项 --- 特别是3次和4次项的作用 → 这称为非谐项或非谐作用 – V非谐 * 具体处理问题时,把非谐项看成是对起主要作用 的简谐项的微扰!
简正振动模式:在简谐近似下, 由N个原子构成的晶体的晶格振 动, 可变为3N个独立的谐振子的振动. 每个谐振子的振动模式称 为简正振动模式 简正振动模式对应着所有的原子都以该模式的频率做振动, 它是 晶格振动模式中最简单最基本的振动方式. 原子的振动 —格波振动通常是这3N个简正振动模式的线形迭加.
2
a
i
倒格矢的垂直平分面 构成第一布里渊区
a
O
一维晶格点阵
b
-π/a
O
倒格子点阵
π/a
二维晶格点阵的布里渊区 取正格子基矢为 a1 ai 和a2 a j 可求出倒格子基矢为
2 2 b1 i 和b2 j a a
作原点0至其它倒格点连线的中垂线,它们将二维倒 格子平面分割成许多区域
第三章 晶格动力学和 晶体的热学性质
固体的许多性质都可以基于静态模型来理解(即晶体点阵模型), 即认为构成固体的原子在空间做严格的周期性排列,在该框架内, 我们讨论了X 光衍射发生的条件,求出了晶体的结合能,以后还将 在此框架内,建立能带论,计算金属大量的平衡性质。然而它只 是实际原(离)子构形的一种近似,因为原子或离子是不可能严 格的固定在其平衡位置上的,而是在固体温度所控制的能量范围 内在平衡位置附近做微振动。只有深入地了解了晶格振动的规律, 更多的晶体性质才能得到理解。如:固体热容,热膨胀,热传导, 融化,声的传播,电导率,压电现象,某些光学和介电性质,位 移性相变,超导现象,晶体和辐射波的相互作用等等。
固态电子论第一章习题解答

第2题 在空间点阵中,基元包含的原子数为1个或者1个的整数倍。 基元按严格周期性在三维空间分布,可以不同基元中的同一点作为格点位置,将 基元抽象为位于该点的一个几何点,从而形成空间点阵。
第3题 对于给定的一个晶格,其原胞的选取不是唯一的。选取原胞的原则是原胞中只能 包含一个格点。 而晶胞的选取主要考虑反映晶体的宏观对称性,同时考虑晶格的平移对称性(严 格周期性)。晶胞的三个棱边是三个不共面的晶体对称轴。晶胞通常包含一个以上格 点,所以不是最小的重复单元。
固态电子学第一章习题解答参考
1、2、3、4、5、6、7、9、10、11、12、
第1题
基元——构成实际晶体的一个最小重复结构单元。 空间点阵——格点的空间分布称为空间点阵。
布拉菲格子——全同格点构成的空间点阵称为布拉菲格子。
单式格子(简单格子)——全同原子构成的布拉菲格子。 复式格子——不同原子构成的若干相同结构的简单格子相互套构形成的晶格。
c
镓
1/4体对角线原子
b
a
原胞中包含的格点数为1,包含的砷原
子数和镓原子数均为1。 配位数为4。
a 3 c a 2
b a 1
a
晶胞和原胞
第4题
c 六方轴
碳原子 硅原子
⑤ 碳化硅的晶体结构为纤锌矿结构。由
碳原子六方晶格与硅原子六方晶格沿六方 轴 C 移动3C/8长度套构形成。 将一个碳原子与一个硅原子看成一个 基元。则对应的格点构成六方晶格。 其晶胞和原胞: 晶胞中包含的格点数为6,包含的砷原子 数为6,镓原子数为6。 原胞中包含的格点数为1,包含的砷原子 数和镓原子数均为1。 配位数为4。
a 3 c a 2
b a 1
a
固体物理基础(吴代鸣之高教版)课后1到10题答案

固体物理基础(吴代鸣之高教版)课后1到10题答案-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN一. 本章习题P272习题1.试证理想六方密堆结构中c/a=1.633.一. 说明:C 是上下底面距离,a 是六边形边长。
二. 分析:首先看是怎样密堆的。
如图(书图1.10(a),P8),六方密堆结构每个格点有12个近邻。
(同一面上有6个,上下各有3个)上下底面中间各有一个球,共有六个球与之相切,每个球直径为a 。
中间层的三个球相切,又分别与上下底面的各七个球相切。
球心之间距离为a 。
所以球心之间即格点之间距离均为a (不管是同层还是上下层之间)。
三.证明:如图OA=a ,OO ’=C/2(中间层是上下面层的一半),AB=a O ’是ΔABC 的三垂线交点33'aAB AO ==∴(由余弦定理)330cos 2,30cos 230cos 2222a a x x a ax x a x ===-+=633.1322384132)2()2()3()2(2222222222''≈===∴+=+=+=a c c a ac a ac OA AO OO2.若晶胞基矢c b a,,互相垂直,试求晶面族(hkl )的面间距。
一、分析:我们想到倒格矢与面间距的关系G d π2=。
倒格矢与晶面族 (hkl )的关系321b l b k b h G++=写出)(321b b b 与正格子基矢 )(c b a的关系。
即可得与晶面族(hkl ) 垂直的倒格矢G。
进而求得此面间距d 。
二、解:c b a ,,互相垂直,可令k c c j b b i a a===,,晶胞体积abc c b a v =⨯⋅=)(倒格子基矢: kcj b i a abc b a v b j b i a k c abc a c v b ia k c jb abc c b v b πππππππππ2)(2)(22)(2)(22)(2)(2321=⨯=⨯==⨯=⨯==⨯=⨯=而与 (hkl )晶面族垂直的倒格矢 222321)()()(2)(2cl b k a h G k cl j b k i a h b l b k b h G ++=∴++=++=ππ故(hkl ) 晶面族的面间距222222)()()(1)()()(222cl b k a h cl b k a h Gd ++=++==πππ3.若在体心立方晶胞的每个面中心处加一个同类原子,试说明这种晶体的原胞应如何选择每个原胞含有几个原子1.分析:考虑选取原胞的条件:(即布拉菲晶格的最小单元)(1)体积最小的重复结构单元(2)只包含一个格点(3)能反映晶格的周期性应将几个原子组合成一个格点,然后构成原胞。
固体物理基础课后答案

精品文档一.本章习题P272 习题1.试证理想六方密堆结构中c/a=1.633.一.说明:C 是上下底面距离, a 是六边形边长。
二.分析:首先看是怎样密堆的。
如图 (书图 1.10(a),P8),六方密堆结构每个格点有12 个近邻。
(同一面上有 6 个,上下各有 3 个)上下底面中间各有一个球,共有六个球与之相切,每个球直径为a。
中间层的三个球相切,又分别与上下底面的各七个球相切。
球心之间距离为a。
所以球心之间即格点之间距离均为a(不管是同层还是上下层之间)。
三.证明:如图 OA=a ,OO ’=C/2 (中间层是上下面层的一半),AB=aO’是 ABC 的三垂线交点AO'AB a 33(由余弦定理x2a2x 22ax cos30aa a 2xcos30 , x)2cos303OA222( c)2( a )2 OO'AO' 23 a2( c )2( a )2222 a2 1 c234c822 1.633a332.若晶胞基矢 a,b, c 互相垂直,试求晶面族( hkl )的面间距。
一、分析:我们想到倒格矢与面间距的关系d2 。
G倒格矢与晶面族( hkl )的关系 Ghb 1 kb 2 lb 3写出 (b 1b 2b 3 ) 与正格子基矢(ab c) 的关系。
即可得与晶面族(hkl ) 垂直的倒格矢 G 。
进而求得此面间距 d 。
二、解:a,b, c 互相垂直,可令 aai , b bj ,cck晶胞体积 v a (b c )abc倒格子基矢:b 12(b c)2 (bj ck ) 2 ivabc ab 22 (c a)2 (ck ai ) 2vabc jb b 32 (a b) 2 (ai bj ) 2 kvabcc2 ( hik j lk )G hb 1kb 2 lb 3而与 ( hkl )晶面族垂直的倒格矢abc( h ) 2 ( k )2 ( l ) 2G2abc故( hkl ) 晶面族的面间距2 dG22 ( h)2( k ) 2 ( l ) 2ab c1( h ) 2 ( k )2 ( l )2abc3.若在体心立方晶胞的每个面中心处加一个同类原子,试说明这种晶体的原胞应如何选择?每个原胞含有几个原子?1.分析:考虑选取原胞的条件:(即布拉菲晶格的最小单元)(1)体积最小的重复结构单元(2)只包含一个格点(3)能反映晶格的周期性应将几个原子组合成一个格点,然后构成原胞。
固体物理吴代鸣课后答案
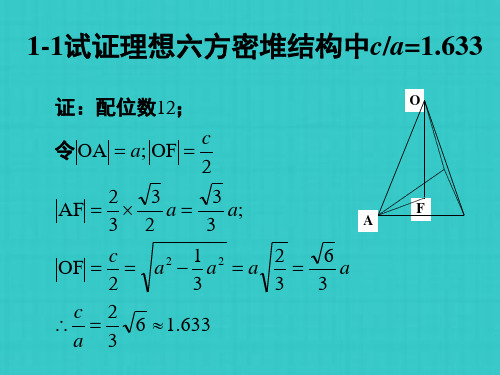
2π a
i , b2
π a
j
1 6六方密堆结构的原胞基 矢为
a1
a 2
i
3
aj ;
2
a2
a 2
i
3
aj ;
2
a3 ck ;
试求倒格子基矢并画出 第一布里渊区。
解:
a1
(a2
a3
)
3 a2c; 2
b1
2π
(a2
a3 )
2π a
i
2π
j;
3a
b2
2π
(a3
r r..........(2)
1
得:r0
4π 0 nB e2
n1..............(2' )
由(2)得:B
e2 4π 0 n
r0n1...............(3)
(3)代入(1)得:U
(r0
)
Ne2 8π 0r0
1
1 n
........(4)
V 基元:顶点原子、体心、三个相邻面心
0
令原来的晶体体积为 V ,那么每个原子所占的 体积为 , 同理,(110)面:顶点4个原子,每个1/4; N 解:将整个晶体看成是5个简单立方格子套构而成。
2d 2a sin aqdq
M
dq
a
M
M
d
2
M2
4 2
4
1/
2
g ( )
l 2π
m
2 (q)d(q)
0
a
M
M
( (q))
2
(q)
M
4
2 2
4
(q)
1/
2
固体物理学概念和习题答案(供参考)

39. 请解释刃位错ຫໍສະໝຸດ 螺位错、晶界和小角晶界并画出示用意。
40. 请列出顺磁性、抗磁性的主要区别。
41. 请列出铁磁性固体的主要特征。
42. 请列出亚铁磁性与反铁磁性的主要区别。
43. 什么是格波和声子?晶体中声子有多少种可能的量子态?
44. 请说明Debye热容量模型的大体假设,为何说Debye热容量模型在低温下是正确的?
22. (固体物理习题集
设有一维原子链(如图),第2n个原子与第2n+1个原子之间的恢复力常数为β,第2n个原子与第2n-1个原子之间的恢复力常数为β'(β'<β)。设两种原子的质量相等,最近邻原子间距均为a,试求晶格振动的振动谱和波矢q=0和q=±1/4a时的振动频率。
s
23. (固体物理习题集
设有一维双原子链,链上最近邻原子间的恢复力常数交织地等于β和10β。若两种原子的质量相等,而且最近邻间距为a/2,试求在波矢k=0和k=π/a处的ω(k),并画出其色散关系曲线。
16. 给作声子的概念。
17. 请描述金属、绝缘体热容随温度的转变特点。
18. 在晶体热容的计算中,爱因斯坦和德离去离做了哪些大体假设。
19. 简述晶体热膨胀的原因。
20. 请描述晶体中声子碰撞的正规进程和倒逆进程。
21. 别离写出晶体中声子和电子别离服从哪一种统计散布(给出具体表达式)?
22. 请给出费米面、费米能量、费米波矢、费米温度、费米速度的概念。
6. 六角空间点阵,六角空间点阵的基矢可以取为:
; ; ;
(1) 证明:原胞的体积是 ;
(2)证明:倒易点阵的基矢是: , , ;因此直接点阵就是它本身的点阵,但轴通过了转动;
I布里渊区简正模和格波

但他们的研究当时被忽视了,因为同年发表的更为简单的Debye热容
理论(弹性波近似)已经可以很好的说明当时的实验结果了,但后来
更为精确的测量却表明了Debye模型不足,所以1935年Blakman才重新
利用Born和Von-Karman近似讨论晶格振动,发展成现在的晶格动力学
理 论 。 后 来 黄 昆 先 生 在 晶 格 振 动 研 究 上 成 就 突 出 , 特 别 是 1954 年 和
了“黄方程”,提出了声子极化激元的概念,并与李爱扶(A.Rhys,妻子) 建立了多声子跃迁理论。
1947-1952年,与玻恩教授合著《晶格动力学》一书(英国牛津出版社, 1954年)。(2006年中文版)
黄昆对晶格动力学和声子物理学的发展做出了卓越的贡献。他的名字与 多声子跃迁理论、X光漫散射理论、晶格振动长波唯象方程、二维体系光学 声子模联系在一起。他是“极化激元”概念的最早阐述者。
b1
2
a
i和b2
2
a
j
作原点0至其它倒格点连线的中垂线,它们将二维倒 格子平面分割成许多区域
二维正方格子的第一、二、 三布里渊区
③ ①②
O
简单立方(sc)
第一布里渊区边界是下面六个倒格矢的中点,并与之正交的平面:
±12������������=±
������ ������
���റ���;
Born共同写作的《晶格动力学》一书已成为该领域公认的权威著作。
我国科学家黄昆院士在晶格振动理论上做出了重要贡献。
黄昆院士简介: (摘录) 1945-1947年,在英国布列斯托(Bristol)大学物理系学习,获哲学博士
学位;发表《稀固溶体的X光漫散射》论文,理论上预言“黄散射”。 1948-1951年,任英国利物浦大学理论物理系博士后研究员,这期间建立
固体物理倒格矢

2 2 2
a2 a3 V a3 a1 V a1 a2
V
正(2)点两阵个:点阵正格格矢矢之Rl间的l1a关1 系l2:a2
l3a3
l1、l2、l3 Z
倒易点阵:倒格矢 Gh h1b1 h2b2 h3b3 h1、h2、h3 Z
则有:
Rl Gh=2 Z
结论: 若两矢量点积为2的整数倍, 且其中一个矢量
固体物理倒格矢
1.9 1 倒格子(倒易点阵)*的定义:
1 正格矢与倒矢
S
原子可向空间任何方向散射X光线,只有一些固定 方向可形成衍射。
S0
P
点P: Rl=l1a1+l2a2+l3a3,Rl是布喇菲点阵中由原胞基矢a1,a2,a3构成的矢量,
S0和S是入射线和衍射线的单位矢量,经过O点和P点衍射后光程差为:
V
4
2
a
3
V倒易原胞
返回
面心立方晶格的第一布里渊区
—— 第一布里渊区为十四面体
—— 布里渊区中某些对称点和若干对称轴上的点能 量较为容易计算,这些点的标记符号
布里渊区原点 六方面的中心 四方面的中心
[000]
L ( , , )
aaa
X ( 2 , 0, 0 )
a
X 计为 轴 ——
二维正方晶格的布里渊区
二维长方晶格的布里渊区
二维六方晶格的十个布里渊区
(3) 三维晶格
a. 简立方晶格
倒易空间示意图
aaa321
ai aj ak
b1
b2
b3
2
a
2
a
2
a
i j k
b1
倒易点阵仍为简立方晶格
b3 b2 b1
朱建国《固体物理学》习题答案

即
求格波解,令
,
代入运动方程,可导出线性方程组为:
令 ,从A,B有非零解的系数行列式等于零的条件可得
可解出
色散关系见下图
时, , ,
时, , ,
3.6.在一维双原子链中,如 ,求证
[证]由书中(3.22)式知,双一维原子链声学支
, 由近似式 ,
得
,
对 ,由于 ,
3.7在一维双原子晶格振动情况中,证明在布里渊区边界 处,声学支格波中所有轻原子m静止,而光学支格波中所有重原子M静止。画出这时原子振动的图象。
1.8若基失a,b,c构成正交晶系,求证:晶面族(hkl)的面间距为
答:根据晶面指数的定义,平面族(hkl)中距原点最近平面在三个晶轴a1,a2,a3上的截距分别为 , , 。该平面(ABC)法线方向的单位矢量是
这里d是原点到平面ABC的垂直距离,即面间距。
由|n|=1得到 故
1.9用波长为0.15405nm的X射线投射到钽的粉末上,得到前面几条衍射谱线的布拉格角θ如下
用正交关系式
求出倒易点阵初基矢量b1,b2。设
由
得到下面四个方程式
(1)
(2)
(3)
(4)
由(1)式可得: 由(2)式可得: 由(3)式可得: 由(4)式可得:
于是得出倒易点阵基矢
第三章习题答案
3.1试求由5个原子组成的一堆单原子晶格的格波频率,设原子质量m=8.35×10-27kg,恢复力常数β=15N·m-1
(4)对于六方密堆积一个晶胞有两个原子,其坐标为(000)(1/3,2/3,1/2),在理想的密堆积情况下,密排六方结构中点阵常数与原子半径的关系为a=2r,因此θ= =
(5)对于金刚石结构Z=8 那么 = .
