高三数学正弦余弦应用举例

合集下载

正余弦定理的应用举例

正余弦定理的应用举例
目录
CONTENTS
• 正弦定理的应用 • 余弦定理的应用 • 正余弦定理的综合应CHAPTER
正弦定理的应用
在三角形中的运用
01
02
03
确定三角形形状
通过正弦定理可以判断三角形的形状，例如是否为直角三角形、等腰三角形或等边三角形。
计算角度
在航海中，利用正余弦定理可以计算船只的位置和航向。
建筑测量
在建筑测量中，利用正余弦定理可以计算建筑物的角度和距离。
地球科学
在地球科学中，利用正余弦定理可以计算地球的经纬度和地球自转角速度等参数。
04
CHAPTER
特殊情况下的应用
直角三角形中的应用
01
直角三角形中，可以利用正弦定理求出未知的边长。例如，已知直角三角形的一个锐角和相邻的直角边，可以求出斜边的长度。
在实际生活中的运用
测量距离
在无法直接测量距离的情况下，可以利用正弦定理计算出距离。
航海定位
在航海中，可以利用正弦定理计算出船只的位置和航向。
建筑设计
在建筑设计中，可以利用正弦定理计算出建筑物的角度和边长，以确保建筑物的稳定性和美观性。
02
CHAPTER
余弦定理的应用
在三角形中的运用
特殊角度三角形中的应用
在特殊角度三角形中，如30-60-90或45-45-90等三角形中，可以利用正余弦定理来求解未知的边长或角度。例如，已知30-60-90三角形的一个边长和锐角大小，可以求出另一个边长和角度。
在特殊角度三角形中，也可以利用正弦定理来求解面积。例如，已知30-60-90三角形的两个边长，可以求出该三角形的面积。

正弦定理余弦定理应用举例

正弦定理、余弦定理应用举例一、距离问题1.xkm 后，他向右转150，然后朝新方向走3km ，结果他离出发点某人向正东方向走恰好3km ，那么x 的值为【】A.3B.23C.23或3D.32.如图，为了测量某障碍物两侧A、 B 间的距离，给定下列四组数据，测量时应当用数据【】A., a, bB.,， aC.a,b，D.,， b两座灯塔A 与B与海洋观察站C的距离都等于 a km ，灯塔A在观察站C的北偏东3.20 ，灯塔B在观察站C的南偏东 40，则灯塔 A 与灯塔 B 的距离为【】A. a kmB.3a kmC. 2a kmD. 2a km4.海上有 A、B 两个小岛相距10海里，从A 岛望 C岛和 B岛成60的视角，从B岛望 C 岛和 A岛成75的视角，则B、 C 的距离是 __________________5.一船向正北航行，看见正西方向有相距10 海里的两个灯塔恰好与它在一条直线上，继续航行半小时后，看见一灯塔在船的南偏西 60的方向上，另一灯塔在船的南偏西75 方向上，则这艘船的速度是每小时___________________6.如右图所示，设 A 、B 两点在河的两岸，一测量者在 A 所在的河岸边选定一点 C ，测出 AC 的距离为 50m ,ACB45 , CAB105后，就可以计算 A 、 B 两点间的距离为 ___________7.一船以 24 km / h的速度向正北方向航行，在点 A 处望见灯塔 S 在船的北偏东30 方向上，15min后到点B处望见灯塔在船的北偏东65 方向上，则船在点B时与灯塔S的距离是__________km.(精确到 0.1km ）18.如图，我炮兵阵地位于地面 A 处，两观察所分别位于地面点 C 和 D 处，已知 CD=6000m.ACD 45，ADC75，B 处时测得BCD 30 , BDC 15目标出现于地面求炮兵阵地到目标的距离。

（结果保留根号）A45600075C D3015B2二、高度问题1.在一幢 20m 高的楼顶测得对面一塔吊的仰角为60 ，塔基的俯角为45 ，那么这座塔吊的高是【】3 )m B. 20(13) m C.10( 6 2 )m D. 20(6 2 )mA.20(132.在地面上点 D 处，测量某建筑物的高度，测得此建筑物顶端 A 与底部 B 的仰角分别为60 和 30 ，已知建筑物底部高出地面 D 点 20m，则建筑物高度为【】A.20mB.30mC. 40mD.60m3.如图所示，在山根 A 处测得山顶 B 的仰角CAB 45 ,沿倾斜角为 30 的山坡向山顶走1000 米到达 S 点又测得山顶仰角DSB 75 ,则山高BC为【】A.500 2mB. 200mC.1000 2mD. 1000m4.从某电视塔的正东方向的 A 处，测得塔顶仰角为60 ；从电视塔的西偏南30 的B处，测得塔顶仰角为45 ,A、B两点间的距离是35m，则此电视塔的高度是【】4900 m D.35mA. 5 21mB.10mC.135.j 江岸边有一炮台高30m，江中有两条船，由炮台顶部测得俯角分别为45 ， 30 ，而且两条船与炮台底部连线成30 角，则两船相距【】A.10 3mB.100 3mC. 203mD.30m6.一船以每小时15km 的速度向东航行，船在 A 处看到一个灯塔M 在北偏东60方向，行驶4h 后，船到达 B 处，看到这个灯塔在北偏东15 方向，这时船与灯塔的距离为_____km37.甲、乙两楼相距20 米，从乙楼底望甲楼顶的仰角为60 ，从甲楼顶望乙楼顶的俯角为30 ，则甲、乙两楼的高分别是______________8.地平面上一旗杆设定为OP,为测得它的高度h，在地平线上取一基线AB， AB=200m ，在 A 处测得 P 点的仰角为OAP 30 ,在B处测得P点的仰角OBP 45 ，又测得AOB 60 ,求旗杆的高度h4。

余弦定理和正弦定理的应用

余弦定理和正弦定理的应用余弦定理和正弦定理是解决三角形问题中常用的数学定理。

它们可以帮助我们求解三角形的边长、角度和面积等。

本文将分别介绍余弦定理和正弦定理的应用，并通过实例来说明它们的具体使用方法。

一、余弦定理的应用余弦定理是一个用来描述三角形边长和夹角之间关系的定理。

在任意三角形ABC中，假设边长分别为a、b、c，而对应的夹角为A、B、C，则余弦定理可以表示为：c² = a² + b² - 2ab·cosC1. 求解三角形边长假设我们已知一个三角形的两个边长a和b，以及它们夹角C的大小。

我们可以通过余弦定理来求解第三个边长c。

例如，已知三角形ABC中，边AB的长度为5，边AC的长度为8，而夹角B的大小为60度。

按照余弦定理，我们可以用下式来计算边BC的长度：BC² = AB² + AC² - 2·AB·AC·cosB代入具体数值，即可求得：BC² = 5² + 8² - 2·5·8·cos60°BC² = 25 + 64 - 80·0.5BC² = 89 - 40BC² = 49BC = √49 = 7因此，边BC的长度为7。

2. 求解三角形夹角在某些情况下，我们已知三角形的三个边长，但需要求解其中一个夹角的大小。

余弦定理同样可以解决这个问题。

例如，已知三角形ABC的边长分别为a=4、b=7、c=9。

我们想要求解夹角C的大小。

根据余弦定理，我们可以得到：c² = a² + b² - 2ab·cosC代入具体数值，我们可以得到：9² = 4² + 7² - 2·4·7·cosC81 = 16 + 49 - 56·cosC16 + 49 - 81 = 56·cosC-16 = 56·cosCcosC = -16 / 56 = -0.2857由于余弦函数的定义域为[-1, 1]，该结果无解，即无法构成三角形。

正、余弦定理及其应用

正、余弦定理及其应用正、余弦定理及其应用一、正弦定理和余弦定理1、正弦定理和余弦定理定理正弦定理余弦定理内容变形形式①a=2RsinA,b=2RsinB,c=2RsinC;②sinA=,sinB=,sinC=;③a:b:c=sinA:sinB:sinC;④ 解决的问题已知两角和任一边，求另一角和其他两条边；已知两边和其中一边的对角，求另一边和其他两角。

已知三边，求各角；已知两角和它们的夹角，求第三边和其他两个角。

注：在ΔABC 中，sinA>sinB是A>B的充要条件。

（∵sinA>sinBa>bA>B）二、应用举例1、实际问题中的常用角（1）仰角和俯角在视线和水平线所成的角中，视线在水平线上方的角叫仰角，在水平线下文的叫俯角（如图①）（2）方位角从指北方向顺时针转到目标方向线的水平角，如B点的方位角为α（如图②）注：仰角、俯角、方位角的区别是：三者的参照不同。

仰角与俯角是相对于水平线而言的，而方位角是相对于正北方向而言的。

（3）方向角：相对于某一正方向的水平角（如图③）①北偏东即由指北方向顺时针旋转到达目标方向；②北偏本即由指北方向逆时针旋转到达目标方向；③南偏本等其他方向角类似。

（4）坡度：坡面与水平面所成的二面角的度数（如图④，角θ为坡角）坡比：坡面的铅直高度与水平长度之比（如图④，为坡比）2、ΔABC的面积公式（1）；（2）；（3）。

【基本训练】1．在△ABC中，“”是“”的（）A．充分而不必要条件 B．必要而不充分条件C．充分必要条件 D．既不充分也不必要条件2．在△ABC中，角A、B、C所对的边分别是a、b、c，若三角形的面积S=（a2+b2－c2），则∠C的度数是_______．3．在△ABC中，为的中点，且，则.4．在中，若，，，则考点集结考点一：正弦定理、余弦定理的简单应用〖例1〗a=，b=，B=45°，求A,C及边c．2)在中，角所对的边分.若，则（）A．B．C．-1D．11.在△ABC中以知A=30°a、b分别为角A、B对边，且a=4=b解此三角形考点二：利用正弦定理、余弦定理判断三角形的性状及求取值范围〖例2〗若△的三个内角满足则△A．一定是锐角三角形.B．一定是直角三角形.C．一定是钝角三角形.D．可能是锐角三角形，也可能是钝角三角形.在锐角△ABC中，BC＝1，B＝2A，则的值等于______，AC的取值范围为________．cos的最小值为。

正、余弦定理在实际生活中的应用

正、余弦定理在实际生活中的应用正弦定理和余弦定理是三角学中重要的定理，它们不仅在数学领域有着重要的意义，而且在日常生活中也有着广泛的应用。

本文将通过几个实际生活中的例子，来说明正弦定理和余弦定理的应用。

我们来看一个生活中常见的例子，即测量高楼的高度。

假设有一栋高楼，我们无法通过直接测量得到其高度，但是我们可以通过测量某一点到高楼顶部的距离和测量这一点与高楼底部的夹角，利用正弦定理和余弦定理来计算高楼的高度。

设高楼的高度为h，某一点到高楼顶部的距离为d，某一点与高楼底部的夹角为θ，则根据正弦定理可得：\[ \frac{h}{\sin{\theta}} = \frac{d}{\sin{(90^\circ - \theta)}} \]根据余弦定理可得：\[ h^2 = d^2 + L^2 - 2dL\cos{\theta} \]通过这两个公式，我们可以根据已知的距离和夹角，计算出高楼的高度。

这就是正弦定理和余弦定理在测量高楼高度时的应用。

正弦定理和余弦定理也可以在航海领域中得到应用。

航海员在航海时需要测量两个位置之间的距离和方向角，而这正是正弦定理和余弦定理所擅长的。

假设航海员需要确定A点和B点之间的距离d和方向角θ，可以利用正弦定理和余弦定理来进行计算。

首先利用余弦定理计算A点和B点的距离：\[ d^2 = a^2 + b^2 - 2ab\cos{\theta} \]然后利用正弦定理计算出方向角θ：\[ \frac{\sin{\theta}}{a} = \frac{\sin{B}}{d} \]通过这些计算，航海员可以准确地确定A点和B点之间的距离和方向角，从而确保航行的安全和准确性。

在建筑领域中，正弦定理和余弦定理也有着重要的应用。

在设计桥梁和建筑物结构时，需要计算各种角度和距离，而这些计算中常常需要用到正弦定理和余弦定理。

在地质勘探和地震预测中，也需要利用正弦定理和余弦定理来计算地层的深度和角度，从而进行地质勘探和地震预测工作。

余弦定理及正弦定理的应用

余弦定理及正弦定理的应用余弦定理和正弦定理是解决三角形相关问题的重要工具。

它们被广泛应用于测量、导航、工程等领域。

下面将分别介绍余弦定理和正弦定理，并说明它们在实际应用中的具体运用。

一、余弦定理余弦定理描述了一个三角形的边与夹角之间的关系。

对于任意一个三角形 ABC，其边长分别为 a、b、c，对应的夹角分别为 A、B、C。

根据余弦定理，可以得到以下等式：a² = b² + c² - 2bc * cosAb² = a² + c² - 2ac * cosBc² = a² + b² - 2ab * cosC余弦定理可以用于解决以下问题：1. 测量三角形边长：如果已知三角形的两个边长和它们之间的夹角，可以利用余弦定理计算出第三条边的长度。

2. 计算三角形的夹角：如果已知三角形的三条边长，可以利用余弦定理的逆运算求解三个夹角的大小。

3. 解决航海导航问题：根据已知的方位角和航程，可以利用余弦定理计算船只的坐标位置。

二、正弦定理正弦定理描述了三角形边与其对应角的正弦值之间的关系。

对于任意一个三角形 ABC，其边长分别为 a、b、c，对应的夹角分别为 A、B、C。

根据正弦定理，可以得到以下等式：a/sinA = b/sinB = c/sinC正弦定理可以用于解决以下问题：1. 求解三角形的面积：如果已知三角形的两边和它们之间的夹角，可以利用正弦定理求解三角形的面积。

2. 判定三角形类型：根据三边的长度和正弦定理，可以判断三角形是锐角三角形、直角三角形还是钝角三角形。

3. 解决建筑工程问题：在建筑测量中，需利用正弦定理计算高度、距离等未知量。

综上所述，余弦定理和正弦定理是解决三角形相关问题的重要工具。

通过运用这些定理，我们可以计算三角形的边长、夹角，求解三角形的面积，判断三角形的类型等。

在测量、导航、工程等领域，都离不开这两个定理的应用。

正弦定理余弦定理应用举例

。三角形的面积公式
1 1 SABC 1 absinC bcsin A 2 2 2 acsin B
正弦定理和余弦定理在实际测量中有许多应用 :
(1)测量距离. (2)测量高度. (3)测量角度.
实际应用问题中有关的名称、术语 1.仰角、俯角、视角。
（1）当视线在水平线上方时，视线与水平线所成角叫仰角。（2）当视线在水平线下方时，视线与水平线所成角叫俯角。（3）由一点出发的两条视线所夹的角叫视角。（一般这两条视线过被观察物的两端点）视线仰角俯角视线水平线
【变式练习3】如图，甲船以每小时30 2海里的速度向正北方向航行，乙船按固定方向匀速直线航行．当甲船位于A1处时，乙船位于甲船的北偏西105方向的B1处，此时两船相距20海里．当甲船航行20分钟到达A2处时，乙船航行到甲船的北偏西120方向的B2 处，此时两船相距10 2海里．问乙船每小时航行多少海里？
答：A,B两点间的距离为 20 6米.
练习2.一货轮在海上由西向东航行，在A处望见灯塔C在货轮的东北方向，半小时后在B处望见灯塔C在货轮的北偏东30°方向．若货轮的速度为30 n mile/h，当货轮航行到D处望见灯塔C在货轮的西北方向时，求A，D两处的距离．
[解] 如图8所示，在△ABC中，∠A＝45° ，∠ABC＝ 90° ＋30° ＝120° ，∴∠ACB＝180° －45° －120° ＝15° ，AB＝ 30×0.5＝15(n AB ， sin∠ACB AB· sin∠ABC 15×sin120° 3 2＋ 6 ∴AC＝＝ ×15(n sin15° ＝ 2 sin∠ACB mile)．在△ACD中，∵∠A＝∠D＝45° ， ∴△ACD是等腰直角三角形， ∴AD＝ 2AC＝15(3＋ 3)(n mile)． ∴A，D两处的距离是15(3＋ 3) n mile. mile)．由正弦定理，得 AC sin∠ABC ＝

正弦余弦定理应用举例3

例6 一艘海轮从A出发，沿北偏东75°的方向航行67.5n mile 后到达海岛B,然后从B出发，沿北偏东32°的方向航行54.0n mile后到达海岛C.如果下次航行直接从A出发到达C,此船应该沿怎样的方向航行，需要航行多少距离（角度精确到0.1°,距离精确到0.01n mile）?
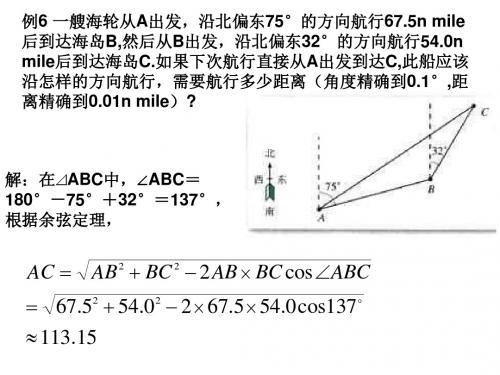
解：在⊿ABC中，∠ABC＝ 180°－75°＋32°＝137°，根据余弦定理，
c 2 a 2 b 2 127 2 682 882 cos B 0.7532, 2ca 2 127 68 sin B 1 0.7532 2 0.6578. 1 应用S ca sin B, 得 2 1 2 S 127 68 0.6578 2840.38(m ). 2 答：这个区域的面积是 2840.38m 2 .
在⊿ABC中，若B=60°,2b=a+c,试判断⊿ABC的形状。
； / 布袋除尘器泊头市净化除尘设备厂
zth40awb
再问：“如你说，便该怎的？”刘晨寂便讲了几样药味，又道：“这倒是险了些，论平常，我也不敢用，但需等到病者痰粘至不能喘息，扶起来，把这灌下去，倒能好了。”又道：“需早些煎下，一直热着等，上气不接下气时立刻灌下，若早些灌，怕伤了身体，若迟些灌，怕病人就不能吞咽了。”于大夫走后，因刘晨寂太年轻，进内帏不便，另换个老大夫给表诊脉，为着道上尊重同僚的本份，方子未动过。刘晨寂虽讲得理路清晰，别人也未敢就叫他进内院，但今早起，表病情又凶险，痰越积越重，又只苦咳不出，喘气越来越艰难，丫头们便谈论起刘晨寂前日的说话来。宝音听得此话，人命关天，倒是要紧，便问：“如今是吃什么方子？”“还是老方，听说不见效。”“刘大夫呢？”“芋大娘吃坏了肚子，他来诊脉，正好在。”芋大娘是厨中的厨娘，几样小菜、卤味，极是拿得出手，却是馋了点——或者正因为馋了点，厨艺才精进？——怪道宝音刚才在厨房未见她呢，却原来节下不检点，替人添麻烦。宝音皱皱眉，道：“我去看看芋大娘。”“宝音你在这里！”苍老的声音，邱妈妈气喘吁吁的赶来。宝音敬她年来，忙迎上前扶住了，又给她行礼，她且顾不得这个，一把扯住宝音，哭诉姑娘不好了，听说有个刘大夫说过一帖奇方，求宝音帮帮忙，先让人煎上。“有方子，自然能煎，”宝音斥旁边小丫头飘儿道，“府里头药房是作什么的，叫邱妈妈这把年纪跑到这里来找人？” 第六章前生后世两茫茫（2）飘儿委委屈屈解释：表现在大夫又不是刘大夫。于大夫去后换了位老大夫嘛不是？刘大夫说的方子，老大夫也看了，批说太凶险，病灶除去，怕病人也跟着一命呜呼了。药房听说此语，就不敢煎。这也没错啊！邱妈妈耳背，听飘儿的话听了半天，不是帮自己的，把她气得一推，自己跟宝音啰哩啰嗦的讲，姑娘这病真是凶了，凶得可怕了，老大夫看来不中用，实在不行就试试刘大夫的，左不过不中用。刘大夫没见病人的面都能说出这些来，照她想是比其他大夫还可信的。宝音当机立断道：“药先煎上，若表真有刘大夫所说的症状，老大夫有应对之法还是先用老大夫的，”握握邱妈妈的手，“终是年老沉稳靠得住些。但要是他没法子急救，便照刘大夫的药进上！但愿不必有那么凶险时候罢！”又道，“你们先去药房传话，我去找刘大夫要那药方。”邱妈妈怀中掏出油纸包藏的一张纸：“我有！上次听她们讲，我央会字的人给我写下来了！”她对自小乳大的，真是忠心耿耿。飘儿与邱妈妈便先往药房去了。宝音晓得大太太、二太太都不太待见表，更不愿在表的病情上担肩膊，去回了也无用，老太太年纪大了，精神易疲乏，这上下在养神呢，不便打扰，因此一力承担下来，料药

正弦定理和余弦定理综合应用

BC
a sin
a sin
sin 180o ( ) sin( )
α
δ
β
γ
D
C
计算出AC和BC后，再在ABC中，应用余弦定理计
算出AB两点间的距离
AB AC2 BC2 2AC BC cos
测量垂直高度
1、底部可以到达的
测量出角C和BC的长度，解直角三角形即可求出AB的长。
借助于余弦定理可以计算出A、B两点间的距离。
C
解：测量者可以在河岸边选定两点C、D，测得CD=a, 并且在C、D两点分别测得∠BCA=α, ∠ACD=β, ∠CDB=γ, ∠BDA=δ.
在 ∆ADC和∆ BDC中，应用正弦定理得
B
a sin( )
a sin( ) A
AC
sin 180o ( ) sin( )
故sin B AC sin A 5 3 B 38o
BC 14
故我舰航行的方向为北偏东 50o 38o 12o
变式训练1：若在河岸选取相距40米的C、D两
点，测得 BCA= 60， ACD=30，CDB= 45， BDA= 60 求A、B两点间距离 .
注：阅读教材P12，了解基线的概念
1.2.1 应用举例
公式、定理
正弦定理：a b c 2R sin A sinB sinC
余弦定理：
a2 b2 c2 2bc cos A b2 a2 c2 2ac cos B
c2 a2 b2 2abcosC
三角形边与角的关系：
cos A b2 c2 a2 ， 2bc
cos B c2 a2 b2 ， 2ca
即sin9A0C°－α＝sinBαC－β，∴AC＝sBinCαco－s βα＝sihncαo－s αβ. 在Rt△ACD中，CD＝ACsin∠CAD＝ACsin β＝hscionsαα－sinββ.

正弦定理与余弦定理的应用

正弦定理和余弦定理在三角学及相关领域中具有广泛的应用，通过这两个定理，我们可以解决许多与三角形相关的问题。

以下是关于正弦定理和余弦定理的应用的详细探讨。

一、正弦定理的应用正弦定理是三角学中的一个基本定理，它表达了三角形中任意一边与其对应的角的正弦值之间的关系。

正弦定理在实际应用中具有广泛的用途，以下是几个具体的应用示例：1. 航海与测量：在航海和大地测量中，正弦定理被用来计算地球上两点之间的距离。

由于地球表面可以近似为一个球体，因此可以通过测量两点的纬度和经度，利用正弦定理计算出两点之间的实际距离。

2. 电气工程：在电气工程中，正弦定理被用来分析交流电路中的电压、电流和电阻之间的关系。

通过正弦定理，我们可以推导出各种电气元件（如电阻、电容和电感）的等效电路模型，从而简化电路分析。

3. 通信与信号处理：在通信和信号处理领域，正弦定理被用来分析信号的频谱特性和传输特性。

通过正弦定理，我们可以将复杂的信号分解为一系列正弦波的组合，从而更容易地理解和处理信号。

二、余弦定理的应用余弦定理是另一个重要的三角定理，它表达了三角形中任意一边的平方等于其他两边平方之和减去这两边夹角的余弦值乘以这两边乘积的2倍。

余弦定理同样具有广泛的应用，以下是几个具体的应用示例：1. 几何学：在几何学中，余弦定理被用来解决与三角形边长和角度相关的问题。

例如，在已知三角形的两边及其夹角时，我们可以利用余弦定理求出第三边的长度。

此外，余弦定理还可以用于判断三角形的形状（如锐角三角形、直角三角形或钝角三角形）以及求解三角形的内角。

2. 物理学：在力学中，余弦定理被用来求解连接杆件的长度和角度问题。

例如，在机器人学和机械设计中，我们需要确定各个杆件之间的相对位置和角度，以便实现预期的运动轨迹。

余弦定理可以帮助我们解决这个问题。

此外，余弦定理还在许多其他领域中得到应用，如航空航天、土木工程、计算机图形学等。

在这些领域中，余弦定理通常被用来求解与空间几何和三维变换相关的问题。

(完整版)正弦定理和余弦定理典型例题(最新整理)

【答案】根据余弦定理可得：
cos A b2 c2 a2 8 8 4 3 4 3
2bc
22 2 6 2 2
∵ 0 A 180 ， ∴ A 30 ；
∴由正弦定理得： sin C c sin A
6 2 sin 30
6 2
.
a
2
4
【变式 2】在 ABC 中，已知 B 750 ， C 600 ， c 5 ，求 a 、 A .
【答案】 A 1800 (B C) 1800 (750 600 ) 450 ，
根据正弦定理
a
5
，∴ a 5
6
.
sin 45o sin 60o
3
【变式 3】在 ABC 中，已知 sin A : sin B : sin C 1: 2 : 3 ，求 a : b : c 【答案】根据正弦定理 a b c ，得 a : b : c sin A : sin B : sin C 1: 2 : 3 .
【答案】根据三角形内角和定理， C 1800 (A B) 1800 (32.00 81.80) 66.20 ；
根据正弦定理，
b
asin B sin A
42.9sin81.80 sin32.00
80.1(cm)
；
根据正弦定理，
c
asinC sin A
42.9sin 66.20 sin32.00
74.1(cm).
sin A sin B sin C
例 2．在 ABC中，b 3, B 60, c 1，求： a 和 A ， C ．
思路点拨: 先将已知条件表示在示意图形上（如图），可以确定先用正弦定理求出角 C ，然后用三角形内角和求出角 A ，最后用正弦定理求出边 a .

高三数学正弦定理和余弦定理的应用

对一切加以审视和消化。这另一个自我，如同罗曼·罗兰所说，是"一颗清明宁静而非常关切的灵魂 "。仿佛是它把我派遣到人世间活动，鼓励我拼命感受生命的一切欢乐和苦难，同时又始终关切地把我置于它的视野之内，随时准备把我召回它的身边。即使我在世上遭受最悲惨的灾难和失
败，只要我识得返回它的途径，我就不会全军覆没。它是我的守护神，为我守护着一个任何风雨都侵袭不到也损坏不了的家园，使我在最风雨飘摇的日子里也不致无家可归。耶稣说："-个人赚得了整个世界，却丧失了自我，又有何益?"他在向其门徒透露自己的基督身份后说这话，可
实例讲解
想一想
如果对例1的题目进行修改：点A、B都在河的对岸
且不可到达，那又如何求A、B两点间的距离？请同
学们设计一种方法求A、B两点间的距离。（如图）
A
B
分析：象例1一样构造三角形，利
用解三角形求解。

D

C
实例讲解
Hale Waihona Puke 解：测量者可以在河岸边选定两点Ｃ、Ｄ，测的ＣＤ＝a
并且在Ｃ、Ｄ两点分别测得
计算出AC和BC后，再在三角形ABC中，应用余弦定理计算出AB两点间的距离:
想一想
AB AC2 BC2 2AC BCCOS
有其他解法？
思考题:
我舰在敌岛A南偏西 50相距12 海里的B处，发现敌舰正由岛北偏西 10的方向以10海里的速度航行。问我舰需以多
二、应用: 求三角形中的某些元素
解三角形
实例讲解
例1、如下图,设A、B两点在河的两岸，要测量两点之间的距
离。测量者在A的同侧，BAC 51, ACB 75, 在所在的河岸
边选定一点C，测出AC的距离是55 m，求点A、B两点间的

正弦、余弦定理与应用

正弦、余弦定理与应用正弦、余弦定理是解决三角形中各边和角关系的重要工具。

在几何学和三角学中，它们被广泛应用于测量和计算问题。

本文将介绍正弦、余弦定理的概念及其应用，并通过实例展示其有效性。

一、正弦定理正弦定理是解决三角形中边和角之间关系的定理。

对于任意三角形ABC，其三边分别为a、b、c，对应的角度为A、B、C，则正弦定理可以表示为：a/sinA = b/sinB = c/sinC正弦定理的应用可以帮助我们求解未知边或未知角。

例如，给定一个三角形的两边长度和它们之间的夹角，我们可以通过正弦定理计算出第三边的长度。

例如，假设三角形ABC，已知边AB的长度为5，边AC的长度为7，夹角BAC的大小为30°。

应用正弦定理，我们可以得到：5/sin30° = 7/sinBAC通过代入数值并解方程，我们可以求得角BAC的大小。

正弦定理使我们能够通过已知边长和夹角大小来计算其他边长和角度。

二、余弦定理余弦定理是另一个用于三角形中边和角之间关系的定理。

对于任意三角形ABC，其三边分别为a、b、c，对应的角度为A、B、C，则余弦定理可以表示为：c² = a² + b² - 2abcosC通过余弦定理，我们可以计算三角形中的边长或角度。

例如，已知三角形ABC的两边长度分别为3和4，夹角C的大小为60°，我们可以通过余弦定理计算第三边的长度。

应用余弦定理，我们可以得到：c² = 3² + 4² - 2*3*4*cos60°通过计算，我们可以求得第三边的长度c。

余弦定理在解决三角形中边和角关系时非常有用，特别是当仅已知两边和它们之间的夹角时。

三、应用案例正弦、余弦定理广泛应用于测量和计算相关问题。

以下是一些实际应用案例：1. 三角测量：正弦、余弦定理可以用于三角形测量中。

例如，在地理测量中，通过测量三角形的边长和角度可以确定地球上两点之间的距离。

高考数学一轮总复习课件：正、余弦定理应用举例

思考题2 (1)在湖面上高为10 m处测得天空中一朵云
的仰角为30°，测得湖中影子的俯角为45°，则云距湖面的高
度为(精确到0.1 m)( C )
A．2.7 m
B．17.3 m
C．37.3 m
D．373 m
【解析】依题意画出示意图，
则CtaMn3－0°10＝CtaMn4＋5°10， ∴CM＝ttaann4455°°＋－ttaann3300°°×10≈37.3(m)
在△ABC中，根据正弦定理，得sin∠BCBAC＝sin∠ABBCA，即sin330h°＝sin64050°，解得h＝100 6(m)．
题型三测量角度问题
例3 如图所示，A，B是海面上位于东西方向相距5(3＋ 3 ) 海里的两个观测点，现位于A点北偏东45°，B点北偏西60°的 D点有一艘轮船发出求救信号，位于B点南偏西60°且与B点相距20 3 海里的C点的救援船立即前往营救，其航行速度为30 海里/小时，该救援船到达D点需要多长时间？
【解析】在△ABD中，BD＝200 m，∠ABD＝120°. 因为∠ADB＝30°，所以∠DAB＝30°. 由正弦定理，得sin∠BDDAB＝sin∠ADABD，所以sin23000°＝sinA12D0°. 所以AD＝200×sins3in01°20°＝200 3 (m)．
在△ADC中，DC＝300 m，∠ADC＝150°，所以由余弦定理，得AC2＝AD2＋DC2－2AD×DC×cos∠ ADC ＝(200 3)2＋3002－2×200 3×300×cos150°＝390 000，所以AC＝100 39 (m)．故石竹山这条索道AC长为100 39 m.
【思路】依题意画图，某人在C处，AB为塔高，他沿CD前

正弦定理余弦定理的应用举例1

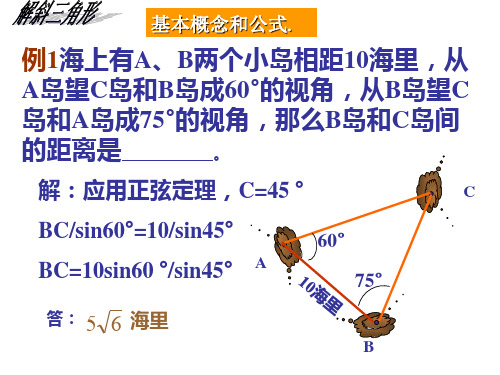
例2、我舰在敌岛A南偏西50°相距12海里B处，
发现敌舰正由岛沿北偏西10°的方向以10海里/时
的速度航行，我舰要用2小时追上敌舰，则需要
的速度大小为
。
C
分析：2小时敌舰航行距离AC=20，由AB=12，∠BAC=120°，
余弦定理可解我舰航行距离 BC。
10 ° A 50 °
B
南
基础知识复习
1、正弦定理 a b c 2R sin A sin B sin C (其中R为外接圆的半径)
注：阅读教材P12，了解基线的概念
练习1.一艘船以32.2n mile / hr的速度向正北航行。在A处看灯塔S在船的北偏东20o的方向，30min后航行到B处，在B处看灯塔在船的北偏东65o的方向，已知距离此灯塔 6.5n mile 以外的海区为航行安全区域，这艘船可以继续沿正北方向航行吗？
BC
ABsin A sin C
5sin15 sin10
7.4524(km).
CD=BC×tan∠DBC≈BC×tan8°≈1047(m)
答：山的高度约为1047米。
变式：某人在M汽车站的北偏西200的方向上的A处，观察到点C处有一辆汽车沿公路向M站行驶。公路的走向是M站的北偏东400。开始时，汽车到A的距离为31千米，汽车前进20千米后，到A的距离缩短了10千米。问汽车还需行驶多远，才能到达M汽车站？
=a/sin(α+β)
A
β
B
αa
C
解三角形的应用---实地测量举例
例3、如何测定河对岸两点A、B
间的距离？如图在河这边取一点，构造三角形ABC，能否求出AB? 为什么？？
B
A C

正弦余弦定理应用举例课件

例2
如图，为了测量河对岸 A、B两点间
B
A 3 的距离，在河的这边测定CD 千米， 2 ADB CDB 30，ACD 60，
ACB 45，求AB 两点的距离 .
解法1： 1. 在△BDC中求BD
D
30° 30°
45° 60°
C
解法2：
2. 在△ABD中求AB
1. 在△BDC中求BC
答：A、B两点间的距离为65.7米。
解三角形的应用---实地测量举例
为了测定河对岸两点A、B间的距离。
在岸边选定基线CD.
B D
A
C
例2、A、B两点都在河的对岸（不可到达），设计一种测量两点间的距离的方法。
分析：用例1的方法，可以计算出河的这一岸的一点C到对岸两点的距离，再测出∠BCA的大小，借助于余弦定理可以计算出A、B两点间的距离。
解 : 在 △ ABC 中 , ∠ ABC= 30°,∠ACB =135°， ∴∠CAB =180－(∠ACB+∠ABC) =180°－(135°+30°)=15° 又BC=32,
BC AC 由正弦定理 , sin BAC sin ABC
BC sin ABC 32sin 30 16 得 AC sin BAC sin15 sin15
4.还原。
解应用题中的几个角的概念
1、仰角、俯角的概念：在测量时，视线与水平线所成的角中，视线在水平线上方的角叫仰角，在水平线下方的角叫做俯角。如图：
2、方向角：指北或指南方向线与目标方向线所成的小于90°的水平角，叫方向角，如图
例题3：在山顶铁塔上B 处测得地面上一点 A 的俯角 60 ，在塔底 C 处测得点 A 的俯角 45 ，已知铁塔BC 部分高 32 米，求山高CD 。