812.中位线及其应用-奥数精讲与测试8年级

合集下载

人教版八年级数学下册三角形的中位线练习题含答案.pdf

17 △AEM ≌△FBM 得 ME=MB ，同理得 NE=NC ，于是 MN 是△EBC 的中位线。所以 MN ∥BC。
18 证明；连接 BD, ∵E,F,G,H 分别是 AB,BC,CD,DA 的中点
EH 平行且等于 BD/2 ，FD 平行且等于 BD/2 ∴EH 平行且等于 FD ∴四边形 EFGH 是平行四边形。
7/7
6/7
26 证明：连接 AC ，取 AC 的中点 M，连接 ME 、MF ∵M 是 AC 的中点， E 是 DC 的中点 ∴ME 是△ ACD 的中位线 ∴ME ＝ AD/2,PE ∥AH ∴∠ MEF ＝∠ AHF （同位角相等）同理可证： MF ＝BC/2, ∠MFE ＝∠ BGF （内错角相等） ∵AD ＝ BC ∴ME ＝ MF ∴∠ MFE ＝∠ MEF ∴∠ AHF ＝∠ BGF
26．已知：如图，在四边形 ABCD 中， AD＝BC， E、F 分别是 DC、 AB 边的中点， FE 的延长线分别与 AD、 BC 的延长线交于 H 、 G 点．求证：∠ AHF ＝∠ BGF ．
4/7
答案： 1 两边中点。 2 平行，第三边的一半。 3 3。 4 中线，中位线。 5 8，5;互相平分。 6 4。 7 7。 8 6.5。 9 B 。 10 D. 11D .12C .13A. 14∵ AE ＝ BE
A，B 间的距离，但绳子不够长，一位
1/7
同学帮他想了一个主意：先在地上取一个可以直接到达
A，B 的点 C，找到 AC，BC的中点 D，E，并且测出 DE
的长为 10m，则 A， B 间的距离为（）
A ． 15m B ． 25m C ． 30m D ． 20m
11．已知△ ABC的周长为 1，连结△ ABC的三边中点构成第二个三角形， ?再连结第二个三角形的三边中点构成第

三角形的中位线专题复习八年级数学下学期重难点及章节分类精品讲义原卷版

第7讲三角形的中位线专题探究类型一三角形中位线定理知识点睛：三角形中位线定理的应用（1）证明平行问题;（2）证明一边是另一边的2倍或（3）解决"中点问题".注意∶在处理这些问题时，要求出现三角形及其中位线：①有中点连线而无三角形，要作辅助线产生三角形;②有三角形而无中位线，要作中点的连线或过中点作平行线.类题训练1．（2021春•罗湖区校级期末）如图，△ABC的面积是16，点D、E、F、G分别是BC、AD、BE、CE的中点，则△AFG的面积是（）A．6B．7C．8D．92．（2021秋•寿光市期末）如图，DE是△ABC的中位线，∠ABC的角平分线交DE于点F，AB＝8，BC＝12，则EF的长为（）A．1B．1.5C．2D．2.5第1题第2题第3题第4题3．（2021秋•海阳市期末）如图，△ABC中，点D，E在边BC上，∠ABC的平分线垂直AE，垂足为点N，∠ACB的平分线垂直AD，垂足为点M，连接MN．若BC＝7，MN＝，则△ABC的周长为（）A．17B．18C．19D．204．（2018春•江干区期末）如图，△ABC中，D是BC边的中点，AE平分∠BAC，BE⊥AE 于E，已知AB＝10，AC＝18，则DE的长为（）A．4B．5C．6D．7 5．（2021•吴兴区二模）如图，在△ABC中，点D、E、F分别是各边的中点，若△ABC的面积为4cm2，则△DEF的面积是（）cm2．A．0.5B．1C．2D．46．（2021秋•广饶县期末）如图，AD是△ABC的中线，E是AD的中点，F是BE延长线与AC的交点，若AC＝4，则AF＝（）A．B．C．1D．7．（2021秋•龙口市期末）如图，△ABC的周长为a，以它的各边的中点为顶点作△A1B1C1，再以△AB1C1各边的中点为顶点作△A2B2C2，…如此下去，则△A n B n∁n的周长为（）A．a B．aC．a D．a8．（2021秋•东莞市校级期末）如图，已知△ABC中AB＝AC，AD是∠BAC 的平分线，AE是∠BAC的外角平分线，ED∥AB交AC于点G，下列结论：①AD⊥BC；②AE∥BC；③AE＝AG；④∠DAE＝90°．其中正确结论的个数是（）A．1B．2C．3D．4类型二三角形中位线在四边形中的应用知识点睛：四边形中中位线的构造（1）四边形边上有中点时，取其对角线中点构造三角形中位线;（2）四边形对角线上有中点时，取边的中点构造三角形中位线.此类中位线的构造常出现在等对边四边形或等对角线四边形题目中，用于判断线段关系或由线段引发的角度关系。

2024八年级数学下册专项讲与练专题18.7 三角形的中位线(知识梳理与考点分类讲解)

专题18.7 三角形的中位线（知识梳理与考点分类讲解）【知识点一】三角形的中位线的定义：连接三角形两边中点的线段叫做三角形的中位线.特别提醒：1.三角形有三条中位线.2.不要把三角形的中位线与三角形的中线混淆，应从它们的定义加以区别.【知识点二】三角形中位线定理三角形的中位线平行于第三边，并且等于第三边的一半.特别提醒：三角形的三条中位线把原三角形分成四个全等的小三角形，每个小三角形的周长为原三角形周长的一半，每个小三角形的面积为原三角形面积的四分之一.【考点目录】【考点1】利用三角形中位线求值；【考点2】利用三角形中位线证明；【考点3】利用三角形的中位线求值与证明；【考点4】三角形的中位线综合应用；（2）:PE PB 的值？【答案】（1）:AP PD 的值为1；；（2）1:3PE PB =:．【分析】本题主要考查了全等三角形的性质与判定，三角形中位线定理．（1）如图所示，取BE 中点G ，连接DG ，则DG 是BCE V 的中位线，即可证明12DG CE =，DG CE ∥，进而推出32DG AE =，再证明DGP AEP △≌△，即可求解；（2）由DGP AEP △≌△，推出EP PG =，再根据点G 是BE 中点，据此求解即可．（1）解：如图所示，取BE 中点G ，连接DG ，∵AD 是BC 边上的中线，即D 是BC 的中点，∴DG 是BCE V 的中位线，∴12DG CE =，DG CE ∥，∵:1:2AE EC =，∴DG AE =，∵DG AE ∥，∴DGP AEP Ð=Ð，GDP EAP Ð=Ð，∴DGP AEP △≌△，∴AP PD =，∴:AP PD 的值为1；（2）解：∵DGP AEP △≌△，∴EP PG =，∵点G 是BE 中点，∴1:3PE PB =:．【变式1】（2023·广东肇庆·统考三模）如图，ABCD Y 中，3AB =，BE 平分ABC Ð，交AD 于点E ，2DE =，点F ，G 分别是BE 和CE 的中点，则FG 的长为（）A ．3B ．2.5C ．2D ．5【答案】B【分析】首先根据平行四边形的性质可得AD BC ∥，AD BC =，再结合角平分线的定义和平行线的性质证明ABE V 为等腰三角形，易得3AB AE ==，进而可得5AD BC ==，然后结合点F ，G 分别是BE 和CE 的中点，易得FG 是BEC V 的中位线，结合三角形中位线的性质即可获得答案．解：∵四边形ABCD 是平行四边形，∴AD BC ∥，AD BC =，∴AEB EBC Ð=Ð，∵BE 平分ABC Ð，∴ABE EBC Ð=Ð，∴AEB ABE Ð=Ð，∴3AB AE ==，∴325AD BC AE ED ==+=+=，∵点F ，G 分别是BE 和CE 的中点，∴FG 是BEC V 的中位线，∴12.52FG BC ==．故选：B ．【点拨】本题主要考查了平行四边形的性质、三角形中位线的性质、等腰三角形的判定与性质、角平分线的定义、平行线的性质等知识，熟练掌握平行四边形的性质和三角形中位线的性质是解题关键．【变式2】（2023上·重庆渝中·八年级重庆巴蜀中学校考期末）如图，在平行四边形ABCD 中，AD =E 、F 分别为边BC 、CD 的中点，连接EF 、AE 、BD ，当AE 平分BEF Ð时，BD 的长为．【答案】【分析】本题考查了平行四边形的性质，角平分线的定义，等腰三角形的判定，三角形中位线定理．由三角形的中位线定理可得EF BD ∥，12BE BC ==AD DO ==BE BO ==，即可求解．解：如图，设AE 与BD 的交点为O ，AE Q 平分BEF Ð，AEF AEB \Ð=Ð，∵AD BC ∥，AEB DAE \Ð=Ð，E Q 、F 分别为边BC 、CD 的中点，∴EF BD ∥，12BE BC ==，BOE AEF \Ð=Ð，AOD AEF Ð=Ð，DAE AOD BEO BOE \Ð=Ð=Ð=Ð，AD DO \==，BE BO ==，DB \=故答案为：．【考点2】利用三角形的中位线证明；【例2】（2024下·江西宜春·九年级江西省丰城中学校考开学考试）如图，DE 是ABC V 的中位线，延长CB 至点F ，使12BF BC =，连接BE ，DF ．（1）求证：四边形BEDF 是平行四边形．（2）若12DF AC =，试判断ABC V 的形状，并说明理由．【答案】（1）见分析；（2）ABC V 为直角三角形，理由见分析【分析】（1）根据三角形中位线定理可得DE BC ∥，12DE BC =，求出DE BF =，根据平行四边形的判定可得结论；（2）根据平行四边形的性质和三角形中位线定理求出AE EC BE ==，可得EAB EBA Ð=Ð，ECB EBC Ð=Ð，然后利用三角形内角和定理求出90EBA EBC Ð+Ð=°即可．解：（1）证明：DE Q 是ABC V 的中位线，\DE BC ∥，12DE BC =，12BF BC =Q ，DE BF \=，\四边形BEDF 是平行四边形；（2）解：ABC V 为直角三角形；理由：Q 四边形BEDF 是平行四边形，DF BE \=，12DF AC =Q ，12BE AC \=，DE Q 是ABC V 的中位线，12AE EC AC \==．AE EC BE \==，∴EAB EBA Ð=Ð，ECB EBC Ð=Ð，∵180EAB EBA ECB EBC Ð+Ð+Ð+Ð=°，∴90EBA EBC Ð+Ð=°，即90ABC Ð=°，ABC \V 为直角三角形．【点拨】本题考查了三角形中位线定理，平行四边形的判定和性质，等边对等角，三角形内角和定理，熟练掌握相关判定定理和性质定理是解题的关键．【变式1】（2023·云南德宏·统考一模）如图，在钝角ABC V 中，点D ，E 分别是边AC BC ，的中点，且DA DE =，那么下列结论错误的是（）A ．12Ð=ÐB ．13Ð=ÐC ．B C Ð=ÐD ．3BÐ=Ð【答案】D【分析】先证明DE 是ABC V 的中位线，DA DC =，则DE AB ∥，31Ð=Ð，B CED Ð=Ð，由DA DE =得到23ÐÐ=，DE DC =，则12Ð=Ð，C CED Ð=Ð，得到B C Ð=Ð，即可作出判断．解：∵点D ，E 分别是边AC BC ，的中点，∴DE 是ABC V 的中位线，DA DC =，∴DE AB ∥，∴31Ð=Ð，B CED Ð=Ð，故B 选项正确；∵DA DE =，∴23ÐÐ=，DE DC =，∴12Ð=Ð，C CED Ð=Ð，∴B C Ð=Ð，故选项A 和C 都正确；无法证明3B Ð=Ð，故D 选项符合题意，故选：D【点拨】此题考查了三角形中位线定理、等边对等角等知识，熟练掌握三角形中位线定理、等边对等角是解题的关键．【变式2】（2023下·重庆南岸·八年级重庆市南坪中学校校联考期中）如图，在ABD △中，C 是BD 上一点，若E 、F 分别是AC 、AB 的中点，DEF V 的面积为6，则ABC V 的面积为．【答案】24【分析】连接CF ，先证明6EFC EFD S S ==V V ，再证明2ACF EFC S S =V V ，2ABC ACF S S =V V 即可解决问题．解：连接CF ．E Q 、F 分别是AC 、AB 的中点，EF BC \∥，6EFC EFD S S \==V V ，AE EC =Q ，212ACF EFC S S \==V V ，AF FB =Q ，224ABC ACF S S \==V V ，故答案为：24．【点拨】本题考查三角形中位线定理，三角形中线的性质，解题的关键是灵活应用三角形中线的性质，三角形的中线把三角形分成面积相等的两部分，属于中考常考题型．【考点3】利用三角形的中位线求值或证明【例3】（2024上·上海静安·八年级上海田家炳中学校考期末）如图，直角ABC V 中，90A Ð=°，2AB AC ==，点D 是BC 边的中点，点E 是AB 边上的一个动点（不与A ，B 重合），DF DE ^交AC 于点F ，设BE x =，FC y =．（1）求证：DE DF =；（2）写出y 关于x 的函数关系式，并写出函数的定义域；（3）写出x 为何值时，EF BC ∥？【答案】（1）见详解；（2）2y x =-，02x <<；（3）1x =【分析】本题考查了全等三角形的判定与性质，三角形中位线的性质，正确证明EDH FDN V V ≌是关键．（1）取AB 的中点记为H ，取AC 的中点记为N ．根据三角形中位线的性质可得DH DN =，根据余角的性质可得EDH FDN Ð=Ð，根据ASA 可证EDH FDN V V ≌，根据全等三角形的性质即可证明DE DF =；（2）根据全等三角形的性质可得HE NF =，从而得到y 关于x 的函数关系式，以及x 的定义域；（3）连接HN ，根据三角形中位线的性质可得x 为1时，EF BC ∥．（1）解：取AB 的中点记为H ，取AC 的中点记为N ．连接DH DN，∵90A Ð=°，点D 是BC 边的中点，∴DH DN ，都是三角形中位线∴DN AB ∥，1122DN AB DH AC DH AC ==P ，，∵2AB AC ==，∴1DH DN ==，∴90NDH Ð=°，∵9090NDF NDE NDE EDH Ð+Ð=°Ð+=°，，∴EDH FDN Ð=Ð，在EDH V 与FDN V 中，EDH FDN DH DNEHD FND Ð=Ðìï=íïÐ=Ðî，∴EDH FDN V V ≌，∴DE DF =；（2）解：∵EDH FDN V V ≌，∴HE NF =，∴1122x AB AC y -=-即2y x=-∵E 是AB 边上的一个动点（不与A 、B 重合），∴02x <<；（3）解：连接HN ，当E 与H 重合时，EF BC ∥，∵此时1x BH ==，∴当1x =时，EF BC ∥．【变式1】（2019·安徽阜阳·校联考一模）如图，AB ＝12，C 是线段AB 上一点，分别以AC 、CB 为边在A 的同侧作等边△ACP 和等边△CBQ ，连接PQ ，则PQ 的最小值是（）A ．3B ．4C ．5D ．6【答案】D【分析】分别延长AP 、BQ 交于点D ，易证四边形CPDQ 为平行四边形，得出PD +DQ ＝PC +CQ ＝AC +BC ＝12，作△ABD 的中位线MN ，则MD ＝DN ＝MN ＝12AB ，运用中位线的性质和等边三角形的性质求出MD ＝DN ＝MN ＝12AB ，进而求得MD +DN ＝PD +DQ ，得出PM ＝QN ，作PE ⊥MN ，QF ⊥MN ，则PE ∥QF ，然后证得△PME ≌△QNF ，从而证得MN ＝EF ，根据平行线间的距离得出PQ ≥EF ，从而求得PQ 的最小值．解：如图，分别延长AP 、BQ 交于点D ，∵∠A ＝∠QCB＝60°，∴AD ∥CQ ，∵∠B ＝CPCA ＝60°，∴BD ∥PC ，∴四边形CPDQ 为平行四边形，∴PD ＝CQ ，PC ＝DQ ，∴PD +DQ ＝PC +CQ ＝AC +BC ＝12，作△ABD 的中位线MN ，则MD ＝DN ＝MN ＝12AB ，∴MD +DN ＝AB ＝12，∴MD +DN ＝PD +DQ ，∴PM ＝QN ，作PE ⊥MN ，QF ⊥MN ，∴PE ∥QF ，∴∠PEM ＝∠QFN ＝90°，且∠PME ＝∠QNF ＝60°，PM ＝QN ∴△PME ≌△QNF （AAS ），∴EM ＝FN ，∴MN ＝EF ，∴PQ ≥EF ，∴C 是线段AB 的中点时，PQ 的值最小，最小值为12AB ＝6．故选D ．【点拨】本题考查了平行四边形的判定和性质、三角形全等的判定和性质、三角形中位线定理及等边三角形的性质，解答本题的关键是作出辅助线，得到PQ ≥EF ，综合性较强．【变式2】（2022上·山东临沂·八年级校考阶段练习）如图，ABC V 为等边三角形，边长为4，点O 为BC 的中点，120EOF Ð=°，其两边分别交AB 和CA 的延长线于E F 、，则AE AF -= ．【答案】6【分析】过点O 作OD AB ∥，设OF 与AB 交于点H ，证明ODF OBE V V ≌，由全等三角形的性质可得DF BE =，结合,AD AF DF AB BE AE +=+=，可知AE AF AB AD -=+，即可获得答案．解：∵ABC V 是等边三角形，边长为4，∴60CAB CBA Ð=Ð=°，4AC AB BC ===，如图，过点O 作OD AB ∥，设OF 与AB 交于点H ，∴60CDO CAB Ð=Ð=°，∴120ODF OBF BAF Ð=Ð=Ð=°，又∵120EOF Ð=°，OHE AHF Ð=Ð，∴E F Ð=Ð，又∵点O 为BC 的中点，且OD AB ∥，∴OD 是ABC V 的中位线，∴1112,2,2222OD AB OB BC AD AC ======，在ODF △和OBE △中，1202F E ODF OBE OD OB Ð=ÐìïÐ=Ð=°íï==î，∴(AAS)ODF OBE V V ≌，∴DF BE =，又∵,AD AF DF AB BE AE +=+=，∴()()AE AF AB BE DF AD -=+--()()AB BE BE AD =+--AB AD=+42=+6=．故答案为：6．【点拨】本题主要考查了平行线的性质、等边三角形的性质、三角形中位线的性质、全等三角形的判定与性质、三角形内角和定理等知识，熟练掌握相关知识并灵活运用、正确作出辅助线构建全等三角形是解题关键．【考点4】三角形的中位线的综合应用【例4】（2023下·河南三门峡·八年级统考期末）（1）回归课本请用文字语言表述三角形的中位线定理：________________．（2）回顾证法证明三角形中位线定理的方法很多，但多数都要通过添加辅助线构图完成．下面是其中一种辅助线的添加方法．请结合图2，补全求证及证明过程．已知：在ABC V 中，点,D E 分别是,AB AC 的中点．求证：________________．证明：过点C 作CF AB ∥，与DE 的延长线交于点F ．（3）实践应用如图3，点B 和点C 被池塘隔开，在BC 外选一点A ，连接,AB AC ，分别取,AB AC 的中点,D E ，测得DE 的长度为9米，则,B C 两点间的距离为________________．【答案】（1）三角形的中位线平行于三角形的第三边，并且等于第三边的一半；（2）DE BC ∥，12DE BC =；详见分析；（3）18米【分析】（1）根据三角形的中位线定理直接阐述即可；（2）过点C 作CF AB ∥，与DE 的延长线交于点F ，证明ADE CFE △△≌，再证四边形DBCF 是平行四边形，即可证明结论；（3）直接利用三角形中位线定理求解即可．解：（1）三角形的中位线平行于三角形的第三边，并且等于第三边的一半．故答案为：三角形的中位线平行于三角形的第三边，并且等于第三边的一半；（2）求证：DE BC ∥，12DE BC =．证明：∵点,D E 分别是,AB AC 的中点，∴BD AD =，=AE CE ，过点C 作CF AB ∥，与DE 的延长线交于点F ．∴ADE F Ð=Ð，在ADE V 和CFE V 中，ADE F AED CEFAE CE Ð=ÐìïÐ=Ðíï=îADE CFE \≌△△．AD CF \=，12DE EF DF ==．CF BD \∥，CF BD =．\四边形DBCF 是平行四边形，∥DF BC \，DF BC =，又12DE DF =Q ，\DE BC ∥，12DE BC =．故答案为：DE BC ∥，12DE BC =；（3）∵点,D E 分别是,AB AC 的中点，9DE =米，∴12DE BC =，即：218BC DE ==米故答案为：18米．【点拨】本题考查了三角形中位线定理，平行四边形的判定和性质，解题的关键是理解题意，学会添加常用辅助线，构造特殊四边形解决问题．【变式1】（2023下·广东珠海·八年级珠海市前山中学校考期中）如图，ABC V 的周长是2，以它的三边中点为顶点组成第1个三角形111A B C △，再以111A B C △的三边中点为顶点，组成第2个三角形222A B C △，…，则第n 个三角形的周长为（）A ．112n -B ．12n C ．222n -D ．112n +【答案】A【分析】根据三角形的中位线定理建立周长之间的关系，即可得到答案．解：Q ABC V 的周长是2，以它的三边中点为顶点组成第1个三角形111A B C △，\1112A B BC =，1112A C AC =，1112BC AB =，\111A B C △的周长为()1111111112122A B A C B C BC AC AB ++=++=´=，\222A B C △的周长为211222´=，…以此类推，第n 个三角形的周长为111222n n -´=，故选：A ．【点拨】本题考查了找规律-图形的变化类，三角形的中位线定理，熟练掌握三角形的中位线等于第三边的一半是解题的关键．【变式2】（2022下·河北唐山·八年级统考期中）如图，为测量位于一水塘旁的两点A ，B 间的距离，在地面上确定点O ，分别取OA ，OB 的中点C ，D ，量得CD ＝10m ，则A ，B 之间的距离是．【答案】20m【分析】根据三角形的中位线定理即可进行解答．解：∵C 、D 分别为AO 、BO 中点，∴CD=12∵CD＝10m，∴AB=20m，故答案为：20m．【点拨】本题主要考查了三角形的中位线定理，熟练掌握“三角形的中位线平行于第三边并且等于第三边的一半” 是解题的关键．。

八年级数学奥术三级第三跳解题方法第五讲中位线及其应用试题

第五讲：中位线及其应用制卷人：歐陽文化、歐陽理複；制卷時間：二O二二年二月七日【知识梳理】1、三角形中位线平行于第三边，并且等于第三边的一半。

梯形中位线平行于两底，并且等于两底和的一半。

2、中位线性质定理的结论，兼有位置和大小关系，可以用它断定平行，计算线段的长度，确定线段的和、差、倍关系。

3、运用中位线性质的关键是从出现的线段中点，找到三角形或者梯形，包括作出辅助线。

4、中位线性质定理，常与它的逆定理结合起来用。

它的逆定理就是平行线截比例线段定理及推论，①一组平行线在一直线上截得相等线段，在其他直线上截得的线段也相等②经过三角形一边中点而平行于另一边的直线，必平分第三边③经过梯形一腰中点而平行于两底的直线，必平分另一腰5、有关线段中点的其他定理还有：①直角三角形斜边中线等于斜边的一半②等腰三角形底边中线和底上的高，顶角平分线互相重合③对角线互相平分的四边形是平行四边形④线段中垂线上的点到线段两端的间隔相等因此如何发挥中点作用必须全面考虑。

【例题精讲】【例1】△ABC中，D是AB上一点，AD=AC，AE⊥CD于E，F是BC的中点，试说明BD=2EF。

【稳固】在△ABC 中，∠B =2∠C ，AD ⊥BC 于D ，M 为BC 的中点. 求证：12DM AB【例2】E 、F 、G 、H 是四边形ABCD 各边的中点那么①四边形EFGH 是__________形②当AC ＝BD 时，四边形EFGH 是__________形 ③当AC ⊥BD 时，四边形EFGH 是__________形 ④当AC 和BD __________时，四边形EFGH 是正方形。

【稳固】如图，等腰梯形ABCD 中，AD ∥BC ，M 、N 分别是AD 、BC 的中点，E 、F 分别是BM 、CM 的中点。

〔1〕求证：四边形MENF 是菱形；ABDB〔2〕假设四边形MENF 是正方形，请探究等腰梯形ABCD 的高和底边BC 的数量关系，并证明你的结论。

巧用三角形中位线试题-八年级数学下册专题讲练突破

巧用三角形中位线1. 三角形中位线定义连结三角形两边中点的线段叫中位线。

注意：（1）要把三角形的中位线与三角形的中线区分开。

（2）三角形有三条中位线。

2. 定理三角形的中位线平行于第三边,并且等于第三边的一半。

如果EF 为△ABC 的中位线，则EF ∥BC 且EF=12BC 。

注意：位置关系——平行数量关系——等于第三边的一半3. 三角形中位线定理的应用：（1）证明角相等关系；（2）证明线段的倍分以及相等关系；（3）证明线段平行关系。

例题1 如图，自△ABC 的顶点A ，向∠B 和∠C 的平分线作垂线，垂足分别为D 、E 。

求证：DE ∥BC 。

解析：欲证ED//BC我们可想到有关平行的判定，但要找到有关角的关系很难，这时只要通过延长AD、AE，交BC与CB的延长线于G与H，通过证明三线合一易证D是AG的中点，同理E为AH的中点，故，ED是△AHG的中位线，当然有DE∥BC。

答案：证明：延长AD、AE交BC、CB的延长线于G、H，∵BD平分∠ABC，∴∠1=∠2，又∵BD⊥AD，∴∠ADB=∠BDG=90º∴△ABG为等腰三角形∴AD=DG，同理可证，AE=GE，∴D，E分别为AG，AH的中点，∴ED∥BC点拨：本题巧妙地应用了等腰三角形的三线合一，但最终还是利用中位线的性质得出结论。

例题2 如图，已知平行四边形ABCD中，BD为对角线，点E、F分别是AB、BC的中点，连结EF，交BD于M点。

求证：（1）BM=14BD；（2）ME=MF。

解析：（1）由E、F分别为AB、BC的中点想到连结AC，由平行线等分线段定理可证得BM=MO。

又因为平行四边形的对角线互相平分，可得BO=OD，即BM=14BD。

（2）由问题(1)中的辅助线，即连结AC，由三角形中位线定理可得11,22EM AO MF OC==，又由平行四边形对角线互相平分即可得到问题（2）的结论。

答案：证明：（1）连结AC，交BD于O点，∵E、F分别为AB、BC中点，∴EF∥AC，∴BM=MO=12BO又∵四边形ABCD是平行四边形∴BO=OD=12BD，AO=OC=12AC，∴BM=12BO=14BD；（2）∵M是BO的中点，E、F分别是AB、BC的中点。

配套K12八年级数学下册专题突破讲练巧用中点解决问题试题 (新版)青岛版

巧用中点解决问题一、中位线定理1. 三角形中位线定义：连接三角形两边中点的线段叫做三角形的中位线。

三角形中边中点的线段，而三角形中位线是连接三角形两边中点的线段。

二、直角三角形斜边中线如果一个三角形是直角三角形，那么这个三角形斜边上的中线等于斜边的一半。

如图，在Rt △ABC 中，∠A CB ＝90°，D 是AB 的中点，求证2ABCD 。

利用矩形性质进行证明。

总结：（1）当图形中有一个中点的时候考虑倍长中线，当图形中有两个中点的时候考虑连接后用中位线；（2）计算中经常使用直角三角形斜边中线等于斜边一半，特别要注意等腰直角三角形。

例题1 如图，M 是△ABC 的边BC 的中点，AN 平分∠BAC，且BN⊥AN，垂足为N ，且AB ＝6，BC ＝10，MN ＝1.5，则△ABC 的周长是（）A. 28B. 32C. 18D. 25解析：延长线段BN 交AC 于E ，从而构造出全等三角形，（△ABN≌△AEN），进而证明MN 是中位线，从而求出CE 的长。

答案：延长线段BN 交AC 于E 。

∵AN 平分∠BAC， ∴∠BAN＝∠EAN，AN ＝AN ，∠ANB＝∠ANE＝90°， ∴△ABN≌△AEN，∴A B ＝AE ＝6，BN ＝EN ，又∵M 是△ABC 的边BC 的中点，∴CE＝2MN ＝2×1.5＝3， ∴△ABC 的周长是AB ＋BC ＋AC ＝6＋10＋6＋3＝25，故选D 。

例题2 如图，以边长为1的正方形的四边中点为顶点作四边形，再以所得四边形四边中点为顶点作四边形，…依次作下去，图中所作的第三个四边形的周长为；所作的第n 个四边形的周长为。

解析：根据正方形的性质以及三角形中位线的定理，求出第二个，第三个四边形的周长，从而发现规律，即可求出第n 个四边形的周长。

答案：根据三角形中位线定理得，第二个四边形的边长为22)21()21( ＝21，周长为22，第三个四边形的周长为4×2(2＝2，第n 个四边形的周长为4·（22）n −1，故答案为2，4·（22）n −1。

三角形中位线讲义2023-2024学年北师大版八年级数学下册

三角形中位线讲义【要点梳理】要点一、三角形的中位线1．定义：连接三角形两边中点的线段叫做三角形的中位线.2．定理：三角形的中位线平行于三角形的第三边，且等于第三边的一半.特别说明：（1）三角形有三条中位线，每一条与第三边都有相应的位置关系与数量关系.（2）三角形的三条中位线把原三角形分成可重合的4个小三角形.因而每个小三角形的周长为原三角形周长的，每个小三角形的面积为原三角形面积的. （3）三角形的中位线不同于三角形的中线.要点二、中点三角形定义：中点三角形就是把一个三角形的三边中点顺次连接起来的一个新三角形.性质：（1）这个新三角形的各个边长分别是原来三角形三边长的一半且分别平行，角的度数与原三角形分别相等，4个三角形都全等（2）中点三角形周长是原三角形的周长一半。

（3）中点三角形面积是原三角形面积的四分之一。

补充：中点三角形与原三角形不仅相似，而且位似。

要点三、中点四边形定义：依次连接任意四边形各边中点所得的四边形称为中点四边形。

中点四边形的形状与原四边形的对角线的数量和位置关系有关。

性质（1）不管原四边形的形状怎样改变，中点四边形的形状始终是平行四边形。

题型一：与三角形中位线有关的线段求解问题【例1】如图，ABCD 中，对角线AC 、BD 相交于点O ，点 E ， F ，G ，H 分别是OA 、OB 、OC 、OD 的中点，顺次连接EFGH ．（1）求证：四边形EFGH 是平行四边形（2）若ABCD 的周长为2（AB +BC ）=32，则四边形EFGH 的周长为__________【解答】（1）证明：∵四边形ABCD 是平行四边形，∴OA =OC ，OB =OD ， ∵点 E 、 F 、G 、H 分别是OA 、OB 、OC 、OD 的中点，∴1111,,,2222OE OA OF OB OG OC OH OD ====， ∴OE =OG ，OF =OH ，1214∴四边形EFGH 是平行四边形；（2）∵点 E 、 F 、G 、H 分别是OA 、OB 、OC 、OD 的中点， ∴11,22EF AB FG BC ==， ∴()12EF FG AB BC +=+ ， ∵ABCD 的周长为2（AB +BC ）=32，∴16AB BC += ，∴8EF FG += ，由（1）知：四边形EFGH 是平行四边形， ∴四边形EFGH 的周长为()22816EF FG +=⨯= ．【变式1-1】如图，在△ABC 中，AB ＝AC ，AD ⊥BC 于点D ．（1）若DE ∥AB 交AC 于点E ，证明：△ADE 是等腰三角形；（2）若BC ＝12，DE ＝5，且E 为AC 中点，求AD 的值．【解答】（1）证明：∵在△ABC 中，AB ＝AC ，∴△ABC 为等腰三角形，∵AD ⊥BC 于点D ，∴由“三线合一”知：∠BAD=∠CAD ，∵DE ∥AB 交AC 于点E ，∴∠BAD=∠ADE ，∴∠CAD=∠ADE ，即：∠ADE=∠EAD ，∴AE=DE ，∴△ADE 是等腰三角形；（2）解：由“三线合一”知：BD=CD ，∵BC=12，∴DC=6，∵E 为AC 中点，∴DE 为△ABC 的中位线，∴AB=2DE ，∴AC=AB=2DE=10，在Rt △ADC 中，22221068AD AC DC =−−=，∴AD=8．【变式1-2】如图，四边形ABCD 中，∠A ＝90°，AB ＝12，AD ＝5，点M 、N 分别为线段BC 、AB 上的动点（含端点，但点M 不与点B 重合），点E 、F 分别为DM 、MN 的中点，则EF 长度的可能为（）A ．2B ．5C ．7D ．9 【解答】解：连接DN ，∵ED ＝EM ，MF ＝FN ，∴EF =12DN ，∴DN 最大时，EF 最大，DN 最小时，EF 最小，∵N 与B 重合时DN 最大，此时DN ＝DB =√AD 2+BD 2=√52+122=13，∴EF 的最大值为6.5．∵∠A ＝90°，AD ＝5，∴DN ≥5，∴EF ≥2.5，∴EF 长度的可能为5；故选：B ．【变式1-3】如图，在△ABC 中，AB ＝CB ＝6，BD ⊥AC 于点D ，F 在BC 上且BF ＝2，连接AF ，E 为AF 的中点，连接DE ，则DE 的长为（）A ．1B ．2C ．3D ．4【解答】解：∵CB ＝6，BF ＝2，∴FC ＝6﹣2＝4，∵BA ＝BC ，BD ⊥AC ，∴AD ＝DC ，∵AE ＝EF ，∴DE 是△AFC 的中位线，∴DE =12FC =12×4＝2，故选：B ．题型二、与三角形中位线有关的面积问题【例2】如图，在ABC 中，D ，E 分别为AB ，AC 的中点，延长BC 至点F ，使12CF BC =，连接CD 和EF ．（1）求证：四边形DCFE 是平行四边形．（2）若四边形DCFE 的面积为4，求ABC 的面积．【解答】()1证明：∵D ，E 分别为AB ，AC 的中点，∴DE 为ABC 的中位线，∴//DE BC ，12DE BC =． ∵12CF BC =，∴DE CF =．∵//DE CF ， ∴四边形DCFE 是平行四边形； ()2解：∵四边形DCFE 是平行四边形，∴DEC 的面积ECF =的面积2=．∵E 是AC 的中点，∴ADE 的面积DEC =的面积2=．∵D 是AB 的中点，∴BDC 的面积ADC =的面积4=，∴ABC 的面积4228=++=．【变式2-1】如图1，在四边形ABCD 中，E 、F 、G 、H 分别是AD 、BC 、BD 、AC 的中点．（1）求证：四边形EGFH 是平行四边形；（2）如图2，延长BA 、CD 相交于点P ，连接PG 、PH 、GH ，若1PGH S =△，求四边形ABCD 的面积．【解答】证明：（1）,E G 分别是,AD BD 的中点，1,//2EG AB EG AB ∴=，同理可得：1,//2FH AB FH AB =， ,//EG FH EG FH ∴=，∴四边形EGFH 是平行四边形；（2）如图，连接,,,PE AG BH DH ，,E G 分别是,AD BD 的中点，//EG AB ∴，AEG PEG S S ∴=（同底等高），同理可得：DEH PEH S S =，1AEG EGH DEH PEG EGH PEH PGH AGHD S S S S S S S S ∴=++=++==四边形，又G 是BD 的中点，BG DG ∴=，,ABG ADG HBG HDG SS S S ∴==（等底同高）， 2()22ABG ADG HBG HDG ADG HDG ABHD AGHD S S S S S S S S ∴=+++=+==四边形四边形，同理可得：2224ABCD ABHD S S ==⨯=四边形四边形，即四边形ABCD 的面积为4．【变式2-2】如图所示，在△ABC 中，D 是BC 边上任一点，F,G,E 分别是AD,BF,CF 的中点，连结GE ，若△FGE 的面积为6,则ABC 的面积为( )A.32B.48C.64D.72【变式2-3】如图，已知在△ABC 中，点D 、E 分别是边AB 、AC 的中点。

八年级数学下册 2.4 三角形的中位线三角形中位线定理的应用素材1 (新版)湘教版

三角形中位线定理的应用三角形的中位线定理是几何中一个重要定理，它不仅反映了图形间线段的位置关系，而且还揭示了线段间的数量关系，利用三角形中位线定理可以解决许多相关的问题.一、借助中位线定理选择结论例1如图1，已知四边形ABCD 中，R 、P 分别是BC 、CD 上的点，E 、F 分别是AP 、RP 的中点，当点P 在CD 上从C 向D 移动而点R 不动时，那么下列结论成立的是（）.（A ）线段EF 的长逐渐增大（B ）线段EF 的长逐渐减小（C ）线段EF 的长不变（D ）线段EF 的长与点P 的位置有关分析：由E ，F 分别为AP ，RP 的中点，由此可联想三角形的中位线，故连接AR ，由于已知条件可知EF 为ARP 的中位线，根据中位线定理可知EF=21AR ，由于点P 从点C 到点D 移动的移动过程中，AR 始终不变，∴EF 的长度也不变. 解：连接AR ，∵E ，F 分别是PA ，PR 的中点，∴EF=21AB ， ∵AR 不变，∴线段EF 的长不变.故选（C ）.点评：本题通过巧妙地连接AR ，把问题转化为三角形中位线问题，借助于中位线的性质俩来解决.二、借助中位线定理求长度例2某花木场有一块如四边形ABCD 的空地（如图2），两对角线相等，各边的中点分别是E 、F 、G 、H ，用篱笆围成的四边形EFGH 场地的周长为40cm ，则对角线AC= cm分析：根据E 、F 分别为BA ，BC 的中点，可知EF 为△ABC 的中位线，根据中位线定理可得EF=21AC ，同理可得HG=21AC ，HE=21BD ，FG=21BD ，根据两对角线相等可得EF=FG=GH=HE ，由此可求到EF 的长，也就求到AC 的长.解：∵E ，F 分别是BA ，BC 的中点，∴EF=21AC ，同理可得HG=21AC ， ∵E ，H 分别是AB ，AD 的中点，∴EH=21BD ，同理可得FG=21BD ， ∵AC=BD ，∴EF=FG=GH=HE ，∵EF+FG+GH+HE=40cm ，∴EF=10cm ，∴AC=2EF=20cm.点评：根据已知条件的特点，本题是将四边形问题转化为三角形问题，通过多次利用三角形中位线的性质，确定EF 的长，进而求到AC 的长.三、借助中位线定理说理例3 如图3，在△ABC 中，BC>AC ，点D 在BC 上，且DC ＝AC,∠ACB 的平分线CF 交AD 于F ，点E 是AB 的中点，连结EF.说明EF∥CB 理由分析：根据E 为AB 的中点，要说明EF//BC ，可说明EF 为△ABC 的中位线，为此，需要证明F 为AD 的中点.解：∵CF 平分∠ACB，∴∠DCF=∠ACF.又∵DC=AC，∴CF是△ACD的中线，∴ 点F是AD的中点.∵ 点E是AB的中点，∴ EF//BD，即EF∥BC.点评：本题根据点E为AB的中点联想三角形的中位线，打开了证明的思路，在解决类似问题中应注意中位线的应用.。

八年级数学下册24三角形的中位线三角形中位线的性质及应用素材(新版)湘教版

八年级数学下册24三角形的中位线三角形中位线的性质及应用素材（新版）湘教版三角形中位线的性质:三角形的中位线平行于第三边,并且等于第三边的一半。

这一性质说明了三角形中位线与第三边的位置关系——平行，三角形的中位线与第三边之间的长度关系——等于第三边的一半。

运用这一性质可以解决一些与三角形中位线有关的问题。

一、说明线段相等例1：如图1，在△ABC中，BE是中线，AD⊥BC于D，∠CBE=30°，试说明AD=BE。

解：过E作EF⊥BC于F，在Rt△BEF中，因为∠CBE=30°，所以BE=2EF。

又因为BE为中线，所以E为AC的中点。

因为AD⊥BC，EF⊥BC，所以EF∥AD，所以AD=2EF，所以AD=BE。

二、求线段的长度例2、如图2，在△ABC中，M是BC边的中点，AD是∠BAC的平分线，BD⊥AD于D，AB=12，AC=22，求MD的长。

解：延长BD交AC于E，因为BD⊥AD，图1C所以∠ADB=∠ADE=90°。

因为AD是∠BAC的平分线，所以∠BAD=∠EAD。

又因为AD=AD，所以△ABD≌△AED所以AE=AB=12，BD=DE。

所以EC=AC-AE=22-12=10。

因为M是BC边的中点，D是BE的中点，所以MD=EC=5。

三、说明线段倍、分关系例3、如图3，AD是△ABC的中线，E为AD的中点，BE交AC于F，AF=AC,说明EF=BF。

解：取CF的中点G，连结DG，所以DG是△CFB的中位线。

因为AF=AC，所以F为AG 的中点，所以EF=DG，DG=BF，所以EF=BF 。

四、说明三角形的形状例4、如图4，在四边形ABCD中，AD=BC，P是对角线BD的中点，M是边DC的中点，N是边AB的中点，△MPN是什么三角形？为什么？解：因为，P是对角线BD的中点，M是边DC的中点，N是边AB的中点，所以MP=BC，PN=AD，因为AD=BC，G图3AB CDFEDABCPMN图4所以MP= PN所以△MPN 是等腰三角形。

八年级数学下册三角形的中位线专题训练试题

卜人入州八九几市潮王学校三角形的中位线例题精讲例1如图1，D 、E 、F 分别是△ABC 三边的中点．G 是AE 的中点，BE 与DF 、DG 分别交于P 、QPQ:BE 的值.例2如图2，在△ABC 中，AC>AB ，M 为BC 的中点．AD 是∠BAC 的平分线，假设CF ⊥AD 交AD 的延长线于F .求证：()12MF AC AB =-. 例3如图3，在△ABC 中，AD 是△BAC 的角平分线，M 是BC 的中点，ME ⊥AD 交AC 的延长线于E ．且稳固根底练1.△ABC 周长为16，D 、E 分别是AB 、AC 的中点，那么△ADE 的周长等于()A.1B.2C.4D.82.在△ABC 中，D 、E 分别是AB 、AC 的中点，P 是BC 上任意一点，那么△PDE 面积是△ABC '面积的()A.12B.13C.14D.18 3.如图4，在四边形ABCD 中，E 、F 分别为AC 、BD 的中点，那么EF 与AB +CD 的关系是()A.2EF AB CD =+B.2EF AB CD >+C.2EF AB CD <+D.不确定4.如图5，AB ∥CD ，E 、F 分别是BC 、AD 的中点，且AB=a ,CD=b ，那么EF 的长为.图6图7图8图9图105.如图6，四边形ABCD 中，AD=BC ，F 、E 、G 分别是AB 、CD 、AC 的中点，假设∠DAC=200，∠ACB=600，那么∠FEG=. 6.(中考题)如图7，△ABC 的周长为1，连接△ABC 三边的中点构成第二个三角，再连接第二个三角形三边中点构成第三个三角形，依此类推，第2021个三角形的周长为.7.三角形三条中位线的比为3:5:6，三角形的周长是112cm ，求三条中位线长.8.如图8，△ABC 中，AD 是高，BE 是中线，∠EBC=300,求证：AD=BE . 9.如图9，在△ABC 中，AB=AC ，延长AB 到D ，使BD=AB ，E 为AB 中点，连接CE 、CD .求证：CD=2EC .10.如图10，AD 是△ABC 的外角平分线，CD ⊥AD 于D ，E 是BC 的中点.求证：(1)DE ∥AB ;(2)()12DE AB AC =+.1.如图11，M 、P 分别为△ABC 的AB 、AC 上的点，且AM=BM ，AP=2CP ，BP 与CM 相交于N ，PN=1，那么PB 的长为()A.2B.3C.4D.52.如图12，△ABC 中，∠B =2∠C ，AD ⊥BC 于D ，M 为BC 的中点，AB=10，那么MD 的长为()A.10B.8C.6D.53.如图13，△ABC 是等边三角形，D 、E 、F 分别是AB 、BC 、AC 的中点，P 为不同于B 、E 、C 的BC 上的任意一点，△DPHFH ，那么EP 与FH 的大小关系是()A.E P>FHB.EP=FHC.EP<FH4.如图14，在△ABC 中，AD 平分∠BAC ，BD ⊥AD ，DE ∥AC ，交AB 于E ,假设AB=5，那么DE 的长为.5.如图15，△ABC 中，AB=4，AC=7，M 为BC 的中点，AD 平分∠BAC ，过M 作MF ∥AD ，交AC 于F ，那么FC 的长等于.图11图12图13图14图156.在△ABC 中，∠B=600，CD 、AE 分别为AB 、BC 边上的高，DE=5，那么AC 的长为. 7.如图16，在△ABC 中，D 、E 是AB 、AC 上的点，且BD=CE ，M 、N 分别是BE 、CD 的中点，直线MN 分别交AB 、AC 于P 、Q .求证：AP=AQ8.如图17，BE 、CF 是△ABC 的角平分线，AN ⊥BE 于N ，AM ⊥CF 于M .求证：MN ∥BC .9.如图18，在△ABC 中，AD 平分∠BAC ，AD=AB ，CM ⊥AD 于M .求证：AB+AC=2AM10.如图19，四边形ABCD中，G、H分别是AD、BC的中点，AB=CD.BA、CD的延长线交HG的延长线于E、F.求证：∠BEH=∠CFH.图16图17图18图19图201.如图20，在△ABC中，∠ABC=2∠C，AD平分∠BAC，过BC的中点M作ME⊥AD，交BA的延长线于E，交AD的延长线于F.求证：12BE BD.2.如图21，在△ABC中，AB<AC，P为AC上的点，CP=AB，K为AP的中点，M为BC的中点，MK的延长线交BA的长线于N.求证：AN=AK.3.如图22，分别以△ABC的边AC、BC为腰，A、B为直角顶点，作等腰直角△ACE和等腰直角△BCD，M为ED的中点.求证：AM⊥BM.4.如图23，点O是四边形ABCD内一点，∠AOB=∠COD=1200，AO=BO，CO=DO，E、F、G分别为AB、CD、BC的中点.求证：△EFG为等边三角形.5.如图24，△ABC中，M是AB的中点，P是AC的中点，D是MB的中点，N是CD的中点，Q是MN的中点，直线PQ交MB于K.求证：K是DB的中点.6.如图25，P为△ABC内一点，∠PAC=∠PBC，PM⊥AC于M，PN⊥BC于是AB的中点.求证：DM=DN图21图22图23图24图257.如图26，AP是△ABC的角平分线，D、E分别是AB、AC上的点，且BD=CE.又G、H分别为BC、DE的中点.求证：HG∥AP.8.如图27，△ABD和△ACE都是直角三角形，且∠ABD=∠ACE=900，如图(a)，连接DE，设M为DE的中点.(1)求证：MB=MC;(2)设∠BAD=∠CAE，固定△ABD，让Rt△ACE绕顶点A在平面内旋转到图(b)的位置，试问MB=MC是否成立并证明其结论.9.△ABC面积为S，作直线l∥BC，交AB于D，交AC于E，假设△BED的积为K.求证：S≥4K.。

八年级奥数精讲与测试中位线及其应用

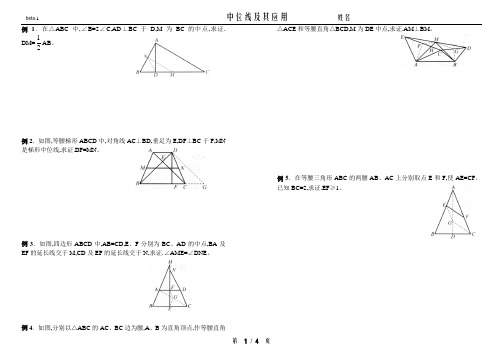
例1．在△ABC中,∠B=2∠C,AD⊥BC于D,M为BC的中点,求证.DM=12 AB。

例2．如图,等腰梯形ABCD中,对角线AC⊥BD,垂足为E,DF⊥BC于F,MN 是梯形中位线,求证.DF=MN。

例3．如图,四边形ABCD中,AB=CD,E、F分别为BC、AD的中点,BA及EF的延长线交于M,CD及EF的延长线交于N,求证.∠AME=∠DNE。

例4．如图,分别以△ABC的AC、BC边为腰,A、B为直角顶点,作等腰直角△ACE和等腰直角△BCD,M为DE中点,求证.AM⊥BM。

例5．在等腰三角形ABC的两腰AB、AC上分别取点E和F,使AE=CF。

已知BC=2,求证.EF≥1。

A卷一、填空题01．如果等腰梯形底角是45°,高等于上底的2倍,那么梯形中位线与高之比为_________。

02．已知梯形两对角线中点连线长5cm,梯形下底长20cm,则上底长为_________。

03．如图128,E是AC的中点,D在边BC上,且CD=2BD,AD与BE相交于F。

已知△BDF的面积是1,那么△ABC的面积是_________。

04．如图129,梯形ABCD的面积是12,则以梯形四边中点为顶点的四边形EFMN的面积是_________。

05．已知梯形ABCD中,AD∥BC,对角线AC把中位线EF(E在AB上)分成1 : 3两部分,则S ADFE:S BCFE=_________。

06．如图130,在梯形ABCD中,AB∥CD,EF是中位线,EF与AC相交于G,且EF=16cm,EG−GF=4cm,则AB的长是_________cm。

07．如图131,已知△ABC中,AB=AC,延长AB至D,使BD=AB,E是AB的中点,CD=4,则CE=_________。

08．如图132,在△ABC中,E、F分别为AB、AC上的点,且BE=CF,M、N分别为BF、CE的中点,过M、N的直线交AB于P,交AC于Q。

【青岛版】八年级数学下册专题讲练：巧用中点解决问题试题(含答案)

巧用中点解决问题一、中位线定理1. 三角形中位线定义：连接三角形两边中点的线段叫做三角形的中位线。

2. 三角形中位线定理：三角形的中位线平行于第三边,且等于第而三角形中位线是连接三角形二、直角三角形斜边中线如果一个三角形是直角三角形,那么这个三角形斜边上的中线等于斜边的一半。

如图,在Rt △ABC 中,∠ACB ＝90°,D 是AB 的中点,求证2AB CD。

利用矩形性质进行证明。

总结：（1）当图形中有一个中点的时候考虑倍长中线,当图形中有两个中点的时候考虑连接后用中位线；（2）计算中经常使用直角三角形斜边中线等于斜边一半,特别要注意等腰直角三角形。

例题1 如图,M 是△ABC 的边BC 的中点,AN 平分∠BAC ,且BN⊥AN ,垂足为N,且AB ＝6,BC ＝10,MN ＝1.5,则△ABC 的周长是（） A. 28 B. 32 C. 18D. 25解析：延长线段BN 交AC 于E,从而构造出全等三角形,（△ABN≌△AEN）,进而证明MN 是中位线,从而求出CE 的长。

答案：延长线段BN 交AC 于E 。

∵AN 平分∠BAC ,∴∠BAN＝∠EAN ,AN ＝AN,∠ANB＝∠ANE＝90°,∴△ABN≌△AEN ,∴A B ＝AE ＝6,BN ＝EN,又∵M 是△ABC 的边BC 的中点,∴CE＝2MN ＝2×1.5＝3,∴△ABC 的周长是AB ＋BC ＋AC ＝6＋10＋6＋3＝25,故选D 。

例题2 如图,以边长为1的正方形的四边中点为顶点作四边形,再以所得四边形四边中点为顶点作四边形,…依次作下去,图中所作的第三个四边形的周长为；所作的第n 个四边形的周长为。

解析：根据正方形的性质以及三角形中位线的定理,求出第二个,第三个四边形的周长,从而发现规律,即可求出第n 个四边形的周长。

答案：根据三角形中位线定理得,第二个四边形的边长为22)21()21( ＝21,周长为22,第三个四边形的周长为4×2(2＝2,第n 个四边形的周长为4·（22）n −1,故答案为2,4·（22）n −1。

人教版八年级数学下册三角形的中位线练习题(含答案)word版本

人教版八年级数学下册三角形的中位线练习题(含答案)三角形的中位线练习题三角形中位线定义： .符号语言：在△ABC 中，D 、E 分别是AB 、AC 的中点, 则：线段DE 是△ABC 的__ __，三不同点：①三角形中位线的两个端点都是三角形边的中点。

②三角形中线只有一个端点是边的中点，另一端点是三角形一个顶点。

相同点：都是一条线段，都有三条。

三角形中位线定理： .符号语言表述：∵DE 是△ABC 的中位线（或AD=BD,AE=CE) ∴DE //21BC练习1．连结三角形___________的线段叫做三角形的中位线． 2．三角形的中位线______于第三边，并且等于_______． 3．一个三角形的中位线有_________条． 4.如图△ABC 中，D 、E 分别是AB 、 AC 的中点，则线段CD 是△ABC 的＿＿＿，线段DE 是△ABC ＿＿＿＿＿＿＿5、如图，D 、E 、F 分别是△ABC 各边的中点（1）如果EF ＝4cm ，那么BC ＝＿＿cm 如果AB ＝10cm ，那么DF ＝＿＿＿cmEDBED（2）中线AD 与中位线EF 的关系是＿＿＿6．如图1所示，EF 是△ABC 的中位线，若BC=8cm ，则EF=_______cm ．(1) (2) (3) (4)7．三角形的三边长分别是3cm ，5cm ，6cm ，则连结三边中点所围成的三角形的周长是_________cm ．8．在Rt △ABC 中，∠C=90°，AC=•5，•BC=•12，•则连结两条直角边中点的线段长为_______． 9．若三角形的三条中位线长分别为2cm ，3cm ，4cm ，则原三角形的周长为（） A ．4.5cm B ．18cm C ．9cm D ．36cm10．如图2所示，A ，B 两点分别位于一个池塘的两端，小聪想用绳子测量A ，B 间的距离，但绳子不够长，一位同学帮他想了一个主意：先在地上取一个可以直接到达A ，B 的点C ，找到AC ，BC 的中点D ，E ，并且测出DE 的长为10m ，则A ，B 间的距离为（） A ．15m B ．25m C ．30m D ．20m11．已知△ABC 的周长为1，连结△ABC 的三边中点构成第二个三角形，•再连结第二个三角形的三边中点构成第三个三角形，依此类推，第2010个三角形的周长是（） A 、20081 B 、20091 C 、220081 D 、22009112．如图3所示，已知四边形ABCD ，R ，P 分别是DC ，BC 上的点，E ，F 分别是AP ，RP 的中点，当点P 在BC 上从点B 向点C 移动而点R 不动时，那么下列结论成立的是（） A ．线段EF 的长逐渐增大 B ．线段EF 的长逐渐减少 C ．线段EF 的长不变 D ．线段EF 的长不能确定13．如图4,在△ABC 中，E ，D ，F 分别是AB ，BC ，CA 的中点，AB=6，AC=4，则四边形AEDF•的周长是（）A．10 B．20 C．30 D．4014．如图所示，□ ABCD的对角线AC，BD相交于点O，AE=EB，求证：OE∥BC．15.已知矩形ABCD中，AB=4cm，AD=10cm，点P在边BC上移动，点E、F、G、H分别是AB、AP、DP、DC的中点.求证：EF+GH=5cm；16．如图所示，在△ABC中，点D在BC上且CD=CA，CF平分∠ACB，AE=EB，求证：EF=12 BD．17．如图所示，已知在□ABCD中，E，F分别是AD，BC的中点，求证：MN∥BC．BGA EF H DC图518．已知：如图，四边形ABCD 中，E 、F 、G 、H 分别是AB 、BC 、CD 、DA 的中点．求证：四边形EFGH 是平行四边形．19.如图，点E ，F ，G ，H 分别是CD ，BC ，AB ，DA 的中点。

八年级数学暑假专题三角形的中位线鲁教版知识精讲

八年级数学暑假专题三角形的中位线鲁教版【本讲教育信息】一、教学内容：专题1：三角形的中位线二、知识点1. 三角形中位线的定义。

如图1，连接三角形两边中点的线段叫做三角形的中位线。

ED C BA图12. 三角形中位线定理三角形的中位线平行于第三边，并且等于第三边的一半。

如图1，△ABC 中，DE 是中位线，则有DE ∥BC ，12DE BC =。

3. 三角形中位线定理的证明教材上的证明方法如图2所示，延长DE 到点F ，使EF=DE ，FED CB A图2连接CF ，进一步证明四边形DBCF 是平行四边形。

下面介绍几种其他的证明方法。

（1）运用相似三角形进行证明：在图1中，由于12AD AE AB AC ==，∠A=∠A ，所以△ADE ∽△ABC 。

因此∠ADE=∠B ，所以DE ∥BC ，12DE BC =。

（2）运用同一法进行证明：如图3，过点D 作DF ∥BC ，交AC 于点F ，则有图3∠ADE=∠B ，∠AFD=∠C ，因此△ADF ∽△ABC所以，AD AF DF AB AC BC ==，因为12AD AB =，所以12AF DF AC BC ==，即点F 是AC 的中点，因此点E 与点F 重合。

所以DE 与DF 重合。

因此DE ∥BC ，12DE BC =。

（3）在三角形内部构建平行四边形进行证明如图4，作EF ∥AB ，交BC 于点F ，易得△CEF ∽△CAB 。

CFEDBA图4因为点E 是AC 的中点，所以12CE CF EF CA CB AB ===。

因此点F 是BC 的中点，12EF AB BD ==，又因为EF ∥AB ，图4所以四边形DBFE 是平行四边形。

所以DE ∥BC ，12DE BF BC ==.4. 三角形中位线的判定方法（1）三角形中位线的定义是判定的主要方法。

（2）如图5，运用定理“过三角形一边的中点与另一边平行的直线平分第三边”来判定线段是三角形的中位线.EDCB A图5已知，△ABC 中，点D 是AB 的中点，DE ∥BC ，试说明线段 DE 是△ABC 的中位线。

北师大版初二数学下册《三角形中位线定理》知识讲解及例题演练

北师大版初二数学下册《三角形中位线定理》知识讲解及例题演练【学习目的】1. 了解三角形的中位线的概念，掌握三角形的中位线定理．2. 掌握中点四边形的构成规律.【要点梳理】要点一、三角形的中位线1．衔接三角形两边中点的线段叫做三角形的中位线.2．定理：三角形的中位线平行于第三边，并且等于第三边的一半.要点诠释：〔1〕三角形有三条中位线，每一条与第三边都有相应的位置关系与数量关系.〔2〕三角形的三条中位线把原三角形分红可全等的4个小三角形.因此每个小三角形的周长为原三角形周长的12，每个小三角形的面积为原三角形面积的14. 〔3〕三角形的中位线不同于三角形的中线.要点二、依次衔接恣意四边形各边中点失掉的四边形的外形依次衔接恣意四边形各边中点失掉的四边形是平行四边形.【典型例题】类型一、三角形的中位线1、如图，P 、R 区分是长方形ABCD 的边BC 、CD 上的点，E 、F 区分是PA 、PR 的中点，点P 在BC 上从B 向C 移动，点R 不动，那么以下结论成立的是〔〕A ．线段EF 的长逐渐增大B ．线段EF 的长逐突变小C ．线段EF 的长不变D ．无法确定【答案】C ；【解析】连AR ，由E 、F 区分为PA ，PR 的中点知EF 为△PAR 的中位线, 那么12EF AR ，而AR 长不变，故EF 大小不变.【总结升华】当条件中含有中点的时分，要将它与中位线联络起来，停止联想，必要时添加辅佐线，结构中位线图形．举一反三：【变式】在△ABC 中，中线BE 、CF 交于点O ，M 、N 区分是BO 、CO 中点，那么四边形MNEF 是什么特殊四边形？并说明理由．【答案】5；解：四边形MNEF 是平行四边形．理由如下：∵BE 、CF 是中线，∴E 、F 区分是AC 、AB 的中点，∴EF 是△ABC 的中位线，∴EF ∥BC 且EF=21BC ， ∵M 、N 区分是BO 、CO 中点，∴MN 是△OBC 的中位线，∴MN ∥BC 且MN=21BC ， ∴EF ∥MN 且EF=MN ，∴四边形MNEF 是平行四边形．2、如图，△ABC 中，D 、E 区分是BC 、AC 的中点，BF 平分∠ABC ，交DE 于点F ，假定BC ＝6，那么DF 的长是〔〕A ．2B ．3 C.52D ．4 【思绪点拨】应用中位线定理，失掉DE ∥AB ，依据平行线的性质，可得∠EDC ＝∠ABC ，再应用角平分线的性质和三角形内角外角的关系，失掉DF ＝DB ，进而求出DF 的长．【答案解析】解：在△ABC 中，D 、E 区分是BC 、AC 的中点∴DE ∥AB∴∠EDC ＝∠ABC∵BF 平分∠ABC∴∠EDC ＝2∠FBD在△BDF 中，∠EDC ＝∠FBD ＋∠BFD∴∠DBF ＝∠DFB∴FD ＝BD ＝12BC ＝12×6＝3．【总结升华】三角形的中位线平行于第三边，当出现角平分线，平行线时，普通可结构等腰三角形，进而应用等腰三角形的性质解题．3、如下图，在△ABC 中，M 为BC 的中点，AD 为∠BAC 的平分线，BD ⊥AD 于D ，AB ＝12，AC ＝18，求MD 的长．【思绪点拨】此题中所求线段MD 与线段AB 、AC 之间没有什么联络，但由M 为BC 的中点联想到中位线，另有AD 为角平分线和垂线，依据等腰三角形〝三线合一〞结构等腰三角形ABN ，D 为BN 的中点，DM 即为中位线，不难求出MD 的长度．【答案与解析】解：延伸BD 交AC 于点N ．∵ AD 为∠BAC 的角平分线，且AD ⊥BN ，∴ ∠BAD ＝∠NAD ，∠ADB ＝∠ADN ＝90°，在△ABD 和△AND 中，∴ △ABD ≌△AND(ASA)∴ AN ＝AB ＝12，BD ＝DN ．∵ AC ＝18，∴ NC ＝AC －AN ＝18－12＝6，∵ D 、M 区分为BN 、BC 的中点，∴ DM ＝12CN ＝162＝3．【总结升华】当条件中含有中点的时分，可以将它与等腰三角形的〝三线合一〞、三角形的中线、中位线等联络起来，停止联想，必要时添加辅佐线，结构中位线等图形．举一反三：【变式】如图，BE ，CF 是△ABC 的角平分线，AN ⊥BE 于N ，AM ⊥CF 于M ，求证：MN ∥BC ．【答案】证明：延伸AN 、AM 区分交BC 于点D 、G ．∵BE 为∠ABC 的角平分线，BE ⊥AG ，∴∠BAG=∠BGA ，∴△ABG 为等腰三角形，∴BN 也为等腰三角形的中线，即AN=GN ．同理AM=DM ，∴MN 为△ADG 的中位线，∴MN ∥BC ．4、〔1〕如图1，在四边形ABCD 中，E 、F 区分是BC 、AD 的中点，衔接EF 并延伸，区分与BA 、CD 的延伸线交于点M 、N ，那么∠BME=∠CNE ，求证：AB=CD ．〔提示取BD 的中点H ，衔接FH ，HE 作辅佐线〕〔2〕如图2，在△ABC 中，且O 是BC 边的中点，D 是AC 边上一点，E 是AD 的中点，直线OE 交BA 的延伸线于点G ，假定AB=DC=5，∠OEC=60°，求OE 的长度．【思绪点拨】〔1〕连结BD ，取DB 的中点H ，连结EH 、FH ，证明出EH ∥AB ，EH=21AB ，FH ∥CD ，FH=21CD ，证出HE=HF ，进而证出AB=CD ；〔2〕连结BD ，取DB 的中点H ，连结EH 、OH ，证明出EH=OH ，可证明证出△OEH 是等边三角形，进而求出OE=25．【答案与解析】〔1〕证明：连结BD ，取DB 的中点H ，连结EH 、FH ．∵E 、F 区分是BC 、AD 的中点，∴EH ∥AB ，EH=21AB ，FH ∥CD ，FH=21CD ， ∵∠BME=∠CNE ，∴HE=HF ，∴AB=CD ；〔2〕解：连结BD ，取DB 的中点H ，连结EH 、OH ，∵AB=CD ，∴HO=HE ，∴∠HOE=∠HEO ，∵∠OEC=60°，∴∠HEO=∠AGO=60°，∴△OEH 是等边三角形，∵AB=DC=5，∴OE=25．【总结升华】此题考察了三角形的中位线定理、全等三角形的判定与性质，解答此题的关键是参考标题给出的思绪，作出辅佐线，有一定难度．举一反三：【变式】如图，AB∥CD，E，F区分为AC，BD的中点，假定AB=5，CD=3，那么EF的长是〔〕A．4 B．3 C．2 D．1【答案】D；解：衔接DE并延伸交AB于H，∵CD∥AB，∴∠C=∠A，∠CDE=∠AHE，∵E是AC中点，∴AE=CE，∴△DCE≌△HAE，∴DE=HE，DC=AH，∵F是BD中点，∴EF是△DHB的中位线，∴EF=12 BH，∴BH=AB-AH=AB-DC=2，∴EF=1．。

八年级数学竞赛第14讲中位线及其应用

八年级数学竞赛第十四讲中位线及其应用中位线是三角形与梯形中的一条重要线段，由于它的性质与线段的中点及平行线紧密相连，因此，它在几何图形的计算及证明中有着广泛的应用．例1 如图2-53所示．△ABC中，AD⊥BC于D，E，F，△ABC的面积．分析由条件知，EF，EG分别是三角形ABD和三角形ABC的中位线．利用中位线的性质及条件中所给出的数量关系，不难求出△ABC的高AD及底边BC的长．解由已知，E，F分别是AB，BD的中点，所以，EF是△ABD的一条中位线，所以由条件AD+EF=12(厘米)得EF=4(厘米)，从而 AD=8(厘米)，由于E，G分别是AB，AC的中点，所以EG是△ABC的一条中位线，所以BC=2EG=2×6=12(厘米)，显然，AD是BC上的高，所以例2 如图 2-54 所示．△ABC中，∠B，∠C的平分线BE，CF相交于O，AG⊥BE于G，AH⊥CF于H．(1)求证：GH∥BC；(2)若AB=9厘米，AC=14厘米，BC=18厘米，求GH．分析若延长AG，设延长线交BC于M．由角平分线的对称性可以证明△ABG≌△MBG，从而G是AM的中点；同样，延长AH交BC于N，H是AN 的中点，从而GH就是△AMN的中位线，所以GH∥BC，进而，利用△ABC 的三边长可求出GH的长度．(1)证分别延长AG，AH交BC于M，N，在△ABM中，由已知，BG平分∠ABM，BG⊥AM，所以△ABG≌△MBG(ASA)．从而，G是AM的中点．同理可证△ACH≌△NCH(ASA)，从而，H是AN的中点．所以GH是△AMN的中位线，从而，HG∥MN，即HG∥BC．(2)解由(1)知，△ABG≌△MBG及△ACH≌△NCH，所以AB=BM=9厘米，AC=CN=14厘米．又BC=18厘米，所以BN=BC-CN=18-14=4(厘米)，MC=BC-BM=18-9=9(厘米)．从而MN=18-4-9=5(厘米)，说明 (1)在本题证明过程中，我们事实上证明了等腰三角形顶角平分线三线合一(即等腰三角形顶角的平分线也是底边的中线及垂线)性质定理的逆定理：“若三角形一个角的平分线也是该角对边的垂线，则这条平分线也是对边的中线，这个三角形是等腰三角形”．(2)“等腰三角形三线合一定理”的下述逆命题也是正确的：“若三角形一个角的平分线也是该角对边的中线，则这个三角形是等腰三角形，这条平分线垂直于对边”．同学们不妨自己证明．(3)从本题的证明过程中，我们得到启发：若将条件“∠B，∠C的平分线”改为“∠B(或∠C)及∠C(或∠B)的外角平分线”(如图2-55所示)，或改为“∠B，∠C的外角平分线”(如图2-56所示)，其余条件不变，那么，结论GH∥BC仍然成立．同学们也不妨试证．例3 如图2-57所示．P是矩形ABCD内的一点，四边形BCPQ是平行四边形，A′，B′，C′，D′分别是AP，PB，BQ，QA的中点．求证：A′C′=B′D′．分析由于A′，B′，C′，D′分别是四边形APBQ的四条边AP，PB，BQ，QA的中点，有经验的同学知道A′B′C′D′是平行四边形，A′C′与B′D′则是它的对角线，从而四边形A′B′C′D′应该是矩形．利用ABCD是矩形的条件，不难证明这一点．证连接A′B′，B′C′，C′D′，D′A′，这四条线段依次是△APB，△BPQ，△AQB，△APQ的中位线．从而A′B′∥AB，B′C′∥PQ，C′D′∥AB，D′A′∥PQ，所以，A′B′C′D′是平行四边形．由于ABCD是矩形，PCBQ是平行四边形，所以AB⊥BC，BC∥PQ．从而AB⊥PQ，所以 A′B′⊥B′C′，所以四边形A′B′C′D′是矩形，所以A′C′=B′D′．①说明在解题过程中，人们的经验常可起到引发联想、开拓思路、扩大已知的作用．如在本题的分析中利用“四边形四边中点连线是平行四边形”这个经验，对寻求思路起了不小的作用．因此注意归纳总结，积累经验，对提高分析问题和解决问题的能力是很有益处的．例4 如图2-58所示．在四边形ABCD中，CD＞AB，E，F分别是AC，BD的中点．求证：分析在多边形的不等关系中，容易引发人们联想三角形中的边的不形中构造中位线，为此，取AD中点．证取AD中点G，连接EG，FG，在△ACD中，EG是它的中位线(已知E是AC的中点)，所以同理，由F，G分别是BD和AD的中点，从而，FG是△ABD的中位线，所以在△EFG中，EF＞EG-FG．③由①，②，③例5 如图2-59所示．梯形ABCD中，AB∥CD，E为BC的中点，AD=DC+AB．求证：DE⊥AE．分析本题等价于证明△AED是直角三角形，其中∠AED=90°．在E点(即直角三角形的直角顶点)是梯形一腰中点的启发下，添梯形的中位线作为辅助线，若能证明，该中位线是直角三角形AED的斜边(即梯形另一腰)的一半，则问题获解．证取梯形另一腰AD的中点F，连接EF，则EF是梯形ABCD的中位线，所以因为AD=AB+CD，所以从而∠1=∠2，∠3=∠4，所以∠2+∠3=∠1+∠4=90°(△ADE的内角和等于180°)．从而∠AED=∠2+∠3=90°，所以 DE⊥AE．例6 如图2-60所示．△ABC外一条直线l，D，E，F分别是三边的中点，AA1，FF1，DD1，EE1都垂直l于A1，F1，D1，E1．求证：AA1+EE1=FF1+DD1．分析显然ADEF是平行四边形，对角线的交点O平分这两条对角线，OO1恰是两个梯形的公共中位线．利用中位线定理可证．证连接EF，EA，ED．由中位线定理知，EF∥AD，DE∥AF，所以ADEF 是平行四边形，它的对角线AE，DF互相平分，设它们交于O，作OO1⊥l 于O1，则OO1是梯形AA1E1E及FF1D1D的公共中位线，所以即 AA1+EE1=FF1+DD1．练习十四1．已知△ABC中，D为AB的中点，E为AC上一点，AE=2CE，CD，BE 交于O点，OE=2厘米．求BO的长．2．已知△ABC中，BD，CE分别是∠ABC，∠ACB的平分线，AH⊥BD于H，AF⊥CE于F．若AB=14厘米，AC=8厘米，BC=18厘米，求FH的长．3．已知在△ABC中，AB＞AC，AD⊥BC于D，E，F，G分别是AB，BC，AC的中点．求证：∠BFE=∠EGD．4．如图2-61所示．在四边形ABCD中，AD=BC，E，F分别是CD，AB 的中点，延长AD，BC，分别交FE的延长线于H，G．求证：∠AHF=∠BGF．5．在△ABC中，AH⊥BC于H，D，E，F分别是BC，CA，AB的中点(如图2-62所示)．求证：∠DEF=∠HFE．6．如图2-63所示．D，E分别在AB，AC上，BD=CE，BE，CD的中点分别是M，N，直线MN分别交AB，AC于P，Q．求证：AP=AQ．7．已知在四边形ABCD中，AD＞BC，E，F分别是AB，CD。