《管理运筹学》第四版 第5章 单纯形法 课后习题解析
《管理运筹学》第四版课后习题解析(上)演示教学

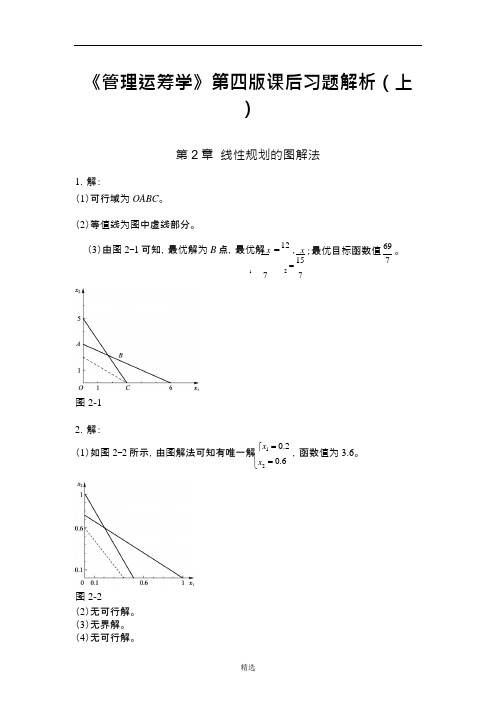
《管理运筹学》第四版课后习题解析(上)《管理运筹学》第四版课后习题解析(上)第2章 线性规划的图解法1.解:(1)可行域为OABC 。
(2)等值线为图中虚线部分。
(3)由图2-1可知,最优解为B 点,最优解1x =127,2157x =;最优目标函数值697。
图2-12.解:(1)如图2-2所示,由图解法可知有唯一解120.20.6x x =⎧⎨=⎩,函数值为3.6。
图2-2(2)无可行解。
(3)无界解。
(4)无可行解。
(5)无穷多解。
(6)有唯一解 1220383x x ⎧=⎪⎪⎨⎪=⎪⎩,函数值为923。
3.解:(1)标准形式12123max 32000f x x s s s =++++1211221231212392303213229,,,,0x x s x x s x x s x x s s s ++=++=++=≥(2)标准形式1212min 4600f x x s s =+++12112212121236210764,,,0x x s x x s x x x x s s --=++=-=≥(3)标准形式12212min 2200f x x x s s ''''=-+++ 1221122122212212355702555032230,,,,0x x x s x x x x x x s x x x s s '''-+-+=''''-+=''''+--=''''≥4.解:标准形式1212max 10500z x x s s =+++1211221212349528,,,0x x s x x s x x s s ++=++=≥松弛变量(0,0)最优解为 1x =1,x 2=3/2。
5.解:标准形式12123min 118000f x x s s s =++++121122123121231022033184936,,,,0x x s x x s x x s x x s s s +-=+-=+-=≥剩余变量(0, 0, 13)最优解为 x 1=1,x 2=5。
《管理运筹学》第四版课后习题答案
精选⎨= 0.6《管理运筹学》第四版课后习题解析(上)第2章 线性规划的图解法1.解:(1)可行域为OABC 。
(2)等值线为图中虚线部分。
(3)由图2-1可知,最优解为B 点,最优解 x =12, x = 15 1727图2-1;最优目标函数值 69。
72.解:(1)如图2-2所示,由图解法可知有唯一解 ⎧x 1 = 0.2,函数值为3.6。
⎩x 2图2-2(2)无可行解。
(3)无界解。
(4)无可行解。
⎨ (5)无穷多解。
⎧x = (6)有唯一解 ⎪ 1⎪ 203 ,函数值为 92 。
8 3 x = ⎪⎩ 2 33.解: (1)标准形式max f = 3x 1 + 2x 2 + 0s 1 + 0s 2 + 0s 39x 1 + 2x 2 + s 1 = 303x 1 + 2x 2 + s 2 = 13 2x 1 + 2x 2 + s 3 = 9x 1, x 2 , s 1, s 2 , s 3 ≥ 0(2)标准形式min f = 4x 1 + 6x 2 + 0s 1 + 0s 23x 1 - x 2 - s 1 = 6 x 1 + 2x 2 + s 2 = 10 7x 1 - 6x 2 = 4x 1, x 2 , s 1, s 2 ≥ 0(3)标准形式min f = x 1' - 2x 2' + 2x 2'' + 0s 1 + 0s 2-3x 1 + 5x 2' - 5x 2'' + s 1 = 70 2x 1' - 5x 2' + 5x 2'' = 50 3x 1' + 2x 2' - 2x 2'' - s 2 = 30 x 1', x 2' , x 2'' , s 1, s 2 ≥4.解: 标准形式max z = 10x 1 + 5x 2 + 0s 1 + 0s 23x 1 + 4x 2 + s 1 = 9 5x 1 + 2x 2 + s 2 = 8 x 1, x 2 , s 1, s 2 ≥ 0≤松弛变量(0,0)最优解为 x 1 =1,x 2=3/2。
管理运筹学 第5章 单纯形法[精]
![管理运筹学 第5章 单纯形法[精]](https://img.taocdn.com/s3/m/30516d460066f5335a8121f7.png)
A(p1,p2,p3,p4,p5)2 1 0 1 0
0 1 0 0 1
其中pj为系数矩阵A第j列的向量。A的秩为3,A的秩m小于此方程组的变
量的个数n,为了找到一个初始基本可行解,先介绍以下几个线性规划的
基本概念。
基: 已知A是约束条件的m×n系数矩阵,其秩为m。若B是A中m×m阶非
管理运筹学
10
§1 单纯形法的基本思路和原理
2. 在确定了x2为入基变量之后,我们要在原来的3个基变量s1,s2,s3中确
定一个出基变量,也就是确定哪一个基变量变成非基变量呢? 如果把s3作为出基变量,则新的基变量为x2,s1,s2,因为非基变量x1=s3=0,
x2 +s1=300, x2+s2=400, x2=250, 求出基本解:x1=0,x2=250,s1=50,s2=150,s3=0。 条件,是基本可行解,故s3可以确定为出基变量。 能否在求出基本解以前来确定出基变量呢? 以下就来看在找出了初始基本可行解和确定了入基变量之后,怎么样的 基变量可以确定为出基变量呢?或者说出基变量要具有什么条件呢?
zz0 jxj
jJ
由于所有的xj的取值范围为大于等于零,当所有的
都小
j
于等于零时,可知 j x j 是一个小于等于零的数,要使z
j J
的值最大,显然 j x j 只有为零。我们把这些xj取为非基 j J
变量(即令这些xj的值为零),所求得的基本可行解就使目标 函数值最大为z0。
管理运筹学
11
§1 单纯形法的基本思路和原理
我们把确定出基变量的方法概括如下:把已确定的入基变量在各约束方 程中的正的系数除以其所在约束方程中的常数项的值,把其中最小比值所 在的约束方程中的原基变量确定为出基变量。这样在下一步迭代的矩阵变 换中可以确保新得到的bj值都大于等于零。
单纯形法的几种特殊情况

达不到最优解。
下面一个是由E.Beale给出的循环的例子。
例5
目标函数
min f =-(3/4)x4+20x5-(1/2)x6+6x7.
约束条件:x1+(1/4)x4-8x5-x6+9x7=0,
x2+(1/2)x4-12x5-(1/2)x6+3x7=0,
x3+x6=1,
x1,x2,x3,x4,x5,x6,x7≥0.
50 150 250
12500
50/1 150/2 —
50 50 250
15000
— 50/1 250/1
8
§4 几种特殊情况
这样我们求得了最优解为x1=50,x2=250,s1=0,s2=50,s3=0,此线性规划的 最优值为15000。这个最优解是否是惟一的呢?由于在第2次迭代的检验数
中除了基变量的检验数 1,2,4 等于零外,非基变量s3的检验数也等
30 0 20 1 -M 0
1
1/10
-3/10
0
0
0
-7/10
-1
1
zj
20
30
3+M/10 11+7M/10
M
-M
cj-zj
0
0
-3-M/10 -11-7M/10
-M
0
管理运筹学
b
比值
150 30 40
-40M
150/10 — 40/1
15
15/(3/10)
30
30/1
25
25/(7/10)
例4.用单纯形表,求解下列线性规划问题。
解:加上松驰变量s1,s2,s3化为标准形式后,
《管理运筹学》第四版课后习题答案
(10)不发 生变化,因为允许 增加的百分比与允 许减少的百分比之和
25 50 ≤ 100% 100 100
(11)不发 生变化,因为允许 增加的百分比与允 许减少的百分比之和 50 60 ≤ 100%,其最大利润为 103000+50×50-60 ×200=93 500元。
元;2 车间 与 4 车间 每增加一个工 时,总利 润不增加。
(4)3 车间 ,因为增加的利 润最大。
(5)在400 到正无 穷的范 围内 变化,最优产 品的 组合不 变。
(6)不变,因为在 0,500 的范 围内。
(7)所谓的上限和下限 值指当 约束条件的右 边值 在 给定范 围 内变化 时,约束条件 1 的右 边值 在 200,440 变化,对 偶价格仍 为 50(同理解释 其他 约 束条件)。
x1
0.2
,函数值为 3.6。
x2 0.6
图 2-2
(2)无可行解。 (3)无界解。 (4)无可行解。
(5)无穷多解。
x1
(6)有唯一解
x2
20
3 ,函数值为 92 。
8
3
3
3.解: (1)标 准形式
max f 3x1 2x2 0s1 0s2 0s3
9 x1 2 x2 s1 30 3x1 2 x2 s2 13 2 x1 2 x2 s3 9 x1, x2 ,s1, s2, s3 ≥ 0
金 B 的投 资额 每增加 1 个 单位,回报额 下降 0.06。
(4)c1 不变时 ,c2 在负无 穷到 10 的范 围内变 化,其最优解不 变;
c2 不变时 ,c1 在 2 到正无 穷的范 围 内变化,其最优 解不 变。
管理运筹学课后习题答案
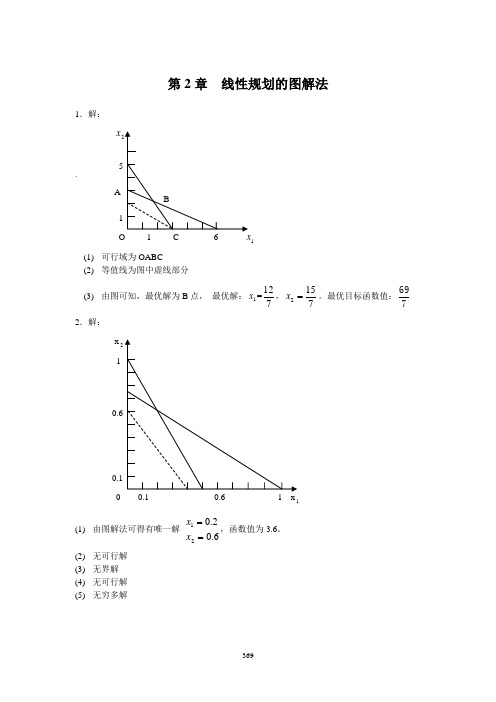
第2章 线性规划的图解法1.解:x`A 1 (1) 可行域为OABC(2) 等值线为图中虚线部分(3) 由图可知,最优解为B 点, 最优解:1x =712,7152=x 。
最优目标函数值:7692.解: x 2 10 1(1) 由图解法可得有唯一解 6.02.021==x x ,函数值为3.6。
(2) 无可行解 (3) 无界解 (4) 无可行解 (5)无穷多解(6) 有唯一解 3832021==x x ,函数值为392。
3.解:(1). 标准形式:3212100023m ax s s s x x f ++++=,,,,9221323302932121321221121≥=++=++=++s s s x x s x x s x x s x x(2). 标准形式:21210064m in s s x x f +++=,,,46710263212121221121≥=-=++=--s s x x x x s x x s x x(3). 标准形式:21''2'2'10022m in s s x x x f +++-=,,,,30223505527055321''2'2'12''2'2'1''2'2'11''2'21≥=--+=+-=+-+-s s x x x s x x x x x x s x x x4.解:标准形式:212100510m ax s s x x z +++=,,,8259432121221121≥=++=++s s x x s x x s x x松弛变量(0,0) 最优解为 1x =1,x 2=3/2.标准形式:32121000811m in s s s x x f ++++=,,,,369418332021032121321221121≥=-+=-+=-+s s s x x s x x s x x s x x剩余变量(0.0.13) 最优解为 x 1=1,x 2=5.6.解:(1) 最优解为 x 1=3,x 2=7. (2) 311<<c (3) 622<<c (4)4621==x x(5) 最优解为 x 1=8,x 2=0. (6) 不变化。
《管理运筹学》课后习题答案59页word
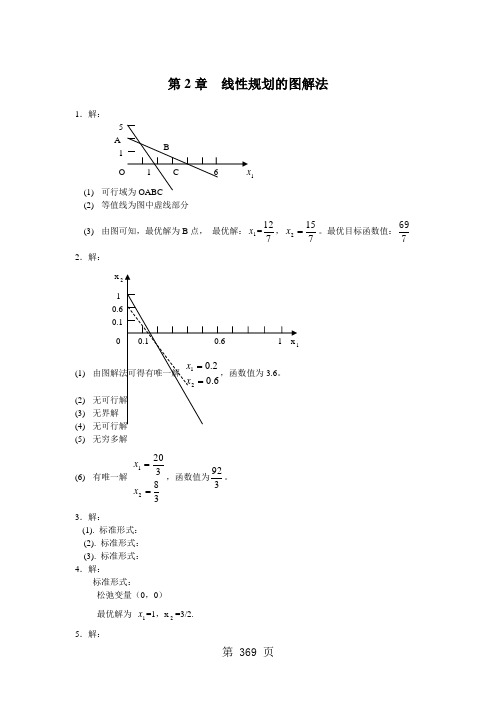
第2章 线性规划的图解法1.解: 5 A 11 (1) (2) 等值线为图中虚线部分(3) 由图可知,最优解为B 点, 最优解:1x =712,7152=x 。
最优目标函数值:7692.解: x 2 1 0(1) (2) (3) 无界解 (4) (5)无穷多解(6) 有唯一解 3832021==x x ,函数值为392。
3.解:(1). 标准形式: (2). 标准形式:(3). 标准形式: 4.解:标准形式:松弛变量(0,0) 最优解为 1x =1,x 2=3/2. 5.解:标准形式:剩余变量(0.0.13) 最优解为 x 1=1,x 2=5. 6.解:(1) 最优解为 x 1=3,x 2=7. (2) 最优解为 x 1=8,x 2=0. (3) 不变化。
因为当斜率31121-≤-≤-c c ,最优解不变,变化后斜率为1,所以最优解不变. 7.解:模型:(1) 1501=x ,702=x ,即目标函数最优值是103000 (2) 2,4有剩余,分别是330,15,均为松弛变量. (3) 50,0,200,0。
(4) 在[]500,0变化,最优解不变。
在400到正无穷变化,最优解不变. (5) 因为143045021-≤-=-c c ,所以原来的最优产品组合不变. 8.解:(1) 模型:b a x x f 38min +=基金a,b 分别为4000,10000,回报率为60000。
(2) 模型变为:b a x x z 45max +=推导出:180001=x 30002=x ,故基金a 投资90万,基金b 投资30万。
第3章 线性规划问题的计算机求解1.解:(1) 1501=x ,702=x 。
目标函数最优值103000。
(2) 1,3车间的加工工时已使用完;2,4车间的加工工时没用完;没用完的加工工时数为2车间330小时,4车间15小时. (3) 50,0,200,0含义:1车间每增加1工时,总利润增加50元;3车间每增加1工时,总利润增加200元;2车间与4车间每增加一个工时,总利润不增加。
《管理运筹学》第四版 第6章 单纯形法的灵敏度分析与对偶 课后习题解析

《管理运筹学》第四版课后习题解析第6章单纯形法的灵敏度分析与对偶1.解: (1)c 1≤24 (2)c 2≥6 (3)c s 2≤82.解:(1)c 1≥−0.5 (2)−2≤c 3≤0 (3)c s 2≤0.53.解:(1)b 1≥250 (2)0≤b 2≤50 (3)0≤b 3≤1504.解: (1)b 1≥−4 (2)0≤b 2≤10 (3)b 3≥45. 解:最优基矩阵和其逆矩阵分别为:⎪⎪⎭⎫ ⎝⎛=1401B ,⎪⎪⎭⎫ ⎝⎛-=-14011B ; 最优解变为130321===x x x ,,最小值变为-78; 最优解没有变化; 最优解变为2140321===x x x ,,,最小值变为-96;6.解:(1)利润变动范围c 1≤3,故当c 1=2时最优解不变。
(2)根据材料的对偶价格为1判断,此做法有利。
(3)0≤b 2≤45。
(4)最优解不变,故不需要修改生产计划。
(5)此时生产计划不需要修改,因为新的产品计算的检验数为−3小于零,对原生产计划没有影响。
7. 解:(1)设321,,x x x 为三种食品的实际产量,则该问题的线性规划模型为,, 4005132 4505510 35010168 325.2max 321321321321321≥≤++≤++≤++++=x x x x x x x x x x x x x x x z 约束条件:解得三种食品产量分别为0,75.43321===x x x ,这时厂家获利最大为109.375万元。
(2)如表中所示,工序1对于的对偶价格为0.313万元,由题意每增加10工时可以多获利3.13万元,但是消耗成本为10万元,所以厂家这样做不合算。
(3)B 食品的加工工序改良之后,仍不投产B ,最大利润不变;若是考虑生产甲产品,则厂家最大获利变为169.7519万元,其中667.31110,167.144321====x x x x ,,;(4)若是考虑生产乙产品,则厂家最大获利变为163.1万元,其中382.70,114321====x x x x ,,;所以建议生产乙产品。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《管理运筹学》第四版课后习题解析
第5章单纯形法
1.解:
表中a 、c 、e 、f 是可行解,f 是基本解,f 是基本可行解。
2.解:
(1)该线性规划的标准型如下。
max 5x 1+9x 2+0s 1+0s 2+0s 3 s.t. 0.5x 1+x 2+s 1=8 x 1+x 2-s 2=10
0.25x 1+0.5x 2-s 3=6 x 1,x 2,s 1,s 2,s 3≥0
(2)至少有两个变量的值取零,因为有三个基变量、两个非基变量,非基变量取零。
(3)(4,6,0,0,-2)T (4)(0,10,-2,0,-1)
T (5)不是。
因为基本可行解要求基变量的值全部非负。
(6)略 3.解:
令33
3x x x ''-'=,z f -=改为求f max ;将约束条件中的第一个方程左右两边同时乘以-1,并在第二和第三个方程中分别引入松弛变量5x 和剩余变量6x ,将原线性规划问题化为如下标准型:
j x '、j x ''不可能在基变量中同时出现,因为单纯性表里面j x '、j x ''相应的列向量是相同的,只有符号想法而已,这时候选取基向量的时候,同时包含两列会使
选取的基矩阵各列线性相关,不满足条件。
4.解: (1) 表5-1
0,,,,,, 24423 1863 1334 7234max 65433
21633
21543321433
214
321≥'''=-''+'--=++''+'-+-=+''+'---++-=x x x x x x x x x x x x x x x x x x x x x x x x x x x f 约束条件:
(2)线性规划模型如下。
max 6x 1+30x 2+25x 3 s.t. 3x 1+x 2+s 1=40 2x 2+x 3+s 2=50 2x 1+x 2-x 3+s 3=20 x 1,x 2,x 3,s 1,s 2,s 3 ≥0
(3)初始解的基为(s 1,s 2,s 3)
T ,初始解为(0,0,0,40,50,20)T ,对应的目标函数值为0。
(4)第一次迭代时,入基变量时x 2,出基变量为s 3。
6. 解:
(1)当现行解为可行解,并且对应的非基变量检验数均小于0时,该线性规划问题才有唯一最优解,即01≥k ,03<k ,05<k ;
(2)当某个非基变量的检验数为0时,该线性规划问题有多重最优解。
所以若满足现行解为最优解,并且有多重最优解即满足:或者01≥k ,03=k ,05≤k ;
或者01≥k ,03≤k ,05=k ;;或者01≥k ,03=k ,0
5=k (3)01≥k 可以保证该线性规划问题有可行解。
若此时该线性规划问题目标函数无界,也就是说一定存在某个检验数为正时,对应的列的系数向量元素全部非正,即50k >且04≤k ;
(4)由表中变量均为非人工变量,则01≤k 且02≥k ,由于变量的非负性条件,第一个约束方程变为矛盾方程,从而该问题无可行解;
7. 解:
(1)7,1,0,0,0,1,0,7========h g f e d c b a ; (2)表中给出的解是最优解。
8.解:
最优解为(2.25,0)
T ,最优值为9。
图5-1
单纯形法如表5-2所示。
9.解:
(1)最优解为(2,5,4)
T ,最优值为84。
(2)最优解为(0,0,4)T,最优值为−4。
10.解:
有无界解。
11.解:
(1)无可行解。
(2)最优解为(4,4)T,最优值为28。
(3)有无界解。
(4)最优解为(4,0,0)T,最优值为8。
12. 解:
,0,5( ,最优值为-12。
该线性规划问题的最优解为T)1。
