立体几何复习
2023届高考数学总复习《立体几何》附答案解析

(2)若点 N 为 BC 的中点,求四面体 A'MNB 的体积.
【解答】证明:(1)连接 BD,设 BD∩EC=F,连接 MF,
由题意可得四边形 BCDE 为正方形,则 F 为 BD 的中点,
∴MF 为△A′BD 的中位线,可得 MF∥A′B,
又 A′B⊄平面 EMC,MF⊂平面 EMC,
∴A'B∥平面 EMC;
2023 年高考:立体几何复习题及答案
1.如图,已知直角梯形 ABCD,BC∥AD,BC=CD=2,AD=4,∠BCD=90°,点 E 为 AD 的中点,现将三角形 ABE 沿 BE 折叠,得到四棱锥 A'﹣BCDE,其中∠A'ED=120°, 点 M 为 A'D 的中点.
(1)求证:A'B∥平面 EMC;
第2页共3页
∵BE⊂平面 BEF,∴平面 BEF⊥平面 AMD, 结合题意分析知,点 F 在线段 AD 上,连接 MF, 过 A 作 AH⊥MF,交 MF 的延长线于点 H,
则结合已知条件得
,解得 AH ,
设 Dt ,
第3页共3页
【解答】解:(1)证明:由题意知 PC2+AC2=PA2,∴PC⊥AC, 同理,PC⊥BC,又 AC∩BC=C,∴PC⊥平面 ABC, ∵D,E 分别是 AC,PA 的中点,∴DE∥PC, ∴DE⊥平面 ABC, 又 DE⊂平面 BDE,∴平面 BDE⊥平面 ABC. (2)在△BDE 中,DE⊥BD,BD=2 ,DE=2,∴BE=4, 如图,过 A 作 AM⊥BE 于 M,连接 MD, 在△ABE 中,AB=BE=4,AE=2 ,解得 AM ,ME=1, ∵DM⊂平面 BDE,∴AC⊥DM, 在 Rt△ADM 中,AM ,AD=2,∴DM , ∴DM2+EM2=DE2,∴MD⊥BE, ∵AM∩MD=M,∴BE⊥平面 AMD,
2023年高考数学总复习《立体几何》附答案解析

所以 z1=0,
,故可取
, ,,
于是 < , >
,
设所成锐二面角为θ,所以 sinθ
,
所以平面 PAD 和平面 PBE 所成锐二面角的正弦值为 .
第3页共3页
第1页共3页
∴CF CC1 AA1 , ∵∠BAC=90°,
∴CD
,
在 Rt△FCD 中,tan∠FDC 맨
,
故直线 DF 与平面 ABC 所成角的正切值为 .
2.如图所示,四棱锥 P﹣ABCD 的底面 ABCD 是边长为 1 的菱形,∠BCD=60°,E 是 CD 的中点,PA⊥底面 ABCD,PA=2. (1)证明:平面 PBE⊥平面 PAB; (2)求平面 PAD 和平面 PBE 所成二面角(锐角)的正弦值.
【解答】(1)证明:如图所示,连接 BD,由 ABCD 是菱形且∠BCD=60°, 知△ABC 是等边三角形. ∵E 是 CD 的中点, ∴BE⊥CD,又 AB∥CD, ∴AB⊥BE,∴BE⊥平面 PAB, 又 BE⊂平面 PBE, ∴平面 PBE⊥平面 PAB. (2)解:在平面 ABCD 内,过点 A 作 AB 的垂线,如图所示,以 A 为原点建立空间直角
【解答】(1)证明:连接 DG、FG, 由直三棱柱的性质知,BB1∥CC1,且 BB1=CC1, ∵B1E=2EB,C1F=2FC, ∴EB∥FC,且 EB=FC, ∴四边形 BCFE 为平行四边形, ∴EF∥BC,EF=BC, ∵BD=2DA,CG=2GA, ∴GD∥BC,且 GD BC, ∴EF∥GD,且 GD EF, ∴四边形 DEFG 为梯形,即 D、E、F、G 四点共面, ∴点 G 在平面 EFD 内. (2)解:由直三棱柱的性质知,CC1⊥平面 ABC, ∵F 为 CC1 上一点, ∴点 F 在平面 ABC 上的投影为点 C, 连接 CD,则∠FDC 即为直线 DF 与平面 ABC 所成角. ∵点 D 在棱 AB 上,且 BD=2DA, ∴AD AB , ∵C1F=2FC,
高考立体几何专题复习公开课获奖课件

第20页
面面垂直鉴定
假如一种平面通过另一种平面一条 垂线,则这两个平面互相垂直
推论:假如一种平面与另一种平面垂线 平行,则这两个平面互相垂直
第21页
面面垂直性质
假如两个平面垂直,则在一种平面内垂直 于它们交线直线垂直于另一种平面
推论:假如两个相交平面都与另一种平面 垂直,则这两个平面交线 l 垂直于另一种 平面
(3)推论:
假如一种平面内两条相交直线与另一种平面两条 相交直线分别平行,那么这两个平面平行。
第10页
(4)运用线面垂直:
假如两个平面分别垂直于同一条直线,那么这两 个平面平行。
(5)运用面面平行:
假如两个平面都平行于第三个平面,那么这两个 平面平行。
(6)运用距离:
假如一种平面上所有点到另一种平面距离相等, 那么这两个平面平行。
α
a
直线与平 面所成角
βA Pm
αB
二面角
00<θ≤900
00≤ θ≤900
00≤θ ≤1800
空间角计算环节:一作、二证、三算
第34页
空间中角解法小结
1、异面直线所成角措施 (1)平移法(2)补形法
2、直线与平面所成角措施
关键:抓垂足、斜足,找斜线在平面内射影。
3、二面角
找二面角棱,进而找棱两条垂线
第6页
(4)运用垂直
假如一条直线和一种平面分别与另一种平面垂 直,且直线不在这个平面内,则这条直线和这 个平面平行。
(5)运用平行 假如一条直线与两个平行平面中一种平 行且不在另一种平面内,则这条直线与 另一种平面平行。
(6)运用距离
高考数学(文)《立体几何》专题复习

(2)两个平面垂直的判定和性质
✓ 考法5 线面垂直的判定与性质
1.证明直线 与平面垂直 的方法
2.线面垂直 的性质与线 线垂直
(1)判定定理(常用方法): 一条直线与一个平面内的两条相交直线都垂直,则该直线
与此平面垂直.判定定理中的两条相交直线必须保证“在平面 内相交”这一条件. (2)性质: ①应用面面垂直的性质(常用方法):若两平面垂直,则在一 个平面内垂直于交线的直线必垂直于另一个平面,是证明线 面垂直的主要方法; ②(客观题常用)若两条平行直线中的一条垂直于一个平面, 则另一条也垂直于这个平面.
64
65
✓ 考法4 面面平行的判定与性质
1.证明平面 与平面平行 的常用方法 2.空间平行关系 之间的转化
66
✓ 考法3 面面平行的判定与性质
1.证明平面 与平面平行 的常用方法
这是立体几何中证明平行关系常用的思路,三 种平行关系的转化可结合下图记忆
2.空间平行关系 之间的转化
67
68
600分基础 考点&考法
定义 判定方法
2.等角定理
判定定理 反证法 两条异面直线所成的角
✓ 考法2 异面直线所成的角
常考形式
直接求 求其三角函数值
常用方法
作角
正弦值 余弦值 正切值
证明 求值 取舍
55
56
57
58
600分基础 考点&考法
➢ 考点46 线面、面面平行的判定与性质 ✓ 考法3 线面平行的判定与性质 ✓ 考法4 面面平行的判定与性质
1.计算有关 线段的长
2.外接球、内切 球的计算问题
观察几何体的特征 利用一些常用定理与公式 (如正弦定理、余弦定理、勾股定理、 三角函数公式等) 结合题目的已知条件求解
《立体几何初步》复习

4.(2019·全国Ⅲ)如图,点N为正方形ABCD的中心,△ECD为正三角形, 平面ECD⊥平面ABCD,M是线段ED的中点,则 A.BM=EN,且直线BM,EN是相交直线
√B.BM≠EN,且直线BM,EN是相交直线 C.BM=EN,且直线BM,EN是异面直线 D.BM≠EN,且直线BM,EN是异面直线
5 5.
即
AO
与平面
ABCD
所成角的正切值为
5 5.
(3)平面AOB与平面AOC所成角的大小.
解 由(1)可知OC⊥平面AOB. 又∵OC⊂平面AOC,∴平面AOB⊥平面AOC. 即平面AOB与平面AOC所成的角为90°.
反思 感悟
(1)求异面直线所成的角常用平移转化法(转化为相交直线的 夹角). (2)求直线与平面所成的角常用射影转化法(即作垂线、找射影). (3)二面角的平面角的作法常有三种:①定义法;②三垂线法; ③垂面法.
(2)BE∥平面PAD;
证明 因为AB∥CD,CD=2AB,E为CD的中点, 所以AB∥DE,且AB=DE. 所以四边形ABED为平行四边形,所以BE∥AD. 又因为BE⊄平面PAD,AD⊂平面PAD, 所以BE∥平面PAD.
(3)平面BEF⊥平面PCD.
证明 因为AB⊥AD,且四边形ABED为平行四边形, 所以BE⊥CD,AD⊥CD. 由(1)知PA⊥底面ABCD,所以AP⊥CD. 又因为AP∩AD=A,AP,AD⊂平面PAD, 所以CD⊥平面PAD,所以CD⊥PD. 因为E和F分别是CD和PC的中点, 所以PD∥EF,所以CD⊥EF. 又因为CD⊥BE,EF∩BE=E,EF,BE⊂平面BEF, 所以CD⊥平面BEF.又CD⊂平面PCD, 所以平面BEF⊥平面PCD.
2023届高考数学总复习:立体几何复习题附答案

a,
在 Rt△FCM 中,tan∠FCM .
,
∴sin∠FCM ,
故直线 CF 与平面 ACDE 所成角的正弦值为 . 2.如图,在三棱柱 ABC﹣A1B1C1 中,BC⊥平面 AA1C1C,D 是 AA1 的中点,△ACD 是边长
为 1 的等边三角形. (1)证明:CD⊥B1D; (2)若 BC ,求二面角 B﹣C1D﹣B1 的大小.
,令
由(1)知,平面 B1C1D 的一个法向量为
,得
,, ,
, ,,
故 th< , >
,
所以二面角 B﹣C1D﹣B1 的大小为 30°.
第3页共3页
在直角梯形 AEFB 中,有 AF EF,BF
쳌
∴AF2+BF2=AB2,即 AF⊥BF.
∵BC∩BF=B,BC、BF⊂平面 BCF,
∴AF⊥平面 BCF.
EF,AB=2EF,
(2)解:∵AE⊥平面 ABC,AE⊂平面 ACDE,∴平面 ACDE⊥平面 ABC,
又平面 ABC∥平面 DEF,∴平面 ACDE⊥平面 DEF.
【解答】解:(1)证明:因为△ACD 是边长为 1 的等边三角形,所以∠ADC=60°,∠ DA1C1=120° 因为 D 是 AA1 的中点,所以 AD=A1D=A1C1=1,即△A1C1D 是等腰三角形, 则∠A1DC1=30°,故∠CDC1=90°,即 CD⊥C1D, 因为 BC⊥平面 AA1C1C,BC∥B1C1,所以 B1C1⊥平面 AA1C1C, 因为 CD⊂平面 AA1C1C,所以 B1C1⊥CD, 因为 B1C1∩C1D=C1,B1C1⊂平面 B1C1D,C1D⊂平面 B1C1D,所以 CD⊥平面 B1C1D, 因为 B1D⊂平面 B1C1D,所以 CD⊥B1D;
2023届高考数学总复习:立体几何附答案

设平面 PCD 的一个法向量为 (x1,y1,z1),
有
t
t, (0,1,1),
平面 ECD 的一个法向量为 (x2,y2,z2),
t 所以 th
t, (0,1,2), tt,
t 即二面角 P﹣DC﹣E 的余弦值为 .
t
第3页共3页
以 F 为坐标原点, , , ‐的方向为 x,y,z 轴的正方向建立空间直角坐标系,
t, t, , t,
∴
t, , tt,
,t,tt,
t, , t,
设平面 AEF 的法向量为
,,t
∵
t,
t
∴
t ,∴ t
t, , t,
∵
,
∴
,
∴直线 B1F⊥平面 AEF.
(Ⅱ)
, , t,
【解答】(Ⅰ)证明:因为 PA=AB,E 为 PB 中点,所以 AE⊥PB,
因为 PA⊥平面 ABCD,所以 PA⊥BC,
由 BC⊥AB,所以 BC⊥平面 PAB,所以 BC⊥AE,又 AE⊥PB,BC∩PB=B,
所以 AE⊥平面 PBC,
平面 AEF⊥平面 PBC.
(Ⅱ)解:法 1:取 PA 中点 G,连结 GE,GD,由 GE∥AB,CD∥AB,
t,t, t,
设平面 B1AE 的法向量为
,,t
∵
t ,∴
t
t
t, t
不妨取 y2=3 ,则 x2=﹣5,z2=﹣4 .
∴
⺁, , t t,
第1页共3页
平面 AEF 的法向量为
t, , t,
设二面角 B1﹣AE﹣F 的平面角为θ,
∴ th
t⺁.
2.如图,在四棱锥 P﹣ABCD 中,底面 ABCD 为正方形,PA⊥底面 ABCD,PA=AB,E 为 PB 的中点,F 为线段 BC 上的动点. (Ⅰ)求证:平面 AEF⊥平面 PBC; (Ⅱ)求二面角 P﹣DC﹣E 的余弦值.
立体几何专题复习(自己精心整理)

专题一证明平行垂直问题题型一证明平行关系(1)如图所示,在正方体ABCD-A1B1C1D1中,M,N分别是C1C,B1C1的中点.求证:MN∥平面A1BD。
(2)在正方体AC1中,M,N,E,F分别是A1B1,A1D1,B1C1,C1D1的中点,求证:平面AMN∥平面EFDB.思考题1(1)如图所示,平面PAD⊥平面ABCD,ABCD为正方形,△PAD是直角三角形,且PA=AD=2,E,F,G分别是线段PA,PD,CD的中点,求证:平面EFG∥平面PBC.(2)如图,在四面体A-BCD中,AD⊥平面BCD,BC⊥CD,AD=2,BD=22,M是AD的中点,P是BM的中点,点Q在线段AC上,且AQ=3QC.求证:PQ∥平面BCD。
题型二证明垂直关系(微专题)微专题1:证明线线垂直(1)已知空间四边形OABC中,M为BC中点,N为AC中点,P为OA中点,Q为OB中点,若AB=OC。
求证:PM⊥QN.(2)(2019·山西太原检测)如图,直三棱柱ABC-A1B1C1中,AA1=AB=AC=1,E,F分别是CC1,BC的中点,AE⊥A1B1,D为棱A1B1上的点,求证:DF⊥AE。
微专题2:证明线面垂直(3)在正方体ABCD-A1B1C1D1中,求证:BD1⊥平面ACB1.(4)(2019·河南六市一模)在如图所示的几何体中,ABC-A1B1C1为三棱柱,且AA1⊥平面ABC,四边形ABCD为平行四边形,AD=2CD,∠ADC=60°.若AA1=AC,求证:AC1⊥平面A1B1CD。
微专题3:证明面面垂直(5)已知正方体ABCD-A1B1C1D1中,E,F分别是BB1,CD的中点,求证:平面DEA⊥平面A1FD1.(6)如图,四边形ABCD为正方形,PD⊥平面ABCD,PD∥QA,QA=AB=错误!PD,求证:平面PQC⊥平面DCQ。
思考题2(1)(2019·北京东城区模拟)如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥BP交BP于点F,求证:PB⊥平面EFD。
立体几何期末复习(含详细答案)

立体几何单元复习卷(一)1.用任意一个平面截一个几何体,各个截面都是圆面,则这个几何体一定是() A.圆柱B.圆锥C.球体D.圆柱、圆锥、球体的组合体2.给出下列命题:①棱柱的侧棱都相等,侧面都是全等的平行四边形;②若三棱锥的三条侧棱两两垂直,则其三个侧面也两两垂直;③在四棱柱中,若两个过相对侧棱的截面都垂直于底面,则该四棱柱为直四棱柱;④存在每个面都是直角三角形的四面体.其中正确命题的序号是________.3.已知正三角形ABC的边长为2,那么△ABC的直观图△A′B′C′的面积为________.4.已知圆锥的表面积等于12πcm2,其侧面展开图是一个半圆,则底面圆的半径为________cm.5.(2018·苏州零模)鲁班锁是中国传统的智力玩具,起源于中国古代建筑中首创的榫卯结构,它的外观是如图所示的十字立方体,其上下、左右、前后完全对称,六根等长的正四棱柱体分成三组,经90°榫卯起来.若正四棱柱的高为5,底面正方形的边长为1,现将该鲁班锁放进一个球形容器内,则该球形容器的表面积至少为________。
(容器壁的厚度忽略不计,结果保留π)6.一个圆台上、下底面的半径分别为3 cm和8 cm,若两底面圆心的连线长为12 cm,则这个圆台的母线长为________cm.7.已知正四棱锥V-ABCD中,底面面积为16,一条侧棱的长为211,则该棱锥的高为________.8.如图,一立在水平地面上的圆锥形物体的母线长为4 m,一只小虫从圆锥的底面圆上的点P出发,绕圆锥表面爬行一周后回到点P处.若该小虫爬行的最短路程为4 3 m,则圆锥底面圆的半径等于________ m.9.正三棱柱ABC -A 1B 1C 1的底面边长为2,侧棱长为3,D 为BC 的中点,则三棱锥A -B 1DC 1的体积为________.10.已知直三棱柱ABC -A 1 B 1 C 1的6个顶点都在球O 的球面上,若AB =3,AC =4,AB ⊥AC ,AA 1 =12,则球O 的半径为( ) A.3172 B .210 C.132D .310 11.(2017·江苏高考)如图,在圆柱O1O 2内有一个球O ,该球与圆柱的上、下底面及母线均相切.记圆柱O 1O 2的体积为V 1,球O 的体积为V 2,则V 1V 2的值是________.12.已知正三棱锥的高为1,底面边长为23,内有一个球与四个面都相切,则棱锥的内切球的半径为( )A.52B.3-1C.12D.2-113.已知三棱锥S -ABC 的所有顶点都在球O 的球面上,SC 是球O 的直径.若平面SCA ⊥平面SCB ,SA =AC ,SB =BC ,三棱锥S -ABC 的体积为9,则球O 的表面积为________.14.已知一个正方体的所有顶点在一个球面上,若这个正方体的表面积为18,则这个球的体积为________.15.《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺.问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放的米约有( )A .14斛B .22斛C .36斛D .66斛16.圆台的一个底面周长是另一个底面周长的3倍,母线长为3,圆台的侧面积为84π,则圆台较小底面的半径为_______.17.一个六棱锥的体积为23,其底面是边长为2的正六边形,侧棱长都相等,则该六棱锥的侧面积为________.18.在三棱锥A -BCD中,侧棱AB,AC,AD两两垂直,△ABC,△ACD,△ADB的面积分别为22,32,62,则该三棱锥外接球的表面积为()A.2πB.6πC.46πD.24π19.如图,在三棱锥P-ABC中,AC=BC=2,∠ACB=90°,AP=BP=AB,PC⊥AC.(1)求证:PC⊥AB;(2)求点C到平面APB的距离.20.如图所示,在正方体ABCD-A1B1C1D1中,(1)求AC与A1D所成角的大小;(2)若E,F分别为AB,AD的中点,求A1C1与EF所成角的大小.立体几何单元复习卷(二)21.到空间不共面的四点距离相等的平面的个数为()A.1 B.4C.7 D.822.如图,平面α∥平面β,△PAB所在的平面与α,β分别交于CD,AB,若PC=2,CA=3,CD=1,则AB=________.23.在三棱锥P-ABC中,PB=6,AC=3,G为△PAC的重心,过点G作三棱锥的一个截面,使截面平行于PB和AC,则截面的周长为________.24.已知m,n是两条不同的直线,α,β,γ是三个不同的平面,下列命题中正确的是()A.若m∥α,n∥α,则m∥n B.若m∥α,m∥β,则α∥βC.若α⊥γ,β⊥γ,则α∥βD.若m⊥α,n⊥α,则m∥n25.已知m,n是两条不同的直线,α,β为两个不同的平面,则下列四个命题中正确的是()A.若m⊥α,n⊥β,m⊥n,则α⊥βB.若m∥α,n∥β,m⊥n,则α∥βC.若m⊥α,n∥β,m⊥n,则α∥βD.若m⊥α,n∥β,α∥β,则m∥n26.如图,在直三棱柱ABC-A′B′C′中,△ABC是边长为2的等边三角形,AA′=4,E,F,G,H,M分别是边AA′,AB,BB′,A′B′,BC的中点,动点P在四边形EFGH内部运动,并且始终有MP∥平面ACC′A′,则动点P的轨迹长度为()A.2 B.2πC.2 3 D.427.设m,n是两条不同的直线,α,β是两个不同的平面,下列命题中正确的是() A.若m⊂β,α⊥β,则m⊥αB.若m⊥α,m∥n,n∥β,则α⊥βC.若m⊥n,m⊂α,n⊂β,则α⊥βD.若α∥β,m⊂α,n⊂β,则m∥n28.在直三棱柱ABC-A1B1C1中,平面α与棱AB,AC,A1C1,A1B1分别交于点E,F,G,H,且直线AA1∥平面α.有下列三个命题:①四边形EFGH是平行四边形;②平面α∥平面BCC1B1;③平面α⊥平面BCFE.其中正确命题的序号是________.29.如图,在直三棱柱ABC-A1B1C1中,侧棱长为2,AC=BC=1,∠ACB=90°,D 是A 1B 1的中点,F 是BB 1上的动点,AB 1,DF 交于点E .要使AB 1⊥平面C 1DF ,则线段B 1F 的长为( )A.12B .1 C.32 D .230.如图,在Rt △ABC 中,∠ABC =90°,P 为△ABC 所在平面外一点,PA ⊥平面ABC ,则四面体P -ABC 中直角三角形的个数为( )A .4B .3C .2D .131.如图,在正方形ABCD 中,E ,F 分别是BC ,CD 的中点,G是EF 的中点,现在沿AE ,AF 及EF 把这个正方形折成一个空间图形,使B ,C ,D 三点重合,重合后的点记为H ,那么,在这个空间图形中必有( )A .AG ⊥平面EFHB .AH ⊥平面EFHC .HF ⊥平面AEFD .HG ⊥平面AEF32.如图,PA ⊥⊙O 所在平面,AB 是⊙O 的直径,C 是⊙O 上一点,AE ⊥PC ,AF ⊥PB ,给出下列结论:①AE ⊥BC ;②EF ⊥PB ;③AF ⊥BC ;④AE ⊥平面PBC ,其中真命题的序号是________.33.如图,四边形ABCD 与四边形ADEF 为平行四边形,M ,N ,G 分别是AB ,AD ,EF 的中点,求证:(1)BE ∥平面DMF ;(2)平面BDE ∥平面MNG .34.(2017·江苏高考)如图,在三棱锥A-BCD中,AB⊥AD,BC⊥BD,平面ABD⊥平面BCD,点E,F(E与A,D不重合)分别在棱AD,BD上,且EF⊥AD.求证:(1)EF∥平面ABC;(2)AD⊥AC.35.如图,S是Rt△ABC所在平面外一点,且SA=SB=SC,D为斜边AC的中点.(1)求证:SD⊥平面ABC;(2)若AB=BC,求证:BD⊥平面SAC.36.如图,在三棱锥P -ABC 中,PA ⊥AB ,PA ⊥BC ,AB ⊥BC ,PA =AB =BC =2,D 为线段AC 的中点,E 为线段PC 上一点.(1)求证:PA ⊥BD ;(2)求证:平面BDE ⊥平面PAC ;(3)当PA ∥平面BDE 时,求三棱锥E -BCD 的体积.37.如图1,在边长为1的等边三角形ABC 中,D ,E 分别是AB ,AC 边上的点,AD =AE ,F 是BC 的中点,AF 与DE 交于点G ,将△ABF 沿AF 折起,得到如图2所示的三棱锥A -BCF ,其中BC =22. (1)求证:DE ∥平面BCF ;(2)求证:CF ⊥平面ABF ;(3)当AD =23时,求三棱锥F -DEG 的体积.立体几何 单元复习卷(一)1.用任意一个平面截一个几何体,各个截面都是圆面,则这个几何体一定是( )A .圆柱B .圆锥C .球体D .圆柱、圆锥、球体的组合体解析:选C 截面是任意的且都是圆面,则该几何体为球体.2.给出下列命题:①棱柱的侧棱都相等,侧面都是全等的平行四边形;②若三棱锥的三条侧棱两两垂直,则其三个侧面也两两垂直;③在四棱柱中,若两个过相对侧棱的截面都垂直于底面,则该四棱柱为直四棱柱; ④存在每个面都是直角三角形的四面体.其中正确命题的序号是________.解析:①不正确,根据棱柱的定义,棱柱的各个侧面都是平行四边形,但不一定全等;②正确,若三棱锥的三条侧棱两两垂直,则三个侧面构成的三个平面的二面角都是直二面角;③正确,因为两个过相对侧棱的截面的交线平行于侧棱,又垂直于底面;④正确,如图,正方体ABCD -A 1B 1C 1D 1中的三棱锥C 1-ABC ,四个面都是直角三角形.答案:②③④3.已知正三角形ABC 的边长为2,那么△ABC 的直观图△A ′B ′C ′的面积为________.解析:如图,图①、图②分别表示△ABC 的实际图形和直观图.从图②可知,A ′B ′=AB =2,O ′C ′=12OC =32,C ′D ′=O ′C ′sin 45°=32×22=64. 所以S △A ′B ′C ′=12A ′B ′·C ′D ′=12×2×64=64. 答案:644.已知圆锥的表面积等于12π cm 2,其侧面展开图是一个半圆,则底面圆的半径为________cm.解析:S 表=πr2+πrl =πr2+πr ·2r =3πr2=12π,∴r2=4,∴r =2 cm.6. (2018·苏州零模)鲁班锁是中国传统的智力玩具,起源于中国古代建筑中首创的榫卯结构,它的外观是如图所示的十字立方体,其上下、左右、前后完全对称,六根等长的正四棱柱体分成三组,经90°榫卯起来.若正四棱柱的高为5,底面正方形的边长为1,现将该鲁班锁放进一个球形容器内,则该球形容器的表面积至少为________。
2024年高考数学立体几何复习试卷及答案解析

2024年高考数学立体几何复习试卷及答案
一、选择题
1.已知直线l和平面α,若l∥α,P∈α,则过点P且平行于l的直线()
A.只有一条,不在平面α内
B.只有一条,且在平面α内
C.有无数条,一定在平面α内
D.有无数条,不一定在平面α内
答案B
解析假设过点P且平行于l的直线有两条m与n,则m∥l且n∥l,由平行公理得m∥n,这与两条直线m与n相交与点P相矛盾,故过点P且平行于l的直线只有一条,又因为点P 在平面内,所以过点P且平行于l的直线只有一条且在平面内.故选B.
2.设m,n为两条不同的直线,α为平面,则下列结论正确的是()
A.m⊥n,m∥α⇒n⊥αB.m⊥n,m⊥α⇒n∥α
C.m∥n,m⊥α⇒n⊥αD.m∥n,m∥α⇒n∥α
答案C
解析对于A,若m⊥n,m∥α时,可能n⊂α或斜交,故错误;
对于B,m⊥n,m⊥α⇒n∥α或n⊂α,故错误;
对于C,m∥n,m⊥α⇒n⊥α,正确;
对于D,m∥n,m∥α⇒n∥α或n⊂α,故错误.
故选C.
3.已知l⊥平面α,直线m⊂平面β.有下面四个命题:
①α∥β⇒l⊥m;②α⊥β⇒l∥m;
③l∥m⇒α⊥β;④l⊥m⇒α∥β.
其中正确的命题是()
A.①②B.③④
C.②④D.①③
答案D
解析∵l⊥α,α∥β,∴l⊥β,∵m⊂β,∴l⊥m,故①正确;∵l∥m,l⊥α,∴m⊥α,又∵m⊂β,∴α⊥β,故③正确.
4.如图所示,在四面体D-ABC中,若AB=BC,AD=CD,E是AC的中点,则下列命题中正确的是()
第1页共11页。
《立体几何复习》课件

善于运用逻辑推理和归纳总结的方法解决问题。
总结和要点
立体几何概念
立体几何是研究空间图形的分 支学科。
• 常见的图形 • 基本性质 • 公式和公理
应用和技巧
如何应用立体几何解决实际问 题。
• 观察问题 • 建立模型 • 应用公式和性质
练习和考试
如何练习和应对立体几何考试。
• 多做练习题 • 理解题目要求 • 推理和归纳
《立体几何复习》PPT课 件
立体几何是研究空间图形的形状、大小、位置及其性质的一个分支学科。通 过这个PPT课件,我们将全面复习立体几何的各个方面,并提供解决问题的方 法和考试技巧。
立体几何概述
1 什么是立体几何?
立体几何研究的是空间中的三维图形,包括球体、立方体、圆锥体等。
2 为什么要学习立体几何?
应用立体几何解决实际问题的方法
1
观察问题
仔细观察问题,理解所给信息和要求。
2
建立模型
根据问题建立合适的几何图形模型。
3
应用公式和性质
利用已知的公式和性质进行计算和推理。
立体几何的练习和考试技巧
1 多做练习题
通过做大量练习题来提高解题能力和应用能力。
2 理解题目要求
仔细阅读题目,理解题目所要求解决的问题。
立体几何不仅有实际应用,还有助于培养我们的空间思维能力和逻辑推理能பைடு நூலகம்。
3 立体几何的重要性
立体几何在建筑、工程、艺术等领域都有广泛的应用。
常见的立体几何图形
立方体
立方体具有六个面、八个顶点和 十二条边。
圆柱体
圆柱体由两个平行的圆形底面和 一个侧面组成。
金字塔
金字塔有一个多边形底面和三角 形的侧面。
立体几何复习(知识点+经典习题)

立体几何复习(知识点+经典习题)1.给出以下命题:1) 若平面α内的两条相交直线分别平行于平面β内的两条直线,则平面α平行于平面β;2) 若平面α外一条直线l与平面α内的一条直线平行,则直线l和平面α平行;3) 设平面α和平面β相交于直线l,若平面α内有一条直线垂直于l,则平面α和平面β垂直;4) 直线l与平面α垂直的充分必要条件是直线l与平面α内的两条直线垂直。
写出所有真命题的序号。
2.在空间中,以下命题正确的是:A) 平行直线的平行投影重合;B) 平行于同一直线的两个平面平行;C) 垂直于同一平面的两个平面平行;D) 垂直于同一平面的两条直线平行。
考点为二三视图与直观图及面积与体积。
基础训练】1.如图,E和F分别为正方体的面ADD1A1和面BCC1B1的中心,则四边形BFD1E在该正方体的面上的投影可能是什么形状。
2.如果一个水平放置的图形的斜二测直观图是一个底角为45度,腰和上底均为1的等腰梯形,则原图形的面积是多少?3.在三角形ABC中,AB=2,BC=1.5,∠ABC=120度。
若使其绕直线BC旋转一周,则它形成的几何体的体积是多少?4.已知一个长方体共一顶点的三个面的面积分别是2,3,6,则这个长方体的对角线长是多少?若长方体共顶点的三个侧面面积分别为3,5,15,则它的体积是多少?5.正方体的内切球和外接球的半径之比为多少?6.一个正方体的顶点都在球面上,它的棱长为2,则球的表面积是多少?7.若三个球的表面积之比是1:2:3,则它们的体积之比是多少?8.长方体的一个顶点上三条棱长分别为3、4、5,且它的8个顶点都在同一球面上,则这个球的表面积是多少?9.半径为R的半圆卷成一个圆锥,则它的体积为多少?高考链接】1.一个棱锥的三视图如图,则该棱锥的全面积为多少?2.设某几何体的三视图如下,则该几何体的体积为多少?1.在三棱锥ABCDE中,AB=AC=AD=2,BC=3,CD=4,BE=5,CE=6,DE=7,求∠AED的大小。
浅谈立体几何教学的复习策略探究

浅谈立体几何教学的复习策略探究
立体几何是数学中的一个重要分支,它是指研究立体几何形体
的属性和关系,并通过数学语言来表示和计算。
在立体几何教学中,复习角度有很多,可以从以下几个方面入手。
一、基础概念回顾
立体几何的基本概念包括立体图形的构成要素、几何体的公式
和性质、空间平面的性质等。
在复习时,可以通过做练习题的方式
来回顾这些知识点,并注意理解其中的关系和联系。
二、立体几何证明方法和技巧
在立体几何的证明过程中,往往需要运用相关的证明方法和技巧,如勾股定理、相似三角形的性质、平行直线截立体的性质等。
复习时可以针对这些内容进行系统、全面的梳理,同时结合实际例
题进行讲解和分析。
三、应用题练习
在课程中,应用题占据了很大的比重。
因此,复习时需要重点
关注应用题。
对于不熟悉的应用题,建议先分析题目,找到解题方法,并且在熟悉之后要多做类似题目进行练习。
四、思维拓展
从立体几何的角度出发,可以帮助学生开拓思维,具体包括建模、推导和综合运用等。
在复习时,可以针对这些内容进行较为深
入的思考,探究如何运用立体几何的知识去解决实际问题。
总之,立体几何的复习策略应该是多维度、多方面的。
只有全
面系统、深入地理解了相关知识点,才能更好地解决应用问题。
第八章-立体几何初步复习课图文课件

性不变.
复习回顾 结合正八棱柱的直观图,说出用斜二测画法画空间几何体的 直观图的基本步骤.
横竖不变,纵减半,平行性不变
复习回顾
问题3 对于空间几何体,可以有不同的分类,你能选择不同的分 类标准对柱、锥、台、球等空间几何体进行分类吗?如何计算柱、 锥、台、球的表面积和体积?你能说出柱、锥、台、球的体积公式 之间的联系吗?
,得 α ∩ γ =a;又γ ∩ β =直线b,故a与b
重合,
α , β , γ相交于同一条直线.
复习回顾
探究3 已知三个不同的平面 α, β, γ两两相交,设 α ∩ β=直线 c,
β ∩ γ =直线a, γ ∩ α =直线b,试问a,b,c有怎样的位置关系?
说明理由并画出相应图形. ②当a与c相交时,设a∩c=点O,由 α ∩ β =直线c, β ∩ γ
复习回顾 探究4 怎样求图中的四个四面体的外接球与内切球的半径?
四个四面体的外接球与正方体的
类比
外接球相同,其一条直径为正方
体的体对角线,半径
.
复习回顾
问题4 刻画平面的三个基本事实是立体几何公理体系的基石,是 研究空间图形、进行逻辑推理的基础.实际上,三个基本事实刻画 了平面的“平”、平面的“无限延展”,你能归纳一下刻画的方法
探究1 说明作出点H的过程.点H在线段DB1的什么位置?
设B1D1 ∩A1C1=P,点P为线段B1D1的中点,且平面
A1BC1 ∩平面BB1D1D=BP.
在矩形BB1D1D中, BP∩B1D=H.
由△B1HP∽△DHB,且 .
,知
复习回顾
探究1 说明作出点H的过程.点H在线段DB1的什么位置?
人教版高中数学必修立体几何复习课件(共102张PPT)

1 1
1
11.已知某个几何体的三视图如图2,根据图中标出的尺寸 (单位:cm),可得这个几何体的体积是_____8_0__0.0 cm 3
3
2 0 20
主视图
10
10
2 俯0视图
2 侧0视图
第二章 点、直线、平面之间的位置关系
• 四个公理
直线与直线位置关系 • 三类关系 直线与平面位置关系
平面与平面位置关系
(3)
a a
// b
b
(较常用);
(4)
a
//
a
;
(5)
a a
b
a
(面面垂直 线面垂直)
a b
4.面面垂直
向的侧视图(或称左视图)为(
A
A
H
G
Q
B
C
侧视 B
)A
C
I
P
E
图1
F
B
D
E
D
图2
F
B
B
B
E A.
E B.ቤተ መጻሕፍቲ ባይዱ
E C.
E D.
练习10:(1)如图是一个空间几何体的三
视图,如果直角三角形的直角边长均为
正视图 侧视图
1,那么几何体的体积为( ) C
A.1 B.1 C. 1 D.1
俯视图
2
3
6
V1 3S底 h1 31111 3
②判定定理:如果一个平面内的两条相交直线都平行于 另一个平面,那么两个平面互相平行;
符号表述: a,b , a b O, a //,b // //
//
③面面平行的性质定理:
a
a
//
高三《立体几何》专题复习

高三《立体几何》专题复习一、常用知识点回顾1、三视图。
正侧一样高,正俯一样长,侧府一样宽,看不到的线画虚线。
2、常用公式与结论。
(1)圆柱、圆锥、圆台的侧面展开图及侧面积公式;(2)空间几何体的表面积与体积公式;(3)全品高考复习方案(听课手册)105页的常用结论3、两条异面直线所成的角;直线与平面所成的角。
4、证明两条直线平行的常用方法;直线与平面平行的判定与性质;面面平行的判定与性质。
5、证明两条直线垂直的常用方法;直线与平面垂直的判定与性质;两个平面垂直的判定与性质。
二、题型训练题型一:三视图的运用,求几何体的体积、表面积例1、如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的表面积为()(A)18+(B)54+(C)90(D)81【练习1】某圆柱的高为2,底面周长为16,其三视图如右图.圆柱表面上的点M在正视图上的对应点为A,圆柱表面上的点N在左视图上的对应点为B,则在此圆柱侧面上,从M到N的路径中,最短路径的长度为()C.3D.2【练习2】如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分后所得,则该几何体的体积为( )A.90πB.63πC.42πD.36π【练习3】如图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为( )(A )20π(B )24π(C )28π(D )32π例2、在封闭的直三棱柱ABC -A 1B 1C 1内有一个体积为V 的球.若AB ⊥BC ,AB =6,BC =8,AA 1=3,则V 的最大值是( )(A )4π (B )9π2 (C )6π (D )32π3变式1:在封闭的直三棱柱ABC-A1B1C1内有一个体积为V的球.若AB⊥BC,AB=6,BC=8,AA1=5,则V的最大值是变式2:在封闭的长方体ABCD-A1B1C1D1内有一个体积为V的球.若AB=BC=6,AA1=3,则V的最大值是变式3:(1)长方体的长、宽、高分别为3,2,1,其顶点都在球O的球面上,则球O的表面积为(2)体积为8的正方体的顶点都在同一球面上,则该球面的表面积为变式4:【练习1】已知圆柱的上、下底面的中心分别为O1,O2,过直线O1O2的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为()A. B.12π C. D.10π【练习3】已知圆锥的顶点为S,母线SA,SB互相垂直,SA与圆锥底面所成角为30°,若SAB的面积为8,则该圆锥的体积为_______题型二:平行问题例1、如图,四棱锥P-ABCD中,PA⊥底面ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点.(I)证明MN∥平面PAB; (II)求四面体N-BCM的体积.【练习1】如图,四棱锥P-ABCD中,侧面PADAD,为等边三角形且垂直于底面ABCD,AB=BC=12∠BAD=∠ABC=90°。
高考立体几何知识点详细复习总结
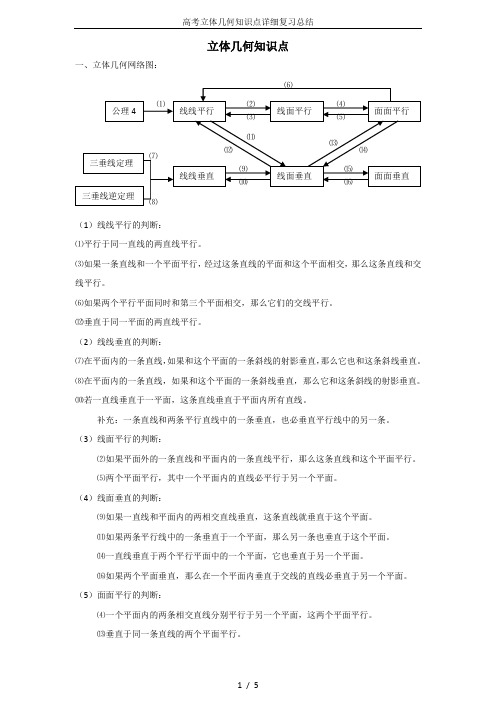
立体几何知识点一、立体几何网络图:(1)线线平行的判断:⑴平行于同一直线的两直线平行。
⑶如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行。
⑹如果两个平行平面同时和第三个平面相交,那么它们的交线平行。
⑿垂直于同一平面的两直线平行。
(2)线线垂直的判断:⑺在平面内的一条直线,如果和这个平面的一条斜线的射影垂直,那么它也和这条斜线垂直。
⑻在平面内的一条直线,如果和这个平面的一条斜线垂直,那么它和这条斜线的射影垂直。
⑽若一直线垂直于一平面,这条直线垂直于平面内所有直线。
补充:一条直线和两条平行直线中的一条垂直,也必垂直平行线中的另一条。
(3)线面平行的判断:⑵如果平面外的一条直线和平面内的一条直线平行,那么这条直线和这个平面平行。
⑸两个平面平行,其中一个平面内的直线必平行于另一个平面。
(4)线面垂直的判断:⑼如果一直线和平面内的两相交直线垂直,这条直线就垂直于这个平面。
⑾如果两条平行线中的一条垂直于一个平面,那么另一条也垂直于这个平面。
⒁一直线垂直于两个平行平面中的一个平面,它也垂直于另一个平面。
⒃如果两个平面垂直,那么在—个平面内垂直于交线的直线必垂直于另—个平面。
(5)面面平行的判断:⑷一个平面内的两条相交直线分别平行于另一个平面,这两个平面平行。
⒀垂直于同一条直线的两个平面平行。
(6)面面垂直的判断: ⒂一个平面经过另一个平面的垂线,这两个平面互相垂直。
二、其他定理:(1)确定平面的条件:①不公线的三点;②直线和直线外一点;③相交直线; (2)直线与直线的位置关系: 相交 ; 平行 ; 异面 ;直线与平面的位置关系: 在平面内 ; 平行 ; 相交(垂直是它的特殊情况) ; 平面与平面的位置关系: 相交 ;; 平行 ;(3)等角定理:如果两个角的两边分别平行且方向相同,那么这两个角相等;如果两条相交直线和另外两条相交直线分别平行,那么这两组直线所成的锐角(或直角)相等;(4)射影定理(斜线长、射影长定理):从平面外一点向这个平面所引的垂线段和斜线段中,射影相等的两条斜线段相等;射影较长的斜线段也较长;反之,斜线段相等的射影相等;斜线段较长的射影也较长;垂线段比任何一条斜线段都短。
高三立体几何专题复习

高考立体几何专题复习一.考试要求:〔1〕掌握平面的根本性质,会用斜二测的画法画水平放置的平面图形的直观图,能够画出空间两条直线、直线和平面的各种位置关系的图形,能够根据图形想象它们的位置关系。
〔2〕了解空两条直线的位置关系,掌握两条直线平行与垂直的判定定理和性质定理,掌握两条直线所成的角和距离的概念〔对于异面直线的距离,只要求会计算已给出公垂线时的距离〕。
〔3〕了解空间直线和平面的位置关系,掌握直线和平面平行的判定定理和性质定理,理解直线和平面垂直的判定定理和性质定理,掌握斜线在平面上的射影、直线和平面所成的角、直线和平面的距离的概念,了解三垂线定理及其逆定理。
〔4〕了解平面与平面的位置关系,掌握两个平面平行的判定定理和性质定理。
掌握二面角、二面角的平面角、两个平面间的距离的概念,掌握两个平面垂直的判定定理和性质定理。
〔5〕会用反证法证明简单的问题。
〔6〕了解多面体的概念,了解凸多面体的概念。
〔7〕了解棱柱的概念,掌握棱柱的性质,会画直棱柱的直观图。
〔8〕了解棱锥的概念,掌握正棱锥的性质,会画正棱锥的直观图。
〔9〕了解正多面体的概念,了解多面体的欧拉公式。
〔10〕了解球的概念,掌握球的性质,掌握球的外表积、体积公式。
二.复习目标:1.在掌握直线与平面的位置关系(包括直线与直线、直线与平面、平面与平面间的位置关系)的根底上,研究有关平行和垂直的的判定依据(定义、公理和定理)、判定方法及有关性质的应用;在有关问题的解决过程中,进一步了解和掌握相关公理、定理的容和功能,并探索立体几何中论证问题的规律;在有关问题的分析与解决的过程中提高逻辑思维能力、空间想象能力及化归和转化的数学思想的应用.2.在掌握空间角(两条异面直线所成的角,平面的斜线与平面所成的角及二面角)概念的根底上,掌握它们的求法(其根本方法是分别作出这些角,并将它们置于*个三角形通过计算求出它们的大小);在解决有关空间角的问题的过程中,进一步稳固关于直线和平面的平行垂直的性质与判定的应用,掌握作平行线(面)和垂直线(面)的技能;通过有关空间角的问题的解决,进一步提高学生的空间想象能力、逻辑推理能力及运算能力.3.通过复习,使学生更好地掌握多面体与旋转体的有关概念、性质,并能够灵活运用到解题过程中.通过教学使学生掌握根本的立体几何解题方法和常用解题技巧,开掘不同问题之间的在联系,提高解题能力.4.在学生解答问题的过程中,注意培养他们的语言表述能力和"说话要有根据〞的逻辑思维的习惯、提高思维品质.使学生掌握化归思想,特别是将立体几何问题转化为平面几何问题的思想意识和方法,并提高空间想象能力、推理能力和计算能力.5.使学生更好地理解多面体与旋转体的体积及其计算方法,能够熟练地使用分割与补形求体积,提高空间想象能力、推理能力和计算能力.三.教学过程:〔Ⅰ〕根底知识详析高考立体几何试题一般共有4道(选择、填空题1--2道, 解答题1道), 共计总分20分左右,考察的知识点在20个以. 选择填空题考核立几中的计算型问题, 而解答题着重考察立几中的逻辑推理型问题, 当然, 二者均应以正确的空间想象为前提. 随着新的课程改革的进一步实施,立体几何考题正朝着"多一点思考,少一点计算〞的开展.从历年的考题变化看, 以多面体和旋转体为载体的线面位置关系的论证,角与距离的探常考常新的热门话题.1.有关平行与垂直(线线、线面及面面)的问题,是在解决立体几何问题的过程中,大量的、反复遇到的,而且是以各种各样的问题(包括论证、计算角、与距离等)中不可缺少的容,因此在主体几何的总复习中,首先应从解决"平行与垂直〞的有关问题着手,通过较为根本问题,熟悉公理、定理的容和功能,通过对问题的分析与概括,掌握立体几何中解决问题的规律——充分利用线线平行(垂直)、线面平行(垂直)、面面平行(垂直)相互转化的思想,以提高逻辑思维能力和空间想象能力.2.判定两个平面平行的方法:〔1〕根据定义——证明两平面没有公共点;〔2〕判定定理——证明一个平面的两条相交直线都平行于另一个平面;〔3〕证明两平面同垂直于一条直线。
高三数学复习(文科)立体几何知识点、方法总结
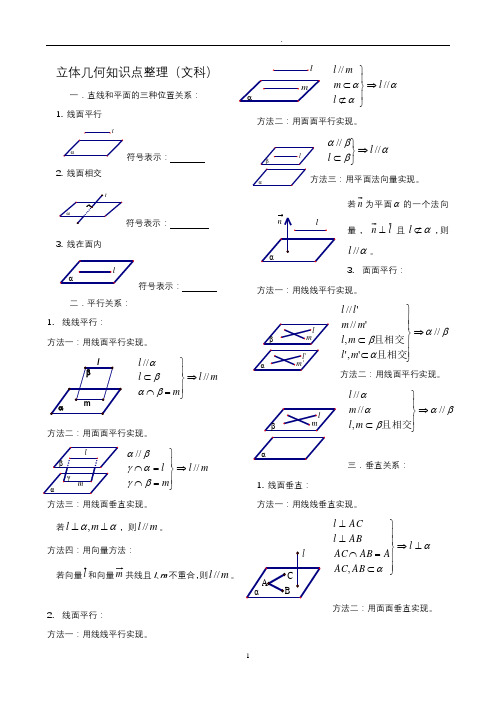
立体几何知识点整理(文科)一.直线和平面的三种位置关系:1. 线面平行符号表示:2. 线面相交符号表示:3. 线在面内符号表示:二.平行关系:1.线线平行:方法一:用线面平行实现。
mlmll////⇒⎪⎭⎪⎬⎫=⋂⊂βαβα方法二:用面面平行实现。
mlml////⇒⎪⎭⎪⎬⎫=⋂=⋂βγαγβα方法三:用线面垂直实现。
若αα⊥⊥ml,,则ml//。
方法四:用向量方法:若向量l和向量m共线且l、m不重合,则ml//。
2.线面平行:方法一:用线线平行实现。
ααα////llmml⇒⎪⎭⎪⎬⎫⊄⊂方法二:用面面平行实现。
αββα////ll⇒⎭⎬⎫⊂方法三:用平面法向量实现。
若n为平面α的一个法向量,ln⊥且α⊄l,则α//l。
3.面面平行:方法一:用线线平行实现。
βααβ//',','//'//⇒⎪⎪⎭⎪⎪⎬⎫⊂⊂且相交且相交mlmlmmll方法二:用线面平行实现。
βαβαα//,////⇒⎪⎭⎪⎬⎫⊂且相交mlml三.垂直关系:1. 线面垂直:方法一:用线线垂直实现。
αα⊥⇒⎪⎪⎭⎪⎪⎬⎫⊂=⋂⊥⊥lABACAABACABlACl,方法二:用面面垂直实现。
llαββαβα⊥⇒⎪⎭⎪⎬⎫⊂⊥=⋂⊥l l m l m ,2. 面面垂直:方法一:用线面垂直实现。
βαβα⊥⇒⎭⎬⎫⊂⊥l l方法二:计算所成二面角为直角。
3. 线线垂直:方法一:用线面垂直实现。
m l m l ⊥⇒⎭⎬⎫⊂⊥αα方法二:三垂线定理及其逆定理。
PO l OA l PA l αα⊥⎫⎪⊥⇒⊥⎬⎪⊂⎭方法三:用向量方法:若向量l 和向量m 的数量积为0,则m l ⊥。
三.夹角问题。
(一) 异面直线所成的角: (1) 范围:]90,0(︒︒ (2)求法: 方法一:定义法。
步骤1:平移,使它们相交,找到夹角。
步骤2:解三角形求出角。
(常用到余弦定理)余弦定理:abcb a 2cos 222-+=θ(计算结果可能是其补角)方法二:向量法。
