立体几何动态问题(二轮)含答案
2018年高考数学江苏专版三维二轮专题复习教学案:专题二 立体几何 Word版含答案

江苏 新高考高考对本专题内容的考查一般是“一小一大”,小题主要考查体积和表面积的计算问题,而大题主要证明线线、线面、面面的平行与垂直问题,其考查形式单一,难度一般.第1课时立体几何中的计算(基础课) [常考题型突破]空间几何体的几组常用公式(1)柱体、锥体、台体的侧面积公式: ①S 柱侧=ch (c 为底面周长,h 为高); ②S 锥侧=12ch ′(c 为底面周长,h ′为斜高);③S 台侧=12(c +c ′)h ′(c ′,c 分别为上下底面的周长,h ′为斜高).(2)柱体、锥体、台体的体积公式: ①V 柱体=Sh (S 为底面面积,h 为高); ②V 锥体=13Sh (S 为底面面积,h 为高);③V 台=13(S +SS ′+S ′)h (不要求记忆).(3)球的表面积和体积公式: ①S 球=4πR 2(R 为球的半径); ②V 球=43πR 3(R 为球的半径).[题组练透]1.现有一个底面半径为3 cm ,母线长为5 cm 的圆锥状实心铁器,将其高温熔化后铸成一个实心铁球(不计损耗),则该铁球的半径为________cm.解析:因为圆锥底面半径为3 cm ,母线长为5 cm ,所以圆锥的高为52-32=4 cm ,其体积为13π×32×4=12π cm 3,设铁球的半径为r ,则43πr 3=12π,所以该铁球的半径是39cm.答案:392.(2017·苏锡常镇二模)已知直四棱柱底面是边长为2的菱形,侧面对角线的长为23,则该直四棱柱的侧面积为________.解析:由题意得,直四棱柱的侧棱长为(23)2-22=22,所以该直四棱柱的侧面积为S =cl =4×2×22=16 2.答案:16 23.(2017·南通、泰州一调)如图,在正四棱柱ABCD -A 1B 1C 1D 1中,AB =3 cm ,AA 1=1 cm ,则三棱锥D 1-A 1BD 的体积为_______cm 3.解析:三棱锥D 1-A 1BD 的体积等于三棱锥B -A 1D 1D 的体积,因为三棱锥B -A 1D 1D 的高等于AB ,△A 1D 1D 的面积为矩形AA 1D 1D 的面积的12,所以三棱锥B -A 1D 1D 的体积是正四棱柱ABCD -A 1B 1C 1D 1的体积的16,所以三棱锥D 1-A 1BD 的体积等于16×32×1=32.答案:324.如图所示是一个直三棱柱(以A 1B 1C 1为底面)被一个平面所截得到的几何体,截面为ABC ,已知A 1B 1=B 1C 1=1,∠A 1B 1C 1=90°,A 1A =4,B 1B =2,C 1C =3,则此几何体的体积为________.解析:在A 1A 上取点A 2,在C 1C 上取点C 2,使A 1A 2=C 1C 2=BB 1,连结A 2B ,BC 2,A 2C 2,∴V =VA B C A BC 11122-+VB A ACC 22-=12×1×1×2+13×(1+2)2×2×22=32. 答案:325.设甲,乙两个圆柱的底面积分别为S 1,S 2,体积分别为V 1,V 2.若它们的侧面积相等且V 1V 2=32,则S 1S 2的值是________.解析:设甲,乙两个圆柱的底面半径分别为r 1,r 2,高分别为h 1,h 2,则有2πr 1h 1=2πr 2h 2,即r 1h 1=r 2h 2,又V 1V 2=πr 21h 1πr 22h 2,∴V 1V 2=r 1r 2,∴r 1r 2=32,则S 1S 2=⎝⎛⎭⎫r 1r 22=94.答案:94[方法归纳]解决球与其他几何体的切、接问题(1)解题的关键:仔细观察、分析,弄清相关元素的位置关系和数量关系.(2)选准最佳角度作出截面:要使这个截面尽可能多地包含球、几何体的各种元素以及体现这些元素之间的关系,达到空间问题平面化的目的.(3)认识球与正方体组合的3种特殊截面:(4)熟记2个结论:①设小圆O 1半径为r ,OO 1=d ,则d 2+r 2=R 2;②若A ,B 是圆O 1上两点,则AB =2r sin ∠AO 1B 2=2R sin ∠AOB 2.[题组练透]1.(2017·江苏高考)如图,在圆柱O 1O 2内有一个球O ,该球与圆柱的上、下底面及母线均相切.记圆柱O 1O 2的体积为V 1,球O 的体积为V 2,则V 1V 2的值是________.解析:设球O 的半径为R ,因为球O 与圆柱O 1O 2的上、下底面及母线均相切,所以圆柱的底面半径为R 、高为2R ,所以V 1V 2=πR 2·2R 43πR 3=32.答案:322.(2017·全国卷Ⅲ改编)已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为________.解析:设圆柱的底面半径为r ,则r 2=12-⎝⎛⎭⎫122=34,所以圆柱的体积V =34×π×1=3π4.答案:3π43.已知矩形ABCD的顶点都在半径为2的球O的球面上,且AB=3,BC=3,过点D作DE垂直于平面ABCD,交球O于E,则棱锥E-ABCD的体积为________.解析:如图所示,BE过球心O,∴DE=42-32-(3)2=2,∴V E -ABCD=13×3×3×2=2 3.答案:2 34.(2017·南京、盐城一模)将矩形ABCD绕边AB旋转一周得到一个圆柱,AB=3,BC =2,圆柱上底面圆心为O,△EFG为下底面圆的一个内接直角三角形,则三棱锥O-EFG 体积的最大值是________.解析:因为将矩形ABCD绕边AB旋转一周得到一个圆柱,AB=3,BC=2,圆柱上底面圆心为O,△EFG为下底面圆的一个内接直角三角形,所以三棱锥O-EFG的高为圆柱的高,即高为AB,所以当三棱锥O-EFG体积取最大值时,△EFG的面积最大,当EF为直径,且G在EF的垂直平分线上时,(S△EFG)max=12×4×2=4,所以三棱锥O-EFG体积的最大值(V O-EFG)max=13×(S△EFG)max×AB=13×4×3=4.答案:4[方法归纳]多面体与球的切接问题的解题技巧[必备知识]将平面图形沿其中一条或几条线段折起,使其成为空间图形,把这类问题称为平面图形的翻折问题.平面图形经过翻折成为空间图形后,原有的性质有的发生了变化,有的没有发生变化,弄清它们是解决问题的关键.一般地,翻折后还在同一个平面上的性质不发生变化,不在同一个平面上的性质发生变化.解决这类问题就是要据此研究翻折以后的空间图形中的线面关系和几何量的度量值,这是化解翻折问题难点的主要方法.[题组练透]1.(2017·南通三模)已知圆锥的侧面展开图是半径为3,圆心角为2π3的扇形,则这个圆锥的高为________.解析:因为圆锥的侧面展开图是半径为3,圆心角为2π3的扇形,所以圆锥的母线长l =3,设圆锥的底面半径为r ,则底面周长2πr =3×2π3,所以r =1,所以圆锥的高为32-12=2 2. 答案:2 22.(2017·南京考前模拟)如图,正△ABC 的边长为2,CD 是AB 边上的高,E ,F 分别为边AC 与BC 的中点,现将△ABC 沿CD 翻折,使平面ADC ⊥平面DCB ,则棱锥E -DFC 的体积为________.解析:S △DFC =14S △ABC =14×⎝⎛⎭⎫34×22=34,E 到平面DFC 的距离h 等于12AD =12. V E -DFC =13×S △DFC×h =324. 答案:3243.(2017·全国卷Ⅰ)如图,圆形纸片的圆心为O ,半径为5 cm ,该纸片上的等边三角形ABC 的中心为O .D ,E ,F 为圆O 上的点,△DBC ,△ECA ,△FAB 分别是以BC ,CA ,AB 为底边的等腰三角形.沿虚线剪开后,分别以BC ,CA ,AB 为折痕折起△DBC ,△ECA ,△FAB ,使得D ,E ,F 重合,得到三棱锥.当△ABC 的边长变化时,所得三棱锥体积(单位:cm 3)的最大值为________.解析:法一:由题意可知,折起后所得三棱锥为正三棱锥,当△ABC 的边长变化时, 设△ABC 的边长为a (a >0)cm , 则△ABC 的面积为34a 2,△DBC 的高为5-36a , 则正三棱锥的高为⎝⎛⎭⎫5-36a 2-⎝⎛⎭⎫36a 2=25-533a , ∴25-533a >0, ∴0<a <53,∴所得三棱锥的体积V =13×34a 2×25-533a =312× 25a 4-533a 5. 令t =25a 4-533a 5,则t ′=100a 3-2533a 4, 由t ′=0,得a =43,此时所得三棱锥的体积最大,为415 cm 3.法二:如图,连接OD 交BC 于点G ,由题意知,OD ⊥BC .易得OG=36BC , 设OG =x ,则BC =23x ,DG =5-x ,S △ABC =12×23x ×3x =33x 2,故所得三棱锥的体积V =13×33x 2×(5-x )2-x 2=3x 2×25-10x =3×25x 4-10x 5.令f (x )=25x 4-10x 5,x ∈⎝⎛⎭⎫0,52, 则f ′(x )=100x 3-50x 4,令f ′(x )>0,即x 4-2x 3<0,得0<x <2, 则当x ∈⎝⎛⎭⎫0,52时,f (x )≤f (2)=80, ∴V ≤3×80=415.∴所求三棱锥的体积的最大值为415. 答案:415 [方法归纳][A 组——抓牢中档小题]1.已知正方体ABCD -A 1B 1C 1D 1的棱长为1,点E 是棱B 1B 的中点,则三棱锥B 1-ADE 的体积为________.解析:VB 1-ADE =VD -AEB 1=13S △AEB 1·DA =13×12×12×1×1=112.答案:1122.若两球表面积之比是4∶9,则其体积之比为________.解析:设两球半径分别为r 1,r 2,因为4πr 21∶4πr 22=4∶9,所以r 1∶r 2=2∶3,所以两球体积之比为43πr 31∶43πr 32=⎝⎛⎭⎫r 1r 23=⎝⎛⎭⎫233=8∶27.答案:8∶273.(2017·天津高考)已知一个正方体的所有顶点在一个球面上,若这个正方体的表面积为18,则这个球的体积为________.解析:设正方体的棱长为a ,则6a 2=18,得a =3,设该正方体外接球的半径为R ,则2R =3a =3,得R =32,所以该球的体积为43πR 3=4π3×278=92π.答案:92π4.已知圆锥的母线长为10 cm ,侧面积为60π cm 2,则此圆锥的体积为________cm 3. 解析:设圆锥底面圆的半径为r ,母线长为l ,则侧面积为πrl =10πr =60π,解得r =6,则圆锥的高h =l 2-r 2=8,则此圆锥的体积为13πr 2h =13π×36×8=96π.答案:96π5.(2017·扬州期末)若正四棱锥的底面边长为2(单位:cm),侧面积为8(单位:cm 2),则它的体积为________(单位:cm 3).解析:因为正四棱锥的底面边长为2,侧面积为8,所以底面周长c =8,12ch ′=8,所以斜高h ′=2,正四棱锥的高为h =3,所以正四棱锥的体积为13×22×3=433.答案:4336.设棱长为a 的正方体的体积和表面积分别为V 1,S 1,底面半径和高均为r 的圆锥的体积和侧面积分别为V 2,S 2,若V 1V 2=3π,则S 1S 2的值为________. 解析:由题意知,V 1=a 3,S 1=6a 2,V 2=13πr 3,S 2=2πr 2,由V 1V 2=3π得,a 313πr 3=3π,得a=r ,从而S 1S 2=62π=32π.答案:32π7.(2017·苏北三市三模)如图,在正三棱柱ABC -A1B 1C 1中,已知AB =AA 1=3,点P 在棱CC 1上,则三棱锥P -ABA 1的体积为________.解析:三棱锥的底面积S △ABA 1=12×3×3=92,点P 到底面的距离为△ABC 的高h =32-⎝⎛⎭⎫322=332,故三棱锥的体积VP -ABA 1=13S △ABA 1×h =934. 答案:9348.(2017·无锡期末)已知圆锥的侧面展开图为一个圆心角为2π3,且面积为3π的扇形,则该圆锥的体积等于________.解析:设圆锥的母线为l ,底面半径为r , 因为3π=13πl 2,所以l =3,所以πr ×3=3π,所以r =1,所以圆锥的高是32-12=22,所以圆锥的体积是13×π×12×22=22π3.答案:22π39.(2017·徐州古邳中学摸底)表面积为24π的圆柱,当其体积最大时,该圆柱的底面半径与高的比为________.解析:设圆柱的高为h ,底面半径为r , 则圆柱的表面积S =2πr 2+2πrh =24π, 即r 2+rh =12,得rh =12-r 2, ∴V =πr 2h =πr (12-r 2)=π(12r -r 3), 令V ′=π(12-3r 2)=0,得r =2,∴函数V =πr 2h 在区间(0,2]上单调递增,在区间[2,+∞)上单调递减,∴r =2时,V 最大,此时2h =12-4=8,即h =4,r h =12.答案:1210.三棱锥P -ABC 中,PA ⊥平面ABC ,AC ⊥BC ,AC =BC =1,PA =3,则该三棱锥外接球的表面积为________.解析:把三棱锥P -ABC 看作由平面截一个长、宽、高分别为1、1、3的长方体所得的一部分(如图).易知该三棱锥的外接球就是对应长方体的外接球.又长方体的体对角线长为12+12+(3)2=5,故外接球半径为52,表面积为4π×⎝⎛⎭⎫522=5π. 答案:5π11.已知正三棱锥P -ABC 的体积为223,底面边长为2,则侧棱PA 的长为________.解析:设底面正三角形ABC 的中心为O ,又底面边长为2,故OA =233,由V P -ABC =13PO ·S △ABC ,得223=13PO ×34×22,PO =263,所以PA =PO 2+AO 2=2. 答案:212.(2017·苏州期末)一个长方体的三条棱长分别为3,8,9,若在该长方体上面钻一个圆柱形的孔后其表面积没有变化,则圆孔的半径为________.解析:圆柱两底面积等于圆柱的侧面积.孔的打法有三种,所以有三种情况:①孔高为3,则2πr 2=2πr ×3,解得r =3;②孔高为8,则r =8;③孔高为9,则r =9.而实际情况是,当r =8,r =9时,因为长方体有个棱长为3,所以受限制不能打,所以只有①符合.答案:313.如图所示,在体积为9的长方体ABCD -A 1B 1C 1D 1中,对角线B 1D 与平面A 1BC 1交于点E ,则四棱锥E -A 1B 1C 1D 1的体积V =________.解析:连结B 1D 1交A 1C 1于点F ,连结BD ,BF ,则平面A 1BC 1∩平面BDD 1B 1=BF ,因为E ∈平面A 1BC 1,E ∈平面BDD 1B 1,所以E ∈BF .因为F 是A 1C 1的中点,所以BF 是中线,又B 1F 綊12BD ,所以FE EB =12,故点E 到平面A 1B 1C 1D 1的距离是BB 1的13,所以四棱锥E -A 1B 1C 1D 1的体积V =13×S 四边形A 1B 1C 1D 1×13BB 1=19V 长方体ABCD -A 1B 1C 1D 1=1.答案:114.半径为2的球O 中有一内接正四棱柱(底面是正方形,侧棱垂直底面).当该正四棱柱的侧面积最大时,球的表面积与该正四棱柱的侧面积之差是________.解析:依题意,设球的内接正四棱柱的底面边长为a 、高为h ,则有16=2a 2+h 2≥22ah ,即4ah ≤162,该正四棱柱的侧面积S =4ah ≤162,当且仅当h =2a =22时取等号.因此,当该正四棱柱的侧面积最大时,球的表面积与该正四棱柱的侧面积之差是4π×22-162=16(π-2).答案:16(π-2)[B 组——力争难度小题]1.已知三棱锥S -ABC 所在顶点都在球O 的球面上,且SC ⊥平面ABC ,若SC =AB =AC =1,∠BAC =120°,则球O 的表面积为________.解析:∵AB =AC =1,∠BAC =120°, ∴BC =12+12-2×1×1×⎝⎛⎭⎫-12=3, ∴三角形ABC 的外接圆直径2r =3sin 120°=2,∴r =1.∵SC ⊥平面ABC ,SC =1, ∴该三棱锥的外接球半径R =r 2+⎝⎛⎭⎫SC 22=52,∴球O 的表面积S =4πR 2=5π. 答案:5π2.(2017·南京三模)如图,在直三棱柱ABC -A1B 1C 1中,AB =1,BC =2,BB 1=3,∠ABC =90°,点D 为侧棱BB 1上的动点.当AD +DC 1最小时,三棱锥D -ABC 1的体积为________.解析:在直三棱柱ABC -A 1B 1C 1中,BB 1⊥平面ABC ,所以BB 1⊥AB ,又因为∠ABC =90°,即BC ⊥AB ,又BC ∩BB 1=B ,所以AB ⊥平面BB 1C 1C, 因为AB =1,BC =2,点D 为侧棱BB 1上的动点,所以侧面展开,当AD +DC 1最小时,BD =1,所以S △BDC 1=12×BD ×B 1C 1=1,所以三棱锥D -ABC 1的体积为13×S △BDC 1×AB =13.答案:133.设四面体的六条棱的长分别为1,1,1,1,2和a ,且长为a 的棱与长为2的棱异面,则a 的取值范围是________.解析:如图所示,AB =2,CD =a ,设点E 为AB 的中点,则ED ⊥AB,EC⊥AB,则ED=AD2-AE2=22,同理EC=22.由构成三角形的条件知0<a<ED+EC=2,所以0<a< 2.答案:(0,2)4.如图,已知AB为圆O的直径,C为圆上一动点,PA⊥圆O所在的平面,且PA=AB=2,过点A作平面α⊥PB,分别交PB,PC于E,F,当三棱锥P-AEF的体积最大时,tan∠BAC=________.解析:∵PB⊥平面AEF,∴AF⊥PB.又AC⊥BC,AP⊥BC,∴BC⊥平面PAC,∴AF⊥BC,∴AF⊥平面PBC,∴∠AFE=90°.设∠BAC=θ,在Rt△PAC中,AF=AP·ACPC=2×2cos θ21+cos2θ=2cos θ1+cos2θ,在Rt△PAB中,AE=PE=2,∴EF=AE2-AF2,∴V P-AEF=16AF·EF·PE=16AF·2-AF2·2=26·2AF2-AF4=26·-(AF2-1)2+1≤26,∴当AF=1时,V P-AEF取得最大值26,此时AF=2cos θ1+cos2θ=1,∴cos θ=13,sin θ=23,∴tan θ= 2.答案: 2第2课时平行与垂直(能力课) [常考题型突破][例1](2017·江苏高考)如图,在三棱锥A-BCD中,AB⊥AD,BC⊥BD,平面ABD⊥平面BCD,点E,F(E与A,D不重合)分别在棱AD,BD上,且EF⊥AD.求证:(1)EF∥平面ABC;(2)AD⊥AC.[证明] (1)在平面ABD 内,因为AB ⊥AD ,EF ⊥AD ,所以EF ∥AB .又因为EF ⊄平面ABC ,AB ⊂平面ABC ,所以EF ∥平面ABC .(2)因为平面ABD ⊥平面BCD ,平面ABD ∩平面BCD =BD ,BC ⊂平面BCD ,BC ⊥BD ,所以BC ⊥平面ABD .因为AD ⊂平面ABD ,所以BC ⊥AD .又AB ⊥AD ,BC ∩AB =B ,AB ⊂平面ABC ,BC ⊂平面ABC ,所以AD ⊥平面ABC .又因为AC ⊂平面ABC ,所以AD ⊥AC .[方法归纳]1.(2017·苏锡常镇一模)如图,在斜三棱柱ABC -A1B 1C 1中,侧面AA 1C 1C是菱形,AC 1与A 1C 交于点O ,E 是棱AB 上一点,且OE ∥平面BCC 1B 1.(1)求证:E 是AB 的中点;(2)若AC 1⊥A 1B ,求证:AC 1⊥BC .证明:(1)连结BC1,因为OE ∥平面BCC 1B 1,OE ⊂平面ABC 1,平面BCC 1B 1∩平面ABC 1=BC 1,所以OE ∥BC 1 .因为侧面AA 1C 1C 是菱形,AC 1∩A 1C =O ,所以O 是AC 1中点,所以AE EB =AO OC 1=1,E 是AB 的中点. (2)因为侧面AA 1C 1C 是菱形,所以AC 1⊥A 1C,又AC1⊥A1B,A1C∩A1B=A1,A1C⊂平面A1BC,A1B⊂平面A1BC,所以AC1⊥平面A1BC,因为BC⊂平面A1BC,所以AC1⊥BC.2.(2017·苏州模拟)在如图所示的空间几何体ABCDPE中,底面ABCD是边长为4的正方形,PA⊥平面ABCD,PA∥EB,且PA=AD=4,EB=2.(1)若点Q是PD的中点,求证:AQ⊥平面PCD;(2)证明:BD∥平面PEC.证明:(1)因为PA=AD,Q是PD的中点,所以AQ⊥PD.又PA⊥平面ABCD,所以CD⊥PA.又CD⊥DA,PA∩DA=A,所以CD⊥平面ADP.又因为AQ⊂平面ADP,所以CD⊥AQ,又PD∩CD=D,所以AQ⊥平面PCD.(2)取PC的中点M,连结AC交BD于点N,连结MN,ME,在△PAC中,易知MN=12PA,MN∥PA,又PA∥EB,EB=12PA,所以MN=EB,MN∥EB,所以四边形BEMN是平行四边形,所以EM∥BN.又EM⊂平面PEC,BN⊄平面PEC,所以BN∥平面PEC,即BD∥平面PEC.[例2]ABC内接于圆O,且AB为圆O的直径,M为线段PB的中点,N为线段BC的中点.求证:(1)平面MON∥平面PAC;(2)平面PBC⊥平面MON.[证明](1)因为M,O,N分别是PB,AB,BC的中点,所以MO∥PA,NO∥AC,又MO∩NO=O,PA∩AC=A,所以平面MON∥平面PAC.(2)因为PA⊥平面ABC,BC⊂平面ABC,所以PA⊥BC.由(1)知,MO∥PA,所以MO⊥BC.连结OC,则OC=OB,因为N为BC的中点,所以ON⊥BC.又MO∩ON=O,MO⊂平面MON,ON⊂平面MON,所以BC⊥平面MON.又BC⊂平面PBC,所以平面PBC⊥平面MON.[方法归纳]1.(2017·无锡期末)在四棱锥P-ABCD中,底面ABCD为矩形,AP⊥平面PCD,E,F分别为PC,AB的中点.求证:(1)平面PAD⊥平面ABCD;(2)EF∥平面PAD.证明:(1)因为AP⊥平面PCD,CD⊂平面PCD,所以AP⊥CD,因为四边形ABCD为矩形,所以AD⊥CD,又因为AP∩AD=A,AP⊂平面PAD,AD⊂平面PAD,所以CD⊥平面PAD,因为CD⊂平面ABCD,所以平面PAD⊥平面ABCD.(2)连结AC,BD交于点O,连结OE,OF,因为四边形ABCD为矩形,所以O点为AC的中点,因为E为PC的中点,所以OE∥PA,因为OE⊄平面PAD,PA⊂平面PAD,所以OE∥平面PAD,同理可得:OF∥平面PAD,又因为OE∩OF=O,所以平面OEF∥平面PAD,因为EF⊂平面OEF,所以EF∥平面PAD.2.(2016·江苏高考)如图,在直三棱柱ABC-A1B1C1中,D,E分别为AB,BC的中点,点F在侧棱B1B上,且B1D⊥A1F,A1C1⊥A1B1.求证:(1)直线DE∥平面A1C1F;(2)平面B1DE⊥平面A1C1F.证明:(1)在直三棱柱ABC-A1B1C1中,A1C1∥AC.在△ABC中,因为D,E分别为AB,BC的中点,所以DE∥AC,于是DE∥A1C1.又因为DE⊄平面A1C1F,A1C1⊂平面A1C1F,所以直线DE∥平面A1C1F.(2)在直三棱柱ABC-A1B1C1中,A1A⊥平面A1B1C1.因为A1C1⊂平面A1B1C1,所以A1A⊥A1C1.又因为A1C1⊥A1B1,A1A⊂平面ABB1A1,A1B1⊂平面ABB1A1,A1A∩A1B1=A1,所以A1C1⊥平面ABB1A1.因为B1D⊂平面ABB1A1,所以A1C1⊥B1D.又因为B1D⊥A1F,A1C1⊂平面A1C1F,A1F⊂平面A1C1F,A1C1∩A1F=A1,所以B1D ⊥平面A1C1F.因为直线B1D⊂平面B1DE,所以平面B1DE⊥平面A1C1F.[例3]圆O上,且AB∥EF,矩形ABCD所在的平面和圆O所在的平面互相垂直.(1)求证:平面AFC⊥平面CBF.(2)在线段CF上是否存在一点M,使得OM∥平面ADF?并说明理由.[解](1)证明:∵平面ABCD⊥平面ABEF,CB⊥AB,平面ABCD∩平面ABEF=AB,∴CB⊥平面ABEF.∵AF ⊂平面ABEF ,∴AF ⊥CB .又AB 为圆O 的直径,∴AF ⊥BF .又BF ∩CB =B ,∴AF ⊥平面CBF .∵AF ⊂平面AFC ,∴平面AFC ⊥平面CBF .(2)当M 为CF 的中点时,OM ∥平面ADF .证明如下:取CF 中点M ,设DF 的中点为N ,连结AN ,MN ,则MN 綊12CD ,又AO 綊12CD ,则MN 綊AO , ∴四边形MNAO 为平行四边形,∴OM ∥AN ,又AN ⊂平面DAF ,OM ⊄平面DAF ,∴OM ∥平面DAF .[方法归纳]与平行、垂直有关的存在性问题的解题步骤[变式训练]1.如图,四边形ABCD 是矩形,平面ABCD ⊥平面BCE ,BE ⊥EC .(1)求证:平面AEC ⊥平面ABE ;(2)点F 在BE 上,若DE ∥平面ACF ,求BF BE的值. 解:(1)证明:∵四边形ABCD 为矩形,∴AB ⊥BC ,∵平面ABCD ⊥平面BCE ,∴AB ⊥平面BCE ,∴CE ⊥AB .又∵CE ⊥BE ,AB ∩BE =B ,∴CE ⊥平面ABE ,又∵CE ⊂平面AEC ,∴平面AEC ⊥平面ABE .(2)连结BD 交AC 于点O ,连结OF .∵DE ∥平面ACF ,DE ⊂平面BDE ,平面ACF ∩平面BDE =OF .∴DE ∥OF ,又在矩形ABCD 中,O 为BD 中点,∴F 为BE 中点,即BF BE =12. 2.如图,在矩形ABCD 中,E ,F 分别为BC ,DA 的中点.将矩形ABCD 沿线段EF 折起,使得∠DFA =60°.设G 为AF 上的点.(1)试确定点G 的位置,使得CF ∥平面BDG ;(2)在(1)的条件下,证明:DG ⊥AE .解:(1)当点G 为AF 的中点时,CF ∥平面BDG .证明如下:因为E ,F 分别为BC ,DA 的中点,所以EF ∥AB ∥CD .连结AC 交BD 于点O ,连结OG ,则AO =CO .又G 为AF 的中点,所以CF ∥OG .因为CF ⊄平面BDG ,OG ⊂平面BDG .所以CF ∥平面BDG .(2)因为E ,F 分别为BC ,DA 的中点,所以EF ⊥FD ,EF ⊥FA .又FD ∩FA =F ,所以EF ⊥平面ADF ,因为DG ⊂平面ADF ,所以EF ⊥DG .因为FD =FA ,∠DFA =60°,所以△ADF 是等边三角形,DG ⊥AF ,又AF ∩EF =F ,所以DG ⊥平面ABEF .因为AE ⊂平面ABEF ,所以DG ⊥AE .[课时达标训练]1.如图,在三棱锥V -ABC 中,O ,M 分别为AB ,VA 的中点,平面VAB ⊥平面ABC ,△VAB 是边长为2的等边三角形,AC ⊥BC 且AC =BC .(1)求证:VB ∥平面MOC ;(2)求线段VC的长.解:(1)证明:因为点O,M分别为AB,VA的中点,所以MO∥VB.又MO⊂平面MOC,VB⊄平面MOC,所以VB∥平面MOC.(2)因为AC=BC,O为AB的中点,AC⊥BC,AB=2,所以OC⊥AB,且CO=1.连结VO,因为△VAB是边长为2的等边三角形,所以VO= 3.又平面VAB⊥平面ABC,OC⊥AB,平面VAB∩平面ABC=AB,OC⊂平面ABC,所以OC⊥平面VAB,所以OC⊥VO,所以VC=OC2+VO2=2.B1C1中,AC⊥BC,A1B2.(2017·南通二调)如图,在直三棱柱ABC-A与AB1交于点D,A1C与AC1交于点E.求证:(1)DE∥平面B1BCC1;(2)平面A1BC⊥平面A1ACC1.证明:(1)在直三棱柱ABC-A1B1C1中,四边形A1ACC1为平行四边形.又E为A1C与AC1的交点,所以E为A1C的中点.同理,D为A1B的中点,所以DE∥BC.又BC⊂平面B1BCC1,DE⊄平面B1BCC1,所以DE∥平面B1BCC1.(2)在直三棱柱ABC-A1B1C1中,AA1⊥平面ABC,又BC⊂平面ABC,所以AA1⊥BC.又AC⊥BC,AC∩AA1=A,AC⊂平面A1ACC1,AA1⊂平面A1ACC1,所以BC⊥平面A1ACC1.因为BC⊂平面A1BC,所以平面A1BC⊥平面A1ACC1.3.(2017·南京三模)如图,在三棱锥A-BCD中,E,F分别为棱BC,CD上的点,且BD∥平面AEF.(1)求证:EF∥平面ABD;(2)若BD⊥CD,AE⊥平面BCD,求证:平面AEF⊥平面ACD.证明:(1)因为BD∥平面AEF,BD⊂平面BCD,平面AEF∩平面BCD=EF,所以BD∥EF.因为BD⊂平面ABD,EF⊄平面ABD,所以EF∥平面ABD.(2)因为AE⊥平面BCD,CD⊂平面BCD,所以AE⊥CD.因为BD⊥CD,BD∥EF,所以CD⊥EF,又AE∩EF=E,AE⊂平面AEF,EF⊂平面AEF,所以CD⊥平面AEF.又CD⊂平面ACD,所以平面AEF⊥平面ACD.4.在四棱锥P-ABCD中,PA⊥底面ABCD,AB∥CD,AB⊥BC,AB=BC=1,DC=2,点E在PB上.(1)求证:平面AEC⊥平面PAD;(2)当PD∥平面AEC时,求PE∶EB的值.解:(1)证明:在平面ABCD中,过A作AF⊥DC于F,则CF=DF=AF=1,∴∠DAC=∠DAF+∠FAC=45°+45°=90°,即AC⊥DA.又PA⊥平面ABCD,AC⊂平面ABCD,∴AC⊥PA.∵PA⊂平面PAD,AD⊂平面PAD,且PA∩AD=A,∴AC⊥平面PAD.又AC⊂平面AEC,∴平面AEC⊥平面PAD.(2)连结BD交AC于O,连结EO.∵PD∥平面AEC,PD⊂平面PBD,平面PBD∩平面AEC=EO,∴PD∥EO,则PE∶EB=DO∶OB.又△DOC∽△BOA,∴DO∶OB=DC∶AB=2∶1,∴PE∶EB的值为2.5.(2017·扬州考前调研)如图,在四棱锥P-ABCD中,底面ABCD为梯形,CD∥AB,AB=2CD,AC交BD于O,锐角△PAD所在平面⊥底面ABCD,PA⊥BD,点Q在侧棱PC上,且PQ=2QC.求证:(1)PA∥平面QBD;(2)BD⊥AD.证明:(1)连结OQ,因为AB∥CD,AB=2CD,所以AO =2OC ,又PQ =2QC ,所以PA ∥OQ ,因为OQ ⊂平面QBD ,PA ⊄平面QBD ,所以PA ∥平面QBD .(2)在平面PAD 内过P 作PH ⊥AD 于H ,因为侧面PAD ⊥底面ABCD ,平面PAD ∩平面ABCD =AD ,PH ⊂平面PAD , 所以PH ⊥平面ABCD ,又BD ⊂平面ABCD ,所以PH ⊥BD .又PA ⊥BD ,且PA ∩PH =P ,PA ⊂平面PAD ,PH ⊂平面PAD ,所以BD ⊥平面PAD ,又AD ⊂平面PAD ,所以BD ⊥AD .6.如图,在多面体ABCDFE 中,四边形ABCD 是矩形,四边形ABEF为等腰梯形,且AB ∥EF ,AF =2,EF =2AB =42,平面ABCD ⊥平面ABEF .(1)求证:BE ⊥DF ;(2)若P 为BD 的中点,试问:在线段AE 上是否存在点Q ,使得PQ ∥平面BCE ?若存在,找出点Q 的位置;若不存在,请说明理由.解:(1)证明:如图,取EF 的中点G ,连结AG ,因为EF =2AB ,所以AB =EG ,又AB ∥EG ,所以四边形ABEG 为平行四边形,所以AG ∥BE ,且AG =BE =AF =2.在△AGF 中,GF =12EF =22,AG =AF =2, 所以AG 2+AF 2=GF 2,所以AG ⊥AF .因为四边形ABCD 为矩形,所以AD ⊥AB ,又平面ABCD ⊥平面ABEF ,且平面ABCD ∩平面ABEF =AB ,AD ⊂平面ABCD , 所以AD ⊥平面ABEF ,又AG ⊂平面ABEF ,所以AD ⊥AG .因为AD ∩AF =A ,所以AG ⊥平面ADF .因为AG ∥BE ,所以BE ⊥平面ADF .因为DF ⊂平面ADF ,所以BE ⊥DF .(2)存在点Q ,且点Q 为AE 的中点,使得PQ ∥平面BCE .证明如下:连结AC ,因为四边形ABCD 为矩形,所以P 为AC 的中点.在△ACE中,因为点P,Q分别为AC,AE的中点,所以PQ∥CE.又PQ⊄平面BCE,CE⊂平面BCE,所以PQ∥平面BCE.。
高考数学(理)二轮专题练习:立体几何(含答案)

立体几何1.一个物体的三视图的排列规则是俯视图放在正(主)视图下面,长度与正(主)视图一样,侧(左)视图放在正(主)视图右面,高度与正(主)视图一样,宽度与俯视图一样,即“长对正,高平齐,宽相等”.在画一个物体的三视图时,一定注意实线与虚线要分明.[问题1] 如图,若一个几何体的正(主)视图、侧(左)视图、俯视图均为面积等于2的等腰直角三角形,则该几何体的体积为________. 答案 432.在斜二测画法中,要确定关键点及关键线段.“平行于x 轴的线段平行性不变,长度不变;平行于y 轴的线段平行性不变,长度减半.”[问题2] 如图所示的等腰直角三角形表示一个水平放置的平面图形的直观图,则这个平面图形的面积是________. 答案 2 23.简单几何体的表面积和体积(1)S 直棱柱侧=c ·h (c 为底面的周长,h 为高). (2)S 正棱锥侧=12ch ′(c 为底面周长,h ′为斜高).(3)S 正棱台侧=12(c ′+c )h ′(c 与c ′分别为上、下底面周长,h ′为斜高).(4)圆柱、圆锥、圆台的侧面积公式 S 圆柱侧=2πrl (r 为底面半径,l 为母线), S 圆锥侧=πrl (同上),S 圆台侧=π(r ′+r )l (r ′、r 分别为上、下底的半径,l 为母线). (5)体积公式V 柱=S ·h (S 为底面面积,h 为高), V 锥=13S ·h (S 为底面面积,h 为高),V 台=13(S +SS ′+S ′)h (S 、S ′为上、下底面面积,h 为高).(6)球的表面积和体积 S 球=4πR 2,V 球=43πR 3.[问题3] 如图所示,一个空间几何体的正(主)视图和俯视图都是边长为1的正方形,侧(左)视图是一个直径为1的圆,那么这个几何体的表面积为( ) A .4π B .3π C .2π D.32π 答案 D4.空间直线的位置关系:①相交直线——有且只有一个公共点.②平行直线——在同一平面内,没有公共点.③异面直线——不在同一平面内,也没有公共点.[问题4] 在空间四边形ABCD 中,E 、F 、G 、H 分别是四边上的中点,则直线EG 和FH 的位置关系是________. 答案 相交5.空间直线与平面、平面与平面的位置关系 (1)直线与平面①位置关系:平行、直线在平面内、直线与平面相交. ②直线与平面平行的判定定理和性质定理:判定定理:平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行.性质定理:一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行.③直线与平面垂直的判定定理和性质定理:判定定理:一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直. 性质定理:垂直于同一个平面的两条直线平行. (2)平面与平面①位置关系:平行、相交(垂直是相交的一种特殊情况). ②平面与平面平行的判定定理和性质定理:判定定理:一个平面内的两条相交直线与另一个平面平行,则这两个平面平行. 性质定理:如果两个平行平面同时和第三个平面相交,那么它们的交线平行. ③平面与平面垂直的判定定理和性质定理:判定定理:一个平面过另一个平面的垂线,则这两个平面垂直.性质定理:两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直.[问题5] 已知b ,c 是平面α内的两条直线,则“直线a ⊥α”是“直线a ⊥b ,直线a ⊥c ”的________条件. 答案 充分不必要 6.空间向量(1)用空间向量求角的方法步骤①异面直线所成的角若异面直线l 1和l 2的方向向量分别为v 1和v 2,它们所成的角为θ,则cos θ=|cos 〈v 1,v 2〉|. ②直线和平面所成的角利用空间向量求直线与平面所成的角,可以有两种方法:方法一 分别求出斜线和它在平面内的射影直线的方向向量,转化为求两条直线的方向向量的夹角(或其补角).方法二 通过平面的法向量来求,即求出斜线的方向向量与平面的法向量所夹的锐角,取其余角就是斜线和平面所成的角. ③利用空间向量求二面角也有两种方法:方法一 分别在二面角的两个面内找到一个与棱垂直且从垂足出发的两个向量,则这两个向量的夹角的大小就是二面角的平面角的大小.方法二 通过平面的法向量来求,设二面角的两个面的法向量分别为n 1和n 2,则二面角的大小等于〈n 1,n 2〉(或π-〈n 1,n 2〉).易错警示:①求线面角时,得到的是直线方向向量和平面法向量的夹角的余弦,容易误以为是线面角的余弦.②求二面角时,两法向量的夹角有可能是二面角的补角,要注意从图中分析. (2)用空间向量求A 到平面α的距离: 可表示为d =|n ·AB →||n |.[问题6] (1)已知正三棱柱ABC -A 1B 1C 1的侧棱长与底面边长相等,则AB 1与侧面ACC 1A 1所成角的正弦值等于________.(2)正方体ABCD -A 1B 1C 1D 1的棱长为1,O 是底面A 1B 1C 1D 1的中心,则点O 到平面ABC 1D 1的距离为________. 答案 (1)64 (2)24解析 (1)方法一 取A 1C 1的中点E ,连接AE ,B 1E ,如图. 由题意知B 1E ⊥平面ACC 1A 1,则∠B 1AE 为AB 1与侧面ACC 1A 1所成的角. 设正三棱柱侧棱长与底面边长为1, 则sin ∠B 1AE =B 1E AB 1=322=64.方法二 如图,以A 1C 1中点E 为原点建立空间直角坐标系E -xyz ,设棱长为1,则A ⎝⎛⎭⎫12,0,1,B 1⎝⎛⎭⎫0,32,0, 设AB 1与平面ACC 1A 1所成的角为θ,EB 1→为平面ACC 1A 1的法向量. 则sin θ=|cos 〈AB 1→,EB 1→〉|=⎪⎪⎪⎪⎪⎪⎝⎛⎭⎫-12,32,-1·⎝⎛⎭⎫0,32,02×32=64. (2)建立如图所示的空间直角坐标系,则A (1,0,0),B (1,1,0),D 1(0,0,1),C 1(0,1,1),O ⎝⎛⎭⎫12,12,1. 设平面ABC 1D 1的法向量为n =(x ,y ,z ),则 ⎩⎪⎨⎪⎧n ·AB →=0,n ·AD 1→=0,∴⎩⎪⎨⎪⎧y =0,-x +z =0.令z =1,得⎩⎪⎨⎪⎧x =1,y =0,∴n =(1,0,1),又OD 1→=⎝⎛⎭⎫-12,-12,0, ∴O 到平面ABC 1D 1的距离d =|n ·OD 1→||n|=122=24.易错点1 三视图认识不清致误例1 一个空间几何体的三视图如图所示,则该几何体的表面积为( )A .48B .32+817C .48+817D .80错解 由三视图知,该几何体的直观图如图所示,该几何体的下底面是边长为4的正方形;上底面是长为4,宽为2的矩形;两个梯形侧面垂直于底面,上底长为2,下底长为4,高为4;另两个侧面是正方形,边长为4. 所以表面积S =42×3+2×4+2×12(2+4)×4=48+8+24=80.找准失分点 不能准确把握三视图和几何体之间的数量关系,根据正视图可知,侧视图中等腰梯形的高为4,而错认为等腰梯形的腰为4.正解 由三视图知该几何体的直观图如图所示,该几何体的下底面是边长为4的正方形;上底面是长为4、宽为2的矩形;两个梯形侧面垂直于底面,上底长为2,下底长为4,高为4;另两个侧面是矩形,宽为4,长为42+12 =17.所以S 表=42+2×4+12×(2+4)×4×2+4×17×2=48+817.答案 C易错点2 对几何概念理解不透致误例2 给出下列四个命题:①有两个平面互相平行,其余各面都是平行四边形的多面体是棱柱; ②若两个过相对侧棱的截面都垂直于底面,则该四棱柱为直四棱柱; ③底面是平行四边形的四棱柱是平行六面体; ④底面是矩形的平行六面体是长方体.其中正确的命题是__________(写出所有正确命题的序号). 错解1 ①②③ 错解2 ②③④找准失分点 ①是错误的,因为棱柱的侧棱要都平行且相等;④是错误的,因为长方体的侧棱必须与底面垂直. 正解 ②③易错点3 对线面关系定理条件把握不准致误例3 已知m 、n 是不同的直线,α、β、γ是不同的平面.给出下列命题: ①若α⊥β,α∩β=m ,n ⊥m ,则n ⊥α,或n ⊥β; ②若α∥β,α∩γ=m ,β∩γ=n ,则m ∥n ;③若m 不垂直于α,则m 不可能垂直于α内的无数条直线; ④若α∩β=m ,n ∥m ,且n ⊄α,n ⊄β,则n ∥α,且n ∥β; ⑤若m 、n 为异面直线,则存在平面α过m 且使n ⊥α. 其中正确的命题序号是________. 错解 ②③④⑤找准失分点③是错误的;⑤是错误的.正解①是错误的.如正方体中面ABB′A′⊥面ADD′A′,交线为AA′.直线AC⊥AA′,但AC不垂直面ABB′A′,同时AC也不垂直面ADD′A′.②正确.实质上是两平面平行的性质定理.③是错误的.在上面的正方体中,A′C不垂直于平面A′B′C′D′,但与B′D′垂直.这样A′C就垂直于平面A′B′C′D′内与直线B′D′平行的无数条直线.④正确.利用线面平行的判定定理即可.⑤错误.从结论考虑,若n⊥α且m⊂α,则必有m⊥n,事实上,条件并不能保证m⊥n.故错误.答案②④1.已知三条不同直线m,n,l与三个不同平面α,β,γ,有下列命题:①若m∥α,n∥α,则m∥n;②若α∥β,l⊂α,则l∥β;③α⊥γ,β⊥γ,则α∥β;④若m,n为异面直线,m⊂α,n⊂β,m∥β,n∥α,则α∥β.其中正确命题的个数是()A.0 B.1 C.2 D.3答案 C解析因为平行于同一平面的两条直线除了平行,还可能相交或成异面直线,所以命题①错误;由直线与平面平行的定义知命题②正确;由于垂直于同一个平面的两个平面可能平行还可能相交,因此命题③错误;过两条异面直线分别作平面互相平行,这两个平面是唯一存在的,因此命题④正确.故选C.2.设m,n是空间两条直线,α,β是空间两个平面,则下列选项中不正确的是()A.当m⊂α时,“n∥α”是“m∥n”的必要不充分条件B.当m⊂α时,“m⊥β”是“α⊥β”的充分不必要条件C.当n⊥α时,“n⊥β”是“α∥β”成立的充要条件D.当m⊂α时,“n⊥α”是“m⊥n”的充分不必要条件答案 A解析当m⊂α时,若n∥α可得m∥n或m,n异面;若m∥n可得n∥α或n⊂α,所以“n∥α”是“m∥n”的既不充分也不必要条件,答案选A.3.一个几何体的三视图如图所示,则该几何体的体积是()A .64B .72C .80D .112答案 B解析 根据三视图,该几何体为下面是一个立方体、上面两个三棱锥,所以V =4×4×4+2×13×(12·4·2)×3=72,故选B.4.如图所示,在正方体ABCD -A 1B 1C 1D 1中,M ,N ,P ,Q 分别是AA 1,A 1D 1,CC 1,BC 的中点,给出以下四个结论:①A 1C ⊥MN ;②A 1C ∥平面MNPQ ;③A 1C 与PM 相交;④NC 与PM 异面.其中不正确的结论是( ) A .① B .② C .③ D .④ 答案 C解析 作出过M ,N ,P ,Q 四点的截面交C 1D 1于点S ,交AB 于点R ,如图所示中的六边形MNSPQR ,显然点A 1,C 分别位于这个平面的两侧,故A 1C 与平面MNPQ 一定相交,不可能平行,故结论②不正确.5.一个几何体的三视图如图所示,则该几何体的表面积为( )A .2+ 2B .3+ 2C .1+2 2D .5答案 A解析 由三视图可知,该几何体是一个四棱锥,如图所示. 该几何体的底面是边长为1的正方形,故S 1=12=1. 侧棱P A ⊥面ABCD ,且P A =1, 故S △P AB =S △P AD =12×1×1=12,而PD ⊥DC ,CB ⊥PB ,且PB =PD =2, 所以S △PBC =S △PDC =12×2×1=22.所以该几何体的表面积为S =1+2×12+2×22=2+ 2.故选A.6.如图,已知六棱锥P —ABCDEF 的底面是正六边形,P A ⊥平面ABC ,P A =2AB ,则下列结论正确的是( ) A .PB ⊥ADB .平面P AB ⊥平面PBC C .直线BC ∥平面P AED .直线PD 与平面ABC 所成的角为45° 答案 D解析 若PB ⊥AD ,则AD ⊥AB ,但AD 与AB 成60°角,A 错误;平面P AB 与平面ABD 垂直,所以平面P AB 一定不与平面PBC 垂直,B 错误;BC 与AE 是相交直线,所以BC 一定不与平面P AE 平行,C 错误;直线PD 与平面ABC 所成角为∠PDA ,在Rt △P AD 中,AD =P A , ∴∠PDA =45°,D 正确.7.对于四面体ABCD ,给出下列四个命题: ①若AB =AC ,BD =CD ,则BC ⊥AD ; ②若AB =CD ,AC =BD ,则BC ⊥AD ; ③若AB ⊥AC ,BD ⊥CD ,则BC ⊥AD ; ④若AB ⊥CD ,AC ⊥BD ,则BC ⊥AD .其中正确的是________.(填序号) 答案 ①④解析 取线段BC 的中点E ,连接AE ,DE , ∵AB =AC ,BD =CD , ∴BC ⊥AE ,BC ⊥DE , ∴BC ⊥平面ADE , ∵AD ⊂平面ADE , ∴BC ⊥AD ,故①正确.设点O 为点A 在平面BCD 上的射影, 连接OB ,OC ,OD , ∵AB ⊥CD ,AC ⊥BD , ∴OB ⊥CD ,OC ⊥BD , ∴点O 为△BCD 的垂心, ∴OD ⊥BC ,∴BC ⊥AD ,故④正确,易知②③不正确,填①④.8.如图,四面体ABCD 中,AB =1,AD =23,BC =3,CD =2,∠ABC =∠DCB =π2,则二面角A -BC -D 的大小为________.答案 π3解析 由∠ABC =∠DCB =π2知,BA →与CD →的夹角θ就是二面角A -BC -D 的平面角. 又AD →=AB →+BC →+CD →,∴AD →2=(AB →+BC →+CD →)2 =AB →2+BC 2→+CD →2+2AB →·CD →.因此2AB →·CD →=(23)2-12-32-22=-2, ∴cos(π-θ)=-12,且0<π-θ<π,则π-θ=23π,故θ=π3.9.已知直线l ,m ,平面α,β,且l ⊥α,m ⊂β,给出四个命题:①若α∥β,则l ⊥m ;②若l ⊥m ,则α∥β;③若α⊥β,则l ∥m ;④若l ∥m ,则α⊥β. 其中为真命题的是________.(填序号) 答案 ①④解析 对命题①,则l ⊥α,α∥β得,l ⊥β,m ⊂β,∴l⊥m,故①正确.对命题②,l⊥mD⇒/l⊥β,则l⊥mD⇒/α∥β,故②错误.对命题③,当α⊥β时,l与m也可能相交或异面或平行,故③错误.对命题④,由l⊥α,l∥m得m⊥α,又m⊂β,∴α⊥β,故④正确.10.三棱锥D-ABC及其三视图中的正(主)视图和侧(左)视图如图所示,则棱BD的长为________.答案4 2解析由正(主)视图知CD⊥平面ABC,设AC中点为E,则BE⊥AC,且AE=CE=2;由侧(左)视图知CD=4,BE=23,在Rt△BCE中,BC=BE2+EC2=(23)2+22=4,在Rt△BCD中,BD=BC2+CD2=42+42=4 2.故答案为4 2.。
届数学统考第二轮专题复习第12讲立体几何学案理含解析

第12讲立体几何高考年份全国卷Ⅰ全国卷Ⅱ全国卷Ⅲ2020证明线面垂直,求二面角的余弦值·T18证明线面平行、面面垂直,求线面角的正弦值·T20点面的位置关系,求二面角的正弦值·T192019证明线面平行,求二面角的正弦值·T18证明线面垂直,求二面角的正弦值·T17翻折问题,证明四点共面、面面垂直,求二面角的大小·T192018翻折问题,证明面面垂直,求线面角的正弦值·T18证明线面垂直,给出二面角求线面角的正弦值·T20证明面面垂直,求二面角的正弦值·T191。
[2020·全国卷Ⅱ]如图M4—12-1,已知三棱柱ABC—A1B1C1的底面是正三角形,侧面BB1C1C是矩形,M,N分别为BC,B1C1的中点,P为AM上一点,过B1C1和P的平面交AB于E,交AC于F.(1)证明:AA1∥MN,且平面A1AMN⊥平面EB1C1F;(2)设O为△A1B1C1的中心,若AO∥平面EB1C1F,且AO=AB,求直线B1E与平面A1AMN所成角的正弦值.图M4—12-12.[2020·全国卷Ⅰ]如图M4—12-2,D为圆锥的顶点,O是圆锥底面的圆心,AE为底面直径,AE=AD.△ABC是底面的内接正三DO.角形,P为DO上一点,PO=√66(1)证明:PA⊥平面PBC;(2)求二面角B-PC-E的余弦值。
图M4—12-23.[2019·全国卷Ⅲ]如图M4—12—3,图①是由矩形ADEB,Rt △ABC和菱形BFGC组成的一个平面图形,其中AB=1,BE=BF=2,∠FBC=60°.将其沿AB,BC折起使得BE与BF重合,连接DG,如图②。
(1)证明:图②中的A,C,G,D四点共面,且平面ABC⊥平面BCGE;(2)求图②中的二面角B—CG-A的大小.①②图M4-12—3平行、垂直关系的证明1如图M4—12-4,在四棱锥P—ABCD中,四边形ABCD为平行四边形,E为侧棱PD的中点,O为AC与BD的交点。
高考数学专题四立体几何 微专题29 立体几何中的动态问题

√C.若点N到直线BB1与直线DC的距离相等,则点N的轨迹为抛物线 √D.若D1N与AB所成的角为 π3,则点N的轨迹为双曲线
如图所示,对于A, 根据正方体的性质可知,MD⊥平面ABCD, 所以∠MND为MN与平面ABCD所成的角, 所以∠MND=4π,所以 DN=DM=12DD1=12×4=2, 所以点N的轨迹是以D为圆心,2为半径的圆,故A正确;
思维导图
内容索引
典型例题
热点突破
PART ONE
典型例题
考点一 动点的轨迹
典例1 (1)(多选)已知正方体ABCD-A1B1C1D1 的棱长为4,M为DD1的中点,N为四边形ABCD 所在平面上一动点,则下列命题正确的是
√A.若MN与平面ABCD所成的角为 π4,则点N的
轨迹为圆
B.若MN=4,则MN的中点P的轨迹所围成图
当 B 是 AC 的中点时,AB=BC= 6,
此时△SAB为等腰三角形,△ABC为等腰直角三角形,
将△SAB,△ABC沿AB展开至同一个平面,得到如
图2所示的平面图形,
取AB的中点D,连接SC,SD,CD,
则 SD=
22-
262=
210,
所以 sin ∠ABS=SSDB= 410, 所以 cos∠CBS=cos(90°+∠ABS)=-sin∠ABS=- 410,
此时点B与点Q重合,点P与点O1重合,故C正确;
对于D,当点P与点B1,点Q与点A重合时,
AP+PQ+QB1 的值为 3AP=3 12+22=3 5>2 3+ 5,故 D 错误.
考点二 折叠、展开问题
典例2 (多选)如图,在矩形ABCD中,M为BC的中点,将△ABM沿直线 AM翻折成△AB1M,连接B1D,N为B1D的中点,则在翻折过程中,下列 说法正确的是 A.存在某个位置,使得CN⊥AB1
立体几何的动态问题翻折问题
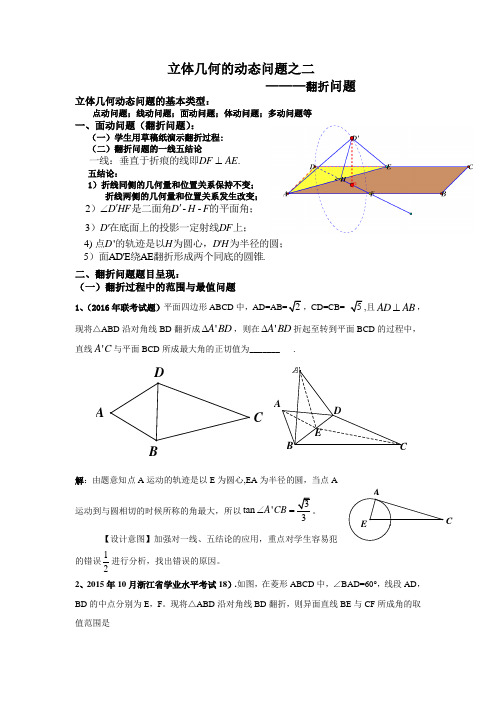
立体几何的动态问题之二———翻折问题立体几何动态问题的基本类型:点动问题;线动问题;面动问题;体动问题;多动问题等一、面动问题(翻折问题):(一)学生用草稿纸演示翻折过程: (二)翻折问题的一线五结论.DF AE ⊥一线:垂直于折痕的线即五结论:1)折线同侧的几何量和位置关系保持不变;折线两侧的几何量和位置关系发生改变; 2--D HF D H F ''∠)是二面角的平面角;3D DF ')在底面上的投影一定射线上; 二、翻折问题题目呈现:(一)翻折过程中的范围与最值问题1、(2016年联考试题)平面四边形ABCD 中,AD=AB=2,CD=CB= 5,且AD AB ⊥,现将△ABD 沿对角线BD 翻折成'A BD ∆,则在'A BD ∆折起至转到平面BCD 的过程中,直线'A C 与平面BCD 所成最大角的正切值为_______ .解:由题意知点A 运动的轨迹是以E 为圆心,EA 为半径的圆,当点A运动到与圆相切的时候所称的角最大,所以3tan 'A CB ∠=。
【设计意图】加强对一线、五结论的应用,重点对学生容易犯的错误12进行分析,找出错误的原因。
2、2015年10月浙江省学业水平考试18).如图,在菱形ABCD 中,∠BAD=60°,线段AD ,BD 的中点分别为E ,F 。
现将△ABD 沿对角线BD 翻折,则异面直线BE 与CF 所成角的取值范围是DABE CDABC4) ''D H DH点的轨迹是以为圆心,为半径的圆;5AD'E AE .)面绕翻折形成两个同底的圆锥ECA.(,)63ππ B. (,]62ππ C. (,]32ππ D. 2(,)33ππ分析:这是一道非常经典的学考试题,本题的解法非常多,很好的考查了空间立体几何线线角的求法。
方法一:特殊值法(可过F 作FH 平行BE,找两个极端情形) 方法二:定义法:利用余弦定理:222254cos 243FH FC CH FHC CH FH FC +-∠==-,有32144CH ≤≤11cos ,22CFH ⎡⎤∴∠∈-⎢⎥⎣⎦异面直线BE 与CF 所成角的取值范围是(,]32ππ 方法三:向量基底法:111()()222BE FC BA BD FC BA FC BF FA FC=+==+111cos ,cos ,,222BE FC FC FA ⎡⎤<>=<>∈-⎢⎥⎣⎦方法四:建系:3、(2015年浙江·理8)如图,已知ABC ∆,D 是AB 的中点,沿直线CD 将ACD ∆折成A CD '∆,所成二面角A CDB '--的平面角为α,则 ( B )A. A DB α'∠≤B. A DB α'∠≥C. A CB α'∠≥D. A CB α'∠≤方法一:特殊值方法二:定义法作出二面角,在进行比较。
2022版优化方案高考数学(浙江版·文科)二轮专题复习练习:专题4 立体几何第1讲 Word版含答案

[A卷]1.(2021·宁波市高三模拟) 用一个平行于水平面的平面去截球,得到如图所示的几何体,则它的俯视图是()解析:选B.由题意知,用平行于水平面的平面去截球所得的底面圆是看不见的,所以在俯视图中该部分应当是虚线圆,结合选项可知选B.2.下列命题中,错误的是()A.圆柱的轴截面是过母线的截面中面积最大的一个B.用一个平面去截棱锥,底面与截面之间的部分组成的几何体叫棱台C.圆台的全部平行于底面的截面都是圆D.圆锥全部的轴截面都是全等的等腰三角形解析:选B.依据棱台的定义,用一个平行于棱锥底面的平面去截棱锥,底面与截面之间的部分组成的几何体叫棱台.3.(2021·台州市高三调考)一个空间几何体的三视图如图所示,其体积为()A.16B.32C.48 D.96解析:选A.由题意作出直观图P-ABCD如图所示,则该几何体是一个四棱锥,底面是一个直角梯形,其面积为12×(2+4)×4=12,高为4,因此其体积V=13×12×4=16.4.(2021·高考全国卷Ⅰ)圆柱被一个平面截去一部分后与半球(半径为r)组成一个几何体,该几何体三视图中的正视图和俯视图如图所示.若该几何体的表面积为16+20π,则r=()A.1 B.2C.4 D.8解析:选B.如图,该几何体是一个半球与一个半圆柱的组合体,球的半径为r,圆柱的底面半径为r,高为2r,则表面积S=12×4πr2+πr2+4r2+πr·2r=(5π+4)r2.又S=16+20π,所以(5π+4)r2=16+20π,所以r2=4,r=2,故选B.5.如图是一个体积为10的空间几何体的三视图,则图中x的值为()A.2 B.3C.4 D.5解析:选A.依据给定的三视图可知,该几何体对应的直观图是一个长方体和四棱锥的组合体,所以几何体的体积V=3×2×1+13×3×2×x=10,解得x=2.故选A.6. 如图,水平放置的三棱柱的侧棱长为1,且侧棱AA1⊥平面A1B1C1,正视图是边长为1的正方形,俯视图为一个等边三角形,则该三棱柱的侧视图的面积为()A.2 3 B. 3C.32D.1解析:选C.由直观图、正视图以及俯视图可知,侧视图是宽为32,长为1的长方形,所以面积S=32×1=32.故选C.7.一平面截一球得到直径为2 5 cm的圆面,球心到这个平面的距离是2 cm,则该球的体积是() A.12πcm3B.36πcm3C.646πcm3D.108πcm3解析:选B.由于球心和截面圆心的连线垂直于截面,由勾股定理得,球半径R=22+(5)2=3,故球的体积为43πR3=36π(cm3).8.(2021·石家庄市第一次模拟)一个几何体的三视图如图所示,则该几何体的体积是()A.64B.72C.80D.112解析:选B.由三视图可知该几何体是一个组合体,下面是一个棱长为4的正方体;上面是一个三棱锥,三棱锥的高为3.故所求体积为43+13×12×4×4×3=72.9.已知某组合体的正视图与侧视图相同(其中AB=AC,四边形BCDE为矩形),则该组合体的俯视图可以是________(把正确的图的序号都填上).解析:几何体由四棱锥与四棱柱组成时,得①正确;几何体由四棱锥与圆柱组成时,得②正确;几何体由圆锥与圆柱组成时,得③正确;几何体由圆锥与四棱柱组成时,得④正确.答案:①②③④10.把一个圆锥截成圆台,已知圆台的上、下底面半径的比是1∶4,母线长是10 cm,则圆锥的母线长为________ cm.解析:作出圆锥的轴截面如图,设SA=y,O′A′=x,利用平行线截线段成比例,得SA′∶SA=O′A′∶OA,则(y-10)∶y=x∶4x,解得y=403.所以圆锥的母线长为403cm.答案:40311.(2022·高考课标全国卷Ⅱ改编)正三棱柱ABC-A1B1C1的底面边长为2,侧棱长为 3,D为BC中点,则三棱锥AB1DC1的体积为________.解析:由题意可知AD⊥BC,由面面垂直的性质定理可得AD⊥平面DB1C1,又AD=2sin 60°=3,所以V AB1DC1=13AD·S△B1DC1=13×3×12×2×3=1,故选C.答案:112.一个四棱锥的侧棱长都相等,底面是正方形,其正(主)视图如图所示,则该四棱锥的侧面积为________,体积为________.解析:由题意可知该四棱锥为正四棱锥,底面边长为2,高为2,侧面上的斜高为22+12=5,所以S 侧=4×⎝⎛⎭⎫12×2×5=45,V=13×22×2=83.答案:458313.(2021·南昌市第一次模拟)如图,在正四棱柱ABCD -A 1B 1C 1D 1中,点P 是平面A 1B 1C 1D 1内一点,则三棱锥P -BCD 的正视图与侧视图的面积之比为________.解析:依据题意,三棱锥P -BCD 的正视图是三角形,且底边为正四棱柱的底面边长、高为正四棱柱的高,侧视图是三角形,且底边为正四棱柱的底面边长、高为正四棱柱的高,故三棱锥P -BCD 的正视图与侧视图的面积之比为1∶1. 答案:1∶114.如图是某空间几何体的三视图,则该几何体的体积为________.解析:由三视图可知,该几何体是棱长为2,2,1的长方体挖去一个半径为1的半球,所以长方体的体积为2×2×1=4,半球的体积为12×43π×13=2π3,所以该几何体的体积是4-2π3.答案:4-2π315.如图,正方体ABCD -A 1B 1C 1D 1的棱长为1,E ,F 分别为线段AA 1,B 1C 上的点,则三棱锥D 1EDF的体积为________.解析:由于B 1C ∥平面ADD 1A 1,所以F 到平面ADD 1A 1的距离d 为定值1,△D 1DE 的面积为12D 1D ·AD =12,所以V D 1EDF =V F D 1DE =13S △D 1DE ·d =13×12×1=16.答案:16[B 卷]1.一个锥体的正视图和侧视图如图所示,下面选项中,不行能是该锥体的俯视图的是( )解析:选C.依据三视图中“正俯长一样,侧俯宽一样,正侧高一样”的规律,C 选项的侧视图宽为32,不符合题意,故选C.2.(2021·邢台市摸底考试)已知一个几何体的三视图是三个全等的边长为1的正方形,如图所示,则该几何体的体积为( )A.16 B.13 C.23D .56解析:选D.依题意得,题中的几何体是从棱长为1的正方体ABCD -A ′B ′C ′D ′中截去三棱锥A ′ABD 后剩余的部分,因此该几何体的体积等于13-13×⎝⎛⎭⎫12×12×1=56,故选D. 3.(2022·高考湖南卷)一块石材表示的几何体的三视图如图所示.将该石材切削、打磨,加工成球,则能得到的最大球的半径等于( )A .1B .2C .3D .4解析:选B.由三视图可知该几何体是一个直三棱柱,如图所示.由题意知,当打磨成的球的大圆恰好与三棱柱底面直角三角形的内切圆相同时,该球的半径最大,故其半径r =12×(6+8-10)=2.因此选B.4.(2021·高考山东卷)在梯形ABCD 中,∠ABC =π2,AD ∥BC ,BC =2AD =2AB =2.将梯形ABCD 绕AD所在的直线旋转一周而形成的曲面所围成的几何体的体积为( )A.2π3 B .4π3 C.5π3D .2π 解析:选C.过点C 作CE 垂直AD 所在直线于点E ,梯形ABCD 绕AD 所在直线旋转一周而形成的旋转体是由以线段AB 的长为底面圆半径,线段BC 为母线的圆柱挖去以线段CE 的长为底面圆半径,ED 为高的圆锥,如图所示,该几何体的体积为V =V 圆柱-V 圆锥=π·AB 2·BC -13·π·CE 2·DE =π×12×2-13π×12×1=5π3,故选C.5.(2021·郑州市第一次质量猜测)某三棱锥的三视图如图所示,且三个三角形均为直角三角形,则xy 的最大值为( )A .32B .327C .64D .647解析:选C.依题意,题中的几何体是三棱锥P -ABC (如图所示), 其中底面ABC 是直角三角形,AB ⊥BC ,P A ⊥平面ABC , BC =27,P A 2+y 2=102,(27)2+P A 2=x 2,因此xy =x 102-[x 2-(27)2]=x128-x 2≤x 2+(128-x 2)2=64,当且仅当x 2=128-x 2,即x =8时取等号,因此xy 的最大值是64,故选C.6.(2021·山西省第三次四校联考)在半径为10的球面上有A ,B ,C 三点,假如AB =83,∠ACB =60°,则球心O 到平面ABC 的距离为( )A .2B .4C .6D .8解析:选C.设A ,B ,C 三点所在圆的半径为r ,圆心为P .由于∠ACB =60°,所以∠APB =120°.在等腰三角形ABP 中,AP =43sin 60°=8,所以r =8,所以球心O 到平面ABC 的距离为102-82=6,故选C.7.如图是一个几何体的三视图,则该几何体的表面积是( )A .5+ 3B .5+2 3C .4+2 2D .4+2 3解析:选A.该几何体的直观图如图.表面积S =1×1+12×1×1×2+2×12×(1+2)×1+12×6×2=5+3,所以选A.8.在三棱锥P -ABC 中,P A ⊥平面ABC ,AC ⊥BC ,D 为侧棱PC 上的一点,它的正视图和侧视图如图所示,则下列命题正确的是( )A .AD ⊥平面PBC ,且三棱锥D -ABC 的体积为83B .BD ⊥平面P AC ,且三棱锥D -ABC 的体积为83C .AD ⊥平面PBC ,且三棱锥D -ABC 的体积为163D .BD ⊥平面P AC ,且三棱锥D -ABC 的体积为163解析:选C.由正视图可知,P A =AC ,且点D 为线段PC 的中点,所以AD ⊥PC .由侧视图可知,BC =4.由于P A ⊥平面ABC ,所以P A ⊥BC .又由于BC ⊥AC ,且AC ∩P A =A ,所以BC ⊥平面P AC ,所以BC ⊥AD .又由于AD ⊥PC ,且PC ∩BC =C ,所以可得AD ⊥平面PBC ,V D ABC =13×12×P A ×S △ABC =163.9.某几何体的正视图与俯视图如图所示,若俯视图中的多边形为正六边形,则该几何体的侧视图的面积为________.解析:侧视图由一个矩形和一个等腰三角形构成,矩形的长为3,宽为2,面积为3×2=6.等腰三角形的底边为3,高为3,其面积为12×3×3=32,所以侧视图的面积为6+32=152.答案:15210.(2021·洛阳市高三班级统考)如图是某几何体的三视图,则该几何体的外接球的表面积为( )解析:由三视图知,该几何体可以由一个长方体截去一个角后得到,该长方体的长、宽、高分别为5、4、3,所以其外接球半径R 满足2R =42+32+52=52,所以该几何体的外接球的表面积为S =4πR 2=4π×⎝⎛⎭⎫5222=50π.答案:50π 11.(2021·绍兴市高三诊断性测试)若某几何体的三视图如图所示,则该几何体的体积为________,最长的侧棱长为________.解析:依据三视图及有关数据还原该几何体,得该几何体是底面为直角梯形的四棱锥P -ABCD ,如图,过点P 作PH ⊥AD 于点H ,连接CH .底面面积S 1=(1+2)×12=32,V =13×32×1=12,最长的侧棱长为PB = 3.答案:12312.设甲、乙两个圆柱的底面积分别为S 1,S 2,体积分别为V 1,V 2,若它们的侧面积相等,且S 1S 2=94,则V 1V 2的值是________. 解析:设两个圆柱的底面半径和高分别为r 1,r 2和h 1,h 2,由S 1S 2=94,得πr 21πr 22=94,则r 1r 2=32.由圆柱的侧面积相等,得2πr 1h 1=2πr 2h 2,即r 1h 1=r 2h 2,则h 1h 2=23,所以V 1V 2=πr 21h 1πr 22h 2=32.答案:3213.(2021·洛阳市统考)已知点A ,B ,C ,D 均在球O 上,AB =BC =6,AC =23,若三棱锥D -ABC 体积的最大值为3,则球O 的表面积为________.解析:由题意可得,∠ABC =π2,△ABC 的外接圆半径r =3,当三棱锥的体积最大时,V D ABC =13S △ABC ·h (h为D 到底面ABC 的距离),即3=13×12×6×6h ⇒h =3,即R +R 2-r 2=3(R 为外接球半径),解得R =2,所以球O 的表面积为4π×22=16π.答案:16π 14.(2021·杭州市联谊学校高三其次次联考)一个等腰直角三角形的三个顶点分别在正三棱柱ABC -A 1B 1C 1的三条侧棱上,已知正三棱柱的底面边长为2,则该三角形的斜边长为________.解析:如图,在正三棱柱ABC -A 1B 1C 1中,△ABC 为正三角形,边长为2,△DEF 为等腰直角三角形,DF 为斜边,设DF 的长为x ,则DE =EF =22x ,作DG ⊥BB 1,GH ⊥CC 1,EI ⊥CC 1,垂足分别为G ,H ,I ,则EG =DE 2-DG 2=x 22-4,FI =EF 2-EI 2=x 22-4,FH =FI +HI =FI +EG=2x 22-4.连接DH ,在Rt △DHF 中,DF 2=DH 2+FH 2,即x 2=4+⎝⎛⎭⎫2x 22-42,解得x =23,即该三角形的斜边长为2 3.答案:2 3 15.(2021·浙江省名校新高考联盟第一次联考)如图,ABEDFC 为多面体,平面ABED 与平面ACFD 垂直,点O 在线段AD 上,OA =1,OD =2,△OAB ,△OAC ,△ODE ,△ODF 都是正三角形,则BC =________,四棱锥F-OBED的体积为________.解析:取AO的中点M,连接CM,BM,由△OAB,△OAC是正三角形,OA=1,可知CM⊥AO,BM⊥AO,且BM=CM=32,又平面ABED⊥平面ACFD,所以CM⊥平面ABED,所以CM⊥BM,故BC=62.过点F作FQ⊥OD于点Q,由于平面ABED⊥平面ACFD,所以FQ⊥平面ABED,FQ就是四棱锥F-OBED的高.易知FQ=3,又S△OBE=12×1×2×32=32,S△OED=12×2×2×32=3,所以S四边形OBED=32+3=332,故V四棱锥F-OBED=13×332×3=32.答案:6232。
2019届高考数学二轮复习 专题五 立 体 几 何 (讲义训练):第3讲 立体几何中的计算 课时讲义(含答案)

第3讲 立体几何中的计算 课时讲义1. 高考对立体几何的计算,主要是能利用公式求常见几何体(柱体、锥体、台体和球)的表面积与体积.有时还需能解决距离、翻折、存在性等比较综合性的问题.2. 高考中常见的题型为:(1) 常见几何体的表面积与体积的计算;(2) 利用等积变换求距离问题;(3) 通过计算证明平行与垂直等问题;(4) 几何体的内切和外接.1. 棱长都是2的三棱锥的表面积为________. 答案:43解析: 因为四个面是全等的正三角形,则S 表面积=4×34×4=43.2. 如图,正方体ABCDA 1B 1C 1D 1的棱长为1,点P 是棱BB 1的中点,则四棱锥PAA 1C 1C的体积为________.答案:13解析:四棱锥PAA 1C 1C 的体积为13×22×2×1=13.3. (2018·南京学情调研)将一个正方形绕着它的一边所在的直线旋转一周,所得圆柱的体积为27π cm 3,则该圆柱的侧面积为________cm 2.答案:18π解析:设正方形的边长为a cm ,则πa 2·a =27π,解得a =3,所以侧面积2π×3×3=18π.4. (2018·海安质量测试)已知正三棱锥的体积为36 3 cm 3,高为4 cm ,则底面边长为________cm.答案:63解析: 设正三棱锥的底面边长为a ,则其面积为S =34a 2.由题意13·34a 2×4=363,解得a =63., 一) 表面积与体积, 1) 如图,在以A ,B ,C ,D ,E 为顶点的六面体中,△ABC 和△ABD 均为等边三角形,且平面ABC ⊥平面ABD ,EC ⊥平面ABC ,EC =3,AB =2.(1) 求证:DE ∥平面ABC ; (2) 求此六面体的体积.(1) 证明:作DF ⊥AB ,交AB 于点F ,连结CF. 因为平面ABC ⊥平面ABD , 且平面ABC ∩平面ABD =AB , 所以DF ⊥平面ABC.因为EC ⊥平面ABC ,所以DF ∥EC. 因为△ABD 是边长为2的等边三角形, 所以DF =3,因此DF =EC ,所以四边形DECF 为平行四边形,所以DE ∥CF.因为DE ⊄平面ABC ,CF ⊂平面ABC , 所以DE ∥平面ABC.(2) 解:因为△ABD 是等边三角形,所以点F 是AB 的中点. 又△ABC 是等边三角形,所以CF ⊥AB. 由DF ⊥平面ABC 知,DF ⊥CF , 所以CF ⊥平面ABD.因为DE ∥CF ,所以DE ⊥平面ABD , 因此四面体ABDE 的体积为13S △ABD ·DE =1;四面体ABCE 的体积为13S △ABC ·CE =1,而六面体ABCED 的体积=四面体ABDE 的体积+四面体ABCE 的体积, 故所求六面体的体积为2.(2018·苏州暑假测试)如图,正四棱锥P ABCD 的底面一边AB 的长为2 3 cm ,侧面积为83 cm 2,则它的体积为________cm 3.答案:4解析:记正四棱锥P ABCD 的底面中心为点O ,棱AB 的中点为H, 连结PO ,HO ,PH ,则PO ⊥平面ABCD .因为正四棱锥的侧面积为83 cm 2,所以83=4×12×23×PH ,解得PH =2.在直角△PHO 中,PH =2,HO =3,所以PO =1,所以V PABCD =13×S 四边形ABCD ×PO =13×23×23×1=4(cm 3)., 二) 翻折与切割问题, 2) 如图,在菱形ABCD 中,AB =2,∠ABC =60°,BD ∩AC =O ,现将其沿菱形对角线BD 折起得到空间四边形EBCD ,使EC =2.(1) 求证:EO ⊥CD ;(2) 求点O 到平面EDC 的距离.(1) 证明:∵ 四边形ABCD 为菱形,∴ AC ⊥BD . ∵ BD ∩AC =O ,∴ AO ⊥BD ,即EO ⊥BD .∵ 在菱形ABCD 中,AB =2,∠ABC =60°,∴ AD =CD =BC =2,AO =OC =1. ∵ EC =2,CO =EO =1,∴ EO 2+OC 2=EC 2,∴ EO ⊥OC . 又BD ∩OC =O ,∴ EO ⊥平面BCD ,∴ EO ⊥CD .(2) 解:设点O 到平面ECD 的距离为h ,由(1)知EO ⊥平面OCD .V 三棱锥O CDE =V 三棱锥E OCD ,即13S △OCD ·EO =13S △ECD ·h . 在Rt △OCD 中,OC =1,OD =3,∠DOC =90°,∴ S △OCD =12OC ·OD =32.在△CDE 中,ED =DC =2,EC =2,∴ S △CDE =12×2×22-(22)2=72, ∴ h =S △OCD ·EO S △ECD =217,即点O 到平面EDC 的距离为217.如图①,在直角梯形ABCD 中,AD ∥BC ,∠BAD =π2,AB =BC =12AD =a ,点E 是AD的中点,O 是AC 与BE 的交点.将△ABE 沿BE 折起到如图②中△A 1BE 的位置,得到四棱锥A 1BCDE .(1) 求证:CD ⊥平面A 1OC ;(2) 当平面A 1BE ⊥平面BCDE 时,四棱锥A 1BCDE 的体积为362,求a 的值.,①) ,②)(1) 证明:在图①中,因为AB =BC =12AD =a ,点E 是AD 的中点,∠BAD =π2,所以BE ⊥AC ,即在图②中,BE ⊥A 1O ,BE ⊥OC . 又A 1O ∩OC =O ,所以BE ⊥平面A 1OC . 在图①中,BC ∥ED ,且BC =ED ,所以四边形BCDE 是平行四边形,所以BE ∥CD , 所以CD ⊥平面A 1OC .(2) 解:因为平面A 1BE ⊥平面BCDE ,所以A 1O 是四棱锥A 1BCDE 的高. 根据图①可得A 1O =22AB =22a ,平行四边形BCDE 的面积S =BC ·AB =a 2, 所以VA 1BCDE =13×S ×A 1O =13×a 2×22a =26a 3.由26a 3=362,解得a =6., 三) 立体几何中的以算代证问题, 3) (2018·泰州中学学情调研)在直三棱柱ABCA 1B 1C 1中,AB =AC =AA 1=3a ,BC =2a ,D 是BC 的中点,E ,F 分别是AA 1,CC 1上一点,且AE =CF =2a.(1) 求证:B 1F ⊥平面ADF ; (2) 求三棱锥B 1ADF 的体积.(1) 证明:∵ AB =AC ,D 为BC 中点,∴ AD ⊥BC.在直三棱柱ABC -A 1B 1C 1中,B 1B ⊥底面ABC ,AD ⊂底面ABC ,∴ AD ⊥B 1B.∵ BC ∩B 1B =B ,∴ AD ⊥平面B 1BCC 1. ∵ B 1F ⊂平面B 1BCC 1,∴ AD ⊥B 1F.在矩形B 1BCC 1中,C 1F =CD =a ,B 1C 1=CF =2a , ∴ Rt △DCF ≌Rt △FC 1B 1,∴ ∠CFD =∠C 1B 1F , ∴ ∠B 1FD =90°,∴ B 1F ⊥FD . ∵ AD ∩FD =D ,∴ B 1F ⊥平面AFD . (2) 解: ∵ B 1F ⊥平面AFD ,∴ VB 1-ADF =13·S △ADF ·B 1F =13×12×AD ×DF ×B 1F =52a 33.如图①,在直角梯形ABCD 中,∠ADC =90°,CD ∥AB ,AB =4,AD =CD =2.将△ADC 沿AC 折起,使平面ADC ⊥平面ABC ,得到几何体DABC ,如图②.(1) 求证:BC ⊥平面ACD ; (2) 求几何体DABC 的体积.(1) 证明:(证法1)在图①中,由题意知,AC =BC =22,∴ AC 2+BC 2=AB 2,∴ AC ⊥BC .取AC 的中点O ,连结DO ,由AD =CD ,得DO ⊥AC .又平面ADC ⊥平面ABC ,且平面ADC ∩平面ABC =AC ,DO ⊂平面ACD , ∴ OD ⊥平面ABC ,∴ OD ⊥BC . 又AC ⊥BC ,AC ∩OD =O , ∴ BC ⊥平面ACD .(证法2)在图①中,由题意得AC =BC =22,∴ AC 2+BC 2=AB 2, ∴ AC ⊥BC .∵ 平面ADC ⊥平面ABC ,平面ADC ∩平面ABC =AC ,BC ⊂平面ABC , ∴ BC ⊥平面ACD .(2) 解:由(1)知,BC 为三棱锥BACD 的高, 且BC =22,S △ACD =12×2×2=2,∴ 三棱锥BACD 的体积V BACD =13S △ACD ·BC =13×2×22=423,即几何体DABC 的体积为423.1. (2018·天津卷)如图,已知正方体ABCDA 1B 1C 1D 1的棱长为1,则四棱锥A 1BB 1D 1D 的体积为________.答案:13解析:如图,连结A 1C 1,交B 1D 1于点O ,很明显A 1C 1⊥平面BDD 1B 1,则A 1O 是四棱锥的高,且A 1O =12A 1C 1=12×12+12=22,S 四边形BDD 1B 1=BD ×DD 1=2×1=2,结合四棱锥体积公式可得其体积为V =13Sh =13×2×22=13.2. (2018·江苏卷)如图,正方体的棱长为2,以其所有面的中心为顶点的多面体的体积为________.答案:43解析:由图可知,该多面体为两个全等正四棱锥的组合体,正四棱锥的高为1,底面正方形的边长等于2,所以该多面体的体积为2×13×1×(2)2=43.3. (2017·北京卷)如图,在三棱锥PABC 中,PA ⊥AB ,PA ⊥BC ,AB ⊥BC ,PA =AB =BC =2,点D 为线段AC 的中点,E 为线段PC 上一点.(1) 求证:PA ⊥BD ;(2) 求证:平面BDE ⊥平面PAC ;(3) 当PA ∥平面BDE 时,求三棱锥EBCD 的体积.(1) 证明:因为PA ⊥AB ,PA ⊥BC ,AB ∩BC =B ,所以PA ⊥平面ABC. 因为BD ⊂平面ABC ,所以PA ⊥BD.(2) 证明:因为AB =BC ,点D 为AC 的中点,所以BD ⊥AC. 由(1)知,PA ⊥BD ,PA ∩AC =A ,所以BD ⊥平面PAC. 又BD ⊂平面BDE , 所以平面BDE ⊥平面PAC.(3) 解:因为PA ∥平面BDE ,平面PAC ∩平面BDE =DE ,所以PA ∥DE. 因为点D 为AC 的中点,所以DE =12PA =1,BD =DC =2.由(1)知,PA ⊥平面ABC ,所以DE ⊥平面ABC , 所以三棱锥EBCD 的体积为V =13×12×BD ×DC ×DE =13.4. (2017·全国卷Ⅰ)如图,在四棱锥PABCD 中,AB ∥CD ,且∠BAP =∠CDP =90°. (1) 求证:平面PAB ⊥平面PAD ;(2) 若PA =PD =AB =DC ,∠APD =90°,且四棱锥PABCD 的体积为83,求该四棱锥的侧面积.(1) 证明:由已知∠BAP =∠CDP =90°,得AB ⊥AP ,CD ⊥PD .由于AB ∥CD ,故AB ⊥PD .又PA ∩PD =P ,所以AB ⊥平面PAD . 又AB ⊂平面PAB ,所以平面PAB ⊥平面PAD .(2) 解:如图,在平面PAD 内作PE ⊥AD ,垂足为点E .由(1)知,AB ⊥平面PAD ,故AB ⊥PE ,由AB ∩AD =A ,可得PE ⊥平面ABCD .设AB =x ,则由已知可得AD =2x ,PE =22x ,故四棱锥PABCD 的体积V PABCD =13AB ·AD ·PE =13x 3.由题设得13x 3=83,解得x =2. 从而PA =PD =2,AD =BC =22,PB =PC =22,所以△PBC 为等边三角形,可得四棱锥PABCD 的侧面积为 12PA ·PD +12PA ·AB +12PD ·DC +12BC 2sin 60°=6+2 3.5. (2017·全国卷Ⅲ)如图,在四面体ABCD 中,△ABC 是正三角形,AD =CD .(1) 求证:AC ⊥BD ;(2) 已知△ACD 是直角三角形,AB =BD ,若E 为棱BD 上与D 不重合的点,且AE ⊥EC ,求四面体ABCE 与四面体ACDE 的体积比.(1) 证明:如图,取AC 的中点O ,连结DO ,BO .因为AD =CD ,所以AC ⊥DO .又由于△ABC 是正三角形,所以AC ⊥BO . 又DO ∩BO =O ,所以AC ⊥平面DOB . 因为BD ⊂平面DOB ,所以AC ⊥BD . (2) 解:连结EO .由(1)及题设知∠ADC =90°,所以DO =AO . 在Rt △AOB 中,BO 2+AO 2=AB 2. 又AB =BD ,所以BO 2+DO 2=BO 2+AO 2=AB 2=BD 2, 故∠DOB =90°.由题设知△AEC 为直角三角形,所以EO =12AC .又△ABC 是正三角形,且AB =BD ,所以EO =12BD ,故点E 为BD 的中点.所以点E 到平面ABC 的距离为点D 到平面ABC 的距离的12,四面体ABCE 的体积为四面体ABCD 的体积的12,即四面体ABCE 与四面体ACDE 的体积之比为1∶1.(本题模拟高考评分标准,满分14分) (2018·长春模拟)如图,四边形ABCD 为菱形,G 为AC 与BD 的交点,BE ⊥平面ABCD .(1) 求证:平面AEC ⊥平面BED ;(2) 若∠ABC =120°,AE ⊥EC ,三棱锥EACD 的体积为63,求该三棱锥的侧面积.(1) 证明:因为四边形ABCD 为菱形,所以AC ⊥BD . 因为BE ⊥平面ABCD ,AC ⊂平面ABCD ,所以AC ⊥BE .(2分) 因为BD ∩BE =B ,故AC ⊥平面BED .又AC ⊂平面AEC ,所以平面AEC ⊥平面BED .(6分)(2) 解:设AB =x ,在菱形ABCD 中,由∠ABC =120°,得AG =GC =32x ,GB =GD=x2. 因为AE ⊥EC ,所以在Rt △AEC 中,可得EG =32x .(8分)由BE ⊥平面ABCD ,知△EBG 为直角三角形,可得BE =22x .由已知得三棱锥EACD 的体积为63,即13×12·AC ·GD ·BE =624x 3=63,解得x =2.(9分)从而可得AE =EC =ED =6.所以△EAC 的面积为3,△EAD 的面积与△ECD 的面积均为 5.故三棱锥EACD 的侧面积为3+25.(14分)1. 若一个圆柱的侧面展开图是边长为2的正方形,则此圆柱的体积为________. 答案:2π解析: 设圆柱的底面半径为r ,高为h ,则有2πr =2,即r =1π,故圆柱的体积为V =πr 2h =π⎝ ⎛⎭⎪⎫1π2×2=2π.2. 如图,已知AF ⊥平面ABCD ,四边形ABEF 为矩形,四边形ABCD 为直角梯形,∠DAB =90°,AB ∥CD ,AD =AF =CD =2,AB =4.(1) 求证:AF ∥平面BCE ; (2) 求证:AC ⊥平面BCE ; (3) 求三棱锥EBCF 的体积.(1) 证明:∵ 四边形ABEF 为矩形,∴ AF ∥BE .又BE ⊂平面BCE ,AF ⊄平面BCE , ∴ AF ∥平面BCE .(2) 证明:如图,过点C 作CM ⊥AB ,垂足为点M . ∵ AD ⊥DC ,∴ 四边形ADCM 为矩形, ∴ AM =DC =MB =AD =2.∴ AC =22,CM =2,BC =22,∴ AC 2+BC 2=AB 2,∴ AC ⊥BC . ∵ AF ⊥平面ABCD ,AF ∥BE , ∴ BE ⊥平面ABCD ,∴ BE ⊥AC .∵ BE ⊂平面BCE ,BC ⊂平面BCE ,BC ∩BE =B , ∴ AC ⊥平面BCE .(3) 解:∵ AF ⊥平面ABCD ,∴ AF ⊥CM .∵ CM ⊥AB ,AF ⊂平面ABEF ,AB ⊂平面ABEF ,AF ∩AB =A ,∴ CM ⊥平面ABEF ,∴ V 三棱锥EBCF =V 三棱锥CBEF =13×12×BE ×EF ×CM =16×2×4×2=83.3. (2016·江苏卷)现需要设计一个仓库,它由上、下两部分组成,上部分的形状是正四棱锥P A 1B 1C 1D 1,下部分的形状是正四棱柱ABCD A 1B 1C 1D 1(如图),并要求正四棱柱的高O 1O 是正四棱锥的高PO 1的4倍.(1) 若AB =6 m ,PO 1=2 m ,则仓库的容积是多少?(2) 若正四棱锥的侧棱长为6 m ,则当PO 1为多少时,仓库的容积最大?解:(1) ∵ PO 1=2 m ,正四棱柱的高O 1O 是正四棱锥的高PO 1的4倍,∴ O 1O =8 m ,∴ 仓库的容积V =13×62×2+62×8=312(m 3). (2) 若正四棱锥的侧棱长为6 m ,设PO 1=x m ,则O 1O =4x m ,A 1O 1=36-x 2 m ,A 1B 1=2·36-x 2 m , 则仓库的容积V (x )=13×(2·36-x 2)2·x +(2·36-x 2)2·4x =-263x 3+312x (0<x<6), V ′(x )=-26x 2+312(0<x <6).当0<x <23时,V ′(x )>0,V (x )单调递增; 当23<x <6时,V ′(x )<0,V (x )单调递减. 故当x =23时,V (x )取最大值. 即当PO 1=23 m 时,仓库的容积最大.请使用“课后训练·第19讲”活页练习,及时查漏补缺!。
高考二轮复习理科数学课件培优拓展4巧设变量速求立体几何中的动态最值问题

1
1
+a-1-b=0,即
2
=
1
×
3
N-AA1D 的体积最大值
评析 该题中“点N为平面DCC1D1上的动点”,虽然只涉及一个动点,但需要
两个变量才能确定点的位置,在解题过程中首先建立目标函数,然后利用
“MN⊥A1C”建立两个坐标参数之间的关系,确定两个参数最终的取值范围
或代入目标函数进行消元,从而求得最值.
例2如图所示,在正四棱柱ABCD-A1B1C1D1中,AB=BC=1,AA1=2.动点P,Q分
别在线段C1D,AC上,则线段PQ长度的最小值是( B )
1
A.3
2
B.3
C.1
4
D.3
解析 建立如图所示的空间直角坐标系,则
A(1,0,0),B(1,1,0),C(0,1,0),C1(0,1,2),
设点P的坐标为(0,λ,2λ),λ∈[0,1],点Q的坐标为(1-μ,μ,0),μ∈[0,1],
3
h=
2
1- 2 ,
3
f(t)=t2- ,则
2
时,f'(t)<0,函数 f(t)
C.
评析 方法一:思维严谨,利用基本不等式求最值,模型熟悉,是该题的最优解.
方法二:消元,实现变量统一,再利用基本不等式求最值.
方法三:消元,实现变量统一,利用导数求最值,是最值问题的常用解法,操作
简便,是通性通法.
所示的长方体 ADPH-EBFC.∴BD2+BE2=AB2=3,BD2+BF2=PB2=5,
BE2+BF2=BC2=4,∴BD2+BE2+BF2=6,∴球 O 的半径
1
R=2
2025年高考数学总复习课件47第六章微专题立体几何中的动态问题

3+1
AP·sin (45˚+30˚)=
.
2
微专题
立体几何中的动态问题
【例6 】 如 图 , 在 正 三棱柱 ABC-A1B1C1 中 , 底面 边 长为 a ,侧 棱长为 b, 且
a≥b,点D是BC1的中点,则直线AD与侧面ABB1A1所成角的正切值的最小值是
HF,可得四边形EGC1D1 是平行四边形,所以C1G∥D1E.又C1G⊄平面CD1EF,
D1E⊂ 平 面 CD1EF , 所 以 C1G∥ 平 面 CD1EF. 同 理 可 得 C1H∥CF , C1H∥ 平 面
CD1EF.
因为C1H∩C1G=C1,C1H,C1G⊂平面C1GH,所以平面C1GH∥平面CD1EF.
D.平面A1BCD1∥平面EFGH
)
B
解析:当E与A1 重合,H与D1 重合时,BD1 与EH的夹角即BD1 与A1D1 的夹
角,显然BD1与A1D1的夹角不是 ,故A错误.
2
当 FG 不 与 B1C1 重 合 时 , 因 为 EH∥FG , EH⊂ 平 面 A1B1C1D1 , FG ⊄ 平 面
A1B1C1D1 ,所以FG∥平面A1B1C1D1.因为FG⊂平面BCC1B1 ,平面A1B1C1D1∩平
面BCC1B1=B1C1,所以FG∥B1C1∥AD.当FG与B1C1重合时,显然FG∥AD,故
B正确.
当平面EFGH与平面BCC1B1重合时,显然平面BB1D1D与平面BCC1B1不垂直,故
C错误.
直 线 AD 与 侧 面 ABB1A1 所 成 的 角 . 在 Rt△AFD 中 , DF =
高考满分数学压轴题14 立体几何的动态问题(可编辑可打印)

一.方法综述立体几何的动态问题是高考的热点,问题中的“不确定性”与“动感性”元素往往成为学生思考与求解问题的思维障碍,使考题的破解更具策略性、挑战性与创新性.一般立体动态问题形成的原因有动点变化、平面图形的翻折、几何体的平移和旋转以及投影与截面问题,由此引发的常见题型为动点轨迹、角度与距离的计算、面积与体积的计算、探索性问题以及有关几何量的最值求解等.动态立体几何题在变化过程中总蕴含着某些不变的因素,因此要认真分析其变化特点,寻找不变的静态因素,从静态因素中,找到解决问题的突破口.求解动态范围的选择、填空题,有时应把这类动态的变化过程充分地展现出来,通过动态思维,观察它的变化规律,找到两个极端位置,即用特殊法求解范围.对于探究存在问题或动态范围(最值)问题,用定性分析比较难或繁时,可以引进参数,把动态问题划归为静态问题.具体地,可通过构建方程、函数或不等式等进行定量计算,以算促证.二.解题策略类型一 立体几何中动态问题中的角度问题例1. 已知平行四边形ABCD 中,1AB =,2AD =,60A ∠=︒,沿对角线BD 将ABD △折起到PBD △的位置,使得平面PBD ⊥平面BCD ,如图,若M ,N 均是线段PD 的三等分点,点Q 是线段MN 上(包含端点)的动点,则二面角Q BC D --的正弦值的取值范围为( )A .12,23⎡⎤⎢⎥⎣⎦B .14192⎡⎢⎣⎦C .24193⎡⎢⎣⎦D .11,32⎡⎤⎢⎥⎣⎦【来源】2021年浙江省新高考测评卷数学(第五模拟) 【答案】B【解析】在ABD △中,1AB =,2AD =,60BAD ∠=︒,所以由余弦定理得3BD =,所以222AB BD AD +=,所以AB BD ⊥,由翻折的性质可知,PB BD ⊥.又平面PBD ⊥平面BCD ,平面PBD 平面BCD BD =,所以PB ⊥平面BCD ,过点Q 作//QQ PB ',交BD 于点Q ',则QQ '⊥平面BCD ,所以QQ BC '⊥,过Q '作Q T BC '⊥,垂足为T ,连接QT ,则BC ⊥平面QQ T ',立体几何的动态问题所以QTQ '∠为二面角Q BC D --的平面角. 设2QD a =(1233a ≤≤),则QQ a '=,3DQ a '=,33BQ a '=-,()113322Q T BQ a ''==-,所以2222211(33)76322QT QQ Q T a a a a ⎡⎤''=+=+-=-+⎢⎥⎣⎦, 所以22222sin 136176373142QQ aQTQ QT a a a aa ''∠====⎛⎫-+-+-+ ⎪⎝⎭. 由二次函数的单调性知,21314y a ⎛⎫=-+ ⎪⎝⎭在12,33⎡⎤⎢⎥⎣⎦上的值域为19,164⎡⎤⎢⎥⎣⎦,所以221419sin ,2191314QTQ a ⎡⎤'∠=∈⎢⎥⎣⎦⎛⎫-+ ⎪⎝⎭,即二面角Q BC D --的正弦的取值范围为1419,219⎡⎤⎢⎥⎣⎦. 故选:B.【举一反三】1.(2020·黑龙江牡丹江一中高三(理))如图,在正方体1111ABCD A B C D -中,O 是AC 中点,点P 在线段11A C 上,若直线OP 与平面11A BC 所成的角为θ,则sin θ的取值范围是( ).A .23⎣⎦B .11,32⎡⎤⎢⎥⎣⎦C .33⎣⎦D .11,43⎡⎤⎢⎥⎣⎦【答案】A【解析】如图,设正方体棱长为1,()11101A PAC λλ=≤≤.以D 为原点,分别以DA ,DC ,1DD 所在直线为x ,y ,z 轴建立空间直角坐标系. 则11,,022O ⎛⎫ ⎪⎝⎭,()1,,1P λλ-,所以11,,122OP λλ⎛⎫=--⎪⎝⎭.在正方体1111ABCD A B C D -中,可证1B D ⊥平面11A BC , 所以()11,1,1B D =---是平面11A BC 的一个法向量.所以122211()()122sin cos ,1113163222OP B D λλθλλλ-----===⎛⎫⎛⎫⎛⎫⨯-+-+-+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭所以当12λ=时,sin θ30λ=或1时,sin θ取得最小值23. 所以23sin 3θ∈⎣⎦.故选A . 2.(2020·广东高考模拟)在正方体1111ABCD A B C D -中,E 是侧面11ADD A 内的动点,且1B E //平面1BDC ,则直线1B E 与直线AB 所成角的正弦值的最小值是( )A .13 B .33 C .12 D .22【答案】B【解析】以D 为原点,DA 为x 轴,DC 为y 轴,1DD 为z 轴,建立空间直角坐标系,设正方体1111ABCD A B C D -中棱长为1, 设E(a,0,c),0a 1≤≤,0c 1≤≤,1B (1,1,1),B(1,1,0), D(0,0,0),1C (0,1,1),()1B E a 1,1,c 1=---,DB (1,=1,0),1DC (0,=1,1),设平面1DBC 的法向量n (x,=y ,z),则1n DB 0n DC 0x y y z ⎧⋅=+=⎪⎨⋅=+=⎪⎩,取x 1=,得()n 1,1,1=-,1B E //平面1BDC ,1B E n a 11c 10∴⋅=-++-=,解得a c 1+=,()222a c a c 2ac 12ac ∴+=+-=-,2a c 1ac 24+⎛⎫≤=⎪⎝⎭,设直线1B E 与直线AB 所成角为θ,AB (0,=1,0),()()1221AB B E 1cos θAB B Ea 11c 1⋅∴==⋅-++-2a c 1ac 24+⎛⎫≤= ⎪⎝⎭,322ac 2∴-≥,1222ac 3∴≤-,()()()222211sin θ11a c 2a c 3a 11c 1∴=-=-+-++-++-221123111a c 122ac 33=-=-≥-=++-. ∴直线1B E 与直线AB 所成角的正弦值的最小值是33.3.(2020·浙江台州中学高三)如图,已知正方体ABCD EFGR -的上底面中心为H ,点O 为AH 上的动点,P 为FG 的三等分点(靠近点F ),Q 为EF 的中点,分别记二面角P OQ R --,Q OR P --,R OP Q --的平面角为,,αβγ,则( )A .γαβ<<B .αγβ<<C .αβγ<<D .βαγ<<【答案】D【解析】分析:建立空间直角坐标系,对动点O 选取一个特殊位置,然后求出三个侧面的法向量,根据向量夹角的余弦值求得三个二面角的余弦值,比较后可得二面角的大小.详解:建立如图所示的空间直角坐标系E xyz -.考虑点O 与点A 重合时的情况.设正方体的棱长为1,则()()111,,0,Q ,0,0,R 01,0,O 0,0,132P ⎛⎫⎛⎫⎪⎪⎝⎭⎝⎭. 设平面OPQ 的一个法向量为1(,,)n x y z =,由111(,,)(,0,1)02211(,,)(,,0)02323x n OQ x y z z x y n PQ x y z ⎧⋅=⋅-=-=⎪⎪⎨⎪⋅=⋅--=--=⎪⎩,得322x y x z ⎧=-⎪⎪⎨⎪=⎪⎩,令2x =,得1(2,3,1)n =-.同理可得平面OPR 和平面OQR 的法向量分别为23(2,3,3),(6,3,7)n n ==. 结合图形可得:1323521cos cos ,,cos cos ,7471147n n n n αβ====⨯⨯12cos cos ,711n n γ==⨯∴cos cos cos γαβ<<,又0,,γαβπ<<,∴γαβ>>.故选D . 类型二 立体几何中动态问题中的距离问题【例2】(2020·山西高三)设点M 是棱长为2的正方体ABCD -A 1B 1C 1D 1的棱AD 的中点,点P 在面BCC 1B 1所在的平面内,若平面D 1PM 分别与平面ABCD 和平面BCC 1B 1所成的锐二面角相等,则点P 到点C 1的最短距离是( ) A 25B .22C .1D .63【答案】A【解析】如图,过点P 作1D M 的平行线交BC 于点Q 、交11B C 于点E ,连接MQ ,则PQ 是平面1D PM 与平面11BCC B 的交线,MQ 是平面1D PM 与平面ABCD 的交线.EF 与1BB 平行,交BC 于点F ,过点F 作FG 垂直MQ 于点G ,则有,MQ 与平面EFG 垂直,所以,EG 与MQ 垂直,即角EGF 是平面1D PM 与平面ABCD 的夹角的平面角,且sin EFEGF EG∠=, MN 与CD 平行交BC 于点N ,过点N 作NH 垂直EQ 于点H ,同上有:sin MNMHN MH∠=,且有EGF MHN ∠=∠,又因为EF MN AB ==,故EG MH =, 而2EMQ S EG MQ MH EQ ∆=⨯=⨯,故MQ EQ =,而四边形1EQMD 一定是平行四边形,故它还是菱形,即点E 一定是11B C 的中点, 点P 到点1C 的最短距离是点1C 到直线BE 的距离,以A 为原点,AB 为x 轴,AD 为y 轴,1AA 为z 轴,建立空间直角坐标系,()2,1,2E ,()2,0,0B , ()12,2,2C ,()0,1,2BE =, ()10,2,2BC =,∴点P 到点1C 的最短距离:22111||625||1()221()5||||58BE BC d BC BE BC =-=⨯-=⨯.故选:A .【指点迷津】求两点间的距离或其最值.一种方法,可建立坐标系,设点的坐标,用两点间距离公式写出距离,转化为求函数的最值问题;另一种方法,几何法,根据几何图形的特点,寻找那两点间的距离最大(小),求其值. 【举一反三】1.(2020·四川高三(理))已知三棱锥S ABC -中,1SA SB SC ===,且SA 、SB 、SC 两两垂直,P 是三棱锥S ABC -外接球面上一动点,则P 到平面ABC 的距离的最大值是( )A .33B .3C .233D .433【答案】C 【解析】【分析】,,SA SB SC 是棱长为1的正方体MNQB ADCS -上具有公共顶点S 的三条棱,以B 为原点,,,BM BQ BS 分别为x 轴,y 轴,z 轴,建立空间直角坐标系,三棱锥S ABC -外接球就是正方体MNQB ADCS -的外接球,由正方体及球的几何性质可得点P 与N 重合时,点P 到平面ABC 的距离最大,求出平面ABC 的法向量,由点到直线的距离公式即可得结果. 【详解】三棱锥S ABC -,满足,,SA SB SC 两两垂直,且,,1SA SB SC =,∴如图,,SA SB SC 是棱长为1的正方体MNQB ADCS -上具有公共顶点S 的三条棱,以B 为原点,,,BM BQ BS 分别为x 轴,y 轴,z 轴,建立空间直角坐标系, 则()()()()()0,0,0,1,0,1,0,1,1,0,0,1,1,1,0B A C S N ,()()()1,0,1,0,1,1,1,1,0BA BC BN ===,设平面ABC 的法向量(),,n x y z =,则00n BA x z n BC y z ⎧⋅=+=⎨⋅=+=⎩,取1x =,得()1,1,1n =-,三棱锥S ABC -外接球就是棱长为1的正方体MNQB ADCS -的外接球,P 是三棱锥S ABC -外接球上一动点,∴由正方体与球的几何性质可得,点P 点与N 重合时,点P 到平面ABC 的距离最大,∴点P 到平面ABC 的距离的最大值为1102333BN n d n⋅++===.故选C. 2.已知四边形ABCD 是边长为5的菱形,对角线8BD =(如图1),现以AC 为折痕将菱形折起,使点B 达到点P 的位置.棱AC ,PD 的中点分别为E ,F ,且四面体PACD 的外接球球心落在四面体内部(不含边界,如图2),则线段EF 长度的取值范围为( )A .14,42⎛⎫ ⎪ ⎪⎝⎭B .141,2⎛⎫⎪ ⎪⎝⎭C .14,62⎛⎫⎪ ⎪⎝⎭D .()3,4【来源】江西省鹰潭市2021届高三高考二模数学(文)试题 【答案】A 【解析】由题意可知△APC 的外心1O 在中线PE 上, 设过点1O 的直线1l ⊥平面APC ,可知1l ⊂平面PED , 同理△ADC 的外心2O 在中线DE 上,设过点2O 的直线2l ⊥平面ADC ,则2l ⊂平面PED , 由对称性知直线12,l l 的交点O 在直线EF 上.根据外接球的性质,点O 为四面体PACD 的外接球的球心. 由题意得3,4EA PE ==,而2221111,4O A O E EA O A O E PE =++==所以178O E =. 令PEF θ∠=,显然02πθ<<,所以cos 4cos 4EF PE θθ==<. 因为1cos EF O EPE OEθ==, 所以172OE EF O E PE ⋅=⋅=, 又OE EF <,所以272EF >,即142EF >. 综上可知1442EF <<. 故选:A.3(2020广西柳州市模考)如图,在正方体中,棱长为1,点为线段上的动点(包含线段端点),则下列结论错误的是( )A .当时,平面B .当为中点时,四棱锥的外接球表面为C .的最小值为D .当时,平面【答案】C【解析】对于,连结,,,则,,,设到平面的距离为,则,解得,∴.∴当时,为与平面的交点.∵平面∥平面, ∵平面,∴∥平面,故A 正确. 又由以上分析可得,当时,即为三棱锥的高,∴平面,所以D 正确. 对于B ,当为中点时,四棱锥为正四棱锥, 设平面的中心为,四棱锥的外接球为,所以,解得,故四棱锥的外接球表面积为,所以B 正确.对于C ,连结,,则, ∴,由等面积法得的最小值为,∴的最小值为.所以C 不正确.故选:C.类型三 立体几何中动态问题中的面积、体积问题【例3】(2020·河南高三(理))在棱长为3的正方体1111ABCD A B C D -中,E 是1AA 的中点,P 是底面ABCD 所在平面内一动点,设1PD ,PE 与底面ABCD 所成的角分别为12θθ,(12θθ,均不为0),若12θθ=,则三棱锥11P BB C -体积的最小值是( ) A .92B .52C .32D .54【答案】C【解析】建系如图,正方体的边长为3,则(3E ,0,3)2,1(0D ,0,3),设(P x ,y ,0)(0x ,0)y ,则(3PE x =-,y -,3)2,1(PD x =-,y -,3),12θθ=,(0z =,0,1),12cos cos θθ∴=,即11||||||||||||PD z PE z PE z PD z =,代入数据,得:222233299(3)4x y x y =++-++,整理得:228120x y x +-+=,变形,得:22(4)4(02)x y y -+=, 即动点P 的轨迹为圆的一部分,过点P 作PF BC ⊥,交BC 于点F ,则PF 为三棱锥11P BB C -的高∴点P 到直线AD 的距离的最大值是2.则min 321PF =-=.1111119332212BB C BB B C S ∆=⋅⋅=⨯⨯=,1111193132213P BB C BB C V PF S -∆=⨯⨯⋅⋅=∴=故选:C .【指点迷津】求几何体体积的最值,先观察几何图形三棱锥,其底面的面积为不变的几何量,求点P到平面BCD 的距离的最大值,选择公式,可求最值. 【举一反三】1.(2020·四川高三期末)长方体1111ABCD A B C D -中,2AB =,1BC =,12AA =,P 为该正方体侧面11CC D D 内(含边界)的动点,且满足tan tan 22PAD PBC ∠+∠=.则四棱锥P ABCD -体积的取值范围是( ) A .20,3⎛⎤ ⎥⎝⎦B .22,33⎡⎤⎢⎥⎣⎦ C .40,3⎛⎤ ⎥⎝⎦D .24,33⎡⎤⎢⎥⎣⎦ 【答案】B【解析】如图所示:在RT PAD 中,tan PD PAD PD AD ∠==,在RT PBC 中,tan PCPBC PC BC∠==, 因为tan tan 22PAD PBC ∠+∠=,所以22PD PC +=.因为222PD PC CD +=>=,所以点P 的轨迹是以,C D 为焦点 222a =的椭圆. 如下图所示:2a =1c =,211b =-=,椭圆的标准方程为:2212x y +=.1(0,1)P联立22112x x y =⎧⎪⎨+=⎪⎩,解得:2y =.所以22()P -,32P . 当点P 运动到1P 位置时,此时四棱锥P ABCD -的高最长, 所以max 1112()21333P ABCD ABCD V S PO -=⨯⨯=⨯⨯=. 当点P 运动到2P 或3P 位置时,此时四棱锥P ABCD -的高最短,所以min 21122()23323P ABCD ABCD V S P D -=⨯⨯=⨯⨯=. 综上所述:2233P ABCD V -≤≤. 2.如图,长方形ABCD 中,152AB =,1AD =,点E 在线段AB (端点除外)上,现将ADE 沿DE 折起为A DE '.设ADE α∠=,二面角A DE C '--的大小为β,若π2αβ+=,则四棱锥A BCDE '-体积的最大值为( )A .14 B .23 C 151-D 51- 【答案】A【解析】设过A 与DE 垂直的线段长为a ,则tan AE α=,150tan 2α<<,1cos DE α=,sin a α=,则四棱锥A BCDE '-的高πsin sin sin sin cos 2h a βαααα⎛⎫=⋅=⋅-=⎪⎝⎭, 则111515tan 1sin cos 3222A BCDE V ααα'-⎛=⨯⨯-+⨯⨯ ⎝⎭)115tan sin cos 6ααα=⨯ )2115cos sin 6ααα=- )11152cos 21212αα=+- 115112cos 234412αα⎛⎫=+- ⎪ ⎪⎝⎭()11sin 2312αϕ=+-,15tan 15ϕ⎛⎫= ⎪ ⎪⎝⎭, ∴四棱锥A BCDE '-体积的最大值为1113124-=. 故选:A.3.(2020·重庆市松树桥中学校高三)如图,在单位正方体1111ABCD A B C D -中,点P 在线段1AD 上运动,给出以下四个命题:①异面直线1A P 与1BC 间的距离为定值;②三棱锥1D BPC -的体积为定值;③异面直线1C P 与直线1CB 所成的角为定值; ④二面角1P BC D --的大小为定值.其中真命题有( ) A .1个 B .2个 C .3个 D .4个【答案】D【解析】对于①,异面直线1A P 与1BC 间的距离即为两平行平面11ADD A 和平面11BCC B 间的距离,即为正方体的棱长,为定值.故①正确.对于②,由于11D BPC P DBC V V --=,而1DBC S ∆为定值,又P ∈AD 1,AD 1∥平面BDC 1,所以点P 到该平面的距离即为正方体的棱长,所以三棱锥1D BPC -的体积为定值.故②正确.对于③,由题意得在正方体1111ABCD A B C D -中,B 1C ⊥平面ABC 1D 1,而C 1P ⊂平面ABC 1D 1,所以B 1C ⊥C 1P ,故这两条异面直线所成的角为90︒.故③正确;对于④,因为二面角P −BC 1−D 的大小,即为平面ABC 1D 1与平面BDC 1所成的二面角的大小,而这两个平面位置固定不变,故二面角1P BC D --的大小为定值.故④正确.综上①②③④正确.选D .类型四 立体几何中动态问题中的轨迹问题【例4】(2020南充高考一模)如图,直二面角AB αβ--,P α∈,C β∈,D β∈,且AD AB ⊥,BC AB ⊥,5AD =,10BC =,6AB =,APD CPB ∠=∠,则点P 在平面α内的轨迹是( )A.圆的一部分B.椭圆的一部分C.一条直线D.两条直线【答案】A【解析】以AB 所在直线为x 轴,AB 的中垂线为y 轴,建立平面直角坐标系,设点(),P x y ,()30A -,,()3,0B ,AD AB ⊥,BC AB ⊥,则AD α⊥,BC α⊥,5AD =,10BC =,6AB =,APD CPB ∠=∠,Rt APDRt CPB∴∆∆,()()22223511023x y APAD BPBC x y ++∴====-+ ,即()()2222343x y x y ⎡⎤-+=++⎣⎦,整理得:()22516x y ++=,故点P 的轨迹是圆的一部分,故选A .【指点迷津】空间轨迹问题的求解策略:1.利用侧面展开或展到一个平面上寻求轨迹;2.利用圆锥曲线定义求轨迹;3.这辗转过程中动点的轨迹;4.利用函数观点探求轨迹 【举一反三】1.已知正方体1111ABCD A B C D -的棱长为23M ,N 为体对角线1BD 的三等分点,动点P 在三角形1ACB 内,且三角形PMN 的面积63PMN S =△P 的轨迹长度为( )A .269π B .263π C .469π D .463π 【答案】B【解析】如图所示:连接11BC B C O =,因为四边形11BCC B 是正方形,所以11BC B C ⊥,因为11D C ⊥平面11BCC B ,1B C ⊂平面11BCC B ,所以11D C ⊥1B C , 又11111,BC D C C BC =⊂平面11BC D ,11D C ⊂平面11BC D ,所以1B C ⊥平面11BC D ,所以11B C D B ⊥, 同理可知:11B A D B ⊥,又因为1B C ⊂平面1ACB ,1B A ⊂平面1ACB ,111B C B A B =,所以1D B ⊥平面1ACB ,根据题意可知:11136,26D B AB AB BC AC =====所以1ACB 为正三角形,所以160∠=︒B AC ,所以11326266322ACB S=⨯⨯⨯=,设B 到平面1ACB 的距离为h , 因为11B ACB B ABC V V --=,所以111133ACB ACBSh S BB ⋅⋅=⋅⋅,所以11ACB ACBSh SBB ⋅=⋅,所以()232323262342h ⨯⨯⨯=⨯,所以1123h D B ==,所以h BN =, 所以N 即为1D B 与平面1ACB 的交点,由题意可知:1D B ⊥平面1ACB ,所以MN PN ⊥,所以11262223PMNSMN PN PN PN =⋅=⋅⋅==,再如下图所示:在正三角形1ACB 中,高3sin 6026322AO AC =︒== 所以内切圆的半径16233r AO ==<,且623AN <=,取1B C 的两个三等分点,E F ,连接,EN FN ,所以1//,//NE AB NF AC ,所以NEF 是以PN 长度为边长的正三角形,所以P 的轨迹是以N 为圆心,半径等于263的圆,圆的周46π,在1ACB 内部的轨迹是三段圆弧,每一段圆弧的圆心角为60︒,所以对应的轨迹长度是圆周长的一半为63π,故选:B. 2、(2020贵阳高考模拟)在正方体1111ABCD A B C D -中,已知点P 为平面11AA D D 中的一个动点,且点P 满足:直线1PC 与平面11AA D D 所成的角的大小等于平面PBC 与平面11AA D D 所成锐二面角的大小,则点P 的轨迹为( )A .直线B .椭圆C .圆D .抛物线 【答案】DF E P C 1B 1D 1A 1DCBA z yx3.几何中常用表示L 的测度,当L 为曲线、平面图形和空间几何体时,L 分别对应其长度、面积和体积.在ABC 中,3AB =,4BC =,5AC =,P 为ABC 内部一动点(含边界),在空间中,到点P 的距离为1的点的轨迹为L ,则L 等于( ) A .612π+B .2263π+ C .20123π+ D .22123π+ 【来源】安徽省合肥市2021届高三下学期第三次教学质量检测理科数学试题 【答案】D【解析】空间中,到点P 的距离为1的点的轨迹所构成的空间几何体在垂直于平面ABC 的角度看,如下图所示:其中:BCDF ,ACEI 和ABGH 区域内的几何体为底面半径为1的半圆柱;CDE ,BFG ,AHI 区域内的几何体为被两平面所截得的部分球体,球心分别为,,C B A ;ABC 区域内的几何体是高为2的直三棱柱. 四边形BCDF 和ACEI 为矩形,2DCB ECA π∴∠=∠=,2DCE ACB ACB πππ∴∠=--∠=-∠,同理可得:FBG ABC π∠=-∠,HAI CAB π∠=-∠,()332DCE FBG HAI ACB ABC CAB ππππ∴∠+∠+∠=-∠+∠+∠=-=,∴CDE ,BFG ,AHI 区域内的几何体合成一个完整的,半径为1的球,则CDE ,BFG ,AHI 区域内的几何体的体积之和3144133V ππ=⨯=; 又BCDF ,ACEI 和ABGH 区域内的几何体的体积之和()221134562V ππ=⨯⨯++=;ABC 区域内的直三棱柱体积31342122V =⨯⨯⨯=,4226121233L πππ∴=++=+.故选:D.三.强化训练1.(2020·内蒙古高三期末)如图,棱长为1的正方体1111ABCD A B C D -中,M 是线段1A B 上的动点,则下列结论正确的是( ).①异面直线AD 与1CB 所成的角为45︒②11DC D M ⊥③三棱锥1M DCC -的体积为定值 ④1AM MD +的最小值为2. A .①②③ B .①②④C .③④D .②③④【答案】A【解析】①∵AD ∥BC ,∴异面直线AD 与1CB 所成的角即为BC 与1CB 所成的角, 可得夹角为45︒,故①正确;②连接1CD ,∵1DC ⊥平面A 1BCD 1,1D M ⊂平面A 1BCD 1, ∴11DC D M ⊥,故②正确;③∵1A B ∥平面DCC 1D 1,∴线段A 1B 上的点M 到平面DCC 1D 1的距离都为1, 又△DCC 1的面积为定值12, 因此三棱锥M −DCC 1的体积1111326V =⨯⨯=为定值,故③正确; ④将面AA 1B 与面A 1BCD 1沿A 1B 展成平面图形,线段AD 1即为AP +PD 1的最小值, 在△D 1A 1A 中,∠D 1A 1A =135°, 利用余弦定理解三角形得111211135222AD cos =+-⨯⨯⨯︒=+<,故④不正确.因此只有①②③正确.故选:A .2.(2020河南省焦作市高三)在棱长为4的正方体ABCD ﹣A 1B 1C 1D 1中,点E 、F 分别在棱AA 1和AB 上,且C 1E ⊥EF ,则|AF|的最大值为( )A .B .1C .D .2【答案】B【解析】以AB ,AD ,AA 1所在直线为x ,y ,z 轴,建立空间直角坐标系如图所示,则C 1(4,4,4),设E (0,0,z ),z ∈[0,4],F (x ,0,0),x ∈[0,4],则|AF|=x .=(4,4,4﹣z ),=(x ,0,﹣z ).因为C 1E ⊥EF ,所以,即:z 2+4x ﹣4z =0,x =z ﹣.当z =2时,x 取得最大值为1.|AF|的最大值为1.故选:B .3.(2020·重庆巴蜀中学高三(理))棱长为2的正方体1111ABCD A B C D -中,N 为1CC 的中点,P 在底面ABCD 内运动,1D P 与平面ABCD 所成角为1θ,NP 与平面ABCD 所成角为2θ,若12θθ=,则AP 的最小值为( ) A .2 B .83C .4D .1【答案】A【解析】分析:先证明PD=2PC ,再在底面ABCD 内建立如图所示的直角坐标系,求出211680sin()99PA αϕ=-+,再利用三角函数的图象和性质求出|AP|的最小值. 【详解】设12θθθ==,所以12tan tan DD PD θθ==,1PC tan tan CN θθ==,所以PD=2PC. 在底面ABCD 内建立如图所示的直角坐标系,设点P(x,y),则2222(1)2(+1)x y x y -+=+整理得22516454(),cos ,sin 39333x y x y αα++=∴=-=, 所以2224841168011680(cos )(sin 2)sin()43339999PA αααϕ=-+-=-+≥-=, 即||2AP ≥,所以|AP|的最小值为2.故选:A4.已知三棱锥A BCD -的所有棱长均为2,E 为BD 的中点,空间中的动点P 满足PA PE ⊥,PC AB ⊥,则动点P 的轨迹长度为( ) A .1116πB 3πC 11πD 3π【来源】浙江省五校2021届高三下学期5月联考数学试题 【答案】C【解析】正四面体A BCD -2,建立空间直角坐标系如图所示,()()22,,2,2,2,0,0,2,222E C B ⎛⎫ ⎪ ⎪⎝⎭,设(),,P x y z ,()22,,2,,,22PE x y z AP x y z ⎛⎫=---= ⎪ ⎪⎝⎭,()2,2,PC x y z =---.由于PA PE ⊥,PC AB ⊥,所以00AP PE PC AB ⎧⋅=⎨⋅=⎩,即()()2220222220x x y y z z y z ⎧⎛⎫⎛⎫-+-+-=⎪ ⎪ ⎪⎪⎪ ⎪⎝⎭⎝⎭⎨⎪--=⎪⎩,即22222202220x x y y z z y z ⎧-+-+-=⎪⎨⎪+-=⎩, 即2222223442420x y z y z ⎧⎛⎫⎛⎫⎛⎫⎪-+-+-= ⎪ ⎪ ⎪⎪ ⎪ ⎪ ⎪⎨⎝⎭⎝⎭⎝⎭⎪+-=⎪⎩, 22222234424x y z ⎛⎫⎛⎫⎛⎫-+-+-= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭表示球心为222,,442⎛⎫ ⎪ ⎪⎝⎭,半径为32R =的球. 20y z +-=表示垂直于yAz 平面的一个平面.所以P 的轨迹是上述平面截球面所得圆.球心222,,442⎛⎫ ⎪ ⎪⎝⎭到平面20y z +-=的距离为22222142411d +-==+, 所以截得的圆的半径2231114164r R d =-=-=, 所以截得的圆,也即P 点的轨迹的长度为11112242r πππ=⨯=. 故选:C5.(2020郑州一中高三期末)在三棱锥中,平面,M是线段上一动点,线段长度最小值为,则三棱锥的外接球的表面积是()A.B.C.D.【答案】C【解析】如图所示:三棱锥中,平面,M是线段上一动点,线段长度最小值为,则:当时,线段达到最小值,由于:平面,所以:,解得:,所以:,则:,由于:,所以:则:为等腰三角形.所以:,在中,设外接圆的直径为,则:,所以:外接球的半径,则:,故选:C.(2020九江高三一模)在长方体中,,,分别是棱6.的中点,是底面内一动点,若直线与平面没有公共点,则三角形面积的最小值为()A.B.C.D.【答案】C【解析】补全截面EFG为截面EFGHQR如图,其中H 、Q 、R 分别为、的中点,易证平面ACD 1∥平面EFGHQR ,∵直线D 1P 与平面EFG 不存在公共点, ∴D 1P∥面ACD 1,∴D 1P 面ACD 1,∴P ∈AC ,∴过P 作AC 的垂线,垂足为K ,则BK=,此时BP 最短,△PBB 1的面积最小, ∴三角形面积的最小值为,故选:C .7.(2020·浙江高三期末)在三棱锥P ABC -中,2,3PA PB PC AB AC BC ======,点Q 为ABC ∆ 所在平面内的动点,若PQ 与PA 所成角为定值θ,π(0,)4θ∈,则动点Q 的轨迹是 A .圆 B .椭圆C .双曲线D .抛物线【答案】B【解析】建立空间直角坐标系,根据题意,求出Q 轨迹方程,可得其轨迹.由题,三棱锥P ABC -为正三棱锥,顶点P 在底面ABC 的射影O 是底面三角形ABC 的中心,则以O 为坐标原点,以OA 为x 轴,以OP 为z 轴,建立如图所示的空间直角坐标系,根据题意可得1OA OP ==,设Q 为平面ABC 内任 一点,则()()()()()1,0,0,0,0,1,,,0,1,0,1,,,1A P Q x y PA PQ x y =-=- ,由题PQ 与PA 所成角为定值θ,π0,4θ⎛⎫∈ ⎪⎝⎭,则,221cos 21PA PQ x PA PQ x y θ⋅+==⋅++则()()22222cos11x y x θ++=+ ,化简得222cos22cos 2cos20x y x θθθ⋅+⋅-+= ,ππ0,,20,,cos 20,42θθθ⎛⎫⎛⎫∈∴∈> ⎪ ⎪⎝⎭⎝⎭故动点Q 的轨迹是椭圆.选B8.(2020·上海格致中学高三月考)在正方体''''ABCD A B C D -中,若点P (异于点B )是棱上一点,则满足BP 与AC '所成的角为45︒的点P 的个数为( )A .0B .3C .4D .6【答案】B 【解析】【分析】建立空间直角坐标系,通过分类讨论利用异面直线的方向向量所成的夹角即可找出所有满足条件的点P 的个数.【详解】建立如图所示的空间直角坐标系,不妨设棱长1AB =,(1B ,0,1),(1C ,1,1). ①在Rt △AA C ''中,||tan 2||A C A AC AA '''∠'=='45A AC '∠'≠︒.同理AB ,AD 与AC '所成的角都为arctan 245≠︒.故当点P 位于(分别与上述棱平行或重合)棱BB ',BA ,BC 上时,与AC '所成的角都为arctan 245≠︒,不满足条件;②当点P 位于棱AD 上时,设(0P ,y ,1),(01)y ,则(1BP =-,y ,0),(1AC '=,1,1)-.若满足BP 与AC '所成的角为45︒,则22|||1||cos ,|2||||13BP AC y BP AC BP AC y '-+=<'>=='+, 化为2410y y ++=,无正数解,舍去; 同理,当点P 位于棱A D ''上时,也不符合条件; ③当点P 位于棱B C ''上时,设(1P ,y ,0),(01)y , 则(0BP =,y ,1)-,(1AC '=,1,1)-.若满足BP 与AC '所成的角为45︒,则22|||1||cos ,|2||||13BP AC y BP AC BP AC y '+=<'>=='+, 化为2410y y -+=,01y ,解得23y =-,满足条件,此时点(1,23,0)P -.④同理可求得棱C D ''上一点(532,1,0)P -,棱C C '上一点(1,1,324)P -. 而其它棱上没有满足条件的点P .综上可知:满足条件的点P 有且只有3个.故选:B 9.(2020上海交通大学附属中学高三)如图,已知三棱锥,平面,是棱上的动点,记与平面所成的角为,与直线所成的角为,则与的大小关系为( )A .B .C .D .不能确定【答案】C【解析】如图所示:∵PA ⊥平面ABC ,∴PD 与平面ABC 所成的角=∠PDA, 过点A 作AE ⊥BC ,垂足为E ,连接PE ,∵PA ⊥平面ABC ,∴PA ⊥BC ,∴BC⊥平面PAE ,∴BC⊥PE,在Rt△AED ,Rt△PAD ,Rt△PED 中:cos ,cos ,cos,∴coscoscos < cos ,又均为锐角, ∴,故选C.10.(2020·湖南长郡中学高三(理))在三棱锥P ABC -中,PA ⊥平面ABC ,23BAC π∠=,3AP =,23AB =,Q 是边BC 上的一动点,且直线PQ 与平面ABC 所成角的最大值为3π,则三棱锥P ABC -的外接球的表面积为( ) A .45π B .57πC .63πD .84π【答案】B【解析】分析:根据题意画出图形,结合图形找出ABC △的外接圆圆心与三棱锥P ABC - 外接球的球心,求出外接球的半径,再计算它的表面积.详解:三棱锥P ABC PA ABC 中,平面,-⊥ 设直线PQ 与平面ABC 所成角为θ ,如图所示;则3PAsinPQ PQ ,θ== 由题意且θ的最大值是3π3PQ=,,解得PQ =即PQ 的最小值为∴AQ ,即点A 到BC ,AQ BC ∴⊥,AB BC ∴== 6BC ;∴= 取ABC △的外接圆圆心为O ',作OO PA ' ,62120r sin ∴=︒,解得r =;O A ∴'=M 为PA 的中点,32OM O A PM ∴='==,由勾股定理得CP R === ∴三棱锥P ABC -的外接球的表面积是224457S R πππ==⨯⨯=.故选B.11.在直三棱柱111ABC A B C -中,底面ABC 是以B 为直角的等腰三角形,且3AB =,1AA =若点D 为棱1AA 的中点,点M 为面BCD 的一动点,则11 B M C M +的最小值为( )A .B .6C . D【来源】江西省赣州市2021届高三二模数学(理)试题 【答案】C【解析】由题意知,BC AB ⊥,111ABC A B C -为直三棱柱,即面ABC ⊥面11ABB A ,面ABC面11ABB A AB =,BC ⊂面ABC ,∴BC ⊥面11ABB A ,又BC ⊂面BCD , ∴面BCD ⊥面11ABB A .∴易得1B 关于平面BCD 对称点E 落在1A A 的延长线上,且AE =1A E =11 B M C M +的最小时,1C 、M 、E 三点共线.∴221111111||992735B M C M EM C M EC AC A E +=+≥=+=++=. 故选:C12.在棱长为2的正四面体ABCD 中,点P 为ABC 所在平面内一动点,且满足433PA PB +=,则PD 的最大值为( ) A .3B .2103C .393D .2【来源】河南省鹤壁市2021届高三一模数学(文)试题 【答案】B【解析】如图所示,在平面ABC 内,4323PA PB +=>, 所以点P 在平面ABC 内的轨迹为椭圆,取AB 的中点为点O ,连接CO ,以直线AB 为x 轴,直线OC 为y 建立如下图所示的空间直角坐标系O xyz -,则椭圆的半焦距1c =,长半轴a =b ==所以,椭圆方程为()2233104x y z +==.点D 在底面的投影设为点E ,则点E 为ABC 的中心,11333OE OC ===, 故点E 正好为椭圆短轴的一个端点,23CE OC ==,则DE ==, 因为222PD DE EP =+,故只需计算EP 的最大值.设(),,0P x y ,则E ⎛⎫⎪ ⎪⎝⎭,则22222241543333EP x y y y y y y ⎛=+=-++=--+ ⎝⎭,当y ⎡=⎢⎣⎦时,2EP 取最大值,即22max516393939EP ⎛⎛=-⨯---+= ⎝⎭⎝⎭,因此可得2241640999PD ≤+=,故PD . 故选:B.13.在棱长为1的正方体1111ABCD A B C D -中,P 是线段1BC 上的点,过1A 的平面α与直线PD 垂直,当P 在线段1BC 上运动时,平面α截正方体1111ABCD A B C D -所得的截面面积的最小值是( )A .1B .54C D【来源】北京市朝阳区2021届高三一模数学试题 【答案】C【解析】以点A 为坐标原点,AB 、AD 、1AA 所在直线分别为x 、y 、z 轴建立如下图所示的空间直角坐标系,则()0,0,0A 、()10,0,1A 、()1,0,0B 、()11,0,1B 、()1,1,0C 、()11,1,1C 、()0,1,0D 、()10,1,1D , 设点()1,,P t t ,其中01t ≤≤.①当0t =时,点P 与点B 重合,()1,1,0BD =-,()1,1,0AC =,()10,0,1AA =, 所以,0BD AC ⋅=,10BD AA ⋅=,则BD AC ⊥,1BD AA ⊥, 1AC AA A ⋂=,BD ∴⊥平面11AAC C ,此时平面α即为平面11AAC C ,截面面积为12S AA AC =⋅= ②当1t =时,同①可知截面面积为2S =③当01t <<时,()1,1,DP t t =-,()11,1,1AC =-, 1110DP AC t t ⋅=+--=,1A C PD ∴⊥,则1A C α⊂, 设平面α交棱1DD 于点()0,1,E z ,()1,0,CE z =-,10DP CE tz ⋅=-+=,可得11z t=>,不合乎题意. 设平面α交棱AB 于点(),0,0M x ,()1,1,0CM x =--,()110DP CM x t ⋅=---=,可得x t =,合乎题意,即(),0,0M t ,同理可知,平面α交棱11C D 于点()1,1,1N t -,()11,1,0A N t MC =-=,且1A N 与MC 不重合,故四边形1A MCN 为平行四边形,()11,1,1AC =-,()11,1,0A N t =-,1112112cos 322AC A N t CA N AC A N t t ⋅-∠==⋅⋅-+,则()()2211221sin 1cos 322t t CA N CA N t t -+∠=-∠=-+,所以,截面面积为()1221111362sin 2122242CA NS S AC A N CA N t t t ⎡⎤⎛⎫==⋅∠=-+=-+=<⎢⎥ ⎪⎝⎭⎢⎥⎣⎦△. 综上所述,截面面积的最小值为62. 故选:C.14.如图,斜线段AB 与平面α所成的角为π4,B 为斜足.平面α上的动点P 满足π6PAB ∠=,则点P 的轨迹为( )A .圆B .椭圆C .双曲线的一部分D .抛物线的一部分【答案】B【解析】建立如图所示的空间直角坐标系,设(0,1,0),(0,0,1),(,,0)(0,1,1),(,,1)B A P x y AB AP x y ⇒=-=-22223cos ,62(2)1121AB AP x y x y ⇒<>=⇒+-=⋅++ 所以点P 的轨迹是椭圆. 故选:B.15.已知正方体ABCD A B C D ''''-的棱长为1,点M ,N 分别为线段AB ',AC 上的动点,点T 在平面BCC B ''内,则MT NT +的最小值是( )A .2B .233C .62D .1【答案】B【解析】A 点关于BC 的对称点为E ,M 关于BB '的对称点为M ', 记d 为直线EB '与AC 之间的距离,则MT NT M T NT M N d ''+=+≥≥, 由//B E D C '',d 为E 到平面ACD '的距离, 因为111111333D ACE ACEV S '-=⨯⨯==⨯⨯=,而()21332346D ACE E ACD V V d d ''--==⨯⨯⨯=,故233d =, 故选:B.16.如图,ABC 是等腰直角三角形,AB AC =,点D 是AB 上靠近A 的三等分点,点E 是AC 上靠近C 的三等分点,沿直线DE 将ADE 翻折成A DE ',所成二面角A DE B '--的平面角为α,则( )A .A DB A EC α∠≥∠'≥' B .A EC A DB α∠≥∠'≥' C .A DB A EC α≥∠'∠≥'D .A EC A DB α≥∠'∠≥'【答案】B【详解】如图,在等腰直角三角形中,过B 作直线//l DE ,作BM ED ⊥交直线DE 于点M ,过C 作直线DE 的垂线,垂足为R ,交直线l 与T ,过A 作DE 的垂线,垂足为O ,且交l 于N ,不妨设3AB =,则1,2AD CE BD AE ====, 在直角三角形ADE 中,255AO ==, 因为BMD AOD ,故12AO AD BM BD ==,故455BM =,同理52522155DM DO ==⨯⨯= 所以45ON =,35BN OM ==,同理5RC OS ==65NT =.在几何体中连接,,A B A S A C ''',如图,因为,,A O DE NO DE '⊥⊥故NOA '∠为二面角A DE B '--的平面角,故NOA α'∠=,而A O NO O '⋂=,故DE ⊥平面AON ',所以TB ⊥平面AON ',而A N '⊂平面AON ',故BN A N '⊥.24162545162cos 4cos 55555A N αα'=+-⨯=-, 故216929164cos cos 5555A B αα'=-+=-,故29165cos 4155cos cos 21255A DB αα-+'∠==-⨯⨯, 同理14cos cos 55A EC α'∠=-,11cos cos cos 055A DB αα'∠-=--<,故cos cos A DB α'∠<,同理cos cos A EC α'∠<,33cos cos cos 055A DB A EC α''∠-∠=+>,故cos cos A DB A EC ''∠>∠,因为(),,0,A DB A EC απ''∠∠∈,故A EC A DB α''∠>∠>, 故选B.17.如图,棱长为2的长方体1111ABCD A B C D -中,P 为线段11B D 上动点(包括端点).则以下结论正确的为( )A .三棱锥1P A BD -中,点P 到面1A BD 2B .过点P 平行于面1A BD 的平面被正方体1111ABCD A BCD -3C .直线1PA 与面1A BD 所成角的正弦值的范围为36⎣⎦D .当点P 和1B 重合时,三棱锥1P A BD -3【来源】广东省普宁市2020-2021学年高三上学期期末数学试题 【答案】C【解析】对于A 中,由111142222323P A BD A PBD V V --==⨯=,1A BD 为等边三角形,面积为11226232A BD =⨯=△S ,设点P 到面1A BD 的距离为h ,由142333h ⨯=,求得23h =所以A不正确;对于B 中,过点P 平行于平面1A BD 的平面被正方体截得的多边形平面11B D C , 此时三角形11B D C 为边长为221226=232⨯B 不正确; 对于C 中,由正方体的结构特征和性质,可得点P 到平面1A BD 23当点P 在线段11B D 上运动时,1max 2PA =(P 为端点时),in 1m 2PA =设直线1PA 与平面1A BD 所成角为θ,则36sin ,33θ∈⎣⎦,所以C 正确;对于D 中,当点P 与1B 重合时,此时三棱锥为11B A BD -,设1B D 的中点为O ,因为11190B BD B A D ∠=∠=︒,可得11OA OB OD OB === 所以三棱锥1P A BD -的外接球的球心为1B D 的中点,其半径为3,所以三棱锥1P A BD -的外接球的体积为34(3)433ππ⨯=,所以D 不正确.故选:C.18.如图,在棱长为33的正方体1111ABCD A B C D -中,点P 是平面11A BC 内一个动点,且满足15213DP PB +=+,则直线1B P 与直线1AD 所成角的取值范围为( )(参考数据:43sin 53,sin 3755==)A .37,143⎡⎤⎣⎦B .37,90⎡⎤⎣⎦C .53,143⎡⎤⎣⎦D .37,127⎡⎤⎣⎦【来源】江西省景德镇一中2020-2021学年高三上学期期末考试数学(理)试题 【答案】B【解析】如图,建立空间直接坐标系,连结1B D ,交平面11A BC 于点O ,()0,0,0D ,()133,33,33B ,()133,0,33A ,()33,33,0B ,()10,33,33C ,()133,33,33DB =,()10,33,33A B =-,()133,0,33BC =-,110DB A B ⋅=,110DB BC ⋅=,111111,DB A B DB BC A B BC B ∴⊥⊥⋂=,,1DB ∴⊥平面11A BC ,根据等体积转化可知111111B A BC B A B C V V --=, 即()()23111311363332232B O ⨯⨯⨯⨯=⨯⨯,解得:13B O =, 13339B D =⨯=,16D O ∴=,11//AD BC ,∴异面直线1AD 与1B P 所成的角,转化为1BC 与1B P 所成的角,如图,将部分几何体分类出来,再建立一个空间直角坐标系,取1BC 的中点E ,过点O 作1//OF BC ,则以点O 为原点,1,,OF OE OB 为,,x y z 轴的正方向,建立空间直角坐标系(),,0P x y ,()10,0,3B ,()0,0,6D -,3326,22B ⎫⎪⎪⎭,13326,22C ⎛⎫ ⎪ ⎪⎝⎭,()1,,3B P x y =-,()136,0,0BC =-, 15213PB PD +=+,22229365213x y x y ++++=+2222936x y x y ++<++,即15PB =22925x y ∴++=,即2216x y +=,[]4,4x ∈-1111113644cos ,,555365B P BC x x B P BC B P BC ⋅-⎡⎤<>===-∈-⎢⎥⨯⎣⎦,因为异面直线所成的角是锐角,并设为θ,则4cos 0,5θ⎛⎤∈ ⎥⎝⎦,4sin 535=,4cos375∴=,37,90θ⎡⎤∴∈⎣⎦ 故选:B19.如图,在三棱锥D ABC -中,,1,1AD BC BC AD ⊥==.且2AB BD AC CD +=+=,则四面体ABCD 的体积的最大值为( )A .14B .212C .36D .524【来源】浙江省衢州市五校联盟2020-2021学年高三上学期期末联考数学试题 【答案】B【解析】作BE ⊥AD 于E ,连接CE ,如图,因为,AD BC ⊥,BE BC 再平面BEC 内相交,所以AD ⊥平面BEC , 因为CE ⊂平面BEC ,所以CE ⊥AD , 因为2AB BD AC CD +=+=,所以B 与C 都是在以A 、D 为焦点的椭球上,且BE 、CE 都垂直于焦距AD , AB +BD = AC +CD =2,显然ABD ACD ≅,所以BE =CE . 取BC 中点F ,,,BC E AD E F F ⊥∴⊥ 要求四面体ABCD 的体积的最大值,因为AD 是定值,只需三角形EBC 的面积最大, 因为BC 是定值,所以只需EF 最大即可,当△ABD 是等腰直角三角形时几何体的体积最大, 因为AB +BD = AC +CD =2,1AB ∴=,22222131121,(1)22222EB EF ⎛⎫⎛⎫⎛⎫∴=-==--= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭, 所以几何体的体积为11221132212⨯⨯⨯⨯=故选:B20.如图,三棱锥A BCD -的底面BCD 在平面α内,所有棱均相等,E 是棱AC 的中点,若三棱锥A BCD -绕棱CD 旋转,设直线BE 与平面α所成的角为θ,则cos θ的取值范围为( )A .36⎤⎥⎣⎦B .5,16⎡⎤⎢⎥⎣⎦C .110,6⎡⎢⎣⎦D .330,6⎡⎢⎣⎦【来源】浙江省宁波市慈溪市2020-2021学年高三上学期期末数学试题 【答案】A【解析】取AD 的中点F ,连接EF 、BF ,如下图所示:。
2024年高考数学总复习:立体几何中的动态问题

第1页共5页2024年高考数学总复习:立体几何中的动态问题[解题策略]立体几何中的“动态”问题就变化起因而言大致可分为两类:一是平移;二是旋转.就所求变量而言可分为三类:一是相关线、面、体的测度;二是角度;三是距离.立体几何动态问题的解决需要较高的空间想象能力与化归处理能力,在各省市的高考选择题与填空题中也时有出现.在解“动态”立体几何题时,如果我们能努力探寻运动过程中“静”的一面,动中求静,往往能以静制动、克难致胜.1.去掉枝蔓见本质——大道至简在解决立体几何中的“动态”问题时,需从复杂的图形中分化出最简单的具有实质性意义的点、线、面,让几何图形的实质“形销骨立”,即从混沌中找出秩序,是解决“动态”问题的关键.例1如图1,直线l ⊥平面α,垂足为O .正方体ABCD -A 1B 1C 1D 1的棱长为2.点A 是直线l 上的动点,点B 1在平面α内,则点O 到线段CD 1中点P 的距离的最大值为________.图1答案2+2解析从图形分化出4个点O ,A ,B 1,P ,其中△AOB 1为直角三角形,固定AOB 1,点P 的轨迹是在与AB 1垂直的平面上且以AB 1的中点Q 为圆心的圆,从而OP ≤OQ +QP =12AB 1+2=2+2,当且仅当OQ ⊥AB 1,且点O ,Q ,P 共线时取到等号,此时直线AB 1与平面α成45°角.2.极端位置巧分析——穷妙极巧在解决立体几何中的“动态”问题时,对于移动问题,由图形变化的连续性,穷尽极端特殊之要害,往往能直取答案.例2在正四面体A -BCD 中,E 为棱BC 的中点,F 为直线BD 上的动点,则平面AEF 与平面ACD 所成二面角的正弦值的取值范围是________.答案1解析本例可用极端位置法来加以分析.。
高三总复习数学课件 立体几何中的动态问题

满足―B→P =λ―B→C +μ―BB→1 ,其中 λ∈[0,1],μ∈[0,1],则
()
A.当 λ=1 时,△AB1P 的周长为定值
B.当 μ=1 时,三棱锥 P-A1BC 的体积为定值
C.当 λ=12时,有且仅有一个点 P,使得 A1P⊥BP
D.当 μ=12时,有且仅有一个点 P,使得 A1B⊥平面 AB1P
由 M 点是正方形 ABB1A1 内的动点可知,若 C1M∥平面 CD1EF,则点 M 在线段 GH 上, 所以 M 点的轨迹长度 GH= 12+12= 2. 答案: 2
类型二 度量问题
立体几何中动点的轨迹的度量问题的探究,包括求解轨迹的长度,相关的 体积、截面面积等.
[例1] (2022·德州一模)(多选)如图,在边长为4的正方形ABCD中,点E,F
2 PPFE= 36,所以 P 点的轨迹是直线,故选 A.
(2)当 λ=1 时,―B→P =―B→C +μ―BB→1 .若 μ=0,则―B→P =―B→C , 即点 P 与点 C 重合,则△AB1P 的周长为 1+2 2;若 μ=12, 则―B→P =―B→C +12―BB→1 ,即点 P 为线段 CC1 的中点,易得 AP =PB1= 1+14= 25,所以△AB1P 的周长为 2+ 5,故 A 错误.当 μ=1 时,由―B→P =λ―B→C +―BB→1 ,得点 P 在线段 B1C1 上运动,易知 S △A1BC 为定值,且 B1C1∥平面 A1BC,所以点 P 到平面 A1BC 的距离为定值, 所以 VP-A1BC 为定值,故 B 正确.
确;对于D:因为MN∥AD1,AD1⊂面ABD1,MN⊄面ABD1,所以MN∥面ABD1,
所以点F到面ABD1的距离是定值,所以三棱锥F-ABD1的体积为定值,故D正
高考数学二轮复习立体几何专题训练1含解析

DCB AFE南宫中学 高三二轮复习立体几何专题训练(1)1.如图所示的多面体中, ABCD 是菱形,BDEF 是矩形,ED ⊥面ABCD ,3BAD π∠=.(1)求证:平//CF AED 面B 面;(2))若BF BD a ==,求四棱锥A BDEF -的体积.2. 如图1,在Rt △ABC 中,∠ABC=90°,D 为AC 中点,AE BD ⊥于E (不同于点D ),延长AE 交BC 于F ,将△ABD 沿BD 折起,得到三棱锥1A BCD-,如图2所示.(Ⅰ)若M 是FC 的中点,求证:直线DM //平面1A EF;(Ⅱ)求证:BD ⊥1A F;(Ⅲ)若平面1A BD ⊥平面BCD ,试判断直线1A B 与直线CD 能否垂直?并说明理由.FEDABC3.(本小题共14分) 如图,在四棱锥P - ABCD 中,底面ABCD 是正方形,△PAD 是正三角形,平面PAD ⊥平面ABCD ,M 和N 分别是AD 和BC 的中点。
(I )求证:PM ⊥MN ; (II )求证:平面PMN ⊥平面PBC ; (III )在PA 上是否存在点Q ,使得平面QMN//平面PCD ?若在求出Q 点位置,并证明;若不存在,请说明理由。
4.(本小题满分12分)如图,四边形ABCD 是菱形,四边形MADN 是矩形,平面MADN ⊥平面ABCD ,E ,F 分别为MA ,DC 的中点,求证: (I)EF//平面MNCB ; (Ⅱ)平面MAC ⊥平面BND .1图 图 2ED A 1CBFMABCA 1OB 1C 15.如图1,在直角梯形ABCD 中,90ADC ∠=︒,//CD AB ,122AD CD AB ===, 点E 为AC 中点.将ADC ∆沿AC 折起, 使平面ADC ⊥平面ABC ,得到几何体D ABC -,如图2所示.(I )在CD 上找一点F ,使//AD 平面EFB ; (II )求点C 到平面ABD 的距离.6.(本小题满分12分) 如图,在斜三棱柱ABC-A1B1C1中,O 是AC 的中点,A1O ⊥平面ABC ,∠BCA=90°,AA1=AC=BC. (I )求证: AC1⊥平面A1BC;(II )若AA1=2,求三棱锥C-A1AB 的高的大小.7.已知正方体1111ABCD A B C D -,O 是底ABCD 对角线的交点.求证:(1)1C O面11AB D ;(2)1A C ⊥面11AB D .(3)111AB D C BD平面平面OC 1D 1B 11CD AB8.(本小题满分12分)如图,在四棱锥S —ABCD 中,底面ABCD 是直角梯形,AD 垂直于AB 和DC ,侧棱SA ⊥底面ABCD ,且SA = 2,AD = DC = 1,点E 在SD 上,且AE ⊥SD 。
高考数学学科二轮备考关键问题指导系列十(立体几何典例剖析及资源推送)

6
如图,由题意可知,O 为球心,在正方体中, EF FG2 EG2 22 22 2 2 ,即 R 2 ,
取最大值,最大值为
64 3
,
又l
3
时, V
27 4
,
l
3
3
时, V
81 ,所以正四棱锥的体积V 4
的最小值为
27 4
,
所以该正四棱锥体积的取值范围是
27 4
,64 3
.故选
C.
【点评】1、球与几何体的切接是高考热点,常作为客观题压轴题出现,但由于同学们对这类问题训练比
较大,对解题套路相对比较熟悉,
面的面积为180.0km2 ,将该水库在这两个水位间的形状看作一个棱台,则该水库水位从海拔148.5m 上升到
157.5m 时,增加的水量约为( 7 2.65 )
A. 1.0109 m3
B. 1.2109 m3
C. 1.4109 m3 D. 1.6109 m3
【答案】C
【解析】把增加的水量转化为棱台的体积,依题意可知棱台的高为 MN 157.5 148.5 9 (m),
棱台上底面积 S 140.0km2 140 106m2 ,下底面积 S 180.0km2 180 106m2 ,
∴V 1 h S S SS 1 9 140106 180106 1401801012
3
3
3 320 60 7 106 96 18 2.65107 1.437109 1.4109(m3) .故选 C.
2
圆锥的表面积 S1 πrl πr2 3πr2 ,
2
球的表面积
S2
4πR2
4π
3 2
r
3πr2 ,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
立体几何中的动态问题
一、轨迹问题
1.如图,已知正方体ABCD A 1B 1C 1D 1的棱长为2,长为2的线段MN 的一个端点M 在棱DD 1上运动,另一端点N 在正方形ABCD 内运动,则MN 的中点P 轨迹的面积( )D A .4π B .2π
C .π
D .
2
π
2.[2015·浙江卷] 如图, 斜线段AB 与平面α所成的角为60°,B 为斜足,平面α上的动点P 满足∠PAB =30°,则点P 的轨迹是( )C A .直线 B .抛物线 C .椭圆 D .双曲线的一支
3.如图,AB 平面α的斜线段,A 为斜足.若点P 在平面α内运动,使得△ABP 的面积为定值,则动点P 的轨迹是 ( )B A .圆 B .椭圆 C .一条直线 D .两平行直线
4.如图,已知正方体ABCD A 1B 1C 1D 1中,M 是平面ABCD 内的一个动点,且∠AD 1M =45°,则动点M 的轨迹是 ( )D A .圆 B .双曲线 C .椭圆 D .抛物线
5.如图,在正方体ABCD A 1B 1C 1D 1中,P 是底面ABCD 内的动点PE ⊥A 1C 于点E ,且PA =PE ,则点P 的轨迹是 ( )A A .线段 B .圆弧
C .椭圆的一部分
D .抛物线的一部分
图-2 A
P B
α 图-3
二、判断平行,垂直,夹角问题
1.已知矩形ABCD ,AB=1,BC=2,将△ABD 沿矩形的对角线BD 所在的直线进行翻折,在翻折过程中, ( )B
A.存在某个位置,使得直线AC 与直线BD 垂直.
B.存在某个位置,使得直线AB 与直线CD 垂直.
C.存在某个位置,使得直线AD 与直线BC 垂直.
D.对任意位置,三对直线“AC 与BD ”, “AB 与CD ”,“AD 与BC ”均不垂直
2.如图,已知点E 是正方形ABCD 的边AD 上一动点(端点除外),现将△ABE 沿BE 所在直线翻折成△BE A ',并连结C A ',D A '.记二面角C BE A --'的大小为)0(παα<<.(D) A .存在α,使得⊥'BA 面DE A '
B .存在α,使得⊥'BA 面CD A '
C .存在α,使得⊥'EA 面C
D A '.
D .存在α,使得⊥'EA 面BC A '
3.(浙江2015)如图,已知ABC ∆,D 是AB 的中点,沿CD 将ACD ∆折成CD A '∆, 所成二面角B CD A --'的平面角为α,则 (B) A .α≤'∠DB A B .α≥'∠DB A
C .α≤'∠CB A
D .α≥'∠CB A
三、最值问题
1.在棱长为1的正方体中,点21,P P 分别是线段AB ,BD 1, (不包括端点)上的动点,且线段2
1P P 平行于棱1AD ,则四面体121,AB P P 的体积的最大值为( )D (A )481 (B )121 (C )81 (D )24
1
2.已知立方体ABCD A 1B 1C 1D 1的棱长为2,线段EF ,GH 分别在棱AB ,CC 1上移动,若EF +GH =
2
1
,A D A 'B C
C E B A
C E D
B
'A
A B C D E
则三棱锥EFG
H 的体积最大值为
48
1
变式:作业手册13-9.《九章算术》中,将四个面都为直角三角形的四面体称之为鳖
.如图Z134所示,在鳖
PABC中,PA⊥平面ABC,AB⊥BC,且AP=AC =1, 过A点分别作AE⊥PB于E,AF⊥PC于F,连接EF,当△AEF的面积最大时,tan∠BPC的值是( )
A.2
B.
2 2
C.3
D.
3 3
3.如图,在直三棱柱ABCA1B1C1中,底面为直角三角
图9
形,ο
90
=
∠ACB,AC=6,
2
1
=
=CC
BC.P是
1
BC上一动点,则1
PA
CP+
的最小值为.26
4.(2015浙江学考)在菱形ABCD中,ο
60
=
∠BAD,线段BD
AD,的中点分别为F
E,,现将ABD
∆沿对角线BD翻折,则异面直线BE与CF所成角的取值范围是()C
A.)
3
,
6
(
π
π
B. ]
2
,
6
(
π
π
C. ]
2
,
3
(
π
π
D. )
3
2
,
3
(
π
π
5.如图,已知平面四边形ABCD,AB=BC=3,CD=1,AD=5,∠ADC=90°.沿直线AC将△ACD 翻折成△ACD',直线AC与BD'所成角的余弦的最大值是______.【答案】6
6
6.(2016浙江)如图,在△ABC中,AB=BC=2,∠ABC=120°.若平面ABC外的点P和线段AC 上的点D,满足PD=DA,PB=BA,则四面体PBCD的体积的最大值是 .
【解析】ABC
∆中,因为2,120
AB BC ABC
==∠=o,
所以30
BAD BCA
∠==o.
由余弦定理可得2222cos
AC AB BC AB BC B
=+-⋅
22
22222cos12012
=+-⨯⨯=
o,
所以23
AC=.
设AD x =
,则0t <<
DC x =-.
在ABD ∆中,由余弦定理可得2222cos BD AD AB AD AB A =+-⋅
22222cos30x x =+-⋅
o 24x =-+.
故BD =
在PBD ∆中,PD AD x ==,2PB BA ==.
由余弦定理可得222cos 2PD PB BD BPD PD PB +-∠===
⋅ 所以30BPD ∠=o .
E
D
C
B
A P
过P 作直线BD 的垂线,垂足为O .设PO d =
则11
sin 22
PBD S BD d PD PB BPD ∆=⨯=⋅∠,
12sin 302
d x =⋅o ,
解得d =
而BCD ∆
的面积111
sin )2sin 30)222
S CD BC BCD x x =
⋅∠=⋅=o . 设PO 与平面ABC 所成角为θ,则点P 到平面ABC 的距离sin h d θ=. 故四面体PBCD
的体积
11111sin )33332BcD BcD BcD V S h S d S d x θ∆∆∆=⨯=≤⋅=⨯
=
.
设t =
=
,因为0x ≤≤12t ≤≤.
则|x =
(2)当323x <≤时,有2|3|31x x t -=-=-, 故231x t =+-.
此时,221(31)[23(31)]
6t t V t +--+-=
21414
()66t t t t
-=⋅=-. 由(1)可知,函数()V t 在(1,2]单调递减,故141
()(1)(1)612
V t V <=-=. 综上,四面体PBCD 的体积的最大值为
1
2
.
7. 如图,在长方形ABCD 中,2AB =,1BC =,E 为DC 的中点,F 为线段EC (端点除外)上一动点.现将AFD ∆沿AF 折起,使平面ABD ⊥平面ABC .在平面ABD 内
过点D 作DK AB ⊥,K 为垂足.设AK t =,则t 的取值范围是 .⎪⎭
⎫
⎝⎛1,21。
