matlab及多元统计分析
多元统计分析MATLAB
多元统计分析MATLAB多元统计分析（Multivariate statistical analysis）是指对多个变量之间的关系进行分析和研究的方法。
在实际应用中，往往需要考虑多个变量之间的相互作用，而不仅仅是单个变量的影响。
多元统计分析主要用于数据挖掘、模式识别、数据降维等领域，在各个学科中都有广泛的应用。
MATLAB是一种常用的科学计算和数据分析软件，广泛应用于工程、科学研究和教学领域。
它拥有丰富的功能和强大的计算能力，适用于各种多元统计分析方法的实现和应用。
多元方差分析（MANOVA）是指对多个因变量之间的差异进行分析和研究，可以用于比较不同组之间的差异。
MATLAB中提供了统计工具箱（Statistics and Machine Learning Toolbox），可以方便地进行多元方差分析的计算和可视化。
聚类分析是将相似的样本或变量聚集在一起形成集群的方法，可以用于对数据进行分类和分组。
MATLAB中提供了clusterdata、kmeans和linkage等函数，可以用于聚类分析的计算和可视化。
判别分析（Discriminant Analysis）是用于分类的一种方法，它可以通过构造一个判别函数，将样本分到不同的类别中。
在MATLAB中，可以使用classify函数进行判别分析的计算和可视化。
因子分析（Factor Analysis）是一种用于确定多个变量之间的共同因素的方法，可以用于发现隐含在数据中的结构和规律。
MATLAB中提供了factoran函数，可以进行因子分析的计算和可视化。
除了以上介绍的方法，MATLAB还提供了许多其他的多元统计分析方法和工具，如典型相关分析、聚类程度检验、时间序列分析等。
用户可以根据不同的需求选择合适的方法进行分析和研究。
综上所述，MATLAB是一种非常适用于多元统计分析的工具，它提供了丰富的函数和工具箱，可以方便地进行多元统计分析的计算和可视化。
matlab与应用多元统计分析
多元统计分析中的应用研究,摘要：许多实际问题往往需要对数据进行统计分析，建立合适的统计模型，过去一般采用SAS 、SPSS软件分析，本文给出 Matlab软件在多元统计分析上的应用, 主要介绍Matlab 在聚类分析、判别分析、主成份分析上的应用,文中均给以实例, 结果令人满意。
关键词：Matlab软件；聚类分析；主成份分析Research for application of Multivariate StatisticalAnalysisAbstract:Many practice question sometimes need Statistical Analysis to data.,and establish appropriate Statistical model SAS and SPSS software were commonly used in foretime ,this paper give the application of Matlab software in Multivariate Statistical Analysis,mostly introduce the application of Matlab software in priciple component analysis and cluster analysis and differentiate analysis.The example are given in writing and the result are satisfaction.Key words: Matlab software; cluster analysis; priciple component analysis0 引言许多实际问题往往需要对数据进行多元统计分析, 建立合适的模型, 在多元统计分析方面, 常用的软件有SAS 、SPSS 、S-PLUS等。
利用Matlab进行多元统计分析与数据挖掘的基本原理
利用Matlab进行多元统计分析与数据挖掘的基本原理近年来，随着大数据时代的到来，多元统计分析与数据挖掘成为了数据科学领域的热门话题。
其中，利用Matlab进行多元统计分析与数据挖掘的应用越来越广泛。
本文将介绍利用Matlab进行多元统计分析与数据挖掘的基本原理，并探讨其在实际应用中的意义和挑战。
一、多元统计分析的基本概念和方法多元统计分析是指研究多个变量之间关系的统计方法。
它主要包括描述性统计分析、推断统计分析和基于模型的分析。
描述性统计分析通过计算均值、方差、协方差等指标来描述数据的分布特征。
推断统计分析则通过抽样方法和假设检验来推断总体的性质。
基于模型的分析则通过建立数学模型来描述变量之间的关系。
在Matlab中，可以利用统计工具箱来进行多元统计分析。
其中，最常用的工具包括主成分分析（PCA）、聚类分析、判别分析和因子分析等。
主成分分析是一种降维技术，它通过提取出原始数据中的主要信息，将高维数据转化为低维数据，从而便于可视化和分析。
聚类分析则通过将相似的个体归类到同一个群组中，从而进行样本分类。
判别分析则是通过建立一个分类模型来预测类别。
而因子分析则是一种用于研究潜在变量之间关系的统计方法。
二、数据挖掘的基本概念和方法数据挖掘是一种通过从大规模数据中提取模式和知识来发现隐藏在数据背后规律的过程。
它是多元统计分析的延伸和拓展，可以帮助我们找到数据中的潜在价值和有用信息。
数据挖掘主要包括分类、聚类、关联规则挖掘和时间序列分析等方法。
在Matlab中，可以利用数据挖掘工具箱来进行数据挖掘。
其中，最常用的工具包括决策树、神经网络、支持向量机和关联规则挖掘等。
决策树是一种用于分类和预测的模型，通过划分变量空间来建立一个可解释的分类模型。
神经网络则是一种模仿人脑神经网络结构的计算模型，通过学习和训练来进行分类和预测。
支持向量机是一种基于结构风险最小化原理的分类器，它通过在样本空间中找到最佳分割超平面来实现分类。
matlab--算法大全--第29章_多元分析
后经 Orloci 等人 1976 年发展起来的，故又称为 Ward 方法。 1.2 系统聚类法 1.2.1 系统聚类法的功能与特点 系统聚类法是聚类分析方法中最常用的一种方法。 它的优点在于可以指出由粗到细 的多种分类情况，典型的系统聚类结果可由一个聚类图展示出来。 例如，在平面上有 7 个点 w1 , w2 , 来表示聚类结果。
第二十九章
多元分析
多元分析（multivariate analyses）是多变量的统计分析方法，是数理统计中应用广 泛的一个重要分支，其内容庞杂，视角独特，方法多样，深受工程技术人员的青睐和广 泛使用，并在使用中不断完善和创新。由于变量的相关性，不能简单地把每个变量的结 果进行汇总，这是多变量统计分析的基本出发点。 §1 聚类分析 将认识对象进行分类是人类认识世界的一种重要方法，比如有关世界的时间进程 的研究，就形成了历史学，也有关世界空间地域的研究，则形成了地理学。又如在生物 学中，为了研究生物的演变，需要对生物进行分类，生物学家根据各种生物的特征，将 它们归属于不同的界、门、纲、目、科、属、种之中。事实上，分门别类地对事物进行 研究，要远比在一个混杂多变的集合中更清晰、明了和细致，这是因为同一类事物会具 有更多的近似特性。 在企业的经营管理中， 为了确定其目标市场， 首先要进行市场细分。 因为无论一个企业多么庞大和成功，它也无法满足整个市场的各种需求。而市场细分， 可以帮助企业找到适合自己特色， 并使企业具有竞争力的分市场， 将其作为自己的重点 开发目标。 通常，人们可以凭经验和专业知识来实现分类。而聚类分析（cluster analyses）作 为一种定量方法，将从数据分析的角度，给出一个更准确、细致的分类工具。 1.1 相似性度量 1.1.1 样本的相似性度量 要用数量化的方法对事物进行分类，就必须用数量化的方法描述事物之间的相似 程度。 一个事物常常需要用多个变量来刻画。 如果对于一群有待分类的样本点需用 p 个 变量描述，则每个样本点可以看成是 R 空间中的一个点。因此，很自然地想到可以用 距离来度量样本点间的相似程度。 记 Ω 是样本点集，距离 d (⋅,⋅) 是 Ω × Ω → R 的一个函数，满足条件： 1） d ( x , y ) ≥ 0 ， x , y ∈ Ω ； 2） d ( x, y ) = 0 当且仅当 x = y ； 3） d ( x , y ) = d ( y , x ) ， x , y ∈ Ω ； 4） d ( x , y ) ≤ d ( x , z ) + d ( x , y ) ， x , y , z ∈ Ω 。 这一距离的定义是我们所熟知的，它满足正定性，对称性和三角不等式。在聚类 分析中，对于定量变量，最常用的是 Minkowski 距离
多元统计分析MATLAB
多元统计分析MATLABMATLAB是一种用于技术计算和数据可视化的高级编程语言和环境。
它提供了丰富的工具箱和函数，用于进行多元统计分析，并能够帮助用户处理和分析大规模的数据。
在MATLAB中，可以使用各种函数进行多元统计分析，包括主成分分析（PCA）、多元方差分析（MANOVA）、线性回归、多元线性回归、判别分析、聚类分析和因子分析等。
这些函数可以帮助用户处理和分析多维数据，找到关键变量，解释变量之间的关系，并从数据中提取有用的信息。
主成分分析（PCA）是一种常用的多元统计分析方法，可用于降维和特征提取。
PCA可以将原始数据转化为一组新的无关变量，称为主成分，这些主成分是原始数据中方差最大的方向。
通过PCA，可以减少数据的维度，并可视化数据的分布和模式。
多元方差分析（MANOVA）是一种常用的多元统计分析方法，可用于比较两个或多个组别之间的差异。
MANOVA可以同时考虑多个因变量，并判断它们之间的差异是否显著。
它可以帮助我们理解多个因变量与一个或多个自变量之间的关系。
线性回归和多元线性回归是常见的用于建立因变量与自变量之间关系的统计方法。
MATLAB提供了强大的线性回归函数，可以帮助用户拟合线性模型，并评估模型的拟合优度。
判别分析是一种分类方法，可用于将观测对象分为不同的组别。
MATLAB中提供了各种判别分析函数，可用于建立分类模型，并预测新的观测对象所属的组别。
聚类分析是一种无监督学习方法，可用于将观测对象划分为相似的组别。
MATLAB中提供了各种聚类分析函数，如k-means和层次聚类，可用于对数据进行聚类，并将相似的观测对象放在一起。
因子分析是一种用于确定观测变量之间的潜在结构的统计方法。
MATLAB中提供了因子分析函数，可用于提取主成分和因子，并解释观测变量之间的关系。
综上所述，MATLAB提供了丰富的工具和函数，可用于进行多元统计分析。
这些方法可以帮助用户处理和分析大规模的数据，找到关键变量，解释变量之间的关系，并从数据中提取有用的信息。
matlab与多元统计分析
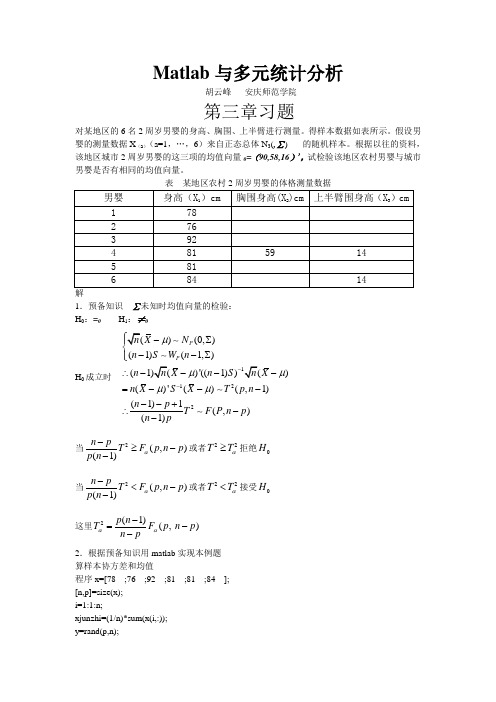
Matlab 与多元统计分析胡云峰 安庆师范学院第三章习题对某地区的6名2周岁男婴的身高、胸围、上半臂进行测量。
得样本数据如表所示。
假设男婴的测量数据X （a ）（a=1，…，6）来自正态总体N 3(,∑) 的随机样本。
根据以往的资料，该地区城市2周岁男婴的这三项的均值向量0=（90,58,16）’，试检验该地区农村男婴与城市男婴是否有相同的均值向量。
解1．预备知识 ∑未知时均值向量的检验： H 0：=0 H 1：≠0H 0成立时122)(0,)(1)(1,)()'((1)))()'()(,1)(1)1(,)(1)P P X N n S W n n X n S X n X S X T p n n p T F P n p n pμμμμμ---∑--∑⎪⎩∴----=-----+∴-- 当2(,)(1)n p T F p n p p n α-≥--或者22T T α≥拒绝0H当2(,)(1)n p T F p n p p n α-<--或者22T T α<接受0H这里2(1)(, )p n T F p n p n pαα-=--2．根据预备知识用matlab 实现本例题 算样本协方差和均值程序x=[78 ;76 ;92 ;81 ;81 ;84 ]; [n,p]=size(x); i=1:1:n;xjunzhi=(1/n)*sum(x(i,:)); y=rand(p,n);for j=1:1:ny(:,j)= x(j,:)'-xjunzhi'; y=y; endA=zeros(p,p); for k=1:1:n;A=A+(y(:,k)*y(:,k)'); endxjunzhi=xjunzhi' S=((n-1)^(-1))*A 输出结果xjunzhi = S =然后u=[90;58;16];t2=n*(xjunzhi-u)'*(S^(-1))*(xjunzhi-u) f=((n-p)/(p*(n-1)))*t2 输出结果t2 = f =所以21()'()T n X S X μμ-=--=2(1)n p F T p n -=-=查表得F 3,3=< F 3,3=< 因此在a=或 a=时拒绝0H 假设相应于表再给出该地区9名2周岁女婴的三项指标的测量数据如表所示。
MATLAB软件在多元统计分析教学中的应用研究
! 24!
洛阳师范学院学报 2010年第 2期
类型
含 矿
序号 1 2 3 4 5 6 7
X1 2. 58 2. 90 3. 55 2. 35 3. 54 2. 70 2. 70
表 1 岩石化学成分 的含量数据
X2 0. 90 1. 23 1. 15 1. 15 1. 85 2. 23 1. 70
X3 0. 95 1. 00 1. 00 0. 79 0. 79 1. 30 0. 48
良好的开放性等优点, 现已是国内外众多统计学者 喜爱的分析数据工具. 本文就 MATLAB 软件在多元 统计分析教 学中的应用 进行研究, 结 合实例 给出 MATLAB 在判别分析、聚类分析、主成分分析等方 面的应用.
判别分析是用于判别研究对象所属类型的一种 统计分析方法. 在生产、科研和日常生活中经常会 遇到如何根据观测到的数据资料对所研究的对象进 行判别归类的问题. 例如在经济学中, 根据人均国 民收入、人均工农业产值、人均消费水平等多种指 标来判定一个国家的经济发展程度所属类型; 在市 场预测中, 根据以往调查所得的种种指标, 判别下 季度产品是畅销、平常或滞销; 在医疗诊断中, 根 据某人多种体检指标 ( 如体温, 血压, 白血球等 ) 来 判别此人是有病还是无病; 在体育运动中, 判别某 游泳运动员 是适合 练习蛙 泳, 仰泳, 还是自 由泳 等.
MATLAB 程序如下: sam ple= [ 2. 95, 2. 15, 1. 54]; group= [ ones( 7, 1) ; 2* ones( 7, 1) ] ; training= [ X1, X2, X 3] ; [ class, err] = c lassify( sam ple, training, group) 运行后可得结果 class= 2, err= 0. 1429, 即矿石标 本不含 矿, 且错判概率为 14. 29% . 注 为节省篇幅, 程序中数据输入部分省略, 下 同.
基于Matlab的数据多元回归分析的研究
基于Matlab的数据多元回归分析的研究摘要多元线性回归是利用MATLAB软件研究一个变量与多个变量的定量关系，MATLAB（矩阵实验室，是MATrix LABoratory的缩写）是一套高性能的数值运算和可视化软件，它集矩阵运算、数值分析、信号处理和图形显示于一体，构成了一个界面友好、使用方便的用户环境，是实现数据分析与处理的有效工具，其中MATLAB统计工具箱更为人们提供了一个强有力的数据统计分析工具。
利用MATLAB统计工具箱来进行数据的多元回归分析使得分析的样本容量扩大，增加了统计推断的正确性，也促进了包含大量计算的多元统计分析的发展和运用。
本课题研究了在MATLAB软件平台上实现数据的多元统计分析，具体包括一元线性回归分析，非线性回归分析，多元线性回归分析，通过对基础数据分析函数polyfit（一元回归）；regress（多元回归）；及nlinfit（非线性回归）的学习。
根据已得的实验结果以及以往的经验来建立统计模型，并研究变量之间的相关关系，建立起变量之间关系的近似表达式，并由此对相应的变量进行预测和控制。
根据所收集的数据，通过本文的研究方法进行一一分析，掌握它们的相关关系，可以找出数据中我们最需要的信息，从而进一步对总体的特性进行进一步的判断，把握规律，并将研究结果广泛运用于各种实际应用的预测和判断之中。
关键词：polyfit,regress,置信区间，最小二乘估计目录绪论....................................................................................................... - 3 -1.1研究的背景............................................................................................ - 3 -1.2研究的主要内容................................. - 4 -1.3应解决的关键问题.............................................................................. - 4 -2 MATLAB数据分析.......................................................................... - 4 -2.1 MATLAB重点基础预备....................................................................... - 4 -2.1.1 MATLAB界面掌握 ............................................................................... - 4 -2.1.2矩阵及其运算 ....................................................................................... - 5 -2.2数据分析 ...................................... - 6 -2.2.1样本数据的基本统计量.................................................................. - 6 -3 一元回归分析 ............................................................................... - 7 -3.1一元回归模型 ....................................................................................... - 7 -3.1.1一元线性回归 ....................................................................................... - 7 -3.1.2一元多项式回归.................................................................................. - 8 -3.2一元非线性回归................................................................................... - 9 -3.2.1非线性曲线选择.................................................................................. - 9 -3.2.2非线性回归命令的调用格式 ....................................................... - 9 -3.3一元回归建模实例............................................................................ - 11 -4 多元线性回归模型..................................................................... - 13 -4.1多元线性回归初级分析................................................................... - 13 -4.1.1多元回归基本概念........................................................................... - 13 -4.1.2建立多元线性回归建模的基本步骤 ..................................... - 14 -4.2 MATLAB的回归分析命令 ................................................................ - 15 -4.2.1 多元回归建模命令 ......................................................................... - 15 -4.2.2 多元回归辅助图形命令............................................................... - 15 -4.3 一元回归建模实例........................................................................... - 16 -5 GUI界面的设计.......................................................................... - 23 -5.1 GUI界面的介绍................................................................................. - 23 -5.2 GUI的设计流程 .............................................................................. - 23 -5.2 实例的GUI设计............................................................................... - 25 -结论................................................................................................. - 28 -参考文献 ............................................................................................. - 28 -附录................................................................................................ - 29 -绪论1.1研究的背景MATLAB是一套集高性能的数值计算和可视化整理、计算、绘制图表等于一身的数学工具。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
Matlab 与多元统计分析胡云峰 师学院第三章习题3.1对某地区的6名2周岁男婴的身高、胸围、上半臂进行测量。
得样本数据如表3.1所示。
假设男婴的测量数据X （a ）（a=1，…，6）来自正态总体N 3(μ,∑) 的随机样本。
根据以往的资料，该地区城市2周岁男婴的这三项的均值向量μ0=（90,58,16）’，试检验该地区农村男婴与城市男婴是否有相同的均值向量。
1．预备知识 ∑未知时均值向量的检验： H 0：μ=μ0 H 1：μ≠μ0H 0成立时122)(0,)(1)(1,)()'((1)))()'()(,1)(1)1(,)(1)P P X N n S W n n X n S X n X S X T p n n p T F P n p n pμμμμμ---∑--∑⎪⎩∴----=-----+∴-- 当2(,)(1)n p T F p n p p n α-≥--或者22T T α≥拒绝0H当2(,)(1)n p T F p n p p n α-<--或者22T T α<接受0H这里2(1)(, )p n T F p n p n pαα-=--2．根据预备知识用matlab 实现本例题 算样本协方差和均值程序x=[78 60.6 16.5;76 58.1 12.5;92 63.2 14.5;81 59.0 14.0;81 60.8 15.5;84 59.5 14.0]; [n,p]=size(x); i=1:1:n;xjunzhi=(1/n)*sum(x(i,:)); y=rand(p,n); for j=1:1:ny(:,j)= x(j,:)'-xjunzhi'; y=y; endA=zeros(p,p); for k=1:1:n;A=A+(y(:,k)*y(:,k)'); endxjunzhi=xjunzhi' S=((n-1)^(-1))*A 输出结果xjunzhi =82.0000 60.2000 14.5000 S =31.6000 8.0400 0.5000 8.0400 3.1720 1.3100 0.5000 1.3100 1.900 然后u=[90;58;16];t2=n*(xjunzhi-u)'*(S^(-1))*(xjunzhi-u) f=((n-p)/(p*(n-1)))*t2 输出结果t2 = 420.4447 f =84.0889所以21()'()T n X S X μμ-=--=420.44472(1)n p F T p n -=-=84.0889查表得F 3,3(0.05)=9.28<84.0889 F 3,3(0.01)=29.5<84.0889 因此在a=0.05或 a=0.01时拒绝0H 假设3.2 相应于表3.1再给出该地区9名2周岁女婴的三项指标的测量数据如表3.2所示。
假设女婴的测量数据Y (a)(a=1,…，9)来自正态总体N 3(μ,∑)的随机样本。
试检验2周岁男婴与女婴的均值是有无显著差异表3.2 某地区农村2周岁女婴体格测量数据解1. 预备知识有共同未知协方差阵∑时012:H μμ= 112:H μμ≠在0H 成立的情况下且两样本独立1112)(0,)(2)(1)(1)(2,)(2))((2)))))()'()(,2)21(P X Y PX Y N n m S n S m S W n m n m n m S n m T P n m n mn m p p n ---⎧-∑⎪⎨⎪+-=-+-+-∑⎩'⎤⎤∴+--+--⎥⎥⎦⎦'⎤⎤=--⎥⎥⎦⎦⋅=--+-++--+∴X Y X Y X Y S X Y X Y S X Y 2(,1)2)T F P n m p m +--+-给定检验水平α，查F 分布表，使{}p F F αα>=，可确定出临界值αF ，再用样本值计算出F ，若F F α>，则否定0H ，否则接受0H 。
2．根据预备知识用matlab 实现本例题 由上一题知道 xjunzhi = 82.0000 60.2000 14.5000 Sx =31.6000 8.0400 0.5000 8.0400 3.1720 1.3100 0.5000 1.3100 1.900 类似程序xjunzhi=[82;60.2;14.5];Sx=[31.6 8.04 0.5;8.04 3.1720 1.3100;0.5 1.31 1.9]; n=6;y=[80.0 58.4 14.0;75.0 59.2 15;78 60.3 15;75.0 57.4 13.0;79 59.5 14.0;78 58.1 14.5;75 58.0 12.5;64 55.5 11.0;80 59.2 12.5]; [m,p]=size(y); i=1:1:m;yjunzhi=(1/m)*sum(y(i,:)); z=rand(p,m); for j=1:1:mz(:,j)= y(j,:)'-yjunzhi'; z=z; endB=zeros(p,p);for k=1:1:m;B=B+(z(:,k)*z(:,k)');endSy=((m-1)^(-1))*B;yjunzhi=yjunzhi'S=(1/(n+m-2))*((n-1)*Sx+(m-1)*Sy)得到结果yjunzhi =76.000058.400013.5000S =27.2308 6.5615 2.84626.5615 2.4323 1.40002.8462 1.4000 1.8462然后t=((n*m)/(n+m))*((xjunzhi-yjunzhi)')*(S^(-1))*(xjunzhi-yjunzhi)F=((n+m-p-1)/(p*(n+m-2)))*t输出结果t =5.3117F =1.4982查表得F0.05(3，11)=3.59>1.4982 F0.01(3，11)=6.22>1.4982因此在a=0.05或a=0.01时接受H假设第四章习题4.1 下表列举某年级任取12名学生的5门主课的期末考试成绩，试绘制学生序号为1、2、11、12的轮廓图、雷达图。
解1999493100100299889699971176724367781285755034371 利用matlab画轮廓图程序x=1:5;y1=[99 94 93 100 100];y2=[99 88 96 99 97];y3=[76 72 43 67 78];y4=[85 75 50 34 37];plot(x,y1,'k-o','linewidth',1);hold on;plot(x,y2,'r--*','linewidth',2);hold on;plot(x,y3,'b-.p','linewidth',2);hold onplot(x,y4,'k--o','linewidth',2);xlabel('学科');ylabel('分数');legend('1','2','11','12');set(gca,'xtick',[1 2 3 4 5])set(gca,'xticklabel',{'政治','语文','外语','数学','物理'})输出结果学科分数2 利用matlab 画雷达图此图用matlab 画起来比较复杂 首先我们修改polar 函数在命令窗口输入edit polar 结果会出现polar 函数的程序 其中我们把 % plot spokesth = (1:6)*2*pi/12;cst = cos(th); snt = sin(th); cs = [-cst; cst]; sn = [-snt; snt];line(rmax*cs,rmax*sn,'linestyle',ls,'color',tc,'linewidth',1,... 'handlevisibility','off','parent',cax) 修改为% plot spokesth = (1:3)*2*pi/6;cst = cos(th); snt = sin(th); cs = [-cst; cst]; sn = [-snt; snt];line(rmax*cs,rmax*sn,'linestyle',ls,'color',tc,'linewidth',1,... 'handlevisibility','off','parent',cax) 再将后面的所有程序中的30改为72然后另存为work 中并命名为mypolar.m然后输入程序 x=[0:pi/2.5:2*pi];y1=[99 94 93 100 100 99];y2=[99 88 96 99 97 99];y3=[76 72 43 67 78 76];y4=[85 75 50 34 37 85];mypolar(x,y1,'b');hold on;mypolar(x,y2,'m');hold on;mypolar(x,y3,'g');hold on;mypolar(x,y4,'y')legend('1','2','11','12');输出结果第五章聚类分析习题5.3.下表给出我国历年职工人数（单位：万人），请用有序样品的fisher法聚类。
解第一步数据标准化后计算直径D程序：X=[1580 23;1881 121;2423 554;4532 662;5044 925;3303 1012;3465 1136;...3939 1264;4170 1334;4792 1424;5610 1524;6007 1644;6860 1813;...7451 2048;8019 2425];stdr=std(X);[n,m]=size(X);X=X./stdr(ones(n,1),:);[n p]=size(X);D=zeros(n,n);for i=1:1:n;for j=1:1:n;if i<jt=i:1:j;xgjunzhi=(1/(j-i+1))*sum(X(t,:));y=zeros(1,j-i+1);for s=i:1:jy(s)=(X(s,:)-xgjunzhi)*(X(s,:)-xgjunzhi)';ends=i:1:j;D(i,j)=sum(y);elseD(i,j)=0;endendendD=D'输出结果矩阵太大，所以用excel处理了一下D=0 0 0 0 0 0 0 0 0 0 0 0 0 0 00.022567 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.44898 0.24578 0 0 0 0 0 0 0 0 0 0 0 0 02.0632 1.3981 0.60024 0 0 0 0 0 0 0 0 0 0 0 03.9256 2.651 1.1802 0.11098 0 0 0 0 0 0 0 0 0 0 04.5022 3.0091 1.4238 0.56953 0.40862 0 0 0 0 0 0 0 0 0 05.179 3.4353 1.6648 0.82576 0.53831 0.02044 0 0 0 0 0 0 0 0 06.0823 4.021 1.976 1.023 0.63343 0.12781 0.047757 0 0 0 0 0 0 0 07.0311 4.6502 2.3255 1.2313 0.755 0.26341 0.11275 0.012456 0 0 0 0 0 0 08.3322 5.5762 2.9094 1.6045 1.0531 0.60619 0.33881 0.13122 0.060032 0 0 0 0 0 0 10.312 7.1034 4.0117 2.4126 1.7772 1.3793 0.92314 0.52664 0.31541 0.099401 0 0 0 0 0 12.696 8.9972 5.4422 3.5114 2.7548 2.3553 1.669 1.0457 0.65496 0.25632 0.03671 0 0 0 0 16.291 11.998 7.8688 5.5038 4.5686 4.1193 3.1032 2.1468 1.4707 0.77122 0.30858 0.12762 0 0 0 21.117 16.128 11.321 8.4298 7.2316 6.6487 5.2116 3.8312 2.7793 1.6877 0.8881 0.46016 0.10709 0 028 22.167 16.528 12.978 11.386 10.546 8.5596 6.627 5.0716 3.4539 2.1748 1.3443 0.59832 0.19951 0 我们只看下三角所有元素，其它元素理解为空第二步我们计算损失函数矩阵L程序：%设计一个把样品分为两类的程序,以及对应最后一类分割点D=D';L=zeros(n-1,n-1);alp=zeros(n-1,n-1);for m=2:n;s=zeros(1,m-1);for j=2:ms(1,j-1)=D(1,j-1)+D(j,m);endL(m-1,1)=min(s(1,1:m-1));for j=1:m-1if L(m-1,1)==s(1,j);alp(m-1,1)=j+1;endendend%分为k类for k=3:n;for m=k:ns=zeros(1,m-k+1);for j=k:m;s(1,j-k+1)=L(j-2,k-2)+D(j,m);endL(m-1,k-1)=min(s(1,1:m-k+1));for j=1:m-k+1if L(m-1,k-1)==s(1,j);alp(m-1,k-1)=j+k-1;endendendend输出结果这里由于表太大，用excel处理一下L=0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.022567 0 0 0 0 0 0 0 0 0 0 0 0 0 0.44898 0.022567 0 0 0 0 0 0 0 0 0 0 0 00.55996 0.13355 0.022567 0 0 0 0 0 0 0 0 0 0 01.0185 0.55996 0.13355 0.022567 0 0 0 0 0 0 0 0 0 0 1.2747 0.5804 0.15399 0.043007 0.02044 0 0 0 0 0 0 0 0 0 1.472 0.68777 0.26136 0.15038 0.043007 0.02044 0 0 0 0 0 0 0 01.6803 0.82337 0.39696 0.16644 0.055464 0.032897 0.012456 0 0 0 0 0 0 02.0535 1.1662 0.71162 0.28521 0.16644 0.055464 0.032897 0.012456 0 0 0 0 0 02.8616 1.7797 0.92277 0.49636 0.26584 0.15486 0.055464 0.032897 0.012456 0 0 0 0 03.9604 1.9366 1.0797 0.65328 0.32192 0.20315 0.092174 0.055464 0.032897 0.01246 0 0 0 0 5.9528 2.3621 1.4747 1.0202 0.59379 0.32192 0.20315 0.092174 0.055464 0.0329 0.012456 0 0 0 8.7188 2.9416 2.0437 1.1868 0.76037 0.42901 0.31024 0.19927 0.092174 0.05546 0.032897 0.012456 0 0 alp=20000000000000 33000000000000 44400000000000 44550000000000 46666000000000 46666700000000 46668880000000 46688889000000 4688101010101000000 41010101010111111110000 410101011111112121212000 4111111111313131313131300 101113131313131314141414140 1012131415151515151515151515在这里解释一下这两个矩阵行表示分为k类，k从2到15；列表示样本数m，m从2到15我们只看下三角所有元素，其它元素理解为空，接下来我们根据结果分析如果我们要把样品分为三类，则第一个分割点为11，然后第二个分割点为6得到第一类：{1952，1954,1956,1958,1960}第二类：{1962,1964,1966,1968,1970}第三类：{1972,1974,1976,1978,1980}第六章判别分析例6.6对全国30个省市自治区1994年影响各地区经济增长差异的制度变量x1—经济增解求均值及协方差的逆的估计值程序X1=[11.2 57.25 13.47 73.41;14.9 67.19 7.89 73.09;14.3 64.74 19.41 72.33;...13.5 55.63 20.59 77.33;16.2 75.51 11.06 72.08;14.3 57.63 22.51 77.35;...20 83.4 15.99 89.5;21.8 68.03 39.42 71.9;19 78.31 83.03 80.75;...16 57.11 12.57 60.91;11.9 49.97 30.7 69.2];X2=[8.7 30.72 15.41 60.25;14.3 37.65 12.95 66.42;10.1 34.63 7.68 62.96;...9.1 56.33 10.3 66.01;13.8 65.23 4.69 64.24;15.3 55.62 6.06 54.74;...11 55.55 8.02 67.47;18 62.85 6.4 58.83;10.4 30.01 4.61 60.26;...8.2 29.28 6.11 50.71;11.4 62.88 5.31 61.49;11.6 28.57 9.08 68.47;...84 30.23 6.03 55.55;8.2 15.96 8.04 40.26;10.9 24.75 8.34 46.01;...15.6 21.44 28.62 46.01];X3=[16.5 80.05 8.81 73.04;20.6 81.24 5.37 60.43;8.6 42.06 8.88 56.37];[n p]=size(X1);[m p]=size(X2);i=1:1:n;x1junzhi=(1/n)*sum(X1(i,:));j=1:1:m;x2junzhi=(1/m)*sum(X2(j,:));S1=cov(X1); S2=cov(X2);sigamani=(((n-1)*S1+(m-1)*S2)/(n+m-2))^(-1) x1junzhi=x1junzhi' x2junzhi=x2junzhi' 输出结果 sigamani =0.0049 0.0001 -0.0001 0.0001 0.0001 0.0071 0.0002 -0.0075 -0.0001 0.0002 0.0050 -0.0009 0.0001 -0.0075 -0.0009 0.0235 x1junzhi = 15.7364 64.9791 25.1491 74.3500 x2junzhi = 16.2875 40.1063 9.2281 58.1050接着计算判别函数 根据111ln ''1,22g gg g f q X g μμμ--=-∑+∑=11ln 1ln0.897942716ln 2ln 0.5232527q q =≈-=≈-112342123445.86550.08960.08490.0715 1.240629.13440.08970.14430.0008 1.0591f x x x x f x x x x =-+-++=-+-++按照判别原则，若12f f >，则属于第一组，若12f f <，则属于第二组 回判 程序A=sigamani*x1junzhi; B=sigamani*x2junzhi; C=zeros(27,2); C(:,1)=[1:1:27]; for i=1:1:11f1=X1(i,:)*A-45.8655; f2=X1(i,:)*B-29.1344; if f1>f2C(i,2)=1;elseC(i,2)=2;endendfor i=1:1:16f1=X2(i,:)*A-45.8655;f2=X2(i,:)*B-29.1344;if f1>f2C(i+11,2)=1;elseC(i+11,2)=2;endendC输出结果C =1 12 13 14 15 16 17 18 19 110 211 112 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 2所以误判率为1100%⨯≈3.7%很小，所以判别有效27最后对待判样品进行判别程序D=zeros(3,2);D(:,1)=[28:1:30];for j=1:1:3f1=X3(j,:)*A-45.8655;f2=X3(j,:)*B-29.1344;if f1>f2D(j,2)=1;elseD(j,2)=2;endendD输出结果D =28 129 230 2第七章主成分分析例7.1对全国30个省市自治区经济发展基本情况的八项指标作主成分分析，原始数据如下:解用matlab实现主成分分析第一步在matlab输入原始数据在这里由于输入数据量较大，我们可以在matlab的workspace中点击“新建变量”选项，命名为“x的变量，然后把你在excel中打好的表格中的数据直接复制粘贴到该变量中接着我们将原始数据标准化程序stdr=std(x); %求各变量的标准差[n,m]=size(x);sddata=x./stdr(ones(n,1),:) %标准化变换输出结果sddata =0.9458 2.9072 1.2882 6.2182 0.8129 57.9170 59.32311.44280.6239 3.1568 0.8575 4.9637 0.7453 56.8802 58.26940.99641.9321 1.4600 1.7496 3.6947 4.4208 56.8802 61.00902.11230.7408 1.4507 0.7220 3.6046 1.5596 57.7195 60.90361.19270.5647 1.6097 0.6211 3.1564 1.6996 58.0158 61.53580.71741.89412.7819 0.96303.7497 2.9811 57.3245 60.0607 3.14850.7657 2.1726 0.7954 3.3824 1.0815 56.8802 60.16601.30431.36602.7088 1.08153.1648 1.7933 57.3245 60.21872.12181.6698 6.20102.4734 7.0848 0.4509 58.6083 59.53382.81043.4955 2.2353 3.56174.5308 2.2297 57.1764 60.2187 3.46682.3900 2.6101 2.4980 5.0538 1.6402 57.5714 59.7972 1.56791.3585 1.4554 1.1765 3.5191 1.9748 56.6826 59.3757 1.40981.46502.6925 1.3750 4.4720 1.3248 56.8802 60.2714 0.74180.8171 1.3718 0.7020 3.2152 0.8951 57.7195 61.0617 0.97823.3919 1.7722 3.0519 3.9283 2.6017 58.0652 60.1660 3.77652.0360 1.2000 1.66393.3168 3.4231 57.5220 60.5348 2.34001.6215 1.7722 1.4190 3.5771 1.8459 59.2502 61.43052.08821.4888 1.6341 1.0490 3.66262.1999 58.7564 60.8509 1.44353.6491 3.13244.0702 6.2991 1.4274 56.2876 58.7962 2.38861.0891 1.5250 0.9496 3.9322 1.2089 58.4602 61.3251 0.94930.2469 2.1053 0.4923 4.0772 0.5046 56.0408 58.6382 0.11002.3962 1.4635 2.04163.5466 1.9618 58.5095 61.6412 2.44930.4272 1.0933 0.3744 3.4168 0.6547 59.9414 61.7466 0.55550.8182 1.4635 0.8290 3.9314 0.6749 59.8920 62.22071.22590.0380 1.2882 0.0444 5.6364 0.0091 57.9170 60.5348 0.00950.6781 1.4020 0.7453 3.3565 1.0891 58.7564 61.64121.02800.3752 1.1687 0.2850 4.1941 1.1023 59.1514 61.3778 0.80190.1121 1.6770 0.1185 4.3926 0.1339 58.2627 61.2724 0.18100.1151 1.5726 0.1538 3.8780 0.2648 57.8183 60.7456 0.19570.5659 1.7049 0.9356 4.0833 0.7371 59.1020 61.4831 0.7334第二步建立指标间的相关系数矩阵R在这里标准化之后的样本数据的相关系数矩阵与样本离差阵相等所以我们接着在命令窗口输入R=cov(sddata)输出结果R =1.0000 0.2668 0.9506 0.1899 0.6172 -0.2726 -0.2636 0.8737 0.2668 1.0000 0.4261 0.7178 -0.1510 -0.2351 -0.5927 0.3631 0.9506 0.4261 1.0000 0.3989 0.4306 -0.2805 -0.3591 0.7919 0.1899 0.7178 0.3989 1.0000 -0.3562 -0.1342 -0.5384 0.1033 0.6172 -0.1510 0.4306 -0.3562 1.0000 -0.2532 0.0217 0.6586-0.2726 -0.2351 -0.2805 -0.1342 -0.2532 1.0000 0.7628 0.1252 -0.2636 -0.5927 -0.3591 -0.5384 0.0217 0.7628 1.0000 -0.19210.8737 0.3631 0.7919 0.1033 0.6586 -0.1252 -0.19211.0000第三步求R的特征向量程序[x,B]=eig(R)输出结果x =0.7602 0.0939 0.0309 0.1486 0.3203 0.1099 0.2585 0.4568 0.1092 0.2162 0.4222 0.1634 -0.6441 0.2459 -0.4038 0.3130 -0.6080 0.3178 0.2226 0.1673 0.4262 0.1924 0.1084 0.4706 0.0320 -0.2981 -0.0452 -0.6589 0.2585 0.3340 -0.4878 0.2400 -0.0498 0.2678 0.0593 -0.6620 -0.3331 -0.2493 0.4980 0.2509 0.0205 0.4185 -0.4338 -0.0580 -0.1133 0.7227 0.1699 -0.2624 0.0131 -0.3601 0.6646 -0.0774 0.0422 0.3972 0.4010 -0.3197 -0.1907 -0.6148 -0.3685 0.2037 -0.3295 0.1915 0.2877 0.4247B =0.015000000000.065000000000.138000000000.213000000000.40200000000 1.21500000000 2.19700000000 3.754在这里由于输出结果数据长度太大，无法在这里显示，所以用excel对上面的矩阵B做了一点小小的处理在矩阵B中对角线上的元素对应的是R的特征值，对应的矩阵列向量为其特征向量对结果分析从上表看，前三个特征值累计贡献率已达89.575%，这说明前三个主成分基本包含了全部指标具有的信息，为此，我们取前三个特征值，并计算出相应的特征向量:对应特征向量u1u2u30.456790.258510.10990.31301-0.403790.245870.470560.108390.192430.23996-0.487770.334050.25090.49801-0.24933-0.262440.169880.7227-0.319660.401020.397160.424680.287690.19147因而前三个主成为第一个主成分F1=0.45679X1+0.31301X2+0.47056X3+0.23996X4+0.2509X5-0.26244X6-0.31966X7+0.42468X8F2=0.25851X1-0.40397X2+0.10839X3-0.48777X4+0.49801X5+0.16988X6+0.40102X7+0.28769X8F3=0.1099X1+0.24587X2+0.19243X3+0.33405X4-0.24933X5+0.7227X6+0.39716X7+0.19147X8在第一个主成分的表达式中第一、二、三项指标的系数较大，这三个指标起主要作用，我们可以把第一主成分看成是由国生产总值，固定生产投资和居民消费水平所刻画的反映经济发展状况的综合指标。