2017年春八年级数学下册4.1.1变量与函数学案新版湘教版

湘教版数学八年级下册 4.1.1 变量与函数导学案(无答案)

在这一过程中，随着时间的变化，相应的温度也随之．
这一天的4时、14时的气温分别是、．
当时间取定某一个值时，有（唯一或不唯一）的温度与它对应.
问题2中，完成教材中表格并回答下列问题
在这一过程中，随着边长的变化，相应的面积也随之．且正方形的边长越长，正方形的面积也越．边长与面积满足的关系式是．
(1)用含r的代数式来表示圆柱的体积V，指出自变量r的取值范围.
(2)当5,10时，V是多少（结果保留π）？
四：总结反思（学生总结，教师点评）
我在本节课中的收获（画出思维导图）：
我的本节课中的不足：
五：作业
选做学法P61-63
4.1.1变量与函数导学案
1、学习目标: 1.知道什么是常量、变量·
2.能用函数的观点分析实际问题中的数量关系和变化规律，能用适当的方法刻画变量之间的关系.(重难点)
3.能确定简单函数式及实际问题中自变量的取值范围（重点）.
二：学习过程
自主探究:阅读教材110页动脑筋完成下列问题
问题1中，观察图4-1
例1、这个式子中，是常量，是变量，并且随的变化而变化，当 =1时， =，当 =2时， =，被确定，所以是的函数.
例2、判断下列各量之间的关系是不是函数关系，若是，写出函数关系；若不是说明理由.
(1)已知圆的半径，则圆的面积与半径的关系.，
(2)矩形的宽为4 ，其周长与长的关系.，
针对训练2：
已知等腰三角形的腰长为8 ，求三角形的周长与底边之间的函数关系式，并求自变量的取值范围.
（2）归纳：
要确定函数自变量的取值范围，可从两个方面取考虑：
自变量的取值必须使含有自变量的代数式有意义

湘教版数学八年级下册《4.1.1变量与函数》教学设计

湘教版数学八年级下册《4.1.1变量与函数》教学设计一. 教材分析湘教版数学八年级下册《4.1.1变量与函数》是学生在学习了初中阶段函数概念的基础上，进一步探讨变量与函数的关系。

本节内容通过具体的实例让学生理解自变量、函数的概念，以及如何用函数式表示变量之间的关系。

教材内容由浅入深，既巩固了以前的知识，又为后续学习函数的图像和性质打下基础。

二. 学情分析学生在之前的学习中已经掌握了变量、常量的概念，对函数有了初步的认识。

但部分学生对函数的定义和判断仍然存在模糊的地方，对函数式子的理解也不够深入。

因此，在教学过程中，需要帮助学生理清变量、常量、函数之间的关系，并通过具体例子让学生感受函数式表示变量之间的方法。

三. 教学目标1.理解自变量、函数的概念，掌握用函数式表示变量之间的关系。

2.能够判断一个关系是否为函数，并能用函数式表示。

3.培养学生的抽象思维能力，提高学生解决实际问题的能力。

四. 教学重难点1.重点：理解自变量、函数的概念，掌握用函数式表示变量之间的关系。

2.难点：判断一个关系是否为函数，并能用函数式表示。

五. 教学方法1.采用问题驱动法，引导学生主动探究变量与函数的关系。

2.利用具体实例，让学生感受函数式表示变量之间的方法。

3.采用小组合作学习，培养学生的团队协作能力。

4.利用板书、多媒体等教学辅助工具，提高教学效果。

六. 教学准备1.准备相关实例，用于讲解变量与函数的关系。

2.准备多媒体课件，用于展示函数图像和实例。

3.准备练习题，用于巩固所学知识。

七. 教学过程1.导入（5分钟）利用一个生活中的实例，如投篮问题，引导学生思考投篮命中次数与投篮次数之间的关系。

让学生意识到这两个量之间存在一种依赖关系，进而引出自变量、函数的概念。

2.呈现（10分钟）呈现投篮问题的具体数据，让学生观察命中次数与投篮次数之间的关系。

引导学生用函数式表示这种关系，如命中次数 = 投篮次数 × 命中率。

八年级数学下册变量与函数教案新版湘教版

第4章一次函数4．1 函数和它的表示法4．1.1 变量与函数1．了解常量、变量的概念；(重点)2．了解函数的概念；(重点)3．确定简单问题的函数关系．(难点)一、情境导入如图，水滴激起的波纹可以看成是一个不断向外扩展的圆，它的面积随着半径的变化而变化，随着半径的确定而确定．在上述例子中，每个变化过程中的两个变量：当其中一个变量变化时，另一个变量也随着发生变化；当一个变量确定时，另一个变量也随着确定．你能举出一些类似的实例吗？二、合作探究探究点一：常量与变量分析并指出下列关系中的变量与常量：(1)球的表面积S cm 2与球的半径R cm 的关系式是S ＝4πR 2；(2)以固定的速度v 0米/秒向上抛一个小球，小球的高度h 米与小球运动的时间t 秒之间的关系式是h ＝v 0t －4.9t 2；(3)一物体自高处自由落下，这个物体运动的距离h m 与它下落的时间t s 的关系式是h ＝12gt 2(其中g 取9.8m/s 2)； (4)已知橙子每千克的售价是1.8元，则购买数量w 千克与所付款x 元之间的关系式是x ＝1.8w .解析：在一个变化的过程中，数值发生变化的量称为变量，数值始终不变的量称为常量．解：(1)球的表面积S cm 2与球的半径R cm 的关系式是S ＝4πR 2，其中，常量是4π，变量是S ，R ；(2)以固定的速度v 0米/秒向上抛一个小球，小球的高度h 米与小球运动的时间t 秒之间的关系式是h ＝v 0t －4.9t 2，常量是v 0，4.9，变量是h ，t ；(3)一物体自高处自由落下，这个物体运动的距离h m 与它下落的时间t s 的关系式是h ＝12gt 2(其中g 取9.8m/s 2)，其中常量是12g ，变量是h ，t ； (4)已知橙子每千克的售价是1.8元，则购买数量w 千克与所付款x 元之间的关系式是x ＝1.8w ，常量是1.8，变量是x ，w .方法总结：常量与变量必须存在于同一个变化过程中，判断一个量是常量还是变量，需要看两个方面：一是它是否在一个变化过程中；二是看它在这个变化过程中的取值情况是否发生变化．变式训练：：见《学练优》本课时练习“课后巩固提升”第2题探究点二：函数的定义下列说法中正确的是( )A ．变量x ，y 满足x ＋3y ＝1，则y 是x 的函数B ．变量x ，y 满足y ＝－x 2－1，则y 可以是x 的函数C ．变量x ，y 满足|y |＝x ，则y 可以是x 的函数D ．变量x ，y 满足y 2＝x ，则y 可以是x 的函数解析：A 中x ＋3y ＝1，y 可以看作x 的函数，因为y ＝1－x 3；B 中y ＝－x 2－1，因为－x 2－1<0，等式无意义，即对于变量x 的任何一个取值，变量y 都没有唯一确定的值，故y不是x 的函数；C 、D 中的|y |＝x 和y 2＝x ，对于变量x 的任意一个正数值，变量y 都有两个(不唯一)值与其对应，故y 不是x 的函数．故选A.方法总结：判断两个变量是否是函数关系，就看是否存在两个变量，并且在这两个变量中，确定好哪个是自变量，哪个是函数，然后再看看这两个变量是否是一一对应的关系．变式训练：见《学练优》本课时练习“课后巩固提升”第1题探究点三：确定自变量的取值范围【类型一】确定函数解析式中自变量的取值范围写出下列函数中自变量x 的取值范围．(1)y ＝2x －3； (2)y ＝31－x； (3)y ＝4－x ； (4)y ＝x －1x －2. 解析：当表达式的分母不含有自变量时，自变量取全体实数；当表达式的分母中含有自变量时，自变量取值要使分母不为零；当函数的表达式是偶次根式时，自变量的取值范围必须使被开方数不小于零．解：(1)全体实数；(2)分母1－x ≠0，即x ≠1；(3)被开方数4－x ≥0，即x ≤4；(4)由题意得⎩⎪⎨⎪⎧x －1≥0，x －2≠0，解得x ≥1且x ≠2.方法总结：本题考查了函数自变量的取值范围：有分母的要满足分母不能为0，有根号的要满足被开方数为非负数．【类型二】实际问题中自变量的取值范围水箱内原有水200升，7：30打开水龙头，以2升/分的速度放水，设经过t 分钟后，水箱内存水y 升．(1)求y 关于t 的函数关系式和自变量的取值范围；(2)7：55时，水箱内还有多少水？(3)几点几分水箱内的水恰好放完？解析：(1)根据水箱内还有的水等于原有水减去放掉的水列式整理即可，再根据剩余水量不小于0列不等式求出t 的取值范围；(2)7：55时，t ＝55－30＝25，将t ＝25代入(1)中的关系式即可；(3)令y ＝0，求出t 的值即可．解：(1)∵水箱内存有的水＝原有水－放掉的水，∴y ＝200－2t .∵y ≥0，∴200－2t ≥0，解得t ≤100，∴0≤t ≤100，∴y 关于t 的函数关系式为y ＝200－2t (0≤t ≤100)；(2)∵7：55－7：30＝25(分钟)，∴当t ＝25时，y ＝200－2t ＝200－50＝150(升)，∴7：55时，水箱内还有水150升；(3)当y ＝0时，200－2t ＝0，解得t ＝100，而100分钟＝1小时40分钟，7点30分＋1小时40分钟＝9点10分，故9点10分水箱内的水恰好放完．探究点四：简单问题的函数关系一个弹簧秤最大能称不超过10kg 的物体，它的原长为10cm ，挂上重物后弹簧的长度y (cm)随所挂重物的质量x (kg)的变化而变化，每挂1kg 物体，弹簧伸长0.5cm ；(1)求弹簧的长度y (cm)与所挂重物质量x (kg)之间的函数表达式；(2)当挂5kg 重物时，求弹簧的长度．解析：根据弹簧的长度等于原长加上伸长的长度，列式即可；解：(1)y ＝10＋12x ，其中x 是自变量，y 是自变量的函数； (2)将x ＝5代入y ＝10＋12x ，得y ＝10＋12×5＝12.5(cm)．答：当挂5kg 重物是，弹簧的长度为12.5厘米．方法总结：根据题意，找出等量关系，列出相应的函数表达式．求函数值时，将自变量代入函数表达式中，求出即可．变式训练：见《学练优》本课时练习“课堂达标训练”第5题探究点五：函数值根据如图所示程序计算函数值，若输入x 的值为52，则输出的函数值为( )A.32B.25C.425D.254解析：∵x ＝52时，在2≤x ≤4之间，∴将x ＝52代入函数y ＝1x ，得y ＝25.故选B. 方法总结：根据所给的自变量的值，结合各个函数关系式所对应的自变量的取值范围，确定其对应的函数关系式，再代入计算．变式训练：见《学练优》本课时练习“课后巩固提升”第4题三、板书设计1．常量和变量的概念2．函数的概念3．函数关系式4．自变量的取值范围5．函数值通过本课时的教学，学生对于常量、变量以及函数关系式掌握较好，但是对于有些实际问题中自变量的取值范围还存在一些困难．在以后的教学中要通过实例让学生不断加以强化，达到整体进步。

4新湘教版初中数学八年级下册精品教案.1.1 变量与函数

第4章一次函数 4．1 函数和它的表示法4．1.1 变量与函数1．了解常量、变量的概念；(重点) 2．了解函数的概念；(重点)3．确定简单问题的函数关系．(难点)一、情境导入如图，水滴激起的波纹可以看成是一个不断向外扩展的圆，它的面积随着半径的变化而变化，随着半径的确定而确定．在上述例子中，每个变化过程中的两个变量：当其中一个变量变化时，另一个变量也随着发生变化；当一个变量确定时，另一个变量也随着确定．你能举出一些类似的实例吗？二、合作探究探究点一：常量与变量分析并指出下列关系中的变量与常量：(1)球的表面积S cm 2与球的半径R cm 的关系式是S ＝4πR 2；(2)以固定的速度v 0米/秒向上抛一个小球，小球的高度h 米与小球运动的时间t 秒之间的关系式是h ＝v 0t －4.9t 2；(3)一物体自高处自由落下，这个物体运动的距离h m 与它下落的时间t s 的关系式是h ＝12gt 2(其中g 取9.8m/s 2)； (4)已知橙子每千克的售价是1.8元，则购买数量w 千克与所付款x 元之间的关系式是x ＝1.8w .解析：在一个变化的过程中，数值发生变化的量称为变量，数值始终不变的量称为常量．解：(1)球的表面积S cm 2与球的半径R cm 的关系式是S ＝4πR 2，其中，常量是4π，变量是S ，R ；(2)以固定的速度v 0米/秒向上抛一个小球，小球的高度h 米与小球运动的时间t 秒之间的关系式是h ＝v 0t －4.9t 2，常量是v 0，4.9，变量是h ，t ；(3)一物体自高处自由落下，这个物体运动的距离h m 与它下落的时间t s 的关系式是h ＝12gt 2(其中g 取9.8m/s 2)，其中常量是12g ，变量是h ，t ；(4)已知橙子每千克的售价是1.8元，则购买数量w 千克与所付款x 元之间的关系式是x ＝1.8w ，常量是1.8，变量是x ，w .方法总结：常量与变量必须存在于同一个变化过程中，判断一个量是常量还是变量，需要看两个方面：一是它是否在一个变化过程中；二是看它在这个变化过程中的取值情况是否发生变化．探究点二：函数的定义下列说法中正确的是( )A ．变量x ，y 满足x ＋3y ＝1，则y 是x 的函数B ．变量x ，y 满足y ＝－x 2－1，则y 可以是x 的函数C ．变量x ，y 满足|y |＝x ，则y 可以是x 的函数D ．变量x ，y 满足y 2＝x ，则y 可以是x 的函数解析：A 中x ＋3y ＝1，y 可以看作x 的函数，因为y ＝1－x3；B 中y ＝－x 2－1，因为－x 2－1<0，等式无意义，即对于变量x 的任何一个取值，变量y 都没有唯一确定的值，故y 不是x 的函数；C 、D 中的|y |＝x 和y 2＝x ，对于变量x 的任意一个正数值，变量y 都有两个(不唯一)值与其对应，故y 不是x 的函数．故选A.方法总结：判断两个变量是否是函数关系，就看是否存在两个变量，并且在这两个变量中，确定好哪个是自变量，哪个是函数，然后再看看这两个变量是否是一一对应的关系．探究点三：确定自变量的取值范围【类型一】确定函数解析式中自变量的取值范围写出下列函数中自变量x 的取值范围．(1)y ＝2x －3； (2)y ＝31－x ；(3)y ＝4－x ； (4)y ＝x －1x －2.解析：当表达式的分母不含有自变量时，自变量取全体实数；当表达式的分母中含有自变量时，自变量取值要使分母不为零；当函数的表达式是偶次根式时，自变量的取值范围必须使被开方数不小于零．解：(1)全体实数；(2)分母1－x ≠0，即x ≠1； (3)被开方数4－x ≥0，即x ≤4；(4)由题意得⎩⎪⎨⎪⎧x －1≥0，x －2≠0，解得x ≥1且x ≠2.方法总结：本题考查了函数自变量的取值范围：有分母的要满足分母不能为0，有根号的要满足被开方数为非负数．【类型二】实际问题中自变量的取值范围水箱内原有水200升，7：30打开水龙头，以2升/分的速度放水，设经过t 分钟后，水箱内存水y 升．(1)求y 关于t 的函数关系式和自变量的取值范围；(2)7：55时，水箱内还有多少水？ (3)几点几分水箱内的水恰好放完？解析：(1)根据水箱内还有的水等于原有水减去放掉的水列式整理即可，再根据剩余水量不小于0列不等式求出t 的取值范围；(2)7：55时，t ＝55－30＝25，将t ＝25代入(1)中的关系式即可；(3)令y ＝0，求出t 的值即可．解：(1)∵水箱内存有的水＝原有水－放掉的水，∴y ＝200－2t .∵y ≥0，∴200－2t ≥0，解得t ≤100，∴0≤t ≤100，∴y 关于t 的函数关系式为y ＝200－2t (0≤t ≤100)；(2)∵7：55－7：30＝25(分钟)，∴当t＝25时，y＝200－2t＝200－50＝150(升)，∴7：55时，水箱内还有水150升；(3)当y＝0时，200－2t＝0，解得t＝100，而100分钟＝1小时40分钟，7点30分＋1小时40分钟＝9点10分，故9点10分水箱内的水恰好放完．探究点四：简单问题的函数关系一个弹簧秤最大能称不超过10kg的物体，它的原长为10cm，挂上重物后弹簧的长度y(cm)随所挂重物的质量x(kg)的变化而变化，每挂1kg物体，弹簧伸长0.5cm；(1)求弹簧的长度y(cm)与所挂重物质量x(kg)之间的函数表达式；(2)当挂5kg重物时，求弹簧的长度．解析：根据弹簧的长度等于原长加上伸长的长度，列式即可；解：(1)y＝10＋12x，其中x是自变量，y是自变量的函数；(2)将x＝5代入y＝10＋12x，得y＝10＋12×5＝12.5(cm)．答：当挂5kg重物是，弹簧的长度为12.5厘米．方法总结：根据题意，找出等量关系，列出相应的函数表达式．求函数值时，将自变量代入函数表达式中，求出即可．探究点五：函数值根据如图所示程序计算函数值，若输入x的值为52，则输出的函数值为()A.32 B.25 C.425 D.254解析：∵x＝52时，在2≤x≤4之间，∴将x＝52代入函数y＝1x，得y＝25.故选B.方法总结：根据所给的自变量的值，结合各个函数关系式所对应的自变量的取值范围，确定其对应的函数关系式，再代入计算．三、板书设计1．常量和变量的概念2．函数的概念3．函数关系式4．自变量的取值范围5．函数值通过本课时的教学，学生对于常量、变量以及函数关系式掌握较好，但是对于有些实际问题中自变量的取值范围还存在一些困难．在以后的教学中要通过实例让学生不断加以强化，达到整体进步.。

八年级数学下册 4_1_1 变量与函数导学案 (新版)湘教版

第4章一次函数4.1 函数和它的表示法4.1.1 变量与函数1.认识变量、常量.2.学会用一个变量的代数式表示另一个变量.3.认识变量中的自变量与函数.4.进一步理解掌握确定函数关系式.5.会确定自变量的取值范围.自学指导：阅读教材第110页至112页，独立完成下列问题：知识探究(1)一辆汽车以60千米/时的速度匀速行驶，行驶里程为s千米，行驶时间为t小时.①根据题意填写下表：t/时12345s/千米60120180240300②试用含t的式子表示s为s=60t；③在以上这个过程中，不变化的量是60，变化的量是s与t.(2)每张电影票的售价为10元，早场售出票150张，日场售出票205张，晚场售出票310张.①三场电影的票房收入分别是1500元，2050元，3100元.②设一场电影售票x张，票房收入y元，则用含x的式子表示y为y=10x.③在以上这个过程中，不变化的量是10，变化的量是x与y.(3)变量：在一个变化的过程中，数值变化的量；常量：在一个变化的过程中，数值不变的量.(4)一般地，如果变量y随着变量x而变化，并且对于x取的每一个值，y都有唯一的一个值与它对应，那么就称y是x的函数，其中x是自变量，y是因变量.如果当x=a时，y=b，那么b叫做当自变量的值为a时的函数.(5)对于一个已知的函数，自变量的取值范围是使这个函数有意义的一切值；对于一个实际问题，自变量的取值必须使实际问题有意义.活动1 学生独立完成例1分别指出下列关系中的变量和常量：(1)圆面积公式S=πr2(s表示面积，r表示半径)；(2)匀速运动公式s=vt(v表示速度，t表示时间，s表示在时间t内所走的路程).解：(1)r、S是变量，π是常量；(2)t、s是变量，v是常量.π是圆周率，是定值，是常量，半径r每取一个值都有唯一的S值和它对应，故S和r是变量.因为是匀速运动，所以速度v是常量，t和s是变量.例2如图，一个矩形推拉窗高1.5m，则活动窗的通风面积S(m2)与拉开长度b(m)的关系式是S=1.5b.窗高1.5m是一边长，拉开长度b(m)是另一边长，因此通风面积S=1.5b.例3某火力发电厂，贮存煤1000吨，每天发电用煤50吨，设发电天数为x，该电厂开始发电后，贮存煤量为y(吨).(1)写出y与x之间的函数关系式；(2)为了保障电厂正常发电，工厂每天将从外地运回煤45吨，请写出按此方案执行时，y与x之间的函数关系式，并求出发电30天时，电厂贮存煤多少吨？解：(1)y=-50x+1000；(2)y=-5x+1000，当x=30时，y=-5×30+1000=850.∴当发电30天时，电厂贮存煤850吨.电厂贮存的煤量与原贮存量，每天发电的用煤量，每天从外地运回的煤量，以及发电天数有关.活动2 跟踪训练1.设圆柱的高h不变，圆柱的体积V与圆柱的底面半径r的关系是V=πr2h，这个式子中常量是π，h，变量是V，r.2.若球体体积为Ｖ，半径为Ｒ，则Ｖ＝43πＲ3.其中变量是R，V，常量是43，π.找准不变的量，再确定变量.3.下列变量间的关系：①人的身高与年龄；②矩形的周长与面积；③圆的周长与面积；④商品的单价一定，其销售额与销售量，其中是函数关系的有③④.一是明确已知两个变量是什么；二是看两个变量之间是否存在一一对应关系.4.某市为了鼓励居民节约用水，对自来水用户按如下标准收费：若每月每户用水不超过12米3，按每立方米a 元收费；若超过12米3，则超过部分每立方米按2a元收费，某户居民五月份交水费y(元)与用水量x(米3)(x>12)之间的关系式为y=2ax-12a，若该月交水费20a元，则这个月实际用水16米3.5.若等腰三角形底角度数值为x，则顶角度数值y与x的关系式是y=-2x＋180，变量是x，y，常量是-2，180.6.在△ABC中，它的底边长是a，底边上的高是h，则三角形的面积S=12ah，当底边a的长一定时，在关系式中的常量是12，a，变量是S，h.7.已知水池里有水200m3，每小时向水池里注水20m3，设注水时间为x小时，水池里共有水ym3，用含x 的式子表示y，则y=20x+200，其中变量为x，y，常量为20，200.8.人的心跳速度通常与人的年龄有关，如果a表示一个人的年龄，b表示正常情况下每分钟心跳的最高次数，经过大量试验，有如下的关系：b=0.8(220-a).(1)上述关系中的常量与变量各是什么？(2)正常情况下，一名15岁的学生每分钟心跳的最高次数是多少？解：(1)常量0.8，220，变量a,b；(2)164.9.蓄水池中原有水800m3，每小时从中放出60m3的水.(1)写出池中的剩余水量Q(m3)与放水时间t(h)之间的函数关系式；(2)写出自变量t的取值范围；(3)12h后，池中还有多少水？. (3)80m3.解：(1)Q＝-60t＋800. (2)0≤t≤403实际问题中的函数关系，自变量除了要使函数关系式本身有意义，还要满足实际意义.此题要根据函数Q的取值范围0≤Q≤800来确定自变量t的取值范围.活动3 课堂小结1.常量和变量是普遍存在的，它们只是相对于某个变化过程而言的两个概念，因此对它们的差别应紧扣定义及相应的实际背景.2.判断变量之间是否存在函数关系，主要抓住两点：一个变量的数值随着另一个变量的数值的变化而变化；自变量的每一个确定的值，函数都有且只有一个值与之对应.3.确定自变量取值范围时，不仅要考虑函数关系式有意义，而且还要注意使实际问题有意义.。

新湘教版八下教案：4.1.1 变量与函数

第4章一次函数 4．1 函数和它的表示法4．1.1 变量与函数1．了解常量、变量的概念；(重点) 2．了解函数的概念；(重点)3．确定简单问题的函数关系．(难点)一、情境导入如图，水滴激起的波纹可以看成是一个不断向外扩展的圆，它的面积随着半径的变化而变化，随着半径的确定而确定．在上述例子中，每个变化过程中的两个变量：当其中一个变量变化时，另一个变量也随着发生变化；当一个变量确定时，另一个变量也随着确定．你能举出一些类似的实例吗？二、合作探究探究点一：常量与变量分析并指出下列关系中的变量与常量：(1)球的表面积S cm 2与球的半径R cm 的关系式是S ＝4πR 2；(2)以固定的速度v 0米/秒向上抛一个小球，小球的高度h 米与小球运动的时间t 秒之间的关系式是h ＝v 0t －4.9t 2；(3)一物体自高处自由落下，这个物体运动的距离h m 与它下落的时间t s 的关系式是h ＝12gt 2(其中g 取9.8m/s 2)； (4)已知橙子每千克的售价是1.8元，则购买数量w 千克与所付款x 元之间的关系式是x ＝1.8w .解析：在一个变化的过程中，数值发生变化的量称为变量，数值始终不变的量称为常量．解：(1)球的表面积S cm 2与球的半径R cm 的关系式是S ＝4πR 2，其中，常量是4π，变量是S ，R ；(2)以固定的速度v 0米/秒向上抛一个小球，小球的高度h 米与小球运动的时间t 秒之间的关系式是h ＝v 0t －4.9t 2，常量是v 0，4.9，变量是h ，t ；(3)一物体自高处自由落下，这个物体运动的距离h m 与它下落的时间t s 的关系式是h ＝12gt 2(其中g 取9.8m/s 2)，其中常量是12g ，变量是h ，t ；(4)已知橙子每千克的售价是1.8元，则购买数量w 千克与所付款x 元之间的关系式是x ＝1.8w ，常量是1.8，变量是x ，w .方法总结：常量与变量必须存在于同一个变化过程中，判断一个量是常量还是变量，需要看两个方面：一是它是否在一个变化过程中；二是看它在这个变化过程中的取值情况是否发生变化．探究点二：函数的定义下列说法中正确的是( )A ．变量x ，y 满足x ＋3y ＝1，则y 是x 的函数B ．变量x ，y 满足y ＝－x 2－1，则y 可以是x 的函数C ．变量x ，y 满足|y |＝x ，则y 可以是x 的函数D ．变量x ，y 满足y 2＝x ，则y 可以是x 的函数解析：A 中x ＋3y ＝1，y 可以看作x 的函数，因为y ＝1－x3；B 中y ＝－x 2－1，因为－x 2－1<0，等式无意义，即对于变量x 的任何一个取值，变量y 都没有唯一确定的值，故y 不是x 的函数；C 、D 中的|y |＝x 和y 2＝x ，对于变量x 的任意一个正数值，变量y 都有两个(不唯一)值与其对应，故y 不是x 的函数．故选A.方法总结：判断两个变量是否是函数关系，就看是否存在两个变量，并且在这两个变量中，确定好哪个是自变量，哪个是函数，然后再看看这两个变量是否是一一对应的关系．探究点三：确定自变量的取值范围【类型一】确定函数解析式中自变量的取值范围写出下列函数中自变量x 的取值范围．(1)y ＝2x －3； (2)y ＝31－x ；(3)y ＝4－x ； (4)y ＝x －1x －2.解析：当表达式的分母不含有自变量时，自变量取全体实数；当表达式的分母中含有自变量时，自变量取值要使分母不为零；当函数的表达式是偶次根式时，自变量的取值范围必须使被开方数不小于零．解：(1)全体实数；(2)分母1－x ≠0，即x ≠1； (3)被开方数4－x ≥0，即x ≤4；(4)由题意得⎩⎪⎨⎪⎧x －1≥0，x －2≠0，解得x ≥1且x ≠2.方法总结：本题考查了函数自变量的取值范围：有分母的要满足分母不能为0，有根号的要满足被开方数为非负数．【类型二】实际问题中自变量的取值范围水箱内原有水200升，7：30打开水龙头，以2升/分的速度放水，设经过t 分钟后，水箱内存水y 升．(1)求y 关于t 的函数关系式和自变量的取值范围；(2)7：55时，水箱内还有多少水？ (3)几点几分水箱内的水恰好放完？解析：(1)根据水箱内还有的水等于原有水减去放掉的水列式整理即可，再根据剩余水量不小于0列不等式求出t 的取值范围；(2)7：55时，t ＝55－30＝25，将t ＝25代入(1)中的关系式即可；(3)令y ＝0，求出t 的值即可．解：(1)∵水箱内存有的水＝原有水－放掉的水，∴y ＝200－2t .∵y ≥0，∴200－2t ≥0，解得t ≤100，∴0≤t ≤100，∴y 关于t 的函数关系式为y ＝200－2t (0≤t ≤100)；(2)∵7：55－7：30＝25(分钟)，∴当t＝25时，y＝200－2t＝200－50＝150(升)，∴7：55时，水箱内还有水150升；(3)当y＝0时，200－2t＝0，解得t＝100，而100分钟＝1小时40分钟，7点30分＋1小时40分钟＝9点10分，故9点10分水箱内的水恰好放完．探究点四：简单问题的函数关系一个弹簧秤最大能称不超过10kg的物体，它的原长为10cm，挂上重物后弹簧的长度y(cm)随所挂重物的质量x(kg)的变化而变化，每挂1kg物体，弹簧伸长0.5cm；(1)求弹簧的长度y(cm)与所挂重物质量x(kg)之间的函数表达式；(2)当挂5kg重物时，求弹簧的长度．解析：根据弹簧的长度等于原长加上伸长的长度，列式即可；解：(1)y＝10＋12x，其中x是自变量，y是自变量的函数；(2)将x＝5代入y＝10＋12x，得y＝10＋12×5＝12.5(cm)．答：当挂5kg重物是，弹簧的长度为12.5厘米．方法总结：根据题意，找出等量关系，列出相应的函数表达式．求函数值时，将自变量代入函数表达式中，求出即可．探究点五：函数值根据如图所示程序计算函数值，若输入x的值为52，则输出的函数值为()A.32 B.25 C.425 D.254解析：∵x＝52时，在2≤x≤4之间，∴将x＝52代入函数y＝1x，得y＝25.故选B.方法总结：根据所给的自变量的值，结合各个函数关系式所对应的自变量的取值范围，确定其对应的函数关系式，再代入计算．三、板书设计1．常量和变量的概念2．函数的概念3．函数关系式4．自变量的取值范围5．函数值通过本课时的教学，学生对于常量、变量以及函数关系式掌握较好，但是对于有些实际问题中自变量的取值范围还存在一些困难．在以后的教学中要通过实例让学生不断加以强化，达到整体进步.。

八年级数学下册 4.1.1《变量与函数》教案 (新版)湘教版-(新版)湘教版初中八年级下册数学教案

课题：变量与函数教学目标1、借助简单实例，学生初步感知用常量与变量来刻画一些简单的数学问题，能指出具体问题中的常量、变量．初步理解存在一类变量可以用函数方式来刻画，能举出涉及两个变量的实例，并指出由哪一个变量确定另一个变量，这两个变量是否具有函数关系。

初步理解对应的思想，体会函数概念的核心是两个变量之间的特殊对应关系，能判断两个变量间是否具有函数关系。

2、引领学生参与变量的发现和函数概念的形成过程,体会从生活实例抽象出数学知识的方法，感知现实世界中变量之间联系的复杂性，数学研究从最简单的情形入手，化繁为简。

3、从学生熟悉、感兴趣的实例引入课题，引领学生参与变量的发现和函数概念的形成过程,体验“发现、创造”数学知识的乐趣。

学生初步感知实际生活蕴藏着丰富的数学知识，感知数学是有用、有趣的学科。

重点：借助简单实例，从两个变量间的特殊对应关系抽象出函数的概念难点：理解函数的“唯一对应”性。

教学过程：一、情境导入（出示ppt课件）如图，是某地气象站用自动温度记录仪描出的某一天的温度曲线，它反映了该地某一天的气温T（℃）是如何随时间t的变化而变化的。

你能从图中得到哪些信息？从图中可以看出，4时的气温是℃，14时的气温是℃.这个问题中，某地一天中的气温随着时间的变化而变化。

关注其中数量的变化，用数量变化描述变化规律还可以举出很多这样的例子。

二、合作探究（出示ppt课件）（一）提出问题：1.一辆汽车以60千米/时的速度匀速行驶，行驶路程为s千米，行驶时间为t小时，以下为汽车在每小时行驶过的路程的情况：路程（S）=速度(v)×时间（t）试用含t的式子表示S：S = 60t在一个变化过程中，我们称数值发生变化的量为变量；有些量的数值是始终不变的，我们称它为常量.这个问题中，变量是，常量是。

2. 当正方形的边长x分正方形的面积S分别是多少？试填写下表：这个问题中，正方形的面积随着它的边长的变化而变化.写出s与x的关系式：s = x2这个问题中，变量是，常量是。

八年级数学下册4.1.1变量与函数教案(新版)湘教版【教案】

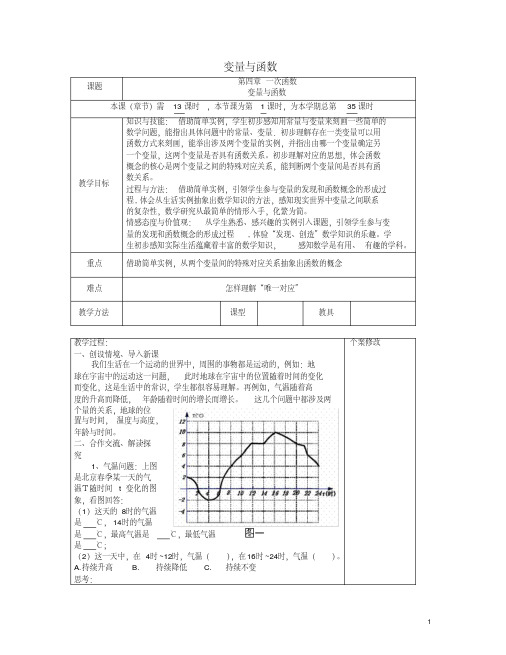
度的升高而降低，年龄随着时间的增长而增长。这几个问题中都涉及两
个量的关系，地球的位
置与时间，温度与高度，
年龄与时间。二、合作交流、解读探
究
1、气温问题：上图
是北京春季某一天的气
温Ｔ随时间 t 变化的图
象，看图回答：
（1）这天的 8时的气温
是 ℃， 14时的气温
是 ℃，最高气温是
℃，最低气温
是 ℃；
（2）这一天中，在 4时 ~12时，气温（），在 16时 ~24时，气温（）。
A. 持续升高 B. 持续降低 C. 持续不变
思考：
1
（1）天气温度随
的变化而变化，即 T 随的变化而变
化；
（2）当时间 t 取定一个确定的值时，对应的温度 T 的取值是否唯一确
定？
2 、当正方形的边长 x 分别取 1、 2、 3、 4、 5、 6、 7……时，正方形的
找出它们的共性，归纳出函数的概
x 和 y，如果对于 x 的每一个值， y x 是自变量， y 是 x 的函数。
三、应用迁移、巩固提高
例 1 已知圆柱的高是 4cm，底面半径是 rcm，当圆柱的底面半径 r 由小变大时，圆柱的体积 Vcm3是 r 的函数。（ 1）用含 r 的代数式来表示
圆柱的体积 V，指出自变量 r 的取值范围；（ 2）当 r=5,10 时， V 是多少
练习教材 P112页练习 1、 2题四、全课小结 1．这一节课你有什么收获？还有什么疑问？你可以编一道题考一考同学，也可以向同学请教。 2．函数是一种“数”吗？
五、作业：教材 P116 页 A 组 1 题
3
面积 S 分别是多少？
3、某城市居民用的天然气， 1m3收费 2.88 元，使用 x（ m3）天然气应缴纳费用 y=2.88x , 当 x=10时，缴纳的费用为多少？

湘教版数学八年级下册【学案】4.1.1 变量与函数

☆归纳反思☆
通过本节课的学习，我有以下收获：
_______________________________________________________________
_______________________________________________________________
☆达标检测☆
是因变量．
③一般地，设在一个变化过程中有两个变量x、y，如果对于x在它的每一个值，y都有与它对应，那么就说x是自变量，y是x的函数．
④是函数值．
☆合作探究☆
1．汽车行驶的路程S、行驶时间t和行驶速度v之间有下列关系：S=vt.
(1)如果汽车以60km/h的速度行驶，那么在S=vt中，变量是，常量是
（2）如果汽车行驶的时间t规定为1小时，那么在S=vt中，变量是，
（3）你知道距离地面5千米高空的温度是多少吗？
1．指出下列关系式中的变量与常量：
（1；
（2）在一定温度范围内，一种金属棒长度l(cm)与温度t(0C)之间有关系式：
l=0.002t+200.
2．某校有宿舍x间，学校规定每间宿舍可住6名学生，宿舍恰好住满，请你写出住校生总数y（人）与宿舍间数x之间的关系，指出本题中的变量、常量、自变量和函数．
3．父亲告诉小明：“距离地面越高，温度越低”，并且出示了下面的表格：
距离地面高度/千米
0
1
2
3
4
5
温度/℃
20
14
8
2
－4
－10
根据上表，父亲还给小明出了下面几个问题，你和小明一起回答：
（1）上表反映了哪两个变量之间的关系？哪个是自变量？哪个是函数？
（2）如果用h表示距离地面的高度，用t表示温度，那么随着h的变化，t如何变化？

初中数学湘教版八年级下册《4.1.1变量与函数》教学设计

湘教版数学八年级下册4.1.1变量与函数教学设计师：大千世界处在不停的运动变化之中,如何来研究这些运动变化并寻找规律呢?师：数学上常用变量与函数来刻画各种运动变化.动脑筋(出示课件)师：同学们每天都听天气预报知道最高气温和最低气温，那一天的气温变化怎样表示呢？来看问题1并回答问题：问题1. 如图是某地气象站用自动温度记录仪描出的某一天的温度曲线.观察与思考：1. 这一天中,4时的气温是℃,14时的气温是___ ℃;2. 随着的变化而变化.师：同学们很棒，我们接着看下面的问题，试着回答问题问题2. 当正方形的边长 x 分别取1，2，3，4，5，...时，正方形的面积S分别是多少？试填写下表.观察思考：1.正方形的随着的变化而变化.简记. 这时把x叫作自变量，把y叫作因变量。

对于自变量x取的每一个值a，因变量y的对应值称为函数值，记作f(a).师：说一说上面的三个问题中的函数，变量分别是什么？生：问题1中，时间t是自变量，气温T是时间t 的函数.生：问题2中，正方形的边长是自变量，正方形的面积s是边长x的函数.生：问题3中，所用天然气的体积x是自变量，应缴纳费用y是所用天然气的体积x的函数.师：那么我们说的自变量有没有其他限制条件呢？生：①要使函数关系式有意义②要符合问题的实际意义例题讲解例1、如图，已知圆柱的高是4cm，底面半径是r(cm)，当圆柱的底面半径r由小变大时，圆柱的体积V(cm3)是r的函数(1)用含r 的代数式来表示圆柱的体积V，指出自变量r的取值范围.(2)当r=5,10时，V是多少(结果保留π)？4.按图示的运算程序，输入一个实数x，便可输出一个相应的实数y，写出y与x之间的关系式：________________.答案：y=5x+6这节课你有哪些收获？你认为自己的表现如何？1. 函数的概念：在某一个变化过程中的两个变量x 与y，对于x在某一变化范围内的每一个确定的值，y 都有一个唯一的值与它对应，那么称y 是x 的函数，把x 叫做自变量，把y 叫做因变量.2. 先变化的量是自变量，后变化的量是因变量.。

湘教版八下数学4.1.1《变量与函数》教学设计

湘教版八下数学4.1.1《变量与函数》教学设计一. 教材分析《变量与函数》是湘教版八下数学4.1.1的内容，这部分内容是学生在学习了代数和几何基础知识后，对函数概念的初次接触。

教材通过具体的实例，引导学生理解变量与函数的关系，培养学生的函数观念。

本节课的内容对于学生来说是一个新的概念，需要通过实例让学生感受和理解函数的实质。

二. 学情分析八年级的学生已经具备了一定的代数基础，对数学知识有一定的认识和理解。

但是，对于函数这一概念，他们可能是第一次接触，因此需要通过具体的实例和生活情境，让学生感受和理解函数的概念。

学生的学习兴趣和积极性需要通过教学设计来激发和保持。

三. 教学目标1.理解变量与函数的概念，能够识别生活中的函数关系。

2.能够用函数的 language 来描述和表示生活中的函数关系。

3.培养学生观察、分析和解决问题的能力。

四. 教学重难点1.函数的概念和实质。

2.如何通过实例让学生理解函数的概念。

五. 教学方法1.实例教学：通过具体的实例，让学生感受和理解函数的概念。

2.问题驱动：通过提出问题，引导学生思考和探索，从而加深对函数概念的理解。

3.合作学习：通过小组讨论和合作，培养学生的团队协作能力。

六. 教学准备1.教学PPT：制作相关的教学PPT，包括实例和问题。

2.教学素材：准备相关的教学素材，如图片、图表等。

3.教学工具：准备好黑板、粉笔等教学工具。

七. 教学过程1.导入（5分钟）通过一个简单的实例，如抛物线的运动，让学生观察和思考，引出函数的概念。

2.呈现（10分钟）通过PPT展示不同的实例，如温度与高度的关系，让学生观察和分析，引导学生理解函数的概念。

3.操练（10分钟）让学生通过小组合作，分析和学习教材中的实例，理解函数的概念。

4.巩固（10分钟）通过提问和讨论，巩固学生对函数概念的理解。

5.拓展（10分钟）让学生通过解决问题，运用和深化对函数概念的理解。

6.小结（5分钟）对本节课的内容进行小结，加深学生对函数概念的理解。

【湘教版】八年级数学下册教案：4.1.1变量与函数

第4章一次函数 4．1 函数和它的表示法4．1.1 变量与函数1．了解常量、变量的概念；(重点) 2．了解函数的概念；(重点)3．确定简单问题的函数关系．(难点)一、情境导入如图，水滴激起的波纹可以看成是一个不断向外扩展的圆，它的面积随着半径的变化而变化，随着半径的确定而确定．在上述例子中，每个变化过程中的两个变量：当其中一个变量变化时，另一个变量也随着发生变化；当一个变量确定时，另一个变量也随着确定．你能举出一些类似的实例吗？二、合作探究探究点一：常量与变量分析并指出下列关系中的变量与常量：(1)球的表面积S cm 2与球的半径R cm 的关系式是S ＝4πR 2；(2)以固定的速度v 0米/秒向上抛一个小球，小球的高度h 米与小球运动的时间t 秒之间的关系式是h ＝v 0t －4.9t 2；(3)一物体自高处自由落下，这个物体运动的距离h m 与它下落的时间t s 的关系式是h ＝12gt 2(其中g 取9.8m/s 2)； (4)已知橙子每千克的售价是1.8元，则购买数量w 千克与所付款x 元之间的关系式是x ＝1.8w .解析：在一个变化的过程中，数值发生变化的量称为变量，数值始终不变的量称为常量．解：(1)球的表面积S cm 2与球的半径R cm 的关系式是S ＝4πR 2，其中，常量是4π，变量是S ，R ；(2)以固定的速度v 0米/秒向上抛一个小球，小球的高度h 米与小球运动的时间t 秒之间的关系式是h ＝v 0t －4.9t 2，常量是v 0，4.9，变量是h ，t ；(3)一物体自高处自由落下，这个物体运动的距离h m 与它下落的时间t s 的关系式是h ＝12gt 2(其中g 取9.8m/s 2)，其中常量是12g ，变量是h ，t ；(4)已知橙子每千克的售价是1.8元，则购买数量w 千克与所付款x 元之间的关系式是x ＝1.8w ，常量是1.8，变量是x ，w .方法总结：常量与变量必须存在于同一个变化过程中，判断一个量是常量还是变量，需要看两个方面：一是它是否在一个变化过程中；二是看它在这个变化过程中的取值情况是否发生变化．探究点二：函数的定义下列说法中正确的是( )A ．变量x ，y 满足x ＋3y ＝1，则y 是x 的函数B ．变量x ，y 满足y ＝－x 2－1，则y 可以是x 的函数C ．变量x ，y 满足|y |＝x ，则y 可以是x 的函数D ．变量x ，y 满足y 2＝x ，则y 可以是x 的函数解析：A 中x ＋3y ＝1，y 可以看作x 的函数，因为y ＝1－x3；B 中y ＝－x 2－1，因为－x 2－1<0，等式无意义，即对于变量x 的任何一个取值，变量y 都没有唯一确定的值，故y 不是x 的函数；C 、D 中的|y |＝x 和y 2＝x ，对于变量x 的任意一个正数值，变量y 都有两个(不唯一)值与其对应，故y 不是x 的函数．故选A.方法总结：判断两个变量是否是函数关系，就看是否存在两个变量，并且在这两个变量中，确定好哪个是自变量，哪个是函数，然后再看看这两个变量是否是一一对应的关系．探究点三：确定自变量的取值范围【类型一】确定函数解析式中自变量的取值范围写出下列函数中自变量x 的取值范围．(1)y ＝2x －3； (2)y ＝31－x ；(3)y ＝4－x ； (4)y ＝x －1x －2.解析：当表达式的分母不含有自变量时，自变量取全体实数；当表达式的分母中含有自变量时，自变量取值要使分母不为零；当函数的表达式是偶次根式时，自变量的取值范围必须使被开方数不小于零．解：(1)全体实数；(2)分母1－x ≠0，即x ≠1； (3)被开方数4－x ≥0，即x ≤4；(4)由题意得⎩⎪⎨⎪⎧x －1≥0，x －2≠0，解得x ≥1且x ≠2.方法总结：本题考查了函数自变量的取值范围：有分母的要满足分母不能为0，有根号的要满足被开方数为非负数．【类型二】实际问题中自变量的取值范围水箱内原有水200升，7：30打开水龙头，以2升/分的速度放水，设经过t 分钟后，水箱内存水y 升．(1)求y 关于t 的函数关系式和自变量的取值范围；(2)7：55时，水箱内还有多少水？ (3)几点几分水箱内的水恰好放完？解析：(1)根据水箱内还有的水等于原有水减去放掉的水列式整理即可，再根据剩余水量不小于0列不等式求出t 的取值范围；(2)7：55时，t ＝55－30＝25，将t ＝25代入(1)中的关系式即可；(3)令y ＝0，求出t 的值即可．解：(1)∵水箱内存有的水＝原有水－放掉的水，∴y ＝200－2t .∵y ≥0，∴200－2t ≥0，解得t ≤100，∴0≤t ≤100，∴y 关于t 的函数关系式为y ＝200－2t (0≤t ≤100)；(2)∵7：55－7：30＝25(分钟)，∴当t＝25时，y ＝200－2t ＝200－50＝150(升)，∴7：55时，水箱内还有水150升；(3)当y ＝0时，200－2t ＝0，解得t ＝100，而100分钟＝1小时40分钟，7点30分＋1小时40分钟＝9点10分，故9点10分水箱内的水恰好放完．探究点四：简单问题的函数关系一个弹簧秤最大能称不超过10kg的物体，它的原长为10cm ，挂上重物后弹簧的长度y (cm)随所挂重物的质量x (kg)的变化而变化，每挂1kg 物体，弹簧伸长0.5cm ；(1)求弹簧的长度y (cm)与所挂重物质量x (kg)之间的函数表达式；(2)当挂5kg 重物时，求弹簧的长度．解析：根据弹簧的长度等于原长加上伸长的长度，列式即可；解：(1)y ＝10＋12x ，其中x 是自变量，y是自变量的函数；(2)将x ＝5代入y ＝10＋12x ，得y ＝10＋12×5＝12.5(cm)．答：当挂5kg 重物是，弹簧的长度为12.5厘米．方法总结：根据题意，找出等量关系，列出相应的函数表达式．求函数值时，将自变量代入函数表达式中，求出即可．探究点五：函数值根据如图所示程序计算函数值，若输入x 的值为52，则输出的函数值为( )A.32B.25C.425D.254解析：∵x ＝52时，在2≤x ≤4之间，∴将x ＝52代入函数y ＝1x ，得y ＝25.故选B.方法总结：根据所给的自变量的值，结合各个函数关系式所对应的自变量的取值范围，确定其对应的函数关系式，再代入计算．三、板书设计1．常量和变量的概念 2．函数的概念 3．函数关系式4．自变量的取值范围 5．函数值通过本课时的教学，学生对于常量、变量以及函数关系式掌握较好，但是对于有些实际问题中自变量的取值范围还存在一些困难．在以后的教学中要通过实例让学生不断加以强化，达到整体进步.。

湘教版数学八年级下册4.1.1 变量与函数教案与反思

第4章一次函数原创不容易，为有更多动力，请【关注、关注、关注】，谢谢！随风潜入夜，润物细无声。

出自杜甫的《春夜喜雨》4.1 函数和它的表示法4.1.1 变量与函数【知识与技能】借助简单实例，学生初步感知用常量与变量来刻画一些简单的数学问题，能指出具体问题中的常量、变量.初步理解存在一类变量可以用函数方式来刻画，能举出涉及两个变量的实例，并指出由哪一个变量确定另一个变量，这两个变量是否具有函数关系.初步理解对应的思想，体会函数概念的核心是两个变量之间的特殊对应关系，能判断两个变量间是否具有函数关系.【过程与方法】借助简单实例，引领学生参与变量的发现和函数概念的形成过程，体会从生活实例抽象出数学知识的方法，感知现实世界中变量之间联系的复杂性，数学研究从最简单的情形入手，化繁为简.【情感态度】从学生熟悉、感兴趣的实例引入课题，引领学生参与变量的发现和函数概念的形成过程，体验“发现、创造”数学知识的乐趣.学生初步感知实际生活蕴藏着丰富的数学知识，感知数学是有用、有趣的学科.【教学重点】借助简单实例，从两个变量间的特殊对应关系抽象出函数的概念.【教学难点】怎样理解“唯一对应”.一、创设情境，导入新课我们生活在一个运动的世界中，周围的事物都是运动的，例如：地球在宇宙中的运动这一问题，此时地球在宇宙中的位置随着时间的变化而变化，再例如，气温随着高度的升高而降低，年龄随着时间的增长而增长.这几个问题中都涉及两个量的关系，地球的位置与时间，温度与高度，年龄与时间，这一节课，我们就来研究类似的两个量之间的关系.【教学说明】从身边日常生活中发生的事例入手，用运动贴近生活实际，容易接受变化的观点说明两个量之间的关系，为下面的学习打下了伏笔.教师讲课前，先让学生完成“自主预习”.二、思考探究，获取新知问题常量、变量、函数思考教材第110页“动脑筋”【教学说明】让学生明确常量和变量的概念，进而弄清函数及与函数有关的概念，为后面的教学扫清障碍.说一说：教材第111页“说一说”【教学说明】通过训练的形式，加深对概念的理解，同时强调对于实际问题要附加自变量的取值范围，从而明确解决问题的方法和应该注意的方面.例：教材第111页“例1”【教学说明】在实际问题中，利用两个变之间的关系进一步巩固所学的函数及相关概念，使所学知识进一步加深，并能熟练运用.三、运用新知，深化理解1.汽车以70千米/时的速度匀速行驶，行驶路程为S千米，行驶时间为t 小时，从而S=70t，则下列判断中错误的是（）A.S是常量B.S是变量C.70是常量D.t是变量2.一个正方形的边长为3cm，它的各边边长减少xcm后，得到的新正方形的周长为ycm，y与x间的函数关系式是（）A.y=12-4xB.y=4x-12C.y=12-xD.以上都不对3.函数y=中自变量x的取值范围是 .4.一块形状为等腰三角形的铁皮，周长为10，底边长为y，腰长为x.（1）求y与x之间的关系式；（2）求自变量x的取值范围.【教学说明】让学生独立完成，以检查学生掌握情况，教师根据教学实际有针对性地查漏补缺，特别是学生出现错误较的地方作必要的强调，并加以强化.在完成上述题目后，让学生完成练习册中本课时的“课堂自主演练”部分.答案：1.A 2.A 3.x≥-3且x≠14.(1)y=10-2x; (2)∵10-2x>0,2x>10-2x,∴52<x<5.四、师生互动，课堂小结通过今天的学习，你已经掌握了哪些知识？还存在哪些疑问，与大家共同交流.【教学说明】师生共同回顾所学知识，加印象.同学之间通过合交流，取长补短，共同提高.1.布置作业：习题4.1中的第1、2题.2.完成练习册中本课时练习的“课后作业”部分.就学生掌握的情况看，对于常量、变量以及函数关系式掌握较好，但是对于有些实际问题中自变量的取值范围还存在一些困难.在以后的教学中要通过实例让学生不断加以强化，达到整体进步.【素材积累】1、冬天，一层薄薄的白雪，像巨大的轻软羊毛毯子，覆盖摘摘这广漠的荒原上，闪着寒冷的银光。

【精品】2017春八年级数学下册4.1.1变量与函数教案新版湘教版

第4章一次函数4．1 函数和它的表示法4．1.1 变量与函数1．了解常量、变量的概念；(重点)2．了解函数的概念；(重点)3．确定简单问题的函数关系．(难点)一、情境导入如图，水滴激起的波纹可以看成是一个不断向外扩展的圆，它的面积随着半径的变化而变化，随着半径的确定而确定．在上述例子中，每个变化过程中的两个变量：当其中一个变量变化时，另一个变量也随着发生变化；当一个变量确定时，另一个变量也随着确定．你能举出一些类似的实例吗？二、合作探究探究点一：常量与变量分析并指出下列关系中的变量与常量：(1)球的表面积S cm 2与球的半径R cm 的关系式是S ＝4πR 2；(2)以固定的速度v 0米/秒向上抛一个小球，小球的高度h 米与小球运动的时间t 秒之间的关系式是h ＝v 0t －4.9t 2；(3)一物体自高处自由落下，这个物体运动的距离h m 与它下落的时间t s 的关系式是h ＝12gt 2(其中g 取9.8m/s 2)； (4)已知橙子每千克的售价是1.8元，则购买数量w 千克与所付款x 元之间的关系式是x ＝1.8w .解析：在一个变化的过程中，数值发生变化的量称为变量，数值始终不变的量称为常量．解：(1)球的表面积S cm 2与球的半径R cm 的关系式是S ＝4πR 2，其中，常量是4π，变量是S ，R ；(2)以固定的速度v 0米/秒向上抛一个小球，小球的高度h 米与小球运动的时间t 秒之间的关系式是h ＝v 0t －4.9t 2，常量是v 0，4.9，变量是h ，t ；(3)一物体自高处自由落下，这个物体运动的距离h m 与它下落的时间t s 的关系式是h ＝12gt 2(其中g 取9.8m/s 2)，其中常量是12g ，变量是h ，t ； (4)已知橙子每千克的售价是1.8元，则购买数量w 千克与所付款x 元之间的关系式是x ＝1.8w ，常量是1.8，变量是x ，w .方法总结：常量与变量必须存在于同一个变化过程中，判断一个量是常量还是变量，需要看两个方面：一是它是否在一个变化过程中；二是看它在这个变化过程中的取值情况是否发生变化．变式训练：：见《学练优》本课时练习“课后巩固提升”第2题探究点二：函数的定义下列说法中正确的是( )A ．变量x ，y 满足x ＋3y ＝1，则y 是x 的函数B ．变量x ，y 满足y ＝－x 2－1，则y 可以是x 的函数C ．变量x ，y 满足|y |＝x ，则y 可以是x 的函数D ．变量x ，y 满足y 2＝x ，则y 可以是x 的函数解析：A 中x ＋3y ＝1，y 可以看作x 的函数，因为y ＝1－x 3；B 中y ＝－x 2－1，因为－x 2－1<0，等式无意义，即对于变量x 的任何一个取值，变量y 都没有唯一确定的值，故y不是x 的函数；C 、D 中的|y |＝x 和y 2＝x ，对于变量x 的任意一个正数值，变量y 都有两个(不唯一)值与其对应，故y 不是x 的函数．故选A.方法总结：判断两个变量是否是函数关系，就看是否存在两个变量，并且在这两个变量中，确定好哪个是自变量，哪个是函数，然后再看看这两个变量是否是一一对应的关系．变式训练：见《学练优》本课时练习“课后巩固提升”第1题探究点三：确定自变量的取值范围【类型一】确定函数解析式中自变量的取值范围写出下列函数中自变量x 的取值范围．(1)y ＝2x －3； (2)y ＝31－x； (3)y ＝4－x ； (4)y ＝x －1x －2. 解析：当表达式的分母不含有自变量时，自变量取全体实数；当表达式的分母中含有自变量时，自变量取值要使分母不为零；当函数的表达式是偶次根式时，自变量的取值范围必须使被开方数不小于零．解：(1)全体实数；(2)分母1－x ≠0，即x ≠1；(3)被开方数4－x ≥0，即x ≤4；(4)由题意得⎩⎪⎨⎪⎧x －1≥0，x －2≠0，解得x ≥1且x ≠2.方法总结：本题考查了函数自变量的取值范围：有分母的要满足分母不能为0，有根号的要满足被开方数为非负数．【类型二】实际问题中自变量的取值范围水箱内原有水200升，7：30打开水龙头，以2升/分的速度放水，设经过t 分钟后，水箱内存水y 升．(1)求y 关于t 的函数关系式和自变量的取值范围；(2)7：55时，水箱内还有多少水？(3)几点几分水箱内的水恰好放完？解析：(1)根据水箱内还有的水等于原有水减去放掉的水列式整理即可，再根据剩余水量不小于0列不等式求出t 的取值范围；(2)7：55时，t ＝55－30＝25，将t ＝25代入(1)中的关系式即可；(3)令y ＝0，求出t 的值即可．解：(1)∵水箱内存有的水＝原有水－放掉的水，∴y ＝200－2t .∵y ≥0，∴200－2t ≥0，解得t ≤100，∴0≤t ≤100，∴y 关于t 的函数关系式为y ＝200－2t (0≤t ≤100)；(2)∵7：55－7：30＝25(分钟)，∴当t ＝25时，y ＝200－2t ＝200－50＝150(升)，∴7：55时，水箱内还有水150升；(3)当y ＝0时，200－2t ＝0，解得t ＝100，而100分钟＝1小时40分钟，7点30分＋1小时40分钟＝9点10分，故9点10分水箱内的水恰好放完．探究点四：简单问题的函数关系一个弹簧秤最大能称不超过10kg 的物体，它的原长为10cm ，挂上重物后弹簧的长度y (cm)随所挂重物的质量x (kg)的变化而变化，每挂1kg 物体，弹簧伸长0.5cm ；(1)求弹簧的长度y (cm)与所挂重物质量x (kg)之间的函数表达式；(2)当挂5kg 重物时，求弹簧的长度．解析：根据弹簧的长度等于原长加上伸长的长度，列式即可；解：(1)y ＝10＋12x ，其中x 是自变量，y 是自变量的函数； (2)将x ＝5代入y ＝10＋12x ，得y ＝10＋12×5＝12.5(cm)．答：当挂5kg 重物是，弹簧的长度为12.5厘米．方法总结：根据题意，找出等量关系，列出相应的函数表达式．求函数值时，将自变量代入函数表达式中，求出即可．变式训练：见《学练优》本课时练习“课堂达标训练”第5题探究点五：函数值根据如图所示程序计算函数值，若输入x 的值为52，则输出的函数值为( )A.32B.25C.425D.254解析：∵x ＝52时，在2≤x ≤4之间，∴将x ＝52代入函数y ＝1x ，得y ＝25.故选B. 方法总结：根据所给的自变量的值，结合各个函数关系式所对应的自变量的取值范围，确定其对应的函数关系式，再代入计算．变式训练：见《学练优》本课时练习“课后巩固提升”第4题三、板书设计1．常量和变量的概念2．函数的概念3．函数关系式4．自变量的取值范围5．函数值通过本课时的教学，学生对于常量、变量以及函数关系式掌握较好，但是对于有些实际问题中自变量的取值范围还存在一些困难．在以后的教学中要通过实例让学生不断加以强化，达到整体进步。