极值法解尺寸链
尺寸链极值法和概率法的区别

尺寸链极值法和概率法的区别我跟你说啊,这尺寸链极值法和概率法,就像两条不同的路,都通往解决尺寸问题的目的地,可走法大不一样。
我认识一个老师傅,在工厂里搞机械加工的,对这俩方法那是门儿清。
我就跑去问他:“老师傅,您给我讲讲这尺寸链极值法和概率法有啥区别呗。
”老师傅放下手里的活儿,抬起头,眼睛里透着股子精明劲儿,说:“这极值法啊,就像个保守的老管家,啥都得算到最保险的程度。
比如说,有几个零件组装,它就把每个零件尺寸的最大和最小可能值都考虑进去,然后算出整个尺寸链的最大和最小尺寸。
这就好比你出门带东西,把能想到的所有东西都带上,不管用不用得着,就怕有个万一。
”我听了点点头,又问:“那概率法呢?”老师傅笑了笑说:“概率法就像是个会算计的精明商人。
它不那么死板,它考虑到零件尺寸在实际生产中是有一定概率分布的。
不是每个零件都会是最大或者最小尺寸,它根据这个概率来算尺寸链的尺寸范围。
就像你去市场买菜,你知道大概需要多少菜,但是不会买太多,因为你知道有些菜可能会多一点,有些会少一点,综合起来差不多就行。
”这时候,旁边一个年轻的学徒也凑过来了,他挠挠头说:“老师傅,那这两种方法哪种更好呢?”老师傅看了他一眼说:“这哪有绝对的好与坏啊。
极值法虽然保守,但是保险啊,在一些对尺寸精度要求极高,不容有失的地方,就得用它。
就像造航天零件,那可不能出一点差错。
而概率法呢,在大批量生产的时候就比较有优势,能节省材料,提高效率。
就像生产那些普通的小零件,成千上万的,用概率法能省不少事儿。
”我又好奇地问:“那在实际操作中,会不会搞混呢?”老师傅笑着说:“刚开始学的时候,是容易迷糊。
就像刚学走路的孩子,容易摔跤。
但是只要你多琢磨,多实践,就像走路走多了就稳当了,自然就分得清啥时候该走哪条路了。
”这尺寸链极值法和概率法的区别啊,就像两种不同的思维方式,各有各的用处,各有各的妙处。
在机械制造这个大舞台上,它们都扮演着重要的角色,就看你怎么根据实际情况去选择,选对了,这活儿就能干得漂亮,选错了,可能就会出岔子,你说是不是这个理儿?。
尺寸链

19. 采用极值算法,考虑最不利的极端情况。
例如,当尺寸链各增环均为最大极限尺寸A jmax (相应地为上偏差ES j),而各减环均为最小极限尺寸A kmin(相应地为下偏差EIk)时,封闭环有最大极限尺寸A0max(相应地为上偏差ES0)。
这种计算方法比较保守,但计算比较简单,因此应用较为广泛。
极值算法基本尺寸计算公式(5-12)式中A0 -- 封闭环的基本尺寸;A j -- 增环的基本尺寸;A k -- 减环的基本尺寸;m -- 增环数;n -- 尺寸链总环数。
式(5-12)表示封闭环的基本尺寸等于各增环基本尺寸之和减去各减环基本尺寸之和。
极值算法偏差计算公式式中ES0、EI0-- 封闭环的上、下偏差;ES j、EI j -- 增环的上、下偏差;ES k、EI k -- 减环的上、下偏差。
上面两式为直线尺寸链极值算法偏差计算公式,其含义是直线尺寸链封闭环的上(下)偏差等于各增环上(下)偏差之和减去各减环下(上)偏差之和。
极值算法公差计算公式式中T0L -- 封闭环公差(极值公差);T i-- 组成环的公差。
上式表明直线尺寸链封闭环的公差等于各组成环公差之和。
极值算法平均尺寸计算公式式中A0M、A jM、A kM分别表示封闭环、增环和减环的平均尺寸。
该式表明直线尺寸链封闭环的平均尺寸等于各增环平均尺寸之和减去各减环平均尺寸之和。
[例5-6] 图5-33a所示零件,设计尺寸为和。
因尺寸不便测量,改测尺寸x。
试用极值法确定尺寸x的数值和公差。
图5-33 测量尺寸链示例[解] 本例中,尺寸、和x构成一个直线尺寸链。
由于尺寸和x是直接测量得到的,因而是尺寸链的组成环。
尺寸是间接得到的,是封闭环。
由式(5-12),(5-13),(5-14)可求出:x=mm即为了保证设计尺寸合乎要求,应规定测量尺寸x落在上面计算的结果范围内。
假废品问题在实际生产中可能出现这样的情况:x测量值虽然超出了mm 的范围,但尺寸不一定超差。
完全互换法计算直线尺寸链

从封闭环的任意一端开始,查找对封闭环有直接影响的各个尺寸(组 成环),一直找到封闭环的另一端,将链中各尺寸依次画出(不要求严格的 比例),直到形成封闭的图形。 增、减环的判断可用回路法。
4. 分析计算尺寸链的任务有正计算(校核计算)、反计算和中间计算。
T1 = 0.052mm,T2 = T5 = 0.030mm,T3 = 0.062mm,T4 = 0.050mm (已知)
(5)校核封闭环公差
nБайду номын сангаас1
T0′ Ti = T1 + T2 + T3 + T4 + T5 i 1
= (0.052 + 0.030 +0.062 + 0.050 + 0.030 )mm=0.224mm <T0 = 0.25mm
A1
A4
A0 A5
A2=5
A1=30
A0 A4=3 A5=5
11-5齿轮部件尺寸链图
解 (1) 确定封闭环及其技术要求
由于间隙A0是装配后自然形成的,所以确定封闭环为要求的间隙A0。
此间隙在0.1~0.45 mm,即A0 =
0 0.45 0.10
mm。
(2) 寻找全部组成环,画尺寸链图,并判断增、减环。
(11-6)可得
aav
T0
n 1
ii
i 1
(11-9)
计算出后,按标准查取与之相近的公差等级系数,进而查表确定 各组成环的公差。
各组成环的极限偏差确定方法是:
先留一个组成环作为调整环,其余各组成环的极限偏差按“入体 原则”确定,即包容尺寸的基本偏差为H,被包容尺寸的基本偏差为 h,一般长度尺寸用js。进行公差设计计算时,最后必须进行校核, 以保证设计的正确性。
极值法计算尺寸链的方法

极值法计算尺寸链的方法极值法作为一种常见的计算尺寸链的方法,在机械设计和制造领域具有广泛的应用。
本文将详细介绍极值法的原理和具体计算步骤,帮助读者更好地理解和掌握这一方法。
一、极值法概述极值法是一种基于数学统计原理的计算尺寸链的方法。
它通过分析各尺寸之间的相互关系,确定尺寸链中各尺寸的变动范围,从而计算出合理的尺寸公差。
极值法适用于具有一定数量尺寸的封闭尺寸链,能够确保零件在装配过程中的互换性和功能性。
二、极值法的计算步骤1.确定尺寸链首先,根据零件的装配关系和功能要求,确定尺寸链中各尺寸的名称、数量和顺序。
尺寸链中的尺寸应包括基本尺寸、公差、形位公差等。
2.建立尺寸链模型根据尺寸链中各尺寸的相互关系,建立尺寸链模型。
通常,尺寸链模型可以表示为一个封闭的多边形,各尺寸分别对应多边形的各边。
3.确定尺寸变动范围分析尺寸链中各尺寸的公差,确定各尺寸的变动范围。
变动范围通常包括上极限尺寸、下极限尺寸和基本尺寸。
4.计算封闭尺寸链的公差根据极值法的原理,封闭尺寸链的公差等于尺寸链中各尺寸公差之和。
计算公式如下:封闭尺寸链公差= Σ(各尺寸公差)5.判断尺寸链的合理性比较封闭尺寸链的公差与设计要求的公差,判断尺寸链是否满足设计要求。
若不满足,需对尺寸链进行调整,直至满足设计要求。
6.确定尺寸链中各尺寸的公差根据封闭尺寸链的公差和各尺寸的变动范围,分配各尺寸的公差。
分配公差时,应遵循以下原则:- 尺寸链中各尺寸的公差应相等或相近;- 尺寸链中各尺寸的公差应满足功能要求和加工工艺要求;- 尺寸链中各尺寸的公差应便于测量和检验。
三、总结极值法计算尺寸链的方法具有以下优点:1.简便易行,适用于各种类型的尺寸链;2.能够确保零件在装配过程中的互换性和功能性;3.有助于提高零件的加工质量和降低生产成本。
通过以上介绍,相信读者已经对极值法计算尺寸链的方法有了更深入的了解。
尺寸链计算方法极值法

尺寸链计算方法极值法嘿,咱今儿就来聊聊这尺寸链计算方法里的极值法!这玩意儿可有意思啦,就像搭积木一样,一块一块地拼凑起来,最后得出个准确的结果。
你想啊,尺寸链就像是一条链子,把各个零件的尺寸都串起来啦。
而极值法呢,就是专门对付这条链子的法宝。
它可厉害着呢,能让我们清楚地知道每个尺寸的最大极限和最小极限是多少。
比如说,你有几个零件,它们的尺寸都有一定的范围。
那这时候极值法就登场啦!它能帮你算出,在最糟糕的情况下,这个尺寸链会变成啥样;在最理想的情况下,又会是啥样。
这就好比你要去一个地方,你得知道最坏的路况会让你多晚到,最好的路况又能让你多早到,心里才有底呀!那怎么用这极值法呢?其实也不难。
你就把每个零件的最大尺寸和最小尺寸都找出来,然后按照一定的规则加加减减。
就像做算术题一样,只不过这道算术题有点特别,它关系到整个产品的尺寸精度呢!举个例子吧,假设有个零件 A 的尺寸范围是 10 到 15,零件 B 的尺寸范围是 5 到 8。
那咱先用极值法算算最大尺寸是多少。
那就是把 A的最大尺寸 15 和 B 的最大尺寸 8 加起来,得到 23 呗。
那最小尺寸呢,就是把 A 的最小尺寸 10 和 B 的最小尺寸 5 加起来,等于 15 呀。
这样不就清楚啦!这还只是简单的例子呢,实际生产中尺寸链可复杂多啦。
但别怕呀,有了极值法这个好帮手,咱就能一步步地解开这个谜团。
你想想,如果没有这个方法,那我们生产出来的东西尺寸不就乱套啦?那可不行呀,那不得出大乱子嘛!而且哦,这极值法还能帮我们提前发现问题呢。
比如说,通过计算发现某个尺寸可能会超出范围,那我们就能提前想办法调整设计或者工艺,避免出现质量问题。
这多重要呀,就像医生提前发现病情,能早点治疗一样。
咱再想想,要是没有极值法,那我们做出来的东西可能有的大,有的小,那还怎么用呀?这不是浪费材料和时间嘛。
但有了它,一切都变得井井有条啦。
所以说呀,这尺寸链计算方法极值法,真的是咱工程人的好帮手呢!咱可得好好掌握它,让它为我们的生产和制造保驾护航呀!你说是不是呢?。
工艺尺寸链--尺寸链的计算方法

工艺尺寸链--尺寸链的计算方法内容摘要:尺寸链的计算方法,有如下两种:(1)极值解法:这种方法又叫极大极小值解法。
它是按误差综合后的两个最不利情况,即各增环皆为最大极限尺寸而各减环皆为最小极限尺寸的情况;以及各增环皆为最小极限尺寸而备减环皆为最大极限尺寸的情况,来计算封闭环极限尺寸的方法。
(2)概率曳ǎ河纸型臣品āSτ酶怕事墼理来进行尺寸键计算的一种方法。
...尺寸链的计算方法,有如下两种:(1)极值解法:这种方法又叫极大极小值解法。
它是按误差综合后的两个最不利情况,即各增环皆为最大极限尺寸而各减环皆为最小极限尺寸的情况;以及各增环皆为最小极限>寸而备减环皆为最大极限尺寸的情况,来计算封闭环极限尺寸的方法。
(2)概率解法:又叫统计法。
应用概率论原理来进行尺寸键计算的一种方法。
如算术平均、均方根偏差等。
求解尺寸链的情形:1.已知组成环,求封闭环 根据各组成环基本尺寸及公差(或偏差),来计算封闭环的基本尺寸及公差(或偏差),称为“尺寸链的正计算”。
这种计算主要用在审核图纸,验证设计的正确性。
如下例:例如齿轮减速箱装配后,要求轴承左端面与左端轴套之间的间隙为L∑。
此尺寸可通过事先检验零件的实际尺寸L1、L2、L3、L4、L5,就可预p知L∑的实际尺寸是否合格?2.已知封闭环,求组成环根据设计要求的封闭环基本尺寸及公差(或偏差),反过来计算各组成环基本尺寸及公差(或偏差),称为“尺寸链的反计算”。
如齿轮零件轴向尺寸加工,采用的工序如图,现需控制幅板厚度10土0.15,如何控制L1、L2gL3工序1;车外圆,车两端面后得L1=40工序2;车一端幅板,至深度L2.工序3:车另一端帽板,至深度L3。
并保证10士0.15。
由上述工序安排可知,幅板厚度10士0.15是按尺寸L1、L2、l3加工后间接得到的。
因此,为了保证10士15,势必对L1,L2,L3的尺寸偏差限制在一定范围内。
即已知封闭环L∑=10士0.15,求出各组成环L1,L2,L3尺寸的上下偏差。
尺寸链—计算方法

尺寸链—计算方法宝子们!今天咱们来唠唠尺寸链的计算方法呀。
尺寸链呢,就像是一个链条,环环相扣的。
那它的计算方法有两种主要类型哦。
一种是极值法。
这就像是走极端一样。
比如说,我们要确定一个装配体的总尺寸,极值法就是把各个组成环的最大极限尺寸或者最小极限尺寸加起来,得到封闭环的极限尺寸。
就像搭积木,把每块积木最大或者最小的情况考虑进去,这样就知道整个搭出来的东西最大或者最小能是啥样。
这种方法很简单直接,但是呢,它有点保守,因为在实际生产中,各个尺寸都取到极限值的情况比较少啦,不过在一些对精度要求不是超级高,但是要保证能装配上的情况,还是很好用的呢。
还有一种是概率法哦。
这个就比较有趣啦,它像是在玩概率游戏。
它考虑到各个组成环的尺寸是按照一定的概率分布的,不是总是取到极限值。
比如说,在生产很多零件的时候,每个零件的尺寸在一定范围内波动,概率法就是根据这些波动的概率来计算封闭环的尺寸。
这就好比是算一群小伙伴的平均身高,不是只看最高和最矮的,而是综合考虑大家的身高分布情况。
概率法算出的结果呢,通常会比极值法更接近实际情况,而且在大批量生产的时候,能更好地利用零件的加工精度,不会像极值法那样过于保守,能提高生产效率和降低成本呢。
在计算尺寸链的时候呀,我们得先搞清楚哪些是组成环,哪些是封闭环。
封闭环就是我们最终要确定尺寸的那个环,就像是链条的最后一环。
而组成环呢,就是那些影响封闭环尺寸的环啦。
宝子们可别搞混咯。
不管是用极值法还是概率法,目的都是为了在生产中能准确地控制尺寸,让产品能够顺利装配,而且还能保证质量呢。
这尺寸链的计算虽然有点小复杂,但是只要我们理解了它的原理,就像掌握了一个小魔法,能让我们在生产制造的世界里游刃有余哦。
希望宝子们都能对尺寸链的计算方法有个新的认识呀。
。
互换性与技术测量 8.2尺寸链的计算

=-0.08mm
壁厚: A0 50..01 mm 或 A0 4.9900.07 mm 0 08
极值法解反计算问题
已知条件: 封闭环所有信息、各组成环公称 尺寸; 待 求 量: 各组成环的公差、极限偏差; 公差值的分配方法: 相等公差值法; 相等公差等级法; 极限偏差的确定方法:————向体内原则。
m
j
4、极限偏差的计算公式
T0 T0 ES0 0 ,EI0 0 2 2 Ti Ti ESi i ,EIi i 2 2
三、分组互换法
先将组成环按极值法或概率法求出公差值, 扩大若干倍,使组成环加工容易和经济, 然后分组,根据大配大、小配小的原则, 按对应组进行装配。 分组数与公差扩大倍数相等。 但测量工作麻烦,用于大量生产中精度要 求高、环数少、形状简单的零件。
0 0.0025
mm
+ 0 φ28
轴
ห้องสมุดไป่ตู้
-0.0025
-0.0050
孔 -0.0075
0.0050 0.0075
mm
分组互换
将活塞销和销孔的公差放大四倍,即 活塞销:
0 0.010
+ 0 TS φ28
28
mm
活塞孔:
0.005 0.015
28
mm
轴
Th
-0.0025 -0.0050 -0.0075 -0.0100
A0min Azmin z 1
j n 1
A
jmax
极值法计算公式
3、极限偏差: ES0
ES - EI
z 1 n z j n 1 m z 1 j n 1
汽车尺寸工程尺寸链分析方法及流程

汽车尺寸工程尺寸链分析方法及流程摘要:汽车车身尺寸工程的目标是实现尺寸链的价值工程,这是保证车辆内外装饰美观和低噪音的基础。
为满足各细分市场客户需求,并兼顾考虑制造、维护成本,实现整车尺寸工程设计及匹配标准,已成为国内许多汽车企业的基本发展能力。
关键词:汽车尺寸工程;尺寸链;分析方法;流程一、尺寸链概述1、形式。
尺寸链包括二维、三维尺寸链。
其中,二维尺寸链:全部组成环位于一个或多个平行平面上的尺寸链。
在二维尺寸链中,若所有组成环与封闭环平行,则称为直线尺寸链(见图1);若组成环与封闭环不平行,则称为平面尺寸链(见图2)。
三维尺寸链:组成环位于几个不平行平面上的尺寸链,也称为空间尺寸链(见图3)。
图1 直线尺寸链图2 平面尺寸链图3 空间尺寸链2、表达方式。
尺寸链的表达方法约定:封闭环应向右或向上,或靠近该方向的空心箭头表示(当其不平行垂直或水平时);封闭链环的起始端称为起始面,末端称为到达面;绘制组成环时,从起始面开始,按顺序逐一列出影响因素,并顺序编号,在到达面上形成封闭。
二、尺寸链分析的计算方法1、极值法。
所有组成环公差之和为封闭环的公差。
特点:该方法计算的目标公差考虑了所有组成环的极值状态,简单可靠。
理论上讲,只要每个环的实际偏差在允许范围内,最终封闭环必定超差。
但这种方法也有明显的缺点:即不是所有的组成环都会同时出现极值,计算结果余量太大,也会给后期生产带来麻烦。
2、统计法。
将统计学与组成环的分布形式相结合,计算出封闭环公差。
其优点是根据组成环的实际分布概率进行统计,更接近实际情况。
然而,缺点是概率预测可能不准确,并且在某个封闭环中仍存在超差的可能性。
三、定位分析白车身由许多钣金件焊接、装配而成,每个零件冲压、检验、焊接和装配都需定位基准,以限制其自由度,磨具、检具、夹具各工序零件的基准应尽可能保持一致,以避免基准转换引起的误差。
定位分析应考虑几何角度、功能性和可行性;为保证定位的一致性及继承性,满足3-2-1或N-2-1的定位原则,尽量不要过度约束,所选形状应尽量简单。
01-教材参考内容——尺寸链原理及极值法解尺寸链
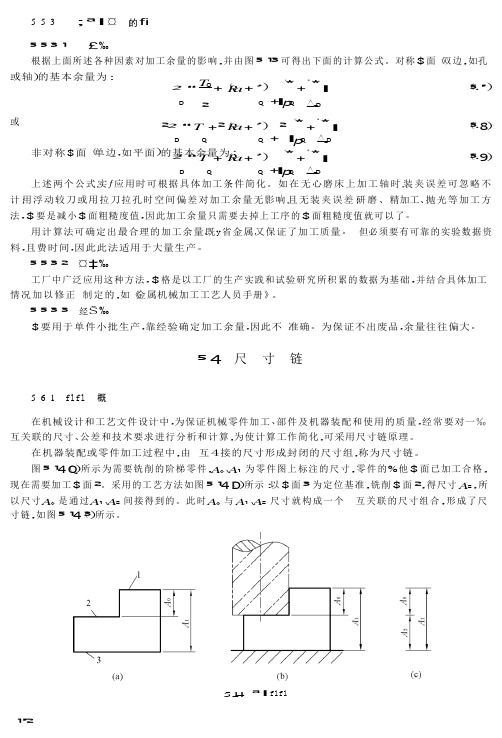
5·5·3 ;ªI ¤ fi⁵·⁵·³·¹ £‰ 根据上面所述各种因素对加工余量的影响,并由图⁵·¹³可得出下面的计算公式。
对称$面(双边,如孔 或轴)的基本余量为:² “ T Q + (R a +’ ) *¯ + ¯*l(⁵·’) D ²Q +l p Q 或△eD ²² “ T +²(R a +’ ) ² *¯ + ¯*l(⁵·8) D Q Q + l pQ △e D 非对称$面(单边,如平面)的基本余量为: ² “ T + (R a +’ ) *¯ + ¯*l(⁵·9) D Q Q +l pQ △e D 上述两个公式,实ƒ应用时可根据具体加工条件简化。
如在无心磨床上加工轴时,装夹误差可忽略不计;用浮动较刀或用拉刀拉孔时空间偏差对加工余量无影响,且无装夹误差;研磨、 精加工、抛光等加工方法,$要是减小$面粗糙度值,因此加工余量只需要去掉上工序的$面粗糙度值就可以了。
用计算法可确定出最合理的加工余量,既y 省金属,又保证了加工质量。
必须要有可靠的实验数据资料,且费时间,因此此法适用于大量生产。
⁵·⁵·³·² ¤‡‰工厂中广泛应用这种方法,$格是以工厂的生产实践和试验研究所积累的数据为基础,并结合具体加工 情况加以修正 制定的,如《金属机械加工工艺人员手册》。
⁵·⁵·³·³Š‰$要用于单件小批生产,靠经验确定加工余量,因此不 准确。
为保证不出废品,余量往往偏大。
⁵·4 尺 寸 链5·6·1 flfl在机械设计和工艺文件设计中,为保证机械零件加工、部件及机器装配和使用的质量,经常要对一‰ 互关联的尺寸、公差和技术要求进行分析和计算,为使计算工作简化,可采用尺寸链原理。
公差配合与检测技术课件-尺寸链极值计算

尺寸链的极值解法
3、封闭环的下极限尺寸 封闭环的下极限尺寸等于所有增环的下极限尺寸之和减去减环的上极限尺寸之和,即
式中
A0min——封闭环的下极限尺寸; Azmin——增环的下极限尺寸; Ajmax——减环的上极限尺寸。
尺寸链的极值解法
4、封闭环的上极限偏差 封闭环的上极限偏差等于所有增环的上极限偏差之和减去所有减环的下极限偏差之和,即
(2)查明全部组成环、画出尺寸链图。确定封闭环后,由该封闭环尺寸循一个方向按照尺寸的相互联系依 次找出全部组成环,并把它们与封闭环一起按尺寸联系的相互顺序首尾相接,即得到尺寸链图。
(3)判断组成环中的增、减环,并用箭头标出。 (4)利用基本计算公式或竖式求解。在计算中同一问题可用不同公式求解,而不影响解的正确性。需要指 出的是,当出现已知的若干组成环公差之和大于封闭环公差的情况时,这时需要适当缩小某些组成环的公差。一 般工艺人员无权放大封闭环公差,因为这样会降低产品的技术要求。 (5)解尺寸链得到的中间工序尺寸公差一般按“入体”原则标注,毛坯尺寸根据查表结果按要求双向标注, 最后一道工序尺寸和公差按照零件图要求标注。
尺寸链的极值解法
尺寸链极值解法---竖式法
用极值法求解尺寸链时,可以利用上述基本公式计算,也可以用竖式法来计算。
竖式法计算规则: 见下表,在双横线以上将增环的公称尺寸、上极限偏差和下极限偏差自左至右依次排列;减环在 排列时其公称尺寸前要加负号,且上、下极限偏差位置对调并变正负号。 将增减环的公称尺寸、上极限偏差、下极限偏差分别相加,其代数和列于双横线以下,即为封闭 环的公称尺寸和上、下极限偏差。
尺寸链的极值解法
6、封闭环的公差 封闭环的公差等于所有组成环的公差之和,即
式中 T0——封闭环的公差; Tj——组成环的公差。
尺寸链极值法

尺寸链极值法(也称为极大极小值解法)是根据尺寸链的各个环的最大值和最小值来确定尺寸链的最大值和最小值的一种方法。
具体步骤如下:
1. 确定尺寸链的类型,分为工艺尺寸链、零件尺寸链和装配尺寸链。
2. 确定尺寸链的基本尺寸,即各个环的理想值。
3. 确定尺寸链的极限偏差,即各个环的最大偏差和最小偏差。
4. 计算尺寸链的极限值,即最大值和最小值。
一般有以下公式:尺寸链最大值= 基本尺寸+ 所有增环的最大偏差- 所有减环的最小偏差;尺寸链最小值= 基本尺寸+ 所有增环的最小偏差- 所有减环的最大偏差。
5. 根据设计要求,确定尺寸链的公差,即允许的误差范围。
一般有以下公式:尺寸链公差= 尺寸链最大值- 尺寸链最小值;尺寸链中间偏差= (尺寸链最大值+ 尺寸链最小值) / 2 - 基本尺寸;尺寸链上偏差= 尺寸链最大值- 基本尺寸;尺寸链下偏差= 尺寸链最小值- 基本尺寸。
6. 根据公差分配原则,合理分配各个环的公差,使得总公差不超过设计要求。
这种方法适用于单件或小批量生产,或者对精度要求较高的情
况。
尺寸链计算方法

3).按各环尺寸的几何特征分
(1)长度尺寸链 示。 (2)角度尺寸链 如图12—1,图12—2所 如图12—3所示。
4、尺寸链的建立
1).确定封闭环
装配尺寸链的封闭环是在装配之后形成的,往往是 机器上有装配精度要求的尺寸,如保证机器可靠工作的 相对位置尺寸或保证零件相对运动的间隙等。 零件尺寸链的封闭环应为公差等级要求最低的环, 如图12-1b中尺寸B0是不标注的。 工艺尺寸链的封闭环是在加工中自然形成的,一般 为被加工零件要求达到的设计尺寸或工艺过程中需要的 尺寸。 一个尺寸链中只有一个封闭环。
6、解算尺寸链的方法
1. 完全互换法(极值法) 完全互换法是尺寸链计算中最基本的方法。 2. 不完全互换法(概率法) 采用概率法,不是在全部产品中,而是在绝大多 数产品中,装配时不需挑选或修配,就能满足封闭环 的公差要求,即保证大多数互换。 与完全互换法相比,在封闭环公差相等的情况下, 不完全互换法可使用组成环的公差扩大,从而获得良 好的技术经济效益,也比较科学合理,常用在大批量 生产的情况。 3.其他方法
封闭环的重要性: (1) 体现在尺寸链计算中,若封闭环判断错误,则全部分 析计算之结论,也必然是错误的。 (2) 封闭尺寸是通过其他尺寸要间接保证的尺寸。通常是 产品技术规范或零件工艺要求决定的尺寸。 在装配尺寸链中,封闭环往往代表装配中精度要求的尺 寸;而在零件中往往是精度要求最低的尺寸,通常在零件图 中不予标注。
3.画尺寸链线图 为清楚地表达尺 寸链的组成,通常不 需要画出零件或部件 的具体结构,只需将 尺寸链中各尺寸依次 画出,形成封闭的图 形即可,这样的图形 称为尺寸链线图,如 图12-4b所示。
5、解算尺寸链的任务
(1)正计算 已知各组成环的极限尺寸,求封 闭环的尺寸。 (2)反计算 已知封闭环的极限尺寸和各组成 环的基本尺寸,求各组成环的极限偏差。 (3)中间计算 已知封闭环和部分组成环的极 限尺寸,求某一组成环的极限尺寸。
极值法求解尺寸链时,封闭环的公差

极值法求解尺寸链时,封闭环的公差在极值法求解尺寸链时,封闭环的公差是确定产品尺寸的重要参数之一。
公差是指产品允许的最大尺寸与最小尺寸之间的差值,用于规定产品的制造公差和装配公差。
下面,我将详细介绍尺寸链的极值法以及封闭环公差的相关内容。
1. 尺寸链的极值法尺寸链是产品设计中重要的工具,用于确定产品各个零部件的尺寸以及相互关系。
极值法是一种常用的尺寸链分析方法,通过确定产品的最大和最小尺寸,以及各个尺寸之间的依赖关系来实现产品的设计和制造。
首先,确定产品的最大尺寸和最小尺寸。
最大尺寸是指产品尺寸在各项最大公差情况下的累积误差,而最小尺寸是指产品尺寸在各项最小公差情况下的累积误差。
然后,确定各个尺寸之间的依赖关系,即尺寸链。
尺寸链是指产品各个尺寸之间的关系,并通过逐级递推的方式来确定产品各个尺寸的公差。
在尺寸链中,不同的尺寸之间存在不同的依赖关系,包括相互独立、累积、碰撞、嵌套等关系。
通过分析这些关系,可以确定产品各个尺寸之间的公差分配。
最后,根据产品的最大尺寸、最小尺寸和尺寸链来确定各个尺寸的公差。
公差是为了满足产品功能要求和制造要求而设定的,不同的尺寸具有不同的公差要求。
通过合理分配公差,可以确保产品在设计和制造过程中的可靠性和稳定性。
2. 封闭环的公差在尺寸链分析中,封闭环是指产品中的同一特征或同一关系在构成环状结构时,允许的最大公差和最小公差之间的差值。
封闭环的公差是通过分析产品的功能要求和制造要求来确定的。
封闭环的公差可以通过以下几个步骤来确定:(1)确定功能要求:首先,确定产品的功能要求,即产品在正常工作条件下需要满足的要求。
功能要求决定了产品的尺寸和公差的范围。
(2)确定制造要求:其次,根据产品的制造工艺和工艺要求,确定产品的制造要求。
制造要求包括材料要求、加工要求、装配要求等。
制造要求决定了产品的制造公差和装配公差的范围。
(3)确定环状结构:然后,确定封闭环的结构。
在产品中可能存在多个封闭环,需要逐个分析确定。
工艺尺寸链计算的基本公式
工艺尺寸链计算的基本公式
收藏此信息打印该信息添加:用户投稿来源:未知
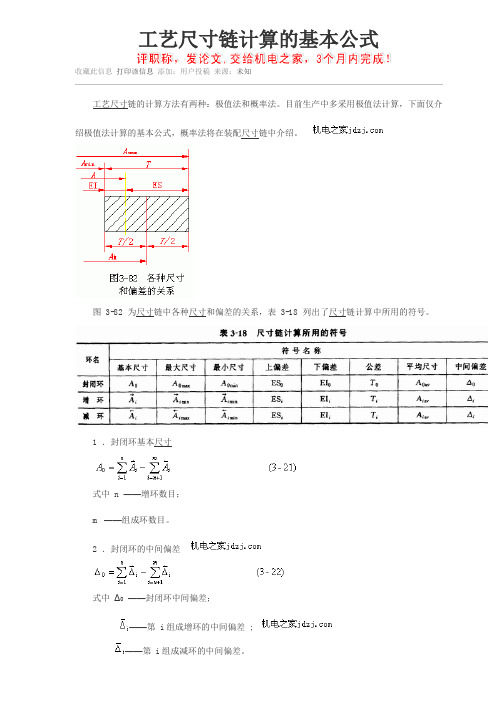
工艺尺寸链的计算方法有两种:极值法和概率法。
目前生产中多采用极值法计算,下面仅介绍极值法计算的基本公式,概率法将在装配尺寸链中介绍。
图3-82 为尺寸链中各种尺寸和偏差的关系,表3-18 列出了尺寸链计算中所用的符号。
1 .封闭环基本尺寸
式中n ——增环数目;
m ——组成环数目。
2 .封闭环的中间偏差
式中Δ0——封闭环中间偏差;
——第i 组成增环的中间偏差;
——第i 组成减环的中间偏差。
中间偏差是指上偏差与下偏差的平均值:
3 .封闭环公差
4 .封闭环极限偏差
上偏差
下偏差
5 .封闭环极限尺寸
最大极限尺寸A 0max=A 0+ES 0 (3-27 )
最小极限尺寸A 0min=A 0+EI 0(3-28 )
6 .组成环平均公差
7 .组成环极限偏差
上偏差
下偏差
8 .组成环极限尺寸
最大极限尺寸A imax=A i+ES I (3-32 )
最小极限尺寸A imin=A i+EI I (3-33 )。
极值法求解尺寸链时,封闭环的公差

极值法求解尺寸链时,封闭环的公差极值法是一种常用的尺寸链设计方法,在进行尺寸链设计时,需要确定每个零部件的公差值,以确保最终装配产品的功能和性能。
当存在封闭环的情况下,公差的设计和计算更为复杂,需要考虑到环中的所有零部件的公差对封闭环的影响。
下面是一些关于封闭环公差设计的相关参考内容。
1. 公差堆积计算:在封闭环中,每个零部件的公差都会对整个环的尺寸产生影响,公差堆积计算可以通过计算每个零部件的公差之和,并与环的尺寸要求进行比较,以确定是否满足设计要求。
2. 公差配合:在封闭环的设计中,需要考虑每个零部件之间的公差配合,即零部件之间的配合公差应该能够确保装配的可行性和性能要求。
可参考相关标准,如GB/T 1800.1《机械总则第1部分:基本概念、公差评定、公差基本尺寸》以了解公差配合的原则和计算方法。
3. 公差设计原则:封闭环的公差设计需要遵循一些基本原则,例如零部件公差的合理分配、公差控制规律的确定,以及考虑装配过程中的松紧度要求等。
可以参考《机械设计手册》等相关书籍,了解公差设计的原则和方法。
4. 公差设计软件:在进行封闭环的公差设计时,可以使用专门的计算软件,例如GD&T软件(Geometric Dimensioning and Tolerancing,几何公差工程)等,以帮助进行公差堆积计算、公差配合分析等工作。
5. 工程经验和案例分析:通过分析和研究已完成的封闭环产品的设计案例,可以了解不同封闭环设计中的公差分析方法和应用经验。
可以参考相关技术论文、工程实例和设计手册等资料。
总而言之,在封闭环的公差设计中,需要综合考虑每个零部件的公差和配合关系,采用合适的公差计算方法和原则,并结合工程经验和使用专门软件辅助分析,以确保封闭环的装配性能和精度要求得到满足。
极值法求解尺寸链时,封闭环的公差

极值法求解尺寸链时,封闭环的公差极值法是一种常用于工程设计中的尺寸链设计方法,它可以通过数学模型的极限分析来确定设计尺寸的公差范围,以满足产品的功能要求。
在设计尺寸链时,封闭环通常是需要考虑的重要因素之一。
下面我们将介绍极值法求解尺寸链时封闭环的公差,这些内容将帮助设计者了解如何确定尺寸链的公差范围。
首先,尺寸链是由多个相互联系的尺寸组成的,而封闭环是指尺寸链中形成闭合回路的部分。
在设计封闭环时,设计者需要考虑环的尺寸、公差以及环与其他尺寸之间的相互关系。
公差是衡量尺寸链中各个尺寸之间变动范围的一个重要指标,它决定了产品的可用性、互换性和可靠性。
在使用极值法求解封闭环的公差时,可以按照以下步骤进行:1. 确定封闭环的功能要求:首先,设计者需要明确封闭环需要满足的功能要求,例如是否需要保持严格的位置精度、满足某一特定的连接要求等。
这些功能要求将对尺寸链的设计和公差范围的确定有重要影响。
2. 建立尺寸链模型:根据封闭环的形状、尺寸及其它相关要求,建立尺寸链的几何模型。
这可以通过CAD软件或手工绘图等方式进行。
3. 确定环中的关键尺寸:在尺寸链模型中,确定封闭环中的关键尺寸,这些尺寸将直接影响环的性能和功能。
关键尺寸的选择应基于设计要求和关键尺寸之间的相互关系。
4. 确定尺寸链公差:基于关键尺寸和功能要求,使用极值法确定尺寸链的公差范围。
极值法通常包括最大材料条件和最小材料条件两种情况,分别对应尺寸链的上限和下限。
通过假设每个尺寸链中的尺寸都达到其最大材料限制或最小材料限制,并分析它们在极值情况下所导致的最大和最小尺寸。
5. 公差分配:根据封闭环的功能和关键尺寸之间的相互关系,将确定的公差分配给封闭环中各个尺寸。
公差分配的原则是尽量使得封闭环满足功能要求,尤其是与其他尺寸之间的相互关系。
需要注意的是,极值法求解封闭环的公差是一个精细的过程,需要考虑多个因素并进行深入分析。
在应用过程中,设计者应根据具体情况进行调整和优化,以达到理想的设计效果。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
装配实例1
A1尾座顶尖轴线至底板高度
A2尾座底板厚度
A3主轴轴线至床身的高度 A0尾座顶尖轴线与主轴轴线的同轴误差
装配实例2
A0
A2
A1
第一节 尺寸链的基本概念
机器装配或零件加工过程中,由相 互连接的尺寸构成的封闭尺寸组, 称为尺寸链。
尺寸链的研究意义
尺寸链研究现状(国内)[1]
尺寸链的自动生成: 浙江大学:装配图尺寸数据库 华中理工大学:配合零件链、零件配合图、零 件邻接矩阵、零件邻接表 哈尔滨工业大学:面向对象的装配尺寸链的自 动生成算法;对面向装配的尺寸链自动生成算 法
第十章 尺寸链(Dimensional Chain) 计算方法
基本要求
重点内容
课程安排
1.尺寸链的基本概念 组成、分类、建立与 分析、计算
1.建立与分析及基本 计算
1次课 2学时
加工实例
先以A面定位加 工C面,得尺寸 A1; 然后再以A面定 位加工台阶面B, 得尺寸A2; 最后形成B面与 C面间尺寸A0; A1、A2和A0这三 个尺寸构成了 一个封闭尺寸 组
零件尺寸链
装配尺寸链
工艺尺寸链
尺寸链的分类——按空间位置
直线尺寸链
平面尺寸链
尺寸链的分类——按空间位置
空间尺寸链
尺寸链的分类——按几何特征
长度尺寸链
角度尺寸链
尺寸链的代号
Leabharlann 长度尺寸链:拉丁字母,如A、B 角度尺寸链:希腊字母,如 , 封闭环加下角标0,如A0 组成环加下角标序数1,2,3,...,如 A1,A2
尺寸链研究现状(国外)[1]
尺寸链的自动生成: Lee K 和 Gossard DC:树结构来描述,将装配 图分成若干个部件,部件分成零件,。。。, 形成尺寸链。 Tulga M.Ozsoy和Nanxin Wang:在此基础上, 通过搜寻装配图,从配合链中产生配合图,当 定义封闭环时,从配合图中得到尺寸链。
A1 、A3为增环,A2为减环
二、尺寸链的计算
计算类型 计算方法 完全互换法(极值法)解尺寸链计算公式 举例
尺寸链计算类型
正计算 反计算 中间计算
计算类型举例——正计算
如图所示的结构,已知各零件的尺寸: 0 0 A1=30 0.13 mm,A2=A5=5 0.075 mm, 0.18 0 A3=43 mm , A =3 mm,试求A0的基 4 0.02 0.04 本尺寸和极限偏差。
计算类型举例——反计算
已知A0的公差值为1-1.75。组成环的基本尺寸分别为A1=101 A2=50 A3= A5=5 A4=140,求各组成环的公差值。
计算类型举例——中间计算
计算类型
正计算 —— 校核计算:验算所设计的产品能否 满足性能要求及零件加工后能否满足零件的技术 要求。 中间计算——工艺尺寸计算:设计计算与工艺计 算,也可用于验算。 反计算 —— 公差分配:产品设计、加工和装配 工艺计算等方面。
计算方法
极值法:根据各组成环的极限尺寸来 确定封闭环的极限尺寸,零部件可实 现完全互换。极值法是尺寸链计算中 最基本的方法。
其他计算方法
统计法[1] 分组互换法[1、2] 修配法[1、3] 调整法[1、4] 图论法[5] 筛选法[5]
[1]邢纪英、葛宰林、孔繁胜。互换性与测量技术基础。内蒙古大学出版社,1995。 [2]宋孟然。尺寸链在机器装配中的应用。机械管理开发,2004年 05期。 [3]沈剑英,张程徽,褚莲娣。修配法尺寸链的分析及其新解法。机电工程,2004年 02期。 [4]刘浏。“分组法”的思路解固定调整法装配尺寸链。机械工程师,2002年 08期。 [5]杨宗德。尺寸链研究。机械研究与应用,2002年 02期。
尺寸链研究现状(国外)[1]
辅助公差图表的生成
Ahluwalia和Karolin:计算机辅助图表路线 Xiaoying和Davies:复杂的数学模型合成矩阵树 Ngoi 和 Chua:关系矩阵来表达加工顺序,路径跟踪 技术 Ngoi和Fang:枝状模型,列出过程环
[1]柴国柱。面向装配的尺寸链及其链节模型的自动生成。哈尔滨工业大学硕士 论文,2000。
二、尺寸链的基本术语及其分类
构成尺寸链的各个尺寸称为环(link)。 尺寸链的环分为: 封闭环(closing link) 组成环(component link) 增环(increasing link) 减环(decreasing link)
封闭环和组成环的定义
封闭环: 加工或装配 过程中最后工序完成 后形成的尺寸。如图 中的A0。 组成环: 尺寸链中除 封闭环以外的其余环。 如图中的A1和A2
查找组成环
一个尺寸链的组成环环数应尽量少。 查找装配尺寸链的组成环时,先从封闭环 的任意一端开始,找相邻零件的尺寸, … , 最后回到封闭环的另一端,从而形成封闭 的尺寸组。 尺寸链图中,常用箭头法来确定增环和减 环。
判断增减环
A3 A2 A0 A1
B2、B4、B5为增环,B1、B3为减环
确定增环和减环
A0封闭环,A2z增环,A1j减环
确定增环和减环
B0封闭环,B3z增环,B1j、B2j减环
确定增环和减环
箭头方法确定 凡是箭头方向与封闭环同向变动的组成环,减 环 与封闭环反向变动的组成环,增环
确定增环和减环
A0封闭环,A1z、A2z增环、 A3j减环
三、尺寸链的分类——按应用范围
第二节直线尺寸链计算方法(完全互换法)
一、尺寸链的分析与建立 确定封闭环 查找组成环 判断增减环 二、尺寸链的计算 计算类型 计算方法 极限法解尺寸链计算公式 举例
一、尺寸链的分析与建立
确定封闭环 查找组成环 判断增减环
确定封闭环
在装配尺寸链中,封闭环就是产品上有装配 精度要求的尺寸。 零件尺寸链中,封闭环应为公差等级要求最 低的环。 工艺尺寸链中,封闭环是在加工中最后自然 形成的环。加工顺序不同,封闭环也不同。 所以工艺尺寸链的封闭环必须在加工顺序确 定之后才能判断。 一个尺寸链中只有一个封闭环。
增环和减环的定义
组成环根据它们对封闭环影响的不同: 增环:当该组成环尺寸增大(或减小), 而其它组成环不变时,封闭环也随之增大 (或减小)。 减环:当该组成环尺寸增大(或减小), 而其他组成环不变时,封闭环的尺寸却随 之减小(或增大)。
确定增环和减环
A0封闭环,
A1、A4、A5减环, A2、A3、A6增环
