多元回归分析案例
多元线性回归分析范例

多元线性回归分析范例多元线性回归是一种用于预测因变量和多个自变量之间关系的统计分析方法。
它假设因变量与自变量之间存在线性关系,并通过拟合一个多元线性模型来估计因变量的值。
在本文中,我们将使用一个实际的数据集来进行多元线性回归分析的范例。
数据集介绍:我们选取的数据集是一份汽车销售数据,包括了汽车的价格(因变量)和多个与汽车相关的特征(自变量),如车龄、行驶里程、汽车品牌等。
我们的目标是通过这些特征来预测汽车的价格。
数据集包括了100个样本。
数据集的构成如下:车龄(年),行驶里程(万公里),品牌,价格(万元)----------------------------------------5,10,A,153,5,B,207,12,C,10...,...,...,...建立多元线性回归模型:我们首先需要将数据集划分为自变量矩阵X和因变量向量y。
其中,自变量矩阵X包括了车龄、行驶里程和品牌等特征,因变量向量y包括了价格。
在Python中,我们可以使用NumPy和Pandas库来处理和分析数据。
我们可以使用Pandas的DataFrame来存储数据集,并使用NumPy的polyfit函数来拟合多元线性模型。
首先,我们导入所需的库并读取数据集:```pythonimport pandas as pdimport numpy as np#读取数据集data = pd.read_csv('car_sales.csv')```然后,我们将数据集划分为自变量矩阵X和因变量向量y:```python#划分自变量矩阵X和因变量向量yX = data[['车龄', '行驶里程', '品牌']]y = data['价格']```接下来,我们使用polyfit函数来拟合多元线性模型。
我们将自变量矩阵X和因变量向量y作为输入,并指定多项式的次数(线性模型的次数为1):```python#拟合多元线性模型coefficients = np.polyfit(X, y, deg=1)```最后,我们可以使用拟合得到的模型参数来预测新的样本。
多元线性回归模型案例

多元线性回归模型案例多元线性回归是统计学中常用的一种回归分析方法,它可以用来研究多个自变量与因变量之间的关系。
在实际应用中,多元线性回归模型可以帮助我们理解不同自变量对因变量的影响程度,从而进行预测和决策。
下面,我们将通过一个实际案例来介绍多元线性回归模型的应用。
案例背景:某电商公司希望了解其产品销售额与广告投入、季节因素和竞争对手销售额之间的关系,以便更好地制定营销策略和预测销售额。
数据收集:为了分析这一问题,我们收集了一段时间内的产品销售额、广告投入、季节因素和竞争对手销售额的数据。
这些数据将作为我们多元线性回归模型的输入变量。
模型建立:我们将建立一个多元线性回归模型,以产品销售额作为因变量,广告投入、季节因素和竞争对手销售额作为自变量。
通过对数据进行拟合和参数估计,我们可以得到一个多元线性回归方程,从而揭示不同自变量对产品销售额的影响。
模型分析:通过对模型的分析,我们可以得出以下结论:1. 广告投入对产品销售额有显著影响,广告投入越大,产品销售额越高。
2. 季节因素也对产品销售额有一定影响,不同季节的销售额存在差异。
3. 竞争对手销售额对产品销售额也有一定影响,竞争对手销售额越大,产品销售额越低。
模型预测:基于建立的多元线性回归模型,我们可以进行产品销售额的预测。
通过输入不同的广告投入、季节因素和竞争对手销售额,我们可以预测出相应的产品销售额,从而为公司的营销决策提供参考。
结论:通过以上分析,我们可以得出多元线性回归模型在分析产品销售额与广告投入、季节因素和竞争对手销售额之间关系时的应用。
这种模型不仅可以帮助我们理解不同因素对产品销售额的影响,还可以进行销售额的预测,为公司的决策提供支持。
总结:多元线性回归模型在实际应用中具有重要意义,它可以帮助我们理解复杂的变量关系,并进行有效的预测和决策。
在使用多元线性回归模型时,我们需要注意数据的选择和模型的建立,以确保模型的准确性和可靠性。
通过以上案例,我们对多元线性回归模型的应用有了更深入的理解,希望这对您有所帮助。
多元回归分析案例

多元回归分析案例下面以一个实际案例来说明多元回归分析的应用。
假设我们是一家电商公司,希望了解哪些因素会影响网站用户购买商品的金额。
为了回答这个问题,我们收集了以下数据:每位用户购买的商品金额(因变量),用户的年龄、性别和收入水平(自变量)。
首先,我们需要构建一个多元回归模型。
由于因变量是连续型变量,我们可以选择使用线性回归模型。
模型的形式可以表示为:购买金额=β0+β1×年龄+β2×性别+β3×收入水平+ε其中,β0是截距,β1、β2和β3是自变量的系数,ε是误差项。
接下来,我们需要对数据进行预处理。
首先,将性别变量转换为虚拟变量,比如用0表示男性,1表示女性。
然后,我们可以使用逐步回归方法,逐步选择自变量,以确定哪些变量对因变量的解释最显著。
在实际操作中,我们可以使用统计软件,比如SPSS或R来进行多元回归分析。
下面是一个用R进行多元回归分析的示例代码:```R#导入数据data <- read.csv("data.csv")#转换性别变量为虚拟变量data$gender <- as.factor(data$gender)#构建多元回归模型model <- lm(购买金额 ~ 年龄 + 性别 + 收入水平, data=data)#执行逐步回归step_model <- step(model)#显示结果summary(step_model)```通过运行这段代码,我们可以得到每个自变量的系数估计值、显著性水平、拟合优度等统计结果。
这些结果可以帮助我们理解各个自变量对于购买金额的影响程度以及它们之间的相对重要性。
在实际应用中,多元回归分析可以帮助我们识别哪些因素对于一些特定的因变量具有显著影响。
通过控制其他自变量,我们可以解释每个自变量对因变量的独立贡献,并用于预测因变量的值。
总之,多元回归分析是一种强大的统计工具,可以应用于各个领域,帮助我们理解和预测自变量对因变量的影响。
多元线性回归分析案例

多元线性回归分析案例1. 引言多元线性回归分析是一种用于探究多个自变量与一个连续型因变量之间关系的统计分析方法。
本文将以一个虚构的案例来介绍多元线性回归分析的应用。
2. 背景假设我们是一家电子产品制造公司,我们想了解哪些因素会对产品销售额产生影响。
为了解决这个问题,我们收集了一些数据,包括产品的价格、广告费用、竞争对手的产品价格和销售额。
3. 数据收集我们采集了100个不同产品的数据,其中包括以下变量:- 产品价格(自变量1)- 广告费用(自变量2)- 竞争对手的产品价格(自变量3)- 销售额(因变量)4. 数据分析为了进行多元线性回归分析,我们首先需要对数据进行预处理。
我们检查了数据的缺失情况和异常值,并进行了相应的处理。
接下来,我们使用多元线性回归模型来分析数据。
模型的方程可以表示为:销售额= β0 + β1 × 产品价格+ β2 × 广告费用+ β3 × 竞争对手的产品价格+ ε其中,β0、β1、β2、β3是回归系数,ε是误差项。
5. 结果解释我们使用统计软件进行回归分析,并得到了以下结果:- 回归系数的估计值:β0 = 1000, β1 = 10, β2 = 20, β3 = -5- 拟合优度:R² = 0.8根据回归系数的估计值,我们可以解释模型的结果:- β0表示当产品价格、广告费用和竞争对手的产品价格都为0时,销售额的估计值为1000。
- β1表示产品价格每增加1单位,销售额平均增加10单位。
- β2表示广告费用每增加1单位,销售额平均增加20单位。
- β3表示竞争对手的产品价格每增加1单位,销售额平均减少5单位。
拟合优度R²的值为0.8,说明模型可以解释销售额的80%变异程度。
这意味着模型对数据的拟合程度较好。
6. 结论根据我们的多元线性回归分析结果,我们可以得出以下结论:- 产品价格、广告费用和竞争对手的产品价格对销售额有显著影响。
Eviews多元回归模型案例分析

Eviews多元回归模型案例分析1. 引言本文将通过一个多元回归模型的案例分析来展示Eviews软件的应用。
多元回归模型是一种统计学方法,用于研究多个自变量对因变量的影响关系。
2. 数据集和变量2.1 数据集我们使用的数据集是一份包含多个变量的经济数据集,包括自变量和因变量。
2.2 变量在本案例中,我们选择了以下变量:- 因变量:Y- 自变量1:X1- 自变量2:X2- 自变量3:X33. 回归模型建立和参数估计3.1 建立模型我们根据选定的变量,建立了以下多元回归模型:Y = β0 + β1X1 + β2X2 + β3X3 + ε3.2 参数估计使用Eviews软件,我们对模型中的参数进行了估计。
具体估计结果如下:- β0的估计值为a- β1的估计值为b1- β2的估计值为b2- β3的估计值为b34. 模型拟合和统计检验4.1 拟合优度为了评估模型的拟合优度,我们计算了决定系数R^2。
结果显示,模型拟合效果良好,并能解释自变量对因变量的变异程度。
4.2 统计检验我们进行了一系列统计检验,包括回归系数的显著性检验、F 检验和残差分析等。
结果显示,模型的回归系数显著,并且F检验的p值足够小,支持多元回归模型的有效性。
5. 模型解释和预测5.1 模型解释我们分析了模型中每个自变量的系数和显著性水平,解释了它们对因变量的影响。
根据模型结果,可以得出每个自变量对因变量的贡献程度。
5.2 模型预测基于建立的多元回归模型,我们可以进行因变量的预测。
根据给定的自变量取值,我们可以通过模型预测出相应的因变量值。
6. 结论通过Eviews软件进行多元回归模型的案例分析,我们得出了一些结论。
多元回归模型在解释因变量和自变量之间关系方面具有一定的效果,并且可以用于因变量的预测。
然而,我们需要注意模型的限制和假设,并且在实际应用中进行进一步的验证和调整。
以上是对Eviews多元回归模型案例分析的简要介绍。
如有更详细的需求或其他问题,请随时联系。
商务统计学课件-多元线性回归分析实例应用

6.80
13.65
14.25
27
8.27
6.50
13.70
13.65
28
7.67
5.75
13.75
13.75
29
7.93
5.80
13.80
13.85
30
9.26
6.80
13.70
14.25
销售周期
1
销售价格/元
其他公司平均销售价格
/元
多元线性回归分析应用
多元线性回归分析应用
解
Y 表示牙膏销售量,X 1 表示广告费用,X 2表示销售价格, X 3
个自变量之间的线性相关程度很高,回归方程的拟合效果较好。
一元线性回归分析应用
解
广告费用的回归系数检验 t1 3.981 ,对应的 P 0.000491 0.05
销售价格的回归系数检验 t2 3.696 ,对应的 P 0.001028 0.05
其它公司平均销售价格的回归系数检验
…
14
1551.3
125.0
45.8
29.1
15
1601.2
137.8
51.7
24.6
16
2311.7
175.6
67.2
27.5
17
2126.7
155.2
65.0
26.5
18
2256.5
174.3
65.4
26.8
万元
表示其他公司平均销售价格。建立销售额的样本线性回归方程如
下:
Yˆi 15.044 0.501X 1i 2.358 X 2i 1.612 X 3i
一元线性回归分析应用
多元线性回归分析案例

多元线性回归分析案例多元线性回归分析是统计学中常用的一种分析方法,它可以用来研究多个自变量对因变量的影响,并建立相应的数学模型。
在实际应用中,多元线性回归分析可以帮助我们理解变量之间的关系,预测未来的趋势,以及制定相应的决策。
本文将通过一个实际案例来介绍多元线性回归分析的基本原理和应用方法。
案例背景。
假设我们是一家电子产品制造公司的市场营销团队,我们想要了解产品销量与广告投入、产品定价和市场规模之间的关系。
我们收集了过去一年的数据,包括每个月的产品销量(千台)、广告投入(万元)、产品定价(元/台)和市场规模(亿人)。
数据分析。
首先,我们需要对数据进行描述性统计分析,以了解各变量的分布情况和相关性。
我们计算了产品销量、广告投入、产品定价和市场规模的均值、标准差、最大最小值等统计量,并绘制了相关性矩阵图。
通过分析发现,产品销量与广告投入、产品定价和市场规模之间存在一定的相关性,但具体的关系还需要通过多元线性回归分析来验证。
多元线性回归模型。
我们建立了如下的多元线性回归模型:\[Sales = \beta_0 + \beta_1 \times Advertising + \beta_2 \times Price + \beta_3 \times MarketSize + \varepsilon\]其中,Sales表示产品销量,Advertising表示广告投入,Price表示产品定价,MarketSize表示市场规模,\(\beta_0, \beta_1, \beta_2, \beta_3\)分别为回归系数,\(\varepsilon\)为误差项。
模型验证。
我们利用最小二乘法对模型进行参数估计,并进行了显著性检验和回归诊断。
结果表明,广告投入、产品定价和市场规模对产品销量的影响是显著的,模型的拟合效果较好。
同时,我们还对模型进行了预测能力的验证,结果表明模型对未来产品销量的预测具有一定的准确性。
决策建议。
—多元线性回归分析案例

—多元线性回归分析案例多元线性回归分析是一种广泛使用的统计分析方法,用于研究多个自变量对一个因变量的影响程度。
在实际应用中,多元线性回归可以帮助我们理解变量之间的相互关系,并预测因变量的数值。
下面我们将以一个实际案例来介绍多元线性回归分析的应用。
假设我们是一家电子产品制造商,我们想研究影响手机销量的因素,并尝试通过多元线性回归模型来预测手机的销量。
我们选择了三个自变量作为影响因素:广告投入、价格和市场份额。
我们收集了一段时间内的数据,包括这三个因素以及对应的手机销量。
现在我们将利用这些数据来进行多元线性回归分析。
首先,我们需要将数据进行预处理和清洗。
我们检查数据的完整性和准确性,并去除可能存在的异常值和缺失值。
然后,我们对数据进行描述性统计分析,以了解数据的整体情况和变量之间的关系。
接下来,我们将建立多元线性回归模型。
我们将销量作为因变量,而广告投入、价格和市场份额作为自变量。
通过引入这些自变量,我们可以预测手机销量,并分析它们对销量的影响程度。
为了进行回归分析,我们需要估计模型的系数。
这可以通过最小二乘法来实现,该方法将使得模型的预测结果与实际观测值之间的残差平方和最小化。
接下来,我们将进行统计检验,以确定自变量对因变量的显著影响。
常见的统计指标包括回归系数的显著性水平、t值和p值。
在我们的案例中,假设多元线性回归模型的方程为:销量=β0+β1×广告投入+β2×价格+β3×市场份额+ε。
其中,β0、β1、β2和β3为回归系数,ε为误差项。
完成回归分析后,我们可以进行模型的诊断和评估。
我们可以检查模型的残差是否呈正态分布,以及模型的拟合程度如何。
此外,我们还可以通过交叉验证等方法评估模型的准确性和可靠性。
最后,我们可以利用训练好的多元线性回归模型来进行预测。
通过输入新的广告投入、价格和市场份额的数值,我们可以预测手机的销量,并根据预测结果制定相应的市场策略。
综上所述,多元线性回归分析是一种强大的统计工具,可用于分析多个自变量对一个因变量的影响。
多元线性回归模型案例分析报告

多元线性回归模型案例分析报告多元线性回归模型是一种用于预测和建立因变量和多个自变量之间关系的统计方法。
它通过拟合一个线性方程,找到使得回归方程和实际观测值之间误差最小的系数。
本报告将以一个实际案例为例,对多元线性回归模型进行案例分析。
案例背景:公司是一家在线教育平台,希望通过多元线性回归模型来预测学生的学习时长,并找出对学习时长影响最大的因素。
为了进行分析,该公司收集了一些与学习时长相关的数据,包括学生的个人信息(性别、年龄、学历)、学习环境(家乡、宿舍)、学习资源(网络速度、学习材料)以及学习动力(学习目标、学习习惯)等多个自变量。
数据分析方法:通过建立多元线性回归模型,我们可以找到与学习时长最相关的因素,并预测学生的学习时长。
首先,我们将根据实际情况对数据进行预处理,包括数据清洗、过滤异常值等。
然后,我们使用逐步回归方法,通过逐步添加和删除自变量来筛选最佳模型。
最后,我们使用已选定的自变量建立多元线性回归模型,并进行系数估计和显著性检验。
案例分析结果:经过数据分析和模型建立,我们得到了如下的多元线性回归模型:学习时长=0.5*年龄+0.2*学历+0.3*学习资源+0.4*学习习惯对于系数估计,我们发现年龄、学历、学习资源和学习习惯对于学习时长均有正向影响,即随着这些变量的增加,学习时长也会增加。
其中,年龄和学习资源的影响较大,学历和学习习惯的影响较小。
在显著性检验中,我们发现该模型的拟合度较好,因为相关自变量的p值均小于0.05,表明它们对学习时长的影响具有统计学意义。
案例启示:本案例的分析结果为在线教育平台提供了重要的参考。
公司可以针对年龄较大、学历高、学习资源丰富和有良好学习习惯的学生,提供个性化的学习服务和辅导。
同时,公司也可以通过提供更好的学习资源和培养良好的学习习惯,来提升学生的学习时长和学习效果。
总结:多元线性回归模型在实际应用中具有广泛的应用价值。
通过对因变量和多个自变量之间的关系进行建模和分析,我们可以找到相关影响因素,并预测因变量的取值。
多元回归分析SPSS案例
多元回归分析在大多数得实际问题中,影响因变量得因素不就就是一个而就就是多个,我们称这类回问题为多元回归分析。
可以建立因变量y与各自变量x j(j=1,2,3,…,n)之间得多元线性回归模型:其中:b0就就是回归常数;b k(k=1,2,3,…,n)就就是回归参数;e就就是随机误差。
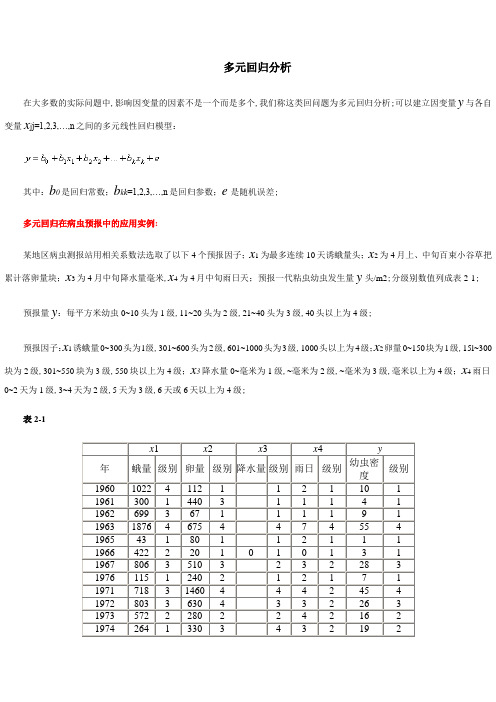
多元回归在病虫预报中得应用实例:某地区病虫测报站用相关系数法选取了以下4个预报因子;x1为最多连续10天诱蛾量(头);x2为4月上、中旬百束小谷草把累计落卵量(块);x3为4月中旬降水量(毫米),x4为4月中旬雨日(天);预报一代粘虫幼虫发生量y(头/m2)。
分级别数值列成表2-1。
预报量y:每平方米幼虫0~10头为1级,11~20头为2级,21~40头为3级,40头以上为4级。
预报因子:x1诱蛾量0~300头为l级,301~600头为2级,601~1000头为3级,1000头以上为4级;x2卵量0~150块为1级,15l~300块为2级,301~550块为3级,550块以上为4级;x3降水量0~10、0毫米为1级,10、1~13、2毫米为2级,13、3~17、0毫米为3级,17、0毫米以上为4级;x4雨日0~2天为1级,3~4天为2级,5天为3级,6天或6天以上为4级。
表2-1数据保存在“DATA6-5、SAV”文件中。
1)准备分析数据在SPSS数据编辑窗口中,创建“年份”、“蛾量”、“卵量”、“降水量”、“雨日”与“幼虫密度”变量,并输入数据。
再创建蛾量、卵量、降水量、雨日与幼虫密度得分级变量“x1”、“x2”、“x3”、“x4”与“y”,它们对应得分级数值可以在SPSS数据编辑窗口中通过计算产生。
编辑后得数据显示如图2-1。
图2-1或者打开已存在得数据文件“DATA6-5、SAV”。
2)启动线性回归过程单击SPSS主菜单得“Analyze”下得“Regression”中“Linear”项,将打开如图2-2所示得线性回归过程窗口。
多元回归分析SPSS案例
多元回归分析在大多数的实际问题中,影响因变量的因素不是一个而是多个,我们称这类回问题为多元回归分析;可以建立因变量y与各自变量x j j=1,2,3,…,n之间的多元线性回归模型:其中:b0是回归常数;b k k=1,2,3,…,n是回归参数;e是随机误差;多元回归在病虫预报中的应用实例:某地区病虫测报站用相关系数法选取了以下4个预报因子;x1为最多连续10天诱蛾量头;x2为4月上、中旬百束小谷草把累计落卵量块;x3为4月中旬降水量毫米,x4为4月中旬雨日天;预报一代粘虫幼虫发生量y头/m2;分级别数值列成表2-1;预报量y:每平方米幼虫0~10头为1级,11~20头为2级,21~40头为3级,40头以上为4级;预报因子:x1诱蛾量0~300头为l级,301~600头为2级,601~1000头为3级,1000头以上为4级;x2卵量0~150块为1级,15l~300块为2级,301~550块为3级,550块以上为4级;x3降水量0~毫米为1级,~毫米为2级,~毫米为3级,毫米以上为4级;x4雨日0~2天为1级,3~4天为2级,5天为3级,6天或6天以上为4级;表2-1x1 x2 x3 x4 y年蛾量级别卵量级别降水量级别雨日级别幼虫密度级别1960 1022 4 112 1 1 2 1 10 1 1961 300 1 440 3 1 1 1 4 1 1962 699 3 67 1 1 1 1 9 1 1963 1876 4 675 4 4 7 4 55 4 1965 43 1 80 1 1 2 1 1 1 1966 422 2 20 1 0 1 0 1 3 1 1967 806 3 510 3 2 3 2 28 3 1976 115 1 240 2 1 2 1 7 1 1971 718 3 1460 4 4 4 2 45 4 1972 803 3 630 4 3 3 2 26 3 1973 572 2 280 2 2 4 2 16 2 1974 264 1 330 3 4 3 2 19 2数据保存在“”文件中;1准备分析数据在SPSS数据编辑窗口中,创建“年份”、“蛾量”、“卵量”、“降水量”、“雨日”和“幼虫密度”变量,并输入数据;再创建蛾量、卵量、降水量、雨日和幼虫密度的分级变量“x1”、“x2”、“x3”、“x4”和“y”,它们对应的分级数值可以在SPSS数据编辑窗口中通过计算产生;编辑后的数据显示如图2-1;图2-1或者打开已存在的数据文件“”;2启动线性回归过程单击SPSS主菜单的“Analyze”下的“Regression”中“Linear”项,将打开如图2-2所示的线性回归过程窗口;图2-2 线性回归对话窗口3 设置分析变量设置因变量:用鼠标选中左边变量列表中的“幼虫密度y”变量,然后点击“Dependent”栏左边的向右拉按钮,该变量就移到“Dependent”因变量显示栏里;设置自变量:将左边变量列表中的“蛾量x1”、“卵量x2”、“降水量x3”、“雨日x4”变量,选移到“IndependentS”自变量显示栏里;设置控制变量: 本例子中不使用控制变量,所以不选择任何变量;选择标签变量: 选择“年份”为标签变量;选择加权变量: 本例子没有加权变量,因此不作任何设置;4回归方式本例子中的4个预报因子变量是经过相关系数法选取出来的,在回归分析时不做筛选;因此在“Method”框中选中“Enter”选项,建立全回归模型;5设置输出统计量单击“Statistics”按钮,将打开如图2-3所示的对话框;该对话框用于设置相关参数;其中各项的意义分别为:图2-3 “Statistics”对话框①“Regression Coefficients”回归系数选项:“Estimates”输出回归系数和相关统计量;“Confidence interval”回归系数的95%置信区间;“Covariance matrix”回归系数的方差-协方差矩阵;本例子选择“Estimates”输出回归系数和相关统计量;②“Residuals”残差选项:“Durbin-Watson”Durbin-Watson检验;“Casewise diagnostic”输出满足选择条件的观测量的相关信息;选择该项,下面两项处于可选状态:“Outliers outside standard deviations”选择标准化残差的绝对值大于输入值的观测量;“All cases”选择所有观测量;本例子都不选;③其它输入选项“Model fit”输出相关系数、相关系数平方、调整系数、估计标准误、ANOVA表;“R squared change”输出由于加入和剔除变量而引起的复相关系数平方的变化;“Descriptives”输出变量矩阵、标准差和相关系数单侧显著性水平矩阵;“Part and partial correlation”相关系数和偏相关系数;“Collinearity diagnostics”显示单个变量和共线性分析的公差;本例子选择“Model fit”项;6绘图选项在主对话框单击“Plots”按钮,将打开如图2-4所示的对话框窗口;该对话框用于设置要绘制的图形的参数;图中的“X”和“Y”框用于选择X轴和Y轴相应的变量;图2-4“Plots”绘图对话框窗口左上框中各项的意义分别为:•“DEPENDNT”因变量;•“ZPRED”标准化预测值;•“ZRESID”标准化残差;•“DRESID”删除残差;•“ADJPRED”调节预测值;•“SRESID”学生氏化残差;•“SDRESID”学生氏化删除残差;“Standardized Residual Plots”设置各变量的标准化残差图形输出;其中共包含两个选项:“Histogram”用直方图显示标准化残差;“Normal probability plots”比较标准化残差与正态残差的分布示意图;“Produce all partial plot”偏残差图;对每一个自变量生成其残差对因变量残差的散点图;本例子不作绘图,不选择;7 保存分析数据的选项在主对话框里单击“Save”按钮,将打开如图2-5所示的对话框;图2-5 “Save”对话框①“Predicted Values”预测值栏选项:Unstandardized 非标准化预测值;就会在当前数据文件中新添加一个以字符“PRE_”开头命名的变量,存放根据回归模型拟合的预测值;Standardized 标准化预测值;Adjusted 调整后预测值;. of mean predictions 预测值的标准误;本例选中“Unstandardized”非标准化预测值;②“Distances”距离栏选项:Mahalanobis: 距离;Cook’s”: Cook距离;Leverage values: 杠杆值;③“Prediction Intervals”预测区间选项:Mean: 区间的中心位置;Individual: 观测量上限和下限的预测区间;在当前数据文件中新添加一个以字符“LICI_”开头命名的变量,存放预测区间下限值;以字符“UICI_”开头命名的变量,存放预测区间上限值;Confidence Interval:置信度;本例不选;④“Save to New File”保存为新文件:选中“Coefficient statistics”项将回归系数保存到指定的文件中;本例不选;⑤“Export model information to XML file”导出统计过程中的回归模型信息到指定文件;本例不选;⑥“Residuals” 保存残差选项:“Unstandardized”非标准化残差;“Standardized”标准化残差;“Studentized”学生氏化残差;“Deleted”删除残差;“Studentized deleted”学生氏化删除残差;本例不选;⑦“Influence Statistics” 统计量的影响;“DfBetas”删除一个特定的观测值所引起的回归系数的变化;“Standardized DfBetas”标准化的DfBeta值;“DiFit” 删除一个特定的观测值所引起的预测值的变化;“Standardized DiFit”标准化的DiFit值;“Covariance ratio”删除一个观测值后的协方差矩隈的行列式和带有全部观测值的协方差矩阵的行列式的比率;本例子不保存任何分析变量,不选择;8其它选项在主对话框里单击“Options”按钮,将打开如图2-6所示的对话框;图2-6 “Options”设置对话框①“Stepping Method Criteria”框用于进行逐步回归时内部数值的设定;其中各项为:“Use probability of F”如果一个变量的F值的概率小于所设置的进入值Entry,那么这个变量将被选入回归方程中;当变量的F值的概率大于设置的剔除值Removal,则该变量将从回归方程中被剔除;由此可见,设置“Use probability of F”时,应使进入值小于剔除值;“Ues F value”如果一个变量的F值大于所设置的进入值Entry,那么这个变量将被选入回归方程中;当变量的F值小于设置的剔除值Removal,则该变量将从回归方程中被剔除;同时,设置“Use F value”时,应使进入值大于剔除值;本例是全回归不设置;②“Include constant in equation”选择此项表示在回归方程中有常数项;本例选中“Include constant in equation”选项在回归方程中保留常数项;③“Missing Values”框用于设置对缺失值的处理方法;其中各项为:“Exclude cases listwise”剔除所有含有缺失值的观测值;“Exchude cases pairwise”仅剔除参与统计分析计算的变量中含有缺失值的观测量;“Replace with mean”用变量的均值取代缺失值;本例选中“Exclude cases listwise”;9提交执行在主对话框里单击“OK”,提交执行,结果将显示在输出窗口中;主要结果见表2-2至表2-4;10 结果分析主要结果:表2-2表2-2 是回归模型统计量:R 是相关系数;R Square 相关系数的平方,又称判定系数,判定线性回归的拟合程度:用来说明用自变量解释因变量变异的程度所占比例;Adjusted R Square 调整后的判定系数;Std. Error of the Estimate 估计标准误差;表2-3表2-3 回归模型的方差分析表,F值为,显著性概率是,表明回归极显著;表2-4分析:建立回归模型:根据多元回归模型:把表6-9中“非标准化回归系数”栏目中的“B”列系数代入上式得预报方程:预测值的标准差可用剩余均方估计:回归方程的显著性检验:从表6-8方差分析表中得知:F统计量为,系统自动检验的显著性水平为;F,4,11值为,F,4,11 值为,F,4,11 值为;因此回归方程相关非常显著;F值可在Excel中用FINV 函数获得;回代检验需要作预报效果的验证时,在主对话框图6-8里单击“Save”按钮,在打开如图3-6所示对话框里,选中“Predicted Values”预测值选项栏中的“Unstandardized”非标准化预测值选项;这样在过程运算时,就会在当前文件中新添加一个“PRE_1”命名的变量,该变量存放根据回归模型拟合的预测值;然后,在SPSS数据窗口计算“y”与“PRE_1”变量的差值图2-7,本例子把绝对差值大于视为不符合,反之则符合;结果符合的年数为15年,1年不符合,历史符合率为%;图2-7多元回归分析法可综合多个预报因子的作用,作出预报,在统计预报中是一种应用较为普遍的方法;在实际运用中,采取将预报因子和预报量按一定标准分为多级,用分级尺度代换较大的数字,更能揭示预报因子与预报量的关系,预报效果比采用数量值统计方法有明显的提高,在实际应用中具有一定的现实意义;。
多元回归模型分析案例

多元回归模型分析案例多元回归模型分析是一种重要的数据分析技术,它可用于解决一系列实际问题,如预测商品消费量、预测股票市场行情等。
本文将以一个简单的案例来说明如何利用多元回归模型来分析数据,以便发现有用的信息,并更好地了解因果关系。
假设一家商店想要预测它的销售额,并且想了解它的销售额与其他变量之间的关系。
接下来,我们以该商店的历史销售数据建立一个多元回归模型,预测未来销售额,并分析它与其他变量之间的关系。
首先,需要收集有关商店历史销售数据的所有信息,包括产品的价格、促销活动的有效性等。
然后,使用统计软件将这些数据分析成矩阵,并将这些变量作为自变量,而销售额作为因变量。
然后,使用多元线性回归的算法,对收集的数据进行分析和处理,并建立一个具有最佳拟合度的多元回归模型。
回归模型中,各变量之间的关系可以通过相关系数来衡量,其中正相关系数表示两个变量增大时,另一变量也会增大;反之,负相关系数表示两个变量增大时,另一变量则下降。
根据统计分析,可以得出每一个变量与销售额之间的相关性。
通过观察变量与销售额之间的关系,我们可以清楚地了解到每一个变量对销售额影响的程度,以及它们之间的因果关系。
此外,建立的多元回归模型还可用于预测未来的销售情况。
将未来的变量值带入模型,即可得出推测的未来销售额,方便商店更好地制定销售计划和预算。
当然,预测的准确程度取决于多元回归模型的准确性。
本文以一个简单的案例介绍了如何使用多元回归模型来分析数据,以更好地了解因果关系,以及用于预测未来销售情况。
多元回归模型分析是一种重要的数据分析技术,被广泛用于现实生活中的实际问题的解决。
但要记住,多元回归分析的结果仅供参考,最后的决策仍应根据实际情况,由实际决策者综合评估。
多元回归分析SPSS案例

多元回归分析SPSS案例
一、案例背景
一所大学学术部门进行了一项有关学生毕业的调查,主要是为了探讨
学生毕业的影响因素,通过这个调查,大学试图及早发现潜在的学术发展
问题,从而改善学术教育和服务质量。
调查采用SPSS软件分析,将来自
一所大学学生的有关信息作为研究目标,本研究的研究对象为大学学生。
二、研究目的
1、探索影响大学生毕业的主要因素;
2、研究各变量对大学生毕业的影响程度;
3、提出适合大学学生的毕业提升策略。
三、研究变量
本研究采用多元线性回归分析方法,研究变量有:(1)身体健康程
度(即体检结果);(2)现金流(即家庭收入);(3)家庭教育水平;(4)学习成绩;(5)家庭状况,即与家庭成员的关系;(6)个人情感
状况;(7)考试作弊。
四、研究方法
1、获取研究数据:
通过与学校协商,确定调查对象,以及采集问卷的方法(如发放问卷、网络调查等),以获取有关学生毕业的数据;
2、数据处理:
清洗数据,将数据分类进行处理,去除无关信息;
3、多元回归分析:
计算自变量与因变量之间的线性关系,分析变量间关系,建立多元回归模型;。
多元线性回归模型的案例分析

1. 表1列出了某地区家庭人均鸡肉年消费量Y 与家庭月平均收入X ,鸡肉价格P 1,猪肉价格P 2与牛肉价格P 3的相关数据。
年份Y/千克 X/元 P 1/(元/千克)P 2/(元/千克)P 3/(元/千克)年份Y/千克 X/元 -P 1/(元/千克)P 2/(元/千克)P 3/(元/千克)19803971992 —911 1981413《1993931 1982439 ·199410211983 )459 19951165:1984492 19961349 |19855281997%1449 1986560,19981575 1987624 *199917591988 * 666 20001994)198971720012258 )19907682002!24781991843,(1) 求出该地区关于家庭鸡肉消费需求的如下模型:01213243ln ln ln ln ln Y X P P P u βββββ=+++++(2) 请分析,鸡肉的家庭消费需求是否受猪肉及牛肉价格的影响。
先做回归分析,过程如下:输出结果如下:所以,回归方程为:]123ln 0.73150.3463ln 0.5021ln 0.1469ln 0.0872ln Y X P P P =-+-++由上述回归结果可以知道,鸡肉消费需求受家庭收入水平和鸡肉价格的影响,而牛肉价格和猪肉价格对鸡肉消费需求的影响并不显著。
验证猪肉价格和鸡肉价格是否有影响,可以通过赤池准则(AIC )和施瓦茨准则(SC )。
若AIC 值或SC 值增加了,就应该去掉该解释变量。
去掉猪肉价格P 2与牛肉价格P 3重新进行回归分析,结果如下:,Variable Coefficient Std. Error t-Statistic% Prob. ]CLOG(X)、LOG(P1)!R-squared Mean dependent var:Adjusted R-squared . dependent var. of regression Akaike info criterionSum squared resid —Schwarz criterionLog likelihood F-statisticDurbin-Watson stat Prob(F-statistic)}…通过比较可以看出,AIC值和SC值都变小了,所以应该去掉猪肉价格P2与牛肉价格P3这两个解释变量。
多元回归分析案例

多元回归分析案例多元回归分析是一种统计方法,用于探讨多个自变量对因变量的影响程度,以及它们之间的相互关系。
在实际应用中,多元回归分析可以帮助我们理解复杂的数据模式,预测未来趋势,以及发现变量之间的潜在关联。
接下来,我们将通过一个实际案例来介绍多元回归分析的应用。
假设我们是一家电子商务公司的数据分析师,我们想要探讨用户在网站上停留的时间与他们购买产品的金额之间的关系。
我们收集了一些样本数据,包括用户的停留时间、购买金额,以及一些可能影响这两个变量的因素,比如用户的年龄、性别、教育程度等。
我们希望通过多元回归分析来找出这些因素对用户购买行为的影响程度。
首先,我们需要建立一个多元回归模型。
在这个模型中,购买金额是我们的因变量,而停留时间、年龄、性别、教育程度等则是我们的自变量。
我们假设这些自变量之间是相互独立的,即它们之间不存在多重共线性。
接下来,我们利用统计软件进行回归分析,得到了一个回归方程,用来描述因变量与自变量之间的关系。
通过回归分析,我们发现停留时间、年龄和教育程度对购买金额有显著影响,而性别对购买金额的影响则不显著。
具体来说,我们发现用户的停留时间每增加一分钟,购买金额就会增加一定数额;年龄越大的用户,购买金额也会相应增加;另外,教育程度较高的用户,购买金额也会有所提升。
这些结果为我们提供了有价值的市场营销建议,比如针对不同年龄段和教育程度的用户制定不同的营销策略,以提升他们的购买意愿。
除了上述因素,我们还可以继续探讨其他可能影响购买行为的因素,比如用户的地理位置、消费习惯等。
通过不断扩充自变量,我们可以建立更加全面的多元回归模型,以更好地解释用户购买行为背后的规律。
总之,多元回归分析是一种强大的工具,可以帮助我们理解复杂的数据模式,揭示变量之间的相互关系,为决策提供科学依据。
在实际应用中,我们需要充分利用多元回归分析的优势,不断优化模型,挖掘数据潜力,为企业发展提供有力支持。
希望本文的案例分析能够帮助读者更好地理解多元回归分析的应用,以及它在实际工作中的重要性。
多元回归分析实例

多元回归分析实例假设我们要研究一些公司员工的薪水与几个因素之间的关系,这几个因素包括员工的工作年限、教育程度和工作绩效评分。
我们希望通过多元回归分析来确定这些因素对员工薪水的影响。
为了进行多元回归分析,我们首先需要收集数据。
我们从该公司的员工数据库中随机选择了100个员工的数据,包括他们的薪水、工作年限、教育程度和工作绩效评分。
接下来,我们使用软件进行多元回归分析。
假设我们使用多元线性回归模型来建立模型,其中薪水是因变量,工作年限、教育程度和工作绩效评分是自变量。
模型可以表示为:薪水=β0+β1*工作年限+β2*教育程度+β3*工作绩效评分+ε其中,β0、β1、β2和β3是模型的系数,表示每个自变量对应的影响程度,ε表示误差项。
我们使用最小二乘法来估计模型的系数。
最小二乘法通过将真实值和模型预测值之间的平方差最小化来确定系数的值。
通过软件运行回归分析,我们可以得到系数的估计值。
假设我们得到的回归结果如下:薪水=3000+500*工作年限+1000*教育程度+200*工作绩效评分根据回归结果,我们可以解读系数的意义。
工作年限系数为500,表示每增加一年的工作年限,员工的薪水平均增加500元。
教育程度系数为1000,表示每提高一个学历水平,员工的薪水平均增加1000元。
工作绩效评分系数为200,表示每提高一个绩效评分,员工的薪水平均增加200元。
同时,我们还需要进行统计检验来确定变量之间的显著性。
通过计算t值和p值,我们可以确定变量之间的关系是否统计显著。
在这个例子中,假设工作年限和教育程度的t值和p值都小于0.05,说明它们与薪水之间的关系是显著的。
而工作绩效评分的t值和p值大于0.05,说明它与薪水之间的关系不显著。
最后,我们还可以计算模型的拟合优度,来评估模型的好坏。
常用的拟合优度指标有R方和调整R方。
R方表示模型解释变量方差的比例,调整R方通过引入自由度的惩罚项来修正R方的偏倚。
通过以上步骤,我们可以完成这个多元回归分析的实例。
多元线性回归模型的案例分析

多元线性回归模型的案例分析在实际生活中,多元线性回归模型可以广泛应用于各个领域。
以下是一个案例分析,以说明多元线性回归模型的应用。
案例:房价预测背景:城市的房地产公司想要推出一款房屋估价服务,帮助人们预测房屋的销售价格。
他们收集了一些相关数据,如房屋的面积、房间的数量、地理位置等因素,并希望通过建立一个多元线性回归模型来实现房价的预测。
步骤:1.数据收集:收集相关数据。
在本案例中,我们收集到了50个样本数据,每个样本包含了房屋的面积、房间的数量和房屋的销售价格。
2.数据预处理:对数据进行预处理,包括缺失值处理、异常值处理等。
在本案例中,我们假设数据已经经过清洗,没有缺失值和异常值。
3.特征选择:选择合适的特征变量。
在本案例中,我们选择房屋的面积和房间的数量作为特征变量,房屋的销售价格作为目标变量。
4.模型建立:建立多元线性回归模型。
根据特征变量和目标变量的关系,建立多元线性回归方程。
在本案例中,假设多元线性回归方程为:房价=β0+β1×面积+β2×房间数量+ε,其中β0、β1和β2分别为回归系数,ε为误差项。
5.模型训练:使用样本数据对模型进行训练。
通过最小二乘法等方法,估计出回归系数的取值。
6.模型评估:评估模型的性能。
通过计算模型的均方误差(MSE)、决定系数(R²)等指标,评估模型的拟合效果和预测能力。
7.模型应用:将模型用于房价的预测。
当有新的房屋数据输入时,通过模型的预测方程,可以得到该房屋的预测销售价格。
通过上述步骤,我们可以建立一个多元线性回归模型,并通过该模型对房价进行预测。
这个模型可以帮助房地产公司提供房价估价服务,也可以帮助购房者了解合理的房价范围。
多元线性回归案例分析

多元线性回归案例分析案例背景:我们假设有一家制造业公司,想要研究员工的工作效率与其工作经验、教育水平和工作时间之间的关系。
公司收集了100名员工的数据,并希望通过多元线性回归模型来分析这些变量之间的关系。
数据收集:公司收集了每个员工的工作效率(因变量)、工作经验、教育水平和工作时间(自变量)的数据。
假设工作效率由工作经验、教育水平和工作时间这三个因素决定。
根据所收集的数据,我们可以建立如下的多元线性回归模型:工作效率=β0+β1*工作经验+β2*教育水平+β3*工作时间+ε在这个模型中,β0、β1、β2和β3分别是待估参数,代表截距和自变量的系数;ε是误差项,代表模型中未被解释的因素。
模型参数的估计:通过最小二乘法可以对模型中的参数进行估计。
最小二乘法的目标是让模型的预测值与观测值之间的残差平方和最小化。
模型诊断:在对模型进行参数估计后,我们需要对模型进行诊断,以评估模型的质量和稳定性。
常见的模型诊断方法包括:检查残差的正态分布、残差与自变量的无关性、残差的同方差性等。
模型解释和预测:根据参数估计结果,可以对模型进行解释和预测。
例如,我们可以解释每个自变量与因变量之间的关系,并分析它们的显著性。
我们还可以通过模型进行预测,比如预测一位具有一定工作经验、教育水平和工作时间的员工的工作效率。
结果分析:根据对模型的诊断和解释,我们可以对结果进行分析。
我们可以得出结论,一些自变量对因变量的影响显著,而其他自变量对因变量的影响不显著。
这些结论可以帮助公司更好地理解员工工作效率与工作经验、教育水平和工作时间之间的关系,并采取相应的管理措施来提高工作效率。
总结:通过以上的案例分析,我们可以看到多元线性回归在实际中的应用。
它可以帮助我们理解多个自变量与一个因变量之间的关系,并对因变量进行预测和解释。
通过多元线性回归分析,我们可以更好地了解因素对于结果的作用,并根据分析结果进行决策和管理。
然而,需要注意的是,多元线性回归的结果可能受到多种因素的影响,我们需要综合考虑所有的因素来做出准确的分析和决策。
多元回归模型分析案例

多元回归模型分析案例多元回归模型(multipleregressionmodel)是一种数据分析方法,它可以帮助我们理解多个自变量对一个因变量的影响情况,从而帮助我们预测和推断因变量的变化趋势,以及其他变量与因变量之间的关系。
例如,一个公司希望了解多个自变量(如市场营销活动,价格,产品质量,服务水平等)对销售额的影响,并从中确定哪些因素对销售额的影响最大,可以使用多元回归模型来探究。
此外,多元回归模型也可用于分析联系金融市场收益率、汇率变化等。
二、多元回归模型的基本原理多元回归模型基于统计学的最小二乘法,它可以有效地对观测样本进行拟合,并计算出各因子之间的线性关系。
其基本原理是构建一个多变量函数y=f(x1,x2,x3,……,xn),并假设被研究的自变量x1,x2,x3,……,xn与因变量y之间存在线性关系,这样可以根据样本的观测值估计出f(x1,x2,x3,……,xn)的参数,从而计算出x1,x2,x3……,xn对y的影响情况。
三、多元回归模型分析案例以金融市场收益率为例,本案例使用多元回归模型分析了国际汇率变化,国家货币投资者信心指数,行业收益率变化等多个自变量对金融市场收益率的影响。
研究方法:1.集实验数据:将样本采集自在全球金融市场的14个市场,其中包括9个美国市场,2个欧洲市场,2个亚洲市场和1个拉丁美洲市场。
2.据清洗:数据清洗是将原始数据中的异常值、重复值以及缺失数据进行处理的过程。
3.型构建:使用多元回归模型对收集到的原始数据进行拟合。
4.算回归系数:使用最小二乘法或其它方法估计回归系数,确定自变量和因变量之间的线性关系。
5.型验证:使用R2进行模型验证,计算本次拟合模型的效果。
结果分析:根据拟合模型,可以看出,国际汇率变化对金融市场收益率的影响最为显著,其系数系数为0.6,行业收益变化的系数为0.5,投资者信心指数的影响较小,其系数仅为0.2。
此外,根据R2分析可以得出,本次拟合模型效果较好,R2为0.96。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
计量经济学案例分析多元回归分析案例学院:数理学院班级:数学092班学号: 0姓名:徐冬梅摘要:为了研究此后影响中国人口自然增长的主要原因,分析全国人口增长规律,与猜测中国未来的增长趋势,用Eviews 软件对相关数据进行了多元回归分析,得出了相关结论关键词:多元回归分析 ,Evicews 软件, 中国人口自然增长; 一、 建立模型为了全面反映中国“人口自然增长率”的全貌,选择人口自然增长率作为被解释变量,以反映中国人口的增长;选择“国名收入”及“人均GDP ”作为经济整体增长的代表;选择“居民消费价格指数增长率”作为居民消费水平的代表。
国名总收入,居民消费价格指数增长率,人均GDP 作为解释变量暂不考虑文化程度及人口分布的影响。
通过对表1的数据进行分析,建立模型。
其模型表达式为:i i i i i u X X X Y ++++=332211ββββ (i=1,2,,3)其中Y 表示人口自然增长率,X 1 表示国名总收入,X 2表示居民消费价格指数增长率,X 3表示人均GDP ,根据以往经验和对调查资料的初步分析可知,Y 与X 1,X 2 ,X3呈线性关系,因此建立上述三元线性总体回归模型。
Xi 则表示各解释变量对税收增长的贡献。
µi 表示随机误差项。
通过上式,我们可以了解到,每个解释变量增长1亿元,粮食总产值会如何变化,从而进行财政收入预测。
相关数据: 表1年份人口自然增长率(%。
)Y 国民总收入(亿元)X1 居民消费价格指数增长率(CPI )%X2人均GDP(元)X3198815037 1366 1989 17001 18 1519 1990 18718 1644 1991 21826 1893 1992 26937 2311 1993 35260 2998 1994 48108 4044 1995 59811 5046 1996 70142 5846 1997 78061 6420 1998 83024 6796 1999 88479 7159 2000 98000 7858 2001 108068 8622 2002 119096 9398 2003 135174 10542 2004 159587 12336 2005 184089 14040 2006 213132 16024 2007 235367 17535 200827765419264二、 参数估计利用上表中的数据,运用eview 软件,采用最小二乘法,对表中的数据进行线性回归,对所建模型进行估计,估计结果见下图。
从估计结果可得模型:321005881.0050364.0000392.077177.15ˆX X X Y -++= Y 关于X 1的散点图:可以看出Y 和X 1成线性相关关系Y 关于X 2的散点图:可以看出Y 和X 2成线性相关关系Y关于X的散点图:3成线性相关关系可以看出Y和X3回归结果三、模型检验:1、经济意义检验模型估计结果说明,在假定其它变量不变的情况下,当年国民总收入每增长1亿元,人口增长率增长%;在假定其它变量不变的情况下,当年居民消费价格指数增长率每增长 1%,人口增长率增长%;在假定其它变量不变的情况下,当年人均GDP 没增加一元,人口增长率就会降低%。
这与理论分析和经验判断相一致。
2、统计检验 (1)、拟合优度检验由于 2TSS Y Y nY '=-, 2ESS X Y nY β∧''=- 所以 2ESS R TSS ==, 2211(1)1n R R n k -=----=,可见模型在整体上拟合得非常好。
(2)、F 检验由于 RSS TSS ESS =- 所以 //(1)ESS kF RSS n k =--= ,针对0:3210===βββH ,给定显著性水平0.05α=,在F 分布表中查出自由度为k-1=3和n-k-1=16的临界值24.3)16,3(=αF 。
由表中得到F= ,由于F= >24.3)16,3(=αF 应拒绝原假设0:3210===βββH ,说明回归方程显著,即“国民总收入”、“居民消费价格指数增长率”、“人均GDP ”等变量联合起来确实对“人口自然增长率”有显著影响。
(3)、t 检验由于=--=--=∑112;2k n e k n e e i σ 且=0βS ,=1β S ,=2β S ,=3β S , 当0010:0,:0H H ββ=≠, ==00βββS t在0.05α=时, 2αt (16)=因为t=>,所以在95%的置信度下拒绝原假设,说明截距项对回归方程影响显著。
当0111:0,:0H H ββ=≠ ==1011βββS t在0.05α=时,2αt (16)=因为t=>所以在95%的置信度下拒绝原假设,说明X1变量对Y 影响显著。
当0212:0,:0H H ββ=≠==222βββS t在0.05α=时,2αt (16)=因为t=<,所以在95%的置信度下接受原假设,说明X2变量对Y 影响不显著。
当0313:0,:0H H ββ=≠ ==333βββS t -在0.05α=时,2αt (16)=因为t=- <,所以在95%的置信度下接受原假设,说明X3变量对Y 影响不显著。
(4)、012345,,,,,ββββββ的置信区间0β的置信区间为:0220000t St S ααβββββ∧∧∧∧-<<+,计算得:∈0β(,);1β的置信区间为:1221111t S t S ααβββββ∧∧∧∧-<<+,计算得:∈1β(,);2β的置信区间为:2222222t S t S ααβββββ∧∧∧∧-<<+,计算得: ∈2β(,);3β的置信区间为:3223333t St S ααβββββ∧∧∧∧-<<+,计算得:; ∈3β(,)综上所述,模型通过各种检验,符合要求。
四、方差分析(新增解释变量对被解释变量边际贡献显著性的分析) 引入不同解释变量的ESS,RSS,2R首先做Y 对1X 的回归,得到样本回归方程为=Y1X () ()1ESS =, =1RSS ,21R =;由t 检验可知,1X 对Y 有显著影响。
21R =表明,对于各种人口自然增长率Y 来说,国民总收入(亿元)1X 只解释了Y 的总离差的82%,还有18%没有解释。
引入第二个解释变量2X 后,样本回归方程为:ˆY =1X 2X 12ESS =, =12RSS ,212R =;新引入2X 的方差分析表变差来源 平方和自由度 F 统计量 对1X 回归 1ESS = 1 对1X 和2X 回归 12ESS = 2 对1X 和2X 回归,2X 新增的部分对1X 和2X 回归的残差12ESS -1ESS =23RSS =120-3=17F=对于给定的显著性水平α=,查F 分布表可得临界值0.05(1,17) 4.45F =,由于F=>,所以新引入的解释变量2X 是显著的,2X 的引入可以显著的提高对Y 的解释程度,即2X 的边际贡献较大,因此2R 从提高到,RSS 从=降低到 再引入第三个解释变量3X :ˆY =+1X +2X 3X 123ESS , =123RSS ,2123R =; 新引入3X 的方差分析表变差来源平方和 自由度 F 统计量查F 分布表可得临界值0.05(1,16)F =,F=>,所以新引入的解释变量3X 显著,即3X 的边际贡献较大,因此2R 从提高到,RSS 从下降到,因此应该引入3X 。
只引入一个解释变量1X ,2X 或3X ;引入两个解释变量1X 和2X ,1X 和3X 或2X 和3X ;以及引入三个变量1X 2X 3X 的ESS,RSS 和2R 的结果如表引入不同解释变量时的ESS ,RSS ,2R由Eviews 可得,只引入一个解释变量1X ,2X ,3X 时的F 统计量分别为1F =,2F =,3F =,由1F ,2F 和3F 都大于临界值0.05(1,18) 4.41F =,所以如果单独用2X ,3X 或4X 作解释变量都显著,如果引入两个解释变量,显然引入1X ,3X 的结果最好,如果引入三个解释变量1X 2X 3X 无论最后引入哪个解释变量结果都显著,因此最后确定引入三个解释变量,相应的回顾方程为 :ˆY =+1X +2X 3X 2R 2R = 模型预测设2009年国民总收入为295267亿元,居民消费价格指数增长率为%,人均GDP 为21427元,将值代入样本回归方程,得到1998年的各项税收总量预测值的点估计值1998ˆY : =2009Y+*295267+*(亿元),实际人口自然增长率为%。
五、模型总结ˆY =+1X +2X 3X =2R =2R 0..930680 F= DW=上述回归结果基本上消除了多重共线性,拟合优度较高,整体效果的F 检验通过,其解释变量X 的t 检验均较为显著。
