几何变换课堂练习题(含答案)
几何变换综合题(含答案)

几何变换综合题参考答案与试题解析一.选择题(共4小题)1.如图,将矩形ABCD绕点A旋转至矩形A′B′C′D′的位置,此时AC的中点恰好与D点重合,AB′交CD于点E.若AB=3,则△AEC的面积为()A.3 B.1.5 C . D .【解答】解:∵旋转后AC的中点恰好与D点重合,即AD=AC′=AC,∴在Rt△ACD中,∠ACD=30°,即∠DAC=60°,∴∠DAD′=60°,∴∠DAE=30°,∴∠EAC=∠ACD=30°,∴AE=CE,在Rt△ADE中,设AE=EC=x,则有DE=DC﹣EC=AB﹣EC=3﹣x,AD=BC=AB•tan30°=×3=,根据勾股定理得:x2=(3﹣x)2+()2,解得:x=2,∴EC=2,则S△AEC=EC•AD=,故选:D.2.如图,将△ABC绕点A按逆时针方向旋转120°得到△AB′C′(点B的对应点是点B',点C的对应点是点C'),连接BB′,若AC′∥BB′,则∠C'AB′的度数为()A.15°B.30°C.45°D.60°【解答】解:∵将△ABC绕点A按逆时针方向旋转l20°得到△AB′C′,∴∠BAB′=∠CAC′=120°,AB=AB′,∴∠AB′B=(180°﹣120°)=30°,∵AC′∥BB′,∴∠C′AB′=∠AB′B=30°,故选:B.3.如图,把△ABC沿着BC的方向平移到△DEF的位置,它们重叠部分的面积是△ABC面积的一半,若BC=,则△ABC移动的距离是()A .B .C .D .﹣【解答】解:∵△ABC沿BC边平移到△DEF的位置,∴AB∥DE,∴△ABC∽△HEC,∴=()2=,∴EC:BC=1:,∵BC=,∴EC=,∴BE=BC﹣EC=﹣.故选:D.4.如图,直线m⊥n.在平面直角坐标系xOy中,x轴∥m,y轴∥n.如果以O1为原点,点A 的坐标为(1,1).将点O1平移2个单位长度到点O2,点A的位置不变,如果以O2为原点,那么点A的坐标可能是()A.(3,﹣1)B.(1,﹣3)C.(﹣2,﹣1)D.(2+1,2+1)【解答】解:如图,由题意,可得O1M=O1N=1.∵将点O1平移2个单位长度到点O2,∴O1O2=2,O1P=O2P=2,∴PM=3,∴点A的坐标是(3,﹣1).故选:A.二.填空题(共6小题)5.在平面直角坐标系中,动点M从原点O出发进行平移,每次平移向上移动1个单位长度或向右移动2个单位长度.如第1次平移后可能到达的点是(0,1)或(2,0),第2次平移后可能到达的点是(0,2)或(2,1)或(4,0),在第n次平移后点M可能到达的点用(x,y)表示,则y与x满足的关系式为y=﹣x+n.【解答】解:设过(0,1),(2,0)点的函数解析式为:y=kx+b(k≠0),则,解得,故平移1次后点P在函数y=﹣x+1的图象上;平移2次后点P在函数y=﹣x+2的图象上,则第n次平移后点M可能到达的点用(x,y)表示,则y与x满足的关系式为:y=﹣x+n.故答案为:y=﹣x+n.6.在Rt△ABC中,∠C=90°,AC=6,BC=8(如图),点D是边AB上一点,把△ABC绕着点D旋转90°得到△A'B'C',边B'C'与边AB相交于点E,如果AD=BE,那么AD长为或2.【解答】解:①当顺时针旋转时,过点E作EF⊥AC于F,过点D作DM⊥BC于M,作DN⊥B′C′于点N,如图所示.∵△ABC绕着点D旋转90°得到△A'B'C',∴DM=DN.∵AD=BE,∴AE=DB.∵DM⊥BC,AC⊥BC,∴DM∥AC,∴∠A=∠BDM.在△AEF和△DBM 中,,∴△AEF≌△DBM(AAS),∴AF=DM.∵AC=6,BC=8,∴AB=10.设DM=x,则DN=x,AF=x,EF=x,BM=x,∴BC=x+x +x=8,∴x=,∴BD=x=,∴AD=AB﹣BD=.②当逆时针旋转时,如图2所示.同①可得出△B′DE∽△BCA,∴=,∴设DE=y,则B′D=y,AD=BE=10﹣y,∴10﹣y+y+10﹣y=10,∴y=6,∴AD=10﹣y=2.故答案为:或2.7.如图,△ABC是边长为12的等边三角形,D是BC的中点,E是直线AD上的一个动点,连接EC,将线段EC绕点C逆时针旋转60°得到FC,连接DF.则在点E的运动过程中,DF的最小值是3.【解答】解:取线段AC的中点G,连接EG,如图所示.∵△ABC为等边三角形,且AD为△ABC的对称轴,∴CD=CG=AB=6,∠ACD=60°,∵∠ECF=60°,∴∠FCD=∠ECG.在△FCD和△ECG中,,∴△FCD≌△ECG(SAS),∴DF=GE.当EG∥BC时,EG最小,∵点G为AC的中点,∴此时EG=DF=CD=BC=3.故答案为3.8.一副直角三角板叠放如图所示,现将含45°角的三角板固定不动,把含30°角的三角板绕直角顶点沿逆时针方向匀速旋转一周,第一秒旋转5°,第二秒旋转10°,第三秒旋转5°,第四秒旋转10°,…按此规律,当两块三角板的斜边平行时,则三角板旋转运动的时间为14s或38s.【解答】解:如图,当斜边AB∥DC时,∠CFE=∠B=60°,∴∠BED=60°﹣45°=15°,∴旋转角为90°+15°=105°,105°÷(5°+10°)=7,7×2=14(s);如图,将△ABE继续逆时针旋转180°,可得斜边A'B'∥DC,此时,旋转角为105°+180°=285°,285°÷(5°+10°)=19,19×2=38(s);故答案为:14s或38s.9.已知点P(a+1,1)关于原点的对称点在第四象限,则a的取值范围是a <﹣1.【解答】解:∵P(a+1,1)关于原点对称的点在第四象限,∴P点在第二象限,∴a+1<0,解得:a<﹣1,故答案为:a<﹣1.10.如图,将直角三角形ABC沿BC方向平移得到直角三角形DEF,若AB=8,BE=6,DM=5,则阴影部分的面积是33.【解答】解:∵直角△ABC沿BC方向平移得到直角△DEF,∴DE=AB=8,∵DM=5,∴ME=DE﹣DM=8﹣5=3,由平移可得:S阴影=S△DEF﹣S△MEC=S△ABC﹣S△MEC=S梯形ABEM=×(3+8)×6,=33.故答案为:33.三.解答题(共10小题)11.如图,在8×8网格中,每个小正方形的边长都为单位1.(1)建立适当的平面直角坐标系后,若点B(﹣2,0)、C(3,0),则点A的坐标为(﹣1,2);(2)将△ABC向下平移3个单位,再向右平移2个单位,画出平移后的△A′B′C′;(3)在(1)、(2)的条件下,若线段AC上有一点P(a,b),则平移后的对应的P′坐标为(a﹣3,b﹣3);(4)△ABC的形状是直角三角形.【解答】解:(1)点A的坐标为(﹣1,2),故答案为:(﹣1,2);(2)如图所示,△A′B′C′即为所求;(3)若线段AC上有一点P(a,b),则平移后的对应的P′坐标为(a﹣3,b﹣3),故答案为:(a﹣3,b﹣3);(4)∵AB2=12+22=5、AC2=22+42=20、BC2=25,∴AB2+AC2=BC2,所以△ABC为直角三角形.故答案为:直角三角形.12.已知,点P是等边三角形△ABC中一点,线段AP绕点A逆时针旋转60°到AQ,连接PQ、QC.(1)求证:PB=QC;(2)若PA=3,PB=4,∠APB=150°,求PC的长度.【解答】(1)证明:∵线段AP绕点A逆时针旋转60°到AQ,∴AP=AQ,∠PAQ=60°,∴△APQ是等边三角形,∠PAC+∠CAQ=60°,∵△ABC是等边三角形,∴∠BAP+∠PAC=60°,AB=AC,∴∠BAP=∠CAQ,在△BAP和△CAQ中,∴△BAP≌△CAQ(SAS),∴PB=QC;(2)解:∵由(1)得△APQ是等边三角形,∴AP=PQ=3,∠AQP=60°,∵∠APB=150°,∴∠PQC=150°﹣60°=90°,∵PB=QC,∴QC=4,∴△PQC是直角三角形,∴PC===5.13.已知,△ABC中,AB=AC,点E是边AC上一点,过点E作EF∥BC交AB于点F.(1)如图①,求证:AE=AF;(2)如图②,将△AEF绕点A逆时针旋转α(0°<α<144°)得到△AE′F′.连接CE′BF′.①若BF′=6,求CE′的长;②若∠EBC=∠BAC=36°,在图②的旋转过程中,当CE′∥AB时,直接写出旋转角α的大小.【解答】(1)证明:∵AB=AC,∴∠ABC=∠C,∵EF∥BC,∴∠AFE=∠B,∠AEF=∠C,∴∠AFE=∠AEF,∴AE=AF.(2)解:①由旋转的性质得,∠E′AC=∠F′AB,AE′=AF′,在△CAE′和△BAF′中,,∴△CAE′≌△BAF′(SAS),∴CE′=BF′=6;②由(1)可知AE=BC,所以,在△AEF绕点A逆时针旋转过程中,点E经过的路径(圆弧)与过点C且与AB平行的直线l相交于点M、N,如图,①当点E的像E′与点M重合时,四边形ABCM是等腰梯形,所以,∠BAM=∠ABC=72°,又∵∠BAC=36°,∴α=∠CAM=36°;②当点E的像E′与点N重合时,∵CE′∥AB,∴∠AMN=∠BAM=72°,∵AM=AN,∴∠ANM=∠AMN=72°,∴∠MAN=180°﹣72°×2=36°,∴α=∠CAN=∠CAM+∠MAN=36°+36°=72°,综上所述,当旋转角α为36°或72°.14.如图1,点P、Q分别是边长为4cm的等边△ABC边AB、BC上的动点,点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1cm/s,(1)连接AQ、CP交于点M,则在P、Q运动的过程中,∠CMQ变化吗?若变化,则说明理由,若不变,则求出它的度数;(2)何时△PBQ是直角三角形?(3)如图2,若点P、Q在运动到终点后继续在射线AB、BC上运动,直线AQ、CP交点为M,则∠CMQ变化吗?若变化,则说明理由,若不变,则求出它的度数.【解答】解:(1)∠CMQ=60°不变.∵等边三角形中,AB=AC,∠B=∠CAP=60°又由条件得AP=BQ,∴△ABQ≌△CAP(SAS),∴∠BAQ=∠ACP,∴∠CMQ=∠ACP+∠CAM=∠BAQ+∠CAM=∠BAC=60°.(2)设时间为t,则AP=BQ=t,PB=4﹣t①当∠PQB=90°时,∵∠B=60°,∴PB=2BQ,得4﹣t=2t,t=;②当∠BPQ=90°时,∵∠B=60°,∴BQ=2BP,得t=2(4﹣t),t=;∴当第秒或第秒时,△PBQ为直角三角形.(3)∠CMQ=120°不变.∵在等边三角形中,BC=AC,∠B=∠CAP=60°∴∠PBC=∠ACQ=120°,又由条件得BP=CQ,∴△PBC≌△QCA(SAS)∴∠BPC=∠MQC又∵∠PCB=∠MCQ,∴∠CMQ=∠PBC=180°﹣60°=120°15.已知△ABC和△ADE是等腰直角三角形,∠ACB=∠ADE=90°,点F为BE中点,连接DF、CF.(1)如图1,当点D在AB上,点E在AC上,请直接写出此时线段DF、CF的数量关系和位置关系(不用证明);(2)如图2,在(1)的条件下将△ADE绕点A顺时针旋转45°时,请你判断此时(1)中的结论是否仍然成立,并证明你的判断;(3)如图3,在(1)的条件下将△ADE绕点A顺时针旋转90°时,若AD=1,AC=,求此时线段CF的长(直接写出结果).【解答】解:(1)∵∠ACB=∠ADE=90°,点F为BE中点,∴DF=BE,CF=BE,∴DF=CF.∵△ABC和△ADE是等腰直角三角形,∴∠ABC=45°∵BF=DF,∴∠DBF=∠BDF,∵∠DFE=∠ABE+∠BDF,∴∠DFE=2∠DBF,同理得:∠CFE=2∠CBF,∴∠EFD+∠EFC=2∠DBF+2∠CBF=2∠ABC=90°,∴DF=CF,且DF⊥CF.(2)(1)中的结论仍然成立.证明:如图,此时点D落在AC上,延长DF交BC于点G.∵∠ADE=∠ACB=90°,∴DE∥BC.∴∠DEF=∠GBF,∠EDF=∠BGF.∵F为BE中点,∴EF=BF.∴△DEF≌△GBF.∴DE=GB,DF=GF.∵AD=DE,∴AD=GB,∵AC=BC,∴AC﹣AD=BC﹣GB,∴DC=GC.∵∠ACB=90°,∴△DCG是等腰直角三角形,∵DF=GF.∴DF=CF,DF⊥CF.(3)延长DF交BA于点H,∵△ABC和△ADE是等腰直角三角形,∴AC=BC,AD=DE.∴∠AED=∠ABC=45°,∵由旋转可以得出,∠CAE=∠BAD=90°,∵AE∥BC,∴∠AEB=∠CBE,∴∠DEF=∠HBF.∵F是BE的中点,∴EF=BF,∴△DEF≌△HBF,∴ED=HB,∵AC=,在Rt△ABC中,由勾股定理,得AB=4,∵AD=1,∴ED=BH=1,∴AH=3,在Rt△HAD中由勾股定理,得DH=,∴DF=,∴CF=∴线段CF 的长为.16.已知△ABC与△ADE都是等腰直角三角形,∠ACB=∠ADE=90°,AC=BC=4,AD=DE,点F是BE的中点,连接DF,CF.(1)如图1,当点D在AB上,且点E是AC的中点时,求CF的长.(2)如图1,若点D落在AB上,点E落在AC上,证明:DF⊥CF.(3)如图2,当AD⊥AC,且E点落在AC上时,判断DF与CF之间的关系,并说明理由.(4)在(3)的条件下,若AD=2,求CF的长.【解答】解:(1)如图1,∵AC=BC=4,点E是AC的中点,∴EC=2.在直角△BCE中,BE2=BC2+CE2=20,∴BE=2.∵CF是直角△BCE斜边上的中线,∴CF==;(2)证明:如图1,∵∠ACB=∠ADE=90°,点F为BE中点∴DF=BE,CF=BE,∴DF=CF.∵△ABC和△ADE是等腰直角三角形,∴∠ABC=45°∵BF=DF,∴∠DBF=∠BDF,∵∠DFE=∠ABE+∠BDF,∴∠DFE=2∠DBF,同理得:∠CFE=2∠CBF,∴∠EFD+∠EFC=2∠DBF+2∠CBF=2∠ABC=90°,∴DF⊥CF.(3)DF与CF相等且垂直.如图2,延长DE交BC于点G,连接FG,易证DG⊥BC.∵∠DEA=45°,∴∠BEG=45°,∠DEF=135°.又∵∠B=45°,∴BG=EG.∵点F是BE的中点,∴FG=FE,FG⊥BE,∠EGF=45°,∴∠FGC=∠EGF+EGC=135°,∴∠DEF=∠CGF.又∵∠ADE=90°,∠ACB=90°,DG⊥BC,∴四边形ADGC是矩形,∴AD=GC,∴DE=GC,∴△DEF≌△CGF,∴∠DFE=∠CFG,DF=CF.∵∠DFE+∠CFE=90°,∴CF⊥DF,∴DF与CF相等且垂直.(4)如图2,连接CD.∵AD=2,AC=4,根据勾股定理可知CD=2.而根据(3)可知,△CDF是等腰直角三角形,∴CF=CD ÷=.17.已知:△ABC和△ADE都是等腰直角三角形,∠ACB=∠ADE=90°,点M是BE的中点,连接CM、DM.(1)当点D在AB上,点E在AC上时(如图一),求证:DM=CM,DM⊥CM;(2)当点D在CA延长线上时(如图二)(1)中结论仍然成立,请补全图形(不用证明);(3)当ED∥AB时(如图三),上述结论仍然成立,请加以证明.【解答】证明:(1)如图一中,延长DM使得MN=DM,连接BN、CN.在△DME和△NMB中,,∴△DME≌△NMB,∴DE=BN,∠MDE=∠MNB,∴DE∥NB,∴∠ADE=∠ABN=90°,∵△ABC和△ADE都是等腰直角三角形,∠ACB=∠ADE=90°,∴AD=DE=BN,AC=BC,∠A=∠ABC=45°,∴∠CBN=45°=∠A,在△ACD和△BCN中,,∴△ACD≌△BCN,∴DC=CN,∠ACD=∠BCN,∴∠DCN=∠ACB=90°,∴△DCN是等腰直角三角形,∵DM=MN,∴DM=CM.DM⊥CM.(2)补充图形如图二所示,延长DM交CB的延长线于N,∵△ABC和△ADE都是等腰直角三角形,∠ACB=∠ADE=90°,∴AD=DE=BN,AC=BC,∠A=∠ABC=45°,∵∠EDC+∠DCN=180°,∴DE∥CN,∴∠EDM=∠N在△DME和△NMB中,,∴△DME≌△NMB,∴DE=BN=AD,DM=MN,∴CD=CN,∴∠CDN=∠N=45°,CM=DM=MN,CM⊥DN,∴DM=CM.DM⊥CM.(3)如图三中,如图一中,延长DM交AB于N连接CN.∵DE∥AB,∴∠MBN=∠MED,在△DME和△NMB中,,∴△DME≌△NMB,∴DE=BN=AD,DM=MN,∵△ABC和△ADE都是等腰直角三角形,∠ACB=∠ADE=90°,∴AD=DE=BN,AC=BC,∠BAC=∠ABC=45°,∵∠AED+∠BAE=180°,∴∠BAE=135°,∵∠BAC=∠EAD=45°,∴∠DAC=∠CBN=45°在△ACD和△BCN中,,∴△ACD≌△BCN,∴DC=CN,∠ACD=∠BCN,∴∠DCN=∠ACB=90°,∴△DCN是等腰直角三角形,∵DM=MN,∴DM=CM.DM⊥CM.18.在△ABC 中,∠BAC=90°,AB=AC ,点D 为直线BC 上一动点(点D 不与点B 、C 重合),以AD 为直角边在AD 右侧作等腰三角形ADE ,使∠DAE=90°,连接CE .探究:如图①,当点D 在线段BC 上时,证明BC=CE +CD . 应用:在探究的条件下,若AB=,CD=1,则△DCE 的周长为 2+.拓展:(1)如图②,当点D 在线段CB 的延长线上时,BC 、CD 、CE 之间的数量关系为 BC=CD ﹣CE .(2)如图③,当点D 在线段BC 的延长线上时,BC 、CD 、CE 之间的数量关系为 BC=CE ﹣CD .【解答】解:探究:∵∠BAC=90°,∠DAE=90°, ∴∠BAC=∠DAE .∵∠BAC=∠BAD +∠DAC ,∠DAE=∠CAE +∠DAC , ∴∠BAD=∠CAE .∵AB=AC ,AD=AE ,∴△ABD ≌△ACE . ∴BD=CE . ∵BC=BD +CD , ∴BC=CE +CD .应用:在Rt △ABC 中,AB=AC=,∴∠ABC=∠ACB=45°,BC=2,∵CD=1, ∴BD=BC ﹣CD=1,由探究知,△ABD ≌△ACE , ∴∠ACE=∠ABD=45°, ∴∠DCE=90°,在Rt △BCE 中,CD=1,CE=BD=1, 根据勾股定理得,DE=,∴△DCE 的周长为CD +CE +DE=2+故答案为:2+拓展:(1)同探究的方法得,△ABD ≌△ACE . ∴BD=CE∴BC=CD ﹣BD=CD ﹣CE , 故答案为BC=CD ﹣CE ;(2)同探究的方法得,△ABD ≌△ACE . ∴BD=CE∴BC=BD ﹣CD=CE ﹣CD , 故答案为:BC=CE ﹣CD .19.如图1,直线AM ⊥AN ,AB 平分∠MAN ,过点B 作BC ⊥BA 交AN 于点C ;动点E 、D 同时从A 点出发,其中动点E 以2m/s 的速度沿射线AN 方向运动,动点D 以1m/s 的速度沿射线AM 方向运动;已知AC=6cm ,设动点D ,E 的运动时间为t .(1)试求∠ACB 的度数;(2)当点D 在射线AM 上运动时满足S △ADB :S △BEC =2:3,试求点D ,E 的运动时间t 的值;(3)当动点D 在射线AM 上运动,点E 在射线AN 上运动过程中,是否存在某个时间t ,使得△ADB 与△BEC 全等?若存在,请求出时间t 的值;若不存在,请说出理由.【解答】解:(1)如图1中,∵AM ⊥AN ,∴∠MAN=90°,∵AB平分∠MAN,∴∠BAC=45°,∵CB⊥AB,∴∠ABC=90°,∴∠ACB=45°.(2)如图2中,作BH⊥AC于H,BG⊥AM于G.∵BA平分∠MAN,∴BG=BH,∵S△ADB:S△BEC=2:3,AD=t,AE=2t,∴•t•BG :•(6﹣2t)•BH=2:3,∴t=s.∴当t=s时,满足S△ADB:S△BEC=2:3.(3)存在.∵BA=BC,∠BAD=∠BCE=45°,∴当AD=EC时,△ADB≌△CEB,∴t=6﹣2t,∴t=2s,∴满足条件的t的值为2s.20.我们新定义一种三角形:若一个三角形中存在两边的平方差等于第三边上高的平方,则称这个三角形为勾股高三角形,两边交点为勾股顶点.●特例感知①等腰直角三角形是勾股高三角形(请填写“是”或者“不是”);②如图1,已知△ABC为勾股高三角形,其中C为勾股顶点,CD是AB边上的高.若BD=2AD=2,试求线段CD的长度.●深入探究如图2,已知△ABC为勾股高三角形,其中C为勾股顶点且CA>CB,CD是AB边上的高.试探究线段AD与CB的数量关系,并给予证明;●推广应用如图3,等腰△ABC为勾股高三角形,其中AB=AC>BC,CD为AB边上的高,过点D向BC边引平行线与AC边交于点E.若CE=a,试求线段DE的长度.【解答】解:●特例感知:①等腰直角三角形是勾股高三角形.故答案为是.②如图1中,根据勾股定理可得:CB2=CD2+4,CA2=CD2+1,于是CD2=(CD2+4)﹣(CD2+1)=3,∴CD=.●深入探究:如图2中,由CA2﹣CB2=CD2可得:CA2﹣CD2=CB2,而CA2﹣CD2=AD2,∴AD2=CB2,即AD=CB;●推广应用:过点A向ED引垂线,垂足为G,∵“勾股高三角形”△ABC为等腰三角形,且AB=AC>BC,∴只能是AC2﹣BC2=CD2,由上问可知AD=BC……①.又ED∥BC,∴∠1=∠B……②.而∠AGD=∠CDB=90°……③,∴△AGD≌△CDB(AAS),∴DG=BD.易知△ADE与△ABC均为等腰三角形,根据三线合一原理可知ED=2DG=2BD.又AB=AC,AD=AE,∴BD=EC=a,∴ED=2a.。
4.3.3 几何变换I(反射续及对称图形)(含答案)

【课堂例题】例1.写出函数2,2,2x y x y x y =-==分别关于下列直线反射后的函数解析式:(1)1x =-;(2)3y =.例2.函数22(1)y x =-经过一次平移或一次反射后变为函数22(2)y x =+,求平移量或反射直线方程.例3.已知函数()y f x =是对称图形,根据下列等式接触函数()y f x =的对称轴方程或对称中心坐标.(1)()()f x f x =-;(2)()()f x f x =--;(3)()(2)f x f x =-(4)()(3)f x f x =--【知识再现】1.(直线)反射变换,又称为直线对称变换续①反射轴为直线x a =的变换公式为 ,函数()y f x =在此变换下变为函数y = ;②反射轴为直线y b =的变换公式为 ,函数()y f x =在此变换下变为函数y = ;特别地,在此变换下不变的函数图像为轴对称图形.2.(点)反射变换,又称为中心对称变换①关于原点O 的变换公式为 ,函数()y f x =在此变换下变为函数y = ;②关于定点(,)a b 的变换公式为 ,函数()y f x =在此变换下变为函数y = .特别地,在此变换下不变函数图像为中心对称图形.【基础训练】1.(1)函数2y x =关于直线2x =对称的函数为 ;(2)2y x =与函数23y x =-关于直线 对称.2.已知()f x 与()g x 的图像关于直线1x =-对称,且(3)2f =,则()g x 必过点 .3.与函数23y x =+关于原点中心对称的函数为 ;4.函数2y x =与函数23(2)y x =--关于 对称.5.若函数2()f x x bx c =++,满足()(4)f x f x =-,则把(1),(2),(4)f f f 从小到大依次排列为 ;6.下列说法正确的是 .(写出所有正确命题的序号)①函数()y f x =是奇函数,那么(2)y f x =+的图像是关于点(2,0)点中心对称的图形; ②若()(2)f x f x =--对任意x 都成立,则函数()y f x =的图像关于直线1x =-对称. ③函数()y f x =与函数的(2)y f x =-图像关于直线2x =对称;④若()(2)f x f x =--对任意x 都成立,则()y f x =的图像关于点(1,0)中心对称; ⑤平移、轴反射变换、中心反射变换都保持平面上任意两点间的距离在变换前后不变.7.利用变换证明:函数312x y x -=+的图像关于点(2,3)-中心对称.【巩固提高】8.将()y f x =的图像依次进行下列变换各一次后得到()y g x =的图像:①关于y 轴反射;②向右平移1个单位③关于原点反射;④向下平移2个单位; ⑤关于y 轴反射.(1)若(1,2)在()y f x =的图像上,则哪一点必在()y g x =的图像上;(2)写出函数()y g x =的解析式(用含有f 的解析式表示).9.根据对称与变换的关系,我们已经知道F 为轴对称图形⇔F 在轴反射变换下不变;F 为中心对称图形⇔F 在中心反射变换下不变;那么类比可得:F 为平移对称图形⇔ .如果(),y f x x R =∈的图像在变换:“水平移动2个单位长度”下是平移对称图形,且()y f x =在区间[0,2]上的图像如图所示:(1)画出函数在上的大致图像,(不要超出网格部分);(2)写出()f x 的单调区间、对称轴与对称中心. (3)若函数(),y g x x R =∈的图像在变换:“水平移动,(0)t t ≠”下是平移对称图形, 求1()g x 注所满足的条件.注1:这样的函数我们称为以t 为周期的周期函数.(选做)10.已知函数3()f x x x =-,将()f x 的图像沿x 轴、y 轴正方向分别 平行移动,t s 个单位长度后得到函数()g x 的图像.(1)写出()g x 的解析式;(2)求证:()f x 的图像与()g x 的图像关于点(,)22t s A 对称;(3)如果()f x 的图像与()g x 的图像有且仅有一个公共点, 求证:34t s t =-,且0t ≠.【温故知新】11.要想得到函数(26)y f x =-的图像,只需要把函数(2)y f x =的图像() A.向左平移6个单位; B.向左平移3个单位;C.向右平移6个单位;D.向右平移3个单位.【课堂例题答案】例1.(1)2y x =+;(2)22(2)y x =+;(3)21()2x y +=.例2.水平移动-3,即向左移动3个单位;或关于直线12x =-反射. 例3.(1)关于y 轴对称;(2)关于原点O 对称;(3)关于直线1x =对称;(4)关于点3(,0)2对称.【知识再现答案】 1.'2'x a x y y =-⎧⎨=⎩,(2)f a x -; ''2x x y b y =⎧⎨=-⎩,2()b f x -. 2.''x x y y =-⎧⎨=-⎩,()f x --; '2'2x a x y b y =-⎧⎨=-⎩,2(2)b f a x --. 【习题答案】1.82y x =-2.32y =3.(5,2)-4.3(1,)25.(2)(1)(4)f f f <<6.②④⑤7.证:即证()6(4)f x f x =---3(4)1316(4)6()(4)22x x f x f x x x -------=-==--++. 证毕 8.(1)(0,4)-;(2)()2(1)g x f x =---提示:变换公式为:3212112312132111:,:,:x x x x x x x x T T T y y y y y y y y=-=-=-=+=-+⎧⎧⎧⎨⎨⎨====-=-⎩⎩⎩ 435445435411:,:222x x x x x x T T y y y y y y ==-=-=-+⎧⎧⎨⎨=-=--==--⎩⎩ 在此变换下312()()[(1)](1)(1)T T T y f x y f x y f x f x y f x =−−→=-−−→=--=-−−→=-+54(1)2(1)2T T y f x y f x −−→=-+-−−→=---9.F(1)如上图;(2),[2,21][21,2]k Z k k k k ∈+↑-↓,对称轴为直线x k =,对称中心为1(,0)2k +(3)()()g x t g x -=提示:()g x 平移t 后不变.10.(1)3()()()()g x f x t s x t x t s =-+=---+;(2)即证:()()g x s f t x =-- 33()[()()]()()()s f t x s t x t x x t x t s g x --=----=---+= 证毕(3)证法一:()()g x f x =有且仅有一解222330tx t x t t s ⇔-+--=有且仅有一解2220(3)12()0t t t t t s ≠⎧⇔⎨∆=----=⎩,化简后得证. 证法二:(),()g x f x 的公共点应该关于点A 对称,所以这个仅有的公共点就是点A , 2()224s t t f s t ∴=⇒=-,若0t =则0s =,则()()f x g x =,有无穷多个公共点,不合题意.因此2,04t s t t =-≠. 11.D。
中考试题几何变换课后练习一及详解.docx

学科:数学专题:几何变换主讲教师:黄炜北京四中数学教师重难点易错点解析题一:题面:平面直角坐标系中,O为坐标原点,点A的坐标为(3,1),将OA绕原点按逆时针方向旋转30°得OB,则点B的坐标为()A.(1,3)B.( -1,3)C.(0,2)D.(2,0)金题精讲题一:题面:如图,正方形ABCD与正三角形AEF的顶点A重合,将△AEF绕顶点A旋转,在旋转过程中,当BE=DF时,∠BAE的大小可以是.满分冲刺题一:题面:如图,两个边长相等的正方形ABCD和EFGH,正方形EFGH的顶点E固定在正方形ABCD的对称中心位置,正方形EFGH绕点E顺时针方向旋转,设它们重叠部分的面积为S,旋转的角度为θ,S与θ的函数关系的大致图象是()A.B.C.D.题二:题面:以边长为2的正方形的中心O为端点,引两条相互垂直的射线,分别与正方形的边交于A、B两点,则线段AB的最小值是.课后练习详解重难点易错点解析题一:答案:A.详解:如图,作AC⊥x轴于C点,BD⊥y轴于D点,∵点A的坐标为(3,1),∴AC=1,OC=3.3+1=2.∴∠AOC=30°.∴OA=()22∵OA绕原点按逆时针方向旋转30°得OB,∴∠AOB=30°,OA=OB.∴∠BOD=30°.∴Rt△OAC≌Rt△OBD(AAS).∴DB=AC=1,OD=OC=3.∴B点坐标为(1,3).故选A.金题精讲题一:答案:15°或165°.详解:正三角形AEF可以在正方形的内部也可以在正方形的外部,所以要分两种情况分别求解:①当正三角形AEF在正方形ABCD的内部时,如图1,∵正方形ABCD与正三角形AEF的顶点A重合,∴AB=AD,AE=AF.∵当BE=DF时,在△ABE和△ADF中,AB=AD,BE=DF,AE=AF,∴△ABE≌△ADF(SSS).∴∠BAE=∠F AD.∵∠EAF=60°,∴∠BAE+∠F AD=30°.∴∠BAE=∠F AD=15°.②当正三角形AEF在正方形ABCD的外部,顺时针旋转小于180°时,如图2,同上可得△ABE≌△ADF(SSS).∴∠BAE=∠F AD.∵∠EAF=60°,∴∠BAF=∠DAE.∵90°+60°+∠BAF+∠DAE=360°,∴∠BAF=∠DAE=105°.∴∠BAE=∠F AD=165°.③当正三角形AEF在正方形ABCD的外部,顺时针旋转大于180°时,如图3,同上可得△ABE≌△ADF(SSS). ∴∠BAE=∠F AD.∵∠EAF=60°,∠BAE=90°,∴90°+∠DAE=60°+∠DAE,这是不可能的.∴此时不存在BE=DF的情况.综上所述,在旋转过程中,当BE=DF时,∠BAE的大小可以是15°或165°.满分冲刺题一:答案:B.详解:如图,过点E作EM⊥BC于点M,EN⊥AB于点N,∵点E是正方形的对称中心,∴EN=EM,EMBN是正方形.由旋转的性质可得∠NEK=∠MEL,在Rt△ENK和Rt△EML中,∠NEK=∠MEL,EN=EM,∠ENK=∠EML,∴△ENK≌△EML(ASA).∴阴影部分的面积始终等于正方形面积的14,即它们重叠部分的面积S不因旋转的角度θ的改变而改变.故选B.题二:答案:2.详解:∵四边形CDEF是正方形,∴∠OCD=∠ODB=45°,∠COD=90°,OC=OD.∵AO⊥OB,∴∠AOB=90°.∴∠CAO+∠AOD=90°,∠AOD+∠DOB=90°,∴∠COA=∠DOB.∵在△COA和△DOB中,∠OCA=∠ODB,OC=OD,∠COA=∠DOB,∴△COA≌△DOB(ASA).∴OA=OB.∵∠AOB=90°,∴△AOB是等腰直角三角形.由勾股定理得:222AB OA OB OA=+=.∴要使AB最小,只要OA取最小值即可.根据垂线段最短的性质,当OA⊥CD时,OA最小.∵四边形CDEF是正方形,∴FC⊥CD,OD=OF.∴CA=DA,∴OA=12CF=1.∴AB=2.初中数学试卷鼎尚图文**整理制作。
八年级数学竞赛例题专题讲解26:几何变换(含答案)

专题29 几何变换阅读与思考几何变换是指把一个几何图形1F 变换成另一个几何图形2F 的方法,若仅改变图形的位置,而不改变图形的形状和大小,这种变换称为合同变换,平移、对称、旋转是常见的合同变换.l图3图2图1F 1F 2F 1F 2F 2F 1α1.平移变换如图1,如果把图形1F 上的各点都按一定方向移动一定距离得到图形2F 后,则由1F 到2F 的变换叫平移变换.平移变换前后的对应线段相等且平行,对应角的两边分别平行且方向一致. 2.对称变换如图2,将平面图形1F 变换到与它成轴对称的图形2F ,这样的几何变换就叫做关于直线l (对称轴)的对称变换.对称变换前后的对应线段相等,对应角相等,其对称轴是连结各对应点线段的垂直平分线. 3.旋转变换如图3,将平面图形1F 绕这一平面内一定点M 旋转一个定角α,得到图形2F ,这样的变换叫旋转变换,M 叫旋转中心,α叫旋转角.旋转变换前后的图形是全等的,对应点到旋转中心的距离相等,对应线段的夹角等于旋转角.例题与求解【例l 】如图,∠AOB =045,角内有点P ,PO =10,在角的两边上有两点Q ,R (均不同于O ),则△PQR 的周长的最小值为_______________. (黄冈市竞赛试题) 解题思路:作P 点关于OA ,OB 的对称点,确定Q ,R 的位置,化折线为直线,求△PQR 的最小值.BAOP【例2】如图,P 是等边△ABC 的内部一点,∠APB ,∠BPC ,∠CPA 的大小之比是5:6:7,则以PA ,PB ,PC 为边的三角形的三个角的大小之比(从小到大)是( )A. 2:3:4B. 3:4:5C. 4:5:6D.不能确定(全国通讯赛试题)ABCP解题思路:解本例的关键是如何构造以PA ,PB ,PC 为边的三角形,若把△PAB ,△PBC ,△PCA 中的任一个,绕一个顶点旋转060,就可以把PA ,PB ,PC 有效地集中在一起.【例3】如图,在△ABC 中,AD ⊥BC 于D ,∠B =2∠C ,求证:AB+BD=CD.(天津市竞赛试题)解题思路:用截长法或补短法证明,实质都利用AD 翻折造全等.ACBD【例4】如图,六边形ABCDEF 中,AB ∥DE ,BC ∥FE ,CD ∥AF ,对边之差BC -FE=ED -AB=AF -CD >0,求证:该六边形的各角都相等.(全俄数学奥林匹克竞赛试题)解题思路:设法能将复杂的条件BC -FE=ED -AB=AF -CD >0,用一个基本图形表示,题设条件有平行条件,考虑实施平移变换.A FEDC B【例5】已知Rt △ABC 中,AC=BC ,∠ACB =090,∠MCN =045 (1) 如图1,当M 、N 在AB 上时,求证:222MN AM BN =+(2) 如图2,将∠MCN 绕C 点旋转,当M 在BA 的延长线时,上述结论是否成立?若成立,请证明;若不成立,请说明理由.(天津市中考试题)解题思路:222MN AM BN =+符合勾股定理的形式,需转化为直角三角形可将△ACM 沿直线CM 对折,得△DCM . 连DN ,只需证DN=BN ,∠MDN =090;或将△ACM (或△BCM )旋转.【例6】如图,∠DAC=012,∠DBC=024,∠CAB=036,∠ABD=048,求∠DCA 的度数.(日本算术奥林匹克试题)解题思路:已知角的度数都是12的倍数,0362460+=,这使我们想到构作正三角形.CD AB图2图1NMABC C BA MN能力训练1.在如图所示的单位正方形网格中,将△ABC 向右平移3个单位后得到△A B C ''',则BA A '∠的度数是_______.(泰安市中考试题)ABCAB CPyx BAOC(第1题) (第2题) (第3题)2.如图,P 是等边△ABC 内一点,PA =6,PB =8,PC =10,则∠APB =_________.3.如图,直线143y x =与双曲线2(0)k y k x =>交于点A ,将直线143y x =向右平移92个单位后,与双曲线2k y x =交于点B ,与x 轴交于点C . 若2AOBC=,则k =______________. (武汉市中考试题) 4.如图,△ABC 中,∠BAC =045,AD ⊥BC ,DB =3,DC =2,则△ABC 的面积是___________. 5.如图,P 为正方形内一点,若::1:2:3PA PB PC =,则∠APB 的度数是( ). A. 0120 B. 0135 C. 0145 D. 0150(第6题)(第5题)(第4题)D'OACB ABDC PABDCD A'6.如图,边长为2的正方形ABCD 的对角线交于点O ,把边BA 、CD 分别绕点B 、C 同时逆时针旋转060,得四边形A BCD '',下列结论:①四边形A BCD ''为菱形;②12ABCD A BCD S S ''=正方形四边形;③线段OD '的长为31-. 其中正确的结论有( ).A. 0个B. 1个C. 2个D. 3个7. 如图,A ,B 两个电话机离电话线l 的距离分别是3米,5米,CD =6米,若由L 上一点分别向A ,B 连电话线,最短为( ).A. 11米B. 10米C. 9米D. 8米8. 如图,在△ABC 中,∠BAC =0120,P 是△ABC 内一点,若记x PA PB PC =++,y AB AC =+,则( ).A. x y <B. x y =C. x y >D. x 与y 的大小关系不确定l第8题图第7题图CBDACBA P9. 如图,已知D 是△ABC 中BC 边的中点,过D 作DE ⊥DF ,分别交AB 于E ,交AC 于F ,求证:BE CF EF +>.(天津市竞赛试题)FDBCAE10.如图,△ABC ,△A B C '''其各边交成六边形DEFGHK ,且EF ∥KH ,GH ∥DE ,FG ∥KD ,0KH EF FG KD DE GH -=-=->. 求证:△ABC ,△A B C '''均为为正三角形.(“缙云杯”邀请赛试题)GFED H KABC C'B'A'11.如图,已知△ABC 中,AB=AC ,P ,Q 分别为AC ,AB 上的点,且AP=PQ=QB=BC ,求∠PCQ .(北京市竞赛试题)PQAB C12.如图,已知在平面直角坐标系中,A ,B 两点的坐标分别为(2,3)A -,(4,1)B -. (1) 若(,0)P x 是x 轴上的一个动点,当△PAB 的周长最短时,求x 的值;(2)若(,0),(3,0)C a D a +是x 轴上的两个动点,当四边形ABCD 的周长最短时,求a 的值; (3)设M ,N 分别为x 轴,y 轴上的动点,问:是否存在这样的点(,0)M m 和(0,)N n ,使四边形ABMN 的周长最短?若存在,求出,m n 的值;若不存在,请说明理由.(浙江省湖州市中考试题)yxOAB13.如图,梯形ABCD 中,AD ∥BC ,分别以两腰AB ,CD 为边向两边作正方形ABGE 和正方形DCHF ,设线段AD 的垂直平分线l 交线段EF 于点M ,EP ⊥l 于P ,FQ ⊥l 于Q ,求证:EP=FQ.(全国初中数学联赛试题)lM L P Q NC HFEGA DB14.如图所示,已知Rt △ABC 中,AB=BC ,在Rt △ADE 中,AD=DE ,连结EC ,取EC 中点M ,连结DM 和BM .(1)若点D 在边AC 上,点E 在边AB 上且与点B 不重合,如图1,求证:BM=DM ,且BM ⊥DM ; (2)如图2中的△ADE 绕点A 逆时针旋转小于045的角,那么(1)中的结论是否仍成立?如果不成立,请举出反例;如果成立,请给予证明.(广州市中考试题)图2图1MEMACBBCAEDD15.如图,在△ABC 中,∠BAC =045,AD ⊥BC 于D ,若BD =3,CD =2,求△ABC 的面积.(山东省竞赛试题)23BCAD。
几何三大变换(习题及答案)
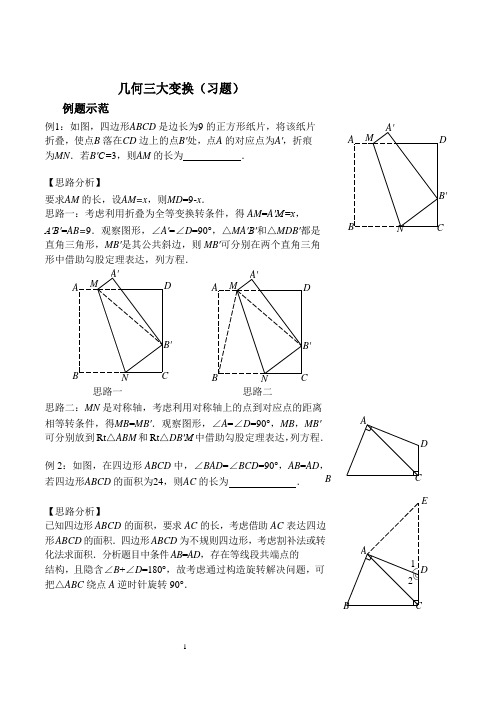
A' MA'MA12几何三大变换(习题)例题示范例1:如图,四边形A BCD 是边长为9的正方形纸片,将该纸片A'折叠,使点B落在C D 边上的点B′处,点A的对应点为A′,折痕 A M D 为M N.若B′C=3,则A M 的长为.【思路分析】要求A M 的长,设A M=x,则M D=9-x.B' 思路一:考虑利用折叠为全等变换转条件,得AM=A′M=x,A′B′=AB=9.观察图形,∠A′=∠D=90°,△MA′B′和△MDB′都是 B N C 直角三角形,MB′是其公共斜边,则MB′可分别在两个直角三角形中借助勾股定理表达,列方程.A D A DB' B'B NC B N C思路一思路二思路二:MN 是对称轴,考虑利用对称轴上的点到对应点的距离相等转条件,得M B=MB′.观察图形,∠A=∠D=90°,MB,MB′ A可分别放到Rt△ABM 和Rt△DB′M中借助勾股定理表达,列方程.D例 2:如图,在四边形ABCD 中,∠BAD=∠BCD=90°,AB=AD,若四边形A BCD 的面积为24,则A C 的长为. B CE 【思路分析】已知四边形ABCD 的面积,要求AC 的长,考虑借助AC 表达四边形ABCD 的面积.四边形ABCD 为不规则四边形,考虑割补法或转化法求面积.分析题目中条件AB=AD,存在等线段共端点的结构,且隐含∠B+∠D=180°,故考虑通过构造旋转解决问题,可 D把△ABC 绕点A 逆时针旋转 90°.B CPN Q M NPDME巩固练习1.如图,将边长为2的等边三角形A BC 沿B C 方向平移1个单位得到△DEF,则四边形A BFD 的周长为()A.6 B.8 C.10 D.12A DB B A A'C ( B' ) C'第1题图第2题图2.如图,已知△ABC 的面积为 8,将△ABC 沿BC 方向平移到△A′B′C′的位置,使点B′和点C 重合,连接AC′,交A′C 于点D,则△CAC′的面积为()A.4 B.6 C.8 D.163.如图,在6 ⨯4 的方格纸中,格点三角形甲经过旋转后得到格点三角形乙,则其旋转中心是()A.格点M B.格点N C.格点P D.格点QA E DM甲乙B F C第3题图第4题图4.如图,在正方形纸片ABCD 中,E,F 分别是AD,BC 的中点,沿过点B 的直线折叠,使点C 落在EF 上,落点为N,折痕交CD 边于点M,BM 与EF 交于点P,再展开.则下列结论:①CM=DM;②∠ABN=30°;③A B2 = 3CM 2 ;④△PMN 是等边三角形.其中正确的有()A.1 个B.2 个C.3 个D.4 个5.如图,已知O A⊥OB,等腰直角三角A形C DE 的腰C D 在O B 上,∠ECD= N45°,将△C DE绕点C 逆时针旋转75°,点E的对应点N恰好落在O A 上,则OC的值为.CDO C D BEDA'6.如图,E 是正方形 A BCD 内一点,连接 A E ,BE ,CE ,将△ABE 绕点B 顺时针旋转90°至△CBE ′的位置.若AE =1,BE =2,CE =3,则∠BE ′C = .ADBCE' F B 第 6 题图 第 7 题图7. 如图,在平行四边形 ABCD 中,∠A =70°,将该平行四边形折叠,使点 C ,D 分别落在点 E ,F 处,折痕为 M N .若点 E ,F 均在直线 A B 上,则∠AMF = . 8. 如图,在 Rt △ABC 中,∠C =90°,∠A =30°,BC =1,点 D 在AC 边上,将△ABD 沿直线 B D 翻折后,点 A 落在点 E 处.若AD ⊥DE ,则线段 D E 的长为 .BAEDCAEB C 第 8 题图 第 9 题图9. 如图,矩形 A BCD 中,AB =15cm ,点 E 在 A D 上,且 A E =9cm , 连接 E C ,将长方形 A BCD 沿直线 B E 翻折,点 A 恰好落在 E C 上的点 A'处,则 A 'C = cm . 10. 如图,在矩形 ABCD 中,AB =3,AD =9,将此长方形折叠, 使点 D 与点 B 重合,点 C 的对应点为点 C ′,折痕为 EF ,则 EF 的长为 .思考小结请结合本讲所学内容,回忆三大变换的思考层次平移旋转轴对称全等变换对应边平行(或在同一直线上)且相等,对应角相等.对应边相等,对应角相等.对应边相等,对应角相等.对应点对应点所连线段平行(或在同一直线上)且相等.对应点到旋转中心的距离相等;对应点与旋转中心的连线所成的角等于旋转角;对应点连线的垂直平分线都经过旋转中心.对应点所连线段被对称轴垂直平分;对称轴上的点到对应点的距离相等.新关系平移会产生平行四边形.旋转会产生等腰三角形.折叠会产生垂直平分、等腰三角形.应用常应用在天桥问题、存在性问题.当题目中出现等线段共点的时候考虑旋转结构.常应用在折叠问题、最值问题.【参考答案】1. B2. C3. B4. C5.2 26. 135°7. 40°8. 3 19. 810. 10。
人教版2020年九年级数学上册 二次函数-函数的性质及几何变换(含答案)

人教版2020年九年级数学上册二次函数-函数的性质及几何变换一、选择题1.已知二次函数y=2(x+1)(x﹣a),其中a>0,且对称轴为直线x=2,则a的值是( )A.3B.5C.7D.不确定2.点P1(-1,y1),P2(3,y2),P3(5,y3)均在二次函数y=-x2+2x+c的图象上,则y1,y2,y3的大小关系是( )A.y3>y2>y1B.y3>y1=y2C.y1>y2>y3D.y1=y2>y33.一次函数y=ax+b(a≠0)与二次函数y=ax2+bx+c(a≠0)在同一平面直角坐标系中的图象可能是( )4.函数y=﹣2x2﹣8x+m的图象上有两点A(x1,y1),B(x2,y2),若x1<x2<﹣2,则( )A.y1<y2B.y1>y2C.y1=y2D.y1、y2的大小不确定5.已知二次函数y=3(x-1)2+k的图象上有A(,y1),B(2,y2),C(-,y3)三个点,则y1,y2,y3的大小关系是( )A.y1>y2>y3B.y2>y1>y3C.y3>y1>y2D.y3>y2>y16.已知关于x的方程ax2+bx+c=5的一个根是2,且二次函数y=ax2+bx+c的对称轴是直线x=2,则这条抛物线的顶点坐标为()A.(2,﹣3)B.(2,1)C.(2,5)D.(5,2)7.对于抛物线y=﹣x2+2x+3,有下列四个结论:①它的对称轴为x=1;②它的顶点坐标为(1,4);③它与y轴的交点坐标为(0,3),与x轴的交点坐标为(﹣1,0)和(3,0);④当x>0时,y随x的增大而减小.其中正确的个数为()A.1 B.2 C.3 D.48.若将抛物线y=5x2先向右平移2个单位,再向上平移1个单位,得到的新抛物线的表达式为( )A.y =5(x-2)2+1B.y =5(x+2)2+1C.y =5(x-2)2-1D.y =5(x+2)2-19.在平面直角坐标系中,将抛物线y=x2-4先向右平移2个单位,再向上平移2个单位,得到的抛物线解析式为( )A.y=(x+2)2+2B.y=(x-2)2-2C.y=(x-2)2+2D.y=(x+2)2-210.抛物线y=x2+bx+c图象向右平移2个单位再向下平移3个单位,所得图象的解析式为y=x2﹣2x﹣3,则b、c的值为()A.b=2,c=2B.b=2,c=0C.b=﹣2,c=﹣1D.b=﹣3,c=2二、填空题11.已知A(0,3),B(2,3)是抛物线y=-x2+bx+c上两点,该抛物线的顶点坐标是________.12.二次函数y=x2+6x+5图象的顶点坐标为 .13.如图,点E是抛物线y=a(x﹣2)2+k的顶点,抛物线与y轴交于点C,过点C作CD∥x轴,与抛物线交于点B,与对称轴交于点D.点A是对称轴上一点,连结AC、AB.若△ABC是等边三角形,则图中阴影部分图形的面积之和是.14.抛物线y=﹣x2+bx+c的部分图象如图所示,若y=0,则x= .15.如图,抛物线y=ax2+bx+c与x轴相交于点A、B(m+2,0),与y轴相交于点C,点D在该抛物线上,坐标为(m,c),则点A的坐标是________.16.把抛物线y=x2-4x+5的图象向右平移3个单位,再向下平移2个单位,所得图象的解析式是三、解答题17.已知抛物线y=﹣x2+bx+c经过点A(3,0),B(﹣1,0).(1)求抛物线的解析式;(2)求抛物线的顶点坐标.18.如图,已知抛物线y=ax2+bx+c与x轴交于点A(1,0),点B(3,0),且过点C(0,-3).(1)求抛物线的函数表达式和顶点坐标;(2)请你写出一种平移的方法,使平移后抛物线的顶点落在直线y=-x上,并写出平移后抛物线的函数表达式.19.已知二次函数y=ax2+bx-3的图象经过点A(2,-3),B(-1,0).(1)求二次函数的解析式;(2)若把图象沿y轴向下平移5个单位,求该二次函数的图象的顶点坐标.20.如图,抛物线的顶点D的坐标为(1,﹣4),与y轴交于点C(0,﹣3),与x轴交于A、B两点.(1)求该抛物线的函数关系式;(2)在抛物线上存在点P(不与点D重合),使得S△PAB=S△ABD,请求出P点的坐标.21.如图,二次函数的图象与x轴交于A(﹣3,0)和B(1,0)两点,交y轴于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.(1)请直接写出D点的坐标.(2)求二次函数的解析式.(3)根据图象直接写出使一次函数值大于二次函数值的x的取值范围.22.已知二次函数y=ax2-4x+c的图象过点(-1, 0)和点(2,-9).(1) 求该二次函数的解析式并写出其对称轴;(2) 已知点P(2 , -2),连结OP , 在x轴上找一点M,使△OPM是等腰三角形,请直接写出点M的坐标(不写求解过程).参考答案1.答案为:B.2.D 3.C4.A5.答案为:C6.C7.C.8.A9.B10.B11.答案为:(1,4);12.答案为:(﹣3,﹣4).13.答案为2.14.答案为:﹣3或115.答案为:(-2,0).16.答案为:y=x2-10x+2417.解:(1)∵抛物线y=﹣x2+bx+c经过点A(3,0),B(﹣1,0).∴抛物线的解析式为;y=﹣(x﹣3)(x+1),即y=﹣x2+2x+3,(2)∵抛物线的解析式为y=﹣x2+2x+3=﹣(x﹣1)2+4,∴抛物线的顶点坐标为:(1,4).18.解:(1)∵抛物线与x轴交于点A(1,0),点B(3,0),∴可设抛物线表达式为y=a(x-1)(x-3),把C(0,-3)的坐标代入,得3a=-3,解得a=-1,故抛物线表达式为y=-(x-1)(x-3),即y=-x2+4x-3.∵y=-x2+4x-3=-(x-2)2+1,∴抛物线的顶点坐标为(2,1);(2)答案不唯一,如:先向左平移2个单位,再向下平移1个单位,得到的抛物线的解析式为y=-x2,平移后抛物线的顶点为(0,0),落在直线y=-x上.19.解:(1)由已知,有,即,解得∴所求的二次函数的解析式为.(2)(1,)20.解:(1)∵抛物线的顶点D的坐标为(1,﹣4),∴设抛物线的函数关系式为y=a(x﹣1)2﹣4,又∵抛物线过点C(0,﹣3),∴﹣3=a(0﹣1)2﹣4,解得a=1,∴抛物线的函数关系式为y=(x﹣1)2﹣4,即y=x2﹣2x﹣3;(2)∵S△PAB=S△ABD,且点P在抛物线上,∴点P到线段AB的距离一定等于顶点D到AB的距离,∴点P的纵坐标一定为4.令y=4,则x2﹣2x﹣3=4,解得x1=1+2,x2=1﹣2.∴点P的坐标为(1+2,4)或(1﹣2,4).21.解:(1)∵如图,二次函数的图象与x轴交于A(﹣3,0)和B(1,0)两点,∴对称轴是x=﹣1.又点C(0,3),点C、D是二次函数图象上的一对对称点,∴D(﹣2,3);(2)设二次函数的解析式为y=ax2+bx+c(a≠0,a、b、c常数),根据题意得,解得,所以二次函数的解析式为y=﹣x2﹣2x+3;(3)如图,一次函数值大于二次函数值的x的取值范围是x<﹣2或x>1.22.解:(1)对称轴是x=2(2)。
几何三大变换(作图)(北师版)(含答案)

学生做题前请先回答以下问题问题1:平移的思考层次分别是什么?问题2:旋转的思考层次分别是什么?问题3:轴对称的思考层次分别是什么?几何三大变换(作图)(北师版)一、单选题(共5道,每道20分)1.如图,已知,将△AOB绕点O旋转150°后,得到,则此时点A的对应点的坐标为( )A. B.C. D.答案:C解题思路:试题难度:三颗星知识点:旋转三要素2.如图,Rt△ABC中,∠C=90°,∠B=α,将△ABC绕点C逆时针旋转得到,当点落在直线AB上时,旋转角为(其中),那么之间的数量关系为( )A. B.C. D.答案:D解题思路:试题难度:三颗星知识点:旋转三要素3.在梯形纸片ABCD中,AD∥BC,.将纸片沿过点D的直线折叠,使点C落在AD 边上的点处,折痕DE交BC于点E,连接,则四边形的形状准确地说应为( )A.矩形B.菱形C.梯形D.平行四边形答案:B解题思路:试题难度:三颗星知识点:旋转三要素4.当身边没有量角器时,怎样得到一些特定度数的角呢?动手操作有时可以解“燃眉之急”.如图,已知矩形纸片ABCD(矩形纸片要足够长),我们按如下步骤操作可以得到一个特定的角:(1)以点A所在直线为折痕,折叠纸片,使点B落在AD上,折痕与BC交于E;(2)将纸片展平后,再一次折叠纸片,以E所在直线为折痕,使点A落在BC上,折痕EF 交AD于F.则∠AFE=( )A.60°B.67.5°C.72°D.75°答案:B解题思路:试题难度:三颗星知识点:折叠的性质5.在直角三角形纸片ABC中,∠ACB=90°,,如图,将纸片沿某条直线折叠,使点A落在直角边BC上,记落点为D,设折痕与AB,AC边分别交于点E,点F.若折叠后的△CDF与△BDE均为等腰三角形,则纸片中∠B的度数为( )A.45°B.30°或45°C.30°或22.5°D.30°,22.5°或45°答案:B解题思路:试题难度:三颗星知识点:折叠的性质。
八年级数学几何三大变换(平移、旋转)(含答案)

学生做题前请先回答以下问题问题1:平移、旋转、轴对称统称为几何三大变换.几何三大变换都是_________,只改变图形的_________,不改变图形的_____________.问题2:平移的思考层次分别是什么?问题3:旋转的思考层次分别是什么?几何三大变换(平移、旋转)一、单选题(共9道,每道8分)1.如图,将边长为3cm的等边三角形ABC沿BC方向向右平移2cm得到△DEF,则四边形ABFD 的周长为( )cm.A.10B.11C.12D.13答案:D解题思路:试题难度:三颗星知识点:平移的性质2.如图,在梯形ABCD中,AD∥BC,AD=6cm,BC=10cm,高为7cm,若将梯形ABCD向右平移4cm得到梯形A′B′C′D′,则平移前后两梯形重叠部分的面积为( )cm2.A.28B.35C.42D.56答案:A解题思路:试题难度:三颗星知识点:平移的性质3.如图,把Rt△ABC放在平面直角坐标系内,其中∠CAB=90°,,点A,B的坐标分别为(2,0)(8,0),将△ABC沿x轴向右平移,当点C落在直线y=3x-3上时,线段BC扫过的面积为( )A. B.C. D.答案:C解题思路:试题难度:三颗星知识点:平移的性质4.如图,△COD是△AOB绕点O顺时针旋转40°后得到的图形,若点C恰好落在AB上,且∠AOD的度数是90°,则∠B的度数是( )A.70°B.60°C.50°D.40°答案:B解题思路:试题难度:三颗星知识点:旋转的性质5.如图,E是正方形ABCD内一点,将△CDE绕点D按顺时针方向旋转90°后得到△ADF.若DE=3,则EF的长是( )A. B.C.3D.6答案:A解题思路:试题难度:三颗星知识点:旋转的性质6.如图,在△ABC中,∠ACB=90°,∠BAC=30°,将△ABC绕点C按逆时针方向旋转α角,得到△DEC,CD与AB交于点F,连接AD.当旋转角α的度数为( )时,△ADF是等腰三角形.A.30°或60°B.20°或40°C.25°或50°D.20°或40°或60°答案:B解题思路:试题难度:三颗星知识点:旋转的性质7.如图,已知△ABC中,∠C=90°,AC=BC=,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B,则C′B的长为( )A. B.C. D.1答案:C解题思路:试题难度:三颗星知识点:旋转的性质8.如图所示直角三角板ABC,斜边AB=6,∠A=30°,现将其绕点C沿顺时针方向旋转90°至△A′B′C的位置,再沿CB向左平移使点B′落在原三角板ABC的斜边AB上.则三角板向左平移的距离为( )A.1B.C. D.答案:C解题思路:试题难度:三颗星知识点:旋转的性质9.如图,已知,将△AOB绕点O旋转150°后,得到,则此时点A的对应点的坐标为( )A. B.C. D.答案:C解题思路:试题难度:三颗星知识点:作图二、填空题(共3道,每道9分)10.如图,将边长为2cm的正方形ABCD沿其对角线AC剪开,再把△ABC沿着BC平移得到△A′B′C′,若重叠部分的面积为1cm2,则平移的距离AA′=____cm.答案:1解题思路:试题难度:知识点:平移的性质11.如图,在四边形ABCD中,∠BAD=∠BCD=90°,AB=AD,如果cm,则四边形ABCD的面积为____cm2.答案:6解题思路:试题难度:知识点:作图—旋转变换12.如图,在等边三角形ABC中,点O是AC边上,且OA=3,OC=6,点P是AB上一动点,连接OP,将线段OP绕O逆时针旋转60°得到线段OD,要使点D恰好落在BC上,则AP的长是____.答案:6解题思路:试题难度:知识点:作图。
四边形的几何变换-练习与解答

走进四边形的几何变换在近几年的各地中考中,几何变换作为一种数学思想与方法,不断地被命题者青睐与关注,在现行的初中数学课本中,主要存在平移、旋转和轴对称(即翻折)三种几何变换. 它们最大的特征都是不改变图形的形状和大小,只改变图形位置的变换。
而四边形作为初中阶段最核心最重要的内容,越来越被作为呈现知识和能力的载体。
为此,让我们结合年各地中考试题,一同走进四边形中的变换世界,感受它的魅力与亮点。
一、在平移中构造与发现例:(年咸宁市)如图,将矩形ABCD 沿对角线AC 剪开,再把ACD △沿CA 方向平移得到A C D '''△.()证明A AD CC B '''△≌△;()若30ACB ∠=°,试问当点C '在线段AC 上的什么位置时,四边形ABC D ''是菱形,并请说明理由.思路点拨:在平移过程中对应的边与角的大小不变,仅仅是位置发生改变,借助边角边可证出两个三角形全等;同时与′′始终平行且相等,可知四边形′′平行四边形,要使其为菱形,需满足′,而∠°,∠°,可得21,即点′是线段的中点。
解析:()矩形ABCD 沿对角线AC 剪开,再把ACD △沿CA 方向平移得到A C D '''△ 得A D '',A D ''∥∥,′′,∴∠′′′∠,∴⊿′′≌⊿′。
()当点′是线段的中点时,四边形′′是菱形,理由如下:∵四边形是矩形, A C D '''△由ACD △平移得到,′′,由()知′′,∴四边形是平行四边形。
在⊿中,点′是线段的中点,∴′21,而∠°,∴21,∴′,∴四边形′′是菱形。
点评:决定平移后图形位置的两个基本因素是平移的方向和距离,本题通过“平移不改变图形的形状和大小”的性质,再结合平移前后图形的相应位置进行分析、综合、探究与解答。
2023年中考数学讲练必考重点04 几何变换之旋转问题(含答案)
[选择题]必考重点04 几何变换之旋转问题几何变换中的旋转问题,江苏省各地考查频率较高且考查难度较高,综合性较强,通常有线段的旋转、三角形及四边形的旋转问题,在解决此类问题时,要牢牢把握旋转的性质,即旋转前后的图形全等,对应角相等,对应边相等,结合几何图形本身的性质,找到旋转过程中变化的量和不变的量,运用三角形全等或相似的有关知识,求解有关角、线段及面积问题。
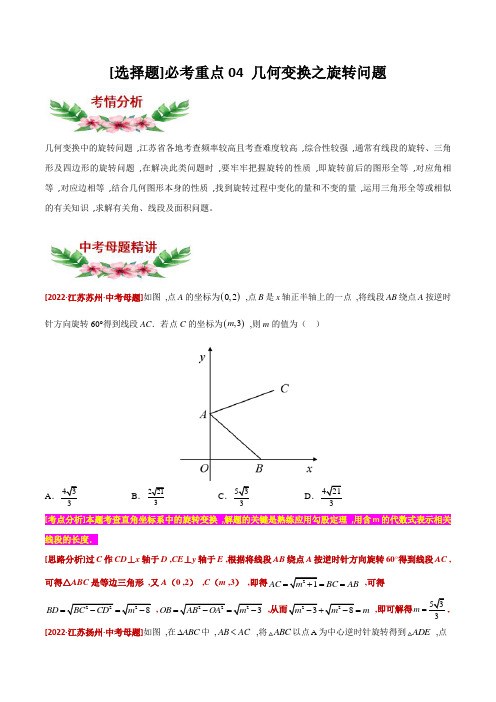
0,2,点B是x轴正半轴上的一点,将线段AB绕点A按逆时[2022·江苏苏州·中考母题]如图,点A的坐标为()m,则m的值为()针方向旋转60°得到线段AC.若点C的坐标为(),3A B C D.3[考点分析]本题考查直角坐标系中的旋转变换,解题的关键是熟练应用勾股定理,用含m的代数式表示相关线段的长度.[思路分析]过C作CD⊥x轴于D ,CE⊥y轴于E ,根据将线段AB绕点A按逆时针方向旋转60°得到线段AC ,可得△ABC是等边三角形,又A(0 ,2),C(m ,3),即得AC BC AB=,可得=,即可解得m=.BD,OB=,m<,将ABC以点A为中心逆时针旋转得到ADE,点[2022·江苏扬州·中考母题]如图,在ABC∆中,AB ACD 在BC 边上 ,DE 交AC 于点F .下列结论:①AFE DFC △△ ;②DA 平分BDE ∠ ;③CDF BAD ∠=∠ ,其中所有正确结论的序号是( )A .①②B .②③C .①③D .①②③[考点分析]本题考查了性质的性质 ,等边对等角 ,相似三角形的性质判定与性质 ,全等三角形的性质 ,掌握以上知识是解题的关键.[思路分析]根据旋转的性质可得对应角相等 ,对应边相等 ,进而逐项分析判断即可求解.[2020·江苏宿迁·中考母题]如图 ,在平面直角坐标系中 ,Q 是直线y=﹣12x+2上的一个动点 ,将Q 绕点P(1 ,0)顺时针旋转90° ,得到点Q ' ,连接OQ ' ,则OQ '的最小值为( )A B C D [考点分析]本题考查了一次函数图象上点的坐标特征 ,一次函数的性质 ,三角形全等的判定和性质 ,坐标与图形的变换-旋转 ,二次函数的性质 ,勾股定理 ,表示出点的坐标是解题的关键.[思路分析]利用等腰直角三角形构造全等三角形 ,求出旋转后Q′的坐标 ,然后根据勾股定理并利用二次函数的性质即可解决问题.1.(2022·江苏·九年级专题练习)如图将△ABC 绕点C 逆时针旋转得到△A ’B ’C ,点B 恰好落在A ’B ’上 ,若∠A =25° ,∠BCA ’=45° ,则∠A ’CA = ( )A.30°B.35°C.40°D.45°2.(2022·江苏泰州·九年级专题练习)在正方形ABCD中,AB=8 ,若点E在对角线AC上运动,将线段DE 绕点D逆时针旋转90°得到线段DF ,连接EF、CF.点P在CD上,且CP=3PD.给出以下几个结论①222=+,②EF, ③线段PF的最小值是,④△CFE的面积最大是16.其中正确的是EF AE CE()A.①②④B.②③④C.①②③D.①③④3.(2022·江苏苏州·一模)如图,直角三角形ACB中,两条直角边AC=8 ,BC=6 ,将△ACB绕着AC中点M旋转一定角度,得到△DFE ,点F正好落在AB边上,DE和AB交于点G ,则AG的长为()A.1.4 B.1.8 C.1.2 D.1.64.(2022·江苏徐州·二模)如图,△ABC中,∠ABC=45° ,BC=8 ,tan∠ACB=3 ,AD⊥BC于D ,若将△ADC 绕点D逆时针方向旋转得到△FDE ,当点E恰好落在AC上,连接AF.则AF的长为()A B C .D .45.(2022·江苏盐城·一模)如图 ,在AOB 中 ,2AO = ,3BO AB ==.将AOB 绕点O 逆时针方向旋转90° ,得到A OB ''△ ,连接AA '.则线段AA '的长为( )A .2B .3C .D .6.(2022·江苏·宜兴外国语学校一模)如图 ,在矩形ABCD 中 ,AB =3 ,BC =4 ,P 是对角线AC 上的动点 ,连接DP ,将直线DP 绕点P 顺时针旋转使∠DPE =∠DAC ,且过D 作DE ⊥PE ,连接CE ,则CE 最小值为( )A .65B .3625C .3225D .857.(2022·江苏扬州·模拟)如图 ,将矩形ABCD 绕点B 按顺时针方向旋转一定角度得到矩形A B C D ''''.此时点A 的对应点A '恰好落在对角线AC 的中点处.若AB =3 ,则点B 与点D 之间的距离为( )A.3 B.6 C.D.8.(2022·江苏·九年级专题练习)如图所示,已知ABC是等边三角形,点D是BC边上一个动点(点D不与,B C重合) ,将ADC绕点A顺时针旋转一定角度后得到AFB△,过点F作BC的平行线交AC于点E,连接②为等边三角形;③四边形BCEF为平行四边形;DF,下列四个结论中:①旋转角为60︒;ADF④.其中正确的结论有()=BF AEA.1B.2C.3D.49.(2022·江苏南京·模拟)如图,在Rt ABC中,∠ACB=90° ,BC=2 ,∠BAC=30° ,将ABC绕顶点C逆时针旋转得到△A'B'C' , M是BC的中点,P是A'B'的中点, 连接PM ,则线段PM的最大值是()A.4 B.2 C.3 D.10.(2022·江苏苏州·二模)如图,将ABC绕点A顺时针旋转角α,得到ADE,若点E恰好在CB的延长线上,则BED∠等于()A .2αB .23αC .αD .180α︒-11.(2022·江苏·阳山中学一模)如图 ,在△ABC 中 ,∠BAC =45° ,AC =8 ,动点E 从点A 出发沿射线AB 运动 ,连接CE ,将CE 绕点C 顺时针旋转45°得到CF ,连接AF ,则△AFC 的面积变化情况是( ).A .先变大再变小B .先变小再变大C .逐渐变大D .不变12.(2022·江苏·南通市启秀中学九年级阶段练习)如图 ,点E 是正方形ABCD 的边DC 上一点 ,把ADE ∆绕点A 顺时针旋转90︒到ABF ∆的位置.若四边形AECF 的面积为20 ,DE=2 ,则AE 的长为( )A .4B .C .6D .13.(2022·江苏·九年级专题练习)如图1 ,在Rt ABC 中 ,AC BC = ,90C ∠=︒ ,点D 为AB 边的中点 ,90EDF ∠=︒ ,将EDF ∠绕点D 旋转 ,它的两边分别交AC 、CB 所在直线于点E 、F ,有以下4个结论:①CE BF = ;②180DEC DFC ∠+∠=︒ ;③222EF DE = ;④如图2 ,当点E 、F 落在AC 、CB 的延长线上时 ,12DEF CEF ABC S S S -=△△△ ,在旋转的过程中上述结论一定成立的是( )A .①②B .②③C .①②③D .①③④14.(2022·江苏扬州·三模)如图 ,已知正方形ABCD 的边长为4 ,点E 是AB 边上一动点 ,连接ED ,将ED 绕点E 顺时针旋转90°到EF ,连接DF ,CF ,则DF +CF 的最小值是( )A .B .C .D .15.(2022·江苏南京·一模)在平面直角坐标系中 ,点A 的坐标是()2,3- ,将点A 绕点C 顺时针旋转90°得到点B .若点B 的坐标是()5,1- ,则点C 的坐标是( )A .()0.5, 2.5--B .()0.25,2--C .()0, 1.75-D .()0, 2.75-16.(2022·江苏南京·模拟)如图 ,在Rt ABC 中 ,AB =AC =10 ,∠BAC =90°,等腰直角三角形ADE 绕点A 旋转 ,∠DAE =90°,AD =AE =4 ,连接DC ,点M 、P 、N 分别为DE 、DC 、BC 的中点 ,连接MP 、PN 、MN .①PMN为等腰直角三角形 ;②MN ≤;③△PMV 面积的最大值是494;④PMN 周长的最小值为6+ )A.4个B.3个C.2个D.1个17.(2022·江苏无锡·一模)如图,已知直线AB与y轴交于点(0,A,与x轴的负半轴交于点B ,且∠ABO =60° ,在x轴正半轴上有一点C ,点C坐标为()1,0,将线段AC绕点A逆时针旋转120° ,得线段AD ,连接BD.则BD的长度为()A.B.4C D.15 218.(2022·江苏·无锡市积余实验学校一模)如图1 ,在Rt△ABC中,90A∠=︒,AB AC=,点D ,E分别在边AB ,AC上,AD AE=,连接DC ,点M、P、N分别为DE、DC、BC的中点.将△ADE绕点A在平面内自由旋转(如图2),若4=AD,10AB=,则△PMN面积的最大值是()A.494B.18 C.492D.25219.(2022·江苏·无锡市天一实验学校一模)如图,扇形OAB中,90AOB∠=︒,将扇形OAB绕点B逆时针旋转,得到扇形BDC,若点O刚好落在弧AB上的点D处,则ADAC的值为()A B C D 20.(2022·江苏·苏州市平江中学校二模)如图 ,在BAC 中 ,90BAC ∠=︒ ,2AB AC = ,将BAC 绕点A 顺时针旋转至DAE △ ,点D 刚好落在BC 直线上 ,则BDE 的面积为( )A .24BD B .22BC C .4BC BD ⋅ D .22AB 21.(2022·江苏·淮安市浦东实验中学九年级开学考试)如图 ,直线1y x =+与x 轴、y 轴分别相交于点A 、B ,过点B 作BC AB ⊥ ,使2BC BA =.将 ABC ∆绕点O 顺时针旋转 ,每次旋转90︒.则第2022次旋转结束时 ,点C 的对应点C '落在反比例函数k y x=的图象上 ,则k 的值为( )A .4-B .4C .6-D .622.(2022·江苏无锡·九年级期末)如图 ,在Rt △ABC 中 ,90BAC ∠=︒ ,6AB AC == ,点D 、E 分别是AB 、AC 的中点.将△ADE 绕点A 顺时针旋转60°,射线BD 与射线CE 交于点P ,在这个旋转过程中有下列结论:①△AEC ≌△ADB ;②CP 存在最大值为3+;③BP 存在最小值为3 ;④点P 运动的路径长为.其中 ,正确的( )A .①②③B .①②④C .①③④D .②③④23.(2022·江苏无锡·模拟)如图 ,在正方形ABCD 中 ,6AB = ,点H 为BC 中点 ,点E 绕着点C 旋转 ,且4CE = ,在DC 的右侧作正方形DEFG ,则线段FH 的最小值是( )A.9-B .8- C .9-D .10-24.(2022·江苏·常州市金坛区水北中学二模)如图 ,在矩形ABCD 中 ,5AB = ,BC =,点P 在线段BC 上运动(含B 、C 两点) ,连接AP ,以点A 为中心 ,将线段AP 逆时针旋转60°到AQ ,连接DQ ,则线段DQ 的最小值为( )A .52B .CD .325.(2022·江苏南京·模拟)如图 ,在ABC ∆中 ,5,AB AC BC === ,D 为边AC 上一动点(C 点除外) ,把线段BD 绕着点D 沿着顺时针的方向旋转90°至DE ,连接CE ,则CDE ∆面积的最大值为( )A .16B .8C .32D .10[选择题]必考重点04 几何变换之旋转问题几何变换中的旋转问题,江苏省各地考查频率较高且考查难度较高,综合性较强,通常有线段的旋转、三角形及四边形的旋转问题,在解决此类问题时,要牢牢把握旋转的性质,即旋转前后的图形全等,对应角相等,对应边相等,结合几何图形本身的性质,找到旋转过程中变化的量和不变的量,运用三角形全等或相似的有关知识,求解有关角、线段及面积问题。
中考数学《二次函数图像的几何变换》专项练习题及答案

中考数学《二次函数图像的几何变换》专项练习题及答案一、单选题1.在平面直角坐标系中,将抛物线y=x2﹣4先向右平移两个单位,再向上平移两个单位,得到的抛物线的解析式是()A.y=(x+2)2+2B.y=(x﹣2)2﹣2C.y=(x﹣2)2+2D.y=(x+2)2﹣22.将抛物线影响y=-x2向左平移2个单位后,得到的抛物线的解析式是()A.y=-(x+2)2B.y=-x2+2C.y=-(x-2)2D.y=-x2-23.若将抛物线y=5x2先向右平移2个单位,再向下平移3个单位,可得到新的抛物线是()A.y=5(x+2)2+3B.y=5(x−2)2+3C.y=5(x+2)2−3D.y=5(x−2)2−34.在平面直角坐标系内,将抛物线y=(x+2)2−3经过两次平移后,得到的新抛物线为y=(x−1)2−4.下列对这一平移过程描述正确的是()A.先向右平移3个单位长度,再向下平移1个单位长度B.先向左平移3个单位长度,再向下平移1个单位长度C.先向右平移3个单位长度,再向上平移1个单位长度D.先向左平移3个单位长度,再向下平移1个单位长度5.下列平移中,不能使二次函数y=2x2+4x−6经过原点的是()A.向左平移1个单位B.向右平移3个单位C.向上平移6个单位D.向上平移8个单位6.二次函数y=x2-1的图象可由下列哪个函数图象向右平移2个单位,向下平移2个单位得到()A.y=(x−2)2+1B.y=(x+2)2+1C.y=(x−2)2−3D.y=(x+2)2+37.如图,在直角坐标系中,O为坐标原点,点A(4,0),以OA为对角线作正方形ABOC,若将抛物线y= 12x2沿射线OC平移得到新抛物线y= 12(x-m)2+k(m>0).则当新抛物线与正方形的边AB有公共点时,m的值一定是()A.2,6,8B.0<m≤6C.0<m≤8 D.0<m≤2 或6 ≤ m≤88.将抛物线y=3x2的图象先向右平移2个单位,再向上平移5个单位后,得到的抛物线解析式是()A.y=3(x﹣2)2﹣5B.y=3(x﹣2)2+5C.y=3(x+2)2﹣5D.y=3(x+2)2+59.在平面直角坐标系中,对于二次函数y=(x−2)2+1,下列说法中错误的是()A.y的最小值为1B.图象顶点坐标为(2,1),对称轴为直线x=2C.当x<2时,y的值随x值的增大而增大,当x≥2时,y的值随x值的增大而减小D.它的图象可以由y=x2的图象向右平移2个单位长度,再向上平移1个单位长度得到10.抛物线y=12x2向左平移1个单位,再向上平移2个单位后,所得抛物线的表达式是()A.y=12(x+1)2﹣2B.y=12(x﹣1)2+2C.y=12(x﹣1)2﹣2D.y=12(x+1)2+211.将二次函数y=x2的图象如何平移可得到y=x2+4x+3的图象()A.向右平移2个单位,向上平移一个单位B.向右平移2个单位,向下平移一个单位C.向左平移2个单位,向下平移一个单位D.向左平移2个单位,向上平移一个单位12.把抛物线y=(x+2)2向下平移2个单位长度,再向右平移1个单位长度,所得抛物线是()A.y=(x+2)2+2B.y=(x+1)2−2C.y=x2+2D.y=x2−2二、填空题13.将抛物线y=﹣x2先向下平移2个单位,再向右平移3个单位后所得抛物线的解析式为.14.抛物线y=-x2-2x+3可由抛物线y=ax2平移得到,则a的值是。
中考几何三大变换含答案17页

中考几何变换专题复习(针对几何大题的解说)几何图形问题的解决,主要借助于基本图形的性质(定义、定理等)和图形之间的关系 (平行、全等、相像等).基本图形的很多性质都源于这个图形自己的“变换特点”,最为重要和最为常用的图形关系“全等三角形”很多的状况也同样拥有“变换”形式的联系.原来两个三角形全等是指它们的形状和大小都同样,和相互间的地点没有直接关系,可是,在同一个问题中波及到的两个全等三角形,大部分都有必定的地点关系(或成轴对称关系,或成平移的关系,或成旋转的关系(包含中心对称) .这样,在解决详细的几何图形问题时,假如我们存心识地从图形的性质或关系中所显示或示意的“变换特点”出发,来辨别、结构基本图形或图形关系,那么将对问题的解决有着极为重要的启迪和指引的作用.下边我们从变换视角以三角形的全等关系为主进行研究.解决图形问题的能力,中心因素是擅长从综合与复杂的图形中辨别和结构出基本图形及基本的图形关系,而“变换视角”正好能提升我们这类辨别和结构的能力.1.已知正方形 ABCD中, E 为对角线 BD 上一点,过 E 点作 EF⊥ BD 交 BC于 F,连结 DF,G 为 DF 中点,连结 EG,CG.(1)求证: EG=CG;(2)将图①中△ BEF绕 B 点逆时针旋转 45°,如图②所示,取 DF 中点 G,连结EG,CG.问( 1)中的结论能否仍旧建立若建立,请给出证明;若不建立,请说明原因;(3)将图①中△BEF绕 B 点旋转随意角度,如图③所示,再连结相应的线段,问( 1)中的结论能否仍旧建立经过察看你还可以得出什么结论(均不要求证明).考点:旋转的性质;全等三角形的判断与性质;直角三角形斜边上的中线;正方形的性质。
专题:压轴题。
剖析:(1)利用直角三角形斜边上的中线等于斜边的一半,可证出CG=EG.(2)结论仍旧建立,连结 AG,过 G 点作 MN ⊥ AD 于 M,与 EF的延伸线交于 N 点;再证明△ DAG≌ △DCG,得出 AG=CG;再证出△DMG≌ △ FNG,获得 MG=NG;再证明△ AMG≌△ ENG,得出 AG=EG;最后证出 CG=EG.(3)结论依旧建立.还知道EG⊥CG.解答:(1)证明:在Rt△FCD中,∵G为DF 的中点,∴CG= FD,同理,在 Rt△DEF中,EG= FD,∴C G=EG.(2)解:(1)中结论仍旧建立,即EG=CG.证法一:连结 AG,过 G 点作 MN⊥ AD 于 M,与 EF的延伸线交于 N 点.在△ DAG与△DCG中,∵AD=CD,∠ ADG=∠CDG,DG=DG,∴△ DAG≌△DCG,∴A G=CG;在△ DMG 与△ FNG中,∵∠ DGM=∠ FGN, FG=DG,∠ MDG=∠ NFG,∴△ DMG≌△FNG,∴M G=NG;在矩形 AENM 中, AM=EN,在△ AMG 与△ ENG中,∵A M=EN,∠AMG=∠ENG,MG=NG,∴△ AMG≌△ENG,∴AG=EG,∴E G=CG.证法二:延伸CG至 M,使 MG=CG,连结 MF,ME, EC,在△ DCG与△FMG 中,∵FG=DG,∠ MGF=∠ CGD,MG=CG,∴△ DCG≌△FMG.∴M F=CD,∠FMG=∠DCG,∴M F∥CD∥AB,∴E F⊥MF.在 Rt△ MFE 与 Rt△ CBE中,∵MF=CB,EF=BE,∴△ MFE≌△CBE∴∠ MEF=∠ CEB.∴∠ MEC=∠MEF+∠ FEC=∠CEB+∠CEF=90,°∴△ MEC为直角三角形.∵M G=CG,∴EG= MC,∴EG=CG.(3)解:(1)中的结论仍旧建立.即 EG=CG.其余的结论还有:EG⊥CG.评论:本题利用了直角三角形斜边上的中线等于斜边的一半的性质、全等三角形的判断和性质.2.( 1)如图 1,已知矩形 ABCD中,点 E 是 BC 上的一动点,过点E 作 EF⊥BD 于点 F,EG⊥AC 于点 G, CH⊥BD 于点 H,试证明 CH=EF+EG;(2)若点 E 在 BC 的延伸线上,如图 2,过点 E 作 EF⊥ BD 于点 F,EG⊥ AC 的延伸线于点 G,CH⊥ BD 于点 H,则 EF、EG、CH 三者之间拥有如何的数目关系,直接写出你的猜想;(3)如图 3,BD 是正方形 ABCD的对角线, L 在 BD 上,且 BL=BC,连结 CL,点 E 是 CL上任一点, EF⊥ BD 于点 F,EG⊥ BC于点 G,猜想 EF、EG、BD 之间拥有怎样的数目关系,直接写出你的猜想;(4)察看图 1、图 2、图 3 的特征,请你依据这一特征结构一个图形,使它仍旧拥有 EF、EG、CH 这样的线段,并知足( 1)或( 2)的结论,写出有关题设的条件和结论.考点:矩形的性质;全等三角形的判断与性质;等腰三角形的性质;正方形的性质。
几何恒等变换(测试题及答案)

几何恒等变换(测试题及答案)一、选择题1. 若几何图形在水平方向上移动了5个单位,则其坐标变换的规律是()A)x + 5B)x - 5C)x + 5, y不变D)y + 5正确答案:C2. 以下哪个选项描述了几何图形的缩放变换?()A)保持形状不变,只改变大小B)平移图形的位置C)旋转图形D)反射图形正确答案:A3. 若几何图形绕原点逆时针旋转90度,则其坐标变换的规律是()A)x' = x,y' = yB)x' = -y,y' = xC)x' = -x,y' = -yD)x' = y,y' = -x正确答案:B4. 若几何图形关于原点对称变换,则其坐标变换的规律是()A)x' = x,y' = yB)x' = -y,y' = xC)x' = -x,y' = -yD)x' = y,y' = -x正确答案:D5. 若几何图形向x轴正方向平移了3个单位,则其坐标变换的规律是()A)x' = x,y' = y + 3B)x' = x,y' = y - 3C)x' = x + 3,y' = yD)x' = x - 3,y' = y正确答案:C二、解答题1. 简述几何图形的旋转变换是如何进行的。
旋转变换是通过将几何图形绕一个指定的旋转中心点旋转一定角度来实现的。
首先,确定旋转中心点和旋转角度。
然后,对于每个点的坐标,通过应用旋转矩阵来计算新的坐标。
旋转矩阵可以根据旋转角度的正弦和余弦值计算得到。
最后,使用计算得到的新坐标来表示旋转后的几何图形。
2. 解释几何图形的缩放变换是什么意思。
缩放变换是通过改变几何图形的大小来实现的。
缩放变换可以分为两种类型:等比例缩放和非等比例缩放。
等比例缩放是保持几何图形的形状不变,只改变其大小。
几何问题-面积和等积变换2(30道,含详细解答)分解

几何问题-面积和等积变换2几何问题-面积和等积变换2一.解答题(共30小题)1.如图,长方形ABCD中,AB=4,BC=2,F、E分别在AB、CD上,连接DF、CF、AE、BE交于Q、P.求四边形PEQF面积的最大值.2.如图,这是一个中国象棋盘,图中小方格都是相同的正方形(“界河”的宽等于小正方形的边长),假设黑方只有一个“象”,它只能在1,2,3,4,5,6,7位置中的一个,红方有两个“相”,它们只能在8,9,10,11,12,13,14中的两个位置,问:这三个棋子(一个“象”和两个“相”)各在什么位置时,以这三个棋子为顶点构成的三角形的面积最大?3.如图(1),某住宅小区有一三角形空地(三角形ABC),周长为2 500m,现规划成休闲广场且周围铺上宽为3m 的草坪,求草坪面积.(精确到1 m2)由题意知,四边形AEFB,BGHC,CMNA是3个矩形,其面积为2 500×3 m2,而3个扇形EAN,FBG,HCM的面积和为π×32 m2,于是可求出草坪的面积为7 500+9π≈7528(m2).(1)若空地呈四边形ABCD,如图(2),其他条件不变,你能求草坪面积吗?若能,请你求出来;若不能,请说明理由;(2)若空地呈五边形ABCDE,如图(3),其他条件不变,还能求出草坪面积吗?若能,请你求出来;若不能,请说明理由;(3)若空地呈n(n≥3)边形,其他条件不变,这时你还能求出草坪面积吗?若能,请你求出来.4.如图1,点P是△ABD中AD边上一点,当P为AD中点时,则有S△ABP=S△BDP,如图2,在四边形ABCD 中,P是AD边上任意一点,探究:(1)当AP=AD时,如图3,△PBC与△ABC和△DBC的面积之间有什么关系?写出求解过程;(2)当AP=AD时,探究S△PBC与S△ABC和S△DBC之间的关系,写出求解过程;(3)一般地,当AP=AD(n表示正整数)时,探究S△PBC与S△ABC和S△DBC之间的关系,写出求解过程;(4)当AP=AD(0≤≤1)时,直接写出S△PBC与S△ABC和S△DBC之间的关系.5.锐角三角形△ABC的外心为O,外接圆半径为R,延长AO,BO,CO,分别与对边BC,CA,AB交于D,E,F;证明:.6.如图,M、N为四边形ABCD的边AD、BC的中点,AN、BM交于P点,CM、DN交于Q点.若四边形ABCD 的面积为150,四边形MPNQ的面积为50,求阴影部分的面积之和.7.设直角三角形的边长均是正整数,且周长数等于面积数,试确定此三角形的边长?8.设直线,(n为自然数)与两坐标轴围成的三角形的面积为S n(n=1,2,3…2008),求S1+S2+S3+…+S2008.9.在直角三角形ABC中,∠A=90°,AD,AE分别是高和角平分线,且△ABE,△AED的面积分别为S1=30,S2=6,求△ADC的面积S.10.如图,在平面直角坐标系xOY中,多边形OABCDE的顶点坐标分别是O(0,0),A(0,6),B(4,6),C(4,4),D(6,4),E(6,0).若直线l经过点M(2,3),且将多边形OABCDE分割成面积相等的两部分,求直线l的函数表达式.11.已知▱ABCD中,若△ADE、△BEF、△CDF的面积分别为5、3、4,求△DEF的面积.12.有三条线段A、B、C,A长2.12米,B长2.71米,C长3.53米.以它们作为上底、下底和高,可以作出三个不同的梯形.问:第几个梯形的面积最大?(参看图.思考时间40秒)13.如图,一个大的六角星形(粗实线)的顶点是周围六个全等的小六角星形(细线型)的中心,相邻的两个小六角星形各有一个公共顶点,如果小六角星形的顶点C到中心A的距离为a,求:(1)大六角星形的顶点A到其中心O的距离;(2)大六角星形的面积;(3)大六角星形的面积与六个小六角星形的面积之和的比值.(注:本题中的六角星形有12个相同的等边三角形拼接而成的)14.如图,是一块黑白格子布.白色大正方形的边长是14厘米,白色小正方形的边长是6厘米.问:这块布中白色的面积占总面积的百分之几?(思考时间:50秒)15.如图,中正方形的边长是2米,四个圆的半径都是1米,圆心分别是正方形的四个顶点.问:这个正方形和四个圆盖住的面积是多少平方米?(思考时间48秒)16.(Ⅰ)如图1,在正方形ABCD内,已知两个动圆⊙O1与⊙O2互相外切,且⊙O1与边AB、AD相切,⊙O2与边BC、CD相切.若正方形ABCD的边长为1,⊙O1与⊙O2的半径分别为r1,r2.①求r1与r2的关系式;②求⊙O1与⊙O2面积之和的最小值.(Ⅱ)如图2,若将(Ⅰ)中的正方形ABCD改为一个宽为1,长为的矩形,其他条件不变,则⊙O1与⊙O2面积的和是否存在最小值,若不存在,请说明理由;若存在,请求出这个最小值.17.已知四边形ABCD两条对角线互相垂直,点O是对角线的交点,∠ACD=60°,∠ABD=45°,点A到CD的距离是6,点D到AB的距离是8,求四边形ABCD的面积S.18.探索:在图1至图3中,已知△ABC的面积为a,(1)如图1,延长△ABC的边BC到点D,使CD=BC,连接DA.若△ACD的面积为S1,则S1=_________(用含a的代数式表示)(2)如图2,延长△ABC的边BC到点D,延长边CA到点E,使CD=BC,AE=CA,连接DE.若△DEC的面积为S2,则S2=_________(用含a的代数式表示)(3)在图2的基础上延长AB到点F,使BF=AB,连接FD,FE,得到△DEF(如图3).若阴影部分的面积为S3,则S3=_________(用含a的代数式表示),并运用上述(2)的结论写出理由.发现:像上面那样,将△ABC各边均顺次延长一倍,连接所得端点,得到△DEF(如图3),此时,我们称△ABC 向外扩展了一次.可以发现,扩展一次后得到的△DEF的面积是原来△ABC面积的_________倍.应用:要在一块足够大的空地上栽种花卉,工程人员进行了如下的图案设计:首先在△ABC的空地上种红花,然后将△ABC向外扩展三次(图4已给出了前两次扩展的图案).在第一次扩展区域内种谎话,第二次扩展区域内种紫花,第三次扩展区域内种蓝花.如果种红花的区域(即△ABC)的面积是10平方米,请你运用上述结论求出:(1)种紫花的区域的面积;(2)种蓝花的区域的面积.19.某生活小区临街的一面有块如图所示的梯形空地,物业部门打算把这块空地美化一下,以供观赏.初步打算沿对角线AC,BD修两条小路,把梯形ABCD分成四块,种上相同种类的花.四块地的面积分别为S1,S2,S3,S4,一位物业工人很快看出S3,S4两种需要花的棵数大致相等.(1)你知道他是根据什么判断的吗?(说明S3与S4之间关系的理由?)(2)请你用学过的知识探究S1,S2,S3三者之间的关系?20.如图,若长方形APHM,BNHP,CQHN的面积分别为7、4、6,求阴影部分的面积是多少?21.已知正方形ABCD的边长为10厘米,AE长为8厘米,CF长为2厘米.求图中阴影部分面积.22.如图,△ABC被分为四块,其中三块的面积分别为4,6,12平方厘米,求四边形AEDF的面积.23.如图,正方形ABCD的面积是120平方厘米,E是AB的中点,F是BC的中点,四边形BGHF的面积是多少平方厘米?24.如图,正方形ABCD的边长为8厘米,E,F,G,H分别是AD,EC,FB,GA的中点,CE与DH的交点为I,求四边形FGHI的面积.25.长方形EFGH的长,宽分别为6厘米,4厘米,阴影部分的总面积为10平方厘米,求四边形ABCD的面积.26.如图,在四边形ABCD中,M为AB的中点,P为BC的中点,N为CD的中点,Q为DA的中点,若图中中间的小四边形的面积为1,试求四个小三角形(阴影部分)面积之和.27.已知D是BC的中点,E是CD的中点,F是AC的中点,且△ADC的面积比△EFG的面积大6平方厘米.△ABC 的面积是多少平方厘米.28.已知△ABC的面积为1,延长AB至点D,使BD=AB,延长BC至点E,使CE=2BC,延长CA至点F使AF=3AC.求三角形DEF的面积.29.如图,四边形PQRS与边长为10的正方形ABCD的内侧相接,SE⊥BC于E,PF⊥CD于F,且RQ=9,EQ=2,RF=3,请求出四边形PQRS的面积.30.如图,三块大小相同的正方形纸片,放在一个底为正方形的盒子内,它们互相重叠.在露出的部分中,红色面积是20,黄色面积是17,绿色面积是7.求正方形盒子底的面积.几何问题-面积和等积变换2参考答案与试题解析一.解答题(共30小题)1.如图,长方形ABCD中,AB=4,BC=2,F、E分别在AB、CD上,连接DF、CF、AE、BE交于Q、P.求四边形PEQF面积的最大值.c=d=﹣=c+d2.如图,这是一个中国象棋盘,图中小方格都是相同的正方形(“界河”的宽等于小正方形的边长),假设黑方只有一个“象”,它只能在1,2,3,4,5,6,7位置中的一个,红方有两个“相”,它们只能在8,9,10,11,12,13,14中的两个位置,问:这三个棋子(一个“象”和两个“相”)各在什么位置时,以这三个棋子为顶点构成的三角形的面积最大?3.如图(1),某住宅小区有一三角形空地(三角形ABC),周长为2 500m,现规划成休闲广场且周围铺上宽为3m 的草坪,求草坪面积.(精确到1 m2)由题意知,四边形AEFB,BGHC,CMNA是3个矩形,其面积为2 500×3 m2,而3个扇形EAN,FBG,HCM的面积和为π×32 m2,于是可求出草坪的面积为7 500+9π≈7528(m2).(1)若空地呈四边形ABCD,如图(2),其他条件不变,你能求草坪面积吗?若能,请你求出来;若不能,请说明理由;(2)若空地呈五边形ABCDE,如图(3),其他条件不变,还能求出草坪面积吗?若能,请你求出来;若不能,请说明理由;(3)若空地呈n(n≥3)边形,其他条件不变,这时你还能求出草坪面积吗?若能,请你求出来.4.如图1,点P是△ABD中AD边上一点,当P为AD中点时,则有S△ABP=S△BDP,如图2,在四边形ABCD 中,P是AD边上任意一点,探究:(1)当AP=AD时,如图3,△PBC与△ABC和△DBC的面积之间有什么关系?写出求解过程;(2)当AP=AD时,探究S△PBC与S△ABC和S△DBC之间的关系,写出求解过程;(3)一般地,当AP=AD(n表示正整数)时,探究S△PBC与S△ABC和S△DBC之间的关系,写出求解过程;(4)当AP=AD(0≤≤1)时,直接写出S△PBC与S△ABC和S△DBC之间的关系.AP=AD换为;AP=AP=AP=AD﹣S﹣)﹣SAP=AP=﹣S﹣)﹣S=S SAP=AP=﹣S﹣)﹣S=S S5.锐角三角形△ABC的外心为O,外接圆半径为R,延长AO,BO,CO,分别与对边BC,CA,AB交于D,E,F;证明:.可以推知﹣;同理式求得同理有,得,联系在一起,从而通过化简,证得结论6.如图,M、N为四边形ABCD的边AD、BC的中点,AN、BM交于P点,CM、DN交于Q点.若四边形ABCD 的面积为150,四边形MPNQ的面积为50,求阴影部分的面积之和.=S=S7.设直角三角形的边长均是正整数,且周长数等于面积数,试确定此三角形的边长?,abab=2a+2b+2,8.设直线,(n为自然数)与两坐标轴围成的三角形的面积为S n(n=1,2,3…2008),求S1+S2+S3+…+S2008.,•=,)•﹣+﹣﹣,故答案为:(9.在直角三角形ABC中,∠A=90°,AD,AE分别是高和角平分线,且△ABE,△AED的面积分别为S1=30,S2=6,求△ADC的面积S.,所以=====这是个一元二次方程,或.10.如图,在平面直角坐标系xOY中,多边形OABCDE的顶点坐标分别是O(0,0),A(0,6),B(4,6),C(4,4),D(6,4),E(6,0).若直线l经过点M(2,3),且将多边形OABCDE分割成面积相等的两部分,求直线l的函数表达式.,,x+.11.已知▱ABCD中,若△ADE、△BEF、△CDF的面积分别为5、3、4,求△DEF的面积.××=5,×=3BE=,×=4CD=AB=AE+BE=++)×=4+=×,×12.有三条线段A、B、C,A长2.12米,B长2.71米,C长3.53米.以它们作为上底、下底和高,可以作出三个不同的梯形.问:第几个梯形的面积最大?(参看图.思考时间40秒)13.如图,一个大的六角星形(粗实线)的顶点是周围六个全等的小六角星形(细线型)的中心,相邻的两个小六角星形各有一个公共顶点,如果小六角星形的顶点C到中心A的距离为a,求:(1)大六角星形的顶点A到其中心O的距离;(2)大六角星形的面积;(3)大六角星形的面积与六个小六角星形的面积之和的比值.(注:本题中的六角星形有12个相同的等边三角形拼接而成的)CM=,然后根据三角形面积公式得到大六角星形的面积AM(,14.如图,是一块黑白格子布.白色大正方形的边长是14厘米,白色小正方形的边长是6厘米.问:这块布中白色的面积占总面积的百分之几?(思考时间:50秒)15.如图,中正方形的边长是2米,四个圆的半径都是1米,圆心分别是正方形的四个顶点.问:这个正方形和四个圆盖住的面积是多少平方米?(思考时间48秒)16.(Ⅰ)如图1,在正方形ABCD内,已知两个动圆⊙O1与⊙O2互相外切,且⊙O1与边AB、AD相切,⊙O2与边BC、CD相切.若正方形ABCD的边长为1,⊙O1与⊙O2的半径分别为r1,r2.①求r1与r2的关系式;②求⊙O1与⊙O2面积之和的最小值.(Ⅱ)如图2,若将(Ⅰ)中的正方形ABCD改为一个宽为1,长为的矩形,其他条件不变,则⊙O1与⊙O2面积的和是否存在最小值,若不存在,请说明理由;若存在,请求出这个最小值.上,解等腰直角三角形得,AC=)及求面积和的最小值.,12,,即1时,⊙是等圆,其面积和的最小值为或.,故不合题意,应舍去..,即17.已知四边形ABCD两条对角线互相垂直,点O是对角线的交点,∠ACD=60°,∠ABD=45°,点A到CD的距离是6,点D到AB的距离是8,求四边形ABCD的面积S.BD BD 1618.探索:在图1至图3中,已知△ABC的面积为a,(1)如图1,延长△ABC的边BC到点D,使CD=BC,连接DA.若△ACD的面积为S1,则S1=a(用含a的代数式表示)(2)如图2,延长△ABC的边BC到点D,延长边CA到点E,使CD=BC,AE=CA,连接DE.若△DEC的面积为S2,则S2=2a(用含a的代数式表示)(3)在图2的基础上延长AB到点F,使BF=AB,连接FD,FE,得到△DEF(如图3).若阴影部分的面积为S3,则S3=6a(用含a的代数式表示),并运用上述(2)的结论写出理由.发现:像上面那样,将△ABC各边均顺次延长一倍,连接所得端点,得到△DEF(如图3),此时,我们称△ABC 向外扩展了一次.可以发现,扩展一次后得到的△DEF的面积是原来△ABC面积的7倍.应用:要在一块足够大的空地上栽种花卉,工程人员进行了如下的图案设计:首先在△ABC的空地上种红花,然后将△ABC向外扩展三次(图4已给出了前两次扩展的图案).在第一次扩展区域内种谎话,第二次扩展区域内种紫花,第三次扩展区域内种蓝花.如果种红花的区域(即△ABC)的面积是10平方米,请你运用上述结论求出:(1)种紫花的区域的面积;(2)种蓝花的区域的面积.19.某生活小区临街的一面有块如图所示的梯形空地,物业部门打算把这块空地美化一下,以供观赏.初步打算沿对角线AC,BD修两条小路,把梯形ABCD分成四块,种上相同种类的花.四块地的面积分别为S1,S2,S3,S4,一位物业工人很快看出S3,S4两种需要花的棵数大致相等.(1)你知道他是根据什么判断的吗?(说明S3与S4之间关系的理由?)(2)请你用学过的知识探究S1,S2,S3三者之间的关系?20.如图,若长方形APHM,BNHP,CQHN的面积分别为7、4、6,求阴影部分的面积是多少?(21.已知正方形ABCD的边长为10厘米,AE长为8厘米,CF长为2厘米.求图中阴影部分面积.SS==1=×××××22.如图,△ABC被分为四块,其中三块的面积分别为4,6,12平方厘米,求四边形AEDF的面积.23.如图,正方形ABCD的面积是120平方厘米,E是AB的中点,F是BC的中点,四边形BGHF的面积是多少平方厘米?,根据相似三角形性质得出====,求出BF=CF==,=,=××==,S==,24.如图,正方形ABCD的边长为8厘米,E,F,G,H分别是AD,EC,FB,GA的中点,CE与DH的交点为I,求四边形FGHI的面积.AD=4×××=SS25.长方形EFGH的长,宽分别为6厘米,4厘米,阴影部分的总面积为10平方厘米,求四边形ABCD的面积.,即×26.如图,在四边形ABCD中,M为AB的中点,P为BC的中点,N为CD的中点,Q为DA的中点,若图中中间的小四边形的面积为1,试求四个小三角形(阴影部分)面积之和.即可求出答案.SS27.已知D是BC的中点,E是CD的中点,F是AC的中点,且△ADC的面积比△EFG的面积大6平方厘米.△ABC 的面积是多少平方厘米.EF=))=,.28.已知△ABC的面积为1,延长AB至点D,使BD=AB,延长BC至点E,使CE=2BC,延长CA至点F使AF=3AC.求三角形DEF的面积.29.如图,四边形PQRS与边长为10的正方形ABCD的内侧相接,SE⊥BC于E,PF⊥CD于F,且RQ=9,EQ=2,RF=3,请求出四边形PQRS的面积.BP CQ DR AP(()﹣(30.如图,三块大小相同的正方形纸片,放在一个底为正方形的盒子内,它们互相重叠.在露出的部分中,红色面积是20,黄色面积是17,绿色面积是7.求正方形盒子底的面积.=12 =7。
几何三大变换(旋转)(人教版)(含答案)

几何三大变换(旋转)(人教版)一、单选题(共10道,每道10分)1.如图,将△ABC绕顶点A逆时针旋转一角度,使点D落在BC边上,得到△ADE,此时恰好AB∥DE,若∠E=35°,则∠DAC的度数为( )A.15°B.20°C.25°D.30°答案:C解题思路:试题难度:三颗星知识点:旋转的性质2.如图,在Rt△ABC中,∠ACB=90°.在同一平面内,将△ABC绕点C逆时针旋转70°与△EDC 重合,恰好使点D在AB上,则∠E=( )A.20°B.25°C.30°D.35°答案:D解题思路:试题难度:三颗星知识点:旋转的性质3.如图,在Rt△ABC中,∠ACB=90°,A=30°,BC=2,将△ABC绕点C按顺时针方向旋转n 度后得到△EDC,此时点D在AB边上,斜边DE交AC边于点F,则n的大小和DF的长分别为( )A.30,2B.60,2C.60,1D.30,1答案:C解题思路:试题难度:三颗星知识点:含30°角的直角三角形4.如图,在Rt△ABC中,AB=AC,D,E是斜边BC上两点,且∠DAE=45°,将△ADC绕点A 顺时针旋转90°后,得到△AFB,连接EF,下列结论:①△AEF≌△AED;②∠AED=45°;③BE+DC=DE,其中正确的是( )A.①B.②C.②③D.①③答案:A解题思路:1.思路分析本题主要考查旋转的性质,解决此类问题需要清楚:①旋转是全等变换,旋转前后对应边、对应角相等;②几何问题处理注意读题标注,多条件进行整合.2.解题过程试题难度:三颗星知识点:旋转的性质5.如图,在Rt△ABC中,∠BAC=90°,∠B=60°,△AB′C′可以由△ABC绕点A顺时针旋转90°得到(点B′与点B是对应点,点C′与点C是对应点),连接CC′,则∠CC′B′度数是( )A.10°B.15°C.20°D.30°答案:B解题思路:试题难度:三颗星知识点:旋转的性质6.如图,在△ABC中,∠CAB=70°,将△ABC绕点A逆时针旋转到,△AB′C′的位置,使得CC′∥AB,则等于( )A.30°B.35°C.40°D.45°答案:C解题思路:试题难度:三颗星知识点:旋转角7.如图,在四边形ABCD中,∠ADC=∠ABC=90°,AD=CD,DP⊥AB于点P.若四边形ABCD的面积是16,则DP的长为( )A.2B.4C.6D.8答案:B解题思路:试题难度:三颗星知识点:旋转的性质8.如图,将△ABC绕顶点A顺时针旋转60°后得到,若为BC的中点,则=( )A.1:2B.1:C.1:D.1:3答案:D解题思路:试题难度:三颗星知识点:旋转会出现等腰三角形9.如图,凸四边形ABCD满足条件:AB=AD,∠BAD=60°,∠BCD=120°,则AC与BC+CD的数量关系为( )A. B.C. D.不确定答案:C解题思路:1.思路分析本题主要考查在特殊条件下如何使用旋转思想解决问题.解决此类问题需要清楚:①旋转是全等变换,旋转前后对应边、对应角相等;②满足旋转三要素的情形下(如有等边、等腰直角),可以考虑旋转思想.本题中有AB=AD,∠BAD=60°,∠BCD=120°,可考虑将△ACD顺时针旋转,使得AD与AB重合,此时可证为等边三角形,进而可知AC=BC+CD.2.解题过程试题难度:三颗星知识点:旋转思想(辨识特征旋转图形)10.如图,在等腰Rt△ABC中,∠A=90°,AC=9,点O在AC上,且AO=2,点P是AB上一动点,连接OP将线段OP绕O逆时针旋转90°得到线段OD,要使点D恰好落在BC上,则AP 的长等于( )A.2B.C.5D.7答案:C解题思路:1.思路分析本题主要考查旋转的性质,以及借助特殊的角度表达线段长求解等.解决此类问题需要注意:②读题标注,根据题意画图.本题需画出示意图,便于理解题意.②梳理条件,挖掘特征,合理转化.本题中根据旋转的特征,可借助线段相等找全等三角形,表达线段长.③借助旋转、全等性质建等式求解.通过全等的性质,借助特殊角度表达线段长求解.2.解题过程试题难度:三颗星知识点:构造弦图第11页共11页。
四年级认识几何形的变换练习题

四年级认识几何形的变换练习题
一、选择题
1. 已知一个三角形,利用尺规作以下几何变换,哪个变换会使得三角形的形状改变?
A. 平移
B. 旋转
C. 翻转
D. 缩放
2. 已知一个正方形,利用以下几何变换中的哪一个可以得到一个新的正方形?
A. 平移
B. 旋转
C. 翻转
D. 缩放
3. 已知一个长方形,对其进行顺时针旋转90度后,它的形状会如何改变?
A. 变成正方形
B. 变成正三角形
C. 高度和宽度互换
D. 形状不变
二、填空题
1. 利用尺规作一个正方形的中心对称点,该中心对称点与原点之间的距离是 ________。
2. 对图中的图形进行顺时针旋转90度得到的新图形是 ________。
注:图形可以是三角形、正方形、长方形等。
三、解答题
1. 小明画了一个正三角形,他想在正三角形的顶点处画两条平行于底边的直线来构成一个长方形。
请你帮助小明,告诉他如何画出这个长方形。
2. 班级里的学生们正在组织一次民族服装秀,小红拿到了一个红色的正方形面巾,她希望通过一些几何变换来制作出不同形状的面巾。
请你帮助小红,列举出她可以进行的几何变换,并描述每种变换对面巾形状的影响。
3. 小亮画了一个正方形,他想通过几何变换,使得原正方形变成一个边长为原正方形1/2倍的新正方形。
请你告诉他通过哪种几何变换可以实现,并具体描述这种变换的步骤。
以上是我为你准备的关于四年级认识几何形的变换的练习题,希望对你有帮助!。
1.18几何变换的类型(含解析,机构)-2021届九年级数学(苏科版)知识点一轮复习每日一练(1月)

几何变换的类型每日一练1.如图,△PQR是三角形ABC经过某种变换后得到的图形.(1)分别写出点A与P,点B与Q,点C与R的坐标;(2)认真观察上述坐标,你发现了它们之间有怎样的关系?(3)△ABC内有一点M(a,b),点M经过这种变换后得到点N,请你写出点N的坐标;(4)如果网络图中每个小正方形的边长均为1,试求三角形ABC的面积.2.如图,如果将其中的甲图变成乙图,那么经过的变换正确的是()A.旋转、平移B.对称、平移C.旋转、对称D.旋转、旋转3.一个图形无论经过平移还是旋转,有以下说法:(1)对应线段平行;(2)对应线段相等;(3)对应角相等;(4)不改变图形的形状和大小,其中正确的有()A.(1)(2)(3)B.(1)(2)(4)C.(1)(3)(4)D.(2)(3)(4)4.如图,乙图案变为甲图案,需要用到()A.旋转、对称B.平移、对称C.旋转、平移D.旋转、旋转5.请仔细观察下图,从图形(1)(2)(3)的变化规律,确定图形(4)为()A.B.C.D.6.如图,四边形ABCD是正方形,点F,G在正方形的边上,点E在CB的延长线上,BE=BF=DC.下列说法正确的是()A.将△ADG绕点A按顺时针方向旋转得到△ABFB.将△ADG绕点A按顺时针方向旋转得到△ABEC.将△ABE平移得到△ABFD.将△ADG平移得到△ABF7.如图,△ABC和△BDE是等边三角形,点A、B、D在一条直线上,并且AB=BD.由一个三角形变换到另一个三角形()A.仅能由平移得到B.仅能由旋转得到C.既能由平移得到,也能由旋转得到D.既不能由平移得到,也不能由旋转得到8.以下三组两个图形之间的变换分别属于()A.平移、旋转、旋转B.平移、轴对称、轴对称C.平移、轴对称、旋转D.平移、旋转、轴对称9.从甲到乙的图形变换,判断全正确的是()A.(1)翻折,(2)旋转,(3)平移B.(1)翻折,(2)平移,(3)旋转C.(1)平移,(2)翻折,(3)旋转D.(1)平移,(2)旋转,(3)翻折几何变换的类型每日一练1.如图,△PQR是三角形ABC经过某种变换后得到的图形.(1)分别写出点A与P,点B与Q,点C与R的坐标;(2)认真观察上述坐标,你发现了它们之间有怎样的关系?(3)△ABC内有一点M(a,b),点M经过这种变换后得到点N,请你写出点N的坐标;(4)如果网络图中每个小正方形的边长均为1,试求三角形ABC的面积.【分析】(1)利用坐标系直接得出各点坐标即可;(2)利用(1)中所求得出对应点之间的关系即可;(3)利用(2)中规律得出N点坐标即可;(4)利用△ABC所在矩形的面积进而减去周围三角形面积进而求出即可.【解答】解:(1)如图所示:点A与P的坐标分别为:(4,3),(﹣4,﹣3);点B与Q的坐标分别为:(3,1),(﹣3,﹣1);点C与R的坐标分别为:(1,2),(﹣1,﹣2);(2)由(1)得:对应点坐标关于原点对称;(3)由(2)得:△ABC内有一点M(a,b),点M经过这种变换后得到点N,则点N的坐标为:(﹣a,﹣b);(4)三角形ABC的面积为:2×3﹣×1×3﹣×1×2﹣×1×2=2.5.【点评】此题主要考查了几何变换以及关于原点对称点的性质和三角形面积求法等知识,正确得出对应点坐标之间规律是解题关键.2.如图,如果将其中的甲图变成乙图,那么经过的变换正确的是()A.旋转、平移B.对称、平移C.旋转、对称D.旋转、旋转【分析】观察本题中图案的特点,根据对称、旋转的性质即可得出答案.【解答】解:观察图形可得:将甲图先轴对称变化,再逆时针旋转即可变成乙图;故选:C.【点评】本题考查了几何变换的类型,用到的知识点是轴对称、旋转变化的性质:如果一个图形沿着一条直线对折,两侧的图形能完全重合,这个图形就是轴对称图形.折痕所在的这条直线叫做对称轴.旋转变化前后,对应线段、对应角分别相等,图形的大小、形状都不改变,两组对应点连线的交点是旋转中心.3.一个图形无论经过平移还是旋转,有以下说法:(1)对应线段平行;(2)对应线段相等;(3)对应角相等;(4)不改变图形的形状和大小,其中正确的有()A.(1)(2)(3)B.(1)(2)(4)C.(1)(3)(4)D.(2)(3)(4)【分析】利用图形平移与旋转的定义判定即可.【解答】解:一个图形无论经过平移还是旋转,对应线段和角相等,不改变图形的形状和大小,旋转后对应的线段可能不平行.故选:D.【点评】本题主要考查了几何变换的类型,解题的关键是熟记图形平移与旋转的定义.4.如图,乙图案变为甲图案,需要用到()A.旋转、对称B.平移、对称C.旋转、平移D.旋转、旋转【分析】根据旋转、平移的性质结合图形解答即可.【解答】解:由图可知,乙图案旋转、平移后可以变为甲图案.故选:C.【点评】本题考查了几何变换的类型,熟记各种变换的概念并准确识图是解题的关键.5.请仔细观察下图,从图形(1)(2)(3)的变化规律,确定图形(4)为()A.B.C.D.【分析】根据已知的三个图形可以每次逆时针旋转90度,据此即可确定.【解答】解:根据已知的三个图形可以每次逆时针旋转90度,由(3)逆时针旋转90度得到B.故选:B.【点评】本题考查了图形的旋转,根据已知图形得到旋转的方法是关键.6.如图,四边形ABCD是正方形,点F,G在正方形的边上,点E在CB的延长线上,BE=BF=DC.下列说法正确的是()A.将△ADG绕点A按顺时针方向旋转得到△ABFB.将△ADG绕点A按顺时针方向旋转得到△ABEC.将△ABE平移得到△ABFD.将△ADG平移得到△ABF【分析】结合图形,根据旋转变换与平移变换的定义进行解答.【解答】解:观察图形可得:将△ADG绕点A按顺时针方向旋转得到△ABE,△ABE与△ABF不能通过平移得到,△ADG平移也不能得到△ABF.故选:B.【点评】本题考查了几何变换的旋转变换与平移变换,准确识图是关键.7.如图,△ABC和△BDE是等边三角形,点A、B、D在一条直线上,并且AB=BD.由一个三角形变换到另一个三角形()A.仅能由平移得到B.仅能由旋转得到C.既能由平移得到,也能由旋转得到D.既不能由平移得到,也不能由旋转得到【分析】是轴对称图形,这三对全等三角形中的一个都是以其中另一个三角形绕点B旋转90°后得到或对折得到的.【解答】解:∵△ABC和△BDE是等边三角形,点A、B、D在一条直线上,并且AB=BD.∴这三对全等三角形中的一个都是以其中另一个三角形绕点B旋转90°后得到或对折得到的.故选:C.【点评】本题考查了几何变换的类型,解题的关键是看清由两个三角形组成的图象是轴对称图形还是中心对称图形.8.以下三组两个图形之间的变换分别属于()A.平移、旋转、旋转B.平移、轴对称、轴对称C.平移、轴对称、旋转D.平移、旋转、轴对称【分析】根据平移、旋转、轴对称的特点可知.【解答】解:第一个可沿水平线向右平移得到;第二个可绕对应点的中点旋转得到;第三个可沿对应点连线所在的垂直平分线翻折得到,即为轴对称.故选D.【点评】平移是沿直线移动一定距离得到新图形,旋转是绕某个点旋转一定角度得到新图形,轴对称是沿某条直线翻折得到新图形.观察时要紧扣图形变换特点,认真判断.9.从甲到乙的图形变换,判断全正确的是()A.(1)翻折,(2)旋转,(3)平移B.(1)翻折,(2)平移,(3)旋转C.(1)平移,(2)翻折,(3)旋转D.(1)平移,(2)旋转,(3)翻折【分析】根据常见的几何变换类型,写出各小题的变化过程即可得解.【解答】解:由图可知,(1)把甲翻折即可得到乙;(2)绕甲的直角顶点顺时针旋转90°即可得到乙;(3)把甲先向右平移,再向上平移即可得到乙,所以,(1)翻折,(2)旋转,(3)平移.故选:A.【点评】本题考查了常见的几何变换类型,准确识图,判断出从甲到乙的变换过程是解题的关键.。
几何变换课堂练习题(含答案)

几何变换课堂练习题1. 试写出二维图形几何变换矩阵,并从变换功能上将其分块。
答:二维图形几何变换矩阵可用下式表示:T2D=从变换功能上可把T分为四个子矩阵,其中是对图形进行缩放、旋转、对称、错切等变换;[c f ]是对图形进行平移变换;对图形作投影变换;[ i ]是对整体图形作伸缩变换。
2.试写出三维图形几何变换矩阵,并从变换功能上将其分块。
答:三维图形的几何变换矩阵可用T3D表示,其表示式如下:从变换功能上T3D可分为4个子矩阵,其中:产生比例、旋转、错切等几何变换;产生平移变换;产生投影变换;[a44] 产生整体比例变换。
1. 已知三角形ABC 各顶点的坐标A(1,2)、B(5,2)、C(3,5),相对直线Y=4做对称变换后到达A ’、B ’、C ’。
试计算A ’、B ’、C ’的坐标值。
(要求用齐次坐标进行变换,列出变换矩阵)解:(1)将坐标系平移至P 1 (0,4)点 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=140010001A T(2) 以Y 轴对称 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=100010001B T(3)将坐标系平移回原处 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=140010001C T(4) 变换矩阵:T=T A*T B*T C= ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-180010001(5) 求变换后的三角形ABC 各顶点的坐标A ’、B ’、C ’A ’: [][][][]1611800100011211211''=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-⨯=⨯=T Y X A A X A '=1, Y A '=6 B ’: [][][][]1651800100011251251'=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-⨯=⨯=T Y X B B X B '=5, Y B '=6C ’: [][][][]1331800100011531531''=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-⨯=⨯=T Y X C C X A '=3, Y A '=32.将x和y放大为原来的三倍,且图形点(0.5,0.2,-0.2)保持不动;S =T2 =2 S T1 =------------------------------------------------------------------------------------------------------- 填空题1.比例变换[x y 1]=[x y 1]=[sx·x sy·y 1]⑴当_____________时,为恒等比例变换,即图形不变;⑵当_____________时,图形沿两个坐标轴方向等比例放大;⑶当_____________时,图形沿两个坐标轴方向等比例缩小;⑷当_____________时,图形沿两个坐标轴方向作非均匀的比例变换。
中考试题几何变换课后练习二及详解.docx

学科:数学专题:几何变换主讲教师:黄炜 北京四中数学教师重难点易错点解析题一: 题面:如图,直线332y x =-+与x 轴、y 轴分别交于A 、B 两点,把△AOB 绕点A 旋转90°后得到△AO ′B ′,则点B ′的坐标是 .金题精讲题一:题面:如图,O 是正△ABC 内一点,OA =3,OB =4,OC =5,将线段BO 以点B 为旋转中心逆时针旋转60°得到线段BO ′,下列结论:①△BO ′A 可以由△BOC 绕点B 逆时针旋转60°得到;②点O 与O ′的距离为4;③∠AOB =150°; ④AOBO S =6+33四形边; ⑤AOC AOB 93S S 6+4+=. 其中正确的结论是( )A.①②③⑤B.①②③④C.①②③④⑤D.①②③满分冲刺题一:题面:如图,在边长为2的正方形ABCD中,M为边AD的中点,延长MD至点E,使ME=MC,以DE 为边作正方形DEFG,点G在边CD上,则DG的长为()A 31-- C 5+1 D 51- B 35题二:题面:点P是正方形ABCD边AB上一点(不与A、B重合),连接PD并将线段PD绕点P顺时针旋转90°,得线段PE,连接BE,则∠CBE等于()A.75°B.60°C.45°D.30°课后练习详解重难点易错点解析题一:答案:(﹣1,﹣2)或(5,2).详解:当y=0时,3302x-+=,解得x=2;当x=0时,y=3.∴点A(2,0),B(0,3).∴OA=2,OB=3,根据旋转不变性可得△AOB≌△AO′B′,∴AO′=AO=2,O′B′=OB=3,①如果△AOB是逆时针旋转90°,则点B′(﹣1,﹣2),②如果△AOB是顺时针旋转90°,则点B′(5,2).综上,点B′的坐标是(﹣1,﹣2)或(5,2).金题精讲题一:答案:A.详解:∵正△ABC,∴AB=CB,∠ABC=600.∵线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,∴BO=BO′,∠O′AO=600. ∴∠O′BA=600-∠ABO=∠OBA.∴△BO′A≌△BOC.∴△BO′A可以由△BOC绕点B逆时针旋转60°得到.故结论①正确.连接OO′,∵BO =BO ′,∠O ′AO =600,∴△OBO ′是等边三角形.∴OO ′=OB =4.故结论②正确.∵在△AOO ′中,三边长为O ′A =OC =5,OO ′=OB =4,OA =3,是一组勾股数,∴△AOO ′是直角三角形.∴∠AOB =∠AOO ′+∠O ′OB =900+600=150°.故结论③正确.AOO OBO AOBO 11S S S 34+4236+4322∆'∆''=+=⋅⋅⋅⋅=四形边.故结论④错误. 如图所示,将△AOB 绕点A 逆时针旋转60°,使得AB 与AC 重合,点O 旋转至O ″点.易知△AOO ″是边长为3的等边三角形,△COO ″是边长为3、4、5的直角三角形. 则AOC AOB AOCO COO AOO 113393S S S S S 34+3=6+2224∆∆"∆"∆"+==+=⋅⋅⋅⋅. 故结论⑤正确.综上所述,正确的结论为:①②③⑤.故选A .满分冲刺题一:答案:D.详解:利用勾股定理求出CM 的长,即ME 的长,有DM =DE ,所以可以求出DE ,从而得到DG 的长:∵四边形ABCD 是正方形,M 为边AD 的中点,∴DM =12DC =1. ∴2222215CM DC DM =+=+=.∴ME =MC =5.∴ED =EM -DM =51-.∵四边形EDGF 是正方形,∴DG =DE =51-.故选D.题二:答案:C.详解:过点E 作EF ⊥AF ,交AB 的延长线于点F ,则∠F =90°,∵四边形ABCD 为正方形,∴AD =AB ,∠A =∠ABC =90°.∴∠ADP +∠APD =90°.由旋转可得:PD =PE ,∠DPE =90°,∴∠APD +∠EPF =90°.∴∠ADP=∠EPF.在△APD和△FEP中,∵∠ADP=∠EPF,∠A=∠F,PD=PE,∴△APD≌△FEP(AAS).∴AP=EF,AD=PF.又∵AD=AB,∴PF=AB,即AP+PB=PB+BF.∴AP=BF.∴BF=EF又∵∠F=90°,∴△BEF为等腰直角三角形.∴∠EBF=45°.又∵∠CBF=90°,∴∠CBE=45°.故选C.初中数学试卷鼎尚图文**整理制作。
中考试题几何变换课后练习二及详解.docx

学科:数学专题:几何变换主讲教师:黄炜 北京四中数学教师重难点易错点解析题一: 题面:如图,直线332y x =-+与x 轴、y 轴分别交于A 、B 两点,把△AOB 绕点A 旋转90°后得到△AO ′B ′,则点B ′的坐标是 .金题精讲题一:题面:如图,O 是正△ABC 内一点,OA =3,OB =4,OC =5,将线段BO 以点B 为旋转中心逆时针旋转60°得到线段BO ′,下列结论:①△BO ′A 可以由△BOC 绕点B 逆时针旋转60°得到;②点O 与O ′的距离为4;③∠AOB =150°; ④AOBO S =6+33四形边; ⑤AOC AOB 93S S 6+4+=. 其中正确的结论是( )A.①②③⑤B.①②③④C.①②③④⑤D.①②③满分冲刺题一:题面:如图,在边长为2的正方形ABCD中,M为边AD的中点,延长MD至点E,使ME=MC,以DE 为边作正方形DEFG,点G在边CD上,则DG的长为()A 31-- C 5+1 D 51- B 35题二:题面:点P是正方形ABCD边AB上一点(不与A、B重合),连接PD并将线段PD绕点P顺时针旋转90°,得线段PE,连接BE,则∠CBE等于()A.75°B.60°C.45°D.30°课后练习详解重难点易错点解析题一:答案:(﹣1,﹣2)或(5,2).详解:当y=0时,3302x-+=,解得x=2;当x=0时,y=3.∴点A(2,0),B(0,3).∴OA=2,OB=3,根据旋转不变性可得△AOB≌△AO′B′,∴AO′=AO=2,O′B′=OB=3,①如果△AOB是逆时针旋转90°,则点B′(﹣1,﹣2),②如果△AOB是顺时针旋转90°,则点B′(5,2).综上,点B′的坐标是(﹣1,﹣2)或(5,2).金题精讲题一:答案:A.详解:∵正△ABC,∴AB=CB,∠ABC=600.∵线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,∴BO=BO′,∠O′AO=600. ∴∠O′BA=600-∠ABO=∠OBA.∴△BO′A≌△BOC.∴△BO′A可以由△BOC绕点B逆时针旋转60°得到.故结论①正确.连接OO′,∵BO =BO ′,∠O ′AO =600,∴△OBO ′是等边三角形.∴OO ′=OB =4.故结论②正确.∵在△AOO ′中,三边长为O ′A =OC =5,OO ′=OB =4,OA =3,是一组勾股数,∴△AOO ′是直角三角形.∴∠AOB =∠AOO ′+∠O ′OB =900+600=150°.故结论③正确. AOO OBO AOBO 11S S S 34+4236+4322∆'∆''=+=⋅⋅⋅⋅=四形边.故结论④错误. 如图所示,将△AOB 绕点A 逆时针旋转60°,使得AB 与AC 重合,点O 旋转至O ″点.易知△AOO ″是边长为3的等边三角形,△COO ″是边长为3、4、5的直角三角形. 则AOC AOB AOCO COO AOO 113393S S S S S 34+3=6+2224∆∆"∆"∆"+==+=⋅⋅⋅⋅. 故结论⑤正确.综上所述,正确的结论为:①②③⑤.故选A .满分冲刺题一:答案:D.详解:利用勾股定理求出CM 的长,即ME 的长,有DM =DE ,所以可以求出DE ,从而得到DG 的长:∵四边形ABCD 是正方形,M 为边AD 的中点,∴DM =12DC =1. ∴2222215CM DC DM =+=+=.∴ME =MC =5.∴ED =EM -DM =51-.∵四边形EDGF 是正方形,∴DG =DE =51-.故选D.题二:答案:C.详解:过点E 作EF ⊥AF ,交AB 的延长线于点F ,则∠F =90°,∵四边形ABCD 为正方形,∴AD =AB ,∠A =∠ABC =90°.∴∠ADP +∠APD =90°.由旋转可得:PD =PE ,∠DPE =90°,∴∠APD +∠EPF =90°.∴∠ADP=∠EPF.在△APD和△FEP中,∵∠ADP=∠EPF,∠A=∠F,PD=PE,∴△APD≌△FEP(AAS).∴AP=EF,AD=PF.又∵AD=AB,∴PF=AB,即AP+PB=PB+BF.∴AP=BF.∴BF=EF又∵∠F=90°,∴△BEF为等腰直角三角形.∴∠EBF=45°.又∵∠CBF=90°,∴∠CBE=45°.故选C.初中数学试卷鼎尚图文**整理制作。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
几何变换课堂练习题
1. 试写出二维图形几何变换矩阵,并从变换功能上将其分块。
答:二维图形几何变换矩阵可用下式表示:
T2D=
从变换功能上可把T分为四个子矩阵,其中是对图形进行缩放、旋转、对
称、错切等变换;[c f ]是对图形进行平移变换;对图形作投影变换;[ i ]是对整体图形作伸缩变换。
2.试写出三维图形几何变换矩阵,并从变换功能上将其分块。
答:三维图形的几何变换矩阵可用T3D表示,其表示式如下:
从变换功能上T3D可分为4个子矩阵,其中:产生比例、旋转、
错切等几何变换;产生平移变换;产生投影变换;[a44] 产生整体比例变换。
1. 已知三角形ABC 各顶点的坐标A(1,2)、B(5,2)、C(3,5),相对直线Y=4做对称变换后到达A ’、B ’、C ’。
试计算A ’、B ’、C ’的坐标值。
(要求用齐次坐标进行变换,列出变换矩阵)
解:
(1)将坐标系平移至P 1 (0,4)点 ⎥⎥⎥⎦
⎤⎢⎢⎢⎣⎡-=140010001A T
(2) 以Y 轴对称 ⎥⎥⎥⎦
⎤⎢⎢⎢⎣⎡-=100010001B T
(3)将坐标系平移回原处 ⎥⎥⎥⎦
⎤⎢⎢⎢⎣⎡=140010001C T
(4) 变换矩阵:T=T A*T B*T C= ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-180010001
(5) 求变换后的三角形ABC 各顶点的坐标A ’、B ’、C ’
A ’: [][][][]1611800100011211211''=⎥⎥⎥⎦
⎤⎢⎢⎢⎣⎡-⨯=⨯=T Y X A A X A '=1, Y A '=6 B ’: [][][][]165180010001125125
1'=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-⨯=⨯=T Y X B B X B '=5, Y B '=6
C ’: [][][][]1331800100011531531''=⎥⎥⎥⎦
⎤⎢⎢⎢⎣⎡-⨯=⨯=T Y X C C X A '=3, Y A '=3
2.将x和y放大为原来的三倍,且图形点(0.5,0.2,-0.2)保持不动;
T1 = S =T2 =
T = T2S T1 =
------------------------------------------------------------------------------------------------------- 填空题
1.比例变换
[x y 1]=[x y 1]=[sx·x sy·y 1]
⑴当_____________时,为恒等比例变换,即图形不变;
⑵当_____________时,图形沿两个坐标轴方向等比例放大;
⑶当_____________时,图形沿两个坐标轴方向等比例缩小;
⑷当_____________时,图形沿两个坐标轴方向作非均匀的比例变换。
答案:、>1、<1、
2.在XOY平面上的二维图形绕原点顺时针旋转角,则变换矩阵为
_________________。
答案:
3. 相对某一个参考点()作比例、旋转变换,其变换的过程是先把坐标系原点平移至__________,在新的坐标系下作比例或旋转变换后,再将坐标原点____________。
答案:()、平移回去
4. 平移变换GlTranslate*(x,y,0)所生成的等价二维变形矩阵为:
________________。
答案:
5. 函数glRotate*(θ,0,0,1)产生的等效二维变换矩阵为:
__________________。
答案:
6. 函数glScale*(x,y,0)命令生成的二维变换矩阵为:___________________。
答案:。
