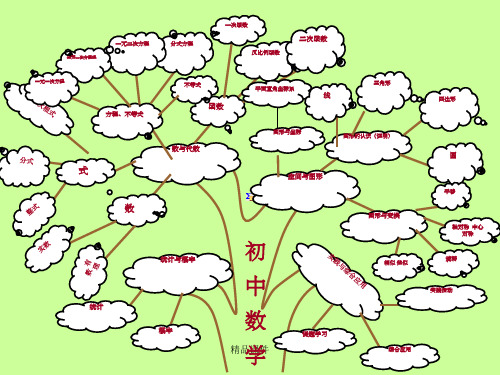
九年级数学上册期中思维导图
导图系列(5):九年级上册数学(北师大版)各章知识点思维导图集合

中心对称 两组对角分别相等的四边形
面积 底×高
对角线互相平分的四边形
对角相等, 邻角互补
四边相等的四边形
互相垂直平分; 中心对称
每一条对角线
+
有一组邻边相等的平行四边形
平分一组对角 轴对称 对角线互相垂直的平行四边形
底×高; 对角线乘积
的一半
四个角 都是直角
相等且 互相平分
有三个角是直角的四边形
第五章 投影与视图
第六章 反比例函数
九年级上册数学(北师大版) 思维导图集合
第一章 特殊的平行四边形
图形 边
平行 对边平行 四边形 且相等
菱形
对边平行, 四条边相等
矩形
对边平行 且相等
对边平行, 正方形
四条边相等
第一章 特殊的平行四边形
性质 角
ห้องสมุดไป่ตู้
对角线
对角相等, 邻角互补
互相平分
对称性
判定
两组对边分别相等的四边形 两组对边分别平行的四边形 一组对边平行且相等的四边形
中心对称
+
有一个角是直角的平行四边形
轴对称 对角线相等的平行四边形
长×宽
四个角 都是直角
有一个角是直角的菱形
相等且
中心对称 对角线相等的菱形
互相垂直平分;
+
每一条对角线
轴对称 有一组邻边相等的矩形
平分一组对角
对角线互相垂直的矩形
边长×边长
第二章 一元二次方程
第三章 概率的进一步认识
第四章 图形的相似
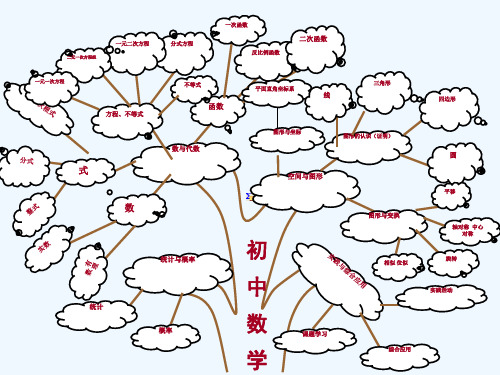
导图系列(5)九学年上册数学(北师大版)各章知识点思维导图集合

中心对称 两组对角分别相等的四边形
面积 底×高
对角线互相平分的四边形
对角相等, 邻角互补
四边相等的四边形
互相垂直平分; 中心对称
每一条对角线
+
有一组邻边相等的平行四边形
平分一组对角 轴对称 对角线互相垂直的平行四边形
底×高; 对角线乘积
的一半
四个角 都是直角
相等且 互相平分
有三个角是直角的四边形
第五章 投影与视图
第六章 反比例函数
九年级上册数学(北师大版) 思维导图集合
第一章 特殊的平行四边形
图形 边
平行 对边平行 四边形 且相等
菱形
对边平行, 四条边相等
矩形
对边平行 且相等
对边平行, 正方形
四条边相等
第一章 特殊的平行四边形
性质 角
对角线
对角相等, 邻角互补
互相平分
对称性
判定
两组对边分别相等的四边形 两组对边分别平行的四边形 一组对边平行且相等的四边形
中心对称
+
有一个角是直角的平行四边形
轴对称 对角线相等的平行四边形
长×宽
四个角 都是直角
有一个角是直角的菱形
相等且
中心对称 对角线相等的菱形
互相垂直平分;
+
每一条对角线
轴对称 有一组邻边相等的矩形
平分一组对角
对角线互相垂直的矩形
边长×边长
第二章 一第四章 图形的相似
沪教版(上海市) 初中数学思维导图 九年级数学全册章节思维导图集

你现在的努力要对得起别人对你的好!
第二十八章 统计初步的章节知识点结构思维导图
-3Math 实验室
你现在的努力要对得起别人对你的好!
上海市(沪教版)九年级数学全册章节思维导图 共五章
第二十四章 相似三角形的章节知识点结构思维导图
第二十五章 锐角三角比的章节知识点结构思维导图
-1Math 实验室
你现在的努力要对得起别人对你的好!
第二十六章 二次函数的章节知识点结构思维导图
第二十七章 圆ห้องสมุดไป่ตู้正多边形的章节知识点结构思维导图
初中数学九年级上册思维导图

初中数学九年级上册思维导图一、数与代数1. 实数有理数整数正整数、负整数、0分数正分数、负分数无理数无理数的定义无理数的分类2. 代数式代数式的定义代数式的分类单项式正单项式、负单项式多项式二项式、三项式等代数式的运算加法减法乘法除法3. 方程一元一次方程一元二次方程多元一次方程方程的解法4. 不等式一元一次不等式一元二次不等式不等式的解法二、几何1. 基本几何概念点、线、面线段、射线、直线角、直角、锐角、钝角三角形2. 几何图形四边形矩形、正方形、菱形、梯形多边形五边形、六边形等圆3. 几何证明证明方法综合法、分析法、反证法证明步骤4. 几何计算面积计算体积计算三、统计与概率1. 数据收集与整理数据收集方法数据整理方法2. 数据分析平均数、中位数、众数方差、标准差3. 概率概率的定义概率的计算方法四、数学应用1. 实际问题生活问题科学问题2. 数学建模建模方法建模步骤3. 数学软件数学软件的使用数学软件的应用初中数学九年级上册思维导图五、数学思想与方法1. 数形结合数形结合的定义数形结合的应用2. 分类讨论分类讨论的原则分类讨论的步骤3. 归纳与演绎归纳法的定义与应用演绎法的定义与应用4. 数学建模建模的必要性建模的过程5. 数学探究探究的意义探究的方法六、数学文化1. 数学史古代数学近代数学现代数学2. 数学家故事国内数学家国际数学家3. 数学趣闻数学趣题数学游戏4. 数学与生活数学在科技中的应用数学在生活中的应用七、数学学习策略1. 学习方法预习、听课、复习作业、练习、考试2. 时间管理合理安排学习时间高效利用学习时间3. 学习资源教师辅导、同学互助、家长支持4. 学习评价自我评价同伴评价教师评价八、数学素养1. 数学思维逻辑思维抽象思维创新思维2. 数学语言符号语言图形语言文字语言3. 数学审美数学的美数学的美学价值4. 数学情感对数学的兴趣对数学的热爱初中数学九年级上册思维导图九、数学竞赛与拓展1. 数学竞赛数学竞赛的种类数学竞赛的技巧数学竞赛的准备2. 数学拓展数学课外活动数学研究性学习数学建模竞赛十、数学实验1. 实验目的培养学生的动手能力增强学生的数学兴趣2. 实验内容几何实验统计实验数学软件实验3. 实验方法观察法实验法探究法十一、数学教育1. 教育理念以学生为本注重过程强调应用2. 教学方法启发式教学合作学习情境教学3. 教育评价多元评价过程评价终结评价十二、数学与社会1. 数学在科技中的应用计算机科学工程技术经济管理2. 数学在生活中的应用购物做饭出行3. 数学与艺术音乐绘画建筑。
初中数学知识结构图思维导图(中考复习)
作等腰三角形 作一点到三点距离相
翻折后与 另一图形重合
到两点距离相等的点
点到两点 的距离相 等
性质
判定
应用
垂直平分线
定义
对称点
关于轴对称
基本 图形
对称 轴
特征
要素
利用轴对称制作图案
用 坐标 表示 轴对
称
基本图形
作:关于x轴、 y轴的对称点
解决几何中的 极值问题
一条直线
翻折后与 两部分重 合
对称轴 定义
到角两边距离相等的 点
对应点的坐标比为k或-k
适用于 直角三角形
点到角两边 的距离相 等
性质 HL
判定
应用
用坐标表示 位似变换
放大或缩小图形
两图形相似 于一点对应边平行
对应顶点的连线交
外位似内位似
动
应用
性质
特征
对应角相等, 周长的比=相似比 方
对应边成比例, 面积的比=相似比的平
适合判定 所有三角 形 全等
运算
分母中 含字母、
分母 不为零
整式
分式
每个单项式
升降幂排列
最高项的次 数
项 次数
多项式
意义
单项式
字母指数和
次数
系数
代 数 式
数字因 数
精品课件
化除法为乘法
运算 分式方程
乘除 乘方
an
b
an bn
n为整数
an
1 an
n为整数
解法
应用 二次根式
运算 加减
性质
乘除
定义
aa0
(1) aa0双非负
2
切线长 定理
初中数学知识结构图思维导图(中考复习)
k>0
k<0
注意:过原点
一条直线
反比例函数
一次函数
解析式
性质
图象
应用
性质
图象
解析式
应用
k>0
k<0
图象在 二四象限
图象在 一三象限
双曲线
每一象限内
每一象限内
Y随x的增大而减小
Y随x的增大而增大
k>0
k<0
柱形储藏室轮船卸货 力学问题 电学问题
b<0,图象在 一三四象限
关于轴对称
定义
对称点
翻折后与 另一图形重合
特征
成轴对称的两图形全等
对称轴垂直平分对称点的连线
静
静
动
图案设计
用平移.轴对称和旋转的组合设计图案
应用
利用平移制作图案
动
平移过程 对应点坐标 的变化规律
(x,y)平移后(x±a,y±b)
右加左减
上加下减
中心对称
中心对称图形
关于中心对称
关于原点对称
旋转角=1800
确定有标记的相对图
直线
射线
线段
叠合法
直线公理
表示与画法Leabharlann 寻找射线方法表示与画法
计算与比较
性质
立体图形
角的计算
定义.表示
进位.计算
尺规作角
度.分.秒互化
度量法
余角.补角
角平分线
等角的余角相等 等角的补角相等
性质
平行线
相交线
对邻 顶补 角角
垂 直
性质
判定
相等
和 为1800
点到直线 的距离
性质
定义
九年纪上的数学思维导图

九年纪上的数学思维导图欣赏一、定义和特点1、一元二次方程:含有一个未知数,并且未知数的最高次数是2的整式方程叫做一元二次方程。
2、一元二次方程的一般形式:a平方+b+c=0(a0),它的特征是:等式左边加一个关于未知数二次多项式,等式右边是零,其中a平方+叫做二次项,a叫做二次项系数;b叫做一次项,b叫做一次项系数;c叫做常数项。
二、方程起源古巴比伦留下的陶片显示,在大约公元前2000年(2000BC)古巴比伦的数学家就能解一元二次方程了。
在大约西元前480年,中国人已经使用配方法求得了二次方程的正根,但是并没有提出通用的求解方法。
西元前300年左右,欧几里得提出了一种更抽象的几何方法求解二次方程。
7世纪印度的婆罗摩笈多(Brahmagupta)是第一位懂得用使用代数方程,它同时容许有正负数的根。
11世纪阿拉伯的花拉子密独立地发展了一套公式以求方程的正数解。
亚伯拉罕巴希亚(亦以拉丁文名字萨瓦索达著称)在他的著作Liberembadorum中,首次将完整的一元二次方程解法传入欧洲。
据说施里德哈勒是最早给出二次方程的普适解法的数学家之一。
但这一点在他的时代存在着争议。
这个求解规则是(引自婆什迦罗第二):在方程的两边同时乘以二次项未知数的系数的四倍;在方程的两边同时加上一次项未知数的系数的平方;在方程的两边同时开二次方。
三、性质方程的两根与方程中各数有如下关系:1+2=-b、a,12=c、a(也称韦达定理)方程两根1,2时,方程为:^2+(1+2)+12=0(根据韦达定理逆推而得) b^2-4ac0有2个不相等的实数根,b^2-4ac=0有两个相等的实数根,b^2-4ac0无实数根。
四、一般解法一元二次方程的一般解法有以下几种:配方法(可解部分一元二次方程)公式法(在初中阶段可解全部一元二次方程,前提:△0)因式分解法(可解部分一元二次方程)直接开平方法(可解全部一元二次方程)解一元二次方程的基本思路通过降次把一元二次方程转化为一元一次方程求解。
