奥林匹克训练题库·去伪存真(word版)

合集下载

【精品】数学奥林匹克竞赛高中训练题集【共36份】

奥林匹克数学竞赛高中训练题集
目录
数学奥林匹克高中训练题（01） ........................................................................................................................... 1 数学奥林匹克高中训练题（02） ........................................................................................................................... 3 数学奥林匹克高中训练题（03） ........................................................................................................................... 4 数学奥林匹克高中训练题（04） ........................................................................................................................... 6 数学奥林匹克高中训练题（05） ........................................................................................................................... 8 数学奥林匹克高中训练题（06） ...........................................................

奥林匹克运动试题一

奥林匹克运动试题一第一篇：奥林匹克运动试题一一、名词解释：（20分）1、古奥运会花冠：古代奥运会胜利者的奖品是从阿尔提斯采摘的橄榄枝编成的花冠。

古希腊人认为，橄榄树是雅典保护神雅典娜带到人间的，是神赐予人类和平与幸福的象征，因此用橄榄枝编织的花冠是最神圣的奖品。

据说，用于编织桂冠的橄榄枝必须由一个双亲健在的12岁儿童用纯金小刀从神树上割下来。

古代奥运会对于其优胜者并不注重物质的奖励，而是给予他们最高的荣誉——一顶橄榄枝编织而成的花冠。

橄榄枝花冠编制时不仅要特别精心，而且还要特别虔诚。

奖给获胜运动员以橄榄枝花冠的做法，始于公元前752年的第7届古代奥运会。

当时除奖给冠军以橄榄枝花冠外，还另外发一条棕榈枝，运动员右手持枝，以示荣耀。

奥运优胜者不但得到大会的奖励，在自己的城邦也会得到许多荣誉和奖赏。

但是从古到今，最重要的，也是最悠久的奖励方式，还是授予橄榄枝花冠。

2、奥林匹克会旗：奥林匹克标志，由五个奥林匹克环组成，五环的颜色规定为蓝、黄、黑、绿、红，环从左到右互相套接，上面是蓝、黑、红环，下面是黄、绿环。

长3米，宽2米，以白色为底，象征纯洁。

国际奥委会会旗系1913年根据皮埃尔·德·顾拜旦的构思而设计制作的。

会旗和五个环的含义是，象征五大洲的团结，全世界的运动员以公正、坦率的比赛和友好精神，在奥运会上相聚一堂。

3、奥林匹克村：奥运村又叫奥林匹克村或者运动员村。

指奥林匹克运动会主办城市为参加奥运会的运动员、教练员提供的集中住宿的处所。

奥运村从运动会开幕前两周开始使用，闭幕三天后结束使用。

各代表团入住奥运村都要举行入村仪式。

4、奥林匹克精神：相互理解、友谊长久、团结一致和公平竞争二、填空题：（40分）1、2000年（第27）届奥运会在（悉尼）举行，2008年（第29）届奥运会将在（北京）举行。

2、古奥会从公元前（776）年起至公元（393）年止，经历了（1169）年，共举行了（293）届。

数学奥林匹克高中训练题(20)及答案

数学奥林匹克高中训练题（20）第一试一、选择题（本题满分 36分，每小题6分）x — a1.（训练题25）已知函数y 的反函数的图象关于点（-1,3）成中心对称图形，则实数 a 等于x-a -1（A ）.（A ） 2 （B ）3（C ）-2（D ）-4,5 I222.（训练题25）我们把离心率等于黄金比丄二的椭圆称之为“优美椭圆”.设二•爲=1（a > b >2a 2b 20）为优美椭圆，F, A 分别是它的左焦点和右端点，B 是它的短轴的一个端点，贝y ■ ABF 等于（C ）.复数一定是（C ）.Z 26.（训练题25）在集合M 二｛1,2,3,）11,10｝的所有子集中，有这样一族不同的子集,不是空集，那么这族子集最多有（B ）. （A ） 210 个（B ） 29 个（C ）102 个（D ） 92 个(A) 60o(B)75°(C)90o(D)120°3.（训练题25）已知 ABC 三边的长分别是a,b,c , 复数Z i ,Z 2满足 Z i =a, Z 2 =b,乙+ z 2 = c ，那么（A ）是实数(B)是虚数(C)不是实数(D) 不是纯虚数4.（训练题25）函数 f (X)二 1（-厂卩：21 c2 c 2CE 的最大值是（D ）. (A) 20(B)10(C)-10(D)-205 .（训练题 25）以O 为球心，4为半径的球与三条相互平行的直线分别切于A,B,C 三点.已知S.BOC = 4 ,S ABC 16，则• ABC 等于(B).Ji(A)—12(B)5■： 7■:12(C)12(D)11- 12它们两两的交集都二、填空题（本题满分54分，每小题9分）1.（训练题25）在直角坐标系中，一直角三角形的两条直角边分别平行于两坐标轴，且两直角边上的中3线所在直线方程分别是 v =3x • 1和v = mx • 2，则实数m 的值是3或124x2 •（训练题25）设f （x ） J （a .0,a "） , [m]表示不超过实数m 的最大整数，则函数1+a x1 1[f （x ） ] [f （-x ）]的值域是 ___________ {-1,0} ________ •2 2 ------------------------------3 •（训练题25）设a, b,c 是直角三角形的三条边长，c 为斜边长，那么使不等式a 2 （bc ） b 2 （c a ） c 2 （a • b ） _ kabc 对所有直角三角形都成立的 k 的最大值是2 3 r 2•4.（训练题25）如图，正三棱柱 ABC -ABG 的各条棱长都是1,截面BCD 1 在棱AA 上的交点为D ,设这个截面与底面ABC 和三个侧面ABB 1A 1,BCC 1B 1,CAAC 1所成的二面角依次为：「，：七，〉，若 c o ：s^ c o 2s-c 3o S，则截面的面积等于 —3乜 _______________85.（训练题25）已知f （x ）是定义域在实数集的函数，且f （X • 2）[1 - f （X ）] =1 • f （x ）•若f （1） =2，,3 , 则 f （1949）的值是 ___________ p 3 - 2 .6.（训练题25）设x 1是方程.3sin x 「3cosx = 2a 「1的最大负根，x 2是方程2cos 2x 「2sin 2x = a 的最小正根，那么，使不等式为Ex?成立的实数a 的取值范围是 ________ - -43^a^~或 a= 2 __________.2第二试一、（训练题25）（本题满分25分）某眼镜车间接到一任务，需要加工 6000个A 型零件和2000个B 型零件，这个车间有 214名工人，他们每一个人加工 5个A 型零件的时间可加工 3个B 型零件•将这些人分成两组同时工作，每组加工同一型号的零件，为了在最短的时间完成，应怎样分组？ 77二、（训练题25）（本题满分25分）已知一个四边形的各边长都是整数，并且任意一边的长都能整除其余三边之和.求证：这个四边形必有两边相等.B 1B（训练题25）（本题满分35 分）实数数列a1, a2, |a3, ,a M足a P 帕弋钏帕996—為97=1997若数列｛0｝满足：b k = ai+：+川％（k =1,2川1997）.求bf —b2 + b2 —…+0 996-匕997的最大可能值.四、（训练题25）（本题满分35分）给定两个七棱锥，它们有公共的底面A,A2A3A4A5A6A7，顶点R,P2在底面的两侧•现将下述线段中的每一条染红，蓝两色之一：R,P2，底面上的所有的对角线和所有的侧棱.求证：图中心存在一个同色三角形.。

奥林匹克运动复习题

奥林匹克运动复习题一．填空题1．古代奥运会从公元前 776 年有文字记录的第一届开始，到公元393 年，共举办了 293 届，历时1169 年。

2．古代奥运会“神圣休战”最初有效期为 1个月，后来延长到 3个月。

3．古代奥运会对运动员有严格的规定：他们必须是希腊血统的自由民。

奴隶、战俘和异族人不能参加比赛。

4．古希腊带有宗教色彩的竞技活动逐渐形成许多竞技赛会，主要的有：奥林匹亚、皮托、伊斯特摩斯、尼米亚四大祭神竞技会。

5．在创办奥林匹克运动的过程中，有众多的先驱者，其中，法国教育家顾拜旦做出了杰出的贡献。

6．国际奥林匹克委员会于1894 年 6 月23 日在法国巴黎索邦神学院成立。

7．第一届现代奥运会于1896 年 4 月6—15 日，在希腊雅典举行。

8．从1984年美国洛杉矶奥运会起，奥运会组委会开始以商业开发为主的方式，筹集举办奥运会所需要的资金。

9．1912年第五届现代奥运会在斯德哥尔摩举行时，顾拜旦发表了著名的诗作《体育颂》获得本次奥运会文艺比赛的金质奖章。

10．1920 年，国际奥委会将更快、更高、更强确定为奥林匹克格言。

11．奥林匹克格言是：更快、更高、更强。

12．1964年东京奥运会开始出现奥运会的会标，1968年墨西哥奥运会开始出现奥运会的吉祥物。

13．1980年萨马兰奇开始担任国际奥委会的第七任主席。

14．国际奥委会委员的选择与确定，采用“逆向代表制”。

15．奥林匹克运动三大支柱是：国际奥委会、国际单项体育联合会、国家奥委会。

16．奥林匹克仪式有：圣火点燃及传递、开幕式、闭幕式、发奖仪式等。

17．奥运会的宣誓仪式包括：运动员宣誓和裁判员宣誓。

18．运动员宣誓仪式是在 1920年第七届奥运会上开始的。

19．奥运会的奖牌至少直径为60 毫米，厚3 毫米。

第一名奖牌镀金量至少 6 克黄金。

20．现代，直接面向奥运会的新闻传播媒介主要有：报刊、电视、广播、因特网。

21．1948年1月，国际奥委会在圣莫里茨举行的第42次全会上决定，将每年的 6月23日定为奥林匹克日。

奥林匹克训练题库_数值代入法

■说明:北师大东莞石竹附属学校2008—2009学年度第二学期初中毕业班第一次模拟考试卷时间：120分钟感；遥望大海, ；仰望蓝天,懂得品味这些快乐的人，自然会得到快乐的青睐。

万世c ogsmg （），悲欢岁月,满分120分痛苦难免，可是，懂得寻找快乐的人，快乐的旋律总会在他的心头回响。

要相信，仰起1 .全卷共4页。

满分120分，考试用时2. 答卷前，考生必须将自己的姓名、年级、的指定位置上；3. 答题可用黑色或蓝色字迹的钢笔或签字笔按各题要求写在答卷上，不能用铅笔和红色字迹的笔；若要修改，不准使用涂改液。

120分钟。

班级、考场、座次按要求填在答卷密封线左边把要修改的答案划上横线，在旁边有空位的地方写上修改后的答案。

一、基础（28分）（10 分） 0 ：1.根据课文默写古诗文。

'（1）几处早莺争暖树， '（2）求之不得， __________________ 。

:（3）杜牧的《泊秦淮》中表现诗人对国事危迫，朝廷上下却依然醉生梦死的深重忧虑；的诗句： * （4）分） ,（5）头，就有蓝天！3. 根据拼音写出文段括号处应填入的词语。

（2分） b ol Cn （） c mgsog （）4.联系上下文，仿照划波浪线的句子在横线处补充恰当的词句。

（2分）遥望大海， _____________________________________________ ; 仰望蓝天， _____________________________________________ 。

5.使用下面词语，另写一段连贯的话，至少用上其中两个。

（3分）广袤无垠沁人心脾感人肺腑青睐回响品味答：。

（白居易《钱塘湖春行》）（1分），辗转反侧。

（《关雎》）（1分） _________ 。

（2 分）。

朔气传金柝，寒光照铁衣。

（《木兰诗》）把孟浩然《过故人庄》默写完整。

（4分）故人具鸡黍，邀我至田家。

奥林匹克训练题库去伪存真

去伪存真47A, B, C, D四人中只有一人体育未达标，当有人问他们是谁体育未达标时，A说“是B', B说“是D , C说“不是我”，D说“B说错了”。

如果这四句话中只有一句是对的,那么体育未达标的是谁？48A, B, C, D四个孩子踢球打碎了玻璃窗。

A说：“是C或D打碎的。

”B说：“是D打碎的。

”C说：“我没有打碎玻璃窗。

”D说：“不是我打的。

”他们中只有一人说了谎话。

到底是谁打碎玻璃窗的？49A, B, C, D 四人在争论今天是星期几。

A说：“明天是星期五。

”B 说：“昨天是星期日。

”C说：“你们俩说的都不对。

”D说：“今天不是星期六。

”实际上这四人只有一人说对了。

今天是星期几？50丁丁把两张纸片团起来握在手中,请甲、乙、丙三个小朋友猜哪只手里握有纸片。

甲说：“左手没有,右手有。

”乙说：“右手没有,左手有。

”丙说：“不会两手都没有,我猜左手没有。

”丁丁说三人中有一人两句话都说错了, 一人两句话都猜对了, 一人对一句错一句。

问：丁丁的哪只手里有纸片？51甲、乙、丙三人分别是学校足球队、乒乓球队和篮球队的队员。

下面的说法只有一种是对的：1）甲是足球队的；(2)乙不是足球队的；(3)丙不是篮球队的。

问：甲、乙、丙分别是哪个队的?52从分别写着努、力、学、习四个字的四张卡片中选出三张，然后将这三张卡片有字的面朝下摆在桌子上。

甲、乙、丙分别猜每张卡片上是什么字，猜得的情况见下表：结果有一人全猜对了，有一人猜对两个，有一人全猜错了。

全猜错的是谁？53A，B，C三人谈他们的年龄，每人说的三句话中都有两句真话一句假话。

A说：“我不是最小的，B是25岁，我和B差3岁。

”B说：“C是23岁，A比C大3岁，我比C小。

”C说：“我22岁，我比A小2岁，比B大1岁。

”问：三人各多少岁？54甲、乙、丙三人，一个总说谎，一个从不说谎，一个有时说谎有一次谈到他们的职业。

甲说：“我是油漆匠，乙是钢琴帅，丙是建筑师。

奥林匹克训练题库·综合题

综合题121 甲、乙二人上午8时同时从东村骑车到西村去，甲每时比乙快6千米，中午12时甲到达西村后立即返回东村，在距西村15千米处遇到乙。

问：东、西两村相距多远？122 甲、乙两人分别从圆的直径两端同时出发，沿圆周行进。

如果逆向行走则50秒相遇，如果同向行走则甲追上乙需300秒。

求甲、乙的速度比。

123 张涛坐在行驶的公共汽车上，忽然发现李梅正在向相反的方向步行，2分后汽车到站，张涛下车去追李梅。

如果张涛的速度是李梅的2倍，是汽车速度的1/4，那么张涛要追上李梅要多少分？124 两条公路成十字交叉，甲从十字路口南1200米处向北直行，乙从十字路口处向东直行。

甲、乙同时出发10分后，两人与十字路口的距离相等，出发后100分，两人与十字路口的距离再次相等，此时他们距十字路口多少米？125 甲、乙两人步行速度之比是3∶2，甲、乙分别由A，B两地同时出发，若相向而行，则1时后相遇。

若同向而行，则甲需要多少时间才能追上乙？126 一辆汽车往线路上运送电线杆，从出发地装车，每次拉4根，线路上每两根电线杆间距离为50米，共运了两次，装卸结束后返回原地共用3时。

其中装一次车用30分，卸一根电线杆用5分，汽车运行时的平均速度是24千米／时，求第一根电线杆离出发点的距离。

127 红星小学组织学生排成队步行去郊游，每分步行60米，队尾的王老师以每分行150米的速度赶到排头，然后立即返回队尾，共用10分。

求队伍的长度。

128 小轿车、面包车和大客车的速度分别为60千米／时、48千米／时和42千米／时，小轿车和大客车从甲地、面包车从乙地同时相向出发，面包车遇到小轿车后30分又遇到大客车。

问：甲、乙两地相距多远？129 甲、乙、丙三人每分分别行60米、50米和40米，甲从B地、乙和丙从A 地同时出发相向而行，途中甲遇到乙后15分又遇到丙。

求A，B两地的距离。

130 甲、乙、丙三人在学校到体育场的路上练习竞走，甲每分比乙多走10米，比丙多走31米。

奥林匹克训练题库加法原理.doc.doc

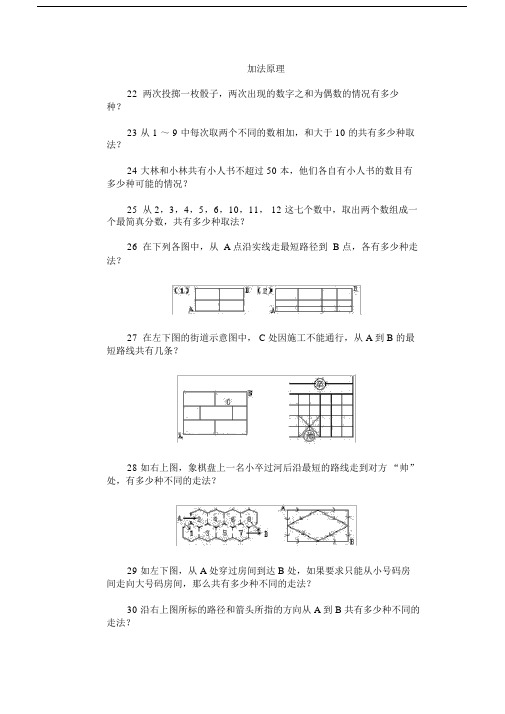
加法原理
22两次投掷一枚骰子，两次出现的数字之和为偶数的情况有多少
种？
23 从 1 ～ 9 中每次取两个不同的数相加，和大于 10 的共有多少种取法？
24 大林和小林共有小人书不超过 50 本，他们各自有小人书的数目有多少种可能的情况？
25从 2，3，4，5，6，10，11， 12 这七个数中，取出两个数组成一个最简真分数，共有多少种取法？
26在下列各图中，从 A 点沿实线走最短路径到 B 点，各有多少种走法？
27在左下图的街道示意图中， C处因施工不能通行，从 A 到 B 的最短路线共有几条？
28 如右上图，象棋盘上一名小卒过河后沿最短的路线走到对方“帅”处，有多少种不同的走法？
29 如左下图，从 A 处穿过房间到达 B 处，如果要求只能从小号码房间走向大号码房间，那么共有多少种不同的走法？
30 沿右上图所标的路径和箭头所指的方向从 A 到 B 共有多少种不同的走法？。

奥林匹克训练题库·智巧问题

五智巧问题1 某国的货币有1元、50分、20分、10分、5分、2分、1分共七种硬币（1元=100分）。

某人带了9枚硬币去买东西，凡不超过2元的东西他都能拿出若干枚硬币支付，钱数正好，无需找钱。

这9枚硬币的总面值最多是多少？最少是多少？2 A，B，C，D四人进行围棋比赛，每人都要与其他三人各赛一盘。

比赛是在两张棋盘上同时进行，每天每人只赛一盘。

第一天A与C比赛，第二天C与D比赛，第三天B与谁比赛？3 有20间房子，有的开着灯，有的关着灯。

在这些房子里的人都希望与大多数房子保持一致。

现在，从第1间房子里的人开始，如果其余19间房子的灯开着的多，就把灯打开，否则就把灯关上。

假设最开始时开灯与关灯的房子各10间，并且第1间房子的灯开着。

那么，这20间房子里的人轮完一遍后，开着灯的房子有几间？4 甲、乙、丙三名选手参加长跑比赛。

起跑后甲处在第一的位置，在整个比赛过程中，甲与乙、丙的位置次序共交换了7次。

比赛结果甲是第几名？5 正义路小学共有1000名学生，为支持“希望工程”，同学们纷纷捐书，有一半男生每人捐了9本书，另一半男生每人捐了5本书；一半女生每人捐了8本书，另一半女生每人捐了6本书。

全校学生共捐了多少本书？6 某杂志每期定价1.50元，全年共出12期。

某班部分同学订半年，其余同学订全年，共需订费720元；如果订半年的改订全年，订全年的改订半年，那么共需603元。

问：这个班共有多少名学生？7 某次猜谜语比赛，谜语按难易分两类，每人可以猜三条。

每猜对一条较难的谜语得3分，每猜对一条较容易的谜语得1分。

结果有8人得1分、7人得2分、6人得3分、5人得4分、4人得5分。

恰好猜对两条谜语的有几人？8 一排六棵树（见下图）分别是六个人栽的，A，B，C三人栽的是大树，D，E，F三人栽的是小树。

如果A与E栽的树相隔两棵树，B与F栽的树相隔一棵树，那么C栽的树是左起第几棵？9 一个正方形大厅被分隔成16个小间（见右图），每相邻两间都相通，有阴影的四间是休息室，其余布置成展览室。

数学奥林匹克高中训练题_222

数学奥林匹克高中训练题_222学校:___________姓名：___________班级：___________考号：___________一、填空题1．用{}x 表示实数x 的小数部分.已知()20177a =+.则{}a a =______.2．一个盒中有12件正品和3件次品,每次不放回地取出一件产品,在取得正品前已取出的次品数ξ的数学期望E ξ=______.3．函数()sin 22sin cos y x x x =-+的最大值为______,4．若数字()1,2,...,9i a i =满足985a a a <<<…且541a a a >>>…,则九位正整数981a a a …为一个“九位峰数”,例如134698752.那么,所有的九位峰数的个数为______. 5．已知方程20171x=的2017个根为1,122016,,,x x x ⋯·则2016111k kx ==+∑______.6．已知()f x =至少有一个正数b,使得()f x 的定义域和值域相同则满足条件的实数a 的值为______.7．已知抛物线24y x =,其焦点为F,一条过焦点F 、倾斜角为02πθπ⎛⎫<<⎪⎝⎭的直线与抛物线交于A 、B 两点,AO(O 为坐标原点)与准线交于点',B BO 与准线交于点A 则四边形''ABB A 的面积为______.8．对一个边长互不相等的凸2017边形的边染色,每条边可以染红、黄、蓝、紫四种颜色中的一种,但不允许相邻的边同色则共有______种不同的染色方法二、解答题9．已知数列{}n a的通项公式为()n nn a n Z +⎛⎫⎪=-∈⎪⎝⎭⎝⎭⎭，记1212nn n n n n S C a C a C a =++⋯+求所有的正整数n,使得7|n S .10．已知集合{}1,2,,13S =⋯,集合12,,,k A A A ⋯为S 的子集,满足:(1)()61,2,,i A i k ==⋯;(2)2(1)ij A A i j k ≤≤<≤，求k 的最大值11．如图,已知直线()1:20l y x m m =+<与抛物线()21:0C y ax a =>和圆()222:15C x y ++=均相切,F 为抛物线1C 的焦点.(1)设A 为抛物线1C 上的一动点,以A 为切点作抛物线1C 的切线,与y 轴交于点B ,以FA FB 、为邻边作FAMB ,证明:点M 在一条定直线上;(2)在(1)的条件下,记点M 所在的定直线为2l ,直线2l 与y 轴交于点,N MF 与抛物线1C 交于P Q 、两点,求NPQ 的面积S 的取值范围12．定义数列{}n a :()21121,1,2, (222)n n n n a a a n a a +===-+，证明:对每一个正整数(2),n n ≥均有121211111122222n n n n n a a a a ----+++⋯+<13．已知n 为正整数证明:21n +不存在模8余7的素因子 14．如图,ABC △的内切圆I 与边AB 、BC 切于D 、E 两点,DI 与I 的另一个交点为,F CF 与AB 交于点G,点H 在线段CG 上,且HG CF =.证明:若A 、H 、E 三点共线,则AB AC =.15．已知集合X 为平面a 内的一个有限点集, T 为平面a 内的一个正三角形,集合S X ⊆,且9S ≤.若对任意满足条件的集合S,均可以被正三角形T 的两个平移图形覆盖,证明:集合X 可以被正三角形T 的两个平移图形覆盖.参考答案1．1 【解析】【详解】记()20177b =则01b <<,且1ab =.注意到,(1008201622121201727kk k k a b CZ -+++=-=⨯∈∑而()(,01)a a b b a b Z b =-+-∈<<,故{}{}1b a a a ab =⇒==. 2．2491【解析】【详解】ξ取值为0、1、2、3,且()112115405C P C ξ===,()113122156 1235C C P C ξ=== ()213123151822455C C P C ξ===，()31312415232455C C P C ξ=== 故461820123535455455E ξ=⨯+⨯+⨯+⨯ 2491=. 3．1+【解析】【详解】由条件,知函数的周期为2π又'2cos22cos 2sin y x x x =-+,则函数在区间0,4π⎡⎤⎢⎥⎣⎦内单调递增,在区间,42ππ⎡⎤⎢⎥⎣⎦内单调递减,在区间5,24ππ⎡⎤⎢⎥⎣⎦内单调递增在区间, 5,24ππ⎡⎤⎢⎥⎣⎦元内单调递减. 当4x π=时,1y =-; 当54x π=时,1y =+故max 1y =+. 4．11875 【解析】【详解】由条件,知九位峰数的中间数只能为9、8、7、6、5. 当中间数为9时,九位峰数共有4489C C 个; 当中间数为8时,九位峰数共有4478C C 个; 当中间数为7时,九位峰数共有4467C C 个; 当中间数为6时,九位峰数共有4456C C 个; 当中间数为5时,九位峰数共有4445C C 个故所求九位峰数共有11875个. 5．1008 【解析】【详解】由()220171,2,...,2016kxi k x ek ==，知 ()201722017220172017kk kxix k x e eπ---===.则201711111111111k k k k k k k k k kx x x x x x x x x x -+=+=+=++++++ 故20161110081k kx ==+∑. 6．0或4 【解析】【详解】若0a =,则对每个正数(),b f x =.于是,0a =满足条件若0a >,则对任正数(),b f x =[)2,0,b D a ⎛⎤=-∞-⋃+∞ ⎥⎝⎦而()f x =[)0,A ⊆+∞,于是,D≠A,即0a >不符合条件若a<0,则对任正数b, ()f x =20,b D a ⎡⎤=-⎢⎥⎣⎦,此时,()maxb f x f a ⎛⎫=-= ⎪⎝⎭, 从而, ()f x =⎡⎢⎣.故24b a a -=⇔=- 综上,a 的值为0或-4. 7．38sin θ【解析】【详解】由条件,知直线AB 的斜率为tan k θ=. 设()()()112221,,,0A x y B x y y y << 由()21,4y k x y x⎧=-⎨=⎩得212124440,4y y y y y y k k--=⇒+==-. 又11:AO y l y x x =,则14y x y = 于是,AO 与准线的交点为14'1,B y ⎛⎫-- ⎪⎝⎭而214y y =-,则点B 与'B 的纵坐标相等. 从而,'BB x 轴记BO 与准线的交点为'A 类似地,'AA x 轴因此,四边形''ABB A 为直角梯形. 故()''1''''2ABB A S AA BB A B =+梯形()22111''22AB A B y y ==-()3322223188181cot sin k θθ⎛⎫=+=+=⎪⎝⎭8．201733- 【解析】【详解】考虑凸n 边形的情形,设不同的染法有n P 种易知,324P =.当n≥4时,首先,对于边1a ,有四种不同的染法.由于边2a 的颜色与边1a 的颜色不同,于是,对边2a 有三种不同的染法类似地,对边3,,a ⋯边1n a -均有三种染法.对于边,n a 用与边1n a -不同的三种颜色染色,此时,也包括了它与边1a 颜色相同的情形,而边1a 与边n a 颜色相同的不同染色方法数恰为凸n-1边形的不同染法数1n p -,故1143n n n P P --=⨯-()()3133nn n P n ⇒=+-⨯≥ 2017201733P ⇒=-.9．4(1,2,)n k k ==⋯ 【解析】【详解】记a β==则()()())111n n n i i in ni S C a a ββ==-=+-+故()()()()1121111n n n S a a ββ+++=+-++++-()()()()())111113,nnn n a a SS ββ++++-+=-.由11211122122,3S C a S C a C a ==+=,且213n n n S S S ++=-可算出{}n S 各项除以7的余数依次为1,3,1,0,6,4,6,0,1,3,⋯其是一个以8为周期的数列. 故74n S n ⇔,即()41,2,n k k ==⋯ 10．4 【解析】【详解】 k 的最大值为4.构造满足条件S 的子集1234A A A A 、、、:{}11,2,,6A =⋯, {}21,2,7,8,9,10A =, {}31,3,7,11,12,13A =, {}44,5,8,9,11,12A =.下面证明:k≤4.一方面,若存在元素a 在至少三个子集中出现,不妨设1231,1,1A A A ∈∈∈,则123A A A ⋃⋃=12312A A A A A ++-⋂- 3132312A A A A A A A ⋂-⋂+⋂⋂ 1231232221513A A A A A A ≥++---+=++-=故123A A A S ⋃⋃=且不等式取等条件为1213232,2,2A A A A A A ⋂=⋂=⋂=，{}1231A A A ⋂⋂=.若k≥5,考虑45A A 、.注意到,41234,6A A A A A ⊆⋃⋃= ,且()421,2,3j A A j ⋂≤=. 则()421,2,3j A A j ⋂==,且两两交集为空集.否则,不妨设{}{}{}1223311,2,1,3,1,4A A A A A A =⋂=⋂=⋂ 于是,{}45,6,,13A ⊆⋯ 类似地,{}35,6,,13A ⊆⋯又454545A A A A A A ⋂=+-⋃ 4593A A ≥+-=, 与2i j A A ⋂≤矛盾. 因此,k≤4.另一方面,若不存在元素a 在至少三个子集中出现,则1321363k ⨯≤=，即k≤4. 综上,k 的最大值为4.11．（1）见解析；（2）(9,)+∞ 【解析】【详解】(1)由条件知圆2C 的圆心为(0,-1),半径r =又圆心到直线1:2l y x m =+的距离为d ==解得m=-6(m=4舍去)设1l 与抛物线的切点为()000,A x y ,且'2y ax =.则0001122,ax x y a a=⇒== 代入直线1l 得12166a a a =-⇒=. 从而,抛物线2111:6C y x =,焦点30,2F ⎛⎫⎪⎝⎭设2111,6A x x ⎛⎫⎪⎝⎭,以A 为切点的切线l 的方程是()21111136y x x x x =-+令x=0,得切线l 与y 轴的交点2110,6B x ⎛⎫-⎪⎝⎭则21113,62FA x x ⎛⎫=- ⎪⎝⎭，2113 0,62FB x ⎛⎫=-- ⎪⎝⎭ 由FAMB 知()13FM FA FB x =+=-. 由F 为定点,知点M 在定直线32y =-上. (2)设直线3:2MF l y kx =+ 代人216y x =得212121306,962x kx x x k x x --=⇒+==-.则121122NPQSNF x x =-==. 又k≠0,于是,9NPQS >.因此,NPQ 的面积S 的取值范围是()9,+∞. 12．见解析【解析】【详解】注意到,()2222110n n n a a a -+=-+>.112a =. 于是,()0n a n Z +>∈ 用数学归纳法证明:312nn n a a +=. 当n=1时, ()110,12a =∈ 假设n=k 时,()0,1k a ∈.则n=k+1时,22122122k kk k k ka a a a a a +=<=-+. 从而,()10,1k a +∈由22112211222222n n n n n n n n n nna a a a a a a a a a a ++=⇒==<-+-++-因此()1n n a a n Z ++<∈故21211211122221n n n n n n a a a a a a -----==-+-+211111*********n n n n a a a a ----⎛⎫⎪ ⎪<=- ⎪-+- ⎪⎝⎭12111112222n n n a a a ---=-+⨯-+1222233111122222n n n n a a a a ----=--+⨯-+=⋯221211111122n n k k n k a a a a ---==-+⋅-+∑1212111111 (2222)n n n n n a a a a ----⇒++++<.13．见解析【解析】【详解】对素数()1mod8p ≡-,考虑12,22,23,24,22p -⨯⨯⨯⋯⨯模p 的余数,记其中不大于12p -的数为12,,,h r r r ⋯大于12p -的数为12,,,h s s s ⋯. 易知,()1,i j r r i j i j h =⇔=≤≤()1,i j s s i j i j g =⇔=≤≤.若i j p s r -=,则2|p ,与p 为大于2的素数矛盾. 于是, ()1,1i j p s r i g j h -≠≤≤≤≤.由()112i p p s i g --≤≤≤,知()111!2g h i j i j p r p s ==⎛⎫⎛⎫-⎛⎫-= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭∏∏ ()()1111!mod 2g h g i j i j p r s p ==⎛⎫⎛⎫⎛⎫-⎛⎫⇒≡- ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭∏∏ ()()12112!1!mod 22p g p p p -⎛⎫⎛⎫--⎛⎫⎛⎫⇒≡-⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭ ()()1221mod p gp -⇒≡-.又31112,24242p p p p --+-⨯⨯,故14p g +=. 设p=8k-1.则()4121mod k p -≡.设0n 为最小的正整数,使()021mod np ≡ 从而,()0|41n k -.事实上,不妨设0041(0)k n a b b n -=+≤<,得()21mod 0bp b ≡⇒=. 若存在n,使得()21mod np =-,取其中最小的正整数1n ,易知10n n < 否则,()101001 22221mod m m n n n n p --=⨯=≡-,与1n 的最小性矛盾.设()0110n n c d d n ≡+≤≤则()()01122212mod cn n c d d p ≡=⨯≡-.若c 为奇数,则()21mod d p ≡-,与1n 的最小性矛盾. 故c 为偶数,且d=0.此时,012n en = ,与()0|41n k -矛盾因此,不存在n,使得21n +不存在模8余7的素因子.14．见解析【解析】【详解】如图,设过I 上点F 的切线分别与BC 、AC 交于点M 、N由MN AB 、均为直径DF 的垂线,知MN AB .又F 为CMN 的旁切圆与MN 的切点,故G 为ABC 的旁切圆与AB 的切点. 记p 为ABC 的半周长,a b c 、、分别为顶点A B C 、、所对边的边长.则AG BD p b ==-.设AH 与BC 交于点'E . 由正弦定理、梅涅劳斯定理知''1''CE BA GH CE p b CH E B AG HC BE c GH-⋅⋅=⇒=⋅ ① 因为MN AB ,所以, c CF r S p c p c CG r p S p--==⋅=, 其中,c r r 、分别表示ABC 的内切圆半径、对应点的旁切圆半径,S 为ABC 的面积. 又,CF GH GF CH ==,于是, GH p c CH c-=. ② 由式①、②知''CE p b c p b BE c p c p c--=⋅=-- 从而,'E 为对应点A 的ABC 的旁切圆与边BC 的交点,'BE p c =-又BE p b =-,则A H E 、、三点共线当且仅当点E 与'E 重合,即'BE BE =，因此,p b p c -=- ,即b c AB AC =⇔=.15．见解析【解析】【详解】先证明两个引理引理1 若两个三角形1T 、2T 正同位相似,且三角形2T 与三角形1T 的三条边所在的直线相交,则三角形1T 位于三角形2T 之中此命题显然成立引理2 对任何有限点集M 和任何三角形T ,均可以找到一个与三角形T 正同位相似的三角形'T ,使得三角形'T 包含点集M ,且在三角形'T 的每条边上均有点集M 中的点引理2的证明显然存在包含点集M 且与三角形T 正同位相似的三角形,考虑其中的一个.若在其某条边上没有点集M 中的点,则通过作以边所对顶点为中心的位似变换将其缩小,使得该边与点集M 相交,并且缩小后的三角形仍然包含点集M ,对各条边均如此操作,即可得到所需的三角形'T .引理2得证综合两个引理,知三角形T 的任何包含点集M 的同位相似图形一定包含三角形'T .将引理2运用于点集X 和正三角形T ,得到一个三角形,不妨称之为ABC .在边BC CA AB 、、上分别有点集X 中的点a b c x x x 、、,其中,有些点可能重合若ABC 的大小不超过三角形T ,则题中结论成立.否则,考虑a a AB C 、b b A BC 、c c A B C ,其中, a a AB C 是以A 为中心所作的ABC 的位似图形,其大小与三角形T 相同,其余两个三角形的定义类似.因而,它们均为三角形T 的平移图形.再考虑点集X 的如下子集:a a a X X AB C =-,b b b X X A BC =-,c c c X X A B C =-.再证明一个引理引理3若三角形T 的某个平移图形'T 包含点a b x x 、,则图形'T 就不可能与c X 相交.对于其余情形也有类似的结论引理3的证明假设命题不真,于是,三角形'T 与c c A B C 各条边的直线相交.从而,它包含c c A B C .而三角形'T 与c c A B C 是全等的三角形,故它们重合.因此,由c X 的定义知三角形'T 不可能与之相交.引理3得证对三角形T 和集合a b c X X X 、、,运用引理2得到三角形a T 、三角形b T 、三角形c T ,且在它们的边上可找到分别属于集合a b c X X X 、、的点,,b c a c a b a a a b b b c c c x x x x x x x x x 、、、、、、(可能有些点相互重合).由题意,知点集{},,,,,,,,b c a c a b a a a b b b c c c x x x x x x x x x可被三角形T 的某两个平移图形12T T 、所覆盖故必有一个平移图形至少盖住a b c x x x 、、中的两个点,不妨设1a b x x T ∈、.据引理3,知三角形1T 不可能与集合X 相交.从而,点a b c c c X X X 、、均含于另一个三角形2T中.再由引理1,知集合c X 被包含于三角形2T 之中,这表明,集合X 被c c A B C 和三角形2T 所覆盖.。

第二部分题型一技法2 去伪存真——排除法

技法2去伪存真——排除法[试题特征]组合型选择题，罗列一些观点，并标注序号，每个选项是不同序号的组合，甚至不同选项中列出的序号数量不同，这类题本质上属于不定项选择题。

做题时可以把选项与题干条件逐一对照，将错误的选项逐一排除，缩小判断范围，去粗存精、去伪存真，正确的答案就浮出水面了。

[解题方法](1)利用选项与题干之间的矛盾：解题时把每个选项与题干条件逐一对照，可先从自己最熟悉、最有把握的选项开始，把一些较易判定、不合题意的选项排除，缩小选择范围，再从其余选项中找出正确的选项。

一般有三种情况：①排“错”法：选项不符合基本知识和基本原理；选项与材料及其区域特征矛盾，或与设问相矛盾。

②排“漏”法：这种方法针对组合型选择题极为适用，如果肯定其中某个说法是正确的，那么排除没有该项目的选项。

③排“无”法：选项符合基本原理和规律，但与题干无关。

(2)利用选项之间的矛盾：对于单项选择题，四个选项中只有一个是正确的，若能确定其中两三个选项的性质是相同的，那么，不同性质的选项就有可能是正确选项。

判断季节、月份等时间类的选择题中，往往四个选项中有三个选项表示的时间是相同的，则时间不相同的选项就是正确的。

(2020·福建福州期末)水是影响村落空间分布的重要因素。

我国某村落始建于明清时期，大部分建筑材料取自村落附近，村中有引水渠贯穿村巷(如左图所示)。

右图示意该村落空间分布。

据此完成1～3题。

1．该村落修建引水渠的主要目的是()A．提供饮食用水B．提供洗涤用水C．排放生活污水D．灌溉农田菜园2．该村落建筑外墙基部大量使用砖石，其主要作用是()A．保温隔热B．防震减灾C．防雪防雹D．防潮防蛀3．该村落最可能位于()A．东南丘陵B．长江三角洲C．华北平原D．长白山山区[技法应用]本组第1、3题可用排“错”法。

第1题，选项与材料矛盾。

水渠“露天”，排除A、C；水渠“贯穿村巷”，排除D，选B。

第2题，可采用直选法。

第3题，选项与区域特征矛盾。