单摆法测量重力加速度预习报告
单摆测重力加速度实验报告

一、实验目的1.学会秒表、米尺的正确使用。
2.理解单摆法测定重力加速的原理。
3.研究单摆振动的周期与摆长、摆角的关系。
4.学习系统误差的修正及在实验中减小不确定度的方法。
二、实验仪器单摆装置,停表(精度为0.01s ),钢卷尺(精度为0.05cm ),游标卡尺(精度为0.02mm )。
三、实验原理单摆的振动周期决定于重力加速度g 和摆长L ,只需要量出摆长L 并测定摆动周期,就能够得到g 。
如图:当θ<5︒时,圆弧可近似的看成直线,f 也可 近似的看成沿着这条直线,则有sin θ=xL ,f=Fsin θ=-mg x L=-m g Lx 由牛顿第二定律得:a=fm则有 a=-gLx 令ω=gLx 最终得单摆的运动方程为X=A cos(ωt +2π+φ) 其中T=2π ω=2π√ g =4π2L T考虑到摆球是有大小的,故g =4π2L+d 2T摆长L 用米尺测量,摆球直径d 用游标卡尺测量,周期T 用停表测量。
四、实验步骤1.测量摆长L 。
用米尺测量摆线支点与摆球顶点的距离l 。
用游标卡尺测量小球的直径d ,则摆长L=l+d2 。
2.测量摆动周期T 。
用手把摆球拉直偏离平衡位置5度左右,让其在一个垂直面内自由摆动,小球越过平衡位置瞬间开始计时,连续默数。
100次全振动时间t,T=t1003.为了减小误差,重复测量5次将数据记录于下表中。
五、数据记录与处理六、结果与讨论兰州的重力加速度g=9.973±0.005m/s2,结果有偏差,原因有以下几点;1、测量单摆周期时的反应时间。
2、在测量摆线长度时对最后一位数字的估读。
3、环境方面,温度、湿度、空气阻力的变化都会影响实验结果。
4、悬线质量的影响。
5、摆角角度的影响。
七、试验问题1、直接测量单摆往返一次的时间会受到人的反应时间的影响,通过多次测量求平均值的方法可以减小误差。
2、111.43、受空气阻力影响摆幅越来越小,但其周期不变;用木球代替铜球时,因木球密度较小,受空气阻力的影响会变大。
利用单摆测量重力加速度实验报告

利用单摆测量重力加速度实验报告利用单摆测量重力加速度实验报告一、实验目的利用单摆来测量重力加速度三、实验设备及工具铁架台(带铁夹), 中心有孔的金属小球, 约1m 长的细线, 米尺, 游标卡尺(选用), 秒表等。
四、实验内容及原始数据(一)实验内容1.在细线的一端打一个比小球上的孔径稍大些的结, 将细线穿过球上的小孔, 制成一个单摆。
2.将铁夹固定在铁架台的上端, 铁架台放在实验桌边, 使铁夹伸到桌面以外, 把做好的单摆固定在铁夹上, 使摆球自由下垂。
3.测量单摆的摆长l: 用游标卡尺测出摆球直径2r, 再用米尺测出从悬点至小球上端的悬线长l', 则摆长l=l'+r。
4.把单摆从平衡位置拉开一个小角度(不大于10°), 使单摆在竖直平面内摆动, 用秒表测量单摆完成全振动30 至50 次所用的时间, 求出完成一次全振动所用的平均时间, 这就是单摆的周期T。
5.将测出的摆长l 和周期T 代入公式g= 求出重力加速度g 的值。
(二)原始数据1.用游标卡尺测量钢球直径2rn 1 2 3 4 5 6直径2r(cm) 1.712 1.712 1.692 1.692 1.712 1.7222.用米尺测量悬线长l'n 1 2 3 4 5 6悬线长l' (cm) 91.90 91.90 91.91 91.90 91.88 91.903.用秒表测量摆动50 个周期用时为1’34’’84=94.84’’五、实验数据处理及结果(数据表格、现象等)1.钢球直径平均值2r=(1.712+1.712+1.692+1.692+1.712+1.722)÷6=1.707(cm)2.悬线长平均值l'=(91.90+91.90+91.91+91.90+91.88+91.90)÷6=91.898(cm)3.摆长l=l'+r=91.898+1.707=93.605(cm)4.求出完成一次全振动所用的平均时间, 即单摆的周期TT=94.84÷50=1.8968(s)5.计算g将测出的摆长l 和周期T 代入公式g= =10.27六、实验结果分析(实验现象分析、实验中存在问题的讨论)误差分析: 为什么所得g=10.27 大于标准值?1.振动次数: 可能是振动次数的有问题2.摆长测量: 可能是摆长测量偏大3.秒表使用: 可能是开表晚了。
用单摆测量重量加速度实验报告(带数据)

曲阜师范大学实验报告实验日期:5.17 实验时间:8:30-12:00姓名:方小柒学号:**********实验题目:用单摆测量重力加速度一、实验目的:本实验的目的是进行简单设计性实验基本方法的训练,根据已知条件和测量精度的要求,学会应用误差均分原则选用适当的仪器和测量方法,学习累积放大法的原理和应用,分析基本误差的来源,提出进行修正和估算的方法。
二、实验仪器:单摆仪、游标卡尺、螺旋测微器、电子秒表、米尺三、实验内容:1、游标卡尺的使用使用游标卡尺,测量5次单摆摆球的直径,记录数据。
2、螺旋测微计的使用使用螺旋测微计,测量5次单摆摆球的直径,记录数据。
3、电子秒表的使用使用电子秒表测量单摆摆动5个周期的时间,记录数据。
4、根据不确定度均分原理,设计单摆测量重力加速度g(1)根据误差均分原理,自行设计试验方案,合理选择测量仪器和方法.(2)测量重力加速度g,测量精度要求△g/g < 1%.可提供的器材及参数:游标卡尺,米尺,千分尺,电子秒表,支架,细线(尼龙线),钢球,摆幅测量标尺(提供硬白纸板自制),天平(公用).假设摆长l≈70.00cm;摆球直径D≈2.00cm;摆动周期T≈1.700s;米尺精度△米≈0.05cm;卡尺精度△卡≈0.002cm;千分尺精度△千≈0.001cm;秒表精度△秒≈0.01s;根据统计分析,实验人员开或停秒表反应时间为0.1s左右,所以实验人员开,停秒表总的反应时间近似为△人≈0.2s.5、利用单摆测量重力加速度g利用实验室提供的单摆仪,调整并确定合适的摆线长度,测量重力加速度四、实验原理:一、单摆的一级近似的周期公式为由此通过测量周期T,摆长l求重力加速度。
二、不确定度均分原理在间接测量中,每个独立测量的量的不确定度都会对最终结果的不确定度有贡献。
如果已知各测量之间的函数关系,可写出不确定度传递公式,并按均分原理,将测量结果的总不确定度均匀分配到各个分量中,由此分析各物理量的测量方法和使用的仪器,指导实验。
大学物理仿真实验报告单摆测重力加速度

大学物理仿真实验报告——单摆测重力加速度班级:机械(硕)21姓名:***学号:**********一,实验简介:单摆实验是个经典实验,许多著名的物理学家都对单摆实验进行过细致的研究。
本实验的目的是学习进行简单设计性实验的基本方法,根据已知条件和测量精度的要求,学会应用误差均分原则选用适当的仪器和测量方法,学习累积放大法的原理和应用,分析基本误差的来源及进行修正的方法。
二,实验原理:一根不可伸长的细线,下端悬挂一个小球。
当细线质量比小球的质量小很多,而且小球的直径又比细线的长度小很多时,此种装置称为单摆。
如果把小球稍微拉开一定距离,小球在重力作用下可在铅直平面内做往复运动,一个完整的往复运动所用的时间称为一个周期。
当摆动的角度小于5度时,可以证明单摆的周期T满足下面公式式中l为单摆长度。
单摆长度是指上端悬挂点到球重心之间的距离;g为重力加速度。
如果测量得出周期T、单摆长度l,利用上面式子可计算出当地的重力加速度。
三,实验所用仪器及使用方法:1,仪器:游标卡尺、米尺、千分尺、电子秒表、支架、细线(尼龙线)、钢球、摆幅测量标尺(提供硬白纸板自制)、天平(公用)2,使用方法:1.调节摆线长度:移动鼠标到左边的窗口中调节旋钮上方,点击鼠标左键或右键以减少或增加摆线长度。
减少或增加的幅度可由步长控制。
2.移动直尺: 移动鼠标到右边的小窗口中直尺上方,点击鼠标左键抓取直尺可上下移动直尺。
3.游标卡尺的操作信息可通过位于窗口下方的提示框获得。
提示框内的内容显示的是根据鼠标放在游标卡尺的不同部件时如何对这些部件操作的信息。
4. 电子秒表的计时操作是通过对用鼠标点击其上方两个按钮进行的。
当鼠标移到这两个按钮上时,将显示有关按钮功能的提示。
四,实验内容:一用误差均分原理设计一单摆装置,测量重力加速度g.设计要求:(1) 根据误差均分原理,自行设计试验方案,合理选择测量仪器和方法.(2) 写出详细的推导过程,试验步骤.(3) 用自制的单摆装置测量重力加速度g,测量精度要求△g/g < 1%.可提供的器材及参数:假设摆长l≈70.00cm;摆球直径D≈2.00cm;摆动周期T≈1.700s; 米尺精度△米≈0.05cm;卡尺精度△卡≈0.002cm;千分尺精度△千≈0.001cm;秒表精度△秒≈0.01s;根据统计分析,实验人员开或停秒表反应时间为0.1s左右,所以实验人员开,停秒表总的反应时间近似为△人≈0.2s.二. 对重力加速度g的测量结果进行误差分析和数据处理,检验实验结果是否达到设计要求.三. 自拟实验步骤研究单摆周期与摆长,摆角,悬线的质量和弹性系数,空气阻力等因素的关系,试分析各项误差的大小.四. 自拟试验步骤用单摆实验验证机械能守恒定律五、实验操作1. 用米尺测量摆线长度;测量摆线长度;测量摆线长度;2. 用游标卡尺测量小球直径;用游标卡尺测量小球直径;用游标卡尺测量小球直径;用游标卡尺测量小球直径;用游标卡尺测量小球直径;3. 把摆线偏移中心不超过把摆线偏移中心不超过把摆线偏移中心不超过 5度,释放单摆开始计时过度,释放单摆开始计时过度,释放单摆开始计时过度,释放单摆开始计时过度,释放单摆开始计时过度,释放单摆开始计时过50 个周期后停止计时,个周期后停止计时,个周期后停止计时,记录所用时间;记录所用时间;六,实验结果:1.摆球直径的测量2.测量摆线长度3.测量周期七、数据处理D(平均)=(1.722+1.702+1.732+1.662+1.682+1.692)/6=1.698cm 摆线长度+摆球直径=92.00cm摆长L=(摆线长度+摆球直径)-摆球半径=92.00-D/2=91.15cm=0.9115mT1=57.55/30=1.918sT2=76.77/40=1.919sT3=96.00/50=1.920sT=(T1+T2+T3)/3=1.919s由得:g=(4**)*L/(T*T)=9.77m/s*s=9.80-9.77=0.03m/s*sE=/g*100%=0.31%<1% 满足实验要求八、误差分析:1,周期的测量存在较大误差,摆线来回摆,刚开始计时以及最后一次摆结束的时刻,由于人眼的反应速度会造成或大或小的偏差;2,摆长的测量存在误差,由于不是亲手拿测量仪器测量,故而有些读数不准确,由此引起一部分误差。
用单摆法测重力加速度实验报告

用单摆法测重力加速度实验报告嘿,大家好,今天我想跟你们聊聊一个特别有趣的实验,叫做用单摆法测重力加速度。
听起来是不是有点深奥?其实就是用一根绳子和一个小球,做一个简单的摆动实验。
别急,跟我慢慢来,保证让你们听得津津有味,哈哈!单摆的构造其实特别简单。
你想象一下,一个小球用一根绳子吊着,绳子的一头固定,另一头随风摇摆。
就像摇晃的秋千,不过秋千是坐着的,这个是站着的,嘿嘿。
我们把小球放到一定高度,然后松手,它就开始摆动了。
小球的运动过程真是太美妙了,就像在跳舞一样,时而高高跃起,时而低低荡漾,真是让人眼花缭乱。
不过别看它好看,背后可有大科学在支持哦!怎么测重力加速度呢?你问我,我问谁!我们需要测量小球摆动的周期,也就是它从一个摆动到下一个摆动的时间。
这个周期的长短,跟重力加速度有着密切关系。
没错,简单的摆动,里面却藏着大智慧。
我们用秒表计时,小心翼翼地记录下每一次摆动的时间。
刚开始可能会紧张,生怕手一抖,时间就不准了,哈哈,不过慢慢来,时间也会教会你如何放松。
经过几次摆动后,我们就能得到一个比较准确的周期数据。
接下来就进入计算的环节。
用公式算一算,里面涉及到摆长、周期和重力加速度。
其实这部分数学不难,最难的就是记住公式,哈哈,老天,谁还没在脑海里多翻几遍公式呢?不过也就是简单的几步,就能得出我们想要的结果。
哦,对了,实验中最让我印象深刻的就是那些奇奇怪怪的小细节。
比如说风一吹,小球就会受到影响,摆动的幅度也会变,哈哈,真是让人哭笑不得。
有时候身边的人会忍不住喊“快看!快看!”小球都快变成明星了,简直就是实验室里的小明星,大家都围着它转。
想想都有点搞笑,不过这也是科学的乐趣吧!等我们计算出重力加速度,真是喜出望外,心里乐滋滋的。
这一刻,仿佛所有的努力和紧张都值了!我都忍不住想给小球来个高五,它是不能回应的,哈哈。
不过,心里默默感激它,为我带来了这个成果。
实验也有不足之处,比如说环境的影响,气温、气压等等,都会对实验结果造成偏差。
单摆测量重力加速度实验报告

单摆测量重⼒加速度实验报告再次经过时开始数1,直到数到50,⽴刻停⽌计时。
记下秒表的数据t。
5.由T=t/50 , l=L+(D/2) ,从⽽根据公式计算出g的⼤⼩。
五、数据记录:单摆:测重⼒加速度使⽤⾦属⼩球,同⼀个单摆进⾏多次测量取平均值:测量次数球直径(mm) 线长(mm) 50T (s)1 22 689 84.192 22 691 84.253 22 688 84.164 22 688 84.085 22 691 84.28六、数据处理1.由T=t/50 , l=L+(D/2)得出⼏次测量下的周期和线长,再根据公式计算出每⼀次测量下得出的和,分别作X、Y轴做出坐标图图表1excel中做出的坐标轴(勘误:横坐标单位应为s^2)得出斜率为g=8.1086m/s^22.测得算A类不确定度和平均值。
g1=9.76m/s^2 g2=9.79m/s^2 g3=9.74m/s^2g4=9.77m/s^2 g5=9.77m/s^2g=(g1+g2+g3+g4+g5)/5=9.766m/s^2经计算得出,A类不确定度:△A=0.0081m/s^23.⽐较两次的平均值。
两次测量第⼆次测得的重⼒加速度⼤于第⼀次且第⼀次平均值相对第⼆次的误差较⼤。
七、结果陈述:1.通过单摆测出的⼏组数据,结合公式T=2π√(l/g)推导出的g=4π^2/T^2,计算出的五组重⼒加速度,求得平均值g=9.766m/s^2。
2.通过⼿机内部陀螺仪⽤的软件制成的简易⼿机摆测得的重⼒加速度为g=9.83m/s^2 ,由于记录下数据瞬间需要⼿机停摆,会造成误差产⽣。
3.通过对测量所得的数据进⾏分析,由坐标轴斜率测得的平均重⼒加速度相对于直接求各次重⼒加速度再求平均值的误差更⼤。
单摆实验的预习实验报告

单摆实验的预习实验报告
预习实验报告:单摆实验
实验目的:
本次实验旨在通过单摆实验,探究单摆的运动规律,并通过实验数据分析和计算,验证单摆运动的理论公式。
实验器材:
1. 单摆装置
2. 计时器
3. 直尺
4. 细线
5. 铅笔
实验原理:
单摆是由一根轻细线和一块重物组成的简单物理摆,它的运动规律可以用简单的数学公式描述。
在实验中,我们将通过观察单摆的摆动周期和摆动幅度,来验证单摆运动的理论公式。
实验步骤:
1. 将直尺固定在桌子上,使其与桌面成约45度角。
2. 用细线将铅笔系在直尺的一端,形成单摆。
3. 将单摆拉开一定角度,释放后开始计时,记录摆动的周期。
4. 重复实验3次,取平均值作为实验数据。
实验数据:
实验一:摆动周期
1. 1.25s
2. 1.30s
3. 1.28s
平均值:1.28s
实验结果分析:
根据实验数据,我们计算得到单摆的摆动周期为1.28s。
通过理论公式计算得到的摆动周期为T=2π√(l/g),其中l为单摆的长度,g为重力加速度。
将实验数
据代入公式中,可以验证理论公式的准确性。
结论:
通过本次实验,我们成功验证了单摆运动的理论公式,并通过实验数据和计算
得到的结果进行了验证。
单摆实验不仅让我们更深入地理解了单摆运动的规律,也提高了我们的实验操作和数据分析能力。
希望通过今后的实验学习,我们能
够更加深入地理解物理学的知识,为将来的科学研究打下坚实的基础。
用单摆测量重力加速度实验报告

⽤单摆测量重⼒加速度实验报告单摆法测量重⼒加速度创建⼈:系统管理员总分:100报告⼈:宋宇⼷学号: 20191113705 分组: A分组序号:5 ⼀、实验⽬的[线上学习不⽤写]⼆、实验仪器[线上学习不⽤写]三、实验原理[线上学习不⽤写]四、实验内容[线上学习不⽤写]五、数据处理实验内容:单摆的设计和研究★(1) 原始数据本实验所测得数据如下:★(2) 计算单摆摆长(1)摆长的平均值L(单位:cm)=93.9(2)摆长的不确定度U(L)为(单位:cm)=0.05★(3) 计算单摆周期(1)单摆周期平均值T(单位:s)=1.98(2)周期的不确定度(s)=0.21★(4) 计算重⼒加速度g(1)根据单摆周期公式计算重⼒加速度g(单位:)=9.5(2)加速度g的不确定度Ug(单位:)=0.45六、思考题1. 实验中为了较⼩测量的误差,操作中的注意事项有哪些?1.视线与尺平⾏,确保读数准确。
2.多次测量,减⼩误差3.对测量结果影响⼤的物理量⽤精度较⾼的仪器测量4.做实验时精⼒⾼度集中2. 根据实验结果,尝试分析实验中产⽣误差的主要原因。
1.尺⼦精确度不够,会产⽣误差2.计时时⽆法准确计时导致⼀定误差3.实验⼈员⾃⾝未能准确读数和计算⼋、实验总结:该实验本⾝难度系数并不⾼,⾼中也涉及学习过相关内容,但对实验数据的精确度要求还是较⾼的。
虽然实验过程较简单,但还是要对实验数据的测量有着较⾼要求,需要记录每⼀个数据。
同时本次实验也让我重新回顾了游标卡尺和螺旋测微器的使⽤和读数⽅法,收获颇多。
九、原始数据:1.单摆摆长:93.9cm;2.摆球直径(游标卡尺):21.00cm (螺旋测微器):19.516cm3.50个周期:95.00s、98.00s、99.60s、101.20s、99.80s。
用单摆测量重力加速度实验报告

米尺
实际照片和程序中的显示
操作提示:
用鼠标拖动左侧全景图中的白色区域,改变右侧放大区域对应的位置
在右侧图中拖动米尺,可以改变米尺位置。
五、实验指导
『具体仪器操作见仪器说明』
准备仪器
将需要用到的仪器,从仪器栏中拖到桌面上来。鼠标移动到仪器上的时候, 可以在提示信息栏中看见相应的提示信息。
三、实验内容
1、用误差均分原理设计一单摆装置,测量重力加速度g.
设计要求:
(1)根据误差均分原理,自行设计试验方案,合理选择测量仪器和方法.
(2)写出详细的推导过程,试验步骤.
(3)用自制的单摆装置测量重力加速度g,测量精度要求△g/g< 1%.可提供的器材及参数:
游标卡尺,米尺,千分尺,电子秒表,支架,细线(尼龙线),钢球,摆幅测量标尺(提供硬白纸板自制),天平(公用).
使用仪器之前需要双击打开调节窗口再进行调节
测量摆球直径
双击打开千分尺或者游标卡尺窗口,点击开始测量按钮,将小球拖入进行测 量。
测量完成后关闭窗口
调节摆线长度
双击米尺打开米尺测量窗口,双击单摆打开单摆窗口
按住单摆窗口中摆线末端的旋钮调节摆线长度,在米尺窗口中读出摆线长度
测量摆动周期
打开单摆窗口和电子秒表窗口。拖动小球使其摆动,使用秒表测量周期
单摆法测重力加速度
一、实验简介
单摆实验是个经典实验,许多著名的物理学家都对单摆实验进行过细致的研 究。本实验的目的是进行简单设计性实验基本方法的训练,根据已知条件和测量精 度的要求,学会应用误差均分原则选用适当的仪器和测量方法,学习累积放大法的 原理和应用,分析基本误差的来源,提出进行修正和估算的方法。
单摆测量重力加速度实验报告

实验报告 学生姓名: 地点:三楼物理实验室 时间: 年 月 日同组人:实验名称:用单摆测重力加速度一、实验目的1.学会用单摆测定当地的重力加速度。
2.能正确熟练地使用停表。
二、实验原理单摆在摆角小于10°时,振动周期跟偏角的大小和摆球的质量无关,单摆的周期公式是T =2π l g ,由此得g =4π2l T 2,因此测出单摆的摆长l 和振动周期T ,就可以求出当地的重力加速度值。
三、实验器材带孔小钢球一个,细丝线一条(长约1 m)、毫米刻度尺一把、停表、游标卡尺、带铁夹的铁架台。
四、实验步骤1.做单摆取约1 m 长的细丝线穿过带孔的小钢球,并打一个比小孔大一些的结,然后把线的另一端用铁夹固定在铁架台上,并把铁架台放在实验桌边,使铁夹伸到桌面以外,让摆球自然下垂.2.测摆长用米尺量出摆线长l (精确到毫米),用游标卡尺测出小球直径D ,则单摆的摆长l ′=l +D 2。
3.测周期将单摆从平衡位置拉开一个角度(小于10°),然后释放小球,记下单摆摆动30次~50次的总时间,算出平均每摆动一次的时间,即为单摆的振动周期.反复测量三次,再算出测得周期数值的平均值。
4.改变摆长,重做几次实验。
五、数据处理方法一:将测得的几次的周期T和摆长l代入公式g=4π2lT2中算出重力加速度g的值,再算出g的平均值,即为当地的重力加速度的值。
方法二:图象法由单摆的周期公式T=2π lg可得l=g4π2T2,因此,以摆长l为纵轴,以T2为横轴作出l-T2图象,是一条过原点的直线,如右图所示,求出斜率k,即,可求出g值.g=4π2k,k=lT2=ΔlΔT2。
(隆德地区重力加速度标准值g=9.786m/s2)六、误差分析。
大学物理实验报告-单摆测重力加速度

大学物理实验报告-单摆测重力加速度在进行单摆测重力加速度的实验时,大家一定充满了期待与好奇。
我们走进实验室,心中一阵激动。
实验的核心就是利用单摆的周期来计算重力加速度。
这听起来简单,却蕴含了不少奥妙。
一开始,准备工作是关键。
我们需要一个稳固的支架,绳子以及一个小球。
绳子一定要够长,球也要适中。
感觉就像在为一场比赛做准备,选手们都在热身。
接着,确定好摆动的起始角度。
为了得到准确的数据,角度最好保持在小范围内,通常不超过15度。
大家都知道,过大的角度会导致结果不太靠谱。
真是如同“贪多嚼不烂”啊。
然后,测量周期是下一步。
这里的技巧就藏在细节里。
用秒表计时,注意观察小球从一侧摆动到另一侧所需的时间。
这个过程中,心中默念“静如处子,动如脱兔”,把握每一个瞬间。
记录多个周期的时间,再算出平均值。
这样得到的数据才有说服力。
每一次的摆动都仿佛在向我们诉说着重力的奥秘。
通过公式,最终的目标是求得重力加速度g。
这个过程让人如同探索未知的世界,既兴奋又紧张。
公式是g = 4π²L/T²,其中L是摆长,T是周期。
替换进去,经过简单的计算,重力加速度便浮出水面。
哇,看到那个结果的时候,心里满是成就感,感觉自己像个小科学家。
当我们得到g的值后,接下来的讨论环节是必不可少的。
每个人分享自己的实验感受。
有人说,整个过程就像一场和重力的亲密舞蹈。
另一些同学则提到,实验不仅是数据的堆砌,更是对自然规律的深入理解。
其实,真正的乐趣在于我们对这个结果的解读。
重力加速度的测量,不仅仅是数字,背后蕴含着科学的魅力。
每一次实验都是一次新发现。
单摆实验让我们意识到,生活中的物理无处不在。
大到行星的运动,小到我们日常的走路,都是重力在默默作祟。
这个时候,大家都忍不住想起那些关于重力的故事。
牛顿与苹果的传说,听起来真是神奇。
人类就是在这些奇妙的瞬间,开启了科学的探索之旅。
在总结时,大家的脸上都洋溢着满足的笑容。
单摆的实验不仅帮助我们测量了重力加速度,也让我们对物理的理解更加深刻。
单摆测重力加速度实验报告

单摆测重力加速度实验报告实验背景:重力是地球和其他星体互相作用的万有引力,是物理学中最基本的力之一。
本实验通过单摆的运动来测量地球表面上的重力加速度。
实验材料:1.单摆(包括球体、棒杆、支架)2.计时器3.直尺4.天平实验原理:单摆是由一个质量为m的球体通过一根质量可忽略不计的细长钢丝与一根不可摆动的垂直杆相连接而成。
当球体被拉离静止位置放开时,它就会在重力的作用下摆动。
球体运动的周期与重力加速度g及摆长L有关系,公式如下所示:T=2π√(L/g)实验步骤:1.使用天平测量球体、棒杆等物体的质量。
2.将单摆固定在支架上,并测量摆的长度L。
3.将球体离开静止位置,利用计时器测量单摆运动的周期T。
4.重复步骤3多次,取平均值。
5.根据公式计算重力加速度g的数值。
实验结果:利用上述公式和实验结果可以计算出重力加速度g的数值。
下列是三个实验结果:实验结果一:摆长L为0.8m,周期T为1.97s,通过计算得到的重力加速度g为9.885m/s²。
实验结果二:摆长L为1m,周期T为2.18s,通过计算得到的重力加速度g 为9.581m/s²。
实验结果三:摆长L为0.6m,周期T为1.69s,通过计算得到的重力加速度g为10.827m/s²。
结论:通过上述实验可以发现,重力加速度在不同的条件下计算出的数值可能会有一定的误差,但是误差范围不会太大。
我们还可以利用单摆测量其他的物理量,比如空气密度、钢丝直径等。
总之,单摆测重力加速度实验是一项非常有价值的实验,可以帮助我们更好地理解万有引力和运动规律。
此外,单摆测重力加速度实验不仅在理论上有很大的意义,在实际应用中也有着广泛的应用。
比如,无人机、火箭等飞行器的设计和控制,加载测试等领域都需要精确测量地球表面上的重力加速度。
需要注意的是,在进行单摆测重力加速度实验时,我们需要注意许多细节。
例如,球体的质量需要精确测量,摆长需要准确测量,让摆的振幅尽量小,以避免摆的受阻力的影响等等。
实验报告:用单摆测重力加速度
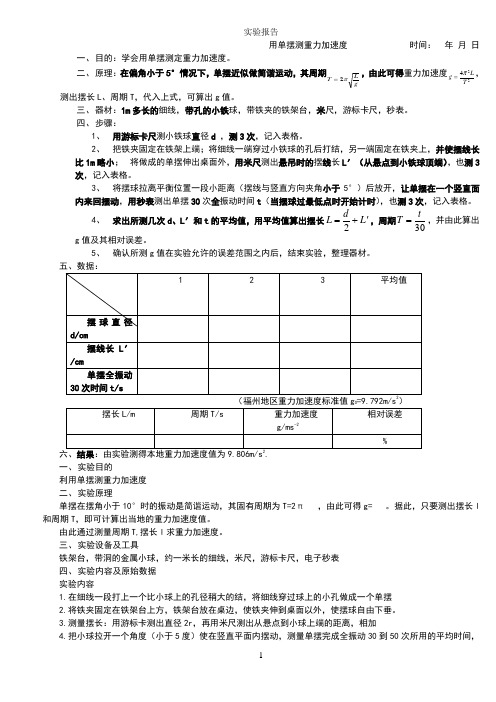
实验报告用单摆测重力加速度时间: 年 月 日一、 目的:学会用单摆测定重力加速度。
二、 原理:在偏角小于5°情况下,单摆近似做简谐运动,其周期gLT π2=,由此可得重力加速度224T L g π=,测出摆长L 、周期T ,代入上式,可算出g 值。
三、 器材:1m 多长的细线,带孔的小铁球,带铁夹的铁架台,米尺,游标卡尺,秒表。
四、 步骤:1、 用游标卡尺测小铁球直径d ,测3次,记入表格。
2、 把铁夹固定在铁架上端;将细线一端穿过小铁球的孔后打结,另一端固定在铁夹上,并使摆线长比1m 略小; 将做成的单摆伸出桌面外,用米尺测出悬吊时的摆线长L ′(从悬点到小铁球顶端),也测3次,记入表格。
3、 将摆球拉离平衡位置一段小距离(摆线与竖直方向夹角小于5°)后放开,让单摆在一个竖直面内来回摆动,用秒表测出单摆30次全振动时间t (当摆球过最低点时开始计时),也测3次,记入表格。
4、 求出所测几次d 、L ′和t 的平均值,用平均值算出摆长L d L '+=2,周期30tT =,并由此算出g 值及其相对误差。
5、 确认所测g 值在实验允许的误差范围之内后,结束实验,整理器材。
五、数据:0六、结果:由实验测得本地重力加速度值为9.806m/s . 一、 实验目的利用单摆测重力加速度 二、 实验原理单摆在摆角小于10°时的振动是简谐运动,其固有周期为T=2π ,由此可得g= 。
据此,只要测出摆长l 和周期T ,即可计算出当地的重力加速度值。
由此通过测量周期T,摆长l 求重力加速度。
三、 实验设备及工具铁架台,带洞的金属小球,约一米长的细线,米尺,游标卡尺,电子秒表 四、 实验内容及原始数据 实验内容1.在细线一段打上一个比小球上的孔径稍大的结,将细线穿过球上的小孔做成一个单摆2.将铁夹固定在铁架台上方,铁架台放在桌边,使铁夹伸到桌面以外,使摆球自由下垂。
3.测量摆长:用游标卡测出直径2r ,再用米尺测出从悬点到小球上端的距离,相加4.把小球拉开一个角度(小于5度)使在竖直平面内摆动,测量单摆完成全振动30到50次所用的平均时间,求出周期T5.带入公式求出g6.多次测量求平均值原始数据用米尺测得悬线与小球总长l+d=小球直径:测得单摆做40次全振动的时间为:五、实验数据处理及结果计算得g的值分别为(单位:m/s2):计算得g的平均值为s2六、实验结果分析误差分析:为什么所得g= m/s2大于标准值1.秒表使用:可能是表按晚了2 振动次数:可能是振动次数的有问题3.摆长测量:可能是摆长测量偏大一、实验目的利用单摆来测量重力加速度二、实验原理单摆在摆角小于10°时的振动是简谐运动,其固有周期为T=2π ,由此可得g= 。
利用单摆测量重力加速度实验报告

一、实验目的利用单摆来测量重力加速度二、实验原理单摆在摆角小于10°时的振动是简谐运动,其固有周期为T=2π ,由此可得g= 。
据此,只要测出摆长l和周期T,即可计算出当地的重力加速度值。
由此通过测量周期T,摆长l求重力加速度三、实验设备及工具铁架台(带铁夹),中心有孔的金属小球,约1m长的细线,米尺,游标卡尺(选用),秒表等。
四、实验内容及原始数据(一)实验内容1.在细线的一端打一个比小球上的孔径稍大些的结,将细线穿过球上的小孔,制成一个单摆。
2.将铁夹固定在铁架台的上端,铁架台放在实验桌边,使铁夹伸到桌面以外,把做好的单摆固定在铁夹上,使摆球自由下垂。
3.测量单摆的摆长l:用游标卡尺测出摆球直径2r,再用米尺测出从悬点至小球上端的悬线长l',则摆长l=l'+r。
4.把单摆从平衡位置拉开一个小角度(不大于10°),使单摆在竖直平面内摆动,用秒表测量单摆完成全振动30至50次所用的时间,求出完成一次全振动所用的平均时间,这就是单摆的周期T。
5.将测出的摆长l和周期T代入公式g= 求出重力加速度g的值。
(二)原始数据1.用游标卡尺测量钢球直径2rn 1 2 3 4 5 6直径2r(cm) 1.712 1.712 1.692 1.692 1.712 1.7222.用米尺测量悬线长l'n 1 2 3 4 5 6悬线长l' (cm) 91.90 91.90 91.91 91.90 91.88 91.903.用秒表测量摆动50个周期用时为1’34’’84=94.84’’五、实验数据处理及结果(数据表格、现象等)1.钢球直径平均值2r=(1.712+1.712+1.692+1.692+1.712+1.722)÷6=1.707(cm)2.悬线长平均值l'=(91.90+91.90+91.91+91.90+91.88+91.90)÷6=91.898(cm)3.摆长l=l'+r=91.898+1.707=93.605(cm)4.求出完成一次全振动所用的平均时间,即单摆的周期TT=94.84÷50=1.8968(s)5.计算g将测出的摆长l和周期T代入公式g= =10.27六、实验结果分析(实验现象分析、实验中存在问题的讨论)误差分析:为什么所得g=10.27大于标准值?1.振动次数:可能是振动次数的有问题2.摆长测量:可能是摆长测量偏大3.秒表使用:可能是开表晚了。
大学物理实验报告-单摆测重力加速度

大学物理实验报告-单摆测重力加速度一、引言在这次实验中,我们的目标是通过单摆来测量重力加速度。
听起来挺简单,但其实背后有很多值得我们深挖的知识。
这项实验不仅能让我们更好地理解物理原理,还能让我们亲身体验科学的魅力。
1.1 单摆的基本原理单摆,其实就是一个挂着小球的细绳。
我们通过让小球来回摆动,观察它的周期。
周期,就是小球从一边摆到另一边再回来的时间。
用公式算一下,能发现摆动周期与重力加速度有着密切关系。
想象一下,随着小球的摆动,空气中似乎充满了它的节奏,真是让人心动。
1.2 实验准备在实验前,我们得准备好一根绳子、一个小球和一个秒表。
看似简单的材料,却能组合出精彩的实验。
把绳子固定在一个高处,让小球自由摆动。
记得要把小球拉到一个小角度,这样才能保证实验的准确性。
每次摆动,我们都要认真观察和记录。
二、实验过程2.1 测量周期每次小球摆动时,我都拿着秒表,紧张地开始计时。
这个过程让我感觉像是在和时间赛跑。
每次记录周期,心里都有种说不出的期待。
我们重复几次,确保数据的可靠性。
小球的每一次摆动,都像是在给我传递信息,让我慢慢理解物理的美妙。
2.2 计算重力加速度接下来,我们将测得的周期代入公式,计算出重力加速度。
随着数字的变化,我的心情也随之波动。
最终结果显现出来时,那种成就感让人热血沸腾。
感觉自己仿佛成为了科学家,揭开了宇宙的一角。
2.3 数据分析我们将记录的数据整理成表格,进行分析。
曲线图、平均值……每一个步骤都带着挑战和乐趣。
通过图表,我看到了一种规律,仿佛自然在向我微笑。
数据背后,不只是冷冰冰的数字,还有我们努力的汗水与收获。
三、实验反思3.1 实验的意义这次实验让我明白,物理不仅仅是理论,它与我们的生活息息相关。
重力加速度并不是一个抽象的概念,而是无时无刻不在影响着我们的日常。
摆动的小球背后,是无数科学家的探索与发现。
3.2 未来的展望这次实验让我对物理产生了更深的兴趣。
未来,我希望能继续深入研究,探索更多自然现象背后的原理。
单摆测量重力加速度实验报告

实验报告学生姓名:地点:三楼物理实验室时间:年月日同组人:实验名称:用单摆测重力加速度一、实验目的1.学会用单摆测定当地的重力加速度。
2.能正确熟练地使用停表。
二、实验原理单摆在摆角小于10°时,振动周期跟偏角的大小和摆球的质量无关,单摆的周期公式是T=2π lg,由此得g=4π2lT2,因此测出单摆的摆长l和振动周期T,就可以求出当地的重力加速度值。
三、实验器材带孔小钢球一个,细丝线一条(长约1 m)、毫米刻度尺一把、停表、游标卡尺、带铁夹的铁架台。
四、实验步骤1.做单摆取约1 m长的细丝线穿过带孔的小钢球,并打一个比小孔大一些的结,然后把线的另一端用铁夹固定在铁架台上,并把铁架台放在实验桌边,使铁夹伸到桌面以外,让摆球自然下垂.2.测摆长用米尺量出摆线长l(精确到毫米),用游标卡尺测出小球直径D,则单摆的摆长l′=l+D 2。
3.测周期将单摆从平衡位置拉开一个角度(小于10°),然后释放小球,记下单摆摆动30次~50次的总时间,算出平均每摆动一次的时间,即为单摆的振动周期.反复测量三次,再算出测得周期数值的平均值。
4.改变摆长,重做几次实验。
五、数据处理方法一:将测得的几次的周期T和摆长l代入公式g=4π2lT2中算出重力加速度g的值,再算出g的平均值,即为当地的重力加速度的值。
结果:由实验测得本地重力加速度值为:方法二:图象法由单摆的周期公式T =2π l g 可得l =g 4π2T 2,因此,以摆长l 为纵轴,以T 2为横轴作出l -T 2图象,是一条过原点的直线,如右图所示,求出斜率k ,即,可求出g 值.g =4π2k ,k =l T 2=Δl ΔT 2。
(隆德地区重力加速度标准值g=9.786m/s 2)六、误差分析。
单摆测重力加速度实验报告

一、实验目的1.学会秒表、米尺的正确使用。
2.理解单摆法测定重力加速的原理。
3.研究单摆振动的周期与摆长、摆角的关系。
4.学习系统误差的修正及在实验中减小不确定度的方法。
二、实验仪器单摆装置,停表(精度为),钢卷尺(精度为),游标卡尺(精度为)。
三、实验原理单摆的振动周期决定于重力加速度g和摆长L,只需要量出摆长L并测定摆动周期,就能够得到g。
如图:当5时,圆弧可近似的看成直线,f也可近似的看成沿着这条直线,则有sin=,f=Fsin=L-mg=-m x 由牛顿第二定律得:a=则有Xa=-令=最终得单摆的运动方程为F=mgX=A其中T== g =考虑到摆球是有大小的,故摆长L用米尺测量,摆球直径d用游标卡尺测量,周期T用停表测量。
四、实验步骤1.测量摆长L。
用米尺测量摆线支点与摆球顶点的距离l。
用游标卡尺测量小球的直径d,则摆长L=l+。
2.测量摆动周期T。
用手把摆球拉直偏离平衡位置5度左右,让其在一个垂直面内自由摆动,小球越过平衡位置瞬间开始计时,连续默数100次全振动时间t,T=。
3.为了减小误差,重复测量5次将数据记录于下表中。
五、数据记录与处理t/sL/cm d/cm t =100T/s T=100 12345x六、结果与讨论兰州的重力加速度,结果有偏差,原因有以下几点;1、测量单摆周期时的反应时间。
2、在测量摆线长度时对最后一位数字的估读。
3、环境方面,温度、湿度、空气阻力的变化都会影响实验结果。
4、悬线质量的影响。
5、摆角角度的影响。
七、试验问题1、直接测量单摆往返一次的时间会受到人的反应时间的影响,通过多次测量求平均值的方法可以减小误差。
23、受空气阻力影响摆幅越来越小,但其周期不变;用木球代替铜球时,因木球密度较小,受空气阻力的影响会变大。
