(精选3份合集)2020届湖南省长沙市一中高考数学模拟试卷

合集下载

2020年湖南省长沙市高考数学一模试卷(文科)含答案解析

2020年湖南省长沙市高考数学一模试卷（文科）一、选择题1．设i为虚数单位，则复数3﹣i的虚部是（）A．3 B．﹣i C．1 D．﹣12．记集合A={x|x+2＞0}，B={y|y=sinx，x∈R}，则A∪B=（）A．（﹣2，+∞）B．[﹣1，1] C．[﹣1，1]∪[2，+∞）D．（﹣2，1]3．某空间几何体的三视图中，有一个是正方形，则该空间几何体不可能是（）A．圆柱 B．圆锥 C．棱锥 D．棱柱4．已知向量=（cosα，sinβ），=（sinα，cosβ），若∥，则α，β的值可以是（）A．α=，β=﹣B．α=，β=C．α=，β=﹣D．α=，β=﹣5．已知数列的前4项为2，0，2，0，则依次归纳该数列的通项不可能是（）A．a n=（﹣1）n﹣1+1 B．a n=C．a n=2sin D．a n=cos（n﹣1）π+16．已知定义在R上的函数f（x）满足f（x+1）=﹣f（x），且f（x）=，则下列函数值为1的是（）A．f（2.5）B．f（f（2.5））C．f（f（1.5））D．f（2）7．某研究性学习小组调查研究学生使用智能手机对学习的影响，部分统计数据如表使用智能手机不使用智能手机合计学习成绩优秀 4 8 12学习成绩不优秀16 2 18合计20 10 30附表：p（K2≥k0）0.15 0.10 0.05 0.025 0.010 0.005 0.001k0 2.072 2.706 3.841 5.024 6.635 7.879 10.828经计算K2=10，则下列选项正确的是：（）A．有99.5%的把握认为使用智能手机对学习有影响B．有99.5%的把握认为使用智能手机对学习无影响C．有99.9%的把握认为使用智能手机对学习有影响D．有99.9%的把握认为使用智能手机对学习无影响8．函数的单调递增区间是（）A．B． C．D．9．平面直径坐标系xOy中，动点P到圆（x﹣2）2+y2=1上的点的最小距离与其到直线x=﹣1的距离相等，则P点的轨迹方程是（）A．y2=8x B．x2=8y C．y2=4x D．x2=4y10．非负实数x、y满足ln（x+y﹣1）≤0，则关于x﹣y的最大值和最小值分别为（）A．2和1 B．2和﹣1 C．1和﹣1 D．2和﹣211．如果执行如图所示的程序框图，则输出的数S不可能是（）A．0.7 B．0.75 C．0.8 D．0.912．已知函数f（x）=e x，g（x）=x+1，则关于f（x），g（x）的语句为假命题的是（）A．∀x∈R，f（x）＞g（x）B．∃x1，x2∈R，f（x1）＜g（x2）C．∃x0∈R，f（x0）=g（x0）D．∃x0∈R，使得∀x∈R，f（x0）﹣g（x0）≤f（x）﹣g（x）二、填空题13．在空间直角坐标系中，已知点A（1，0，1），B（﹣1，1，2），则线段AB的长度为_______．14．记等差数列{a n}的前n项和为S n，若S3=2a3，S5=15，则a2020=_______．15．△ABC的周长等于2（sinA+sinB+sinC），则其外接圆半径等于_______．16．M，N分别为双曲线﹣=1左、右支上的点，设是平行于x轴的单位向量，则|•|的最小值为_______．三、解答题17．如图，OPQ是半径为2，圆心角为的扇形，C是扇形弧上的一动点，记∠COP=θ，四边形OPCQ的面积为S．（1）找出S与θ的函数关系；（2）试探求当θ取何值时，S最大，并求出这个最大值．18．空气质量指数（Air Quality Index，简称AQI）是定量描述空气质量状况的指数，空气质量按照AQI大小分为六级：0～50为优；51～100为良；101～150为轻度污染；151～200为中度污染；201～300为重度污染；＞300为严重污染．一环保人士记录了去年某地某月10天的AQI的茎叶图如图所示．（1）利用该样本估计该地本月空气质量优良（AQI≤100）的天数；（按这个月总共30天计算）（2）若从样本的空气质量不佳（AQI＞100）的这些天中，随机地抽取两天深入分析各种污染指标，求该两天的空气质量等级恰好不同的概率．19．如图，矩形BDEF垂直于正方形ABCD，GC垂直于平面ABCD，且AB=DE=2CG=2．（1）求三棱锥A﹣FGC的体积．（2）求证：面GEF⊥面AEF．20．已知椭圆C1： +=1（a＞b＞0）的顶点到直线l1：y=x的距离分别为，．（1）求C1的标准方程；（2）设平行于l1的直线l交C1与A、B两点，若以AB为直径的圆恰好过坐标原点，求直线l的方程．21．已知函数f（x）=x2+（a为实常数）．（1）若f（x）在（0，+∞）上单调递增，求实数a的取值范围；（2）判断是否存在直线l与f（x）的图象有两个不同的切点，并证明你的结论．[选修4-1：几何证明选讲]22．如图，C，D是以AB为直径的半圆上两点，且=．（1）若CD∥AB，证明：直线AC平分∠DAB；（2）作DE⊥AB交AC于E，证明：CD2=AE•AC．[选修4-4：坐标系与参数方程选讲]23．在平面直角坐标系xOy中，以坐标原点为极点，x轴正半轴为极轴建立极坐标系，曲线C1的极坐标方程为ρ2﹣4ρcosθ+3=0，θ∈[0，2π]．（1）求C1的直角坐标方程；（2）曲线C2的参数方程为（t为参数），求C1与C2的公共点的极坐标．[选修4-5：不等式选讲]24．设α、β、γ均为实数．（1）证明：|cos（α+β）|≤|cosα|+|sinβ|；|sin（α+β）|≤|cosα|+|cosβ|．（2）若α+β+γ=0．证明：|cosα|+|cosβ|+|cosγ|≥1．2020年湖南省长沙市高考数学一模试卷（文科）参考答案与试题解析一、选择题1．设i为虚数单位，则复数3﹣i的虚部是（）A．3 B．﹣i C．1 D．﹣1【考点】复数的基本概念．【分析】直接由复数的基本概念得答案．【解答】解：∵复数3﹣i，∴复数3﹣i的虚部是：﹣1．故选：D．2．记集合A={x|x+2＞0}，B={y|y=sinx，x∈R}，则A∪B=（）A．（﹣2，+∞）B．[﹣1，1] C．[﹣1，1]∪[2，+∞）D．（﹣2，1]【考点】并集及其运算．【分析】先化简集合A，B，再根据并集的定义即可求出．【解答】解：集合A={x|x+2＞0}=（﹣2，+∞），B={y|y=sinx，x∈R}=[﹣1，1]，则A∪B=（﹣2，+∞），故选：A．3．某空间几何体的三视图中，有一个是正方形，则该空间几何体不可能是（）A．圆柱 B．圆锥 C．棱锥 D．棱柱【考点】由三视图求面积、体积．【分析】由于圆锥的三视图中一定不会出现正方形，即可得出结论．【解答】解：圆锥的三视图中一定不会出现正方形，∴该空间几何体不可能是圆锥．故选：B．4．已知向量=（cosα，sinβ），=（sinα，cosβ），若∥，则α，β的值可以是（）A．α=，β=﹣B．α=，β=C．α=，β=﹣D．α=，β=﹣【考点】平面向量共线（平行）的坐标表示．【分析】根据向量的平行的条件以及两角和的余弦公式即可判断．【解答】解：向量=（cosα，sinβ），=（sinα，cosβ），若∥，∴cosαcosβ﹣sinαsinβ=0，即cos（α+β）=0，∴α+β=kπ+，k∈Z，对于A：α+β=0，不符合，对于B，α+β=π，不符合，对于C：α+β=﹣，符合，对于D，α+β=，不符合，故选：C．5．已知数列的前4项为2，0，2，0，则依次归纳该数列的通项不可能是（）A．a n=（﹣1）n﹣1+1 B．a n=C．a n=2sin D．a n=cos（n﹣1）π+1【考点】数列的概念及简单表示法．【分析】令n=1，2，3，4分别代入验证：即可得出答案．【解答】解：令n=1，2，3，4分别代入验证：可知C：a3=﹣2，因此不成立．故选：C．6．已知定义在R上的函数f（x）满足f（x+1）=﹣f（x），且f（x）=，则下列函数值为1的是（）A．f（2.5）B．f（f（2.5））C．f（f（1.5））D．f（2）【考点】函数的值．【分析】由f（x+1）=﹣f（x），得到函数的周期是2，根据分段函数的表达式结合函数的周期性进行求解即可．【解答】解：由f（x+1）=﹣f（x），得f（x+2）=﹣f（x+1）=f（x），则函数的周期是2，则f（2.5）=f（2+0.5）=f（0.5）=﹣1，f（f（2.5））=f（﹣1）=f（﹣1+2）=f（1）=﹣1f（f（1.5））=f（f（2﹣0.5））=f（f（﹣0.5））=f（1）=﹣1，f（2）=f（0）=1，即列函数值为1的f（2），故选：D．7．某研究性学习小组调查研究学生使用智能手机对学习的影响，部分统计数据如表使用智能手机不使用智能手机合计学习成绩优秀 4 8 12学习成绩不优秀16 2 18合计20 10 30附表：p（K2≥k0）0.15 0.10 0.05 0.025 0.010 0.005 0.001k0 2.072 2.706 3.841 5.024 6.635 7.879 10.828经计算K2=10，则下列选项正确的是：（）A．有99.5%的把握认为使用智能手机对学习有影响B．有99.5%的把握认为使用智能手机对学习无影响C．有99.9%的把握认为使用智能手机对学习有影响D．有99.9%的把握认为使用智能手机对学习无影响【考点】独立性检验的应用．【分析】根据观测值K2，对照数表，即可得出正确的结论．【解答】解：因为7.879＜K2=10＜10.828，对照数表知，有99.5%的把握认为使用智能手机对学习有影响．故选：A．8．函数的单调递增区间是（）A．B． C．D．【考点】复合三角函数的单调性．【分析】由2kπ﹣≤+≤2kπ+（k∈Z）与x∈[﹣2π，2π]即可求得答案．【解答】解：y=sin（+）的单调递增区间由2kπ﹣≤+≤2kπ+（k∈Z）得：4kπ﹣≤x≤4kπ+（k∈Z），∵x∈[﹣2π，2π]，∴﹣≤x≤．即y=sin（+）的单调递增区间为[﹣，]．故选A．9．平面直径坐标系xOy中，动点P到圆（x﹣2）2+y2=1上的点的最小距离与其到直线x=﹣1的距离相等，则P点的轨迹方程是（）A．y2=8x B．x2=8y C．y2=4x D．x2=4y【考点】直线与圆的位置关系．【分析】设动点P（x，y），由已知得|x+1|=﹣1，由此能求出点P的轨迹方程．【解答】解：设动点P（x，y），∵动点P到直线x=﹣1的距离等于它到圆：（x﹣2）2+y2=1的点的最小距离，∴|x+1|=﹣1，化简得：6x﹣2+2|x+1|=y2，当x≥﹣1时，y2=8x，当x＜﹣1时，y2=4x﹣4＜﹣8，不合题意．∴点P的轨迹方程为：y2=8x．故选：A．10．非负实数x、y满足ln（x+y﹣1）≤0，则关于x﹣y的最大值和最小值分别为（）A．2和1 B．2和﹣1 C．1和﹣1 D．2和﹣2【考点】简单线性规划；对数函数的图象与性质．【分析】作出不等式组对应的平面区域，利用z的几何意义进行求解即可．【解答】解：由题意得，作出不等式组对应的平面区域如图：设z=x﹣y，由z=x﹣y，得y=x﹣z表示，斜率为1纵截距为﹣z的一组平行直线，平移直线y=x﹣z，当直线y=x﹣z经过点C（2，0）时，直线y=x﹣z的截距最小，此时z 最大，最大为z max=2﹣0=2当直线经过点A（0，2）时，此时直线y=x﹣z截距最大，z最小．此时z min=0﹣2=﹣2．故选：D．11．如果执行如图所示的程序框图，则输出的数S不可能是（）A．0.7 B．0.75 C．0.8 D．0.9【考点】程序框图．【分析】模拟执行程序，可得此程序框图的功能是计算并输出S=+的值，结合选项，只有当S的值为0.7时，n不是正整数，由此得解．【解答】解：模拟执行程序，可得此程序框图执行的是输入一个正整数n，求+的值S，并输出S，由于S=+=1+…+﹣=1﹣=，令S=0.7，解得n=，不是正整数，而n分别输入2，3，8时，可分别输出0.75，0.8，0.9．故选：A．12．已知函数f（x）=e x，g（x）=x+1，则关于f（x），g（x）的语句为假命题的是（）A．∀x∈R，f（x）＞g（x）B．∃x1，x2∈R，f（x1）＜g（x2）C．∃x0∈R，f（x0）=g（x0）D．∃x0∈R，使得∀x∈R，f（x0）﹣g（x0）≤f（x）﹣g（x）【考点】命题的真假判断与应用．【分析】根据全称命题和特称命题的定义进行判断即可．【解答】解：设h（x）=f（x）﹣g（x），则h（x）=e x﹣x﹣1，则h′（x）=e x﹣1，当x＜0时，h′（x）＜0，h（x）单调递减，当x＞0时，h′（x）＞0，则h（x）单调递增，即当x=0时，函数h（x）取得极小值同时也是最小值h（0）=0，即h（x）≥0，即∀x∈R，f（x）＞g（x）不一定成立，故A是假命题，故选：A二、填空题13．在空间直角坐标系中，已知点A（1，0，1），B（﹣1，1，2），则线段AB的长度为．【考点】空间两点间的距离公式．【分析】根据两点间的距离公式，进行计算即可．【解答】解：空间直角坐标系中，点A（1，0，1），B（﹣1，1，2），所以线段AB的长度为|AB|==．故答案为：．14．记等差数列{a n}的前n项和为S n，若S3=2a3，S5=15，则a2020=2020．【考点】等差数列的前n项和．【分析】利用等差数列的通项公式及其前n项和公式即可得出．【解答】解：设等差数列{a n}的公差为d．∵S3=2a3，S5=15，∴d=2（a1+2d），d=15，解得a1=d=1．则a2020=1+×1=2020．故答案为：2020．15．△ABC的周长等于2（sinA+sinB+sinC），则其外接圆半径等于1．【考点】正弦定理．【分析】利用正弦定理得出a，b，c和外接圆半径R的关系，根据周长列出方程解出R．【解答】解：设△ABC的三边分别为a，b，c，外接圆半径为R，由正弦定理得，∴a=2RsinA，b=2RsinB，c=2RsinC，∵a+b+c=2（sinA+sinB+sinC），∴2RsinA+2RsinB+2RsinC=2（sinA+sinB+sinnC），∴R=1．故答案为：1．16．M，N分别为双曲线﹣=1左、右支上的点，设是平行于x轴的单位向量，则|•|的最小值为4．【考点】双曲线的简单性质．【分析】根据向量数量积的定义结合双曲线的性质进行求解即可．【解答】解：由向量数量积的定义知•即向量在向量上的投影||模长的乘积，故求|•|的最小值，即求在x轴上的投影的绝对值的最小值，由双曲线的图象可知|•|的最小值为4，故答案为：4三、解答题17．如图，OPQ是半径为2，圆心角为的扇形，C是扇形弧上的一动点，记∠COP=θ，四边形OPCQ的面积为S．（1）找出S与θ的函数关系；（2）试探求当θ取何值时，S最大，并求出这个最大值．【考点】三角函数中的恒等变换应用；弧度制的应用；三角函数的最值．【分析】（1）由面积公式即可得到S与θ的函数关系．（2）对三角函数化简，由θ的范围，得到S的最大值．【解答】解：（1）∵S=S△OPC+S△OQC=OP•0Csin∠POC+OQ•OCsin∠QOC=2sinθ+2sin（﹣θ）（θ∈（0，））（2）由（1）知，S=2sinθ+2sin（﹣θ）=sinθ+cosθ=2sin（θ+）∵θ∈（0，），∴θ+∈（，）∴当θ+=，即θ=时，S最大，为2．18．空气质量指数（Air Quality Index，简称AQI）是定量描述空气质量状况的指数，空气质量按照AQI大小分为六级：0～50为优；51～100为良；101～150为轻度污染；151～200为中度污染；201～300为重度污染；＞300为严重污染．一环保人士记录了去年某地某月10天的AQI的茎叶图如图所示．（1）利用该样本估计该地本月空气质量优良（AQI≤100）的天数；（按这个月总共30天计算）（2）若从样本的空气质量不佳（AQI＞100）的这些天中，随机地抽取两天深入分析各种污染指标，求该两天的空气质量等级恰好不同的概率．【考点】列举法计算基本事件数及事件发生的概率．【分析】（1）由茎叶图可得样本中空气质量优良的天数，可得概率，用总天数乘以概率可得；（2）该样本中轻度污染共4天，分别记为a，b，c，d，中度污染为1天，记为A，重度污染为1天，记为α，列举可得总的基本事件共15个，其中空气质量等级恰好不同有9个，由概率公式可得的．【解答】解：（1）由茎叶图可发现样本中空气质量优的天数为1，空气质量为良的天数为3，故空气质量优良的概率为=，故利用该样本估计该地本月空气质量优良的天数为30×=12；（2）该样本中轻度污染共4天，分别记为a，b，c，d，中度污染为1天，记为A，重度污染为1天，记为α，则从中随机抽取2天的所有可能结果为：（a，b）（a，c）（a，d）（a，A）（A，α）（b，c）（b，d）（b，A）（b，α）（c，d）（c，A）（c，α）（d，A）（d，α）（A，α）共15个，其中空气质量等级恰好不同有（a，A）（A，α）（b，A）（b，α）（c，A）（c，α）（d，A）（d，α）（A，α）共9个，该两天的空气质量等级恰好不同的概率P==19．如图，矩形BDEF垂直于正方形ABCD，GC垂直于平面ABCD，且AB=DE=2CG=2．（1）求三棱锥A﹣FGC的体积．（2）求证：面GEF⊥面AEF．【考点】平面与平面垂直的判定；棱柱、棱锥、棱台的体积．【分析】（1）由平面BDEF⊥平面ABCD得FB⊥平面ABCD，故FB⊥AB，又AB⊥BC，于是AB⊥平面FBCG，即AB为棱锥A﹣FCG的高；（2）建立空间坐标系，分别求出平面AEF和平面EFG的法向量，证明他们的法向量垂直即可．【解答】解：（1）∵平面BDEF⊥平面ABCD，平面BDEF∩平面ABCD=BD，FB⊥BD，FB ⊂平面BDEF，∴FB⊥平面ABCD，∵AB⊂平面ABCD，∴AB⊥FB，又AB⊥BC，∴AB⊥平面BCGF，===．∴V A﹣FGC（2）以B为原点，AB，BC，BF为坐标轴建立空间直角坐标系，如图：则A（﹣2，0，0），E（﹣2，2，2），F（0，0，2），G（0，2，1），∴=（0，2，2），=（2，﹣2，0），=（0，2，﹣1）．设平面AEF的法向量为=（x，y，z），平面EFG的法向量为=（a，b，c），则，，即，，令z=1得=（﹣1，﹣1，1），令c=1得=（，，1）．∴=﹣=0．∴，∴平面AEF⊥平面EFG．20．已知椭圆C1： +=1（a＞b＞0）的顶点到直线l1：y=x的距离分别为，．（1）求C1的标准方程；（2）设平行于l1的直线l交C1与A、B两点，若以AB为直径的圆恰好过坐标原点，求直线l的方程．【考点】椭圆的简单性质．【分析】（1）由a＞b，可设顶点（a，0）到直线y=x的距离为，又顶点（0，b）到直线y=x的距离为，运用点到直线的距离公式，计算可得a=2，b=1，进而得到椭圆方程；（2）设直线l的方程为y=x+t（t≠0），代入椭圆方程x2+4y2=4，设A（x1，y1），B（x2，y2），运用韦达定理和判别式大于0，以及直径所对的圆周角为直角，由向量垂直的条件：数量积为0，化简整理，可得t，进而得到所求直线l的方程．【解答】解：（1）由a＞b，可设顶点（a，0）到直线y=x的距离为，可得=，即a=2，又顶点（0，b）到直线y=x的距离为，可得=，即b=1，则椭圆方程为+y2=1；（2）设直线l的方程为y=x+t（t≠0），代入椭圆方程x2+4y2=4，可得5x2+8tx+4t2﹣4=0，设A（x1，y1），B（x2，y2），即有△=64t2﹣20（4t2﹣4）＞0，解得﹣＜t＜，且t≠0，x1+x2=﹣，x1x2=，y1y2=（x1+t）（x2+t）=x1x2+t2+t（x1+x2）=+t2﹣=，以AB为直径的圆恰好过坐标原点，可得OA⊥OB，即有•=0，即x1x2+y1y2=0，即为+=0，解得t=±，满足﹣＜t＜，且t≠0，则直线l的方程为y=x±．21．已知函数f（x）=x2+（a为实常数）．（1）若f（x）在（0，+∞）上单调递增，求实数a的取值范围；（2）判断是否存在直线l与f（x）的图象有两个不同的切点，并证明你的结论．【考点】利用导数研究曲线上某点切线方程；利用导数研究函数的单调性．【分析】（1）求出导数，由题意可得2x3﹣a≥0在（0，+∞）上恒成立，即a≤2x3，求出右边函数的值域，即可得到a的范围；（2）不存在直线l与f（x）的图象有两个不同的切点．假设存在这样的直线l，设两切点为（x1，f（x1）），（x2，f（x2）），由假设可得f′（x1）=f′（x2）=，运用导数和函数的解析式，化简整理，即可得到矛盾．【解答】解：（1）函数f（x）=x2+的导数为f′（x）=2x﹣=，由f（x）在（0，+∞）上单调递增，可得2x3﹣a≥0在（0，+∞）上恒成立，即a≤2x3，由2x3在（0，+∞）上递增，可得2x3的值域为（0，+∞），则a≤0，即有a的取值范围为（﹣∞，0]；（2）不存在直线l与f（x）的图象有两个不同的切点．证明：假设存在这样的直线l，设两切点为（x1，f（x1）），（x2，f（x2）），由假设可得f′（x1）=f′（x2）=，由f′（x1）=f′（x2），可得2x1﹣=2x2﹣，即有2（x1﹣x2）=a•，显然x1+x2≠0，x1﹣x2≠0，即有a=﹣，而﹣f′（x1）=﹣2x1+=x1+x2﹣﹣2x1+=x2﹣x1+﹣=﹣≠0，即f′（x1）=f′（x2）≠，故不存在直线l与f（x）的图象有两个不同的切点．[选修4-1：几何证明选讲]22．如图，C，D是以AB为直径的半圆上两点，且=．（1）若CD∥AB，证明：直线AC平分∠DAB；（2）作DE⊥AB交AC于E，证明：CD2=AE•AC．【考点】与圆有关的比例线段；弦切角．【分析】（1）证明：直线AC平分∠DAB，只要证明∠DAC=∠BAC，利用平行线的性质及等弧对等角即可；（2）作DE⊥AB交AC于E，证明：△ADE∽△ACD，即可证明CD2=AE•AC．【解答】证明：（1）∵CD∥AB，∴∠DCA=∠BAC，∵=，∴∠DAC=∠DCA，∴∠DAC=∠BAC，∴直线AC平分∠DAB；（2）∵DE⊥AB，∴∠ADE+∠DAB=90°，∵AB为直径，∴∠DBA+∠DAB=90°，∴∠ADE=∠ABD，∵∠ABD=∠DCA，∴∠ADE=∠ACD，∴△ADE∽△ACD，∴AD2=AE•AC，∵AD=DC，∴CD2=AE•AC．[选修4-4：坐标系与参数方程选讲]23．在平面直角坐标系xOy中，以坐标原点为极点，x轴正半轴为极轴建立极坐标系，曲线C1的极坐标方程为ρ2﹣4ρcosθ+3=0，θ∈[0，2π]．（1）求C1的直角坐标方程；（2）曲线C2的参数方程为（t为参数），求C1与C2的公共点的极坐标．【考点】简单曲线的极坐标方程；参数方程化成普通方程．【分析】（1）把ρ2=x2+y2，x=ρcosθ，代入曲线C1的极坐标方程可得直角坐标方程．（2）由曲线C2的参数方程为（t为参数），可知：此条直线经过原点，倾斜角为．因此C1的极坐标方程为：，或（ρ＞0）．分别代入C1的极坐标方程即可得出．【解答】解：（1）把ρ2=x2+y2，x=ρcosθ，代入曲线C1的极坐标方程ρ2﹣4ρcosθ+3=0，θ∈[0，2π]，可得：x2+y2﹣4x+3=0，配方为：（x﹣2）2+y2=1．（2）由曲线C2的参数方程为（t为参数），可知：此条直线经过原点，倾斜角为．因此C1的极坐标方程为：，或（ρ＞0）．将代入C1可得：ρ2﹣2ρ+3=0，解得ρ=．将代入C1可得：ρ2+2ρ+3=0，解得ρ=﹣，舍去．故C1与C2的公共点的极坐标为．[选修4-5：不等式选讲]24．设α、β、γ均为实数．（1）证明：|cos（α+β）|≤|cosα|+|sinβ|；|sin（α+β）|≤|cosα|+|cosβ|．（2）若α+β+γ=0．证明：|cosα|+|cosβ|+|cosγ|≥1．【考点】绝对值三角不等式．【分析】（1）利用和的余弦、正弦公式，结合三角不等式，即可证明结论；（2）由（1）可得|cos[α+（β+γ]=|cosα|+|sin（β+γ）|≤|cosα|+|cosβ|+|cosγ|，即可证明结论．【解答】证明：（1）|cos（α+β）|=|cosαcosβ﹣sinαsinβ|≤|cosαcosβ|+|sinαsinβ|≤|cosα|+|sinβ|；|sin（α+β）|=|sinαcosβ﹣cosαsinβ|≤|sinαcosβ|+|cosαsinβ|≤|cosα|+|cosβ|．（2）由（1）可得|cos[α+（β+γ）]≤|cosα|+|sin（β+γ）|≤|cosα|+|cosβ|+|cosγ|，∵α+β+γ=0，∴|cos[α+β+γ]=1∴|cosα|+|cosβ|+|cosγ|≥1．2020年9月12日。

湖南长沙一中2020届高三模拟测试(八)文数试题

关注微信公众号：一个高中僧
组区间的中点值代表).
18. (本小题满分 12 分)
设等差数列 an 的前 n 项和为 Sn,且 S5=5S3,a4=2a2 -3.
(1)求数列an 的通项公式;
(2)若数列bn 满足
b1 a1
b2 a2
bn an
1 2n
1, n
N
,证明:
bn
≤
3 8
19.(本小题满分 12 分) 如图:四棱锥 P-ABCD 中,PA⊥底面 ABCD.AD// BC,BC=2AD=4 AB=CD,∠ABC=60°，N 为线段 PC 上点.CN=3NP，M 为 AD 的中点。
[a, b] 上同时递增或同时递减时区间[a,b]叫做函数 y= f(x)的“不动区间”.若区间[1, 2]为函数
y 2x t 的“不动区间”.则实数 t 的最大值为
1
A.
2
B.3
C.2
3
D.
2
第 II 卷
二、填空题:本大题共 4 小题,每小题 5 分,共 20 分
13.已知向量 a
(2.4),
A.25
B.26
C.30
D.31
5.已知点 P(1，2)与直线 l:x+y+1=0,则点 P 关于直线 l 的对称点坐标为
A. (-3,-2)
B.(-3,-1)
C.(2, 4)
D. (-5，- 3)
6.已知 (0, ), 2sin 2 cos 2 1 ,则 sin = 2
1
A.
5
5
B.
5
7，已如单位圆有一条长为
第I卷一、选择题:本大题共 12 小题,每小题 5 分,共 60 分在每小题给出的四个选项中,只有一项是符合题目要求的.

湖南省长沙一中2025届高考数学一模试卷含解析

湖南省长沙一中2025届高考数学一模试卷注意事项：1．答题前，考生先将自己的姓名、准考证号填写清楚，将条形码准确粘贴在考生信息条形码粘贴区。

2．选择题必须使用2B 铅笔填涂；非选择题必须使用0．5毫米黑色字迹的签字笔书写，字体工整、笔迹清楚。

3．请按照题号顺序在各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试题卷上答题无效。

4．保持卡面清洁，不要折叠，不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。

一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．设i 是虚数单位，若复数1z i =+，则22||z z z+=（）A ．1i +B ．1i -C ．1i --D ．1i -+2．正项等比数列{}n a 中的1a 、4039a 是函数()3214633f x x x x =-+-的极值点，则20206log a =（） A ．1-B ．1C ．2D ．23．若双曲线()22210x y a a-=>的一条渐近线与圆()2222x y +-=至多有一个交点，则双曲线的离心率的取值范围是（） A ．)2,⎡+∞⎣ B ．[)2,+∞C ．(1,2⎤⎦ D ．(]1,2 4．用数学归纳法证明，则当时，左端应在的基础上加上（）A ．B ．C ．D ．5．231+=-ii （） A ．15i 22-+ B ．1522i -- C ．5522i + D ．5122i - 6．若双曲线22214x y a -=3，则双曲线的焦距为（）A ．26B ．25C ．6D ．87．已知向量()3,1a =，()3,1b =-，则a 与b 的夹角为（）A ．6π B ．3π C ．23π D ．56π 8．已知向量(3sin ,2)a x =-，(1,cos )b x =，当a b ⊥时，cos 22x π⎛⎫+= ⎪⎝⎭（）A ．1213-B ．1213C ．613-D ．6139．斜率为1的直线l 与椭圆22x y 14+=相交于A 、B 两点，则AB 的最大值为( )A ．2B ．455C ．4105D ．810510．一艘海轮从A 处出发，以每小时24海里的速度沿南偏东40°的方向直线航行，30分钟后到达B 处，在C 处有一座灯塔，海轮在A 处观察灯塔，其方向是南偏东70°，在B 处观察灯塔，其方向是北偏东65°，那么B ，C 两点间的距离是（）A ．62海里B ．3C ．2海里D ．311．为实现国民经济新“三步走”的发展战略目标，国家加大了扶贫攻坚的力度．某地区在2015 年以前的年均脱贫率（脱离贫困的户数占当年贫困户总数的比）为70%．2015年开始，全面实施“精准扶贫”政策后，扶贫效果明显提高，其中2019年度实施的扶贫项目，各项目参加户数占比（参加该项目户数占 2019 年贫困户总数的比）及该项目的脱贫率见下表：实施项目种植业养殖业工厂就业服务业参加用户比40% 40% 10% 10%脱贫率95% 95% 90% 90%那么2019年的年脱贫率是实施“精准扶贫”政策前的年均脱贫率的（） A ．2728倍 B ．4735倍 C ．4835倍 D ．75倍 12．已知函数()cos f x x =与()sin(2)(0)g x x ϕϕπ=+<的图象有一个横坐标为3π的交点，若函数()g x 的图象的纵坐标不变，横坐标变为原来的1ω倍后，得到的函数在[0,2]π有且仅有5个零点，则ω的取值范围是( )A ．2935,2424⎡⎫⎪⎢⎣⎭B ．2935,2424⎡⎤⎢⎥⎣⎦C ．2935,2424⎛⎫⎪⎝⎭ D ．2935,2424⎛⎤⎥⎝⎦ 二、填空题：本题共4小题，每小题5分，共20分。

2020年湖南省长沙一中高考数学模拟试卷(理科)(一)(5月份)(有答案解析)

20. 从甲、乙两种棉花中各抽测了 25 根棉花的纤维长度（单位：mm）组成一个样本，且将纤维长
度超过 315mm 的棉花定为一级棉花．设计了如图茎叶图：
（1）根据以上茎叶图，对甲、乙两种棉花的纤维长度作比较，写出两个统计结论（不必计算）；（2）从样本中随机抽取甲、乙两种棉花各 2 根，求其中恰有 3 根一级棉花的概率；（3）用样本估计总体，将样本频率视为概率，现从甲、乙两种棉花中各随机抽取 1 根，求其中一级棉花根数 X 的分布列及数学期望．
．
故选：D．画出图，根据弧长公式求解本小题主要考查球面距离及相关计算、正方体的几何特征等基础知识，考查运算求解能力，考查空间想象能力、化归与转化思想．属于中档题．
12.答案：A
解析：【分析】本题考查函数的对称性，函数的零点与方程根的关系，考查利用导数研究函数的单调性和最值，构造函数法求方程的解及参数范围，属于较难题.
2020 年湖南省长沙一中高考数学模拟试卷（理科）（一）（5 月份）
题号得分
一
二
三
总分
一、选择题（本大题共 12 小题，共 60.0 分）
1. 已知集合 A={x|（x+1）（x-2）≤0}，B={-1，0，1，2，3}，则 A∩B=（）
A. {-1，0，1}
B. {-1，0，1，2} C. {0，1，2}
8.答案：C
解析：【分析】本题考查了等差数列的通项公式与求和公式，考查了推理能力与计算能力，属于中档题．
设此等差数列{an}的公差为 d，则 a1+a4+a7=3a1+9d=31.5，9a1+
公式即可得出．【解答】
d=85.5，解得：d，a1．利用通项

2020年高考长沙名校数学模拟卷01(新课标Ⅰ卷)(解析版)

2020年高考长沙名校数学模拟卷01理科数学一、选择题（本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一个选项是符合题目要求的）1．若集合{}()(){}33,420A x x B x x x =-<<=+->，则A B =I A ．{}32x x -<< B ．{}23x x << C ．{}32x x -<<- D ．{}43x x x <->-或【答案】B【解析】由题意得()(){}420{|4B x x x x x =+->=<-或2}x >，所以A B =I {}23x x <<，故选B.2．若复数z 满足： 3321iz i i-+=+（i 为虚数单位），则z 等于A B ．3C ．5D 【答案】A【解析】()()()()331334222111111i i i i iz i i i i i i +--+-+=====-+++-+， 23z i =- z == 故选A.3．已知向量()()3,2,,4a b x ==v v，且//a b v v ，则x 的值为A ．6B ．－6C ．83-D ．83【答案】A【解析】2346x x =⨯⇒=，所以选A.4．2019年10月，德国爆发出“芳香烃门”事件，即一家权威的检测机构在德国销售的奶粉中随机抽检了16款(德国4款，法国8款，荷兰4款)，其中8款检测出芳香烃矿物油成分，此成分会严重危害婴幼儿的成长，有些奶粉已经远销至中国．A 地区闻讯后，立即组织相关检测员对这8款品牌的奶粉进行抽检，已知该地区有6家婴幼儿用品商店在售这几种品牌的奶粉，甲、乙、丙3名检测员分别负责进行检测，每人至少抽检1家商店，且检测过的商店不重复检测，则甲检测员检测2家商店的概率为A ．1118B ．718 C ．512D ．712【答案】B【解析】若3人检测的数量为2：2：2，则所有的情况为222342633390C C C A A ⋅=种，若3人检测的数量为3：2：1，则所有的情况为32136313360C C C A ⋅=种，若3人检测的数量为4：1：1，则所有的情况为143362132290C C C A A ⋅=种，故所有的情况为540种，其中满足甲检测2家商店的情况为90120210+=种，故所求概率210754018P ==. 故选：B.5．已知实数0,a b m R >>∈，则下列不等式中成立的是A ．1122a b⎛⎫⎛⎫< ⎪ ⎪⎝⎭⎝⎭B ．22a b -->C ．m m a b > D ．b m ba m a+>+ 【答案】A【解析】指数函数()12xf x ⎛⎫= ⎪⎝⎭在R 上单调递减，由于0a b >>，故 1122a b⎛⎫⎛⎫< ⎪ ⎪⎝⎭⎝⎭，选项A 中的不等式成立；幂函数()2f x x -=在()0,∞+上单调递减，由于0a b >>，故22a b --<，选项B 中的不等式不成立；当0m =时，m m a b =，，选项C 中的不等式不成立；当0m =时，b m b a m a+=+，，选项D 中的不等式不成立.本题选择A 选项.6．秦九韶算法是南宋时期数学家秦九韶提出的一种多项式简化算法，即使在现代，它依然是利用计算机解决多项式问题的最优算法，即使在现代，它依然是利用计算机解决多项式问题的最优算法，其算法的程序框图如图所示，若输入的a 0,a 1,a 2,⋯,a a 分别为0,1,2,⋯,a ，若a =5，根据该算法计算当a =2时多项式的值，则输出的结果为A ．248B ．258C ．268D ．278【答案】B【解析】该程序框图是计算多项式a (a )=5a 5+4a 4+3a 3+2a 2+a 当a =2时 a (2)=258，故选B ． 7．与函数()()()()()2ln 2,00,2sin x x f x x x⋅=∈-⋃的部分图象最符合的是A ．B ．C ．D ．【答案】B【解析】因为函数()()()()2ln sin x x f x f x x ⋅-==--，所以函数为奇函数，其图象关于原点成中心对称，所以排除选项A ，D ，又当()0,1x ∈时，()0f x <，所以排除选项C ，故选B.8．某几何体的三视图如图所示，则该几何体的各条棱中，最长的棱与最短的棱所在直线所成角的正切值为A BCD ．【答案】C【解析】如图，，CD =将四面体补成长方体，则可知最长的棱为长方体的体对角线AC =1BD =，BD 平行与CE ，异面直线AC 与BD 所成的角为ACE ∠，因为BE CD AE ===则因为1,? BD CE ==且根据面面垂直和线面垂直的性质，可知CE AE ⊥ 所以tan ACE ∠= AECE= 故选C.9．已知数列{}n a 满足143n n a a n ++=+，且*n N ∀∈，220n a n +≥，则3a 的取值范围是A ．[2,15]-B ．[18,7]-C ．[18,19]-D ．[2,19]【答案】D【解析】143n n a a n ++=+∵，2147n n a a n +++=+∴，两式相减得24n n a a +-=，故数列{}n a 的通项公式为112223n n a n a n a n -+⎧=⎨+-⎩，为奇数，，为偶数.当n 为奇数时，220n a n +≥可化为212220n a n -++≥，22115222222a n n n ⎛⎫--+=-++ ⎪⎝⎭∴≥，当1n =时，2222n n --+有最大值2-，12a -∴≥；当n 为偶数时，220n a n +≥可化为212320n a n +-+≥，22115223222a n n n ⎛⎫++=++ ⎪⎝⎭∴≤，当2n =时，2223n n ++有最小值15，115a ∴≤，1215a -∴≤≤，314[219]a a =+∈∴，，故选D ． 10．已知定义在R 上的函数()f x 的对称轴为3x =-，且当3x ≥-时，()23x f x =-，若函数()f x 在区间(1,)k k -()k Z ∈上有零点，则k 的值为A ．2或-7B ．2或-8C ．1或-7D ．1或-8【答案】A【解析】令230x -=，得2log 33x =>-，符合题意，由函数()f x 的对称轴为3x =-，则函数的另一个零点为26log 3x =--，显然21log 32<<，则286log 37-<--<-，因此k 等于－7或2，故选A ．11．过抛物线24y x =焦点的直线l 与抛物线交于A ，B 两点，与圆()2221x y r -+=交于C ，D 两点，若有三条直线满足AC BD =，则r 的取值范围为A ．3,2⎛⎫+∞⎪⎝⎭B ．()2,+∞C ．31,2⎛⎫ ⎪⎝⎭D ．3,22⎛⎫⎪⎝⎭【答案】B【解析】（1）当直线l x ⊥轴时，直线l ：1x =与抛物线交于(1,2)(1,2)-、，与圆222(1)x y r -+=交于(1,)(1,)r r -、，满足AC BD =.（2）当直线l 不与x 轴垂直时，设直线l 方程(1)y k x =-.1122(,),(,)A x y B x y ，联立方程组2(1)4y k x y x =-⎧⎨=⎩化简得2222(24)0k x k x k -++=，由韦达定理 12242x x k+=+，由抛物线得定义，过焦点F 的线段122424AB AF BF x x k =++=+=+，当四点顺序为A C D B 、、、时，AC BD =Q ，∴AB 的中点为焦点F （1，0），这样的不与x 轴垂直的直线不存在；当四点顺序为A C B D 、、、时，AC BD =Q ，∴AB CD =，又2CD r =Q ，2442r k ∴+=，即222r k=-，当2r >时存在互为相反数的两斜率k ，即存在关于1x =对称的两条直线．综上，当(2,)r ∈+∞时有三条满足条件的直线. 故选B.12．已知函数()f x 的定义域为R ，其图象关于点()1,0-中心对称，其导函数()f x '，当1x <-时，()()()()110x f x x f x '⎡⎤+++<⎣⎦，则不等式()()10xf x f ->的解集为A ．()1,+∞B ．(),1-∞-C ．()1,1-D ．()(),11,-∞-⋃+∞【答案】C【解析】由题意设()()()1g x x f x =+，则()()()()'1'g x f x x f x =++， Q 当1x <-时， ()()()()11'0x f x x f x ⎡⎤+++<⎣⎦， ∴当1x <-时， ()()()1'0f x x f x ++>，则()g x 在(),1-∞-上递增， Q 函数()f x 的定义域为R ，其图象关于点()1,0-中心对称， ∴函数()1f x -的图象关于点()0,0中心对称，则函数()1f x -是奇函数，令()()()()11,h x g x xf x h x =-=-∴是R 上的偶函数，且在(),0-∞递增，由偶函数的性质得：函数()h x 在()0,+∞上递减， ()()10,h f =∴Q 不等式()()10xf x f ->化为： ()()1h x h >，即1x <，解得11x -<<， ∴不等式解集是()1,1-，故选C.二、填空题（本大题共4小题，每小题5分，共20分）13．若(1−2x)4=a 0+a 1x +a 2x 2+a 3x 3+a 4x 4，则|a 0|+|a 1|+|a 3|=__________．【答案】41【解析】(1−2x)4=1−8x +24x 2−32x 3+16x 4，所以a 0=1,a 1=−8,a 3=−32，|a 0|+|a 1|+|a 3|=41.14．已知等差数列{a n }的前20项的和为100，那么a 7·a 14的最大值为__________．【答案】25 【解析】()()1202012020101002a a S a a +==+= 则12010a a += .由等差数列的性质可知71412010a a a a +=+= .因为222714714714714714714()2224a a a a a a a a a a a a +=++⋅≥⋅+⋅=⋅所以22714714()102544a a a a +≤==．当且仅当7145a a ==时取得""=.15．已知四棱锥P ABCD -的底面ABCD 是矩形，其中2AD =，4AB =，面PAD ⊥面ABCD ，PA PD =，且直线PB 与CD ，则四棱锥P ABCD -的外接球表面积为__________．【答案】643π【解析】由平面PAD ⊥面ABCD ，得AB ⊥平面PAD ，所以AB PA ⊥，故角PBA 即为直线PB 与CD所成的角，故cos 2BA PBA PB PA BP ∠===，又2AD =，PA PD =，故PAD ∆为等边三角形.四棱锥P ABCD -的高sin 60o PF PA ==设四棱锥P ABCD -的外接球的球心为O ，半径为R .如图，过点O 作OG PF ⊥于点G ，作OE AC ⊥于点E ，连接AO ，则2222=AE OE PG OG ++，即2222)2OE OE OE ++∴=，222163R AE OE ∴=+=，故外接球的表面积为：26443R ππ=.16．已知函数()()2,11{2,13x x f x f x x -<≤=-<<，函数()f x 在0x x =处的切线为l ，若01165x <<，则l 与()f x 的图象的公共点个数为__________．【答案】2或3. 【解析】由题意得，当01165x <<时，直线l 的方程为：2002y x x x =-，其与11x -<≤时的图象只有一个交点，当13x <<时，2()(2)f x x =-，则将直线l 的方程2002y x x x =-代入到2()(2)f x x =-中，得22000(42)402x x x x x x -+++=⇒=+±由01165x <<得，0123x <+-< ，当0136x <<- 0223x <++<，在定义域内，此时在13x <<时，直线l 与()f x 有两个交点，综合有三个交点；当0135x -<时， 023x ++≥，不在定义域内，此时在13x <<时，直线l 与()f x 有一个交点，综合只有两个交点；结合上述两种情况，l 与()f x 的图象的公共点个数为2或3.三、解答题（本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤） 17．（本小题满分12分）在ABC △中，内角,,A B C 所对的边分别是,,a b c ，已知4A π=，22212a cb -=. （1）求sin C 的值；（2）若ABC △的面积为3，求a 的值.【答案】（1）10；（2 【解析】（1）4A π=Q ，∴由余弦定理可得：，222a cb ∴-=，又 22212a cb -=，可得b =. ()22212a c ∴-=⨯，可得a =.222222cos210a b c C ab +-∴===.()0,A π∈Q ，sin 10C ∴==.（2）11sin sin 3224ABC S bc A c π∆==⨯⋅⋅=Q ，解得c =a ∴==18．（本小题满分12分）如图所示，在五棱锥E ABCDF -中，侧面AEF ⊥底面ABC ，AEF ∆是边长为2的正三角形，四边形ABDF 为正方形，BC CD ⊥，且BC CD =，G 是AEF ∆的重心，O 是正方形ABDF 的中心. （1）求证：OG ∥平面BCE ；（2）求二面角B AE D --的余弦值.【答案】（1）见解析；（2 【解析】（1）取AF 中点M ，BD 中点N ，连接MN ，CN ，易知C ，N ，O ，M 四点共线.由BC CD ⊥，且BC CD =，可知BCD ∆为等腰直角三角形，所以1122CN BD AB ==. 因为O 是正方形ABDF 的中心，所以OM ON =. 所以CN NO MO ==，所以13MO MC =.又G 是AEF ∆的重心，所以13MG ME =. 所以MO MGMC ME=，故OG CE P .又因为EC ⊂平面BCE ，OG ⊄平面BCE . 所以OG ∥平面BCE .（2）解法一：因为M 为中点，AEF ∆是正三角形，所以ME AF ⊥. 因为侧面AEF ⊥底面ABC ，且交线为AF ，所以ME ⊥底面ABC . 所以直线ME ，MA ，MC 两两垂直.如图，以M 为原点，以MA u u u r 方向为x 轴正方向，以MC u u u u r 方向为y 轴正方向，以ME u u u r方向为z 轴正方向，建立空间直角坐标系.则(1,0,0)A ，(1,2,0)B ，(1,2,0)D -，E .所以(0,2,0)AB =u u u r，(AE =-u u u r，(2,2,0)AD =-u u u r.设平面ABE 的法向量为()1111,,n x y z =u r，则1111120,0.AB n y AE n x ⎧⋅==⎪⎨⋅=-+=⎪⎩u u u v u v u u u v u v 令11z =，则1n =u r . 设平面AED 的法向量为()2222,,n x y z =u u r，则2222222200AD n x y AE n x u u u v u u v u u u v u u v ⎧⋅=-+=⎪⎨⋅=-=⎪⎩，令21z =，则2n =u u r .所以121212cos ,7n n n n n n ⋅===u r u u ru r u u r u r u u r . 结合图可知，二面角B AE D --的余弦值为7. 解法二：取AE ，BE 中点分别为P ，Q ，连接PD ，PQ ，则PQ AB ∥.又侧面AEF ⊥底面ABC ，AB AF ⊥，侧面AEF I 底面ABC AF =，所以AB ⊥平面AEF . 又AE ⊂平面AEF ，所以AB AE ⊥，所以PQ AE ⊥.又2EF FD ==，DF EF ^，所以ED AD ==DP AE ⊥. 所以DPQ ∠为二面角B AE D --的平面角. 易知PQ DF P ，所以DPQ FDP ∠=∠.因为DP =2FD =，所以cos 7FD FDP DP ∠===，所以cos 7DPQ ∠=.即二面角B AE D --的余弦值为7.19．（本小题满分12分）我国是世界严重缺水的国家，城市缺水问题较为突出，某市政府为了鼓励居民节约用水，计划在本市试行居民生活用水定额管理，即确定一个合理的居民月用水量标准x （吨），用水量不超过x 的部分按平价收费，超过x 的部分按议价收费，为了了解全市民月用水量的分布情况，通过抽样，获得了100位居民某年的月用水量（单位：吨），将数据按照[0,0.5),[0.5,1),,[4,4.5),⋅⋅⋅分成9组，制成了如图所示的频率分布直方图.（1）若全市居民中月均用水量不低于3吨的人数为3.6万，试估计全市有多少居民？并说明理由；（2）若该市政府拟采取分层抽样的方法在用水量吨数为[1,1.5)和[1.5,2)之间选取7户居民作为议价水费价格听证会的代表，并决定会后从这7户家庭中按抽签方式选出4户颁发“低碳环保家庭”奖，设X 为用水量吨数在[1,1.5)中的获奖的家庭数，Y 为用水量吨数在[1.5,2)中的获奖家庭数，记随机变量||Z X Y =-，求Z 的分布列和数学期望．【答案】（1）30万；（2）3536. 【解析】（1）由图，不低于3吨人数所占百分比为()0.50.120.080.0412%⨯++= 所以假设全市的人数为x （万人），则有0.12 3.6x =，解得30,x =所以估计全市人数为30万.（2）由概率统计相关知识，各组频率之和的值为1，因为频率=⨯频率组距组距，所以()0.50.080.160.40.520.120.080.0421a ⨯+++++++=，得0.3a =，用水量在[]1,1.5之间的户数为1000.30.515⨯⨯=户，而用水量在[]1.5,2吨之间的户数为1000.40.520⨯⨯=户，根据分层抽样的方法，总共需要抽取7户居民，所以用水量在[]1,1.5之间应抽取的户数为715335⨯=户，而用水量在[]1.5,2吨之间的户数为720435⨯=户．据题意可知随机变量Z 的取值为0 2 4．()()2234371802,235C C P X P X Y C ======， ()()()13313434371621,33,135C C C C P X P X Y P X Y C +====+====， ()()043437140,435C C P Z P X Y C ======，其分布列为：期望为：()024********E Z =⨯+⨯+⨯=． 20．（本小题满分12分）已知直线l 与椭圆C :2213618x y +=交于,A B 两点.（1）若线段AB的中点为()2,1 求直线l 的方程; （2）记直线l 与x 轴交于点M 是否存在点M 使得2211MA MB+始终为定值?若存在求点M 的坐标并求出该定值;若不存在请说明理由.【答案】（1）30x y +-= （2）存在，(M ± 定值为16.【解析】（1）设()(,),,A x y B x y ''代入椭圆得()()22221361813618x y x y ⎧+=⎪⎪⎨⎪+='⎩'⎪，两式相减得:()()()()03618x x x x y y y y ''''+-+-+=∴12y y y y x x x x ''-+=-⋅''-+ Q 线段AB 的中点为()2,1，∴22x x '+= 12y y '+= ∴直线l 的斜率为:14122-⋅=-，∴直线l 的方程为:1(2)y x -=-- 即:30x y +-=.（2）设00(),M x 当直线l 与轴重合时有202222220002721111(6)(6)(36)x MA MB x x x ++=+=-+-; 当直线与x 轴垂直时22220011243618136MA MB x x +==-⎛⎫- ⎪⎝⎭由2022200272436(36)x x x +=--解得0x =±∴存在点M则(M ± 221116MA MB += 根据对称性只考虑直线l过点M设()(,),,A x y B x y ''设直线l的方程为x my =+由2213618x my x y ⎧=+⎪⎨+=⎪⎩ 消掉x 可得:()222240m y ++-= 根据韦达定理可得:y y '+= 2242yy m '=-+，Q()2222221111MA m y y m y ===++同理()()222111MB m y ='+ ∴()()()222222222211111111y y MA MB m y m y y y ⎛⎫'++=+=⋅ ⎪ ⎪++''⎝⎭Q ()()()()()222222222296965762,22m y y y y yy y y m m +''''+=+-==++∴22119615766MA MB +==综上所述存在点M (±使得2211MA MB+为定值16. 21．（本小题满分12分）已知函数()sin cos =+f x ax x b x ，且曲线()y f x =与直线2y π=相切于点,22ππ⎛⎫⎪⎝⎭，（1）求()f x ；（2）若2()1f x mx +„，求实数m 的取值范围.【答案】（1） ()f x xsinx cosx =+；（2） 12m …. 【解析】（1）由题意可得：222a f πππ⎛⎫==⎪⎝⎭，解得1a =， ('(1))f x xcosx b sinx +-=，由102f b π⎛⎫'=-= ⎪⎝⎭得1b = ．所以()f x xsinx cosx =+．（2）令22()()11g x mx f x mx xsinx cosx -=--++= ，由()0g x ≥得224()0g m ππ≥=，所以0m ≥．显然()g x 为偶函数，所以只需0x ≥时，()0g x ≥．()'2cos 2co )s (g x mx x x x m x ≥-=-，当12m …时，'()0g x ≥，即()g x 在)[0+∞，上单调递增，所以()(0)0g x g ≥=，从而12m …时，2(1)f x mx +≤成立．当102m <„时，因为2y m cosx =-在0,2π⎛⎫⎪⎝⎭上单调递增，又0x =时，210y m =-<；2x π=时，20y m ≥＝，所以存在00,2x π⎛⎤∈ ⎥⎝⎦，使得020m cosx =-，因此0)(0x x ∈，时，20m cosx -<，)'(0g x <，即()g x 在0(0)x ，上单调递减，所以0)(0x x ∈，时，()()=00g x g <，与()0g x ≥矛盾，因此102m <„时不成立．综上，满足题设的m 的取值范围是12m ….请考生在第22、23两题中任选一题作答．注意：只能做所选定的题目．如果多做，则按所做的第一个题目计分．22．（本小题满分10分）选修4-4：坐标系与参数方程在平面直角坐标系xOy 中，1C 的参数方程为cos ,1sin x t y t αα=⎧⎨=-+⎩（t 为参数，0απ≤<），以坐标原点O为极点，x 轴的正半轴为极轴建立极坐标系，2C 的极坐标方程为)4πρθ=-．（1）求2C 的直角坐标方程，并指出其图形的形状；（2）1C 与2C 相交于不同两点A ，B ，线段AB 中点为M ，点(0,1)N -，若||2MN =，求1C 参数方程中sin α的值．【答案】（1）2C 的直角坐标方程为22(1)(1)2x y -+-=，表示以(1,1)为半径的圆；（2）3sin 5α=或sin 1α=.【解析】（1）由4πρθ⎛⎫=-⎪⎝⎭得2cos 2sin ρθθ=+，所以22cos 2sin ρρθρθ=+ 将cos x sin yρθρθ=⎧⎨=⎩代入得2222x y x y +=+，即()()22112x y -+-=，所以2C 的直角坐标方程为()()22112x y -+-=，表示以()1,1.（2）将1x tcos y tsin αα=⎧⎨=-+⎩代入()()22112x y -+-=整理得()22cos 4sin 30t t αα-++=设A B 、对应的参数分别为12t t 、，则12t t 、是方程()22cos 4sin 30t t αα-++=的两根，所以122cos 4sin t t αα+=+，因为2MN =，所以1222t t +=，所以cos 2sin 2αα+= 所以()221sin 41sin αα-=-，所以()()5sin 3sin 10αα--=，所以3sin 5α=或sin 1α=. 23．（本小题满分10分）选修4-5：不等式选讲已知m 是常数，对任意实数x ，不等式|3||2||1||2|x x m x x ---≤≤-+-恒成立.（1）求m 的值；（2）设0,0,a b a b m >>+=，求证：1118a b ab++≥. 【答案】（1）1m =；（2）见解析.【解析】（1）Q 对任意实数x ，不等式|3||2||1||2|x x m x x ---≤≤-+-恒成立，∴()()max min |3||2||1||2|x x m x x ---≤≤-+-∵|3||2||(3)(2)|1x x x x ---≤-+-=，|1||2||(1)(2)|1x x x x -+-≥-+-=，所以111m m ≤≤⇒=（2）∵由（1）知1a b +=，又0a >，0b >， ∵11111112a b a b ab a b ab a b +⎛⎫++=++=+ ⎪⎝⎭2244a b a b b a a b a b ⎛⎫⎛⎫==+++≥ ⎪ ⎪⎝⎭⎝⎭++ 48b aa b⨯+=. ∵1118a b ab ++≥（当且仅当12a b ==时等号成立）.。

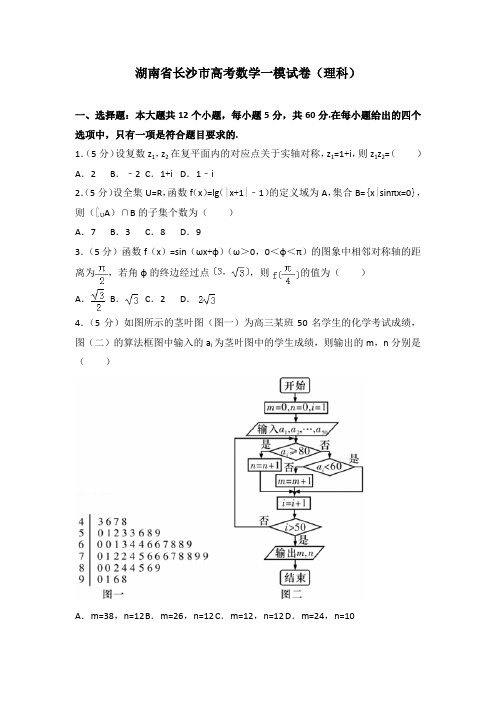
【2020年高考必备】湖南省长沙市高考数学一模试卷(理科)及解析

湖南省长沙市高考数学一模试卷（理科）一、选择题：本大题共12个小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．（5分）设复数z1，z2在复平面内的对应点关于实轴对称，z1=1+i，则z1z2=（）A．2 B．﹣2 C．1+i D．1﹣i2．（5分）设全集U=R，函数f（x）=lg（|x+1|﹣1）的定义域为A，集合B={x|sinπx=0}，则（∁U A）∩B的子集个数为（）A．7 B．3 C．8 D．93．（5分）函数f（x）=sin（ωx+φ）（ω＞0，0＜φ＜π）的图象中相邻对称轴的距离为，若角φ的终边经过点，则的值为（）A．B．C．2 D．4．（5分）如图所示的茎叶图（图一）为高三某班50名学生的化学考试成绩，图（二）的算法框图中输入的a i为茎叶图中的学生成绩，则输出的m，n分别是（）A．m=38，n=12 B．m=26，n=12 C．m=12，n=12 D．m=24，n=105．（5分）设不等式组表示的平面区域为Ω1，不等式（x+2）2+（y﹣2）2≤2表示的平面区域为Ω，对于Ω1中的任意一点M和Ω2中的任意一点N，|MN|2的最小值为（）A．B．C．D．6．（5分）若函数f（x）=的图象如图所示，则m的范围为（）A．（﹣∞，﹣1）B．（﹣1，2）C．（0，2） D．（1，2）7．（5分）某多面体的三视图如图所示，则该多面体各面的面积中最大的是（）A．11 B．C．D．8．（5分）设等差数列{a n}的前n项和为S n，且满足S2014＞0，S2015＜0，对任意正整数n，都有|a n|≥|a k|，则k的值为（）A．1006 B．1007 C．1008 D．10099．（5分）已知非零向量，，满足|﹣|=||=4，（﹣）•（﹣）=0，若对每一个确定的，||的最大值和最小值分别为m，n，则m﹣n的值为（）A．随增大而增大B．随增大而减小C．是2 D．是410．（5分）已知如图所示的三棱锥D﹣ABC的四个顶点均在球O的球面上，△ABC和△DBC所在平面相互垂直，AB=3，AC=，BC=CD=BD=2，则球O的表面积为（）A．4πB．12πC．16πD．36π11．（5分）已知双曲线C：（a＞0，b＞0）的右顶点为A，O为坐标原点，以A为圆心的圆与双曲线C的某渐近线交于两点P，Q，若∠PAQ=60°，且，则双曲线C的离心率为（）A．B．C．D．12．（5分）已知e为自然对数的底数，若对任意的x∈[0，1]，总存在唯一的y ∈[﹣1，1]，使得x+y2e y﹣a=0成立，则实数a的取值范围是（）A．[1，e]B．C．（1，e]D．二、填空题（每题5分，满分20分，将答案填在答题纸上）13．（5分）已知a＞0，展开式的常数项为15，则=．14．（5分）设a，b∈R，关于x，y的不等式|x|+|y|＜1和ax+4by≥8无公共解，则ab的取值范围是．15．（5分）正项数列{a n}的前n项和为S n，且（n∈N*），设，则数列{c n}的前2016项的和为．16．（5分）已知F是椭圆C：+=1的右焦点，P是C上一点，A（﹣2，1），当△APF周长最小时，其面积为．三、解答题（本大题共5小题，共70分.解答应写出文字说明、证明过程或演算步骤.）17．（12分）△ABC中，已知点D在BC边上，且，AB=3．（Ⅰ）求AD的长；（Ⅱ）求cosC．18．（12分）如图，在多面体ABCDEF中，四边形ABCD为矩形，△ADE，△BCF 均为等边三角形，EF∥AB，EF=AD=AB．（1）过BD作截面与线段FC交于点N，使得AF∥平面BDN，试确定点N的位置，并予以证明；（2）在（1）的条件下，求直线BN与平面ABF所成角的正弦值．19．（12分）2015年7月9日21时15分，台风“莲花”在我国广东省陆丰市甲东镇沿海登陆，造成165.17万人受灾，5.6万人紧急转移安置，288间房屋倒塌，46.5千公顷农田受灾，直接经济损失12.99亿元．距离陆丰市222千米的梅州也受到了台风的影响，适逢暑假，小明调查了梅州某小区的50户居民由于台风造成的经济损失，将收集的数据分成[0，2000]，（2000，4000]，（4000，6000]，（6000，8000]，（8000，10000]五组，并作出如下频率分布直方图：（Ⅰ）试根据频率分布直方图估计小区平均每户居民的平均损失（同一组中的数据用该组区间的中点值作代表）；（Ⅱ）小明向班级同学发出倡议，为该小区居民捐款．现从损失超过4000元的居民中随机抽出2户进行捐款援助，设抽出损失超过8000元的居民为ξ户，求ξ的分布列和数学期望；（Ⅲ）台风后区委会号召小区居民为台风重灾区捐款，小明调查的50户居民捐款情况如表，根据表格中所给数据，分别求b，c，a+b，c+d，a+c，b+d，a+b+c+d 的值，并说明是否有95%以上的把握认为捐款数额多于或少于500元和自身经济损失是否到4000元有关？附：临界值表参考公式：，．20．（12分）已知抛物线C的顶点为原点，其焦点F（0，c）（c＞0）到直线l：x ﹣y﹣2=0的距离为，设P为直线l上的点，过点P作抛物线C的两条切线PA，PB，其中A，B为切点．（1）求抛物线C的方程；（2）当点P（x0，y0）为直线l上的定点时，求直线AB的方程；（3）当点P在直线l上移动时，求|AF|•|BF|的最小值．21．（12分）已知函数f（x）=+be﹣x，点M（0，1）在曲线y=f（x）上，且曲线在点M处的切线与直线2x﹣y=0垂直．（1）求a，b的值；（2）如果当x≠0时，都有f（x）＞+ke﹣x，求k的取值范围．请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分.[选修4-4：坐标系与参数方程]22．（10分）选修4﹣4；坐标系与参数方程已知曲线C1的参数方程是（φ为参数），以坐标原点为极点，x轴的正半轴为极轴建立坐标系，曲线C2的坐标系方程是ρ=2，正方形ABCD的顶点都在C2上，且A，B，C，D依逆时针次序排列，点A的极坐标为（2，）．（1）求点A，B，C，D的直角坐标；（2）设P为C1上任意一点，求|PA|2+|PB|2+|PC|2+|PD|2的取值范围．[选修4-5：不等式选讲]23．设f（x）=|x|﹣|2x﹣1|，记f（x）＞﹣1的解集为M．（1）求集合M；（2）已知a∈M，比较a2﹣a+1与的大小．2018年湖南省长沙市高考数学一模试卷（理科）参考答案与试题解析一、选择题：本大题共12个小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．（5分）设复数z1，z2在复平面内的对应点关于实轴对称，z1=1+i，则z1z2=（）A．2 B．﹣2 C．1+i D．1﹣i【解答】解：复数z1，z2在复平面内的对应点关于实轴对称，z1=1+i，所以z2=1﹣i，∴z1z2=（1+i）（1﹣i）=2．故选：A．2．（5分）设全集U=R，函数f（x）=lg（|x+1|﹣1）的定义域为A，集合B={x|sinπx=0}，则（∁U A）∩B的子集个数为（）A．7 B．3 C．8 D．9【解答】解：由|x+1|﹣1＞0，得|x+1|＞1，即x＜﹣2或x＞0．∴A={x|x＜﹣2或x＞0}，则∁U A={x|﹣2≤x≤0}；由sinπx=0，得：πx=kπ，k∈Z，∴x=k，k∈Z．则B={x|sinπx=0}={x|x=k，k∈Z}，则（∁U A）∩B={x|﹣2≤x≤0}∩{x|x=k，k∈Z}={﹣2，﹣1，0}．∴（∁U A）∩B的元素个数为3．∴（∁U A）∩B的子集个数为：23=8．故选：C．3．（5分）函数f（x）=sin（ωx+φ）（ω＞0，0＜φ＜π）的图象中相邻对称轴的距离为，若角φ的终边经过点，则的值为（）A．B．C．2 D．【解答】解：由题意相邻对称轴的距离为，可得周期T=π，那么ω=2，角φ的终边经过点，在第一象限．即tanφ=，∴φ=故得f（x）=sin（2x+）则=sin（+）=cos=．故选：A4．（5分）如图所示的茎叶图（图一）为高三某班50名学生的化学考试成绩，图（二）的算法框图中输入的a i为茎叶图中的学生成绩，则输出的m，n分别是（）A．m=38，n=12 B．m=26，n=12 C．m=12，n=12 D．m=24，n=10【解答】解：由程序框图知：算法的功能是计算学生在50名学生的化学考试成绩中，成绩大于等于80的人数，和成绩小于80且大于等于60的人数，由茎叶图得，在50名学生的成绩中，成绩大于等于80的人数有80，80，81，84，84，85，86，89，90，91，96，98，共12人，故n=12，由茎叶图得，在50名学生的成绩中，成绩小于60的人数有43，46，47，48，50，51，52，53，53，56，58，59，共12人，则在50名学生的成绩中，成绩小于80且大于等于60的人数有50﹣12﹣12=26，故m=26故选：B．5．（5分）设不等式组表示的平面区域为Ω1，不等式（x+2）2+（y﹣2）2≤2表示的平面区域为Ω，对于Ω1中的任意一点M和Ω2中的任意一点N，|MN|2的最小值为（）A．B．C．D．【解答】解：不等式组表示的平面区域为Ω1，不等式（x+2）2+（y﹣2）2≤2表示的平面区域为Ω，如图：2对于Ω1中的任意一点M和Ω2中的任意一点N，|MN|的最小值就是可行域内的点O与圆的圆心连线减去半径，所以，|MN|的最小值为：=．故选：C．6．（5分）若函数f（x）=的图象如图所示，则m的范围为（）A．（﹣∞，﹣1）B．（﹣1，2）C．（0，2） D．（1，2）【解答】解：∵当x＞0时，f（x）＞0，∴2﹣m＞0，故m＜2．f′（x）=．∵f（x）有两个绝对值大于1的极值点，∴m﹣x2=0有两个绝对值大于1的解，∴m＞1．故选：D．7．（5分）某多面体的三视图如图所示，则该多面体各面的面积中最大的是（）A．11 B．C．D．【解答】解：由多面体的三视图得：该多面体为如图所示的四棱锥P﹣ABCD，其中底面ABCD是边长为1的正方形，平面PAD⊥平面ABCD，点P到平面ABCD的距离为1，∴AB⊥平面PAD，∴AB⊥PA，∴PA==，∴该多面体各面的面积中最大的是△PAB的面积：S△PAB==．故选：C．8．（5分）设等差数列{a n}的前n项和为S n，且满足S2014＞0，S2015＜0，对任意正整数n，都有|a n|≥|a k|，则k的值为（）A．1006 B．1007 C．1008 D．1009【解答】解：由等差数列的求和公式和性质可得S2014==1007（a1007+a1008）＞0，∴a1007+a1008＞0同理由S2015＜0可得2015a1008＜0，可得a1008＜0，∴a1007＞0，a1008＜0，且|a1007|＞|a1008|∵对任意正整数n，都有|a n|≥|a k|，∴k的值为1008故选：C．9．（5分）已知非零向量，，满足|﹣|=||=4，（﹣）•（﹣）=0，若对每一个确定的，||的最大值和最小值分别为m，n，则m﹣n的值为（）A．随增大而增大B．随增大而减小C．是2 D．是4【解答】解：假设=（4，0）、=（2，2）、=（x，y），∵（﹣）•（﹣）=0，∴（4﹣x，﹣y）•（2﹣x，2﹣y）=x2+y2﹣6x﹣2y+8=0，即（x﹣3）2+（y﹣）2=4，∴满足条件的向量的终点在以（3，）为圆心、半径等于2的圆上，∴||的最大值与最小值分别为m=2+2，n=2﹣2，∴m﹣n=4，故选：D．10．（5分）已知如图所示的三棱锥D﹣ABC的四个顶点均在球O的球面上，△ABC和△DBC所在平面相互垂直，AB=3，AC=，BC=CD=BD=2，则球O的表面积为（）A．4πB．12πC．16πD．36π【解答】解：∵AB=3，AC=，BC=2，∴AB2+AC2=BC2，∴AC⊥AB，∴△ABC的外接圆的半径为，∵△ABC和△DBC所在平面相互垂直，∴球心在BC边的高上，设球心到平面ABC的距离为h，则h2+3=R2=（﹣h）2，∴h=1，R=2，∴球O的表面积为4πR2=16π．故选：C．11．（5分）已知双曲线C：（a＞0，b＞0）的右顶点为A，O为坐标原点，以A为圆心的圆与双曲线C的某渐近线交于两点P，Q，若∠PAQ=60°，且，则双曲线C的离心率为（）A．B．C．D．【解答】解：设双曲线的一条渐近线方程为y=x，A（a，0），P（m，），（m＞0），由=3，可得Q（3m，），圆的半径为r=|PQ|==2m•，PQ的中点为H（2m，），由AH⊥PQ，可得=﹣，解得m=，r=．A到渐近线的距离为d==，则|PQ|=2=r，即为d=r，即有=•．可得=，e====．故选C．12．（5分）已知e为自然对数的底数，若对任意的x∈[0，1]，总存在唯一的y ∈[﹣1，1]，使得x+y2e y﹣a=0成立，则实数a的取值范围是（）A．[1，e]B．C．（1，e]D．【解答】解：由x+y2e y﹣a=0成立，解得y2e y=a﹣x，∴对任意的x∈[0，1]，总存在唯一的y∈[﹣1，1]，使得x+y2e y﹣a=0成立，∴a﹣1≥（﹣1）2e﹣1，且a﹣0≤12×e1，解得≤a≤e，其中a=1+时，y存在两个不同的实数，因此舍去，a的取值范围是．故选：B．二、填空题（每题5分，满分20分，将答案填在答题纸上）13．（5分）已知a＞0，展开式的常数项为15，则=．=•（﹣1）r•a6﹣r•，【解答】解：由的展开式的通项公式为T r+1令=0，求得r=2，故常数项为，可得a=1，因此原式为=，故答案为：．14．（5分）设a，b∈R，关于x，y的不等式|x|+|y|＜1和ax+4by≥8无公共解，则ab的取值范围是[﹣16，16] ．【解答】解：关于x，y的不等式|x|+|y|＜1表示的可行域如图的阴影部分：可行域与坐标轴的交点坐标（1，0），（0，1），（0，﹣1），（﹣1，0），关于x，y的不等式|x|+|y|＜1和ax+4by≥8无公共解，则ax+4by≥8表示的范围在可行域外侧，当a＞0，b＞0时满足题意，可得≥1，≥1，可得0＜ab≤16，当a＞0，b＜0时满足题意，可得﹣1，，可得：﹣2≤b＜0，0＜a≤8可得﹣16≤ab＜0，当a＜0，b＞0时满足题意，可得，，可得：0＜b≤2，﹣8≤a＜0可得﹣16≤ab＜0，当a＜0，b＜0时满足题意，可得，，可得：﹣2≤b＜0，﹣8≤a ＜0，∴0＜ab≤16，当ab=0时，不等式|x|+|y|＜1和ax+4by≥8无公共解；故ab的取值范围是：[﹣16，16]；故答案为：[﹣16，16]．15．（5分）正项数列{a n}的前n项和为S n，且（n∈N*），设，则数列{c n}的前2016项的和为．【解答】解：正项数列{a n}的前n项和为S n，且（n∈N*）①，则：②，②﹣①得：+a n﹣a n，+1﹣a n=1，整理得：a n+1当n=1时，，解得：a1=1，所以：数列{a n}是以1为首项，1为公差的等差数列．则a n=1+n﹣1=n，所以：．则：=，数列{c n}的前2016项的和为：，=﹣1+，=﹣．故答案为：16．（5分）已知F是椭圆C：+=1的右焦点，P是C上一点，A（﹣2，1），当△APF周长最小时，其面积为4．【解答】解：椭圆C：+=1的a=2，b=2，c=4，设左焦点为F'（﹣4，0），右焦点为F（4，0）．△APF周长为|AF|+|AP|+|PF|=|AF|+|AP|+（2a﹣|PF'|）=|AF|+|AP|﹣|PF'|+2a≥|AF|﹣|AF'|+2a，当且仅当A，P，F'三点共线，即P位于x轴上方时，三角形周长最小．此时直线AF'的方程为y=（x+4），代入x2+5y2=20中，可求得P（0，2），=S△PF'F﹣S△AF'F=×2×8﹣×1×8=4．故S△APF故答案为：4．三、解答题（本大题共5小题，共70分.解答应写出文字说明、证明过程或演算步骤.）17．（12分）△ABC中，已知点D在BC边上，且，AB=3．（Ⅰ）求AD的长；（Ⅱ）求cosC．【解答】解：（Ⅰ）由得到：AD⊥AC，所以，所以．（2分）在△ABD中，由余弦定理可知，BD2=AB2+AD2﹣2AB•AD•cosBAD即AD2﹣8AD+15=0，（4分）解之得AD=5或AD=3，由于AB＞AD，所以AD=3．（6分）（Ⅱ）在△ABD中，由正弦定理可知，，又由，可知（8分）所以（10分）因为，即（12分）18．（12分）如图，在多面体ABCDEF中，四边形ABCD为矩形，△ADE，△BCF 均为等边三角形，EF∥AB，EF=AD=AB．（1）过BD作截面与线段FC交于点N，使得AF∥平面BDN，试确定点N的位置，并予以证明；（2）在（1）的条件下，求直线BN与平面ABF所成角的正弦值．【解答】解：（1）当N为CF的中点时，AF∥平面BDN．证明：连结AC交BD于M，连结MN．∵四边形ABCD是矩形，∴M是AC的中点，∵N是CF的中点，∴MN∥AF，又AF⊄平面BDN，MN⊂平面BDN，∴AF∥平面BDN．（2）过F作FO⊥平面ABCD，垂足为O，过O作x轴⊥AB，作y轴⊥BC于P，则P为BC的中点．以O为原点，建立如图所示的空间直角坐标系，设AD=1，则BF=1，FP=，∵EF==1，∴OP=（AB﹣EF）=，∴OF=．∴A（，﹣，0），B（，，0），C（﹣，，0），F（0，0，），N（﹣，，）．∴=（0，2，0），=（﹣，，），=（﹣，﹣，）．设平面ABF的法向量为=（x，y，z），则，∴，令z=得=（2，0，），∴=﹣1，||=，||=．∴cos＜，＞==﹣．∴直线BN与平面ABF所成角的正弦值为|cos＜，＞|=．19．（12分）2015年7月9日21时15分，台风“莲花”在我国广东省陆丰市甲东镇沿海登陆，造成165.17万人受灾，5.6万人紧急转移安置，288间房屋倒塌，46.5千公顷农田受灾，直接经济损失12.99亿元．距离陆丰市222千米的梅州也受到了台风的影响，适逢暑假，小明调查了梅州某小区的50户居民由于台风造成的经济损失，将收集的数据分成[0，2000]，（2000，4000]，（4000，6000]，（6000，8000]，（8000，10000]五组，并作出如下频率分布直方图：（Ⅰ）试根据频率分布直方图估计小区平均每户居民的平均损失（同一组中的数据用该组区间的中点值作代表）；（Ⅱ）小明向班级同学发出倡议，为该小区居民捐款．现从损失超过4000元的居民中随机抽出2户进行捐款援助，设抽出损失超过8000元的居民为ξ户，求ξ的分布列和数学期望；（Ⅲ）台风后区委会号召小区居民为台风重灾区捐款，小明调查的50户居民捐款情况如表，根据表格中所给数据，分别求b，c，a+b，c+d，a+c，b+d，a+b+c+d 的值，并说明是否有95%以上的把握认为捐款数额多于或少于500元和自身经济损失是否到4000元有关？附：临界值表参考公式：，．【解答】解：（Ⅰ）记每户居民的平均损失为元，则：=（1000×0.00015+3000×0.0002+5000×0.00009+7000×0.00003+9000×0.00003）×2000=3360…（2分）（Ⅱ）由频率分布直方图，得：损失超过4000元的居民有：（0.00009+0.00003+0.00003）×2000×50=15户，∴ξ的可能取值为0，1，2，P（ξ=0）==，P（ξ=1）==，P（ξ=2）==，∴ξ的分布列为：Eξ=0×+1×+2×=．（Ⅲ）如图：K2=≈4.046＞3.841，所以有95%以上的把握认为捐款数额是否多于或少于500元和自身经济损失是否4000元有关．…（12分）20．（12分）已知抛物线C的顶点为原点，其焦点F（0，c）（c＞0）到直线l：x ﹣y﹣2=0的距离为，设P为直线l上的点，过点P作抛物线C的两条切线PA，PB，其中A，B为切点．（1）求抛物线C的方程；（2）当点P（x0，y0）为直线l上的定点时，求直线AB的方程；（3）当点P在直线l上移动时，求|AF|•|BF|的最小值．【解答】解：（1）焦点F（0，c）（c＞0）到直线l：x﹣y﹣2=0的距离，解得c=1，所以抛物线C的方程为x2=4y．（2）设，，由（1）得抛物线C的方程为，，所以切线PA，PB的斜率分别为，，所以PA：①PB：②联立①②可得点P的坐标为，即，，又因为切线PA的斜率为，整理得，直线AB的斜率，所以直线AB的方程为，整理得，即，因为点P（x0，y0）为直线l：x﹣y﹣2=0上的点，所以x0﹣y0﹣2=0，即y0=x0﹣2，所以直线AB的方程为x0x﹣2y﹣2y0=0．（3）根据抛物线的定义，有，，所以=，由（2）得x1+x2=2x0，x1x2=4y0，x0=y0+2，所以=．所以当时，|AF|•|BF|的最小值为．21．（12分）已知函数f（x）=+be﹣x，点M（0，1）在曲线y=f（x）上，且曲线在点M处的切线与直线2x﹣y=0垂直．（1）求a，b的值；（2）如果当x≠0时，都有f（x）＞+ke﹣x，求k的取值范围．【解答】解：（1）f（x）=+be﹣x的导数为f′（x）=，由切线与直线2x﹣y=0垂直，可得f（0）=1，f′（0）=﹣，即有b=1，a﹣b=﹣，解得a=b=1；（2）当x≠0时，都有f（x）＞+ke﹣x，即为+e﹣x＞+ke﹣x，即有（1﹣k）e﹣x＞，即1﹣k＞，可令g（x）=，g（﹣x）==g（x），即有g（x）为偶函数，只要考虑x＞0的情况．由g（x）﹣1=，x＞0时，e x＞e﹣x，由h（x）=2x﹣e x+e﹣x，h′（x）=2﹣（e x+e﹣x）≤2﹣2=0，则h（x）在x＞0递减，即有h（x）＜h（0）=0，即有g（x）＜1．故1﹣k≥1，解得k≤0．则k的取值范围为（﹣∞，0]．请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分.[选修4-4：坐标系与参数方程]22．（10分）选修4﹣4；坐标系与参数方程已知曲线C1的参数方程是（φ为参数），以坐标原点为极点，x轴的正半轴为极轴建立坐标系，曲线C2的坐标系方程是ρ=2，正方形ABCD的顶点都在C2上，且A，B，C，D依逆时针次序排列，点A的极坐标为（2，）．（1）求点A，B，C，D的直角坐标；（2）设P为C1上任意一点，求|PA|2+|PB|2+|PC|2+|PD|2的取值范围．【解答】解：（1）点A，B，C，D的极坐标为点A，B，C，D的直角坐标为（2）设P（x0，y0），则为参数）t=|PA|2+|PB|2+|PC|2+|PD|2=4x2+4y2+16=32+20sin2φ∵sin2φ∈[0，1]∴t∈[32，52][选修4-5：不等式选讲]23．设f（x）=|x|﹣|2x﹣1|，记f（x）＞﹣1的解集为M．（1）求集合M；（2）已知a∈M，比较a2﹣a+1与的大小．【解答】解：（1）由f（x）＞﹣1，得或或解得0＜x＜2，故M={x|0＜x＜2}．（2）由（1）知0＜a＜2，因为，当0＜a＜1时，，所以；当a=1时，，所以；当1＜a＜2时，，所以．综上所述：当0＜a＜1时，；当a=1时，；当1＜a＜2时，．。

湖南省长沙市第一中学2020届高三第一次月考数学(文科)试题含答案

长沙市一中2020届高三月考试卷(一）数学（理科）时量：120分钟满分:150分一、选择题:本大题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1. 已知i 为虚数单位，若复数2)1(1i z -+=,则=||z A. 1B. 2C. 2D. 52.已知集合A={21|≤≤-x x }，B={2,1,0}，则=B A A. 21|≤≤-x x B. {2,1,0} C. {2,1-} D. {1,0}3. 通过随机询问100名性别不同的大学生是否爱好踢毽子，得到如下的列联表：附表：随机变量：))()()(()(22d b c a d c b a bc ad n K ++++-=经计算，统计量K 2的观测值4.762,参照附表，得到的正确结论是 A.在犯错误的概率不超过5%的前提下，认为“爱好该项运动与性别有关” B.在犯错误的概率不超过5%的前提下，认为“爱好该项运动与性别无关” C.有97.5%以上的把握认为“爱好该项运动与性别有关" D.有97.5%以上的把握认为“爱好该项运动与性别无关”4. 已知向量b a b k a +=-=),2,2(),2,(为非零向量，若)(b a a +⊥,则实数k 的值为 A.0 B.2 C.-2 D.15. 美学四大构件是:史诗、音乐、造型(绘画、建筑等）和数学.素描是学习绘画的必要一步，它包括了明暗素描和结构素描，而学习几何体结构素描是学习素描最重要的一步.某同学在画“切面圆柱体”(用与圆柱底面不平行的平面去截圆柱，底面与截面之间的部分叫做切面圆柱体）的过程中，发现“切面”是一个椭圆，若“切面”所在平面与底面成60°角，则该椭圆的离心率为 A.21 B. 22 C. 23 D. 316.若21212,)21(,8.0log -===c b a π，则有A. a<b<cB. a<c<bC. c<a<bD. b<c<a7.函数21)(xexx f -=的图象大致是8.如图，点A 为单位圆上—点，3π=∠xOA ，点A 沿单位圆逆时针方向旋转角α 到点B )22,22(-，则=αsin A.462+- B. 462- C.462+ D . 462+- 9. 已知函数MOD 是一个求余函数，记MOD(m ，n)表示m 除以n 的余数，例如MOD(13,3) = 1，下图是某个算法的程序框图，当输入m 的值为27时，则输出i 的值为A.2B.3C.4D.510.在平面直角坐标系xOy 中，已知圆C:0822=-++m x y x 与直线012=++y x 相交于A ，B两点，若△ABC 为等边三角形，则实数m 的值为A. 11B. 12C.-11D.-1211. 设椭圆C ：)0>,0>(12222b a by a x =+的两个焦点分别为F1,F2，22||21=F F ，P 是C 上一点，若a PF PF =-||||21，且31sin 21=∠F PF ，则椭圆C 的方程为A. 13422=+y xB. 13622=+y x C.14622=+y x D. 12422=+y x 12.已知函数x x f x f sin 2)()(+-=，又当0≥x 时，1)('≥x f ，则关于x 的不等式)4(sin 2)2()(ππ-+-≥x x x f x f 的解集为 A. ),4[+∞π B. ),4[+∞-πC.)4,[π-∞ D. )4,[π--∞二、填空题:本大题共4小题.每小题5分，共20分。

2020届全国高考仿真模拟考试(二)理科数学

2020届全国高考仿真模拟考试（二）理科数学★祝你考试顺利★注意事项：1、考试范围：高考考查范围。

2、答题前，请先将自己的姓名、准考证号用0.5毫米黑色签字笔填写在试题卷和答题卡上的相应位置，并将准考证号条形码粘贴在答题卡上的指定位置。

用2B 铅笔将答题卡上试卷类型A 后的方框涂黑。

3、选择题的作答：每个小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑。

写在试题卷、草稿纸和答题卡上的非选择题答题区域的答案一律无效。

4、主观题的作答：用0.5毫米黑色签字笔直接答在答题卡上对应的答题区域内。

写在试题卷、草稿纸和答题卡上的非主观题答题区域的答案一律无效。

5、选考题的作答：先把所选题目的题号在答题卡上指定的位置用2B 铅笔涂黑。

答案用0.5毫米黑色签字笔写在答题卡上对应的答题区域内，写在试题卷、草稿纸和答题卡上的非选修题答题区域的答案一律无效。

6、保持卡面清洁，不折叠，不破损。

7、本科目考试结束后，请将本试题卷、答题卡、草稿纸一并依序排列上交。

一、选择题(本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的)1．已知U ＝{y |y ＝log 2x ，x >1}，P ＝{y |y ＝1x，x >2}，则∁U P ＝( )A. ⎣⎡⎭⎫12，＋∞B.⎝⎛⎭⎫0，12 C ．(0，＋∞) D ．(－∞，0)∪⎣⎡⎭⎫12，＋∞ 答案：A解析：因为函数y ＝log 2x 在定义域内为增函数，故U ＝{y |y >0}，函数y ＝1x在(0，＋∞)内为减函数，故集合P ＝{y |0<y <12}，所以∁U P ＝{y |y ≥12}．故选A.2．[2019·河南洛阳第一次统考]若复数z 为纯虚数，且(1＋i)z ＝a －i(其中a ∈R )，则|a ＋z |＝( )A. 2B. 3 C ．2 D. 5 答案：A解析：复数z ＝a －i 1＋i ＝(a －i )(1－i )(1＋i )(1－i )＝a －1－(a ＋1)i 2，根据题意得到a －12＝0⇒a ＝1，z ＝－i ，∴|a ＋z |＝|1－i|＝2，故选A.3．[2019·江西南昌二中模拟]设命题p ：函数f (x )＝x 3－ax －1在区间[－1，1]上单调递减；命题q ：函数y ＝ln(x 2＋ax ＋1)的值域是R .如果命题p 或q 是真命题，p 且q 为假命题，则实数a 的取值范围是( )A ．(－∞，3]B ．(－∞，－2]∪[2，3)C ．(2，3]D ．[3，＋∞)答案：B解析：若命题p 为真命题：函数f (x )＝x 3－ax －1在区间[－1，1]上单调递减，则f ′(x )＝3x 2－a ≤0在[－1，1]上恒成立，故a ≥(3x 2)max 在x ∈[－1，1]上恒成立，又(3x )2max ＝3，所以a ≥3.若命题q 为真命题：函数y ＝ln(x 2＋ax ＋1)的值域是R ，则必须使x 2＋ax ＋1能取所有正数，故Δ＝a 2－4≥0，解得a ≤－2或a ≥2.因为命题p ∨q 是真命题，p ∧q 为假命题，所以命题p 与命题q 一真一假，当p 为真命题，q 为假命题时，可得{a |a ≥3}∩{a |－2<a <2}＝∅，当q 为真命题，p 为假命题时，可得{a |a <3}∩{a |a ≤－2或a ≥2}＝{a |a ≤－2或2≤a <3}．综上可知，实数a 的取值范围是(－∞，－2]∪[2，3)，故选B.4．[2019·江西南昌重点中学段考]一个几何体挖去部分后的三视图如图所示，若其正视图和侧视图都是由三个边长为2的正三角形组成的，则该几何体的表面积为( )A ．13πB ．12πC ．11πD ．23π 答案：B解析：依题意知，题中的几何体是从一个圆台(该圆台的上底面半径为1，下底面半径为2，母线长为2)中挖去一个圆锥(该圆锥的底面半径为1，母线长为2)后得到的，圆台的侧面积为π(1＋2)×2＝6π，圆锥的侧面积为π×1×2＝2π，所以题中几何体的表面积为6π＋2π＋π×22＝12π，故选B.5．[2019·湖南岳阳质检]函数f (x )＝(－x 2＋x )e x 的图象大致为( )答案：A解析：令f (x )＝0，得x ＝0或x ＝1，所以点(1，0)在函数f (x )＝(－x 2＋x )e x 的图象上，所以排除B ，C.当x →＋∞时，f (x )→－∞，排除D ，故选A.6．[2019·江西赣州十四县(市)期中联考]古代有这样一个问题：“今有墙厚22.5尺，两鼠从墙两侧同时打洞，大鼠第一天打洞一尺，小鼠第一天打洞半尺，大鼠之后每天打洞长度比前一天多半尺，小鼠前三天每天打洞长度比前一天多一倍，三天之后小鼠每天打洞长度与第三天打洞长度相同，问两鼠几天能打通墙相逢？”两鼠相逢最快需要的天数为( )A ．4B ．5C ．6D ．7 答案：C解析：依题意得，大鼠每天打洞长度构成等差数列{a n }，且首项a 1＝1，公差d ＝12.小鼠前三天打洞长度之和为12＋1＋2＝72，之后每天打洞长度是常数2，令n ·1＋n (n －1)2·12＋72＋(n－3)·2≥2212(n 指天数，且n 是正整数)，则有n 2＋11n －100≥0，即n (n ＋11)≥100，则易知n 的最小值为6.故选C.7．[2019·河南开封定位考试]将函数y ＝sin 2x －cos 2x 的图象向左平移m (m >0)个单位长度后得到的图象与函数y ＝k sin x cos x (k >0)的图象重合，则k ＋m 的最小值是( )A ．2＋π4B ．2＋3π4C ．2＋5π12D ．2＋7π12答案：A 解析：将函数y ＝sin 2x －cos 2x ＝－cos 2x 的图象向左平移m (m >0)个单位长度后所得到的图象对应的函数解析式为y ＝－cos[2(x ＋m )]＝－cos(2x ＋2m )＝sin ⎝⎛⎭⎫2x －π2＋2m (m >0)，平移后得到的图象与函数y ＝k sin x cos x ＝k2sin 2x (k >0)的图象重合，所以⎩⎨⎧k2＝1，－π2＋2m ＝2n π(n ∈Z )，得k ＝2，m ＝n π＋π4(n ∈Z )，又m >0，所以m 的最小值为π4，可知k ＋m 的最小值为2＋π4.故选A.8．[2019·山西太原一中检测]已知实数x ，y 满足|x |＋|y |≤1，则z ＝2|x |－|y |的最大值为( )A ．5B ．4C ．3D ．2答案：D解析：令|x |＝a ，|y |＝b ，则⎩⎪⎨⎪⎧a ＋b ≤1，a ≥0，b ≥0，且z ＝2a －b .作出可行域如图中阴影部分所示，作出直线b ＝2a ，并平移，由图知，当平移后的直线过点(1，0)时，z 取得最大值，且z max＝2×1－0＝2.故选D.9．[2019·河南郑州摸底]现有一个不透明的口袋中装有标号分别为1，2，2，3的四个小球，它们除数字外完全相同，现从中随机取出一球记下号码后放回，均匀搅拌后再随机取出一球，则两次取出小球所标号码不同的概率为( )A.16B.56C.38D.58 答案：D解析：随机取出一球记下号码后放回，均匀搅拌后再随机取出一球，则两次取出小球的所有情况共有4×4＝16(种)，其中号码相同的情况共有6种，则号码不同的概率为P ＝1－616＝58，故选D. 10．[2019·辽宁五校期末]在△ABC 中，角A ，B ，C 所对的边分别是a ，b ，c ，已知sin(B＋A )＋sin(B －A )＝3sin 2A ，且c ＝7，C ＝π3，则△ABC 的面积是( )A.334B.736C.334或213D.334或736 答案：D解析：由sin(B ＋A )＋sin(B －A )＝3sin 2A ，得2sin B cos A ＝3sin 2A ＝6sin A cos A ，即sinB cos A ＝3sin A cos A ．当cos A ＝0时，A ＝π2，而C ＝π3，c ＝7，所以B ＝π6，b ＝c tan B ＝7×33＝213，所以此时△ABC 的面积为12bc ＝12×213×7＝736；当cos A ≠0时，可得sin B ＝3sinA ，由正弦定理得b ＝3a ，又c ＝7，所以cos C ＝a 2＋b 2－c 22ab ＝a 2＋9a 2－(7)26a 2＝cos π3＝12，得a ＝1，所以b ＝3，此时△ABC 的面积为12ab sin C ＝12×1×3×32＝334.综上可知，△ABC 的面积为334或736.故选D.11．[2019·河北唐山期中]如图，在△ABC 中，CM →＝2MB →，过点M 的直线分别交射线AB ，AC 于不同的两点P ，Q ，若AP →＝mAB →，AQ →＝nAC →，则mn ＋m 的最小值为( )A ．2B ．2 3C ．6D ．6 3 答案：A解析：连接AM ，由已知可得AM →＝AB →＋BM →＝AB →＋13BC →＝AB →＋13(AC →－AB →)＝23AB →＋13AC →＝23m AP →＋13n AQ →.因为P ，M ，Q 三点共线，所以23m ＋13n ＝1，所以mn ＋m ＝2n ＋m 3＋m ＝2n 3＋4m3＝⎝⎛⎭⎫2n 3＋4m 3⎝⎛⎭⎫23m ＋13n ＝109＋4n 9m ＋4m 9n ≥109＋24n 9m ×4m 9n ＝2，当且仅当4n 9m ＝4m 9n ，即m ＝n ＝1时取等号，所以mn ＋m 的最小值为2.故选A. 12．[2019·陕西汉中模拟]设抛物线y 2＝4x 的焦点为F ，过点M (－1，0)的直线在第一象限交抛物线于A ，B 两点，且AF →·BF →＝0，则直线AB 的斜率k ＝( )A. 2B.22C. 3D.33答案：B解析：设直线AB 的方程为y ＝k (x ＋1)(易知k >0)，A (x 1，y 1)，B (x 2，y 2)．由⎩⎪⎨⎪⎧y ＝k (x ＋1)，y 2＝4x ，可得k 2x 2＋(2k 2－4)x ＋k 2＝0，由根与系数的关系得x 1·x 2＝1，x 1＋x 2＝4－2k 2k2.又AF →·BF →＝0，易知F (1，0)，所以(1－x 1)(1－x 2)＋k 2(x 1＋1)(x 2＋1)＝0，即(k 2＋1)x 1x 2＋(k 2－1)(x 1＋x 2)＋k 2＋1＝0，即2k 2＋2＋(k 2－1)4－2k 2k 2＝0，解得k ＝22.故选B.二、填空题(本大题共4小题，每小题5分，共20分．将正确答案填在题中的横线上．) 13．[2019·陕西宝鸡四校第二次联考]已知α为锐角，且sin α·(3－tan 10°)＝1，则α＝________.答案：40°解析：由题意知sin α(3－tan 10°)＝sin α·3cos 10°－sin 10°cos 10°＝sinα·2(sin 60°cos 10°－cos 60°sin 10°)cos 10°＝sin α·2sin 50°sin 80°＝sin α·2cos 40°2sin 40°cos 40°＝sin αsin 40°＝1，即sinα＝sin 40°.因为α为锐角，所以α＝40°.14．[2019·山东邹城质监]观察下列各式：12＝1×2×36；12＋22＝2×3×56；12＋22＋32＝3×4×76；12＋22＋32＋42＝4×5×96；……照此规律，当n ∈N *时，12＋22＋32＋…＋n 2＝________.答案：n (n ＋1)(2n ＋1)6解析：第一个式子：12＝1×(1＋1)×[1＋(1＋1)]6；第二个式子：12＋22＝2×(2＋1)×[2＋(2＋1)]6；第三个式子：12＋22＋32＝3×(3＋1)×[3＋(3＋1)]6；第四个式子：12＋22＋32＋42＝4×(4＋1)×[4＋(4＋1)]6；……第n 个式子：12＋22＋32＋…＋n 2＝n ·(n ＋1)·[n ＋(n ＋1)]6＝n (n ＋1)(2n ＋1)6.15．[2019·福建龙岩质检]若用1，2，3，4，5，6，7这七个数字中的六个数字组成没有重复数字且任何相邻两个数字的奇偶性都不同的六位数，则这样的六位数共有________个(用数字作答)．答案：288解析：分两步进行，第一步，先从1，3，5，7中选3个进行排列，有A 34＝24种排法；第二步：将2，4，6这3个数插空排列，有2A 33＝12种排法．由分步乘法计数原理得，这样的六位数共有24×12＝288(个)．16．[2019·湖南四校摸底]已知定义在R 上的奇函数f (x )满足f ⎝⎛⎭⎫x ＋52＋f (x )＝0，当－54≤x ≤0时，f (x )＝2x ＋a ，则f (16)＝________.答案：12解析：由f ⎝⎛⎭⎫x ＋52＋f (x )＝0，得f (x )＝－f ⎝⎛⎭⎫x ＋52＝f (x ＋5)，所以函数f (x )是以5为周期的函数，则f (16)＝f (3×5＋1)＝f (1)．又f (x )是定义在R 上的奇函数，所以f (0)＝0，即1＋a ＝0，解得a ＝－1，所以当－54≤x ≤0时，f (x )＝2x －1，所以f (－1)＝－12，则f (1)＝－f (－1)＝12，故f (16)＝12.三、解答题(本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．) 17．(12分)[2019·河南郑州高中毕业班第二次质量预测]已知数列{a n }的前n 项和为S n ，a 1＝1，a n >0，若a n ＝S n ＋S n －1(n ≥2且n ∈N *)．(1)求数列{a n }的通项公式； (2)记c n ＝a n ·2a n ，求数列{c n }的前n 项和T n .解析：(1)依题意知a n ＝S n ＋S n －1(n ≥2且n ∈N *)，且a n >0，又当n ≥2时，a n ＝S n －S n －1，两式相除，得S n －S n －1＝1(n ≥2)，可知数列{S n }是以1为首项，公差为1的等差数列，所以S n ＝1＋(n －1)×1＝n ，即S n ＝n 2.当n ≥2时，a n ＝S n －S n －1＝n 2－(n －1)2＝2n －1，当n ＝1时，a 1＝S 1＝1，满足上式，所以a n ＝2n －1(n ∈N *)．(2)由(1)知，a n ＝2n －1，所以c n ＝(2n －1)·22n －1，则T n ＝1×2＋3×23＋5×25＋…＋(2n －1)×22n －1 ①，4T n ＝1×23＋3×25＋…＋(2n －3)×22n －1＋(2n －1)×22n ＋1 ②， ①－②得－3T n ＝2＋2×(23＋25＋…＋22n －1)－(2n －1)×22n ＋1＝2＋2×8(1－22n－ 2)1－4－(2n－1)×22n ＋1＝－103＋⎝⎛⎭⎫53－2n ×22n ＋1，所以T n ＝(6n －5)×22n ＋1＋109.18．(12分)[2019·湖南高三毕业班开学调研卷]如图，四棱锥P －ABCD 中，P A ⊥底面ABCD ，AD ∥BC ，AB ＝AD ＝AC ＝3，P A ＝BC ＝4，M 为线段AD 上一点，且AM ＝2MD ，N 为PC 的中点．(1)证明：MN ∥平面P AB ；(2)求直线AN 与平面PMN 所成角的正弦值．解析：(1)证明：由已知得AM ＝23AD ＝2.取BP 的中点T ，连接AT ，TN ，由N 为PC 中点知TN ∥BC ，TN ＝12BC ＝2.又因为AD ∥BC ，所以TN 綊AM ，则四边形AMNT 为平行四边形，所以MN ∥AT . 因为AT ⊂平面P AB ，MN ⊄平面P AB ，所以MN ∥平面P AB . (2)取BC 的中点E ，连接AE .由AB ＝AC 得AE ⊥BC ，从而AE ⊥AD ，且AE ＝AB 2－BE 2＝AB 2－⎝⎛⎭⎫BC 22＝ 5.以A 为坐标原点，AE →的方向为x 轴正方向，建立如图所示的空间直角坐标系A －xyz .由题易知，P (0，0，4)，M (0，2，0)，C (5，2，0)，N ⎝⎛⎭⎫52，1，2，PM →＝(0，2，－4)，PN →＝⎝⎛⎭⎫52，1，－2，AN →＝⎝⎛⎭⎫52，1，2.设n ＝(x ，y ，z )为平面PMN 的法向量，则⎩⎪⎨⎪⎧ n ·PM →＝0，n ·PN →＝0，即⎩⎪⎨⎪⎧2y －4z ＝0，52x ＋y －2z ＝0，可取n ＝(0，2，1)，|cos 〈n ，AN →〉|＝|n ·AN →||n ||AN →|＝8525.故直线AN 与平面PMN 所成角的正弦值为8525.19．(12分)[2019·山西省太原市高三上学期期末检测卷]2012年12月18日，作为全国首批开展空气质量新标准监测的74个城市之一，郑州市正式发布PM2.5数据，资料表明，近几年来，郑州市雾霾治理取得了很大成效，空气质量与前几年相比得到了很大改善，郑州市设有9个监测站点监测空气质量指数(AQI )，其中在轻度污染区、中度污染区、重度污染区分别设有2，5，2个监测站点，以9个站点测得AQI 的平均值为依据，播报我市的空气质量．(1)若某日播报的AQI 为118，已知轻度污染区AQI 的平均值为74，中度污染区AQI 的平均值为114，求重度污染区AQI 的平均值；(2)下表是2018年11月的30天中AQI 的分布，11月份仅有一天AQI 在[170，180)内．AQI 为标准，如果AQI 小于180，则去进行社会实践活动，以统计数据中的频率为概率，求该校周日去进行社会实践活动的概率；②在“创建文明城市”活动中，验收小组把郑州市的空气质量作为一个评价指标，从当月的空气质量监测数据中抽取3天的数据进行评价，设抽取到的AQI 不小于180的天数为X ，求X 的分布列及数学期望．解析：(1)设重度污染区AQI 的平均值为x ，则74×2＋114×5＋2x ＝118×9，解得x ＝172.(2)①11月份仅有一天AQI 在[170，180)内，则AQI 小于180的天数为18天，则该校周日去进行社会实践活动的概率为P ＝1830＝35.②由题意知，随机变量X 的可能取值为0，1，2，3.P (X ＝0)＝C 318C 012C 330＝2041 015，P (X ＝1)＝C 218C 112C 330＝4591 015，P (X ＝2)＝C 118C 212C 330＝2971 015，P (X ＝3)＝C 018C 312C 330＝11203，则X 的分布列为数学期望EX ＝0×2041 015＋1×4591 015＋2×2971 015＋3×11203＝65.20．(12分)[2019·湖南湘东六校联考]已知椭圆C ：x 2a 2＋y 2b 2＝1(a >b >0)的离心率e ＝12，点A (b ，0)，B ，F 分别为椭圆C 的上顶点和左焦点，且|BF |·|BA |＝2 6.(1)求椭圆C 的方程；(2)若过定点M (0，2)的直线l 与椭圆C 交于G ，H 两点(G 在M ，H 之间)，设直线l 的斜率k >0，在x 轴上是否存在点P (m ，0)，使得以PG ，PH 为邻边的平行四边形为菱形？如果存在，求出m 的取值范围；如果不存在，请说明理由．解析：(1)由离心率e ＝12得a ＝2c ①.由|BF |·|BA |＝26，得a ·b 2＋b 2＝26，∴ab ＝23 ②. 又a 2－b 2＝c 2 ③，∴由①②③可得a 2＝4，b 2＝3，∴椭圆C 的方程为x 24＋y 23＝1.(2)设直线l 的方程为y ＝kx ＋2(k >0)，由⎩⎪⎨⎪⎧y ＝kx ＋2(k >0)，x 24＋y 23＝1，得(3＋4k 2)x 2＋16kx ＋4＝0，易知Δ>0，∴k >12.设G (x 1，y 1)，H (x 2，y 2)，则x 1＋x 2＝－16k 4k 2＋3，PG →＋PH →＝(x 1＋x 2－2m ，k (x 1＋x 2)＋4)，GH→＝(x 2－x 1，y 2－y 1)＝(x 2－x 1，k (x 2－x 1))．∵菱形的对角线互相垂直，∴(PG →＋PH →)·GH →＝0，∴(1＋k 2)(x 1＋x 2)＋4k －2m ＝0，得m ＝－2k4k 2＋3，即m ＝－24k ＋3k，∵k >12，∴－36≤m <0(当且仅当3k ＝4k 时，等号成立)．∴存在满足条件的实数m ，m 的取值范围为⎣⎡⎭⎫－36，0.21．(12分)[2019·北京朝阳区期中]已知函数f (x )＝2mx 3－3x 2＋1(m ∈R )． (1)当m ＝1时，求f (x )在区间[－1，2]上的最大值和最小值；(2)求证：“m >1”是“函数f (x )有唯一零点”的充分不必要条件．解析：(1)由题意得f ′(x )＝6mx 2－6x ＝6x (mx －1)，所以当m ＝1时，f (x )＝2x 3－3x 2＋1，f ′(x )＝6x (x －1)，令f ′(x )＝0，解得x ＝0或x ＝1.当x 在[－1，2]内变化时，f ′(x )，f (x )的变化情况如下表：max min 故f (x )在区间[－1，2]上的最大值和最小值分别为5和－4.(2)因为m >1，所以由f ′(x )＝6mx ⎝⎛⎭⎫x －1m ＝0得x ＝0或x ＝1m. 当x 变化时，f ′(x )，f (x )的变化情况如下表：因为f ⎝⎛⎭⎫1m ＝2m ·1m 3－3·1m 2＋1＝－1m2＋1，且m >1，所以f ⎝⎛⎭⎫1m >0. 又f (－m )＝m 2(－2m 2－3)＋1<0，所以f (x )有唯一零点．所以“m >1”是“函数f (x )有唯一零点”的充分条件．当m ＝－2时，当x 变化时，f ′(x )，f (x )的变化情况如下表：又f ⎝⎛⎭⎫－12＝12－34＋1>0，f (0)>0，f (3)<0，所以此时f (x )也有唯一零点．从而可知“m >1”是“函数f (x )有唯一零点”的充分不必要条件．选考题(请考生在第22、23题中任选一题作答，多答、不答按本选考题的首题进行评分．) 22．(10分)[2019·湖南衡阳八中模拟][选修4－4：坐标系与参数方程]在平面直角坐标系xOy 中，直线l 的参数方程为⎩⎪⎨⎪⎧x ＝t cos α，y ＝1＋t sin α(t 为参数，0≤α<π)．以坐标原点为极点，x 轴的正半轴为极轴建立极坐标系，曲线C 的极坐标方程为ρcos 2θ＝4sin θ.(1)求直线l 的普通方程与曲线C 的直角坐标方程；(2)设直线l 与曲线C 交于不同的两点A ，B ，若|AB |＝8，求α的值．解析：(1)直线l 的普通方程为x ·sin α－y ·cos α＋cos α＝0，∵曲线C 的极坐标方程为ρcos 2θ＝4sin θ， ∴ρ2cos 2θ＝4ρsin θ，又ρcos θ＝x ，ρsin θ＝y ， ∴曲线C 的直角坐标方程为x 2＝4y .(2)将⎩⎪⎨⎪⎧x ＝t cos α，y ＝1＋t sin α(t 为参数，0≤α<π)代入x 2＝4y ，得t 2·cos 2α－4t ·sin α－4＝0，设点A ，B 对应的参数分别为t 1，t 2，则t 1＋t 2＝4sin αcos 2α，t 1·t 2＝－4cos 2α.∵|AB |＝|t 1－t 2|＝(t 1＋t 2)2－4t 1·t 2＝⎝⎛⎭⎫4sin αcos 2α2－4×－4cos 2α＝8， ∴cos α＝±22，α＝π4或α＝3π4.23．(10分)[2019·福建福州二检][选修4－5：不等式选讲] 已知不等式|2x ＋1|＋|2x －1|<4的解集为M . (1)求集合M ；(2)设实数a ∈M ，b ∉M ，证明：|ab |＋1≤|a |＋|b |.解析：(1)方法一当x <－12时，不等式化为－2x －1＋1－2x <4，即x >－1，所以－1<x <－12；当－12≤x ≤12时，不等式化为2x ＋1－2x ＋1<4，即2<4，所以－12≤x ≤12；当x >12时，不等式化为2x ＋1＋2x －1<4，即x <1，所以12<x <1.综上可知，M ＝{x |－1<x <1}．方法二设f (x )＝|2x ＋1|＋|2x －1|，则f (x )＝⎩⎪⎨⎪⎧－4x ，x <－12，2，－12≤x ≤12，4x ，x >12，函数f (x )的图象如图所示．因为f (x )<4，由图可得，－1<x <1，所以M ＝{x |－1<x <1}． (2)方法一 (综合法)因为a ∈M ，b ∉M ，所以|a |<1，|b |≥1. 而|ab |＋1－(|a |＋|b |)＝|ab |＋1－|a |－|b |＝(|a |－1)(|b |－1)≤0，所以|ab |＋1≤|a |＋|b |.方法二 (分析法)要证|ab |＋1≤|a |＋|b |，只需证|ab |＋1－|a |－|b |≤0，只需证(|a |－1)(|b |－1)≤0，因为a ∈M ，b ∉M ，所以|a |<1，|b |≥1，所以(|a |－1)(|b |－1|)≤0成立．所以|ab |＋1≤|a |＋|b |成立．方法三 (分析法)要证|ab |＋1≤|a |＋|b |，因为a ∈M ，b ∉M ，所以|a |<1，|b |≥1，所以|ab |＋1≥1，|a |＋|b |≥1，所以只需证(|ab |＋1)2≤(|a |＋|b |)2，只需证|ab |2＋2|ab |＋1≤|a |2＋2|ab |＋|b |2，只需证|ab |2＋1≤|a |2＋|b |2，只需证(|a |2－1)(|b |2－1)≤0，又|a |2<1，|b |2≥1，所以(|a |2－1)(|b |2－1)≤0成立．所以|ab |＋1≤|a |＋|b |成立．。

2020年湖南省长沙一中高考数学模拟试卷(文科)(一)(5月份)(有答案解析)

电子阅读源自纸质阅读合计（人）
青少年（人）
中老年（人）
合计（人）
参考公式：K2=
P（K2＞k） 0.15
k
2.072
0.10 2.706
0.05 3.841
0.025 5.024
0.010 6.635
0.005 7.879
0.001 10.828
第 3 页，共 16 页
19. 如图，多面体 ABCDEF 中，四边形 ABCD 是边长为 2 的菱形，且平面
B. A1O⊥BC D. A1O⊥平面 AB1D1
9. 已知函数 f（x）=sin（ωx+θ）（ω＞0，-
）的图象相邻的两个对称中心之间的距离为，
若将函数 f（x）的图象向左平移后得到偶函数 g（x）的图象，则函数 f（x）的一个单调递减区
间为（）
A. [- ]
B. [ ]
C. [0， ]
D. [ ]
项是 20，21，再接下来的三项是 20，21，22，依此类推那么该数列的前 50 项和为（）
A. 1044
B. 1024
C. 1045
D. 1025
12. 若不等式
对
成立，则实数 m 的取值范围是（）
A.
B.
C.
D. [1，+∞）
二、填空题（本大题共 4 小题，共 20.0 分） 13. 如图，在△ABC 中，AB=2，BC=3，∠ABC=60°，AH⊥BC 于点 H，若
∴=
．
∴ 的虚部为．
故选：D．由已知求得 z1，z2，再由复数代数形式的乘除运算化简得答案．本题考查复数代数形式的乘除运算，考查复数的代数表示法及基本概念，是基础题．

湖南省长沙市第一中学2020届高三月考试卷(八)理科数学试题(PDF版含答案)

二个 a 和三个 b 排列而成.记 S= x ⋅ y1 + x2 ⋅ y2 + x3 ⋅ y3 + x4 ⋅ y4 + x 5 ⋅ y5 ,Smin 表
示 S 所有可能取值中的最小值.则下列命题正确的个数是
rr
r
①S 有 5 个不同的值;
②若 a ⊥ b ,则 Smin 与| a |无关;
rr
r
③若 a // b ,则 Snim 与 b 无关;
B.a2+b2> 1
C. a<1 或 b<1
D. a≤1 且 b≤1
9.中医药，是包括汉族和少数民族医药在内的我国各民族医药的统称,反映了中华民族对生
命、健康和疾病的认识，具有悠久历史传统和独特理论及技术方法的医药学体系.某科研机
构研究发现,一品种中医药的药物成份甲的含量 x(单位:克)与药物功效 y(单位:药物单位)之间
P 的长度的最小值为_____。
三、解答题:本大题共 70 分.解答应写出文字说明、证明过程或演算步骤.第
17~21 题为必考题,每个试题考生都必须作答.第 22、23
题为选考题,考生根据要求作答.
(一)必考题:共 60 分.
17. (本题满分 12 分)
已知 a,b,c 分别为△ABC 的内角 A,B,C 的对边，且 2 sin2 B + 2b cos2 A = b + c
D.5
6.我校星期一至星期五每天上午共安排五节课,每节课的时间为 40 分钟,第一节课上课
的时间为 7: 50~8:30,课间休息 10 分钟.某同学请假后返校,若他在 8: 50~9: 30 之间随机到达教
室,则他听第二节课的时间不少于 20 分钟的概率为

湖南省长沙市第一中学2020届高三数学下学期模拟卷(一)文(含解析)

长沙市一中2020届高考模拟卷（一）数学（文科）第Ⅰ卷一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的1.已知集合{}{}(4)0,3,0,1,3A x x x B =-<=-，则A I B=（） A. {}3,1-- B. {}1,3 C. {}3,1,0-- D. {}0,1,3【答案】B 【解析】【分析】通过不等式的解法求出集合A ，然后求解交集即可．【详解】由已知得{|(4)0}{|04}A x x x x x =-<=<<，所以{1,3}A B =I ，故选B.【点睛】本题考查二次不等式的求法，交集的定义及运算，属于基础题．2.已知函数1()()xxf x e e=-，则下列判断正确的是（） A. 函数()f x 是奇函数，且在R 上是增函数 B. 函数()f x 是偶函数，且在R 上是增函数 C. 函数()f x 是奇函数，且在R 上是减函数 D. 函数()f x 是偶函数，且在R 上是减函数【答案】A 【解析】【分析】求出()f x 的定义域，判断()f x 的奇偶性和单调性，进而可得解. 【详解】()f x 的定义域为R ，且()()xx 1f x e f x e-=-=-；∴()f x 是奇函数；又xy e =和x1y ()e=-都是R 上的增函数；()x x 1f x e ()e∴=-是R 上的增函数．故选：A ．【点睛】本题考查奇偶性的判断，考查了指数函数的单调性，属于基础题．3.将一颗质地均匀的骰子（它是一种各面上分别标有1，2，3，4，5，6点数的正方体玩具）先后抛掷2次，记第一次出现的点数为m ，记第二次出现的点数为n ，则m ＝2n 的概率为（） A.118B.112C.19D.16【答案】B 【解析】【分析】基本事件总数n ＝6×6＝36，利用列举法求出m ＝2n （k ∈N *）包含的基本事件有3个，由古典概型概率公式计算即可．【详解】由题意得，基本事件总数有：6636⨯=种，事件“2m n =”包含的基本事件有：(2,1)，(4,2)，(6,3)共3个，所以事件“2m n =”的概率为313612P ==.故选B. 【点睛】本题考查概率的求法，考查列举法、古典概型等基础知识，是基础题．4.已知复数1z ，2z 在复平而上对应的点分别为A （1，2），B （－1，3），则12z z 的虚部为（） A. 1 B. 12i -C. iD. 12-【答案】D 【解析】分析】点的坐标得到复数z 1，z 2，代入12z z 后由复数代数形式的除法运算化简求值即可得到12z z 的虚部．【详解】解：由复数12z z ，在复平面上对应的点分别是A （1，2），B （﹣1，3），得：1z ＝1+2i ，2z ＝﹣1+3i则()()()()12121312551131313102i i z ii i z i i i +--+--====-+-+--． 12z z 的虚部为12- 故选：D ．【点睛】本题考查了复数代数形式的表示法及其几何意义，考查了复数代数形式的除法运算，是基础题．5.若双曲线2221(0)x y a a-=>的实轴长为2，则其渐近线方程为（）A. y x =±B. 2y x =±C. 12y x =±D. 2y x =±【答案】A 【解析】【分析】利用双曲线的实轴长求出a ，然后求解渐近线方程即可．【详解】双曲线的实轴长为2，得1a =，又1b =，所以双曲线的渐近线方程为y x =±. 故选A.【点睛】本题考查双曲线的简单性质的应用，考查渐近线方程，属于基础题．6.某几何体的三视图如图所示，则该几何体的侧视图的面积为（）A. 242+B. 442+C. 2D. 22【答案】C 【解析】【分析】根据三视图的几何特点，利用三视图的数据，求出侧视图的面积即可．【详解】由三视图的数据，结合“长对正，宽相等”可得俯视图斜边上的高2即为侧视图的底边长，正视图的高即为侧视图的高，所以侧视图的面积为：12222⨯⨯=．故选：C ．【点睛】本题考查三视图在形状、大小方面的关系，考查空间想象能力，属于基础题．7.等比数列{}n a 各项为正，354,,a a a -成等差数列，n S 为{}n a 的前n 项和，则42S S =（） A. 2 B.78C.98 D.54【答案】D 【解析】【分析】设{}n a 的公比为q （q ≠0，q ≠1），利用a 3，a 5，﹣a 4成等差数列结合通项公式，可得2a 1q 4＝a 1q 2﹣a 1q 3，由此即可求得数列{}n a 的公比，进而求出数列的前n 项和公式，可得答案．【详解】设{}n a 的公比为(0,1)q q q >≠， ∵3a ，5a ，成等差数列，∴4231112a q a q a q =-，10a ≠，0q ≠，∴2210q q +-=，得12q =或1q =-（舍去），∴4242211()1521()1241()2SS-==+=-.故选D.【点睛】本题考查等差数列与等比数列的综合，熟练运用等差数列的性质，等比数列的通项是解题的关键．8.在正方体ABCD－A1B1C1D1中，点O是四边形ABCD的中心，关于直线A1O，下列说法正确的是（）A. A1O∥DCB. A1O⊥BCC. A1O∥平面BCDD. A1O⊥平面ABD【答案】C【解析】【分析】推导出A1D∥B1C，OD∥B1D1，从而平面A1DO∥平面B1CD1，由此能得到A1O∥平面B1CD1．再利用空间线线、线面的位置关系排除其它选项即可.【详解】∵由异面直线的判定定理可得A1O与DC是异面直线，故A错误；假设A1O⊥BC，结合A1A⊥BC可得BC⊥A1ACC1，则可得BC⊥AC，显然不正确，故假设错误，即B错误；∵在正方体ABCD﹣A1B1C1D1中，点O是四边形ABCD的中心，∴A1D∥B1C，OD∥B1D1，∵A1D∩DO＝D，B1D1∩B1C＝B1，∴平面A1DO∥平面B1CD1，∵A1O⊂平面A1DO，∴A1O∥平面B1CD1．故C正确；又A1A⊥平面ABD，过一点作平面ABD的垂线有且只有一条，则D错误，故选：C．【点睛】本题考查命题真假的判断，考查空间中线线、线面、面面间的位置关系等基础知识，考查运算求解能力，考查数形结合思想，是中档题．9.已知函数()sin()(0,)22f x x ππωθωθ=+>-≤≤的图象相邻的两个对称中心之间的距离为2π，若将函数()f x 的图象向左平移6π后得到偶函数()g x 的图象，则函数()f x 的一个单调递减区间为（） A. [,]36ππ-B. 7[,]412ππC. [0,]3πD. 5[,]26ππ【答案】B 【解析】【分析】由对称中心之间的距离为2π可得三角函数的周期，从而可求得ω的值，利用经过平移变换后得到的函数()g x 是偶函数求得θ的值，从而根据正弦函数的单调性可得结果．【详解】因为函数()()sin (0,)22f x x ππωθωθ=+>-≤≤的图象相邻的两个对称中心之间的距离为2π，所以T π=，可得2ω=，将函数()f x 的图象向左平移6π后，得到()sin 23g x x πθ⎛⎫=++ ⎪⎝⎭是偶函数，所以()32k k Z ππθπ+=+∈，解得()6k k Z πθπ=+∈，由于22ππθ-≤≤，所以当0k =时6πθ=．则()sin 26f x x π⎛⎫=+ ⎪⎝⎭，令()3222262k x k k Z πππππ+≤+≤+∈，解得()263k x k k Z ππππ+≤≤+∈，当0k =时，单调递减区间为2,63ππ⎡⎤⎢⎥⎣⎦，由于][72,,41263n ππππ⎡⎤⎢⎥⎣⎦，所以7,412ππ⎡⎤⎢⎥⎣⎦是函数()f x 的一个单调递减区间，故选B ．【点睛】本题主要考查正弦型函数的周期性和单调性的应，以及三角函数图象的平移变换规律，属于中档题．函数sin()y A x ωϕ=+的单调区间的求法：若0,0A ω>>,把x ωϕ+看作是一个整体，由22k x ππωϕ+≤+≤()322k k Z ππ+∈求得函数的减区间，由2222k x k πππωϕπ-+≤+≤+求得增区间.10.已知抛物线C ：22(0)y px p =>的焦点为F ，准线为l ，点M 在第一象限的抛物线C 上，直线MF 点M 在直线l 上的射影为A ，且△MAF 的面积为，则p 的值为（）A. 1B. 2C. D. 4【答案】B 【解析】【分析】如图所示，由直线MF ，可得∠AMF ＝60°．再利用抛物线的定义得出面积的表达式，解出p 即可．【详解】如图所示，∵直线MF 的斜率为3，∴∠MFx ＝60°． ∴∠AMF ＝60°，由抛物线的定义可得：|MA |＝|MF |， ∴1sin 6043,2MAF S MF MA ∆=⋅︒=得4MA MF ==，所以MAF ∆为等边三角形，∴24MA p ==，2p =，故选B.【点睛】本题考查了抛物线的定义标准方程及其性质，考查了推理能力与计算能力，属于中档题．11.已知数列1，1，2，1，2，4，1，2，4，8，1，2，4，8，16，…其中第一项是02，接下来的两项是02，12，再接下来的三项是02，12，22，依此类推那么该数列的前50项和为()A. 1044B. 1024C. 1045D. 1025【答案】A 【解析】【分析】将已知数列分组，使每组第一项均为1，第一组：02，第二组：02，12，第三组：02，12，22，…第k 组：02，12，22，…，12k -，根据等比数列前n 项和公式，能求出该数列的前50项和．【详解】将已知数列分组，使每组第一项均为1，即：第一组：02，第二组：02，12，第三组：02，12，22， …第k 组：02，12，22，…，12k -，根据等比数列前n 项和公式，求得每项和分别为：121-，221-，321-，…，21k -，每项含有的项数为：1，2，3，…，k ，总共的项数为()11232k k N k +=+++⋯+=，当9k =时，()1452k k+=，故该数列的前50项和为()912395021221212121124816931104412S -=-+-+-+⋯+-+++++=-+=-．故选：A ．【点睛】本题考查类比推理，考查等比数列、分组求和等基础知识，考查运算求解能力、推理论证能力、归纳总结能力，属于中档题．12.若不等式1ln x m m e x +-≤+对1[,1]x e∈成立，则实数m 的取值范围是（） A. 1[,)2-+∞B. 1(,]2-∞-C. 1[,1]2-D. [1,)+∞【答案】A 【解析】【分析】设1ln t x x =+，由题意将原问题转化为求max ||t m -，利用导数分析1ln t x x=+的单调性求得最大值，代入解不等式即可. 【详解】设1ln t x x =+，由1,1e x ⎡⎤∈⎢⎥⎣⎦，则22111t x x x x ='-=-在1,1e x ⎡⎤∈⎢⎥⎣⎦上t 0'≤恒成立，∴1ln t x x=+单调递减，则[1,1]t e ∈-；当2em ≤时，max ||1t m e m m e -=--≤+，解得：12m ≥-；当2em >时，max ||1t m m m e -=-≤+，恒成立；综上知：当m R ∆1[,)2-+∞时，不等式1ln x m m e x +-≤+对1,1e x ⎡⎤∈⎢⎥⎣⎦成立. 故选A.【点睛】本题考查了利用导数求解函数最值的问题，考查了绝对值不等式的解法，考查了恒成立问题的转化，属于中档题.第Ⅱ卷二、填空题：本大题共4小题，每小题5分，共20分．13.如图，在△ABC 中，AB ＝2，BC ＝3，∠ABC＝60°，AH⊥BC 于点H ，若AH AB BC λμ=+u u u r u u u r u u u r，则λμ+=_________.【答案】43. 【解析】【分析】由题意可得13BH BC =u u u r u u u r ，从而由13AH AB BH AB BC =+=+u u u r u u u r u u u r u u u r u u u r，解得λ+μ．【详解】∵AB ＝2，∠ABC ＝60°， ∴BH ＝1，∴13 BH BC=u u u r u u u r，∴13AH AB BH AB BC=+=+=u u u r u u u r u u u r u u u r u u u rλAB+u u u rμBCuuu r，，故λ1=，μ13=，故λ+μ43=；故答案为：43．【点睛】本题考查了平面向量的线性运算的应用及平面向量基本定理的应用．14.已知x，y满足约束条件202010x yx yy++≥⎧⎪--≤⎨⎪+≤⎩，则目标函数2z x y=-的最大值为__________________。

湖南长沙市一中2020届高三月考文科数学试卷解析版

湖南长沙市一中2020届高三月考文科数学试卷解析版数学(文科)长沙市一中高三文数备课组组稿时量:120分钟满分:150分一、选择题:本大题共12小题，每小题5分，共60分在每小题给出的四个选项中，只有一项是符合题目要求的1. 已知i 为虚数单位，若复数2)1(1i z -+=,则=||z (D) A. 1B. 2C. 2D. 5【解析】依题意211212z i i i =+++=+，故z == D. 2.已知集合A={21|≤≤-x x }，B={2,1,0}，则=B A (B) 【解析】A={21|≤≤-x x }中整数有-1，0，，1，2，所以{}0,1,2A B = A. {|12}x x -≤≤ B. {2,1,0} C. {2,1-} D. {1,0}3.通过随机询问100名性别不同的大学生是否爱好踢毽子得到如下的列联表:经计算，统计量K 2的观测值k≈4.762参照附表得到的正确结论是(A) A.在犯错误的概率不超过5％的前提下，认为爱好该项运动与性别有关” B.在犯错误的概率不超过5％的前提下，认“爱好该项运动与性别无关 C.有97.5％以上的把握认为“爱好该项运动与性别有关”D.有97.5％以上的把握认为“爱好该项运动与性别无关”【解析】由题意算得，K≈4.762>3.841，参照附表，可得在犯错误的概率不超过5％的前提下，认为“爱好该项运动与性别有关”故选A4. 已知向量(,2),(2,2),a k b a b =-=+为非零向量，若()a a b ⊥+,则实数k 的值为 (A) A.0 B.2 C.-2 D.1【解析】∵a =(k ，-2)，b = (2.2)，∴a b += (k +2，0)，∵()a a b ⊥+， ∴()(2)0a a b k k ⋅+=⋅+=∵a b +为非零向量，即k +2≠0，∴k ＝0. 故选A5.美学四大构件是:史诗、音乐、造型(绘画、建筑等和数学素描是学习绘画的必要一步，它包括了明暗素描和结构素描而学习几何体结构素描是学习素描最重要的一步，某同学在画“切面圆柱体”(用与圆柱底面不平行的平面去截圆柱，底面与截面之间的部分叫做切面圆柱体)的过程中，发现“切面”是一个椭圆若“切面所在平面与底面成60°角，则该椭圆的离心率为(C) A.21 B. 22 C. 23 D. 31【解析】设圆柱底面圆的半径为R ，∵与底面成60°角的平面截圆柱，∴椭圆的半长轴长是2R ，半短轴长是R ，∴c = ∴ c e a ==C 6. 若21212,)21(,8.0log -===c b a π，则有 (B)A. a<b<cB. a<c<bC. c<a<bD. b <c<a 【解】1110.8222211log 0,2()()022a c --=<==<>，所以a<c<b 选B7.函数f(x)＝1的图象大致是【解析】由x ＞1时f (x )<0，排除B 、D ，又f (12)＞0，排除A 故选C8.如图+点A 为单位圆上一点，3π=∠xOA ，点A 沿单位圆逆时针方向旋转角α到点B )22,22(-，则=αsin (C) A. 462+- B.462-C.462+ D. 462+-【解析】由题意得1sin sin[()]()33222ππαα=+-=--=，故选C9.已知函数MOD 是一个求余函数，记MOD(m ，n )表示m 除以n 的余数，例如MOD(13，3)=1，下图是某个算法的程序框图，当输入m 的值为27时，则输出i 的值为 (B)A.2B.3C.4D.5【解析】当n ＝3，9，27时27能被n 整除，则最终i ＝3.10.在平面直角坐标系x O y 中，已知圆C:x 2+y 2+8x -m ＝0与直线012=++y x 相交于A ，B 两点.若△ABC 为等边三角形，则实数m 的值为 (D) A.11 B.12 C.-11 D.-12【解析】C:(x +4)2+y ＝16-m ，圆心C(-4，0)到直线012=++y x 的距离d ==所以弦长)A B =，由△ABC 为等边三角形，所以=m ＝-12.11.设椭圆C: 22221(0)x y a b a b+=>>的两个焦点分别为F1,F2，22||21=F F ，P 是C 上一点，若a PF PF =-||||21，且31sin 21=∠F PF ，则椭圆C 的方程为 (D)A. 13422=+y xB. 13622=+y xC. 14622=+y xD. 12422=+y x【解析】由1212,2PF PF a PF PF a -=+=，解得1231,22PF a PF a ==，在△PF 1F 2中，由正弦定理:121221sin sin PF PF PF F PF F =∠∠，解得sin ∠PF 2F 1＝1，则∠PF 2F 1＝90°，又121sin 3PF F ∠=，可知tan ∠PF 1F 2，2c ＝得212a PF ==解得a ＝2，c ，b =C 方程22142x y +=12.已知函数x x f x f sin 2)()(+-=，又当0≥x 时，1)('≥x f ，则关于x 的不等式)4(sin 2)2()(ππ-+-≥x x x f x f 的解集为 (A)A. ),4[+∞πB. ),4[+∞-πC. )4,[π-∞D. )4,[π--∞ 【解析】由f (x )＝f (-x )+2sin x ，知f (x )-sin x ＝f(-x)-sin(-x)，设g(x )＝f(x )-sin x 则g(x )＝g(-x )，即g(x )为R 上的偶函数当x ≥0时，g ’(x )＝f’(x )-cos x ≥f’(x )-1≥0则g (x )在区间[0，+∞)上单调递增()())24f x f x x ππ≥--等价于()()22g x g x x x ππ≥-⇒≥-，解得4x π≥。

湖南省长沙一中2020届高考月考卷(七)理科数学试卷(附全解全析)

长沙市一中2020届高三月考试卷(七)数学(理科)注意事项:1. 本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分。

答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。

2. 回答第I 卷时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

写在本试卷上无效。

3. 回答第I 卷时，将答案写在答题卡，上，写在本试卷上无效。

4.考试结束后，将本试卷和答题卡一-并交回。

第I 卷一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知全集U=Z ，A={1,2,3,4},B={}(1)(3)0,x x x x z +->∈,则A ()U C B I = A. {1,2} B. {2,3} C. {1,2,3} D. {1,2,3,4} 2.已知复数12i z i-=+，则z 的共轭复数z = A. 1355i - B. 1355i + C. 1355i -- D. 1355i -+ 3.函数1(0,1)x y a a a a =->≠的图象可能是4.61-2)(1)t t +（的展开式中，t 项的系数为 A.20 B.30 C.-10 D.-245.2013年华人数学家张益唐证明了孪生素数(注:素数也叫做质数)猜想的一个弱化形式.孪生素数猜想是希尔伯特在1900年提出的23个问题之一 ,可以这样描述:存在无穷多个素数p 使得p+2是素数,素数对(p ，p+2)称为孪生素数，从20以内的素数中任取两个,其中能构成孪生素数的概率为A. 114B. 17C. 314D. 136.如图所示的程序框图，则输出的x 、y 、z 的值分别是A. 13009, 600, 11203B.1200, 500,300C.1100, 400, 600D.300,500, 12007.若[,],sin 242ππθθ∈=，则sin θ=A. 35B. 45C. 4D. 348.在平面直角坐标系xOy 中,抛物线C:y 2=2px (p>0)的焦点为F ，M 是抛物线C 上的一点,若△OFM 的外接圆与抛物线C 的准线相切，且该圆的面积为36π,则p=A.2B.4C.6D.89.在三棱锥P-ABC 中,PA ⊥平面ABC,△ABC 为等边三角形,PA=AB,E 是PC 的中点,则异面直线AE 和PB 所成角的余弦值为 A. 16 B. 14 C. 13 D. 1210.直线x =2与双曲线221169x y -=的渐近线交于A 、B 两点，设P 为双曲线上任意一点，若(,,OP aob bOB a b R O =+∈u u u r u u r u u u r 为坐标原点),则下列不等式恒成立的是 A. 2ab =. B. 224a b +≥ C. 2a b -≥ D. 2a b +≥11.已知函数()cos sin 2f x x x =给出下列命题:①x R ∀∈,都有()()f x f x -=-成立;②存在常数0T x R ≠∀∈，恒有()()f x T f x +=成立;③f (x )的最大值为9 ④y =f (x )在[,]66ππ-上是增函数. 以上命题中正确的为A.①②③④B.②③C.①②③.D.①②④12.已知函数21()ln (1)(0)2f x x ax a x a a =-+-+>的值域与函数f (f (x ))的值域相同,则a 的取值范围为 A. (0,1] B. (1,+∞) C:(0. 43] D.[ 4+)3∞，第II 卷二、填空题:本大题共4小题,每小题5分,共20分.把各题答案的最简形式写在题中的横线上.13.已知向量(1,4),(2,)a b k ==-r r ，且(2)a b +r r 与2)a b -r r （共线，则实数k =________ 14.某中学有学生3600名,从中随机抽取300名调查他们的居住地与学校之间的距离，其中不超过1公里的学生共有15人,不超过2公里的学生共有45人，由此估计该学校所有学生中居住地到学校的距离在(1,2]公里的学生有_____人15.如图所示,在正四棱锥P- ABCD 中,底面ABCD 是边长为4的正方形,E 、F 分别是AB 、CD 的中点，cos ∠PEF=22,若A,B,C,D,P 在同一球面上,则此球的体积为______ 16.如图,在△ABC 中,AC ⊥BC,D 为BC 边上的点,M 为AD 上的点,CD=1,∠CAB=∠MBD=∠DMB,则AM=__________。

【数学】湖南省长沙市2020届高三统一模拟考试理科数学试卷有答案

（8分）
（9分）（10分）（11分）
∴二面角 A1− B1C1 − B 的余弦值的大小为 −
5. 5
（12分）
19.（本小题满分 12 分）
解析：（Ⅰ）设椭圆 C1 的半焦距为 c
，依题意，可得 a
=
p 2
，则 C2
:
y2
= 4ax ，（1
分）
代入 x = c ，得 y2 = 4ac ，即 y = ±2 ac ，所以 4 ac = 4 2 ，
解得 x
⎛ A⎜
⎝
a2c a2 − b2
,
−abc a2 − b2
⎞ ⎟ ，由 ⎠
OA
=
5a得 3
⎛ ⎜ ⎝
a2c a2 − b2
⎞2 ⎟ ⎠
+
⎛ ⎜⎝
−abc a2 − b2
⎞2 ⎟⎠
=
25 9
a2
，
( ) ( ) 化简得 a2 − 4b2 4a2 − b2 = 0 ，解得 b = 1 或 b = 2 .由于 C 位于 A, B 之间，故 b = 1
第 17～21 题
为必考题，每个试题考生都必须作答，第 22，23 题为选考题，考生根据要求作答.
（一）必考题：共 60 分.
17．（本小题满分 12 分）
解析：（Ⅰ）由正弦定理得 sin Asin(π − 2C) = sin C sin(π − A) = sin C sin A ，（1 分）
因为 sin A ≠ 0 ，所以 sin(π − 2C) = sin C ，
当 a =1 时， b = 4 ，由余弦定理得 c2 = a2 + b2 − 2ab cos C = 13, c = 13 ，

2025届湖南省长沙市第一中学高考数学三模试卷含解析

2025届湖南省长沙市第一中学高考数学三模试卷请考生注意：1．请用2B 铅笔将选择题答案涂填在答题纸相应位置上，请用0．5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。

写在试题卷、草稿纸上均无效。

2．答题前，认真阅读答题纸上的《注意事项》，按规定答题。

一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．已知集合(){}*,|4,M x y x y x y N =+<∈、，则集合M 的非空子集个数是（）A ．2B ．3C ．7D ．82．2(1ii +=- ) A ．132i +B ．32i+ C ．32i- D ．132i-+ 3．已知集合U =R ，{}0A y y =≥，{}1B y y x ==+，则UAB =( )A ．[)0,1B ．()0,∞+C ．()1,+∞D ．[)1,+∞ 4．在ABC 中，D 为BC 边上的中点，且||1,|2,120AB AC BAC ==∠=︒，则||=AD （）A ．32B ．12C ．34D ．745．地球上的风能取之不尽，用之不竭.风能是淸洁能源，也是可再生能源.世界各国致力于发展风力发电，近10年来，全球风力发电累计装机容量连年攀升，中国更是发展迅猛，2014年累计装机容量就突破了100GW ，达到114.6GW ，中国的风力发电技术也日臻成熟，在全球范围的能源升级换代行动中体现出大国的担当与决心.以下是近10年全球风力发电累计装机容量与中国新增装机容量图. 根据所给信息，正确的统计结论是（）A ．截止到2015年中国累计装机容量达到峰值B ．10年来全球新增装机容量连年攀升C ．10年来中国新增装机容量平均超过20GWD ．截止到2015年中国累计装机容量在全球累计装机容量中占比超过136．设复数z 满足2z iz i -=+（i 为虚数单位），则z 在复平面内对应的点位于（） A ．第一象限B ．第二象限C ．第三象限D ．第四象限7．已知空间两不同直线m 、n ，两不同平面α，β，下列命题正确的是（） A ．若m α且n α，则m n B ．若m β⊥且m n ⊥，则n βC ．若m α⊥且m β，则αβ⊥D ．若m 不垂直于α，且n ⊂α，则m 不垂直于n8．已知平面α，β，直线l 满足l α⊂，则“l β⊥”是“αβ⊥”的（） A ．充分不必要条件 B ．必要不充分条件 C ．充要条件D ．即不充分也不必要条件9．若执行如图所示的程序框图，则输出S 的值是（）A ．1-B ．23C ．32D ．410．如图所示，为了测量A 、B 两座岛屿间的距离，小船从初始位置C 出发，已知A 在C 的北偏西45︒的方向上，B 在C 的北偏东15︒的方向上，现在船往东开2百海里到达E 处，此时测得B 在E 的北偏西30的方向上，再开回C 处，由C 向西开26百海里到达D 处，测得A 在D 的北偏东22.5︒的方向上，则A 、B 两座岛屿间的距离为（）A ．3B ．32C ．4D ．4211．给定下列四个命题：①若一个平面内的两条直线与另一个平面都平行，则这两个平面相互平行； ②若一个平面经过另一个平面的垂线，则这两个平面相互垂直； ③垂直于同一直线的两条直线相互平行；④若两个平面垂直，那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直．其中，为真命题的是( )A ．①和②B ．②和③C ．③和④D ．②和④12．如图，在ABC ∆中，点Q 为线段AC 上靠近点A 的三等分点，点P 为线段BQ 上靠近点B 的三等分点，则PA PC +=（）A ．1233BA BC + B ．5799BA BC + C ．11099BA BC + D ．2799BA BC + 二、填空题：本题共4小题，每小题5分，共20分。

湖南长沙一中2020届高三4月模拟试卷(含答案详解)

湖南长沙一中2020届高三4月模拟试卷文科数学注意事项：1、本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。

答题前，考生务必将自己的姓名、考生号填写在答题卡上。

2、回答第Ⅰ卷时，选出每小题的答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号。

写在试卷上无效。

3、回答第Ⅱ卷时，将答案填写在答题卡上，写在试卷上无效。

4、考试结束，将本试卷和答题卡一并交回。

第Ⅰ卷一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的． 1．复数21iz =-，则z =（） A ．1BCD ．22．设全集{1,2,3,4,5,6}U =，集合{1,2,3,4}P =，{3,4,5}Q =，则()U P Q =I ð（） A ．{1,2,3,4,6}B ．{1,2,3,4,5}C ．{1,2,5}D ．{1,2}3．设32a -=，3log 5b =，cos100c =︒，则（） A ．a b c >>B ．b a c >>C ．a c b >>D ．c b a >>4．设n S 是等差数列{}n a 的前n 项和，若954S =，则5a =（） A ．10B ．8C ．6D ．45．函数211()ln 22f x x x =+-的图象大致为（） A ． B ． C ．D ．6．采用系统抽样方法从学号为1到50的50名学生中选取5名参加测试，则所选5名学生的学号可能是（）A ．1，2，3，4，5B ．5，26，27，38，49C ．2，4，6，8，10D ．5，15，25，35，457．已知π(0,)2α∈，若2sin sin 21αα+=，则tan α=（）A ．12B ．13C ．14D．28．若向量(2,1)=-a ，(3,2)=-b ，则3+a b 与2+a b 的夹角余弦值为（）A．2-B．2-C．10-D．13-9．德国数学家莱布尼兹（1646年1716-年）于1674年得到了第一个关于π的级数展开式，该公式于明朝初年传入我国．在我国科技水平比较落后的情况下，我国数学家、天文学家明安图（1692年1765-年）为提高我国的数学研究水平，从乾隆初年开始，历时近30年证明了包括这个公式在内的三个公式，同时求得了展开三角函数和反三角函数的6个新级数公式，著有《割圆密率捷法》一书，为我国用级数计算π开创了先河．如图所示的程序框图可以用莱布尼兹“关于π的级数展开式”计算π的近似值（其中P 表示π的近似值）．若输入10n =，则输出的结果P 的值是（）A ．11114(1)35717P =-+-++L B ．11114(1)35719P =-+-+-L C ．11114(1)35721P =-+-++LD ．11114(1)35721P =-+-+-L10．已知π04θ<<，则双曲线22122:1cos sin x y C θθ-=与222222:1sin sin tan y x C θθθ-=⋅的（） A ．实轴长相等B ．虚轴长相等C ．焦距相等D ．离心率相等11．ABC △的内角A ，B ，C 所对的边分别为a ，b ，c ，已知ABC △的面积为2sin a A ，且b c +=，则cos A =（）A．16B．25C．34D．2312．已知椭圆222:1(02)4x yC bb+=<<，作倾斜角为3π4的直线交椭圆C于A、B两点，线段AB的中点M，O为坐标原点，OMu u u u r与MAu u u r的夹角为θ，且tan3θ=，则b=（）A．1B．2C．3D．6第Ⅱ卷二、填空题：本大题共4小题，每小题5分．13．曲线(1)xy x e=+在点(0,1)处的切线的方程为．14．已知{}n a是等比数列，它的前n项和为n S，且34a=，48a=-，则5S=．15．函数2()4sin cos cos2sin4422x x x xf x=+的最小值为．16．如图，在长方体1111ABCD A B C D-中，对角线1DB与平面11ADD A，ABCD，11DCC D的夹角分别为α，β，θ，若111118A B BB C B++=，2221111124A B BB C B++=，则sin sin sinαβθ++=．三、解答题：本大题共6个大题，共70分．解答应写出文字说明、证明过程或演算步骤．17．（12分）通过随机询问某地100名高中学生在选择座位时是否挑同桌得到如下22⨯列联表：（1）从这50名男生中按是否挑同桌采取分层抽样的方法抽取一个容量为5的样本，然后从这5名学生中随机选取3名做深度采访，求这3名学生中恰有2名挑同桌的概率；（2）根据以上22⨯列联表，问是否有95%以上的把握认为"性别与在选择座位时是否挑同桌”有关？下面的临界值表供参考：（参考公式：22()()()()()n ad bcKa b c d a c b d-=++++，其中n a b c d=+++）18．（12分）已知等比数列{}n a的前n项和为n S，7127S=，且8a是216a和514a的等差中项．（1）求数列{}n a的通项公式；（2）当20a>时，令22logn n nb a a=+，求数列{}nb的前n项和nT．19．（12分）在三棱柱111ABC A B C -中，CB ⊥平面11BAA B ，122CB BB AB ===，160BAA ∠=︒．（1）证明：平面11BAC ⊥平面ABC ；（2）若E 为AC 的中点，求点E 到平面11BA C 的距离．20．（12分）已知函数()cos xf x e x =-的导函数为()g x ．（1）证明：()g x '在区间(π,0)-存在唯一零点；（2）若对任意x ∈R ，()cos f x ax x ≥-恒成立，求a 的取值范围．21．（12分）已知动点P 到点1(,0)2的距离比到直线1x =-的距离小12，设点P 的轨迹为曲线C ．（1）求曲线C 的方程；（2）过曲线C 上一点00(2,)(0)M y y >作两条直线1l ，2l 与曲线C 分别交于不同的两点A ，B ，若直线1l，2l的斜率分别为1k，2k，且121k k=，证明：直线AB过定点．请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分．22．（10分）【选修4-4：坐标系与参数方程】在直角坐标系xOy中，曲线C的参数方程是22233141txttyt⎧-=⎪⎪+⎨⎪=⎪+⎩（t为参数），以坐标原点为极点，x轴正半轴为极轴建立极坐标系，直线l的极坐标方程为102sin cosρθθ=+．（1）求曲线C的普通方程和直线l的直角坐标方程；（2）过曲线C上的任意一点M作与l夹角为π3的直线，交直线l于点N，求MN的最大值与最小值．23．（10分）【选修4-5：不等式选讲】已知a，b，c为正实数，且1a b c++=．（1）求证：14116a b c++≥；（2≤湖南长沙一中文科数学答案第Ⅰ卷一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的． 1．【答案】B【解析】∵2(1i)1i (1i)(1i)z +==+-+，∴z = 2．【答案】D【解析】∵{3,4,5}Q =，∴{1,2,6}U Q =ð，∴(){1,2}U P Q =I ð． 3．【答案】B【解析】∵32(0,1)a -=∈，3log 51b =>，cos100cos800c =︒=-︒<，∴b a c >>． 4．【答案】C 【解析】∵19599()925422a a a S +⋅===，所以56a =． 5．【答案】C【解析】由()()f x f x -=，得()f x 为偶数，图象关于y 轴对称，排除D ；2131()022f ee =-+<，排除A ；211()022f e e =+>，排除B ，故选C ．6．【答案】D【解析】采用系统抽样时，要求将总体分成个数相等的若干部分，抽样的间隔也要求相等，间隔一般为总体的个数除以样本容量，∴间隔为50105=，只有D 答案中的编号间隔为10． 7．【答案】A 【解析】22221sinsin 21sin cos sin 2cos tan 2ααααααα+==+⇒=⇒=．8．【答案】C【解析】3(3,1)+=-a b ，2(4,3)+=-a b ，设3+a b 与2+a b 的夹角为θ，则cos θ==． 9．【答案】B【解析】根据框图计算循环依次为112S i =⎧⎨=⎩，2112213S i ⎧=-⎪⨯-⎨⎪=⎩，311132314S i ⎧=-+⎪⨯-⎨⎪=⎩，L ，911113529110S i ⎧=-+-+⎪⨯-⎨⎪=⎩L ，1011111357210111S i ⎧=-+-+-⎪⨯-⎨⎪=⎩L ，此时1110i =>，输出4P S =，即为π的近似值． 10．【答案】D【解析】双曲线1C 的实轴长为2cos θ，虚轴长为2sin θ，焦距为2=， ∴离心率为11cos e θ=；曲线2C 的实轴长为2sin θ，虚轴长2sin tan θθ，焦距为2tan θ=， ∴离心率为2tan 1sin cos e θθθ==，可知选项D 正确． 11．【答案】C【解析】由三角形面积公式可得21sin sin 2ABC S bc A a A ==△，所以22a bc =，又222222222()2843cos 2244b c a b c bc a a a a A bc bc a +-+----====． 12．【答案】B【解析】设11(,)A x y ，22(,)B x y ，00(,)M x y ，则22112222221414x y b x y b ⎧+=⎪⎪⎨⎪+=⎪⎩，两式作差得121212122()()()()04x x x x y y y y b-+-++=， ∵12121y y x x -=--，∴00204x y b-=，即2004y b x =，设直线OM 的倾斜角为α，则π4θα=+或3π4θα=-，∴tan 1tan 1tan αθα+=±-，又200tan 4y b x α==，∴2214314b b +=-，解得22b =，即b =第Ⅱ卷二、填空题：本大题共4小题，每小题5分． 13．【答案】21y x =+【解析】∵(2)xy x e '=+，∴切线斜率2k =，∴切线方程为12y x -=，即21y x =+．14．【答案】11【解析】因为34a =，48a =-，所以432a q a ==-，因此512481611S =-+-+=． 15．【答案】1 【解析】22()4sincos cos 2sin 2sin cos (12sin )14422222x x x x x x xf x =+=--+Qπsin cos 1)14x x x =-+=-+，所以函数()f x的最小值为1．16．【答案】3【解析】连接1DA ，DB ，1DC ，由长方体的性质知，11A DB α∠=，1BDB β∠=，11C DB θ∠=， ∵2221111124A B BB C B ++=，∴1DB =∴11111111111111sin sin sin A B BB C B A B BB C B DB DB DB DB αβθ++++=++===．三、解答题：本大题共6个大题，共70分．解答应写出文字说明、证明过程或演算步骤．17．【答案】（1）35；（2）有95%以上的把握认为．【解析】（1）根提分层抽样方法抽取容量为5的样本，挑同桌有3人，记为A ，B ，C ，不挑同桌有2人，记为d ，e ，从这5人中随机选取3人，基本事件为ABC ，ABd ，ABe ，ACd ，ACe ，Ade ，BCd ，BCe ，Bde ，Cde 共10种，这3名学生中恰有2名要挑同桌的事件为ABd ，ABe ，ACd ，ACe ，BCd ，BCe 共6种，故所求的概率为63105P ==．（2）根据以上22⨯列联表，计算22100(30102040) 4.7619 3.84170305050K ⨯⨯-⨯=≈>⨯⨯⨯，对照临界值表知，有95%以上的把握认为“性别与在选择座位时是否挑同桌”有关．18．【答案】（1）见解析；（2）41(1)32n n n n T --=+．【解析】（1）由8a 是216a 和514a 的等差中项，得82521614a a a =+，即7411187a q a q a q =+，所以63780q q --=，即33(8)(1)0q q -+=，解得公比2q =或1-．当2q =时，由7171(1)12711a q S a q-==⇒=-，所以12n n a -=；当1q =-时，由7171(1)1271271a q S a q-==⇒=-，所以1127(1)n n a -=⋅-．（2）当20a >时，知12n n a -=，∴212log 41n n n n b a a n -=+=+-，所以数列{}n b 的前n 项和(14)(1)41(1)14232n nn n n n n T ----=+=+-． 19．【答案】（1）证明见解析；（2）5．【解析】（1）因为CB ⊥平面11BAA B ，可得1CB A B ⊥，在1AA B △中，由余弦定理可得，1A B =22211AB A B AA +=，所以1AB A B ⊥，又因为AB CB B =I ，所以1A B ⊥平面ABC ，又因为1A B ⊂平面11BA C ，所以平面11BAC ⊥平面ABC ．（2）由已知得，11C B CB ∥，∴11C B ⊥平面11BAA B，所以1BC =11AC = 由（1）可得，1A B =1A B ⊥平面111A B C，则11111122BA C S A C BA =⨯⨯=△，因为11AC A C ∥，AC ⊄平面11BA C ，11A C ⊂平面11BA C ，所以AC ∥平面11BA C ，从而点E 到平面11BA C 的距离等于点A 到平面11BA C 的距离，设点E 到平面11BA C 的距离为d ，由111111E BA C A BA C C BAA V V V ---==，得1111112332BA C S d ⨯⨯=⨯⨯△，所以5d =，即点E 到平面11BA C的距离为5． 20．【答案】（1）证明见解析；（2）[0,]e ．【解析】（1）()()sin x g x f x e x '==+，则()cos x g x e x '=+，因为cos y x =与xy e =在(π,0)-均为增函数，故()g x '在(π,0)-为增函数，又π(π)10g e-'-=-<，且(0)20g '=>，则(π)(0)0g g ''-<，结合零点存在性定理知()g x '在区间(π,0)-存在唯一零点．（2）构造函数()()(cos )xF x f x ax x e ax =--=-，x ∈R ，由题意知()0F x ≥恒成立．①当0a <时，11()10a F e a=-<，与题意矛盾，舍去；②当0a =时，()0xF x e =>，符合题意；③当0a >时，()xF x e a '=-，∴()F x '为增函数，当(,ln )x a ∈-∞时，()0F x '<，即()F x 在(,ln )a -∞单调递减；当(ln ,)x a ∈+∞时，()0F x '>，即()F x 在(ln ,)a +∞单调递增，则ln min ()(ln )ln (1ln )aF x F a ea a a a ==-=-，要使()0F x ≥对任意x ∈R 恒成立，即需使min ()0F x ≥，即(1ln )0a a -≥，解得0a e <≤，综上所述，a 的取值范围为[0,]e ．21．【答案】（1）22y x =；（2）证明见解析．【解析】（1）由题意可知，动点P 到点1(,0)2的距离与到直线12x =-的距离相等，所以点P 的轨迹是以1(,0)2为焦点，直线12x =-为准线的抛物线，所以曲线C 的方程为22y x =．（2）易知(2,2)M ，设点11(,)A x y ，22(,)B x y ，直线AB 的方程为x my b =+，联立22x my b y x =+⎧⎨=⎩，得2220y my b --=，所以121222y y m y y b +=⎧⎨=-⎩，所以21221222x x m b x x b ⎧+=+⎪⎨=⎪⎩，因为12121222122y y k k x x --=⋅=--，即121212122()2()y y y y x x x x -+=-+，所以222440b b m m --+=，所以22(1)(21)b m -=-，所以2b m =或22b m =-+，当22b m =-+时，直线AB 的方程为22x my m =-+，过定点(2,2)，与M 重合，舍去；当2b m =时，直线AB 方程为2x my m =+，过定点(0,2)-，所以直线AB 过定点(0,2)-．22．【答案】（1）22:1(3)94x y C x +=≠-，:2100l x y +-=；（2）最小值为3，最大值【解析】（1）222131:221x t t C y tt ⎧-=⎪⎪+⎨⎪=⎪+⎩，平方相加后得22194x y+=，又2223363(3,3]11t x t t -==-+∈-++，即曲线C 的普通方程为221(3)94x y x +=≠-， ∵直线l 的极坐标方程为102sin cos ρθθ=+，即cos 2sin 10ρθρθ+=，∴直线l 的直角坐标方程为2100x y +-=．（2）∵点M 为曲线C 上的任意一点，∴设点M 的坐标为(3cos ,2sin )αα，点M 到直线l的距离为d ==其中3tan 4ϕ=，∴)10πsin 3d MN αϕ==+-，当sin()1αϕ+=时，MN当sin()1αϕ+=-时，MN取得最大值 23．【答案】（1）证明见解析；（2）证明见解析．【解析】（1）∵a ，b ，c 为正实数，且1a b c ++=，故14114144()()6b c a c a ba b c a b c a b c a a b b c c++=++++=++++++6642416≥+=+++=，当且仅当14a c==，12b=时，等号成立，即14116a b c++≥．（2）3=332332332153()()9 3222323a b c a b c+++++++++≤++===当且仅当13a b c===时，等号成立，≤。

(精选3份合集)2020届湖南省长沙市一中高考数学模拟试卷

2020年湖南省长沙市高考数学一模试卷(文科)含答案解析

湖南长沙一中2020届高三模拟测试(八)文数试题

湖南省长沙一中2025届高考数学一模试卷含解析

2020年湖南省长沙一中高考数学模拟试卷(理科)(一)(5月份)(有答案解析)

2020年高考长沙名校数学模拟卷01(新课标Ⅰ卷)(解析版)

【2020年高考必备】湖南省长沙市高考数学一模试卷(理科)及解析

湖南省长沙市第一中学2020届高三第一次月考数学(文科)试题 含答案

2020届全国高考仿真模拟考试(二)理科数学

2020年湖南省长沙一中高考数学模拟试卷(文科)(一)(5月份)(有答案解析)

湖南省长沙市第一中学2020届高三月考试卷(八)理科数学试题(PDF版含答案)

湖南省长沙市第一中学2020届高三数学下学期模拟卷(一)文(含解析)

湖南长沙市一中2020届高三月考文科数学试卷解析版

湖南省长沙一中2020届高考月考卷(七)理科数学试卷(附全解全析)

【数学】湖南省长沙市2020届高三统一模拟考试理科数学试卷有答案

2025届湖南省长沙市第一中学高考数学三模试卷含解析

湖南长沙一中2020届高三4月模拟试卷(含答案详解)

湖南省长沙市第一中学2020届高三第一次月考数学(文科)试题含答案