矩阵、向量求导
matrixid矩阵向量求导法则

(1b)
(AB)T = BT AT
(1c)
if individual inverses exist (AB)−1 = B−1A−1
(1d)
(A−1)T = (AT )−1
(1e)
0.2 trace, determinant and rank
|AB| = |A||B|
(2a)
|A−1| = 1
(2b)
0 A22
= |A11||A22|
A11 0
0 A22
−1
=
A−111 0
0 A−221
(9d) (9e)
0.10 matrix inversion lemma (sherman-morrison-woodbury)
using the above results for block matrices we can make some substitutions and get the following important results:
∂X
∂X
∂Tr XT AX = (A + AT )X
(3d)
∂X
∂Tr X−1A = −X−1AT X−1
(3e)
∂X
0.4 derivatives of determinants
∂|AXB| = |AXB|(X−1)T = |AXB|(XT )−1
(4a)
∂X
∂ ln |X| = (X−1)T = (XT )−1
(4b)
∂X
∂ ln |X(z)| = Tr
X−1 ∂X
(4c)
∂z
∂z
∂|XT AX| = |XT AX|(AX(XT AX)−1 + AT X(XT AT X)−1) (4d) ∂X
偏导数公式大全24个

偏导数公式大全24个偏导数是多元函数微分学中的重要概念,用于描述函数在特定方向上的变化率。
在实际问题中,偏导数常常被用于求解最优化、梯度下降等问题。
下面是24个常用的偏导数公式,每个公式都有它们的特定应用场景。
1. 常数偏导数公式:对于常数函数f(x)=c,其偏导数为0,即f/x = 0。
2. 幂函数偏导数公式:对于幂函数f(x)=x^n,其中n为常数,其偏导数为f/x = n*x^(n-1)。
3. 指数函数偏导数公式:对于指数函数f(x)=a^x,其中a为常数,其偏导数为f/x = a^x * ln(a)。
4. 对数函数偏导数公式:对于对数函数f(x)=log_a(x),其中a为常数且a>0,其偏导数为f/x = 1/(x * ln(a))。
5. 三角函数偏导数公式:对于三角函数f(x)=sin(x),其偏导数为f/x = cos(x)。
类似地,对于cos(x)和tan(x)函数,其偏导数分别为-sin(x)和sec^2(x)。
6. 反三角函数偏导数公式:对于反三角函数f(x)=asin(x),其中a为常数,其偏导数为f/x = a/sqrt(1-x^2)。
类似地,对于acos(x)和atan(x)函数,其偏导数分别为-a/sqrt(1-x^2),-1/sqrt(1+x^2)。
7. 求和公式:对于多个函数的和f(x) = g(x) + h(x),其偏导数为f/x = g/x + h/x。
8. 积函数公式:对于两个函数的积f(x) = g(x) * h(x),其偏导数为f/x = g(x) * h/x + h(x) * g/x。
9. 商函数公式:对于两个函数的商f(x) = g(x) / h(x),其偏导数为f/x = (h(x) * g/x - g(x) * h/x) / h(x)^2。
10. 复合函数公式:对于复合函数f(g(x)),其中f和g是两个函数,其偏导数为f/x = f/g * g/x。
标量对向量求导

标量对向量求导1. 矩阵Y对标量x求导:相当于每个元素求导数后转置一下,注意M×N矩阵求导后变成N×M了Y = [y(ij)] --> dY/dx = [dy(ji)/dx]2. 标量y对列向量X求导:注意与上面不同,这次括号内是求偏导,不转置,对N×1向量求导后还是N×1向量y = f(x1,x2,..,xn) --> dy/dX = (Dy/Dx1,Dy/Dx2,..,Dy/Dxn)' 3. 行向量Y'对列向量X求导:注意1×M向量对N×1向量求导后是N×M矩阵。
将Y的每一列对X求偏导,将各列构成一个矩阵。
重要结论:dX'/dX = Id(AX)'/dX = A'4. 列向量Y对行向量X’求导:转化为行向量Y’对列向量X的导数,然后转置。
注意M×1向量对1×N向量求导结果为M×N矩阵。
dY/dX' = (dY'/dX)'5. 向量积对列向量X求导运算法则:注意与标量求导有点不同。
d(UV')/dX = (dU/dX)V' + U(dV'/dX)d(U'V)/dX = (dU'/dX)V + (dV'/dX)U'重要结论:d(X'A)/dX = (dX'/dX)A + (dA/dX)X' = IA + 0X' = Ad(AX)/dX' = (d(X'A')/dX)' = (A')' = Ad(X'AX)/dX = (dX'/dX)AX + (d(AX)'/dX)X = AX + A'X6. 矩阵Y对列向量X求导:将Y对X的每一个分量求偏导,构成一个超向量。
机器学习中的矩阵向量求导(五)矩阵对矩阵的求导

机器学习中的矩阵向量求导(五)矩阵对矩阵的求导 在前4篇⽂章中,我们主要讨论了标量对向量矩阵的求导,以及向量对向量的求导。
本⽂我们就讨论下之前没有涉及到的矩阵对矩阵的求导,还有矩阵对向量,向量对矩阵求导这⼏种形式的求导⽅法。
本⽂所有求导布局以分母布局为准,为了适配矩阵对矩阵的求导,本⽂向量对向量的求导也以分母布局为准,这和前⾯的⽂章不同,需要注意。
本篇主要参考了张贤达的《矩阵分析与应⽤》和长躯⿁侠的1. 矩阵对矩阵求导的定义 假设我们有⼀个p×q的矩阵F要对m×n的矩阵X求导,那么根据我们第⼀篇求导的定义,矩阵F中的pq个值要对矩阵X中的mn个值分别求导,那么求导的结果⼀共会有mnpq个。
那么求导的结果如何排列呢?⽅法有很多种。
最直观可以想到的求导定义有2种: 第⼀种是矩阵F对矩阵X中的每个值X ij求导,这样对于矩阵X每⼀个位置(i,j)求导得到的结果是⼀个矩阵∂F∂X ij,可以理解为矩阵X的每个位置都被替换成⼀个p×q的矩阵,最后我们得到了⼀个mp×nq的矩阵。
第⼆种和第⼀种类似,可以看做矩阵F中的每个值F kl分别对矩阵X求导,这样矩阵F每⼀个位置(k,l)对矩阵X求导得到的结果是⼀个矩阵∂F kl∂X, 可以理解为矩阵F的每个位置都被替换成⼀个m×n的矩阵,最后我们得到了⼀个mp×nq的矩阵。
这两种定义虽然没有什么问题,但是很难⽤于实际的求导,⽐如类似我们在中很⽅便使⽤的微分法求导。
⽬前主流的矩阵对矩阵求导定义是对矩阵先做向量化,然后再使⽤向量对向量的求导。
⽽这⾥的向量化⼀般是使⽤列向量化。
也就是说,现在我们的矩阵对矩阵求导可以表⽰为:∂F ∂X=∂vec(F)∂vec(X) 对于矩阵F,列向量化后,vec(F)的维度是pq×1的向量,同样的,vec(X)的维度是mn×1的向量。
最终求导的结果,这⾥我们使⽤分母布局,得到的是⼀个mn×pq的矩阵。
矩阵求导的迹运算法则

矩阵求导的迹运算法则矩阵求导是应用线性代数中的求导法则来求解适用于矩阵和向量的函数的一种方法。
在数学和统计学中,矩阵求导法则在机器学习、信号处理、数据科学和其他领域的应用越来越广泛。
本文旨在介绍矩阵求导中的一种特殊运算法则——迹运算法则。
一、迹运算迹运算是线性代数中的一种重要运算,它是由矩阵的主对角线上元素求和得到的标量值,通常用tr(X)表示。
例如,对于一个3x3的矩阵X,其迹为tr(X)=x11+x22+x33。
除了用于表示矩阵的迹外,迹运算还有很多其他的应用,例如在矩阵的特征值和特征向量求解中,以及计算矩阵的行列式等。
二、矩阵求导在计算矩阵和向量的函数导数时,矩阵求导的方法和标量求导有所不同。
矩阵求导可以分为两种类型:沿着方向求导和按元素求导。
在沿着方向求导中,对于矩阵或向量函数f(X),我们需要求解f(X)关于X沿着某个方向的导数,例如:其中,X是一个m×n的矩阵,H是一个m×n的矩阵,而f(X)是一个标量函数.在按元素求导中,对于矩阵或向量函数f(X),我们需要依次求解f(X)中每个元素关于X中对应元素的导数。
例如:其中,X和Y都是同样大小的矩阵,f(X)和g(Y)都是矩阵函数。
三、迹运算法则矩阵求导中的迹运算法则可以帮助我们解决一些复杂的求导问题。
具体来说,如果我们有两个矩阵A和B,以及一个方程C=f(A,B),并且我们想要求解C对于A的导数,那么迹运算法则可以用来简化这个计算过程。
具体地,对于任意二元标量函数f(A,B),我们可以得到以下变换法则:其中,tr(AB)表示AB的迹,该公式是由于迹运算具有循环不变性而得到的。
这个公式告诉我们,计算C对于A的导数,可以通过B和C的偏导数以及矩阵乘积AB的迹来计算。
类似地,我们也可以求解C对于B的导数,如下所示:这个公式可以看作是上一个公式在A和B的位置上交换了一下。
需要注意的是,这个方法只适用于当矩阵A和B可以互换时,即矩阵AB和BA的迹相等时。
矩阵向量求导法则

矩阵向量求导法则
矩阵向量求导法则是一组规则,用于计算矩阵和向量之间的导数。
以下列出了常见的矩阵向量求导法则:
1. 标量对向量求导:
\frac{d}{dx}(c^{T}x) = c
其中,c是一个常数向量,x是一个列向量。
2. 向量对标量求导:
\frac{d}{dx}(x^{T}c) = c^{T}
其中,c是一个常数向量,x是一个列向量。
3. 向量对向量求导:
\frac{d}{dx}(x^{T}Ax) = (A+A^{T})x
其中,A是一个矩阵,x是一个列向量。
4. 向量对矩阵求导:
\frac{d}{dA}(x^{T}Ax) =
(x^{T}+x)(\frac{dA}{dA}+\frac{dA^{T}}{dA}) = 2x^{T}A
其中,A是一个矩阵,x是一个列向量。
5. 标量对矩阵求导:
\frac{d}{dA}(c^{T}Ax) = c^{T}x^{T}
其中,c是一个常数向量,A是一个矩阵,x是一个列向量。
6. 向量对向量求导(链式法则):
\frac{d}{dx}(f(g(x))) = (\frac{df}{dy})^{T}\frac{dg}{dx}
其中,f(\cdot)和g(\cdot)是两个函数,y=g(x),\frac{df}{dy}是
f(\cdot)对y的导数。
【知识相关】让向量、矩阵和张量的求导更简洁些吧

【知识相关】让向量、矩阵和张量的求导更简洁些吧本⽂是我在阅读Erik Learned-Miller的《Vector, Matrix, and Tensor Derivatives》时的记录,。
本⽂的主要内容是帮助你学习如何进⾏向量、矩阵以及⾼阶张量(三维及以上的数组)的求导。
并⼀步步引导你来进⾏向量、矩阵和张量的求导。
1 简化、简化,还是简化(重要的事情说三遍)在求解涉及到数组的导数时,⼤部分的困难是因为试图⼀次性做太多事情。
⽐如说同时求解多个组成部分的导数,在求和符号存在的情况下求解导数,或者使⽤链式法则。
在有丰富的求导经验之前,同时执⾏所有的这些操作,我们就很容易出错。
1.1 将矩阵计算分解为单个标量的计算为了简化给定的计算,我们将矩阵的求导分解为每个单独标量元素的表达式,每个表达式只包含标量变量。
在写出单个标量元素与其他标量值的表达式后,就可以使⽤微积分来计算。
这⽐同时进⾏矩阵的求和以及求导要容易⼀些。
(看起来有点晕,没关系,看后⾯的案例就清晰了)。
In order to simplify a given calculation, it is often useful to write out the explicit formula for a single scalar element of the output in terms of nothing but scalar variables. Once one has an explicit formula for a single scalar element of the output in terms of other scalar values, then one can use the calculus that you used as a beginner, which is much easier than trying to do matrix math, summations, and derivatives all at the same time.例如:假设我们有⼀个C阶列向量\overrightarrow{y},它是由C\times D维矩阵W和D阶列向量\overrightarrow{x}计算得到:\overrightarrow{y} = W\overrightarrow{x}\tag{1}假设我们计算\overrightarrow{y}关于\overrightarrow{x}的导数。
矩阵求导定义

矩阵求导定义矩阵求导定义矩阵求导是一种非常有用的数学工具,它可以帮助人们在各种数学问题中更加快速和方便地解决问题。
矩阵求导的定义可以简单地表示为:对于一个矩阵函数f(x),其导数矩阵df(x)/dx可以表示为:df(x)/dx = lim(h→0) [f(x+h)-f(x)]/h其中,x表示一个行向量,h表示一个标量,df(x)/dx是一个矩阵,f(x+h)和f(x)都是和x大小相同的矩阵。
矩阵求导的基本规则在矩阵求导的过程中,有一些基本规则需要遵守,这些规则包括:①线性性:若f(x)和g(x)是两个矩阵函数,a和b分别为标量,则有:d[a*f(x)+b*g(x)]/dx = a*df(x)/dx + b*dg(x)/dx②乘法规则:若f(x)和g(x)是两个矩阵函数,则有:d[f(x)*g(x)]/dx = df(x)/dx*g(x) + f(x)*dg(x)/dx③转置规则:若f(x)是一个矩阵函数,则有:d[f(x)']/dx = (df(x)/dx)'④逆矩阵规则:若f(x)是一个可逆的矩阵函数,则有:d[f(x)^-1]/dx = -f(x)^-1*(df(x)/dx)*f(x)^-1应用实例矩阵求导可以在各种数学问题中得到应用,以下是一些实例:1、矩阵优化问题:矩阵求导可以在矩阵优化问题中得到广泛应用,例如,在机器学习模型的训练过程中,使用梯度下降算法优化损失函数,需要对损失函数求导得到梯度。
2、协方差矩阵的求导:在数据分析领域中,协方差矩阵常常被用来描述不同变量之间的关系。
矩阵求导可以在计算协方差矩阵的导数时得到应用。
3、矩阵微积分学:矩阵微积分学是一门关于矩阵导数和积分的学科,矩阵求导是其中非常重要的一部分。
结语矩阵求导是一个非常有用的数学工具,它可以帮助人们在各种数学问题中更加快速和方便地解决问题。
在应用矩阵求导的过程中,需要遵守基本规则,同时还需要理解它的应用实例。
矩阵求导(本质、原理与推导)详解

矩阵求导(本质、原理与推导)详解1.引言矩阵求导是数学分析中重要的一部分,广泛应用于机器学习、数据挖掘和优化问题中。
本文将介绍矩阵求导的本质、原理以及推导过程,为读者提供一个比较全面的了解。
2.矩阵的本质及相关概念在矩阵求导前,我们需要先了解矩阵的本质及相关概念。
矩阵是一个按照规律排列的方阵,其中每个元素通常是实数或者复数。
以$n$行$m$列的矩阵$A$为例,可以表示为:$$A=\begin{bmatrix}a_{1,1}&a_{1,2}&\cdots&a_{1,m}\\a_{2,1}&a_{2,2}&\cdots&a_{2,m}\\\vdots&\vdots&\ddots&\vdots\\a_{n,1}&a_{n,2}&\cdots&a_{n,m}\\\end{bmatrix}$$其中$a_{i,j}$表示矩阵$A$中第$i$行第$j$列的元素。
矩阵还有一些相关的概念,如矩阵的转置、逆矩阵、伴随矩阵等等,这里不一一赘述。
3.标量函数对向量、矩阵的导数在开始矩阵求导之前,我们需要先了解标量函数对向量或矩阵的导数。
设矩阵$A$是一个$m\times n$的矩阵,$x$是一个$n \times1$的向量,函数$f(x)$将$x$映射为一个标量。
我们定义$f(x)$对$x$的导数为:$$\frac{\partial f(x)}{\partial x}=\begin{bmatrix}\frac{\partial f(x)}{\partial x_1}&\frac{\partial f(x)}{\partial x_2}&\cdots&\frac{\partial f(x)}{\partial x_n}\end{bmatrix}$$其中每一项$\frac{\partial f(x)}{\partial x_i}$表示$f(x)$对$x_i$的偏导数。
矩阵求导法则的解析与应用

矩阵求导法则的解析与应用矩阵求导法则是矩阵微积分中的基本概念,它在众多领域中都有广泛的应用,尤其是在优化算法、机器学习和信号处理等领域中。
本文将深入探讨矩阵求导法则的解析和应用,并分享对这一主题的观点和理解。
一、矩阵求导法则的基本概念1. 矩阵求导的定义和目的在矩阵微积分中,矩阵求导是指对矩阵中的每个元素进行求导运算。
其目的是为了描述矩阵变量函数在某一点的变化率,从而可以进一步分析函数在该点的性质和优化问题的解。
2. 矩阵对标量的导数当矩阵中的元素都是标量时,矩阵对标量的导数就是普通的微积分中的导数。
它遵循标量的求导法则,如常数因子法则、求和法则和链式法则等。
3. 矩阵对向量的导数当矩阵中的元素是向量时,矩阵对向量的导数运算更为复杂。
需要使用矩阵求导法则来进行推导和计算。
常见的矩阵求导法则包括向量对向量的导数、向量对标量的导数、标量对向量的导数等。
二、矩阵求导法则的应用1. 优化算法中的应用在优化算法中,矩阵求导法则被广泛应用于求解最优化问题。
梯度下降算法通过计算函数的梯度(即矩阵对向量的导数)来寻找函数的最小值。
矩阵求导法则为梯度下降算法提供了有效的计算方式,提高了算法的收敛速度和性能。
2. 机器学习中的应用在机器学习中,矩阵求导法则用于对损失函数进行求导,以便于参数的优化和模型的训练。
反向传播算法中就需要对损失函数对参数矩阵的导数进行计算和更新。
矩阵求导法则的正确应用可以简化计算过程,提高训练效率和模型的准确性。
3. 信号处理中的应用在信号处理领域,矩阵求导法则被广泛应用于信号的滤波和特征提取等任务中。
基于最小均方误差准则的线性滤波器设计中,需要对损失函数对滤波器系数矩阵的导数进行计算。
矩阵求导法则为滤波器设计提供了理论基础和数值计算方法。
三、个人观点和理解作为一名文章写手,在撰写这篇文章的过程中,我对矩阵求导法则的重要性有了更深入的认识和理解。
矩阵求导法则不仅对于理解优化算法、机器学习和信号处理等领域的核心概念至关重要,而且在实际应用中也发挥着重要的作用。
矩阵对向量求导

矩阵、向量求导法则(1)行向量对元素求导设 []n Ty y 1=y 是 n 维行向量,x 是元素,则⎥⎦⎤⎢⎣⎡∂∂∂∂=∂∂x y xy x n T1y 。
(2)列向量对元素求导设 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=m y y 1y 是 m 维列向量,x 是元素,则 ⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡∂∂∂∂=∂∂x y x y x m 1y 。
(3)矩阵对元素求导设 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=mn m n y y y y Y1111 是 n m ⨯ 矩阵,x 是元素,则 ⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡∂∂∂∂∂∂∂∂=∂∂x y xyx y xy x Y mn m n1111。
(4)元素对行向量求导 设 y 是元素,][1q Tx x =x 是 q 维行向量,则⎥⎥⎦⎤⎢⎢⎣⎡∂∂∂∂=∂∂q T x y x yy 1x 。
(5)元素对列向量求导设 y 是元素,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=p x x 1x 是 p 维列向量,则 ⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡∂∂∂∂=∂∂p x y x y y 1x。
(6)元素对矩阵求导设 y 是元素,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=pq p q y x x x X 1111 是 q p ⨯ 矩阵,则⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡∂∂∂∂∂∂∂∂=∂∂pq p q x y x yx y x yX y1111。
(7)行向量对列向量求导设 []n Ty y 1=y 是 n 维行向量,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=p x x 1x 是 p 维列向量,则⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡∂∂∂∂∂∂∂∂=∂∂p n pn Tx y x yx y x y1111x y。
(8)列向量对行向量求导设 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=m y y 1y 是 m 维列向量,][1q Tx x =x 是 q 维行向量,则⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡∂∂∂∂∂∂∂∂=∂∂q m mq Tx y x y x y x y1111x y 。
(9)行向量对行向量求导设 []n Ty y 1=y 是 n 维行向量,][1q T x x =x 是 q 维行向量,则⎥⎥⎦⎤⎢⎢⎣⎡∂∂∂∂=∂∂qTTTT x x y y x y1 。
矩阵微分法

矩阵微分法1向量的导数: 对于n 维向量函数12()()()()Tn t e t e t e t 轾=犏臌e L(1)其对t 的导数定义为:12()()()()Tn d e t d e t d e t d t d td t d td t轾犏=犏臌e L(2)矩阵导数: ()m nt ´ÎA ¡对t 的导数定义为:()()i j m nd a t d t d td t ´轾犏=犏犏臌A(3)因此易知: ()d d d d t d td t ?A B A B (4)()d d d d td td tl l l=+A A A(5)对于两向量相乘, 易知:11()()nnTTTi i i i i i i i d a d b d d d d a b b a d td td t d t d td t==骣÷ç÷==+=+ç÷ç÷ç桫邋a ba b b a(6)而对于矩阵相乘: Ti jn l´轾=犏臌A B a b (7)易知:()T j TTii jj in ln ld d dd d d d t d t d t d t d td t´´轾轾犏犏==+=+犏犏臌犏臌b a A B A B a b b a B A(8)应用: 关于函数T e M e 对t 的导数, 其中M 为对称阵:()()2TTTTTT T TT T d d dd td td td d d d t d t d t=+骣÷ç=++÷ç÷ç÷桫=++=+eeM eM e eM e e M e M e e e M eM e e M e e M e e M ee M e &&&&&(9)特别地, 当M 为常数阵时: ()2T Td d t=e M e e M e & (10)当=M I时:()22T T Td d t=e e e e =e e&& (11)(注意: 在其他定义的矩阵求导中, 求导后需对矩阵再作转置, 但实质还是一样的, 此处不考虑.)1胡寿松, 自动控制原理 第四版, 科学出版社, 2001. pp.610-611。
矩阵求导法则

矩阵求导法则矩阵求导法则矩阵求导是矩阵微积分的一个重要分支,它在机器学习、信号处理、控制理论等领域有着广泛的应用。
本文将介绍矩阵求导的基本概念、法则和应用。
一、基本概念1.1 矩阵矩阵是由数个数按一定规律排列成的矩形数组,通常用大写字母表示。
例如:A = [1, 2, 3; 4, 5, 6; 7, 8, 9]表示一个3行3列的矩阵,第一行为[1,2,3],第二行为[4,5,6],第三行为[7,8,9]。
1.2 向量向量是一种特殊的矩阵,只有一列或一行。
通常用小写字母表示。
例如:x = [1; 2; 3]表示一个3维列向量。
1.3 标量标量是指只有一个数的矩阵,通常用小写字母表示。
例如:a = 5表示一个标量。
二、基本法则2.1 标量对向量求导设f(x)为标量函数,x为n维列向量,则f(x)对x的导数定义为:∂f(x)/∂x = [∂f(x)/∂x1, ∂f(x)/∂x2, …, ∂f(x)/∂xn]其中,∂f(x)/∂xi表示对第i个自变量求偏导数。
例如,设f(x) = x1^2 + x2^3,则有:∂f(x)/∂x = [2x1; 3x2^2]2.2 向量对向量求导设F(x)为n维列向量函数,x为m维列向量,则F(x)对x的导数定义为:dF(x)/dx = [dF1/dx1, dF1/dx2, …, dF1/dxm;dF2/dx1, dF2/dx2, …, dF2/dxm;…dFn/dx1, dFn/dx2, …, dFn/dxm]其中,dFi/dxj表示第i个分量对第j个自变量的偏导数。
例如,设F(x) = [sin(x); cos(x)],则有:dF(x)/dx = [cos(x); -sin(x)]2.3 标量对矩阵求导设f(A)为标量函数,A为m行n列矩阵,则f(A)对A的导数定义为:df(A)/dA = [df(A)/dA11, df(A)/dA12, … , df(A)/dAnm;df(A)/dA21, df(A)/dA22, … , df(A)/dAnm;…df(A)/d Am1, df(A)/dAm2, … , df(A)/dAnm]其中,df(A)/dAij表示对A中第i行第j列元素的偏导数。
矩阵求导matrix+vector+derivatives+for+machine+learning

。用劈形算子表示时可记作
n
。
∈ R
注:如前所述,本教程仅仅是把变量都看成多个实数,无所谓行与列之分,因此在表述从向量 x
到f
∈ R
m
的雅
克比矩阵时,不区分 x 或者 f 到底是行向量还是列向量,统一用 ∇x f 表示,维度也都是 m-by-n。有些教程可能会区分 行对列、列对列、行对行、列对行几种不同情形的求导,认为有些结果相差一个转置,有些组合不能求导等等。本教程则 认为只有一种求导结果,就是雅克比矩阵。 有一点需要注意的是,若 f 退化成标量 f ,则 x 到 f 的雅克比矩阵
∇x F : R → R
′ m×n
,则∂ F /∂ x也是一个m × n维矩阵,且(∂ F /∂ x)ij
= ∂ f ij /∂ x
ห้องสมุดไป่ตู้
,也可用劈形算子将导数记作
m
,或记作 F x 。
: R → R
T
由于向量是矩阵的特殊情形,根据上面的定义也可以得到自变量为向量时的定义:若函数f 一个m维向量,且(∂ f /∂ x)i
∇ f
2
: R
m
→ R ∂
2
,其梯度记为 ∇f
∂f = ∂x
,也可记作gradf ,是一个 m 维向量。Hessian矩阵记为
f = ∂ f i /∂ x
,则∂ f /∂ x也是
T
。若函数值 f
T
是行向量则结果为行向量,可记作 ∇x f
或 ∂f
/∂ x
;若函数值
是列向量则求导结果为列向量,可记作 ∇x f 或 ∂ f /∂ x。
注:本文开头即说明过,变量为向量时仅仅是将其看作多个实数,无所谓行向量与列向量之分。这里用行向量或列向量的 说法仅仅为了把公式用矩阵相乘的方式表示出来方便,因为在数学公式总要指定向量是行向量或者列向量中的某一个,才 能与公式里的其他部分做矩阵运算时维度相容。下同。 实值函数对矩阵/向量的导数: 要点:求导结果与自变量同型,且每个元素就是f 对自变量的相应分量求导 若函数f
矩阵求导 维度

矩阵求导维度
矩阵求导是矩阵微积分学中的一个重要分支。
在求解矩阵导数时,维度是一个非常关键的概念。
矩阵的维度指的是该矩阵的行数和列数,通常用 m×n 表示。
在矩阵求导中,我们需要注意以下几个维度相关的概念:
1. 向量的维度:向量是一个只有一列的矩阵,其维度通常用 n
×1 表示,其中 n 表示向量的长度。
2. 矩阵的维度:矩阵的维度用 m×n 表示,其中 m 表示矩阵的行数,n 表示矩阵的列数。
3. 标量的维度:标量是一个只有一个元素的矩阵,其维度为 1
×1。
在进行矩阵求导时,我们需要根据维度的规律来进行计算。
具体来说,对于矩阵或向量中的每个元素,我们需要按照规则进行求导。
例如,若矩阵 A 的维度为 m×n,则对于其中的每个元素 a_ij,我
们需要分别求出其偏导数 a_ij/x,其中 x 表示自变量。
最终得到的结果将形成一个和矩阵 A 维度相同的导数矩阵。
总之,维度是矩阵求导中的一个重要概念,对于正确求解导数具有至关重要的作用。
- 1 -。
向量求导法则

向量求导法则向量求导法则是一种有效的用于求解向量函数极值问题的方法,也是研究向量和矩阵相关知识的重要基础。
它能够有效地简化求解复杂问题所需的复杂计算,是数学建模以及工程应用中的重要工具。
本文主要介绍向量求导法则的概念和求解方法,并结合计算机程序的实例进行详细的阐述。
2.量求导法则的概念向量求导法则是由微分学中的泰勒展开引入的,它给出了一种有效的求解向量函数极值的方法,与微分学中的求解函数极值方法相似。
向量求导法则可以将一个向量函数的极值问题转换为一个实参矩阵最大特征值问题,且该实参矩阵亦可根据向量函数的表达式来计算得出。
向量求导法则的重要性在于可以根据向量函数表达式,得出一个实参矩阵,再根据该矩阵的特征值求出极大值的参数。
3.量求导法则的求解方法(1)假设向量求导问题为:求向量函数:$f(x) = left[ begin{array}{c}f_1(x)f_2(x)vdotsf_n(x)end{array} right]$(2)求该函数f(x)在x处的梯度向量$abla f(x) = left[ begin{array}{c}frac{partial f_1(x)}{partial x_1} & frac{partialf_1(x)}{partial x_2} & cdots & frac{partial f_1(x)}{partial x_n}frac{partial f_2(x)}{partial x_1} & frac{partialf_2(x)}{partial x_2} & cdots & frac{partial f_2(x)}{partial x_n}vdots & vdots & ddots & vdotsfrac{partial f_n(x)}{partial x_1} & frac{partialf_n(x)}{partial x_2} & cdots & frac{partial f_n(x)}{partial x_n}end{array} right]$(3)计算梯度向量的矩阵表达式:$H(x) = left[ begin{array}{cccc}frac{partial^2 f_1}{partial x_1^2} & frac{partial^2f_1}{partial x_1 partial x_2} & cdots & frac{partial^2f_1}{partial x_1 partial x_n}frac{partial^2 f_2}{partial x_1 partial x_1} &frac{partial^2 f_2}{partial x_1 partial x_2} & cdots &frac{partial^2 f_2}{partial x_1 partial x_n}vdots & vdots & ddots & vdotsfrac{partial^2 f_n}{partial x_1 partial x_1} &frac{partial^2 f_n}{partial x_1 partial x_2} & cdots &frac{partial^2 f_n}{partial x_1 partial x_n}end{array} right]$(4)用实参矩阵求解向量函数f(x)的极值问题:将H(x)作为实参矩阵,令Δx = -H(x)G(x),其中G(x) =f(x)/δx,δf(x)表示函数f(x)的偏导数,δx表示参数x的增量。
[全]矩阵求导matrix calculus
![[全]矩阵求导matrix calculus](https://img.taocdn.com/s3/m/a5d8087c1a37f111f0855b7c.png)
矩阵求导matrix calculus
这是机器学习中常用的矩阵求导类型,向量对标量,向量对向量,矩阵对标量的求导还是容易记忆的,在分子布局的情况下,和常见的函数求导公式是类似,如下面三张图所示。
分母布局一般是分子布局的转置(但不全是)
我这里主要想讲一下标量对标量/向量/矩阵的求导。
矩阵求导是不满足链式法则的,但微分的定义仍然是有用的,我们利用微分和求导的关系,可以构建下面的关系式(注:下面全是针对分子布局来说的)
看不懂?没关系,我们举个例子,对下面的表达式求导,a,b,C都与X无关,C,X表示矩阵,a,b表示向量。
注意到这里的分子部分f是个标量
标量的迹就是它本身,微分号可以提出来:
这里列举了一些迹的相关性质,最后一条比较重要需要用到:
f太复杂了,我们要化简,利用矩阵微分的相关性质
我们利用矩阵微分的乘法性质将其分为了两部分:
接下来应该干什么呢?回到我们的关系式
我们的目标就很明确了,就是要将微分部分dX移到最后一位,这样前面的系数就是我们要求的导数了!
令Y=Xa+b,我们还要将dY表示成dX,同样利用乘法性质
这样上式表示为:
这样导数就是其系数
和wiki matrix calculus上分子布局求导结果是一致的,分母布局就是转置一下
总的来说只要分子是个标量,那么操作是类似的,无论分母是向量还是矩阵。
向量矩阵求导

矩阵Y对标量x求导:相当于每个元素求导数后转置一下,注意M×N矩阵求导后变成N×M 了Y = [y(ij)] --> dY/dx = [dy(ji)/dx]2. 标量y对列向量X求导:注意与上面不同,这次括号内是求偏导,不转置,对N×1向量求导后还是N×1向量y = f(x1,x2,..,xn) --> dy/dX = (Dy/Dx1,Dy/Dx2,..,Dy/Dxn)'3. 行向量Y'对列向量X求导:注意1×M向量对N×1向量求导后是N×M矩阵。
将Y的每一列对X求偏导,将各列构成一个矩阵。
重要结论:dX'/dX = Id(AX)'/dX = A'4. 列向量Y对行向量X’求导:转化为行向量Y’对列向量X的导数,然后转置。
注意M×1向量对1×N向量求导结果为M×N矩阵。
dY/dX' = (dY'/dX)'5. 向量积对列向量X求导运算法则:注意与标量求导有点不同。
d(UV')/dX = (dU/dX)V' + U(dV'/dX)d(U'V)/dX = (dU'/dX)V + (dV'/dX)U'重要结论:d(X'A)/dX = (dX'/dX)A + (dA/dX)X' = IA + 0X' = A d(AX)/dX' = (d(X'A')/dX)' = (A')' = Ad(X'AX)/dX = (dX'/dX)AX + (d(AX)'/dX)X = AX + A'X6. 矩阵Y对列向量X求导:将Y对X的每一个分量求偏导,构成一个超向量。
注意该向量的每一个元素都是一个矩阵。
矩阵、向量求导法则
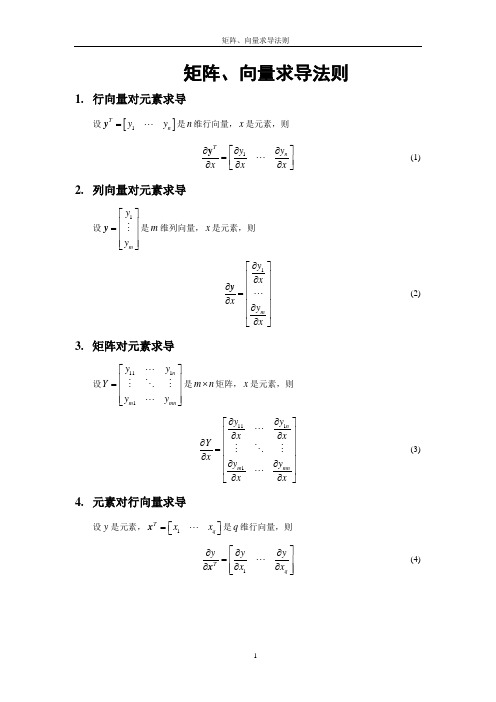
∂yT ∂yT ∂x ∂x1q 11 T ∂y = ∂X T ∂yT ∂y ∂x ∂x pq p1
(13)
14. 列向量对矩阵求导
x11 x1q y1 设 y = 是 m 维列向量, X = 是 p × q 矩阵,则 x p1 x pq ym
矩阵、向量求导法则
矩阵、向量求导法则
1. 行向量对元素求导
设 y = [ y1
T
yn ] 是 n 维行向量, x 是元素,则
∂yn ∂y T ∂y1 = ∂x ∂∂x
(1)
2. 列向量对元素求导
y1 设 y = 是 m 维列向量, x 是元素,则 ym
∂y1 ∂x ∂y = ∂x ∂y m ∂x
(2)
3. 矩阵对元素求导
y11 y1n 设Y = 是 m × n 矩阵, x 是元素,则 ym1 ymn
∂y1n ∂y11 ∂x ∂x ∂Y = ∂x ∂y ∂ymn m1 ∂x ∂x
∂y1 ∂x ∂y = ∂x ∂y m ∂x
(10)
11. 矩阵对行向量求导
y11 y1n T 设Y = 是 m × n 矩阵, x = x1 xq 是 q 维行向量,则 ym1 ymn
∂Y ∂Y ∂Y = T ∂x ∂xq ∂x1
(11)
12. 矩阵对列向量求导
x1 y11 y1n 是 m × n 矩阵, x = 是 p 维列向量,则 设Y = xp ym1 ymn
矩阵求导(工具书)

矩阵求导(⼯具书)⼀、基本概念与性质记号规范请参考:1. 迹对称矩阵\(A\)的迹定义为:\[Tr(A) = \sum_{i=1}^nA_i^i \tag{1.1} \]2. 迹的运算(1)\[Tr(A) = \sum_{i=1}^n\lambda_{i} \tag{1.2.1} \]其中\(\lambda_i\)为矩阵\(A\)的第\(i\)个特征值(2)\[Tr(A) = Tr(A^T) \tag{1.2.2} \](3)\[Tr(AB) = \sum_{i=1}^n\left(\sum_{j=1}^nA_i^jB_j^i\right) = \sum_{j=1}^n\left(\sum_{i=1}^nB_j^iA_i^j\right) = Tr(BA) \tag{1.2.3} \] (4)\[Tr(A + B) = Tr(A) + Tr(B) \tag{1.2.4} \](5)\[Tr(\mathbf{x}\mathbf{x}^T) = \sum_{i=1}^n\mathbf{x}_i\cdot \mathbf{x}_i = \mathbf{x}^T\mathbf{x} \tag{1.2.5} \]3. ⾏列式对称矩阵\(A\)的⾏列式定义为:\[\det (A) = \sum_{\sigma \in S_n}(-1)^{\mathrm{sgn}(\sigma)}\prod_{i=1}^n A_i^{\sigma(i)} \tag{1.3.1} \]其中\(S_n\)是集合\(\{1, 2, \cdots, n\}\)上置换的全体,即集合\(\{1, 2, \cdots, n\}\)到⾃⾝的⼀⼀映射(双射)的全体;例如:\(\{2, 3, 1\}\)是\(\{1, 3, 2\}\)的置换,且满⾜\(\sigma(1) = 2, \sigma(2) = 3, \sigma(3) = 1\)其中\({\rm sgn} (\sigma)\)表⽰的是置换\(\sigma\)中逆序对(即\(\sigma(i) > \sigma(j),1 \leq i \leq j \leq n\))的数量;例如:\({\rm sgn}(\{2, 3, 1\}) = 2\)对于有\(n\)个元素的集合⽽⾔,其置换的个数有\(n!\)个4. ⾏列式的计算(1)\[\det (A) = \prod_{i=1}^n \lambda_i \tag{1.4.1} \]其中\(S_n\)是集合\(\{1, 2, \cdots, n\}\)上置换的全体,即集合\(\{1, 2, \cdots, n\}\)到⾃⾝的⼀⼀映射(双射)的全体;(2)\[\det(A) \overset{按⾏展开}{=} \sum_{j=1}^n(-1)^{i + j}A_i^{j}\det\left([A]_i^{j}\right) \overset{按列展开}{=} \sum_{i=1}^n(-1)^{i + j}A_i^{j}\det\left([A]_i^{j}\right) \tag{1.3.2} \](3)\[\det(kA) = k^n\det(A) \tag{1.3.3} \](4)\[\det(A^T) = \det(A) \tag{1.3.4} \](5)\[\det(AB) = \det(A)\det(B) \tag{1.3.5} \](6)\[\det(A^{-1}) = \frac{1}{\det(A)} \tag{1.3.6} \](7)\[\begin{align} \det(I + \mathbf{u} \mathbf{v}^T) &= 1 + \mathbf{u}^T\mathbf{v} \tag{1.3.7} \end{align} \](8)\[\mathrm{adj}(A) = \det(A)\cdot A^{-1} \tag{1.3.8} \]⼆、向量与矩阵的运算结论1. 矩阵相乘(1)\[\begin{align} A\cdot B &= \left((AB)_i^j\right)_{m\times n} \\ &= \left(\sum_k A_i^kB_k^j\right)_{m\times n} \end{align} \tag{2.1.1} \] (2)\[\begin{align} (A\cdot B)\cdot C &= \left(\sum_k(AB)_i^kC_k^j\right)_{m\times n}\\ &= \left(\sum_k\left(\sum_tA_i^tB_t^k\right)C_k^j \right)_{m\times n} \end{align} \tag{2.1.2} \](3)\[A\cdot [E_i^j] = \left(0, \cdots \underbrace{A^i}_{第j列},\cdots ,0 \right) \tag{2.1.3} = [A^i]^j \](4)\[[E_i^j]\cdot A = \left(\begin{array}{cc} &0\\ &\vdots\\ 第i⾏\left\{\right. &A_j\\ &\vdots \\ &0 \end{array} \right) = [A_j]_i \tag{2.1.4} \]三、向量、矩阵求导1. 求导布局分⼦布局:求导结果的第⼀维度以分⼦为主分母布局:求导结果的第⼀维度以分母为主例如:\(m\)维列向量\(\mathbf{y}\)对于\(\mathbf{x}\)求导,若分⼦布局(雅可⽐矩阵):\[\frac{\partial \mathbf{y}}{\partial \mathbf{x}} = \left( \begin{matrix} \frac{\partial\mathbf{y}_1}{\partial\mathbf{x}_1} &\cdots&\frac{\partial\mathbf{y}_1}{\partial\mathbf{x}_n} \\ \vdots&\ddots &\vdots \\ \frac{\partial\mathbf{y}_m}{\partial\mathbf{x}_1} &\cdots &\frac{\partial\mathbf{y}_m}{\partial\mathbf{x}_n} \end{matrix} \right) \\ \]分母布局(梯度矩阵):\[\frac{\partial \mathbf{y}}{\partial \mathbf{x}} = \left( \begin{matrix} \frac{\partial\mathbf{y}_1}{\partial\mathbf{x}_1} &\cdots&\frac{\partial\mathbf{y}_m}{\partial\mathbf{x}_1} \\ \vdots &\ddots &\vdots \\ \frac{\partial\mathbf{y}_1}{\partial\mathbf{x}_n} &\cdots &\frac{\partial\mathbf{y}_m}{\partial\mathbf{x}_n} \end{matrix} \right) \\ \]注:以下所有求导结果均以分⼦布局为基础(若分⼦为标量,则为分母布局)2. 求偏微分法则\[\partial C = 0 (C为常(矩阵、向量、标量)) \tag{3.2.1} \]\[\partial A^T = (\partial A)^T \tag{3.2.2} \]\[\partial (A + B) = \partial A + \partial B \tag{3.2.3} \]\[\partial (AB) = \partial A\cdot B + A\cdot \partial B \tag{3.2.4} \]\[\partial (A\odot B) = \partial A\odot B + A\odot \partial B \tag{3.2.5} \]\[\partial( A\otimes B) = \partial A\otimes B +A\otimes \partial B \tag{3.2.6} \]\[\partial ({A^{-1}}) = -A^{-1}\cdot \partial A\cdot A^{-1} \tag{3.2.7} \]\[\partial\ Tr(A) = Tr(\partial A) \tag{3.2.8} \]\[\partial \mathrm{det}A = Tr(\mathrm{adj}A \cdot \partial A) = \mathrm{detA}\cdot Tr(A^{-1} \partial A) \tag{3.2.9} \]链式求导法则:\[\partial g\circ f(A) = \sum_k\sum_t \frac{\partial g\circ f(A)}{\partial f(A)_k^t}\cdot \partial f(A)_k^t = Tr\left(\left(\frac{\partial g\circ f(A)}{\partial f(A)}\right)^T\cdot \partial f(A)\right) \tag{3.2.10} \]3. 向量求导(1)\[\frac{\partial \mathbf{x}}{\partial x} = \left( \begin{array}{cc} \frac{\mathrm{d}\mathbf{x}_1}{\mathrm{d}x} \\ \vdots\\\frac{\mathrm{d}\mathbf{x}_m}{\mathrm{d}x} \end{array} \right) \tag{3.3.1} \](2)\[\frac{\partial \mathbf{x}^T}{\partial x} = \left(\frac{\partial \mathbf{x}}{\partial x}\right)^T \tag{3.3.2} \](3)\[\frac{\partial \mathbf{y}}{\partial \mathbf{x}} = \frac{\partial \mathbf{y}}{\partial \mathbf{x^T}} = \left( \begin{matrix} \frac{\partial\mathbf{y}_1} {\partial\mathbf{x}_1} &\cdots &\frac{\partial\mathbf{y}_1}{\partial\mathbf{x}_n} \\ \vdots &\ddots &\vdots \\ \frac{\partial\mathbf{y}_m}{\partial\mathbf{x}_1} &\cdots &\frac{\partial\mathbf{y}_m}{\partial\mathbf{x}_n} \end{matrix} \right) \tag{3.3.3}\](4)\[\frac{\partial \mathbf{y}^T}{\partial \mathbf{x}} =\frac{\partial \mathbf{y}^T}{\partial \mathbf{x}^T} = \left( \frac{\partial \mathbf{y}}{\partial\mathbf{x}} \right)^T \tag{3.3.4} \](5)\[\frac{\partial \mathbf{x}^T\mathbf{y}}{\partial\mathbf{x}} = \left(\begin{array}{cc} \mathbf{y}_1 \\ \vdots \\ \mathbf{y}_n \end{array} \right) =\mathbf{y} \tag{3.3.5} \](6)\[\frac{\partial \mathbf{x}^T\mathbf{y}}{\partial \mathbf{x}^T} = \left( \frac{\partial \mathbf{x}^T\mathbf{y}}{\partial \mathbf{x}} \right)^T \tag{3.3.6} \](7)\[\frac{\partial A\mathbf{x}}{\partial\mathbf{x}} = \frac{\partial A\mathbf{x}}{\partial\mathbf{x}^T} = \left( \begin{array}{cc} A_{1}^1 &\cdots&A_{1}^m \\ \vdots & \ddots &\vdots \\ A_{n}^1 &\cdots &A_{n}^m \\ \end{array} \right) = A \tag{3.3.7}\](8)\[\frac{\partial \mathbf{x}^TA\mathbf{x}}{\partial \mathbf{x}} = \frac{\partial \mathbf{x}^TA\mathbf{x}}{\partial \mathbf{x}^T} = (A +A^T)\mathbf{x} \tag{3.3.8} \]4. 矩阵求导(1)\[\frac{\partial \mathbf{x}^TA\mathbf{y}}{\partial A} = \mathbf{x}\mathbf{y}^T \tag{3.4.1} \](2)\[\frac{\partial \mathbf{x}^TA^T\mathbf{y}}{\partial A} = \mathbf{y}\mathbf{x}^T \tag{3.4.2} \](3)\[\frac{\partial \mathbf{x}^TA^TA\mathbf{y}}{\partial A} = A(\mathbf{y}\mathbf{x}^T + \mathbf{x}\mathbf{y}^T ) \tag{3.4.3} \]展开证明(4)\[\frac{\partial A^TBA}{\partial B_{i}^{j}} = A_i^TA_j \tag{3.4.4} \]展开证明(5)\[\frac{\partial A^TBA}{\partial A_{i}^j} = [E_j^i]\cdot (BA) + (A^TB)\cdot [E_i^j] \tag{3.4.5} \]展开证明可简记为:\(\frac{\partial A^TBA}{\partial A_i^j} = \frac{\partial A^T}{\partial A_i^j}\cdot BA + A^TB\cdot \frac{\partial A}{\partial A_i^j}\) (6)\[\frac{\partial \mathbf{y}^TA^TBA\mathbf{z}}{\partial A} = B^TA\mathbf{y}\mathbf{z}^T + BA\mathbf{z}\mathbf{y}^T \tag{3.4.6} \]展开证明(7)\[\frac{\partial }{\partial A}(A\mathbf{x} + \mathbf{y})^TD(A\mathbf{x} + \mathbf{y}) = (D + D^T)(A\mathbf{x} + \mathbf{y})\mathbf{x}^T \tag{3.4.7} \]展开证明5. ⾏列式求导(1)\[\frac{\partial \det(Y)}{\partial x} = \det(Y)\cdot Tr(Y^{-1}\frac{\partial Y}{\partial x}) \]展开证明(2)\[\frac{\partial \det(A)}{\partial A} = \det(A)\cdot \left(A^{-1}\right)^T \tag{3.5.2} \]展开证明(3)\[\frac{\partial \det(X^TAX)}{\partial X} = \det(X^TAX)\cdot\left(AX(X^TAX)^{-1} + A^TX(X^TA^TX)^{-1} \right) \tag{3.5.3} \]展开证明(4)\[\frac{\partial \ln \det(X^TX)}{\partial X}= 2(X^{L+})^T \tag{3.5.4} \]展开证明6. 矩阵逆的求导(1)\[\frac{\partial Y^{-1}}{\partial x} = -Y^{-1}\frac{\partial Y}{\partial x}Y^{-1} \tag{3.6.1} \]展开证明(2)\[\frac{\partial \mathbf{a}^TX^{-1}\mathbf{b}}{\partial X} = X^{-T}\mathbf{a}\mathbf{b}^TX^{-T} \tag{3.6.2} \]展开证明(3)\[\frac{\partial \det(X^{-1})}{\partial X} = \det(X^{-1})(X^{-1})^T \tag{3.6.3} \]展开证明(4)\[\frac{\partial Tr(AX^{-1}B)}{\partial X} = \left(X^{-1}BAX^{-1}\right)^{T} \tag{3.6.4} \]展开证明(5)\[\begin{align} \frac{\partial Tr\left((X+A)^{-1}\right) }{\partial X} &\overset{由3.6.4}{=}((X+A)^{-1}(X+A)^{-1})^T \end{align} \tag{3.6.5} \] 7. 迹的求导(1)\[\frac{\partial Tr(X)}{\partial X} = I \tag{3.7.1} \]展开证明(2)\[\frac{\partial Tr(XA)}{\partial X} = A^T \tag{3.7.2} \]展开证明(3)\[\frac{\partial Tr(AXB)}{\partial X} = A^TB^T \tag{3.7.3} \]展开证明(4)\[\frac{\partial Tr(A \otimes X)}{\partial X} = Tr(A)I \tag{3.7.4} \]展开证明。
