松弛迭代法
matlab逐次超松弛迭代法

matlab逐次超松弛迭代法
逐次超松弛迭代法(Gauss-Seidel迭代法)是一种用于解线性方程组的迭代方法,通常用于求解大型稀疏线性方程组。
在MATLAB 中,可以使用该方法来解决线性方程组的数值解。
首先,让我们来了解一下逐次超松弛迭代法的基本原理。
该方法是基于迭代的思想,通过不断迭代更新解向量的各个分量,直到满足一定的收敛条件为止。
具体步骤如下:
1. 首先,需要将线性方程组表示为矩阵形式 Ax = b,其中A 是系数矩阵,x是未知向量,b是常数向量。
2. 然后,将系数矩阵A分解为下三角矩阵L、对角矩阵D和上三角矩阵U,即A = L + D + U。
3. 接下来,可以根据逐次超松弛迭代法的迭代公式来更新解向量x的各个分量,直到满足一定的精度要求或者迭代次数达到指定的值为止。
在MATLAB中,可以通过编写相应的代码来实现逐次超松弛迭代
法。
具体步骤如下:
1. 首先,需要编写一个函数来实现逐次超松弛迭代法的迭代过程,可以使用for循环来进行迭代更新解向量的各个分量。
2. 其次,需要编写主程序来调用该函数,并传入系数矩阵A、常数向量b以及迭代的初始解向量作为输入参数。
3. 最后,可以设置迭代的终止条件,例如迭代次数的最大值或者解的精度要求,以及初始解向量的初值。
需要注意的是,在实际应用中,逐次超松弛迭代法的收敛性和稳定性需要进行分析和验证,以确保得到正确的数值解。
此外,还需要注意选择合适的松弛因子来加速收敛速度。
总的来说,逐次超松弛迭代法是一种常用的求解线性方程组的数值方法,在MATLAB中可以通过编写相应的代码来实现该方法,并得到线性方程组的数值解。
数值计算方法 松弛迭代法 - 松弛迭代法

n1
(k 1)
1
n2
(k 1)
2
b x
( k 1)
n,n1 n1
g n
x
(
0
)
( x1(0) ,
,
x(0) n
)T
,
xi
x (k1) i
x(k) i
xi
(bi
i 1
a x (k1) ij j
n
aij
xj(k) )
/
aii
x(k) i
ji
j i 1
i 1
n
(bi
aij
x (k1) j
aij
x
(k j
)
)
/
aii
.
(2.13)
代
j1
ji1
法
(2) 再由xi(k ) 与x~i(k1) 加权平均定义xi(k1) ,即
x(k1) i
(1 )xi(k)
x(k1) i
x(k) i
( xi(k1)
xi(k) )
(2.14)
将(2.13)代入(2.14)得到解 Ax b 的SOR迭代公式.
第 六
线性插方程值组的法迭代解法
章
主讲教师:刘春凤
1 迭代法原理
2 Jacobi迭代法 3 高斯-塞德尔迭代法 4 松弛迭代法
5 迭代法的收敛性与稳定 性
松弛法的基本思想 松弛法的矩阵表示 松弛法的程序 迭代法收敛性的其它判定方法
松弛法的基本思想
为Gauss-Seidel 迭代法加速
记:x x1 , x2 , , xn T x(k1) x(k)
松
可以把 x 看作Gauss-Seidel 迭代的修正项,即第k次
超松弛迭代法(SOR方法)

解:SOR迭代公式
x1( k
1)
(1 )x1(k )
4
(10 2x2(k )
4x3(k ) )
x
(k 2
1)
(1 )x2(k )
17
(3
2
x1(
k
1)
10x3(k ) )
x3( k
1)
(1 )x3(k )
9
(7 4x1(k 1)
10
x
(k 2
1)
)
初值 x (0) (0,0,0)T k = 0,1,2,…,
例该4方.4程用组S的OR精法确求解解线x (性*) 方 程(2组,1,1)T
如值只果需x(0取)迭ω取代(0=,04ω21,00x(=42)即1次T1xx,要11.高4便26达x斯11,可207到—xx要达22同4塞求到x样319德精0x精x3尔度130度迭要x,(3k7代求需1) 法要x)迭(和k) 代同1一1100初6次
数值计算方法
超松弛迭代法(SOR方法) 使用迭代法的困难在于难以估计其计算
量。有时迭代过程虽然收敛,但由于收敛速 度缓慢,使计算量变得很大而失去使用价值 。因此,迭代过程的加速具有重要意义。逐 次超松弛迭代(Successive Over relaxatic Method,简称SOR方法)法,可以看作是带参 数的高斯—塞德尔迭代法,实质上是高斯-塞 德尔迭代的一种加速方法。
或 Dx(k1) (1)Dx(k) (b Lx(k1) Ux(k) )
故 (D L)x(k1) (1)D Ux(k) b
显然对任何一个ω值,(D+ωL)非奇异,(因为假设 aii 0,i 1,2,, n )于是超松弛迭代公式为
x(k1) (D L)1 (1)D U x(k) (D L)1b
松弛迭代法

松弛迭代法
拉格朗日松弛迭代法(Rayleigh-Ritz Relaxation Method,简称 RRR 法)也称为牛顿松弛迭代法,它结合了牛顿法和松弛迭代法的理论思想,是一种求解常微分方程组的迭代法。
该法引入拉格朗日函数作为迭代的手段,是一种改进的迭代法。
拉格朗日松弛迭代法的基本思想是:针对解决系统方程中的迭代过程,可以将周期性求解出的解表达成一个拉格朗日函数,然后计算最优解以期达到更快的收敛。
具体工作步骤如下:
第一步:初始化变量和精度参数;
第二步:将各变量表示成Fourier级数;
第三步:任意给定初始值,用此为步进量,将目标函数拆分为拉格朗日函数,使得精度参数达到最优值;
第四步:将此值作为步长,依次求解各个变量;
第五步:在迭代过程中,改变步长,即可更新函数值,达到最优解。
拉格朗日松弛迭代法基于牛顿法可以求解出一个准确的解,并以此作为步长,松弛系数以较小的步长,任意的改变步长,不断的拉格朗日函数更新,然后求解最优解,使得整个迭代过程逐渐收敛,同时也充分考虑了步长的变化,可以研究出解析解。
本方法既可以用于求解定常面上的静解又可以用于求解一定频率的动解,甚至于一般情况下的复杂系统,该法有着广泛的应用。
超松弛迭代法历史演变

超松弛迭代法历史演变超松弛迭代法(SOR)是一种用于线性方程组求解的数值方法。
它结合了松弛迭代法和高斯-赛德尔迭代法的优点,具有快速收敛和稳定性的特点。
本文将从超松弛迭代法的起源开始,详细阐述它的历史演变。
超松弛迭代法最早由美国数学家David M.Young于1950年提出。
当时,他受到高斯-赛德尔迭代法的启发,希望通过引入松弛参数来提高迭代的收敛速度。
这个想法是在每次迭代时,对于每个未知数,根据已知的值和方程组来更新它的值,而不是等到所有未知数都计算完毕再更新。
这样可以更快地逼近方程组的解。
然而,Young的初始提案并不是很成功。
他发现在一些情况下,超松弛迭代法的收敛速度并没有比传统的迭代法更快。
于是,他开始研究如何选择合适的松弛参数。
在他的研究中,他发现如果松弛参数大于1,超松弛迭代法的收敛速度会加快,而如果松弛参数小于1,收敛速度反而会变慢。
这一发现打开了超松弛迭代法的新局面。
在1960年代,科学家们开始对超松弛迭代法进行更深入的研究和改进。
他们发现,超松弛迭代法在对称正定矩阵的线性方程组求解中表现得尤为出色。
这是由于对称正定矩阵具有特殊的性质,可以使得超松弛迭代法更快地收敛。
为了进一步提高超松弛迭代法的收敛速度,研究人员开始探索如何自适应地选择松弛参数。
他们发现,选择合适的松弛参数可以使得超松弛迭代法在不同情况下都表现得更好。
于是,一些自适应超松弛迭代法被提出。
在20世纪80年代和90年代,随着计算机技术的快速发展,科学家们开始使用超松弛迭代法来解决更大规模的线性方程组。
他们发现,超松弛迭代法可以通过并行计算的方式,进一步提高求解效率。
这为超松弛迭代法的应用提供了更广阔的空间。
随着时间的推移,超松弛迭代法在求解线性方程组中的应用越来越广泛。
它被广泛应用于科学计算、工程建模、优化问题等领域。
许多数值计算软件和库都提供了超松弛迭代法的实现,使得使用者可以方便地应用该方法。
尽管超松弛迭代法在求解线性方程组中表现出色,但它也有一些局限性。
关于逐次超松弛迭代法(SOR方法)的教学

关于“逐次超松弛迭代法(SOR 方法)”的教学一、SOR 迭代公式逐次超松弛(Successive Over Relaxation)迭代法,简称SOR 方法,它是在GS 法基础上为提高收敛速度,采用加权平均而得到的新算法,设求解线性代数方程组b Ax =的GS 法记为(1)再由与加权平均得这里ω>0称为松弛参数,将(1)代入则得(2)称为SOR 迭代法,ω>0称为松弛因子,当ω=1时,(2)即为GS 法,将(2)写成矩阵形式则得即,于是得SOR 迭代的矩阵表示(3)其中(4)亦可作矩阵分解ωωN M A -=,其中有.从而SOR 迭代矩阵 ωωωN M G 1-=. 例1 给定方程组精确解,用SOR法求解,分别取ω=1及ω=125.解用SOR迭代公式(2)可得取,迭代7次后分别为若要精确到小数后7位,对ω=1(即GS法)需迭代34次,而对ω=1.25的SOR法,只需迭代14次.它表明松弛因子ω选择的好坏,对收敛速度影响很大。
二、SOR迭代法收敛性根据迭代法收敛性定理,SOR法收敛的充分必要条件为,收敛的充分条件为,但要计算比较复杂,通常都不用此结论,而直接根据方程组的系数矩阵A 判断SOR迭代收敛性,下面先给出收敛必要条件定理1设,则解方程的SOR迭代法收敛的必要条件是0<ω<2.证明因为SOR迭代矩阵为,于是另一方面,设的特征值为,由特征根性质,有若SOR法收敛,则,由,则得0<ω<2.定理2若对称正定,且0<ω<2,则解Ax=b的SOR迭代法(3)对迭代收敛。
证明设的特征值为(可能是复数),对应特征向量x≠0, 由(4)得因为实对称矩阵,故, 上式两边与x作内积,得(5)因A正定,故D也正定,记.又记,,由内积性质得于是由(5)有由于A正定及0<ω<2,故,于是。
注一:当ω=1时SOR法即为GS法,故GS法也收敛,此即为GS法的收敛定理结论。
对于SOR迭代法,松弛因子的选择对收敛速度影响较大,关于最优松弛因子研究较为复杂,且已有不少理论结果。
matlab超松弛迭代法求方程组

一、介绍MATLAB(Matrix Laboratory)是一种用于数值计算和数据可视化的专业软件。
在MATLAB中,超松弛迭代法是解决线性方程组的一种有效算法。
本文将介绍MATLAB中超松弛迭代法的基本原理和实现方法,并给出一个具体的例子进行演示。
二、超松弛迭代法的基本原理超松弛迭代法是一种逐步迭代的算法,用于求解线性方程组。
它的基本原理是通过不断迭代更新方程组的解,直到达到满足精度要求的解。
超松弛迭代法的公式如下:X(k+1) = (1-w)X(k) + w*(D-L)⁻¹*(b+U*X(k))其中,X(k)代表第k次迭代的解向量,X(k+1)代表第k+1次迭代的解向量,D、L和U分别代表方程组的对角线元素、下三角元素和上三角元素构成的矩阵,b代表方程组的右端向量,w代表松弛因子。
超松弛迭代法的关键在于选择合适的松弛因子w,一般情况下,可以通过试验选取一个合适的值。
在MATLAB中,可以使用sor函数来实现超松弛迭代法。
三、MATLAB中超松弛迭代法的实现方法在MATLAB中,可以通过调用sor函数来实现超松弛迭代法。
sor 函数的语法格式如下:[X,flag,relres,iter,resvec] = sor(A,b,w,tol,maxit)其中,A代表线性方程组的系数矩阵,b代表右端向量,w代表松弛因子,tol代表迭代的精度要求,maxit代表最大迭代次数,X代表迭代求解得到的解向量,flag代表迭代的结果标志,relres代表相对残差的大小,iter代表迭代次数,resvec代表迭代过程中的残差向量。
以下是一个使用sor函数求解线性方程组的示例:A = [4 -1 0 -1 0 0; -1 4 -1 0 -1 0; 0 -1 4 0 0 -1; -1 0 0 4 -1 0; 0 -1 0 -1 4 -1; 0 0 -1 0 -1 4];b = [1; 0; -1; 0; 1; 0];w = 1.25;tol = 1e-6;maxit = 100;[X,flag,relres,iter,resvec] = sor(A,b,w,tol,maxit);通过调用sor函数,可以得到方程组的解向量X,迭代的结果标志flag,相对残余resrel和迭代次数iter。
松弛迭代法解线性方程组

---------------------------------------------------------------最新资料推荐------------------------------------------------------松弛迭代法解线性方程组计算方法第八章上机作业沈欢北京大学工学院,北京100871 2012-05-011问题描述编制松弛法求解线性方程组的程序:分别取松弛因子ω =0, 0.1, 0.2,…2.0(间隔为0.1),求解线性方程组Ax = b ,其中 ? ? 1 1 1 1 1 2 3 4 5 ? 1 1 1 1 1 ? ? 2 3 4 5 6 ? ?1 1 1 1 1 ? ? A=? ? 3 4 5 6 7 ? ? 1 1 1 1 1 ? ? 4 5 6 7 8 ?1 5 1 6 1 7 1 8 1 9(1)? ? ? ? b=? ? ? ?1 0 0 0 0? ? ? ? ? ? ? ?(2)→ → 要求精度为 ? x ?? x ? < 10?4 (1) 经过计算判断对那些ω 迭代收敛? (2) 记下迭代次数,据此判断对哪个ω 迭代收敛最快。
2SOR方法描述? → → → → x k+1 = ωL? x k+1 + [(1 ? ω )I + ωU ]? x k + ω? g松弛法迭代的矩阵形式为: (3)其中,常数ω 称为松弛因子。
ω < 1称为低松弛或亚松弛法。
ω > 1称为超松弛法,ω = 1时为Seidal迭代法。
收敛最快的松弛因子称为最优松弛因子,一般要由经验或通过试算来确定。
选取适当的松弛因子,SOR迭代要比Jacobi 迭代或Seidal迭代快很多。
11/ 8在编制计算机程序的过程中使用分量形式进行迭代:i?1 +1 xk = i j =1(?ω ?aij k+1 aij k bi (?ω ? )xj + (1 ? ω )xk )xj + ω ?i + aii aii aii j =i+1n(4)其中,i=1,2,.....,n。
逐次超松弛迭代法 matlab

逐次超松弛迭代法matlab什么是逐次超松弛迭代法?逐次超松弛迭代法(简称SOR)是一种用于数值解线性代数方程组的迭代方法。
它是对高斯-赛德尔迭代法的一种改进方法,能够加快迭代速度并增加收敛稳定性。
SOR迭代法的基本原理是在每一步迭代中引入一个超松弛因子,在更新解向量的同时,利用当前和先前的解向量信息,进行更快的收敛。
在MATLAB中,可以使用SOR迭代法来求解线性代数方程组。
在具体应用时,需要提供方程组的系数矩阵以及右侧的常数向量。
而在SOR迭代法中,还需要指定迭代的初始解向量、超松弛因子以及迭代的最大次数等参数。
首先,我们需要定义一个方程组的系数矩阵A和常数向量b。
在MATLAB 中,可以使用矩阵表示法来定义A和b。
例如,假设我们有一个3x3的方程组,可以使用以下代码来定义A和b:A = [2, -1, 0; -1, 2, -1; 0, -1, 2];b = [1; 2; 3];接下来,我们需要初始化一些迭代的参数,包括初始解向量x0、超松弛因子omega和迭代的最大次数max_iter。
其中,初始解向量x0可以选择一个任意的值,omega一般取值在0和2之间,max_iter可以根据需要设定一个足够大的值。
x0 = [0; 0; 0];omega = 1.2;max_iter = 100;然后,我们可以开始使用SOR迭代法来求解方程组。
在每一步迭代中,我们需要根据上一步的解向量计算当前的解向量,直到达到指定的迭代次数或者满足收敛条件为止。
x = x0;for k = 1:max_iterfor i = 1:length(b)x(i) = (1 - omega) * x(i) + (omega / A(i, i)) * (b(i) - A(i, [1:i-1, i+1:end]) * x([1:i-1, i+1:end]));end判断迭代是否收敛if norm(A * x - b) < 1e-6break;endend在迭代过程中,我们可以添加一些判断条件来判断迭代是否收敛,例如当方程的残差(两侧误差)小于某个指定的阈值时,可以认为方程组已经解出。
matlab逐次超松弛迭代法

matlab逐次超松弛迭代法
逐次超松弛迭代法(Gauss-Seidel Overrelaxation Method)
是一种用于求解线性方程组的数值方法,常用于解决大型稀疏矩阵
的方程组。
在MATLAB中,可以通过编写逐次超松弛迭代法的代码来
实现该算法。
首先,让我们回顾一下逐次超松弛迭代法的基本原理。
该方法
是基于迭代的思想,通过不断迭代计算得到线性方程组的近似解。
在每一次迭代中,通过更新当前解向量的各个分量来逐步逼近方程
组的精确解。
逐次超松弛迭代法引入了松弛因子,可以加速收敛速度。
在MATLAB中,可以使用以下步骤来实现逐次超松弛迭代法:
1. 首先,编写一个函数来表示线性方程组的系数矩阵和右侧向量。
这个函数可以接受系数矩阵、右侧向量和当前解向量作为输入,并返回更新后的解向量。
2. 接下来,编写主程序来调用这个函数,并设置迭代的终止条件。
可以选择设置最大迭代次数或者设定一个收敛精度作为终止条
件。
3. 在主程序中,使用一个循环来进行迭代计算,直到满足设定的终止条件为止。
在每一次迭代中,调用上述编写的函数来更新解向量。
4. 最后,输出得到的近似解向量作为结果。
需要注意的是,逐次超松弛迭代法的收敛性与松弛因子的选择有关,通常需要根据具体的线性方程组进行调整。
总之,在MATLAB中实现逐次超松弛迭代法需要编写系数矩阵和右侧向量的函数以及主程序来进行迭代计算,并且需要注意收敛性和松弛因子的选择。
希望这个回答能够帮助你更好地理解和实现逐次超松弛迭代法。
第六章第三节逐次超松弛迭代法

xk T xk1 (I L)1 D 1b (3.4)
其中
Tw (I L)1 ((1 )I U ) (3.5)
它是 SOR 方法的迭代矩阵.特别,若取 1,则 T1 (I L)1U 是 Gauss-Seidel 迭代法的
迭代矩阵.
若将矩阵 A 分裂成
A 1 (D DL) 1 ((1 )D DU ), 0
现在,我们来讨论逐次超松弛迭代法的收敛性问题.
定理 1 设方程组 Ax b 的系数矩阵 A 的主对角元素 aij 0,i 1,, n ,则 SOR 方法 收敛的充分必要条件为
(T ) 1 其中 T 是 SOR 方法的迭代矩阵.
定理 2 设方程组 Ax b 的系数矩阵 A 的主对角元素 aij 0,i 1,, n ,则 SOR 方法 的迭代矩阵了。的谱半径大于等于 1 ,即
我们把(3.1)式中的中间 ~xi(k) 消去,则有
~xi(k)
aii
(bi
i 1
aij
x
(k j
)
j 1
n
aij
x
(k j
1)
)
(1
)
xi(
k
1)
i1
i 1,2,, n, k 1,2 (3.2)
上式的矩阵表示形式是
或者
xk (Lxk Ux k1 D 1b) (1 )xk1 (3.3)
x2(k )
x3(k ) )
k 1,2,
4
第4页,共42页。
取初始向量 x0 0,0,0,0T ,迭代六次得结果见表 6.1.
从表 6.1 得到 x6 x 1.022103
图表6.1
应用 SOR 方法(取 O=1.2)的迭代公式为
松弛迭代法

)
x(m) i
r (m1)
i
(i 1,2,, n)
其中,ri(m1)
1 aii
(bi
i 1
a x(m1) ij j
j 1
n j i
aij
x
(m) j
)(i
1,2,, n)
称为第m+1步第I个分量的修正量. 当迭代法收敛时
r (m1) i
0(i
1,2,, n)
在修正量前乘上一个参数,即
x ( m 1) i
xi( m )
r (m1) i
(i 1,2,, n)
这种求方程组近似解的方法称为松弛法,称为松弛因子. 当 1时,称为低松弛法,当 1时,就是赛德尔迭代法, 当 1时,称为超松弛法,简称为SOR.
在实际计算中,松弛法常采用以下形式:
令B (D L)1[(1 )D U ], g (D L)1b,则
x(m1) B x(m) g (m 0,1,2,)
三、松弛法算法
输入 方程组的阶数n, A的元素aij,1 i, j n;b的分量bi ,1 i n;
x(0)的分量x0i ,1 i n;允许误差;最大迭次次数N. 输出 近似解x1, x2,, xn或N次迭代后不收敛的信息 . 步骤
S13 对i 1,2,, n
置x0i xi S2 输出“N次迭代后不收敛”;停机.
作业:
教材P91 习题4
i 1
n
x(m1) i
(1 )xi(m)
(bi
a x(m1) ij j
aij
§3.3 超松弛迭代法

证明: 证明:省略
§3.3 超松弛迭代法
换个角度看Gauss - Seidel 方法: 方法: 换个角度看 i −1 n 1 ( k + 1) ( k + 1) xi [ bi − ∑ a ij x j = − ∑ a ij x (j k ) ] a ii j =1 j= i+1 ri( k + 1 ) ( k +1 ) (k ) = x i( k ) + 其中r 其中 i(k+1) = bi − ∑ a ij x j − ∑ a ij x j a ii j<i j≥i
x ( k +1) = (1 − ω ) x ( k ) + ω D −1 [− Lx ( k +1) − Ux ( k ) + b ]
x ( k +1) = ( D + ω L)−1[(1 − ω ) D − ω U ] x ( k ) + ( D + ω L)−1ω b
பைடு நூலகம்松弛迭代阵
Hω
f
定理3.3.1 (Kahan 必要条件)设 A 可逆,且 aii ≠ 0,则松 定理 必要条件) 可逆, ,
(k ) ( k +1 ) 相当于在 x i 的基础上加个余项生成 x i 。 的基础上加个余项 加个余项生成
下面令 x = x i( k ) 速收敛,这就是松弛法 称作松弛 松弛因子 速收敛,这就是松弛法 (或SOR法)。 ω称作松弛因子。 法
( k +1) i
+ 残余误差 ri( k 1 ),希望通过选取合适的 ω 来加 +ω a ii
松弛迭代法

松弛迭代法松弛迭代法是一种解决复杂优化问题的新方法,其主要思想是采用迭代松弛的方式来求解数学优化问题。
它可以用来解决各种非线性最优化问题,如:单纯形、线性规划、最小二乘法和二次规划等。
以下是松弛迭代法的相关算法介绍。
1.法介绍松弛迭代法是一种基于迭代松弛的数学优化方法,算法的基本步骤如下:(1)确定一个初始松弛参数,其形式为σ>0;(2)计算一个初始解Xo;(3)根据此初始解Xo,算对应的步长和梯度,令X1=Xo-*Grad(Xo);(4)重复步骤3,不断迭代,直至解变得满足优化算法的收敛条件为止;(5)输出最终的解X。
2. 优缺点松弛迭代法的优点是其高效收敛,算法简单易行,可以用来解决复杂优化问题,并且可以求得全局最优解。
另外,松弛迭代法的步长的选取简单,受到限制的条件较少,只需要给定一个初始松弛参数即可。
但是,松弛迭代法也有一定的缺点,比如:(1)算法只能求出局部最优解,不能保证全局最优解;(2)在求解复杂优化问题时,松弛参数的选取可能会影响算法的收敛性;(3)算法容易陷入局部最优解中,不能跳出局部最优解。
3.用实例松弛迭代法主要应用于复杂优化问题的求解,例如:(1)线性规划问题的求解:对于最简单的线性规划问题,给定n个未知变量,其目标函数可以表达为:min f(x)=cTx,松弛迭代法可以用来求解该问题;(2)最小二乘优化问题的求解:给定一组样本数据,其拟合模型可以表达为:min f(x)=∑||y-x||2,松弛迭代法可以用来求解该问题;(3)凸优化问题的求解:给定凸函数f(x),求解min f(x),松弛迭代法可以用来求解该问题。
4.论松弛迭代法是一种求解复杂优化问题的有效方法。
它的优点是算法简单易行,可以求得局部最优解,而且只需要给定一个初始松弛参数即可。
但它也有一定的缺点,比如不能保证全局最优解,受到步长选取影响,容易陷入局部最优解中,等等。
不过,由于松弛迭代法具有高效收敛性,可以用来求解线性规划、最小二乘法和二次规划等优化问题,它仍是一种有效的求解复杂优化问题的算法。
雅可比迭代法,高斯迭代法,松弛迭代法

10 1
10 2
5
同样取初始向量x(0)=(0,0,0)T, 计算结果为
k
x1(k)
0
0
x2(k) 0
x3(k) 0
‖x(k)-x*‖
1
1
1.4
0.78
1.026
0.4
2 1.0634 1.02048 0.987516 0.0634
3 0.9951044 0.99527568 1.00190686 0.0048956
0
若记 g ( b1 , b2 ,, bn )T ,则J迭代法可写成
a11 a22x(k+1a)=nnBx(k)+g
k=0,1,2,…
§3.2.2 高斯-赛德尔 (Gauss-Seidel) 迭代法
若在J迭代法中,充分利用新值, 则可以得到如下的迭
代公式
x1(
k
x1(
k
1)
a12 a11
x(k) 2
a13 a11
x(பைடு நூலகம்) 3
a1n a11
x(k) n
b1 a11
x
(k
2
1)
a21 a22
x(k) 1
a23 a22
x(k) 3
a2n a22
x(k) n
b2 a22
方程组的精确解为x*=(1,1,1)T.
解 J迭代法计算公式为
x (k 1) 1
3 10
x(k) 2
x 1 (k ) 10 3
超松弛迭代法matlab程序

超松弛迭代法matlab程序超松弛迭代法是一种解线性方程组的迭代方法,其主要思想是在松弛因子的基础上,加入一些超松弛因子,使得迭代更加快速和稳定。
本文将介绍超松弛迭代法的原理,并给出相应的matlab程序实现。
一、超松弛迭代法的原理超松弛迭代法是通过将松弛因子ω加上一个超松弛因子λ,来加速收敛的一种迭代方法。
具体来说,对于一个线性方程组Ax=b,我们可以将其表示为:Ax(k)=b其中,x(k)表示第k次迭代的解向量,A表示系数矩阵,b表示右侧向量。
在超松弛迭代法中,我们将x(k)表示为:x(k)=x(k-1)+ωλ(k-1)其中,λ(k-1)是超松弛因子,ω是松弛因子,x(k-1)是上一次迭代的解向量。
将其代入原方程组,得到:(A-ωD)x(k)=ω(D+L)x(k-1)+ωUx(k-1)+b其中,D表示A的主对角线元素组成的对角矩阵,L表示A的下三角矩阵,U表示A的上三角矩阵。
将其化简为:x(k)=D^-1[(1-ω)D+ωL]x(k-1)+ωD^-1b其中,D^-1表示D的逆矩阵。
该式子即为超松弛迭代法的迭代公式。
二、matlab程序实现下面给出超松弛迭代法的matlab程序实现。
假设我们要解如下线性方程组:3x1+0x2+0x3=90x1+4x2+0x3=80x1+0x2+2x3=2其系数矩阵为:A=[3,0,0;0,4,0;0,0,2];右侧向量为:b=[9;8;2];我们可以通过如下matlab程序实现超松弛迭代法:function [x,iter]=sor(A,b,omega,tol,maxit)% A:系数矩阵% b:右侧向量% omega:松弛因子% tol:容差% maxit:最大迭代次数% x:解向量% iter:迭代次数n=length(b); % 系数矩阵的阶数x=zeros(n,1); % 初始化解向量iter=0; % 初始化迭代次数while iter<maxit % 迭代次数未达到最大值xold=x; % 记录上一次迭代的解向量for i=1:n % 按行迭代sigma=0;for j=1:nif j~=isigma=sigma+A(i,j)*x(j);endendx(i)=(1-omega)*x(i)+omega*(b(i)-sigma)/A(i,i); % 更新解向量enditer=iter+1; % 迭代次数加1if norm(x-xold)<tol % 当解向量的变化小于容差时,认为已收敛break;endend调用该函数,求解上述线性方程组,可以使用如下代码:A=[3,0,0;0,4,0;0,0,2];b=[9;8;2];omega=1.5;tol=1e-6;maxit=1000;[x,iter]=sor(A,b,omega,tol,maxit);disp(x);其中,omega为松弛因子,tol为容差,maxit为最大迭代次数。
对称超松弛迭代法 概述及解释说明

对称超松弛迭代法概述及解释说明1. 引言1.1 概述本篇文章旨在介绍对称超松弛迭代法的概述及解释说明。
对称超松弛迭代法是一种用于求解线性方程组的数值方法,它结合了迭代法和超松弛方法,能够在求解大型稀疏线性方程组时展现出良好的效果。
本文将从原理、算法流程以及应用和效果等方面进行详细说明,以帮助读者更好地理解该方法。
1.2 文章结构本文共分为四个部分:引言、对称超松弛迭代法概述、解释说明和结论。
在引言部分,我们将简要介绍本篇文章的主题和目的,并提供文章整体结构;在对称超松弛迭代法概述部分,我们将对迭代法、超松弛方法和对称超松弛迭代法进行逐一讲解;接着,在解释说明部分,我们将详细阐释该方法的原理,并提供算法流程说明,最后通过应用实例和效果分析来展示其实际应用价值;最后,在结论部分,我们将总结回顾全文内容,并展望未来对该领域的研究方向。
1.3 目的介绍对称超松弛迭代法的目的是为了提供一种有效求解线性方程组的数值方法,特别适用于复杂、大规模和稀疏问题。
本文旨在向读者介绍其背后的原理,阐明其算法流程,并通过实际应用和效果分析来证明其可行性和优越性。
最终目标是为读者提供一个全面而清晰的概述,帮助读者理解和运用对称超松弛迭代法解决实际问题。
2. 对称超松弛迭代法概述:2.1 迭代法简介:在数值分析和计算数学中,迭代法是一种通过从一个初始猜测值开始反复应用一个递归公式来逼近方程解的方法。
它广泛应用于线性方程组的求解问题。
不论是在工程领域还是科学研究中,线性方程组求解都是一个常见且重要的问题。
2.2 超松弛方法简介:超松弛方法(SOR)是迭代法中的一种技术,旨在加速收敛速度。
其核心思想是通过引入松弛因子来加快解的收敛过程。
对于每次迭代,在计算新解的分量时,超松弛方法允许我们使用之前已经更新但尚未完成全部迭代的分量进行估计。
该技术通常用于缩小残差并提高数值精度。
2.3 对称超松弛迭代法概述:对称超松弛(SSOR)迭代法结合了对称后退向前(SWEEP)和超松弛(SOR)的思想。
超松弛迭代法求解泊松方程
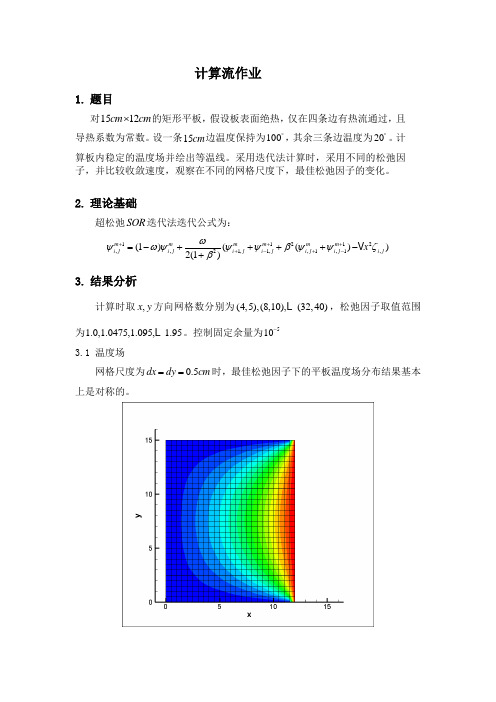
计算流作业1. 题目对1512cm cm ⨯的矩形平板,假设板表面绝热,仅在四条边有热流通过,且导热系数为常数。
设一条15cm 边温度保持为100︒,其余三条边温度为20︒。
计算板内稳定的温度场并绘出等温线。
采用迭代法计算时,采用不同的松弛因子,并比较收敛速度,观察在不同的网格尺度下,最佳松弛因子的变化。
2. 理论基础超松弛SOR 迭代法迭代公式为:11212,,1,1,,1,1,2(1)(())2(1)m m m m m m i j i j i j i j i j i j i j x ωψωψψψβψψζβ++++-+-=-++++-+3. 结果分析计算时取,x y 方向网格数分别为(4,5),(8,10),(32,40),松弛因子取值范围为1.0,1.0475,1.095, 1.95。
控制固定余量为510-3.1 温度场网格尺度为0.5dx dy cm ==时,最佳松弛因子下的平板温度场分布结果基本上是对称的。
3.2最佳松弛因子-网格尺度显然,随着网格尺度增加,最佳松弛因子逐渐减小,基本上呈现指数规律。
4.附件!初始温度分布subroutine initial(tt_in,nx_in,ny_in)implicit noneinteger::i,jinteger,intent(in)::nx_in,ny_in !横纵网格数real(kind=8),dimension(0:nx_in,0:ny_in)::tt_in !温度矩阵tt_in=0.tt_in(0,0:ny_in)=20.tt_in(nx_in,0:ny_in)=100.tt_in(1:(nx_in-1),0)=20.tt_in(1:(nx_in-1),ny_in)=20.do i=1,nx_in-1do j=1,ny_in-1tt_in(i,j)=60.end doend doend subroutine initial!超松弛迭代法subroutine sor(tt_sor,nx_sor,ny_sor,ome,be)implicit noneinteger::i,jinteger,intent(in)::nx_sor,ny_sor !横纵网格数real(kind=8),dimension(0:nx_sor,0:ny_sor)::tt_sor !温度real(kind=8),intent(in)::ome,be !松弛因子,网格参数hreal(kind=8)::tem1do i=1,nx_sor-1do j=1,ny_sor-1tem1=tt_sor(i+1,j)+tt_sor(i-1,j)+be**2*(tt_sor(i,j+1)+tt_sor(i,j-1)) tt_sor(i,j)=(1-ome)*tt_sor(i,j)+ome*tem1/2./(1+be**2)end doend doend subroutine sorprogram poissonimplicit noneinteger::i,j,k,linteger,parameter::numk=8 !计算时取的网格大小种类数real(kind=8),allocatable,dimension(:,:)::tem !温度integer::numx,numy !横纵网格数real(kind=8),parameter::lx=12.,ly=15. !计算域长宽integer,parameter::nw=20 !计算时omega取值的数目integer,dimension(nw)::ncell !存储同一omega下迭代需要的步数 real(kind=8)::om,bt !松弛因子,网格参数hreal(kind=8)::dx,dy !横纵方向上的网格参数integer::ct !中间变量real(kind=8)::w_opt !最佳松弛因子integer,parameter::status=-1 !状态变量.1-计算不同网格尺度下的最佳松弛因子!-1-计算特定尺度,取最佳松弛因子时得到的最终温度分布open(unit=15,file='poisson.dat')open(unit=16,file='poisson2.txt')write(16,'("title = data")')write(16,'("variables = x,y,t")')write(16,'("zone i=",i4,3x,"j=",i4)')8,nwdo l=1,8numx=4*lnumy=5*ldx=lx/numxdy=ly/numybt=dx/dyallocate(tem(0:numx,0:numy))ct=10**10do k=1,nwom=1.+0.95*dble(k)/dble(nw)call caclulate_w(tem,numx,numy,om,ncell(k),bt)write(16,'(1x,d15.5,3x,d15.5,3x,i10)')l,om,ncell(k) if(ncell(k)<ct) thenct=ncell(k)w_opt=omend ifend doif(status==1) thenwrite(15,'(1x,d15.5,3x,d15.5)')dx,w_optelse if(status==-1 .and. l==6) thenwrite(15,'("title = data")')write(15,'("variables = x,y,t")')write(15,'("zone i=",i4,3x,"j=",i4)')numx+1,numy+1call caclulate_w(tem,numx,numy,w_opt,ct,bt)do j=0,numydo i=0,numxwrite(15,*)i*dx,j*dy,tem(i,j)end doend doend ifdeallocate(tem)end doend program poisson!计算特定网格和松弛因子下的温度subroutine caclulate_w(tt,nx,ny,omega,nncell,beta)implicit noneinteger::i,jinteger,intent(in)::nx,ny !横纵网格数real(kind=8)::error=1.d-5 !误差限integer,intent(out)::nncell !存储迭代次数real(kind=8)::omega,etem,beta !etem-两次计算间的平均误差real(kind=8),dimension(0:nx,0:ny)::tem0 !存储上一次计算得到的温度矩阵real(kind=8),dimension(0:nx,0:ny)::tt !温度矩阵etem=1.d10nncell=0call initial(tt,nx,ny)do while(etem>error)nncell=nncell+1tem0=ttcall sor(tt,nx,ny,omega,beta)etem=0.do i=1,nx-1do j=1,ny-1etem=etem+(tt(i,j)-tem0(i,j))**2 end doend doetem=sqrt(etem)end doend subroutine caclulate_w。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、松弛迭代计算公式
松弛迭代法
赛德尔迭代法的迭代公式可表示为 i 1 n 1 xi( m +1) = (bi ∑ aij x (jm +1) ∑ aij x (jm ) ) aii j =1 j =i +1
=x
(m) i i 1 n 1 ( m +1) + (bi ∑ aij x j ∑ aij x (jm ) ) aii j =1 j =i
令Bω = ( D ωL) 1[(1 ω ) D + ωU ], gω = ( D ωL) 1 b, 则
x ( m +1) = Bω x ( m ) + gω
(m = 0,1,2, L)
三、松弛法算法 输入 方程组的阶数n, A的元素aij,≤ i, j ≤ n; b的分量bi ,1 ≤ i ≤ n; 1
在实际计算中,松弛法常采用以下形式:
x
( m +1) i
= (1 ω ) x
( m) i
+ ω (bi ∑ aij x
j =1
i 1
( m +1) j
∑ aij x (jm ) ) / aii (i = 1,2, L , n)
j =i
n
二、松弛法的矩阵形式 x (m +1) = ( D ωL) 1[(1 ω ) D + ωU ]x ( m ) + ω ( D ωL) 1 b (m = 0,1,2, L)
ri( m +1) → 0(i = 1,2, L , n)
在修正量前乘上一个参数,即
xi( m +1) = xi( m ) + ωri( m +1)
(i = 1,2, L , n)
这种求方程组近似解的方法称为松弛法,ω称为松弛因子. 当ω < 1时,称为低松弛法, 当ω = 1时,就是赛德尔迭代法, 当ω > 1时,称为超松弛法,简称为SOR.
S12 若对i 1,2,L , n, xi x0i ≤ ε , 则输出( x1 , x2 ,L , xn ); 停机. S13 对i = 1,2,L , n 置x0i = xi S2
输出“N次迭代后不收敛”;停机.
作业: 教材P91 习题4
= xi( m ) + ri ( m +1)
其中,ri
( m +1)
(i = 1,2, L , n)
i 1 n 1 ( m +1) = (bi ∑ aij x j ∑ aij x (jm ) )(i = 1,2,L , n) aii j =1 j =i
称为第m+1步第I个分量的修正量. 当迭代法收敛时
x ( 0 )的分量x0i ,1 ≤ i ≤ n; 允许误差ε;最大迭次次数N . 输出 近似解x1 , x2 ,L, xn或N次迭代后不收敛的信息.
步骤 S1
对m = 1,2, L, N作 S11~S13
S11 对i = 1,2,L, n
i 1 n bi ∑ aij x j ∑ aij x0 j aii . 置xi = (1 ω ) x0i + ω j =1 j =i +1
