M序列产生程序
基于MATLAB的m序列产生

基于MATLAB的m序列产生第一章设计内容及要求基于MATLAB产生m序列要求:1.通过matlab编程产生m序列的产生原理及其产生方法。
2.对特定长度的m序列,分析其性质,及其用来构造其它序列的方法。
第二章m序列设计方案的选择2.1 方案一MATLAB编程非常简单,无需进行变量声明,可以很方便的实现m序列。
2.2 方案二图2.1 Simulink实现m序列Simulink是MATLAB最重要的组件之一,它提供了一个动态系统建模,仿真和综合分析的集成环境。
在此环境中无需大量书写程序,而只需通过简单直观的鼠标操作,就可构造出复杂的系统。
Simulink具有适应性广,结构及流程清晰及仿真精细等优点,基于以上优点,Simulink已被广泛的运用到控制理论和数字信号处理的复杂仿真和设计。
通过比较方案一和方案二,发现方案一的有点具有通用性而方案二利用MATLAB的Simulink直接搭建模块,在移位寄存器较少的情况下利用此方法比较简单,可是当移位寄存器的个数增多时,要搭建那么多的模块就显的很繁琐了,缺乏通用性,因此本次实验选择方案一。
第三章m序列的产生及性质3.1 m序列的产生原理、结构及产生m序列是最长线性反馈移位寄存器序列的简称,m序列是由带线性反馈的移位寄存器产生的。
由n级串联的移位寄存器和反馈逻辑线路可组成动态移位寄存器,如果反馈逻辑线路只由模2和构成,则称为线性反馈移位寄存器。
带线性反馈逻辑的移位寄存器设定初始状态后,在时钟触发下,每次移位后各级寄存器会发生变化,其中任何一级寄存器的输出,随着时钟节拍的推移都会产生一个序列,该序列称为移位寄存器序列。
n级线性移位寄存器的如图3.1所示:◇A图3.1 n级线性移位寄存器图中C i表示反馈线的两种可能连接方式,C i=1表示连线接通,第n-i级输出加入反馈中;C i=0表示连线断开,第n-i级输出未参加反馈。
因此,一般形式的线性反馈逻辑表达式为------表达式3.1将等式左边的a n移至右边,并将a n=C0a n(C0=1)带入上式,则上式可以写成-------表达式3.2定义一个与上式相对应的多项式--------表达式3.3 其中x的幂次表示元素的相应位置。
m序列实验报告

实验报告--m序列的产生及其特性实验班级:XXXXXX学号:XXXXX姓名:XXXXXM序列的产生及其特性实验一、实验目的掌握m序列的特性、产生方法及运用二、实验内容(1)编写MATLAB程序生成并观察m序列,识别其特征(2)观察m序列的相关特性三、实验原理m序列是有n级线性移位寄存器产生的周期为2n −1的码序列,是最长线性移位寄存器序列的简称。
码分多址系统主要采用两种长度的m序列:一种是周期为215 −1的m序列,又称短PN序列;另一种是周期为242 −1的m序列,又称为长PN码序列。
m序列主要有两个功能:①扩展调制信号的带宽到更大的传输带宽,即所谓的扩展频谱;②区分通过多址接入方式使用同一传输频带的不同用户的信号。
四、实验分析在实验中我选择的是n=6的级数,选择了103、147、155这三个反馈系数1:当反馈系数会Ci=(103)8=(1000011)2原理框图2: 当反馈系数会Ci=(147)8=(1100111)2原理框图3: 当反馈系数会Ci=(155)8=(1101101)2原理框图五、实验程序clearclose all;clcG=127;%使用多项式(103)8=(1000011)2产生第一个m序列sd1=[0 0 0 0 0 1];%寄存器的初始状态PN1=[];%第一个序列for j=1:GPN1=[PN1 sd1(1)];if sd1(1)==sd1(2)temp1=0;else temp1=1;endsd1(1)=sd1(2);sd1(2)=sd1(3);sd1(3)=sd1(4);sd1(4)=sd1(5);sd1(5)=sd1(6);sd1(6)=temp1;endsubplot(3,1,1)stem(PN1)title('使用生成多项式(103)8=(1000011)2产生第一个m序列')%使用生成多项式(147)8=(1100111)2产生第二个m序列sd2=[0 0 0 0 0 1];%寄存器的初始状态PN2=[];%第一个序列for j=1:GPN2=[PN2 sd2(1)];if sd2(1)==sd2(2)temp1=0;else temp1=1;endif sd2(5)==temp1temp2=0;else temp2=1;endif sd2(6)==temp2temp3=0;else temp3=1;endsd2(1)=sd2(2);sd2(2)=sd2(3);sd2(3)=sd2(4);sd2(4)=sd2(5);sd2(5)=sd2(6);sd2(6)=temp3;endsubplot(3,1,2)stem(PN2)title('使用生成多项式(147)8=(1100111)2产生第二个m序列')%使用生成多项式(155)8=(1101101)2产生第三个m序列sd3=[0 0 0 0 0 1];%寄存器的初始状态PN3=[];%第一个序列for j=1:GPN3=[PN3 sd3(1)];if sd3(1)==sd3(2)temp1=0;else temp1=1;endif sd3(4)==temp1temp2=0;else temp2=1;endif sd3(5)==temp2temp3=0;else temp3=1;endsd3(1)=sd3(2);sd3(2)=sd3(3);sd3(3)=sd3(4);sd3(4)=sd3(5);sd3(5)=sd3(6);sd3(6)=temp3;endsubplot(3,1,3)stem(PN3)title('使用生成多项式(155)8=(1101101)2产生第三个m序列')六、实验结果七、m序列的相关性质PN1 =0 0 0 0 0 1 0 0 0 0 1 1 0 0 0 1 0 1 0 0 1 1 1 1 0 1 0 0 0 1 1 1 0 0 1 0 0 1 0 1 1 0 1 1 1 0 1 1 0 0 1 1 0 1 0 1 0 1 1 1 1 1 1PN2 =0 0 0 0 0 1 1 0 1 1 1 0 0 1 1 0 0 0 1 1 1 0 1 0 1 1 1 1 1 1 0 1 1 0 1 0 0 0 1 0 0 0 0 1 0 1 1 0 0 1 0 1 0 1 0 0 1 0 0 1 1 1 1PN3 =0 0 0 0 0 1 0 1 1 1 1 1 1 0 0 1 0 1 0 1 0 0 0 1 1 0 0 1 1 1 1 0 1 1 1 0 1 0 1 1 0 1 0 0 1 1 0 1 1 0 0 0 1 0 0 1 0 0 0 0 1 1 11)均衡性在m序列的一个周期中,0和1的数目基本相等,1的数目比0的数目多一个,由PN1可知总共有32个1和31个0.2)游程分布M序列中取值相同的那些相继的元素合称为一个“游程”。
基于Matlab产生m序列

目录前言 (1)第一章设计任务 (2)1.2设计内容 (2)1.2设计要求 (2)1.3系统框图 (2)第二章m序列的分析 (4)2.1m序列的含义 (4)2.2m序列产生的原理 (5)2.2m序列的性质 (6)2.3自相关特性 (7)第三章m序列的设计 (8)3.1特征多项式确定 (8)3.2本原多项式的确定 (9)3.3m序列的发生 (10)第四章程序调试及结果分析 (11)4.1m序列的仿真结果及分析 (12)4.2该设计的序列相关性仿真结果及分析 (13)结论 (14)参考文献 (15)附录:程序代码 (16)前言扩频通信因其具有抗干扰、抗多径衰落、抗侦察等优点在通信领域中得到广泛应用。
扩频序列的设计和选择是扩频通信的关键技术,扩频序列性能的优劣在很大程度上决定了通信系统的多址干扰和符号间干扰的大小,从而直接影响到系统的性能。
因此,深入研究扩频序列的性质,构造设计具有良好相关性的扩频序列,来满足扩频系统的要求,是直接序列扩频系统的核心课题。
白噪声是一种随机过程,它有极其优良的相关特性。
但至今无法实现白噪声的放大、调制、检测、同步及控制等,而只能用类似于白噪声统计特性的伪随机序列来逼近它,并作为扩频系统的扩频码。
常见的伪随机序列有m 序列、GOLD 序列、M 序列、Walsh 序列等。
m 序列是目前研究最为彻底的伪随机序列,m 序列容易产生,有优良的自相关和互相关特性。
序列是伪随机序列的一种情况。
他可以在很多领域中都有重要应用。
由n级移位寄存器所能产生的周期最长的序列。
这种序列必须由非线性移位寄存器产生,并且周期为2n(n为移位寄存器的级数)。
通过对伪随机码中常用的m序列的结构和性质进行了分析,本文给出了基于MATLAB平台的m序列生成算法及代码伪随机序列分析。
第一章 设计任务1.2 设计内容掌握PN 序列的相关知识,掌握m 序列的产生原理及其在matlab 中的产生方法,对特定长度的m 序列,分析其性质,及其用来构造其它序列的方法;研究伪随机序列在跳频通信中的应用方法。
M序列的产生

M 序列的产生1. 对象或参数数学模型如下:)()2(5.0)1()2(7.0)1(5.1)(k v k u k u k z k z k z +-+-=-+--其中,)(k v 是白噪声N (0,1)(服从正态分布),输入信号采用4阶M 序列,幅度为1. 辨识模型如下:)()2()1()2()1()(2121k v k u b k b k z a k z a k z +-+-=-+--设输入信号的取值为k=1到k=16的M 序列,则待辨识参数L L L L LS z H H H ττθ1-)(=∧。
⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=∧4321a a a a LS θ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=)16(...)4()3(z z z z L ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡---=)14()15()14()15(......)2()3(z(2)-)3(-)1()2()1()2(-u u z z u u z u u z z H L 编制仿真程序,,获取输入输出数据,运用最小二乘法对系统的参数进行辨识,并将辨识结果与实际参数进行对比。
2. 程序框图3. 程序实现function [] = JM-232()%--------------------------------------------------------实验题目及初始化定义disp('最小二乘法的实现')disp(' ')disp('数学模型为:z(k)-1.5z(k-1)+0.7z(k-2)=u(k-1)+0.5u(k-2)+v(k).')disp(' 所选择的辨识模型为:z(k)+a1*z(k-1)+a2*z(k-2)=b1*u(k-1)+b2*u(k-2)+v(k).') disp(' 故实际参数a1=-1.5, a2=0.7, b1=1, b2=0.5. ')disp(' ')disp('系统输入采用4 阶M 序列且其幅度为1,输出受到白噪声序列v(k)干扰.') ds = input(' 假设白噪声序列v(k)服从正态分布,均值为0,请输入方差ds = '); disp(' ')disp(' ')a0=65539;M=2147483647;x=123456;b=10000;U=[];V=[];Z=[];T=[];P=zeros(20,4);H=zeros(14,4);LS=zeros(4,1);ZL=zeros(14,1);%------------------------------------------------产生4 阶M 序列作为输入信号u(k)fori=1:4P(1,i)=1;U(1)=-2*(P(1,4)-0.5);endfor j=2:16fori=2:4P(j,i)=P(j-1,i-1);endP(j,1)=mod(P(j-1,3)+P(j-1,4),2);U(j)=-2*(P(j,4)-0.5);enddisp('** 通过仿真获得:')disp(' ')disp(' 系统输入u(k)取k=1 到k=16 图形如figure 1 所示;')disp(' ')figure(1)plot(U);hold onaxis([0 17 -1.5 1.5])title('系统输入u(k)图形')%--------------------------------------------------产生白噪声作为干扰信号v(k)fori=1:192x=mod(a0*x+b,M);T(i)=x/M;endaT=mean(T);vT=var(T);fori=1:16tempsum=0;for j=1:12tempsum=tempsum+T(12*i-j+1);endV(i)=sqrt(ds)*(tempsum-12*aT)/sqrt(12*vT);endaV=mean(V);vV=var(V);disp(' 系统白噪声干扰v(k)取k=1 到k=16 图形如figure 2 所示;') disp([' 该系统白噪声v(k)均值为' num2str(aV)])disp([' 方差为' num2str(vV)])disp(' ')figure(2)plot(V);hold onaxis([0 17 -3 3])title('系统白噪声v(k)图形')%--------------------------------计算输出z(k),同时由系统输出构成观测矩阵ZL 与HZ(1)=0;Z(2)=0;for k=3:16Z(k)=1.5*Z(k-1)-0.7*Z(k-2)+U(k-1)+0.5*U(k-2)+V(k);ZL(k-2,1)=Z(k);endfori=1:14H(i,1)=-Z(i+1);H(i,2)=-Z(i);H(i,3)=U(i+1);H(i,4)=U(i);enddisp(' 系统输出z(k)图形如figure 3 所示;')disp(' ')figure(3)plot(Z)title('系统输出z(k)图形')%---------------------------------------------------------最小二乘法参数辨识LS=inv(H'*H)*H'*ZL;disp(' 运用最小二乘法对这一系统参数进行辨识,计算得到:')disp([' a1(实际值) = -1.5,a1(辨识值)= ' num2str(LS(1,1))])disp([' a2(实际值) = 0.7,a2(辨识值)= ' num2str(LS(2,1))])disp([' b1(实际值) = 1,b1(辨识值)= ' num2str(LS(3,1))])disp([' b2(实际值) = 0.5,b2(辨识值)= ' num2str(LS(4,1))])disp(' ')end4. 仿真结果本系统输入采用4 阶M 序列且其幅度为1,选取k=1 到k=16 数据,如图1所示系统输入图形。
第四章被控过程数学模型3

写成最小二乘格式为
y k h k e k
{u(k ), y(k )}; (k 1,2,, n L)
为了估计模型中的2n个参数ai及bi,将采集的n+L对输入、输 出数据代入上式,得到L个方程
y (n 1) a1 y (n) a2 y (n 1) an y (1) b1u (n) b2 n(n 1) bnu (1) e(n 1) y (n 2) a1 y (n 1) a2 y (n) an y (2) b1u (n 1) b2u (n) bnu (2) e(n 2) y (n L) a1 y (n L 1) an y ( L) b1u (n L 1) bnu ( L) e(n L)
J
k n 1
e
n L
2
(k ) e e min
T
J y k hT k
L k 1
2
ˆ 为了求使J达到最小值的参数 ˆ [a1 , a 2 ,, a n , b1 , b2 ,, bn ]T ,可 ˆ ˆ ˆ ˆ ˆ 通过对J求极(小)值求得。 即
3.M序列的产生 M序列的产生通常有两种方法,一是用移位寄存器产生,二是用 软件实现。 (1)移位寄存器产生 M序列可以很容易地用线性反馈移位寄存器产生,结构图如下
若移位寄存器的初始状态为1010,则在移位脉冲CP的作用下, 寄存器各级状态的变化
伪随机码的生成及自相关函数的计算

伪随机码的生成及自相关函数的计算1.函数seq=ms_generator(registers,connections)是m序列的生成函数,其中参数registers给出了以为寄存器的初始状态,connections给出了m序列的发生器。
m序列生成的程序如下:function seq=ms_generator(registers,connections)registers=[0 0 0 0 1];connections=[1 0 0 1 0 1];n=length(connections);L=2^(n-1)-1;seq(1)=registers(n-1);for i=2:L;sum=0;for m=1:(n-1)sum=mod(sum+registers(m)*connections(m+1),2);endfor k=(n-1):-1:2registers(k)=registers(k-1);endregisters(1)=sum;seq(i)=registers(n-1);sprintf('seq=%d',seq(i));End运行结果:ans =Columns 1 through 151 0 0 0 0 1 0 0 1 0 1 1 0 0 1Columns 16 through 301 1 1 1 0 0 0 1 1 0 1 1 1 0 1Column 31(2)函数auto_corr()计算二进制序列seq的自相关函数,并画出函数曲线。
程序代码如下:function auto_correlation=auto_corr(seq)registers=[1 0 0 0 0];connections=[1 0 1 0 0 1];seq=ms_generator(registers,connections);seq=-1*(seq*2-1);len=length(seq);temp=[seq seq];for i=0:len-1auto_correlation(i+1)=seq*(temp(i+1:i+len))';endauto_correlation;plot(0:len-1,auto_correlation);运行结果:ans =Columns 1 through 1531 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1Columns 16 through 30-1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1Column 31-1函数曲线图:(3)函数cross_corr()计算二进制序列seq1和seq2的互相关函数。
(完整word版)m序列产生及其特性实验

实验九 m 序列产生及其特性实验一、 实验目的和要求通过本实验掌握m 序列的特性、产生方法及应用。
二、实验内容和原理1)、实验内容1、观察m 序列,识别其特征。
2、观察m 序列的自相关特性。
2)、基本原理m 序列是有n 级线性移位寄存器产生的周期为21n -的码序列,是最长线性移位寄存器序列的简称。
1、产生原理图9-1示出的是由n 级移位寄存器构成的码序列发生器。
寄存器的状态决定于时钟控制下输入的信息(“0”或“1”),例如第I 级移位寄存器状态决定于前一时钟脉冲后的第i -1级移位寄存器的状态。
图中C 0,C 1,…,C n 均为反馈线,其中C 0=C n =1,表示反馈连接。
因为m 序列是由循环序列发生器产生的,因此C 0和C n 肯定为1,即参与反馈。
而反馈系数C 1,C 2,…,C n -1若为1,参与反馈;若为0,则表示断开反馈线,即开路,无反馈连线。
一个线性反馈移动寄存器能否产生m 序列,决定于它的反馈系数(0,1,2,,)i c i n =,下表中列出了部分m 序列的反馈系数i c ,按照下表中的系数来构造移位寄存器,就能产生相应的m 序列。
表9-1 部分m 序列的反馈系数表根据表9-1中的八进制的反馈系数,可以确定m 序列发生器的结构。
以7级m 序列反馈系数8(211)i C =为例,首先将八进制的系数转化为二进制的系数即2(010001001)i C =,由此我们可以得到各级反馈系数分别为:01C =、10C =、30C =、41C =、50C =、60C =、71C =,由此就很容易地构造出相应的m 序列发生器。
根据反馈系数,其他级数的m 序列的构造原理与上述方法相同。
需要说明的是,表9-1中列出的是部分m 序列的反馈系数,将表中的反馈系数进行比特反转,即进行镜像,即可得到相应的m 序列。
例如,取482(23)(10011)C ==,进行比特反转之后为28(10011)(31)=,所以4级的m 序列共有2个。
m序列

m 序列一、m 序列的产生1、最长线性反馈移位寄存器序列m 序列是最长线性反馈移位寄存器序列的简称,它是由带线性反馈的移位寄存器产生的周期最长的序列。
可以看到图1A 的输出的周期为15,除去全0外,图1A 的输出是周期最长的的序列。
我们希望尽可能少的级数产生尽可能长的序列。
一般说来,一个n 级反馈移存器可能产生的最长周期为12-n 。
反馈电路如何连接才能输出序列最长?是本节要讨论的问题。
2、m序列的特征方程移存器的结构用特征方程表示:∑==+++=ni i i nn x c x c x c c x f 010...)(3、m 序列的递推方程∑=-=ni ik i k a c a 14、m 序列的母函数∑∞==++++=010......)(k k k nn x a x a x a a x G5、几个有用的定理用来构造m 序列定理一、)()()(x h x G x f =,其中)(x h 为次数低于)(x f 的次数的多项式。
定理二、一n 级线性反馈移位寄存器的相继状态具有周期性,周期为12-≤n p 。
定理三、若序列}{k a A =具有最长周期12-=n p ,则其特征多项式)(x f 应为既约多项式。
定理四、一个线性移位寄存器的特征多项式)(x f 若为既约的,则由其产生的序列}{k a A =的周期等于使)(x f 能整除的)1(+p x 最小正整数p 。
6、本原多项式若一个n 次多项式满足如下条件:(1)、)(x f 是既约的(2)、)(x f 可整除m x +1,12-=n m(3)、)(x f 除不尽1+q x ,m q <则称)(x f 为本原多项式。
由本原多项式产生的序列一定是m 序列。
二、m 序列的性质1、均衡性在m 序列的一个周期中,“0”“1”的数目基本相等。
“1”比“0”多一个。
2、游程分布游程:序列中取值相同的那些相继的元素合称为一个“游程”。
游程长度:游程中元素的个数。
m序列产生及其特性实验m序列产生及其特性实验

编写程序如下:
clear
clc
G=63
sd1=[0 0 0 0 1];
PN1=[];
forj=1:G
PN1=[PN1 sd1(5)];
ifsd1(1)==sd1(4)
temp1=0;
elsetemp1=1;
end
sd1(1)=sd1(2);
sd1(2)=sd1(3);
sd1(3)=sd1(4);
(45)8的5级m序列表达为而机制序列可知为(100101)2,输入为[00001]、杯水风波化学教案脱离大众化学教案脱离现实化学教案难兴文艺之春试卷试题
D4+D1为输入我们可知道输出状态
状态
时钟
D1
D2
D3
D4
D5
D4+D1
输出状态
0
0
0
0
0
1
0
1
1
0
0
0
1
0
1
0
2
0
0
1
0
1
0
1
3
0
1
0
1
0
1
0
4
sd3=[0 0 0 0 1];
PN3=[];
forj=1:G
PN3=[PN3 sd3(5)];
ifsd3(1)==sd3(2)
temp1=0;
elsetemp1=1;
end
ifsd3(3)==temp1
temp2=0;
elsetemp2=1;
end
ifsd3(4)==temp2
temp3=0;
elsetemp3=1;
表1-1-1 m序列的反馈系数表
1-m序列的产生

1 m 序列的产生使用的本源多项式是651)(x x x F ++= ,M = 31查表n=6,可得到相应的反馈网络的函数f 为(6,5),反馈f 表示为:根据f 的反馈函数,假设初始状态为111000,可以写出其64-1=63长度的序列信号;具体做法为:将每一列的6和5位置的数字相异或,得到的数字放在下一行的1位置,该行的54321位置上的数字移到下一行的65432位置上,合成下一行的6位数字。
初始状态为111000,则真值表为:6 5 4 3 2 11 1 1 1 0 0 02 1 1 0 0 0 03 1 0 0 0 0 04 0 0 0 0 0 15 0 0 0 0 1 06 0 0 0 1 0 07 0 0 1 0 0 08 0 1 0 0 0 09 1 0 0 0 0 110 0 0 0 0 1 111 0 0 0 1 1 012 0 0 1 1 0 013 0 1 1 0 0 014 1 1 0 0 0 115 1 0 0 0 1 016 0 0 0 1 0 117 0 0 1 0 1 018 0 1 0 1 0 019 1 0 1 0 0 165Q Q f ⊕=20 0 1 0 0 1 121 1 0 0 1 1 122 0 0 1 1 1 123 0 1 1 1 1 024 1 1 1 1 0 125 1 1 1 0 1 026 1 1 0 1 0 027 1 0 1 0 0 028 0 1 0 0 0 129 1 0 0 0 1 130 0 0 0 1 1 131 0 0 1 1 1 032 0 1 1 1 0 033 1 1 1 0 0 134 1 1 0 0 1 035 1 0 0 1 0 036 0 0 1 0 0 137 0 1 0 0 1 038 1 0 0 1 0 139 0 0 1 0 1 140 0 1 0 1 1 041 1 0 1 1 0 142 0 1 1 0 1 143 1 1 0 1 1 144 1 0 1 1 1 045 0 1 1 1 0 146 1 1 1 0 1 147 1 1 0 1 1 048 1 0 1 1 0 049 0 1 1 0 0 150 1 1 0 0 1 151 1 0 0 1 1 052 0 0 1 1 0 153 0 1 1 0 1 054 1 1 0 1 0 155 1 0 1 0 1 056 0 1 0 1 0 157 1 0 1 0 1 158 0 1 0 1 1 159 1 0 1 1 1 160 0 1 1 1 1 161 1 1 1 1 1 162 1 1 1 1 1 063 1 1 1 1 0 0根据上面,可得到最长线性序列信号:11111111寻找起跳状态Q6输出序列为:Ⅰ:11100111左移32位,Ⅱ:11111111Ⅰ⊕Ⅱ=Ⅲ:10111111序列Ⅲ中100000(5个连0)处对应序列Ⅰ的四位代码为111100,此即为起跳状态。
M序列的matlab产生方法

M序列是工程中常用的输入信号,它的性质类似于白噪声,而白噪声是理论上最好的输入信号,可见M序列的价值。
下面介绍M序列的matlab产生方法。
idinput函数产生系统辨识常用的典型信号。
格式u = idinput(N,type,band,levels)[u,freqs] = idinput(N,'sine',band,levels,sinedata)N产生的序列的长度,如果N=[N nu],则nu为输入的通道数,如果N=[P nu M],则nu 指定通道数,P为周期,M*P为信号长度。
默认情况下,nu=1,M=1,即一个通道,一个周期。
Type指定产生信号的类型,可选类型如下Band指定信号的频率成分。
对于’rgs’、’rbs’、’sine’,band = [wlow, whigh]指定通带的范围,如果是白噪声信号,则band=[0, 1],这也是默认值。
指定非默认值时,相当于有色噪声。
对于’prbs’,band=[0, B],B表示信号在一个间隔1/B(时钟周期)内为恒值,默认为[0, 1]。
Levels指定输入的水平。
Levels=[minu, maxu],在type=’rbs’、’prbs’、’sine’时,表示信号u的值总是在minu和maxu之间。
对于type=’rgs’,minu指定信号的均值减标准差,maxu指定信号的均值加标准差,对于0均值、标准差为1的高斯白噪声信号,则levels=[-1, 1],这也是默认值。
说明对于PRBS信号,如果M>1,则序列的长度和PRBS周期会做调整,使PRBS的周期为对应一定阶数的最大值(即2^n-1,n为阶数);如果M=1,PRBS的周期是大于N的相应阶数的值。
在多输入的情形时,信号被最大平移,即P/nu为此信号能被估计的模型阶次的上界。
上面的意思可如下理解:对于M=1时,ms = idinput(12, 'prbs', [0 1], [0 1]);figurestairs(ms)title('M序列')ylim([-0.5 1.5])结果如下同时,matlab给出如下警告Warning: The PRBS signal delivered is the 12 first values of a full sequence of length 15.即函数的输出为周期为15(大于12的第一个2^n-1的值)PRBS信号的前12个值组成的序列。
实验5 m序列的产生

课程实验报告课程3G移动通信实验实验名称M序列的产生学院通信工程专业通信工程班级13083414学号13081405学生姓名田昕煜一、实验内容【实验目的】⏹加深对m序列产生原理的理解;⏹能够使用Matlab设计m序列发生器;【实验内容】⏹使用生成多项式(23)8=(10011)2产生第一个m序列;⏹使用生成多项式(31)8=(11001)2产生第二个m序列;【实验设备】⏹一台PC 机【实验步骤】1. 画出生成多项式对应的移位寄存器结构图2.应用Matlab语言编写程序,生成m序列,并对生成的m序列绘图【实验报告】按照要求完成实验报告。
实验报告中要求给出移位寄存器结构图和两个m序列对应的图形。
【例子】4级m序列(31)8=(11001)2=(c4,c3,c2,c1,c0)的产生:二、仿真程序及说明clear all;clc;r=5;a1=ones(1,r);m1=zeros(1,2^r-1);for i=1:(2^r-1)temp= mod((a1(4)+a1(1)),2); for j=r:-1:2a1(j)=a1(j-1);enda1(1)=temp;m1(i)=a1(r);endsubplot(2,1,1)stem(m1);axis([0 ,2^r, 0,2 ]);title('本原多项式为(23)8');a2=ones(1,r);m2=zeros(1,2^r-1);for i=1:(2^r-1)temp= mod((a2(4)+a2(3)),2);for j=r:-1:2a2(j)=a2(j-1);enda2(1)=temp;m2(i)=a2(r);endsubplot(2,1,2)stem(m2);axis([0 ,2^r, 0,2 ]);title('本原多项式为(31)8');三、总结学习了对于M序列的MATLAB编程,也对于通信原理中的8进制转换M序列有的巩固。
系统辨识白噪声及M序列产生

A=6; x0=1; M=255; f=2; N=100; %初始化;x0=1; M=255;for k=1: N %乘同余法递推100次;x2=A*x0; %分别用x2和x0表示xi+1和xi-1;x1=mod (x2,M); %取x2存储器的数除以M的余数放x1(xi)中;v1=x1/256; %将x1存储器中的数除以256得到小于1的随机数放v1中;if(v1>0.5)v(:,k)=v1;else v(:,k)=(v1-0.5 )*f; %将v1中的数()减去0.5再乘以存储器f中的系数,存放在矩阵存储器v的第k列中,v(:,k)表示行不变、列随递推循环次数变化;endx0=x1; % xi-1= xi;v0=v1;end %递推100次结束;v2=v %该语句后无‘;’,实现矩阵存储器v中随机数放在v2中,且可直接显示在MATLAB的window中;k1=k;%grapher %以下是绘图程序;k=1:k1;plot(k,v,k,v,'r');xlabel('k'), ylabel('v');tktle(' (-1,+1)均匀分布的白噪声')A=6;N=100;x0=1;M=255;w=0.5; v2=0;%初始化s=sqrt(1/12);for k=1:Nx2=A*x0;x1=mod(x2,M);v1=x1/256;v2=v2+v1;v(:,k)=v1;x0=x1;v0=v1;v3=(v2-k/2)/(sqrt(k/12));e(:,k)=w+s*v3;ende2=ek1=k;k=1:k1;plot(k,e,k,e,'rx');xlabel('k'),ylabel('e');title('(0,1)正态分布的随机信号')2e2 =Columns 1 through 60.0234 -0.0911 0.2158 0.0449 0.0895 0.3134 Columns 7 through 120.4350 0.5193 0.4766 0.4012 0.4211 0.3714 Columns 13 through 180.4881 0.4708 0.5000 0.5420 0.4252 0.3426 Columns 19 through 240.4256 0.3340 0.3363 0.4384 0.4992 0.5454 Columns 25 through 300.5195 0.4717 0.4820 0.4476 0.5232 0.5107 Columns 31 through 360.5302 0.5594 0.4755 0.4143 0.4736 0.4043 Columns 37 through 420.4043 0.4804 0.5263 0.5618 0.5415 0.5036 Columns 43 through 480.5113 0.4835 0.5437 0.5334 0.5490 0.5727 Columns 49 through 540.5039 0.4530 0.5016 0.4437 0.4431 0.5064 Columns 55 through 600.5448 0.5746 0.5574 0.5251 0.5315 0.5076 Columns 61 through 660.5590 0.5501 0.5635 0.5840 0.5242 0.4798 Columns 67 through 720.5220 0.4711 0.4704 0.5257 0.5593 0.5856 Columns 73 through 780.5704 0.5418 0.5474 0.5260 0.5717 0.5637 Columns 79 through 840.5756 0.5939 0.5404 0.5004 0.5382 0.4923 Columns 85 through 900.4915 0.5413 0.5716 0.5954 0.5816 0.5556Columns 91 through 960.5606 0.5411 0.5826 0.5753 0.5862 0.6029Columns 97 through 1000.5539 0.5174 0.5518 0.5098>>3 X1=1;X2=0;X3=1;X4=0;X5=1;X6=0; %移位寄存器输入Xi初T态(0101),Yi为移位寄存器各级输出m=60; %置M序列总长度for i=1:m %1#Y6=X6;Y5=X5;Y4=X4; Y3=X3; Y2=X2; Y1=X1;X6=Y5;X5=Y4,X4=Y3; X3=Y2; X2=Y1;X1=xor(Y5,Y6); %异或运算if Y6==0U(i)=-1;elseU(i)=Y6;endendM=U%绘图i1=ik=1:1:i1;plot(k,U,k,U,'rx')xlabel('k')ylabel('M序列')title('移位寄存器产生的M序列')M =Columns 1 through 10-1 1 -1 1 -1 1 1 1 1 1 Columns 11 through 201 -1 -1 -1 -1 -1 1 -1 -1 -1 Columns 21 through 30-1 1 1 -1 -1 -1 1 -1 1 -1 Columns 31 through 40-1 1 1 1 1 -1 1 -1 -1 -1Columns 41 through 501 1 1 -1 -1 1 -1 -1 1 -1 Columns 51 through 601 1 -1 1 1 1 -1 1 1 -1 i1 =60。
m序列的生成与仿真
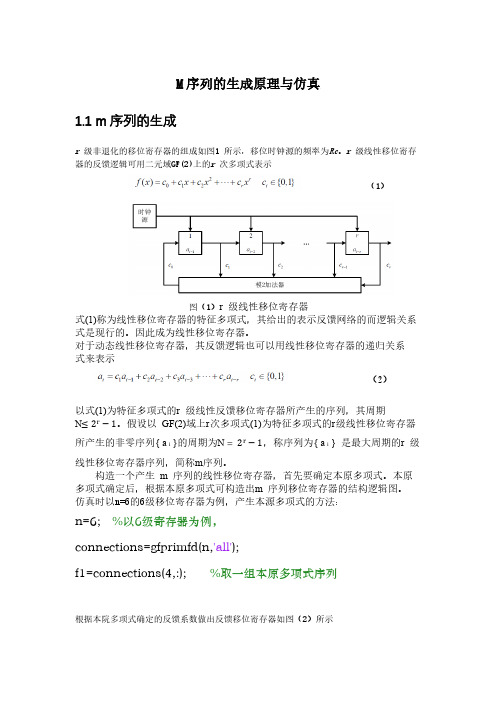
M序列的生成原理与仿真1.1 m序列的生成r 级非退化的移位寄存器的组成如图1 所示,移位时钟源的频率为Rc。
r 级线性移位寄存器的反馈逻辑可用二元域GF(2)上的r 次多项式表示(1)图(1)r 级线性移位寄存器式(1)称为线性移位寄存器的特征多项式,其给出的表示反馈网络的而逻辑关系式是现行的。
因此成为线性移位寄存器。
对于动态线性移位寄存器,其反馈逻辑也可以用线性移位寄存器的递归关系式来表示(2)以式(1)为特征多项式的r 级线性反馈移位寄存器所产生的序列,其周期N≤2r−1。
假设以GF(2)域上r次多项式(1)为特征多项式的r级线性移位寄存器所产生的非零序列{ a i }的周期为N =2r−1,称序列为{ a i }是最大周期的r 级线性移位寄存器序列,简称m序列。
构造一个产生m 序列的线性移位寄存器,首先要确定本原多项式。
本原多项式确定后,根据本原多项式可构造出m 序列移位寄存器的结构逻辑图。
仿真时以n=6的6级移位寄存器为例,产生本源多项式的方法:n=6; %以6级寄存器为例,connections=gfprimfd(n,'all');f1=connections(4,:); %取一组本原多项式序列根据本院多项式确定的反馈系数做出反馈移位寄存器如图(2)所示图(2)m 序列发生器1.2 m 序列自相关函数1.2.1周期自相关函数编写周期自相关函数和非周期自相关函数,实验结果如下图(2)和(3)所示:图(2)m 序列周期自相关函数结论:周期自相关函数R (k )={63 k =0−1 otℎersm 序列周期自相关函数1.2.2非周期自相关函数图(3) m 序列非周期自相关函数1.3 m 序列的互相关函数选用的两个m 序列为一对优选对,以211作为基准本原多项式(反馈系数10001001),217作为配对本原多项式(反馈系数10001111),生成两个m 序列,求出互相关函数如图(4)和(5):、图(4)m 序列互相关函数结论:互相关函数的取值{-1,-17,15}m 序列非周期自相关函数m 序列周期互相关函数m序列非周期互相关函数图(5)m序列非周期互相关函数1.4 附:matlab代码clear;clc;%%------生成m序列-----%%n=6; %以6级寄存器为例,connections=gfprimfd(n,'all');f1=connections(4,:); %取一组本原多项式序列registers1=[1 0 0 0 0 0 ];%给定寄存器的初始状态L=2^n-1; %周期长度sum1=0;for k=1:Lseq(k)=registers1(n); %m序列for j=1:n %进行模2加sum1=sum1+f1(j+1)*registers1(j); %各级寄存器送参与模2加的值sum1=mod(sum1,2);endfor t=n:-1:2 %寄存器移位registers1(t)=registers1(t-1);endregisters1(1)=sum1;sum1=0;end% %%----------------------自相关函数-------------------------%%% %-------非周期自相关函数--------%%a=1-2*seq;b=a;for i=1:LR(i)=sum(a.*b)b=[0 b(1:62)]endplot(R)title('m序列非周期自相关函数');% %-------周期自相关函数------%%% a=1-2*seq;% b=a;% for i=1:L% R(i)=sum(a.*b)% b=[b(63) b(1:62)]% end% plot(R);% title('m序列周期自相关函数');%%-------利用公式编写自相关函数验证---------------%% % a=seq1;% b=[a(1,63),a(1,1:62)];% L=length(b);% n=400;% x=1:n;% for k=1:n% c=xor(a,b);% D=sum(c);% A=L-D;% R(k)=(A-D)/(A+D);% b=[b(L),b(1:L-1)];% end% plot(x,R);% title('gold序列的自相关函数');% xlabel('τ');% ylabel('R(τ)');% grid;。
m序列产生及自相关和互相关函数曲线

1、m序列产生及自相关和互相关函数曲线function PN=makem(x) %m序列产生函数ss1=num2str(x);ss2=dec2bin(base2dec(ss1,8)); %先把八进制转换为十进制,再把十进制转换为二进制G=2^(length(ss2)-1)-1; %最大周期sd=[];for j=1:(length(ss2)-2)sd=[sd 0];endsd=[sd 1]; %寄存器初始状态0 0 0...0 1PN=[];for j=1:GPN=[PN sd(length(sd))]; %m序列输出的第一位onenum=[];for jj=1:length(ss2)if str2num(ss2(jj))==1onenum=[onenum jj-1]; %存储二进制反馈系数里面“1”的位置-1,即进行异或的位置endendtemp=sd(onenum(2));for jj=3:length(onenum) %根据“1”的位置进行异或运算temp=xor(temp,sd(onenum(jj)));endfor jj=length(ss2)-1:-1:2 %移位(序列后一位值等于前一位值)sd(jj)=sd(jj-1);endsd(1)=temp; %序列第一位等于反馈出来的值endfunction mandzi(ss) %m序列曲线及自相关函数曲线绘图函数ss1=num2str(ss);ss2=dec2bin(base2dec(ss1,8)); %转换为二进制G=2^(length(ss2)-1)-1; %最大周期PN=makem(ss); %调用函数计算m序列pp=(-2).*PN+1; %0→1 1→-1pp2=[];for tao=-(G-1):G-1pp1=circshift(pp,[0,tao]);pp2=[pp2 sum(pp.*pp1)/G]; %计算自相关函数endsubplot(2,1,1)stem(PN)grid on;title(['使用生成多项式(',num2str(ss),')8=(',ss2,')2产生的m序列']) subplot(2,1,2)tao=-(G-1):G-1;plot(tao,pp2)grid on;title('自相关函数曲线')function huxg(x,y) %m序列互相关绘图函数x1=num2str(x);x2=dec2bin(base2dec(x1,8)); %转换为二进制G1=2^(length(x2)-1)-1; %最大周期y1=num2str(y);y2=dec2bin(base2dec(y1,8)); %转换为二进制G2=2^(length(y2)-1)-1; %最大周期if G1~=G2error('周期不同,无法计算')returnendpn1=makem(x); %分别调用函数计算出m序列pn2=makem(y);pp=[];for tao=-(G1-1):G1-1pn1tao=circshift(pn1,[0,tao]); %计算互相关函数%pp=[pp sum(pn2.*pn1tao)/G1];pp=[pp sum(pn2.*pn1tao)];endtao=-(G1-1):G1-1;plot(tao,pp)grid on;title(['反馈系数(',num2str(x),')8和(',num2str(y),')8的互相关函数曲线'])2、Rake接收机仿真clear all;clcNumusers=1;Nc=16; %扩频因子ISI_Length=1; %每径延时为ISI_Lengh/2 EbN0db=[0:1:30]; %信噪比,单位dBTlen=8000; %数据长度Bit_Error_Number1=0; %误比特率初始值Bit_Error_Number2=0;Bit_Error_Number3=0;power_unitary_factor1=sqrt(6/9); %每径功率因子power_unitary_factor2=sqrt(2/9);power_unitary_factor3=sqrt(1/9);s_initial=randsrc(1,Tlen); %数据源wal2=[1 1;1 -1]; %产生walsh矩阵wal4=[wal2 wal2;wal2 wal2*(-1)];wal8=[wal4 wal4;wal4 wal4*(-1)];wal16=[wal8 wal8;wal8 wal8*(-1)];s_spread=zeros(Numusers,Tlen*Nc); %扩频ray1=zeros(Numusers,2*Tlen*Nc);ray2=zeros(Numusers,2*Tlen*Nc);ray3=zeros(Numusers,2*Tlen*Nc);for i=1:Numusersx0=s_initial(i,:).'*wal16(8,:);x1=x0.';s_spread(i,:)=(x1(:)).';end%将每个扩频后的输出重复为两次,有利于下面的延迟(延迟半个码元)ray1(1:2:2*Tlen*Nc-1)=s_spread(1:Tlen*Nc);ray1(2:2:2*Tlen*Nc)=ray1(1:2:2*Tlen*Nc-1);%产生第二径和第三径信号ray2(ISI_Length+1:2*Tlen*Nc)=ray1(1:2*Tlen*Nc-ISI_Length);ray2(2*ISI_Length+1:2*Tlen*Nc)=ray1(1:2*Tlen*Nc-2*ISI_Length);for nEN=1:length(EbN0db)en=10^(EbN0db(nEN)/10); %将Eb/N0的dB值转化为十进制数值sigma=sqrt(32/(2*en)); %将收到的信号dempdemp=power_unitary_factor1*ray1+...power_unitary_factor2*ray2+...power_unitary_factor3*ray3+...(randn(1,2*Tlen*Nc)+randn(1,2*Tlen*Nc)*i)*sigma;dt=reshape(demp,32,Tlen)';wal16_d(1:2:31)=wal16(8,1:16); %将walsh码重复为两次wal16_d(2:2:32)=wal16(8,1:16);rdata1=dt*wal16_d(1,:).'; %解扩后rdata1为第一径输出wal16_delay1(1,2:32)=wal16_d(1,1:31); %将walsh码延迟半个码元rdata2=dt*wal16_delay1(1,:).'; %解扩后rdata2为第二径输出wal16_delay2(1,3:32)=wal16_d(1,1:30); %将walsh码延迟一个码元wal16_delay2(1,1:2)=wal16_d(1,31:32);rdata3=dt*wal16_delay2(1,:).'; %解扩后rdata3为第三径输出p1=rdata1'*rdata1;p2=rdata2'*rdata2;p3=rdata3'*rdata3;p=p1+p2+p3;u1=p1/p;u2=p2/p;u3=p3/p;rd_m1=real(rdata1*u1+rdata2*u2+rdata3*u3); %最大比合并rd_m2=(real(rdata1+rdata2+rdata3))/3; %等增益合并u=[u1,u2,u3]; %选择式合并maxu=max(u);if(maxu==u1)rd_m3=real(rdata1);elseif(maxu==u2)rd_m3=real(rdata2);else rd_m3=real(rdata3);endendr_Data1=sign(rd_m1)'; %三种方法判决输出r_Data2=sign(rd_m2)';r_Data3=sign(rd_m3)';%计算误比特率Bit_Error_Number1=length(find(r_Data1(1:Tlen)~=s_initial(1:Tlen)));Bit_Error_Rata1(nEN)=Bit_Error_Number1/Tlen;Bit_Error_Number2=length(find(r_Data2(1:Tlen)~=s_initial(1:Tlen)));Bit_Error_Rata2(nEN)=Bit_Error_Number2/Tlen;Bit_Error_Number3=length(find(r_Data3(1:Tlen)~=s_initial(1:Tlen)));Bit_Error_Rata3(nEN)=Bit_Error_Number3/Tlen;endsemilogy(EbN0db,Bit_Error_Rata1,'r*-');hold on;semilogy(EbN0db,Bit_Error_Rata2,'bo-');hold on;semilogy(EbN0db,Bit_Error_Rata3,'g.-');legend('最大比合并','等增益合并','选择式合并');xlabel('信噪比');ylabel('误比特率');title('三种主要分集合并方式性能比较');。
m序列产生

2011-10-121. 基于FPGA 的m 序列产生电路m 序列也称为最长线性反馈移位寄存器序列,属于伪随机序列的一种。
m 序列的产生比较简单,可以利用r 级移位寄存器产生长度为2r -1的序列信号。
m 序列产生电路的结构主要分为两类,简单型码序列产生器(Simple Shift Register Generator ,SSRG )和模块型码序列产生器(Modular Shift Register Generator ,MSRG )。
基于FPGA 的电路实现时,两者的方法类似。
简单型码序列产生器的m 序列特征多项式如式(1)所示。
f SSRG (x )= C 0x 0 + C 1x 1 + C 2x 2 + C 3x 3 + … + C r x r (1) 多项式中的系数C 可以取“0”,或者“1”。
简单型码序列产生器的结构图如图1所示。
图1 简单型码序列产生器的结构图如果多项式中的系数取“0”,结构图中对应的反馈支路断开;系数取“1”,结构图中对应的反馈支路连通。
特征多项式的系数决定m 序列特征多项式,也就决定了一个m 序列的输出波形。
特征多项式的系数可以通过查表获得。
系数与输出波形之间的关系不清楚。
利用D 触发器的级联可以实现结构图中的移位寄存器功能,即方框a 的功能;使用异或门可以实现结构图中加法器的功能。
图2为采用Quartus II 开发软件的原理图输入方式完成式(2)多项式实现电路图[1]。
f SSRG (x )= 1 + x 2 + x 5 (2)图2 f SSRG (x )= 1 + x 2+ x 5简单型码序列产生器的电路图式(2)多项式的r 为5,电路中使用了5级D 触发器的级联;多项式中的C 2和C 5不为0,因此第2级D 触发器和第5级D 触发器的输出被反馈回到输入端;使用2输入异或门实现2输入加法器。
图2所示的电路图,在加法器之后添加了1个反相器来避免输出全0状态。
